Prerpints.org logo
Preprint
Review

A Review of Photonic Real-Time Signal Processing

Altmetrics

Downloads

104

Views

47

Comments

0

David Moss  *

This version is not peer-reviewed

Submitted:

21 September 2024

Posted:

23 September 2024

You are already at the latest version

Alerts
Abstract
The simultaneous progress of integrated op- tical frequency comb (OFC) and radio frequency (RF) photonic signal processing technique have promoted the rapid development of real-time signal processing. Integrated optical frequency comb offer multiple wave- lengths as a powerful source for RF photonic sig- nal transversal filter. Here, we review development of real-time signal processing system consisting of inte- grated OFC and RF photonic signal transversal filter in chronological order, and focus on the applications of this system such as differentiator, integrator, Hilbert transformer, and image processor. We also discuss and present our outlook on more parallel functions and fur- ther integration of real-time signal processing system.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

With the rapid development of the technology, information density has increased. The speed of information transmission and processing has been restricted by the electronic bottleneck defined by moore’s Law, which makes it difficult to meet the needs of information age. Compared with conventional real-time signal processing technology, RF photonics can modulate real-time signal into the optical domain which can be transmitted and processed by optical technology and further realize high speed and wide bandwidth [1,2,3,4,5].
RF photonics is an interdisciplinary technology that combines RF and photonic technology, which can utilize the advantage of broad bandwidth, ultrahighspeed and low loss offered by photonics to generate, transmit and process real-time signal [6,7]. RF photonics can be used in radar systems, wireless communication, radio frequency identification, biomedical imaging, astronomy and quantum information processing [8,9,10]. Conventional real-time signal processing technologies typically operate in frequency range from tens of kilohertz to tens of gigahertz for processing low frequency real-time signals and the speed of conventional real-time signal processing technology is limited by electronic devices [11,12,13]. Compared with conventional real-time signal processing technology, the realtime signal processing based RF photonics can operate in frequency range from hundreds of megahertz to hundreds of terahertz for processing higher frequency realtime signal in higher speed. Real-time signal processing based RF photonics utilize light to transmit realtime signal and then have greater resilience to electromagnetic interference resulting in higher signal quality [14,15].
Optical frequency comb (OFC) is a multiple-wavelength light source that offers numerous coherent wavelength channels. The adjacent channels are equally spaced in the OFC spectrum. Conventional OFC generation approaches feature large size, high cost, and limited wavelengths [16,17,18,19]. By contrast, micro-ring resonators with ultra-high Q factor have a point that offers a wide bandwidth in a little space, and can serve as an ideal platform for OFC generation [20,21,22]. In 2015, OFC based on a micro-ring resonator was first applied to RF photonics for real-time ultra-fast signal processing, establishing the connection between optical frequency and RF frequency [23].

2. RF Photonic Signal Processing

The RF photonic signal processing is a rapidly developing technology which has been widely used in many fields such as image processing, telecommunication, photon radar and photon neural network [8,9,10]. Compared to the conventional RF link filters, the RF signal processing system has higher bandwidth up to THz, lower loss about 0.15 dB/km and more suitable for long-distance transmission [13]. It transforms the electrical signals into optical signals to use optical methods to process signals then transform the optical signals back to the electrical signals as an output. A conventional RF photonic signal processing system contains light source, electro-optical conversion, optical signal processing unit and photoelectric conversion. Figure 2 [M1] is the model of the typical RF photonic signal processing system. For example a RF photonic signal processing system first generate a Kerr combs then shaping the combs which is the impluse response of the system in order to obtain the required system functions then modulating the RF signal through the Mach-Zehnder modulator (MZM). After modulating the RF signal the system uses the time-delay fiber to Implement convolution and finally transform the optical signals back to the electrical signal as an output. The MZM has two optical paths, a RF signal input and a bias voltage input which can transform the phase information into intensity information with the advantages of fast speed, good thermal stability, high extinction ratio, and low chirp [68]. [M2] The optical signal is equally distributed across two optical paths according to power and the RF input signal is loaded into two optical paths. Under the effect of the electric field, the propagation speed of light in an optical waveguide will change, resulting in phase difference so that the RF signal could be modulated into the optical signal. The transfer function of the MZM is a cosine function, so it is necessary to adjust the bias voltage to ensure that the modulator operates in the linear region.
The demonstration of RF photonic signal Processing system could be date back to 1977 by Chang [70]. He used 15 multi-mode fibers to create 15 different intervals with a delay of 5.2 ns demonstrating a filter which has 193 MHz fundamental passband. Later in 1995 Lindsay demonstrated the 20 GHz bandwidth photonic mixers and applied to superheterodyne receivers [34]. Frankel used 8 different fibers demonstrating a 8 taps tunable filter and this system used a low voltage control to change the wavelength of the laser continuously which enable the filter to continuously change the passband [24]. Another research of the mixer is demonstrated by Michael who extended the frequency band range to 1 THz [35]. Yongwoo Park used the similar structure to demonstrate the photonic intensity high order temporal differentiator in 2009 [47]. He used the variable attenuator to change the amplitude of the taps which is more reconfigurable and flexible. Junqiang Zhou also proposed a LiNbO3 phase modulator photonic differentiator [46]. The more complex RF photonic signal processing system used a tunable laser source to connect a set of 1×8 Bragg gratings through a power divider, each grating equipped with an attenuator to achieve different tap weights, and thus demonstrating an 8-tap filter [71]. However, filters based on Bragg gratings have the disadvantages of narrow bandwidth and poor low-frequency cutoff performance, which is because it is difficult to manufacture gratings that strictly meet the requirements [72,73,74]. The RF photonic signal processing system also applied in the neural network. In 2012 Lager and Paquot used intensity encoding calculation to implement a photonic neural network which had faster computing speed than the traditional neural network [51]. At the same time, the photonic mixer continued enhancing their dynamic range to 127 dB·Hz4/5 [38] and the conversion efficiency to 11.3 dB [36] through the Brillouin scattering and the dual-parallel Mach-Zehnder modulator (DPMZM). The photonic filters, the photonic Hilbert transformer and the photonic neural network also developed at the direction of higher bandwidth, higher integration by the use of the DPMZM [63], the brillouin scattering [26,28], the crystal delay line [27] and the ring resonator [59].
Thach used the RF photonic signal Processing system based on the kerr combs to demonstrate a Hilbert transformer with impulse response in hyperbolic cosine function which has 20 taps and a wide 3 dB bandwidth above 5 octave [65]. After the demonstration of the 20 taps Hilbert transformer, Xingyuan Xu demonstrated a 80 taps microwave photonic bandpass filter [33]. The record number of tap enabled the filters to achieve excellent performance which was the Four times higher than the previous Q value, 0.5 GHz-4.6 GHz 3 dB bandwidth and 48.9 dB out of band inhibition. The experimental data was highly consistent with the simulation results, indicating that this method is effective. Moss further improved the performance of the Hilbert converter [62]. In addition, the Kerr comb also was applied in the integrator [61] the differentiator [50,75] and the neural network [56,76]. Along with the application of soliton crystal frequency combs in neural networks, research had also been conducted on the training [53] and reinforcement learning of photonic neural networks [52]. Futhermore, multiplication and accumulation operations had been achieved by using photonic neural networks [54]. There are also some filters based on the electric optical frequency comb [25].
Preprints 118923 g001
Figure 1. The development of the photonic signal processing including. (a) Filters [24,25,26,27,28,29,30,31,32,33]. (b) Mixers [34,35,36,37,38,39,40,41,42,43,44,45]. (c) Differentiators [46,47,48,49,50]. (d) Neural networks [51,52,53,54,55,56,57,58]. (e) Integrators [59,60,61]. (f) Hilbert transformers [62,63,64,65]. (g) Others [66,67].
Figure 1. The development of the photonic signal processing including. (a) Filters [24,25,26,27,28,29,30,31,32,33]. (b) Mixers [34,35,36,37,38,39,40,41,42,43,44,45]. (c) Differentiators [46,47,48,49,50]. (d) Neural networks [51,52,53,54,55,56,57,58]. (e) Integrators [59,60,61]. (f) Hilbert transformers [62,63,64,65]. (g) Others [66,67].
Preprints 118923 g001
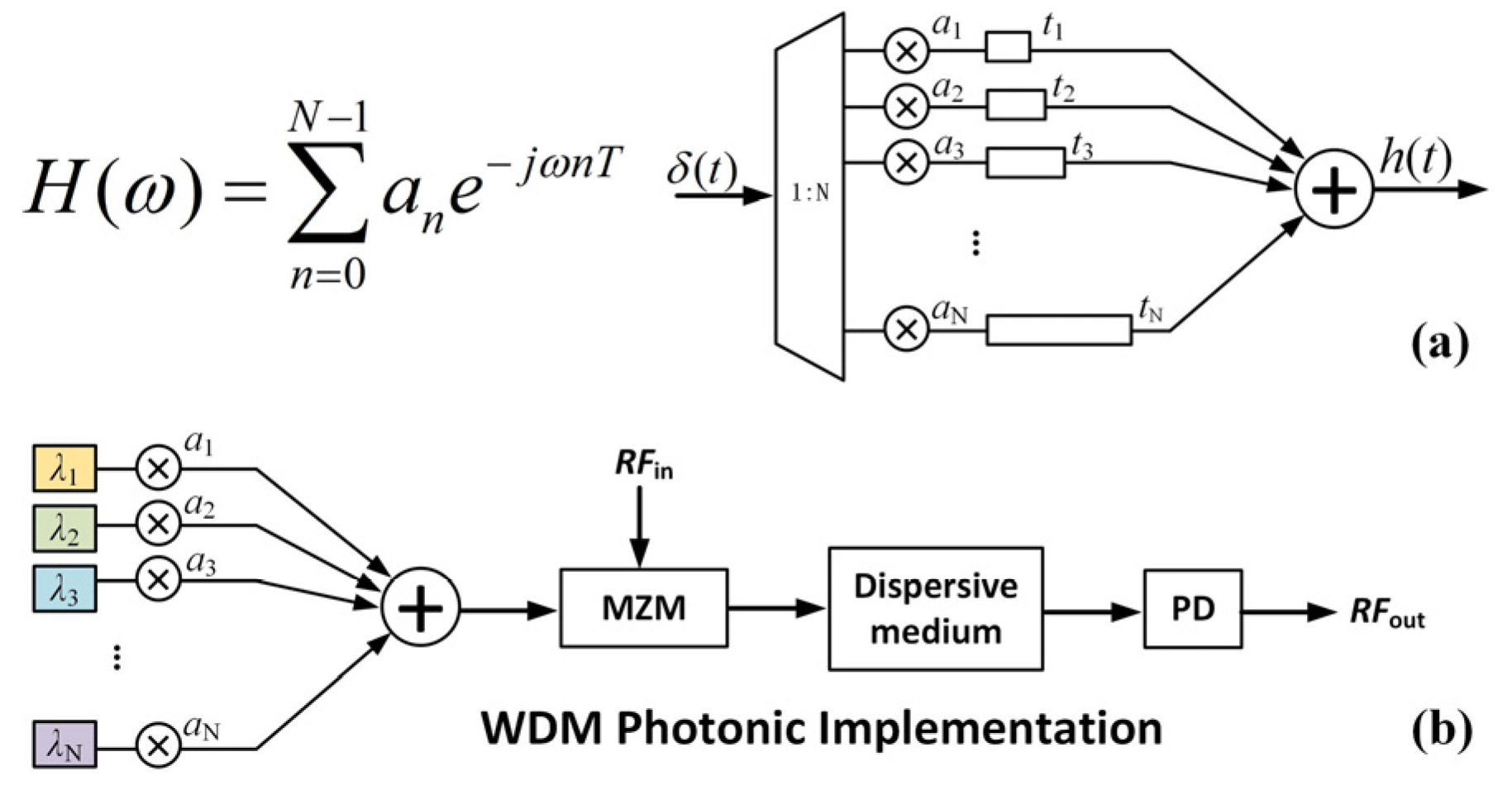
Preprints 118923 g002
Figure 2. (a) The structure of the RF signal processing system. (b) The actual composition of the system, weight coefficient is provided by the the length of the optical frequency comb, the signal mode fiber provide the different time-delay depending on the different wavelength and then calculate them all by the photodetector [69]. PD: photodetector; MZM: Mach-Zehnder modulator.
Figure 2. (a) The structure of the RF signal processing system. (b) The actual composition of the system, weight coefficient is provided by the the length of the optical frequency comb, the signal mode fiber provide the different time-delay depending on the different wavelength and then calculate them all by the photodetector [69]. PD: photodetector; MZM: Mach-Zehnder modulator.
Preprints 118923 g002
After 2020s, the RF photonic signal processing system are developing in the direction of silion intergrated [29,30,45,58,67] lower noise [32,43,44] and higher bandwidth [62,66]. Due to the advantages of high processing speed, integration, low loss, and large bandwidth, photonic signal processing systems have broad research prospects. For example, Mengxi Tan applied a RF photonic signal processing system based on Kerr comb in the field of image processing. This system achieved high reconfigurability and had the potential for integration [77]. The signal processing speed of the system reached an astonishing 17 TBit/s, and it can simultaneously perform 34 image processing functions on about 400,000 video signals. Currently, the integration methods of the RF photonic signal processing system still need further research.

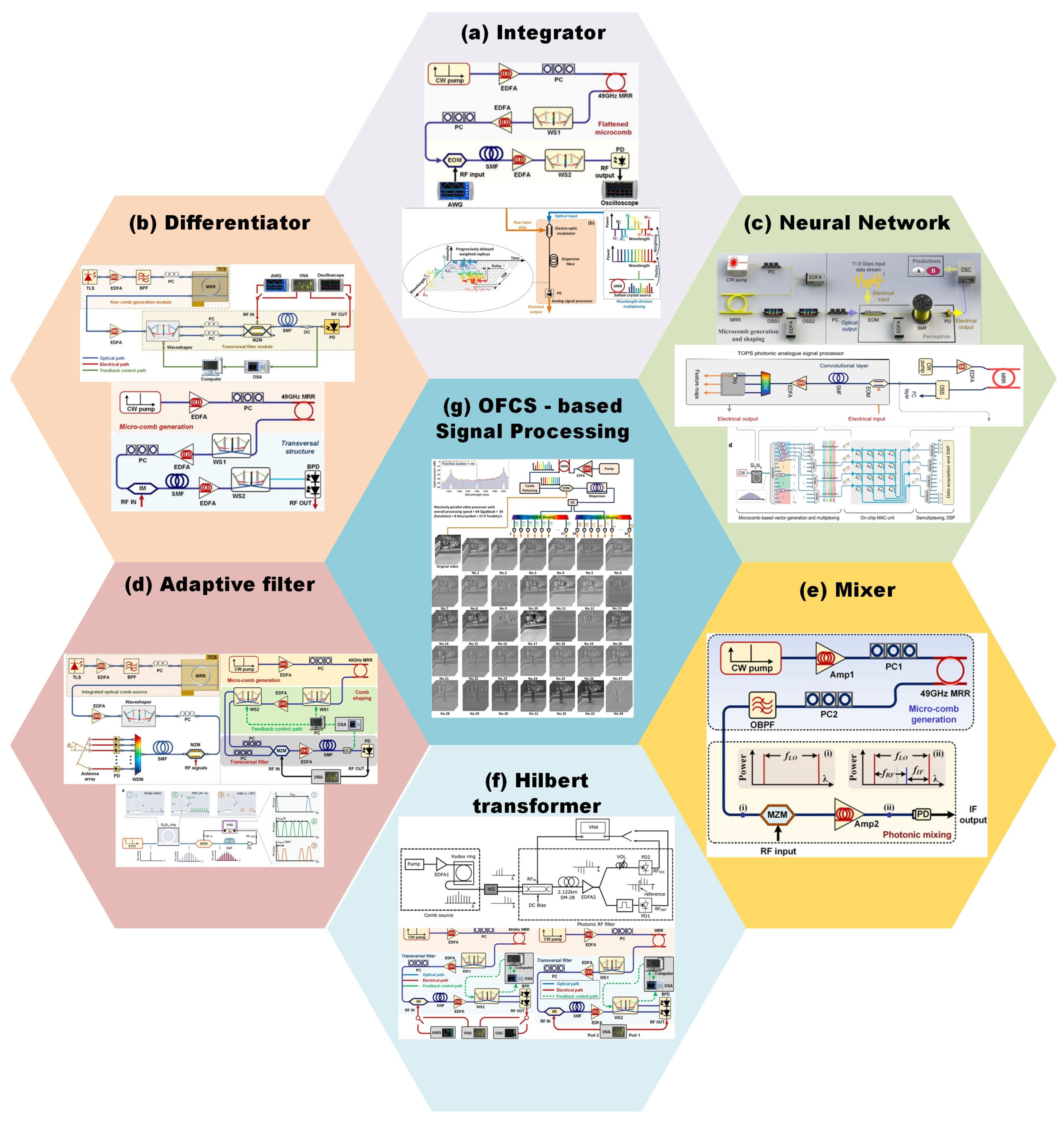
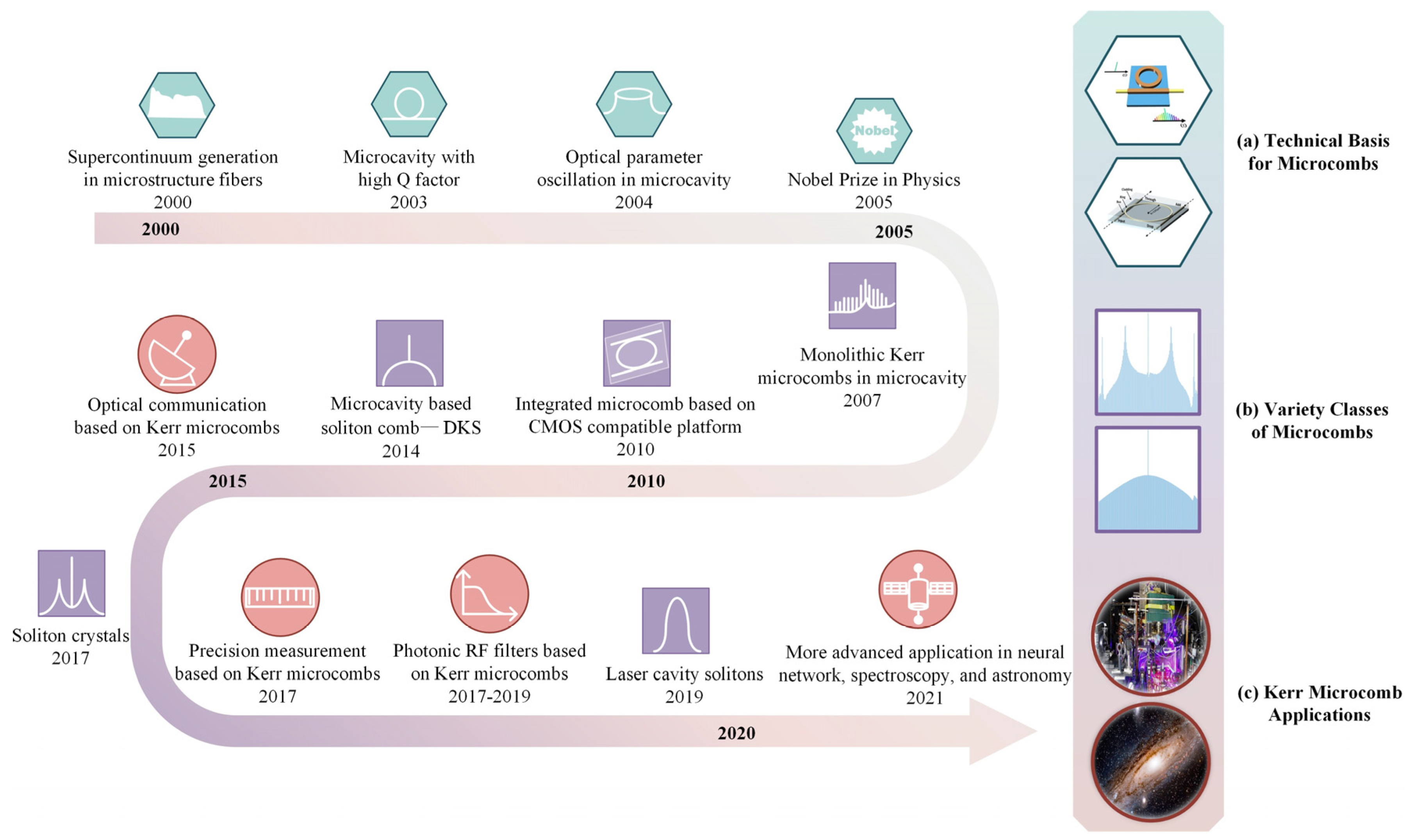
3. Optical Frequency Comb

Optical frequency combs (OFCs) comprise discrete and equidistant phase-locked frequency components, which can cover a range of hundreds THz [96]. The OFCs’ time domain is showcased in Figure 3a, appearing as an ultra-short optical pulse sequence. The frequency domain spectrum in Figure 3b owns the shape of a comb and is obtained through the Fourier transform of the temporal waveform. The OFCs’ appearance provides a bridge between optical and RF, allowing the precise measurement of the laser frequency through the electrical means of the RF [97]. The importance of the OFCs was recognized and the scientists, T.W. HĂ€nsch and J. Hall, who made vital breakthroughs in the OFCs field were awarded the 2005 Nobel Prize in Physics. With an increasingly deeper understanding of the OFCs, they attracted enormous attention for various applications in RF photonics [96,98].
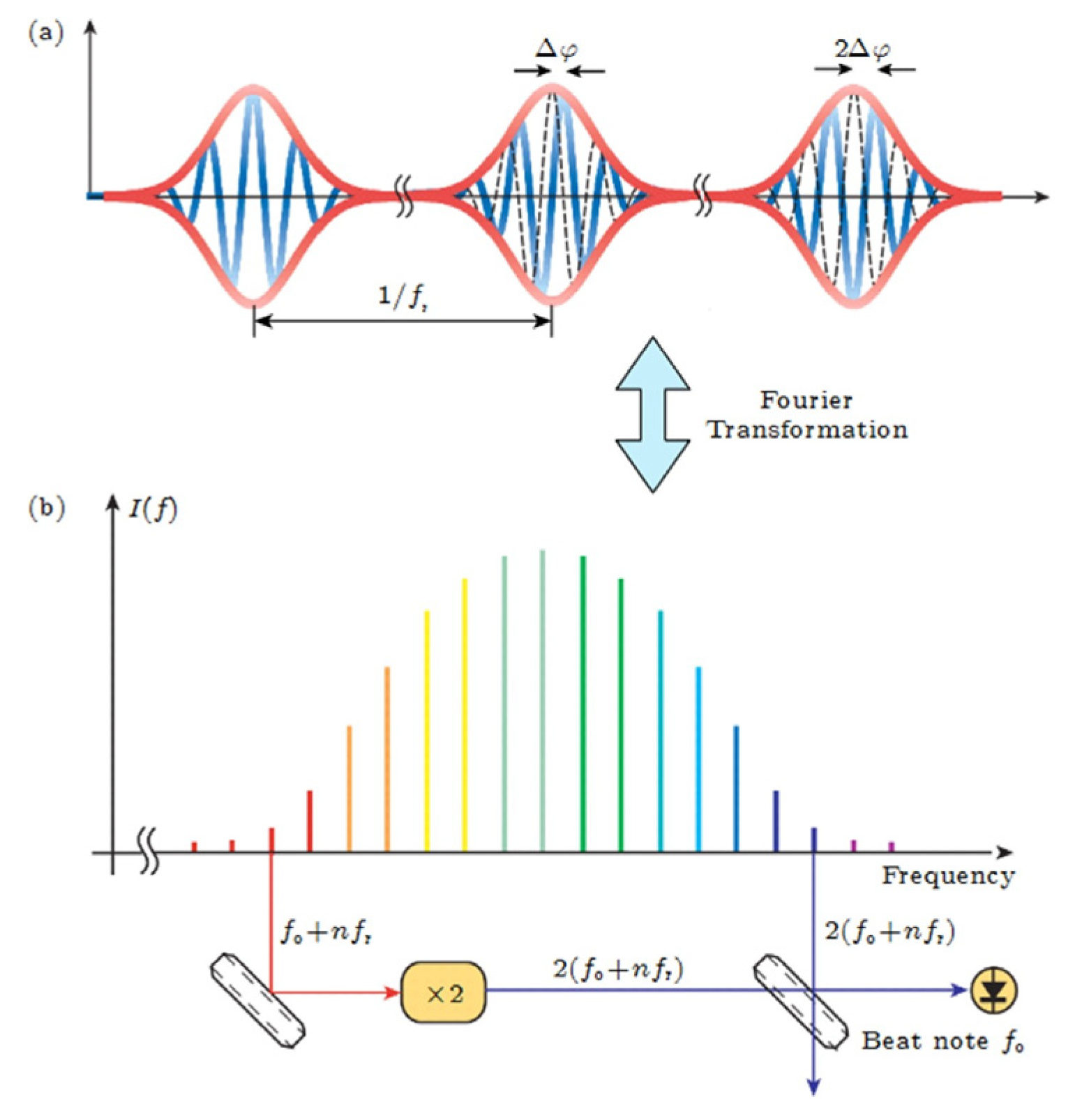
Preprints 118923 g003
Figure 3. (a) The temporal waveform of the OFC. (b) The optical spectrum of OFC and the two plots have a Fourier relationship [78].
Figure 3. (a) The temporal waveform of the OFC. (b) The optical spectrum of OFC and the two plots have a Fourier relationship [78].
Preprints 118923 g003
The techniques for generating OFCs include electro-optical modulation, mode-locked laser, or laser array, which result in bulky system size and limited bandwidth [99,100,101,102,103,104]. To address the limitations, the researcher explored new platforms that produce smallsized and broad bandwidth combs. The development of microcavity with an ultra-high quality factor (Q factor) enables the Kerr microcomb to be a crucial alternative to OFC technology [20,78,105].
The discovery of the Kerr microcomb could be traced back to the beginning of the 21st century when Ranka generated the supercontinuum spectrum in microstructured fibers [83]. These materials own anomalous dispersion that stimulates non-linear optical effects such as four-wave mixing and soliton propagation, which are the formation basis for the Kerr combs [83,85,106]. In 2003, the silicon-based microcavity with the 108 Q factor was fabricated, in which the optical parameter oscillation was observed in the following year [79,80,81,82]. Although only few optical teeth were produced, the results saw the beginning of the Kerr microcombs. Then in 2007, Kippenberg’s group produced broadband OFCs in microcavity using the continuous wave (CW) laser, indicating an important node of the microcomb development, after which researchers started to generate Kerr comb in different cavities except for silicon ones, including CMOS-compatible platforms based on Silicon Nitride or high-index doped silica glass [20,22,84]. From 2014 to 2019, an increasing number of Kerr comb generation works were conducted, and various soliton combs were observed, namely dissipative Kerr solitons (DKSs), soliton crystal (SCs), and laser cavity solitons (LCSs) [85,86,87]. The appearance of these low-power consumption and chipscaled microcombs contributed to the wide application in various fields including RF photon signal processing [88,89,90], optical communication [76,91,92], precision measurement [93,94], neural networks [107,108], and spectroscopy [95], and has a promising future in both the academic and industrial world.

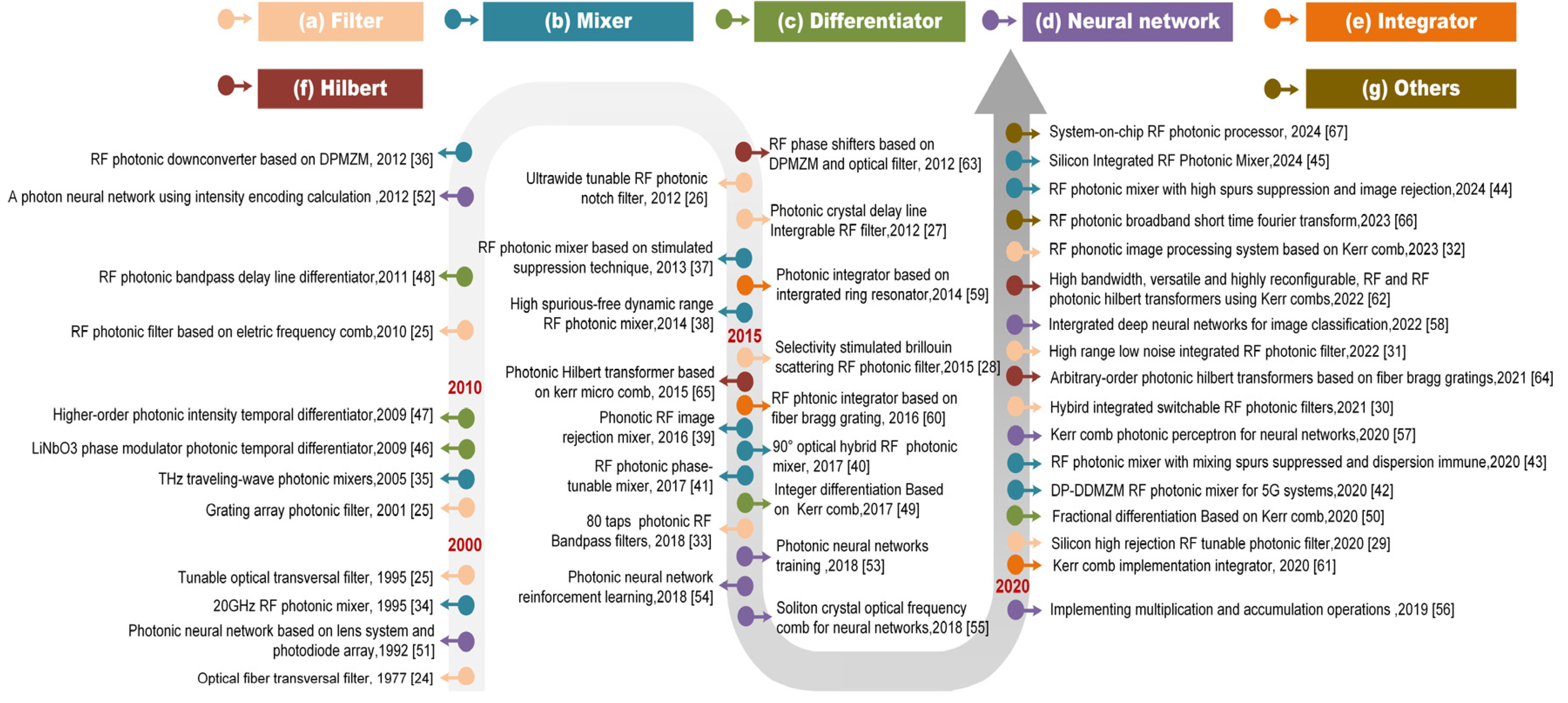
4. Real-Time Signal Processing Based on OFC

There are many approaches to realize RF photonic signal processing. One is that the optical filter response is mapped onto the RF domain [121,122,123,124,125,126] and Brillouin scattering by on-chip is the one of the most important approaches [123,124,125]. Another approach is reconfigurable transfer function for adaptive signal processing based on transversal filter [124,125,126]. It works by generating weighted and delayed copies of the real-time RF signal in the optical domain and then combing them during photo-detection. Transversal filters can achieve arbitrary RF transfer functions by changing the weight of taps. The taps usually are offered by multi-wavelength source such as discrete laser arrays [127,128,129], Bragg grating arrays [130,131], electro-optical generated combs [16], or mode-locked fiber lasers [132]. However, taps offered by these approaches are limited in quantity and the complexity. Compared to the methods mentioned above, integrated OFC based on micro-ring resonators have distinct advantages in offering multi-wavelength sources with smaller in size, more conducive to integration and achieve larger free spectrum range (FSR) [133,134,135,136,137,138].
In 2015, Thach for the first time combined an OFC based on micro-ring with a RF photonic transversal filter to realize a 20-tap Hilbert transformer, and we called this system “the real-time signal processing system”, leading the research upsurge of RF photonic filter based on OFC [23]. The real-time signal processing system proposed in this paper consists of three main sections: OFC generation, comb shaping, and RF photonic filtering. In the generation of OFC, pump wave generated by a continuous-wave tunable laser is amplified by a high power Erbium-doped fiber amplifier (EDFA1) and then the pump wave enters into the micro-ring resonator and generate OFC. In the second section of the RF photonic signal processing system, a reconfigurable filter (WaveShaper) shapes the comb lines of OFC according to the required tap coefficients. Afterwards, the comb lines of OFC as a multiplewavelength source enter into the last section of this system with going through a 2x2 balanced Mach-Zehnder modulator for modulating comb lines to realize negative and positive tap coefficients, 2.122 km single-mode fiber (SMF) for delaying the different filter taps, and a second fiber amplifier (EDFA2) for compensating for loss and separating the comb. The optical signals are finally detected by photodiodes to output RF signals. The real-time signal processing system’s frequency response is measured with an RF vector network analyzer (VNA). Afterwards, this real-time signal processing system also realized a reconfigurable RF photonic intensity differentiator [49] including the first, second and third order intensity differentiator and a reconfigurable true RF time delay capable of yielding a phased array antenna [109]. The first multi-channel RF tunable microwave true time delay lines for phased array antenna based on this real-time signal processing system has higher performance and lower size. By shaping the comb lines of OFC, this system realized the antenna which achieved high angular resolution, wide range of beam steering angles, and small variation in beam steering angle. In [111], the photodetector of the system was replaced by balanced photodetector which consisted of two mutually matched and consistent photodiodes. Two photodiodes could differentially subtract the current signal and the signal was amplified and output. Compared with previous photodetector, balanced photodetector could effectively counteract the influence of both light source and environmental noise, thereby enhancing the signal-tonoise ratio. In this work, Sim not only realized a significantly finer 50 GHz FSR offering up to 80 comb lines based on a Kerr micro-comb but also realized a fractional Hilbert transformer with arbitrary fractional orders. In [112], a broadband Local Oscillator (LO)-free photonic RF mixer was also proposed based on this real-time signal processing system which could convert RF frequency to the U-band. The comb lines offered by OFC served as a RF local oscillator for RF signal conversion. Finally, this work realized a low ratio of -6.8 dB between output RF power and IF power and the spurious suppression of signal was up to 43.5 dB. Following this mixer, Xingyuan Xu el at. further proposed a novel approach to Optical artificial networks (ONN) based on this real-time signal processing system [113]. ONN is a novel approach to neural network computation that utilizes principles and technologies of photonics [139,140]. In traditional electronic neural networks, information transmission occurs through electronic signals processed and transmitted on silicon chips [141,142,143]. In contrast, optical neural networks leverage the properties of light for information transmission and processing, potentially offering advantages in speed and energy efficiency [144,145,146,147,148,149].
Preprints 118923 g004
Figure 4. [M3] Timeline for the development of Kerr microcombs. (a) Technical basis for microcombs [79,80,81,82,83]. (b) Variety classes of microcombs generated in the development process [20,22,84,85,86,87]. (c) Applications of the Kerr microcombs [76,88,89,90,91,92,93,94,95].
Figure 4. [M3] Timeline for the development of Kerr microcombs. (a) Technical basis for microcombs [79,80,81,82,83]. (b) Variety classes of microcombs generated in the development process [20,22,84,85,86,87]. (c) Applications of the Kerr microcombs [76,88,89,90,91,92,93,94,95].
Preprints 118923 g004
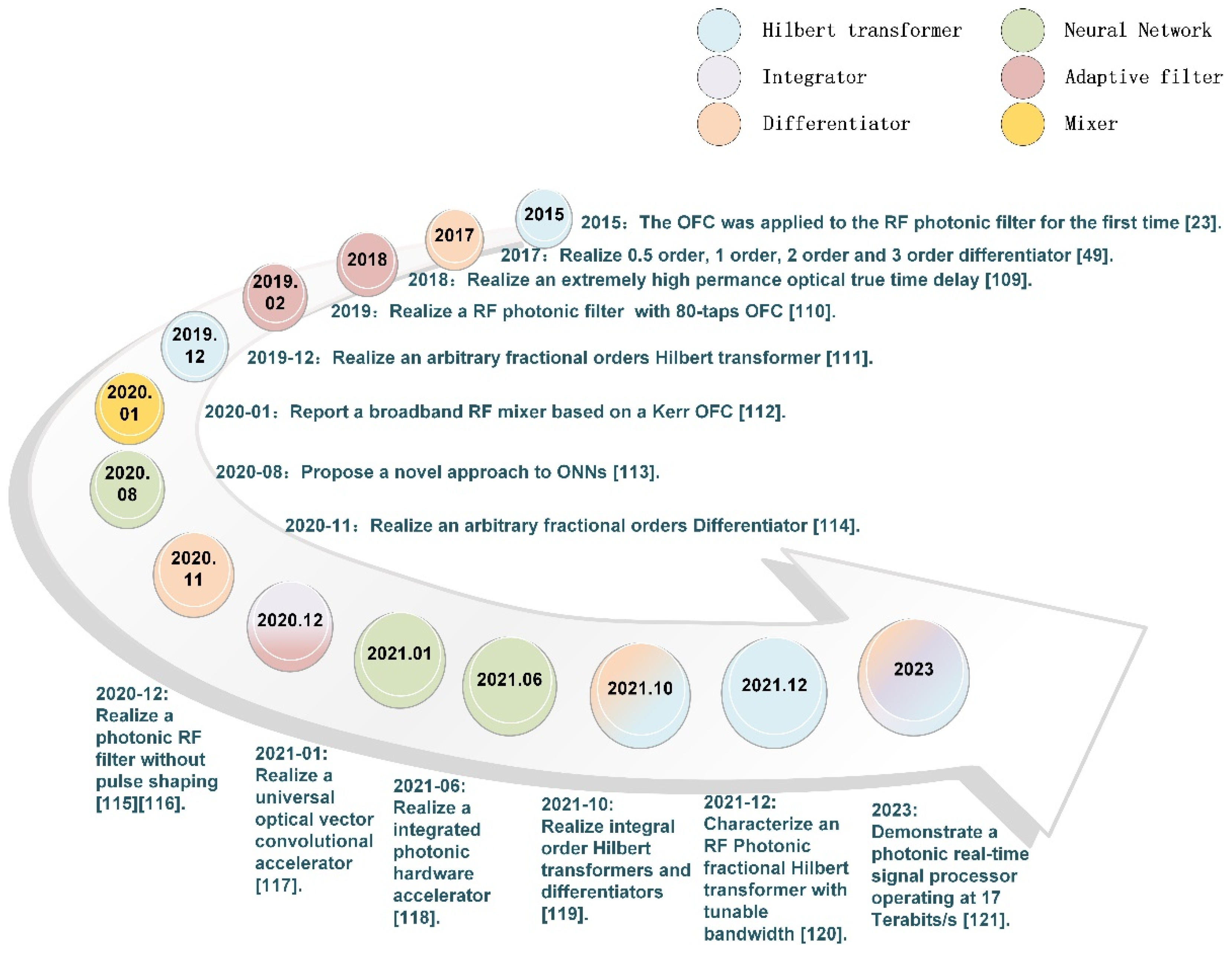
Preprints 118923 g005
Figure 5. [M4] Timeline for the development of real-time signal processing based on OFC [23,49,108,109,110,111,112,113,114,115,116,117,118,119,120].
Figure 5. [M4] Timeline for the development of real-time signal processing based on OFC [23,49,108,109,110,111,112,113,114,115,116,117,118,119,120].
Preprints 118923 g005
Preprints 118923 g006
Figure 6. [M5] The results of real-time signal processing system for different applications based on OFC. (a) Integrator [115,120]. (b) Differentiator [49,114,118,120]. (c) Neural network [108,113,117]. (d) Adaptive filter [109,110]. (e) Mixer [112]. (f) Hilbert transformer [23,111,118,119,120].
Figure 6. [M5] The results of real-time signal processing system for different applications based on OFC. (a) Integrator [115,120]. (b) Differentiator [49,114,118,120]. (c) Neural network [108,113,117]. (d) Adaptive filter [109,110]. (e) Mixer [112]. (f) Hilbert transformer [23,111,118,119,120].
Preprints 118923 g006
The basic idea behind ONN is to use light’s properties for information transmission and processing between neurons. Typically composed of components such as light sources, modulators, amplifiers, and detectors, optical neural networks simulate the functionality of neurons and process information through optical signals.
In this paper, a new approach based on the realtime signal processing system including OFC utilized wavelength, time, spatial, multiplexing to compute vector dot products, which could use straightforward flatting to convert dot products into vectors for performing matrix operation. The novel ONN finally achieved a record throughput of 95.2 Gbps per unit and then it was applied to the standard benchmark tests including handwritten digits and predicting benign/maglignant cancer classes, capable of achieving >93% accuracy and >85% accuracy, respectively. In 2020, a novel differentiator was demonstrated based on this real-time signal processing system [114]. In contrast to previous differentiator [49], this differentiator not only operated directly on the real-time RF signal rather than the optical domain but also was based on a novel the form of OFC named “soliton crystals”, thus effectively realized reconfigurable arbitrary fractional orders ranging from 0.15 to 0.9. At the same time, Kippenberg’s team also designed an RF photonic filter, but the signal processing system they constructed was slightly different from this real-time signal processing system in this paper [116]. The signal processing system They designed didn’t have a WaveShaper and adjusted the OFC spacing by triggering a perfect soliton crystals.
A novel photonic integrator based on the real-time signal processing system with transversal structures was reported [115], which offered multiple wavelength channels because of OFC so that each path could be controlled independently and thus improving high reconfigurability and accuracy. What’s more, in contrast to previous real-time signal processing system, the comb shaping approach of this system was optimized from optical power shaping to impulse response shaping in order to reduce errors. This photonic integrator was capable of offering a large integration time window of 6.8 ns and a time resolution of 84 ps.
After optimizing this system, Xu proposed a universal optical vector convolutional accelerator using the same hardware of real-time signal processing system, which could operate at more than 10 TOPS and generate a 250,000 pixels images convolutions [108]. At the same year, Kippenberg et al. also proposed a novel integrated photonic accelerator involved in ONN based on soliton microcombs and was capable of operating multiply-accumulate at speed of 1012 MAC operations per second [117].
In 2021, after demonstrating fractional order differentiator, Sim Tan proposed a integral order differentiator including 1st, 2nd and 3rd order three kinds based on this real-time signal processing system [118]. Soon after, Sim Tan demonstrated an configurable RF photonic Hilbert transformer with tunable bandwidths as well as centre frequency on the basis of the same system [119]. This Hilbert transformer could achieve a tunable bandwidth ranging from 1.2 GHz to 15.3 GHz as well as a tunable centre frequency from baseband to 9.5 GHz by adjusting the weight of taps and programming. Following this, Sim Tan further first proposed a video images processor based on this real-time signal processing system which was highly reconfigurable by programmable control [120]. This video images processor could perform not only different functions such as integral and fractional order differentiation, fractional order Hilbert transforms, and integration but also images processing approaches including edge detection, motion blur and edge enhancement without changing the physical hardware as show in Figure 7g[M6] . This work demonstrated that this video images processor could simultaneously process over 399,061 real-time signals with an ultrahigh bandwidths of 17 Tbs/s. In addition, This result confirmed that the theory was in good agreement with the measurement, and laid a foundation for the integration of ultrahigh-bandwidth realtime signal processing system.
Preprints 118923 g007
Figure 7. different structure of real-time signal processing system for different applications based on OFC. (a) Integrator [115,120]. (b) Differentiator [49,114,118,120]. (c) Neural network [108,113,117]. (d) Adaptive filter [109,110]. (e) Mixer [112]. (f) Hilbert transformer [23,111,118,119,120].
Figure 7. different structure of real-time signal processing system for different applications based on OFC. (a) Integrator [115,120]. (b) Differentiator [49,114,118,120]. (c) Neural network [108,113,117]. (d) Adaptive filter [109,110]. (e) Mixer [112]. (f) Hilbert transformer [23,111,118,119,120].
Preprints 118923 g007

5. Discussion

We review the development of real-time signal processing system based on Kerr OFC in chronological order in Figure 5. The first part reviews the development process of RF photonic signal processing methods. The second part introduces the classification and development trend of OFC in detail. In the final part, we further review the development of real-time signal processing system based on OFC and the different parallel functions implemented in chronological order. Thereby, we review the timeline of this real-time signal processing system and we operated a series of optimization for this system.
The real-time signal processing system realized many parallel functions such as integrator, differentiator, neural network, adaptive filter, mixer and Hilbert transformer showcased in Figure 6a–f and Figure 7a–g. For Hilbert transformer and differentiator, the number of wavelength determines the number of comb lines while the number of taps in turn directly determines the performance of this system. Arbitrary fractional and integral orders differentiators and tunablebandwidth Hilbert transformers were proposed based on this real-time signal processing system with excellent performance.
For the system mentioned in this article, the performance of the optical frequency comb has reached a high state, and many record-setting functions have been completed including that the optical vector convolutional accelerator, and the new world record (up to 17 Terabits/s) photonic real-time signal processor. Nonetheless, there are still many applications as well as more parallel functions that ultimately could be implemented based on this system.
In terms of the comb lines shaping, tap errors during comb shaping can lead to deviations between experimental results and theory, as well as non-ideal impulse responses in the system. These errors stem from various sources such as optical micro-comb instability, waveshaper inaccuracies, wavelength-dependent gain variation in optical amplifiers, chirp induced by optical modulators, and third-order dispersion in dispersive fibers. To mitigate these issues, real-time feedback control loops can be employed. Initially, the power of comb lines is detected by an optical spectrum analyzer (OSA) and compared with ideal tap weights to generate an error signal. This signal is then fed back into the waveshaper for system calibration, enhancing comb shaping accuracy. Alternatively, to further refine tap errors and improve accuracy, the feedback loop’s error signal can be derived directly from the measured impulse response instead of raw optical power. This involves measuring RF Gaussian pulse replicas across all wavelengths to obtain the system’s impulse response, from which peak intensities are extracted to determine RF-to-RF wavelength channel weights accurately. Subsequently, the extracted channel weights are compared with desired weights to derive an error signal for programming the loss of waveshaper. Through multiple iterations of this comb shaping loop, an accurate impulse response is achieved, compensating for system non-idealities and enhancing the accuracy of RF photonic transversal filter-based signal processors. Importantly, this calibration process is conducted only once. As for the integration of real-time signal processing system, the potential of this system is significant due to its integration capabilities with current nanofabrication techniques [150]. The microcomb source is already integrated and fabricated using CMOS-compatible processes [151,152]. The several key components of this system have been successfully integrated using cutting-edge nanofabrication techniques [153,154,155]. These include the optical pump source [151,152], optical spectral shapers [153], LiNO3 modulators [155], dispersion media [154], and photodetectors. Furthermore, advanced integrated microcombs have demonstrated reliable generation of soliton crystals in operational settings [152,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179]. Monolithic integration of the entire real-time signal processing system promises enhanced performance, compactness, and energy efficiency. Despite lacking complete integration, employing discrete integrated OFC instead of laser arrays already provides significant advantages for RF systems in terms of performance, size, cost, and complexity. This will be greatly assisted by the development of ultra high nonlinearity 2D materials such as graphene oxide [180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195,196,197,198,199,200,201,202,203,204,205,206,207,208,209,210].
Recent advancements have shown that soliton crystals can achieve various RF functions without requiring spectral shaping, solely through different pumping conditions that produce varied spectra [116]. This expands the capabilities of OFC beyond what is achievable with DKS states. Such developments are particularly advantageous as they eliminate the need for spectral shapers, components in RF systems that ultimately require integration efforts.

References

  1. J. Yao, “Microwave photonics,” Journal of lightwave technology, vol. 27, no. 3, pp. 314–335, 2009.
  2. C. Cox III, “Analog photonic links: Theory and practice,” 2004.
  3. C. H. Cox, E. I. Ackerman, G. E. Betts, and J. L. Prince, “Limits on the performance of rf-over-fiber links and their impact on device design,” IEEE Transactions on Microwave Theory and Techniques, vol. 54, no. 2, pp. 906–920, 2006. [CrossRef]
  4. H. V. Roussell, M. D. Regan, J. L. Prince, C. H. Cox, J. X. Chen, W. K. Burns, G. E. Betts, E. I. Ackerman, and J. C. Campbell, “Gain, noise figure and bandwidth-limited dynamic range of a low-biased external modulation link,” in Microwave Photonics, 2007 Interntional Topical Meeting on. IEEE, 2007, pp. 84–87.
  5. I. Gasulla and J. Capmany, “Analytical model and figures of merit for filtered microwave photonic links,” Optics Express, vol. 19, no. 20, pp. 19 758–19 774, 2011. [CrossRef]
  6. J. Capmany and D. Novak, “Microwave photonics combines two worlds,” Nature photonics, vol. 1, no. 6, p. 319, 2007. [CrossRef]
  7. W. S. Chang, RF photonic technology in optical fiber links. Cambridge University Press, 2002.
  8. D. Marpaung, J. Yao, and J. Capmany, “Integrated microwave photonics,” Nature photonics, vol. 13, no. 2, pp. 80–90, 2019. [CrossRef]
  9. J. Azaña, “Ultrafast analog all-optical signal processors based on fiber-grating devices,” IEEE Photonics Journal, vol. 2, no. 3, pp. 359–386, 2010. [CrossRef]
  10. J. Capmany, B. Ortega, and D. Pastor, “A tutorial on microwave photonic filters,” Journal of Lightwave Technology, vol. 24, no. 1, pp. 201–229, 2006. [CrossRef]
  11. A. J. Seeds and K. J. Williams, “Microwave photonics,” Journal of lightwave technology, vol. 24, no. 12, pp. 4628– 4641, 2006. [CrossRef]
  12. S. Iezekiel, Microwave photonics: devices and applications. John Wiley & Sons, 2009.
  13. C. Rumelhard, C. Algani, and A.-L. Billabert, Microwaves Photonic Links: Components and Circuits. John Wiley & Sons, 2013.
  14. T. Berceli and P. R. Herczfeld, “Microwave photonics—a historical perspective,” IEEE transactions on microwave theory and techniques, vol. 58, no. 11, pp. 2992–3000, 2010. [CrossRef]
  15. A. Vilcot, B. Cabon, and J. Chazelas, Microwave Photonics: from components to applications and systems. Springer Science & Business Media, 2003.
  16. V. Supradeepa, C. M. Long, R. Wu, F. Ferdous, E. Hamidi, D. E. Leaird, and A. M. Weiner, “Comb-based radiofrequency photonic filters with rapid tunability and high selectivity,” Nature Photonics, vol. 6, no. 3, pp. 186–194, 2012. [CrossRef]
  17. A. Malacarne, R. Ashrafi, M. Li, S. LaRochelle, J. Yao, and J. Azaña, “Single-shot photonic time-intensity integration based on a time-spectrum convolution system,” Optics Letters, vol. 37, no. 8, pp. 1355–1357, 2012. [CrossRef]
  18. V. Torres-Company and A. M. Weiner, “Optical frequency comb technology for ultra-broadband radio-frequency photonics,” Laser & Photonics Reviews, vol. 8, no. 3, pp. 368– 393, 2014. [CrossRef]
  19. Z. Jiang, C.-B. Huang, D. E. Leaird, and A. M. Weiner, “Optical arbitrary waveform processing of more than 100 spectral comb lines,” nature photonics, vol. 1, no. 8, pp. 463–467, 2007. [CrossRef]
  20. P. Del’Haye, A. Schliesser, O. Arcizet, T. Wilken, R. Holzwarth, and T. Kippenberg, “Optical frequency comb generation from a monolithic microresonator,” Nature, vol. 450, pp. 1214–7, 01 2008. [CrossRef]
  21. W. Liang, D. Eliyahu, V. S. Ilchenko, A. A. Savchenkov, A. B. Matsko, D. Seidel, and L. Maleki, “High spectral purity kerr frequency comb radio frequency photonic oscillator,” Nature communications, vol. 6, no. 1, p. 7957, 2015. [CrossRef]
  22. J. S. Levy, A. A. Gondarenko, M. A. Foster, A. C. Turner-Foster, A. L. Gaeta, and M. Lipson, “Cmoscompatible multiple-wavelength oscillator for on-chip optical interconnects,” Nature Photonics, vol. 4, pp. 37–40, 2010. [Online]. Available: https://api.semanticscholar.org/ CorpusID:122006845. [CrossRef]
  23. T. G. Nguyen, M. Shoeiby, S. T. Chu, B. E. Little, R. Morandotti, A. Mitchell, and D. J. Moss, “Integrated frequency comb source based hilbert transformer for wideband microwave photonic phase analysis,” Optics express, vol. 23, no. 17, pp. 22 087–22 097, 2015. [CrossRef]
  24. M. Frankel and R. Esman, “Fiber-optic tunable microwave transversal filter,” IEEE Photonics Technology Letters, vol. 7, no. 2, pp. 191–193, Feb. 1995. [CrossRef]
  25. E. Hamidi, D. E. Leaird, and A. M. Weiner, “Tunable Programmable Microwave Photonic Filters Based on an Optical Frequency Comb,” IEEE Transactions on Microwave Theory and Techniques, vol. 58, no. 11, pp. 3269–3278, Nov. 2010. [CrossRef]
  26. W. Zhang and R. A. Minasian, “Ultrawide Tunable Microwave Photonic Notch Filter Based on Stimulated Brillouin Scattering,” IEEE Photonics Technology Letters, vol. 24, no. 14, pp. 1182–1184, Jul. 2012. [CrossRef]
  27. J. Sancho, J. Bourderionnet, J. Lloret, S. CombriĂ©, I. Gasulla, S. Xavier, S. Sales, P. Colman, G. Lehoucq, D. Dolfi, J. Capmany, and A. De Rossi, “Integrable microwave filter based on a photonic crystal delay line,” Nature Communications, vol. 3, no. 1, p. 1075, Sep. 2012. [CrossRef]
  28. D. Marpaung, B. Morrison, M. Pagani, R. Pant, D.-Y. Choi, B. Luther-Davies, S. J. Madden, and B. J. Eggleton, “Lowpower, chip-based stimulated Brillouin scattering microwave photonic filter with ultrahigh selectivity,” Optica, vol. 2, no. 2, p. 76, Feb. 2015. [CrossRef]
  29. S. Gertler, E. A. Kittlaus, N. T. Otterstrom, and P. T. Rakich, “Tunable microwave-photonic filtering with high out-of-band rejection in silicon,” APL Photonics, vol. 5, no. 9, p. 096103, Sep. 2020. [CrossRef]
  30. Y. Tao, H. Shu, X. Wang, M. Jin, Z. Tao, F. Yang, J. Shi, and J. Qin, “Hybrid-integrated high-performance microwave photonic filter with switchable response,” Photonics Research, vol. 9, no. 8, p. 1569, Aug. 2021. [CrossRef]
  31. S. Gertler, N. T. Otterstrom, M. Gehl, A. L. Starbuck, C. M. Dallo, A. T. Pomerene, D. C. Trotter, A. L. Lentine, and P. T. Rakich, “Narrowband microwave-photonic notch filters using Brillouin-based signal transduction in silicon,” Nature Communications, vol. 13, no. 1, p. 1947, Apr. 2022. [CrossRef]
  32. O. Daulay, G. Liu, K. Ye, R. Botter, Y. Klaver, Q. Tan, H. Yu, M. Hoekman, E. Klein, C. Roeloffzen, Y. Liu, and D. Marpaung, “Ultrahigh dynamic range and low noise figure programmable integrated microwave photonic filter,” Nature Communications, vol. 13, no. 1, p. 7798, Dec. 2022. [CrossRef]
  33. X. Xu and et al., “Advanced adaptive photonic rf filters with 80 taps based on an integrated optical micro-comb source,” Journal of Lightwave Technology, vol. 37, no. 4, pp. 1288–1295, 2019. [CrossRef]
  34. A. Lindsay, G. Knight, and S. Winnall, “Photonic mixers for wide bandwidth RF receiver applications,” IEEE Transactions on Microwave Theory and Techniques, vol. 43, no. 9, pp. 2311–2317, Sept./1995. [CrossRef]
  35. E. A. Michael, B. Vowinkel, R. Schieder, M. Mikulics, M. Marso, and P. Kordoơ, “Large-area traveling-wave photonic mixers for increased continuous terahertz power,” Applied Physics Letters, vol. 86, no. 11, p. 111120, Mar. 2005. [CrossRef]
  36. E. H. W. Chan and R. A. Minasian, “Microwave Photonic Downconverter With High Conversion Efficiency,” Journal of Lightwave Technology, vol. 30, no. 23, pp. 3580–3585, Dec. 2012. [CrossRef]
  37. E. H. Chan and R. A. Minasian, “High conversion efficiency microwave photonic mixer based on stimulated brillouin scattering carrier suppression technique,” Optics letters, vol. 38, no. 24, pp. 5292–5295, 2013. [CrossRef]
  38. A. Altaqui, E. H. W. Chan, and R. A. Minasian, “Microwave photonic mixer with high spurious-free dynamic range,” Applied Optics, vol. 53, no. 17, p. 3687, Jun. 2014. [CrossRef]
  39. S. Pan and Z. Tang, “A highly reconfigurable photonic microwave frequency mixer,” SPIE Newsroom, Feb. 2015. [CrossRef]
  40. J. Zhang, E. H. W. Chan, X. Wang, X. Feng, and B. Guan, “High Conversion Efficiency Photonic Microwave Mixer With Image Rejection Capability,” IEEE Photonics Journal, vol. 8, no. 4, pp. 1–11, Aug. 2016. [CrossRef]
  41. T. Jiang, R. Wu, S. Yu, D. Wang, and W. Gu, “Microwave photonic phase-tunable mixer,” Optics Express, vol. 25, no. 4, p. 4519, Feb. 2017. [CrossRef]
  42. A. Kumar, A. Gautam, and V. Priye, “Microwave Photonic Mixer Using DP-DDMZM for Next Generation 5G Cellular Systems,” Fiber and Integrated Optics, vol. 39, no. 4, pp. 149–168, Jul. 2020. [CrossRef]
  43. T. Lin, Z. Zhang, J. Liu, S. Zhao, J. Li, C. Zou, J. Wang, K. Zhang, and W. Jiang, “Reconfigurable Photonic Microwave Mixer With Mixing Spurs Suppressed and Dispersion Immune for Radio-Over-Fiber System,” IEEE Transactions on Microwave Theory and Techniques, vol. 68, no. 12, pp. 5317–5327, Dec. 2020. [CrossRef]
  44. G. Shen and Y. Zhou, “Broadband Microwave Photonic Mixer With High Spurs Suppression and Image Rejection,” IEEE Photonics Journal, vol. 16, no. 1, pp. 1–8, Feb. 2024. [CrossRef]
  45. F. Liu, Z. Tang, R. Wu, L. Tang, D. Van Thourhout, and S. Pan, “Silicon Integrated Microwave Photonic Mixer Based on Cascaded Microring Resonator Modulators,” IEEE Photonics Technology Letters, vol. 36, no. 5, pp. 333–336, Mar. 2024. [CrossRef]
  46. J. Zhou, S. Fu, S. Aditya, P. Ping, C. Lin, V. Wong, and D. Lim, “Photonic Temporal Differentiator based on Polarization Modulation in a LiNbO3 Phase Modulator.”.
  47. Y. Park, M. H. Asghari, and J. Azana, “Reconfigurable higher-order photonic intensity temporal differentiator,” in 2009 IEEE LEOS Annual Meeting Conference Proceedings. Belek-Antalya: IEEE, Oct. 2009, pp. 731–732.
  48. Yichen Han, Ze Li, and Jianping Yao, “A Microwave Bandpass Differentiator Implemented Based on a Nonuniformly-Spaced Photonic Microwave Delay-Line Filter,” Journal of Lightwave Technology, vol. 29, no. 22, pp. 3470–3475, Nov. 2011. [CrossRef]
  49. X. Xu, J. Wu, M. Shoeiby, T. G. Nguyen, S. T. Chu, B. E. Little, R. Morandotti, A. Mitchell, and D. J. Moss, “Reconfigurable broadband microwave photonic intensity differentiator based on an integrated optical frequency comb source,” Apl Photonics, vol. 2, no. 9, 2017. [CrossRef]
  50. M. Tan, X. Xu, B. Corcoran, J. Wu, A. Boes, T. G. Nguyen, S. T. Chu, B. E. Little, R. Morandotti, A. Mitchell, and D. J. Moss, “ RF and Microwave Fractional Differentiator Based on Photonics,” IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 67, no. 11, pp. 2767–2771, Nov. 2020. [CrossRef]
  51. D. Woods and T. J. Naughton, “Photonic neural networks,” Nature Physics, vol. 8, no. 4, pp. 257–259, Apr. 2012. [CrossRef]
  52. J. Bueno, S. Maktoobi, L. Froehly, I. Fischer, M. Jacquot, L. Larger, and D. Brunner, “Reinforcement learning in a large-scale photonic recurrent neural network,” Optica, vol. 5, no. 6, p. 756, Jun. 2018. [CrossRef]
  53. T. W. Hughes, M. Minkov, Y. Shi, and S. Fan, “Training of photonic neural networks through in situ backpropagation and gradient measurement,” Optica, vol. 5, no. 7, p. 864, Jul. 2018. [CrossRef]
  54. M. A. Nahmias, T. F. De Lima, A. N. Tait, H.-T. Peng, B. J. Shastri, and P. R. Prucnal, “Photonic Multiply-Accumulate Operations for Neural Networks,” IEEE Journal of Selected Topics in Quantum Electronics, vol. 26, no. 1, pp. 1–18, Jan. 2020. [CrossRef]
  55. B. Corcoran, M. Tan, X. Xu, A. Boes, J. Wu, T. G. Nguyen, S. T. Chu, B. E. Little, R. Morandotti, A. Mitchell, and D. J. Moss, “Ultra-dense optical data transmission over standard fibre with a single chip source,” Nature Communications, vol. 11, no. 1, p. 2568, May 2020. [CrossRef]
  56. X. Xu, M. Tan, B. Corcoran, J. Wu, T. G. Nguyen, A. Boes, S. T. Chu, B. E. Little, R. Morandotti, A. Mitchell, D. G. Hicks, and D. J. Moss, “Photonic Perceptron Based on a Kerr Microcomb for High-Speed, Scalable, Optical Neural Networks,” Laser & Photonics Reviews, vol. 14, no. 10, p. 2000070, Oct. 2020. [CrossRef]
  57. S. Zarei, M.-r. Marzban, and A. Khavasi, “Integrated photonic neural network based on silicon metalines,” Optics Express, vol. 28, no. 24, p. 36668, Nov. 2020. [CrossRef]
  58. F. Ashtiani, A. J. Geers, and F. Aflatouni, “An on-chip photonic deep neural network for image classification,” Nature, vol. 606, no. 7914, pp. 501–506, Jun. 2022. [CrossRef]
  59. W. Liu, M. Li, R. S. Guzzon, E. J. Norberg, J. S. Parker, L. A. Coldren, and J. Yao, “A Photonic Temporal Integrator With an Ultra-Long Integration Time Window Based on an InP-InGaAsP Integrated Ring Resonator,” Journal of Lightwave Technology, vol. 32, no. 20, pp. 3654–3659, Oct. 2014. [CrossRef]
  60. J. Zhang and J. Yao, “Microwave photonic integrator based on a multichannel fiber Bragg grating,” Optics Letters, vol. 41, no. 2, p. 273, Jan. 2016. [CrossRef]
  61. X. Xu, M. Tan, J. Wu, A. Boes, B. Corcoran, T. G. Nguyen, S. T. Chu, B. E. Little, R. Morandotti, A. Mitchell, and D. J. Moss, “Photonic RF and Microwave Integrator Based on a Transversal Filter With Soliton Crystal Microcombs,” IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 67, no. 12, pp. 3582–3586, Dec. 2020. [CrossRef]
  62. D. Moss, “High bandwidth, versatile and highly reconfigurable, RF and microwave photonic Hilbert transformers using Kerr micro-combs.”.
  63. J. Shen, G. Wu, W. Zou, and J. Chen, “A Photonic RF Phase Shifter Based on a Dual-Parallel Mach–Zehnder Modulator and an Optical Filter,” Applied Physics Express, vol. 5, no. 7, p. 072502, Jul. 2012. [CrossRef]
  64. Y. Li, X. Liu, X. Shu, and L. Zhang, “Arbitrary-Order Photonic Hilbert Transformers Based on Phase-Modulated Fiber Bragg Gratings in Transmission,” Photonics, vol. 8, no. 2, p. 27, Jan. 2021. [CrossRef]
  65. T. G. Nguyen and et al., “Integrated frequency comb source based hilbert transformer for wideband microwave photonic phase analysis,” Optics Express, vol. 23, no. 17, pp. 22 087–22 097, 2015. [CrossRef]
  66. J. Li, S. Fu, X. Xie, M. Xiang, Y. Dai, F. Yin, and Y. Qin, “Low-Latency Short-Time Fourier Transform of Microwave Photonics Processing,” Journal of Lightwave Technology, vol. 41, no. 19, pp. 6149–6156, Oct. 2023. [CrossRef]
  67. W. Zhang, J. C. Lederman, T. Ferreira De Lima, J. Zhang, S. Bilodeau, L. Hudson, A. Tait, B. J. Shastri, and P. R. Prucnal, “A system-on-chip microwave photonic processor solves dynamic RF interference in real time with picosecond latency,” Light: Science & Applications, vol. 13, no. 1, p. 14, Jan. 2024. [CrossRef]
  68. C. Han and et al., “Proton radiation effects on high-speed silicon mach-zehnder modulators for space application,” Science China Information Sciences, vol. 65, no. 12, p. 222401, 2022. [CrossRef]
  69. M. Tan, “Microcomb-based ultra-fast signal processing,” 2021.
  70. C. T. Chang, J. A. Cassaboom, and H. F. Taylor, “Fibre-optic delay-line devices for rf signal processing,” Electronics Letters, vol. 22, no. 13, pp. 678–680, 1977. [CrossRef]
  71. G. Yu, W. Zhang, and J. A. R. Williams, “Highperformance microwave transversal filter using fiber bragg grating arrays,” IEEE Photonics Technology Letters, vol. 12, no. 9, pp. 1183–1185, 2000. [CrossRef]
  72. C. Sima and et al., “Phase controlled integrated interferometric single-sideband filter based on planar bragg gratings implementing photonic hilbert transform,” Optics Letters, vol. 38, no. 5, pp. 727–729, 2013. [CrossRef]
  73. M. Li and J. Yao, “All-fiber temporal photonic fractional hilbert transformer based on a directly designed fiber bragg grating,” Optics Letters, vol. 35, no. 2, pp. 223–225, 2010. [CrossRef]
  74. M. Li and Y. Jianping, “Experimental demonstration of a wideband photonic temporal hilbert transformer based on a single fiber bragg grating,” IEEE Photonics Technology Letters, vol. 22, no. 21, pp. 1559–1561, 2010. [CrossRef]
  75. X. Xu, J. Wu, M. Shoeiby, T. G. Nguyen, S. T. Chu, B. E. Little, R. Morandotti, A. Mitchell, and D. J. Moss, “Reconfigurable broadband microwave photonic intensity differentiator based on an integrated optical frequency comb source,” APL Photonics, vol. 2, no. 9, p. 096104, Sep. 2017. [CrossRef]
  76. B. Corcoran, M. Tan, X. Xu, A. Boes, J. Wu, T. G. Nguyen, S. T. Chu, B. E. Little, R. Morandotti, A. Mitchell et al., “Ultra-dense optical data transmission over standard fibre with a single chip source,” Nature communications, vol. 11, no. 1, p. 2568, 2020. [CrossRef]
  77. M. Tan and et al., “Photonic signal processor based on a kerr microcomb for real-time video image processing,” Communications Engineering, vol. 2, no. 1, p. 94, 2023. [CrossRef]
  78. T. Udem, R. Holzwarth, and T. W. HĂ€nsch, “Optical frequency metrology,” Nature, vol. 416, no. 6877, pp. 233–237, 2002. [CrossRef]
  79. K. J. Vahala, “Optical microcavities,” Nature, vol. 424, pp. 839–846, 2003. [Online]. Available: https://api.semanticscholar.org/CorpusID:4349700. [CrossRef]
  80. T. J. Kippenberg, D. K. Armani, S. M. Spillane, and K. J. Vahala, “Ultra-high-q toroid microcavity on a chip,” Nature, vol. 421, pp. 925–928, 2003. [Online]. Available: https://api.semanticscholar.org/CorpusID:4420078. [CrossRef]
  81. T. J. Kippenberg, S. M. Spillane, and K. J. Vahala, “Kerr-nonlinearity optical parametric oscillation in an ultrahigh-q toroid microcavity.” Physical review letters, vol. 93 8, p. 083904, 2004. [Online]. Available: https://api.semanticscholar.org/CorpusID:11378974. [CrossRef]
  82. A. A. Savchenkov, A. B. Matsko, D. Strekalov, M. Mohageg, V. S. Ilchenko, and L. Maleki, “Low threshold optical oscillations in a whispering gallery mode caf2 resonator,” Phys. Rev. Lett., vol. 93, p. 243905, Dec 2004. [CrossRef]
  83. J. Ranka, R. Windeler, and A. Stentz, “Visible continuum generation in air-silica microstructure optical fibers with anomalous dispersion at 800 nm,” Optics letters, vol. 25, pp. 25–7, 02 2000. [CrossRef]
  84. L. Razzari, D. Duchesne, M. Ferrera, R. Morandotti, S. T. Chu, B. E. Little, and D. J. Moss, “Cmos-compatible integrated optical hyper-parametric oscillator,” Nature Photonics, vol. 4, pp. 41–45, 2010. [Online]. Available: https://api.semanticscholar.org/CorpusID:120307174. [CrossRef]
  85. T. Herr, V. Brasch, J. Jost, C. Wang, N. Kondratiev, M. Gorodetsky, and T. Kippenberg, “Temporal solitons in optical microresonators,” Nature Photonics, vol. 8, 11 2012. [CrossRef]
  86. H. Bao, A. Cooper, M. Rowley, L. D. Lauro, J. S. T. Gongora, S. T. Chu, B. E. Little, G.-L. Oppo,R. Morandotti, D. J. Moss, B. Wetzel, M. Peccianti, and A. Pasquazi, “Laser cavity-soliton microcombs,” Nature Photonics, vol. 13, pp. 384–389, 2019. [Online]. Available: https://api.semanticscholar.org/CorpusID:85502173. [CrossRef]
  87. D. Cole, E. Lamb, P. Del’Haye, S. Diddams, and S. Papp, “Soliton crystals in kerr resonators,” Nature Photonics, vol. 11, 10 2017. [CrossRef]
  88. Y. Sun, J. Wu, M. Tan, X. Xu, Y. Li, R. Morandotti, A. Mitchell, and D. J. Moss, “Applications of optical micro-combs”, Advances in Optics and Photonics Vol. 15 (1) 86-175 (2023). [CrossRef]
  89. X. Xue, Y. Xuan, H.-J. Kim, J. Wang, D. Leaird, M. Qi, and A. Weiner, “Programmable single-bandpass photonic rf filter based on kerr comb from a microring,” Lightwave Technology, Journal of, vol. 32, pp. 3557–3565, 10 2014. [CrossRef]
  90. X. Xu, M. Tan, J. Wu, R. Morandotti, A. D. Mitchell, and D. J. Moss, “Microcomb-based photonic rf signal processing,” IEEE Photonics Technology Letters, vol. 31, pp. 1854–1857, 2019. [Online]. Available: https://api.semanticscholar.org/CorpusID:203075392. [CrossRef]
  91. P. Marin-Palomo, J. N. Kemal, M. Karpov, A. Kordts, J. Pfeifle, M. H. P. Pfeiffer, P. Trocha, S. Wolf, V. Brasch, M. H. Anderson, R. Rosenberger, K. Vijayan, W. Freude, T. J. Kippenberg, and C. Koos, “Microresonatorbased solitons for massively parallel coherent optical communications,” Nature, vol. 546, pp. 274–279, 2016. [Online]. Available: https://api.semanticscholar.org/ CorpusID:15027009. [CrossRef]
  92. A. FĂŒlöp, M. Mazur, A. Lorences-Riesgo, P.-H. Wang, Y. Xuan, D. Leaird, M. Qi, P. Andrekson, A. Weiner, and V. Torres Company, “High-order coherent communications using mode-locked dark-pulse kerr combs from microresonators,” Nature Communications, vol. 9, 04 2018. [CrossRef]
  93. M.-G. Suh and K. J. Vahala, “Soliton microcomb range measurement,” Science, vol. 359, pp. 884 – 887, 2017. https://api.semanticscholar.org/ CorpusID:3447410. [CrossRef]
  94. P. Trocha, D. Ganin, M. Karpov, M. H. P. Pfeiffer, A. Kordts, J. Krockenberger, S. Wolf, P. MarinPalomo, C. Weimann, S. Randel, W. Freude, T. J. Kippenberg, and C. Koos, “Ultrafast optical ranging using microresonator soliton frequency combs,” Science, vol. 359, pp. 887 – 891, 2017. [Online]. Available: https://api.semanticscholar.org/CorpusID:262504772. [CrossRef]
  95. M.-G. Suh, Q. Yang, K. Y. Yang, X. Yi, and K. J. Vahala, “Microresonator soliton dual-comb spectroscopy,” Science, vol. 354, pp. 600 – 603, 2016. [Online]. Available: https://api.semanticscholar.org/CorpusID:11249028. [CrossRef]
  96. A. Pasquazi, M. Peccianti, L. Razzari, D. J. Moss, S. Coen, M. Erkintalo, Y. K. Chembo, T. Hansson, S. Wabnitz, P. Del’Haye et al., “Micro-combs: A novel generation of optical sources,” Physics Reports, vol. 729, pp. 1–81, 2018. [CrossRef]
  97. S. A. Diddams, D. J. Jones, J. Ye, S. T. Cundiff, J. L. Hall, J. K. Ranka, R. S. Windeler, R. Holzwarth, T. Udem, and T. W. HĂ€nsch, “Direct link between microwave and optical frequencies with a 300 thz femtosecond laser comb,” Physical review letters, vol. 84, no. 22, p. 5102, 2000. [CrossRef]
  98. X. Xu, M. Tan, J. Wu, R. Morandotti, A. Mitchell, and D. J. Moss, “Microcomb-based photonic rf signal processing,” IEEE Photonics Technology Letters, vol. 31, no. 23, pp. 1854–1857, 2019. [CrossRef]
  99. D. J. Jones, S. A. Diddams, J. K. Ranka, A. Stentz, R. S. Windeler, J. L. Hall, and S. T. Cundiff, “Carrier-envelope phase control of femtosecond mode-locked lasers and direct optical frequency synthesis,” Science, vol. 288, no. 5466, pp. 635–639, 2000. [CrossRef]
  100. L. Jia-ming, Photonic Devices. Cambridge University Press, 2005.
  101. D. E. Spence, P. N. Kean, and W. Sibbett, “60-fsec pulse generation from a self-mode-locked ti:sapphire laser.” Optics letters, vol. 16 1, pp. 42–4, 1991. [Online]. Available: https://api.semanticscholar.org/CorpusID:32748074. [CrossRef]
  102. K. R. Tamura, E. P. Ippen, H. A. Haus, and L. E. Nelson, “77-fs pulse generation from a stretchedpulse mode-locked all-fiber ring laser.” Optics letters, vol. 18 13, p. 1080, 1993. [Online]. Available: https://api.semanticscholar.org/CorpusID:19639214. [CrossRef]
  103. H. Murata, A. Morimoto, T. Kobayashi, and S. Yamamoto, “Optical pulse generation by electrooptic-modulation method and its application to integrated ultrashort pulse generators,” IEEE Journal of Selected Topics in Quantum Electronics, vol. 6, no. 6, pp. 1325–1331, 2000. [CrossRef]
  104. A. Parriaux, K. Hammani, and G. Millot, “Electro-optic frequency combs,” Adv. Opt. Photon., vol. 12, no. 1, pp. 223–287, Mar 2020. [Online]. Available: https://opg.optica.org/aop/abstract.cfm?URI=aop-12-1-223. [CrossRef]
  105. T. J. Kippenberg, S. M. Spillane, and K. J. Vahala, “Kerr-nonlinearity optical parametric oscillation in an ultrahigh-q toroid microcavity.” Physical review letters, vol. 93 8, p. 083904, 2004. [Online]. Available: https://api.semanticscholar.org/CorpusID:11378974. [CrossRef]
  106. M. Haelterman, S. Trillo, and S. Wabnitz, “Dissipative modulation instability in a nonlinear dispersive ring cavity,” Optics Communications, vol. 91, pp. 401–407, 1992. [Online]. Available: https://api.semanticscholar.org/ CorpusID:122501011. [CrossRef]
  107. X. Xu, M. Tan, B. Corcoran, J. Wu, T. Nguyen, A. Boes, S. Chu, B. Little, R. Morandotti, A. Mitchell, D. Hicks, and D. Moss, “Photonic perceptron based on a kerr microcomb for high-speed, scalable, optical neural networks,” Laser & Photonics Reviews, vol. 14, 08 2020. [CrossRef]
  108. X. Xu, M. Tan, B. Corcoran, J. Wu, A. Boes, T. G. Nguyen, S. T. Chu, B. E. Little, D. G. Hicks, R. Morandotti et al., “11 tops photonic convolutional accelerator for optical neural networks,” Nature, vol. 589, no. 7840, pp. 44–51, 2021. [CrossRef]
  109. X. Xu, J. Wu, T. G. Nguyen, M. Shoeiby, S. T. Chu, B. E. Little, R. Morandotti, A. Mitchell, and D. J. Moss, “Advanced rf and microwave functions based on an integrated optical frequency comb source,” Optics Express, vol. 26, no. 3, pp. 2569–2583, 2018. [CrossRef]
  110. X. Xu, M. Tan, J. Wu, T. G. Nguyen, S. T. Chu, B. E. Little, R. Morandotti, A. Mitchell, and D. J. Moss, “Advanced adaptive photonic rf filters with 80 taps based on an integrated optical micro-comb source,” Journal of Lightwave Technology, vol. 37, no. 4, pp. 1288–1295, 2019. [CrossRef]
  111. M. Tan, X. Xu, B. Corcoran, J. Wu, A. Boes, T. G. Nguyen, S. T. Chu, B. E. Little, R. Morandotti, A. Mitchell et al., “Microwave and rf photonic fractional hilbert transformer based on a 50 ghz kerr micro-comb,” Journal of Lightwave Technology, vol. 37, no. 24, pp. 6097–6104, 2019. [CrossRef]
  112. X. Xu, J. Wu, M. Tan, T. G. Nguyen, S. T. Chu, B. E. Little, R. Morandotti, A. Mitchell, and D. J. Moss, “Broadband microwave frequency conversion based on an integrated optical micro-comb source,” Journal of Lightwave Technology, vol. 38, no. 2, pp. 332–338, 2020. [CrossRef]
  113. X. Xu, M. Tan, B. Corcoran, J. Wu, T. G. Nguyen, A. Boes, S. T. Chu, B. E. Little, R. Morandotti, A. Mitchell et al., “Photonic perceptron based on a kerr microcomb for highspeed, scalable, optical neural networks,” Laser & Photonics Reviews, vol. 14, no. 10, p. 2000070, 2020. [CrossRef]
  114. M. Tan, X. Xu, B. Corcoran, J. Wu, A. Boes, T. G. Nguyen, S. T. Chu, B. E. Little, R. Morandotti, A. Mitchell et al., “Rf and microwave fractional differentiator based on photonics,” IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 67, no. 11, pp. 2767–2771, 2020. [CrossRef]
  115. X. Xu, M. Tan, J. Wu, A. Boes, B. Corcoran, T. G. Nguyen, S. T. Chu, B. E. Little, R. Morandotti, A. Mitchell et al., “Photonic rf and microwave integrator based on a transversal filter with soliton crystal microcombs,” IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 67, no. 12, pp. 3582–3586, 2020. [CrossRef]
  116. J. Hu, J. He, J. Liu, A. S. Raja, M. Karpov, A. Lukashchuk, T. J. Kippenberg, and C.-S. Brùs, “Reconfigurable radiofrequency filters based on versatile soliton microcombs,” Nature communications, vol. 11, no. 1, p. 4377, 2020. [CrossRef]
  117. J. Feldmann, N. Youngblood, M. Karpov, H. Gehring, X. Li, M. Stappers, M. Le Gallo, X. Fu, A. Lukashchuk, A. S. Raja et al., “Parallel convolutional processing using an integrated photonic tensor core,” Nature, vol. 589, no. 7840, pp. 52–58, 2021. [CrossRef]
  118. M. Tan, X. Xu, J. Wu, B. Corcoran, A. Boes, T. G. Nguyen, S. T. Chu, B. E. Little, R. Morandotti, A. Mitchell et al., “Integral order photonic rf signal processors based on a soliton crystal micro-comb source,” Journal of Optics, vol. 23, no. 12, p. 125701, 2021. [CrossRef]
  119. M. Tan, X. Xu, A. Boes, B. Corcoran, J. Wu, T. G. Nguyen, S. T. Chu, B. E. Little, A. J. Lowery, R. Morandotti et al., “Highly versatile broadband rf photonic fractional hilbert transformer based on a kerr soliton crystal microcomb,” Journal of Lightwave Technology, vol. 39, no. 24, pp. 7581–7587, 2021. [CrossRef]
  120. M. Tan, X. Xu, A. Boes, B. Corcoran, T. G. Nguyen, S. T. Chu, B. E. Little, R. Morandotti, J. Wu, A. Mitchell et al., “Photonic signal processor based on a kerr microcomb for real-time video image processing,” Communications Engineering, vol. 2, no. 1, p. 94, 2023. [CrossRef]
  121. Y. Liu, J. Hotten, A. Choudhary, B. J. Eggleton, and D. Marpaung, “All-optimized integrated rf photonic notch filter,” Optics letters, vol. 42, no. 22, pp. 4631–4634, 2017. [CrossRef]
  122. Y. Liu, D. Marpaung, A. Choudhary, J. Hotten, and B. J. Eggleton, “Link performance optimization of chip-based si 3 n 4 microwave photonic filters,” Journal of lightwave technology, vol. 36, no. 19, pp. 4361–4370, 2018. [CrossRef]
  123. Y. Liu, Y. Yu, S. Yuan, X. Xu, and X. Zhang, “Tunable megahertz bandwidth microwave photonic notch filter based on a silica microsphere cavity,” Optics Letters, vol. 41, no. 21, pp. 5078–5081, 2016. [CrossRef]
  124. D. Marpaung, B. Morrison, M. Pagani, R. Pant, D.-Y. Choi, B. Luther-Davies, S. J. Madden, and B. J. Eggleton, “Low-power, chip-based stimulated brillouin scattering microwave photonic filter with ultrahigh selectivity,” Optica, vol. 2, no. 2, pp. 76–83, 2015. [CrossRef]
  125. A. Choudhary, B. Morrison, I. Aryanfar, S. Shahnia, M. Pagani, Y. Liu, K. Vu, S. Madden, D. Marpaung, and B. J. Eggleton, “Advanced integrated microwave signal processing with giant on-chip brillouin gain,” Journal of lightwave technology, vol. 35, no. 4, pp. 846–854, 2016. [CrossRef]
  126. D. Marpaung, B. Morrison, R. Pant, and B. J. Eggleton, “Frequency agile microwave photonic notch filter with anomalously high stopband rejection,” Optics letters, vol. 38, no. 21, pp. 4300–4303, 2013. [CrossRef]
  127. S. Mansoori and A. Mitchell, “Rf transversal filter using an aotf,” IEEE Photonics Technology Letters, vol. 16, no. 3, pp. 879–881, 2004. [CrossRef]
  128. J. Leng, W. Zhang, and J. A. Williams, “Optimization of superstructured fiber bragg gratings for microwave photonic filters response,” IEEE Photonics technology letters, vol. 16, no. 7, pp. 1736–1738, 2004. [CrossRef]
  129. M. Delgado-Pinar, J. Mora, A. Diez, M. Andres, B. Ortega, and J. Capmany, “Tunable and reconfigurable microwave filter by use of a bragg-grating-based acousto-optic super-lattice modulator,” Optics letters, vol. 30, no. 1, pp. 8–10, 2005. [CrossRef]
  130. G. Yu, W. Zhang, and J. Williams, “High-performance microwave transversal filter using fiber bragg grating arrays,” IEEE Photonics Technology Letters, vol. 12, no. 9, pp.1183–1185, 2000. [CrossRef]
  131. D. Hunter, R. Minasian, and P. Krug, “Tunable optical transversal filter based on chirped gratings,” Electronics Letters, vol. 31, no. 25, pp. 2205–2207, 1995. [CrossRef]
  132. A. Ortigosa-Blanch, J. Mora, J. Capmany, B. Ortega, and D. Pastor, “Tunable radio-frequency photonic filter based on an actively mode-locked fiber laser,” Optics letters, vol. 31, no. 6, pp. 709–711, 2006. [CrossRef]
  133. B. Toby, “Microresonator-based optical frequency combs,” DOC 2022 Abstract Book, p. 11, 2011.
  134. M. A. Foster, J. S. Levy, O. Kuzucu, K. Saha, M. Lipson, and A. L. Gaeta, “Silicon-based monolithic optical frequency comb source,” Optics Express, vol. 19, no. 15, pp. 14 233–14 239, 2011. [CrossRef]
  135. M. Peccianti, A. Pasquazi, Y. Park, B. E. Little, S. T. Chu, D. J. Moss, and R. Morandotti, “Demonstration of a stable ultrafast laser based on a nonlinear microcavity,” Nature communications, vol. 3, no. 1, p. 765, 2012. [CrossRef]
  136. A. Pasquazi, L. Caspani, M. Peccianti, M. Clerici, M. Ferrera, L. Razzari, D. Duchesne, B. E. Little, S. T. Chu, D. J. Moss et al., “Self-locked optical parametric oscillation in a cmos compatible microring resonator: a route to robust optical frequency comb generation on a chip,” Optics express, vol. 21, no. 11, pp. 13 333–13 341, 2013. [CrossRef]
  137. D. J. Moss, R. Morandotti, A. L. Gaeta, and M. Lipson,“New cmos-compatible platforms based on silicon nitride and hydex for nonlinear optics,” Nature photonics, vol. 7, no. 8, pp. 597–607, 2013. [CrossRef]
  138. L. Razzari, D. Duchesne, M. Ferrera, R. Morandotti, S. Chu, B. E. Little, and D. J. Moss, “Cmos-compatible integrated optical hyper-parametric oscillator,” Nature Photonics, vol. 4, no. 1, pp. 41–45, 2010. [CrossRef]
  139. Y. Shen, N. C. Harris, S. Skirlo, M. Prabhu, T. Baehr-Jones, M. Hochberg, X. Sun, S. Zhao, H. Larochelle, D. Englund et al., “Deep learning with coherent nanophotonic circuits,” Nature photonics, vol. 11, no. 7, pp. 441–446, 2017. [CrossRef]
  140. X. Lin, Y. Rivenson, N. T. Yardimci, M. Veli, Y. Luo, M. Jarrahi, and A. Ozcan, “All-optical machine learning using diffractive deep neural networks,” Science, vol. 361, no. 6406, pp. 1004–1008, 2018. [CrossRef]
  141. S. K. Esser, R. Appuswamy, P. Merolla, J. V. Arthur, and D. S. Modha, “Backpropagation for energy-efficient neuromorphic computing,” Advances in neural information processing systems, vol. 28, 2015.
  142. A. Graves, G. Wayne, M. Reynolds et al., “Hybrid computing using a neural network with dynamic external memory,” Nature, vol. 538, no. 7626, pp. 471–476, 2016. [CrossRef]
  143. D. A. Miller, “Attojoule optoelectronics for low-energy information processing and communications,” Journal of Lightwave Technology, vol. 35, no. 3, pp. 346–396, 2017. [CrossRef]
  144. P. Antonik, N. Marsal, D. Brunner, and D. Rontani, “Human action recognition with a large-scale brain-inspired photonic computer,” Nature Machine Intelligence, vol. 1, no. 11, pp. 530–537, 2019. [CrossRef]
  145. L. Appeltant, M. C. Soriano, G. Van der Sande, J. Danckaert, S. Massar, J. Dambre, B. Schrauwen, C. R. Mirasso, and I. Fischer, “Information processing using a single dynamical node as complex system,” Nature communications, vol. 2, no. 1, p. 468, 2011. [CrossRef]
  146. H.-T. Peng, M. A. Nahmias, T. F. De Lima, A. N. Tait, and B. J. Shastri, “Neuromorphic photonic integrated circuits,” IEEE Journal of Selected Topics in Quantum Electronics, vol. 24, no. 6, pp. 1–15, 2018. [CrossRef]
  147. A. N. Tait, M. A. Nahmias, B. J. Shastri, and P. R. Prucnal, “Broadcast and weight: an integrated network for scalable photonic spike processing,” Journal of Lightwave Technology, vol. 32, no. 21, pp. 3427–3439, 2014. [CrossRef]
  148. N. Tait, J. Chang, B. J. Shastri, M. A. Nahmias, and P. R. Prucnal, “Demonstration of wdm weighted addition for principal component analysis,” Optics Express, vol. 23, no. 10, pp. 12 758–12 765, 2015. [CrossRef]
  149. J. Feldmann, N. Youngblood, C. D. Wright, H. Bhaskaran, and W. H. Pernice, “All-optical spiking neurosynaptic networks with self-learning capabilities,” Nature, vol. 569, no. 7755, pp. 208–214, 2019. [CrossRef]
  150. V. J. Urick, “Considerations and application opportunities for integrated microwave photonics,” in Optical Fiber Communication Conference. Optica Publishing Group, 2016, pp. M2B–1.
  151. Stern, X. Ji, Y. Okawachi, A. L. Gaeta, and M. Lipson, “Battery-operated integrated frequency comb generator,” Nature, vol. 562, no. 7727, pp. 401–405, 2018. [CrossRef]
  152. Shen, L. Chang, J. Liu, H. Wang, Q.-F. Yang, C. Xiang, R. N. Wang, J. He, T. Liu, W. Xie et al., “Integrated turnkey soliton microcombs,” Nature, vol. 582, no. 7812, pp. 365–369, 2020. [CrossRef]
  153. A. J. Metcalf, H.-J. Kim, D. E. Leaird, J. A. Jaramillo-Villegas, K. A. McKinzie, V. Lal, A. Hosseini, G. E. Hoefler, F. Kish, and A. M. Weiner, “Integrated line-by-line optical pulse shaper for high-fidelity and rapidly reconfigurable rffiltering,” Optics Express, vol. 24, no. 21, pp. 23 925–23 940, 2016. [CrossRef]
  154. Sahin, K. Ooi, C. Png, and D. Tan, “Large, scalable dispersion engineering using cladding-modulated bragg gratings on a silicon chip,” Applied Physics Letters, vol. 110, no. 16, 2017. [CrossRef]
  155. C. Wang, M. Zhang, X. Chen, M. Bertrand, A. Shams-Ansari, S. Chandrasekhar, P. Winzer, and M. Lončar, “Integrated lithium niobate electro-optic modulators operating at cmoscompatible voltages,” Nature, vol. 562, no. 7725, pp. 101–104, 2018. [CrossRef]
  156. Pasquazi, et al., “Sub-picosecond phase-sensitive optical pulse characterization on a chip”, Nature Photonics, vol. 5, no. 10, pp. 618-623 (2011). [CrossRef]
  157. M Ferrera et al., “On-Chip ultra-fast 1st and 2nd order CMOS compatible all-optical integration”, Optics Express vol. 19 (23), 23153-23161 (2011). [CrossRef]
  158. Bao, C., et al., Direct soliton generation in microresonators, Opt. Lett, 42, 2519 (2017). [CrossRef]
  159. M.Ferrera et al., “CMOS compatible integrated all-optical RF spectrum analyzer”, Optics Express, vol. 22, no. 18, 21488 21498 (2014). [CrossRef]
  160. M. Kues, et al., “Passively modelocked laser with an ultra-narrow spectral width”, Nature Photonics, vol. 11, no. 3, pp. 159, 2017. [CrossRef]
  161. M. Ferrera, et al., “Low-power continuous-wave nonlinear optics in doped silica glass integrated waveguide structures,” Nature Photonics, vol. 2, no. 12, pp. 737-740, 2008. [CrossRef]
  162. M.Ferrera et al.“On-Chip ultra-fast 1st and 2nd order CMOS compatible all-optical integration”, Opt. Express, vol. 19, (23)pp. 23153-23161 (2011). [CrossRef]
  163. Duchesne, M. Peccianti, M. R. E. Lamont, et al., “Supercontinuum generation in a high index doped silica glass spiral waveguide,” Optics Express, vol. 18, no, 2, pp. 923-930, 2010. [CrossRef]
  164. H Bao, L Olivieri, M Rowley, ST Chu, BE Little, R Morandotti, DJ Moss, ... “Turing patterns in a fiber laser with a nested microresonator: Robust and controllable microcomb generation”, Physical Review Research vol. 2 (2), 023395 (2020). [CrossRef]
  165. M. Ferrera, et al., “On-chip CMOS-compatible all-optical integrator”, Nature Communications, vol. 1, Article 29, 2010. [CrossRef]
  166. A. Pasquazi, et al., “All-optical wavelength conversion in an integrated ring resonator,” Optics Express, vol. 18, no. 4, pp. 3858-3863, 2010. [CrossRef]
  167. Pasquazi, Y. Park, J. Azana, et al., “Efficient wavelength conversion and net parametric gain via Four Wave Mixing in a high index doped silica waveguide,” Optics Express, vol. 18, no. 8, pp. 7634-7641, 2010. [CrossRef]
  168. Peccianti, M. Ferrera, L. Razzari, et al., “Subpicosecond optical pulse compression via an integrated nonlinear chirper,” Optics Express, vol. 18, no. 8, pp. 7625-7633, 2010. [CrossRef]
  169. M Ferrera, Y Park, L Razzari, BE Little, ST Chu, R Morandotti, DJ Moss, ... et al., “All-optical 1st and 2nd order integration on a chip”, Optics Express vol. 19 (23), 23153-23161 (2011). [CrossRef]
  170. M. Ferrera et al., “Low Power CW Parametric Mixing in a Low Dispersion High Index Doped Silica Glass Micro-Ring Resonator with Q-factor > 1 Million”, Optics Express, vol.17, no. 16, pp. 14098–14103 (2009). [CrossRef]
  171. M. Peccianti, et al., “Demonstration of an ultrafast nonlinear microcavity modelocked laser”, Nature Communications, vol. 3, pp. 765, 2012. [CrossRef]
  172. A.Pasquazi, et al., “Self-locked optical parametric oscillation in a CMOS compatible microring resonator: a route to robust optical frequency comb generation on a chip,” Optics Express, vol. 21, no. 11, pp. 13333-13341, 2013. [CrossRef]
  173. Pasquazi, et al., “Stable, dual mode, high repetition rate mode-locked laser based on a microring resonator,” Optics Express, vol. 20, no. 24, pp. 27355-27362, 2012. [CrossRef]
  174. H. Bao, et al., Laser cavity-soliton microcombs, Nature Photonics, vol. 13, no. 6, pp. 384-389, Jun. 2019. [CrossRef]
  175. Antonio Cutrona, Maxwell Rowley, Debayan Das, Luana Olivieri, Luke Peters, Sai T. Chu, Brent L. Little, Roberto Morandotti, David J. Moss, Juan Sebastian Totero Gongora, Marco Peccianti, Alessia Pasquazi, “High Conversion Efficiency in Laser Cavity-Soliton Microcombs”, Optics Express Vol. 30, Issue 22, pp. 39816-39825 (2022). [CrossRef]
  176. M.Rowley, P.Hanzard, A.Cutrona, H.Bao, S.Chu, B.Little, R.Morandotti, D. J. Moss, G. Oppo, J. Gongora, M. Peccianti and A. Pasquazi, “Self-emergence of robust solitons in a micro-cavity”, Nature vol. 608 (7922) 303–309 (2022). [CrossRef]
  177. A. Cutrona, M. Rowley, A. Bendahmane, V. Cecconi,L. Peters, L. Olivieri, B. E. Little, S. T. Chu, S. Stivala, R. Morandotti, D. J. Moss, J. S. Totero-Gongora, M. Peccianti, A. Pasquazi, “Nonlocal bonding of a soliton and a blue-detuned state in a microcomb laser”, Nature Communications Physics 6 Article 259 (2023). [CrossRef]
  178. Aadhi A. Rahim, Imtiaz Alamgir, Luigi Di Lauro, Bennet Fischer, Nicolas Perron, Pavel Dmitriev, Celine Mazoukh, Piotr Roztocki, Cristina Rimoldi, Mario Chemnitz, Armaghan Eshaghi, Evgeny A. Viktorov, Anton V. Kovalev, Brent E. Little, Sai T. Chu, David J. Moss, and Roberto Morandotti, “Mode-locked laser with multiple timescales in a microresonator-based nested cavity”, APL Photonics 9 031302 (2024). [CrossRef]
  179. A. Cutrona, M. Rowley, A. Bendahmane, V. Cecconi,L. Peters, L. Olivieri, B. E. Little, S. T. Chu, S. Stivala, R. Morandotti, D. J. Moss, J. S. Totero-Gongora, M. Peccianti, A. Pasquazi, “Stability Properties of Laser Cavity-Solitons for Metrological Applications”, Applied Physics Letters vol. 122 (12) 121104 (2023). [CrossRef]
  180. Wu, J. et al. “2D layered graphene oxide films integrated with micro-ring resonators for enhanced nonlinear optics”, Small Vol. 16, 1906563 (2020). [CrossRef]
  181. Wu, J. et al., “Graphene oxide waveguide and micro-ring resonator polarizers”, Laser and Photonics Reviews Vol. 13, 1900056 (2019). [CrossRef]
  182. Zhang, Y. et al., “Enhanced Kerr nonlinearity and nonlinear figure of merit in silicon nanowires integrated with 2d graphene oxide films”, ACS Applied Material Interfaces Vol. 12, 33094-33103 (2020). [CrossRef]
  183. Qu, Y. et al., “Enhanced four-wave mixing in silicon nitride waveguides integrated with 2d layered graphene oxide films”, Advanced Optical Materials Vol. 8, 2001048 (2020). [CrossRef]
  184. Yuning Zhang, Jiayang Wu, Yunyi Yang, Yang Qu, Linnan Jia, Houssein El Dirani, SĂ©bastien Kerdiles, Corrado Sciancalepore, Pierre Demongodin, Christian Grillet, Christelle Monat, Baohua Jia, and David J. Moss, “Enhanced supercontinuum generated in SiN waveguides coated with GO films”, Advanced Materials Technologies 8 (1) 2201796 (2023). [CrossRef]
  185. Yuning Zhang, Jiayang Wu, Linnan Jia, Yang Qu, Baohua Jia, and David J. Moss, “Graphene oxide for nonlinear integrated photonics”, Laser and Photonics Reviews 17 2200512 (2023). [CrossRef]
  186. Jiayang Wu, H.Lin, David J. Moss, T.K. Loh, Baohua Jia, “Graphene oxide for electronics, photonics, and optoelectronics”, Nature Reviews Chemistry 7 (3) 162–183 (2023). [CrossRef]
  187. Yang Qu, Jiayang Wu, Yuning Zhang, Yunyi Yang, Linnan Jia, Baohua Jia, and David J. Moss, “Photo thermal tuning in GO-coated integrated waveguides”, Micromachines Vol. 13 1194 (2022). [CrossRef]
  188. Yuning Zhang, Jiayang Wu, Yunyi Yang, Yang Qu, Houssein El Dirani, Romain Crochemore, Corrado Sciancalepore, Pierre Demongodin, Christian Grillet, Christelle Monat, Baohua Jia, and David J. Moss, “Enhanced self-phase modulation in silicon nitride waveguides integrated with 2D graphene oxide films”, IEEE Journal of Selected Topics in Quantum Electronics Vol. 29 (1) 5100413 (2023). [CrossRef]
  189. Yuning Zhang, Jiayang Wu, Yunyi Yang, Yang Qu, Linnan Jia, Baohua Jia, and David J. Moss, “Enhanced spectral broadening of femtosecond optical pulses in silicon nanowires integrated with 2D graphene oxide films”, Micromachines Vol. 13 756 (2022). [CrossRef]
  190. Jiayang Wu, Yuning Zhang, Junkai Hu, Yunyi Yang, Di Jin, Wenbo Liu, Duan Huang, Baohua Jia, David J. Moss, “Novel functionality with 2D graphene oxide films integrated on silicon photonic chips”, Advanced Materials Vol. 36 2403659 (2024). [CrossRef]
  191. Di Jin, Jiayang Wu, Junkai Hu, Wenbo Liu1, Yuning Zhang, Yunyi Yang, Linnan Jia, Duan Huang, Baohua Jia, and David J. Moss, “Silicon photonic waveguide and microring resonator polarizers incorporating 2D graphene oxide films”, Applied Physics Letters vol. 125, 000000 (2024). [CrossRef]
  192. Yuning Zhang, Jiayang Wu, Linnan Jia, Di Jin, Baohua Jia, Xiaoyong Hu, David Moss, Qihuang Gong, “Advanced optical polarizers based on 2D materials”, npj Nanophotonics Vol. 1, (2024). [CrossRef]
  193. Junkai Hu, Jiayang Wu, Wenbo Liu, Di Jin, Houssein El Dirani, SĂ©bastien Kerdiles, Corrado Sciancalepore, Pierre Demongodin, Christian Grillet, Christelle Monat, Duan Huang, Baohua Jia, and David J. Moss, “2D graphene oxide: a versatile thermo-optic material”, Advanced Functional Materials 34 2406799 (2024). [CrossRef]
  194. Yang Qu, Jiayang Wu, Yuning Zhang, Yunyi Yang, Linnan Jia, Houssein El Dirani, SĂ©bastien Kerdiles, Corrado Sciancalepore, Pierre Demongodin, Christian Grillet, Christelle Monat, Baohua Jia, and David J. Moss, “Integrated optical parametric amplifiers in silicon nitride waveguides incorporated with 2D graphene oxide films”, Light: Advanced Manufacturing 4 39 (2023). [CrossRef]
  195. Di Jin, Wenbo Liu, Linnan Jia, Junkai Hu, Duan Huang, Jiayang Wu, Baohua Jia, and David J. Moss, “Thickness and Wavelength Dependent Nonlinear Optical Absorption in 2D Layered MXene Films”, Small Science 4 2400179 (2024). [CrossRef]
  196. Linnan Jia, Jiayang Wu, Yuning Zhang, Yang Qu, Baohua Jia, Zhigang Chen, and David J. Moss, “Fabrication Technologies for the On-Chip Integration of 2D Materials”, Small: Methods Vol. 6, 2101435 (2022). [CrossRef]
  197. Yuning Zhang, Jiayang Wu, Yang Qu, Linnan Jia, Baohua Jia, and David J. Moss, “Design and optimization of four-wave mixing in microring resonators integrated with 2D graphene oxide films”, Journal of Lightwave Technology Vol. 39 (20) 6553-6562 (2021). [CrossRef]
  198. Yuning Zhang, Jiayang Wu, Yang Qu, Linnan Jia, Baohua Jia, and David J. Moss, “Optimizing the Kerr nonlinear optical performance of silicon waveguides integrated with 2D graphene oxide films”, Journal of Lightwave Technology Vol. 39 (14) 4671-4683 (2021). [CrossRef]
  199. Yang Qu, Jiayang Wu, Yuning Zhang, Yao Liang, Baohua Jia, and David J. Moss, “Analysis of four-wave mixing in silicon nitride waveguides integrated with 2D layered graphene oxide films”, Journal of Lightwave Technology Vol. 39 (9) 2902-2910 (2021). [CrossRef]
  200. Jiayang Wu, Linnan Jia, Yuning Zhang, Yang Qu, Baohua Jia, and David J. Moss, “Graphene oxide: versatile films for flat optics to nonlinear photonic chips”, Advanced Materials Vol. 33 (3) 2006415, pp.1-29 (2021). [CrossRef]
  201. Y. Qu, J. Wu, Y. Zhang, L. Jia, Y. Yang, X. Xu, S. T. Chu, B. E. Little, R. Morandotti, B. Jia, and D. J. Moss, “Graphene oxide for enhanced optical nonlinear performance in CMOS compatible integrated devices”, Paper No. 11688-30, PW21O-OE109-36, 2D Photonic Materials and Devices IV, SPIE Photonics West, San Francisco CA March 6-11 (2021). [CrossRef]
  202. Yang Qu, Jiayang Wu, Yunyi Yang, Yuning Zhang, Yao Liang, Houssein El Dirani, Romain Crochemore, Pierre Demongodin, Corrado Sciancalepore, Christian Grillet, Christelle Monat, Baohua Jia, and David J. Moss, “Enhanced nonlinear four-wave mixing in silicon nitride waveguides integrated with 2D layered graphene oxide films”, Advanced Optical Materials vol. 8 (21) 2001048 (2020). arXiv:2006.14944. [CrossRef]
  203. Yuning Zhang, Yang Qu, Jiayang Wu, Linnan Jia, Yunyi Yang, Xingyuan Xu, Baohua Jia, and David J. Moss, “Enhanced Kerr nonlinearity and nonlinear figure of merit in silicon nanowires integrated with 2D graphene oxide films”, ACS Applied Materials and Interfaces vol. 12 (29) 33094−33103 June 29 (2020). [CrossRef]
  204. Jiayang Wu, Yunyi Yang, Yang Qu, Yuning Zhang, Linnan Jia, Xingyuan Xu, Sai T. Chu, Brent E. Little, Roberto Morandotti, Baohua Jia, and David J. Moss, “Enhanced nonlinear four-wave mixing in microring resonators integrated with layered graphene oxide films”, Small vol. 16 (16) 1906563 (2020). [CrossRef]
  205. Jiayang Wu, Yunyi Yang, Yang Qu, Xingyuan Xu, Yao Liang, Sai T. Chu, Brent E. Little, Roberto Morandotti, Baohua Jia, and David J. Moss, “Graphene oxide waveguide polarizers and polarization selective micro-ring resonators”, Paper 11282-29, SPIE Photonics West, San Francisco, CA, 4 7 February (2020). [CrossRef]
  206. Jiayang Wu, Yunyi Yang, Yang Qu, Xingyuan Xu, Yao Liang, Sai T. Chu, Brent E. Little, Roberto Morandotti, Baohua Jia, and David J. Moss, “Graphene oxide waveguide polarizers and polarization selective micro-ring resonators”, Laser and Photonics Reviews vol. 13 (9) 1900056 (2019). [CrossRef]
  207. Yunyi Yang, Jiayang Wu, Xingyuan Xu, Sai T. Chu, Brent E. Little, Roberto Morandotti, Baohua Jia, and David J. Moss, “Enhanced four-wave mixing in graphene oxide coated waveguides”, Applied Physics Letters Photonics vol. 3 120803 (2018). [CrossRef]
  208. Linnan Jia, Yang Qu, Jiayang Wu, Yuning Zhang, Yunyi Yang, Baohua Jia, and David J. Moss, “Third-order optical nonlinearities of 2D materials at telecommunications wavelengths”, Micromachines (MDPI), 14, 307 (2023). [CrossRef]
  209. Linnan Jia, Dandan Cui, Jiayang Wu, Haifeng Feng, Tieshan Yang, Yunyi Yang, Yi Du, Weichang Hao, Baohua Jia, David J. Moss, “BiOBr nanoflakes with strong nonlinear optical properties towards hybrid integrated photonic devices”, Applied Physics Letters Photonics vol. 4 090802 vol. (2019). [CrossRef]
  210. Linnan Jia, Jiayang Wu, Yunyi Yang, Yi Du, Baohua Jia, David J. Moss, “Large Third-Order Optical Kerr Nonlinearity in Nanometer-Thick PdSe2 2D Dichalcogenide Films: Implications for Nonlinear Photonic Devices”, ACS Applied Nano Materials vol. 3 (7) 6876–6883 (2020). [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated