1. Euler’s product and zeta function are reciprocal relationship
The Riemann zeta function is defined by the following infinite series:
The Euler product formula and the Riemann zeta function have the following relation:
This can be written more concisely as an infinite product over all primes
p:
This equation shows that Euler’s product and zeta function have a reciprocal relationship.
If we plot on the y-axis and on the x-axis, the curve will be a hyperbola with asymptotes along the axes. This hyperbola is symmetric with respect to the line y=x.
Dividing both sides by everything but the ζ(s) we obtain:
The
Euler product formula is an alternative expression of the
Riemann ζ
function in terms of prime numbers. We define it as a function of
.
Originally the function was defined for real arguments of . It is convergent when is greater than 1. It was Riemann who extended the real-valued function to be a complex function with a complex variable rather than a real variable . Through the extension onto the entire complex plane , the Riemann zeta function is now expressed as:
2. Fourier series and vector dot product expressions
Each term in the eq. (5) can be expressed as:
The complex conjugate of is:
Combining the Complex Power Function and its Conjugate
Dividing by
:
With the help of the following relations:
Hence, the Riemann zeta function for real arguments can be expressed as:
where,
, k is the positive integers,
.
We can also express the eq. (11) more concisely as
When
, we have
Equation (10) can be expressed as:
Thus, the eq. (11) or (12) still holds.
With the Euler formula
eq. (11) can also be rewritten as:
If we define a basis vector for angular frequencies
and an amplitude coefficient vector:
Hence, for real arguments, eq. (11) is the Fourier series for Euler product formula with complex Fourier coefficients:
It should be paid attention that the function
is a real-valued function. Accordingly, the coefficients for positive and negative angular frequency flow are conjugated with each other.
3. Physical Interpretations
The series of powers of natural numbers with real arguments, defined by eq. (11), is convergent, if the real argument is greater than one, .
Physically, it can be imagined as two rotational particles with opposite rotational signs, namely, one particle is rotating clockwise and another one anticlockwise. If we view the two particles as a whole system, then the total rotational momentum (the sum of the rotational momentum of the two particles) will be zero. But the total rotational energy is , the greater the parameter, , is, the smaller the total energy will be.
Initially, the two particles are located at the coordinate origin, they are rotating in an over-damping field, this over-damping field finally causes the entangled oscillators to return to equilibrium without oscillating.
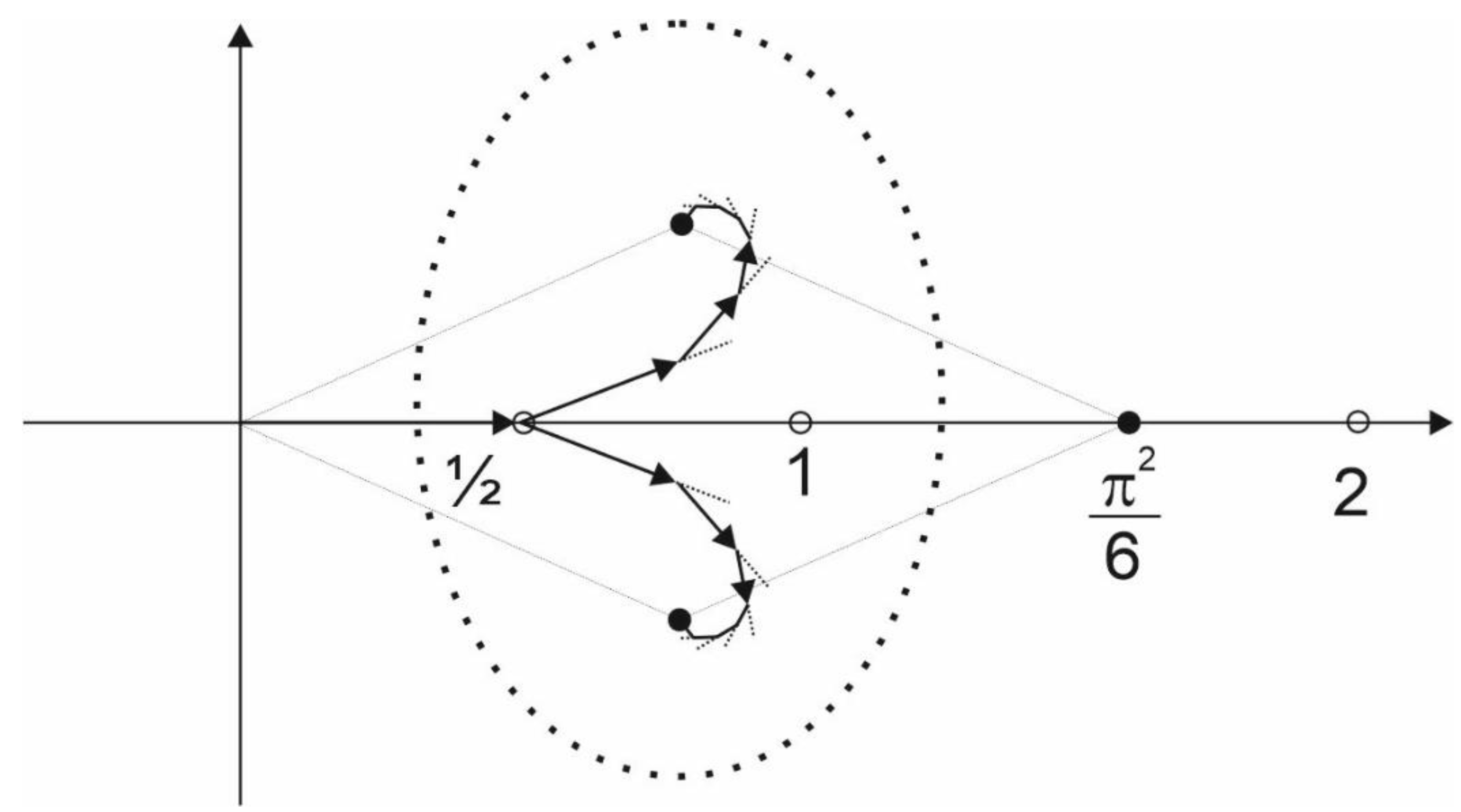
Figure 1 gives an example of
. Oscillators move slowly toward the equilibrium state.
Figure 1.
Initially entangled two particles is viewed as a system: total rotational energy is . After the decay the total vorticity.
Figure 1.
Initially entangled two particles is viewed as a system: total rotational energy is . After the decay the total vorticity.
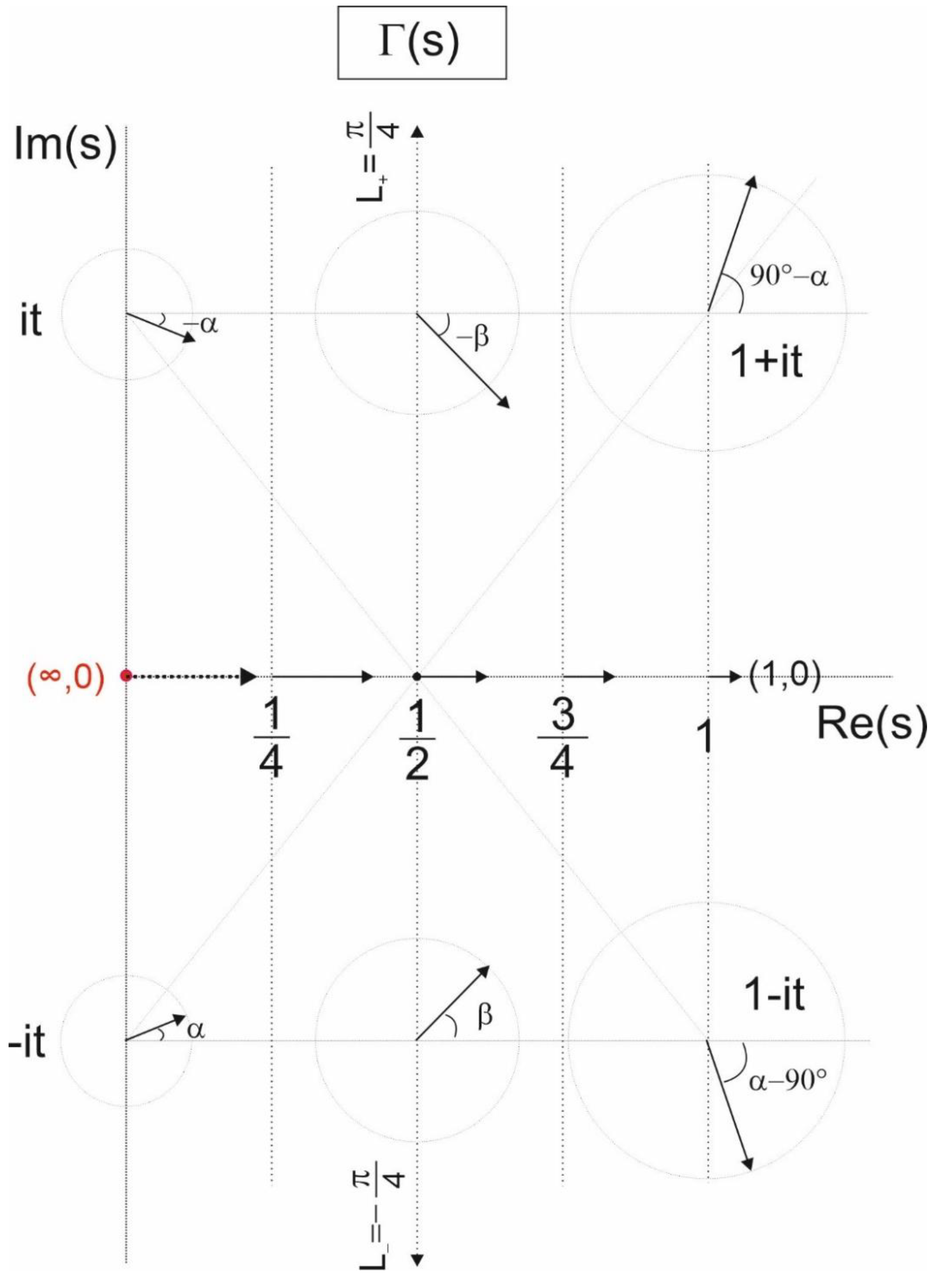
4. Riemann’s functional equation holds at
One of Riemann’s functional equations is
Recalling the infinite series definition of the Riemann zeta function of eq. (1), this equation can be expressed explicitly as
In this case, the amplitude vectors for negative and positive angular frequencies are:
and the angular frequency vectors are:
Hence, eq. (22) can be expressed more compactly as:
We define a complex function as:
Hence, the amplitude vectors of eq. (23) can be rewritten as:
Both sides of eq. (25) are infinite series, each term must be equal.
Isolating the function of
:
The magnitudes of both sides must be equal. Therefore
The amplitude of the RHS of eq. (31) multiplies a scaling factor of
. For amplitudes to match with the
factor, we should consider special values of
:
That is, given
, the amplitude conditions for both sides of the infinite series, eq. (25) are satisfied.
The arguments of the complex functions are related by modulo 2π:
That means, for the infinite series, eq. (25) to hold, the complex variable s must have its real part
equal to
. Thus, s can be written as:
Namely, the real part of s is fixed at 1/2, and the imaginary part t can vary.
Given these conditions, the Fourier coefficients can be written explicitly:
Thus, eq. (25) can be expressed explicitly as:
From eq. (37) We know that each term
Adding both terms together:
Thus, the Fourier expansion of the Euler
product formula at
is
This is a real-valued function, thus, this equation implies that the absolute values of the arguments of
at
equal the basis vectors of
, but with opposite signs.
In other words, equation (40) represents the complex form of the Fourier expansion of the Euler product formula at . Or we can say that the Riemann zeta function at can be expressed as a complex Fourier series. The complex coefficients of the negative and positive angular frequency flow are and , respectively.
It has been proved by Siegel [
3] that at
, the Riemann functional equation (21) is a real-valued function:
Hence, the amplitude vectors can be rewritten as:
and its arguments have an opposite sign of
, namely have the following form:
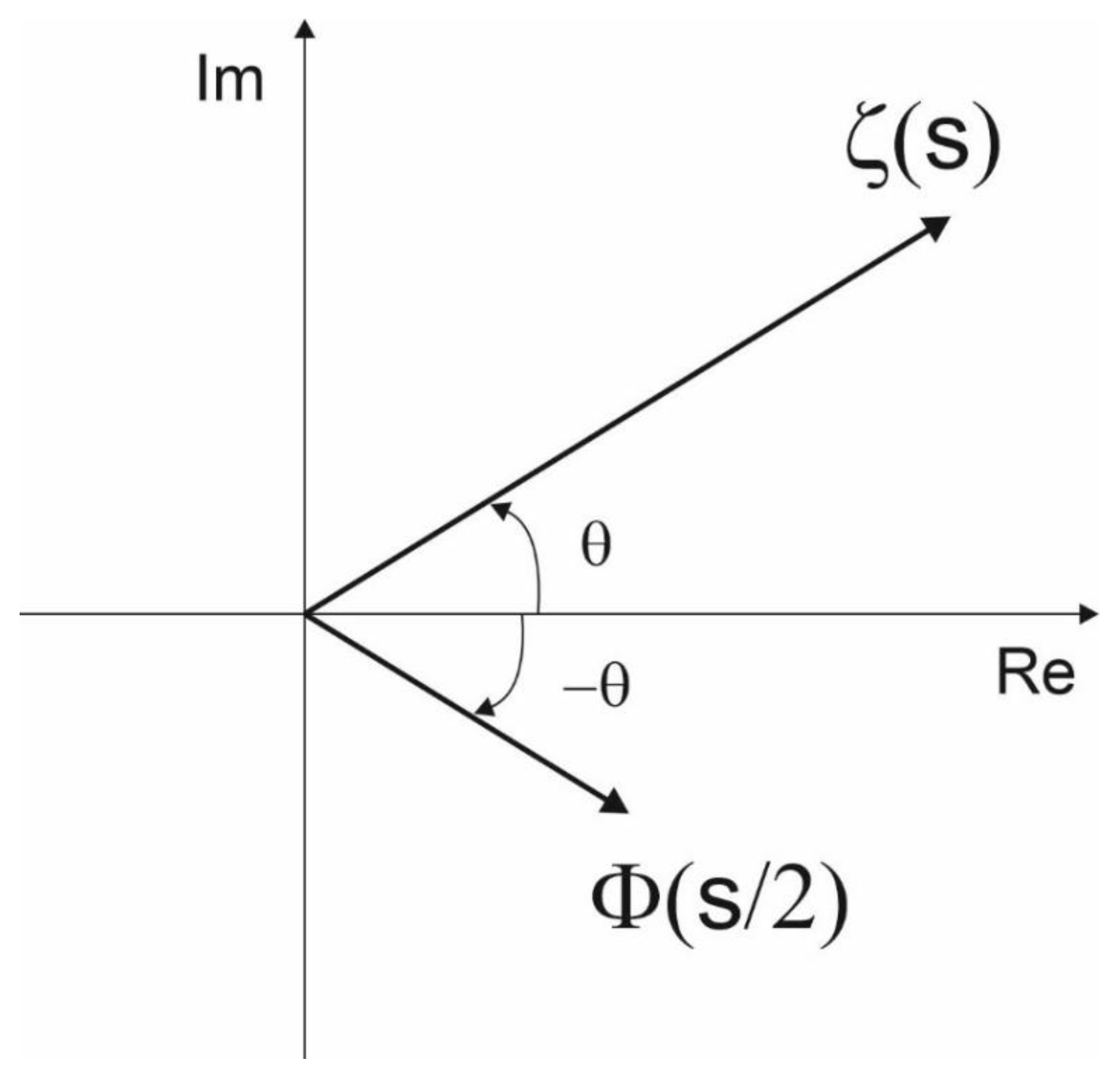
Figure 2.
The absolute values of the arguments of the functions and equal to each other, but with opposite signs.
Figure 2.
The absolute values of the arguments of the functions and equal to each other, but with opposite signs.
Recalling the definition of Riemann’s Xi function,
At
, the complex numbers of s and (1-s) are conjugates, hence, in the complex plane, along the line
, the Riemann’s Xi function of (42) is a real-valued function.
5. Holomorphic extensions of the Riemann zeta function
There are two versions of the functional equation:
Except for two points of s=0 and 1-s=0. Because the gamma function at s=0 has a pole.
Where the gamma function is defined:
We define two complex functions:
It can be proved that they behave as multiplicative inverses in complex plane, with one function being the inverse of the other for all points in their domain where both functions are non-zero:
Hence, two Riemann zeta functions, eq. (45), can be rewritten as
If we define the amplitude and argument of
to be r and
, respectively, because of the complex multiplicative inversion behavior of g(s) and g(1-s) of the eq. (48), thus, the Riemann zeta function in the complex plane can be expressed as:
where
is the argument of
at the point of
.
This implies that in the general case, the amplitudes of and are not equal to each other, rather, they behave as multiplicative inverses:
If we plot
on the y-axis and
on the x-axis, the curve of the amplitudes will be a hyperbola with asymptotes along the axes. This amplitude hyperbola is symmetric with respect to the line y=x, this is at the location of
.
Especially, in the complex plane, along the vertical line , the amplitudes of g(s) and g(1-s) are equal to each other, and both equal one:
They are conjugates, thus, along the line
, the Riemann zeta functions, eq. (49), can be expressed as:
where
is the argument of
at the point of
:
and where
is the argument of gamma function at the points of
:
Thus, the operating effect of
on the
leads the
to rotate an angle of
clockwise, while
leads the
to rotate an angle of
anticlockwise, but the scaling factor of
and
keeps as constant, both factors are equal to one.
Moreover, if the argument , we have the following trivial equations:
In this case, both equations take the same amplitude and argument simultaneously. The non-trivial zero points of the Riemann zeta function will be located at these points.
Hence, along the vertical line , the amplitudes of and are the same for all cases, and the difference of their arguments is equal to , namely, the rotation radii of and equal each other. If one function is rotating and passing through the coordinate origin clockwise, another one must be rotating and passing through the origin anticlockwise, and furthermore, they will be located at the points of .
In the general case, the amplitudes of and are not equal to each other, because of their multiplicative inversion relationship, eq.(51). If the rotation radius of one function is bigger, another one must be smaller, hence, both functions cannot pass through the coordinate origin, otherwise, the multiplicative inversion relationship of eq. (51) cannot be held, unless the amplitude, r, of the function is zero for all cases in the definition domain. But from the definition of the eq. (47), it cannot be equal to zero.