Prerpints.org logo
Preprint
Article

About Stability of One System of Stochastic Difference Equations with Exponential Nonlinearity

Altmetrics

Downloads

48

Views

28

Comments

0

This version is not peer-reviewed

Submitted:

25 September 2024

Posted:

26 September 2024

You are already at the latest version

Alerts
Abstract
A system of two nonlinear difference equations under stochastic perturbations is considered. Nonlinearity of the exponential type in each equation of the system under consideration depends on all variables of the system. The stability in probability of a positive equilibrium of the system is studied via the general method of Lyapunov functionals construction and the method of linear matrix inequalities (LMIs). The obtained results are illustrated via examples and figures with numerical simulations of solutions of a considered system of stochastic difference equations. The proposed way of investigation can be applied to nonlinear systems of higher dimension and with other types of nonlinearity, for both difference equations and for delay differential equations.
Keywords: 
Subject: Computer Science and Mathematics  -   Mathematics

MSC:  39A30; 39A50

1. Introduction

Systems of both difference and differential equations with different forms of exponential nonlinearities are very popular in research and various applications (see, for instance, [1,2,3,4,5,6,7,8,9,10] and references therein).
Here, similarly to [9], the stability of the positive equilibrium of a system with exponential nonlinearity is investigated under stochastic perturbations via the general method of Lyapunov functionals construction [10,11,12,13] and the method of linear matrix inequalities (LMIs) [14,15,16,17,18,19,20,21,22]. However, unlike, for instance, [1,9], where the exponential nonlinearity in each equation depends on only one variable, here each equation exponentially depends on all variables of the system under consideration. The obtained results are illustrated via examples and figures with numerical simulations of solutions of a considered system of difference equations. Numerical analysis of the considered LMIs is carried out using MATLAB.
Consider the system of two nonlinear difference equations
x 1 ( n + 1 ) = a 1 + b 1 x 1 ( n − 1 ) + c 1 x 1 ( n − 1 ) e − p 1 x 1 ( n ) − q 1 x 2 ( n ) , x 2 ( n + 1 ) = a 2 + b 2 x 2 ( n − 1 ) + c 2 x 2 ( n − 1 ) e − p 2 x 1 ( n ) − q 2 x 2 ( n ) , n ∈ N = { 0 , 1 , … } ,
with positive parameters, b i < 1 , i = 1 , 2 , and positive initial conditions x i ( j ) = ϕ i ( j ) , i = 1 , 2 , j ∈ N 0 = { − 1 , 0 } .
The equilibrium ( x 1 , x 2 ) of system (1) is defined by the system of two algebraic equations
x 1 = a 1 + b 1 x 1 + c 1 x 1 e − p 1 x 1 − q 1 x 2 , x 2 = a 2 + b 2 x 2 + c 2 x 2 e − p 2 x 1 − q 2 x 2 .
Theorem 1. 
The system (2) has a unique positive solution.
Proof. 
Presenting the first equation (2) in the form
e q 1 x 2 1 − b 1 − a 1 x 1 = c 1 e − p 1 x 1
and calculating the logarithm, we get
x 2 = 1 q 1 ln c 1 − p 1 x 1 − ln 1 − b 1 − a 1 x 1 , x 1 > a 1 1 − b 1 .
Similarly, from the second equation (2) we have
e p 2 x 1 1 − b 2 − a 2 x 2 = c 2 e − q 2 x 2
and
x 1 = 1 p 2 ln c 2 − q 2 x 2 − ln 1 − b 2 − a 2 x 2 , x 2 > a 2 1 − b 2 .
It is clear that the function x 2 = f 1 ( x 1 ) given by (4) is defined and positive if x 1 ∈ ( x 1 m i n , x 1 m a x ) , where x 1 m i n = a 1 1 − b 1 and x 1 m a x is a unique root of the equation
1 − b 1 − a 1 x 1 = c 1 e − p 1 x 1 ,
which follows from (3) by x 2 = 0 .
Calculating the derivative
x 2 ′ = 1 q 1 − p 1 − a 1 ( ( 1 − b 1 ) x 1 − a 1 ) x 1 < 0 ,
it is easy to see that x 2 = f 1 ( x 1 ) is strictly decreasing function. Moreover, lim x 1 → x 1 m i n f 1 ( x 1 ) = + ∞ and f 1 ( x 1 m a x ) = 0 .
Calculating the derivative of the function x 2 = f 2 ( x 1 ) given by (6), we have
p 2 = − q 2 + a 2 ( ( 1 − b 2 ) x 2 − a 2 ) x 2 x 2 ′ > 0 ,
i.e., x 2 ′ < 0 . It means that x 2 = f 2 ( x 1 ) is strictly decreasing function for x 1 ≥ 0 . Moreover, lim x 1 → ∞ f 2 ( x 1 ) = a 2 1 − b 2 and x 2 = f 2 ( 0 ) is a unique root of the equation
1 − b 2 − a 2 x 2 = c 2 e − q 2 x 2 ,
which follows from (5) by x 1 = 0 . It is easy to see that the root x 2 of this equation satisfies the condition x 2 > a 2 1 − b 2 .
Two decreasing functions x 2 = f 1 ( x 1 ) and x 2 = f 2 ( x 1 ) has one general point, which is a solution of the system (2) and is the unique equilibrium ( x 1 * , x 2 * ) of the system (1). The proof is completed. □
Corollary 1.1. 
The equilibrium ( x 1 * , x 2 * ) of the system (1) satisfies the conditions
x 1 * ∈ a 1 1 − b 1 , x 1 m a x , x 2 * ∈ a 2 1 − b 2 , x 2 m a x ,
where x 1 m a x and x 2 m a x are roots of the equations (7) and (8) respectively.
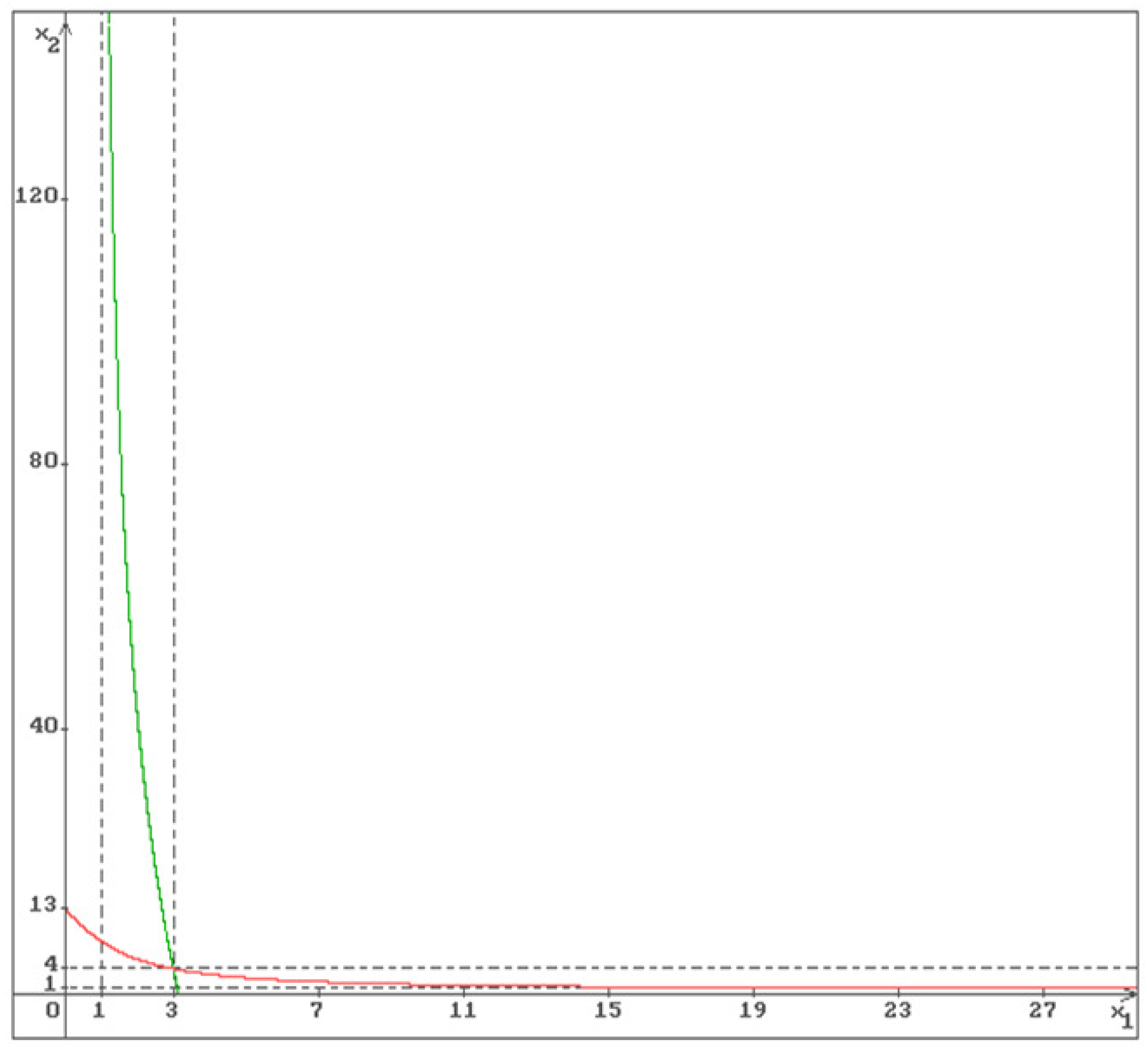
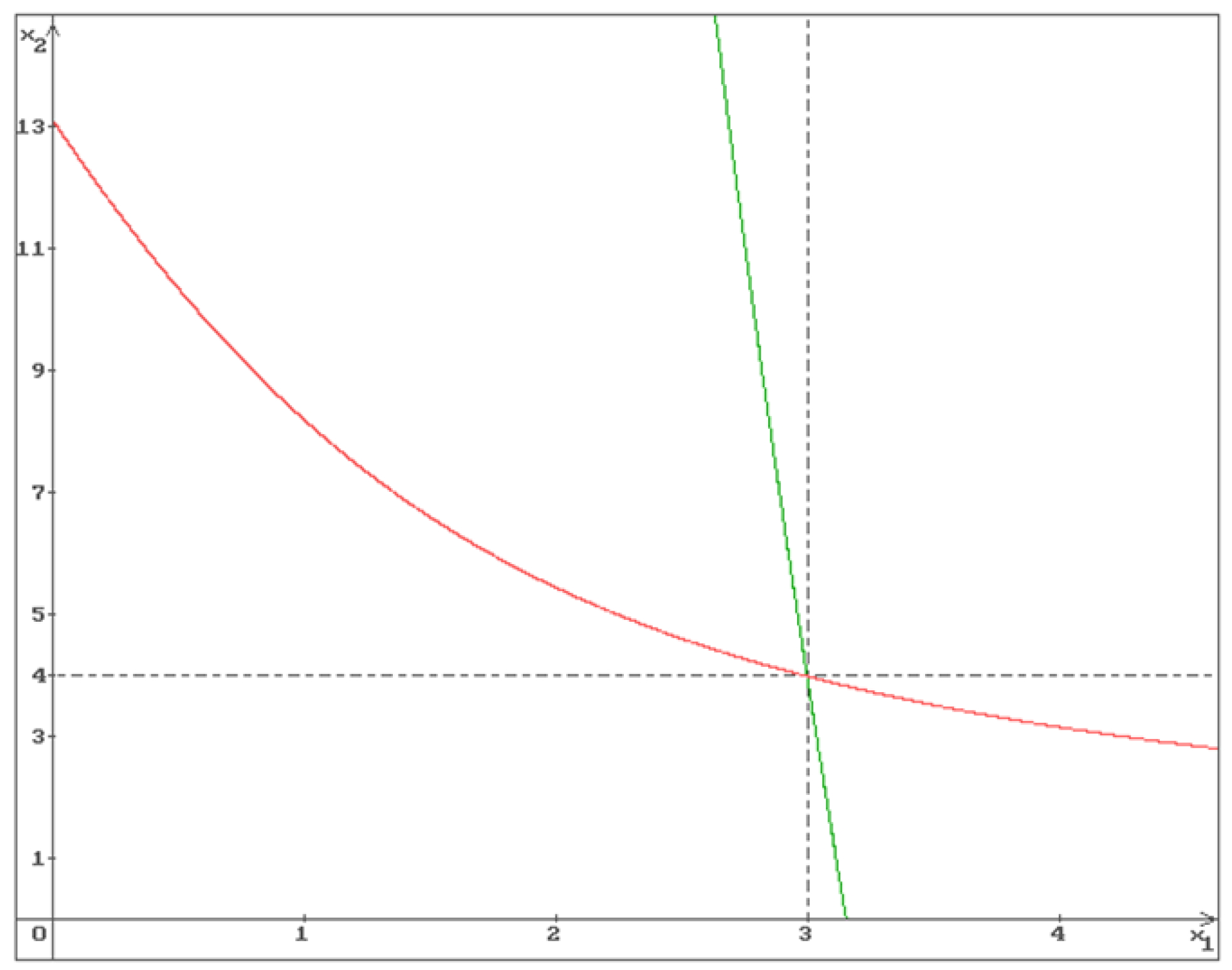
Example 1. 
Consider the system (1) with
a 1 = 0.3 , a 2 = 0.4 , b 1 = 0.7 , b 2 = 0.6 , c 1 = 0.2810 , c 2 = 0.4215 , p 1 = p 2 = 0.1 , q 1 = q 2 = 0.01 .
Then the solution of the system (2) is ( x 1 * , x 2 * ) = ( 3 , 4 ) , from (9) and (7), (8) it follows that x 1 m i n = 1 , x 2 m i n = 1 , x 1 m a x = 3.156 , x 2 m a x = 13.147 . In Figure 1 and 2 the graphs of the functions x 2 = f 1 ( x 1 ) (green), x 2 = f 2 ( x 1 ) (red) and the equilibrium ( x 1 * , x 2 * ) are shown.

2. Stochastic Perturbations and the System Transformation

Let { Ω , F , P } be a basic probability space, F n ∈ F , n ∈ N , be a nondecreasing family of sub- σ -algebras of F , i.e., F n 1 ⊂ F n 2 for n 1 < n 2 , E be the mathematical expectation with respect to the measure P , ξ 1 ( n ) and ξ 2 ( n ) , n ∈ N , be two mutually independent sequences with F n -adapted mutually independent random values such that [10]
E ξ i ( n ) = 0 , E ξ i 2 ( n ) = 1 , E ξ i ( n ) ξ j ( m ) = 0 if i ≠ j or n ≠ m , i , j = 1 , 2 .
Let us assume that the system (1) is exposed to stochastic perturbations that are directly proportional to the deviation of the system state ( x 1 ( n ) , x 2 ( n ) ) from the equilibrium ( x 1 * , x 2 * ) . Then the system (1) takes the form
x 1 ( n + 1 ) = a 1 + b 1 x 1 ( n − 1 ) + c 1 x 1 ( n − 1 ) e − p 1 x 1 ( n ) − q 1 x 2 ( n ) + σ 1 ( x 1 ( n ) − x 1 * ) ξ 1 ( n + 1 ) , x 2 ( n + 1 ) = a 2 + b 2 x 2 ( n − 1 ) + c 2 x 2 ( n − 1 ) e − p 2 x 1 ( n ) − q 2 x 2 ( n ) + σ 2 ( x 2 ( n ) − x 2 * ) ξ 2 ( n + 1 ) .
Remark 1. 
Note that the such type of stochastic perturbations was firstly proposed in [23] for a system of Ito’s stochastic delay differential equations and was later used in many other works for both differential and difference equations (see, for instance, [10,13] and references therein). With this type of stochastic perturbations, the equilibrium of the original deterministic system remains also a solution of the stochastically perturbed system.
Presenting the solution of the system (11) in the form ( x 1 ( n ) , x 2 ( n ) ) = ( y 1 ( n ) + x 1 * , y 2 ( n ) + x 2 * ) , we get
y 1 ( n + 1 ) + x 1 * = a 1 + b 1 ( y 1 ( n − 1 ) + x 1 * ) + c 1 ( y 1 ( n − 1 ) + x 1 * ) e − p 1 y 1 ( n ) − q 1 y 2 ( n ) e − p 1 x 1 * − q 1 x 2 * + σ 1 y 1 ( n ) ξ 1 ( n + 1 ) , y 2 ( n + 1 ) + x 2 * = a 2 + b 2 ( y 2 ( n − 1 ) + x 2 * ) + c 2 ( y 2 ( n − 1 ) + x 2 * ) e − p 2 y 1 ( n ) − q 2 y 2 ( n ) e − p 2 x 1 * − q 2 x 2 * + σ 2 y 2 ( n ) ξ 2 ( n + 1 ) .
Substituting (2) into (12), from the first equation we have
y 1 ( n + 1 ) = a 1 + b 1 x 1 * − x 1 * + b 1 y 1 ( n − 1 )   + c 1 ( y 1 ( n − 1 ) + x 1 * ) e − p 1 y 1 ( n ) − q 1 y 2 ( n ) e − p 1 x 1 * − q 1 x 2 * + σ 1 y 1 ( n ) ξ 1 ( n + 1 ) = b 1 y 1 ( n − 1 ) − c 1 x 1 * e − p 1 x 1 * − q 1 x 2 *   + c 1 ( y 1 ( n − 1 ) + x 1 * ) e − p 1 y 1 ( n ) − q 1 y 2 ( n ) e − p 1 x 1 * − q 1 x 2 * + σ 1 y 1 ( n ) ξ 1 ( n + 1 ) = b 1 + c 1 e − p 1 x 1 * − q 1 x 2 * e − p 1 y 1 ( n ) − q 1 y 2 ( n ) y 1 ( n − 1 )   − c 1 x 1 * e − p 1 x 1 * − q 1 x 2 * 1 − e − p 1 y 1 ( n ) − q 1 y 2 ( n ) + σ 1 y 1 ( n ) ξ 1 ( n + 1 ) .
Similarly, for the second equation (12) we get
y 2 ( n + 1 ) = a 2 + b 2 x 2 * − x 2 * + b 2 y 2 ( n − 1 )   + c 2 ( y 2 ( n − 1 ) + x 2 * ) e − p 2 y 1 ( n ) − q 2 y 2 ( n ) e − p 2 x 1 * − q 2 x 2 * + σ 2 y 2 ( n ) ξ 2 ( n + 1 ) = b 2 y 2 ( n − 1 ) − c 2 y * e − p 2 x 1 * − q 2 x 2 *   + c 2 ( y 2 ( n − 1 ) + x 2 * ) e − p 2 y 1 ( n ) − q 2 y 2 ( n ) e − p 2 x 1 * − q 2 x 2 * + σ 2 y 2 ( n ) ξ 2 ( n + 1 ) = b 2 + c 2 e − p 2 x 1 * − q 2 x 2 * e − p 2 y 1 ( n ) − q 2 y 2 ( n ) y 2 ( n − 1 )   − c 2 x 2 * e − p 2 x 1 * − q 2 x 2 * 1 − e − p 2 y 1 ( n ) − q 2 y 2 ( n ) + σ 2 y 2 ( n ) ξ 2 ( n + 1 ) .
As a result we obtain the nonlinear system
y 1 ( n + 1 ) = b 1 + c 1 e − p 1 x 1 * − q 1 x 2 * e − p 1 y 1 ( n ) − q 1 y 2 ( n ) y 1 ( n − 1 ) − c 1 x 1 * e − p 1 x 1 * − q 1 x 2 * 1 − e − p 1 y 1 ( n ) − q 1 y 2 ( n ) + σ 1 y 1 ( n ) ξ 1 ( n + 1 ) , y 2 ( n + 1 ) = b 2 + c 2 e − p 2 x 1 * − q 2 x 2 * e − p 2 y 1 ( n ) − q 2 y 2 ( n ) y 2 ( n − 1 ) − c 2 x 2 * e − p 2 x 1 * − q 2 x 2 * 1 − e − p 2 y 1 ( n ) − q 2 y 2 ( n ) + σ 2 y 2 ( n ) ξ 2 ( n + 1 ) ,
with the zero solution.
Remark 2. 
Note that stability of the zero solution of the system (13) is equivalent to stability of the equilibrium ( x 1 * , x 2 * ) of the system (11).
Using (2) and the linear approximation e − x = 1 − x + o ( x ) , where lim x → 0 o ( x ) x = 0 , we obtain the linear part of the system (13)
z 1 ( n + 1 ) = 1 − a 1 x 1 * z 1 ( n − 1 ) − ( ( 1 − b 1 ) x 1 * − a 1 ) ( p 1 z 1 ( n ) + q 1 z 2 ( n ) ) + σ 1 z 1 ( n ) ξ 1 ( n + 1 ) , z 2 ( n + 1 ) = 1 − a 2 x 2 * z 2 ( n − 1 ) − ( ( 1 − b 2 ) x 2 * − a 2 ) ( p 2 z 1 ( n ) + q 2 z 2 ( n ) ) + σ 2 z 2 ( n ) ξ 2 ( n + 1 ) .
Representing the linear system (14) in the matrix form, we get
z ( n + 1 ) = − A z ( n ) + B z ( n − 1 ) + ∑ i = 1 2 C i z ( n ) ξ i ( n + 1 ) ,
where
z ( n ) = z 1 ( n ) z 2 ( n ) , A = α 1 p 1 α 1 q 1 α 2 p 2 α 2 q 2 , B = β 1 0 0 β 2 , C 1 = σ 1 0 0 0 , C 2 = 0 0 0 σ 2 ,
and
α i = ( 1 − b i ) x i * − a i , β i = 1 − a i x i * , i − 1 , 2 .

3. Stability

3.1. Some Necessary Definitions and Statements

Let ′ be the transposition sign. Put now
y ( n ) = ( y 1 ( n ) , y 2 ( n ) ) ′ , z ( n ) = ( z 1 ( n ) , z 2 ( n ) ) ′ , n ∈ N , ϕ ( j ) = ( ϕ 1 ( j ) , ϕ 2 ( j ) ) ′ , j ∈ N 0 .
Definition 3.1.([10]). The zero solution of the system (13) is called stable in probability if for any ε > 0 and ε 1 ∈ ( 0 , 1 ) there exists a δ > 0 such that the solution y ( n ) = y ( n , ϕ ) of the system (13) satisfies the inequality P { sup n ∈ N | y ( n ) | > ε } < ε 1 for any initial function ϕ ( j ) such that P { ∥ ϕ ∥ 0 < δ } = 1 , where ∥ ϕ ∥ 0 = max j ∈ N 0 | ϕ ( j ) | .
Definition 3.2.([10]). The zero solution of the system (14) is called mean square stable if for each ε > 0 there exists a δ > 0 such that E | z ( n ) | 2 < ε , n ∈ N , for any initial function ϕ ( j ) such that ∥ ϕ ∥ 2 = max j ∈ N 0 E | ϕ ( j ) | 2 < δ ; asymptotically mean square stable if it is mean square stable and for each initial function ϕ ( j ) such that ∥ ϕ ∥ 2 < ∞ the solution z ( n ) of the system (14) satisfies the condition lim n → ∞ E | z ( n ) | 2 = 0 .
Let E n = E { . / F n } be the conditional expectation with respect to the σ -algebra F n , U ε = { y : | y | ≤ ε } , ε > 0 , and Δ V ( n ) = V ( n + 1 ) − V ( n ) .
Theorem 2.([10]). Let for the system (13) there exists a functional V ( n ) = V ( n , y ( − 1 ) , . . . , y ( n ) ) which satisfies the conditions
V ( n , y ( − 1 ) , . . . , y ( n ) ) ≥ c 0 | y ( n ) | 2 , V ( 0 , φ ( − 1 ) , φ ( 0 ) ) ≤ c 1 ∥ φ ∥ 0 2 , E n Δ V ( n , y ( − 1 ) , . . . , y ( n ) ) ≤ 0 , y ( j ) ∈ U ε , − 1 ≤ j ≤ n , n ∈ N ,
where ε > 0 , c 0 > 0 , c 1 > 0 . Then the zero solution of the system (13) is stable in probability.
Theorem 3.([10]). Let for the system (14) there exists a nonnegative functional V ( n ) = V ( n , z ( − 1 ) , . . . , z ( n ) ) which satisfies the conditions
E V ( 0 , ϕ ( − 1 ) , ϕ ( 0 ) ) ≤ c 1 ∥ ϕ ∥ 2 , E Δ V ( n ) ≤ − c 2 E | z ( n ) | 2 , n ∈ N ,
where c 1 > 0 , c 2 > 0 . Then the zero solution of the system (14) is asymptotically mean square stable.
Remark 3.. Note that the system (13) has an order of nonlinearity higher than one. It is known [10] that in this case sufficient conditions for asymptotic mean square stability of the zero solution of the linear system (14) are also sufficient conditions for stability in probability of the zero solution of the nonlinear system (13).

3.2. Stability conditions

Theorem 4.. Let there exist positive definite 2 × 2 -matrices P and R such that the following linear matrix inequality (LMI)
A ′ P A + S 0 + R − P A ′ P B B ′ P A B ′ P B − R < 0
holds, where
S 0 = ∑ i = 1 2 C i ′ P C i = σ 1 2 p 11 0 0 σ 2 2 p 22 ,
the matrices C 1 , C 2 are defined in (16) and p 11 , p 22 are diagonal elements of the matrix P. Then the equilibrium ( x 1 * , x 2 * ) of the system (11) is stable in probability.
Proof. 
Following the general method of Lyapunov functionals construction [10,11,12,13], consider the functional V ( n ) in the form V ( n ) = V 1 ( n ) + V 2 ( n ) , where V 1 ( n ) = z ′ ( n ) P z ( n ) , P > 0 , z ( n ) is defined in (16) and the additional functional V 2 ( n ) will be chosen below. For the functional V 1 ( n ) via (15) we have
E Δ V 1 ( n ) = E [ V 1 ( n + 1 ) − V 1 ( n ) ] = E [ z ′ ( n + 1 ) P z ( n + 1 ) − z ′ ( n ) P z ( n ) ] = E [ − z ′ ( n ) A ′ + z ′ ( n − 1 ) B ′ + ∑ i = 1 2 z ′ ( n ) C i ′ ξ i ( n + 1 ) * P − A z ( n ) + B z ( n − 1 ) + ∑ i = 1 2 C i z ( n ) ξ i ( n + 1 ) − z ′ ( n ) P z ( n ) ] .
From here via (10) and (20) it follows that
E Δ V 1 ( n ) = E [ z ′ ( n ) ( A ′ P A + S 0 − P ) z ( n ) + z ′ ( n ) A ′ P B z ( n − 1 ) + z ′ ( n − 1 ) B ′ P A z ( n ) + z ′ ( n − 1 ) B ′ P B z ( n − 1 ) ]
or in the matrix form
E Δ V 1 ( n ) = E z ( n ) z ( n − 1 ) ′ A ′ P A + S 0 − P A ′ P B B ′ P A B ′ P B z ( n ) z ( n − 1 ) .
Using the additional functional V 2 ( n ) = z ′ ( n − 1 ) R z ( n − 1 ) , R > 0 , with Δ V 2 ( n ) = z ′ ( n ) R z ( n ) − z ′ ( n − 1 ) R z ( n − 1 ) , for the functional V ( n ) = V 1 ( n ) + V 2 ( n ) we obtain
E Δ V ( n ) = E z ( n ) z ( n − 1 ) ′ A ′ P A + S 0 + R − P A ′ P B B ′ P A B ′ P B − R z ( n ) z ( n − 1 ) .
From (22) and the LMI (19) for some c > 0 we have E Δ V ( n ) ≤ − c E | z ( n ) | 2 , i.e., the constructed functional V ( n ) satisfies the conditions of Theorem 3. Therefore, the zero solution of the linear equation (15) is asymptotically mean square stable. Via Remarks 3 and 2 it means that the equilibrium ( x 1 * , x 2 * ) of the system (11) is stable in probability. The proof is completed. □
Remark 4. 
Note that instead of the LMI (19) for definition of stability some other LMIs also can be used. Using, for instance, the additional functional V 2 ( n ) in the form V 2 ( n ) = z ′ ( n − 1 ) ( R + B ′ P B ) z ( n − 1 ) instead of the LMI (19) we obtain the LMI
A ′ P A + B ′ P B + S 0 + R − P A ′ P B B ′ P A − R < 0 .
If at least one from the LMIs (19) and (23) holds then the equilibrium ( x 1 * , x 2 * ) of the system (11) is stable in probability. Other ways to get appropriate LMIs are shown also in [9].
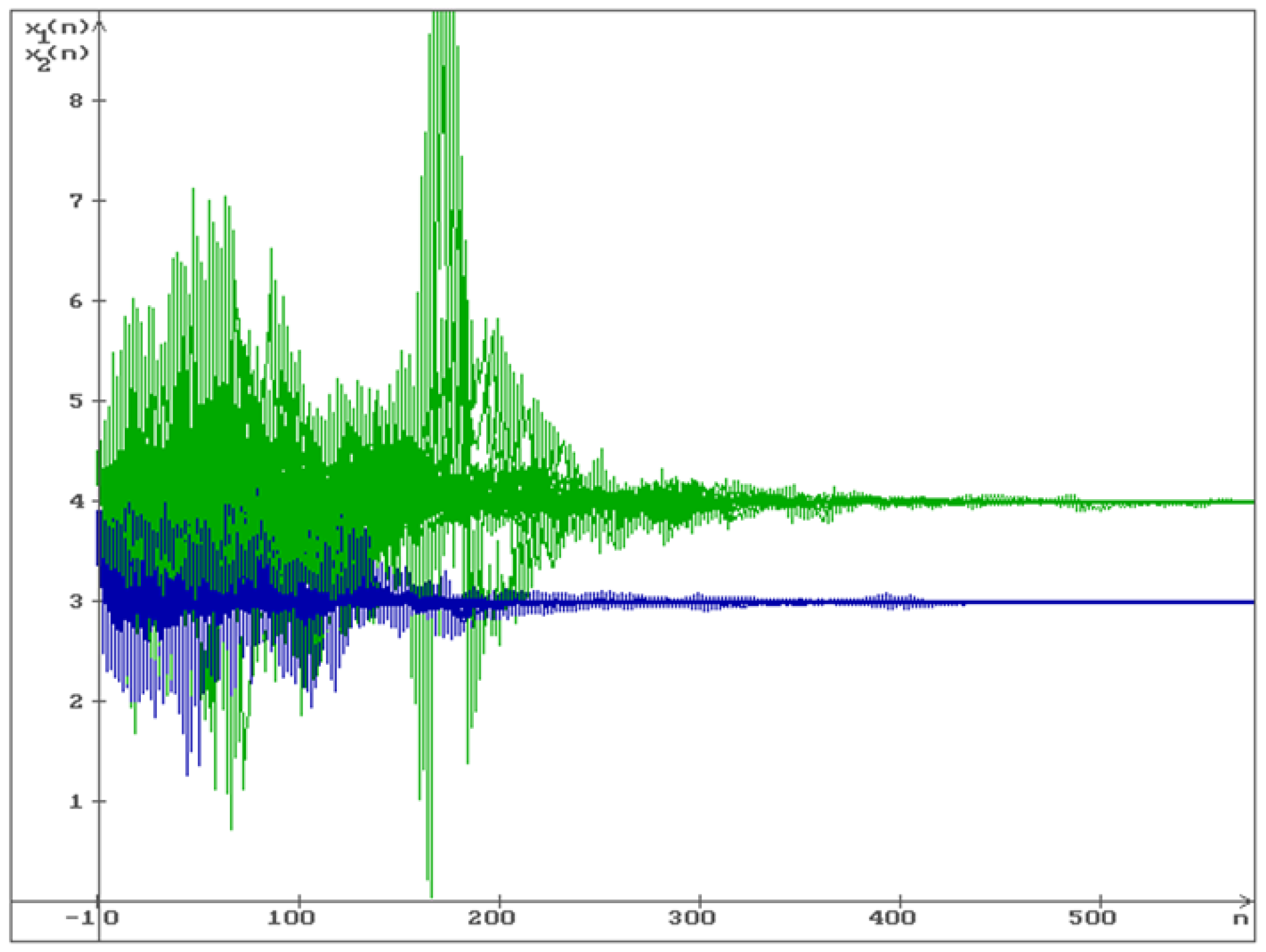
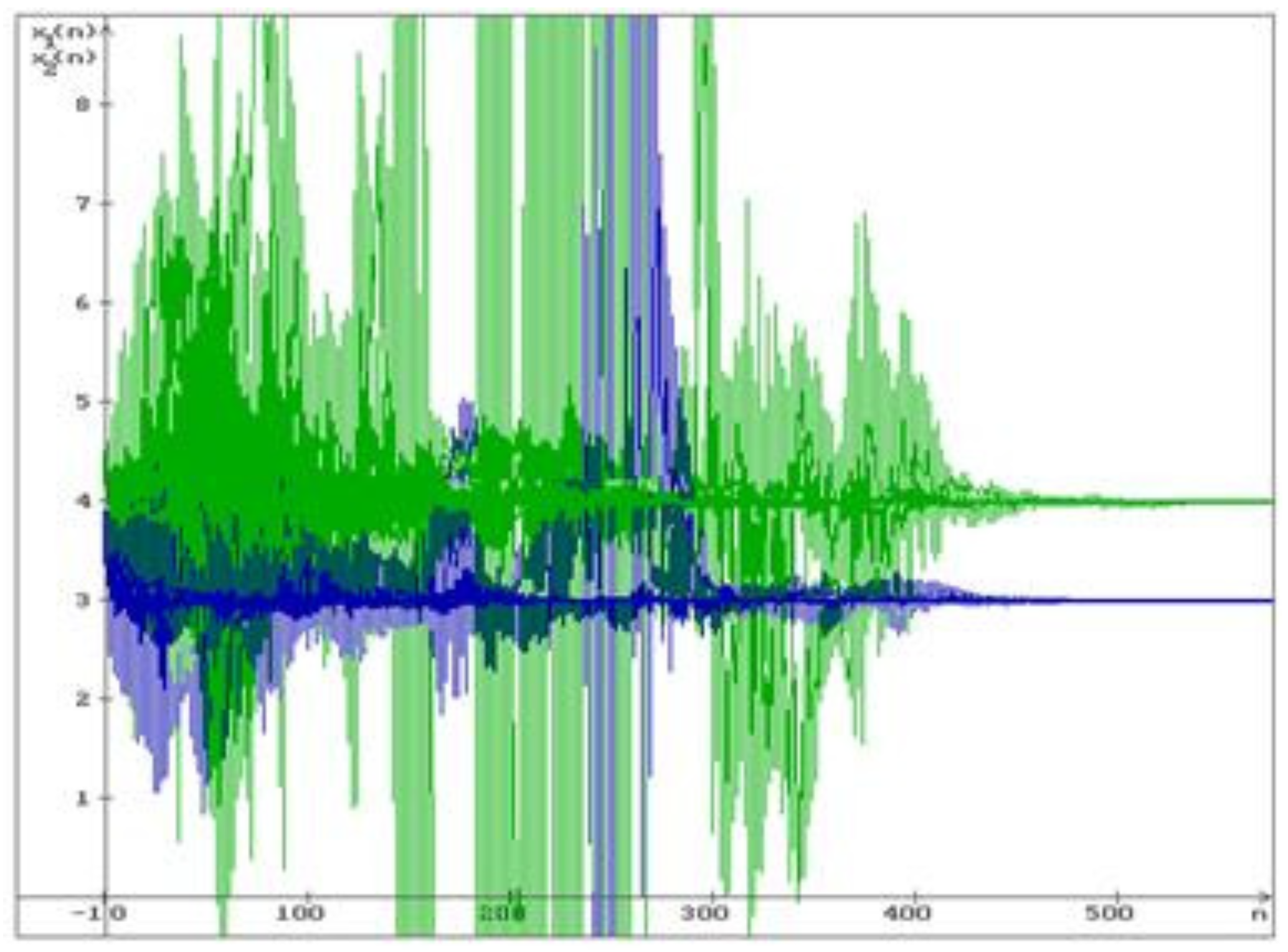
Example 2. 
Consider the system (11) with the values of the parameters given in Example 1. Via MATLAB it was obtained that by σ 1 = 0.23 , σ 2 = 0.38 the LMIs (19) and (23) hold. In Figure 3 and Figure 4 two different implementations of the solution of the system (11) are shown. In both cases, all trajectories of the solution converge to the stable equilibrium ( x 1 * , x 2 * ) = ( 3 , 4 ) .

4. Conclusions

Stability of a system of nonlinear difference equations under stochastic perturbations is investigated. The nonli-nearity of exponential form in each equation depends on all variables of the system under consideration. The conditions of stability in probability for positive equilibrium of the considered system are obtained using the general method of Lyapunov functionals construction, are formulated in terms of linear matrix inequalities (LMIs) and are illustrated by numerical examples and figures. The method of stability investigation, used in the paper, can be applied to many other types of nonlinear systems for both difference and differential equations in various applications.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Papaschinopoulos, G.; Radin, M.A.; Schinas, C.J. On the system of two difference equations of exponential form: xn+1=a+bxn-1e-yn, yn+1=c+dyn-1e-xn. Mathematical and Computer Modelling 2011, 54, 2969–2977. [Google Scholar] [CrossRef]
  2. Papaschinopoulos, G.; Radin, M.A.; Schinas, C.J. Study of the asymptotic behavior of the solutions of three systems of difference equations of exponential form. Applied Mathematics and Computation 2012, 218, 5310–5318. [Google Scholar] [CrossRef]
  3. Papaschinopoulos, G.; Fotiades, N.; Schinas, C.J. On a system of difference equations including negative exponential terms. Journal of Differential Equations and Applications 2014, 20, 717–732. [Google Scholar] [CrossRef]
  4. Papaschinopoulos, G.; Ellina, G.; Papadopoulos, K.B. Asymptotic behavior of the positive solutions of an exponential type system of difference equations. Applied Mathematics and Computation 2014, 245, 181–190. [Google Scholar] [CrossRef]
  5. Shaikhet, L. Stability of equilibrium states for a stochastically perturbed exponential type system of difference equations. Journal of Computational and Applied Mathematics 2015, 290, 92–103. [Google Scholar] [CrossRef]
  6. Thai, T.H.; Dai, N.A.; Anh, P.T. Global dynamics of some system of second-order difference equations. Electronic Research Archive 2021, 29, 4159–4175. [Google Scholar] [CrossRef]
  7. Khan, A.Q. Global Dynamics of a Nonsymmetric System of Difference Equations. Mathematical Problems in Engineering 2022, 14, 4435613. [Google Scholar] [CrossRef]
  8. Shaikhet, L. Stability of the exponential type system of stochastic difference equations. Special Issue "Nonlinear Stochastic Dynamics and Control and Its Applications". Mathematics 2023, 11, 3975, 20p. Available online: https://www.mdpi.com/2227-7390/11/18/3975. [CrossRef]
  9. Shaikhet, L. Stability of equilibria of exponential type system of three differential equations under stochastic perturbations. Mathematics and Computers in Simulation 2023, 206, 105–117. [Google Scholar] [CrossRef]
  10. Shaikhet, L. Lyapunov Functionals and Stability of Stochastic Difference Equations; Springer Science & Business Media: London, UK, 2011. [Google Scholar]
  11. Kolmanovskii, V. , Shaikhet, L. Some peculiarities of the general method of Lyapunov functionals construction. Applied Mathematics Letters. 2002, 15(3), 355–360. [Google Scholar] [CrossRef]
  12. Kolmanovskii, V.; Shaikhet, L. About one application of the general method of Lyapunov functionals construction. International Journal of Robust and Nonlinear Control (Special Issue on Time Delay Systems, RNC) 2003, 13, 805–818. [Google Scholar] [CrossRef]
  13. Shaikhet, L. Lyapunov Functionals and Stability of Stochastic Functional Differential Equations. Springer Science & Business Media: Berlin, 2013. [Google Scholar]
  14. Boyd, S.; El-Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; SIAM: Philadelphia, PA, USA, 1994. [Google Scholar]
  15. Choi, H.H. A new method for variable structure control system design: A linear matrix inequality approach. Automatica 1997, 33, 2089–2092. [Google Scholar] [CrossRef]
  16. Niculescu, S.I. H∞ memory less control with an α-stability constraint for time delays systems: an LMI approach. IEEE Transactions on Automatic Control 1998, 43, 739–743. [Google Scholar] [CrossRef]
  17. Nguang, S.K. Robust H∞ control of a class of nonlinear systems with delayed state and control: an LMI approach. In Proceedings of the 37th IEEE Conference on Decision and Control, Tampa, Florida, USA, 1998; pp. 2384–2389. [Google Scholar]
  18. Gouaisbaut, F.; Dambrine, M.; Richard, J.P. Robust control of delay systems: a sliding mode control design via LMI. Systems & Control Letters 2002, 46, 219–230. [Google Scholar]
  19. Seuret, A.; Gouaisbaut, F. Hierarchy of LMI conditions for the stability analysis of time-delay systems. Systems & Control Letters 2015, 81, 1–7. [Google Scholar]
  20. Fridman, E.; Shaikhet, L. Stabilization by using artificial delays: an LMI approach. Automatica 2017, 81, 429–437. [Google Scholar] [CrossRef]
  21. Fridman, E.; Shaikhet, L. Delay-dependent LMI conditions for stability of stochastic systems with delay term in the form of Stieltjes integral. In Proceedings of the 57th IEEE Conference on Decision and Control, Fontainebleau, Miami Beach, Florida, USA, 2018; pp. 6567–6572. [Google Scholar]
  22. Fridman, E.; Shaikhet, L. Simple LMIs for stability of stochastic systems with delay term given by Stieltjes integral or with stabilizing delay. Systems & Control Letters 2019, 124, 83–91. Available online: https://www.sciencedirect.com/science/article/abs/pii/S016769111830224X.
  23. Beretta, E.; Kolmanovskii, V.; Shaikhet, L. Stability of epidemic model with time delays influenced by stochastic perturbations. Mathematics and Computers in Simulation, (Special Issue "Delay Systems") 1998, 45, 269–277. Available online: https://www.sciencedirect.com/science/article/pii/S0378475497001067. [CrossRef]
Preprints 119324 g001
Figure 1. The graphs of the functions x 2 = f 1 ( x 1 ) (green) and x 2 = f 2 ( x 1 ) (red).
Figure 1. The graphs of the functions x 2 = f 1 ( x 1 ) (green) and x 2 = f 2 ( x 1 ) (red).
Preprints 119324 g001
Preprints 119324 g002
Figure 2. The intersection point of the graphs of the functions x 2 = f 1 ( x 1 ) (green) and x 2 = f 2 ( x 1 ) (red) is the equilibrium ( x 1 * , x 2 * ) = ( 3 , 4 ) .
Figure 2. The intersection point of the graphs of the functions x 2 = f 1 ( x 1 ) (green) and x 2 = f 2 ( x 1 ) (red) is the equilibrium ( x 1 * , x 2 * ) = ( 3 , 4 ) .
Preprints 119324 g002
Preprints 119324 g003
Figure 3. 50 trajectories of the system (11) solution: x 1 ( n ) (blue) and x 2 ( n ) (green). The solution converges to the stable equilibrium ( x 1 * , x 2 * ) = ( 3 , 4 ) . The first implementation.
Figure 3. 50 trajectories of the system (11) solution: x 1 ( n ) (blue) and x 2 ( n ) (green). The solution converges to the stable equilibrium ( x 1 * , x 2 * ) = ( 3 , 4 ) . The first implementation.
Preprints 119324 g003
Preprints 119324 g004
Figure 4. 50 trajectories of the system (11) solution: x 1 ( n ) (blue) and x 2 ( n ) (green). The solution converges to the stable equilibrium ( x 1 * , x 2 * ) = ( 3 , 4 ) . The second implementation.
Figure 4. 50 trajectories of the system (11) solution: x 1 ( n ) (blue) and x 2 ( n ) (green). The solution converges to the stable equilibrium ( x 1 * , x 2 * ) = ( 3 , 4 ) . The second implementation.
Preprints 119324 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated