Preprint
Article
Contribution to the Statistical Mechanics of Static Triplet Correlations and Structures in Quantum Fluids
This version is not peer-reviewed.
Submitted:
25 September 2024
Posted:
26 September 2024
You are already at the latest version
A peer-reviewed article of this preprint also exists.
Abstract
The current developments in the theory of quantum static triplet correlations and their associated structures (real r-space and Fourier k-space) in monatomic fluids are reviewed. The main framework utilized is Feynman’s path integral formalism (PI) and the issues addressed cover quantum diffraction effects and zero-spin bosonic exchange. The structures are associated with the external weak fields that reveal their nature, and due attention is paid to the underlying pair level structures. Without the pair level one cannot fully grasp the triplet extensions in the hierarchical ladder of structures, as both the pair and the triplet structures are essential ingredients in the triplet response functions. Three general classes of PI structures do arise: centroid, total continuous linear response, and instantaneous. Use of functional differentiation techniques is widely made and, as a bonus, this leads to identify an exact extension of the “classical isomorphism” when the centroid structures are considered. In this connection, the direct correlation functions, as borrowed from classical statistical mechanics, play a key role (either exact or approximate) in the corresponding quantum applications. Additionally, as an auxiliary framework, the traditional closure schemes for triplets are also discussed, owing to their potential usefulness for rationalizing PI triplet results. To illustrate some basic concepts, new numerical calculations (path integral Monte Carlo PIMC and closures) are reported. They are focused on the purely diffraction regime and deal with supercritical helium-3 and the quantum hard-sphere fluid.
Keywords:
Quantum triplets
; quantum fluids
; path integral Monte Carlo
; triplet closures
; Ornstein-Zernike treatments
; supplementary.zip (179.43KB )
1. Introduction
The study of the correlations between the particles of a system is key to the understanding of its behavior, classical or quantum. Without trying to be exhaustive, one may mention the following main lines in which are involved: (a) equilibrium thermodynamics [1,2,3,4,5,6,7,8,9,10,11,12,13]; (b) time-dependent phenomena [12,13,14,15,16,17,18,19,20,21,22]; (c.1) the experimental [23,24,25,26,27,28,29,30,31] and/or (c.2) computational [7,8,9,10,11,12,13,17,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46] techniques for their practical determinations; and (d) the fundamental questions related to entanglement and separability [47,48,49,50,51,52,53]. Each of these lines forms a whole body of knowledge with direct/indirect practical applications, ranging from phase equilibria and stability to quantum networks and information. Furthermore, all of them taken together display useful and revealing intersection areas. In this connection, the present article will focus on statistical mechanics issues at the intersection between lines (a) and (c.2), by selecting the somewhat forgotten topic of the triplet correlations in equilibrium quantum monatomic fluids (in 3-D space) at nonzero temperatures. This situation contrasts sharply with that of the classical fluid, for which insightful theoretical and computational developments have been available in the literature for a long time (see for instance References [37,38,41,42,43,44,45]).
As a convention, the concept “monatomic fluids” can imply either actual fluids composed of atoms or model fluids composed of structureless particles (one-site). In this work, both terms atom and particle will be used indistinctly. Also, it is convenient to stress that in a broad sense the general concept of equilibrium “correlations” encompasses the usual fluid structures in the real r-space and the response functions in the reciprocal Fourier k-space (n refers to the number of particles involved in their formulations). Both types of static structures are connected essentially through Fourier transforms, which are far from trivial for [3,7,9,11,41]. One also notes that an extended use has assigned the names correlation functions and structure factors to the and the respectively. This is the convention followed in this article, although depending on the context “correlations” or “structures” will be used occasionally in the global sense.
For homogeneous and isotropic monatomic fluids, at the pair level one deals with 2-D structural functions, whilst at the triplet level one deals with 4-D structural functions. Contrarily to the pair functions, the triplet functions cannot be extracted from radiation scattering experiments, because the triplet contribution to the scattering intensity is negligible as compared to the rest of the contributions that shape the differential cross section [24]. Therefore, a comprehensive quantum fluid triplet study, which goes beyond the time-honored closure-theory attempts [3,39,40], entails an appropriately developed theoretical framework, which must be complemented with very powerful computational means. In this way, one can perform the extensive numerical calculations needed (the experiments here). From recent path-integral Monte Carlo plus approximate closure works by the present author [54,55,56,57,58,59,60], one may feel that the time is becoming ripe to start undertaking the triplet topic. As in the classical domain the interest in this quantum task does justify by itself, if only because it makes statistical mechanics go beyond the usual pair level. But for those more application-orientated, one may point out that there are many questions which can benefit from such development (e.g., further fluid structural characterizations of the fluid-solid transition [6,41,61,62], phonon-phonon interactions in superfluids [40], time-dependent phenomena [16,17,18,19,20,21,22,23,33,34] (see Reference [24] to infer the possible connections), colloid suspension properties [63,64], etc.). In relation to this, it may be motivating to mention the empirical relationships found for the maxima of the equilateral correlations in r-space of the quantum hard-sphere (QHS) fluid along the crystallization line [59], and the surprising success of closures in capturing significant quantum fluid triplet features [59,60]. The reader should be aware however that the quantum fluid complexity is far greater than that of its classical fluid counterpart, as will be discussed in detail in this article.
The outline of this article is as follows. Section 2 is devoted to giving an introductory global description of the context in which the quantum triplet topic is inserted, together with its current state of development. Section 3 contains a condensed presentation of the pair and triplet structures in classical statistical mechanics. Why? Because, although there are radical differences between the classical and the quantum domains, both share a good deal of the general notations involved, plus a significant number of basic concepts and tools used (e.g., functional differentiation and closures). This excursion into the classical background is expected to ease the way to the quantum fluid discussion. Section 4 reviews the basic theory of Feynman’s path integrals PI in (thermal) imaginary time [4,7,9]. When complemented with computer simulations (resembling somehow the classical ones), PI can be utilized for the complete study of quantum fluid static triplets (r-space and k-space) in the diffraction and the bosonic exchange regime (more on the exchange issues later). Section 5 focuses upon the higher complexity of the quantum fluid structures as revealed by PI, concentrating on the quantum diffraction regime by reason of its fundamental role. Thus, one finds that the single structural class present in the classical domain, C, composed of pairs splits into three different structural classes, namely instantaneous ETn, total continuous linear response TLRn, and centroids CMn, [7,9,11]. The discussion focuses on , although paying due attention to , by reason of its importance when studying triplets. The parallel extension to zero-spin particles and bosonic fluids is deferred to an Appendix. To illustrate some of the main points discussed, a set of various results are included in this Section 5. The studied systems are helium-3 under supercritical conditions, and the quantum hard-sphere fluid on its crystallization line. For helium-3 the results are related to the r- and k-spaces, while for quantum hard spheres are on k-space. Section 6 gives a summary description of the systems, and the methods used to facilitate the understanding of the reported results. The methods are path integral Monte Carlo simulations (PIMC) and a significant number of closures, such as Kirkwood superposition (KS3) [37], Jackson-Feenberg (JF3) [40], the intermediate AV3 (KS3+JF3)/2 [59], Barrat-Hansen-Pastore (BHP3) [41], and Denton-Ashcroft [65]. Section 7 contains a series of final remarks together with directions for future research. Finally, two Appendices, I the boson fluid and II a list of acronyms and basic associated references for the reader’s convenience, close this work.
2. Setting Quantum Fluid Triplets in Their Context
Before entering the mathematical formulations, it
seems useful to give an introductory guide for situating the triplet topic in
its statistical mechanics context. This will also serve the purpose of
introducing some basic concepts and notations. Unrestricted reference to the
classical domain is made in what follows. By doing so, the fundamental quantum
departures from the common ground are expected to be fully grasped by readers
not very familiar with the structural issues.
2.1. The Tackling of the Classical and the Quantum Domains
The use of computers has given a definitive impulse to every aspect of modern research activities. As regards condensed matter physics, the related computer applications have been guided by the numerical implementations of two central lines of thought: approximate theories about the fluid behavior (e.g., see References [2,3,4,5,6]), and the powerful simulation techniques which started from the works by Metropolis et al. (Monte Carlo MC) [66] and Alder and Wainwright (molecular dynamics MD) [67]. In fact, all these methodologies have made it possible to circumvent both theoretical and experimental difficulties that impeded further developments in statistical mechanics. In this connection, suffice it to recall two examples directly relevant to the triplet question: (a) the practical solution of the problem posed by the hierarchical nature of the n-particle correlation functions in r-space (i.e., the exact Bogolyubov-Born-Green-Kirkwood-Yvon BBGKY hierarchy [2,3,4,5,6]), enabling one to compute via simulations the independently of one another [13,42]; and (b) the possibilities of devising computational alternatives for remedying the lack of experimental techniques [24] to determine structure factors in k-space (and thus correlation functions in r-space) beyond the pair level .
The approximate theories in their most useful forms utilize closures, which allow one to tackle the calculations of the and the functions. These two types of objects are in general connected through nontrivial Fourier transforms [3,7,8,9,11,13,24,41]. Closures in r-space hypothesize relationships between a correlation function and the set of lower-order correlation functions (e.g., KS3 [37], JF3 [40], or other choices [26,27,38]). To compute the which are far more complicated objects, additional correlation functions in r-space are introduced. The latter are the so-called direct correlation functions which are based on Ornstein-Zernike OZn concepts [1,68] (e.g., for Percus-Yevick [5,69,70,71], hypernetted chain [6,69,70,71], or Baxter’s partition [72]; and for Barrat-Hansen-Pastore [41], or Denton-Ashcroft [65]). Nowdays the relative importance of closures has obviously decreased in favor of simulation, but one should not adopt a cavalier attitude towards them. Indeed, these closure-theories may yield, at a much lower cost, excellent results as compared to simulation or experiments for key pair quantities (e.g., classical and quantum k-space pair structure factors [13,46,72] and, also, insightful pictures of the complex structural problems at the triplet level [37,38,39,40,41,58,59,60,65].
The two basic simulation techniques, MC and MD, exploit the properties of the statistical mechanics ensembles using a finite sample to model the real fluid behavior (e.g., in the canonical ensemble number of particles, volume of the simulation box, temperature) [2,5,6,12,13,17,71]. These applications are consistent with the concept of thermodynamic limit, : for , such that , the intensive quantities are independent of the system size [5] (surface effects from a container are not considered). MC is an elaborate stochastic Markov process that generates particle configurations compatible with the equilibrium state of the fluid being modelled. MD is based on the solving of the equations of motion (e.g., Newton’s) for the particles in the modelled fluid, either in equilibrium or in nonequilibrium states. MC provides “exact” results, since it is essentially a multi-dimensional numerical integration method, and it can be extended to deal with quantum many-body systems at non-zero temperatures [9,13,16]. However, the MD reliability is different depending on the classical or the quantum nature of the application. Thus, although for the time-evolution in classical fluids MD provides a perfectly defined calculational framework [13,17], the same does not occur for quantum fluids because of Heisenberg’s uncertainty principle. Hence, the related quantum dynamics applications are of limited validity, this being a general issue that remains an open problem. (See the appealing formulations and results, based on the PI formalism [4], reported in References [18,19,21,22,33,34]). It must be stated that within the quantum domain PI is the theoretical framework that has led to the implementation of the most powerful simulation techniques to date for investigating equilibrium states. The two basic techniques are path-integral Monte Carlo (PIMC) and path-integral molecular dynamics (PIMD), the latter being an equilibrium construction that bears no connection with the actual time evolution of the system [7,9,10,11,35,36,46,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97]. All these developments of Feynman’s PI owe much to the pioneering works by Barker [73], Chandler and Wolynes [7], Berne et al. [16,74,81], and Ceperley and Pollock [9,77,78]. It is worthwhile to mention that, in addition to the diffraction and the bosonic exchange regimes [9,35,36,78], a further PI extension involving Wigner’s formulation (WPIMC) has been used recently by Filinov et al. to study in a practical way fermionic exchange [98,99], an issue that remained far from accurate PIMC computations owing to the so-called “sign problem” [98,100,101].
2.2. Hamiltonians and Interparticle Potentials
Any of the foregoing computer applications must incorporate as a key ingredient a model for describing the interactions between the actual particles composing the fluid. These models are built by employing any (or all) of the following methods [13,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118]: geometrical arguments (e.g., hard spheres), experimental data, and quantum mechanical reasoning/computations. In this regard, it is well-known that the Born-Oppenheimer approximation (BOA) [119], aided again by the availability of increasing computational resources, has been instrumental in developing the quantum study of real systems. Among its many applications, those of interest in the structural study of fluids may be listed as follows: interatomic/intermolecular interactions [102,103,104,105,106,107,108,109], molecular properties in condensed phases [109,110,111,112], properties of atomic/molecular clusters or far larger assemblies, etc. [113,114,115,116,117,118]. Note that for an isolated polyatomic system BOA defines its electronic energy (including obviously the nuclear repulsions) as the potential energy for the motions of the nuclei within the overall atomic structure. Consequently, for a set of N atoms, from the consideration of a number of geometries of the nuclei at fixed positions in 3-D space, operational forms of the global potential energy can be determined quantum mechanically as sums of n-body contributions (two-body, three-body, etc.) that depend only on the positions The point is that a quantum average over the electronic coordinates is to be performed, and this leads to a model of the polyatomic system in which the effective centers for the interactions are placed at the positions of the nuclei, i.e., the non-collapsing and tempered function [5].
Therefore, for an isolated monatomic fluid one can write the model Hamiltonian in the conveniently simplified form:
where is the momentum of atom j and m is the atom mass. (The and are to be interpreted as classical dynamical functions or as quantum operators, depending on the application; explicit spin interactions are disregarded). Among the constructions, the success of the pairwise approach, has been fundamental. The latter form usually contains “averaged” many-body effects in the “pair” potential [13] and has yielded a thorough understanding of fluid systems. Particularly, this is true of monatomic fluids at equilibrium, regardless of their classical or quantum behavior [9,13,17]. One also notes that the use of explicit many-body sums for becomes necessary when the relative orientations of three [102,103,108] or more atoms (or particles in general) play an important role, as for example at very high densities in the solid state [115,116,117], or when the fixing of the n-body terms is strictly individualized with the use of quantum chemical computations [108,114].
The final test of an interaction model is the comparison with experiment of the calculated properties (e.g., for fluids: the pair structures and the internal energies E, the pressures p, etc.). In this regard, one must realize that the form Equation (1) for the Hamiltonian is perfectly suited for comparisons of the related fluid pair structures, fixed via computations, with those determined through radiation scattering experiments (X-ray, neutron diffraction) [5,6,23,28,29,30]. In turn, from these comparisons one can improve the predictive power of the interaction model via further fittings of its parameters [13].
Also, it is important to point out that although the fluid particle correlations are induced by the particle interactions (including those coming from quantum symmetries), both concepts are generally not the same thing. Thus, the many-body correlations may not be specifically associated with an explicit inclusion in the calculations of three-body or higher-order potential energy contributions. Note, for example, that in a monatomic gas described with just a pair potential , one can identify correlations of any order between the atoms. Within such a context, a key fact that may guarantee the high quality of the computed triplet structures is associated with the fluid description achieved via albeit this might not be sufficient and evaluations with alternative interaction models, or calculations of special fluid properties involving these structures [3,40,44], could be necessary to settle the question.
2.3. Classical Calculations
As mentioned earlier, the classical and PI-quantum applications share several basic features and problems (thermodynamic evaluations can be carried out alongside those of the equilibrium structures and/or utilize the latter [9,13]). Therefore, consideration is given first to the classical case, and the specific quantum characteristics will be discussed afterwards.
The equilibrium classical developments have focused mainly on the pair and the triplet levels, the two basic sets being: [13,24,41,42,43,44,45,120,121,122,123,124]. The distances r, s, and u define a triplet configuration of three generic atoms: The k variables of the response Fourier functions are the wavenumbers of the related (elastic) momentum transfers from an external weak field to the fluid is the angle between and and can be used in lieu of in [5,6,41]. Recall that in going from to the expected computational load must increase greatly, since the dimensionality of the problem goes from 2-D to 4-D.
The classical pair level can be solved via simulation to a high degree of accuracy. However, the calculations are more affordable and straightforward than those of which encounter some difficulties. The latter are brought about by the necessity of: (a) scanning wavevectors k commensurate with the simulation box, i.e., for the usual cubic box with integers and L the box length; and (b) the use of equal-modulus sets of vectors for a given value . Accordingly, the simulation task is far more expensive than that of and, more critically, does not permit the direct calculation of the component, which is a central thermodynamic quantity: the dimensionless isothermal compressibility, where is the bulk (number) density and [13]. These features are well known by statistical mechanics practitioners and, instead of employing extended simulation schemes looking for reliable (and unnecessarily expensive) extrapolations one can utilize methods based on the direct MC/MD simulation of complemented with well-grounded closure procedures [13,71,72,125,126,127]. The latter involve the OZ2 framework, which yields the pair direct correlation function a function that shows a very rapid decay to zero with increasing distances. This function is decisive in circumventing the difficulties mentioned above and provides, through its Fourier transform, a highly accurate and cost-effective answer to the whole pair structure factor problem: that is for
As regards triplets, the whole situation is not so well developed. The simulation techniques are certainly possible in this context [41,42,44,45,120,121,122,123,124], albeit the abovementioned drawbacks at the pair level are clearly augmented. To diminish the cost of full 4-D computations in both r-space and k-space, the triplet studies have concentrated mainly on the considered as the most characteristic features, namely the statistical properties of the equilateral and isosceles features. The descriptions so obtained are not complete, but one can expect them to be sufficiently informative for many practical purposes [41,120,121,122,123,124]. However, if more detailed triplet results are needed, they can be fixed for in r-space through affordable simulations [44], albeit for in k-space the computational load increases largely. At this juncture one might think of using a combination of simulation and closures [41,120,121,122,123,124], as achieved at the pair level, that is, using the simulated (and !) to fix Nevertheless, the computations of would have to be quite complete over the three spatial dimensions for the Fourier transforms to be obtained accurately [120,121]. In addition, the alternative based on OZ3 direct correlation functions, i.e., Baxter’s hierarchy [68], remains in general uncertain due to the lack of a univocal formulation that cuts the hierarchy in a generally significant way [41,65,68,128,129]. Despite these difficulties, the use of closures is a very useful source of information (e.g., for Kirkwood superposition KS3 [37], Jackson-Feenberg JF3 [40], the intermediate AV3 (KS3+JF3)/2 [59], and/or for Barrat et al. BHP3 [41], Denton-Ashcroft DAS3 [65]).
For the current purposes, it seems natural to characterize the structural complexity associated with a classical monatomic fluid by the class Cn = Such class might be extended to include thus separating the two ways to obtain (simulation and direct correlation functions), but given the direct relationships between the and the that measure does not seem necessary. By doing so, the comparison with the quantum case is expected to be clearer by avoiding unnecessary complications to the essence of the related discussion. Moreover, direct correlation functions in the quantum case do not have the same general status as in the classical domain, which makes their absence from Cn a reasonable choice.
2.4. Quantum Calculations: Path Integrals
The consideration of the structural study of quantum monatomic fluids at equilibrium is in order now. The classical approach is an idealization in which thermal quantum effects can be neglected at sufficiently high temperature T. However, as T is lowered, the quantum diffraction regime becomes non-negligible, its importance being greater with diminishing temperatures and increasing densities. Furthermore, for sufficiently low T quantum exchange regimes (Bose-Einstein or Fermi-Dirac spin statistics) show up and must be taken into account [9,36,98,99]. All the classical simulation difficulties are also present in this context, with the added intricacies arising from the variety of quantum effects. In this regard, diffraction effects and zero-spin bosonic statistics can be tackled, broadly speaking, along lines of thought that are somewhat parallel. These are the subjects of the present article, whose interest is clear if one considers that every fluid can undergo diffraction effects, and that helium-4 as being composed of zero-spin particles is a paradigm for boson superfluids. Nevertheless, the treatment of quantum fluids with non-zero spin statistics is far more complex, owing to the roles that can be played by: (a) the multiplicity of spin states, (b) the intrinsic half-integer spin statistics difficulties (fermionic fluids), or (c) the magnetic interactions with external fields. All these more general cases will not be addressed in this work, which is focused on the current state of equilibrium triplet structure studies.
To begin with, the quantum monatomic fluid under diffraction effects displays three structural classes, which can be seen as arising from the particle delocalizations that produce a splitting of the classical Cn. These new classes are associated with three different forms of linear response from the quantum fluid to an external weak field. This means that if the structural complexity of the classical monatomic fluid is taken as a reference, the complexity of this quantum counterpart is (at least) three times higher. These quantum classes are revealed by the PI formalism [7,9,18,19,55,84,130], and are known as: instantaneous (ETn), total continuous linear response (TLRn), and centroids (CMn). The general scheme for any of them is just the same as before, correlation functions and structure factors, but with TLRn involving self-particle correlations; such a fact makes this latter class a distinct one. For notational convenience [11] these quantum classes will be denoted as: and . Their connections with external weak fields are as follows: (a) as ETn is a close “analogous” to Cn, then the corresponding fields are those of elastic neutron scattering or X-ray diffraction [23,28]; (b) TLRn arises from the action of continuous fields [11]; and (c) CMn is a particular case of the latter and corresponds to a field of constant strength [19,130], also showing a truly deep classical-like character [55,130]. On the one hand, the first two classes can be measured experimentally at the pair level , that is, ET2 and TLR2; from a wider perspective, these measurements also show connections with dynamic quantities via sum rules [23,29,30]. On the other hand, CM2 cannot be fixed directly through experiments, although it is very useful as an auxiliary object for theoretical developments [18,19,33,34,130,131,132,133,134,135,136,137]. (Beyond recall that no structural measurement is experimentally obtainable today).
To get a first feeling of the PI-origin of these classes, a simple image will suffice [4]. Under diffraction conditions at temperature T every actual particle with mass m delocalizes in the form of a thermal packet, its size being related to the thermal de Broglie wavelength . Accordingly, there are many possibilities for defining interparticle distances, but within the current response context three sorts of physically significant PI interparticle distances arise [7,9,11,84,130], each associated with one of the three PI classes. Although their exact nature will be discussed in Section 5 of this article, just for visualization purposes notice that the CMn class is built on the distances between the thermal packet centers, which are termed centroids or “centers of mass”. The other two classes involve more elaborate forms of distances between the particle thermal packets. Although the higher complexity of the structural quantum case should be clear at this point, there is still more to this issue that deserves consideration, as the following PI calculational facts reveal.
The quantum PI simulations in the diffraction-effects regime (PIMC, PIMD) describe the delocalized atoms in real 3-D space through a statistical distribution of (closed) elastic “necklaces” with P “beads” apiece (i.e., the thermal packets: one P-necklace per actual atom) [4,7,9]. is a positive integer, greater than 1, which is to be optimized and represents a compromise between statistical convergence and theoretical accuracy. The latter is given by the Trotter’s limit [138], in which necklaces transform into continuous closed paths in Euclidean (imaginary) time and an exact representation of the actual atoms and the fluid is retrieved [9]. (There is an alternate and equivalent PI formulation based on the Fourier expansions of the paths [139,140], but it will not be analyzed in this work). An actual fluid composed of N atoms is thus modelled by a set of beads. Therefore, P plays a decisive role in the simulation studies of the quantum structures (of course, using a reduced sample it makes them far more expensive than those of the classical case where Furthermore, apart from such an increase in the computational effort just to generate the equilibrium configurations, and of the usual N-dependences of any of the n-th order structure calculations [2,13], to obtain the structures it is crucial to point out that: the instantaneous (ETn) calculations scale as P, the total continuous linear response (TLRn) do as and the centroid (CMn) do as in the classical case.
As stressed, when diffraction effects dominate the fluid behavior, and thus exchange interactions can be neglected, the PI necklaces are closed. However, if quantum exchange cannot be neglected, one faces complicated mixtures of closed and open necklaces, the latter interlinking with one another, in response to the corresponding permutations among atoms [7,9,35,36,78]. Within the PI-description, the physically significant interparticle distances are defined by specific inter-bead distances (ETn and TLRn), or by constructions that use the bead positions (CMn), as will be shown in detail in Section 5 (diffraction effects) and Appendix I (zero-spin bosonic exchange) [9,35,130,132,133,134,135].
Therefore, the quantum structural complexity extremely exceeds in practice that of the classical case. Even if one only wishes to perform a full structural study including up to the triplet level, the PI computational effort appears today as a daunting task. As an aside, one may mention the approximate frameworks arising from the exact PI formalism (i.e., Feynman-Hibbs potentials [4,140] and their generalizations [141,142]), which can be utilized to carry out thermodynamic and structural studies of fluids with weak quantum behavior [11,131,143,144,145]. Although their applicability is certainly limited, they are far from being computationally expensive, and turn out to be very useful due to the intuitive structural pictures they provide at both the pair and the triplet levels [11].
2.5. Quantum Calculations: Closures
As regards closure-theories, their applications to quantum fluids may be carried out by following/adapting the same methodologies as those employed for classical fluids in both the r-space and the k-space. Actually, these adaptations have gone both ways (classical ↔ quantum), which has been a normal practice throughout the years [3,37,38,39,40,41,65,68,69,70,71,72,125,126,127,128]. However, the related theoretical quantum grounds deserve especial consideration, which becomes clear when applying OZn schemes.
Thus, by focusing on diffraction effects, it is very interesting that OZn turns out to be a rigorous framework for the centroid class CMn [55], albeit OZn is only approximate for ETn and TLRn [11]. Surprisingly, despite such mathematical observation, excellent results, as compared to experiment and simulation, have been obtained when fixing the three pair structure factors, , and by OZ2-treating the corresponding PI-simulated correlation functions [11,46,55,60,62,131,136,144,145]. The OZ2 calculations are much less demanding than those carried out with PIMC in k-space, and the results for obtained with PIMC and OZ2 are almost indistinguishable from one another [46]. Moreover, the OZ2 evaluations of the components are obtained with great accuracy as part of the whole determinations. Furthermore, according to the extended compressibility theorem [130], there is the exact formulation of the isothermal compressibility of the fluid that can be achieved with OZ2 through the centroid component . This implies that the OZ2 applications to the CM2 correlations produce, in principle, exact values for (within the accuracy and precision of the calculations performed) [130,136]. For the cases ET2 and TLR2, which in rigor must share that same centroid value [130], one can obtain approximate, though very valuable, estimates via OZ2 [46,60,62]. As regards triplet closures, the question is open and must be settled through comparison with exact PIMC/PIMD results. Although uncertainties larger than in the classical domain might be expected here, some promising results have been obtained lately [58,59,60] as summarized below. In relation to bosonic exchange, even though closures were employed in the past to deal with zero-spin/charged fluids [3,39,40,69], their use is not so straightforward, and some consideration will be given in Appendix I.
2.6. Some Recent Quantum Triplet Facts
To close this overview, three motivating pieces of information on quantum fluid triplets in the diffraction regime, obtained recently with PIMC and closures, may be worth giving here.
(i) For the quantum hard-sphere fluid on the crystallization line [59], the PIMC absolute maximum amplitudes of the instantaneous (ET) and centroid (CM) pair and equilateral structures, i.e., and do follow empirical behaviors of the type where is the degeneracy parameter, and and b are positive constants.
(ii) A preliminary PIMC triplet study of liquid para-hydrogen in k-space [58] suggests that on the quantum crystallization line there might exist an almost “constancy” (i.e., values in a relatively narrow interval) of a salient trait in the centroid triplet structure factor (e.g., the maximum of the equilateral components or an isosceles amplitude located nearby). If confirmed, this could be a parallel to the quantum freezing constancy observed at the pair level of the centroid maximum amplitude for a given fluid [62]. (At the pair level there is no general quantum extension of the classical Hansen-Verlet rule [6] for the centroid maximum amplitudes ).
(iii) The applicability of closures to quantum triplets could have a broader scope than suspected and be very helpful to provide physically significant pictures of the different quantum triplet behaviors in cost-effective ways. Even though the available information on closure applications to quantum triplets is scarce [54,55,56,57,58,59,60], for a wide range of quantum diffraction conditions (quantum hard spheres [59] and supercritical helium-3 [60], the intermediate triplet closure AV3 = (KS3+JF3)/2 in r-space captures significant features of the correlation functions and . Consequently, improvements on the AV3 closure, e.g., via adaptations of Abe’s expansion [38], should be well-worth exploring.
3. Equilibrium Classical Fluid Triplets
A homogeneous and isotropic classical monatomic
fluid is considered, which will serve as a reference for basic notations,
concepts, and tools, when presenting the quantum fluid discussion. A summary
description of both the pair and the triplet levels is given because a complete
study of the triplet level already involves the consideration of the pair
level [37,38,39,40,41]. The
grand canonical ensemble is employed in all the derivations, with the mean
number density being , and the interatomic distances denoted by The partition function reads as [2]:
where is the chemical potential, the inverse temperature the partition function of the canonical ensemble z the activity , and is the 3N-dimensional element of volume for
N atoms. Throughout this article, the ensemble averages are denoted by which in their definitions contain the division by
the corresponding partition function.
3.1. r-Space Correlation Functions
The one-point density dynamical function is simply
given by its ensemble average being The pair and triplet correlation functions are probability density
functions (not normalized to unity) derived from the partition function [2]. These
functions can be defined with the help of Dirac’s as [5]:
Note that and are intensive quantities which depend on and T and, essentially, they are given by
the ensemble averages of the two- and three- point density dynamical functions
(notice the avoidance of self-contributions). Their normalizations read as [2]:
A powerful alternate way to formulate the foregoing
correlation functions is based on the use of the functional differentiation of with respect to the variations in an external weak field which acts on every particle as [5,6,146,147,148]. The resulting equations are somewhat involved, but they lead to the physical interpretation of these functions as directly related to the response from the fluid to By starting from given by
one obtains the following set of equations:
The foregoing development can be easily generalized
to obtain the hierarchy of functionals which can be seen as the recursive definition of
the properties) of the inhomogeneous fluid in the presence of the
external field By letting , the functionals/properties on the right-hand sides of
Equations (8a)-(8c) transform into properties of the isolated fluid
which, as shown in Equations (9b)-(9c), give the
two- and three- body spontaneous fluctuations of the fluid density. The
explicit formulas for and are standard knowledge in classical statistical
mechanics [41,146,147,148], and for brevity are
not written here. It is easy to see, however, that contains contributions of the type. Note that the pair correlation function is contained in the formula of and that both correlation functions and are in that of . As an aside, note that for the canonical
component the following complementary identities hold:
which is the expected behavior of this type of
integrals, since there are no fluctuations in the number of particles in a
canonical ensemble. The analogous integrals involving are nonvanishing and are related to the true
number fluctuations, which are consistently defined in a grand canonical
ensemble. In this connection, given the formal equivalence between the
structural classes classical Cn and PI-centroid CMn [55,130],
the explicit and formulas and many other features are deferred to
the treatment of such PI quantum correlations. Hence, only some important facts
and consequences are to be considered in what follows.
3.2. k-Space Structure Factors
By approximating the right-hand sides of Equations
(8) by the zero-field Equations (9) and Fourier transforming, one obtains the
response functions in k-space from the fluid to the action of at the pair and the triplet levels [6,41]. These functions are the static structure
factors that read as:
In writing Equations (10) and (11) use of the
homogeneity and isotropy of the fluid is made. The response functions and are thus related to the density-density and the
density-density-density correlation functions of the isolated fluid,
respectively.
Note that in a broad sense one enters a general
linear response framework when takes on the right-hand sides of the hierarchy and
carries out the Fourier transforms on both sides of the equations. In this
regime, the fluid “does not know” if what is being undergone is due to an
external field or is just the result of its own spontaneous fluctuations.
Therefore, each of the (variations in the) fluid properties in k-space can be formulated in terms of
its corresponding isolated fluid property in r-space, and in such a way that the
functional dependence on the external field is linear [5,6]. In this connection, for clarity, it is worth writing here the well-known relationship at the pair level [6,148]: and also that at the triplet level: The static structure factors, or response
functions, are thus the proportionality factors between the variations in the
properties and the variations in the external field. Accordingly, the
associated wavenumbers k, ,and are the moduli of the wavevectors that
define the (elastic) momentum transfers from the field to the fluid i.e., . These characteristics linked to the use of the
linear response regime will be maintained when studying the quantum domain.
Some important points to be noticed are the
following:
(i) can be determined experimentally, while cannot [24].
(ii) and are real-valued quantities [41].
(iii) The general form of expanded in terms of the Fourier transforms of the
different contributions built with and is quite involved and will be given in connection
with the quantum CMn discussion.
(iv) For its direct theoretical and experimental
interest, note that the term in Equation (10a) represents the subtraction
of the forward scattering of radiation (elastic scattering). This operation is
an integral part of the complete definition of this pair structure function
(note that for large wavenumbers). Obviously, a
generalization of this operation also applies to the case, as will be shown later on.
Some Concomitant Problems and Their OZ Solutions
In this connection a deeper consideration is
necessary. Note that the term subtraction in Equation (10a) is also linked
to the theoretical asymptotic value of i.e., for in the grand canonical ensemble [2], which gives full meaning to the Fourier
transform in Equation (10b). Moreover, it is customary in simulation work to
omit this term, as the component is strictly unattainable due to the
finite sample size (i.e., finite and/or which imposes commensurability with the simulation
box on the wavevectors to be scanned (clearly, this also negatively affects the
calculation of the low-k region). Such omission is acceptable when
dealing with the simulation techniques but neglects the key fact that the component makes the connection with the
thermodynamics of the fluid [3,6,13], since as stressed earlier. The previous connection
yields an appealing way to determine the equation of state of the fluid via integration, an operation that is formally
independent of the many-body form selected to represent the potential energy (obviously, does need to be calculated). However, in calculating via Equation (10b) one faces the problem of
the long-ranged oscillations of about unity [2],
which forces one to have a knowledge of the pair correlations over a
sufficiently long range of interparticle distances Otherwise, accuracy in the
Fourier transform is doomed to fail [13]
(e.g., unphysical estimates for can result from that naïve use of the transform).
In addition, as the optimal determination of is accomplished via simulation, this already poses
a practical problem derived from the need for more expensive computations by
increasing the simulation sample sizes [13].
Furthermore, although the canonical ensemble is a very convenient
calculational tool, the necessarily finite combined with the intrinsically bad asymptotic
behavior of in this ensemble, i.e., [2,3], present
one with another important drawback to be dealt with.
The same discussion, but with augmented
difficulties, applies to the computation of in which the in Equation (11) involve and/or Under these circumstances, irrespective of
the mighty computational facilities at one’s disposal, targets that appear as
most desirable are: the saving of electrical power, the shortening of the time
to get answers through more rapid calculations, and the possibilities of
obtaining physical pictures of the underlying processes.
The obvious advantage of using functional
techniques is that they give the physically complete answers of the classical
structural problems at one stroke, although, inevitably, some problems stand
out and others arise. Nevertheless, there is more to using functional
techniques in this context, since they can be employed to build insightful
solutions to these drawbacks. In relation to this, the additional role played
by the inverse functional derivatives (e.g., in the derivation of the Ornstein-Zernike (OZn)
equations is to be highlighted [41,65,68,69,70,71,72,146,147].
The OZn equations define a further type of structural functions: the direct
correlation functions etc. By restricting up to the triplet level for
simplicity, and yield compact and efficient formulations of the
structure factors and The key point is that the direct correlation
functions are short-ranged (i.e., they decay to zero rapidly with increasing
distances), which allows one to fix very accurately the Fourier transforms
involved.
Given that the OZn framework at the pair and the
triplet levels will be considered in detail when dealing with the isomorphic
PI-centroid CMn class, for brevity, the classical situation may be summarized
here in the following basic equations [1,41,68]:
- -
- OZ2 equation
- -
- OZ2 pair structure factor
- -
- Baxter’s hierarchy related results
- -
- OZ3 triplet structure factor
Some further comments are in order now. First, the
OZ2 equation takes a single form, whereas one finds four different, though
equivalent, versions of the OZ3 equation [70].
Second, the terms appearing in Equations (10a) and (11) are
fully included in their reformulations given by Equations (13) and (15).
Therefore, the incompleteness associated with simulation
schemes appears formally OZn-circumvented. Third, note the important role of
the pair level in k-space, as shown in the triplet Equations (14)-(15)
where the pair quantities give a solution to the simulation-intractable
situations at and/or (also , and are indispensable building blocks. Fourth,
however, the OZn equations are void in themselves, and they need further
approaches (closures) to be solved. This is easy to grasp by observing
the structure of the Equations (12) and (14): both are integral equations for
the unknown and , which add new difficulties to the whole
structural question [24,26,27,37,38,39,40,41,45,65,68,69,70,71,72,121,122,123,124,125,126,127,128,129].
Further formal considerations (triplet symmetries and asymptotics, consistency
relationships, etc.) and analyses to fix the pending issues (e.g., closures,
the vexing canonical long-range behavior, etc.) are given in the next
subsections.
3.3. Grand Canonical Triplet Symmetries and Asymptotic Behaviors
(i) In r-space, by renumbering the atom
labels, the triplet and functions satisfy the following symmetries:
Also, when two particles get very close together
the triplet function obviously vanishes [150,151].
Technically, one writes
although, as at the pair level, the zero value is
reached for interparticle distances greater than zero. The asymptotic behaviors are [2,151]:
(conventionally, one may take particle 1 as the
origin of coordinates for the three generic particles). For the equilateral and
isosceles correlations these conditions are usually written as
In the canonical ensemble Equation (17e) and its
analogous at higher orders are not so neat because of terms [2,3], but this
theoretical feature is not central at this stage. (More on asymptotic
properties later).
(iii) Note that for in r-space one expects a decay to zero when
any of the particles increasingly separates from the other two, because this is
a reasonable physical behavior that can be drawn from Equations (14). However,
for and in k-space their explicit behaviors may
become involved, since they depend on the angles between and (e.g., for is the observed behavior).
3.4. The Interplay between Simulation Techniques and Closures
There are well known MC and MD simulation
techniques to obtain and [13,17,41,42,43,44,45,120,121,122,123,124],
and they will not be described here. Rather, the interest is to be focused on
some significant facts that show the interplay and complementarity between the
simulation calculations and the approximations that can be obtained via
closures.
(i) In the OZ2 case there are highly accurate
methods that yield and [5,6,13,71,72,125,126,127,152].
It is useful to point out that the knowledge of the latter functions allows one
to extend the range of distances obtained for via simulation which, for instance, using a cubic
box is limited to half the box length In addition to Equations (13), the basic formulas
are:
As stressed earlier, the access to the fluid
equation of state via and is a key OZ2 feature. Moreover, the knowledge of and hence of an extended
is useful for further studies, such as especial asymptotic decay properties of the pair correlations (pure exponential and exponentially damped oscillatory decays) [153,154,155] or some triplet correlation evaluations [3,41,156].
Among the OZ2 methods, Baxter’s partition of Equation (12) deserves especial attention [72,125], since it per se does not need any explicit knowledge of the underlying interactions between the particles: the only input
parameters to carry out calculations are (and T to extract the actual value of ) [46,130,136]. This contrasts sharply with typical OZ2 approaches, such as Percus-Yevick or the hypernetted chain [5,6,71,152], and makes Baxter’s applicability more general and powerful. Although the latter is a theoretical development in classical statistical mechanics, a good deal of its applications have been performed in the context of fluids with quantum behavior. Therefore, for the quantum purposes of this work, it is convenient at this point to give some specific details of Baxter’s partition [72] and its practical implementation, which involving a minimization procedure [125] (BDH Baxter-Dixon-Hutchinson) also needs a further
analysis of its results [46,60,62,127,131,136].
Baxter’s partition for a disordered fluid and its
practical implementation (BDH) are based on: (a) vanishes for distances greater than a cut-off
distance (b) obtained via simulation is known for ; (c) is limited by the range of distances set by half
the simulation box length , and is fixed through a minimization procedure
that preserves the continuity of at such cut off; (d) the minimization yields in
general a set of possible cut-off distances which are the “zeros” of an auxiliary function; a
practical convergence of the observable property, i.e., occurs within an upper subset of these zeros; (e)
there are ways to treat the situation in which no zeros arise [125] and, also, to extract the physically
significant information from the upper zeros [46,62,136].
Clearly, the longer the L value is, the better the OZ2 results should
be. In this connection, to minimize the defects of the fixed with a finite size in a simulation (e.g., canonical ensemble
calculations), an additional combination of OZ2 and simulation is highly
recommended. As a matter of fact, the iterative improvement on with grand-canonical corrections [126,127] leads to a better-defined convergence along the sequence An example of the latter iterations can be
summarized in the useful algorithm put forward by Baumketner and Hiwatari (BHw)
[127]:
where the initial conditions are the simulated and its associated OZ2- that yield the first correction , which in turn is OZ2 analyzed to obtain its giving the second correction and so on, until convergence in is reached. When using OZ2-(BDH+BHw), the value can be fixed at every step as the mean value
of the arising from the upper set associated with the
resulting zeros [136]. For
further applications (e.g., triplet calculations [41,55,60])
involving a specific single function as an intermediate quantity, i.e., or the selection within the final upper -range of convergence of one of them as a
representative is sufficient to give perfectly consistent results.
(ii) For OZ3 the situation involves the design of
accurate closure methods for obtaining or and which still remains a non-closed problem. For the functions key closures are:
- -
- Kirkwood superposition (KS3) [37]
The interesting point is that KS3 and JF3 are
pivotal references in general triplet studies. In this regard, one may
distinguish between triplets in r-space and
triplets in k-space: KS3 plays a central role in r-space [38,39,40,41,121,150,151], whereas JF3 does it in k-space
because [41,70]. The
forms adopted by the KS3 and JF3 triplet structure factors can be found in
Reference [41], from which the case AV3 is a
trivial matter (note that for JF3 the formula reduces to the product of the three factors in Equation (15)). KS3 was derived in the context of classical statistical mechanics, while JF3 was in the context of quantum statistical mechanics. Despite these different conceptual frameworks, these two closures have been applied to both classical and quantum fluids indistinctly [26,27,32,37,38,39,40,41,54,55,56,57,58,59,60,121,150,151]. (In relation to this, recent results for fluids with quantum behavior show that AV3 performs very well as compared to KS3 or JF3 [59,60]). As regards their behaviors under limiting conditions, note that KS3 and JF3 satisfy the long range Equations (17b)-(17e); KS3 also satisfies the short-range Equation (17a), whilst JF3 fails to describe this latter situation [150,151].
Other triplet closures are orientated towards k-space [41,65,122,123,124,128]. Among them the insightful Barrat-Hansen-Pastore (BHP3) closure deals with [41]. By starting
from Equation (14a), the BHP3 closure introduces an auxiliary pair function such that:
which is fixed through the minimization of the
following nonnegative functional:
To initiate the iterations is the recommended choice [41]. The convergence is assessed via the quotient which involves the value of the functional being
minimized and the (squared) norm of the density derivative of the pair direct
correlation function, which serves as a reference. For the pertinent formal
details of this type of minimization, the reader is referred to Reference [41] (gradients), or to References [45,55,56] (conjugate gradients). After fixing the application of Fourier transforms to obtain yields the approximation [41]. BHP3
satisfies Equations (14) and has been applied to classical and quantum fluids [41,45,55,56,57,58,60,121,122,123,124].
Along the same k-line of thought, another
example is Denton-Ashcroft symmetrized approach (DAS3) [65], which can be cast as:
in which the following definitions are to be used:
DAS3 satisfies the key Equation (14b) only at , and has been applied to classical and
quantum fluids [55,65].
(iii) The validity of the closure-based approaches
is to be established by comparison with exact simulation results. On the one
hand, closures at the pair level have proven their value as was mentioned
earlier. On the other hand, there are missing traits when triplets are
described in terms of pair properties, and one would not expect much success in
utilizing closures for triplets. Nonetheless, the triplet results reveal that
closures may capture salient features in both the r-space and the k-space.
Therefore, their usefulness as interpretive tools may be greater than imagined
(see References [41] and [122] for the classical domain and [59] and [60] for the quantum domain).
3.5. Other Theoretical Features
(i) There is another functional calculus way to
obtain the formulation of the pair Equation (3). Using the pairwise approach for the
interactions between particles in the fluid, this alternative is based on the
functional derivative of with respect to the variations in the
interparticle potential : such first functional derivative leads to . If one iterates the procedure, the second
functional derivative produces a highly intricate expression. Given that
no external field is considered, the usefulness of these formal manipulations
seems rather reduced. The reader is referred to Reference [6] for the derivation of in the canonical ensemble. This issue will be
reconsidered when analyzing the quantum fluid instantaneous structures (Section 5).
(ii) An interesting relationship is obtained from
the grand canonical average of a function that depends on the particle
coordinates, (e.g., the n-point density dynamical
functions), and reads as [150,151,157]:
For the two-point density one arrives at an exact connection between
where This relationship may be useful for checking the
consistency of the results computed for and or for testing approximate triplet closures. This
latter issue will also be discussed in connection with fluids with quantum
behavior.
4. Basic Path Integral Concepts
4.1. PI Partition Functions
The starting point is the quantum grand-canonical
partition function which for an isolated quantum system composed of N
identical particles can be cast as [4,5,7]
where Tr denotes the trace operation, is given by Equation (1), the mean number
density is given again by , and the other symbols retain the meanings seen
earlier.
If attention is focused on monatomic fluids at low
temperatures, such that exchange interactions can be neglected, the partition
function for diffraction effects can be written in the
coordinate representation as [5,7]:
where stands for the volume element of the N
distinguishable particles, and is the configurational state-ket. Now, with the
use of the path-integral approach (PI), can be reduced to [7,9,11,74,77,78,79,81,84,90]
in which every actual particle j (=1,2,…,N,…)
is transformed into a closed elastic necklace j with P beads
labelled Thus, one finds a PI-model system composed of -sized canonical ensembles each ruled by an
“effective potential” depending upon all the corresponding bead
coordinates , such that
The parameter is a generalized activity that reads as follows:
which helps to identify the expression of the
canonical A crucial step in PI work is to give suitably
operational forms to by resorting to propagator calculus. In addition,
the formal generalizations to tackle quantum exchange regimes rely heavily on
the basic development for distinguishable particles [4,7,9].
4.2. Sum over Histories and Propagators
The PI-P picture (31a) becomes exact in the
limit (Trotter’s theoretical accuracy [9,138]), although one can find optimal finite P values
that yield sufficiently precise and accurate representations of the actual
system. The optimal P is thus a compromise between theoretical accuracy
and statistical convergence for properties. All of this is related to the
design of (thermal) propagators that serve to build [7,9,75,81,82,83,84]. A
brief explanation of how the practical image of beads-and-necklaces arises is
worth giving here.
The basic idea is to split the density matrix
diagonal elements into, in general, a number X of factors
involving operators and to employ the completeness relationship in the
coordinate representation . By doing so, one obtains the exact convolution
property [9]:
which leads to the canonical partition function:
where , and the (*) in the product implies the cyclic property . The thermal propagator is the generic nonnegative matrix element [9], which clearly corresponds to dealing with a density matrix at a higher temperature than the actual.
The whole process contained in Equations (32) and (33) can be visualized in an appealing way by resorting to the image of the periodic “motion” of the system in imaginary time (period [4,140]. Thus, in Equation (32) the system may be viewed as if it “travelled” from to by following every possible broken path (in configuration space) defined by the intermediate stages that can be associated with the equally spaced -“instants” in imaginary time. Every particle j follows then a closed path (necklace), marked out by the -“instants” (beads). In the language of continuous paths one speaks of the basic interval for the motion in imaginary time to take place, and there is the obvious equivalence as is customary in every Fourier series analysis. (Warning: this does not imply by any means that The partition function as given in Equation (33) closes the situation by integrating over every possible starting point and, in this way, the “sum over histories” in imaginary time arises. It is easy to see that there is equivalence among all the X imaginary-time instants (translational invariance in imaginary time).
To give operational forms to the propagator one needs approximations to tackle the problem posed by the nonzero commutator [7,9,81,82,83]. In relation to this, several possibilities are available in the PI literature. The accuracy attainable with the approximation depends strongly on the propagator selected and the X value employed is defined in Equations (31)). For the purposes of this work, only a few guiding lines are to be commented, the reader being referred to the pertinent references cited below for complete details.
In the study of quantum many-body systems three main types of constructions for the propagator stand out, which lead to: (i) the primitive propagator (PP), for which conventionally the number of beads is and yields an accuracy for [4,7,9,61,80]; (ii) the fourth-order propagator (SCVJ), arising from the works by Suzuki [82], Chin [83], and Voth et al. [84], for which the final number of beads P must be even and yields an accuracy for and (iii) the pair actions (PA) based on the developments put forward by Ceperley [9] and by Cao and Berne (a specific PA for quantum hard spheres, CBHSP) [81], for which the number of beads is again and there is no systematic recipe for their accuracies. It is useful to recall at this point that another version of a fourth-order propagator, the Takahasi-Imada propagator [75,76], is not very useful for computing correlations and structures [10,11,75]. Consequently, the PI computational effort depends on the size of the optimal P value, which depends on the propagator effectiveness, a property that varies from type to type. One may summarize this issue by saying that: pair actions are more efficient since they appear to require lower optimal P values, whereas high-order propagator expressions can be improved, seeking to reduce P, in a systematic way. (For early hard-sphere PA’s constructions and applications based on Barker’s work [73] see References [79,158,159], and also [11] for a general discussion of this issue).
The expressions of the PP, CBHSP and SCVJ propagators are given in what follows. Hereafter, the P value is assumed to be the optimal, and the (final) P beads are numbered correlatively The three cases can be written as
where is common to the three and can be cast as [4,7]
with the (*) implying the cyclic property This contribution arises from the free particle behaviors, which within PI take the form of harmonic couplings between adjacent beads in every necklace.
By assuming for simplicity pairwise interactions between the actual particles, and denoting the inter-necklace bead-bead distances by (the equal t label is to be noticed) the contributions and read as [7,9,62,81,84]:
(a) Primitive propagator
(b) Cao-Berne propagator for quantum hard spheres (diameter
(c) SCVJ propagator
where is a unit vector, and the parameter although for a good deal of applications is a recommended value [84]. (In Equations (38) note that necessarily ).
4.3. The Classical Isomorphism, Bead Roles, and Notational Conventions
(i) The comparison of the quantum given in Equations (31) with the classical given in Equation (2) leads to the so-called classical isomorphism [7,9,16], or more properly semi-classical isomorphism, due to the dependences shown in Equation (31b) (see References [2,11,13] for the semiclassical approach forms). This fact makes the PI computational study of quantum fluids amenable to using well-known basic classical simulation techniques (MC and MD), such as path integral Monte Carlo (PIMC) and path integral molecular dynamics (PIMD). The latter basic techniques (and its variants) have become standard tools in modern quantum condensed matter research [9,10,11,18,19,21,22,33,34,35,36,54,55,56,57,58,59,60,61,62,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101]. Naturally, there are unavoidable differences between the classical and the PI developments and computations, since the language of classical dynamical functions is radically different from that of quantum operators [4,5]. However, as regards the studies of the structures of fluids with quantum behavior, the relevance of such isomorphism runs deeper than one might think at first sight [9,11,18,19,55,93].
(ii) The inter-necklace interactions are uniquely defined as averages involving equal imaginary time t-bead interactions, which is connected to the diagonal character of the potential energy operator (iii) contains kinetic effects between consecutive imaginary times (beads) in different necklaces.
(iv) The singularity of the potential (37a) in CBHSP prevents the numerical evaluation of its derivative for a given (“frozen”) configuration of necklaces [136,160].
(v) An inspection of the PP, SCVJ, and CBHSP formulas indicates that, when using these propagators, careful attention must be paid to the equivalence among the beads. The point is that while there is full equivalence between all the beads in PP and CBHSP applications, such symmetry is broken when use of SCVJ is made. The SCVJ beads are classified into two groups, conventionally the odd-numbered and the even-numbered In thermodynamic calculations the general roles played by the beads are as follows: the same in PP [7,9,74,80], the same in CBHSP [9,81], but different in SCVJ depending on the odd/even group they belong to [62,84]. Moreover, for the current purposes of structural evaluations, it is worth stressing that: (a) in PP and CBHSP all the beads play the same role in the corresponding ensemble averages [9,11,79,80,81], whereas (b) in SCVJ only the odd-numbered beads are physically significant, thereby playing the same role in such ensemble averages [11,84] (the even-numbered beads must be discarded). Technically, these different traits arise from the use of a double-time step when constructing SCVJ [82,83,84] instead of the usual single-time step applied in the PP and CBHSP derivations (the reader is referred to the quoted references for full details). These structural bead features will be formalized in Section 5.
In order not to burden the notations, the conventions for structures followed in this article are worth summarizing now. Given the optimal number of beads per necklace:
- The three symbols for denoting beads are: t, and depending on the context.
- Label t runs over and is associated with every necklace j.
- Label runs over and is associated with every necklace j.
- Label runs over , and serves the purpose of a whole renumbering of all the structurally significant beads in a canonical sample, such that they are associated with the necklaces as .
Depending on the propagator the above conventions mean:
- For the PP and CBHSP propagators, in which and
- For the SCVJ propagator, in which , and the global picking of the odd-numbered t-beads in every necklace. (Note that the even-numbered beads represent intermediate stages that fit mathematically into the whole picture of P-membered necklaces).
4.4. Quantum Exchange Interactions
The situation gets much more complex when one deals with monatomic fluids in which quantum exchange interactions cannot be neglected. For now, it is worthwhile to remark that bosonic exchange can be successfully tackled with PI computations, as shown about forty years ago by Ceperley and Pollock [78] and by others later [9,35,36,91,96,97]. However, the known as the “sign problem” [100,101] made fermionic exchange remain out of the PI reach. However, this situation has changed for the better very recently, thanks to the appealing approach put forward by Filinov et al. using the Wigner extension of the usual PI formalism (WPIMC) [98,99].
The intricacies of the exchange issue can be grasped by observing the form of the canonical partition function for the general case of N particles not only identical, but also indistinguishable, all of them in the same spin state [4,9,100]:
where runs over the permutations of the particles, for every if there is bosonic exchange, if there is fermionic exchange and such that holds for even and holds for odd and is defined as which is meant to denote the action of the permutation on the ordered ket denoting the position states of N distinguishable particles. As seen, a pure summation of nonnegative terms arises from the bosonic case, whereas an alternating summation does from the fermionic case. Accordingly, feasible calculations can be carried out for bosons since a well-defined probability density is always involved. However, given the enormous size that can reach, the same does not occur for fermions, for which large uncertainties plague in practice PI direct calculations (it seems out of the question that one could have access today to unlimited computational resources that would yield the exact answer to the whole fermionic sum). In their WPIMC works, Filinov et al. overcome the “sign problem” by treating the fermionic exchange determinant via a positive semidefinite Gram determinant [161].
Some observations regarding Equation (39) are in order. (a) By keeping the identity permutation alone, one retrieves the pure diffraction effects as given in Equations (30)-(31); this results in the non-classical Boltzmann statistics associated with (b) Note that the presence of guarantees the correct transition to the classical partition function and also the access to thermal properties (free energies, entropy) [162]; this is a factor which must always be written when dealing with (c) If more than one spin state were involved, the expression (39) would have to be generalized by including every spin possibility [100,163].
The PI triplet structural issues of a zero-spin bosonic fluid will be addressed in Appendix I. However, this does not yet seem the time to enter a detailed discussion of the PI fermionic fluid case, and the interested reader is referred to the following references for basic information [98,99,164,165,166,167,168,169].
4.5. The PI-Centroid Variable
A particularly interesting PI quantity is the centroid variable which is the necklace “center of mass” (all the necklaces are equivalent, so are their centroids) [4,18,19,140,141,142]. The corresponding definitions for the propagators discussed above are the following [61,80,84,159]:
This variable is of paramount importance in both the thermodynamic and the structural studies of fluids with quantum behavior. As regards equilibrium situations, one may mention the structural relationships (OZ2!) with the equation of state [130,136], the structural extension of the semi-classical isomorphism [11,55,130], the connections with observable quantities and special situations [62,135,137,143,144,145], or the applications to deal with quantum exchange interactions [130,132,133,134], as will be discussed later for the zero-spin bosonic case in Appendix I. Furthermore, centroids are key to building interesting approaches to quantum dynamics in condensed phases [18,19,33,34,93].
5. Theory of Equilibrium Quantum Fluid Triplet Structures under Diffraction Effects
A homogeneous and isotropic quantum monatomic fluid is considered. Exchange interactions are neglected and the Hamiltonian Equation (1) is selected. The correlation functions and their associated structure factors can be grouped into three classes [7,9,11,84]: centroids (CMn), total continuous linear response (TLRn), and instantaneous (ETn). Each class is associated with the linear response from the fluid to an external weak field . When use of functional calculus techniques is made, a good deal of the developments for the CMn class are parallel to that of the classical monatomic fluid, and the same may be said of the TLRn class, though to a significantly lesser extent [7,11,55,130]. The ETn case has a different nature, the functional techniques that can be applied to CMn and TLRn are inapplicable to ETn, and this latter class is to be treated separately [3,6,9,84,135].
The grand-canonical partition function for the study of the CMn and TLRn classes incorporates the action of and reads as follows [11,62]:
where the operator is defined as The key point here is how to deal with the exponential of the sum of two non-commutative operators, i.e., , which can be accomplished in the standard way via the Baker-Campbell-Hausdorff formula [163]. For the current purposes, the density matrix elements in Equation (41) are split into X steps and one applies the basic approximation:
which is accurate up to terms (as occurs in the PP propagator derivation). This approximation leads to the partition function:
is diagonal in the coordinate representation). By observing Equation (43) one notes that the nonnegative density matrix elements may be given the final PI propagator form desired or needed for PI convergence reasons. In relation to this, notice that: (a) functional derivations involving are independent of such form, (b) the linear response from the fluid is characterized by functions in the limit and (c) the optimal value for X can therefore be conveniently adapted. By recalling that, regardless of the propagator employed, the final optimal number of beads in PI calculations is conventionally taken as P, the latter remark (c) is unimportant for PP and CBHSP (or PA’s in general), since . However, it turns out to be crucial for SCVJ for which and the physically significant beads for structural purposes are just those contained in Equation (43): . (Note that is the primary object that serves to define the structural ensemble averages). As stressed earlier, such significant beads are the odd-numbered t ones when SCVJ is fully developed and the intermediate beads completing the whole P-set do arise, i.e., [11,84]. Consequently, can be approximated by the general PI form [11,62]:
Now, it is worthwhile to point out that the action of the field expressed in Equation (44) is consistent with a thermalized -interaction, but not with a “sudden” interaction such as that of the radiation-atom elastic collisions. On the one hand, examples of the fields in 3-D space involved in Equation (44) are: static continuous fields in r-space and continuous fields in imaginary time, such as a gravitational field or the special case of a set of neutrons thermalized with a fluid sample composed of zero-spin particles, as is the case of fluid helium-4 [30]. (For the latter, such continuous interaction takes place in Trotter’s limit , which is PI treated in (44) via the finite number of beads, P or . The classes CMn and TLRn are associated with these types of continuous -fields. On the other hand, examples of related fields not involved in Equation (44) correspond to the elastic scattering of radiation experiments, e.g., neutrons for fluid helium-4, X-rays for fluids helium-4 and helium-3 [6,28] (from a conceptual statistical mechanical point of view there is no difference between the static response functions to both radiation probes [6]). Thus, within the framework set in subsection 2.2, the inadequacy of the static picture related to Equation (44) can be illustrated, for simplicity, by considering the interaction between a neutron and a spinless particle, which is essentially given by the neutron-nucleus Fermi’s potential (a Dirac-) [6,23]: the (elastic) collision between an incoming neutron and a thermally delocalized atom localizes the atom at just a position in the sample (the “collapse” by the position measurement); afterwards the atom must delocalize again according to the fluid equilibrium state. “Viewed” from the foregoing PI approach, the neutron-atom collision should take place at the position of a given bead, which would imply the immediate disappearance of the associated necklace distribution and its ensuing reappearance [11,170]. This quantum phenomenon cannot therefore be analyzed via the functional derivatives of (44), which cannot cope with the disappearance/ reappearance of the atom quantum thermal packet, and a full quantum time-dependent treatment is the way to understand it [6]. Therefore, for the class ETn, which is associated with localizing -fields, Equation (44) is not appropriate (more about this in subsections 5.3 and 5.4). In sharp contrast, under classical conditions the radiation-atom elastic collision phenomena pose no problems to the functional derivations and their static linear response interpretation [5,6,148]. Now, a detailed discussion of the three classes of equilibrium quantum structures follows.
5.1. The PI-Centroid CMn Class
This class behaves from the structural standpoint in the classical way. This is a remarkable result that arises from the explicit consideration of a continuous weak field of constant strength, acting on the fluid [19,33,55,84,130]:
Inclusion of this field leads to the general PI partition function [130]:
where use of Equation (40) is made. For clarity reasons, it is convenient to rewrite the previous formula as:
It is straightforward to show that the functional derivatives of are formally identical to those of the classical case contained in Equations (8)-(9). Thus, one finds up to the third order [11,57,130]:
where the inhomogeneities caused by are reflected in the fluid centroid functionals/properties The CMn hierarchy can be obtained by iterating the procedure to higher orders. As explained earlier in the classical case, if one makes on the right-hand sides, the isolated fluid properties arise:
where and use is made of the total pair correlation function of centroids Incidentally, note that the factor accompanying may be abbreviated to , consistently with the subtraction from of the asymptotic behaviors Note that Equations (49b) and (49c) can be formulated in a concise manner with the use of the spontaneous fluctuations of the centroid density (analogous with Equations (9b) and (9c)).
The formal expressions for the grand-canonical averages giving and are identical to those of the classical case Equations (3) and (4) (Figure 1):
5.1.1. PI-Centroid Linear Response
By integrating (48b) and (48c) with the substitutions (49b) and (49c) on the right-hand sides, and taking the Fourier transforms, the two- and three-body centroid response functions arise as [11,55]:
The same dependences on the moduli of the wavevectors (e.g., and similar comments as those made in connection to the classical Equations (10)-(11) do apply here. In particular, the terms are key to formulating completely and , and correspond to the especial situations: (a) ; (b) and/or , and Explicitly, the CM3 triplet structure factor can be cast as:
where stands for the Fourier transform of does for that of , etc. Given the analogies between the structural formulations for quantum centroids and classical monatomic particles, it would be a significant step forward if such parallelism could be extended to also include the OZn direct correlation function schemes for centroids. This is indeed the case as discussed in detail below [55,130].
5.1.2. PI-Centroid Direct Correlation Functions
There is the direct axiomatic way, consisting in checking that the OZn relationships satisfied in the classical domain by the set (see the insightful work by Lee [70]) are also satisfied by a set of PI-centroid functions which is defined accordingly in the same manner (see Reference [130] for OZ2). This procedure finds support in: (a) the formal equivalence between the PI-centroid and the classical hierarchies arising from their partition functions, and (b) the fact that the external field is switched off when deriving the usual OZn equations [70], which serve to analyze the structures of the isolated fluid equilibrium states. Nonetheless, it seems useful to obtain the centroid OZn equations via a free-energy argument closely related to the standard procedures [171,172,173,174,175]. The reasoning below expands in a more comprehensive manner the early theoretical sketch reported in [55], and hinges heavily on the external field of constant force as the cause for the PI-centroid structures to show up. Recall that the PI-centroid (a “center-of-mass” variable) is an auxiliary mathematical object which, as such, cannot interact with external fields in an experimentally measurable direct way. Therefore, no claim can be made regarding any general validity of the centroid OZn() derivations under other weak external potentials , as is usual in the general functional OZn-context of classical fluids. The following development is an adaption to PI-centroids of the procedure that can be found in Haymet et al.’s insightful works [173,174,175].
(i) The starting point is the differential of the fluid energy:
where S is the entropy, p the pressure, the one-body number density distribution of actual particles, and a (constant) variation in the field acting on such particles. The key point is that under these conditions Equation (55) can be rewritten in terms of the centroids:
because it so happens that
Equation (57) can be obtained directly by integrating the functional derivative (see Equation (48a) and subsection 5.2). However, at this point it seems better to consider the role of the normalized thermal packet representing a delocalized atom in the inhomogeneous fluid. The function is a probability density necessarily normalized to unity:
where is the position vector of the atom, and the position vector of the centroid. To grasp this concept, consider the simpler example of the homogeneous Gaussian thermal packet provided by the semiclassical Feynman-Hibbs picture (GFH) [4,11,143,144]), in which a particle of mass m in a fluid is described as a thermal packet of width [4]. The corresponding may be visualized as a deformation of the Gaussian packet adopting the symmetry of the external field. The derivation of Equation (57) uses the following facts: (a) the centroid is the “center of mass” of the probability density ; (b) the actual atom density is obviously related to the centroid density through a smearing out operation involving the inhomogeneous packet; and (c) the external force undergoes a constant variation The proof goes as follows :
(ii) Following the steps in References [173,174,175] one defines an auxiliary energy via a Legendre transformation:
and a Helmholtz free energy for the fluid in the form:
(iii) A discussion of the selection of reference ideal systems in classical and quantum studies can be found in References [172,173,174,175]. This is a very important matter, for the application of functional differentiation to the corresponding excess free energy will yield a hierarchy of direct correlation functions. The direct correlation functions so obtained may or may not coincide with the usual for classical simple fluids [70,146,147,171,172,173,174,175]. In the current case of PI-centroids, which are quantum intermediate objects [4,11,18,19,140], given the classical-like form of the derivatives of the grand canonical potential, , with respect to the field given in Equations (48), the selection of the ideal Boltzmann system in the field seems the appropriate choice. By doing so, a classical-like hierarchy of PI-centroid direct correlation functions will be obtained. For the present structural purposes, focused on the usual Ornstein-Zernike framework at this choice is going to be rewarding. Therefore, the Boltzmann-system reference [171] yields [55]:
and the excess free energy reads as:
(iv) The functional differentiation of leads to the hierarchy of the PI-centroid direct correlation functions which, up to the third order, reads as follows:
Of particular interest is the pair function which can be developed in the convenient form:
where attention should be drawn to the inverse derivative which is perfectly consistent with the use of the grand canonical ensemble, for density variations independent of the external field can be made [147].
5.1.3. OZ2 and OZ3 Frameworks
Inserting Equations (48b) and (65) into Equation (66), one arrives at the inhomogeneous OZ2 equation in the field
which transforms into the conventional homogeneous version if the field is switched off
By Fourier transforming Equation (68) and combining the result with Equation (52c), the static pair structure factor for PI-centroids is:
formally identical to the classical form Equation (13a). It can be demonstrated that for the quantum fluid [130]
a result that should not be surprising, since the fluctuations in the number of particles can be counted with the centroids. Therefore, the PI-centroid component fixed via formally provides an exact way to obtain the equation of state of a fluid with quantum diffraction behavior. As in the classical case, is expected to decay effectively to zero within a short range of distances, which is indeed the case and leads to highly accurate results in k-space [46,62]. In this connection, recall that direct correlation functions show generally a tail in their decays [149], but its importance is negligible beyond a certain cut off (see References [130,136] and Figure 2).
At this point, and following Reference [41], it is worth introducing a new hierarchy arising from the functional derivatives of the total free energy . As before, the following formulas are limited to the third order, the iteration to higher orders being straightforward. For brevity, detailed reference to the various dependences of the functionals are omitted in what follows. At first order one finds:
where the terms containing come from the ideal system contributions. In Equation (71) one identifies the actual chemical potential as the algebraic sum of the external field and an intrinsic contribution, in agreement with the expected constancy of the chemical potential in the presence of the external field [171,172].
The interest of the hierarchy lies in the fact that, together with the hierarchy they allow the OZn frameworks to be formulated in compact ways [41]. Thus, OZ2 as given in Equation (67) can be cast as:
which reduces to Equation (68) in the limit Furthermore, via functional differentiation of Equation (74) one obtains the OZ3 framework. One of the four equivalent OZ3 equations can be derived by following closely References [41] and [70]. First, by taking the functional derivative with respect to the one-particle density a new identity arises:
Second, with application to of intermediate differentiation with respect to , and renumbering the particle labels, one arrives at the final form:
which, again, reduces to the homogeneous OZ3 equation in the limit The triplet linear response function for PI-centroids of the homogeneous quantum fluid arises from the Fourier transform of Equation (76) combined with the definition given in Equation (53b). Thus, by noting that:
one finds the triplet structure factor:
which is equivalent to Equation (54) but formulated in terms of direct correlation functions [55], with all the advantages and problems associated with these objects commented earlier. In this connection, if the variations in the density are uniform, the general hierarchy sketched in Equations (64) takes the simpler and operative Baxter’s form [68]. In particular, the analogous to Equations (14) read as:
5.1.4. Some Additional Relationships and Further Remarks
For the hierarchy the partition function leads to all the relationships that are applicable in the classical context [70]. A straightforward calculation yields:
which at zero field gives the corresponding centroid equations for the isolated quantum fluid. Completing with the first order derivative , the first three of the related equations read as:
Besides, note the classical-like additional identities that hold in the PI-centroid context:
where is the in-the-field PI canonical partition function, and the relations to the number fluctuations are clearly displayed. These number fluctuations refer to the in-the-field fluid; the formulas on the right-hand sides remain the same when but obviously the meaning is not the same.
Finally, several remarks are in order. It is worthwhile to point out that the formal OZn derivations applied in the classical domain and related to the bijective connection external fieldequilibrium density [171,172,175,176,177], hold here for . This is guaranteed by the form of the quantum partition function Equation (44) which is isomorphic to its classical counterpart Equation (2). Another point is that there is no defined interparticle potential between PI centroids (compare to the variational approximations arising from the PI formalism [4,140,141,142], which yield versions of such a potential), but this is not relevant to this discussion [171]. In this regard, nor is the fact that under the same conditions two different densities are included in Equation (57), namely the true particle density and the centroid density, because: (a) one is the actual and the other is an auxiliary quantity, (b) each corresponds to a distinct object, and (c) both are intimately related. (The situation is analogous to a distribution of mass and the consideration of its center of gravity). To bring this subsection to a close, note that the applicability of the classical OZn numerical schemes to the quantum CMn class is perfectly possible and rewarding: (i) at the pair level, OZ2(BDH+BHw) is a powerful way to fix the equations of state of quantum fluids [46,62,130,136,137]; and (ii) at the triplet level, first OZ3 applications were reported in References [55,56,58].
5.2. The PI Total Continuous Linear Response TLRn Class
For this class the fluid undergoes a general external weak field which is continuous either spatially or in imaginary time (no magnetic interactions are considered). The PI partition function can be cast as [7,11,57]:
The functional derivatives for this model now can be cast as:
In the foregoing formulas a vector stands for the position vector of a structurally significant bead in the grand-canonical sample (i.e., is any of the Recall that for structural evaluations each canonical ensemble has significant particles, and that X is held fixed throughout the grand canonical ensemble. Therefore, by following the standard procedures [2,11,57] one sets the definitions:
and obtains the relationships:
where the number fluctuations refer to the in-the-field fluid. The formulas on the right-hand sides remain the same when although the meaning is therefore not the same.
The linear response cases in this case arise by making on the right-hand sides of Equations (82). In r-space this can be summarized in the following equations [57]:
where it is important to note the role played by X in Equations (84). Equations (84b) and (84c) can be formulated in concise forms with Equations (82) and the spontaneous fluctuations of the bead density at the two- and three-body levels respectively.
For notational simplicity, by arranging correlatively the NX beads present in each canonical ensemblethe pair and triplet correlation functions are defined by the ensemble averages [57]:
Note that the correlations between beads include both: equal and different imaginary times. The foregoing averages (85a)-(85b) can be split into actual atom components: one-particle, two-particle, and three-particle. In this regard, (a) for : the bead-bead pair correlations can correspond to beads in the same necklace (one-atom self-correlations ) or to beads in different necklaces (two-atom correlations ) [11}:
and (b) for the bead-bead-bead triplet correlations can correspond to three beads in the same necklace (one-atom self correlations ), two beads in the same necklace and the third in another necklace (mixture of one-atom self-correlations and two-atom correlations ), and the three beads in different necklaces (three-atom correlations . At the triplet level this can be cast as [11,57]:
where for clarity reasons the vector notation and vertical bars to separate necklaces in the cases are used.
The pair and triplet static structure factors arise from Equations (84b)-(84c) via the Fourier transform process explained earlier. They can be cast as [11,55,56,57]:
which in expanded form can be written as:
More information about these structural functions in the r- and the k- spaces can be found in works by this author [11,46,54,55,56,57,62].
The fixing of the and spatial structures can be accomplished with PIMC or PIMD simulations. Note that their computations scale as and respectively, which makes a demanding task. To date these calculations have focused on full evaluations of [11,46,62], but only on restricted evaluations of covering equilateral and isosceles features of the three-particle part of quantum hard spheres [54]. As for the structure factors and the PIMC/PIMD situation regarding the X-scaling is similar but further aggravated by the necessity to scan sets of commensurate wavevectors and, also, by the drawbacks associated with the low-k regions. Again, a significant part of , not very close to can be determined with reasonable PI simulation effort [46]. Nonetheless, the simulations of over a significant range of wavevectors, excluding obviously the unattainable and/or, and , remain today daunting (at least for most researchers).
OZ2 and OZ3 Frameworks
In view of the present-day PI-simulation difficulties in obtaining even restricted descriptions of the structure factors TLR2 and (above all) TLR3, one might think of resorting to direct correlation functions. However, the delocalization of quantum particles brings about several complications if one tries to construct OZn frameworks by following classical-like ways. A couple of examples will suffice to illustrate this knotty issue. Firstly, just at the pair level, one can consider Haymet et al.’s approach [173,174,175]. Here, the pair part of the TLR2 case Equation (87a), which depends only on and is normalized to unity for large wavevectors (see below), was the object of interest as applied to freezing in fluid helium-4 [175]. Broadly speaking, some of the main features are: (a) the ideal system was defined as the Feynman ideal system; (b) the direct use of inverse derivatives led to a need for effective particle masses in the ideal system to deal with the self correlations, though this measure could not be implemented under diminishing temperatures; and (c) in the end, a generalized OZ2 framework was obtained, but “effective” structure factors had to be defined, and unnatural amplifications in that pair part of TLR2 were detected for large wavevectors k. Secondly, another generalized OZ2 framework is that put forward by Shinoda et al. [178,179], in which the time-honored molecular approach RISM [7,71] was adapted to tackling the PI-model of a fluid with quantum behavior, as if it were a classical molecular fluid (RISM = reference interaction site model). This approach also focused on the same pair part of TLR2 mentioned above, and self interactions did appear when working the related OZ2 scheme arising from RISM (i.e., a given particle “interacts” with itself at different imaginary times). Accordingly, further approaches to cope with this fact of the model were to be taken.
At this juncture, the following two observations may be useful to help grasp the difficulties in this context. (i) First, a simple exercise. By assuming that for the TLR2 unrestricted bead-bead correlations one might define a direct correlation function in the conventional manner [5]:
it is straightforward to check the strange behavior that application of an identity analogous to (66) would yield with increasing X As in the two foregoing approaches, one can rederive the classical OZ2 equation for but the expression for the Trotter limit turns out to be meaningless. (ii) Second, a mathematical fact. Note that most of the OZ2 frameworks (e.g., Percus-Yevick, hypernetted chain, and their variants [69,71]) are formulated with reference to interatomic potentials The point is that the potential energy operators are diagonal in the coordinate representation, which means that beads do interact via if and only if they belong to different necklaces and are at the same imaginary time step (e.g., as shown in Equations (36a), (37a), and (38)). Hence, there cannot be any particle self interactions in a PI context.
The approximation proposed by the present author to deal with consists in separating the intra-necklace bead-bead correlations from the inter-necklace bead-bead correlations and applying directly the classical OZ2 framework to the latter (the pair part mentioned above) [180]. This (lucky) choice found some support by the applicability of this procedure to the GFH picture of fluids with (weak) quantum behavior [11,143,144,180]. This approach can be summarized as follows:
where is defined by the first two terms in Equation (89a), being a sort of “form factor” for the one-particle thermal packet, and adopts the well-known classical form associated with the overall inter-necklace correlations The self correlations do not contribute to the isothermal compressibility of the fluid (i.e., the component), which can also be formulated in the usual way only with [130]. Application to of the standard OZ2 Equation (12), which defines its associated yields after Fourier transforming:
where one notes that admits approximate analytical representations [131,180], a very useful one being that derived within the GFH picture [131]
One way or another, quantum approximations that involve classical schemes provide this context with reasonable alternatives to handle k-space difficulties [46,173,178,180], although their corresponding ranges of validity are to be analyzed a posteriori. Surprisingly, for the approximation given by Equation (90a), such range turns out to exceed expectations, since even under very strong diffraction effects the comparisons with experiment and PI-simulations are excellent. In this respect, at for supercritical helium-3 and for normal liquid helium-4 at and near SVP (saturated vapor pressure) conditions, the TLR2 results based on OZ2(BDH+BHw) were found to be almost indistinguishable from those obtained via PIMC, and/or very close to experiment [30,46,170,181]. Under diffraction effects and at the pair level, the conclusion when conducting OZ2 treatments is clear: the intra- and inter-necklace bead-bead correlations can be separated safely for most practical purposes. Two more observations: (a) with increasing quantum effects, the very low-k region may be affected by the OZ2 approximations used (see subsection 5.4); and (b) when exchange interactions are not negligible, this sort of bead-bead separation cannot be applied.
So far, to this author’s knowledge, no related OZ3 schemes have been reported for TLR3. The intricacy of these triplet features is certainly greater than at the pair level. In relation to this, one notes that the straightforward procedure followed in the pair linear response structures, Equations (86a)-(89)-(90), cannot be used in the functions leading to , as shown in Equations (86b) and (87c). Accordingly, whether this type of OZ ideas might be fruitful when studying the triplet remains to be investigated. The use of approximations, extending those in Equations (90), for treating the terms displayed in Equation (86b) will be necessary.
5.3. The PI Instantaneous ETn Class
This last class is not amenable to being treated with functional derivatives involving an external weak field, because of the collapse of the thermal packet under an instantaneous localization process. To obtain the definitions of the related pair correlation function and its associated structure factor which are in many ways analogues to their classical counterparts the standard quantum reasoning is based on the study of: (a) neutron scattering, with the time-dependent treatment using Born’s approximation and Fermi’s potential, plus the elastic sum rule applied to the dynamic structure factor [6,23,29]; or (b) the elastic scattering of X-rays, plus the consideration only of the pair coherent part associated with the nuclei (i.e., the single-atom actual form factor due to the electrons is dealt with separately) [6,28]. For the diffraction quantum effects the final expressions are [3,6,9,11]:
where the ensemble averages refer to Equation (29), both being formally equivalent to the classical definitions . The latter remark implies that both quantum averages reduce to the usual formulas in the classical limit. Explicitly, the pair correlations are defined via the ensemble average:
and the PI approach gives:
or in compact form
where the selection of the structurally significant (and equivalent) equal -time beads is to be highlighted; this is the distinctive trait of the ETn class. Likewise, the instantaneous structure factor can be calculated within PI as [9,11]:
It is a simple matter to extend the formulation for the instantaneous triplets in r-space, the PI average being (Figure 3):
The spontaneous fluctuations in the density at the pair and the triplet levels can be expressed by formulas, involving Equation (30), analogous to the classical Equations (9b)-(9c):
and, therefore, the actual and the PI definitions of the pair and triplet instantaneous structure factors can be written as:
Once again, this definition of the triplet structure factor is very convenient, since it reduces to the classical formulation when neglecting quantum effects [3]. For completeness, note that within PI one finds the explicit triplet formulas [55]:
Some related remarks are the following. (a) From the simulation standpoint: note that the ETn structural computations scale as X, which make them more expensive than those of the classical case (but far less expensive than those of TLRn which scale as as shown in Equation (87b). (b) The development of Equation (100) is formally the same as that of the classical case or, equivalently, that of the PI centroids given in Equation (54), where one only has to substitute the CMn quantities for the ETn ones. (c) As stressed earlier, there is a full formal equivalence among the Cn, CMn, and ETn basic formulations of the isolated fluid quantities in r-space and k-space
5.3.1. OZ2 and OZ3 Frameworks
At this stage of the presentation, it is clear that no exact OZn frameworks are available for analyzing the structural functions of the ETn class. However, as occurred in the TLRn class, the adoption of classical schemes/ideas, either as such [3] or modified [69], seems unavoidable if one tries to use the device of direct correlation functions. In this regard, and again based on the applicability of the classical-OZn to the PI-based variational pictures [11,143,144,145,180], there was nothing to lose by trying the direct use of the classical OZ2 and OZ3 schemes. It goes without saying that the OZ2(BDH+BHw) results were beyond expectations. Thus, under very strong quantum diffraction effects (e.g., helium-4 and helium-3 fluids at ), the overall agreement with experiment and PI simulation was excellent [28,29,46,55,170,181], the very low-k region being the most sensitive to this approximation (see subsection 5.4). As regards OZ3, applications of the classical scheme have been made to helium-3 [55,60], the quantum hard sphere fluid (bare of with Yukawa attractions) [56], and liquid parahydrogen [57,58], but no full tests of validity have been conducted.
The two basic equations here are the adaptations of the classical Equations (13) and (15), i.e., formally the same as in CMn, although now they are approximations:
where the direct correlation functions and are introduced as arising from the standard OZ2 and OZ3 classical procedures (Figure 4 and Figure 5).
5.3.2. An ETn Functional Digression
Before going any further, it is worthwhile to remark that there is a functional approach to the ET2 correlation function [6,135]. The point is that, by focusing on the variations of the partition function with respect to the variations in the interparticle potential one obtains an expression in which the correlation function shows up. The general usefulness of this development seems scarce because there is no response from the fluid to an external field. However, for completeness, it is noticeable that one can obtain useful relations at the pair-level involving both the ET2 and the CM2 structures [135]. To simplify the following discussion, only the PP propagator is used in what follows.
The PP grand canonical partition function for the homogeneous and isotropic fluid can be cast as [7,90]:
A straightforward calculation yields the related first functional derivative:
which is formally identical to the classical or to the PI-ET2 counterpart in the canonical ensemble that can be found in [6] and [135], respectively.
As regards the extensions to higher orders, the situation is rather inconclusive. To get a feeling of the drawbacks posed by this type of formulation, it seems instructive to consider the development of :
the main problem being that different imaginary times are mixed. One might even think of extracting artificially equal-imaginary time quantities by “tinkering” with the t-sums, but these manipulations are of no interest to ET correlations. Furthermore, beyond the pair level expressed in Equation (103), these derivatives become increasingly entangled. Although the latter might be related to spontaneous effects within the quantum fluid, they seem to be of no use for the current study of static quantum fluid structures.
5.4. A Joint Consideration of CMn, TLRn, and ETn
(i) Apart from the general consideration that the three quantum classes of linear response functions are directly related to different forms of density-correlation functions in the isolated fluid (as in the classical case), there are some properties exactly shared by the three classes. These properties obviously belong to the isolated quantum fluid and can be identified at zero-field, . A most interesting case arises for the structure factors at zero momentum transfer(s) , because the distinct response functions of the (isolated) fluid must take the same value regardless of the pair, or the triplet, structure considered.
At the pair level there is the extended compressibility theorem [130] that states:
It is worth remarking that the foregoing exact result can be distorted when classical-like OZ2 calculations with ET2 and LR2 are carried out. On the one hand, the discrepancies from the OZ2-CM2 exact estimate remain in general controlled and do not alter the overall representation of the k-space structures determined. On the other hand, the importance of the disagreement may be a matter to analyze in certain cases (e.g., near changes of phase), as both the density and the temperature play roles in this issue [46,62,130,136,137,180].
The generalization of Equation (105) to the triplet level, involving the double-zero momentum transfer, reads as [57]:
By taking advantage of the OZn formulation for centroids, Equation (106) can be written in terms of Using Equations (69), (77c) and (78b), one finds
which in view of Equations (105) and (106) leads to the following result valid irrespective of the response class [57]:
The quantity is a quantum fluid property related to higher-order fluctuations in the number of the atoms (particles), and it is a simple matter to prove that:
The trivial connections of the zero-field Equations (105) and (108b) with the functional Equations (80d)-(80e) and (83f)-(83g), at zero field, are to be noticed (ET and CM are completely parallel in this regard).
Also, for the single-zero momentum transfer one finds the exact CM relationship [57]
whilst for ET an analogous equation can also be written, but owing to the OZn properties utilized it is an approximation:
It seems worthwhile to explore in future work the possibility of obtaining an equation for based on the connection between the instantaneous and centroid pair correlation functions [135]. If successful, this could help to solve the ET problems for low-k wavenumbers, generalizing in this way the exact result connecting the properties of the centroid and the delocalized particle within the GFH picture [131,180]. So far, no further formulas based on direct correlation functions for TLR3 have been derived.
(ii) The symmetry properties in r-space and in k-space of the structures CMn, TLRn, and ETn, are translations of the classical ones seen in subsection 3.3. CMn and ETn behave in the classical way regarding the limits of increasing/decreasing distances between atoms and, also, in the limit of increasing wavenumbers (see also Figures 1, 2b, and 3). However, the class TLRn (unrestricted bead-bead-… correlations) presents some striking differences. In relation to this, suffice it to mention that for the TLR2 functions one finds in r-space: (a) at increases with the P discretization, because of its one-atom component , and tends to unity for long distances due to the two-atom component ; (b) for long distances, and does not necessarily vanish when two atoms come close together (it may even be nonzero at ); (c) for large wavenumbers. The magnitudes of these discrepancies from the standard classical behaviors depend on the intensity of the quantum effects, and the reader is referred to [46,54,55,62,170,180] for related results. Consequently, one may expect an interesting variety of patterns when studying TLR3 functions.
(iii) Another set of exact PI relationships can be obtained [54] by following the classical developments [26,150,151,157] given in Equations (27) and (28). It is easy to establish that for the two-point densities (referring to actual two-particle correlations) given by:
one obtains the classical-like relationships:
The latter formula leads to the classical-like equations:
where the functions stand for:
and, for consistency, corresponds to its associated pair structure (recall that in practice the values may show deviations from the exact Equation (105)).
Note that the total continuous linear response TLR is not contained in the LR relationships, since the self-correlations do not fit into this scheme. Equations (113) arise only from the pure actual two- and three-atom correlations.
For the purposes of this work, it is also worthwhile to remark that Equation (113b) can be transformed and split into two parts as :
where
Given that is just a pair quantity that can be fixed with high accuracy, whilst is a quantity that depends explicitly on the use of these two quantities yields consistency tests of possible closures for . In this connection, one uses KS3 as a reference by expressing the triplet closure in the form:
By substituting a closure to be tested in Equation (113f), two comparison tests are between: (a) and , and (b) the values of the density derivative determined with the computed pair results and the corresponding estimates arising from the closure.
In relation to this, for completeness, the three basic closures KS3 Equation (22), JF3 Equation (23), and AV3 Equation (24), lead to the following expressions for their quantities in Equation (113d) (Figure 6):
- -
- KS3:
- -
- JF3:
- -
- AV3:
(iv) Furthermore, as regards OZn schemes, application of the classical and quantum reasonings [38,39,40,41,59,60,72,125,126,127] is a possible and rewarding way to obtain information on the quantum triplet CM3 and ET3 structures. Recall that the CM2 calculations have, in the end, an exact OZ2 framework, but that under any other circumstances approximations are involved. Despite the latter remark, the usual PIMC/PIMD (“raw”) pair radial structures CM2, ET2, LR2, arising from the canonical simulations, can be: (a) utilized to carry out OZ2 studies of the asymptotic decay properties [183,184], and (b) improved using OZ2-based treatments and corrections (e.g., the BDH+BHw analysis considered in Section 3.4). By doing so, grand-canonical approximations for these pair functions can be determined, which may be viewed as better intermediate quantities for an intensive use of direct correlation functions in triplet calculations via closures. In this connection, although for r-space triplets the PI simulations in the canonical ensemble are sufficient to give very useful information, note that for k-space triplets there are no complete OZ3 tests regarding the (density-temperature) ranges of validity. The huge PI computational load involved, covering significant ranges of the two wavevectors and physical conditions, and the variety of closures for triplets are reasons for explaining this lack of knowledge (Figure 4, Figure 5 and Figure 7).
(v) Finally, it is worthwhile to write the connections (“sum rules”) of the dynamic structure factor which can be obtained through inelastic neutron diffraction experiments [23], with the PI quantities and
where stands for the angular frequencies of the neutron radiation. arises as a density-density relaxation function [23] (Equation (87a)). The latter expressions have been utilized in fluid helium-4 studies (e.g., see References [29,30,170,178]).
6. Systems Studied in This Work, Computational Details and Related Observations
The main structural concepts reviewed in the previous Sections are illustrated in this work with further numerical applications to supercritical helium-3, and the QHS fluid on the crystallization line, thus expanding the scope of previous works on these key systems [54,55,59,60]. For helium-3 the focus is on pair and triplet structures in r-space and triplet structures in k-space, whereas for quantum hard spheres is on triplets in k-space. The computational techniques employed are PIMC simulations in the canonical ensemble (or better complemented with OZ2 and OZ3 treatments, by using the closures and relationships addressed in this work. The simulations utilize sample sizes inside a central cubic box of side L, with the usual periodic boundary conditions, and the Metropolis sampling scheme involving the normal-mode algorithm (acceptance ratio 50%) [74,145]. One PIMC kpass is defined as attempted bead moves, and one PIMC Mpass is kpasses. The computed structural classes are the centroid (CMn) and the instantaneous (ETn) at the pair and triplet levels, the latter being focused on some equilateral and isosceles features. Representative results are contained in the Supplementary Material.
The state points studied are listed below:
(i) For helium-3: (; , (; (; The pair interatomic potential selected is Janzen-Aziz’s SAPT2 [106], and PIMC calculations involve the SCVJ propagator with [84]. Information obtained in Reference [46] on auxiliary state points about the state point at : is also employed.
(ii) For the QHS fluid [59,62,137] only k-space results for one state point are reported, Complementary structures for two state points about the latter, by varying at constant , are also obtained in the present work; these variations are: , which for a system with amount to . (Other pilot applications along the crystallization line, at [62,79], have also been carried out and will be commented later). PIMC calculations involve the CBHSP propagator [81]. Recall that there is a unique way to characterize a state point in the QHS system by using reduced units [59,62]: i.e., the length unit is the hard-sphere diameter, .
PIMC canonical simulations focus on the instantaneous and centroid pair and/or triplet correlation functions. The sample sizes employed are as follows: (a) for and in helium-3, at , at , and at [46]; (b) for in the QHS fluid, at the auxiliary state points analyzed, and the same at the target state point taking its pair information from calculations in Reference [59].
The pair structures in r-space are computed in the usual way utilizing histograms [13], the width of the bins being Most of the “raw” pair canonical structures are subsequently OZ2-analyzed and improved in the form already described [46,136]: application of the OZ2 Baxter-Dixon-Hutchinson’s (BDH) procedure [72,125] plus Baumketner-Hiwatari (BHw) corrections [127]. By doing so, access to every k-space related property at the pair level is obtained with high accuracy (Figure 2).
As regards the MC/MD calculations of triplets, they present a number of nontrivial subtleties, as discussed by Tanaka and Fukui [42], Baranyai and Evans [43,44], and Barrat et al. [41]. In the current PIMC applications, the method followed in r-space is based on References [42,43,44], which for the study of quantum fluids was firstly used in Reference [54]. The interested reader is referred to the latter reference for specific details. To facilitate the understanding of the reported results, however, suffice to say that triplet correlations are determined via:
where is the number of times that mutual distance triplets lie within the ranges and (again: the previous notation should be obvious: In addition, to avoid redundancies in the counting, the conservative (and less time-consuming) condition is imposed [42]. The run lengths of the PIMC computations for helium-3 in r-space are as follows: in between 1233-1300 kpasses for fixing the pair structures and gathering statistics every 8000-12500 accepted configurations; and in between 2470-2560 kpasses for fixing the triplet structures and , where is included, gathering statistics every 8000-10000 accepted configurations. Statistical errors (one-standard deviation) are fixed with block subaverages and remain very small: at the main peaks they are below 0.8% (see main details in Figure 1 and Figure 3).
The calculations of the triplet structures in k-space turn out to be much more involved, and a few remarks are to be made. The PIMC simulations involve the sample sizes : (a) for helium-3 at (Figure 5); and (b) at the QHS fluid state point (Figure 7). These calculations are focused only on the equilateral components instantaneous for helium-3, and instantaneous and centroid for the QHS state point. Twelve sets of vectors commensurate with the simulation box, are scanned; each set is composed of 8 pairs such that: the vectors being at an angle and with the constraint [58]. This implies that for helium-3 at the resulting moduli (wavenumbers) are in , whilst for the QHS fluid state point, the moduli are in Also, the sampling is more focused on the low-k wavenumbers and the regions of the main peaks. PIMC run lengths are as follows: for helium-3 in between 30 and 120 Mpasses, gathering statistics every 5000 accepted configurations; and for the QHS fluid state point in between 6.5 and 60 Mpasses, gathering statistics every 8000 accepted configurations. Statistical errors (one-standard deviation) are fixed with block subaverages and remain controlled: at the main amplitudes they are: 1.8% for the instantaneous case in helium-3; for the centroid case and for the instantaneous case in the QHS fluid (see main details in Figure 5 and Figure 7)). As a complementary result, the (mean) imaginary components, which must be identically zero [41], at the main amplitudes turn out to be: for the instantaneous case at the helium-3 state point; for the centroid case and for the instantaneous case at the QHS fluid state point. Clearly, although the QHS sampling is highly informative, it must be improved. In addition, all these results give an idea of the slowness of this sort of calculations when dealing with fluids with quantum behavior. This drawback becomes more acute if the fluid state point investigated belongs to the actual crystallization line of the potential model selected to describe the fluid. In this case, the sample size cannot be small (i.e., about one hundred particles, as the used in helium-3): the “flipping” back and forth in the simulation between the fluid and solid branches [13] must be avoided. This is the case in the current QHS fluid application. After monitoring such an effect, it has not been observed with but it is rather conspicuous with . This monitoring has involved the configurational centroid CM2 structure factor defined as normalized to unity at its crystal-structure maxima [137]. For the current QHS study with the latter configurational quantity remains below the maximal fluid value estimate [61].
Closure calculations reported here for triplets (instantaneous and centroid) in r-space are carried out utilizing KS3, JF3 and AV3, whereas in k-space are with BHP3 [41,55,56] and DAS3 [65]. These calculations necessitate the corresponding pair structures, and . Detailed descriptions of the related procedures can be found in works by this author [54,55,56,57,58,59,60], although for the reader to better grasp the reported results it may be worthwhile to mention the following facts.
(i) JF3 and BHP3 share a common type of integral [39,41,156], which in each case is utilized in this work as follows:
- BHP3 (k-space) [55]
where the stand for the standard Legendre polynomials, and the upper limit is utilized. (In the limit the -expansions are exact [41,156]).
(ii) For the closure analyses at constant temperature, the numerical density-derivatives of the pair and the direct correlation functions, and are evaluated with the centered algorithms: Stirling’s (two-point) and Richardson’s (four-point) [182] (Figures 5 to 7). By denoting a generic radial pair function by , the previous algorithms can be written as:
(iii) As regards JF3 and AV3, the following observations are worth making. Comparison with PIMC results for the equilateral components of the helium-3 triplet structure factors indicates that (Figure 5 and Table 1): (a) JF3 cannot capture the negative behavior within the low-k region and its usefulness reduces to the large-k wavenumbers, since it gives the asymptotic behavior of the structure factor; and (b) AV3 as reported in Reference [60] yields lower values for both the negative depth in the low-k region and the height of the main amplitude. In view of the results in Figure 6, it is highly likely that AV3 can be improved using Abe’s developments [38] and gives better triplet results in both r-space and k-space.
(iv) BHP3 minimizations for ET3 helium-3 at the state point at were reported in [60], where use of conjugate gradients [185] was made, as explained elsewhere [55,56]. Discretizations of the functions into 7001 points covered the distance interval . Convergence as assessed via was rapid and without any problems, the latter quotient reaching values in a few hundred iterations. The explored ranges of wavenumbers for have been extended, for checking the properties in k-space as k increases: JF3 appears as the limit with increasing k wavenumbers, and the results are consistent. Figure 4 and Figure 5 and Table 1 collect representative results for this system. As seen, for the equilateral components, BHP3 [60] gives a nice representation of the PIMC values, particularly in capturing the negative behavior for
Nevertheless, some pilot BHP3 minimizations for the QHS fluid (CM3 and ET3) along the crystallization line [79,137] have turned out to be affected from convergence problems. These latter results are therefore far from conclusive from a physical standpoint and only a brief comment follows. The key observation is that the convergence in this case (tested with both gradients and conjugate gradients) appears to be strongly dependent on the value of the norms in such a way that the larger this value is, the slower and more physically doubtful the convergence path turns out to be. These norm values are clearly associated with the depths at the origin of the pair direct correlation function . To get a better feeling of this situation some data related to the pair direct correlation functions analyzed in this work are worth quoting here:
(i) For helium-3 at ( the five instantaneous values , corresponding to the five state points involved, are in [60], and no BHP3 problems with the convergence were observed.
(ii) For the QHS fluid at : the three instantaneous values involved at the origin of the interparticle distances are in while the three centroid values are in
(iii) The reference values given by the squared norms turn out to be as follows:
- -
- For helium-3, using Richardson four-point derivative the instantaneous reference is .
- -
As seen, there is a significant BHP3 difference between the foregoing results for helium-3 and the QHS fluid. Note that the comparison is better made using the actual values in for distances, since the modelling via hard spheres for helium-3 is not consistent [55] for the current structural purposes. In relation to this, the distinct features of the interparticle potentials involved are to be remarked: for helium-3, continuous for and weakly attractive at the minimum [106], whilst for QHS there is an infinite discontinuity at . These potentials are obviously connected to the shapes of the pair direct correlation functions, and hence to their density derivatives. Consequently, although applications of BHP3 are clearly dependent on the latter derivatives by reason of their construction Equation (25b), in intricate regions such as the freezing transition this dependence becomes extremely sensitive to the quality of the numerical derivatives. (Recall the basic density increments about the target state points: for helium-3, and for QHS). Therefore, a very careful fixing of the QHS intermediate and by diminishing for increasing the accuracy in the density derivative calculations, could fix this BHP3 situation. However, apart from the computational overload, possibly including an augmented precision in the calculations, one can still foresee some difficulties. Firstly, the slow minimization of a large quantity which, together with the fine details of the density derivatives of the pair direct correlation function involved, might misdirect the convergence path and lead to unphysical solutions. Secondly, although OZ2 for centroids is formally exact, OZ2 is an approximation for the instantaneous case, which means for the latter that extra problems can be encountered in the freezing region when applying simple corrections such as BHw. Furthermore, there is the question of the complete calculation of the triplet structure factors by including its general components. Obviously, detailed work to clarify the ranges of applicability of BHP3 is needed.
(v) On the contrary the current DAS3 calculations of are directly worked out in k-space and, once the necessary pair information is available, they are straightforward. Apart from the numerical derivative problems, no intrinsic procedural problems appear. As shown in Figure 5 and Figure 7 and Table 1, DAS3 also gives good representations of the equilateral PIMC results, albeit apparently not so good as BHP3 in the instantaneous low-k region These applications use the two-point derivative Equation (118a) for the QHS-fluid CM3 and ET3 evaluations, and the four-point derivative Equation (118b) for the helium-3 ET3 evaluations. For this closure the underlying OZ2 problems with the instantaneous class also exist, and its basic assumptions Equations (26) remain to be fully tested. Again, detailed work to clarify the ranges of applicability of DAS3 is needed.
7. Final Remarks and Future Directions
The investigation of the static triplet structures in quantum condensed matter (fluids and solids) via path integrals is a promising and challenging avenue. Although it may be said that an initial background to this topic is already established, key theoretical and computational aspects in both the real (r-space) and the reciprocal Fourier (k-space) remain to be explored and understood. The theoretical issues should focus on: (a) expanding further the limits set by the usual pair-level approach (solid phases [59]), and (b) the treatment of systems composed of nonzero-spin particles, particularly fermionic systems. The computational issues should mainly address the questions of cost-effectiveness posed by the required accuracy when determining the variety of different quantum triplet structures (dimensionality 4-D), with a view to increasing the simulation sample size and, also, the possible integration of proper two- and three-body potentials (e.g., [107,108]) in the structure computational schemes. In this regard, exascale computations, when widely available, could alleviate the effort to be made. (Just as a high hope, if quantum computers became a reality in practice some day, the quantum triplet problems might provide an excellent test bed). All these developments can provide very useful guidance for materials research and future higher-order structural studies.
Some specific theoretical goals within the path integral framework can be the following. (i) The consideration of general external fields including magnetic interactions and/or situations involving more than one spin state in monatomic fluids; the latter can give rise to a special set of treatments for fermionic fluids when studied with the insightful Wigner path integral schemes [98,99]. (ii) A formulation of the actual triplet structures in molecular fluids (e.g., hydrogen fluids) that, going beyond the overall one-site picture [57,58], gives full meaning to the direct atom-atom constructions [11], or yields more global molecular approaches.
As regards the specific computational goals, one can mention the following pending path integral tasks in homogeneous and isotropic monatomic fluids (4-D problems). In the diffraction regime: (iii) the determination of the total continuous linear response functions TLR3, which remain virtually untouched [54]; and (iv) the completion of the ET3 and CM3 structures by fixing their behaviors over significant ranges of the three significant variables which characterize them (i.e, three independent interparticle distances, or two wavenumbers and an angle). In the quantum exchange regimes, there is nothing yet related to calculations of triplet structures that has been undertaken and work on this should be welcome.
As complements to the exact path integral calculations of triplets, one may try a variety of closures. These closures are not as efficient and clear-cut defined as those at the pair level. Despite this remark, there are some results indicating that, when studying the instantaneous and centroid and functions within the quantum diffraction regime, closures may be a great source of information. Triplets in r-space have been discussed at length elsewhere [54,55,56,57,59,60], and suffice it to say that the results obtained through the AV3 closure Equation (24) [59,60] point to the possibility of achieving significant improvements based on Abe’s expansion [38]. In this regard, it is expected that the negative effects of increasing densities on the long-range isosceles correlations could be fixed to a significant extent, which may reflect in better k-space results. Nonetheless, closure results for quantum triplets in k-space remain comparatively an unknown issue. For the time being, the closures BHP3 Equations (25) and DAS3 Equations (26) give results equilateral components) that make them worth exploring in depth. They may capture traits of the sensitive low-k (negative) region of the equilateral ET3 and/or CM3 structure factors and, also, the behavior of the important main amplitude region. In connection with the low-k region, BHP3 seems better adapted than DAS3. However, and based on pilot calculations, BHP3 variational calculations seem less appropriate for investigating intricate regions, such as the quantum hard-sphere crystallization line, whereas DAS3 calculations appear here as a more robust option for both ET3 and CM3. For large-k wavenumbers the basic JF3 closure (Equation (15) with , which is part of both closures, dominates the triplet behavior.
The k-space closure results obtained so far are just a beginning (e.g., [58], and Figure 5 and Figure 7 herein), and more work is needed to substantiate their relevance, particularly regarding the non-equilateral components. Searching for the limits of applicability of closures, even for qualitative purposes related to the CM3 and ET3 cases in the diffraction regime, seems a rewarding task. The case TLR3 does not seem amenable to closure studies because of self correlations, although there is nothing against trying closure treatments of the pure triplet-atom part ([54] and Equations (113)).
Supplementary Materials
Detailed numerical results are contained in the zip file LMSfiles_QR2024.zip, which is organized in seven directories, each being associated to its corresponding figure in this work.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
Appendix I: A Formal Analysis of Zero-Spin Bosonic Exchange Structures
Within the PI approach the derivation of the physically significant structures of a homogeneous and isotropic zero-spin bosonic fluid can be carried out along essentially the same ideas reviewed in the main text of this article. The key point is that the partition function can be expressed as containing a weighting function which is nonnegative everywhere in configuration space, thereby being a proper probability density. The three classes of structures ETn, TLRn, and CMn can be studied by generalizing the pair level treatments [7,9,35,36,78,130,133,134]. In what follows, for illustrating the main features of the bosonic triplets, use of the PP propagator is made [130].
The Hamiltonian for N atoms to be dealt with in the linear response regime is now taken of the global form:
where is the Hamiltonian operator for the isolated N-atom system given in Equation (1), and stand for the action of an external (continuous or non-localizing) weak field: , which in the case of CMn is a constant-strength field The Bose-Einstein (BE) grand canonical partition function for zero-spin atoms can be written as [7,9]:
where runs over the permutations of the N atom labels, and with denoting the specific action of a given permutation on label j. Application of the PP propagator using P beads (the optimal discretization) leads to the PI approximation [7,9,130]:
In Equation (A.3) several features are to be remarked. (a) are positive constants. (b) leads to if leaves j invariant, or to an otherwise ). (c) There is complete symmetry in the treatment of the corresponding beads in each canonical ensemble, owing to the mathematical group property of the permutations. Two consequences of (c) are: (c.1) translational invariance in imaginary time holds, and (c.2) the effect of the external field can be factored out of the weighting function for each canonical ensemble. Therefore, note that Equation (A.3) can be compacted as [130]:
where is the Bose-Einstein weighting function, nonnegative everywhere and including all the permutational effects:
Although the form shown in (A.3) is well-known [7,9], it may be worthwhile to recall that, for permutations different from the identity, there appear P-membered “open-necklaces”. In a P-open-necklace there is no harmonic coupling between, conventionally, its beads (head) and (tail). Thus, any of such permutations is represented within PI by a mixture of P-membered necklaces and/or P-open-necklaces. The latter necklaces interlink with each other harmonically in a head-tail fashion, thus building membered (closed) necklaces (i.e., is the identity permutation). A brief description of what arises from PI follows.
(i) The identity permutation reduces to the picture of distinguishable particles dealt with in the main part of this article, which gives N individual necklaces with P beads apiece. (ii) For the permutation in which only the exchange 1 occurs, i.e., (2,1,3,4,…,N), one finds individual necklaces with P beads apiece (particles 3,4,…, N) and one 2P-membered necklace corresponding to that permutation and built in a head-tail fashion from the open-necklaces 1 and 2: bead in open-necklace links with bead in open-necklace , and bead in open-necklace links with bead in open-necklace , the rest of beads being linked in the normal way found in the identity permutation. (iii) For the permutation in which there is only a triple exchange cycle i.e., (2,3,1,4,…,N), one finds individual necklaces with P beads apiece (particles 4,…,N) and one 3P-membered necklace corresponding to that permutation and built in a head-tail fashion: bead in open-necklace links with bead in open-necklace , bead in open-necklace links with bead in open-necklace , and bead in open-necklace links with bead in the open-necklace the rest of beads being linked in the normal way found for the identity permutation. (iv) The process continues, mixtures of membered necklace configurations arise, and so on.
As a result, for a given permutation one finds, in the end, a mixture of -membered necklaces such that where some of the can be zero . Also, the potential energy contributions are invariant under the group of permutations and, therefore, the final expression in terms of bead interactions is the same regardless of the permutation and coincides with the form obtained for the identity permutation. (Illustrative graphs of mixtures of necklaces can be seen in References [9,11]). The beads are equivalent and when entering an membered necklace lose their appurtenance to an initial P-necklace (translational invariance), although for keeping track of the particle positions and correlations an ordering must be retained, which can be updated consistently throughout the simulation, etc. [9,35]. Although the latter are crucial matters from the simulator’s practical point of view, in any case, the correctly formulated ensemble averages imply integrations over the bead configurational space with a weighting function that already contains these symmetry characteristics. The practical importance of the bosonic full symmetry to the fluid structural study is to be highlighted. Most of the basic derivations carried out in the case of distinguishable particles can be applied in this further context.
Firstly, for the instantaneous pair (ET2) and triplet (ET3) cases in r-space one must give form to the standard quantum averages:
The PI partition function for dealing with the instantaneous class ETn is
At this point, it may be useful to renumber the beads consecutively, as done earlier by using the labels being:
By using the indices j, l, m, t, as counting devices, Equations (A5.a) [9] and (A5.b) are approximated by the PI equal-time averages:
It is also straightforward to derive the associated instantaneous pair structure factors:
The expanded form of Equation (A.5h) is analogous to Equation (54). As seen, translational invariance in imaginary time holds true for every ET equation written above.
Secondly, the class PI-TLRn can be worked out in the manner shown earlier. By taking the functional derivatives with respect to the external field of:
the results are somewhat analogous to those of TLR in Section 5, since separations of the forms displayed in Equations (86a) and (86b) do not make sense in the BE context and cannot be employed here. Accordingly, by renumbering the beads as before (A.5d), the TLR2 and TLR3 levels can be summarized in the response functions (they are defined by at zero field ) [130]:
where is the overall bead-bead correlation function under BE statistics, and:
which involves both the pair and the triplet overall bead-bead and bead-bead-bead correlation functions under BE statistics, respectively. (In relation to the separation comment above, compare for instance Equation (A.6b) with Equations (87a) and (89a)). Again, translational invariance in imaginary time holds true for every PI-TLR equation written above.
Thirdly, the class CMn is somewhat especial. The introduction of a constant-strength field, leads formally to a partition function in which conventional centroids do appear [130]:
which using Equation (40) is:
In this regard, it is worth insisting on the fact that the centroids are defined as if they were associated with the original closed P-necklaces of the N distinguishable particles, although now one must include the possibility of dealing with P-open-necklaces. The centroid still is a “center of mass”, either of a closed P necklace or of a broken P line, which agrees with Voth et al.’s proposal [133]. However, this definition presents the problem of violating the invariance under imaginary-time translations [134], a feature that must hold under bosonic exchange. Such inconsistency is resolved by the integration over the centroid coordinates [133,134] all over the configuration space. Nevertheless, this forces one to have a detailed description of the function inside the integral at fixed centroid positions, which does not seem very efficient from a computational point of view. Therefore, from a purely formal perspective, for the centroids so defined their usual role in the counting of number fluctuations [130] can also be identified under bosonic exchange. The functional derivatives with respect to that can be obtained from Equation (A.7b) are analogous to those given in Equations (48). Consequently, the linear response functions and arising at can be formally written in the same manner as Equations (52)-(54).
The bosonic pair and triplet structure factors discussed above must share the same values at zero-momentum transfer [130], as in Equations (105)-(106). This extended compressibility theorem for boson fluids obviously excludes the pure two-body case LR2 considered for distinguishable particles. Recall that closures were used in the past to study bosonic fluids in an approximate way [3,39,40,69]). Therefore, one might also think of postulating classical-like OZ2 and OZ3 frameworks for the current centroid correlations, but the situation seems far from promising in practice, if only for the necessity of obtaining accurate pair centroid correlation functions derived from the constrained Equation (A.7b) at zero field. Moreover, theoretical questions regarding whether a hierarchy for direct correlation functions in this centroid context can be defined should also be cleared up. Furthermore, classical-like OZ applications to the bosonic ET and TLR correlations, incorporating or not quantum corrections, would be approximations whose final reliability could only be tested a posteriori. Finally, note that the present centroid discussion is not intended to go any further than the number fluctuation questions, since there is a one-to-one correspondence between the number of particles and the number of centroids which, by construction, respects the features of bosonic exchange in the development of this CM framework. For discussions covering a more rigorous centroid definition and related dynamical schemes the reader is referred to References [133,134].
Appendix II: List of Main Acronyms and Their Basic References
| AV3 | Intermediate closure for triplet structures [59,60]. |
| BDH | OZ2 Baxter-Dixon-Hutchinson variational procedure [72,125,136]. |
| BHw | OZ2 Baumketner-Hiwatari grand canonical corrections [127]. |
| BHP3 | OZ3 Barrat-Hansen-Pastore variational procedure [41]. |
| BOA | Born-Oppenheimer approximation [119]. |
| CBHSP | Cao-Berne hard-sphere propagator for quantum hard spheres [81]. |
| CMn | Path integral Centroid class of structures at the n-th level [18,19,55,130]. |
| DAS3 | Denton-Ashcroft symmetrized closure for triplet structures [65]. |
| ETn | Path integral Instantaneous class of structures at the n-th level [9,11,35,84]. |
| GFH | Gaussian Feynman-Hibbs picture [4,140,180]. |
| JF3 | Jackson-Feenberg closure for triplet structures [3,40]. |
| kpass | attempted bead moves in a PIMC simulation. |
| KS3 | Kirkwood superposition closure for triplet structures [37]. |
| MC | Monte Carlo simulation method [13,17,66]. |
| MD | Molecular dynamics simulation method [13,17,67]. |
| Mpass | attempted bead moves in a PIMC simulation. |
| OZn | Classical Ornstein-Zernike framework at the n-th level [1,6,41,68,70]. |
| OZ2 | Classical Ornstein-Zernike framework at the pair level. |
| OZ3 | Classical Ornstein-Zernike framework at the triplet level. |
| PA’s | Pair actions for path integral simulations [9,81]. |
| PI | Path integral formalism [4,140]. |
| PIMC | Path integral Monte Carlo computational scheme [7,9,16,35]. |
| PIMD | Path integral molecular dynamics computational scheme [10,89,94]. |
| PP | Primitive propagator [7,9,80]. |
| RISM | OZ2 reference interaction site model [7,71,178,179]. |
| QHS | Quantum hard spheres [62,79,81,136]. |
| SAPT2 | Janzen-Aziz pair potential between two helium atoms [106]. |
| SCVJ | Suzuki-Chin-Voth-Jang-Jang fourth order propagator [82,83,84]. |
| SVP | Saturated vapor pressure conditions. |
| TLRn | Path integral total continuous linear response class of structures at the n-th level [7,11,57,62]. |
| WPIMC | Wigner path integral Monte Carlo [98,99,169]. |
References
- Ornstein, L.S.; Zernike, F. Accidental Deviations of Density and Opalescence at the Critical Point of a Single Substance. Proc. Acad. Sci. Amsterdam 1914, 17, 793–806. [Google Scholar]
- Hill, T.L. Statistical Mechanics; Dover: New York, NY, USA, 1987; ISBN 978-0-486-65390-7. [Google Scholar]
- Feenberg, E. Theory of Quantum Fluids; Academic Press: New York, NY, USA, 1969; ISBN 978-0-122-50850-9. [Google Scholar]
- Feynman, R.P. Statistical Mechanics; Benjamin: Reading, Massachusetts, USA, 1972; ISBN 978-0-805-32509-6. [Google Scholar]
- Balescu, R. Equilibrium and Nonequilibrium Statistical Mechanics; John Wiley & Sons: New York, NY, USA, 1975; ISBN 978-0-471-04600-4. [Google Scholar]
- Hansen, J.P.; McDonald, I.R. Theory of Simple Liquids; Academic Press: London, UK, 1976; ISBN 978-0-123-23850-4. [Google Scholar]
- Chandler, D.; Wolynes, P.G. Exploiting the Isomorphism Between Quantum Theory and Classical Statistical Mechanics of Polyatomic Fluids. J. Chem. Phys. 1981, 74, 4078–4095. [Google Scholar] [CrossRef]
- Schiff, D.; Verlet, L. Ground State of Liquid Helium-4 and Helium-3. Phys. Rev. 1967, 160, 208–219. [Google Scholar] [CrossRef]
- Ceperley, D.M. Path Integrals in the Theory of Condensed Helium. Rev. Mod. Phys. 1995, 67, 279–355. [Google Scholar] [CrossRef]
- Pérez, A.; Tuckerman, M.E. Improving the Convergence of closed and open Path Integral Molecular Dynamics Via Higher-Order Trotter Factorization Schemes. J. Chem. Phys. 2011, 135, 064104. [Google Scholar] [CrossRef]
- Sesé, L.M. Path Integrals and Effective Potentials in the Study of Monatomic Fluids at Equilibrium. In Advances in Chemical Physics; Rice, S.A., Dinner, A.R., Eds.; Wiley: New York, NY, USA, 2016; Volume 160, pp. 49–158. [Google Scholar] [CrossRef]
- Wood, W.W. Computer studies on Fluid Systems of Hard-Core Particles. In Fundamental Problems in Statistical Mechanics; Cohen, E.D.G., Ed.; North-Holland: Amsterdam, The Netherlands, 1975; Volume 3, pp. 331–388. [Google Scholar]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Clarendon: Oxford, UK, 1989; ISBN 978-0-198-55645-9. [Google Scholar]
- Alder, B.J. Computer Dynamics. Annu. Rev. Phys. Chem. 1973, 24, 325–337. [Google Scholar] [CrossRef]
- Hoover, W.G. Nonequilibrium Molecular Dynamics. Annu. Rev. Phys. Chem. 1983, 34, 103–127. [Google Scholar] [CrossRef]
- Berne, B.J.; Thirumalai, D. On the Simulation of Quantum Systems: Path Integral Methods. Annu. Rev. Phys. Chem. 1986, 37, 401–424. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation; Academic Press: San Diego, USA, 2002; ISBN 978-0-122-67351-1. [Google Scholar]
- Voth, G.A. Path Integral Centroid Methods in Quantum Statistical Mechanics and Dynamics. In Advances in Chemical Physics; Prigogine, I., Rice, S.S., Eds.; Wiley: New York, NY, USA, 1996; Volume 93, pp. 135–218. [Google Scholar] [CrossRef]
- Ramírez, R.; López-Ciudad, T. The Schrödinger Formulation of the Feynman Path Centroid Density. J. Chem. Phys. 1999, 111, 3339–3348. [Google Scholar] [CrossRef]
- Götze, W. Complex Dynamics of Glass-Forming Liquids; Oxford University Press: Oxford, UK, 2012; ISBN 978-0-19-965614-1. [Google Scholar]
- Markland, T.E.; Morrone, J.A.; Miyazaki, K.; Berne, B.J.; Reichman, D.R.; Rabani, E. Theory and Simulations of Quantum Glass-Forming Liquids. J. Chem. Phys. 2012, 136, 074511. [Google Scholar] [CrossRef]
- Cendagorta, J.R.; Bacic, Z.; Tuckerman, M. An Open-Chain Imaginary-Time Path- Integral Sampling Approach to the Calculation of Approximate Symmetrized Quantum Time Correlation Functions. J. Chem. Phys. 2018, 148, 102340. [Google Scholar] [CrossRef] [PubMed]
- Lovesey, S.W. Theory of Neutron Scattering from Condensed Matter; Clarendon: Oxford, UK, 1987; Volume 1, ISBN 978-0-198-52028-3. [Google Scholar]
- Egelstaff, P.A. The Structure of Simple Liquids. Annu. Rev. Phys. Chem. 1973, 24, 159–187. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Leonard, A. Multiple Scattering of Neutrons in the Static Approximation. Phys. Rev. 1962, 128, 2188–2190. [Google Scholar] [CrossRef]
- Egelstaff, P.A.; Page, D.I; Heard, C.R.T. Experimental Study of the Triplet Correlation Function for Simple Liquids. J. Phys. C: Solid St. Phys. 1971, 4, 1453–1465. [Google Scholar] [CrossRef]
- Winfield, D.J.; Egelstaff, P.A. Short Range Triplet Correlations in Krypton Near the Critical Point. Can. J. Phys. 1973, 51, 1965–1970. [Google Scholar] [CrossRef]
- Hallock, R.B. X-Ray Scattering from Gaseous 3He and 4He at Small Momentum Transfer. Phys. Rev. A 1973, 8, 2143–2159. [Google Scholar] [CrossRef]
- Woods, A.D.B.; Svensson, E.C.; Martel, P. Neutron Scattering from Nonsuperfluid 4He. Can. J. Phys. 1978, 56, 302–310. [Google Scholar] [CrossRef]
- Woods, A.D.B.; Svensson, E.C.; Martel, P. The Dynamic Structure Factor of 4He at 4.2 K. In Low Temperature Physics-LT14, Krusius, M., Vuorio, M, Eds.; North-Holland: Amsterdam, The Netherlands, 1975; Volume 1, pp. 187–190. ISBN 978-0-720-49301-6. [Google Scholar]
- Montfrooij, W.; de Graaf, L.A.; van den Bosch, P.J.; Soper, A.K.; Howells, W.S. Density and Temperature Dependence of the Structure Factor of Dense Fluid Helium. J. Phys.: Condens. Matter 1991, 3, 4089–4096. [Google Scholar] [CrossRef]
- Raveché, H.J.; Mountain, R.D. Structure Studies in Liquid 4He. Phys. Rev. A 1974, 9, 435–447. [Google Scholar] [CrossRef]
- Ramírez, R.; López-Ciudad, T.; Noya, J.C. Feynman Effective Classical Potential in the Schrödinger Formulation. Phys. Rev. Lett. 1998, 81, 3303–3306. [Google Scholar] [CrossRef]
- Miura, S.; Okazaki, S.; Kinugawa, K. A Path Integral Centroid Molecular Dynamics Study of Nonsuperfluid Liquid Helium-4. J. Chem. Phys. 1999, 110, 4523–4532. [Google Scholar] [CrossRef]
- Boninsegni, M. Permutations Sampling in Path Integral Monte Carlo. J. Low Temp. Phys. 2005, 141, 27–46. [Google Scholar] [CrossRef]
- Boninsegni, M.; Prokof’ev, N.V.; Svistunov, B.V. Worm Algorithm and Diagrammatic Monte Carlo: A New Approach to Continuous-Space Path Integral Monte Carlo Simulations. Phys. Rev. E 2006, 74, 036701. [Google Scholar] [CrossRef] [PubMed]
- Kirkwood, J.G. Statistical Mechanics of Fluid Mixtures. J. Chem. Phys. 1935, 3, 300–313. [Google Scholar] [CrossRef]
- Abe, R. On the Kirkwood Superposition Approximation. Prog. Theor. Phys. 1959, 21, 421–430. [Google Scholar] [CrossRef]
- Jackson, H.W.; Feenberg, E. Perturbation Methods for Low States of a Many-Particle Boson System. Ann. Phys. 1961, 15, 266–295. [Google Scholar] [CrossRef]
- Jackson, H.W.; Feenberg, E. Energy Spectrum of Elementary Excitations in Helium II. Rev. Mod. Phys. 1962, 34, 686–693. [Google Scholar] [CrossRef]
- Barrat, J.L.; Hansen, J.P.; Pastore, G. On the Equilibrium Structure of Dense Fluids. Triplet Correlations, Integral Equations and Freezing. Mol. Phys. 1988, 63, 747–767. [Google Scholar] [CrossRef]
- Tanaka, M.; Fukui, Y. Simulation of the Three-Particle Distribution Function in a Long-Range Oscillatory Potential Liquid. Prog. Theor. Phys. 1975, 53, 1547–1565. [Google Scholar] [CrossRef]
- Baranyai, A.; Evans, D.J. Direct Entropy Calculation from Computer Simulation of Liquids. Phys. Rev A 1989, 40, 3817–3822. [Google Scholar] [CrossRef]
- Baranyai, A.; Evans, D.J. Three-Particle Contribution to the Configurational Entropy of Simple Fluids. Phys. Rev. A 1990, 42, 849–857. [Google Scholar] [CrossRef] [PubMed]
- Jorge, S.; Kahl, G.; Lomba, E.; Abascal, J.L.F. On the Triplet Structure of Binary Liquids. J. Chem. Phys. 2000, 113, 3302–3309. [Google Scholar] [CrossRef]
- Sesé, L.M. Path-Integral and Ornstein-Zernike Computations of Quantum Fluid Structures under Strong Fluctuations. AIP Advances 2017, 7, 025204. [Google Scholar] [CrossRef]
- Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum Mechanical Description of Physical Reality Be Considered Complete. Phys. Rev. 1935, 47, 777–780. [Google Scholar] [CrossRef]
- Bell, J.S. On the Problem of Hidden-Variables in Quantum Mechanics. Rev. Mod. Phys. 1966, 38, 447–452. [Google Scholar] [CrossRef]
- Freedman, S.J.; Clauser, J.F. Experimental Test of Local Hidden-Variable Theories. Phys. Rev. Lett. 1972, 28, 938–941. [Google Scholar] [CrossRef]
- Aspect, A.; Dalibard, J.; Roger, G. Experimental Test of Bell’s Inequalities Using Time-Varying Analyzers. Phys. Rev. Lett. 1982, 49, 1804–1807. [Google Scholar] [CrossRef]
- Pan, J.-W.; Bouwmeester, D.; Wienfurter, H. Experimental Entanglement Swapping: Entangling Photos that Never Interacted. Phys. Rev. Lett. 1998, 80, 3891–3894. [Google Scholar] [CrossRef]
- Werlang, T.; Ribeiro, G.A.P.; Rigolin, G. Interplay Between Quantum Phase Transitions and the Behavior of Quantum Correlations at Finite Temperatures. Int. J. Modern Phys. B 2013, 27, 1345032. [Google Scholar] [CrossRef]
- Duplij, S.; Vogl, R. Innovative Quantum Computing. IOP Publishing, 2023, Chps. 5-6. [CrossRef]
- Sesé, L.M. Triplet Correlations in the Quantum Hard-Sphere Fluid. J. Chem. Phys. 2005, 123, 104507. [Google Scholar] [CrossRef]
- Sesé, L.M. Computational Study of the Structures of Gaseous Helium-3 at Low Temperatures. J. Phys. Chem. B 2008, 112, 10241–10254. [Google Scholar] [CrossRef] [PubMed]
- Sesé, L.M. A Study of the Pair and Triplet Structures of the Quantum Hard-Sphere Yukawa Fluid. J. Chem. Phys. 2009, 130, 074504. [Google Scholar] [CrossRef] [PubMed]
- Sesé, L.M. On Static Triplet Structures in Fluids with Quantum Behavior. J. Chem. Phys. 2018, 148, 102312. [Google Scholar] [CrossRef] [PubMed]
- Sesé, L.M. Computation of Static Quantum Triplet Structure Factors of Liquid Para-Hydrogen. J. Chem. Phys. 2018, 149, 124507. [Google Scholar] [CrossRef]
- Sesé, L.M. Real Space Triplets in Quantum Condensed Matter: Numerical Experiments Using Path Integrals, Closures, and Hard Spheres. Entropy 2020, 22, 1338. [Google Scholar] [CrossRef]
- Sesé, L.M. A Glimpse into Quantum Triplet Structures in supercritical 3He. Entropy 2023, 25, 283. [Google Scholar] [CrossRef]
- Melrose, J.R.; Singer, K. An Investigation of Supercooled Lennard-Jones Argon by Quantum Mechanical and Classical Monte Carlo Simulations. Mol. Phys. 1989, 66, 1203–1214. [Google Scholar] [CrossRef]
- Sesé, L. M. Path-Integral and Ornstein-Zernike Study of Quantum Fluid Structures on the Crystallization Line. J. Chem. Phys. 2016, 144. [Google Scholar] [CrossRef]
- Ho, H.M.; Lin, B.; Rice, S.A. Three-Particle Correlation Functions of Quasi-Two-Dimensional One-Component and Binary Colloid Suspensions. J. Chem. Phys. 2006, 125, 184715. [Google Scholar] [CrossRef]
- Nguyen, M.-T.; Monchiet, V.; Bonnet, G.; To, Q.-D. Conductivity Estimates of Spherical-Particle Suspensions Based on Triplet Structure Factors. Phys. Rev. E 2016, 93, 022105. [Google Scholar] [CrossRef]
- Denton, A.R.; Ashcroft, N.W. High-Order Direct Correlation Functions of Uniform Classical Liquids. Phys. Rev. A 1989, 39, 426–429. [Google Scholar] [CrossRef] [PubMed]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Alder, B.J.; Wainwright, T.E. Phase transition for a hard sphere system. J. Chem. Phys. 1957, 27, 1208–1209. [Google Scholar] [CrossRef]
- Baxter, R.J. Direct Correlation Functions and Their Derivatives with Respect to Particle Density. J. Chem. Phys. 1964, 41, 553–558. [Google Scholar] [CrossRef]
- Chihara, J. Integral Equations for Neutral and Charged Quantum Fluids Including Extension of the Percus-Yevick Equation. Prog. Theor. Phys. 1973, 50, 1156–1181. [Google Scholar] [CrossRef]
- Lee, L.L. Correlation Functions of Classical Fluids III. The method of Partition Function Variation Applied to the Chemical Potential: Cases of PY and HNC2. J. Chem. Phys. 1974, 60, 1197–1207. [Google Scholar] [CrossRef]
- Gray, C.G.; Gubbins, K.E. Theory of Molecular Fluids; Clarendon: Oxford, UK, 2011; Volume 1, ISBN 978-0-19-855602-2. [Google Scholar]
- Baxter, R.J. Ornstein-Zernike Relation for a Disordered Fluid. Aust. J. Phys. 1968, 21, 563–569. [Google Scholar] [CrossRef]
- Barker, J.A. A Quantum-Statistical Monte Carlo Method; Path Integrals with Boundary Conditions. J. Chem. Phys. 1979, 70, 2914–2918. [Google Scholar] [CrossRef]
- Herman, M.F.; Bruskin, E.J.; Berne, B.J. On Path Integral Monte Carlo Simulations. J. Chem. Phys. 1982, 76, 5150–5155. [Google Scholar] [CrossRef]
- Takahashi, M.; Imada, M. Monte Carlo Calculation of Quantum System. II Higher-Order Correction. J. Phys. Soc. Japan 1984, 53, 3765–3769. [Google Scholar] [CrossRef]
- Li, X.-P.; Broughton, J.Q. High-Order Correction to the Trotter Expansion for Use in Computer Simulation. J. Chem. Phys. 1987, 86, 5094–5100. [Google Scholar] [CrossRef]
- Pollock, E.L.; Ceperley, D.M. Simulation of Quantum Many-Body Systems by Path-Integral Methods. Phys. Rev. B 1984, 30, 2555–2568. [Google Scholar] [CrossRef]
- Ceperley, D.M.; Pollock, E.L. Path-Integral Computation of the Low-Temperature Properties of Liquid 4He. Phys. Rev. Lett. 1986, 56, 351–354. [Google Scholar] [CrossRef] [PubMed]
- Runge, K.J.; Chester, G.V. Solid-Fluid Phase Transition of Quantum Hard Spheres at Finite Temperatures. Phys. Rev. B 1988, 38, 135–162. [Google Scholar] [CrossRef]
- Singer, K.; Smith, W. Path-Integral Simulations of Condensed Phase Lennard-Jones Systems. Mol. Phys. 1988, 64, 1215–1231. [Google Scholar] [CrossRef]
- Cao, J.; Berne, B.J. A New Quantum Propagator for Hard Sphere and Cavity Systems. J. Chem. Phys. 1992, 97, 2382–2385. [Google Scholar] [CrossRef]
- Suzuki, M. New Scheme of Hybrid Exponential Product Formulas with Applications to Quantum Monte Carlo Simulations. In Computer Simulation Studies in Condensed Matter Physics VIII, Springer Proceedings in Physics, Volume 80; Landau, D.P., Mon, K.K., Schüttler, H.-B., Eds.; Springer-Verlag: Berlin, Germany, 1995; pp. 169–174. ISBN 978-3-642-79993-8. [Google Scholar]
- Chin, S.A. Symplectic Integrators from Composite Operator Factorizations. Phys. Letters A 1997, 226, 344–348. [Google Scholar] [CrossRef]
- Jang, S.; Jang, S.; Voth, G.A. Applications of Higher-Order Composite Factorization Schemes in Imaginary Time Path Integral Simulations. J. Chem. Phys. 2001, 115, 7832–7842. [Google Scholar] [CrossRef]
- Müser, M.H.; Berne, B.J. Path Integral Monte Carlo Scheme for Rigid Tops: Application to the Quantum Rotator Phase Transition in Solid Methane, Phys. Rev. Lett. 1996, 77, 2638–2641. [Google Scholar] [CrossRef]
- Marx, D.; Müser, M.H. Path Integral Simulations of Rotors: Theory and Applications. J. Phys. Condens. Matter 1999, 11, R117–R155. [Google Scholar] [CrossRef]
- Noya, E.G.; Sesé, L.M.; Ramírez, R.; McBride, C.; Conde, M.M.; Vega, C. Path Integral Monte Carlo Simulations for Rigid Rotors and their Application to Water. Mol. Phys. 2011, 109, 149–168. [Google Scholar] [CrossRef]
- Herrero, C.P.; Ramírez, R. Path-Integral Simulation of Solids. J. Phys.: Condens. Matter 2014, 26, 233201. [Google Scholar] [CrossRef] [PubMed]
- Scharf, D.; Martyna, G.J.; Klein, M. Path-Integral Monte Carlo Study of a Lithium Impurity in Para-Hydrogen: Clusters and the Bulk Liquid. J. Chem. Phys. 1993, 99, 8997–9012. [Google Scholar] [CrossRef]
- Wang, Q.; Johnson, J.K.; Broughton, J.Q. Path Integral Grand Canonical Monte Carlo. J. Chem. Phys. 1997, 107, 5108–5117. [Google Scholar] [CrossRef]
- Grüter, P.; Ceperley, D.M.; Laloë, F. Critical Temperature of Bose-Einstein Condensation of Hard-Sphere Gases. Phys. Rev. Lett. 1997, 79, 3549–3552. [Google Scholar] [CrossRef]
- Ruggeri, M.; Moroni, S.; Boninsegni, M. Quasi-2D Liquid 3He. Phys. Rev. Lett. 2013, 111, 045303. [Google Scholar] [CrossRef]
- Sinitskiy, A.V.; Voth, G.A. A Reductionist Perspective on Quantum Statistical Mechanics: Coarse-Graining of Path Integrals. J. Chem. Phys. 2015, 143, 094104. [Google Scholar] [CrossRef] [PubMed]
- Martyna, G.J.; Hughes, A.; Tuckerman, M.E. Molecular Dynamics Algorithms for Path Integrals at Constant Pressure. J. Chem. Phys. 1999, 110, 3275–3290. [Google Scholar] [CrossRef]
- Ramírez, R.; Herrero, C.P.; Antonelli, A.; Hernández, E.R. Path Integral Calculation of Free Energies: Quantum Effects on the Melting Temperature of Neon. J. Chem. Phys. 2008, 129, 064110. [Google Scholar] [CrossRef]
- Miura, S.; Okazaki, S. Path Integral Molecular Dynamics Method Based on a Pair Density Matrix Approximation: An Algorithm for Distinguishable and Identical Particle Systems. J. Chem. Phys. 2001, 115, 5353–5361. [Google Scholar] [CrossRef]
- Miura, S.; Tanaka, J. Path-Integral Hybrid Monte Carlo Algorithm for Correlated Bose Fluids. J. Chem. Phys. 2004, 120, 2160–2168. [Google Scholar] [CrossRef] [PubMed]
- Filinov, V.; Levashov, P.; Larkin, A. Density of States of a 2D System of Soft-Sphere Fermions by Path Integral Monte Carlo Simulations. J. Phys. A: Math. and Theor. 2023, 56, 345201. [Google Scholar] [CrossRef]
- Filinov, V.S.; Syrovatka, R.A.; Levashov, P.R. Exchange-Correlation Bound States of the Triplet Soft-Sphere Fermions by Path Integral Monte Carlo Simulations. Phys. Rev E 2023, 108, 024136. [Google Scholar] [CrossRef] [PubMed]
- Ceperley, D.M. Path Integral Calculations of Normal Liquid 3He. Phys. Rev. Lett. 1992, 69, 331–334. [Google Scholar] [CrossRef]
- Holzmann, M.; Bernu, B.; Ceperley, D.M. Many-Body Wavefunctions for Normal Liquid 3He. Phys. Rev. B 2006, 74, 104510. [Google Scholar] [CrossRef]
- Axilrod, B.M.; Teller, E. Interaction of the Van der Waals Type Between Three Atoms. J. Chem. Phys. 1943, 11, 299–300. [Google Scholar] [CrossRef]
- Bruch, L.W.; McGee, I.J. Calculations and Estimates of the Ground State Energy of Helium Trimers. J. Chem. Phys. 1973, 59, 409–413. [Google Scholar] [CrossRef]
- Kistenmacher, H.; Popkie, H.; Clementi, E.; Watts, R.O. Study of the Structure of Molecular Complexes VII. Effect of Correlation Energy Corrections to the Hartree-Fock Water-Water Potential on Monte Carlo Simulations of Liquid Water. J. Chem. Phys. 1974, 60, 4455–4465. [Google Scholar] [CrossRef]
- Aziz, R.A; Slaman, M.J. An Analysis of the ITS-90 Relations for the Non-Ideality of 3He and 4He: Recommended Relations Based on a New Interatomic Potential for Helium. Metrologia 1990, 27, 211–219. [Google Scholar] [CrossRef]
- Janzen, A.R.; Aziz, R.A. An Accurate Potential Energy Curve for Helium Based on Ab-Initio Calculations. J. Chem. Phys. 1997, 107, 914–919. [Google Scholar] [CrossRef]
- Cencek, W.; Przybytek, M.; Komasa, J.; Mehl, J.B.; Jeziorski, B.; Szalewicz, K. Effects of Adiabatic, Relativistic, and Quantum Electrodynamics Interactions on the Pair Potential and Thermophysical Properties of Helium. J. Chem. Phys. 2012, 136, 224303. [Google Scholar] [CrossRef] [PubMed]
- Cencek, W.; Patkowski, K.; Szalewicz, K. Full Configuration-Interaction Calculation of Three-Body Nonadditive Contribution to Helium Interaction Potential. J. Chem. Phys. 2009, 131, 064105. [Google Scholar] [CrossRef]
- Sesé, L.M.; Gómez, P.C.; Sueiro, F. An Application of Quantum Chemical Methodology to Liquid Phase Studies: Monte Carlo Simulation of Nonrigid Acetone Dissolved in Carbon Disulfide. J. Mol. Liq. 1986, 32, 235–258. [Google Scholar] [CrossRef]
- Sesé, L.M. Molecular Electronic States in Liquid Phase: Configuration Interaction States. J. Mol. Liq. 1988, 37, 45–57. [Google Scholar] [CrossRef]
- Fernández, M.; Tortajada, J.; Sesé, L.M. A Theoretical Analysis of the Ultraviolet Spectrum (180-260 nm) of Pure Liquid Benzene. Z. Phys. D: Atoms, Molecules and Clusters 1988, 9, 243–251. [Google Scholar] [CrossRef]
- Sesé, L.M. Environmental Effects on Molecules Immersed in Liquids. Z. Phys. D: Atoms, Molecules and Clusters 1990, 17, 195–202. [Google Scholar] [CrossRef]
- Jordan, H.F.; Fosdick, L.D. Three-Particle Effects in the Pair Distribution Function for 4He Gas. Phys. Rev. 1968, 171, 128–149. [Google Scholar] [CrossRef]
- Kistenmacher, H.; Lie, G.C.; Popkie, H.; Clementi, E. Study of the Structure of Molecular Complexes VI. Dimers and Small Clusters of Water Molecules in the Hartree-Fock Approximation. J. Chem. Phys. 1974, 61, 546–561. [Google Scholar] [CrossRef]
- Boninsegni, M.; Pierleoni, C.; Ceperley, D.M. Isotopic Shift of Helium Melting Pressure: Path Integral Monte Carlo Study. Phys. Rev. Lett. 1994, 72, 1854–1857. [Google Scholar] [CrossRef]
- Moroni, S.; Pederiva, F.; Fantoni, S.; Boninsegni, M. Equation of State of Solid 3He. Phys. Rev. Lett. 2000, 84, 2650–2653. [Google Scholar] [CrossRef]
- Barnes, A.L.; Hinde, R.J. Three-Body Interactions and the Elastic Constants of HCP Solid 4He. J. Chem. Phys. 2017, 147, 114504. [Google Scholar] [CrossRef] [PubMed]
- Nam, P.T.; Ricaud, J.; Triay, A. Dilute Bose Gas with Three-Body Interaction: Recent Results and Open Questions. J. Math. Phys. 2022, 63, 061103. [Google Scholar] [CrossRef]
- Sutcliffe, B.T. Fundamentals of Computational Quantum Chemistry. In Computational Techniques in Quantum Chemistry and Molecular Physics, Diercksen, G.H.F., Sutcliffe, B.T, Veillard, A., Eds.; NATO Advanced Study Institutes Series; Springer: Dordrecht, Holland, 1975; Volume 15, pp. 1–105. [Google Scholar] [CrossRef]
- Bildstein, B.; Kahl, G. Triplet Correlation Functions for Hard Spheres: Computer Simulation Results. J. Chem. Phys. 1994, 100, 5882–5893. [Google Scholar] [CrossRef]
- Bildstein, B.; Kahl, G. Triplet Correlation Functions for Hard Spheres: Comparison of Different Approaches. Phys. Rev. E 1993, 47, 1712–1726. [Google Scholar] [CrossRef] [PubMed]
- Sciortino, F.; Kob, W. Debye-Waller Factor of Liquid Silica: Theory and Simulation. Phys. Rev. Lett. 2001, 86, 648–651. [Google Scholar] [CrossRef]
- Jorge, S.; Lomba, E.; Abascal, J.L.F. Theory and Simulation of the Triplet Structure Factor and Triplet Direct Correlation Functions in Binary Mixtures. J. Chem. Phys. 2002, 116, 730–736. [Google Scholar] [CrossRef]
- Coslovich, D. Static Triplet Correlations in Glass-Forming Liquids: A Molecular Dynamics Study. J. Chem. Phys. 2013, 138, 12A539. [Google Scholar] [CrossRef]
- Dixon, M.; Hutchinson, P. A Method for the Extrapolation of Pair Distribution Functions. Mol. Phys. 1977, 33, 1663–1670. [Google Scholar] [CrossRef]
- Salacuse, J.J.; Denton, A.R.; Egelstaff, P.A. Finite-Size Effects in Molecular Dynamics Simulations: Static Structure Factor and Compressibility I. Theoretical Method. Phys. Rev. E 1996, 53, 2382–2389. [Google Scholar] [CrossRef]
- Baumketner, A.; Hiwatari, Y. Finite-Size Dependence of the Bridge Function Extracted from Molecular Dynamics Simulations. Phys. Rev. E 2001, 63, 061201. [Google Scholar] [CrossRef]
- Curtin, W.A.; Ashcroft, N.W. Weighted-Density-Functional Theory of Inhomogeneous Liquids and the Freezing Transition. Phys. Rev. A 1985, 32, 2909–2919. [Google Scholar] [CrossRef] [PubMed]
- Lee, L.L. Constructing a New Closure Theory Based on the Third-Order Ornstein-Zernike Equation and a Study of the Adsorption of Simple Fluids. J. Chem. Phys. 2011, 135, 204706. [Google Scholar] [CrossRef] [PubMed]
- Sesé, L.M. The Compressibility Theorem for Quantum Simple Fluids at Equilibrium. Mol. Phys. 2003, 101, 1455–1468. [Google Scholar] [CrossRef]
- Sesé, L.M. Determination of the Quantum Static Structure Factor of Liquid Neon within the Feynman-Hibbs Picture. Mol. Phys. 1996, 89, 1783–1802. [Google Scholar] [CrossRef]
- Roy, P.-N.; Jang, S.; Voth, G.A. Feynman Path Centroid Dynamics for Fermi-Dirac Statistics. J. Chem. Phys. 1999, 111, 5303–5305. [Google Scholar] [CrossRef]
- Blinov, N.V.; Roy, P.-N.; Voth, G.A. Path Integral Formulation of Centroid Dynamics for Systems Obeying Bose-Einstein Statistics. J. Chem. Phys. 2001, 115, 4484–4495. [Google Scholar] [CrossRef]
- Blinov, N.; Roy, P.-N. Operator Formulation of Centroid Dynamics for Bose-Einstein and Fermi-Dirac Statistics. J. Chem. Phys. 2001, 115, 7822–7831. [Google Scholar] [CrossRef]
- Blinov, N.; Roy, P.-N. Connection Between the Observable and Centroid Structural Properties of a Quantum Fluid: Application to Liquid Para-Hydrogen. J. Chem. Phys. 2004, 120, 3759–3764. [Google Scholar] [CrossRef]
- Sesé, L.M. On the Accurate Direct Computation of the Isothermal Compressibility for Normal Quantum Simple Fluids: Application to Quantum Hard Spheres. J. Chem. Phys. 2012, 136, 244504. [Google Scholar] [CrossRef]
- Sesé, L.M. Path Integral Monte Carlo Study of Quantum-Hard Sphere Solids. J. Chem. Phys. 2013, 139, 044502. [Google Scholar] [CrossRef]
- Trotter, H.F. Approximation of Semi-Groups of Operators. Pacific J. Math. 1958, 8, 887–919. [Google Scholar] [CrossRef]
- Doll, J.D.; Freeman, D.L.; Beck, T.L. Equilibrium and Dynamical Fourier Path Integral Methods. Adv. Chem. Phys. 1990, 78, 61–127. [Google Scholar] [CrossRef]
- Feynman, R.P.; Hibbs, A.R. Quantum Mechanics and Path Integrals; McGraw-Hill: New York, NY, USA, 1965; ISBN 978-0-070-20650-2. [Google Scholar]
- Feynman, R.P.; Kleinert, H. Effective Classical Partition Function. Phys. Rev. A 1986, 34, 5080–5084. [Google Scholar] [CrossRef] [PubMed]
- Giachetti, R.; Tognetti, V. Variational Approach to Quantum Statistical Mechanics of Nonlinear Systems with Applications to Sine-Gordon Chains. Phys. Rev. Lett. 1985, 55, 912–915. [Google Scholar] [CrossRef] [PubMed]
- Sesé, L.M. Feynman-Hibbs Quantum Effective Potentials for Monte Carlo Simulations of Liquid Neon. Mol. Phys. 1993, 78, 1167–1177. [Google Scholar] [CrossRef]
- Sesé, L.M. Quantum Effects on the Static Structure Factor of Lennard-Jones Fluids. Mol. Phys. 1997, 92, 693–703. [Google Scholar] [CrossRef]
- Sesé, L.M. An Application of the Self-Consistent Variational Effective Potential Against the Path-Integral to Compute Equilibrium Properties of Quantum Simple Fluids. Mol. Phys. 1999, 97, 881–896. [Google Scholar] [CrossRef]
- Percus, J.K. Approximation Methods in Classical Statistical Mechanics. Phys. Rev. Lett. 1962, 8, 462–463. [Google Scholar] [CrossRef]
- Lebowitz, J.L.; Percus, J.K. Statistical Thermodynamics of Nonuniform Fluids. J. Math. Phys. 1963, 4, 116–123. [Google Scholar] [CrossRef]
- Yvon, J. Note sur un Calcul de Perturbation en Mécanique Statistique. Suppl. Nuovo Cimento 1958, 9, 144–151. [Google Scholar] [CrossRef]
- Groot, R.D.; van der Eerden, J.P.; Faber, N.M. The Direct Correlation Function in Hard Sphere Fluids. J. Chem. Phys. 1987, 87, 2263–2270. [Google Scholar] [CrossRef]
- Raveché, H.J.; Mountain, R.D. Three-Body Correlations in Simple Dense Fluids. J. Chem. Phys. 1970, 53, 3101–3107. [Google Scholar] [CrossRef]
- Raveché, H.J.; Mountain, R.D. Three Atom Correlations in Liquid Neon. J. Chem. Phys. 1972, 57, 3987–3991. [Google Scholar] [CrossRef]
- Stell, G. The Percus-Yevick Equation for the Radial Distribution Function of a Fluid. Physica 1963, 29, 517–534. [Google Scholar] [CrossRef]
- Fisher, M.E.; Widom, B. Decay of Correlations in Linear Systems. J. Chem. Phys. 1969, 50, 3756–3772. [Google Scholar] [CrossRef]
- Tago, Y.; Smith, W.R. Decay of Pair Correlation Functions. Can. J. Phys. 1997, 55, 761–766. [Google Scholar] [CrossRef]
- Evans, R.; Henderson, J.R.; Hoyle, D.C.; Parry, A.D.; Sabeur, Z.A. Asymptotic Decay of Liquid Structure: Oscillatory Liquid-Vapour Density Profiles and the Fisher-Widom line. Mol. Phys. 1993, 80, 755–775. [Google Scholar] [CrossRef]
- Haymet, A.D.J; Rice, S.A.; Madden, W.G. An Accurate Integral Equation for the Pair and Triplet Distribution Functions of a Simple Liquid. J. Chem. Phys. 1981, 74, 3033–3041. [Google Scholar] [CrossRef]
- Gubbins, K.E.; Gray, C.G.; Egelstaff, P.A. Thermodynamic Derivatives of Correlation Functions. Mol. Phys. 1978, 35, 315–328. [Google Scholar] [CrossRef]
- Jacuzzi, G.; Omerti, E. Monte Carlo Calculation of the Radial Distribution Function of Quantum Hard Spheres at Finite Temperatures Using Path Integrals with Boundary Conditions. J. Chem. Phys. 1983, 79, 3051–3054. [Google Scholar] [CrossRef]
- Sesé, L.M.; Ledesma, R. Path-Integral Monte Carlo Energy and Structure of the Quantum Hard-Sphere System Using Efficient Propagators. J. Chem. Phys. 1995, 102, 3776–3786. [Google Scholar] [CrossRef]
- Fierz, M. Connection Between Pair Density and Pressure for a Bose Gas Consisting of Rigid Spherical Atoms. Phys. Rev. 1957, 106, 412–413. [Google Scholar] [CrossRef]
- Filinov, V.; Levashov, P.; Larkin, A. Monte Carlo Simulation of the Electron Short-Range Quantum Ordering in Coulomb Systems and the ‘Fermionic Sign Problem’. J. Phys. A: Mathematical and Theoretical 2022, 55, 035001. [Google Scholar] [CrossRef]
- Adams, D.J. Chemical Potential of Hard Sphere fluids by Monte Carlo Methods, Mol. Phys. 1974, 28, 1241–1252. [Google Scholar] [CrossRef]
- Kleinert, H. Path Integrals in Quantum Mechanics, Statistical Physics, and Polymer Physics; Chp. 7; World Scientific: Singapore, 1995; ISBN 981-0-21472-3. [Google Scholar]
- Kalos, M.H.; Levesque, D.; Verlet, L. Helium at Zero Temperature with Hard-Sphere and other Forces. Phys. Rev. A 1974, 9, 2178–2195. [Google Scholar] [CrossRef]
- Ceperley, D.; Chester, G.V.; Kalos, M.H. Monte Carlo Simulation of a Many-Fermion Study. Phys. Rev. B 1977, 16, 3081–3099. [Google Scholar] [CrossRef]
- Stirling, W.G.; Scherm, R.; Hilton, P.A.; Cowley, R.A. Neutron inelastic scattering from Liquid Helium Three. J. Phys. C.: Solid State Phys. 1976, 9, 1643–1663. [Google Scholar] [CrossRef]
- Sköld, K.; Pelizzari, C.A. Neutron inelastic scattering from Liquid 3He at 40mK and at 1.2 K. J. Phys. C. Solid State Phys. 1978, 11, L589–L592. [Google Scholar] [CrossRef]
- Hilton, P.A.; Cowley, R.A.; Scherm, R.; Stirling, W.G. Lifetime of zero sound in Liquid Helium Three. J. Phys. C.: Solid State Phys. 1980, 13, L295–L299. [Google Scholar] [CrossRef]
- Filinov, V.S.; Levashov, P.R.; Larkin, A.S. The Quantum Density of States and Distribution Functions of the Helium-3: Wigner Approach in Path Integral Monte Carlo simulations. Mol. Phys. 2024, e2323645. [Google Scholar] [CrossRef]
- Sesé, L.M. Structural and Response Functions at Equilibrium in Path-Integral Quantum Simple Fluids. Mol. Phys. 2002, 100, 927–940. [Google Scholar] [CrossRef]
- Evans, R. The Nature of the Liquid-Vapour Interface and other topics in the Statistical Mechanics of Non-Uniform Classical Fluids. Adv. Phys. 1979, 28, 143–200. [Google Scholar] [CrossRef]
- Evans, R. Density Functionals in the Theory of Nonuniform Fluids. In Fundamentals of Inhomogeneous Fluids; Henderson, D., Ed.; Marcel Dekker: New York, NY, USA, 1992; ISBN 0-8247-8711-0. [Google Scholar]
- Haymet, A.D.J. Freezing. In Fundamentals of Inhomogeneous Fluids; Henderson, D., Ed.; Marcel Dekker: New York, NY, USA, 1992; ISBN 0-8247-8711-0. [Google Scholar]
- McCoy, J.D.; Rick, S.W.; Haymet, A.D.J. Density Functional Theory of Freezing for Quantum Systems. I. Path Integral Formulation of General Theory. J. Chem. Phys. 1990, 92, 3034–3039. [Google Scholar] [CrossRef]
- Rick, S.W.; McCoy, J.D.; Haymet, AD.J. Density Functional Theory of Freezing for Quantum Systems. II. Application to Helium. J. Chem. Phys. 1990, 92, 3040–3047. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Mermin, N.D. Thermal Properties of the Inhomogeneous Electron Gas. Phys. Rev. 1965, 137, A1441–A1443. [Google Scholar] [CrossRef]
- Shinoda, K.; Miura, S.; Okazaki, S. A Molecular Approach to Quantum Fluids Based on a Generalized Ornstein-Zernike Equation. J. Chem. Phys. 2001, 114, 7497–7505. [Google Scholar] [CrossRef]
- Shinoda, K.; Miura, S.; Okazaki, S. A Generalized Ornstein-Zernike Integral Equation Study of Atomic Impurities in Quantum Fluids. J. Chem. Phys. 2001, 115, 4161–4168. [Google Scholar] [CrossRef]
- Sesé, L.M. Properties of the Path-Integral Quantum Hard-Sphere Fluid in k-Space. J. Chem. Phys. 2002, 116, 8492–8503. [Google Scholar] [CrossRef]
- Bogoyavlenski, I.V.; Karnatsevich, I.V.; Konareva, V.G. Experimental Investigation of the Equation of State of Helium Isotopes (He4 and He3) in the Temperature Range from 3.3 K to 14 K. Sov. J. Low Temp. Phys. 1978, 4, 265-277.
- Ralston, A.; Rabinowitz, P. A First Course in Numerical Analysis; Dover: New York, NY, USA, 2001; ISBN 0-486-41454-X. [Google Scholar]
- Bailey, L.E.; Sesé, L.M. The Asymptotic Decay of Pair Correlations in the Path-Integral Quantum Hard-Sphere Fluid. J. Chem. Phys. 2001, 115, 6557–6568. [Google Scholar] [CrossRef]
- Bailey, L.E.; Sesé, L.M. The Decay of Pair Correlations in Quantum Hard-Sphere Fluids. J. Chem. Phys. 2004, 121, 10076–10087. [Google Scholar] [CrossRef]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes; Cambridge University Press: Cambridge, UK, 1988; ISBN 0-521-30811-9. [Google Scholar]
Figure 1.
Helium-3 equilateral centroid and instantaneous correlations in r-space at state point ; 0.0228717687 Results obtained with PIMC canonical simulation , with improved with respect to Reference [60]. Representative errors bars (one-standard deviation) in the vicinity of the main maxima: .
Figure 1.
Helium-3 equilateral centroid and instantaneous correlations in r-space at state point ; 0.0228717687 Results obtained with PIMC canonical simulation , with improved with respect to Reference [60]. Representative errors bars (one-standard deviation) in the vicinity of the main maxima: .
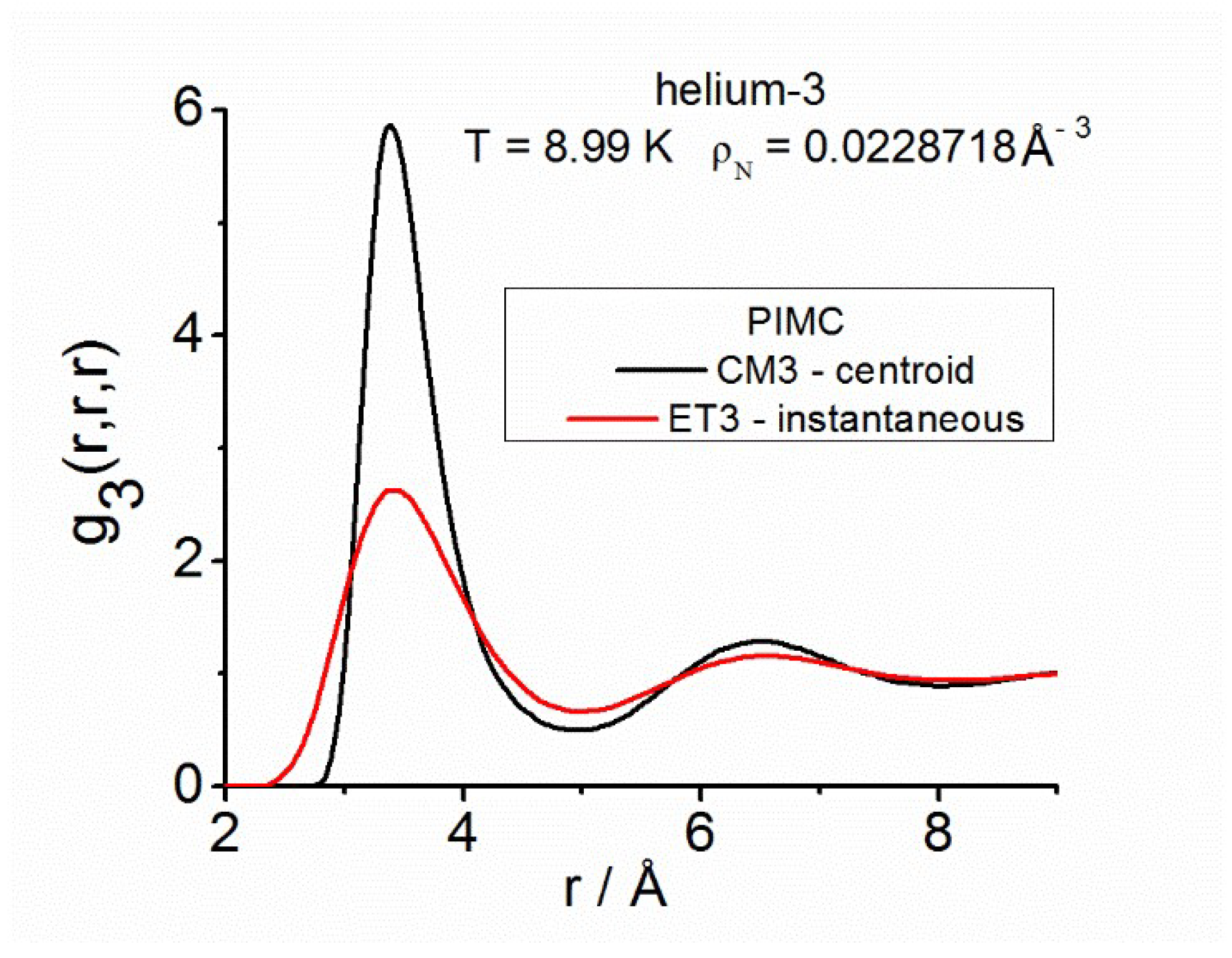
Figure 2.
Quantum hard-sphere fluid basic results at state point on the fluid side of the crystallization line [59,137]. Use of reduced units is made: and (hard-sphere diameter). (a) Pair direct correlation functions and for the centroid and instantaneous correlations, obtained by OZ2-treating the PIMC and canonical correlation functions . Shown are representative results for centroids CM2 along the convergence region marked by the zeros (from BDH+BHw/5- iterations there arise a total of fourteen ) [59,72,125,127]. For the instantaneous case ET2 only the largest result obtained with a single application of BDH is displayed. The different widths of the centroid functions are intended to serve as a guide to the eye. (b) Centroid and instantaneous pair structure factors at selected values. Note the more pronounced centroid features.
Figure 2.
Quantum hard-sphere fluid basic results at state point on the fluid side of the crystallization line [59,137]. Use of reduced units is made: and (hard-sphere diameter). (a) Pair direct correlation functions and for the centroid and instantaneous correlations, obtained by OZ2-treating the PIMC and canonical correlation functions . Shown are representative results for centroids CM2 along the convergence region marked by the zeros (from BDH+BHw/5- iterations there arise a total of fourteen ) [59,72,125,127]. For the instantaneous case ET2 only the largest result obtained with a single application of BDH is displayed. The different widths of the centroid functions are intended to serve as a guide to the eye. (b) Centroid and instantaneous pair structure factors at selected values. Note the more pronounced centroid features.
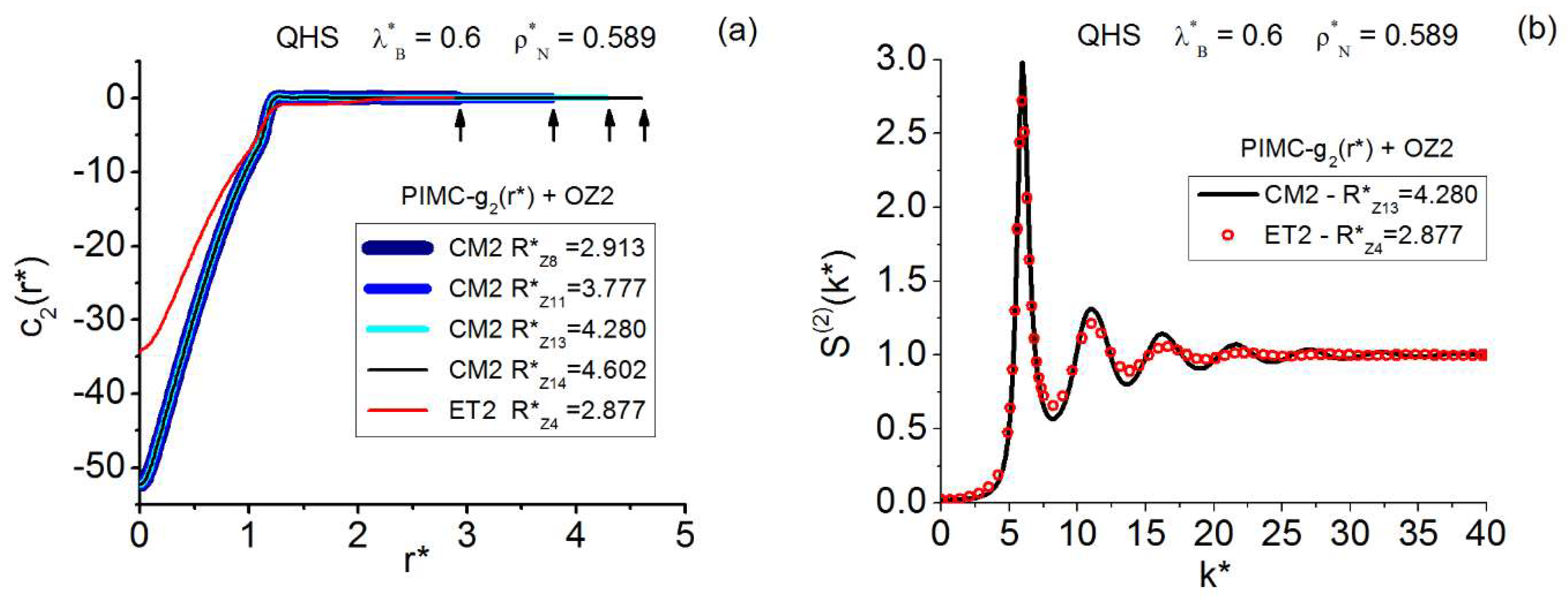
Figure 3.
Helium-3 instantaneous correlation function at state point ; 0.0025 obtained through PIMC canonical simulations (a) Pair and equilateral arising from PIMC plus OZ2 (BDH+BHw/5-iterations) [46,72,125,127] and only PIMC, respectively. To be noticed the long-range behaviors towards unity with increasing r. Representative PIMC errors bars (one-standard deviation) in the vicinity of the main maxima: and , the OZ2 corrected result for the latter height being (b) Isosceles at selected r-slices. To be noticed the long-range behaviors towards the pair values at each r value with increasing s (recall the canonical effect on the structures).
Figure 3.
Helium-3 instantaneous correlation function at state point ; 0.0025 obtained through PIMC canonical simulations (a) Pair and equilateral arising from PIMC plus OZ2 (BDH+BHw/5-iterations) [46,72,125,127] and only PIMC, respectively. To be noticed the long-range behaviors towards unity with increasing r. Representative PIMC errors bars (one-standard deviation) in the vicinity of the main maxima: and , the OZ2 corrected result for the latter height being (b) Isosceles at selected r-slices. To be noticed the long-range behaviors towards the pair values at each r value with increasing s (recall the canonical effect on the structures).
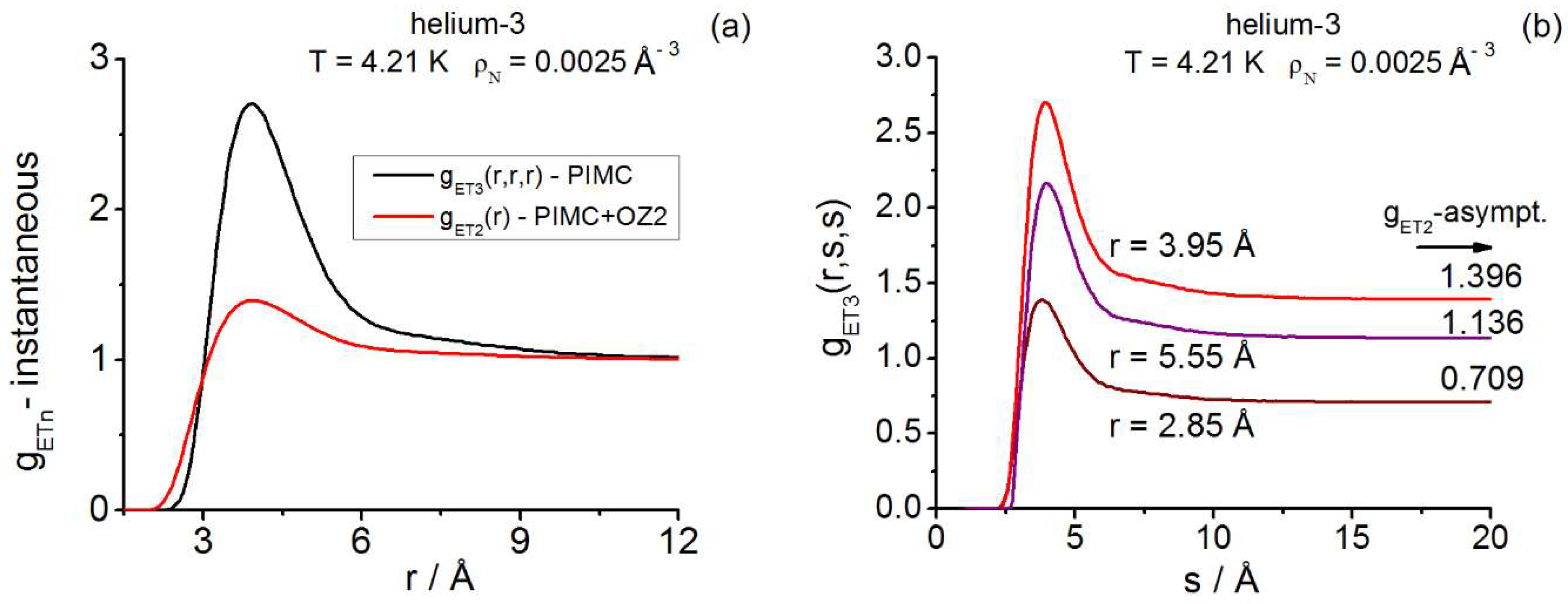
Figure 4.
Helium-3 instantaneous direct correlation function at state point ; 0.02286713 obtained with OZ2 and OZ3 procedures applied to PIMC canonical data. (a) Pair and equilateral arising from OZ2(BDH+BHw/5-iterations) [46,72,125,127] and OZ3(BHP3) [41,60], respectively. To be noticed the more rapid evolution of triplets towards zero with increasing r. (b) Isosceles at selected r-slices.
Figure 4.
Helium-3 instantaneous direct correlation function at state point ; 0.02286713 obtained with OZ2 and OZ3 procedures applied to PIMC canonical data. (a) Pair and equilateral arising from OZ2(BDH+BHw/5-iterations) [46,72,125,127] and OZ3(BHP3) [41,60], respectively. To be noticed the more rapid evolution of triplets towards zero with increasing r. (b) Isosceles at selected r-slices.
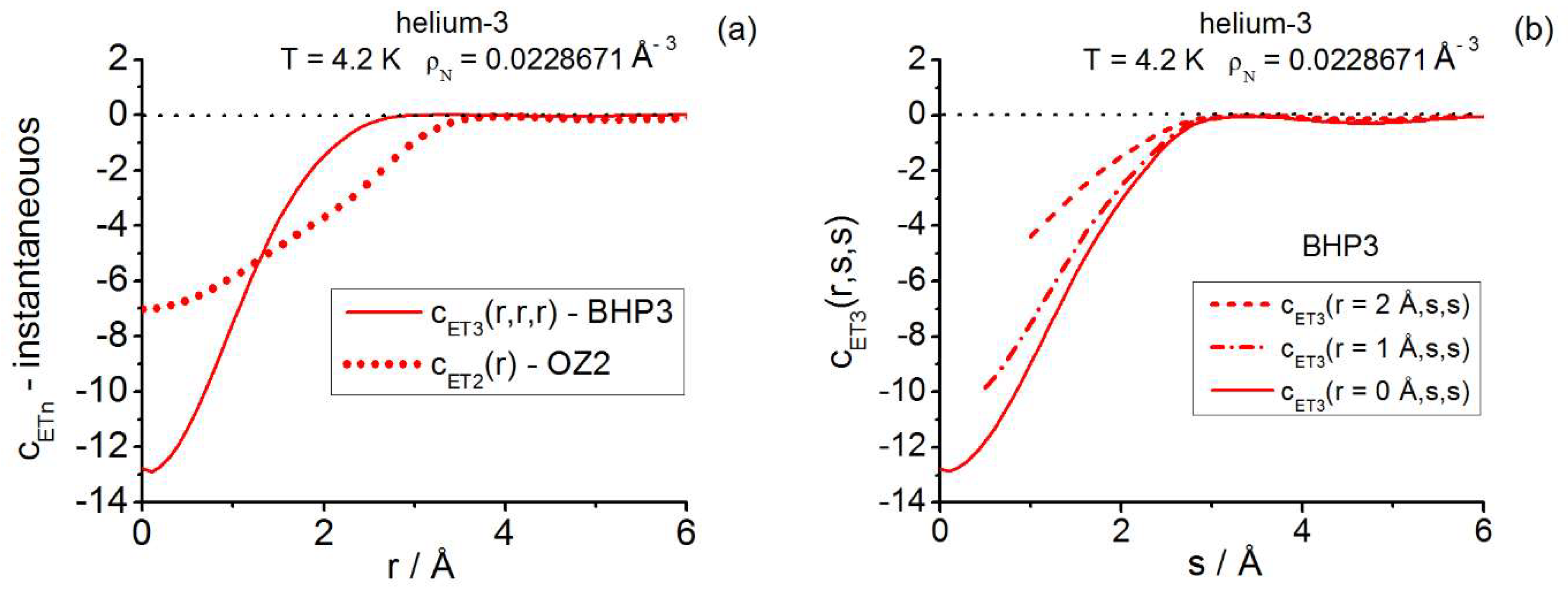
Figure 5.
Helium-3 equilateral components of several determinations of the instantaneous triplet structure factor at state point ; 0.02286713 Density-dependent intermediate data calculated in Reference [46]. (a) Results obtained with PIMC in the canonical ensemble and OZ3(BHP3) [41,60]. To be remarked: the PIMC and BHP3 negative values for the double-zero component fixed via the (classical) sum rule Equation (14b); and the small PIMC error bars (one-standard deviation), the greater being near the main amplitude . (b) Results obtained with PIMC and closures JF3 [41,60] and DAS3 [65]. To be noticed the positiveness of the whole behavior of JF3, and the very reduced negative behavior of DAS3 near the origin , at which it is also .
Figure 5.
Helium-3 equilateral components of several determinations of the instantaneous triplet structure factor at state point ; 0.02286713 Density-dependent intermediate data calculated in Reference [46]. (a) Results obtained with PIMC in the canonical ensemble and OZ3(BHP3) [41,60]. To be remarked: the PIMC and BHP3 negative values for the double-zero component fixed via the (classical) sum rule Equation (14b); and the small PIMC error bars (one-standard deviation), the greater being near the main amplitude . (b) Results obtained with PIMC and closures JF3 [41,60] and DAS3 [65]. To be noticed the positiveness of the whole behavior of JF3, and the very reduced negative behavior of DAS3 near the origin , at which it is also .
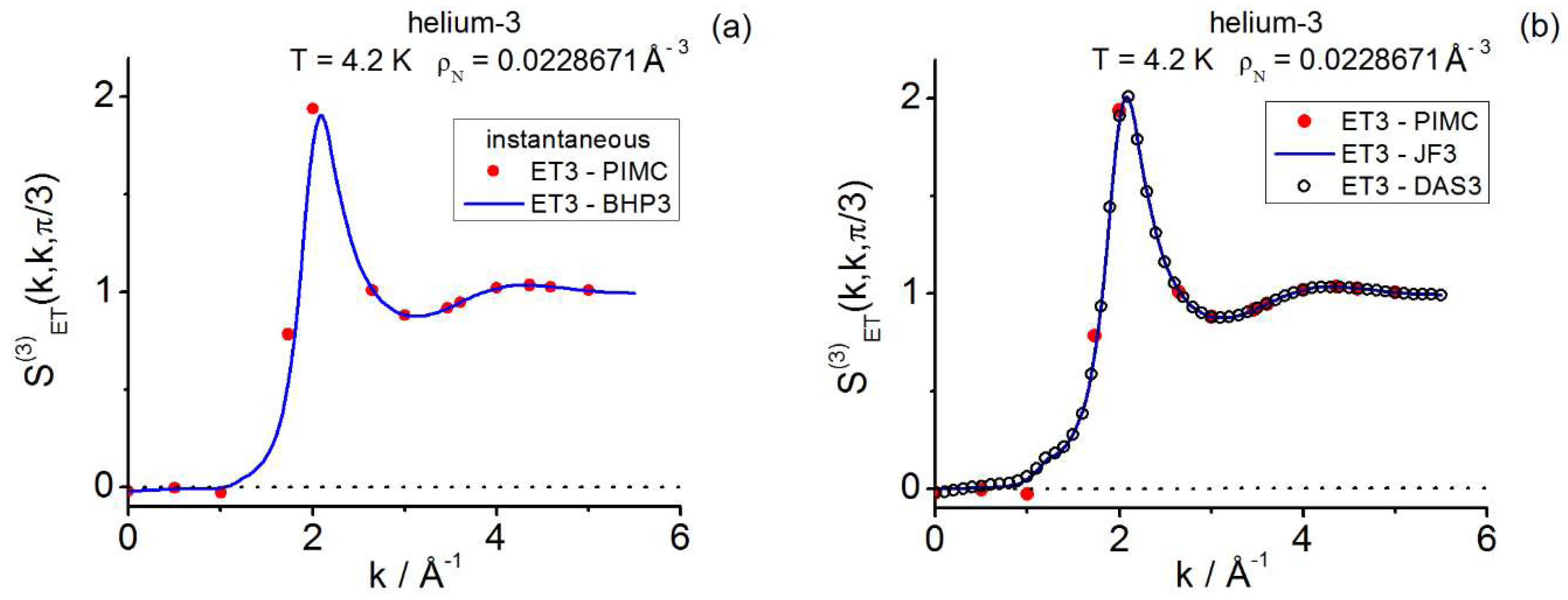
Figure 6.
Helium-3 closure consistency calculations (Equations (113)) for the instantaneous triplet correlation function at state point ; 0.02286713 Density-dependent intermediate data calculated in Reference [46]. (a) Density derivative at constant temperature of the pair radial correlation function Closures KS3 [37], JF3 [40], and their average AV3 [59], are compared to the numerical result (“exact”) fixed with Richardson extrapolation (four-point estimate [182]). To be noticed the greater closeness between AV3 and the “exact” values. (b) Functional at constant temperature fixed with Richardson extrapolation (four-point estimate) compared with its closure approximations arising from KS3, JF3, and AV3. To be noticed the greater closeness between AV3 and the “exact” values past the region where JF3 behaves wrongly.
Figure 6.
Helium-3 closure consistency calculations (Equations (113)) for the instantaneous triplet correlation function at state point ; 0.02286713 Density-dependent intermediate data calculated in Reference [46]. (a) Density derivative at constant temperature of the pair radial correlation function Closures KS3 [37], JF3 [40], and their average AV3 [59], are compared to the numerical result (“exact”) fixed with Richardson extrapolation (four-point estimate [182]). To be noticed the greater closeness between AV3 and the “exact” values. (b) Functional at constant temperature fixed with Richardson extrapolation (four-point estimate) compared with its closure approximations arising from KS3, JF3, and AV3. To be noticed the greater closeness between AV3 and the “exact” values past the region where JF3 behaves wrongly.
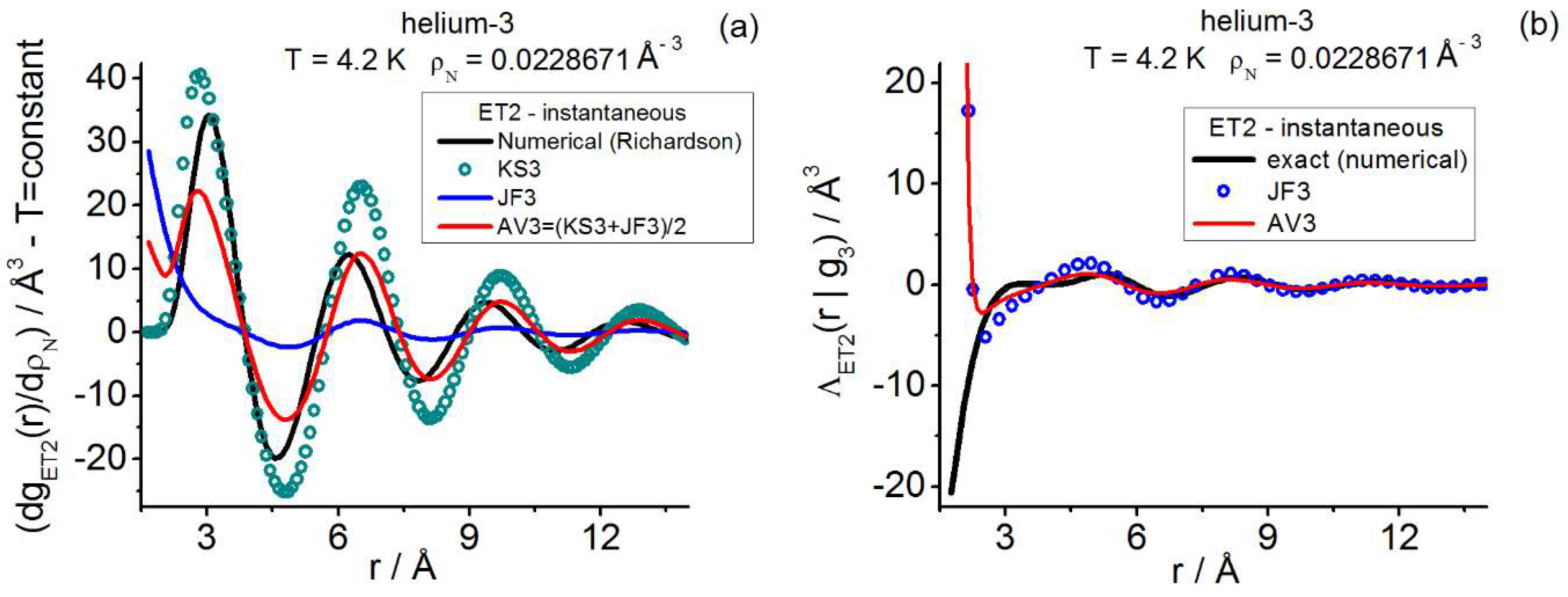
Figure 7.
Quantum hard-sphere fluid equilateral components of triplet structure factors at state point on the fluid side of the crystallization line [59,62,137]. Use of reduced units is made: (hard-sphere diameter). (a) Centroid triplet structure factors CM3 obtained with PIMC canonical simulation and the closures JF3 [41] and DAS3 [65]. To be noticed the PIMC largest error bars (one-standard deviation) at the main amplitude, which is near , and the negative values at the double-zero component fixed with the classical Equation (14b)) and at . Also, JF3 results are always positive, while DAS3 results (obtained via Stirling two-point derivatives) remain below zero for . (b) Instantaneous triplet structure factors ET3 obtained with the same methods as above. To be noticed the PIMC largest error bars (one-standard deviation) at the main amplitude, which is near , and the negative values at the double-zero component fixed with Equation (14b))) and at . Also, JF3 results are always positive, while DAS3 results remain below zero for .
Figure 7.
Quantum hard-sphere fluid equilateral components of triplet structure factors at state point on the fluid side of the crystallization line [59,62,137]. Use of reduced units is made: (hard-sphere diameter). (a) Centroid triplet structure factors CM3 obtained with PIMC canonical simulation and the closures JF3 [41] and DAS3 [65]. To be noticed the PIMC largest error bars (one-standard deviation) at the main amplitude, which is near , and the negative values at the double-zero component fixed with the classical Equation (14b)) and at . Also, JF3 results are always positive, while DAS3 results (obtained via Stirling two-point derivatives) remain below zero for . (b) Instantaneous triplet structure factors ET3 obtained with the same methods as above. To be noticed the PIMC largest error bars (one-standard deviation) at the main amplitude, which is near , and the negative values at the double-zero component fixed with Equation (14b))) and at . Also, JF3 results are always positive, while DAS3 results remain below zero for .
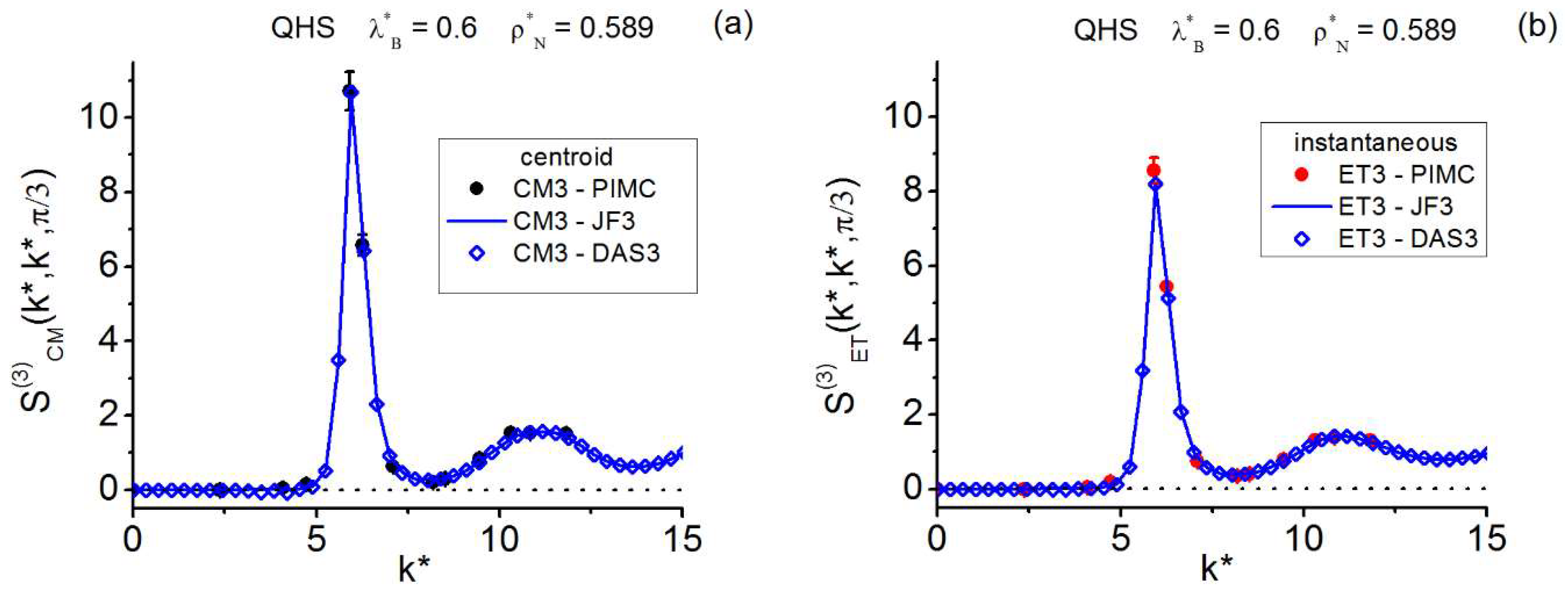
Table 1.
Detail of the instantaneous results for helium-3 . AV3 and BHP3 data taken from [60].
Table 1.
Detail of the instantaneous results for helium-3 . AV3 and BHP3 data taken from [60].
| Instantaneous— | |||||
| PIMC | JF3 | AV3 | BHP3 | DAS3 | |
| 0 | ------ | ||||
| 0.5 | |||||
| 1 | |||||
| 2 | |||||
| 2.1 | ------ | ||||
| 5 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Downloads
65
Views
27
Comments
0
Subscription
Notify me about updates to this article or when a peer-reviewed version is published.
MDPI Initiatives
Important Links
© 2025 MDPI (Basel, Switzerland) unless otherwise stated






