Study on Influencing Factors of Vertical Bearing Capacity of Pile Foundation in Multi‐Layer Cave

In order to study the influence factors of vertical bearing capacity of pile foundation under the special address condition of multi-layer karst cave, the finite element model of foundation pile in double-layer karst area was established by using a commercial general finite element software Ansys, the bearing capacity of concrete pile foundation with different rock height, different ec-centricity and different elastic modulus under the gradually increasing load was studied. The results show that: (1) Under the condition of constant external load, the maximum displacement of pile foundation increases with the increase of eccentricity; (2) With the increase of concrete strength, the maximum displacement decreases gradually, but the corresponding maximum stress is roughly the same; (3) The height of the rock cave has a great influence on the bearing capacity of the pile foundation. In the construction process, it is necessary to minimize or avoid passing through the area with higher karst caves.

Keywords:

Subject: Engineering - Civil Engineering

1. Introduction

China is one of the countries with wide distribution, large distribution area and many types of karst landforms in the world. As the most important foundation treatment method in karst area, pile foundation has been widely used in practical engineering. With the implementation of China ‘s western development strategy, a large number of high-grade highway construction will pass through the western mountainous areas, and a large number of engineering pile foundations will pass through the karst development areas. The complex and changeable karst areas have brought great difficulties to the construction of highway bridge pile foundations. Therefore, it is of practical engineering significance to study the bearing characteristics of bridge pile foundation in karst area [1,2,3,4].

At present, many scholars have systematically studied the vertical bearing characteristics of pile foundations in karst development areas. Wang et al. [1] calculated the influence of the height and length of the pile side hole on the vertical bearing capacity of the pile foundation by numerical analysis. Chen et al. [2] studied the bearing characteristics and load transfer mechanism of pile foundation crossing karst caves with different scales and layers by centrifugal model test, and gave the sensitivity of vertical bearing capacity of pile foundation to three factors. Liu et al. [3] established a regression model of the load-settlement relationship of pile foundation by using the field static load test data. Compared with the numerical simulation results, it shows that the model can effectively predict the settlement of pile foundation. Su et al. [4] studied the influence of cave radius, cave vertical spacing and cave height on the vertical bearing characteristics of foundation pile under the condition of double-layer cave by numerical simulation method. The results show that the cave span affects the side friction of the whole upper, middle and lower sections of the foundation pile, and the vertical spacing of the cave has a great influence on the side friction of the middle section of the foundation pile. Ai et al. [5] used finite element to simulate the influence of rock thickness on the stress characteristics of bridge pile foundation in karst area. From the simulation results, it can be seen that when the rock thickness is thin, the upper load is borne by the pile end resistance. When the thickness of the rock layer is thick, the pile end resistance and the pile side friction bear the load together. Feng et al. [6] used the theoretical model to predict the bearing capacity of pile foundation under the influence of the underlying karst cave. The results show that the theoretical model can well predict the bearing capacity of pile foundation. Jiang et al. [7] analyzed the calculation method of bearing capacity of pile foundation under the action of underlying karst cave, and put forward a new calculation method of roof thickness. Huang et al. [8] used the numerical modeling of pile foundation in karst area of Chongqing-Guizhou Railway to analyze the vertical bearing characteristics of pile foundation crossing multi-layer karst cave, and put forward two different shear failure modes of karst cave roof. The thickness of rock stratum and the span ratio of karst cave are different, and the failure modes of rock stratum are different. The lateral friction resistance of pile foundation in karst cave is greatly attenuated. On the basis of the measured data, HORVATH et al. [9] established the relationship between the pile side resistance and the saturated uniaxial compressive strength of rock. CARRUBBA et al. [10] carried out field tests to obtain the relationship between pile side resistance and uniaxial compressive strength of bedrock. Based on the modified Hoek-Brown strength criterion, SERRANO et al. [11,12] proposed a calculation method for the ultimate bearing capacity of rock-socketed piles in soft and hard rocks, and analyzed its bearing mechanism. KHAN et al. [13] used the finite element model to simulate the pile-rock interface, and analyzed the influence of the roughness of the pile-rock interface on the bearing capacity of the pile foundation. SINGH et al. [14] studied the bearing characteristics of rock-socketed piles under inclined load by numerical simulation, and analyzed the influence of rock-socketed depth and other factors on the bearing capacity of pile foundation. To sum up, although a large number of scholars have studied the influence of karst cave on bridge pile foundation, most of them consider the influence of single karst cave [15,16]. In practical engineering, pile foundation needs to cross multi-layer karst cave and the design and calculation method of bearing capacity of pile foundation crossing multi-layer karst cave is not given in the current code [17,18,19].

In order to study the influence factors of vertical bearing capacity of pile foundation under the special condition of multi-layer karst. The finite element model of double-layer karst pile foundation is established by using Ansys Workbench commercial general finite element software. The bearing capacity of concrete pile foundation with different rock height, different eccentricity and different elastic modulus under gradually increasing load is studied. The above research results can better guide the design and construction of pile foundation in multi-layer karst area.

2. Engineering Geological Survey and Working Condition Setting

2.1. Engineering Geological Survey

The project is located on the east side of the intersection of the entrance and exit of Dunan Expressway in Mashan County, Nanning City, Guangxi Province and the provincial highway 20324 line. The site landform belongs to the karst basin. The geological conditions are shown in Figure 1. The first layer is back fill soil with a height of 3.8 m. The second layer is broken limestone with a height of 0.6 m. The third layer is karst cave with a height of 4.5 m. The fourth layer is broken limestone with a height of 2.4 m. The fifth layer is karst cave with a height of 3.2 m. The sixth layer is relatively complete limestone. The height of the pile is 15 m, and the most complete limestone is 0.5 m.

2.2. Working Condition Setting

The pile foundation in karst geology is easily affected by various factors. This paper will mainly analyze the influence of different eccentricity, different diameter and different elastic modulus on the bearing capacity of pile foundation. According to 5.3.5 in ‘Technical code for building pile foundation’ (JGJ94-2008) [18]

Q_{u k} = Q_{s k} + Q_{p k} = μ \sum q_{s i k} l_{i} + q_{p k} A_{p}

(1)

Where

q_{s i k}

is the standard value of the ultimate lateral resistance of the first layer of soil on the pile side,

q_{p k}

is the standard value of the ultimate end resistance.

The standard value

Q_{u k}

of vertical ultimate bearing capacity of single pile with pile diameter of 1.0 m is estimated. ZK05 drilling hole is selected. When the pile end enters the broken limestone layer of 2.00 m, the standard value

Q_{u k}

of vertical ultimate bearing capacity of single pile can reach 8842.87 KN (pile length is about 22.72 m). ZK19 borehole is selected. When the pile end enters the more complete limestone layer 1.00 m, the standard value of the vertical ultimate bearing capacity of the single pile

Q_{u k}

can reach 9132.47 KN (the pile length is about 16.10 m), of which the more broken limestone layer

f_{r k}

is 21.6 MPa, and the more complete limestone layer

f_{r k}

is 51.9 MPa. In this paper, the design bearing capacity of the AB type punched cast-in-place pile with an outer diameter of 500 mm and a wall thickness of 125 mm is 3701 KN. Therefore, three different working conditions are established for these three factors

Condition 1: The AB type punched cast-in-place pile with an outer diameter of 500 mm and a wall thickness of 125 mm is used to design the loading steps. The initial loading value is 2000 KN, the loading step is 500 KN, and the ultimate loading value is 5000 KN. The maximum displacement of the pile and the change of the maximum stress are studied under different eccentricity conditions. (2) The stress and strain of the same eccentricity and the same force are loaded. (3) Under the same force, the stress and strain changes under different eccentricity conditions.

Working condition 2: Using 500 mm AB type punching pile, under the loading condition of working condition 1, the Young’s modulus of pile foundation material is changed, and the displacement and stress changes of concrete with different strength under the eccentricity of 0.005 and 0.01 are studied.

Condition 3: Change the height of the fourth layer of broken limestone, and use the AB type punched cast-in-place pile with an outer diameter of 500 mm. The design value of the vertical bearing capacity of the pile body is 3701 KN, and the influence of the height of the karst cave on the bearing capacity of the pile foundation is studied.

3. Numerical Simulation

3.1. Finite Element Model

Due to the special conditions of karst geology and most of the broken limestone around the pile foundation, the stress mode of the pile used in this model is mainly the end force. The pile established by the finite element has a 50 mm interval with the surrounding soil. The contact relationship between the pile body and the surrounding limestone and soil layer and the contact relationship between the pile bottom and the limestone in contact with it are set to frictional. The friction coefficient is set to 0 [7,8]. The pile body is set as the active contact surface, and the surrounding limestone and soil are set as the passive contact surface. The contact between the first layer of backfill soil and the second layer of broken limestone is set to bonded. Fixed constraints are set on the surface of soil and limestone and the bottom of the lowest limestone. Because the stiffness of the pile is much larger than that of the surrounding rock and soil, the pile material is set to be linear elastic material, and the surrounding soil is set to be ideal elastic-plastic model, and the Drucker-Proger model is used to reflect its elastic-plastic characteristics. Due to the small influence on the soil outside a certain range, the soil with a diameter of 10 times of the pile body and 2.5m deep soil under the pile body are taken to establish the finite element model. The finite element model is shown in Figure 2, and the required material parameters are shown in Table 1.

3.2. Numerical Simulation Results Analysis

According to the above three specific conditions, three different numerical simulations of parameter analysis are established. The influence of these three factors on the displacement and stress of pile foundation is reflected by changing the eccentric distance, Young’s modulus and pile diameter. This paper mainly discusses several kinds of eccentricity in the following Table 2.

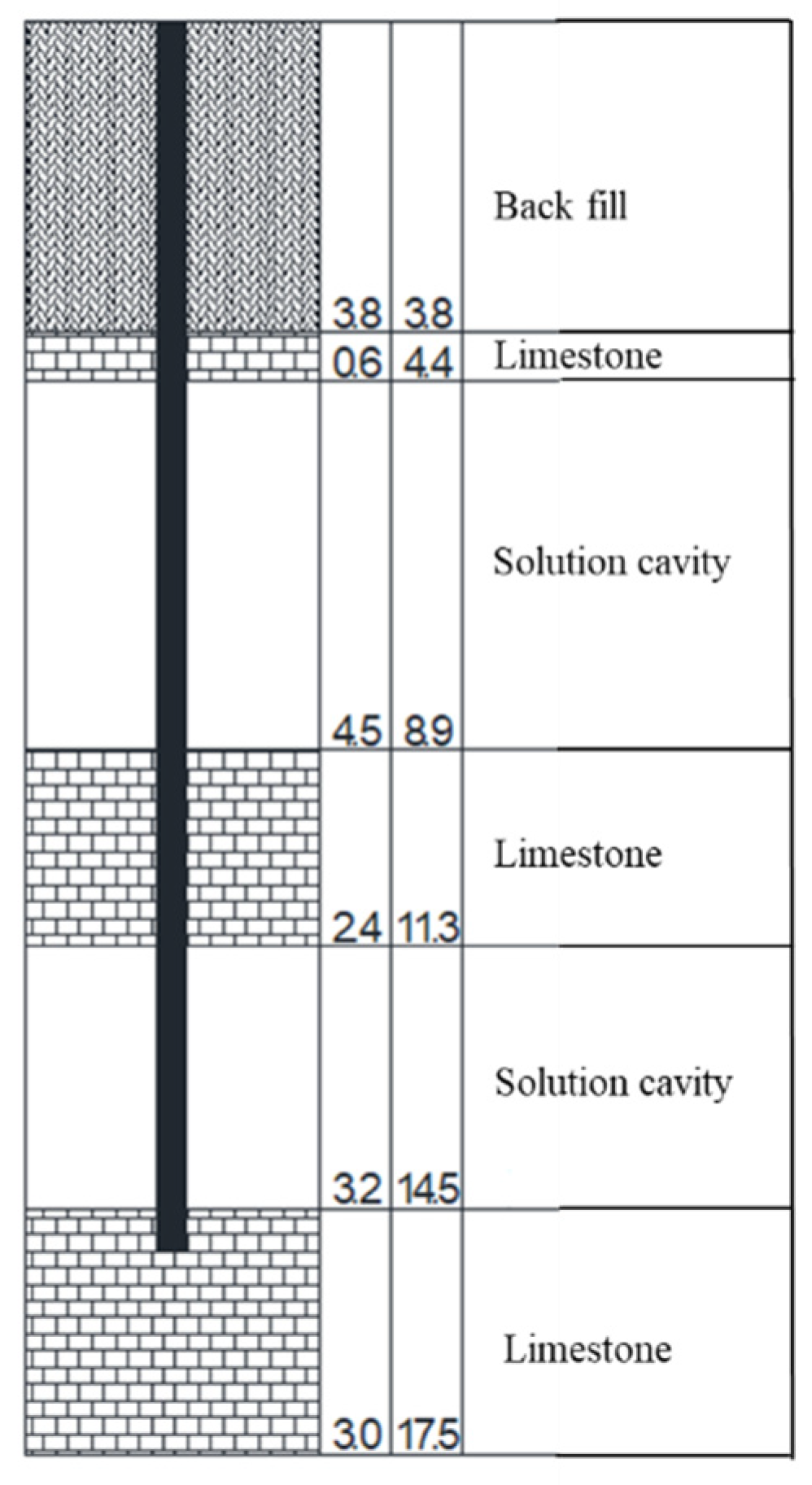
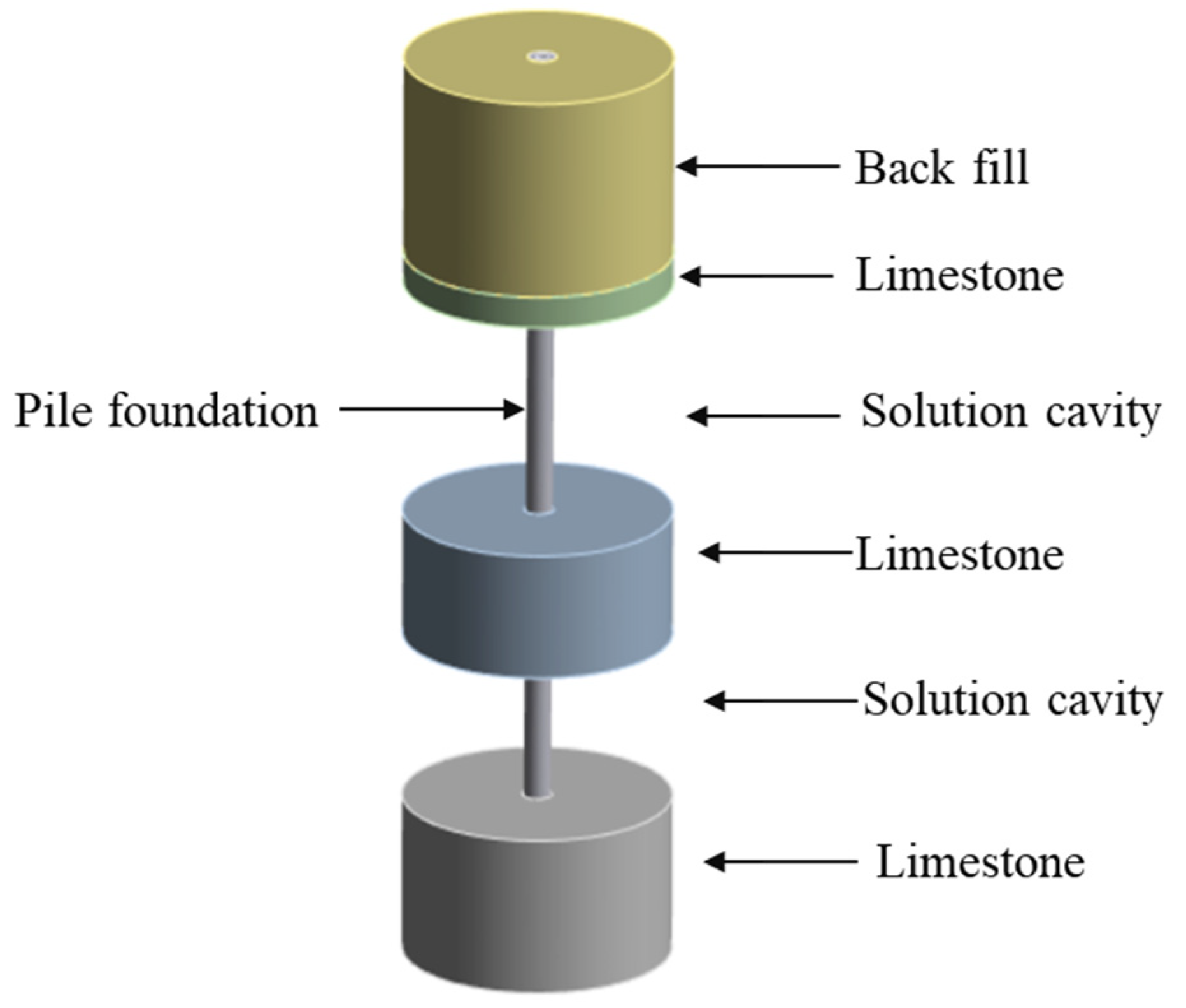
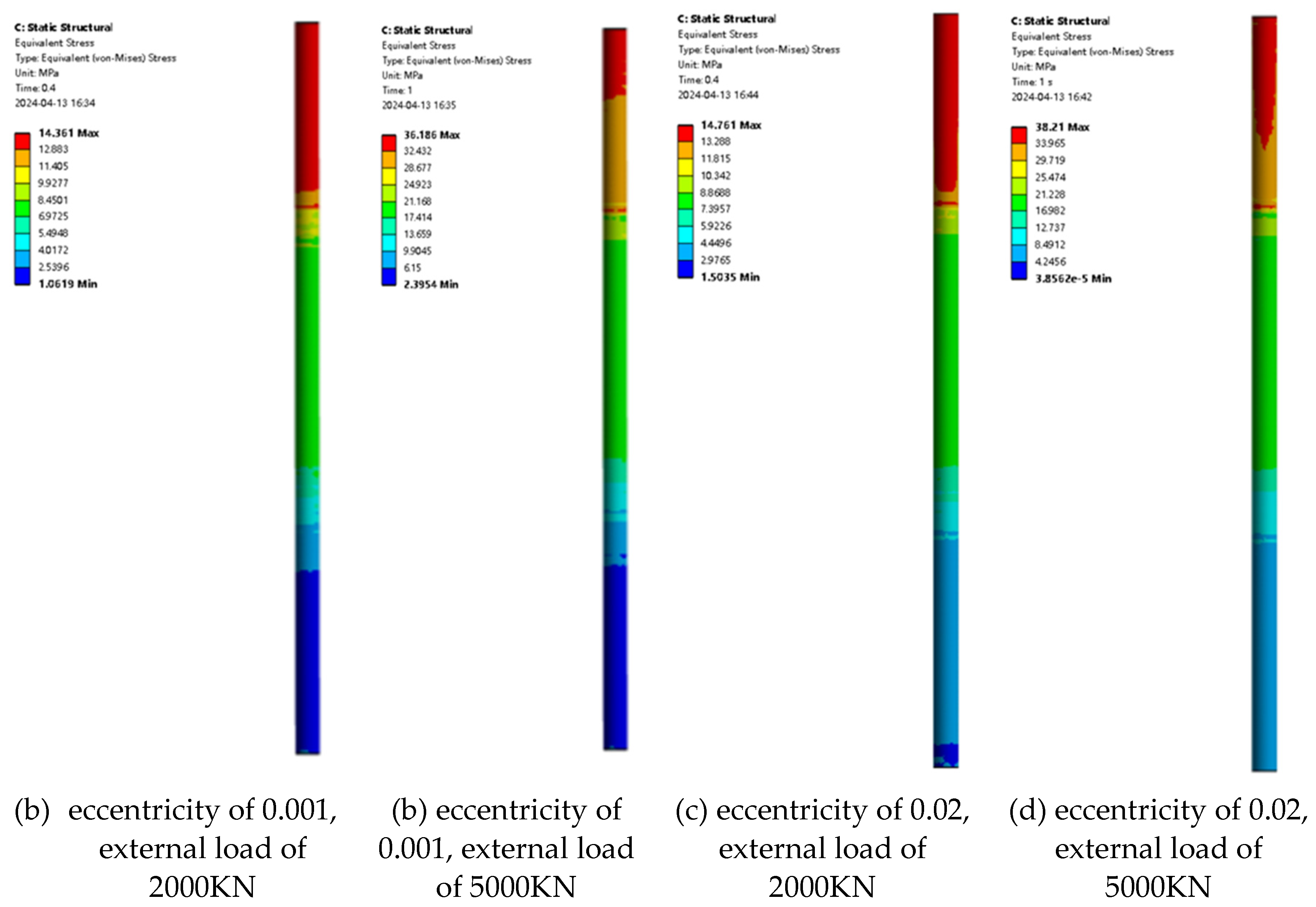
3.2.1. Effect of Eccentricity on Pile Deformation and Bearing Capacity

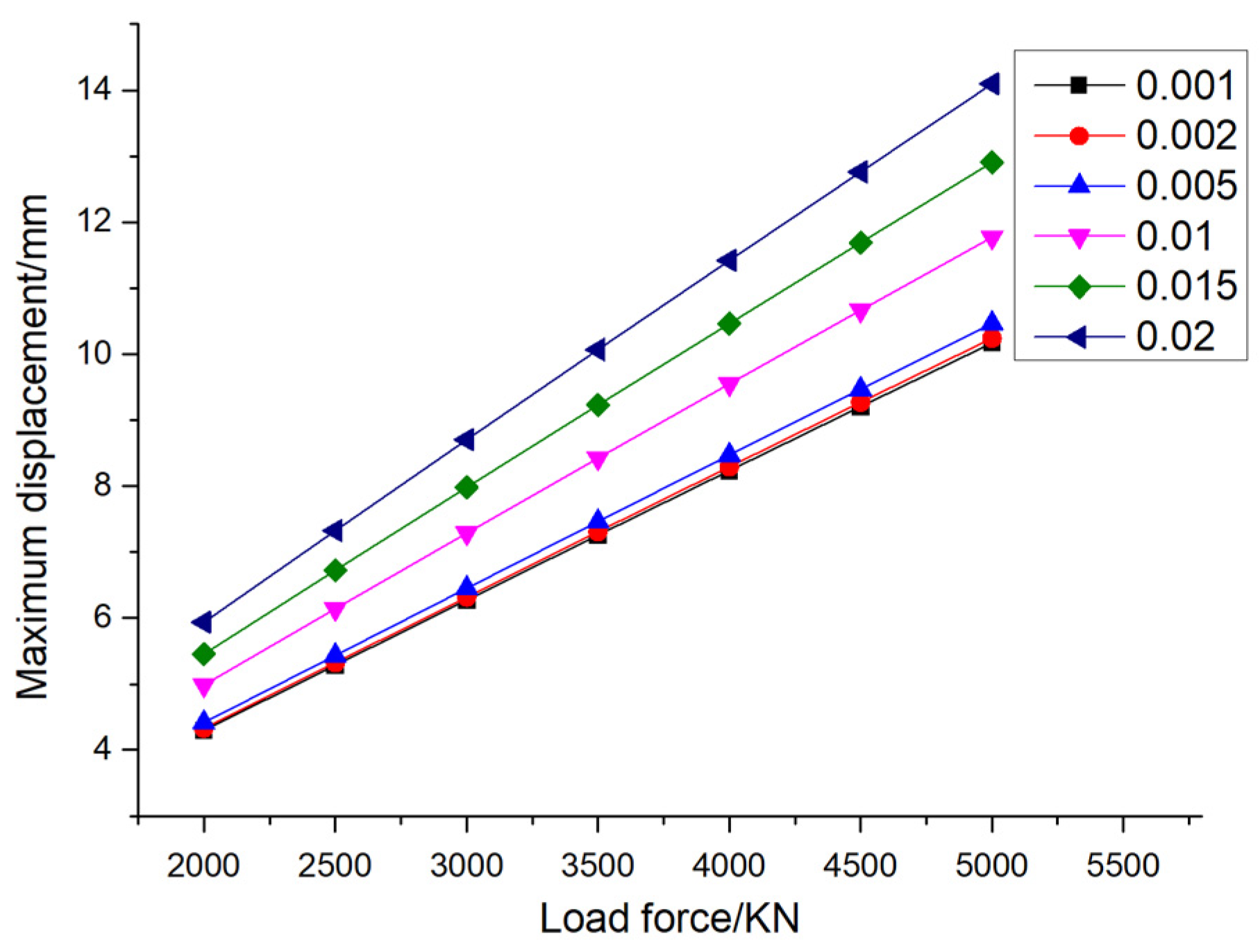
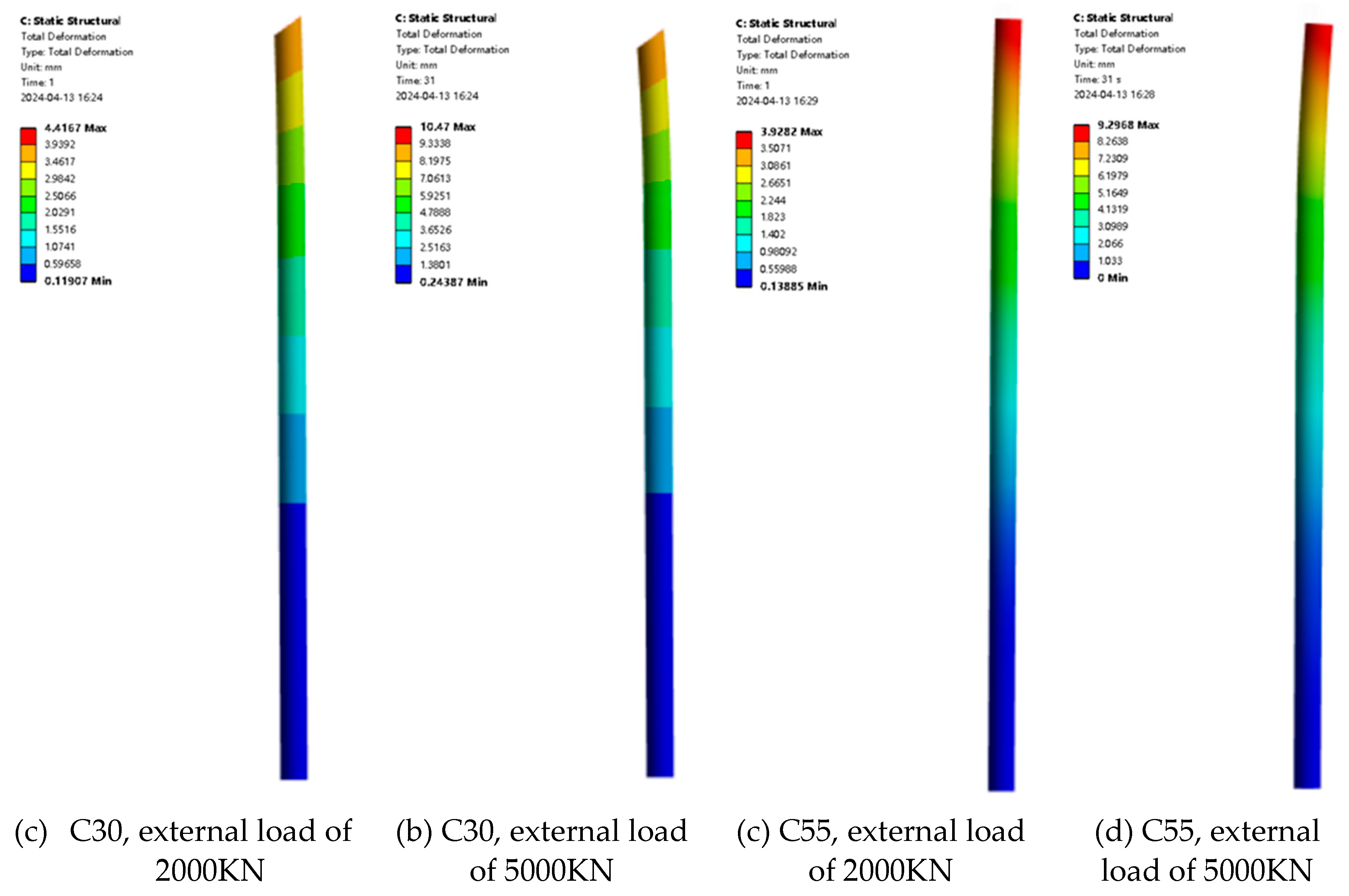
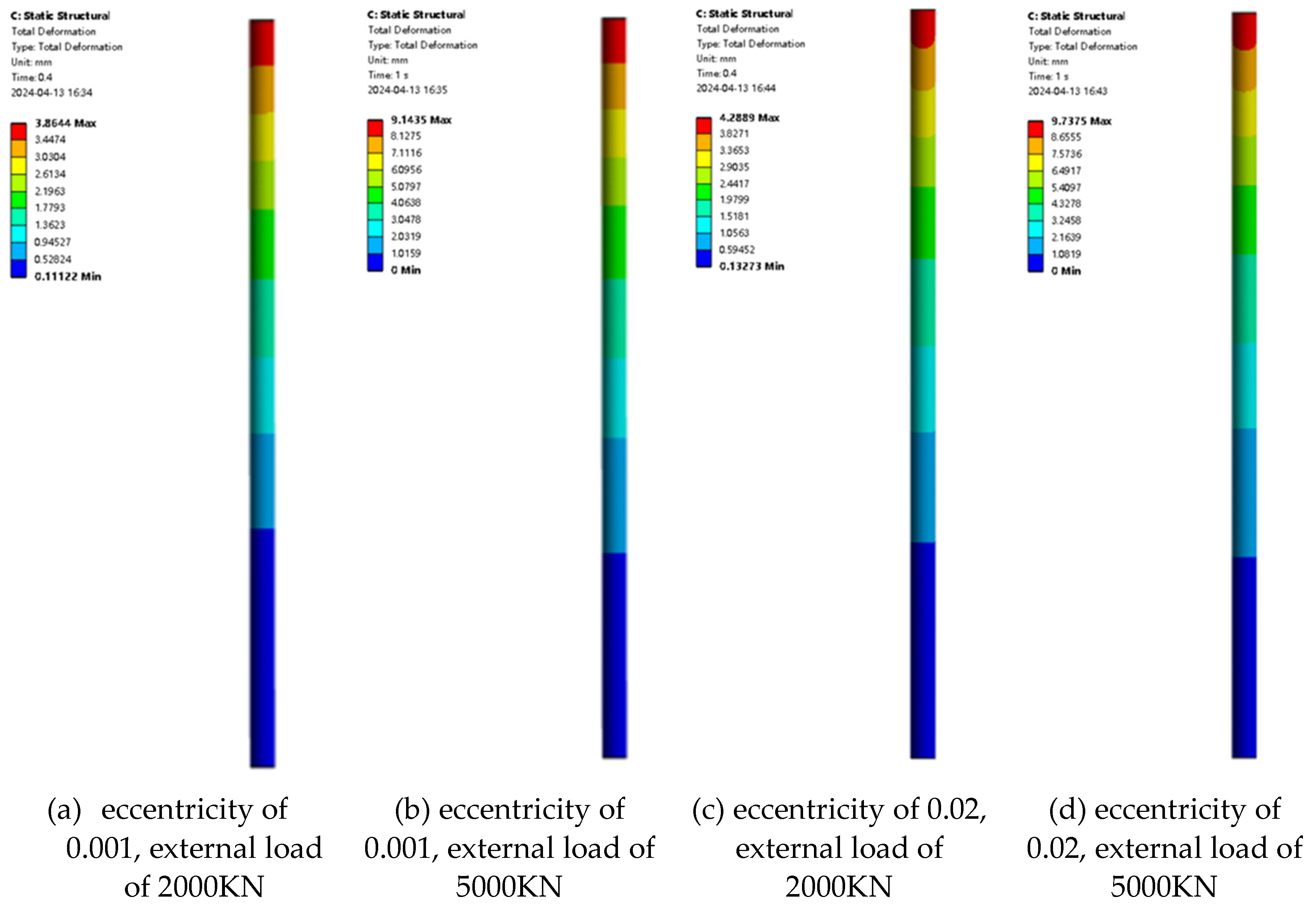
Figure 3 and Figure 4 show the maximum displacement and the displacement contour of pile foundation under different eccentricity and different loading, respectively. It can be seen from the figure that when the eccentricity is determined, the maximum displacement of the pile foundation increases with the increase of loading. Taking the eccentricity of 0.001 as an example, when the external load is divided into 2000KN, 2500KN, 3000KN, 3500KN, 4000KN, 4500KN and 5000KN, the maximum displacement of the pile foundation is 4.30mm, 5.29mm, 6.27mm, 7.26mm, 8.24mm, 9.21mm and 10.17mm, respectively. Taking the eccentricity of 0.02 as an example, when the external load is divided into 2000KN, 2500KN, 3000KN, 3500KN and 4000KN, 4500KN and 5000KN, the maximum displacement of the pile foundation is 5.94mm, 7.32mm, 8.70mm, 10.07mm, 11.42mm, 12.76mm and 14.10mm, respectively. From the above data, it can be seen that the increase rate of the maximum displacement of the pile foundation increases with the increase of the eccentricity. When the external load is determined, the maximum displacement of the pile foundation increases with the increase of eccentricity. Taking the external load of 2000 KN as an example, when the eccentricity is 0.001,0.002,0.005,0.01,0.015 and 0.02, the maximum displacement of the pile foundation is 4.30 mm, 4.33 mm, 4.41 mm, 4.99 mm, 5.45 mm and 5.94 mm, respectively. Taking the external load of 5000 KN as an example, when the eccentricity is 0.001, 0.002, 0.005, 0.01, 0.015 and 0.02, the maximum displacement of the pile foundation is 10.17 mm and 10.24 mm, 10.47mm, 11.77mm, 12.91mm and 14.10mm, respectively. When the eccentricity is determined, the maximum displacement of the pile foundation increases with the increase of the external load.

Figure 5 and Figure 6 show the maximum stress and the stress contour of pile foundation under different eccentricity and different loading, respectively. It can be seen from the figure that when the eccentricity is determined, the maximum stress of the pile foundation increases with the increase of loading. Taking the eccentricity of 0.001 as an example, when the external load is divided into 2000KN, 2500KN, 3000KN, 3500KN, 4000KN, 4500KN and 5000KN, the maximum displacement of the pile foundation is 15.10MPa, 18.84MPa, 22.59MPa, 26.34MPa, 30.09MPa, 33.84MPa and 37.60MPa. Taking the eccentricity of 0.02 as an example, when the external load is divided into 2000KN, 2500KN, 3000KN, 3500KN, 4000KN, 4500KN and 5000KN, the maximum stress of the pile foundation is 17.37MPa, 21.69MPa,26.05MPa,30.44MPa,34.85MPa, 39.27MPa and 43.70 MPa, respectively. From the above data, it can be seen that the increase rate of the maximum stress of the pile foundation increases with the increase of the eccentricity. When the external load is determined, the maximum stress of the pile foundation increases with the increase of eccentricity. Taking the external load of 2000 KN as an example, when the eccentricity is 0.001,0.002,0.005,0.01,0.015 and 0.02, the maximum stress of the pile foundation is 15.10MPa, 15.11MPa, 15.29MPa, 15.79MPa, 16.65MPa and 17.37 MPa, respectively. Taking the external load of 5000 KN as an example, when the eccentricity is 0.001,0.002,0.005,0.01,0.015 and 0.02, the maximum stress of the pile foundation is 37.61MPa, 37.58MPa, 38.02MPa, 39.83MPa, 42.03MPa and 43.699MPa, respectively. When the eccentricity is determined, the maximum stress of the pile foundation increases with the increase of the external load.

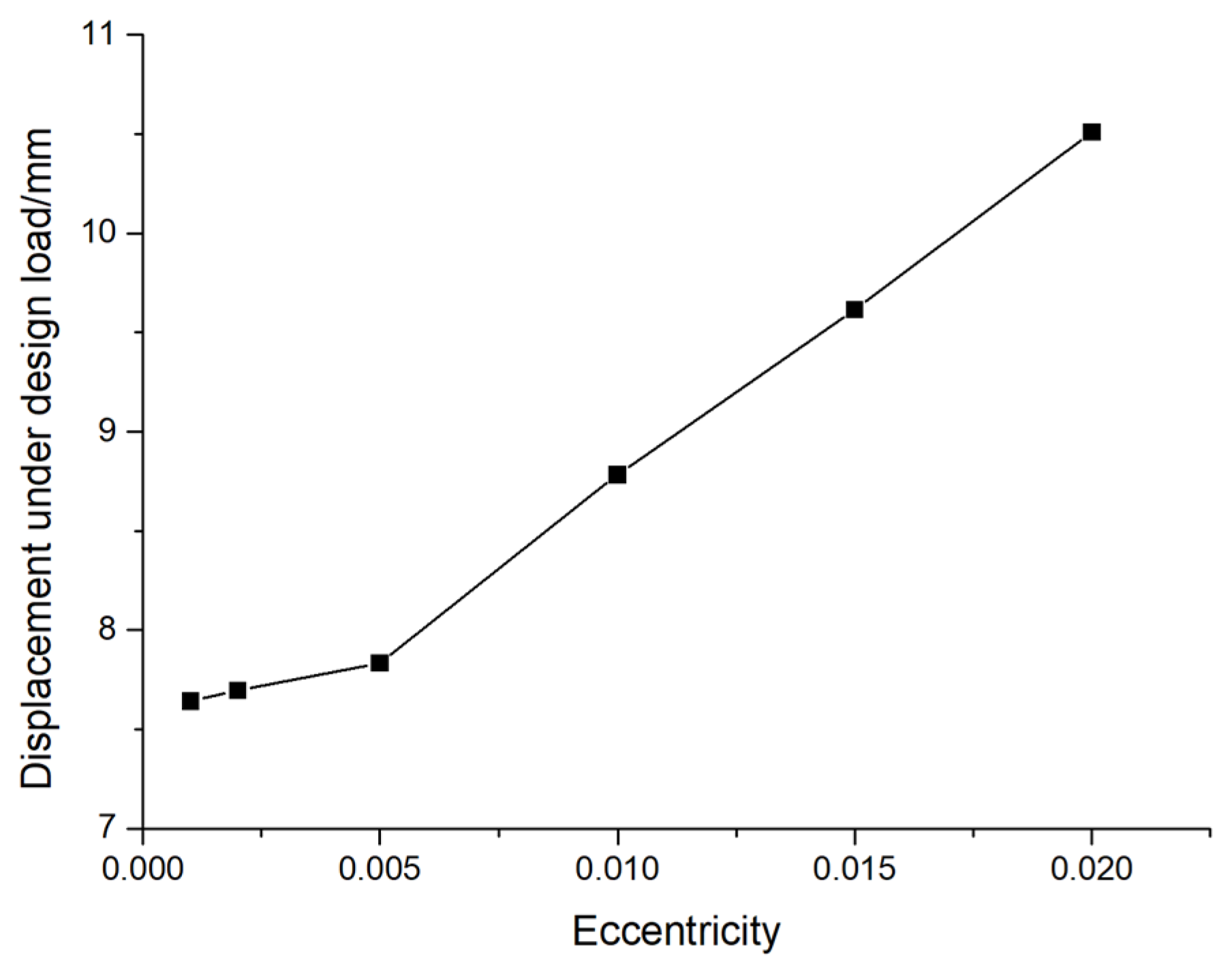
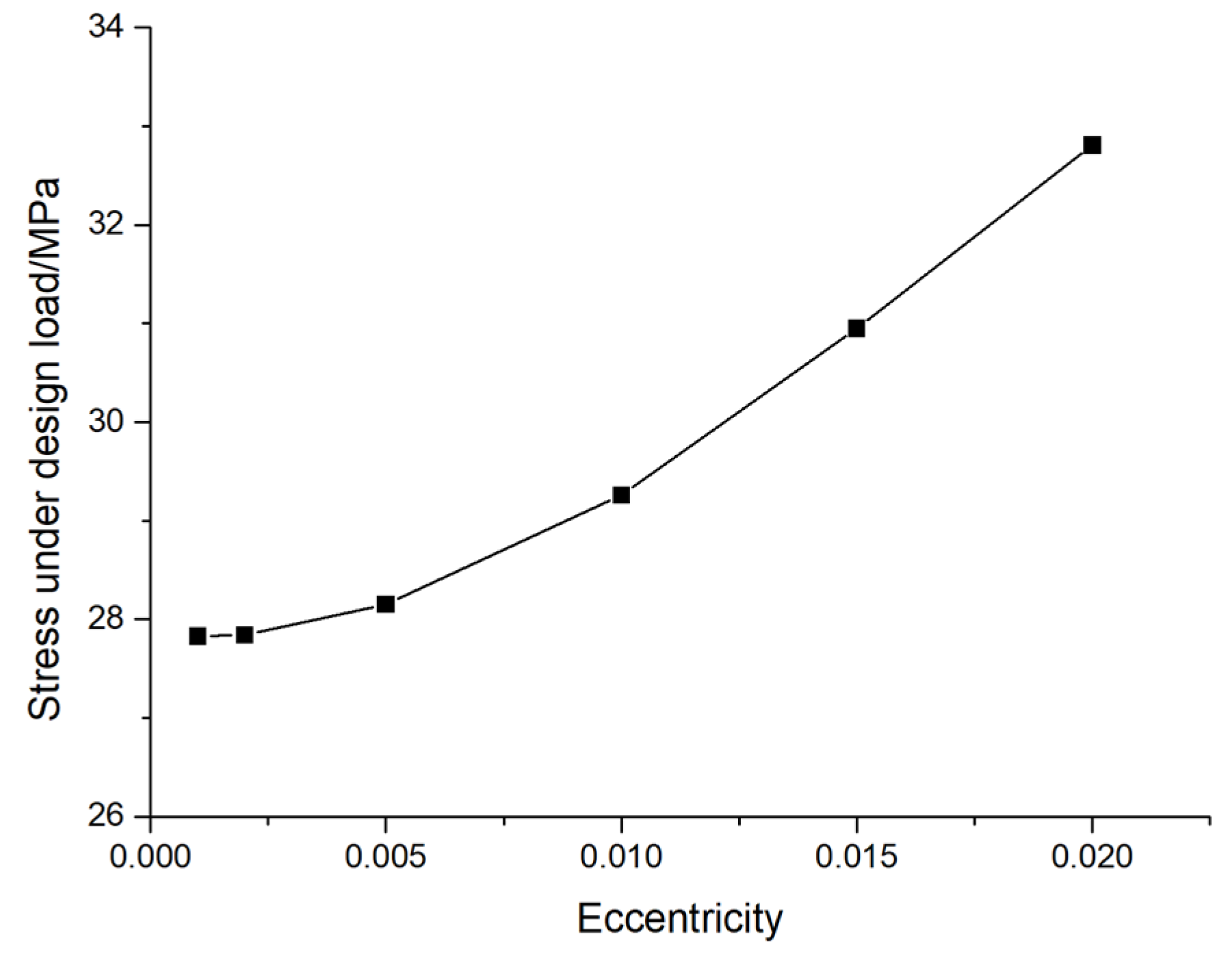
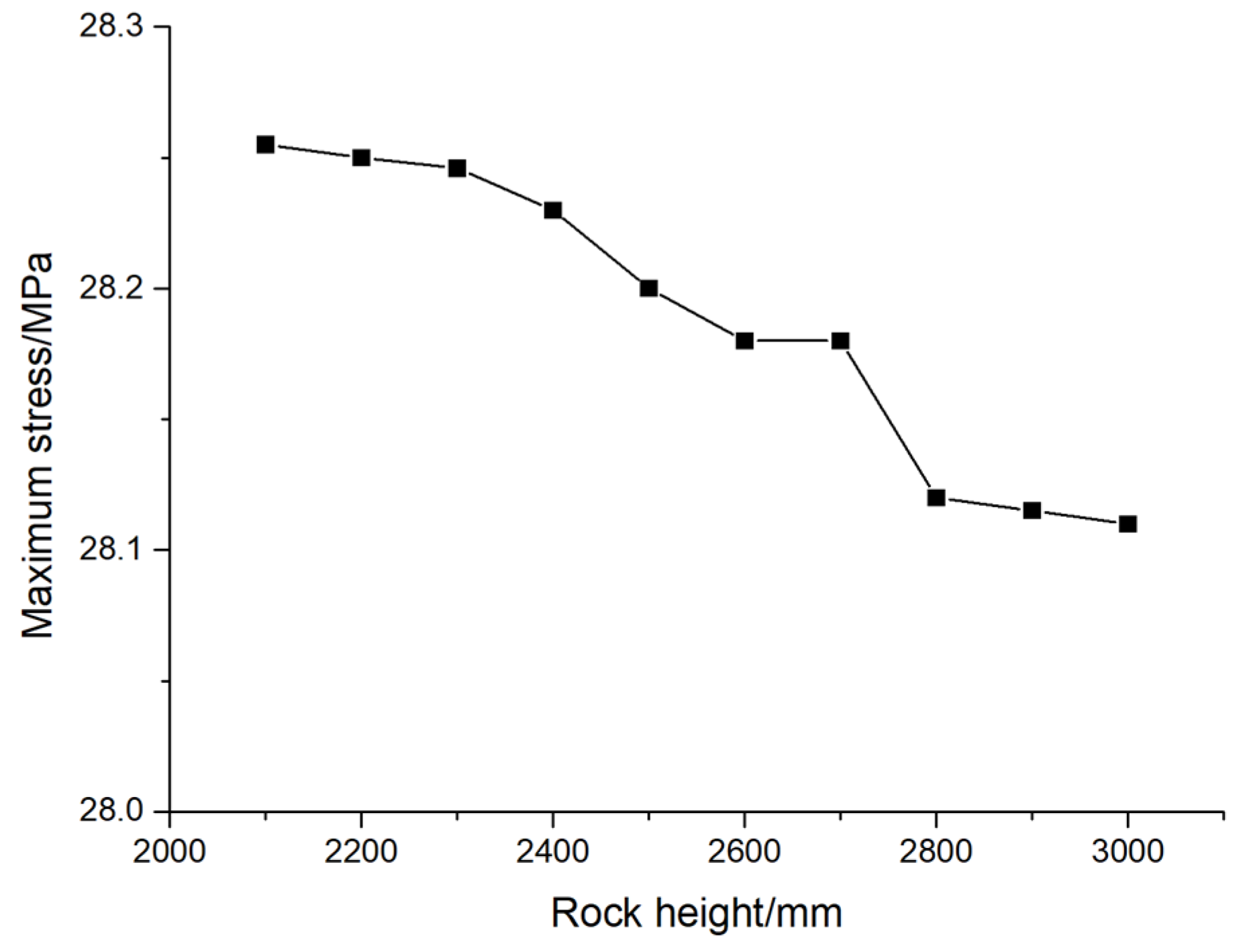
In order to study the performance of pile foundation under the design value of its vertical bearing capacity, the AB type prestressed concrete pipe pile with an outer diameter of 500 mm and a wall thickness of 125 mm is taken as an example, and the displacement and stress under the design bearing capacity are calculated respectively. The variation law of eccentricity, as shown in Figure 7 and Figure 8. From the diagram, it can be seen that the maximum displacement of the pile foundation increases with the increase of the eccentricity, and the slope of the change curve also increases, that is, the increase rate of the maximum displacement also increases with the increase of the eccentricity. When the eccentricity is 0.001,0.002,0.005,0.01,0.15 and 0.02, the maximum displacements at the design load are 7.64mm, 7.70mm, 7.83mm, 8.78mm, 9.62mm and 10.51mm, respectively. At the same time, the stress of the pile foundation also increases with the increase of the eccentricity, and the slope of the change curve also increases, that is, the increase rate of the stress also increases with the increase of the eccentricity. When the eccentricity is 0.001,0.002,0.005,0.01,0.15 and 0.02, the stress at the design load is 27.83 MPa, 27.84 MPa, 28.15 MPa, 29.26 MPa, 30.95 MPa and 32.21 MPa, respectively. The variation of displacement and stress with eccentricity is consistent with the law observed in Figure 3 and Figure 5. The reason for the above phenomenon is that there is a 50 mm interval between the pile body and the soil boundary. When the eccentricity is small, there is mainly the bottom rock embedded in the pile foundation to resist the external force, and its deformation does not contact with the surrounding soil. When the eccentricity is large, the pile foundation bears a large lateral load, which will contact with the surrounding soil, resulting in the above change law.

3.2.2. Effect of Elastic Modulus on Pile Deformation and Bearing Capacity

In order to study the influence of the elastic modulus of the pile foundation’s own material on the deformation and bearing capacity of the pile foundation, this section keeps the geometric size of the pile foundation unchanged, the external loading method unchanged, and the eccentricity unchanged, and only modifies the elastic modulus of the pile foundation’s own material. The elastic modulus parameters of pile foundation materials considered in this paper are shown in Table 3.

According to the previous research, the displacement and bearing capacity of pile foundation increase with the increase of eccentricity. In order to better discuss the influence of elastic modulus of pile foundation material, two cases of eccentricity of 0.005 and 0.01 are selected for analysis.

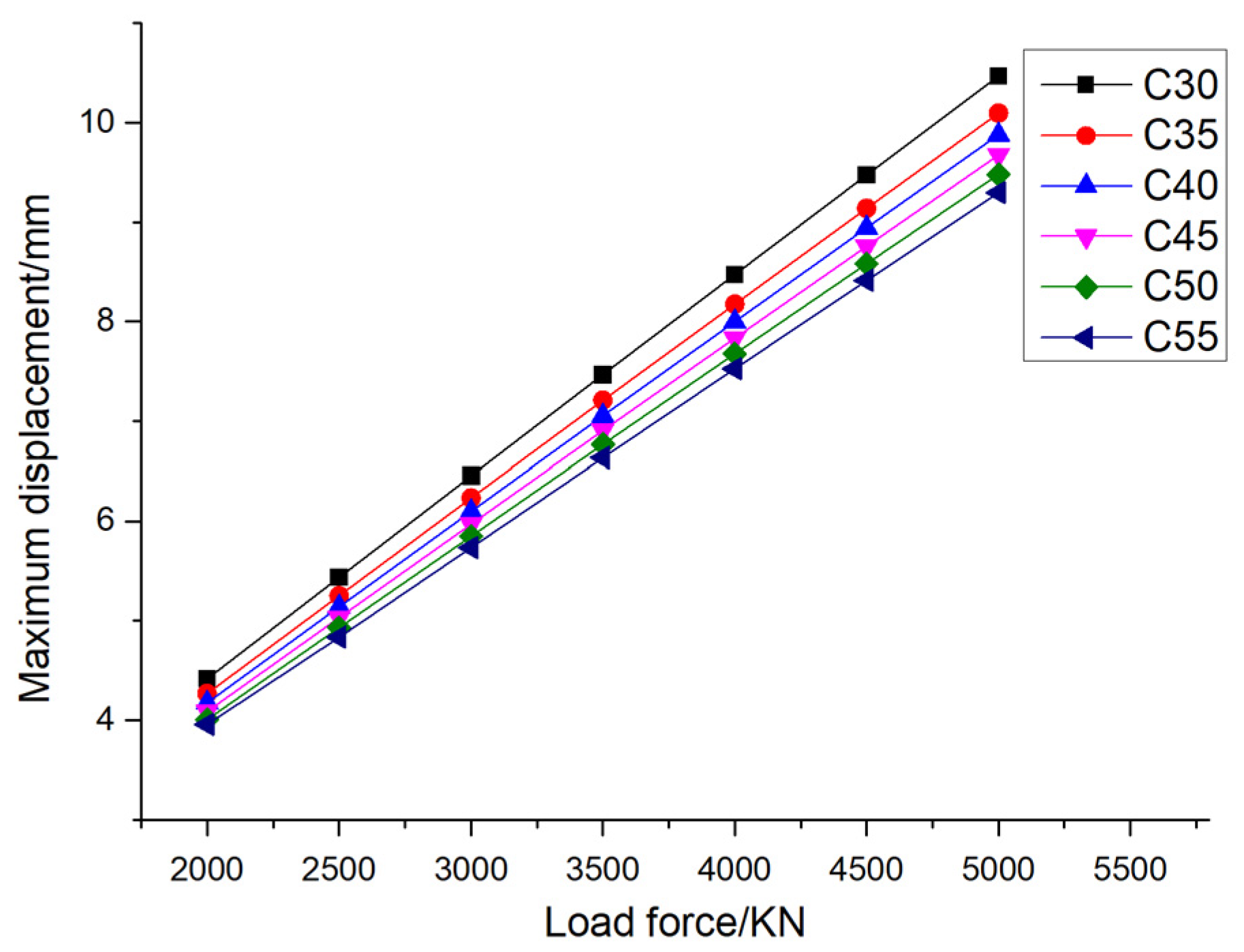
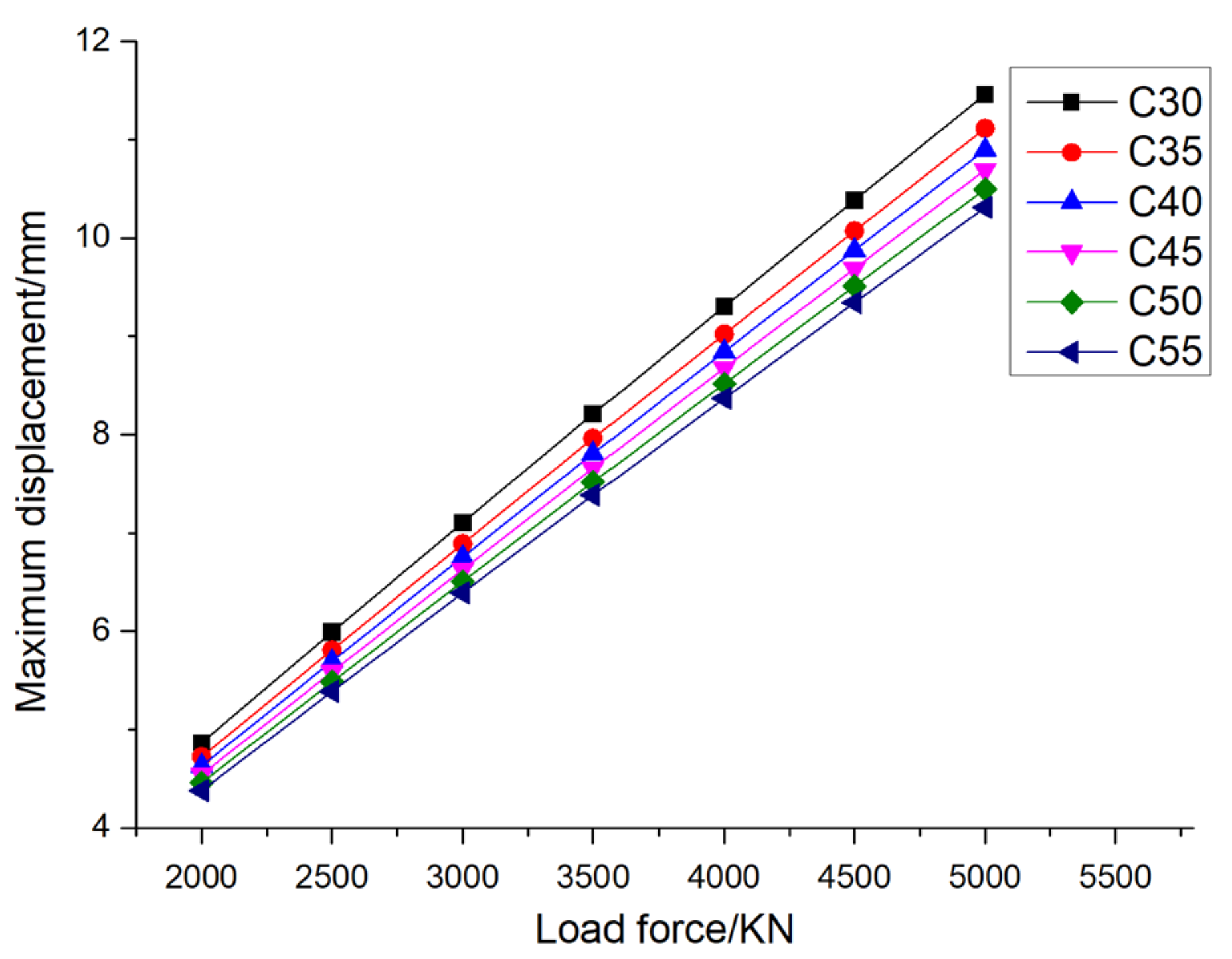
Figure 9 gives the variation of the maximum displacement of the pile foundation with the material properties of the pile foundation itself under different loading conditions when the eccentricity is 0.005. It can be seen from the figure that when the pile foundation material is determined, the maximum displacement of the pile foundation increases with the increase of loading. Taking the pile foundation material C30 as an example, when the external load is divided into 2000KN, 2500KN, 3000KN, 3500KN, 4000KN, 4500KN and 5000KN, the maximum displacement of the pile foundation is 4.42mm, 5.44mm, 6.45mm, 7.47mm, 8.47mm, 9.47mm and 10.47mm. Taking the pile foundation material C55 as an example, when the external load is divided into 2000KN, 2500KN, 3000KN, 3500KN, 4000KN. The maximum displacements of pile foundation are 3.96mm, 4.83mm, 5.74mm, 6.63mm, 7.53mm, 8.41mm and 9.30mm at 4500KN and 5000KN, respectively. Through the above data, it can be seen that the increase rate of the maximum displacement of the pile foundation decreases with the increase of the elastic modulus of the pile foundation material. When the external load is determined, the maximum displacement of pile foundation decreases with the increase of elastic modulus of pile foundation material. Taking the external load of 2000 KN as an example, when the pile foundation materials are C30, C35, C40, C45, C50 and C55, the maximum displacements of the pile foundation are 4.42 mm, 4.27 mm, 4.17 mm, 4.09 mm, 4.01 mm and 3.96 mm, respectively. Taking the external load of 5000 KN as an example, when the pile foundation materials are C30, C35, C40, C45, C50 and C55, the maximum displacements of the pile foundation are 10.47 mm, 10.10 mm and 9.88 mm, respectively. 9.68mm, 9.48mm and 9.30mm. When the pile foundation material is determined, the maximum displacement of the pile foundation decreases with the increase of the elastic modulus of the pile foundation material.

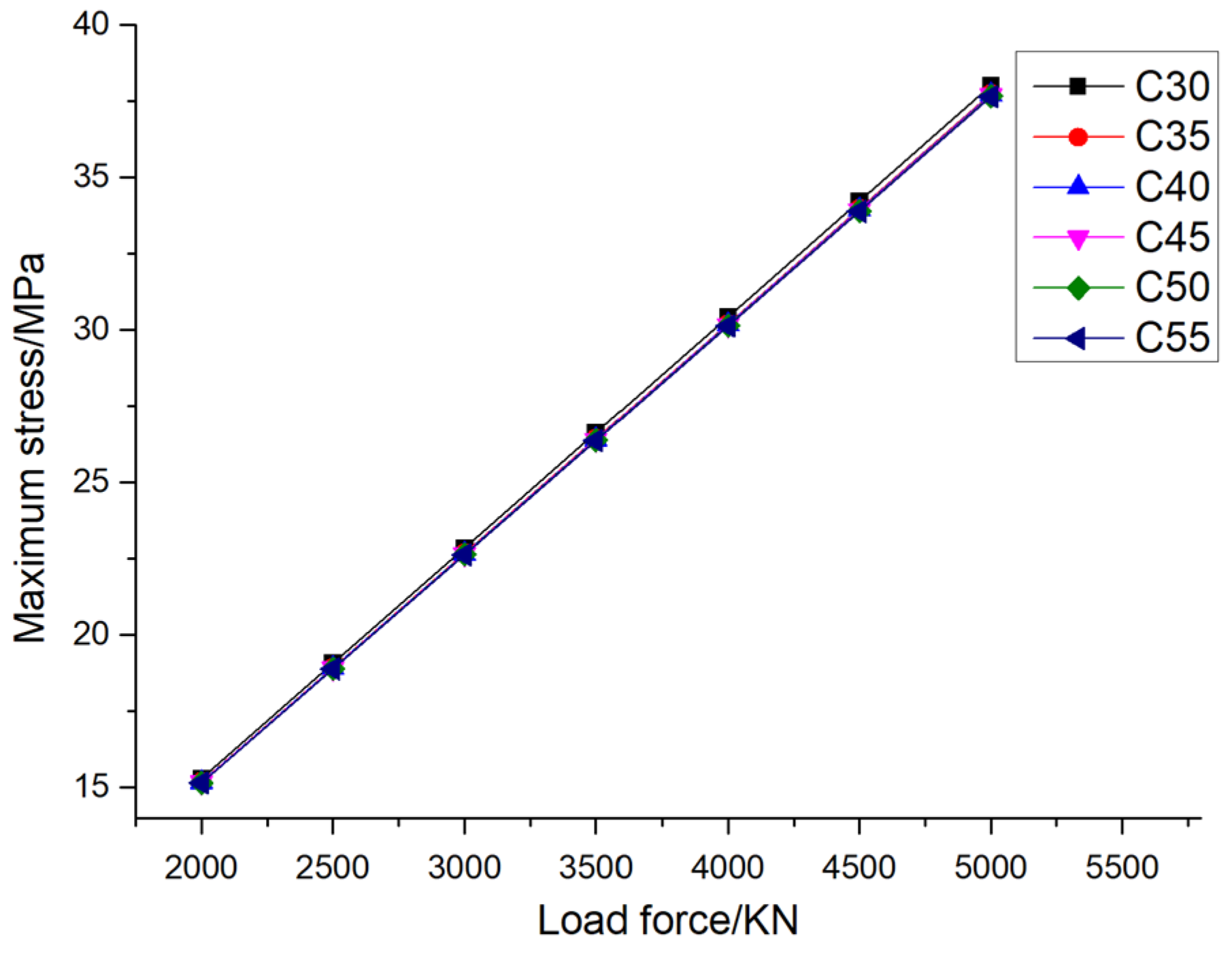
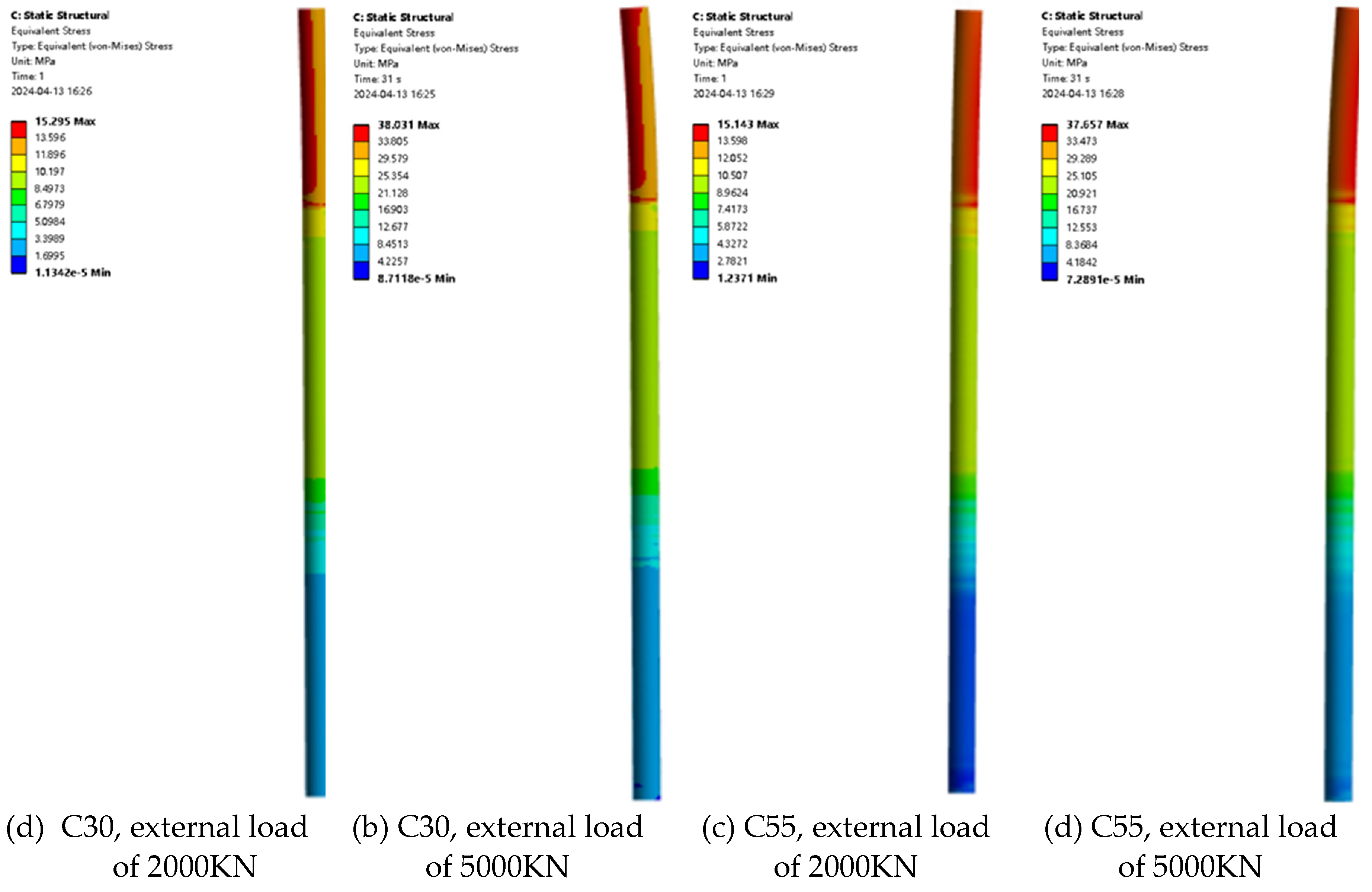
Figure 10 shows the variation of the maximum stress of the pile foundation with the material properties of the pile foundation itself under different loading conditions when the eccentricity is 0.005. It can be seen from the figure that when the pile foundation material is determined, the maximum stress of the pile foundation increases with the increase of loading. Taking the pile foundation material C30 as an example, when the external load is divided into 2000 KN, 2500 KN, 3000 KN, 3500 KN, 4000 KN, 4500 KN and 5000 KN, the maximum stress of the pile foundation is 15.30 MPa, 19.10 MPa, 22.85 MPa, 26.64 MPa, 30.43 MPa, 34.23 MPa and 38.03 MPa, respectively. Different from the change law of the maximum stress of the pile foundation, when the external load is determined. The maximum stress of pile foundation remains basically unchanged with the increase of elastic modulus of pile foundation material. Taking the external load of 2000 KN as an example, when the pile foundation materials are C30, C35, C40, C45, C50 and C55, the maximum stresses of the pile foundation are 15.30 MPa, 15.18 MPa, 15.17 MPa, 15.16 MPa, 15.15 MPa and 15.14 MPa, respectively. Taking the external load of 5000 KN as an example, when the pile foundation materials are C30, C35, C40, C45, C50 and C55, the maximum stress of the pile foundation is 38.03 MPa, 37.75 MPa, 37.72 MPa, 37.70 MPa, 37.68 MPa and 37.66 MPa, respectively. When the external load is determined, the maximum stress of the pile foundation has little to do with the strength grade of the concrete and does not belong to the main influencing factor.

The reason for the above phenomenon is that when the geometric size of the pile foundation is unchanged, the main influencing factor of the stress is the external load. When it is in the elastic deformation stage, the elastic modulus of the pile foundation itself has little effect on the stress. The deformation is different, which is equal to the product of strain and length. When the stress is constant, the increase of the strength of the material itself can reduce its own strain, thereby reducing its own deformation.

Figure 11 and Figure 12 respectively show the variation of the maximum displacement and the maximum stress of the pile foundation with the material properties of the pile foundation itself under different loading conditions when the eccentricity is 0.01. Figure 13 and Figure 14 show the displacement contour and the stress contour of the pile foundation with the material properties of the pile foundation itself under different loading conditions when the eccentricity is 0.01, respectively. It is consistent with the change law of the maximum displacement and maximum stress of the pile foundation under step loading when the eccentricity is 0.005. When the eccentricity is 0.01, when the pile foundation material is determined, the maximum displacement of the pile foundation increases with the increase of loading. When the external load is determined, the maximum displacement of pile foundation decreases with the increase of elastic modulus of pile foundation material. Different from the change law of the maximum stress of pile foundation, when the external load is determined, the maximum stress of pile foundation remains basically unchanged with the increase of the elastic modulus of pile foundation material. When the external load is determined, the maximum stress of the pile foundation is not related to the strength grade of the concrete, and it is not the main influencing factor.

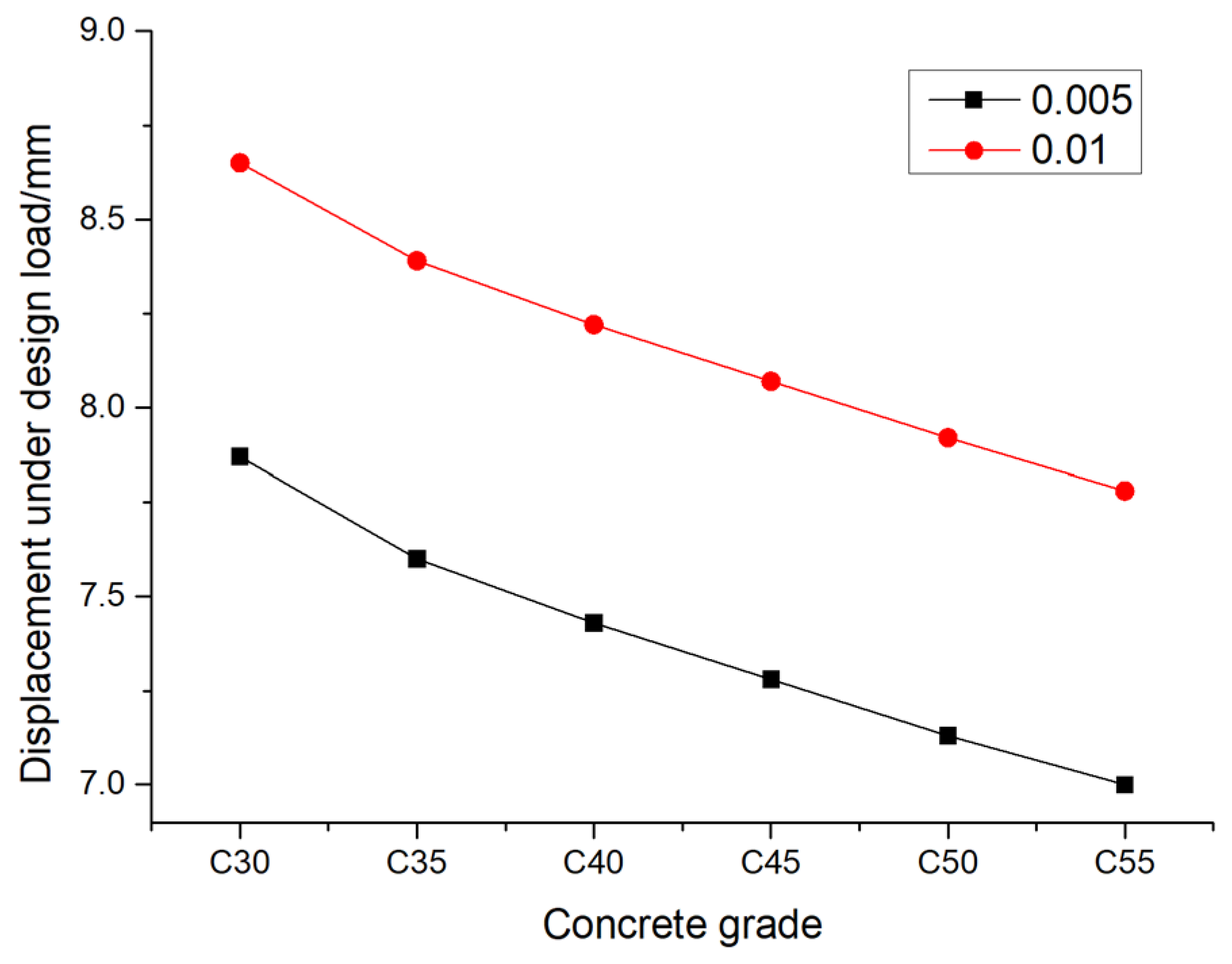
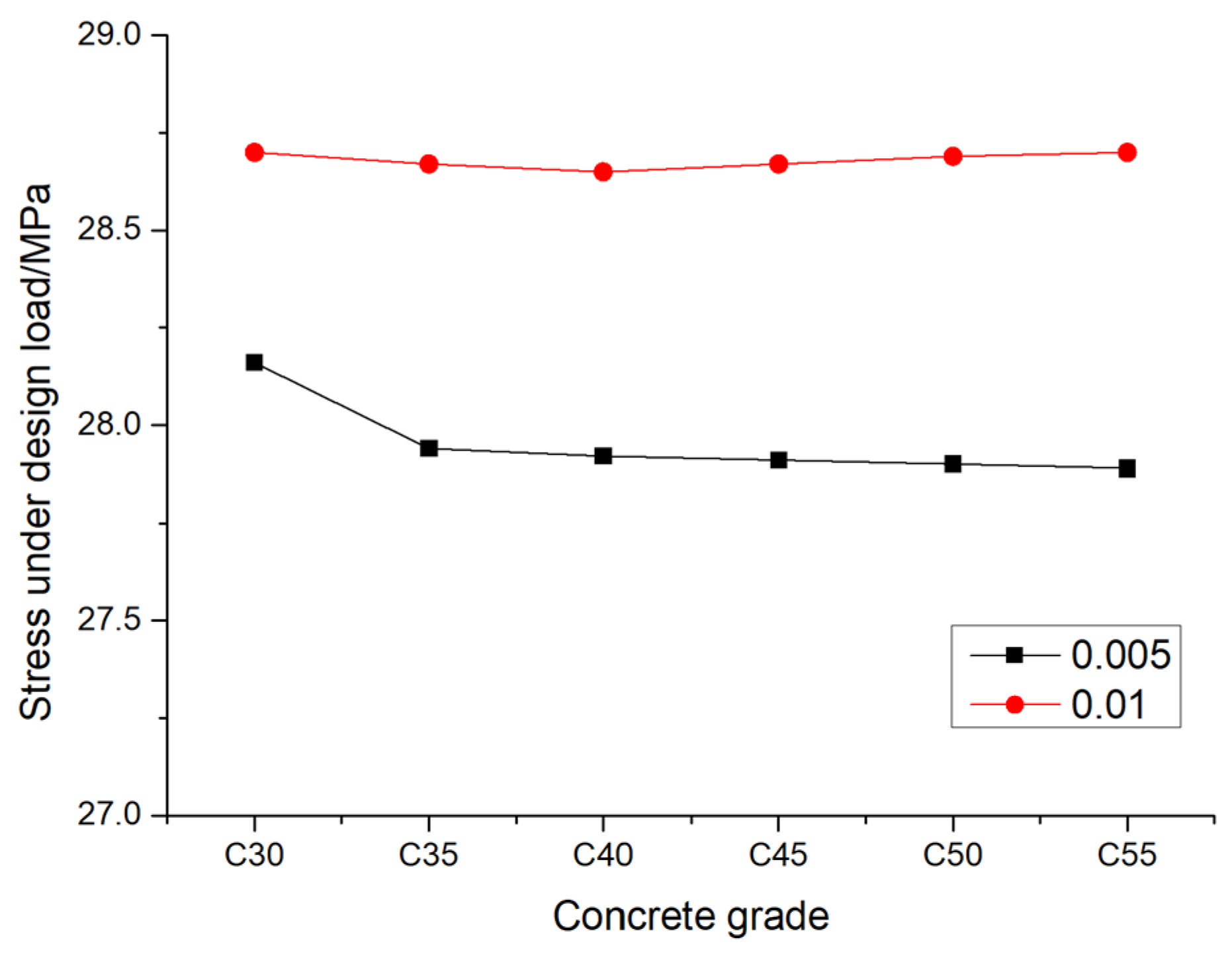
In order to further understand the maximum displacement and maximum stress of pile foundation under its design bearing capacity. The variation of the maximum displacement and the maximum stress with the elastic modulus of the pile foundation material is calculated under the eccentricity of 0.005 and 0.01, as shown in Figure 15 and Figure 16. It can be seen from the Figure 11 that the maximum displacement of the pile foundation under the design load decreases with the increase of the strength of the concrete material of the pile foundation, and when the eccentricity is 0.005 and the eccentricity is 0.01, the decreasing trend of the maximum displacement is roughly the same as the decreasing speed. When the eccentricity is 0.005, when the pile foundation materials are C30, C35, C40, C45, C50 and C55, the maximum displacement of the pile foundation is 7.87 mm, 7.60 mm, 7.43 mm, 7.28 mm, 7.13 mm and 7.00 mm, respectively. When the eccentricity is 0.01, when the pile foundation materials are C30, C35, C40, C45, C50 and C55, the maximum displacement of the pile foundation is 8.65 mm, 8.39 mm, 8.22 mm, 8.07 mm, 7.92 mm and 7.78 mm, respectively. 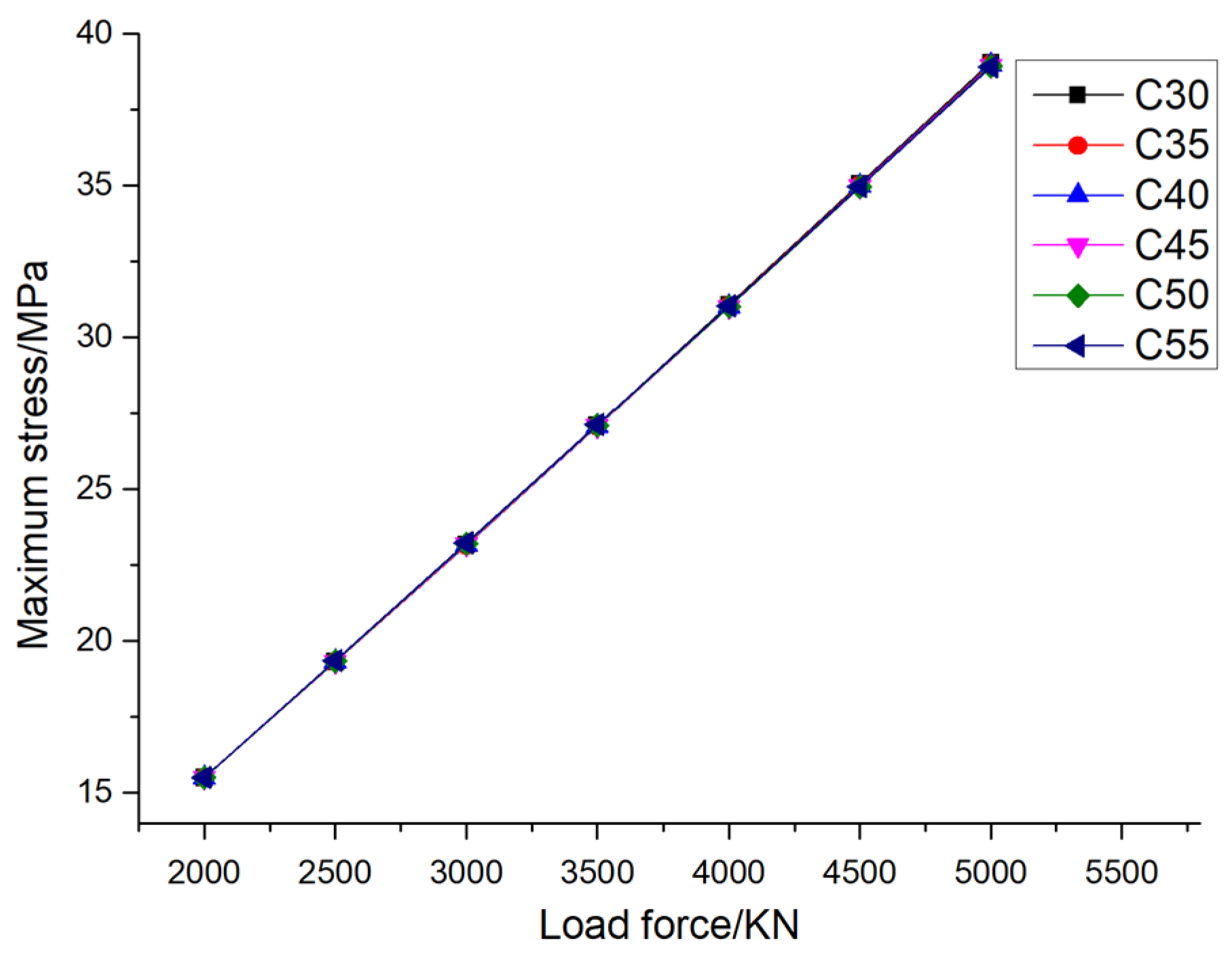It can be seen from the Figure 12 that the maximum stress of the pile foundation under the design load basically remain unchanged with the increase of the strength of the concrete material of the pile foundation, When the eccentricity is 0.005, when the pile foundation materials are C30, C35, C40, C45, C50 and C55, the maximum stress of the pile foundation is 28.16 MPa, 27.94MPa, 27.92MPa, 27.91MPa, 27.90MPa and 27.89MPa, respectively. When the eccentricity is 0.01, when the pile foundation materials are C30, C35, C40, C45, C50 and C55, the maximum stress of the pile foundation is 28.70MPa mm, 28.67MPa, 28.65MPa, 28.67MPa, 28.69MPa and 28.70MPa, respectively. The reason for the above phenomenon is that the strain of the pile foundation remains basically unchanged when the geometric size of the pile foundation and the external load remain unchanged. When the stress is constant, the strain will decrease with the increase of the elastic modulus of the pile foundation material itself. Deformation is equal to the product of strain and pile length, so its change rule is consistent with the change rule of strain. That is, the deformation of the pile foundation decreases with the increase of the elastic modulus of its own concrete material.

3.2.3. Effect of Rock Height on Pile Deformation and Bearing Capacity

In order to study the influence of rock height on the deformation and bearing capacity of pile foundation. Under the condition of keeping the eccentricity constant and the pile foundation material unchanged, that is, the load unchanged, only the height of the rock stratum is changed. Figure 17 shows the variation of the maximum displacement of the pile foundation with the height of the rock stratum. It can be seen from the figure that the maximum displacement of the pile foundation decreases with the increase of the height of the rock stratum. When the rock height increases from 2100mm to 3000mm, the maximum displacement decreases from 7.931mm to 7.686mm, and the reduction rate is 3.1%. Figure 18 shows the variation of the maximum stress of the pile foundation with the height of the rock stratum. It can be seen from the figure that the maximum stress of the pile foundation decreases with the increase of the height of the rock stratum. When the rock height increases from 2100 mm to 3000 mm, the maximum stress decreases from 28.25 MPa to 28.11 MPa, and the reduction rate is 0.5%. The reason for the above phenomenon is that with the increase of rock height, there are more external constraints around the pile foundation, so that the maximum displacement and maximum stress will decrease accordingly.

4. Conclusions

In this paper, a finite element model of foundation pile in double-layer karst area was established by using a commercial general finite element software Ansys, the bearing capacity of concrete pile foundation with different rock height different eccentricity and different elastic modulus under the gradually increasing load was studied.

The following conclusions are obtained:

(1) When the external load is constant, the maximum displacement of pile foundation increases with the increase of eccentricity. And when the eccentricity is greater than 0.015, the increase rate of the maximum displacement is gradually accelerated. It shows that the eccentricity should be strictly controlled not more than 1.5% in the construction. If it is greater than the need to increase the pile cap, increase the column section, modify the superstructure by the designer, and increase the number of piles to solve the eccentricity problem.

(2) By changing the Young’s modulus of pile foundation, it can be seen that with the increase of concrete strength, the maximum displacement decreases gradually, but the corresponding maximum stress is roughly the same. Therefore, the maximum displacement in the design of pile foundation construction needs more attention than the stress.

(3) By changing the height of the rock stratum, it can be seen that the rock cave has a great influence on the bearing capacity of the pile foundation, and it is necessary to pay attention to the karst cave with too high height. The karst cave with too high height has a great influence on the vertical bearing capacity of the pile foundation compared with the karst cave with small height but intermittent up and down. Therefore, it is necessary to understand the height and number of karst caves at the corresponding position in the construction, so as to minimize or avoid passing through the area with high karst caves.

Author Contributions

Methodology, Yi Wang; Writing—review & editing, Fenghui Dong.

Funding

Natural Science Foundation of Jiangsu Province (Grant No. BK20200793).

Data Availability Statement

The data used to support the findings of this study are available from the corresponding author upon request.

Acknowledgments

The authors wish to express their sincere to the Natural Science Foundation of Jiangsu Province (Grant No. BK20200793).

Conflicts of Interest

The authors declare no conflict of interest.

References

WANG P, DING H, ZHANG P. Influence of karst caves at pile side on the bearing capacity of super-long pile foundation[J]. Mathematical Problems in Engineering, 2020, 2020(2): 1-13.
CHEN H Y, FENG Z J, LI T, et al. Study on the vertical bearing performance of pile across cave and sensitivity of three parameters[J]. Scientific Reports, 2021, 2021(1): 17342.
LIU J K, WANG J P, ZHU M, et al. The settlement prediction of pile foundation based on grey linear regression model[J]. Applied Mechanics and Materials, 2012, 204-208: 320-325.
Su Guanfeng, He Guoing, Yi Jin, et al. Experimental study onthe vertical bearing capacity of bridge pile in multi-layer cave [ J]. Highway Engineering, 2017,42(1):80-84.
AI Kai, WANG Jing. Study of piles foundation in karst area[J]. Rock and Soil Mechanics, 2003, 24(Suppl.1):124-126.
Feng Z J,Hu HB, DongY X,et al. Effect steel casing on vertical bearing characteristics steel tube-reinforced concrete piles in loess area []Applied Sciences, 2019,9(14):2827.
Jiang C, Liu L,Wu J. A new method determining safe thickness of karst cave roof under pile tip [J]. Journal of Central South University,2014, 21(3),1190-1196.
HUANG Ming, ZHANG Bing-qi, CHEN Fu-quan, et al. Numerical calculation on load transfer progress of pile foundation in beaded karst cave stratum[J]. Journal of Engineering Geology, 2017, 25(6): 1574-1582.
HORVATH R G, KENNEY T C, KOZICKI P. Methods of improving the performance of drilled piers in weak rock [J]. Canadian geotechnical journal,1983,20(4):758-772.
CARRUBBA, P. Skin fiction on large-diameter piles socketed into rock [J]. Canadian geotechnical journal,1997,34 (2):230-240.
SERRANO A,OLALLA C. Shaft resistance of a pile embedded in rock [J]. International journal of rock mechanics and mining sci-ences,2004,41(1):21-35.
SERRANO A,OLALLA C,GALINDO R A. Ultimate bearing capacity at the tip of a pile in rock based on the modified Hoek-Brown criterion [J]. International journal of rock mechanics and mining sciences,2014,71:83-90.
KHAN A. Numerical modelling of shear socketed piers [J]. International journal for numerical and analytical methods in geomechanics,2000,24(11):853-867.
SINGH A P, BHANDARI T,AYOTHIRAMAN R, et al. Numerical analysis of rock socketed piles under combined vertical-lateral loading [J]. Procedia engineering,2017,191:776-784.
Nie O K, Li XL, Yuan W, et al. Calculation method for the critical thickness of a karst cave roof at the bottom of a socketed pile[J]. Advances in Materials Science and Engineering, 2021.14:1669410.
Yuan W, LI X, Li ZH, et al. A strength reduction method based on the generalized Hoek-Brown (GHB)criterion for rock slope stability analysis[J]. Computers and Geotechnics, 2020.117:103240.
Ministry of Housing and Urban-Rural Development of the People’sRepublic of China. General specification for building and municipalfoundation:GB55003-2021[S]. Beijing: China Architecture and Building Press, 2021.
Ministry of Housing and Urban-Rural Development of the People’sRepublie of China. Technical code for building pile foundation: JG]94-2008[S]. Beijing: China Architecture and Building Press2008.
Ministry of Housing and Urban-Rural Development of the People’sRepublic of China. Code for investigation of geotechnical engineer-ing:GB 50021-2001[S]. Beijing: China Architecture and Building Press, 2009.

Figure 1. Schematic diagram of the geological survey.

Figure 2. Finite element model.

Figure 3. The maximum displacement of pile foundation under different eccentricity and different loading force.

Figure 4. The displacement contour of pile foundation under different eccentricity and different loading force.

Figure 5. The maximum stress of pile foundation under different eccentricity and different loading force.

Figure 6. The stress contour of pile foundation under different eccentricity and different loading force.

Figure 7. The variation law of pile foundation displacement with eccentricity under design load.

Figure 8. The variation law of pile foundation stress with eccentricity under design load.

Figure 9. The maximum displacement of pile foundation under different elastic modulus and different loading force (the eccentricity is 0.005).

Figure 10. The maximum stress of pile foundation under different elastic modulus and different loading force (the eccentricity is 0.005).

Figure 11. The maximum displacement of pile foundation under different elastic modulus and different loading force (the eccentricity is 0.01).

Figure 12. The maximum stress of pile foundation under different elastic modulus and different loading force (the eccentricity is 0.01).

Figure 13. The displacement contour of pile foundation under different elastic modulus and different loading force (the eccentricity is 0.01).

Figure 14. The stress contour of pile foundation under different elastic modulus and different loading force (the eccentricity is 0.01).

Figure 15. The variation law of pile foundation displacement with concrete grade under design load.

Figure 16. The variation law of pile foundation stress with concrete grade under design load.

Figure 17. The variation curve of maximum displacement of pile foundation with the height of rock.

Figure 18. The variation curve of maximum stress of pile foundation with the height of rock.

Table 1. Material parameters used in numerical simulation.

Material	$ρ$ (kg/m³)	E(Pa)	$μ$	Cohesion(Pa)	Internal frictional angle(°)
Concrete	2500	3e10	0.3	-	-
Back fill	1580	3.5e7	0.27	1.78e4	30.2
Broken limestone	2700	3.2e9	0.275	1.5e6	45
Limestone	2700	5e9	0.275	2e6	45

Table 2. Eccentricity and eccentricity distance.

Eccentricity	0.001	0.002	0.005	0.01	0.015	0.02
Eccentricity distance/mm	15	30	75	150	225	300

Table 3. Concrete strength grade table for pile foundation.

Strength grade	C30	C35	C40	C45	C50	C55
Elastic modulus (Pa)	3e10	3.15e10	3.25e10	3.35 e10	3.45 e10	3.55 e10

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer