Prerpints.org logo
Preprint
Article

Energy-Resolved Mass Spectrometry and Mid-Infrared Microscopy for Purity Assessment of a Synthetic Peptide Cyclised by Intramolecular Click Chemistry

Altmetrics

Downloads

51

Views

33

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

25 September 2024

Posted:

26 September 2024

You are already at the latest version

Alerts
Abstract
Cyclic peptides have higher stability and better properties as therapeutic agents than their linear peptide analogues. Consequently, intramolecular click chemistry is becoming an increasingly popular method for the synthesis of cyclic peptides from their isomeric linear peptides. However, assessing the purity of these cyclic peptides by mass spectrometry is a significant challenge, as the linear and cyclic peptides have identical masses. In this paper, we have evaluated the analytical capabilities of energy-resolved mass spectrometry (ER MS) and mid-infrared microscopy (IR) to address this challenge. On the one hand, mixtures of both peptides were subjected to Collision Induced Dissociation tandem mass spectrometry (CID MS/MS) experiments in an ion trap mass spectrometer at several excitation energies. Two different calibration models were used: a univariate model (at a single excitation voltage) and a multivariate model (using multiple excitation voltages). The multivariate model demonstrated slightly enhanced analytical performance, which can be attributed to more effective signal averaging when multiple excitation voltages are considered. On the other hand, IR microscopy was used for the quantification of the relative amount of linear peptide. This was achieved through univariate calibration, based on the absorbance of an alkyne band specific to the linear peptide, and through Partial Least Squares (PLS) multivariate calibration. The PLS calibration model demonstrated superior performance in comparison to univariate calibration, indicating that consideration of the full IR spectrum is preferable to focusing on the specific peak of the linear peptide. The advantage of IR microscopy is that it is linear across the entire working interval, from linear peptide molar ratios of 0 (equivalent to pure cyclic peptide) up to 1 (pure linear peptide). In contrast, the ER MS calibration models exhibited linearity only up to 0.3 linear peptide molar ratio. However, ER MS showed better performances in terms of limit of detection, intermediate precision and root-mean-square-error of calibration. Therefore, ER MS is the optimal choice for the detection and quantification of the lowest relative amounts of linear peptide.
Keywords: 
Subject: Chemistry and Materials Science  -   Analytical Chemistry

1. Introduction

Cyclic peptides are abundant in nature and have remarkable biological activities. More than 40 cyclic peptides from nature or derivatives are used as therapeutics today. [1,2]. The cyclic structure of peptides offers improved properties compared to their linear analogues, such as proteolytic stability, lower toxicity and higher membrane permeability, binding affinity and specificity. Therefore, cyclic peptides have numerous pharmaceutical applications such as antibiotics, antifungals, hormone analogues, immunosuppressants and anti-tumour agents. [1,2,3,4]
Cyclic peptides can be obtained by either genetic or synthetic methods. Several strategies can be used to cyclize linear peptides by synthetic methods: disulfide cyclization, macrolactamization, thiol alkylation, and “click chemistry” with the Huisgen reaction. [2,5,6] The Huisgen reaction is a Cu-catalyzed cycloaddition of an azide with an alkyne to form a triazole. The added advantage of this reaction is that it is compatible with many other functional groups and that the triazole moiety incorporated into the peptide structure provides greater rigidity and stability against protease degradation. [2,7,8] However, since there is no atom loss in this “click” reaction, the cyclic peptide and its linear precursor are isomers and have exactly the same mass. Therefore, they cannot be distinguished by single-stage mass spectrometry.
Isomeric mixtures can be readily distinguished in tandem MS by selecting, if feasible, transitions by Multiple Reaction Monitoring (MRM) that are specific to each isomer. [9,10] Nevertheless, several studies on synthetic polymers and peptides cyclized with the Huisgen reaction have demonstrated that the most significant fragment ions obtained from the cyclic form and its linear precursor are also isomers and originate from the loss of N2, either from the triazole group or from the azide moiety. [11,12,13] Consequently, the detection of residual linear precursor in the sample of cyclized products is not feasible through the simple visual inspection of MS/MS spectra. This renders the usual quantification methods, such as MRM, inapplicable for Huisgen cyclized peptides. Therefore, alternative analytical strategies must be employed to assess the purity of these cyclic peptides and the absence of their isomeric linear precursors.
While other techniques have been developed to analyse isomeric mixtures, including the kinetic method [14,15,16,17] and, more recently, Ion Mobility Mass Spectrometry [18,19,20,21,22], Energy-Resolved Mass Spectrometry (ER MS) can also provide reliable results for quantitative analysis in the presence of isomeric mixtures. [12,13,17,23,24,25,26,27,28] ER MS involves performing Collision Induced Dissociation (CID) experiments to obtain MS/MS spectra at several excitation voltages. Bartolucci et al. have demonstrated that accurate quantification of co-eluted isomers can be achieved through multilinear regression of ER MS data [17,23,24,25,26]. This approach is further complemented by that of Memboeuf et al., who have demonstrated that ER MS, and in particular the Survival Yield (SY) plots, can be employed as a tool for structural analysis [29], to quantify isomeric and isobaric mixtures [12,13,27] and to remove isobaric interferences in liquid chromatography[30,31]. The SY curves of isomeric mixtures can be expressed as a linear combination of the SY curves of the pure isomeric compounds[13,29]. Typically, the SY curves of isomeric mixtures will lie between the SY curves of both pure compounds, with their position being related to the relative concentration of each isomer in the mixture. Subsequently, linear and multivariate calibration models can be calculated to establish the relationship between the SY and the relative amount of both isomers in the sample mixtures.[13] In this context, we have previously demonstrated that this method can be employed to assess the purity of a Huisgen cyclised polylactic polymer [11,12] as well as a Huisgen cyclised peptide [13].
Fourier Transform Infrared (FT-IR) microscopy represents a rapid alternative to traditional analytical techniques. [32] One of the key advantages of this technique is that it requires only a small amount of sample, minimal sample preparation, and allows for the examination of small spatial regions, providing molecular-level information, such as functional groups, bonding types, and molecular conformations. The distribution of chemical entities can be investigated based on specific marker bands [33]. A wide range of biological investigations have been conducted by FT-IR microspectroscopy, including cancer detection [34], plant tissue analysis [35] and conformational studies of proteins and peptides [36], among others. The combination of advances in IR instrumentation with the application of chemometric tools has also rendered this technology an optimal choice for rapid screening of a wide range of analytes in food analysis. In this context, it has been successfully applied to detect acrylamide in potato chips [37] and milk adulteration [38]. To the best of our knowledge, FT-IR microscopy has not yet been applied to assess the purity of peptides cyclised with the Huisgen reaction.
The objective of this paper is to evaluate the analytical capabilities of energy-resolved mass spectrometry and mid-infrared microscopy for the detection and quantification of a linear isomeric peptide present in a sample of a cyclic peptide synthesized with the Huisgen reaction. To this end, a model linear peptide with the sequence LAIFPWFLHPVAIGHA was synthesized and cyclized with the Huisgen reaction to obtain its isomeric cyclic peptide. Subsequently, both isomeric peptides, as well as their mixtures, were analysed by ER MS and IR microscopy. The relative amount of linear peptide was calculated by univariate and multivariate calibration. The analytical performance of IR microscopy was then compared with that of energy-resolved mass spectrometry in terms of detection limits, precision, root-mean-square error of calibration and linearity interval.

2. Materials and Methods

2.1. Chemicals and Sample Preparation

Methanol (HPLC-MS grade) and cesium chloride (purity > 98%) were purchased from Sigma-Aldrich. The linear and cyclic peptides were synthesised at the Nanobio Platform (Université Grenoble Alpes, Grenoble, France). The structures of the two peptides are shown in Figure 1. The linear peptide precursor (2007.2 Da) contains a basic histidine residue and has the following structure X-LAIFPWFLHPVAIGHA-βA-Z (where X is the azide moiety, βA is the beta-alanine amino acid and Z is the group with the alkyne function). The linear peptide was assembled on a Syro II peptide synthesiser using the same Fmoc strategy as previously described.[13]
Separate stock solutions of the linear and cyclic peptides were prepared at 50 μM in water/methanol (1:1). Cesium chloride was added to all solutions at 180 μM to form the cesium adducts of the peptides. Calibration standards were prepared in water/methanol (1:1). The total concentration of linear and cyclic peptides was 5 μM. The mixtures were prepared with the following linear/cyclic peptide ratios: 1:0; 0.5:9.5; 1:9; 1.5:8.5; 2:8; 3:7; 4:6; 5:5, 6:4 and 0:1.
The samples measured by IR microscopy were prepared at a total concentration of 5-10-4 M in water/methanol (1:1). In this case, CsCl was not added to the samples. The mixtures were prepared with the following linear/cyclic peptide ratios: 0:1; 0.5:9.5; 1:9; 1.5:8.5; 2:8; 3:7; 4:6; 5:5; 6:4; 8:2 and 1:0. All stock and working solutions were stored at -20 °C until use.

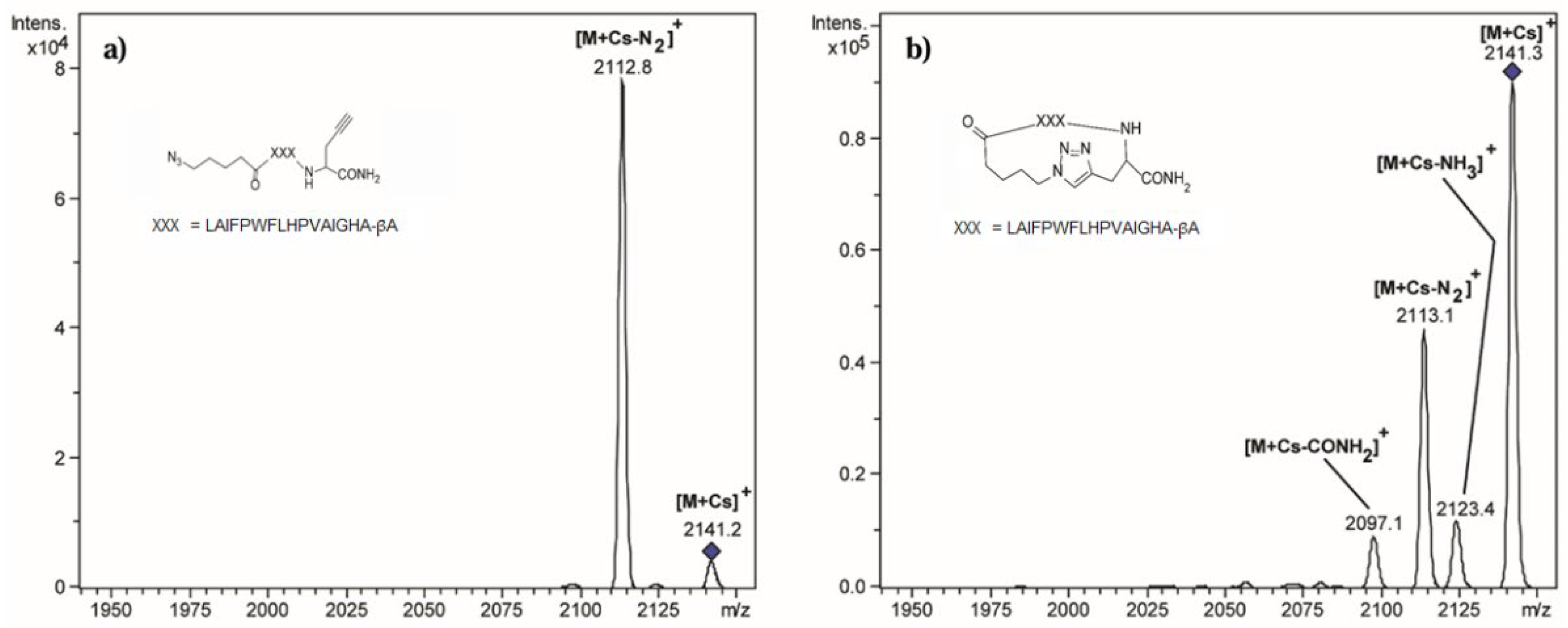
2.2. Energy Resolved Mass Spectrometry

Mass spectrometry experiments were performed in positive ion mode using an ion trap mass spectrometer (HCTplus, Bruker Daltonics) equipped with an electrospray ionization source (ESI, Agilent Technologies). The solutions were introduced by direct injection and electrosprayed via a syringe pump at a 2 µL·min-1 flow rate. The nebulizing gas (N2) pressure was set at 10 psi and the N2 drying gas flow rate at 5 L·min-1 heated at 300°C. Helium was used as trapping and collision gas at 3.00·10-5 mbar (uncorrected gauge reading). The settings of the instrument were the following: capillary voltage 3.8 kV, end plate −0.5 kV, skimmer 40 V, and a trap drive at 110. MS/MS spectra were performed by isolating precursor ions with an isolation window of 1 m/z followed by a fragmentation delay of 200 ms, fragmentation time of 100 ms, and a fragmentation width of 10 m/z. 1 minute acquisition was performed at each excitation voltage. For an improved statistic and repeatability, data are further summed up over the last 45 seconds of the acquisition stage in order to generate a MS/MS spectrum from which peaks intensities can be further extracted. The software DataAnalysis 3.3 (Bruker Daltonics, Bremen, Germany) was used for data acquisition and mass spectra processing. Default software parameters were used for data processing (back ground reduction, smoothing, and peak centering). Survival Yield curves were calculated using the freely available LibreOffice software package.[39] The SciDAVis software (freely available) was used for data visualization.[40] The SY curves were fitted using the SciDAVis built-in Boltzmann model.

2.3. Infrared Microscopy

A ThermoFisher Scientific Nicolet iN10 MX microscope was used to obtain mid-infrared (675-4000 cm-1) spectra by specular reflectance. Background noise was recorded before each acquisition and subtracted from the spectra. The spectra of each peptide mixture are obtained by creating a grid of 800 µm by 600 µm. The grid contains 100 evenly spaced points. During acquisition, the Omnic Picta software (Thermo Scientific) averaged 16 spectra per point and provided 1 average spectrum per point. 100 spectra were collected per mixture. Three replicates were performed for each mixture. Reflective aluminium-coated slides with 12 numbered spots were used to facilitate identification of the peptide mixture during IR acquisition. 2 µL of the peptide mixture at 5·10-4 M was added to the spot. Preprocessing of IR spectra and multivariate calibration models were performed with Matlab R2024a (The Mathworks, Inc.) and the PLS_Toolbox 9.3.1 (2024) (Eigenvector Research, Inc., Manson, WA USA).

3. Results and Discussion

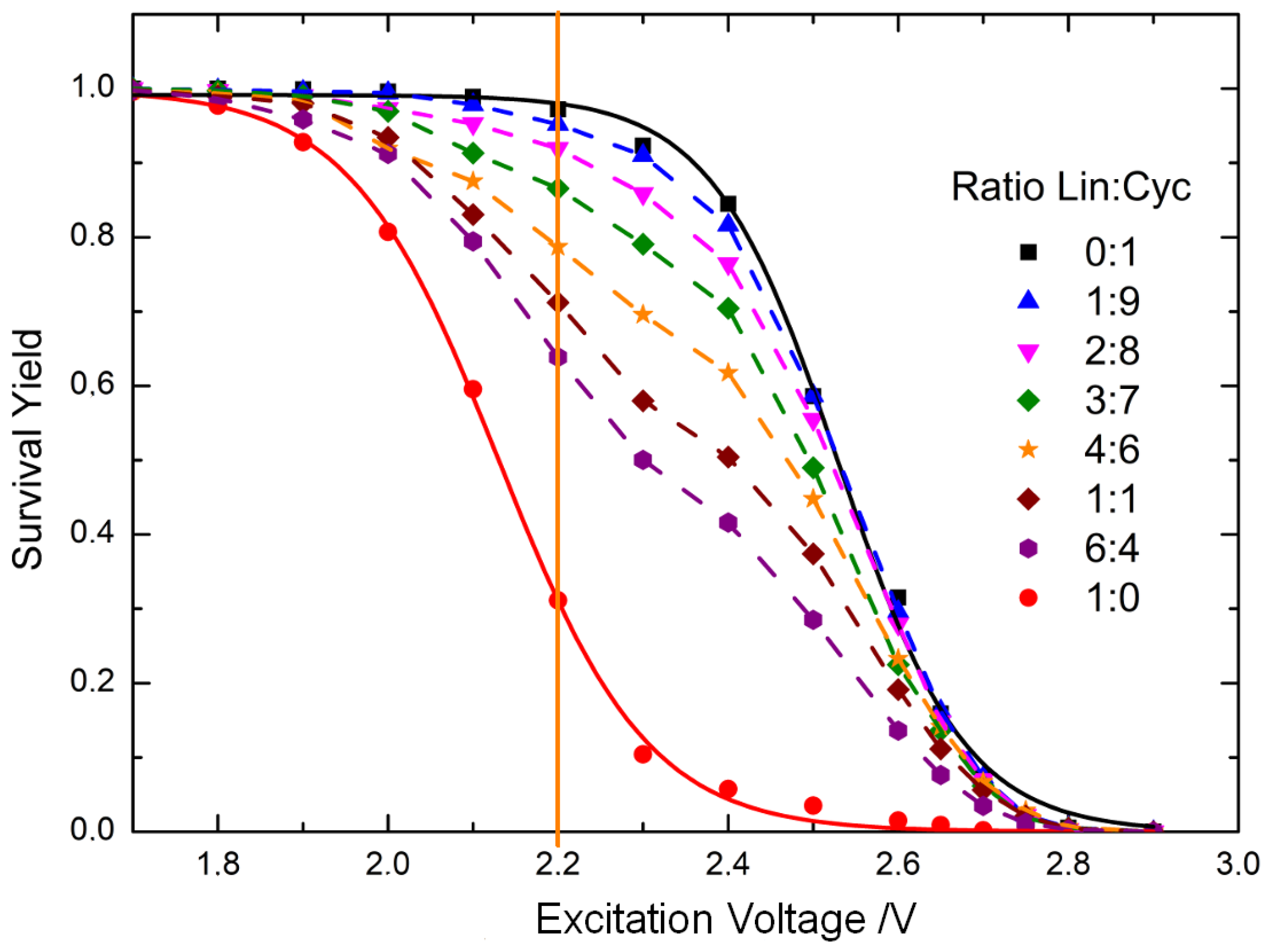
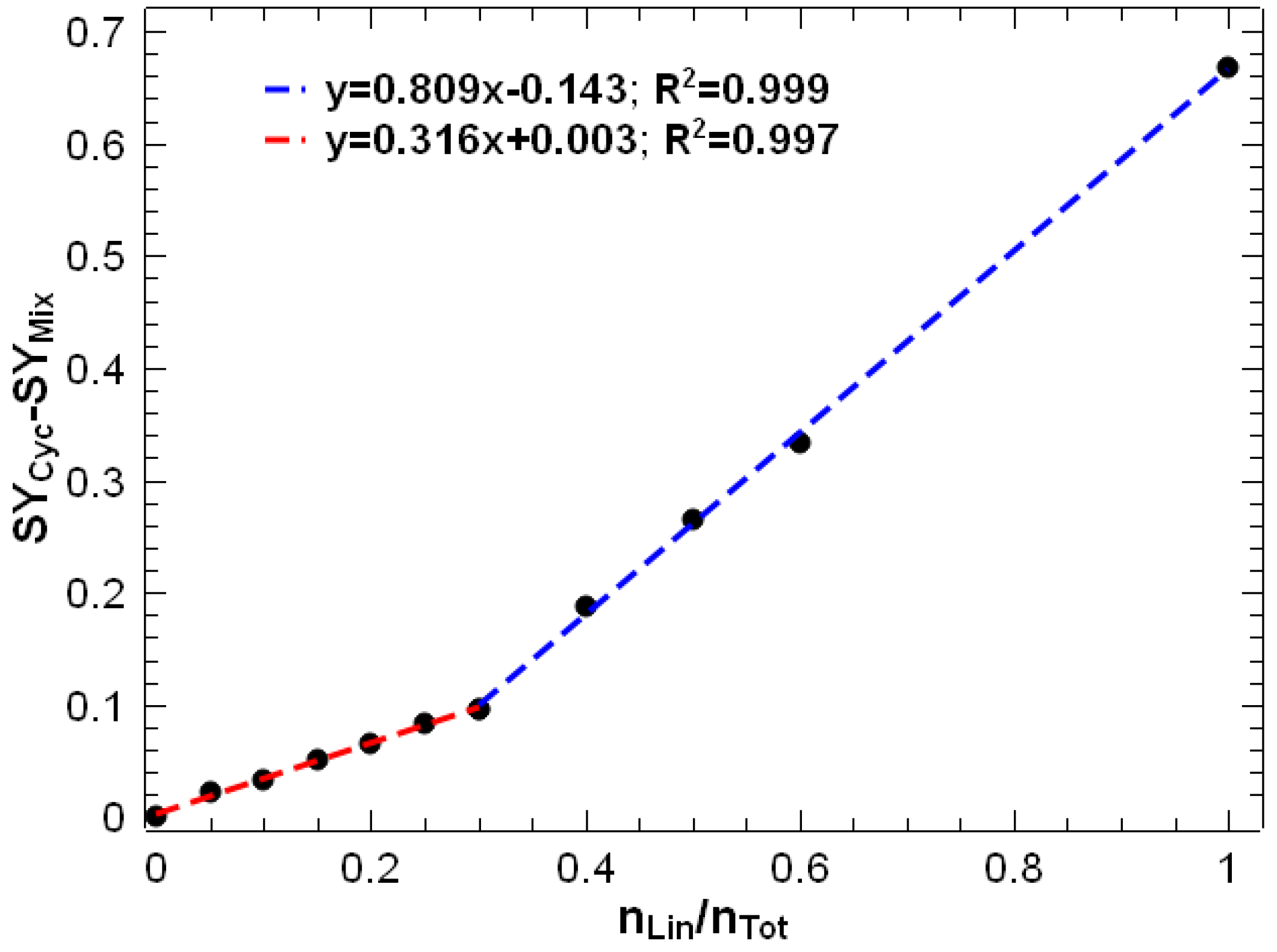
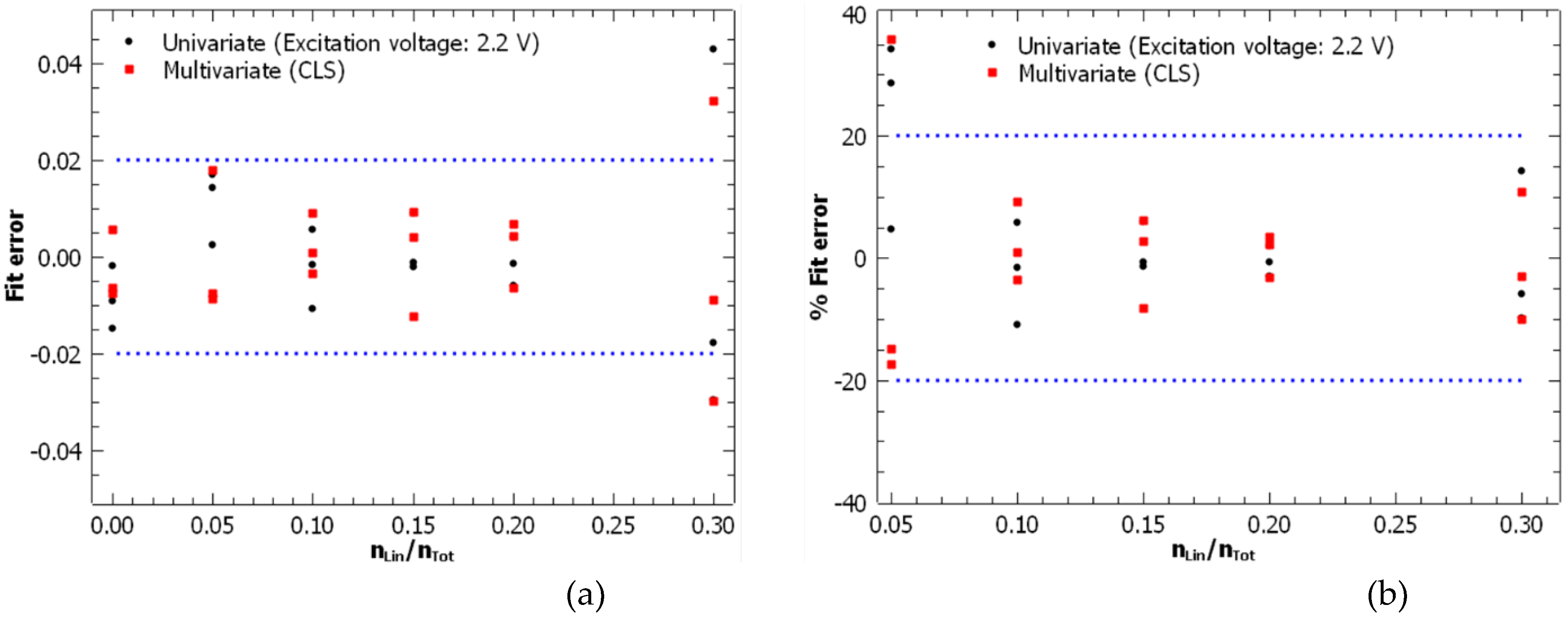
3.1. Energy-Resolved Mass Spectrometry and the Survival Yield Technique

ER MS experiments were performed by measuring the MS/MS spectra of the cesium cationised peptides at different excitation voltages ranging from 1.7 V to 2.9 V. Figure 2 shows the MS/MS spectra of the cyclic and linear peptides at 2.5 V. At this excitation voltage the linear peptide is almost completely fragmented, whereas the cyclic peptide is slightly fragmented and the precursor ion peak (at 2141.3 m/z) has the higher intensity. The major fragment of the linear peptide corresponds to the loss of N2 (at 2112.8 m/z). This fragment is also observed for the cyclic peptide. As there are no specific fragments for the linear peptide, it is not possible to detect the presence of the linear peptide by visual inspection of the MS/MS spectra of the cyclic peptide samples. However, the difference in excitation energy required to fragment both peptides can be used to detect the presence of linear peptide. In this sense, energy resolved mass spectrometry and, more specifically, the survival yield (SY) was used to detect and quantify the relative amount of linear peptide.
The Survival Yield (SY) was calculated at each excitation voltage as the ratio of the precursor ions peak intensity and the Total Ion Current (TIC).[11,12,13,28,29,30,31]
S Y = I p r e c u r s o r I p r e c u r s o r + ∑ I f r a g m e n t
where Iprecursor is the intensity of the precursor ions peak and Ifragment is the intensity of each fragment ions peak obtained from the MS/MS experiment. SY curves were then obtained by plotting SY against the excitation voltage (see Figure 3).
Figure 3 shows the SY curves of the pure cyclic and linear cesium cationised peptides, which are sigmoidal. The SY curve of the cyclic peptide shows a significant shift towards higher excitation voltages compared to that of the linear peptide. This is consistent with the MS/MS spectra in Figure 2. The SY curves of the mixtures of cyclic and linear peptides lie between the SY curves of the pure peptides. The position of the SY curves is related to the relative amount of linear and cyclic peptide[13,27]. The higher the relative amount of cyclic peptide, the closer the SY curve of the mixture is to the SY curve of the cyclic peptide.
The difference between the SY of the mixtures and the SY of the cyclic peptide was plotted against the molar ratio of linear peptide. This plot was made at an excitation voltage of 2.2 V (orange vertical line in Figure 3) as we observed the best results to detect lower amounts of linear peptide under these conditions. Figure 4 shows that two different linear relationships are observed: a linear model for molar ratios of linear peptide between 0 and 0.3, and another linear model with a higher slope for molar ratios from 0.3 to 1. The large difference in sensitivity between the two models is due to matrix effects due to ion suppression, which are commonly observed in electrospray sources in mass spectrometry. It can be clearly observed that the ionisation of linear peptides is suppressed by the presence of cyclic peptides. Therefore, for lower proportions of linear peptides, the slope of the calibration model is much lower. Conversely, for linear peptide ratios exceeding 0.3, ion suppression is less pronounced due to the reduced relative abundance of cyclic peptide. This is evidenced by the slope of the calibration curve, which is approximately 2.5 times higher than for lower ratios, indicating that sensitivity is diminished in the low range of linear peptide contamination.
Univariate and multivariate calibration models were calculated for the lower interval of linear peptide molar ratios (i.e., from 0 to 0.3) because the aim of the study is to detect the presence of small traces of linear precursor in samples of cyclic peptide. For this range, we measured the SY of each mixture three times. For comparative purposes, the linear peptide molar ratios of the mixtures were the same as the ones measured by IR microscopy: 0, 0.05, 0.1, 0.15, 0.20 and 0.30. Figure 5a shows the univariate calibration model at an excitation voltage of 2.2 V (orange vertical line in Figure 3). This regression model was obtained by calculating at 2.2 V the difference between the SY of the cyclic peptide and the SY of each calibration standard and by plotting this difference against the linear peptide molar ratio of the calibration standards.
Figure 5b shows the results obtained by multivariate calibration to quantify the molar ratio of linear peptide by applying the Classical Least Squares (CLS) algorithm. In this case, instead of using the SY at only one excitation voltage, the SY curve as a whole was used. The SY curve of a calibration standard can indeed be described as a linear combination of the SY curves of cesium cationised linear and cyclic peptides obtained from pure samples.[13,27] A linear combination coefficient (a) can then be obtained, which minimizes the sum of squares of residuals (e) of the following expression:
S Y Mixture   =   a   ×   S Y Linear +   ( 1 − a )   . S Y Cyclic + e
where SYLinear and SYCyclic correspond, respectively, to the SY curves of the cesium-cationised linear and cyclic peptides obtained from pure samples (bolded variables describe vectors). Linear coefficients (a) obtained for each calibration standard were then plotted against the molar ratio of linear peptide to calculate an univariate regression curve. In this way, the linear coefficient obtained by CLS can be related to the molar ratio of linear peptide of the calibration samples. In absence of matrix effects due to ionisation efficiency, the slope of this curve should be close to 1. In this case, the slope is only 0.483, much lower than 1. This is because there is ionisation suppression of the linear peptide in the presence of the cyclic peptide (as it was already observed in Figure 4 for the interval 0-0.3 of linear peptide molar ratio).
Both calibration models showed good coefficients of determination, R2, with the multivariate model slightly better. Three of the calibration standards initially prepared to be measured by IR microscopy (at molar ratios of linear peptide of 0.1, 0.2 and 0.3) were also measured by ER MS (red circles in Figure 5). The IR standards were diluted 100 times in water/methanol (1:1) and CsCl was added at 180 μM in order to be in the same conditions as the calibration standards used for the ER MS calibration models (black squares in Figure 5). The SY values and the CLS coefficients (a) obtained for the IR samples are very similar to the ones obtained for the MS samples. These results confirm that the ER MS measurements are reproducible and that the IR calibration standards were correctly prepared.
The limit of detection, LD, was then calculated by using the information from the calibration model and the formula:
L D = 3.3 · s e b 1
where se corresponds to the standard deviation of the residuals of the calibration line (defined also as standard error) and b1 to its slope. This approach is recommended in LC-MS methods as it gives conservative estimates when the LD is calculated from calibration graphs.[41,42] The factor of 3.3 is associated with a probability of a false positive decision (type I or α-error) of 0.05 and a probability of a false negative decision (type II or β-error) of 0.05.[43,44] The LD calculated for the univariate model was 0.053 molar ratio of linear peptide. The LD calculated for the multivariate model was 0.045, slightly better than the univariate model.
The performance of both calibration models was evaluated by calculating the fit error of each calibration standard as the difference between the predicted value of the linear peptide molar ratio, (nLin//nTotal) predicted, and the reference value of the linear peptide molar ratio, (nLin//nTotal) reference. The proportional fit error was calculated as:
% F i t   e r r o r = ( n L i n / n T o t a l ) p r e d i c t e d − ( n L i n / n T o t a l ) r e f e r e n c e n ( n L i n / n T o t a l ) r e f e r e n c e · 100
Figure 6a shows the fit error of each calibration standard calculated for the univariate and multivariate calibration models. All fit errors were randomly distributed around 0 and less than 0.02 (except for the standard at 0.3). Figure 6b shows the percentage of fit error for each calibration standard. Both models show similar values of fit error. The percentage of fit errors was less than 20% except for the standard at 0.05 molar ratio of linear peptide. The Root-Mean-Square Error of Calibration (RMSEC) was calculated to obtain an average fit error for each calibration model:
R M S E C = ∑ i = 1 n F i t   e r r o r i 2 n
where n corresponds to the number of calibration standards, i.e., 6*3=18. The RMSEC values calculated for both models were quite similar and slightly better for the multivariate model: for the univariate model it was 0.015 and for the multivariate model it was 0.013.
The intermediate precision was calculated as the pooled variance of all the three replicates measured for each calibration standard.[44] The intermediate precision (expressed as standard deviation) was 1.71·10-2 for the univariate model and 1.58·10-2 for the CLS, showing that precision is slightly improved when the entire SY curve is used to calculate the molar ratio of linear peptides. Although the performance of the linear and multivariate calibration models is quite similar, the multivariate model shows slightly better performance in terms of limit of detection, RMSEC and intermediate precision. However, it is important to note that the multivariate model requires the measurement of the entire SY curve and is more time consuming than the univariate model which only requires the measurement at one excitation voltage.

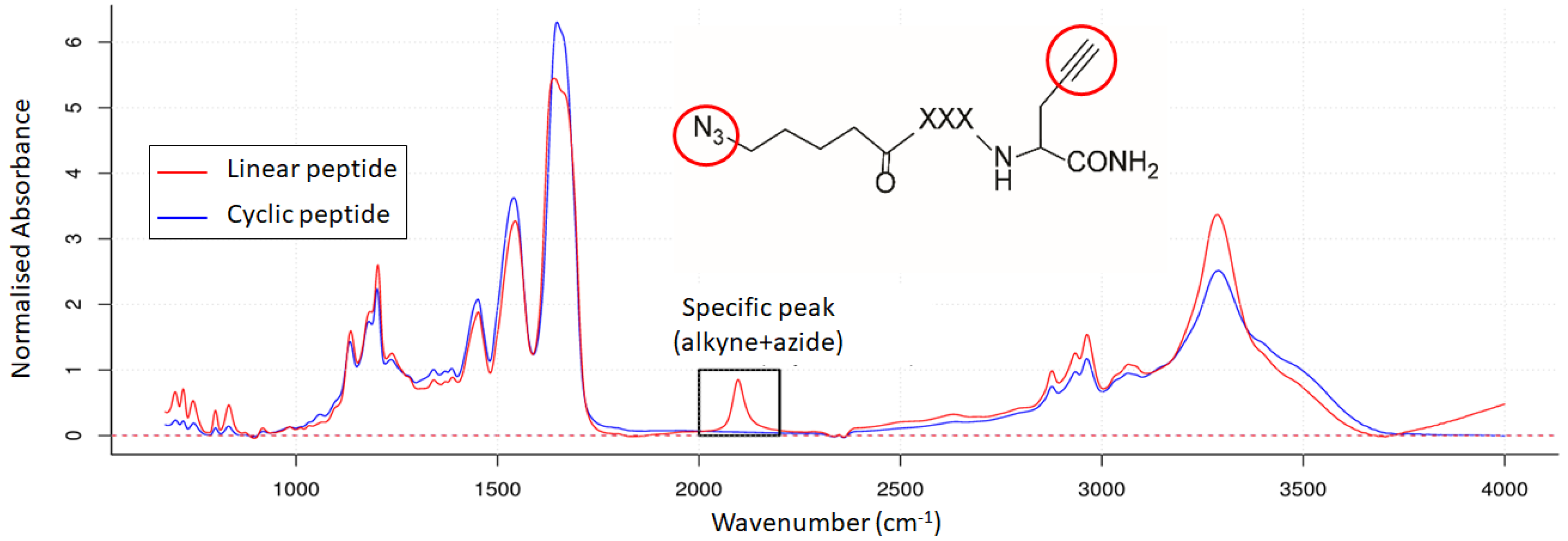
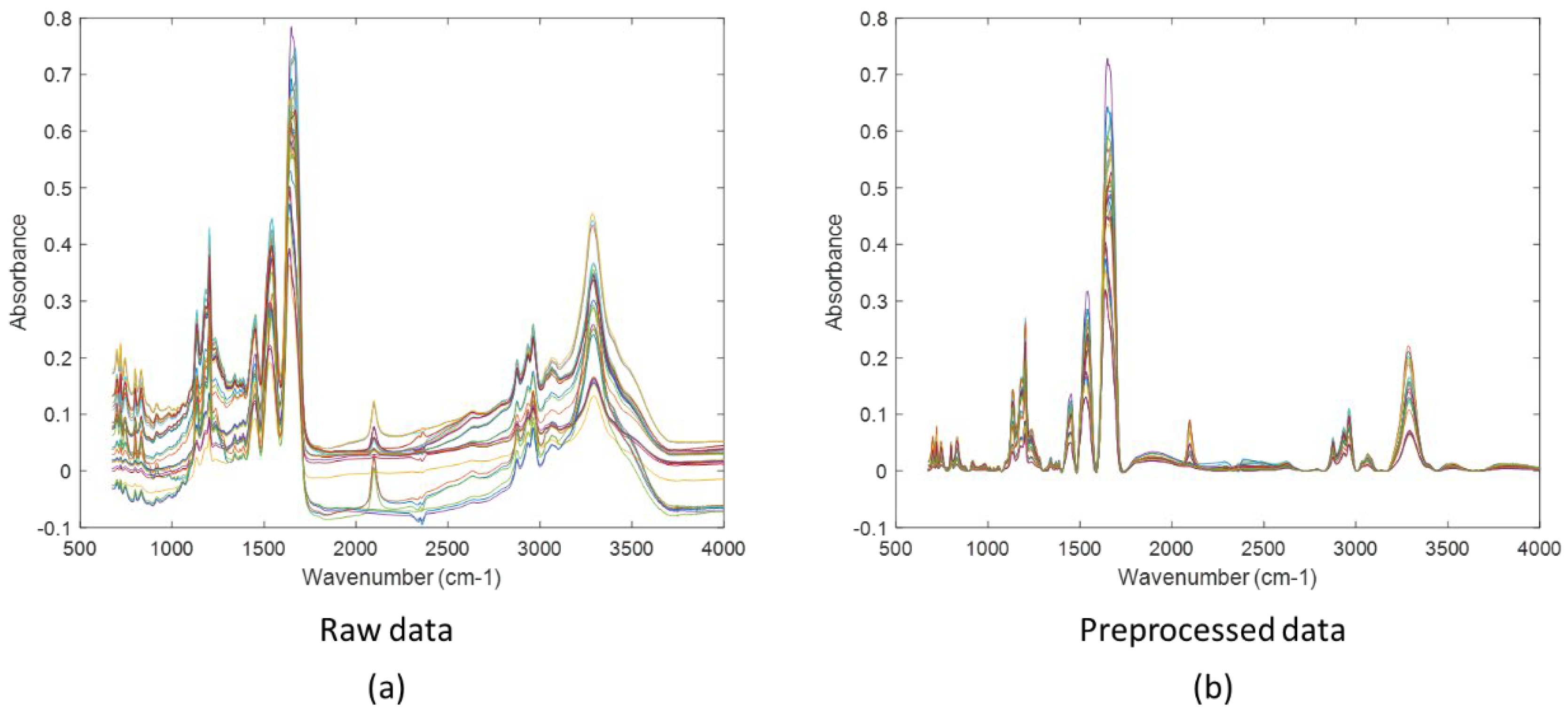
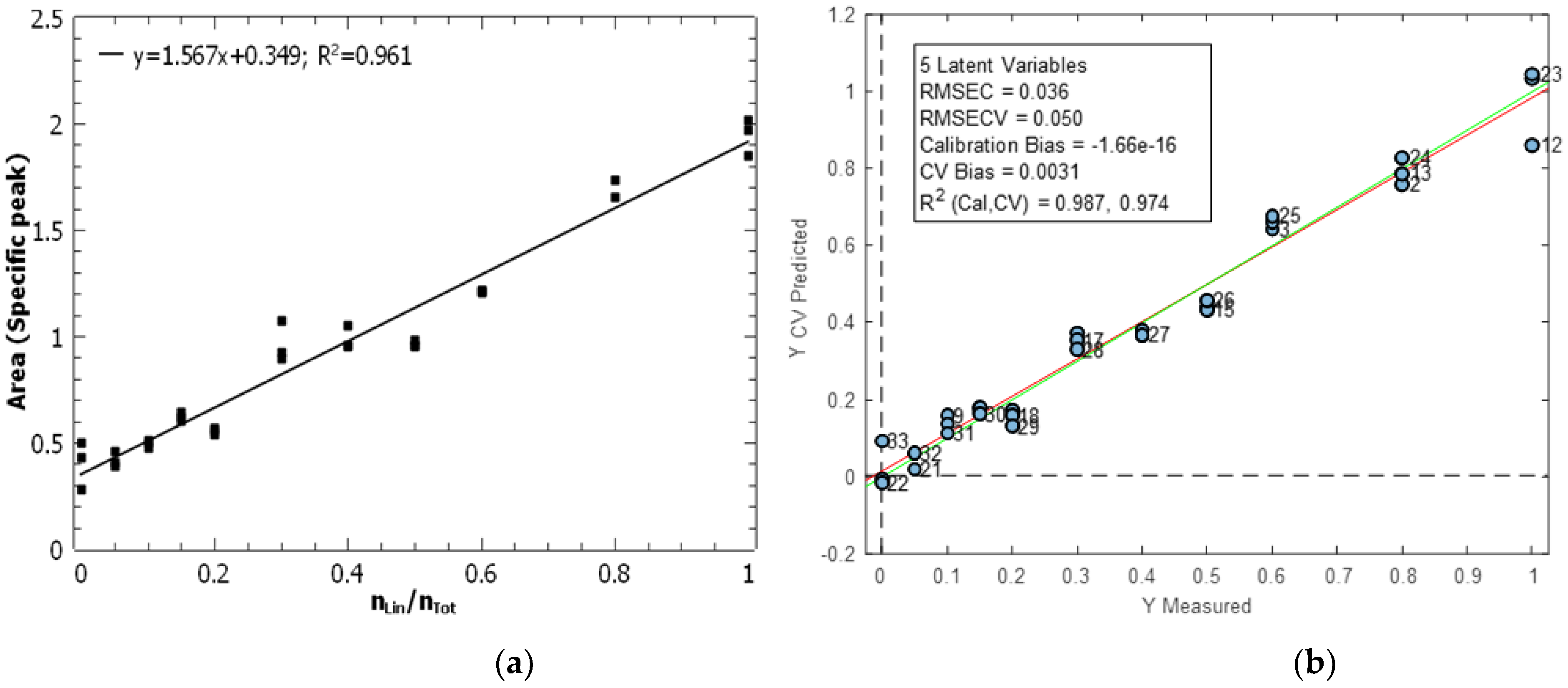
3.2. Mid-Infrared Microscopy

The pure linear and cyclic peptides were measured by IR microscopy. Figure 7 shows the superposition of the two IR spectra. Each spectrum was normalised to the mean absorbance and baseline corrected. Both spectra show the same absorption bands except for a wavelength region from 2040 to 2170 cm-1,which is observed only for the linear peptide. In fact, this band is characteristic of the linear peptide, since it corresponds to the alkyne ( C ≡ C ) and/or azide (N3) functions, which usually appear between 2140-2100 cm-1 and 2160-2120 cm-1, respectively.
Several mixtures of the cyclic and linear peptides were measured by IR microscopy. Each mixture was measured in triplicate. For each triplicate, 100 spectra were measured and averaged (see Experimental section). Figure 8 shows the average spectrum for each triplicate. A total of 33 spectra are shown (i.e., 3 replicates*11 concentration levels). Figure 8a shows that the spectra are baseline shifted. This is usually the case in IR data due to background variations, mainly due to scattering.
Figure 8b shows the IR spectra corrected by Asymmetric Least Squares.[45,46] Asymmetric Least Squares (AsLS) is a spectral baseline correction method that separates the baseline from the signal. AsLS is widely used in spectroscopy and chromatography for accurate baseline correction, effectively distinguishing sharp peaks from smooth baseline components. The advantage of this method is that no prior information about peak shapes or baselines is required. It minimizes an objective function combining residuals and a smoothness penalty. Weights are iteratively adjusted: higher for points below the baseline (assumed to be noise) and lower for points above (assumed to be peaks). Parameters include lambda for smoothness and p for asymmetry. Both parameters have to be tuned to the data at hand and be chosen by data visualization. In AsLS, p (for asymmetry) usually varies between 0.1 and 0.001, and lambda (for smoothness) between 102 to 109.[45] In our case, the best baseline correction of the IR spectra was obtained with p=0.001 and λ=1·104. These values were used to correct the baseline of all the IR spectra. Figure 8b shows that the preprocessed spectra were successfully baseline corrected.
The molar ratio of linear peptide was quantified through univariate and multivariate calibration, as illustrated in Figure 9. The univariate calibration model (Figure 9a) corresponds to the area of the specific peak against the molar ratio of linear peptide. A high determination coefficient (R2=0.961) was observed for the univariate model, indicating a strong correlation between the two variables.
For the multivariate model, the PLS (Partial Least Squares) regression method was applied, between the matrix X (33 x 1725) containing the IR spectra and the vector y (33 x 1) containing the molar ratio of linear peptide. The model was validated using contiguous-block cross validation, with 11 data splits (3 samples per split). The optimal PLS model had 5 latent variables and had quite good figures of merit (Figure 9b), with an RMSEC = 0.036 and a Root Mean-Square Error of Cross-Validation, RMSECV = 0.050. The model had practically no bias and the coefficients of determination, R2, for calibration and validation were 0.987 and 0,974, respectively.
Figure 10 shows the fit errors calculated for the calibration standards with the univariate and PLS models. The PLS model displays superior predictive capabilities in comparison to the univariate model. This is clearly observed in Figure 10a, which shows that the fit errors of the univariate model are higher than those of the PLS model. The fit errors of the PLS model were less than 0.07 (with the exception of one sample at nLin/nTot=1), whereas the univariate model exhibited calibration standards with fit errors reaching up to 0.15. Figure 10b also demonstrates that the PLS model is more predictive in terms of percentage of fit error. For the PLS model, the percentage of fit error of the calibration samples is less than 20%, with the exception of the samples with molar ratios of linear peptide less than 0.15. This is not the case for the univariate model, which shows that almost all the calibration samples are predicted with higher percentages of fit error.
The RMSEC of the univariate model was of 0.062, while the RMSEC of the PLS model was of 0.036. This confirms that the PLS model is more predictive than the univariate model. As for ER MS, the intermediate precision was calculated as the pooled variance of all the three replicates measured for each calibration standard.[44] The intermediate precision (expressed as standard deviation) was 5.06·10-2 for the univariate model and 2.63·10-2 for the PLS model. This shows that precision is clearly improved when the entire IR spectra is used to calculate the molar ratio of linear peptides. The limit of detection of the univariate model (calculated with Eq. 3) was of 0.21. The limit of detection of the multivariate model was calculated as 3.3·RMSEC, which corresponds in multivariate calibration to the equivalent expression of Eq. 3. The limit of detection was 0.12, which is considerably lower than that of the univariate calibration. The PLS model demonstrates superior performance in terms of limit of detection, RMSEC and intermediate precision. It is therefore preferable to consider the full IR spectrum rather than focusing on the specific peak of the linear peptide.

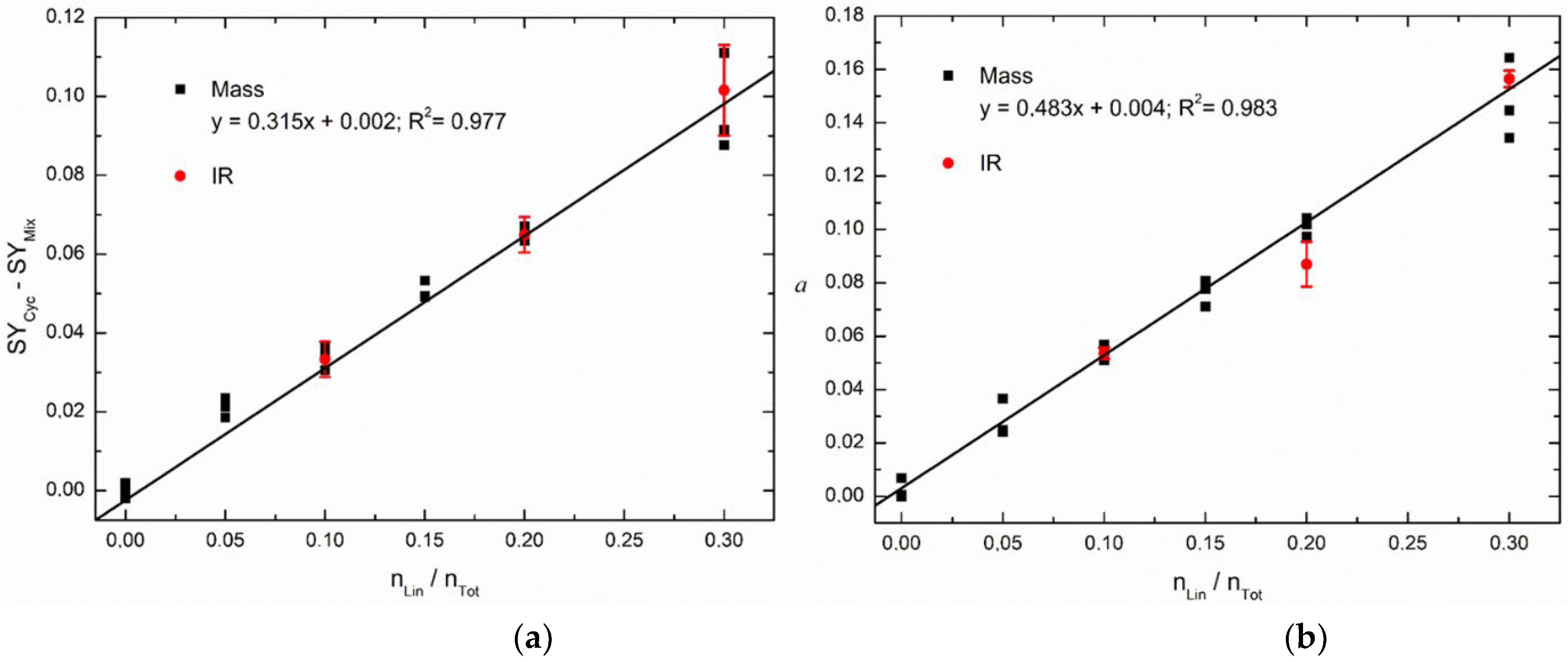
3.3. Comparison of Energy-Resolved Mass Spectrometry and Mid-Infrared Microscopy

Table 1 presents a summary of the analytical performances obtained for energy-resolved mass spectrometry and mid-infrared microscopy. The results demonstrate that ER MS exhibits superior performance to IR-microscopy in terms of root-mean-square error of calibration (RMSEC), intermediate precision and limit of detection. One limitation of ER MS is that the calibration models are only linear up to a linear peptide molar ratio of 0.3. In contrast, IR-microscopy is linear across the entire working interval, from linear peptide molar ratios of 0 (equivalent to pure cyclic peptide) up to 1 (pure linear peptide). Therefore, energy-resolved mass spectrometry is the optimal choice for the detection and quantification of the smallest amounts of linear peptide. However, infrared microscopy is more suitable for samples with higher molar ratios of linear peptide.

4. Conclusions

The successful quantification of mixtures of synthetic linear and cyclic isomeric peptides has been achieved through the utilisation of energy-resolved mass spectrometry (ER MS) and mid-infrared microscopy. The ER MS method was based on univariate and multivariate calibration models, calculated from Survival Yield (SY) data. The multivariate model demonstrated slightly enhanced analytical performance, which can be attributed to more effective signal averaging when SY curves are considered as a whole, resulting in a greater number of data points and more robust statistics. However, the multivariate model requires the entire SY curve to be measured, making it a more time-consuming process than the univariate model, which only requires the measurement of SY at one excitation voltage.
The feasibility of infrared microscopy as an alternative technique for quantifying the relative amount of linear peptide has also been demonstrated. In this case, the Partial Least Squares (PLS) calibration model exhibited superior performance in comparison to univariate calibration, indicating that it is preferable to consider the full IR spectrum rather than focusing on the specific peak of the linear peptide.
The comparative analysis of the two analytical techniques reveals that ER MS demonstrates superior performance compared to IR microscopy. It can therefore be concluded that ER MS is the optimal technique for the detection and quantification of the smallest amounts of linear peptide. However, one limitation of ER MS is that the linearity interval is more restricted than that of IR microscopy. This is due to matrix effects originating in the electrospray source, whereby the ion suppression of the linear peptide in the presence of cyclic peptide results in a restricted linearity interval. In contrast, IR microscopy is linear across the entire working interval, from linear peptide molar ratios of 0 (equivalent to pure cyclic peptide) up to 1 (pure linear peptide). Consequently, infrared microscopy is more appropriate for samples exhibiting higher molar ratios and greater variability in the relative concentration values of linear peptide.

Author Contributions

Conceptualization, A.M (Alicia Maroto), R.B. and A.M. (Antony Memboeuf); methodology, D.J.D.F ; software, A.M (Alicia Maroto) and R.B.; validation, A.M (Alicia Maroto), R.B. and A.M. (Antony Memboeuf); formal analysis, A.M (Alicia Maroto) and R.B.; investigation, D.J.D.F; R.B. and A.M. (Antony Memboeuf); data curation, D.J.D.F, A.M (Alicia Maroto) and R.B.; writing—original draft preparation, A.M (Alicia Maroto); writing—review and editing, R.B. and A.M. (Antony Memboeuf).; visualization, A.M (Alicia Maroto), R.B. and A.M. (Antony Memboeuf); supervision, A.M (Alicia Maroto), R.B. and A.M. (Antony Memboeuf); project administration, A.M. (Antony Memboeuf); funding acquisition, A.M. (Antony Memboeuf). All authors have read and agreed to the published version of the manuscript.

Funding

Funding was obtained from the Université de Brest (UBO) through BQR program.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are contained within the article.

Acknowledgments

The authors are grateful to the University of Brest for providing the necessary facilities to carry out this research.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Abdalla, M.A.; McGaw, L.J. Natural Cyclic Peptides as an Attractive Modality for Therapeutics: A Mini Review. Molecules 2018, 23, 2080. [CrossRef]
  2. Ji, X.; Nielsen, A.L.; Heinis, C. Cyclic Peptides for Drug Development. Angewandte Chemie International Edition 2024, 63, e202308251. [CrossRef]
  3. Ramadhani, D.; Maharani, R.; Gazzali, A.M.; Muchtaridi, M. Cyclic Peptides for the Treatment of Cancers: A Review. Molecules 2022, 27, 4428. [CrossRef]
  4. Gisemba, S.A.; Ferracane, M.J.; Murray, T.F.; Aldrich, J.V. A Bicyclic Analog of the Linear Peptide Arodyn Is a Potent and Selective Kappa Opioid Receptor Antagonist. Molecules 2024, 29, 3109. [CrossRef]
  5. Li, P.; Roller, P.P. Cyclization Strategies in Peptide Derived Drug Design. Curr Top Med Chem 2002, 2, 325–341. [CrossRef]
  6. Li, H.; Aneja, R.; Chaiken, I. Click Chemistry in Peptide-Based Drug Design. Molecules 2013, 18, 9797–9817. [CrossRef]
  7. Jagasia, R.; Holub, J.M.; Bollinger, M.; Kirshenbaum, K.; Finn, M.G. Peptide Cyclization and Cyclodimerization by CuI-Mediated Azide−Alkyne Cycloaddition. J. Org. Chem. 2009, 74, 2964–2974. [CrossRef]
  8. Tahoori, F.; Balalaie, S.; Sheikhnejad, R.; Sadjadi, M.; Boloori, P. Design and Synthesis of Anti-Cancer Cyclopeptides Containing Triazole Skeleton. Amino Acids 2014, 46, 1033–1046. [CrossRef]
  9. Uclés, S.; Lozano, A.; Sosa, A.; Parrilla Vázquez, P.; Valverde, A.; Fernández-Alba, A.R. Matrix Interference Evaluation Employing GC and LC Coupled to Triple Quadrupole Tandem Mass Spectrometry. Talanta 2017, 174, 72–81. [CrossRef]
  10. Yan, Z.; Maher, N.; Torres, R.; Cotto, C.; Hastings, B.; Dasgupta, M.; Hyman, R.; Huebert, N.; Caldwell, G.W. Isobaric Metabolite Interferences and the Requirement for Close Examination of Raw Data in Addition to Stringent Chromatographic Separations in Liquid Chromatography/Tandem Mass Spectrometric Analysis of Drugs in Biological Matrix. Rapid Communications in Mass Spectrometry 2008, 22, 2021–2028. [CrossRef]
  11. Josse, T.; Winter, J.D.; Dubois, P.; Coulembier, O.; Gerbaux, P.; Memboeuf, A. A Tandem Mass Spectrometry-Based Method to Assess the Architectural Purity of Synthetic Polymers: A Case of a Cyclic Polylactide Obtained by Click Chemistry. Polym. Chem. 2014, 6, 64–69. [CrossRef]
  12. Jeanne Dit Fouque, D.; Maroto, A.; Memboeuf, A. Purification and Quantification of an Isomeric Compound in a Mixture by Collisional Excitation in Multistage Mass Spectrometry Experiments. Anal. Chem. 2016, 88, 10821–10825. [CrossRef]
  13. Jeanne Dit Fouque, D.; Lartia, R.; Maroto, A.; Memboeuf, A. Quantification of Intramolecular Click Chemistry Modified Synthetic Peptide Isomers in Mixtures Using Tandem Mass Spectrometry and the Survival Yield Technique. Anal Bioanal Chem 2018, 410, 5765–5777. [CrossRef]
  14. Tao, W.A.; Cooks, R.G. Peer Reviewed: Chiral Analysis by MS. Anal. Chem. 2003, 75, 25 A-31 A. [CrossRef]
  15. Majumdar, T.K.; Clairet, F.; Tabet, J.C.; Cooks, R.G. Epimer Distinction and Structural Effects on Gas-Phase Acidities of Alcohols Measured Using the Kinetic Method. J. Am. Chem. Soc. 1992, 114, 2897–2903. [CrossRef]
  16. Tao, W.A.; Wu, L.; Cooks, R.G. Differentiation and Quantitation of Isomeric Dipeptides by Low-Energy Dissociation of Copper(II)-Bound Complexes. J. Am. Soc. Mass Spectrom. 2001, 12, 490–496. [CrossRef]
  17. Crotti, S.; Menicatti, M.; Pallecchi, M.; Bartolucci, G. Tandem Mass Spectrometry Approaches for Recognition of Isomeric Compounds Mixtures. Mass Spectrometry Reviews n/a, e21757. [CrossRef]
  18. Hanozin, E.; Morsa, D.; De Pauw, E. Energetics and Structural Characterization of Isomers Using Ion Mobility and Gas-Phase H/D Exchange: Learning from Lasso Peptides. PROTEOMICS 2015, 15, 2823–2834. [CrossRef]
  19. Lapthorn, C.; Pullen, F.; Chowdhry, B.Z. Ion Mobility Spectrometry-Mass Spectrometry (IMS-MS) of Small Molecules: Separating and Assigning Structures to Ions. Mass Spectrom Rev 2013, 32, 43–71. [CrossRef]
  20. Morsa, D.; Defize, T.; Dehareng, D.; Jérôme, C.; De Pauw, E. Polymer Topology Revealed by Ion Mobility Coupled with Mass Spectrometry. Anal. Chem. 2014, 86, 9693–9700. [CrossRef]
  21. Hanozin, E.; Grifnée, E.; Gattuso, H.; Matagne, A.; Morsa, D.; Pauw, E.D. Covalent Cross-Linking as an Enabler for Structural Mass Spectrometry. Anal. Chem. 2019, 91, 12808–12818. [CrossRef]
  22. Wu, Q.; Wang, J.-Y.; Han, D.-Q.; Yao, Z.-P. Recent Advances in Differentiation of Isomers by Ion Mobility Mass Spectrometry. TrAC Trends in Analytical Chemistry 2020, 124, 115801. [CrossRef]
  23. Menicatti, M.; Guandalini, L.; Dei, S.; Floriddia, E.; Teodori, E.; Traldi, P.; Bartolucci, G. The Power of Energy-Resolved Tandem Mass Spectrometry Experiments for Resolution of Isomers: The Case of Drug Plasma Stability Investigation of Multidrug Resistance Inhibitors. Rapid Commun Mass Spectrom 2016, 30, 423–432. [CrossRef]
  24. Menicatti, M.; Guandalini, L.; Dei, S.; Floriddia, E.; Teodori, E.; Traldi, P.; Bartolucci, G. Energy Resolved Tandem Mass Spectrometry Experiments for Resolution of Isobaric Compounds: A Case of Cis/Trans Isomerism. Eur J Mass Spectrom (Chichester) 2016, 22, 235–243. [CrossRef]
  25. Menicatti, M.; Pallecchi, M.; Bua, S.; Vullo, D.; Di Cesare Mannelli, L.; Ghelardini, C.; Carta, F.; Supuran, C.T.; Bartolucci, G. Resolution of Co-Eluting Isomers of Anti-Inflammatory Drugs Conjugated to Carbonic Anhydrase Inhibitors from Plasma in Liquid Chromatography by Energy-Resolved Tandem Mass Spectrometry. J Enzyme Inhib Med Chem 2018, 33, 671–679. [CrossRef]
  26. Pallecchi, M.; Lucio, L.; Braconi, L.; Menicatti, M.; Dei, S.; Teodori, E.; Bartolucci, G. Isomers Recognition in HPLC-MS/MS Analysis of Human Plasma Samples by Using an Ion Trap Supported by a Linear Equations-Based Algorithm. International Journal of Molecular Sciences 2023, 24, 11155. [CrossRef]
  27. Memboeuf, A.; Jullien, L.; Lartia, R.; Brasme, B.; Gimbert, Y. Tandem Mass Spectrometric Analysis of a Mixture of Isobars Using the Survival Yield Technique. J. Am. Soc. Mass Spectrom. 2011, 22. [CrossRef]
  28. Jeanne Dit Fouque, D.; Maroto, A.; Memboeuf, A. Internal Standard Quantification Using Tandem Mass Spectrometry of a Tryptic Peptide in the Presence of an Isobaric Interference. Anal. Chem. 2018, 90, 14126–14130. [CrossRef]
  29. Maroto, A.; Jeanne Dit Fouque, D.; Memboeuf, A. Ion Trap MS Using High Trapping Gas Pressure Enables Unequivocal Structural Analysis of Three Isobaric Compounds in a Mixture by Using Energy-Resolved Mass Spectrometry and the Survival Yield Technique. J Mass Spectrom 2020, 55, e4478. [CrossRef]
  30. Maroto, A.; dit Fouque, D.J.; Lartia, R.; Memboeuf, A. Removal of Isobaric Interference Using Pseudo-Multiple Reaction Monitoring and Energy-Resolved Mass Spectrometry for the Isotope Dilution Quantification of a Tryptic Peptide. Journal of Mass Spectrometry 2024, 59, e5025. [CrossRef]
  31. Maroto, A.; Fouque, D.J. dit; Lartia, R.; Memboeuf, A. LC-MS Accurate Quantification of a Tryptic Peptide Co-Eluted with an Isobaric Interference by Using in-Source Collisional Purification. Anal Bioanal Chem 2023, 415, 7211–7221. [CrossRef]
  32. Katon, J.E. Infrared Microspectroscopy. A Review of Fundamentals and Applications. Micron 1996, 27, 303–314. [CrossRef]
  33. Muchaamba, F.; Stephan, R. A Comprehensive Methodology for Microbial Strain Typing Using Fourier-Transform Infrared Spectroscopy. Methods and Protocols 2024, 7, 48. [CrossRef]
  34. Bunaciu, A.A.; Fleschin, Ş.; Aboul-Enein, H.Y. Biomedical Investigations Using Fourier Transform-Infrared Microspectroscopy. Crit Rev Anal Chem 2014, 44, 270–276. [CrossRef]
  35. Türker-Kaya, S.; Huck, C.W. A Review of Mid-Infrared and Near-Infrared Imaging: Principles, Concepts and Applications in Plant Tissue Analysis. Molecules 2017, 22, 168. [CrossRef]
  36. Lin, S.-Y.; Chu, H.-L. Fourier Transform Infrared Spectroscopy Used to Evidence the Prevention of Beta-Sheet Formation of Amyloid Beta(1-40) Peptide by a Short Amyloid Fragment. Int J Biol Macromol 2003, 32, 173–177. [CrossRef]
  37. Ayvaz, H.; Plans, M.; Riedl, K.M.; Schwartz, S.J.; Rodriguez-Saona, L.E. Application of Infrared Microspectroscopy and Chemometric Analysis for Screening the Acrylamide Content in Potato Chips. Anal. Methods 2013, 5, 2020–2027. [CrossRef]
  38. Santos, P.M.; Pereira-Filho, E.R.; Rodriguez-Saona, L.E. Rapid Detection and Quantification of Milk Adulteration Using Infrared Microspectroscopy and Chemometrics Analysis. Food Chemistry 2013, 138, 19–24. [CrossRef]
  39. Download LibreOffice | LibreOffice - Free and Private Office Suite - Based on OpenOffice - Compatible with Microsoft Available online: https://www.libreoffice.org/download/download-libreoffice/ (accessed on 19 September 2024).
  40. SciDAVis Available online: https://scidavis.sourceforge.net/ (accessed on 19 September 2024).
  41. Kruve, A.; Rebane, R.; Kipper, K.; Oldekop, M.-L.; Evard, H.; Herodes, K.; Ravio, P.; Leito, I. Tutorial Review on Validation of Liquid Chromatography–Mass Spectrometry Methods: Part I. Analytica Chimica Acta 2015, 870, 29–44. [CrossRef]
  42. Evard, H.; Kruve, A.; Leito, I. Tutorial on Estimating the Limit of Detection Using LC-MS Analysis, Part I: Theoretical Review. Analytica Chimica Acta 2016, 942, 23–39. [CrossRef]
  43. Currie, L.A. Detection and Quantification Limits: Origins and Historical Overview. Analytica Chimica Acta 1999, 391, 127–134. [CrossRef]
  44. Massart, D.L.; Vandeginste, B.G.M.; Buydens, L.M.C.; De Jong, S.; Lewi, P.J.; Smeyers-Verbeke, J. Handbook of Chemometrics and Qualimetrics: Part A; Elsevier: Amsterdam. The Netherlands, 1997; ISBN 0-444-89724-0.
  45. Eilers, P.; Boelens, H. Baseline Correction with Asymmetric Least Squares Smoothing. Unpubl. Manuscr 2005.
  46. Eilers, P.H.C. A Perfect Smoother. Anal. Chem. 2003, 75, 3631–3636. [CrossRef]
Preprints 119383 g001
Figure 1. Synthesis of the cyclic peptide from the linear peptide by “click chemistry” using the Huisgen reaction.
Figure 1. Synthesis of the cyclic peptide from the linear peptide by “click chemistry” using the Huisgen reaction.
Preprints 119383 g001
Preprints 119383 g002
Figure 2. MS/MS spectra of linear (a) and cyclic (b) cesium cationised peptides at 2.5 V excitation voltage. No peaks were observed outside of the mass range displayed in these MS/MS spectra.
Figure 2. MS/MS spectra of linear (a) and cyclic (b) cesium cationised peptides at 2.5 V excitation voltage. No peaks were observed outside of the mass range displayed in these MS/MS spectra.
Preprints 119383 g002
Preprints 119383 g003
Figure 3. Survival Yield (SY) curves of mixtures of linear and cyclic peptides at different molar ratios. The SY is calculated from the MS/MS spectra of the cesium cationised peptides. The SY of the mixtures lie between the SY curves of the linear and cyclic peptides. The orange vertical line corresponds to the excitation voltage at which the univariate calibration model was calculated to relate the SY to the molar ratio of the linear peptide.
Figure 3. Survival Yield (SY) curves of mixtures of linear and cyclic peptides at different molar ratios. The SY is calculated from the MS/MS spectra of the cesium cationised peptides. The SY of the mixtures lie between the SY curves of the linear and cyclic peptides. The orange vertical line corresponds to the excitation voltage at which the univariate calibration model was calculated to relate the SY to the molar ratio of the linear peptide.
Preprints 119383 g003
Preprints 119383 g004
Figure 4. SY at an excitation voltage of 2.2 V for cesium-cationised mixtures of cyclic and linear peptides at different molar ratios. Two regression models were calculated: one for molar ratios of linear peptide from 0 to 0.3 (in red) and another from 0.3 to 1 (in blue).
Figure 4. SY at an excitation voltage of 2.2 V for cesium-cationised mixtures of cyclic and linear peptides at different molar ratios. Two regression models were calculated: one for molar ratios of linear peptide from 0 to 0.3 (in red) and another from 0.3 to 1 (in blue).
Preprints 119383 g004
Preprints 119383 g005
Figure 5. Calibration models of SY data with three replicates (black squares) for mixtures of cesium cationized linear and cyclic peptides obtained with (a) univariate calibration at an excitation voltage of 2.2 V and, with (b) multivariate calibration (coefficient (a) in Eq. 2). The IR samples (red circles) correspond to mixtures initially prepared for IR microscopy and measured by ER MS. The red circles correspond to the mean value of three measurements and the error bar correspond to the standard deviation of the three measurements.
Figure 5. Calibration models of SY data with three replicates (black squares) for mixtures of cesium cationized linear and cyclic peptides obtained with (a) univariate calibration at an excitation voltage of 2.2 V and, with (b) multivariate calibration (coefficient (a) in Eq. 2). The IR samples (red circles) correspond to mixtures initially prepared for IR microscopy and measured by ER MS. The red circles correspond to the mean value of three measurements and the error bar correspond to the standard deviation of the three measurements.
Preprints 119383 g005
Preprints 119383 g006
Figure 6. Performance of the univariate (black circles) and multivariate calibration models (red squares) in terms of: (a) fit error and (b) percentage of fit error.
Figure 6. Performance of the univariate (black circles) and multivariate calibration models (red squares) in terms of: (a) fit error and (b) percentage of fit error.
Preprints 119383 g006
Preprints 119383 g007
Figure 7. IR spectra of the linear peptide (in red) and the cyclic peptide (in blue). A specific peak is observed for the linear peptide.
Figure 7. IR spectra of the linear peptide (in red) and the cyclic peptide (in blue). A specific peak is observed for the linear peptide.
Preprints 119383 g007
Preprints 119383 g008
Figure 8. IR spectra of the mixtures of linear and cyclic peptides: a) Raw data, b) Preprocessed spectra with baseline correction by AsLS.
Figure 8. IR spectra of the mixtures of linear and cyclic peptides: a) Raw data, b) Preprocessed spectra with baseline correction by AsLS.
Preprints 119383 g008
Preprints 119383 g009
Figure 9. Calibration models to quantify the molar ratio of linear peptide by IR microscopy. (a) Univariate calibration based on the area of the specific peak of linear peptide (Figure 7). (b) PLS calibration model calculated from the whole IR spectra. .
Figure 9. Calibration models to quantify the molar ratio of linear peptide by IR microscopy. (a) Univariate calibration based on the area of the specific peak of linear peptide (Figure 7). (b) PLS calibration model calculated from the whole IR spectra. .
Preprints 119383 g009
Preprints 119383 g010
Figure 10. Performance of the univariate (black circles) and PLS (red squares) calibration models in terms of: (a) fit error and (b) percentage of fit error.
Figure 10. Performance of the univariate (black circles) and PLS (red squares) calibration models in terms of: (a) fit error and (b) percentage of fit error.
Preprints 119383 g010
Table 1. Analytical performance of univariate and multivariate calibration models for the quantification of the molar ratio of linear peptide by energy-resolved mass spectrometry (ER MS) and IR microscopy.
Table 1. Analytical performance of univariate and multivariate calibration models for the quantification of the molar ratio of linear peptide by energy-resolved mass spectrometry (ER MS) and IR microscopy.
Analytical technique Calibration model Linearity interval
 R2 Fit error
(RMSEC)		 Intermediate precision Detection limit (LD)

ER MS		 Univariate 0 - 0.3 0.977 0.015 1.71·10-2 0.053
Multivariate (CLS) 0 - 0.3 0.983 0.013 1.58·10-2 0.045
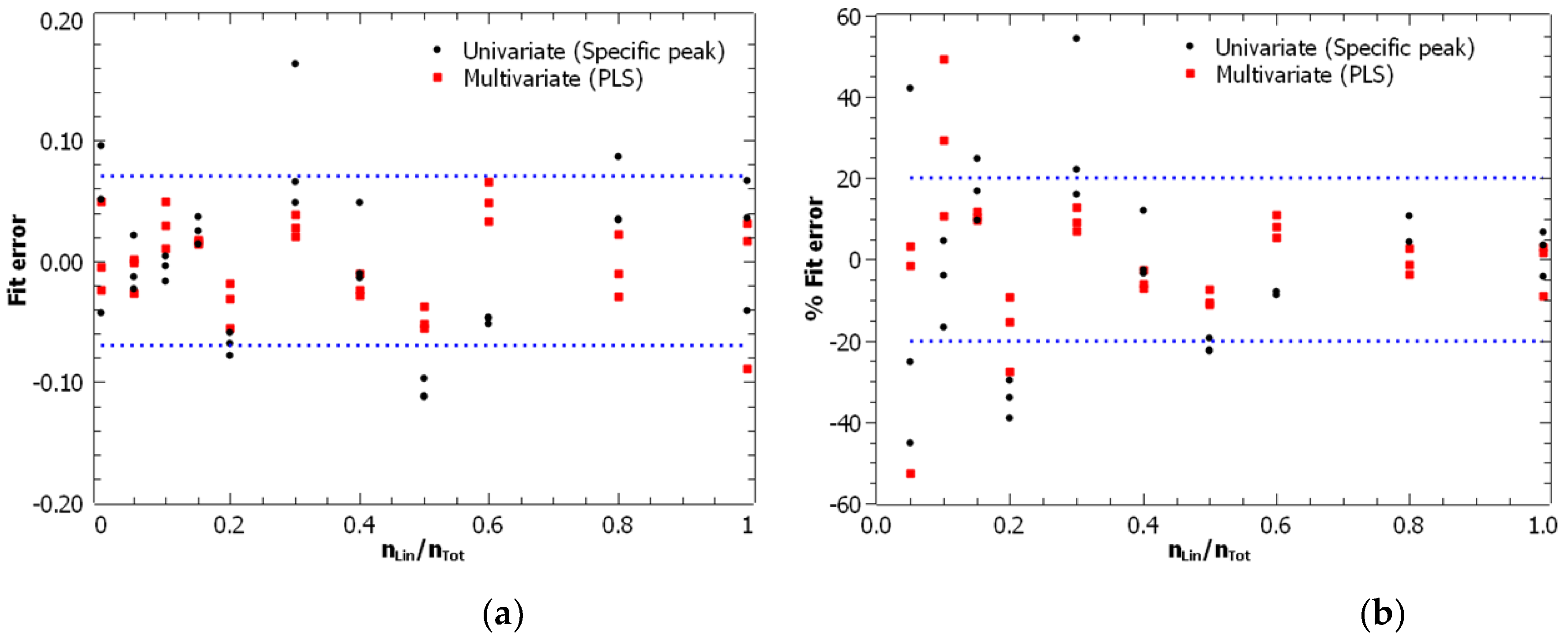
IR
microscopy		 Univariate 0 - 1 0.961 0.062 5.06·10-2 0.21
Multivariate (PLS) 0 - 1 0.987 0.036 2.63·10-2 0.11
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated