Prerpints.org logo
Preprint
Article

Analytical Prediction of Multi-Phase Texture in Laser Powder Bed Fusion

Altmetrics

Downloads

47

Views

29

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

26 September 2024

Posted:

29 September 2024

You are already at the latest version

Alerts
Abstract
For advancing manufacturing, arising AM, with an inverse philosophical approach compared to conventional procedures, has benefits that include intricate fabrication, reduced material waste, flexible design, and more. Regardless of its potential, AM must overcome several challenges due to multi-physical processes with miscellaneous physical stimuli in diverse materials systems and situations, such as anisotropic microstructure and mechanical properties, a restricted choice of materials, defects, and high cost. Unlike conventional experimental work that requires extensive trial and error resources and FEM, which generally consumes substantial computational power, the analytical approach based on physics is an exceptional choice. Understanding the relationship between the microstructure and material properties of the fabricated parts is a crucial focus in AM research. Texture is a vital factor in almost every modern industry. This study first proposed a physics-based model to foreshadow the multi-phase crystallographic orientation distribution in Ti-6Al-4V LPBF while considering the part boundary conditions due to the importance of part geometry in real industry. The thermal distribution obtained from this function operates as the information for the single-phase crystallographic texture model. In this model, we forerun and validate the orientations of single-phase materials utilizing three Euler Angles with the principles of CET and thermodynamics, as well as the intensity of the texture by approximating them with published results. Then, we transform the single-phase texture into a dual-phase texture in Bunge calculation, illustrating visualized by pole figures of both BCC and HCP phases. This texture evolution model provides a new paradigm for future researchers to model the texture or microstructure evolution semi-analytically and save many computational resources in a real-world perspective. Others have not yet done this work about simulating the multi-phase texture in an analytical approach, so this work bridges the gap in this field. Furthermore, this paper establishes the foundation for future research on materials properties affected by microstructure or texture in academic and industrial environments. The precision and dependability of the results obtained through this method make it a valuable tool for ongoing research and advancement.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

The world is undergoing an industrial revolution driven by bio-inspired artificial intelligence [1], growing accumulated data, and increasing yet limited computational resources. These driving forces are reshaping human society more profoundly than ever before. Undoubtedly, Sir Isaac Newton’s analytical philosophy of science established in the seventeenth century [2] still dominates academic research. The combination of the two has demonstrated exceptional performance in industries and academia. In addition, decarbonization, green, and sustainable manufacturing have been a shared consensus around the globe, as pointed out in many national technological strategy reports such as [3]. Throughout the long history of human eras, various materials and manufacturing processes have been playing a core role, and there has been significant progress in materials discovery [4,5] and synthesis [6] within Industry 4.0 [7]. For advancing manufacturing, emerging AM [8,9] provides an inverse philosophical approach compared to traditional procedures. Its benefits include intricate fabrication, reduced material waste, flexible design, and more. This process replaces conventional manufacturing techniques and generates economic impact [10]. Regardless of its potential, AM still needs to overcome several challenges due to multi-physical processes with miscellaneous physical stimuli in diverse materials systems and situations, which usually require more convoluted unraveling than materials find and synthesis. These challenges must be addressed before they can supersede [11] conventional manufacturing practices in more fields. Even with AM’s advantages, limitations such as anisotropic microstructure and mechanical properties, a restricted choice of materials, defects, and high cost are weighty [12]. Due to the vast number of landscapes that require exploration and the challenge of selecting restricted materials for 3D printing, solely conventional experimental work is impractical, as it necessitates extensive trial and error resources. On the other hand, FEM, another mainstream methodology, generally consumes substantial computational power. Regarding this high cost, the analytical approach based on physics would be an outstanding choice.
The two most common techniques for printing metals are powder bed fusion and direct energy deposition [12]. LPBF is a commonly used metal AM method in which a high-density laser beam melts layers of powder to create parts layer by layer [13], and can be selected as a representative research technique with merely thermal stimuli. In LPBF, understanding the relationship between the microstructure and material properties of the fabricated parts is a crucial focus in AM research [14,15]. Texture is a critical factor in almost every modern industry. It affects things as different as the weight of beer cans, automotive industries [16], and the potential of high-temperature superconducting cables. The evolution of texture determines many of the physical, chemical, and mechanical properties of polycrystalline materials [17]. Remember, one of the challenges mentioned in the introduction is anisotropy, an essential issue in situations such as microelectronic devices, fiber composites, polycrystalline metal, etc. This means the microstructure and properties are anisotropic, usually closely related to grain structure in terms of grain orientations or texture, which are still contested when modeling quantitatively. Many research papers implementing numerical models, experimental methods, and machine learning conducted predictions of the materials microstructure or characterizations of materials microstructure evolution caused by factors including processing parameters, original materials properties, etc. L. Thijs et al. [18] investigated the microstructure evolution of titanium alloy processed by LPBF, the effect of scanning parameters, and the procedure on microstructure mainly using characterization methods. H. Azizi et al. [19] characterizing the impact of produce direction on the microstructure development of Al-Si alloy constructed by the LPBF technique.
The research work involving similar kinds of experimental characterizations or FEM modeling has the disadvantage of being time-consuming. The texture explorations included in the microstructure evolution also share this impediment, particularly for AM, where there are anisotropic giant grains (around a hundred microns). An adequate microstructure size can be on the hierarchy of a micrometer, and the existing FEM cannot handle such a large quantity of data. Therefore, proper analytical models become increasingly important on the eve of this intelligence industrial revolution regarding usually limited computational capacity or experimental facilities. For quantitative texture evolution prediction in LPBF, some early efforts focused on heat treating, melting with laser scanning, electron beam, welding [20,21], and so on by analytics. J. Goldak et al. [22] developed a FEM mathematical model for traditional weld heat sources based on space’s Gaussian power density distribution. J. D. Hunt’s [23] CET standard helps obtain the processing-microstructure space map. Gäumann et al. [24,25] developed it in the background of single-crystal superalloys with laser deposition. J. Gockel et al. [26] innovatively translated the solidification map into G- R S space, paving the way for a more comprehensive understanding of the subject. A. Basak et al. [27] discussed the processing map under various materials systems and metal additive manufacturing processes. J. Liu et al. [28] employed these findings to create a reasonably speedy model for foretelling the grain orientation of the Titanium alloy materials system after solidification in LPBF. However, the model’s precision could not be assured because of the need for a robust thermal model. A. Chadwick et al. [29] incorporated solid-liquid interfacial stability consideration, forming a semi-analytical model. However, their employed Rosenthal thermal model is simple for calculating texture evolution in LPBF, and the iterative process consumed about 1 minute, which would still be too long for actual industrial application. Additionally, they did not give clear grain orientation information, and this would make subsequent properties modeling, if any, difficult. Recent related research [30,31,32] shared similar problems to those mentioned above.
This work proposes new quantitative models considering heat input and heat loss with a more accurate molten pool and temperature distribution for microstructure evolution simulation, addressing the flaws mentioned above that no previous research solves. Additionally, the model established in this research is analytical-based, and the approach is prone to being data-driven, which is much faster. Currently, materials testing is expensive in the industry, and historical data has not yet been fully utilized, though they were recorded; there is an urgent need to develop a computational, cost-effective paradigm to quickly take up the leading role in this emerging AI and data-driven industrial revolution. Plus, this work expands the range of quantitative texture prediction to multi-phase materials cases. Still, in academia, it is essential to develop a better authentic analytical framework for crystallographic orientation distributions of materials to facilitate further study of the development of material properties in the AM process. This study initially employs a computational approach [33] to father a singular β -phase texture established on thermal narrative, representing the liquidus of Ti-6Al-4V materials in melting. Then, the second HCP phase is modeled and incorporated. This study employs the thoughtful temperature model [34], Hunt’s model [23], and several past publications’ empirical parameters. The outcomes indicate that the models utilized in this study perform admirably and attain a more increased accuracy rank in forecasting the multi-phase surface of materials.

2. Methodology

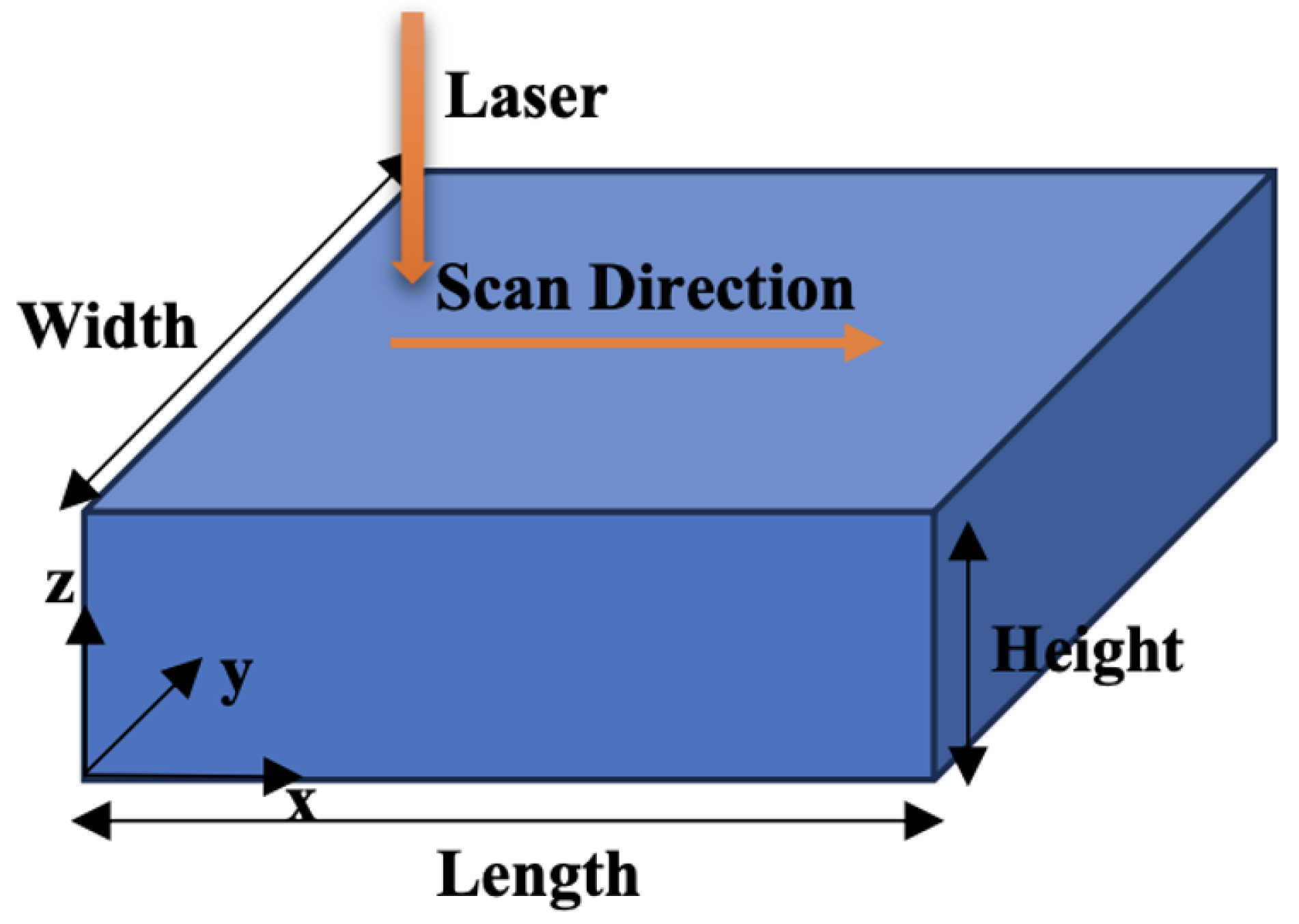
2.1. Thermal Model

This study initially applies a physics-focused analytical framework established by Ning et al. [34] to estimate the three-dimensional thermal distribution in LPBF. Geometry and build edges are essential in real applications, so a closed-form solution should be implemented here, considering heat transfer boundary conditions and taking their effects. This framework takes into account the impact of heat conduction, convection, and radiation on the heat loss at the part boundary, affecting the molten pool geometry and the induced thermal gradient. These factors have not been considered in the context of analytical modeling by previous researchers. In elaborate, the boundary faces have been segmented into multiple heat sinks with equivalent areas in order to determine heat loss. For a point-moving heat source, the employed solution was first suggested in literature [35] and presupposed a 3D semi-infinite body:
T ( x , y , z ) = P η 4 π K R exp − V ( R + x ) 2 κ + T 0
where η is the laser absorption coefficient and P is the laser power. The distance from the heat source ( x 0 , y 0 , z 0 ) to the point of analysis (x, y, z) is R = ( x − x 0 ) 2 + ( y − y 0 ) 2 + ( z − z 0 ) 2 . The expression for κ is κ = K / ρ c , where K denotes thermal conductivity, ρ is density, and c is heat capacity.
In terms of the dissipation of thermal energy, the mechanisms of heat conduction, convection, and radiation are addressed through the utilization of the subsequent equations, as follows:
Q cond = A k p Δ T R
Q conv = A h ( T − T 0 )
Q rad = A ε σ ( T 4 − T 0 4 )
where h is the heat convection coefficient, ε is the emissivity, σ is the Stefan-Boltzmann constant, and k p is the powder’s thermal conductivity. T is the temperature that can be determined using the point-moving heat source solution, and A is the area comprising each heat sink on the surface of the melt pool. The following is the expression for the three-dimensional temperature distribution when heat input and heat losses are added up:
T ( x , y , z ) = 1 4 π k R P η exp − V ( R + x ) 2 κ − A h ( T − T 0 ) + ε σ ( T 4 − T 0 4 ) + k p ( T − T 0 ) R + T 0
Figure 1 illustrates a schematic depiction of the construction component employed for the examination of the thermal distribution in LPBF. Its main objective is to corroborate the model. This investigation exclusively focuses on the single-track scanning strategy.
The molten pool geometry can be ascertained by comparing the temperature distribution calculated with the thermal model with the material’s melting temperature.

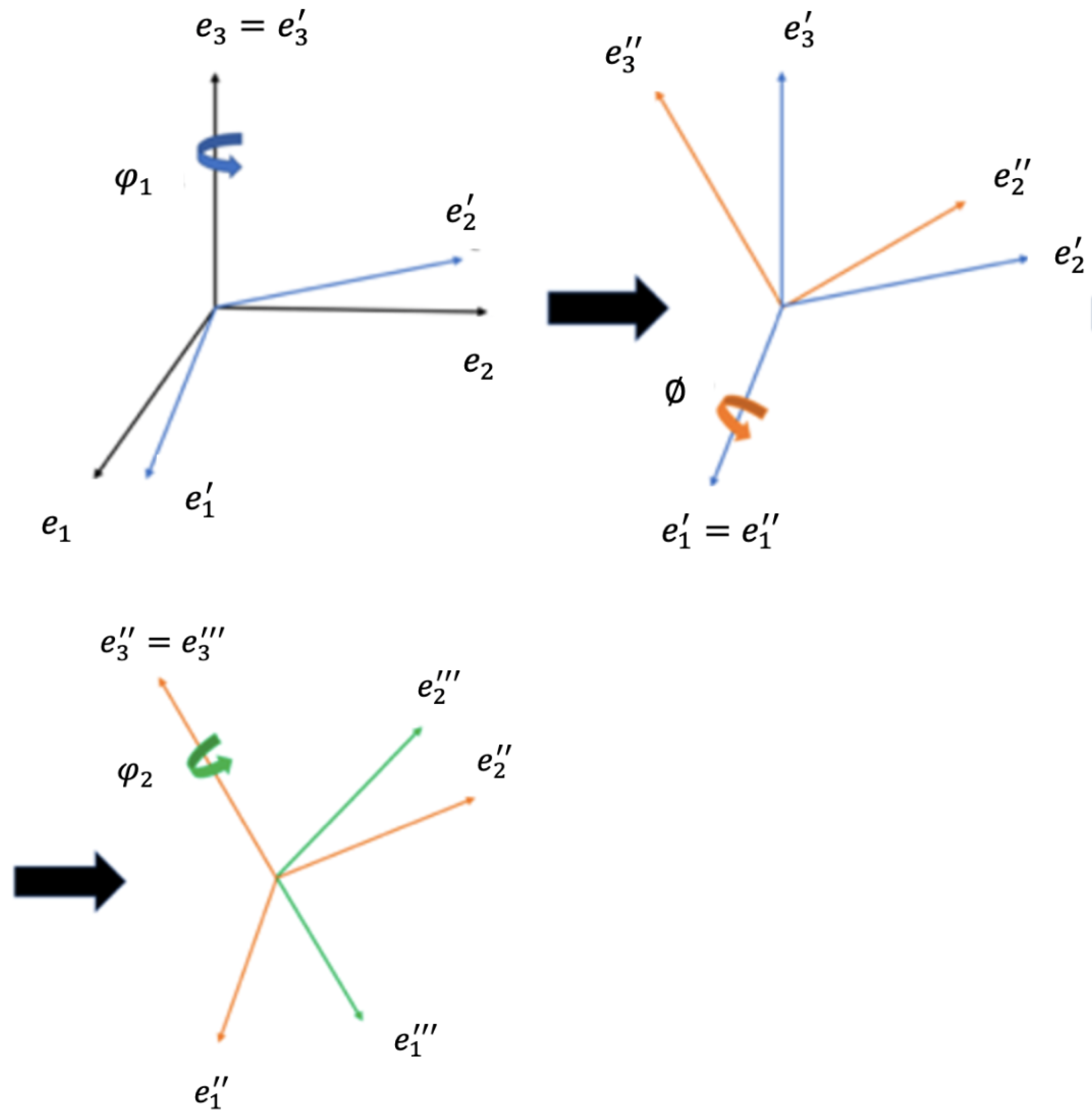
2.2. Single-Phase Texture Model

In this work, the liquidus components of Ti-6Al-4V during melting were represented by a single BCC beta phase texture. Three Euler angles represent the crystallographic orientation of each individual grain in the material. These angles specify the three rotations needed to convert the crystallographic lattice frame from the lab reference frame. Among numerous conventions, the Bunge convention was picked to depict the Euler angles, as seen in Figure 2.
By analyzing the temperature distribution profile, it is possible to calculate the thermal gradient within the molten pool using the formula G = | ∇ T | . The solidification rate, R S , which affects grain growth and is dependent on factors such as the beam velocity and the shape of the melt pool, can subsequently be obtained by
R S = V cos θ
where θ is the angle between the directions of growth and scanning, and V is the scanning speed. The CET is expressed by the G n R S ratio in Hunt’s model. If the ratio surpasses a certain value ∅, the solidification process becomes entirely columnar, and arms of dendrites will sprout from the interface between liquid and solid states. Kobryn et al. [37] have experimentally calibrated a solidification map in the G − R S space for Ti-6Al-4V, which is being utilized here. The final orientation of the materials is greatly influenced by the substrate texture, which is an important factor in the solidification process. As a result, careful consideration of the substrate’s orientation must be given. This study utilized a polycrystalline powder substrate with multiple random orientations instead of a single crystal base, allowing for a substrate that is closer to industrial reality. Columnar grains will develop epitaxially from the seed crystal once the solidification location has been identified. Maximizing the cosine value of the angle formed by two vectors will reveal the direction in which the terminal dendrite of a given location point grows. The formula cos ϕ = m · G G represents this angle, with m denoting the unique crystallographic orientation vector of the seed crystal that yields the greatest value of cos ϕ . The location’s thermal gradient vector is G . This idea is predicated on the fundamental precept that the most stable configuration can be obtained by decreasing the energy of the system. The polycrystal base, which offers seed crystals in many orientations, is seen in Figure 3 along with the melt pool and thermal gradient.
The texture orientations will grow along the orientation based on the random substrate texture at its location once the solidification area is identified for the growth of equiaxed grains. The liquid behind the melt pool hardens as the laser travels along a single track, working its way up from the bottom. Following the completion of the first layer scanning, the second layer will be constructed on top of the first layer, with the first layer serving as the new seed crystals for the grain growth in the second layer. This process will continue layer by layer. The texture-related calculation algorithm was coded in MATLAB with the input parameters of physical constants, LPBF process conditions, and materials properties. Columnar/equiaxed transition coefficients are referred to in literature [38].

2.3. Multi-Phase Texture Model

The multi-phase texture model has two main components. The first involves calculating thermal gradients grounded on input processing parameters and material properties. Once the thermal gradients have been figured, the second component uses Bunge calculations to estimate the texture. While the single-phase texture is modeled using solidification rates, the second and subsequent phases are constructed upward employing precipitation rotational matrices. For the Ti-6Al-4V materials system, the first phase is the BCC beta structure, and the HCP alpha phase could be considered the child phase. As the materials are melted, it is entirely the BCC beta phase, and the HCP phase comes into being when precipitation occurs during cooling and there would be both BCC beta and HCP alpha phases. [39]. Further, it was assumed that alpha-phase precipitation would orient itself based on the parent texture but in a manner described in the literature [40]. Then, it comes to the percentage or frequency at which the HCP alpha phase precipitates. Over the years, the documentation extensively covers the variety of alpha phase sizes, orientations, and their relation to solidification rates. Extensive research has been conducted to study the development of the alpha phase in Ti-6Al-4V alloy during additive manufacturing. They have enabled the mapping of thermal gradients versus growth rate (G vs. R S ) [41] and the detailed identification of six specific types of alpha-phase precipitates along with their relative distributions [42]. According to the literature [42], the frequency documented of the six alpha-phase precipitates rotational matrices and their distribution are: D − 1 E = 1 0 0 0 1 0 0 0 1 (17.8%), D − 1 C 23 + = 1 2 3 2 0 3 2 − 1 2 0 0 0 − 1 (13.2%), D − 1 C 3 z + = − 1 2 − 3 2 0 3 2 − 1 2 0 0 0 − 1 (11.3%), D − 1 C 21 + = 1 0 0 0 − 1 0 0 0 − 1 (14.4%), D − 1 C 22 + = − 1 2 3 2 0 3 2 1 2 0 0 0 − 1 (16.9%), D − 1 C 6 z + = 1 2 − 3 2 0 3 2 1 2 0 0 0 1 (26.4%). The material’s Euler angles in the single-phase BCC texture undergo one of six rotation transformations to simulate the alpha-phase HCP texture precipitates. Although previous studies have described the rotational symmetry elements and any additional misorientation effects caused by grain boundaries [43], defect-caused stresses [44], we will not consider them here due to their instability across various processing situations. Each element of the single-phase BCC matrix was broken down by converting the Euler angles into a 3*3 matrix using Bunge’s method. Then, they were multiplied by one of the six alpha-phase precipitation operators at the coefficient representing their documented accurate distributions stated above. After combining the two phases, the final texture was a mix of the two textures at a ratio of 85:15 HCP: BCC, with a slight random fluctuation of 0.38. This ratio was chosen to visualize the beta phase better, but the BCC phase is usually less common when the alloy is completely cooled [45].
In real-world applications, multiple rows and layers are expected to be used in manufacturing bulk materials and their microstructure using LPBF. Therefore, it is essential to simulate these scenarios to guide industrialization. When developing the stacked-fault microstructure, the texture was modeled from the bottom to the top, while the remelted depth was calculated at each step to ensure accurate height was achieved. Similarly, in multi-row situations, the sections covered between the rows were precisely measured to ensure the correctness of the results. Lastly, they were integrated into multiple rows and layers and stored in relevant variables for further visualization and mathematical analysis. Therefore, this model can simulate texture evolution in any complicated scanning strategy with multiple rows, layers, or even different angles.

3. Results and Discussion

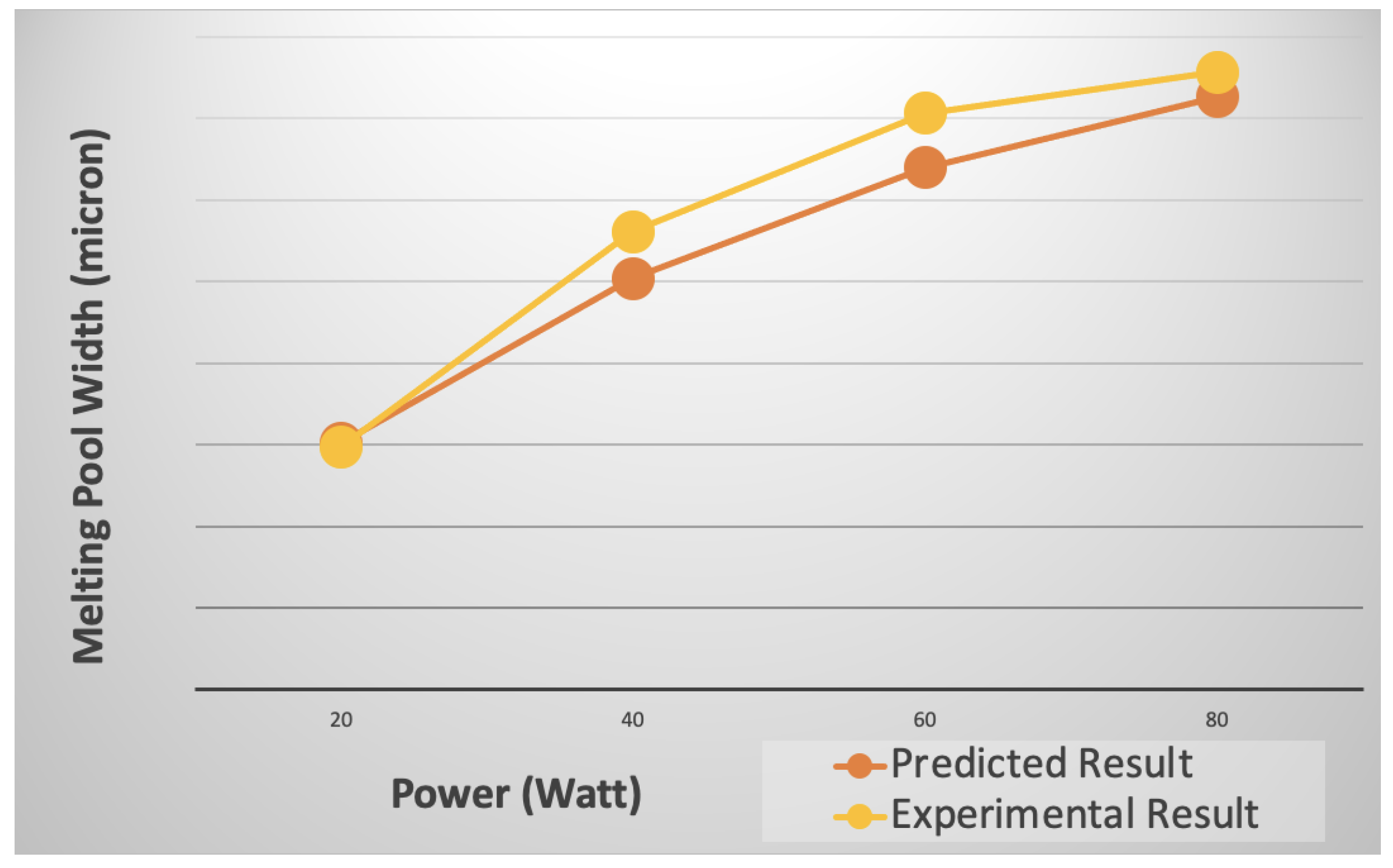
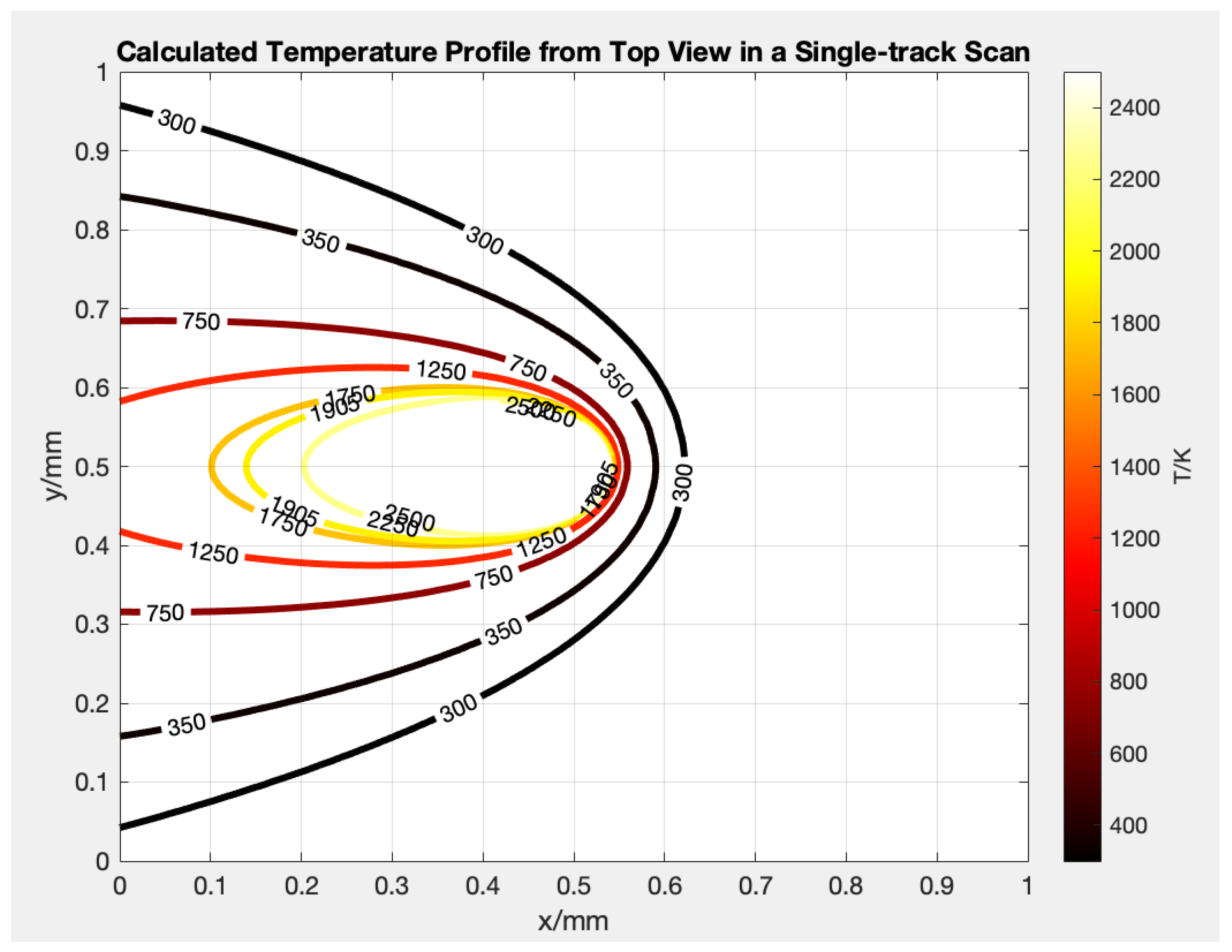
3.1. Thermal Model

In order to estimate the temperature distribution in Ti-6Al-4V LPBF while accounting for part boundary conditions, a model was suggested in this study. It was supposed that the build component and the platform were made of the same material. Table 1 displays the Ti-6Al-4V thermal material parameters that were gathered from the literature. The laser absorption value of 0.818 was taken from a previous study [46]. This value was determined through an analytical simulation of the heat transfer model claimed by Gusarov et al. [47]. It was then included in the suggested model as a laser power coefficient. By comparing it to the melting temperature of the material, the geometry of the molten pool is found. If the predicted temperature exceeds the melting point, the area should be included in the molten pool. Otherwise, it falls outside of the molten pool. The dimensions of the build part were set as follows: length - 4mm, width - 1mm, and height - 0.5mm. The boundary heat loss should be equal to the sum of the heat sinks on each surface, with nine heat sinks applied. The predicted temperature dispersion and melt pool size are based on specific processing conditions.
A series of thermal simulations were conducted to demonstrate the power and accurateness of the proposed thermal model. The results obtained from these simulations were validated against experimental measurements [50]. The temperature profiles obtained from the simulations were compared with the melting point of Ti-6Al-4V to estimate the size and shape of molten pools. As seen in Figure 4, the experimentally measured molten pool size was contrasted with the projected molten pool dimensions. The comparison revealed that the simulation predictions and the experimental data agreed satisfactorily, demonstrating the validity of the thermal model working at this study.
To verify the single-phase and multi-phase texture, the simulated texture should be compared under the same processing parameters of past experimental data [51], so the laser power and scanning speed were first set as 157W and 225mm/s. The 3D temperature distribution near the laser source location was heralded, as depicted in Figure 5, where the temperature profiles were on the top surface. The dimensions of the molten pool are 181.82 μ m (Width), 88.89 μ m (Depth), 393.94 μ m (Length).
According to J. Liu et al. [28], modifications to the power and scanning velocity processing parameters only impact the magnitude—not the direction or texture. However, the power and scanning speed can affect the texture of 3D-printed objects. The main issue that needs to be addressed is the temperature distribution caused by Rosenthal’s solution. This calculation should be done by considering the heat loss due to various factors such as heat conduction, heat convection, and heat radiation at the borders of the print. All these factors are related to temperature and can be calculated using their respective equations. To provide more evidence, Figure 6 and Figure 7 below display some running outcomes with various processing parameters based on the thoughtful thermal models. After obtaining the thermal gradients in the X, Y, and Z directions, the angle α between the X and Y components of the thermal gradient can be computed and exhibited in the histogram format. The calculation equation is:
α = arctan ( G Y / G X )
where GY, GX are components of G in the Y and X directions. Figure 6 and Figure 7 display the simulated angle α calculated, illustrating the different distribution of thermal gradient angles between the two scenarios. It has been demonstrated that the thermal gradient and consequent texture can be impacted by processing parameters including laser power and scanning velocity. Their prior single-phase texture model has been improved upon by this study, as the researchers identified and addressed a flaw in their previous model’s heat transfer consideration that caused deviations from experimental data.

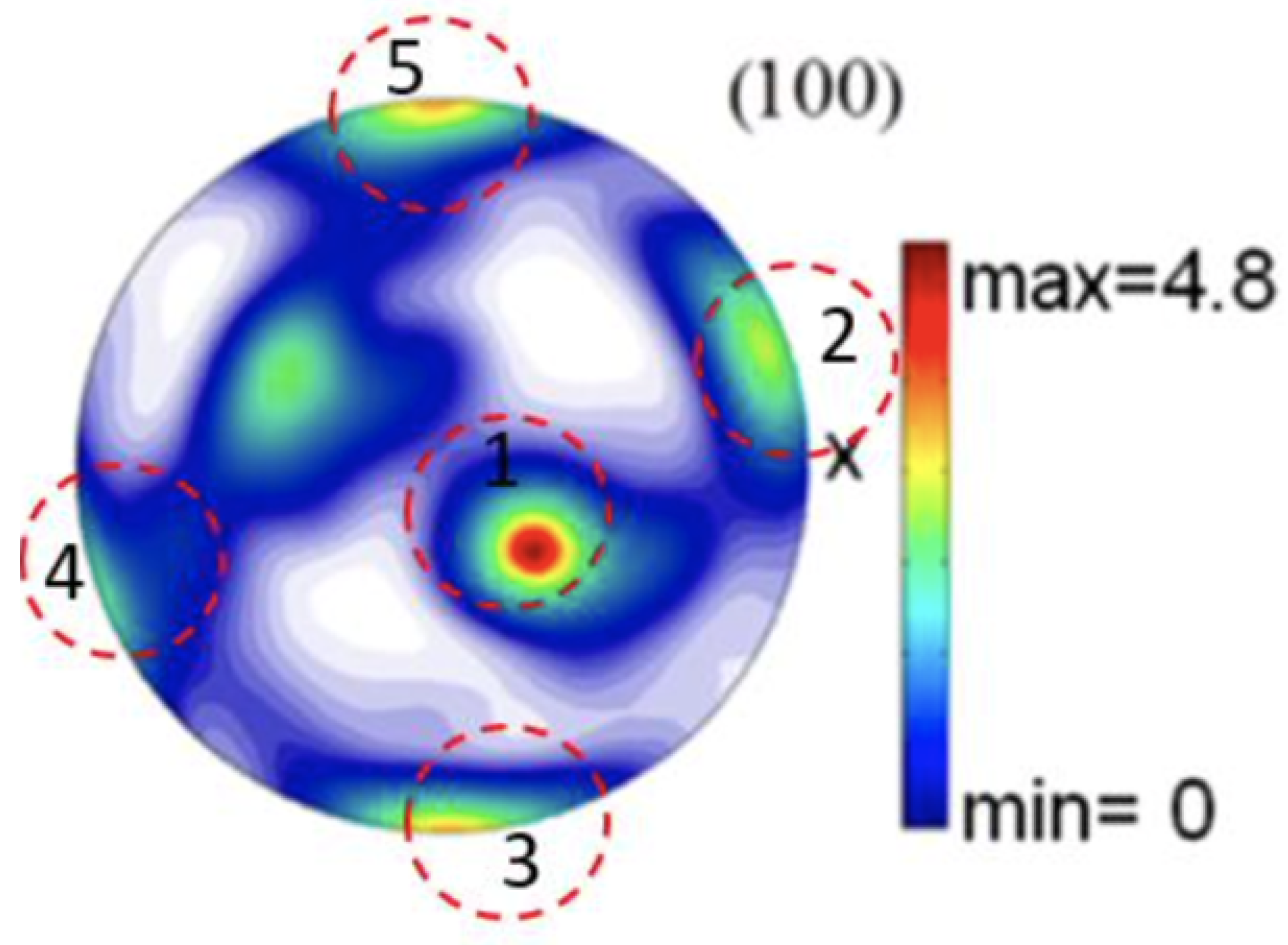
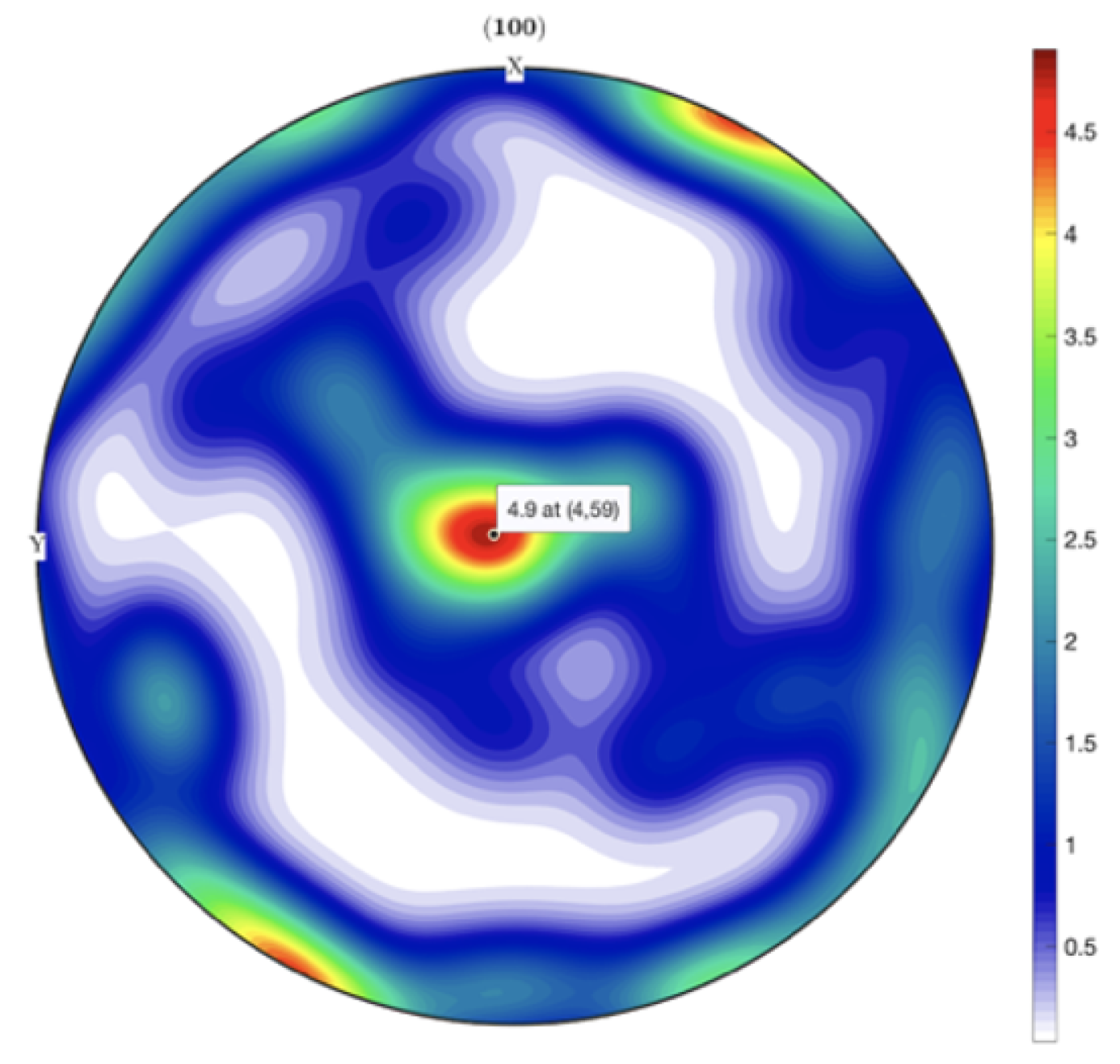
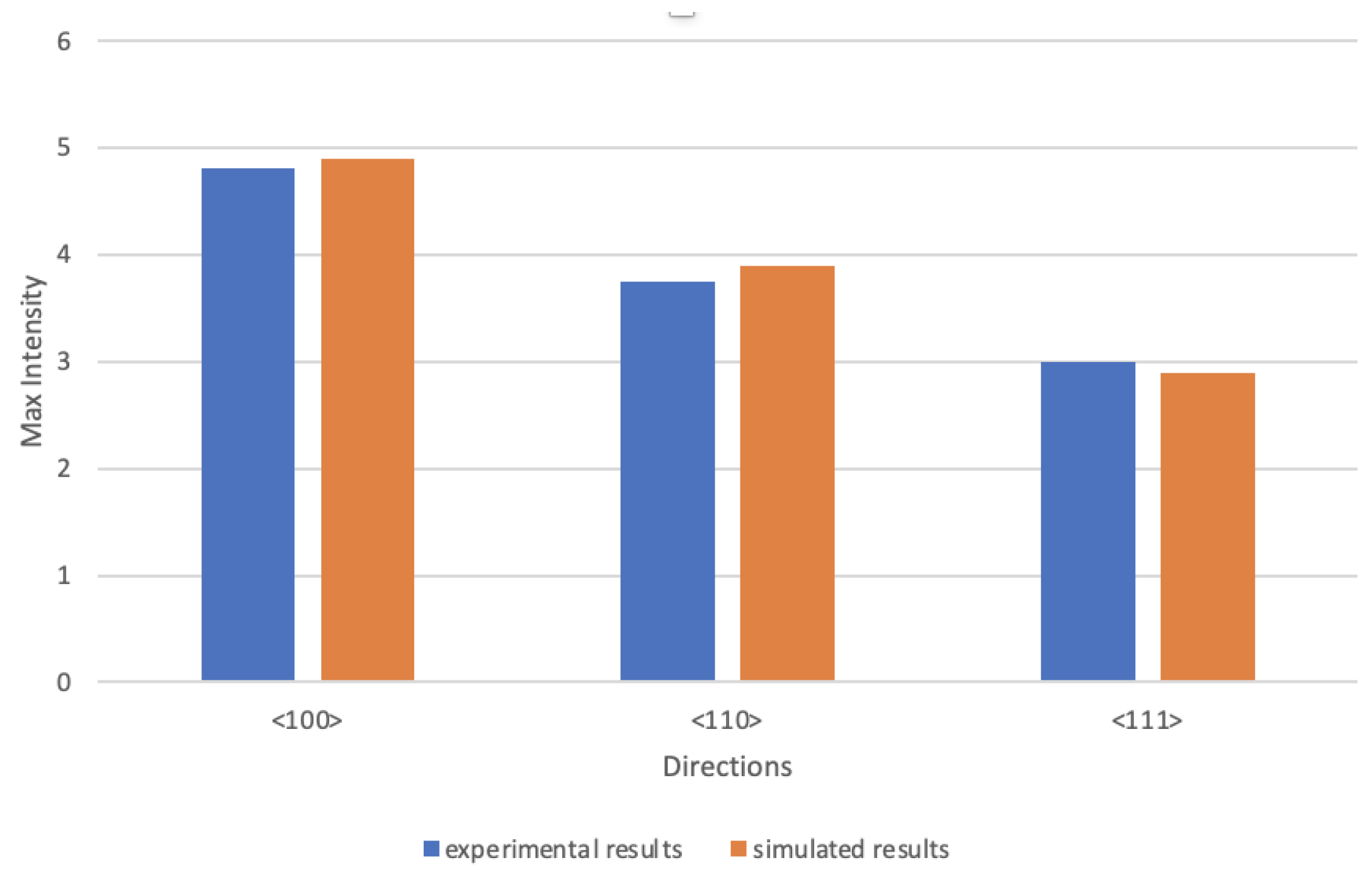
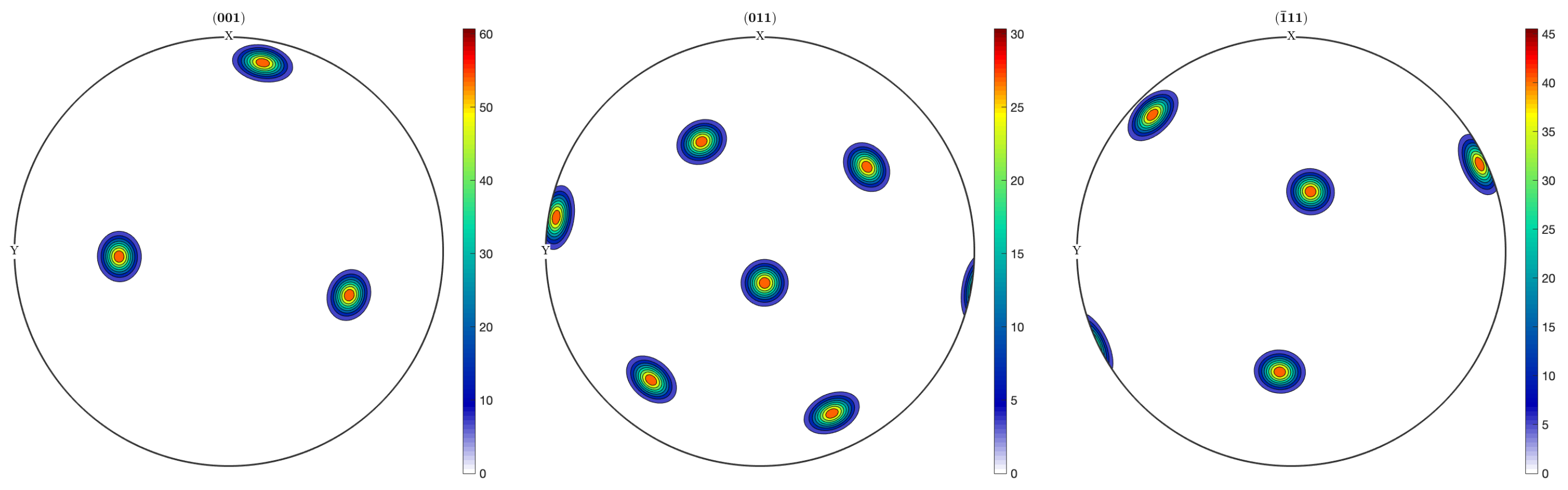
3.2. Single-Phase Texture Model

The building settings for the texture evolution of Ti-6Al-4V in LPBF are displayed in Table 2. The beta phase texture results of the experimental study conducted by M. Simonelli et al. [51] and the current simulation study are represented in Figure 8 and Figure 9, respectively. The experimental and simulated results show a similar pattern in the beta phase texture. The maximum intensity peaks in both of the two (100) patterns are located somewhat off of the < 100 > direction, implying that the majority of grains are orientated in that direction. The simulation result has a texture intensity of 4.9, which is very close to the experimental result 4.8. Regarding the peak positions, the modified simulation result agrees with the experimental result exactly. However, the experimental study also includes the alpha/HCP phase along with the beta/BCC phase following the solidification of the liquid phase. This could be the cause of the little discrepancy between the experimental result and the simulation result reported in this study. Additionally, Figure 10 shows the comparison between the simulated and experimental results regarding maximum texture intensity in all of the three directions of < 100 > < 110 > < 111 > . The close agreement also suggests the accuracy of this model.

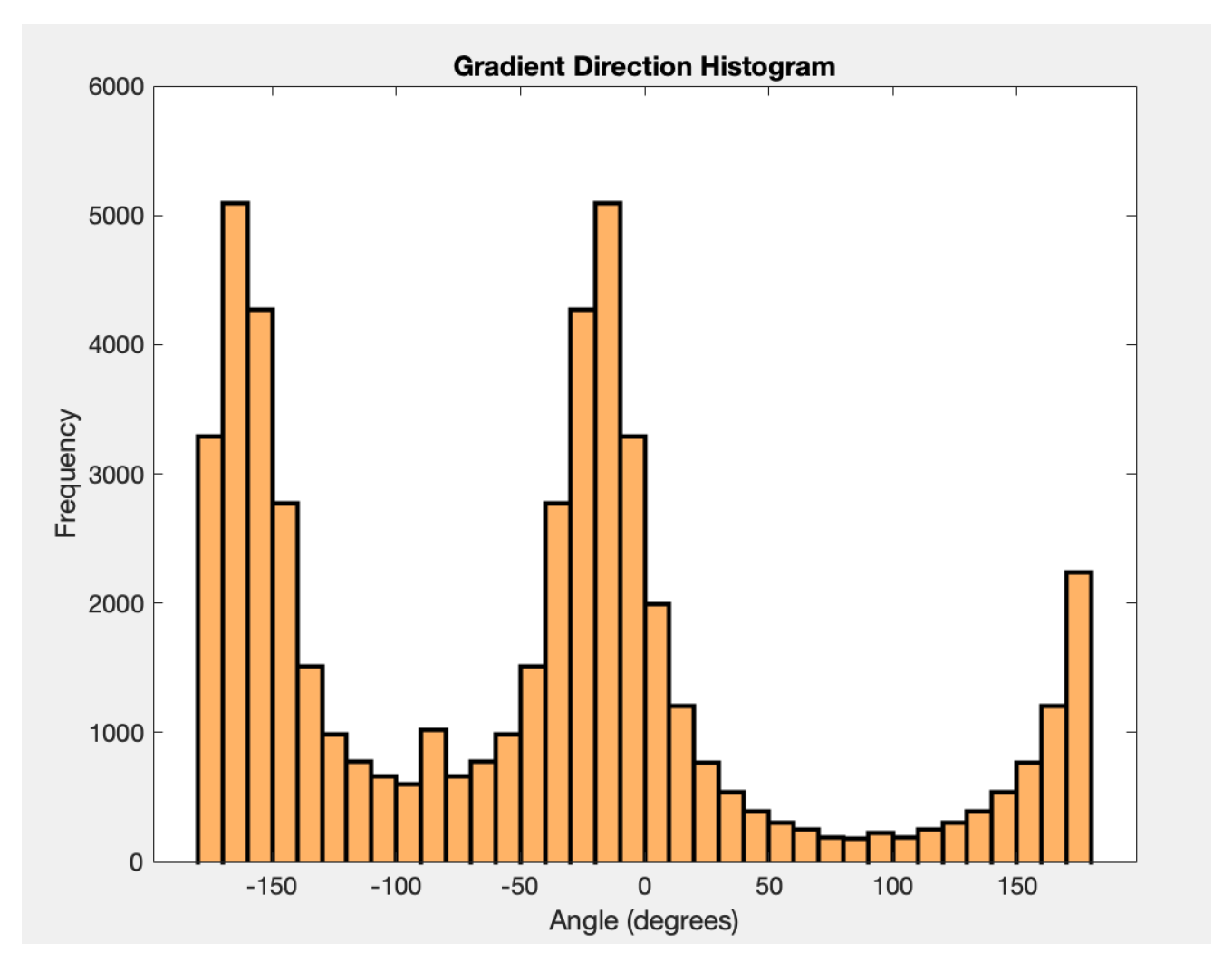
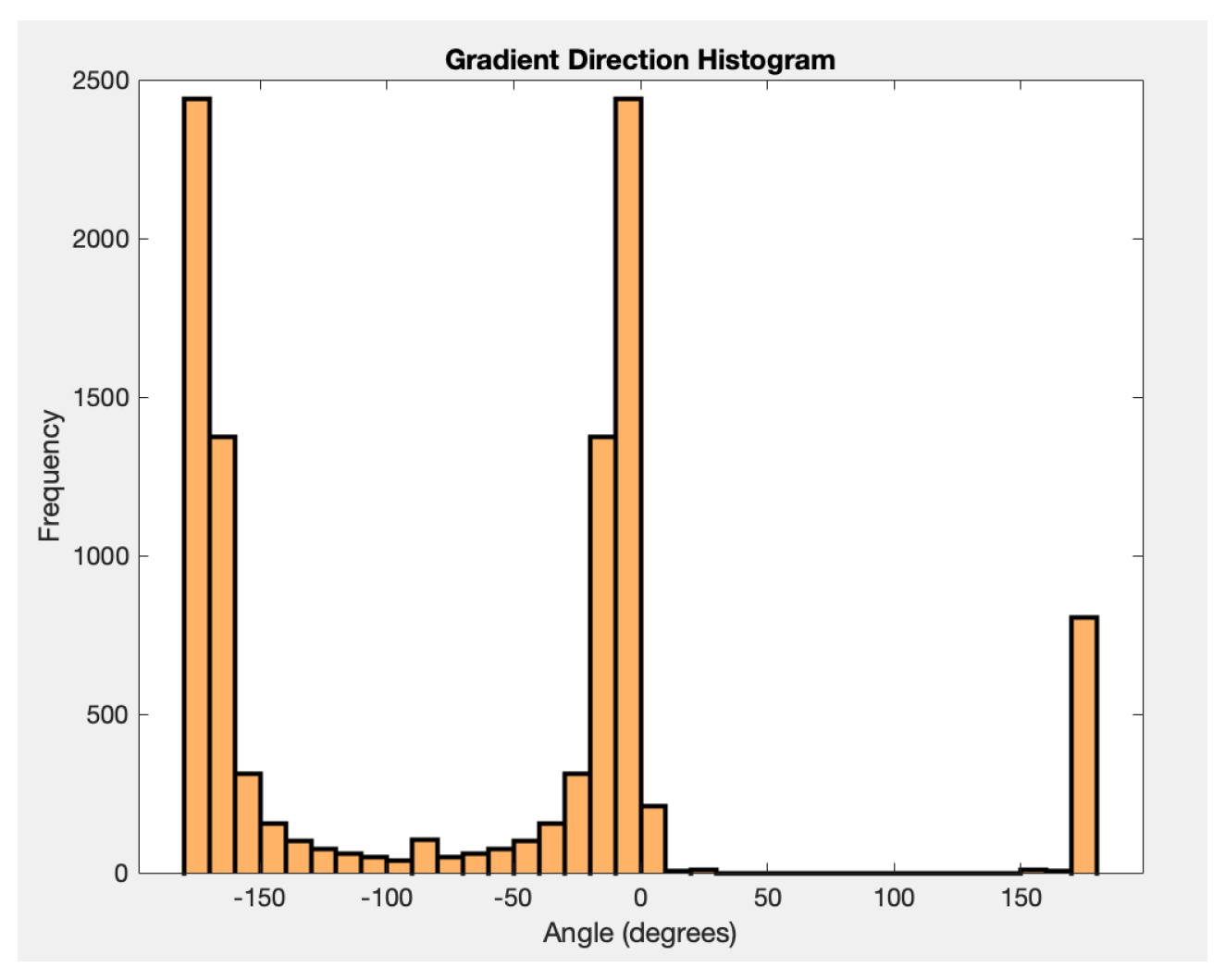
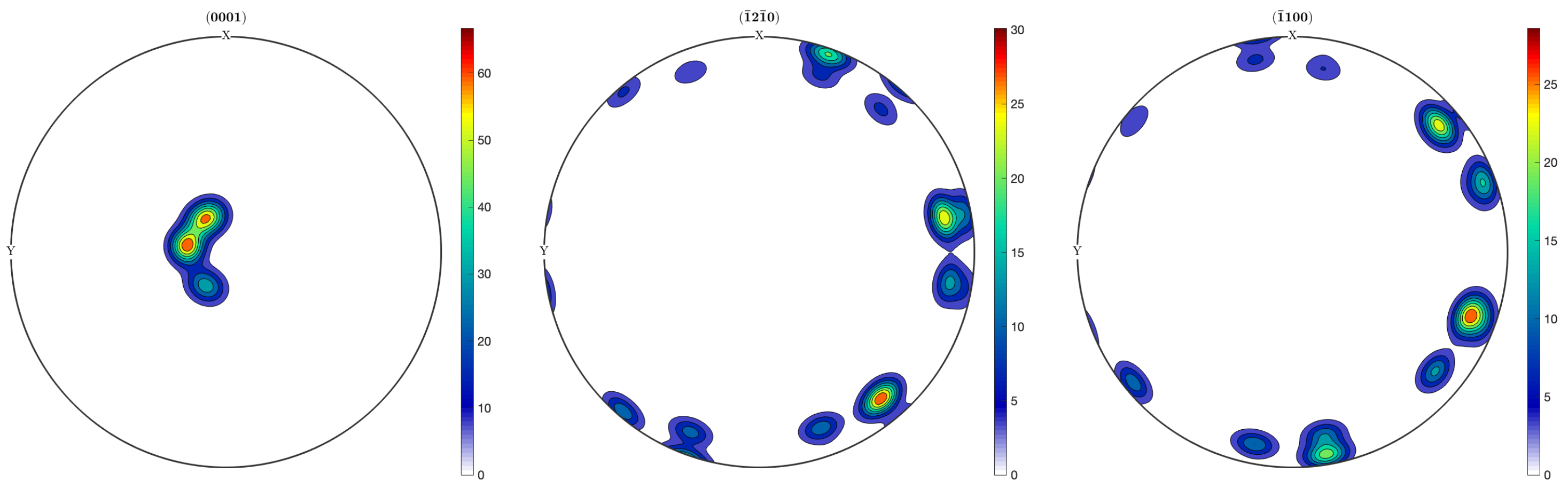
3.3. Multi-Phase Texture Model

In simulating multi-phase texture, to simplify the model and not lose important information, the laser point was still set at the center of the part, and the layer thickness and hatching space are all 50 μ m . With the help of the relevant software and toolbox, the texture, or in other words, the crystallization orientations, which are characterized by three Euler Angles, were mapped out as pole figures (Figure 11, Figure 12).
According to a study [52], the BCC’s beta phase’s pole figures exhibit a lack of central intensity nodes in their (100) plane, but they have separate nodes represented in the three planes shown. The intensity peak results agree with the (100), (011), and (-111) outcomes in the research. On the other hand, the findings for the alpha HCP phase were also compatible, showing that a central intensity appeared in the (0001) orientation [39]. In contrast, the intensities of other orientations drove outward to the perimeter of the (-12-10) and (-1100) pole figures, as reported in previous studies [52]. Although the simulated figures do not look like they match the experimentally plotted figures done by Muiruri et al. [52], the primary trend and appearance of BCC and HCP phases mentioned above agree well. To explain the deviation, past research [53] disclosed that experimental samples are created using different build directions, such as horizontal, vertical, and diagonal, which can impact the pole figure results. Different orientations would be produced depending on the sample orientation and volume. Furthermore, the addition of reheating the samples as additional layers are added and introducing defects such as grain boundaries, twinning, and residual stresses further complicate the process of matching experimental results. Last but not least, the whole process of doing the calculation generally took a time scale of several seconds or within twenty seconds on an ordinary personal laptop, which shows the promising future to be applied in the industry or further academic investigation, such as further exploration of materials properties manufactured by LPBF.

4. Conclusions

This investigation has materialized a quantitative analytical method that connects the microstructure and process prerequisites. We have updated the temperature model in LPBF metal AM to comprise heat loss, such as heat conduction, heat convection, and heat radiation, in order to convey the thermal yore closer to fact. The thermal distribution obtained from this functions as the intake to the single-phase crystallographic texture model. In this model, we forerun and validate the orientations of single-phase materials (specifically, Ti-6Al-4V) using three Euler Angles and the intensity of the texture by corresponding them with observed results. Then, we transform the single-phase texture into a dual-phase texture, illustrating it with three Euler Angles visualized by pole figures of both BCC and HCP phases.
This analytical semi-empirical representative, the multi-phase texture instance, is based on CET circumstances, previous practical data of typical materials, and physical laws with the aim of minimizing system energy. Specifically, this texture evolution model considers multi-phase texture situations, providing a new paradigm for future researchers to model the texture or microstructure evolution semi-analytically and save many computational resources. From a real-world perspective, the advantage of this model is that the more accurate it is, the more likely it can be used to replace laboratory testing. That would save time, reduce material waste, and allow substantially larger sample replicates with adjustable sizes and geometries. This work about simulating the multi-phase texture in an analytical approach has not yet been done by others, so this work bridges the gap in this field.
Moreover, the materials investigated are flexible and could be similarly converted to other materials systems, so this is general. Meanwhile, some critical assumptions of this research are made, including that defects and distortion did not occur, and interatomic energy interactions were overlooked in this work. Since the material properties vary throughout the whole process, the values of these properties are assumed to be static in this work. Thus, real-time properties or at least prone-to-be properties values might be incorporated into the model. Hence, the considerations could be based on eliminating these assumptions for future directions to perfect texture or microstructure evolution if reality permits, such as the computational cost allowed in the industry. Plus, some machine learning approaches that could more conveniently utilize a large amount of materials data would be promising to be combined to make it more robust and generalized.

Author Contributions

W. Huang conceived and developed the proposed analytical model, validated the model, and wrote the paper. M. Standish helped develop the analytical model. W. Wang, J. Ning, L. Cai, and H. Garmestani provided general help and did the paper review. S. Y. Liang provided general guidance and proofread the paper writing.

Acknowledgments

This work was supported by the Boeing Company.

Conflicts of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Abbreviations

The following abbreviations are used in this manuscript:
LPBF Laser powder bed fusion
CET Columnar-to-equiaxed transition
FEM Finite element method
AI Artificial intelligence
BCC Body-centered cubic
HCP Hexagonal tightly packed
P Laser power
T Temperature
η Laser absorption coefficient
x, y, z Coordinates
V Laser scanning velocity
R The distance between the source of heat and the analysis point
K Thermal conductivity
x 0 , y 0 , z 0 Coordinates of the heat source
κ Thermal diffusivity
T 0 Room temperature
c Heat capacity
ρ Density
Q c o n d Heat of conduction
Q c o n v Heat of convection
Q r a d Heat of radiation
A Each heat sink’s area on the surface of the melt pool
k p Powder thermal conductivity
Δ T Temperature change
h Heat convection coefficient
ε Radiation emissivity
σ Stefan-Boltzmann constant
G Thermal gradient vector
R S Solidification rate
θ The angle formed by the growth and scanning directions
n Exponent
∅ Certain value in Hunt’s model
m The exact texture vector of the seed crystal that yields the maximum value of cos ϕ
PX Polycrystal base
N s e e d Number of possible seed crystals
T m Melting temperature
k t Bulk thermal conductivity
nn, kk Columnar/equiaxed transition coefficient
X, Y, Z Coordinate axis
GX, GY The X and Y directions’ components of the thermal gradient vector
α Angle between the X and Y components of the thermal gradient

References

  1. Zhu, S.; Yu, T.; Xu, T.; Chen, H.; Dustdar, S.; Gigan, S.; Gunduz, D.; Hossain, E.; Jin, Y.; Lin, F.; et al. Intelligent computing: The latest advances, challenges, and future. Intelligent Computing 2023, 2, 0006. [CrossRef]
  2. Newton, I. Philosophiæ Naturalis Principia Mathematica. 1687.
  3. NSTC Subcommittee on Advanced Manufacturing, N.S.; Council, T. NATIONAL STRATEGY FOR ADVANCED MANUFACTURING. Technical report, Office of Science and Technology Policy, 2022.
  4. Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [CrossRef]
  5. Merchant, A.; Batzner, S.; Schoenholz, S.S.; Aykol, M.; Cheon, G.; Cubuk, E.D. Scaling deep learning for materials discovery. Nature 2023, 624, 80 – 85. [CrossRef]
  6. Szymanski, N.J.; Rendy, B.; Fei, Y.; Kumar, R.E.; He, T.; Milsted, D.; McDermott, M.J.; Gallant, M.; Cubuk, E.D.; Merchant, A.; et al. An autonomous laboratory for the accelerated synthesis of novel materials. Nature 2023, 624, 86 – 91. [CrossRef]
  7. Schwab, K. The fourth industrial revolution: What it means, how to respond. 2016.
  8. Gibson, I.; Rosen, D.W.; Stucker, B.E.; Khorasani, M. Additive Manufacturing Technologies. 2021.
  9. Wohlers, T.T.; Gornet, T.J.; Mostow, N.; Campbell, I.; Diegel, O.; Kowen, J.; Huff, R.; Stucker, B.E.; Fidan, I.; Doukas, A.; et al. History of Additive Manufacturing. SSRN Electronic Journal 2023. [CrossRef]
  10. Carr, T.; Chewning, E.; Doheny, M.; Madgavkar, A.; Padhi, A.; Tingley, A. Delivering the US manufacturing renaissance. Technical report, McKinsey’s Operations Practice and the McKinsey Global Institute, 2022.
  11. Conner, B.P.; Manogharan, G.P.; Martof, A.N.; Rodomsky, L.M.; Rodomsky, C.M.; Jordan, D.C.; Limperos, J.W. Making sense of 3-D printing: Creating a map of additive manufacturing products and services. Additive manufacturing 2014, 1, 64–76. [CrossRef]
  12. Ngo, T.D.; Kashani, A.R.; Imbalzano, G.; Nguyen, K.T.; Hui, D. Additive manufacturing (3D printing): A review of materials, methods, applications and challenges. Composites Part B: Engineering 2018.
  13. Yap, C.Y.; Chua, C.K.; Dong, Z.L.; Liu, Z.H.; Zhang, D.Q.; Loh, L.E.; Sing, S.L. Review of selective laser melting: Materials and applications. Applied physics reviews 2015, 2. [CrossRef]
  14. Vrancken, B.; Thijs, L.; Kruth, J.P.; van Humbeeck, J. Heat treatment of Ti6Al4V produced by Selective Laser Melting: Microstructure and mechanical properties. Journal of Alloys and Compounds 2012, 541, 177–185. [CrossRef]
  15. dong Gu, D.; Shi, X.; Poprawe, R.; Bourell, D.L.; Setchi, R.; Zhu, J. Material-structure-performance integrated laser-metal additive manufacturing. Science 2021, 372.
  16. Hirsch, J.; Al-Samman, T. Superior light metals by texture engineering: Optimized aluminum and magnesium alloys for automotive applications. Acta Materialia 2013, 61, 818–843. [CrossRef]
  17. Margulies, L.; Winther, G.; Poulsen, H.F. In Situ Measurement of Grain Rotation During Deformation of Polycrystals. Science 2001, 291, 2392 – 2394. [CrossRef]
  18. Thijs, L.; Verhaeghe, F.; Craeghs, T.; Van Humbeeck, J.; Kruth, J.P. A study of the microstructural evolution during selective laser melting of Ti–6Al–4V. Acta materialia 2010, 58, 3303–3312. [CrossRef]
  19. Azizi, H.; Ebrahimi, A.; Ofori-Opoku, N.; Greenwood, M.; Provatas, N.; Mohammadi, M. Characterizing the microstructural effect of build direction during solidification of laser-powder bed fusion of Al-Si alloys in the dilute limit: A phase-field study. Acta Materialia 2021, 214, 116983. [CrossRef]
  20. Klemens, P. Heat balance and flow conditions for electron beam and laser welding. Journal of Applied physics 1976, 47, 2165–2174. [CrossRef]
  21. Cline, H.; Anthony, T. Heat treating and melting material with a scanning laser or electron beam. Journal of Applied Physics 1977, 48, 3895–3900. [CrossRef]
  22. Goldak, J.; Chakravarti, A.; Bibby, M. A new finite element model for welding heat sources. Metallurgical transactions B 1984, 15, 299–305. [CrossRef]
  23. Hunt, J.D. Steady state columnar and equiaxed growth of dendrites and eutectic. Materials science and engineering 1984, 65, 75–83. [CrossRef]
  24. Gäumann, M.; Henry, S.; Cléton, F.; Wagnière, J.D.; Kurz, W. Epitaxial laser metal forming: analysis of microstructure formation. Materials Science and Engineering: A 1999, 271, 232–241. [CrossRef]
  25. Gäumann, M.; Bezencon, C.; Canalis, P.; Kurz, W. Single-crystal laser deposition of superalloys: processing–microstructure maps. Acta materialia 2001, 49, 1051–1062. [CrossRef]
  26. Gockel, J.; Beuth, J. Understanding Ti-6Al-4V microstructure control in additive manufacturing via process maps. In Proceedings of the 2013 International Solid Freeform Fabrication Symposium. University of Texas at Austin, 2013.
  27. Basak, A.; Das, S. Epitaxy and microstructure evolution in metal additive manufacturing. Annual Review of Materials Research 2016, 46, 125–149. [CrossRef]
  28. Liu, J.; To, A.C. Quantitative texture prediction of epitaxial columnar grains in additive manufacturing using selective laser melting. Additive Manufacturing 2017, 16, 58–64. [CrossRef]
  29. Chadwick, A.F.; Voorhees, P.W. The development of grain structure during additive manufacturing. Acta Materialia 2021, p. 116862.
  30. Chadwick, A.F.; Voorhees, P.W. The Effects of Melt Pool Geometry and Scan Strategy on Microstructure Development During Additive Manufacturing. IOP Conference Series: Materials Science and Engineering 2023, 1274. [CrossRef]
  31. Elahi, S.M.; Tavakoli, R.; Boukellal, A.K.; Isensee, T.; Romero, I.; Tourret, D. Multiscale simulation of powder-bed fusion processing of metallic alloys. Computational Materials Science 2022. [CrossRef]
  32. Zhang, J.; Chadwick, A.F.; Chopp, D.L.; Voorhees, P.W. Phase field modeling with large driving forces. npj Computational Materials 2023, 9, 1–9. [CrossRef]
  33. Huang, W.; Wang, W.; Ning, J.; Garmestani, H.; Liang, S.Y. Analytical Model of Quantitative Texture Prediction Considering Heat Transfer Based on Single-Phase Material in Laser Powder Bed Fusion. Journal of Manufacturing and Materials Processing 2024. [CrossRef]
  34. Ning, J.; Mirkoohi, E.; Dong, Y.; Sievers, D.E.; Garmestani, H.; Liang, S.Y. Analytical modeling of 3D temperature distribution in selective laser melting of Ti-6Al-4V considering part boundary conditions. Journal of Manufacturing Processes 2019. [CrossRef]
  35. Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids. 1952.
  36. Bunge, H.J. Texture analysis in materials science: mathematical methods; 2013.
  37. Kobryn, P.A.; Semiatin, S.L. Microstructure and texture evolution during solidification processing of Ti–6Al–4V. Journal of Materials Processing Technology 2003, 135, 330–339. [CrossRef]
  38. Welsch, G.; Boyer, R.; Collings, E. Materials properties handbook: titanium alloys; 1993.
  39. Takajo, S.; Tomida, T.; Caspi, E.N.; Pesach, A.; Tiferet, E.; Vogel, S.C. Property Improvement of Additively Manufactured Ti64 by Heat Treatment Characterized by In Situ High Temperature EBSD and Neutron Diffraction. Metals 2021. [CrossRef]
  40. Simonelli, M.; Tse, Y.Y.; Tuck, C. On the Texture Formation of Selective Laser Melted Ti-6Al-4V. Metallurgical and Materials Transactions A 2014, 45, 2863–2872. [CrossRef]
  41. Al-Bermani, S.S.; Blackmore, M.; Zhang, W.; Todd, I. The Origin of Microstructural Diversity, Texture, and Mechanical Properties in Electron Beam Melted Ti-6Al-4V. Metallurgical and Materials Transactions A 2010, 41, 3422–3434. [CrossRef]
  42. Glavicic, M.G.; Kobryn, P.A.; Bieler, T.R.; Semiatin, S.L. An automated method to determine the orientation of the high-temperature beta phase from measured EBSD data for the low-temperature alpha-phase in Ti–6Al–4V. Materials Science and Engineering A-structural Materials Properties Microstructure and Processing 2003, 351, 258–264. [CrossRef]
  43. Wang, S.; Aindow, M.; Starink, M.J. Effect of self-accommodation on α/α boundary populations in pure titanium. Acta Materialia 2003, 51, 2485–2503. [CrossRef]
  44. Shi, R.; Wang, Y. Variant selection during α precipitation in Ti–6Al–4V under the influence of local stress – A simulation study. Acta Materialia 2013, 61, 6006–6024. [CrossRef]
  45. Chen, W.; Boehlert, C.J. The elevated-temperature fatigue behavior of boron-modified Ti-6Al-4V(wt.%) castings. Materials Science and Engineering A-structural Materials Properties Microstructure and Processing 2008, 494, 132–138. [CrossRef]
  46. Yang, Y.; Knol, M.F.; van Keulen, A.; Ayas, C. A semi-analytical thermal modelling approach for selective laser melting. Additive manufacturing 2018, 21, 284–297. [CrossRef]
  47. Gusarov, A.V.; Yadroitsev, I.; Bertrand, P.; Smurov, I.Y. Model of Radiation and Heat Transfer in Laser-Powder Interaction Zone at Selective Laser Melting. Journal of Heat Transfer-transactions of The Asme 2009, 131, 072101. [CrossRef]
  48. Boyer, R.R.; Welsch, G.; Collings, E.W. Materials Properties Handbook: Titanium Alloys. 1994.
  49. Yadroitsev, I.; Yadroitsava, I. Evaluation of residual stress in stainless steel 316L and Ti6Al4V samples produced by selective laser melting. Virtual and Physical Prototyping 2015, 10, 67 – 76. [CrossRef]
  50. Fu, C.H.; Guo, Y.B. Three-Dimensional Temperature Gradient Mechanism in Selective Laser Melting of Ti-6Al-4V. Journal of Manufacturing Science and Engineering-transactions of The Asme 2014, 136, 061004. [CrossRef]
  51. Simonelli, M.; Tse, Y.Y.; Tuck, C.J. Effect of the build orientation on the mechanical properties and fracture modes of SLM Ti–6Al–4V. Materials Science and Engineering A-structural Materials Properties Microstructure and Processing 2014, 616, 1–11. [CrossRef]
  52. Muiruri, A.M.; Maringa, M.; du Preez, W.B. Crystallographic Texture Analysis of As-Built and Heat-Treated Ti6Al4V (ELI) Produced by Direct Metal Laser Sintering. Crystals 2020. [CrossRef]
  53. Hadadzadeh, A.; Hadadzadeh, A.; Amirkhiz, B.S.; Li, J.Y.; Mohammadi, M. Columnar to equiaxed transition during direct metal laser sintering of AlSi10Mg alloy: Effect of building direction. Additive Manufacturing 2018. [CrossRef]
Preprints 119508 g001
Figure 1. Diagrammatic representation of the single scan and the build component
Figure 1. Diagrammatic representation of the single scan and the build component
Preprints 119508 g001
Preprints 119508 g002
Figure 2. Bunge Euler angle convention[36]
Figure 2. Bunge Euler angle convention[36]
Preprints 119508 g002
Preprints 119508 g003
Figure 3. Columnar grain growth on polycrystal base (PX means polycrystal base; N seed implies the number of possible seed crystals)[28]
Figure 3. Columnar grain growth on polycrystal base (PX means polycrystal base; N seed implies the number of possible seed crystals)[28]
Preprints 119508 g003
Preprints 119508 g004
Figure 4. Measurements of the molten pool’s size were made under several process scenarios. Laser power varied from 20 W to 80 W, with a constant scanning velocity of 0.2 m/s. Experimental and projected measurements are indicated by yellow and orange colors, respectively.
Figure 4. Measurements of the molten pool’s size were made under several process scenarios. Laser power varied from 20 W to 80 W, with a constant scanning velocity of 0.2 m/s. Experimental and projected measurements are indicated by yellow and orange colors, respectively.
Preprints 119508 g004
Preprints 119508 g005
Figure 5. 3D temperature profile predicted from top view close to the laser position
Figure 5. 3D temperature profile predicted from top view close to the laser position
Preprints 119508 g005
Preprints 119508 g006
Figure 6. The Ti-6Al-4V in LPBF, with P = 300W and V = 0.1m/s, has a simulated thermal gradient direction angle α histogram between the X and Y directions.
Figure 6. The Ti-6Al-4V in LPBF, with P = 300W and V = 0.1m/s, has a simulated thermal gradient direction angle α histogram between the X and Y directions.
Preprints 119508 g006
Preprints 119508 g007
Figure 7. The Ti-6Al-4V in LPBF, with P = 700W and V = 1m/s, has a simulated thermal gradient direction angle α histogram between the X and Y directions.
Figure 7. The Ti-6Al-4V in LPBF, with P = 700W and V = 1m/s, has a simulated thermal gradient direction angle α histogram between the X and Y directions.
Preprints 119508 g007
Preprints 119508 g008
Figure 8. The experimentally observed beta phase pattern of LPBF Ti-6Al-4V [51]
Figure 8. The experimentally observed beta phase pattern of LPBF Ti-6Al-4V [51]
Preprints 119508 g008
Preprints 119508 g009
Figure 9. LPBF Ti-6Al-4V’s simulated beta phase texture and outcome
Figure 9. LPBF Ti-6Al-4V’s simulated beta phase texture and outcome
Preprints 119508 g009
Preprints 119508 g010
Figure 10. Comparison between the simulated and experimental maximum texture intensity in the directions of < 100 > < 110 > < 111 > .
Figure 10. Comparison between the simulated and experimental maximum texture intensity in the directions of < 100 > < 110 > < 111 > .
Preprints 119508 g010
Preprints 119508 g011
Figure 11. Simulated pole figure of Ti-6Al-4V beta BCC phase in (001), (011), (-111) planes.
Figure 11. Simulated pole figure of Ti-6Al-4V beta BCC phase in (001), (011), (-111) planes.
Preprints 119508 g011
Preprints 119508 g012
Figure 12. Simulated pole figure of Ti-6Al-4V alpha HCP phase in (0001), (-12-10), (-1100) planes.
Figure 12. Simulated pole figure of Ti-6Al-4V alpha HCP phase in (0001), (-12-10), (-1100) planes.
Preprints 119508 g012
Table 1. Materials Properties and Values of Ti-6Al-4V [46,48,49]
Table 1. Materials Properties and Values of Ti-6Al-4V [46,48,49]
Properties of Material Value Unit
Surrounding Temperature ( T 0 ) 20 °C
Melting Temperature ( T m ) 1655 °C
Density ( ρ ) 4428 k g / m 3
Bulk Thermal Conductivity ( k t ) 5-35 W / ( m K )
Powder Thermal Conductivity ( k p ) 0.21 W / ( m K )
Heat Capacity (C) 500-800 J / ( K g K )
Heat Convection Coefficient (h) 24 W / ( m 2 K )
Radiation Emissivity ( ε ) 0.9 1
Stefan-Boltzmann Constant ( σ ) 5.67 × 10 − 8 W / ( m 2 K )
CET (nn) 3.2 1
CET (kk) 10 25 1
Table 2. Build Configuration for Ti-6Al-4V Texture Evolution in LPBF
Table 2. Build Configuration for Ti-6Al-4V Texture Evolution in LPBF
Construct Parameters Value
Layers 10
Seeds 100
Sections 1000
Grains 20
Track 1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated