Prerpints.org logo
Preprint
Concept Paper

Optimizing Exotic Option Pricing: Monte Carlo Simulation and Variance Reduction Techniques

Altmetrics

Downloads

61

Views

31

Comments

0

This version is not peer-reviewed

Submitted:

26 September 2024

Posted:

29 September 2024

You are already at the latest version

Alerts
Abstract
This study investigates the pricing of exotic options, specifically Barrier and Asian options, through the application of Monte Carlo simulation. The research commences by establishing the theoretical foundations and closed-form solutions within the Black-Scholes framework. Subsequently, three distinct random walk models are introduced to generate underlying asset paths for simulation purposes. The antithetic variate technique is demonstrated to significantly reduce standard error and accelerate convergence in the pricing of both options, thereby enhancing the precision of Monte Carlo estimates. Notably, the selection of underlying random walk models is found to have a minimal impact on accuracy, suggesting avenues for further research in advanced variance reduction techniques. This study provides valuable insights into the pricing of exotic options, offering implications for finance professionals and researchers, and driving innovation in option pricing methodologies for dynamic financial markets. The research underscores the efficacy of Monte Carlo simulation and variance reduction techniques in pricing complex options, contributing to the advancement of financial modelling and derivatives pricing.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

This study inquiry aims to examine the application of Monte Carlo (MC) simulation techniques for the valuation of exotic options, specifically Asian and Barrier options. The study will integrate the Black-Scholes model to capture the dynamics of the underlying asset's price behaviour, acknowledging the challenges posed by exotic options' complex payoffs, non-linear characteristics, and path dependencies. Traditional frameworks, such as the Black-Scholes model, may not effectively price these options due to unrealistic assumptions and the absence of closed-form solutions. MC simulation has gained prominence in the financial sector for estimating exotic option prices with high accuracy. This investigation will assess the efficacy of MC simulation in pricing Barrier and Asian options, employing the Antithetic Variate method to enhance efficiency and precision. The technical requirements of this study involve utilizing Python for implementing MC simulation and conducting an in-depth analysis of the simulated data. Therefore, the research objectives are:
  • To investigate the utilization of MC simulation techniques for valuing exotic options.
  • To integrate the Black-Scholes model to capture the dynamics of the underlying asset's price behaviour.
  • To assess the efficacy of MC simulation in pricing Barrier and Asian options.
  • To employ the Antithetic Variate method to enhance the efficiency and precision of the simulations.
  • To conduct an in-depth analysis of the simulated data using Python.
This study's significance lies in its contribution to the development of more accurate and efficient methods for valuing exotic options, which is crucial for financial institutions and investors. The research will provide valuable insights into the application of MC simulation techniques in finance and the potential for future research in this area.
The study is as follows; the background will be seen in the next section. The related works are listed in Section III. The experimental analysis is carried out in Section IV, and in Section V, we provide a conclusion and future directions for the research.

2. Background

This study examination delves into the realm of financial derivatives, specifically options contracts, which are categorized into two primary types: call and put options. Call options grant the purchaser the right, but not the obligation, to acquire an underlying asset at a predetermined strike price on or before a specified expiration date. Conversely, put options provide the right to sell the underlying asset under identical conditions. The execution of these rights is referred to as the exercise of the option. A pivotal concern in option pricing is the determination of the premium without prior knowledge of future fluctuations in the underlying asset's price. The most basic options, denominated "plain vanilla" options, are classified into two categories: European and American options. European options can solely be exercised on the expiration date, whereas American options can be exercised at any point prior to the expiration date. This investigation primarily focuses on European options, as more complex options, such as exotic options, share analogous structures. The payoff of European options is contingent upon whether they are in the money, at the money, or out of the money at expiry. For a European call option, the holder profits if the asset's price at expiry exceeds the strike price, generating a payoff equal to the difference between the two. Conversely, for a European put option, the holder profits when the asset's price is less than the strike price, enabling them to sell the asset at the higher strike price. If these conditions are not met, the options expire with no value, i.e., the payoff is zero. A crucial concept in options pricing is the put-call parity, which relates the prices of call and put options on the same underlying asset, with the same strike price and expiration date. This relationship ensures that the combined portfolio of a long call and a short put position mirrors holding the asset and shorting cash. Utilizing this parity, if one knows the price of a call option, they can readily determine the price of the corresponding put option, and vice versa. Notwithstanding their utility, vanilla options possess limitations, particularly in volatile markets where fixed strike prices may diminish their effectiveness as hedging tools. Additionally, they are often priced using models like Black-Scholes, which assume constant volatility and may fail to accurately reflect market behaviour. To address these limitations, exotic options have been developed. Exotic options offer more flexible and customized risk management strategies and can hedge against more complex risks than vanilla options. Exotic options differ fundamentally from vanilla options because they are path-dependent. While vanilla options are path-independent, meaning their payoff depends solely on the underlying asset's price at expiration, exotic options also consider the path that the asset price followed to reach its final value. There are two types of path dependency: strong and weak. Strong path-dependent options, like Asian options, require additional variables to model price paths, while weakly path-dependent options, like barrier options, do not. These exotic options offer more complex hedging and trading strategies, rendering them valuable for sophisticated investors [1,2,3,4,5].

2.1. Black-Scholes Model

The Black-Scholes model, introduced by Fischer Black and Myron Scholes in 1973, is a seminal tool in quantitative finance for pricing European call and put options. This mathematical framework facilitates the estimation of fair premiums for options by incorporating key factors such as the underlying asset price, expiration time, volatility, drift rate, risk-free interest rate, and strike price. Grounded in the efficient market hypothesis, the model posits that asset prices reflect all available information and adjust instantaneously to new data. Asset prices are assumed to follow a Markov process, evolving solely based on their current state, independent of past behaviour. This randomness in price movements is modelled using a stochastic process known as Brownian motion, or the Wiener process, which combines deterministic and random components. The deterministic part represents predictable returns, akin to interest earned from a risk-free investment, while the random part simulates unpredictable price changes caused by market shocks. The combination of these components yields a stochastic differential equation known as Geometric Brownian Motion (GBM), where asset prices change proportionally to their current value. The Black-Scholes model relies on several assumptions, including the log-normal distribution of asset prices, constant volatility and interest rates, allowance for short selling, and the absence of transaction costs, dividends, or arbitrage opportunities. Under these conditions, the model constructs a delta-hedged portfolio, comprising a long position in the underlying asset and a short position in the option, continuously adjusted to eliminate risk and ensure a risk-free return at the interest rate r. The model yields two pivotal formulas for pricing European options: the call option value and the put option value. Despite criticisms regarding its unrealistic assumptions, the Black-Scholes model remains a powerful tool in quantitative finance, providing closed-form solutions that simplify the pricing of European options and offer a valuable framework for understanding the relationship between options and their underlying assets. The model continues to serve as a benchmark for more advanced numerical methods and simulations employed in the financial industry [6,7,8,9,10,11].

2.2. Barrier Options

The market for barrier options, a type of financial derivative, has experienced rapid growth, with demand doubling annually since 1992. These complex options are valued for their unique feature of being activated or nullified based on the underlying asset's price crossing a predetermined barrier level. Researchers have made significant contributions to the development of pricing models for various types of barrier options. The pioneering work of Robert C. Merton in 1973 introduced an analytical solution for down-and-out call options. Subsequent advancements were made in the early 1990s, who developed techniques for pricing knock-in calls and puts. Barrier options are path-dependent, meaning their payoffs are influenced by the actual price path of the underlying asset. These options can be categorized as either "in" or "out" and can be placed above or below the current price level of the underlying asset. The pricing of barrier options is complex due to the introduction of restrictions on potential payoffs. One of the key pricing relationships in barrier options is the "in-out parity", which mirrors the put-call parity in vanilla options. In practice, most barrier options are monitored discretely, whereas theoretical models often assume continuous monitoring. This discrepancy leads to challenges in pricing, as discrete monitoring introduces discontinuities in the option's payoff function. Research has highlighted considerable price differences between options monitored discretely versus continuously. To address this issue, approximation methods have been proposed, such as the continuity correction approach introduced in 1997.

2.3. Asian Options

Asian options are distinct from European options because their payoff depends on the average price of the underlying asset over a specified period, rather than the asset's price at a single point in time, typically at expiration. This averaging process, which can span the entire life of the option or a defined portion, reduces the overall volatility of the option and, consequently, its cost compared to traditional European options. The average price feature introduces path dependency, making Asian options more complex to model and price. Unlike standard options, which are valued primarily based on the asset price and time to expiration, Asian options require an additional variable that tracks the average price of the underlying asset over time. To adapt the pricing of Asian options within the Black-Scholes framework, this path dependency is accounted for by introducing a state variable. This state variable captures the average price of the underlying asset and evolves based on the asset’s price path. Mathematically, this can be expressed as an integral over time of a function of the asset’s price and time. The state variable’s form can change depending on the specific type of path dependency required. The standard assumption is that the asset price follows a lognormal random walk, as it does in the Black-Scholes model, but the inclusion of the state variable makes the option value a function of three variables: the current asset price, the average price, and time to expiration. To hedge the risk associated with Asian options, a delta-hedged portfolio is constructed, which includes holding one path-dependent option and shorting a certain amount of the underlying asset. The averaging method for determining the average price in Asian options can be flexible, depending on the buyer’s requirements. The function used to compute the average price can involve either continuous or discrete sampling of the asset’s price. In continuous averaging, the asset price is integrated over time, while in discrete averaging, the price is sampled at specific intervals. Discrete averaging is often preferred in practice because of its practical advantages—continuous data can be unreliable due to factors like network delays or the imprecision of trades, while discrete monitoring, typically relying on key prices such as daily closing prices, offers verifiable prices for calculating the average. However, this practical preference for discrete sampling adds complexity to the option valuation, as closed-form solutions are generally unavailable. Numerical methods, such as MC simulations, are frequently employed to price Asian options with discrete averaging. The valuation of Asian options is inherently complex due to their dependence not only on the price at expiration but also on the price path of the underlying asset during the averaging period. This path dependency complicates the development of closed-form analytical solutions. While closed-form approximations are available, particularly for continuously monitored Asian options, numerical methods such as MC simulations are often necessary for pricing. Under certain assumptions, however, closed-form solutions do exist for specific types of Asian options. For example, continuously sampled geometric average rate Asian options can be priced using closed-form solutions because the geometric average of lognormal random variables follows a lognormal distribution, allowing standard mathematical methods to be applied. Despite their complexity, Asian options are popular in financial markets because they reduce the risk of price manipulation near expiration and provide better hedging opportunities, particularly for companies dealing with commodities that are thinly traded, such as rare earth metals or agricultural products. These features make Asian options a valuable tool for managing market risk across a range of industries.

2.4. Monte Carlo Simulations

The MC method, widely used in financial modelling, is a prominent numerical technique for estimating option prices, especially in the absence of closed-form solutions. Developed during World War II, the MC method was initially designed to improve decision-making under uncertainty. The method draws its name from the gambling city of Monaco, highlighting the role of probability in decision-making. Essentially, it estimates expected values through random sampling, relying on the solution to Stochastic Differential Equations (SDEs). In 1977, Boyle first applied this method to the pricing of European options, marking its entry into financial modelling. Subsequently, Boyle, Broadie, and Glasserman (1997) extended the technique with variance reduction methods to enhance its accuracy. Later works by Glasserman (2004) and Asmussen and Glynn (2007) provided further refinements, and Kloeden and Platen (1992) detailed numerical solutions to SDEs, making the method more robust. The core concept of MC simulation involves generating random inputs, simulating a large number of outcomes, and then calculating an average to estimate an expected value. Repeated simulations, according to the law of large numbers, improve the accuracy of the results as the estimated outcomes converge to the actual value. In financial applications, MC simulations are used to estimate the expected payoff of an option by simulating multiple price paths for the underlying asset. The MC method has distinct advantages when applied to exotic options, such as barrier or Asian options, which require the modelling of complex conditions. For barrier options, one must determine whether each simulated price path crosses a predefined barrier, while for Asian options, it is necessary to track the entire price path to compute the average value of the underlying asset. The method's flexibility makes it adaptable to a variety of option types. However, the main drawback is its computational intensity. Obtaining accurate estimates often requires tens of thousands of simulations, which can be time-consuming. Moreover, computing "Greeks" (sensitivities of the option price with respect to different parameters) is inefficient, as MC relies on small changes to the inputs and averaging results, a process that may be computationally expensive and less accurate than alternative methods. Despite these challenges, the MC method remains a valuable tool for pricing options. The steps in the process are straightforward:
  • Simulate the price path of the underlying asset using a risk-neutral random walk starting from the current value over the required time frame.
  • Calculate the payoff of the option for this realization, considering the specific features of the option.
  • Repeat this simulation for a large number of price paths.
  • Compute the average payoff over all simulations.
  • Discount the average payoff to present value using the risk-free interest rate, which provides the option's price.

3. Related Works

The study of hedging strategies and pricing methods for barrier options has seen various advancements, combining traditional financial models with modern computational techniques. [12] proposed a hedging strategy for barrier options using the Black-Scholes model alongside the MC method. Their findings indicated that this strategy not only effectively reduced hedging costs but also provided satisfactory performance in managing the associated risks, as observed through their analysis of the Greek letters (sensitivities of the option price). [13] introduced a novel modification to the MC algorithm for pricing down-and-out call options and double barrier options. They utilized random variables drawn from a uniform distribution to improve the algorithm's accuracy. Their primary focus was on calculating the first hitting time, a critical aspect in the valuation of barrier options, and they found that their modified method significantly reduced prediction errors, leading to more precise option pricing. In contrast, [14] employed the Crank-Nicolson finite difference method to calculate barrier option prices. By increasing the steps of discretization, they observed convergence in their results and examined the impact of changing interest rates on option values. Their study revealed that both the Crank-Nicolson method and the antithetic MC approach yielded more accurate results than the standard MC method, highlighting the advantages of these numerical techniques in option pricing. [15] tackled the pricing of American barrier options within uncertain environments, deriving formulas based on uncertain differential equations. Their research offers a framework that could potentially be extended to other types of options, paving the way for further exploration of option pricing under uncertainty. In a related study, [16] focused on basket options with barriers, where they selected several stocks as the underlying assets and used the MC method to simulate the prices of these complex financial instruments. Their testing confirmed the robustness and accuracy of the MC simulations in pricing such options. [17] applied machine learning techniques, including support vector machines, nearest neighbour classification, and decision trees, to predict option prices in the Indian stock market. Their use of ensemble methods like bagging improved prediction accuracy. They also experimented with cascaded neural networks combined with optimization algorithms, achieving better forecasting results compared to deep neural networks alone. [18] focused on pricing geometric and arithmetic Asian options using traditional numerical methods. To enhance computational efficiency, they trained a back propagation neural network, which significantly reduced the runtime, indicating the potential of machine learning in speeding up complex financial computations. Finally, [19] modified the MC method by adjusting strike prices, time to maturity, and volatility parameters. They used decision trees, neural networks, and ensemble learning techniques to forecast the values of call and put options. Their research also explored the relationship between stock prices and volatility, providing insights into the predictive power of machine learning models in option pricing [20,21,22,23,24,25].

4. Experimental Analysis

4.1. Barrier Options

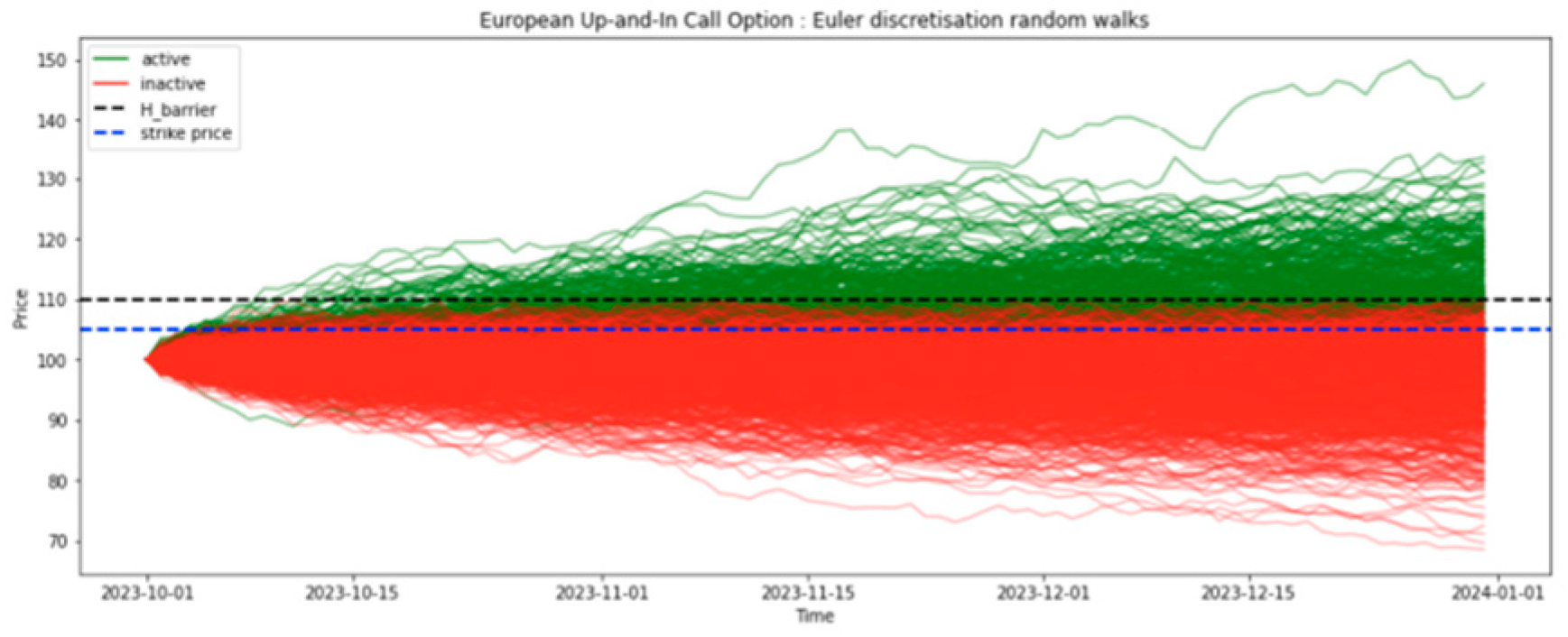
This analysis examines the pricing of an up-and-in call option using closed-form solutions and MC simulation methods. The parameters used include an initial stock price of $100, volatility of 0.2, risk-free rate of 0.03, barrier price of $110.6772, exercise price of $105, and option maturity from January 1, 2024, to December 31, 2024. 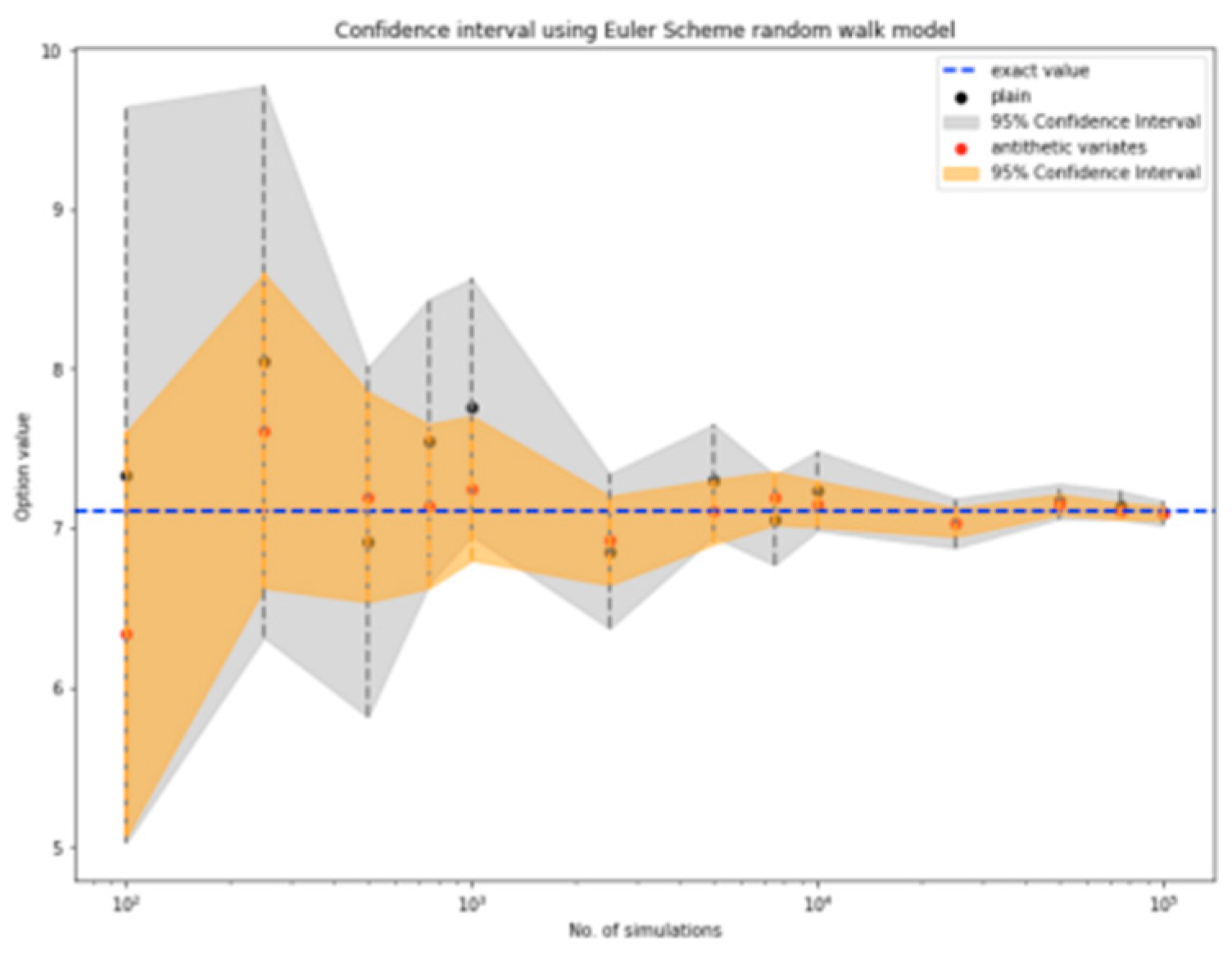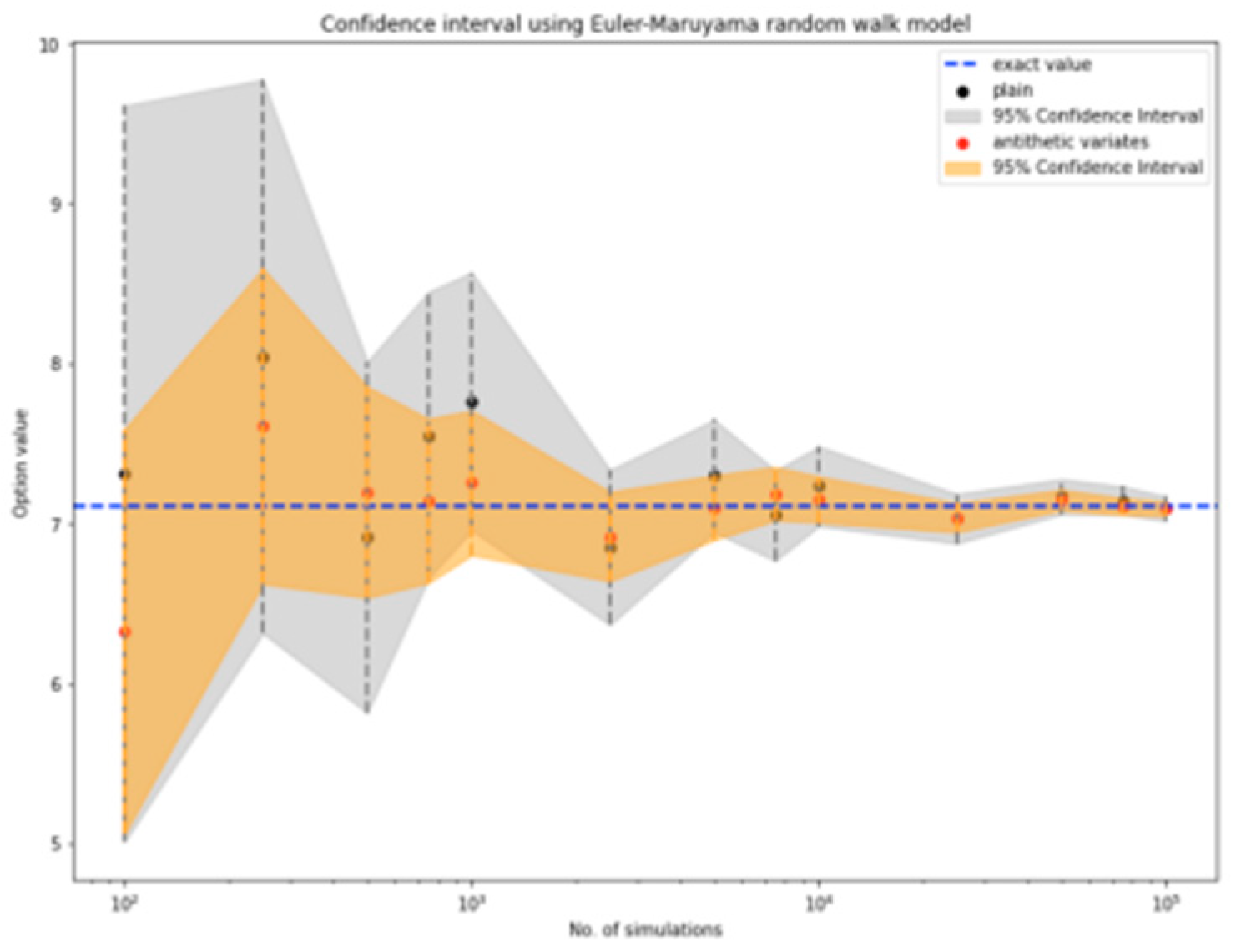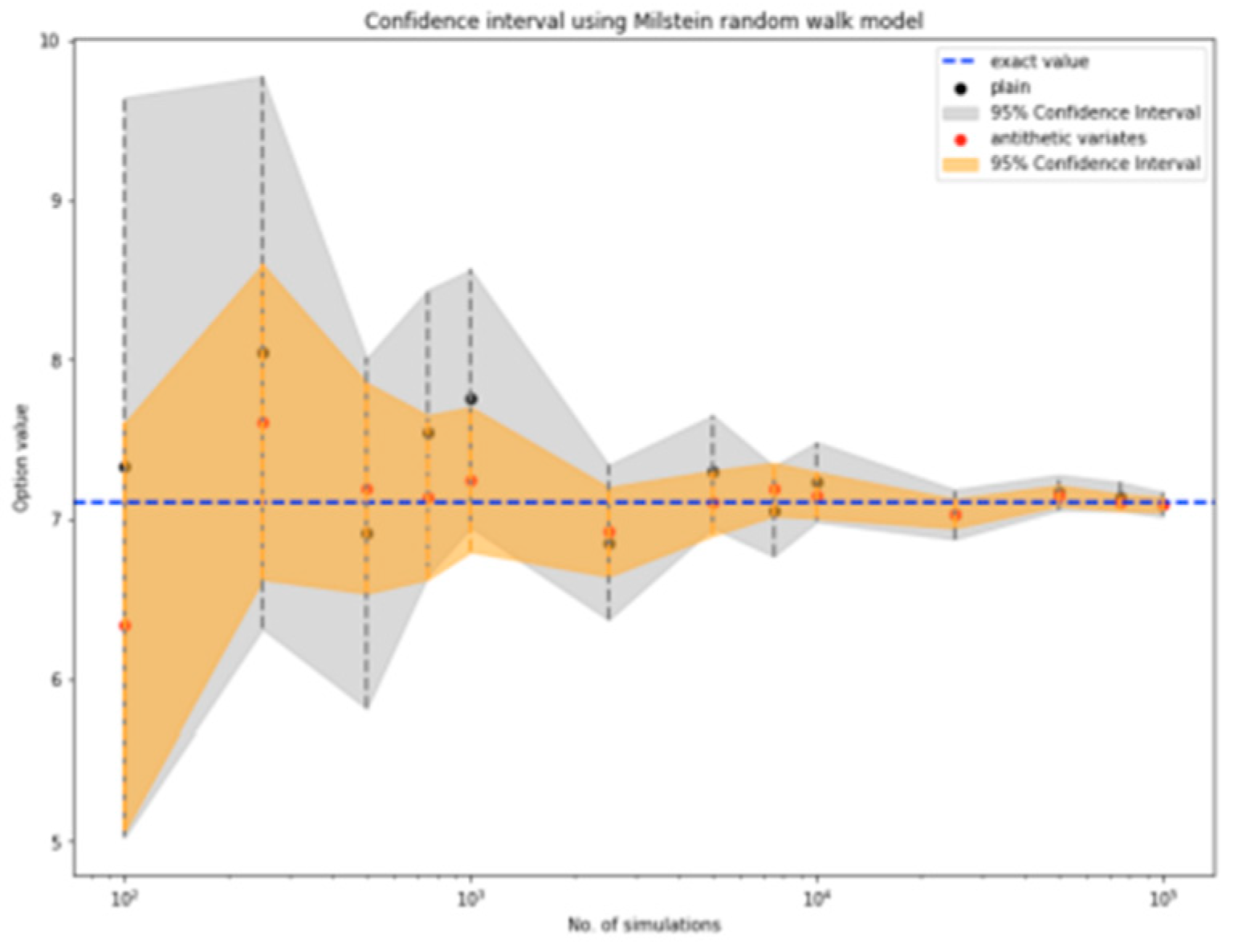The exact price of the up-and-in call option is calculated using a closed-form formula as shown in Figure 1, yielding a value of 7.1055. 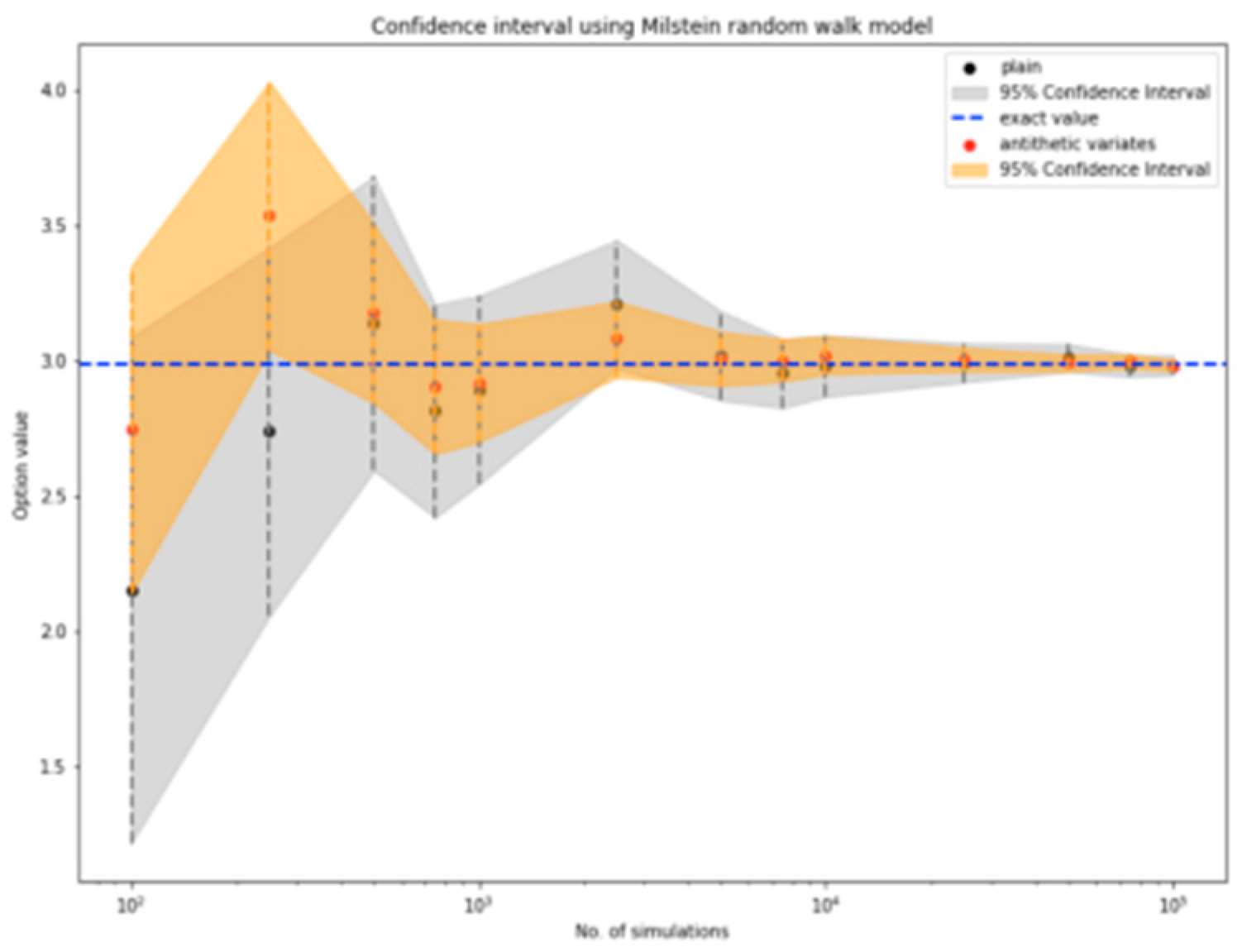MC simulations are also employed to estimate the option price, with three different random walk models used to model the underlying asset's price movements as shown in Figures 2 to 4. The results demonstrate convergence to the exact value as the number of simulations increases. The antithetic variates method is applied as a variance reduction technique to improve the accuracy of the estimated option price. This method significantly enhances the stability of the estimates and allows for faster convergence to the true value. The choice of random walk model is found to have minimal impact on the estimated option price, suggesting that practitioners should prioritize the use of variance reduction techniques. Confidence intervals are constructed to visualize the accuracy of the estimates, with the exact price from the closed-form solution lying within the 95% confidence intervals for all three models. The antithetic variates method is shown to produce narrower confidence intervals, further demonstrating its effectiveness in reducing variance and improving precision.
Preprints 119478 g001
Figure 1. Up-and-in call option simulation using MC.
Figure 1. Up-and-in call option simulation using MC.
Preprints 119478 g001
Preprints 119478 g002
Figure 2. Euler scheme model's confidence interval for up-and-in barrier options.
Figure 2. Euler scheme model's confidence interval for up-and-in barrier options.
Preprints 119478 g002
Preprints 119478 g003
Figure 3. Euler Maruyama model's confidence interval for an up-and-in barrier option.
Figure 3. Euler Maruyama model's confidence interval for an up-and-in barrier option.
Preprints 119478 g003
Preprints 119478 g004
Figure 4. Milstein model's confidence interval for up and-in barrier option.
Figure 4. Milstein model's confidence interval for up and-in barrier option.
Preprints 119478 g004

4.2. Asian Options

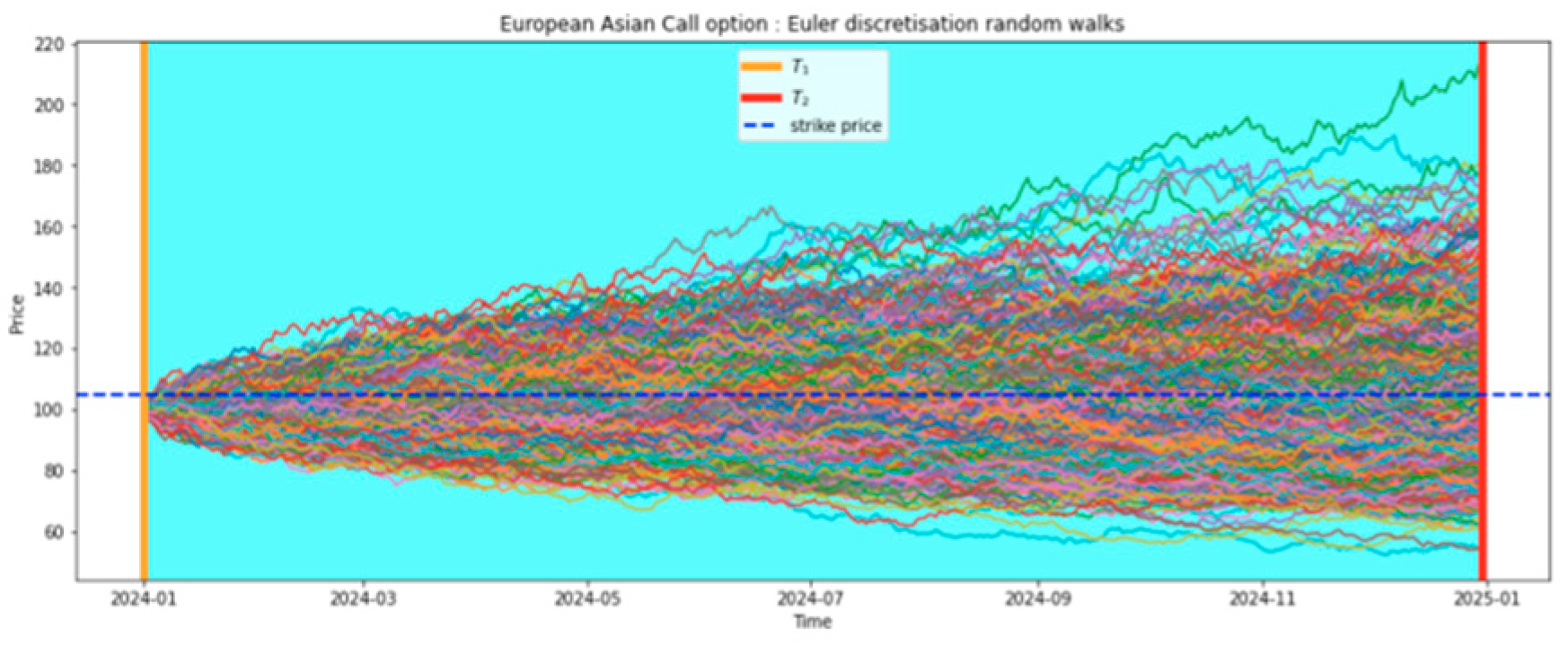
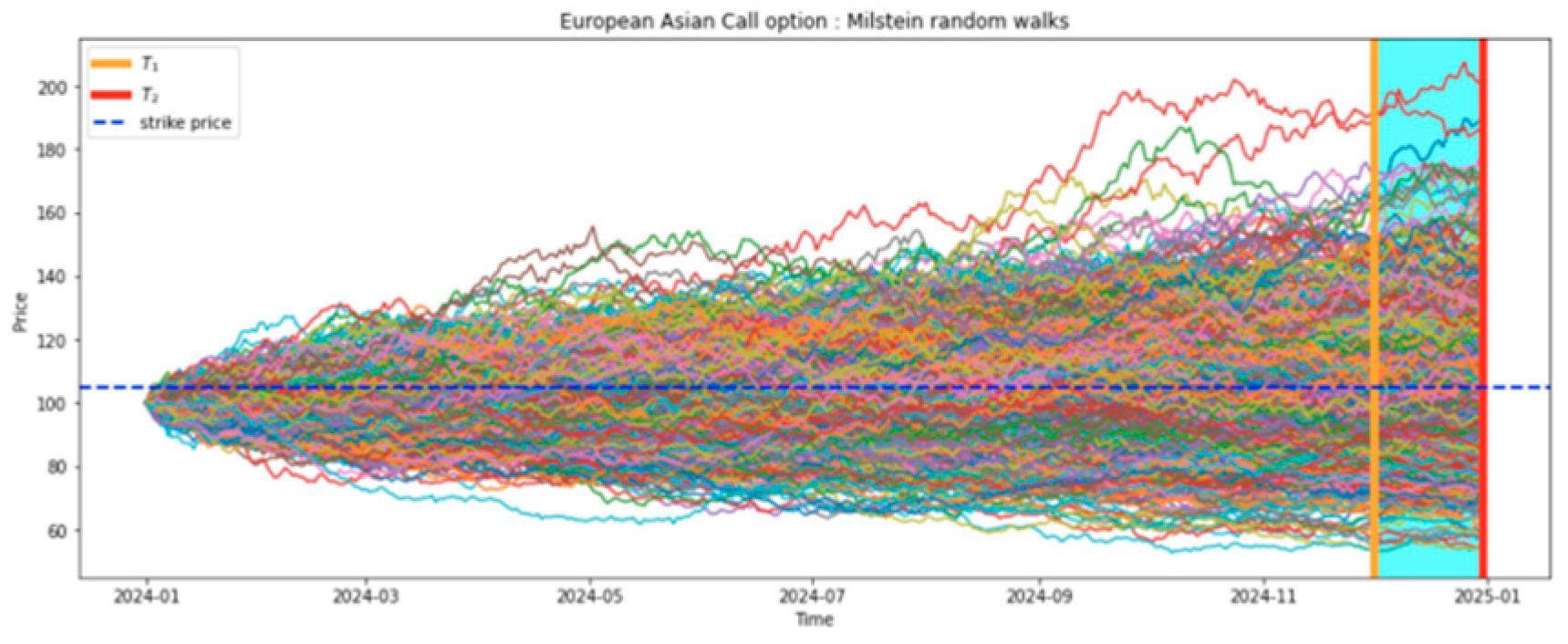
This study presents a comprehensive examination of the pricing of geometric average rate Asian options as shown in Figure 5, utilizing various methods including exact closed-form solutions, MC simulations, and antithetic variate techniques. The examples provided illustrate the impact of averaging periods and simulation techniques on the pricing accuracy and convergence of option values. The first example considers a geometric average rate call option with a full contract duration averaging period, demonstrating the convergence of Monte Carlo estimates to the exact closed-form solution as shown in Figure 6. The antithetic variate technique is shown to improve efficiency and accelerate convergence. 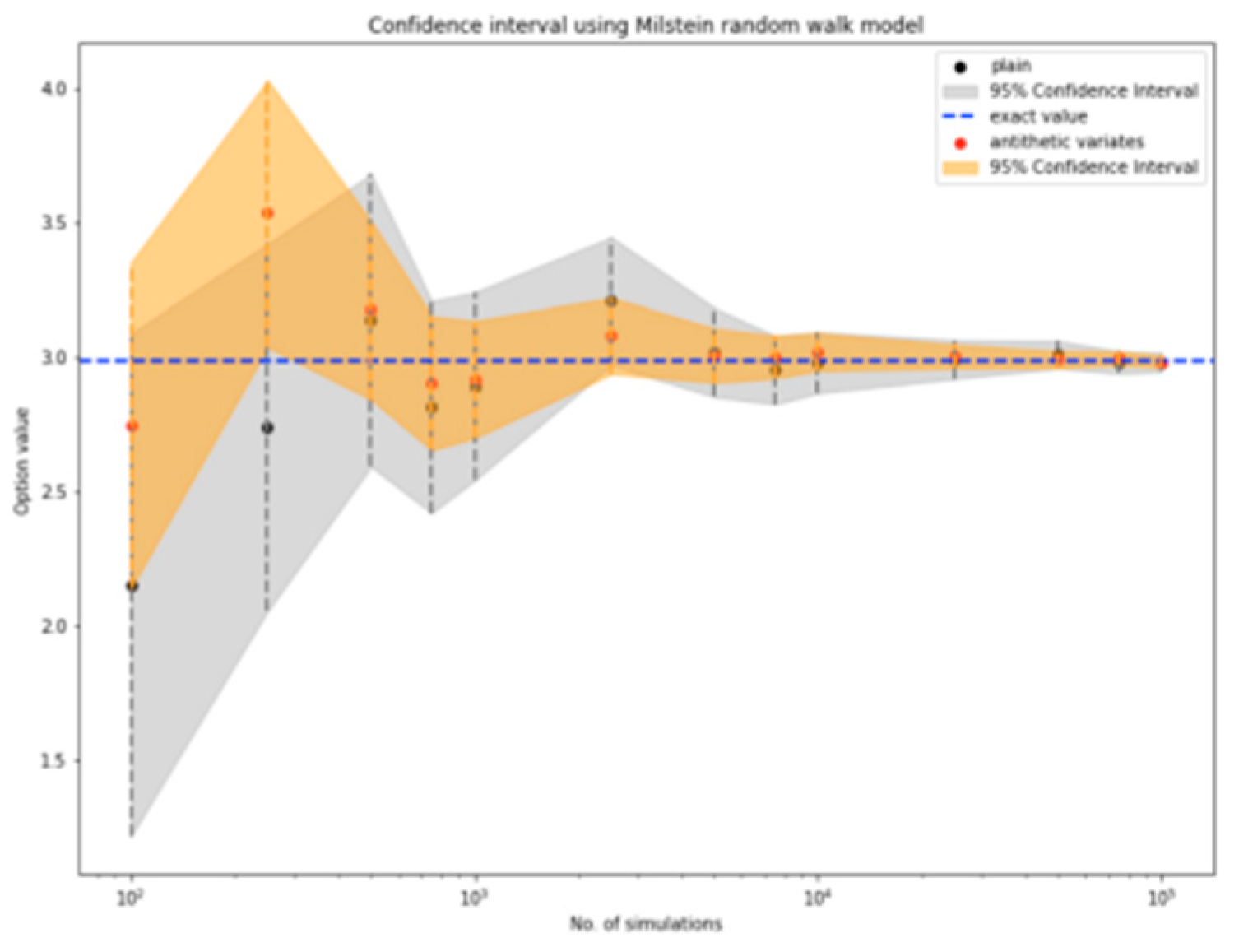The second example focuses on a geometric average rate put option, again demonstrating the convergence of MC estimates to the exact solution as shown in Figure 7. Confidence interval plots illustrate the accuracy of the estimates as shown in Figure 8. 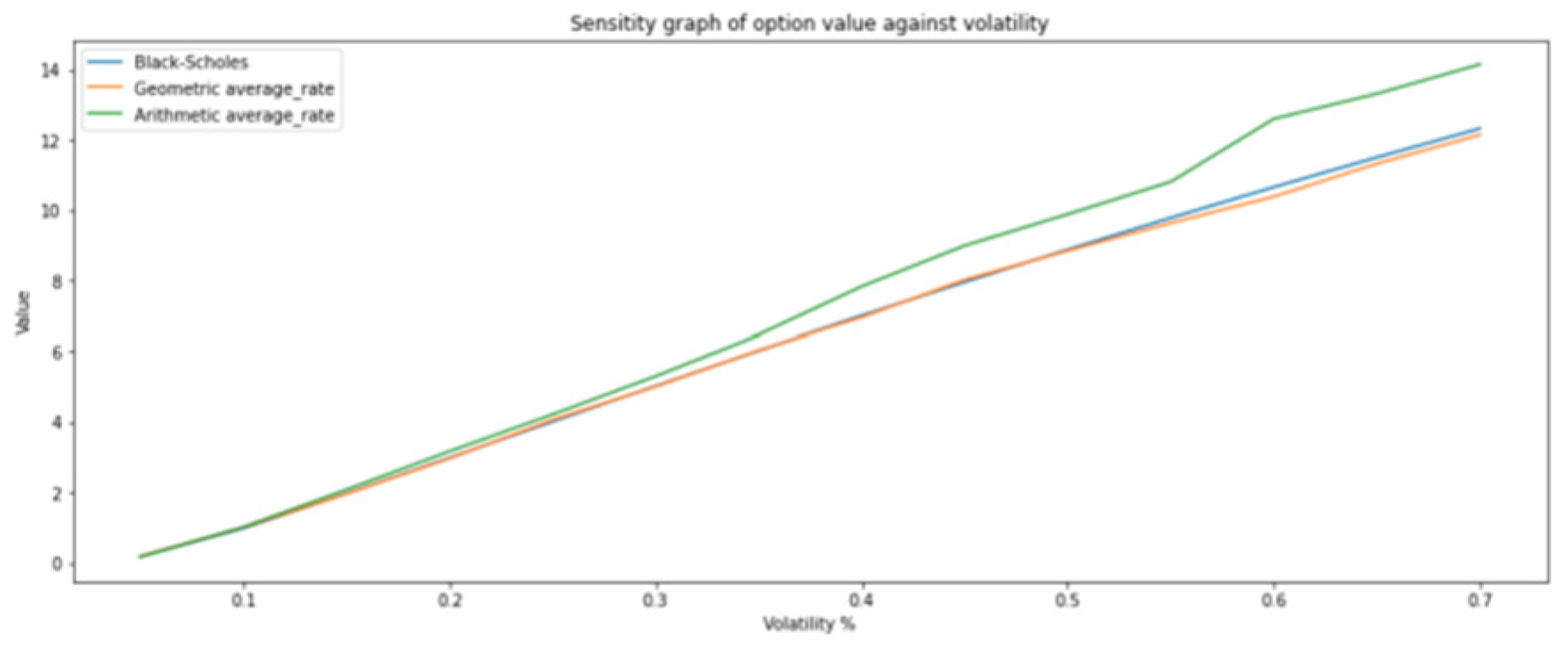The third example examines a geometric average rate call option with an averaging period spanning the final 30 days of the contract as shown in Figure 9. Despite the change in averaging period, the exact closed-form solution remains identical to the previous examples. MC simulations provide a more accurate estimate, and the results demonstrate that exotic options are generally cheaper than vanilla options due to their averaging feature.

5. Conclusion and Future Works

This study presents a comprehensive examination of the MC method's efficacy in pricing Barrier and Asian options, demonstrating convergence stabilization at approximately 5000 simulations for Barrier options and 750-1000 for Asian options. The research findings indicate that the choice of random walk model, including the Euler Scheme, Euler-Maruyama, and Milstein's method, has a negligible impact on simulation accuracy within the Black-Scholes framework. However, the incorporation of the antithetic variate technique significantly enhances convergence, reducing variance and accelerating the process by 1.5 times for Barrier options and 1.3 times for Asian options, despite increased computational time. These results suggest that future research efforts should prioritize the development of variance reduction techniques over the creation of new random walk models for basic MC testing. Furthermore, this study acknowledges the limitations of the Black-Scholes model and recommends exploring alternative models that account for evolving volatility and interest rates to better align with real-world trading conditions. By addressing these limitations, future research can improve the accuracy and applicability of option pricing models.

Funding

No funds, grants, or other support was received.

Data Availability

Data will be made on reasonable request.

D. Code Availability

Code will be made on reasonable request.

Conflict of Interest

The authors declare that they have no known competing for financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. V. K. Kanaparthi, “Examining the Plausible Applications of Artificial Intelligence & Machine Learning in Accounts Payable Improvement,” FinTech, vol. 2, no. 3, pp. 461–474, Jul. 2023. [CrossRef]
  2. V. Kanaparthi, “Transformational application of Artificial Intelligence and Machine learning in Financial Technologies and Financial services: A bibliometric review,” Jan. 2024. [CrossRef]
  3. V. Kanaparthi, “Exploring the Impact of Blockchain, AI, and ML on Financial Accounting Efficiency and Transformation,” Jan. 2024, Accessed: Feb. 04, 2024. [Online]. Available online: https://arxiv.org/abs/2401.15715v1.
  4. V. Kanaparthi, “Examining Natural Language Processing Techniques in the Education and Healthcare Fields,” Int. J. Eng. Adv. Technol., vol. 12, no. 2, pp. 8–18, Dec. 2022. [CrossRef]
  5. V. Kanaparthi, “The Role of Machine Learning in Predicting and Understanding Inflation Dynamics: Insights from the COVID-19 Pandemic,” in 2024 3rd International Conference on Artificial Intelligence for Internet of Things, AIIoT 2024, Institute of Electrical and Electronics Engineers Inc., 2024. [CrossRef]
  6. M. Kanojia, P. Kamani, G. S. Kashyap, S. Naz, S. Wazir, and A. Chauhan, “Alternative Agriculture Land-Use Transformation Pathways by Partial-Equilibrium Agricultural Sector Model: A Mathematical Approach,” Aug. 2023, Accessed: Sep. 16, 2023. [Online]. Available online: https://arxiv.org/abs/2308.11632v1.
  7. G. S. Kashyap, K. Malik, S. Wazir, and R. Khan, “Using Machine Learning to Quantify the Multimedia Risk Due to Fuzzing,” Multimed. Tools Appl., vol. 81, no. 25, pp. 36685–36698, Oct. 2022. [CrossRef]
  8. P. Kaur, G. S. Kashyap, A. Kumar, M. T. Nafis, S. Kumar, and V. Shokeen, “From Text to Transformation: A Comprehensive Review of Large Language Models’ Versatility,” Feb. 2024, Accessed: Mar. 21, 2024. [Online]. Available online: https://arxiv.org/abs/2402.16142v1.
  9. S. Wazir, G. S. Kashyap, and P. Saxena, “MLOps: A Review,” Aug. 2023, Accessed: Sep. 16, 2023. [Online]. Available online: https://arxiv.org/abs/2308.10908v1.
  10. N. Marwah, V. K. Singh, G. S. Kashyap, and S. Wazir, “An analysis of the robustness of UAV agriculture field coverage using multi-agent reinforcement learning,” Int. J. Inf. Technol., vol. 15, no. 4, pp. 2317–2327, May 2023. [CrossRef]
  11. H. Habib, G. S. Kashyap, N. Tabassum, and T. Nafis, “Stock Price Prediction Using Artificial Intelligence Based on LSTM– Deep Learning Model,” in Artificial Intelligence & Blockchain in Cyber Physical Systems: Technologies & Applications, CRC Press, 2023, pp. 93–99. [CrossRef]
  12. G. Schrimpf, J. Schneider, H. Stamm-Wilbrandt, and G. Dueck, “Record Breaking Optimization Results Using the Ruin and Recreate Principle,” J. Comput. Phys., vol. 159, no. 2, pp. 139–171, Apr. 2000. [CrossRef]
  13. S. R. Cook, A. Gelman, and D. B. Rubin, “Validation of software for Bayesian models using posterior quantiles,” J. Comput. Graph. Stat., vol. 15, no. 3, pp. 675–692, 2006. [CrossRef]
  14. J. Ekblom and J. Blomvall, “Importance sampling in stochastic optimization: An application to intertemporal portfolio choice,” Eur. J. Oper. Res., vol. 285, no. 1, pp. 106–119, Aug. 2020. [CrossRef]
  15. N. Lee, N. M. An, and J. Thorne, “Can Large Language Models Infer and Disagree Like Humans?,” May 2023, Accessed: Aug. 23, 2023. [Online]. Available online: https://arxiv.org/abs/2305.13788v1.
  16. L. Yu, W. Zhang, J. Wang, and Y. Yu, “SeqGAN: Sequence generative adversarial nets with policy gradient,” in 31st AAAI Conference on Artificial Intelligence, AAAI 2017, AAAI press, Feb. 2017, pp. 2852–2858. [CrossRef]
  17. Ghorbani and J. Zou, “Data shapley: Equitable valuation of data for machine learning,” in 36th International Conference on Machine Learning, ICML 2019, PMLR, May 2019, pp. 4053–4065. Accessed: May 20, 2023. [Online]. Available online: https://proceedings.mlr.press/v97/ghorbani19c.html.
  18. N. Zhang, “Learning Adversarial Transformer for Symbolic Music Generation,” IEEE Trans. Neural Networks Learn. Syst., pp. 1–10, Jul. 2020. [CrossRef]
  19. M. Lopez de Prado, “Hierarchical Portfolio Construction: Dispelling Markowitz’s Curse,” SSRN Electron. J., May 2016. [CrossRef]
  20. S. Naz and G. S. Kashyap, “Enhancing the predictive capability of a mathematical model for pseudomonas aeruginosa through artificial neural networks,” Int. J. Inf. Technol. 2024, pp. 1–10, Feb. 2024. [CrossRef]
  21. G. S. Kashyap, A. Siddiqui, R. Siddiqui, K. Malik, S. Wazir, and A. E. I. Brownlee, “Prediction of Suicidal Risk Using Machine Learning Models,” Dec. 25, 2021. Accessed: Feb. 04, 2024. [Online]. Available online: https://papers.ssrn.com/abstract=4709789.
  22. F. Alharbi, G. S. Kashyap, and B. A. Allehyani, “Automated Ruleset Generation for ‘HTTPS Everywhere’: Challenges, Implementation, and Insights,” Int. J. Inf. Secur. Priv., vol. 18, no. 1, pp. 1–14, Jan. 2024. [CrossRef]
  23. S. Wazir, G. S. Kashyap, K. Malik, and A. E. I. Brownlee, “Predicting the Infection Level of COVID-19 Virus Using Normal Distribution-Based Approximation Model and PSO,” Springer, Cham, 2023, pp. 75–91. [CrossRef]
  24. G. S. Kashyap et al., “Revolutionizing Agriculture: A Comprehensive Review of Artificial Intelligence Techniques in Farming,” Feb. 2024. [CrossRef]
  25. F. Alharbi and G. S. Kashyap, “Empowering Network Security through Advanced Analysis of Malware Samples: Leveraging System Metrics and Network Log Data for Informed Decision-Making,” Int. J. Networked Distrib. Comput., pp. 1–15, Jun. 2024. [CrossRef]
Preprints 119478 g005
Figure 5. Geometric average rate simulation using MC methods dial the number.
Figure 5. Geometric average rate simulation using MC methods dial the number.
Preprints 119478 g005
Preprints 119478 g006
Figure 6. Geometric average rate call option's confidence interval is the average of the entire contract length, according to the Milstein model.
Figure 6. Geometric average rate call option's confidence interval is the average of the entire contract length, according to the Milstein model.
Preprints 119478 g006
Preprints 119478 g007
Figure 7. The contract's average duration represents the option value against volatility.
Figure 7. The contract's average duration represents the option value against volatility.
Preprints 119478 g007
Preprints 119478 g008
Figure 8. Geometric average rate put option's confidence interval is the average of the entire contract length, according to the Milstein model.
Figure 8. Geometric average rate put option's confidence interval is the average of the entire contract length, according to the Milstein model.
Preprints 119478 g008
Preprints 119478 g009
Figure 9. Geometric average rate simulation using MC methods call options with a 30-day expiration date and an average price.
Figure 9. Geometric average rate simulation using MC methods call options with a 30-day expiration date and an average price.
Preprints 119478 g009
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated