Investigating the Riemann Hypothesis with HQF ASA and Modular Surfaces - a Detailed Description

Preprint

Article

Investigating the Riemann Hypothesis with HQF ASA and Modular Surfaces - a Detailed Description

Altmetrics

Downloads

Views

Comments

Supplementary Material

supplementary.tex (25.48KB )

Hime Oliveira^*

This version is not peer-reviewed

Submitted:

27 September 2024

Posted:

30 September 2024

You are already at the latest version

Alerts

Abstract

This article describes a new application of the global optimization method HQF ASA to the investigation of the Riemann hypothesis, in the sense of searching for zeros of the Riemann zeta function ζ outside the critical line but inside the (open) subset of the critical strip ((0,1/2)∪(1/2,1))×(−∞,∞). The underlying idea is very simple: a complex root r of a given complex function f : C → C must satisfy the condition ||f(r)|| = 0, that is, f(r) must have 2-dimensional Eu- clidean norm equal to 0, considering r as a point of R2. In the opposite direction, for any r ∈ C, ||f(r)|| = 0 implies f(r) = 0 and r is a root of f. Focusing again on the Riemann zeta function ζ, the open and simply connected region Rc = (1/2,1)×(0,∞) is used along the text, taking into account the symmetries of zeros of ζ in the critical strip. In this fashion, finding a global optimizer for ||ζ|| is equivalent to finding a root of ζ. Therefore, and taking into account the well-known efficacy of HQF ASA, a good sign of the trueness of RH would be not finding global minima in several optimization sessions with expanding subsets of Rc. In practical terms, several optimization sessions are executed using QMF ASA with increasing subsets of Rc, searching for global minima of ||ζ||. After presenting numerical results and figures, the adequacy of the proposed approach as a tool for preliminary empirical analysis for this type of problem is discussed.

Keywords:

Subject: Computer Science and Mathematics - Mathematics

1. Introduction

This work describes a new computational approach that may be useful when starting investigations about existence of zeros of complex functions inside extensive (complex) domains. In truth it was used in a recent research about the Riemann hypothesis, furnishing early information about its feasibility and possible trueness [11] . After this preliminary phase, and considering that no root could be found, the mathematical proof may proceed, endowed with valuable information obtained in an empirical way.

In general terms, the Riemann hypothesis is the conjecture that the Riemann zeta function only has nontrivial roots in the set of complex numbers with real part 1/2, that is, the critical line in

C

. It is considered by many people the most important unsolved problem in pure mathematics, and also very significant in analytic number theory because of its connections with the distribution of prime numbers and many other scientific problems. Its trivial zeros occur at all negative even integers

{- 2 i : i \in N - {0}}

, and the known nontrivial roots supposedly occur somewhere on the critical line, and only there. The Riemann hypothesis is concerned with the locations of these nontrivial zeros:

Figure 1. Part of open critical strip and critical line.

In this fashion, if the hypothesis is true, all nontrivial zeros must be located on the critical line, that is, the subset of

C

with real part equal to 1/2 .

Furthermore, as said above, the study will be conducted only in the open region

(1 / 2, 1) \times (0, \infty)

. This is valid because roots are vertically symmetric (the conjugate of a zero is a zero as well), and horizontally symmetric relatively to the critical line - please, for more details, refer to [1]. In this case the discovery of one root in

A \overset{Δ}{=} (1 / 2, 1) \times (0, \infty)

results in finding four roots, symmetrically located relatively to the x axis and the critical line.

At this point it is important to highlight an important but usually unperceived fact, mainly for non-mathematicians: numerical calculations typically produce approximated results and although they can seem to be exact, they could not be so. Accordingly, in the present case, an apparent root may not be a true one, and a theoretical proof is needed, mathematically speaking. For example, in [2] it iis stated that "All the (nontrivial) zeros computed so far appear to be irrational numbers...". Incredibly, even the nontrivial zeros found by Riemann himself seem to lack such an essential theoretical validation!

Another significant issue is related to the choice of HQF ASA [10] as the basic tool for the task at hand - as an evolutionary method, designed to deal with nonlinear, multimodal and high-dimensional problems, it seemed (and was) well-equipped to go the distance.

In the next section, several optimization sessions will be presented and discussed so as to better explain the described approach and its benefits whenever starting a new research.

2. Searching for Roots Outside the Critical Line—Riemann Zeta Function

In what follows the results of some simulations are presented and interpreted so as to illustrate the proposed ideas. The optimization sessions were realized with increasing complex domains, contained in A, and no global optimum with value equal to zero was found, signaling towards a positive answer to the Riemann conjecture. Actually, the foiund optima correspond to points very near certain zeros on the critical line.

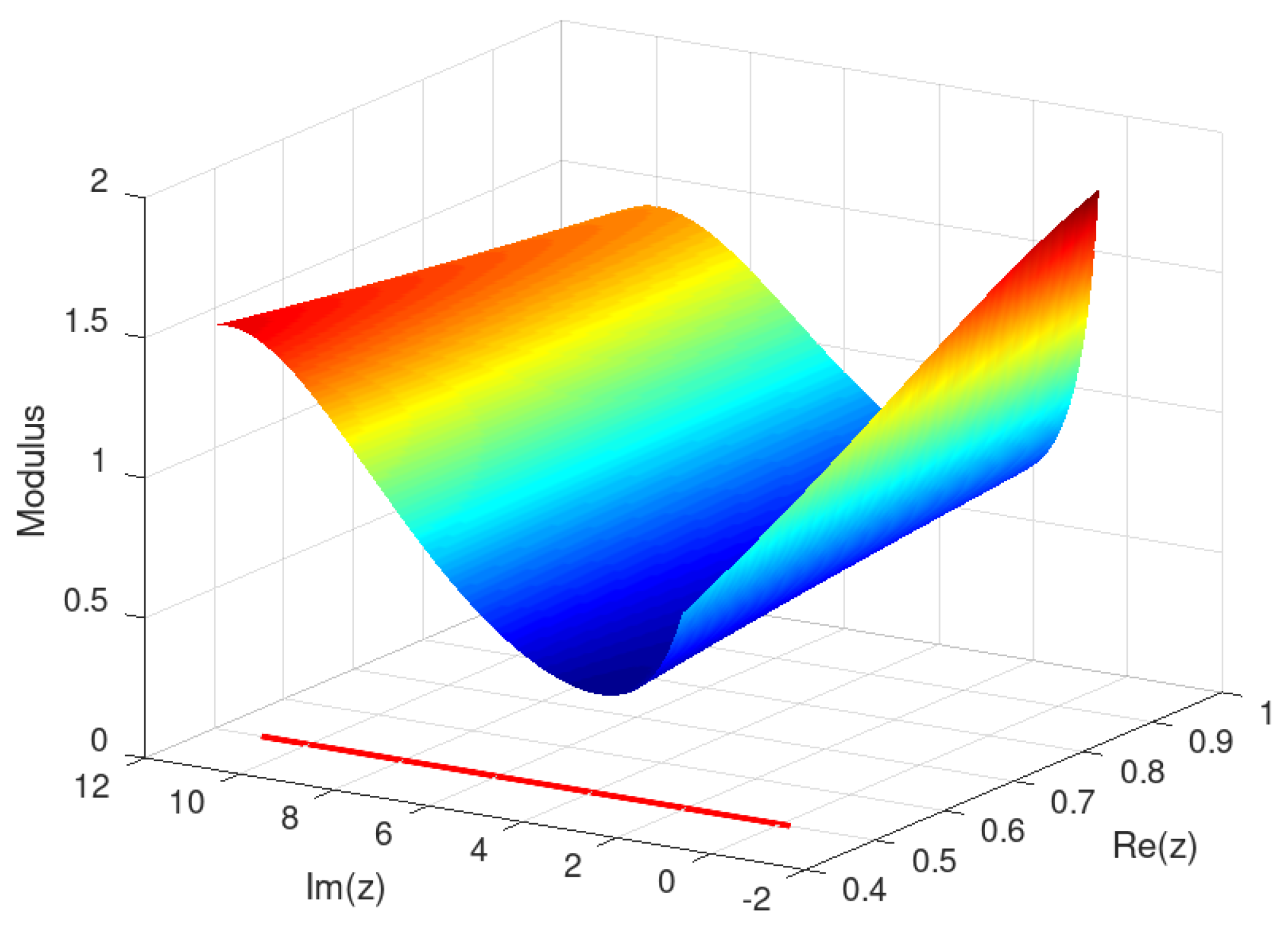
2.1. Domain $(0.50001, 0.99999) \times (0.000010, 10]$

In this first domain the modular surface stays far from the

C

complex plane, with minimum value of 0.526256339271718331929 and minimizer (0.50001253297613657 , 2.475747919503654249 ). This is so because the first known zero of

ζ

(departing from zero) is 14.134725, once more signaling favorably to RH.

Figure 2. Modular surface for

ζ

restricted to

(0.50001, 0.99999) \times (0.000010, 10]

Figure 2. Modular surface for

ζ

restricted to

(0.50001, 0.99999) \times (0.000010, 10]

Therefore, it is assumed that

ζ

has no roots inside the current region.

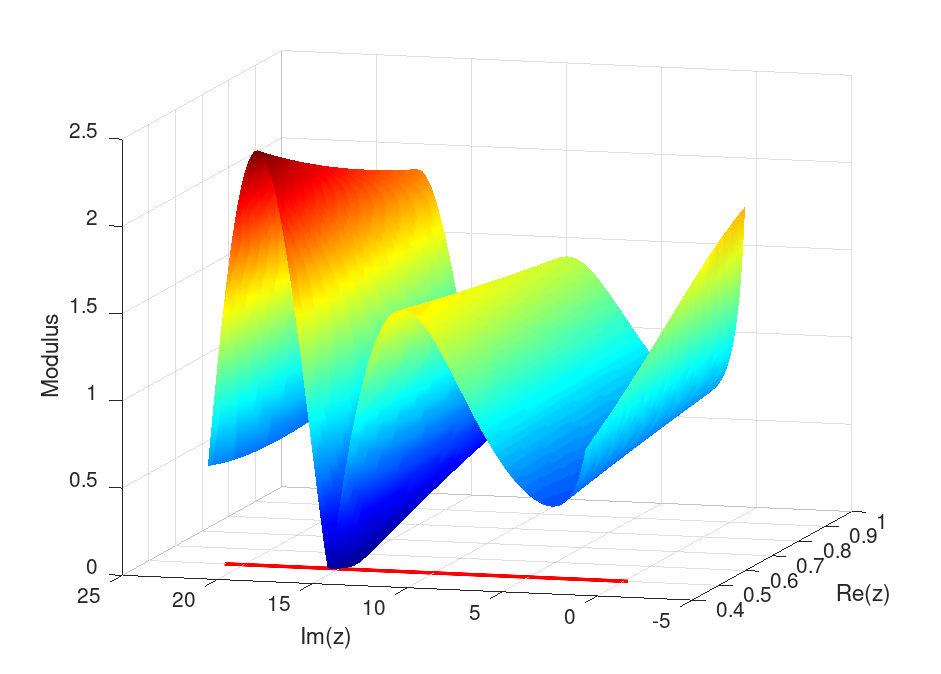
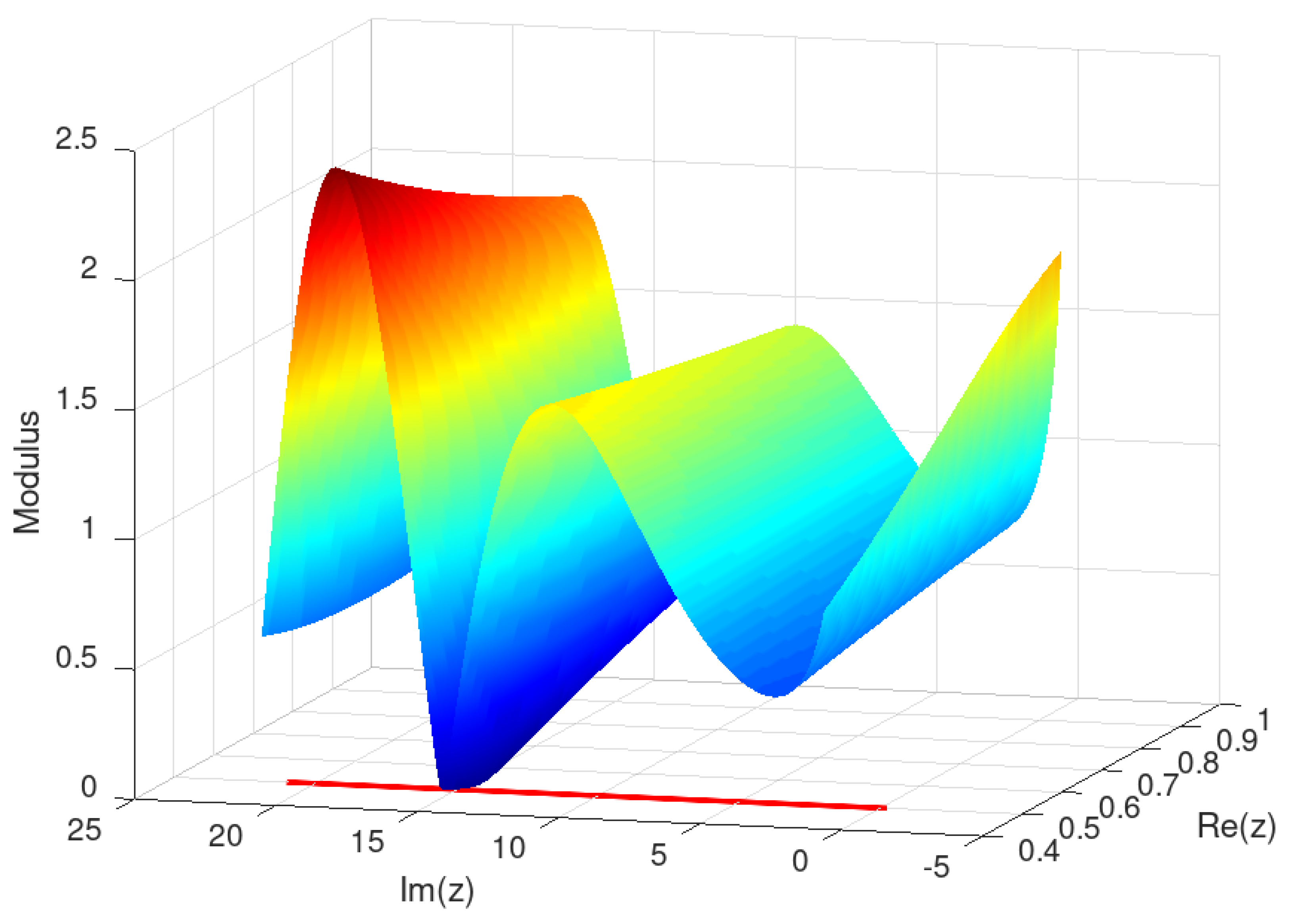
2.2. Domain $(0.50001, 0.99999) \times (0.000010, 20]$

In this larger domain the modular surface reaches a neighborhood of a nontrivial zero of zeta in the critical line, with minimum value of 7.93157218836881838797e-06 and minimizer ( 0.5000100000000001765 , 14.13472514160298488 ). Here, the first known zero of

ζ

(departing from zero) is approximated, once more signaling favorably to RH.

Figure 3. Modular surface for

ζ

restricted to

(0.50001, 0.99999) \times (0.000010, 20]

Figure 3. Modular surface for

ζ

restricted to

(0.50001, 0.99999) \times (0.000010, 20]

The minimizer found by HQF ASA corresponds to the (nowadays historical) nontrivial root nearby 0.5 + 14.1347251416 i, but surely it is not a root of

ζ

. Again, it is assumed that

ζ

has no roots inside the current region.

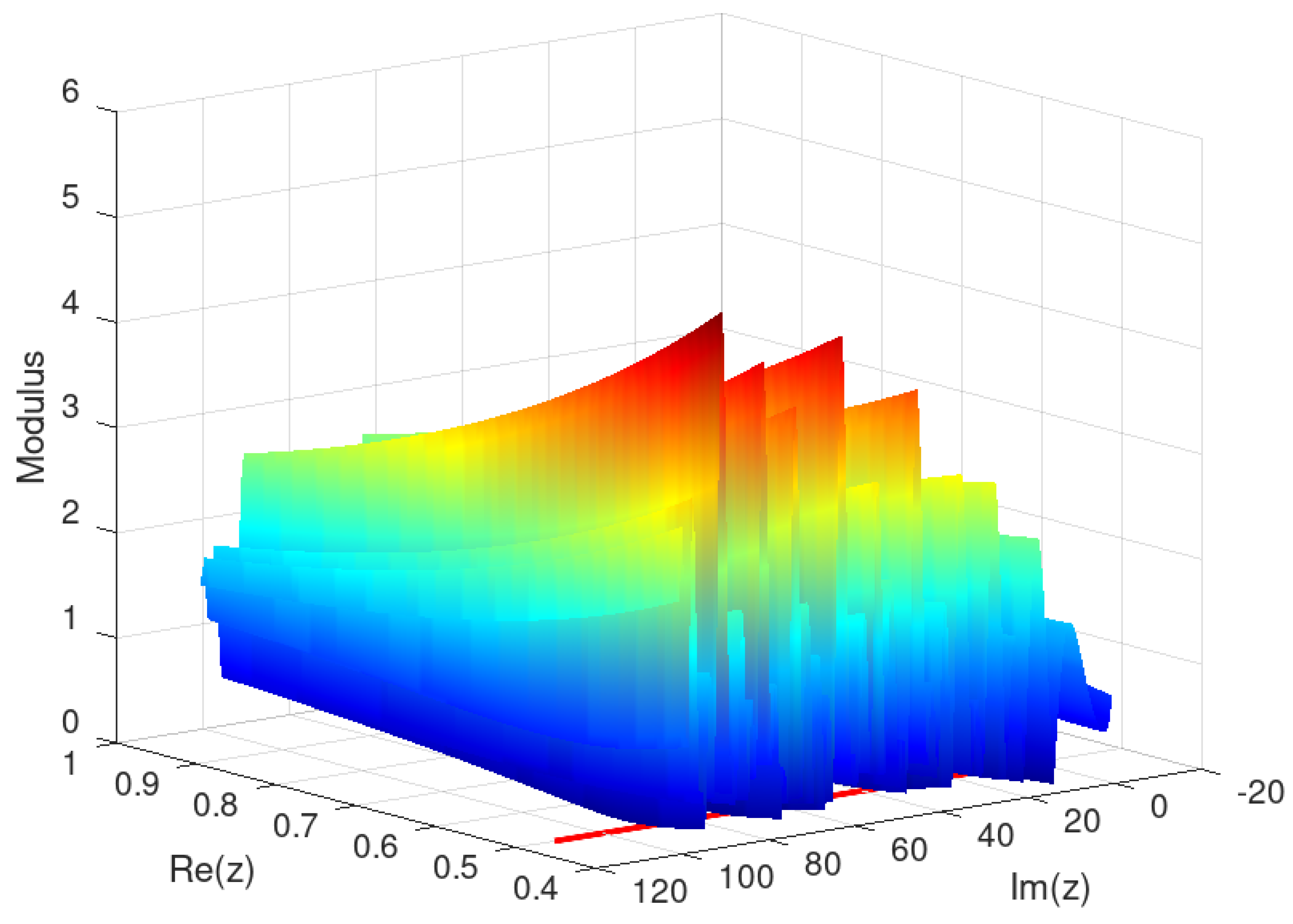
2.3. Domain $(0.50001, 0.99999) \times (0.000010, 100]$

In this domain the modular surface reaches neighborhoods of several nontrivial zeros of zeta in the critical line, HQF ASA converged to a point corresponding to one of them, with minimum value of 1.65412942330078749364e-05 and minimizer ( 0.5000100000000006206 , 60.83177852461846413 ).

In this simulation, the minimizer found by HQF ASA , which is not a root of

ζ

, corresponds to the nontrivial root nearby 0.5 + 60.8317785 i . Of course, other roots on the critical line could have "attracted" the algorithmic dynamics, depending on the location of the initial seed. Again, it is assumed that

ζ

has no roots inside the current complex domain.

Figure 4. Modular surface for

ζ

restricted to

(0.50001, 0.99999) \times (0.0000100, 100]

Figure 4. Modular surface for

ζ

restricted to

(0.50001, 0.99999) \times (0.0000100, 100]

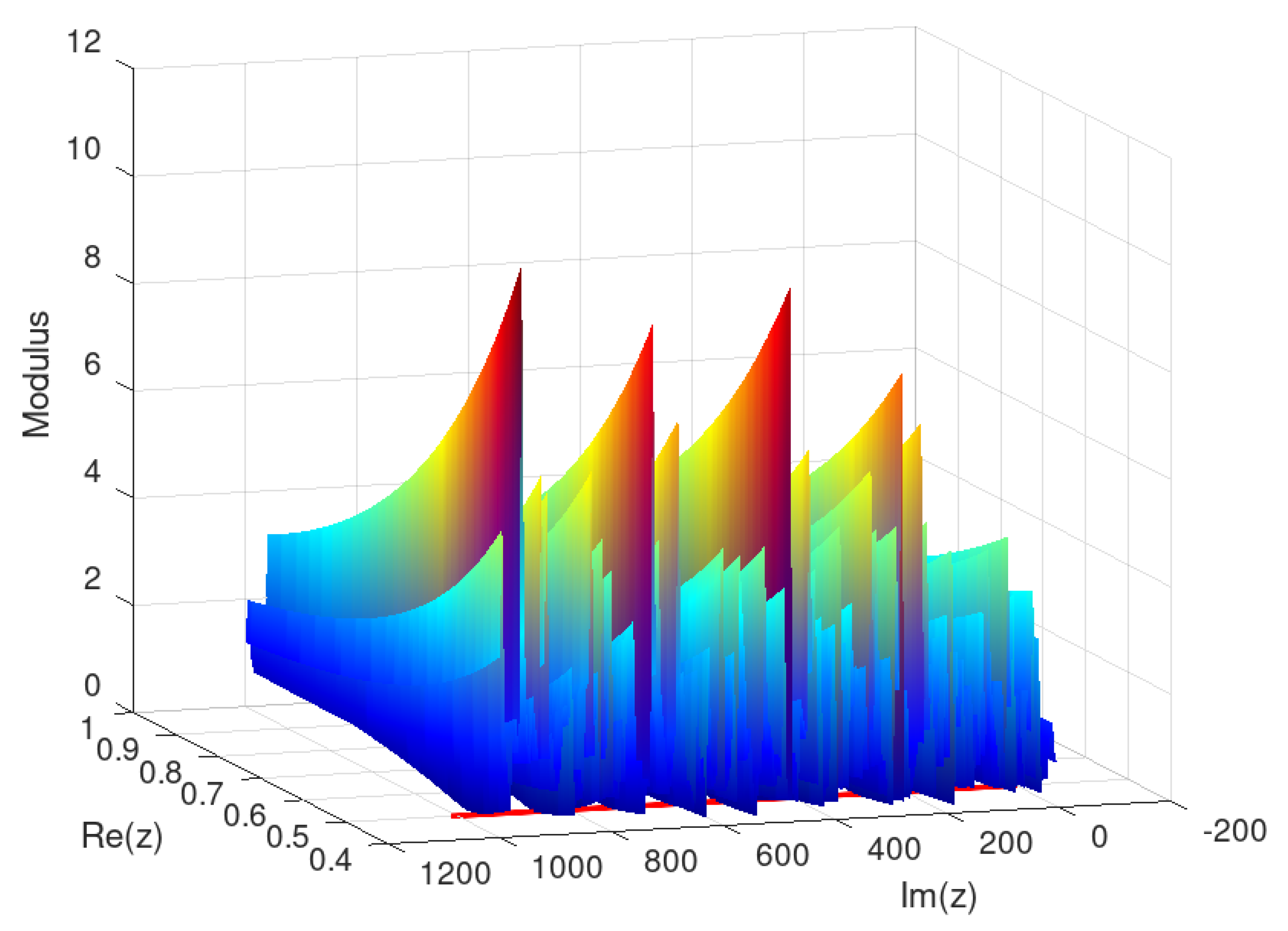
2.4. Domain $(0.50001, 0.99999) \times (0.000010, 1000]$

and minimizer ( 0.5000099999999999545 , 572.4199841326216074e+02 ).

In this simulation, the minimizer found by HQF ASA , which is not a root of

ζ

, corresponds to the nontrivial root nearby 0.5 + 572.419984132 i . Of course, other roots on the critical line could have "attracted" the algorithmic dynamics, depending on the location of the initial seed. Again, it is assumed that

ζ

has no roots inside the current complex domain.

Figure 5. Modular surface for

ζ

restricted to

(0.50001, 0.99999) \times (0.000010, 1000]

Figure 5. Modular surface for

ζ

restricted to

(0.50001, 0.99999) \times (0.000010, 1000]

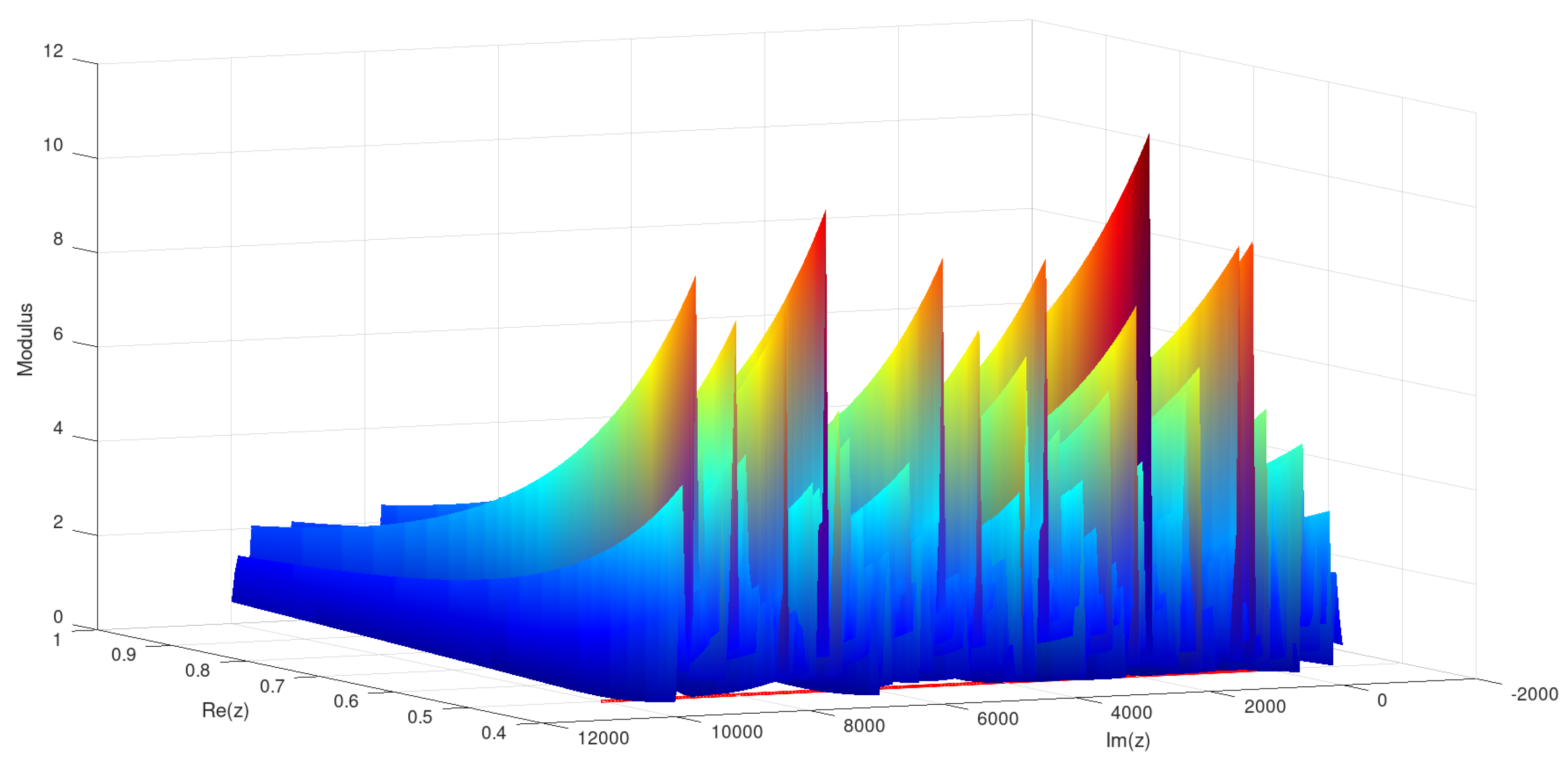
2.5. Domain $(0.50001, 0.99999) \times (0.000010, 10000]$

and minimizer ( 0.5000100000000001765 , 4035.10559902981413 ).

In this simulation, the minimizer found by HQF ASA , which is not a root of

ζ

, corresponds to the nontrivial root nearby 0.5 + 4035.105599030 i . Of course, other roots on the critical line could have "attracted" the algorithmic dynamics, depending on the location of the initial seed. Again, it is assumed that

ζ

has no roots inside the current complex domain.

Figure 6. Modular surface for

ζ

restricted to

(0.50001, 0.99999) \times (0.000010, 10000]

Figure 6. Modular surface for

ζ

restricted to

(0.50001, 0.99999) \times (0.000010, 10000]

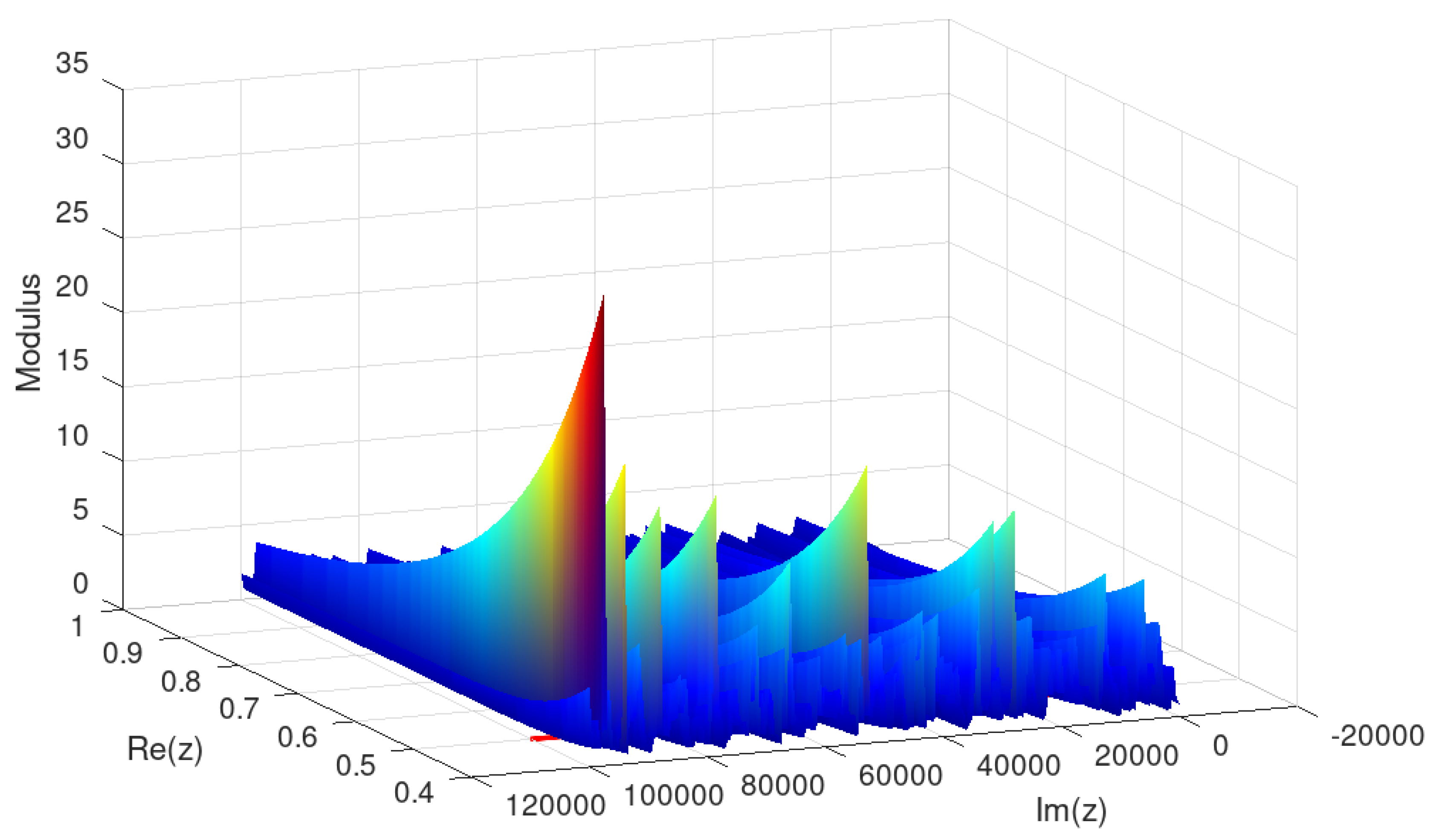
2.6. Domain $(0.50001, 0.99999) \times (0.000010, 100000]$

and minimizer ( 0.5000100000000001765 , 68995.52289638234652 ).

In this simulation, the minimizer found by HQF ASA , which is not a root of

ζ

, corresponds to the nontrivial root nearby 0.5 + 68995.522896385 i . Of course, other roots on the critical line could have "attracted" the algorithmic dynamics, depending on the location of the initial seed. Again, it is assumed that

ζ

has no roots inside the current complex domain.

Figure 7. Modular surface for

ζ

restricted to

(0.50001, 0.99999) \times (0.000010, 100000]

Figure 7. Modular surface for

ζ

restricted to

(0.50001, 0.99999) \times (0.000010, 100000]

3. Practical Directives, Unfoldings and Results Relative to the Previous Evidences

As said above, the presented ideas have already produced significant results and some considerations may be helpful.

First, it is worth saying that the number of optimization sessions should be chosen so as to give the researcher enough information about the geometry of the given objective function (global optimization is basically a geometric problem) and the likelihood for the existence of global optima inside the desired region. So, there is not a rigid rule or limit for such a choice.

After this initial phase, the information obtained by means of the simulations certainly will help in creating proof strategies, rigorously demonstrating the final theoretical targets. One well-succeeded case in which the whole cycle really took place is described in [11] (without including the preliminary step) and the theoretical proof itself has nothing to do with optimization or related subjects, but the initial prospection was fundamental to complete the overall task.

4. Conclusions

This paper exposed an heuristic way to preliminarily investigate the existence of roots for complex functions using evolutionary global optimization techniques in a given complex domain. Even though this experimental step does not represent a theoretical contribution to the subject, it can furnish strong evidences about whether such roots exist or not in that specific region and where they could be located, in the affirmative case. In any circumstance, the chosen global optimization paradigm needs to be very effective, in order not to get stuck in local minima. In the present work the selected method was HQF ASA [10].

In a concrete case [11] there was substantial likelihood to arrive at a satisfactory conclusion about the Riemann hypothesis. The underlying method used in this paper may be directed to any complex function, provided it satisfies certain regularity conditions, this including Dirichlet L-functions and so many others [9].

References

N. ARWASHAN, THE RIEMANN HYPOTHESIS AND THE DISTRIBUTION OF PRIME NUMBERS, Nova Science Publisher Inc, 2021.
J. Derbyshire, Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York, Penguin, 2004.
Edwards, H. M. Riemann’s Zeta Function. New York: Dover, 2001.
S. Lang, Complex Analysis, 4th ed., Springer-Verlag, 1999.
C. H.C. Little, K. L. Teo, B. van Brunt, Real Analysis via Sequences and Series, Springer, New York, 2015.
M. Mureşan, A Concrete Approach to Classical Analysis, Springer-Verlag, New York, 2009.
T. Needham, Visual Complex Analysis, OUP, Oxford, 2023.
Z. Nitecki, Differentiable Dynamics - An Introduction to the Orbit Structure of Diffeomorphisms. The MIT Press, New York, 1971.
H. Oliveira. Existence of Zeros for Holomorphic Complex Functions: A Dynamical Systems Approach. Preprints 2023, 2023090357. [CrossRef]
H. Oliveira. Homotopic quantum fuzzy adaptive simulated annealing [HQF ASA], Information Sciences, Vol. 669, 2024.
Oliveira, H. A Modest Contribution to the Riemann Hypothesis Using the Poincaré Index. Preprints 2023, 2023090513. [Google Scholar] [CrossRef]
E. C. Titchmarsh.. The Theory of the Riemann Zeta Function, 2nd edition, Oxford University Press, 1986.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Investigating the Riemann Hypothesis with HQF ASA and Modular Surfaces - a Detailed Description

Abstract

1. Introduction

2. Searching for Roots Outside the Critical Line—Riemann Zeta Function

2.1. Domain ( 0.50001 , 0.99999 ) × ( 0.000010 , 10 ]

2.2. Domain ( 0.50001 , 0.99999 ) × ( 0.000010 , 20 ]

2.3. Domain ( 0.50001 , 0.99999 ) × ( 0.000010 , 100 ]

2.4. Domain ( 0.50001 , 0.99999 ) × ( 0.000010 , 1000 ]

2.5. Domain ( 0.50001 , 0.99999 ) × ( 0.000010 , 10000 ]

2.6. Domain ( 0.50001 , 0.99999 ) × ( 0.000010 , 100000 ]

3. Practical Directives, Unfoldings and Results Relative to the Previous Evidences

4. Conclusions

References

MDPI Initiatives

Important Links

Subscribe

2.1. Domain $(0.50001, 0.99999) \times (0.000010, 10]$

2.2. Domain $(0.50001, 0.99999) \times (0.000010, 20]$

2.3. Domain $(0.50001, 0.99999) \times (0.000010, 100]$

2.4. Domain $(0.50001, 0.99999) \times (0.000010, 1000]$

2.5. Domain $(0.50001, 0.99999) \times (0.000010, 10000]$

2.6. Domain $(0.50001, 0.99999) \times (0.000010, 100000]$