1. Introduction

2. Literature

3. Methodology

3.1. Modeling

The model used is inspired by previous works such as Detragiache et al. (2006), Hermes and Lensink (2004), and Claessens et al. (2001). These studies explain bank profitability and efficiency based on bank-specific characteristics and the macroeconomic environment in which banks operate. Our model assesses the impact of foreign bank entry on the efficiency of domestic banks in developing countries using sustainability proxies related to efficiency, bank characteristics, and macroeconomic factors.

Our model is specified as follows:

Y_btp = α + ξ Presence_tp + φβ B_btp + δ M_tp + γ Inter + ε_btp.

(1)

where b, t, and p, respectively, reflect the bank b in year t and the country p;

b = 1, .. ..., n, t = 1, ...., T and p = 1, .. ..., P.

Ybtp: Efficiency of domestic banks; serving as the proxy for financial sustainability.

Presence_tp represents the "presence of foreign banks" (measured by the proportion of foreign-controlled assets), which serves as a proxy for their influence on financial stability and sustainability.

B_tp: includes bank characteristics, such as size (total assets), capital adequacy ratio, and loan portfolio composition (e.g., proportion of green or SME loans), which reflect financial, social, and environmental sustainability.

M_tp includes macroeconomic variables like GDP growth, inflation rate, and interest rate, which affect banks' overall financial sustainability.

Inter: includes interaction terms (Presence * Performance Gap between domestic and foreign banks) to measure the moderating effect of foreign bank presence on domestic bank characteristics, allowing us to test how competition influences sustainability.

εb_tp: The stochastic component of the error is assumed to be uncorrelated with the explanatory variables and follows the normal distribution N (0, σε). It is independent and identically distributed (iid).

This study uses two different methods to measure each bank's efficiency level. The first is to calculate the intermediation margin ratio, which has been widely used in the literature to assess the effect of the entry of foreign banks on the efficiency of local banks in developing countries. The second method is based on the estimated efficiency level by the "Meta frontier approach." This approach calculates the technical efficiency of banks operating different production technologies, and they are subject to different environmental conditions (economic, political, social ... etc.). It provides a measure of the efficiency level of banks operating in different countries while considering the existing technological gap between these countries.

Suppose we have "P" in different countries, and each country 'p' contains Np banks that face the same input prices and pursue the goal of cost minimization given the output level. The stochastic cost frontier model for each bank "b" of the country "p" at the time "t" can be formulated as follows:

$$C{T}_{bt(p)}=f(X_{bt(p)};\varphi {}_{(p)})e^{v_{bt(p)}+u_{bt(p)}}$$

(2)

$$b=1,\hspace{0.33em}2,\hspace{0.33em}\mathrm{3..........}{N}_p\hspace{1em};t=1,\hspace{0.17em}2,\mathrm{...............}T.\hspace{1em}\hspace{1em}\hspace{1em}p=1,\hspace{0.17em}\hspace{0.17em}2,\mathrm{..........}P.$$

where CTbt(p) is the total cost, Xbt (p) is the vector of output and input prices. φ (p) is the vector of unknown parameters to be estimated. Vbt (p) is the usual error term that follows the normal distribution N (0, σ2); it is independent of Ubt(p). It is a white noise used to control measurement errors and determinants of costs beyond the control of managers. The term also captures the luck (bad) of the bank having experienced a favorable (unfavorable) exogenous shock that (increases) decreases the total cost of the bank. Ubt(p) is the deviation of the cost of the firm b compared to the efficiency frontier. It serves as an approximation of technical and allocative inefficiency. It is positively defined with an independent distribution Vbt(p).

To facilitate the equation (2-29), it can be formulated as follows:

$$C{T}_{bt(p)}=e^{X_{bt(p)}{\varphi }_{(p)}+}{v}_{bt(p)}+u_{bt(p)}$$

(3)

Following Battese et al. (2004), this model assumes that for each country, there is only one data generation process for banks that use a given technology.

Therefore, this model is applied to each country to assess its stochastic frontier cost. Meta-frontier takes the same functional form as an individual stochastic frontier for each country. Thus, the function of the Meta-cost frontier that envelops the frontiers of specific costs for each country can be formulated as follows:

$$C{T}_{bt}^{\ast }=f(X_{bt};{\varphi }^{\ast })\equiv e^{X_{bt}{\varphi }^{\ast }}$$

(4)

$C{T}_{bt}^{\ast }$ Is the optimal expense for the bank "b" at the time "t" required to produce the given output amount under exogenous input price conditions?

${\varphi }^{\ast }$ Is the vector of parameters associated with the Meta-frontier cost function that satisfies the condition (C1) below:

$$X_{bt}{\varphi }^{\ast }\le X_{bt}{\varphi }_{(p)}$$

(C1)

Meta-frontier is the deterministic function parameter that envelops the deterministic part of the individual cost frontiers. Its values must be less or equal to the deterministic components of the estimated stochastic cost frontier for each country. The cost Meta-frontier function can reflect the minimum production cost to produce a given output level. This is the minimum cost associated with the technique of more efficient production. The inequality constraint given by equation (C1) must be satisfied for all countries throughout the period. Meta-frontier is considered the curve enveloping the individual frontier cost countries.

Figure 1 illustrates how the Meta-frontier cost envelops the stochastic frontiers function of different countries in the case of a single output.

In this figure, the frontier 1, 2, and 3 represent four stochastic frontiers for 3 countries. The cost of the Meta-frontier function that encompasses the three stochastic frontiers indicates the possibility of producing at a total cost below the deterministic costs correlated with the stochastic cost frontiers of the four countries. Frontiers 1 and 2 are arbitrarily chosen to be tangent to the Meta-frontier, and frontier 3 is not. Thus, as the stochastic cost frontiers 1 and 2 are closest to the Meta-frontier, we can say that banks in countries 1 and 2 adopt more production technology developed than those in the third country.

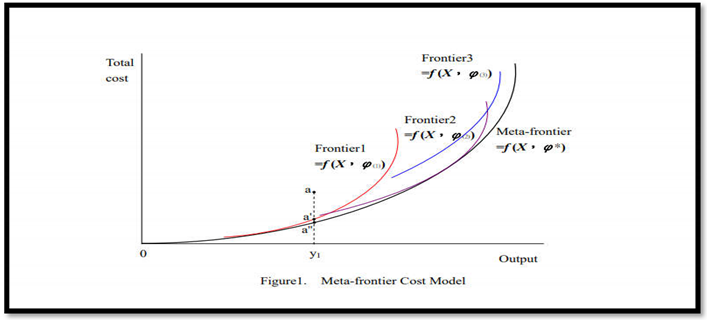
3.2. The Efficiency Score and the Technology Gap Ratio "TGR"

A company's cost efficiency is evaluated by the minimum cost (taken from the frontier) to the observed current cost for the same given production and conditions price. It is a measure of cost deviation versus best performance.

The Meta-frontier cost efficiency."$C{T}_{bt(p)}^{\ast }$" of a bank "b" in a year "t" in the country "p" can be estimated using the Meta-frontier model, as specified in equation (5) :

$$C{E}_{bt(p)}^{\ast }={\displaystyle \frac{e^{X_{bt}{\varphi }^{\ast } \hspace{0.17em}+\hspace{0.17em}{v}_{bt(p)}}}{C{T}_{bt(p)}}}$$

(5)

Integrate the equation (3) into equation (5):

$$C{E}_{bt(p)}^{\ast }={\displaystyle \frac{e^{X_{bt}{\varphi }^{\ast } \hspace{0.17em}+\hspace{0.17em}{v}_{bt(p)}}}{e^{X_{bt}{\varphi }_{(p)}+v_{bt(p)}+u_{bt(p)}}}}=e^{-u_{bt(p)}}\ast {\displaystyle \frac{e^{X_{bt}{\varphi }^{\ast }}}{e^{X_{bt}{\varphi }_{(p)}}}}$$

(6)

where the first term on the right reflects the level of technical efficiency (EC) on the stochastic cost frontier of the country "p."1

$$C{E}_{bt(p)}={\displaystyle \frac{e^{X_{bt}{\varphi }_{(p)} \hspace{0.17em}+\hspace{0.17em}{v}_{bt(p)}}}{e^{X_{bt}{\varphi }_{(p)}+v_{bt(p)}+u_{bt(p)}}}}=e^{-u_{bt(p)}}$$

(7)

It must be between 0 and 1 because $u_{bt(p)}$It is considered a non-negative random variable.

For the second term, it is the technology gap ratio "TGR."

$$TG{R}_{bt(p)}={\displaystyle \frac{e^{X_{bt}{\varphi }^{\ast }}}{e^{X_{bt}{\varphi }_{(p)}}}}$$

(8)

The ratio "$TGR$" measures the technology gap for country "p" where production technology adopted by its firms is less developed than that available for all countries. It is obtained from the Meta-frontier cost function.

According to the constraint (C1), this measurement is between 0 and 1. A country's high value of the ratio "TGR" reflects its adoption of advanced production technology.

Finally, the cost efficiency relative to the Meta-frontier as measured by the equation (5) can then be formulated as follows:

$$C{E}_{bt(p)}^{\ast }=C{E}_{bt(p)}\ast TG{R}_{bt(p)}$$

(9)

The vector ${\stackrel{⌢}{\varphi }}^{\ast }$It is obtained after solving the following optimization problem:

$$\begin{array}{l}Min\hspace{0.33em}L={\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{b=1}^N\left|Ln\hspace{0.17em}f\left(X_{bt}{\stackrel{⌢}{\varphi }}_{(p)}\right)-Ln\hspace{0.17em}f\left(X_{bt}{\varphi }^{\ast }\right)\right|}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}(10-37)\\ \\ s/c:Ln\hspace{0.17em}f\left(X_{bt}{\varphi }^{\ast }\right)\le Ln\hspace{0.17em}f\left(X_{bt}{\stackrel{⌢}{\varphi }}_{(p)}\right)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}(C2)\end{array}$$

As all deviations are positive according to the constraint (C2), all the absolute differences are equal to the differences. Using equations (3) and (4), we can convert the optimization problem above (10, C2) to a linear programming problem "LP" :

$$\begin{array}{l}Min\hspace{0.33em}L={\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{b=1}^N\left(X_{bt}{\stackrel{⌢}{\varphi }}_{(p)}-X_{bt}{\varphi }^{\ast }\right)}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}\hspace{0.17em}(11)\\ \\ \hspace{1em}s/c:X_{bt}{\varphi }^{\ast }\le X_{bt}{\stackrel{⌢}{\varphi }}_{(p)}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(C3)\end{array}$$

The functional form of the cost function adopted for calculating the level of efficiency is the type of translog cost function; it is as follows:

$${(\mathrm{Ln} \mathrm{CT})}_{\mathrm{b},\mathrm{t}}= \mathsf{\alpha } + ({\displaystyle \sum _{i:1}^3}{\mathsf{\phi }}_{\mathrm{i}} \mathrm{Ln} {\mathrm{w}}_{\mathrm{i}}{)}_{\mathrm{b},\mathrm{t}}+({\displaystyle \frac{1}{\begin{array}{l}2\\ \end{array}}}{\displaystyle \sum _{i:1}^3}{\displaystyle \sum _{j:1}^3}{\mathsf{\phi }}_{\mathrm{ij}} \mathrm{Ln} {\mathrm{w}}_{\mathrm{i}} \mathrm{Ln} {\mathrm{w}}_{\mathrm{j}} {)}_{\mathrm{b},\mathrm{t}}+({\displaystyle \sum _{k:1}^3}{\mathsf{\gamma }}_{\mathrm{k}} \mathrm{L}\mathrm{n} {\mathrm{y}}_{\mathrm{k}}{)}_{\mathrm{b},\mathrm{t}}$$

$$+({\displaystyle \frac{1}{\begin{array}{l}2\\ \end{array}}}{\displaystyle \sum _{k:1}^3}{\displaystyle \sum _{m:1}^3}{\mathsf{\gamma }}_{\mathrm{km}} \mathrm{Ln} {\mathrm{y}}_{\mathrm{k}} \mathrm{Ln} {\mathrm{y}}_{\mathrm{m}}{)}_{\mathrm{b},\mathrm{t}}+({\displaystyle \sum _{i:1}^3}{\displaystyle \sum _{k:1}^3}{\mathsf{\lambda }}_{\mathrm{ik}} \mathrm{L}\mathrm{n} {\mathrm{w}}_{\mathrm{i}} \mathrm{L}\mathrm{n} {\mathrm{y}}_{\mathrm{k}}{)}_{\mathrm{b},\mathrm{t}}$$

$$+({\mathsf{\tau }}_{\mathrm{f}} \mathrm{Ln} \mathrm{F} {)}_{\mathrm{b},\mathrm{t}}+{\displaystyle \frac{1}{\begin{array}{l}2\\ \end{array}}}({\mathsf{\tau }}_{\mathrm{ff}} \mathrm{LnF} \mathrm{LnF} {)}_{\mathrm{b},\mathrm{t}}+({\displaystyle \sum _{k:1}^3}{\mathsf{\omega }}_{\mathrm{fi}} \mathrm{L}\mathrm{n} \mathrm{F} \mathrm{L}\mathrm{n} {\mathrm{y}}_{\mathrm{k}}{)}_{\mathrm{b},\mathrm{t}}$$

$$+({\displaystyle \sum _{i:1}^3}{\mathsf{\psi }}_{\mathrm{fi}} \mathrm{L}\mathrm{n}\mathrm{F} \mathrm{L}\mathrm{n} {\mathrm{w}}_{\mathrm{i}}{)}_{\mathrm{b},\mathrm{t}}+{\mathrm{U}}_{\mathrm{b}\mathrm{t}}+{\mathrm{V}}_{\mathrm{b}\mathrm{t}}$$

(12)

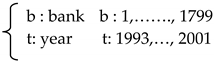where (Ln CT) is the natural logarithm of the total cost of the b^th bank in the period t, (Ln w_{i bt}) is the natural logarithm of its i^th input prices, (Ln y_k) represents the natural logarithm of its k^th output, (Ln F) denotes its capitalization ratio used to control observable heterogeneity among banks.

Technical inefficiency, due to the excessive use of inputs to produce a given volume of output resulting from the choice of the wrong combination of inputs given their relative prices in the market, would be captured by the inefficiency term U_bt. The term V_bt is used to control measurement errors and determinants of costs beyond the control of managers. This term also captures the (bad) luck of the bank having experienced an exogenous shock (unfavorable) favorable that (increases) decreases the total cost of the bank.

To be consistent with the economic theory, the cost function should be: (i) non-negative, (ii) twice continuously differentiable in its domain, (iii) symmetric, (iv) linear homogeneous in input prices, (v) monotonically increasing in input prices and outputs, (vi) concave in input prices. The parameters need to satisfy the following restrictions :

φ_ij = φ_ji, γ_km = γ_mk ⇒ pour que la fonction de coût soit symétrique

${\displaystyle \sum _{i:1}^3}$ φ_i = 1, ${\displaystyle \sum _{i:1}^3}$φ_ij = 0, ${\displaystyle \sum _{k:1}^3}$λ_ik = 0, ${\displaystyle \sum _{i:1}^3}$_ψfi = 0 ∀ i

In this work, we refer to the intermediation approach to define the inputs and outputs bank.

The independent variables included in the model reflect the characteristics of the banks and the environment in which they operate. We select variables that can be measured for all banks in different countries.

4. Results

5. Conclusions

References

1. Abut D., S. Bigio et D.A. Siller, 1999. The independent local bank in Latin America. Goldman Sachs Investment Research. November 23.
2. Agénor P., 2001. Benefits and costs of international financial integration: Theory and Facts. Paper prepared for the conference on Financial Globalization: Issues and Challenges for Small States (Saint Kitts, March 27-28, 2001), organized by the Word Bank Institute in collaboration with the Malta Institute for Small States and the Eastern Caribbean Central Bank.
3. Angbazo L.,1997. Commercial bank net interest margins, default risk, interest-rate risk, and off-balance sheet banking. Journal of Banking and Finance, (21), pp 55-87.
4. Atkinson S.E., et C. Cornwell, 1993. Measuring technical efficiency with panel data: A dual approach. Journal of Econometrics 59, pp 257-261. [CrossRef]
5. Aziz I., W. Bailey, C.X. Mao, F. Siddik et W. Thorbecke, 2002. Firm behavior, economic vulnerability, and the credit crunch: an analysis of micro-macro interactions, mimeo. Asian Development Bank Institute.
6. Barajas A, R. Steiner, et N. Salazar, 2000. The impact of liberalization and foreign investment in Colombia’s financial sector, Journal of Development Economics, Vol 63, pp 157–196. [CrossRef]
7. Barth J. R, G. Caprio et R. Levine, 2001. The regulation and supervision of banks around the world a new data base, The world banks.
8. Berger A. N., et R. DeYoung, 2001. The effects of geographic expansion on bank efficiency, Journal of Financial Services Research, Vol 19, N° 2-3, pp 163-184. [CrossRef]
9. Berger A.N., et R. Deyoung, 1997. Problem loans and cost efficiency in commercial banks, Journal of Banking and Finance 21 N 6, pp 849-870.
10. Berger A.N., et T.H. Hannan, 1998. The Efficiency cost of market power in the banking industry: A test of the « Quiet Life » and related hypotheses, The Review of Economics and Statistics, Vol 80, No.3, pp 454-465. [CrossRef]
11. Bhattacharya J., 1993. The role of foreign banks in developing countries: A survey of evidence, Unpublished manuscript, Cornell University.
12. Bonaccorsi di Patti E., et D.C. Hardy, 2005. Financial sector liberalization, bank privatization, and efficiency: Evidence from Pakistan, Journal of Banking & Finance 29, pp 2381–2406. [CrossRef]
13. Bosco M.G., 2003. Are foreign banks more efficient than domestic banks? An empirical study of transition and MED countries, Proceedings of the Global economic Modelling Network, International Conference on Policy Modelling, July 2003.
14. Buch C.M., 1997. Opening up for foreign banks: how central and Eastern Europe can benefit, Economics of Transition, Vol 5 (2), pp 339-366. [CrossRef]
15. Cao M., et S. Shi, 2000. Screening, bidding, and the loan market, Queen S. University, mimeo.
16. Chantapong S., 2003. Comparative study of domestic and foreign bank performance in Thailand: The regression Analysis, Economic Change and Restructuring, Vol 38, N° 1, pp 63-83. [CrossRef]
17. Claessens S., A. Demirgüç-Kunt et H. Huizinga, 2001. How does foreign entry affect the domestic banking market? Journal of Banking and Finance 25, pp 891-911.
18. Claessens S., et M. Jansen, 2000. The internationalization of financial services: Issues and lessons for developing countries: overview, In The internationalization of financial services: issues and lessons for developing countries, Kluwer law international, The Hague.
19. Claessens S., et T. Glaessner, 1999. Internationalization of financial services in Asia In Hanson, J. and S. Kathuria (eds.), India: A Financial Sector For the Twenty-First Century. Washington, D.C.: World Bank, New York, Oxford University Press.
20. Clarke G., R. Cull, L. D’Amato et A. Molinari, 1999. The effect of foreign entry on Argentina’s domestic banking sector, The World Bank Series: Policy Research Working Paper Series Number 2158.
21. Clarke G., R. Cull, M. Martinez Peria et S.M. Sanchez, 2001. Foreign bank entry: experience, implication for developing countries, and agenda for further research, The World Bank in its series, Policy Research Working Paper Series, N° 2698.
22. CNB, 1998. Banking supervision in the Czech Republic, Czech National Bank, Prague.
23. Crystal J.S, G.B. Dages et L.S. Goldberg, 2002. Has foreign bank entry led to sounder banks in Latin America, Current Issues in Economics and Finance, Federal Reserve Bank of New York, V 8, N° 1, pp 1-6.
24. Daniel Ofori-Sasu, L. Mensah, J.K. Akuma et| I. Doku 2019. Banking efficiency in emerging economies: Does foreign banks entry matter in the Ghanaian context? International Journal of Finance & Economics, vol 24, Issue 3, pp 1091-1108. [CrossRef]
25. Dell’Ariccia G., 2000. Learning by lending, competition, and screening incentives in the banking industry, International Monetary Fund, mimeo.
26. Demirguç-Kunt A., et H. Huizinga, 1999. Determinants of commercial bank interest margins and profitability: some international evidence, The World Bank Economic Review, vol. 13, Nº 2, pp 379-408. [CrossRef]
27. Demirgüç-Kunt A., R. Levine et H.G. Min 1998. Opening to foreign banks: issues of stability, efficiency, and growth, In Proceedings of the Bank of Korea Conference on the Implications of Globalization of World Financial Markets, pp 83-105.
28. Demsetz H., 1973. Industry structure, market rivalry, and public policy, Journal of Law and Economics, 16, pp 1-9.
29. Denizer C., 1999. Foreign entry in Turkeys banking sector, 1980–1997 The World Bank.
30. Detragiache E. et P. Gupta, 2004. Foreign banks in emerging market crises: Evidence from Malaysia, IMF Working Paper.
31. Detragiache E., T. Tressel, et P. Gupta, 2006. Foreign Banks in Poor Countries: Theory and Evidence, IMF Working Paper, WP/06/18. [CrossRef]
32. Deyoung R., et G. Whalen, 1994. Is a consolidated banking industry a more efficient banking industry?, Office of The Comptroller of The Currency, Quarterly Journal, Vol 13, N° 3, pp 11-21.
33. Dietsch M., 1996. Efficience et prise de risque dans les banques en France , Revue économique, Vol47, N 3, pp 745 – 754.
34. Drakos K., 2003. Assessing the success of reform in transition banking 10 years later: an interest margins analysis, Journal of Policy Modelling, (25), pp 309–317. [CrossRef]
35. Esho N., 2001. The determinants of cost efficiency in cooperative financial institution: Australian evidence, Journal of Banking and Finance, V 25, N 35, pp 941-964. [CrossRef]
36. Feldstein M., 2002. Economic and financial crises in emerging markets economies: overview of prevention and management, NBER Working paper.
37. Fries S., et A. Taci, 2005. Cost efficiency of banks in Transition: Evidence From 289 Banks in 15 Post-Communist Countries, Journal of Banking and Finance, Vol 29, pp 55-81. [CrossRef]
38. Garber P.M., 2000. What you see vs. what you get: derivatives in international capital flows, paper prepared for World Bank–Brookings–IMF Financial Markets and Development Conference on “Emerging Markets in the New Financial System: Managing Financial and Corporate Distress,” Florham Park, New Jersey, March 30–31.
39. Goldberg L., 2001. When is U.S. bank lending to emerging markets volatile? Federal Reserve Bank of New York, Mimeo.
40. Goldberg L., B.G. Dages et D. Kinney, 2000. Foreign and domestic bank participation in emerging markets: lessons from Mexico and Argentina, FRBNY Economic Policy Review, 6 (3), pp 17-36.
41. Hainz C., et M. Schnitzer, 2001. “The development of the banking sector in Eastern Europe : the next decade”, In: Winkler, Adalbert (Hrsg.): Banking and Monetary Policy in Eastern Europe – The First Ten Years, Palgrave, Houndsmills/Basingstoke, pp 205–216.
42. Haiyan Yina, J. Yangb et Xing Lu 2020. Bank globalization and efficiency: Host- and home-country effects. Research in Internaional Business and Finance, Vol 54.
43. Hermes N., et R. Lensink, 2004. The short–term effects of foreign bank entry on domestic bank behavior: does economic development matter?, Journal of banking and finance, vol 28, pp 553-568. [CrossRef]
44. Huang T.H., et T.L. Kao, 2006. Joint estimation of technical efficiency and production risk for multi-output banks under a panel data cost frontier model, Journal of Productivity Analysis, 26, pp 87–102. [CrossRef]
45. Kaminsky G., et C. M. Reinhart., 1999. The twin crises: the causes of banking and balance of payments problems, American Economic Review; 89(3), pp 473-500.
46. Keeton W.R., 1999. Does faster loan growth lead to higher loan losses? Federal Reserve Bank of Kansas City Economic Review, 84 (2), pp 57-75.
47. Kraft E., R. Hofler et J. Payne, 2002. Privatization foreign bank entry and bank efficiency in croatia A fourier-flexible function stochastic cost frontier analysis, Working Paper: The Croatian National Bank.
48. Kroszner R., 1998. On the political economy of banking and financial regulatory reform in emerging markets, CRSP Working Paper, N° 472.
49. Leightner J.E., et C.C. Knox Lovell, 1998. The Impact of financial liberalization on the performance of Thai banks, Journal of Economic and Business, (50), pp 115-131. [CrossRef]
50. Levine R, 1996. Foreign banks, financial development, and economic growth, In: Claude, E., Barfied, (eds), International Financial Markets. AEi Press, Washington, DC.
51. Levine.R, 1999. Foreign bank entry and capital control liberalization: effects on growth and stability, mimeo. University of Minnesota.
52. Liu L., 2002a. Beyond sequencing: A risk management approach to financial liberalization, ADB Institute.
53. Liu L., 2002b. Sequencing PRC.s banking sector reform after the WTO: options and strategy ADB Institute.
54. Mathieson D., et J. Roldos, 2001. The role of foreign banks in emerging markets, Paper prepared for the FMI-World Bank-Brookings institution Conference on Financial Markets and Development, 19-21 April, New York.
55. Mc Fadden C., 1994. Foreign banks in Australia, The World Bank.
56. Montgomery H., 2003. The role of foreign banks in Post-crisis Asia: The importance of method of entry, Asian Development Bank Institute, Research Paper, N° 51.
57. Nikiel E.M., et T.P. Opiela, 2002. Customer type and bank efficiency in Poland: implication for emerging market banking, Comptemporary Economic Policy, Vol 20, N° 3, pp 255-271. [CrossRef]
58. Palinski A., 1999. Evaluation of bank debt restructuring in 1992-1998 for selected polish bank’s, Bank and Credit, National Bank of Poland, 12.
59. Peek J., et E. Rosengren, 2000b. Implications of the globalization of the banking sector: the Latin American experience, Federal Reserve Bank of Boston New England Economic Review September/October 2000.
60. Rojas-Suarez L., 1998. Early warning indication of banking crises: what works for emerging markets? With Application to Latin America, Deutsche Bank Securities Working paper.
61. Shaffer S., 1998. The winner curse in banking, Journal of Financial Intermediation, 7, pp 359-92. [CrossRef]
62. Tschoegl A.E., 2003. Financial crises and the presence of foreign banks, Paper presented at the World Bank conference on Systemic financial distress: containment and resolution, 7-8 October 2003.
63. Unite A., et M. Sullivan, 2003. The effect of foreign entry and ownership structure on the Philippine domestic banking market Journal of Banking & Finance 27, pp 2323–2345. [CrossRef]
64. Weill L., 2003. Banking efficiency in transition economies the role of foreign ownership Economic of Transition :September 2003, Vol 11, N° 3, pp 569-592. [CrossRef]
65. Weller C.E, et A.S. Hersh, 2002. Increased competition from large foreign lenders threaten domestic banks, raises financial instability, Economic Policy Institute, Issue Brief N° 178.
66. Weller C.E., 2000a. Financial liberalization, multinational banks and credit supply: the case of Poland”, International review of Applied Economics, Vol 14, N° 2, pp 193-211. [CrossRef]
67. Williams B., 1998. Factors affecting the performance of foreign owned banks in Australia: a cross sectional study, Journal of Banking and Finance, (22), pp197-219. [CrossRef]
68. Williams B., 2003. Domestic and international determinants of bank profits: foreign banks in Australia, Journal of Banking and Finance, V 27, N° 6, pp 1185-1210. [CrossRef]
69. Williamson J., et M. Mahar, 1998. A survey of financial liberalization, Princeton Essays in International Finance, N° 211, November.