Prerpints.org logo
Preprint
Article

Evaluation of the Cooling Effect of an Outdoor Misting Fan for Workers in Hot Environments Wearing Personal Protective Equipment (PPE)

Altmetrics

Downloads

61

Views

36

Comments

0

This version is not peer-reviewed

Submitted:

30 September 2024

Posted:

02 October 2024

You are already at the latest version

Alerts
Abstract
Heat stress on workers wearing PPE(Personal protective equipment) in hot outdoor environments is of rising concern, especially in cases when rest breaks and clothing changes are impractical. Mist fan evaporative cooling could provide low-energy continuous cooling even during work activity. The cooling effect of a misting fan was compared to that of a fan alone, as well as natural convection. A thermal mannequin with heat flux sensors at 8 body locations was exposed to an outdoor misting fan while clothed in typical work clothes and PPE. Work clothes were dry or saturated with water to simulate sweat. The distance from the misting fan ranged from 4m (wetting common) to 7m (wetting unlikely). On average, the misting fan had a cooling effect of 0.31met (18.3W/m2) higher than natural convection when PPE with wet work clothes are worn, and 0.35met (10.63W/m2) higher when dry work clothes with PPE were worn. This equates to reducing thermal metabolic load from light industrial work to walking about in office work, or from standing to reclining. Under international standards for workers in hot environments based on metabolic rate and WBGT(wet bulb globe temperature), such as ISO 7243, this equate to an average of about a 0.35ºC (dry clothes with PPE) to 0.61ºC (wet clothes with PPE) increase in acceptable WBGT.
Keywords: 
Subject: Public Health and Healthcare  -   Public, Environmental and Occupational Health
Authors’ note: Short progress reports on this research project were presented at AIJ 2023, SHASEJ 2023, SHASEJ 2022 national conferences in Japan.

1. Introduction

Climate change is projected to greatly increase the frequency of dangerous levels of heat stress worldwide, even in regions where is currently almost never occurs [1]. Workers have increased risk from heat stress working in hot environments both indoors and outdoors. Heat stress on can lead to heat-related illness including heat cramps, heat exhaustion, and heat stroke, and increase risk of injuries resulting from dizziness [2]. During the years 2019-2023, there were 4,282 hospitalizations for heat stroke in Japan, including 128 deaths. 20% of cases including 18 deaths were in manufacturing settings [3]. Activities requiring Personal Protective Equipment (PPE), such as COVID-19 testing sites or the Fukushima nuclear reactor cleanup, present a challenge to worker wellbeing, especially during hot weather. The PPE material which protects workers from contaminants often inhibits the evaporation of sweat, which can increase thermal stress response even at mild temperatures [4]. Situations requiring PPE may make typical cooling methods ineffective or impractical.
Workers in hot environments may need frequent breaks to reduce heat stress in accord with worker health and safety standards and guidelines such as ISO 7933 [5], but this reduces productivity [6]. The JIS Z8504 standard (based on ISO 7243) uses the wet bulb globe temperature (WBGT) as an index to indicate potential heat stress, where a clothing adjustment value (CAV) can be used to find the effective WBGT. A water-vapor impermeable clothing layer adds a massive 10 – 12 degrees to the effective WBGT [7].
Methods to relieve thermal stress at work sites while workers are still wearing PPE are desirable. For workers to remove and then put on the PPE for every rest break to promote cooling, it may be impractical in terms of time, costs and effort for workers. Further, increased cycles of removing PPE may increase contamination risks [8]. One cooling solution is use of dedicated air conditioned spaces. However, this comes with high cost and is energy intensive, especially when high ventilation is required. Recirculation of air may pose added contamination risk. If an open space is used, the energy consumption for cooling would increase dramatically.
Some solutions which avoid the need to remove PPE were reviewed by Foster et al. [8]. They include the use of phase change material (such as water ice packets) in cooling vests either below or over the PPE, or eating crushed ice or drinking ice slurry as internal body cooling. Both methods have limits to the time of effect; the melting time of the vest, or the capacity of each person to eat ice or drink slurry while also adding the need to remove masks, which may be impractical and risk contamination. Cooling of hands/arms in running water or ice water while wearing PPE and gloves is another possible solution. Tokizawa et al. [9] found that 1 hour of walking activity in a 33°C, 60%RH environment while wearing PPE resulted in an average 0.8°C increase in body core temperature of test subjects. A combination of the vest with hand and foot pre-cooling yielded a 0.2°C increase. These solutions all require some sort of cooler unit and the energy and preparation to pre-cool vests, make ice, etc.
Unlike these methods, it may be possible to continuously use evaporation cooling on workers in the outdoor work areas, even during their work activity. Evaporation cooling takes advantage of the exchange of sensible heat from air for latent heat of water evaporation, reducing the air temperature. In this adiabatic process, the largest possible reduction in air temperature is to the wet bulb temperature, with the air reaching a saturated state [10].
Fine mist sprays greatly increase the rate of evaporation by increasing the surface area of the water. The source water does not need to be pre-cooled, as micron-scale mist droplets almost instantaneously reach the wet bulb temperature upon being sprayed [11]. Even if the only water available onsite is warm, hot water at 60°C can be sprayed without significant reduction in the cooling effect [12].
Fine mist sprays are vulnerable to being carried away by light breezes. However, combination with a fan can direct the cooled air and mist. A fan can project the mist-cooled air as far as its “throw”, which can be several or tens of meters. This could be oriented to continually reduce thermal stress even during work activity, possibly reducing the need for rest breaks.
Generally, human thermal comfort in hot environments is reduced when skin is wet due to sweating. However, skin wetted by mist on hot summer days, even in tropical climates has been evaluated as pleasant [13]. This is likely due to the evaporation of the mist droplets from the skin surface, with some contribution from their relatively low temperature also yielding some sensible heat transfer, while there also may be some perception bias [14].

1.1. Scope and Design of the Experiment

The goal of the experiment is to determine if the evaporative and convective cooling effect of a misting fan can be effective in the outdoor environment even for workers wearing PPE with low vapor permeability. The primary measurement of cooling evaluated here is the heat flux at the skin/surface of a thermal mannequin, with skin surface temperature also included. Skin heat flux of the thermal mannequin with and without PPE and/or standard work clothes are then compared to quantify the change in cooling effect due to wearing PPE. The effect of the misting fan (combining forced convection, air temperature reduction and possible wetting leading to contact evaporation) is compared to the effect of the fan with the misting function turned off (convection cooling only) as well as the natural convection state (no fan or mist)..
The thermal mannequin is a non-sweating type, so the possible effect of sweat is simulated by applying the base layer of work clothing as either dry or wet, in a method similar to the dry thermal mannequin experiments of Havenith et al. [15]. Further, the effect of wind speed and mist density is examined by varying the distance from the misting fan. This includes conditions where wetting is common with higher air velocity (within 4m of this fan), as well as conditions where wetting is rare (7m from this fan). Intermediate ranges (5m and 6m) were also tested. Air temperature, globe temperature and humidity measurements were made to determine environment conditions.
In this case, the typical outdoor conditions are in Japan’s humid subtropical climate, which is classified as Cfa per the Koppen climate [16] classification system. This is similar to many other locations worldwide with major urban centers, such as eastern China, South America including southern Brazil and northeastern Argentina, some Mediterranean climates in Europe, parts of eastern coastal Australia, and much of the southeastern quadrant of the USA.

2. Theory

2.1. Heat Balance of the Body

The complex system of heat transfer within the human body and with the environment is often simplified for evaluation using a two-node model, including in ASHRAE [17] and ISO algorithms. The body core and the skin comprise the 2 nodes, with a single layer of clothing, each with its own average temperature to represent the whole body. The heat generation of the body is expressed in terms of metabolic rate units (met), or as an equivalent heat flux at the skin surface. The metabolic rate while seated and quiet is defined as 1 met corresponding to 58W/m2 of skin surface area. Workers have increased metabolic rates, expressed as larger met values; such as 1.7 met for “walking about” in office work, 2.0-2.4 for light machine work, or 4.0 met for handling 50kg bags [18]. These metabolic rates are used along with the environment WBGT (wet bulb globe temperature) to determine any restrictions on activity to help reduce heat stress, such as in the JIS Standard Z8504 [19] (based on ISO 7243), where an increase in metabolic rate of about 30W/m2 reduces the acceptable WBGT by 1ºC.
The heat flux from the skin surface Qsk for a person wearing clothing with an insulation value of Rcl in an environment with operative temperature To can be found by [20],
Qsk = (Tsk –To)/(Rcl + Ra,cl)
where Tsk is the skin surface temperature and Ra,cl is the thermal resistance of the outermost boundary (skin or clothing), which can be taken as the inverse of the heat transfer coefficient with the environment, thus Ra,cl = 1/h. In the characterization experiments in still for the unclothed mannequin used here, Ra,cl had a whole-body average of 0.115m2K/W, which corresponds to a net heat transfer coefficient of 8.7W/m2K.
The above equation incorporates both convection and radiant heat transfer through use of operative temperature. Separate evaluation of these two components at the bare skin surface is the sum of the convective heat flux Qc and the radiant heat flux Qr
Qc + Qr = hc (Tair – Ts) + hr (Tr – Ts)
where hc and hr are the convective and radiant heat transfer coefficients, Tair is the environment air temperature, Ts is the skin surface temperature and Tr is the mean radiant temperature. The radiant heat transfer coefficient for a standing human is taken as 4.7 W/m2K as per ASHRAE. If net surface heat flux, skin surface temperature, and environment temperatures are measured, they can be substituted into Eq (2) to find the convective heat transfer coefficient during each experiment trial or the total thermal insulation value of clothing plus the surface air layer Itot [21],
Itot = (Rcl + Ra,cl) = (Tsk – Tair) / (Qc + Qr)
Evaporative cooling at the skin surface Esk for a person wearing clothes with an evaporative heat transfer resistance of Re,cl in an environment with water vapor pressure of Pair can be found by
Esk = w(Psk – Pair) / [Re,cl + 1/(fcl he)]
where Psk is the water vapor pressure at the skin (normally assumed as that of the saturated state), w is the skin wettedness, fcl is the clothing area factor (the ratio of clothing area to skin area), and he is the evaporative heat transfer coefficient. However, this formulation assumes one value of wettedness, while misting onto PPE would yield a second wet layer, possibly at different locations than natural sweat. Evaporation due to mist wetting may in part be evaluated by a method explained below.

2.2. Evaporation Cooling Effect on Air

The cooling effect of water evaporation Qev is from the latent heat of evaporation L, plus any sensible heat exchange as the water temperature Tw changes before evaporation by
Qev = mevL + mwCp,w (Tw – Ta,i)
where mev is the evaporated mass, mw is the mass of water interacting with air, and CP,w is the specific heat of liquid water taken as 4.184kJ/kg-K. The latent heat of water evaporating in air at 25ºC is about 2450kJ/kg. When a packet of air of mass mair at initial temperature Ta,i into which water evaporates yielding a cooling of Qev, the average cooled air temperature Tc can be found substituting into
Qev = mairCp,air (Tc – Ta,i)
where CP,air is the specific heat of air, taken as 1.005kJ/kg-K. Generally, the lowest possible evaporation-cooled air temperature in this adiabatic process is the wet bulb temperature. The ratio of change in air temperature to this maximum possible air temperature change (called the “wet bulb depression”) is the evaporation efficiency ηev.
ηev = (Ta,i – Tc) / (Ta,i – Twb)
As water evaporates, it also increases the amount of water vapor in air. The change from the initial vapor pressure Pa,i to that in the cooled air pc is proportional to the evaporation efficiency, where the maximum potential water vapor pressure is to the saturated state psat at the same specific enthalpy in the initial state in the adiabatic process.
(Pa,i – Pc) = ηev (Pa,i – Psat)
In a case with well-defined boundaries, such as an air duct, with complete evaporation of all water, this calculation can be relatively simple. In the case of mist evaporation cooling in open spaces, it is difficult to evaluate the amount of air being cooled, and its ratio to the amount of water evaporated at any given point.

2.3. Mist Droplet Evaporation Time

A rough estimate of the potential for a misting fan to cause wetting can simply be judged by the air velocity field of the fan, and the mist droplet evaporation time. The rate of evaporation of water mist droplets can be expressed as inversely proportional to the wet bulb depression ΔTwb, the difference between the environment moist air wet bulb temperature and the saturated state wet bulb temperature at the same enthalpy level, as evaporation in air is an adiabatic process (this can also be expressed in terms of vapor pressure depression). In terms of wet bulb depression, the time for a single droplet to fully evaporate in moist air can be expressed as [22],
tev = D2/(80ΔTwb)
where D is the droplet diameter expressed in terms of microns, tev is the time to complete evaporation expressed in seconds, ΔTwb is the wet bulb depression expressed in K, and 80 is a constant based on water’s latent heat of evaporation, thermal conductivity of air, unit conversion, etc. For example, a 20μm diameter water droplet in moist air with a 10K wet bulb depression (such as at 35ºC air temperature and 45% relative humidity) will evaporate in about 0.5s, while a 40μm droplet would evaporate in about 2s. However, this simple calculation for a single drop does not account for the decreasing wet bulb depression (increasing vapor pressure) within an evaporating mist cloud. Actual evaporation times will tend to be slower when mist is more dense.

2.4. Maximum Convection and Radiation Heat Transfer without Wetting

The maximum possible convection heat transfer due to mist cooling without surface/skin evaporation wetting effects at the outer surface can be found using Eq.(10), taking Ts as the initial surface/skin temperature with the air temperature reduced to the wet bulb temperature. This would represent a case with air reaching the minimum possible temperature and the surface not having yet cooled.
Qc,max = hc (Ts – Twb)
The radiant heat transfer could reach a maximum with the mist cloud completely blocking any environmental thermal radiation and solely producing a radiant temperature of the wet bulb temperature cloud,
Qr,max = hr (Ts – Twb)
The convection heat transfer coefficient hc needed in Eq.(10) can be taken from the literature, or found for each body location in each experiment trial from the net heat flux Qc + Qr measured during forced convection cooling with only the fan while taking hr as 4.7 and substituting into Eq.(2), such that
hc = [(Qc + Qr) - hr (Ts – Tr)] / (Ts – Ta)
Any heat transfer above the total of these amounts (Qc,max + Qr,max) may be due to wetting yielding evaporation cooling at the outer surface.
The heat flux from the skin surface can rapidly change when mist cooling occurs. In our previous research with misting fans, it was found that human skin, or a heated silicone rubber surface similar to human skin, showed temperature drops more than 2K in under 5 seconds even when exposed to short (about 3s) passes of an oscillating mist fan with a 45s cycle [23]. When mist-cooled air reaches the outer surface, and the skin surface rapidly cools, the temperature differences in the above equations change rapidly, resulting in change in total heat flux over time. In general, the initial arrival of mist cooled air should have the highest heat flux (cooling) as the difference between cooled air temperature and warm skin is likely large. The heat flux should then drop as the skin temperature decreases while the mist-cooled air temperature is roughly constant. This trend should appear in the experiment data.
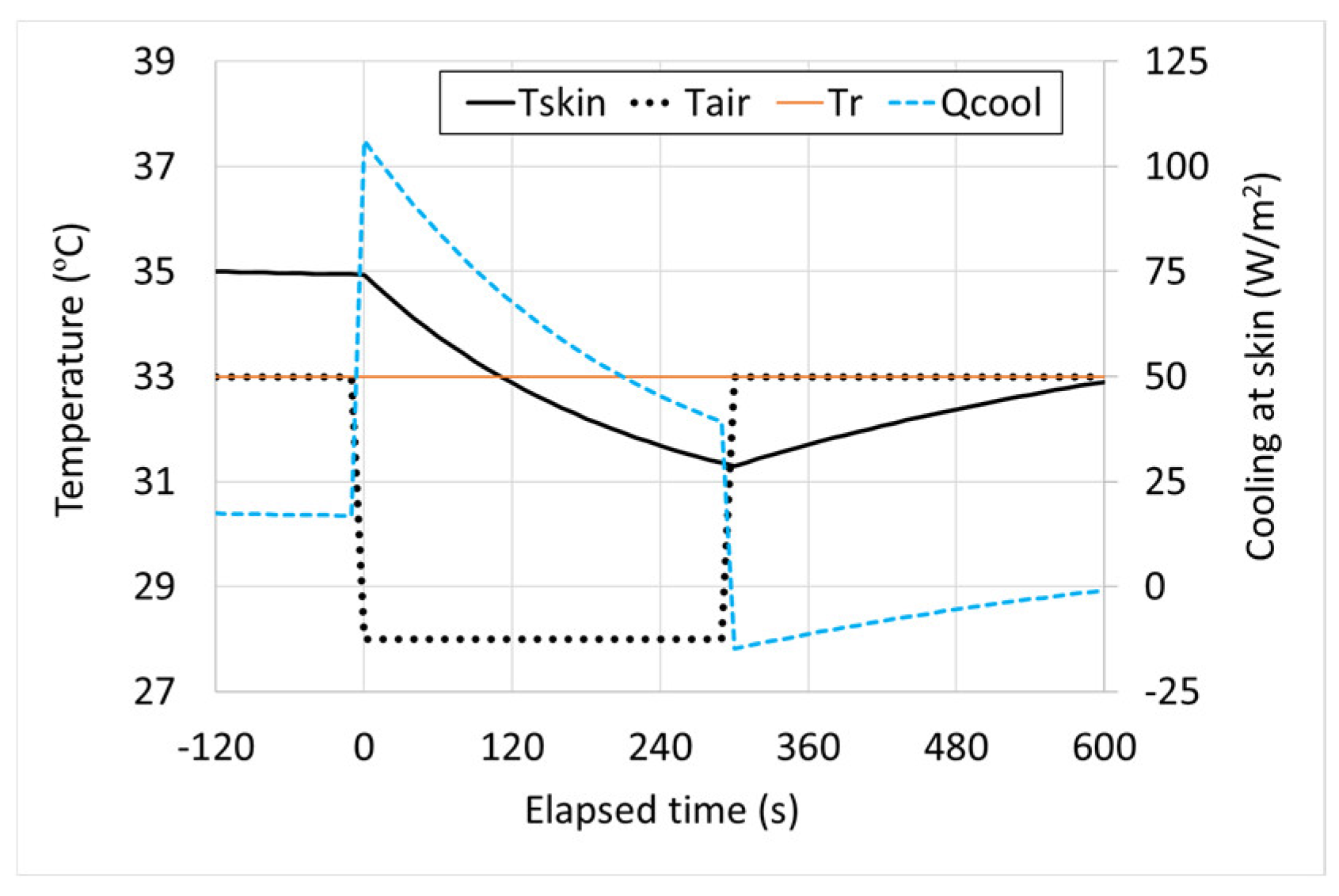
Two theoretical examples of the change in skin temperature and heat flux are created in Figure 1 and Figure 2. In the first case, the air temperature Tair and radiant temperature Tr are initially 33ºC, lower than the skin temperature Tskin is 35ºC. Mist fan cooling causes a 5K drop in air temperature for 5 minutes, then stops. Heat transfer coefficients are taken from the above system of equations. For this simple simulation case, the skin compartment reaction is set as a lumped sum thermal capacitance model with internal heating. The cooling effect, Qcool, starts at a peak and slowly decreases as the skin temperature decreases, thus the temperature difference driving the cooling effect becomes smaller. When misting stops, the skin temperature is lower than the environment temperature, so the heat flux at skin becomes negative (heating) and the skin returns toward the initial temperature.
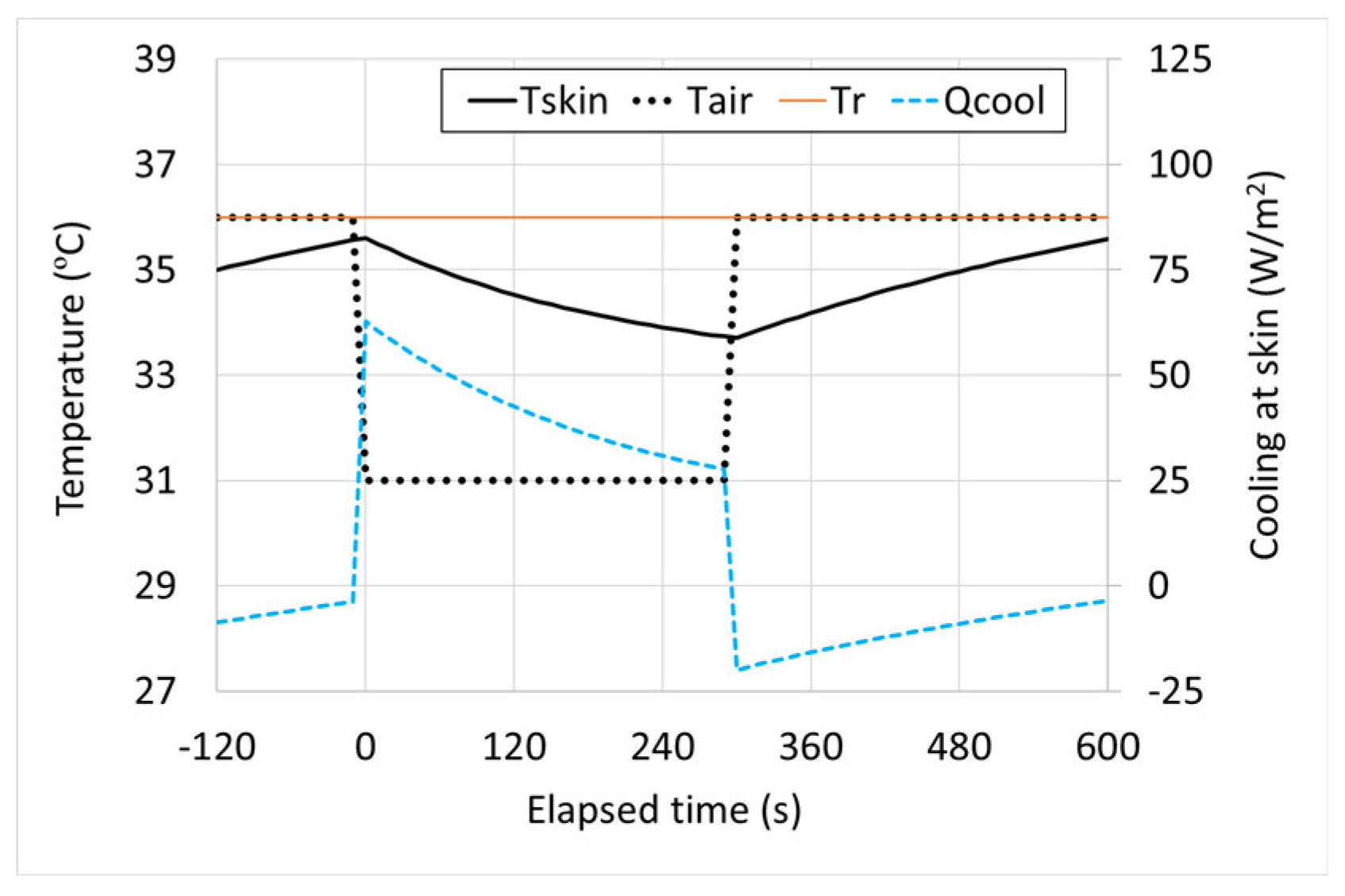
In the second case, the air and radiant temperatures are set at 36ºC, higher than the skin temperature at 35ºC. There is a similar initial peak in mist cooling, but when mist is not active, the skin is being heated by the environment.
As an example case of heat flux values, a hot summer day in Osaka of 35°C and 45%RH has a Twb of about 25°C. According to ASHRAE, the convection heat transfer coefficient hc for a standing person in air moving at speed v is 14.8v0.69 W/m2K, while in still air it is 4.0 W/m2K [24].
If skin temperature is initially 34°C, the globe temperature in shade is the same as air temperature, hc is the value for a human standing in 1m/s moving air 14.8 W/m2K, and hr is 4.7, the maximum non-wet cooling effect from a misting fan (Qc,max + Qr,max) would be about 175W/m2, while in still air it would be about 78W/m2. At the highest air velocity examined in these experiments, where v = 2.6m/s, the maximum non-wet cooling effect of the misting fan would be about 300 W/m2.
High cooling heat flux values above this theoretical maximum, which is determined from the measured heat transfer with fan convection alone in each trial, would likely indicate that wetting of the outer surface has occurred. Wetting the skin surface or clothing would add evaporative cooling to the case where the natural evaporative cooling from sweat is restricted.
The cooling due to evaporation from a wet surface depends on the difference in vapor pressure between the wet surface, taken as the saturated vapor pressure Psat, and the environment vapor pressure Pair and the fraction of the surface that is wet, w.
Qev = whe (Psat – Pair)
The evaporation heat transfer coefficient he is related to the convection heat transfer coefficient by the Lewis relation.
LR = he / hc ≈16.5 K/hPa
If a surface becomes wetted by the misting fan, it will tend to drop toward the wet bulb temperature, both due to the mist droplets already being at the wet bulb temperature Twb, and added forced convection of the fan bringing conditions similar to an aspirated wet bulb thermometer. The net cooling effect can no longer be explained by Eqs (2), (10) and (11). Evaporation cooling E is added, and surface temperature Ts tends to fall toward Twb, while Tair is at some value between the initial environment air temperature and the wet bulb temperature, depending on the density of the mist.
Qc + Qr + E = hc (Tair – Twb) + hr (Tr – Twb) + E
Accurate evaluation of this process requires sensors that can reliably measure air and surface temperature while wet as well as the wettedness ratio of skin and clothing. This is beyond the scope of this experiment.

3. Experiment

The purpose of the experiment was to explore the effect of PPE inhibiting misting fan evaporation cooling. The clothing set was simple; 1 layer of work clothing covered by 1 set of PPE. These were fitted to a constant-temperature-control type mannequin with surface heat flux sensors to determine the cooling effect at the mannequin’s skin. There were 5 clothing combinations; dry work clothes, dry work clothes with PPE, wet work clothes, wet work clothes with PPE, and bare skin (no clothes). The mannequin was exposed to natural convection, forced convection from the fan alone, and the misting fan cooling.
The primary outputs of the experiment were changes in heat flux at the skin for the various clothing and mist fan configurations. The overall heat transfer coefficient from skin to environment can also be derived from the data. Repeated application and removal of clothing to a thermal mannequin each day made it impractical to conduct additional measurements within the clothing layers. Further, wetting of the layers would lead to the issue of unreliable temperature readings when sensors become wet.
If the results show mist evaporation cooling is still effective even when PPE are worn, a detailed examination of the heat transfer through the clothing layers can be performed in the future in a more controlled environment. That is, this experiment is a proof-of-concept. The results indicate the potential of mist cooling for workers in PPE, which may need more detailed investigation.
Use of a misting fan meant for outdoor cooling made an experiment in a controlled indoor environment impractical. A typical climate-controlled chamber is far too small for the outdoor misting fan used here, which has a throw of air velocity 0.5m/s at over 10m distance. Recirculation of misted air back into the fan would occur. Humidity levels would significantly increase even in spaces large enough to handle the fan throw. The misting fan’s 19L/hr spray would increase the indoor absolute humidity level by an average of 3g/kgDA even if ventilated at 5ach, with localized increases likely higher.
Thus, experiments were conducted outdoors, using tents and barriers aligned to form a wind tunnel, blocking direct sunlight and reducing interference from natural wind. Varying environment conditions were expected to cause some variance in the results. We conducted as many experiment trials as possible during a hot, summer season to help find if the results are statistically significant.

3.1. Apparatus

This experiment evaluates the effect of a misting fan on a thermal mannequin wearing work clothes with or without PPE by recording heat flux and temperature values at the thermal mannequin’s skin surface.

3.1.1. Characteristics of the Misting Fan

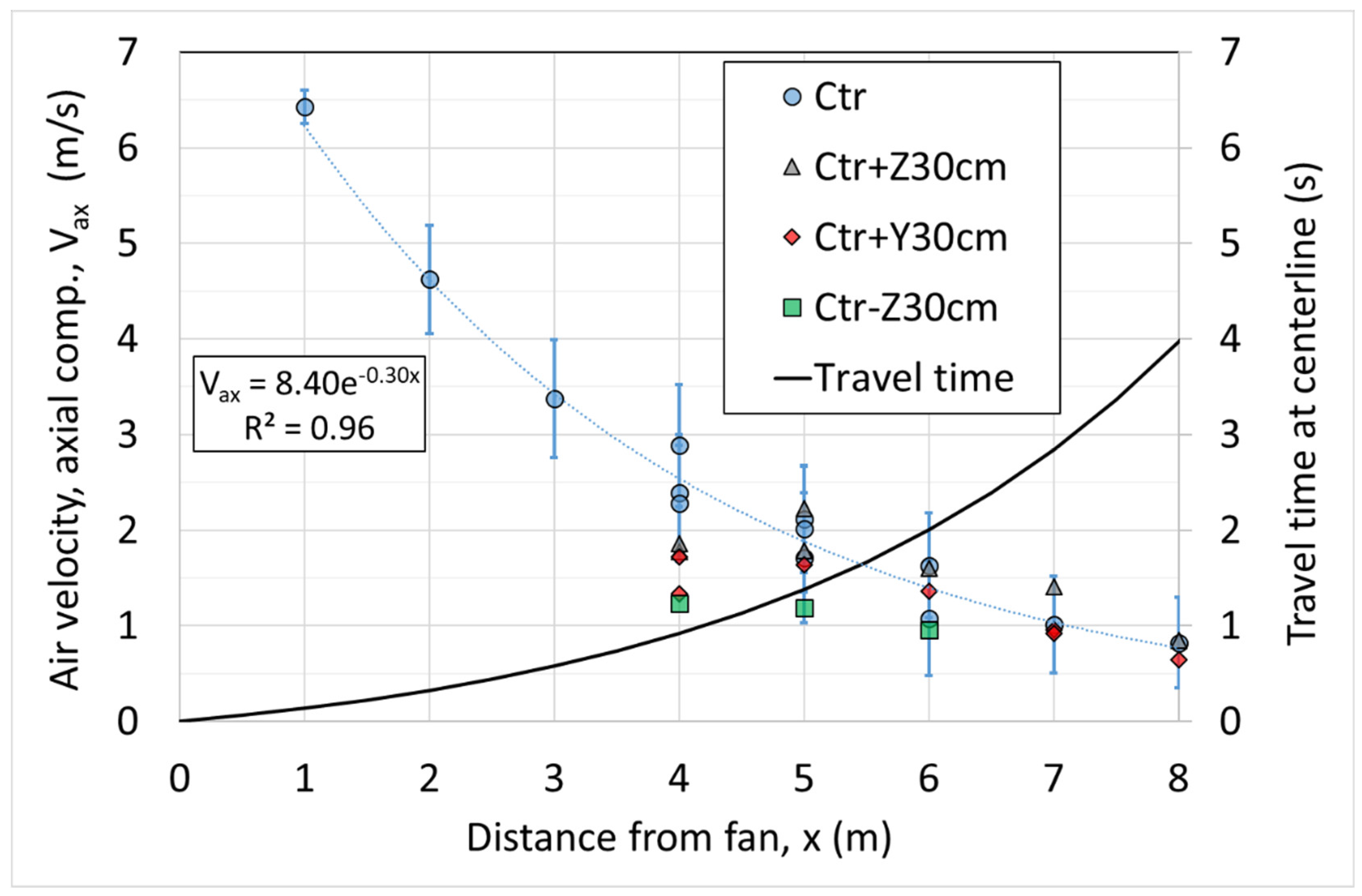
The misting fan used here blows 40m3/min of air with a throw of 0.5m/s velocity over 10m along the centerline. The axial velocity profile as measured by a 3D ultrasonic anemometer at 10Hz is shown in Figure 3, where the points represent 1 minute time-averaged values and the bars represent +/- 1 standard deviation. The figure includes values along the fan axis centerline, and 30cm above and below (Z axis) as well as 30cm to the side (Y-axis). The travel time to distance x from the fan outlet is also shown in the figure integrated from the centerline velocity.
The misting fan has 8 hydraulic mist spray nozzles attached at the fan’s 30cm diameter as a ring header. The nozzles each spray 2.1 liters/hour when supplied with high-pressure water at 6 MPa. The Sauter mean diameter (SMD) of the droplets is 25 microns. The fan and high-pressure water pump consume about 400W of electric power. In the subtropical summer conditions of Japan (wet bulb depression typically about 7 - 10K), the mist tends to fully evaporate at about 5m – 6m distance from the fan. This matches predictions of droplet evaporation times from Eq.(9).

3.1.2. Characteristics of the Work Clothing

The work clothing was a long sleeve work shirt and pants commercially-available in Japan. The material was polyester, meant as summer-use with light brown color. The cloth thickness was 0.3mm with a dry weight of 180g/m2. There is no thermal data available for these specific clothes, but similar work clothing sets measured by Japanese researchers have a thermal insulation value of 0.85 – 0.9 clo [25,26].
The PPE was a Tyvek® Model 400 hooded coat and pants set. According to the maker, the high-density polyethylene (HDPE) fiber cloth has a thickness of 0.14mm and weight of 43.4g/m2. Air permeability is 0.2cm3/cm2-s. Thermal resistance is 16.3x10-3 m2K/W. The clo value of the set is 1.05 [27]. This thermal resistance is determined in accordance with ISO 11092 standard, where the surface/skin temperature is held at 35°C, the air temperature is 20°C and environment air speed is at 1 m/s [28].
According to ASHRAE, the convection heat transfer coefficient for a standing person in moving air is 14.8 W/m2K at air velocity 1m/s, while in still air it is 4.0 W/m2K [29].
Water vapor resistance is 11.3 m2Pa/W. Under the JIS T8115 (based on ISO 16602) standard, it meets Type 5 (airborne dust) and Type 6 (mist spray) classification for protection against chemicals [30]. The mist nozzles used here spray particle diameters much larger than those used in the standard, thus the mist droplets were not expected to penetrate the PPE.

3.2. Construction of a Low-Cost, Simple Thermal Mannequin

In the measurement of thermal resistance of clothing, the ISO 11092 Standard involves use of a heated 3mm metal plate with temperature sensor and controller set for a temperature of 35°C, which must be maintained constant to within 0.1K during testing [31]. This type of typical standard-compliant test unit, as well as thermal mannequins of similar function, may not provide a realistic match to the human skin response and heat transfer in rapid thermal transients (as explained above, see Figure 1 and Figure 2), such as the use of misting fans.
For this pilot study, a low-cost, simple thermal mannequin using skin-temperature control was built, tested, and adjusted until it reasonably matched expected human skin responses.
The thermal mannequin had 8 measurement cells located at the chest, abdomen, back, head, right (facing forward) and left (facing laterally left) upper arm, and right and left thigh (both facing forward) to simulate warm, dry skin. The cells used liquid water as thermal mass similar to the body, covered by natural rubber. Each cell consisted of a polyethylene water tank of 0.5L (head, chest, abdomen, back, upper things) or 0.2L(upper arms). These were filled with still water. A 10mm ID copper pipe coil was placed in the center of each cell to circulate warm water as a heat exchanger. The tanks were then sealed to prevent evaporation of the still water. The outward facing surface was covered with two 3mm thick rubber sheets, then a 5cm X 5cm heat flux/temperature sensor, and outermost a 0.4mm thick silicone rubber sheet with thermal emissivity of about 0.93, similar to human skin. The hardness 65 natural rubber density was measured by weight as 1510kg/m3. The thermal conductivity of natural rubber is 0.15-0.20 W/mK.
Such that there were no air gaps, the layers were held in place by 0.015mm-thick double-sided tape. The outermost silicone sheet was held in place by mechanical tension with clamps, because the tape did not stick to silicone. The cells were secured onto a urethane foam mannequin. Cavities were cut into the foam at each location, fitting the size of the cell tanks, thus acting as insulation on all sides except the exposed outer surface. The 8 heat exchanger units were connected with thermally insulated 16mm ID hoses in series to a 400W water temperature control unit (both heating and cooling) with circulation pump. The circulation flow rate was 3L/min. The water temperature was set to 37°C. At times the circulating water temperature rose to near 38°C on hotter days.

3.2.1. Characteristics of Sensors

The heat flux/temperature sensors (Eto Denki heat flux sensor Model M55A) were 5cm X 5cm non-flexible square wafers made of a matrix of T-type thermocouples which yield both sensor (surface) temperature and heat flux. According to the manufacturer, sensitivity is to 0.4W/m2 in heat flux based on sensitivity to 0.001°C. In calibration tests of these sensors in an enclosed environment with still air, the measurement error for temperature was +/-0.2K and for heat flux was +/-2.1W/m2.
Environment conditions were measured with temperature/relative humidity loggers (Espec RS-14) with accuracy of +/- 0.5°C and +/-5%RH up to 90% relative humidity. Circulating water tank temperatures and globe temperature (inside a standard 15cm matte black copper globe) were measured with T-type thermocouples connected to data logger (Graphtec GL820) with an accuracy of +/- 0.2°C.
If this setup succeeds in replicating qualities of thermal mannequins that have been used by researchers in the history of the field of thermal comfort, then it may be seen as sufficient for this pilot study.

3.3. Procedure

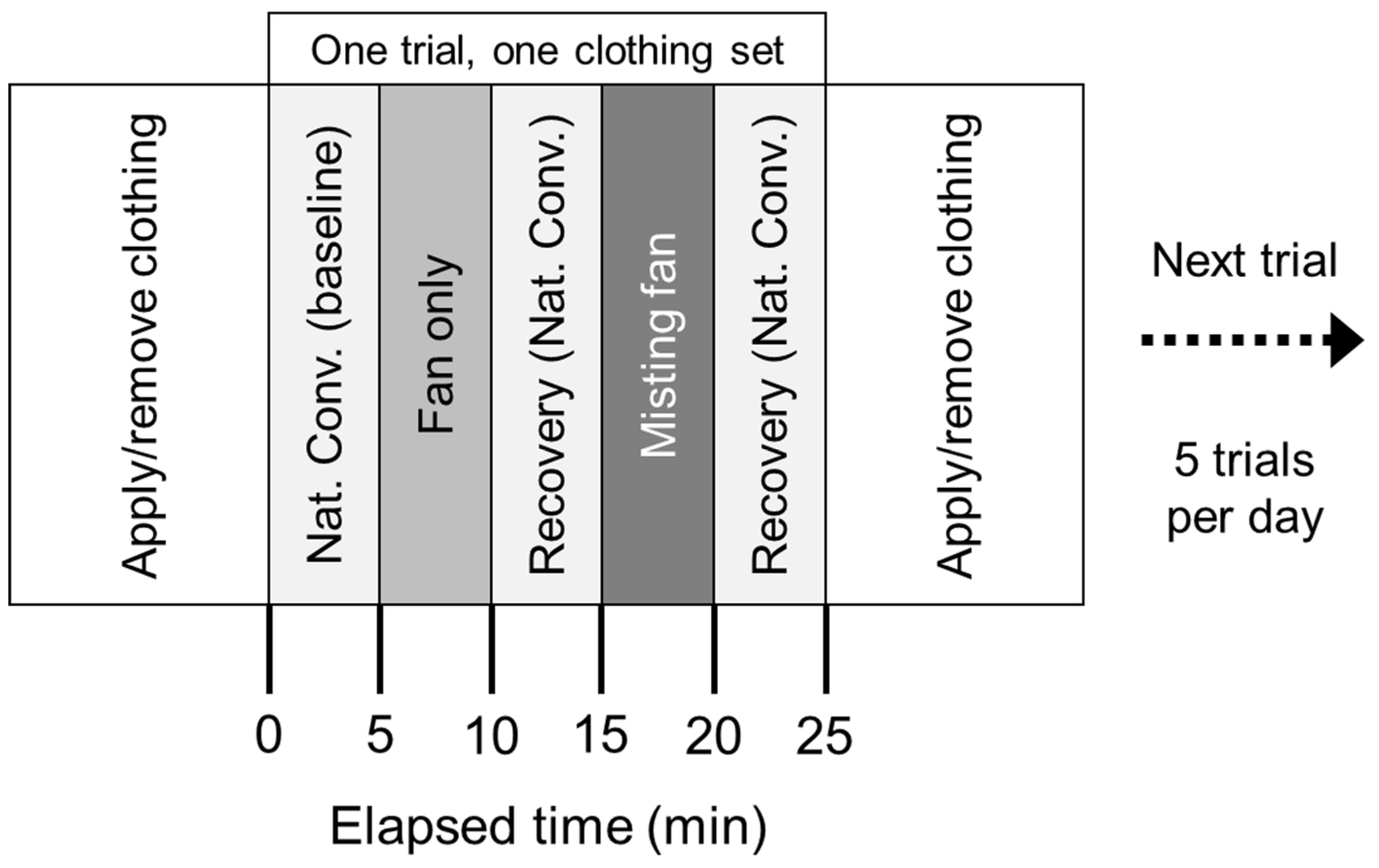
The main experiments consisted of 533 measured cases in multiple outdoor trials on 22 days from July to October, 2022. Most experiment days consisted of 5 trials, one for each clothing combination. Each trial consisted of 5 minutes at the base natural convection heat flux conditions, then 5 minutes of fan forced convection, then 5 minutes of natural convection again as a recovery period, then 5 minutes of mist fan cooling. An additional 5 minute recovery period at natural convection was done after the mist cooling, for a total of 25 minutes per trial as shown in Figure 4. Then clothing was applied or removed, and the next trial performed. The same 3 experimenters performed all trials.

3.3.1. Tabulation of the Cooling Effect

The outdoor environment conditions were not uniform through the experiment trials, both due to taking place on different days and the change in conditions over the day during the approximately 3 hours of a 5 trial experiment set. The difference in heat flux values as different clothing configurations were tested was not solely be due to the differences in applied fan or mist cooling and clothing. The air temperature, humidity, globe temperature and wind conditions changed during the trials. However, each individual clothing set trial took 25 minutes in total. The environment conditions did not greatly change during the short period of each trial. However, in cases where windy conditions made directing the mist onto the mannequin impossible, or still air changed into such a windy condition, or a sudden outbreak of rain, that day’s experiments were cancelled and the interrupted trial data was not included in the 22 days of successful trials.

3.3.2. Environment Conditions during the Experiment Trials

The change in environment conditions over each 25-minute period was relatively small. The difference between maximum and minimum air temperature in all trial periods averaged 0.6K with a standard deviation of 0.6K. The average span for wet bulb temperature was 0.3K with a standard deviation of 0.2K. The globe temperate of all cases averaged 0.3°C lower than the environment air temperature, with a RMSE of 2.1K.

3.4. Characterization Experiments

To be used as an experimental platform to evaluate cooling effects, a thermal mannequin should have skin temperature, skin surface heat flux and thermal response times similar to humans, as can be predicted by thermal comfort and heat stress models.
During construction of the thermal mannequin, characterization experiments of the bare mannequin were conducted indoors in still air on 2 days at air temperatures 20°C and 24.5°C, with globe temperature within 0.5°C of air temperature. Various combinations of 1mm, 3mm and 5mm thick rubber sheets were tested to find the combination that yielded the closest to human skin temperature and skin heat flux (total of convection and radiant) as predicted by the ISO7933 heat stress model [32]. Weighted averages were created using the mean skin approximation of Houdas and Ring [33] adjusted to the 8 points. It was found 2 layers of 3mm-thick rubber yielded the closest results. These results are shown in Table 1.
Further characterization experiments were performed with the 5 clothing combinations. Net heat transfer coefficients h = (hc + hr) for the clothing sets, were measured outdoors in nearly still air (v < 0.15m/s) over 30 minutes at time-averaged conditions of Tair=21.2℃, RH=37%, Tg=21.9℃, Twb=12.9℃, Tsk,avg = 33.8℃. The results are shown in Table 2. Dry work clothing reduced h compared to bare skin, addition of PPE reduced h further. Application of wet work clothes caused higher heat flux, which results as a higher value of h than bare skin, while addition of PPE lowered h. The fit of the clothing yields a tight fit at the chest sensor with little or no air gap, but a loose fit at the abdomen and the back, with air gaps of approximately 1-3cm. Fit is tight at the thighs, slightly loose (about 1cm) at the upper arms. The PPE hood is applied to the head, but does not cover the heat flux cell. The head heat flux could serve as a control case for the various clothing combinations, though the clothing may have some effect on the flow of air around the head, such as warmed air flowing upward from the shirt collar.

3.4.1 Time Constants of the Thermal Mannequin Warm Water Cells

In the ISO 7933 heat stress model, the thermal time constant of human skin in response to a change in the thermal environment is 3 minutes. When Tanabe developed a thermal mannequin, one goal was to have a thermal time constant of under or about 5 minutes [34].
This experiment focused on skin heat flux in short term trials. If the heated water cells had a similar response time, they may be suitable. The thermal time constant for a steady-state environment condition can be found when mist cooling and fan is stopped and the mannequin skin temperatures recover to the initial thermal state. The elapsed time when the fraction 1-1/e (63%) of temperature had recovered is taken as the thermal time constant. The average values for each of the 8 cells are shown in Table 3. The average value is higher than that of the ISO human model and lower than the goal of Tanabe’s thermal mannequin. Thus, it might be judged as sufficiently similar to a human.
Thermal mannequins used in major laboratories often have much shorter thermal response times, designed to maintain constant temperature or constant heat flux with integrated electric heaters behind the simulated skin material for steady-state evaluations. Research shows time constants of approximately 10 seconds after a programmed change in skin temperature settings, or sudden application or removal of an external heat load [35]. This type of mannequin is not suitable here, where skin temperature is expected to change and affect the heat transfer result.
Here, the low-cost thermal mannequin as a whole was taken to fairly well replicate expected dry skin temperature, surface heat flux, heat transfer coefficient, and thermal time constant. Lessons learned in these trials can be used to further improve the mannequin in later experiments.

3.5. Outdoor Experiments

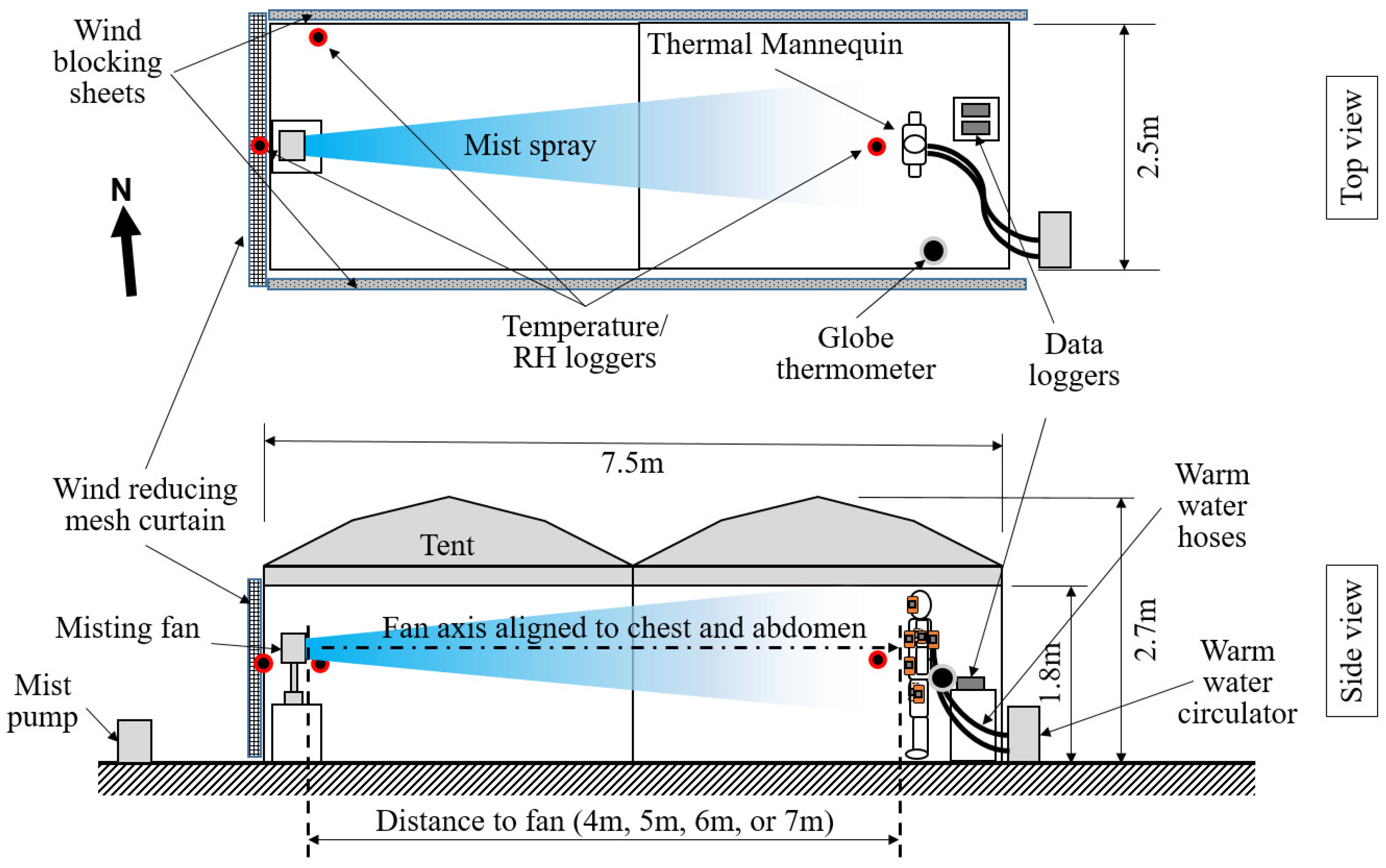
An outdoor experiment space was made to reduce the influence of natural wind and sunlight while still allowing flow of air in a layout similar to a wind tunnel. Two canopy tents were aligned east- west with waterproof sheets attached to the north and south walls. Prevailing winds on site are generally from the west. The misting fan was placed at the west opening. A wind-reducing mesh sheet was attached to the west opening. The east opening was left open, as shown in Figure 5. The thermal mannequin was placed inside the tent area at distances of 4m, 5m, 6m or 7m, with the misting fan axis centerline at the same height and aimed at the chest and abdomen. The entire tent setup was located in a U-shape courtyard with buildings at north, west, and south blocking most natural wind. The tents were placed about 3m distant from the south building, which is 3-storeys tall, thus shading the setup from direct sunlight in nearly all experiments. The east side of the courtyard is open. On some days, when natural wind shifted to the east, the misting fan spray was blown back into the fan, not reliably reaching the mannequin. On these days, experiments were cancelled. However, during some experiments, the effect of natural wind did temporarily increase or reduce the speed of blown air. This was a likely source of variance in the heat flux measurements.

3.5.1. Application of Work Clothes

The goal of each daily experiment was to compare the 5 clothing states within a short time period. The connection to the warm water circulator hoses, the temperature and heat flux sensor wiring to the data loggers, and the mannequin mounting-stand made it impractical to apply clothing quickly. To help quickly change the clothing, the 2 sleeves of the work shirt were cut off, and then applied as a vest and 2 separate sleeves. The sleeves were then attached back onto the vest with safety pins and hook-and-loop tape. The workpants were slit along the sides and hook-and-loop tape sewn in such that they could be quickly removed or applied. The PPE overalls were cut and applied in the same manner.

3.5.2. Wetting of Work Clothes

To simulate a worker wearing clothing saturated with sweat, the work clothes were dampened with tap water. In each day’s trials, the clothes were weighed on an electronic scale of 0.1g precision for the initial dry weight. The clothes were then put in a bucket full of tap water and removed. After removal, the clothes were hand wrung (by the same experimenter in all cases) until they were damp but not dripping any water. The clothes were then weighed again. This yielded a consistent moisture fraction in the clothes. After each trial set, the still-wet clothes were removed and weighed again to yield the remaining moisture fraction. These values are included in Table 4. However, some moisture was likely lost during the process of weighing, by placing and removing the clothing, by evaporation during the elapsed time over the 2 wet trials, or by contact transfer of moisture from the clothing to the mannequin surface.
The sleeves and vest portion had an average moisture fraction of 84-85% with standard deviation of 2%. The pants had an average of 62% with a slightly larger standard deviation. Moisture fraction for the sleeves and vest was likely higher due to the pockets, cuffs, etc. as more layers of cloth to absorb more water. However, the locations of the heat flux sensors were not under the pockets nor cuffs. This method was determined to yield consistent moisture fraction in the work clothes. It is likely that a person literally dripping with sweat could show a higher clothing moisture fraction if the dripping wet clothes were weighed. However, ASHRAE notes that when sweat is literally dripping from clothes [36], it has no additional effect on evaporative cooling.
Initial water weight and remaining moisture at the end of each experiment day are shown in Table 4. The remaining moisture at the end of each trial was about 42-81% of the initial amount of water, with an overall higher standard deviation of about 4-11%. In the trials where PPE were used over wet clothing, more water tended to remain at the end of each trial, indicating the PPE had prevented evaporation, as expected. However, that amount is small (about 5-16% of the initial water weight), indicating that much water loss occurred in the period other than the fan and misting fan periods.

4. Results

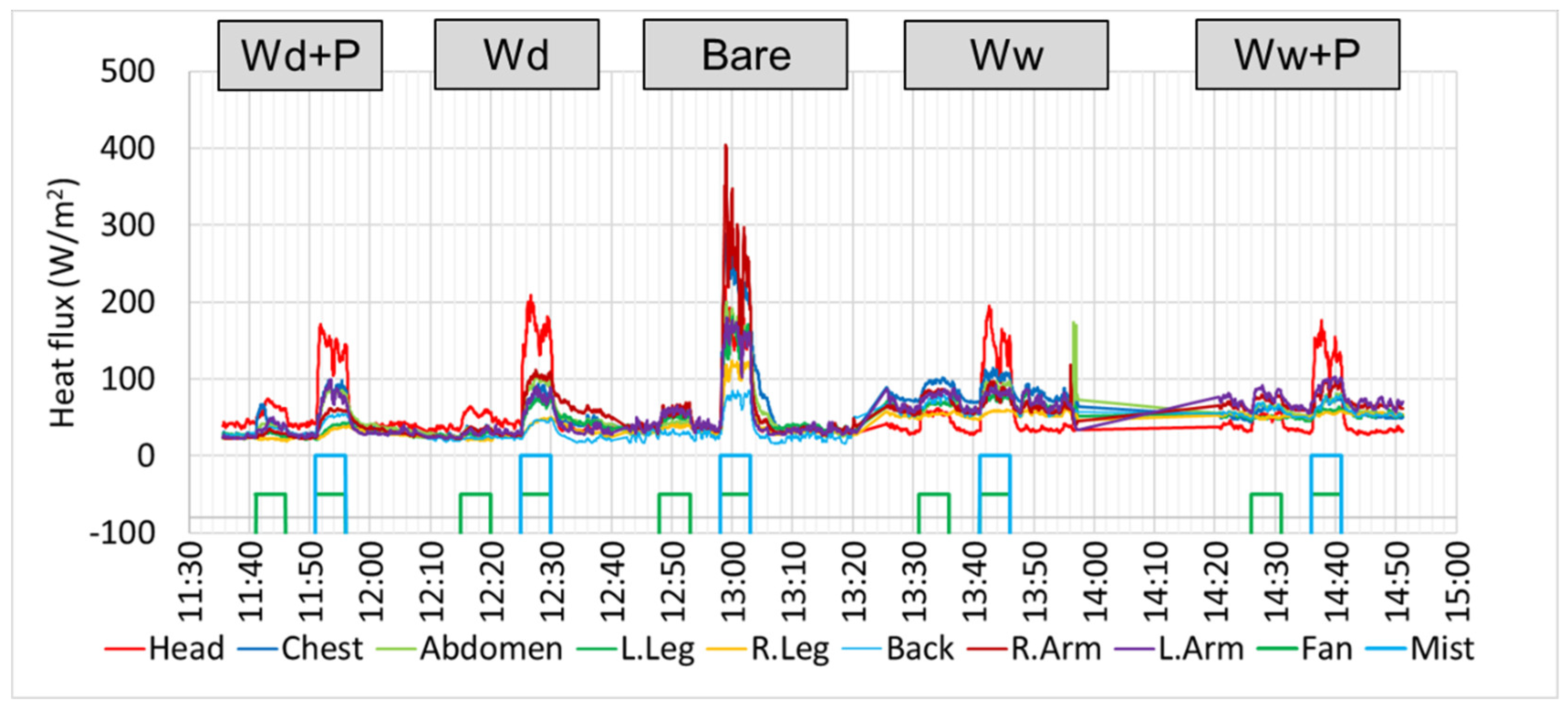
The surface heat flux values at all 8 locations, as well as the surface temperature changes showed a clear dependency on the clothing set. An example of the raw data for heat flux for one experiment day (Sept. 13, 2022 where Tair =32.4℃, RH=48%, Twb= 24.3℃, distance to fan 4m) consisting of 5 trials is shown in Figure 6. In the figure, fan use is shown as a green step line and misting fan use is both a blue step line and green step line at the bottom of each figure. Clothing set type is shown in the grey text boxes at the top of each figure. “Bare” means the mannequin without clothes, “Wd” is Work clothes in a dry state, “Wd+P” is work clothes in a dry state with PPE, “Ww” is work clothes in the wet state, and “Ww+P” is work clothes in the wet state with PPE.
Bare skin always showed the highest heat flux (cooling effect) in some cases nearly 400W/m2, which is 30% higher than the expected maximum cooling from non-wet mist fan cooling. Misting fan use shows higher heat flux values than fan convection alone for each clothing set. PPE clothing tends to show slightly lower heat flux than the same clothing without PPE. The heat flux values tend to have peaks near the beginning of each 5-minute misting period, as expected by theory.

4.1. Net Cooling Effect

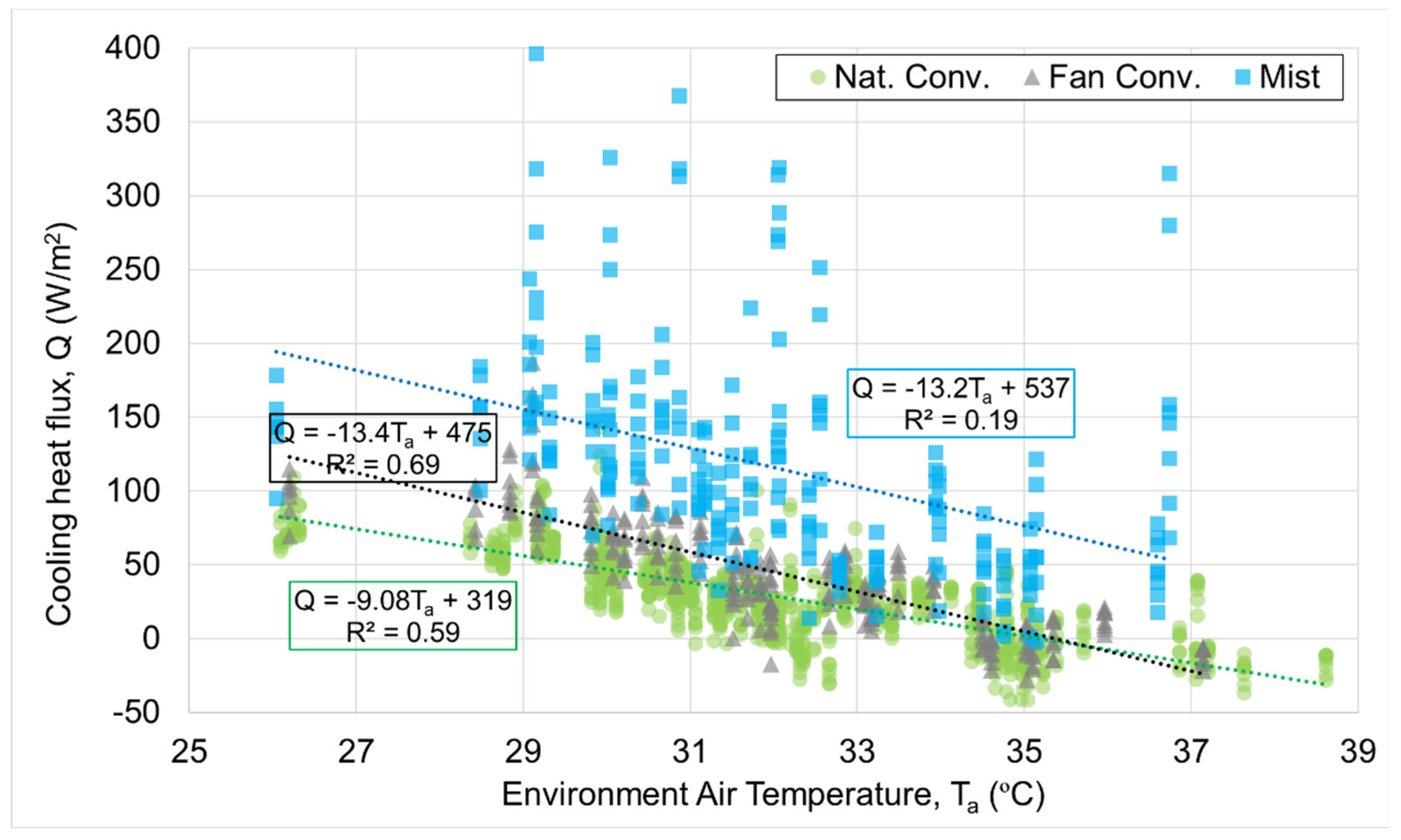
The cooling effect is evaluated by comparison of the 3 states examined in this experiment; natural convection, fan convection, and fan convection with mist cooling. As an illustration of the overall cooling effect without influence of clothing, the heat flux at all 8 locations of all experiments for the bare, dry skin case (no clothing) are plotted in Figure 7. As can be expected, at higher air temperatures, the cooling effect decreases, and can become heating when air temperatures exceed skin temperature. Natural convection cooling sometimes falls to negative values (representing heating of the skin by the environment) at air temperatures over 32°C, frequently so at air temperature over 34°C. Fan convection cooling also tends to the negative over 34°C, indicating heating. Mist cooling values are much higher than fan convection, with a larger variance. The best–fit lines have similar slopes, and the y-axis intersection values show that mist cooling is on average about 60W/m2 stronger than fan convection alone.
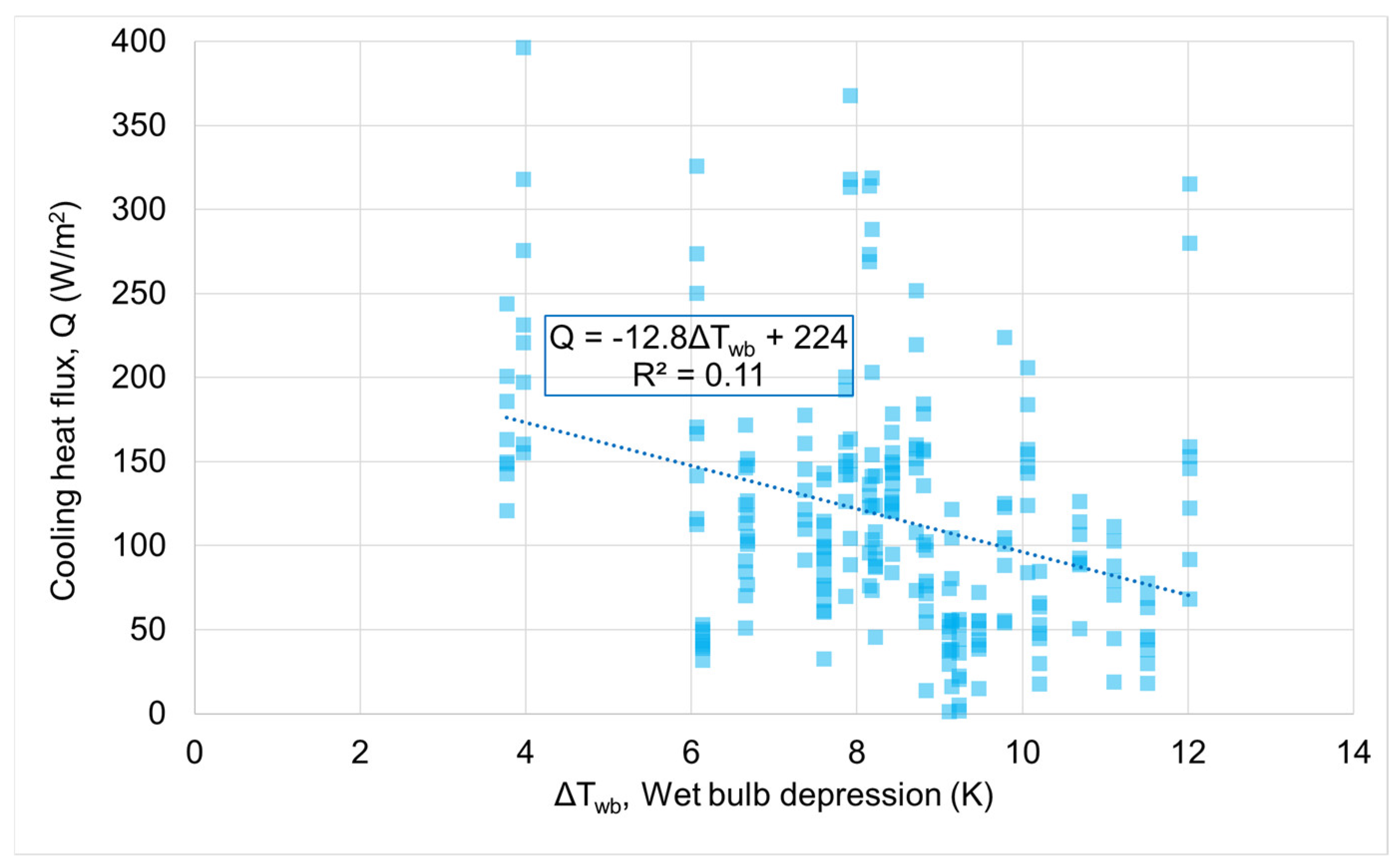
Mist evaporation cooling is not solely dependent on air temperature, but also humidity. One index of evaporation cooling potential is the wet bulb depression. A plot of all misting fan cooling heat flux against the wet bulb depression shows a slight trend to be stronger when the wet bulb depression is lower. When the wet bulb depression is low, the speed of mist droplet evaporation is slowed, so wetting is more likely to occur. This suggests that there is a slight trend that when humidity levels are higher, the mist is more likely to cause wetting, which may lead to some increased cooling effect form contact evaporation.
Preprints 119787 g008
Figure 8. Net cooling heat flux on bare skin surface for all misting fan cases compared to the wet bulb depression.
Figure 8. Net cooling heat flux on bare skin surface for all misting fan cases compared to the wet bulb depression.
Preprints 119787 g008

4.2. Cooling Effect of Fan Alone on Various Clothing Combinations

The cooling effect of the fan is taken as the difference between the time-averaged heat flux while the mannequin is exposed to 5 minutes of fan cooling, and the time-averaged heat flux due to natural convection in the 5 minutes immediately before the activation of the fan. The difference in heat flux is either due to the forced convection of the fan, any small fluctuations in the outdoor environment over the total 10-minute time span, or the change in mannequin surface temperature as it is cooled. Although outdoor conditions likely do not change significantly in just 10 minutes, it is possible that the total fan effect as calculated may be evaluated as negative. This would happen if some natural wind was occurring during the natural convection period to boost the natural convection cooling level for that trial. It could also happen if some natural wind suddenly blew in the opposite direction of the fan, reducing the relative wind velocity onto the mannequin. On several days where natural winds were clearly interfering with the mist fan, the entire day of experiment trials were cancelled.
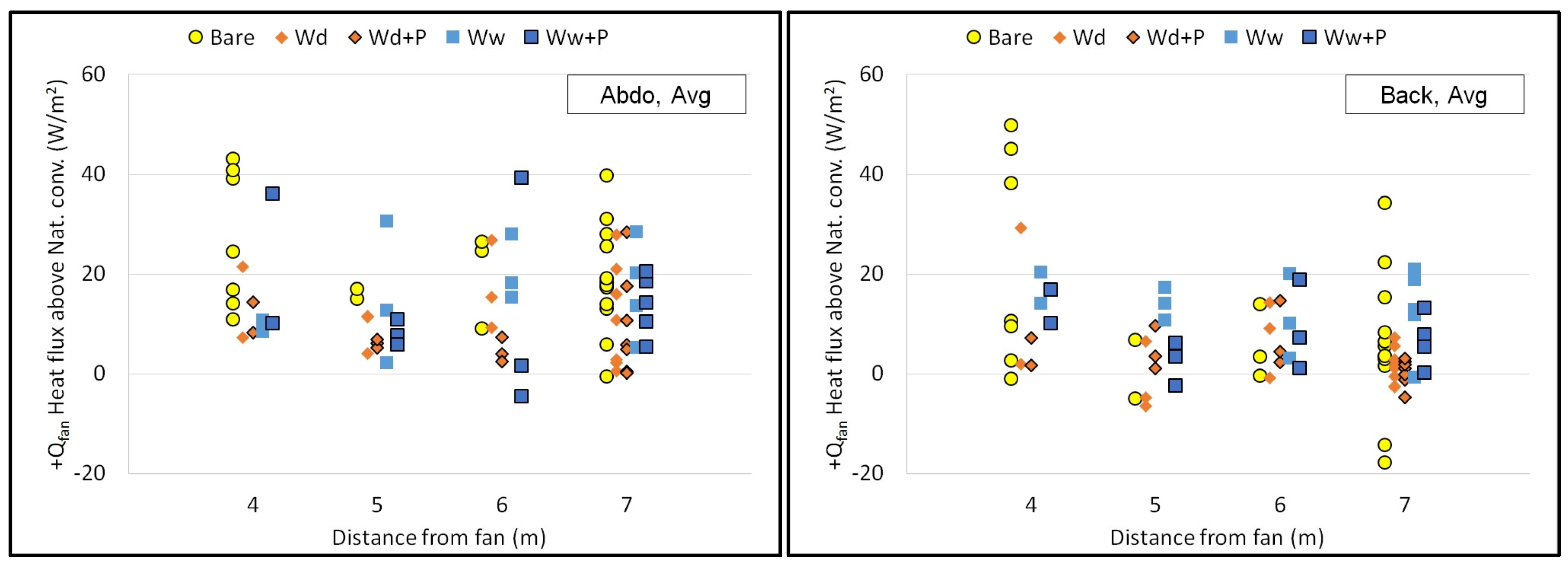
The net heat flux of the fan alone are shown in Figure 9, where the x-axis shows the distance from the fan, and the different colors and shapes of the points show the clothing condition. In these figures;
In most cases, “Bare” has the largest heat flux, as can be expected due to direct exposure of the measured skin surface with no insulation from clothing.

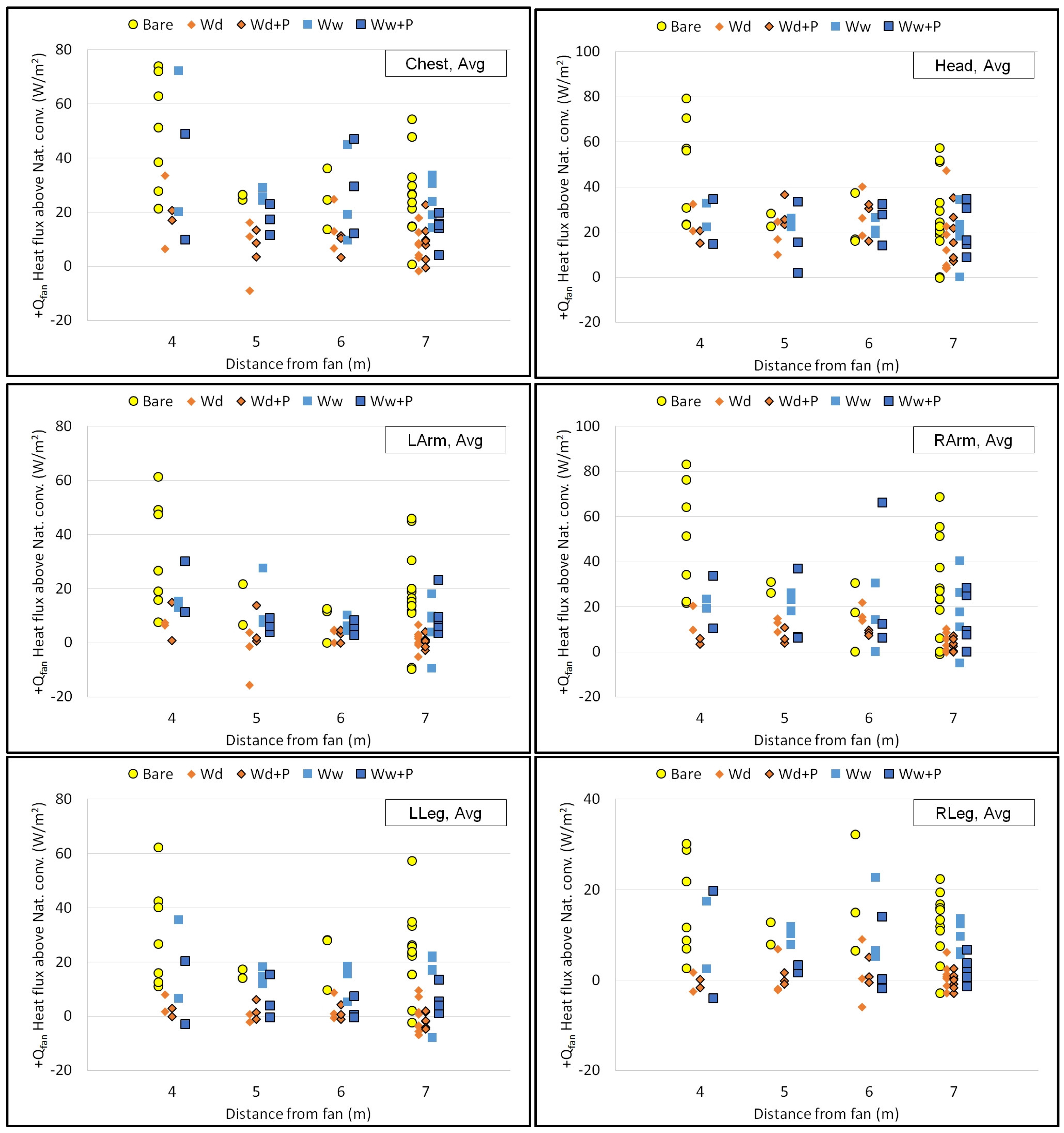
4.3. Cooling Effect of Misting Fan on Various Clothing Combinations

The cooling effect of the misting fan is taken as the difference between the time-averaged heat flux while the mannequin is exposed to 5 minutes of misting fan cooling, and the time-averaged heat flux due to natural convection in the 5 minutes immediately before the activation of the fan (not the 5 minutes immediately before the misting, as the heat flux and temperature values were recovering from the fan alone cooling period). These values are shown in Figure 10.
Values are higher than fan cooling. Bare cases tend to be much higher than clothed cases. Mist cooling effects are strongest at 4m distance (where wetting is likely), but the results for 5m, 6m, and 7m seem about the same in the graphs. Overall, there were far more trials done at 7m distance, numbering 30 sets in total. Many of the first trials were done at 7m to avoid complications from wetting.
As explained in the theory section including in Figure 1 and Figure 2, the cooling effect can have a peak value at the start of cooling, then becoming smaller as the skin surface temperature changes. To check is this might yield significantly different results than the 5-minute time average results above, the difference between the peak value and the 5-minute time averaged value of all cases is shown in Table 5. The fan cooling effect peak ranges 1.3 to -2.6 W/m2 different from the time-average. The value is about the same as the measurement error of the heat flux sensor. For mist fan cooling, the peak values tend to be significantly higher than the time average, up to about 20W/m2.
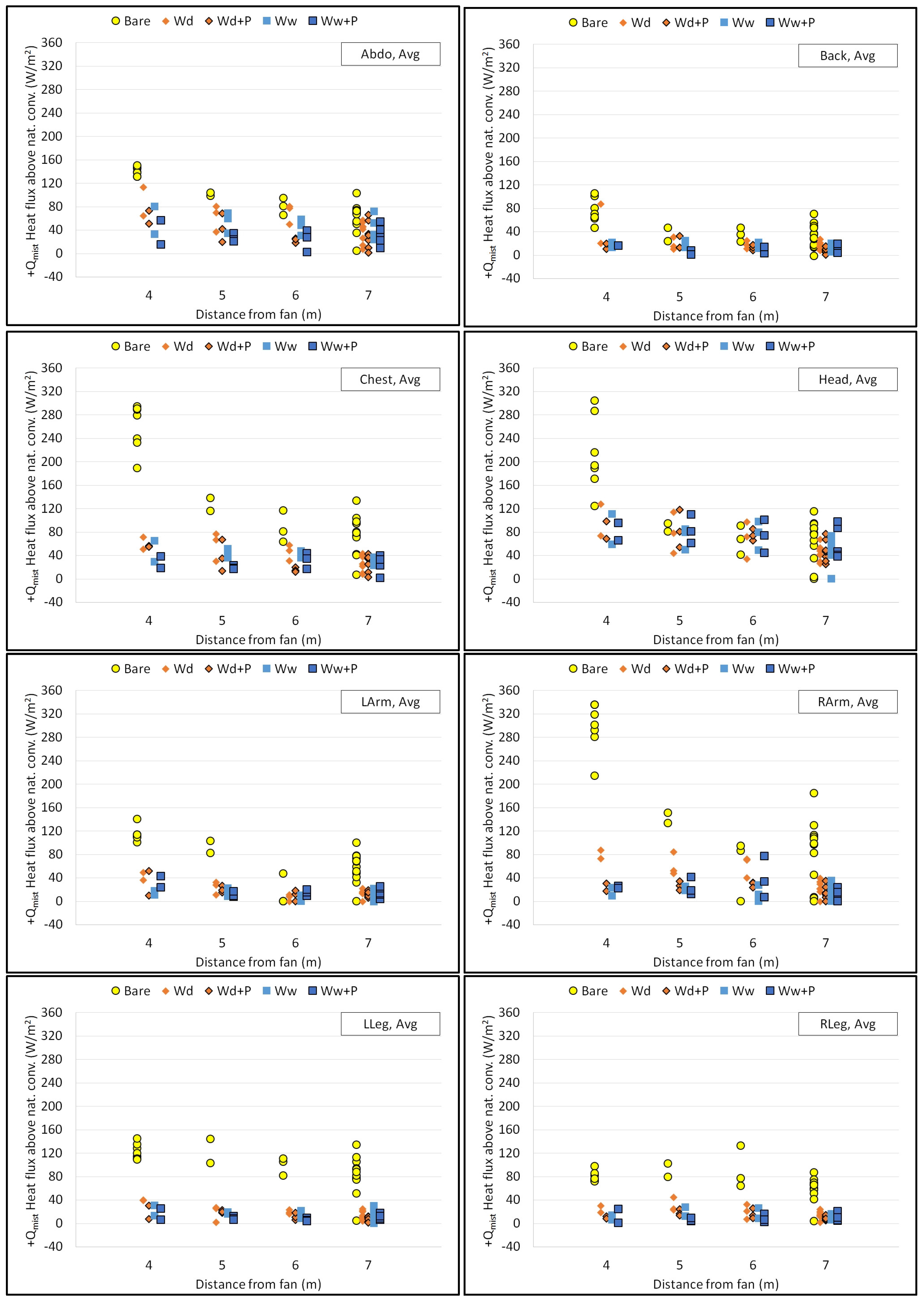
The average fan cooling effect above the natural convection value +Qfan, and the average mist fan cooling effect above the natural convection value +Qmist for each clothing combination at each distance from the fan is shown in Table 6. The same data is shown in terms of met values in Table 7. Mist fan cooling is stronger than fan alone in all cases. The strongest cooling effects are at 4m, where the mist is dense and some wetting is likely. The weakest effect tends to be at 7m, where wetting is unlikely and the mist is more scattered. The difference between +Qfan and +Qmist is smaller for the wet clothing cases, as can be expected. Already wet clothing will experience evaporation cooling even with the fan only cooling, but misting adds the effect of decreased air temperature and possible added wetting. PPE values are lower than non-PPE values for both dry and wet cases.
In terms of met values, the average cooling is the mist fan cooling yielding 0.31-0.35met when PPE are worn. This is the difference between the metabolic rate of light machine work (2.1met) and walking about in an office (1.8met), or standing (1.0 met) compared to reclining or sleeping (0.7 met). ON average, PPE reduced the mist cooling effect by 9.3 W/m2 (31% lower) for dry clothing, and by 1.7 W/m2 (16% lower) for wet clothing.
The difference between fan cooling and misting fan cooling effects at each body location for the bare and dry clothing combinations are fairly clear in Figure 9 and Figure 10 and Table 6 and Table 7. The difference is less clear for the wet clothing combinations. A two-tailed, paired t-test was done to check the null hypothesis that there is no statistical difference between the +Qfan and +Qmist values for each location and clothing combination, including all distances from the fan. The results are shown in Table 8, where P values under 0.05 are taken as invalidating the null hypothesis, thus the average +Qfan and +Qmist values are significantly different. The level of P-value is indicated by the * marks as shown in the legend at the right of the figure. The P-value is above 0.05 for 9 out of the 16 of the wet clothing cases, though still borderline (P<0.1) for 5 of those cases. The head location was clearly different for all cases, as could be expected because clothing was not directly applied to the head. It serves as a control case. The 4 least statistically significant cases includes 3 of the arm cases.

5. Discussion

As this is a pilot study, the goal was to confirm the possibility of a misting fan yielding significant cooling for workers wearing water-impermeable PPE, then suggest where further investigation can help better understand and optimize any effect.
As could be expected, as air temperature rises, the cooling effect of the fan alone decreases, and can become heating when air temperatures exceed skin temperature. Mist cooling values were much higher than fan convection, with a larger variance on average about 60W/m2 stronger than fan convection alone for all cases, including bare skin.
There was a weak correlation between increased mist fan cooling effect and lower wet bulb depression. This may indicate that when evaporation is slowed, wetting of clothing surfaces increases, to yield more cooling effect. However, more detailed evaluation of the amount of wetting of clothing is needed.
The mist fan cooling for the work clothes and PPE combination yielded about 0.35 met of cooling above background natural convection levels on average in hot summer outdoor conditions, which was higher than 0.08 met from fan convection alone. When the work clothing layer was wet, PPE still yielded a stronger effect of 0.31 met than fan convection alone at 0.18met.
A shift of about -0.3 met can significantly reduce total thermal load. The net heat stress of activity equivalent to light machine work in PPE with constant mist fan cooling could be reduced to the same as walking at low speed or “walking about” in office or clinic work without a misting fan. The metabolic heat stress of standing in PPE with mist fan cooling would be reduced to about the same as reclining. International standards calling for rest for workers in hot environments based on metabolic rate and WBGT (JIS Z8504, based on ISO 7243) allow for about a 1ºC increase in acceptable WBGT per 30W/m2 of metabolic rate decrease. This equates to an average of about a 0.35ºC (dry clothes + PPE) to 0.61ºC (wet clothes + PPE) increase in acceptable WBGT when mist fan cooling is used.
The mist fan cooling effect was shown as statistically different from the fan alone cooling for bare and dry clothing combinations, including PPE. When the work clothing layer was wet, in about half the locations and cases (9 of 16), there was not a statistically significant difference between the average mist fan cooling effect and the fan alone cooling. However, 5 of those 9 cases were borderline (0.05<P<0.1). The lowest significance was concentrated at the arms. Measurement of the moisture fraction of the clothes showed the PPE prevented some evaporation. However, the amount of evaporation in all steps of the experiment is not known. An experiment protocol in which clothing weight is weighed at each point in the process is needed.
A more detailed examination of the temperature of each clothing layer will help to better understand the heat transfer process. Here, the work clothing was either completely dry (wettedness of 0), or saturated with moisture. A test of middle-range wettedness values is needed. This should include an examination of the humidity level in the air spaces between clothing layers and skin will help to characterize vapor mass and heat exchange within clothing layers even under mist fan cooling. This would give evidence to support the hypothesis that the mist cooling on the outer layer is the contributor to the increased cooling recorded in these experiments when PPE are present. It would further lead to finding the maximum limit of such cooling given the environment conditions.
Further optimization of the misting fan deployment or use of multiple fans may increase these effects. A much more detailed examination of the effect of contact evaporation and air velocity is needed to help optimize the system. It may be that is very slight wetting with high air velocity is the most effective, or strong wetting with low air velocity, or some middle ground.
A new heat exchange model which can account for two separate wettedness ratios, of the skin and of the outer layer of clothing if wetted by mist, may better simulate the effect of contact evaporation of mist on clothing.

6. Conclusions

Mist fan evaporative cooling could provide low-energy cooling for workers in PPE. The cooling effect of a misting fan was compared to that of a fan alone, as well as natural convection using a thermal mannequin with heat flux probes at 8 locations. On average, the misting fan had a cooling effect of 0.31met (18.3W/m2) higher than natural convection when PPE with wet work clothes are worn, and 0.35met (10.63W/m2) higher when dry work clothes with PPE were worn. This equates to reducing thermal metabolic load from light industrial work to walking about in office work, or from standing to reclining. It would also equate to an average of about a 0.35ºC (dry clothes + PPE) to 0.61ºC (wet clothes + PPE) increase in acceptable WBGT, according to international standards for workers in hot environments based on metabolic rate and WBGT(wet bulb globe temperature). With higher values (up to 1.0ºC average acceptable WBGT increase) if the workers are closer to the fan such that wetting is likely.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org, To be determined after consultation with journal editor.

Author Contributions

Conceptualization, C.F.; methodology, C.F..; software, C.F..; validation, C.F., J.Y. and K.E.; formal analysis, C.F..; investigation, C.F..; data curation, C.F, J.Y..; writing—original draft preparation, C.F..; funding acquisition, C.F.; writing—review and editing, J.Y.; K.E.; resources, C.F., J.Y.; K.E.; supervision, C.F.; project administration, C.F.,J.Y.

Funding

This research was in large part funded by the Japan Society for Promotion of Science “Kakenhi” Grant No. N21K04567.

Data Availability Statement

Full original measurement data sets and data analysis files will be provided upon reasonable request.

Acknowledgments

The outstanding efforts of students Hayato Kiyose and Yuji Sakata for their aid in conducting the experiment trials in harsh summer conditions as well as their aid in collating the massive amount of data is also greatly appreciated.

Conflicts of Interest

The authors declare no conflicts of interest.

Published Materials

This article is the full version of research presented as short summary progress reports entitled “Experiments on the Effect of Clothing and PPE(Personal Protection Equipment) on the Cooling Effect of a Water Mist Fan” at the SAHSEJ 2022 national conference[37], “Measurements of the Effect of Work Clothing and Personal Protective Equipment(PPE) on the Cooling Effect of a Mist Fan”[in Japanese] at the SHASEJ 2023 national conference[38], and “Measurements of the Effect of Work Clothing and Personal Protective Equipment(PPE) on the Cooling Effect of a Mist Fan”[in Japanese] at the Arch. Inst. of Japan AIJ2023 national conference[39].

References

  1. Vargas Zeppetello, L.R., Raftery, A.E. & Battisti, D.S. “Probabilistic projections of increased heat stress driven by climate change.”, Commun. Earth Environ 3, 183 (2022). [CrossRef]
  2. National Institute for Occupational Safety and Health (NIOSH), (2020) “Workplace Safety and Health Topics – Heat Stress” https://www.cdc.gov/niosh/topics/heatstress/default.html [Accessed Aug 22, 2024].
  3. Japan Ministry of Health Labor and Welfare (MLHW) “2023 (confirmed) data on number of casualties due to heat stroke at workplaces” [in Japanese] https://www.mhlw.go.jp/content/11200000/000900487.pdf [Accessed July 15, 2024].
  4. White MK, Vercruyssen M, Hodous TK. (1989) Work tolerance and subjective responses to wearing protective clothing and respirators during physical work. Ergonomics; 32: 1111–23.
  5. International Organization for Standardization (ISO), Ergonomics of the thermal environment - Analytical determination and interpretation of heat stress using calculation of the predicted heat strain. ISO Standard No. 7933:2004. https://www.iso.org/standard/37600.html.
  6. Ioannou LG, Tsoutsoubi L, Samoutis G, Bogataj LK, Kenny GP, Nybo L, Kjellstrom T, Flouris AD. “Time-motion analysis as a novel approach for evaluating the impact of environmental heat exposure on labor loss in agriculture workers.”, Temperature (Austin). 2017 Jul 12;4(3):330-340. [CrossRef]
  7. Japanese Industrial Standards Committee (JISC). (2017) “Ergonomics of the thermal environment – Assessment of heat stress using the WBGT (wet bulb globe temperature) index”, JIS Standard No. Z8504:2017. [Accessed July 12, 2024 at JISC website] JIZ Z8504.
  8. Foster, J., Hodder, S., Goodwin, J., Havenith, G., (2020). “Occupational Heat Stress and Practical Cooling Solutions for Healthcare and Industry Workers During the COVID-19” Annals of Work Exposures and Health, 2020, 1–8. [CrossRef]
  9. Tokizawa, K., Oka, T., (2019) “Bougofuku chakuyou-ji no shonetsuu futan keigen taisaku : teashi precooling to suijunkan vest no heiyou kouka“ (Measures to reduce heat stress when wearing protective clothing- Combined effect of hand and foot precooling and water circulation vest) [in Japanese] Special Research Report of the (Japan) National Institute of Occupational Safety and Health (JNIOSH)-SRR-No.49-2-1.
  10. ASHRAE, (2023). Ch 53. Evaporative Cooling in ASHRAE Handbook 2023 – HVAC Applications. Online version [Accessed Jul 11, 2024].
  11. Holterman H. (2003) “Kinetics and evaporation of water drops in air.” IMAG Report 2003-12/Wageningen UR. Wageningen, The Netherlands.
  12. Farnham C., Nakao M, Nishioka M, Nabeshima M, Mizuno T. (2015) “Effect of water temperature on evaporation of mist sprayed from a nozzle” J. Heat Island Inst. Intl. 10, 35-44.
  13. Yeoh KZ, Yuan C, Wong NH, Cen C., (2019) “Dry Mist Systems and its impact on Thermal Comfort for the Tropics” Sustainable Cities and Society 51(2):101727. [CrossRef]
  14. Farnham C., Yuan J., (2021) “Possible Perception Bias in the Thermal Evaluation of Evaporation Cooling with a Misting Fan” Clean Technologies 3(1), 183-205. [CrossRef]
  15. Havenith G, Bröde P, Hartog E, Kuklane K, et al. (2013) “Evaporative cooling: effective latent heat of evaporation in relation to evaporation distance from the skin.” J. Appl. Physiol. 114, 778-785. [CrossRef]
  16. Kottek M, Grieser J, Beck C, Rudolf B, and Rubel F. (2006) “World Map of Köppen-Geiger Climate Classification updated.” Meteorol. Z., 15, 259-263. [CrossRef]
  17. ASHRAE, (2020) “ANSI/ASHRAE Standard 55, Thermal Environmental Conditions for Human Occupancy”. Atlanta, GA.
  18. ASHRAE, (2021). Ch. 9 Thermal Comfort in ASHRAE Handbook 2021 –Fundamentals, ASHRAE, Atlanta, GA.
  19. JIZ Z8504, Ibid.
  20. ASHRAE, (2021). Ch. 9 Thermal Comfort in ASHRAE Handbook 2021 –Fundamentals, ASHRAE, Atlanta, GA.
  21. Holmer, I., (2006) “protective clothing in hot environments” Industrial Health 44, 404-413.
  22. Farnham, C., Zhang, L., Yuan, J., Emura, K., Alam, M.A., and Mizuno, T., (2017) “Measurement of the evaporative cooling effect: oscillating misting fan” Building Research & Information 45, 783-799. [CrossRef]
  23. Ibid.
  24. ASHRAE, (2021). Ch. 9 Thermal Comfort in ASHRAE Handbook 2021 –Fundamentals, ASHRAE, Atlanta, GA.
  25. Yamada, T. (2011) “Evaluation Methods for Business Energy Savings – Measurement of clothing thermal resistance using thermal mannequins”, [in Japanese]. Tiri News, Vol 065 p.7 https://www.iri-tokyo.jp/uploaded/attachment/1708.pdf [Accessed July 1, 2024].
  26. Matsushitataka Kensetu Corp.: Kyushu Living Environment Research Society. “The importance of managing clothing insulation and metabolic rate!” White paper #142 [in Japanese]. https://www.ecoq21.jp/latest-article/no142/no142.pdf [Accessed June 15, 2024].
  27. DuPont de Nemours, Inc. “SafeSPEC Products Selector”. https://www.safespec.dupont.asia/content/dupont/apac/ap/en/ products/personal- protection/safespec/tyvek-400-model-ty198s-wh.html. [Accessed: June 11, 2024].
  28. British Standards Institution (BSI), (2014) “Textiles. Physiological effects. Measurement of thermal and water-vapour resistance under steady-state conditions (sweating guarded-hotplate test)”, BS EN ISO 11092:2014.
  29. ASHRAE, (2021). Ch. 9 Thermal Comfort in ASHRAE Handbook 2021 –Fundamentals, ASHRAE, Atlanta, GA.
  30. Japanese Industrial Standards Committee (JISC). (2015) “Protective clothing for protection against chemicals.”, JIS Standard No. T8815:2015. [Accessed July 10, 2024 at JISC website].
  31. British Standards Institution, (2014) BS EN ISO 11092:2014 Textiles — Physiological effects— Measurement of thermal and water-vapour resistance under steady-state conditions (sweating guarded-hotplate test) (ISO 11092:2014).
  32. International Organization for Standardization (ISO), (2004) “ISO7993 Ergonomics of the thermal environment – Analytical determination and interpretation of heat stress using calculation of the predicted heat strain”.
  33. Houdas, Y., Ring, E.F.J., 1982. Human Body Temperature - its Measurement and Regulation. [CrossRef]
  34. Tanabe S., Arena E.A., Bauman F.S., Zhang H., Madsen T.L. (1994) “Evaluating thermal environments by using a thermal manikin with controlled skin surface temperature”.
  35. Farrington, R., Rugh, J., Bharathan D., Burke, R. (2004) Use of a Thermal Manikin to Evaluate Human Thermoregulatory Responses in Transient, Non-Uniform, Thermal Environments, NREL white paper #2004-01-2345. https://www.nrel.gov/transportation/assets/pdfs/2004_01_2345.pdf [Accessed July 10, 2024].
  36. ASHRAE, (2021). Ch. 9 Thermal Comfort in ASHRAE Handbook 2021 –Fundamentals, ASHRAE, Atlanta, GA.
  37. Farnham, C. “Experiments on the Effect of Clothing and PPE(Personal Protection Equipment) on the Cooling Effect of a Water Mist Fan”, Proc. of SHASEJ 2022 national conference, Sept 2022, Kobe, Japan.
  38. Farnham, C. “Mist fan no reikyaku koua ni tai suru sagyoufuku to bougofuku ni eikyou ni kan suru jikken (Measurements of the Effect of Work Clothing and Personal Protective Equipment(PPE) on the Cooling Effect of a Mist Fan)” [in Japanese] Proc. of SHASEJ 2023 national conference, Sept 2023, Fukui, Japan.
  39. Farnham, C. “Mist fan no reikyaku kouka ni tai suru sagyoufuku no eikyou ni kan suru jikken (Measurements of the Effect of Work Clothing and Personal Protective Equipment(PPE) on the Cooling Effect of a Mist Fan)” [in Japanese] `Proc. of Arch. Inst. of Japan national nonference, Sept 2023, Kinki, Japan.
Preprints 119787 g001
Figure 1. Theoretical example of skin temperature change during mist fan cooling when environment temperature is lower than skin temperature.
Figure 1. Theoretical example of skin temperature change during mist fan cooling when environment temperature is lower than skin temperature.
Preprints 119787 g001
Preprints 119787 g002
Figure 2. Theoretical example of skin temperature change during mist fan cooling when environment temperature is lower than skin temperature.
Figure 2. Theoretical example of skin temperature change during mist fan cooling when environment temperature is lower than skin temperature.
Preprints 119787 g002
Preprints 119787 g003
Figure 3. Profile of misting fan air velocity (axial component) at centerline, 30cm above and below (+Z30cm, -Z30cm) and 30cm to the side (Y+30cm) with approx. integrated travel time to distance x at the centerline.
Figure 3. Profile of misting fan air velocity (axial component) at centerline, 30cm above and below (+Z30cm, -Z30cm) and 30cm to the side (Y+30cm) with approx. integrated travel time to distance x at the centerline.
Preprints 119787 g003
Preprints 119787 g004
Figure 4. Diagram of the experiment trial procedure timing.
Figure 4. Diagram of the experiment trial procedure timing.
Preprints 119787 g004
Preprints 119787 g005
Figure 5. Outdoor experiment setup of misting fan with thermal mannequin.
Figure 5. Outdoor experiment setup of misting fan with thermal mannequin.
Preprints 119787 g005
Preprints 119787 g006
Figure 6. Raw data of heat flux values for the 8 mannequin locations over 1 day of trials.
Figure 6. Raw data of heat flux values for the 8 mannequin locations over 1 day of trials.
Preprints 119787 g006
Preprints 119787 g007
Figure 7. Net cooling heat flux on bare skin surface for all cases compared to air temperature.
Figure 7. Net cooling heat flux on bare skin surface for all cases compared to air temperature.
Preprints 119787 g007
Preprints 119787 g009aPreprints 119787 g009b
Figure 9. Average heat flux of fan over natural convection on same day and conditions for 8 mannequin locations. Sensor location at upper right in each graph. (Note: Bare = No clothing, Wd = Work clothing dry, Ww = Work clothing wet, P = Protective clothing).
Figure 9. Average heat flux of fan over natural convection on same day and conditions for 8 mannequin locations. Sensor location at upper right in each graph. (Note: Bare = No clothing, Wd = Work clothing dry, Ww = Work clothing wet, P = Protective clothing).
Preprints 119787 g009aPreprints 119787 g009b
Preprints 119787 g010
Figure 10. Average heat flux of misting fan above natural convection on same day and conditions for 8 mannequin locations.
Figure 10. Average heat flux of misting fan above natural convection on same day and conditions for 8 mannequin locations.
Preprints 119787 g010
Table 1. Heat flux and heat transfer coefficients for the unclothed thermal mannequin, measured indoors in still air at 20.0℃ and 24.5℃.
Table 1. Heat flux and heat transfer coefficients for the unclothed thermal mannequin, measured indoors in still air at 20.0℃ and 24.5℃.
Location Tair = 20℃ Tair = 24.5℃
Heat flux (W/m2) Tskyufen(℃) hyufen(m2K/W) Heat flux (W/m2) Tskyufen(℃) hyufen(m2K/W)
Head 98 32.0 8.0 73 33.4 8.3
Chest 95 31.8 7.9 70 33.2 8.1
Abdomen 119 34.0 8.4 91 34.5 9.1
Back 112 32.2 9.1 83 33.7 9.1
R Leg 100 31.8 8.3 77 33.1 9.1
R Arm 117 31.5 10.0 92 32.7 11.37
L Leg 100 32.4 8.0 74 33.7 8.1
L Arm 109 31.9 9.0 82 33.2 9.6
Wt. Avg. 106 32.8 8.6 80 33.4 9.0
ISO 7993 112 32.5 9.1 73 33.2 8.8
Table 2. Net heat transfer coefficients of clothing sets in characterization experiments.
Table 2. Net heat transfer coefficients of clothing sets in characterization experiments.
Location Bare Dry WC Dry WC + PPE Wet WC Wet WC + PPE
Head 9.0 12.4 9.1 11.7 10.2
Chest 8.5 8.4 8.0 7.6 7.4
Abdomen 8.0 4.9 4.2 8.1 6.8
Back 11.0 7.8 6.2 12.0 12.2
R Leg 9.1 6.1 5.6 13.4 11.7
R Arm 11.2 5.3 4.7 9.4 7.8
L Leg 9.1 8.1 6.8 8.1 7.7
L Arm 11.8 8.2 6.1 10.5 13.3
Wt. Avg 9.7 7.5 6.2 10.4 9.9
Table 3. Average thermal time constants of the warm water cells.
Table 3. Average thermal time constants of the warm water cells.
Location Avg. thermal time constant Std. Dev
Head 3m08s 1m17s
Chest 3m52s 1m29s
Abdomen 3m34s 1m59s
Back 4m06s 1m43s
R Leg 4m36s 2m06s
R Arm 4m37s 2m06s
L Leg 2m47s 1m02s
L Arm 3m12s 2m03s
Avg of all 3m44s
Table 4. Amount of water measured in wetted work clothing. Average and SD of all trials.
Table 4. Amount of water measured in wetted work clothing. Average and SD of all trials.
Value Sleeves Vest Pants
Dry weight Avg 153.2g 334.6g 465.1g
SD 0.7g 1.0g 0.3g
Surface area 0.4m2 0.7m2 1.3m2
Wetted weight Avg 282.7g 620.3g 752.2g
SD 3.7g 7.7g 17.9g
Initial water weight (% of clothing wt) Avg 129.5g (85%) 285.7g (85%) 287.1g (62%)
SD 3g (2%) 7g (2%) 17g (4%)
Remaining moisture (% of initial) without PPE Avg 54g (42%) 167g (58%) 185g (64%)
SD 12g (9%) 20g (7%) 32g (11%)
Remaining moisture (% of initial) with PPE Avg 69g (53%) 182g (64%) 232g (81%)
SD 6g (5%) 10g (4%) 14g (5%)
Evap. prevented by PPE (% of initial water weight) Avg 15g (12%) 15g (5%) 47g (16%)
Table 5. Difference between instantaneous maxima and time-averaged values during all 5-minute periods of fan cooling and mist cooling. Average of all cases (all clothing and distances) at each location. [Units: W/m2].
Table 5. Difference between instantaneous maxima and time-averaged values during all 5-minute periods of fan cooling and mist cooling. Average of all cases (all clothing and distances) at each location. [Units: W/m2].
Stat Abdo Back Chest Head LArm RArm LLeg RLeg
+Qfan 1.3 -1.0 1.2 -0.6 -2.6 -0.6 -0.3 -0.2
+Qmist 12.6 3.0 14.4 20.6 5.3 17.1 6.8 6.6
Table 6. Whole body weighted average of fan cooling and misting fan cooling effects.
Table 6. Whole body weighted average of fan cooling and misting fan cooling effects.
+Qfan (W/m2) +Qmist (W/m2)
Dist Bare Wd Wd+P Ww Ww+P Bare Wd Wd+P Ww Ww+P
4m 30.8 10.6 6.1 19.3 16.0 141.9 53.9 30.0 27.0 25.2
5m 14.7 1.7 5.8 16.2 7.7 96.4 37.0 28.7 26.9 17.1
6m 16.6 8.9 5.9 14.3 11.4 69.8 32.2 20.2 23.2 19.6
7m 18.7 3.8 3.1 14.2 8.9 63.2 20.9 15.9 20.4 18.7
ALL 20.5 5.8 4.6 14.5 10.6 84.2 29.6 20.3 21.8 18.3
Table 7. Whole body weighted average of fan cooling and misting fan cooling effects in terms of met units.
Table 7. Whole body weighted average of fan cooling and misting fan cooling effects in terms of met units.
+Qfan (met) +Qmist (met)
Dist Bare Wd Wd+P Ww Ww+P Bare Wd Wd+P Ww Ww+P
4m 0.53 0.18 0.10 0.33 0.28 2.45 0.93 0.52 0.47 0.44
5m 0.25 0.03 0.10 0.28 0.13 1.66 0.64 0.50 0.46 0.29
6m 0.29 0.15 0.10 0.25 0.20 1.20 0.55 0.35 0.40 0.34
7m 0.32 0.06 0.05 0.24 0.15 1.09 0.36 0.27 0.35 0.32
ALL 0.35 0.10 0.08 0.25 0.18 1.45 0.51 0.35 0.38 0.31
Table 8. Statistical significance of difference between fan only cooling and misting fan cooling effects. Two-tailed, paired t-test of each clothing combination and location.
Table 8. Statistical significance of difference between fan only cooling and misting fan cooling effects. Two-tailed, paired t-test of each clothing combination and location.
Bare Wd Wd+P Ww Ww+P
Back **** ** *** 0.09 *
Head **** **** **** **** ****
Chest **** **** *** 0.08 0.08 Symbol Meaning
LArm **** **** *** 0.37 * Numerical P >0.05
Abdo **** **** *** **** * * P ≤0.05
LLeg **** **** **** 0.19 0.06 ** P ≤0.01
RLeg **** **** **** 0.09 * *** P ≤0.001
RArm **** **** **** 0.35 0.24 **** P ≤0.0001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated