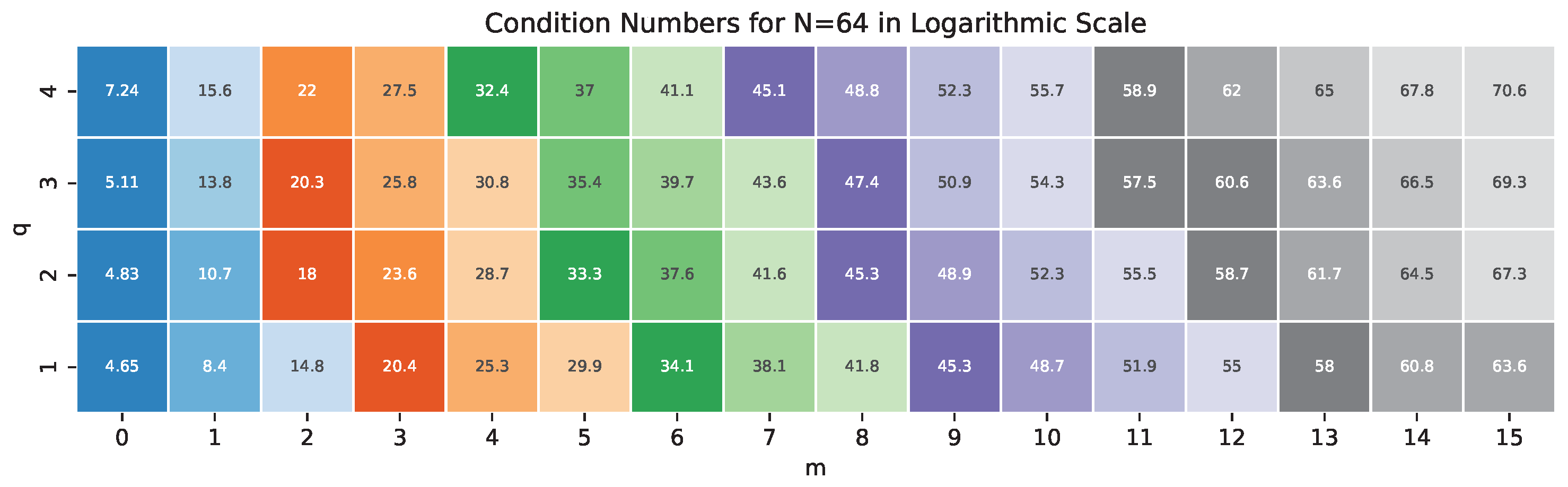Prerpints.org logo
Preprint
Article

On a Convergence of Quasi-Periodic Interpolations Exact for the Polyharmonic-Neumann Eigenfunctions

Altmetrics

Downloads

42

Views

24

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

30 September 2024

Posted:

30 September 2024

You are already at the latest version

Alerts
Abstract
Fourier expansions by the polyharmonic-Neumann eigenfunctions showed improved convergence compared to the Fourier expansions by the classical trigonometric system due to the rapid decay of the corresponding Fourier coefficients. Based on this evidence, we investigate interpolations on a finite interval that are exact for the polyharmonic-Neumann eigenfunctions and show the same benefits. Further, we improve the convergence of the interpolations by applying the idea of quasi-periodicity, where the basis functions are periodic on a slightly extended interval. We show that those interpolations have much better convergence rates away from the endpoints of the approximation interval. Moreover, the interpolations are more accurate on the entire interval. We prove those properties for a specific case of the polyharmonic-Neumann eigenfunctions known as the modified Fourier system. For other basis functions, we provide evidence based on the results of numerical experiments.
Keywords: 
Subject: Computer Science and Mathematics  -   Mathematics

1. Introduction

It is well known that trigonometric expansions and interpolations by the classical system
H c l a s s = { cos π n x : n ∈ Z + } ∪ { sin π n x : n ∈ N } , x ∈ [ − 1 , 1 ] ,
suffer from degraded convergence while approximating non-periodic functions on a finite interval [ − 1 , 1 ] even with sufficient smoothness. There is ample literature devoted to the methods that improve convergence or overcome the Gibbs phenomenon. It is impossible to summarize such a great amount of work. Individual articles include [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61]. We will follow only the ideas related to the current paper: quasi-periodic (QP) interpolations and the expansions by the polyharmonic-Neumann eigenfunctions. The main purpose of this paper is to combine those ideas and explore QP interpolations that are exact on the polyharmonic-Neumann eigenfunctions.
The main idea of the QP approach is to extend basis functions from 2-periodic to ( 2 + ε ) -periodic, where ε tends to zero as the number of terms in the expansions tends to infinity. It generally does not eliminate the Gibbs phenomenon at the points x = ± 1 but mitigates its impacts. Meanwhile, it accelerates the convergence rate away from the endpoints. The idea of such expansions was introduced in [62]. Papers [63,64,65,66,67] investigate the pointwise convergence of the QP interpolation and its convergence in the L 2 -norm. It can be combined with the polynomial correction method with improved convergence ([67]) for complete elimination of the Gibbs phenomenon and additional convergence acceleration.
Another efficient idea is the utilization of the polyharmonic-Neumann eigenfunctions. The eigenfunctions of the following even-order operator
L 0 = ( − 1 ) q d 2 q d x 2 q , q ≥ 1 ,
have been investigated by numerous authors (see [61,68] with references therein) with some Neumann boundary conditions that provide the possible fastest decay of the corresponding expansion coefficients:
L 0 ϕ ( x ) = α 2 q ϕ ( x ) , x ∈ [ − 1 , 1 ] ,
ϕ ( r ) ( ± 1 ) = 0 , r = q , q + 1 , ⋯ , 2 q − 1 .
Those eigenfunctions are known as polyharmonic-Neumann eigenfunctions.
It is known ([69]) that
L 0 ϕ ( x ) = 0
iff ϕ is a polynomial of degree q − 1 . The corresponding orthonormal eigenfunctions are ϕ 0 , n , n = 0 , ⋯ , q − 1 , where ϕ 0 , n is the n-th Legendre polynomial. All other eigenvalues are positive and simple. The corresponding system of eigenfunctions
H q = { ϕ 0 , n ( x ) : n = 0 , ⋯ , q − 1 } ∪ { ϕ n ( x ) : n ∈ N } , q ≥ 1
form a dense orthonormal subset of L 2 ( − 1 , 1 ) .
Following [61], we denote the truncated expansion of a function f ∈ L 2 ( − 1 , 1 ) in polyharmonic-Neumann eigenfunctions as
F N q [ f ] ( x ) : = ∑ n = 0 q − 1 f ^ 0 , n ϕ 0 , n ( x ) + ∑ n = 1 N f ^ n ϕ n ( x ) , x ∈ [ − 1 , 1 ] ,
where
f ^ 0 , n : = ∫ − 1 1 f ( x ) ϕ 0 , n ( x ) d x , f ^ n : = ∫ − 1 1 f ( x ) ϕ n ( x ) d x .
Approximations by F N q [ f ] ( x ) are better than those based on the classical truncated Fourier series. Let H r be the Sobolev space with index r. Then, the following estimates are true ([61]):
a)
The coefficients f ^ n of a function f ∈ H q + 1 ( − 1 , 1 ) are O ( n − q − 1 ) as n → ∞ ([61]).
b)
If f ∈ H q + 2 ( − 1 , 1 ) , the rate of convergence of F N q [ f ] to f is O ( N − q − 1 ) as N → ∞ in compact subsets of ( − 1 , 1 ) and O ( N − q ) as N → ∞ if x = ± 1 .
c)
All those results are valid without any periodical conditions contrary to the classical truncated Fourier series.
Particular case, q = 1 , is of special interest. The corresponding system of eigenfunctions is also known as the modified Fourier basis:
H 1 = { cos π n x : n ∈ Z + } ∪ { sin π ( n − 1 2 ) x : n ∈ N } , x ∈ [ − 1 , 1 ] .
It was originally proposed by Krein [70] and then thoroughly investigated in a series of papers [59,60,61,68,71,72,73,74,75].
Paper [76] considers interpolations on a uniform grid and exact for the eigenfunctions from the system H 1 . It explores the pointwise convergence of the interpolations and proves the convergence rate O ( N − 3 ) for compact subsets of ( − 1 , 1 ) , which is better than the convergence rate of the corresponding Fourier expansions. Moreover, the paper proves the convergence rate on [ − 1 , 1 ] as O ( N − 1 ) , the same as for the expansions. The convergence rate of the interpolation in the L 2 ( − 1 , 1 ) norm is O ( N − 3 / 2 ) , which is again the same as for the corresponding expansions. Hence, the main benefit of applying interpolations is faster convergence at the points away from the singularities x = ± 1 .
One of the goals of the current paper is to improve the results of [76] by applying the idea of QP interpolations. We show how this idea works for the interpolations based on the modified system. We prove some convergence theorems and provide the results of numerical experiments. Comparisons with the Fourier expansions and interpolations from [76] confirm our expectations. QP interpolations have improved convergence rates at the points away from x = ± 1 . Interestingly, better convergence is also detected on the entire interval, although not by the convergence rate. The next goal is to apply the idea to all polyharmonic-Neumann systems with q > 1 . We don’t prove convergence theorems but provide some evidence via numerical experiments. They showed the same behavior for q > 1 compared to q = 1 : much faster convergence inside the interval and moderately better pointwise convergence on the entire interval than for Fourier expansions.
The paper is constructed as follows. Section 2 describes the idea of the QP interpolation applied to the classical trigonometric system H c l a s s according to papers [63,64,65,66,67]. Section 3 deals with the modified Fourier system. We derive explicit formulae that realize the idea of the quasi-periodicity applied to the modified Fourier system. Section 4 proves some preliminary lemmas we need for the main theorems in the next section. Section 5 proves the main convergence results for the QP interpolations based on the modified Fourier basis. Here, we show the benefits of the idea. Section 6 shows how the QP extensions can be applied to polyharmonic eigenfunctions. Section 7 provides the results of numerical experiments and outlines the main benefits of the QP interpolations compared to the classical Fourier expansions. Section 8 concludes the main contributions of this paper.

2. The Quasi-Periodic Interpolations for the Classical Trigonometric System

Let us consider the QP interpolations that are exact for the system H c l a s s in more detail. Assume a trigonometric interpolation problem of a function f for a uniform grid { x k } ∈ [ − 1 , 1 ] . Let us assume that
x k : = 2 k 2 N + 1 , | k | ≤ N .
To resolve the convergence problem, we assume interpolation of the function f on the extended interval [ − 1 / σ , 1 / σ ] and for the uniform grid { x k * } ∈ [ − 1 , 1 ] including both endpoints:
x k * : = k N , | k | ≤ N ,
and exact for the following system of functions
{ e i π n σ x } n = − N N ,
where
σ N , m : = σ : = 2 N N m , N m = 2 N + 2 m + 1 , m = 1 , 2 , ⋯ .
All basis functions have the period 2 / σ , which tends to 2 as N tends to infinity. That is how the term quasi-periodic appeared in the works. To clarify further the essence of the QP interpolation, we perform the following change of variable
t = σ x , t ∈ [ − 1 , 1 ] , x ∈ [ − 1 / σ , 1 / σ ]
that transforms the grid { x k * } ∈ [ − 1 , 1 ] into { x k m } , | k | ≤ N .
x k m : = 2 k 2 N + 2 m + 1 , | k | ≤ N .
Hence, in the variable t, we must solve the problem of the classical trigonometric interpolation on the nonuniform grid { x k m } , | k | ≤ N as some of the 2 m points are missing from the uniform grid { x k m } , | k | ≤ N + m . As a result, the QP interpolation requires the solution of a system of linear equations with 2 m unknowns. In the case of the classical trigonometric system, the matrix of the system is Vandermonde, providing an explicit solution for the unknowns. This process is shown in [63]. Let us denote the QP interpolation for the system H c l a s s as I N , m 0 [ f ] ( x ) . Then,
I N , m 0 [ f ] ( x ) : = ∑ k = − N N f k N c k ( x ) ,
where
c k ( x ) : = 1 N m ∑ n = − N N ω 2 n − k e i π n σ x − ∑ ℓ = 1 2 m ω 2 ℓ + 2 N N + 2 m − k ∑ j = 1 2 m v ℓ , j − 1 ∑ n = − N N ω 2 n j + N e i π n σ x ,
and
ω n ( N , m ) : = ω n : = e i π n N m .
Here, v ℓ , j − 1 are the elements of the inverse of the following Vandermonde matrix
v j , ℓ : = ω 2 ℓ + 2 N j − 1 , j , ℓ = 1 , ⋯ , 2 m .
The elements v ℓ , j − 1 have the following explicit form
v ℓ , j − 1 = − 1 ω 2 ℓ + 2 N j ∏ k = 1 k ≠ ℓ 2 m ( ω 2 ℓ + 2 N − ω 2 k + 2 N ) ∑ t = 0 j − 1 γ t ω 2 ℓ + 2 N t , ℓ , j = 1 , ⋯ , 2 m ,
where γ j are the coefficients of the following polynomial
∏ k = 1 2 m ( x − ω 2 k + 2 N ) = ∑ t = 0 2 m γ t x t .
The QP interpolation I N , m 0 [ f ] ( x ) can be rewritten in the terms of Fourier discrete coefficients:
I N , m 0 [ f ] ( x ) = ∑ n = − N N f ˇ n , m 0 − ∑ ℓ = 1 2 m θ n , ℓ f ˇ ℓ + N , m 0 e i π n σ x ,
where
f ˇ n , m 0 : = 1 N m ∑ k = − N N f k N ω k − 2 n ,
and
θ n , ℓ : = ω 2 ℓ + 2 N − N − 1 ∑ j = 1 2 m v ℓ , j − 1 ω 2 n j + N .
Papers [63,64,65,67] investigated the convergence of the QP interpolations in different frameworks. They prove:
a)
The pointwise convergence rate of the QP interpolation I N , m 0 [ f ] ( x ) , m ≥ 1 is O ( N − 2 m − 1 ) as N → ∞ away from the endpoints | x | < 1 . The classical interpolation has O ( N − 1 ) rate as N → ∞ . Hence, the improvement is of the order O ( N 2 m ) .
b)
The convergence of the QP interpolation I N , m 0 [ f ] ( x ) , m ≥ 1 is O ( N − 1 / 2 ) as N → ∞ in the L 2 ( − 1 , 1 ) norm. The convergence rate is the same as that for classical interpolation. However, the QP interpolation is strongly more accurate.
c)
The QP and classical interpolations are O ( 1 ) at the endpoints x = ± 1 due to the Gibbs phenomenon. It can be improved by the polynomial correction methods.

3. Quasi-Periodic Interpolations for the Modified Trigonometric System

The first results concerning the convergence of the expansions by the modified Fourier system H 1 appeared in the works [59,71,72,73]. We present two theorems for further comparisons.
Theorem 1.
[72,73] Assume f ∈ C 2 [ − 1 , 1 ] and f ′ ′ ∈ B V [ − 1 , 1 ] . If | x | < 1 , then
f ( x ) − F N 1 [ f ] ( x ) = O ( N − 2 ) , N → ∞ .
Otherwise,
f ( ± 1 ) − F N 1 [ f ] ( ± 1 ) = O ( N − 1 ) , N → ∞ .
Overall, we see better convergence rates than for classical Fourier expansions ([77]) and the improvement is of order O ( N ) . This can be explained by faster decay of coefficients f ^ n
f ^ n = O ( n − 2 ) , n → ∞
compared to the classical ones when f is enough smooth but non-periodic on [ − 1 , 1 ] . Estimate (27) can be explained by a non-periodicity of the basis functions sin π ( n − 1 2 ) x on [ − 1 , 1 ] .
Now, we will deal with exact interpolations for the functions from the modified system H 1 . Upcoming theorems prove the improved convergence of interpolations compared to the expansions F N 1 [ f ] .
The basis functions of the system H 1 can be rewritten in the following complex form, which is more convenient for further derivations
φ n ( x ) : = 1 2 , n = 0 1 2 ( − 1 ) n e i π n x 2 + e − i π n x 2 , n ∈ N
The corresponding interpolations we denote by I N 1 [ f ] ( x ) and the derivation can be found in [76]
I N 1 [ f ] ( x ) : = ∑ n = 0 2 N f ˇ n 1 φ n ( x ) ,
where
f ˇ n 1 = 2 2 N + 1 ∑ k = − n N f ( x k ) φ ¯ n ( x k ) , x k = 2 k 2 N + 1 .
Let
A s ( f ) : = A s : = f ( s ) ( 1 ) + ( − 1 ) s − 1 f ( s ) ( − 1 ) .
Theorem 2.
[76] Let f be an odd function on [ − 1 , 1 ] . Assume that f ∈ C 4 [ − 1 , 1 ] and f ( 4 ) ∈ B V [ − 1 , 1 ] . Then, the following estimate holds for | x | < 1
f ( x ) − I N 1 [ f ] ( x ) = A 1 ( f ) ( − 1 ) N π 32 N 3 sin π ( N + 1 2 ) x cos 2 π x 2 + O ( N − 4 ) , N → ∞ .
Theorem 3.
[76] Let f be an odd function on [ − 1 , 1 ] . Assume that f ∈ C 2 [ − 1 , 1 ] and f ( 2 ) ∈ B V [ − 1 , 1 ] . Then, the following estimate holds
f ( ± 1 ) − I N 1 [ f ] ( ± 1 ) = ± A 1 ( f ) ( − 1 ) N + 1 2 π N + o ( N − 1 ) , N → ∞ .
The comparison of Theorem 1 to Theorems 2 and 3 reveals the expectations from interpolations: better convergence inside the interval of interpolation, away from the endpoints. Now, we will deal with QP interpolations for the system H 1 and will show improved convergence compared to both I N 1 [ f ] and F N 1 [ f ] .
According to the idea of the QP interpolations, we modify functions φ n ( x ) into φ n , m ( x ) as follows:
φ n , m ( x ) : = 1 2 , n = 0 1 2 ( − 1 ) n e i π n σ x 2 + e − i π n σ x 2 , n = 1 , ⋯ , 2 N
We search for the QP interpolation for the H 1 in the following form
I N , m 1 [ f ] ( x ) : = ∑ k = − N N f k N a k ( x ) ,
where the coefficient-functions a k ( x ) will be determined from the requirement that I N , m 1 [ f ] ( x ) is exact for the basis functions φ n , m :
I N , m 1 [ φ n , m ] ( x ) ≡ φ n , m ( x ) , n = 0 , 1 , ⋯ , 2 N .
We have
∑ k = − N N 1 2 ( − 1 ) n ω n k + ω − n k a k ( x ) ≡ 1 2 ( − 1 ) n e i π n σ x 2 + e − i π n σ x 2 , n = 0 , 1 , ⋯ , 2 N .
Taking into account that φ − n , m ( x ) = ( − 1 ) n φ n , m ( x ) , we see that (37) is exact also for φ − n , m ( x ) , n = 1 , ⋯ , 2 N . Hence, we can extend the system (37) by adding some new unknowns
∑ k = − N m + 1 N m − 1 1 2 ( − 1 ) n ω n k + ω − n k a k * ( x ) + ϵ n ( x ) ≡ 1 2 ( − 1 ) n e i π n σ x 2 + e − i π n σ x 2 , | n | ≤ N m − 1 ,
where
ϵ n ( x ) ≡ 0 , | n | ≤ 2 N ,
and
a k * ( x ) ≡ a k ( x ) , k = − N , ⋯ , N , 0 , | k | > N .
Then, we multiply the both sides of (38) by ω n j for | j | ≤ N + 2 m and sum over n:
∑ k = − N m + 1 N m − 1 a k * ( x ) 2 ∑ n = − N m + 1 N m − 1 ( − 1 ) n ω n k + j + ω − n k − j + ∑ n = − N m + 1 N m − 1 ω n j ϵ n ( x ) = ∑ n = − N m + 1 N m − 1 ω n j 2 ( − 1 ) n e i π n σ x 2 + e − i π n σ x 2 .
Based on the relations
∑ n = − N m + 1 N m − 1 ( − 1 ) n ω n k + j + ω − n k − j = 2 N m , k = j , 2 N m , | k + j | = N m , 0 , | k + j | ≠ N m , k ≠ j ,
we get
N m a j * ( x ) + ∑ n = 2 N + 1 N m − 1 ω n j ϵ n * ( x ) + ∑ n = − N m + 1 − 2 N − 1 ω n j ϵ n * ( x ) = ∑ n = − 2 N 2 N ω n j 2 ( − 1 ) n e i π n σ x 2 + e − i π n σ x 2 , | j | ≤ N + 2 m ,
where
ε n * ( x ) = ε n ( x ) − 1 2 ( − 1 ) n e i π n σ x 2 + e − i π n σ x 2 , | n | = N + 1 , ⋯ , N + 2 m .
Taking into account (40), we rewrite (43) as follows
∑ n = 2 N + 1 N m − 1 ω n j ϵ n * ( x ) + ∑ n = − N m + 1 − 2 N − 1 ω n j ϵ n * ( x ) = ∑ n = − 2 N 2 N ω n j 2 ( − 1 ) n e i π n σ x 2 + e − i π n σ x 2 , | j | = N + 1 , ⋯ , N + 2 m .
From (38) and (44), we have
ϵ − n * ( x ) = ( − 1 ) n ϵ n * ( x ) .
For negative j-es, the equations of (45) can be written in the following form
∑ n = 2 N + 1 2 N + 2 m ( − 1 ) n ω n j ε n * ( x ) + ∑ n = − 2 N − 2 m − 2 N − 1 ( − 1 ) n ω n j ε n * ( x ) = ∑ n = − 2 N 2 N ω n j 2 e i π n σ x 2 + ( − 1 ) n e − i π n σ x 2 , j = N + 1 , ⋯ , N + 2 m .
After adding the equations of (47) to the corresponding equations of (45), we will get a system for unknowns ε n * ( x ) having only even indices
∑ n = N + 1 N + m ω 2 n j ε 2 n * ( x ) + ∑ n = − N − m − N − 1 ω 2 n j ε 2 n * ( x ) = ∑ n = − N N ω 2 n j 2 e i π n σ x + e − i π n σ x , j = N + 1 , ⋯ , N + 2 m .
Taking into account the relations
∑ n = − N − m − N − 1 ω 2 n j ε 2 n * ( x ) = ∑ n = N + m + 1 N + 2 m ω 2 n j ε 2 n − 2 N m * ( x ) , j = N + 1 , ⋯ , N + 2 m ,
we obtain the following linear system of equations
∑ ℓ = 1 2 m v j , ℓ b 2 N + 2 ℓ ( x ) = ∑ n = − N N ω 2 n j 2 e i π n σ x + e − i π n σ x , j = 1 , ⋯ , 2 m ,
with the Vandermonde matrix (19) and unknowns
b 2 n ( x ) : = ω 2 n N + 1 ε 2 n * ( x ) , n = N + 1 , ⋯ , N + m , ω 2 n N + 1 ε 2 n − 2 N m * ( x ) , n = N + m + 1 , ⋯ , N + 2 m .
Now, subtracting the equations of (47) from the corresponding equations of (45), we will get the following system of equations for unknowns ε n * ( x ) having only odd indices
∑ n = N N + m − 1 ω 2 n + 1 j ε 2 n + 1 * ( x ) + ∑ n = − N − m − N − 1 ω 2 n + 1 j ε 2 n + 1 * ( x ) = ∑ n = − N N − 1 ω 2 n + 1 j 2 − e i π ( 2 n + 1 ) σ x 2 + e − i π ( 2 n + 1 ) σ x 2 , j = N + 1 , ⋯ , N + 2 m .
Based on the relations
∑ n = − N − m − N − 1 ω 2 n + 1 j ε 2 n + 1 * ( x ) = ∑ n = N + m + 1 N + 2 m ω 2 n + 1 j ε 2 n − 2 N m + 1 * ( x ) , j = N + 1 , ⋯ , N + 2 m ,
we get the following linear system of equations
∑ ℓ = 1 2 m V j , ℓ b 2 ℓ + 2 N + 1 ( x ) = ∑ n = − N N − 1 ω 2 n + 1 j + N 2 − e i π ( 2 n + 1 ) σ x 2 + e − i π ( 2 n + 1 ) σ x 2 , j = 1 , ⋯ , 2 m
with Vandermonde matrix
V j , ℓ = β ℓ j − 1 , j = 1 , ⋯ , 2 m , ℓ = 1 , ⋯ , 2 m ,
where
β ℓ ( N , m ) : = β ℓ : = ω 2 ℓ + 2 N − 1 , ℓ = 1 , ⋯ , m , ω 2 ℓ + 2 N + 1 , ℓ = m + 1 , ⋯ , 2 m .
and unknowns
b 2 n + 1 ( x ) : = ω 2 n − 1 N + 1 ε 2 n − 1 * ( x ) , n = N + 1 , ⋯ , N + m , ω 2 n + 1 N + 1 ε 2 n − 2 N m + 1 * ( x ) , n = N + m + 1 , ⋯ , N + 2 m .
Similar to (19), the inverse of V j , ℓ j , ℓ = 1 2 m can be calculated explicitly. The corresponding elements of the inverse can be written as follows
V ℓ , j − 1 = − 1 β ℓ j ∏ k = 1 , k ≠ l 2 m β ℓ − β k ∑ t = 0 j − 1 δ t β ℓ t , ℓ , j = 1 , ⋯ , 2 m ,
where
∏ k = 1 2 m x − β k = ∑ t = 0 2 m δ t x t .
Now, taking into account (43) and (40), we determine the coefficients a k :
a k ( x ) = 1 N m ∑ n = − 2 N 2 N ω n k 2 ( − 1 ) n e i π n σ x 2 + e − i π n σ x 2 − ∑ n = 2 N + 1 N m − 1 ω n k ϵ n * ( x ) − ∑ n = − N m + 1 − 2 N − 1 ω n k ϵ n * ( x ) , | k | ≤ N .
Then, the QP interpolation for the system H 1 has the following explicit form
I N , m 1 [ f ] ( x ) = ∑ n = 0 2 N φ n , m ( x ) f ˇ n , m 1 + 2 ∑ n = 0 N − 1 φ 2 n + 1 , m ( x ) ∑ j = 1 2 m φ 2 n + 1 , m 1 + j N ∑ ℓ = 1 m ω 2 N + 2 ℓ − 1 − N − 1 V ℓ , j − 1 f ˇ 2 N + 2 ℓ − 1 , m 1 − 2 ∑ n = 0 N φ 2 n , m ( x ) ∑ j = 1 2 m φ 2 n , m 1 + j N ∑ ℓ = 1 m ω 2 N + 2 ℓ − N − 1 V ℓ , j − 1 f ˇ 2 N + 2 ℓ , m 1 ,
where
f ˇ n , m 1 : = 2 N m ∑ k = − N N f k N φ ¯ n , m k N .
Let us proof that I N , m 1 [ f ] interpolates f on the grid x k = k / N , | k | ≤ N . For even functions, the QP interpolations for the system H 1 coincide with the QP interpolations for the system H c l a s s . Any function can be represented as a sum of even and odd functions, making enough to consider only odd ones. For odd functions f ˇ 2 n , m = 0 , n = 0 , ⋯ , N + m , and
I N , m 1 [ f ] ( x ) = ∑ n = 0 N − 1 F n , m sin π ( 2 n + 1 ) σ x 2 ,
where
F n , m : = f ˇ n , m 1 − ∑ ℓ = 1 m Θ n , ℓ f ˇ N + ℓ − 1 , m 1 = f ˇ n , m 1 − ∑ ℓ = m + 1 2 m Θ n , ℓ f ˇ N + ℓ , m 1 ,
f ˇ n , m 1 = 2 N m ∑ k = − N N f k N s 2 n + 1 , k ,
with
s n , k ( N , m ) : = s n , k : = sin π n k N m ,
and
Θ n , ℓ ( N , m ) : = Θ n , ℓ : = 2 i β ℓ − N − 1 ∑ j = 1 2 m s 2 n + 1 , j + N V ℓ , j − 1 .
Theorem 4.
Let f ∈ C [ − 1 , 1 ] be an odd function. Then I N , m 1 [ f ] ( x ) interpolates f on the grid x k = k N , k = − N , ⋯ , N .
Proof. 
Let f be an odd function. Taking into account
2 ∑ n = 0 N − 1 φ 2 n + 1 , m k N ∑ j = 1 2 m φ 2 n + 1 , m 1 + j N = 1 2 ∑ τ = 1 2 m ∑ j = 1 2 m β τ − k + j + N − β τ k + j + N ,
together with (55) and (56), we can write
I N , m 1 [ f ] k N = 2 N m ∑ t = − N N f t N ∑ n = 0 N − 1 φ 2 n + 1 , m k N φ ¯ 2 n + 1 , m t N + 2 ∑ n = 0 N − 1 φ 2 n + 1 , m k N ∑ j = 1 2 m φ 2 n + 1 , m 1 + j N ∑ ℓ = 1 m β ℓ − N − 1 V ℓ , j − 1 φ ¯ 2 N + 2 ℓ − 1 , m t N = 2 N m ∑ t = − N N f t N ∑ n = 0 N + m − 1 φ 2 n + 1 , m k N φ ¯ 2 n + 1 , m t N = f k N ,
which completes the proof. □
Further, we need the following estimates based on (56) and (58), we have
V ℓ , s − 1 = O N 2 m − 1 .
Then, given (67), we derive
Θ n , ℓ = O N 2 m − 1 .
The goal of the next two sections is the investigation of the pointwise convergence of the QP interpolation for the system H 1 . The next section reveals some preliminary results and Section 5 proves the main results where Theorems 5, refth6 show the exact convergence rate of the pointwise convergence away from the singularities x = ± 1 , and Theorems 7, 8 explore the pointwise convergence at the points x = ± 1 .

4. Preliminary Lemmas

In this section, we prove some preliminary results needed for further convergence theorems.
Lemma 1.
Let f ∈ C [ − 1 , 1 ] be an odd function. Then,
F N + k , m = 0 , k = 0 , ⋯ , 2 m .
Proof. 
For k = 0 , ⋯ , m − 1 ,
F N + k , m = f ˇ N + k , m 1 − ∑ ℓ = 1 m β ℓ − N − 1 ∑ j = 1 2 m β k + 1 j + N − β 2 m − k j + N V ℓ , j − 1 f ˇ N + ℓ − 1 , m 1 = f ˇ N + k , m 1 − β k + 1 − N − 1 β k + 1 N + 1 f ˇ N + k , m 1 = 0 .
The proof is similar for k = m + 1 , ⋯ , 2 m . Since, f ˇ N + m , m 1 = 0 , and Θ N + m , ℓ = 0 for ℓ = 1 , ⋯ 2 m , it is true also for k = m . □
Let f ∈ C α [ − 1 , 1 ] , α ≥ 0 . We define
f * ( x ) : = f l e f t ( x ) , x ∈ − 1 , − σ , f x σ , x ∈ − σ , σ , f r i g h t ( x ) , x ∈ σ , 1 ,
where
f l e f t ( x ) = ∑ j = 0 α f ( j ) ( − 1 ) j ! x σ + 1 j , f r i g h t ( x ) = ∑ j = 0 α f ( j ) ( 1 ) j ! x σ − 1 j .
Obviously, f * ∈ C α [ − 1 , 1 ] . If f is an odd function, then f * is odd either. Also, we will use the following notation
f n * : = ∫ − 1 1 f * ( x ) sin π n + 1 2 x d x .
Lemma 2.
Let f be an odd function such that f ( 2 p + 2 v + 2 ) ∈ A C [ − 1 , 1 ] for some p , v ≥ 0 , m ≥ 1 , and
f ( k ) ( − 1 ) = f ( k ) ( 1 ) = 0 , k = 1 , ⋯ , 2 p .
Then, the following estimate holds as n → ∞
f n * = ( − 1 ) n ∑ j = 2 p + 1 2 p + 2 v + 2 A j N m N j μ m , j 2 n + 1 N m + o n − 2 p − 2 v − 3 .
where
μ m , j ( x ) : = ∑ k = 0 j − 1 2 ( − 1 ) k ( 2 m + 1 ) j − 2 k − 1 2 2 k + 2 − j ( j − 2 k − 1 ) ! π x 2 k + 2 .
Proof. 
Taking into account the smoothness of f and f * with α = 2 p + 2 v + 2 , we get after integration by parts
f n * = ∑ k = 0 p + v ( − 1 ) n + k π n + 1 2 2 k + 2 f * ( 2 k + 1 ) ( 1 ) + f * ( 2 k + 1 ) ( − 1 ) − ( − 1 ) p + v π n + 1 2 2 p + 2 v + 3 ∫ − 1 1 f * ( 2 p + 2 v + 3 ) ( x ) cos π n + 1 2 x d x = ∑ k = 0 p + v ( − 1 ) n + k π n + 1 2 2 k + 2 f r i g h t ( 2 k + 1 ) ( 1 ) + f l e f t ( 2 k + 1 ) ( − 1 ) − ( − 1 ) p + v π n + 1 2 2 p + 2 v + 3 ∫ − σ σ f * ( 2 p + 2 v + 3 ) ( x ) cos π n + 1 2 x d x ,
where
f l e f t ( 2 k + 1 ) ( − 1 ) = 1 σ 2 k + 1 ∑ j = 2 k + 1 2 p + 2 v + 2 ( − 1 ) j − 1 f ( j ) ( − 1 ) ( 2 m + 1 ) j − 2 k − 1 ( j − 2 k − 1 ) ! ( 2 N ) j − 2 k − 1 ,
and
f r i g h t ( 2 k + 1 ) ( 1 ) = 1 σ 2 k + 1 ∑ j = 2 k + 1 2 p + 2 v + 2 f ( j ) ( 1 ) ( 2 m + 1 ) j − 2 k − 1 ( j − 2 k − 1 ) ! ( 2 N ) j − 2 k − 1 .
In view of the generalized Riemann-Lebesgue theorem ([77]), we have
f n * = ∑ k = 0 p + v 1 σ 2 k + 1 ( − 1 ) n + k π n + 1 2 2 k + 2 ∑ j = 2 k + 1 2 p + 2 v + 2 A j ( 2 m + 1 ) j − 2 k − 1 ( j − 2 k − 1 ) ! ( 2 N ) j − 2 k − 1 + o n − 2 p − 2 v − 3 = ( − 1 ) n ∑ j = 2 p + 1 2 p + 2 v + 2 A j ( 2 N ) j ∑ k = 0 j − 1 2 ( − 1 ) k ( 2 m + 1 ) j − 2 k − 1 ( N m ) 2 k + 1 ( j − 2 k − 1 ) ! π n + 1 2 2 k + 2 + o n − 2 p − 2 v − 3 ,
which completes the proof. □
Let
g ( x ) : = ∑ r = − ∞ ∞ ( − 1 ) r r + x = 2 i π e i π x − e − i π x .
Then,
Φ k , m e i π x : = e i π ( 2 m − 1 ) x 2 ∑ r = − ∞ ∞ ( − 1 ) r + 1 r + x 2 2 k + 2 = e i π ( 2 m − 1 ) x 2 g ( 2 k + 1 ) x 2 ( 2 k + 1 ) ! .
Also, denote
η n , k ( N , m ) : = η n , k : = ∑ r ≠ 0 ( − 1 ) r r + n N m 2 k + 2 .
Lemma 3.
Let f be an odd function and f ( 2 p + 2 v + 2 m + 2 ) ∈ A C [ − 1 , 1 ] for some p , v ≥ 0 , m ≥ 1 and
f ( k ) ( − 1 ) = f ( k ) ( 1 ) = 0 , k = 1 , ⋯ , 2 p .
Then, the following estimate holds for | n | ≤ N + c (c is a constant)
F n , m − f n * = ( − 1 ) n N m ∑ j = 2 p + 1 2 p + 2 v + 2 m + 2 A j 2 j + 1 N j ∑ k = 0 j − 1 2 ( − 1 ) k ( 2 m + 1 ) j − 2 k − 1 ( j − 2 k − 1 ) ! π 2 k + 2 × ( 2 η n + 1 2 , k + ω 2 n + 1 − m + 1 2 ∑ τ = 0 2 m − 1 Φ k , m ( τ ) ( − 1 ) τ ! ω 2 n + 1 + 1 τ + ω 2 n + 1 m − 1 2 ∑ τ = 0 2 m − 1 Φ k , m ( τ ) ( − 1 ) τ ! ω − 2 n − 1 + 1 τ + 2 ( − 1 ) n ∑ ℓ = 1 2 m ∑ j = 1 2 m s 2 n + 1 , j + N V ℓ , j − 1 ∑ τ = 2 m 2 v + 2 m + 1 1 τ ! Φ k , m ( τ ) ( − 1 ) β ℓ + 1 τ ) + o N − 2 p − 2 v − 4 .
Proof. 
First, let us prove the following property
F n , m = ∑ r = − ∞ ∞ f n + r N m * − 1 2 ∑ ℓ = 1 m Θ n , ℓ ∑ r = − ∞ ∞ f N + ℓ − 1 + r N m * − 1 2 ∑ ℓ = m + 1 2 m Θ n , ℓ ∑ r = − ∞ ∞ f N + ℓ + r N m * .
Equations (64) and (65) imply
F n , m = 2 N m ∑ k = − N N f k N s 2 n + 1 , k − 1 4 i ∑ ℓ = 1 2 m Θ n , ℓ β ℓ k − β ℓ − k .
Taking into account definition (74) of f * with α = 2 p + 2 v + 2 m + 2 , we derive
f k N = f * 2 k N m = ∑ t = 0 ∞ f t * sin π ( 2 t + 1 ) k N m = 1 2 i ∑ t = − ∞ ∞ f t * ω 2 t + 1 k .
Hence,
F n , m = 1 2 N m ∑ k = − N N ∑ t = − N − m N + m ∑ r = − ∞ ∞ f t + r N m * ( ω t − n 2 k − ω t + n + 1 2 k − 1 2 ∑ ℓ = 1 m Θ n , ℓ ω t − N − ℓ + 1 2 k − ω t + N + ℓ 2 k − 1 2 ∑ ℓ = m + 1 2 m Θ n , ℓ ω t − N − ℓ 2 k − ω t + N + ℓ + 1 2 k ) .
According to (67), we can write for k = N + 1 , ⋯ , N + 2 m
− 1 2 ∑ ℓ = 1 m Θ n , ℓ ω t − N − ℓ + 1 2 k − ω t + N + ℓ 2 k − 1 2 ∑ ℓ = m + 1 2 m Θ n , ℓ ω t − N − ℓ 2 k − ω t + N + ℓ + 1 2 k = 2 i ω 2 t + 1 k s 2 n + 1 , k = ω t + n + 1 2 k − ω t − n 2 k .
Then,
F n , m = 1 2 N m ∑ k = − N N + 2 m ∑ t = − N − m N + m ∑ r = − ∞ ∞ f t + r N m * ( ω t − n 2 k − ω t + n + 1 2 k − 1 2 ∑ ℓ = 1 m Θ n , ℓ ω t − N − ℓ + 1 2 k − ω t + N + ℓ 2 k − 1 2 ∑ ℓ = m + 1 2 m Θ n , ℓ ω t − N − ℓ 2 k − ω t + N + ℓ + 1 2 k ) .
Now, taking into account that
1 N m ∑ k = − N − m N + m ω t − n 2 k = δ t , n , − N − m ≤ t , n ≤ N + m ,
we obtain
F n , m = 1 2 ∑ r = − ∞ ∞ ( f n + r N m * − f − n − 1 + r N m * − 1 2 ∑ ℓ = 1 m Θ n , ℓ f N + ℓ − 1 + r N m * − f − N − ℓ + r N m * − 1 2 ∑ ℓ = m + 1 2 m Θ n , ℓ f N + ℓ + r N m * − f − N − ℓ − 1 + r N m * ) ,
which proves (89). Then,
F n , m − f n * = ∑ r ≠ 0 f n + r N m * − 1 2 ∑ ℓ = 1 m Θ n , ℓ ∑ r = − ∞ ∞ f N + ℓ − 1 + r N m * − 1 2 ∑ ℓ = m + 1 2 m Θ n , ℓ ∑ r = − ∞ ∞ f N + ℓ + r N m * .
We continue the modifications of (97). Lemma 2, Equations (67) and (71) lead to the following estimate
1 2 ∑ ℓ = 1 m Θ n , ℓ ∑ r = − ∞ ∞ f N + ℓ − 1 + r N m * + 1 2 ∑ ℓ = m + 1 2 m Θ n , ℓ ∑ r = − ∞ ∞ f N + ℓ + r N m * = 1 N m ∑ j = 2 p + 1 2 p + 2 v + 2 m + 2 A j 2 j N j ∑ k = 0 j − 1 2 ( − 1 ) k + 1 ( 2 m + 1 ) j − 2 k − 1 ( j − 2 k − 1 ) ! π 2 k + 2 ∑ ℓ = 1 2 m Φ k , m ( β ℓ ) ∑ i = 1 2 m s 2 n + 1 , i + N V ℓ , i − 1 + o N − 2 p − 2 v − 4 .
The Taylor expansion
Φ k , m β ℓ = ∑ τ = 0 2 v + 2 m + 1 1 τ ! Φ k , m ( τ ) ( − 1 ) β ℓ + 1 τ + O ( N − 2 v − 2 m − 2 ) ,
together with the following relation
∑ ℓ = 1 2 m ∑ i = 1 2 m ω n i + N V ℓ , i − 1 β ℓ + 1 τ = ω n N + 1 ω n + 1 τ , τ = 0 , ⋯ , 2 m − 1
and Equation (71) imply
1 2 ∑ ℓ = 1 m Θ n , ℓ ∑ r = − ∞ ∞ f N + ℓ − 1 + r N m * + 1 2 ∑ ℓ = m + 1 2 m Θ n , ℓ ∑ r = − ∞ ∞ f N + ℓ + r N m * = ( − 1 ) n N m ∑ j = 2 p + 1 2 p + 2 v + 2 m + 2 A j 2 j + 1 N j ∑ k = 0 j − 1 2 ( − 1 ) k + 1 ( 2 m + 1 ) j − 2 k − 1 ( j − 2 k − 1 ) ! π 2 k + 2 × ( ω 2 n + 1 − m + 1 2 ∑ τ = 0 2 m − 1 Φ k , m ( τ ) ( − 1 ) τ ! ω 2 n + 1 + 1 τ + ω − 2 n − 1 − m + 1 2 ∑ τ = 0 2 m − 1 Φ k , m ( τ ) ( − 1 ) τ ! ω − 2 n − 1 + 1 τ + 2 ( − 1 ) n ∑ ℓ = 1 m ∑ i = 1 2 m s 2 n + 1 , i + N V ℓ , i − 1 ∑ τ = 2 m 2 v + 2 m + 1 1 τ ! Φ k , m ( τ ) ( − 1 ) β ℓ + 1 τ ) + o N − 2 p − 2 v − 4 .
Equations (101) and (97) completes the proof. □
Lemma 4.
Let f be an odd function and f ( 2 p + 4 m + 2 ) ∈ A C [ − 1 , 1 ] for some p ≥ 0 , m ≥ 1 and
f ( k ) ( − 1 ) = f ( k ) ( 1 ) = 0 , k = 1 , ⋯ , 2 p .
Then, the following estimates hold as N → ∞
F N − t , m = C p , m [ f ] ( − 1 ) N + t N 2 p + 2 m + 3 2 m + t 2 m + 1 + O N − 2 p − 2 m − 4 , t ≥ 1 ,
where
C p , m [ f ] : = A 2 p + 1 2 2 p + 2 ∑ k = 0 p ( − 1 ) k ( 2 m + 1 ) 2 p − 2 k π 2 m − 2 k − 1 ( 2 p − 2 k ) ! Φ k , m ( 2 m + 1 ) ( − 1 ) .
Proof. 
Following the steps of the proof of Lemma 3, we obtain
F N − t , m = ( − 1 ) N + t + 1 N m ∑ j = 2 p + 1 2 p + 4 m + 2 A j ( 2 N ) j ∑ k = 0 j − 1 2 ( − 1 ) k ( 2 m + 1 ) j − 2 k − 1 ( j − 2 k − 1 ) ! π 2 k + 2 × ω 2 N − 2 t + 1 − m + 1 2 Φ k , m ω 2 N − 2 t + 1 + ∑ ℓ = 1 2 m Φ k , m β ℓ ∑ i = 1 2 m ( − 1 ) i − m V ℓ , i − 1 s m + t , 2 i − 2 m − 1 + o N − 2 p − 2 m − 4 .
Taking into account the relation
ω 2 N − 2 t + 1 − m + 1 2 Φ k , m ω 2 N − 2 t + 1 = ω − 2 N + 2 t − 1 − m + 1 2 Φ k , m ω − 2 N + 2 t − 1 ,
we can rewrite (105) as follows
F N − t , m = ( − 1 ) N + t + 1 2 N m ∑ j = 2 p + 1 2 p + 4 m + 2 A j ( 2 N ) j ∑ k = 0 j − 1 2 ( − 1 ) k ( 2 m + 1 ) j − 2 k − 1 ( j − 2 k − 1 ) ! π 2 k + 2 × ω 2 N − 2 t + 1 − m + 1 2 S 1 + ω − 2 N + 2 t − 1 − m + 1 2 S 2 + o N − 2 p − 2 m − 4 ,
where
S 1 : = Φ k , m ω 2 N − 2 t + 1 − ∑ ℓ = 1 2 m Φ k , m β ℓ ∑ t = 1 2 m V ℓ , t − 1 ω 2 N − 2 t + 1 t − 1 ,
and
S 2 : = Φ k , m ω − 2 N + 2 t − 1 − ∑ ℓ = 1 2 m Φ k , m β ℓ ∑ t = 1 2 m V ℓ , t − 1 ω − 2 N + 2 t − 1 t − 1 .
Let us estimate S 1 by rewriting it as follows
S 1 = ∑ j = 1 2 m r e s z = β j γ β − t Φ k , m ( z ) γ ( z ) z − β − t + r e s z = β − t γ β − t Φ k , m ( z ) γ ( z ) z − β − t ,
where β − t = ω 2 N − 2 t + 1 and γ ( z ) = ∏ ℓ = 1 2 m z − β ℓ . Hence,
S 1 = 1 2 π i ∫ Γ γ β − t Φ k , m ( z ) γ ( z ) z − β − t d z ,
where Γ contains the points β ℓ ℓ = 1 2 m and β − t . Then,
S 1 = ( − 1 ) m i π 2 m + 1 Φ k , m ( 2 m + 1 ) ( − 1 ) N 2 m + 1 2 m + t 2 m + 1 + O N − 2 m − 2 , N → ∞ .
Similarly, we estimate S 2
S 2 = ( − 1 ) m + 1 i π 2 m + 1 Φ k , m ( 2 m + 1 ) ( − 1 ) N 2 m + 1 2 m + t 2 m + 1 + O N − 2 m − 2 , N → ∞ .
The required statement can be proved based on (112), (113) and (107). □
Similarly can be proved the next one.
Lemma 5.
Let f be an odd function and f ( 2 p + 2 m + 2 ) ∈ A C [ − 1 , 1 ] for some p ≥ 0 , m ≥ 1 and
f ( k ) ( − 1 ) = f ( k ) ( 1 ) = 0 , k = 0 , ⋯ , 2 p .
Then, the following estimate holds as n → ∞
F n , m − f n * = ( − 1 ) n N m A 2 p + 1 N 2 p + 1 ν m , 2 p + 1 2 n + 1 N m + O N − 2 p − 3 ,
where
ν m , j ( x ) : = 1 2 j + 1 ∑ k = 0 j − 1 2 ( − 1 ) k ( 2 m + 1 ) j − 2 k − 1 ( j − 2 k − 1 ) ! π 2 k + 2 ∑ r ≠ 0 2 ( − 1 ) r r + x 2 2 k + 2 + e − i π x m − 1 2 ∑ τ = 0 2 m − 1 1 τ ! Φ k , m ( τ ) ( − 1 ) e i π x + 1 τ + e i π x m − 1 2 ∑ τ = 0 2 m − 1 1 τ ! Φ k , m ( τ ) ( − 1 ) e − i π x + 1 τ .

5. The Convergence of the QP Interpolations by the Modified Fourier System

This section proves the main theorems for the pointwise convergence of the QP interpolations for the system H 1 .
We will use the sequences of finite differences defined as follows
δ n 0 { y t } t = − ∞ ∞ = δ n 0 { y t } t = y n ,
δ n p { y t } t = − ∞ ∞ = δ n p { y t } t = δ n + 1 p − 1 { y t } t + 2 δ n p − 1 { y t } t + δ n − 1 p − 1 { y t } t , p ≥ 1 ,
where { y t } t = − ∞ ∞ is a sequence of complex numbers.
The following theorem proves one of the main results of this paper, showing the benefits of QP interpolations over Fourier expansions and traditional trigonometric interpolations. Theorems 5 and 6 show the exact convergence rate for | x | < 1 , and Theorems 7, 8 at the points x = ± 1 .
Let
R N , m 1 [ f ] ( x ) : = f ( x ) − I N , m 1 [ f ] ( x ) .
Theorem 5.
Let f be an odd function and f ( 2 p + 4 m + 2 ) ∈ A C [ − 1 , 1 ] for some p ≥ 0 , m ≥ 1 and
f ( k ) ( − 1 ) = f ( k ) ( 1 ) = 0 , k = 1 , ⋯ , 2 p .
Then, the following estimate holds for | x | < 1 as N → ∞
R N , m 1 [ f ] ( x ) = D N , m , p [ f ] ( x ) N 2 p + 2 m + 3 + o ( N − 2 p − 2 m − 3 ) ,
where
D N , m , p [ f ] ( x ) : = C p , m [ f ] sin π σ ( 2 N + 1 ) x 2 ∑ k = 0 m 2 m − k + 1 k ( − 1 ) k + N 2 2 k + 2 cos 2 k + 2 π σ x 2 − sin π σ ( 2 N − 1 ) x 2 ∑ k = 0 m − 1 2 m − k − 1 k ( − 1 ) k + N 2 2 k + 4 cos 2 k + 4 π σ x 2 ,
and C p , m [ f ] is defined by (104).
Proof. 
We define f * (see (74)) for α = 2 p + 4 m + 2 . Consequently, f * ( 2 p + 4 m + 2 ) ∈ A C [ − 1 , 1 ] . The error R N , m 1 [ f ] can be decomposed as follows for x ∈ [ − 1 , 1 ] :
R N , m 1 [ f ] ( x ) = ∑ n = 0 N − 1 ( f n * − F n , m ) sin π σ ( 2 n + 1 ) x 2 + ∑ n = N ∞ f n * sin π σ ( 2 n + 1 ) x 2 .
To estimate the components of R N , m 1 [ f ] , we use the following transformation (see [49,78] for derivation of similar transformations)
R N , m 1 [ f ] ( x ) = sin π σ ( 2 N − 1 ) x 2 ∑ k = 0 m δ N k F t , m t 1 + e − i π σ x k + 1 1 + e i π σ x k + 1 − sin π σ ( 2 N + 1 ) x 2 ∑ k = 0 m δ N − 1 k F t , m t 1 + e − i π σ x k + 1 1 + e i π σ x k + 1 + r N , m [ f ] ( x ) ,
where
r N , m [ f ] ( x ) = 1 4 m + 1 cos 2 m + 2 π σ x 2 ∑ n = 0 N − 1 δ n m + 1 f t * − F t , m t sin π σ ( 2 n + 1 ) x 2 + 1 4 m + 1 cos 2 m + 2 π σ x 2 ∑ n = N ∞ δ n m + 1 f t * t sin π σ ( 2 n + 1 ) x 2 .
We start by proving that
r N , m [ f ] ( x ) = o ( N − 2 p − 2 m − 3 ) , N → ∞ , | x | < 1 .
Similar to (124), we obtain the following decomposition of r N , m [ f ] :
r N , m [ f ] ( x ) = δ N m + 1 F t , m t sin π σ ( 2 N − 1 ) x 2 − δ N − 1 m + 1 F t , m t sin π σ ( 2 N + 1 ) x 2 4 m + 2 cos 2 m + 4 π σ x 2 + 1 4 m + 2 cos 2 m + 4 π σ x 2 ∑ n = 0 N − 1 δ n m + 2 f t * − F t , m t sin π σ ( 2 n + 1 ) x 2 + 1 4 m + 2 cos 2 m + 4 π σ x 2 ∑ n = N ∞ δ n m + 2 f t * t sin π σ ( 2 n + 1 ) x 2 .
To estimate δ n m + 2 f t * t as | n | > N , N → ∞ , we use Lemma 2 for v = 2 m :
δ n m + 2 f t * t = ∑ j = 2 p + 1 2 p + 4 m + 2 A j 2 j N j ∑ k = 0 j − 1 2 ( − 1 ) k ( 2 m + 1 ) j − 2 k − 1 N m 2 k + 1 ( j − 2 k − 1 ) ! π 2 k + 2 × δ n m + 2 ( − 1 ) t t + 1 2 2 k + 2 t + o ( n − 2 p − 4 m − 3 ) .
It is easy to verify (see Lemma 3.2 in [78]) that
δ n m + 2 ( − 1 ) t t + 1 2 2 k + 2 t = O ( n − 2 m − 2 k − 6 ) , n → ∞ .
Then,
δ n m + 2 f t * t = O ( N − 2 p − 1 n − 2 m − 5 ) + o ( n − 2 p − 4 m − 2 ) , | n | > N , N → ∞ .
Hence, the last term of (127) is o ( N − 2 p − 2 m − 3 ) as N → ∞ .
Then, to estimate δ n m + 2 F t , m − f t * t for | n | ≤ N as N → ∞ , we use Equation (88) of Lemma 3 for v = m :
δ n m + 2 F t , m − f t * t = 1 N m ∑ j = 2 p + 1 2 p + 4 m + 2 A j 2 j + 1 N j ∑ k = 0 j − 1 2 ( − 1 ) k ( 2 m + 1 ) j − 2 k − 1 ( j − 2 k − 1 ) ! π 2 k + 2 × ( 2 δ n m + 2 ( − 1 ) t η t + 1 2 , k t + ∑ τ = 0 2 m − 1 Φ k , m ( τ ) ( − 1 ) τ ! δ n m + 2 ( − 1 ) t ω 2 t + 1 − m + 1 2 ω 2 t + 1 + 1 τ t + ∑ τ = 0 2 m − 1 Φ k , m ( τ ) ( − 1 ) τ ! δ n m + 2 ( − 1 ) t ω − 2 t − 1 − m + 1 2 ω − 2 t − 1 + 1 τ t ) + 2 ∑ ℓ = 1 2 m ∑ j = 1 2 m δ n m + 2 s 2 t + 1 , N + j t V ℓ , j − 1 ∑ τ = 2 m 4 m + 1 1 τ ! Φ k , m ( τ ) ( − 1 ) β ℓ + 1 τ + o N − 2 p − 2 m − 4 .
By using the following estimates
δ n m + 2 ( − 1 ) t η t + 1 2 , k t = O N − 2 m − 4 , δ n m + 2 ( − 1 ) t e i π β t N m t = O N − 2 m − 4
from [78] and [65], respectively, and the fact that V ℓ , p − 1 = O N 2 m − 1 , we get
δ n m + 2 F t , m − f t * t = o N − 2 p − 2 m − 4 , | n | ≤ N , N → ∞ .
Consequently, the second term of (127) is o ( N − 2 p − 2 m − 3 ) as N → ∞ .
Now, to estimate the first term of (127), we use the relation
δ N m + 1 F t , m = ∑ t = 0 2 m + 2 2 m + 2 t F N + m + 1 − t , m = ∑ t = m + 2 2 m + 2 2 m + 2 t F N + m + 1 − t , m ,
which follows from Lemma 1. Then, given Lemma 4
δ N m + 1 F t , m = C p , m [ f ] ( − 1 ) N + m + 1 N 2 p + 2 m + 3 ∑ t = m + 2 2 m + 2 ( − 1 ) t 2 m + 2 t m + t − 1 2 m + 1 + O N − 2 p − 2 m − 4 ,
and the identity (see [79,80])
∑ t = m + 2 2 m + 2 ( − 1 ) t 2 m + 2 t m + t − 1 2 m + 1 = 0 ,
we obtain that
δ N m + 1 F t , m t = O N − 2 p − 2 m − 4 .
We can similarly estimate δ N − 1 m + 1 F t , m t and prove (126).
Now, we return to the first two terms on the right-hand side of (124), which we denote by I 1 and I 2 , respectively.
Taking into account Lemma 1, we write the first term of (124) in the form
I 1 = sin π σ ( 2 N − 1 ) x 2 ∑ k = 0 m δ N k F t , m t 1 + e − i π σ x k + 1 1 + e i π σ x k + 1 = sin π σ ( 2 N − 1 ) x 2 ∑ k = 0 m 1 2 2 k + 2 cos 2 k + 2 π σ x 2 ∑ t = 0 k − 1 2 k t + k + 1 F N − t − 1 , m .
By the application of Lemma 4, we obtain
I 1 = C p , m [ f ] ( − 1 ) N + 1 N 2 p + 2 m + 3 sin π σ ( 2 N − 1 ) x 2 × ∑ k = 1 m 1 2 2 k + 2 cos 2 k + 2 π σ x 2 ∑ t = 0 k − 1 ( − 1 ) t 2 k t + k + 1 2 m + t + 1 2 m + 1 + O ( N − 2 p − 2 m − 4 ) .
The application of the following identity
∑ t = 0 k − 1 ( − 1 ) t 2 k t + k + 1 2 m + t + 1 2 m + 1 = ( − 1 ) k + 1 2 m − k k − 1
deduces
I 1 = C p , m [ f ] ( − 1 ) N + 1 N 2 p + 2 m + 3 sin π σ ( 2 N − 1 ) x 2 ∑ k = 0 m − 1 2 m − k − 1 k ( − 1 ) k 2 2 k + 4 cos 2 k + 4 π σ x 2 + O ( N − 2 p − 2 m − 4 ) .
Similarly can be estimated the second term of (124):
I 2 = C p , m [ f ] ( − 1 ) N N 2 p + 2 m + 3 sin π σ ( 2 N + 1 ) x 2 ∑ k = 0 m 2 m − k + 1 k ( − 1 ) k 2 2 k + 2 cos 2 k + 2 π σ x 2 + O ( N − 2 p − 2 m − 4 ) ,
which completes the proof. □
A similar estimate can be proved for even functions on [ − 1 , 1 ] . As we mentioned before, interpolation I N , m 1 [ f ] ( x ) coincides with I N , m 0 [ f ] ( x ) for even functions. Hence, the proof can be performed according to the results of [65] or similar to the proof of Theorem 5. Theorem 1 of [65] is an example of the proof which can be improved specifically for even functions on [ − 1 , 1 ] .
We present the final result by omitting the proof. Let
B j ( f ) : = f ( j ) ( 1 ) + ( − 1 ) j f ( j ) ( − 1 ) , j = 0 , 1 , ⋯ .
Theorem 6.
Let f be an even function and f ( 2 p + 4 m + 2 ) ∈ A C [ − 1 , 1 ] for some p ≥ 0 , m ≥ 1 and
f ( k ) ( − 1 ) = f ( k ) ( 1 ) = 0 , k = 1 , ⋯ , 2 p .
Then, the following estimate holds for | x | < 1 as N → ∞
R N , m 1 [ f ] ( x ) = B 2 p + 1 ( f ) 2 2 p + 4 N 2 p + 2 m + 3 ∑ k = 0 p ( − 1 ) k ( 2 m + 1 ) 2 p − 2 k π 2 m − 2 k − 1 ( 2 p − 2 k ) ! Φ k , m ( 2 m + 1 ) ( − 1 ) × cos π ( N + 1 ) σ x ∑ k = 0 m 2 2 m − k + 1 k − 2 m − k k ( − 1 ) k + N 2 2 k + 1 cos 2 k + 2 π σ x 2 − cos π N σ x ∑ k = 0 m − 1 2 2 m − k − 1 k − 2 m − k − 2 k ( − 1 ) k + N 2 2 k + 3 cos 2 k + 4 π σ x 2 + o N − 2 p − 2 m − 3 .
The next two theorems reveal the behavior of the QP interpolations at the endpoints x = ± 1 .
Theorem 7.
Let f be an odd function and f ( 2 p + 2 m + 2 ) ∈ A C [ − 1 , 1 ] for some p ≥ 0 , m ≥ 1 and
f ( k ) ( − 1 ) = f ( k ) ( 1 ) = 0 , k = 1 , ⋯ , 2 p .
Then, the following estimate holds
lim N → ∞ N 2 p + 1 R N , m 1 [ f ] 1 − h N = A 2 p + 1 ( f ) ℓ 2 p + 1 , m ( h ) , h ≥ 0 ,
where
ℓ j , m ( h ) = − 1 2 ∫ 0 1 ν m , j ( t ) cos π t h + m + 1 / 2 d t + 1 2 ∫ 1 ∞ μ m , j ( t ) cos π t h + m + 1 / 2 d t ,
and functions μ m , j and ν m , j are defined in Lemmas 2 and 5, respectively.
Proof. 
We define f * (see (74)) for α = 2 p + 2 m + 2 and decompose R N , m 1 [ f ] ( x ) as follows
R N , m 1 [ f ] ( x ) = ∑ n = 0 N − 1 ( f n * − F n , m ) sin π σ ( 2 n + 1 ) x 2 + ∑ n = N ∞ f n * sin π σ ( 2 n + 1 ) x 2 .
Then,
R N , m 1 [ f ] 1 − h N = ∑ n = 0 N − 1 ( − 1 ) n ( f n * − F n , m ) cos π ( 2 n + 1 ) h + m + 1 2 N m + ∑ n = N ∞ ( − 1 ) n f n * cos π ( 2 n + 1 ) h + m + 1 2 N m .
Lemmas 2 and 5 lead to
N 2 p + 1 R N , m 1 [ f ] 1 − h N = − A 2 p + 1 N m ∑ n = 0 N − 1 ν m , 2 p + 1 2 n + 1 N m cos π ( 2 n + 1 ) h + m + 1 2 N m + A 2 p + 1 N m ∑ n = N ∞ μ m , 2 p + 1 2 n + 1 N m cos π ( 2 n + 1 ) h + m + 1 2 N m + O 1 N .
We get the required estimate by tending N to infinity and replacing the sums with the corresponding integrals. □
Similar estimate can be proved for even functions on [ − 1 , 1 ] .
Theorem 8.
Let f be an even function and f ( 2 p + 2 m + 2 ) ∈ A C [ − 1 , 1 ] for some p ≥ 0 , m ≥ 1 and
f ( k ) ( − 1 ) = f ( k ) ( 1 ) = 0 , k = 1 , ⋯ , 2 p .
Then, the following estimate holds
lim N → ∞ N 2 p + 1 R N , m 1 [ f ] 1 − h N = B 2 p + 1 ( f ) ℓ 2 p + 1 , m ( h ) , h ≥ 0 ,
where
ℓ j , m ( h ) = − 1 2 ∫ 0 1 ν m , j ( t ) cos π t h + m + 1 / 2 d t + 1 2 ∫ 1 ∞ μ m , j ( t ) cos π t h + m + 1 / 2 d t ,
and functions μ m , j and ν m , j are defined in Lemmas 2 and 5, respectively.
The comparison of Theorems 1, 2, and 5,6 reveals the benefit of the QP interpolations for smooth functions inside the interval of approximation | x | < 1 . According to Theorems 5, 6 the exact convergence rate of the QP interpolations is O ( N − 2 p − 2 m − 3 ) as N → ∞ . For example, when p = 0 , the convergence rate is O ( N − 2 m − 3 ) . Hence, compared to the traditional interpolation, the improvement is of order O ( N − 2 m ) , m ≥ 1 . Compared to the Fourier expansion by the system H 1 , the improvement is of order O ( N − 2 m − 1 ) , m ≥ 1 .
The comparison of Theorems 1, 3, and 7, 8 reveals the convergence properties at the points x = ± 1 . All theorems show the same convergence rate O ( N − 2 p − 1 ) . However, as our experiments show, the QP interpolations for m ≥ 1 are more accurate compared to the Fourier expansions. However, for a fair comparison, we must remember that a higher accuracy requires more smoothness from the function on interval [ − 1 , 1 ] .

6. Expansions and Interpolations by Polyharmonic-Neumann Eigenfunctions

In this section, we describe the derivation of eigenfunctions (see the system H q in (6)) and eigenvalues of the operator L 0 for realization of the corresponding expansions F N q [ f ] ( x ) , interpolations I N q [ f ] ( x ) and QP interpolations I N , m q [ f ] ( x ) . We follow [61] and briefly describe well-known results for completeness.
The eigenfunctions of the problem (3)-(4) corresponding to α ≠ 0 can be expressed as a finite sum of products of trigonometric and hyperbolic functions with real coefficients given as a solution of q × q algebraic eigenproblem. The explicit calculation of the eigenfunctions requires the separation of cases corresponding to even and odd q. When q is even, the eigenfunction takes one of two possible forms ϕ [ i ] which is even if i = 0 and odd if i = 1 :
ϕ [ 0 ] ( x ) = ∑ r = 0 q 2 c r [ 0 ] cos α [ 0 ] x sin π r q cosh α [ 0 ] x cos π r q + ∑ r = 1 q 2 − 1 d r [ 0 ] sin α [ 0 ] x sin π r q sinh α [ 0 ] x cos π r q ,
and
ϕ [ 1 ] ( x ) = ∑ r = 0 q 2 − 1 c r [ 1 ] cos α [ 1 ] x sin π r q sinh α [ 1 ] x cos π r q + ∑ r = 1 q 2 d r [ 1 ] sin α [ 1 ] x sin π r q cosh α [ 1 ] x cos π r q .
In case of odd q:
ϕ [ 0 ] ( x ) = ∑ r = 0 q − 1 2 c r [ 0 ] cos α [ 0 ] x sin π r + 1 2 q cosh α [ 0 ] x cos π r + 1 2 q + ∑ r = 0 q − 3 2 d r [ 0 ] sin α [ 0 ] x sin π r + 1 2 q sinh α [ 0 ] x cos π r + 1 2 q ,
and
ϕ [ 1 ] ( x ) = ∑ r = 0 q − 3 2 c r [ 1 ] cos α [ 1 ] x sin π r + 1 2 q sinh α [ 1 ] x cos π r + 1 2 q + ∑ r = 0 q − 1 2 d r [ 1 ] sin α [ 1 ] x sin π r + 1 2 q cosh α [ 1 ] x cos π r + 1 2 q .
The parameters c r [ i ] , d r [ i ] , and α [ i ] are specified by enforcing the boundary conditions, which results in an algebraic q × q eigenproblem.
The eigenfunctions ϕ n are exponentially close to regular oscillators in compact subsets of ( − 1 , 1 )
ϕ n ( x ) = cos 1 4 ( 2 n + q − 1 ) π x + 1 2 ( n + q − 1 ) π + O ( e − 1 2 γ q ( 1 − | x | ) n π ) , n > > 1 , x ∈ ( − 1 , 1 ) .
The latest can be applied to accelerate the computation of the corresponding expansions.
The n-th eigenvalue α n has the following asymptotic:
α n = 1 4 ( 2 n + q − 1 ) π + O ( e − γ q n π ) , n > > 1 ,
for some γ q > 0 depending only on q. This asymptotic can be used to calculate eigenvalues with any predefined precision. In general, the eigenvalues can be calculated as the roots of the determinants of the mentioned systems. Computation can be carried out extremely easily using iterations. The values α n ≈ 1 / 4 ( 2 n + q − 1 ) π can be used as the starting points of iterations. Having calculated the values α n and functions φ n ( x ) and φ 0 , n ( x ) , we can experiment with the expansions F N q [ f ] .
The traditional interpolation for the system H q and for the grid x k = 2 k / ( 2 N + 1 ) , | k | ≤ N , we seek in the following form:
I N q [ f ] ( x ) = ∑ k = − N N a k ( x ) f ( x k ) ,
where the unknown-functions a k , we determine requiring that the interpolation is exact for the eigenfunctions of H q :
∑ k = − N N φ 0 , n ( x k ) a k ( x ) ≡ φ 0 , n ( x ) , n = 0 , ⋯ , q − 1 ,
and
∑ k = − N N φ n ( x k ) a k ( x ) ≡ φ n ( x ) , n = 1 , ⋯ , 2 N − q + 1 .
Denoting by { M n , k } , n = 0 , ⋯ , 2 N , k = − N , ⋯ , N the matrix of the system, we can write I N q [ f ] ( x ) as follows
a k ( x ) = ∑ n = 0 q − 1 M k , n − 1 φ 0 , n ( x ) + ∑ n = 1 2 N − q + 1 M k , n − 1 φ n ( x ) ,
and
I N q [ f ] ( x ) = ∑ n = 0 q − 1 φ 0 , n ( x ) ∑ k = − N N f ( x k ) M k , n − 1 + ∑ n = 1 2 N − q + 1 φ n ( x ) ∑ k = − N N f ( x k ) M k , n − 1 .
Again, by denoting
f ˇ 0 , n q = ∑ k = − N N f ( x k ) M k , n − 1 , n = 0 , ⋯ , q − 1 ,
and
f ˇ n q = ∑ k = − N N f ( x k ) M k , n − 1 , n = 1 , ⋯ , 2 N − q + 1 ,
we can write
I N q [ f ] ( x ) = ∑ n = 0 q − 1 f ˇ 0 , n q φ 0 , n ( x ) + ∑ n = 1 2 N − q + 1 f ˇ n q φ n ( x ) .
By the same procedure, we derive the corresponding QP interpolations for the system H q and for the grid x k = k / N , | k | ≤ N that includes also the endpoints. Let us denote it as I N , m q [ f ] and seek in the form:
I N , m q [ f ] ( x ) = ∑ k = − N N a k ( x ) f ( x k ) ,
where the unknown functions a k , we find assuming that I N , m q [ f ] is exact for φ 0 , n ( σ x ) and φ n ( σ x ) :
∑ k = − N N a k ( x ) φ 0 , n ( σ x k ) ≡ φ 0 , n ( σ x ) , n = 0 , ⋯ , q − 1 ,
and
∑ k = − N N a k ( x ) φ n ( σ x k ) ≡ φ n ( σ x ) , n = 1 , ⋯ , 2 N − q + 1 .
Denoting by { P n , k } , n = 0 , ⋯ , 2 N , k = − N , ⋯ , N the matrix of the system, we can write I N , m q [ f ] ( x ) as follows
a k ( x ) = ∑ n = 0 q − 1 P k , n − 1 φ 0 , n ( σ x ) + ∑ n = 1 2 N − q + 1 P k , n − 1 φ n ( σ x ) ,
and
I N , m q [ f ] ( x ) = ∑ n = 0 q − 1 φ 0 , n ( σ x ) ∑ k = − N N f ( x k ) P k , n − 1 + ∑ n = 1 2 N − q + 1 φ n ( σ x ) ∑ k = − N N f ( x k ) P k , n − 1 .
Again, by denoting
f ˇ 0 , { n , m } q = ∑ k = − N N f ( x k ) P k , n − 1 , n = 0 , ⋯ , q − 1 ,
and
f ˇ n , m q = ∑ k = − N N f ( x k ) P k , n − 1 , n = 1 , ⋯ , 2 N − q + 1 ,
we can write
I N , m q [ f ] ( x ) = ∑ n = 0 q − 1 f ˇ 0 , { n , m } q φ 0 , n ( σ x ) + ∑ n = 1 2 N − q + 1 f ˇ n , m q φ n ( σ x ) .
We don’t have convergence theory for the interpolations I N q and I N , m q , when q > 1 . However, in the next section, our experiments show that overall conclusions are the same as for q = 1 .

7. The Results of Numerical Experiments and Discussions

In this section, we compare the behaviors of expansions and interpolations based on numerical experiments. Let
f ( x ) = 1 11 / 10 + x ,
which we use in the experiments. This is a non-periodic function (in the sense that 2-periodic extension on R is not continuous), and although infinitely differentiable on [ − 1 , 1 ] , its derivatives are very large around x = − 1 .
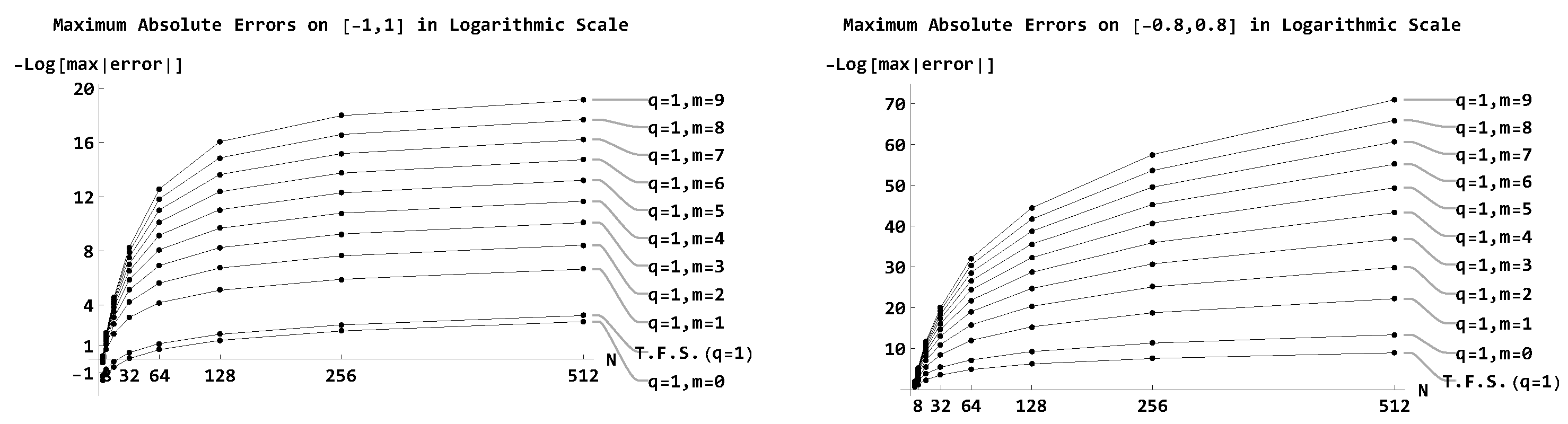
Let us start with the results for the system H 1 , known as the modified Fourier basis/system. Figure 1 presents the maximums of the absolute errors in the logarithmic scale on different intervals. The left figure deals with the entire [ − 1 , 1 ] interval, and the right one shows the errors away from the endpoints on the interval [ − 0.8 , 0.8 ] . The "T.F.S." stands for the truncated Fourier series F N q [ f ] (see (7)). The value m = 0 corresponds to the traditional interpolation based on H 1 (see (168) with q = 1 ).
The left part of Figure 1 confirms our previous statement that although all expansions and interpolations have the same convergence rate on [ − 1 , 1 ] , the QP interpolations are better due to a smaller constant of the leading term of the asymptotic error. The traditional interpolations are less accurate than the expansions on [ − 1 , 1 ] , which was expected as the expansions are the best in the L 2 [ − 1 , 1 ] norm. However, the QP interpolations starting from m = 1 outperform expansions and traditional interpolations. This is also one of the benefits of the QP interpolations.
The right part of Figure 1 confirms that interpolations have asymptotically better convergence rates than Fourier expansions, and the accuracy is higher as larger is the value of parameter m. The traditional interpolations corresponding to m = 0 have a better convergence rate than the expansions on [ − 0.8 , 0.8 ] .
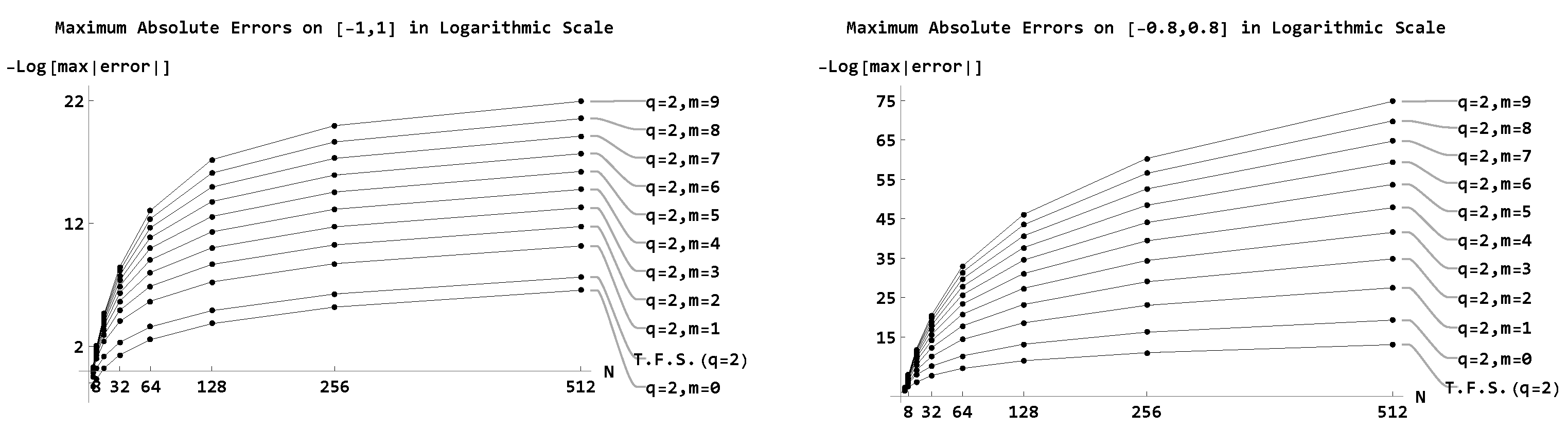
Figure 2 demonstartes similar results for the expansions and interpolations for the system H 2 corresponding to q = 2 . Interpolations are more accurate away from the endpoints x = ± 1 than the expansions (T.F.S (q=2)) and interpolations for q = 1 . On the entire interval, the expansions are more accurate than the traditional interpolation but less accurate than the QP interpolations for the system H 2 .
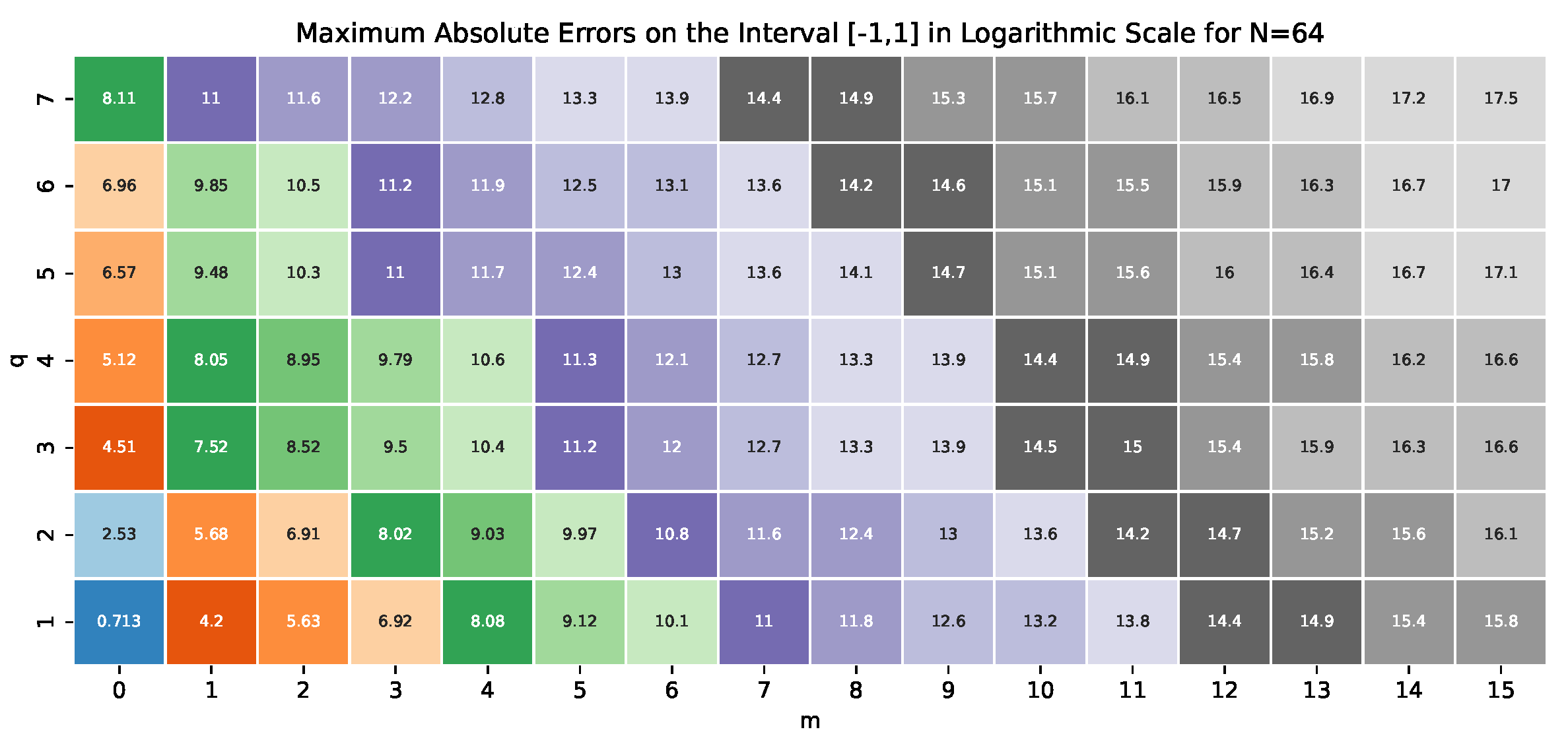
The same behavior was observed for the expansions and interpolations for other systems H q . We can conclude that by increasing the value of parameter q, we increase the convergence rate by O ( N ) away from the endpoints x = ± 1 . On the entire interval, [ − 1 , 1 ] , the convergence rate is O ( N − 1 ) , but the constant at the leading term of the asymptotic error is decreasing while increasing the values of q and m. In the following two figures, we show the maximum absolute errors on [ − 0.8 , 0.8 ] and [ − 1 , 1 ] in the logarithmic scale to reveal these dynamics. We used a moderate number of coefficients N = 64 , the values of 1 ≤ q ≤ 7 and 0 ≤ m ≤ 15 . The value m = 0 corresponds to the traditional interpolation.
Preprints 119841 g004
Figure 4. The maximum of the absolute errors of interpolations on interval [ − 0.8 , 0.8 ] in the logarithmic scale. The value m = 0 corresponds to the traditional interpolation. The values m ≥ 1 correspond to the QP interpolations. The value q = 1 corresponds to the QP interpolations by the modified Fourier system H 1 with the explicit implementation (61) where N = 64 .
Figure 4. The maximum of the absolute errors of interpolations on interval [ − 0.8 , 0.8 ] in the logarithmic scale. The value m = 0 corresponds to the traditional interpolation. The values m ≥ 1 correspond to the QP interpolations. The value q = 1 corresponds to the QP interpolations by the modified Fourier system H 1 with the explicit implementation (61) where N = 64 .
Preprints 119841 g004
Both figures show that the accuracy of the QP interpolation is proportional to q + 2 m . This means that the convergence properties of the QP interpolations can be improved by increasing either q or m. However, calculating the eigenvalues for large q is connected with more computational difficulties than increasing the value of m for the fixed value of q. It is possible to tend m do infinity slowly as log ( N ) . The latest will provide convergence at an exponential rate for infinitely differentiable functions. For example, q = 7 and m = 8 provides the same accuracy as q = 1 and m = 12 on [ − 0.8 , 0.8 ] . It is worth noting that the eigenvalues of the systems H 1 and H 2 are known explicitly and can be calculated with high accuracy.
The QP interpolations (except q = 1 ) don’t have explicit forms. They require the calculation of the inverses of matrices M in (164) with a high accuracy. Hence, it is essential to reveal the condition numbers of the matrices for different q and m. Figure 5 shows the numbers. The condition number for q = 4 and m = 7 is approximately the same as for q = 1 and m = 9 . Moreover, in the case of the modified Fourier basis corresponding to q = 1 , the realization is explicit as the corresponding matrix is a Vandermonde type. There are efficient algorithms ([81]) for calculating the inverses of the Vandermonde matrices with high accuracy.

8. Conclusion

We analyzed the convergence of the quasi-periodic (QP) interpolations, which are exact for the eigenfunctions of the systems H q , q ≥ 1 , composed of the polyharmonic-Neumann eigenfunctions. We proved convergence theorems for q = 1 , showing better convergence of the QP interpolations compared to the corresponding Fourier expansions and traditional interpolations. The QP interpolations depend on a parameter m ≥ 1 that, together with parameter q, determines the convergence rate of order O ( N − 2 m − 3 − q ) as N → ∞ , where N is the number of the eigenfunctions involved in the interpolation. We proved it for q = 1 and assumed for q > 1 based on the results of numerical experiments. The theoretical convergence rate and numerical experiments demonstrate that the accuracy of the QP interpolations can be improved by increasing the value either of q or m. The latest is more feasible as calculating the eigenfunctions for large values of q is connected with computational problems. The best choice can be the utilization of the QP interpolations based on the system H 1 by slowly tending parameter m to infinity. In this case, the eigenfunctions are known explicitly, and the interpolations can be implemented by effectively calculating the inverse of the Vandermonde matrices.

Author Contributions

Conceptualization, Arnak Poghosyan; Investigation, Arnak Poghosyan, Lusine Poghosyan and Rafayel Barkhudaryan; Methodology, Arnak Poghosyan, Lusine Poghosyan and Rafayel Barkhudaryan; Project administration, Arnak Poghosyan; Software, Arnak Poghosyan and Lusine Poghosyan; Supervision, Arnak Poghosyan; Validation, Arnak Poghosyan and Lusine Poghosyan; Writing – original draft, Arnak Poghosyan, Lusine Poghosyan and Rafayel Barkhudaryan; Writing – review & editing, Arnak Poghosyan, Lusine Poghosyan and Rafayel Barkhudaryan.

Funding

This research received no external funding.

Data Availability Statement

No external research data were used. Everyone can simulate data used in this research with any available software like Python, Matlab, Wolfram Mathematica, etc.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Levin, D. Development of non-linear transformations of improving convergence of sequences. Internat. J. Comput. Math. 1973, 3, 371–388. [Google Scholar] [CrossRef]
  2. Majda, A.; McDonough, J.; Osher, S. The Fourier method for nonsmooth initial data. Math. Comp. 1978, 32, 1041–1081. [Google Scholar] [CrossRef]
  3. Wimp, J. Sequence transformations and their applications; Vol. 154, Mathematics in Science and Engineering, Academic Press: New York, 1981; pp.xix+257. [Google Scholar]
  4. Smith, D.A.; Ford, W.F. Numerical comparisons of nonlinear convergence accelerators. Math. Comp. 1982, 38, 481–499. [Google Scholar] [CrossRef]
  5. Biringen, S.; Kao, K.H. On the application of pseudospectral FFT techniques to nonperiodic problems. Internat. J. Numer. Methods Fluids 1989, 9, 1235–1267. [Google Scholar] [CrossRef]
  6. Boyd, J.P. Sum-accelerated pseudospectral methods: the Euler-accelerated sinc algorithm. Appl. Numer. Math. 1991, 7, 287–296. [Google Scholar] [CrossRef]
  7. Vandeven, H. Family of spectral filters for discontinuous problems. J. Sci. Comput. 1991, 6, 159–192. [Google Scholar] [CrossRef]
  8. Brezinski, C.; Redivo Z., M. Extrapolation methods; Vol. 2, Studies in Computational Mathematics, North-Holland Publishing Co.: Amsterdam, 1991; pp.x+464. [Google Scholar]
  9. Gottlieb, D.; Shu, C.W.; Solomonoff, A.; Vandeven, H. On the Gibbs phenomenon. I. Recovering exponential accuracy from the Fourier partial sum of a nonperiodic analytic function. J. Comput. Appl. Math. 1992, 43, 81–98. [Google Scholar] [CrossRef]
  10. Gottlieb, D. Issues in the application of high order schemes. In Algorithmic trends in computational fluid dynamics (1991); ICASE/NASA LaRC Ser., Springer: New York, 1993; pp. 195–218. [Google Scholar]
  11. Homeier, H.H.H. Some Applications of Nonlinear Convergence Accelerators. IJQC 1993, 45, 545–562. [Google Scholar] [CrossRef]
  12. Boyd, J.P. A lag-averaged generalization of Euler’s method for accelerating series. Appl. Math. Comput. 1995, 72, 143–166. [Google Scholar] [CrossRef]
  13. Dillmann, A.; Grabitz, G. On a method to evaluate Fourier-Bessel series with poor convergence properties and its application to linearized supersonic free jet flow. Quart. Appl. Math. 1995, 53, 335–352. [Google Scholar] [CrossRef]
  14. Gottlieb, D.; Shu, C.W. On the Gibbs phenomenon. IV. Recovering exponential accuracy in a subinterval from a Gegenbauer partial sum of a piecewise analytic function. Math. Comp. 1995, 64, 1081–1095. [Google Scholar]
  15. Gottlieb, D.; Shu, C.W. On the Gibbs phenomenon. V. Recovering exponential accuracy from collocation point values of a piecewise analytic function. Numer. Math. 1995, 71, 511–526. [Google Scholar] [CrossRef]
  16. Gottlieb, D.; Shu, C.W. On the Gibbs phenomenon. III. Recovering exponential accuracy in a sub-interval from a spectral partial sum of a piecewise analytic function. SIAM J. Numer. Anal. 1996, 33, 280–290. [Google Scholar] [CrossRef]
  17. Vozovoi, L.; Israeli, M.; Averbuch, A. Analysis and application of Fourier-Gegenbauer method to stiff differential equations. SIAM J. Numer. Anal. 1996, 33, 1844–1863. [Google Scholar] [CrossRef]
  18. Oleksy, C. A convergence acceleration method of Fourier series. Comput. Phys. Comm. 1996, 96, 17–26. [Google Scholar] [CrossRef]
  19. Geer, J.; Banerjee, N.S. Exponentially accurate approximations to piece-wise smooth periodic functions. J. Sci. Comput. 1997, 12, 253–287. [Google Scholar] [CrossRef]
  20. Gelb, A.; Gottlieb, D. The resolution of the Gibbs phenomenon for ’spliced’ functions in one and two dimensions. Computers Math. Applic. 1997, 33, 35–58. [Google Scholar] [CrossRef]
  21. Gottlieb, D.; Shu, C.W. On the Gibbs phenomenon and its resolution. SIAM Rev. 1997, 39, 644–668. [Google Scholar] [CrossRef]
  22. Vozovoi, L.; Weill, A.; Israeli, M. Spectrally accurate solution of nonperiodic differential equations by the Fourier-Gegenbauer method. SIAM J. Numer. Anal. 1997, 34, 1451–1471. [Google Scholar] [CrossRef]
  23. Boyd, J.P. Two comments on filtering (artificial viscosity) for Chebyshev and Legendre spectral and spectral element methods: preserving boundary conditions and interpretation of the filter as a diffusion. J. Comput. Phys. 1998, 143, 283–288. [Google Scholar] [CrossRef]
  24. Kvernadze, G. Determination of the jumps of a bounded function by its Fourier series. J. Approx. Theory 1998, 92, 167–190. [Google Scholar] [CrossRef]
  25. Marshall, S.L. Convergence acceleration of Fourier series by analytical and numerical application of Poisson’s formula. J. Phys. A 1998, 31, 2691–2704. [Google Scholar] [CrossRef]
  26. Gelb, A.; Tadmor, E. Detection of edges in spectral data. Appl. Comput. Harmon. Anal. 1999, 7, 101–135. [Google Scholar] [CrossRef]
  27. Gelb, A.; Tadmor, E. Detection of edges in spectral data. II. Nonlinear enhancement. SIAM J. Numer. Anal. 2000, 38, 1389–1408. [Google Scholar] [CrossRef]
  28. Kvernadze, G.; Hagstrom, T.; Shapiro, H. Detecting the singularities of a function of Vp class by its integrated Fourier series. Comput. Math. Appl. 2000, 39, 25–43. [Google Scholar] [CrossRef]
  29. Gelb, A. A hybrid approach to spectral reconstruction of piecewise smooth functions. J. Sci. Comput. 2000, 15, 293–322. [Google Scholar] [CrossRef]
  30. Mhaskar, H.N.; Prestin, J. On the detection of singularities of a periodic function. Adv. Comput. Math. 2000, 12, 95–131. [Google Scholar] [CrossRef]
  31. Wright, R.K. A robust method for accurately representing non-periodic functions given Fourier coefficient information. J. Comput. and Appl. Math. 2002, 140, 837–848. [Google Scholar] [CrossRef]
  32. Tadmor, E.; Tanner, J. Adaptive mollifiers for high resolution recovery of piecewise smooth data from its spectral information. Found. Comput. Math. 2002, 2, 155–189. [Google Scholar] [CrossRef]
  33. Gelb, A.; Tadmor, E. Spectral reconstruction of piecewise smooth functions from their discrete data. Math. Model. Numer. Anal. 2002, 36, 155–175. [Google Scholar] [CrossRef]
  34. Jung, J.H.; Shizgal, B.D. Generalization of the inverse polynomial reconstruction method in the resolution of the Gibbs phenomenon. J. Comput. Appl. Math. 2004, 172, 131–151. [Google Scholar] [CrossRef]
  35. Wright, R.K. Local spline approximation of discontinuous functions and location of discontinuities, given low-order Fourier coefficient information. J. Comput. and Appl. Math. 2004, 164-165, 783–795. [Google Scholar] [CrossRef]
  36. Archibald, R.; Gelb, A.; Yoon, J. Polynomial fitting for edge detection in irregularly sampled signals and images. SIAM J. Numer. Anal. 2005, 43, 259–279. [Google Scholar] [CrossRef]
  37. Jung, J.H.; Shizgal, B.D. Inverse polynomial reconstruction of two dimensional Fourier images. J. Sci. Comput. 2005, 25, 367–399. [Google Scholar] [CrossRef]
  38. Tadmor, E.; Tanner, J. Adaptive filters for piecewise smooth spectral data. IMA J. Numer. Anal. 2005, 25, 635–647. [Google Scholar] [CrossRef]
  39. Nersessian, A.; Poghosyan, A. Accelerating the convergence of trigonometric series. Cent. Eur. J. Math. 2006, 4, 435–448. [Google Scholar] [CrossRef]
  40. Jung, J.H.; Shizgal, B.D. On the numerical convergence with the inverse polynomial reconstruction method for the resolution of the Gibbs phenomenon. J. Comput. Phys. 2007, 224, 477–488. [Google Scholar] [CrossRef]
  41. Paszkowski, S. Convergence acceleration of orthogonal series. Numer. Algorithms 2008, 47, 35–62. [Google Scholar] [CrossRef]
  42. Boyd, J.P. Large-degree asymptotics and exponential asymptotics for Fourier, Chebyshev and Hermite coefficients and Fourier transforms. J. Engrg. Math. 2009, 63, 355–399. [Google Scholar] [CrossRef]
  43. Adcock, B. Gibbs phenomenon and its removal for a class of orthogonal expansions. BIT 2011, 51, 7–41. [Google Scholar] [CrossRef]
  44. Poghosyan, A. Asymptotic behavior of the Eckhoff approximation in bivariate case. Anal. Theory Appl. 2012, 28, 329–362. [Google Scholar]
  45. Poghosyan, A. On an auto-correction phenomenon of the Eckhoff interpolation. Aust. J. Math. Anal. Appl. 2012, 9, 1–31. [Google Scholar]
  46. Poghosyan, A. On an auto-correction phenomenon of the Krylov-Gottlieb-Eckhoff method. IMA J. Numer. Anal. 2011, 31, 512–527. [Google Scholar] [CrossRef]
  47. Poghosyan, A. On a convergence of the Fourier-Pade approximation. Armen. J. Math. 2012, 4, 49–79. [Google Scholar]
  48. Nersessian, A.; Poghosyan, A. On a rational linear approximation of Fourier series for smooth functions. J. Sci. Comput. 2006, 26, 111–125. [Google Scholar] [CrossRef]
  49. Nersessian, A.; Poghosyan, A. Accelerating the convergence of trigonometric series. Cent. Eur. J. Math. 2006, 4, 435–448. [Google Scholar] [CrossRef]
  50. Poghosyan, A. On a convergence of the rational-trigonometric-polynomial approximations realized by the roots of the Laguerre polynomials. Journal of Contemporary Mathematical Analysis 2013, 48, 339–347. [Google Scholar] [CrossRef]
  51. Poghosyan, A. On a fast convergence of the rational-trigonometric-polynomial interpolation. Advances in Numerical Analysis 2013. [Google Scholar] [CrossRef]
  52. Poghosyan, A. Asymptotic behavior of the Eckhoff method for convergence acceleration of trigonometric interpolation. Anal. Theory Appl. 2010, 26, 236–260. [Google Scholar] [CrossRef]
  53. Barkhudaryan, A.; Barkhudaryan, R.; Poghosyan, A. Asymptotic behavior of Eckhoff’s method for Fourier series convergence acceleration. Anal. Theory Appl. 2007, 23, 228–242. [Google Scholar] [CrossRef]
  54. Poghosyan, A. On a convergence of the Fourier-Pade interpolation. Armen. J. Math. 2013, 5, 1–25. [Google Scholar]
  55. Nersessian, A. On Some Fast Implementations of Fourier Interpolation. Operator Theory and Harmonic Analysis; Karapetyants, A.N.; Kravchenko, V.V.; Liflyand, E.; Malonek, H.R., Eds. Springer International Publishing, 2021, pp. 463–477.
  56. Nersessian, A. A fast method for numerical realization of Fourier tools. IntechOpen 2020. [Google Scholar] [CrossRef]
  57. Nersessian, A. On an over-convergence phenomenon for Fourier series. Basic approach. Armen. J. Math. 2018, 10, 1–22. [Google Scholar] [CrossRef]
  58. Nersessian, A. Acceleration of Convergence of Fourier Series Using the Phenomenon of Over-Convergence. Armenian Journal of Mathematics 2022, 14, 1–31. [Google Scholar] [CrossRef]
  59. Iserles, A.; Nørsett, S., P. From high oscillation to rapid approximation. I. Modified Fourier expansions. IMA J. Numer. Anal. 2008, 28, 862–887. [Google Scholar] [CrossRef]
  60. Huybrechs, D.; Iserles, A.; Nørsett, S., P. From high oscillation to rapid approximation IV: accelerating convergence. IMA J. Numer. Anal. 2011, 31, 442–468. [Google Scholar] [CrossRef]
  61. Adcock, B. Modified Fourier expansions: theory, construction and applications. PhD thesis, Trinity Hall, University of Cambridge, 2010.
  62. Nersessian, A.; Oganesyan, N. Quasiperiodic interpolation. Reports of NAS RA 2001, 101, 115–121. [Google Scholar]
  63. Poghosyan, L.; Poghosyan, A. Asymptotic estimates for the quasi-periodic interpolations. Armen. J. Math. 2013, 5, 34–57. [Google Scholar]
  64. Poghosyan, L. On L2-convergence of the quasi-periodic interpolation. Dokl. Nats. Akad. Nauk Armen. 2013, 113, 240–247. [Google Scholar]
  65. Poghosyan, L.; Poghosyan, A. On the pointwise convergence of a quasiperiodic trigonometric interpolation. Izv. Nats. Akad. Nauk Armenii Mat. 2014, 49, 68–80. [Google Scholar]
  66. Poghosyan, A.; Poghosyan, L. On a pointwise convergence of quasi-periodic-rational trigonometric interpolation. Int. J. Anal. 2014, 2014, 1–10. [Google Scholar] [CrossRef]
  67. Poghosyan, L. Convergence acceleration of quasi-periodic and quasi-periodic-rational interpolations by polynomial corrections. Armen. J. Math. 2013, 5, 123–138. [Google Scholar]
  68. Adcock, B.; Iserles, A.; Nørsett, S., P. From high oscillation to rapid approximation II: expansions in Birkhoff series. IMA J. Numer. Anal. 2012, 32, 105–140. [Google Scholar] [CrossRef]
  69. Levitan, B.M.; Sargsjan, I.S. Introduction to spectral theory: selfadjoint ordinary differential operators; Vol. Vol. 39, Translations of Mathematical Monographs, American Mathematical Society, Providence, RI, 1975; pp. xi+525. Translated from the Russian by Amiel Feinstein.
  70. Krein, M.G. On a special class of differential operators. Doklady AN USSR 1935, 2, 345–349. [Google Scholar]
  71. Iserles, A.; Nørsett, S., P. From high oscillation to rapid approximation. III. Multivariate expansions. IMA J. Numer. Anal. 2009, 29, 882–916. [Google Scholar] [CrossRef]
  72. Adcock, B. Univariate modified Fourier methods for second order boundary value problems. BIT 2009, 49, 249–280. [Google Scholar] [CrossRef]
  73. Olver, S. On the convergence rate of a modified Fourier series. Math. Comp. 2009, 78, 1629–1645. [Google Scholar] [CrossRef]
  74. Adcock, B. Multivariate modified Fourier series and application to boundary value problems. Numer. Math. 2010, 115, 511–552. [Google Scholar] [CrossRef]
  75. Adcock, B. Convergence acceleration of modified Fourier series in one or more dimensions. Math. Comp. 2011, 80, 225–261. [Google Scholar] [CrossRef]
  76. Poghosyan, A.; Bakaryan, T. On interpolation with respect to a modified trigonometric system. Izv. Nats. Akad. Nauk Armenii Mat. 2018, 53, 72–83. [Google Scholar] [CrossRef]
  77. Zygmund, A. Trigonometric Series. Vol. 1,2; Cambridge Univ. Press, 1959.
  78. Poghosyan, A. Asymptotic behavior of the Krylov-Lanczos interpolation. Anal. Appl. (Singap.) 2009, 7, 199–211. [Google Scholar] [CrossRef]
  79. Riordan, J. Combinatorial identities; John Wiley & Sons Inc.: New York, 1968; pp.xiii+256. [Google Scholar]
  80. Riordan, J. An introduction to combinatorial analysis; Princeton University Press: Princeton, N.J, 1980. [Google Scholar]
  81. Åke Björck. ; Pereyra, V. Solution of Vandermonde Systems of Equations. Mathematics of Computation 1970, 24, 893–903. [Google Scholar] [CrossRef]
Preprints 119841 g001
Figure 1. The errors of expansions and interpolations for the system H 1 corresponding to q = 1 .
Figure 1. The errors of expansions and interpolations for the system H 1 corresponding to q = 1 .
Preprints 119841 g001
Preprints 119841 g002
Figure 2. The errors of expansions and interpolations for the system H 2 corresponding to q = 2 .
Figure 2. The errors of expansions and interpolations for the system H 2 corresponding to q = 2 .
Preprints 119841 g002
Preprints 119841 g003
Figure 3. The maximum of the absolute errors of interpolations on interval [ − 1 , 1 ] in the logarithmic scale. The value m = 0 corresponds to the traditional interpolation. The values m ≥ 1 correspond to the QP interpolations. The value q = 1 corresponds to the QP interpolations by the modified Fourier system H 1 with the explicit implementation (61) where N = 64 .
Figure 3. The maximum of the absolute errors of interpolations on interval [ − 1 , 1 ] in the logarithmic scale. The value m = 0 corresponds to the traditional interpolation. The values m ≥ 1 correspond to the QP interpolations. The value q = 1 corresponds to the QP interpolations by the modified Fourier system H 1 with the explicit implementation (61) where N = 64 .
Preprints 119841 g003
Preprints 119841 g005
Figure 5. The condition numbers of the matrices { P n , k } in Equation (172) for N = 64 in the logarithmic scale.
Figure 5. The condition numbers of the matrices { P n , k } in Equation (172) for N = 64 in the logarithmic scale.
Preprints 119841 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated