Prerpints.org logo
Preprint
Article

Enhancing Short- and Medium-term Solar Power Generation Forecasting Based on Prophet and Gate Recurrent Unit

Altmetrics

Downloads

58

Views

24

Comments

0

This version is not peer-reviewed

Submitted:

30 September 2024

Posted:

03 October 2024

You are already at the latest version

Alerts
Abstract
Accurate solar power forecasting is pivotal for the effective planning, management, and operation of power systems, ensuring a sustainable energy supply for consumers while optimizing the integration of renewable energy sources and the functioning of electricity markets. Recent advancements have focused on developing predictive models that offer precise daily forecasts for solar power generation, which are critical for power usage planning and production efficiency. These models typically leverage a diverse range of data inputs, including solar power metrics and meteorological variables such as temperature, humidity, precipitation, solar radiation, and wind speed—factors that significantly influence solar power generation due to their weather-dependent nature. This study introduces a novel hybrid forecasting model that synergizes the capabilities of the Prophet model and Gated Recurrent Units (GRU), leveraging their respective strengths to enhance predictive performance. The proposed model is rigorously evaluated across short-term (2 days, 7 days) and medium-term (15 days, 30 days) forecasting horizons. Experimental results demonstrate that the hybrid model significantly outperforms the existing models, delivering superior accuracy in solar power generation forecasts.
Keywords: 
Subject: Environmental and Earth Sciences  -   Environmental Science

1. Introduction

The global focus on renewable energy sources has intensified in response to energy crises, air pollution, and concerns over global warming. It is projected that renewable energy will contribute to approximately 40% of global energy consumption by 2030 [1]. Among renewable energy technologies, solar photovoltaic (PV) power generation stands out for its direct conversion of solar power into electrical energy using solar modules. This method is highly regarded for its environmental benefits, including minimal air, water, and noise pollution, adaptability to local conditions, low installation costs, and potential for grid integration [2,3].
Recent data underscores the rapid growth of solar power capacity worldwide. According to Rethink Energy, global installations in the first nine months of 2022 increased by 54GW, reaching a total installed capacity of approximately 142.5GW, with projections indicating an annual installation capacity of 222GW [4]. Similarly, in the European Union, new PV installations totaled 41.4GW in 2022, bringing the cumulative installed capacity to 208.9GW by the year's end [5]. China reported a cumulative installed capacity of 396.261GW by the end of 2022, following a significant annual installation of 87.41GW [6]. In Korea, the implementation of the 'Renewable Energy 3020 Implementation Plan' has substantially increased solar power capacity from 1,362MW in 2017 to 4,658MW in 2020 [7].
Solar power forecasting has been a focal point of research, particularly in regions with established solar observation infrastructure like Europe and the United States. Early efforts in solar power forecasting leveraged advanced technologies, equipment, and extensive data availability. As global solar power installations continue to expand, so does the advancement in solar power forecasting methodologies. The primary objective of this research is to enhance prediction accuracy through developing and synthesizing diverse forecasting models, addressing economic considerations and enhancing overall performance [8,9].
Solar power forecasting methods encompass a spectrum of approaches, including traditional physics and statistics-based models, new machine learning techniques, optimization algorithms, deep learning, and hybrid models [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34]. These methods cater to different forecasting timeframes: short-term (hours to weeks), medium-term (weeks to months), and long-term (months to years) [10,11,12].
For short-term forecasting, methods such as exponential smoothing, ARIMA, k-nearest neighbors (KNN), decision trees, support vector machines (SVM), particle swarm optimization (PSO), and artificial intelligence (AI) have been applied [13,14,15,16,17,18,19]. Medium-term forecasting expands into weeks and months, incorporating variables like weather data, events, and economic indicators, utilizing models such as linear regression, neural networks, recurrent neural networks (RNN), long short-term memory (LSTM), convolutional neural networks (CNN), among others [20,21,22,23,24,25]. Long-term forecasting, spanning months to years, necessitates more comprehensive consideration of system elements and utilizes algorithms like time series analysis, ARIMA, and ensemble methods [26,27,28].
Each forecasting algorithm possesses distinct strengths and limitations. For instance, ARIMA excels in short-term predictions but struggles with seasonal and non-stationary data, while LSTM is suitable for capturing long-term dependencies but demands significant computational resources [26,27,28]. Hybrid models, combining multiple algorithms based on data characteristics and forecasting objectives, have emerged as a promising approach in solar power forecasting [29,30,31,32,33,34]. By integrating the strengths of different models, hybrid approaches aim to enhance prediction accuracy and robustness.
This study proposes a hybrid forecasting method for medium- and short-term solar power generation, combining GRU for long-term forecasting and Prophet for seasonality and event handling. The methodology includes data collection, preprocessing, and experimentation with GRU using multivariate datasets derived from Prophet predictions and observed data residuals in 15-minute intervals. We conduct experiments for short-term (2 days and 7 days) and medium-term (15 days and 30 days) power generation predictions.
The structure of this paper is as follows: Section 2 reviews related research on Prophet and GRU models. Section 3 identifies limitations in existing Prophet models and proposes solution methods. Section 4 describes the data collection, the pre-processing method for collected data, the data splitting method for learning and testing, and the proposed method using Prophet and GRU. Section 5 outlines the methodology and presents experimental results. Finally, Section 6 concludes with a discussion of the potential impact of the proposed hybrid approach and future research directions.

2. Related Works

2.1. Prophet Model

The Prophet model, developed by Facebook, is a robust open-source time series forecasting library widely employed across diverse domains including marketing, advertising, demand forecasting, energy prediction, and financial forecasting [35]. It comprises three key components: trend, seasonality, and holidays. The trend component, denoted as g(t), captures the long-term growth or decline in the time series data, allowing the model to adapt to gradual changes over time. The seasonality component, represented by s(t), accounts for periodic variations that occur at regular intervals, such as daily, weekly, or yearly patterns. This enables the model to capture recurring fluctuations in the data. The holidays component, denoted as h(t), incorporates information about one-off events or special occurrences that may impact the time series, such as public holidays, festivals, or significant events. Considering these factors, the model can adjust its forecasts for deviations from regular patterns during specific periods.
The Prophet model's structure is shown as in Equation (1), where y(t) represents the observed value at time t, and ε(t) denotes the error term, capturing any noise or randomness present in the data. Overall, Prophet's flexibility and capability to accommodate various time series patterns make it a highly versatile and effective tool for accurate forecasting in various applications.
y(t) = g(t) + s(t) + h(t) + ε(t)
Figure 1 shows the power generation data of Company W collected from July 1, 2018, to November 30, 2019. In Korea, solar power generation decreases during the winter months, particularly from December to February, due to several factors. Firstly, these months experience shorter daylight hours, reducing the amount of sunlight available for solar panels to convert into electricity. Secondly, the sun's angle is lower during winter, leading to less direct sunlight and lower solar irradiance levels. Weather conditions such as frequent cloud cover and precipitation diminish solar power output. Conversely, solar power generation increases during summer, especially from June to August. During this period, Korea experiences longer daylight hours and higher solar irradiance levels due to the sun being at a higher angle in the sky. Clearer skies and reduced cloud cover also contribute to optimal conditions for solar power production. These seasonal variations in solar power generation in Korea highlight the significant influence of sunlight availability and weather conditions on renewable energy production throughout the year.
Figure 2 and Figure 3 illustrate the prediction outcomes of the Prophet model applied to the training data over one year (July 2018 to June 2019), considering only the holiday effect. These results were obtained through simulations utilizing default parameter values without customization. In Figure 2, the black dots represent the observed data values from July 2018 to June 2019, while the dark blue line represents the model's predicted values from July 2018 to October 2019. The light blue line indicates the uncertainty interval. Notably, the period up to July 2019 demonstrates the in-sample fit, where the model is fitted to the training data. Beyond that point, the out-of-sample forecast is depicted, representing predictions for the test data.
Figure 3 displays the components of the fitted model, including trends, holidays, weekly, and daily variations. In Figure 3, the trend shows a stable trend with little fluctuation every month but has a large error during the forecast period (light blue shadow). The holiday component exhibits intermittent large deviations in development. Daytime indicates that advances occur Monday through Friday and no advances occur on weekends. Finally, the daily component shows that solar power is mainly generated from 8:00 a.m. to 8:00 p.m., which corresponds to solar time, and little solar power is generated during the rest of the time.

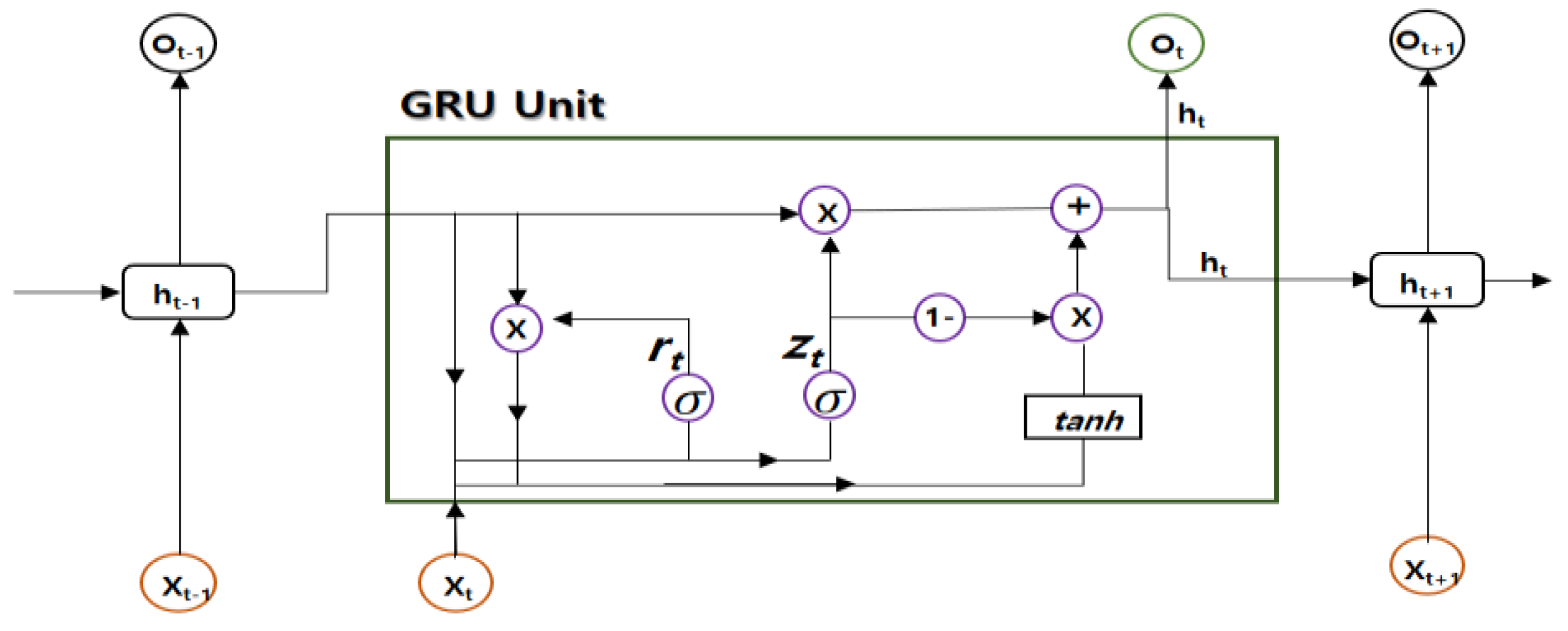
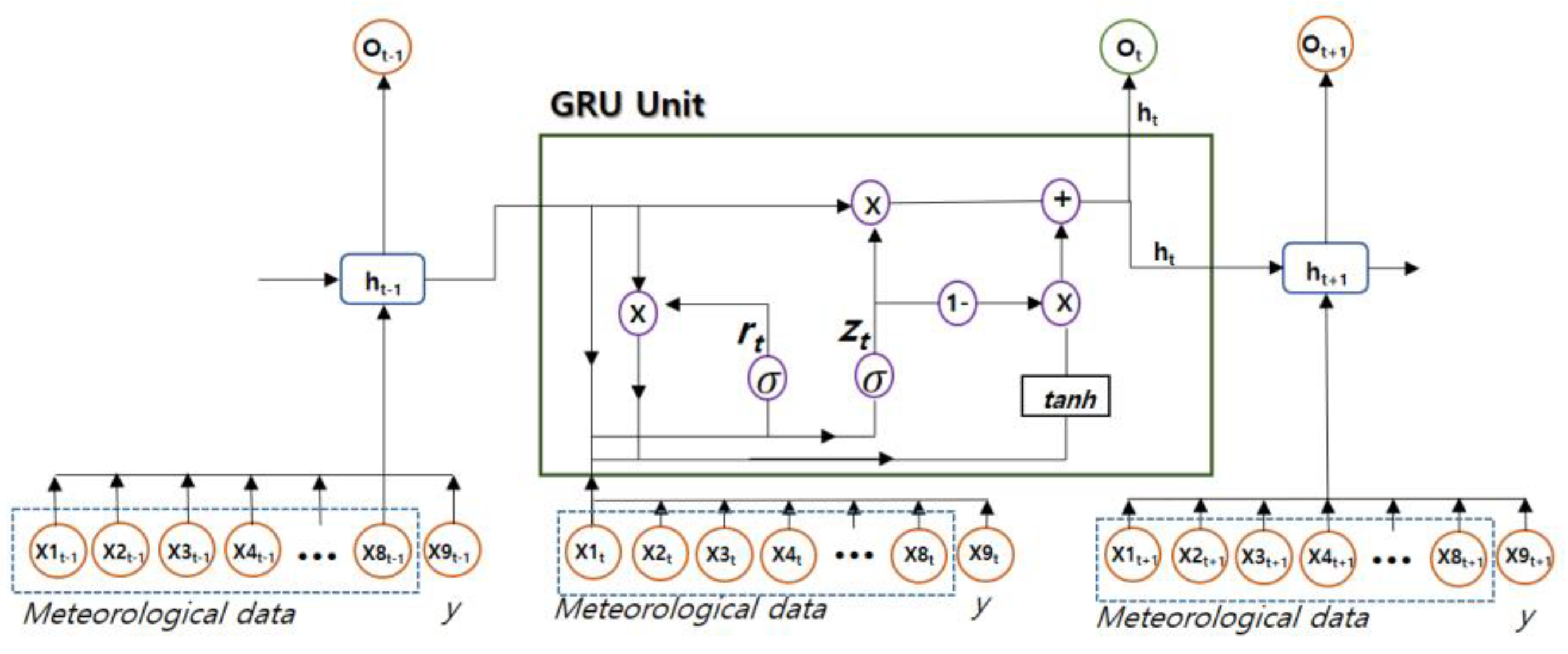
2.2. GRU(Gated Recurrent Unit)

GRU, which stands for Gated Recurrent Unit, is a type of recurrent neural network (RNN) used for processing sequence data [36]. GRU offers similar functionality to LSTM, but with a simpler structure, as depicted in Figure 4.
It addresses the vanishing gradient problem and reduces computational costs while learning long-term dependencies in sequence data. The components of GRU are the update gate, reset gate, and hidden state. Equation (2) represents the formulation of GRU. In this equation,   r t denotes the reset gate, z t represents the update gate, h t is the hidden state, and   x t signifies the current input. W z and   W r are the weights for the update and reset gates, respectively.
z t = σ W z · h t − 1 , x t r t = σ W r · h t − 1 , x t h t ˜ = t a n h W · r t ∗ h t − 1 , x t h t = 1 − z t ∗ h t − 1 + z t ∗ h t
The update gate ( z t ) determines how much information to retain based on the current input and the previous hidden state. The reset gate ( r t ) determines how much past information to forget based on the current input and the previous hidden state. The hidden state ( h t ) is computed based on the previous hidden state and the current input, generating a new hidden state. GRU's ability to manage long-term dependencies, handle the vanishing gradient problem, and reduce computational overhead makes it a valuable model for processing sequential data.

3. Problem Definition and Solution Methods

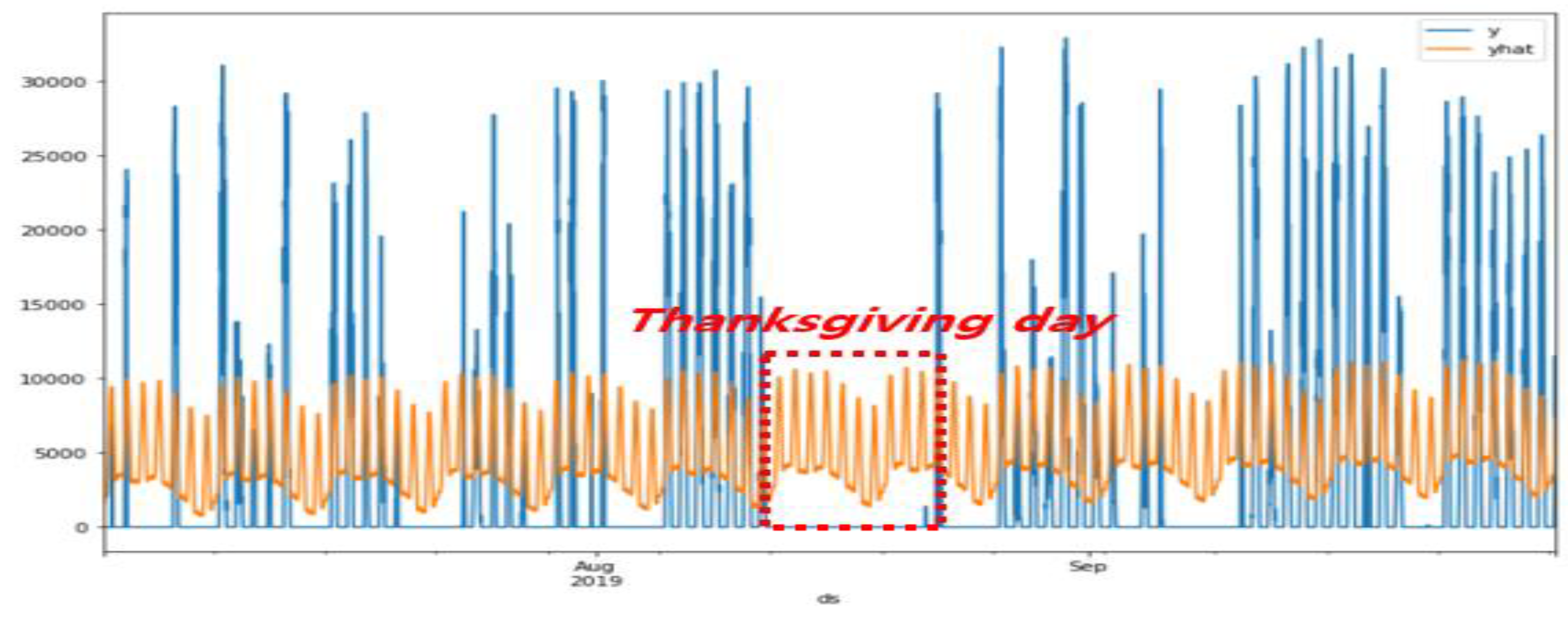
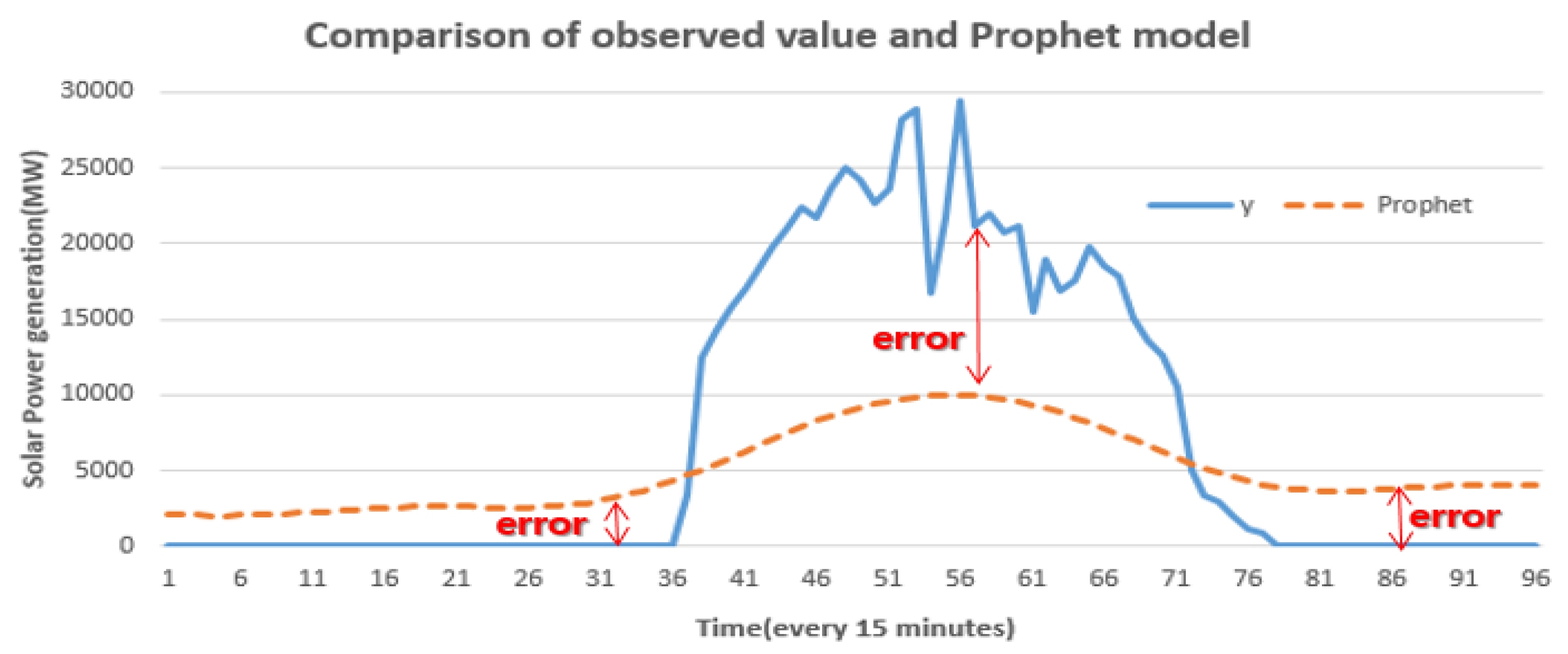
3.1. Prophet Model’s Problem

One of the advantages of the Prophet model is its ability to incorporate seasonality and events (holidays, public holidays) in the predictions. However, as shown in Figure 5, when applying the Prophet model to the data from September 1st to September 30th, 2019, it exhibits a drawback in accurately predicting the observed values (y) during the four-day Thanksgiving day period (from September 12th to September 15th). While the observed values (y) during this period are close to zero, the Prophet model predictions (yhat) fail to capture this pattern accurately.
To address this issue, adjustments in the parameters of the Prophet model are required. Specifically, the holiday information (duration and names) needs to be properly configured to account for its impact on power generation during those specific days. Additionally, flexibility adjustments in the trend and setting appropriate parameters for yearly seasonality are necessary to better align the model's predictions with the observed power generation data.

3.2. Solution Methods

Figure 6 shows the errors between the Prophet model (Prophet) and the observed values (y) for Aug. 5, 2019, at 15-minute intervals. The GRU model, known for its effectiveness in medium-term forecasting based on meteorological data influencing power generation, addresses these discrepancies. However, a limitation of the GRU model in this study is its inability to account for information related to holidays and special events. To mitigate this issue, long-term predictions are made using the Prophet model, which is adept at incorporating seasonal and event-related variations. In contrast, short-term predictions are refined by integrating the GRU model's outputs.

4. Proposed Methods

4.1. Data Collection

4.1.1. Solar PV System Install Location

Table 1 presents the location and detailed information of the solar power generation system installed in Building W of the Company in Naju, Jeollanam-do, South Korea, to validate the effectiveness of the proposed method. The primary objective of the building is to utilize solar power generation for self-consumption. The total area of the building consists of three wings, totaling 600,983m2. The building structure is constructed using H-beams, and the exterior walls are made of sandwich panels. The installed photovoltaic (PV) system has a capacity of 50KW, the PCS (Power Conversion System) has a capacity of 100KW, and the battery capacity is 200KW.

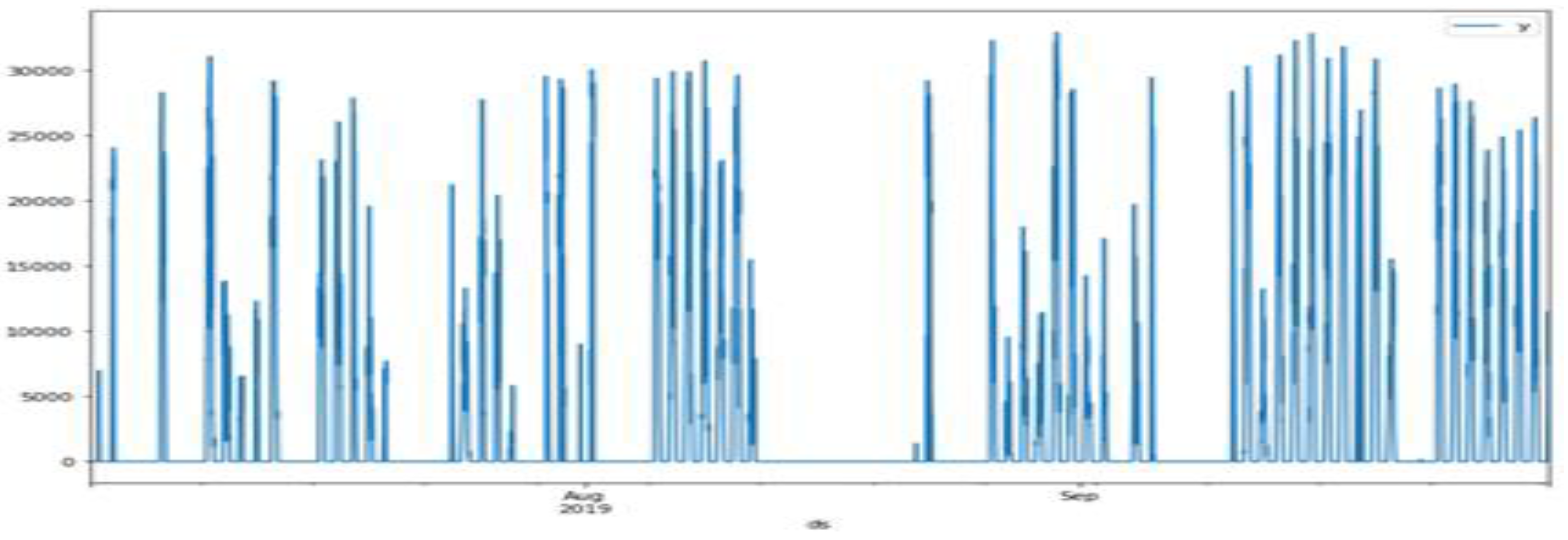
4.1.2. Power Generation and Meteorological Data

This study's power generation data was collected from July 1, 2018, to September 30, 2019, at 15-minute intervals from W Company (Petrochemical) located in Naju, Jeollanam-do, South Korea. Korean holiday data, including substitute holidays, election days, and traditional holidays, were generated using the work calendar package [37]. Additionally, weather data including time, precipitation, temperature, wind direction, wind speed, humidity, and atmospheric pressure for the location in Naju were collected at hourly intervals from the Korea Meteorological Administration's weather data portal (https://data.kma.go.kr/cmmn/main.do).
The most relevant variables for power generation were selected among the weather data. These variables include precipitation-related parameters such as rain, rain15, and rain day, as well as temperature, wind speed, humidity, sunshine duration, and cloud cover [38].

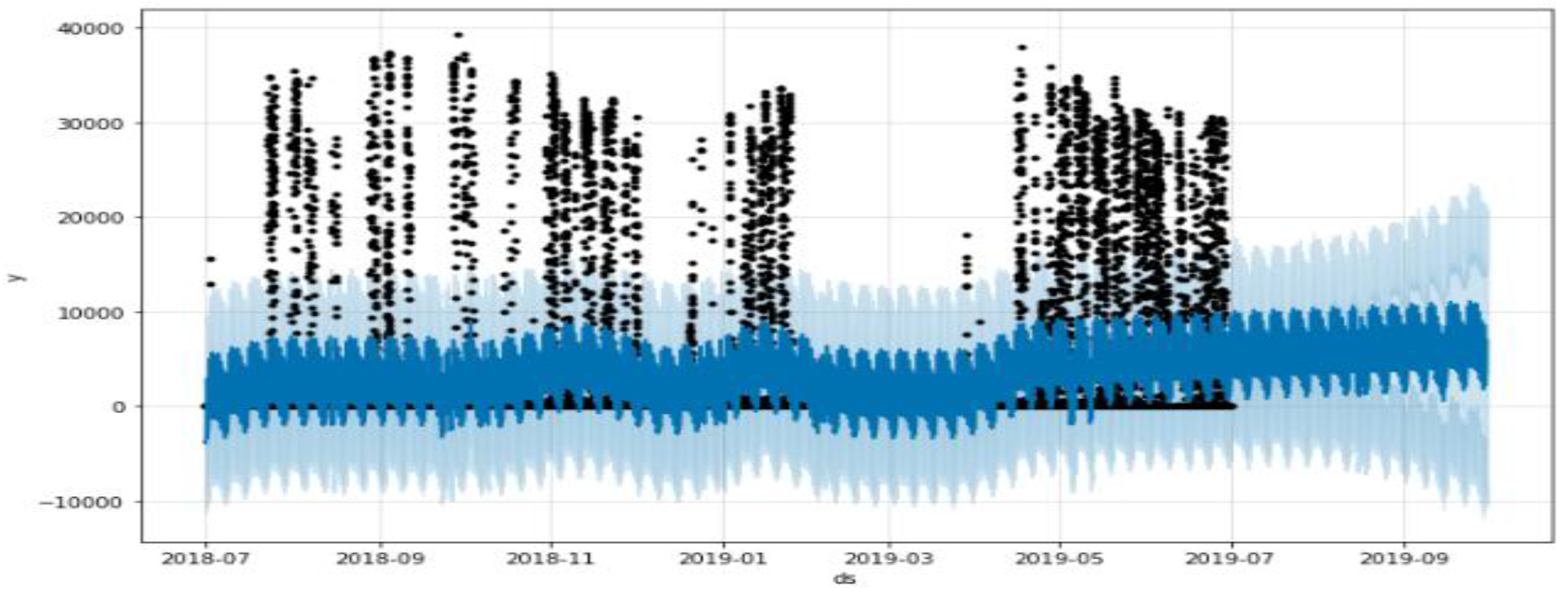
4.2. Data Pre-Processing

To align the time intervals of power data (15 minutes) and weather data (hourly), linear interpolation is used to resample the weather data to 15-minute intervals. This ensures that both datasets have matching timestamps. Additionally, any missing values in the power and weather data are replaced with zero values. To minimize the impact of outliers on the analysis, the data scale is normalized using RobustScaler [39]. The equation for RobustScaler normalization is as follows:
X s c a l e d = x − Q 1 x Q 3 x − Q 1 x
In Equation (3), x is the original data value, X s c a l e d is the normalized data value, Q1(x) is the first quartile (25th percentile) of the data, and Q3(x) is the third quartile (75th percentile) of the data. By using Robust Scaler, we ensure that the data is normalized while being less sensitive to the influence of outliers.

4.3. Data Partition for Training and Test Data

The training data, spanning from July 1, 2018, to June 30, 2019, and the test data, spanning from July 1, 2019, to September 30, 2019, were divided into 80% and 20% respectively for the experiments. The data is divided into an 80% (365 days * 24 hours * 15 minutes) portion for training and a 20% (92 days * 24 hours * 15 minutes) portion for testing to conduct the experiments. Time series data is sensitive to temporal order, so shuffling the data randomly can lead to the model making inaccurate predictions of future data. Therefore, in this study, we did not apply cross-validation.

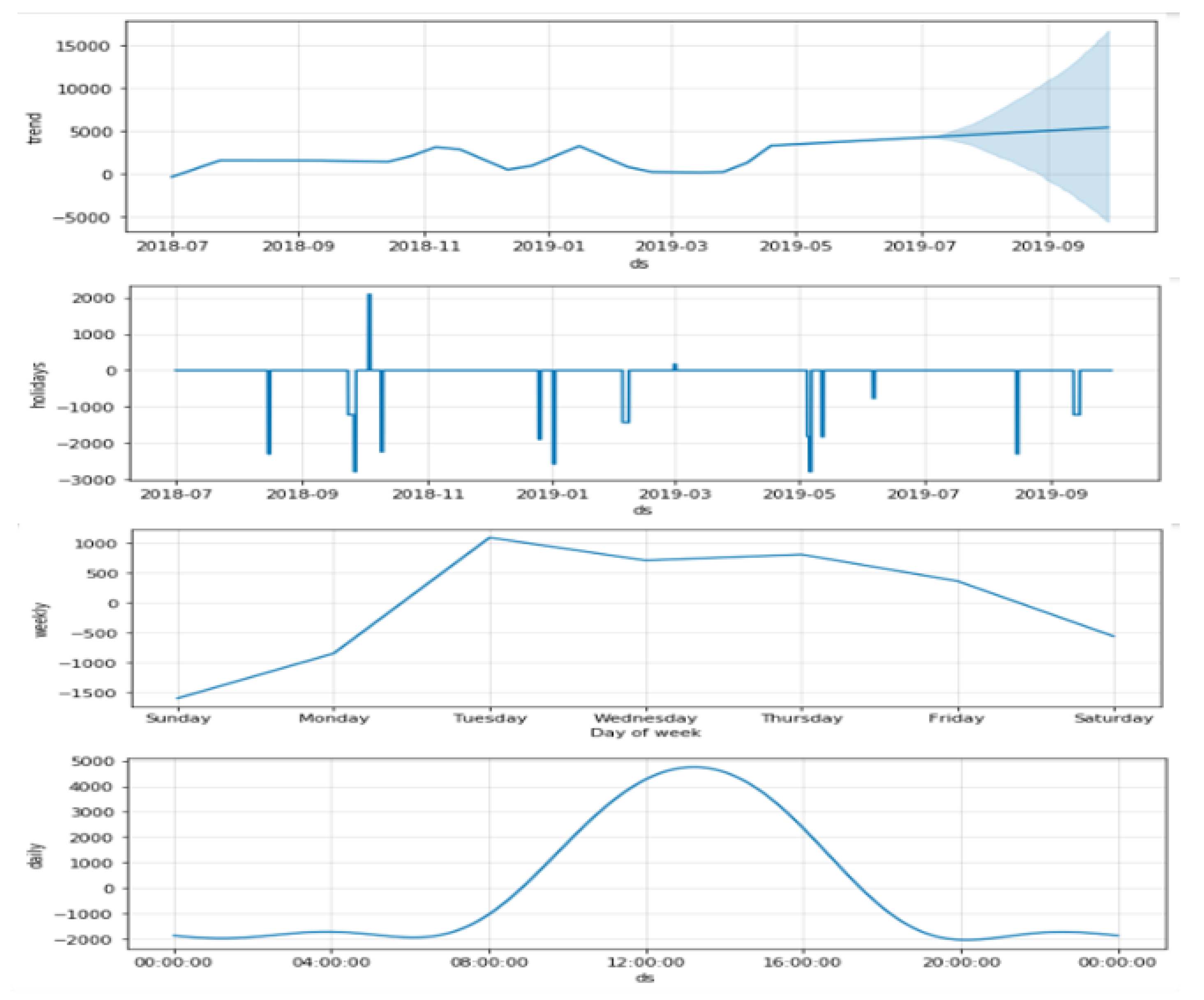
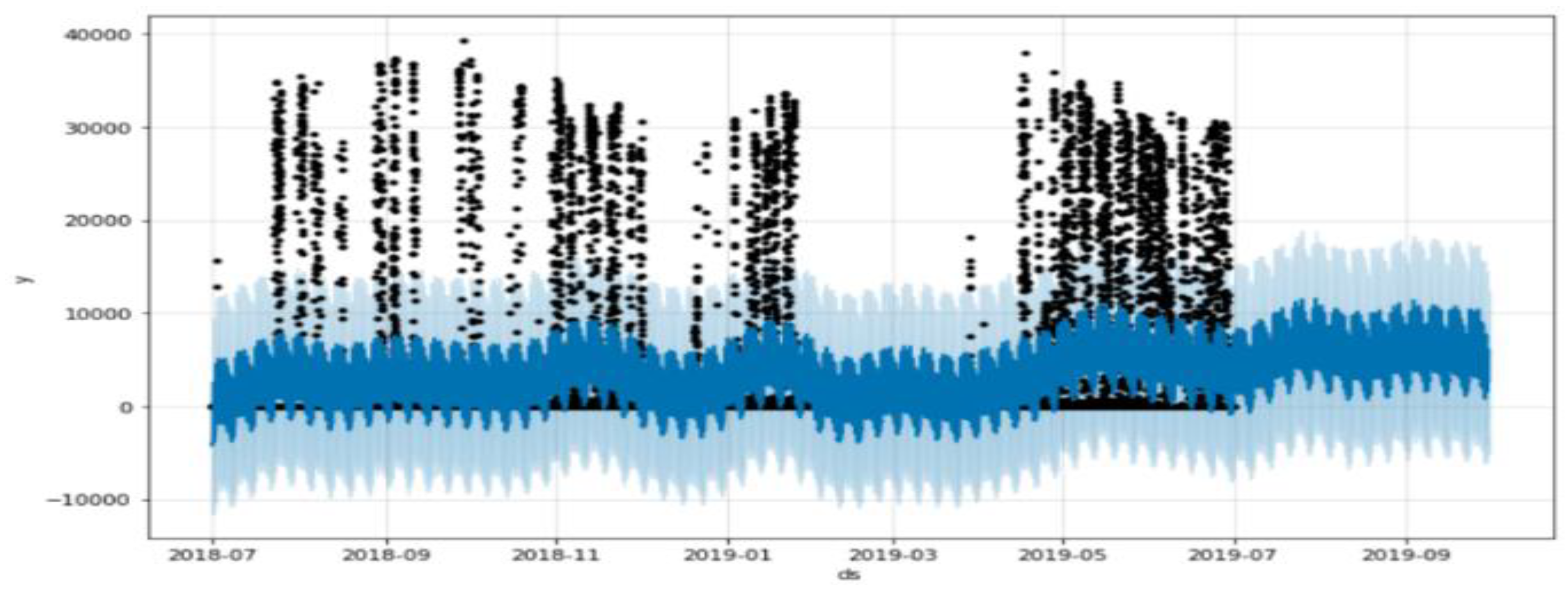
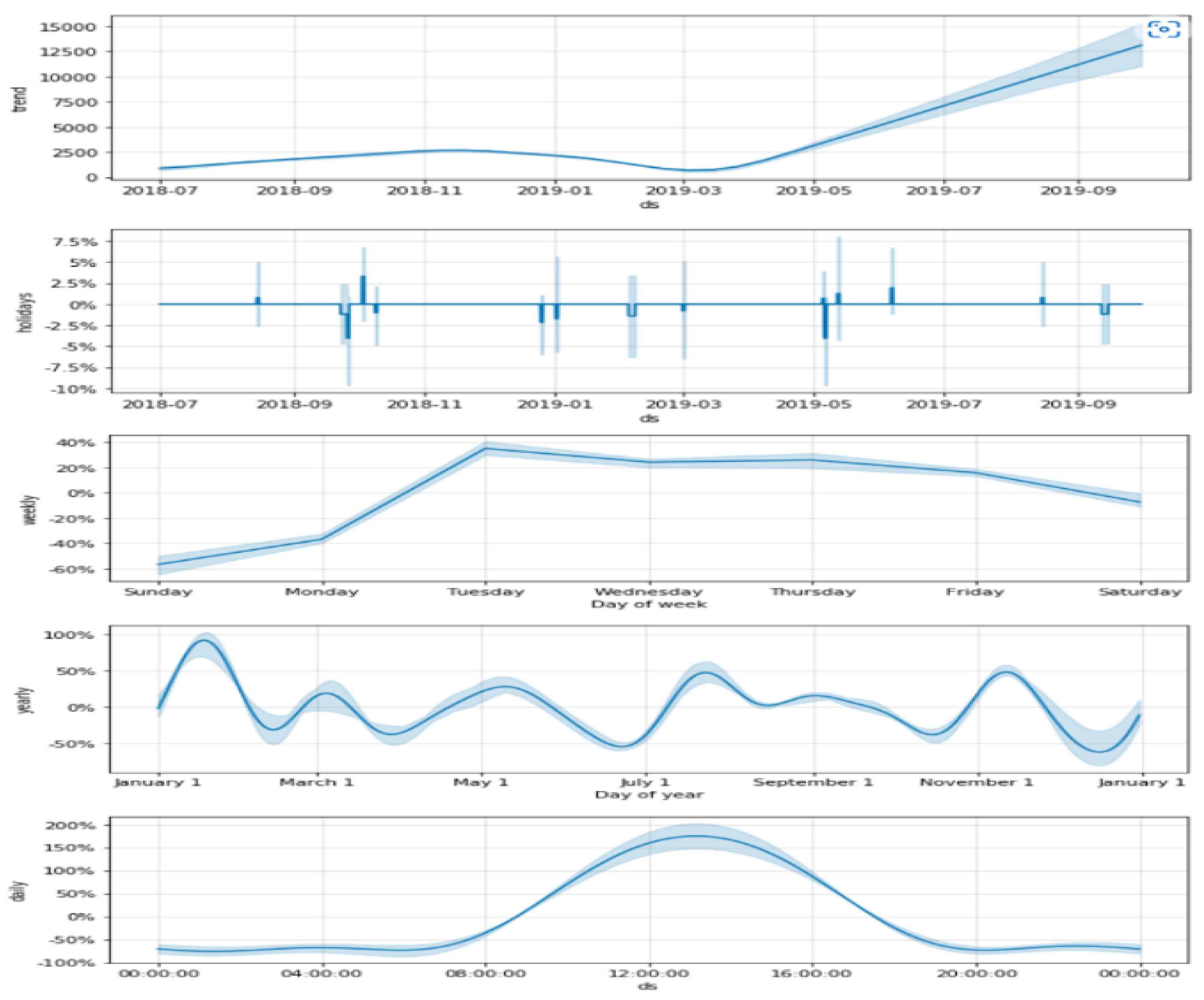
4.4. Modified Prophet Model

The experimental training data used in this study consists of power generation data collected from July 1, 2018, to June 30, 2019. During this period, holidays and alternative holidays (such as election days and traditional holidays) were considered to enhance the accuracy of power generation predictions. Specifically, when applying the Prophet model, various parameters such as trend (change_point_prior_scale = 0.01), holiday effect (holiday_prior_scale = 0.25), yearly seasonality (yearly_season_ability = 10), and adding to meteorological data (‘rain’, ‘’rain15’, rainday’, ‘temp’, ‘wind’, and ‘atm’) were tuned through simulations. The simulation results are shown in Figure 7 and Figure 8.
Table 2. Proposed prophet model parameter setting.
Table 2. Proposed prophet model parameter setting.
Parameter Nature Parameter Name Value
Trend Parameters growth linear
changepoints None
n_changepoints 25
changepoint_range 0.8
changepoint_prior_scale 0.01
Seasonality parameters yearly_seasonality 10
weekly_seasonality False
daily_seasonality False
seasonality_mode multiplicative
seasonality_prior_scale 10
holidays parameters Holidays
holidays_prior_scale 		df
0.25
Flow parameters flow flow
flow_prior_scale 10
Other parameters mcmc_samples 0
interval_width 0.8
Figure 7 and Figure 8 show stable predictions compared to Figure 2 and Figure 3, which are the results of the existing prophet, respectively. In Figure 2, the prediction direction is not constant and shows increase and decrease in various directions, whereas in Figure 3, the prediction direction is constant.

4.5. Proposed Hybrid Model

To reduce the error between Prophet's prediction and the actual measurement as shown in Figure 6, we propose reducing the error rate of power generation prediction by applying the residuals of the long-term trend (yearly and monthly) between predicted and actual values as shown in Equation (4).
E r r o r = P r o p h e t p r e d − y
In Equation (4), the Error is the difference between the predicted values from the original Prophet model (Prophetpred) and the actual values (y).
The Error term, defined as the difference in Equation (4), is utilized as an input for the GRU model, as illustrated in Figure 9. The input dataset comprises nine variables, including various meteorological parameters: precipitation (rain, rain15, rainy days), temperature, wind speed, humidity, sunshine duration, cloud cover, and an Error term. In Figure 9, x 1 t − 1 ~ x 8 t − 1 represents the previous time (t-1) values of rainfall (rain, rain15, and rain day), temperature, wind speed, humidity, sunshine duration, cloud cover, while x 9 t − 1 represents the Error term.
The proposed hybrid model's training and testing data are derived from the same dataset. The input layer of the GRU model consists of 9 variables, which include 8 meteorological data variables including rainfall (rain, rain15, and rain day), temperature, wind speed, humidity, sunshine duration, cloud cover, and one error variable. The hidden layer of the GRU model contains 9 nodes. Table 3 shows the training and testing options for simulating GRU. The initial learning rate is set to 0.005, and the maximum number of iterations is 500. The mean square error (MSE) for the loss function, ADAM [40] for the optimizer, and ReLU [41] for the activity function are employed during both training and testing.

5. Simulation Metrics and Results

5.1. Simulation Metrics

To validate the proposed method in this study, several error metrics, including CC (Correlation Coefficient) [42], RMSE (Root Mean Square) [43], RMSSE (Root Mean Squared Scaled Error) [44], and SMAPE (Symmetric Mean Absolute Percentage Error) [45] were employed. These metrics were used to evaluate the performance and accuracy of the proposed approach compared to other methods. Equations (5) and (8) are CC, RMSE, RMSSE, and SMAPE formulas, respectively.
The correlation coefficient [42] was used to assess the accuracy of the actual values and predictions.
r X , Y = 1 k ∑ i = 1 k x i − x ¯ y i − y ¯ σ x σ y
In Equation (5), x ¯ and y ¯ represent the means of X and Y, respectively, while σ x and σ y represent the standard deviations of X and Y, respectively. k is the number of data points.
R M S E = 1 n ∑ i = 1 n y i − y i ¯ 2
R M S S E = 1 n ∑ i = m + 1 n + m y i − y i ¯ 2 1 m − 1 ∑ i = 2 n y i − y i − 1 2
S M A P E = 100 n × ∑ i = 1 n y i − y i ¯ y i + y i ¯ / 2
In Equations (6) and (8), y i is the actual observed value, y i ¯ is the predicted value, m is the number of training data, and n is the number of test data.

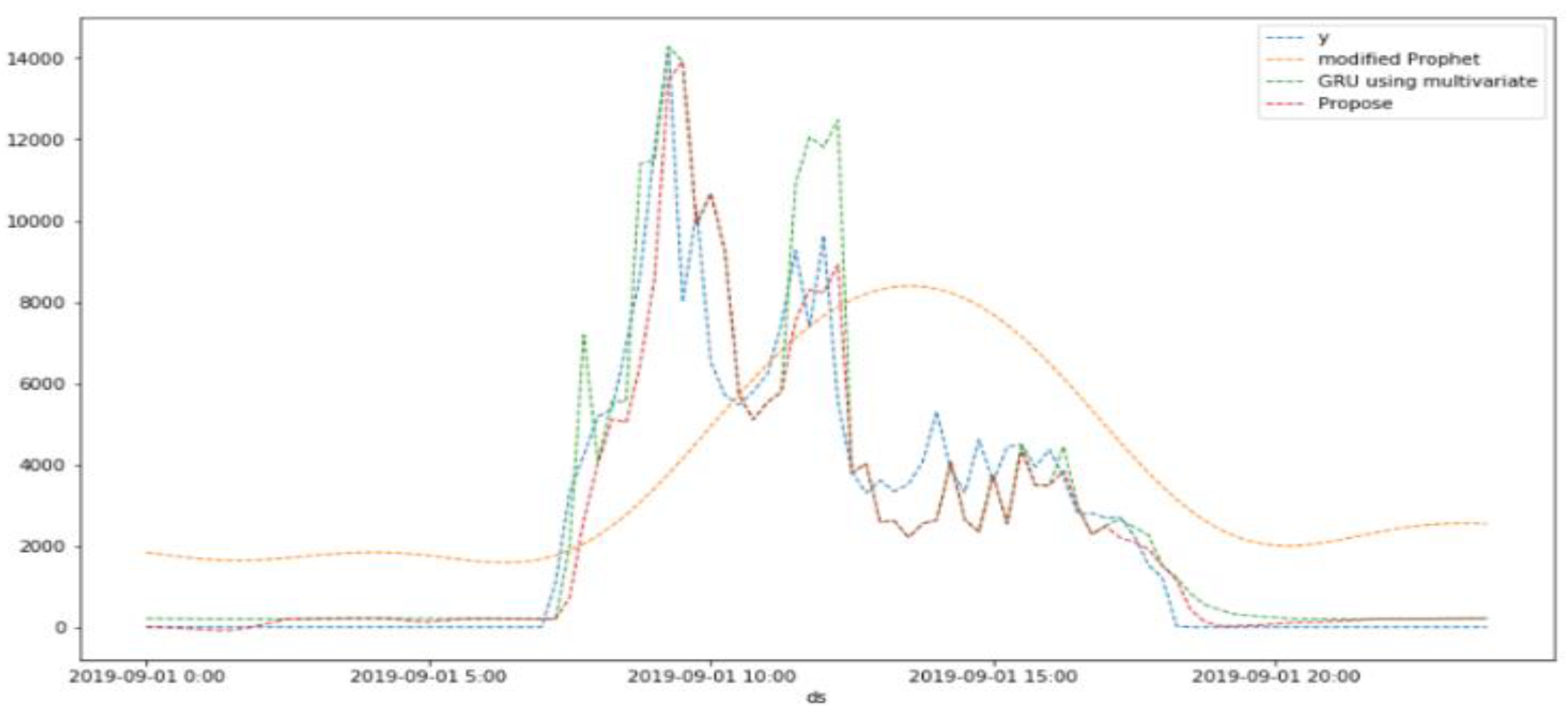
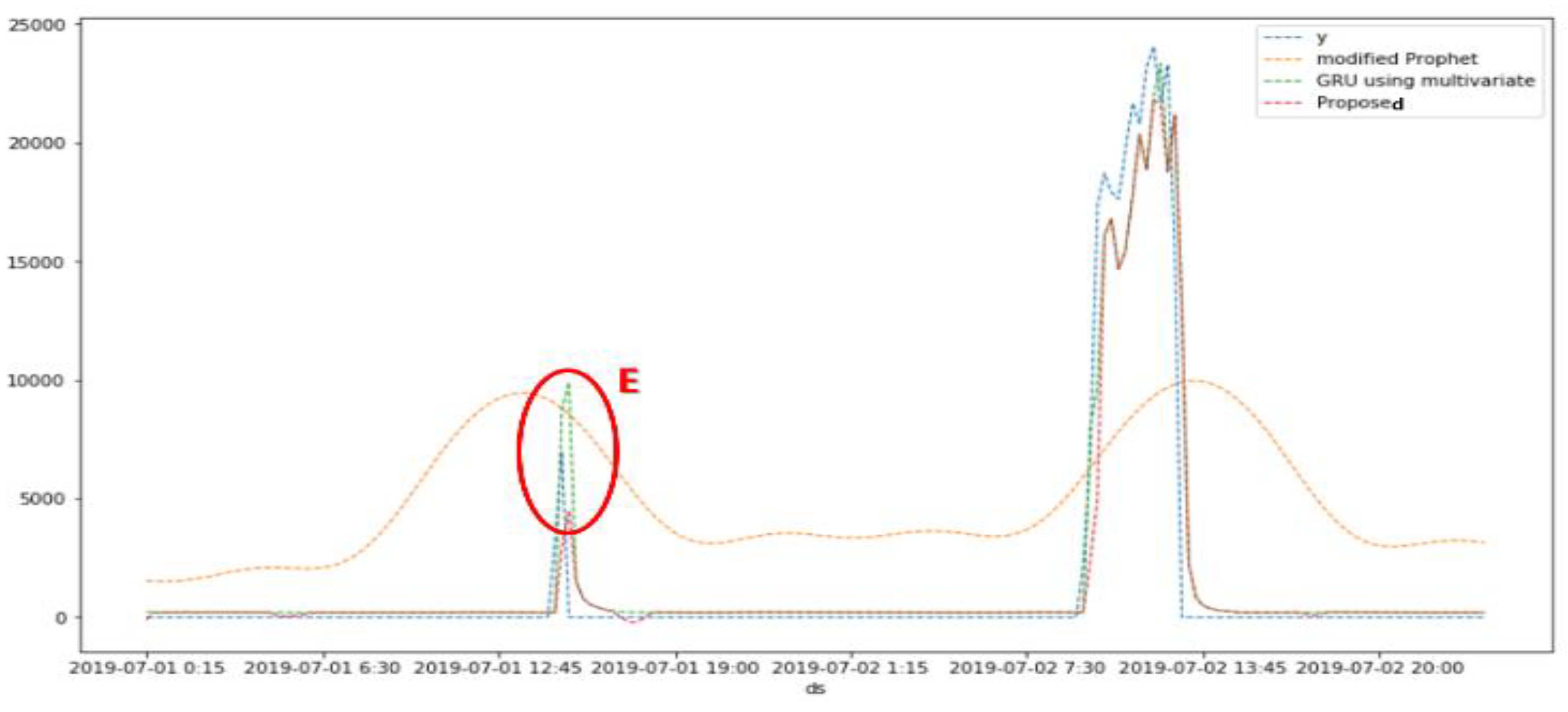
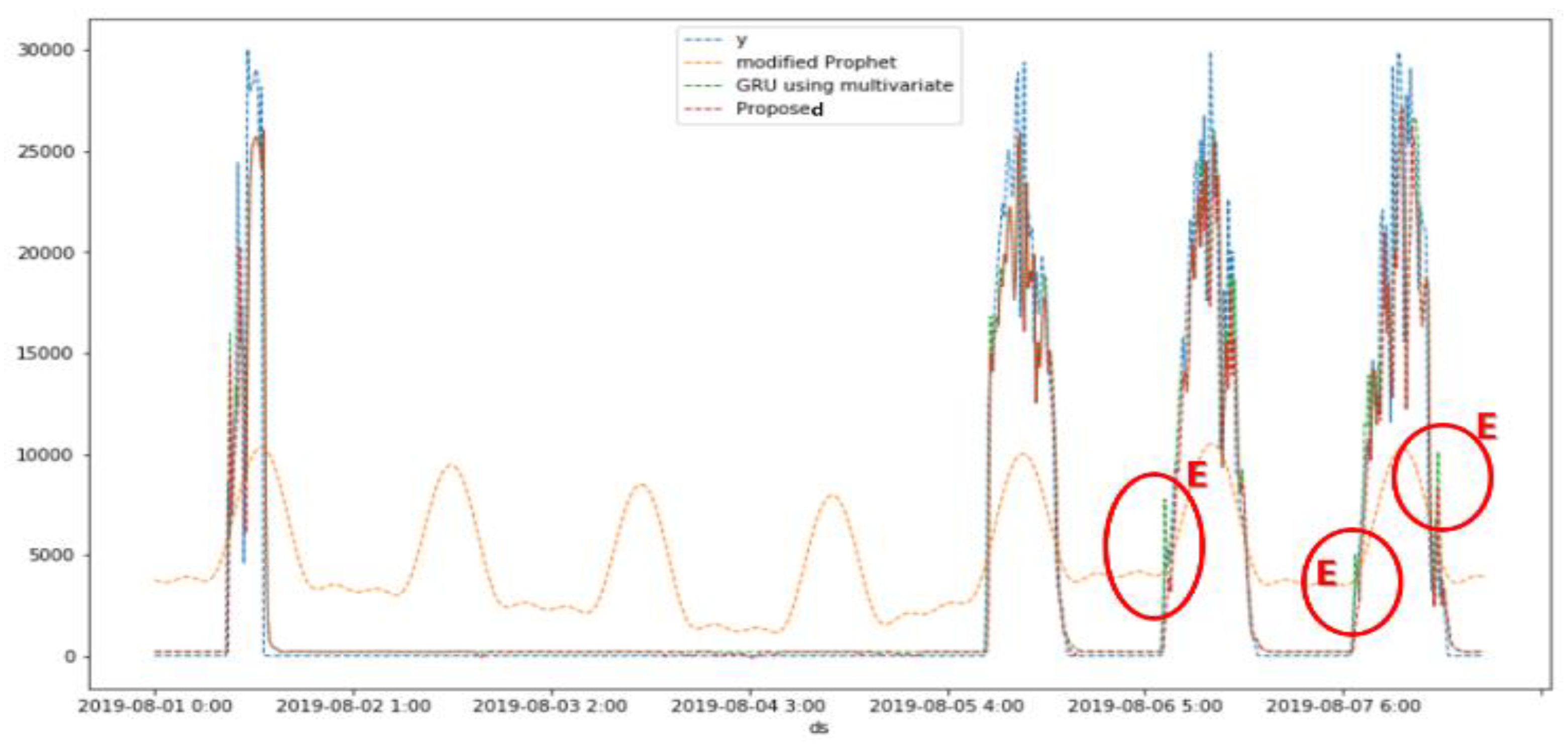
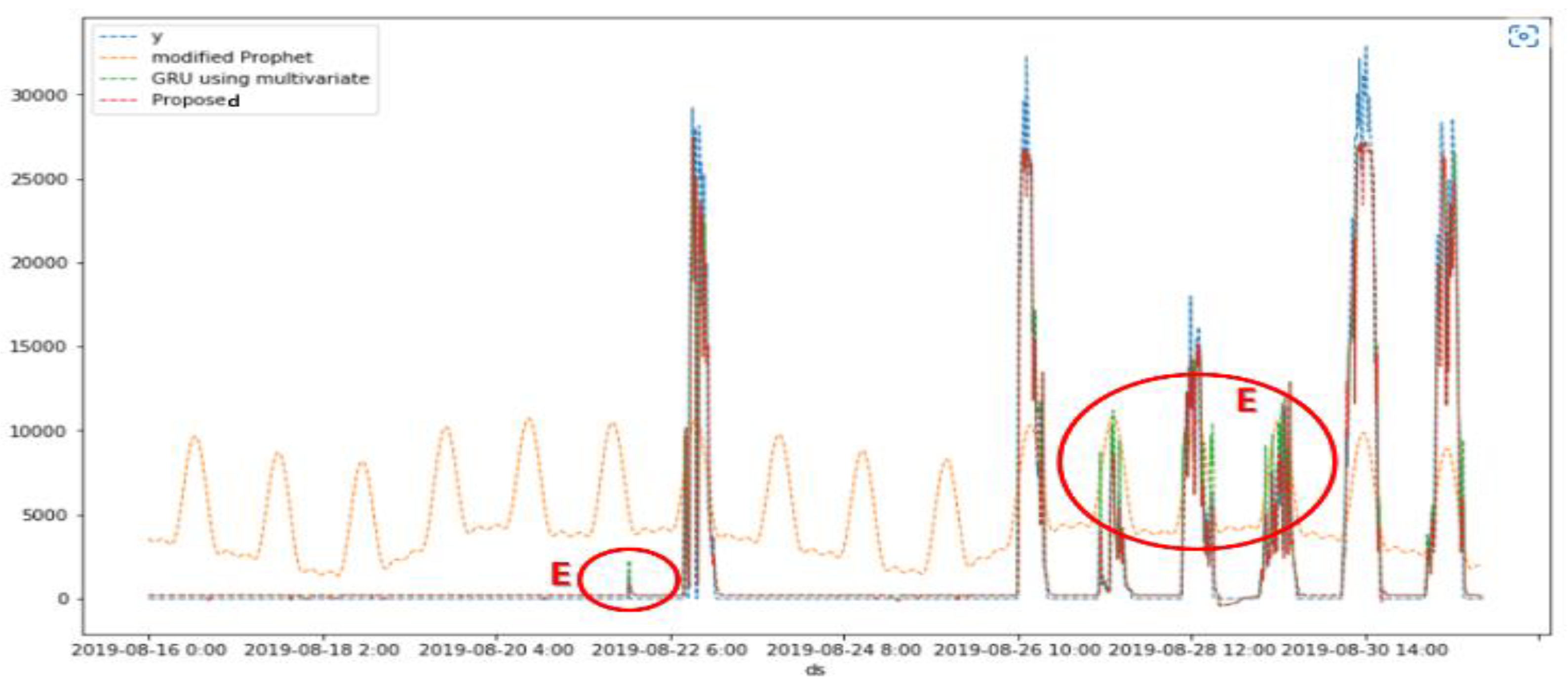
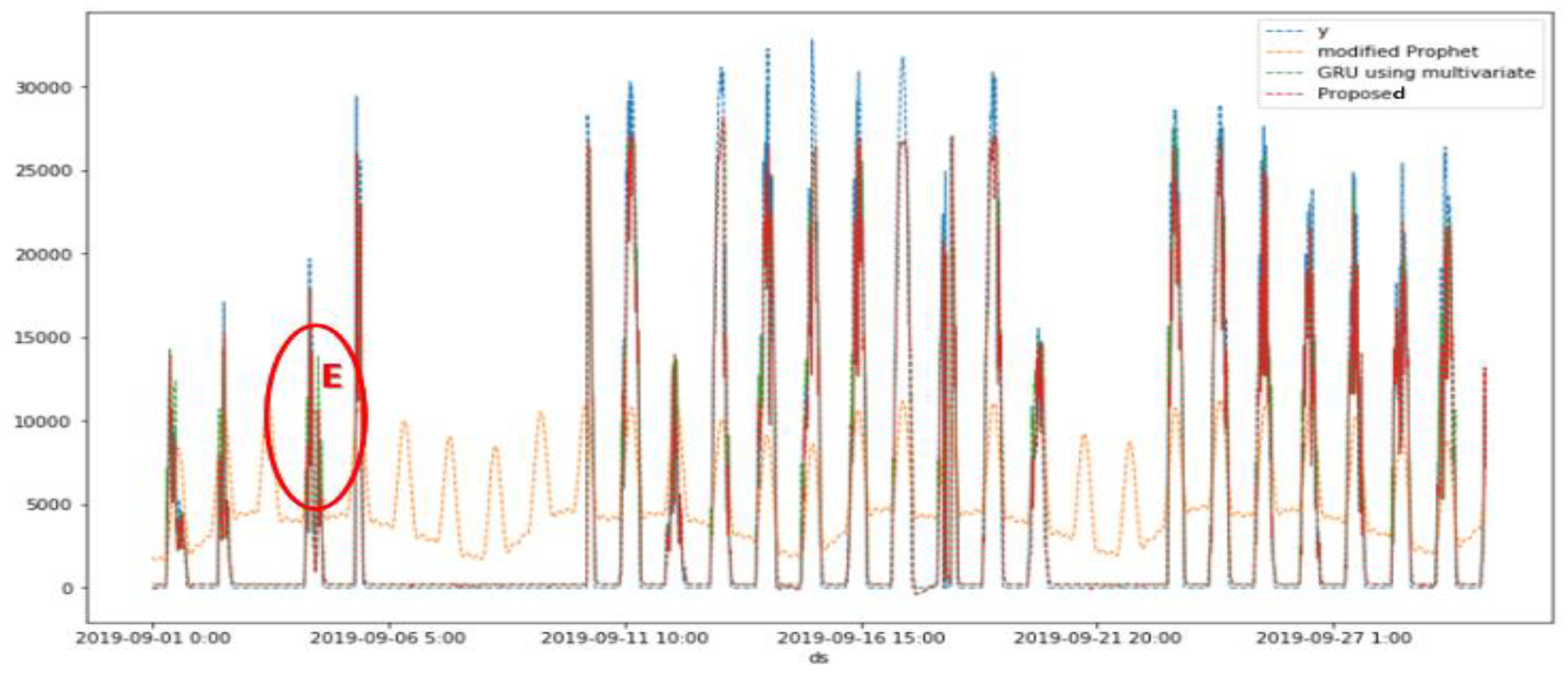
5.2. Simulation Results

Table 4 presents a performance comparison among modified Prophet, ‘GRU using multivariate’, and the proposed method. The GRU using multivariate was trained and tested similarly to the proposed method, utilizing eight input variables: rainfall (rain, rain15, and rain day), temperature, wind speed, humidity, sunshine duration, and cloud cover, excluding error term.
As the prediction period increased, the correlation coefficient of the modified Prophet model decreased, while the correlation coefficients of ‘GRU using multivariate’ and the proposed method remained consistently higher than those of the modified Prophet model. Regardless of the prediction period, the RMSE of the modified Prophet model was approximately twice as high as that of ‘GRU using multivariate’ and two to three times higher than that of the proposed method. Additionally, the RMSE of ‘GRU using multivariate’ was 1.5 to 2 times higher than that of the proposed method. Therefore, the proposed method outperformed both the modified Prophet and ‘GRU using multivariate’ models. The SMAPE of the modified Prophet model was higher than that of GRU using multivariate and the proposed method, while the SMAPE of ‘GRU using multivariate’ and the proposed method were almost similar.
Figure 10 compares graphic visualization performance between actual observed values (y) and other methods from September 1, 2019 (one day). In Figure 10, solar power generation is heavily influenced by solar irradiance, with generation occurring predominantly from 7:00 AM to 5:00 PM. At the same time, there is minimal generation during the remaining hours from 6:00 PM to 6:00 AM. Even during the hours of solar irradiance from 7:00 AM to 5:00 PM, differences in generation indicate significant influence from meteorological data. Particularly, the modified Prophet exhibits a consistent pattern regardless of meteorological data, while the proposed method and other methods predict power generation similar to actual measurements.
Figure 11 to Figure 12 compare the short-term power generation predictions for 2 days (from July 1 to July 2, 2019) and 7 days (from August 1 to August 7, 2019). Figure 13 to Figure 14 compare the medium-term power generation predictions for 15 days (from August 16 to August 30, 2019) and 30 days (from September 1 to September 30, 2019). In these figures, 'y' represents the measured power generation during the observation period, the modified Prophet represents the proposed Prophet model in Section 4.4, ‘GRU using multivariate’ represents the prediction values obtained using meteorological data and observed values, and Proposed represents the predicted power generation values using the proposed approach.
In Figure 11, Figure 12, Figure 13 and Figure 14, the proposed method and 'GRU using multivariate' closely resemble the actual observed values (y), while the 'modified Prophet' shows higher errors than the observed values (y). ‘GRU using multivariate’ exhibits intermittent prediction errors, indicated by "E" in the graphs, particularly due to the challenge of accurately predicting power generation on the day following consecutive occurrences of holidays or events (alternative holidays, holidays, and vacations). In contrast, the proposed method closely predicts the actual observed values (y).

6. Conclusion

The proposed hybrid model exhibits a marked improvement in the accuracy of solar power generation forecasts, which is essential for the strategic planning, management, and operation of power systems. This model supports the maintenance of a continuous and sustainable energy supply while enhancing the operational efficiency of renewable energy systems and power markets. By integrating the Prophet model's capacity to handle long-term trends and seasonality with the GRU's ability to capture complex, non-linear patterns in meteorological data, this study presents a robust algorithm for forecasting solar power generation over both short- and medium-term periods. The comprehensive evaluation underscores the hybrid model's superiority over existing models, positioning it as a reliable tool for advancing the accuracy and reliability of solar power generation forecasts.
Looking ahead, future research could focus on extending the model’s capabilities to real-time or near-real-time forecasting. Such an advancement would allow for more dynamic and responsive predictions, which would be especially valuable for grid operators in need of real-time data for load balancing and resource optimization. Additionally, integrating more advanced deep learning models and exploring the model’s scalability across different geographical regions and climatic conditions would further enhance its applicability. Finally, addressing the computational efficiency of the hybrid model could enable its use in resource-constrained environments, broadening its practical relevance.

Author Contributions

N.S., summarized the results and supervised; E.K., analyzed the data and simulation. All authors have read and agreed to the published version of the manuscript.

Funding

This study received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable

Data Availability Statement

Not applicable.

Acknowledgments

This study was supported by a research fund from Honam University, 2024.

Conflicts of Interest

Not applicable.

References

  1. The Presidential Commission on Carbon Neutrality and Green Growth. 2050 Presidential Commission on Carbon Neutrality and Green Growth. 2030 Nationally Determined Contributions. Policy Report, Sejong-si, Republic of Korea, 2021.
  2. International Energy Agency; Renewable Energy Market Update. International Energy Agency, 2023, Paris, France.
  3. Lee, S.H.; Cho, I.H. International Renewable Energy Policy Change and Market Analysis. Korea Energy Economics Institute, 2018, Seongan-dong, Korea.
  4. Rethink Energy-Solar Service. Solar Industry growing rapidly with DER skew post-pandemic., Rethink Energy, Mar. 29, 2023.
  5. European Commission. EU strategic dependencies and capacities: second stage of in-depth reviews. Feb. 2, 2022.
  6. Huang, B.B.; Zhang, Y.Z.; Wang, C.X. Judgment of China’s 14th five-year plan new energy development and issues needing attention. Electr. Power 2020, 53, 1089–1094. [Google Scholar]
  7. Korea Energy Economics Institute (KEEI). Modified CFI 2030 Plan to Implement Energy Self-Reliance Island. KEEI: Ulsan, Korea, 2019.
  8. Noh, C.H.; Jang, W.H.; Kim, C.H. Recent Trends in Renewable Energy Resources for Power Generation in the Republic of Korea. Resources. 2015, 4, 751–764. [Google Scholar] [CrossRef]
  9. Rashid, M.M.U.; Granelli, F.; Hossain, M.A.; Alam, M.S.; Alismail, F.S.; Karmaker, A.K.; Rahaman, M.M. Development of Home Energy Management Scheme for a Smart Grid Community. Energies 2020, 13, 4288. [Google Scholar] [CrossRef]
  10. Raza, M.Q.; Khosravi, A. A review on artificial intelligence based load demand forecasting techniques for smart grid and buildings. Renew. Sustain Energy Rev. 2015, 50, 1352–1372. [Google Scholar] [CrossRef]
  11. Willis, H.L.; Northcote-Green, J.E.D. Spatial electric load forecasting: A tutorial review. Proc. Of the IEEE 1983, 71, 232–253. [Google Scholar] [CrossRef]
  12. Enea, M. A review of machine learning algorithms used for load forecasting at micro-grid level. In Sinteza 2019—International Scientific Conference on Information Technology and Data Related Research, Singidunum University, Belgrade, Serbia, pp.452–458, 2019.
  13. Brown, R.G. Smoothing Forecasting and Prediction of Discrete Time Series; Prentice-Hall: Englewood Cliffs, NJ, USA, 1963. [Google Scholar]
  14. Ohtsuka, Y.; Oga, T.; Kakamu, K. Forecasting electricity demand in Japan: A Bayesian spatial autoregressive ARMA approach. Comput. Stat. Data Anal. 2010, 54, 2721–2735. [Google Scholar] [CrossRef]
  15. Fix, E.E.; Hodges, J.L., Jr. Discriminatory Analysis-Nonparametric Discrimination: Consistency Properties; International Statistical Institute: Voorburg, The Netherlands, 1989; Vol. 57, pp. 238–247. [Google Scholar] [CrossRef]
  16. Yu, Z.; Haghighat, F.; Fung, B.C.M.; Yoshino, H. A decision tree method for building energy demand modeling. Energy Build 2010, 42, 1637–1646. [Google Scholar] [CrossRef]
  17. Dong, B.; Cao, C.; Lee, S.E. Applying support vector machines to predict building energy consumption in tropical region. Energy Build. 2005, 37, 545–553. [Google Scholar] [CrossRef]
  18. Bonyadi, M.R.; Michalewicz, Z. Particle swarm optimization for single objective continuous space problems: A review. Evol. Comput. 2017, 25, 1–54. [Google Scholar] [CrossRef]
  19. Kalogirou, S.A; Neocleous, C.C; Schizas, C.N. Building heating load estimation using artificial neural networks. In Proceedings of the 17th International Conference on Parallel Architectures and Compilation Techniques, San Francisco, CA, USA, 10–14 November 1997. [Google Scholar]
  20. Freedman, D.A. Statistical Models: Theory and Practice; Cambridge University Press, 2009; Volume 26. [Google Scholar]
  21. Bagnasco, A.; Fresi, F.; Saviozzi, M.; Silvestro, F.; Vinci, A. Electrical consumption forecasting in hospital facilities: An application case. Energy Build. 2015, 103, 261–270. [Google Scholar] [CrossRef]
  22. Graves, A.; Liwicki, M.; Fernandez, F.; Bertolami, R.; Bunke, H.; Schmidhuber, J. A Novel Connectionist System for Improved Unconstrained Handwriting Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 855–868. [Google Scholar] [CrossRef] [PubMed]
  23. Gers, F.; Schmidhuber, J.; Cummins, F. Learning to Forget: Continual Prediction with LSTM. In Proceedings of the 9th International Conference on Artificial Neural Networks, ICANN’99, Edinburgh, UK, 7–10 September 1999; pp. 850–855. [Google Scholar]
  24. Ian, G.; Yoshua, B.; Aaron, C. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
  25. Valenzuela, P.; Gorricho, J.; Iglesia, D.L. Automatic model and feature selection for time series forecasting: Achieving good performance and interpretability. Information Sciences 2018, 157–174. [Google Scholar]
  26. Sanguansat, E.; Klomjit, N. A comparative study of machine learning techniques for short-term load forecasting. Energies 2019, 12. [Google Scholar]
  27. Fung, G.; Shih, E. Evaluating the Forecasting Performance of Facebook's Prophet Model for Time Series Data. Journal of Open Source Software 2019, 4. [Google Scholar]
  28. Bashir, B.; Haoyong, C. Short-term electricity load forecasting using hybrid prophet-LSTM model optimized by BPNN. Energy Reports 2022, 8, 1678–1686. [Google Scholar] [CrossRef]
  29. Arslan, S. A hybrid forecasting model using LSTM and Prophet for energy consumption with decomposition of time series data. PeerJ Computer Science 2022, 8. [Google Scholar] [CrossRef]
  30. Pin, L.; Zhang, J.S. A New Hybrid Method for China’s Energy Supply Security Forecasting Based on ARIMA and XGBoost. Energies 2018, 11. [Google Scholar]
  31. Yuanhua, C.; Muhammad, S.B.; Muhammad, A.; Dingtian, X. Evaluation of Machine Learning Models for Smart Grid Parameters: Performance Analysis of ARIMA and Bi-LSTM. Sustainability 2023, 15. [Google Scholar] [CrossRef]
  32. Pooniwala, N.; Sutar, R. Forecasting Short-Term Electric Load with a Hybrid of ARIMA Model and LSTM Network. International Conference on Computer Communication and Informatics, 2021.
  33. Agbessi, A.P.; Salami, A.A.; Agbosse, K.S.; Birregah, B. Peak Electrical Energy Consumption Prediction by ARIMA, LSTM, GRU, ARIMA-LSTM and ARIMA-GRU Approaches. Energies 2023, 16. [Google Scholar] [CrossRef]
  34. Taylor, S.J.; Letham, B. Prophet: forecasting at scale. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp.1389-1397, 2017.
  35. Taylor, S.J.; Letham, B. Prophet: forecasting at scale. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp.1389-1397, 2017.
  36. Cho, K.; Merriënboer, B.V.; Bahdanau, D.; Bengio, Y. On the properties of neural machine translation: Encoder-decoder approaches. Proceedings of SSST-8, Eighth Workshop on Syntax, Semantics and Structure in Statistical Translation, 2014.
  37. Work Calendar Library Package. Available online: https://pypi.org/project/workalendar/ (accessed on 20 August 2024).
  38. Namrye, S.; Mina, J. Analysis of Meteorological Factor Multivariate Models for Medium- and Long-Term Photovoltaic Solar Power Forecasting using Long Short-Term Memory. Applied Sciences 2021, 11, 316. [Google Scholar]
  39. Robust Scaler Documentation in Scikit-Learn. Available online: https://www.itl.nist.gov/div898/software/dataplot/refman2/auxillar/iqrange.htm (accessed on 20 August 2024).
  40. Kingma, D.; Ba, J. Adam: A method for stochastic optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar]
  41. Nair, V.; Hinton, G. Rectified linear units improve restricted Boltzmann machines. In Proceedings of the 27th International Conference on International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010. [Google Scholar]
  42. Sethna, J.P. Chapter 10: Correlations, response, and dissipation. In Statistical Mechanics: Entropy, Order Parameters, and Complexity; Oxford University Press: Oxford, UK, 2006; ISBN 978-0198566779. [Google Scholar]
  43. RMSE. Available online: https://en.wikipedia.org/wiki/Root_mean_square_deviation (accessed on 20 August 2024).
  44. RMSSE. Available online: https://www.pmorgan.com.au/tutorials/mae%2C-mape%2C-mase-and-the-scaled-rmse/ (accessed on 20 August 2024).
  45. SMAPE. Available online: https://en.wikipedia.org/wiki/Symmetric_mean_absolute_percentage_error (accessed on 20 August 2024).
Preprints 119790 g001
Figure 1. Power generation data of Company W collected from July 1, 2018, to Nov. 30, 2019.
Figure 1. Power generation data of Company W collected from July 1, 2018, to Nov. 30, 2019.
Preprints 119790 g001
Preprints 119790 g002
Figure 2. Simulation using the prophet model considering the holiday effect for one year (July 2018 to June 2019).
Figure 2. Simulation using the prophet model considering the holiday effect for one year (July 2018 to June 2019).
Preprints 119790 g002
Preprints 119790 g003
Figure 3. Trend, holidays, weekly, and daily prediction analysis of prophet model. The blue line shows the trend the model fits from the test data, and the light blue shade shows the predicted trend.
Figure 3. Trend, holidays, weekly, and daily prediction analysis of prophet model. The blue line shows the trend the model fits from the test data, and the light blue shade shows the predicted trend.
Preprints 119790 g003
Preprints 119790 g004
Figure 4. Structure of GRU.
Figure 4. Structure of GRU.
Preprints 119790 g004
Preprints 119790 g005
Figure 5. Comparison of performance of the prophet model (yhat) and actual observed value (y) from July to September 2019.
Figure 5. Comparison of performance of the prophet model (yhat) and actual observed value (y) from July to September 2019.
Preprints 119790 g005
Preprints 119790 g006
Figure 6. Performance comparison between observed value (y) and prophet model (prophet) on July 2, 2019.
Figure 6. Performance comparison between observed value (y) and prophet model (prophet) on July 2, 2019.
Preprints 119790 g006
Preprints 119790 g007
Figure 7. Error forecast of the proposed Prophet model. The black dots represent the historical input data, the blue line represents the predicted trend line after model fitting, and the light blue area above and below the blue curve represents the confidence interval.
Figure 7. Error forecast of the proposed Prophet model. The black dots represent the historical input data, the blue line represents the predicted trend line after model fitting, and the light blue area above and below the blue curve represents the confidence interval.
Preprints 119790 g007
Preprints 119790 g008
Figure 8. Trend, holidays, weekly, and daily prediction analysis of the proposed prophet model. The blue line shows the trend the model fits from the test data, and the light blue shade shows the predicted trend.
Figure 8. Trend, holidays, weekly, and daily prediction analysis of the proposed prophet model. The blue line shows the trend the model fits from the test data, and the light blue shade shows the predicted trend.
Preprints 119790 g008
Preprints 119790 g009
Figure 9. Proposed hybrid model.
Figure 9. Proposed hybrid model.
Preprints 119790 g009
Preprints 119790 g010
Figure 10. Comparison of performance between observed values (y) and other methods for 1 September 2019 (one day).
Figure 10. Comparison of performance between observed values (y) and other methods for 1 September 2019 (one day).
Preprints 119790 g010
Preprints 119790 g011
Figure 11. Comparison of performance between observed values (y) and other methods from 1 July to 2 July 2019 (2 days). The area “E” shows the largest prediction error in ‘GRU using multivariate’.
Figure 11. Comparison of performance between observed values (y) and other methods from 1 July to 2 July 2019 (2 days). The area “E” shows the largest prediction error in ‘GRU using multivariate’.
Preprints 119790 g011
Preprints 119790 g012
Figure 12. Comparison of performance between observed values (y) and other methods from 1 October to 7 October 2019 (7 days). The area “E” shows the largest prediction error in ‘GRU using multivariate’.
Figure 12. Comparison of performance between observed values (y) and other methods from 1 October to 7 October 2019 (7 days). The area “E” shows the largest prediction error in ‘GRU using multivariate’.
Preprints 119790 g012
Preprints 119790 g013
Figure 13. Comparison of performance between observed values (y) and other methods from 15 August to 30 August 2019 (15 days). The area “E” shows the largest prediction error in ‘GRU using multivariate’.
Figure 13. Comparison of performance between observed values (y) and other methods from 15 August to 30 August 2019 (15 days). The area “E” shows the largest prediction error in ‘GRU using multivariate’.
Preprints 119790 g013
Preprints 119790 g014
Figure 14. Comparison of performance between observed values (y) and other methods from 1 September to 30 September 2019 (30 days). The area “E” shows the largest prediction error in ‘GRU using multivariate’.
Figure 14. Comparison of performance between observed values (y) and other methods from 1 September to 30 September 2019 (30 days). The area “E” shows the largest prediction error in ‘GRU using multivariate’.
Preprints 119790 g014
Table 1. Solar power generation system installation location and information.
Table 1. Solar power generation system installation location and information.
Division Information
Location Naju, Jeollanam-do, South Korea
The main purpose of usage Self-generated solar power generation
Building area Total 3 building, 600,983m2
Number of floors 1st floor of the factory building and one other building
Building structure H-beam
Outer wall Sandwich panels
PV system capacity 50KW
ESS PCS: 100KW, battery: 200KW
Table 3. Training and testing option by proposed hybrid model.
Table 3. Training and testing option by proposed hybrid model.
Parameter GRU
Number of layers 9
Number of neurons 9
Number of epochs 500
Learning rate 0.005
Loss function MSE
Optimization ADAM
Weight initializer 1
Activation function ReLU
Table 4. Comparison of the performance of modified Prophet, GRU, and proposed method.
Table 4. Comparison of the performance of modified Prophet, GRU, and proposed method.
Term Metrics Modified
Prophet		 GRU
using multivariate		 Proposed
Short-
term		 2 days
(July 1~2)		 CC 0.39 0.94 0.95
RMSE 5765.38 1660.25 1588.59
RMESE 36732.30 10577.77 10121.23
SMAPE (%) 189.47 187.43 186.45
7 days
(Aug. 1~7)		 CC 0.69 0.95 0.95
RMSE 6393.15 2521.99 2510.73
RMSSE 76202.52 30060.66 29926.40
SMAPE (%) 169.36 160.89 160.38
Medium-
term		 15 days
( Aug. 16~30)		 CC 0.47 0.96 0.96
RMSE 6141.05 1822.63 1756.73
RMSSE 110664.40 32844.71 31657.08
SMAPE (%) 177.34 170.66 170.62
30 days
(Sep. 1~30)		 CC 0.67 0.96 0.96
RMSE 6601.82 2272.38 2227.31
RMSSE 161311.70 55524.48 54423.11
SMAPE (%) 158.2 146.84 146.70
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated