Bioconvection and Mixed Convection Flow around a Vertical Thin Needle with Variable Surface Fluxes

Preprint

Article

Bioconvection and Mixed Convection Flow around a Vertical Thin Needle with Variable Surface Fluxes

Altmetrics

Downloads

Views

Comments

Nayema Islam Nima

Mohammed Abdul Hannan^*

Nayema Islam Nima

Mohammed Abdul Hannan^*

This version is not peer-reviewed

Submitted:

01 October 2024

Posted:

02 October 2024

You are already at the latest version

Alerts

Abstract

This work investigates mixed convection flow over a vertical thin needle with variable surface heat, mass, and microbial flux, incorporating the influence of gyrotactic microorganisms. The governing partial differential equations are transformed into ordinary differential equations using appropriate similarity transformations. These transformed equations are then numerically solved employing MATLAB's Bvp4c solver. The study's primary focus lies in examining the influence of various dimensionless parameters, including the mixed convection parameter, power-law index, buoyancy parameters, bioconvection parameters, and needle size parameter, on the velocity, temperature, concentration, and microbe profiles. The results demonstrate that these parameters significantly impact surface (wall) temperature, surface fluid concentration, surface motile microbe concentration, and the corresponding velocity, temperature, concentration, and microorganism profiles. The study's findings offer valuable insights into the intricate dynamics of mixed convection flow with bioconvection and have potential applications in diverse fields such as biomedicine and engineering.

Keywords:

Subject: Engineering - Bioengineering

1. Introduction

Researchers have paid special attention to mixed convection, which incorporates both forced and free convection, in the last several decades. The primary reason, according to references [1,2,3], is its wide range of technological and industrial uses. Heat exchanges in low-velocity situations, wind-current-exposed solar collectors, atmospheric boundary layer flows, nuclear reactor emergency shutdown cooling, and others are examples. Mixed convection flow across diverse surfaces was studied by many authors, including [4,5,6,7]. Heat flux is a critical factor in the study of mixed convection boundary layer flow, where the movement of fluid is influenced by both buoyancy forces and external forces such as pressure gradients or mechanical pumps. The role of heat flux in this context is paramount, as it directly impacts the distribution of temperature within the fluid and along solid surfaces. This, in turn, affects how efficiently heat is transferred in various systems. Understanding heat flux is essential for accurately predicting temperature profiles and optimizing thermal processes across a wide range of applications. In mixed convection, the dynamic interplay between forced convection driven by external forces and natural convection resulting from buoyancy effects creates complex heat transfer scenarios. The effectiveness of this heat transfer process hinges on the ability to manage heat flux at the boundaries where fluid meets solid surfaces. By carefully monitoring and analyzing heat flux, engineers can design more efficient thermal systems. This involves optimizing convective heat exchange at solid boundaries, such as those found in heat exchangers, electronic cooling systems, and industrial reactors. For instance, in electronics cooling, precise control of heat flux is crucial to prevent overheating and ensure the reliable operation of components. Similarly, in environmental processes like geothermal energy extraction or climate control systems, managing heat flux is key to maintaining desired temperature conditions. Accurate heat flux analysis also plays a vital role in predicting the behavior of the boundary layer the thin region of fluid near a solid surface where velocity and temperature gradients are most significant. Properly managing this boundary layer is essential for achieving effective heat dissipation in cooling systems or retaining heat in processes where insulation is critical. The ability to control and predict heat flux enables the development of systems with enhanced thermal performance and energy efficiency. This knowledge is vital across a spectrum of industries, from the design of more efficient power plants and HVAC systems to the creation of sustainable environmental technologies. By leveraging a deep understanding of heat flux in mixed convection scenarios, engineers can develop innovative solutions that improve the thermal management of a wide range of systems, leading to greater reliability, performance, and sustainability. Multiple studies [8,9,10,11,12,13] have shown the importance of fluid flow and uniform or varied heat flux in some manufacturing processes. Recently, Ahmed et al. [14] studied mixed convective Williamson fluid flow with variable thermal conductivity. Everts et al. [15] observed forced convective flow through horizontal tube with constant surface heat flux.

Bioconvection in fluid dynamics refers to the phenomenon where self-propelled microorganisms, such as algae and bacteria, react to oxygen gradients (oxytaxis), rotation (gyrotaxis), or gravity. Motile bacteria swim upwards in the system due to their greater density compared to the surrounding liquid. This behavior leads to the formation of various flow patterns, as explained in references [16,17,18]. Gyrotactic bacteria play a crucial role in bioconvection by coordinating group movements that have a substantial impact on ecological dynamics. Their navigational proficiency in locating nutrient-abundant areas plays a role in the transportation of nutrients, hence impacting the spatial arrangement of microorganisms in aquatic habitats. The bioconvection patterns that are created also contribute to the biological pump by enabling the upward movement of organic materials and nutrients. Moreover, the ability of gyrotactic microorganisms to respond to light gradients improves their capacity to perceive and understand their surroundings. In addition to ecological ramifications, the examination of these microorganisms offers significant understanding of thermo-bioconvection, microbial augmentation, bio-Microsystems, biofuels, and other bioengineering systems [19,20,21,22,23,24]. Alharbi et al. [25] investigated the importance of gyrotactic microorganisms in a tangent hyperbolic nanofluid flowing across a thin surface.Alam et al. [26] studied gyrotactic microbial flow under thermal radiative condition over dual stretched surface. Chemical reaction and heat generation effect with microorganism are by Ferdows et al. [27] through non-isothermal horizontal surface. In recent studies, Khan et al. [28] and Yasmin [29] both investigated hydromagnetic bioconvection flow with nanofluid over stretching surfaces. Stefan blowing and gyrotactic bacteria affected bionanoconvective flow past a needle, as observed by Amirsom et al. [30] and Beg et al. [31].

Researchers are studying the fluid dynamics surrounding a thin needle because of its importance in biomedical engineering applications including cancer treatment and transdermal medicine delivery. Experimental research on momentum and heat transfer by analyzing slender needle flow is important. This phenomenon arises due to the movement of the needle, which causes disturbances in the flow of the free stream. Thus, this topic is important for hot anemometers used to measure wind velocity, transportation systems, geothermal power generation, fiber technology, lubrication, aerospace, wire coating, metal spinning, micro/nanoscale equipment, and underground nuclear waste disposal. Thin needles have paraboloid of revolution geometry and are thinner than boundary layer thickness. Grosan and Pop [32] were the first to study nanoparticles' effect on thin needle flow. Soid et al. [33] applied this to a needle in a nanofluid. Hayat et al. [34] studied nanoliquid flow where a thin needle near a stagnation point changed surface heat flux. Ali et al. [35] studied mixed convective nanofluid flow over a needle. Salleh et al. [36] examined how a heat source and chemical reaction affect nanofluid flow around a thin needle in a stability analysis. Waini et al. [37] and Khan et al. [38] studied hybrid nanofluid flow through a thin needle.

The aforementioned investigations on free or mixed convection boundary layer flow over vertical thin needles pertain to stationary needles submerged in a viscous and incompressible fluid. Furthermore, the study has mostly focused on analyzing heat and mass transfer under either isothermal or non-isothermal conditions, as well as constant or variable wall heat flux needles. However, the current study is motivated by the recent studies [31,39,40] fact that there is no existing literature on the flow of a mixed convective boundary layer via a vertical thin needle that contains gyrotactic microorganisms and has variable surface heat, mass, and motile microbe flux. Considering the frequent occurrence of this specific changing surface heat flow scenario in engineering practice, it deserves distinct consideration. As far as I know, the findings derived from this study are novel and unique, and have not been previously published. The findings of this study have potential applications in several industries such as food and pharmaceuticals, chemical processing equipment, fuel cell technology, and enhanced oil recovery.

2. Model Formulation

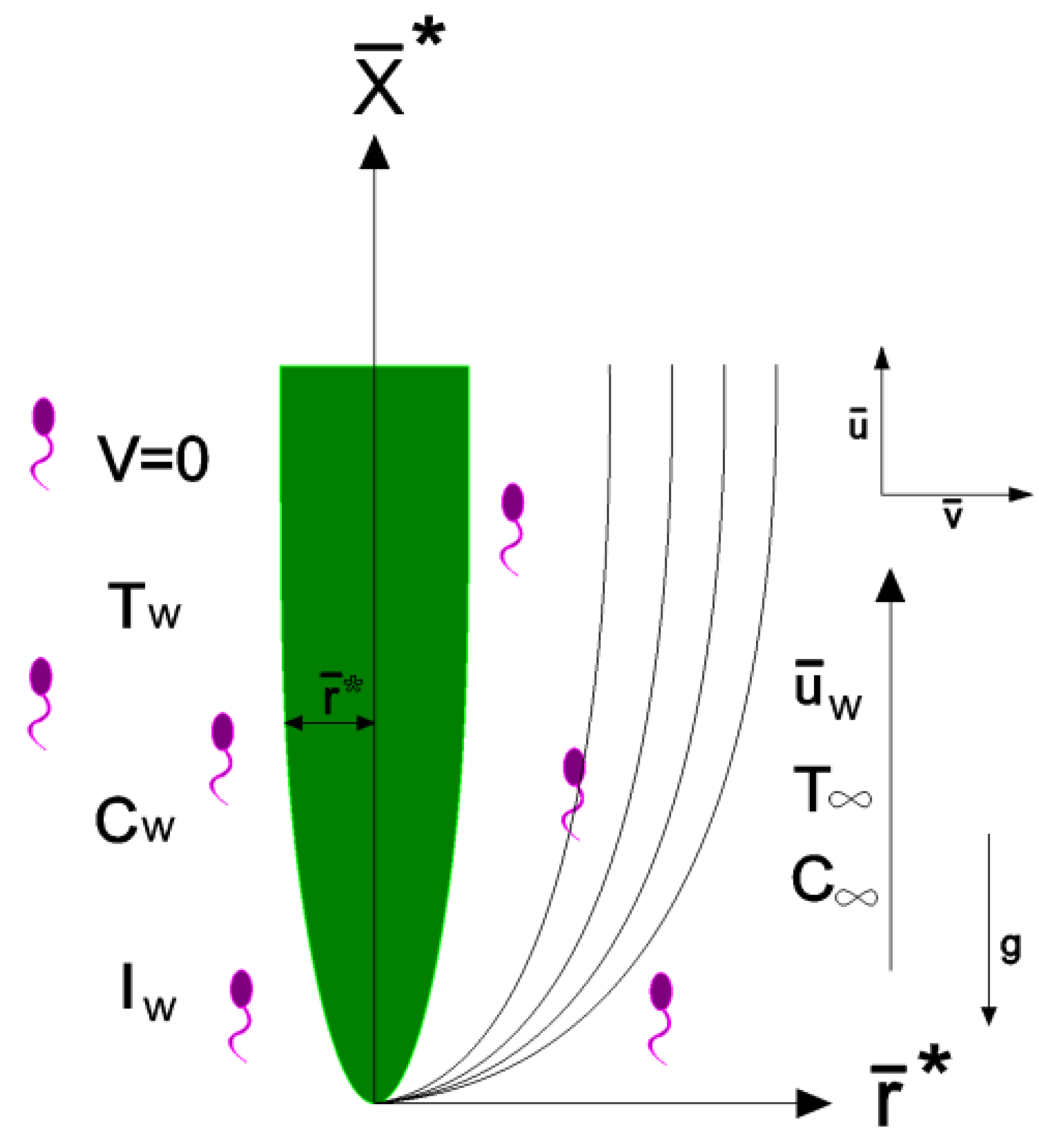
Figure 1 examines the 2-D laminar flow of a fluid surrounding a vertical thin needle. The flow is influenced by variations in heat, mass, and the movement of microorganisms. Additionally, the presence of gyrotactic bacteria is taken into account. A vertical, thin needle with a radius

{\bar{r}}^{*} = {\bar{R}}^{*} ({\bar{x}}^{*})

defined by is displayed alongside the flow model and system coordinates, where the -

{\bar{x}}^{*}

axis is measured from the leading edge of the needle, and the axial and radial coordinates are,

{\bar{x}}^{*}

and

{\bar{r}}^{*}

respectively. A needle is deemed thin when its thickness is not greater than the boundary layer that forms over it. Following [30,31,41], the Boussinesq approximations yield the dimensionless equations in cylindrical coordinates are:

\frac{1}{r^{*}} \frac{\partial^{2} ψ}{\partial r^{* 2}} = λ^{3} [\frac{\partial T}{\partial r^{*}} + N_{c} \frac{\partial C}{\partial r^{*}} + N_{m} \frac{\partial I}{\partial r^{*}}]

(1)

\frac{1}{r^{*}} \frac{\partial ψ}{\partial r^{*}} \frac{\partial T}{\partial x} - \frac{1}{r^{*}} \frac{\partial ψ}{\partial r^{*}} \frac{\partial T}{\partial r^{*}} = \frac{1}{r^{*}} \frac{\partial}{\partial r^{*}} (r^{*} \frac{\partial T}{\partial r^{*}})

(2)

L e [\frac{1}{r^{*}} \frac{\partial ψ}{\partial r^{*}} \frac{\partial C}{\partial x^{*}} - \frac{1}{r^{*}} \frac{\partial ψ}{\partial r^{*}} \frac{\partial C}{\partial r^{*}}] = \frac{1}{r^{*}} \frac{\partial}{\partial r^{*}} (r^{*} \frac{\partial C}{\partial r^{*}})

(3)

L b [\frac{1}{r^{*}} \frac{\partial ψ}{\partial r^{*}} \frac{\partial I}{\partial x^{*}} - \frac{1}{r^{*}} \frac{\partial ψ}{\partial r^{*}} \frac{\partial I}{\partial r^{*}}] + P e [\frac{\partial}{\partial r^{*}} (I \frac{\partial C}{\partial r^{*}})] \frac{1}{x^{* 2 m - 1}} = \frac{1}{r^{*}} \frac{\partial}{\partial r^{*}} (r^{*} \frac{\partial I}{\partial r^{*}})

(4)

\frac{\partial ψ}{\partial x^{*}} = 0, \frac{\partial T}{\partial r^{*}} = - q_{w} (x^{*}), \frac{\partial C}{\partial r^{*}} = - q_{c} (x^{*}), \frac{\partial I}{\partial r^{*}} = - q_{i} (x^{*})

(5)

\frac{1}{r^{*}} \frac{\partial ψ}{\partial r^{*}} = U_{w} (x^{*}), T \to T_{\infty}, C \to C_{\infty}, I \to 0 at r^{*} \to \infty

(6)

The non-dimensionalizing analysis made use of the following variables:

x^{*} = \frac{{\bar{x}}^{*}}{L}, r^{*} = P e^{\frac{1}{2}} \frac{{\bar{r}}^{*}}{L}, u = \frac{\bar{u}}{u_{\infty}}, v = P e^{\frac{1}{2}} \frac{\bar{v}}{u_{\infty}}, R^{*} (x^{*}) = P e^{\frac{1}{2}} \frac{{\bar{R}}^{*} (x^{*})}{L}, r^{*} = P e^{\frac{1}{2}} \frac{{\bar{r}}^{*}}{L}, U_{w} = \frac{{\bar{U}}_{w}}{u_{\infty}}

T = \frac{k P e^{\frac{1}{2}} (\bar{T} - T_{\infty})}{q_{w} L}, C = \frac{D_{c} P e^{\frac{1}{2}} (\bar{C} - C_{\infty})}{q_{c} L}, I = \frac{D_{i} P e^{\frac{1}{2}} \bar{I}}{q_{i} L}, q_{w} = \frac{{\bar{q}}_{w}}{k}, q_{c} = \frac{{\bar{q}}_{c}}{D_{c}}, q_{i} = \frac{{\bar{q}}_{i}}{D_{i}}

The parameters can be defined as

R a = \frac{g β_{T} q_{w} L^{2}}{ν α}, P e = \frac{u_{\infty} L}{α}, ε = \frac{R a^{\frac{1}{3}}}{P e^{\frac{1}{2}}}, N_{c} = \frac{β_{c} q_{c} k}{β_{T} q_{w} D_{c}}, N_{m} = \frac{β_{n} q_{i} k}{β_{T} q_{w} D_{i}}, L e = \frac{α}{D_{c}}, L b = \frac{α}{D_{i}}, P e = \frac{b W_{c}}{D_{i}}

Similarity transformations now are

ξ = x^{* m * - 1} r^{*}, ψ = x^{*} f (η), T = x^{* 2 m * - 1} θ (ξ), C = x^{* 2 m * - 1} φ (ξ), I = x^{* 2 m * - 1} χ (ξ)

U_{w} = x^{* 2 m * - 1}, q_{w} = x^{* 3 m * - 2}, q_{c} = x^{* 3 m * - 2}, q_{i} = x^{* 3 m * - 2}

Setting

ξ = p

the relationship

ξ = \frac{r^{*}}{x^{* (1 - m *)}}

explains the body's shape and size with its surface assumed by

R^{*} (x^{*}) = p x^{* (1 - m *)}

m * = 1

is a cylinder,

m * = 0.5

is a paraboloid (blunt-nosed shape), and

m * = 0

is a cone.

Transformations of ordinary differential equations are:

f^{″} = {(ε)}^{3} ξ [θ^{'} + N_{c} φ^{'} + N_{m} χ^{'}]

(7)

ξ θ^{″} + θ^{'} + f θ^{'} - (2 m * - 1) f^{'} θ = 0

(8)

ξ ϕ^{″} + ϕ^{'} + L e . f ϕ^{'} - (2 m * - 1) L e . f^{'} φ = 0

(9)

ξ χ^{″} + χ^{'} + L b . f χ^{'} - L b . (2 m * - 1) f^{'} χ - P e (ξ φ^{'} χ^{'} + χ ϕ^{'} + ξ φ^{″}) = 0

(10)

Modified boundary conditions are:

ξ = p, f (p) = 0, θ^{'} (p) = - 1, φ^{'} (p) = - 1, χ (p) = - 1 and

(11)

ξ \to \infty, f^{'} \to p, θ \to 0, φ \to 0, χ \to 0

(12)

To define surface temperature

T_{w}

, surface fluid concentration

C_{w}

and surface motile microorganism concentration

I_{w}

are

T_{w} = \frac{k P e^{\frac{1}{2}} ({\bar{T}}_{w} - T_{\infty})}{q_{w} L}, C_{w} = \frac{D_{c} P e^{\frac{1}{2}} ({\bar{C}}_{w} - C_{\infty})}{q_{c} L}, I_{w} = \frac{D_{i} P e^{\frac{1}{2}} {\bar{I}}_{w}}{q_{i} L}

Finally using non-dimensional and similarity transformations, we get,

T = x^{* 2 m - 1} θ (p), C = x^{* 2 m * - 1} φ (p), I = x^{* 2 m * - 1} χ (p)

3. Numerical Method

In solving boundary value problems (BVPs) using MATLAB's bvp4c function, the first step involves defining the system of ordinary differential equations (ODEs) representing the problem and specifying the corresponding boundary conditions. A crucial aspect is providing an accurate initial guess for the solution. The bvp4c function is then employed, with the ODEs, boundary conditions, and initial guess as inputs. The solver can be fine-tuned using optional parameters. Post-solving, the solution is extracted from the output structure, and visualization and analysis are carried out using MATLAB's plotting functions. If the solution does not meet desired criteria, an iterative process may involve refining the initial guess or adjusting solver options. This methodology enables users to effectively utilize the BVP4C solver for a broad range of problems, provided careful consideration of the ODEs, boundary conditions, and the iterative refinement process. In the context of bvp4c function described above we need to transform the governing equations into first order differential equation. At first Equations (7-10) can be rearranged in the following way

\begin{array}{l} f^{″} = ε^{3} ξ [θ^{'} + N_{c} φ^{'} + N_{m} χ^{'}] \\ θ^{″} = \frac{- θ^{'} - f θ^{'} + (2 m * - 1) f^{'} θ}{ξ} \\ φ^{″} = \frac{- φ^{'} - L e f φ^{'} + (2 m * - 1) L e f^{'} φ}{ξ} \\ χ^{″} = \frac{- χ^{'} - L b f χ^{'} + (2 m * - 1) L b f^{'} χ + P e (ξ φ^{'} χ^{'} + χ φ^{'} + ξ φ^{″})}{ξ} \end{array}

Next, we'll convert the problem to a differential equation of the first order. For this let

ξ = p

and

s_{1} = f, s_{2} = f^{'}, s_{3} = θ, s_{4} = θ^{'}, s_{5} = φ, s_{6} = φ^{'}, s_{7} = χ, s_{8} = χ^{'}

These differential equations of first order are

\begin{array}{l} \frac{d h_{1}}{d x} = f^{'} = s_{2} \\ \frac{d h_{2}}{d x} = f^{″} = ε^{3} p [s {}_{4}+ s_{6} N_{c} + s_{8} N_{m}] \\ \frac{d h_{4}}{d x} = θ^{″} = \frac{- s_{4} - s_{1} s_{4} + (2 m * - 1) s_{2} s_{3}}{p} \\ \frac{d h_{6}}{d x} = φ^{″} = \frac{- s_{6} - s_{1} s_{6} L e + (2 m * - 1) s_{2} s_{5} L e}{p} \\ \frac{d h_{8}}{d x} = χ^{″} = \frac{- s_{8} - s_{1} s_{8} L b + (2 m * - 1) s_{2} s_{8} L b + P e (p s_{6} s_{8} + s_{7} s_{6} + s_{7} (- s_{6} - L e s_{1} s_{6} + (2 m * - 1) L e s_{2} s_{5}))}{p} \end{array}

The boundary conditions are defined by

y a^{*}

as the left boundary and

y b^{*}

as the right boundary.

\begin{array}{l} y a * (1) = 0, y b * (2) - p = 0 \\ y a * (4) + 1 = 0, y b * (3) = 0 \\ y a * (6) + 1 = 0, y b * (5) = 0 \\ y a * (8) + 1 = 0, y b * (7) = 0 \end{array}

To validate the findings, the differential equations are once again solved numerically using Maple's dsolve command. The asymptotic boundary conditions (11)-(12) are substituted by setting the similarity variable

η_{m a x}

to a value of 5. The outcomes for both situations are presented in Table 1. demonstrate strong concordance and precision in numerical computations.

To assess the additional accuracy of the obtained findings from both the MATLAB Bvp4c and Maple schemes, an error analysis is done, and the results are appended to Table 2. Calculating error percentages is an important step in validating numerical algorithms and assuring their accuracy. A smaller mistake percentage shows that the method is more accurate in this particular problem.

To do error analysis between MATLAB Bvp4c and Maple scheme, absolute and relative error were calculated using the following formulas:

Absolute error = |N_{M A P L E} - N_{B V P 4 C}|

Relative error = \frac{|N_{M A P L E} - N_{B V P 4 C}|}{M a x (|N_{M A P L E}|, |N_{B V P 4 C}|)}

Then percentage error is calculated expressing the relative error as a percentage, which is often easier to interpret and compare.

Percentage Error = \frac{|N_{M A P L E} - N_{B V P 4 C}|}{M a x (|N_{M A P L E}|, |N_{B V P 4 C}|)} \times 100

These above formulas allow quantifying the error between two methods, facilitating the comparison and validation of numerical results.

4. Analysis and Interpretation of the Outcome

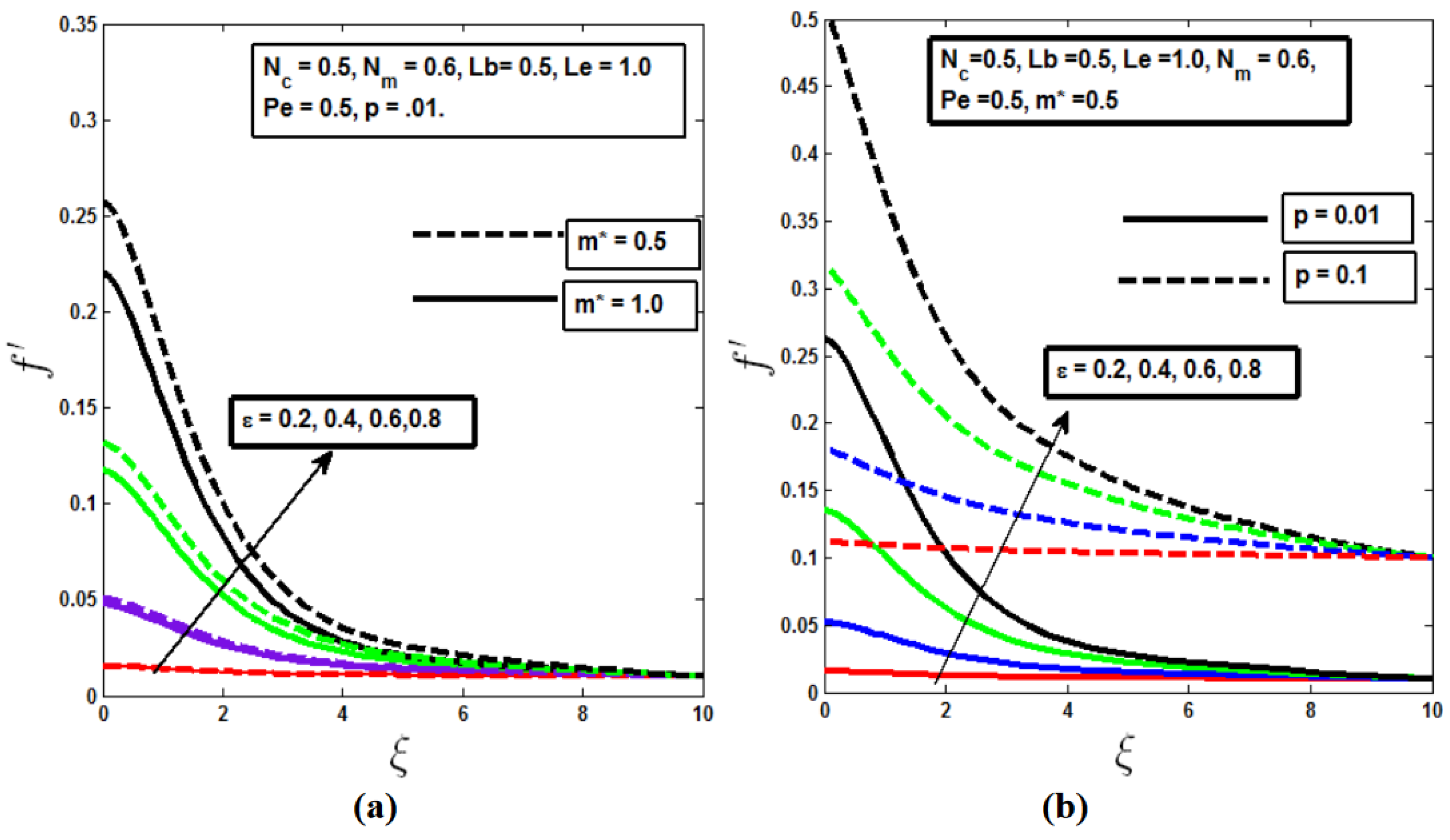
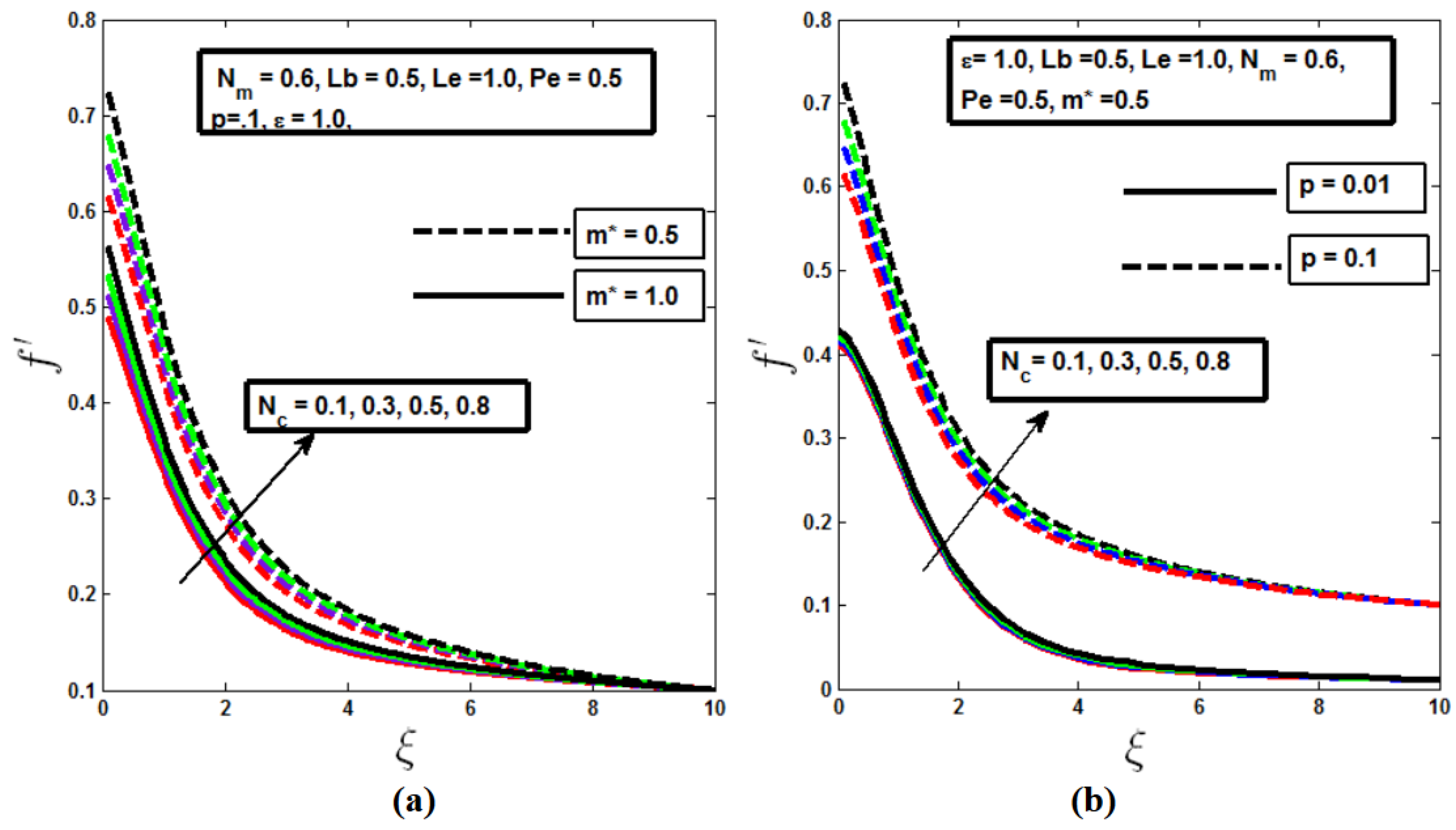
Figure 2 and Figure 3 show the distribution of the velocity profile for various values of the buoyancy parameter

N_{c}

and the mixed convection parameter

ε

. In both isothermal (m* = 0.5) and non-isothermal (m* = 1.0) needle scenarios, as shown in Figure 2(a) and Figure 3(a), and across different needle sizes, as depicted in Figure 2(b) and Figure 3(b), the velocity profile increases as the values of

N_{c}

and

ε

rise. This increase is driven by the buoyant forces that enhance fluid motion. The velocity boundary layer becomes thicker when using an isothermal needle compared to a non-isothermal one, and increasing the needle thickness further improves the velocity profile. This enhanced flow profile is due to momentum diffusion, facilitated by the needle’s larger contact area with the fluid. On the other hand, as the needle size decreases, less of its surface interacts with the fluid particles, leading to restricted fluid flow due to the frictional forces acting on the needle surface. In practical applications, this insight is particularly useful in fields such as chemical processing or biomedical engineering, where controlling fluid flow around needles or similar structures is crucial. For example, optimizing needle size and the buoyancy effects can enhance the efficiency of processes like drug delivery or heat exchangers, where precise control overflow profiles is necessary for optimal performance.

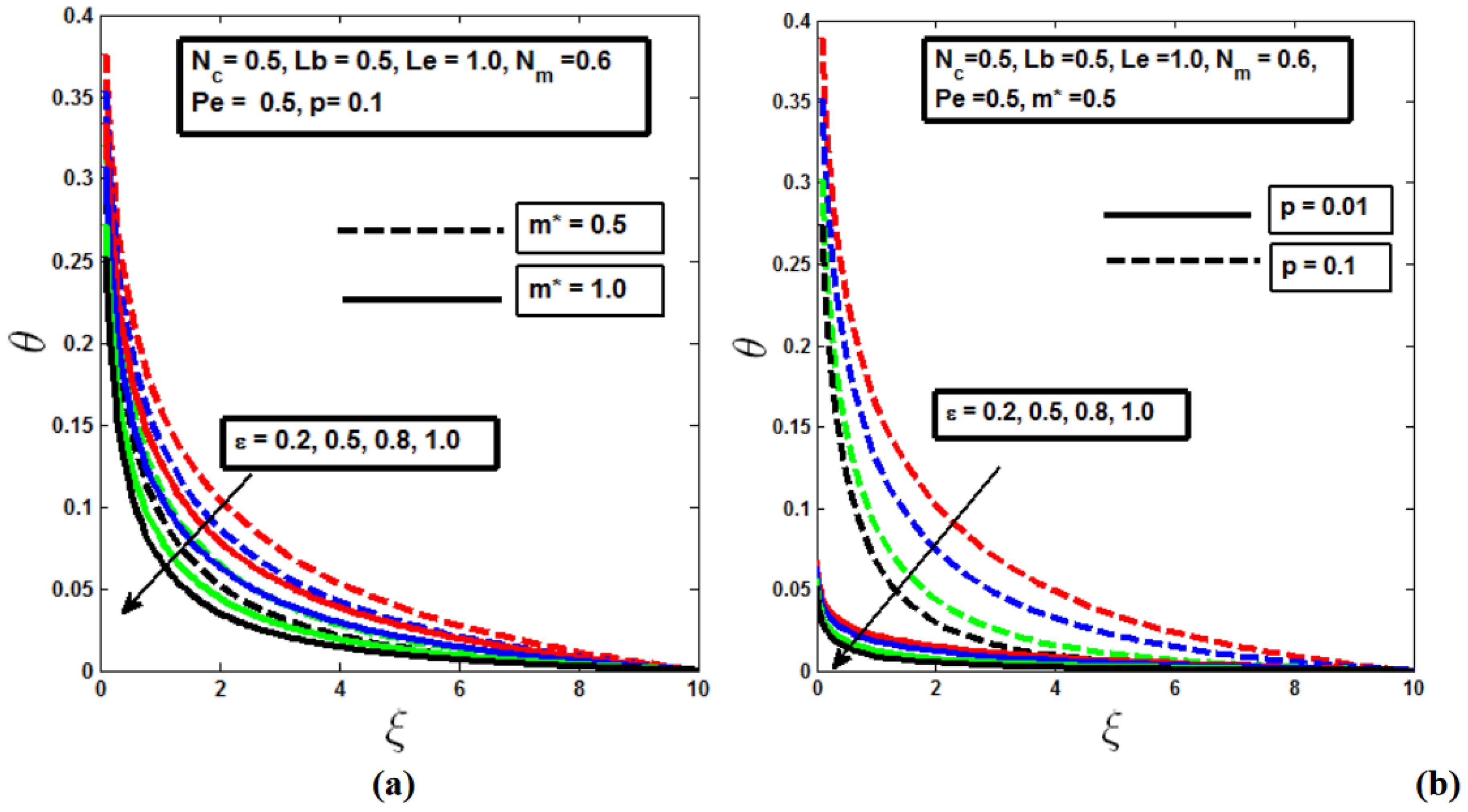
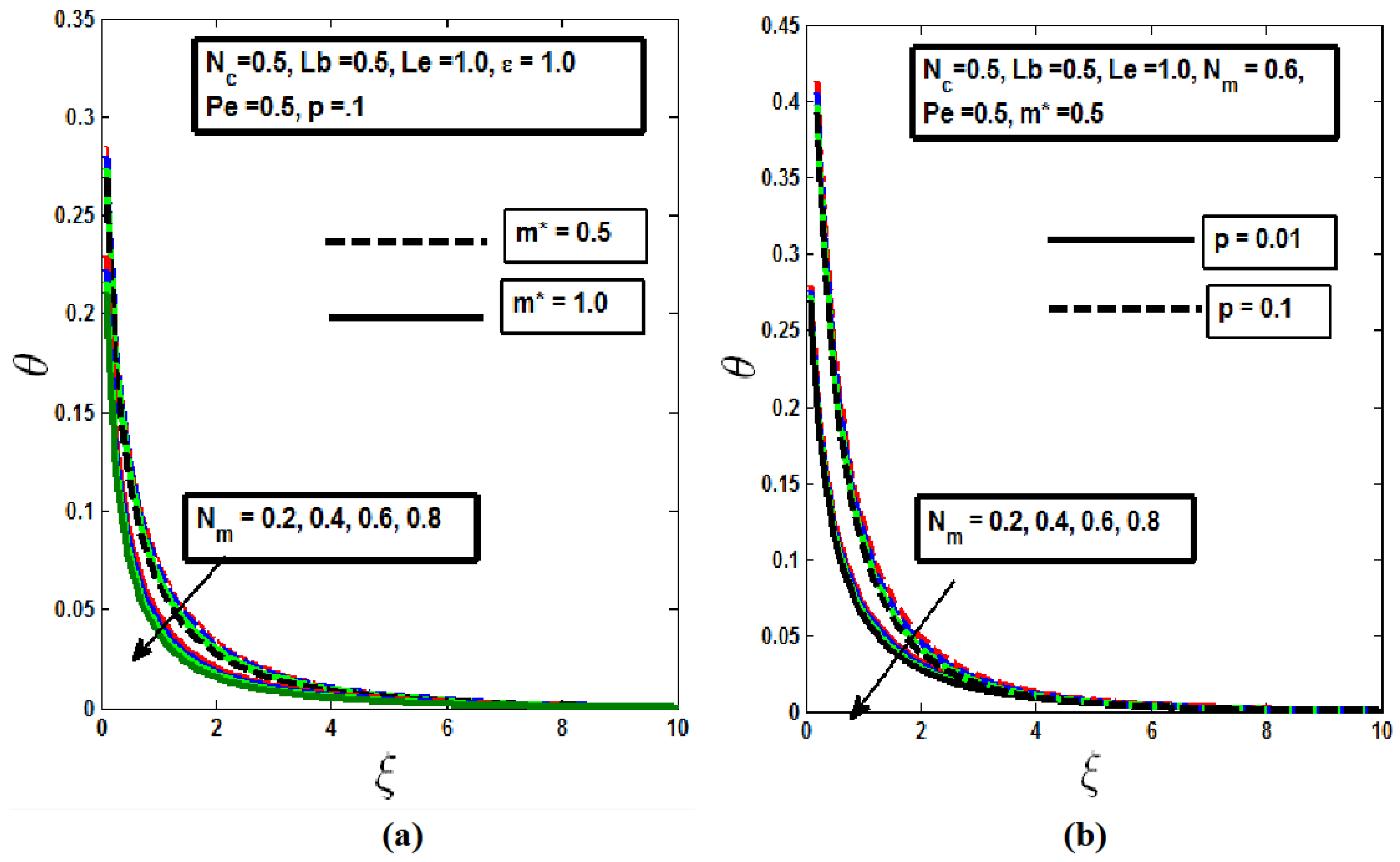
As illustrated in Figure 4 and Figure 5, the temperature profile decreases with an increase in the mixed convection parameter

ε

. This effect is more pronounced for a non-isothermal needle (m* = 1.0), where the temperature drop is greater, in contrast to the behavior observed in the velocity profile. Additionally, increasing the needle thickness leads to a thicker thermal boundary layer, which in turn lowers the temperature at the needle's surface, as depicted in Figure 4(b) and Figure 5(b). This phenomenon is further explained by the fact that a higher rate of momentum diffusion hinders thermal diffusion, resulting in the cooling of the boundary layer and a subsequent reduction in its thickness, as supported by reference [21].

In practical terms, this understanding is crucial in industries where precise thermal management is needed, such as in the design of cooling systems for microelectronics or in biomedical applications where controlled temperature profiles around needles are critical. By optimizing the mixed convection parameter and needle geometry, engineers can effectively manage heat transfer to maintain optimal operating conditions or enhance the performance of thermal systems.

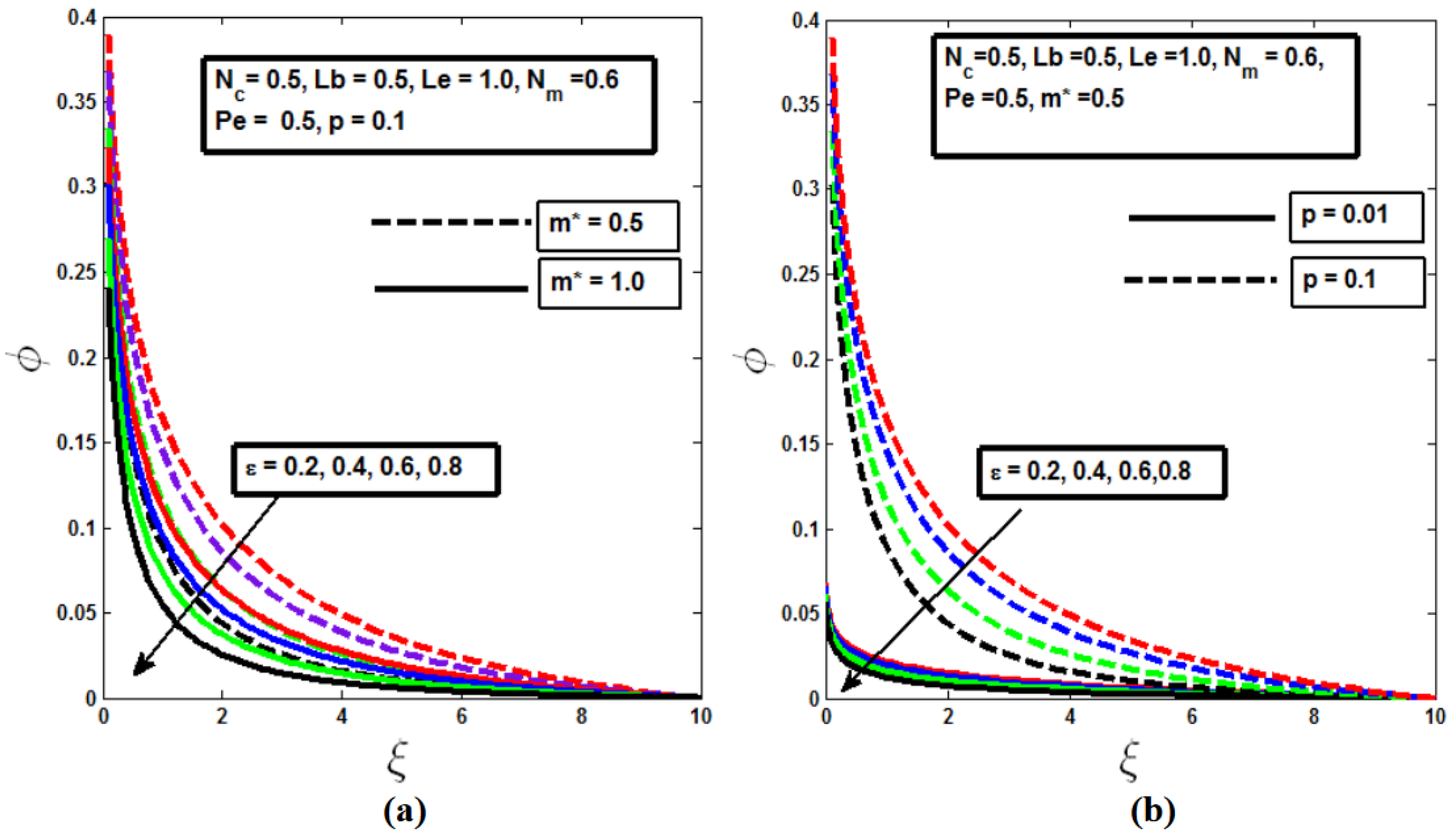
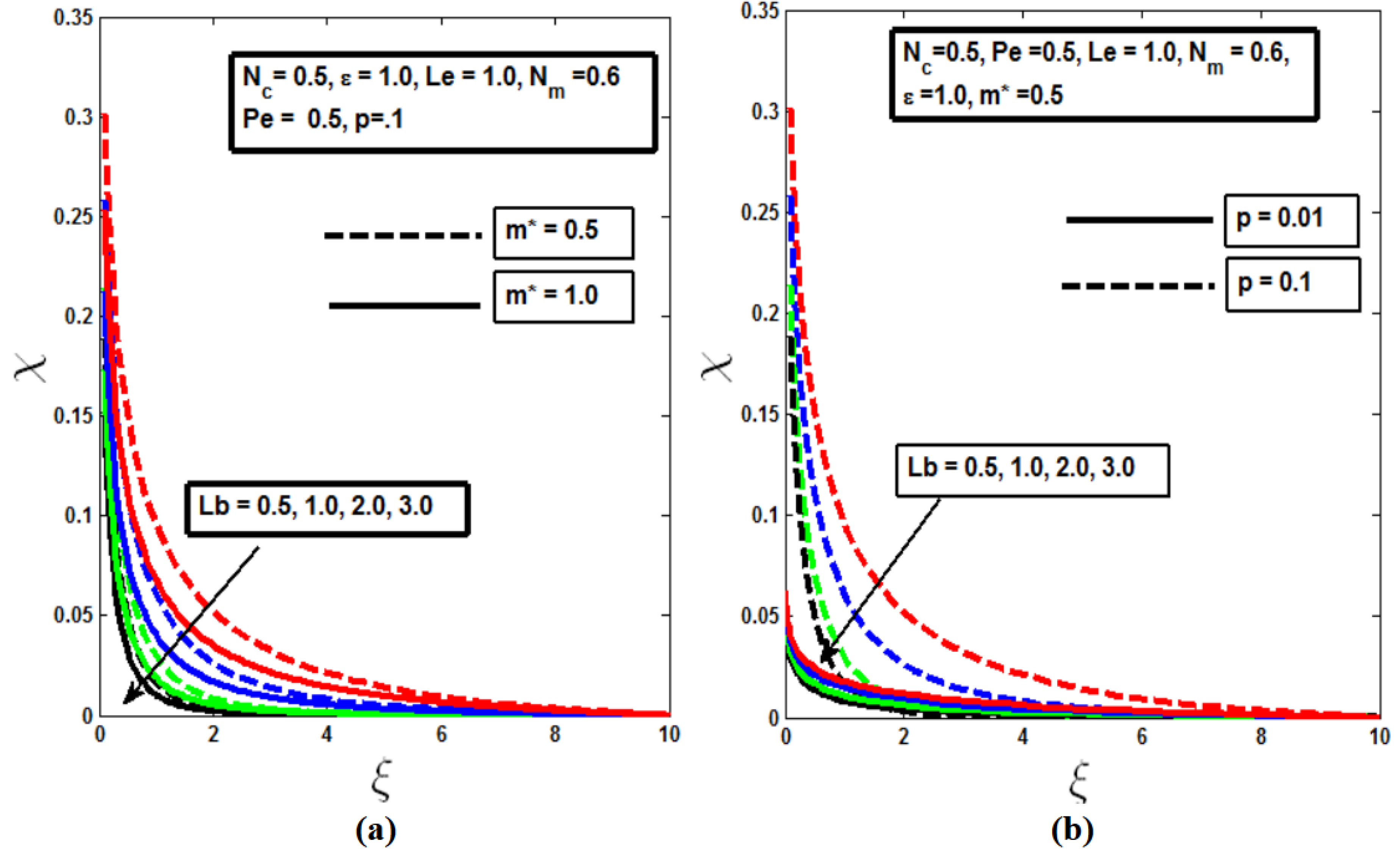
As shown in Figure 6, the concentration profile decreases with increasing values of the Lewis number

L e

, particularly in the non-isothermal case (m* = 1). This effect is further amplified by the slender surface of the needle, as illustrated in Figure 6(b), which leads to an even greater reduction in the concentration profile.

L e

is a dimensionless parameter representing the ratio of thermal diffusivity to mass diffusivity, playing a critical role in the analysis of heat and mass transfer processes. As the Lewis number increases, the boundary layer thickness of the concentration profile diminishes for both isothermal and non-isothermal needle configurations, as seen in Figure 7.

In practical applications, such as in the design of biosensors or microfluidic devices, understanding how the Lewis number and needle geometry affect microbial flow is essential. For instance, in scenarios where precise control of microbial concentration is required, optimizing the needle's slenderness and adjusting the Lewis number can be key to achieving desired outcomes in processes involving heat and mass transfer.

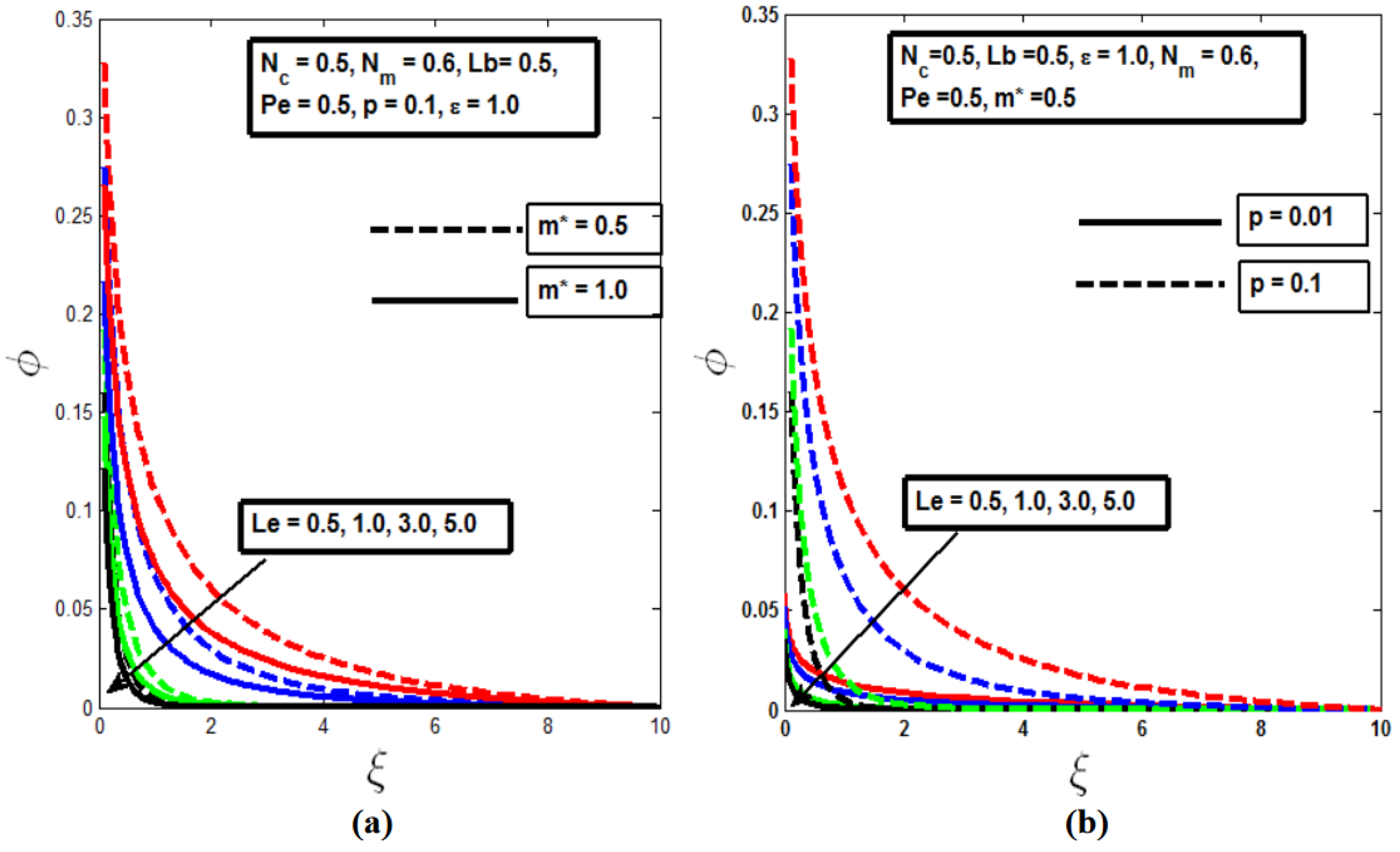
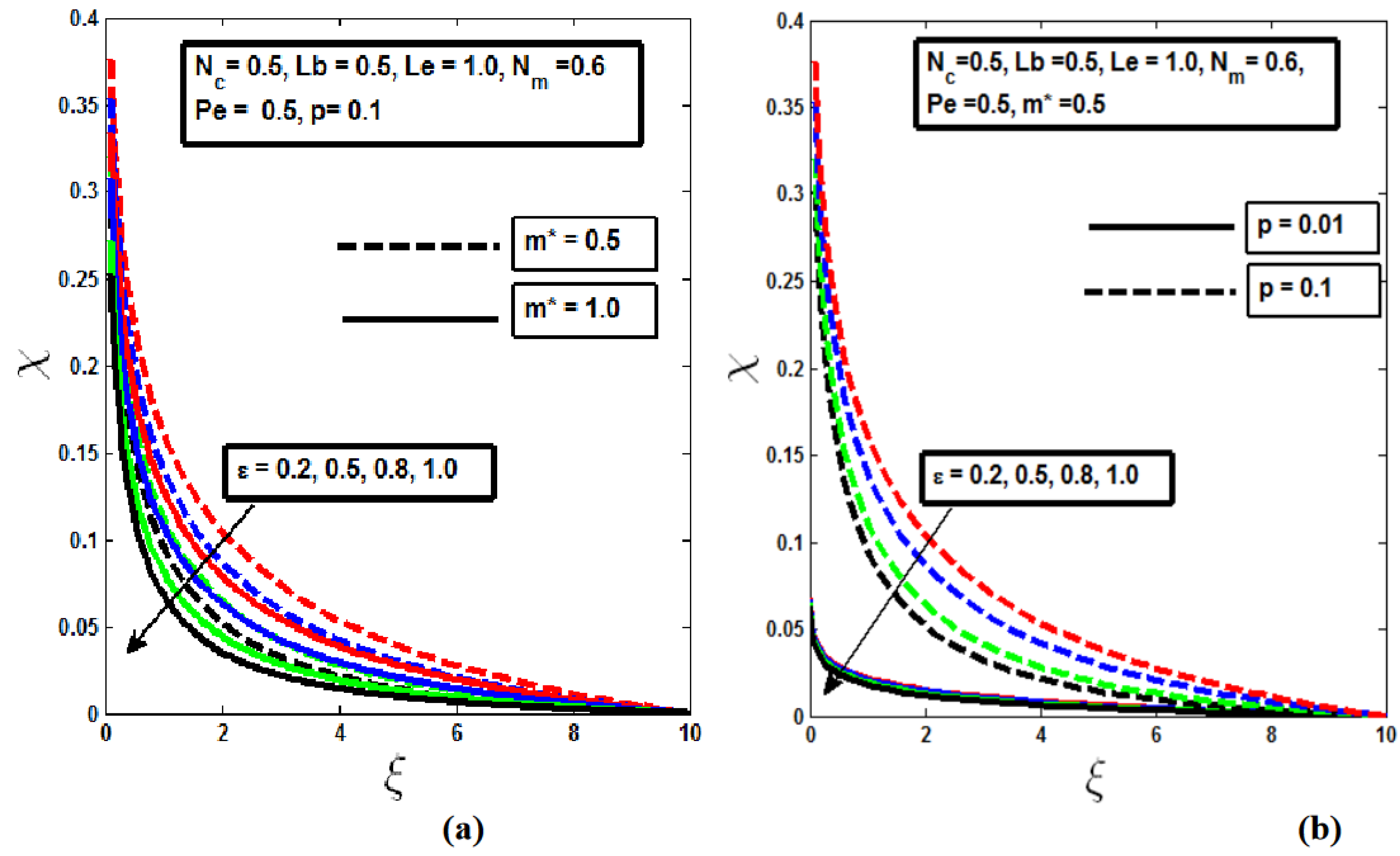
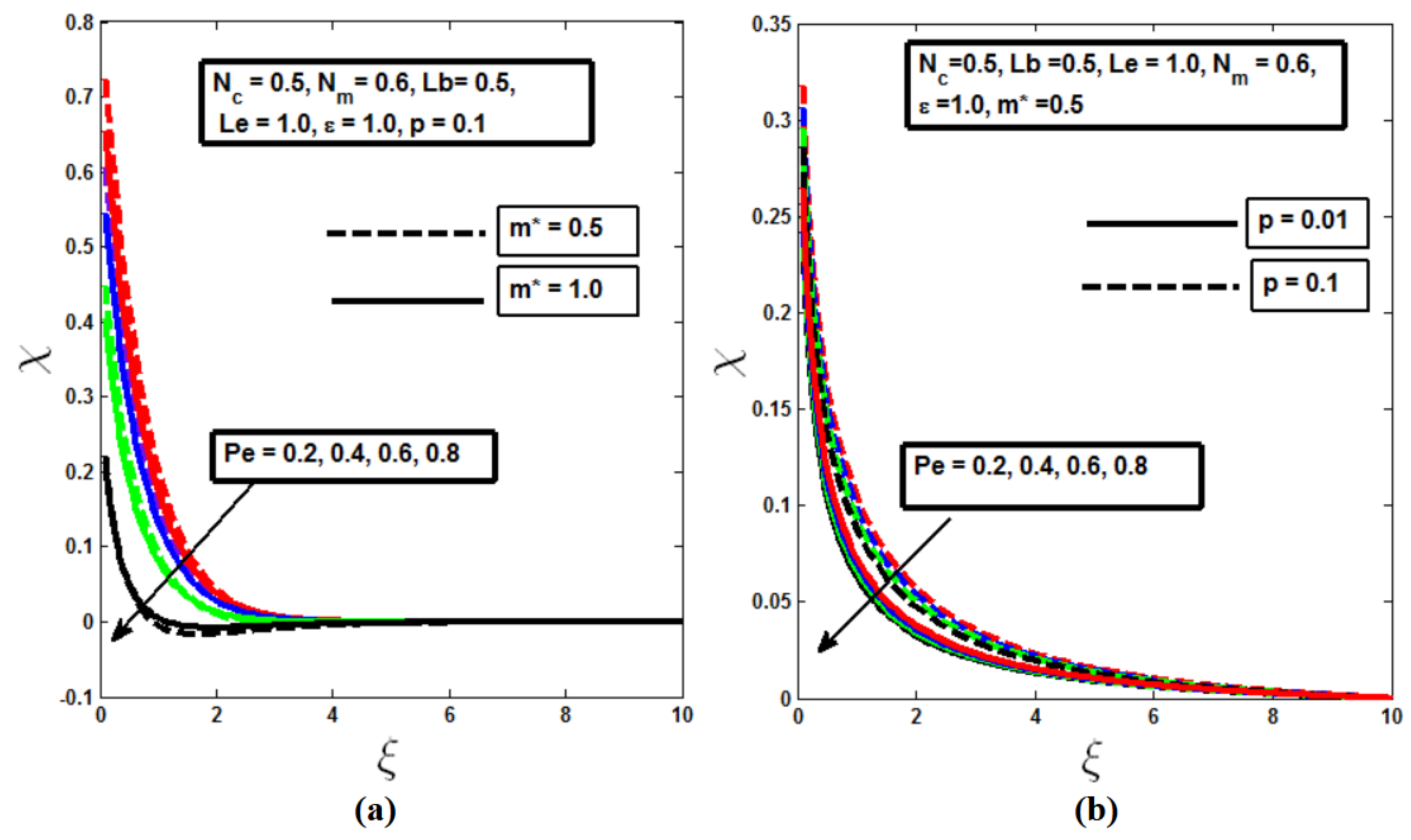
Figure 8, Figure 9 and Figure 10 illustrate that as the mixed convection parameter

ε

, Bioconvection Lewis number

L b

, and Bioconvection Peclet number

P e

increase, there is a noticeable reduction in the microorganism profiles. An increase in

P e

and

L b

enhances the fluid's mobility, which in turn thins the layer of motile microbes. This behavior is consistent across both isothermal (m* = 0.5) and non-isothermal (m* = 1.0) conditions, as depicted in Figure 8(b), Figure 9(b) and Figure 10(b). Additionally, Figure 8(b), Figure 9(b) and Figure 10(b) show that decreasing the diameter of the needle leads to a thinner boundary layer in the microorganism profile. This occurs because a smaller needle size accelerates the transport of motile microorganisms, resulting in a reduced thickness of the boundary layer. This practical insight is particularly relevant in applications where controlling the thickness of microbial layers is critical, such as in bioengineering processes or designing efficient cooling systems where microbial presence must be minimized.

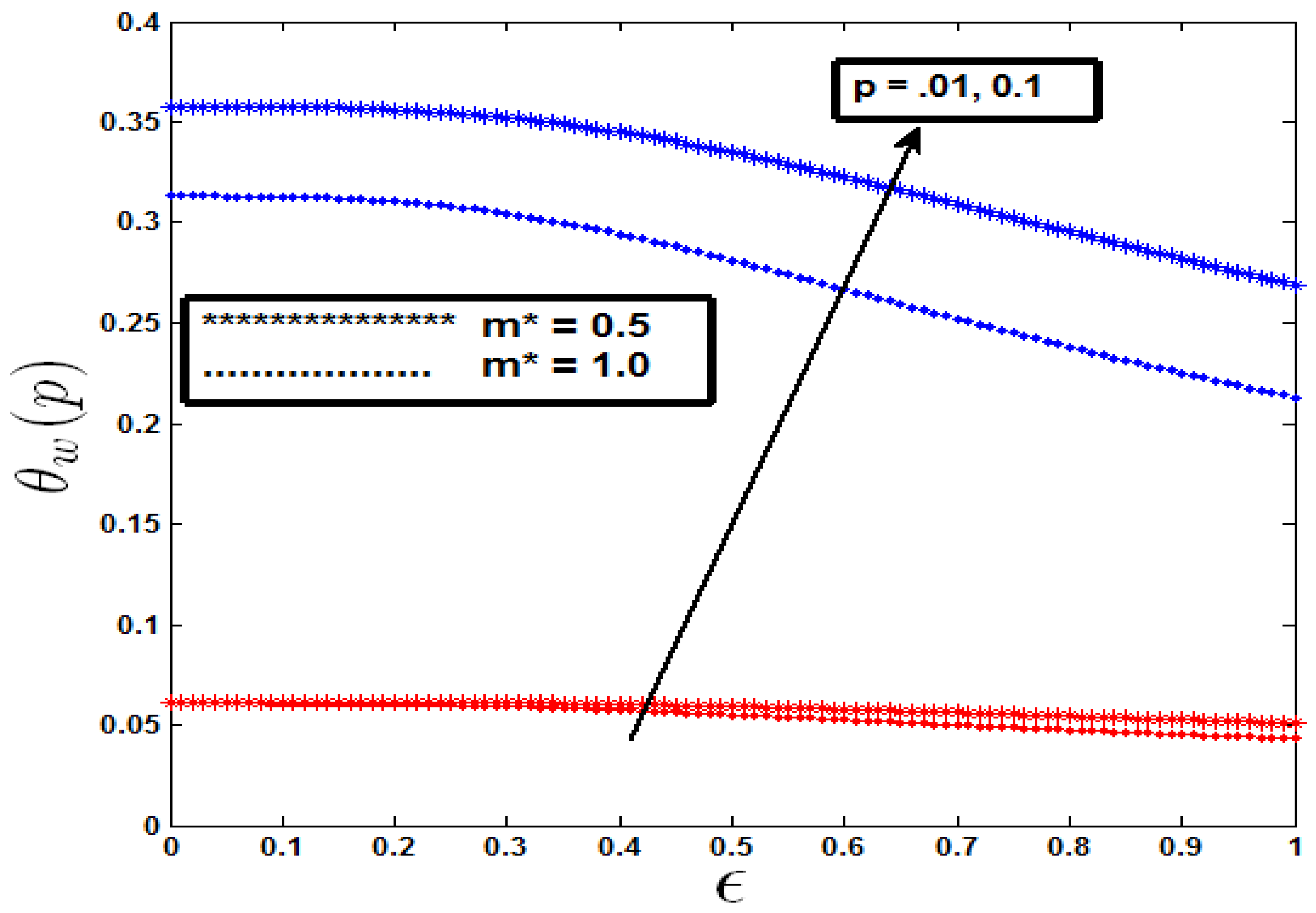
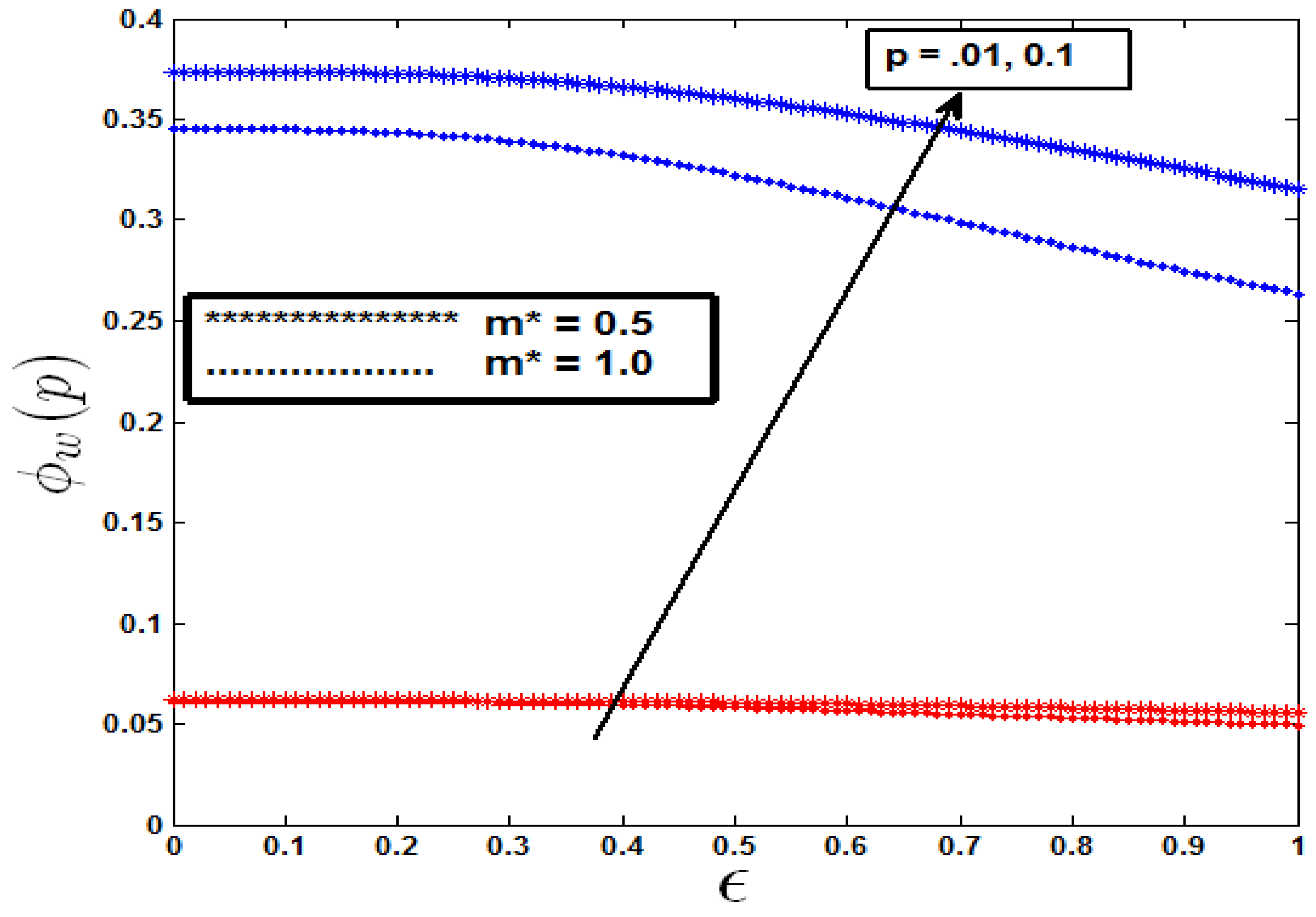
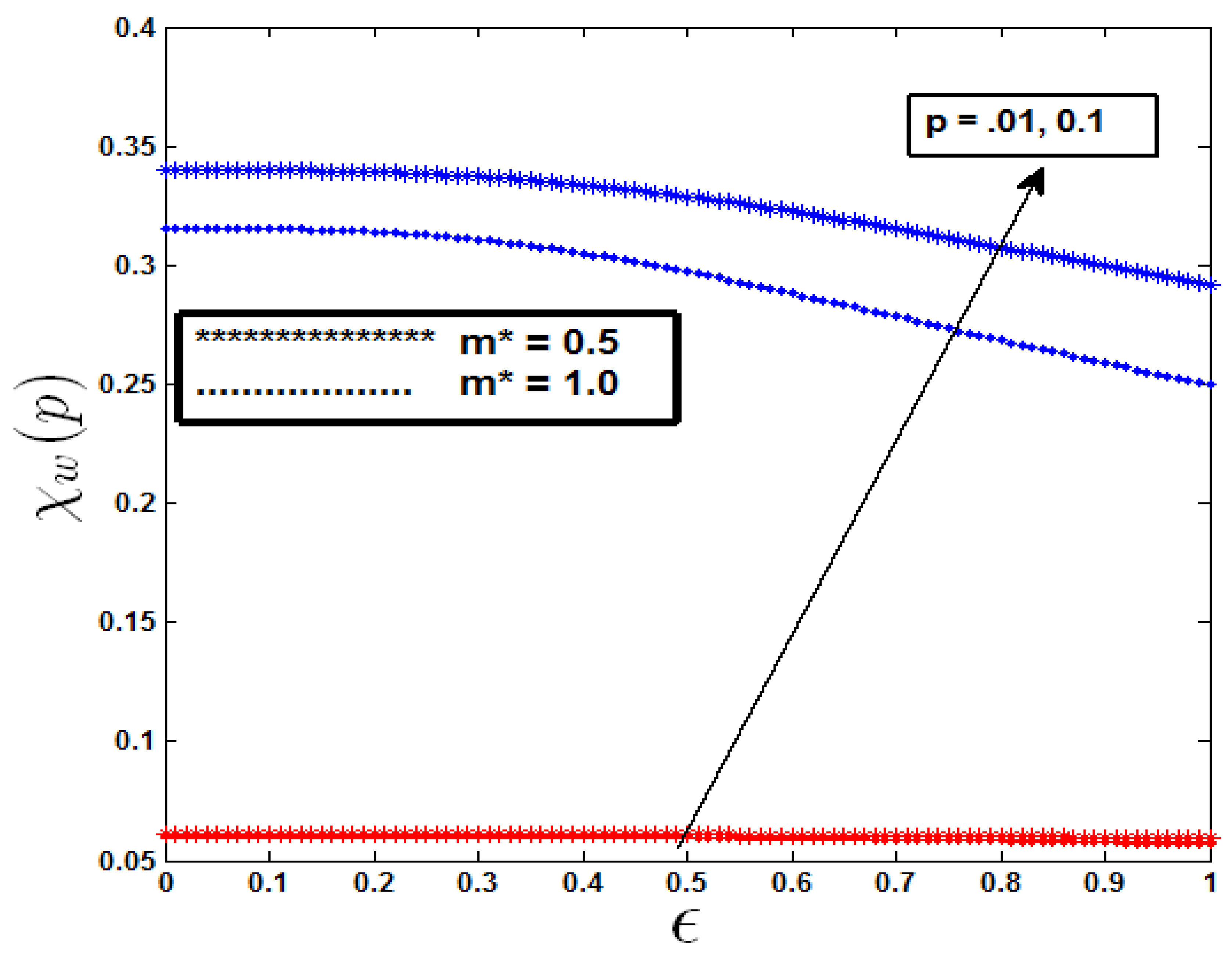
Figure 11, Figure 12 and Figure 13 demonstrate how surface temperature, fluid concentration, and motile microbe concentration change with varying values of the mixed convection parameter

ε

. As

ε

increases, there is a corresponding decrease in surface temperature, fluid concentration, and motile microbe density. This inverse relationship is particularly evident as the values of m rise, leading to a more significant reduction in non-isothermal cases. Additionally, the use of a slender needle further reduces the wall temperature, fluid concentration, and motile microorganism concentration, as shown in Figure 11, Figure 12 and Figure 13. This understanding is vital for optimizing operations where temperature and concentration control are critical, such as in biomedical devices or chemical reactors. For example, by modifying the mixed convection parameter and needle geometry, these systems can be fine-tuned to accomplish desired outcomes, such as increasing the efficiency of cooling mechanisms or improving the precision of microbial growth control in bioreactors.

5. Conclusions

The present study introduces a novel theoretical and numerical analysis of a constant two-dimensional mixed convection flow model. The model incorporates the effects of gyrotactic microorganisms and variable surface heat, mass, and motile microbe flux. The investigation encompasses both isothermal and non-isothermal needles with varying diameters. The impact of key parameters on flow, heat, mass, and microorganism characteristics is thoroughly examined. The study's findings can be summarized as follows:

The velocity profile exhibits an upward trend with increasing values of the mixed convection parameter (λ), while the temperature, concentration, and microorganism profiles show a decreasing trend.
The buoyancy parameters contribute to a decrease in the temperature profile and an increase in the velocity profile.
The Lewis parameter (Le) significantly influences the concentration profile, resulting in a reduction in the thickness of the concentration boundary layer.
The thickness of the microorganism profile boundary layer decreases with an increase in the bioconvection Lewis number (Lb) and Peclet number (Pe).
The non-isothermal power-law index leads to a decrease in all physical quantities.
An increase in needle thickness results in a higher velocity profile. In contrast, slim needles lead to a decrease in temperature and microorganism profiles.

The insights gained from this study contribute to a deeper understanding of mixed convection flow with bioconvection, offering potential applications in various fields, including biomedicine, chemical engineering, and environmental science. The findings highlight the complex interplay between physical parameters and their impact on flow behavior, heat and mass transfer, and microorganism distribution. The study's outcomes can inform the design and optimization of systems involving mixed convection and bioconvection phenomena, leading to advancements in areas such as drug delivery, bioreactors, and microbial enhanced oil recovery. Future research can build upon these findings by exploring additional complexities, such as non-Newtonian fluids, time-dependent effects, and the influence of external forces.

References

Nasir, N. A. A. M., Ishak, A., & Pop, I. (2017). Stagnation-point flow and heat transfer past a permeable quadratically stretching/shrinking sheet. Chinese Journal of Physics, 55(5), 2081-2091. [CrossRef]
Aly, A. M., &Raizah, Z. A. S. (2019). Mixed convection in an inclined nanofluid filled-cavity saturated with a partially layered porous medium. Journal of Thermal Science and Engineering Applications, 11(4), 041002.
Rashid, A., Ayaz, M., & Islam, S. (2023). Numerical investigation of the magnetohydrodynamic hybrid nanofluid flow over a stretching surface with mixed convection: A case of strong suction. Advances in Mechanical Engineering, 15(6), 16878132231179616. [CrossRef]
Al-Omar, S. O. O., & Ali, O. M. (2023). Mixed convection from two horizontally aligned hot and cold circular cylinders in a vented square enclosure. Ain Shams Engineering Journal, 14(8), 102048.
Ferdows, M., Alshuraiaan, B., &Nima, N. I. (2022). Effects of non-Darcy mixed convection over a horizontal cone with different convective boundary conditions incorporating gyrotactic microorganisms on dispersion. Scientific Reports, 12(1), 16581.
Raju, B. H. S., Nath, D., Pati, S., &Baranyi, L. (2020). Analysis of mixed convective heat transfer from a sphere with an aligned magnetic field. International Journal of Heat and Mass Transfer, 162, 120342.
Ahmad, U., Ashraf, M., Abbas, A., Rashad, A. M., &Nabwey, H. A. (2021). Mixed convection flow along a curved surface in the presence of exothermic catalytic chemical reaction. Scientific Reports, 11(1), 12907.
Ibrahim, W., &Zemedu, C. (2020). MHD nonlinear mixed convection flow of micropolarnanofluid over nonisothermal sphere. Mathematical Problems in Engineering, 2020, 1-20.
Megahed, A. M., Ghoneim, N. I., Reddy, M. G., & El-Khatib, M. (2021). Magnetohydrodynamic fluid flow due to an unsteady stretching sheet with thermal radiation, porous medium, and variable heat flux. Advances in Astronomy, 2021, 1-9. [CrossRef]
You, X., & Li, S. (2021). Fully developed opposing mixed convection flow in the inclined channel filled with a hybrid nanofluid. Nanomaterials, 11(5), 1107. [CrossRef]
A Mashkour, M. (2021). Analysis of Transient Mixed Convection in a Horizontal Channel Partially Heated From Below. Eastern-European Journal of Enterprise Technologies, 4(8), 112.
Ahmad, I., Faisal, M., Zan-Ul-Abadin, Q., Loganathan, K., Javed, T., &Pattanaik, B. (2022). Dynamics of nanoplatelets in mixed convective radiative flow of hybridized nanofluid mobilized by variable thermal conditions. Mathematical Problems in Engineering, 2022.
Ahmed, M. M., Nourhan, I. G., Reddy, M.G. & El-Khatib, M. Magnetohydrodynamic Fluid Flow due to an Unsteady Stretching Sheet with Thermal Radiation, Porous Medium, and Variable Heat Flux. Advances in Astronomy, 2021, Article ID 6686883, 9 pages, 2021.
Ahmed, K., Akbar, T., Ahmed, I., Muhammad, T., &Amjad, M. (2023). Mixed convective MHD flow of Williamson fluid over a nonlinear stretching curved surface with variable thermal conductivity and activation energy. Numerical Heat Transfer, Part A: Applications, 1-16.
Everts, M., Mahdavi, M., Meyer, J. P., &Sharifpur, M. (2023). Development of the hydrodynamic and thermal boundary layers of forced convective laminar flow through a horizontal tube with a constant heat flux. International Journal of Thermal Sciences, 186, 108098.
Khan, W. A., Rashad, A. M., Abdou, M. M. M., &Tlili, I. (2019). Natural bioconvection flow of a nanofluid containing gyrotactic microorganisms about a truncated cone. European Journal of Mechanics-B/Fluids, 75, 133-142.
Saleem, S., Rafiq, H., Al-Qahtani, A., El-Aziz, M. A., Malik, M. Y., &Animasaun, I. L. (2019). Magneto Jeffrey nanofluidbioconvection over a rotating vertical cone due to gyrotactic microorganism. Mathematical Problems in Engineering, 2019.
Mahdy, A., &Nabwey, H. A. (2020). Microorganisms time-mixed convection nanofluid flow by the stagnation domain of an impulsively rotating sphere due to Newtonian heating. Results in Physics, 19, 103347.
Sudhagar, P., Kameswaran, P. K., & Kumar, B. R. (2019). Gyrotactic microorganism effects on mixed convective nanofluid flow past a vertical cylinder. Journal of Thermal Science and Engineering Applications, 11(4), 041018.
Mallikarjuna, B., Rashad, A. M., Chamkha, A., &Abdou, M. M. M. (2018). Mixed bioconvection flow of a nanofluid containing gyrotactic microorganisms past a vertical slender cylinder. Frontiers in Heat and Mass Transfer (FHMT), 10.
Rashad, A. M., &Nabwey, H. A. (2019). Gyrotactic mixed bioconvection flow of a nanofluid past a circular cylinder with convective boundary condition. Journal of the Taiwan Institute of Chemical Engineers, 99, 9-17.
Mahdy, A. (2021). Unsteady Mixed Bioconvection Flow of Eyring–Powell Nanofluid with Motile Gyrotactic Microorganisms Past Stretching Surface. BioNanoScience, 11(2), 295-305.
Waqas, H., Manzoor, U., Shah, Z., Arif, M., &Shutaywi, M. (2021). Magneto-burgers nanofluid stratified flow with swimming motile microorganisms and dual variables conductivity configured by a stretching cylinder/plate. Mathematical Problems in Engineering, 2021, 1-16.
Bilal, S., Rehman, K. U., Shatanawi, W., Shflot, A. S., & Malik, M. Y. (2024). Heat Transfer Analysis of Carreau Nanofluid Flow with Gyrotactic Microorganisms: A Comparative Study. Case Studies in Thermal Engineering, 104617. [CrossRef]
Alharbi, K. A. M., Bilal, M., Ali, A., Eldin, S. M., Alburaikan, A., &Khalifa, H. A. E. W. (2023). Significance of gyrotactic microorganisms on the MHD tangent hyperbolic nanofluid flow across an elastic slender surface: Numerical analysis. Nanotechnology Reviews, 12(1), 20230106.
Alam, M. M., Arshad, M., Alharbi, F. M., Hassan, A., Haider, Q., Al-Essa, L. A., ... &Galal, A. M. (2023). Comparative dynamics of mixed convection heat transfer under thermal radiation effect with porous medium flow over dual stretched surface. Scientific Reports, 13(1), 12827.
Ferdows, M., Nima, N. I., & Shit, G. C. (2023). Chemical reactions and heat generation influence on mixed convection flow with gyrotactic microorganisms over a non-isothermal horizontal surface. International Journal for Computational Methods in Engineering Science and Mechanics, 24(4), 296-306. [CrossRef]
Khan, Z., Thabet, E. N., Habib, S., Abd-Alla, A. M., Bayones, F. S., Alharbi, F. M., &Alwabli, A. S. (2024). Numerical study of hydromagnetic bioconvection flow of micropolar nanofluid past an inclined stretching sheet in a porous medium with gyrotactic microorganism. Journal of Computational Science, 78, 102256.
Yasmin, H. (2024). Numerical investigation of heat and mass transfer study on MHD rotatory hybrid nanofluid flow over a stretching sheet with gyrotactic microorganisms. Ain Shams Engineering Journal, 15(9), 102918. [CrossRef]
Amirsom, N.A., Uddin, M.J. & Ismail, A.I.M. MHD boundary layer bioconvection non-Newtonian flow past a needle with Stefan blowing. Heat. Trans. Asian Res. 48(2): 727-743 (2019).
Beg, 0. A, Zohra, F.T, Uddin, M.J, Ismail, and A.I.M. &Sathasivam, S. Energy conservation of nanofluids from a biomagnetic needle in the presence of Stefan blowing: Lie symmetry and numerical simulation, Case Studies in Thermal Engineering24, (100861), (2021).
Grosan, T., & Pop, I. (2011). Forced convection boundary layer flow past nonisothermal thin needles in nanofluids. [CrossRef]
Lai, F. C., Choi, C. Y., &Kulacki, F. A. (1990). Coupled heat and mass transfer by natural convection from slender bodies of revolution in porous media. International communications in heat and mass transfer, 17(5), 609-620.
Hayat, T., Khan, M. I., Farooq, M., Yasmeen, T., &Alsaedi, A. (2016). Water-carbon nanofluid flow with variable heat flux by a thin needle. Journal of Molecular Liquids, 224, 786-791.
Ali, B., Jubair, S., Al-Essa, L. A., Mahmood, Z., Al-Bossly, A., &Alduais, F. S. (2023). Boundary layer and heat transfer analysis of mixed convective nanofluid flow capturing the aspects of nanoparticles over a needle. Materials Today Communications, 35, 106253.
Salleh, S. N. A., Bachok, N., Arifin, N. M., & Ali, F. M. (2020). Influence of Soret and Dufour on forced convection flow towards a moving thin needle considering Buongiorno’snanofluid model. Alexandria engineering journal, 59(5), 3897-3906.
Waini, I., Ishak, A., & Pop, I. (2020). Hybrid nanofluid flow past a permeable moving thin needle. Mathematics, 8(4), 612.
Khan, A., Saeed, A., Tassaddiq, A. et al. Bio-convective and chemically reactive hybrid nanofluid flow upon a thin stirring needle with viscous dissipation. Sci Rep 11, 8066 (2021).
Khan, A., Saeed, A., Tassaddiq, A., Gul, T., Mukhtar, S., Kumam, P., ... & Kumam, W. (2021). Bio-convective micropolar nanofluid flow over thin moving needle subject to Arrhenius activation energy, viscous dissipation and binary chemical reaction. Case Studies in Thermal Engineering, 25, 100989. [CrossRef]
Waqas, H., Alqarni, M. S., Muhammad, T., & Khan, M. A. (2021). Numerical study for bioconvection transport of micropolar nanofluid over a thin needle with thermal and exponential space-based heat source. Case Studies in Thermal Engineering, 26, 101158. [CrossRef]
Ahmad, S., Arifin, N.M., Nazar, R. et al. Mixed convection boundary layer flow along vertical moving thin needles with variable heat flux. Heat Mass Transfer 44:473 (2008). [CrossRef]

Figure 1. Flow diagram and graphical system.

Figure 2. Velocity profile with mixed convection parameter

ε

change for a) different m* values and b) varied needle diameters.

Figure 2. Velocity profile with mixed convection parameter

ε

change for a) different m* values and b) varied needle diameters.

Figure 3. Buoyancy parameter

N_{C}

fluctuating velocity distribution for a) varying m* values and b) various needle diameters.

Figure 3. Buoyancy parameter

N_{C}

fluctuating velocity distribution for a) varying m* values and b) various needle diameters.

Figure 4. Effect of mixed convection parameter

ε

on Temperature profile for a) different values of m* b) different needle sizes.

Figure 4. Effect of mixed convection parameter

ε

on Temperature profile for a) different values of m* b) different needle sizes.

Figure 5. Effect of buoyancy parameter

N_{m}

on Temperature profile for a) different values of m* b) different needle sizes.

Figure 5. Effect of buoyancy parameter

N_{m}

on Temperature profile for a) different values of m* b) different needle sizes.