Prerpints.org logo
Preprint
Article

Synthesis and Study of Sorption Properties of Zinc-Imprinted Polymer

Altmetrics

Downloads

52

Views

31

Comments

0

Submitted:

02 September 2024

Posted:

02 October 2024

You are already at the latest version

Alerts
Abstract
Imprinted polymers with imprints of Zn2+ ions (ZnIP) and reference polymers without imprints (NIP) were synthesized based on humic and methacrylic acids. Comparative studies of the physical parameters of ZnIP and NIP were carried out using elemental analysis, IR spectroscopy and electron microscopy. Kinetic parameters of Zn2+ ion sorption on ZnIP and NIP were determined. It was found that the sorption kinetics on both ZnIP and NIP are approximated by a pseudo-first-order equation. The sorption rate constant for ZnIP is higher than that of NIP, indicating a higher adsorption rate of Zn2+ ions onto the surface of ZnIP. This may be due to more accessible sites on ZnIP. Adsorption of Zn2+ ions is best described by the Langmuir model, indicating monolayer adsorption on a homogeneous surface. The Langmuir model also shows that ZnIP is effective at low adsorbate concentrations. The Freundlich model describes the adsorption with less accuracy, which may indicate monolayer adsorption and less surface homogeneity. ZnIP shows better adsorption capacity and higher efficiency compared to NIP and can be proposed as a selective sorption material for Zn2+ ions.
Keywords: 
Subject: Chemistry and Materials Science  -   Applied Chemistry

1. Introduction

Recently, the development of polymers with a molecular imprints has become an important area of research [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]. These polymers are created with targeted molecular sites that recognize specific target molecules. We are particularly interested in molecular imprinted polymers, which provide promising solutions for the selective separation and concentration of components of complex mixtures [16,17,18,19,20]. Due to its ability for selective recognition, simplicity of synthesis and high thermal and chemical stability, the number of studies in the field of molecular imprinted polymers is growing rapidly, demonstrating the development of molecular imprinting technologies [17,19,20].
Modern research shows great prospects for rapidly developing molecular imprinting technologies to create a new generation of sorption materials. The possibility of developing imprinted polymers for wastewater treatment from heavy metals is particularly attractive. The interest in this area of research is due to the fact that imprinted polymers are used not only in scientific research, but are already being introduced into the chemical [9,12,14], pharmaceutical [21,22] and biotechnological [23,24,25,26] industries, especially at the stages of purification of end products. A key aspect of the use of molecular imprinted polymers in sorption materials is their ability to effectively remove pollutants, including trace concentrations, and their exceptional stability under harsh conditions (high temperature, pressure, organic solvents) simplifies the process of water purification [4,6,7,9,10,12,13,14,27,28].
The synthesis of molecular imprinted polymers with specified properties and their ability to selectively recognize is a difficult task. Nevertheless, the possibilities of their application are practically unlimited. This is due to the fact that compounds of various classes can be used as a matrix, capable of absorbing pollutants from both organic and aquatic environments.
The review [5] presents the results of studies of ion-imprinted polymers for the selective removal of transition metal ions (including heavy metal ions, precious metal ions, radionuclides and rare earth metal ions) from an aqueous solution by critically analyzing the most relevant literature studies over the past decade.
In this context, polymers developed based on the molecular imprinting methodology, especially those that use natural polymers as a base, represent an innovative solution. The most promising raw materials for such polymers are humic acids, products of coal waste processing.
Humic acids are used as natural sorbents for purification of technogenic media from heavy metals [29,30,31,32,33]. Their ability to interact with various types of pollutants is due to the presence of many oxygen-containing functional groups, aromatic and heterocyclic structures. These acids have a wide range of beneficial properties and are able to bind almost all types of ecotoxicants, including heavy metal ions.
Water pollution has become a serious problem due to the uncontrolled discharge of heavy metals, which are highly toxic pollutants. Zinc, which is often found in wastewater, is particularly dangerous because its salts can negatively affect ecosystems. Excess or deficiency of zinc can damage the systems of living organisms. Therefore, zinc water purification is an important part of industrial water treatment processes.
Previously, we synthesized molecular imprinted polymers to remove heavy metals from water [34,35]. In this work, research on the development of molecular imprinted polymers is continued. The purpose of this study is the synthesis of a zinc-imprinted polymer based on humic acids and a functional monomer, as well as their study of its sorption properties.

2. Materials and Methods

2.1. Chemicals

In the synthesis of imprinted zinc-imprinted polymers (ZnIP) and non-imprinted comparison polymers (NIP), humic acids (HA) obtained from oxidized coal from the Shubarkol deposit (Karaganda, Kazakhstan) [35]. Zinc acetate (Merck, Darmstadt, Germany; CAS:5970-45-6) was used as a template molecule for obtaining prints. Methacrylic acid (MAA; Merck, Darmstadt, Germany; CAS:79-41-4) was used as a monomer. Ethylene glycol dimethacrylate (EGDMA; Merck, Darmstadt, Germany; CAS:97-90-5) was used as a crosslinking agent; benzoyl peroxide (BP; Merck, Darmstadt, Germany; CAS:94-36-0) – as a reaction initiator. The objects of sorption research were aqueous solutions of zinc acetate, which were prepared by dissolving precise Zn(CH3COO)2·H2O attachments in distilled water.

2.2. Synthesis of Imprinted Polymers with a Molecular Zinc Imprint

The synthesis of an imprinted polymer with a molecular zinc imprint (ZnIP) was carried out according to the method of non-covalent imprinting developed by us using radical polymerization. A solution of Zn(CH3COO)2 (0.1 mmol) was added to an aqueous solution of HA (1 mmol) and treated with ultrasound (US) for 30 minutes. Further, the mixture was kept under stirring for 6 hours until a stable pre-polymerization complex was formed between the HA molecules and the template molecule. Then a functional monomer (methacrylic acid, 1 mmol), a crosslinking agent (EGDMA, 10 mmol) and an initiator (benzoyl peroxide, 0.1 mmol) were introduced into this complex. To prevent oxygen exposure, the reaction mixture was purged with argon for 15 minutes. Polymerization was carried out for 180 minutes in a thermostat (Termex, Tomsk, Russia) at a temperature of 60°C. After completion of copolymerization, the resulting product was centrifuged (centrifuge Hermle Labortechnik GmbH, Wechingen, Germany) at a speed of 14,000 rpm, washed with water to a neutral medium, dried, crushed (shredder IKA-Werke GmbH & Co., Staufen, Germany), sieved on laboratory sieves and a fraction with a particle size of 200-400 microns was selected. The template was removed from the crushed sorbent by acid hydrolysis with 0.1 N HCl solution, heated to 50-60°C and kept for 30 minutes. The resulting product was filtered and the precipitate was rinsed with water until the Cl- ions disappeared.
An unprinted comparison polymer (NIP) was synthesized using a similar technique, but without the addition of a template.

2.3. Characterization Studies

The structural properties of ZnIP and NIP were studied using Fourier transform infrared spectroscopy with attenuated total internal reflection. The IR spectra for ZnIP and NIP were obtained using the FSM-1201 IR Fourier spectrometer (Infraspec Company, St. Petersburg, Russia) in the range of wave numbers 4000-400 cm-1, the error is not more than 2 cm-1.
To assess the content of oxygen-containing groups in ZnIP and NIP, the conductometric method of reverse titration using the laboratory conductometer Anion-4100 (Infraspak-Analyte, Novosibirsk, Russia) was used. The measurements were carried out sequentially on three hitches, and the average value was obtained from three experiments.
Elemental analysis of carbon, hydrogen, nitrogen and oxygen content in ZnIP and NIP was performed on an elemental analyzer (Elementar Unicube, Langenselbold, Germany).
The morphology of ZnIP and NIP was characterized using scanning electron microscopy on a MIRA 3 device (Tescan Orsay Holding, Brno-Kohoutovice, Czech Republic) equipped with detectors registering various signals. Images with topographic contrast were obtained using secondary electron detectors, and the elemental composition on the surface was determined using X-ray energy dispersive microanalysis.
The Ultrasonic Homogenizer JY92-IIDN with a maximum power of 900 watts and a frequency of 25 kHz (Scientz, China) was used as an ultrasound source. The equipment is equipped with a 7-inch touchscreen to control the instruments. The ultrasonic power step is smoothly adjustable by 1%, with pulse and continuous operation, as well as with a testing function. All operating parameters of the device, including temperature, can be adjusted individually.

2.4. Adsorption of Zn2+ Ions

Sorption of imprinted polymers with a molecular imprint of zinc and comparison polymers was carried out in a static mode. To do this, a 0.1 g suspension of sorption material was placed in a flat-bottomed flask with a lapped stopper. Further, 25 cm3 solutions of zinc acetate with an increasing concentration from 100 to 2000 mg/dm3 were poured into the flasks.
The solutions were mixed for 6 hours using a laboratory shaker (PE-6410, St. Petersburg, Russia). After the adsorption equilibrium was established, the suspended particles were separated from the solution by filtration. Further, the equilibrium concentrations of Zn2+ ions in the filtrate were determined using an inductively coupled plasma iCAR6500 atomic emission spectrometer (SPECTRO ARCOS EOP SPECTRO Analytical instruments GmbH, Germany). The number of Zn2+ ions adsorbed on ZnIP was calculated as the ratio of the difference in concentrations of Zn2+ ions in solution before and after sorption, related to the unit mass of the imprinted polymer:
А = ( С 0 − C р ) · V m
where A is the number of sorbed Zn2+ ions (mmol/g); C0 is the concentration of Zn2+ ions in the initial solution before sorption (mmol/dm3); Ceq – the equilibrium concentration of Zn2+ ions in the solution after sorption (mmol/dm3); m – the mass of ZnIP (g), V – the volume of the analyzed solution (cm3).
According to the obtained values of the sorption capacity (A, mmol/g) adsorption isotherms were constructed in the studied ZnIP at different equilibrium concentrations of Zn2+ ions (Ceq, mg/dm3).
At the same time, the sorption characteristics were calculated: the degree of extraction (R, %), the coefficient of distribution of Zn2+ ions on an imprinted polymer with molecular imprints of zinc (D) and the imprinting factor (IF) according to the equations:
R = c 0 − c p c 0 · 100 %
D = R ( 100 − R ) · V m
I F = D Z n I P D N I P
Similarly, the sorption properties for the comparison polymer were studied using the above method.
The effect of pH and time on the adsorption capacity was studied. The measurements were repeated 3 times and the results were analyzed. The effect of pH on adsorption capacity was studied in the range 3.0-9.0. To construct kinetic adsorption curves, zinc acetate solutions were prepared, 0.1 g of ZnIP sorbent was added, mixed on a laboratory shaker (PE-6410, St. Petersburg, Russia), samples were taken through 5, 10, 20, 30, 40, and 60 minutes . According to the obtained values of the degree of sorption of Zn2+ ions (R, %) of the studied ZnIP and NIP at different times, isotherms calculated by the equation were constructed:
R = С 0 − С t C 0 · 100 %
where: R is the degree of extraction (%); C0 is the initial molar concentration of metal ions (mmol/dm3); Ct is the molar concentration of metal ions at a time (mmol/dm3).
The obtained sorption isotherms can theoretically be described on the basis of two equations:
1) the Langmuir monomolecular sorption model equation describing the sorption isotherm over the entire concentration range:
A = A m a x · ( K s o r b · C p ) 1 + K s o r b · C p
or in a linear form:
C p A = 1 K s o r b · A m a x + 1 A m a x · C p
where Ksorb is the sorption constant, dm3/mmol; A – maximum sorption capacity, mmol/g.
2) the empirical Freundlich equation, which is usually used to represent the average section of the sorption isotherm:
A = K F r · C p 1 / n
or in a linear form:
l g A = l g K F r + 1 n · l g C p
where KFr is the Freundlich constant, which represents the amount of adsorption substance at an equilibrium concentration equal to one; 1/n– a constant whose value is equal to the correct fraction.

3. Results and Discussion

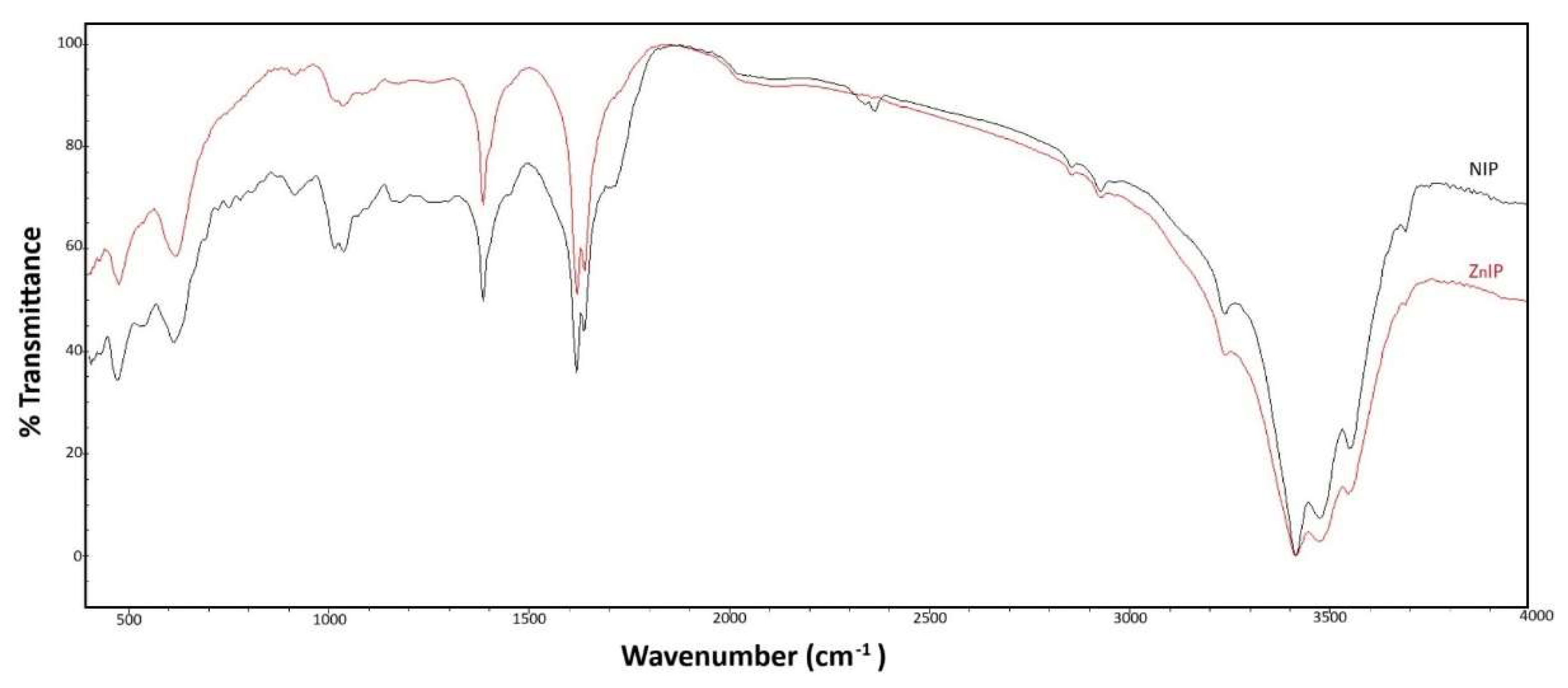
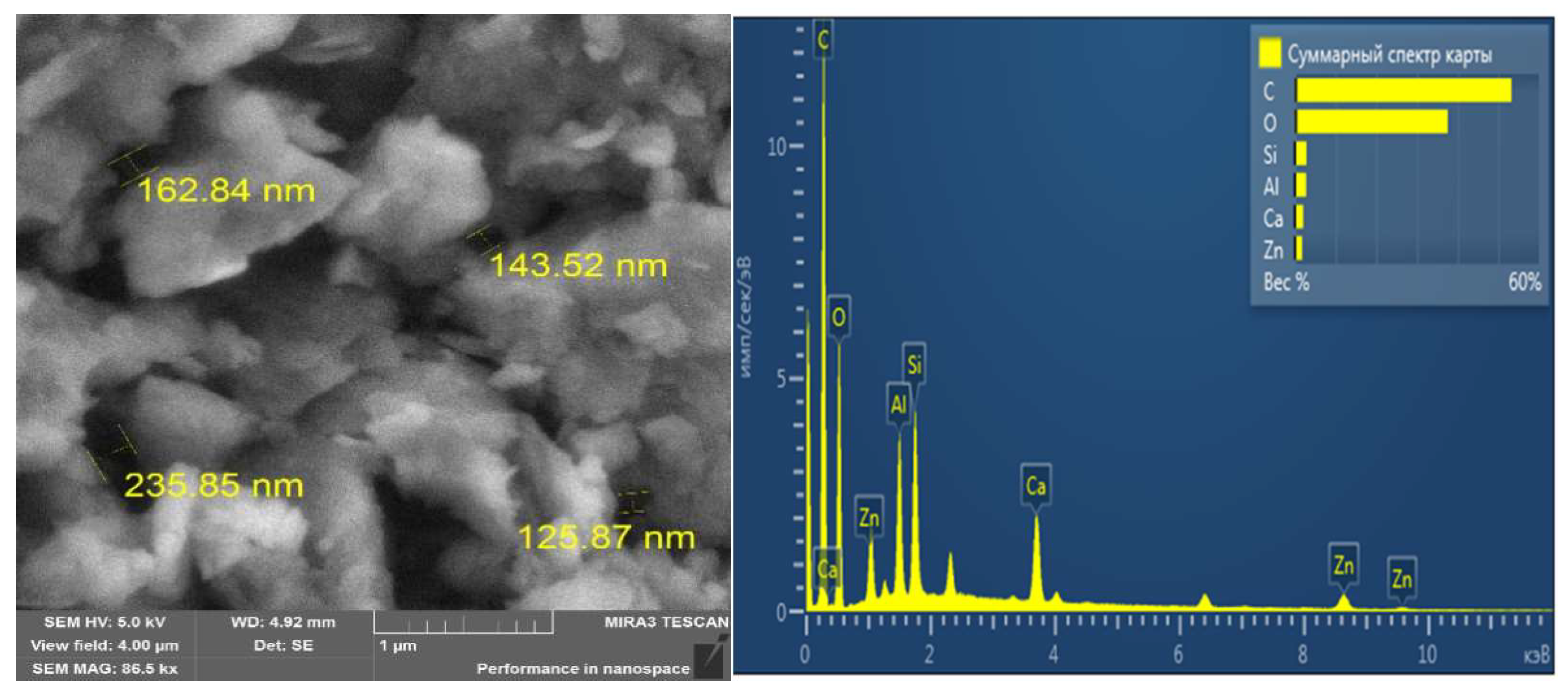
3.1. Characterisation Analysis

The zinc-imprinted polymer (ZnIP) was prepared in three stages. The first stage is the synthesis of a pre–polymerization complex consisting of a polymer (humic acid, HA) and a template molecule (Zn(CH3COO)2) under the influence of ultrasound (US). The second stage – a functional monomer (methacrylic acid, MAA), a crosslinking agent (ethylene glycol dimethacrylate, EGDMA) and an initiator (benzoyl peroxide, BP) were added to the pre-polymerization complex. The mixture was subjected to heat treatment at 60°C for 180 minutes. The third stage is the removal of the template molecule from the polymer mesh by acid hydrolysis. An unprinted reference polymer (NIP) was synthesized under similar conditions without the participation of a template molecule. Table 1 shows the initial components used for the synthesis of ZnIP and NIP.
The results of chemical studies of synthesized ZnIP and NIP are confirmed by data from elemental analysis, IR spectroscopy, X-Ray phase analysis, conductometry and electron microscope. The physico-chemical characteristics of ZnIP and NIP are given in Table 2.
The results of the elemental analysis (Table 2) showed a decrease in the oxygen content of ZnIP by 4.12% compared to NIP. This indicates the interaction of Zn2+ ions with the carboxyl and hydroxyl groups of the polymer, which leads to a decrease in their number in the ZnIP structure. A decrease in the content of oxygen-containing groups in ZnIP also confirms the possibility of binding of these groups to Zn2+ ions by the mechanism of complexation. The values of the Σ(COOH+OH) content in ZnIP are 4.43 mg-eq/g, and in NIP – 4.95 mg-eq/g. This may indicate that some of the Zn2+ ions were used to bind to oxygen-containing functional groups of the polymer, which confirms the effectiveness of imprinting. The ZnIP yield is 76.54% and the NIP yield is 77.98%. These values are quite close, which indicates that the imprinting process does not significantly affect the overall yield of the polymer, despite changes in its composition and structure. Thus, the results of the elemental analysis confirm that ZnIP binds Zn2+ ions to the functional groups of the polymer, which may be important for its applications as a molecular imprint.
IR spectroscopy methods were used to determine the structural characteristics of ZnIP and NIP (Figure 1).
It was found that the IR spectra obtained by ZnIP and NIP were very similar, since these samples were synthesized using the same methodology and initial reagents. The images of the ZnIP and NIP samples showed peaks in the region of 1010-1139 cm-1, which correspond to the stretching of the C–O bonds of carbohydrates, alcohol and ether groups, indicating the presence of these functional groups in the ZnIP and NIP polymers. Bands with a maximum at 913 cm-1 are associated with the presence of substituted aromatic structures. The changes in the 1385 cm-1 region can be explained by destructive processes that affect the structure of both ZnIP and NIP polymers, leading to a reduction in the length of the aliphatic chain and an increase in the number of annular –CH3 groups. The appearance of a band in the 1600-1650 cm-1 region in both ZnIP and NIP is associated with fluctuations in the C=C double bond of methacrylic acid. The presence of an absorption band in the region of 1700-1720 cm-1 is associated with the stretching of C=O in carboxyl groups. Their presence in the IR spectrum of NIP, but their absence in the spectrum of ZnIP, indicates that a coordination complex is formed in ZnIP, which may make it difficult to detect carboxyl groups. The stretching of peaks in the range of 3200-3560 cm-1, characteristic of hydroxyl groups, may indicate a possible binding of zinc ions in the ZnIP sample by the mechanisms of ion exchange and complexation. Distinct peaks in the 450 and 612 cm-1 regions represent Zn–O bonds.
The surface morphology of ZnIP and NIP was studied using a scanning electron microscope (SEM) (Figure 2 and Figure 3).
Micrographs of the ZnIP sample surface show a more porous structure with globular aggregates 125-235 nm thick. These globular aggregates form a porous network, which is characteristic of ZnIP after the removal of Zn2+ ions.
Removal of Zn2+ ions. From the polymer network, ZnIP creates accessible active sites that can specifically interact with Zn2+ ions. during the adsorption process. The presence of these accessible sites is clearly demonstrated in raster microscopic images (Figure 2). As can be seen from the figure, ZnIP samples have a unique structure, which is characterized by spherical cavities. This is due to the fact that imprinting of Zn2+ ions. In the polymer network, ZnIP creates special "targets" for Zn2+ ions, which improves their capture rate compared to the fingerprint-free polymer (NIP), which does not have such a specific structural organization.
ZnIP, due to its structure with imprints of Zn2+ ions, has a large number of available active sites, which accelerates the adsorption process and improves interaction with Zn2+ ions. An analysis of the elemental composition and a multilayer EDS map confirm the absence of Zn2+ ions in the resulting product after acid hydrolysis (ZnIP).
A smoother and more uneven surface without visible aggregated inclusions is observed on the scanned surface of the NIP sample (Figure 3). The results of the analysis of the elemental composition and the multilayer EDS map confirm the characteristics of NIP, demonstrating the absence of specific structural changes characteristic of ZnIP.

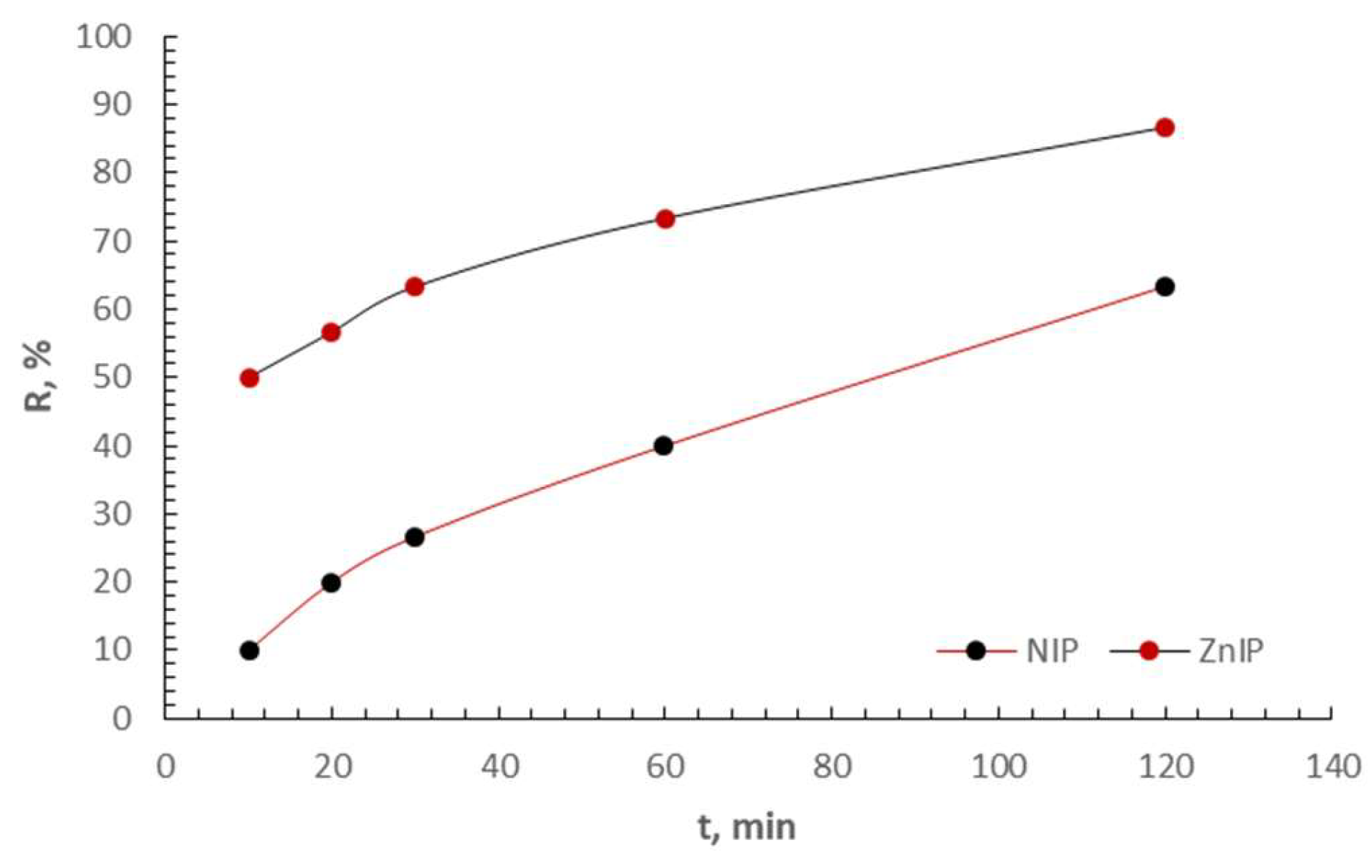
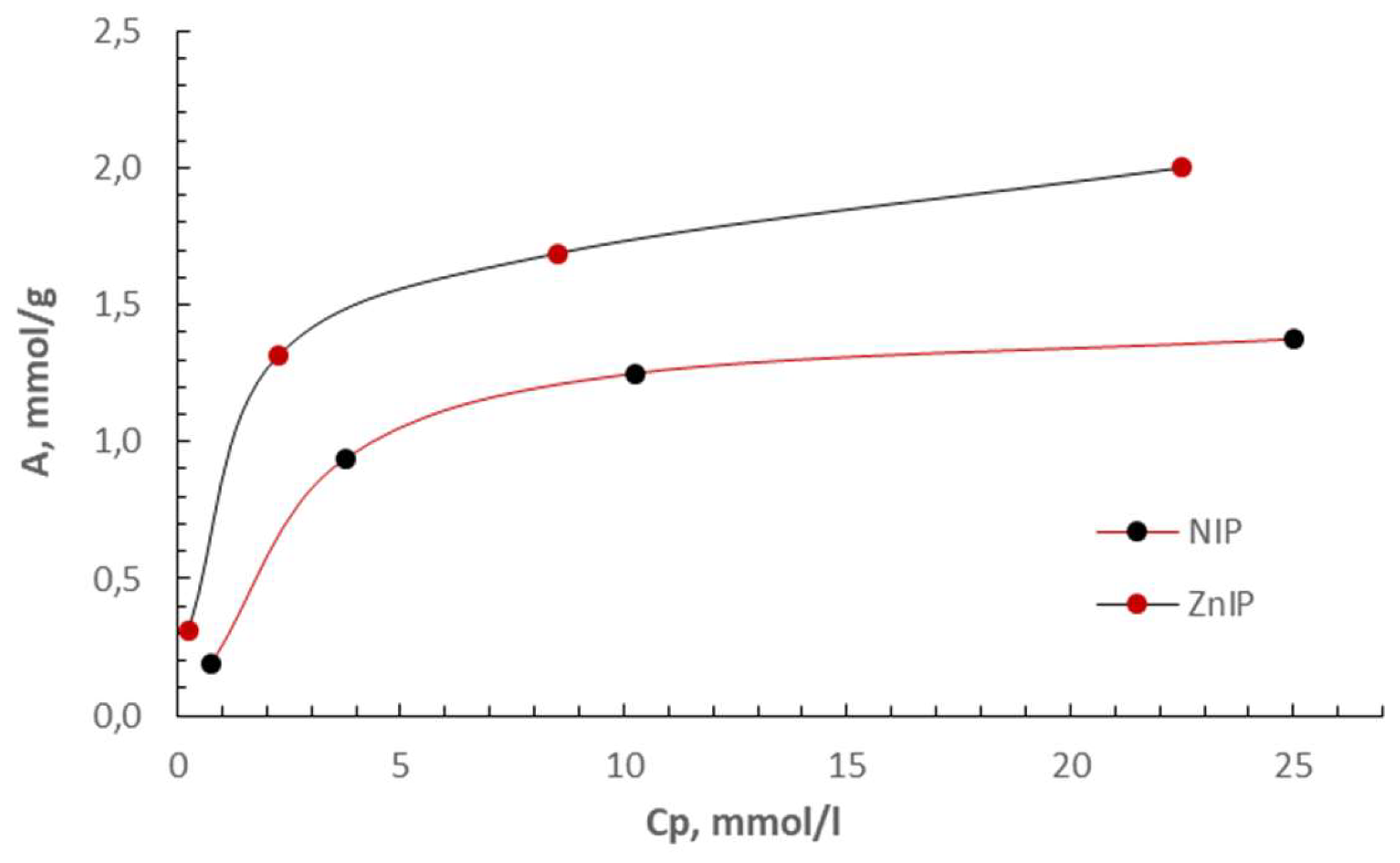
3.2. Adsorption Study

Figure 4 shows the time dependences of the degree of sorption of Zn2+ ions calculated by equation (5).
If we assume that the number of ligands in the ZnIP structure significantly exceeds the initial concentration of Zn2+ ions, then the law of effective masses for the sorption process can switch to a pseudo-order relative to the metal cation.
To determine the pseudo-order, a graphical method was chosen using kinetic equations for reactions of integer order – the first (10), second (11) and third (12):
l n C = l n C 0 − k 1 t
1 С = k 2 t + 1 C 0 2
1 С 2 = k 3 t + 1 C 0 2
where: ki is the rate constant of the ith order of reaction; t is the reaction time (min).
Based on experimental data, the parameters of three types of linear dependencies were calculated and correlation coefficients were determined (Table 3).
Higher correlation coefficients were noted when describing experimental data using the kinetic equation of the pseudo-first order reaction. Thus, the first order for ZnIP demonstrates high accuracy, with a correlation coefficient of r=0.9973, for NIP a correlation coefficient of r=0.9970. This confirms that the adsorption reaction for both ZnIP and NIP is best described in the first order. The rate constant for ZnIP (k1=0.0118) is higher than for NIP k1=0.0079, which indicates a higher rate of adsorption of Zn2+ ions for ZnIP. This may indicate that ZnIP has more accessible active sites than NIP.
Thus, the first order is the most accurate model for describing the adsorption kinetics for both ZnIP and NIP. The adsorption rate for ZnIP is significantly higher in all orders of magnitude, which is confirmed by the large values of the rate constants. Second- and third-order models can be used, but they exhibit lower accuracy.
As is known, the quantitative characteristic of sorption is Gibbs specific excess sorption, calculated by equation (1). We experimentally determined the sorption isotherms for Zn2+ ions at a temperature of 298.0 K. The results are shown in Figure 5.
According to the obtained equations, the calculated concentrations of the initial molar ion concentrations (C0i) for the pseudo-first-order model are close to experimental ones.
When analyzing sorption properties, not only the percentage of extraction was considered, but also the distribution coefficients and the imprinting factor. The distribution coefficients (D) and the imprinting factor (IF), calculated according to equations (3) and (4), respectively, are presented in Table 4.
Table 4 shows that the extraction degrees and the values of the distribution coefficients for ZnIP are higher compared to NIP. ZnIP has been found to have a better adsorption capacity than NIP.
The adsorption of Zn2+ ions from aqueous solutions was studied in the pH range 3.0-9.0. The nature of the pH dependence indicates that the Zn2+ ions are extracted by both ZnIP and NIP.
The maximum degree of extraction is observed in the pH range 5.0 at which the imprinting process takes place. Sorption decreases with increasing pH.
The correspondence of the experimental data to the Langmuir and Freundlich equations is proved on the basis of their linear forms by plotting graphs in the appropriate coordinates – if the points fit on a straight line, then this serves as a criterion for the possibility of using these equations to describe sorption isotherms.
Figure 7 shows the experimental data in the coordinates of the linear form of the Freundlich equation.
Based on the determination of linear regression coefficients, the parameters of the Freundlich equations for ZnIP and NIP were calculated (Table 5).
Expressions (13) and (14) represent the processing of an array of experimental points according to the linear regression equation for Zn2+ ions of ZnIP and NIP samples, respectively:
l g A = l g 1.1832 + 1 2.4060 · l g C p
l g A = l g 2.0526 + 1 1.7348 · l g C p
Figure 8 shows the experimental data in the coordinates of the linear form of the Langmuir monomolecular adsorption equation.
Based on the determination of linear regression coefficients, the parameters of the equations were calculated – ion sorption constants and their maximum sorption per unit mass of ZnIP and NIP (Table 6).
Expressions (15) and (16) represent the processing of an array of experimental points according to the linear regression equation for Zn2+ ions of ZnIP and NIP samples, respectively:
C p A = 1 0.6177 · 2.1262 + 1 2.1262 · C p
C p A = 1 0.2471 · 1.6269 + 1 1.6269 · C p
The high correlation coefficients for equations (15) and (16) allow us to assert that the model Langmuir monomolecular adsorption equation adequately describes the isotherms of sorption of Zn2+ ions in the entire range of concentrations studied. The ZnIP sample shows a higher maximum adsorption – 2.1262 mmol/g, compared to NIP – 1.6269 mmol/g and a significantly higher adsorption equilibrium constant of 0.6177 l/mmol for ZnIP and 0.2471 l/mmol for NIP. The correlation coefficients for the ZnIP (r=0.9985) and NIP (r=0.9837) samples indicate that the Langmuir model describes adsorption on the ZnIP sample almost perfectly and well on the NIP.
The Freundlich constant (KFr=1.1832) for ZnIP shows a slightly lower adsorbent capacity compared to NIP (KFr=2.0526). However, the correlation coefficient in the Freundlich equation for the ZnIP sample (r=0.9125) indicates a higher, but not ideal, accuracy of data description by the Freundlich model compared to the Langmuir model compared to NIP (r=0.8670).
The difference between the Langmuir and Freundlich models can be explained as follows. The Langmuir model assumes that adsorption occurs on a homogeneous surface with a fixed number of adsorption centers and the formation of an adsorbate monolayer. The high correlation coefficients r for both ZnIP and NIP indicate that the adsorption on these samples corresponds well to the assumptions of the Langmuir model. This means that the adsorption is most likely limited to a single layer, and the surface of the adsorbent is homogeneous. The Freundlich model describes adsorption on heterogeneous surfaces and takes into account the possibility of multilayer adsorption. However, lower r values for this model compared to the Langmuir model indicate that the assumptions of the Freundlich model correspond less accurately to the actual adsorption process on these samples. This may mean that multilayer adsorption or strong surface heterogeneity are not the dominant factors in this case.
Thus, ZnIP demonstrates better adsorption capacity and is better described by the Langmuir model, which is confirmed by a high r value. This may indicate that adsorption on this sample occurs predominantly in a single layer and on a homogeneous surface. However, Langmuir's model emphasizes that ZnIP is particularly effective at low concentrations of adsorbate, due to its high constant and maximum adsorption. NIP is also well described by the Langmuir model, although its adsorption capacity is somewhat lower. The Freundlich model describes adsorption on this sample with less accuracy, which may be due to the fact that adsorption on this sample is closer to monolayer. The differences in the correlation coefficients between the Langmuir and Freundlich models are due to the fact that the Langmuir model better corresponds to the physical nature of adsorption on these samples, assuming monolayer adsorption on homogeneous surfaces.

4. Conclusions

Thus, imprinted polymers (ZnIP) specially tuned for the sorption of Zn2+ ions and comparison polymers (NIP) that do not contain fingerprints were synthesized using the molecular imprinting method. The composition and structure of the obtained ZnIP and NIP were confirmed using modern physico-chemical methods: During the study of the sorption properties of ZnIP and NIP, it was found that ZnIP exhibit a higher sorption capacity with respect to Zn2+ ions compared with NIP. The maximum adsorption of Zn2+ ions is 2.1262 mmol/g for ZnIP and 1.6269 mmol/g for NIP. The difference in the maximum adsorption is statistically significant. The sorption of ions of Zn2+ ions on ZnIP and NIP is described by kinetic equations of the pseudo-first order, which confirms the correspondence of the model. The sorption rate constant for ZnIP is higher than for NIP. This indicates a higher rate of adsorption of Zn2+ ions on ZnIP. The higher sorption rate constant and high maximum adsorption for ZnIP indicate its greater efficiency in capturing Zn2+ ions. ZnIP is the preferred choice for applications requiring fast and efficient sorption of Zn2+ ions, due to its higher sorption capacity and adsorption rate. The use of the molecular imprinting method to create ZnIP made it possible to obtain a polymer with significantly improved sorption properties with respect to Zn2+ ions compared with an unprinted polymer. ZnIP demonstrates higher sorption efficiency and speed, which makes it a promising material for practical applications in the field of wastewater treatment and other technological processes where effective removal of Zn2+ ions is required.

Author Contributions

Conceptualization, A.Kh.Zh.; methodology, A.Kh.Zh.; software, A.Kh.Zh.; validation, A.M.Zh.; formal analysis, Ye.P.V., O.V.A.; investigation, Ye.P.V., O.V.A.; data curation, A.Kh.Zh.; writing—original draft preparation, A.Kh.Zh., writing—review and editing, A.Kh.Zh; visualization, Ye.P.V., O.V.A.; supervision, A.Kh.Zh.; project administration, A.Kh.Zh. All authors have read and agreed to the published version of the manuscript.

Funding

This research is funded by the Science Committee of the Ministry of Science and Higher Education of the Republic of Kazakhstan (Grant No. AP19678338) “Fundamentals of creating molecularly imprinted polymers from coal waste”.

Institutional Review Board Statement

Not applicable.

Conflicts of Interest

The authors declare no conflicts of interest

References

  1. Okutucu, B. Waste in Textile and Leather Sectors. IntechOpen; A. Körlü: Izmir, Turkey, 2020; pp. 1-12. [CrossRef]
  2. Stevens, M.G.F. Batlokwa, B.S. Multi-templated Pb-Zn-Hg Ion Imprinted Polymer for the Selective and Simultaneous Removal of Toxic Metallic Ions from Wastewater. International Journal of Chemistry. 2017, 9. https://dx.doi.org/10.5539/ijc.v9n2p10.
  3. Kuras, M.J.; Perz, K.; Kołodziejski, W.L. Synthesis, characterization and application of a novel zinc(II) ion-imprinted polymer. Polym. Bull. 2017, 74:5029-5048. [CrossRef]
  4. Wirawan, T.; Supriyanto, G.; Soegianto, A. Adsorption of Zinc(II) onto Zn(II)-Ionic Imprinted Polymer. 2019, IOP Conf. Ser.: Mater. Sci. Eng. 546, 022036 . [CrossRef]
  5. Lazar, M.M.; Ghiorghita, C.-A.; Dragan, E.S.; Humelnicu, D.; Dinu, M.V. Ion-Imprinted Polymeric Materials for Selective Adsorption of Heavy Metal Ions from Aqueous Solution. Molecules. 2023, 28, 2798. [CrossRef]
  6. Su, S.; Huang, Y.; Han, G.; Guo, Z.; Liu, F. Study of the Adsorption of Humic Acid with Zn2+ by Molecular Dynamic Simulation and Adsorption Experiments. In: Li, B., et al. Characterization of Minerals, Metals, and Materials 2019. The Minerals, Metals & Materials Series. Springer, Cham., 31-41. [CrossRef]
  7. Putri, T.; Zulfikar, M.A.; Wahyuningrum, D.; Saputra I.S. Synthesis and Characterization of Molecularly Imprinted Polymers (MIPs) Using Humic Acid. J. Pure App. Chem. Res. 2022, 11, 175-181. http://dx.doi.org/10.21776/ub.jpacr.2022.011.03.656.
  8. Bakhshi, A.; Daryasari, A.P.; Soleimani, M. A Molecularly Imprinted Polymer as the Adsorbent for the Selective Determination of Oxazepam in Urine and Plasma Samples by High-Performance Liquid Chromatography with Diode Array Detection. J. Anal. Chem. 2021, 76, 1414-1421. [CrossRef]
  9. Bivián-Castro, E.Y.; Zepeda-Navarro, A.; Guzmán-Mar, J.L.; Flores-Alamo, M.; Mata-Ortega, B. Ion-Imprinted Polymer Structurally Preorganized Using a Phenanthroline-Divinylbenzoate Complex with the Cu(II) Ion as Template and Some Adsorption Results. Polymers. 2023, 15, 1186. [CrossRef]
  10. Özgecan, E.; Yeşeren, S.; Müge, A.; Adil, D. Molecularly Imprinted Polymers for Removal of Metal Ions: An Alternative Treatment Method. Biomimetics. 2018, 3, 38. [CrossRef]
  11. Hasanah, A.N.; Safitri, N.; Zulfa, A.; Neli, N.; Rahayu, D. Factors Affecting Preparation of Molecularly Imprinted Polymer and Methods on Finding Template-Monomer Interaction as the Key of Selective Properties of the Materials. Molecules. 2021, 26, 5612. [CrossRef]
  12. Abdou, M.M.; Soliman, A.-G.A.; Kobisy, A.S.; Abu-Rayyan, A.; Al-Omari, M.; Alshwyeh, H.A.; Ragab, A.H.; Al Shareef, H.F.; Ammar, N.S. Preparation and Evaluation of Phenol Formaldehyde-Montmorillonite and Its Utilization in the Adsorption of Lead Ions from Aqueous Solution. ACS Omega. 2024, 9, 12015-12026. [CrossRef]
  13. Meza López, F.d.L.; Hernández, C.J.; Vega-Chacón, J.; Tuesta, J.C.; Picasso, G.; Khan, S.; Sotomayor, M.D.P.T.; López, R. Smartphone-Based Rapid Quantitative Detection Platform with Imprinted Polymer for Pb (II) Detection in Real Samples. Polymers. 2024, 16, 1523. [CrossRef]
  14. Elsayed, N.H.; Monier, M.; Alatawi, R.A.S.; Albalawi, M.A.; Alhawiti, A.S. Preparation of Chromium (III) Ion-Imprinted Polymer Based on Azo Dye Functionalized Chitosan. Carbohydr Polym. 2022, 284:119139. [CrossRef]
  15. Vargas-Berrones, K.; Ocampo-Perez, R.; Rodríguez-Torres, I.; Medellín-Castillo, N.A.; Flores-Ramírez, R. Molecularly Imprinted Polymers (MIPs) as Efficient Catalytic Tools for the Oxidative Degradation of 4-nonylphenol and its by-products. Environ. Sci. Pollut. Res. 2023, 30, 90741–90756. [CrossRef]
  16. Singhal, A.; Singh, A.; Shrivastava, A.; Khan, R. Epitope Imprinted Polymeric Materials: Application in Electrochemical Detection of Disease Biomarkers. J. Mat. Chem. B. 2023, 11, 936-954. [CrossRef]
  17. Dietl, S.; Sobek, H.; Mizaikoff, B. Epitope-imprinted polymers for biomacromolecules: Recent Strategies, Future Challenges and Selected Applications. TrAC Trends in Analytical Chem. 2021, 143, 116414. [CrossRef]
  18. Cruz, A.G.; Haq, I.; Cowen, T.; Di Masi, S.; Trivedi, S.; Alanazi, K.; Piletska, E.; Mujahid, A.; Piletsky, S.A. Design and Fabrication of a Smart Sensor Using in Silico Epitope Mapping and Electro-Responsive Imprinted Polymer Nanoparticles for Determination Of Insulin Levels in Human Plasma. Biosensors and Bioelectronics. 2020, 169, 112536. [CrossRef]
  19. Rapacz, D.; Smolinska-Kempisty, K.; Wolska, J. Molecularly imprinted polymers toward herbicides – Progress in Development and the Current State of the Art Depending on the Polymerization Environment – Short review. Journal of Environmental Chemical Engineering. 2024, 12, 112159. [CrossRef]
  20. Piletska, E.; Magumba, K.; Joseph, L.; Cruz, A.G.; Norman, R.; Singh, R.; Tabasso, A.F.S.; Jones, D. J.L.; Macip, S.; Piletsky, S. Molecular Imprinting as a Tool for Determining Molecular Markers: a Lung Cancer Case. RSC Advances. 2022, 12, 17747-17754. [CrossRef]
  21. Piletsky, S.S.; Piletska, E.; Poblocka, M.; Macip, S.; Jonese, D.J.L.; Braga, M.; Cao,T.H.; Singh, R.; Spivey, A.C.; Aboagye, E.O.; Piletsky, S.A. Snapshot Imprinting: Rapid Identification of Cancer Cell Surface Proteins and Epitopes Using Molecularly Imprinted Polymers. Nano Today. 2021, 41, 101304. [CrossRef]
  22. Piletska, E.; P.Veron, B. Bertin, F. Mingozzi, D. Jones, Norman, R. L., J. Earley MSc, Karim, K.; Garcia-Cruz, A.; Piletsky, S.A. Analysis of Adeno-Associated Virus Serotype 8 (AAV8)-Antibody Complexes Using Epitope Mapping by Molecular Imprinting Leads to the Identification of Fab Peptides That Potentially Evade AAV8 Neutralisation. Nanomedicine: Nanotechnology, Biology and Medicine. 2023, 52, 102691. [CrossRef]
  23. 23. Yin, Z-Z.; Cheng, S-W.; Xu, L-B.; Liu, H-Y.; Huang, K.; Li, L.; Zhai, Y-Y.; Zeng, Y-B.; Liu, H-Q.; Shao, Y.; Zhang, Z-L.; Lu, Y-X. Highly Sensitive And Selective Sensor for Sunset Yellow Based on Molecularly Imprinted Polydopamine-Coated Multi-Walled Carbon Nanotubes. Biosensors and Bioelectronics. 2018, 100, 565-570. [CrossRef]
  24. Choi, D.Y.; Yang, J.C.; Hong, S.W.; Park, J. Molecularly Imprinted Polymer-Based Electrochemical Impedimetric Sensors on Screen-Printed Carbon Electrodes for the Detection of Trace Cytokine IL-1β. Biosensors and Bioelectronics. 2022, 204, 114073. [CrossRef]
  25. Erdem, Ö.; Eş, I.; Saylan, Y.; Atabay, M.; Gungen, M.A.; Ölmez, K.; Denizli, A.; Inci, F. In situ Synthesis and Dynamic Simulation of Molecularly Imprinted Polymeric Nanoparticles on a Micro-Reactor System. Nat. Commun. 2023, 14, 4840. [CrossRef]
  26. Brueckl, H.; Shoshi, A.; Schrittwieser, S.; Schmid, B.; Schneeweiss, P.; Mitteramskogler, T.; Haslinger, M.J.; Muehlberger, M.; Schotter, J. Nanoimprinted Multifunctional Nanoprobes for a Homogeneous Immunoassay in a Top-Down Fabrication Approach. Sci. Rep. 2021, 11, 6039. [CrossRef]
  27. Gaurav, S.; Balasubramanian, K. Molecularly Imprinted Polymers for Selective Recognition and Extraction of Heavy Metal Ions and Toxic Dyes. J. Chem. Eng. 2020, 65, 396–418. [CrossRef]
  28. Kuras, M.J.; Perz, K.; Kołodziejski, W.L. Synthesis, Characterization and Application of a Novel Zinc(II) Ion-Imprinted Polymer. Polym. Bull. 2017, 74, 5029–5048. [CrossRef]
  29. Klučáková, M.; Pavlíková, M. Lignitic Humic Acids as Environmentally Friendly Adsorbent for Heavy Metals. Journal of Chemistry. 2017, 1-5. [CrossRef]
  30. Linnik, R.P.; Zaporozhets, O.; Mariychuk, A.R.; Lisnyak, V.V. Zinc Removal from Waters by Hybrid Sorbent with Humic Acid. 2019. https://10.1109/ICTEP48662.2019.8968971.
  31. Masoud, M.S.; Zidan, A.A.; El Zokm, G.M.; Elsamra, R.M. I.; Okbah, M.A. Humic acid and Nano-Zeolite NaX as low cost and Eco-Friendly Adsorbents for removal of Pb (II) and Cd (II) From Water: Characterization, Kinetics, Isotherms and Thermodynamic Studies. Biomass Conv. Bioref. 2024, 14, 3615-3632. [CrossRef]
  32. Menad, K.; Feddag, A.; Juhna, T. Copper (II)–Humic Acid Adsorption Process Using Microporous-Zeolite Na-X. J Inorg Organomet Polym. 2019, 29, 1-16. [CrossRef]
  33. Faisal, A.A.H.; Abdul-Kareem, M.B.; Mohammed, A. K.; Naushad, M.; Ghfar, A.A.; Ahamad, T. Humic Acid Coated Sand as a Novel Sorbent in Permeable Reactive Barrier for Environmental Remediation of Groundwater Polluted With Copper And Cadmium Ions. Journal of Water Process Engineering. 2020, 36, 101373. [CrossRef]
  34. Zhakina, A.Kh.; Rakhimova, B.B.; Vassilets, Ye.P.; Arnt, O.V.; Muldakhmetov, Z. Synthesis and Modification of a Natural Polymer with the Participation of Metal Nanoparticles, Study of Their Composition and Properties. Polymers. 2024, 16, 264. [CrossRef]
  35. Muldakhmetov, Z.M.; Gazaliev, A.M.; Zhakina, A.Kh.; Vassilets, Ye.P.; Arnt, O.V. Synthesis of a Composite Based on Humic Acid Tuned to Sorbed Copper Ion. Bull. Univ. Karaganda Chem. Ser. 2022, 108, 182-189. [CrossRef]
Preprints 117000 g001
Figure 1. IR spectra of imprinted polymers.
Figure 1. IR spectra of imprinted polymers.
Preprints 117000 g001
Preprints 117000 g002
Figure 2. ZnIP microstructure with elemental analysis.
Figure 2. ZnIP microstructure with elemental analysis.
Preprints 117000 g002
Preprints 117000 g003
Figure 3. NIP microstructure with elemental analysis.
Figure 3. NIP microstructure with elemental analysis.
Preprints 117000 g003
Preprints 117000 g004
Figure 4. Kinetics of sorption of Zn2+ ions by zinc-imprinted polymer and polymer comparisons.
Figure 4. Kinetics of sorption of Zn2+ ions by zinc-imprinted polymer and polymer comparisons.
Preprints 117000 g004
Preprints 117000 g005
Figure 5. Isotherms of sorption of Zn2+ ions.
Figure 5. Isotherms of sorption of Zn2+ ions.
Preprints 117000 g005
Preprints 117000 g006
Figure 6. Dependence of the degree of extraction of Zn2+ ions on pH on ZnIP and NIP.
Figure 6. Dependence of the degree of extraction of Zn2+ ions on pH on ZnIP and NIP.
Preprints 117000 g006
Preprints 117000 g007
Figure 7. The isotherm of the sorption of Zn2+ ions on ZnIP and NIP in the coordinates of the linear form of the Freundlich equation.
Figure 7. The isotherm of the sorption of Zn2+ ions on ZnIP and NIP in the coordinates of the linear form of the Freundlich equation.
Preprints 117000 g007
Preprints 117000 g008
Figure 8. The isotherm of the sorption of Zn2+ ions on ZnIP and NIP in the coordinates of the linear form of the Langmuir equation.
Figure 8. The isotherm of the sorption of Zn2+ ions on ZnIP and NIP in the coordinates of the linear form of the Langmuir equation.
Preprints 117000 g008
Table 1. Initial components for the synthesis of zinc-imprinted polymers and comparison polymers.
Table 1. Initial components for the synthesis of zinc-imprinted polymers and comparison polymers.
№ Polymer HA (mmol) MAA (mmol) Zn(CH3COO)2 (mmol) Crosslinking agent (EGDMA, mmol) Initiator (BP, mmol)
1 ZnIP 1 1 1.00 10 0.1
2 NIP 1 1 – 10 0.1
Table 2. Characteristics of imprinted polymers.
Table 2. Characteristics of imprinted polymers.
№ Polymer Cg, % Hg, % Ng, % Og, % Σ(COOH+OH) mg-eq/g Yield, %
1 ZnIP 61.32±0.2 3.97±0.1 0.67±0.1 34.04±0.3 4,43±0.2 76.54
2 NIP 57.32±0.2 3.85±0.1 0.67±0.1 38.16±0.3 4.95±0.2 77.98
Table 3. Kinetic equations of sorption of Zn2+ ions by zinc-imprinted and non-imprinted polymer at T=298.0 K and pH=5.0 and correlation coefficients (r).
Table 3. Kinetic equations of sorption of Zn2+ ions by zinc-imprinted and non-imprinted polymer at T=298.0 K and pH=5.0 and correlation coefficients (r).
The pseudo-order of the reaction Sorbed ion Zn2+ zinc-imprinted polymer
First lnC=1.4083-0.0118t r=0.9973 k1=0.0118
Second 1/C=0.1665+0.0067t r=0.9813 k2=0.0067
Third 1/C2=0.1001+0.0085t r=0,9341 k3=0.0085
The pseudo-order of the reaction Sorbed ion Zn2+ by a non-imprinted polymer
First lnC=1.9653-0.0079t r=0.9970 k1=0.0079
Second 1/C=0.1234+0,0019t r=0,9863 k2=0.0019
Third 1/C2=0.0047+0.001t r=0.9571 k3=0.0010
Table 4. Degrees of extraction (R, %), distribution coefficients (D) and values of imprinting factors (IF).
Table 4. Degrees of extraction (R, %), distribution coefficients (D) and values of imprinting factors (IF).
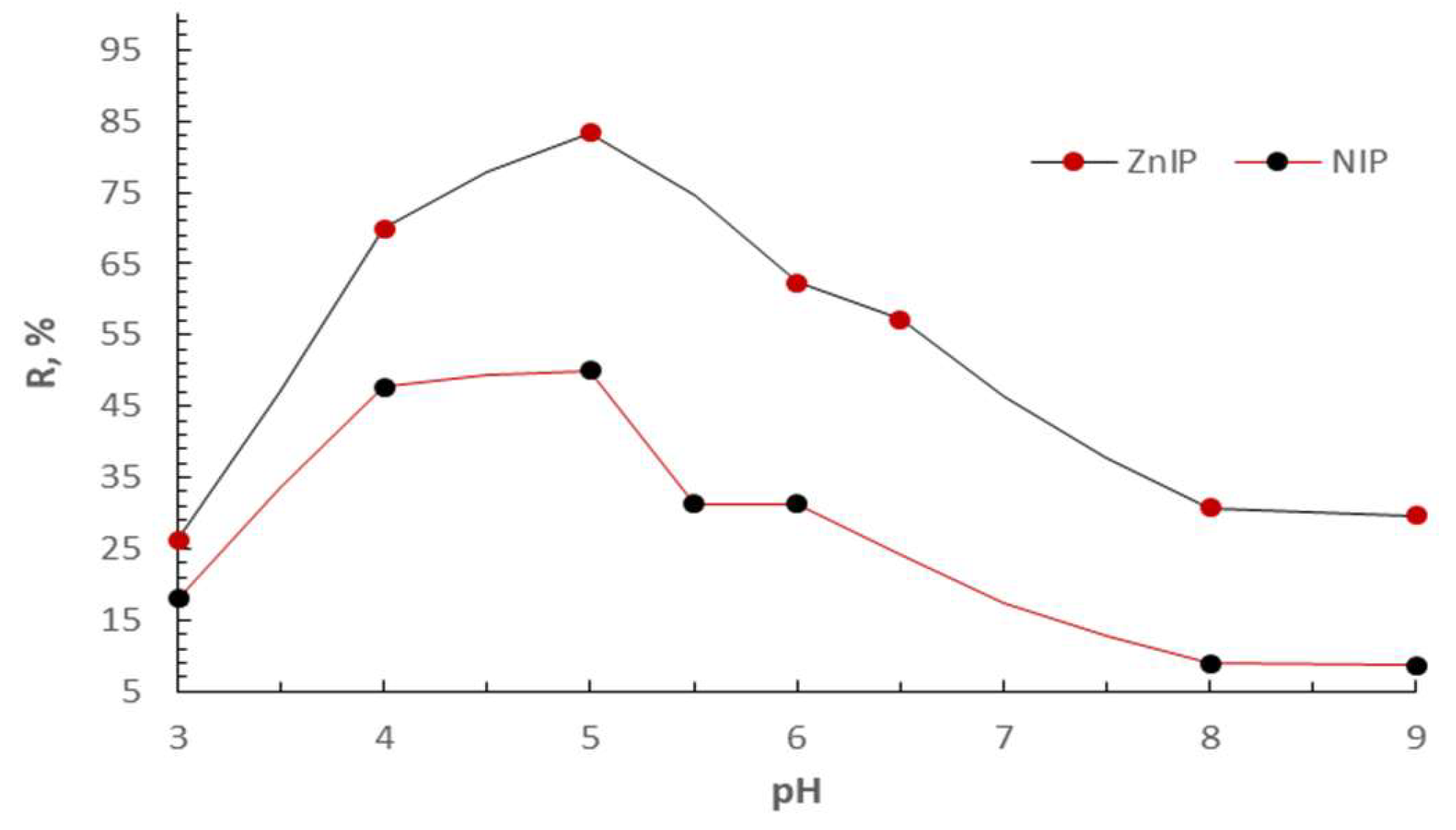
R, % D·10-2 IF
ZnIP NIP ZnIP NIP ZnIP
83.33 50.00 12.50 2.50 5.00
70.00 50.00 5.83 2.50 2.33
44.26 32.79 1.99 1.22 1.63
26.23 18.03 0.89 0.55 1.62
Table 5. Linear approximation coefficients (y=kx+b), Freundlich equation parameters and correlation coefficients (r).
Table 5. Linear approximation coefficients (y=kx+b), Freundlich equation parameters and correlation coefficients (r).
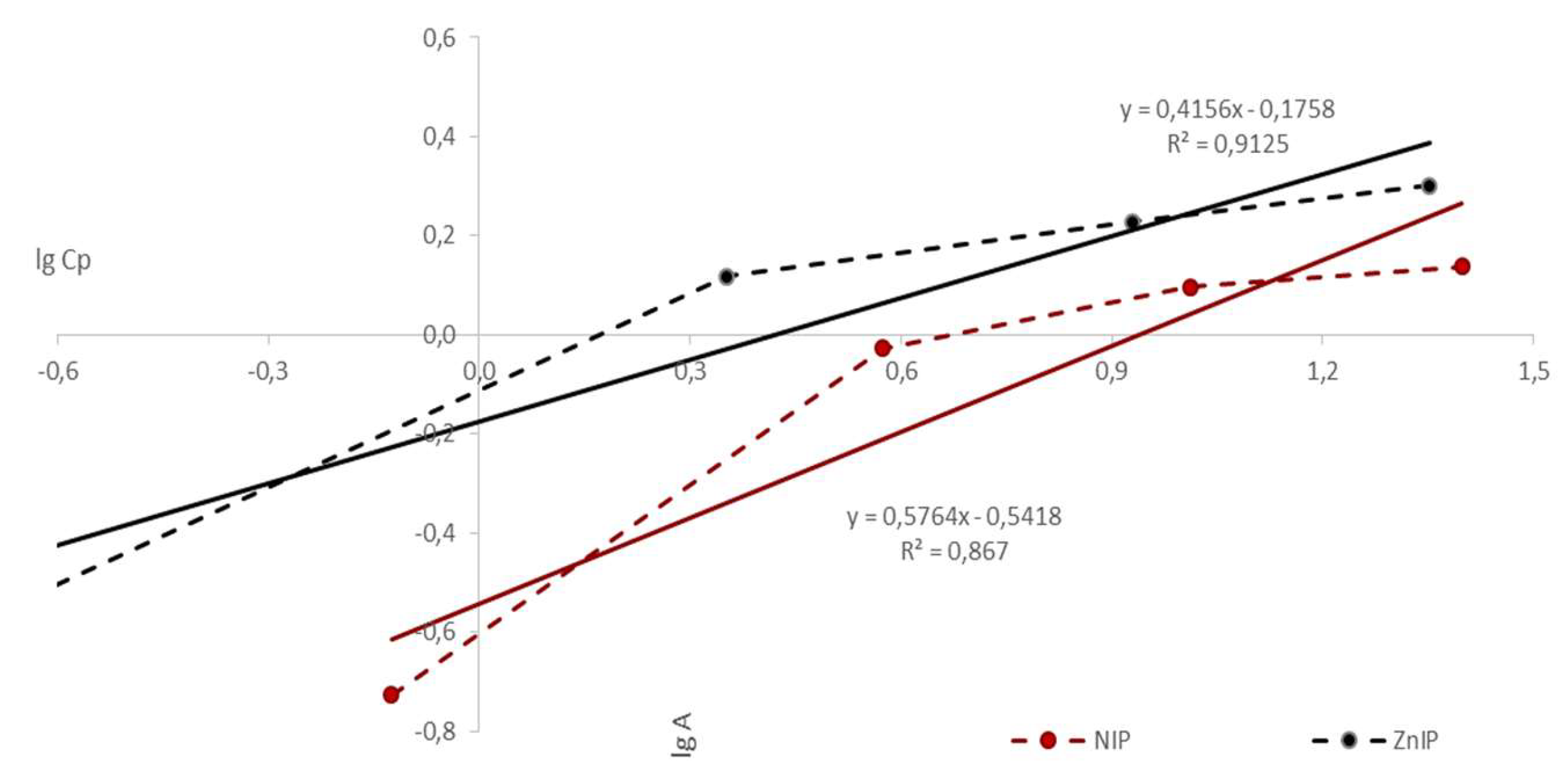
Polymer k b KFr n r
ZnIP 0.4156 -0.1758 1.1832 2.4060 0.9125
NIP 0.5764 -0.5418 2.0526 1.7348 0.8670
Table 6. Linear approximation coefficients (y=kx+b), Langmuir equation parameters and correlation coefficients (r).
Table 6. Linear approximation coefficients (y=kx+b), Langmuir equation parameters and correlation coefficients (r).
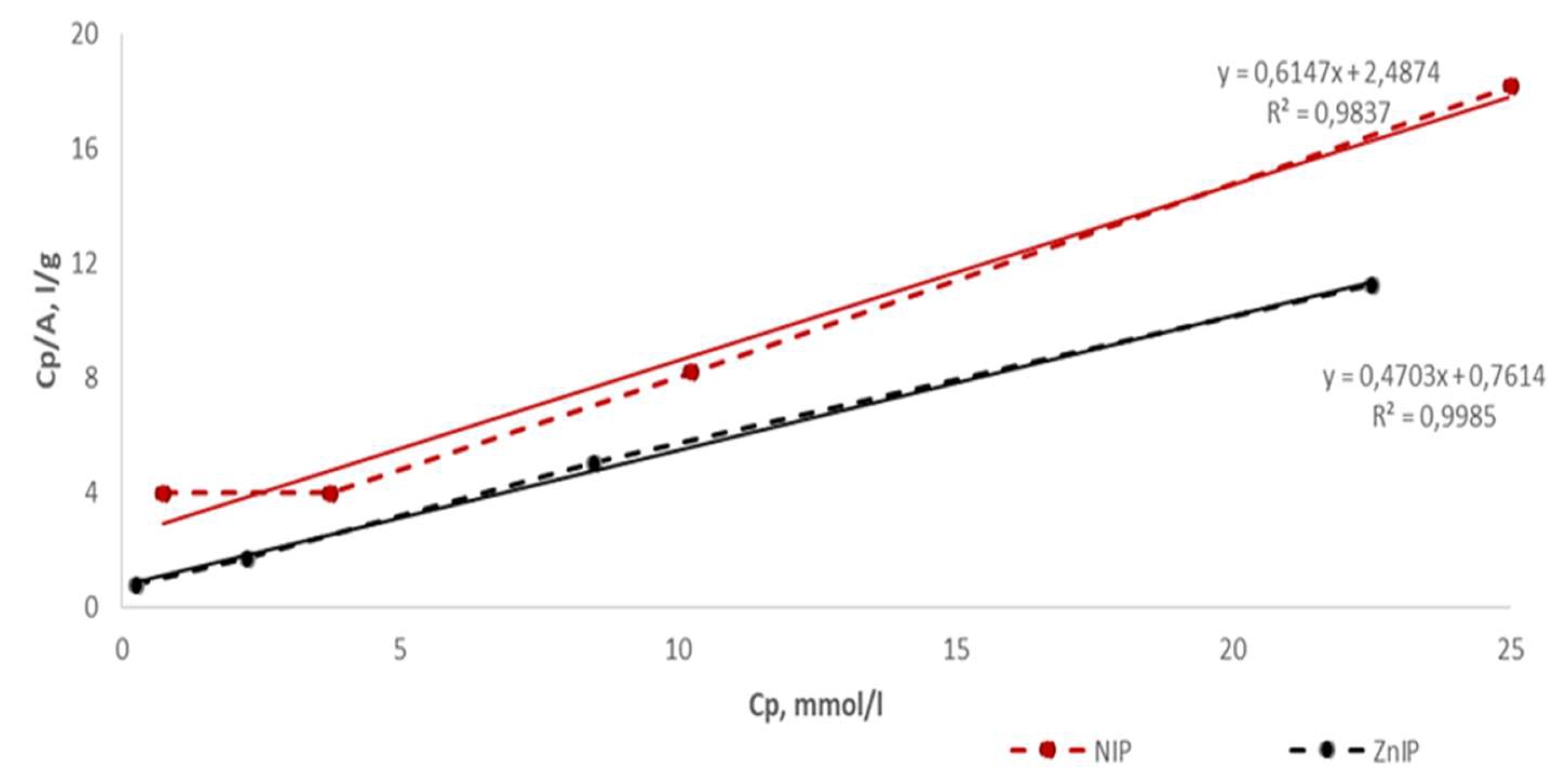
Polymer k b Maximum specific adsorption, A∞, mmol/g Adsorption equilibrium constant, KL, l/mmol r
ZnIP 0.4703 0.7614 2.1262 0.6177 0.9985
NIP 0.6147 2.4874 1.6269 0.2471 0.9837
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated