Prerpints.org logo
Preprint
Article

Robust Soliton Crystal Generation

Altmetrics

Downloads

109

Views

38

Comments

0

This version is not peer-reviewed

Submitted:

02 October 2024

Posted:

03 October 2024

You are already at the latest version

Alerts
Abstract
The deterministic generation of robust soliton comb has significant meaning for the optical frequency combs to be widely used in various applications. As a novel form of microcomb, Soliton crystal holds the advantages of easy generation, high conversion efficiency, and excellent thermal robustness. Here, we report the turnkey deterministic generation of ‘Palm-like’ soliton crystal with a free-running scheme. The robustness of the turnkey soliton crystal generation is also investigated in multiple aspects, including the success rate, the thermal robustness, and the long-term stability. The experiment results reveal our turnkey soliton crystal can achieve nearly a 100% success rate with a power variation less than ±1.5 dB over one hundred trials of two samples, is insensitive to thermal effects, and is robust to the environment during four-hour laboratory time.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

It has been over two decades since octave spanning optical frequency combs (OFCs) were developed, [1,2] enabling absolute frequency referencing. Kerr microcombs [3] – OFCs realized in micro-resonators – offer the possibility of realizing combs in a compact footprint, and the first reports [4,5,6] of fully integrated microcombs in CMOS compatible platforms triggered a tremendous wave of activity that has captured the imagination of the community since [7,8,9,10] and is still an extremely active field of research [11,12,13]. Beyond this, high repetition rates, high efficiencies and broad spectral coverage have made OFCs attractive for demonstrations focused on applications that span optical communications [14,15,16], frequency synthesis [17,18], quantum optics [19,20,21,22,23], microwave photonics [10,11,12,13,24,25,26,27], astronomical detection [28], and artificial intelligence [29,30,31,32]. Among many different types of microcombs of microcombs that have been reported, soliton microcombs are especially preferred for their high coherence and low noise [33], and these properties are linked to solitons being self-reinforcing waves. There are various categories of soliton microcombs, such as bright dissipative Kerr solitons (DKSs) [34,35], dark pulses, [36] soliton crystals (SCs) [15,37], and laser-cavity solitons [38,39].
Bright DKS microcomb states were the earliest discovered soliton microcomb that could be generated in micro-ring resonators (MRRs) [34,35], and operate in the red-detuned regime of MRRs having anomalous dispersion. However, when generating these soliton states, overcoming the fast resonance drift caused by the sudden decline of intracavity power that occurs at the onset of soliton generation, can be extremely challenging unless mitigated. Various control schemes have been applied to do this, such as fast frequency sweeping [40], power-kicking [41], integrated thermal-tuning [42], auxiliary laser pumping [43], self-injection locking [44], and forward and backward frequency sweeping [45]. Moreover, the typical internal conversion efficiency of DKSs is still only around 1% [46].
Using a shifted resonant mode within a microresonator, either through coupled resonators or through mode interactions in a single resonator, enables higher efficiency microcomb generation [47,48]. These mode shifts can enable bright single solitons [48], dark pulses [47,49] and SCs [15]. Bright, single soliton states have been demonstrated recently with efficiencies up to 54% [48], although this is achieved by reducing the pump power after soliton generation, which means that the per-line power is not increased significantly. Dark pulse states have reached up to 50% [49], but lack the intrinsic self-reinforcing nature of bright states. Laser cavity soliton microcombs have achieved the highest efficiency of all microcombs to date, [38,39] with the capability of reaching 100% since they do not operate via the LLE and so do not require a CW background that limits the efficiency. They have also achieved self-starting and self recovering, and operate by embedding a microring resonator in a nested cavity fiber loop configuration.
SCs are self-organized ensembles of co-propagating solitons that fill the resonator in the angular domain, and can show efficiencies up to 40% [15]. Their generation is a function of pump power, pump wavelength, cavity dispersion, and modes shifted by an avoided mode crossing (AMX) which is characterized by its wavelength location and strength. For SCs, the AMX enables an extended background wave into the soliton waveform in the resonator, which forms an attractive soliton-soliton interation, in turn enabling the ensemble of solitons to stably form [50,51]. A key property of SCs is that there is little intracavity power change when forming the SC state, so the intracavity temperature (and hence optical the resonance undergoing pumping) does not have the significant shift that is associated with DKS states. Therefore, no complex pumping scheme is needed, and the robust SCs can be obtained by slow frequency sweeping or temperature tuning of the pump wavelength. This greatly simplifies the system required to generate a SC state, which can be experimentally obtained by slow frequency sweeping of the pump laser or temperature tuning of the resonator.
Recent years have witnessed a surge in research on Kerr comb generation and applications with the aim moving microcombs out of the laboratory. This has been highlighted by advanced integrated photonics fabrication processes and packaging methods in order to greatly reduce the system size, weight, and power consumption (SWaP) as well as investigating the autonomous, deterministic, and robust generation of soliton combs. While deterministic generation has been shown for DKS states [43,52,53,54,55,56,57,58,59], other than for nested-cavity LCS microcombs, it has not been conclusively shown for high efficiency microcombs.
Attempts to demonstrate deterministic, and robust generation of SCs have focused on so-called “perfect” soliton crystals (PSCs) that have been deterministically generated with a 100% success rate [60] by forward tuning with low pump power. Here, the mode shift is synthesized using an auxiliary laser [51], to generate SCs with a mode spacing of 1 to 32 FSRs when soliton number is over 10 (490 GHz FSR repetition rate), the success rate of the PSC state generation is 100%, and when soliton number is below 10, the success rate, while not 100%, is still over 50%, which reduces with decreasing soliton number. However, PSCs tend to have wide comb line spacings, or relatively low numbers of comb lines with significant power, which limits their use in many applications. Soliton crystals with defects, in contrast, can have comb lines at the resonator FSR, and many comb lines with significant power – leading to many different proof-of-concept demonstrations for a wide range of applications [15,37,61,62,63] These can be generated with a high likelihood of success, with [50] showing a probability of over 60% for certain SC state. In [64], the desired SCs, with s line spacings of 48.9 to 150 GHz, can be generated by employing genetic algorithms as part of a closed-loop feedback control algorithm. However, these techniques for deterministic generation involve challenges such as complex setups resulting in wide mode spacings. Hence, while soliton crystals featuring defects look to be promising microcomb states, there has so far not been a simple, turn-key set up to generate these on demand.
The pump-to-comb conversion efficiency (CE) of the soliton combs is also important for turnkey operation. Dark pulse turnkey generation using two coupled SiN ring resonators was previously reported [53] with a CE of 41%. In addition, self-injection locking [57] has achieved a CE of 40% and 25% for bright solitons with repetition rates of 3 THz and 1.2 THz respectively. This wide comb line spacing greatly reduces their range of applications. In contrast, bounded bright solitons have been generated in zero-dispersion rings with a CE of 26% [58], but there the comb spectrum led to flaws – either highly structured spectra featuring a broad bandwidth with a considerably lower power, or a relatively smooth spectrum with a less structured shape but with a much more limited bandwidth. To date, there have been no demonstrations repeatability generating the same soliton state simultaneously with stable comb line powers, together with turnkey operation.
In this work, we demonstrate deterministically generated turnkey ‘Palm’ like 100 GHz (single FSR) SC microcombs using a free-running scheme. The turnkey SC generation is repeated 100 times using two different devics, both achieving a 100% success rate. Further, we repeat the experiments over a range of operating temperatures, still maintaining turnkey comb generation. Finally, we show that these states are robust to typical laboratory environmental variations, with line-by-line power variations lower than ±0.5 dB over the course of several hours, at the same time achieving a high efficiency of over 49%. This is the first report of deterministic turnkey generation of robust SCs using an open-loop (no feedback) system, demonstrating perfect consistency. These results conclusively show that turnkey deterministic generation of ‘Palm-like’ SC combs, in different devices, at different temperatures, and robust over significant time frames can be achieved.

2. ‘Palm-Like’ SC Generation and Simulation

In this work we generate ‘Palm-like’ SCs in two different 100 GHz FSR 4-port (add-drop) MRRs fabricated on a complementary-metal- oxide-semiconductor (CMOS) compatible high-index doped silica glass platform. These ‘Palm-like’ states have supported a number of applications [15,37,61,62,63], demonstrating that they are very useful microcombs. The radius of the MRRs is 270 µm with a waveguide that is is 3 µm wide and 1.5 µm thick. The device is pigtailed with a single mode fiber array to ensure the MRR is portable and reliably fiber coupled with very low loss – typically 1.0 - 1.5dB/facet. To help understand how ‘Palm- like’ SCs can be generated in these devices, the dispersion of the MRRs was measured to determine the AMX wavelength and strength.
The dispersion measurement setup is depicted in Figure 1(a). The tunable pump laser was swept across the MRR resonances as well as the Mach-Zehnder interferometer (MZI) and H13C14N (HCN) gas cell slowly at low power to eliminate effects of thermal drift on the MRR resonances, with the oscilloscope triggered to record the traces when the pump laser started sweeping. The MZI acted as a reference to find the resonances with high resolution while the HCN cell was for the calibration of wavelengths. Using the data from MZI and HCN, the MRR resonant wavelengths could be accurately calculated using a Lorentzian resonance profile fit. The cavity mode (µ) frequencies (ω) are ωµ = ω0 + µD1 + Dint, where the ω0 is the center wavelength, D1/(2π) is the FSR of the cavity and the Dint the integrated dispersion of the MRR which can be expressed as: Dint = ω − ω0 − · · · etc. We chose the reference frequency (ω0) to match the frequency of the resonance closest to 1550 nm. In the absence of any AMXs, the Dint is smooth and approximately parabolic. With the perturbation of the AMX, Dint shows some discontinuities around the AMX location. The measured dispersion of the two rings used in the experiment is shown in Figure 1 (b) and (c). The AMX strength (the largest difference between the Dint of the modes shifted by the AMX) of sample 1 with the TM mode and sample 2 with the TE mode is 131.78 MHz and 109.80 MHz respectively, and the corresponding AMX locations are 1522.435 nm and 1587.970 nm. As an approximate indication of pump wavelength, past experiments led us to link the AMX at 1522.435 nm of the TM mode and 1587.970 nm of the TE mode, to the ability to generate a ‘Palm-like’ SC state if pumped close to 1550 nm and 1560 nm.
The experimental setup for the ‘Palm-like’ SCs generation is shown in Figure 2 (a). The device was mounted on a thermo-electric cooler (TEC) to stabilize the MRR resonances. The continuous wave (CW) tunable pump laser was connected to an Erbium-doped fiber amplifier (EDFA) directly to guarantee enough power (up to 2W CW) for the SC generation. The output of EDFA was connected to a fiber polarization controller (FPC), which enabled the polarization of the incident light in the MRR to be set to the desired state. An attenuator was added at the drop port of MRR, then the light from the microcomb was passed into an optical spectrum analyzer (OSA). The TEC temperature was fixed at 25 ◦C, and the wavelength of the CW laser manually tuned from shorter to longer wavelength until a ‘Palm-like’ SC was generated. When pumping the sample 1 (sample 2) with 950 mW (1.6W) at 1550.33 (1559.76) nm, the desired ‘Palm-like’ state was generated, the experimental spectrum of two samples is depicted in Figure 2 (b) and (c) with blue. Simulations were carried out using the normalized Lugiato-Lefever Equation (LLE) in Equation (1) and the results are shown in Figure 2 (b) and (c) with orange, with the simulation broadly replicating the features of the experimentally generated comb.
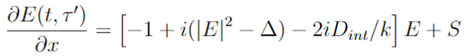
Preprints 120045 i001
where τ is the fast time corresponding to the azimuthal position in the ring, ∆ is the detuning, k = 2πf0/Q is the total loss rate, E is the intracavity field and S is the normalized input field.

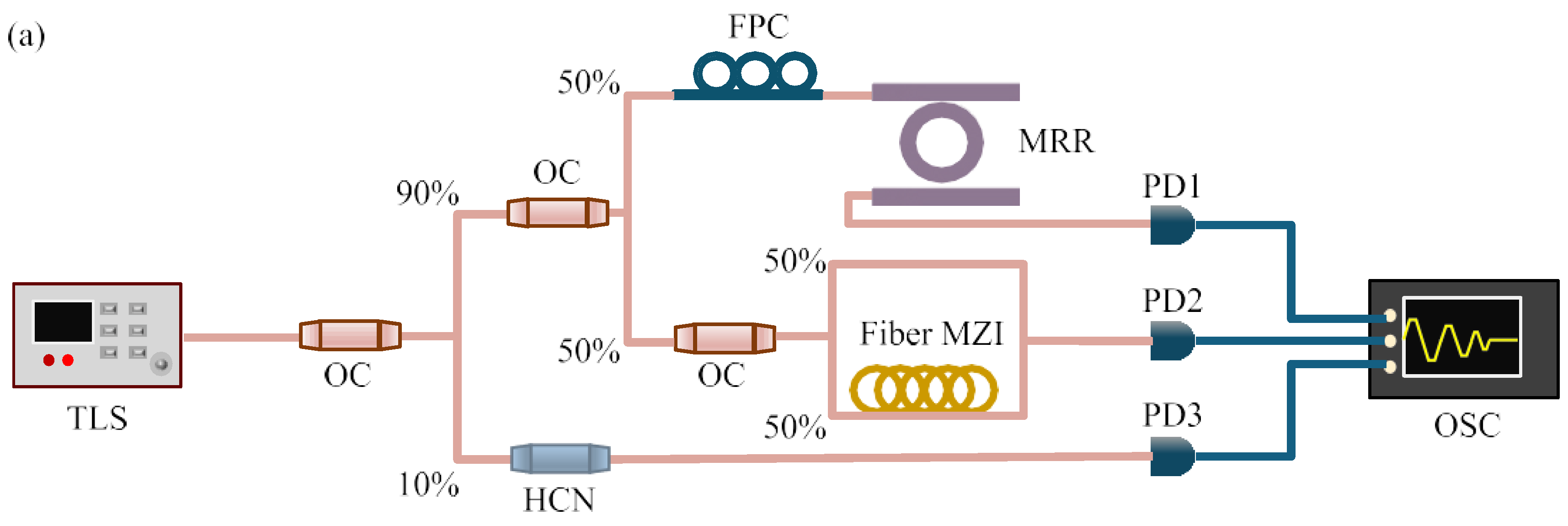
3. Deterministic Turnkey Generation

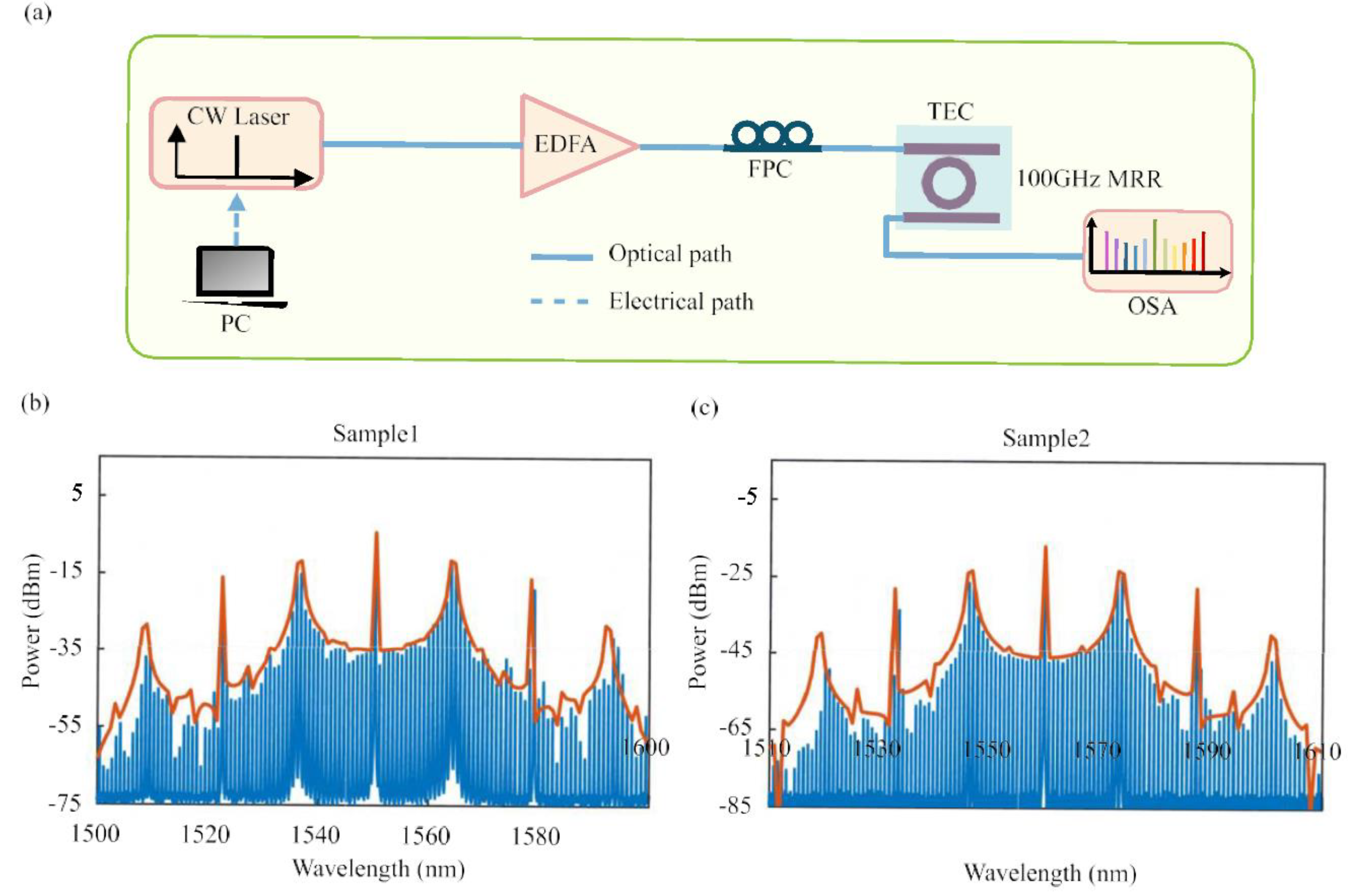
3.1. Repeatable Turnkey SC Generation

Knowing that ‘Palm-like’ SCs could be generated at 1550.33 nm for sample 1 and 1559.76 nm for sample 2 using manually tuning, a program was then applied to control the laser for wavelength sweeping. To achieve turnkey generation, we set the start wavelength to 1540 nm and 1557 nm, then swept the laser wavelength to 1550.33 nm and 1559.76 nm for the two samples, respectively, resulting in the deterministic generation of the SC combs. To verify the repeatability of the turnkey SC generation, 100 cycles were executed, with the results showing that the same states were generated on completion of the laser sweep to the target wavelengths. The power distribution from 1530 nm to 1570 nm of sample 1 with 100 cycles

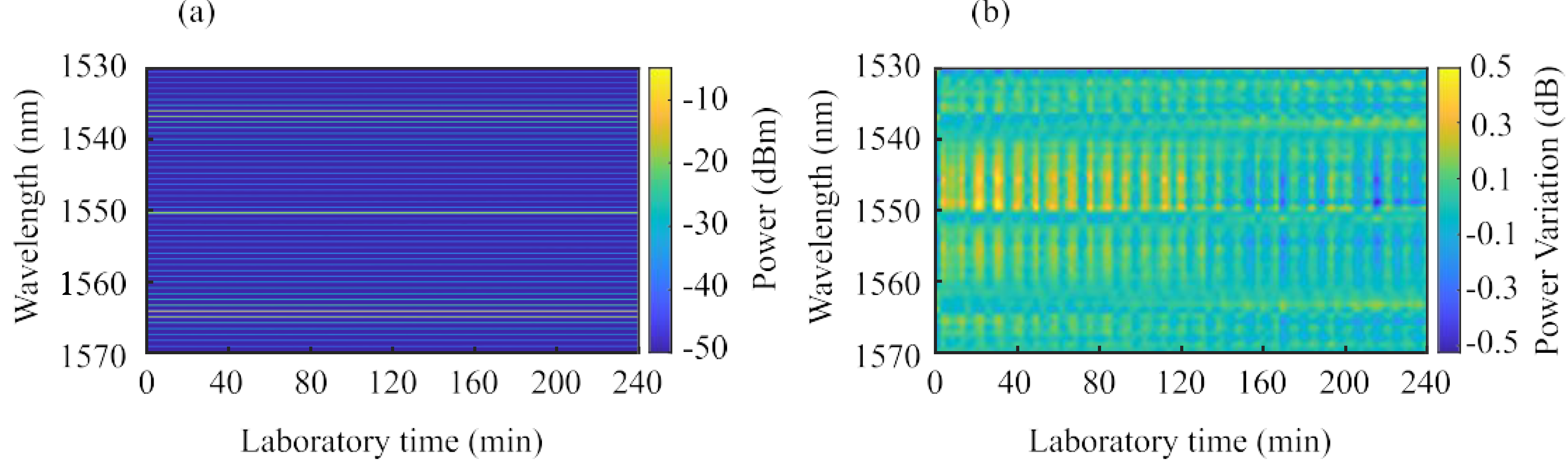
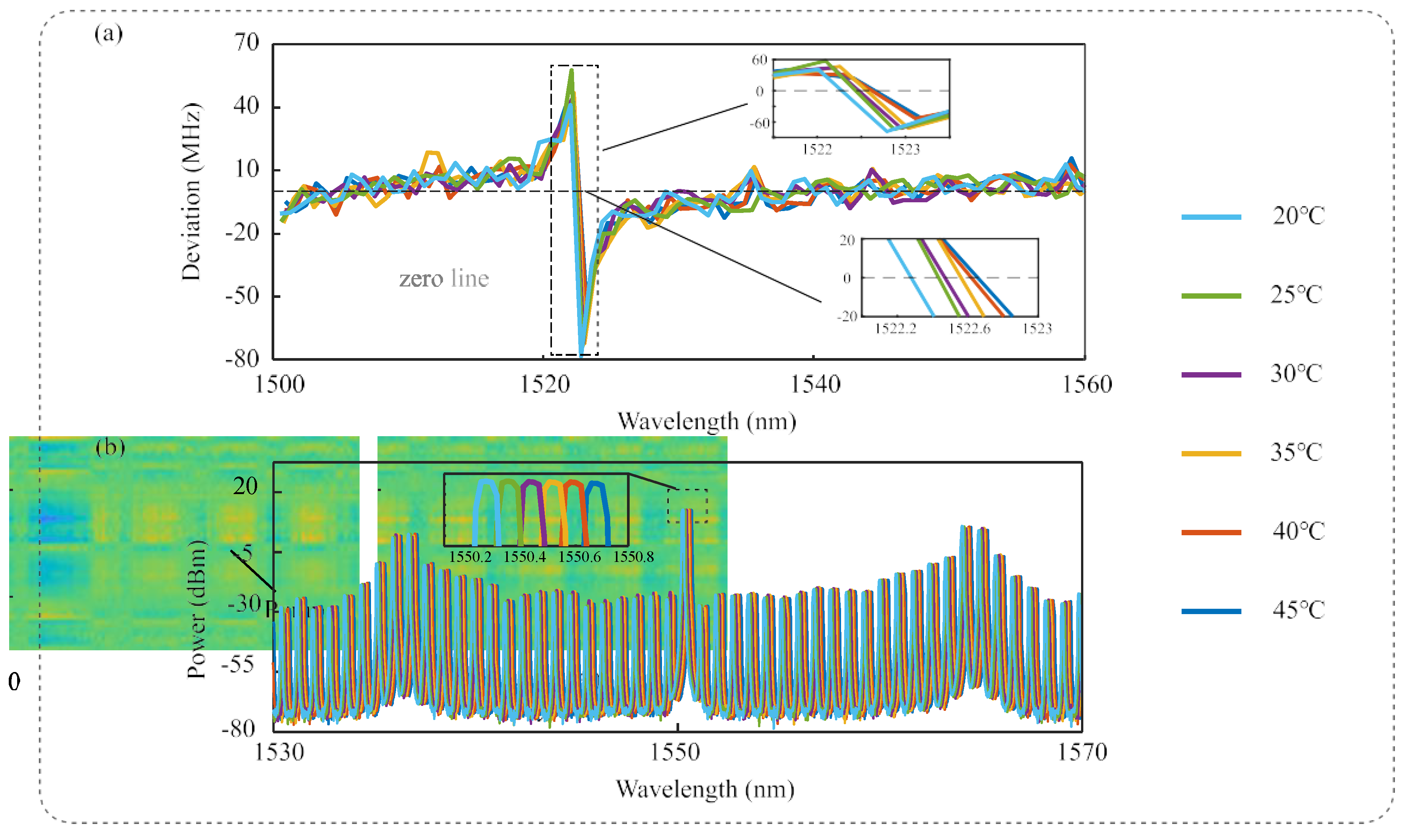
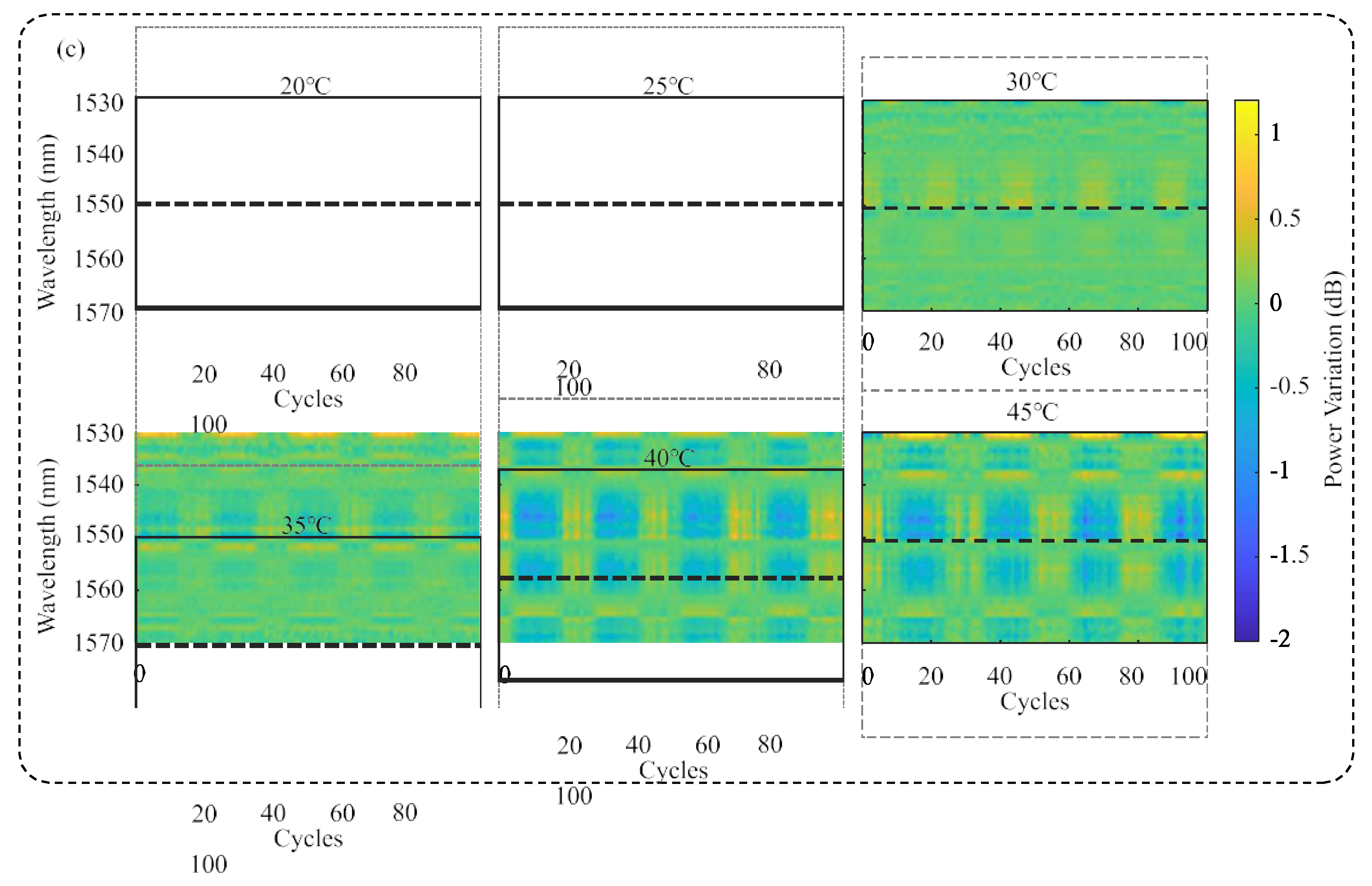
3.2. Turnkey SC Characterization at Different Operating Temperatures

Is depicted in Figure 3 (a), where the color bar shows the power spectrum density, and it can be seen that the power was ultra-stable over the 100 repeated experiments. Figure 3 (b) shows the power variation map of resonances between 1530 and 1570 nm of sample 1 over 100 cycles, where the variation is shown with respect to the mid-value of the 100-cycle resonance power as a baseline, showing a variation within ±1.5 dB. Figure 3 (c) shows the power distribution between 1540 and 1580 nm for sample 2 over 100 cycles and Figure 3 (d) is the power variation, which is also within ±1.5 dB. The internal conversion efficiency (CE) was calculated for the two samples, defined as the ratio between all the comb line powers minus the pump power, to the total power. By analyzing the spectrum on OSA (1530-1570 nm for sample 1, 1540-1580 nm for sample 2), a CE for both MRRs was 49.07% and 40.35% respectively, the high value representing attractive performance for practical devices.
In addition to the repeatability, the long-term stability is also an important factor that is important for practical microcomb operation. Measurements of the microcomb spectra over 4 hours were performed at 25 ◦C for sample 1 - the same conditions as for experiments described above, with the turnkey generated ‘Palm-like’ SCs spectra recorded every 3 minutes on an OSA. Figure 4 (a) shows the temporal evolution of a SC optical spectrum, where the color bar represents the optical power spectral density. Figure 4 (b) illustrates the variation of power in the resonances over 4 hours showing a variation within ±0.5 dB.

3.3. Turnkey SC Characterization at Different Operating Temperatures

Temperature changes cause an effective index change in the MRR, further shifting the resonance and affecting the AMXs [65]. To investigate whether thermal drifts affected the turnkey SC generation, a series of experiments were performed under a range of temperatures from 20 ◦C to 45 ◦C with a step s of 5 ◦C. Here, only sample 1 was investigated since the two devices had performed similarly. To determine the thermal properties of the AMX, the dispersion was measured versus temperature [65]. As shown in Figure 5 (a) the AMX wavelength shifted about
0.38 nm to longer wavelength when the temperature changed from 20 ◦C to 45 ◦C, representing a shift of much less than one FSR (˜0.8 nm), with the change in AMX wavelengths between 12.37 MHz and 53.6 MHz. The pump wavelength was swept sto generate ‘Palm-like’ SC at different temperature after characterizing the dispersion, with the generated spectra shown in Figure 5 (b). As the pump wavelength was tuned to longer wavelength, with increasing temperature the calculated slope of the pump wavelength shift with temperature drift is 0.0169 nm/◦C. During the dispersion measurements, the resonance shifts were also measured simultaneously, being about 0.0166 nm/◦C and showing high consistency with the pump wavelength shift. These results reveal the small change in AMXs caused by temperature shifts did not affect the SC generation or the pump wavelength but rather can be predicted according to the thermal coefficient, similar to [65].To further explore the turnkey generation of ‘Palm-like’ SCs at different temperatures, repeatable experiments as described in section 3.1 were performed. The initial wavelength was kept at 1540 nm with the final wavelengths being the target wavelength for each temperature. The repeatable turnkey experiments of the six temperatures are illustrated in Figure 5 (c), and the spectra variation for different temperatures for the 100 repetitions being smooth while the pump wavelength displayed a minor drift. This work will benefit all microcomb based applications, [66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89] particularly microwave photonics [90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124].

4. Conclusions

In conclusion, we demonstrate turnkey generation of 100 GHz ‘Palm-like’ SC combs with open-loop control (no feedback) and investigate its repeatability and robustness. For 100 attempts at turnkey generation, with two different samples, we achieve a perfect 100% success rate in generating ‘Palm-like’ states, with line-by-line power variations over the entire 40 nm comb bandwidth being less than than ±1.5 dB. The effect of temperature is investigated, showing that SC combs can be generated in a turnkey way over a wide range of operation temperatures. The temperature shifts have no influence on the deterministic generation of the SC combs and its repeatability. Moreover, in a standard lab environment over the course of a 4-hour trial, line- by-line power variations are within ±0.5 dB, showing that the comb is stable under open-loop controls built into a commercial-off-the-shelf (COTS) laser and TEC. Our work shows that we achieved the deterministic generation of robust SC combs without any complex stabilizing schemes, which guarantees simple, stable, repeatable and predictable the comb generation. Deterministic generation of these soliton crystal combs opens up opportunities for these states to be used in applications where highly robust combs are desired, and where complex control loops would be problematic.

References

  1. Theodor W. Hänsch, “Nobel Lecture: Passion for Precision”, Reviews of Modern Physics Vol. 78 1297 (2006). [CrossRef]
  2. John L. Hall, “Nobel Lecture: Defining and measuring optical frequencies”, Reviews of Modern Physics Vol. 78 1279 (2006). [CrossRef]
  3. P. Del’Haye, A. Schliesser, O. Arcizet, T. Wilken, R. Holzwarth, T. J. Kippenberg, Nature 2007, 450, 7173 1214.
  4. Moss, D. J., Morandotti, R., Gaeta, A. L. & Lipson, M. “New CMOS compatible platforms based on silicon nitride and Hydex for nonlinear optics”, Nature Photonics 7, 597-607 (2013). [CrossRef]
  5. L.Razzari, D.Duchesne, M.Ferrera, R.Morandotti, B.E Little, S.T. Chu and D.J Moss, “CMOS compatible integrated optical hyper-parametric oscillator”, Nature Photonics 4 41-44 (2010). [CrossRef]
  6. J. S. Levy, A. Gondarenko, M. A. Foster, A. C. Turner-Foster, A. L. Gaeta, and M. Lipson, "CMOS-compatible multiple-wavelength oscillator for on-chip optical interconnects," Nature Photonics 4 37-40 (2010). [CrossRef]
  7. A. Pasquazi, M. Peccianti, L. Razzari, D. J. Moss, S. Coen, M. Erkintalo, Y. K. Chembo, T. Hansson, S. Wabnitz, P. DelHaye, X. Xu, A. M. Weiner, and R. Morandotti, “Micro-Combs: A Novel Generation of Optical Sources”, Physics Reports 729 1–81 (2018). [CrossRef]
  8. T. J. Kippenberg, A. L. Gaeta, M. Lipson, and M. L. Gorodetsky, "Dissipative Kerr solitons in optical microresonators," Science 361 (2018). [CrossRef]
  9. A. L. Gaeta, M. Lipson, and T. J. Kippenberg, "Photonic-chip-based frequency combs," Nature Photonics 13, 158-169 (2019). [CrossRef]
  10. Yang Sun, Jiayang Wu, Mengxi Tan, Xingyuan Xu, Yang Li, Roberto Morandotti, Arnan Mitchell, and David J. Moss, “Applications of optical micro-combs”, Advances in Optics and Photonics 15 (1) 86-175 (2023).
  11. Shuman Sun, Beichen Wang, Kaikai Liu, Mark W. Harrington, Fatemehsadat Tabatabaei, Ruxuan Liu, Jiawei Wang, Samin Hanifi, Jesse S. Morgan, Mandana Jahanbozorgi, Zijiao Yang, Steven M. Bowers, Paul A. Morton, Karl D. Nelson, Andreas Beling, Daniel J. Blumenthal, and Xu Yi, “Integrated optical frequency division for microwave and mmWave generation”, Nature 627 540 (2024). [CrossRef]
  12. Igor Kudelin, William Groman, Qing-Xin Ji, Joel Guo, Megan L. Kelleher, Dahyeon Lee, Takuma Nakamura, Charles A. McLemore, Pedram Shirmohammadi, Samin Hanifi, Haotian Cheng, Naijun Jin, Lue Wu, Samuel Halladay, Yizhi Luo, Zhaowei Dai, Warren Jin, Junwu Bai, Yifan Liu, Wei Zhang, Chao Xiang, Lin Chang, Vladimir Iltchenko, Owen Miller, Andrey Matsko, Steven M. Bowers, Peter T. Rakich, Joe C. Campbell, John E. Bowers, Kerry J. Vahala, Franklyn Quinlan, and Scott A. Diddams, “Photonic chip-based low-noise microwave oscillator”, Nature 627 534 (2024). [CrossRef]
  13. Yun Zhao, Jae K. Jang, Garrett J. Beals, Karl J. McNulty, Xingchen Ji, Yoshitomo Okawachi, Michal Lipson, and Alexander L. Gaeta, “All-optical frequency division on-chip using a single laser” Nature 627 546 (2024).
  14. B. Corcoran, A. Mitchell, R. Morandotti, L. K. Oxenlowe, and D. J. Moss, “Microcombs for Optical Communications”, Nature Photonics 18 (2024).
  15. B. Corcoran, M. Tan, X. Xu, A. Boes, J. Wu, T. G. Nguyen, S. T. Chu, B. E. Little, R. Morandotti Mitchell, et al., Nature communications 2020, 11, 1 2568.
  16. P. Marin-Palomo, J. N. Kemal, M. Karpov, A. Kordts, J. Pfeifle, M. H. Pfeiffer, P. Trocha, S. Wolf, V. Brasch, M. H. Anderson, et al., Nature 2017, 546, 7657 274.
  17. D. T. Spencer, T. Drake, T. C. Briles, J. Stone, L. C. Sinclair, C. Fredrick, Q. Li, D. Westly, B. R. Ilic, A. Bluestone, et al., Nature 2018, 557, 7703 81.
  18. N. Singh, M. Xin, N. Li, D. Vermeulen, A. Ruocco, E. S. Magden, K. Shtyrkova, E. Ippen, F. X. Ka¨rtner, M. R. Watts, Laser & Photonics Reviews 2020, 14, 7 1900449.
  19. H.-H. Lu, A. M. Weiner, P. Lougovski, J. M. Lukens, IEEE Photonics Technology Letters 2019, 31, 23 1858.
  20. Kues, M. et al. “Quantum optical microcombs”, Nature Photonics vol. 13, (3) 170-179 (2019).
  21. C. Reimer et al., “Generation of multiphoton entangled quantum states by means of integrated frequency combs,” Science, vol. 351, no. 6278, pp. 1176-1180, 2016. [CrossRef]
  22. M. Kues, et al., “On-chip generation of high-dimensional entangled quantum states and C. Reimer, et al., “High-dimensional one-way quantum processing implemented on d-level cluster states”, Nature Physics, vol. 15, no.2, pp. 148–153, 2019. [CrossRef]
  23. X. Xu, J. Wu, T. G. Nguyen, M. Shoeiby, S. T. Chu, B. E. Little, R. Morandotti, A. Mitchell, D. J. Moss, Optics Express 2018, 26, 3 2569.
  24. Y. Wei, X. Wang, Y. Miao, J. Chen, X. Wang, C. Gong, Applied Optics 2022, 61, 23 6834.
  25. J.Wu, X. Xu, T.G. Nguyen, S.T. Chu, B.E. Little, R.Morandotti, A.Mitchell, and D.J. Moss, “RF photonics: An optical micro-combs’ perspective”, IEEE Journal of Selected Topics in Quantum Electronics 24 (4), 1-20 Article: 6101020 (2018).
  26. M. Tan, X. Xu, J.Wu, R. Morandotti, A. Mitchell, and D. J. Moss, “RF and microwave photonic temporal signal processing with Kerr micro-combs”, Advances in Physics X, VOL. 6, NO. 1, 1838946 (2021). [CrossRef]
  27. R. A. Probst, D. Milakovi´c, B. Toledo-Padro´n, G. Lo Curto, G. Avila, A. Brucalassi, B. L. Canto Martins, I. de Castro Lea˜o, M. Esposito, J. I. Gonz´alez Herna´ndez, et al., Nature Astronomy 2020, 4, 6 603.
  28. X. Xu, M. Tan, B. Corcoran, J. Wu, A. Boes, T. G. Nguyen, S. T. Chu, B. E. Little, D. G. Hicks,.
  29. R. Morandotti, et al., Nature 2021, 589, 7840 44.
  30. J. Feldmann, N. Youngblood, M. Karpov, H. Gehring, X. Li, M. Stappers, M. Le Gallo, X. Fu, A. Lukashchuk, A. S. Raja, J. Liu, C. D. Wright, A. Sebastian, T. J. Kippenberg, W. H. P. Pernice, and H. Bhaskaran, “Parallel convolutional processing using an integrated photonic tensor core”, Nature 2021, 589, 7840 52. [CrossRef]
  31. M. Tan, X. Xu, A. Boes, B. Corcoran, T. G. Nguyen, S. T. Chu, B. E. Little, R. Morandotti, J. Wu, Mitchell, et al., Communications Engineering 2023, 2, 1 94.
  32. B. J. Shastri, A. N. Tait, T. Ferreira de Lima, W. H. Pernice, H. Bhaskaran, C. D. Wright, P. R. Prucnal, Nature Photonics 2021, 15, 2 102.
  33. W. Wang, L. Wang, W. Zhang, Advanced Photonics 2020, 2, 3 034001.
  34. T. Herr, M. L. Gorodetsky, T. J. Kippenberg, Nonlinear optical cavity dynamics: from microresonators to fiber lasers 2016, 129–162.
  35. T. Herr, V. Brasch, J. D. Jost, C. Y. Wang, N. M. Kondratiev, M. L. Gorodetsky, T. J. Kippenberg, Nature Photonics 2014, 8, 2 145.
  36. V. Lobanov, G. Lihachev, T. Kippenberg, M. Gorodetsky, Optics express 2015, 23, 6 7713.
  37. D. C. Cole, E. S. Lamb, P. Del’Haye, S. A. Diddams, S. B. Papp, Nature Photonics 2017, 11, 10 671.
  38. M. Rowley, P.-H. Hanzard, A. Cutrona, H. Bao, S. T. Chu, B. E. Little, R. Morandotti, D. J. Moss, G.-L. Oppo, J. Sebastian T. Gongora, M. Peccianti and A. Pasquazi, “Self-emergence of robust solitons in a micro-cavity”, Nature 608 (7922) 303 – 309 (2022).
  39. Hualong Bao, Andrew Cooper, Maxwell Rowley, Luigi Di Lauro, Juan Sebastian Totero Gongora, Sai T. Chu, Brent E. Little, Gian-Luca Oppo, Roberto Morandotti, David J. Moss, Benjamin Wetzel, Marco Peccianti and Alessia Pasquazi, “Laser Cavity-Soliton Micro-Combs”, Nature Photonics 13 (6) 384–389 (2019).
  40. L. Gaeta, M. Lipson, T. J. Kippenberg, nature photonics 2019, 13, 3 158.
  41. V. Brasch, M. Geiselmann, T. Herr, G. Lihachev, M. H. Pfeiffer, M. L. Gorodetsky, T. J. Kippenberg, Science 2016, 351, 6271 357.
  42. C. Joshi, J. K. Jang, K. Luke, X. Ji, S. A. Miller, A. Klenner, Y. Okawachi, M. Lipson, A. L. Gaeta, Optics letters 2016, 41, 11 2565.
  43. H. Zhou, Y. Geng, W. Cui, S.-W. Huang, Q. Zhou, K. Qiu, C. Wei Wong, Light: Science & Applications 2019, 8, 1 50.
  44. V. Brasch, M. Geiselmann, M. H. Pfeiffer, T. J. Kippenberg, Optics express 2016, 24, 25 29312.
  45. H. Guo, M. Karpov, E. Lucas, A. Kordts, M. H. Pfeiffer, V. Brasch, G. Lihachev, V. E. Lobanov, M. L. Gorodetsky, T. J. Kippenberg, Nature Physics 2017, 13, 1 94.
  46. C. Bao, L. Zhang, A. Matsko, Y. Yan, Z. Zhao, G. Xie, A. M. Agarwal, L. C. Kimerling, J. Michel, L. Maleki, et al., Optics letters 2014, 39, 21 6126.
  47. X. Xue, Y. Xuan, Y. Liu, P.-H. Wang, S. Chen, J. Wang, D. E. Leaird, M. Qi, A. M. Weiner, Nature Photonics 2015, 9, 9 594.
  48. O´. B. Helgason, M. Girardi, Z. Ye, F. Lei, J. Schro¨der, V. Torres-Company, Nature Photonics 2023, 17, 11 992.
  49. A. Fu¨l¨op, M. Mazur, A. Lorences-Riesgo, O´. B. Helgason, P.-H. Wang, Y. Xuan, D. E. Leaird, M. Qi, P. A. Andrekson, A. M. Weiner, et al., Nature communications 2018, 9, 1 1598.
  50. W. Wang, Z. Lu, W. Zhang, S. T. Chu, B. E. Little, L. Wang, X. Xie, M. Liu, Q. Yang, L. Wang, et al., Optics letters 2018, 43, 9 2002.
  51. Z. Lu, H.-J. Chen, W. Wang, L. Yao, Y. Wang, Y. Yu, B. Little, S. Chu, Q. Gong, W. Zhao, et al., Nature communications 2021, 12, 1 3179.
  52. M. Zhang, S. Ding, X. Li, K. Pu, S. Lei, M. Xiao, X. Jiang, Nature Communications 2024, 15, 1 1661.
  53. B. Y. Kim, Y. Okawachi, J. K. Jang, M. Yu, X. Ji, Y. Zhao, C. Joshi, M. Lipson, A. L. Gaeta, Optics letters 2019, 44, 18 4475.
  54. B. Shen, L. Chang, J. Liu, H. Wang, Q.-F. Yang, C. Xiang, R. N. Wang, J. He, T. Liu, W. Xie, et al., Nature 2020, 582, 7812 365.
  55. W. Jin, Q.-F. Yang, L. Chang, B. Shen, H. Wang, M. A. Leal, L. Wu, M. Gao, A. Feshali, M. Paniccia, et al., Nature Photonics 2021, 15, 5 346.
  56. H. Shu, L. Chang, Y. Tao, B. Shen, W. Xie, M. Jin, A. Netherton, Z. Tao, X. Zhang, R. Chen, et al., Nature 2022, 605, 7910 457.
  57. N. Y. Dmitriev, S. N. Koptyaev, A. S. Voloshin, N. M. Kondratiev, K. N. Min’kov, V. E. Lobanov, M. V. Ryabko, S. V. Polonsky, I. A. Bilenko, Physical Review Applied 2022, 18, 3 034068.
  58. Q.-X. Ji, W. Jin, L. Wu, Y. Yu, Z. Yuan, W. Zhang, M. Gao, B. Li, H. Wang, C. Xiang, et al., Optica 2023, 10, 2 279.
  59. H. Weng, M. McDermott, A. A. Afridi, H. Tu, Q. Lu, W. Guo, J. F. Donegan, Optics Express 2024, 32, 3 3123.
  60. M. Karpov, M. H. Pfeiffer, H. Guo, W. Weng, J. Liu, T. J. Kippenberg, Nature Physics 2019, 15, 10 1071.
  61. M. Tan, X. Xu, Y. Li, Y. Sun, D. Hicks, R. Morandotti, J. Wu, A. Mitchell, D. J. Moss, In Laser Resonators, Microresonators, and Beam Control XXIV, volume 11987. SPIE, 2022 1198702.
  62. X. Xu, M. Tan, J. Wu, T. G. Nguyen, S. T. Chu, B. E. Little, R. Morandotti, A. Mitchell, D. J. Moss, Journal of Lightwave Technology 2019, 37, 4 1288.
  63. X. Xu, M. Tan, J. Wu, A. Boes, B. Corcoran, T. G. Nguyen, S. T. Chu, B. E. Little, R. Morandotti, Mitchell, D. J. Moss, IEEE Transactions on Circuits and Systems II: Express Briefs 2020, 67, 12 3582.
  64. C. Mazoukh, L. Di Lauro, I. Alamgir, B. Fischer, N. Perron, A. Aadhi, A. Eshaghi, B. E. Little, S. T. Chu, D. J. Moss, et al., Communications Physics 2024, 7, 1 81.
  65. 65. C. E. Murray, M. Tan, C. Prayoonyong, X. Zhu, S. T. Chu, B. E. Little, R. Morandotti, A. Mitchell, D. J. Moss, B. Corcoran, Optics Express 2023, Vol. 31, 23 37749.
  66. A.Pasquazi, et al., “Sub-picosecond phase-sensitive optical pulse characterization on a chip”, Nature Photonics, vol. 5, no. 10, pp. 618-623 (2011).
  67. M Ferrera et al., “On-Chip ultra-fast 1st and 2nd order CMOS compatible all-optical integration”, Optics Express vol. 19 (23), 23153-23161 (2011).
  68. Bao, C., et al., Direct soliton generation in microresonators, Opt. Lett, 42, 2519 (2017). [CrossRef]
  69. M.Ferrera et al., “CMOS compatible integrated all-optical RF spectrum analyzer”, Optics Express, vol. 22, no. 18, 21488 - 21498 (2014).
  70. M. Kues, et al., “Passively modelocked laser with an ultra-narrow spectral width”, Nature Photonics, vol. 11, no. 3, pp. 159, 2017. [CrossRef]
  71. M. Ferrera, et al., “Low-power continuous-wave nonlinear optics in doped silica glass integrated waveguide structures,” Nature Photonics, vol. 2, no. 12, pp. 737-740, 2008. [CrossRef]
  72. M.Ferrera et al.“On-Chip ultra-fast 1st and 2nd order CMOS compatible all-optical integration”, Opt. Express, vol. 19, (23)pp. 23153-23161 (2011).
  73. D. Duchesne, M. Peccianti, M. R. E. Lamont, et al., “Supercontinuum generation in a high index doped silica glass spiral waveguide,” Optics Express, vol. 18, no, 2, pp. 923-930, 2010. [CrossRef]
  74. H Bao, L Olivieri, M Rowley, ST Chu, BE Little, R Morandotti, DJ Moss, ... “Turing patterns in a fiber laser with a nested microresonator: Robust and controllable microcomb generation”, Physical Review Research vol. 2 (2), 023395 (2020). [CrossRef]
  75. M. Ferrera, et al., “On-chip CMOS-compatible all-optical integrator”, Nature Communications, vol. 1, Article 29, 2010. [CrossRef]
  76. Pasquazi, et al., “All-optical wavelength conversion in an integrated ring resonator,” Optics Express, vol. 18, no. 4, pp. 3858-3863, 2010.
  77. Pasquazi, Y. Park, J. Azana, et al., “Efficient wavelength conversion and net parametric gain via Four Wave Mixing in a high index doped silica waveguide,” Optics Express, vol. 18, no. 8, pp. 7634-7641, 2010.
  78. Peccianti, M. Ferrera, L. Razzari, et al., “Subpicosecond optical pulse compression via an integrated nonlinear chirper,” Optics Express, vol. 18, no. 8, pp. 7625-7633, 2010. [CrossRef]
  79. M Ferrera, Y Park, L Razzari, BE Little, ST Chu, R Morandotti, DJ Moss, ... et al., “All-optical 1st and 2nd order integration on a chip”, Optics Express vol. 19 (23), 23153-23161 (2011).
  80. M. Ferrera et al., “Low Power CW Parametric Mixing in a Low Dispersion High Index Doped Silica Glass Micro-Ring Resonator with Q-factor > 1 Million”, Optics Express, vol.17, no. 16, pp. 14098–14103 (2009).
  81. M. Peccianti, et al., “Demonstration of an ultrafast nonlinear microcavity modelocked laser”, Nature Communications, vol. 3, pp. 765, 2012.
  82. Pasquazi, et al., “Self-locked optical parametric oscillation in a CMOS compatible microring resonator: a route to robust optical frequency comb generation on a chip,” Optics Express, vol. 21, no. 11, pp. 13333-13341, 2013.
  83. Pasquazi, et al., “Stable, dual mode, high repetition rate mode-locked laser based on a microring resonator,” Optics Express, vol. 20, no. 24, pp. 27355-27362, 2012.
  84. H. Bao, et al., Laser cavity-soliton microcombs, Nature Photonics, vol. 13, no. 6, pp. 384-389, Jun. 2019. [CrossRef]
  85. Antonio Cutrona, Maxwell Rowley, Debayan Das, Luana Olivieri, Luke Peters, Sai T. Chu, Brent L. Little, Roberto Morandotti, David J. Moss, Juan Sebastian Totero Gongora, Marco Peccianti, Alessia Pasquazi, “High Conversion Efficiency in Laser Cavity-Soliton Microcombs”, Optics Express Vol. 30, Issue 22, pp. 39816-39825 (2022). https://doi.org/10.1364/OE.470376. [CrossRef]
  86. M.Rowley, P.Hanzard, A.Cutrona, H.Bao, S.Chu, B.Little, R.Morandotti, D. J. Moss, G. Oppo, J. Gongora, M. Peccianti and A. Pasquazi, “Self-emergence of robust solitons in a micro-cavity”, Nature vol. 608 (7922) 303–309 (2022).
  87. Cutrona, M. Rowley, A. Bendahmane, V. Cecconi,L. Peters, L. Olivieri, B. E. Little, S. T. Chu, S. Stivala, R. Morandotti, D. J. Moss, J. S. Totero-Gongora, M. Peccianti, A. Pasquazi, “Nonlocal bonding of a soliton and a blue-detuned state in a microcomb laser”, Nature Communications Physics6Article 259 (2023). [CrossRef]
  88. Aadhi A. Rahim, Imtiaz Alamgir, Luigi Di Lauro, Bennet Fischer, Nicolas Perron, Pavel Dmitriev, Celine Mazoukh, Piotr Roztocki, Cristina Rimoldi, Mario Chemnitz, Armaghan Eshaghi, Evgeny A. Viktorov, Anton V. Kovalev, Brent E. Little, Sai T. Chu, David J. Moss, and Roberto Morandotti, “Mode-locked laser with multiple timescales in a microresonator-based nested cavity”, APL Photonics 9 031302 (2024). DOI:10.1063/5.0174697. [CrossRef]
  89. Cutrona, M. Rowley, A. Bendahmane, V. Cecconi,L. Peters, L. Olivieri, B. E. Little, S. T. Chu, S. Stivala, R. Morandotti, D. J. Moss, J. S. Totero-Gongora, M. Peccianti, A. Pasquazi, “Stability Properties of Laser Cavity-Solitons for Metrological Applications”, Applied Physics Letters vol. 122 (12) 121104 (2023); doi: 10.1063/5.0134147. [CrossRef]
  90. X. Xu, J. Wu, M. Shoeiby, T. G. Nguyen, S. T. Chu, B. E. Little, R. Morandotti, A. Mitchell, and D. J. Moss, “Reconfigurable broadband microwave photonic intensity differentiator based on an integrated optical frequency comb source,” APL Photonics, vol. 2, no. 9, 096104, Sep. 2017. [CrossRef]
  91. Xu, X., et al., Photonic microwave true time delays for phased array antennas using a 49 GHz FSR integrated micro-comb source, Photonics Research, vol. 6, B30-B36 (2018). [CrossRef]
  92. X. Xu, M. Tan, J. Wu, R. Morandotti, A. Mitchell, and D. J. Moss, “Microcomb-based photonic RF signal processing”, IEEE Photonics Technology Letters, vol. 31 no. 23 1854-1857, 2019. [CrossRef]
  93. Xu, et al., “Advanced adaptive photonic RF filters with 80 taps based on an integrated optical micro-comb source,” Journal of Lightwave Technology, vol. 37, no. 4, pp. 1288-1295 (2019).
  94. X. Xu, et al., “Photonic RF and microwave integrator with soliton crystal microcombs”, IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 67, no. 12, pp. 3582-3586, 2020. DOI:10.1109/TCSII.2020.2995682. [CrossRef]
  95. X. Xu, et al., “High performance RF filters via bandwidth scaling with Kerr micro-combs,” APL Photonics, vol. 4 (2) 026102. 2019. [CrossRef]
  96. M. Tan, et al., “Microwave and RF photonic fractional Hilbert transformer based on a 50 GHz Kerr micro-comb”, Journal of Lightwave Technology, vol. 37, no. 24, pp. 6097 – 6104, 2019. [CrossRef]
  97. M. Tan, et al., “RF and microwave fractional differentiator based on photonics”, IEEE Transactions on Circuits and Systems: Express Briefs, vol. 67, no.11, pp. 2767-2771, 2020. DOI:10.1109/TCSII.2020.2965158. [CrossRef]
  98. M. Tan, et al., “Photonic RF arbitrary waveform generator based on a soliton crystal micro-comb source”, Journal of Lightwave Technology, vol. 38, no. 22, pp. 6221-6226 (2020). DOI: 10.1109/JLT.2020.3009655. [CrossRef]
  99. M. Tan, X. Xu, J. Wu, R. Morandotti, A. Mitchell, and D. J. Moss, “RF and microwave high bandwidth signal processing based on Kerr Micro-combs”, Advances in Physics X, VOL. 6, NO. 1, 1838946 (2021). DOI:10.1080/23746149.2020.1838946. [CrossRef]
  100. X. Xu, et al., “Advanced RF and microwave functions based on an integrated optical frequency comb source,” Opt. Express, vol. 26 (3) 2569 (2018). [CrossRef]
  101. M. Tan, X. Xu, J. Wu, B. Corcoran, A. Boes, T. G. Nguyen, S. T. Chu, B. E. Little, R. Morandotti, A. Lowery, A. Mitchell, and D. J. Moss, “"Highly Versatile Broadband RF Photonic Fractional Hilbert Transformer Based on a Kerr Soliton Crystal Microcomb”, Journal of Lightwave Technology vol. 39 (24) 7581-7587 (2021). [CrossRef]
  102. Wu, J. et al. RF Photonics: An Optical Microcombs’ Perspective. IEEE Journal of Selected Topics in Quantum Electronics Vol. 24, 6101020, 1-20 (2018).
  103. T. G. Nguyen et al., “Integrated frequency comb source-based Hilbert transformer for wideband microwave photonic phase analysis,” Opt. Express, vol. 23, no. 17, pp. 22087-22097, Aug. 2015. [CrossRef]
  104. X. Xu, et al., “Broadband RF channelizer based on an integrated optical frequency Kerr comb source,” Journal of Lightwave Technology, vol. 36, no. 19, pp. 4519-4526, 2018. [CrossRef]
  105. X. Xu, et al., “Continuously tunable orthogonally polarized RF optical single sideband generator based on micro-ring resonators,” Journal of Optics, vol. 20, no. 11, 115701. 2018. [CrossRef]
  106. X. Xu, et al., “Orthogonally polarized RF optical single sideband generation and dual-channel equalization based on an integrated microring resonator,” Journal of Lightwave Technology, vol. 36, no. 20, pp. 4808-4818. 2018. [CrossRef]
  107. X. Xu, et al., “Photonic RF phase-encoded signal generation with a microcomb source”, J. Lightwave Technology, vol. 38, no. 7, 1722-1727, 2020. [CrossRef]
  108. X. Xu, et al., Broadband microwave frequency conversion based on an integrated optical micro-comb source”, Journal of Lightwave Technology, vol. 38 no. 2, pp. 332-338, 2020. [CrossRef]
  109. M. Tan, et al., “Photonic RF and microwave filters based on 49GHz and 200GHz Kerr microcombs”, Optics Comm. vol. 465,125563, Feb. 22. 2020. [CrossRef]
  110. X. Xu, et al., “Broadband photonic RF channelizer with 90 channels based on a soliton crystal microcomb”, Journal of Lightwave Technology, Vol. 38, no. 18, pp. 5116 – 5121 (2020). doi: 10.1109/JLT.2020.2997699. [CrossRef]
  111. M. Tan et al, “Orthogonally polarized Photonic Radio Frequency single sideband generation with integrated micro-ring resonators”, IOP Journal of Semiconductors, Vol. 42 (4), 041305 (2021). DOI: 10.1088/1674-4926/42/4/041305. [CrossRef]
  112. Mengxi Tan, X. Xu, J. Wu, T. G. Nguyen, S. T. Chu, B. E. Little, R. Morandotti, A. Mitchell, and David J. Moss, “Photonic Radio Frequency Channelizers based on Kerr Optical Micro-combs”, IOP Journal of Semiconductors Vol. 42 (4), 041302 (2021). DOI:10.1088/1674-4926/42/4/041302. [CrossRef]
  113. B. Corcoran, et al., “Ultra-dense optical data transmission over standard fiber with a single chip source”, Nature Communications, vol. 11, Article:2568, 2020.
  114. X. Xu et al, “Photonic perceptron based on a Kerr microcomb for scalable high speed optical neural networks”, Laser and Photonics Reviews, vol. 14, no. 8, 2000070 (2020). DOI: 10.1002/lpor.202000070. [CrossRef]
  115. Xingyuan Xu, Weiwei Han, Mengxi Tan, Yang Sun, Yang Li, Jiayang Wu, Roberto Morandotti, Arnan Mitchell, Kun Xu, and David J. Moss, “Neuromorphic computing based on wavelength-division multiplexing”, IEEE Journal of Selected Topics in Quantum Electronics29 (2) 7400112 (2023). DOI:10.1109/JSTQE.2022.3203159. [CrossRef]
  116. Yunping Bai, Xingyuan Xu,1, Mengxi Tan, Yang Sun, Yang Li, Jiayang Wu, Roberto Morandotti, Arnan Mitchell, Kun Xu, and David J. Moss, “Photonic multiplexing techniques for neuromorphic computing”, Nanophotonics vol. 12 (5): 795–817 (2023). DOI:10.1515/nanoph-2022-0485. [CrossRef]
  117. Chawaphon Prayoonyong, Andreas Boes, Xingyuan Xu, Mengxi Tan, Sai T. Chu, Brent E. Little, Roberto Morandotti, Arnan Mitchell, David J. Moss, and Bill Corcoran, “Frequency comb distillation for optical superchannel transmission”, Journal of Lightwave Technology vol. 39 (23) 7383-7392 (2021). DOI: 10.1109/JLT.2021.3116614. [CrossRef]
  118. Mengxi Tan, Xingyuan Xu, Jiayang Wu, Bill Corcoran, Andreas Boes, Thach G. Nguyen, Sai T. Chu, Brent E. Little, Roberto Morandotti, Arnan Mitchell, and David J. Moss, “Integral order photonic RF signal processors based on a soliton crystal micro-comb source”, IOP Journal of Optics vol. 23 (11) 125701 (2021). https://doi.org/10.1088/2040-8986/ac2eab. [CrossRef]
  119. Yang Sun, Jiayang Wu, Yang Li, Xingyuan Xu, Guanghui Ren, Mengxi Tan, Sai Tak Chu, Brent E. Little, Roberto Morandotti, Arnan Mitchell, and David J. Moss, “Optimizing the performance of microcomb based microwave photonic transversal signal processors”, Journal of Lightwave Technology vol. 41 (23) pp 7223-7237 (2023). DOI: 10.1109/JLT.2023.3314526. [CrossRef]
  120. Mengxi Tan, Xingyuan Xu, Andreas Boes, Bill Corcoran, Thach G. Nguyen, Sai T. Chu, Brent E. Little, Roberto Morandotti, Jiayang Wu, Arnan Mitchell, and David J. Moss, “Photonic signal processor for real-time video image processing based on a Kerr microcomb”, Communications Engineering vol. 2 94 (2023). DOI:10.1038/s44172-023-00135-7. [CrossRef]
  121. Mengxi Tan, Xingyuan Xu, Jiayang Wu, Roberto Morandotti, Arnan Mitchell, and David J. Moss, “Photonic RF and microwave filters based on 49GHz and 200GHz Kerr microcombs”, Optics Communications, vol. 465, Article: 125563 (2020). doi:10.1016/j.optcom.2020.125563. doi.org/10.1063/1.5136270. [CrossRef]
  122. Yang Sun, Jiayang Wu, Yang Li, Mengxi Tan, Xingyuan Xu, Sai Chu, Brent Little, Roberto Morandotti, Arnan Mitchell, and David J. Moss, “Quantifying the Accuracy of Microcomb-based Photonic RF Transversal Signal Processors”, IEEE Journal of Selected Topics in Quantum Electronics vol. 29 no. 6, pp. 1-17, Art no. 7500317 (2023). 10.1109/JSTQE.2023.3266276. [CrossRef]
  123. Yang Li, Yang Sun, Jiayang Wu, Guanghui Ren, Bill Corcoran, Xingyuan Xu, Sai T. Chu, Brent. E. Little, Roberto Morandotti, Arnan Mitchell, and David J. Moss, “Processing accuracy of microcomb-based microwave photonic signal processors for different input signal waveforms”, MDPI Photonics 10, 10111283 (2023). DOI:10.3390/photonics10111283. [CrossRef]
  124. Yang Sun, Jiayang Wu, Yang Li, and David J. Moss, “Comparison of microcomb-based RF photonic transversal signal processors implemented with discrete components versus integrated chips”, MDPI Micromachines 14, 1794 (2023). https://doi.org/10.3390/mi14091794. [CrossRef]
Preprints 120045 g001
Figure 1. The dispersion measurement setup and the results of 100 GHz MRR. TLS: tunable laser source; OC: optical coupler; FPC: fiber polarization controller; MZI: Mach-Zehnder interferometer; HCN: H13C14N calibration cell; PD: photodetector; OSC: oscilloscope. (a) The dispersion measurement setup; (b) The integrated dispersion of sample 1 with TM mode; (c) The integrated dispersion of sample 2 with TE mode.
Figure 1. The dispersion measurement setup and the results of 100 GHz MRR. TLS: tunable laser source; OC: optical coupler; FPC: fiber polarization controller; MZI: Mach-Zehnder interferometer; HCN: H13C14N calibration cell; PD: photodetector; OSC: oscilloscope. (a) The dispersion measurement setup; (b) The integrated dispersion of sample 1 with TM mode; (c) The integrated dispersion of sample 2 with TE mode.
Preprints 120045 g001
Preprints 120045 g002
Figure 2. The generation setup and results of ‘Palm-like’ SC. EDFA: Erbium-doped fiber amplifier; TEC: thermo-electric cooler; OSA: optical spectrum analyzer; PC: personal computer. (a) The ‘Palm-like’ SC generation setup; (b) The ‘Palm-like’ SC generation and simulation results of sample 1; (c) The ‘Palm-like’ SC generation and simulation results of sample 2.
Figure 2. The generation setup and results of ‘Palm-like’ SC. EDFA: Erbium-doped fiber amplifier; TEC: thermo-electric cooler; OSA: optical spectrum analyzer; PC: personal computer. (a) The ‘Palm-like’ SC generation setup; (b) The ‘Palm-like’ SC generation and simulation results of sample 1; (c) The ‘Palm-like’ SC generation and simulation results of sample 2.
Preprints 120045 g002
Preprints 120045 g003
Figure 3. The repeatable turnkey ‘Palm-like’ SC generation. (a) The spectra evolution of 100 times deterministic turnkey ‘Palm-like’ SC generation of sample 1; (b) The power variation of 100 times for sample 1; (c) The spectra evolution of 100 times deterministic turnkey ‘Palm-like’ SC generation of sample 2; (d) The power variation of 100 times for sample 2.
Figure 3. The repeatable turnkey ‘Palm-like’ SC generation. (a) The spectra evolution of 100 times deterministic turnkey ‘Palm-like’ SC generation of sample 1; (b) The power variation of 100 times for sample 1; (c) The spectra evolution of 100 times deterministic turnkey ‘Palm-like’ SC generation of sample 2; (d) The power variation of 100 times for sample 2.
Preprints 120045 g003
Preprints 120045 g004
Figure 4. The long-term stability of SC. (a) The temporal evolution of the SC optical spectrum; (b) The power variation of the spectra within 4 hours.
Figure 4. The long-term stability of SC. (a) The temporal evolution of the SC optical spectrum; (b) The power variation of the spectra within 4 hours.
Preprints 120045 g004
Preprints 120045 g005aPreprints 120045 g005b
Figure 5. The repeatable turnkey ‘Palm-like’ SC generation with different temperatures. (a) The AMX measurement results with the temperature from 20 ◦C to 45 ◦C; (b) The generated SCs spectrum under different temperatures; (c) Power variation of the 100-cycle deterministic turnkey generation of ‘Palm-like’ SCs under 20 ◦C, 25 ◦C, 30 ◦C, 35 ◦C, 40 ◦C and 45 ◦C.
Figure 5. The repeatable turnkey ‘Palm-like’ SC generation with different temperatures. (a) The AMX measurement results with the temperature from 20 ◦C to 45 ◦C; (b) The generated SCs spectrum under different temperatures; (c) Power variation of the 100-cycle deterministic turnkey generation of ‘Palm-like’ SCs under 20 ◦C, 25 ◦C, 30 ◦C, 35 ◦C, 40 ◦C and 45 ◦C.
Preprints 120045 g005aPreprints 120045 g005b
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated