Reinforcement Learning Model-Based and Model-Free Paradigms for Optimal Control Problems in Power Systems: Comprehensive Review and Future Directions

Preprint

Review

Reinforcement Learning Model-Based and Model-Free Paradigms for Optimal Control Problems in Power Systems: Comprehensive Review and Future Directions

Altmetrics

Downloads

105

Views

Comments

A peer-reviewed article of this preprint also exists.

Submitted:

01 October 2024

Posted:

04 October 2024

You are already at the latest version

Alerts

Abstract

This paper reviews recent works related to applications of reinforcement learning in power system optimal control problems. Based on an extensive analysis of works in the recent literature, we attempt to better understand what is the gap between reinforcement learning methods that rely on complete or incomplete information about the model dynamics, and data-driven reinforcement learning approaches. More specifically we ask how such models change based on the application or the algorithm, what are the currently open theoretical and numerical challenges in each of the leading applications, and which reinforcement-based control strategies will rise in the following years. The reviewed research works are divided to ``model-based'' methods and ``model-free'' methods, in order to highlight the current developments and trends within each of these two groups. The optimal control problems reviewed are energy markets, grid stability and control, energy management in buildings, electrical vehicles and energy storage.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

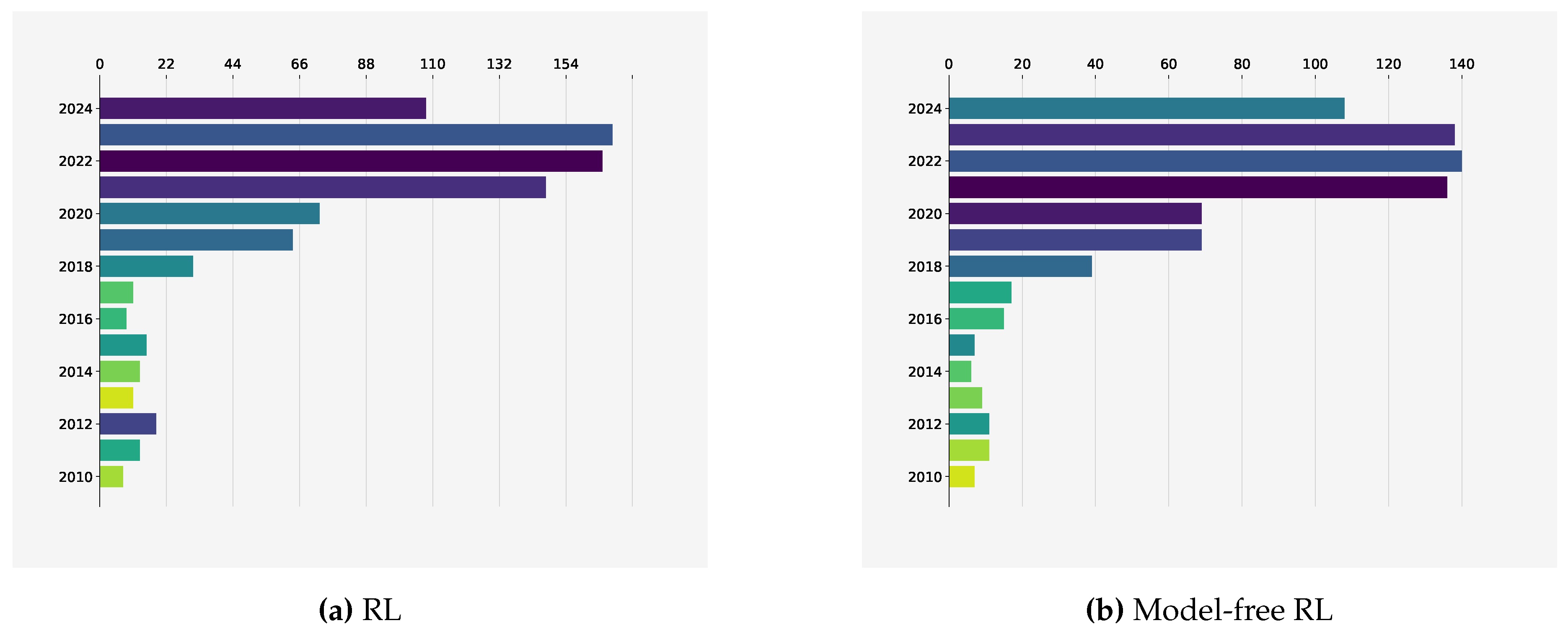
1. Introduction

Nowadays, power systems and energy markets experience rapid growth. As the population grows and economies develop, the demand for electricity rises. This necessitates larger and more intricate power systems to meet a larger demand of energy [1,2,3]. Moreover, as technological developments march forward, modern power systems incorporate a wider variety of energy sources, including renewables like solar and wind power, alongside traditional sources such as coal and natural gas. Managing this diverse mix requires complex infrastructure and control systems. Not only that, but the emergence of renewable energy sources complicates the grid topology in more than one way; it also stimulates the integration of energy storage devices, such as batteries into power grids. While beneficial for balancing supply and demand and integrating renewables, this introduces new challenges related to managing and optimizing storage assets within the system. Some of these considerations are presented in [4,5]. Additional complexity induced by renewable energy sources is caused by the trend towards decentralization in power generation, with emphasis on distributed energy resources (DERs) like rooftop solar panels and small-scale wind turbines. Integrating these decentralized sources into the grid complicates its behavior and dynamics, as discussed in [6,7,8].

On top of that, outdated infrastructure in many countries requires upgrades to improve reliability, efficiency, and resilience. This often involves the implementation of advanced technologies such as smart grids, which introduce additional complication, as one can examine in the following works [9,10]. In the light of these advances, there is an increase in cyber-security threats, which create the need to deal with not only intricate and unpredictable, but sometimes even malicious surrounding. This necessitates using redundant components, or the development of cyber-security protocols to ensure systems robustness and resilience. All of which contribute to system complexity [11,12,13]. Finally, regulatory frameworks governing the power sector are becoming more strict, requiring utilities to meet various standards related to environmental impact, reliability, and safety, such as addressed in [14,15]. Compliance with these regulations often involves implementing complex technologies and processes.

Overall, the combination of technological advancements, changing energy landscapes, regulatory demands, and the need for greater resiliency, is driving the increased complexity of power systems in the modern era. The preceding factors are enough to conclude that in today’s world, well-known and widely studied control problems in power systems, such as grid stability control or storage energy management, escalate into large-scale problems with extremely high dimensions. The computational burden and intricate dynamics of nowadays power systems establish the need for more advanced, and efficient algorithms to solve different control problems in this domain. To address these challenges, power experts are motivated to leverage various machine learning models, that exhibit remarkable performance in a variety of different domains, to aid in the assessment and control of these intricate systems. Specifically, one major study of interest is the field of reinforcement learning, which is mainly used for control problems that involve a continuous decision-making process. Several other works in recent literature review different applications in power systems, and present multiple reinforcement learning techniques for solving them, including [16,17,18,19].

Nonetheless, bearing in mind the aforementioned aspects, this paper presents a comprehensive review of the state-of-the-art reinforcement learning techniques used for optimal control problems in power systems. While similar works already exist, we focus here specifically on the comparison between model-based and model-free configurations, introducing recent challenges and trends. Thus, in this work, we systematically review the latest model-based and model-free reinforcement learning models and their application for control problems in power systems. In the model-based configuration, agents learn the probability distribution from which the transition function and reward are generated. On the contrary, in model-free configurations, the agent follows the optimal strategy, which maximizes the cumulative reward, without explicitly learning the mapping of the transition function and reward function. We strive to gain a deeper understanding of how well both of these methods perform under different environments, and also aim to fundamentally understand what properties of the state and action space affect the learning process. Furthermore, we aim to assess the implications of deterministic and stochastic policy definitions. Finally, our most basic question is to conclude whether there are types of control problem settings where the model-based method outperforms the model-free one, or visa-versa. In this light, we also attempt to emphasize current trends, highlight intriguing theoretical and practical open challenges that arise in this domain, and suggest exciting future research directions.

The paper is organized as follows: Section 2 sets a framework of fundamental reinforcement learning terminology and how it is used in power systems, and presents an overview of core algorithms that are used for various control applications. In addition, the terms model-free and model-based are defined. Section 3 concerns with model-based paradigm of reinforcement learning applied in various control problems in power systems, and reviews recent work in five main control applications that include energy market management, power grid stability and control, building energy management, electrical vehicles control problems and energy storage control problems. The section ends with a discussion of notable trends. Section 4 is structured similarly to the previous one, only it focuses on model-free paradigm in reinforcement learning. Next, Section 6 lists the latest open challenges that are yet to be solved for leveraging reinforcement learning approaches to address optimal control in power systems, highlighting specific considerations for model-based and model-free paradigms, and suggests future research ideas. Consequently, Section 7 concludes the article.

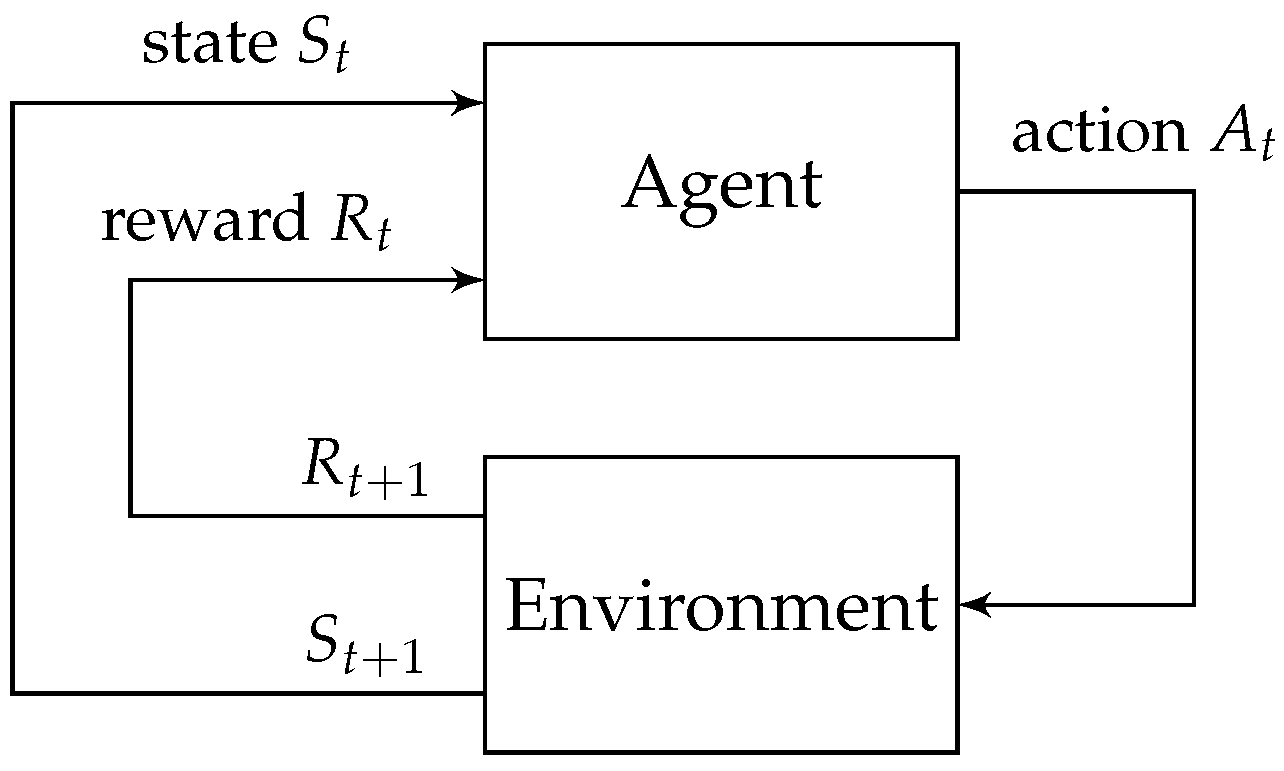
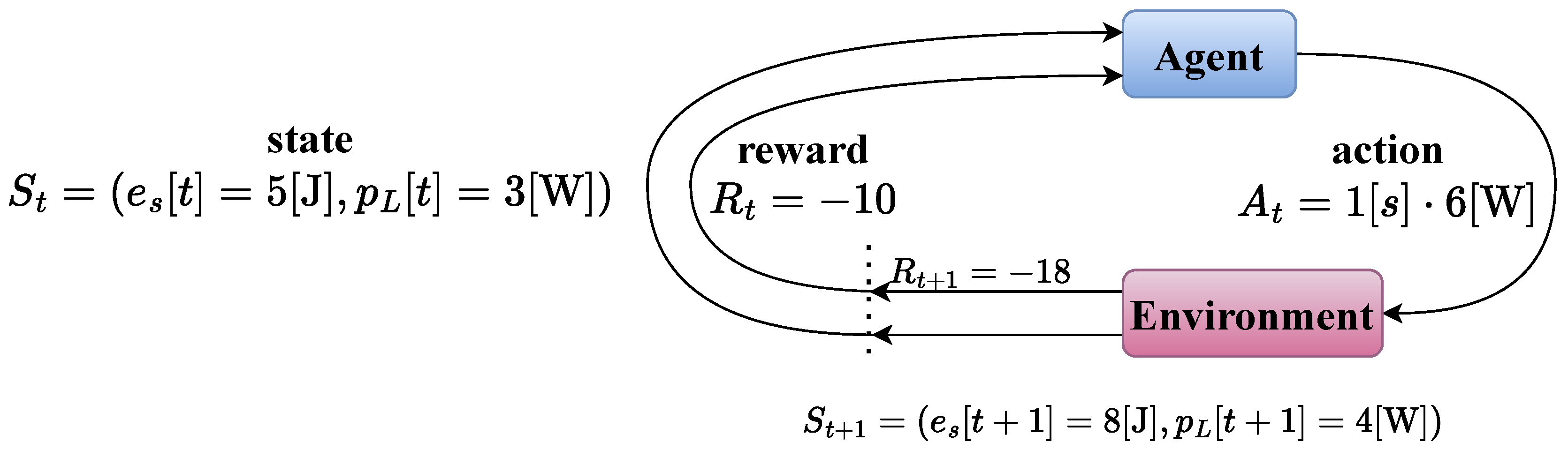
2. Technical Background on Reinforcement Learning

2.1. Markov Decision Processes

Reinforcement learning (RL) provides a framework for analyzing sequential-decision making problems, where the focus is on learning from interaction to achieve a goal [20,21,22,23]. In this context, the entity that learns and performs the decision-making is called an “agent”, while the element it interacts with is called the “environment”. This process is depicted in Figure 1.

This type of tasks are assumed satisfy Markovian properties, and thus in most scenarios, the reinforcement learning problem is formulated as a Markov Decision Process (MDP). To formally define a reinforcement learning problem as an MDP, we must specify each element of the following tuple

〈 S, A, R, P 〉

, where

S

defines the state-space of the environment,

A

induces the action space of the agent,

R

is the set of all possible numeric rewards the agent may receive, and

P

represents the distribution probability of the states, that is, given a state s and action a, the probability to transfer to a new state

s^{'}

and achieve a reward r is given by

P (s^{'}, r ∣ s, a) = \Pr {S_{t + 1} = s^{'}, R_{t + 1} = r ∣ S_{t} = s, A_{t} = a} .

(1)

The flow of the process is as follows: The agent continually interacts with the environment by choosing actions, while the environment responds to those actions by presenting the agent new situations and by giving him rewards. More specifically, at each discrete time step

t = 0, 1, 2, \dots

, the agent receives some representation of the environments state

S_{t} \in S

, where

S

is the set of possible states, and relying on that information, the agent chooses an action

A_{t} \in A (S_{t})

, where

A (S_{t})

is the set of actions available in state

S_{t}

. In the next time step, in part influenced by its actions, the agent receives a numerical reward

R_{t + 1} \in R \subset R

, and observes a new state of the environment

S_{t + 1}

At each time step, the agent implements a mapping from states to probabilities of choosing each possible action. This mapping is called the agent’s policy, and it is denoted by

π

, where

π (a ∣ s)

is the probability that

A_{t} = a

S_{t} = s

. Reinforcement learning methods outline how an agent adapts its policy based on its experiences, as the agent’s primary objective, is to maximize the cumulative reward it receives over time.

To demonstrate how reinforcement learning is adopted in a power systems optimal control framework, let us examine a system consisting of a single controllable generator, single storage device and a load as depicted in Figure 2. In such a system it is necessary to decide at every moment in time how much energy should be generated, and how much energy should be stored. The best combination is found by solving an optimization problem, in which the objective is to minimize the overall cost. To simplify the analysis it is assumed that the load profile can be estimated with reasonable accuracy, meaning that the power

p_{L} (\cdot) \in R_{\geq 0}

consumed over the time interval

[0, T]

is known. The generator has an output power

p_{g} (\cdot) \in R_{\geq 0}

that can be controlled, and is characterized by a cost function

F (p_{g})

. It is assumed that

p_{g} (t) = p_{s} (t) + p_{L} (t)

, where

p_{s} (\cdot)

is the power that flows into the storage. Now, formulating this problem as an MDP, we represent the generator’s controller as the agent, and the storage as the environment. The agent is defined by its action-space

A

, which represents all the possible values that the generator can produce. The environment is represented by its state-space and rewards, where the state-space denotes all the possible states of charge of the storage, while the instantaneous rewards are

R_{t} = - F (p_{g} (t))

. The agent’s objective is to find a policy

π

, which determines what action to take at each state, meaning, how much to power generate according to the storage’s state of charge, to maximize the cumulative reward

\sum_{t = 0}^{T} R_{t} = \sum_{t = 0}^{T} - F (p_{g} (t))

Consider a numerical example, where

F (p_{g}) = p_{g}^{2} / 2

, and the storage capacity is

e_{max} = 10 [J]

. The current state is

S_{t} = (e_{s} [t] = 5 [J], p_{L} [t] = 3 [W])

, where

e_{s} [t]

is the state of charge of the storage at time step t, and

p_{L} [t]

is the power demand of the load at time step t; the previous reward was

R_{t} = - 10

. The agent decides to produce

p_{g} (t) = 1 [s] \cdot 6 [W]

where

1 [s]

is the time resolution we sample in. As a result, assuming deterministic setting, the load demand is satisfied, and the rest flows into the storage, meaning the new energy value that is stored now, is

e_{s} [t + 1] = 8 [J]

and the resulting next state is

S_{t + 1} = (e_{s} [t + 1] = 8 [J], p_{L} [t + 1] = 4 [W])

, where

p_{L} [t + 1] = 4 [W]

is the load power demand at the next time step. The resulting reward is calculated by

R_{t + 1} = - 0.5 \cdot {(6)}^{2} = 18

. The sequential decision-making process is described in Figure 3. Table 1 presents some additional examples for optimal control problems in power systems, and their adequate MDP formulation.

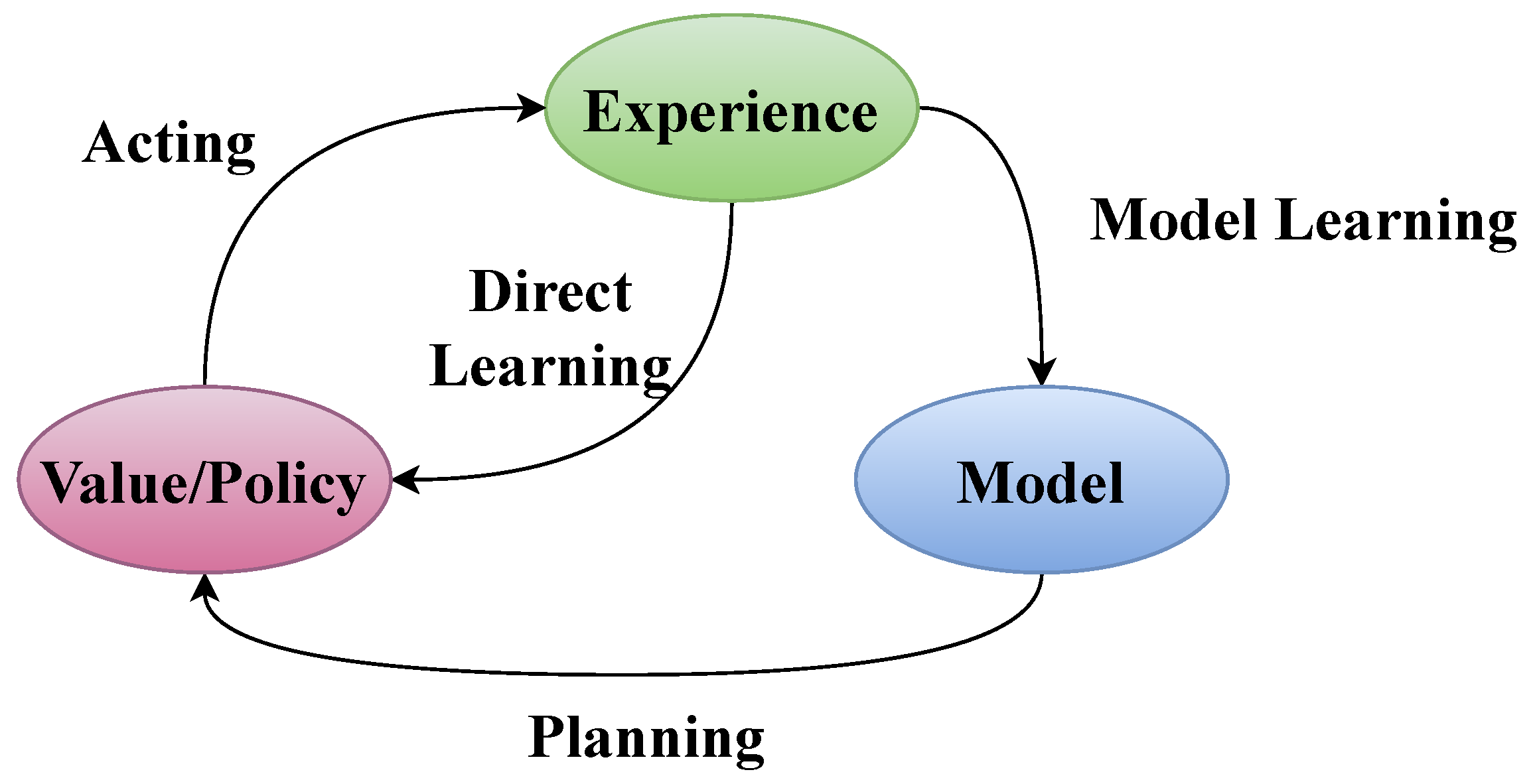
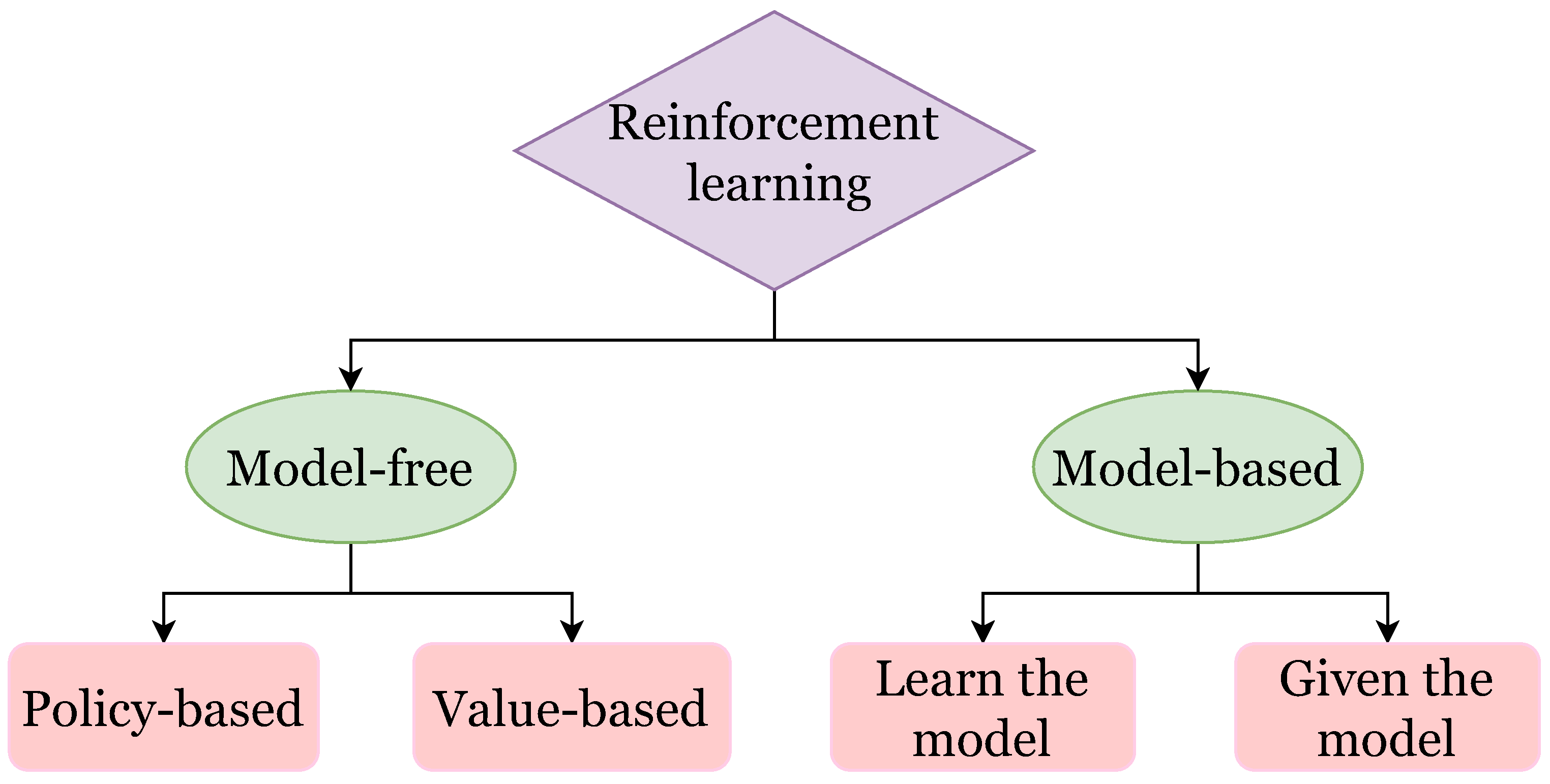
2.2. Model Based and Model Free Reinforcement Learning

In reinforcement learning, the key distinction between model-based and model-free paradigms lies in how they learn and plan. Model-based methods involve learning a model of the environment’s dynamics, including transition probabilities and rewards, which is then used for planning and decision-making. In contrast, model-free approaches directly learn a policy or value function from experience without explicitly modeling the environment. They rely solely on observed interactions with the environment to optimize the policy, without requiring knowledge of its underlying dynamics. Nonetheless, these two paradigms are in no sense two contradicting approaches, but rather these two configurations are the edges of a full spectrum of solutions, such that each algorithm on the spectrum combines different traits from each of them. For more perspectives on the topic one may look at the following works [24,25,26]. While model-based methods may potentially leverage a learned model for more efficient planning, model-free methods often offer greater simplicity and flexibility, especially in complex or uncertain environments where it is hard to learn an accurate model. Figure 4 presents the inherent difference between both methods. Furthermore, a graphical summary of the different approaches to each paradigm is given in Figure 5.

2.3. Model Computation

In this section, we present analytical algorithms from control theory that may be used to solve analytically the model of the environment, and then use planning approaches to find the optimal policy.

2.3.1. Dynamic Programming

Dynamic programming is an optimization technique that tackles complex problems by breaking them down into smaller, manageable sub-problems, through a multi-stage decision process [27,28]. Unlike many other optimization methods, dynamic programming algorithms explore all possible solutions to find the globally optimal one. Given the impracticality of directly scanning the entire solution space, these algorithms solve the problem step-by-step using a recursive formula. They are versatile, applicable to both linear and nonlinear objective functions and constraints, whether convex or non-convex. If a globally optimal solution exists, dynamic programming guarantees convergence. However, dynamic programming is constrained by several factors. It relies on a recursive formulation of the cost function, necessitating knowledge of all past and future signals, which can be unrealistic in practice. Moreover, it suffers from the “curse of dimensionality” [29]. Specifically, in power systems control problems like those involving energy storage, the method’s complexity increases linearly with the number of time samples but exponentially with the number of storage devices and the number of state variables describing each device. To demonstrate a basic dynamic-programming solution, recall the energy balancing problem Figure 3. We will base our example on [30]. We denote the discrete time steps by

k = 0, \dots, T

, where T is given and known. We may denote the power generated at a discrete time step k as

p^{(k)} \in R

, of which a portion

d^{(k)} \in R

is fed to the grid to meet the load demand. Let us assume that the values of

d^{(k)}

are given and known. The part that remains, denoted by

u^{(k)} \in R

is stored in the storage device, meaning

p^{(k)} = u^{(k)} + d^{(k)}

. The energy of the storage at each time step k is denoted by

e^{(k)}

and is bounded by the storage energy capacity

e_{max}

. The cost of the production is given by

f (u^{(k)} + d^{(k)})

, thus, the total cumulative cost that we aim to minimize is given by:

F_{tot} (u^{(k)}, d^{(k)}) = Δ \sum_{k} f (u^{(k)} + d^{(k)}),

(2)

where

Δ

is the time resolution. The arising optimization problem is:

\begin{matrix} \underset{{u^{(k)}}}{minimize} & Δ \sum_{k = 1}^{N} f (u^{(k)} + d^{(k)}), \\ s . t . & u^{(k)} = \frac{e^{(k)} - e^{(k - 1)}}{Δ \cdot η (e^{(k)})}, for k = 1, \dots, N \\ 0 \leq e^{(k)} \leq e_{max}, for k = 1, \dots, N \\ e_{0} = 0 . \end{matrix}

(3)

Now, let us define an auxiliary cost function as

V_{k} = Δ \sum_{k = 1}^{k} f (u^{(k)} + d^{(k)}),

(4)

with

V_{0} = 0

. In this light, for

k = 1

we have

V_{1} (e^{(1)}) = Δ \cdot f (u^{(1)} + d^{(1)}),

(5)

where

u^{(1)} = e^{(1)} / (Δ \cdot η (e^{(1)}))

, and

0 \leq e^{(1)} \leq e_{max}

For

k = 2, \dots, N

V_{k} (e_{(k)}) = min_{0 \leq e_{(k - 1)} \leq e_{max}} \{V_{k - 1} (e_{(k - 1)}) + Δ \cdot f (u^{(k)} + d^{(k)})\},

(6)

where

u^{(k)} = (e^{(k)} - e^{(k - 1)}) / (Δ \cdot η (e^{(k)}))

, and

0 \leq e^{(k)} \leq e_{max}

. Now we can compute the optimal energies

{(e^{(N)})}^{*} = \underset{0 \leq e^{(N)} \leq e_{max}}{arg min} \{V_{N} (e^{(N)})\}

(7)

and for each

k = 2, \dots, N

{(e^{(k - 1)})}^{*} = \underset{0 \leq e_{(k - 1)} \leq e_{max}}{arg min} \{V_{k - 1} (e^{(k - 1)}) + Δ \cdot f (u^{(k)} + d^{(k)})\}

(8)

with

u^{(k)} = ({(e^{(k - 1)})}^{*} - e^{(k - 1)}) / (Δ \cdot η ({(e^{(k)})}^{*}))

. Finally, we have that

{(e^{(0)})}^{*} = 0

The optimal powers are:

{(u^{(k)})}^{*} = \frac{{(e^{(k)})}^{*} - {(e^{(k - 1)})}^{*}}{Δ \cdot η ({(e^{(k)})}^{*})}

(9)

for

k = 1, \dots, N

2.3.2. Model Predictive Control (MPC)

Model Predictive Control (MPC) is a control strategy used in engineering and control theory to optimize the performance of dynamic systems subject to constraints. It involves repeatedly solving an optimization problem over a finite time horizon, using a model of the system dynamics to predict future behavior and adjust control inputs accordingly. By iteratively updating the control actions, MPC aims to minimize a cost function while satisfying system constraints, thus achieving desired performance objectives as explained in [31,32,33]. The system’s model in concern is presented as

x_{k + 1} = f (x_{k}, u_{k}),

(10)

where

x_{k}

represents the state of the system at time step k, and

u_{k}

is the control input at time step k, and f is the system dynamics function describing how the state evolves over time. The cost function is given by

J = \sum_{0}^{N - 1} L (x_{k}, u_{k}) + M (x_{N}),

(11)

where L is the stage cost function penalizing deviations of state and control from desired values at each time step, M is the terminal cost function penalizing the final state, and N is the prediction horizon.

The system is assumed to operate under constraints of the following form

\begin{matrix} g (x_{k}, u_{k}) \leq 0 \forall k, \\ h (x_{k}, u_{k}) = 0 \forall k, \end{matrix}

(12)

where g and h are inequality and equality constraint functions, respectively, representing limits on the state and control inputs over the prediction horizon. Concluding, the optimization problem may be formulated as

\begin{matrix} min_{U} & J, \\ s . t . & x_{k + 1} = f (x_{k}, u_{k}), \\ g (x_{k}, u_{k}) \leq 0 \forall k, \\ h (x_{k}, u_{k} = 0 \forall k, \\ x_{0} = x_{i n i t} . \end{matrix}

(13)

Here,

U = [u_{0}, u_{1}, \dots, u_{N - 1}]

represents the sequence of control inputs over the prediction horizon N, and the optimization problem is solved at each time step to determine the optimal control sequence

U^{*}

that minimizes the cost function while satisfying system dynamics and constraints. The first element of the optimal control sequence,

u_{0}^{*}

, is applied to the system, and the optimization problem is solved again at the next time step, considering the updated state and constraints. This process repeats at each time step to achieve closed-loop control. There are some disadvantages to this method, some of them are the high computational cost and the requirement for an accurate system model.

2.4. Policy Learning Basic Concepts

In the following section, we discuss the two approaches of the model-free learning paradigm. First, we present the foundational concepts of many of the most common model-free algorithms which are based on policy iteration, such as Monte Carlo, Temporal Differences, and Q-learning. The main ideas are encapsulated in the “Value Function”, “Policy Iteration” and “Value Iteration”; for a deeper discussion one may refer to [20]. Finally, we will present a model-free algorithm that relies on policy optimization, this is the “Policy Gradient” basic algorithm.

2.4.1. Value Function

Almost all reinforcement learning algorithms involve estimating value functions (functions of states or of stateaction pairs) that is for the agent to be in a given state (or how good it is to perform a given estimate how good action in a given state). The notion of “how good” here is defined in terms of future rewards that can be expected, or, to be precise, in terms of expected return. The rewards the agent can expect to receive in the future depend on what actions it will take. Accordingly, value functions are defined with respect to particular policies. the value of a state s under a policy

π

, denoted by

v_{π} (s)

, is the expected return when starting in s and following

π

thereafter. For MDPs, we can define

v_{π} (s)

formally as

v_{π} (s) = E_{π} [G_{t} ∣ S_{t} = s] = E_{π} [\sum_{k = 0}^{\infty} γ^{k} R_{t + k + 1} ∣ S_{t} = s],

(14)

where

E_{π} [\cdot]

denotes the expected value of a random variable given that the agent follows policy

π

. We call the function

v_{π} (\cdot)

the state-value function for policy

π

. For all

s \in S

, the state-value function may be calculated recursively:

v_{π} (s) = \sum_{a} π (a ∣ s) \sum_{s^{'}, r} p (s^{'}, r ∣ s, a) [r + γ v_{π} (s^{'})],

(15)

where

π (a ∣ s)

is the probability of taking action a in state s under policy

π

, and the expectations are subscripted by

π

to indicate that they are conditional on

π

being followed. The existence and uniqueness of

v_{π}

are guaranteed as long as either

γ < 1

or eventual termination is guaranteed from all states under the policy

π

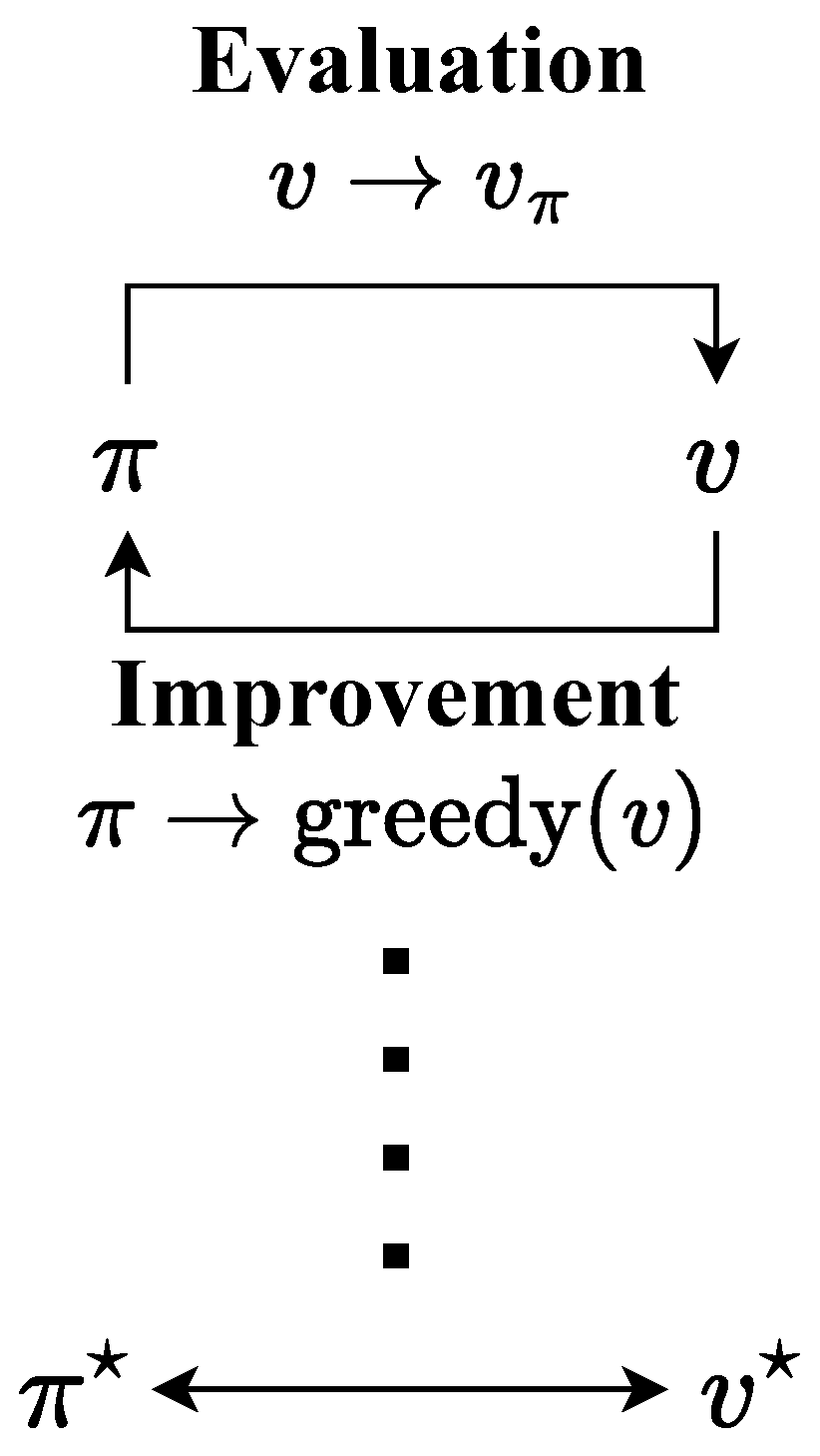
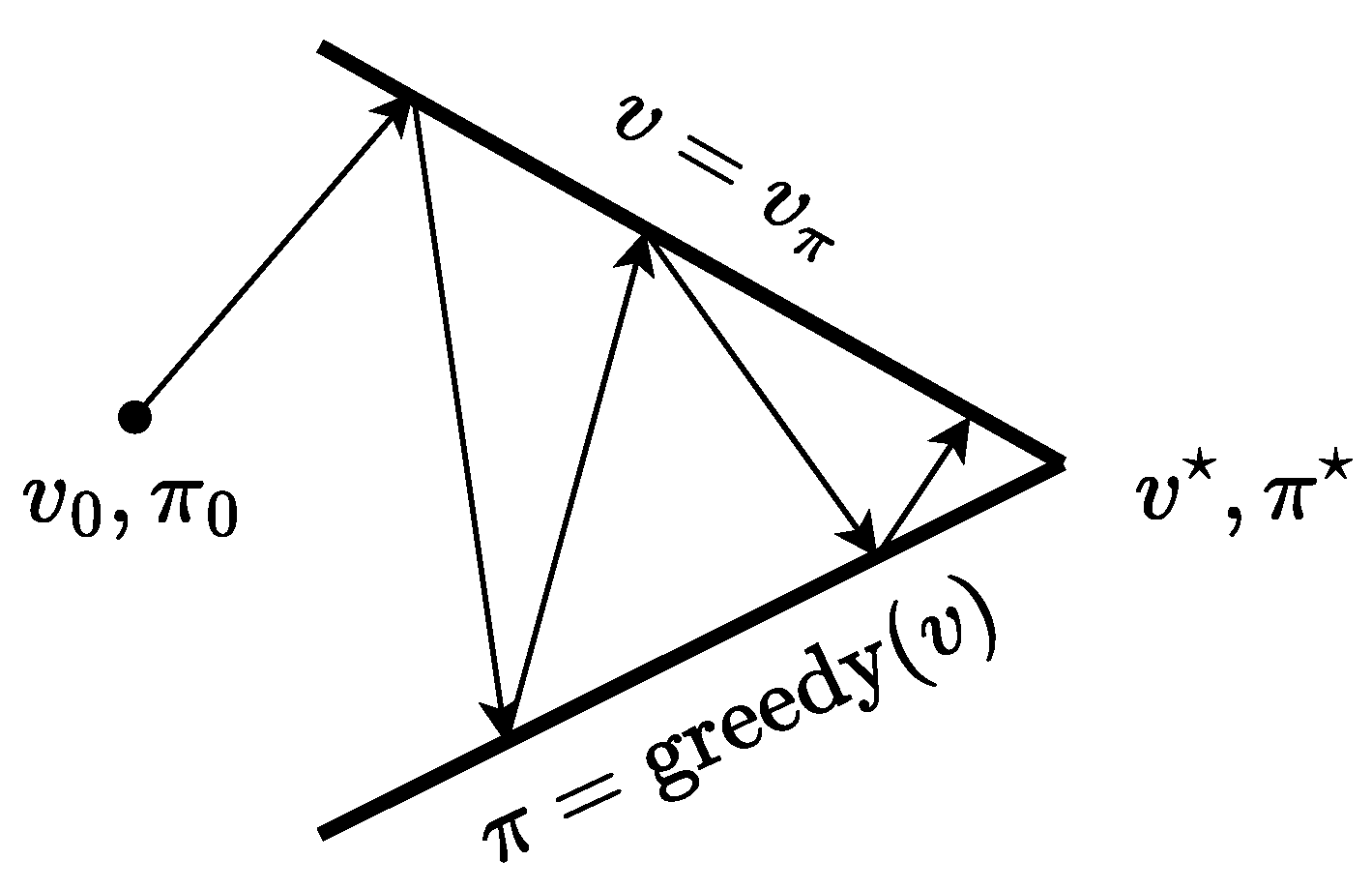
2.4.2. Policy Iteration

First, we consider how to compute the state-value function

v_{π}

for an arbitrary policy

π

. This process is called policy evaluation. The initial approximation value function,

v_{0}

, is chosen arbitrarily and each successive approximation is obtained by using the Bellman equation for

v_{π}

as an update rule:

v_{π} (s) = \sum_{a} π (a ∣ s) \sum_{s^{'}, r} p (s^{'}, r ∣ s, a) [r + γ v_{π} (s^{'})]

(16)

for all

s \in S

. It is clear that

v_{k} = v_{π}

. It can be shown that the sequence

{v_{k}}

converges to

v_{π}

k \to \infty

. This process is called iterative policy evaluation. We compute the value function for a policy to help discover improved policies. Consider we have determined the value function

v_{π}

for an arbitrary deterministic policy

π

. For some state s we would like to know whether or not we should change the policy to deterministically choose an action

a \neq π (s)

. We have an estimation of how good it is to follow the current policy from s, that is

v_{π} (s)

, but perhaps there is a better one. To answer this question, we can consider selecting an action a in s and following the existing policy

π

thereafter. The value of this behavior is given by the q-value function

q_{π} (s, a) = E_{π} [R_{t + 1} + γ v_{π} (S_{t + 1}) ∣ S_{t} = s, A_{t} = a] = \sum_{s^{'}, r} p (s^{'}, r ∣ s, a) [r + γ v_{π} (s^{'})] .

(17)

If this value is greater than

v_{π} (s)

, meaning it is better to select a in s and follow

π

thereafter than to follow

π

all the time, one would expect that it is better to select a every time s is encountered, which introduces a new policy. Fundamentally, if for all

s \in S

q_{π} (s, π^{'} (s) \geq v_{π} (s),

(18)

then it may be inferred that policy

π^{'}

is at least as good as policy

π

, meaning it must obtain at least the same expected return from all states

s \in S

v_{π^{'}} (s) \geq v_{π} (s) .

(19)

This result is addressed as the policy improvement theorem.

Following this procedure of continuous policy evaluation and improvement composes the “policy iteration” algorithm that is presented in Figure 6.

2.4.3. Value Iteration

The major drawback of policy iteration is that the policy evaluation stage may itself be a lengthy iterative process, that scans many states. Another formulation for the policy evaluation stage is given by

\begin{matrix} v_{k + 1} (s) & = max_{a} E [R_{t + 1} + γ v_{k} (S_{t + 1}) ∣ S_{t} = s, A_{t} = a] \\ = max_{a} \sum_{s^{'}, r} p (s^{'}, r ∣ s, a) [r + γ v_{k} (s^{'})], \end{matrix}

(20)

for all

s \in S

. The interaction between evaluation and improvement processes is presented in Figure 7. Here, each process drives the value function or policy toward one of the lines representing a solution to one of the two goals.

2.4.4. Policy Gradient

In reinforcement learning, policy gradient methods are algorithms designed to directly optimize the policy, represented as

π_{θ} (a | s)

, which defines a probability distribution over actions a given states s, as elaborated in [34]. The main goal of these methods is to maximize the expected return,

J (π_{θ}) = E_{τ \sim π_{θ}} [R (τ)]

, which is the cumulative reward an agent accumulates over time, where

R (τ)

represents the finite-horizon un-discounted return. To achieve this, policy gradient methods use a gradient ascent algorithm to evaluate the expected return, by adjusting the policy parameters

θ

in a way that gradually increases this expected return. By iteratively following the gradient of the expected return, the policy parameters are refined to enhance the agent’s performance. These methods are particularly effective for environments characterized by continuous action spaces, and also for learning stochastic policies that are crucial for managing uncertainty and exploration.

Directly optimizing the policy often results in more stable and efficient learning, making policy gradient methods powerful tools for tackling complex reinforcement learning challenges. In this context, there are two approaches, the “policy-based” and “value-based”. policy-based methods are a class of algorithms that directly optimize the policy

π_{θ} (a | s)

, where

θ

represents the parameters of the policy, s is the state, and a is the action. These methods differ from value-based methods, which focus on learning a value function and deriving the policy from it. Policy-based methods aim to directly find the optimal policy by maximizing the expected return and are the most commonly used approaches.

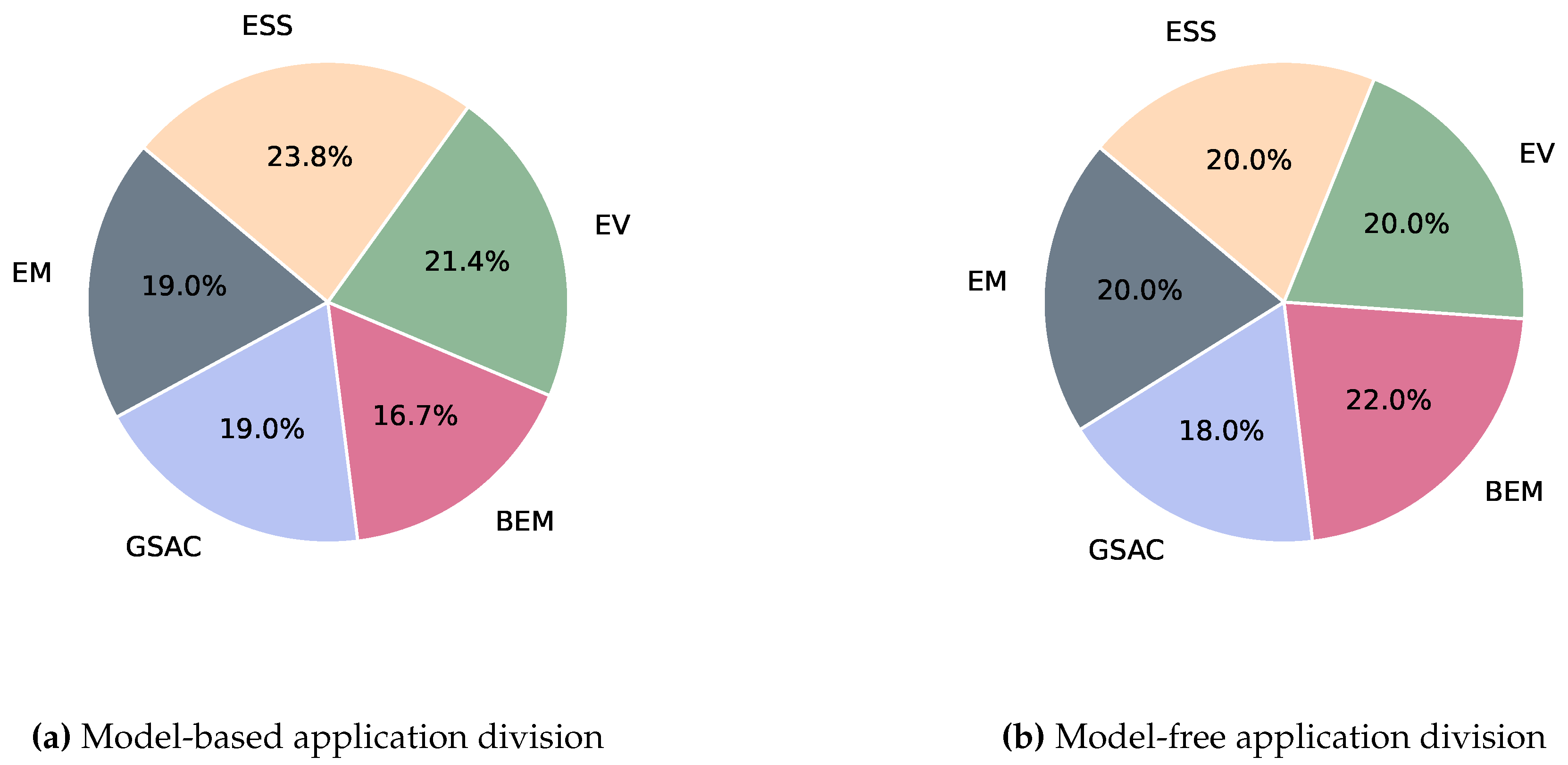
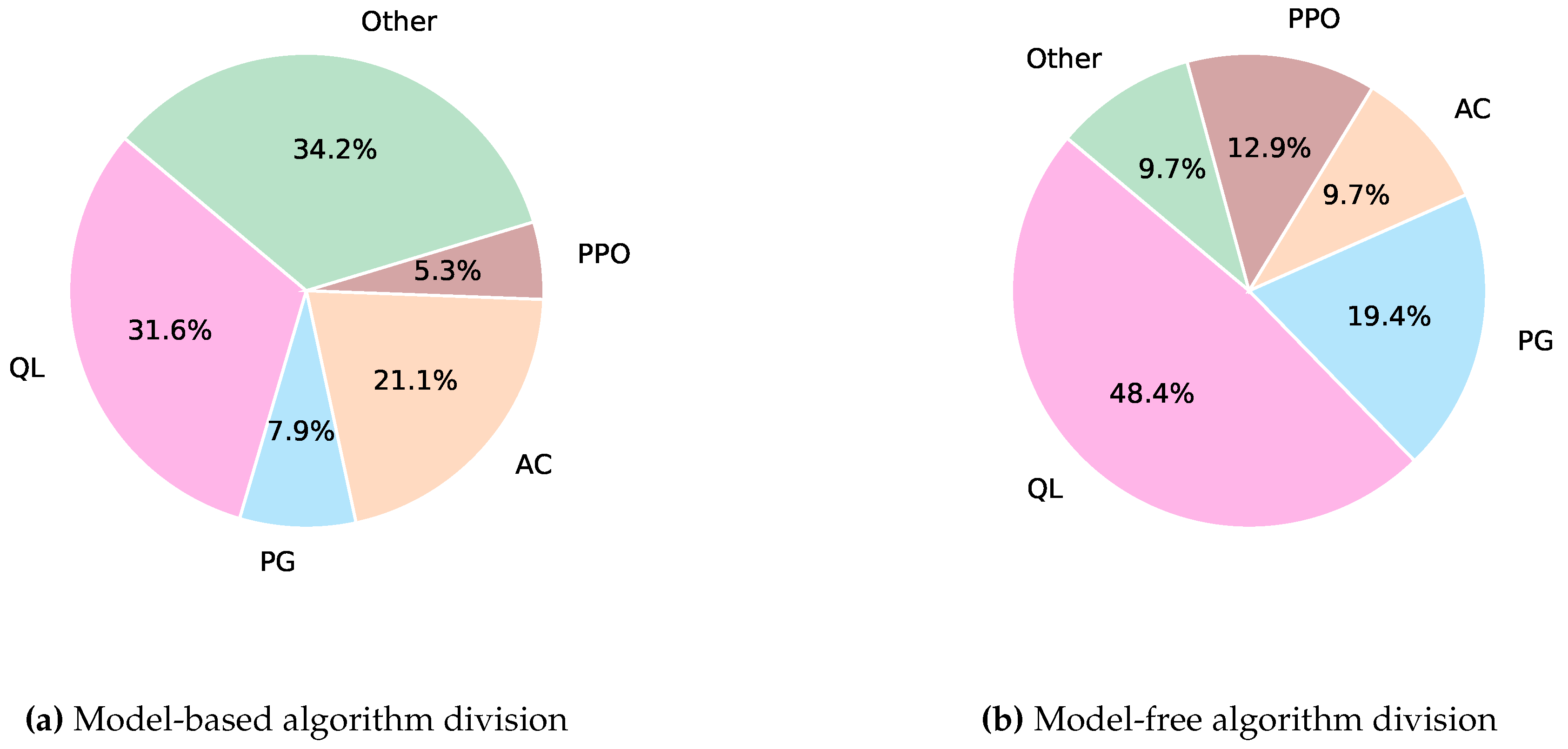
3. Model-Based Paradigm

From here forward, we review how these various concepts and methods are used in power system applications, starting with the important applications that arise in the context of energy markets.

3.1. Energy Markets Management

Reinforcement learning (RL) has become increasingly popular in analyzing energy markets, since it effectively addresses the complexity and unpredictability of its related tasks. RL’s strength lies in its ability to learn optimal strategies through interaction with the environment, enabling it to adapt to changing conditions and uncertainties like fluctuating demand, renewable energy variability, and volatile market prices. This adaptability makes RL particularly valuable in energy markets where dynamic decision-making is a key attribute. Within RL, model-based approaches offer greater sample efficiency by using predictive models of the environment, allowing for faster convergence, while model-free methods, though more flexible, require more interactions with the environment to learn optimal policies. This balance between efficiency and adaptability makes RL a powerful tool for managing the complexities of modern energy markets.

Among the many applications of RL in the energy market, energy bidding policies are a notable example, where model-based approaches have shown substantial improvements. For instance, in paper [35] the authors applied the MB-A3C algorithm to optimize wind energy bidding strategies, significantly enhancing profit margins in the face of market volatility. Similarly, RL has been applied to the optimization of energy bidding in general market-clearing processes, as seen in [36], where model-based RL approaches reduced training times and streamlined market-clearing decisions under regulatory frameworks. Peer-to-peer (P2P) energy trading is another field where RL excels, enabling efficient energy trades among prosumers. Model-based approaches, such as the MB-A3C3 model developed in [37], have optimized these trades by forecasting prices and energy availability, leading to significant cost reductions. Moreover, study [38] proposes a green power certificate trading (GC-TS) system for China, leveraging Q-learning, smart contracts, and a multi-agent Nash strategy to improve trading efficiency and collaboration. It integrates green certificate, electricity, and carbon markets, using a multi-agent reinforcement learning equilibrium model, resulting in increased trading prices and significantly improved transaction success rates. The proposed system outperforms similar models with higher convergence efficiency in trading quotes. Additionally, in [39] the authors focus on energy dispatch problem for wind-solar-thermal power system with non-convex models. The authors propose a combination of the federated reinforcement learning (FRL) with the model-based method. They use grid-connected renewable energy and thermal power at a bus are aggregated as a virtual power plant, in such manner, they ensure private operation with limited but effective information exchange. Numerical studies validate the effectiveness of the proposed framework for handling the short-time scale power sources operation with nonconvex constraints.

Examining paper [40], the authors use an average reward reinforcement learning (ARRL) model to optimize bidding strategies for power generators in an electricity market. They uses Constrained Markov Decision Process (CMDP) to simulate market conditions and update reinforcement values based on the rewards received from market interactions, and incorporate forecasts of system demand and prices as part of the state information used by the RL agent to make informed decisions. Furthermore, study [41] presents an energy management strategy for residential microgrids using a Model Predictive Control (MPC)-based Reinforcement Learning (RL) approach, and the Shapley-value method for fair cost distribution. The authors parameterize the MPC model to approximate the optimal policy, and used a Deterministic Policy Gradient (DPG) optimizer to adjust these parameters, effectively reducing the monthly collective cost by handling system uncertainties. The paper highlight the reduction of the monthly collective cost by about 17.5%, and provided a fair and equitable method for distributing the cost savings among the residents. Continue this line of thought, work [42] deals with energy management for residential aggregators, specifically in managing uncertainties related to renewable energy and load demand. They use a two-level Model Predictive Control (MPC) framework, integrated with Q-learning, to optimize day-ahead and real-time energy management decisions. The solution demonstrated improved performance in reducing operational costs and maintaining system stability while managing the energy needs of a residential community.

In conclusion, reinforcement learning has emerged as a powerful tool in analyzing problems that arise in energy markets, due to its ability to handle the complex and dynamic nature of real-time energy management. Its applications, such as optimizing energy bidding strategies and peer-to-peer trading, have demonstrated substantial improvements in efficiency and profitability, especially when model-based approaches are employed to enhance learning and decision-making. A summary of the studies reviewed is presented in Table 2.

3.2. Power Grid Stability and Control

Many studies cover various aspects of grid stability and control, based on advanced reinforcement learning techniques. Although data-driven techniques have been proven useful in many cases, there are a number of advantages to using model-based paradigms, or at least incorporating some domain knowledge in the learning process, especially in this application. The analysis of grid stability and control is divided into many sub-domains such as voltage control, frequency control, and reactive power control. Each of these has a specific and known structure of which the underlying physics may be rigorously modeled. This observation motivates many researchers to leverage this information, and guide the learning process to accelerate it and result in a more robust and resilient model, with increased generalization abilities. For instance, considering voltage control applications, study [49] focuses on examining load shedding control for large-scale grid emergency voltage control. The authors propose derivative-free deep reinforcement learning algorithm named PARS, that uses the domain knowledge for voltage control problems to handle computational inefficiency and poor scalability RL algorithms. The method was tested on both the IEEE 39-bus and IEEE 300-bus systems, and the latter is by far the largest scale for such a study. Test results show that, compared to other methods including model-predictive control (MPC) and proximal policy optimization (PPO) methods, PARS shows better computational efficiency (faster convergence), and was able to infer more complicated scenarios requiring higher abilities of generalization. Another example concerning this application may be seen in [50], which focuses on short-term voltage stability problem. In this paper, the authors propose a deep reinforcement learning framework, using deep neural network and dynamic surrogate model instead of a real-world power grid or physics-based simulation for the policy learning framework. However, to deal with the complex system dynamics of large-scale power systems, they incorporate imitation learning at the beginning of the training. The results show 97.5% reduction in samples, and 87.7% reduction in training time for an application to the IEEE 300-bus test system when compared to baseline PARS. From a slightly different perspective, work [51] examines the challenges of fast voltage fluctuations in an unbalanced distribution system. This work proposes a model-free approach that incorporates physical domain knowledge, ultimately guiding the training process, thus combining the model-based and model-free approaches. Specifically, they train a surrogate model in a supervised manner using recorded historical data to learn the interaction between power injections and voltage fluctuations of each node. Then, the deep reinforcement learning algorithm, based on actor-critic with slight modifications, is applied to learn an optimal control strategy from the experiences obtained by continuous interactions with the surrogate model. Simulation results on an unbalanced IEEE 123-bus system are presented and compared to other methods including double deep Q-learning, stochastic programming, MPC and deep deterministic policy gradient. On top of that, a different perspective on emergency voltage control is discussed in [52]. This article focuses on the new challenges that arise in off-line emergency control schemes in power systems, highlighting adaptiveness and robustness issues. The authors propose a deep reinforcement learning frameworks, utilizing a Q-learning algorithm, to deal with the growing complexity of the problem. They model the environment using prior domain knowledge from system theory, thus aiding the training process to converge faster, thus extending the models ability to generalize. Furthermore, in this work, an open-source platform named Reinforcement Learning for Grid Control (RLGC) is designed for the first time, to assist in the development and benchmarking of DRL algorithms for power system control, which is an important step toward a unified evaluation platform. The model was assessed for its robustness, using different scenarios, and various noise types in the observations. Finally, a few case studies are discussed, including a four-machine system and the IEEE 39-bus system.

A different application concerning grid stability and control is microgrid management. Microgrids can enhance grid stability, but can also introduce challenges in grid management. For instance, paper [53] considers a hybrid energy storage systems (HESS) control problem in ac-dc microgrids, with a photovoltaic energy production source and diesel generator. The low inertia inherent to the system may cause power quality disturbances if the charging and discharging process of the energy storage is unregulated. The authors propose reinforcement-learning-based online optimal (RL-OPT) control method, based on policy iteration, where the optimal control theory is applied to optimize the C&D profile and to suppress the disturbances caused by integrating HESS. Neural networks are devised to estimate the nonlinear dynamics of HESS based on the input/output measurements, and for learning the optimal control input for bidirectional-converter-interfaced HESS using the estimated system dynamics. The effectiveness of the method is evaluated through HIL experiments to assess performance on real hardware, where unpredicted challenges such as communication delay and measurement noises may appear. Continue this line of thinking, in another study presented in [54], the problem examined is the optimal control of off-grid microgrids, which rely mainly on renewable energy sources coupled with storage systems, to supply electrical consumption. The researchers propose a model-based reinforcement learning algorithm, utilizing a variation of PPO. The proposed algorithm is compared against a rule-based policy and a model predictive controller with look-ahead. The benchmark uses empirically measured data from small village in Bolivia, and emphasizes the improved performance this algorithm achieves over the other methods. Examining another aspect of grid stability and control, it is clear that optimal power flow planning plays a crucial role. In this application domain, various approaches were proposed. For instance, [55] analyzes a scenario with high-level penetration of intermittent renewable energy sources, which necessitates a rapid and economical respinse to the changes in power system operating state. This study suggests a real-time optimal power flow approach using Lagrangian-based deep reinforcement learning, leveraging deep deterministic policy gradient for policy optimization. The DRL action-value function is designed to simultaneously model RT-OPF objective and constraints. Instead of using the critic network, the deterministic gradient is derived analytically. The evaluation is performed on IEEE 118-bus system and compared with advanced methods such as interior-point method, DC optimal power flow and a supervised learning method. A different approach may be seen in [56], which addresses safety considerations in distribution network between interconnected microgrids, against false data injection. They propose a reinforcement learning framework with multi-objectives, using actor-critic algorithm, and incorporate various constraints based on a domain knowledge of the system into the training process, such as voltage and frequency stability considerations, and power flow limitations. Simulations on open-source data are presented. Finally, studies employing model-based RL approaches for grid stability and control applications demonstrate the potential of these methods to enhance the reliability and resilience of power systems. By modeling the complex dynamics of the grid and predicting the impact of various control actions, model-based RL enables precise regulation of voltage, frequency, and power flows. This results in improved fault tolerance and the ability to handle fluctuations from renewable energy sources more effectively. As the integration of distributed energy resources and smart grids becomes more prevalent, model-based RL will be essential for maintaining grid stability and ensuring the efficient operation of future power networks. A summary of the studies reviewd is presented in Table 3.

3.3. Building Energy Management

In this subsection, we review several recent studies from the literature that utilize model-based reinforcement learning to manage energy usage in buildings. Managing the electricity consumption in buildings is essential to reduce peak-demand, and may assist in maintain grid stability. Efficient power distribution and utilization by this type of consumers, especially when considering large-scale office buildings that sustain hundreds of offices, may substantially aid to renewable energy integration, and reduce carbon emissions. For example article [60] develops a method for using DRL for energy management of heating, ventilation, and air-conditioning (HVAC) optimal control. The proposed method is demonstrated in a case-study on a radiant heating system. The authors use a “EnergyPlus” simulator to create a model of the building, and soft actor critic is used to train a DRL agent to develop the optimal control policy for the system supply water temperature set-point. Following, a different study [61] focuses on utilizing a physics-based modeling method for building energy simulation, called “whole building energy model”, in HVAC optimal control problem. The authors use a deep deterministic policy gradient (DDPG) algorithm. By analyzing the real-life control deployment data, it is found that proposed method achieves 16.7% heating demand reduction with more than 95% probability compared to the old rule-based control. In a different approach, presented in [62], the authors implement a reinforcement learning algorithm for HVAC energy management. The model is trained offline over past data and simulated data by imitation-learning from a differential MPC model. Next, they use online transfer learning with real-time data to improve performance utilizing a PPO agent. Results show a reduction in the HVAC system energy consumption, yet maintaining a satisfactory human comfort on simulated data. Moreover, they show a reduction of about 16% in energy consumption when applying the proposed model to the aggregated real-world data. One analytic solution approach to optimal energy management in residential buildings is the MPC method, which incorporates prior knowledge about the systems dynamics to develop a control policy iteratively. Study [63] focuses on mitigating the large overhead required for applying MPC algorithm, by proposing an approximate model utilizing machine learning techniques. They propose an easy implementation scheme of advanced control strategies suitable for low-level hardware, by combining different multivariate regression, such as regression trees, and dimensionality reduction algorithms, such as PCA. The approach is demonstrated on a case study, in which the objective is to optimize temperature control in a six-zone building, modeled using a large state-space and various disturbance types. The results indicate a great reduction in both implementation costs and computational overhead, while preserving satisfactory performance. Taking this idea a step further, in [64] the authors introduce a combination between two control methods of reinforcement learning and MPC, called “RL-MPC”. The proposed algorithm can meet constraints and provide similar performance to MPC, while enabling continuous learning and the possibility to deal with highly uncertain environments that the standard MPC cannot handle. When tested on deterministic environment, the proposed algorithm achieves results as good as a regular MPC, and outperforms it in a stochastic environment. In another related work [65], a new deep learning-based constrained control method inspired by MPC is introduced, called “Differentiable Predictive Control” (DPC). The proposed algorithm begins with a system identification using a physics-constrained neural state space model. Next, a closed loop dynamics model is obtained. From these learned dynamics, the model can infer the optimal control law. The results show that the DPC overcomes the main limitation of imitation learning-based approaches with a lower computational overhead. Looking from a different perspective, work [66] addresses an optimal control of dispatch in building energy management, by coordinating the operation of distributed renewable energy resources to meet economic, reliability and environmental objectives in a building. The authors use a parameterized Q-learning algorithm to achieve the optimal control of dispatch policy of the various power sources. The agent interacts with the environment which is model by an MPC algorithm, that provides the transition dynamics. The efficiency and effectiveness of the policy are demonstrated through simulation.

To summarize, in the domain of energy management for buildings, model-based RL approaches offer several benefits by optimizing heating, cooling, lighting, and other energy-intensive processes. These methods utilize detailed models of building dynamics and environmental conditions to predict energy consumption patterns and adjust control strategies accordingly. By doing so, they can reduce energy costs, improve occupant comfort, and decrease the environmental footprint of buildings. The growing emphasis on sustainable architecture and smart buildings underscores the importance of model-based RL in advancing energy-efficient building management solutions. A summary of the studies reviewed is presented in Table 4.

3.4. Electrical Vehicles

Model-based reinforcement learning methods are increasingly used in electric vehicle (EV) applications, due to their ability to incorporate complex system dynamics and optimize long-term decision-making. By leveraging detailed models of the environment, these methods can predict the impact of actions more accurately, and optimize various aspects of EV operations, such as charging, cost management, and resource allocation. This section discusses several studies that utilize model-based RL approaches to enhance EV-related tasks, including power control, cost savings, pricing strategies, and navigation planning. One study presented in [70] addresses the optimal power control problem for fuel-cell EVs, focusing on reducing hydrogen consumption. The vehicle’s speed and power demands are modeled as a discrete-time Markov chain, with parameters learned via Q-learning. Another paper [71], examines a cost-saving charging policy for plug-in EVs, using a fitted Q-iteration algorithm to estimate usage and future costs. This approach shows a significant reduction in charging costs, ranging from 10% to 50%. Examining work [72], price reduction for EV charging is explored in another study, where a Long Short-Term Memory network predicts future prices. White Gaussian Noise is added to the actions to prevent the model from settling at non-optimal working points. A related study, [73] focuses on increasing the profitability of fast charging stations (FCSTs) through dynamic pricing. This model predicts traffic flow and demand while scoring based on a user satisfaction model. Dynamic pricing is shown to increase the average number of EVs utilizing the FCSTs, improve user satisfaction, reduce waiting times, and boost overall profits. In the domain of navigation, one study [74] aims to provide an efficient charging scheme for urban electric vehicles. This article proposes a new platform for real-time EV charging navigation, based on graph reinforcement learning, that utilizes a deep Q-learning agent. The platform’s main objective is to help EV owners decide when and where to charge, aiming to minimize charging costs and travel time. Case studies are conducted within a practical zone in Nanjing, China, and the authors verify based on simulation results the effectiveness of the developed platform and the solving method. Similarly, another study [75], addresses the navigation task using a network that extracts features from simulations and employs deep Q-learning (DQL) agent to determine the optimal path, demonstrating performance comparable to known optimal solutions. Further, examining the work introduced in [76], a combined approach is taken in a study that involves planning charging needs for a day in advance and making real-time charging decisions based on this plan. This model performs well, matching benchmarked results. Another paper, [77], deals with scheduling EV charging in a power network that includes PV production. It uses a nodal multi-target (NMT) model to ensure that actions are valid (e.g., not charging an EV that doesn’t need it), resulting in improved charging scheduling, faster convergence, and lower costs which are assessed through simulation. Finally, work [78], examines charging control from three perspectives of the user, the power distribution network, and the grid operator. The model’s actions are stochastic, normally distributed with parameters generated by a deep RL model. Each EV is managed by a separate RL model, with a global model coordinating all individual models. The use of this federated approach yields better results than state-of-the-art models. In summary, these studies illustrate the significant potential of model-based RL methods to enhance various aspects of EV management, offering promising solutions for optimizing power control, reducing costs, and improving overall efficiency. By incorporating detailed models of the environment, these approaches can effectively handle the complexities of EV operations, leading to better outcomes for both users and service providers. A summary of the studies reviewed is presented in Table 5.

3.5. Energy Storage Management

Model-based reinforcement learning methods are increasingly being recognized as essential tools for optimizing energy management in systems that integrate renewable energy and energy storage. These methods enable precise control and decision-making by leveraging models that capture the dynamics of the environment, leading to improved efficiency and sustainability. In particular, the application of model-based RL to energy storage management is crucial, as it not only enhances the efficiency of energy usage but also plays a pivotal role in stabilizing the grid and supporting the integration of renewable energy sources. Thus, this section covers various studies that utilize advanced model-based RL approaches to optimize energy management in various storage device applications. The papers collectively present advanced methods for optimizing energy management in various systems, including residential settings, industrial parks, and hybrid vehicles, focusing on integrating renewable energy and energy storage systems. For instance, paper [79], introduces a model-based control algorithm that optimizes photovoltaic power generation and energy storage under dynamic electricity pricing, using convex optimization and reinforcement learning to improve cost savings. Another study discussed in [80] develops an optimization model for energy management in large industrial parks, employing Deep Deterministic Policy Gradient, Greedy algorithms, and Genetic Algorithms to manage energy storage and consumption, addressing the variability of renewable energy sources. In the context of hybrid electric vehicles (HEVs), several papers explore reinforcement learning techniques, such as Q-learning, Dyna, and Sarsa, to optimize fuel efficiency and energy management. These approaches integrate transition probability matrices and recursive algorithms to dynamically adjust control policies based on real-time driving data, significantly improving fuel economy and adaptability compared to traditional methods [81,82,83]. Additionally, one study specifically focuses on minimizing battery degradation costs in Battery Energy Storage Systems (BESS) for power system frequency support, using a deep reinforcement learning approach with an actor-critic model and Deep Deterministic Policy Gradient [84]. Another paper introduces an adaptive control strategy for managing residential energy storage systems paired with PV modules, enhancing grid stability and reducing electricity costs through advanced forecasting techniques and a two-tier control system [85]. In a related study, a comprehensive energy consumption model for tissue paper machines is developed using machine learning techniques, with XGBoost identified as the most effective method for optimizing electricity and steam consumption [86]. Further, study [87], presents a near-optimal storage control algorithm for households with PV systems integrated into the Smart Grid, utilizing convex optimization to manage battery charging and discharging based on dynamic pricing. This approach reduces household electricity expenses by up to 36% compared to baseline systems, highlighting significant advancements in smart energy management. These papers demonstrate the potential of integrating advanced control algorithms, machine learning, and optimization techniques to enhance energy efficiency and operational performance across a range of applications. In summary, these studies illustrate the great interest of researchers, who are trying to employ model-based RL approaches in optimizing energy storage management across diverse applications. By effectively incorporating environmental dynamics and leveraging predictive modeling, these methods achieve superior performance in cost reduction, system efficiency, and resource utilization. As the demand for sustainable energy solutions grows, model-based RL will continue to play a crucial role in advancing smart energy management and supporting the integration of renewable energy into modern power systems. A summary of the studies reviewed is presented in Table 6.

3.6. Prominent Trends

Reviewing Table 2, Table 3, Table 4, Table 5 and Table 6, it is clear that model-based reinforcement learning has shown considerable potential across various domains in energy management, with each application showcasing unique trends and challenges. In power grid stability, particularly voltage control, there is a noticeable trend towards using continuous state spaces and stochastic policies as presented in Figure 8. Conversely, applications like electric vehicle charging schedules often employ discrete state spaces with deterministic policies due to the unpredictable nature of influencing factors such as weather conditions and driver behavior. These discrepancies underscore the challenge of achieving perfect knowledge of the environmental dynamics, often leading to sub-optimal policies produced by RL models. The complexity in modeling these systems highlights the need for adaptive and robust model-based RL methods that can handle such uncertainties. Another point worth mentioning is the clear standardization for the domain of voltage control. This further emphasizes the dire need for standardized tools to conduct qualitative evaluations and promote extensive, in-depth research of new methods and algorithms for various optimal control problems. In energy management for buildings, one might expect similarities with residential energy management due to apparent similarities in the objectives. However, empirical evidence suggests that even different households may require entirely different policies, highlighting the variability in dynamic models. For example, the energy consumption patterns of a person living in a small apartment can vary dramatically depending on their work schedule. The person’s consumption could differ significantly week-to-week if their shift times change. This variability makes it nearly impossible to model consumption profiles accurately ahead of time, thereby necessitating RL algorithms capable of dynamically adapting to these changes. Consequently, model-based RL approaches for building energy management need to be flexible enough to account for diverse and evolving consumption patterns. Most research in energy management for buildings focuses on optimizing the same objective: reducing energy costs while maintaining comfort. While these are crucial considerations, several underexplored applications could benefit from RL. For instance, integrating demand-response programs into building energy management systems could enhance grid stability by adjusting demand in real time based on grid conditions. Another promising area is the integration of renewable energy sources, such as solar panels, into building energy management systems, requiring RL algorithms to manage intermittent supply while ensuring energy efficiency and stability of the power grid. Additionally, using buildings as energy reservoirs and supplying necessary electricity in emergency event may be another area where model-based RL could provide substantial benefits. These applications highlight the need for further exploration and innovation in applying model-based RL to the multifaceted challenges of energy management.

4. Model-Free Paradigms

We now turn our attention to model-free paradigms. In contrast to model-based paradigms, model-free paradigms utilize only statistical data to shape an optimal control policy, without considering any information about the model physics or dynamics. Naturally, such methods rely on aggregated data, and are useful when the dynamical model under consideration is too complicated to learn, as is often the case. Therefore, such methods are increasingly used in power system optimal control problems, and are gaining popularity in recent years. The readers may note that we repeat here the same applications as above, to provide comparisons and to draw conclusions regarding the differences, advantages and disadvantages of each approach.

4.1. Energy Markets Management

Model-free reinforcement learning methods have gained attention in energy market management due to their ability to handle complex, decentralized systems without requiring a model of the environment. These techniques are particularly valuable in situations where the system dynamics are difficult to model or are constantly changing, allowing the RL agent to learn optimal strategies directly from interactions with the environment. Model-free RL approaches, such as Deep Deterministic Policy Gradient and others, have shown promise in various energy market applications. One use case for example is in the management of decentralized energy systems. For instance, in paper [92], the authors demonstrate the effectiveness of a model-free RL approach in optimizing multi-energy systems in residential areas, reducing energy costs without the need for a predefined environmental model. Work [93] addresses the optimization of local energy markets using reinforcement learning through the Autonomous Local Energy Exchange (ALEX) framework, which combines multi-agent learning and a double auction mechanism. They found that weak budget balancing and market truthfulness are essential for effective learning and market performance. ALEX-based pricing improved demand-response functionality and reduced electricity bills by a median of 38.8% compared to traditional net billing, showcasing the efficiency of this approach. Examining study [94], a new method for optimizing energy trading is proposed. They focus on local markets, and perform the optimization using a modified Erev-Roth algorithm for agent bidding strategies. Simulations showed improved self-sufficiency and reduced electricity costs through demand response and peer-to-peer trading. Furthermore, the authors of [95] focus on optimizing real-time bidding and energy management for solar-battery systems to reduce solar curtailment and enhance economic viability. They developed a model-free deep reinforcement learning algorithm (AC-DRL) using an attention mechanism and multi-grained feature convolution to make better-informed bidding decisions. The results showed that AC-DRL significantly outperforms traditional methods, reducing solar curtailments by 76% and increasing revenue by up to 23%. Considering a different context, for example when examining [96], the researchers aim to facilitate community-based virtual power plants (cVPPs) to promptly provide ancillary services to the grid. They establish a decision-making model to minimize the operation cost of the cVPP, and transform it into a partially observable Markov game model. Numerical simulation demonstrates that the proposed method can effectively support cVPPs to autonomously generate energy bidding and management strategies without acquiring other cVPPs’ private information. From a different perspective, paper [97], also focuses on the challenge of integrating distributed energy resources in the grid and their implications on energy trading in local markets. The authors propose new market model to coordinate between the distributed sources, which represent the environment, and explore a model-free prosumer-centric coordination approach through a multi-agent deep reinforcement learning method. Case studies in a real-world setting validate that the proposed market design, demonstrate its effectiveness and show a comparison to other methods. Another work that considered energy trading applications in peer-to-peer setting is [98]. In this study, the authors consider a new;y emerging trend of consumer to consumer trading that redisgn local energy markets. This form of trading diversifies the energy market eco-system and can be used to further support grid stability although it introduces additional uncertainty to energy trading strategies. The researchers present an Markov decision process formulation for this market model, and analyze beneficial trading strategies using multi-agent reinforcement learning methods that rely on data-driven approach. The proposed model is evaluated using simulation, and the results are discussed to highlight the benefits and disadvantages of the method. Energy markets in microgrids are also an interesting subapplication since they can detach themselves from the grid at any time, making them a highly uncertain environment for planning. For example, in work [99], their objective is to achieve distributed energy scheduling and strategy-making in double auction-based microgrid. To address this issue, a multi-agent reinforcement learning approach is adopted. The authors propose an optimal equilibrium selection mechanism to improve performance of model and enhance fairness, execution efficiency, and privacy protection. Simulation results validate the capabilities of the proposed method. To continue this line of thinking, paper [100] uses multi-agent reinforcement learning to control a microgrid in a mixed cooperative and competitive setting. The agents observe energy demand, changing electricity prices, and renewable energy production. Based on this information, they decide upon storage system scheduling to maximize the utilization of the renewables and reduce the energy costs when purchasing from the grid. The evaluation is performed in two settings: single and multi-agent. In the multi-agent setting, the researchers design the individual reward function that each agent receives by leveraging the concept of marginal contribution to better assess how the agents’ actions impacted the joint goal of reducing energy costs. Another paper that considers energy trading in microgrids is [101]. Here, they present an online reinforcement learning approach that is base on imitation learning, to mimick a mixed-integer linear programming (MILP) solver. The proposed method is compared to an agent that learns the policy from scratch, and to a Q-learning agent. Numerical simulations on both simulated and real-world data highlight the performance advantage of the proposed approach as compared to a few other methods. In conclusion, model-free RL approaches offer flexibility and adaptability, making them well-suited for managing decentralized and multi-agent systems in the energy market. Their ability to optimize complex systems without a predefined model opens up new possibilities for advancing real-time decision-making in dynamic energy environments. A summary of the studies reviewed is presented in Table 7.

4.2. Power Grid Stability and Control

Despite the remarkable achievements of model-based reinforcement learning paradigms, in many power system applications, particularly in optimal control problems of power grid stability and management, it is impossible to acquire a perfect knowledge of the system dynamics. As a results, data-driven methods leverage statistical learning, to produce optimal control policies without any knowledge of the system, but relying solely on aggregated data. For example, examining the same task of voltage control regulation, paper [106] implements an autonomous control framework “Grid mind”, for voltage control and secure operation of power grids. The authors use deep Q-network and deep deterministic policy gradient, and feed the model with the current system conditions detected by real-time measurements from supervisory control and data acquisition or phasor measurement units. A case studies on a realistic 200-bus test system is demonstrated. Alternatively, work [107], focuses on the management of active distribution networks, which face frequent and rapid voltage violations due to renewable energy integration. In this work, they propose a fast control of PV inverters. To achieve this, they partition the existing network into sub-networks based on coltage-reasctive power sensitivity. Next, they formulate the scheduling of PV inverters in the sub-networks as a Markov game, and produce a policy using a multi-agent soft actor-critic algorithm, where each sub-network is modeled as an intelligent agent. All agents are trained in a centralized manner to learn a coordinated strategy, but they are executed based on local information for fast response. For the slower time-scale control, OLTCs and switched capacitors are coordinated by a single agent-based SAC algorithm. To show the effectiveness of the method, various comparative tests with different benchmark methods, such as stochastic programming and several others, on IEEE 33- and 123-bus systems and 342-node low voltage distribution system. To continue this line of thinking, consider study [108] which discusses autonomous, real-time voltage contol for economic and safe grid operation. This paper laid the foundation for “Grid mind” which was further extended in [106] to include continuous state space. Here, the researchers proposed a deep q-learning algorithm to effectively learn the voltage corrections required for grid stabilization. They tested the proposed method on the standard IEEE 140-bus system with various scenarios and voltage perturbations. As was previously mentioned, power grid stability and cotrol has many aspects. So, if we continue our analysis of literature in this domain of research, frequency control is another widely discussed problem. For instance, consider the following paper [109], which adresses power systems stability margins, and especially is interested in poorly damped or unstable low-frequency oscillations. The authors aim to propose a reinforcement learning framework to effectively control these oscillations, in order to ensure the stability of the system’s operation. They design a network of real-time close-loop wide-area decentralized power system stabilizer. The data is measured by a Comparative tests with different benchmark methods on IEEE 33- and 123-bus systems and 342-node low voltage distribution system demonstrate system, and processed by a set of decentralized “stability” agents, implementing a variation of Q-learning algorithm. Finally, a Matlab simulation is designed to assess the performance of the method. Moreover, in work [110], they address the problem of frequency regulation in emergency control plans. The writers begin with a model that is designed for limited emergency scenarios utilizing a variation of Q-learning algorithm, and train it off-line. Next, they use transfer learning and extend the generalization ability by using a deep deterministic policy gradient (DDPG) algorithm. They employ this system on-line to learn near-optimal solutions. Using Kundur’s 4-unit-13 bus system and the New England 68-bus system they verify the capabilities of the proposed schemes. The integration of renewable energy, and the latest technological advancments have increased the phenomena of micrdogrids, which can dettach at any time from the main grid, causing malfunction and jeopardizing its standard operation. This has given rise to a new sort of optimal control problems concerning power grid stability and domain. The literature contains many studies that investigate this problem but have different objectvies, emphasizing the many variables that are needed to be considered when mangaing microgrid formations, and the great complexity they introduce into the system. Namely, work [111] inspects a networks of interconnected microgrids that can share power with each other, called multi-microgrid formation, and aim to propose a control policy for the power flow to enhance power system resilience. Thay propose a deep reinforcement learning scheme, based on double deep q-learning algorithm, with a CNN for effective learning of Q-values. The authors evaluate the performance of the proposed scheme using 7-bus system and the IEEE 123-bus system with different environmental conditions. Furthermore, in study [112], the reserchers are also interested in the control and management of multi-microgrid setting, only here they underscore the distribution system operator perspective, whose target is to reduce the demand-side peak-to-average ratio (PAR), and to maximize the profit from selling energy, along with protecting the usedrs privacy. The microgrids are modeled without direct acess to user’s information, and the retail pricing strategy via a Monte Carlo method, based on prediction. Consequtively, to evaluate and compare the proposed framework, the authors use simulation and run few conventional methods, to assess the behavior of the model under uncertainty conditions, where there is only partial information. Another core sub-application that hs to be mentioned in the context of power grid stability and control is the management of the power flow. This involves balancing of supply and demand to prevent grid overloads and maintain stability. There’s a need to optimize the dispatch of power from various sources, including renewable energy and storage systems, to ensure efficient power distribution and minimize losses. Dynamically adjusting the division of the power flow, helps enhance system resilience against disturbances, reduce the risk of blackouts and improve overall grid reliability. In the analysis suggested in [113], they highlight the importance of fast and accurate corrective control actions in real time of the power flow to ensure the system security and reduce costs. The authors propose a method to derive real-time alternating current (AC) optimal power flow (OPF) solutions when considering the uncertainties induced by varying renewable energy sources incorporation in the system, and topological changes. They suggest a deep reinforcement learning framework, using a PPO agent, to assist grid operators. They validate the proposed scheme on the Illinois 200-bus system with wind generation variation and topology changes, to demonstrate its generalization ability. Additional study concerning the optimal power flow can be viewed in [114]. Here, the objective is to analyze the optimal power flow of the distribution network embedded with renewable-energy sources and storage devices. The analytical problem is formulated as a Markov Decision Process and a PPO agent is trained. Using off-line statistical learning on historical data, and a stochastic policy the authors aim to reduce prediction error and address the uncertainty of the environment. A comparative evaluation to double deep Q-learning and stochastic programming methods is performed, assessing the capabilities of the proposed framework. In essence, model-free RL methods have proven to be highly effective for grid stability and control applications by learning optimal control policies through direct interaction with the grid environment. These approaches are particularly advantageous in scenarios where system dynamics are too complex or unpredictable to model accurately. By continuously adapting to changing conditions and unforeseen disturbances, model-free RL can enhance grid stability, manage load balancing, and support the integration of intermittent renewable energy sources. As power systems become more decentralized and dynamic, model-free RL will play a crucial role in ensuring reliable and stable grid operation. A summary of the studies reviewed is presented in Table 8.

4.3. Building Energy Management

A few factors contribute to the development of statistical learning methods for energy management in buildings. First, the high dimension of the data imposes complicated dynamics, that are hard to model precisely, leading to sub-optimal policies produced by model-based algorithms. Moreover, smart grids, and smart metering devices, along with other technological advancements for aggregating and measuring data, provide further motivation for the utilization of data-driven methods. In this subsection, we review recent studies from the literature dealing with model-free reinforcement learning solutions to manage energy in buildings. Examining HVAC application, in [117] the study addresses the problem of optimal control for building HVAC systems. The proposed method is based on model-free Q-learning RL algorithm, and is validated with the measured data from a real central chilled water system. The authors present a comparative evaluation with the basic controller, showing a conservation of 11% of the systems energy in the first applied cooling season in comparison to the old rule-based method that was used until then. Alongside, in [118], the paper addresses both demand-response (DR) and HVAC problems. It focuses on optimizing the demand-response problem while maintaining comfort in residential buildings. The authors develop a novel global-local policy search method. This method utilizes an RL algorithm based on zero-order gradient estimation to search for the optimal policy globally. Next, the obtained policy is fine-tuned locally to bring the first-stage solution closer to that of the original un-smoothed problem. Experiments on simulated data show that the learned control policy outperforms many existing solutions. A different perspective on encountering both demand-response and residential comfort objectives in energy management schemes of buildings is discussed in [119]. The authors aim to propose an cost-effective automation systems that can be widely adopted, to utilize buildings, which may be prominent energy consumers, in demand-response programs. Existing optimization-based smart building control algorithms suffer from high costs due to building-specific modeling and computing resources. To tackle these issues, this paper proposes a solution using reinforcement learning, specifically actor-critic agent. Simulation results demonstrate the control efficacy and the learning efficiency in buildings of different sizes. A preliminary cost analysis on a 4-zone commercial building shows the annual cost for optimal policy training is only 2.25% of the DR incentive received. Results of this study show a possible approach with higher return on investment for buildings to participate in DR programs. Another DR and HVAC solution approach is suggested in [120], where they address the demand side scheduling in a residential building to reduce electricity costs while maintaining resident comfort. The schedule optimization is performed on-line and it is controlled by a deep reinforcement model, combining deep Q-learning and deep policy gradient algorithms. The proposed approach was validated on the large-scale Pecan Street Inc. database, and it includes multiple features that hold information about photovoltaic power generation, electric vehicles parked in the building’s parking lot, and various building appliances. Moving forward, in [121], the authors develop a data-driven approach based on deep reinforcement learning, using a q-learning agent, to address scheduling problem of HVAC systems in residential buildings. The main objective of this work is to reduce energy costs. To asses the performance of their algorithm, the writers performed multiple simulations using the “EnergyPlus” tool. Experiments demonstrate that the proposed DRL-based algorithm is more effective in energy cost reduction compared with the traditional rule-based approach, while maintaining the comfort of the users. Similarly, in [122] the authors intend to minimize the energy cost of an HVAC system in a multi-zone commercial building with the consideration of random zone occupancy, thermal comfort, and indoor air quality comfort. They suggest a Markov game formulation to represent the energy cost minimization. Next, they propose an HVAC control algorithm to solve the Markov game based on multi-agent deep reinforcement learning with attention mechanism, without any prior knowledge of uncertain parameters and without knowing the thermal dynamics models of the building. Experiments on real-world data show the effectiveness, robustness and scalability of the proposed algorithm. Continuing the same line of thinking, [123] addresses optimal HVAC control methods that reduce energy consumption while maintaining the thermal comfort of the occupants. It introduces a model-free reinforcement learning-based HVAC systems that can be controlled dynamically, and relying on a weather forcasting data. In this study, the authors propose a new deep reinforcement learning problem called “WDQN-temPER”, a hybrid HVAC control method combining a deep Q-network with a gated recurrent unit model that predicts the future outdoor temperature and is used as a state variable in the RL model. They experimentally demonstrate in “EnergyPlus” software with simulated data, that their proposed model outperforms a rule-based baseline model in terms of HVAC control, with energy savings of up to 58.79%. Moreover, paper [124] approaches the HVAC problem by optimizing a cost minimization function that jointly considers the energy consumption of the HVAC and the occupants’ thermal comfort. In this study, the authors propose a model that consists of two sub-modules. The first one is a deep feed-forward neural network for predicting the occupants’ thermal comfort, and the second one is a deep deterministic policy gradient algorithm for learning the optimal thermal comfort control policy. They implement a building thermal comfort control simulation environment and evaluate the performance under various settings, which showed improved results comparing to the previous rule-based algorithm. Combining energy management alongside with residential comfort objectives, the researchers who conducted study [125] consider a multi-objective control problem of energy management in residential building, while trying to optimize occupant comfort, energy use, and grid interactivity. They try to utilize an efficient RL control algorithm, based on PPO agent. They address a few major drawbacks associated with RL models, including the need for large training data, long training time, and unstable control behavior during the early exploration process, which makes it infeasible for a real-time application in building control tasks. To address this issue, imitation learning is used, and reliance on a policy transferred from accepted rule based model, to guide the agent in the first crucial stages. This approach showed high performance, fast running time in comparison to some rule-based models under simulated data. Moreover, this technique prevented successfully the unstable early exploration behavior. Considering multi-energy system (MES) control applications refer to integrated systems that combine multiple forms of energy (such as electricity, heat, and gas) to optimize their generation, storage, and consumption. By leveraging the synergies between different energy carriers, MES aim to improve overall efficiency, reliability, and sustainability in energy management. For instance, in work [126], they minimize MES cost by optimizing the scheduling of the MES. Their solution finds an optimal energy usage for the MES. They introduce DDPG - a deep deterministic policy gradient, with a prioritized experience replay strategy for improving sample efficiency, which doesn’t rely on knowledge about the system or any statistical knowledge from forecasting. A different perspective is presented in paper [127] which addresses both electric water heater management and DR. Here, the authors harness electric water heaters for energy storage in buildings, to address residential demand-response control problem. In this work, they propose a Reinforcement learning method, using an auto-encoder network and fitted Q-iteration algorithm to handle the stochastic and nonlinear dynamics of the electric water heaters. The results of the conducted experiment, indicate that compared to a thermostat controller, the presented approach was able to reduce the total cost of energy consumption of the electric water heater by 15%. In conclusion, for energy management in buildings, model-free RL methods offer a flexible and adaptive solution by learning from real-time energy consumption data and occupant behavior patterns. Without needing a predefined model of the building’s dynamics, these methods can autonomously adjust energy usage to optimize for cost savings and comfort. This makes them particularly suitable for managing the energy demands of smart buildings, which may have complex interactions and varying usage patterns. As the adoption of smart building technologies increases, model-free RL will be key to enabling efficient and responsive energy management strategies. A summary of the studies reviewed is presented in Table 9.

4.4. Electrical Vehicles

Model-free reinforcement learning methods are also increasingly crucial in electric vehicle (EV) applications due to their ability to learn and adapt to dynamic environments without requiring explicit models of the system dynamics. These methods offer promising solutions to various challenges associated with EV charging and energy management, optimizing performance while reducing computational complexity. This review highlights several studies that showcase the effectiveness of different RL algorithms in enhancing EV-related tasks, such as charging time minimization, cost reduction, and real-time scheduling. For example, in study [133] the authors aim to minimize EV charging times using a deep learning method, achieving a charging time reduction of 60% compared to the best classical methods available. Another work, [134] the objective is to reduce operative costs. The researchers leverage a deep reinforcement algorithm, using a deep Q-learning agent, to optimize the utilization of photovoltaic systems and battery storage. This model proves to be more effective than simpler DQL models by reducing costs by 15% and increasing the utilization rate of PV by 4%. Furthermore, a different perspective on real-time pricing and scheduling control for charging stations is explored in paper [135]. In this work, the authors apply the SARSA algorithm, which demonstrates higher profitability for charging stations while maintaining low average charging prices. This approach also offers computational efficiency compared to other advanced algorithms which are presented in the evaluation section. Examining the work discussed in [136], they are also interested in cost reduction as their main objective, and try to optimize costs using a genetic algorithm. The proposed model is utilized to determine optimal charging fees, framing the problem as a bi-level optimization involving both power distribution and urban transportation networks. Although this model performs well in smaller networks, it has some limitations in when applied to larger-scale settings. Another approach presented in study [137], introduces a dynamic pricing model that integrates quality of service considerations. Using an actor-critic model, this method achieves results comparable to dynamic programming solutions but with significantly faster computation times. In contrast, concerning the optimal control problem that arises from EV charging schedule, work [138], applies a deep Q-learning model to decide which EVs to charge based on known departure times and energy demands. Tested on real-world data, this model outperforms uncontrolled scenarios by up to 37% and approaches optimal performance, though it struggles with scalability over long time frames. Examining the work [139], the authors aim to suggest an optimal battery management policy, to allow for longer ranges and battery preservation. They design a simplified car model and utilize a DQL agent for action selection, combined with model predictive control (MPC) for actual control, showing slight improvements in range and battery usage, particularly in challenging driving conditions like uphill driving. A separate study, presented in [140], objectives to increase photovoltaic self-consumption and EV state of charge at departure. The study compares three deep reinforcement learning (DRL) models, including DDQN, DDPG, and parameterized DQN, with model predictive control, for simple charging control involving building energy needs and PV utilization. While these DRL models perform well concerning time efficiency, their performance is similar to that of rule-based control methods in the sense of finding the optimal point that satisfies the trade-off between the available PV surplus, after answering the building demands, and the available charge capacity in the EV battery. Additionally, a demand response scheme is analyzed in work [141]. Here, the main focus lies on which devices to turn on to stabilize the grid in terms of power conservation, while keeping user satisfaction in mind. This model ranks devices based on priority and measures total dissatisfaction scores, balancing demand management with user preferences. Lastly, referring to work [142], a simple energy management scenario involving appliances like air conditioners, washing machines, and energy storage systems is analyzed. Using weather forecasts and Q-learning agent, the model achieves a 14% reduction in electricity costs under dynamic pricing scenarios. Overall, these studies highlight the versatility and potential of model-free RL methods in EV applications, offering substantial improvements in operational efficiency, cost-effectiveness, and computational simplicity. A summary of the studies reviewed is presented in Table 10.

4.5. Energy Storage Management

Model-free reinforcement learning methods are becoming increasingly important for energy storage management due to their ability to learn optimal policies directly from interactions with the environment, without requiring explicit models of system dynamics. These approaches offer flexibility and adaptability in complex and uncertain energy management scenarios, making them highly suitable for integrating renewable energy sources and enhancing grid stability. By leveraging real-time data and continuously improving their decision-making strategies, model-free RL techniques can optimize energy usage, reduce costs, and manage storage systems more effectively, addressing the challenges of modern energy systems. The papers collectively explore advanced control and optimization techniques across energy systems, microgrids, and hybrid vehicles, using methods such as deep reinforcement learning and Particle Swarm Optimization (PSO). Consider for example paper [143], which introduces an Adaptive Deadbeat (ADB) controller, optimized with PSO, for managing frequency stability in Scottish power systems with high renewable energy penetration, showing superior performance over traditional controllers. Another study [144] presents a DRL-based framework for optimizing battery energy storage arbitrage, incorporating a lithium-ion battery degradation model and a hybrid CNN-LSTM architecture to predict electricity prices. This model improves profitability and manages battery health efficiently. Further research, such as [145], employs Double Deep Q-Learning to optimize community battery energy storage systems within microgrids, reducing bias and stabilizing learning, particularly under fluctuating market conditions. Alternatively, in work [146], a Q-learning-based strategy is also introduced for optimizing community battery storage, utilizing an enhanced epsilon-greedy policy to balance exploration and exploitation, optimizing performance in both grid-connected and islanded modes. In another paper [147], the objective is to propose a trading policy in the energy market, to incentivize private producers that use renewable energy sources to participate fairly in the energy trading market. The authors tailor a DRL model for modeling prosumer behavior in local energy trading markets using a modified deep Q-network technique, enhancing learning through experience replay. Examining another application, in the study presented in [148], an actor-critic architecture enhanced by Deep Deterministic Policy Gradient is employed to optimize Battery Energy Storage Systems (BESS) for power system frequency support, minimizing operational costs while maintaining stability. Looking at a different perspective, paper [149] introduces a multi-agent DRL method for optimizing energy management in microgrids, where agents share Q-values to achieve correlated equilibrium, significantly enhancing profitability. Additionally, in study [144], the authors propose a DRL with a noisy network approach to optimize battery storage arbitrage, combining CNN-LSTM for market forecasting and balancing financial gains with long-term operational costs. Moreover, study [150] employs a Deep Q-Network for dynamic energy management, integrating real-time data to minimize operating costs and ensure stable microgrid operation. Finally, work [151] integrates Markov Chain models with reinforcement learning to optimize energy management in hybrid vehicles, demonstrating significant improvements in energy efficiency. In summary, these studies highlight model-free RL approaches in optimizing energy storage management across various applications, from residential settings to large-scale industrial systems. By learning directly from the environment, these methods can adapt to changing conditions and uncertainties, offering robust solutions for enhancing energy efficiency and cost-effectiveness. As model-free RL techniques continue to evolve, they hold significant potential for advancing sustainable energy management and supporting the integration of renewable energy sources into the grid.

4.6. Prominent Trends

Reviewing the summaries presented in Table 7, Table 9, Table 8, Table 10, and Table 11 it is clear that model-free reinforcement learning has shown considerable promise across various domains, with each application showcasing unique trends and challenges. In power grid stability, particularly voltage control, there is a noticeable trend towards using stochastic policies. This approach leverages the simple underlying statistics, which are inherent to these control problems. Conversely, applications like electric vehicle charging schedules often employ discrete state spaces with deterministic policies, as may be viewed in Figure 9, due to the complex statistical relations, and due to the unpredictable nature of influencing factors such as weather conditions and driver behavior. These discrepancies underscore the challenge of statistical learning when the uncertainty of the environment is high, often leading to sub-optimal policies produced by model-free RL models. This complexity in the underlying statistical information highlights the need for flexible model-free RL methods that can generalize well under such uncertainties. Another point worth mentioning is the clear standardization for the domain of voltage control. As above, this further emphasizes the dire need for standardized tools to conduct qualitative evaluations and promote extensive, in-depth research of new methods and algorithms for various optimal control problems. Furthermore, it is clear that in order to learn such complicated statistical relations, there is a need for large-scale amounts of data. Currently, this is a major challenge in many domains of power systems, since the technological advances that allow data metering and aggregation are relatively new, and incorporating them into existing systems not only poses a major technological challenge but also subjects the power grid to security threats. In energy management for buildings, one might expect similarities with residential energy management due to apparent similarities in objectives. However, empirical evidence suggests that even different households may require entirely different policies, highlighting the variability in dynamic models. For example, the energy consumption patterns of a person living in a small apartment can vary dramatically depending on their work schedule. This variability makes it nearly impossible to learn and predict consumption profiles accurately ahead of time, thereby necessitating model-free RL algorithms capable of dynamically adapting to these changes. Consequently, model-free RL approaches for building energy management need to be flexible enough to account for diverse and evolving consumption patterns. Due to the rising complexity of optimal control problems in the power systems field of research, and the high dimensions of these problems, statistical learning emerges as a powerful and promising tool. Hence, there is a need for further exploration and innovation in applying model-free RL to the multifaceted challenges of energy management.

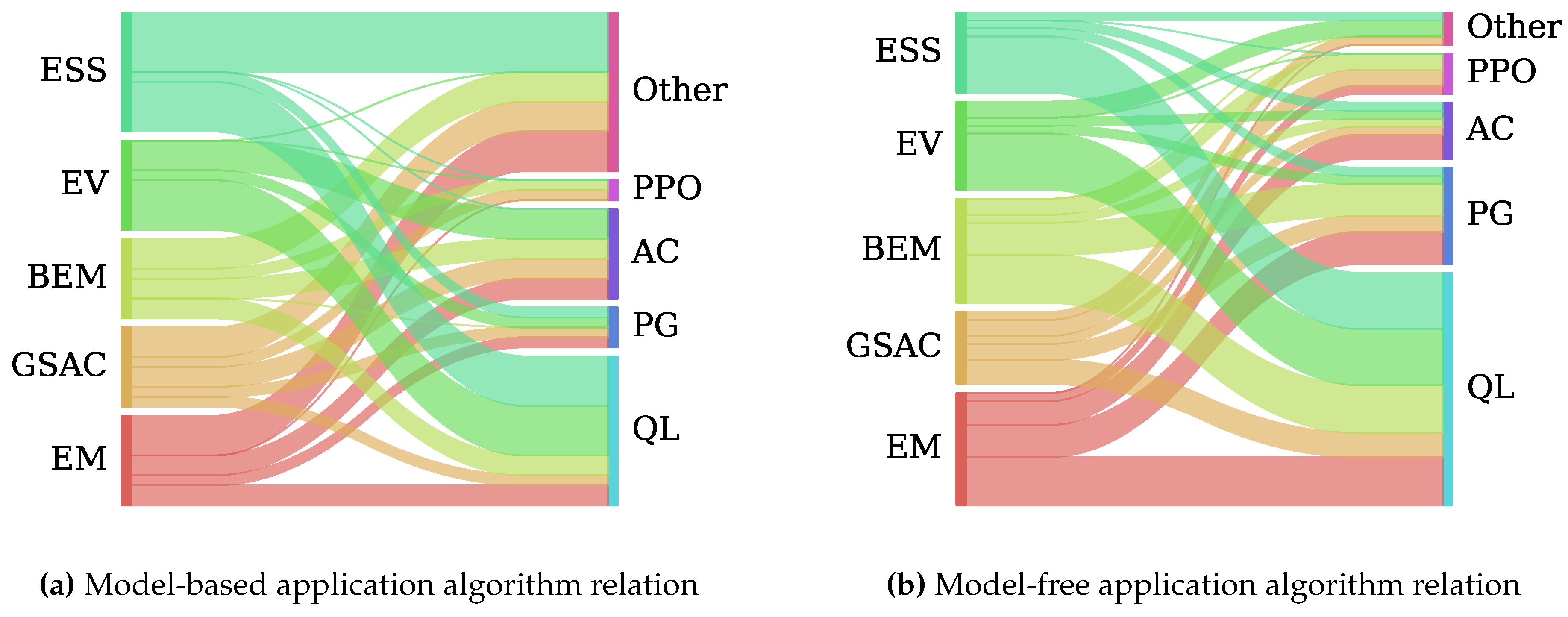
5. Comparison and Discussion

The analysis presented above reveals a few interesting trends. First, it clearly shows that reinforcement learning methods gain more and more interest, and are being vastly deployed for various optimal control problems in power systems. Since 2010 we have seen a steady growth in the number of publications concerning botch model-based and model-free approaches for various applications, as shown in Figure 10. It is important to note that when looking for model-based papers, there is a lack of consensus regarding the definition of it. In many cases, researchers use “model-base” for describing traditional optimal control solutions, such as MPC. Indeed, the differentiation is not exactly clear, since a specific approach for reinforcement learning solutions is based on a known and given model, which degenerates the problem to a planning problem, as was described in Figure 5. Not only that but to ensure efficient search, the terms of “model-based” and “reinforcement learning” were often written separately, in different parts of the sentence to avoid this problem, as may be seen in the search strings presented in Table 12. The distribution between various applications is quite the same, as may be viewed in Figure 11. Similarly, in Figure 12, it may be observed that variations of the “Q-learning” algorithm are by far the most popular, afterwards, in model-based approaches, “Actor-critic” variations are the second most used, while in model-free it is the “Policy gradient” algorithms. Moreover, “Q-learning” dominates the algorithms used when it comes to data-driven approaches, as may be seen in Table 13, or visually in Figure 13. To summarize, the comparison highlights the growing popularity of reinforcement learning in power system applications, emphasizing the connection between various applications, the arising MDP formulations, and the selected reinforcement learning algorithms. These trends underscore the field’s evolving dynamics and the adaptability of reinforcement learning algorithms in addressing complex optimal control challenges in power systems while also pointing to future possibilities.

6. Challenges and Future Research Work

6.1. Challenges

6.1.1. Limited Real-World Data And Standardized Tools

One major challenge when utilizing reinforcement learning methods in control problems for power systems is the limited real-world data [153,154]. Typically, reinforcement learning problems require vast amounts of data and repeated interactions with the environment to produce high-fidelity predictions and avoid injecting bias during training. Currently, there is only a limited amount of data that may be collected from real-world power systems, which impairs performance and limits the generalizability and robustness of the models. Therefore, it is highly interesting to find solutions that can promise performance guarantees, despite the limited amount of data. Alternatively, it is interesting to find ways to generate high-quality data that can be used for benchmarking.

With great caution we also claim that the power systems area of research somewhat lags behind, in terms of available data and standard data-sets, when compared to other disciplines such as computer vision or natural language processing [155,156]. The major challenge is due to the stochastic nature of the environment, and the complex dynamics of the physical systems involved. The uncertainty is high, which degrades the performance of the model. Moreover, most existing solutions do not offer a closed systematic, in-depth formulation of the physical consideration of the network. This lack of standardization hinders the ability to consistently measure and compare the performance of different reinforcement learning approaches, making it difficult to gauge their effectiveness and reliability in real-world applications. Furthermore, the diversity and complexity of power systems, coupled with the need for high levels of safety, stability, and efficiency, require robust testing environments that accurately reflect operational conditions. Without standardized benchmarks, researchers and practitioners face difficulties in replicating results, validating models, and advancing the state-of-the-art in reinforcement learning applications for power systems.

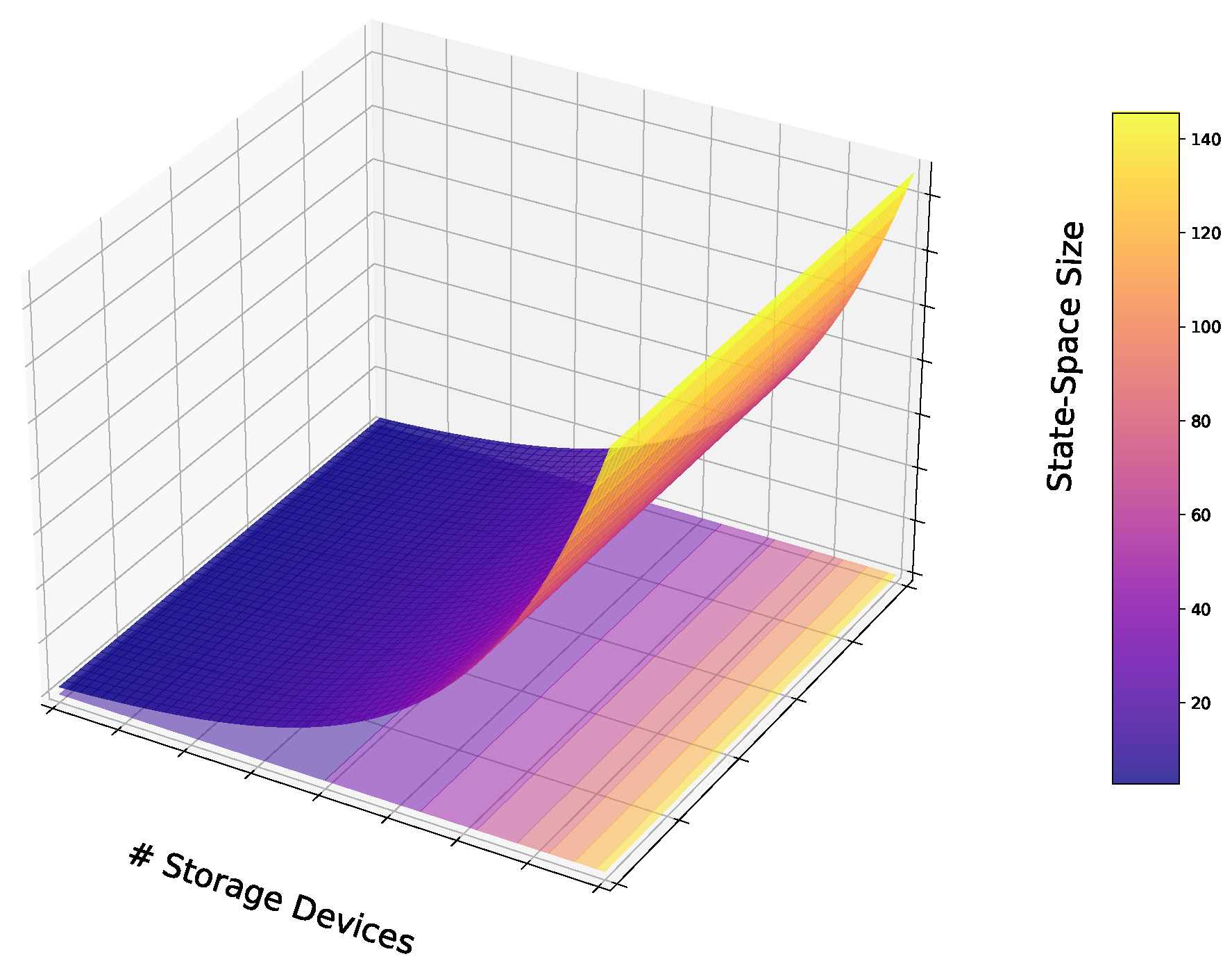
6.1.2. Limited Scalability, Generalization, And The Curse Of Dimensionality

The limited generalization ability of current reinforcement learning solutions arises from numerous factors. Model-free configurations, which rely on large-scale data sets, suffer from a lack of data, or use data that was validated on small-scale, simplified systems. On the contrary, model-based methods often converge to a dynamic model that does not represent accurately the real-life model, which affects the resilience, robustness, flexibility, and generalization ability of the model. This hurdle degrades the generalization ability to handle new samples and prevents the incorporation of such solutions by power system operators. An extensive discussion is presented in [157,158,159].

Extending this idea, the curse of dimensionality in reinforcement learning refers to the exponential growth in computational complexity and data requirements as the number of state or action variables increases. In model-based reinforcement learning, this issue arises because constructing and solving a model that captures all possible state transitions and rewards becomes infeasible with high-dimensional state spaces. On the other hand, model-free reinforcement learning methods, which learn policies or value functions directly from interactions with the environment, also struggle as the amount of experience needed to accurately estimate values or policies scales exponentially with the number of dimensions. This leads to slower learning and the need for more data to achieve reliable performance. Both approaches require sophisticated techniques such as function approximation, dimensionality reduction, or hierarchical learning to manage the complexity and make high-dimensional problems tractable. To understand the extent of the problem, consider any optimal control problem of storage devices. As mentioned in [160], the dimensions of the problem grow exponentially with the number of storage devices, as illustrated in Figure 14.

6.1.3. Limited Robustness And Safety For Real-Time Applications

Reinforcement learning methods, both model-based and model-free, often exhibit limited robustness in power systems control problems [157,158,159]. Model-based reinforcement learning relies on accurate system models, and any discrepancies between the model and the real system can lead to sub-optimal or unsafe control actions. This lack of robustness to modeling errors or system changes can significantly impact performance. Model-free reinforcement learning, which learns directly from interaction with the environment, can struggle with the variability and uncertainty inherent in power systems. It requires extensive and diverse training data to generalize well, but even then, it might not handle unseen scenarios or rare events effectively. Both approaches need mechanisms for robust adaptation to changing conditions, such as continuous learning, domain adaptation, or integrating domain knowledge to enhance reliability and safety in dynamic power system environments.

In addition, implementing learning algorithms in the power systems domain for real-time applications presents numerous challenges. The dynamic and stochastic nature of power systems demands that reinforcement learning models continuously adapt to fluctuating conditions and uncertainties, such as variable renewable energy sources and unexpected equipment failures. These algorithms must make real-time decisions with limited data and computational resources in high-stakes environments where errors can lead to significant financial losses, equipment damage, or blackouts. The need for immediate, reliable decision-making requires reinforcement learning models to learn quickly, while ensuring high accuracy and robustness. Additionally, integrating reinforcement learning into existing control systems, which rely on deterministic methods, poses significant challenges, especially given the stringent regulatory and safety standards governing power systems operations.

Moreover, learning algorithms deployed in real-time, must continuously learn and adapt as new data becomes available, requiring advanced techniques to maintain performance and prevent “catastrophic forgetting”. Ensuring the stability and convergence of these algorithms in a dynamic environment is complex, highlighting the need for ongoing research to develop robust, adaptable, and safe reinforcement learning solutions for real-time power system applications. Different works addressing this challenge are emerging in recent years, such as [161,162,163]. A summary of the challenges is presented in Table 14.

6.2. Future Work

6.2.1. Explainability

Reinforcement learning solutions for power system control problems is a rapidly evolving field of research. It provides powerful tools for analyzing complex problems while reducing computation time, and is highly promising for future applications. Nonetheless, one major drawback of those algorithms, model-based as well as model-free, is their low interpretability for humans, due to the large scale of the network. The underlying dynamics and the decision-making process of those algorithms is poorly understood, even by experts in the domain, since the network may consist of dozens of layers and millions of parameters, with non-linear functions connecting them. Moreover, the design of the architecture demands multiple experiments, and is considered more a form of art than a rigorous, methodical process. Users consider the “black-box” nature of the reinforcement learning models as unreliable, and will not always trust their predictions, therefore, they will be reluctant to use it.

This challenge may be addressed by increasing the interpretability of the models, by using Explainable Artificial intelligence, which will allow researchers, developers, and users to better understand the outcomes of the reinforcement learning models while preserving their performance and accuracy, as illustrated in Figure 15. This will add transparency to the operational mechanism of the models, and will allow us to improve them, even in cases where the analysis procedure was faulty but produced the correct result. This concept starts to emerge in recent literature, as may be seen in work [164,165,166].

6.2.2. Neural Architecture Search

Regardless of their remarkable performance, the design of neural network architecture is in itself a major challenge. Due to the complex structure of the network, and the need to tune millions of parameters, designing neural networks is an art, which often relies on a trial and error process. Furthermore, the design and tuning of the network require significant computational power and often has no tight theoretical bounds on computing time and performance. These facts limit the integration of machine learning in general, and reinforcement learning in particular. In light of this challenge, there is a great need to search and develop new efficient methods, requiring low computational resources, to plan and design neural network architectures. A potential solution may be found in the form of Neural Architecture Search [167,168,169]. This technique allows to discover the optimal neural network architecture for a specific task without human intervention.

6.2.3. Physics-Informed Neural Networks

Although model-free methods exhibit remarkable performance in various applications in power systems, they do not take into account the underlying physical constraints and dynamics of real-world systems, which may be crucial for a more accurate and robust solution. To address this gap, an interesting field of study could be the incorporation of Physics-informed neural networks (PINN) into reinforcement learning models [170,171]. The difference between PINN and a fully model-based configuration is that PINN lacks the knowledge of the perfect model of the world, but instead integrates physical laws or dynamics equations into the reinforcement learning framework, guiding agents to make decisions that align with the underlying physics of the system. This approach not only accelerates learning by reducing the sample complexity but also enhances the robustness and interpretability of the learned policies. Implementation involves incorporating physics-based constraints or dynamics equations as additional terms in the reinforcement learning objective function, enabling agents to learn policies that respect the laws of the environment. This method may improve the learning efficiency and generalization ability of the model.

6.2.4. Public Data-Sets

One of the major challenges in utilizing reinforcement learning methods for power systems control problems lies in the lack of real-world, high-quality data [172,173]. Currently, the data existing represents mostly small-scale networks, and may be insufficient for qualitative training or validation. Incorporating new technologies based on IoT devices to collect large-scale data from a variety of scenarios, may enable reinforcement learning algorithms to converge to real-world dynamic models and reliably represent normal behaviors of the system in concern. Nowadays, there are multiple techniques for processing information in real time and efficiently storing it in remote databases [174,175,176]. These abilities may be leveraged to create unifies and robust datasets, which will lead to more resilient and scalable models, with high generalization abilities.

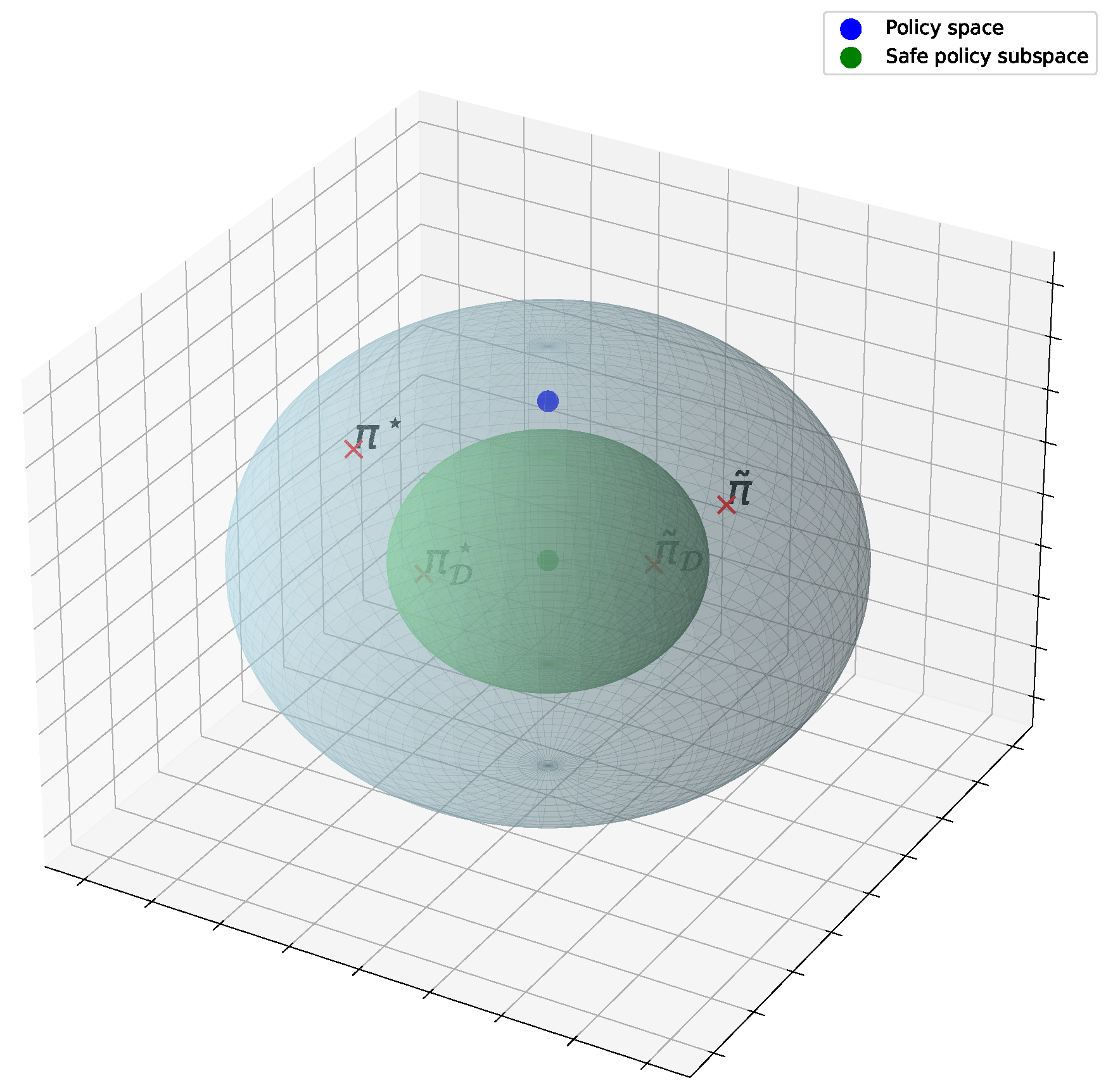
6.2.5. Safety For Real-Time Applications

Safety considerations in critical power systems control using reinforcement learning are paramount due to the high stakes involved in maintaining system stability and preventing failures [177,178,179]. In model-based reinforcement learning, ensuring safety involves accurately modeling the system dynamics and incorporating safety constraints directly into the optimization process to avoid unsafe actions. However, inaccuracies in the model can lead to unsafe decisions. In model-free reinforcement learning, the challenge is even greater as the system learns directly from interaction with the environment, potentially exploring unsafe actions during training. Safe exploration strategies, such as incorporating safety constraints into the reward function are crucial. Both approaches require extensive validation and testing in simulated environments before deployment to ensure that safety is not compromised in real-world operations. As an illustration, one may examine Figure 16, showing the space spanned by the set of all existing policies. This space, naturally, includes the optimal policy

π^{*}

, and its approximation

\tilde{π}

. Focusing now on the subset of all policies that ensure safe system operation we may denote by

π_{C}^{*}

the optimal constrained policy that ensure stable behavior, and by

\tilde{π_{C}}

its approximation. The goal should be, in our opinion, to develop approaches that guide the training process to occur within this safe operation subspace.

Edge AI

Edge AI refers to the deployment of artificial intelligence algorithms and models that operate directly on edge devices, which are located close to or at the source of data generation [180,181,182]. Such edge devices can include smartphones, IoT devices, sensors, cameras, and other embedded systems. By processing data locally, Edge AI reduces the need for constant communication with central cloud servers, leading to several significant benefits, among which is low latency, since processing data on the edge of a network minimizes delays, thus enabling real-time decision-making and responses, which are crucial for applications like autonomous vehicles, industrial automation, and healthcare monitoring. Another benefit is the reduced bandwidth usage. Since data is processed locally, only the most relevant information needs to be transmitted to the cloud, reducing the amount of data sent over networks and easing bandwidth constraints. Moreover, enhanced privacy and security is achieved by keeping data processing local, which means sensitive information does not have to be sent to external servers, thereby reducing the risk of data breaches and enhancing privacy. Additionally, this contributes to reliability, since edge AI systems can continue to function even when there is limited or no internet connectivity, ensuring continuous operation in remote or network-constrained environments. Lastly, scalability is also achieved, since distributed processing across numerous edge devices can lead to better scalability, as the computational load is spread out rather than concentrated in centralized servers.

7. Conclusions

A comprehensive understanding of the differences between model-based and model-free reinforcement learning approaches is important for effectively addressing optimal control problems in the power systems domain. As is evident by the review above, each approach has unique strengths and limitations, and their applications can vary significantly depending on the specific characteristics and requirements of the problem at hand. Model-based RL, which leverages predefined models of environmental dynamics, enables efficient learning which is guided by domain knowledge, and faster convergence, making it well-suited for tasks like grid stability and control, where continuous state spaces and predictable dynamics are common. Conversely, model-free RL does not require a model of the environment and learns optimal policies through direct interaction, making it ideal for applications characterized by high complexity, dynamic changes, and high uncertainty, such as energy management in buildings, electric vehicle charging, and energy storage management that support renewable sources integration. Understanding these trade-offs may allow researchers and practitioners to tailor RL strategies to specific demands, improving the efficiency and robustness of power systems, while facilitating the integration of emerging technologies and renewable energy sources.

In this review, we chose to focus on recent papers that employ both model-based and model-free reinforcement learning paradigms, to study methods and techniques for the solution of optimal control problems in modern power systems. We highlight five application areas: energy market management, grid stability and control, energy management in buildings, electrical vehicles, and energy storage systems. One central conclusion is that model-based solutions are better adapted for control problems with a clear mathematical structure, mostly seen in physical applications such as voltage control for grid stability. On the contrary, for applications with complicated underlying statistical structures, such as optimizing energy costs in buildings, are better suited for model-free approaches which rely solely on aggregated data, and do not require any prior knowledge of the system. However, they do require a large-scale dataset to learn from, which often does not exist. Another important aspect covered in this work is the challenges and limitations of both model-based and model-free approaches when implemented in optimal control problems of power systems. While an emerging and exciting field of study, there are a few obstacles to overcome before reinforcement learning solutions can be used as feasible and reliable solutions in real-world problems, including standardization, safety during training, and generalization ability.

Author Contributions

Conceptualization, E.G. and R.M.; software, E.G.; validation, E.G., R.M, Y.L. and S.K.; writing—original draft preparation, E.G. I.S, A.B, E.S and S.K.N; writing—review and editing, E.G., R.M, Y.L., J.B. and S.K.; visualization, J.B.; supervision, Y.L. and S.K; project administration, L.K.; Funding Acquisition J.B. All authors have read and agreed to the published version of the manuscript.

Funding

The work of J. Belikov was partly supported by the Estonian Research Council grant PRG1463.

Institutional Review Board Statement

Not applicable.

Data Availability Statement

No data was used in this study.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:

RL	Reinforcement learning
MDP	Markov decision process
EM	Energy market
GSAC	Grid stability and control
BEM	Building energy management
EV	Electric vehicle
ESS	Energy storage system
PV	Photovoltaic
MG	Micro-grid
DR	Demand-response
ET	Energy trading
AC	Actor-critic & varitations
PG	Policy gradient & varitations
QL	Q-learning & varitations

References

Schneider, N. Population growth, electricity demand and environmental sustainability in Nigeria: Insights from a vector auto-regressive approach. International Journal of Environmental Studies 2022, 79, 149–176. [CrossRef]
Begum, R.A.; Sohag, K.; Abdullah, S.M.S.; Jaafar, M. CO2 emissions, energy consumption, economic and population growth in Malaysia. Renewable and Sustainable Energy Reviews 2015, 41, 594–601. [CrossRef]
Rahman, M.M. Exploring the effects of economic growth, population density and international trade on energy consumption and environmental quality in India. International Journal of Energy Sector Management 2020-10-08, 14, 1177–1203. [CrossRef]
Comello, S.; Reichelstein, S.; Sahoo, A. The road ahead for solar PV power. Renewable and Sustainable Energy Reviews 2018, 92, 744–756. [CrossRef]
Fathima, A.H.; Palanisamy, K. Energy storage systems for energy management of renewables in distributed generation systems. Energy Management of Distributed Generation Systems 2016, 157. [CrossRef]
Heldeweg, M.A.; Séverine Saintier. Renewable energy communities as ‘socio-legal institutions’: A normative frame for energy decentralization? Renewable and Sustainable Energy Reviews 2020, 119, 109518. [CrossRef]
Urishev, B. Decentralized Energy Systems, Based on Renewable Energy Sources. Applied Solar Energy 2019, 55, 207–212. [CrossRef]
Yaqoot, M.; Diwan, P.; Kandpal, T.C. Review of barriers to the dissemination of decentralized renewable energy systems. Renewable and Sustainable Energy Reviews 2016, 58, 477–490. [CrossRef]
Avancini, D.B.; Rodrigues, J.J.; Martins, S.G.; Rabêlo, R.A.; Al-Muhtadi, J.; Solic, P. Energy meters evolution in smart grids: A review. Journal of Cleaner Production 2019, 217, 702–715. [CrossRef]
Alotaibi, I.; Abido, M.A.; Khalid, M.; Savkin, A.V. A Comprehensive Review of Recent Advances in Smart Grids: A Sustainable Future with Renewable Energy Resources. Energies 2020, 13, e25705. [CrossRef]
Alimi, O.A.; Ouahada, K.; Abu-Mahfouz, A.M. A Review of Machine Learning Approaches to Power System Security and Stability. IEEE Access 2020, 8, 113512–113531. [CrossRef]
Krause, T.; Ernst, R.; Klaer, B.; Hacker, I.; Henze, M. Cybersecurity in Power Grids: Challenges and Opportunities. Sensors 2021, 21. [CrossRef]
Yohanandhan, R.V.; Elavarasan, R.M.; Manoharan, P.; Mihet-Popa, L. Cyber-Physical Power System (CPPS): A Review on Modeling, Simulation, and Analysis With Cyber Security Applications. IEEE Access 2020, 8, 151019–151064. [CrossRef]
Guerin, T.F. Evaluating expected and comparing with observed risks on a large-scale solar photovoltaic construction project: A case for reducing the regulatory burden. Renewable and Sustainable Energy Reviews 2017, 74, 333–348. [CrossRef]
Garcia, A.; Alzate, J.; Barrera, J. Regulatory design and incentives for renewable energy. Journal of Regulatory Economics 2011, 41, 315–336. [CrossRef]
Glavic, M. (Deep) Reinforcement learning for electric power system control and related problems: A short review and perspectives. Annual Reviews in Control 2019, 48, 22–35. [CrossRef]
Perera, A.; Kamalaruban, P. Applications of reinforcement learning in energy systems. Renewable and Sustainable Energy Reviews 2021, 137, 110618. [CrossRef]
Al-Saadi, M.; Al-Greer, M.; Short, M. Reinforcement Learning-Based Intelligent Control Strategies for Optimal Power Management in Advanced Power Distribution Systems: A Survey. Energies 2023, 16. [CrossRef]
Chen, X.; Qu, G.; Tang, Y.; Low, S.; Li, N. Reinforcement Learning for Selective Key Applications in Power Systems: Recent Advances and Future Challenges. IEEE Transactions on Smart Grid 2022, 13, 2935–2958. [CrossRef]
Sutton, R.S.; Barto, A.G. Reinforcement learning: An introduction; MIT press, 2018.
Graesser, L.; Keng, W. Foundations of Deep Reinforcement Learning: Theory and Practice in Python; Addison-Wesley data and analytics series, Addison-Wesley, 2020.
Qiang, W.; Zhongli, Z. Reinforcement learning model, algorithms and its application. International Conference on Mechatronic Science, Electric Engineering and Computer (MEC); , 2011; pp. 1143–1146. [CrossRef]
Zhang, K.; Yang, Z.; Başar, T., Multi-Agent Reinforcement Learning: A Selective Overview of Theories and Algorithms. In Handbook of Reinforcement Learning and Control; Springer International Publishing: Cham, 2021; pp. 321–384. [CrossRef]
Moerland, T.M.; Broekens, J.; Plaat, A.; Jonker, C.M. Model-based Reinforcement Learning: A Survey. Foundations and Trends in Machine Learning 2023, 16, 1–118. [CrossRef]
Huang, Q. Model-based or model-free, a review of approaches in reinforcement learning. 2020 International Conference on Computing and Data Science (CDS); , 2020; pp. 219–221. [CrossRef]
Freed, B.; Wei, T.; Calandra, R.; Schneider, J.; Choset, H. Unifying Model-Based and Model-Free Reinforcement Learning with Equivalent Policy Sets. Reinforcement Learning Journal 2024, 1, 283–301.
Bayón, L.; Grau, J.; Ruiz, M.; Suárez, P. A comparative economic study of two configurations of hydro-wind power plants. Energy 2016, 112, 8–16. [CrossRef]
Riffonneau, Y.; Bacha, S.; Barruel, F.; Ploix, S. Optimal power flow management for grid connected PV systems with batteries. IEEE Transactions on sustainable energy 2011, 2, 309–320. [CrossRef]
Powell, W.B. Approximate Dynamic Programming: Solving the curses of dimensionality; John Wiley & Sons, 2007.
Zargari, N.; Ofir, R.; Chowdhury, N.R.; Belikov, J.; Levron, Y. An Optimal Control Method for Storage Systems With Ramp Constraints, Based on an On-Going Trimming Process. IEEE Transactions on Control Systems Technology 2023, 31, 493–496. [CrossRef]
García, C.E.; Prett, D.M.; Morari, M. Model predictive control: Theory and practice—A survey. Automatica 1989, 25, 335–348. [CrossRef]
Schwenzer, M.; Ay, M.; Bergs, T.; Abel, D. Review on model predictive control: An engineering perspective - The International Journal of Advanced Manufacturing Technology; SpringerLink, 2021. [Accessed 13-05-2024].
Morari, M.; Garcia, C.E.; Prett, D.M. Model predictive control: Theory and practice. IFAC Proceedings Volumes 1988, 21, 1–12. [CrossRef]
Agarwal, A.; Kakade, S.M.; Lee, J.D.; Mahajan, G. On the Theory of Policy Gradient Methods: Optimality, Approximation, and Distribution Shift. Journal of Machine Learning Research 2021, 22, 1–76. [CrossRef]
Sanayha, M.; Vateekul, P. Model-based deep reinforcement learning for wind energy bidding. International Journal of Electrical Power & Energy Systems 2022, 136, 107625. [CrossRef]
Wolgast, T.; Nieße, A. Approximating Energy Market Clearing and Bidding With Model-Based Reinforcement Learning. ArXiv 2023, abs/2303.01772. [CrossRef]
Sanayha, M.; Vateekul, P. Model-Based Approach on Multi-Agent Deep Reinforcement Learning With Multiple Clusters for Peer-To-Peer Energy Trading. IEEE Access 2022, 10, 127882–127893. [CrossRef]
He, Q.; Wang, J.; Shi, R.; He, Y.; Wu, M. Enhancing renewable energy certificate transactions through reinforcement learning and smart contracts integration. Scientific Reports 2024, 14. [CrossRef]
Zou, Y.; Wang, Q.; Xia, Q.; Chi, Y.; Lei, C.; Zhou, N. Federated reinforcement learning for Short-Time scale operation of Wind-Solar-Thermal power network with nonconvex models. International Journal of Electrical Power & Energy Systems 2024, 158, 109980. [CrossRef]
Nanduri, V.; Das, T.K. A Reinforcement Learning Model to Assess Market Power Under Auction-Based Energy Pricing. IEEE Transactions on Power Systems 2007, 22, 85–95. [CrossRef]
Cai, W.; Kordabad, A.B.; Gros, S. Energy management in residential microgrid using model predictive control-based reinforcement learning and Shapley value. Engineering Applications of Artificial Intelligence 2023, 119, 105793. [CrossRef]
Ojand, K.; Dagdougui, H. Q-Learning-Based Model Predictive Control for Energy Management in Residential Aggregator. IEEE Transactions on Automation Science and Engineering 2022, 19, 70–81. [CrossRef]
company, N.P. Nord Pool wholesale electricity market data, 2024. [Online] Available https://data.nordpoolgroup.com/auction/day-ahead/prices?deliveryDate=latest&currency=EUR&aggregation=Hourly&deliveryAreas=AT, Accessed September 19, 2024.
company, A. Australia gird data, 2024. [Online] Available https://www.ausgrid.com.au/Industry/Our-Research/Data-to-share/Average-electricity-use, Accessed September 19, 2024.
Chinese listed companies, C. Carbon emissions data, 2024. [Online] Available https://www.nature.com/articles/s41598-024-60527-3/tables/1, Accessed September 19, 2024.
Hiskens, I. IEEE PES task force on benchmark systems for stability controls, 2013.
company, E. Belgium grid data, 2024. [Online] Available https://www.elia.be/en/grid-data/, Accessed September 19, 2024.
company, C. Chicago electricity price data, 2024. [Online] Available https://hourlypricing.comed.com/live-prices/, Accessed September 19, 2024.
Huang, R.; Chen, Y.; Yin, T.; Li, X.; Li, A.; Tan, J.; Yu, W.; Liu, Y.; Huang, Q. Accelerated Derivative-Free Deep Reinforcement Learning for Large-Scale Grid Emergency Voltage Control. IEEE Transactions on Power Systems 2022, 37, 14–25. [CrossRef]
Hossain, R.R.; Yin, T.; Du, Y.; Huang, R.; Tan, J.; Yu, W.; Liu, Y.; Huang, Q. Efficient learning of power grid voltage control strategies via model-based Deep Reinforcement Learning - machine learning. SpringerLink 2023, 113, 2675–2700. [CrossRef]
Cao, D.; Zhao, J.; Hu, W.; Ding, F.; Yu, N.; Huang, Q.; Chen, Z. Model-free voltage control of active distribution system with PVs using surrogate model-based deep reinforcement learning. Applied Energy 2022, 306, 117982. [CrossRef]
Huang, Q.; Huang, R.; Hao, W.; Tan, J.; Fan, R.; Huang, Z. Adaptive Power System Emergency Control Using Deep Reinforcement Learning. IEEE Transactions on Smart Grid 2020, 11, 1171–1182. [CrossRef]
Duan, J.; Yi, Z.; Shi, D.; Lin, C.; Lu, X.; Wang, Z. Reinforcement-Learning-Based Optimal Control of Hybrid Energy Storage Systems in Hybrid AC–DC Microgrids. IEEE Transactions on Industrial Informatics 2019, 15, 5355–5364. [CrossRef]
Totaro, S.; Boukas, I.; Jonsson, A.; Cornélusse, B. Lifelong control of off-grid microgrid with model-based reinforcement learning. Energy 2021, 232, 121035. [CrossRef]
Yan, Z.; Xu, Y. Real-Time Optimal Power Flow: A Lagrangian Based Deep Reinforcement Learning Approach. IEEE Transactions on Power Systems 2020, 35, 3270–3273. [CrossRef]
Zhang, H.; Yue, D.; Dou, C.; Xie, X.; Li, K.; Hancke, G.P. Resilient Optimal Defensive Strategy of TSK Fuzzy-Model-Based Microgrids’ System via a Novel Reinforcement Learning Approach. IEEE Transactions on Neural Networks and Learning Systems 2023, 34, 1921–1931. [CrossRef]
Huang, Q.; Huang, R.; Hao, W.; Tan, J.; Fan, R.; Huang, Z. Adaptive Power System Emergency Control Using Deep Reinforcement Learning. IEEE Transactions on Smart Grid 2020, 11, 1171–1182. [CrossRef]
Aghaei, J.; Niknam, T.; Azizipanah-Abarghooee, R.; Arroyo, J.M. Scenario-based dynamic economic emission dispatch considering load and wind power uncertainties. International Journal of Electrical Power & Energy Systems 2013, 47, 351–367. [CrossRef]
Zhang, H.; Yue, D.; Xie, X.; Dou, C.; Sun, F. Gradient decent based multi-objective cultural differential evolution for short-term hydrothermal optimal scheduling of economic emission with integrating wind power and photovoltaic power. Energy 2017, 122, 748–766. [CrossRef]
Zhang, Z.; Zhang, C.; Lam, K.P. A deep reinforcement learning method for model-based optimal control of HVAC systems. SURFACE at Syracuse University 2018. [CrossRef]
Zhang, Z.; Chong, A.; Pan, Y.; Zhang, C.; Lam, K.P. Whole building energy model for HVAC optimal control: A practical framework based on deep reinforcement learning. Energy and Buildings 2019, 199, 472–490. [CrossRef]
Chen, B.; Cai, Z.; Bergés, M. Gnu-rl: A precocial reinforcement learning solution for building hvac control using a differentiable mpc policy. Proceedings of the 6th ACM international conference on systems for energy-efficient buildings, cities, and transportation; , 2019; pp. 316–325.
Drgoňa, J.; Picard, D.; Kvasnica, M.; Helsen, L. Approximate model predictive building control via machine learning. Applied Energy 2018, 218, 199–216. [CrossRef]
Arroyo, J.; Manna, C.; Spiessens, F.; Helsen, L. Reinforced model predictive control (RL-MPC) for building energy management. Applied Energy 2022, 309, 118346. [CrossRef]
Drgoňa, J.; Tuor, A.; Skomski, E.; Vasisht, S.; Vrabie, D. Deep learning explicit differentiable predictive control laws for buildings. IFAC-PapersOnLine 2021, 54, 14–19. [CrossRef]
Kowli, A.; Mayhorn, E.; Kalsi, K.; Meyn, S.P. Coordinating dispatch of distributed energy resources with model predictive control and Q-learning. Coordinated Science Laboratory Report no. UILU-ENG-12-2204, DC-256 2012.
Bianchi, C.; Fontanini, A. TMY3 Weather Data for ComStock and ResStock, 2021. [Online] Available https://data.nrel.gov/submissions/156, Accessed September 19, 2024.
Blum, D.; Arroyo, J.; Huang, S.; Drgoňa, J.; Jorissen, F.; Walnum, H.T.; Chen, Y.; Benne, K.; Vrabie, D.; Wetter, M.; others. Building optimization testing framework (BOPTEST) for simulation-based benchmarking of control strategies in buildings. Journal of Building Performance Simulation 2021, 14, 586–610. [CrossRef]
company, N. Wind data, 2024. [Online] Available https://www.nrel.gov/wind/data-tools.html, Accessed September 19, 2024.
Lee, H.; Cha, S.W. Energy management strategy of fuel cell electric vehicles using model-based reinforcement learning with data-driven model update. IEEE Access 2021, 9, 59244–59254.
Chiş, A.; Lundén, J.; Koivunen, V. Reinforcement learning-based plug-in electric vehicle charging with forecasted price. IEEE Transactions on Vehicular Technology 2016, 66, 3674–3684.
Zhang, F.; Yang, Q.; An, D. CDDPG: A deep-reinforcement-learning-based approach for electric vehicle charging control. IEEE Internet of Things Journal 2020, 8, 3075–3087.
Cui, L.; Wang, Q.; Qu, H.; Wang, M.; Wu, Y.; Ge, L. Dynamic pricing for fast charging stations with deep reinforcement learning. Applied Energy 2023, 346, 121334.
Xing, Q.; Xu, Y.; Chen, Z.; Zhang, Z.; Shi, Z. A graph reinforcement learning-based decision-making platform for real-time charging navigation of urban electric vehicles. IEEE Transactions on Industrial Informatics 2022, 19, 3284–3295.
Qian, T.; Shao, C.; Wang, X.; Shahidehpour, M. Deep reinforcement learning for EV charging navigation by coordinating smart grid and intelligent transportation system. IEEE transactions on smart grid 2019, 11, 1714–1723.
Vandael, S.; Claessens, B.; Ernst, D.; Holvoet, T.; Deconinck, G. Reinforcement learning of heuristic EV fleet charging in a day-ahead electricity market. IEEE Transactions on Smart Grid 2015, 6, 1795–1805.
Jin, J.; Xu, Y. Optimal policy characterization enhanced actor-critic approach for electric vehicle charging scheduling in a power distribution network. IEEE Transactions on Smart Grid 2020, 12, 1416–1428.
Qian, J.; Jiang, Y.; Liu, X.; Wang, Q.; Wang, T.; Shi, Y.; Chen, W. Federated Reinforcement Learning for Electric Vehicles Charging Control on Distribution Networks. IEEE Internet of Things Journal 2023.
Wang, Y.; Lin, X.; Pedram, M. Accurate component model based optimal control for energy storage systems in households with photovoltaic modules. 2013 IEEE Green Technologies Conference (GreenTech); , 2013; pp. 28–34. [CrossRef]
Gao, Y.; Li, J.; Hong, M. Machine Learning Based Optimization Model for Energy Management of Energy Storage System for Large Industrial Park. Processes 2021, 9. [CrossRef]
Liu, T.; Zou, Y.; Liu, D.; Sun, F. Reinforcement learning of adaptive energy management with transition probability for a hybrid electric tracked vehicle. IEEE Transactions on Industrial Electronics 2015, 62, 7837–7846. [CrossRef]
Kong, Z.; Zou, Y.; Liu, T. Implementation of real-time energy management strategy based on reinforcement learning for hybrid electric vehicles and simulation validation. PloS one 2017, 12, e0180491. [CrossRef]
Hu, X.; Liu, T.; Qi, X.; Barth, M. Reinforcement learning for hybrid and plug-in hybrid electric vehicle energy management: Recent advances and prospects. IEEE Industrial Electronics Magazine 2019, 13, 16–25. [CrossRef]
Yan, Z.; Xu, Y.; Wang, Y.; Feng, X. Deep reinforcement learning-based optimal data-driven control of battery energy storage for power system frequency support. IET Generation, Transmission & Distribution 2020, 14, 6071–6078. [CrossRef]
Wang, Y.; Lin, X.; Pedram, M. Adaptive control for energy storage systems in households with photovoltaic modules. IEEE Transactions on Smart Grid 2014, 5, 992–1001.
Zhang, H.; Li, J.; Hong, M. Machine learning-based energy system model for tissue paper machines. Processes 2021, 9, 655.
Wang, Y.; Lin, X.; Pedram, M. A Near-Optimal Model-Based Control Algorithm for Households Equipped With Residential Photovoltaic Power Generation and Energy Storage Systems. IEEE Transactions on Sustainable Energy 2016, 7, 77–86. [CrossRef]
company, N. Measurement and Instrumentation Data Center, 2021. [Online] Available https://midcdmz.nrel.gov/apps/sitehome.pl?site=LMU, Accessed September 19, 2024.
company, B. Baltimore load profile data, 2021. [Online] Available https://supplier.bge.com/electric/load/profiles.asp, Accessed September 19, 2024.
Liu, T.; Zou, Y.; Liu, D.; Sun, F. Reinforcement learning–based energy management strategy for a hybrid electric tracked vehicle. Energies 2015, 8, 7243–7260. [CrossRef]
Baah, G.K.; Podgurski, A.; Harrold, M.J. The Probabilistic Program Dependence Graph and Its Application to Fault Diagnosis. IEEE Transactions on Software Engineering 2010, 36, 528–545. [CrossRef]
Ye, Y.; Qiu, D.; Wu, X.; Strbac, G.; Ward, J. Model-Free Real-Time Autonomous Control for a Residential Multi-Energy System Using Deep Reinforcement Learning. IEEE Transactions on Smart Grid 2020, 11, 3068–3082. [CrossRef]
Zhang, S.; May, D.; Gül, M.; Musilek, P. Reinforcement learning-driven local transactive energy market for distributed energy resources. Energy and AI 2022, 8, 100150. [CrossRef]
Bose, S.; Kremers, E.; Mengelkamp, E.M.; Eberbach, J.; Weinhardt, C. Reinforcement learning in local energy markets. Energy Informatics 2021, 4, 7. [CrossRef]
Li, J.; Wang, C.; Wang, H. Attentive Convolutional Deep Reinforcement Learning for Optimizing Solar-Storage Systems in Real-Time Electricity Markets. IEEE Transactions on Industrial Informatics 2024, 20, 7205–7215. [CrossRef]
Li, X.; Luo, F.; Li, C. Multi-agent deep reinforcement learning-based autonomous decision-making framework for community virtual power plants. Applied Energy 2024, 360, 122813. [CrossRef]
Ye, Y.; Papadaskalopoulos, D.; Yuan, Q.; Tang, Y.; Strbac, G. Multi-Agent Deep Reinforcement Learning for Coordinated Energy Trading and Flexibility Services Provision in Local Electricity Markets. IEEE Transactions on Smart Grid 2023, 14, 1541–1554. [CrossRef]
Chen, T.; Su, W. Indirect Customer-to-Customer Energy Trading With Reinforcement Learning. IEEE Transactions on Smart Grid 2019, 10, 4338–4348. [CrossRef]
Fang, X.; Zhao, Q.; Wang, J.; Han, Y.; Li, Y. Multi-agent Deep Reinforcement Learning for Distributed Energy Management and Strategy Optimization of Microgrid Market. Sustainable Cities and Society 2021, 74, 103163. [CrossRef]
Harrold, D.J.; Cao, J.; Fan, Z. Renewable energy integration and microgrid energy trading using multi-agent deep reinforcement learning. Applied Energy 2022, 318, 119151. [CrossRef]
Gao, S.; Xiang, C.; Yu, M.; Tan, K.T.; Lee, T.H. Online Optimal Power Scheduling of a Microgrid via Imitation Learning. IEEE Transactions on Smart Grid 2022, 13, 861–876. [CrossRef]
Chen, D.; Irwin, D. SunDance: Black-box Behind-the-Meter Solar Disaggregation. Proceedings of the Eighth International Conference on Future Energy Systems; , 2017; e-Energy ’17, p. 45–55. [CrossRef]
Mishra, A.K.; Cecchet, E.; Shenoy, P.J.; Albrecht, J.R. Smart: An Open Data Set and Tools for Enabling Research in Sustainable Homes, 2012. [Online] Available https://api.semanticscholar.org/CorpusID:6562225, Accessed September 19, 2024.
company, A. Electricity distribution and prices data, 2024. [Online] Available https://aemo.com.au/en/energy-systems/electricity/national-electricity-market-nem/data-nem/data-dashboard-nem, Accessed September 19, 2024.
Operator, C.I.S. California electrical power system operational data, 2024. [Online] Available https://www.caiso.com/, Accessed September 19, 2024.
Duan, J.; Shi, D.; Diao, R.; Li, H.; Wang, Z.; Zhang, B.; Bian, D.; Yi, Z. Deep-Reinforcement-Learning-Based Autonomous Voltage Control for Power Grid Operations. IEEE Transactions on Power Systems 2020, 35, 814–817. [CrossRef]
Cao, D.; Zhao, J.; Hu, W.; Yu, N.; Ding, F.; Huang, Q.; Chen, Z. Deep Reinforcement Learning Enabled Physical-Model-Free Two-Timescale Voltage Control Method for Active Distribution Systems. IEEE Transactions on Smart Grid 2022, 13, 149–165. [CrossRef]
Diao, R.; Wang, Z.; Shi, D.; Chang, Q.; Duan, J.; Zhang, X. Autonomous Voltage Control for Grid Operation Using Deep Reinforcement Learning. 2019 IEEE Power & Energy Society General Meeting (PESGM); , 2019; pp. 1–5. [CrossRef]
Hadidi, R.; Jeyasurya, B. Reinforcement Learning Based Real-Time Wide-Area Stabilizing Control Agents to Enhance Power System Stability. IEEE Transactions on Smart Grid 2013, 4, 489–497. [CrossRef]
Chen, C.; Cui, M.; Li, F.; Yin, S.; Wang, X. Model-Free Emergency Frequency Control Based on Reinforcement Learning. IEEE Transactions on Industrial Informatics 2021, 17, 2336–2346. [CrossRef]
Zhao, J.; Li, F.; Mukherjee, S.; Sticht, C. Deep Reinforcement Learning-Based Model-Free On-Line Dynamic Multi-Microgrid Formation to Enhance Resilience. IEEE Transactions on Smart Grid 2022, 13, 2557–2567. [CrossRef]
Du, Y.; Li, F. Intelligent Multi-Microgrid Energy Management Based on Deep Neural Network and Model-Free Reinforcement Learning. IEEE Transactions on Smart Grid 2020, 11, 1066–1076. [CrossRef]
Zhou, Y.; Lee, W.; Diao, R.; Shi, D. Deep Reinforcement Learning Based Real-time AC Optimal Power Flow Considering Uncertainties. Journal of Modern Power Systems and Clean Energy 2022, 10, 1098–1109. [CrossRef]
Cao, D.; Hu, W.; Xu, X.; Wu, Q.; Huang, Q.; Chen, Z.; Blaabjerg, F. Deep Reinforcement Learning Based Approach for Optimal Power Flow of Distribution Networks Embedded with Renewable Energy and Storage Devices. Journal of Modern Power Systems and Clean Energy 2021, 9, 1101–1110. [CrossRef]
Birchfield, A.B.; Xu, T.; Gegner, K.M.; Shetye, K.S.; Overbye, T.J. Grid Structural Characteristics as Validation Criteria for Synthetic Networks. IEEE Transactions on Power Systems 2017, 32, 3258–3265. [CrossRef]
Chen, C.; Zhang, K.; Yuan, K.; Zhu, L.; Qian, M. Novel Detection Scheme Design Considering Cyber Attacks on Load Frequency Control. IEEE Transactions on Industrial Informatics 2018, 14, 1932–1941. [CrossRef]
Qiu, S.; Li, Z.; Li, Z.; Li, J.; Long, S.; Li, X. Model-free control method based on reinforcement learning for building cooling water systems: Validation by measured data-based simulation. Energy and Buildings 2020, 218, 110055. [CrossRef]
Zhang, X.; Chen, Y.; Bernstein, A.; Chintala, R.; Graf, P.; Jin, X.; Biagioni, D. Two-stage reinforcement learning policy search for grid-interactive building control. IEEE Transactions on Smart Grid 2022, 13, 1976–1987. [CrossRef]
Zhang, X.; Biagioni, D.; Cai, M.; Graf, P.; Rahman, S. An Edge-Cloud Integrated Solution for Buildings Demand Response Using Reinforcement Learning. IEEE Transactions on Smart Grid 2021, 12, 420–431. [CrossRef]
Mocanu, E.; Mocanu, D.C.; Nguyen, P.H.; Liotta, A.; Webber, M.E.; Gibescu, M.; Slootweg, J.G. On-Line Building Energy Optimization Using Deep Reinforcement Learning. IEEE Transactions on Smart Grid 2019, 10, 3698–3708. [CrossRef]
Wei, T.; Wang, Y.; Zhu, Q. Deep reinforcement learning for building HVAC control. Proceedings of the 54th annual design automation conference 2017; , 2017; pp. 1–6. [CrossRef]
Yu, L.; Sun, Y.; Xu, Z.; Shen, C.; Yue, D.; Jiang, T.; Guan, X. Multi-Agent Deep Reinforcement Learning for HVAC Control in Commercial Buildings. IEEE Transactions on Smart Grid 2021, 12, 407–419. [CrossRef]
Shin, M.; Kim, S.; Kim, Y.; Song, A.; Kim, Y.; Kim, H.Y. Development of an HVAC system control method using weather forecasting data with deep reinforcement learning algorithms. Building and Environment 2024, 248, 111069. [CrossRef]
Gao, G.; Li, J.; Wen, Y. DeepComfort: Energy-Efficient Thermal Comfort Control in Buildings Via Reinforcement Learning. IEEE Internet of Things Journal 2020, 7, 8472–8484. [CrossRef]
Dey, S.; Marzullo, T.; Zhang, X.; Henze, G. Reinforcement learning building control approach harnessing imitation learning. Energy and AI 2023, 14, 100255. [CrossRef]
Ye, Y.; Qiu, D.; Wu, X.; Strbac, G.; Ward, J. Model-Free Real-Time Autonomous Control for a Residential Multi-Energy System Using Deep Reinforcement Learning. IEEE Transactions on Smart Grid 2020, 11, 3068–3082. [CrossRef]
Ruelens, F.; Claessens, B.J.; Quaiyum, S.; De Schutter, B.; Babuška, R.; Belmans, R. Reinforcement Learning Applied to an Electric Water Heater: From Theory to Practice. IEEE Transactions on Smart Grid 2018, 9, 3792–3800. [CrossRef]
weather service, T. Weather data, 2024. [Online] Available https://en.tutiempo.net/climate/ws-486980.html, Accessed September 19, 2024.
company, D. Thermal comfort field measurements, 2024. [Online] Available https://datadryad.org/stash/dataset/, Accessed September 19, 2024. [CrossRef]
company, P.S. Consumption data, 2024. [Online] Available https://www.pecanstreet.org/, Accessed September 19, 2024.
company, E. Commercial Buildings Energy Consumption Data, 2024. [Online] Available https://www.eia.gov/consumption/commercial/data/2012/bc/cfm/b6.php, Accessed September 19, 2024.
Ulrike Jordan, K.V. Hot-Water Profiles, 2001. [Online] Available https://sel.me.wisc.edu/trnsys/trnlib/iea-shc-task26/iea-shc-task26-load-profiles-description-jordan.pdf, Accessed September 19, 2024.
Zhang, C.; Liu, Y.; Wu, F.; Tang, B.; Fan, W. Effective charging planning based on deep reinforcement learning for electric vehicles. IEEE Transactions on Intelligent Transportation Systems 2020, 22, 542–554.
Wang, R.; Chen, Z.; Xing, Q.; Zhang, Z.; Zhang, T. A modified rainbow-based deep reinforcement learning method for optimal scheduling of charging station. Sustainability 2022, 14, 1884.
Wang, S.; Bi, S.; Zhang, Y.A. Reinforcement learning for real-time pricing and scheduling control in EV charging stations. IEEE Transactions on Industrial Informatics 2019, 17, 849–859.
Qian, T.; Shao, C.; Li, X.; Wang, X.; Shahidehpour, M. Enhanced coordinated operations of electric power and transportation networks via EV charging services. IEEE Transactions on Smart Grid 2020, 11, 3019–3030.
Zhao, Z.; Lee, C.K. Dynamic pricing for EV charging stations: A deep reinforcement learning approach. IEEE Transactions on Transportation Electrification 2021, 8, 2456–2468.
Sadeghianpourhamami, N.; Deleu, J.; Develder, C. Definition and evaluation of model-free coordination of electrical vehicle charging with reinforcement learning. IEEE Transactions on Smart Grid 2019, 11, 203–214.
Yeom, K. Model predictive control and deep reinforcement learning based energy efficient eco-driving for battery electric vehicles. Energy Reports 2022, 8, 34–42.
Dorokhova, M.; Martinson, Y.; Ballif, C.; Wyrsch, N. Deep reinforcement learning control of electric vehicle charging in the presence of photovoltaic generation. Applied Energy 2021, 301, 117504.
Wen, Z.; O’Neill, D.; Maei, H. Optimal demand response using device-based reinforcement learning. IEEE Transactions on Smart Grid 2015, 6, 2312–2324.
Lee, S.; Choi, D.H. Reinforcement learning-based energy management of smart home with rooftop solar photovoltaic system, energy storage system, and home appliances. Sensors 2019, 19, 3937.
Yan, Z.; Xu, Y.; Wang, Y.; Feng, X. Deep reinforcement learning-based optimal data-driven control of battery energy storage for power system frequency support. IET Generation, Transmission & Distribution 2020, 14, 6071–6078. [CrossRef]
Cao, J.; Harrold, D.; Fan, Z.; Morstyn, T.; Healey, D.; Li, K. Deep Reinforcement Learning-Based Energy Storage Arbitrage With Accurate Lithium-Ion Battery Degradation Model. IEEE Transactions on Smart Grid 2020, 11, 4513–4521. [CrossRef]
Bui, V.H.; Hussain, A.; Kim, H.M. Double Deep Q -Learning-Based Distributed Operation of Battery Energy Storage System Considering Uncertainties. IEEE Transactions on Smart Grid 2020, 11, 457–469. [CrossRef]
Bui, V.H.; Hussain, A.; Kim, H.M. Q-Learning-Based Operation Strategy for Community Battery Energy Storage System (CBESS) in Microgrid System. Energies 2019, 12. [CrossRef]
Chen, T.; Su, W. Local Energy Trading Behavior Modeling With Deep Reinforcement Learning. IEEE Access 2018, 6, 62806–62814. [CrossRef]
Liu, F.; Liu, Q.; Tao, Q.; Huang, Y.; Li, D.; Sidorov, D. Deep reinforcement learning based energy storage management strategy considering prediction intervals of wind power. International Journal of Electrical Power & Energy Systems 2023, 145, 108608. [CrossRef]
Zhou, H.; Erol-Kantarci, M. Correlated deep q-learning based microgrid energy management. 2020 IEEE 25th International Workshop on Computer Aided Modeling and Design of Communication Links and Networks (CAMAD); , 2020; pp. 1–6. [CrossRef]
Ji, Y.; Wang, J.; Xu, J.; Fang, X.; Zhang, H. Real-time energy management of a microgrid using deep reinforcement learning. Energies 2019, 12, 2291. [CrossRef]
Liu, T.; Hu, X. A bi-level control for energy efficiency improvement of a hybrid tracked vehicle. IEEE Transactions on Industrial Informatics 2018, 14, 1616–1625. [CrossRef]
government, U. UK wholesale electricity market prices, 2024. [Online] Available https://tradingeconomics.com/united-kingdom/electricity-price, Accessed September 19, 2024.
Lopes, J.P.; Hatziargyriou, N.; Mutale, J.; Djapic, P.; Jenkins, N. Integrating distributed generation into electric power systems: A review of drivers, challenges and opportunities. Electric Power Systems Research 2007, 77, 1189–1203. [CrossRef]
Pfenninger, S.; Hawkes, A.; Keirstead, J. Energy systems modeling for twenty-first century energy challenges. Renewable and Sustainable Energy Reviews 2014, 33, 74–86. [CrossRef]
Nafi, N.S.; Ahmed, K.; Gregory, M.A.; Datta, M. A survey of smart grid architectures, applications, benefits and standardization. Journal of Network and Computer Applications 2016, 76, 23–36. [CrossRef]
Ustun, T.S.; Hussain, S.M.S.; Kirchhoff, H.; Ghaddar, B.; Strunz, K.; Lestas, I. Data Standardization for Smart Infrastructure in First-Access Electricity Systems. Proceedings of the IEEE 2019, 107, 1790–1802. [CrossRef]
Ren, C.; Xu, Y. Robustness Verification for Machine-Learning-Based Power System Dynamic Security Assessment Models Under Adversarial Examples. IEEE Transactions on Control of Network Systems 2022, 9, 1645–1654. [CrossRef]
Zhang, Z.; Yau, D.K. CoRE: Constrained Robustness Evaluation of Machine Learning-Based Stability Assessment for Power Systems. IEEE/CAA Journal of Automatica Sinica 2023, 10, 557–559. [CrossRef]
Ren, C.; Du, X.; Xu, Y.; Song, Q.; Liu, Y.; Tan, R. Vulnerability Analysis, Robustness Verification, and Mitigation Strategy for Machine Learning-Based Power System Stability Assessment Model Under Adversarial Examples. IEEE Transactions on Smart Grid 2022, 13, 1622–1632. [CrossRef]
Machlev, R.; Zargari, N.; Chowdhury, N.; Belikov, J.; Levron, Y. A review of optimal control methods for energy storage systems - energy trading, energy balancing and electric vehicles. Journal of Energy Storage 2020, 32, 101787. [CrossRef]
Hadidi, R.; Jeyasurya, B. Reinforcement Learning Based Real-Time Wide-Area Stabilizing Control Agents to Enhance Power System Stability. IEEE Transactions on Smart Grid 2013, 4, 489–497. [CrossRef]
Zhou, Y.; Lee, W.; Diao, R.; Shi, D. Deep Reinforcement Learning Based Real-time AC Optimal Power Flow Considering Uncertainties. Journal of Modern Power Systems and Clean Energy 2022, 10, 1098–1109. [CrossRef]
Yan, Z.; Xu, Y. Real-Time Optimal Power Flow: A Lagrangian Based Deep Reinforcement Learning Approach. IEEE Transactions on Power Systems 2020, 35, 3270–3273. [CrossRef]
Machlev, R.; Heistrene, L.; Perl, M.; Levy, K.; Belikov, J.; Mannor, S.; Levron, Y. Explainable Artificial Intelligence (XAI) techniques for energy and power systems: Review, challenges and opportunities. Energy and AI 2022, 9, 100169. [CrossRef]
Zhang, K.; Zhang, J.; Xu, P.D.; Gao, T.; Gao, D.W. Explainable AI in Deep Reinforcement Learning Models for Power System Emergency Control. IEEE Transactions on Computational Social Systems 2022, 9, 419–427. [CrossRef]
Zhang, K.; Zhang, J.; Xu, P.D.; Gao, T.; Gao, D.W. Explainable AI in Deep Reinforcement Learning Models for Power System Emergency Control. IEEE Transactions on Computational Social Systems 2022, 9, 419–427. [CrossRef]
Ren, P.; Xiao, Y.; Chang, X.; Huang, P.y.; Li, Z.; Chen, X.; Wang, X. A Comprehensive Survey of Neural Architecture Search: Challenges and Solutions. ACM Comput. Surv. 2021, 54, 1–34. [CrossRef]
Jalali, S.M.J.; Osório, G.J.; Ahmadian, S.; Lotfi, M.; Campos, V.M.A.; Shafie-khah, M.; Khosravi, A.; Catalão, J.P.S. New Hybrid Deep Neural Architectural Search-Based Ensemble Reinforcement Learning Strategy for Wind Power Forecasting. IEEE Transactions on Industry Applications 2022, 58, 15–27. [CrossRef]
Wang, Q.; Kapuza, I.; Baimel, D.; Belikov, J.; Levron, Y.; Machlev, R. Neural Architecture Search (NAS) for designing optimal power quality disturbance classifiers. Electric Power Systems Research 2023, 223, 109574. [CrossRef]
Huang, B.; Wang, J. Applications of Physics-Informed Neural Networks in Power Systems - A Review. IEEE Transactions on Power Systems 2023, 38, 572–588. [CrossRef]
Misyris, G.S.; Venzke, A.; Chatzivasileiadis, S. Physics-Informed Neural Networks for Power Systems. 2020 IEEE Power & Energy Society General Meeting (PESGM); , 2020; pp. 1–5. [CrossRef]
Sami, N.M.; Naeini, M. Machine learning applications in cascading failure analysis in power systems: A review. Electric Power Systems Research 2024, 232, 110415. [CrossRef]
Miraftabzadeh, S.M.; Foiadelli, F.; Longo, M.; Pasetti, M. A Survey of Machine Learning Applications for Power System Analytics. 2019 IEEE International Conference on Environment and Electrical Engineering and 2019 IEEE Industrial and Commercial Power Systems Europe (EEEIC / I&CPS Europe); , 2019; pp. 1–5. [CrossRef]
Bedi, G.; Venayagamoorthy, G.K.; Singh, R.; Brooks, R.R.; Wang, K.C. Review of Internet of Things (IoT) in Electric Power and Energy Systems. IEEE Internet of Things Journal 2018, 5, 847–870. [CrossRef]
Ngo, V.T.; Nguyen Thi, M.S.; Truong, D.N.; Hoang, A.Q.; Tran, P.N.; Bui, N.A. Applying IoT Platform to Design a Data Collection System for Hybrid Power System. 2021 International Conference on System Science and Engineering (ICSSE); , 2021; pp. 181–184. [CrossRef]
Sayed, H.A.; Said, A.M.; Ibrahim, A.W. Smart Utilities IoT-Based Data Collection Scheduling. Arabian Journal for Science and Engineering 2024, 49, 2909–2923. [CrossRef]
Chen, X.; Qu, G.; Tang, Y.; Low, S.; Li, N. Reinforcement Learning for Selective Key Applications in Power Systems: Recent Advances and Future Challenges. IEEE Transactions on Smart Grid 2022, 13, 2935–2958. [CrossRef]
Li, H.; He, H. Learning to Operate Distribution Networks With Safe Deep Reinforcement Learning. IEEE Transactions on Smart Grid 2022, 13, 1860–1872. [CrossRef]
Vu, T.L.; Mukherjee, S.; Yin, T.; Huang, R.; Tan, J.; Huang, Q. Safe Reinforcement Learning for Emergency Load Shedding of Power Systems. 2021 IEEE Power & Energy Society General Meeting (PESGM); , 2021; pp. 1–5. [CrossRef]
Gooi, H.B.; Wang, T.; Tang, Y. Edge Intelligence for Smart Grid: A Survey on Application Potentials. CSEE Journal of Power and Energy Systems 2023, 9, 1623–1640. [CrossRef]
Sodhro, A.H.; Pirbhulal, S.; de Albuquerque, V.H.C. Artificial Intelligence-Driven Mechanism for Edge Computing-Based Industrial Applications. IEEE Transactions on Industrial Informatics 2019, 15, 4235–4243. [CrossRef]
Lv, L.; Wu, Z.; Zhang, L.; Gupta, B.B.; Tian, Z. An Edge-AI Based Forecasting Approach for Improving Smart Microgrid Efficiency. IEEE Transactions on Industrial Informatics 2022, 18, 7946–7954. [CrossRef]

Figure 1. Reinforcement learning diagram, adopted from [20].

Figure 2. System configuration, consisting of a generator, a load and a storage device.

Figure 3. Desicion making sequential process for grid-connected storage system.

Figure 4. Visualization of the difference between model-based and model-free decision-making, adopted from [20].

Figure 5. Model-free and model-based approaches.

Figure 6. Generalized policy iteration, where “greedy” operator means that the policy is greedy with respect to the value function. Value and policy interact until they are optimal and become consistent with each other, adopted from [20].

Figure 7. Interaction of evaluation and improvement of the policy, adopted from [20].

Figure 8. State space representation and policy modeling in various power systems applications under model-based paradigm.

Figure 9. State space representation and policy modeling in various power systems applications under model-free paradigm.

Figure 10. Year-wise distribution of publications on reinforcement learning techniques in energy and power system applications. Figure (a) presents articles regarding both model-based and model-free paradigms, while figure (b) shows papers focusing on model-free approach.

Figure 11. Classification of papers based on the type of application and the reinforcement learning approach. Figure (a) presents application division for model-based paradigm, and figure (b) shows the application division for model-free paradigm.

Figure 12. Classification of papers based on the type of algorithm and the reinforcement learning approach. Figure (a) presents algorithm division for model-based paradigm, and figure (b) shows the algorithm division for model-free paradigm.

Figure 13. Visualization of the relation between the selected reinforcement learning algorithm and optimal control problems in power systems. (a) presents the relation between control problem and algorithm for model-based paradigm, and (b) shows the relation between control problem and algorithm for model-based paradigm.

Figure 14. Exponential growth of problem dimensions as a function of number of storage devices controlled.

Figure 15. Explainable reinforcement learning models are easier to trust by power experts and other shareholders.

Figure 16. Safe operational subspace containing robust policies.

Table 1. Examples of MDP formulation for power systems control problems.

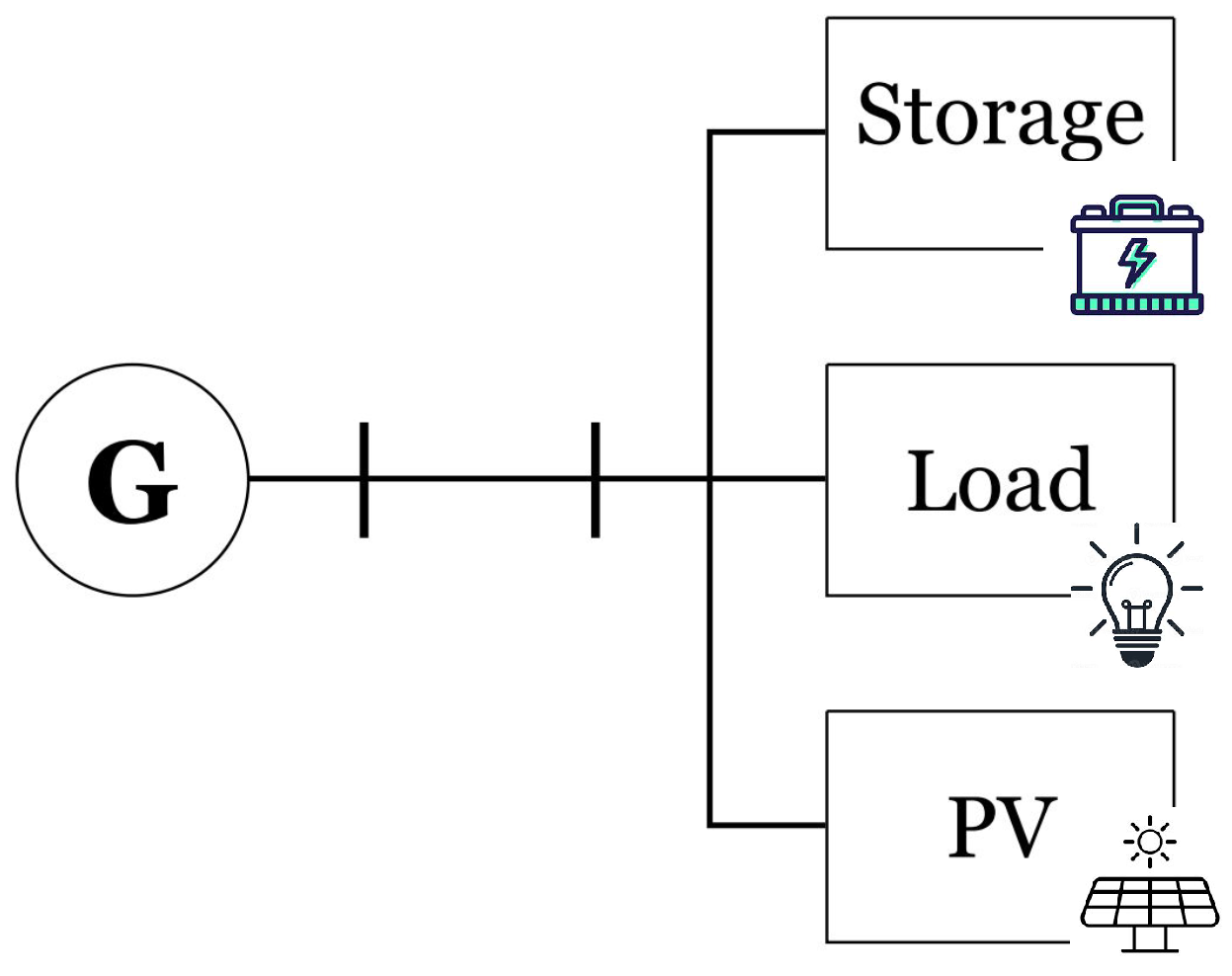
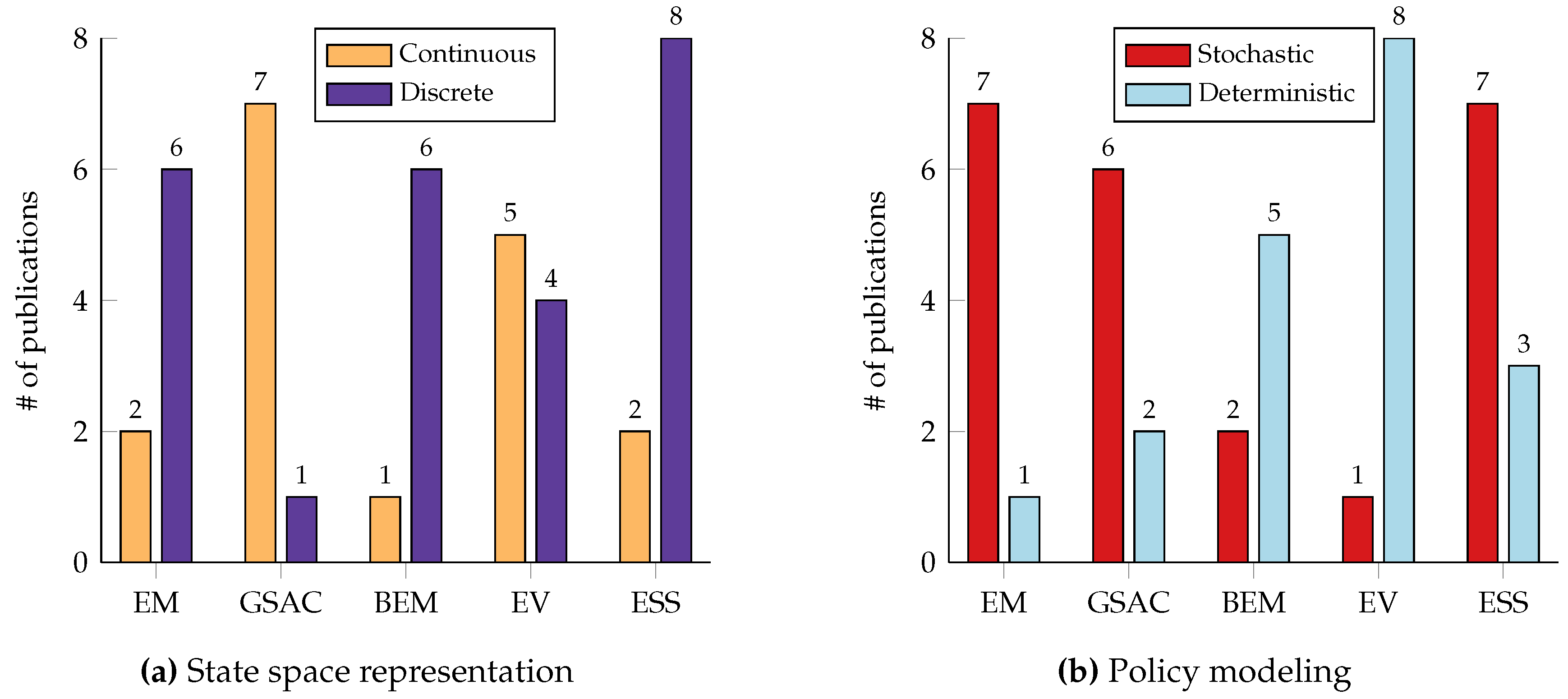
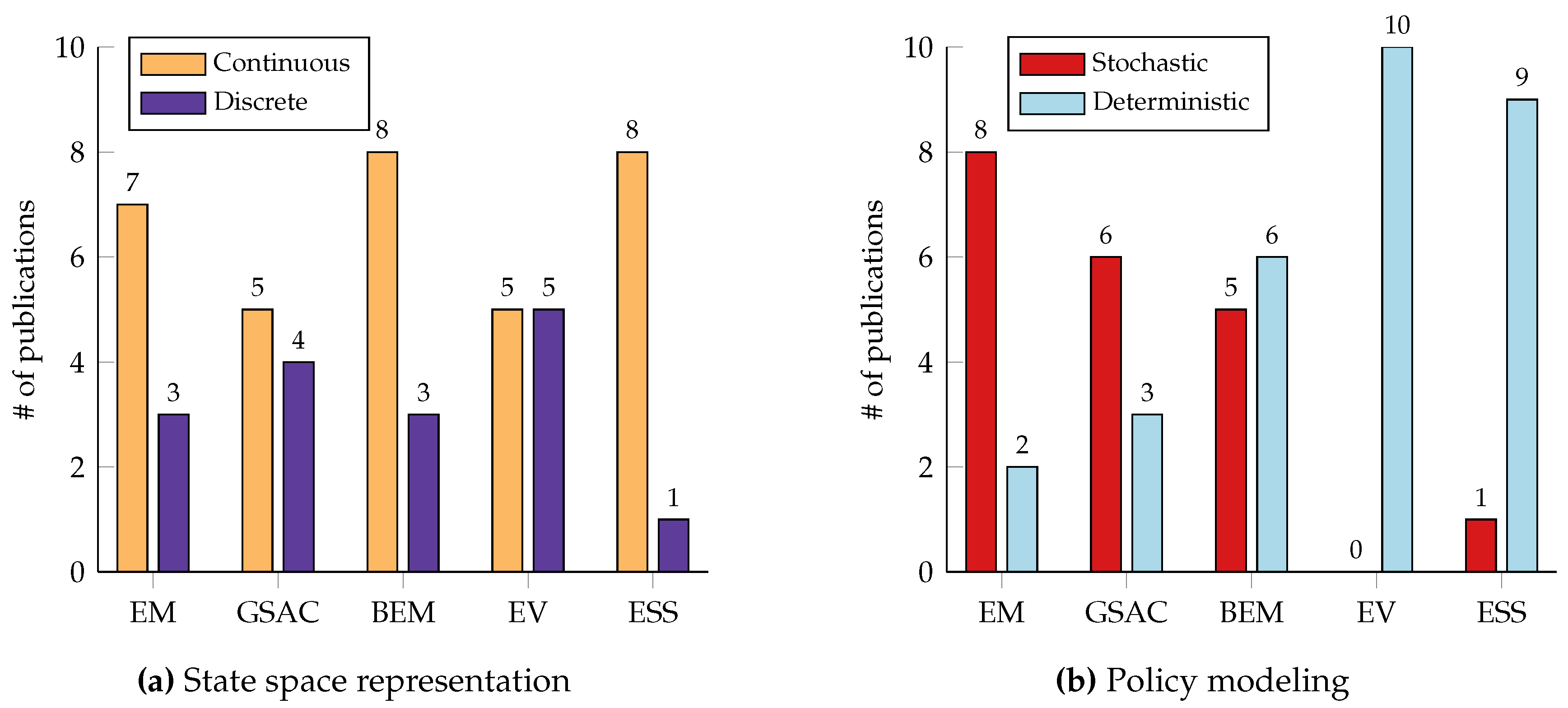
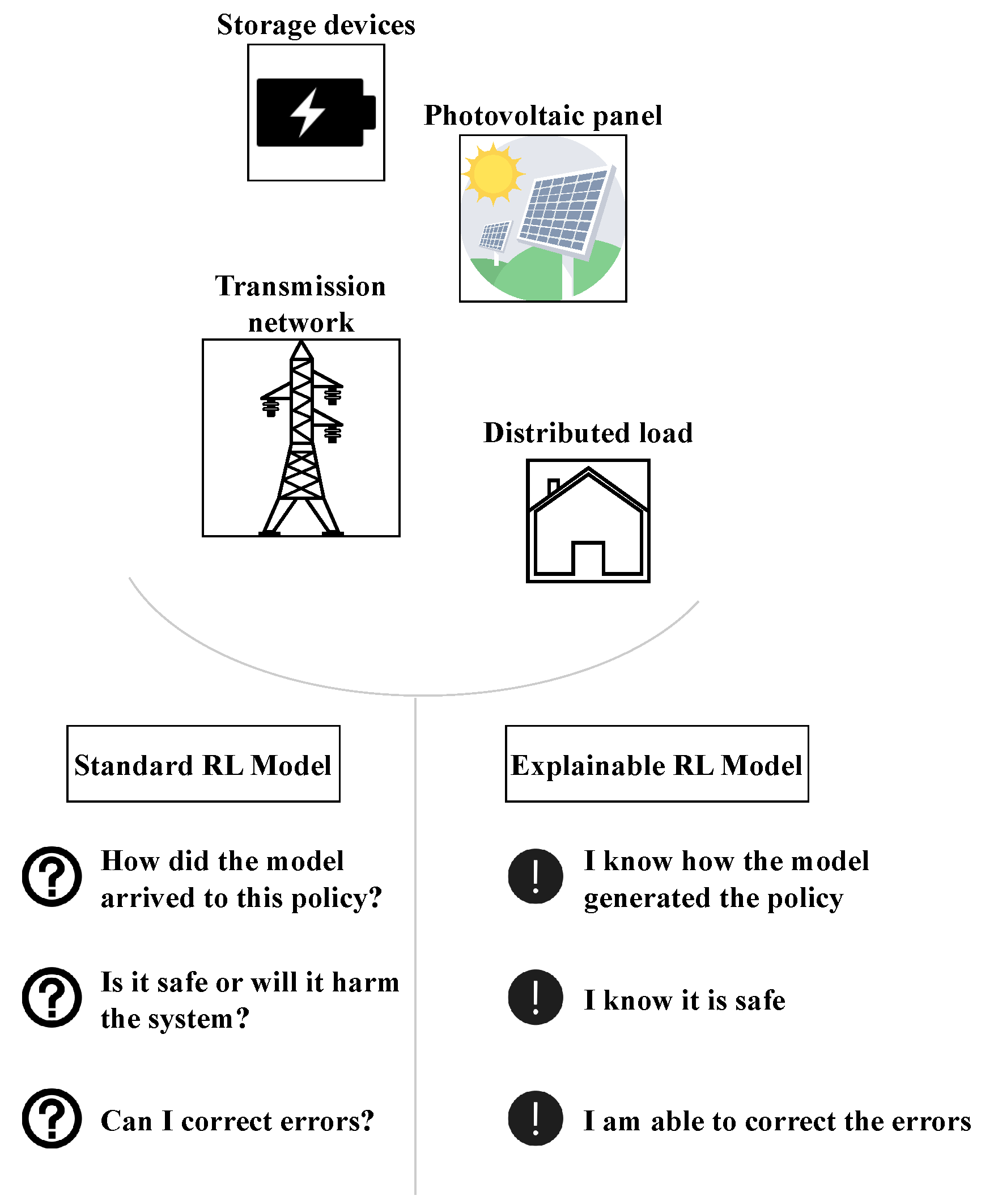
Problem	States	Actions	Reward
EM	System operator decides upon a power flow distribution	Firms set their bid	The firms’ rewards are the net profit achieved
GSAC	Voltage levels at different nodes	Adjusting the output of power generators	Cost of deviating from nominal voltage levels
BEM	Indoor temperature and humidity levels	Adjusting thermostat setpoints for heating and cooling	Cost of electricity
EV	Traffic conditions and route information	Selecting a route based on traffic and charging station availability	Cost of charging, considering electricity prices and charging station fees
ESS	Battery state of charge and current consumer power demand	The controller decides how much power to produce using the generator	The power generation cost the controller must pay

Table 2. Model-based approaches for different applications in energy market management and the MDP setting.

Ref.	Application	Algorithm	State-space	Policy	Dataset & simulator
[35]	ET	AC	Continuous	Deterministic	[43]
[37]	ET	AC	Discrete	Stochastic	[44]
[38]	ET	QL	Continuous	Deterministic	[45]
[40]	ET	Other	Discrete	Stochastic	Simulated data
[41]	ET	PG, Other	Continuous	Deterministic	Real data
[36]	Dispatch	PG	Continuous	Deterministic	Simulated data
[39]	Dispatch	AC, Other	Continuous	Deterministic	[46,47]
[42]	DR, Microgrid	QL	Continuous	Deterministic	Real data, [48]

Table 3. Model-based approaches in different power systems grid stability and control applications and the MDP setting.

Ref.	Application	Algorithm	State-space	Policy	Dataset
[49]	Voltage control	Other	Continuous	Stochastic	IEEE 300, IEEE 9, [57]
[50]	Voltage control	Other	Continuous	Stochastic	IEEE 300
[51]	Voltage control	AC	Continuous	Deterministic	IEEE 123
[52]	Voltage control	QL	Continuous	Stochastic	IEEE 39, [57]
[53]	Microgrid	Other	Discrete	Deterministic	HIL platform “dSPACE MicroLabBox”
[54]	Microgrid	PPO	Continuous	Stochastic	Empirical measurments
[56]	Power flow, Microgrid	AC	Continuous	Stochastic	[58,59]
[55]	Power flow	PG	Continuous	Stochastic	IEEE 118

Table 4. Model-based approaches for different applications in energy management in buildings and the MDP setting.

Ref.	Application	Algorithm	State-space	Policy	Dataset
[60]	HVAC	AC	Discrete	Deterministic	[67]
[61]	HVAC	AC	Continuous	Stochastic	Real data [Upon request]
[63]	HVAC	Other	Discrete	Deterministic	Simulated data
[65]	HVAC	Other	Discrete	Deterministic	Simulated data
[64]	HVAC	QL, Other	Discrete	Deterministic	[68]
[62]	HVAC	PPO	Discrete	Stochastic	“EnergyPlus”
[66]	Dispatch	QL, Other	Discrete	Deterministic	[69], Simulated data

Table 5. Model-based approaches for different applications in electrical vehicles and the MDP setting.

Ref.	Application	Algorithm	State-space	Policy	Dataset
[70]	Power flow	QL	Discrete	Deterministic	MATLAB simulation
[71]	Charge control	QL	Mixed	Deterministic	Historic prices
[72]	Charge control	PG	Continuous	Deterministic	Simulated
[73]	Charge control	AC	Continuous	Deterministic	Simulated
[74]	Charge control	QL	Discrete	Deterministic	Open street map, ChargeBar
[75]	Charge control	QL	Discrete	Deterministic	Simulated
[77]	Charge scheduling	AC	Continuous	Deterministic	Simulated
[78]	Charge control	AC	Continuous	Stochastic	Historic prices
[76]	Load balancing	QL	Continuous	Deterministic	Simulated

Table 6. Model-based approaches for different applications in energy storage management and the MDP setting.

Ref.	Application	Algorithm	State-space	Policy	Dataset
[87]	Smart Grid	QL	Discrete	Stochastic	Simulated data
[79]	Smart Grid	Other	Discrete	Stochastic	Simulated data
[85]	Smart Grid	Other	Discrete	Stochastic	[88,89]
[81]	EV	QL	Discrete	Stochastic	Simulated data
[90]	EV	QL, Other	Discrete	Deterministic	Simulated data
[82]	EV	QL	Continuous	Deterministic	Simulated data
[83]	EV	QL, Other	Discrete	Stochastic	Simulated data
[80]	Renewable energy	Other [91]	Discrete	Stochastic	Simulated data
[84]	Battery ESS, frequency support	PG, AC	Continuous	Deterministic	Simulated data
[86]	Energy system modeling	Other	Discrete	Stochastic	Simulated data

Table 7. Model-free approaches for different applications in energy market management and the MDP setting.

Ref.	Application	Algorithm	State-space	Policy	Dataset
[92]	ET	PG	Continuous	Deterministic	Real data
[93]	ET	QL	Discrete	Deterministic	[102,103]
[95]	ET	PG	Continuous	Deterministic	[104]
[96]	ET	AC	Continuous	Stochastic	Simulated data
[97]	ET	QL	Continuous	Deterministic	Real data
[99]	Microgrid, Dispatch	QL	Continuous	Stochastic	[105]
[100]	Microgrid	PG	Continuous	Stochastic	Simulated data
[101]	Microgrid	Other	Continuous	Deterministic	Real and Simulated data

Table 8. Model-free approaches in different power systems grid stability and control applications and the MDP setting.

Ref.	Application	Algorithm	State-space	Policy	Dataset
[106]	Voltage control	PG	Continuous	Stochastic	Powerflow & Short circuit Assessment Tool (PSAT), 200-bus system [115]
[107]	Voltage control	AC	Continuous	Stochastic	IEEE 33-, 123-, and 342-node systems
[108]	Voltage control	QL	Discrete	Stochastic	IEEE 14-bus system
[109]	Frequency control	QL	Discrete	Deterministic	Simulted data
[110]	Frequency control	PG	Discrete	Deterministic	Kundur’s 4-unit-13 bus system, New England 68-bus system, [116]
[111]	Microgrid	QL	Continuous	Stochastic	7-bus system and the IEEE 123-bus system
[112]	Microgrid	Other	Discrete	Deterministic	Simulated data
[113]	Power flow	PPO	Continuous	Stochastic	Illinois 200-bus system
[114]	Power flow	PPO	Continuous	Stochastic	Simulated data, West Denmark wind data

Table 9. Model-free approaches for different applications in energy management in buildings and the MDP setting.

Ref.	Application	Algorithm	State-space	Policy	Dataset
[117]	HVAC	QL	Discrete	Deterministic	Simulated data
[125]	HVAC	PPO	Continuous	Deterministic	“EnergyPlus”
[121]	HVAC	QL	Continuous	Stochastic	“EnergyPlus”
[123]	HVAC	QL	Discrete	Deterministic	Simulated data
[124]	HVAC	PG	Continuous	Stochastic	[128,129]
[122]	HVAC	AC	Continuous	Stochastic	[130]
[118]	HVAC,DR	PPO	Continuous	Deterministic	“EnergyPlus”
[120]	HVAC, DR	QL, PG	Continuous	Stochastic	[130]
[119]	DR	QL, PG	Discrete	Deterministic	[131]
[126]	Dispatch	PG	Continuous	Deterministic	Simulated data
[127]	Dispatch	QL	Continuous	Stochastic	[47,132]

Table 10. Model-free approaches for different applications in electrical vehicles and the MDP setting.

Ref.	Application	Algorithm	State-space	Policy	Dataset
[133]	Scheduling	QL	Discrete	Deterministic	“Open street map”, “ChargeBar”
[134]	Scheduling	QL	Continuous	Deterministic	Simulated
[135]	Scheduling	Other	Continuous	Deterministic	Historic data
[136]	Scheduling	Other	Continuous	Deterministic	Simulated
[138]	Scheduling	QL	Discrete	Deterministic	“ElaadNL”
[137]	Cost reduction	Other	Mixed	Deterministic	Simulated
[139]	Cost reduction	QL	Continuous	Deterministic	Simulated
[142]	Cost reduction	QL	Discrete	Deterministic	Simulated
[141]	DR	QL	Discrete	Deterministic	Simulated
[140]	SoC control	QL, PG	Continuous	Deterministic	Historic data

Table 11. Model-free approaches for different applications in energy storage management and the MDP setting.

Ref.	Application	Algorithm	State-space	Policy	Dataset
[145]	Microgrids	QL	Continuous	Deterministic	Simulated data
[146]	Microgrids	QL	Discrete	Deterministic	Simulated data
[149]	Microgrids	QL	Continuous	Deterministic	Simulated data
[150]	Microgrids	QL	Continuous	Deterministic	[105]
[148]	Frequency control	Other	Continuous	Deterministic	Simulated data
[143]	Frequency control	PG, AC	Continuous	Deterministic	Simulated data
[144]	Energy trading	QL	Continuous	Deterministic	[152]
[147]	Energy trading	QL	Continuous	Deterministic	Simulated data
[151]	EV	QL	Continuous	Stochastic	Simulated data

Table 12. Keywords for different application areas of the model-based and model-free paradigms.

RL expressions	Power systems application expressions
“model-based”	“energy market management”
OR	OR
“model learning”	“voltage control”
OR	OR
“model-free”	“frequency control”
OR	OR
“data-driven”	“reactive power control”
AND/OR	OR
“reinforcement learning”	“grid stability”
	OR
	“microgrid”
	OR
	“building energy management”
	OR
	“building”
	OR
	“electrical vehicles”
	OR
	“EV”
	OR
	“energy storage control problems”
	OR
	“battery energy storage system”
	OR
	“local energy trading”

Table 13. Relations [in %] between common reinforcement learning algorithms and optimal control problems, as shown in Figure 13.

	QL		PG		AC		PPO		Other
	MB	MF	MB	MF	MB	MF	MB	MF	MB	MF
ESS	5	7	1	1	0	1	0	0	6	1
EV	5	7	1	1	3	1	0	0	0	2
BEM	2	6	0	4	2	1	1	2	3	0
GSAC	1	3	1	2	2	1	1	2	3	1
EM	2	3	2	3	3	1	0	0	3	2

Table 14. Open challenges for application of RL algorithms in power systems control problems.

Category	Challenges
Lack of standardization	Lack of real-world data for different control tasks in power systems. No qualitative simulator to efficiently integrate between accurate physical models of energy systems and reinforcement learning libraries. No standardized benchmarks algorithms or datasets that represent a quality norm for various reinforcement learning algorithms.
Lack of generalization	Lack of data causes limited generalization ability in model-free algorithms. Complex models in power systems are difficult to learn, thus model-based algorithms converge to inaccurate model, which does not generalize well. As the state or action variables increase, there is an exponential growth in the computational requirements of the model.
Limited safety	Model-free methods produce suboptimal policy due to small acquired data, which may not perform well when unexpected events occur. The complexity of the environment’s dynamics causes model-based algorithms to produce suboptimal policies, jeopardizing the stability of the system when uncertainty is encountered. During training the models focus on exploration and perform mainly random actions, in real-time applications for power systems it may be catastrophic and lead to blackouts.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Reinforcement Learning Model-Based and Model-Free Paradigms for Optimal Control Problems in Power Systems: Comprehensive Review and Future Directions

Abstract

1. Introduction

2. Technical Background on Reinforcement Learning

2.1. Markov Decision Processes

2.2. Model Based and Model Free Reinforcement Learning

2.3. Model Computation

2.3.1. Dynamic Programming

2.3.2. Model Predictive Control (MPC)

2.4. Policy Learning Basic Concepts

2.4.1. Value Function

2.4.2. Policy Iteration

2.4.3. Value Iteration

2.4.4. Policy Gradient

3. Model-Based Paradigm

3.1. Energy Markets Management

3.2. Power Grid Stability and Control

3.3. Building Energy Management

3.4. Electrical Vehicles

3.5. Energy Storage Management

3.6. Prominent Trends

4. Model-Free Paradigms

4.1. Energy Markets Management

4.2. Power Grid Stability and Control

4.3. Building Energy Management

4.4. Electrical Vehicles

4.5. Energy Storage Management

4.6. Prominent Trends

5. Comparison and Discussion

6. Challenges and Future Research Work

6.1. Challenges

6.1.1. Limited Real-World Data And Standardized Tools

6.1.2. Limited Scalability, Generalization, And The Curse Of Dimensionality

6.1.3. Limited Robustness And Safety For Real-Time Applications

6.2. Future Work

6.2.1. Explainability

6.2.2. Neural Architecture Search

6.2.3. Physics-Informed Neural Networks

6.2.4. Public Data-Sets

6.2.5. Safety For Real-Time Applications

7. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Data Availability Statement

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe