Multiplicity Counting Deadtime Corrections for Correlated Neutron Pulse Streams

Vladimir Nizhnik

doi:10.20944/preprints202410.0260.v1

Submitted:

02 October 2024

Posted:

03 October 2024

You are already at the latest version

Abstract

We offer a generalization of the conventionally used dead-time correction formulas, provided by Dytlewski, for neutron multiplicity counting. This aims to take into account the conditional effects of gate opening and in-gate neutron losses, and thus, extends to correlated pulse streams. The provided formulas are simple and include explicitly corrected rates obtained with the conventional method. In the limit of weakly correlated pulses with low count rates the generalized formulas reduce to Dytlewski’s expressions. We also performed the numerical validation of the method by simulating pulse-trains sets, evaluating the generalized dead-time correction accuracy and comparing it to the conventional one.

Keywords:

Neutron multiplicity

;

deadtime correction

;

neutron counter

;

correlated counting

Subject:

Physical Sciences - Nuclear and High Energy Physics

Motivation

For large Pu and mixed oxide items, including the impure ones, when measured with neutron counters, the analysed Pu mass accuracy exhibits significant degradation. In addition to the well understood statistical component, there are substantial biases which increase with item size and impurity level. These deviations we largely attribute to the dead-time effect, and in particular to the dead-time correction when using the conventional method, which relies on assumption that the neutron pulse sequence is of a Poisson type i.e., random.

Background

The raw data of the neutron multiplicity counting is the acquired multiplicity distributions in the reals plus accidentals (RA) and accidentals (A) gates, most commonly, using the shift register technique. For the convention in this article, we use normalized multiplicity distributions denoting them as p and q for the RA and A gate, correspondingly.

The cumulative research work, among which [1,2,3] are recognized as decisive advancements, allow the link between the measured distributions and normalized input1 distributions, denoted P and Q, in the presence of extended (paralyzable) dead-time. Specifically, under assumption that neutron emission-detection is a Poisson type process, [3] provides the transition probability coefficients

C_{n \to m}

from n input pulses to m registered pulses, such that when expressed in linear algebra form:

$p_{m} = \sum_{n = m}^{m a x} C_{n \to m} \cdot P_{n}$	$q_{m} = \sum_{n = m}^{m a x} C_{n \to m} \cdot Q_{n}$	(1)
$C_{n \to m} = \frac{(n - 1)!}{(m - 1)!} \sum_{k = 0}^{n - m} \frac{{(- 1)}^{n - m - k} \cdot {(1 - (n - k - 1) \cdot φ)}^{n}}{(n - m)! \cdot (n - m - k)!}$

Additionally,

C_{n \to 0} = 0^{n}

, where

φ = δ / G

, δ – dead-time parameter, G – gate length

The input distributions P and Q then can be, theoretically, restored by the matrix inversion method. This, however, has two computational obstacles. At first, one can note that the summation terms in the

C_{n \to m}

coefficients formula are alternating in signs while exhibiting quasi-polynomial grows with the (n-m) term. This, when using the standard double precision floating point calculations, limits the adequate precision of calculation by multiplicity histogram range of 25-30, depending on φ value. This is far below the requirement for a conventional shift register with multiplicity range 0 to 255 or 511. However, recently, the Arbitrary Precision Arithmetic engines have become available that can be run on a desktop computer, which allows the calculation of the coefficients with required precision in a time efficient manner.

The second obstacle is that the matrix inversion is an ill-posed problem since the

C_{n \to m}

coefficients vanish for some (n-m) combinations, leading to exploding elements of the inverse matrix. This can be overcome by use of regularization techniques, but introduces certain computational complexity.

Dytlewski in [4] showed that for the factorial moments and multiplicity rates, the dead-time corrections can be calculated in an explicit manner without the need to restore the input distributions. He provided the expressions for dead-time corrected factorial multipliers for the first and second reduced factorial moments:

$α_{n} = 1 + \sum_{k = 0}^{n - 2} (\binom{n - 1}{k + 1}) \frac{{(k + 1)}^{k} φ^{k}}{{(1 - (k + 1) φ)}^{k + 2}}$	$β_{n} = α_{n} - 1 + \sum_{k = 0}^{n - 3} (\binom{n - 1}{k + 2}) \frac{(k + 1) {(k + 2)}^{k} φ^{k}}{{(1 - (k + 2) φ)}^{k + 3}}$	(2)
$n = 2 t o m a x, α_{1} = 1$	${n = 3 t o m a x, β}_{2} = α_{2} - 1$	(2)

And the corrected doubles and triples rates are then calculated as following:

D_{c}^{D y t} = \sum_{n = 1}^{m a x} α_{n} \cdot (p_{n} - q_{n}) \cdot S_{c} \times {C f}_{D}

(3)

T_{c}^{D y t} = (\sum_{n = 2}^{m a x} β_{n} \cdot (p_{n} - q_{n}) - \sum_{n = 1}^{m a x} α_{n} \cdot q_{n} \cdot \sum_{n = 1}^{m a x} α_{n} \cdot (p_{n} - q_{n})) \cdot S_{c} \times {C f}_{T}

(4)

Here, Cf are additional multiplicative factors introduced empirically to correct for observed discrepancies between the theoretical formula and measurement or simulation data, such as in [6] and [7]. Cf is usually assigned as exponential, linear, or polynomial function of measured or corrected count rates with adjustable parameters: e.g.,

e x p (c \cdot S)

or

(1 + c_{1} \cdot S + c_{2} \cdot S^{2} + \dots)

.

Method for Correlated Pulse Streams

Let us consider an instant count rate

S_{n}

, which corresponds to the number of neutrons in the gate at an instance of a trigger, namely for n neutrons in the gate

S_{n} = n / G

. If i is the registered number of neutrons in the gate as a result of a detection process with extended dead-time δ, and the corresponding instant input count rate S_n (n input neutrons in the gate), then their relation can be expressed as:

S_{i} = S_{n} \cdot \exp (- S_{n} \cdot δ)

or

i = n \cdot \exp (- δ \cdot n / G)

The coefficients α_i given in eq. (2) represent dead-time corrected multipliers of the first factorial moment, and with good accuracy, approximates the number of input neutrons in the gate which would result in i registered neutrons:

i ≅ α_{i} \cdot \exp (- δ \cdot α_{i} / G)

(5)

For a more accurate approximation for Dytlewski’s α_i multiplier we modify the above expression as:

i ≅ (α_{i} - 1) \cdot \exp (- δ \cdot α_{i} / G) + 1

(6)

Here one count is excluded from being affected by dead-time, which manifesting the fact that derivations for eq. (1) and (2) were made with the assumption of a gate with free input, meaning the first pulse (if any) in the gate is not affected by dead-time and is always registered.

β_i is the second reduced factorial multiplier, approximated as:

β_{i} ≅ \frac{α_{i} \cdot (α_{i} - 1)}{2}

(7)

For further deductions in this article, we assume the high accidentals approximation, given by

G \cdot S^{2} ≫ D

or

G \cdot S ≫ D / S

where S and D – input singles and doubles rates

i.e. when the accidentals rate is much higher than the reals rate. This is a typical case for large Pu items and/or items with high (α,n) terms, producing high count rates and thus high accidentals, when the dead-time correction accuracy is crucial.

The approach outlined in [1,2,3,4] considers a Poisson type process and treats the dead-time count loss for individual neutrons as independent events. It also implies that the event of real coincidence detection treats loss of the gate opening neutron and the correlated in-gate neutron as independent too, which is applicable only to uncorrelated neutron pulses. An event of coincidence detection occurs when the gate opening neutron is not lost under the condition that the in-gate neutron is also not lost. On average, the coincidence event will undergo higher loss probability under condition (if) the gate opening and the in-gate neutron come from the same fission chain, i.e. when the coincidence is real. This is because the local count rates for both gate opening and in-gate correlated neutrons are higher than average.

It is simple to show that the coincidence counting of neutron pulse streams is a time reversible process, when pre-delay and dead-time are zero. Non-zero pre-delay and dead-time, depending on count rates, introduce certain bias between forward and backword counting schemes. However, this relative bias in forward/backward rates is usually a small fraction of

P / G

and/or

δ \cdot S

, as experimentally shown in [8] with implementation of forward/backward counting electronics. Therefore, we infer that the gate opening neutrons on average undergo the same dead-time loss probability as the neutrons in the RA gate.

Doubles Rate

To account for the difference between reals and accidentals for the doubles rate dead-time correction, we introduce factorial multipliers

\tilde{α}

for the RA gate (

p_{n}

distribution) as

{\tilde{α}}_{n} = a_{n} + {c α}_{n}

where

{c α}_{n}

is a correction term to account for the conditional effects of doubles coincidence counting in the RA gate.

D_{c} = \sum_{n = 1}^{m a x} ({\tilde{α}}_{n} \cdot p_{n} - α_{n} \cdot q_{n}) \cdot S_{c}

(8)

Consider the multiplicity distribution of detected input neutrons

d_{n}

,

n = 1 t o m a x

,

\sum_{i = n}^{m a x} d_{n} = 1

, such that

d_{1}

- relative frequency of events that one neutron from same the chain is detected,

d_{2}

- relative frequency of events that two neutrons from the same chain are detected, etc. We account uncorrelated neutrons, such as (α,n) and random background, as a single neutron chain.

In the case of one input neutron, the gate is opened once with zero correlated neutrons in it. In case of two input neutrons, the gate is opened twice:

-: first: with $f_{d}$ probability of one correlated in-gate neutron, $(1 - f_{d})$ probability of zero correlated in-gate neutrons;
-: second: with zero correlated in-gate neutrons, etc.

f_{d}

is the doubles gate fraction. We assume that neutron origin-to-detection waiting time has an exponential shape. Denoting the fission chain detection rate as R, we can write the measured rate (frequency) of gate opening with presence of dead-time,

F_{m}

.

F_{m} = R \cdot \exp (- S \cdot δ) \cdot (d_{1} + d_{2} \cdot f_{d} \cdot \exp (- \frac{δ}{G}) + d_{2} \cdot (1 - f_{d}) + d_{3} \cdot f_{d}^{2} \cdot \exp (- \frac{2 δ}{G}) + d_{3} \cdot 2 {\cdot f}_{d} \cdot| (1 - f_{d}) \cdot \exp (- \frac{δ}{G}) + d_{3} \cdot {(1 - f_{d})}^{2} + d_{4} \cdot f_{d}^{3} \cdot \exp (- \frac{3 \cdot δ}{G}) + \dots)

Here we use the time reversal property to account for trigger loss probability, e.g., if for an input neutron stream at gate opening instance there are two correlated neutrons in the gate, then the probability that the gate opening count is not lost is

\exp (- (S \cdot δ + 2 δ / G))

, where

S \cdot G

is the average number of accidental input neutrons in the gate. With the high accidental assumption, the multiplicity of the detected input neutron chain

n ≪ G / δ

. Thus, we can limit the Taylor expansion of

\exp (- n \cdot δ / G)

to the first term:

F_{m} = R \cdot \exp (- S \cdot δ) \cdot (\sum_{n = 1}^{m a x} d_{n} \cdot n - \sum_{n = 2}^{m a x} d_{n} \cdot \frac{n \cdot (n - 1)}{2} \cdot f_{d} \cdot \frac{δ}{G})

Recalling that

R \cdot \sum_{n = 1}^{m a x} d_{n} \cdot n = S

and

R \cdot \sum_{n = 2}^{m a x} d_{n} \cdot \frac{n \cdot (n - 1)}{2} \cdot f_{d} = D

we rewrite:

F_{m} = S_{m} = (S - D \cdot δ / G) \cdot \exp (- S \cdot δ)

Applying

\exp (S \cdot δ)

as the correction factor for the singles rate, we can determine the correction term

+ D \cdot δ / G

for the RA gate opening rate due to the conditional probability for reals coincidences counting, thus:

D_{c} = S_{c} \cdot \sum_{n = 1}^{m a x} (α_{n} \cdot p_{n} + D \cdot δ \cdot p_{n} + \frac{D^{2}}{S^{2}} \cdot \frac{δ}{G} \cdot p_{n} - α_{n} \cdot q_{n})

{\tilde{α}}_{n} = α_{n} + D \cdot δ + \frac{D^{2}}{S^{2}} \cdot \frac{δ}{G}

(9)

Substituting input rates with corrected rates in the correction term, we finally obtain:

D_{c} = \frac{1}{1 - S_{c} \cdot δ - \frac{D_{c}}{S_{c}} \cdot \frac{δ}{G}} \cdot \sum_{n = 1}^{m a x} α_{n} \cdot (p_{n} - q_{n}) \cdot S_{c}

(10)

The term

\frac{D_{c}}{S_{c}} \cdot \frac{δ}{G}

is small, and for most practical cases can be omitted. For a more precise result, however, the corrected doubles rate can be calculated iteratively, setting

D_{c} = D_{c}^{D y t}

for the first iteration step.

It is easy to see that the multiplicative term

{(1 - S_{c} \cdot δ)}^{- 1}

brings physical meaning to the correction, since for the extended type dead-time the measured count rate reaches the maximum at

S \cdot δ = 1

and decreases with further input rate increase. This means that in the presence of correlated neutrons, the RA gate will have a smaller number of measured coincidences than the A gate at

S \cdot δ ≳ 1

, and the measured doubles rate turns negative, requiring the negative multiplier for correction. Also, note that this term does not vanish for the case of a weakly correlated (quasi-Poisson) source when the singles count rate is not small, still holding the correction for doubles. This is essential for impure Pu items, where the main neutron source is random.

Triples Rate

Introducing the second reduced factorial multiplier for the RA gate

{\tilde{β}}_{i} ≅ \frac{{\tilde{α}}_{i} \cdot ({\tilde{α}}_{i} - 1)}{2}

, recalling eq.(9) for

\tilde{α}

, and following similar induction reasoning as for the doubles rate, we find:

T_{c} = (\sum_{n = 2}^{m a x} β_{n} \cdot (p_{n} - q_{n}) + \sum_{n = 2}^{m a x} α_{n} \cdot p_{n} \cdot D \cdot δ + \frac{D^{2} \cdot δ^{2}}{2} - \sum_{n = 1}^{m a x} α_{n} \cdot q_{n} \cdot \sum_{n = 1}^{m a x} α_{n} \cdot (p_{n} - q_{n} + D \cdot δ) + T \cdot δ) \cdot S_{c}

Limiting the correction terms by second order, we can further obtain the expression for the corrected triples rate:

T_{c} = \frac{(\sum_{n = 2}^{m a x} β_{n} \cdot (p_{n} - q_{n}) + - \sum_{n = 1}^{m a x} α_{n} \cdot q_{n} \cdot \sum_{n = 1}^{m a x} α_{n} \cdot (p_{n} - q_{n})) \cdot S_{c}}{1 - S_{c} \cdot δ} + D_{c}^{2} \cdot δ + \frac{D_{c}^{2} \cdot S_{c} \cdot δ^{2}}{2}

(11)

Both the obtained doubles and triples rate corrections include explicitly the corrected rates calculated with Dytlewski’s expressions (3) and (4), marked with Dyt superscript in the below formulas.

D_{c} = \frac{D_{c}^{D y t}}{1 - S_{c} \cdot δ - \frac{D_{c}}{S_{c}} \cdot \frac{δ}{G}}

(12)

T_{c} = \frac{T_{c}^{D y t}}{1 - S_{c} \cdot δ} + D_{c}^{2} \cdot δ \cdot (1 + \frac{S_{c} \cdot δ}{2})

(13)

Later in the article we refer to the above equations as the generalized correction formulas. One can see that in the limit of a weakly correlated source and low count rate, they reduce to conventional Dytlewski rates.

Refinements for Factorial Multipliers

As outlined in [9], the count loss probability for the first in-gate input neutron depends on selection of the gate opening time, and for the general case has no closed form. However, from naive intuition and as shown later in the numerical validation section, even the approximate evaluation of the first count loss probability yields more accurate corrections in comparison to the assumption of free input for the gate opening. Under the high accidentals assumption, the waiting time distribution can be approximated by that of a Poisson process. We thus can obtain the additive correction

ε_{n}

for

α_{n}

, to account for first in-gate input neutron loss probability, using eq. (5) and (6) as follows:

(α_{n} - 1) \cdot \exp (- α_{n} \cdot φ) + 1 = (α_{n} + ε_{n}) \cdot \exp (- (α_{n} + ε_{n}) \cdot φ)

Given

ε_{n} ≪ α_{n}

and considering

α_{n} \cdot φ

is not a large fraction of unity, we get the updates for

α_{n}

and

β_{n}

:

ε_{n} ≅ α_{n} \cdot φ \cdot (1 + α_{n} \cdot φ) β_{n}^{*} = β_{n} \cdot {(1 + ε_{n} / α_{n})}^{2} α_{n}^{*} = α_{n} + ε_{n}

(14)

Numerical Validation

To validate the obtained dead-time correction formulas, we performed high fidelity neutron pulse train simulations with and without dead-time effects, with statistics (depending on test purpose) of up to 10¹¹ total counts per pulse train. This enabled the precise evaluation of count rates and corresponding dead-time correction factors even when the modelled neutron correlation term was much smaller than random.

We simulated three sets of 300 pulse trains in each as following:

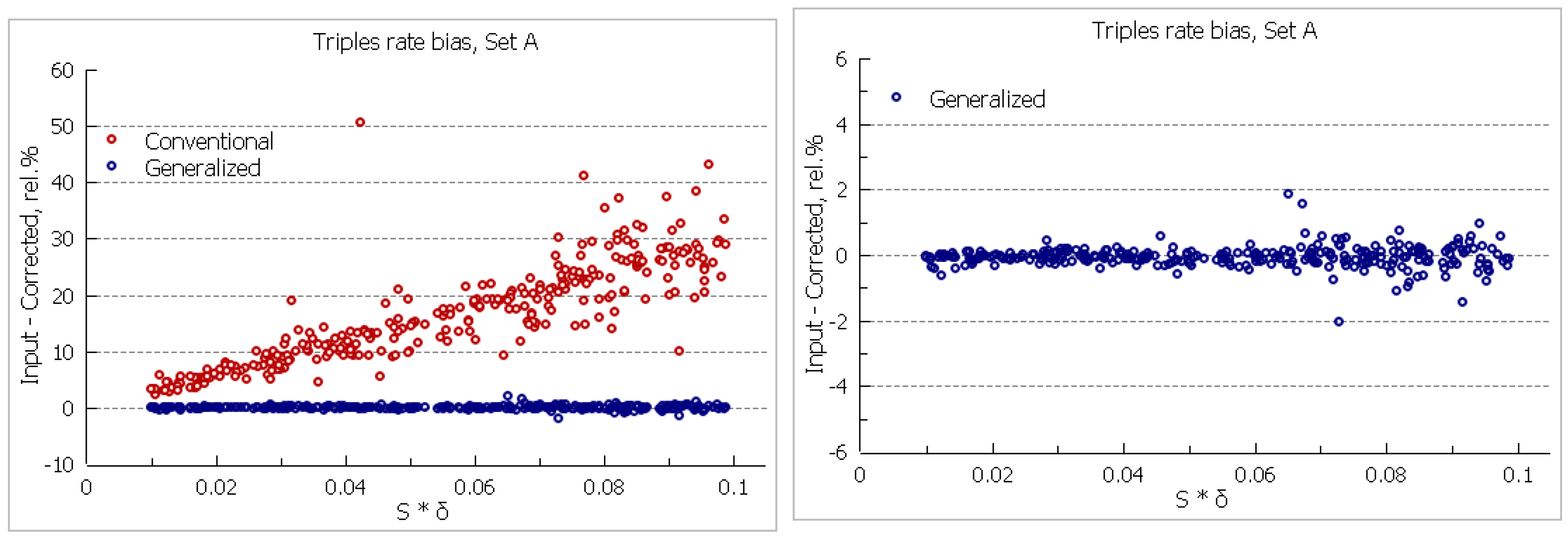
Set A Requiring that dead-time corrections should hold for any input neutron multiplicity (irrespective of the underlying physics of neutron emission and multiplication), for the first set of pulse trains, we modelled arbitrary input multiplicities with combinations from 1 to 5 neutrons, including cases when all neutrons come with the same multiplicity. The input count rate and neutron waiting time since origin were also varied. We also applied various combinations of dead-time

δ

, gate length G and pre-delay P for the pulse trains processing. The simulations were performed with statistics of at least 5∙10¹⁰ counts per pulse train.

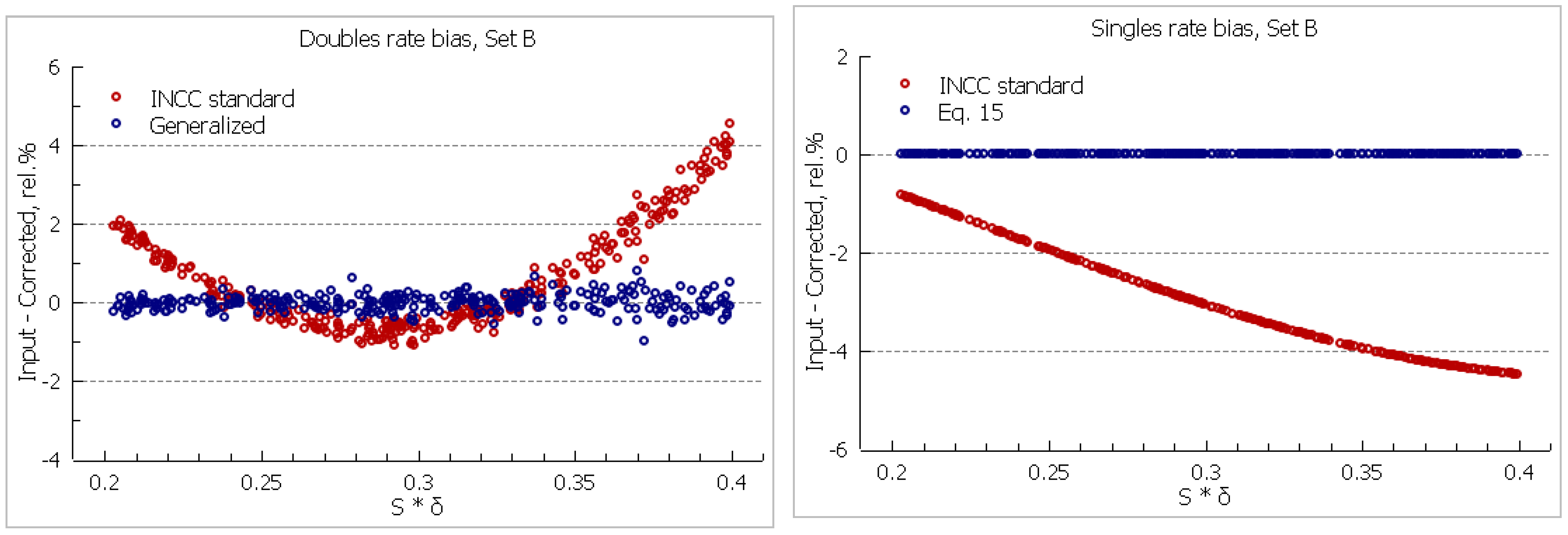
Set B In neutron coincidence counting of Pu items, the dead-time effects can be massive, with

S \cdot δ

values up to 0.4-0.5. This pulse train set is intended for simulation of typical Pu canister assay system [9] measurements with high count rates, by modelling the fission, multiplication and detection process for items of various Pu mass, with detection efficiency

ε = 14.5 %

, die-away time τ = 50 μs,

δ = 180 n s

,

G = 64

μs and P = 4.5 μs. The counting statistics are equivalent to a 30 min measurement time.

Set C For this set, we simulated pulse trains of Pu item measurements with various Pu mass, multiplication and alpha values with Plutonium scrap multiplicity counter (PSMC) [9], with counting statistics equivalent to a 30 min measurement time, with an intent to evaluate the performance of dead-time corrections for typical passive multiplicity measurements. For the modelling we used the detector parameters of one of the PSMC used for safeguards verification:

ε = 54 %

, τ = 48 μs,

δ = 95 n s

,

G = 64

μs and P = 3 μs.

The performance of the dead-time correction methods, specifically conventional given in eq.(3)-(4) and generalized given in eq.(12)-(13), was evaluated against the relative bias between the corrected and input (true) rates,

(i n p - c o r) \cdot 100 % / i n p

, and is shown in Figure 1.

We can see better performance for generalized corrections which show no statistically significant bias or trend against

S \cdot δ

. It is also clear that the empirical corrections using the

S \cdot δ

parameter for conventional method would not much improve its figures, leaving large scattering of the points, since as follows from eq. (13), the correction must also include

D^{2} \cdot δ

and

D^{2} S \cdot δ^{2} / 2

additive terms.

For set A, the average bias for the triples rate generalized correction is -0.08%, without statistically significant slope vs

S \cdot δ

. The mean value for bias-to-relative standard deviation ratio2 is 0.64. It is also observed that for the generalized corrections, the larger biases correspond to smaller

T / S

ratios when triples statistics is small. This is contrary to the conventional correction for which the bias increases for higher

T / S

ratios, i.e., higher pulse correlations.

The above figures utilize the refined factorial multipliers from eq. (14). Use of the original

α_{n}

and

β_{n}

for the generalized correction introduces a small bias with a mean value of +0.42%.

Among the simulated data, the most challenging case for singles and doubles rate dead-time correction is set B with modelling of measurements of large MOX canisters, where input rate and dead-time product reaches 0.4. Having the simulated data with high statistics, we also tested various singles dead-time corrections. One of these is given by formula (15), which follows from the first order approximation (with respect to

δ

) of the dead-time loss probability when applying to the waiting time distribution obtained from the Rossi-alpha counts density profile, [12,13], and is shown in Figure 2.

S_{m} = (S_{c} - \frac{D_{c} \cdot δ}{f_{d} \cdot τ}) \cdot e x p (- S_{c} \cdot δ)

(15)

The generalized correction with refined factorial multipliers for the doubles rate gives no bias and minor, though statistically significant, slope of 0.0023 % per %

S \cdot δ

. The use of the original factorial multipliers introduces a small bias of 0.21% and increases the slope to 0.0079 % per %

S \cdot δ

. The correction using eq.(15) for the singles rate shows excellent performance with bias below 0.01%. The INCC standard correction applies shared parameters A and B for both doubles and singles. When correcting for such high-count rates, the method shows systematic deviation for the corrected singles and doubles rates with opposite sings of their biases.

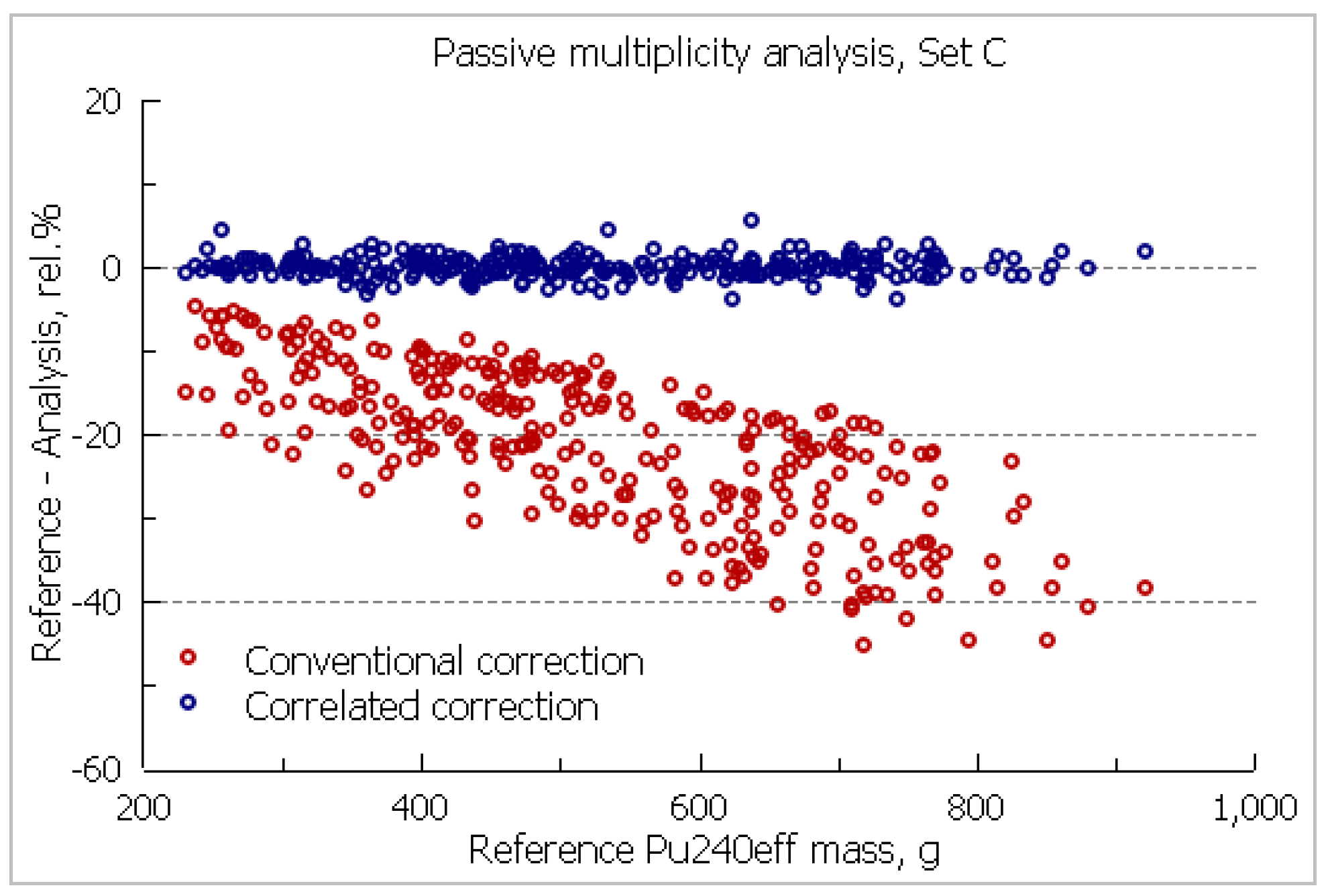
For the pulse trains of set C, we performed the passive multiplicity analysis with comparison of the analysed ²⁴⁰Pu effective mass against the reference modelled mass employing the conventional and generalized dead-time corrections. For the conventional method we did not use the empirical corrections for doubles and triples rates.

Figure 3. Passive multiplicity analysis bias versus modelled Pu240 effective mass.

The RSD value obtained for the generalized correction is 1.27 %. This also includes the statistical component of pulse train counting given the acquisition time of 30 min, chosen to represent a typical verification measurement duration for large MOX and Pu inventory items.

Discussion

Recalling the point model equations for the passive multiplicity rates for Pu, the relative contribution of the additive term to the corrected triples rate in formula (13) can be qualitatively expressed as:

\frac{D_{c}^{2} \cdot δ}{T_{c}} \cdot (1 + \frac{S_{c} \cdot δ}{2}) ~ \frac{m_{240 e} \cdot ε \cdot M}{1 - (3 / 2) {\cdot S}_{c} \cdot δ}

m_{240 e} ε M

- ²⁴⁰Pu effective mass
- detection efficiency
- leakage neutron multiplication

This term, thus increases with item mass, multiplication, counter efficiency and dead-time parameter. Table 1 below shows the relative differences between the corrected triples rates obtained with the conventional and generalized formulas for a few examples of Pu items of various mass and level of impurities (alpha value excess). It also lists the triples relative differences for combination of ²⁵²Cf and AmLi sources of varying yields. The values are calculated for the PSMC counter with parameters as described earlier.

This demonstrates that the additional terms provided by the generalized formula for the triples rate vary significantly even for cases with equal singles rate, and cannot be accurately accounted for using the conventional method with the empirical functionals of singles rate. This concerns not only item measurements, but also counter dead-time characterization measurements which are usually performed with use of ²⁵²Cf and AmLi sources with yields covering the whole or substantial fraction of singles rate range expected for verification measurements.

The considered correction models rest on multiple assumptions, which may not perfectly hold for a real counter. These assumptions are: single channel; single dead-time of rectangular shape, constant length and extended type; exponential waiting time from neutron origin, etc. Additionally, the detector may output a fraction of neutron detections with double pulsing, exhibit nonlinear behaviour of effective dead-time parameter versus count rate, along with other effects. This suggests that the empirical corrections are still to be maintained regardless of the dead-time model in use.

Also, we would like to make a note regarding the empirical correction scheme. In some cases, such as [14], the multiplicity dead-time parameter is determined without invoking additional empirical corrections. With use of the conventional method, this results in an overestimated parameter which changes with count rate. The additional corrections are then introduced post factum as necessary to further correct measurement rates. Another approach, e.g., [7] and [15], uses simultaneous optimization of the multiplicity dead-time parameter along with free parameter(s) for additional empirical correction. The latter approach yields more consistent results and smaller correction biases along the count rate range.

Acknowledgments

This researched was greatly supported by Adam Shephard and Andriy Berlizov, who provided expertise in revising the paper and much improved its content.

For time efficient pulse trains’ simulation and processing, we employed vectorized, GPU-accelerated computations on Kaggle platform. The code is available at https://github.com/V-Nizhnik/Neutron_PT

References

A.F. Para and M.M. Bettoni, “Counting Statistics of Nuclear Detectors”, NIM 70 (1969), 52-56. [CrossRef]
J.W. Muller, “Interval Densities for Extended Dead Times”, report B.I.P.M.-112 (1971).
C.H. Vincent, “Type II dead-time losses between detections occurring at random times within a gate-open time”, NIM-A, vol.269/1 (1988), 335-337. [CrossRef]
N. Dytlewski, “Dead-time Corrections for Multiplicity Counters”, NIM-A, vol.305 (1991), 492-494. [CrossRef]
M. Swinhoe et al., “Deployable Dead Time Corrections for Neutron Multiplicity Measurements Accounting for Neutron Correlations and Multiple Detector Chains”, INMM (2011).
M.S. Krick, W.C. Harker, “Multiplicity Neutron Coincidence Counting User’s Manual”, LANL report LA-UR-93-1394 (1993).
N. Menaa et al., “Experimental Determination of the Multiplicity Deadtime Parameter”, WM2008 symposium (2008).
J.E. Stewart et al., “New Shift-Register Electronics for Improved Precision of Neutron Coincidence and Multiplicity Assays of plutonium and Uranium Mass”, LANL report LA-UR-99-4927 (1999).
J.W. Muller, “Counting statistics of a Poisson process with dead time”, report B.I.P.M.-111 (1970).
H. Menlove et al., “PFPF Canister Counter for Foreign Plutonium (PCAS-3)”, LANL report LA-12485-M (1993).
M. Abhold et al., “Design of the Improved Plutonium Canister Assay System”, LANL report LA-UR-01-3000 (2001).
W. Matthes, R. Haas, “Deadtime correction for ‘updating deadtime’ counters”. Annuals of Nuclear Energy 1985, 12, 693–698. [CrossRef]
M. Bruggeman et al., “Neutron Coincidence Counting Based on Time Interval Analysis with Dead Time Corrected One and Two Dimensional Rossi-alpha Distributions”, SCK-CEN report, BLG-711 (1996).
H.O. Menlove et al., “Manual for the Epithermal Neutron Multiplicity Detector (ENMC) for Measurement of Impure MOX and Plutonium Samples”, LANL report LA-14088 (2004).
M.M. Ferrer et al., “Design and Performance of the Scrap Neutron Multiplicity Counter”, NIM-A, vol.574 (2007), 297-314. [CrossRef]

1	Under term input in this article, we mean true, unaffected by deadtime: e.g. input doubles rate – true doubles rate; input neutron waiting time – waiting time for neutron assuming no deadtime effect; etc.
2	The ratio is lower than unity since the processing with and without deadtime were done on the same pulse train set.
3	$D_{c} = D_{m} \cdot e x p ({A \cdot S}_{m} + B \cdot S_{m}^{2})$ , $S_{c} = S_{m} \cdot e x p ({1 / 4 \cdot (A \cdot S}_{m} + B \cdot S_{m}^{2}))$ , ref. [7].

Figure 1. Relative bias for the generalized and conventional dead-time corrected triples rates vs

S \cdot δ

for the pulse trains of set A. Left: both correction models with (-10; +60) % scale. Despite of the large-scale range, a few points of the conventional correction are off the range reaching about +100%. Right: (-6; +6) % scale for zoomed view of the generalized dead-time correction.

Figure 1. Relative bias for the generalized and conventional dead-time corrected triples rates vs

S \cdot δ

for the pulse trains of set A. Left: both correction models with (-10; +60) % scale. Despite of the large-scale range, a few points of the conventional correction are off the range reaching about +100%. Right: (-6; +6) % scale for zoomed view of the generalized dead-time correction.

Figure 2. Left: corrected doubles rate bias with use of generalized corrections and INCC standard correction3 with best fit for A and B parameters; right: corrected singles rate bias using eq. (15) and INCC standard correction.

Table 1. Relative difference between the corrected triples rates calculated for various Pu items and neutron sources.

Pu240e, g	M	α	$S$	$T_{c}^{D y t}$	$T_{c}^{G e n}$	rel. diff. %
10	1.01	1.0	1.13∙10⁴	3.61∙10³	3.62∙10³	0.2
100	1.07	25.0	1.56∙10⁶	3.09∙10⁴	3.64∙10⁴	17.5
600	1.30	2.5	1.75∙10⁶	4.53∙10⁵	5.53∙10⁵	22.0
1,000	1.40	1.5	1.96∙10⁶	9.60∙10⁵	1.23∙10⁶	27.7

²⁵²Cf	AmLi	Sum yield s^-1	$S$	$T_{c}^{D y t}$	$T_{c}^{G e n}$	rel. diff. %
100 %	0 %	1.0∙10⁶	5.40∙10⁵	8.99∙10⁴	1.05∙10⁵	16.8
10 %	90 %	2.0∙10⁶	1.08∙10⁶	1.84∙10⁴	2.10∙10⁴	13.9
100 %	0 %	2.0∙10⁶	1.08∙10⁶	1.51∙10⁵	2.10∙10⁵	39.2
10 %	90 %	3.0∙10⁶	1.62∙10⁶	2.58∙10⁴	3.15∙10⁴	22.3
100 %	0 %	3.0∙10⁶	1.62∙10⁶	1.85∙10⁵	3.15∙10⁵	70.4

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.