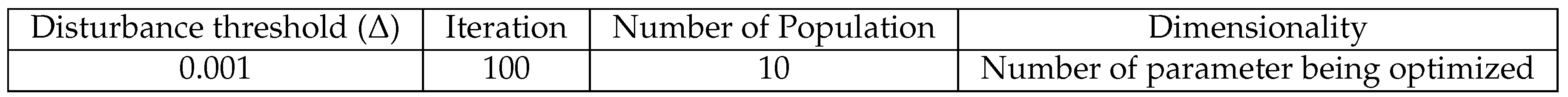3 Dimensional DC Placement: Drone Placement for Optimal Coverage

Preprint

Article

3 Dimensional DC Placement: Drone Placement for Optimal Coverage

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Aniket Basu^*

Hooman Oroojeni

Georgios Samakovitis

Mohammad Majid Al-Rifaie^*

Aniket Basu^*

Hooman Oroojeni

Georgios Samakovitis

Mohammad Majid Al-Rifaie^*

This version is not peer-reviewed

Submitted:

05 October 2024

Posted:

07 October 2024

You are already at the latest version

Alerts

Abstract

Using Drone Cells to optimize Radio Access Networks is an exemplary way to enhance the capabilities of terrestrial Radio Access Networks. Drones fitted with communication and relay modules can act as Drone Cells. The multi Drone Cell placement problem is solved using an adapted Dispersive Flies Optimization alongside with other meta-heuristic algorithms such as Particle Swarm Optimization and Differential Evolution. A home-brewed simulator has been used to test the effectiveness of the different implemented algorithms. Specific environment respective parameter tuning have been explored to better highlight possible advantages of one algorithm over other in any particular environment. Algorithmic diversity has been explored, leading to several modifications and improvements in the implemented models. The results show that using tuned parameters there is a performance uplift in coverage probability when compared to the default meta-heuristic parameters while still remaining within the constraints implied by the problem’s requirements and resource limitation. The paper concludes by offering a study between multiple meta-heuristic approaches and comparison between the methods, investigating the impact of parameter-tuning as well as analyzing the impact of intermittent restart for algorithms persistent diversity.

Keywords:

Subject: Computer Science and Mathematics - Computer Networks and Communications

1. Introduction

Due to the ever-growing demand for mobile and communication networks, future Radio Access Network (RAN) will be put under unprecedented strain to fulfill the needs for all the connected users and devices. Providing pervasive connectivity to the users and connected devices will have to be the main objective of future RAN architectures, guaranteed Quality of Service (QoS) is expected by users. Instead of addition of more Base Station (BS) which are increasingly expensive to built and maintain, a novel approach of Drone Cells (DCs) or Drone Base Station, can be used to alleviate some of connectivity demands and also effectively act as network expansion [1]. Drones fitted with communication and relay modules can act as Drone Cells to provide on-demand network access in both temporal and spatial domains. DCs act as rely station between the connected users and their respective BSs, extending the wireless communication range for user in Coverage Holes or Demanding Areas. Due to their flexibility, DCs can be deployed in emergency scenarios such as any temporary occurring event, natural disasters or ground BS failure to enhance network throughput [2]. DCs with their on-demand wireless coverage capabilities are also more economical with it’s operational expenditure [3]. The term Drone Assisted Radio Access Network was coined to refer to this field of research.

One of the most critical parts of the DC communication model is its’ limited range and power which calls for an efficient usage of DCs. Like terrestrial networks DCs are subjected to many factors that dictates the QoS of DA-RAN architecture. Free space pathloss, signal reflection and blocking due to natural or artificial obstructions are some of the reasons [4]. As such the optimal placement of DCs have been the main focus for many researchers for achieving a high QoS.

In this work, a concise overview of the DA-RAN’s functionality is presented in Section 2, followed by the problem formulation and methodology in Section 3. Lastly, Section 4 covers a series of experiments conducted using the base algorithm parameters, which sparked further exploration into algorithmic diversity and parameter tuning, culminating in a analysis of the resulting trade-offs.

2. Background

The design challenge that Drone Assisted-Radio Access Network (DA-RAN) aims to achieve is to optimize multiple DC flying altitudes and also have maximum radio coverage in a specified area while keeping within the constraints boundaries. The advantages of DA-RAN are that each BS can deploy multiple DCs to operate within a specified Demanding Area (DA) or Coverage Hole (CH) such as a crowded stadium, traffic-congested area, areas suffering from communication loss due to any natural or artificial disaster, etc. They can also act as edge servers to connect more DCs in a mesh network outside the typical range of a BS. CHs created by special events such as concerts or sporting events, etc are dynamically changing in spatial and temporal domains, hence DCs need to be deployed or redeployed accordingly.

3-Dimensional (3D) DC deployment problems have been an area of extensive research and multiple experiments have been conducted where DC are deployed to act as an extension of BS or as edge servers and improve signal strength [5]. Bor-Yaliniz, Irem et al. introduced a multi-tier-drone cell complementing the terrestrial Heterogeneous Networks (HetNet) [6], challenges regarding multi-tier-drone networks are also discussed and addressed in the same paper. Finally, a Drone-cell Management Framework (DMF) was proposed and the benefits of the proposed solution and its benefits in future RAN is demonstrated via a case study. Lyu, Jiangbin et al. proposed a polynomial-time algorithm with successive DC placement to minimize the number of UAV Mobile Base Stations (MBs) or DC needed to maximize the radio coverage for a group of Ground Terminals (GT) [7]. In this scenario, macro-BSs are placed one after the other starting along the perimeter and then in a spiral pattern towards the center for any uncovered GT until all the GTs are covered by the DC [7]. Spectrum Sharing network of DCs was researched by Zhang, Chiya et al. [8], where 3D Poisson Point process is used to find the optimal density of DCs to maximize the network throughput while satisfying the cellular network efficiency constraint.

One of the most key research was the creation of a dedicated communication model for Air-to-Ground (A2G) wireless link. The DC placement is a 3D problem and hence the terrestrial RAN communication channels are not apt for communication between hovering UAVs and terrestrial devices. Al-Hourani in his paper has proposed an Air to Ground communication model that takes into consideration the Line of Sight (LoS) and non-Line of Sight (nLoS) probability links in different urban scenarios [9]. It has been mainly used to focus on a single performance metric and optimal deployment positions. Mozaffari, Mohammad et al. used a constrained K-means clustering approach to minimize the total transmitting power of DC for optimal trajectory and deployment while enabling a reliable up-link of information from the ground Internet-of-Things (IoT) devices [10]. Based on simulations and testing, the approach reduced the total transmit power of the IoT devices by 45% when compared to a static DC. Similarly, another optimal DC placement algorithm was developed by Alzenad, Mohamed et al. to maximize the number of covered users with minimum power consumption. Alzenad, Mohamed et al. proposed the solution by decoupling the Unmanned Aerial Vehicle Mounted Base Stations (UAV-BS) into vertical and horizontal dimensions, simplifying the placement problem and solving then respectively [11]. Zhang, Chiya et al. also adopted the 3D Poisson Point process to optimize the density of DC and also maximize the DC network throughput while satisfying the cellular network efficiency constraints [8]. The downlink coverage probability for the Rayleigh fading channel was derived in terms of an explicit equation by Zhou, Lai et al., and the optimal height, maximum, coverage probability and density of DC were studied [12]. Taking into account the user mobility Ghanavi, Rozhina et al. derived a Reinforced Learning approach using Q learning as the base to guarantee the QoS to users through optimal DC deployment. Through simulations it was proved that given enough time to learn the environment and processing time, the DC are able to improve the QoS to the network considering the user’s movement. With this approach, the agility and the flexibility of future DA-RAN infrastructure can be kept intact [13].

A few constraints dictate the sufficient working and optimization of DA-RAN such as Drone-to-User (D2U), Drone-to-Base (D2B) links, operational constraints due to limited battery, interference from other DCs, interference from terrestrial RAN, weather conditions etc. Most important from the above constraints is the D2B and Drone-to-Ground (D2G) connection link. It is essential for the DCs to be connected to existing terrestrial RAN to function properly, since the main purpose of the DCs are to reliably relay data between the BS and connected users in DAs. Kalantari, Elham et al. did extensive research on the D2B back-haul links regarding multiple DC deployments with a minimum number of DCs needed for user coverage by implementing a heuristic algorithm. As part of related research in [14,15], the authors also investigated the optimal 3D back-haul placement of DC by two different approaches namely, user-centric and network-centric [15]. It was concluded that the network-centric approach maximizes the total number of users served regardless of the network required data rate while the user-centric approach maximizes their sum rate.

Among the techniques used to deal with network coverage and resource allocation was Particle Swarm Optimization (PSO), where PSO was adapted by Kalantari, Elham et al. in their paper and was modified to fit a particular problem i.e. 3D placement of DBSs or DCs in DA-RAN. Kalantari, Elham et al. implemented a utility function into PSO to maintain the capacity and find the coverage constraint for each drone. The utility function that successfully satisfied the coverage constraints while maintaining the capacity constraints was marked as the placement for the DBS. The proposed solution was later simulated in a 2D and 3D environment. Through simulations, it was noted that DBS decreases its altitude in dense areas to reduce the interference to the uncovered users and increases its altitude in low-density regions to cover large areas [14]. PSO was implemented by Ghazzai, Hakim et al. [16] for the cell planning problem for fourth-generation (4G) cellular networks. The main aim of the research was to satisfy both the cell coverage and the capacity constraints simultaneously. PSO was used to find the sub-optimal location for BS that satisfied both the aforementioned constraints in any DAs. For the coverage and cell capacity constraints, many other factors such as the subarea category, user density, resource allocation, and inter-cellular-interference were also taken into account. Subsequent measures were also taken to remove the possibility of redundant BS placement and keep the inter-cellular-interference and the number of BS placements to a minimum. PSO was again adapted by Shi, Weisen et al. to solve the 3D spatial deployment problem of DC in DA-RAN. The proposed solution took inspiration from the D2U, and D2B Pathloss models explained in [9] and proposed a model where PSO was implemented in every DC independently and the algorithm was further optimized to cancel a portion of the search space when an optimal position for the DC has been found. The resulting algorithm was called per Drone Iterated Particle Swarm Optimization (DI-PSO). This results in the algorithm reaching global optimum with much higher probability, and since the search space for the DC is being updated after each iteration with only uncovered DAs remaining, the inter-drone interference is also kept to a minimum . Simulation testing and results also show that there is a much higher convergence rate in DI-PSO when compared with standard PSO [17].

Other related work in terms of network coverage, resource allocation and capacity include [16], where instead of relying on Drone Cells, the algorithm finds the optimal place for setting up new Base Stations, implementing both PSO and Grey Wolf Optimization (GWO) [18] and studying their performances. The proposed method for optimal Base Station location first includes placing the Base Stations in a location owning the random behavior of PSO and GWO and then eliminating the eventually redundant Base Stations. The redundant Base Stations are removed based on the assumption that if the absence of a Base Station affects at least one of the optimization problem constraints, then the Base Station has to be kept and assumed indispensable for a safe network operation [16]. Balanced-Grey Wolf Optimization (B-GWO) has been proposed for multi-UAV deployment and power allocation in Non-Orthogonal Multiple Access (NOMA) , although different from DA-RAN, this implementation can be used for comparison or to gain insight on DC deployment and allocation [19]. Another proposed usage of GWO is in Path Planning, where a Hybrid Discrete Grey Wold Optimizer (HDGWO) has been used to optimize a multi-UAV path planning model with energy constraints (MUPPEC). GWO was also used by Pliatsios, Dimitrios et al. as one of many swarm intelligence algorithm for DC placement and then later, all the implemented algorithms were compared. Among the implemented algorithms GWO was found to be the most effective in DC placement according to the Friedman and Wilcox tests [20].

Similar to user coverage using DCs, Differential Evolution (DE) has been employed to form a UAV-Assisted IoT Data Collection System with a variable population named Differential Evolution with a Variable Population Size (DEVIPS) [21]. Similar to user coverage, the DCs in DEVIPS are deployed to have the best possible deployment position for the coverage of IoT devices. DE has been also implemented for a single unmanned aerial vehicle multitasking, since as an optimized problem, the efficiency of standard DE to obtain the global optimal solution is very low, therefore an Improved Adaptive Differential Evolution algorithm has been implemented for this purpose [22]. The proposed algorithm then can adopt the mutation factor and crossover factor into a dynamic adaptive function which makes the above-mentioned factors able to adjust with the number of population iterations and individual fitness values. Much more recent development in on-demand connectivity enablers have been conducted in [23], where Flying Base Station or FBS are deployed on the demanded network and user specific requirements. Two different meta-heuristic models, Cuckoo search and Differential Evolution were implemented with feasible results being provided by a novel repair operator and compared against in various scenarios under constraints such as uplink and downlink rates, capacity of the FBS etc. Extensive testing has shown that both models performs relatively well in covering all associated users in the demanding area with the only major difference being that DE is three to six times faster in computation than Cuckoo search algorithm.

3. Problem Formulation

Expanding more on the A2G communication links, Al-Hourani has proposed the A2G communication model that takes into consideration the Line of Sight (LoS) and Non-Line of Sight (NLoS) probability links in different urban scenarios [9], the link is calculated as:

P_{L o S} (r, h) = \frac{1}{1 + a exp (- b (arctan (\frac{h}{r}) - a))}

(1)

where h is the height of the DC (altitude), r is the horizontal distance between the user and DC, i.e.

r = \sqrt{{(x_{i} - x_{D})}^{2} + {(y_{i} - y_{D})}^{2}}

), where (

x_{D}, y_{D}

) is the location of the DC in the horizontal dimension, (

x_{i}, y_{i}

) denotes the location of the user and a and b are constant values which are determined by the terrestrial environment of the DC operation. Moreover, the probability of Non-Line of Sight is:

P_{N L o S} = 1 - P_{L o S}

(2)

In addition to the pathloss suffered in free space propagation there is additional pathloss experienced due to the random behavior and structure of specific environment. In this report, only the mean pathloss values are taken into consideration since DC or BS placement deals with long-term variation rather than short-term behavioral changes in the signal model [16]. From the previous model, the pathloss model for NLoS and LoS are:

L o S = 20 log (\frac{4 π f_{c} d}{c}) + η_{L o S}

(3)

N L o S = 20 log (\frac{4 π f_{c} d}{c}) + η_{N L o S}

(4)

where,

d = \sqrt{h^{2} + r^{2}}

, d is the distance between DC and user,

η_{L o S}

and

η_{N L o S}

are the average additional losses for LoS and NLoS links, these were calculated depending on the environment [24].

The mean Pathloss covered by the LoS and NLoS probability link is [24]:

P L (r, h) = P_{LoS} (r, h) η_{LoS} + P_{LoS} (r, h) η_{NLoS}

(5)

where

f_{c}

is the frequency of the carrier and c is the speed of light.

For an UAV flying at height h, the coverage can be classified as a circular disk of radius R. Any users within the radius R can be considered as covered since the pathloss experienced is less than or equal to the threshold(

P L_{t h}

{R = r |}_{Λ = P L_{m a x}}

(6)

The optimal height of DC was calculated in [24]. It can be said that for a given path loss, coverage region R there can be only one altitude h that maximizes the coverage region. Since R is an implicit function of h, the optimal height or the stationary point can be found by [11]:

\frac{\partial R}{\partial h} = \frac{\partial R}{\partial θ} \frac{\partial θ}{\partial h} = 0

(7)

where,

θ

is the angle of elevation between the user and DC, the optimal elevation angle or

θ_{o p t}

was calculated numerically for all environment [11]:

Table 1. Optimal Elevation Angle

Environment	Elevation Angle(Degree)
High rise Urban	$75 . 52^{\circ}$
Dense Urban	$54 . 62^{\circ}$
Urban	$42 . 44^{\circ}$
Suburban	$20 . 34^{\circ}$

With

P L_{t h}

θ_{o p t}

known, the maximum coverage radius was calculated using:

P_{L o S} (r, h) = \frac{A}{1 + a exp (- b (\frac{180}{π} θ_{o p t} - a))} + 20 log (\frac{R}{c o s θ_{o p t}} + B)

(8)

and finally the optimal height can be found by:

h = R t a n (θ_{o p t})

(9)

Total coverage region can be calculated by:

C = 2 π R

(10)

Based on these experiments it was discovered that the optimal DC height can exceed beyond the earth’s atmosphere and hence it was advised to add a height constraint on the DC placement problem [24].

This iteration of the DC problem is devoid of any power consumption or transmission power criteria. Future version of DC placement will have the power criteria added on the work shown in this report.

Three meta-heuristic algorithms have been implemented to address the DC placement problem, namely Particle Swarm Optimization, Differential Evolution, and Dispersive Flies Optimization. A brief overview of each algorithm’s functioning is provided, along with their corresponding pseudo code.

3.1. Particle Swarm Optimization

Particle Swarm Optimization (PSO) is a meta-heuristic algorithm first proposed by James Kennedy and Russel Eberhart in 1995 inspired by the swarm behavior of flocking birds, and fish schools in nature [25]. As the name suggests PSO works by having a swarm (population) of possible solutions. The movement of the particles in the search space is dictated by the particle’s best-known position and the best position of the swarm. The best-known position determines the direction of the entire swarm. These steps are repeated in its standard form for a number of iterations until a probable solution is found.

PSO works as a globally connected swarm where all particles share information between each other and knows the best position ever visited by any particle in the swarm. Each particle’s position and velocity are given as [26]:

x_{i d}^{t + 1} = x_{i d}^{t} + v_{i d}^{t + 1}

(11)

\begin{matrix} v_{i d}^{t + 1} & = v_{i d}^{t} \end{matrix}

(12)

\begin{matrix} + c_{1} r_{1} (p_{i d}^{t} - x_{i d}^{t}) \end{matrix}

(13)

\begin{matrix} + c_{2} r_{2} (g_{i d}^{t} - x_{i d}^{t}) \end{matrix}

(14)

where i is the particle index, d is the dimension (each particle has a position and velocity for each dimension),

x_{i d}^{t}

and

v_{i d}^{t}

is the position and the velocity of the particle i in dimension d at iteration t respectively.

c_{1}

and

c_{2}

are the acceleration constant for the cognitive and social component,

r_{1}

and

r_{2}

are the stochastic component of PSO in the limit [0, 1].

p_{i d}

is location of the best visited location in dimension d for particle i and

g_{i d}

is the best particle in the swarm in dimension d [26]. The pseudo code for PSO is presented in algorithm 1.

Algorithm 1: Particle Swarm Optimization (PSO)

1:: Initialize particles’ positions $X^{0}$
2:: Initialize particles’ velocities $V^{0}$
3:: Initialize personal best positions $P^{0} = X^{0}$
4:: Initialize global best position $G^{0} = argmin {f (X_{i}^{0})}$
5:: for each iteration $t = 1$ to T do
6:: for each particle $i = 1$ to N do
7:: Update velocity: $V_{i}^{t} = w V_{i}^{t - 1} + c_{1} r_{1} (P_{i}^{t - 1} - X_{i}^{t - 1}) + c_{2} r_{2} (G^{t - 1} - X_{i}^{t - 1})$
8:: Update position: $X_{i}^{t} = X_{i}^{t - 1} + V_{i}^{t}$
9:: if $f (X_{i}^{t}) < f (P_{i}^{t - 1})$ then
10:: Update personal best: $P_{i}^{t} = X_{i}^{t}$
11:: end if
12:: if $f (X_{i}^{t}) < f (G^{t - 1})$ then
13:: Update global best: $G^{t} = X_{i}^{t}$
14:: end if
15:: end for
16:: end for

3.2. Differential Evolution

DE or Differential Evolution Algorithm [27] optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. DE was first introduced by Storn, Rainer et al. as an effective evolutionary technique that can be utilized in a continuous domain to address global optimization issues. DE first creates a population of candidate solution which are chosen at random as if nothing is known about the system [28]. The candidate solution with the best objective values are kept in the next iteration in such a manner that the new values of an individual is improved forming a consequent part of the population, otherwise the new values are discarded. These steps are repeated until the termination criteria. For every iteration DE uses the mutation function to produce a donor vector for each individual in the population. The mutant vector for each target vector can be produced using a specific mutation function [29]. The mutation function used in the report is:

” D E / b e s t / 2 ” V_{i} = X_{b e s t} + F (X_{r_{1}} - X_{r_{2}}) + F (X_{r_{3}} - X_{r_{4}})

(15)

where

r 1, r 2, r 3, r 4 \in [1, N * P]

are integers and are mutually exclusive and

F \in [0, 2]

. The integers are chosen at random from the interval and are different from the index i. F is a real and constant factor (scaling factor) that controls the intensification of the differential evolution and

X_{b e s t}

is the best individual vector [29]. The main advantage of DE is that it requires adjustment of only three parameters and the selection of the mutation strategy: the population size, the mutation factor F, and the crossover parameter

C R \in [0, 1]

. The mutation factor is a scaling parameter, where smaller values of F lead to smaller steps in the mutation process, resulting in a longer convergence time. Conversely, higher values of F can accelerate convergence but may also cause the algorithm to overshoot the optimal solution. The crossover parameter CR affects the diversity within the population; higher values of CR introduce more variation, enhancing the algorithm’s ability to perform both local and global searches effectively. Finding an appropriate CR value is crucial for balancing exploration and exploitation capabilities [29]. The pseudo code for DE is presented in Algorithm 2.

Algorithm 2: Differential Evolution (DE)

1:: Initialize population $P$ with random solutions
2:: Set generation counter $t = 0$
3:: while stopping criterion is not met do
4:: Evaluate fitness for each solution in $P$
5:: for each solution $X_{i} \in P$ do
6:: Randomly select three distinct solutions $X_{r 1}$ , $X_{r 2}$ , and $X_{r 3}$ from $P$
7:: Generate trial vector: $V_{i} = X_{b e s t} + F (X_{r_{1}} - X_{r_{2}}) + F (X_{r_{3}} - X_{r_{4}})$ ▹ Equation 15
8:: Clip elements of $V_{i}$ to search space boundaries if necessary
9:: Apply mutation and crossover to create trial vector $U_{i}$
10:: Select $U_{i}$ or $X_{i}$ based on fitness: $X_{i}^{(t + 1)} = \{\begin{matrix} U_{i} & if f (U_{i}) < f (X_{i}) \\ X_{i} & otherwise \end{matrix}$
11:: end for
12:: Increment generation counter: $t = t + 1$
13:: end while
14:: return Best solution found in $P$

3.3. Dispersive Flies Optimization

DFO will be treated as base-mark algorithm. It has been proposed in this paper since it has been proven to outperform generic population-based algorithms such as Differential Evolution Algorithm (DE), PSO, Genetic Algorithm (GA) and is more effective and reliable in 84.62% and 90% of cases respectively when tested over a set of standard benchmark, and if there exists a statically significant difference, DFO converged the solution in 71.05% of the problem set [30]. DFO requires fewer parameters for its function in comparison to the other aforementioned swarm intelligence algorithms. Dispersive Flies Optimisation (DFO) is a minimalist, component-stripped swarm optimizer that relies exclusively on the particles’ positions at time t to determine their positions at time

t + 1

. Unlike other algorithms such as PSO, which uses memory and velocity vectors, or DE, which employs mutant and trial vectors, DFO does not use any additional vectors in its process. The pseudo code for DFO is presented in Algorithm 3.

Algorithm 3: Dispersive Flies Optimization (DFO)

1:: procedure DFO( $N, D, X_{m i n}, X_{m a x}, f$ )
2:: for $i = 0 \to N - 1$ do ▹ Initialization
3:: for $d = 0 \to D - 1$ do
4:: $x_{i d}^{0} \leftarrow U (x_{m i n, d}, x_{m a x, d})$
5:: end for
6:: end for
7:: while ! termination criteria do ▹ Main DFO loop
8:: for $i = 0 \to N - 1$ do
9:: $X_{i} . f i t n e s s \leftarrow f (X_{i})$
10:: end for
11:: $X_{s} =$ arg min $[f (X_{i})]$ , $i \in {0, 1, 2, . . . . . N - 1}$
12:: for $i = 0 \to N - 1$ and $i \neq s$ do
13:: $X_{i_{n}} =$ arg min $[f (X_{(i - 1) % N}), f (X_{(i + 1) % N})]$
14:: for $d = 0 \to D - 1$ do
15:: if $U (0, 1) < Δ$ then
16:: ${x_{i d}}^{t + 1} \leftarrow U (x_{m i n, d}, x_{m a x, d})$ ▹ Restart
17:: else
18:: $u \leftarrow U (0, 1)$
19:: ${x_{i d}}^{t + 1} \leftarrow x_{i_{n} d}^{t} + u (x_{s d}^{t} - x_{i d}^{t})$ ▹ Update
20:: if $x_{i d}^{t + 1} < x_{m i n, d}$ or $x_{i d}^{t + 1} > x_{m a x, d}$ then
21:: $x_{i d}^{t + 1} \leftarrow U (x_{m i n, d}, x_{m a x, d})$
22:: end if
23:: end if
24:: end for
25:: end for
26:: end while
27:: return $X_{s}$
28:: end procedure

These three meta-heuristic algorithms were selected due to their operational diversity and frequent use in the DA-RAN domain. Particle Swarm Optimization has been the most widely used meta-heuristic by leading researchers in the field, as discussed in section 2. Differential Evolution is also a well-established algorithm, applied in a variety of contexts, with its use cases explored in [31]. Dispersive Flies Optimization, while relatively new, is a simple yet effective algorithm, demonstrating performance that can match or surpass others in certain scenarios, as detailed in sub-section 3.3. Through the implementation of these algorithms, this paper aims to provide an overview of the most commonly used methods for DC placement, while also highlighting lesser-known approaches that can deliver results comparable to those achieved by the pioneers in the field.

4. Experiment and Results

Two sets of experiments were conducted, firstly DC placement using default parameters and secondly using tuned parameters. The results of final experiment was evaluated using the Nyeman Hypothesis test and a statistical significant value for all environment to generate a final score to evaluate algorithmic performance.

4.1. Experiments

For the experiments a height constraint has been taken into consideration based on the geographical location of the research conducted to make sure the maximum height of the DC placed does not exceed the maximum legal height of any drones in the United Kingdom [32]. The experimental parameters for the experiments conducted are listed in Table 2.

Here instead of iterations, function evaluation (FE) has been implemented as the main criteria for algorithm termination to make sure the implemented algorithms are more in line with the previous experiments done in the field. FE is calculated based on the number of times the algorithm calls the fitness function to calculate potential solution (fitness) in the search space. Based on the research conducted in [20] maximum the number of FEs allowed has been fixed at 2500, calculated by:

F E = m a x I T * N

(16)

where

m a x I T

is the number of iteration and N is the population size, number of DCs is fixed at 10 making the obtained results parallel with the research done by pioneers in the field. Total FE has been divided into 10 segments, each having 250 FEs. The search agents (flies, particles or chromosomes) are deployed (initialized) in the search space for 250 FE, upon reaching this criteria the covered users along with it’s associated DC is removed from the search space allowing every DC to be deployed one after the rather than all at once. This process continues until all 10 DCs have been deployed. A fourth algorithm or Random Search (RS) has also been implemented on the basis of same theory where one DC is randomly deployed in the search space and the covered users and the associated DC is removed from the search space, continuing until all 10 DCs are deployed in the same process. RS was implemented to visualize the complex nature of the problem and serve as a control to illustrate the potential improvements achievable with more sophisticated algorithms like DFO, PSO, and DE, demonstrating the effectiveness when using a hyper-heuristic method. Each experiment has been executed for 1000 times and the mean of those executions has been compiled into a graph showcasing the coverage probability of each algorithm.

Figure 1. Experiment Tree

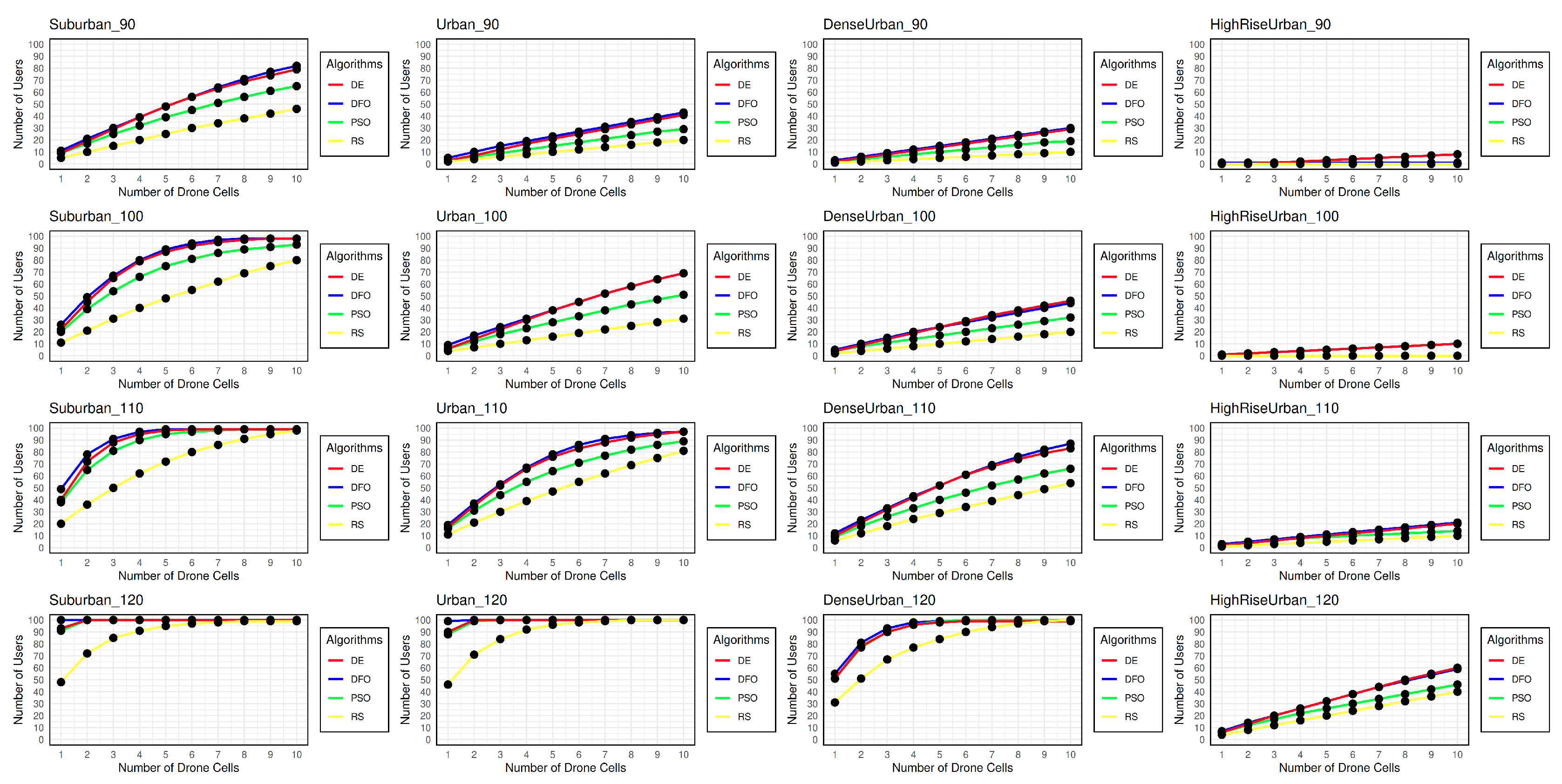
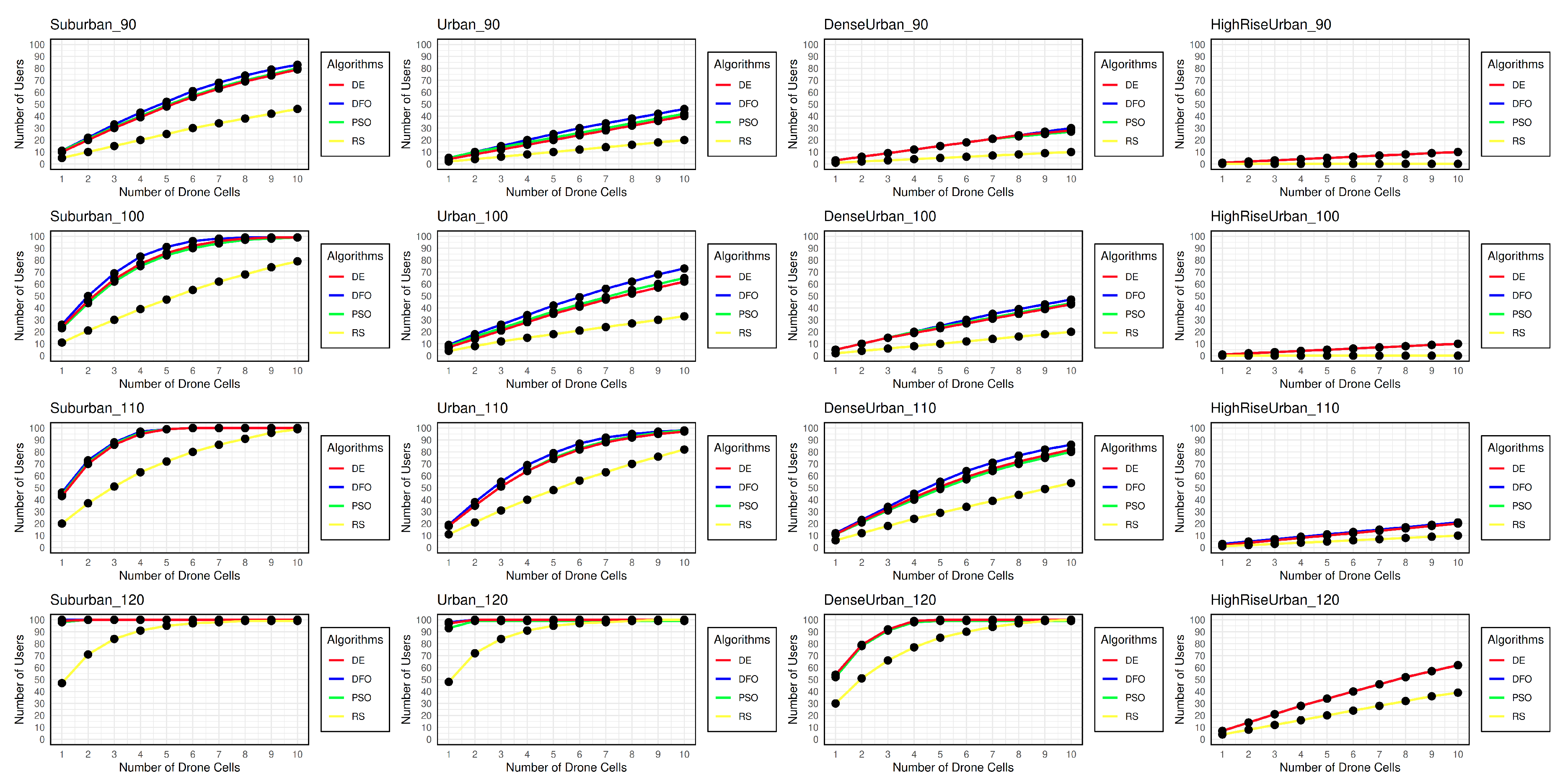
Figure 2 depicts the coverage probability for DE, DFO, PSO and RS for four different terrestrial environment for four pathloss values using default parameters. During initial experimentation some irregularities were found with PSO and DE, where these implementation were prone to being stuck in the local minima after initial users were identified and removed. This phenomenon can be due to low diversity in PSO and DE, the diversity of said algorithms have been reported in [30]. Positional diversity was calculated with the implemented algorithms based on [33]:

Diversity = \frac{1}{N P} \sum_{i = 1}^{N} \sqrt{\sum_{d = 1}^{D} {(x_{i}^{d} - {\bar{x}}^{d})}^{2}}

(17)

{\bar{x}}^{d} = \frac{1}{N} \sum_{i = 1}^{N} x_{i}^{d}

(18)

where N is the number of search agents (flies, chromosomes or particles), D is the dimentionality of the problem,

x_{i}^{d}

is the value at dimension d for agent i and

{\bar{x}}^{d}

is the average value of dimension d for all search agents.

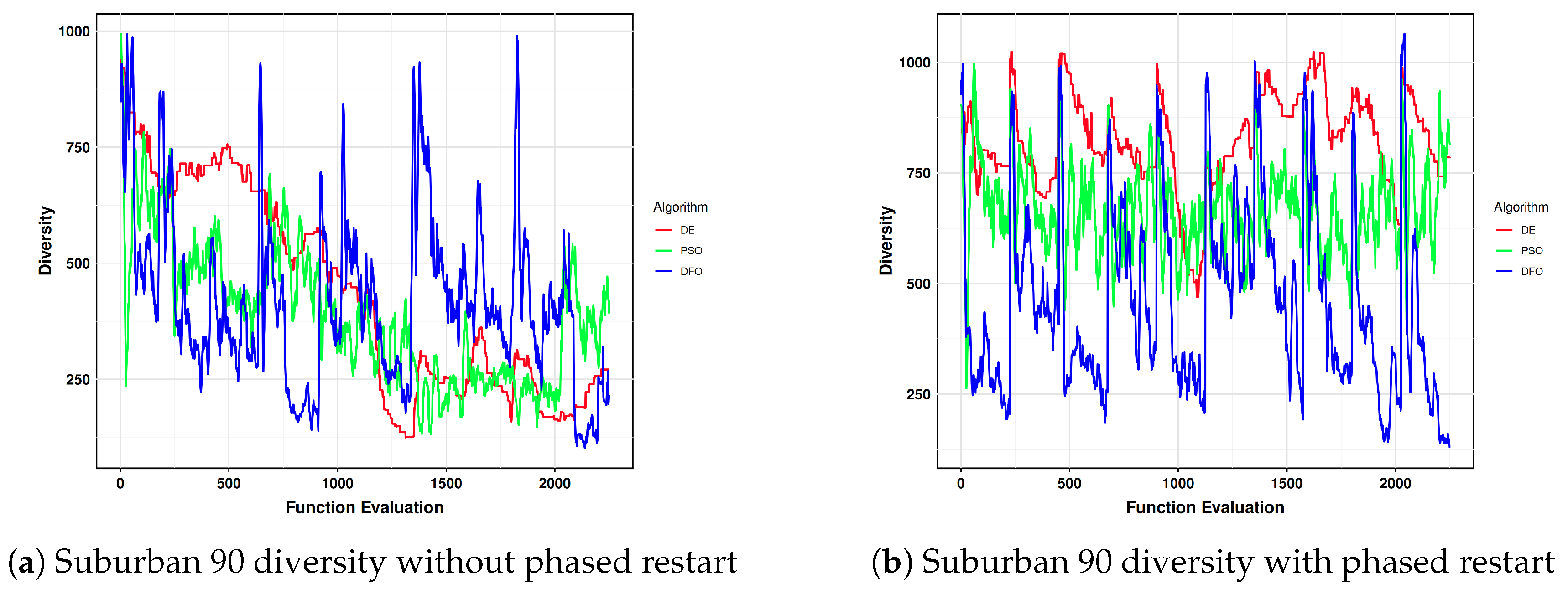
The diversity vs FEs graph in Figure 3a is in line with similar experiments conducted in [30]. In this implementation of DA-RAN, PSO and DE decrease in diversity as function evaluation increases while DFO diversity stays relatively higher owing to its disturbance threshold that enables the flies/search agents to be re-initialized to the search space. The lack of such technique in PSO and DE can create problem where low diversity can cause lower exploration in certain scenarios leading to the algorithms being stuck on a particular solution and not exploration of other potential solution in the search space as depicted in Figure 4a. Since diversity changes with change to the environment and pathloss threshold, the results could be more skewed towards the DFO implementation. To solve this problem, a phased-restart strategy has been introduced to re-initialization the search agents in the search space after each FE segment to promote exploration and reduce the probability of the search agents being stuck on the local minima.

Plotting the diversity again using the phased-restart strategy in Figure 3b and Figure 4b shows that diversity of all algorithms are comparable throughout the process only getting low at the end of each segment where the probable best solution has been found. It is to be noted that DFO inherently does not require phased-restart, but it has been implemented in DFO as well to make sure that all the algorithms are at par with each other.

To further optimize the effectiveness of the algorithms meta-meta-heuristic parameter tuning has been conducted on all the environments for all pathloss threshold to gather the best suitable parameter for each combination of environment.

4.2. Parameter Tuning

DFO has been implemented as the meta-meta-heuristic to optimize all the algorithms including itself. The meta-meta-heuristic algorithm has been compiled for a total of 100 iteration, 5 sets of parameters have been gathered for each of the combination in Figure 6. The set of parameters that results in the highest user coverage has been used for rest of the experimentation. Table 5 contains the parameters for the meta-meta-heuristic parameter tuning.

Figure 5. DFO Optimizer Parameters

Figure 6. Parameter Tuning Tree

Algorithm 4: DFO Meta-meta-optimizer pseudo code

1:: Initialize the flies within the Search Space
2:: while Termination Criteria do
3:: for i = 1 : N flies do
4:: Calculate the fitness for each fly where fitness is user coverage of the respective meta-heuristic algorithm DFO, PSO and DE
5:: end for
6:: for $i = 0 \to N - 1 a n d i \neq s$ do
7:: Find the best neighbour
8:: for $d = 0 \to D - 1$ do
9:: if $U (0, 1) < Δ$ then
10:: Update particle position ▹ see Algorithm 3
11:: Check boundary within parameter range and clamp if outside
12:: end if
13:: end for
14:: end for
15:: end while

The pseudo code the meta-meta-optimizer is presented in Algorithm 4. Based on previous experiments done in the field in regards to parameter-tuning of the implemented algorithm the upper and lower bounds were selected from several pioneers in the field [30,34,35,36,37]. The default and optimized parameters for DFO, PSO and DE are tabulated in Table 3.

4.3. Results

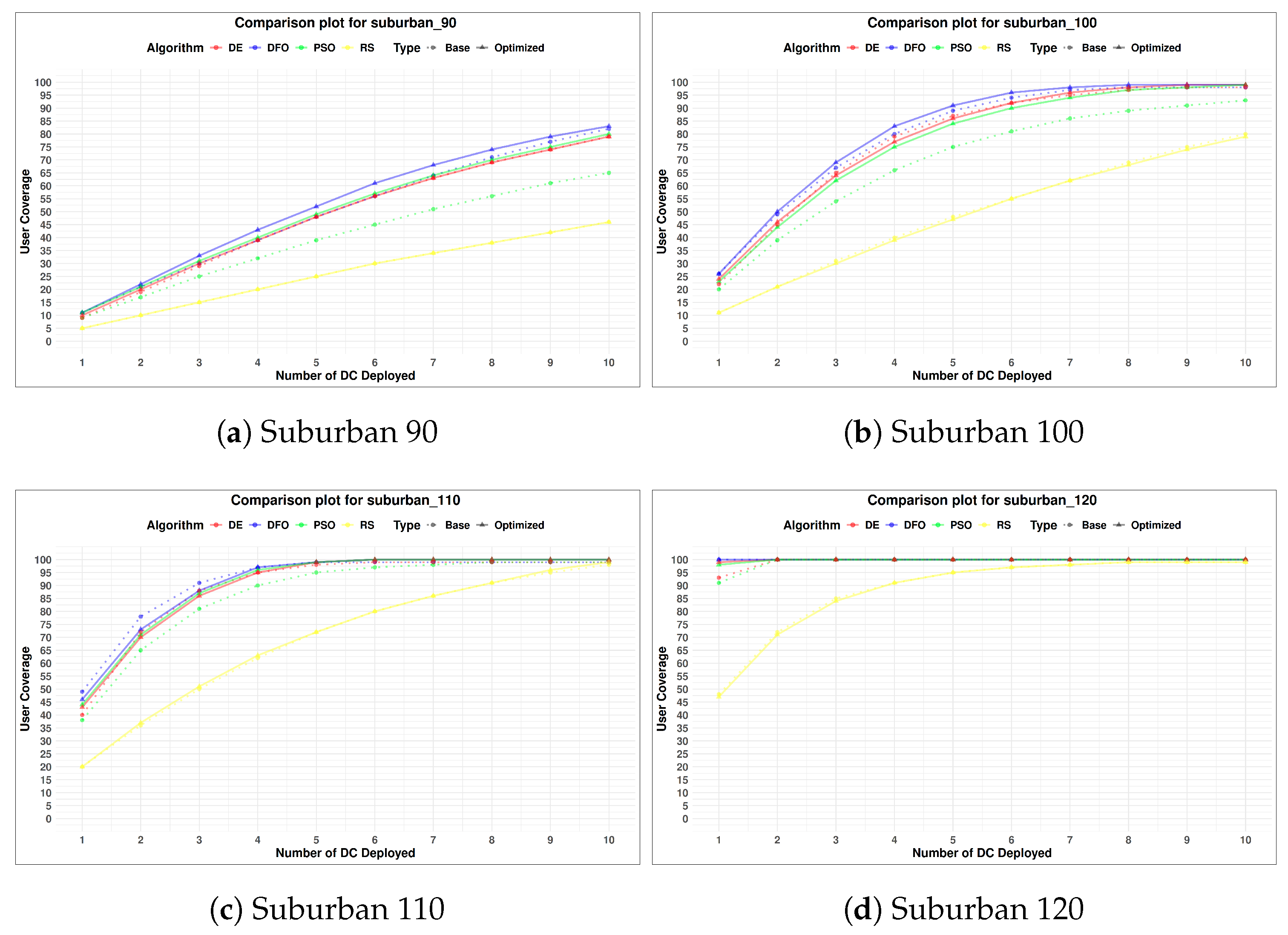
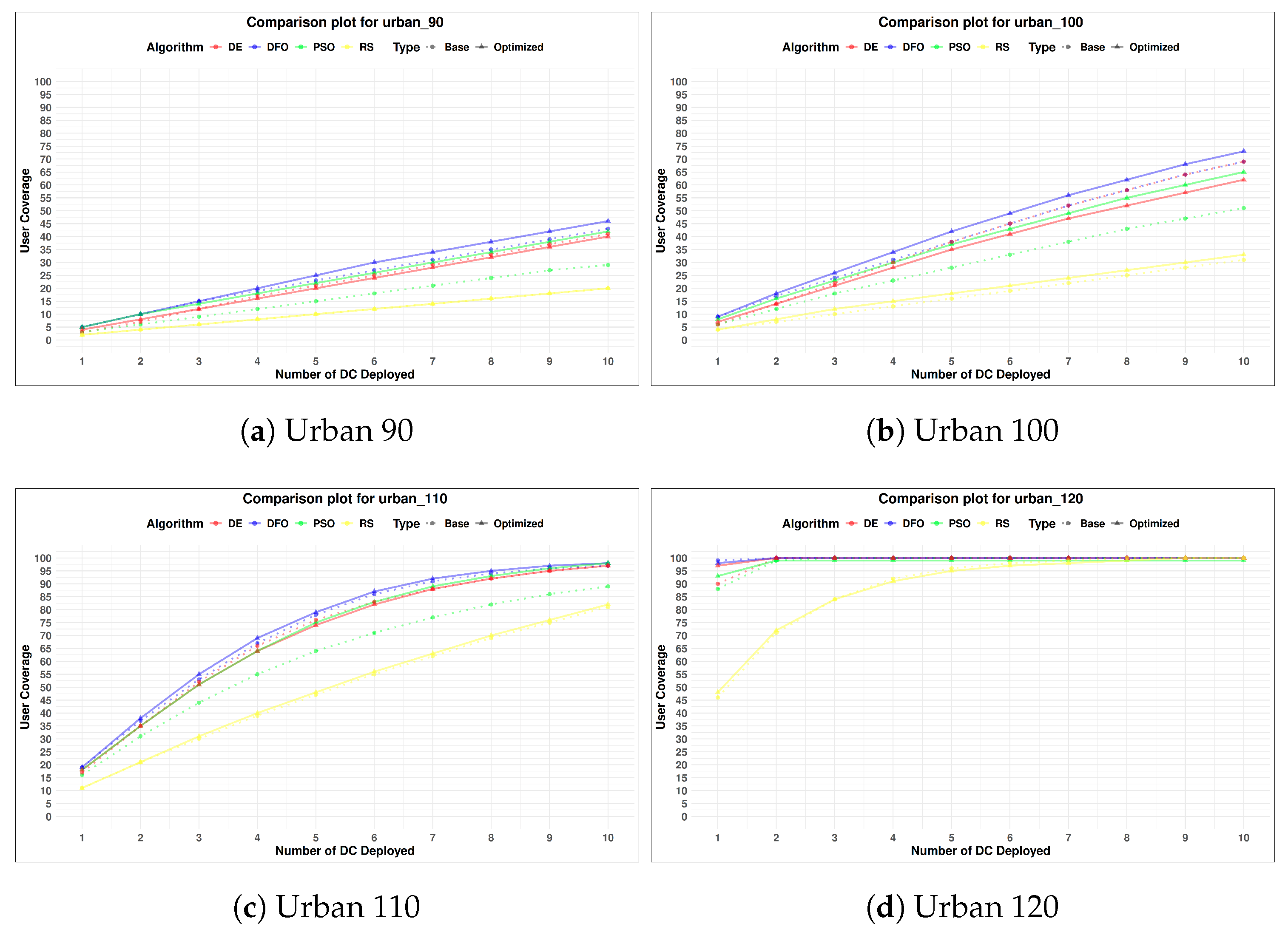
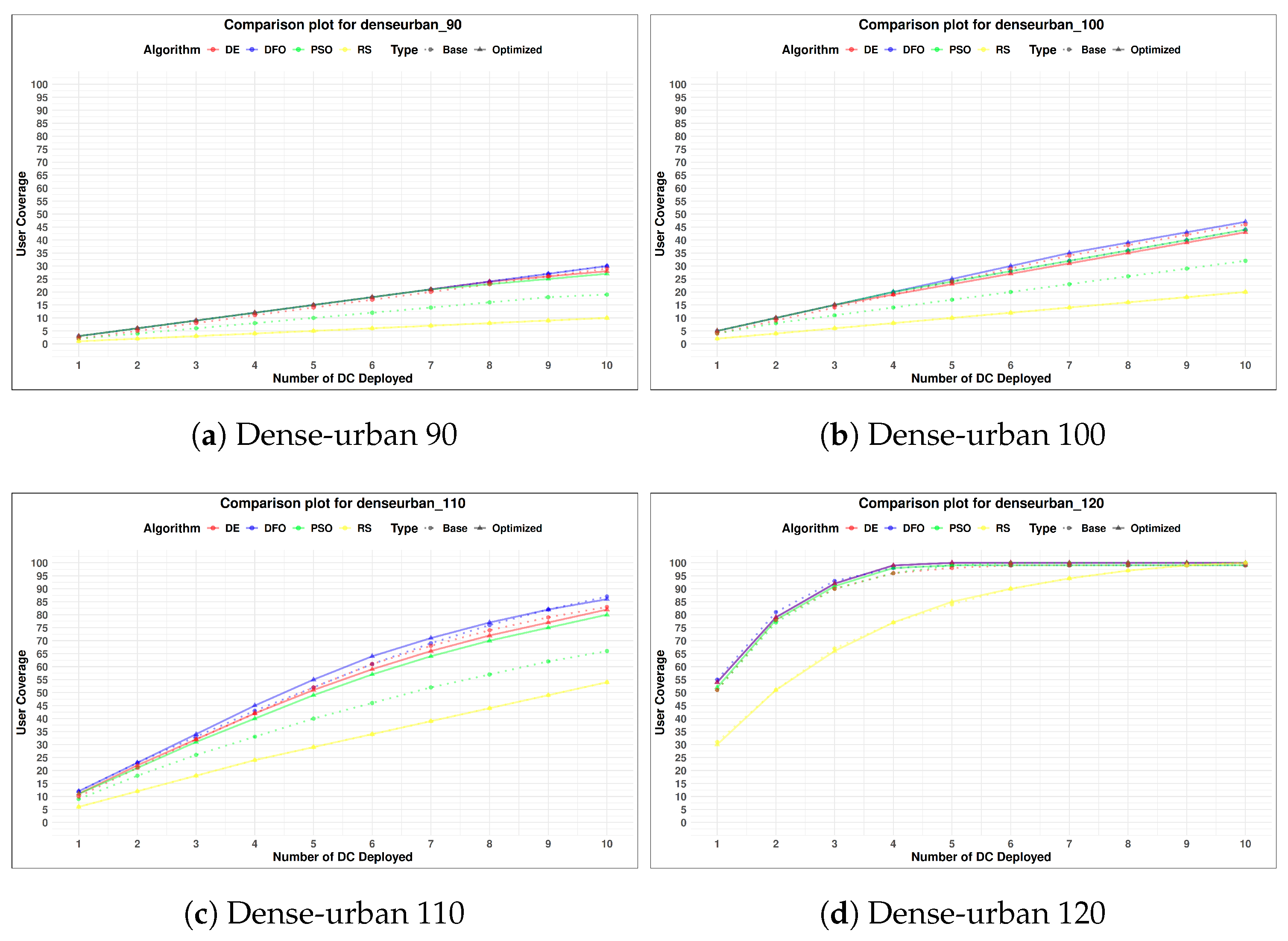
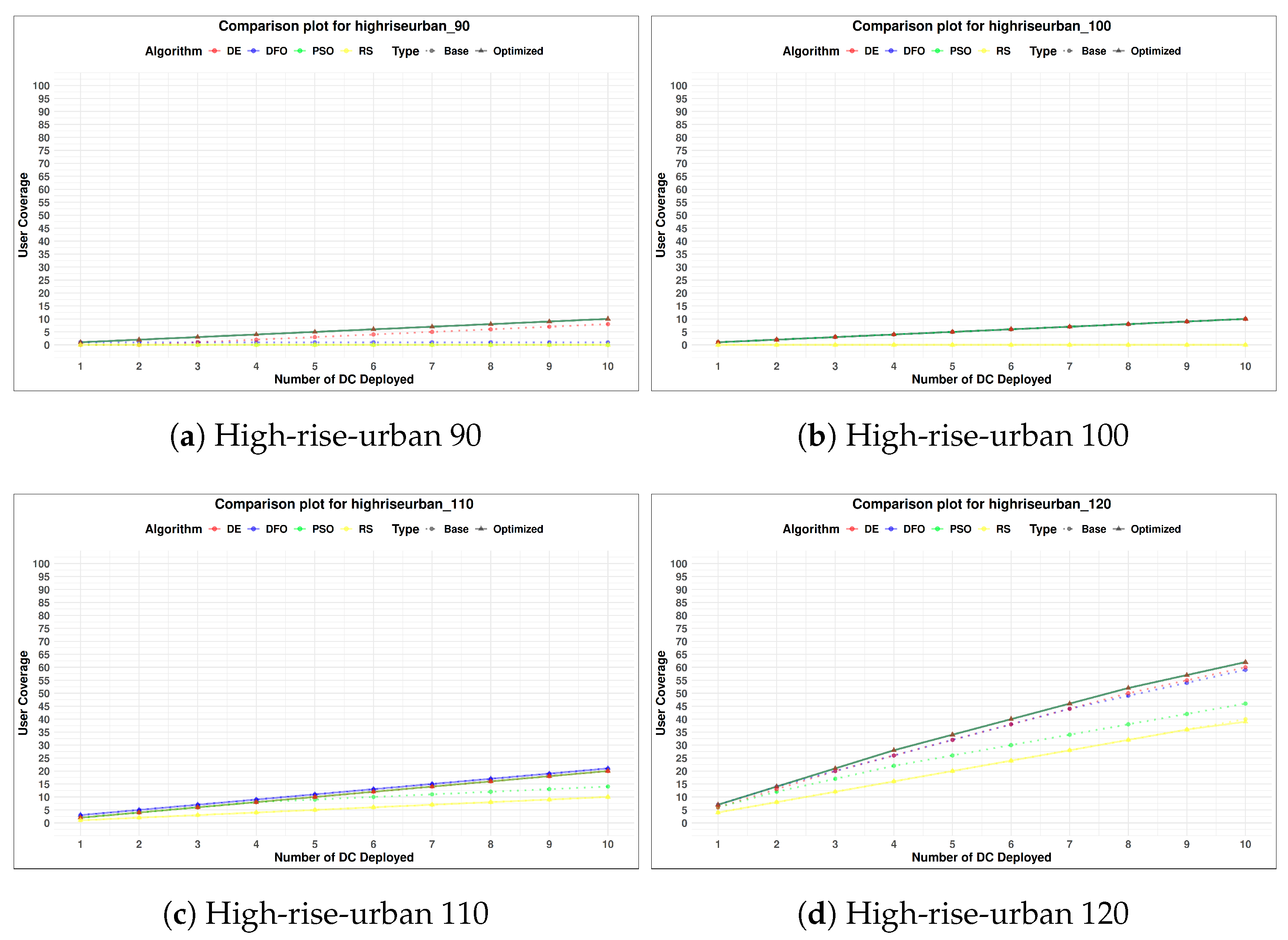
Figure 7, represents the final coverage probability of the algorithms with all the above experiments accounted for. There has been a noticeable improvement in user coverage among most of the environment.

Figure 8, Figure 9, Figure 10 and Figure 11 visualizes the difference between the coverage probability of the implemented algorithm for the default and tuned parameter values. DFO, due to the restart mechanic with higher diversity has the least improvement in user coverage probability. Although with DFO’s advantage in diversity from disturbance threshold the coverage probability of DFO and DE are very similar in all instances. The DC placement problem on its own although being a complex problem can be converted to a simpler one when broken down into multiple sub-parts. In case of the problem presented in this paper, it’s complexity has been minimized. It is hypothesized that for the DE implementation with its 250 FEs per segment, the search agents are not converging fast enough to the local minima and the scattered agents are leading to its higher diversity, while PSO converges faster initially leading to its less than optimal user coverage. Given increased FEs or iterations DE will converge to the local minima leading to less than optimal coverage. Any additional constraints or changes to the parameter tuning process for finding the user coverage could affect algorithms performance.

In some cases, Figure 9a, Figure 9b, Figure 10b, Figure 10c, mainly in case of DFO and DE, the base coverage sometimes exceeds the coverage with tuned parameters. This behavior could be accounted to the heuristic nature of the algorithms. A Wilcoxon Signed-Rank test was conducted between the two sets of results, the result of statistical test in Table 4 illustrates the lack of any significant difference between the performance of standard and tuned algorithm. Although there has been a noticeable improvement in user coverage in some environment, paired test illustrates that the different implementation of PSO are significantly different (highlighted in red) than that of DFO and DE.

Not all scenarios have seen an improvement in user coverage. The major factors affecting the improvement in user coverage can be separated into two parts

Pathloss Threshold: Scenarios with low pathloss threshold have had the most improvement. Lower pathloss dictates smaller coverage radius and vice versa. Due to the smaller coverage area there is a greater possibility for improvement in such scenarios. Figure 8a, Figure 8b, Figure 9a, Figure 9b, Figure 10a, Figure 10b and Figure 11a are such cases where parameter tuning had a bigger impact, except for Figure 11b where the type of environment also affects the coverage. Scenarios with higher threshold such as Figure 8c, Figure 8d, Figure 9c, Figure 9d and Figure 10d have had the least improvement in user coverage because most available users being already covered by a large coverage radius (with a few exception). However it is to be noted that not always a higher threshold dictates a greater coverage radius, as we change the environment type the coverage radius is also affected.
Environment: Environments such as sub-urban, urban and considered as easy environment since there are a limited number of factors obstructing LoS, while environments such as high-rise-urban and dense-urban are considered as hard environment where multiple artificial structures can easily obstruct LoS with High-rise-urban being considered the hardest of all the given environment. As the environment changes from easy to difficult the coverage radius also starts decreasing, leading to less user coverage as can be seen from Figure 8, Figure 9, Figure 10 and Figure 11. Among all the environments High-rise-urban has had the least improvement in user coverage. In Figure 11a, Figure 11b, Figure 11c and Figure 11d there is little to no change in user coverage and it can be considered that given the constraints and environment there can be no better solution that can be found in that particular scenario. Dense-urban while still being a challenging environment has had some improvement in coverage radius in all scenarios.

Among all the implemented algorithms PSO implementation have benefited the most from parameter tuning and phased-restart. RS values remains consistent throughout the experiments, although the placement is random, after averaging a thousand placements the results achieved have reached a stable value. Optimized results for PSO, DE and DFO have reached nearly the same user coverage in all environment and hence the results obtained can be perceived as the "feasible peak" in that scenario, which is an improvement over the default algorithm configuration. Finally a Friedman test was conducted for all environment, the results are presented in Table 5.

The Friedman test shows that there are no significant difference between the implemented algorithms with the introduction of phased restart and parameter tuning except with RS which is to be expected. Highlighted in red are the scenarios where there is significant difference in performance between the implemented algorithms. The rest are cases where all the algorithms have reached a similar level of performance. With addition of more constraints or more complicated methods such as power efficiency or resource allocation, dynamic users etc. there is expected to be a much greater difference between the implemented algorithms.

Table 5. Friedman test statistics, p-values, and Nemenyi post hoc test results for all environment, highlighted cells indicate significant difference between the implemented algorithms

Friedman Test and Nemenyi Post Hoc Test Results
Suburban 90					Urban 90				Dense-urban 90				High rise urban 90
Test Statistic	23.10				26.31				27.00				30.00
P-value	3.84e-05				8.22e-06				5.89e-06				1.38e-06
Algorithm	DFO	PSO	DE	RS	DFO	PSO	DE	RS	DFO	PSO	DE	RS	DFO	PSO	DE	RS
DFO	1.000	0.900	0.750	0.001	1.000	0.702	0.404	0.001	1.000	0.848	0.702	0.001	1.000	0.900	0.900	0.003
PSO	0.900	1.000	0.900	0.007	0.702	1.000	0.900	0.006	0.848	1.000	0.900	0.010	0.900	1.000	0.900	0.003
DE	0.750	0.900	1.000	0.017	0.404	0.900	1.000	0.029	0.702	0.900	1.000	0.004	0.900	0.900	1.000	0.003
RS	0.001	0.007	0.017	1.000	0.001	0.006	0.029	1.000	0.001	0.010	0.004	1.000	0.003	0.003	0.003	1.000
Suburban 100					Urban 100				Dense-urban 100				High rise urban 100
Test Statistic	0.36				27.94				26.62				30.00
P-value	0.949				3.73e-06				7.06e-06				1.38e-06
Algorithm	DFO	PSO	DE	RS	DFO	PSO	DE	RS	DFO	PSO	DE	RS	DFO	PSO	DE	RS
DFO	1.000	0.900	0.900	0.900	1.000	0.226	0.058	0.001	1.000	0.848	0.702	0.001	1.000	0.900	0.900	0.003
PSO	0.900	1.000	0.900	0.900	0.226	1.000	0.900	0.013	0.848	1.000	0.900	0.010	0.900	1.000	0.900	0.003
DE	0.900	0.900	1.000	0.900	0.058	0.900	1.000	0.073	0.702	0.900	1.000	0.072	0.900	0.900	1.000	0.003
RS	0.900	0.900	0.900	1.000	0.001	0.013	0.073	1.000	0.001	0.010	0.072	1.000	0.003	0.003	0.003	1.000
Suburban 110					Urban 110				Dense-urban 110				High rise urban 110
Test Statistic	4.18				26.62				16.89				28.71
P-value	0.242				0.954				0.00074				2.57e-06
Algorithm	DFO	PSO	DE	RS	DFO	PSO	DE	RS	DFO	PSO	DE	RS	DFO	PSO	DE	RS
DFO	1.000	0.900	0.900	0.404	1.000	0.900	0.900	0.002	1.000	0.556	0.799	0.004	1.000	0.900	0.900	0.002
PSO	0.900	1.000	0.900	0.556	0.900	1.000	0.900	0.004	0.556	1.000	0.900	0.160	0.900	1.000	0.900	0.004
DE	0.900	0.900	1.000	0.556	0.900	0.900	1.000	0.007	0.799	0.900	1.000	0.058	0.900	0.900	1.000	0.004
RS	0.404	0.556	0.556	1.000	0.002	0.004	0.007	1.000	0.004	0.160	0.058	1.000	0.002	0.004	0.004	1.000
Suburban 120					Urban 120				Dense-urban 120				High rise urban 120
Test Statistic	11.57				14.23				9.72				30.00
P-value	0.009				0.0026				0.021				1.38e-06
Algorithm	DFO	PSO	DE	RS	DFO	PSO	DE	RS	DFO	PSO	DE	RS	DFO	PSO	DE	RS
DFO	1.000	0.900	0.900	0.160	1.000	0.900	0.900	0.073	1.000	0.900	0.900	0.191	1.000	0.900	0.900	0.003
PSO	0.900	1.000	0.900	0.160	0.900	1.000	0.900	0.073	0.900	1.000	0.900	0.160	0.900	1.000	0.900	0.003
DE	0.900	0.900	1.000	0.160	0.900	0.900	1.000	0.073	0.900	0.900	1.000	0.133	0.900	0.900	1.000	0.003
RS	0.160	0.160	0.160	1.000	0.073	0.073	0.073	1.000	0.191	0.160	0.133	1.000	0.003	0.003	0.003	1.000

5. Conclusions

Motivated by the emergence of DC communication practices and its associated challenges in terms of its coverage and placement, different swarm intelligence approaches has been investigated for optimal DC placement with different constraints on multiple scenarios. The DC placement problem has been investigated with three different models and a base line has been achieved with previous research done in the field. Parameter tuning has been performed across all environments, followed by additional experiments using the optimized parameters. The results and statistical test show that there has been a noticeable improvement over the default algorithm, with the adoption of parameter tuning and re-initialization all three algorithms have shown to be capable of DC placement, even when optimizing DC placement in a challenging environment. DFO implementation has demonstrated to be competitive for both default and re-initialized algorithms, any further experimentation would be conducted with DFO as the base for DC placement.

The objective of this research was to provide an overview of the various techniques used for DC placement and to implement meta-heuristic approaches for a comparative study. The diversity of the algorithms was analyzed, leading to the introduction of phased restarts, particularly for PSO. This enhancement has increased the algorithms’ ability to explore the solution space, resulting in an overall performance boost. Parameter tuning was carried out to maximize the performance of each algorithm across different scenarios and threshold values. Despite its minimalist design, DFO maintained consistent performance across all tests, while DE, even without phased restarts, proved to be an effective algorithm for DC placement. The inherent diversity in DE may become even more valuable in cases where the need for exploration is not as evident.

However, the study also identified several limitations. First, energy efficiency was not a primary focus, leaving room for improvement in minimizing power consumption while maintaining system performance. Second, inter-DC communication was not considered in this work, which could impact data flow and redundancy, especially in large-scale distributed systems. Finally, while the algorithms handled static scenarios well, dynamic user behavior—such as frequent user connections and disconnections—was not modeled, which could affect the adaptability of the solutions in real-time operational environments.

Building on these findings and limitations, future research should address several critical areas to improve DC placement strategies. Incorporating dynamic user behavior into DC placement models can lead to more adaptive solutions capable of maintaining optimal performance under varying load conditions. Additionally, exploring the chaining of multiple DCs to form a distributed network could enhance load balancing, redundancy, and data flow efficiency. Addressing power consumption is crucial for developing sustainable operations, and future work should focus on minimizing energy usage without compromising system performance. Finally, extending research to larger-scale scenarios and real-world applications will help validate and refine these strategies, ensuring their effectiveness and scalability in practical environments.

Author Contributions

Conceptualization, A.B. and M.M.A; methodology, A.B. and M.M.A.; investigation, A.B. and M.MA.; simulation development, A.B.; experiments, A.B; writing–original draft preparation, A.B.; writing–review and editing, A.B., M.M.A, H.O. and G.S.; visualization, A.B.; supervision, M.M.A, H.O. and G.S.

Funding

This research received no external funding

Institutional Review Board Statement

Not applicable

Informed Consent Statement

Not applicable

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:

RAN	Radio Access Networks
DC	Drone Cell
BS	Base Station
CH	Coverage Hole
DA	Demanding Area
QoS	Quality-of-Service
DA-RAN	Drone Assisted Radio Access Network
3D	3-Dimensional
4G	Fourth-Generation
DFO	Dispersive Flies Optimization
PSO	Particle Swarm Optimization
DE	Differential Evolution
RS	Random Search
DMF	Drone-cell Management Framework
GT	Ground Terminals
A2G	Air-to-Ground
UAV-BS	Unmanned Aerial Vehicle Base Station
IoT	Internet-of-Thing
GWO	Grey Wolf Optimization
B-GWO	Balanced-Grey Wolf Optimization
NOMA	Non-orthogonal Multiple Access
HDGWO	Hybrid Discrete Grey Wolf Optimization

MUPPEC	multi-UAV planning model with energy constraints
DEVIPS	Differential Evolution with a variable population size.
FBS	Flying Base Station
LoS	Line-of-Sight
NLoS	non-Line of sight

References

Mozaffari, M.; Taleb Zadeh Kasgari, A.; Saad, W.; Bennis, M.; Debbah, M. Beyond 5G With UAVs: Foundations of a 3D Wireless Cellular Network. IEEE Transactions on Wireless Communications 2019, 18, 357–372. [Google Scholar] [CrossRef]
Naqvi, S.A.R.; Hassan, S.A.; Pervaiz, H.; Ni, Q. Drone-Aided Communication as a Key Enabler for 5G and Resilient Public Safety Networks. IEEE Communications Magazine 2018, 56, 36–42. [Google Scholar] [CrossRef]
Sharma, N.; Magarini, M.; Jayakody, D.N.K.; Sharma, V.; Li, J. On-Demand Ultra-Dense Cloud Drone Networks: Opportunities, Challenges and Benefits. IEEE Communications Magazine 2018, 56, 85–91. [Google Scholar] [CrossRef]
Amorim, R.; Nguyen, H.; Mogensen, P.; Kovács, I.Z.; Wigard, J.; Sørensen, T.B. Radio Channel Modeling for UAV Communication Over Cellular Networks. IEEE Wireless Communications Letters 2017, 6, 514–517. [Google Scholar] [CrossRef]
Dhekne, A.; Gowda, M.; Choudhury, R.R. Cell Tower Extension through Drones: Poster; Association for Computing Machinery: New York, NY, USA, 2016; MobiCom’16; pp. 456–457. [Google Scholar] [CrossRef]
Bor-Yaliniz, I.; Yanikomeroglu, H. The New Frontier in RAN Heterogeneity: Multi-Tier Drone-Cells. IEEE Communications Magazine 2016, 54, 48–55. [Google Scholar] [CrossRef]
Lyu, J.; Zeng, Y.; Zhang, R.; Lim, T.J. Placement Optimization of UAV-Mounted Mobile Base Stations. IEEE Communications Letters 2017, 21, 604–607. [Google Scholar] [CrossRef]
Zhang, C.; Zhang, W. Spectrum Sharing for Drone Networks. IEEE Journal on Selected Areas in Communications 2017, 35, 136–144. [Google Scholar] [CrossRef]
Al-Hourani, A.; Kandeepan, S.; Jamalipour, A. Modeling air-to-ground path loss for low altitude platforms in urban environments. 2014 IEEE Global Communications Conference, 2014, pp. 2898–2904. [CrossRef]
Mozaffari, M.; Saad, W.; Bennis, M.; Debbah, M. Mobile Unmanned Aerial Vehicles (UAVs) for Energy-Efficient Internet of Things Communications. IEEE Transactions on Wireless Communications 2017, 16, 7574–7589. [Google Scholar] [CrossRef]
Alzenad, M.; El-Keyi, A.; Lagum, F.; Yanikomeroglu, H. 3-D Placement of an Unmanned Aerial Vehicle Base Station (UAV-BS) for Energy-Efficient Maximal Coverage. IEEE Wireless Communications Letters 2017, 6, 434–437. [Google Scholar] [CrossRef]
Zhou, L.; Yang, Z.; Zhou, S.; Zhang, W. Coverage Probability Analysis of UAV Cellular Networks in Urban Environments. 2018 IEEE International Conference on Communications Workshops (ICC Workshops), 2018, pp. 1–6. [CrossRef]
Ghanavi, R.; Kalantari, E.; Sabbaghian, M.; Yanikomeroglu, H.; Yongacoglu, A. Efficient 3D aerial base station placement considering users mobility by reinforcement learning. 2018 IEEE Wireless Communications and Networking Conference (WCNC), 2018, pp. 1–6. [CrossRef]
Kalantari, E.; Yanikomeroglu, H.; Yongacoglu, A. On the Number and 3D Placement of Drone Base Stations in Wireless Cellular Networks. 2016 IEEE 84th Vehicular Technology Conference (VTC-Fall), 2016, pp. 1–6. [CrossRef]
Kalantari, E.; Shakir, M.Z.; Yanikomeroglu, H.; Yongacoglu, A. Backhaul-aware robust 3D drone placement in 5G+ wireless networks. 2017 IEEE International Conference on Communications Workshops (ICC Workshops), 2017, pp. 109–114. [CrossRef]
Ghazzai, H.; Yaacoub, E.; Alouini, M.S.; Dawy, Z.; Abu-Dayya, A. Optimized LTE Cell Planning With Varying Spatial and Temporal User Densities. IEEE Transactions on Vehicular Technology 2016, 65, 1575–1589. [Google Scholar] [CrossRef]
Shi, W.; Li, J.; Xu, W.; Zhou, H.; Zhang, N.; Shen, X. 3D Drone-cell deployment optimization for drone assisted radio access networks. 2017 IEEE/CIC International Conference on Communications in China (ICCC), 2017, pp. 1–6. [CrossRef]
Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Advances in Engineering Software 2014, 69, 46–61. [Google Scholar] [CrossRef]
Gupta, A.; Trivedi, A.; Prasad, B. B-GWO based multi-UAV deployment and power allocation in Noma Assisted Wireless Networks - Wireless Networks, 2022.
Pliatsios, D.; Goudos, S.K.; Lagkas, T.; Argyriou, V.; Boulogeorgos, A.A.A.; Sarigiannidis, P. Drone-Base-Station for Next-Generation Internet-of-Things: A Comparison of Swarm Intelligence Approaches. IEEE Open Journal of Antennas and Propagation 2022, 3, 32–47. [Google Scholar] [CrossRef]
Huang, P.Q.; Wang, Y.; Wang, K.; Yang, K. Differential Evolution With a Variable Population Size for Deployment Optimization in a UAV-Assisted IoT Data Collection System. IEEE Transactions on Emerging Topics in Computational Intelligence 2020, 4, 324–335. [Google Scholar] [CrossRef]
li Su, J.; Wang, H. An improved adaptive differential evolution algorithm for single unmanned aerial vehicle multitasking. Defence Technology 2021, 17, 1967–1975. [Google Scholar] [CrossRef]
Pokorny, J.; Seda, P.; Seda, M.; Hosek, J. Modeling Optimal Location Distribution for Deployment of Flying Base Stations as On-Demand Connectivity Enablers in Real-World Scenarios. Sensors 2021, 21. [Google Scholar] [CrossRef] [PubMed]
Al-Hourani, A.; Kandeepan, S.; Lardner, S. Optimal LAP Altitude for Maximum Coverage. IEEE Wireless Communications Letters 2014, 3, 569–572. [Google Scholar] [CrossRef]
Kennedy, J.; Eberhart, R. Particle swarm optimization. Proceedings of ICNN’95 - International Conference on Neural Networks, 1995, Vol. 4, pp. 1942–1948 vol.4. [CrossRef]
Pereira, G. Particle Swarm Optimization 2011. Accessed: 2024-01-10.
Storn, R. On the usage of differential evolution for function optimization. Proceedings of North American Fuzzy Information Processing, 1996, Vol. 0, pp. 519–523. [CrossRef]
Storn, R.; Price, K. Differential Evolution - A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. Journal of Global Optimization 1997, 11, 341–359. [Google Scholar] [CrossRef]
Georgioudakis, M.; Plevris, V. A Comparative Study of Differential Evolution Variants in Constrained Structural Optimization. Frontiers in Built Environment 2020, 6. [Google Scholar] [CrossRef]
al Rifaie, M.M. Dispersive Flies Optimisation. 2014 Federated Conference on Computer Science and Information Systems, 2014, pp. 529–538. [CrossRef]
Das, S.; Suganthan, P.N. Differential Evolution: A Survey of the State-of-the-Art. IEEE Transactions on Evolutionary Computation 2011, 15, 4–31. [Google Scholar] [CrossRef]
Where you can fly drones | UK Civil Aviation Authority. https://register-drones.caa.co.uk/drone-code/where-you-can-fly#:~:text=3.,normally%20fly%20higher%20than%20this., 2019. Accessed: 2024-01-10.
Olorunda, O.; Engelbrecht, A.P. Measuring exploration/exploitation in particle swarms using swarm diversity. 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence), 2008, pp. 1128–1134. [CrossRef]
al Rifaie, M.M.; Cavazza, M. Evolutionary Optimisation of Beer Organoleptic Properties: A Simulation Framework. Foods 2022, 11. [Google Scholar] [CrossRef]
Wang, H.; Geng, Q.; Qiao, Z. Parameter tuning of particle swarm optimization by using Taguchi method and its application to motor design. 2014 4th IEEE International Conference on Information Science and Technology, 2014, pp. 722–726. [CrossRef]
Meissner, M.; Schmuker, M.; Schneider, G. Optimized Particle Swarm Optimization (OPSO) and its application to artificial neural network training. BMC bioinformatics 2006, 7, 125. [Google Scholar] [CrossRef] [PubMed]
Centeno-Telleria, M.; Zulueta, E.; Fernandez-Gamiz, U.; Teso-Fz-Betoño, D.; Teso-Fz-Betoño, A. Differential evolution optimal parameters tuning with artificial neural network. Mathematics 2021, 9, 427. [Google Scholar] [CrossRef]

Figure 2. Coverage Probability for all environment with default parameters

Figure 3. Default and phased restart diversity for Suburban 90 environment

Figure 4. Default and phased restart diversity for Suburban 120 environment

Figure 7. Coverage Probability for all environment with optimal parameters

Figure 8. User Coverage for Suburban Environments

Figure 9. User Coverage for Urban Environments

Figure 10. User Coverage for Dense-urban Environments

Figure 11. User Coverage for High-rise-urban Environments

Table 2. Experimental Parameters

Parameters	Values
Environment	Urban, Suburban, Dense Urban, High-rise Urban
Pathloss Threshold	90, 100, 110, 120
Area	5 $k m^{2}$
Population Size	25
Function Evaluation	2500
Number of DCs	10
Height min, max	0,120
Carrier Frequency	$2 * 10^{9}$ Hz
Speed of Light	299792458 m/s

Table 3. Comparison of standard and optimized parameters

Algorithms		DFO		PSO					DE
	Parameter	N	$Δ$	N	W	c1	c2	Wd	N	F	CR
Environment		N	$Δ$	N	W	c1	c2	Wd	N	F	CR
Standard Parameters		25	0.001	25	1	1.5	2.0	0.99	25	0.8	0.9
Sub-urban 90		34	0.05	213	0.36	0.43	0.5	0.3	72	0.39	0.87
Sub-urban 100		36	0.056	109	1	0.31	1.14	0.73	211	0.79	0.8
Sub-urban 110		235	0.069	137	0.49	2.15	0.2	0.17	50	0.33	0.1
Sub-urban 120		55	0.032	106	0.14	0.8	2.05	0.9	183	0.11	0.89
Urban 90		19	0.055	245	0.24	1.5	1.05	0.48	168	0.35	0.54
Urban 100		5	0.048	195	0.86	0.78	0.8	0.22	110	0.71	0.19
Urban 110		83	0.089	102	0.52	0.96	0.87	0.55	94	0.62	0.52
Urban 120		86	0.019	66	0.07	1.83	2.22	0.16	89	0.21	0.72
Dense-urban 90		37	0.018	212	0.34	0.68	0.46	0.36	238	0.41	0.77
Dense-urban 100		25	0.012	220	0.73	1.05	2.2	0.25	201	0.58	0.18
Dense-urban 110		65	0.029	111	0.11	0.72	1.52	0.93	197	0.46	0.67
Dense-urban 120		73	0.067	57	0.38	1.51	1.35	0.53	197	0.46	0.67
Highrise-urban 90		192	0.016	149	0.46	1.99	1.97	0.22	197	0.46	0.67
Highrise-urban 100		190	0.014	135	0.27	0.44	0.94	0.84	197	0.46	0.67
Highrise-urban 110		32	0.021	179	0.49	1.8	0.96	0.42	197	0.46	0.67
Highrise-urban 120		139	0.067	185	0.21	0.67	1.89	0.43	208	0.43	0.61

Table 4. Wilcoxon Paired test for base and tuned parameter coverage, highlighted cells indicate significant difference between the two sets of results

	DFO		PSO		DE		RS
Environment	DFO		PSO		DE		RS
	W Statistics	P-value	W Statistics	P-value	W Statistics	P-value	W Statistics	P-value
Sub-urban 90	25.5	0.8322	0.5	0.0047	27.5	1.0	27.5	1.0
Sub-urban 100	23.5	0.6754	19.5	0.4102	24.5	0.7559	23.0	0.6329
Sub-urban 110	24.5	0.7564	17.5	0.3004	20.5	0.4652	23.0	0.6329
Sub-urban 120	27.5	1.0	27.5	1.0	27.5	1.0	27.5	1.0
Urban 90	14.0	0.1519	0.0	0.0019	23.0	0.6329	27.5	1.0
Urban 100	10.5	0.0741	0.0	0.0019	6.5	0.0198	18.0	0.3046
Urban 110	23.0	0.6329	11.0	0.0884	27.5	1.0	22.5	0.5791
Urban 120	27.5	1.0	23.5	0.6718	27.5	1.0	25.0	0.7949
Dense-urban 90	27.5	1.0	1.5	0.0049	23.0	0.6329	27.5	1.0
Dense-urban 100	14.0	0.1519	0.0	0.0019	15.5	0.2090	27.5	1.0
Dense-urban 110	24.0	0.7102	0.5	0.0050	23.5	0.6754	27.5	1.0
Dense-urban 120	22.5	0.5964	26.5	0.9167	27.0	0.9588	27.5	1.0
High-rise-urban 90	0.5	0.0027	0.0	0.0019	18.0	0.3046	27.5	1.0
High-rise-urban 100	27.5	1.0	27.5	1.0	27.5	1.0	27.5	1.0
High-rise-urban 110	27.5	1.0	5.0	0.0181	27.5	1.0	27.5	1.0
High-rise-urban 120	14.0	0.1519	0.0	0.0019	18.0	0.3046	22.5	0.5791

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

3 Dimensional DC Placement: Drone Placement for Optimal Coverage

Abstract

1. Introduction

2. Background

3. Problem Formulation

3.1. Particle Swarm Optimization

3.2. Differential Evolution

3.3. Dispersive Flies Optimization

4. Experiment and Results

4.1. Experiments

4.2. Parameter Tuning

4.3. Results

5. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe