Stability Analysis of Boost PFC Considering the External Impedance

Preprint

Article

Stability Analysis of Boost PFC Considering the External Impedance

Altmetrics

Downloads

Views

Comments

This version is not peer-reviewed

Submitted:

05 October 2024

Posted:

08 October 2024

You are already at the latest version

Alerts

Abstract

This stability analysis method is simply represented and understood on a Bode plot of two impedances without complex equations. The external impedance of the charging system is properly quantified and designed based on the stability criteria by analyzing.

Keywords:

Subject: Engineering - Automotive Engineering

1. Introduction

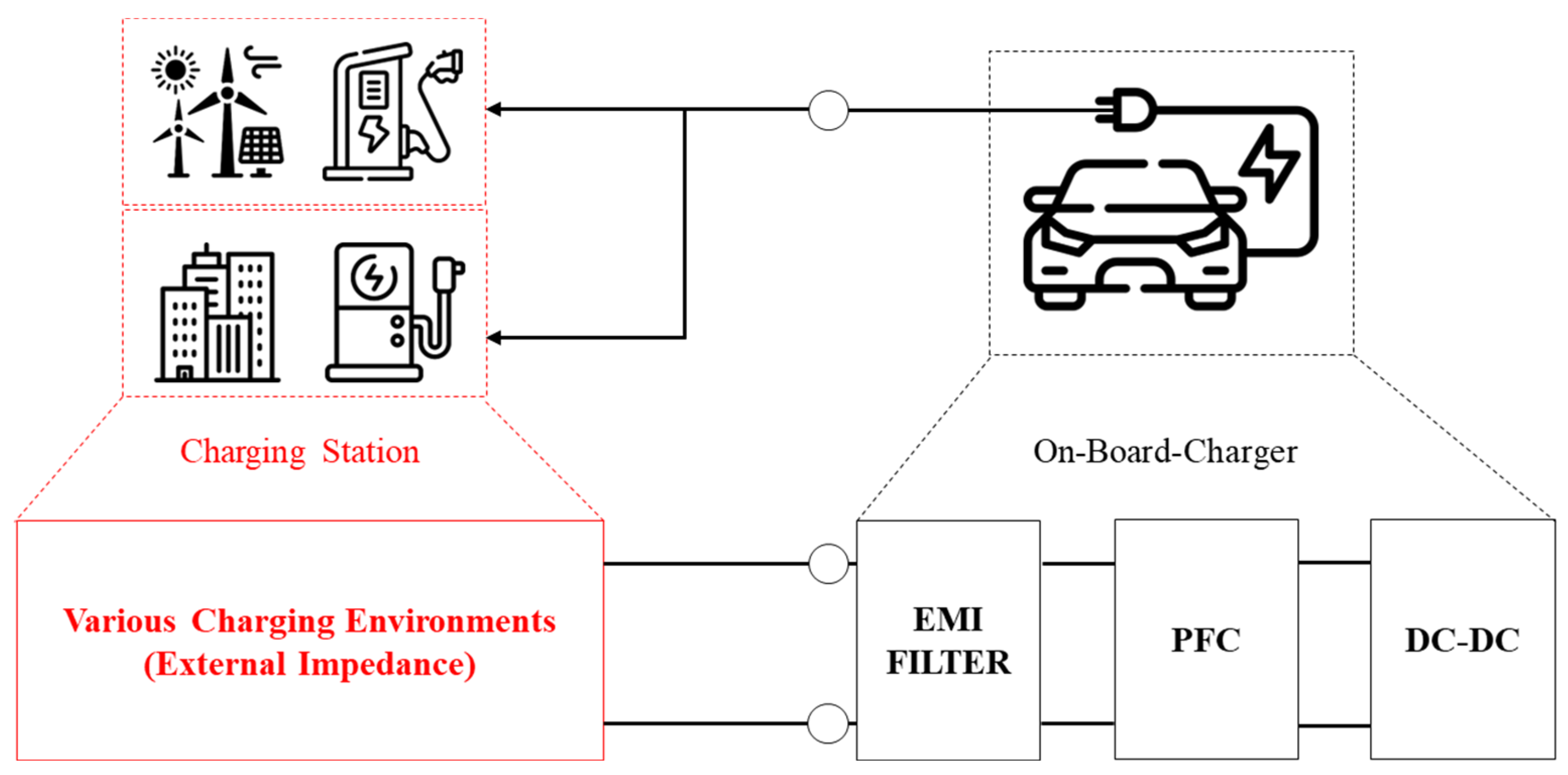
The charging system installed in electric vehicles typically comprises three components, as illustrated in Figure 1: an Electromagnetic Interference (EMI) filter for compliance with electromagnetic regulations, a Power Factor Correction (PFC) circuit for reactive power compensation, and a DC-DC circuit to meet a wide output voltage range.

Electric vehicles charge at various charging stations depending on the situation. Therefore, the charging system of an electric vehicle, unlike conventional power conversion devices, encounters various external impedances (External block in Figure 1). Such external impedances affect the response characteristics and stability of the charging system. To ensure the reliability of the charging system, it is necessary to assess the stability based on the external impedance.

In this paper, for the sake of simplicity, the stability of the DC-DC circuit within the charging system is assumed to be stable. Subsequently, the stability of the system, composed of external impedance, EMI filter, and boost PFC, is analyzed. Specifically, The stability is determined by employing the relationship between the output impedance, which includes external impedance and the EMI filter, and the input impedance of the boost PFC, similar to the approach taken in the study by R. D. Middlebrook [1].

2. Impedance Analysis

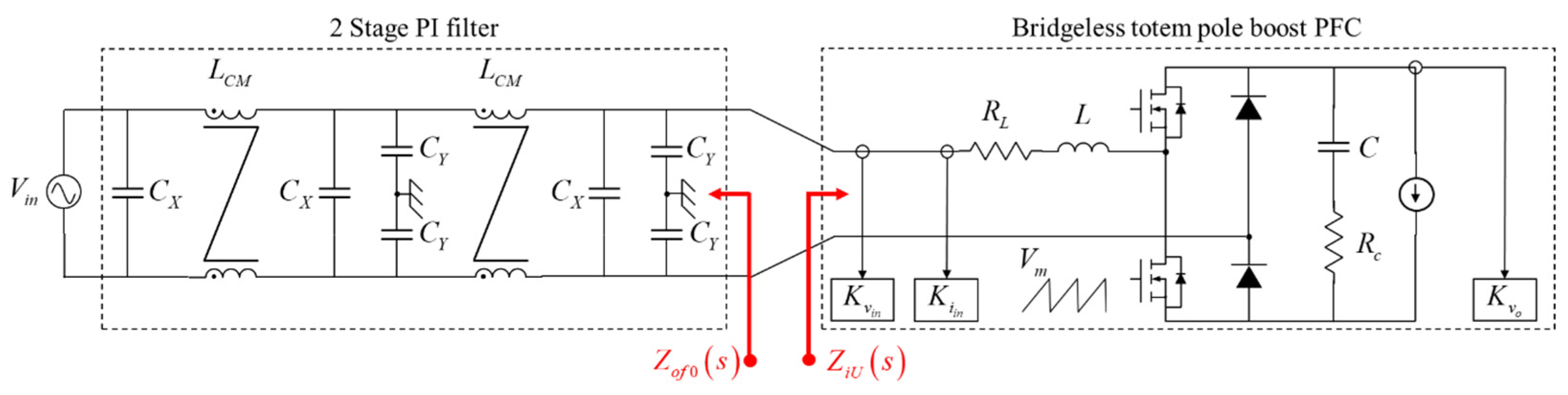
In this paper, as shown in Figure 2, the system is composed of a 2-stage PI filter and a bridgeless totem pole boost PFC converter.

Z_{o f 0} (s)

is the output impedance of an EMI filter, and

Z_{i U} (s)

is the input impedance of the boost PFC.

2.1. EMI Filter Output Impedance with the External Impedance

In this section, discuss the impedance analysis of the EMI filter and explore the impedance analysis when external impedance is considered.

2.1.1. Differential Mode Loop

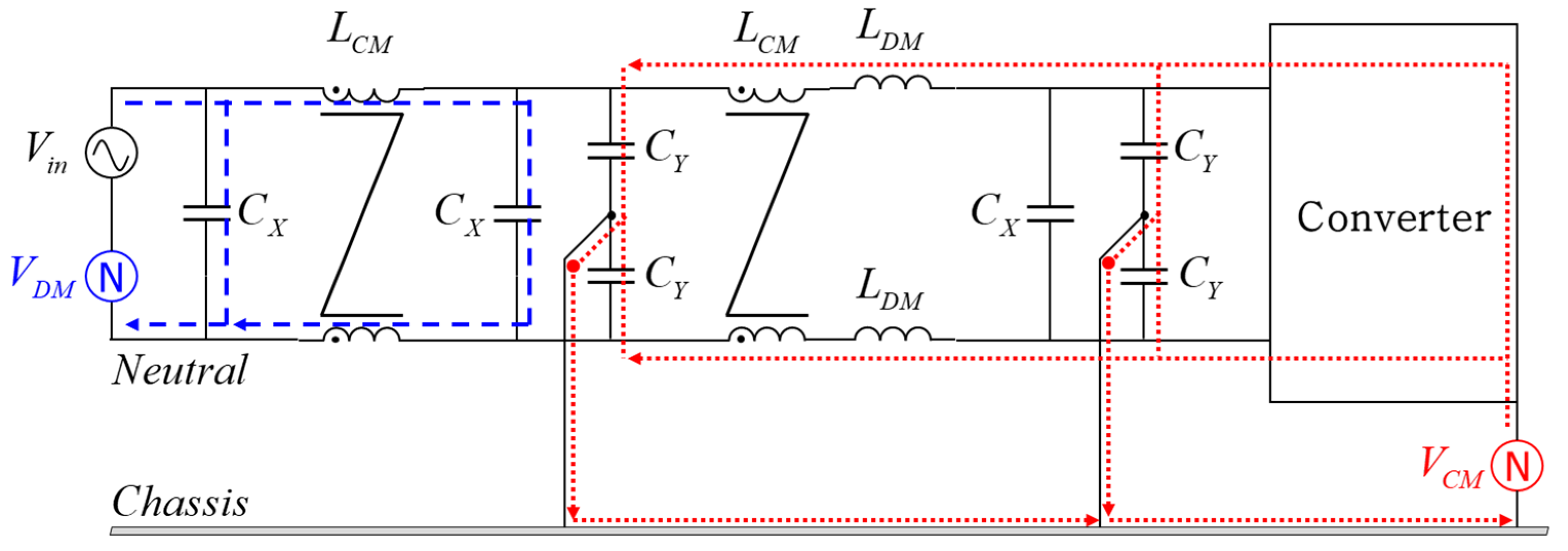
EMI filters are generally classified into two types based on the type of noise : CM (Common Mode) noise and DM (Differential Mode) noise. CM components include CM inductors and Y-capacitors, while DM components include DM inductors and X-capacitors. Figure 3 illustrates the typical structure of an EMI filter. There is CM noise forming a loop through the chassis and DM noise forming a loop through the neutral line.

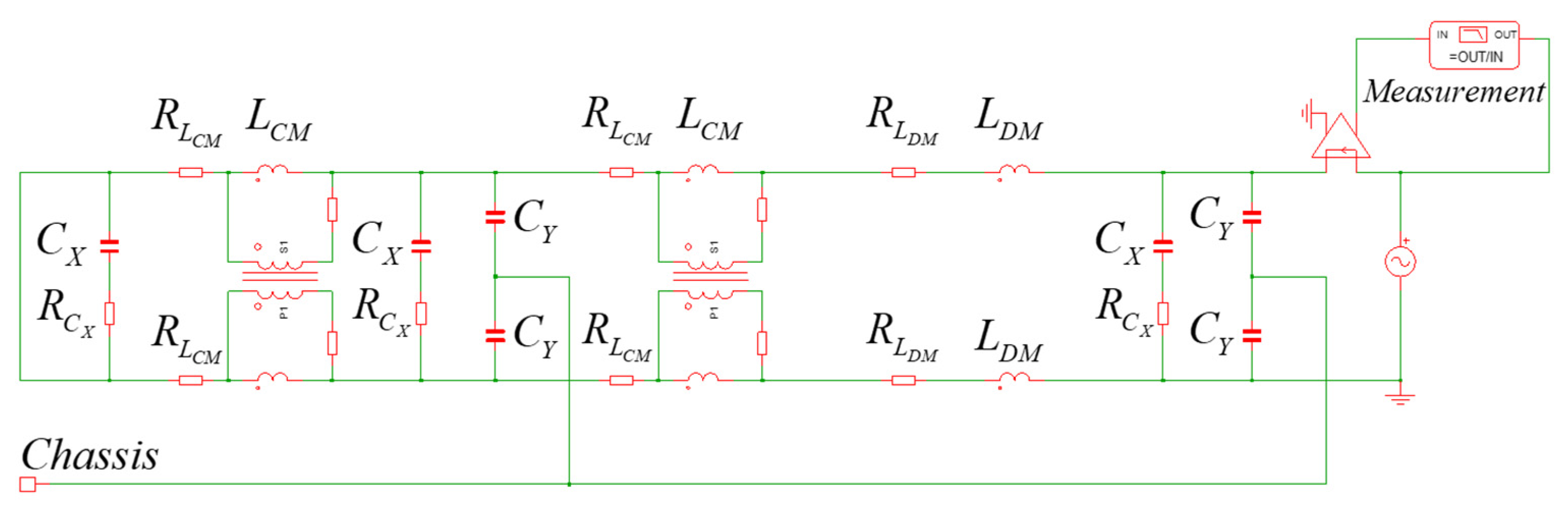
Figure 4 depicts the entire EMI filter with a chassis. Figure 5 represents the circuit of the DM loop. Figure 6 illustrates the input shorted output impedance of the two circuits. The parameters of the EMI filter used in the simulation are indicated in Table 1.

C_{X}

C_{Y}

L_{C M}

L_{D M}

R_{C_{X}}

R_{L_{C M}}

R_{L_{D M}}

Even when considering only the components of the DM loop, as shown in Figure 6, it has the same effect as considering the impedance of the entire circuit. In other words, in the stability analysis of complex EMI filters, the effects of the CM loop can be eliminated to simplify the analysis.

The stability analysis in power conversion devices is defined when input and output form a loop. In the case of the EMI filter, the loop formed by DM noise affects stability. On the contrary, the loop formed by CM noise does not affect stability. Therefore, from the perspective of the EMI filter at the input, only the components forming the loop with the input voltage are considered. In other words, only the X-capacitors related to DM noise are taken into account.

2.1.2. Impedance Analysis with the External Impedance

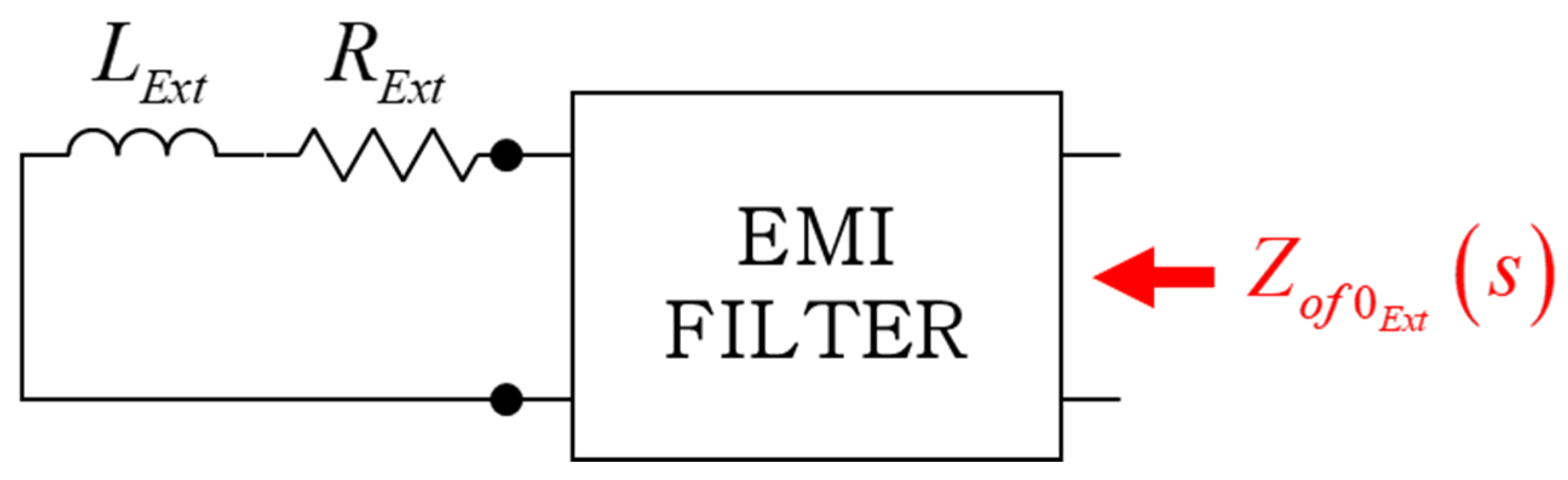
Generally, the grid impedance of a power system consists of inductive and resistive components. In this paper, the term 'external impedance' is used instead of 'grid impedance' for a more conventional stability analysis.

When external impedance is added, define the impedance

Z_{o f 0_{E x t}} (s)

by shorting the voltage source side, not the termination side of the EMI filter, as indicated in Figure 7.

2.2. Boost PFC Input Impedance

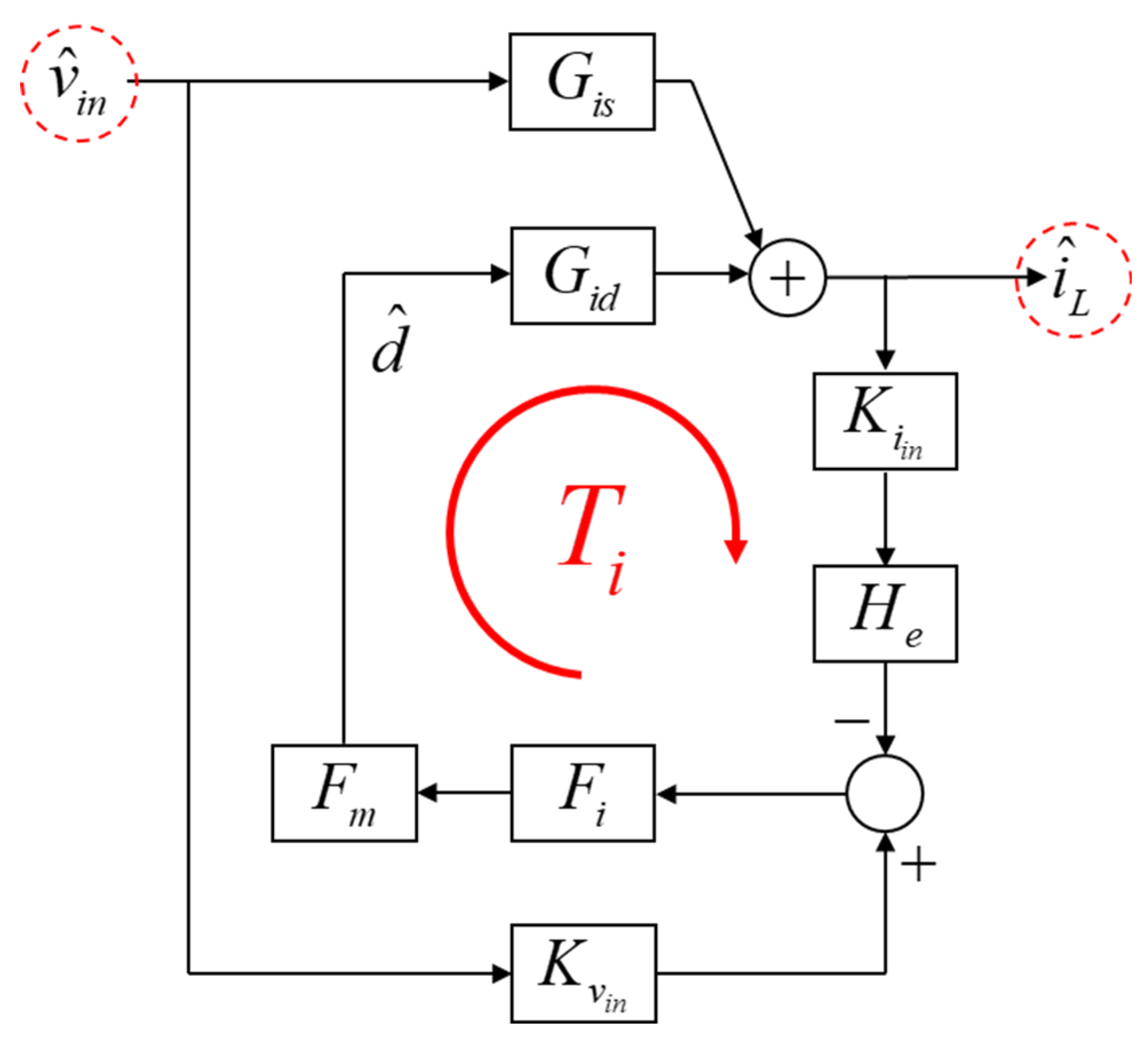
The control block diagram for deriving the input impedance of the boost PFC is illustrated in Figure 8, and the input impedance is represented by Equation (1). The boost PFC input impedance

Z_{i U} (s)

is influenced by the current control loop. Assuming that the voltage control loop has a crossover frequency significantly lower than the current control loop crossover frequency, it is considered to have no impact. After the crossover frequency, the Boost PFC inductor leads the phase by +90° [3].

Z_{i U} (s) = \frac{1 + T_{i} (s)}{K_{v_{i n}} \cdot F_{m} \cdot F_{i} (s) \cdot G_{i d} (s) + G_{i s} (s)}

(1)

3. Stability Analysis of Boost PFC Considering the External Impedance

The stability of the system with coupled external impedance is defined by a new characteristic equation, known as the minor loop gain

T_{m n} (s)

. The uncoupled loop gain

T_{m U} (s)

represents the loop gain of the converter with ideal input and output. It is equivalent to the loop gain commonly used in practice [10]. For stability analysis considering the influence of the input impedance,

T_{m U} (s)

is assumed to be stable, and the minor loop gain

T_{m n} (s)

is analyzed.

Using SIMPLIS to simulate in the frequency-domain and time-domain, it was confirmed that

T_{m n} (s)

determines the stability of the whole system. For the convenience of analysis, the simulation considers only the external impedance, EMI filter, and boost PFC in the OBC system.

The EMI filter consists of a 2-stage PI filter with CM filters, as shown in Figure 2. The parameters related to the EMI filter are presented in Table 2. The boost PFC is a Bridgeless Totem Pole Boost PFC converter, as illustrated in Figure 2. The parameters associated with the boost PFC are presented in Table 3. For current control and voltage control, a Type II compensator, as represented Equation (2), was implemented..

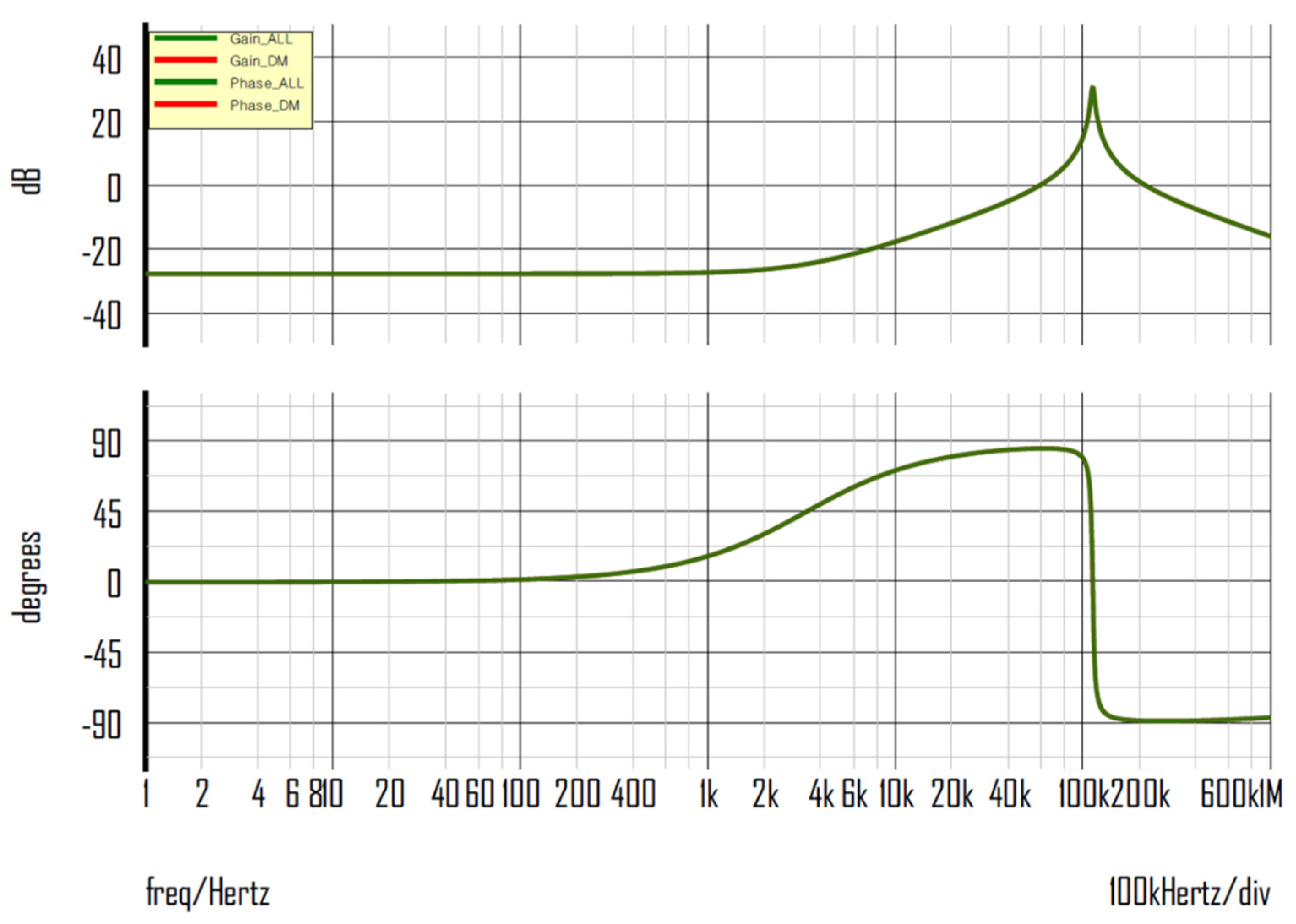
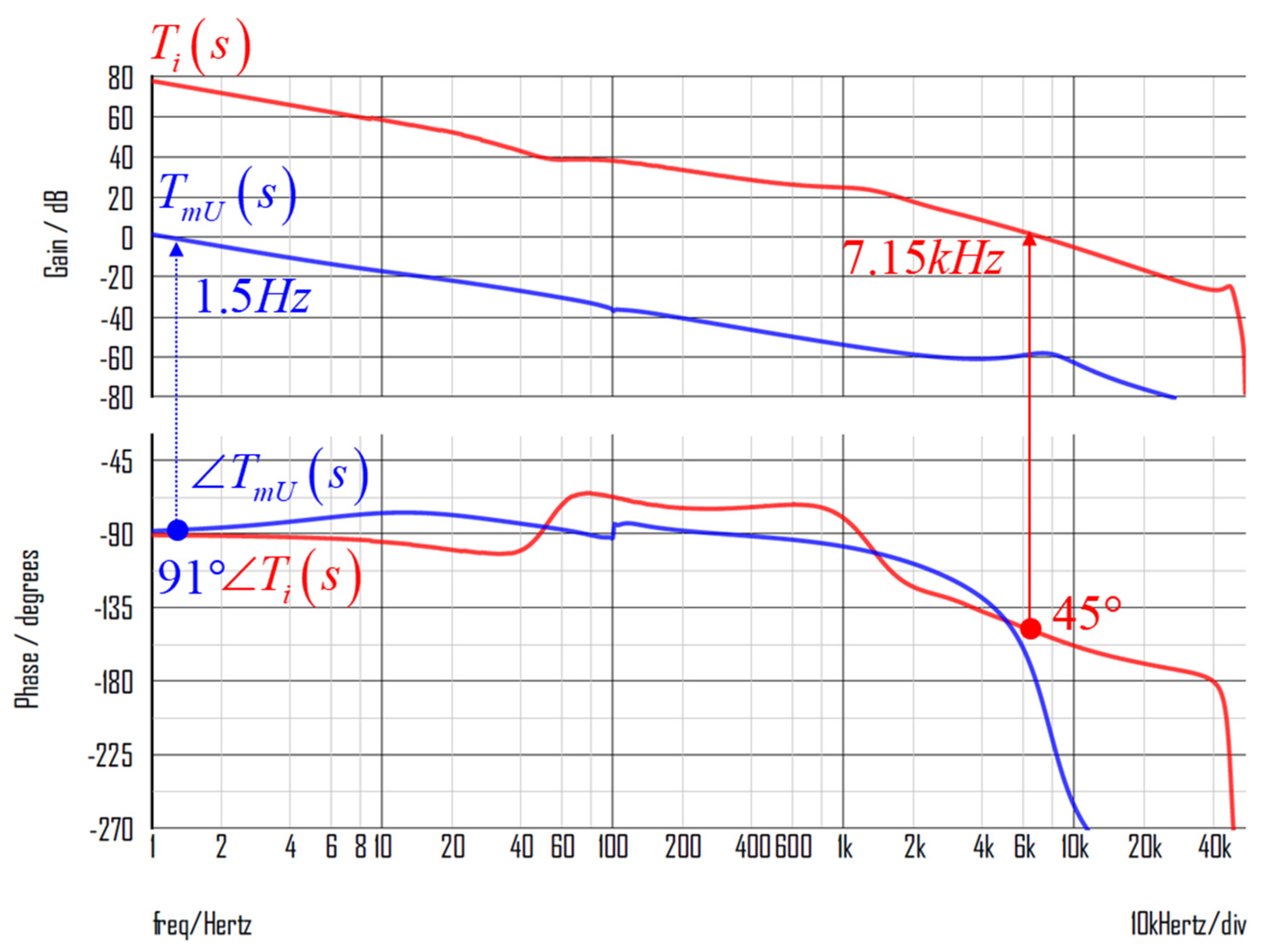
Figure 9 illustrates the current loop gain

T_{i} (s)

and

T_{m U} (s)

using the parameters that were mentioned earlier. The crossover frequency of

T_{i} (s)

is 7.15 kHz, and the phase margin is 45°. And The crossover frequency of

T_{m U} (s)

is 1.5 Hz, and the phase margin is 91°.

C_{X}

C_{Y}

L_{C M}

R_{C_{X}}

R_{L_{C M}}

V_{i n, r m s}

F_{V_{i n}}

V_{o}

I_{o}

F_{s w}

L

R_{L}

R_{C}

V_{m}

K_{V_{i n}}

K_{I_{i n}}

K_{V_{o}}

K_{F_{i}}

ω_{i, z}

ω_{i, p}

ω_{i, c}

K_{F_{i}}

ω_{v, z}

ω_{v, p}

ω_{v, c}

1 \cdot 2 π

5 \cdot 2 π

7.15 \cdot 2 π

10 \cdot 2 π

37.5 \cdot 2 π

1.5 \cdot 2 π

F_{c o n} (s) = K_{c o n} \frac{1}{s} \frac{(1 + \frac{s}{ω_{c o n, z}})}{(1 + \frac{s}{ω_{c o n, p}})}

(2)

3.1. Stability Criteria with the External Impedance

The minor loop gain

T_{m n} (s)

describes the relationship between the output impedance

Z_{o f 0_{E x t}} (s)

of an EMI filter with external impedance included, and the input impedance

Z_{i U} (s)

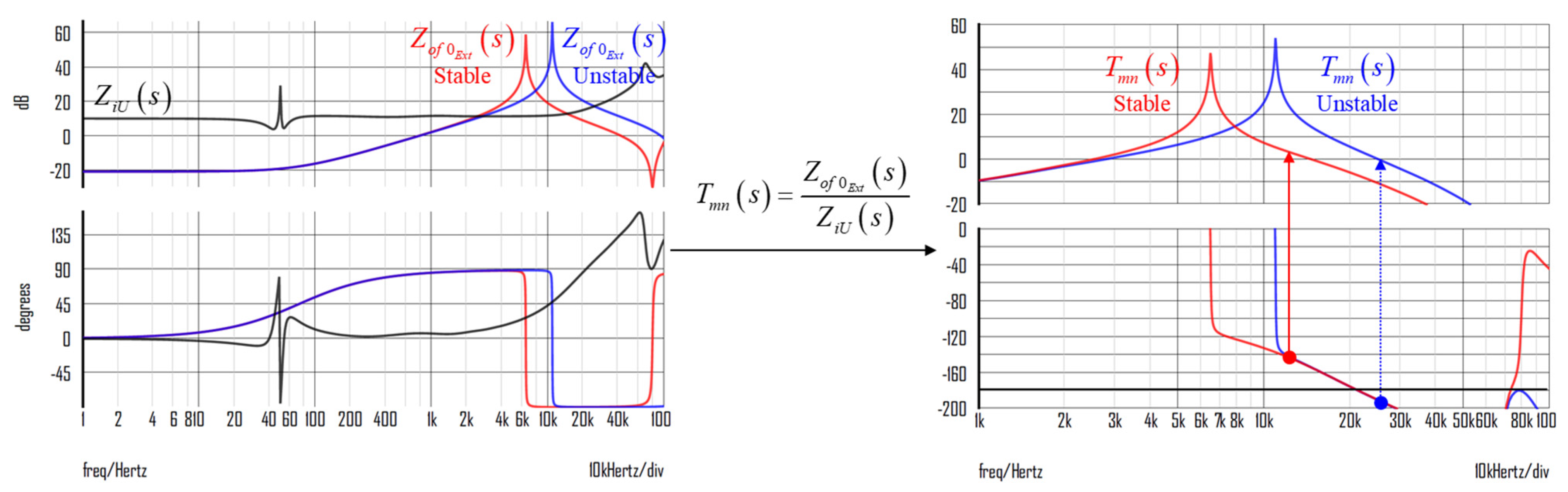
of a boost PFC. The stability criteria of the minor loop gain can be performed in the same manner as the conventional loop gain. These relationships are represented in equation (3). Figure 10 depicts the bode plot of

T_{m n} (s)

using

Z_{i U} (s)

and

Z_{o f 0_{E x t}} (s)

[1 + T_{m U} (s)] [1 + \frac{Z_{o f 0_{E x t}} (s)}{Z_{i U} (s)}] = [1 + T_{m U} (s)] [1 + T_{m n} (s)]

(3)

3.2. Converter Performance under System Interaction

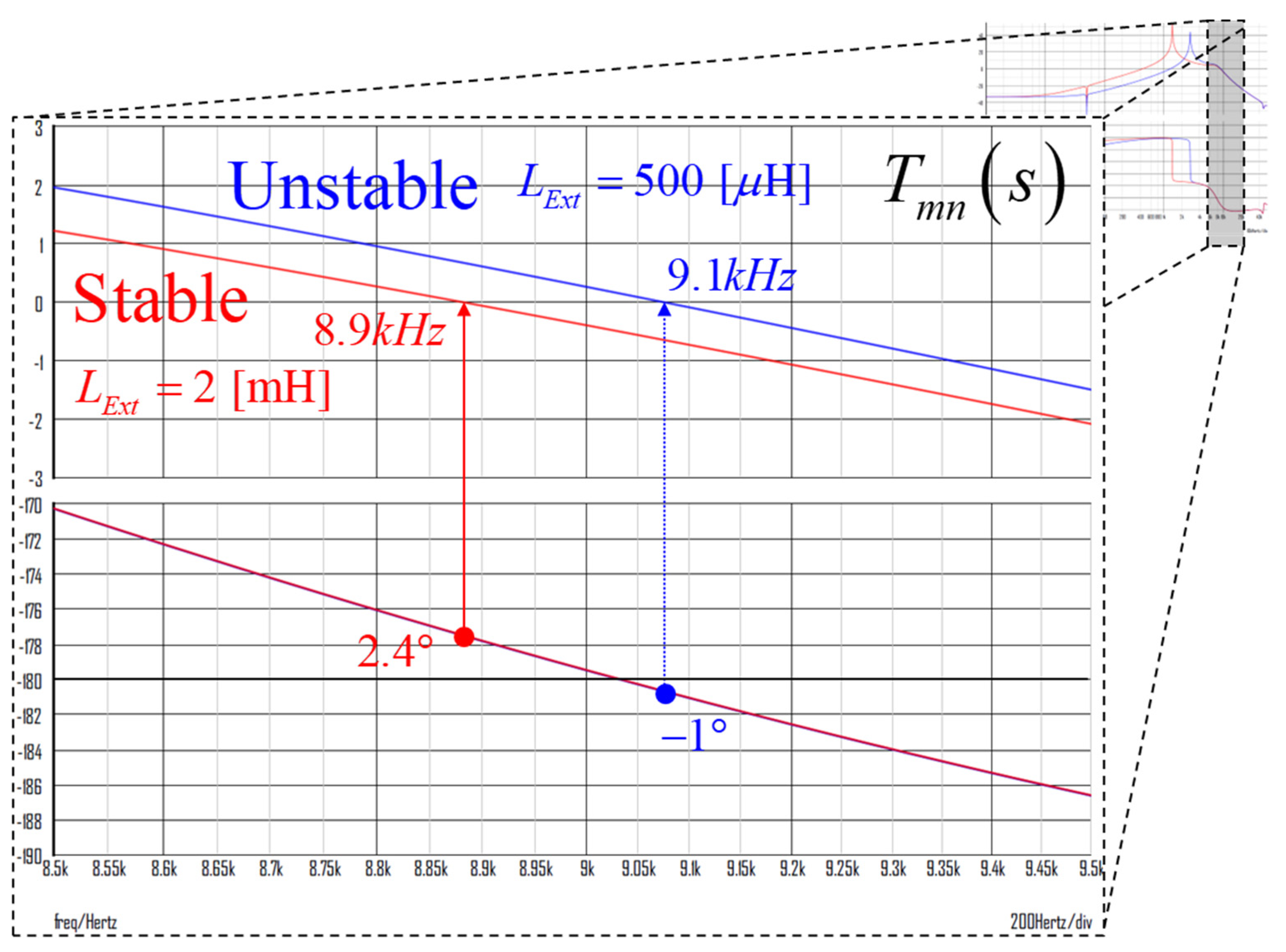
While varying the inductance

L_{E x t}

of the external impedance, consider scenarios where the minor loop gain becomes stable or unstable. In this case, the resistance of the external impedance

R_{E x t}

is fixed at 100mΩ.

Figure 11 represents the minor loop gain

T_{m n} (s)

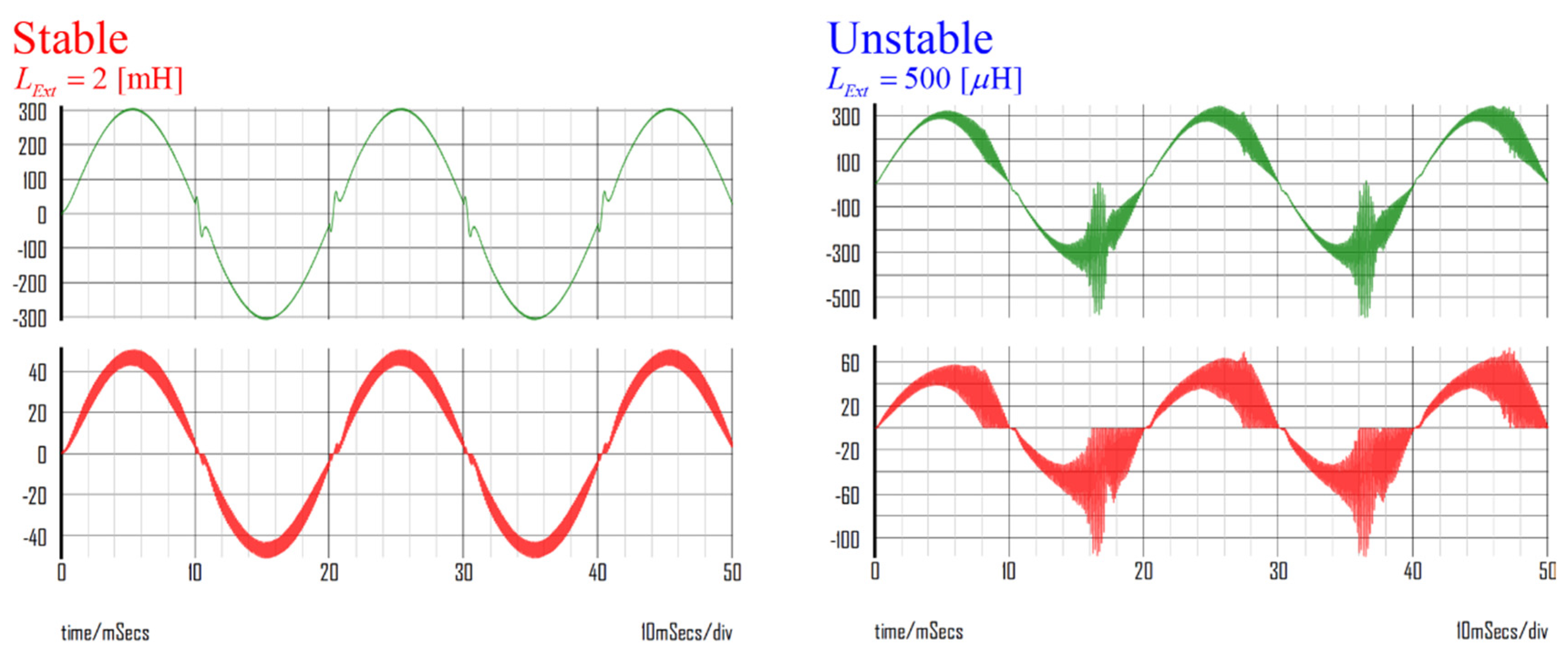
, while Figure 12 depicts the input voltage and current of the boost PFC.

When

L_{E x t}

is 2mH, the phase margin is 2.4°, system is stable. On the other hand, when

L_{E x t}

is 500uH, the phase margin is -1°, system is unstable. The effectiveness of the stability criteria is confirmed through simulations in both the frequency domain and time domain. As predicted in the frequency domain, in an unstable condition, the input voltage and current resonate. Therefore, it can be concluded that the stability criteria through the minor loop gain

T_{m n} (s)

is verified.

4. Conclusions

This paper has summarized the stability analysis approach considering external impedance. The relationship between

Z_{o f 0_{E x t}} (s)

and

Z_{i U} (s)

, in other words, using the minor loop gain

T_{m n} (s)

, can be employed to determine stability. The results were validated through simulations, confirming the effectiveness of the stability analysis approach. Generally, instability occurs when the phase difference (

∠ Z_{o f 0_{E x t}} (s) - ∠ Z_{i U} (s)

) at the intersection point of two impedances is greater than -180°

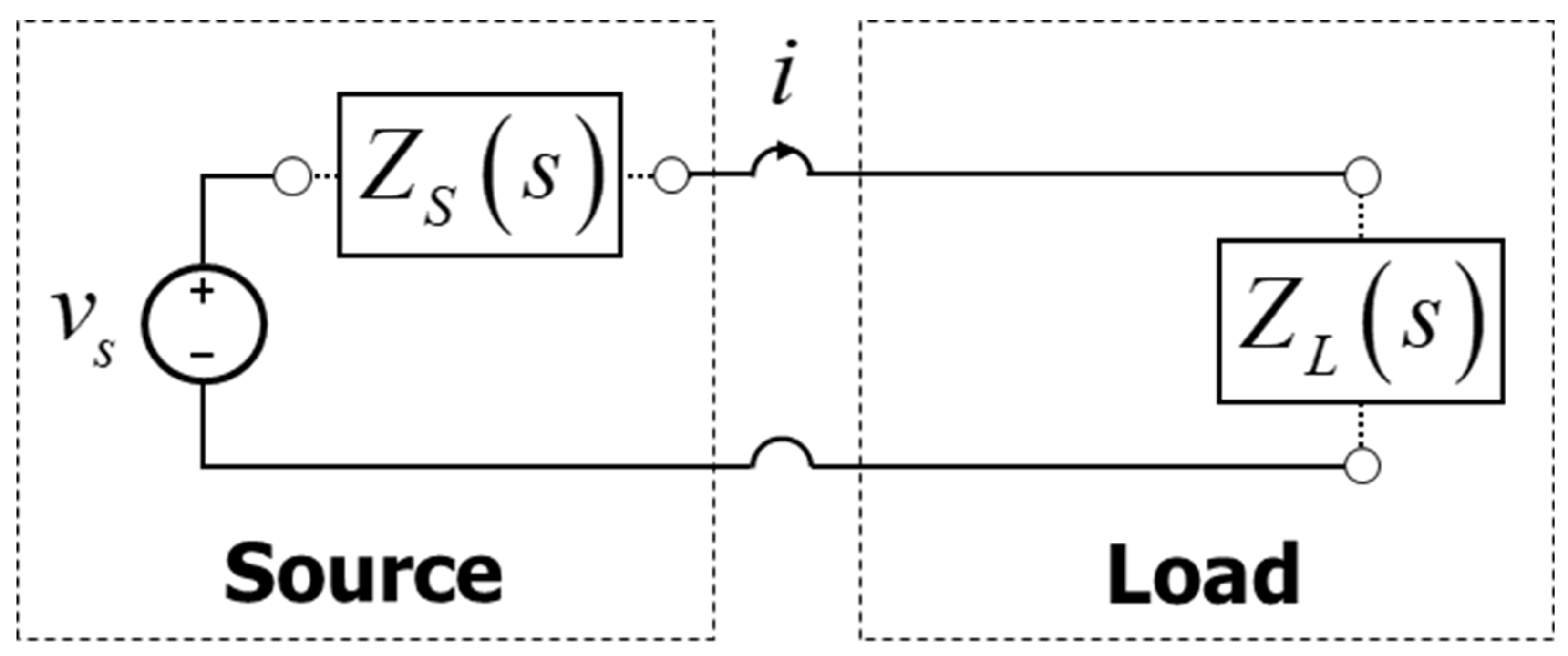
To simplify the explanation for better understanding using circuit theory, it can be described as follows. As depicted in Figure 13, most power conversion devices are divided into a source and a load. And there are source impedance and load impedance. If the magnitudes of the source impedance and load impedance are equal, and their phases are opposite, the current will flow to infinity. Therefore, this can be considered as the system being unstable. In the charging system, the source impedance can be thought of as

Z_{o f 0_{E x t}} (s)

, and the load impedance as

Z_{i U} (s)

. Thus, as indicated in equation (4) the minor loop gain

T_{m n} (s)

can be defined with the numerator as the source impedance

Z_{S} (s)

and the denominator as the load impedance

Z_{L} (s)

The charging system installed in electric vehicles must operate in various charging environments. The system might become unstable and, in certain situations, could face the possibility of being destroyed. Therefore, an analysis of the impedance specifications for which the system can operate is required. The external impedance of the system is properly quantified and designed based on the stability criteria by analyzing

T_{m n} (s)

T_{m n} (s) = \frac{Z_{S} (s)}{Z_{L} (s)}

(4)

Appendix A: Input Filter Interaction Example with SIMPLIS Elements

In this section, explain the example from the Conclusion using the SIMPLIS Elements version. In the given example, a Buck converter was employed, and the system interaction was observed by modifying the resistance of the filter. Following the parameters and elements depicted in the figures makes it easy to verify the system interaction.

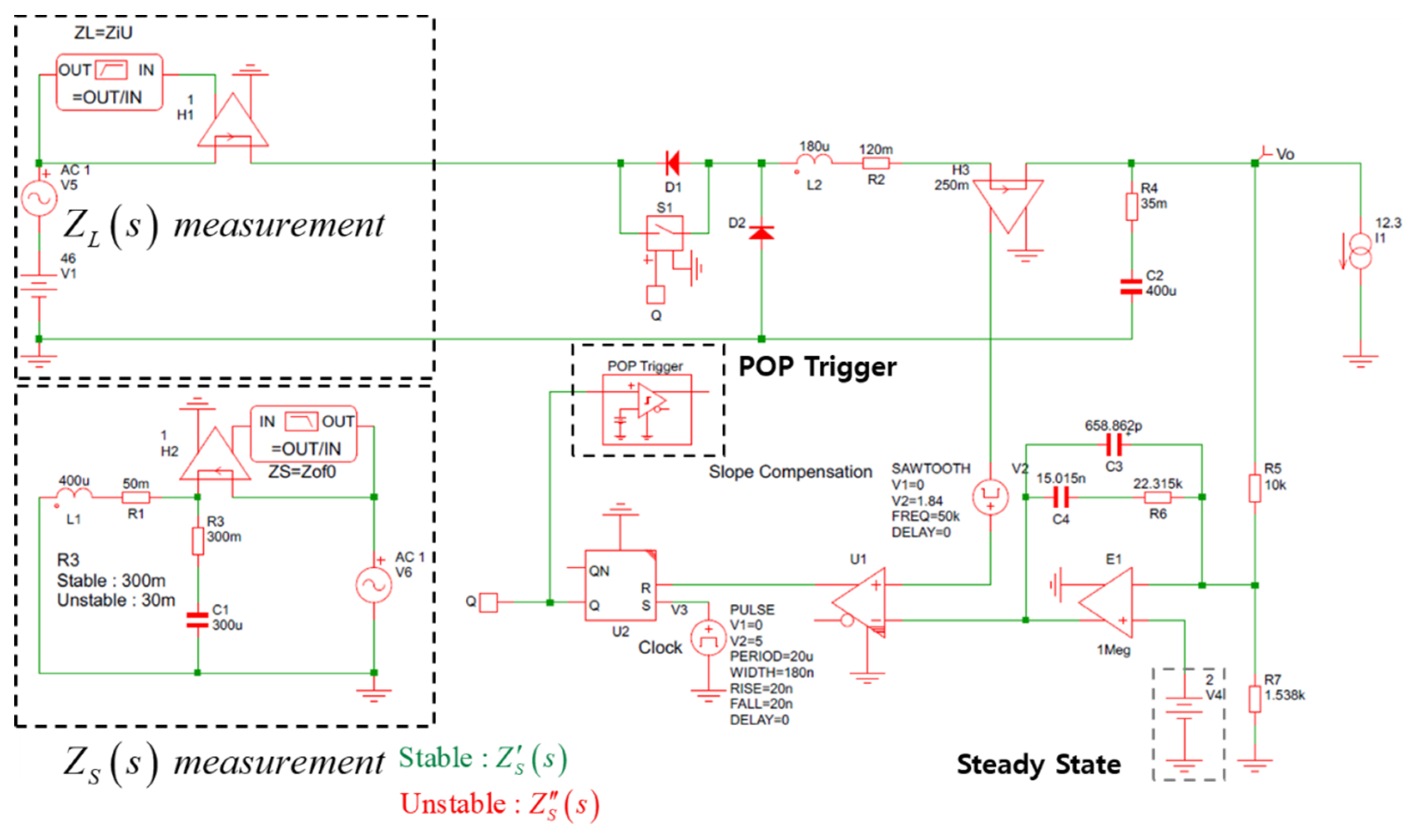
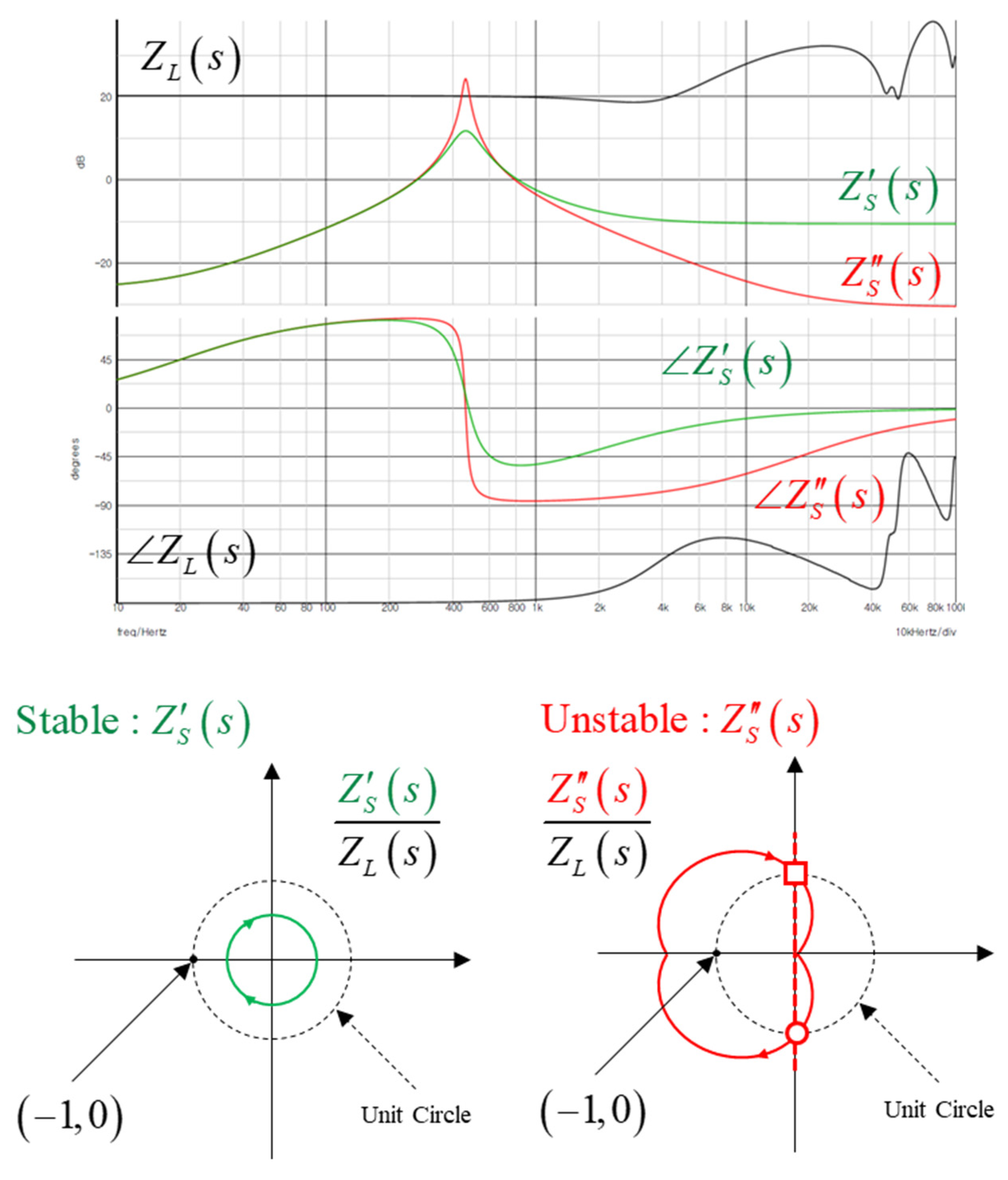
When configuring the SIMPLIS schematic as shown in Figure A1, frequency domain measurements become possible. In this case, it is necessary to add SIMPLIS's unique feature, the POP Trigger element. Setting the resistance value R3 of the filter to 300mΩ results in stability, while setting it to 30mΩ leads to instability. Subsequently, the measurement results in the frequency domain are illustrated in Figure A2.

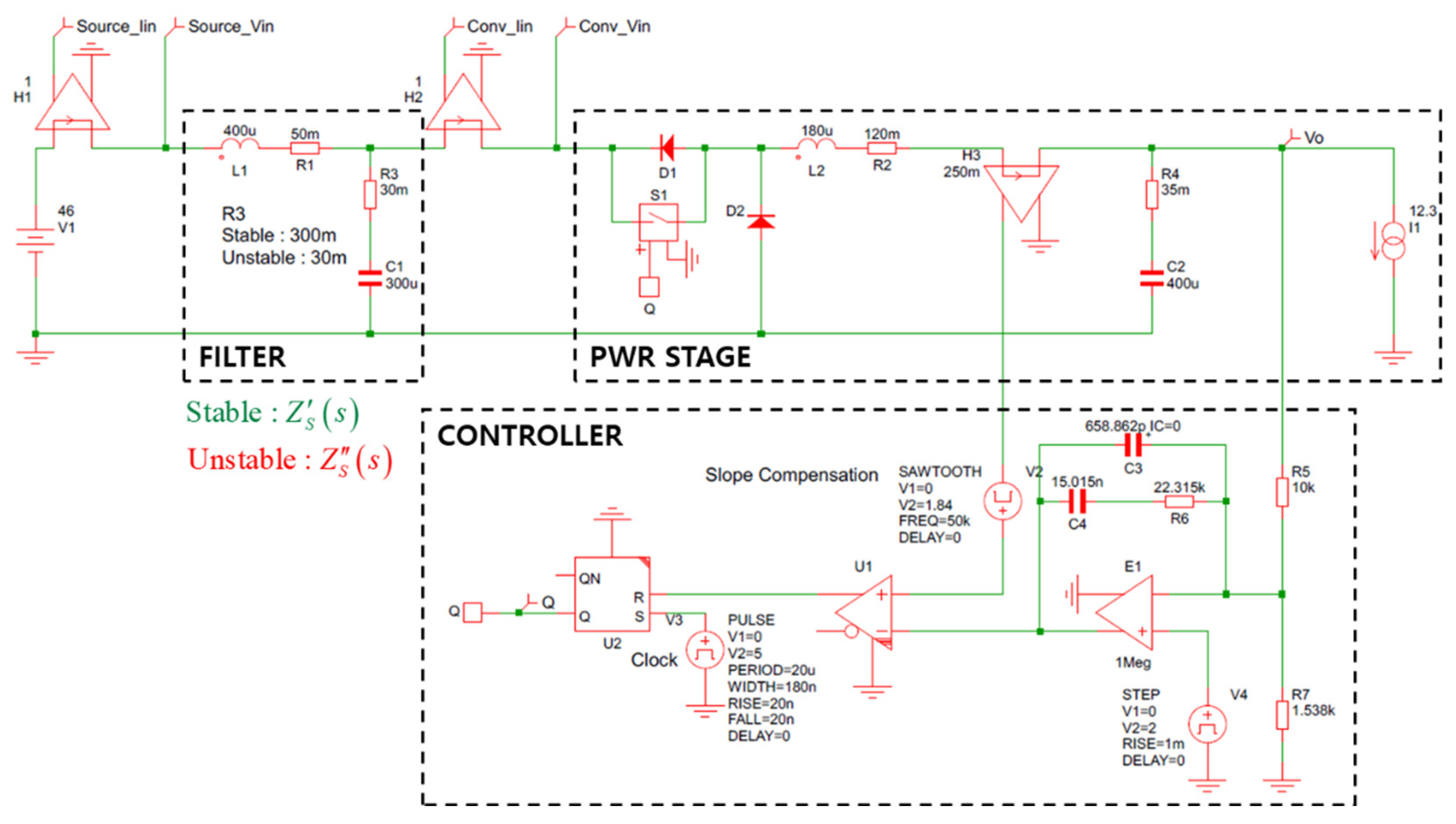
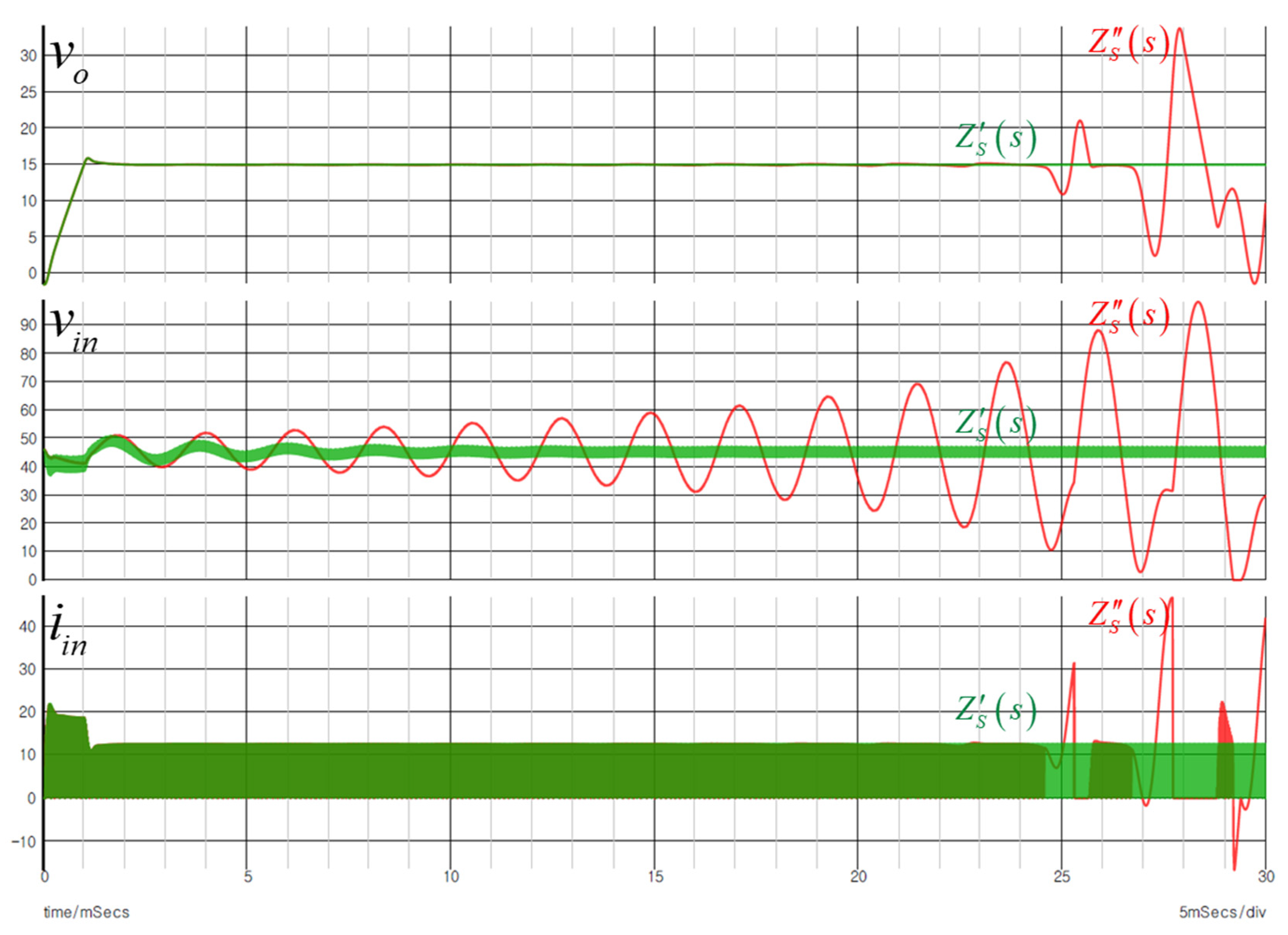
To validate the stability criteria, a time-domain simulation is performed. As illustrated in Figure A3, configure the schematic accordingly and perform a transient analysis. The results of the time-domain simulation in Figure A4 display that in unstable conditions, the input and output voltages and currents exhibit divergence.

Figure A1. SIMPLIS schematic for frequency domain measurements.

Figure A2. The stability criteria in frequency domain of buck converter.

Figure A3. SIMPLIS schematic for time domain measurements.

Figure A4. Converter performance in time domain of buck converter.

References

R. D. Middlebrook, Input filter considerations in design and application of switching regulators, in Conf. Rec. IEEE-IAS Annu. Meeting, 1976, pp. 366-382.
R. D. Middlebrook, Measurement of loop gain in feedback systems†, International Journal of Electronics, vol. 38, no. 4. Informa UK Limited, pp. 485–512, Apr-1975.
J. Sun, Input Impedance Analysis of Single-Phase PFC Converters, IEEE Transactions on Power Electronics, vol. 20, no. 2. Institute of Electrical and Electronics Engineers (IEEE), pp. 308–314, Mar-2005.
Pidaparthy, S.K.; Choi, B. Input Impedances of PWM DC-DC Converters: Unified Analysis and Application Example, Journal of Power Electronics, vol. 16, no. 6. The Korean Institute of Power Electronics, pp. 2045–2056, 20-Nov-2016. [CrossRef]
Spiazzi, G.; Pomilio, J. Interaction between EMI filter and power factor preregulators with average current control: analysis and design considerations, APEC ’99. Fourteenth Annual Applied Power Electronics Conference and Exposition. 1999 Conference Proceedings (Cat. No.99CH36285). IEEE, 1999. [CrossRef]
Huliehel, F.; Lee, F.; Cho, B. Small-signal modeling of the single phase boost high power factor converter with constant frequency control, in Proc. IEEE PESC, 1992, pp. 475-482.
Shin, J.-W.; Cho, B.-H. Digitally Implemented Average Current-Mode Control in Discontinuous Conduction Mode PFC Rectifier, IEEE Trans. Power Electron., vol. 27, no. 7, pp. 3363-3373, Jul. 2012. [CrossRef]
R. B. Ridley, A New Small-Signal Model for Current Mode Control, Ph. D. Dissertation, Virginia Polytechnic Institute and State University, Blacksburg, VA, Nov. 1990.
Tang, W.; Lee, F.; Ridley, R. Small-signal modeling of average current mode control, IEEE Trans. on Power Electron., vol. 8, no. 2, pp.112-119, Apr. 1993.
Byungcho Choi, Pulsewidth Modulated DC-to-DC Power Conversion: Circuits, Dynamics, Control, and DC Power Distribution Systems, 2nd ed., Wiley-IEEE Press, 2021.

Figure 1. External impedance-connected On-Board Charger system.

Figure 2. Figure 2. System configuration.

Figure 3. Figure 3. The typical structure of an EMI filter.

Figure 4. Figure 4. The entire circuit of the EMI filter with a chassis.

Figure 5. Figure 5. The circuit of the DM loop.

Figure 6. Figure 6. The input shorted output impedance

Z_{o f 0} (s)

of the two circuits.

Figure 6. Figure 6. The input shorted output impedance

Z_{o f 0} (s)

of the two circuits.

Figure 7. The input shorted output impedance

Z_{o f 0_{E x t}} (s)

with external impedance.

Figure 7. The input shorted output impedance

Z_{o f 0_{E x t}} (s)

with external impedance.

Figure 7. The boost PFC control block diagram.

Figure 9. Figure 9. The bode plot of

T_{i} (s)

and

T_{m U} (s)

Figure 9. Figure 9. The bode plot of

T_{i} (s)

and

T_{m U} (s)

Figure 10. Figure 10. The minor loop gain

T_{m n} (s)

Figure 10. Figure 10. The minor loop gain

T_{m n} (s)

Figure 11. Figure 11. The minor loop gain

T_{m n} (s)

Figure 11. Figure 11. The minor loop gain

T_{m n} (s)

Figure 12. Figure 12. Converter performance in the time domain.

Figure 13. Figure 13. The simplified structure of most power conversion devices.

Table 1. The parameters of the EMI filter

	$C_{X}$	$C_{Y}$	$L_{C M}$	$L_{D M}$	$R_{C_{X}}$	$R_{L_{C M}}$	$R_{L_{D M}}$
Value	1	47	2	1	10	10	1
Unit	μF	nF	mH	μH	mΩ	mΩ	mΩ

Table 2. The parameters of the EMI filter consists of a 2-stage PI filter

	$C_{X}$	$C_{Y}$	$L_{C M}$	$R_{C_{X}}$	$R_{L_{C M}}$
Value	2.2	47	2	1	10
Unit	μF	nF	mH	mΩ	mΩ

Table 3. The parameters of the Bridgeless Totem Pole Boost PFC converter

	Power	$V_{i n, r m s}$	$F_{V_{i n}}$	$V_{o}$	$I_{o}$	$F_{s w}$	$L$	$R_{L}$	C	$R_{C}$	$V_{m}$
Value	7.4	220	50	400	18.5	55	200	5	900	22	10
Unit	kW	V	Hz	V	A	kHz	μH	mΩ	μF	mΩ	V

Table 4. The parameters of the boost PFC converter controller

	Sensor Gain			Current Controller				Voltage Controller
	$K_{V_{i n}}$	$K_{I_{i n}}$	$K_{V_{o}}$	$K_{F_{i}}$	$ω_{i, z}$	$ω_{i, p}$	$ω_{i, c}$	$K_{F_{i}}$	$ω_{v, z}$	$ω_{v, p}$	$ω_{v, c}$
Value	5	30	3.5	85000	$1 \cdot 2 π$	$5 \cdot 2 π$	$7.15 \cdot 2 π$	20	$10 \cdot 2 π$	$37.5 \cdot 2 π$	$1.5 \cdot 2 π$
Unit	mV/A	mV/A	mV/V	-	krad/s	krad/s	krad/s	-	rad/s	krad/s	rad/s

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Stability Analysis of Boost PFC Considering the External Impedance

Abstract

1. Introduction

2. Impedance Analysis

2.1. EMI Filter Output Impedance with the External Impedance

2.1.1. Differential Mode Loop

2.1.2. Impedance Analysis with the External Impedance

2.2. Boost PFC Input Impedance

3. Stability Analysis of Boost PFC Considering the External Impedance

3.1. Stability Criteria with the External Impedance

3.2. Converter Performance under System Interaction

4. Conclusions

Appendix A: Input Filter Interaction Example with SIMPLIS Elements

References

MDPI Initiatives

Important Links

Subscribe