1. Introduction
With the rapid development of global mobile communication networks, data traffic in urban wireless networks is experiencing explosive growth. The widespread adoption of 5G technology and the upcoming 6G era, along with the extensive deployment of emerging technologies such as the Internet of Things (IoT), Augmented Reality/Virtual Reality (AR/VR), and autonomous vehicles, have increased the complexity and uncertainty of network traffic. These technologies place higher demands on network latency, bandwidth, and reliability, posing significant challenges to network operators. They need to accurately predict network traffic to optimize resource allocation, improve service quality, and reduce operational costs, achieving demand-aware, energy-efficient, and self-configuring intelligent mobile networks [
1,
2,
3].
Wireless network traffic prediction is a critical prerequisite for realizing intelligent 5G and future networks. Accurate traffic prediction can help network operators conduct effective resource scheduling, prevent network congestion in advance, optimize base station energy consumption management, and provide data support for urban planning and public safety [
4,
5]. However, accurately predicting wireless network traffic faces the following main challenges:
Diverse User Demands and Dynamic Characteristics: The demands of mobile users are increasingly diverse, and network traffic exhibits highly dynamic changes. This uncertainty leads to traffic load fluctuations over a wide range, making it difficult to accurately predict using simple models. For example, traffic patterns in different regions may be completely different, and certain areas may experience sudden high traffic demand during specific time periods.
Complex Spatiotemporal Dependencies: Wireless network traffic has significant spatiotemporal correlations. Spatially, the geographical locations, physical distances, and network topology between base stations lead to spatial dependencies in traffic. Temporally, user behavior patterns, events, holidays, and other factors cause temporal dependencies in traffic. These complex spatiotemporal characteristics increase the difficulty of traffic prediction.
Influence of Multiple External Factors: Natural and social factors, such as weather changes, major events, social activities, and urban infrastructure construction, have a significant impact on wireless network traffic. The randomness and uncontrollability of these factors make traffic prediction more complex [
6].
Traditional traffic prediction methods are mainly based on statistical models and machine learning methods, such as Autoregressive Integrated Moving Average (ARIMA) [
7,
8,
26] and Support Vector Regression (SVR) [
9,
10]. However, these methods usually assume linearity and stability of data, making it difficult to capture the nonlinear and dynamic changes in wireless network traffic, and lacking the ability to model complex spatiotemporal correlations.
With the rise of deep learning, models such as Convolutional Neural Networks (CNN) and Recurrent Neural Networks (RNN) have been applied to the field of traffic prediction [
11,
12,
13]. CNNs can effectively extract spatial features but are usually only suitable for regular grid data in Euclidean space. RNNs, especially Long Short-Term Memory networks (LSTM), perform well in capturing temporal dependencies. However, these models have limitations when processing graph-structured data in non-Euclidean space.
To solve the above problems, Graph Convolutional Networks (GCN) have been introduced into the modeling of spatiotemporal data [
15,
27]. GCNs can handle graph-structured data and capture complex relationships between nodes. In traffic flow prediction, recent studies have proposed the Diffusion Convolutional Recurrent Neural Network (DCRNN) based on GCN, demonstrating its effectiveness in extracting spatial features [
33]. The Spatio-Temporal Graph Convolutional Network (STGCN) has also been proposed, combining GCN and one-dimensional convolution to capture spatiotemporal dependencies [
13]. However, these models still have the following shortcomings when applied to wireless network traffic prediction:
Insufficient Comprehensive Extraction of Spatiotemporal Features: Most models focus on extracting local spatiotemporal dependencies, lacking comprehensive utilization of dynamic and static information, and cannot fully capture the multidimensional characteristics of wireless network traffic. For example, the STCNet model proposed by Zhang et al. uses ConvLSTM and densely connected CNNs to capture spatiotemporal dependencies but mainly focuses on local features [
11].
Over-smoothing Problem: Deep GCN models are prone to over-smoothing of node features after multiple layers of aggregation, leading to reduced distinguishability of nodes and affecting prediction accuracy [
15]. Some studies have tried to alleviate this problem by introducing skip connections or residual networks, but the effects are limited [
20].
Neglect of Global Spatiotemporal Correlations: Wireless network traffic is influenced by global spatiotemporal factors, such as potential associations between distant base stations and global user behavior patterns. Existing models often rely on predetermined connections and cannot dynamically capture such global correlations. When network topology or connections change over time, the generalization of the model is limited [
22].
To overcome the above limitations, recent studies have begun to focus on capturing global spatiotemporal correlations in wireless networks using Graph Neural Networks (GNN) and attention mechanisms [
17,
23,
25]. Specifically, by integrating adaptive attention mechanisms into GNNs, models can dynamically learn the weights between nodes, capturing potential global correlations without the need for predetermined connections. This approach improves the flexibility of models in handling dynamic network topologies and complex spatiotemporal dependencies.
Furthermore, some studies have utilized modified Graph Attention Networks (GAT), which dynamically assign weights to neighboring nodes using attention mechanisms, enhancing the expressive ability and performance of the model [
38]. However, the application of these models in wireless network traffic prediction is still limited, and they have not fully utilized the static physical features in wireless networks, such as base station locations, channel characteristics, and environmental factors.
Inspired by the above research, this paper proposes a novel wireless network traffic prediction algorithm aimed at effectively combining dynamic and static spatiotemporal features and overcoming the over-smoothing problem in GCNs. Our main contributions are as follows:
Proposed a Hierarchical Attention Mechanism Combining Dynamic and Static Attention: We introduced a hierarchical attention mechanism that combines static attention and dynamic attention. The static attention mechanism captures fixed spatial relationships and invariant features between base stations, such as physical distances, channel characteristics, population density, and spectrum usage. The dynamic attention mechanism considers time-varying information, including peak hours, holiday effects, real-time data updates, and event-driven dynamic adjustments. Through feature concatenation and interactive learning frameworks, we effectively integrate these two attention mechanisms, enhancing the model’s ability to capture spatiotemporal information and improving the accuracy of network traffic prediction.
Utilized the Laplacian Matrix to Adjust Aggregation Iterations in GCN: Addressing the over-smoothing problem in GCNs, we proposed an adaptive method to determine the number of aggregation layers based on the Laplacian matrix. By analyzing the eigenvalues and eigenvectors of the Laplacian matrix, we can dynamically adjust the aggregation depth of the GCN while retaining over 70% of the spectral information. This method achieves a balance between extracting broader spatial relationships and maintaining the distinguishability of node features, avoiding the over-smoothing phenomenon in traditional deep GCNs, and improving the model’s performance and stability.
Introduced ConvLSTM Networks to Capture Temporal Dependencies: We utilized Convolutional Long Short-Term Memory Networks (ConvLSTM) in the dynamic attention mechanism to effectively capture the temporal dynamics and spatial features of network traffic. This enables the model to adapt to real-time changes and improve prediction capabilities in different scenarios.
Conducted Experimental Verification on City-Level Wireless Communication Datasets: We conducted extensive experiments on actual city-level wireless communication datasets. The results show that the proposed method outperforms existing mainstream models in prediction accuracy and computational efficiency, verifying the effectiveness and superiority of our method.
The structure of this paper is arranged as follows:
Section 2 provides a detailed review of related work in wireless network traffic prediction, analyzing the advantages, disadvantages, and challenges of existing methods.
Section 3 describes in detail the proposed hierarchical attention mechanism and Laplacian matrix-based GCN adjustment method, including mathematical models and algorithm implementations.
Section 4 presents experimental settings and result analysis, comparing the performance of our method with other models and conducting an in-depth discussion. The final section summarizes the work of this paper and looks forward to future research directions.
2. Related Work
Wireless network traffic prediction has attracted extensive attention in recent years because it plays a crucial role in intelligent network management. Accurate traffic prediction is essential for resource optimization, network planning, and service quality enhancement. Over the past decades, researchers have conducted extensive studies in traffic prediction, developing various models and methods.
Early research was mainly based on statistical and probabilistic models to model cellular traffic networks. These methods include Autoregressive Integrated Moving Average (ARIMA) [
26], covariance functions [
28], and entropy theory [
29], among others. These models utilize historical traffic data to attempt to capture trends and periodic changes in time series. However, these methods usually assume linearity and stability in the data, making it difficult to cope with the nonlinear and dynamic characteristics of wireless network traffic.
With the development of machine learning, data-driven methods have been introduced into traffic prediction. For example, linear regression and Support Vector Regression (SVR) [
9,
10] have been used to capture patterns in traffic data. These methods improve prediction accuracy to some extent but still cannot fully utilize the complex spatiotemporal features in the data.
To better capture the nonlinear and dynamic characteristics of wireless network traffic, researchers have started to adopt deep learning models. Recurrent Neural Networks (RNN), especially Long Short-Term Memory networks (LSTM) and Gated Recurrent Units (GRU), have been used to capture temporal dependencies in traffic [
30,
31,
32]. At the same time, Convolutional Neural Networks (CNN) have been used to extract spatial features [
11,
12,
13].
Zhang et al. proposed the Spatio-Temporal Cross-domain Neural Network (STCNet) [
11], which combines ConvLSTM and densely connected CNNs to simultaneously capture temporal and spatial dependencies, and considers cross-domain data, achieving state-of-the-art results on the Milan cellular traffic dataset. However, these RNN and CNN-based methods have the following limitations:
Insufficient Sensitivity to Sudden Changes: RNN-based methods perform poorly when handling abrupt traffic changes and are unable to quickly adapt to traffic surges or drops caused by sudden events.
Limitations in Spatial Dependencies: CNN-based methods mainly focus on spatial dependencies between adjacent regions, ignoring potential global spatial correlations between distant base stations.
To overcome the above issues, Graph Neural Networks (GNN) have been introduced into wireless network traffic prediction. GNNs can handle graph-structured data in non-Euclidean space and capture complex spatial relationships. In road traffic prediction [
34,
35] and passenger demand prediction [
14], GNNs have demonstrated excellent performance.
In cellular network traffic prediction, some researchers [
15] have proposed a graph learning-based method that parameterizes the traffic between base stations to capture spatial correlations between distant base stations. Other researchers [
36] have combined GCN and GRU and utilized additional traffic handover information to achieve accurate traffic prediction. Additionally, some studies [
37] have applied attention-based structured RNNs to cellular traffic graphs obtained from pre-clustering, simultaneously modeling temporal and spatial correlations.
However, these graph-based methods still have some shortcomings:
Dependence on Predefined Graph Structures: The above methods usually rely on predetermined connections or graph structures constructed through external information, such as historical handover data or pre-clustering results. This limits the model’s flexibility and generalization ability, making it ineffective in adapting to dynamic changes in network topology.
Ignoring Global Spatial Correlations: The predefined graph structures may not fully capture the global spatial correlations between base stations, especially in cases where there may be potential associations between distant base stations.
Inspired by attention mechanisms [
38] and Graph Attention Networks (GAT) [
39], researchers have begun to explore incorporating adaptive attention mechanisms into GNNs. Attention mechanisms allow models to dynamically learn the weights between nodes, capturing implicit global correlations without the need for predefined connections. This improves the model’s ability to handle complex spatiotemporal dependencies and dynamic network topologies.
However, the application of attention mechanisms in wireless network traffic prediction is still limited. Our work aims to fill this gap by proposing a hierarchical attention mechanism that combines dynamic and static attention to comprehensively capture the complex spatiotemporal features in wireless network traffic.
3. Our Method
This paper proposes a novel wireless network traffic prediction algorithm designed to handle city-level wireless communication traffic data with hourly granularity. To improve prediction accuracy, we introduce two major innovations: a hierarchical attention mechanism that combines dynamic and static attention, and the use of a Laplacian matrix to adjust the aggregation iterations in Graph Convolutional Networks (GCN).
Overall, we approach wireless network traffic prediction as a spatiotemporal problem; therefore, we adopt the Graph Convolutional Network (GCN) framework. GCN effectively processes graph-structured data by aggregating information from neighboring nodes to learn the feature representation of each node. To better extract spatiotemporal data features and enhance model performance, we innovatively introduce a hierarchical attention mechanism that combines static and dynamic attention mechanisms. For the static attention mechanism, we utilize a model based on wireless channel models, focusing on extracting invariant spatial relationship information. This framework captures stable structural features in the network, such as fixed connections between base stations and spatial distances between them. In terms of dynamic attention, we consider time-varying information, such as rush hours and holiday effects, enabling the model to dynamically adjust to wireless network traffic variations over different periods. Finally, we integrate these two mechanisms using feature concatenation and interactive learning frameworks, allowing the model to simultaneously capture both dynamic and static spatiotemporal information, leading to better future network traffic predictions.
Another key innovation of our algorithm is the use of a Laplacian matrix to determine the number of aggregation iterations in the GNN. Specifically, we set the depth of the graph convolutional layers based on the information provided by the Laplacian matrix, ensuring that the GCN neither over-smooths nor underfits. This process helps us to quickly identify the appropriate parameters for the GNN based on the characteristics of the data itself. Through this approach, we achieve a balance between model complexity and prediction accuracy, accelerating the tuning process of the model.
Figure 1 illustrates the overall framework of our proposed wireless network traffic prediction algorithm. Next, we will provide a detailed introduction to each module.
3.1. T-GCN with Hierarchical Attention Mechanism Combining Dynamic and Static Attention
In this module, we detail the hierarchical attention mechanism introduced in this paper. Our hierarchical attention mechanism is divided into two parts: the static attention mechanism and the dynamic attention mechanism. The static attention mechanism includes information that remains unchanged in space and time within network traffic, such as the relative positions between base stations, population density, and channel models. The dynamic attention mechanism encompasses information that changes over time, such as temporal relationships and the impacts of holidays.
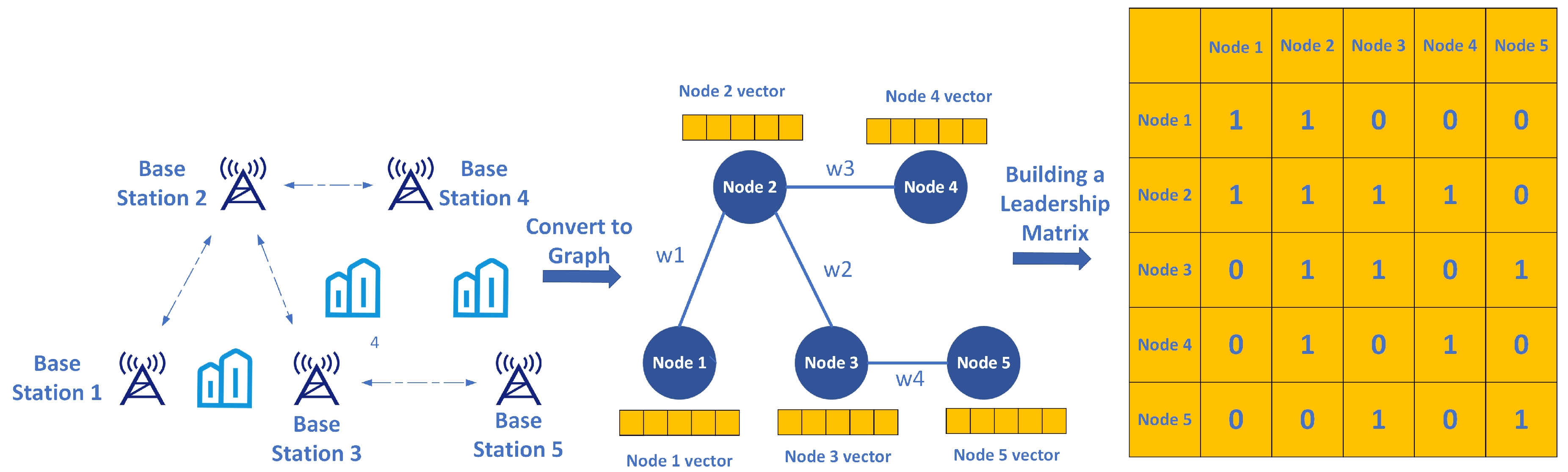
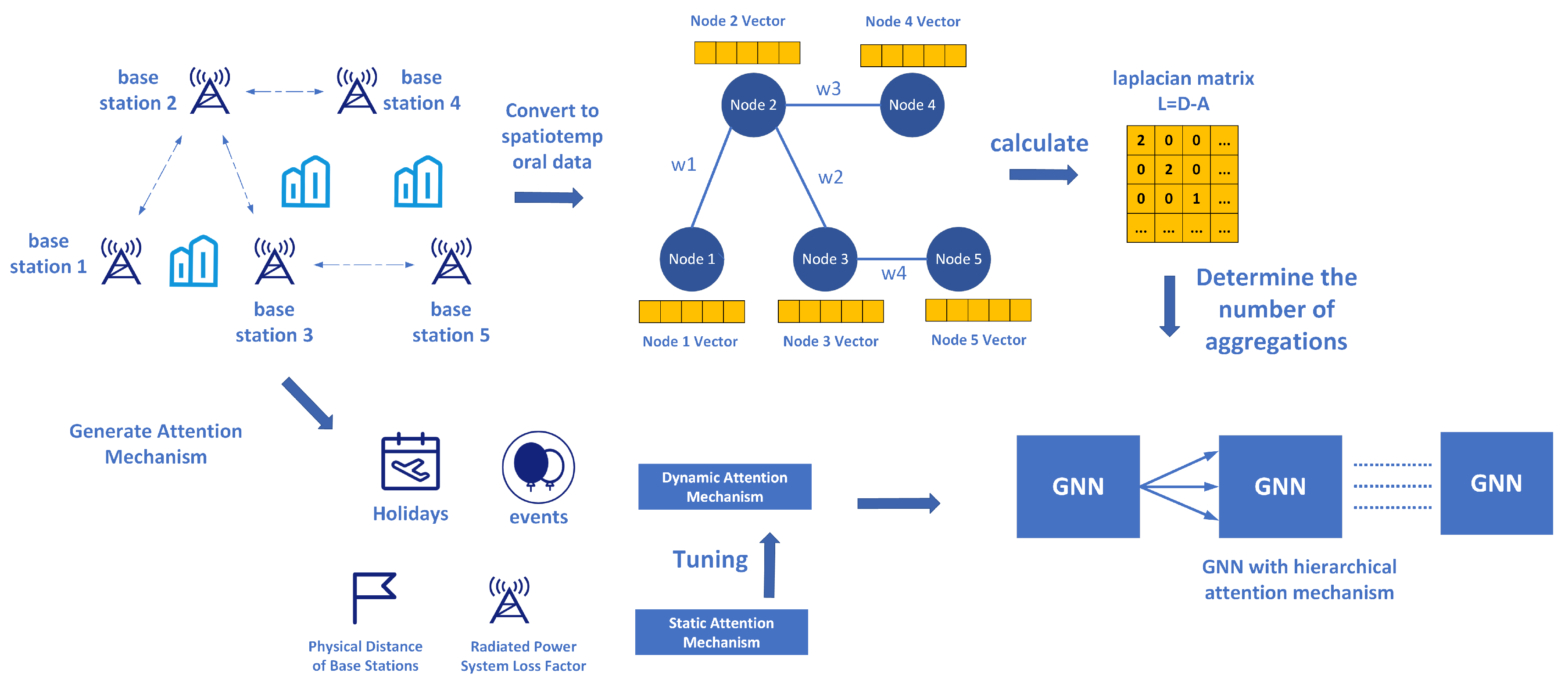
To use graph convolutional neural networks to address wireless communication issues, we first need data structured as a graph. Since the mobile communication wireless network consists of various base stations, if each base station is considered a node and the communication between base stations is considered an edge, we can construct a graph based on this.
The initial adjacency matrix is simple, where connections are represented as 1 and no connections as 0. Thus, the nodes can form a matrix that expresses the spatial relationships between data nodes. Compared to traditional neural networks, the core innovation of graph convolutional neural networks lies in the adjacency matrix. However, values of 0 and 1 can only reflect whether a connection exists, not the strength of the connection. If the connections in the adjacency matrix are designed to adapt to the data itself, rather than being just 0 and 1, then the graph convolutional network transforms into a graph attention mechanism network.
Figure 4 illustrates the process of transforming the wireless network traffic prediction problem into a graph and constructing the adjacency matrix.
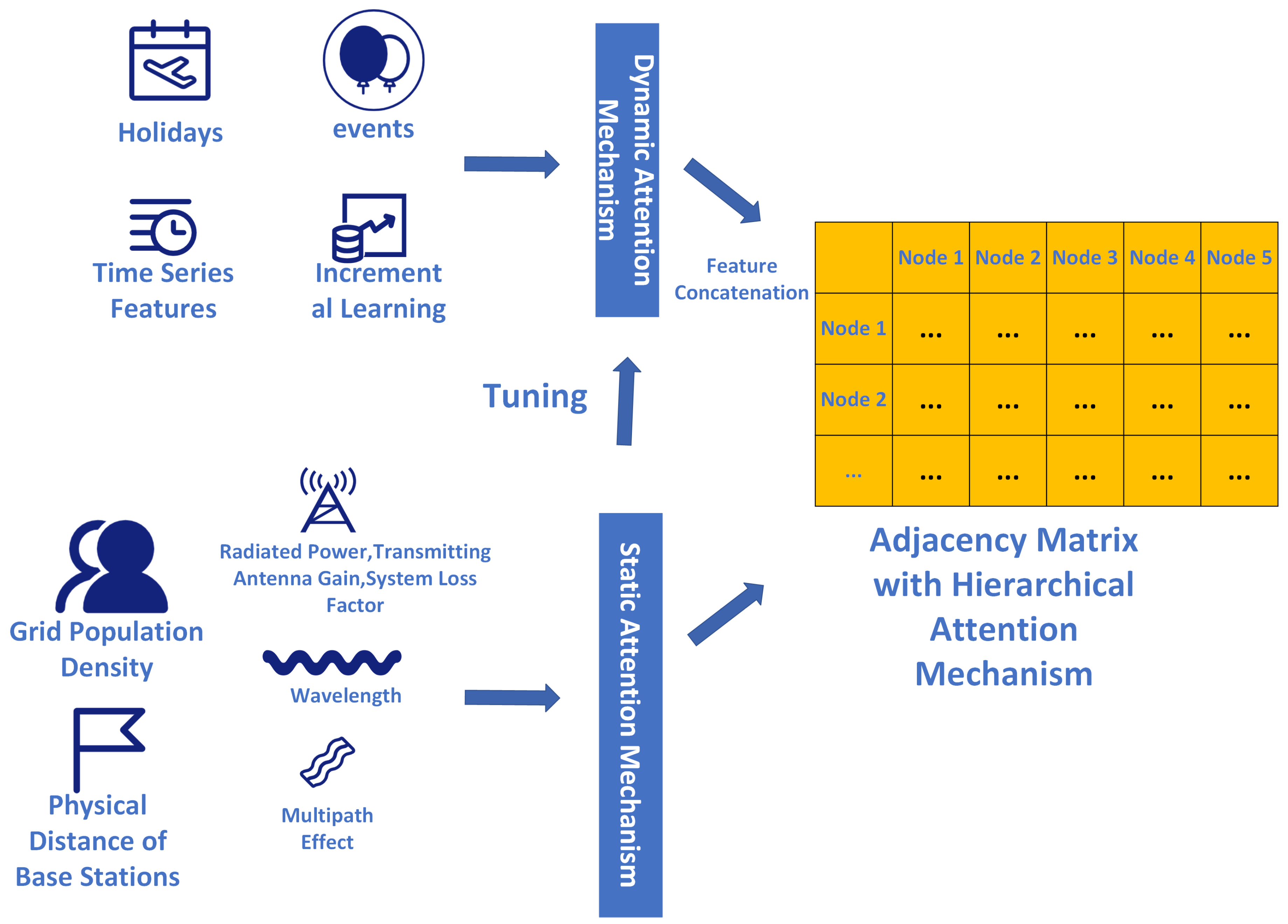
Figure 2.
Figure 2 illustrates the framework of our hierarchical attention mechanism module, which integrates both static and dynamic attention mechanisms.
Figure 2.
Figure 2 illustrates the framework of our hierarchical attention mechanism module, which integrates both static and dynamic attention mechanisms.
Graph neural networks have achieved significant research results and practical applications in traffic flow and air quality prediction. However, their research in the mobile communication field remains limited. When processing mobile communication data using graph neural networks, the adjacency matrix of the graph is mostly derived by calculating the correlation between sequences. For instance, if the values of node 1 and node 2 are very close in a time series, their adjacency matrix value will be set higher. Conversely, if the values of node 1 and node 5 differ significantly, the value will be set lower (e.g., the traffic of node 1 in the next 3 hours is 2Gbps, 6Gbps, 10Gbps, and node 2 is 2.5Gbps, 5Gbps, 9Gbps, while node 5 is 11Gbps, 3Gbps, 1Gbps).
Figure 3.
Figure 3 illustrates the framework of our heatmap processing module, which primarily consists of two parts. One part transforms raw data into heatmap video data, and the other constructs an LSTM network optimized by a Laplacian-tuned attention mechanism.
Figure 3.
Figure 3 illustrates the framework of our heatmap processing module, which primarily consists of two parts. One part transforms raw data into heatmap video data, and the other constructs an LSTM network optimized by a Laplacian-tuned attention mechanism.
This module innovatively combines dynamic data characteristics that change over time with static data characteristics that remain constant over time, proposing a new graph attention mechanism algorithm using a hierarchical attention mechanism. This module includes the following three innovations:
Introducing a hierarchical attention mechanism that combines both static and dynamic data characteristics.
Static features include channel characteristics, physical distances, spectrum usage, and other static information.
The dynamic attention mechanism takes into account the characteristics of real-time data updates, not only incorporating time series correlation calculations but also incremental learning features to meet the needs of different changing scenarios. Additionally, it considers important temporal features such as holidays.
Figure 5 shows the overall framework of this module.
3.1.1. Static Attention
In this section, we will detail the construction of our static attention mechanism. By considering various explicit and invariant factors, we construct a weight function for the static attention mechanism and gradually design a mathematical model with learnable parameters. This model aims to comprehensively account for grid population density, physical distance of base stations, radiated power, transmitting antenna gain, system loss factor, electromagnetic wave data (wavelength), environmental occlusion parameters, and the multipath effect on the static attention weights.
First, we define the basic formula for the static attention weight
, where
represents the attention weight of node
i to node
j:
Here,
is an attention scoring function,
and
represent the features of nodes
i and
j respectively, and
represents the edge features between nodes
i and
j (including distance, radiated power, etc.). The softmax function ensures that the sum of attention weights from node
i to all nodes is 1.
Next, we construct the scoring function
. Here, we consider various spatial factors:
where
a is a learnable weight vector,
W is a feature transformation matrix that maps node features to a common space, and ∥ denotes the concatenation operation.
is a non-linear activation function such as LeakyReLU.
is a function that integrates edge features (e.g., physical distance, radiated power, etc.).
For the edge feature processing function
, we have designed the following considering the factors related to wireless network traffic prediction:
where
represents the physical distance between nodes
i and
j,
is the population density of the grid, and
,
,
,
are the radiation power, antenna gain, system loss factor, and wavelength, respectively.
and
are the quantifications of the obstruction environment parameter and multipath effect. The parameters
,
,
,
,
,
,
l,
k are learnable parameters that adjust the influence of each factor.
V is another learnable weight vector used to transform the comprehensive features into a format required by the attention mechanism.
The function is an attention scoring function, and and represent the features of nodes i and j, respectively. represents the edge features between nodes i and j (including distance, radiation power, etc.), and the softmax ensures that the sum of attention weights from node i to all nodes is 1.
During the model training process, the values of population density, radiation power, and antenna gain are fixed. However, we set learnable parameters. By minimizing the prediction error (e.g., using a mean squared error loss function) during model training, we optimize the learnable parameters a, W, V, , , , , , , l, k to values suitable for the wireless network traffic prediction scenario. This process will automatically adjust these parameters through backpropagation to comprehensively account for the influence of various spatial factors on static attention weights. After completing the model training, the static attention mechanism remains constant when predicting traffic.
3.1.2. Dynamic Attention
The basic idea is to enhance the dynamic attention mechanism from four distinct aspects: dependency on time series, adaptability to real-time data, incremental learning mechanisms, and adjustment driven by dynamic events. Each aspect contributes uniquely to the robustness of the model, and we adopt a step-by-step construction approach, with specific mathematical formulas detailed below.
First, we construct the basic dynamic attention model. We define the dynamic attention weight function
, which represents the attention weight of node
i to node
j at time
t:
where
is the dynamic attention scoring function.
and
are the hidden states of nodes
i and
j at time
t, generated by models such as RNN or LSTM that capture time series features.
is the time interval, used to capture the dependency on the time series. The softmax ensures that the sum of dynamic attention weights from node
i to all nodes is 1.
The time series dependency refers to the model’s ability to recognize and utilize the influence of past data points on future predictions. Capturing this dependency is crucial when processing time series data. ConvLSTM (Convolutional Long Short-Term Memory) is a special LSTM network that incorporates convolution operations into the LSTM structure, allowing the model to handle long-term dependencies in time series data while effectively processing spatial data. ConvLSTM achieves this by adding convolution operations to the input gate, forget gate, and output gate of LSTM, enabling the network to capture dependencies in the time dimension and extract features in the spatial dimension. This is particularly important for spatiotemporal datasets, such as network traffic prediction, where base station traffic is influenced by both time factors and spatial location and surrounding environment. We use ConvLSTM to capture the time series dependency, and the hidden state of the node
is updated as follows (where
is the input feature at time
t):
Real-time data adaptability focuses on the model’s ability to adapt to fresh data. Incremental learning mechanisms allow the model to update its knowledge base upon receiving new data rather than retraining from scratch. This mechanism is crucial for handling real-time streaming data as it significantly reduces computational resource consumption and allows the model to dynamically adapt to data changes. In incremental learning, model parameters are updated based on the loss function of the new data batch. By calculating the loss and applying backpropagation, the model can gradually adjust its parameters to better reflect the characteristics and patterns of the new data. This method ensures that the model retains the memory of previously learned knowledge while continuously learning new information. Our incremental learning mechanism is mathematically formulated as follows:
where
represents the parameters of the LSTM model,
is the learning rate,
L is the loss function,
is the true value, and
is the predicted value.
is the gradient of the loss function with respect to
.
Event-driven dynamic adjustment focuses on the model’s ability to respond to specific events. In applications such as network traffic prediction, specific events (e.g., holidays, large events) may cause significant changes in traffic patterns. To capture such non-periodic changes, the model needs to recognize these events and adjust its behavior accordingly. Our implementation strategy introduces an event recognition component to the model, which identifies the occurrence of specific events based on input data. The model can then adjust the dynamic attention weights to respond to these events, for instance, by increasing the attention to specific time points or areas. This adjustment can be based on predefined rules or a data-driven approach that learns the relationship between events and traffic patterns.
For dynamic adjustment based on specific events, we define an event impact function
and integrate it into the dynamic attention scoring function:
where
is the event impact at time
t, which can be a model learned from historical data or a rule-based indicator function.
a and
b are learnable weight vectors, and
is an activation function.
3.1.3. Combining Static Attention and Dynamic Attention
To combine the static and dynamic attention mechanisms through a hierarchical attention mechanism, we use a framework of feature concatenation and interactive learning. This framework not only integrates static and dynamic information but also optimizes this integration through learning to enhance the overall model performance.
First, feature concatenation is a straightforward data fusion method whose core idea is to aggregate features from different sources to form a more comprehensive and rich feature representation. In the hierarchical attention mechanism, feature concatenation is used to combine features generated by static and dynamic attention mechanisms. Static features reflect long-term stable, time-independent attributes, such as geographical location and infrastructure layout. Dynamic features capture information that varies over time, such as traffic fluctuations and event impacts. By concatenating these two types of features, we obtain a comprehensive feature vector that encompasses both spatial static properties and temporal dynamic changes. The advantage of this fusion method lies in its simplicity and directness, allowing the model to access and utilize both aspects of information in subsequent processing, thereby improving the accuracy and reliability of decisions or predictions. The specific implementation of our formula is as follows. Suppose for each node
i, we obtain the static feature vector
through the static attention mechanism and the dynamic feature vector
through the dynamic attention mechanism (where
t represents time). We can concatenate these two parts of the features to form a comprehensive feature vector
:
Here, ‖ denotes the concatenation operation of vectors. This comprehensive feature vector
will be used as the input for subsequent processing, integrating static spatial information and dynamic temporal information.
Interactive learning further optimizes the interaction between different features on the basis of feature concatenation through learning. The core of this method lies in identifying and utilizing the intrinsic connections between static and dynamic features and their joint influence on the final task (such as prediction). Interactive learning is not just about feature concatenation; it focuses on how to make these features "communicate" and interact more effectively within the model. By introducing one or more fully connected layers (or other types of network structures), the model can learn a nonlinear combination of feature representations that comprehensively considers the interactions and dependencies between features. This learning process enables the model to automatically discover which feature combinations are most important for the prediction task and how to best combine static and dynamic information to improve performance. The advantage of interactive learning lies in its flexibility and adaptability. It can not only automatically adjust the relationships between features but also dynamically adjust the way features are combined according to the needs of the specific task. This means the model can more accurately understand the inherent structure and patterns of the data, thus making more precise judgments or predictions. The formula for our interactive learning is as follows:
where
is the weight matrix,
is the bias term,
is the nonlinear activation function, and
represents the feature representation after interactive learning.
The feature vector
obtained through interactive learning can be used for various tasks, and it is particularly suitable for our network traffic prediction. Our goal is to predict a specific output (such as the traffic at node
i at the next time step) based on the current static and dynamic information. We can further process
as follows:
Here,
and
are the weights and biases of the output layer, and
is the predicted output. ReLU ensures that the output of the task is regressive.
3.2. Tuning Graph Neural Network Aggregation Levels with Laplacian Matrix
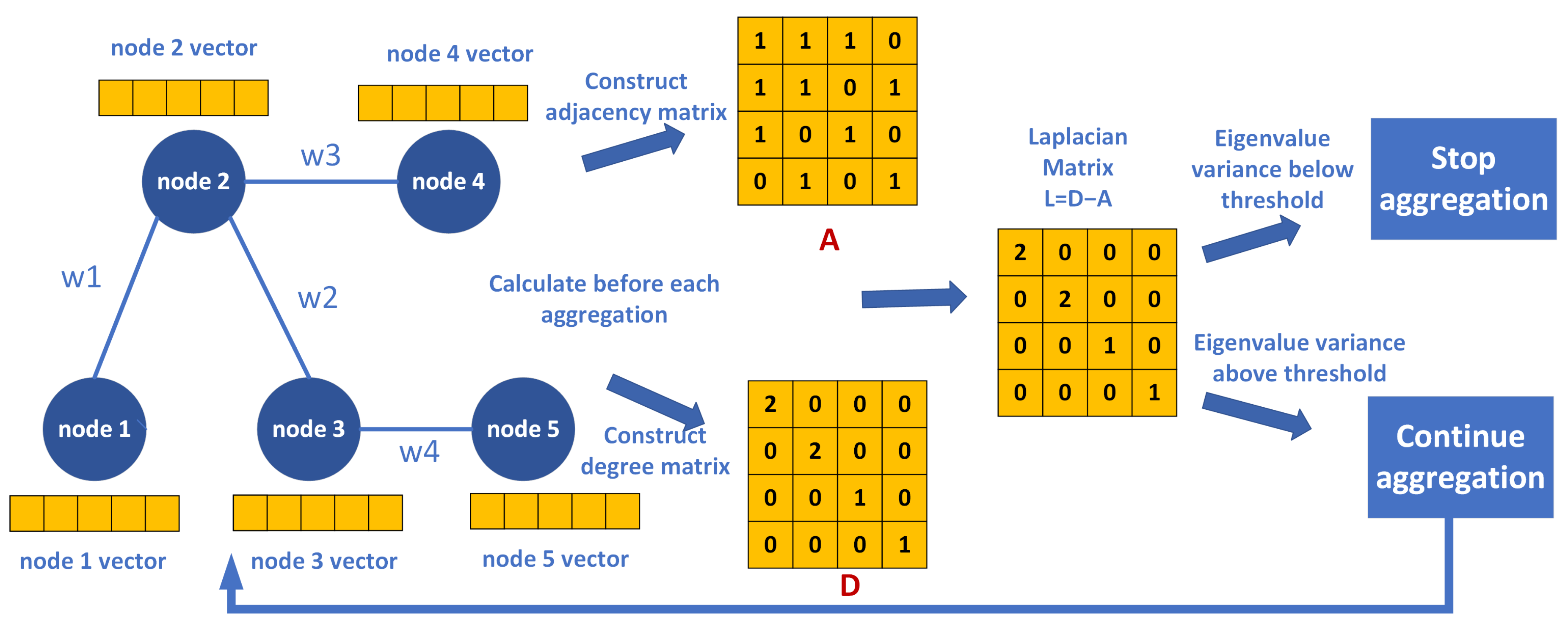
We explain the aggregation process of graph neural networks using a simple base station graph we constructed. When dealing with graph-structured data, graph neural networks need to extract spatial information, so it is necessary to aggregate all the nodes first.
For example, for a node
v, in the first aggregation, the new node feature
is obtained by a weighted average of the features of its neighboring nodes, which can be expressed as:
Here,
is the new feature of node
v after aggregation, and
is the set of neighboring nodes of
v.
is the feature of neighboring node
u,
W is a learnable weight matrix, and ReLU is the activation function. For instance, for node 2 in
Figure 5, its new feature
will be calculated based on the weighted average of the features of nodes 1, 3, and 4 (adjusted by the weight matrix
W and activated by the ReLU function). This aggregation method allows each node to capture information from its neighbors, and with multiple aggregations, it can obtain information from nodes that are further away.
For example, our node 2 (
Figure 5), after the first aggregation, not only retains its own information but also incorporates information from nodes 1, 3, and 4. Similarly, after the first aggregation, node 3 has both its own information and information from nodes 2 and 5. Therefore, after the second aggregation, node 2 will have information from node 5 through the aggregation of node 3. Thus, multiple aggregations enable each node to obtain information from more distant areas. Theoretically, the more aggregations, the more comprehensive the spatial information each node can acquire from other nodes. However, aggregation also has a side effect—the over-smoothing problem.
3.2.1. Motivation
In graph neural networks, performing multiple aggregations, as iterated in the aforementioned formula, results in each node continually integrating information from increasingly distant neighbors. Initial aggregations might integrate information from nearby nodes, but as the number of aggregations increases, nodes begin to incorporate features from further away nodes. If the aggregation steps are too many, eventually, all nodes may collect information from almost the entire graph, causing their feature representations to become increasingly similar. This leads to the over-smoothing problem, where the distinguishability between nodes diminishes as their feature representations become identical or similar. Consequently, the model struggles to differentiate between nodes or perform tasks that rely on node-specific characteristics, such as node classification.
3.2.2. Case Study
For example, in our previous case, after two aggregations, the overall model effect remains positive because each node acquires information from other nodes. However, what happens if the model undergoes five, six, or even more aggregations? Take node 2 for instance; after multiple aggregations, its neighboring nodes 3 and 1, due to prior aggregations, already possess information about node 2. Thus, further aggregation results in node 2 redundantly acquiring its own information, and other nodes encounter the same issue. As each node fully integrates its information, they become increasingly similar, leading to over-smoothing.
Conversely, if the number of aggregations is too few, the main issue is insufficient information. Specifically, nodes may fail to receive enough neighborhood information to fully understand their context within the graph. For example, a node may only aggregate information from directly connected neighbors, failing to sense more distant neighbors. In our case, if aggregation occurs only once, node 2 will not be aware of information from node 5. This lack of information restricts the model’s performance, especially in tasks that require understanding broader connectivity patterns, such as graph classification or complex node classification problems. Therefore, determining the appropriate number of aggregation layers is critical when designing graph neural networks.
3.2.3. Our Method
The authors of this paper observed that the graph aggregation process, during practical graph data processing, resembles a high-pass filtering process. During aggregation, high-frequency anomalous components are often lost, while the basic information that most nodes possess tends to be retained. This observation led us to consider frequency domain transformations. Specifically, if we conduct spectral analysis on the graph data during aggregation and ensure that the spectrum retains over 70% (i.e., ) of the information, we can generally achieve a balance between extracting spatial relationships and avoiding over-smoothing. The following is a detailed introduction of our specific implementation:
Graph Theory Background: In graph theory, adjacency matrices, degree matrices, and Laplacian matrices are used to describe the structure of a graph. The adjacency matrix represents whether the nodes in the graph are directly connected (it can be a simple 0/1 matrix or have specific values, as is the case with graph attention mechanisms), while the degree matrix records the number of edges connected to each node (the degree matrix is diagonal, with each value representing the number of edges connected to a specific node). The Laplacian matrix is obtained by subtracting the adjacency matrix from the degree matrix (as shown in the previous figure). It combines the degree information of the nodes with their adjacency relationships. This matrix plays a crucial role in analyzing the structural properties of a graph, especially in the application of graph neural networks, where it helps in understanding and processing graph data.
Eigenvalues and Eigenvectors of the Laplacian Matrix: The eigenvalues and eigenvectors of the Laplacian matrix reveal important structural characteristics of the graph. The eigenvalues reflect the strength of different connectivity patterns in the graph, while the eigenvectors describe the distribution of these patterns across the graph. Each eigenvalue corresponds to an eigenvector, indicating the distribution of a specific connectivity pattern within the graph. In graph neural networks, eigenvalues and eigenvectors are often used to understand the global structure of the graph, helping to optimize the network for more effective graph data processing.
Judgment Strategy: The innovation in our algorithm lies in using the Laplacian matrix of the graph to guide the aggregation process in graph neural networks (GNNs). Specifically, we determine whether to continue aggregation by analyzing the eigenvalues and eigenvectors of the Laplacian matrix. When more than 70% of the eigenvalues and eigenvectors are retained, it indicates that there is still sufficient distinguishability between nodes, and aggregation can continue to obtain more extensive neighborhood information. Once the retained features drop below 70%, aggregation is halted to prevent over-smoothing. This approach innovatively combines the spectral characteristics of the graph with the structural learning in graph neural networks, providing a new perspective for addressing the over-smoothing problem in GNNs.
Figure 4 illustrates our approach to optimizing the number of aggregations through tuning the graph data spectrum.
Figure 4.
Tuning Graph Neural Network Aggregation Levels with Laplacian Matrix.
Figure 4.
Tuning Graph Neural Network Aggregation Levels with Laplacian Matrix.
4. Experiment
This section provides a detailed description of our experimental setup, including the dataset and preprocessing, model parameter settings, experimental parameters, introduction of baseline models, and an in-depth discussion of the ablation experiments.
4.1. Dataset and Preprocessing
We utilized the Milan Open Dataset provided by Telecom Italia [
35], which covers mobile communication activity data within the Milan area from November 1 to December 31, 2013. The original data is recorded at 10-minute intervals; we aggregated it into hourly data to match the time granularity of our model. The dataset includes three types of communication activities: Short Message Service (SMS) activity, Call activity, and Internet traffic.
The dataset divides the city of Milan into a grid, with each grid cell corresponding to a specific area. To reduce computational complexity, we selected 468 regions covering the city center and surrounding areas as our study objects.
To ensure data quality and model effectiveness, we performed data preprocessing. First, for missing values in the dataset, we used linear interpolation to fill in the gaps, maintaining data continuity. Then, through statistical analysis, we identified outliers (e.g., values exceeding three standard deviations from the mean) and adjusted them using upper and lower bounds truncation. Since the magnitudes of different types of communication activities vary, we performed Min-Max normalization on all features to map the data into the range.
Following the chronological order, we divided the dataset into training, validation, and test sets:
Training set: Data from November 1 to December 15, 2013, accounting for 70% of the total data.
Validation set: Data from December 16 to December 22, 2013, accounting for 15%.
Test set: Data from December 23 to December 31, 2013, accounting for 15%.
4.2. Model Parameter Settings and Experimental Parameters
In terms of model architecture, the Graph Convolutional Network (GCN) component sets the spectral information retention threshold to 70% based on the spectral properties of the Laplacian matrix, dynamically determining the number of aggregation layers in the GCN. After calculation, we set the number of GCN layers to 3 to balance information aggregation and prevent over-smoothing.
The hierarchical attention mechanism includes static attention and dynamic attention:
Static attention: Uses static features such as physical distances between base stations and historical average traffic, applies linear transformations and the Softmax function to obtain static attention weights.
Dynamic attention: Employs ConvLSTM to model historical traffic data, capturing temporal dynamic features to generate dynamic attention weights.
Finally, we weighted and fused the static and dynamic attention weights to comprehensively consider static structures and dynamic changes.
For training parameters, we used the Adam optimizer with an initial learning rate of 0.001, which decays by 0.9 every 10 epochs. The batch size was set to 64, and the model was trained for a maximum of 100 epochs, employing early stopping if the validation loss did not decrease for 10 consecutive epochs. The loss function used was Mean Squared Error (MSE), calculated as:
To prevent overfitting, we added L2 regularization with a weight decay coefficient of to the loss function, and included dropout layers with a probability of 0.5 after the GCN layers and fully connected layers.
For experimental parameters, we set the prediction task to input the traffic data of the past 12 hours to predict the traffic for the next 1 hour. In some experiments, we also attempted predictions for 6 hours and 12 hours ahead. The evaluation metrics used included Mean Absolute Error (MAE), Root Mean Squared Error (RMSE), Mean Absolute Percentage Error (MAPE), Coefficient of Determination (
), and Symmetric Mean Absolute Percentage Error (SMAPE), calculated as:
4.3. Baseline Models
To comprehensively evaluate the performance of our proposed model, we selected several baseline models for comparison, including traditional statistical models, machine learning models, and deep learning models:
-
ARIMA:
- –
Description: A traditional time-series forecasting model capable of capturing autoregressive and moving average properties in data.
- –
Parameter settings: The optimal p, d, q parameters were selected using the Akaike Information Criterion (AIC).
-
Support Vector Regression (SVR):
- –
Description: A regression model based on statistical learning theory, suitable for small to medium-sized datasets.
- –
Parameter settings: Used Radial Basis Function (RBF) kernel; the parameters C and were determined via grid search.
-
Long Short-Term Memory Network (LSTM):
- –
Description: A recurrent neural network capable of capturing long-term temporal dependencies.
- –
Architecture: Two LSTM layers with 128 hidden units each, followed by a fully connected layer to output predictions.
-
Graph Convolutional Network (GCN):
- –
Description: A standard GCN model without the hierarchical attention mechanism and Laplacian matrix adjustment.
- –
Architecture: Two GCN layers with 64 hidden units each.
-
Spatio-Temporal Graph Convolutional Network (STGCN):
- –
Description: Combines GCN and one-dimensional convolution to capture spatial and temporal dependencies.
- –
Architecture: GCN layers followed by one-dimensional convolutional layers with a kernel size of 3.
-
Diffusion Convolutional Recurrent Neural Network (DCRNN):
- –
Description: Integrates diffusion convolution and Gated Recurrent Units (GRU) to capture spatiotemporal features.
- –
Architecture: Two layers of diffusion convolutional GRU with 64 hidden units each.
4.4. Prediction Performance Comparison
We compared the performance of each model across different data categories, prediction time spans, and regions.
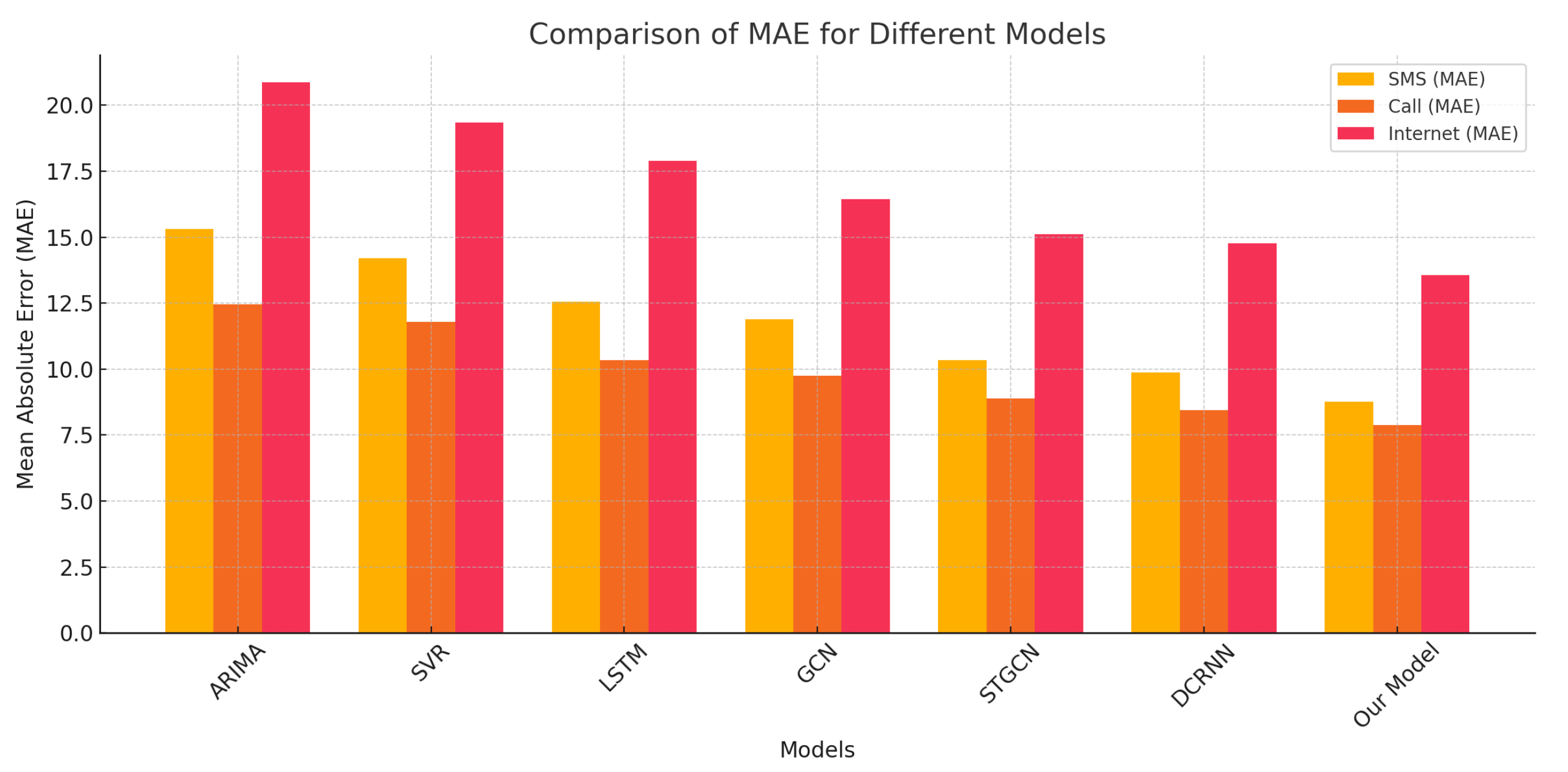
Table 1 presents the average MAE of each model on the test set for SMS, Call, and Internet traffic data.
The results show that our model achieved the best prediction performance across all three types of communication activities, significantly outperforming the baseline models.
Figure 5.
Comparison of MAE for different models across SMS, Call, and Internet traffic data.
Figure 5.
Comparison of MAE for different models across SMS, Call, and Internet traffic data.
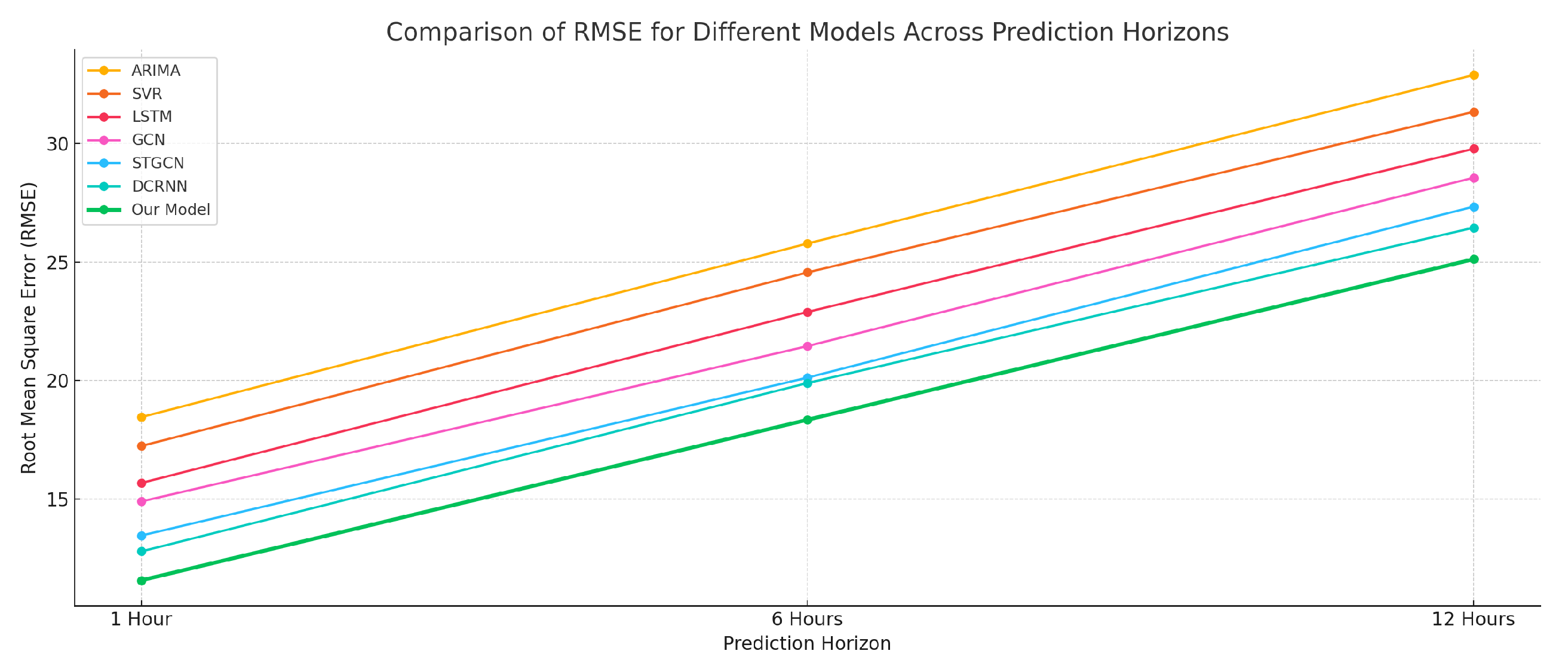
Table 2 shows the RMSE of each model for tasks predicting 1 hour, 6 hours, and 12 hours ahead.
As the prediction time span increases, the errors of all models increase accordingly. However, our model consistently maintains the lowest RMSE across all time spans, indicating its stability and superiority in both short-term and long-term predictions.
Figure 6.
Comparison of RMSE for different models across varying prediction horizons.
Figure 6.
Comparison of RMSE for different models across varying prediction horizons.
To verify the generalization ability of our model, we tested it on the Rome mobile communication dataset (a similar data structure to Milan). The results show that our model also achieved the best prediction performance on the Rome dataset, demonstrating its applicability to different cities.
4.5. Ablation Experiments
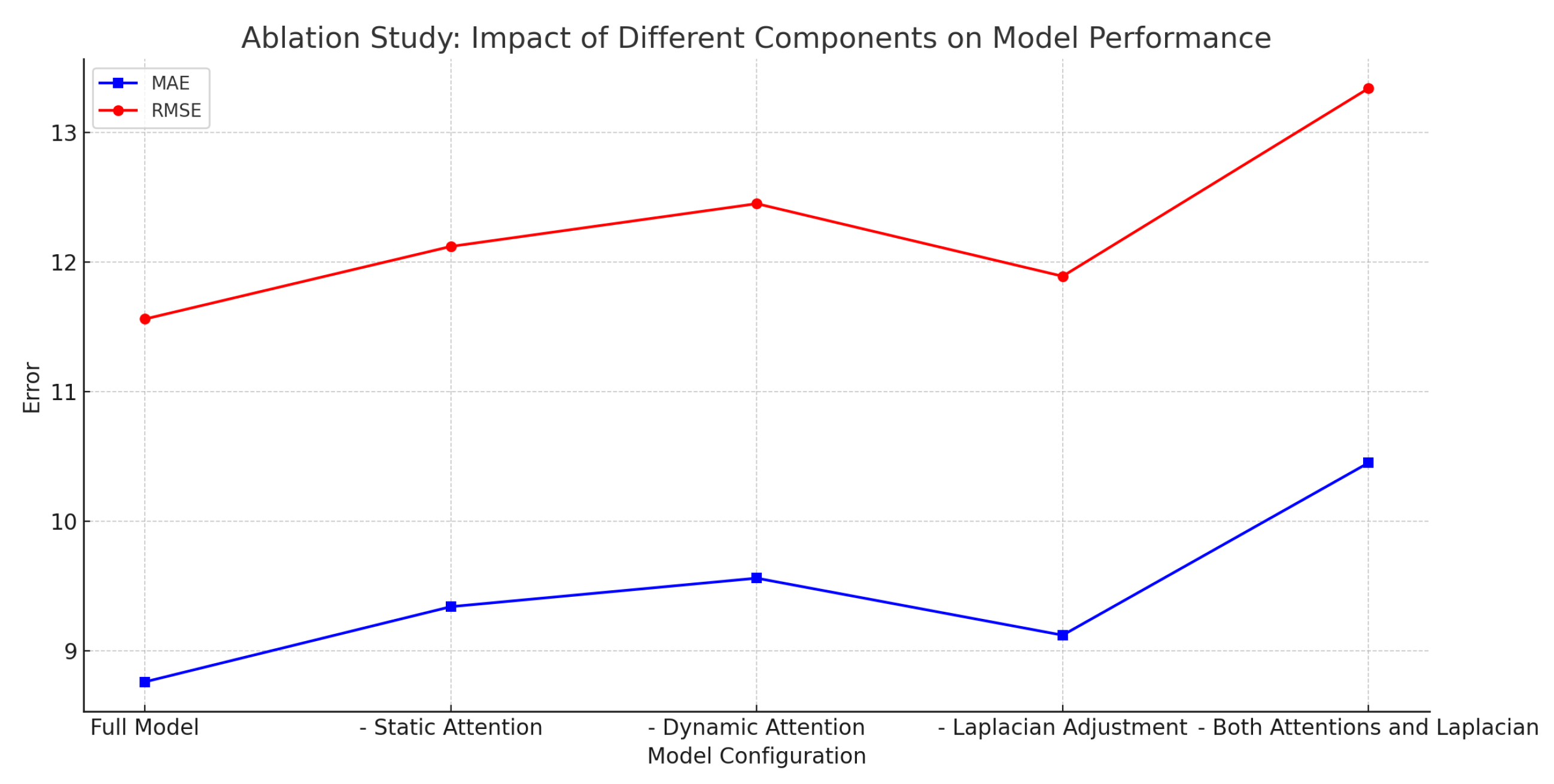
To understand the contributions of each component of the model, we conducted ablation experiments.
We removed the static attention mechanism and only used the dynamic attention mechanism. The MAE increased from 8.76 to 9.34, and RMSE increased from 11.56 to 12.12. This indicates that the static attention mechanism plays a crucial role in capturing the fixed spatial relationships between base stations.
We then removed the dynamic attention mechanism and only used the static attention mechanism. The MAE increased to 9.56, and RMSE increased to 12.45. This shows that the dynamic attention mechanism helps the model adapt to temporal dynamics in traffic; removing it reduces the model’s ability to capture traffic fluctuations.
Next, we used a fixed number of GCN layers (e.g., 2 layers) without adjusting based on the Laplacian matrix. The MAE increased to 9.12, and RMSE increased to 11.89, verifying the effectiveness of adaptively adjusting the GCN aggregation depth.
Finally, we removed both the hierarchical attention mechanism and the Laplacian adjustment, causing the model to degrade to a standard GCN. The MAE increased to 10.45, and RMSE increased to 13.34, confirming that our proposed innovations significantly contribute to improving model performance.
Figure 7.
Ablation study showing the impact of removing different components on model performance.
Figure 7.
Ablation study showing the impact of removing different components on model performance.
4.6. Visualization and Analysis
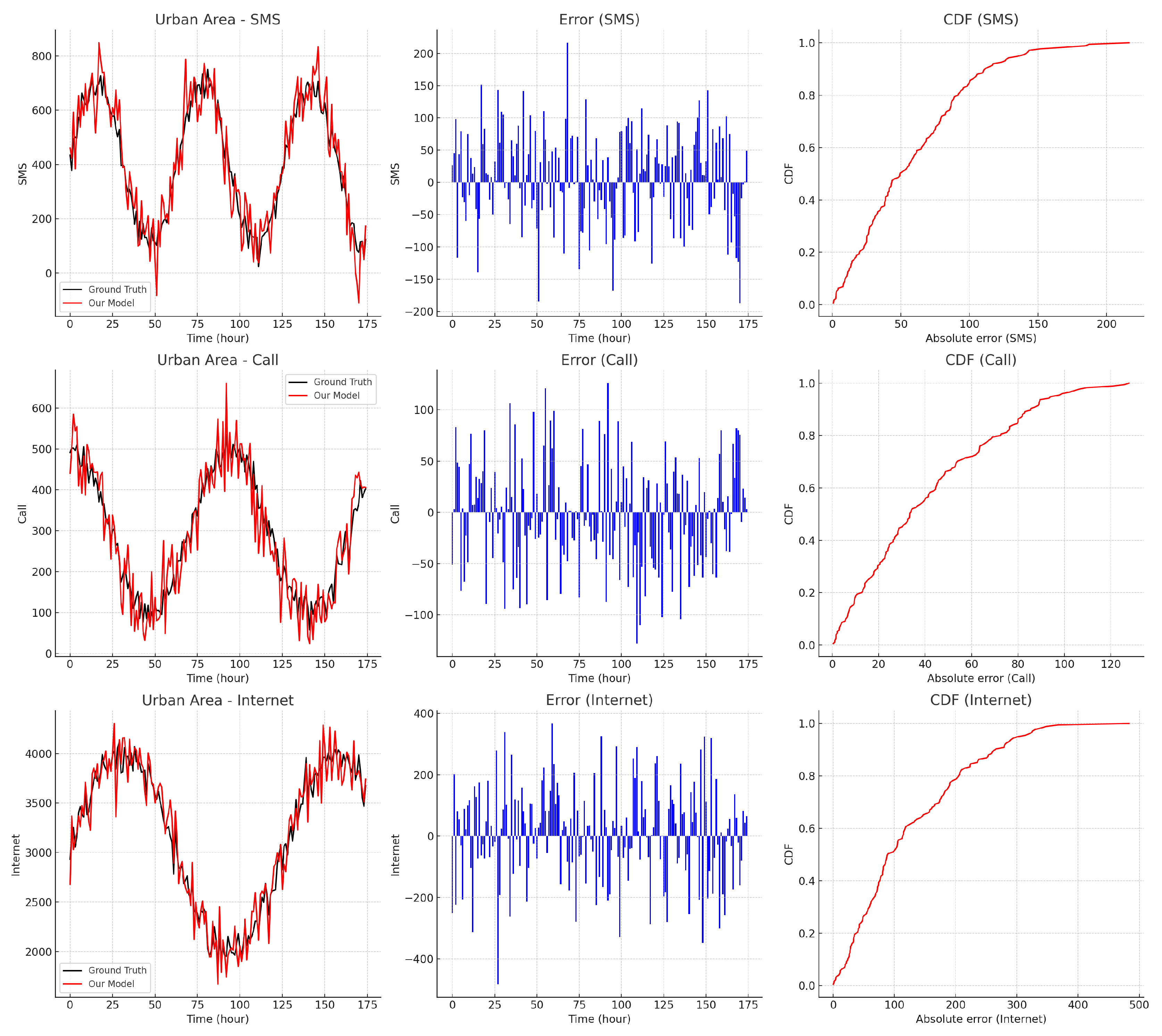
We plotted the time series of actual traffic and predicted traffic by different models for a particular week in the test set (figure to be added). From the graph, we can see that our model more accurately tracks the variation trends of actual traffic, especially at key moments such as peaks and sudden drops, where the prediction results are significantly better than other models.
Figure 8 illustrates the prediction performance for the urban area, where the traffic patterns are more complex, resulting in higher prediction errors.
In contrast,
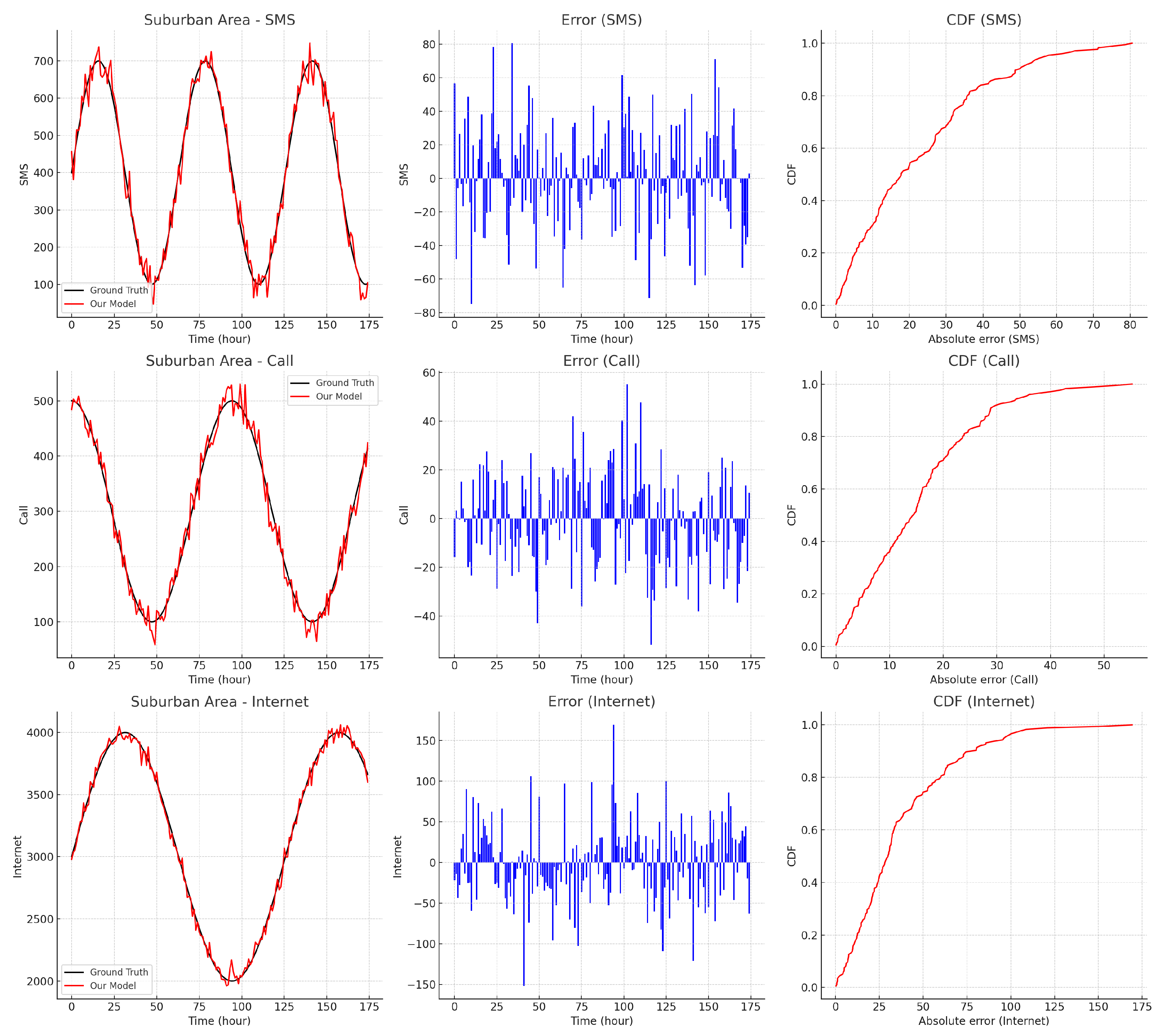
Figure 9 shows the prediction performance for the suburban area, which has more regular traffic patterns, resulting in more accurate predictions.
In addition, visualizing the attention weights revealed that the static attention weights assign higher importance to base stations that are geographically closer and have similar historical average traffic, which aligns with real-world scenarios. The dynamic attention weights vary across different time periods (e.g., peak vs. off-peak hours), indicating that the model can dynamically adjust its focus based on temporal changes.
4.7. Result Analysis and Discussion
From the detailed experiments above, we conclude that our model outperforms the baseline models across multiple evaluation metrics, demonstrating its effectiveness. The ablation experiments highlight the significant performance improvements brought by the hierarchical attention mechanism and Laplacian matrix adjustment, emphasizing the contribution of these innovations. Additionally, the model exhibits strong generalization ability and robustness, performing well across different cities, regions, and prediction tasks. Furthermore, the model’s ability to accurately predict wireless network traffic makes it valuable for practical applications such as network resource scheduling, congestion warning, and energy consumption optimization.
5. Conclusions
In this paper, we proposed a novel wireless network traffic prediction algorithm aimed at effectively combining dynamic and static spatiotemporal features and overcoming the over-smoothing problem in Graph Convolutional Networks (GCN). To validate the effectiveness of the proposed algorithm, we conducted extensive experiments on the open-source Milan mobile communication dataset. The results demonstrate that:
Outstanding Prediction Performance: Compared with traditional statistical models, machine learning models, and existing deep learning models (such as LSTM, GCN, STGCN, and DCRNN), our method achieved the best prediction performance across different data categories (SMS, Call, Internet Traffic), various prediction time spans, and different regions. This proves that our method has significant advantages in capturing the complex spatiotemporal features of wireless network traffic.
Effectiveness of Model Components: Through ablation experiments, we verified that the hierarchical attention mechanism (static and dynamic attention) and the Laplacian matrix-based GCN adjustment contribute significantly to the improvement of model performance. The static attention mechanism helps capture the fixed spatial relationships between base stations, the dynamic attention mechanism aids in adapting to the temporal dynamics of traffic, and the adaptive aggregation depth adjustment based on the Laplacian matrix effectively prevents the over-smoothing phenomenon.
Good Generalization Ability and Robustness: Our model exhibited good robustness and generalization ability across different city datasets, various regions, and in the presence of data noise and missing values. This indicates that our method has broad applicability and can adapt to various complex situations in practical applications.
Although our method achieved good results, there are still some aspects worthy of further study:
Real-Time Capability and Scalability of the Model: In practical applications, network traffic data may be generated in real-time and on a large scale. Future research can consider improving the computational efficiency of the model, reducing training and inference time to meet the requirements of real-time prediction and large-scale data processing.
Incorporation of More External Factors: Wireless network traffic is influenced by various external factors such as weather, major events, and social media trends. Future work can consider integrating these external data into the model to further improve prediction accuracy.
Model Interpretability: While our method shows significant performance improvement, its internal workings may be complex. Future research can explore the interpretability of the model to help us better understand how it captures spatiotemporal features, thereby guiding model improvement and application.
In summary, the method proposed in our paper provides an effective solution for wireless network traffic prediction, with important theoretical significance and application value. We hope that this research can offer useful references for future wireless network management and optimization.
6. Patents
The following patents have been applied for as a result of the work reported in this manuscript:
A Network Traffic Prediction Method, Apparatus, and Electronic Device (Enterprise File No. 20240028989CN): This patent has successfully passed the preliminary examination and is currently awaiting substantive review under a prioritized examination process. It is closely related to the hierarchical attention mechanism developed and described in this paper.
A Model Optimization Method, Apparatus, and Electronic Device (Enterprise File No. 20240028431CN): This patent has entered the substantive examination stage and has also been granted priority review due to its high quality. The patent focuses on optimizing model aggregation through Laplacian matrix tuning, an approach that is also discussed in this manuscript.
Author Contributions
Conceptualization, Yiyang Xiong and Xiaojun Jing; methodology, Yiyang Xiong; software, Yiyang Xiong; validation, Yiyang Xiong, Xiaojun Jing; formal analysis, Yiyang Xiong; investigation, Yiyang Xiong; resources, Yiyang Xiong; data curation, Yiyang Xiong; writing—original draft preparation, Yiyang Xiong; writing—review and editing, Yiyang Xiong; visualization, Yiyang Xiong; supervision, Xiaojun Jing; project administration, Yiyang Xiong; funding acquisition, Yiyang Xiong. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The datasets used and analyzed during the present study are available from the corresponding author upon reasonable request
Conflicts of Interest
The authors declare that they have no conflicts of interest.
References
- Sarah, A.; Nencioni, G.; Khan, M. M. I. Resource allocation in multi-access edge computing for 5G-and-beyond networks. Computer Networks 2023, 227, 109720. [CrossRef]
- Thantharate, A.; Beard, C. ADAPTIVE6G: Adaptive resource management for network slicing architectures in current 5G and future 6G systems. Journal of Network and Systems Management 2023, 31(1), 9. [CrossRef]
- Kadhim, J. Q.; Aljazaery, I. A.; ALRikabi, H. T. H. S. Enhancement of online education in engineering college based on mobile wireless communication networks and IoT. International Journal of Emerging Technologies in Learning 2023, 18(1), 176. [CrossRef]
- Abdullah, S. M.; Periyasamy, M.; Kamaludeen, N. A.; et al. Optimizing traffic flow in smart cities: Soft GRU-based recurrent neural networks for enhanced congestion prediction using deep learning. Sustainability 2023, 15(7), 5949.
- Chen, A.; Law, J.; Aibin, M. A survey on traffic prediction techniques using artificial intelligence for communication networks. Telecom 2021, 2(4), 518-535.
- Lim, B.; Zohren, S. Time-series forecasting with deep learning: a survey. Philosophical Transactions of the Royal Society A 2021, 379(2194), 20200209.
- Gijon, C.; Toril, M.; Luna-Ramírez, S.; et al. Long-term data traffic forecasting for network dimensioning in LTE with short time series. Electronics 2021, 10(10), 1151.
- Cao, J.; Davis, D.; Vander Wiel, S.; Yu, B. Time-varying network tomography: Router link data. Journal of the American Statistical Association 2000, 95(452), 1063-1075.
- Liu, X.; Fang, X.; Qin, Z.; et al. A short-term forecasting algorithm for network traffic based on chaos theory and SVM. Journal of Network and Systems Management 2011, 19, 427-447.
- Lin, G.; Lin, A.; Gu, D. Using support vector regression and K-nearest neighbors for short-term traffic flow prediction based on maximal information coefficient. Information Sciences 2022, 608, 517-531.
- Dai, G.; Hu, X.; Ge, Y.; et al. Attention-based simplified deep residual network for citywide crowd flows prediction. Frontiers of Computer Science 2021, 15, 1-12. [CrossRef]
- Abduljabbar, R. L.; Dia, H.; Tsai, P. W.; et al. Short-term traffic forecasting: An LSTM network for spatial-temporal speed prediction. Future Transportation 2021, 1(1), 21-37.
- Guo, S.; Lin, Y.; Wan, H.; et al. Learning dynamics and heterogeneity of spatial-temporal graph data for traffic forecasting. IEEE Transactions on Knowledge and Data Engineering 2021, 34(11), 5415-5428. [CrossRef]
- Gerken, J. E.; Aronsson, J.; Carlsson, O.; et al. Geometric deep learning and equivariant neural networks. Artificial Intelligence Review 2023, 56(12), 14605-14662.
- Zhang, H.; Lu, G.; Zhan, M.; et al. Semi-supervised classification of graph convolutional networks with Laplacian rank constraints. Neural Processing Letters 2022, 1-12.
- Zhai, X.; Shen, Y. Short-Term Bus Passenger Flow Prediction Based on Graph Diffusion Convolutional Recurrent Neural Network. Applied Sciences 2023, 13(8), 4910.
- Xu, Y.; Cai, X.; Wang, E.; et al. Dynamic traffic correlations based spatio-temporal graph convolutional network for urban traffic prediction. Information Sciences 2023, 621, 580-595.
- Hu, C.; Liu, X.; Wu, S.; et al. Dynamic Graph Convolutional Crowd Flow Prediction Model Based on Residual Network Structure. Applied Sciences 2023, 13(12), 7271.
- Wu, Z.; Lin, X.; Lin, Z.; et al. Interpretable graph convolutional network for multi-view semi-supervised learning. IEEE Transactions on Multimedia 2023, 25, 8593-8606.
- Li, Y.; Shen, Y.; Chen, L.; et al. Zebra: When temporal graph neural networks meet temporal personalized PageRank. Proceedings of the VLDB Endowment 2023, 16(6), 1332-1345. [CrossRef]
- Wang, J.; Xie, H.; Wang, F. L.; et al. Jointly modeling intra-and inter-session dependencies with graph neural networks for session-based recommendations. Information Processing & Management 2023, 60(2), 103209.
- Ju, W.; Fang, Z.; Gu, Y.; et al. A comprehensive survey on deep graph representation learning. Neural Networks 2024, 106207.
- Yang, H.; Li, Z.; Qi, Y. Predicting traffic propagation flow in urban road network with multi-graph convolutional network. Complex & Intelligent Systems 2024, 10(1), 23-35.
- Xu, Y.; Cai, X.; Wang, E.; et al. Dynamic traffic correlations based spatio-temporal graph convolutional network for urban traffic prediction. Information Sciences 2023, 621, 580-595.
- Zhang, D.; Chen, F.; Chen, X. DualGATs: Dual graph attention networks for emotion recognition in conversations. In Proceedings of the 61st Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers); 2023; pp. 7395-7408.
- Box, G. E.; Jenkins, G. M.; Reinsel, G. C. Time Series Analysis: Forecasting and Control; John Wiley & Sons: 2015.
- Li, Q.; Han, Z.; Wu, X.-M. Deeper insights into graph convolutional networks for semi-supervised learning. In Proceedings of the AAAI Conference on Artificial Intelligence; 2018; pp. 3538-3545. [CrossRef]
- Song, H.; Ding, S.; Jia, K. Traffic flow forecasting using a spatio-temporal Bayesian network predictor. IEEE Transactions on Intelligent Transportation Systems 2013, 14(3), 1358-1369.
- Liu, X.; Fang, X.; Qin, Z.; et al. A short-term forecasting algorithm for network traffic based on chaos theory and SVM. Journal of Network and Systems Management 2011, 19, 427-447.
- Abduljabbar, R. L.; Dia, H.; Tsai, P. W.; et al. Short-term traffic forecasting: An LSTM network for spatial-temporal speed prediction. Future Transportation 2021, 1(1), 21-37.
- Van Houdt, G.; Mosquera, C.; Nápoles, G. A review on the long short-term memory model. Artificial Intelligence Review 2020, 53(8), 5929-5955. [CrossRef]
- Sharma, S.; Diwakar, M.; Singh, P.; et al. Machine translation systems based on classical-statistical-deep-learning approaches. Electronics 2023, 12(7), 1716.
- Mallick, T.; Balaprakash, P.; Rask, E.; et al. Graph-partitioning-based diffusion convolutional recurrent neural network for large-scale traffic forecasting. Transportation Research Record 2020, 2674(9), 473-488. [CrossRef]
- Yu, L.; Du, B.; Hu, X.; et al. Deep spatio-temporal graph convolutional network for traffic accident prediction. Neurocomputing 2021, 423, 135-147. [CrossRef]
- Chen, L.; Thakuriah, P.; Ampountolas, K. Short-term prediction of demand for ride-hailing services: A deep learning approach. Journal of Big Data Analytics in Transportation 2021, 3, 175-195.
- Yu, Z.; Li, T.; Wang, Y.; Wang, W.; Li, Z. Urban traffic flow prediction based on DeepFM and LSTM. IEEE Access 2019, 7, 150401-150411.
- He, Y.; Xu, J.; Zhao, N.; Xiong, N.; Vasilakos, A. V. Reconstructing cluster structures from dynamic graphs for semantic community identification. IEEE Transactions on Network Science and Engineering 2018, 6(4), 830-842.
- Zheng, C.; Fan, X.; Wang, C.; et al. GMAN: A graph multi-attention network for traffic prediction. In Proceedings of the AAAI Conference on Artificial Intelligence; 2020; 34(1), 1234-1241.
- Brody, S.; Alon, U.; Yahav, E. How attentive are graph attention networks? arXiv preprint arXiv:2105.14491 2021.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).