Prerpints.org logo
Preprint
Article

High Resolution Building Indicator Mapping Using Airborne LiDAR Data

Altmetrics

Downloads

94

Views

40

Comments

1

Submitted:

14 October 2024

Posted:

14 October 2024

You are already at the latest version

Alerts
Abstract
Urban indicators characterize a specific urban space through calculated values, such as building coverage, building height, floor area ratio, and many others. Urban indicators established in spatial development plans should ensure the preservation of spatial order when introducing new construction investments. They should also harmonize with the existing urban structure, and even modernize it towards sustainable development. When determining these indicators, surrounding space is analyzed. Conventionally, building indicators in the existing space are determined based on available documents, usually 2D spatial data such as large-scale maps or cadastral maps. The aim of this research is to investigate the method of calculating building indicators using 3D urban building models that will be created from airborne Light Detection and Ranging (LiDAR) measurements. In the discussion of the results, indicators calculated based on LiDAR data are compared with calculated from 2D cadastral data. The calculated 3D indicators correlate with the classically calculated indicators. The accuracy of computed building area, volume, and other indicators depends on the LiDAR point cloud density and accuracy. The indicators calculated from 3D data align with new trends in defining Building Morphology Indicators (BMI).
Keywords: 
Subject: Engineering  -   Other

1. Introduction

In the era of creating digital twins of the real world, we should more frequently utilize available 3D spatial data in daily tasks to support the development of smart cities and sustainable urban growth. 3D data enable the calculation of urban [1,2,3], environmental [4], ecological [5], social, economic, and institutional indicators [6,7], as well as programming indicators [8]. In urban spaces, recommended transport indicators (ISO) [9], accessibility indicators for various urban services [10], public green spaces, public utility facilities, and many others [11,12] are assessed. Various analyses are also conducted, aimed at identifying specific areas in urban spaces, such as heat islands [13].
In urban planning and spatial development, to better understand the environment and built structures, solutions based on 3D city models should be widely implemented [12,14,15]. This is essential when making decisions regarding new investments [16,17] based on necessary indicators that ensure not only sustainable development but also the preservation of landscape values, such as those related to shading in urban spaces [9], visibility of the sky [18], and the perception of buildings by people [19].
Digital data sets, such as LiDAR, offer a new perspective on space by enabling the automatic generation of 3D object-vector representations and analyses of urban spaces. An example of this is the capability to create digital models of individual buildings [20,21,22,23] and to generate 3D models of entire cities at LoD2 level [23,24]. These proposed solutions are becoming increasingly advanced [26,27,28,29,30,31] through the integration of LiDAR data with remote sensing datasets and the use of machine learning and deep learning techniques [32,33,34].
In addition to algorithms for modeling entire cities' buildings, there are also algorithms available that allow for the automatic creation of urban greenery models, including the generation of individual tree models, green complexes, and the calculation of biomass in biologically active areas [35,36,37,38,39,40]. The use of deep learning methods for 3D object recognition and vectorization of other urban space elements will, in the future, enable the widespread use of 3D, and even 4D, digital data for monitoring urban spaces and calculating indicators that better describe spatial structures using existing [40,41,42] and new parameters [43].
Urban areas, both existing and planned, are described in urban planning using indicators that define land use and building parameters [44,45]. These indicators include, among others, building height, maximum and minimum number of floors, building coverage, and floor area ratio. Other indicators relate to the distance between buildings, the number of parking spaces, recreational areas, and biologically active areas [46]. The methods for calculating these indicators are widely known and documented in standards and local legal documents [47,48], primarily related to spatial planning. Currently, the calculation of indicator values for existing areas is based on data from cadastral and topographic maps. The set of indicators in local spatial development plans (MPZP) for areas designated for development are the result of separate analyses of urban spaces, based on large-scale 2D maps and other data sets from thematic portals and remote sensing results, such as LiDAR, orthophotos, street view, and many others. 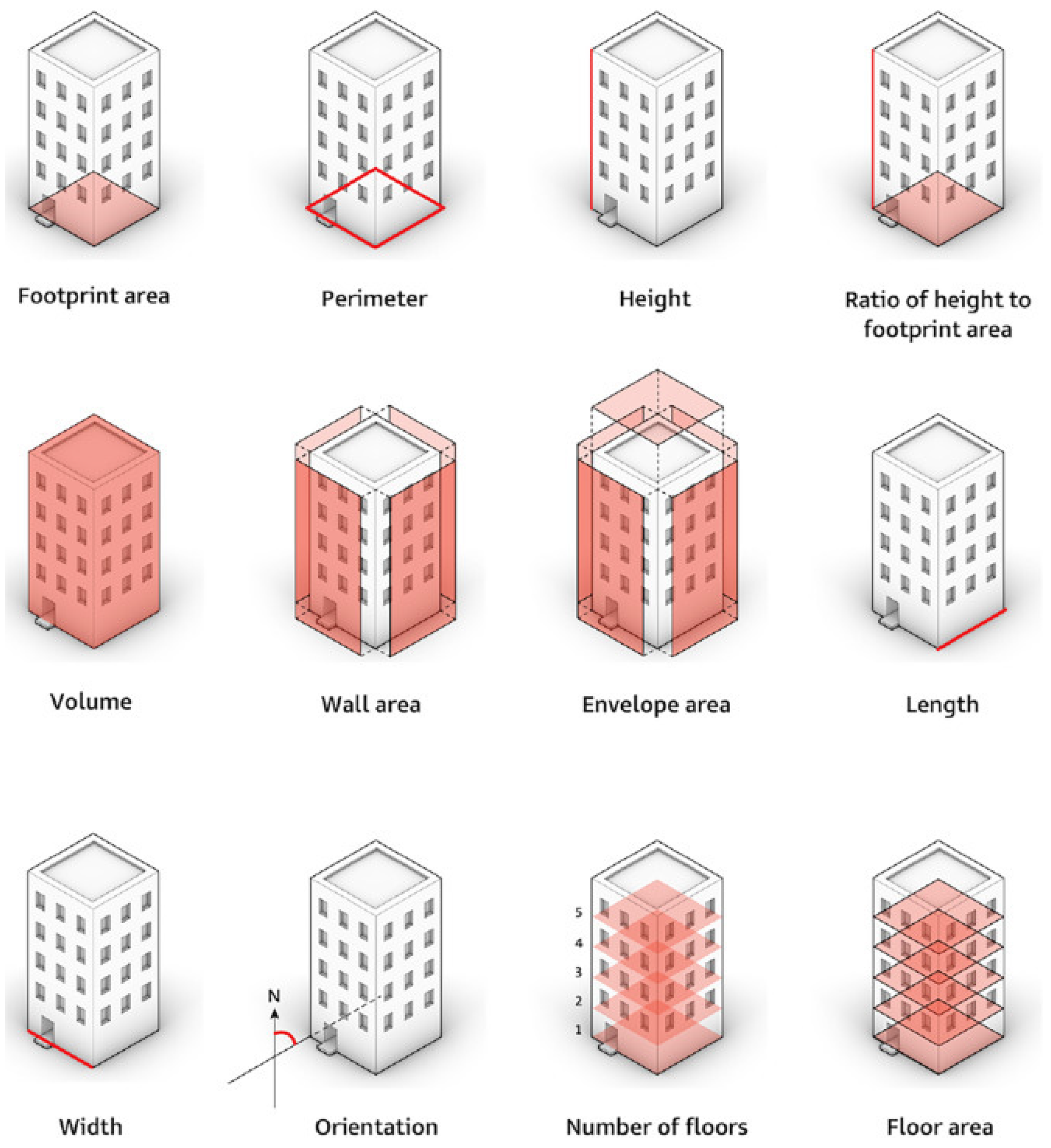New solutions [49,50] are being promoted [51], introducing (Figure 1) global Building Morphology Indicators (BMI).
The aim of the study is to assess the possibility of using airborne LiDAR measurements, to calculate indicators at the buildings. The research methods will be related to an attempt to determine 3D indicators and compare them with indicators calculated on the basis of 2D spatial data from cadastral maps. The research is part of the BMI issue.
At this point, it is inevitable to highlight the novelty and the contribution of this paper which can be summarized as follows:
  • Automatic creation of building indicators from LiDAR point cloud.
  • Evaluation of the building area and volume calculations using LiDAR data.
  • Accuracy assessment and formulation of the target indicators.

2. Datasets

For this study, a fragment of the housing estate is used with single-family buildings built in 1970 in the form of cuboids with flat roofs (Figure 2). Most of the examined buildings were modernized and expanded in the following years. Out of 10 surveyed buildings, only four (4) retained their original shape of flat roof.
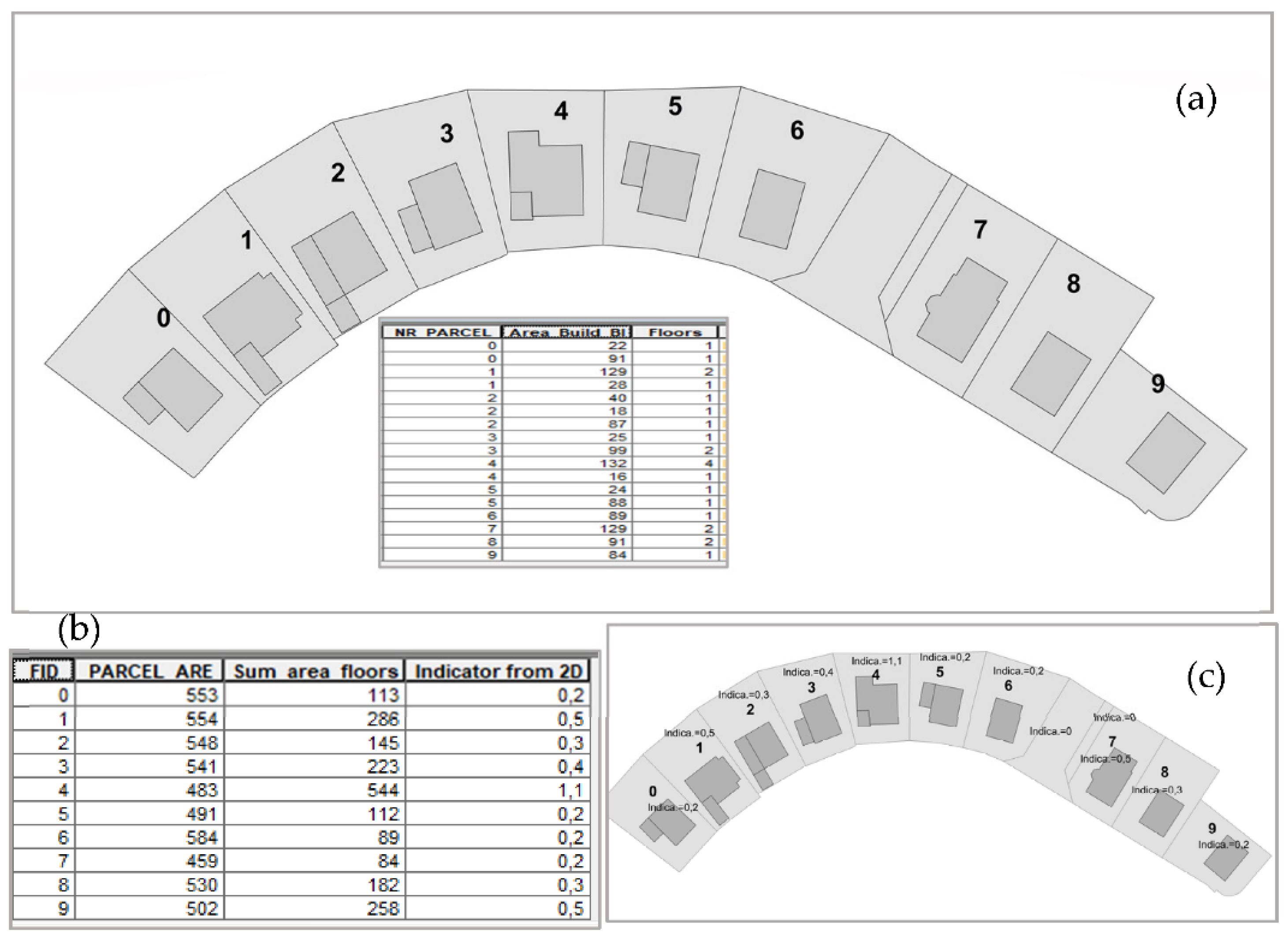
The 2D cadastral data (Figure 3 a) were used to present the research object in 2D and to calculated the building indicators of parcels. The building intensity indexes of the parcels were s calculated as the quotients of the sum of the areas of individual floors of buildings on a parcel to the area of ​​parcels.
The presented data (Figure 2 and Figure 3) are taken as reference data for the accepted studies. They will allow for verification of the results obtained from LiDAR data processing.

3. Suggested Approach

Buildings may be located in urban or rural areas. The density of buildings is incomparable between cites and outside city zones. Furthermore, within the cities, a complicated texture of urban typologies is expected, where great variance of building architectural and geometrical forms can be noticed, e.g., single, connected, multi-stories, skyscrapers, houses, administration, religious and historical buildings. To calculate a building volume, several kinds of measurements can be carried out to realize this purpose, such as direct dimensional measurements, using building plan, Geographic Information System (GIS) database, Building Information Model (BIM), photogrammetry data acquisition, terrestrial laser scanning, and airborne LiDAR data. Each one of these methods has advantages and disadvantages regarding the applicability, speed of data acquisition and processing, resultant accuracy, availability of data or data acquisition technologies, and the measurement cost.
To calculate building volume in urban areas, airborne laser scanning is an efficient data acquisition tool due to its high speed and accuracy. For this purpose, two kinds of airborne LiDAR can be used according to the project scale and the domestic civil aviation safety authority rules [51], i.e., the scanning by Unmanned Aerial Vehicle (UAV) (drone) and the use of manned aircraft (plane or helicopter). Despite the difference between the point clouds obtained by manned and unmanned aircraft regarding the point density, accuracy, speed, flying height, and privacy respecting, scanning using aerial planes is still more employed in urban areas. Unfortunately, when an aerial plane is used to do scanning, the building facades may only be covered partially and have lower point density than that of the roofs [52].
In this context, once the target area is scanned, the measured point cloud should be classified to extract the building class. This procedure will not only help to recognize the building mask, but it is also helpful to detect the individual building point clouds. Once the single building LiDAR point cloud is available, the calculation of building volume can be carried out.
Three assumptions are applied in calculating a building volume starting from the LiDAR point cloud. First, one building represents a mass based on a plane base. Of course, it is impossible to guess the geometric form of the ground located directly under the building because it is covered by the building itself. Moreover, the area surrounding the building may be obstructed by objects, such as trees and other attachments. Hence, to simplify the question of building volume calculation, the building mass is considered above the plane. The second assumption is that the building ground plane is horizontal and the building volume is calculated as the building located on this horizontal plane. Although this hypothesis may not always reflect the truth, it is accurate enough to represent the actual building volume for most scenarios. Also, the hardship of determining the ground plane equation due to the presence of obstacles of different heights surrounding the buildings, such as trees, cars, and other miscellaneous objects represents a great challenge to estimate the accurate ground plane boundary. The third assumption concerns the building facades. To consider the general case of airborne laser scanning, where the building facades are not covered completely and regularly by LiDAR points. This assumption assumes that the building facades are vertical plans.
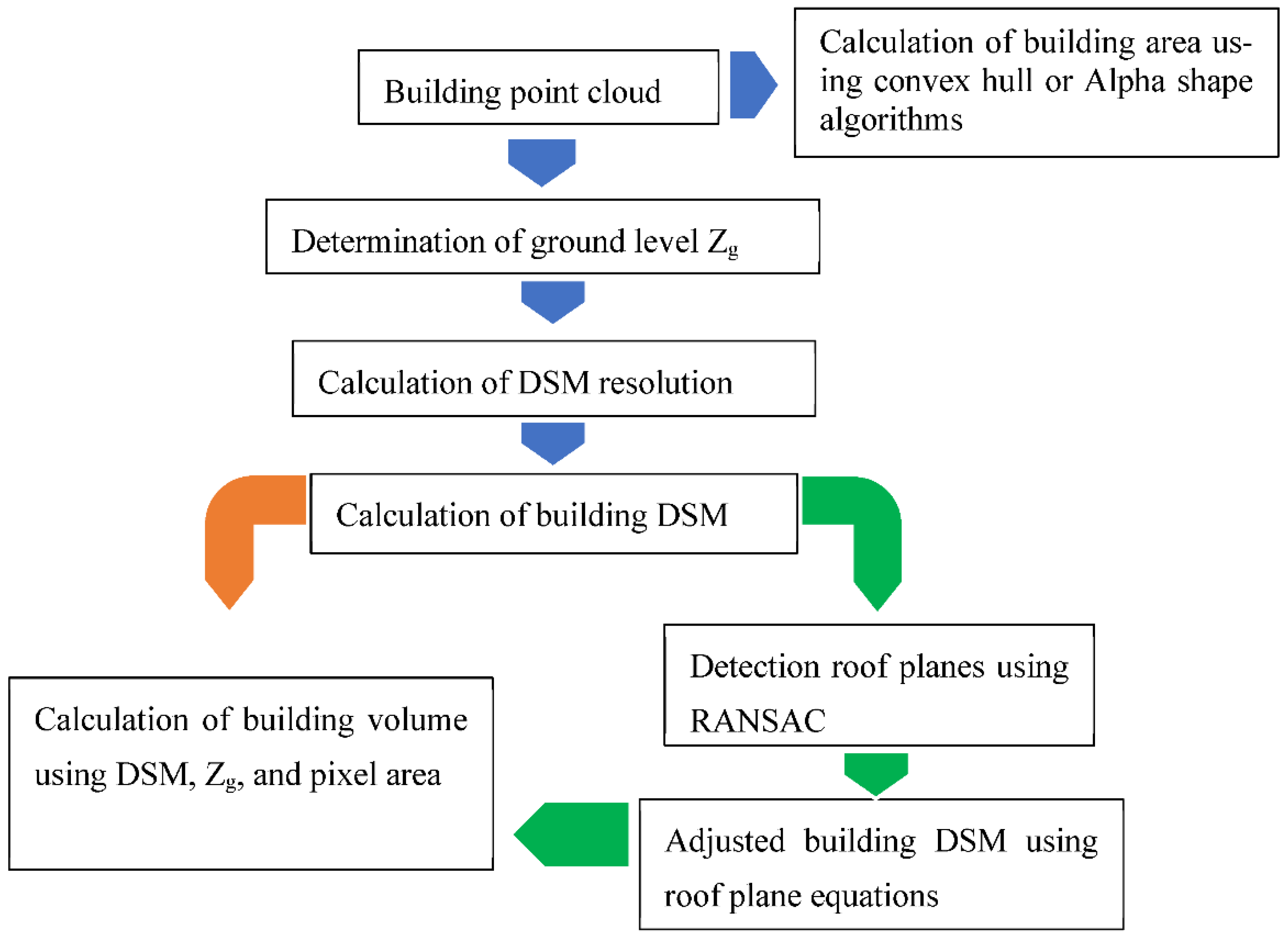
To calculate the building volume starting from the airborne LiDAR point cloud, considering the above three assumptions, two approaches are suggested. Figure 4 contains three kinds of different colored arrows. The blue arrows belong to the two approaches, whereas the orange arrow and green arrows are respectively for the first and second approach.
To determine the ground level Zg, the lowest point in the building neighborhood is detected and its Z coordinate is assigned to the ground level.

3.1. DSM Resolution Calculation

These approaches start with projecting the building point cloud on a grid defined in the horizontal plane OXY. This grid consists of n rows and m columns and consequently of n × m pixels. To calculate the grid resolution (pixel size), the point density should be calculated. For this purpose, using the Theoretical point Density (TD) provided by the scanning company, the Theoretical Mean Distance (TMD) between two neighboring points is calculated (Equation 1) [53].
T M D = 1 T D
Supposing the pixel size equals TMD, the building Digital Surface Model (DSM) can be calculated. From this model, the values of empty pixels inside the building body are calculated using a gradient filter. Thereafter, the number of building LiDAR points is divided on the building area to calculate the practical point density.

3.2. Calculation of Building DSM

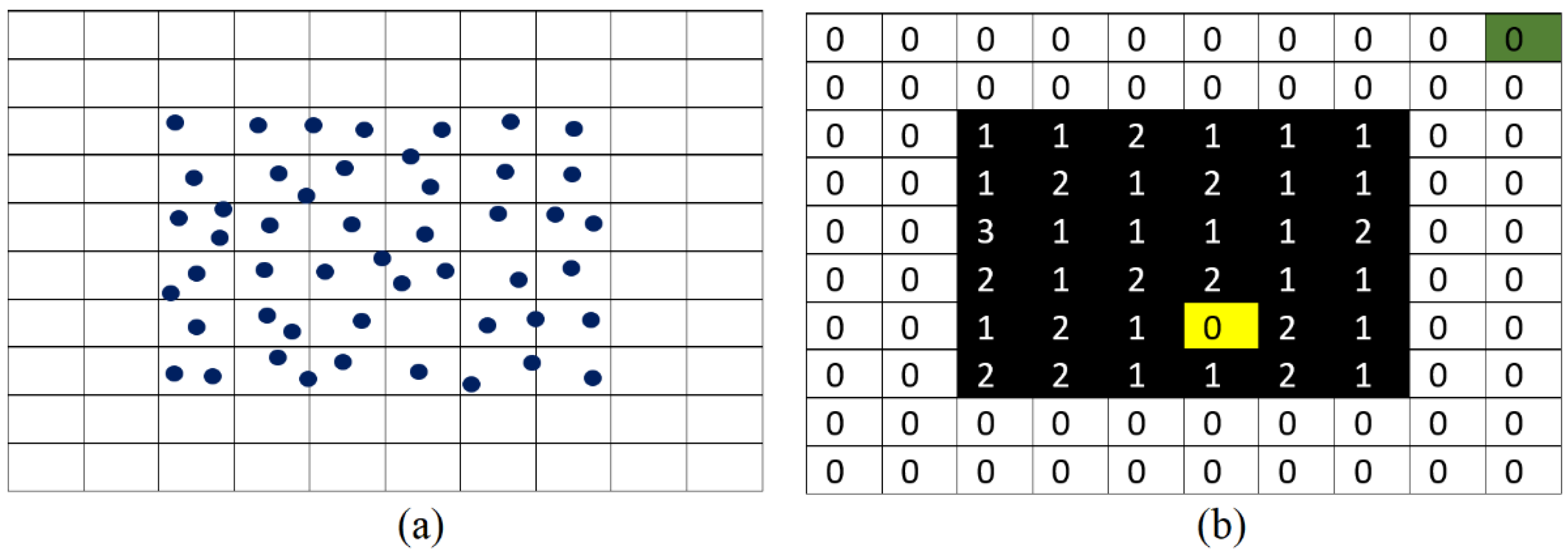
Once the resolution of the building DSM is calculated, the building point cloud is superimposed on the constructed grid and the pixel values are assigned according to the presence of LiDAR points inside or surrounding the pixel. In this context, the pixel value is calculated depending on the Z coordinates of points within the pixel. We take the maximum Z coordinate values of the LiDAR points located inside the pixel. This choice has been adopted to conserve the Z coordinate from interpolation and then the LiDAR points will keep expressing the roof geometry.
At this stage, four kinds of empty pixels can be distinguished: First, the empty pixels located outside the building boundaries, e.g., the green cell in Figure 5 b; Second, empty pixels located inside the building boundaries, e.g., the yellow cell in Figure 5 b; Third, pixels belonging to the building body and contain only one LiDAR point; and finally, pixels belonging to the building body and containing more than one LiDAR point (Figure 5 b). Indeed, the irregular distribution of LiDAR points on the building roof regarding the LiDAR point accuracy, the roof texture, the presence of vertical surfaces such as building facades and noisy points, may produce a variant number of LiDAR points located inside each pixel.
Hence, the application of a gradient filter allows the recognition of the last type of empty pixels. If an empty pixel is located inside the building boundary, the mean Z coordinate value of the LiDAR points located in the neighborhood of the pixel boundaries is assigned to this pixel.
The calculation of building DSM permits eliminating vertical surface points such as building facades which may have low point density and their role for building volume calculation is negligible. Also, it allows us to compensate for the missing points on the roof as well as to eliminate extra points regarding the mean point density. Moreover, the DSM matrixial form not only lightens the data volume, but it helps save the topological relationships between the neighboring points, which facilitates the modelling step. On the other hand, during calculation of building DSM and filling in the missing points inside the building body, extra pixels outside the building body and adjacent to the building boundaries will be added (see red arrow in Figure 6d). Indeed, boundary pixels have similar topological values to the empty pixels inside the building's body (see red arrow in Figure 6d). In fact, these added extra pixels outside a building's body will increase the area of the building (Table 1). Also, the DSM resolution value (pixel size) affects the building area (Table 1). Because one boundary pixel will be considered completely covered by a building body, but the truth is it can be partially covered by a building body. Such boundary error will increase when the DSM resolution decreases (Table 1). In addition to the last listed factors that affect the calculated building area, classification uncertainty may also be considered. When some non-building points connected to the building body are classified as building points, these misclassified points will increase the calculated building area.
From Table 1, it can be noted that the area values, in the case of non-filling the empty pixels inside the building body, greatly increase when the DSM pixel size increases. Also, when the resolution value is smaller than the resolution calculated from the point density (0.1 m), the difference will be very large because the voids will occupied a large area inside the building body DSM. To clarify this idea, let us compare the number of building pixels containing LiDAR points to the number of building empty pixels when different pixel sizes are considered (Table 1). It can be noted in building number 0 that when pixel size is very small (0.1 m), the number of empty pixels equal 86 % of total number of building pixels. Whereas, for the same building, when pixel size become great (0.6 m), the number of empty pixels equal 3.6 % of total number of building pixels. This huge difference of the percentage of empty pixels inside building body DSM is the main responsible of the great building area value difference when the empty pixels are filled or not. Also, when the DSM pixel size is getting smaller, the missing point influence will decrease, but unfortunately, the boundary error influence will continue to be added. Conversely, in the case of filling the empty pixels inside a building body, only the boundary error influence will continue to be added.

3.3. Building Area Calculation and Accuracy Estimation

At this stage, one question arises: is the building DSM a better choice to calculate the building area and volume, or the direct use of building point cloud? To calculate the building area, of course, the direct use of building point cloud will provide accurate results because the boundary errors and empty pixel issue will not be present. In this context, convex hull and alpha shape algorithms can be used to calculate the building area starting from the LiDAR building point cloud [54]. On the other hand, the missing of building ground part due to the roof and façade presence, in addition to the low point density or/and missing façade sections in the building point cloud, the building point cloud will not be sufficient to directly calculate the building volume. To conclude, to calculate the building area starting from the LiDAR building point cloud, the direct use of point cloud will provide an accurate result. Conversely, to calculate the building volume starting from the LiDAR building point cloud, the direct use of point cloud will not provide an accurate result because the heterogeneous distribution of LiDAR points, that is why the use of building DSM will be unavoidable.
To calculate the building footprint area starting from the LiDAR building point cloud, first the point cloud is projected on the horizontal plane OXY. This operation allows converting the 3D point cloud into a 2D point cloud. Second, the polygon boundary of the 2D building point cloud is detected using convex hull or alpha shape algorithms. Finally, the area of this polygon represents the building footprint area. This approach does not only provide an accurate result, but it guarantees the stability of the area value.
At this stage, it is important to highlight the different concepts of building areas. Two kinds of building areas can be distinguished. First, the building footprint area where the underhung and overhung parts are considered simultaneously. Second, underhung areas where overhung parts are not considered. In fact, the calculation of the building intensity index uses the underhung area, whereas the LiDAR building point cloud allows calculating the building footprint area. That is why it is understandable that if the allowed overhung parts percentage is known, then the LiDAR building point cloud can provide an accurate value of the intensity index.
To estimate the accuracy of the calculated area of the target building, several kinds of errors are defined. First, Error due to the point density and error due to the point planimetric accuracy can be estimated. On a 2D LiDAR point inside one pixel, despite the fact that it is assumed that this point is situated in the pixel center, but it can exist anywhere inside this pixel boundary. The distance between the pixel center and the extreme location of the lidar point inside the target pixel equals d L d = 0.5 × T M D where TMD is the mean distance between two neighboring points. Also, another error should be considered, which is the error related to the LiDAR points planimetric accuracy ( d L a ) . The third source of error for building area calculation is the point cloud Classification Error (CE). Supposing that Ar is the building footprint area, the building’s footprint geometrical form is square, and this square side length equals L, then A r = L 2 . According to the error propagation law, the total building area error (dAr) can be described by Equation 2.
d A r = 2 × L × d L d 2 + 2 × L × d L a 2 + A r × C E 2 d A r = 4 × A r × d L d 2 + d L a 2 + A r × C E 2
To understand more Equation 2, let us see this example, e.g., for T M D = 0.25 m , d L a = ∓ 0.15 m , A r = 150 m 2 , C E = 3 % , it can be found that d L d = 0.5 × 0.25 = ± 0.125 m and then d A r = ± 6.57 m 2 .

3.4. Multi-Storey Building Area and Building Intensity Index

To calculate the building intensity index, the summation of all building level areas is divided by the parcel area. For this purpose, the building Multi Levels Area (MLA) should be calculated. In this context, the building point cloud is segmented according to the number of levels. As the ground level is already calculated (see Section 3), the subtraction of the ground level value from the Z coordinated of LiDAR points will provide the height of LiDAR point above the ground level. This value can help to determine the number of building levels related to the concerned LiDAR point. Unfortunately, the noise presence may generate considerable errors when LiDAR points are processed point by point. That is why it is advised to carry out this procedure by considering the roof facets (See Section 3.5). The average building level height can be made as an input, then the number of levels can be calculated for each roof plane where one building can be composed of several different masses of levels.

3.5. Building Volume Calculation and 3D Building Intensity Index

At this stage, the building DSM is calculated from the LiDAR point cloud in addition to the ground level which was estimated in Section 3. These two elements are the input data for this operation. At this point, the two approaches of building volume calculation shown in Figure 4 will be presented and discussed. The first suggested approach of building volume calculation (see green and blue arrows in Figure 4 is based on a hypothesis that the building roof is composed of a list of planar surfaces. But this algorithm will still be efficient despite the obtained roof deformations when no planer surfaces are present. Indeed, non-planar surface will be detected as several neighboring patches where each one will present a local plane. Therefore, this method can be adopted to calculating volumes of generic buildings.
To segment the building roof according to the planer elements, the extended RANdom SAmple Consensus (RANSAC) paradigm [55] is consecutively applied on the building DSM points within a loop to detect all roof planar facets. This algorithm selects three points randomly and fits the plane containing the selected points. Thereafter, it detects all points behaving at a minimal distance (inferior of the given threshold) to the fitted plane. This operation is iterative, where in each iteration, the number of points and the standard deviation of the newly detected plane are compared to the saved plane. If the new plane is better than the saved one regarding the two used criteria, the new plane will replace the previously saved plane. The number of iterations is calculated using a chi-square ( χ 2) distribution density function, which is a continuous probability distribution. Furthermore, the extended RANSAC algorithm loop will be stopped when the number of remaining points becomes smaller than a given threshold (3 % of the building point cloud), or when the algorithm fails to detect any more planes. In each loop iteration, the detected plane will be assessed if some plane points do not belong to the main detected plane body. Hence, these points will be eliminated and reassigned to the building point cloud.
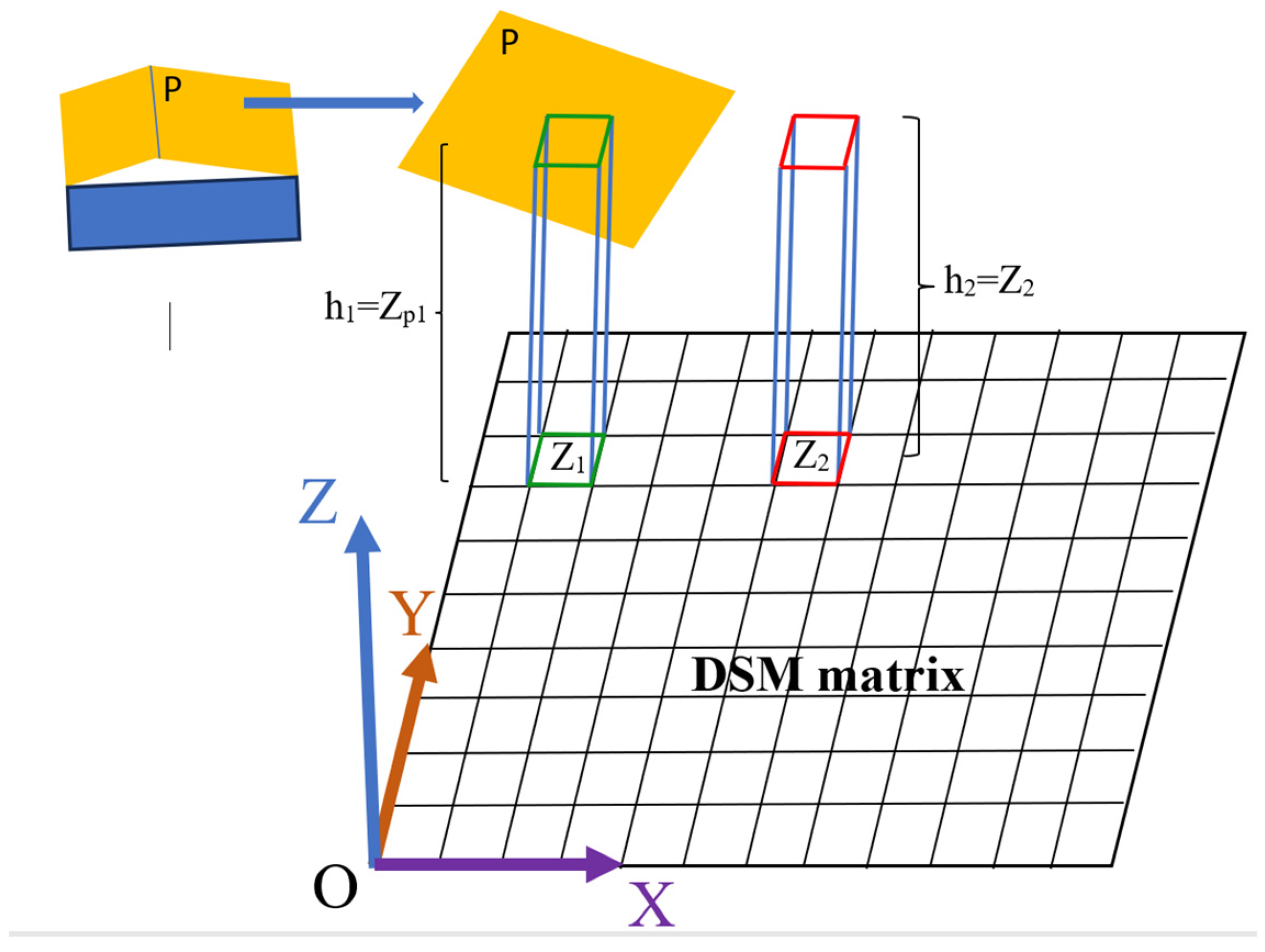
Once the roof planes are detected, the building DSM pixel values are recalculated (adjusted) according to the plane equation which they belong to. In the last step, considering the ground level, each pixel in the adjusted building DSM forms a rectangular parallelepiped, where its height equals the subtraction of the ground level value from the pixel value, and the base area equals the square of pixel length which was calculated in Section 3.1. In Figure 7, the pixel of the green boundary illustrates the calculation approach. Finally, the summation of all rectangular parallelepipeds formed by building body pixels will produce the building volume.
In this context, to obtain an accurate building volume, three additional rules will be applied as follows:
  • Eliminating all building DSM pixels located outside the building boundary polygon, which was calculated in Section 3.3.
  • For building boundary pixels located on the boundary polygon, only the parts situated inside that polygon will be considered.
  • Pixels belonging to the building body and having values smaller than a given threshold will be neglected. This threshold is related to the level height i.e., the threshold will equal ground level + l e v e l   h e i g h t 2 . Indeed, this kind of pixels can be in connection to the building boundary, and they may represent a confusion noise. That is why they are kept at the classification stage.
One building may consist of several parts where the number of levels for each part is different from other parts. In fact, the building roof segmentation allows the recognition of the number of levels for different roof patches. If two neighboring patches have the same number of levels, they can be merged. This operation helps calculate a new matrix named different level building map.
If we intend to calculate the building volume regardless the number of levels, the second approach shown in Figure 4 can be applied. According to Figure 4 (blue and orange arrows), it is similar to the first approach for building volume calculation, except that the building roof planes will not be detected and the building DSM pixel values will not be adjusted. To calculate the building volume, the building DSM calculated in Section 3.2 will be used as the input. By considering the ground level, each pixel in the building DSM forms a rectangular parallelepiped, where its height equals the subtraction of the ground level value from the pixel value, and the base area equals the square of pixel length which was calculated in Section 3.1. In Figure 7, the pixel of the red boundary illustrates the calculation approach. Finally, the summation of all rectangular parallelepipeds formed by building body pixels will produce the building volume.
Concerning the accuracy of the building volume calculated from the LiDAR point cloud, it is supposed that the building geometrical form is cubic, and the cube side length equals L, where the building volume V = L 3 . Similar to the building area accuracy calculation, three errors are envisaged: error caused by the point density, error due to the accuracy of LiDAR points, and error due to LiDAR data classification accuracy.
d V = 9 × V 4 3 × d L d 2 + d L a 2 + V × C E 2
To understand Equation 3 more, let T M D = 0.25 m , d L a = ∓ 0.15 m , A r = 500 m 3 , C E = 3 % , it can then be found that d L d = 0.5 × 0.25 = ± 0.125 m and d V = ± 36.5 m 3 .

4. Results and Discussion

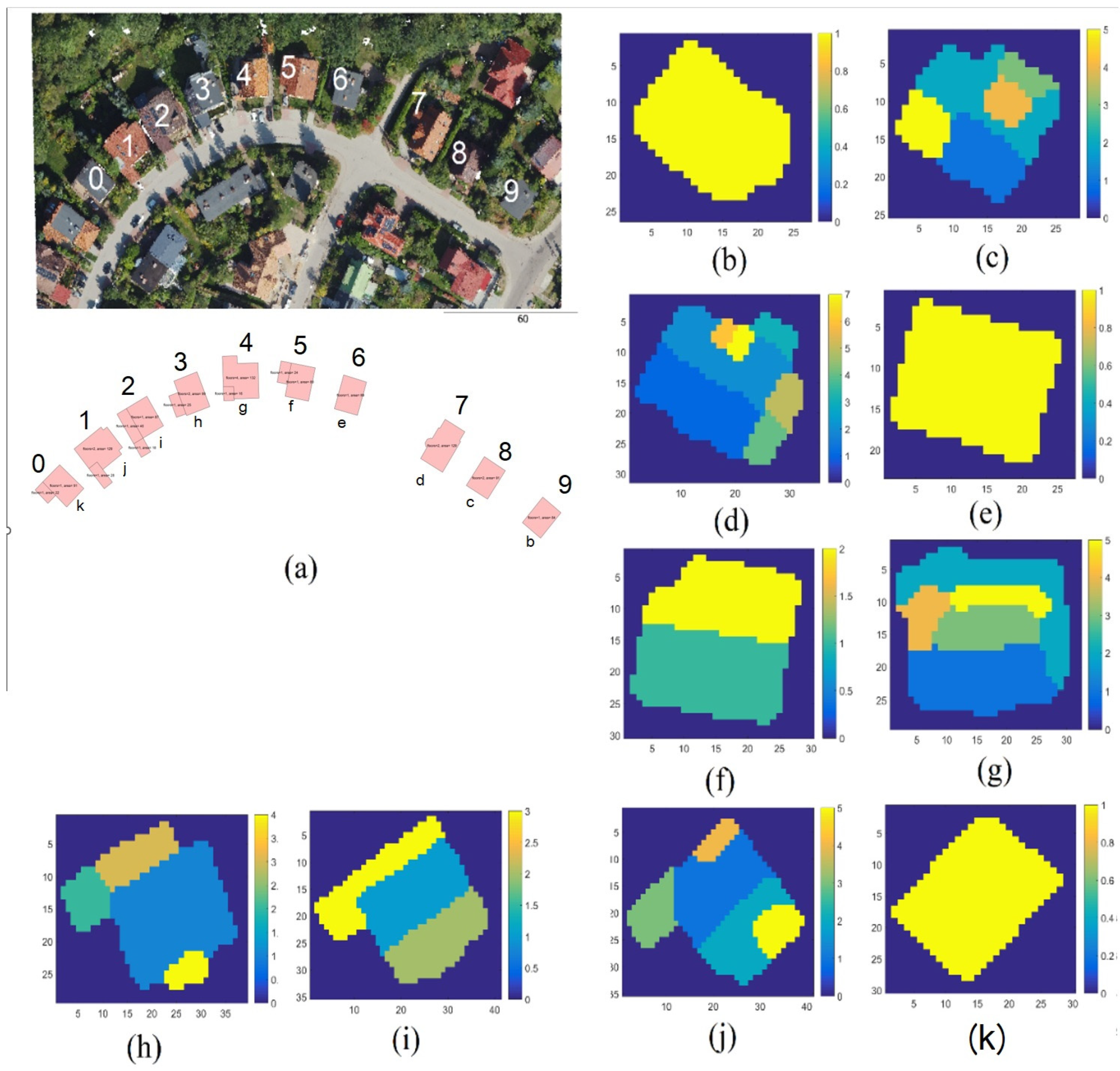
Figure 8 shows the visualization of the study site point cloud using Red, Green, and Blue (RGB) colors in addition to the target building plans. Ten target buildings are enumerated from 0 to 9 in the study area. Also, the same figure illustrates the results of building roof point cloud segmentation. These shown results will be used to calculate the building volumes using the first and second proposed approaches presented in Figure 4.
Table 2 and Table 3 show the obtained results for buildings numbers 0 to 6 in Figure 8. The underhung reference data are measured directly from architectural building plans. The footprint reference data are measured by direct digitizing the point clouds. From Table 2, it can be noted that obtained building footprint areas are accurate enough regarding the reference’s values. Also, the great differences between the footprint and the underhung areas can be explained by the fact that the LiDAR data was measured from above, and then all underhung parts are considered for area calculating. At this stage, it is important to note that the area errors are considerable because the point cloud has a sparse point density (4 point/m2) and the point cloud planimetric accuracy is about ± 0.15 m, in addition to the classification uncertainty of 3%. These factors also affect the volume accuracy shown in Table 3. Of course, to improve the accuracy of the obtained area and volume results, more accurate and dense LiDAR data should be used.
As underhung building areas cannot be measured from the LiDAR building point clouds, the building intensity indices are estimated using the building footprint areas (Table 2) where the results are rounded to the nearest ten centimeters. It can be noted that despite the considerable size differences between the underhung and footprint areas, some intensity index values match the reference values, and others increase slightly (about 0.1 more than the reference value). However, if the allowed overhung parts percentage is given as input, then the LiDAR building point cloud can provide an accurate value of the intensity index.
Regarding the building volume results presented in Table 3, negligible difference can be noted between the volume values obtained by the two suggested approaches. Indeed, fitting the mean plane equation will not be able to reduce the influence of LiDAR point errors. Nevertheless, the application of the extended RANSAC algorithm to segment the building roofs will be essential to calculate one building MLA. Actually, the number of building levels can be determined accurately for each roof patch, and the noisy points will be adjusted. Moreover, to calculate the Volume Relative Accuracy (VRA), Volume 2 of buildings is used. In fact, the high value of VRA may be explained by the low point density and accuracy. To improve the volume accuracy, the LiDAR point density and accuracy should be improved as well as the classification accuracy. Finally, the 3D building Intensity Index (3D II) is calculated two times using both building volume values: Volume 1 and Volume 2. It can be noted that both results are practically identical because the building volume values obtained by the two proposed approached are very similar.
Volume 1 is calculated according to the first suggested approach, while Volume 2 is calculated according to the second suggested approach (see Figure 4); VRA is the Volume Relative Accuracy; 3D II is the 3D building Intensity Index.
As conclusion, the calculated 3D indicators correlate with the classically calculated indicators and with the point-based indicators using two methods.

5. Conclusion

The presented research shows that in the absence of reference data, e.g., BIM data, cadaster, and having data from remote measurements, we still can calculate the development intensity indicators. Simplicity of the calculation, based on remote sensing measurements, can replace cumbersome classic measurements.
The calculated 3D building intensity indexes show a high correlation with classical indices calculated from 2D data. This result indicates the possibilities of using 3D indicators, as they more accurately reflect the built-up space. The 3D approach should be used when calculating other suggested indicators related to e.g., insolation of buildings, and sky visibility.
When the LiDAR data is used to calculate the intensity indicators, the calculation of building area directly from the LiDAR point cloud provides more accurate results than using the building DSM. On the other hand, using the DSM matrixial representation of the building point cloud is essential to calculate the building volume because of the irregular distribution of LiDAR points covering the facades. However, the accuracy of computed building area, volume, and other indicators depends on the LiDAR point cloud density and accuracy. Also, the accuracy of building class extraction from the scanned scene plays a major role in the calculation.
In future research, other building indicators such as footprint perimeter, ratio of building height to footprint area, wall areas, envelope area, and orientation will be investigated. Furthermore, other Laser scanning data acquisition techniques such as UAV scanning and terrestrial mobile scanning will also be assessed.

Author Contributions

Conceptualization, TK.F., L.E., S.J, and G.Z.; methodology, TK.F., L.E.; software, TK.F.; validation, TK.F., formal analysis, TK.F.; resources, L.E., data curation, TK.F., L.E.; writing—original draft preparation, TF.F., E.L.; writing—review and editing, G.Z., S.J.; visualization, TK.F., L.E.; All authors have read and agreed to the published version of the manuscript.”

Funding

Not funding

Data Availability Statement

The publication uses LAS measurement data obtained from an open Polish portal run by the Central Office of Geodesy and Cartography and data from Spatial Information Systems of Olsztyn.

Acknowledgments

Acknowledgments: We would like to thank the Central Office of Geodesy and Cartography (GUGiK) in Poland for providing Lidar measurement data and for making data from 3D portal available.

Conflicts of Interest

No conflict of interest.

References

  1. Huang, L.; Wu, J.; Yan, L. Defining and Measuring Urban Sustainability: A Review of Indicators. Landscape Ecol 2015, 30, 1175–1193. [Google Scholar] [CrossRef]
  2. Pira, M. A Novel Taxonomy of Smart Sustainable City Indicators. Humanit Soc Sci Commun 2021, 8, 197. [Google Scholar] [CrossRef]
  3. Angelakoglou, K.; Nikolopoulos, N.; Giourka, P.; Svensson, I.-L.; Tsarchopoulos, P.; Tryferidis, A.; Tzovaras, D. A Methodological Framework for the Selection of Key Performance Indicators to Assess Smart City Solutions. Smart Cities 2019, 2, 269–306. [Google Scholar] [CrossRef]
  4. Olewiler, N. Environmental Sustainability for Urban Areas: The Role of Natural Capital Indicators. Cities 2006, 23, 184–195. [Google Scholar] [CrossRef]
  5. Nassauer, J.I.; Wu, J.G.; Xiang, W.-N. Actionable Urban Ecology in China and the World: Integrating Ecology and Planning for Sustainable Cities. Landscape and Urban Planning 2014, 125, 207–208. [Google Scholar] [CrossRef]
  6. Jorge-Ortiz, A.; Braulio-Gonzalo, M.; Bovea, M.D. Assessing Urban Sustainability: A Proposal for Indicators, Metrics and Scoring—a Case Study in Colombia. Environ Dev Sustain 2023, 25, 11789–11822. [Google Scholar] [CrossRef]
  7. Garcia, C.; López-Jiménez, P.A.; Sánchez-Romero, F.-J.; Pérez-Sánchez, M. Assessing Water Urban Systems to the Compliance of SDGs through Sustainability Indicators. Implementation in the Valencian Community. Sustainable Cities and Society 2023, 96, 104704. [Google Scholar] [CrossRef]
  8. Gavaldà, O.; Gibbs, C.; Eicker, U. A Review of Current Evaluation Urban Sustainability Indicator Frameworks and a Proposal for Improvement. Sustainability 2023, 15, 15425. [Google Scholar] [CrossRef]
  9. Geoff Boeing, PhD Carl Higgs, MPH Shiqin Liu, MS Prof Billie Giles-Corti, PhD Prof James F Sallis, PhD Prof Ester Cerin, PhD et . Using open data and open-source software to develop spatial indicators of urban design and transport features for achieving healthy and sustainable cities. URBAN DESIGN, TRANSPORT, AND HEALTH| VOLUME 10, ISSUE 6, E907-E918. [CrossRef]
  10. Tan, Shukui, et al. "Regional differences and dynamic evolution of urban land green use efficiency within the Yangtze River Delta, China." Land Use Policy 2021 : 105449.
  11. Pozoukidou, G.; Angelidou, M. Urban Planning in the 15-Minute City: Revisited under Sustainable and Smart City Developments until 2030. Smart Cities 2022, 5, 1356–1375. [Google Scholar] [CrossRef]
  12. Krüger, A.; Kolbe, T.H. BUILDING ANALYSIS FOR URBAN ENERGY PLANNING USING KEY INDICATORS ON VIRTUAL 3D CITY MODELS – THE ENERGY ATLAS OF BERLIN. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2012, XXXIX-B2, 145–150. [Google Scholar] [CrossRef]
  13. Liu, B.; Guo, X.; Jiang, J. How Urban Morphology Relates to the Urban Heat Island Effect: A Multi-Indicator Study. Sustainability 2023, 15, 10787. [Google Scholar] [CrossRef]
  14. Hu, Y.; Dai, Z.; Guldmann, J.-M. Modeling the Impact of 2D/3D Urban Indicators on the Urban Heat Island over Different Seasons: A Boosted Regression Tree Approach. Journal of Environmental Management 2020, 266, 110424. [Google Scholar] [CrossRef] [PubMed]
  15. Biljecki, F.; Stoter, J.; Ledoux, H.; Zlatanova, S.; Çöltekin, A. Applications of 3D City Models: State of the Art Review. ISPRS Int. J. Geo-Inf. 2015, 4, 2842-2889. [Google Scholar] [CrossRef]
  16. Bruno Willenborg, Maximilian Sindram et al. Applications of 3D City Models for a Better Understanding of the Built Environment. Geotechnologies and the Environment, 19 https://doi.org/10.1007/978-3-319-52522-8_9 ,in Understanding of the Built Environment. In: Behnisch, M., Meinel, G. (eds) Trends in Spatial Analysis and Modelling. Geotechnologies and the Environment, vol 19. Springer, Cham. [CrossRef]
  17. Yuan E. Kang; Visualization analysis of urban planning assistant decision network 3D system based on intelligent computing Heliyon, 10, 11, 6 2024 Volume 10, Issue 11, 15 June 2024, e31321 https://www.sciencedirect.com/science/article/pii/S2405844024073523?via%3Dihub.
  18. M. Brasebin1a, J. Perret1b, S. Mustière1c and C. Weber. Measuring the impact of 3D data geometric modeling on spatial analysis: Illustration with Skyview factor. 2012 Usage, Usability, and Utility of 3D City Models, 02001. Owned by the authors, published by EDP Sciences, 2012. [CrossRef]
  19. Xiucheng Liang, Jiat Hwee Chang, Song Gao, Tianhong Zhao, Filip Biljecki, Evaluating human perception of building exteriors using street view imagery, Building and Environment, Volume 263, 2024, 111875. [CrossRef]
  20. Gui, S., and Qin, R., 2021. Automated LoD-2 model reconstruction from very-high-resolution satellite-derived digital surface model and orthophoto. ISPRS Journal of Photogrammetry and Remote Sensing, 181, 1–19. [CrossRef]
  21. Lewandowicz, E.; Tarsha Kurdi, F.; Gharineiat, Z. 3D LoD2 and LoD3 Modeling of Buildings with Ornamental Towers and Turrets Based on LiDAR Data. Remote Sens. 2022, 14, 4687. [Google Scholar] [CrossRef]
  22. Tarsha Kurdi, F.; Lewandowicz, E.; Gharineiat, Z.; Shan, J. Modeling Multi-Rotunda Buildings at LoD3 Level from LiDAR Data. Remote Sens. 2023, 15, 3324. [Google Scholar] [CrossRef]
  23. Tarsha Kurdi, F.; Gharineiat, Z.; Campbell, G.; Dey, E.K.; Awrangjeb, M. Full Series Algorithm of Automatic Building Extraction and Modelling from LiDAR Data. In Proceedings of the 2021 Digital Image Computing: Techniques and Applications (DICTA), Gold Coast, Australia, 29 November–1 December 2021; pp. 1–8. [Google Scholar]
  24. Peters, R., Dukai, B., Vitalis, S., van Liempt, J., & Stoter, J. (2022). Automated 3D Reconstruction of LoD2 and LoD1 Models for All 10 Million Buildings of the Netherlands. Photogrammetric Engineering and Remote Sensing, 88(3), 165-170. [CrossRef]
  25. Zhang, Z., et al., 2022. Vectorized rooftop area data for 90 cities in China. Scien-tific Data, 9 (1), 66. [CrossRef]
  26. Wang, X.; Luo, Y.P.; Jiang, T.; Gong, H.; Luo, S.; Zhang, X.W. A new classification method for LIDAR data based on unbalanced support vector machine. In Proceedings of the 2011 International Symposium on Image and Data Fusion, Tengchong, China, 9–11 August 2011; pp. 1–4. [Google Scholar] [CrossRef]
  27. Wen, C.; Yang, L.; Li, X.; Peng, L.; Chi, T. Directionally constrained fully convolutional neural network for airborne LiDAR point cloud classification. ISPRS Journal of Photogrammetry and Remote Sensing, 2020, vol. 162, pp. 50-62. [CrossRef]
  28. Maltezos, E.; Doulamis, A.; Doulamis, N.; Ioannidis, C. Building extraction from LiDAR data applying deep convolutional neural networks. IEEE Geoscience and Remote Sensing Letters, 2018, vol. 16, no. 1, pp. 155-159, 2018. [CrossRef]
  29. Yuan, J. Learning building extraction in aerial scenes with convolutional networks. IEEE transactions on pattern analysis and machine intelligence 2017. vol. 40, no. 11, pp. 2793-2798. [CrossRef]
  30. Kuras, A.; Brell, M.; Rizzi, J.; Burud, I. Hyperspectral and Lidar Data Applied to the Urban Land Cover Machine Learning and Neural-Network-Based Classification: A Review. Remote Sens. 2021, 13, 3393. [Google Scholar] [CrossRef]
  31. Zhou, L.; Geng, J.; Jiang, W. Joint Classification of Hyperspectral and LiDAR Data Based on Position-Channel Cooperative Attention Network. Remote Sens. 2022, 14, 3247. [Google Scholar] [CrossRef]
  32. Pang, H.E.; Biljecki, F. 3D building reconstruction from single street view images using deep learning. International Journal of Applied Earth Observation and Geoinformation, 2022, 112, 102859. [Google Scholar] [CrossRef]
  33. Xu, Y.; Stilla, U. Towards Building and Civil Infrastructure Reconstruction from Point Clouds: A Review on Data and KeyTechniques. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2857–2885. [Google Scholar] [CrossRef]
  34. Junling ZhuangGuanhong LiHang XuShow all 5 authorsRunjia Tian et all. TEXT-TO-CITY Controllable 3D Urban Block Generation with Latent Diffusion Model. Available from: https://www.researchgate.net/publication/380124047_TEXT-TO-ITY Controllable_3D_Urban_Block_Generation_with_Latent_Diffusion_Model [accessed Aug 14 2024].Proceedings of the 29th International Conference of the Association for Computer-Aided Architectural Design Research in Asia (CAADRIA) 2024, Volume 2, 169-178. © 2024 and published bythe Association for Computer-Aided Architectural Design Research in Asia (CAADRIA), Hong Kong. https://www.researchgate.net/publication/380124047_TEXT-TO-CITY Controllable_3D_Urban_Block_Generation_with_Latent_Diffusion_Model.
  35. Tarsha Kurdi, F.; Lewandowicz, E.; Shan, J. Gharineiat, Z.; 3D modeling and visualization of single tree Lidar point cloud using matrixial form. 2024. IEEE, Journal of selected topics in applied earth observations and remote sensing, VOL. 17, 2024.
  36. Tarsha Kurdi, F.; Amakhchan, W.; Gharineiat, Z. Random Forest machine learning technique for automatic vegetation detection and modeling in LiDAR data. Int. J. Environ. Sci. Nat. Resour. 2021, 28, 556234. [Google Scholar]
  37. Tarsha Kurdi, F.; Lewandowicz, E.; Gharineiat, Z.; Shan, J. Accurate Calculation of Upper Biomass Volume of Single Trees Using Matrixial Representation of LiDAR Data. Remote Sens. 2024, 16, 2220. [Google Scholar] [CrossRef]
  38. Dong L, Du H, Han N, Li X, Zhu D, Mao F, Zhang M, Zheng J, Liu H, Huang Z, et al. Application of Convolutional Neural Network on Lei Bamboo Above-Ground-Biomass (AGB) Estimation Using Worldview-2. Remote Sensing. 2020; 12(6):958. [CrossRef]
  39. Zhou, Lv, Xuejian Li, Bo Zhang, Jie Xuan, Yulin Gong, Cheng Tan, Huaguo Huang, and Huaqiang Du. 2022. "Estimating 3D Green Volume and Aboveground Biomass of Urban Forest Trees by UAV-Lidar" Remote Sensing 14, no. 20: 5211. [CrossRef]
  40. Lucchi, A. Buda, Urban green rating systems: Insights for balancing sustainable principles and heritage conservation for neighbourhood and cities renovation planning, Renewable and Sustainable Energy Reviews, Vol 161, 2022, 112324, ISSN 1364-0321. [CrossRef]
  41. Richa, J.P.; Deschaud, J.-E.; Goulette, F.; Dalmasso, N. AdaSplats: Adaptive Splatting of Point Clouds for Accurate 3D Modeling and Real-Time High-Fidelity LiDAR Simulation. Remote Sens. 2022, 14, 6262. [Google Scholar] [CrossRef]
  42. Biljecki, F.; Lim, J.; Crawford, J.; Moraru, D.; Tauscher, H.; Konde, A.; Adouane, K.; Lawrence, S.; Janssen, P.; Stouffs, R. Extending CityGML for IFC-sourced 3d city models. Autom. Constr. 2021, 121, 103440. [Google Scholar] [CrossRef]
  43. Filip Biljecki, Yoong Shin Chow, Global Building Morphology Indicators, Computers, Environment and Urban Systems, 2022, Volume 95. [CrossRef]
  44. Pira, M. A Novel Taxonomy of Smart Sustainable City Indicators. Humanit Soc Sci Commun 2021, 8, 197. [Google Scholar] [CrossRef]
  45. Bibri, Simon Elias. "A novel model for data-driven smart sustainable cities of the future: the institutional transformations required for balancing and advancing the three goals of sustainability." Energy Informatics 4.1 (2021): 4.
  46. Chen, Jinjin, Chuanbin Zhou, and Feng Li. "Quantifying the green view indicator for assessing urban greening quality: An analysis based on Internet-crawling street view data." Ecological Indicators 113 (2020): 106192.
  47. USTAWA z dnia 27 marca 2003 r. o planowaniu i zagospodarowaniu przestrzennym. Tekst jednolity z 2023 r. t.j. Dz. U. z 2023 r. poz. 977, 1506, 1597, 1688, 1890, 2029, 2739. (ACT of 27 March 2003 on Spatial Planning and Development. Consolidated text of 2023, i.e. Journal of Laws of 2023, items 977, 1506, 1597, 1688, 1890, 2029, 2739.).
  48. ROZPORZĄDZENIE MINISTRA ROZWOJU I TECHNOLOGII z dnia 15 lipca 2024 r. w sprawie sposobu ustalania wymagań dotyczących nowej zabudowy i zagospodarowania terenu w przypadku braku miejscowego planu zagospodarowania przestrzennego. (REGULATION OF THE MINISTER OF DEVELOPMENT AND TECHNOLOGY of 15 July 2024 on the method of determining the requirements for new development and land development in the absence of a local spatial development plan.).
  49. Sargent, I.; Holland, D.; Harding, J. The Building Blocks of User-Focused 3D City Models. ISPRS Int. J. Geo-Inf. 2015, 4, 2890–2904. [Google Scholar] [CrossRef]
  50. Anthony Jjumba, Suzana Dragićević. Sppatial indices for measuring three-dimensional patterns in a voxel-based space. Journal of Geographical Systems, 18, 3, 7 2016. [CrossRef]
  51. McTegg, S.J., Tarsha Kurdi, F., Simmons, S., Gharineiat, Z. 2022. Comparative approach of unmanned aerial vehicle restrictions in controlled airspaces. Remote Sens. 2022, 14, 822. [CrossRef]
  52. Tarsha Kurdi, F., Awrangjeb, M., Munir, N. 2021. Automatic filtering and 2D modelling of LiDAR building point cloud. Transactions in GIS Journal, Vol 25 n° 1 (February 2021) . - pp 164 – 188. [CrossRef]
  53. Tarsha Kurdi, F., Landes, T., Grussenmeyer, P., Smigiel, E. 2006. New approach for automatic detection of buildings in airborne laser scanner data using first echo only. ISPRS Comm. III Symposium, Photogrammetric Computer Vision, Bonn, Sept. 20-22, Germany. International Archives of Photogrammetry and Remote Sensing and Spatial Information Sciences, ISSN: 1682-1750, Vol. XXXVI, Part 3, pp. 25-30.
  54. Dey, E.K., Awrangjeb, M., Tarsha Kurdi, F., Stantic, B. 2021. Building boundary point extraction from LiDAR point cloud data. 20201 Digital Image Computing: Techniques and Applications (DICTA), pp. 1-8, doi:10.1109/DICTA52665.2021.9647371 , Gold Coast, Australia. [CrossRef]
  55. Tarsha Kurdi, F., Landes, T., Grussenmeyer, P. 2008. Extended RANSAC algorithm for automatic detection of building roof planes from Lidar data. The Photogrammetric Journal of Finland. Vol. 21, n°1, 2008, pp.97-109.
Preprints 121160 g001
Figure 1. Illustration of independent indicators at the building level [43].
Figure 1. Illustration of independent indicators at the building level [43].
Preprints 121160 g001
Preprints 121160 g002
Figure 2. Selected buildings for research; (a) Orthophotomap, (b) Cadastral data, (c-d) LIDAR data.
Figure 2. Selected buildings for research; (a) Orthophotomap, (b) Cadastral data, (c-d) LIDAR data.
Preprints 121160 g002
Preprints 121160 g003
Figure 3. Cadastral data; (a) graphical and attribute data, (b) data for the calculation of plot building intensity indicators, (c) visualization of the calculated indicators.
Figure 3. Cadastral data; (a) graphical and attribute data, (b) data for the calculation of plot building intensity indicators, (c) visualization of the calculated indicators.
Preprints 121160 g003
Preprints 121160 g004
Figure 4. Two workflows of building volume calculation using LiDAR point cloud; Blue arrows belong to both approaches; the orange arrow and green arrows are respectively for the first and second approach.
Figure 4. Two workflows of building volume calculation using LiDAR point cloud; Blue arrows belong to both approaches; the orange arrow and green arrows are respectively for the first and second approach.
Preprints 121160 g004
Preprints 121160 g005
Figure 5. Building DSM calculation; (a) Superimposition of LiDAR point cloud on the 2D grid; Blue circles represent LiDAR points; (b) Black pixels represent building body, the numbers represent the number of LiDAR points inside the pixel; the yellow pixel is example of empty pixel inside building body, while the green pixel is an empty pixel outside the building body.
Figure 5. Building DSM calculation; (a) Superimposition of LiDAR point cloud on the 2D grid; Blue circles represent LiDAR points; (b) Black pixels represent building body, the numbers represent the number of LiDAR points inside the pixel; the yellow pixel is example of empty pixel inside building body, while the green pixel is an empty pixel outside the building body.
Preprints 121160 g005
Preprints 121160 g006
Figure 6. Building DSM; (a) and (b) are for Building 0; (c) and (d) are for Building 1; (a) and (c) Without filling empty pixels inside the building body; (b) and (d) With filling empty pixels inside the building body; Red arrow points extra pixels outside the building body and adjacent to the building boundaries are added to building area.
Figure 6. Building DSM; (a) and (b) are for Building 0; (c) and (d) are for Building 1; (a) and (c) Without filling empty pixels inside the building body; (b) and (d) With filling empty pixels inside the building body; Red arrow points extra pixels outside the building body and adjacent to the building boundaries are added to building area.
Preprints 121160 g006
Preprints 121160 g007
Figure 7. Calculation of roof height for two building DSM pixels using two proposed approaches; Z1 and Z2 are DSM pixel values for green and red pixels; h1 is roof height calculated from roof plane equation; h2 is roof height considered directly from DSM; P is a roof plane.
Figure 7. Calculation of roof height for two building DSM pixels using two proposed approaches; Z1 and Z2 are DSM pixel values for green and red pixels; h1 is roof height calculated from roof plane equation; h2 is roof height considered directly from DSM; P is a roof plane.
Preprints 121160 g007
Preprints 121160 g008
Figure 8. Results of building roof segmentation; (a) LiDAR point cloud visualization and buildings are enumerated, and enumerated building plans; (b) to (k) visualization of roof segmentation results for building number 9 to zero (in Figure 8 a, Figure 3).
Figure 8. Results of building roof segmentation; (a) LiDAR point cloud visualization and buildings are enumerated, and enumerated building plans; (b) to (k) visualization of roof segmentation results for building number 9 to zero (in Figure 8 a, Figure 3).
Preprints 121160 g008
Table 1. Areas of Buildings 0 and 1 at different DSM resolutions for two cases with and without filling empty pixels inside the building body.
Table 1. Areas of Buildings 0 and 1 at different DSM resolutions for two cases with and without filling empty pixels inside the building body.
Number
of points		 DSM
Pixel size (m)		 Number of building pixels containing LiDAR points Number of empty building pixels Area without filling
empty pixels (m2)		 Area with filling
empty pixels (m2)		 Reference
area (m2)
Building 0 2094 0.10 1977 12102 19.77 140.79 113
0.25 1470 815 91.88 142.81
0.40 861 49 137.76 145.6
0.60 400 15 144 149.4
Building 1 3272 0.10 3055 20252 30.55 233.07 157
0.25 2320 1431 145 234.44
0.40 1334 150 213.38 237.44
0.60 620 57 223.2 243.72
Table 2. Calculation of building areas; Building numeration are taken from Figure 3 and Figure 8.
Table 2. Calculation of building areas; Building numeration are taken from Figure 3 and Figure 8.
Building number Footprint Area (m2) Footprint ref Area (m2) Underhung ref area (m2) Footprint MLA (m2) Underhung MLA ref (m2) Area error (m2) Parcel area (m2) II % II Ref %
0 131.35 129.99 113 131.35 113 14.28 553 0.2 0.2
1 205.26 200.53 157 339.52 286 20.31 554 0.6 0.5
2 218.71 221.97 145 218.71 145 20.52 548 0.4 0.3
3 163.08 162.62 124 263.09 223 12.86 541 0.5 0.4
4 196.78 193.67 148 602.31 544 23.32 483 1.2 1.1
5 175.1 171.51 112 175.1 112 19.91 491 0.4 0.2
6 112.6 108.52 89 112.60 89 8.61 584 0.2 0.2
Ref: Reference; MLA: Multi Levels Area; II: building Intensity Index.
Table 3. Calculation of building volumes and 3D building Intensity Index.
Table 3. Calculation of building volumes and 3D building Intensity Index.
Building
number		 Volume 1 (m3) Volume 2 (m3) Volume
Error (m3)		 VRA (%) 3D II 1 3D II 2
0 860.56 860.32 58.95 6.9 0.3 0.3
1 1454.25 1454.35 86.93 6.0 0.5 0.5
2 1371.75 1371.25 83.21 6.1 0.5 0.5
3 914.82 914.67 61.65 6.7 0.3 0.3
4 1621.71 1623.82 94.36 5.8 0.7 0.7
5 1423.81 1429.36 85.56 6.0 0.6 0.6
6 619.46 618.01 46.45 7.5 0.2 0.2
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Extracting and Evaluating China’s Urban Entities From 2000 to 2020 Based on Snpp-Viirs-Like Data

Neel Chaminda Withanage

et al.

,

2023

Improve Building Façades in Open Lidar Data Using Ground Imagery

Shenman Zhang

et al.

,

2018

A Simple Yet Effective Approach of Building Footprint Extraction in Indonesia

Danang Budi Susetyo

et al.

,

2020

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated