Prerpints.org logo
Preprint
Article

“Quantum Jumps” as Bifurcations in Non-Linear Soliton-Type Models

This version is not peer-reviewed.

Submitted:

15 October 2024

Posted:

17 October 2024

You are already at the latest version

Abstract
Non-linear superposition of solitons provide almost linear branches as well as ``quantum jumps" to stable particle-like cores. Can the quest for possible non--linearity of quantum mechanics and the ``collapse paradox" of the wave function in (non-)linear quantum mechanics be resolved by transitions between different quasi-linear branches of the corresponding Whitney surface?
Keywords: 
Subject: 
Physical Sciences  -   Theoretical Physics

1. Introduction

In classical mechanics, Hook`s law for the spring is linear only for small elongations. Unharmonic oscillations or even a branching into “catastrophic" deformations [1] may occur. On the other hand, quantum mechanics (QM) is built upon the canonical Schrödinger or Dirac equation and the strict postulate of linear superposition principle. Nevertheless, Yang-Mills theory or Einstein’s gravity are based on nonlinear classical equations. Even in Maxwell’s theory of electromagnetism, effectively non-linear theories a la Born-Infeld or Heisenberg-Euler are induced by field quantization. Lateron, Heisenberg proposed a fundamental nonlinear spinor equation, cf. [23], as an alternative to QCD with its nonlinearly coupled gauge fields.
De Broglie, the founder of matter waves, regarded the ψ of QM as “pilot waves” for the universal wave function u govern by a possible nonlinear dynamics [9]. Already in 1919, Einstein has contemplated in a letter to Lorentz the need for nonlinear differential equations, cf. Colins et al. [8], p. 21. In continuing our previous outline [22] of nonlinear QM, one would regard point-like particles as represented by “quantum solitons” [15] whose regular density centers are guided by an almost linear tail in a quasi monistic concept of matter waves (coined ϕ in the scalar case).
According to Penrose [33], the Schrödinger equation determines an unitary evolution of the wave function, but NOT the reduction to one state during measurements.
Similarly, Bjorken [3], hold the view that a “small amount of ...nonlinearity” in the foundamental equations ...“ may effectively eliminate paradoxes such as the “collapse of the wave packet” during measurements, cf. Mielnik [28,29]. Soliton-like localized quasi-stable solutions would be ideal candidates for realizing De Broglies program of Nonlinear Wave Mechanics (NLWM), cf. Colins et al. [8] for a recent assessment. Spreading due to dispersion needs to be compensated by non-linear effects ensuring stability of solitons representing particles. Thus spontaneous transitions between different quasi linear branches of the Whitney surface would provide an “inner fusion of the statistical and causal laws” [5]. Such nonlinear corrections avoiding the “spooky action at a distance” according to the critizism of Einstein on standard QM, were tested, to some extent, by Weinberg [37].
In our relativistic example below, solitons are rather stable entities, to some extent, behaving effectively like colliding particles, i.e. after leaving the interaction region, where they may deform due to a temporally inelastic relativistic interference. Due to an inherent self-focusing mechanism, here regarded as entanglement, they eventually return to their original shapes and velocities [23].
“Quantum jumps” [5] or the “spontaneous” collapse of the wave function ψ should arise from a irreversable transition between different almost linear branches in the projection of a continous Whitney surface (modelling the nonlinear Lagranging) [1]. For example, a “swallow tail” catastrophe, cf. Mielke [26], Figure 3, exhibits both an almost linear branch and a region of nonlinear dynamics. This rather “holistic” wave approach a la Penrose [34], p. 187, would be induced via a (physically hidden?) control parameter of the corresponding Whitney surface.

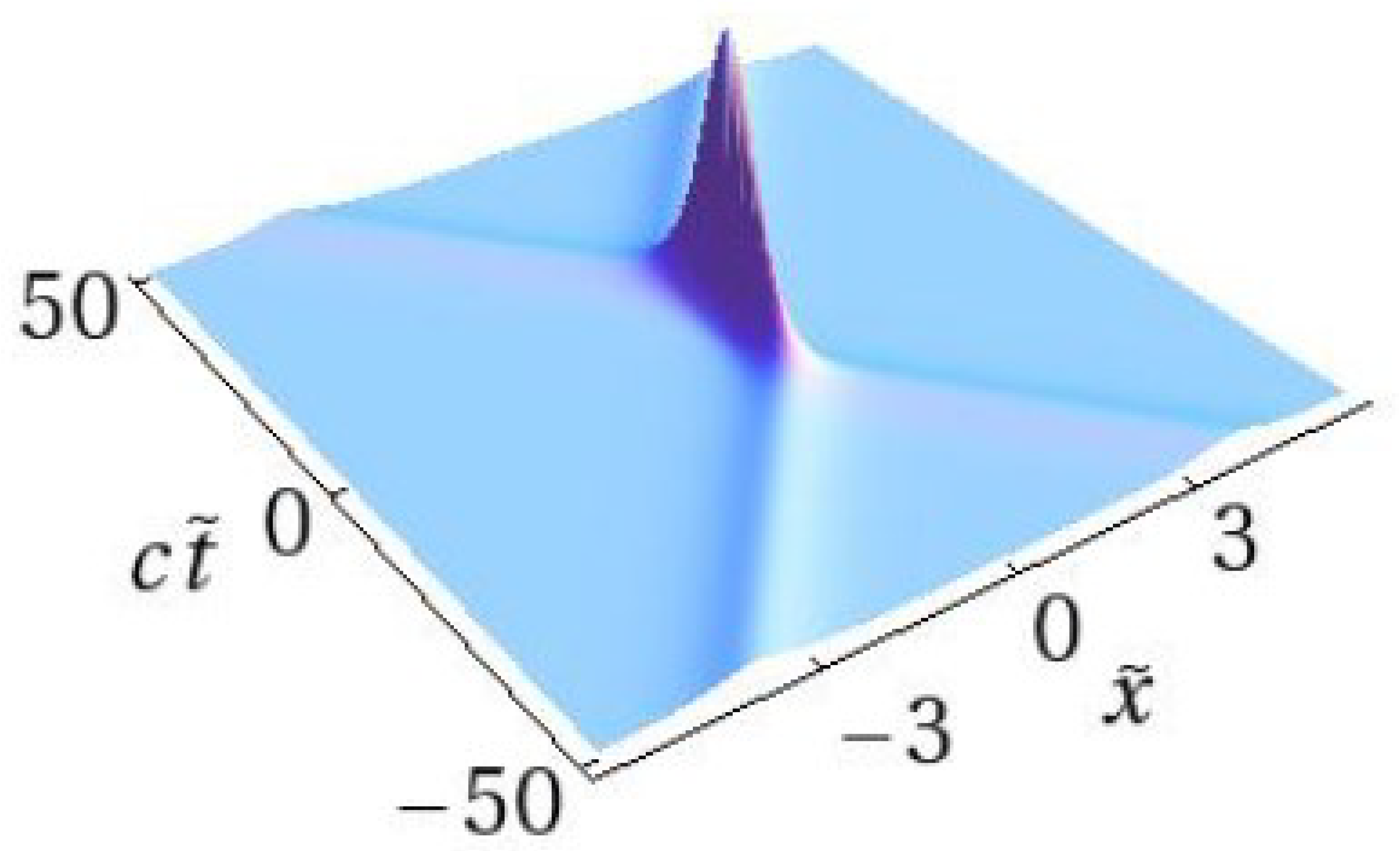
2. Soliton Collisions with Interference

As an instructive example, let us depart from the nonlinear Klein-Gordon (NLKG) equation
□ ϕ = ∂ U ϕ ∂ ϕ ,
where □ : = ∇ • ∇ − ∂ 2 / c 2 ∂ t 2 is the hyperbolic Lorentz-invariant wave operator of d’Alembert.
In quantum chromodynamics (QCD), e.g. hypothetical axions with inertial mass m are self-interacting via the effective [26] periodic potential
U a ( ϕ ) = m 4 λ 1 − cos λ m ϕ ≃ U LE ( ϕ ) − λ 4 ! ϕ 4 − ⋯
which, at higher order of | ϕ | , deviates from the Lane-Emden (LE) potential U LE ( ϕ ) = m 2 ϕ 2 1 − χ ϕ 4 / 2 and, effectively, alters the mass of a propagating particle.
In two dimensions (2D), the sine-Gordon equation results as a well known example. The first term of the Taylor series of the potential (2) corresponds to the mass in the relativistic invariant Klein-Gordon equation; the next one would give rise to the famous ϕ 4 -theory. Combining the first and third term, it can be reckonized as the modified ϕ 6 -theory of LE [14].
For constructing multi-solitons, the well-established Bäcklund transformation (BT) [18,20], can be employed, for which solitons in an optical lattice have been studied [19].
When employing dimensionless light-cone coordinates ξ : = 1 2 ( x ˜ + c t ˜ ) and η : = 1 2 ( x ˜ − c t ˜ ) , thereby absorbing the coupling constants, the sine-Gordon (sG) equation acquires the form
θ ξ η = sin θ
and is CPT invariant. In a moving frame, with γ : = 1 / 1 − v 2 / c 2 as Lorentz factor, it has the exact kink solution
θ = 4 C arctan exp γ x ˜ − v t ˜ .
with charge operator C = 1 , or C = − 1 for an anti-kink. In order to avoid step functions, let us monitor here its spatial derivative
θ x ˜ = 2 γ C s e c h γ x ˜ − v t ˜
which turns out to be localized and square-integrable, as required for the statistical interpretation a la Max Born. In contradistinction, we regard this as an example of “Anschaulichkeit, the possibility of seeing the process in space”, cf. [5]. Thus its absolute value is a template which will facilitate a subsequent comparison with the scattering behavior of solitons or lumps. In nonlinear time evolutions, a topological space of square integrable functions can thus be maintained in NLQM, cf. Natterman [30].
More concretely, Bianchi’s permutability theorem of BTs provides a nonlinear superposition
tan ( θ 3 − θ 0 ) / 4 = B tan ( θ 1 − θ 2 ) / 4 ,
where B < 1 is a common or `average’ relativistic velocity. Still the superposed solitons appear to remain, to some extent, “entangled” (in German verschränkt according to Schrödinger) at spatial infinity, due to the long-range effect of non-linearity.
The CPT invariance of our relativistic KG equation allows us to distinguish solitons from anti-solitons: In the case of the collision of two kinks (instead of a collision of a kink and its CP odd anti-kink, as in Ref. [6]) the trivial seed solution θ 0 = 0 leads to the exact solution
θ k k = 4 arctan K ( ζ 1 , ζ 2 ) .
When C ˜ = C exp ( γ 1 δ 1 + γ 2 δ 2 ) and B = exp ( γ 1 δ 1 ) , the kinetic factor
K ( ζ 1 , ζ 2 ) : = B exp ( ζ 1 ) + C ˜ exp ( ζ 2 ) exp ( ζ 1 + ζ 2 ) − C = exp ( ζ 1 + γ 1 δ 1 ) + C exp ( ζ 2 + γ 2 δ 2 ) exp ( ζ 1 + ζ 2 ) − C ≃ exp ( ζ 1 + γ 1 δ 1 ) + C exp ( ζ 2 + γ 2 δ 2 )
depends on the initial velocities and the inverse Lorentz transformations ζ i : = γ i ( x ˜ + v i t ˜ ) characterized by the opposite sign of the relative velocity occuring in the individual phases δ i . Observe the occurence of a non-linear “soliton resonance” or interference pattern (Figure 1) during collision, when monitored via the derivative of the kinks.
Qualitatively, it resembles De Broglie’s hypothesis of the double solution, where the interference would result from the pilot wave part of ψ . To some extent, such nonlinear QM realizes De Broglie’s original ideas via “pilot waves without pilot waves”, to use a Wheeler type phrase.
At large separations from the interaction region, cf. Figure 1, the solution (7) clearly decouples asymptotically into a (non-interacting) kink–kink or kink–antikink pair [7] distinguished by the sign C = ± 1 of the topological charge. The global stability of solitons has been established and analyzed by Kusmartsev [16] again via Whitney’s theory of bifurcations.
A generalization to (2+1) D has been attempted in Ref. [6], following [10]. Although thereby exact integrability has been lost, certain mappings from solitons to 3D lumps of the Lane-Emden type are instrumental, cf. Figure 2.

3. Interference Patter of Electrons

Claus Jönsson repeated in 1961 the double slit experiment of Thomas Young, however for electrons [13]. At that time it has been regarded as the most beautiful experiment of physics. More recently, for electrons with higher kinetic energy, the gradual built-up of an interference patter has been demonstrated in an double slit type experiment by Tonomura, cf. Figure 3 of Ref. [36]. It reveals both, the statistical behavior of (soliton-like?) electrons, as well as the particle-wave duality, to some extent resembling a more recent version of De Broglie’s “pilot wave” interpretation of quantum mechanics (QM).
Preprints 121382 g003
Figure 3. (Color online) Interference patter of electrons in a double slit type experiment, cf. Tonomura [36]. It is gradually built-up by 140 000 electrons, the corresponding matter waves “collapsing” onto the (scintilator) screen.
Figure 3. (Color online) Interference patter of electrons in a double slit type experiment, cf. Tonomura [36]. It is gradually built-up by 140 000 electrons, the corresponding matter waves “collapsing” onto the (scintilator) screen.
Preprints 121382 g003
However, in nonlinear models, soliton-like solutions exhibit a point particle behaviour only for their respective centers of mass, as well as interference patterns during collisions. The Heisenberg inequality or uncertainty relation in the Lieb form was analyzed in Ref. [38] but not the corresponding interference patterns. Like in Everett’s relative state interpretation of QM, “the world appears indeterministic ...but largely objective through quantum correlations (entanglement) “, cf. Lindgren [21].

4. Cosmic Bell Test?

Colliding solitons of our template behave like “entangled particle pairs”. Due to the nonlinearity, there occurs an overlap of their backward light cones. [4]). A cosmic Bell test [11] does “not rule out models with hidden variables in the overlap of past light cones ... or their overlap”. For soliton scattering, these are mimicized by the asymptotic tails of the exact solutions (7) for nonlinearly superposed solitons.
Moreover, their tails may affect the out-come of the (non-linear) particle wave duality and Wheeler’s delayed-choice Gedanken experiment, cf. Jacques et al. [12]. “Decoherence produces ... an effect that looks like collapse” cf. [2].
There are even speculations [31] that entanglement could be effected via Einstein–Rosen bridges or “wormholes” in space, cf. [25].

5. Discussion: “Collapse” of the Wave Function Triggered by Self-Gravity?

According to Penrose [33], a spontaneous collapse of the wave function could also be induced by the gravitational self-energy of the De Broglie matter wave of a particle. In a self-consistent approach this “departure from linearity” would resemble the (meta-stable) geons of Wheeler for electromagnetic fields or even the (mini-) Boson Stars of T.D. Lee arising in the gravitationally coupled Klein-Gordon equation, cf. [24]. The stability of these Boson Stars in a certain mass range is again assured for the lower branches in the projected Whitney surface [17] moniturizing their nonlinear dynamics. A coupling to higher order curvature invariants a la Kretschmer may even ensure a mass renormalization, cf. [32].

References

  1. V.I. Arnol’d: Catastrophe Theory, Third, revised and expanded edition (Springer, Berlin 1992).
  2. A. Aspect: “Closing the Door on Einstein and Bohr’s Quantum Debate, ” Physics 8 123 (16 December 2015).
  3. J. Bjorken: The Future of the Quantum Theory (Beam Line, Sommer/Fall 2000).
  4. Carl, H. Brans: “Bell’s theorem does not eliminate fully causal hidden variables,” Int. J. Theor. Phys. 27, 219 (1988).
  5. M. Born: “The Interpretation of Quantum Mechanics,” Max Born’s response to two articles in The British Journal for the Philosophy of Science by Erwin Schrödinger entitled "Are There Quantum Jumps?" (Part I and Part II). August and Noviember 1952, pages 95-106, received 29. 1. 1953.
  6. D. Castañeda Valle and E. W. Mielke: “Relativistic soliton collisions of axion type dark matter,” Phys. Lett. B 758, 93 (2016). [CrossRef]
  7. I. Christov and C.I. Christov: “Physical dynamics of quasi-particles in nonlinear wave equations", Phys. Lett. A 372, 841–848 (2008). [CrossRef]
  8. S. Colin, T. Durt and R. Willox: “L. de Broglie’s double solution program: 90 years later,” Annales de la Fondation Louis de Broglie, 42, numero special, 19-71 (2017). [CrossRef]
  9. L. de Broglie: Nonlinear Wave Mechanics (Elsevier, Amsterdam 1960).
  10. D. R. Gulevich, F. V. Kusmartsev, Sergey Savel’ev, V. A. Yampol’skii, and Franco Nori: “Shape and wobbling wave excitations in Josephson junctions: Exact solutions of the (2+1)-dimensional sine-Gordon model", Phys. Rev. B 80, 094509 (2009). [CrossRef]
  11. J. Handsteiner et al. “Cosmic Bell Test: Measurement Settings from Milky Way Stars", Phys. Rev. Lett. 118, 060401 (2017).
  12. V. Jacques et al.: “Experimental Realization of Wheeler’s Delayed-Choice Gedanken Experiment", Science 315, Issue 5814 pp. 966–968 (16 Feb 2007).
  13. C. Jönsson: Electron Diffraction at Multiple Slits, American Journal of Physics 42, 4 (1974).
  14. A. Khare, I.C. Christov, and A. Saxena: “Successive phase transitions and kink solutions in ϕ8, ϕ10, and ϕ12 field theories", Phys. Rev. E 90, 023208 (2014).
  15. T. Kibble: “Relativistic models of Nonlinear Quantum Mechanics,” Commun. Math. Phys. 64, 73 (1978).
  16. F. V. Kusmartsev: “Application of catastrophe theory to molecules and solitons,” Phys. Rept. 183, 1 (1989).
  17. F. V. Kusmartsev, E. W. Mielke and F. E. Schunck: “Gravitational stability of boson stars,” Phys. Rev. D 43, 3895 (1991); “Stability of neutron and boson stars: A new approch based on catastrophe theory", Phys. Lett. A 157, 465 –468.
  18. V. G. Ivancevic and Tijana T. Ivancevic: “Sine-Gordon solitons, kinks and breathers as physical models of nonlinear excitations in living cellular structures,” J. Geometry and Symmetry in Physics 31, 1 – 56 (2013). [CrossRef]
  19. J. Javanainen and Uttam Shrestha: “Nonlinear Phenomenology from Quantum Mechanics: Soliton in a Lattice,” Phys. Rev. Lett. 101, 170405 (2008).
  20. C. Rogers and W.K. Schief: Bäcklund and Darboux Transformations: Geometry and Modern Applications in Soliton Theory (Cambridge University Press, Cambridge 2002).
  21. I. Lindgren: “Interpretation of Quantum Mechanics. A view of our universe,” AIP Conference Proceedings 1177, 10 (2009. [CrossRef]
  22. E.W. Mielke: “Outline of a Nonlinear, Relativistic Quantum Mechanics of Extended Particles,” Fortschritte der Physik 30, 551–585 (1981).
  23. E.W. Mielke: “Toward exact solutions of the nonlinear Heisenberg Pauli-Weyl spinor equation,” J. Math. Phys. 22, 2034 (1981).
  24. E.W. Mielke: “Rotating Boson Stars,” Part of the Fundamental Theories of Physics book series (Fontier FTPH, Springer volume 183, 2016).
  25. E.W. Mielke: Geometrodynamics of Gauge Fields: On the Geometry of Yang-Mills and Gravitational Gauge Theories" (Mathematical Physics Studies) 2nd ed. (Springer, 2017).
  26. E. W. Mielke: “Soliton model of dark matter and natural inflation,” J. Phys. Conf. Ser. 1208, 1, 012012 (2019); “Bifurcations of a soliton model of dark matter towards natural inflation,” Physics Letters B 807 (2020) 135538.
  27. E. W. Mielke and R. Scherzer: “Geon-type solutions of the nonlinear Heisenberg-Klein-Gordon equation,” Phys. Rev. D 24, 2111 (1981).
  28. B. Mielnik: “Is Nonlinear Quantum Mechanics possible??", in Quantum Theory And Symmetries - Proceedings of the International Symposium edited by V. K. Dobrev, Heinz-Dietrich Doebner, J.-D. Hennig, W Lucke p. 124 - 133 (World Scientific, Singapore 1981).
  29. B. Mielnik: “ Nonlinear quantum mechanics: a conflict with the Ptolomean structure?,” Physics Letters A 289, pages 1-8 (2001).
  30. P. Nattermann: “On (Non)linear Quantum Mechanics,” Symmetry in Nonlinear Mathematical Physics, Vol.2, 270– 278 (1997).
  31. B. Nordén: “Quantum entanglement: facts and fiction – how wrong was Einstein after all?", Quarterly Reviews of Biophysics (2016) 49, page 1 of 13. [CrossRef]
  32. Yu P. Rybakov and B. Saha: “Soliton model of the atom,” Foundations of Physics 25 (12):1723-1731 (1995); “Soliton Model of Extended Quantum Particles,” Annales de la Fondation Louis de Broglie 26, 381 (2001).
  33. R. Penrose: “On the Gravitization of Quantum Mechanics 1: Quantum State Reduction,” Found. Phys. 44 557–575 (2014).
  34. R. Penrose: Fashion, Faith, and Fantasy in the New Physics of the Universe (Princeton University Press, 2016).
  35. M. Tegmark and John Archibald Wheeler: “ 100 Years of the Quantum,” Sci. Am. 284, 68–75 (2001).
  36. A. Tonomura: “Direct Observation of thitherto unobservable Quantum Phenomena by using Electrons. PNAS 102, No. 42, 14952 – 14959 (October 18, 2005).
  37. St. Weinberg: “Testing quantum mechanics,” Annals of Physics 194, 336-386 (1989).
  38. Luis Vásquez: Time-energy Heisenberg-type relations for nonlinear classical fields, Phys. Rev. D 33, 2478 (1986).
Preprints 121382 g001
Figure 1. (Color online) Kink-kink collision monitored via the absolute value of its spatial derivative. After passing the interference region, again a nonlinear self-focusing of the solitons occur. The interference resulting from a kind of “pilote wave” part induces a phase shift and displacement in the localization of the moving solitons.
Figure 1. (Color online) Kink-kink collision monitored via the absolute value of its spatial derivative. After passing the interference region, again a nonlinear self-focusing of the solitons occur. The interference resulting from a kind of “pilote wave” part induces a phase shift and displacement in the localization of the moving solitons.
Preprints 121382 g001
Preprints 121382 g002
Figure 2. (Color online) In three dimensions, a regular Lane-Emden lump is viewed as a template for a meta-stable soliton.
Figure 2. (Color online) In three dimensions, a regular Lane-Emden lump is viewed as a template for a meta-stable soliton.
Preprints 121382 g002
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated