1. Introduction
Three-phase two-level inverters are the most widely used power converters in power electronics and motor drives. The main components of the inverters are controllable power switches such as IGBTs, MOSFETs, GTOs, etc. [
1]. By implementing appropriate control strategies, they can output active and reactive power as required, meanwhile operate with desirable performance in terms of good current quality, high power efficiency, and strong robustness against disturbances. In real applications, the inverter faces uncertain conditions including time-varying grid voltage, filter capacitance and inductance changes, measurement delays, and environment noises. To effectively control the inverter, all these uncertainties should be taken into account [
2,
3].
Linear parameter-varying (LPV) systems are used to describe systems with time-varying parameters. Since the seminal work of Shamma in 1991 [
4], the LPV control and filtering approach has attracted a lot of attention from the control field. This is because
it is effective to cope with nonlinearities and time-varying dynamics of the system, and
the maturely developed LTI control methodologies, such as sensitivity shaping and modeling tools, can be extended to LPV systems. During the past decades, several advances in theoretical and practical aspects have been done. Among others, theoretical works are related to analysis and synthesis issues [
5,
6], robust filtering problems [
7,
8], fault detection and isolation [
9], etc. Practical engineering works are also popular, for instance, an LPV static output feedback control method is proposed to improve lateral stability and driving comfort of narrow tilting vehicles [
10], LPV modeling method is adopted to ensure large signal stability for multi-mode buck-boost converters [
11], the uncertain robot system is controlled by an LPV controller with sliding mode optimization [
12]. Time delays exist in many practical systems, such as network controlled systems, electronic networks, hydraulic systems, and chemical processes, which are mostly nonlinear systems. Time delays may cause instability and oscillation in these systems and severely degrade performance [
13,
14]. To target this problem, research on time-delayed LPV system starts coming on stage in recent years, see [
15,
16].
Stochastic systems are used to model systems with stochastic perturbations. This approach is used in several fields and engineering applications, such as mechanical systems, economic systems, etc. Over the past decades, the study of stabilization and filtering problems for stochastic systems has received much attention, and many valuable results have been obtained. For stabilization problems, the asymptotic stability of semiswitched stochastic systems has been investigated in [
17], the problem of input-to-state stability for nonlinear systems with stochastic impulses is systematically studied [
18]. For filtering problems, the recursive filtering problem for a class of uncertain stochastic systems with amplify and forward relays has been investigated in [
19], the problem of distributed robust filtering for switched stochastic time-delay systems with fading measurements over sensor networks is addressed in [
20].
This paper aims to propose a stochastic LPV model approach to deal with the uncertain conditions and time delay faced by a three-phase two-level inverter, where the grid voltage, filter capacitance, and inductance are treated as time-varying parameters, and the environment noises as stochastic disturbances. Sufficient conditions for stability analysis and controller synthesis are obtained for the stochastic LPV system. The theoretical results obtained are applied to the inverter, whose currents are treated as state variables and controlled to reach the equilibrium point. The contributions of this paper are of three folds: 1) the LPV approach is used to model the three-phase two-level inverter, which is a new practical method; 2) comparing with previous theoretical works, this paper further considers the stochastic perturbation and parameter-varying time delay, based on which the stochastic LPV model is established and the stability conditions are obtained; 3) the slack matrix technique is adopted to improve the feasibility of the stability conditions, which facilitates the controller design process. The remaining of this work includes system description and inverter modeling in Section II. Main theoretical analysis is presented in Section III. Simulations to validate the proposal are provided in Secition IV. Finally, conclusioms are addressed in Section V.
2. System Description and Inverter Modeling
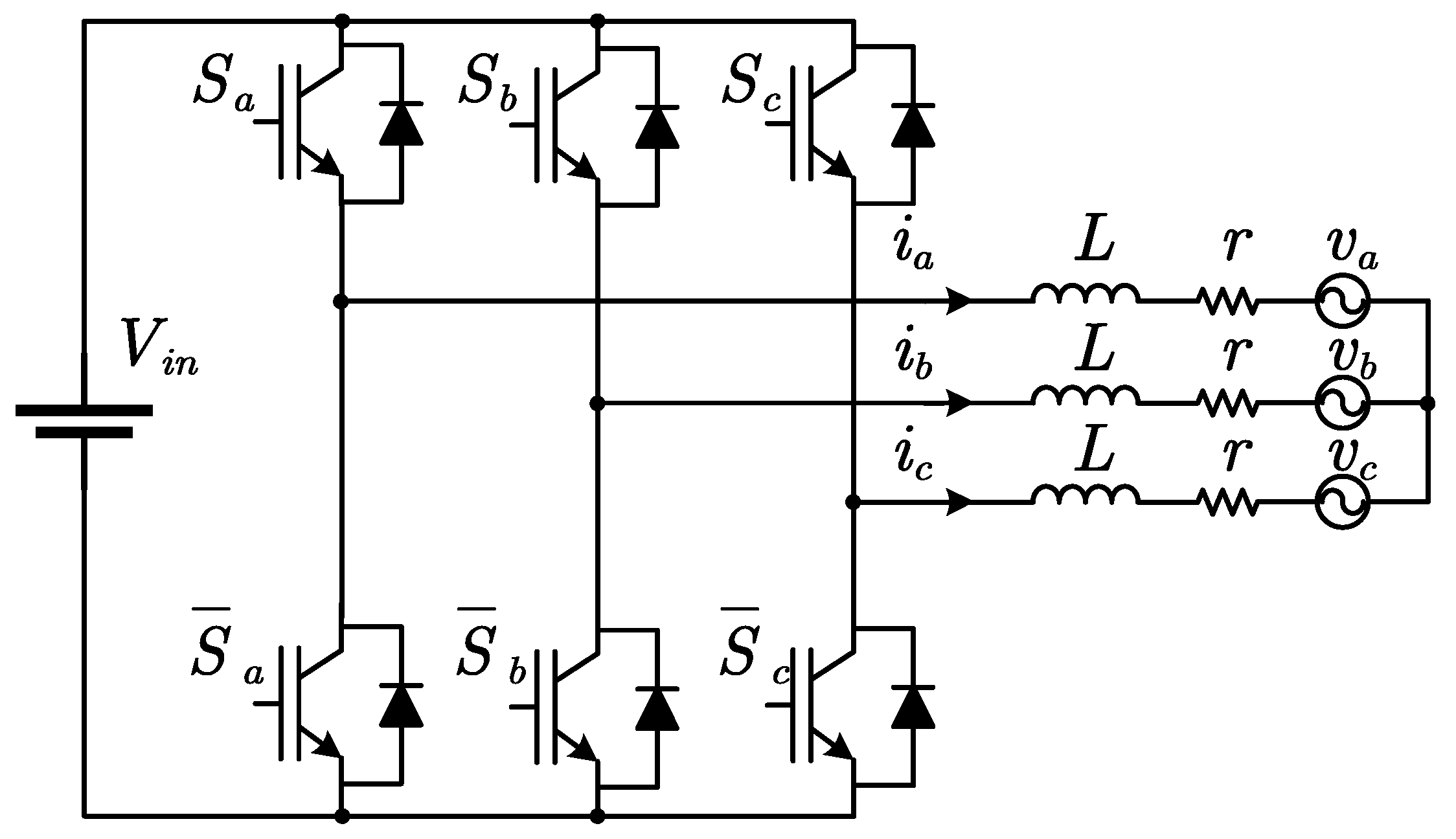
Figure 1 is a two-level three-phase inverter, which is normally used as grid-connecting power converter (the case in this paper) or motor drive. In ideal case, the inverter can be modelled in synchronous reference frame as follows [
21]:
where
is the input dc power source,
is the frequency of grid voltage,
L is the filtering inductor and
r is its equivalent series resistance, and the
dq variables are transformed from the three-phase
abc variables, i.e.,
are grid voltages transformed from
,
and
,
are grid currents transformed from
,
and
, and
are switching functions generated by controller, which is to be used to generate the switching signals
,
and
, though PWM modulator. To provide required power to grid, the
dq currents must be controlled to desired value. Taking into account the inverter parameter variations, stochastic grid perturbations, and control/communication delays, the inverter model can be formulated as a general time-delayed stochastically perturbed LPV system:
where
is the state vector,
is the system matrix related to
L,
r,
;
is the control input,
is the control matrix related to
L;
belonging to
, is either a disturbance input or a reference signal;
is a one-dimensional (1-D) Brownian motion satisfying
and
;
is vector-valued parameter evolving continuously over time and its range is limited to a compact subset;
is the parameter varying delay and satisfies:
where
H and
are constant scalars;
is the initial data function given in the time interval
. The value of
is unknown, but can be measured in real time.
Disregarding the control input
, the autonomous system of (2) is formulated as:
On the other hand, to carry out stability analysis and synthesis, the exogenous disturbance “
” in (2) is considered to be zero, yielding following system:
Therefore the autonomous system of (4) can be formulated as
For simplicity, will be used instead of in the rest of this paper. Before going further, some definitions and lemmas should be given, which are important for deriving main results.
Definition 1: For any initial state
, the time-delayed LPV stochastic system (3) is said to be robustly stable with disturbance attenuation index
if for all
and all parameter trajectories, it holds that
Also, the system is asymptotically mean square stable according to Definition 1 in [
22].
3. System Analysis and Controller Design
3.1. Stability Analysis and Synthesis
Proposition 1: If there exists a family of parameter-dependent continuous differentiable symmetric positive matrices
and
, such that for all the parameter trajectories, it satisfies
where
,
, then system (5) is asymptotically mean square stable.
Proof. Choose Lyapunov-Krasovskii functional as:
According to Itô’s formula [
23],
where
with
, and
. Thus, according to [
24], system (5) is asymptotically mean square stable if
, which is equal to the inequality (
7) with Schur complement transformation. Proof is completed.
Proposition 2: If there exists a family of parameter-dependent continuous differentiable symmetric positive matrices
,
and matrices
, such that for all the parameter trajectories, it holds that
where
then system (4) is mean square stable under
with
.
Proof. Consider system (4) with , is a parameter-dependent state feedback controller.
Substitute
in (
7) with
, and perform a congruence transformation to it with diag
, it is obtained that
where
Let matrix
,
,
, then it is obtained that (
10), and
. Proof is completed.
Remark 1: denotes the varying rate of parameter i which is assumed to be measurable in real time. If is not measurable, but its bound is known a prior, i.e. , then can be approximated by to obtain a new stability condition. represents the sum of every combination of and , which contains a total of combinations.
Proposition 3: If there exists a family of parameter-dependent continuous differentiable symmetric positive matrices
,
and matrix
W, such that for all the parameter trajectories, it satisfies that
where
,
, then system (5) is asymptotically mean square stable.
Proof. The inequality (
12) can be written as
The null spaces of
and
are
According to Projection Lemma [
25], following inequalities are obtained:
where
The inequality (
14) equals to the inequality (
7) with Schur complement transformation, which indicates (
12) can ensure the system to be asymptotically mean square stable. Proof is completed.
Remark 2: With the introduction of a new additional matrix W, the matrix in the Lyapunov function is separated from the system matrix. This extra degree of freedom reduces the usually strong interrelations between plant data and Lyapunov variables, hence improves the solution feasibility and reduces the conservatism.
Theorem 1: If there exists a family of parameter-dependent continuous differentiable symmetric positive matrices
,
,
and matrices
,
V, such that for all the parameter trajectories, it holds that
where
then system (4) is mean square stable under
with
.
Proof. Consider system (4) with
, substituting
in (
12) with
, and perform a congruence transformation with diag
, it is obtained that
where
Let matrix
,
,
,
, (
16) is obtained, and
. Proof is completed.
3.2. Performance Analysis and Synthesis
Proposition 4: The time-delayed LPV stochastic system (3) is said to be robustly stable with disturbance attenuation
if there exists a family of parameter-dependent continuous differentiable symmetric positive matrices
and
, such that for all the parameter trajectories, it holds that
where
Proof. Assume that the system has zero initial state, i.e.,
when
, then according to Itô’s formula, it can be obtained that
Let
where
with
With Schur complement, condition (
18) ensures
, thus
, meaning
. Thus system (3) is robustly stable in the sense of definition 2. Proof is completed.
Proposition 5: The time-delayed LPV stochastic system (2) is said to be robustly stabilized by state feedback controller
with disturbance attenuation
if there exists a family of parameter-dependent continuous differentiable symmetric positive matrices
,
and matrices
, such that for all the parameter trajectories, it holds that
where
and
.
Proof. Consider system (2) with
, substituting
in (
18) with
, and perform a congruence transformation with diag
, it is obtained that
where
Let matrix
,
,
, then (
21) is obtained, and
. Proof is completed.
Proposition 6: The time-delayed LPV stochastic system (3) is said to be robustly stable with disturbance attenuation
if there exists a family of parameter-dependent continuous differentiable symmetric positive matrices
,
and matrix
W, such that for all the parameter trajectories, it holds that
where
,
,
.
Proof. The inequality (
23) can be written as:
The null spaces of
and are
,
respectively. According to Projection Lemma, (
24) is obtained,
with
and
with
and
.
The inequality (
24) equals to the inequality (
18) with Schur complement transformation, which indicates (
23) can ensure the system to be robustly stable. Proof is completed.
Theorem 2: The time-delayed LPV stochastic system (2) is said to be robustly stabilized by state feedback controller
with disturbance attenuation
if there exists a family of parameter-dependent continuous differentiable symmetric positive matrices
,
,
and matrices
,
V, such that for all the parameter trajectories, it holds that
where
and
.
Proof. Consider system (2) with
, substituting
in (
23) with
, and perform a congruence transformation with diag
, it is obtained that
where
Let matrix
,
,
,
, (
26) is obtained, and
. Proof is completed.
4. Simulation Results
For following simulation, the grid and inverter parameters are chosen as follows:
V,
V,
V,
H,
,
rad/s. These values are chosen to comply with European low voltage grid, which has a voltage of 400V, a frequency of 50Hz, with small line resistance and inductance. The matrices of the LPV inverter model (2) are as follows:
where
and
are time-varying parameters, satisfying
,
,
, and
;
is the parameter varying delay with a bounded varying rate. The initial states are set as
, where
.
To deal with the problem of infinite LMIs to be solved during controller synthesis, gridding technique and basis functions should be adopted. The basis functions are chosen as
leading to
therefore the controller synthesis problem becomes finding matrices
and
to satisfy (
10), (
16), (
21), and (
26).
4.1. Stabilization
The state feedback control
is designed to ensure that system (4) is asymptotically mean square stable. By solving the conditions in (
10) in Proposition (2), it is obtained that,
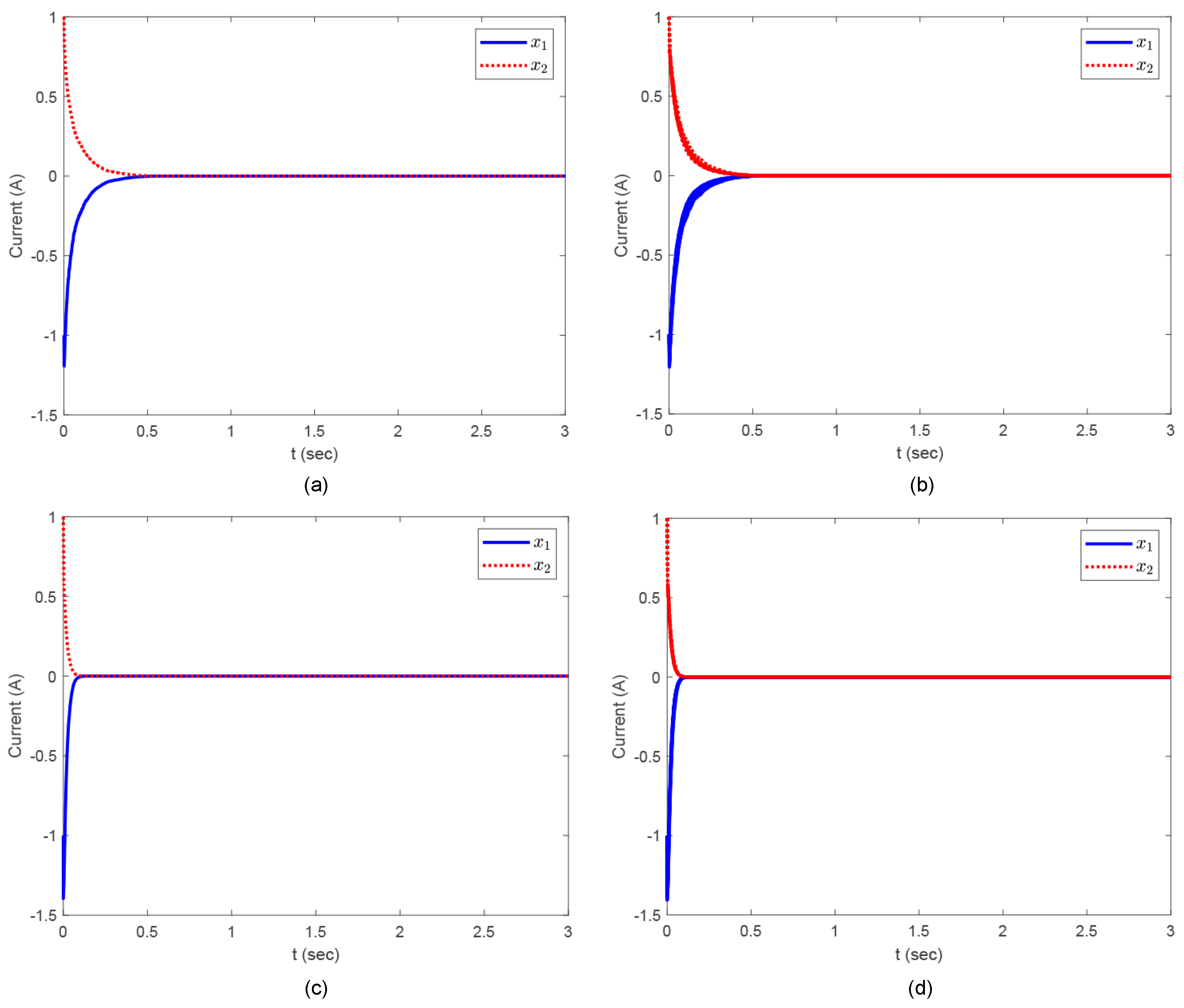
Figure 2-(a) shows the state response of one arbitrarily chosen set, which means a random set of currents can be controlled to a certain reference.
Figure 2-(b) shows the state response of ten arbitrarily chosen sets, which shows that the states of all the sets converge to zero. As can be seen, the stochastic phenomenon can influence the trajectories of currents, but does not affect the stability. Therefore, the time-delayed LPV inverter system is asymptotically stabilized under the stochastic perturbations.
4.2. Stabilization with Slack Matrix
Using slack matrix technique and solve the conditions in (
16) in Theorem 1, it is obtained that:
Similar as in the previous subsection,
Figure 2-(c) shows the state response of one arbitrarily chosen set, and
Figure 2-(d) shows the state response of ten arbitrarily chosen sets. As can be seen, with the controller obtained by adopting slack matrix, the currents converge to the equilibrium with faster speed, compared to the controller obtained in previous subsection, which demonstrates the advantage of slack matrix technique.
4.3. Disturbance Attenuation
Let’s consider in the system a disturbance signal
. Then, the state feedback control
is designed to ensure the system (2) is stabilized and achieves some disturbance attenuation index
. By solving the conditions in (
21) in Theorem 2, it is obtained that,
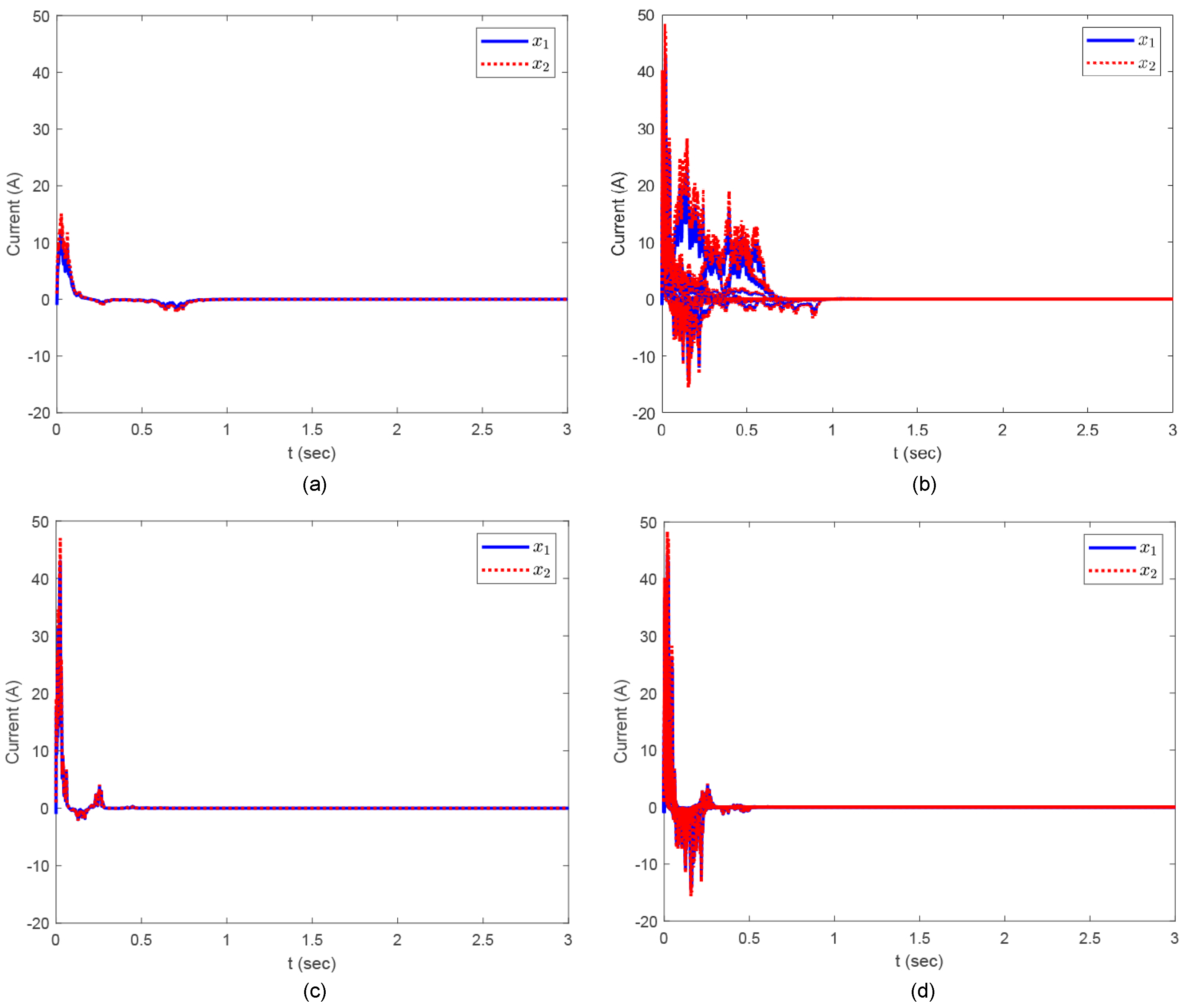
With this controller, the currents converge to equilibrium and the system is stabilized under stochastic perturbations, as shown in
Figure 3-(a) and
Figure 3-(b), and the achieved disturbance attenuation index is
is
.
4.4. Disturbance Attenuation with Slack Matrix
Similar to
Section 4-C, let’s consider in the system a disturbance signal
. By solving the conditions in (
26) in Proposition (5), it is obtained that,
Applying the controller to the inverter system, as shown in
Figure 3-(c) and
Figure 3-(d), the currents converge at faster speed, comparing to the controller obtained without adopting slack matrix technique. Furthermore, the achieved disturbance attenuation index
is
, which is smaller than the previous method. These results again demonstrate the advantage of slack matrix technique.
5. Conclusions
A stochastic LPV approach has been proposed to control the three-phase two-level inverter. The time-delayed stochastic LPV system is first established, for which the analysis and synthesis of the system are carried out. With the parameter-dependent Lyapunov functionals, sufficient conditions have been proposed for stability analysis and control synthesis in terms of parameter-dependent LMIs. The slack matrix approach has been used to derive a new set of stability LMIs, which improves the feasibility and reduces the conservatism of the solution. The theoretical results are verified on the inverter, whose currents are controlled to reach the equilibrium point. Simulation results validate the effectiveness of the proposed theories and demonstrate the advantages of adopting a slack matrix, in terms of faster state response and lower disturbance attenuation index.
Author Contributions
Conceptualization, W. Luo and L. Wu; methodology, W. Luo; validation, W. Luo, R. Zhang and J. Zhang; formal analysis, W. Luo; investigation, W. Luo; data curation, R. Zhang and J. Zhang; writing—original draft preparation, W. Luo, R. Zhang and J. Zhang; writing—review and editing, W. Luo and S. Vazquez; supervision, L. G. Franquelo. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (62003114, 62033005, 62320106001), the China Postdoctoral Science Foundation (2020M681097), the Heilongjiang Postdoctoral Fund (LBH-Z20134), the Natural Science Foundation of Heilongjiang Province (ZD2021F001), the Fundamental Research Funds for the Central Universities (Grant No. HIT.NSFJG202207).
References
- W. Luo, S. Stynski, A. Chub, L. G. Franquelo, M. Malinowski and D. Vinnikov, “Utility-Scale Energy Storage Systems: A Comprehensive Review of Their Applications, Challenges, and Future Directions,” in IEEE Industrial Electronics Magazine, vol. 15, no. 4, pp. 17–27, 2021. [CrossRef]
- Y. Yin, S. Vazquez, A. Marquez, J. Liu, J. I. Leon, L. Wu, and L. G. Franquelo, “Observer-based sliding-mode control for grid-connected power converters under unbalanced grid conditions,” IEEE Transactions on Industrial Electronics, vol. 69, no. 1, pp. 517–527, 2022. [CrossRef]
- E. Zafra, J. Granado, V. B. Lecuyer, S. Vazquez, A. M. Alcaide, J. I. Leon, and L. G. Franquelo, “Computationally Efficient Sphere Decoding Algorithm Based on Artificial Neural Networks for Long-Horizon FCS-MPC,” IEEE Transactions on Industrial Electronics, vol. 71, no. 1, pp. 39–48, 2024. [CrossRef]
- J. S. Shamma and M. Athans, “Guaranteed properties of gain scheduled control for linear parameter-varying plants,” Automatica, vol. 27, no. 3, pp. 559–564, 1991. [CrossRef]
- C. Briat, “Stability analysis and state-feedback control of LPV systems with piecewise constant parameters subject to spontaneous poissonian jumps,” IEEE Control Systems Letters, vol. 2, no. 2, pp. 230–235, 2018. [CrossRef]
- L. O. de Araújo, P. C. Pellanda, J. F. Galdino, and A. M. Simões, “Haar-based stability analysis of LPV systems,” IEEE Transactions on Automatic Control, vol. 60, no. 1, pp. 192–198, 2015. [CrossRef]
- M. S. de Oliveira and R. L. Pereira, “LMI-based filter design conditions for discrete-time LPV systems with bounded parameter variation,” IEEE Transactions on Automatic Control, vol. 66, no. 2, pp. 910–915, 2021. [CrossRef]
- A. P. Pandey and M. C. de Oliveira, “On the necessity of LMI-based design conditions for discrete time LPV filters,” IEEE Transactions on Automatic Control, vol. 63, no. 9, pp. 3187–3188, 2018. [CrossRef]
- J. Tan, S. Olaru, F. Xu, and X. Wang, “Toward a convex design framework for online active fault diagnosis of LPV systems,” IEEE Transactions on Automatic Control, vol. 67, no. 8, pp. 4154–4161, 2022. [CrossRef]
- A.-T. Nguyen, P. Chevrel, and F. Claveau, “LPV static output feedback for constrained direct tilt control of narrow tilting vehicles,” IEEE Transactions on Control Systems Technology, vol. 28, no. 2, pp. 661–670, 2020. [CrossRef]
- J. Ma, M. Zhu, Y. Li, and X. Cai, “Dynamic analysis of multimode buck–boost converter: An LPV system model point of view,” IEEE Transactions on Power Electronics, vol. 36, no. 7, pp. 8539–8551, 2021. [CrossRef]
- G. P. Incremona, A. Ferrara, and V. I. Utkin, “Sliding mode optimization in robot dynamics with LPV controller design,” IEEE Control Systems Letters, vol. 6, pp. 1760–1765, 2022. [CrossRef]
- Y. Shen, Z.-G. Wu, P. Shi, Z. Shu, and H. R. Karimi, “H∞ control of Markov jump time-delay systems under asynchronous controller and quantizer,” Automatica, vol. 99, pp. 352–360, 2019. [CrossRef]
- L. Wu, X. Su, and P. Shi, “Sliding mode control with bounded L2 gain performance of Markovian jump singular time-delay systems,” Automatica, vol. 48, no. 8, pp. 1929–1933, 2012. [CrossRef]
- X. Yang, S. Yin, and O. Kaynak, “Robust identification of LPV time-delay system with randomly missing measurements,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 48, no. 12, pp. 2198–2208, 2018. [CrossRef]
- X. Yang and S. Yin, “Robust global identification and output estimation for LPV dual-rate systems subjected to random output time-delays,” IEEE Transactions on Industrial Informatics, vol. 13, no. 6, pp. 2876–2885, 2017. [CrossRef]
- Q. Wang, Baoand Zhu, “Stability analysis of semi-Markov switched stochastic systems,” Automatica, vol. 94, pp. 72–80, 2018. [CrossRef]
- Y. Tang, X. Wu, P. Shi, and F. Qian, “Input-to-state stability for nonlinear systems with stochastic impulses,” Automatica, vol. 113, p. 108766, 2020. [CrossRef]
- H. Tan, B. Shen, P. Kaixiang, and H. Liu, “Robust recursive filtering for uncertain stochastic systems with amplify-and-forward relays,” International Journal of Systems Science, vol. 51, no. 7, pp. 1188–1199, 2020. [CrossRef]
- Y. Chen, Z. Wang, Y. Yuan, and P. Date, “Distributed H∞ filtering for switched stochastic delayed systems over sensor networks with fading measurements,” IEEE Transactions on Cybernetics, vol. 50, no. 1, pp. 2–14, 2020. [CrossRef]
- W. Luo, S. Vazquez, J. Liu, F. Gordillo, L. G. Franquelo, and L. Wu, “Control system design of a three-phase active front end using a sliding-mode observer,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 52, no. 2, pp. 739–748, 2022. [CrossRef]
- W. Luo, S. Li, S. Vazquez, J. Du, L. Wu, and L. G. Franquelo, “Grid-connected inverter control via linear parameter-varying system approach,” in IECON 2022 – 48th Annual Conference of the IEEE Industrial Electronics Society, 2022, pp. 1–6. [CrossRef]
- X. Mao, “Stability of stochastic differential equations with Markovian switching,” Stochastic Processes and Their Applications, vol. 79, no. 1, pp. 45–67, 1999. [CrossRef]
- S. Xu and T. Chen, “Robust H∞ control for uncertain stochastic systems with state delay,” IEEE Transactions on Automatic Control, vol. 47, no. 12, pp. 2089–2094, 2002. [CrossRef]
- P. Gahinet and P. Apkarian, “A linear matrix inequality approach to H∞ control,” International Journal of Robust and Nonlinear Control, vol. 4, no. 4, pp. 421–448, 1994. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).