Efficiency Analysis and Optimization of Two Speed Regions Operation of PMSM Taking into Account Iron Losses Based on Linear Non-Equilibrium Thermodynamics

Preprint

Article

Efficiency Analysis and Optimization of Two Speed Regions Operation of PMSM Taking into Account Iron Losses Based on Linear Non-Equilibrium Thermodynamics

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

21 October 2024

Posted:

24 October 2024

You are already at the latest version

Alerts

Abstract

In this article, the linear non-equilibrium thermodynamic approach is used to analyze the energy regularities of the interior permanent magnet synchronous motor (IPMSM) taking into account iron losses. The IPMSM is considered a linear power converter (PC) that is multiple linearized at operating points with given angular velocity and load torque. A universal description of such a PC by a system of dimensionless parameters and characteristics made it possible to analyze the perfection of energy conversion in the object. For IPMSM, taking into account iron losses, a mathematical model of the corresponding PC has been built, and an algorithm and research program have been developed, which is valid in a wide range of machine speed regulations. This allows you to obtain the efficiency maps for IPMSM and choose the optimal points of PC operation according to the maximum efficiency criteria. The results of the studies demonstrate the effectiveness of the proposed method for determining the optimal reference of the components d and q of the armature current for both the MTPA strategy at motor speed adjusting below the nominal value and for the FW strategy at its adjusting above the nominal value.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

Permanent magnet synchronous machines (PMSM) are widely used in industry and transport. This is due to their high specific power and torque indicators, high efficiency, reliability, good controllability, rapid torque response and low maintenance requirements [1]. Especially promising are PMSMs for drives of electric vehicles (EV) [2]. For light EVs, synchronous machines controlled by the principle of brushless direct current (BLDC) motor or surface-mounted PMSM (SPMSM) are mainly used, which are easier to implement since the permanent magnets (PM) are placed on the rotor surface. However, this significantly limits the maximum angular velocity of the SPMSM in the range higher than the nominal one. For higher power EVs, a wide angular velocity control range is an important factor due to the ability to operate at speeds significantly higher than rated by the flux weakening (FW). A special type of these machines is used here – interior permanent magnet synchronous machines (IPMSM). They have the PMs placed inside the rotor, thanks to that the magnetic conductivity along the d and q axes related to the rotor are different, which makes it possible to weaken the PM magnetic flux by adjusting the d-component of the armature current [3]. This is ensured by vector control of components d and q of the armature current [4]. Many works have been devoted to the study of the peculiarities of such control and limitations on the angular velocity and electromagnetic torque due to the FW, which are reviewed in [5].

For all applications of PMSMs, and especially for EVs, an important indicator of an electric machine operation is its high efficiency, and in the widest possible range of changes in angular velocity and electromagnetic torque. Research on ensuring the high efficiency of PMSMs is carried out in two interconnected directions – the justification of optimal machine coordinates and the implementation of control algorithms. These directions differ among themselves for the cases of angular velocity adjustment from zero to the nominal value (the first range of speed regulation) and its adjustment above the nominal value (the second range of speed regulation).

For the first range, the main optimal strategy from the point of view of energy efficiency is the strategy of maximum torque per ampere (MTRA) [6,7,8,9]. In its classic form, this strategy ensures minimum losses in the copper of the armature winding. This is explained by two factors: the first one is the clear predominance of losses in copper in the total power losses of the machine during its operation in the first range; the second one is the possibility of analytically obtaining expressions for the assignment of components d and q of the armature current, which are obtained from the basic mathematical model of PMSM. However, due to the relative complexity of these mathematical expressions, their online calculations requires complex controllers, so the main method of control is the use of an offline method – pre-calculated look-up tables (LUT) [10]. This approach also enables the practical implementation of a more accurate preliminary calculation of the trajectories of optimal control of PMSM operation, taking into account losses in steel [11], magnetic saturation and cross-saturation effects [12]. As shown in [13], optimal control based on the minimum of total losses in the machine has significant advantages over the classic MTPA method. Various modern approaches are used for offline determination of these losses: the use of a refined resistive model to justify optimal control coordinates from an energy point of view [14], calculation of losses in steel based on particle swarm optimization (PSO) and a recurrent neural network (NN) [15], a hybrid analytical model for predicting the electromagnetic losses, which is based on the combination of analytical calculations with the results of the FEM analysis of the machine magnetic field [16].

In contrast to offline methods, more complex online methods of IPMSM energy optimization in the first range of their operation have recently been used to implement the MTPA strategy [6,9]. Among them, online MTPA tracking of IPMSM based on min-max optimization [17], Perturb and Observe (P&O) online algorithm [18], fractional-order extremum seeking method for MTPA [19], NN-based with cloud-based training for MTPA [20], NN-based P&O algorithm [21].

In the second range of IPMSM angular velocity regulation, the main limitation is included in the justification of the optimal control coordinates – according to the armature voltage, which is determined by the DC supply voltage of the voltage inverter (VI). In addition, there is also a limitation of the armature current, which is caused by the permissible heating of the machine in a long-term mode operation [22]. Therefore, the optimal from the point of view of energy efficiency control coordinates – components d and q of the armature current – in the steady state should be, as a rule, within the specified limits. As in the first range, these coordinates are determined analytically for the classical approach, taking into account only losses in the copper of the machine [4,5,22,24]. However, in the second range, due to the increase in the IPMSM angular velocity, the frequency of the armature current also increases proportionally, which leads to an approximately quadratic increase in losses in steel [5]. Already at a relatively low angular velocity, losses in steel begin to dominate losses in copper. Therefore, ignoring them leads to a significant error in the justification of the optimal components of the armature current for the given coordinates of the angular velocity at the static load torque of the machine. In order to take into account losses in steel, as well as other factors, such as magnetic saturation and cross-saturation effects, in the second range of IPMSM speed regulation, the above-mentioned offline methods of substantiating optimal coordinates [11,14,15,16] and online methods of optimal control are also used [17,18,19,20,21,25]. However, offline methods are characterized by the complexity of preliminary research, and online methods are differed by the complexity of real-time calculations and hence the need for powerful and expensive controllers.

An effective approach to solving the problem of increasing the energy efficiency of various objects, which work combines physical phenomena of different nature, can be the application of methods of linear non-equilibrium thermodynamics (LNTD) [26,27]. The peculiarity of this approach is the ability to describe complex, including non-linear, steady-state processes of work of various physical, chemical, biological systems according to the universal principle of linearization of the relationship between input and output power coordinates at specific operating points. At the same time, the system is considered a power converter (PC) with a certain number of its inputs and outputs, but the simplest and most often - with single input and single output (SISO). For the latter case, a universal method of the PC describing by a system of dimensionless parameters and characteristics of its performance was developed [28,29]. The most important indicator of the PC is the degree of coupling between its input and output, which unambiguously determines the maximum achievable value of the PC efficiency, as well as the operating point, at which this maximum value is reached. This makes it possible to optimize the operation modes of the PC depending on the adopted optimization criteria [29]. This universal method was most widely used in bioenergetics to describe free energy transformations in bio systems, but it can be successfully used to analyze established processes of energy transformations in systems of any nature. For example, in [30], it was successfully applied to analyze the efficiency of energy conversion in an electromechanical converter – an induction motor, and in [31], it was applied to an aeromechanical converter – a wind turbine.

In this work, the system of linear equations was obtained for the first time and the steady-state modes of IPMSM were described using the universal method taking into account the iron losses, with the aim of model-based optimization of the machine operation in both the first and second ranges of angular velocity regulation. In addition to the main task, the proposed approach makes it possible to analyze energy regularities and explore the possibilities of increasing the efficiency of the IPMSM in different operating modes. Taking into account the non-linear nature of steady-state processes in the machine, the system of linear equations is obtained by linearizing the dependence of the module of the input voltage vector on the angular velocity of the IPMSM at different operating points depending on the d-component of the armature current. The obtained universal dependencies in p. u. for the PC, which simulates the IPMSM operation taking into account iron losses, made it possible to analyze the perfection of energy conversion in such an object and understand its limitations.

The novelty and contribution of this work is the proposal of a new method for modelling the energy regularities of the operation of such a rather complex nonlinear object as IPMSM taking into account iron losses. Within the framework of this method, the necessary mathematical models were obtained, and a research algorithm was developed and implemented in the MathCad environment. With the help of the created program, the analysis of the IPMSM operation in two ranges of its angular velocity regulation with different possibilities was carried out.

The paper is structured as follows. In Section 2, the research method is presented, in particular, the research object is shown in the form of a circular model of IPMSM with consideration of iron losses, and the main provisions of the LNTD and the universal method of describing and evaluating the performance indicators of linear PC are briefly highlighted. In Section 3, the main results of the research are presented and discussed: the mathematical models of SPMSM and IPMSM were obtained, taking into account iron losses as linear PCs; their research was carried out and the energy regularities of operation in both ranges of the machine angular velocity regulation were analyzed; the optimal coordinates of the armature current components were obtained to implement model-based vector control. Concluding remarks are given in Section 4.

2. Research Method

2.1. Mathematical Description of IPMSM Dynamics Taking into Account Iron Losses

The IPMSM mathematical model is traditionally presented in the rotating orthogonal d-q reference frame linked with the rotor, in which the d axis is directed along the flux lincage vector caused by the PM. We will assume the absence of saturation of the magnetic circuit and independence of the inductances of the motor armature winding from the rotor position. Under such conditions, the substitute scheme of the IPMSM taking into account iron losses will take the view shown in Figure 1 [32,33], where v_d and v_q are the projection on the d i q axis of the voltage vector applied to the armature windings, R is the resistance of the armature winding, R_с is the resistance simulating iron losses, L_d, L_q are the inductances of the armature windings relative to the d and q axes, р_р is the the number of pairs of poles of the IPMSM rotor, ω is the angular velocity of the motor rotor, and ψ_pm is the amplitude of the flux linkage created by one PM pole.

Based on the substitute scheme presented in Figure 1, the equations of the electrical balance of the IPMSM in the rotating reference frame, oriented along the rotor field, can be described by the next systems of equations

\{\begin{cases} i_{d} = i_{d 0} + \frac{1}{R_{c}} (L_{d} \frac{d}{d t} i_{d 0} - p_{p} ω L_{q} i_{q 0}) \\ i_{q} = i_{q 0} + \frac{1}{R_{c}} (L_{q} \frac{d}{d t} i_{q 0} + p_{p} ω L_{d} i_{d 0} + p_{p} ω ψ_{pm}) \end{cases}

(1)

\{\begin{cases} v_{d} = i_{d} R + L_{d} \frac{d}{d t} i_{d 0} - p_{p} ω L_{q} i_{q 0} \\ v_{q} = i_{q} R + L_{q} \frac{d}{d t} i_{q 0} + p_{p} ω L_{d} i_{d 0} + p_{p} ω ψ_{pm} \end{cases}

(2)

Substituting (1) into (2), we get

\{\begin{cases} L_{d} \frac{d}{d t} i_{d 0} = - L_{d} i_{d 0} \frac{R}{L_{d} A} + p_{p} ω L_{q} i_{q 0} + \frac{1}{A} v_{d} \\ L_{q} \frac{d}{d t} i_{q 0} = - L_{q} i_{q 0} \frac{R}{L_{q} A} - p_{p} ω (L_{d} i_{d 0} + ψ_{pm}) + \frac{1}{A} v_{q} \end{cases}

(3)

where

A = 1 + \frac{R}{R_{c}}

(4)

In addition to the system of equations of electromagnetic balance (3), the IPMSM mathematical model also includes the differential equation of balance of moments on the motor shaft

J_{m} \frac{d}{d t} ω = T - T_{L}

(5)

where J_m is the moment of inertia of the drive brought to the motor shaft, T is the electromagnetic torque of the motor, and T_L is the static load torque on the motor shaft.

The electromagnetic torque of the studied IPMSM is described by the equation [3,4]

T = \frac{3}{2} p_{p} [ψ_{pm} i_{q 0} + (L_{d} - L_{q}) i_{d 0} i_{q 0}]

(6)

Thus, the total dynamic mathematical model of IPMSM taking into account iron losses has the following view

\{\begin{cases} L_{d} \frac{d}{d t} i_{d 0} = - i_{d 0} \frac{R}{A} + p_{p} ω L_{d} i_{q 0} + \frac{1}{A} v_{d} \\ L_{q} \frac{d}{d t} i_{q 0} = - i_{q 0} \frac{R}{A} - p_{p} ω (L_{d} i_{d 0} + ψ_{pm}) + \frac{1}{A} v_{q} \\ J_{m} \frac{d}{d t} ω = \frac{3}{2} p_{p} [ψ_{pm} i_{q 0} + (L_{d} - L_{q}) i_{d 0} i_{q 0}] - T_{L} \end{cases}

(7)

2.2. Steady-State Equations

For the mathematical description of the steady-state operating mode of the IPMSM taking into account iron losses system (7) is transformed into the form

\{\begin{cases} v_{d} = R i_{d 0} - A p_{p} ω L_{q} i_{q 0} \\ v_{q} = R i_{q 0} + A p_{p} ω (L_{d} i_{d 0} + ψ_{pm}) \\ T_{L} = \frac{3}{2} p_{p} [ψ_{pm} i_{q 0} + (L_{d} - L_{q}) i_{d 0} i_{q 0}] \end{cases}

(8)

Useful dependences between the currents in the steady-state operation of the IPMSM taking into account iron losses can be obtained from the original systems of equations (1) and (2). Having determined

L_{d} \frac{d}{d t} i_{d 0}

from the first equation of system (1) and substituting it into the first equation of system (2), as well as having determined

L_{q} \frac{d}{d t} i_{q 0}

from the second equation of system (1) and substituting it into the second equation of system (2), after transformations we obtain

\{\begin{cases} i_{d} = \frac{1}{A} i_{d 0} + \frac{1}{R_{c} A} v_{d} \\ i_{q} = \frac{1}{A} i_{q 0} + \frac{1}{R_{c} A} v_{q} \end{cases}

(9)

2.3. Performance Indicators of the Universal PC

According to the LNTD, for two conjugate processes, to which any PC belongs, since its output parameters (o – output) are determined by input parameters (i – input), the following system of equations can be written [26]:

\{\begin{cases} J_{i} = L_{ii} X_{i} + L_{io} X_{o} \\ J_{o} = L_{oi} X_{i} + L_{oo} X_{o} \end{cases}

(10)

where the kinetic or "phenomenological" coefficients are from the expressions

L_{jk} = {(\frac{\partial J_{j}}{\partial X_{k}})}_{X_{j} = const}

(11)

By definition, X_i, X_o and J_i are positive, and J_o is negative, which means asorption of energy at the input and its formation at the output, therefore, L_ii, L_oo and (-L_io) must be positive.

According to Onsager's principle of reciprocity [28], L_jk = L_kj. That is, in the vicinity of the equilibrium state, the linear dependence of any flow J_j on any force X_k coincides with the analogous dependence of the flow J_k on the force X_j. Onsager reciprocity ratios make it possible to significantly reduce the number of independent coefficients in systems of type (10).

The above-described main provisions of the LNTD are the basis of the theory of thermodynamic analysis of PC [28,29].

From the analysis of system (10), it is clear that the more negative the value of L_io (compared to the values of the remaining L coefficients), the higher the degree of influence of the input force on the output flow. In addition, with more negative values L_io the degree of suppression of the input flow by the force at the output increases. Thus, the coefficient L_io is related to the degree of coupling q between the input and output processes in PC. To avoid the effect on q values of other kinetic coefficients, the degree of coupling was defined as the coefficient L_io normalized to the coefficients L_ii and L_oo [29]:

q = \frac{L_{io}}{\sqrt{L_{ii} L_{oo}}}

(12)

According to this definition, q will be negative and will acquire values from –1 to 0.

To obtain universal PC characteristics in p. u., two more indicators are introduced [29]:

relation of forces

χ = X_{o} / X_{i}

(13)

phenomenological relationship

Z = \sqrt{L_{oo} / L_{ii}}

(14)

Having normalized the input and output fluxes to the input flux at zero output force (short circuit), the system of equations (10) can be rewritten using the introduced notations

\{\begin{cases} \frac{J_{i}}{L_{ii} X_{i}} = q (Z χ) + 1 \\ \frac{J_{o}}{Z L_{ii} X_{i}} = (Z χ) + q \end{cases}

(15)

and determine the flow ratio as follows:

j = \frac{J_{o}}{J_{i}} = Z \frac{(Z χ) + q}{q \cdot (Z χ) + 1}

(16)

In expressions (15) and (16), the product Zχ is a dimensionless number that expresses the reduced force ratio. The content of q also becomes clear: when q = -1 the output flow differs from the input flow always by –Z times. Therefore, the flows are rigidly (completely) coupled. When

q = 0

the input and output flows are caused only by their own forces and flow in the direction of their decrease, which means that the flows are not coupled at all. For values of q from –1 to 0 the output flow is supported by the input flow in the "downhill" direction, but the ratio of these flows changes along with the change of Zχ, which means that the input and output processes in this case are partially coupled [31].

An important characteristic of PC is the thermodynamic efficiency η of their operation, i.e. the ratio of the rate at which the PC produces free output energy to the rate at which it consumes free input energy. The expression for η can be easily obtained from (16) and (13) in the form

η = - \frac{J_{o} X_{o}}{J_{i} X_{i}} = - j χ = - (Z χ) \frac{(Z χ) + q}{q \cdot (Z χ) + 1}

(17)

Graphical dependence (17) at different values of q is shown in Figure 2. From (17), it is easy to find the optimal ratio of forces from the point of view of thermodynamic efficiency:

{(Z χ)}_{opt - η} = - \frac{q}{1 + \sqrt{1 - q^{2}}}

(18)

at which the thermodynamic efficiency has a maximum value equal to

η_{\max} = {(Z χ)}_{opt - η}^{2}

(19)

Other important indicators of PС operation are the normalized output flow j_o and normalized output power p [29]:

j_{o} = - \frac{J_{2}}{Z L_{11} X_{1}} = - (Z χ) - q

(20)

p = - \frac{J_{o} X_{o}}{L_{ii} X_{i}^{2}} = - (Z χ) [q + (Z χ)]

(21)

Based on of the obtained universal dependencies of the criteria for the operation of a universal PC (17), (20) and (21), it is possible to easily form other criteria for optimal operation appropriate for specific PCs by combining two indicators, for example [29]: the maximum output flow at optimal efficiency, the maximum output power at optimum efficiency, etc.

Using two relative parameters of the universal PC – q and Zχ – it is also possible to determine in p. u. all components of power – the input power P_in*, the output power P_out*, and the total power losses ΔP_Σ*. Moreover, we can also define separate components of the total power losses: the part caused by the nonequilibrium of the process ΔP_R*, that is, the load of the system, and the part caused by its incomplete coupling ΔP_q*. To obtain these components in p. u., all absolute values of powers are normalized to L_iiX_i², as can be seen from (21). For example, we will be interested in the power loss components:

Δ {P_{R}}^{*} = \frac{Δ P_{R}}{L_{ii} X_{i}^{2}} = {[1 + q (Z χ)]}^{2}

(22)

Δ {P_{q}}^{*} = \frac{Δ P_{q}}{L_{ii} X_{i}^{2}} = {(Z χ)}^{2} (1 - q^{2})

(23)

3. Results and Their Discussion

3.1. Parameters of the Experimental Machine

For further research, an experimental IPMSM with the parameters listed in Table 1 was taken.

A separate important task for this study is the modelling of iron losses in IPMSM, which are especially manifested at high angular velocities of the machine. When modelling iron losses, it is assumed that the magnetic flux in the core of the armature has a sinusoidal character.

Let us find with a reasonable approximation the value of resistance R_c, which simulates iron losses given the value of relative power losses in steel in the nominal mode of operation of the machine at a level of δ_Fe = 0.05. From the substitute scheme of the IPMSM shown in Figure 1 this relative power can be approximately written as

δ_{Fe} = \frac{{(1.2 p_{p} ω_{n} ψ_{pm})}^{2}}{R_{c . n} P_{n}}

(24)

where R_c.n is the value of resistance R_c in the nominal mode of operation of the IPMSM, the coefficient of 1.2 makes it possible to approximately estimate the influence of the flux linkage of the armature reaction at a level of 20% of the flux linkage from the PMs.

For the experimental IPMSM with the parameters given in Table 1, the value of R_c calculated by (24) is 14.1 Ohms. Since power losses due to hysteresis and eddy currents, which together make up losses in steel, depend differently on the angular velocity of the machine, the resistance value decreases as the speed decreases. As shown in [34], such a trend can be modeled by the following equation:

R_{c} = R_{c . n} \frac{\frac{K_{f}}{K_{h}} + 1}{\frac{K_{f}}{K_{h}} + \frac{1}{ω^{*}}}

(25)

where K_h and K_f are the coefficients characterizing, respectively, hysteresis losses and eddy currents at nominal values of magnetic flux and frequency; ω^* is the relative value of the angular velocity of the machine, which is equal to one of its nominal value.

According to experimental data [34], K_f/K_h = 0.5694 is accepted.

3.2. PMSM as Linear PC

As a PC, the PMSM converts electrical power at the input of the armature winding into mechanical power on the motor shaft. A force acts in the form of an armature voltage vector

X_{i} = {\vec{v}}_{a}

at the input of this PC, which determines the input flow in the form of an armature current vector

J_{i} = {\vec{i}}_{a}

. At the output of the PC, the force in the form of the angular velocity of the PMSM X_o = ω determines the electromagnetic torque of the machine, which in the steady-state is equal to the machine load torque J_o = T_L. The output power of the PC is equal to –P_o = ω T_L, and the active power at its input is the dot product of the armature voltage and current vectors. The latter looks like this:

P_{i} = ({\vec{v}}_{a} \cdot {\vec{i}}_{a}) = \frac{3}{2} (v_{d} i_{d} + v_{q} i_{q})

(26)

where the factor 3/2 is due to the transformation of the two-phase reference frame to the three-phase one.

The dot product of the armature voltage and current vectors, in order to separate the voltage and current, can also be represented as

P_{i} = ({\vec{v}}_{a} \cdot {\vec{i}}_{a}) = |{\vec{v}}_{a}| |{\vec{i}}_{a}| \cos φ = \frac{3}{2} \sqrt{v_{d}^{2} + v_{q}^{2}} \sqrt{i_{d}^{2} + i_{q}^{2}} \cos (atan \frac{v_{d}}{v_{q}} - atan \frac{i_{d}}{i_{q}})

(27)

where φ is the angle between the voltage and armature current vectors.

From (27), the input power and flow of the PC can be chosen as follows:

X_{i} = \sqrt{\frac{3}{2}} \sqrt{v_{d}^{2} + v_{q}^{2}}, J_{i} = \sqrt{\frac{3}{2}} \sqrt{i_{d}^{2} + i_{q}^{2}} \cos (atan \frac{v_{d}}{v_{q}} - atan \frac{i_{d}}{i_{q}})

(28)

Similarly to (10), the system of linear equations that describes the operation of the PMSM as a linear PC will have the form

\{\begin{cases} \sqrt{\frac{3}{2}} \sqrt{i_{d}^{2} + i_{q}^{2}} \cos (atan \frac{v_{d}}{v_{q}} - atan \frac{i_{d}}{i_{q}}) = L_{ii} (\sqrt{\frac{3}{2}} \sqrt{v_{d}^{2} + v_{q}^{2}}) + L_{io} ω \\ - Т = L_{oi} (\sqrt{\frac{3}{2}} \sqrt{v_{d}^{2} + v_{q}^{2}}) + L_{oo} ω \end{cases}

(29)

Control of the PMSM electromagnetic torque is carried out, most often, in a vector method using a transistor VI, which is implemented by forming the armature current vector, respectively, the EMF vector according to the corresponding law. This law depends on the type of PMSM and its angular velocity control region and directly affects the machine efficiency.

3.3. Efficiency Optimization of SPMSM Operation below Rated Speed

In the SPMSM, the magnets are fixed on the surface of the rotor, therefore, taking into account the fact that the magnetic permeability of PMs is close to the magnetic permeability of air, the inductances along the d and q axes have the same value: L_d = L_q = L = 2 mH. This leads to the presence of only an active component in the electromagnetic torque (6):

T = \frac{3}{2} p_{p} ψ_{pm} i_{q 0}

(30)

In this regard, the energy-efficient SPMSM vector control strategy is the condition i_d = 0 [6]. Under this condition, the input active power (26) will take the form

P_{i} = (\sqrt{\frac{3}{2}} v_{q}) (\sqrt{\frac{3}{2}} i_{q})

(31)

Based on (31), the input power and flow of the PC will be equal to

X_{i} = \sqrt{\frac{3}{2}} u_{q}

J_{i} = \sqrt{\frac{3}{2}} i_{q}

, and the system of linear equations describing the operation of SPMSM as PC will have the form

\{\begin{cases} (\sqrt{\frac{3}{2}} i_{q}) = L_{ii} (\sqrt{\frac{3}{2}} v_{q}) + L_{io} ω \\ - Т_{L} = L_{oi} (\sqrt{\frac{3}{2}} v_{q}) + L_{oo} ω \end{cases}

(32)

Let us determine the kinetic coefficients in the system of equations (32) using the mathematical model of the PMSM steady-state operation (8) and (9).

Under the condition of i_d = 0, from the first equation of system (9), we obtain

i_{d 0} = \frac{1}{R_{c}} v_{d}

(33)

Substituting (33) into the first equation of system (9), we get

v_{d} = - p_{p} ω L_{q} i_{q 0}

(34)

Substituting (34) into (33), and then the resulting expression into the second equation of system (8), after transformations we get

i_{q 0} (1 + A {(\frac{p_{p} ω}{R})}^{2} L_{d} L_{q}) = - \frac{1}{R} v_{q} - \frac{A}{R} p_{p} ψ_{pm} ω

(35)

The second term in parentheses can be neglected due to its smallness.

By substituting the obtained value i_q₀ into the second equation of system (9), as well as into the third equation of system (9), we obtain

i_{q} = \frac{1}{R} v_{q} - \frac{p_{p} ψ_{pm}}{R} ω

(36)

T_{L} = \frac{3}{2} \frac{p_{p} ψ_{pm}}{R} v_{q} - \frac{3}{2} \frac{A {(p_{p} ψ_{pm})}^{2}}{R} ω

(37)

Equations (36) and (37) are reduced to system of equations (32):

\{\begin{cases} (\sqrt{\frac{3}{2}} i_{q}) = \frac{1}{R} (\sqrt{\frac{3}{2}} v_{q}) - \sqrt{\frac{3}{2}} \frac{p_{p} ψ_{pm}}{R} ω \\ - Т_{L} = - \sqrt{\frac{3}{2}} \frac{p_{p} ψ_{pm}}{R} (\sqrt{\frac{3}{2}} v_{q}) + \frac{3}{2} \frac{A {(p_{p} ψ_{pm})}^{2}}{R} ω \end{cases}

(38)

From the equations of system (38), we obtain the expressions for the kinetic coefficients of the PC, which describe the operation of the vector-controlled SPMSM:

L_{ii} = \frac{1}{R}, L_{io} = - \sqrt{\frac{3}{2}} \cdot \frac{p_{p} ψ_{pm}}{R}, L_{oo} = \frac{3}{2} \cdot \frac{A}{R} {(p_{p} ψ_{pm})}^{2}

(39)

Based on kinetic coefficients (39), expressions for the main dimensionless parameters of this PC can be obtained from (12)-(14):

q = - {(A)}^{- 0.5}, Z = \sqrt{\frac{3 A}{2}} p_{p} ψ_{pm}, χ = \sqrt{\frac{3}{2}} \cdot \frac{v_{q}}{ω}, Z χ = \frac{3}{2} \sqrt{A} p_{p} ψ_{pm} \frac{v_{q}}{ω}

(40)

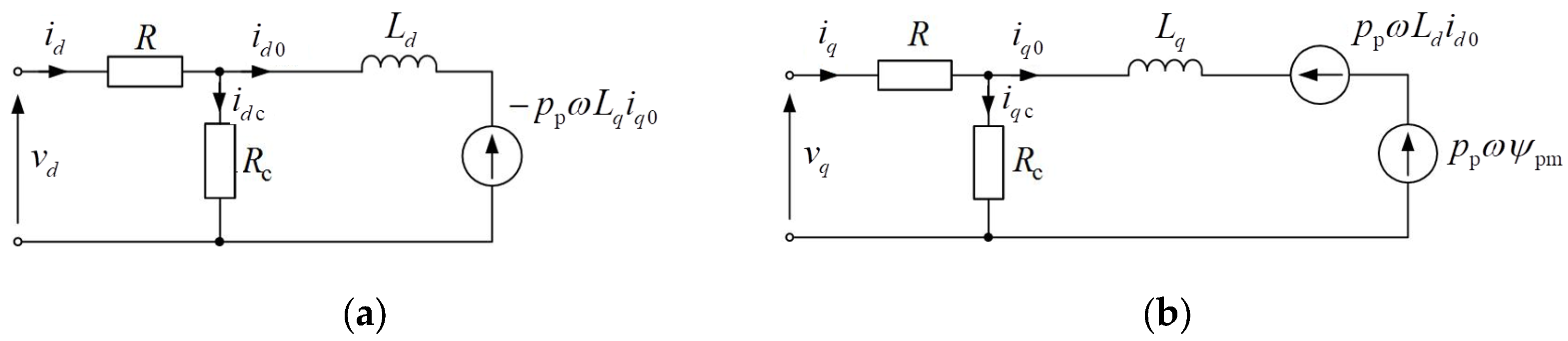
As can be seen from the obtained results (40), the coefficient of coupling q of the PC modelling the SPMSM vector controlled by the i_d = 0 method, for the case without taking into account iron losses, is equal to –1 and does not depend on the mode parameters of the machine. In this case, the SPMSM is modeled by only one substitute scheme determined by the coordinate q, but without resistance R_c (Figure 1(b)). Therefore, the current i_q completely forms an electromagnetic torque, that is, it is directly linked with the output current. For the case of taking into account iron losses, the resistance R_c appears in the substitute circuit, through which a part of the input current is closed. In this way, there is already an incomplete coupling between the input and output of the PC, and the coefficient of coupling is determined through the value A according to (40). 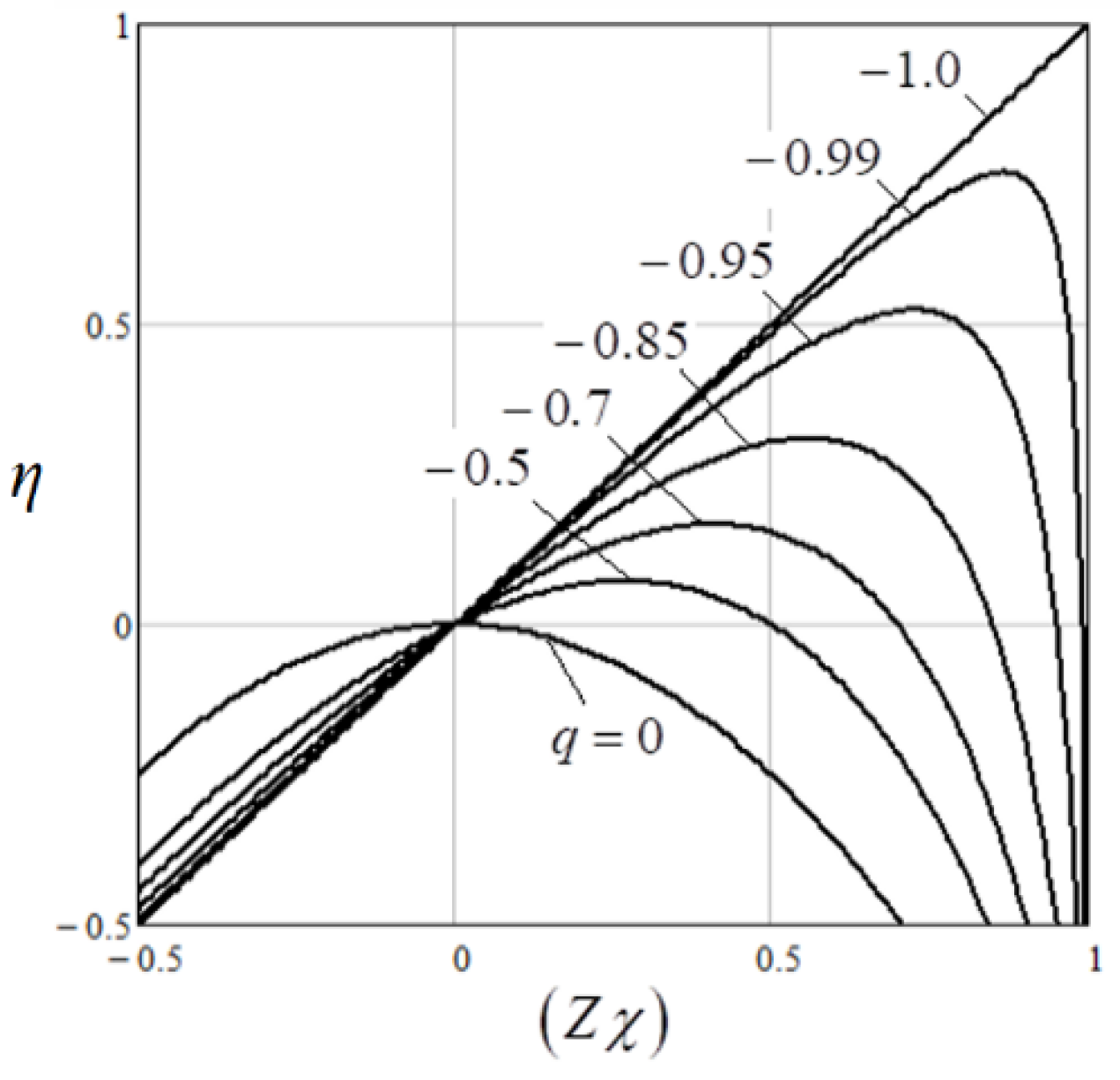With a decrease in the angular velocity of the machine, A decreases because, according to (25), the value of the resistance R_c decreases. For the machine under study, when the relative angular velocity ω^* decreases from 1 to 0.25, the value of q changes from -0.9965 to -0.9898. The maximum energy efficiency of such a machine, according to (17), also decreases from 0.845 to 0.751 (Figure 3). The value of (Zχ)_opt also decreases from 0.919 to 0.867.

The value of the SPMSM operating point Zχ, in turn, depends on the values of two main variables – the angular velocity of the machine ω and the load torque T_L, which directly affect the value of v_q. The value of the latter was calculated from equations (6), (8) and (9) under the following conditions:

i_{q 0} = \frac{2 T_{L}}{3 p_{p} ψ_{pm} i_{q 0}}, v_{d} = - p_{p} ω L_{q} i_{q 0}, i_{d 0} = - \frac{v_{d}}{R_{c}}, v_{q} = R i_{q 0} + A p_{p} ω (L_{d} i_{d 0} + ψ_{pm})

(41)

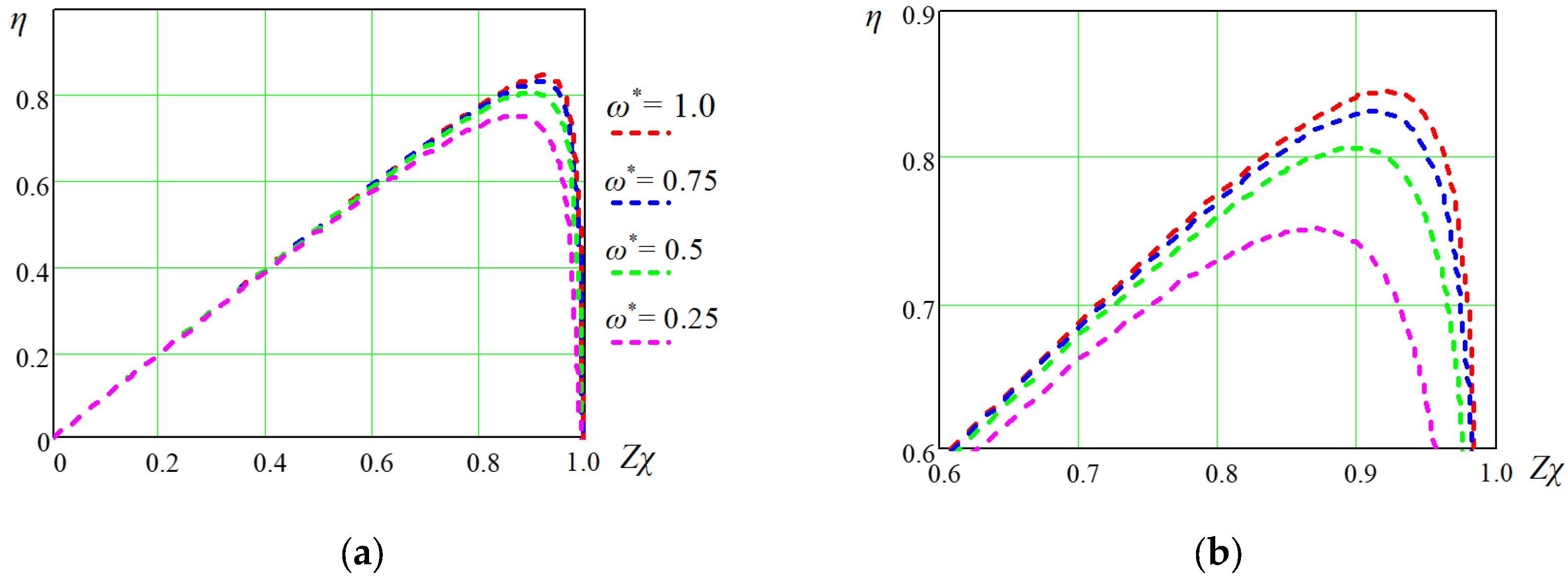
Figure 4 shows how the dimensionless indicator Zχ of the operating mode of the experimental machine depends on the fixed values of the main variables ω and T_L. As can be seen from this figure, the optimal value of (Zχ)_opt, and therefore the maximum efficiency of the machine, is achieved only with a certain combination of values ω and T_L. The following relationship between the variables ω and T_L corresponds to (Zχ)_opt curve:

T_{L} = - 14.03 + 1.442 ω + 0.006377 ω^{2}

(42)

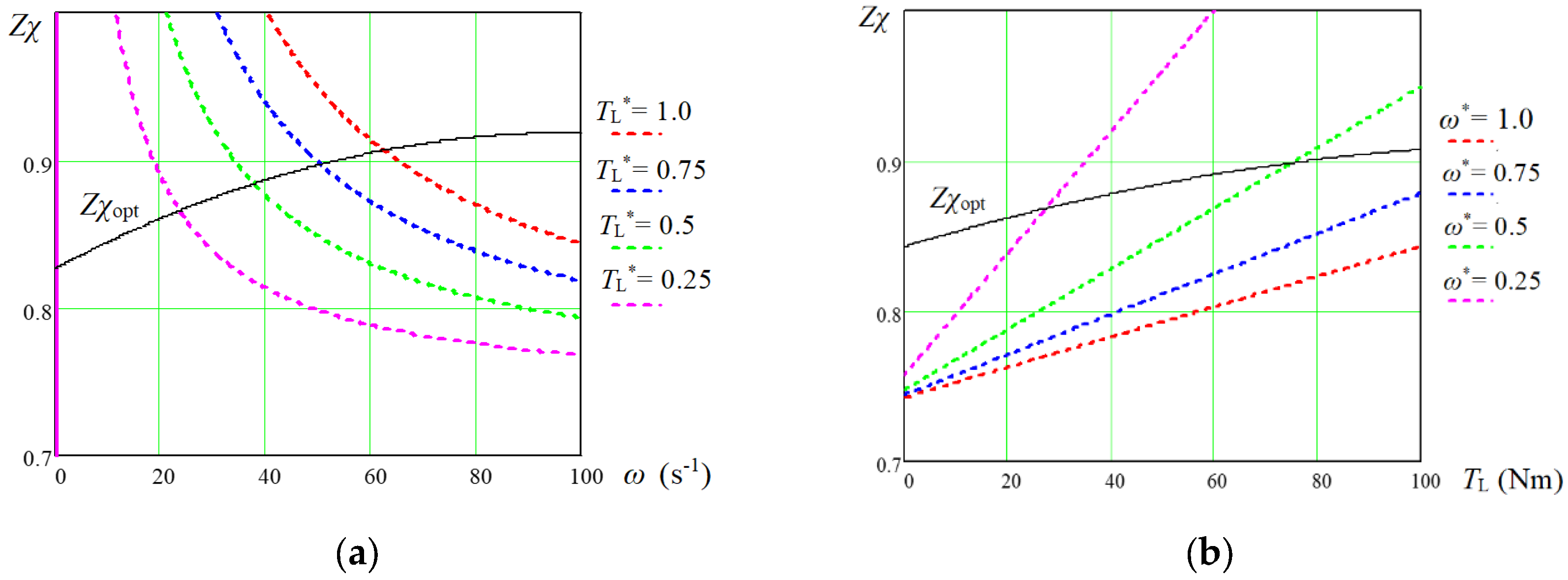
In Figure 4 both above and below the curves shown (Zχ)_opt, the energy efficiency of the SPMSM decreases, and the lower part corresponds to the left side of the η(Zχ) characteristics shown in Figure 3, and the upper part is on the right side of the η(Zχ) characteristics. As can be seen from Figure 4(a), the parts of the obtained dependences, which lie below the (Zχ)_opt curve, correspond to higher angular velocities of the machine. For them, the value of Zχ does not decrease below 0.76. This means that energy efficiency will not be less than 0.75 even at the nominal load torque. The situation can be worse at low motor angular velocities, which are characterized by the upper parts of the dependences in relation to the (Zχ)_opt curves in Figure 4. 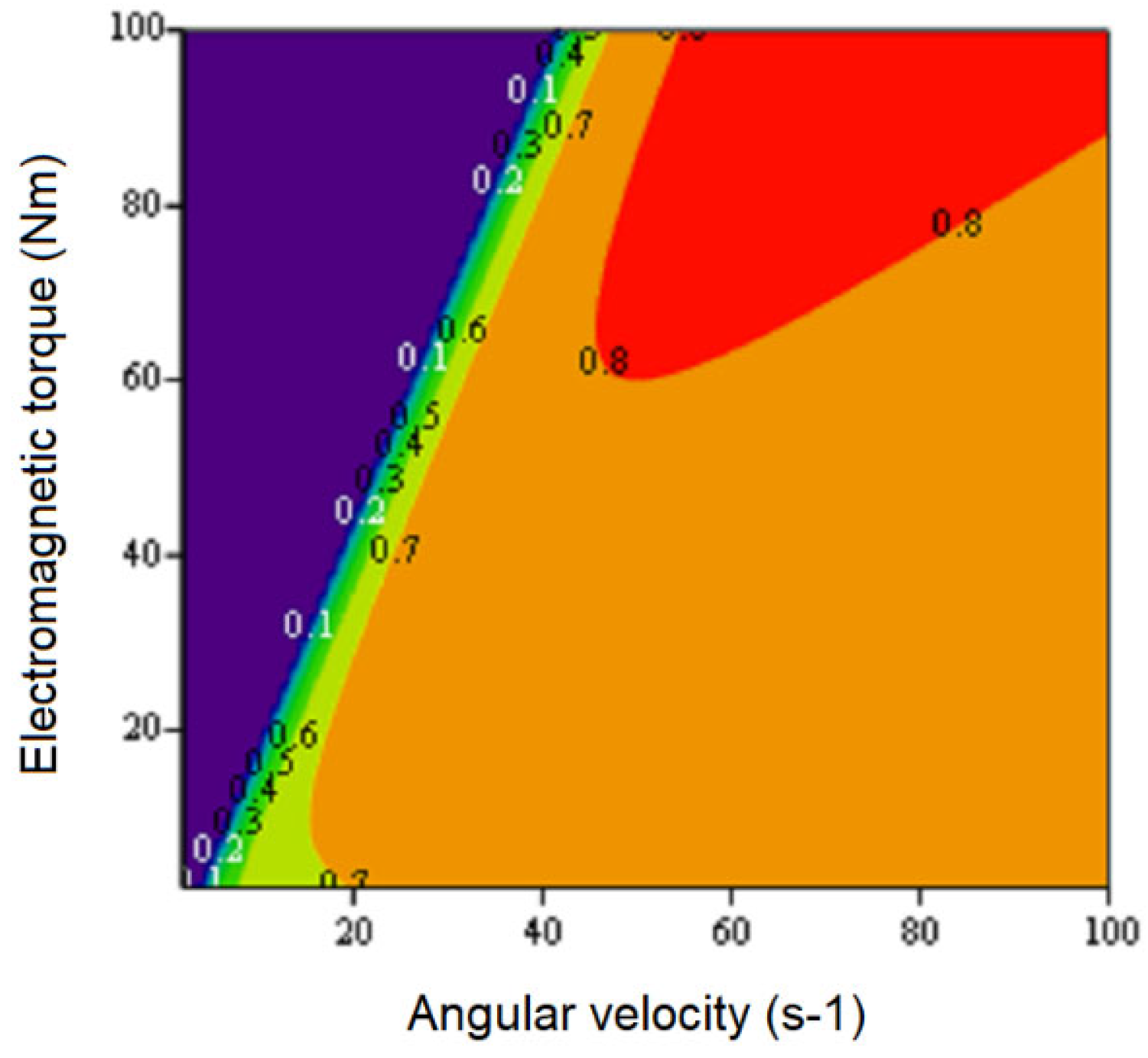As can be seen from Figure 4(a), there is a limitation regarding the maximum load torque, below which the energy efficiency can rapidly decrease to zero. At the same time, the smaller the angular velocity of the SPMSM, the smaller the load torque permissible for a given level of efficiency. The obtained regularity can be clearly seen from the efficiency map, which is constructed for the experimental SPMSM in Figure 5. As the resulting map shows, high energy efficiency is ensured in a fairly wide range starting from the minimum angular speed, at which the machine starts to develop an electromagnetic torque, up to the nominal load and higher. However, it can be seen from the obtained efficiency map that the SPMSM, which is controlled according to the i_d = 0 criterion, cannot provide sufficient electromagnetic torque for EVs at low drive speeds. During acceleration of the experimental machine, as can be seen from Figure 5, its electromagnetic torque will increase gradually, and will reach its nominal value only after half of the nominal value of the angular velocity. Unfortunately, there are no other options to change the SPMSM performance map.

3.4. Efficiency Optimization of IPMSM Operation Below the Rated Speed

As can be seen from the nonlinear mathematical model of IPMSM for its steady-state operation – from systems of equations (8) and (9), as well as from complex expressions for the input force and flow (28), obtain analytical expressions for the kinetic coefficients of the PC that describe the operation of this machine, is impossible. Therefore, the research method for this case remains only numerical. Since the system is clearly nonlinear, the PC parameters will change depending on the working point of the machine - the set values of the angular velocity ω₀ and the load torque T_L0. For a given pair of values of these variables, it is necessary to linearize the system and obtain the PC parameters.

As is known [9], already in the first range of angular velocity regulation of the IPMSM, the energy efficiency of its operation also depends on the value of the armature current component i_d. Even for the classic case – without taking into account iron losses – it is not possible to obtain analytical expressions for the dependencies of the optimal values of the components of the armature current on the value of only the load torque - the MTPA curve [35]. If iron losses are also taken into account, even with the help of such a simple model, which is used in this work, it will not be possible to obtain such analytical dependencies. Therefore, for the purpose of numerical energy optimization of IPMSM taking into account iron losses, it is necessary to introduce one more variative variable. As the analysis showed, it is easiest to choose the component of the armature current i_d₀, which determines the reactive component of the electromagnetic torque. Therefore, further calculations should be carried out as a function of this variable.

Therefore, it is advisable to build the IPMSM mathematical model taking into account iron losses, for successive numerical calculations, based on the systems of equations (8), (9) and expressions (28) in the following view:

i_{q 0} (i_{d 0}) = \frac{2 T_{L}}{3 p_{p} [ψ_{pm} + (L_{d} - L_{q}) i_{d 0}]}

(43)

v_{d} (i_{d 0}) = R i_{d 0} - A p_{p} ω L_{q} i_{q 0} (i_{d 0})

(44)

v_{q} (i_{d 0}) = R i_{q 0} + A p_{p} ω (L_{d} i_{d 0} + ψ_{pm})

(45)

i_{d} (i_{d 0}) = \frac{1}{A} i_{d 0} + \frac{1}{R_{c} A} v_{d} (i_{d 0})

(46)

i_{q} (i_{d 0}) = \frac{1}{A} i_{q 0} (i_{d 0}) + \frac{1}{R_{c} A} v_{q} (i_{d 0})

(47)

v_{a} (i_{d 0}) = \sqrt{\frac{3}{2}} \sqrt{v_{d}^{2} (i_{d 0}) + v_{q}^{2} (i_{d 0})}

(48)

i_{a} (i_{d 0}) = \sqrt{\frac{3}{2}} \sqrt{i_{d}^{2} + i_{q}^{2}} \cos (atan \frac{v_{d} (i_{d 0})}{v_{q} (i_{d 0})} - atan \frac{i_{d} (i_{d 0})}{i_{q} (i_{d 0})})

(49)

Having the set parameters of the working point of the machine ω = ω₀ and T_L = T_L0, as a result of cyclic calculations according to expressions (43)-(49) for points in the range i_d₀ = 0 – (-100) A, the final dependences v_a(i_d₀) and i_a(i_d₀), which characterize the input power of the PC depending on the value of component of the armature current i_d₀, are obtained at a given output power P_o(ω₀, T_L0). Thus, for each value of i_d₀ there is a pair of the PC input and output coordinates - flow X and force J. However, these values are not enough to determine three kinetic coefficients from two equations in system (29). To obtain one more point of the linear PC, it is necessary to linearize the obtained dependences of the input force v_a(i_d₀) and the input flow i_a(i_d₀) of the PC on the output coordinates of the force ω and the flow T_L at the given point (ω₀, T_L0). To obtain such linear dependences, similar calculations were carried out according to expressions (43)-(49), but for points equidistant to the left and right of the given point at some insignificant distances: once by the value of ω₀ for T_L = T_L0, and the second time by the value of T_L0 for ω = ω₀. Four linear dependences of the input flow and force on the output flow and force at the given point (ω₀, T_L0) were found based on the pairs of values v_a(i_d₀) and i_a(i_d₀) obtained at these points, and depending on i_d₀. Attempts to apply points from the obtained linear dependencies to determine the kinetic coefficients showed that if even two points from different dependencies are taken, then the values of the kinetic coefficients L_io and L_oi determined from the two equations of system (29) will be different. Therefore, only one linearized dependence was taken – v_a(i_d₀) in the function ω, which the least of all obtained differs from the linear character that leads to the smallest calculation error. From this dependence, one point was determined – the voltage value v_a(i_d₀) at ω = 0:

v_{a . ω = 0} (i_{d 0}) = v_{a 0} (i_{d 0}) - k_{v (ω)} (i_{d 0}) ω_{0}

(50)

where

k_{v (ω)} (i_{d 0})

are the angular coefficients of the linear dependences of v_a on ω found for different values of i_d₀.

The value of the kinetic coefficients was carried out in the following order.

From the second equation of system (29) for ω = 0 is obtained

L_{o i} (i_{d 0}) = \frac{- T_{L 0}}{v_{a . ω = 0} (i_{d 0})}

(51)

From the first equation of system (29) for the working point of the PC is found

L_{ii} (i_{d 0}) = \frac{i_{a 0} (i_{d 0}) - L_{o i} (i_{d 0}) ω_{0}}{v_{a 0} (i_{d 0})}

(52)

From the second equation of system (29) for the working point of the PС is determined

L_{oo} (i_{d 0}) = \frac{- T_{L 0} - L_{o i} (i_{d 0}) v_{a 0} (i_{d 0})}{ω_{0}}

(53)

With the use of kinetic coefficients (51)-(53) according to expressions (12)-(14), dependences on the main parameters of the PC and the indicator of the energy efficiency of the experimental IPMSM taking into account iron losses were obtained: q(i_d₀), Zχ(i_d₀), and η(i_d₀).

According to the described algorithm, a program was created in the MathCad environment that allows you to calculate the specified parameters and performance indicators of the PC, which models the operation of the experimental IPMSM taking into account iron losses for different operating points of the machine depending on the component of the armature current i_d₀.

To check the correctness of the algorithm, the first computational experiment was conducted for the variant whose results can be determined analytically – for the IPMSM without taking into account iron losses. Having set three orders of magnitude higher than the real value of R_c in the model, the results were obtained for the nominal angular velocity of the machine and for the values of the load torque of 0.25T_n, 0.5 T_n, 0.75 T_n, and 1.0 T_n, which are shown in Figure 6.

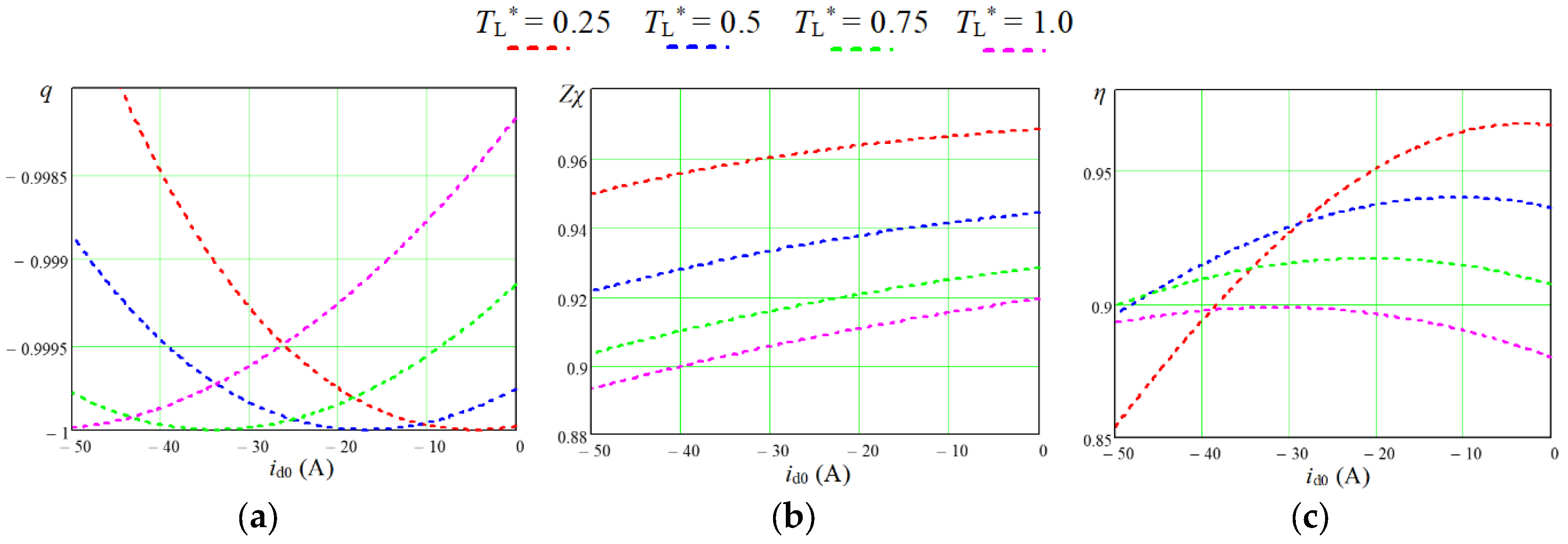
From the dependences η(Zχ) shown in Figure 6, the value of the current component i_d₀, at which the maximum energy efficiency is achieved, were obtained that are listed in Table 2. Since in the case of not taking into account iron losses, i_d₀ = i_d, these values should correspond to the values of the MTPA curve. In [24], the dependence in p. u. between the electromagnetic torque and the component of the armature current i_d for IPMSM at the points of the MTPA curve is given as

T^{*} = 1.5 \sqrt{- i_{d}^{*} {(1 - i_{d}^{*})}^{3}}

(54)

where the relative values are normalized to the corresponding base values

T_{b} = p_{p} ψ_{pm} i_{b}, i_{b} = ψ_{pm} / (L_{q} - L_{d})

(55)

For calculation, a numerical dependence was obtained from expression (54) in [24]:

i_{d}^{*} = 0.01 T^{* 2} - 0.298 T^{*} + 0.0481

(56)

Calculated using (54)-(56) for the experimental IPMSM i_d values from the MTPA curve are given in Table 2. The deviation obtained according to the developed algorithm from the corresponding values obtained analytically does not exceed 1.5 A for medium and high loads, which is less than 10% for medium loads and less than 5% for the nominal motor load torque. This is an acceptable result for these studies and indicates the adequacy of the proposed research method and algorithm for calculating the parameters and performance indicators of IPMSM taking into account iron losses.

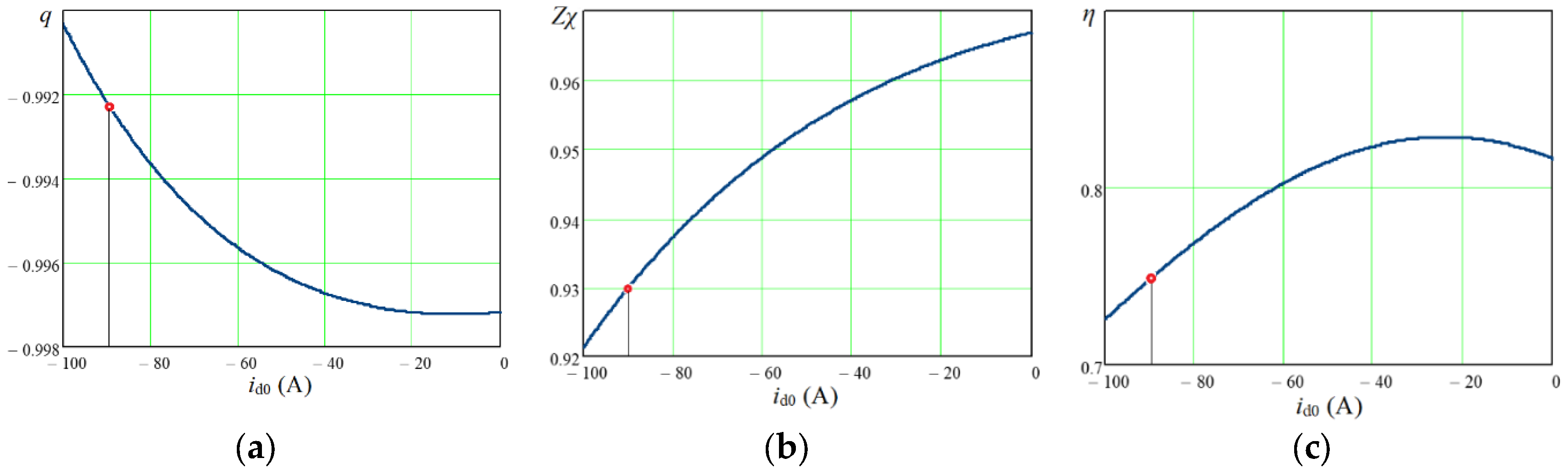
From Figure 6, it can be seen that even without taking into account in the IPMSM iron losses the coefficient of coupling decreases. q = –1, i.e. full coupling for each loads occurs only for the one value of i_d₀, i.e. for a certain optimal ratio between the components of the armature current id₀ and i_q₀. With other ratios between these components, which also provide the required electromagnetic torque of the machine, the coupling between the input and output will already be incomplete. This can be explained by the different contribution of the components of the armature current to the production of the electromagnetic torque according to (6) and the two substitute circuits that work in this case (Figure 1). With different from the optimal ratios between the components of the armature current, there is a "slippage" of power in one of the circuits or in two circuits together.

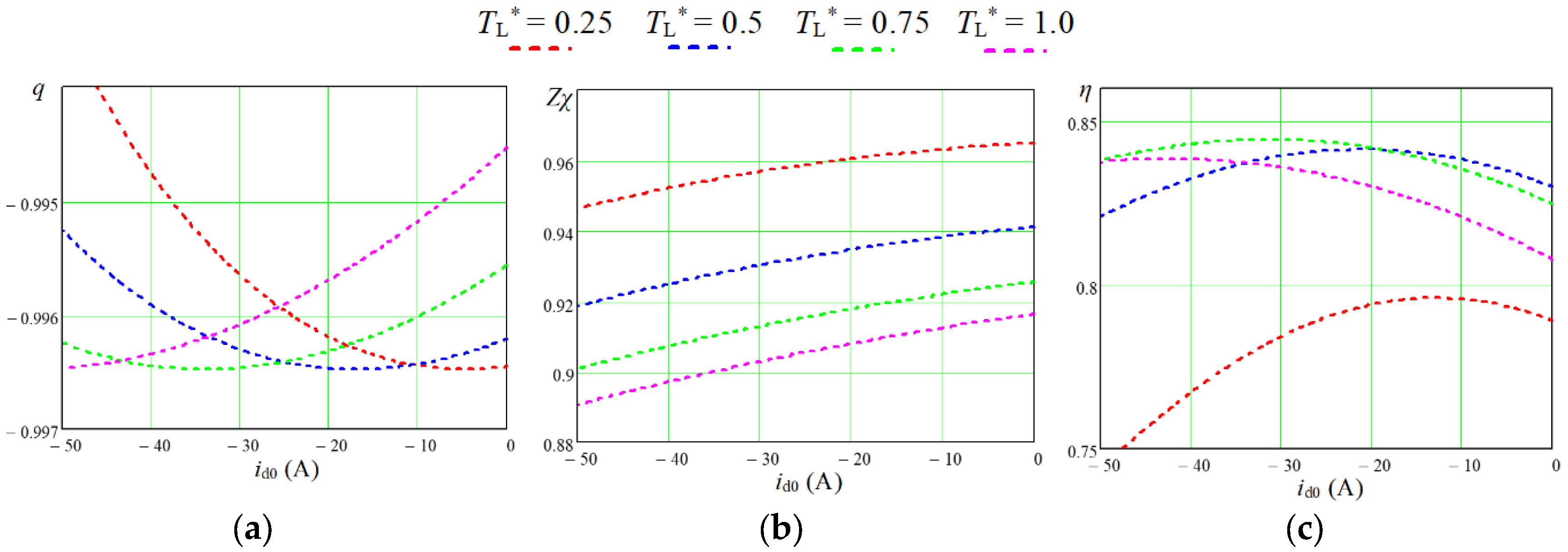
In Figure 7 are similar to those shown in Figure 6 dependencies obtained by the developed calculation program for the experimental IPMSM taking into account iron losses.

Comparison of the results shown in Figure 7 with the similar ones shown in Figure 6 makes it possible to draw the following conclusions. Taking into account iron losses leads to a decrease in the modulus of the PC coefficient of coupling, which simulates the operation of the machine (Figure 7(a)) and a shift of its maximum towards higher values of the id0 current component. The values of the maximum energy efficiency under medium and high loads of the drive (T_L^* = 0.5 – 1.0) are reduced by taking into account the iron losses by 5-9% compared to the option without taking into account these losses (Figure 7(c)). In the case of low drive load (T_L^* = 0.25), η is reduced by as much as 17%, which is explained by the relative increase in the effect on η of losses in steel compared to reduced losses in copper. The points of maximum energy efficiency are also shifted towards larger values of the i_d₀ current component, which are very close to similar values of this current, at which the maximum value of the coefficient of coupling is ensured. Similar regularities also occur for other values of IPMSM angular velocity.

Thus, the presence of one more variable coordinate – the i_d₀ current component – makes it possible to ensure the operation of the IPMSM taking into account the iron losses at the points of maximum energy efficiency. The developed technique makes it possible to obtain optimal values of i_d_0.opt for each pair of values of the operating point of the drive - angular velocity and load torque.

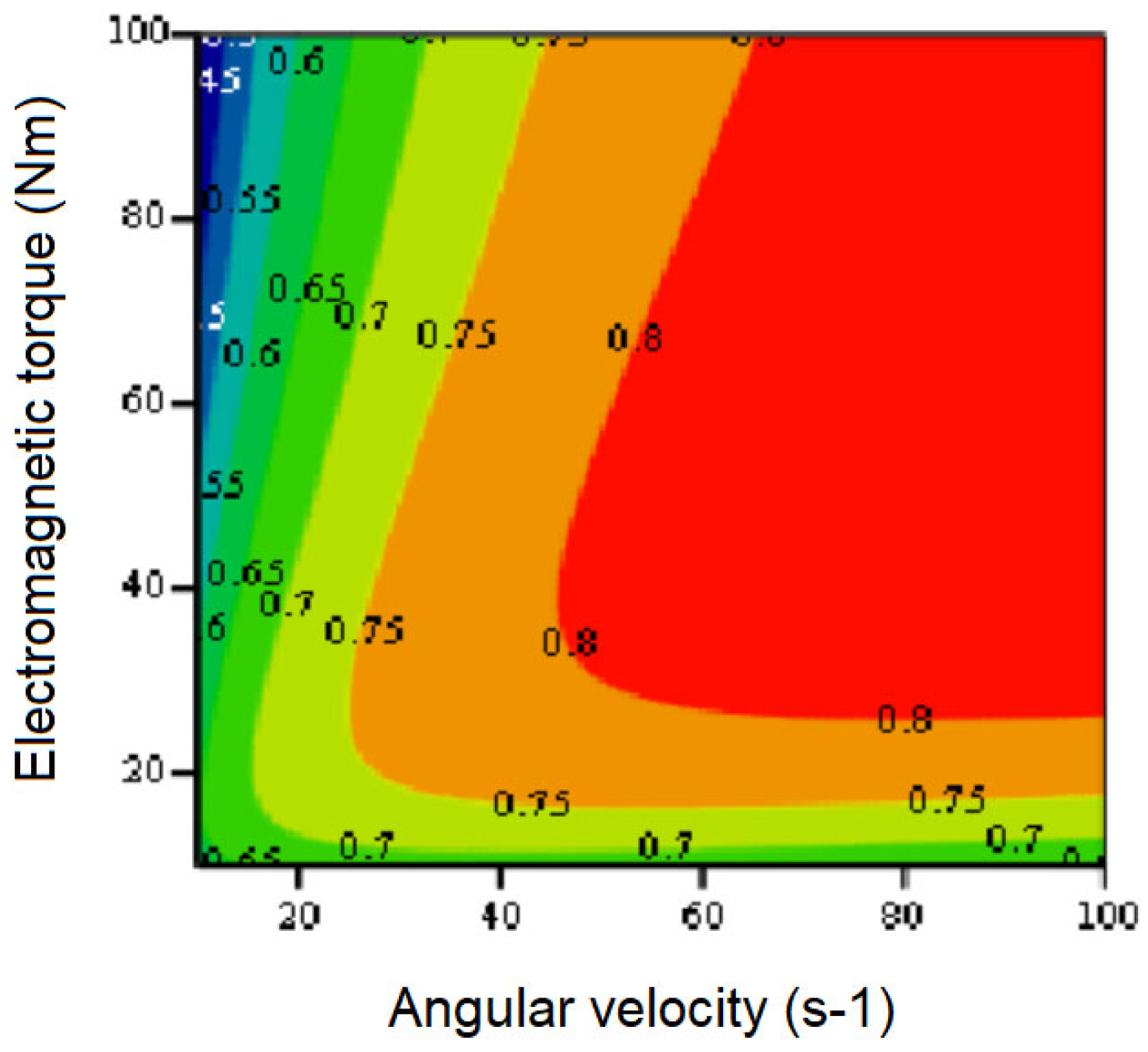
Figure 8 presents the efficiency map obtained for the experimental IPMSM taking into account iron losses, which operates at the points of maximum energy efficiency at optimal values of the i_d_0.opt current component. The map is calculated using the same created program; however, i_d_0.opt is needed at each step of the calculations for the running values of the machine's angular velocity and torque. Such values were obtained in the program by interpolation from the dependence i_d_0.opt (ω,T_L), previously obtained from experiments similar to those shown in Figure 7 carried out for a number of angular velocities of the experimental machine. Since the above dependence is smooth, the interpolation error did not exceed 2%. A comparison of the obtained efficiency map for IPMSM with the efficiency map for SPMSM (Figure 5) shows the advantages of the first over the second, which are the ability to provide a large starting torque and a wider zone of maximum energy efficiency – more than 0.8.

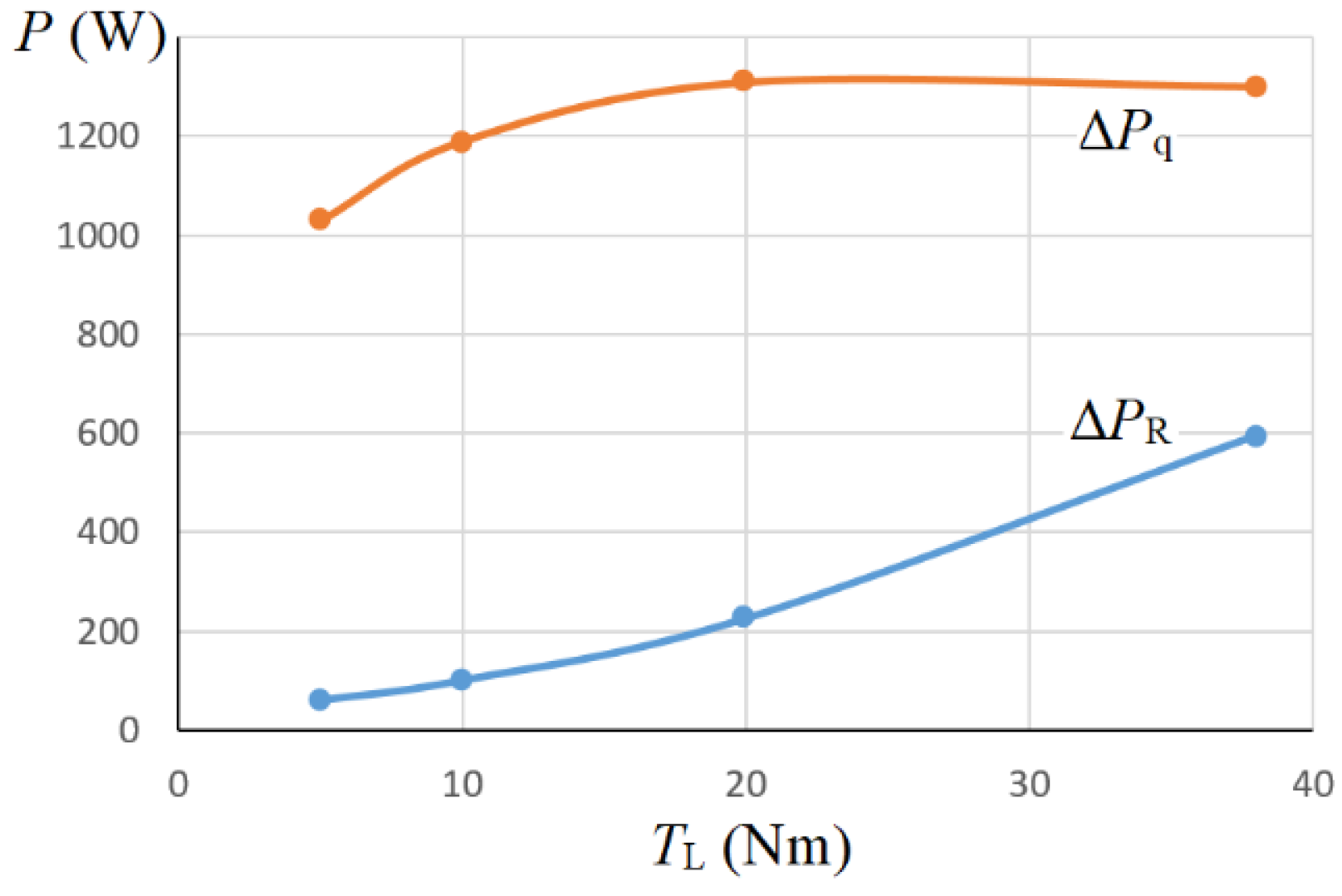
Based on the given results of the IPMSM operation with different loads at the nominal angular velocity, it is possible to easily calculate, based on (22) and (23), the power loss components caused by the imbalance of the power conversion process ΔP_R and incomplete coupling of the PC ΔP_q. The calculation procedure is as follows. From Figure 7(b), the values of the current component i_d_0.opt for each load are obtained. For each of i_d_0.opt from Figures 7(a) and 7(b), the values of q and Zχ are defined, which are used to find the power loss components in p. u. using (22) and (23). For each of the loads, the value of the input force X_i = v_s(i_d_0.opt) and the kinetic coefficient L_ii(i_d_0.opt) are determined from the program. Based on the obtained data, the absolute values of the components of power losses were found using the same expressions (22) and (23). Their dependence on the IPMSM load is shown in Figure 9.

As can be seen from the obtained results, the losses from incomplete coupling ΔPq, which are caused primarily by losses in steel, at a constant motor angular velocity depend very little on the drive load, while the losses from the imbalance of the process ΔP_R, which are the heating losses in the armature windings, rapidly increase with an increase in the load torque of the drive.

3.5. Efficiency Optimization of IPMSM Operation Above the Rated Speed

The numerical simulation algorithm of the IPMSM taking into account iron losses operation developed with the use of the LNTD is quite suitable for modelling their operation in the second region of angular velocity regulation - above its nominal value. The difference between IPMSM operation in the second region compared to the first one is the presence of a limitation on the armature voltage that is caused by the value of the DC voltage V_DC of the VI power supply, as well as a limitation on the armature current in the long-term operating mode that is caused by the heating of the motor. These restrictions are described by the following inequalities [5]:

\sqrt{v_{d}^{2} + v_{q}^{2}} \leq v_{s . \max}

(57)

\sqrt{i_{d}^{2} + i_{q}^{2}} \leq i_{s . \max}

(58)

where v_s.max is the maximum value of the armature voltage amplitude in the two-phase reference frame and i_s.max is the maximum value of the armature current amplitude in the two-phase reference frame in the long-term motor operating mode.

The v_s.max value is related to V_DC by the following relationship:

V_{DC} = \sqrt{3} v_{s . \max}

(59)

With the use of the developed calculation program in the MathCad environment, work was simulated in the second region of the experimental IPMSM taking into account the iron losses, similarly as it was done for the first region.

At the beginning, for the nominal operating mode of the machine – the nominal values of the angular velocity and the load torque – the v_s.max and i_s.max values were determined by (57) and (58): v_s.max = 87 V and i_s.max = 93.5 A. According to (59), the required value for this is V_DC = 150 V.

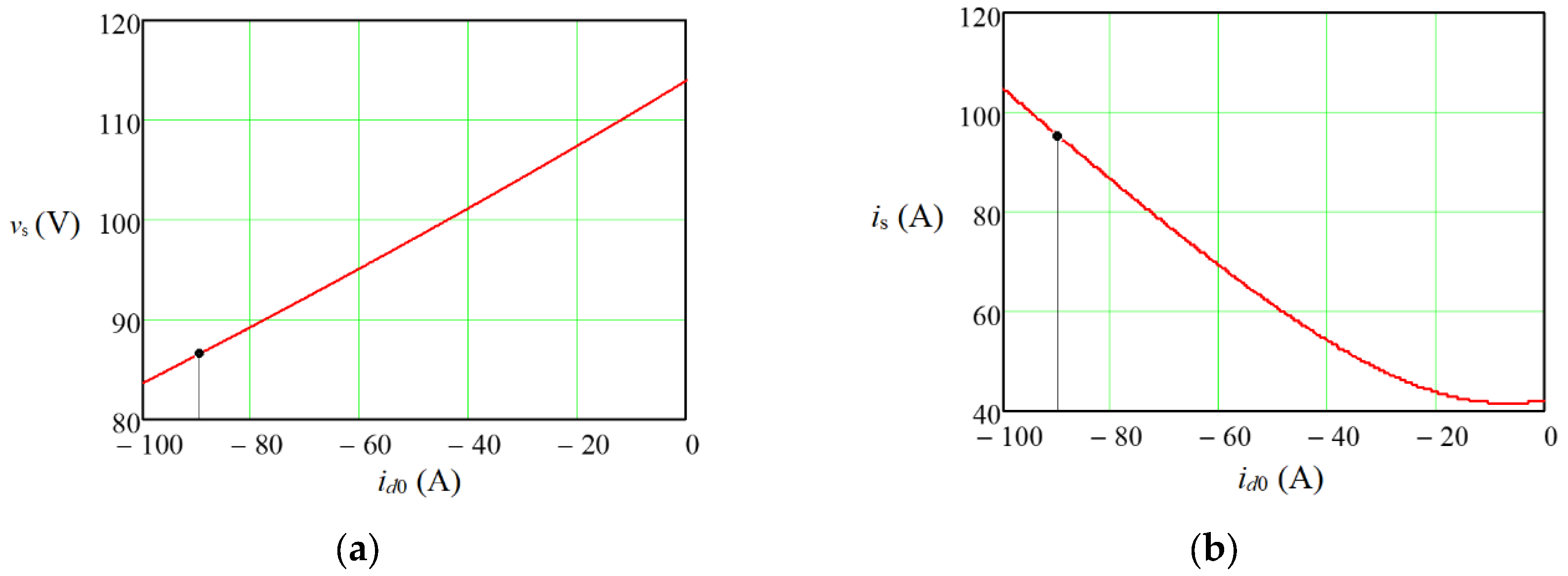
Further studies were carried out for the relative angular velocity of IPMSM equal to ω^* = 1.5. The research methodology consisted in reducing the motor load torque to such a value that the voltage vs decreased to v_s.max. As a result, the value of the load torque T_L = 38 Nm, which was permissible from the point of view of current limitation, was obtained (Figure 10). At the same time, the optimal i_d0 value for ensuring the specified maximum torque was -90A. Dependencies of the main parameters and characteristics for the PC, which models of the experimental IPMSM operation on the value of such armature current component i_d0 during machine operation in the second region with an angular velocity of 150 s-1 for the maximum value of a load torque of 38 Nm are shown in Figure 11. As can be seen from the figure, at the operating point, the degree of coupling is q = –0.9923, and the energy efficiency of the IPMSM is η = 0.750. At the same time, for the optimal value i_d0 = –23 A for this load η = 0.828. However, for such a regime, the required value of v_s is 107 V, which is significantly more than the nominal value (Figure 10(a)).

Analyzing the dependencies presented in Figure 11, it can be concluded that the operation of the IPMSM in the second angular velocity control region is characterized by a significant shift of the operating point from the point of maximum energy efficiency. This is explained by the need to set such a value of the armature current component i_d0, which would provide the task of increased angular velocity while limiting the value of the armature voltage at the nominal level. When the angular velocity increases, the armature voltage remains unchanged, but the armature current increases (Figure 10(b)), which leads to a decrease in energy efficiency. The higher the given angular velocity, the larger the id0 value will be, and the lower the energy efficiency will be. That is, when working in the second region, the i_d0 value is assigned a different task than energy optimization, as it was in the first region. Hence, accordingly, a decrease in the energy efficiency of the machine. When the load torque decreases below the permissible value of 38 Nˑm for a given angular velocity, the energy efficiency decreases even more. Thus, at the same angular velocity of the machine of 150 s^-1, the decrease of T_L to 18 Nˑm leads to a decrease of i_d0 to -70 A, but η decreases already to 0.657.

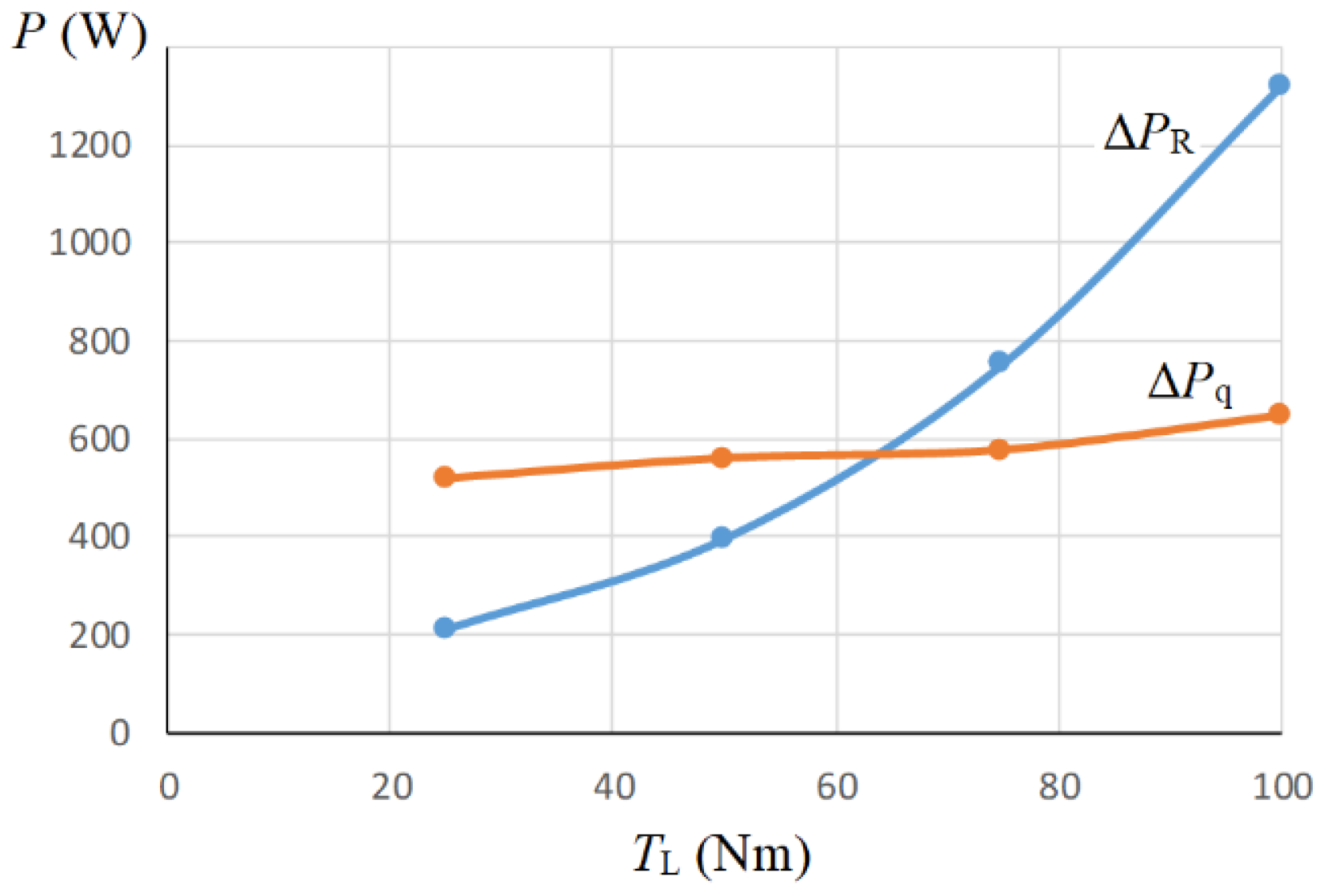
To analyze the energy regularities of IPMSM operation in the second region of angular velocity regulation, for the last experiment, the components of power loss due to process imbalance ΔP_R and the PC incomplete coupling ΔP_q on the drive load torque T_L were calculated according to the algorithm described in subsection 3.4 (Figure 12). The T_L varied from 5 Nm to the maximum permissible value of 38 Nm for a given angular velocity of 150 s^-1.

The nature of the components of power losses in IPMSM during its operation in the second region of angular velocity regulation obtained in Figure 12 is radically different from the nature of these losses in the first region shown in Figure 9. Although the total value of power losses at the maximum load of the drive differs slightly, and, in the second region, the iron losses clearly prevail over the copper losses. As in the previous case, the iron losses slightly depend on the drive load, since the motor angular velocity is unchanged, but in the second region, these losses are approximately twice as large as in the first one. Losses in copper are also higher in the second region than in the first one for the same value of the load torque. This is explained by the significant value of the current component id0, at the level of (–65) – (–90) A, compared to this component in the range (–13) – (–43) A in the first region. As a result of the significant losses and the low value of the electromagnetic torque of the motor, despite its higher angular velocity, the energy efficiency of the IPMSM in the second region decreases (from 0.365 to 0.745 in the computational experiment) compared to the first region (from 0.795 to 0.845).

4. Conclusions

Due to the rapid development of EVs, the requirements for the energy efficiency of PMSMs in a wide range of their angular velocity and torque are increasing. Therefore, the substantiation of optimal from the point of view of maximum energy efficiency of the set coordinates – the d and q components of the armature current, which is used for the vector control of the PMSMs torque, is an urgent task.

The LNTD approach, in particular, the method of universal description of objects as PC, is promising for the analysis of energy processes and improving the efficiency of various systems, in particular electromechanical converters as a PMSM. This approach makes it possible to evaluate the energy quality of systems of different natures from one universal point of view without delving into the physical, chemical or other features of the processes.

The method of mathematical modelling of IPMSM operation taking into account iron losses as a universal PC operating at a given point, developed in this work based on the LNTD, makes it possible to evaluate the quality of energy conversion in the system and, if possible, to choose the optimal values of regulating coordinates to increase its energy efficiency. Conducting research for SPMSM during its operation below the nominal angular velocity according to the vector criterion i_d = 0 made it possible to obtain analytical expressions for PC indicators, which showed that the maximum possible values of energy efficiency are achieved only for certain ratios between the values of angular velocity and electromagnetic torque. The algorithm and research program have been developed for IPMSM, taking into account iron losses, which makes it possible to obtain the indicators of the universal PC for each working point of the machine depending on the values of the armature current component i_d. For the operation of the machine below the nominal angular velocity, the values d and q of the armature current components that are optimal from the point of view of maximum energy efficiency were obtained for the implementation of the MTPA strategy at each operating point. For the second region of IPMSM angular velocity regulation, the value of the armature current component i_d ensures the machine's operation on the armature voltage limitation curve, where optimal operation in terms of energy efficiency is ensured. The proposed method also makes it possible to easily determine the main components of power losses – from process imbalance, which are losses in copper, and from incomplete coupling between the input and output of PC, which in this case are losses in steel. For IPMSM operation in the ranges below and above the nominal angular velocity, the structure of these losses is different: in the first range, as a rule, losses in copper prevail and increase with increasing load, and in the second region, losses in steel dominate and increase with increasing angular velocity of the machine. The methodology developed based on the LNTD makes it possible to obtain the energy efficiency maps for IPMSM operation, taking into account iron losses, in the entire range of changes in the coordinates of the electric drive – angular velocity and load torque.

Further research in this topic will be aimed specifically at improving the accuracy of modelling the steady-state operation of IPMSM, both structurally and parametrically, which will make it possible to increase the accuracy of determining all types of losses and thereby increase the effectiveness of the proposed method of substantiating optimal control coordinates.

Author Contributions

Conceptualization, I.S. and Y.B.; methodology, I.S. and Y.B.; software, Y.B.; validation, B.K.; formal analysis, B.K.; investigation, I.S. and Y.B.; resources, I.S. and B.K.; data curation, I.S. and Y.B.; writing—original draft preparation, I.S. and Y.B.; writing—review and editing, I.S. and B.K.; visualization, Y.B.; supervision, I.S.; project administration, I.S.; funding acquisition, I.S. and B.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:

DC	Direct Current
EV	Electric Vehicle
FEM	Finite Element Method
FW	Flux Weakening
IPMSM	Interior PMSM
LNTD	Linear Non-Equilibrium Thermodynamics
LUT	Look-up Table
MTPA	Maximum Torque per Ampere
NN	Neural Network
PC	Power Converter
PM	Permanent Magnet
PMSM	Permanent Magnet Synchronous Machine
PSO	Particle Swarm Optimization
P&O	Perturb and Observe
SISO	Single Input and Single Output
SPMSM	Surface-Mounted PMSM
VI	Voltage Inverterч

References

Wang, H.; Leng, J. Summary on Development of Permanent Magnet Synchronous Motor. In. Proceedings of the 2018 Chinese Control and Decision Conference (CCDC), Shenyang, China, 09-, 689-693. 11 June. [CrossRef]
Loganayaki, A.; Kumar, R.B. Permanent Magnet Synchronous Motor for Electric Vehicle Applications. Proceedings of the 2019 5th International Conference on Advanced Computing & Communication Systems (ICACCS), Coimbatore, India, 15-, 1064-1069. 16 March. [CrossRef]
Liu, X.; Chen, H.; Zhao, J.; Belahcen, A. Research on the performances and parameters of interior PMSM used for electric vehicles. IEEE Trans. Ind. Electr. 2016, 63, 3533–3545. [Google Scholar] [CrossRef]
Vaclavek, P.; Blaha, P. Interior Permanent Magnet Synchronous Machine Field Weakening Control Strategy – the Analytical Solution. Proceedings of the SICE Annual Conference 2008, 20-, Chofu, Japan, 753-757. 22 August. [CrossRef]
Bianchi, N.; Carlet, P.G.; Cinti, L.; Ortombina, L. A review about flux-weakening operating limits and control techniques for synchronous motor drives. Energies 2022, 15, 1930. [Google Scholar] [CrossRef]
Tinazzi, F.; Bolognani, S.; Calligaro, S.; Kumar, P.; Petrella, R.; Zigliotto, M. Classification and review of MTPA algorithms for synchronous reluctance and interior permanent magnet motor drives. Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE '19 ECCE Europe), Genova, Italy, 03-05 Sept. 2019, P.1-P.10. [CrossRef]
Li, Z.; O’Donnell, D.; Li, W.; Song, P.; Balamurali, A.; Kar, N.C. A Comprehensive Review of State-of-the-Art Maximum Torque per Ampere Strategies for Permanent Magnet Synchronous Motors. Proceedings of the 2020 10th International Electric Drives Production Conference (EDPC), Ludwigsburg, Germany, 08-09 Dec. 2020, 1-8. [CrossRef]
Zhuoyonga, W.; Xiaodonga, Y.; Jiakanga, L.; Liangxua, X.; Huia, T.; Kea, L. Research on IPMSM control based on MTPA. Procedia Computer Science 2022, 208, 635–641. [Google Scholar] [CrossRef]
Dianov, A.; Tinazzi, F.; Calligaro, S.; Bolognani, S. Review and classification of MTPA control algorithms for synchronous motors. IEEE Trans. Power Electr. 2022, 37, 3990–4007. [Google Scholar] [CrossRef]
Shen, Y.; Zhou, B.; Yuan, X.; Zhang, X. Efficiency Optimization Control of PMSM in Electric Vehicle-A Comparative Study. Proceedings of the 2023 7th CAA International Conference on Vehicular Control and Intelligence (CVCI), Changsha, China, 27-29 Oct. 2023, 1-6. [CrossRef]
Ba, X.; Gong, Z.; Guo, Y.; Zhang, C.; Zhu, J. Development of equivalent circuit models of permanent magnet synchronous motors considering core loss. Energies 2022, 15, 1995. [Google Scholar] [CrossRef]
Chandrasekaran, V.; Jose, B.; Muralidharan, A. K.; Mohan, N.; Basu, K. Offline Model Based MTPA Methodology for Optimum Performance of Interior Permanent Magnet Machines over Full Range of Speed and Torque. Proceedings of the 2022 IEEE Transportation Electrification Conference & Expo (ITEC), Anaheim, CA, USA, 15-, 383-390. 17 June. [CrossRef]
Ni, R.; Xu, D.; Wang, G.; Ding, L.; Zhang, G.; Qu, L. Maximum efficiency per ampere control of permanent-magnet synchronous machines. IEEE Trans. Ind. Electr. 2015, 62, 2135–2143. [Google Scholar] [CrossRef]
Ma, Y.; Yang, R.; Yang, H.; Liu, G.; Yao, S. Electromagnetic resistance model based maximum efficiency control for IPMSM with reduced experimental cost. IEEE Trans. Transp. Electr. 2024, 10, 6989–7002. [Google Scholar] [CrossRef]
Xu, K.; Guo, Y.; Lei, G.; Zhu, J. Estimation of iron loss in permanent magnet synchronous motors based on particle swarm optimization and a recurrent neural network. Magnetism 2023, 3, 327–342. [Google Scholar] [CrossRef]
Li, Z.; Huang, X.; Ma, J.; Chen, Z.; Liu, A.; Peretti, L. Hybrid analytical model for predicting the electromagnetic losses in surface-mounted permanent-magnet motors. IEEE Trans. Transp. Electr. 2024, 10, 1388–1397. [Google Scholar] [CrossRef]
Park, J.; Cho, H. -J.; Yun, J.; Sul, S. -K. Online MTPA Tracking of IPMSM Based on Min-Max Optimization. Proceedings of the 2023 11th International Conference on Power Electronics and ECCE Asia (ICPE 2023 - ECCE Asia), Jeju Island, Korea, 22-, 199-204. 25 May. [CrossRef]
Wu, Z.; Tian, D.; Liu, H. Research on MTPA Control of IPMSM for Electric Vehicle. Proceedings of the 2024 IEEE 7th International Electrical and Energy Conference (CIEEC), Harbin, China, 10-, 837-842. 12 May. [CrossRef]
Song, H.; Duan, D.; Yan, Y.; Li, X.; Xie, M. Fractional-order extremum seeking method for maximum torque per ampere control of permanent magnet synchronous motor. Fractal Fract 2023, 7, 858. [Google Scholar] [CrossRef]
Dong, W.; et al. Neural network with cloud-based training for MTPA, flux-weakening, and MTPV control of IPM motors and drives. IEEE Trans. Transp. Electr. 2024, 10, 1012–1030. [Google Scholar] [CrossRef]
Sun, L.; Guo, J.; Kawaguchi, T.; Hashimoto, S.; Jiang, W. Online MTPA control of IPM motor using NN-based perturb and observe algorithm. IEEE Access 2023, 11, 122458–122469. [Google Scholar] [CrossRef]
Zhang, H.; Li, H.; Wu, Y.; Wang, L.; Xue, Y. Model Based Flux Weakening Control Strategy of Permanent Magnet Synchronous Motor with Voltage Feedback Compensation. Proceedings of the 2024 IEEE 10th International Power Electronics and Motion Control Conference (IPEMC2024-ECCE Asia), Chengdu, China, 17-, 933-939. 20 May. [CrossRef]
Olarescu, N.V.; Weinmann, M.; Zeh, S.; Musuroi, S. Novel flux weakening control algorithm for PMSMS. Proceedings of the 2009 International Conference on Power Engineering, Energy and Electrical Drives, Lisbon, Portugal, 18-, 123-127. 20 March. [CrossRef]
Huang, Sh.; Chen, Z.; Huang, K.; Gao, J. Maximum Torque Per Ampere and Flux-Weakening Control for PMSM Based on Curve Fitting. Proceedings of the 2010 IEEE Vehicle Power and Propulsion Conference, Lille, France, 01-03 Sept. 2010, 1-5. [CrossRef]
Zuo, K.; Wang, F.; Li, Z.; Ke, D.; Kennel, R.; Heldwein, M.L. A robust unified strategy for maximum torque per ampere and field weakening in permanent magnet synchronous motor. IEEE Trans. Power Electr. 2024, 39, 5286–5297. [Google Scholar] [CrossRef]
Kondepudi, D.; Prigogine, I. Modern Thermodynamics: From Heat Engines to Dissipative Structures; Publisher: John Wiley & Sons, 2015. [Google Scholar]
Christen, T. Efficiency and Power in Energy Conversion and Storage: Basic Physical Concepts; Publisher: CRC Press. Taylor & Francis Group, 2019. [Google Scholar]
Demirel, Y. Nonequilibrium Thermodynamics: Transport and Rate Processes in Physical, Chemical and Biological Systems, 2-nd ed.; Publisher: Elsevier Science & Technology Books, 2007. [Google Scholar]
Westerhoff, H.V.; van Dam, K. Thermodynamics and Control of Biological Free-Energy Transduction; Publisher: Elsevier, 1987. [Google Scholar]
Shchur, I.; Rusek, A.; Lis, M. Optimal frequency control of the induction electric drive based on the thermodynamics of irreversible processes. Electromechanical and computerized systems 2011, 3, 377–380. [Google Scholar]
Shchur, І.; Lis, M.; Biletskyi, Y. A Non-equilibrium thermodynamic approach for analysis of power conversion efficiency in the wind energy system. Energies 2023, 16, 5234. [Google Scholar] [CrossRef]
Windisch, T.; Hofmann, W. A novel approach to MTPA tracking control of AC drives in vehicle propulsion systems. IEEE Trans. Vehic. Techn. 2018, 67, 9294–9302. [Google Scholar] [CrossRef]
Shchur, I.; Rusek, A.; Mandzyuk, M. Power effective work of PMSМ in electric vehicles at the account of magnetic saturation and iron losses. Przeglad Elektrotechniczny (Electrical Review) 2015, 1, 199–202. [Google Scholar] [CrossRef]
Fernandez-Bernal, F.; Garcia-Cerrada, A.; Faure, R. Determination of parameters in interior permanent-magnet synchronous motors with iron losses without torque measurement. IEEE Trans. Ind. Appl. 2001, 37, 1265–1272. [Google Scholar] [CrossRef]
Nicola, M. ; Nicola, C-I.; Prejbeanu, R.; Popescu, M. IPMSM Control System Based on Maximum Torque Per Ampere Strategy. Proceedings of the 2024 6th Global Power, Energy and Communication Conference (GPECOM), Budapest, Hungary, 04-, 132-137. 07 June. [CrossRef]

Figure 1. Substitute scheme of the IPMSM taking into account iron losses: (a) in relation to the coordinate d, (b) in relation to the coordinate q.

Figure 2. Dependency of the PC efficiency on the reduced force ratio at different degrees of coupling.

Figure 3. Dependencies obtained for the experimental SPMSM taking into account iron losses:(a) in the entire range of changes in Zχ; (b) enlarged fragment in the zone of maximum values of η.

Figure 4. Dependencies of the operating mode parameter Zχ on the main operating coordinates of the experimental machine: (a) from the angular velocity ω at constant values of the relative load torque T_L^*; (b) from the load torque T_L at constant values of the relative angular velocity ω^*.

Figure 5. Efficiency map obtained for the experimental SPMSM.

Figure 6. Dependencies of the PC coefficient of coupling q (a), the operating point parameter Zχ (b), and the energy efficiency η (c) of IPMSM operation without taking into account the iron losses on the value of the armature current component i_d₀ at the nominal angular velocity of the machine for a series values of the load torque.

Figure 7. Dependencies of the PC coefficient of coupling q (a), the operating point parameter Zχ (b), and the energy efficiency η (c) of IPMSM operation with taking into account the iron losses on the value of the armature current component i_d₀ at the nominal angular velocity of the machine for a series values of the load torque.

Figure 8. Efficiency map obtained for the experimental IPMSM.

Figure 9. Dependencies of the components of IPMSM power losses taking into account iron losses from the load torque at the nominal motor angular velocity.

Figure 10. Dependences of the amplitudes of the armature voltage (a) and current (b) vectors of the IPMSM on the value of the armature current component i_d₀ at a machine angular velocity of 150 s^-1 for the maximum value of the load torque of 38 Nm.

Figure 11. Dependencies of the PC coefficient of coupling q (a), the operating point parameter Zχ (b), and the energy efficiency η (c) of IPMSM operation with taking into account the iron losses on the value of the armature current component i_d₀ at a machine angular velocity of 150 s^-1 for the maximum value of the load torque of 38 Nm.

Figure 12. Dependencies of the components of IPMSM power losses from the load torque at the relative angular velocity of the motor ω^* = 1.5.

Table 1. The parameters of the experimental machine.

Parameter	Value
Rated power, Pn (kW)	10
Rated DC voltage, VDC.n (V)	150
Rated angular velocity, ωn (s-1)	100
Rated torque, TG.n (Nm)	100
Rated rms phase current, in (A)	63
Number of pole pairs, pp	2
PM flux linkage, ψpm (Vs)	0.35
Winding resistance, R (Ω)	0.1
d-axis winding inductance, Ld (mH)	1
q-axis winding inductance, Lq (mH)	3
Rated equivalent iron loss resistance, Rc.n (Ω)	14.1

Table 2. Comparison of the optimal values of the i_d current component obtained by the developed algorithm with the corresponding values obtained analytically.

T_L, Nm	25	50	75	100
i_d₀, A	-3.0	-11.5	-21.5	-31.5
T^*	0.2041	0.4082	0.6122	0.8163
i_d^*	-0.0123	-0.0719	-0.1306	-0.1885
i_d, A	-2.15	-12.58	-22.86	-32.99

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Efficiency Analysis and Optimization of Two Speed Regions Operation of PMSM Taking into Account Iron Losses Based on Linear Non-Equilibrium Thermodynamics

Abstract

1. Introduction

2. Research Method

2.1. Mathematical Description of IPMSM Dynamics Taking into Account Iron Losses

2.2. Steady-State Equations

2.3. Performance Indicators of the Universal PC

3. Results and Their Discussion

3.1. Parameters of the Experimental Machine

3.2. PMSM as Linear PC

3.3. Efficiency Optimization of SPMSM Operation below Rated Speed

3.4. Efficiency Optimization of IPMSM Operation Below the Rated Speed

3.5. Efficiency Optimization of IPMSM Operation Above the Rated Speed

4. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe