Compartmental Description of the Cosmological Baryonic Matter Cycle. II. Inclusion of Triggered Star Formation

1. Introduction

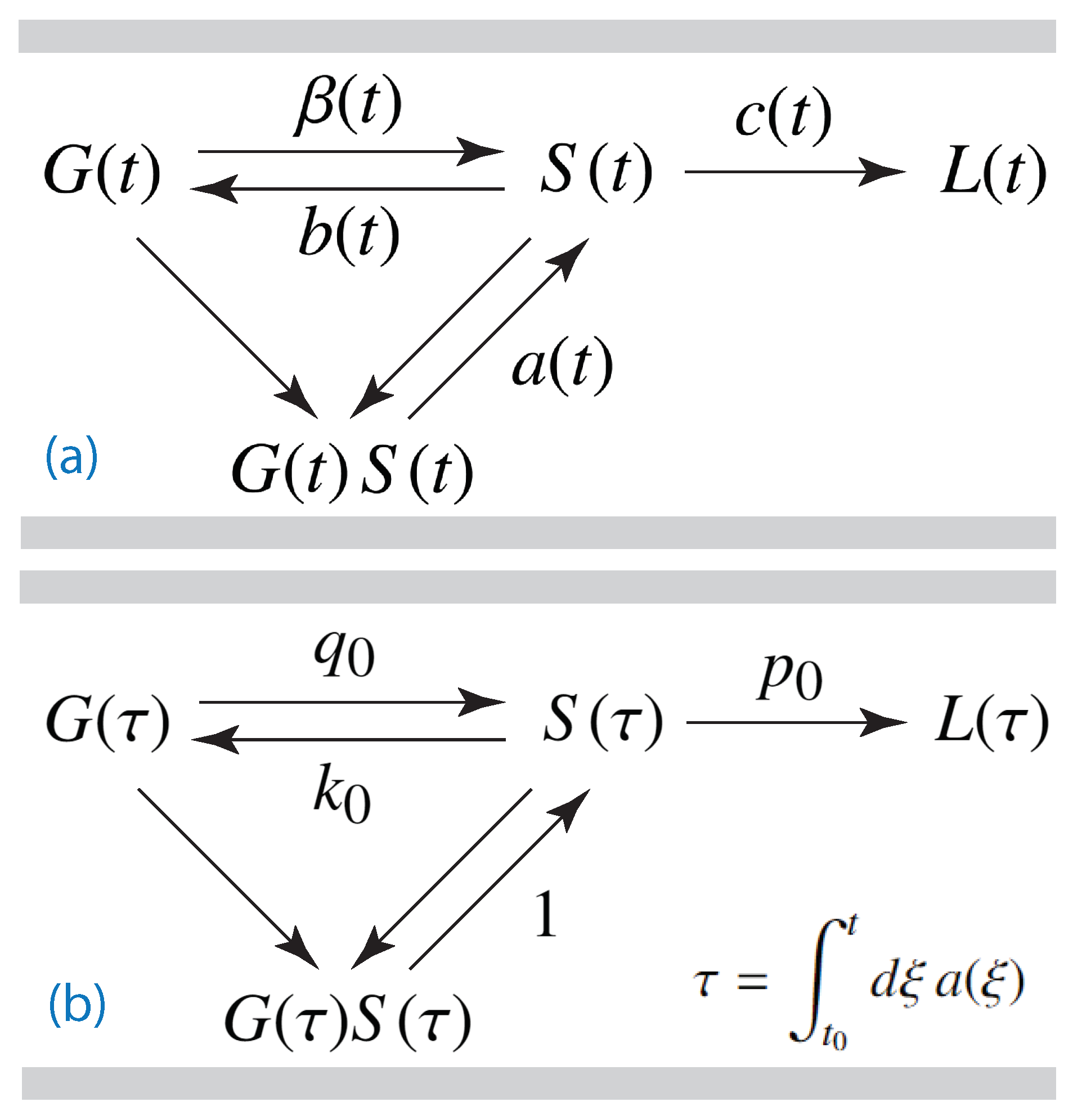
Recently ([1] - hereafter referred to as part I) the compartmental description, well-known from the description of infection diseases and epidemics, has been introduced to describe the temporal evolution of the baryonic matter in interstellar gas and stars. Such a description makes use of gaseous and stellar fractions of the total baryonic matter and transition rates between these fractions. In particular, the respective rates of spontaneous ($\beta \left(t\right)G\left(t\right)$) and triggered ($a\left(t\right)S\left(t\right)G\left(t\right)$) star formation regulate the transfer $G\left(t\right)\to S\left(t\right)$ from gas to luminous main-sequence stars, whereas the stellar feedback rate ($b\left(t\right)S\left(t\right)$) determines the feedback $S\left(t\right)\to G\left(t\right)$ from luminous stars to gas. Thirdly the stellar evolution rate ($c\left(t\right)S\left(t\right)$) regulates the transfer $S\left(t\right)\to L\left(t\right)$ from luminous stars to locked-in stellar matter in the form of white dwarfs, neutron stars and black holes which are much less luminous and have no significant stellar feedback to the gaseous matter compartment.

In part I the process of triggered star formation has been ignored and the resulting exact analytical solutions for stationary rates of spontaneous formation, feedback and evolution have been compared with the observed cosmological star formation rate and the integrated stellar density. It has been demonstrated that the simplified GS-model ignoring stellar evolution cannot explain the observations. The comparison of the full gas-stars-locked-in (GSL) model including stellar evolution is more favorable but still far from being perfect. The non-perfect agreement of the GSL-model with only spontaneous star formation process therefore is a strong motivation to investigate the role of the additional triggered star formation process, which is the subject of the present part II.

Here, the competition of triggered and spontaneous star formation, stellar feedback and stellar evolution was theoretically investigated with analytical and numerical solutions of the nonlinear dynamical GSL equations. Following part I, baryonic matter exists as interstellar and intergalactic gas with the fraction $G\left(t\right)$ and in two forms of stellar matter: $S\left(t\right)$ denotes the fraction of luminous stellar matter in main-sequence stars while $L\left(t\right)$ refers to the fraction of weakly luminous matter in white dwarfs, neutron stars and black holes (referred to as locked-in matter) which have no significant stellar feedback to the gaseous matter compartment. The temporal evolution of the three fractions is controlled by the respective rates of spontaneous star formation ($\beta \left(t\right)G\left(t\right)$) and of triggered star formation ($a\left(t\right)G\left(t\right)S\left(t\right)$ of gas to stellar matter, of stellar feedback ($b\left(t\right)S\left(t\right)$) of stellar to gaseous matter, and of the formation ($c\left(t\right)S\left(t\right)$) of white dwarfs, neutron stars and black holes from stellar evolution. Obviously, the inclusion of triggered star formation introduces a nonlinearity in the GSL equations as it is depends on the product $G\left(t\right)S\left(t\right)$.

The organization of this manuscript is as follows. The GSL-compartmental model for the baryonic matter cycle is revisited in Section 2. While Section 3 is concerned with the GS-limit for negligible stellar evolution, the full GSL model for stationary ratios is investigated in Section 4. Having obtained general relationships between the compartments, and their limiting, stationary values, approximate solutions are derived and tested in Section 5. Section 6 connects the GSL fractions with the cosmic star formation history and discusses observational constraints that help us identifying the parameters of the GSL model. The resulting redshift dependency of the gas and stellar fractions is presented in Section 7. A summary and conclusions are provided in Section 8.

2. GSL-Compartmental Model for the Baryonic Matter Cycle

As in part I we considered the total system of matter either in stars or in interstellar gas and introduce the compartments G (gas), S (stars) and L (locked-in matter in white dwarfs, neutron stars and black holes) where $G\left(t\right)$, $S\left(t\right)$ and $L\left(t\right)$ denote the relative fractions of luminous matter in the three compartments, respectively, as a function of time t.

2.1. Starting Equations

The three fractions obey the sum constraint

$$G\left(t\right)+S\left(t\right)+L\left(t\right)=1,$$

(1)

holding at all times t after the begin of the baryonic evolution at time $t=t_0$. The dynamical evolution of the three fractions is described by the nonlinear dynamical GSL equations (Figure 1)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dG}{dt}}& =& -a\left(t\right)G\left(t\right)S\left(t\right)-\beta \left(t\right)G\left(t\right)+b\left(t\right)S\left(t\right),\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dS}{dt}}& =& a\left(t\right)G\left(t\right)S\left(t\right)+\beta \left(t\right)G\left(t\right)-b\left(t\right)S\left(t\right)-c\left(t\right)S\left(t\right),\hfill \end{array}$$

(3)

and

$${\displaystyle \frac{dL}{dt}}=c\left(t\right)S\left(t\right),$$

(4)

respectively. As initial condition in the presence of spontaneous star formation ($\beta \left(t\right)>0$) we adopted

$$G\left(t_0\right)=1,S\left(t_0\right)=0,L\left(t_0\right)=0.$$

(5)

As an aside we note that in the absence of spontaneous star formation ($\beta =0$) the initial conditions (5) had to be modified to $G\left(t_0\right)=1-\eta$, $S\left(t_0\right)=\eta$, $L\left(t_0\right)=0$, with the small initial stellar fraction $\eta \ll 1$. Without a finite albeit tiny initial fraction the process of triggered star formation does not start. The initial time $t_0$ corresponds to the redshift $z=1100$.

Of particular interest is the formation rate $\mathring{J}\left(t\right)$ of new stars as a function of time,

$$\mathring{J}\left(t\right)=a\left(t\right)G\left(t\right)S\left(t\right)+\beta \left(t\right)G\left(t\right).$$

(6)

The first term represents the rate from triggered star formation, whereas the second term is the rate from spontaneous star formation.

In contrast to part I we included in the analysis also the process of triggered star formation which is nonlinear as it depends on the product $G\left(t\right)S\left(t\right)$. Exact and approximate analytical solutions of the dynamical equations of the GSL-model (1)–(5) were derived which hold for stationary rates as well as for the case of the same time dependency of all rates.

2.2. Stationary Ratios

We here introduced the three ratios

$$k\left(t\right)={\displaystyle \frac{b\left(t\right)}{a\left(t\right)}},q\left(t\right)={\displaystyle \frac{\beta \left(t\right)}{a\left(t\right)}},p\left(t\right)={\displaystyle \frac{c\left(t\right)}{a\left(t\right)}},$$

(7)

indicating the strength of stellar feedback, spontaneous star formation and stellar evolution with respect to triggered star formation, respectively.

For ease of exposition we considered, similar to part I, the case of stationary ratios $k\left(\tau \right)=k_0=$ const, $q\left(\tau \right)=q_0=$ const, and $p\left(\tau \right)=p_0=$ const, as shown in Figure 1. This case applies to stationary values of the rates $a\left(t\right)=a_0$, $b\left(t\right)=b_0$, $\beta ={\beta }_0$ and $c\left(t\right)=c_0$ as well as to any time-dependent star formation rate $a\left(t\right)$, provided $b\left(t\right)\propto a\left(t\right)$, $\beta \left(t\right)\propto a\left(t\right)$, and $c\left(t\right)\propto a\left(t\right)$ have the same time variation while their absolute values can be different.

It is appropriate to introduce the dimensionless reduced time variable

$$\tau ={\int }_{t_0}^{t}d\xi a\left(\xi \right)=a_0(t-t_0)$$

(8)

in terms of the stationary triggered star formation rate $a_0$. This reduced time scale differs from the one introduced in part I: $\tilde{t}={\beta }_0(t-t_0)$. Obviously for stationary rates the relation

$$\tau ={\displaystyle \frac{a_0}{{\beta }_0}}\tilde{t}$$

(9)

holds. In a flat $\Lambda$CDM Friedmann cosmology with ${\Omega }_m=0.3$ and the Hubble constant $H_0=70h_{70}$ km^s−1 Mpc^s−1 the relation (9) implies with Equations (I-42)1 the redshift dependency (for details see Appendix A)

$$\begin{array}{ccc}\hfill \tau \left(z\right)& \simeq & {\displaystyle \frac{\varphi \left(z\right)}{{(1+z)}^{3/2}}},\varphi \left(z\right)=\varphi \zeta \left(z\right),\varphi ={\displaystyle \frac{5.37{\tilde{a}}_0}{h_{70}}},\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill \zeta \left(z\right)& =& {\displaystyle \frac{{(1+z)}^{3/2}}{\sqrt{\frac{7}{3}+{(1+z)}^3}}}\simeq 1-\left(1-\sqrt{{\displaystyle \frac{3}{10}}}\right)e^{-4z/3},\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill \zeta \left(0\right)& =& \sqrt{0.3}=0.548,\hfill \end{array}$$

(12)

In the following the modification introduced by the factor (11) entered only Section 7 to calculate the present-day quantities at redshift $z=0$ whereas for finite redshift we set $\zeta \left(z\right)=1$. In Equation (10) the triggered star formation rate is scaled as

$$a_0={10}^{-17}{\tilde{a}}_0\mathrm{Hz}.$$

(13)

The Equations (1)–(4) then read

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dG}{d\tau }}& =& -G\left(\tau \right)S\left(\tau \right)-q_{0}G\left(\tau \right)+k_{0}S\left(\tau \right),\hfill \end{array}$$

(14a)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dS}{d\tau }}& =& G\left(\tau \right)S\left(\tau \right)+q_{0}G\left(\tau \right)-[k_0+p_0]S\left(\tau \right),\hfill \end{array}$$

(14b)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dL}{d\tau }}& =& p_{0}S\left(\tau \right),\hfill \end{array}$$

(14c)

$$\begin{array}{ccc}\hfill 1& =& G\left(\tau \right)+S\left(\tau \right)+L\left(\tau \right),\hfill \end{array}$$

(14d)

obeying the initial conditions

$$G(\tau =0)=1,S(\tau =0)=0,L(\tau =0)=0.$$

(15)

In Equations (14) we introduced the dimensionless constant ratios

$$k_0={\displaystyle \frac{b_0}{a_0}},q_0={\displaystyle \frac{{\beta }_0}{a_0}},p_0={\displaystyle \frac{c_0}{a_0}}.$$

(16)

The formation rate of new stars (6) as a function of reduced time is given by

$$j\left(\tau \right)=G\left(\tau \right)S\left(\tau \right)+q_{0}G\left(\tau \right).$$

(17)

At $\tau =\infty$ Equation (14) attain a stationary state where all time derivatives vanish. For finite $p_0>0$ Equation (14c) then implies $S_{\infty }=0$, so that $G_{\infty }=0$ according to Equation (14a) leading to $L(\infty )=1$ according to the sum constraint (14d). For later use we thus note

$$G_{\infty }=S_{\infty }=0,L(\infty )=1$$

(18)

Equation (14) could be simplified upon introducing

$$M\left(\tau \right)=G\left(\tau \right)-k_0,N\left(\tau \right)=S\left(\tau \right)+q_0.$$

(19)

Using $M\left(\tau \right)$ and $N\left(\tau \right)$ yielded for Equations (14)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dM}{d\tau }}& =& -M\left(\tau \right)N\left(\tau \right)-q_0{k}_0,\hfill \end{array}$$

(20a)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dN}{d\tau }}& =& M\left(\tau \right)N\left(\tau \right)+q_0{k}_0-p_0[N\left(\tau \right)-q_0],\hfill \end{array}$$

(20b)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dL}{d\tau }}& =& p_0[N\left(\tau \right)-q_0],\hfill \end{array}$$

(20c)

$$\begin{array}{ccc}\hfill 1& =& M\left(\tau \right)+N\left(\tau \right)+L\left(\tau \right)+k_0-q_0,\hfill \end{array}$$

(20d)

with the initial conditions

$$M(\tau =0)=1-k_0,N(\tau =0)=q_0,L(\tau =0)=0.$$

(21)

In the following two sections we investigated analytical solutions of Equations (14)–(21): first, for the special GS-case of negligible stellar evolution ($c_0=p_0=0$) in Section 3, before we investigated the general GSL-case (Section 4).

3. GS-Limit for Negligible Stellar Evolution

In the case of vanishing stellar evolution, $c_0=p_0=0$, implying $L\left(\tau \right)=0$ at all times (Figure 1). In that case the reduced GSL model Equations (14a)–(14b) and (14d) simplified to the GS model equation

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dG}{d\tau }}& =& -G\left(\tau \right)S\left(\tau \right)-q_{0}G\left(\tau \right)+k_{0}S\left(\tau \right),\hfill \end{array}$$

(22a)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dS}{d\tau }}& =& G\left(\tau \right)S\left(\tau \right)+q_{0}G\left(\tau \right)-k_{0}S\left(\tau \right),\hfill \end{array}$$

(22b)

$$\begin{array}{ccc}\hfill 1& =& G\left(\tau \right)+S\left(\tau \right),\hfill \end{array}$$

(22c)

so that with Equations (19) we obtained

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dM}{d\tau }}& =& -M\left(\tau \right)N\left(\tau \right)-q_0{k}_0,\hfill \end{array}$$

(23a)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dN}{d\tau }}& =& M\left(\tau \right)N\left(\tau \right)+q_0{k}_0.\hfill \end{array}$$

(23b)

Equation (23a) readily provided

$$N\left(\tau \right)=-{\displaystyle \frac{\frac{dM}{d\tau }+k_0{q}_0}{M\left(\tau \right)}},$$

(24)

so that

$$S\left(\tau \right)=-q_0-{\displaystyle \frac{\frac{d(G\left(\tau \right)-k_0)}{d\tau }+k_0{q}_0}{G\left(\tau \right)-k_0}}=-q_0-{\displaystyle \frac{\frac{dG\left(\tau \right)}{d\tau }+k_0{q}_0}{G\left(\tau \right)-k_0}}.$$

(25)

Upon insertion of Equation (25) the sum constraint (22c) became

$$1+q_0=G\left(\tau \right)-{\displaystyle \frac{\frac{dG\left(\tau \right)}{d\tau }+k_0{q}_0}{G\left(\tau \right)-k_0}},$$

(26)

or equivalently,

$${\displaystyle \frac{dG\left(\tau \right)}{d\tau }}=G^2\left(\tau \right)-(1+q_0+k_0)G\left(\tau \right)+k_0.$$

(27)

According to Equation (27) the fraction $G\left(\tau \right)$ approaches a stationary value $G_{\infty }$ at $\tau \to \infty$, which is given by

$$\begin{array}{ccc}\hfill G_{\infty }& =& {\displaystyle \frac{1}{2}}({\chi }_0-{\omega }_0)\hfill \\ & =& {\displaystyle \frac{1}{2}}[1+q_0+k_0-\sqrt{{(1+q_0)}^2+k_0^2-2k_0(1-q_0)}],\hfill \end{array}$$

(28)

where

$${\chi }_0\equiv 1+k_0+q_0>1,{\omega }_0\equiv \sqrt{{\chi }_0^2-4k_0}\ge 0.$$

(29)

Taking into account the initial conditions (15), the solution of Equation (27) could be written as

$$\begin{array}{ccc}\hfill \tau & =& {\int }_1^{G\left(\tau \right)}{\displaystyle \frac{dx}{x^2-(1+q_0+k_0)x+k_0}}\hfill \\ & =& -{\int }_1^{G\left(\tau \right)}{\displaystyle \frac{dx}{(x-G_{\infty })({\chi }_0-G_{\infty }-x)}}\hfill \\ & =& -{\int }_{1-G_{\infty }}^{G\left(\tau \right)-G_{\infty }}{\displaystyle \frac{dy}{y({\chi }_0-2G_{\infty }-y)}}\hfill \\ & =& -{\displaystyle \frac{1}{{\omega }_0}}{\int }_{1-G_{\infty }}^{G\left(\tau \right)-G_{\infty }}dy\left[{\displaystyle \frac{1}{y}}+{\displaystyle \frac{1}{{\omega }_0-y}}\right].\hfill \end{array}$$

(30)

This integral evaluated to

$$\begin{array}{ccc}\hfill {\omega }_0\tau & =& -{\left[ln{\displaystyle \frac{y}{{\omega }_0-y}}\right]}_{1-G_{\infty }}^{G-G_{\infty }}={\left[ln\left({\displaystyle \frac{{\omega }_0}{y}}-1\right)\right]}_{1-G_{\infty }}^{G-G_{\infty }}\hfill \\ & =& ln{\displaystyle \frac{\frac{{\omega }_0}{G-G_{\infty }}-1}{\frac{{\omega }_0}{1-G_{\infty }}-1}},\hfill \end{array}$$

(31)

or equivalently

$$G\left(\tau \right)=G_{\infty }+{\displaystyle \frac{{\omega }_0}{1+\left(\frac{{\omega }_0}{1-G_{\infty }}-1\right)e^{{\omega }_0\tau }}}.$$

(32)

The sum constraint (22c) then readily yielded

$$S\left(\tau \right)=1-G\left(\tau \right)=1-G_{\infty }-{\displaystyle \frac{{\omega }_0}{1+\left(\frac{{\omega }_0}{1-G_{\infty }}-1\right)e^{{\omega }_0\tau }}},$$

(33)

providing

$$\begin{array}{ccc}\hfill S_{\infty }& =& 1-G_{\infty }\hfill \\ & =& {\displaystyle \frac{1}{2}}\left[1-q_0-k_0+\sqrt{{(1+q_0)}^2+k_0^2-2k_0(1-q_0)}\right].\hfill \end{array}$$

(34)

Consequently, the dimensionless star formation rate (17) became

$$\begin{array}{ccc}\hfill j\left(\tau \right)& =& G\left(\tau \right)[S\left(\tau \right)+q_0]=\left[G_{\infty }+{\displaystyle \frac{{\omega }_0}{1+\left(\frac{{\omega }_0}{1-G_{\infty }}-1\right)e^{{\omega }_0\tau }}}\right]\times \hfill \\ & & \left[1+q_0-G_{\infty }-{\displaystyle \frac{{\omega }_0}{1+\left(\frac{{\omega }_0}{1-G_{\infty }}-1\right)e^{{\omega }_0\tau }}}\right]\hfill \end{array}$$

(35)

where we recall that ${\omega }_0$ and $G_{\infty }$ are both known in terms of $k_0$ and $q_0$. The maximum of $j\left(\tau \right)$ is attained at ${\tau }_j$ solving $dj\left(\tau \right)/d\tau =0$. This yielded the dimensionless peak time

$${\tau }_j={\displaystyle \frac{1}{{\omega }_0}}ln\left[{\displaystyle \frac{1+q_0-2(G_{\infty }+{\omega }_0)}{\left(\frac{{\omega }_0}{1-G_{\infty }}-1\right)(2G_{\infty }-q_0-1)}}\right],$$

(36)

as well, upon inserting ${\tau }_j$ into Equation (28), the peak amplitude

$$j_{\max }={\displaystyle \frac{{(1+q_0)}^2}{4}},$$

(37)

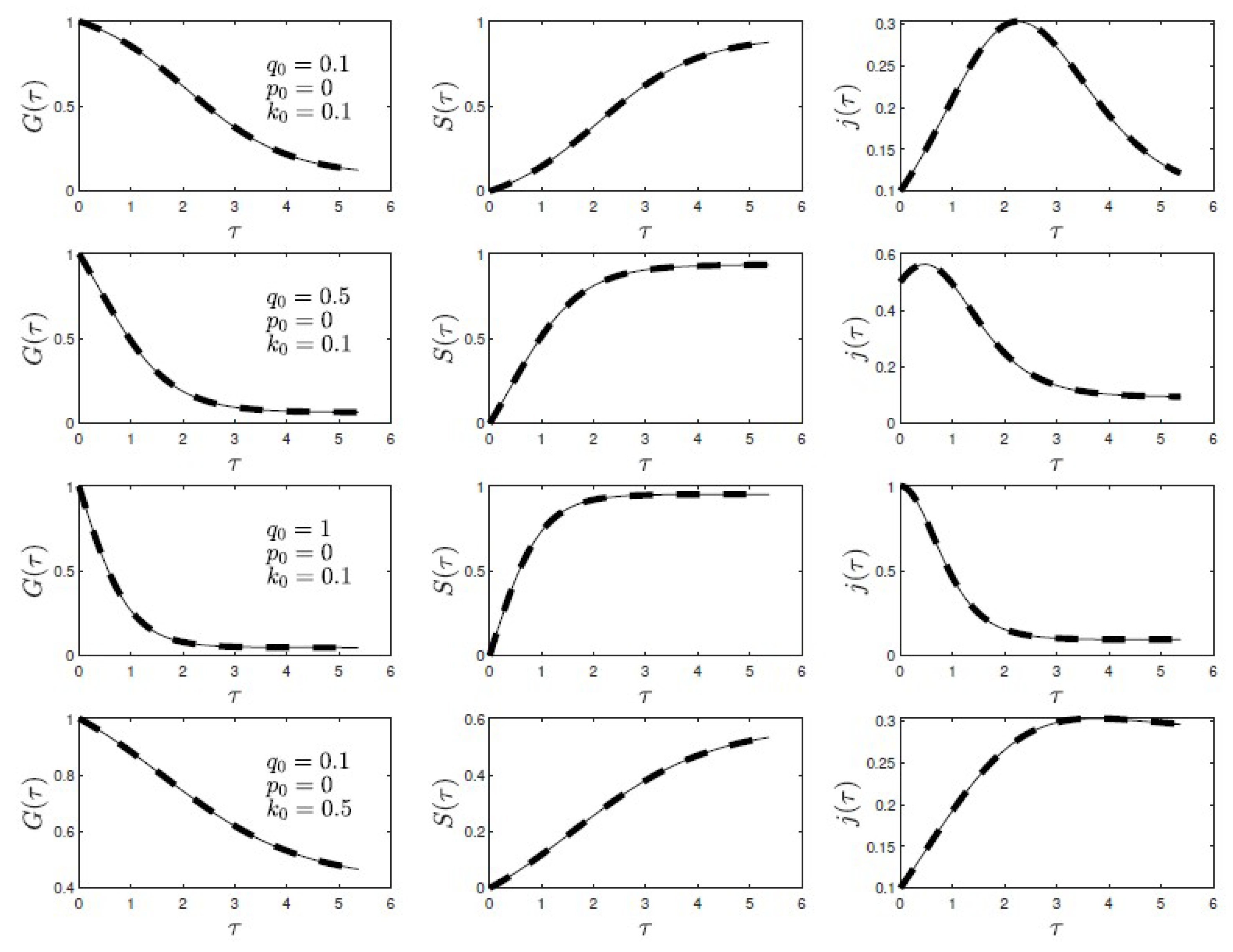
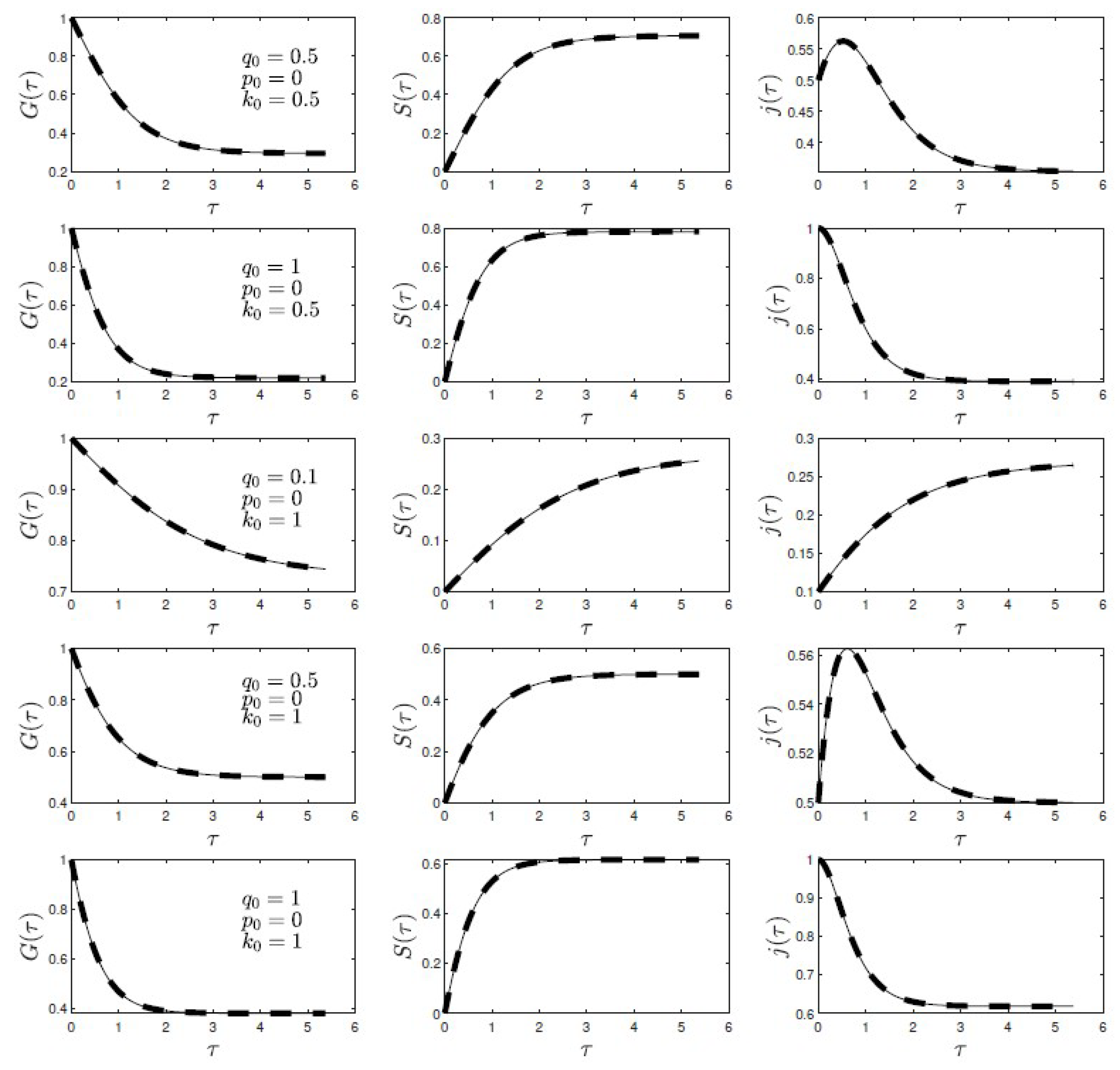
where we made use of the definitions of ${\chi }_0$, ${\omega }_0$, and $G_{\infty }$ according to Equation (28) to simplify the final expression. For the present case of $p_0=0$ the analytical solutions (32), (33), (28) are shown to be identical with the numerical solution in Figure for various choices of $q_0$ and $k_0$. Following [2] the numerical solution of the GSL equations we obtained using the 10th order predictor–corrector Adams method ([3,4]). Within 0.1% precision, a single-step solver based on a modified Rosenbrock formula of order 2, implemented by [5] as ode23s in Matlab^TM yielded practically indistinguishable results. The excellent agreement between the numerical and analytical solutions in Figure confirms the validity of our derivations.

4. The Full GSL Model for Stationary Ratios

4.1. Further Reduction

For the full GSL-model including stellar evolution $p_0>0$ we first reduced Equations (14) further. Equation (20a) readily yielded

$$N\left(\tau \right)=-{\displaystyle \frac{\frac{dM\left(\tau \right)}{d\tau }+q_0{k}_0}{M\left(\tau \right)}},$$

(38)

and Equation (20b) could be written as

$$\begin{array}{ccc}\hfill p_0& =& M\left(\tau \right)+{\displaystyle \frac{q_0(k_0+p_0)}{N\left(\tau \right)}}-{\displaystyle \frac{dlnN\left(\tau \right)}{d\tau }}.\hfill \end{array}$$

(39)

Substituting

$$N\left(\tau \right)=q_0(k_0+p_0)X\left(\tau \right)$$

(40)

the Equation (39) reads

$$p_0-M\left(\tau \right)={\displaystyle \frac{1}{X\left(\tau \right)}}-{\displaystyle \frac{dlnX\left(\tau \right)}{d\tau }}={\displaystyle \frac{1}{X\left(\tau \right)}}\left[1-{\displaystyle \frac{dX\left(\tau \right)}{d\tau }}\right],$$

(41)

or equivalently,

$${\displaystyle \frac{dX\left(\tau \right)}{d\tau }}+[p_0-M\left(\tau \right)]X\left(\tau \right)=1.$$

(42)

This last Equation (42) was readily solved by

$$X\left(\tau \right)=\left[c_0+{\int }_0^{\tau }dx{e}^{p_{0}x-{\int }_0^{x}d{\tau }^{\prime }M\left({\tau }^{\prime }\right)}\right]e^{-p_0\tau +{\int }_0^{\tau }d{\tau }^{\prime }M\left({\tau }^{\prime }\right)}$$

(43)

with the integration constant $c_0=X\left(0\right)$. The solution (43) implied

$$N\left(\tau \right)=q_0(k_0+p_0)\left[c_0+{\int }_0^{\tau }dx{e}^{p_{0}x-{\int }_0^{x}d{\tau }^{\prime }M\left({\tau }^{\prime }\right)}\right]e^{-p_0\tau +{\int }_0^{\tau }d{\tau }^{\prime }M\left({\tau }^{\prime }\right)}.$$

(44)

The initial value $N(\tau =0)=q_0$ then provided $c_0=1/(k_0+p_0)$, so that

$$\begin{array}{ccc}\hfill S\left(\tau \right)& =& N\left(\tau \right)-q_0\hfill \\ & =& q_0\left[1+(k_0+p_0){\int }_0^{\tau }dx{e}^{-U\left(x\right)}\right]e^{U\left(\tau \right)}-q_0,\hfill \end{array}$$

(45)

where we introduced

$$U\left(\tau \right)={\int }_0^{\tau }d{\tau }^{\prime }M\left({\tau }^{\prime }\right)-p_0\tau ,$$

(46)

implying

$$\begin{array}{ccc}\hfill M\left(\tau \right)& =& G\left(\tau \right)-k_0={\displaystyle \frac{dU\left(\tau \right)}{d\tau }}+p_0,\hfill \\ \hfill {\displaystyle \frac{dM\left(\tau \right)}{d\tau }}& =& {\displaystyle \frac{dG\left(\tau \right)}{d\tau }}={\displaystyle \frac{d^{2}U\left(\tau \right)}{d{\tau }^2}},\hfill \end{array}$$

(47)

with

$$\begin{array}{ccc}\hfill U\left(0\right)& =& 0,U^{\prime \prime }\left(0\right)=G^{\prime }\left(0\right)=-q_0,\hfill \\ \hfill U^{\prime }\left(0\right)& =& G\left(0\right)-k_0-p_0=1-k_0-p_0.\hfill \end{array}$$

(48)

Inserting Equations (45) and (47) yielded for Equation (38)

$$\begin{array}{ccc}\hfill -q_0{k}_0& =& {\displaystyle \frac{d^{2}U}{d{\tau }^2}}+q_0\left[{\displaystyle \frac{dU\left(\tau \right)}{d\tau }}+p_0\right]e^{U\left(\tau \right)}\times \hfill \\ & & \left[1+(k_0+p_0){\int }_0^{\tau }dx{e}^{-U\left(x\right)}\right].\hfill \end{array}$$

(49)

With

$${\displaystyle \frac{dU\left(\tau \right)}{d\tau }}{e}^{U\left(\tau \right)}={\displaystyle \frac{d}{d\tau }}{e}^{U\left(\tau \right)},$$

(50)

and

$${\displaystyle \frac{d{e}^{U\left(\tau \right)}}{d\tau }}{\int }_0^{\tau }dx{e}^{-U\left(x\right)}={\displaystyle \frac{d}{d\tau }}\left[e^{U\left(\tau \right)}{\int }_0^{\tau }dx{e}^{-U\left(x\right)}\right]-1$$

(51)

the Equation (49) could be further reduced to

$${\displaystyle \frac{d}{d\tau }}\left[{\displaystyle \frac{dU\left(\tau \right)}{d\tau }}+q_0{e}^{U\left(\tau \right)}\left(1+(k_0+p_0){\int }_0^{\tau }dx{e}^{-U\left(x\right)}\right)\right]$$

$$=q_0{p}_0\left[1-e^{U\left(\tau \right)}\left(1+(k_0+p_0){\int }_0^{\tau }dx{e}^{-U\left(x\right)}\right)\right].$$

(52)

Setting

$$Z\left(\tau \right)={\displaystyle \frac{dU\left(\tau \right)}{d\tau }}+q_0{e}^{U\left(\tau \right)}\left(1+(k_0+p_0){\int }_0^{\tau }dx{e}^{-U\left(x\right)}\right),$$

(53)

Equation (52) reads

$$q_0{p}_0+p_0{\displaystyle \frac{dU\left(\tau \right)}{d\tau }}={\displaystyle \frac{dZ\left(\tau \right)}{d\tau }}+p_{0}Z\left(\tau \right)=e^{-p_0\tau }{\displaystyle \frac{d}{d\tau }}\left[Z\left(\tau \right)e^{p_0\tau }\right].$$

(54)

With the initial conditions $U\left(0\right)=0$ and

$$Z\left(0\right)=U^{\prime }\left(0\right)+q_0=1+q_0-k_0-p_0=ϵ,$$

(55)

Equation (54) integrated to

$$Z\left(\tau \right)=q_0+(ϵ-q_0)e^{-p_0\tau }+p_0{e}^{-p_0\tau }{\int }_0^{\tau }dx{e}^{p_{0}x}{\displaystyle \frac{dU\left(x\right)}{dx}}.$$

(56)

Inserting Equation (56) then provided for Equation (53)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dU\left(\tau \right)}{d\tau }}& +& q_0{e}^{U\left(\tau \right)}\left(1+(k_0+p_0){\int }_0^{\tau }dx{e}^{-U\left(x\right)}\right)\hfill \\ & =& q_0+(ϵ-q_0)e^{-p_0\tau }+p_0{e}^{-p_0\tau }{\int }_0^{\tau }dx{e}^{p_{0}x}{\displaystyle \frac{dU\left(x\right)}{dx}}.\hfill \end{array}$$

(57)

We note that with $U^{\prime }\left(0\right)=1-(k_0+p_0)=ϵ-q_0$

$$(ϵ-q_0)e^{-p_0\tau }=ϵ-q_0-p_0{e}^{-p_0\tau }{\int }_0^{\tau }dx{e}^{p_{0}x}{U}^{\prime }\left(0\right),$$

(58)

so that Equation (57) could be written as

$$\begin{array}{ccc}\hfill {\displaystyle \frac{dU\left(\tau \right)}{d\tau }}& +& q_0{e}^{U\left(\tau \right)}\left(1+(k_0+p_0){\int }_0^{\tau }dx{e}^{-U\left(x\right)}\right)\hfill \\ & =& ϵ+p_0{e}^{-p_0\tau }{\int }_0^{\tau }dx{e}^{p_{0}x}\left[{\displaystyle \frac{dU\left(x\right)}{dx}}-{\left({\displaystyle \frac{dU}{dx}}\right)}_{x=0}\right].\hfill \end{array}$$

(59)

Equations (49), (52) and (59) represent exact determining nonlinear differential equations for the function $U\left(\tau \right)$ defined in Equation (46). In the Section 5 we solved Equation (59) approximately.

4.2. Final Values

As

$$G\left(\tau \right)=U^{\prime }\left(\tau \right)+k_0+p_0,G_{\infty }=U^{\prime }(\infty )+k_0+p_0$$

(60)

we inspected the limiting value of $U(\infty )$ and $U^{\prime }(\infty )$. We considered first the limiting values of Equations (53) and (56) using L’Hospital’s rule for

$$\begin{array}{ccc}\hfill \underset{\tau \to \infty }{lim}{\displaystyle \frac{(k_0+p_0){\int }_0^{\tau }dx{e}^{-U\left(x\right)}}{e^{-U\left(\tau \right)}}}& =& -{\displaystyle \frac{k_0+p_0}{U^{\prime }(\infty )}},\hfill \end{array}$$

(61)

$$\begin{array}{ccc}\hfill \underset{\tau \to \infty }{lim}{\displaystyle \frac{p_0{\int }_0^{\tau }dx{e}^{p_{0}x}{U}^{\prime }\left(x\right)}{e^{p_0\tau }}}& =& U^{\prime }(\infty ),\hfill \end{array}$$

(62)

so that Equation (56) provided

$$Z(\infty )=q_0+U^{\prime }(\infty ),$$

(63)

whereas Equation (53) yielded

$$Z(\infty )=-{\displaystyle \frac{q_0(k_0+p_0)}{U^{\prime }(\infty )}}+U^{\prime }(\infty )+q_0{e}^{U(\infty )}.$$

(64)

The last two Equations (63) and (64) only agree if

$$e^{U(\infty )}=1+{\displaystyle \frac{k_0+p_0}{U^{\prime }(\infty )}}.$$

(65)

Likewise, the limit (61) yielded for Equation (45)

$$S_{\infty }=q_0\left[e^{U(\infty )}-1-{\displaystyle \frac{k_0+p_0}{U^{\prime }(\infty )}}\right]=0,$$

(66)

if we inserted Equation (65).

The additional requirement $U(\infty )=-\infty$ so that $e^{U(\infty )}=0$ then demanded according to Equation (65) that

$$U^{\prime }(\infty )=-(k_0+p_0),$$

(67)

implying

$$G_{\infty }=0,L(\infty )=1-G_{\infty }-S_{\infty }=1.$$

(68)

thus reproducing correctly the earlier noted stationarity property (18).

5. Approximate Solutions of Equation (59)

5.1. Ansatz

The ansatz

$$Y\left(\tau \right)=e^{-U\left(\tau \right)}=c_1{e}^{{\alpha }_1\tau }+(1-c_1)e^{{\alpha }_2\tau },$$

(69)

where without loss of generality ${\alpha }_1>{\alpha }_2$, ensures that $U\left(0\right)=0$ and implies

$$\begin{array}{ccc}\hfill U^{\prime }\left(\tau \right)& =& -{\alpha }_1-{\displaystyle \frac{(1-c_1)({\alpha }_2-{\alpha }_1)e^{({\alpha }_2-{\alpha }_1)\tau }}{c_1+(1-c_1)e^{({\alpha }_2-{\alpha }_1)\tau }}}\hfill \\ & =& -{\alpha }_1+{\displaystyle \frac{{\alpha }_1-{\alpha }_2}{\frac{c_1}{1-c_1}{e}^{({\alpha }_1-{\alpha }_2)\tau }+1}}.\hfill \end{array}$$

(70)

The constants $c_1,{\alpha }_1$ and ${\alpha }_2$ will be determined later. We wrote Equation (59) as

$${\displaystyle \frac{dU\left(\tau \right)}{d\tau }}+q_0{e}^{U\left(\tau \right)}\left(1+(k_0+p_0){\int }_0^{\tau }dx{e}^{-U\left(x\right)}\right)=ϵ+R\left(\tau \right),$$

(71)

with

$$R\left(\tau \right)=p_0{e}^{-p_0\tau }{\int }_0^{\tau }dx{e}^{p_{0}x}[U^{\prime }\left(x\right)-U^{\prime }\left(0\right)].$$

(72)

By multiplying with $e^{-U\left(\tau \right)}$, the Equation (71) in terms of $Y\left(\tau \right)=e^{-U\left(\tau \right)}$ reads

$${\displaystyle \frac{dY\left(\tau \right)}{d\tau }}+[ϵ+R\left(\tau \right)]Y\left(\tau \right)-q_0(k_0+p_0){\int }_0^{\tau }dxY\left(x\right)=q_0,$$

(73)

which is still exact.

5.1.1. Small Times

For small times $\tau \ll p_0^{-1}$, where $U^{\prime }\left(\tau \right)\simeq U^{\prime }\left(0\right)$, the function (72) vanishes

$$R(\tau \le p_0^{-1})\simeq R(\tau =0)=0,$$

(74)

which in the special case of vanishing stellar evolution ($p_0=0$) holds at all times. The next subsection investigates the solution at small times using the approximation (74).

5.1.2. Parameter Relation for Non-Zero Values $p_0\ne 1$

For finite values of $p_0$ we noted that with the limits (61) and (67) Equation (71) for $\tau =\infty$ provides

$$ϵ+R(\infty )=U^{\prime }(\infty )-{\displaystyle \frac{q_0(p_0+k_0)}{U^{\prime }(\infty )}}=-(p_0+k_0)+q_0,$$

(75)

so that

$$R(\infty )=q_0-(p_0+k_0)-ϵ=-1.$$

(76)

According to Equation (70)

$$U^{\prime }\left(x\right)-U^{\prime }\left(0\right)=({\alpha }_1-{\alpha }_2)\left[{\displaystyle \frac{1}{\frac{c_1}{1-c_1}{e}^{({\alpha }_1-{\alpha }_2)x}+1}}-(1-c_1)\right],$$

(77)

so that Equation (72) became

$$\begin{array}{ccc}\hfill R\left(\tau \right)& =& p_0({\alpha }_1-{\alpha }_2)e^{-p_0\tau }({\int }_0^{\tau }dx{\displaystyle \frac{e^{p_{0}x}}{\frac{c_1}{1-c_1}{e}^{({\alpha }_1-{\alpha }_2)x}+1}}\hfill \\ & & -(1-c_1){\int }_0^{\tau }dx{e}^{p_{0}x}).\hfill \end{array}$$

(78)

Substituting $y=e^{({\alpha }_1-{\alpha }_2)\tau }$ allowed us to express the function (78) in terms of the hypergeometric ${}_{2}F_1$ function

$$\begin{array}{ccc}\hfill R\left(\tau \right)& =& p_0({\alpha }_1-{\alpha }_2)e^{-p_0\tau }[{\displaystyle \frac{1}{{\alpha }_1-{\alpha }_2}}{\int }_1^{e^{({\alpha }_1-{\alpha }_2)\tau }}dy{\displaystyle \frac{y^{\mu -1}}{1+\frac{c_1}{1-c_1}y}}\hfill \\ & & -{\displaystyle \frac{1-c_1}{p_0}}(e^{p_0\tau }-1)]\hfill \\ & =& ({\alpha }_1-{\alpha }_2)\{{}_{2}F_1\left(1,\mu ;1+\mu ;-{\displaystyle \frac{c_1}{1-c_1}}{e}^{({\alpha }_1-{\alpha }_2)\tau }\right)-(1-c_1)\hfill \\ & & -e^{-p_0\tau }\left[{}_{2}F_1\left(1,\mu ;1+\mu ;-{\displaystyle \frac{c_1}{1-c_1}}\right)-(1-c_1)\right]\},\hfill \end{array}$$

(79)

with $\mu =p_0/({\alpha }_1-{\alpha }_2)$. With the help of the linear transformation formula ([6])

$${}_{2}F_1(a,b;c;z)={(1-z)}^{-a}{}_{2}F_1\left(a,c-b;c;{\displaystyle \frac{z}{z-1}}\right),$$

(80)

we found for Equation (79)

$$\begin{array}{ccc}\hfill R\left(\tau \right)& =& ({\alpha }_1-{\alpha }_2)(1-c_1)[{\displaystyle \frac{{}_{2}F_1\left(1,1;1+\mu ;\frac{1}{1+\frac{1-c_1}{c_1}{e}^{({\alpha }_2-{\alpha }_1)\tau }}\right)}{1+\frac{c_1}{1-c_1}{e}^{({\alpha }_1-{\alpha }_2)\tau }}}-1\hfill \\ & -& e^{-p_0\tau }\left({}_{2}F_1(1,1;1+\mu ;c_1)-1\right)],\hfill \end{array}$$

(81)

indicating that for infinitely large times

$$R(\infty )=-({\alpha }_1-{\alpha }_2)(1-c_1).$$

(82)

The function $R\left(\tau \right)$ is negative and monotonically decreases with $\tau$. Equating the two limits (76) and (82) then required

$$1-c_1={({\alpha }_1-{\alpha }_2)}^{-1},c_1=1-{\displaystyle \frac{1}{{\alpha }_1-{\alpha }_2}}.$$

(83)

With this choice we obtained for Equation (70)

$$U^{\prime }\left(\tau \right)=-{\alpha }_1+{\displaystyle \frac{1}{1-c_1+c_1{e}^{\frac{\tau }{1-c_1}}}},$$

(84)

implying immediately for $0<c_1<1$

$$U^{\prime }\left(0\right)=1-{\alpha }_1,U^{\prime }(\infty )=-{\alpha }_1,$$

(85)

so that with

$${\alpha }_1=p_0+k_0$$

(86)

the initial (48) and final conditions (67) for $U^{\prime }\left(0\right)$ are exactly fulfilled. Consequently, Equation (84) reads

$$U^{\prime }\left(\tau \right)=-(p_0+k_0)+{\displaystyle \frac{1}{1-c_1+c_1{e}^{\frac{\tau }{1-c_1}}}},$$

(87)

depending on the single parameter $c_1$. Equation (87) is used in subsection to derive an approximative solution for all times. However, we emphasize that the relation (83) between $c_1$ and ${\alpha }_1-{\alpha }_2$, respectively, and therefore Equation (87) are valid only for finite values of $p_0$ and $R\left(\tau \right)$.

5.2. Approximate Solution for Small Times

5.2.1. Solution

With the approximation (74) the ansatz (69) exactly solves Equation (73) being equivalent to

$${\displaystyle \frac{dY\left(\tau \right)}{d\tau }}+ϵY\left(\tau \right)-q_0(k_0+p_0){\int }_0^{\tau }dxY\left(x\right)=q_0,$$

(88)

if

$${\alpha }_1={\displaystyle \frac{\omega -ϵ}{2}},{\alpha }_2=-{\displaystyle \frac{\omega +ϵ}{2}}={\alpha }_1-\omega ,$$

(89)

with

$$\omega =\sqrt{{ϵ}^2+4q_0(k_0+p_0)}\ge ϵ$$

(90)

and

$$c_1{\alpha }_2+(1-c_1){\alpha }_1={\alpha }_1-\omega c_1={\displaystyle \frac{{\alpha }_1{\alpha }_2}{p_0+k_0}}={\displaystyle \frac{{ϵ}^2-{\omega }^2}{4(p_0+k_0)}}=-q_0,$$

(91)

providing

$$c_1={\displaystyle \frac{\omega -ϵ+2q_0}{2\omega }},\alpha ={\displaystyle \frac{c_1}{1-c_1}}={\displaystyle \frac{\omega -ϵ+2q_0}{\omega +ϵ-2q_0}}.$$

(92)

The solution (69) then became

$$Y\left(\tau \right)=c_1{e}^{{\alpha }_1\tau }[1+{\alpha }^{-1}{e}^{-\omega \tau }],$$

(93)

implying

$$U_s\left(\tau \right)=-lnY\left(\tau \right)=-ln\left(c_1\right)+{\displaystyle \frac{ϵ-\omega }{2}}\tau -ln\left[1+{\alpha }^{-1}{e}^{-\omega \tau }\right],$$

(94)

and

$$U_s^{\prime }\left(\tau \right)={\displaystyle \frac{ϵ-\omega }{2}}+{\displaystyle \frac{\omega }{1+\alpha e^{\omega \tau }}},$$

(95)

so that

$$\begin{array}{ccc}\hfill G_s\left(\tau \right)& =& k_0+p_0+{\displaystyle \frac{ϵ-\omega }{2}}+{\displaystyle \frac{\omega }{1+\alpha e^{\omega \tau }}}\hfill \\ & =& {\displaystyle \frac{1+p_0+k_0+q_0}{2}}-{\displaystyle \frac{\omega }{2}}tanh{\displaystyle \frac{\omega \tau +ln\alpha }{2}}.\hfill \end{array}$$

(96)

Here the subscript s indicates that we consider the small time limit. Equations (94)–(96) correctly reproduce $U_s\left(0\right)=0$, $U_s^{\prime }\left(0\right)=ϵ-q_0=1-(k_0+p_0)$ and $G_s\left(0\right)=1$.

In Figure 3 we compared the resulting fractions $G_s\left(\tau \right)$ with the numerically calculated ones for several different choices of the parameters $p_0$, $k_0$ and $q_0$. The agreement is reasonably good for small times but fails at large times. We therefore considered a modified approximate approach valid at all times in Sestion Section 5.3. We first note an important feature of the present solution for vanishing $p_0=0$.

5.2.2. Comparison with Earlier Results for Vanishing Stellar Evolution $p_0=0$

In the case of vanishing stellar evolution ($p_0=0$) considered before in Section 3 the solution (96) holds for all times. Moreover, in this case the un-approximated full Equation (59) agrees exactly with the approximated Equation (88). Therefore the derived solution (96) had to agree with the solution (32). We checked this consistency noting that for $p_0=0$ one has according to Equation (55), $ϵ=1+q_0-k_0={ϵ}_0$, so that according to Equation (90)

$$\omega =\sqrt{{(1+q_0+k_0)}^2-4k_0}=\sqrt{{\chi }_0^2-4k_0}={\omega }_0$$

(97)

in terms of the quantities defined in Equation (29) in Section 3. Then Equation (96) reduced to

$$G\left(\tau \right)=G_{\infty }^0+{\displaystyle \frac{{\omega }_0}{1+{\alpha }_0{e}^{\omega \tau }}},$$

(98)

with

$$G_{\infty }^0=k_0+{\displaystyle \frac{{ϵ}_0-{\omega }_0}{2}}={\displaystyle \frac{{\chi }_0-{\omega }_0}{2}},$$

(99)

and

$${\alpha }_0={\displaystyle \frac{{\omega }_0-{ϵ}_0+2q_0}{{\omega }_0+{ϵ}_0-2q_0}}={\displaystyle \frac{{\omega }_0+q_0+k_0-1}{{\omega }_0+1-q_0-k_0}}={\displaystyle \frac{{\omega }_0}{1-G_{\infty }^0}}-1,$$

(100)

as

$$\begin{array}{ccc}\hfill {\displaystyle \frac{{\omega }_0}{1-G_{\infty }^0}}-1& =& {\displaystyle \frac{{\omega }_0-1+G_{\infty }^0}{1-G_{\infty }^0}}={\displaystyle \frac{2{\omega }_0-1+{\chi }_0-{\omega }_0}{2+{\omega }_0-{\chi }_0}}\hfill \\ & =& {\displaystyle \frac{{\omega }_0+q_0+k_0-1}{{\omega }_0+1-q_0-k_0}}.\hfill \end{array}$$

(101)

Consequently, Equation (98) agrees exactly with the earlier solution (32). This completes the proof of consistency.

5.3. Modified Approximation for General Times

For non-zero values of $p_0>0$ we used the earlier derived Equation (87) based on relation (83) to obtain for the gas fraction

$$G\left(\tau \right)=k_0+p_0+U^{\prime }\left(\tau \right)={\displaystyle \frac{1}{1-c_1+c_1{e}^{\frac{\tau }{1-c_1}}}}.$$

(102)

We noted before that with the relation (83) the initial and final conditions for $U^{\prime }\left(\tau \right)$ are fulfilled, as can also be seen from Equation (102) yielding $G\left(0\right)=G_{\infty }=0$. Equation (102) readily provided

$$G^{\prime }\left(\tau \right)=U^{\prime \prime }\left(\tau \right)=-{\displaystyle \frac{c_1{e}^{\frac{\tau }{1-c_1}}}{(1-c_1){[1-c_1+c_1{e}^{\frac{\tau }{1-c_1}}]}^2}}.$$

(103)

In order to determine the remaining parameter $c_1$ we here used the exact condition (48) for $G^{\prime }\left(0\right)=-q_0$ yielding

$${\displaystyle \frac{c_1}{1-c_1}}=q_0,$$

(104)

so that

$$\begin{array}{ccc}\hfill c_1& =& {\displaystyle \frac{q_0}{1+q_0}},{\alpha }_2=p_0+k_0-1-q_0=-ϵ,\hfill \\ \hfill {\alpha }_1& =& p_0+k_0,ϵ=1+q_0-(p_0+k_0)\hfill \end{array}$$

(105)

We then found for the gas fraction (102)

$$G\left(\tau \right)={\displaystyle \frac{1+q_0}{1+q_0{e}^{(1+q_0)\tau }}}={\displaystyle \frac{1+q_0}{1+e^{(1+q_0)(\tau -{\tau }_G)}}},$$

(106)

with

$${\tau }_G=-{\displaystyle \frac{ln{q}_0}{1+q_0}}.$$

(107)

This time scale is solely determined by the ratio $q_0$ of spontaneous to triggered star formation. Likewise, Equation (69) reads

$$Y\left(\tau \right)={\displaystyle \frac{q_0{e}^{{\alpha }_1\tau }+e^{-ϵ\tau }}{1+q_0}},$$

(108)

providing for the luminous stellar matter fraction (45)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{S\left(\tau \right)+q_0}{q_0}}& =& {\displaystyle \frac{1+(k_0+p_0){\int }_0^{\tau }dxY\left(x\right)}{Y\left(\tau \right)}}\hfill \\ & =& {\displaystyle \frac{1+q_0{e}^{{\alpha }_1\tau }+\frac{{\alpha }_1}{ϵ}(1-e^{-ϵ\tau })}{q_0{e}^{{\alpha }_1\tau }+e^{-ϵ\tau }}}\hfill \\ & =& 1+{\displaystyle \frac{(1+\frac{{\alpha }_1}{ϵ})(1-e^{-ϵ\tau })}{q_0{e}^{{\alpha }_1\tau }+e^{-ϵ\tau }}},\hfill \end{array}$$

(109)

so that

$$\begin{array}{ccc}\hfill S\left(\tau \right)& =& {\displaystyle \frac{q_0({\alpha }_1+ϵ)[1-e^{-ϵ\tau }]}{ϵ[q_0{e}^{{\alpha }_1\tau }+e^{-ϵ\tau }]}}={\displaystyle \frac{q_0(1+q_0)[1-e^{-ϵ\tau }]}{ϵ[q_0{e}^{{\alpha }_1\tau }+e^{-ϵ\tau }]}}\hfill \\ & =& {\displaystyle \frac{q_0(1+q_0)[e^{ϵ\tau }-1]}{ϵ[q_0{e}^{(1+q_0)\tau }+1]}}={\displaystyle \frac{q_0(1+q_0)[e^{ϵ\tau }-1]}{ϵ[1+e^{(1+q_0)(\tau -{\tau }_G)}]}}\hfill \\ & =& {\displaystyle \frac{q_0[e^{ϵ\tau }-1]}{ϵ}}G\left(\tau \right),\hfill \end{array}$$

(110)

which correctly reproduces $S\left(0\right)=S_{\infty }=0$. The first derivative of the fraction (110) vanishes at the time ${\tau }_S$ given by the solution of the Eq.

$$[q_0{e}^{(1+q_0){\tau }_S}+1]ϵe^{ϵ{\tau }_S}=q_0(1+q_0)e^{(1+q_0){\tau }_S}[e^{ϵ{\tau }_S}-1],$$

(111)

leading to

$$(p_0+k_0)e^{(1+q_0){\tau }_S}-(1+q_0)e^{(p_0+k_0){\tau }_S}={\displaystyle \frac{ϵ}{q_0}}.$$

(112)

As the first term dominates the left-hand side of the last Eq. we obtained approximately

$${\tau }_S\simeq {\displaystyle \frac{1}{1+q_0}}\left(-ln\left(q_0\right)+ln{\displaystyle \frac{ϵ}{p_0+k_0}}\right)={\tau }_G+{\displaystyle \frac{ln\frac{ϵ}{p_0+k_0}}{1+q_0}},$$

(113)

which is slightly larger than the time scale (107). Replacing $\tau$ in Equation (110) by ${\tau }_S$ from Equation (113) we found for the peak stellar matter ratio

$$S_{\max }=S\left({\tau }_S\right)\simeq e^{-(p_0+k_0){\tau }_S}\simeq {\left[{\displaystyle \frac{q_0(1+q_0)}{1+q_0-p_0-k_0}}\right]}^{{\displaystyle \frac{p_0+k_0}{1+q_0}}}.$$

(114)

According to Equations (14a) and (17) one has

$$j\left(\tau \right)=-{\displaystyle \frac{dG\left(\tau \right)}{d\tau }}+k_{0}S\left(\tau \right),$$

(115)

where

$$-{\displaystyle \frac{dG\left(\tau \right)}{d\tau }}=-U^{\prime \prime }\left(\tau \right)={\displaystyle \frac{{(1+q_0)}^2}{4{cosh}^2\frac{(1+q_0)(\tau -{\tau }_G)}{2}}}.$$

(116)

For small values of $k_0$, that is $k_0\ll 1$,

$$k_{0}S\left(\tau \right)\le k_0{S}_{\max }\simeq k_0{\left[{\displaystyle \frac{q_0(1+q_0)}{1+q_0-p_0-k_0}}\right]}^{{\displaystyle \frac{p_0+k_0}{1+q_0}}}$$

(117)

is negligibly smaller than $|G^{\prime }\left(\tau \right)|$, so that the formation rate of new stars (115) reduced to

$$j\left(\tau \right)\simeq -G^{\prime }\left(\tau \right)={\displaystyle \frac{{(1+q_0)}^2}{4{cosh}^2\frac{(1+q_0)(\tau -{\tau }_G)}{2}}}.$$

(118)

This formation rate attains its maximum value

$$j_{\max }={\left({\displaystyle \frac{1+q_0}{2}}\right)}^2$$

(119)

at the peak time ${\tau }_j\simeq {\tau }_G$, where ${\tau }_G$ is was introduced in Equation (107). Most noteworthy, both the maximum value and the peak time are solely determined by the ratio $q_0$ of the spontaneous to triggered star formation rates, whereas the two other ratios $p_0$ and $k_0$ do not enter here.

Finally, the fraction of locked-in matter followed from the sum constraint as

$$\begin{array}{ccc}\hfill L\left(\tau \right)& =& 1-G\left(\tau \right)-S\left(\tau \right)\hfill \\ & =& 1-{\displaystyle \frac{1+q_0}{1+e^{(1+q_0)(\tau -{\tau }_G)}}}-{\displaystyle \frac{q_0(1+q_0)[e^{ϵ\tau }-1]}{ϵ[q_0{e}^{(1+q_0)\tau }+1]}}\hfill \\ & =& 1-{\displaystyle \frac{1+q_0}{1+e^{(1+q_0)(\tau -{\tau }_G)}}}\left[1+{\displaystyle \frac{q_0(e^{ϵ\tau }-1)}{ϵ}}\right],\hfill \end{array}$$

(120)

where we inserted Equations (106) and (110). The derived expressions (106), (110), and (120) for $G\left(\tau \right)$, $S\left(\tau \right)$, and $L\left(\tau \right)$ were used in the following sections.

6. Cosmic Star Formation History

As in part I we considered the cosmic star formation history (SFH) of the universe which is proportional to the star formation rate (6). In the following the SFR density and the integrated stellar density using our results from the earlier Section 5.3 are calculated, and compared with data collected by [7].

According to Equations (I-46) and (I-47) as well as Equations (9)–(10) for general $j\left(\tau \right)$ the theoretical cosmic SFR density and the integrated stellar density as a function of redshift are

$${\psi }_{\mathrm{GSL}}\left(z\right)=A_1{\displaystyle \frac{j\left(\tau \right(z\left)\right)}{{(1+z)}^{5/2}}}$$

(121)

with

$$A_1=2.78·{10}^{-10}{a}_0^2{h}_{70}=2.78·{10}^{-44}{\tilde{a}}_0^2{h}_{70}\mathrm{kg}{\mathrm{m}}^{-3}\mathrm{s},$$

(122)

and

$$\begin{array}{ccc}\hfill {\rho }_{\mathrm{GSL}}^{*}\left(z\right)& =& B_1{\int }_z^{1100}d{z}^{\prime }[1-L\left(z^{\prime }\right)-G\left(z^{\prime }\right)]{\displaystyle \frac{j\left(\tau \left(z^{\prime }\right)\right)}{{(1+z^{\prime })}^5}}\hfill \\ & =& B_1{\int }_z^{1100}d{z}^{\prime }S\left(z^{\prime }\right){\displaystyle \frac{j\left(\tau \left(z^{\prime }\right)\right)}{{(1+z^{\prime })}^5}},\hfill \end{array}$$

(123)

with

$$B_1=2.24·{10}^8{a}_0^2=2.24·{10}^{-26}{\tilde{a}}_0^2\mathrm{kg}{\mathrm{m}}^{-3}.$$

(124)

In part I we have argued that the factor $1-L\left(z\right)$ enters the calculation of ${\rho }_{\mathrm{GSL}}^{*}\left(z\right)$ but not the calculation of the SFR density (121) because all stars are born as luminous main sequence stars but only the fraction $1-L\left(z\right)$ contributes to the observed integrated density of luminous stars. Here we refined this reduction factor to $1-L\left(z\right)-G\left(z\right)=S\left(z\right)$ as also the baryonic gas does not contribute to the integrated luminous stellar density.

6.1. Observational Constraints

For the comparison with the predictions of the GSL-model we required the same five constraints as in part I.

First, the observed peak SFR density is given by ´

$$\begin{array}{ccc}\hfill \psi \left(z_E\right)& =& 0.{178}_{-0.044}^{+0.372}{M}_{\odot }{\mathrm{yr}}^{-1}{\mathrm{Mpc}}^{-3}\hfill \\ & =& (3.{83}_{-0.95}^{+8.00})·{10}^{-46}\mathrm{kg}{\mathrm{s}}^{-1}{\mathrm{m}}^{-3},\hfill \end{array}$$

(125)

and occurs in the redshift range $1.62-1.88$ ([8]) and $1.7-2.5$ ([9]).

Secondly, we required for the observed peak redshift

$$z_E=2.0\pm 1.0.$$

(126)

As third constraint we used the observed integrated stellar mass density at $z=0$ ([10,11])

$$\begin{array}{ccc}\hfill {\rho }^{*}\left(0\right)& =& (5.{62}_{-1.35}^{+1.79})·{10}^8{\displaystyle \frac{M_{\odot }}{{\mathrm{Mpc}}^3}}\hfill \\ & =& (3.{80}_{-0.91}^{+1.21})·{10}^{-29}\mathrm{kg}{\mathrm{m}}^{-3}\hfill \end{array}$$

(127)

As fourth constraint we demanded that ${(d\psi /dz)}_{z=0}>0$ in order to have at least one maximum of $\psi \left(z\right)$ at positive z. As fifth more stringent constraint we required that ${\psi }_{\mathrm{GSL}}\left(z\right)$ exhibits exactly one maximum within the redshift range $z\in [0,8]$.

6.2. SFR Density

Using Equation (118) for $j\left(\tau \right)$ and Equation (10) for $\tau \left(z\right)$ the SFR density (121) became

$$\begin{array}{ccc}\hfill {\psi }_{\mathrm{GSL}}\left(\tau \left(z\right)\right)& =& {\displaystyle \frac{A_1{(1+q_0)}^2\Psi \left(\tau \right)}{4{\varphi }^{5/3}}},\hfill \end{array}$$

(128a)

$$\begin{array}{ccc}\hfill \Psi \left(\tau \right)& =& {\displaystyle \frac{{\tau }^{5/3}}{{cosh}^2\frac{(1+q_0)(\tau -{\tau }_G)}{2}}}.\hfill \end{array}$$

(128b)

This SFR density (128) fulfills the fourth and fifth constraint mentioned in the last Section 6.1. With the first derivative

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d\Psi \left(\tau \right)}{d\tau }}& =& {\displaystyle \frac{5}{3}}{\displaystyle \frac{{\tau }^{2/3}}{{cosh}^2\frac{(1+q_0)(\tau -{\tau }_G)}{2}}}\times \hfill \\ & & \left[1-{\displaystyle \frac{3}{5}}(1+q_0)\tau tanh{\displaystyle \frac{(1+q_0)(\tau -{\tau }_G)}{2}}\right]\hfill \end{array}$$

(129)

we found that a single maximum occurs at ${\tau }_E$ given by the solution of the transcendental equation

$$tanh{\displaystyle \frac{(1+q_0)({\tau }_E-{\tau }_G)}{2}}={\displaystyle \frac{5}{3(1+q_0){\tau }_E}},$$

(130)

while

$${\Psi }_{\max }={\tau }_E^{-1/3}\left[{\tau }_E^2-{\displaystyle \frac{25}{9{(1+q_0)}^2}}\right].$$

(131)

Using the following abbreviations,

$$X={\displaystyle \frac{(1+q_0){\tau }_E}{2}},X_u={\displaystyle \frac{(1+q_0){\tau }_G}{2}}=-{\displaystyle \frac{ln{q}_0}{2}},$$

(132)

Equation (130) simplified to

$$tanh(X-X_u)={\displaystyle \frac{5}{6X}}.$$

(133)

For values of $0\le X_u<3$, corresponding to $e^{-6}=2.48·{10}^{-3}\le q_0\le 1$, the positive solution of Equation (133) with a maximum relative deviation of 0.9% from the exact solution is given by

$$\begin{array}{ccc}\hfill X(q_0\le 1)& =& {\displaystyle \frac{(1+q_0){\tau }_E}{2}}\simeq 1.06\left(1+{\displaystyle \frac{X_u^{1.3}}{2}}\right)\hfill \\ & \simeq & 1.06\left[1+0.192{(-ln{q}_0)}^{1.3}\right],\hfill \end{array}$$

(134)

where $X\simeq 1.06$ is the numerical solution of $tanh\left(X\right)=5/\left(6X\right)$. Values $q_0\in [0.01,1]$ correspond to values of $X_u\in [0,2.3]$. For values $X_u<0$, corresponding to values of $q_0>1$, the positive solution of Equation (133) with a maximum relative deviation of 0.4% from the exact solution is given by

$$\begin{array}{ccc}\hfill X(q_0>1)& \simeq & {\displaystyle \frac{5}{6}}+\left(1.06-{\displaystyle \frac{5}{6}}\right)e^{5X_u/3}\hfill \\ & =& {\displaystyle \frac{5}{6}}[1+0.272e^{5X_u/3}]={\displaystyle \frac{5}{6}}\left[1+{\displaystyle \frac{0.272}{q_0^{5/6}}}\right].\hfill \end{array}$$

(135)

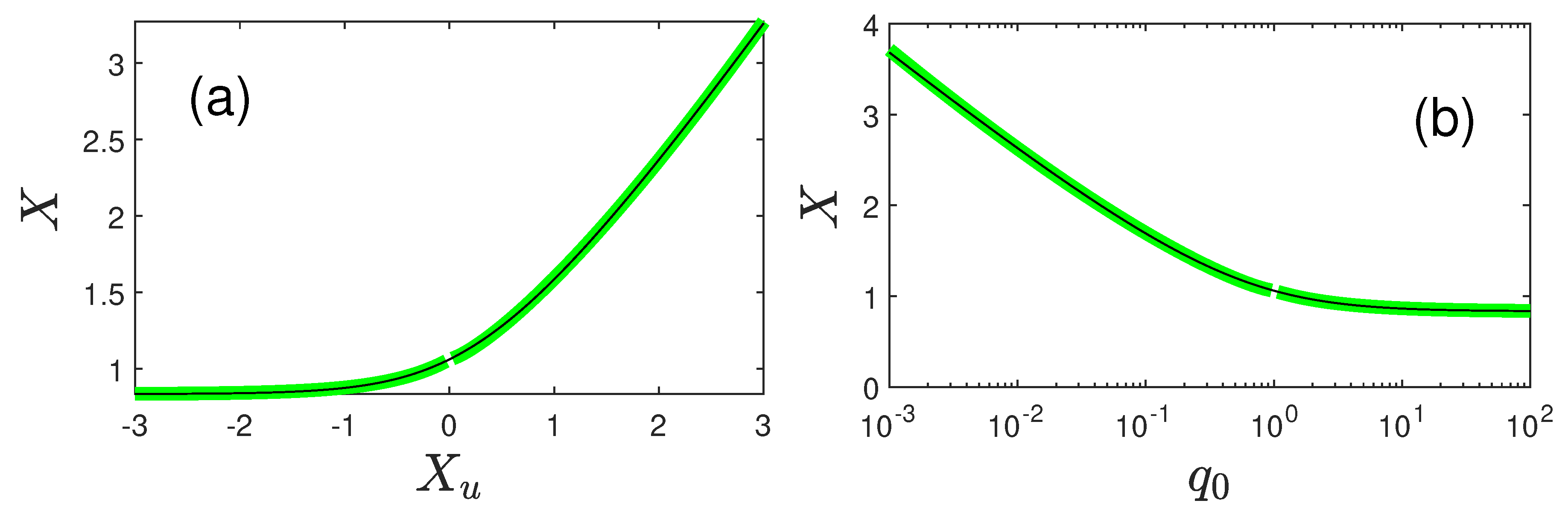
This approximation is exact at $X_u=0$ and $X_u\to -\infty$, and compared with the numerical solution in Figure 4. The cases $q_0\le 1$ and $q_0>1$ will be discussed in turn.

6.2.1. Values $q_0\le 1$

With Equations (10) and (134) we found for the peak time

$${\tau }_E(q_0\le 1)={\displaystyle \frac{2.12[1+0.192{(-ln{q}_0)}^{1.3}]}{1+q_0}},$$

(136)

the peak redshift

$$z_E(q_0\le 1)={\left({\displaystyle \frac{2.533{\tilde{a}}_0(1+q_0)}{h_{70}\left[1+0.192{(-ln{q}_0)}^{1.3}\right]}}\right)}^{2/3}-1$$

(137)

and the the peak SFR density

$$\begin{array}{ccc}\hfill {\Psi }_{\max }(q_0\le 1)& =& 3.4986{\left({\displaystyle \frac{1+0.192{(-ln{q}_0)}^{1.3}]}{1+q_0}}\right)}^{5/3}\times \hfill \\ & & \left[1-{\displaystyle \frac{0.618}{{[1+0.192{(-ln{q}_0)}^{1.3}]}^2}}\right],\hfill \end{array}$$

(138)

so that

$${\psi }_{\mathrm{GSL}}(z_E,q_0\le 1)=4.2205·{10}^{-46}{\tilde{a}}_0^{1/3}{h}_{70}^{8/3}{(1+q_0)}^2{\Psi }_{\max }$$

$$=1.477·{10}^{-45}{\tilde{a}}_0^{1/3}{h}_{70}^{8/3}{(1+q_0)}^{1/3}{\left(1+0.067{(-ln{q}_0)}^{3/2}\right)}^{5/3}\times$$

$$\left[1-{\displaystyle \frac{0.618}{{[1+0.192{(-ln{q}_0)}^{1.3}]}^2}}\right]\mathrm{kg}{\mathrm{s}}^{-1}{\mathrm{m}}^{-3},$$

(139)

Equating Equation (137) with the observed peak redshift (126) readily yielded

$${\tilde{a}}_0(q_0\le 1)=(2.{05}_{-0.93}^{+1.11}){\displaystyle \frac{h_{70}\left[1+0.192{(-ln{q}_0)}^{1.3}\right]}{1+q_0}},$$

(140)

while the equality of Equation (139) with the observed peak SFR density (125) lead to

$${\tilde{a}}_0(q_0\le 1)={\displaystyle \frac{(0.{0174}_{-0.010}^{+0.496})h_{70}^{-8}{(1+q_0)}^{-1}}{{\left[1+0.192{(-ln{q}_0)}^{1.3}\right]}^5{[1-\frac{0.618}{{[1+0.192{(-ln{q}_0)}^{1.3}]}^2}]}^3}}.$$

(141)

Note that for $q_0=1$ Equations (140) and (141) provide (Figure 5)

$$\begin{array}{ccc}\hfill {\tilde{a}}_0(q_0=1)& =& (1.{03}_{-0.47}^{+0.56})h_{70},\hfill \end{array}$$

(142a)

$$\begin{array}{ccc}\hfill {\tilde{a}}_0(q_0=1)& =& (0.{156}_{-0.089}^{+4.449})h_{70}^{-8},\hfill \end{array}$$

(142b)

which overlap very well.

6.2.2. Values $q_0>1$

With Equations (10) and (135) we obtained for the peak time

$${\tau }_E(q_0>1)={\displaystyle \frac{5}{3}}{\displaystyle \frac{0.272+q_0^{5/6}}{q_0^{5/6}(1+q_0)}},$$

(143)

the peak redshift

$$z_E(q_0>1)={\left({\displaystyle \frac{3.222{\tilde{a}}_0{q}_0^{5/6}(1+q_0)}{h_{70}[0.272+q_0^{5/6}]}}\right)}^{2/3},-1$$

(144)

and the peak SFR density

$$\begin{array}{c}\hfill {\Psi }_{\max }(q_0>1)=2.343\left[1-{\displaystyle \frac{q_0^{5/3}}{{(0.272+q_0^{5/6})}^2}}\right]{\left({\displaystyle \frac{0.272+q_0^{5/6}}{q_0^{5/6}(1+q_0)}}\right)}^{5/3},\end{array}$$

(145)

so that

$${\psi }_{\mathrm{GSL}}(z_E,q_0>1)$$

$$=4.2205·{10}^{-46}{\tilde{a}}_0^{1/3}{h}_{70}^{8/3}{(1+q_0)}^2{\Psi }_{\max }$$

$$=9.889·{10}^{-46}{\tilde{a}}_0^{1/3}{h}_{70}^{8/3}{(1+q_0)}^2{\left({\displaystyle \frac{0.272+q_0^{5/6}}{q_0^{5/6}(1+q_0)}}\right)}^{5/3}\times$$

$$\left[1-{\displaystyle \frac{q_0^{5/3}}{{(0.272+q_0^{5/6})}^2}}\right]\mathrm{kg}{\mathrm{s}}^{-1}{\mathrm{m}}^{-3}.$$

(146)

Equating Equation (144) with the observed peak redshift (126) readily yielded

$${\tilde{a}}_0(q_0>1)=(1.{61}_{-0.74}^{+0.87}){\displaystyle \frac{h_{70}[0.272+q_0^{5/6}]}{q_0^{5/6}(1+q_0)}},$$

(147)

while the equality of Equation (146) with the observed peak SFR density (125) lead to

$$\begin{array}{ccc}\hfill {\tilde{a}}_0(q_0>1)& =& {\displaystyle \frac{(0.{0581}_{-0.0334}^{+1.653})}{h_{70}^8(1+q_0)}}{\left[{\displaystyle \frac{q_0^{5/6}}{0.272+q_0^{5/6}}}\right]}^5\times \hfill \\ & & {\left[1-{\displaystyle \frac{q_0^{5/3}}{{\left(0.272+q_0^{5/6}\right)}^2}}\right]}^{-3}.\hfill \end{array}$$

(148)

All four expressions (140)–(141) and (147)–(148) for ${\tilde{a}}_0$ are displayed in Figure 5. As parameter values consistent with the observational constraints values we inferred from Figure 5

$$\begin{array}{ccc}\hfill {\tilde{a}}_0& =& 0.{62}_{-0.29}^{+0.33},q_0=2.0_{-1.1}^{+1.2},\hfill \end{array}$$

(149)

implying

$$\begin{array}{ccc}\hfill a_0& =& (0.{62}_{-0.29}^{+0.33})·{10}^{-17}\mathrm{Hz},\hfill \end{array}$$

(150a)

$$\begin{array}{ccc}\hfill {\beta }_0& =& a_0{q}_0=(1.{24}_{-0.94}^{+1.80})·{10}^{-17}\mathrm{Hz}.\hfill \end{array}$$

(150b)

Consequently, the spontaneous and triggered star formation processes operate on time scales of $t_{\mathrm{spont}}\simeq 2.{57}_{-1.52}^{+8.15}$ Gyr and $t_{\mathrm{trig}}\simeq 5.{13}_{-1.78}^{+4.52}$ Gyr, respectively. The partly large error bars resulted from the large error bars on the observed SFR peak density (125).

Note that for $q_0=1$ the Equations (147) and (148) provide

$$\begin{array}{ccc}\hfill {\tilde{a}}_0(q_0=1)& =& (1.{02}_{-0.47}^{+0.55})h_{70},\hfill \end{array}$$

(151a)

$$\begin{array}{ccc}\hfill {\tilde{a}}_0(q_0=1)& =& (0.{157}_{-0.090}^{+4.455})h_{70}^{-8},\hfill \end{array}$$

(151b)

which agree perfectly with the earlier estimate (142). For very large values of $q_0\gg 1$ Equations (147) and (148) yielded

$$\begin{array}{ccc}\hfill {\tilde{a}}_0(q_0\gg 1)& =& (1.{61}_{-0.74}^{+0.87}){\displaystyle \frac{h_{70}}{q_0}},\hfill \end{array}$$

(152a)

$$\begin{array}{ccc}\hfill {\tilde{a}}_0(q_0\gg 1)& =& (0.{0581}_{-0.0334}^{+1.653})·6.21q_0^{3/2}{h}_{70}^{-8}.\hfill \end{array}$$

(152b)

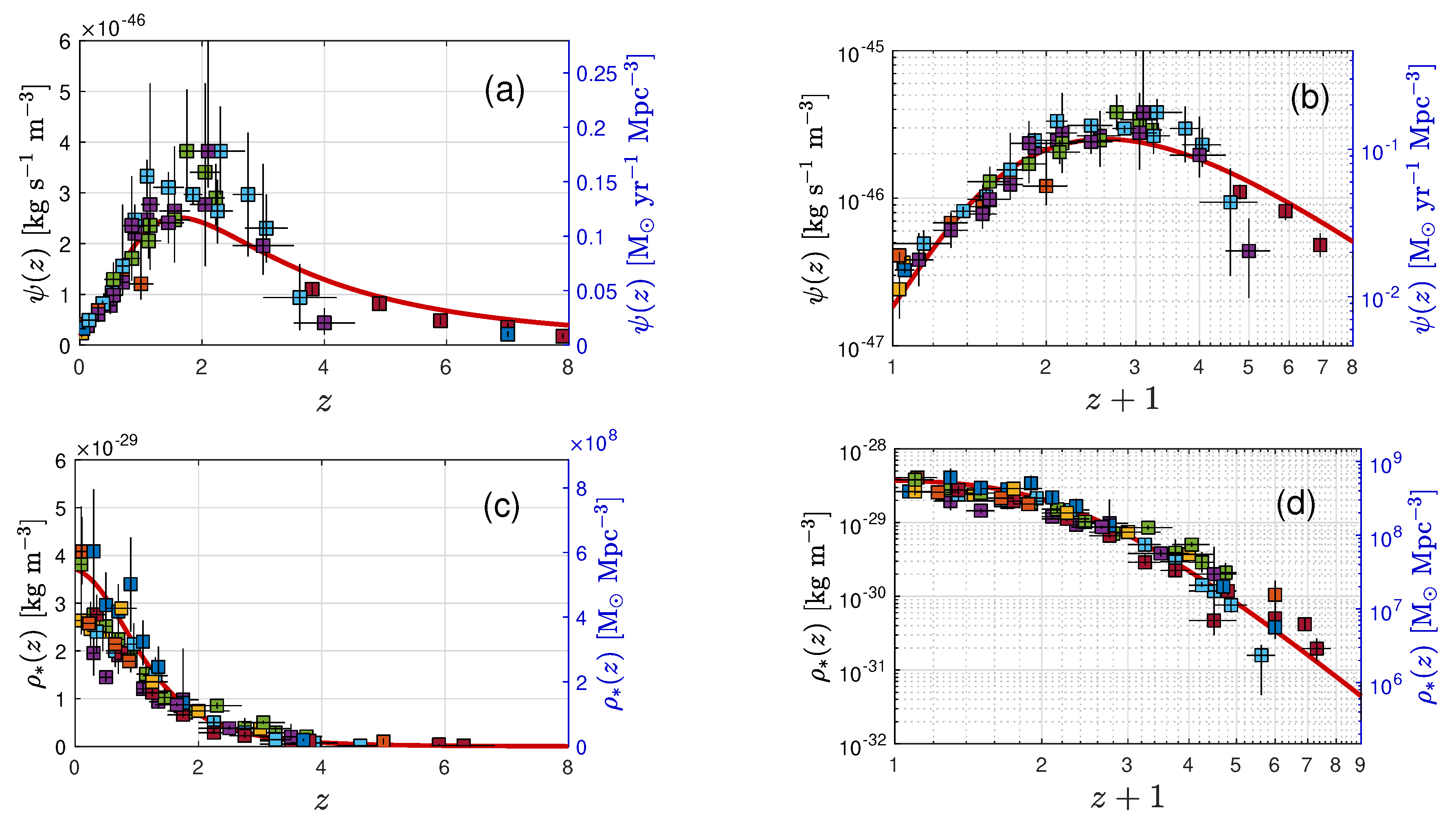
In panels (a) and (c) of Figure 6 we compared the theoretical SFR density (128) with the observations collected by [7] where we varied freely the parameters ${\tilde{a}}_0$ and $q_0$. As can be seen we obtained excellent agreement with the observations for the parameter choice ${\tilde{a}}_0=0.368$ and $q_0=2.67$. Both values are consistent with the range of parameter values (149) implied by the observational constraints discussed before. In panels (b) and (d) we show the corresponding fit to the observations of the integrated stellar density, to be discussed next. Here again we found excellent agreement if additionally the parameter values $k_0=0.0039$ and $p_0=0.656$ so that $k_0+p_0=0.66$ was chosen.

6.3. Integrated Stellar Density

Likewise, the integrated stellar density (123) is given by

$${\rho }_{\mathrm{GSL}}^{*}\left(z\right)={\displaystyle \frac{2B_1}{3{\varphi }^{8/3}}}{\int }_{{\displaystyle \frac{\varphi }{{1101}^{3/2}}}}^{{\displaystyle \frac{\varphi }{{(1+z)}^{3/2}}}}d\tau j\left(\tau \right)S\left(\tau \right){\tau }^{5/3}$$

$$\simeq {\displaystyle \frac{B_1{q}_0{(1+q_0)}^3}{6ϵ{\varphi }^{8/3}}}{\int }_0^{{\displaystyle \frac{\varphi }{{(1+z)}^{3/2}}}}d\tau {\displaystyle \frac{{\tau }^{5/3}}{{cosh}^2\frac{(1+q_0)(\tau -{\tau }_G)}{2}}}{\displaystyle \frac{e^{ϵ\tau }-1}{1+e^{(1+q_0)(\tau -{\tau }_G)}}}$$

$$={\displaystyle \frac{B_1{q}_0{(1+q_0)}^3}{12ϵ{\varphi }^{8/3}}}{\int }_0^{{\displaystyle \frac{\varphi }{{(1+z)}^{3/2}}}}d\tau {\displaystyle \frac{{\tau }^{5/3}{e}^{-\frac{(1+q_0)(\tau -{\tau }_G)}{2}}}{{cosh}^3\frac{(1+q_0)(\tau -{\tau }_G)}{2}}}\left(e^{ϵ\tau }-1\right)$$

$$={\displaystyle \frac{2^{2/3}{B}_1{q}_0^{1/2}{(1+q_0)}^{1/3}}{3ϵ{\varphi }^{8/3}}}J\left({\displaystyle \frac{(1+q_0)\varphi }{2{(1+z)}^{3/2}}}\right),$$

(153)

where we used Equations (10), (110) and (118), substituted according to Equation (132), and introduced the integral

$$\begin{array}{ccc}\hfill J\left(A\right)& =& {\int }_0^{A}dX{\displaystyle \frac{X^{5/3}{e}^{-X}[e^{\frac{2ϵX}{1+q_0}}-1]}{{cosh}^3(X-X_u)}}.\hfill \end{array}$$

(154)

6.3.1. Asymptotics of the Integral (154)

We investigated the asymptotic behavior of the integral (154) for small values of A with respect to unity, corresponding to large values of the redshift z. We obtained

$$\begin{array}{ccc}\hfill J(A\ll 1)& \simeq & {\displaystyle \frac{2ϵ}{1+q_0}}{\int }_0^{A}dX{\displaystyle \frac{X^{8/3}}{{cosh}^3(X-X_u)}}\hfill \\ & \simeq & {\displaystyle \frac{6ϵA^{11/3}}{11(1+q_0){cosh}^3\left(X_u\right)}}={\displaystyle \frac{48ϵq_0^{3/2}{A}^{11/3}}{11{(1+q_0)}^4}}.\hfill \end{array}$$

(155)

As $A\left(z\right)=(1+q_0)\varphi /\left(2{(1+z)}^{3/2}\right)$ the asymptotics (155) corresponds to

$$J(z\ge z_c)\simeq {\displaystyle \frac{3·2^{1/3}ϵq_0^{3/2}{\varphi }^{11/3}}{11{(1+q_0)}^{1/3}{(1+z)}^{11/2}}},$$

(156)

with the characteristic redshift

$$z_c={\left[{\displaystyle \frac{1+q_0)\varphi }{2}}\right]}^{2/3}-1=1.93{\left[{\displaystyle \frac{(1+q_0){\tilde{a}}_0}{h_{70}}}\right]}^{2/3}-1$$

(157)

of order unity. We then obtained for Equation (153) in this limit

$$\begin{array}{ccc}\hfill {\rho }_{\mathrm{GSL}}^{*}(z\ge z_c)& \simeq & {\displaystyle \frac{2B_1{q}_0^2\varphi }{11{(1+z)}^{11/2}}}\hfill \\ & =& {\displaystyle \frac{2.19·{10}^{-26}{q}_0^2{\tilde{a}}_0^3}{h_{70}{(1+z)}^{11/2}}}\mathrm{kg}{\mathrm{m}}^{-3}.\hfill \end{array}$$

(158)

This asymptotic is significantly steeper than the ${(1+z)}^{-4}$ behavior obtained in part I for neglected triggered star formation.

In the alternative case of large arguments $A\gg 1$ the integral (154) was approximated in Appendix B as

$$\begin{array}{ccc}\hfill J(A\gg 1)& \simeq & {\displaystyle \frac{3}{2{cosh}^3\left(X_u\right)}}\left[{\left({\displaystyle \frac{4}{3}}+{\displaystyle \frac{2(k_0+p_0)}{1+q_0}}\right)}^{-8/3}-0.04\right]\hfill \\ & =& {\displaystyle \frac{12q_0^{3/2}}{{(1+q_0)}^3}}\left[{\left({\displaystyle \frac{4}{3}}+{\displaystyle \frac{2(k_0+p_0)}{1+q_0}}\right)}^{-8/3}-0.04\right].\hfill \end{array}$$

(159)

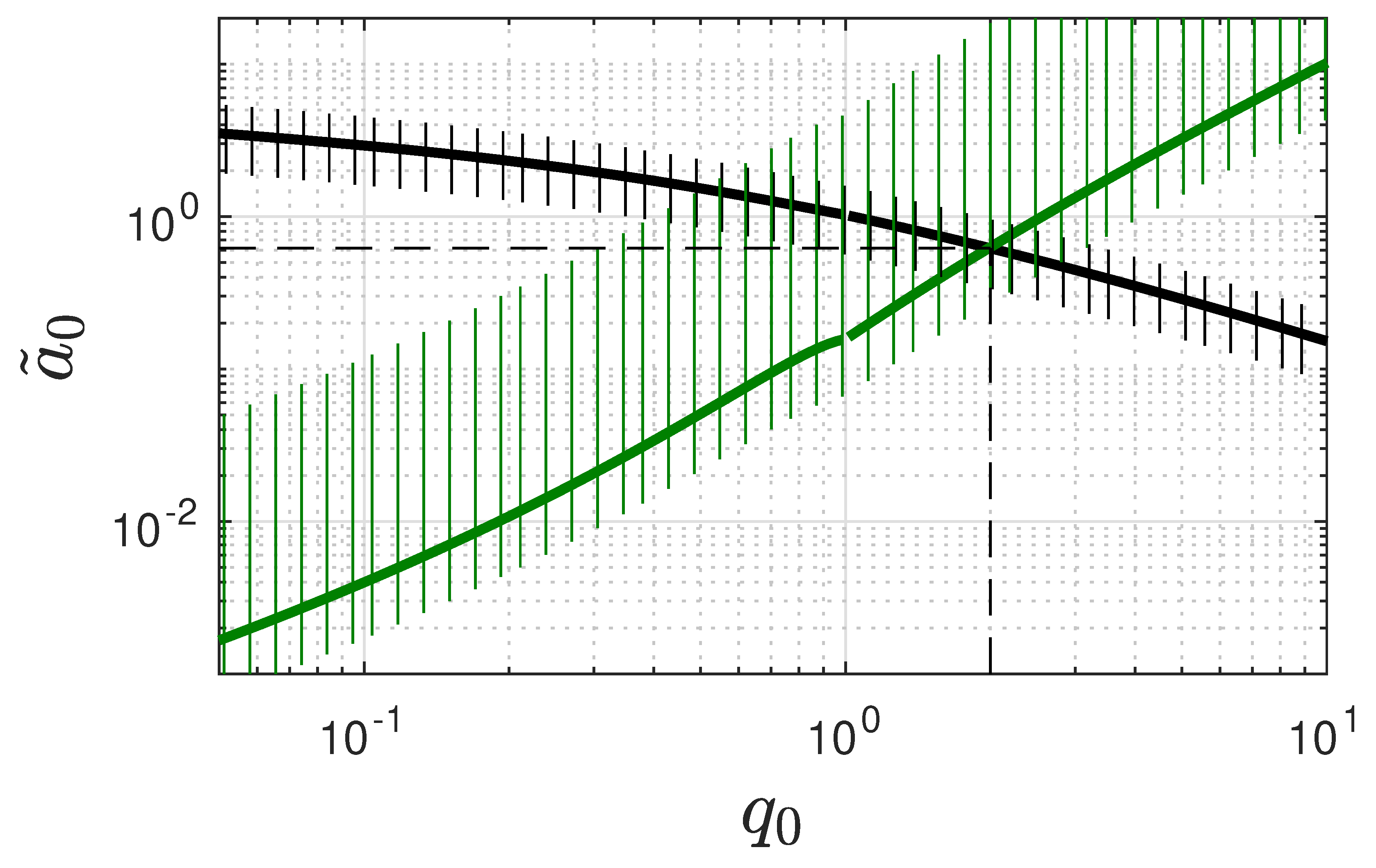
6.3.2. Present-Day Integrated Stellar Density

For the present-day integrated stellar density at redshift $z=0$ we note that with our earlier parameter estimates (149) $A(z=0)=2.69(1+q_0){\tilde{a}}_0{h}_{70}^{-1}\simeq 4.99$ is large compared to unity so that we used the approximation (159) providing for Equation (153)

$${\rho }_{\mathrm{GSL}}^{*}\left(0\right)\simeq {\displaystyle \frac{2^{8/3}{B}_1{q}_0^2}{ϵ{(1+q_0)}^{8/3}{\varphi }^{8/3}}}\left[{\left({\displaystyle \frac{4}{3}}+{\displaystyle \frac{2(k_0+p_0)}{1+q_0}}\right)}^{-8/3}-0.04\right]$$

$$={\displaystyle \frac{1.61·{10}^{-27}{h}_{70}^{8/3}{q}_0^2}{{\tilde{a}}_0^{2/3}ϵ{(1+q_0)}^{8/3}}}\left[{\left({\displaystyle \frac{4}{3}}+{\displaystyle \frac{2(k_0+p_0)}{1+q_0}}\right)}^{-8/3}-0.04\right]\mathrm{kg}{\mathrm{m}}^{-3}.$$

(160)

Equating the constraint (127) with Equation (160) then yielded

$${\tilde{a}}_0={\displaystyle \frac{\left({276}_{-94}^{+140}\right)h_{70}^4{q}_0^3}{{(1+q_0-p_0-k_0)}^{3/2}{(1+q_0)}^4}}{\left[{\left({\displaystyle \frac{4}{3}}+{\displaystyle \frac{2(k_0+p_0)}{1+q_0}}\right)}^{-8/3}-0.04\right]}^{3/2}.$$

(161)

In contrast with the earlier constraints (140) and (141) the constraint (161) depends on the sum $p_0+k_0$ of the additional ratios $k_0$ and $p_0$ characterizing the strength of stellar evolution and feedback, respectively. For ${\tilde{a}}_0$ and $q_0$ from Equation (149), Equation (161) yielded $k_0+p_0=0.{585}_{-0.317}^{+0.574}$ in excellent agreement with the numerical fit in Figure 7.

7. Redshift Dependency of the Gas and Stellar Fractions and Future of the Baryonic Universe

Here the best fit parameter values for the three ratios $q_0$, $p_0$ and $k_0$ and the triggered star formation rate $a_0$ from the last Section were used to determine the present-day ($z=0$) gas and stellar fractions. The three panels in Figure 8 display the resulting reduced time and redshift dependencies of the fractions using Equations (106), (110), and (120). The error bars according to Equations (149) and $k_0+p_0\in [0.25,1.14]$ from the fits in Figure 7 are represented as gray lines, whose darkness moderately increases with their probability, assuming Gaussian distributed ${\tilde{a}}_0$ and $q_0$.

These panels not only show the history of the cosmological gas and stellar fractions as a function of redshift z in panel (b), but also their future evolution as a function of the reduced time $\tau$ in panel (a). Note that the present-day epoch depending on ${\tilde{a}}_0$ corresponds to about $\tau (z=0)=1.83$, so that future starts beyond this time. In panel (a) of Figure 8 we marked the future epochs in green colour. It is clear, however, that ultimately at $\tau =\infty$ the stationary state with values

$$G_{\infty }=0,{\displaystyle \frac{G_{\infty }}{1-G_{\infty }}}=0,{\displaystyle \frac{G_{\infty }}{S_{\infty }}}=0$$

(162)

is attained.

Next we considered the present-day ($z=0$) gas and stellar fractions. As present-day quantities have to be calculated, we used the modification $\zeta \left(0\right)$ in Equations (10)–(12) for $\tau (z=0))$.

7.1. Present-Day Gas Fraction

According to Equation (106) the Equation (10) predicts for the present-day gas fraction

$$\begin{array}{ccc}\hfill G(z=0)& =& {\displaystyle \frac{1+q_0}{1+q_0{e}^{(1+q_0)\tau \left(0\right)}}}={\displaystyle \frac{1+q_0}{1+q_0{e}^{2.94(1+q_0){\tilde{a}}_0{h}_{70}^{-1}}}},\hfill \end{array}$$

(163)

which can be contrasted with the observed Milky Way gas fraction of $\approx 0.1$ ([12]). With the parameters (149) we obtained for $h_{70}=1$

$$G(z=0)=0.{00631}_{-0.00629}^{+0.278}$$

(164)

Within the large error bars this prediction is consistent with the observed gas fraction of about 10 percent.

The gas fraction (164) also provided the present-day interstellar gas mass to total (including locked-in matter) stellar mass

$$\begin{array}{ccc}\hfill {\displaystyle \frac{G(z=0)}{S(z=0)+L(z=0)}}& =& {\displaystyle \frac{G(z=0)}{1-G(z=0)}}=0.00635\hfill \end{array}$$

(165)

for the nominal parameter values $q_0=2$ and ${\tilde{a}}_0=0.62$.

7.2. Stellar Fractions

Likewise, from Equation (110) we obtained

$$\begin{array}{ccc}\hfill S(z=0)& =& {\displaystyle \frac{q_0[e^{ϵ\tau \left(0\right)}-1]G(z=0)}{ϵ}}\hfill \\ & =& {\displaystyle \frac{q_0[e^{2.94ϵ{\tilde{a}}_0{h}_{70}^{-1}}-1]G(z=0)}{ϵ}}.\hfill \end{array}$$

(166)

For the nominal values $q_0=2$, ${\tilde{a}}_0=0.62$, $p_0+k_0=0.66$, so that $ϵ=2.34$, we found

$$S(z=0)=0.{379}_{-0.191}^{+0.224},L(z=0)=0.{615}_{-0.378}^{+0.197}$$

(167)

for the ratio of the present-day interstellar gas mass to luminous stellar mass

$$\begin{array}{ccc}\hfill {\displaystyle \frac{G(z=0)}{S(z=0)}}& =& 0.{01665}_{-0.01665}^{+0.5627}.\hfill \end{array}$$

(168)

The last ratio could be compared with the observed gas/stellar mass fraction in $z\sim 0$ galaxies ([13,14]) as the stellar component has been obtained from large galaxy surveys in the optical/infrared band where locked-in stellar matter contributes negligibly small emission. The observations reveal ratios as a function of stellar mass in the range $[0.01,0.7]$. The estimate (168) is consistent with the observations but excluded the large positive error bar.

The estimates (167) indicated that at the present time the majority of the baryons (more than 72 percent) resides in the form of stellar matter with $61.5_{-37.8}^{+19.7}$ percent in locked-in stellar matter (white dwarfs, neutron stars and black holes) and $37.9_{.19.1}^{+22.4}$ percent in the form of luminous main-sequence stars. These estimates had to be contrasted with expectations from stellar evolution models. In these models, for a reasonable choice of the initial mass function (see for example [15,16]), a stellar population of approximately 13 Gyr has only returned about $R\sim$ 40% of its originally formed mass to the ISM, with $(1-R)\sim$ 60% remaining as surviving stars or remnants. Of that ∼ 60%, only around ∼ 25% consists of remnants (white dwarfs, black holes, and neutron stars) — see section 2.1.2 of the review by [17]. Within their uncertainties the estimates (167) are consistent with the stellar evolution model calculations which have their own uncertainties.

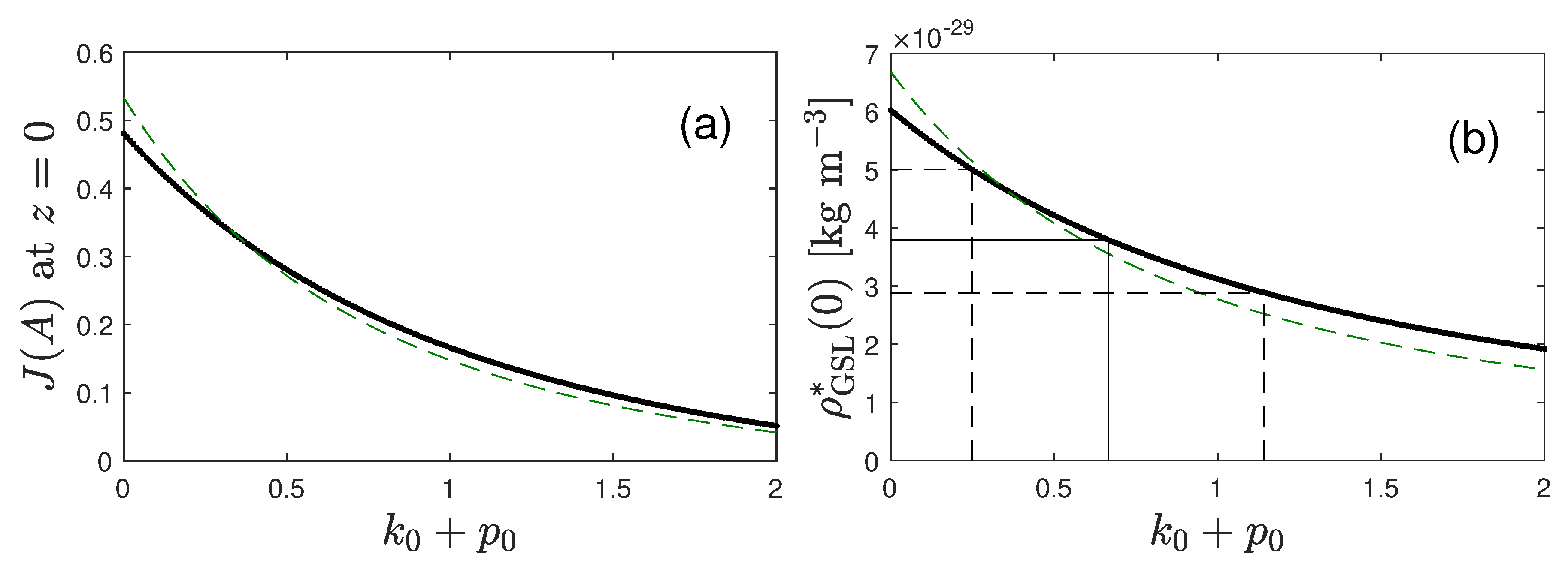
7.3. Remarks

We can conclude this Section with two important remarks:

(1) It had not escaped from our attention that we can only constraint analytically the sum of the two parameters $p_0+k_0$ from the comparison of the integrated stellar light as well as the stellar fractions. This is a drawback of our approximation of the exact Equation (73): without the function $R\left(\tau \right)$ this equation indeed only involves the sum $p_0+k_0$. Therefore any dependence on the individual values of $p_0$ and $k_0$ only stems from the function $R\left(\tau \right)$ calculated in Equation (81). However, with the adopted relation (83) involving only $R(\infty )$, which with the choice (84) then also depends only on the sum $p_0+k_0$, any dependency on the individual values of $p_0$ und $k_0$ was not possible anymore. 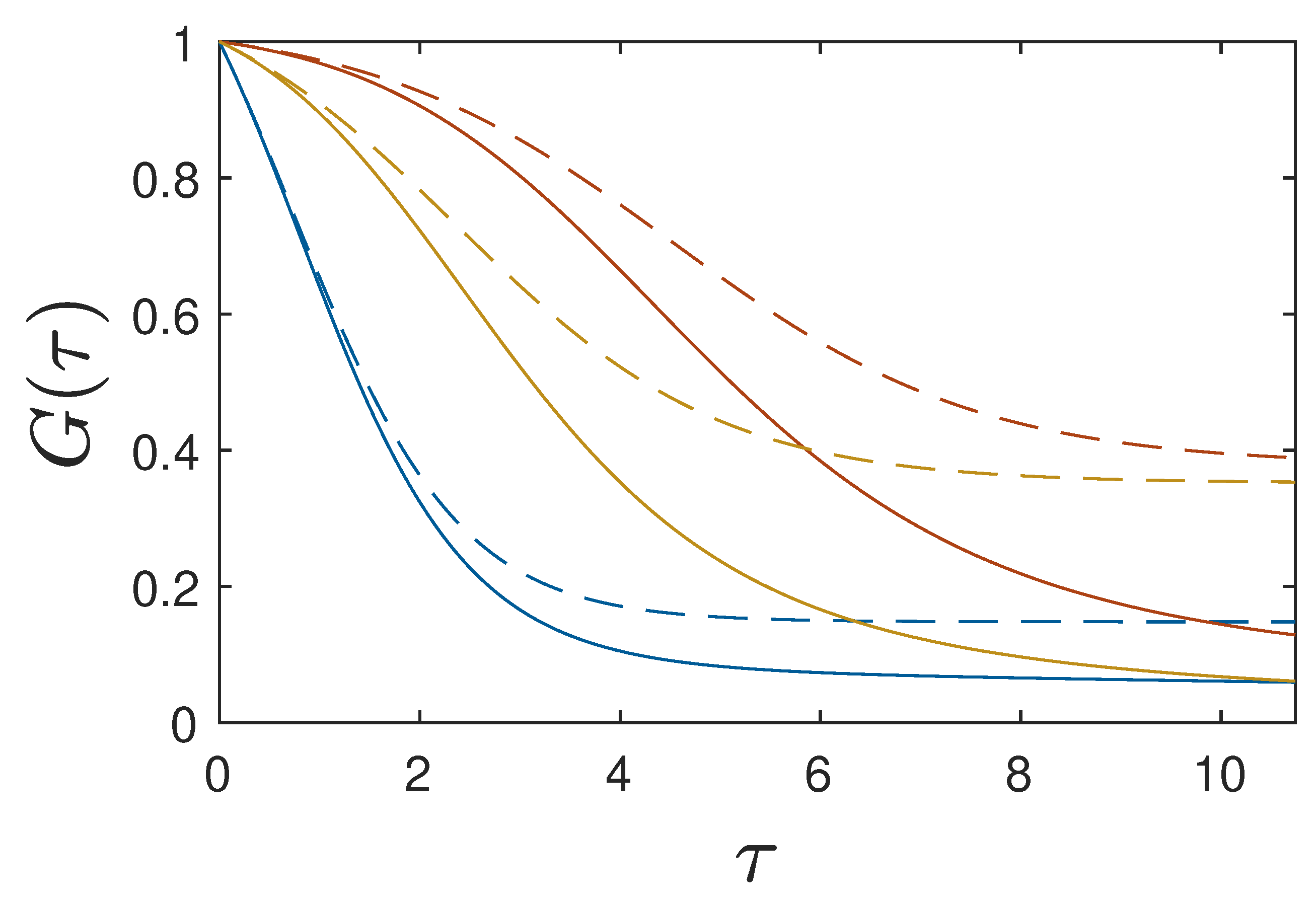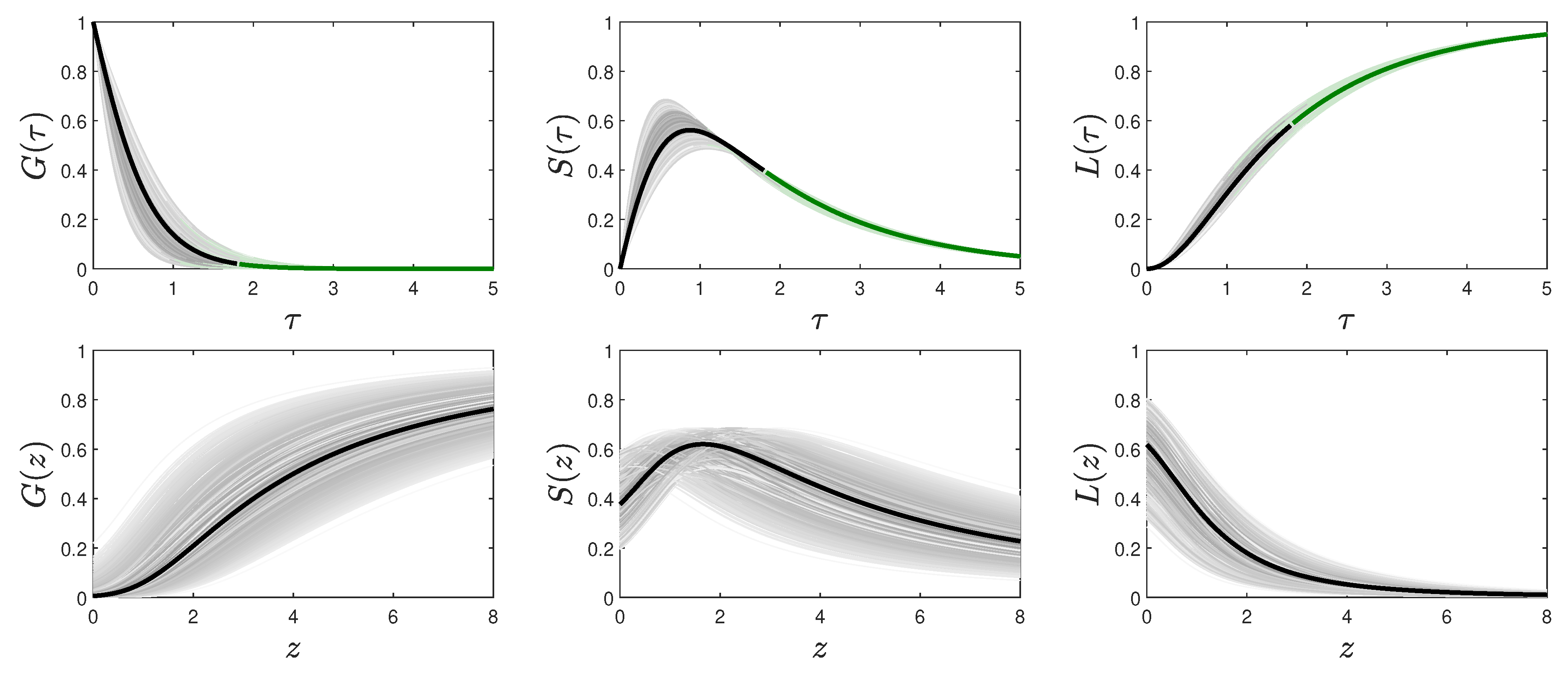This could be proven by comparing the exact numerical solutions of $S\left(\tau \right)$ for the two cases $(k_0=0.2,p_0=0.5)$ and $(k_0=0.5,p_0=0.2$) shown in Figure 9. As in both cases the sum $p_0+k_0=0.7$ is the same our approximation yielded the same time dependence of $S\left(\tau \right)$, whereas the exact numerically calculated variations were different.

(2) The second remark concerns the value of the Hubble constant. In contrast to part I we here were in accord with all observational constraints for the standard value $h_{70}=1$ of the Hubble constant and did not have to speculate on substantially smaller values of the Hubble constant as in part I.

8. Summary and Conclusions

In this work we extended the analysis of the compartmental description of the temporal evolution of the baryonic matter in stars and interstellar gas, pioneered in part I, by the inclusion of the triggered star formation process. As in part I the introduction of gaseous and stellar fractions of the total baryonic matter as the basic dynamical variables is advantageous because it allows to apply the analysis to a variety of astrophysical systems. The competition of triggered and spontaneous star formation, stellar feedback and stellar evolution is theoretically investigated with analytical and numerical solutions of the nonlinear dynamical GSL equations for the interstellar and intergalactic gas fraction $G\left(t\right)$, the luminous stellar matter fraction $S\left(t\right)$, and the locked-in matter fraction $L\left(t\right)$.

By introducing the dimensionless reduced time variable $\tau$ (8) for arbitrarily but given time-dependent triggered SFR coefficient $a\left(t\right)$, as well as the dimensionless ratios $q\left(t\right)=\beta \left(t\right)/a\left(t\right)$, $k\left(t\right)=b\left(t\right)/a\left(t\right)$ and $p\left(t\right)=c\left(t\right)/a\left(t\right)$, the derived exact solutions of the GSL equations for stationary ratios $q_0$, $k_0$ and $p_0$ hold for stationary rates as well as for the case of the same time-dependency of all rates. The accuracy of the analytical solutions is confirmed by comparison with the exact numerical solutions of the GSL equations. Once again of particular interest is the understanding of the cosmic star formation history, the present-day gas and stellar fraction, and their ultimate future fate with compartmental models. For a flat $\Lambda$CDM Friedmann cosmology the relationship between the reduced time variable $\tau \left(z\right)$ and the cosmological redshift z is used to calculate the effect of redshift on the cosmological star formation rate, the integrated stellar density, and the present-day gas and stellar fractions. In contrast to part I the cosmological star formation rate now has two contributions from the spontaneous and triggered formation processes.

The inclusion of the nonlinear triggered star formation process enormously complicated the derivation of analytical solutions. Exact solutions of the GSL equations were derived in Section 3 for the case of negligible stellar evolution and served an important dual purpose, namely to test the accuracy of the numerical code solving the GSL equations as well as comparing with the analytical approximations derived in the most general case in the respective limit of negligible stellar evolution. For the most general case of all four competing processes operating simultaneously with stationary ratios, we reduced the coupled dynamical GSL equations in Section 3 to one exact nonlinear differential equation (see Equations (59) and (73)) determining the time evolution for $U\left(\tau \right)={\int }_0^{\tau }d{\tau }^{\prime }G\left({\tau }^{\prime }\right)-(p_0+k_0)\tau$ from which the gas and stellar fractions can be determined. Approximate analytical solutions were derived in Section 5 for the case of small times $\tau \le p_0^{-1}$ and for general times for positive values of the ratio $p_0$ characterizing the stellar evolution process. The small times solution in the case of negligible stellar evolution ($p_0=0$) holds at all times and agrees exactly with the earlier derived exact solutions in this special case in Section 5. The accuracy of the approximate solution in the general case of finite $p_0$ is demonstrated by comparison with the numerical solutions. Most noteworthy, for small enough rates of stellar feedback determining the ratio $k_0$ the derived gas fraction and the formation rate (118) of new stars as a function of the reduced time $\tau$ are solely determined by the ratio $q_0$ of spontaneous to triggered star formation, whereas the remaining two ratios $k_0$ and $p_0$ exhibit themselves in the temporal evolution of the stellar fractions $S\left(\tau \right)$ and $L\left(\tau \right)$. This is in accord with the starting reduced GSL equations Equations (14a) and (17) that do not directly involve the ratio $p_0$.

The near independency of the formation rate (118) of new stars as a function of the reduced time $\tau$ significantly facilitates the calculation of the cosmological SFR as a function of redshift (Section 6) which, for an adopted constant triggered star formation rate $a_0$, depends only on the two parameters $a_0$ and $q_0={\beta }_0/a_0$. The comparison with the observed SFR provides as best fit values $a_0=0.368$ and $q_0=2.97$, $k_0=0.0039$ and $p_0=0.656$ so that $p_0+k_0=0.66$. Due to the partly large uncertainties in the observed peak SFR rate the error bars on these parameters are ${\tilde{a}}_0=0.{62}_{-0.29}^{+0.39}$, $q_0=2.0_{-1.1}^{+1.2}$ and $k_0+p_0=0.{585}_{-0.317}^{+0.574}$. In Section 7 we calculated the resulting reduced and redshift dependencies of the three gas and stellar fractions. These not only show the history of the cosmological gas and stellar fractions as a function of redshift z, but also predict their future evolution as a function of the reduced time $\tau$. Within the error bars the calculated present day gas and stellar fractions are consistent with the observed Milky Way gas fraction of 0.1 as well as the observed gas/stellar mass fraction in $z\sim 0$ galaxies. They also agree reasonably well with expectations from stellar evolution models.

As most important result of this investigation we found that the inclusion of the triggered star formation process explains the observed cosmological star formation rate and the integrated stellar density as well as the present-day gas and stellar fractions much better than the simplified GSL-model of part I ignoring triggered star formation. The best fit parameter values to the observations indicate that the spontaneous and triggered star formation processes dominate the dynamical evolution of baryonic matter in the universe indicated by the best-fit value of the sum of ratios $p_0+k_0$ being significantly smaller than unity. For an adopted constant triggered star formation rate $a_0$, the spontaneous and triggered star formation processes operate on time scales of $t_{\mathrm{spont}}\simeq 2.{57}_{-1.52}^{+8.15}$ Gyr and $t_{\mathrm{trig}}\simeq 5.{13}_{-1.78}^{+4.52}$ Gyr, respectively. Interestingly, the spontaneous formation process is about twice more effective than the triggered formation process.

After the non-perfect agreement of the simplified GSL-model with only spontaneous star formation process investigated in part I, we can now conclude that the inclusion of the triggered star formation process has improved the situation significantly. This generalized GSL-model is consistent with all observational constraints from the cosmological star formation history and the corresponding integrated stellar density. The model provides excellent fits to the observed redshift dependencies of the star formation rate and the integrated stellar density. Moreover, it explains the observed present-day gas and stellar fractions in the universe, and it makes predictions on the future evolution of these fractions in the universe. The presented analysis of the GSL compartmental model has lead to new and original insights on the cosmological baryonic matter cycle in the universe.