Prerpints.org logo
Preprint
Article

The Impact of Wetting and Drying Cycles on the Architecture and Complexity of Intra-Aggregate Soil Pores

Altmetrics

Downloads

67

Views

46

Comments

0

Submitted:

23 October 2024

Posted:

24 October 2024

You are already at the latest version

Alerts
Abstract
In many soil processes, including solute and gas dynamics, the architecture of intra-aggregate pores is a crucial component. Soil management practices and wetting-drying (W-D) cycles—the latter having a significant impact on pore aggregation—are two key factors that shape pore structure. This study examines the effects of W-D cycles on the architecture of intra-aggregate pores under three different soil management systems: no-tillage (NT), minimum tillage (MT), and conventional tillage (CT). The soil samples were subjected to 0 and 12 W-D cycles, and the resulting pore structures were scanned using X-ray micro-computed tomography, generating reconstructed 3D volumetric data. The analysis was conducted in terms of multifractal spectra, normalized Shannon entropy, lacunarity, porosity, anisotropy, connectivity, and tortuosity. The morphological and geometric properties of the soil pores indicated that W-D cycles did not cause significant changes across the management systems studied. Furthermore, multifractal analysis revealed that the porous systems exhibited fractal behavior rather than multifractality. The results demonstrate that, within the resolution limits of the microtomography analysis, pore architecture remained resilient to changes, despite some observable trends in specific parameters.
Keywords: 
Subject: Environmental and Earth Sciences  -   Soil Science

1. Introduction

The structure of soil is crucial for various processes that occur within this porous system. It is formed by the bonding of primary particles present in the soil, as well as the action of organic material, iron and aluminum oxides, and soil fauna, among other factors [1]. Soil structure directly impacts plant growth, water retention, erosion resistence, and the availability of water and nutrients to plants.
Soil structure directly influences the pore arrangement within it [2]. This structure can be easily changed due to physical processes, which affect the shape, arrangement, and continuity of the pores within the soil [3]. Different soil management systems also have a direct impact on soil structure. For instance, conventional tillage (CT) significantly affects the topsoil due to intense mobilization caused by turning over the soil surface [4].
In contrast, practices like no-tillage (NT) and minimum tillage (MT) minimize topsoil disturbance. NT, in particular, preserves soil structure by maintaining vegetation cover and surface residues, involving little to no soil disruption [5]. Due to these characteristics, NT and MT are often regarded as conservation practices.
In addition to management practices, wetting and drying (W-D) cycles also cause significant changes in the soil’s pore structure [6]. These cycles, in combination with organic matter, play a key role in soil aggregation [7]. However, W-D cycles can also affect soil aggregates, thereby influencing pore distribution [8]. Since aggregates are integral to soil structure, understanding their behavior under repeated W-D cycles is essential [9]. Soil aggregates are particularly important for processes such as aeration, plant growth, water infiltration, carbon sequestration, and other critical soil functions.
More scientific research is needed to assess the changes in intra-aggregate pores, particularly during wetting and drying cycles, since they significantly impact water retention and redistribution [10]. In this context, noninvasive image analysis techniques, such as X-ray micro-computed tomography (X- μ CT), are necessary for studying the dynamics of soil pore architecture at high resolution [11].
X- μ CT offers a significant advantage over traditional techniques. It allows for measurements on the same sample and assessment of different pore sizes in the soil [12,13]. Furthermore, it allows for detailed analysis of pore distribution within samples [14]. X- μ CT also provides insights into pore continuity and tortuosity, both of which are essential for understanding solute dynamics in soil [15]. The ability to easily measure morphological and geometric parameters of soil pores makes X- μ CT an attractive tool for characterizing soil aggregates.
Despite this, the parameters classically obtained by X- μ CT may often not be sufficient to express the changes in soil pore architecture, especially related to pore complexity. For this, we rely on advanced mathematical tools such as fractal [16] and multifractal analysis [17]. For example, multifractal analysis presents a spectral view of the structural heterogeneity in soils. Other parameters, such as entropy and lacunarity, are also especially alternatives for characterizing the soil pore system [18].
In this paper, we discuss how the structure of soil pores is impacted by wetting and drying cycles at the microscopic level within soil aggregates. We aimed to examine how different soil management practices affect the soil structure when exposed to wetting and drying cycles. Our focus is solely on the impact of these cycles, without comparing different management practices. We characterized the soil’s porous system by examining its various morphological and geometric properties. Additionally, we analyzed its complexity using multifractal analysis, entropy, and lacunarity.
Compared to previously published studies, this paper introduces detailed analyses of changes in the pore architecture of small aggregates of highly weathered soil, studies the influence of wet-dry cycles on intra-aggregate pore scale, and the behavior of soils under different management systems in response to wet-dry cycles. Furthermore, techniques that use multifractal analysis are important tools for evaluating dynamic processes in the soil. Thus, this study, focused on the effects of W-D cycles, is based on the following hypotheses: 1) at the intra-aggregate pore scale, modifications in pore architecture tend to be small, and 2) intra-aggregate pore distribution expresses multifractal behavior.
The structure of the article is as follows. Section 2 details the experimental methodology and mathematical framework, outlining the equations and all material resources used. Section 3 presents the numerical results, while Section 4 provides an in-depth discussion of these findings. Finally, Section 5 summarizes the main conclusions drawn from the study, highlighting the key results

2. Materials and Methods

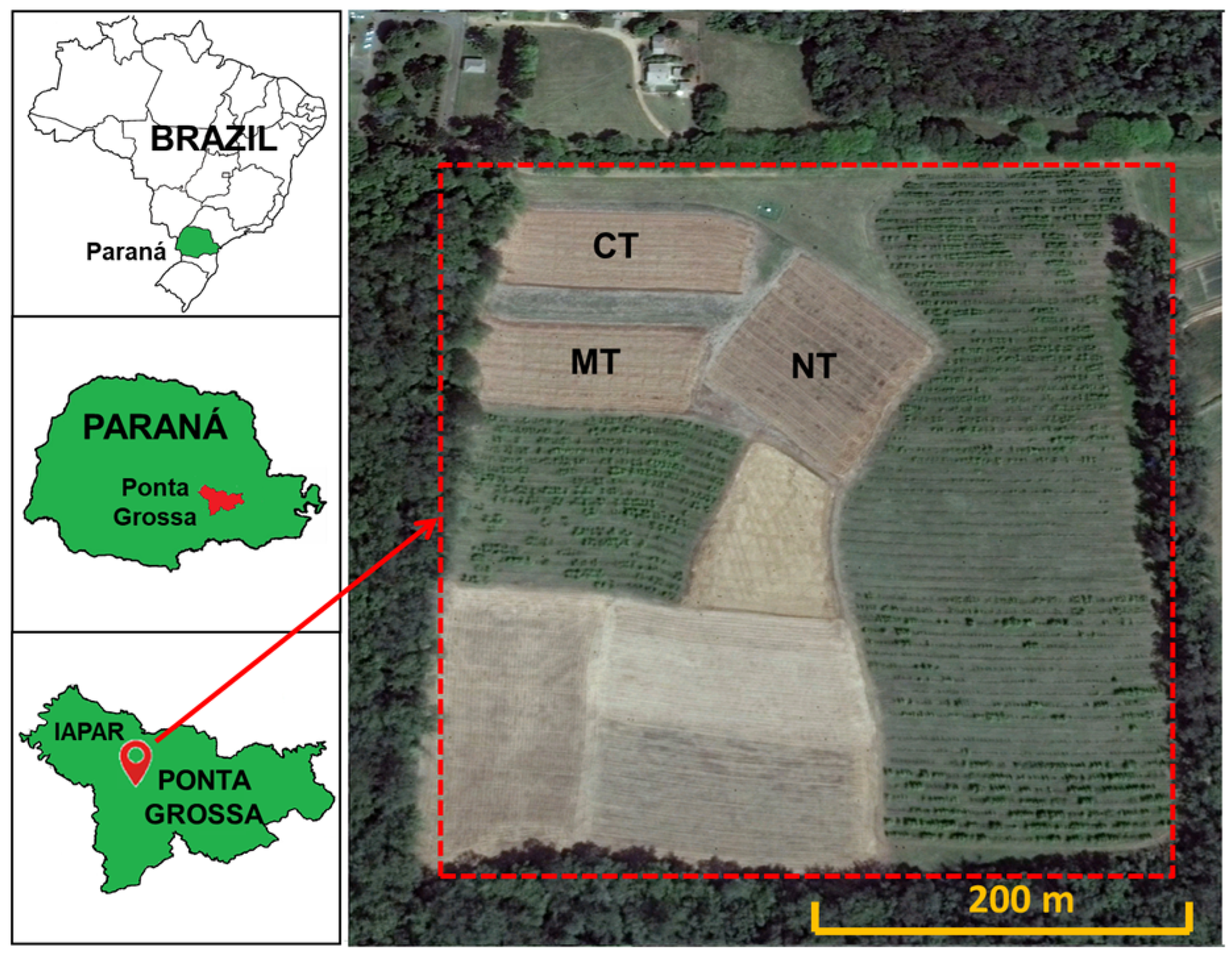
2.1. Experimental Area and Soil Sampling

The soil samples analyzed in this study were collected from a Rhodic Hapludox (Soil Survey Staff) at the IAPAR (Instituto de Desenvolvimento Rural do Paraná) experimental farm (Figure 1), located in Ponta Grossa, Paraná, Brazil (25°06’ S, 50°09’ W; 875 m asl). The region experiences an average annual precipitation of 1400-1600 mm and an average temperature of 17-18°C. The soil’s textural composition consists of 14% clay, 28% silt, and 58% sand, and according to the Köppen classification system, the climate is classified as Cfb, humid subtropical [19].
The experimental area has been subjected to different soil management practices for over 40 years, divided into plots managed by conventional tillage (CT), minimum tillage (MT), and no-tillage (NT). In 2017, undisturbed soil samples were collected from the topsoil layer (0-0.10 m) using steel cylinders (approximately 0.05 m in diameter and 0.05 m in height). In these areas (Figure 1), crop rotations have been carried out with the cultivation of oats (Avena strigosa), vetch (Vicia sativa), or wheat (Triticum aestivum L.) in the winter and corn (Zea mays) and soybean (Glycins max) in the summer. Standard agricultural machinery was employed for soil preparation, including operations such as clearing, cutting, plowing, harrowing, and planting.
A total of 18 soil samples were analyzed, with each sample subjected to one of two W-D cycle treatments: no cycles (0 W-D) or twelve cycles (12 W-D). The samples were further divided across the three different management practices (CT, MT, and NT), with three samples analyzed per treatment combination (2 W-D cycles × 3 management practices × 3 samples per combination).

2.2. Wetting and Drying (W-D) Cycles

The collected core samples were wrapped in plastic film to protect them from potential damage during transport and handling in the laboratory. Upon arrival, the samples underwent a trimming process, during which excess soil was carefully removed using a knife. Half of the samples (three from each management practice) were then saturated for 48 hours using the traditional capillary rise method. This method involved placing a 5 mm layer of water at the base of each sample, gradually adding 5 mm of water per hour until it reached the top edge of the steel cylinder. Once fully saturated, the samples were transferred to an Eijkelkamp 08.01 Sandbox, where they were subjected to a -6 kPa matric potential until reaching thermodynamic equilibrium, which took approximately 3 to 4 days. After each drying phase, the samples were re-saturated, and this process was repeated 12 times (12 W-D cycles). The number of W-D cycles was chosen to correspond to the average number of annual rainfall events exceeding 30 mm.

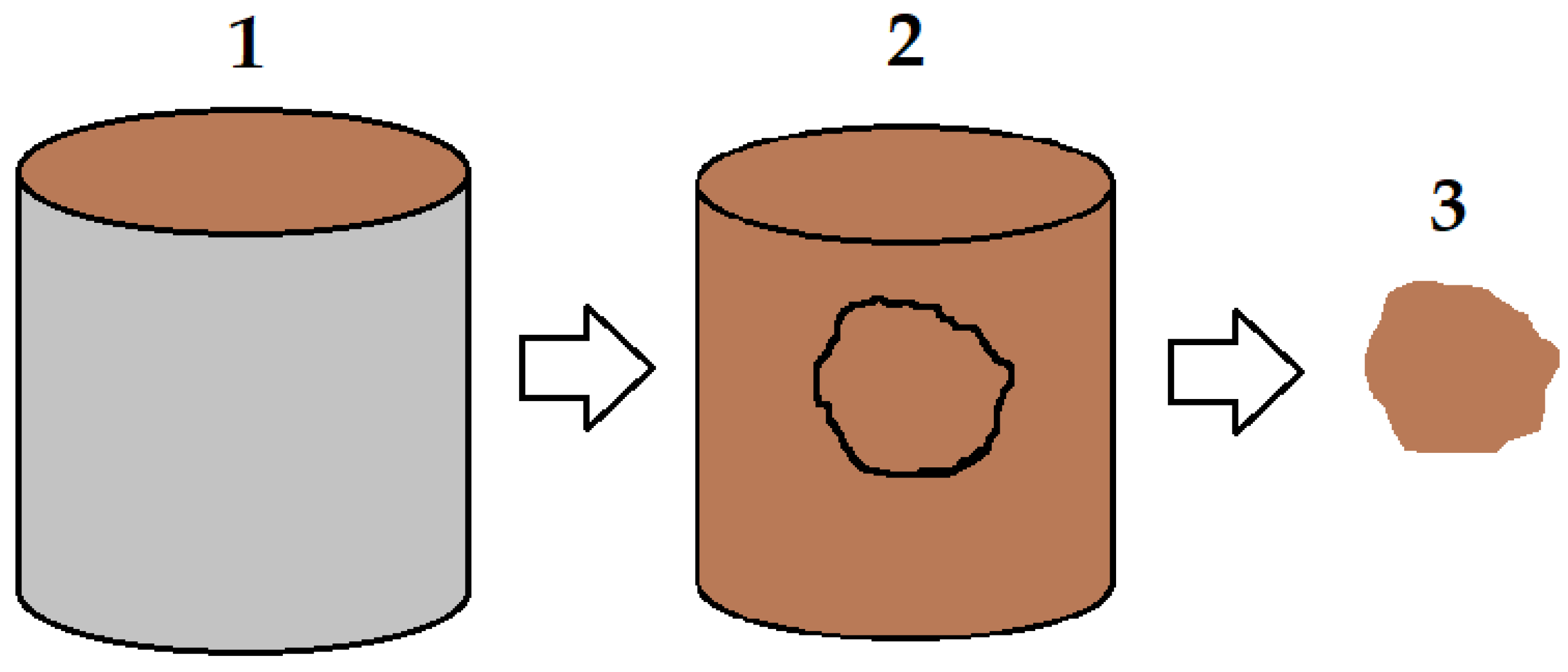
2.3. X-ray Micro-Computed Tomography (X- μ CT)

After completing the W-D cycles, soil aggregates measuring approximately 1-2 cm were carefully extracted from the steel cylinders after being dried at 40 °C in an oven for several days (see Figure A1).Extracting the aggregates was necessary to enhance the resolution of the images compared to those obtained from the intact samples in the cylinders. Once dried, the most stable aggregates were scanned using a GE Nanotom X-ray Computed Tomography (X- μ CT) system installed at the Hounsfield Facility, University of Nottingham, Sutton Bonington Campus, UK [20].
The X- μ CT system, rated at 180 kV / 15 W, was configured to operate at 90 kV and 70 μ A, with an acquisition time of 250 ms per sample. To minimize beam hardening effects, a 0.1 mm copper (Cu) filter was placed near the X-ray source. The images were initially captured in 32-bit grayscale and subsequently cropped by 7 to 10 mm from each edge using ImageJ 1.42 software [21] to eliminate border effects. Before 3D reconstruction, the images were processed with a 2-pixel radius Median 3D filter to reduce noise, followed by the application of a 1-pixel Unsharp Mask filter (size 0.8) to sharpen the solid portions of the aggregates.
After filtering the 900 TIFF images with a voxel size of 5.3 µm, the grayscale images were processed using ImageJ 1.42 software [21] with the non-parametric method. This method separates gray tones into distinct classes by forming a histogram. When two distinct classes of gray tones are present due to material characteristics, the histogram is bimodal, showing two characteristic peaks. This allows for the selection of a binary threshold, segmenting and converting the 32-bit grayscale images into 8-bit binary images, where white represents the solid and black the pores. The initial threshold value was determined using Otsu’s algorithm [22] and then refined through visual inspection of the histogram.

2.4. Quantification of Physical and Morphometric Properties Analyzed Using 3D Imaging

3D lacunarity, Λ ( ε ) , describes the distribution patterns of empty spaces within a porous medium and reflects the degree of heterogeneity in pore clusters. To quantify the 3D lacunarity of soil aggregates, a Matlab®[23] script was developed based on equation 1 and the box-counting method. The analysis was conducted using cubic box sizes ε = {1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 25, 30, 50, 60, 75, 100, 150, 300}. Lacunarity, Λ ( ε ) , is defined as:
Λ ( ε ) = ∑ s s 2 P ( s , ε ) ∑ s s P ( s , ε ) 2 ,
P ( s , ε ) = n ( s , ε ) N ( ε ) ,
where, s represents the number of voxels corresponding to pores within each box of size ε , and P ( s , ε ) (Equation 2) denotes the probability distribution of s for each box size ε . A cubic box of length ε is selected and its number of occupied voxels (pore count) within the box (denoted by s) is determined. The box is then moved along the data set, and the process is repeated over the entire set. This produces a frequency distribution of box masses, n ( s , ε ) , which is converted into the probability distribution P ( s , ε ) by dividing by the total number of boxes N ( ε ) of size ε .
The 3D multifractal analysis was conducted by examining the multifractal spectra of the samples, based on equations 3 and 4 [18,24,25], calculated using the NASS (Non-linear Analysis Scaling System) software [26]. The analysis employed selected box sizes, ε = {50, 60, 75, 90, 150, 180, 300, 450}, with statistical moments (q-values) ranging from 0.5 to 2.0 , in regular increments by 0.1 . The multifractal spectrum was then calculated as follows [17].
f ( α ( q ) ) = lim ε → 0 ∑ i μ i ( q , ε ) log e μ i ( q , ε ) log e ε ,
α ( q ) = lim ε → 0 ∑ i μ i ( q , ε ) log e P i ( ε ) log e ε ,
where μ i represents the partition function or normalized measure of the distribution, q is the statistical moment that characterizes the scaling properties, f ( α ( q ) ) is the multifractal singularity spectrum, α ( q ) refers to the Lipschitz-Hölder exponent associated with the singularity strength, and P i ( ε ) denotes the probability of finding pores within a box i of size ε . The singularity spectrum f ( α ( q ) ) provides a description of the distribution of singularities, while α ( q ) quantifies the intensity or regularity of the measure at different locations within the medium.
Additionally, NASS computes the normalized Shannon entropy, based on equation 5, which provides further insights into the distribution heterogeneity. Normalized Shannon entropy measures the uncertainty or unpredictability in counting voxels corresponding to pores within a volume of size ε × ε × ε . Because it is a scale-dependent property, it is extremely sensitive and can reveal the heterogeneity of the pore system within aggregates to some extent [18,27]. These cubic boxes sizes were: ε = { 1-10, 12, 15, 18, 20, 25, 30, 36, 45, 50, 60, 100, 225}. Due to the sensitivity of this entropy, additional boxes were added for better refinement.
H ∗ ( ε ) = H ( ε ) H M ( ε ) = − ∑ i = 0 P i ( ε ) log P i ( ε ) log ( ε 3 + 1 ) ,
Another geometric property NASS provides is the generalized fractal dimension ( D q ) (Equation 6), which serves as a parameter for measuring and analyzing the geometric aspects of porous systems.
D q = 1 q − 1 lim ε → 0 ∑ i = 1 ∞ log 2 μ i ( q , ε ) log 2 ε ,
Porosity, degree of anisotropy, connectivity, and tortuosity of the pores analyzed using ImageJ 1.42 software [21]. The voxel counter plugin was employed for measuring the imaged porosity ( Φ ):
Φ porosity ( % ) = ∑ i = 1 n V i , pore V total ,
where V i , p o r e is the volume of pores and V t o t a l is the aggregate volume (300 × 300 × 900 voxels or 1.6 × 1.6 × 5.8 mm3).
To better analyze the contribution of different pore sizes to the imaged porosity, the pores were divided into the following volume ranges: 0.0001-0.01 Φ 1 , 0.01-0.1 Φ 2 , 0.1-1.0 mm3 Φ 3 , and >1.0 mm3 Φ 4 . The pores were also classified in terms of shape using the classification suggested by [28]. The pores were divided into the following types of shape: equant, triaxial, prolate, and oblate. The shape of the pores was defined by calculating the ratio between the semi-axes of ellipsoids inscribed within the pores [29]. The contribution of each type of pore to the imaged porosity was analyzed, as was the contribution of the number of pores. All these parameters were calculated using the Particle Analyzer function in ImageJ. The degree of anisotropy ( D A ) and is the aggregate volume connectivity (C) were determined by the BoneJ plugin [30].
D A = 1 − λ min λ max ,
E C = n v − C v ,
C = 1 − E C ,
where E C refers to Euler-Poincaré characteristic, n v is the number of isolated pores (disconnected parts) in the sample volume, C v is the pore connectivity, and the minimum ( λ min ) and maximum ( λ max ) eigenvalues correspond to the shortest and longest radii of an ellipsoid along the x, y, and z axes. D A is a parameter that expresses how a porous media is isotropic ( D A = 0 ) or anisotropic ( D A = 1 ). In the case of pores, it may provide its preferential directions. C is a geometric attribute that reveals a degree of interconnection between pores, i.e., how connected or disconnected the pores are from one another [30].
Pore tortuosity ( τ ) is another geometric attribute that describes the degree of sinuosity in the porous system. This parameter was calculated as the ratio between the geodetic distance ( L G ) and the Euclidean distance ( L E ) between two points connected within the pore network [31].
τ = L G L E

3. Results

3.1. Image Analysis

The microtomography images of the MT samples taken before (Figure 2a) and after (Figure 2b) the application of 12 W-D cycles reveal no significant differences in pore distribution or overall porosity. No noticeable concentrations of pores were observed in specific regions of the samples. However, after 12 W-D, the pores appear more interconnected, particularly in the top portion of the image. Additionally, the post-W-D image shows a higher percentage of isolated pores, suggesting an increase in the total number of pores.
For the samples under CT (Figure 2c,d), a noticeable reduction in porosity can be observed after 12 W-D cycles (Figure 2d). Following the W-D cycles, there was a higher concentration of pores in the upper region of the image, whereas in the 0 W-D sample, pores were more concentrated in the central region. These variations in pore concentration could influence the anisotropy of the pore system. The darker regions in the images indicate areas of higher pore density, which may reflect increased connectivity, as seen in the 0 W-D case. Additionally, the application of W-D cycles led to a rise in the number of isolated pores, suggesting an overall increase in pore count.
For the samples under NT (Figure 2e,f), a reduction in porosity after 12 W-D cycles (Figure 2f) is noticeable, similar to the trend observed for CT. In the 0 W-D sample, there is a higher concentration of pores in specific regions (upper, middle, and lower portions of the image). The darker regions in the 0 W-D image also suggest a higher pore concentration and potentially greater connectivity between pores. However, unlike CT, the presence of isolated pores in NT remains relatively consistent before and after the W-D cycles.

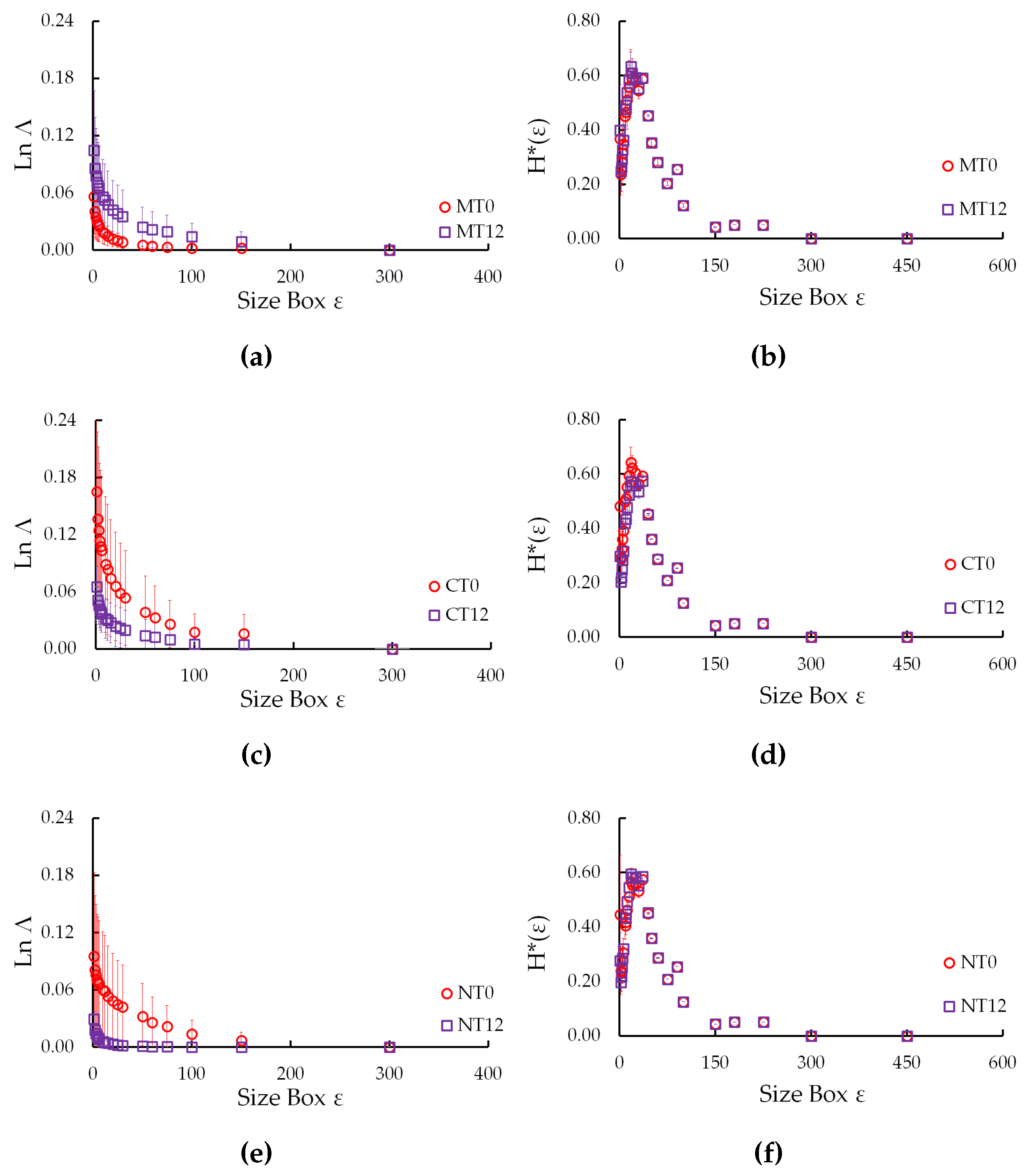
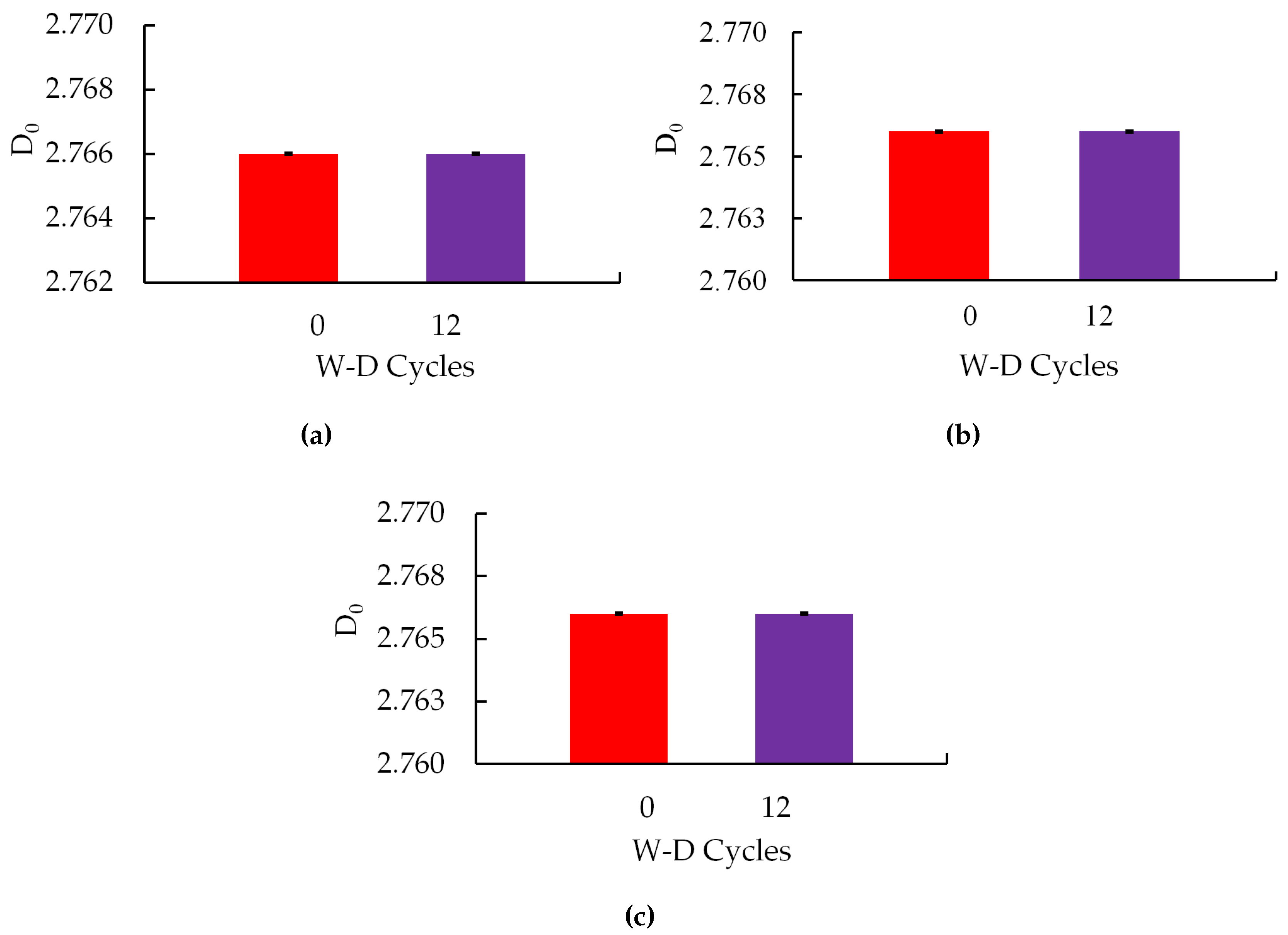
3.2. 3D Lacunarities, 3D Multifractal Spectra, Normalized Shannon Entropy, and Generalized Fractal Dimensions

The 3D lacunarity (Figure 3b,d,f) exhibited a decrease following the implementation of 12 W-D cycles for the CT and MT samples. In contrast, the MT samples displayed an increase in lacunarity after the same number of cycles. The area beneath the lacunarity curves indicates that, for CT (Figure 3c) and NT (Figure 3e) , the difference between the measurements taken at 0 and 12 W-D cycles was approximately 2.9 and 18.9 times greater, respectively. Conversely, for MT (Figure 3a), the samples subjected to 12 W-D cycles revealed an area roughly 4.1 times larger than that observed at 0 W-D cycles. Nonetheless, when accounting for the variability represented by the error bars in the lacunarity values across samples, it becomes evident that there were no significant differences between the samples before and after the W-D cycles were applied.
The normalized 3D Shannon entropy Figure 3b,d,f) exhibited minimal variations among the samples subjected to W-D cycles, particularly in the smallest box sizes. The area calculations beneath the curves revealed nearly identical values for MT (Figure 3b) and NT (Figure 3f) both before and after the W-D cycles, with differences of less than 2%. In contrast, for CT (Figure 3d), there was a 5% difference in areas, accompanied by a reduction following the application of 12 W-D cycles. For MT and NT, a slight increase was noted after 12 W-D cycles. Notably, for the largest box sizes, the values for samples subjected to both 0 and 12 W-D cycles remained unchanged. These findings indicate that, for the analyzed soil aggregates, W-D cycles did not significantly alter pore complexity.
The assessment of the generalized fractal dimension (Figure 4) indicated no significant differences among the samples after the W-D cycles were applied. This consistent finding across all analyzed management practices suggests that multifractality is absent for the studied aggregate sizes. The data for the generalized fractal dimensions, obtained from the multifractal spectra (see Figure A2), typically displayed only slight variations among the samples, which fell within the range of statistical error, for all management practices examined (see Table A1).

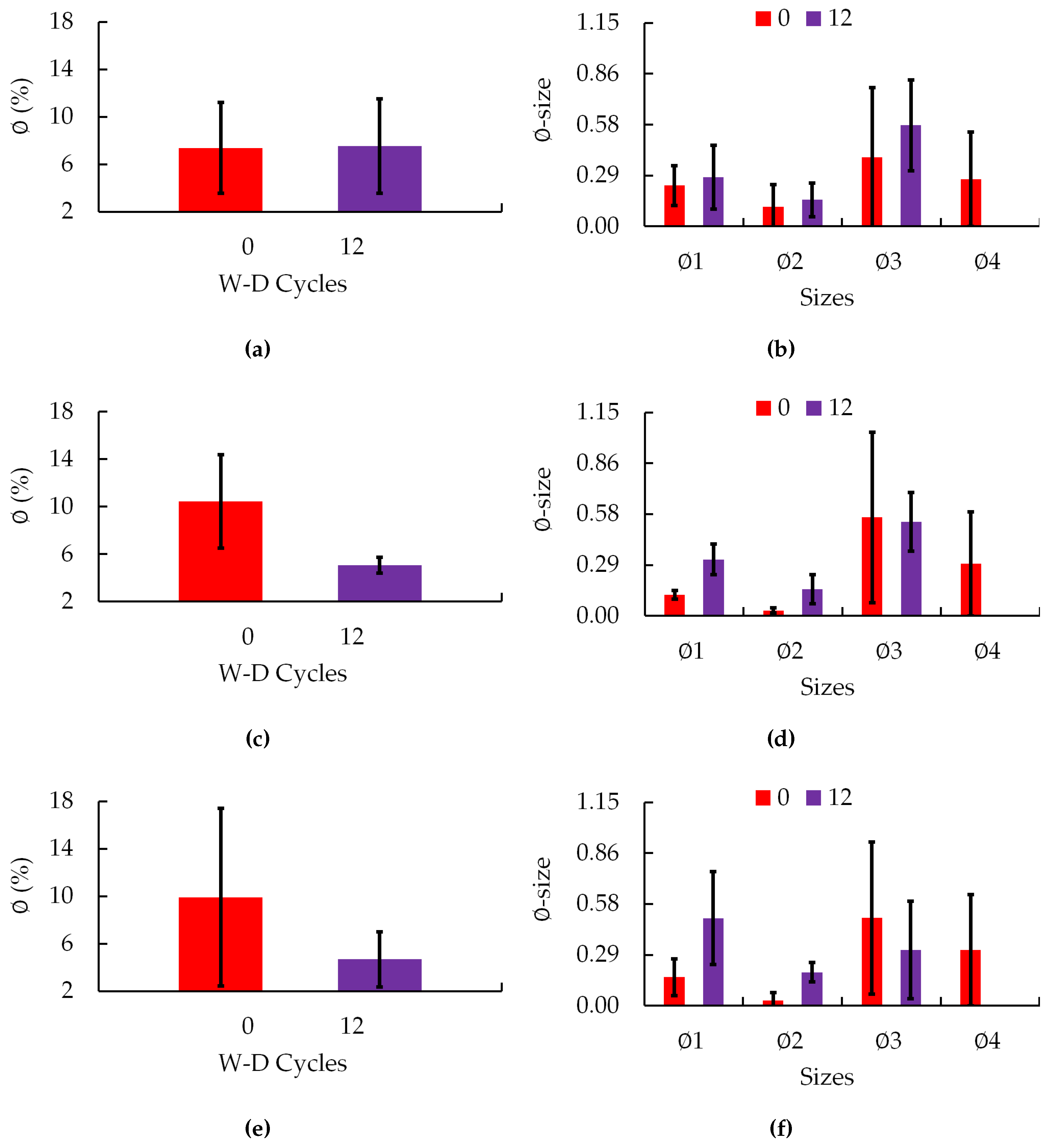
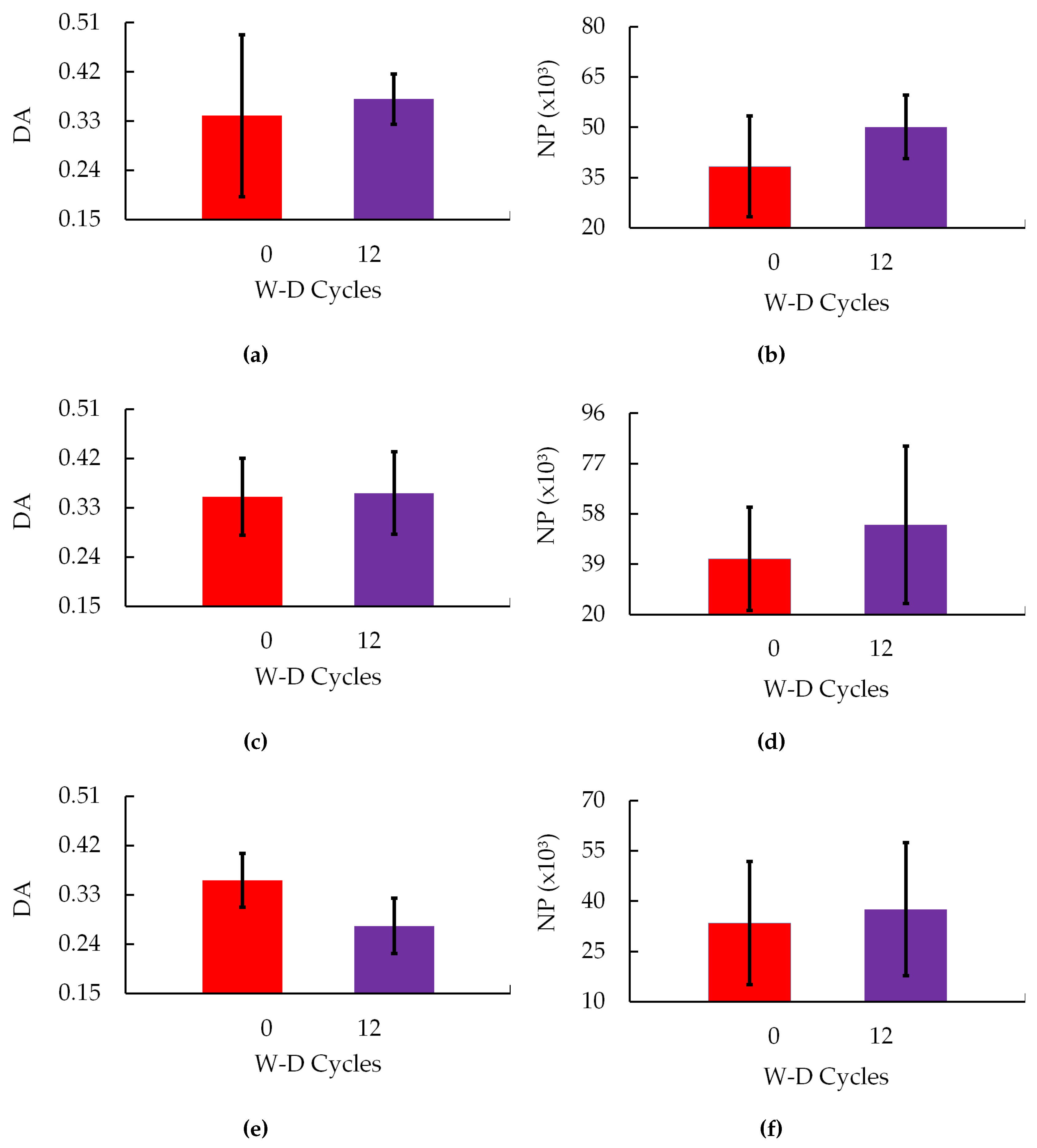
3.3. Physical Properties: Porosity, Degree of Anisotropy and Number of Pores

The assessment of imaged porosity (Figure 5a,c,e) revealed differences (as indicated by error bars) between the W-D cycles solely for the samples under CT. In contrast, no notable differences were found for the MT (Figure 5a) and NT (Figure 5e) samples before and after the W-D cycles. The imaged porosity values for MT were approximately 7.5%. For both CT and NT (Figure 5c,e), there was a trend towards a decrease in imaged porosity after 12 W-D cycles, with reductions of about 52% and 53%, respectively. Concerning pore distribution by shape (Figure 5b,d,f), no differences were detected between W-D cycles across all size classes for the MT samples. The largest pores contributed significantly to the imaged porosity for MT (Figure 5b), accounting for 66% during W-D and 57% after 12 W-D cycles. In the CT samples (Figure 5d), differences were only noted in the smallest pore sizes ( Φ 1 and Φ 2 ) between the 0 and 12 W-D cycles. However, the largest pores contributed to a significant portion of the imaged porosity, representing 85% (0 W-D) and 53% (12 W-D). For NT (Figure 5f), differences were observed only for Φ 2 pores between the W-D cycles. In the 0 W-D samples, the largest pores accounted for 81% of the imaged porosity, while after 12 W-D cycles, the smallest pores ( Φ 1 ) emerged as the primary contributors to imaged porosity, contrasting with the results of the other management practices. Notably, the implementation of 12 W-D cycles completely eliminated the contribution of the largest pores ( Φ 4 ) to the imaged porosity.
The degree of anisotropy showed slight increases for the samples under MT (Figure 6a) and CT (Figure 6c) after 12 W-D. The increase was 9% for MT and 2% for CT, respectively. In the case of NT (Figur Figure 6e), an inverse behavior was observed with a reduction in the degree of anisotropy after 12 W-D cycles. This reduction was equivalent to 23%. However, looking at the variability of the data (error bars) it is possible to state that there are no differences between the samples before and after the application of W-D cycles in terms of the degree of anisotropy. For the number of pores (Figure 6b,d,f), an upward trend was observed in all management practices after 12 W-D cycles. The differences between 0 and 12 W-D cycles were 31% (MT), 30% (CT) and 13% (NT). However, considering the variability between samples, no differences were observed between W-D cycles for all the management practices studied.

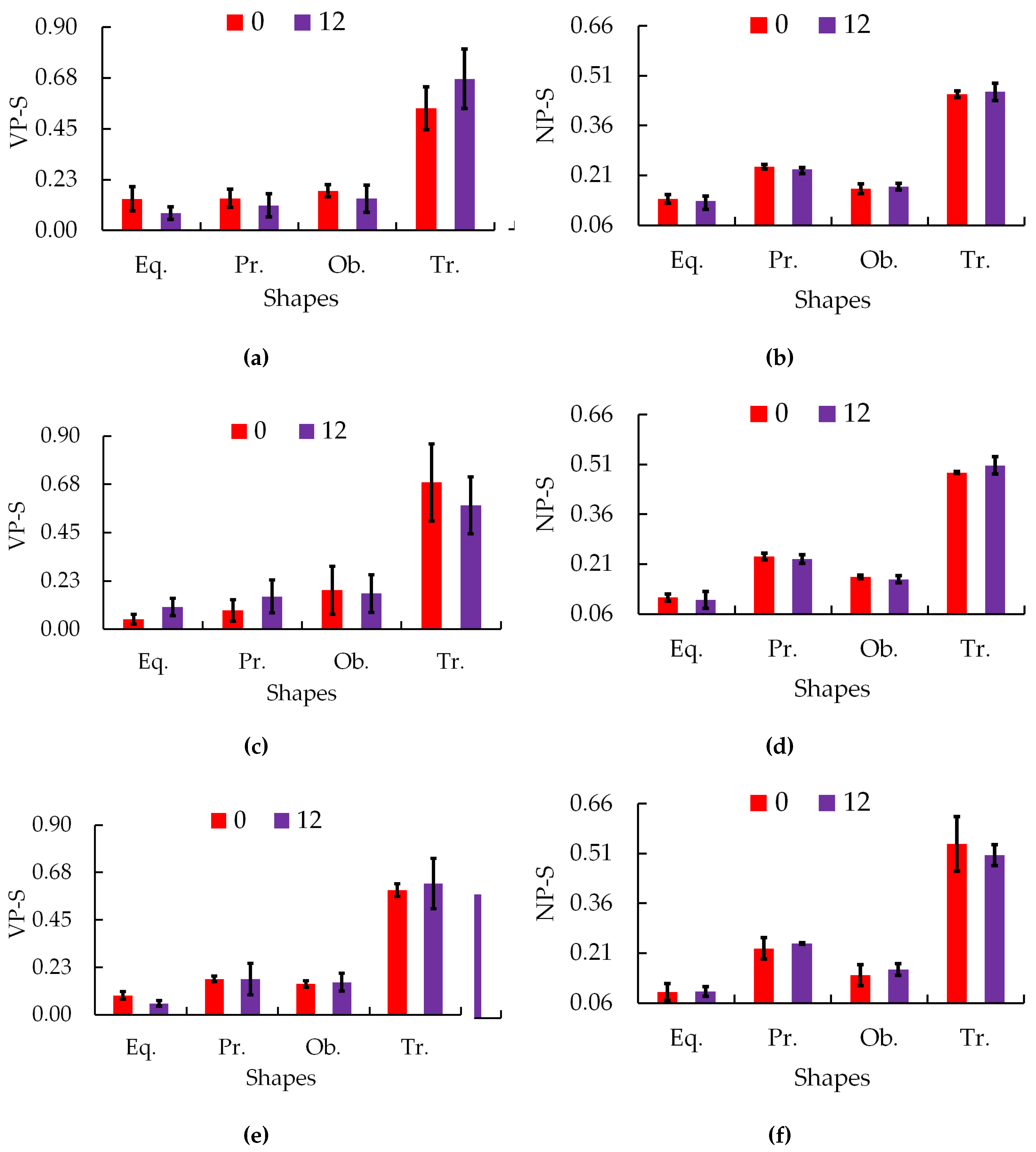
3.4. Morphometric Properties: Connectivity of Pores, Tortuosity, Volume and Number of Pores by Shape

Pore connectivity (Figure 7a,c,e) showed an upward trend of 19% for the samples under MT (Figure 7a) after 12 W-D. For CT (Figure 7c) and NT (Figure 7e), a reduction trend of 20% and 45% was observed, respectively, after the application of W-D cycles. These results indicate that the W-D cycles caused a worsening in pore connectivity after 12 W-D for CT and NT. However, when we consider the variability (error bars) between the samples for pore connectivity, it is not possible to say that the W-D cycles significantly affected this morphological parameter of the soil. Tortuosity showed a slight tendency to increase by 2% for MT (Figure 7b) and decrease by 2% for CT (Figure 7d) after 12 W-D. The greatest variation was observed for NT (Figure 7f) with a tendency to increase by 20% after 12 W-D. For the aggregate samples analyzed, it was not possible to observe a relationship between pore connectivity and tortuosity for the different management practices studied.
The W-D cycles did not significantly affect the contribution of pore shape to the imaged porosity for the different management practices (Figure 8a,c,e). It is worth mentioning that unclassified pores were excluded from the analysis. It was not possible to define a shape for these pores. The greatest contribution to the porosity imaged is due to the triaxial shaped pores (MT: 54% 0 W-D and 67% 12 W-D; CT: 68% 0 W-D and 58% 12 W-D; NT: 59% 0 W-D and 62% 12 W-D). For MT (Figure 8a) these pores increased by 24% after 12 W-D. For CT (Figure 8c) a reduction of 15% was observed, while for NT (Figure 8e) a slight increase of 5%, respectively. The number of pores (Figure 8b,d,f) followed a similar trend to the pore volume.
The greatest contribution to the number of pores is due to the triaxial shaped pores, showing a direct relationship between the volume and number of pores. Again, no differences were observed between the samples in terms of pore shape after the application of W-D cycles for the number of pores. The contribution of triaxial pores to the number of pores was 45% (0 W-D) and 46% (12 W-D) for MT (Figure 8b), 49% (0 W-D) and 51% (12 W-D) for CT (Figure 8d) and 54% (0 W-D) and 51% (12 W-D) for NT (Figure 8f). Therefore, there was a slight upward trend for MT (4%) and CT (2%) and a decrease for NT (6%) in triaxial shaped pores after 12 W-D. Prolate shaped pores made the second largest contribution to the number of pores.

4. Discussion

In this study, we chose to use three different soil management practices to investigate whether the changes caused to soil structure by management show different responses in pore architecture after wetting and drying cycles. The main idea of the study was to see how small soil aggregates are affected by W-D cycles. For this purpose, images with a voxel size of approximately 5 μ m were analyzed. It was also decided to investigate changes in the complexity of the soil pore system using multifractal analysis. Lacunarity and 3D Shannon entropy were calculated to complement the multifractal analysis.
The lacunarity and 3D Shannon entropy curves showed no differences between the W-D cycles (Figure 3). This result was similar for all management practices. The downward trend in lacunarity for CT and NT after 12 W-D indicates a reduction in the degree of dispersion of the pore clusters. In the case of MT, the opposite was observed with an increase in the degree of dispersivity of the pore clusters. [32] working with the same type of soil and larger samples, showed similar results for NT to those found in this study. However, these authors observed no differences for CT. The results found for MT also differ from those observed in our study. In our study we mainly accessed the intra-aggregate pores in comparison to the different study by [32]. In the case of CT, soil disturbance through plowing and harrowing breaks down the aggregates. Therefore, the application of W-D cycles favors soil aggregation in this management [9,33]. This may favor the clustering of pores. It is worth mentioning that the soil analyzed has a more clayey texture, which favors the formation of aggregates [34,35]. Samples were also taken from the surface layer, which is richer in organic material [6]. The higher content of organic material in NT, as well as the action of soil fauna and the presence of roots, can lead to the appearance of pores that are susceptible to changes when the soil undergoes successive W-D cycles [36,37]. The same can happen with MT, which can also be considered a less invasive management practice. The physicochemical forces that exist between soil particles and aggregates and the action of cementing agents are important factors in soil structure changes under W-D cycles [38].
The results of the normalized 3D Shannon entropy (Figure 3) are in agreement with the results of [32] for samples of the same soil with images of a voxel size of 35 μ m . These authors also observed no significant differences in the entropy curves after the W-D cycles. Shannon entropy is used in porous systems to quantify the uncertainty or variability in pore size and shape distribution [39]. Therefore, small differences in this property are an indication that there were no major variations in the complexity of the pore architecture, as observed in our study. Generally, higher entropy values are associated with a more varied soil structure [40]. Soils with more connected pores also tend to have lower entropy, due to the way the pores are arranged [32]. The analysis of the capacity dimension ( D 0 – fractal dimension in 3D) (Figure 4) revealed no significant differences between the W-D cycles across various management practices. This finding aligns with [40], who also observed no variation in soil pore distribution following rainfall events. Similarly, [32] reported comparable results for samples under CT and MT, noting that soils in these systems exhibited moderate multifractality. In contrast, our study indicates that the pore architecture in our system demonstrates monofractal behavior (see Table A1). The D 0 values found in our study, approximately 2.78, are consistent with those reported by [41] and [32], who found D 0 values ranging from 2.34 to 2.85 in areas under organic farming and various management practices.
The image porosity showed a difference only for CT (Figure 5), decreasing with 12 W-D. The same behavior was observed for NT. However, no significant differences were observed for NT and MT. Authors such as [42,43,44] observed an increase in porosity as a function of W-D cycles. In the case of the latter authors, the same type of soil was investigated. However, it is worth mentioning that these authors applied the W-D cycles to samples confined in cylinders. Changes in the volume of the sample with wetting and the friction of the soil with the cylinder walls often lead to irreversible changes in the volume (height) of the soil, increasing large pores. It is worth mentioning that our study analyzed aggregates extracted from the inside of the cylinder containing the soil. Nevertheless, other authors have shown that porosity can decrease after the application of W-D cycles [45]. This result is often associated with instabilities in soil structure due to slaking and dispersing of soil or coalescence of soil aggregates [46]. Often, the migration of small soil particles due to W-D cycles can reduce the contribution of larger pores to soil porosity and induce the formation of smaller pores [47,48]. Consequently, the larger pores inside the aggregates can be reduced.
This was the result observed in our study, which showed a drastic reduction in larger pores, responsible for the downward trend in the imaged porosity for CT and NT after 12 W-D (Figure 5). In the case of MT, there was an increase in the contribution of smaller pores (<1 mm3) to the imaged porosity which compensated for the reduction in larger pores (> 1 mm3). The same was observed for CT and NT for the Φ 1 and Φ 2 size ranges. Our results differ from those of [44,49], but these authors worked with larger samples and probably accessed inter-aggregate pores. In our study, due to the size of the samples, intra-aggregate pores were probably accessed. [8] showed that soil drying can reduce structural porosity due to the coalescence of aggregates, explaining the increase in smaller pores with W-D cycles. However, [9] showed that even small soil aggregates can increase porosity with W-D cycles, contrasting with our results.
The degree of anisotropy (Figure 6) showed small differences for MT and CT after 12 W-D. A downward trend was observed only for NT after the W-D cycles. The DA values found show more isotropic structures without the preferential distribution of pores in different regions of the samples. For NT, it can be said that 12 W-D better distributed the pores throughout the volume of the aggregate, but it is important to say that considering the variability between the samples there were no differences in DA for the different management practices. The DA values are also consistent with other studies that show small variations in this property due to the drying and wetting of the soil [32,34]. [50] recently showed DA values ranging from 0.27 to 0.37 for samples under native pasture and corn-soybean systems, which are consistent with the values in our study. The number of pores (Figure 6) also showed no differences after the W-D cycles for all management practices. However, an upward trend was noted in NP after 12 W-D. This increase in the number of pores may be associated with the fragmentation of larger pores after successive wetting and drying of the soil [51,52], which could explain the greater contribution of smaller pores to the imaged porosity, especially for MT and CT (Figure 5). The results show that the reduction in imaged porosity (Figure 5) for CT and NT was not accompanied by a reduction in NP, which shows the importance of larger pores for porosity. The number of pores found in our study is also consistent with the study by [50] who found values varying between 31,835 (integrated crop-livestock system) and 42,264 (native pasture), respectively.
Considering the variability of the data, pore connectivity (Figure 7) was not significantly affected by the W-D cycles. A slight upward trend was observed for MT, with a downward trend for CT and NT. [47] also observed a reduction in pore connectivity with the application of 3 W-D. These authors associated the reduction in pore connectivity with an increase in the number of isolated pores. This result indicates that the soil pores have been displaced or deformed, which would indicate changes in shape. [49] showed the opposite result, but these authors worked with granite residual soil. They associated the increase in pore connectivity with the expansion and connection of small pores to other pores after successive W-D [34]. In our study we showed a reduction in the largest pores (Figure 5), which indicates that on the scale of the aggregates analyzed this process did not occur. Tortuosity (Figure 7) did not differ between management practices and W-D cycles. The samples under MT and CT showed practically the same tortuosity values. In the case of NT, there was an increase in tortuosity after 12 W-D and consequently a reduction in pore connectivity, as expected. The greater contribution of the smaller volume pores (Figure 5) to the imaged porosity may explain this result, as it is an indication of smaller and more isolated pores, which increases tortuosity. More aligned pores (lower tortuosity) tend to indicate a more interconnected pore system [53]. The tortuosity values found indicate a slightly tortuous pore system for all management practices, which facilitates fluid flow [50,54].
The shape of the pores (Figure 8) showed a greater contribution from triaxial pores to the porosity imaged. These pores tend to be slightly elongated, influenced by the arrangement of the soil particles. Larger quantities of these pores indicate good soil capacity for conducting solutes and for circulating air in the soil, which is vital for root respiration and plant health [55]. The presence of these pores may also be associated with greater pore connectivity, as observed for MT and CT. Triaxial pores also made a greater contribution to the number of pores (Figure 8), showing a relationship for the aggregates analyzed between VP and NP. [56] point out that W-D cycles change the shape and geometry of the soil pore space. According to these authors, these changes are associated with competition between cohesive and adhesive forces in the soil during wetting and drying. The competition between these forces generates tensions that cause changes in pore architecture [57]. [9] showed increases in the proportion of elongated pores with W-D cycles, which is in line with the trend observed in our study for MT and NT. [50] also observed higher triaxial pore contributions to both porosity and pore number for different management practices and native pasture. Pore shapes have a direct influence on root growth and the transmission of water and air in the soil [58].
Our results showed that for the aggregate size analyzed, there were no significant changes in pore architecture based on their morphological and geometric properties. This result corroborates one of the hypotheses of this study, which may be associated with greater stability of the soil’s intra-aggregate pore system. However, a study with different types of soil and with a greater number of repetitions may provide different results than ours. An increase in the number of repetitions could influence the variability between samples. The second hypothesis concerns to multifractal analysis. Our results, based on the generalized values of the fractal dimension, indicate that the analyzed porous space exhibits monofractal behavior, suggesting a homogeneous rather than heterogeneous system. However, future studies involving different soil types are necessary to broaden these findings and achieve new insights using the multifractal analysis technique.

5. Conclusions

The main objective of this study was to analyze how the intra-aggregate pore architecture of soil aggregates is influenced by wetting and drying (W-D) cycles. The results of the morphological, geometric, and complexity-based properties of the pore system indicate that there were no significant differences in soil structure after 12 W-D cycles. This finding suggests that, for the soil studied, at the pore scale evaluated, the pore architecture demonstrated resilience to changes, regardless of the management practices applied.
The soil pore system exhibited monofractality, indicating a more homogeneous rather than heterogeneous structure. The lacunarity curves showed no significant differences between the wetting-drying (W-D) cycles across all management practices, though a downward trend was observed for conventional tillage (CT) and no-tillage (NT) after 12 W-D cycles. Conversely, the opposite trend was observed for minimum tillage (MT). The lacunarity curves followed the pattern of imaged porosity, with the reduction in porosity after 12 W-D cycles attributed exclusively to a decrease in large pores for both CT and NT. In contrast, for MT, the reduction in the proportion of large pores was offset by an increase in the proportion of smaller pores. Additionally, the 3D Shannon entropy remained consistent across W-D cycles for all management practices, indicating no substantial changes in pore size distribution.
The degree of anisotropy (DA) indicated that the porous systems remained isotropic, with very similar DA values observed before and after the wetting and drying (W-D) cycles. Following 12 W-D cycles, there was a slight increase in the number of pores across the different management practices, but the difference between the cycles was not statistically significant. Pore connectivity and tortuosity exhibited minimal change after 12 W-D cycles in both MT and CT management practices, while NT showed a slight downward trend in connectivity and an increase in tortuosity, although these changes were not significant. Regarding the shape distribution of pores, the majority contribution to the imaged porosity came from pores with a triaxial shape, which were found in greater abundance within the aggregates across all management practices.
The findings of this study align with existing literature on different pore size scales, indicating that wetting and drying (W-D) cycles did not significantly alter the pore architecture of the tropical soil analyzed at the scale considered. These results are notable given the importance of pore architecture in key soil processes, such as the movement of solutes and air, and root development. However, further studies are needed to determine whether the same behavior occurs in other soil types. Additionally, it is important to analyze other wetting and drying mechanisms to see if the patterns observed in our study are consistent.

Author Contributions

Conceptualization, L.F.P.; methodology, J.A.T.O., J.V.G. and A.L.F.L.; software, A.N.D.P. and A.L.F.L.; validation, J.A.T.O., A.N.D.P. and A.L.F.L.; formal analysis, J.A.T.O. and J.V.G.; investigation, J.A.T.O. and J.V.G.; resources, L.F.P. and A.N.D.P.; writing—original draft preparation, L.F.P., J.A.T.O. and L.F.P.; writing—review and editing, L.F.P., J.A.T.O., L.F.P, A.N.D.P. and A.L.F.L.; project administration, L.F.P.; funding acquisition, L.F.P. and A.N.D.P..

Funding

This research was partially funded by “Conselho Nacional de Desenvolvimento Científico e Tecnológico” (CNPQ) (Grants 303950/2023-4 and 404058/2021-3) and “Coordenação de Aperfeiçoamento de Pessoal de Nível Superior” (Capes) (Grant Code 001).

Institutional Review Board Statement

Not applicable

Data Availability Statement

All data are available upon reasonable request to lfpires@uepg.br.

Acknowledgments

In this section you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
W-D wetting-drying
NT no-tillage
MT minimum tillage
CT conventional tillage
X- μ CT X-ray micro-computed tomography
IAPAR Instituto de Desenvolvimento Rural do Paraná
3D three dimensional
TIFF Tag Image File Format
NASS Non-linear Analysis Scaling System

Appendix A

Figure A1 shows the procedure for removing the soil aggregate from the inside of the samples collected in the steel cylinder.
Preprints 122180 g0a1
Figure A1. Diagram for extracting the soil aggregate sample. (1) Soil sample inside the cylinder; (2) Volume of soil carefully extracted from the cylinder; (3) Soil aggregate extracted from the center of the sample.
Figure A1. Diagram for extracting the soil aggregate sample. (1) Soil sample inside the cylinder; (2) Volume of soil carefully extracted from the cylinder; (3) Soil aggregate extracted from the center of the sample.
Preprints 122180 g0a1
Table A1 shows the parameters obtained in the multifractal analysis for the different management practices before (0) and after (12) the application of the wetting and drying cycles.
Table A1. Multifractal parameters and generalized fractal dimensions.
Table A1. Multifractal parameters and generalized fractal dimensions.
Management Cycles Parameters
Replicates Δ A f( α min ) α min D 0 D 1 D 2
CT 0 R1 0.26 0.40 2.77 2.99 2.77 2.75 2.73
R2 0.07 1.51 2.77 2.81 2.77 2.75 2.75
R3 0.06 1.64 2.77 2.81 2.77 2.75 2.74
12 R1 0.05 1.59 2.77 2.80 2.77 2.76 2.75
R2 0.05 1.64 2.77 2.82 2.77 2.75 2.75
R3 0.08 1.21 2.77 2.82 2.77 2.75 2.75
MT 0 R1 0.05 1.69 2.77 2.80 2.77 2.76 2.75
R2 0.05 1.54 2.77 2.81 2.77 2.75 2.75
R3 0.08 1.64 2.77 2.81 2.77 2.75 2.74
12 R1 0.10 1.34 2.77 2.79 2.77 2.75 2.74
R2 0.05 1.57 2.77 2.80 2.77 2.75 2.75
R3 0.06 1.59 2.77 2.81 2.77 2.75 2.75
NT 0 R1 0.06 1.38 2.77 2.81 2.77 2.75 2.74
R2 0.25 0.77 2.77 2.96 2.77 2.75 2.74
R3 0.08 1.50 2.77 2.82 2.77 2.75 2.74
12 R1 0.05 1.52 2.77 2.80 2.77 2.76 2.75
R2 0.05 1.55 2.77 2.80 2.77 2.75 2.75
R3 0.05 1.52 2.77 2.80 2.77 2.76 2.75
Λ : Degree of multifractality; A: Degree of asymmetry; f ( α m a x ) : Parameter associated with global system entropy; α m a x : Parameter associated with the internal energy of the system; D 0 : Capacity dimension or box count dimension; D 1 : Correlation dimension; D 2 : Information dimension.
Figure A2 shows the multifractal spectra obtained for the samples of the different management practices before (0) and after (12) applications of the wetting and drying cycles.
Preprints 122180 g0a2
Figure A2. Multifractal spectra for samples subjected to different (0 and 12) wetting and drying 565 cycles (W-D). MT: minimum tillage; CT: conventional tillage; NT: no-tillage; R: replicate.
Figure A2. Multifractal spectra for samples subjected to different (0 and 12) wetting and drying 565 cycles (W-D). MT: minimum tillage; CT: conventional tillage; NT: no-tillage; R: replicate.
Preprints 122180 g0a2

References

  1. Bronick, C.; Lal, R. Soil structure and management: a review. Geoderma 2005, 124, 3–22. [Google Scholar] [CrossRef]
  2. Alaoui, A.; Lipiec, J.; Gerke, H. A review of the changes in the soil pore system due to soil deformation: A hydrodynamic perspective. Soil and Tillage Research 2011, 115–116, 1–15. [Google Scholar] [CrossRef]
  3. Schlüter, S.; Sammartino, S.; Koestel, J. Exploring the relationship between soil structure and soil functions via pore-scale imaging. Geoderma 2020, 370, 114370. [Google Scholar] [CrossRef]
  4. Weidhuner, A.; Hanauer, A.; Krausz, R.; Crittenden, S.J.; Gage, K.; Sadeghpour, A. Tillage impacts on soil aggregation and aggregate-associated carbon and nitrogen after 49 years. Soil and Tillage Research 2021, 208, 104878. [Google Scholar] [CrossRef]
  5. Aziz, I.; Mahmood, T.; Islam, K.R. Effect of long term no-till and conventional tillage practices on soil quality. Soil and Tillage Research 2013, 131, 28–35. [Google Scholar] [CrossRef]
  6. Diel, J.; Vogel, H.J.; Schlüter, S. Impact of wetting and drying cycles on soil structure dynamics. Geoderma 2019, 345, 63–71. [Google Scholar] [CrossRef]
  7. Hochman, D.; Dor, M.; Mishael, Y. Diverse effects of wetting and drying cycles on soil aggregation: Implications on pesticide leaching. Chemosphere 2021, 263, 127910. [Google Scholar] [CrossRef] [PubMed]
  8. Leij, F.J.; Ghezzehei, T.A.; Or, D. Modeling the dynamics of the soil pore-size distribution. Soil and Tillage Research 2002, 64, 61–78. [Google Scholar] [CrossRef]
  9. Ma, R.; Cai, C.; Li, Z.; Wang, J.; Xiao, T.; Peng, G.; Yang, W. Evaluation of soil aggregate microstructure and stability under wetting and drying cycles in two Ultisols using synchrotron-based X-ray micro-computed tomography. Soil and Tillage Research 2015, 149, 1–11. [Google Scholar] [CrossRef]
  10. Yudina, A.; Klyueva, V.; Romanenko, K.; Fomin, D. Micro- within macro: How micro-aggregation shapes the soil pore space and water-stability. Geoderma 2022, 415, 115771. [Google Scholar] [CrossRef]
  11. Wang, W.; Kravchenko, A.N.; Smucker, A.J.M.; Liang, W.; Rivers, M.L. Intra-aggregate Pore Characteristics: X-ray Computed Microtomography Analysis. Soil Science Society of America Journal 2012, 76, 1159–1171. [Google Scholar] [CrossRef]
  12. Singh, N.; Kumar, S.; Udawatta, R.P.; Anderson, S.H.; de Jonge, L.W.; Katuwal, S. X-ray micro-computed tomography characterized soil pore network as influenced by long-term application of manure and fertilizer. Geoderma 2021, 385, 114872. [Google Scholar] [CrossRef]
  13. Meira Cássaro, F.A.; Posadas Durand, A.N.; Gimenez, D.; Pedro Vaz, C.M. Pore-Size Distributions of Soils Derived using a Geometrical Approach and Multiple Resolution MicroCT Images. Soil Science Society of America Journal 2017, 81, 468–476. [Google Scholar] [CrossRef]
  14. Ngom, N.F.; Garnier, P.; Monga, O.; Peth, S. Extraction of three-dimensional soil pore space from microtomography images using a geometrical approach. Geoderma 2011, 163, 127–134. [Google Scholar] [CrossRef]
  15. Ferreira, T.R.; Pires, L.F.; Wildenschild, D.; Heck, R.J.; Antonino, A.C. X-ray microtomography analysis of lime application effects on soil porous system. Geoderma 2018, 324, 119–130. [Google Scholar] [CrossRef]
  16. Pachepsky, Y.; Crawford, J. Fractal analysis of soils. Encyclopedia of Soils in the Environment.
  17. Posadas, A.N.D.; Giménez, D.; Quiroz, R.; Protz, R. Multifractal Characterization of Soil Pore Systems. Soil Science Society of America Journal 2003, 67, 1361–1369. [Google Scholar] [CrossRef]
  18. Chun, H.C.; Giménez, D.; Yoon, S.W. Morphology, lacunarity and entropy of intra-aggregate pores: Aggregate size and soil management effects. Geoderma 2008, 146, 83–93. [Google Scholar] [CrossRef]
  19. Nitsche, P.; Caramori, P.; Ricce, W.; Pinto, L. Atlás Climático do Estado do Paraná. IAPAR, Londrina, 2019.
  20. The University of Nottingham. Our facilities: Nanotom microCT scanner. https://www.nottingham.ac.uk/microct/facilities/nanotom.aspx, accessed on 16.10.2024.
  21. Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nature Methods 2012, 9, 671–675. [Google Scholar] [CrossRef] [PubMed]
  22. Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Transactions on Systems, Man, and Cybernetics 1979, 9, 62–66. [Google Scholar] [CrossRef]
  23. The MathWorks, I. MATLAB. https://www.mathworks.com, 2018. Version R2018a.
  24. Dong, P. Lacunarity analysis of raster datasets and 1D, 2D, and 3D point patterns. Computers & Geosciences 2009, 35, 2100–2110. [Google Scholar] [CrossRef]
  25. Monreal, J.C.; Martínez, F.S.J.; Martí, J.I.; Pérez-Gómez, R. Lacunarity of the Spatial Distributions of Soil Types in Europe. Vadose Zone Journal 2013, 12, 1–9. [Google Scholar] [CrossRef]
  26. Posadas, A.N.D.; Lourenço, A.L.F. NASS: Non-linear Analysis Scaling System, 2019. Software developed with the support of the Department of Environmental Science, Rutgers, The State University of New Jersey, USA.
  27. Andraud, C.; Beghdadi, A.; Haslund, E.; Hilfer, R.; Lafait, J.; Virgin, B. Local entropy characterization of correlated random microstructures. Physica A: Statistical Mechanics and its Applications 1997, 235, 307–318. [Google Scholar] [CrossRef]
  28. Bullock, P.; Fedoroff, N.; Jongerius, A.; Stoops, G.; Tursina, T. Handbook for soil thin section description.; Waine Research: Albrighton, UK, 1985. [Google Scholar]
  29. Galdos, M.; Pires, L.; Cooper, H.; Calonego, J.; Rosolem, C.; Mooney, S. Assessing the long-term effects of zero-tillage on the macroporosity of Brazilian soils using X-ray Computed Tomography. Geoderma 2019, 337, 1126–1135. [Google Scholar] [CrossRef] [PubMed]
  30. Odgaard, A.; Gundersen, H. Quantification of connectivity in cancellous bone, with special emphasis on 3-D reconstructions. Bone 1993, 14, 173–182. [Google Scholar] [CrossRef] [PubMed]
  31. Roque, W.L.; Costa, R.R. A plugin for computing the pore/grain network tortuosity of a porous medium from 2D/3D MicroCT image. Applied Computing and Geosciences 2020, 5, 100019. [Google Scholar] [CrossRef]
  32. de Oliveira, J.A.T.; Cássaro, F.A.M.; Posadas, A.N.D.; Pires, L.F. Soil Pore Network Complexity Changes Induced by Wetting and Drying Cycles—A Study Using X-ray Microtomography and 3D Multifractal Analyses. International Journal of Environmental Research and Public Health 2022, 19, 10582. [Google Scholar] [CrossRef] [PubMed]
  33. Tang, C.S.; Shi, B. Swelling and shrinkage behaviour of expansive soil during wetting-drying cycles. Chinese Journal of Geotechnical Engineering 2011, 33, 1376–1384. [Google Scholar]
  34. Fomin, D.S.; Yudina, A.V.; Romanenko, K.A.; Abrosimov, K.N.; Karsanina, M.V.; Gerke, K.M. Soil pore structure dynamics under steady-state wetting-drying cycle. Geoderma 2023, 432, 116401. [Google Scholar] [CrossRef]
  35. Kravchenko, A.; Wang, A.N.W.; Smucker, A.J.M.; Rivers, M.L. Long-term Differences in Tillage and Land Use Affect Intra-aggregate Pore Heterogeneity. Soil Science Society of America Journal 2011, 75, 1658–1666. [Google Scholar] [CrossRef]
  36. Cheik, S.; Jouquet, P.; Maeght, J.; Capowiez, Y.; Tran, T.; Bottinelli, N. X-ray tomography analysis of soil biopores structure under wetting and drying cycles. European Journal of Soil Science 2021, 72, 2128–2132. [Google Scholar] [CrossRef]
  37. Galdos, M.V.; Brown, E.; Rosolem, C.A.; Pires, L.F.; Hallett, P.D.; Mooney, S.J. Brachiaria species influence nitrate transport in soil by modifying soil structure with their root system. Scientific Reports 2020, 10. [Google Scholar] [CrossRef]
  38. Tang, C.S.; Wang, D.Y.; Shi, B.; Li, J. Effect of wetting–drying cycles on profile mechanical behavior of soils with different initial conditions. CATENA 2016, 139, 105–116. [Google Scholar] [CrossRef]
  39. Caniego, F.; Martí, M.; San José, F. Rényi dimensions of soil pore size distribution. Geoderma 2003, 112, 205–216. [Google Scholar] [CrossRef]
  40. Vázquez, E.V.; Ferreiro, J.P.; Miranda, J.G.V.; González, A.P. Multifractal Analysis of Pore Size Distributions as Affected by Simulated Rainfall. Vadose Zone Journal 2008, 7, 500–511. [Google Scholar] [CrossRef]
  41. Soto-Gómez, D.; Pérez-Rodríguez, P.; Vázquez Juíz, L.; Paradelo, M.; López-Periago, J.E. 3D multifractal characterization of computed tomography images of soils under different tillage management: Linking multifractal parameters to physical properties. Geoderma 2020, 363, 114129. [Google Scholar] [CrossRef]
  42. Sartori, G.; Ferrari, G.; Pagliai, M. Changes in soil porosity and surface shrinkage in a remolded, saline clay soil treated with compost. Soil Science 1985, 139, 523. [Google Scholar] [CrossRef]
  43. Zemenu, G.; Martine, A.; Roger, C. Analyse du comportement d’un sol argileux sous sollicitations hydriques cycliques. Bulletin of Engineering Geology and the Environment 2009, 68, 421–436. [Google Scholar] [CrossRef]
  44. Pires, L.F.; Auler, A.C.; Roque, W.L.; Mooney, S.J. X-ray microtomography analysis of soil pore structure dynamics under wetting and drying cycles. Geoderma 2020, 362, 114103. [Google Scholar] [CrossRef] [PubMed]
  45. Guo, X.M.; Guo, N.; Liu, L. Effects of Wetting-Drying Cycles on the CT-Measured Macropore Characteristics under Farmland in Northern China. Eurasian Soil Science 2023, 56, 747–755. [Google Scholar] [CrossRef]
  46. Bodner, G.; Scholl, P.; Kaul, H.P. Field quantification of wetting–drying cycles to predict temporal changes of soil pore size distribution. Soil and Tillage Research 2013, 133, 1–9. [Google Scholar] [CrossRef]
  47. Wen, T.; Chen, X.; Shao, L. Effect of multiple wetting and drying cycles on the macropore structure of granite residual soil. Journal of Hydrology 2022, 614, 128583. [Google Scholar] [CrossRef]
  48. Pires, L.F.; Villanueva, F.C.; Dias, N.M.; Bacchi, O.O.S.; Reichardt, K. Chemical migration during soil water retention curve evaluation. Anais da Academia Brasileira de Ciências 2011, 83, 1097–1108. [Google Scholar] [CrossRef] [PubMed]
  49. An, R.; Kong, L.; Zhang, X.; Li, C. Effects of dry-wet cycles on three-dimensional pore structure and permeability characteristics of granite residual soil using X-ray micro computed tomography. Journal of Rock Mechanics and Geotechnical Engineering 2022, 14, 851–860. [Google Scholar] [CrossRef]
  50. Dhaliwal, J.K.; Kumar, S. 3D-visualization and quantification of soil porous structure using X-ray micro-tomography scanning under native pasture and crop-livestock systems. Soil and Tillage Research 2022, 218, 105305. [Google Scholar] [CrossRef]
  51. Tang, C.S.; Cheng, Q.; Gong, X.; Shi, B.; Inyang, H.I. Investigation on microstructure evolution of clayey soils: A review focusing on wetting/drying process. Journal of Rock Mechanics and Geotechnical Engineering 2023, 15, 269–284. [Google Scholar] [CrossRef]
  52. Ye, W.m.; Qi, Z.y.; Chen, B.; Xie, J.; Huang, Y.; Lu, Y.r.; Cui, Y.J. Mechanism of cultivation soil degradation in rocky desertification areas under dry/wet cycles. Environmental Earth Sciences 2010, 64, 269–276. [Google Scholar] [CrossRef]
  53. Peth, S.; Horn, R.; Beckmann, F.; Donath, T.; Fischer, J.; Smucker, A.J.M. Three-Dimensional Quantification of Intra-Aggregate Pore-Space Features using Synchrotron-Radiation-Based Microtomography. Soil Science Society of America Journal 2008, 72, 897–907. [Google Scholar] [CrossRef]
  54. Chakraborty, P.; Singh, N.; Bansal, S.; Sekaran, U.; Sexton, P.; Bly, A.; Anderson, S.H.; Kumar, S. Does the duration of no-till implementation influence depth distribution of soil organic carbon, hydro-physical properties, and computed tomography-derived macropore characteristics? Soil and Tillage Research 2022, 222, 105426. [Google Scholar] [CrossRef]
  55. Pagliai, M.; Vignozzi, N.; Pellegrini, S. Soil structure and the effect of management practices. Soil and Tillage Research 2004, 79, 131–143. [Google Scholar] [CrossRef]
  56. Mady, A.Y.; Shein, E.V. Assessment of pore space changes during drying and wetting cycles in hysteresis of soil water retention curve in Russia using X-ray computed tomography. Geoderma Regional 2020, 21, e00259. [Google Scholar] [CrossRef]
  57. Hillel, D. Introduction to environmental soil physics; Elsevier, 2003.
  58. Ambus, J.V.; Awe, G.O.; Faccio Carvalho, P.C.d.; Reichert, J.M. Integrated crop-livestock systems in lowlands with rice cultivation improve root environment and maintain soil structure and functioning. Soil and Tillage Research 2023, 227, 105592. [Google Scholar] [CrossRef]
Preprints 122180 g001
Figure 1. Map location of the state of Paraná, the municipality of Ponta Grossa and the experimental area where the samples were collected. IAPAR: “Instituto de Desenvolvimento Rural do Paraná”; CT: conventional tillage; NT: no–tillage; MT: minimum tillage
Figure 1. Map location of the state of Paraná, the municipality of Ponta Grossa and the experimental area where the samples were collected. IAPAR: “Instituto de Desenvolvimento Rural do Paraná”; CT: conventional tillage; NT: no–tillage; MT: minimum tillage
Preprints 122180 g001
Preprints 122180 g002
Figure 2. 3D images of the soil pore system (terracotta color) for: (a,b) Minimum tillage for 0 and 12 wetting and drying (W-D) cycles; (c,d) Conventional tillage for 0 and 12 W-D cycles; (e,f) No-tillage for 0 and 12 W-D cycles.
Figure 2. 3D images of the soil pore system (terracotta color) for: (a,b) Minimum tillage for 0 and 12 wetting and drying (W-D) cycles; (c,d) Conventional tillage for 0 and 12 W-D cycles; (e,f) No-tillage for 0 and 12 W-D cycles.
Preprints 122180 g002
Preprints 122180 g003
Figure 3. 3D Shannon entropy ( H * ( ε ) ) and lacunarity ( L n ( Λ )) curves for: (a,b) Minimum tillage for 0 and 12 wetting and drying (W-D) cycles; (c,d) Conventional tillage for 0 and 12 W-D cycles; (e,f) No-tillage for 0 and 12 W-D cycles.
Figure 3. 3D Shannon entropy ( H * ( ε ) ) and lacunarity ( L n ( Λ )) curves for: (a,b) Minimum tillage for 0 and 12 wetting and drying (W-D) cycles; (c,d) Conventional tillage for 0 and 12 W-D cycles; (e,f) No-tillage for 0 and 12 W-D cycles.
Preprints 122180 g003
Preprints 122180 g004
Figure 4. Variation of the capacity dimension ( D 0 ) as a function of the application of wetting and drying cycles (W-D) for: (a) Minimum tillage for 0 and 12 W-D cycles; (b) Conventional tillage for 0 and 12 W-D cycles; (c) No-tillage for 0 and 12 W-D cycles.
Figure 4. Variation of the capacity dimension ( D 0 ) as a function of the application of wetting and drying cycles (W-D) for: (a) Minimum tillage for 0 and 12 W-D cycles; (b) Conventional tillage for 0 and 12 W-D cycles; (c) No-tillage for 0 and 12 W-D cycles.
Preprints 122180 g004
Preprints 122180 g005
Figure 5. Variation in porosity ( Φ ) and pore size distribution ( Φ − s i z e ) as a function of the application of wetting and drying cycles (W-D) for: (a,b) Minimum tillage for 0 and 12 W-D cycles; (c,d) Conventional tillage for 0 and 12 W-D cycles; (e,f) No-tillage for 0 and 12 W-D cycles.
Figure 5. Variation in porosity ( Φ ) and pore size distribution ( Φ − s i z e ) as a function of the application of wetting and drying cycles (W-D) for: (a,b) Minimum tillage for 0 and 12 W-D cycles; (c,d) Conventional tillage for 0 and 12 W-D cycles; (e,f) No-tillage for 0 and 12 W-D cycles.
Preprints 122180 g005
Preprints 122180 g006
Figure 6. Variation in degree of anisotropy (DA) and number of pores (NP) as a function of the application of wetting and drying cycles (W-D) for: (a,b) Minimum tillage for 0 and 12 W-D cycles; (c,d) Conventional tillage for 0 and 12 W-D cycles; (e,f) No-tillage for 0 and 12 W-D cycles.
Figure 6. Variation in degree of anisotropy (DA) and number of pores (NP) as a function of the application of wetting and drying cycles (W-D) for: (a,b) Minimum tillage for 0 and 12 W-D cycles; (c,d) Conventional tillage for 0 and 12 W-D cycles; (e,f) No-tillage for 0 and 12 W-D cycles.
Preprints 122180 g006
Preprints 122180 g007
Figure 7. Variation in pore connectivity (C) and tortuosity ( τ ) as a function of the application of wetting and drying cycles (W-D) for: (a,b) Minimum tillage for 0 and 12 W-D cycles; (c,d) Conventional tillage for 0 and 12 W-D cycles; (e,f) No-tillage for 0 and 12 W-D cycles.
Figure 7. Variation in pore connectivity (C) and tortuosity ( τ ) as a function of the application of wetting and drying cycles (W-D) for: (a,b) Minimum tillage for 0 and 12 W-D cycles; (c,d) Conventional tillage for 0 and 12 W-D cycles; (e,f) No-tillage for 0 and 12 W-D cycles.
Preprints 122180 g007
Preprints 122180 g008
Figure 8. Contribution of the different pore shapes to the volume (VP-S) and number of pores (NP-S) for: (a,b) Minimum tillage for 0 and 12 wetting and drying (W-D) cycles; (c,d) Conventional tillage for 0 and 12 W-D cycles; (e,f) No-tillage for 0 and 12 W-D cycles. Eq.: equant; Pr.: prolate; Ob.: oblate; Tr.: triaxial.
Figure 8. Contribution of the different pore shapes to the volume (VP-S) and number of pores (NP-S) for: (a,b) Minimum tillage for 0 and 12 wetting and drying (W-D) cycles; (c,d) Conventional tillage for 0 and 12 W-D cycles; (e,f) No-tillage for 0 and 12 W-D cycles. Eq.: equant; Pr.: prolate; Ob.: oblate; Tr.: triaxial.
Preprints 122180 g008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated