A System of Tensor Equations over the Dual Split Quaternion Algebra with an Application

Preprint

Article

A System of Tensor Equations over the Dual Split Quaternion Algebra with an Application

This version is not peer-reviewed.

This version is not peer-reviewed.

Altmetrics

Downloads

Views

Comments

Submitted:

25 October 2024

Posted:

29 October 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract

In this paper, we propose the definition of block tensors and the real representation of tensors. Equipped with the simplification method, i.e., the real representation along with the M-P inverse, we demonstrate the conditions that are necessary and sufficient for the system of dual split quaternion tensor equations (A*NX,X*SC)=(B,D) when its solution exists. Furthermore, the general expression of the solution is also provided when the solution of the system exists and we use a numerical example to validate it in the last section. To the best of our knowledge, it is the first time that the aforementioned tensor system has been examined on dual split quaternion algebra. Additionally, we provide its equivalent conditions when its Hermitian solution X=X* and η-Hermitian solutions X=Xη* exist. Subsequently, we discuss two special dual split quaternion tensor equations. Last but not least, we propose an application for encrypting and decrypting two color videos and we validate this algorithm through a specific example.

Keywords:

Subject:

Physical Sciences - Mathematical Physics

MSC: 11R52; 15A09; 15A69

1. Introduction

Irish mathematician W.R. Hamilton pioneered the related research about the concept of quaternions in 1843 [1]. There has been a rapid development in quaternions during recent years. There exist various kinds of related work about quaternions that achieve valuable results [2,3]. Most recently, researchers focus on the theories of solving quaternion matrix equations, i.e., general and special solutions of quaternion matrix equations [4]. Quaternions and quaternion matrices have been comprehensively applied to multiple areas including algebra, analysis, topology, and physics. In particular, they are crucial in several fields, such as signal processing [5], image processing [6], and quantum physics [7].

In 1849, building upon Hamilton’s work, James Cockle further introduced "split quaternions" [8]. The set of split quaternions is denoted as:

\begin{matrix} H_{S} = {q = q_{0} + q_{1} i + q_{2} j + q_{3} k : q_{0}, q_{1}, q_{2}, q_{3} \in R}, \end{matrix}

where

\begin{matrix} i^{2} = - j^{2} = - k^{2} = - 1, i j = - j i = k, j k = - k j = - i, k i = - i k = j . \end{matrix}

As a derivative version of quaternions, its form is similar to the original definition of quaternions, but they are indeed two different algebras. The definition proposed by James Cockle has a more complex algebraic structure. Split quaternions play a significant role in various fields, e.g., physics, quantum mechanics, signal processing, and deep learning. Split quaternions have been applied to denote Lorentz rotations, and Lorentz transformations can be represented as

2 \times 2

unitary matrices of split quaternions, which reveals the geometric and physical importance of split quaternions [10,11,12,13,14,38,39].

Clifford [42] later proposed dual numbers and dual quaternions in 1873 and they have already become the basis of handling some typical engineering problems [15]. Dual split quaternions, like dual quaternions, expand the idea of dual numbers to include split quaternions. Building on the principles of split quaternions, dual split quaternions have been applied to diverse disciplines including algebra, geometry, and physics [9,16,17,18].

Below is a typical matrix equation system that this paper mainly focuses on. There exists some related work providing solutions to it, while this paper will explore this equation system defined in the domain of dual split quaternion tensor.

\{\begin{matrix} A X = B, \\ X C = D . \end{matrix}

(1)

Due to its wide applications in fields such as biology, inverse problems in vibration theory and linear programming, system (1) has been extensively studied. Rao and Mitra [19] established the criteria for the solvability of the system (1). They also presented their general solutions. Khatri and Mitra [20] examined their Hermitian solutions within the complex field. Wang [21] derived conditions for solvability and provided solutions for bi-symmetric cases of system (1) in the quaternion skew field. Li and others [22] examined generalized reflexive solutions for complex system (1). Yuan [23] used spectral decomposition to investigate least squares solutions for system (1). Xie [24] applied the M-P inverse as well as the rank of quaternion matrices to determine the equivalent conditions when there exist solutions and then propose the general solution. Si and others [39] used real representations to establish various solutions of system (1) and their equivalent conditions over split quaternion field.

It is revealed that tensors are useful in engineering and science, and there are some papers focusing on the solutions of tensor equations [25,26,27,28,29,35]. Based on the extensive applications of tensors, this paper focuses on solving system (1) defined on the space of dual split quaternion tensors. To the best of our knowledge, it is the first exploration of the above system within the dual split quaternion tensor algebra. Specifically, it aims to solve the following system of dual split quaternion tensor equations:

\{\begin{matrix} A *_{N} X = B, \\ X *_{S} C = D . \end{matrix}

(2)

This paper is designed with such structure: Section 2 describes essential definitions and corollaries that are essential to our subsequent analysis. Section 3 investigates the conditions that are equivalent for system (2) when there exist solutions. In this section, We further demonstrate its general solution in cases where solutions are attainable. Furthermore, we present the sufficient and necessary criteria when system (2) have

η

-Hermitian solutions. Based on these results, we will introduce the equivalent condition for the Hermitian solution, along with the general expressions of solutions for two specific dual split quaternion tensor equations. Ultimately, we will present a specific numerical example and an encryption and decryption algorithm as an application.

In this paper, the dual number field, quaternion field, split quaternion field, dual quaternion field, and dual split quaternion field are represented by

D

H

H_{s}

DQ

, and

{DQ}_{s}

respectively. All

I_{1} \times \dots \times I_{M} \times J_{1} \times \dots \times J_{N}

tensors over

{DQ}_{s}

are represented using

{DQ}_{s}^{I_{1} \times \dots \times I_{M} \times J_{1} \times \dots \times J_{N}}

2. Preliminary

In this section, there are three parts to provide fundamental knowledge for the subsequent demonstration of this paper. In the first part, we will give the definition of dual split quaternion tensors. The second part will cover some definitions and propositions about tensors. Lastly, we will present various real representations of split quaternion tensors.

2.1. Dual Split Quaternion Tensors

A = {(a_{j_{1} \dots j_{M}})}_{1 \leq j_{k} \leq J_{k} (k = 1, \dots, M)}

is a multidimensional array tensor with

J_{1} \times J_{2} \times \dots \times J_{M}

entries. Let

R^{J_{1} \times \dots \times J_{M}}

H^{J_{1} \times \dots \times J_{M}}

, and

H_{s}^{J_{1} \times \dots \times J_{M}}

respectively represent the sets of the order M tensors with

J_{1} \times \dots \times J_{M}

dimensions over the real field

R

, real quaternion algebra

H

, and real split quaternion algebra

H_{s}

For

A = (a_{i_{1} \dots i_{M} l_{1} \dots l_{N}}) \in H_{s}^{I_{1} \times \dots \times I_{M} \times L_{1} \times \dots \times L_{N}}

B = (b_{l_{1} \dots l_{N} i_{1} \dots i_{M}}) \in H_{s}^{L_{1} \times \dots \times L_{N} \times I_{1} \times \dots \times I_{M}}

. When

b_{l_{1} \dots l_{N} i_{1} \dots i_{M}} = a_{i_{1} \dots i_{M} l_{1} \dots l_{N}}

B

is referred to as the transpose of

A

and is denoted by

A^{T}

. When

b_{l_{1} \dots l_{M} i_{1} \dots i_{N}} = {\bar{a}}_{i_{1} \dots i_{N} l_{1} \dots l_{M}}

B

is the conjugate transpose of

A

, represented as

A^{*}

. A diagonal tensor

D = (d_{t_{1} \dots t_{M} t_{1} \dots t_{M}}) \in H_{s}^{T_{1} \times \dots \times T_{M} \times T_{1} \times \dots \times T_{M}}

has all zero entries except for the elements

d_{t_{1} \dots t_{M} t_{1} \dots t_{M}}

. When all diagonal elements of

D

are equal to 1,

D

is referred to as a unit tensor, expressed as

I

. Specifically, if

I \in H_{s}^{T_{1} \times \dots \times T_{M} \times T_{1} \times \dots \times T_{M}}

, it is expressed as

I_{M}

O

denotes the zero tensor whose elements are all zero.

Definition 1

([30,42]). The field of dual numbers is expressed as:

D = {q = q_{0} + q_{1} ϵ : q_{0}, q_{1} \in R, ϵ \neq 0, ϵ^{2} = 0},

where ϵ is the infinitesimal unit.

By extending quaternions and split quaternions to include dual numbers, we derive the definitions of dual quaternions and dual split quaternions:

DQ = {q = q_{0} + q_{1} ϵ : q_{0}, q_{1} \in H, ϵ \neq 0, ϵ^{2} = 0},

{DQ}_{s} = {q = q_{0} + q_{1} ϵ : q_{0}, q_{1} \in H_{s}, ϵ \neq 0, ϵ^{2} = 0} .

The sets of dual quaternion tensors and dual split quaternion tensors [9,30] are represented as follows:

\begin{matrix} {DQ}^{I_{1} \times \dots \times I_{M} \times J_{1} \times \dots \times J_{N}} = {Q = Q_{0} + Q_{1} ϵ : Q_{0}, Q_{1} \in H^{I_{1} \times \dots \times I_{M} \times J_{1} \times \dots \times J_{N}}, ϵ \neq 0, ϵ^{2} = 0}, \\ {DQ}_{s}^{I_{1} \times \dots \times I_{M} \times J_{1} \times \dots \times J_{N}} = {Q = Q_{0} + Q_{1} ϵ : Q_{0}, Q_{1} \in H_{s}^{I_{1} \times \dots \times I_{M} \times J_{1} \times \dots \times J_{N}}, ϵ \neq 0, ϵ^{2} = 0} . \end{matrix}

For

X = X_{0} + X_{1} ϵ, Y = Y_{0} + Y_{1} ϵ \in {DQ}_{s}^{I_{1} \times \dots \times I_{M} \times L_{1} \times \dots \times L_{N}}

X = Y

means that

X_{0} = Y_{0}

and

X_{1} = Y_{1}

, and vice versa.

X^{*} = X_{0}^{*} + X_{1}^{*} ϵ

is called the conjugate transpose of

X

X^{η *} = X_{0}^{η *} + X_{1}^{η *} ϵ

are called the

η

-conjugate transposes of

X

, where

η = {i, j, k}

For

X \in H_{s}^{I_{1} \times \dots \times I_{M} \times L_{1} \times \dots \times L_{N}}

X

is uniquely identified as

X = X_{0} + X_{1} i + X_{2} j + X_{3} k

, where

X_{0}, X_{1}, X_{2}

and

X_{3} \in R^{I_{1} \times \dots \times I_{M} \times L_{1} \times \dots \times L_{N}}

. The conjugate transpose of

X

satisfies

X^{*} = X_{0}^{T} - X_{1}^{T} i - X_{2}^{T} j - X_{3}^{T} k

. Additionally, for

η \in {i, j, k}

, the

η

-conjugates and

η

-conjugate transposes [36] of

X

have following forms:

\begin{matrix} X^{i} & = i^{- 1} X i = X_{0} + X_{1} i - X_{2} j - X_{3} k, \\ X^{j} & = j^{- 1} X j = X_{0} - X_{1} i + X_{2} j - X_{3} k, \\ X^{k} & = k^{- 1} X k = X_{0} - X_{1} i - X_{2} j + X_{3} k, \end{matrix}

and

\begin{matrix} X^{i *} = i^{- 1} X^{*} i = X_{0}^{T} - X_{1}^{T} i + X_{2}^{T} j + X_{3}^{T} k, \\ X^{j *} = j^{- 1} X^{*} j = X_{0}^{T} + X_{1}^{T} i - X_{2}^{T} j + X_{3}^{T} k, \\ X^{k *} = k^{- 1} X^{*} k = X_{0}^{T} + X_{1}^{T} i + X_{2}^{T} j - X_{3}^{T} k . \end{matrix}

Definition 2.

Let

X \in {DQ}_{s}^{I_{1} \times \dots \times I_{N} \times I_{1} \times \dots \times I_{N}}

. Provided that

X

fulfills subsequent criteria:

X = X^{η *} : = η^{- 1} X^{*} η, η \in {i, j, k},

we refer to

X

as a η-Hermitian tensor.

For

X = X_{0} + X_{1} ϵ, Y = Y_{0} + Y_{1} ϵ \in {DQ}_{s}^{T_{1} \times \dots \times T_{M} \times J_{1} \times \dots \times J_{N}}

, then we can derive that

{(X + Y)}^{η *} = X^{η *} + Y^{η *}

and

{(X^{η *})}^{η *} = X

. And

X = Y

means that

X_{0}^{η *} = Y_{0}^{η *}

and

X_{1}^{η *} = Y_{1}^{η *}

, and vice versa.

2.2. Basic theory with Einstein product

Definition 3

([31]). Let

X \in {DQ}_{s}^{I_{1} \times \dots \times I_{M} \times L_{1} \times \dots \times L_{N}}

and

Y \in {DQ}_{s}^{L_{1} \times \dots \times L_{N} \times K_{1} \times \dots \times K_{S}}

, then we can define the Einstein product of tensors

X

and

Y

through the operation

*_{N}

as follows:

\begin{matrix} {(X *_{N} Y)}_{i_{1} \dots i_{M} k_{1} \dots k_{S}} = \sum_{l_{1} \dots l_{N}} x_{i_{1} \dots i_{M} l_{1} \dots l_{N}} y_{l_{1} \dots l_{N} k_{1} \dots k_{S}} \in {DQ}_{s}^{I_{1} \times \dots \times I_{M} \times K_{1} \times \dots \times K_{S}} . \end{matrix}

Proposition 1.

Let

X \in {DQ}_{s}^{I_{1} \times \dots \times I_{M} \times L_{1} \times \dots \times L_{S}}

and

Y \in {DQ}_{s}^{L_{1} \times \dots \times L_{S} \times K_{1} \times \dots \times K_{T}}

, then

${(X *_{S} Y)}^{*} = Y^{*} *_{S} X^{*}$ ;
$I_{S} *_{S} Y = Y$ and $Y *_{T} I_{T} = Y$ .

Definition 4

([32,35]). Let

A \in H_{s}^{I_{1} \times \dots \times I_{M} \times L_{1} \times \dots \times L_{T}}

and

Y \in H_{s}^{L_{1} \times \dots \times L_{T} \times I_{1} \times \dots \times I_{M}}

Y

is referred to as the Moore-Penrose inverse of

A

, expressed as

A^{†}

, if the subsequent conditions are all fulfilled:

$A *_{T} Y *_{M} A = A$ ;
$Y *_{M} A *_{T} Y = Y$ ;
${(A *_{T} Y)}^{*} = A *_{T} Y$ ;
${(Y *_{M} A)}^{*} = Y *_{M} A$ .

Furthermore, projectors

L_{A}

and

R_{A}

have following forms:

L_{A} = I - A^{†} *_{M} A, R_{A} = I - A *_{T} A^{†} .

Similar to block matrices, reference [32] provides the definition of block tensors and reference [33] provides the definition of block tensors when their sizes are same. Next, we extend the definitions from references [32,33] to split quaternion tensors to give the definition of block tensors with the same size.

Definition 5.

Let

X = (x_{l_{1} \dots l_{T} k_{1} \dots k_{N}})

and

Y = (y_{l_{1} \dots l_{T} k_{1} \dots k_{N}}) \in H_{s}^{L_{1} \times \dots \times L_{T} \times K_{1} \times \dots \times K_{N}}

, then

The ’row block tensor’ formed by $X$ and $Y$ is $[X Y] \in H_{s}^{L_{1} \times \dots \times L_{T} \times K_{1} \times \dots \times K_{N - 1} \times 2 K_{N}}$ , and

$\begin{matrix} {[X Y]}_{l_{1} \dots l_{T} k_{1} \dots k_{N}} \\ = \{\begin{matrix} x_{l_{1} \dots l_{T} k_{1} \dots k_{N}}, & l_{1} \dots l_{T} \in [L_{1}] \times \dots \times [L_{T}], k_{1} \dots k_{N} \in [K_{1}] \times \dots \times [K_{N}]; \\ y_{l_{1} \dots l_{T} k_{1} \dots (k_{N} - K_{N})}, & l_{1} \dots l_{T} \in [L_{1}] \times \dots \times [L_{T}], k_{1} \dots k_{N} \in [K_{1}] \times \dots \times Γ, \end{matrix} \end{matrix}$

where $Γ = {K_{N} + 1, K_{N} + 2 \dots, 2 K_{N}}$ .
The ’column block tensor’ formed by $X$ and $Y$ is $[\begin{matrix} X \\ Y \end{matrix}] \in H_{s}^{L_{1} \times \dots \times L_{T - 1} \times 2 L_{T} \times K_{1} \times \dots \times K_{N}}$ , and

$\begin{matrix} {[\begin{matrix} X \\ Y \end{matrix}]}_{l_{1} \dots l_{T} k_{1} \dots k_{N}} \\ = \{\begin{matrix} x_{l_{1} \dots l_{T} k_{1} \dots k_{N}}, & l_{1} \dots l_{T} \in [L_{1}] \times \dots \times [L_{T}], k_{1} \dots k_{N} \in [K_{1}] \times \dots \times [K_{N}]; \\ y_{l_{1} \dots (l_{T} - L_{T}) k_{1} \dots k_{N}}, & l_{1} \dots l_{T} \in [L_{1}] \times \dots \times Γ, k_{1} \dots k_{N} \in [K_{1}] \times \dots \times [K_{N}], \end{matrix} \end{matrix}$

where $Γ = {L_{T} + 1, L_{T} + 2 \dots, 2 L_{T}}$ .

In particular, let

X_{11}

X_{12}

X_{21}

and

X_{22} \in H_{s}^{L_{1} \times \dots \times L_{T} \times K_{1} \times \dots \times K_{N}}

, then

\begin{matrix} [\begin{matrix} X_{11} X_{12} \\ X_{21} X_{22} \end{matrix}] \in H_{s}^{L_{1} \times \dots \times L_{T - 1} \times 2 L_{T} \times K_{1} \times \dots \times K_{N - 1} \times 2 K_{N}} . \end{matrix}

Remark 1.

X_{i j}

is the tensor located at row i, column

j (i, j = 1, 2)

in the aforementioned block tensor and it will be used in the following statement.

Lemma 1

([32]). Let

X_{i} \in H_{s}^{I_{1} \times \dots \times I_{M} \times J_{1} \times \dots \times J_{N}}, i = {1, 2, 3, 4}

Y_{j} \in H_{s}^{J_{1} \times \dots \times J_{N} \times T_{1} \times \dots \times T_{S}}

j = {1, 2}

, and

Z_{k} \in H_{s}^{S_{1} \times \dots \times S_{N} \times I_{1} \times \dots \times I_{M}}

k = {1, 2}

, then

$\begin{matrix} [\begin{matrix} X_{1} & X_{3} \\ X_{2} & X_{4} \end{matrix}] *_{N} [\begin{matrix} Y_{1} \\ Y_{2} \end{matrix}] = [\begin{matrix} X_{1} *_{N} Y_{1} + X_{3} *_{N} Y_{2} \\ X_{2} *_{N} Y_{1} + X_{4} *_{N} Y_{2} \end{matrix}]; \end{matrix}$
$\begin{matrix} [\begin{matrix} Z_{1} & Z_{2} \end{matrix}] *_{M} [\begin{matrix} X_{1} & X_{3} \\ X_{2} & X_{4} \end{matrix}] = [\begin{matrix} Z_{1} *_{M} X_{1} + Z_{2} *_{M} X_{2} & Z_{1} *_{M} X_{3} + Z_{2} *_{M} X_{4} \end{matrix}] . \end{matrix}$

Next, we will introduce the definition of the transformation t between a tensor and a matrix within split quaternion algebra [34,35]. Under this definition, we can simplify the tensor into a matrix.

Definition 6.

The transformation

t : T_{I_{1}, I_{2}, \dots, I_{M}, L_{1}, L_{2}, \dots, L_{N}} (H_{s}) \to M_{I_{1} \cdot I_{2} \dots I_{M}, L_{1} \cdot L_{2} \dots L_{N}} (H_{s})

with

t (X) = X

is defined as follows:

\begin{matrix} {(X)}_{i_{1} i_{2} \dots i_{M} l_{1} l_{2} \dots l_{N}} \overset{t}{\to} {(X)}_{[i_{1} + \sum_{k = 2}^{M} (i_{k} - 1) \prod_{s = 1}^{k - 1} I_{s}] [l_{1} + \sum_{k = 2}^{N} (l_{k} - 1) \prod_{s = 1}^{k - 1} L_{s}]}, \end{matrix}

where

X \in T_{I_{1}, I_{2}, \dots, I_{M}, L_{1}, L_{2}, \dots, L_{N}} (H_{s})

and

X \in M_{I_{1} \cdot I_{2} \dots I_{M}, L_{1} \cdot L_{2} \dots L_{N}} (H_{s})

Lemma 2

([35]). Let

X \in H_{s}^{I_{1} \times \dots \times I_{M} \times L_{1} \times \dots \times L_{N}}

and

Y \in H_{s}^{L_{1} \times \dots \times L_{N} \times K_{1} \times \dots \times K_{S}}

. Then t satisfies following properties:

The map t is bijective and its inverse map $t^{- 1}$ exists as follows:

$\begin{matrix} M_{I_{1} \cdot I_{2} \dots I_{M - 1} \cdot I_{M}, L_{1} \cdot L_{2} \dots L_{N - 1} \cdot L_{N}} (H_{s}) \overset{t^{- 1}}{\to} T_{I_{1}, I_{2}, \dots, I_{M - 1}, I_{M}, L_{1}, L_{2}, \dots, L_{N - 1}, L_{N}} (H_{s}); \end{matrix}$
t satisfies: $t (X *_{N} Y) = t (X) \cdot t (Y)$ and $t (X^{†}) = t {(X)}^{†}$ .

Example 1.

Let

A \in H_{s}^{2 \times 2 \times 2 \times 2}

is defined by

\begin{matrix} {(A)}_{1111} = i + 2 k, {(A)}_{1121} = k, {(A)}_{1112} = 3 i, {(A)}_{1122} = 2, \\ {(A)}_{2111} = 0, {(A)}_{2121} = i + j, {(A)}_{2112} = 2 k, {(A)}_{2122} = i + 2 j, \\ {(A)}_{1211} = - i + 2 j, {(A)}_{1221} = 4 k, {(A)}_{1212} = 0, {(A)}_{1222} = 3 j, \\ {(A)}_{2211} = 4 i + 2 k, {(A)}_{2221} = i + 3 j, {(A)}_{2212} = 2 + 3 i + j, {(A)}_{2222} = 1 + 2 j + 5 k . \end{matrix}

Then

\begin{matrix} A = t (A) & = (\begin{matrix} {(A)}_{1111} & {(A)}_{1121} & {(A)}_{1112} & {(A)}_{1122} \\ {(A)}_{2111} & {(A)}_{2121} & {(A)}_{2112} & {(A)}_{2122} \\ {(A)}_{1211} & {(A)}_{1221} & {(A)}_{1212} & {(A)}_{1222} \\ {(A)}_{2211} & {(A)}_{2221} & {(A)}_{2212} & {(A)}_{2222} \end{matrix}) \\ = (\begin{matrix} i + 2 k & k & 3 i & 2 \\ 0 & i + j & 2 k & i + 2 j \\ - i + 2 j & 4 k & 0 & 3 j \\ 4 i + 2 k & i + 3 j & 2 + 3 i + j & 1 + 2 j + 5 k \end{matrix}) . \end{matrix}

Consequently, there is a one-to-one correspondence between the elements of the split quaternion matrix and the split quaternion tensor. Thus, we can make use of the above definition to transform the tensor into a matrix for further calculations.

2.3. Real Representations of Split Quaternion Tensors

In this section, we will provide various real representations using the definition of block tensors in the above section.

Let

X = X_{0} + X_{1} i + X_{2} j + X_{3} k \in H_{s}^{I_{1} \times \dots \times I_{M} \times J_{1} \times \dots \times J_{N}}

, where

X_{i} \in R^{I_{1} \times \dots \times I_{M} \times J_{1} \times \dots \times J_{N}}

i = {0, 1, 2, 3}

. We will define three kinds of real representations of

X

based on the real representation in [12]:

X^{σ_{i}} : = [\begin{matrix} X_{0} & X_{1} & X_{2} & X_{3} \\ - X_{1} & X_{0} & - X_{3} & X_{2} \\ X_{2} & - X_{3} & X_{0} & - X_{1} \\ X_{3} & X_{2} & X_{1} & X_{0} \end{matrix}] \in R^{I_{1} \times \dots \times 4 I_{M} \times J_{1} \times \dots \times 4 J_{N}} .

Definition 7

([36,39]). Let

X = X_{0} + X_{1} i + X_{2} j + X_{3} k \in H_{s}^{I_{1} \times \dots \times I_{M} \times J_{1} \times \dots \times J_{N}}

, where

X_{0}

X_{1}

X_{2}

X_{3} \in R^{I_{1} \times \dots \times I_{M} \times J_{1} \times \dots \times J_{N}}

I_{M} \in R^{I_{1} \times \dots \times I_{M} \times I_{1} \times \dots \times I_{M}}

. Then we define

\begin{matrix} X^{σ_{j}} : = V_{M} *_{M} X^{σ_{i}} = [\begin{matrix} X_{0} & X_{1} & X_{2} & X_{3} \\ X_{1} & - X_{0} & X_{3} & - X_{2} \\ - X_{2} & X_{3} & - X_{0} & X_{1} \\ X_{3} & X_{2} & X_{1} & X_{0} \end{matrix}], & V_{M} = [\begin{matrix} I_{M} & O & O & O \\ O & - I_{M} & O & O \\ O & O & - I_{M} & O \\ O & O & O & I_{M} \end{matrix}]; \end{matrix}

\begin{matrix} X^{σ_{k}} : = W_{M} *_{M} X^{σ_{i}} = [\begin{matrix} X_{0} & X_{1} & X_{2} & X_{3} \\ X_{1} & - X_{0} & X_{3} & - X_{2} \\ X_{2} & - X_{3} & X_{0} & - X_{1} \\ - X_{3} & - X_{2} & - X_{1} & - X_{0} \end{matrix}], & W_{M} = [\begin{matrix} I_{M} & O & O & O \\ O & - I_{M} & O & O \\ O & O & I_{M} & O \\ O & O & O & - I_{M} \end{matrix}]; \end{matrix}

\begin{matrix} X^{σ_{1}} : = P_{M} *_{M} X^{σ_{i}} = [\begin{matrix} X_{0} & X_{1} & X_{2} & X_{3} \\ - X_{1} & X_{0} & - X_{3} & X_{2} \\ - X_{2} & X_{3} & - X_{0} & X_{1} \\ - X_{3} & - X_{2} & - X_{1} & - X_{0} \end{matrix}], & P_{M} = [\begin{matrix} I_{M} & O & O & O \\ O & I_{M} & O & O \\ O & O & - I_{M} & O \\ O & O & O & - I_{M} \end{matrix}], \end{matrix}

where

V_{M}, W_{M}

and

P_{M} \in R^{I_{1} \times \dots \times 4 I_{M} \times I_{1} \times \dots \times 4 I_{M}}

As shown in the next proposition, we present the relevant characteristics of real representations discussed previously. These properties will play a crucial role in subsequent sections and can be easily obtained through simple calculations. Let

\begin{matrix} R_{M} = [\begin{matrix} O & - I_{M} & O & O \\ I_{M} & O & O & O \\ O & O & O & - I_{M} \\ O & O & I_{M} & O \end{matrix}], S_{M} = [\begin{matrix} O & O & I_{M} & O \\ O & O & O & - I_{M} \\ I_{M} & O & O & O \\ O & - I_{M} & O & O \end{matrix}], T_{M} = [\begin{matrix} O & O & O & I_{M} \\ O & O & I_{M} & O \\ O & I_{M} & O & O \\ I_{M} & O & O & O \end{matrix}] . \end{matrix}

Proposition 2.

For

η = {i, j, k}

, let

X, Y \in H_{s}^{I_{1} \times \dots \times I_{M} \times J_{1} \times \dots \times J_{N}}, P \in H_{s}^{J_{1} \times \dots \times J_{N} \times K_{1} \times \dots \times K_{T}}

, and

λ \in R

. Then

$X = Y \Leftrightarrow X^{η *} = Y^{η *}$ ;
${(X + Y)}^{σ_{η}} = X^{σ_{η}} + Y^{σ_{η}}, {(λ X)}^{σ_{η}} = λ X^{σ_{η}};$
${(X *_{N} P)}^{σ_{i}} = X^{σ_{i}} *_{N} P^{σ_{i}}, {(X *_{N} P)}^{σ_{j}} = X^{σ_{j}} *_{N} V_{N} *_{N} P^{σ_{j}}, {(X *_{N} P)}^{σ_{k}} = X^{σ_{k}} *_{N} W_{N} *_{N} P^{σ_{k}}, {(X *_{N} P)}^{σ_{1}} = X^{σ_{1}} *_{N} P_{N} *_{N} P^{σ_{1}}$ ;
- $R_{M}^{T} *_{M} X^{σ_{i}} *_{N} R_{N} = X^{σ_{i}}, S_{M}^{T} *_{M} X^{σ_{i}} *_{N} S_{N} = X^{σ_{i}}, T_{M}^{T} *_{M} X^{σ_{i}} *_{N} T_{N} = X^{σ_{i}}$ ;
- $R_{M}^{T} *_{M} X^{σ_{j}} *_{N} R_{N} = - X^{σ_{j}}, S_{M}^{T} *_{M} X^{σ_{j}} *_{N} S_{N} = - X^{σ_{j}}, T_{M}^{T} *_{M} X^{σ_{j}} *_{N} T_{N} = X^{σ_{j}}$ ;
- $R_{M}^{T} *_{M} X^{σ_{k}} *_{N} R_{N} = - X^{σ_{k}}, S_{M}^{T} *_{M} X^{σ_{k}} *_{N} S_{N} = X^{σ_{k}}, T_{M}^{T} *_{M} X^{σ_{k}} *_{N} T_{N} = - X^{σ_{k}}$ ;
${(X^{*})}^{σ_{1}} = {(X^{σ_{1}})}^{T}, {(X^{η *})}^{σ_{η}} = {(X^{σ_{η}})}^{T}$ ;
- $X = \frac{1}{2} [\begin{matrix} I_{M} & i I_{M} & j I_{M} & k I_{M} \end{matrix}] *_{M} X^{σ_{i}} *_{N} [\begin{matrix} I_{N} \\ i I_{N} \\ j I_{N} \\ k I_{N} \end{matrix}]$ ;
- $X = \frac{1}{2} [\begin{matrix} I_{M} & - i I_{M} & - j I_{M} & k I_{M} \end{matrix}] *_{M} X^{σ_{j}} *_{N} [\begin{matrix} I_{N} \\ i I_{N} \\ j I_{N} \\ k I_{N} \end{matrix}]$ ;
- $X = \frac{1}{2} [\begin{matrix} I_{M} & - i I_{M} & j I_{M} & - k I_{M} \end{matrix}] *_{M} X^{σ_{k}} *_{N} [\begin{matrix} I_{N} \\ i I_{N} \\ j I_{N} \\ k I_{N} \end{matrix}]$ ;
${(X^{i})}^{σ_{1}} = P_{M} *_{M} X^{σ_{1}} *_{N} P_{N}, {(X^{k})}^{σ_{j}} = V_{M} *_{M} X^{σ_{j}} *_{N} V_{N}, {(X^{j})}^{σ_{k}} = W_{M} *_{M} X^{σ_{k}} *_{N} W_{N}$ .

3. The General Solution to System (2)

Using the definitions and lemmas outlined above, this part will examine the solutions to system (2). At the beginning of this section, we present two lemmas. Utilizing Definition (6), we can transform tensors into matrices. Consequently, the subsequent lemmas can be readily proven using matrix proof techniques found in references [24,37], so this paper will not delve into the details. Building on these lemmas, split quaternion tensors’ real representations are used for obtaining the necessary and sufficient criteria when system (2) exists solutions as well as the general solution expression.

Lemma 3

([37]). Let

A_{1}, A_{2} \in H^{I_{1} \times \dots \times I_{M} \times J_{1} \times \dots \times J_{N}}

B_{1}, B_{2} \in H^{L_{1} \times \dots \times L_{S} \times K_{1} \times \dots \times K_{T}}

, and

C_{1}, C_{2} \in H^{I_{1} \times \dots \times I_{M} \times K_{1} \times \dots \times K_{T}}

. Set

\begin{matrix} K & = A_{2} *_{N} L_{A_{1}}, F = R_{B_{1}} *_{S} B_{2}, G = C_{2} - A_{2} *_{N} A_{1}^{†} *_{M} C_{1} *_{T} B_{1}^{†} *_{S} B_{2}, H = R_{K} *_{M} A_{2}, \\ Q & = A_{1}^{†} *_{M} C_{1} *_{T} B_{1}^{†} + L_{A_{1}} *_{N} K^{†} *_{M} G *_{T} B_{2}^{†} - L_{A_{1}} *_{N} K^{†} *_{M} A_{2} *_{N} H^{†} *_{M} R_{K} *_{M} G *_{T} B_{2}^{†} \\ + H^{†} *_{M} R_{K} *_{M} G *_{T} F^{†} *_{S} R_{B_{1}} . \end{matrix}

Then

\begin{matrix} \{\begin{matrix} A_{1} *_{N} X *_{S} B_{1} & = C_{1}, \\ A_{2} *_{N} X *_{S} B_{2} & = C_{2} \end{matrix} \end{matrix}

(3)

is consistent if and only if

\begin{matrix} R_{A_{1}} *_{M} C_{1} = 0, C_{1} *_{T} L_{B_{1}} = 0, R_{A_{2}} *_{M} C_{2} = 0, C_{2} *_{T} L_{B_{2}} = 0, R_{K} *_{M} G *_{T} L_{F} = 0 . \end{matrix}

Building on this, the general solution for system (3) is stated in the following form:

\begin{matrix} X = Q + L_{A_{1}} *_{N} L_{K} *_{N} W_{1} + W_{2} *_{S} R_{F} *_{S} R_{B_{1}} + L_{A_{1}} *_{N} W_{3} *_{S} R_{B_{2}} + L_{A_{2}} *_{N} W_{4} *_{S} R_{B_{1}}, \end{matrix}

where

W_{i} (i = \bar{1, 4})

are arbitrary tensors of appropriate size defined on

H

Lemma 4

([24]). Suppose that

A = A_{0} + A_{1} ϵ \in {DQ}^{I_{1} \times \dots \times I_{M} \times J_{1} \times \dots \times J_{N}}

B = B_{0} + B_{1} ϵ \in {DQ}^{I_{1} \times \dots \times I_{M} \times K_{1} \times \dots \times K_{S}}

C = C_{0} + C_{1} ϵ \in {DQ}^{K_{1} \times \dots \times K_{S} \times L_{1} \times \dots \times L_{T}}

, and

D = D_{0} + D_{1} ϵ \in {DQ}^{J_{1} \times \dots \times J_{N} \times L_{1} \times \dots \times L_{T}}

. Set

\begin{matrix} A_{2} & = A_{1} *_{N} L_{A_{0}}, C_{2} = R_{C_{0}} *_{S} C_{1}, B_{2} = B_{1} - A_{1} *_{N} (A_{0}^{†} *_{M} B_{0} + L_{A_{0}} *_{N} D_{0} *_{T} C_{0}^{†}), \\ A_{3} & = R_{A_{0}} *_{M} A_{2}, B_{3} = R_{C_{0}}, D_{2} = D_{1} - (A_{0}^{†} *_{M} B_{0} + L_{A_{0}} *_{N} D_{0} *_{T} C_{0}^{†}) *_{S} C_{1}, \\ C_{3} & = R_{A_{0}} *_{M} B_{2}, A_{4} = L_{A_{0}}, B_{4} = C_{2} *_{T} L_{C_{0}}, C_{4} = D_{2} *_{T} L_{C_{0}}, A_{5} = A_{4} *_{N} L_{A_{3}}, \\ B_{5} & = R_{B_{3}} *_{S} B_{4}, C_{5} = C_{4} - A_{4} *_{N} A_{3}^{†} *_{M} C_{3} *_{S} B_{3}^{†} *_{S} B_{4}, D_{5} = R_{A_{5}} *_{N} A_{4}, \\ F & = A_{3}^{†} *_{M} C_{3} *_{S} B_{3}^{†} + L_{A_{3}} *_{N} A_{5}^{†} *_{N} C_{5} *_{T} B_{4}^{†} - L_{A_{3}} *_{N} A_{5}^{†} *_{N} A_{4} *_{N} D_{5}^{†} *_{N} R_{A_{5}} *_{N} C_{5} *_{T} B_{4}^{†} \\ + D_{5}^{†} *_{N} R_{A_{5}} *_{N} C_{5} *_{T} B_{5}^{†} *_{S} R_{B_{3}} . \end{matrix}

Then the subsequent descriptions are equivalent:

The system (2) is solvable.
$\begin{matrix} R_{A_{0}} *_{M} B_{0} = 0, D_{0} *_{T} L_{C_{0}} = 0, A_{0} *_{N} D_{0} = B_{0} *_{S} C_{0}, \\ A_{0} *_{N} D_{1} - B_{0} *_{S} C_{1} = B_{1} *_{S} C_{0} - A_{1} *_{N} D_{0}, R_{A_{3}} *_{M} C_{3} = 0, \\ C_{3} *_{S} L_{B_{3}} = 0, R_{A_{4}} *_{N} C_{4} = 0, C_{4} *_{T} L_{B_{4}} = 0, R_{A_{5}} *_{N} C_{5} *_{T} L_{B_{5}} = 0 . \end{matrix}$

Based on these, the general solution for the system (2) is represented as

X = X_{0} + X_{1} ϵ

, where

\begin{matrix} X_{0} & = A_{0}^{†} *_{M} B_{0} + L_{A_{0}} *_{N} D_{0} *_{T} C_{0}^{†} + L_{A_{0}} *_{N} W *_{S} R_{C_{0}}, \\ X_{1} & = A_{0}^{†} *_{M} (B_{2} - A_{2} *_{N} W *_{S} R_{C_{0}}) + L_{A_{0}} *_{N} (D_{2} - L_{A_{0}} *_{N} W *_{S} C_{2}) *_{T} C_{0}^{†} \\ + L_{A_{0}} *_{N} W_{1} *_{S} R_{C_{0}}, \\ W & = F + L_{A_{3}} *_{N} L_{A_{5}} *_{N} W_{2} + W_{3} *_{S} R_{B_{5}} *_{S} R_{B_{3}} + L_{A_{3}} *_{N} W_{4} *_{S} R_{B_{4}} + L_{A_{4}} *_{N} W_{5} *_{S} R_{B_{3}}, \end{matrix}

and

W_{i} (i = \bar{1, 5})

are random tensors with suitable dimensions.

Remark 2.

Note that the set of real tensors is included within the set of quaternion tensors since real numbers are special cases of quaternions with all imaginary parts set to 0. Thus, the conclusions above also hold in the field of real tensors.

Theorem 1.

Suppose that

A = A_{00} + A_{01} ϵ \in {DQ}_{s}^{I_{1} \times \dots \times I_{M} \times J_{1} \times \dots \times J_{N}}

B = B_{00} + B_{01} ϵ \in {DQ}_{s}^{I_{1} \times \dots \times I_{M} \times K_{1} \times \dots \times K_{S}}

C = C_{00} + C_{01} ϵ \in {DQ}_{s}^{K_{1} \times \dots \times K_{S} \times L_{1} \times \dots \times L_{T}}

, and

D = D_{00} + D_{01} ϵ \in {DQ}_{s}^{J_{1} \times \dots \times J_{N} \times L_{1} \times \dots \times L_{T}}

. Set

\begin{matrix} A_{0} = A_{00}^{σ_{i}}, A_{1} = A_{01}^{σ_{i}}, B_{0} = B_{00}^{σ_{i}}, B_{1} = B_{01}^{σ_{i}}, C_{0} = C_{00}^{σ_{i}}, C_{1} = C_{01}^{σ_{i}}, D_{0} = D_{00}^{σ_{i}}, D_{1} = D_{01}^{σ_{i}}, \\ A_{11} = A_{1} *_{N} L_{A_{0}}, C_{11} = R_{C_{0}} *_{S} C_{1}, B_{11} = B_{1} - A_{1} *_{N} (A_{0}^{†} *_{M} B_{0} + L_{A_{0}} *_{N} D_{0} *_{T} C_{0}^{†}), \\ D_{11} = D_{1} - (A_{0}^{†} *_{M} B_{0} + L_{A_{0}} *_{N} D_{0} *_{T} C_{0}^{†}) *_{S} C_{1}, A_{2} = R_{A_{0}} *_{M} A_{11}, B_{2} = R_{C_{0}}, \\ C_{2} = R_{A_{0}} *_{M} B_{11}, A_{3} = L_{A_{0}}, B_{3} = C_{11} *_{T} L_{C_{0}}, C_{3} = D_{11} *_{T} L_{C_{0}}, A_{4} = A_{3} *_{N} L_{A_{2}}, \\ B_{4} = R_{B_{2}} *_{S} B_{3}, C_{4} = C_{3} - A_{3} *_{N} A_{2}^{†} *_{M} C_{2} *_{S} B_{2}^{†} *_{S} B_{3}, D_{4} = R_{A_{4}} *_{N} A_{3}, \\ F = A_{2}^{†} *_{M} C_{2} *_{S} B_{2}^{†} + L_{A_{2}} *_{N} A_{4}^{†} *_{N} C_{4} *_{T} B_{3}^{†} - L_{A_{2}} *_{N} A_{4}^{†} *_{N} A_{3} *_{N} D_{4}^{†} *_{N} R_{A_{4}} *_{N} C_{4} *_{T} B_{3}^{†} \\ + D_{4}^{†} *_{N} R_{A_{4}} *_{N} C_{4} *_{T} B_{4}^{†} *_{S} R_{B_{2}} . \end{matrix}

Then the subsequent descriptions are equivalent:

The system of dual split quaternion tensor equations (2) is solvable.
The system of real tensor equations

$\begin{matrix} \{\begin{matrix} A_{0} *_{N} X_{0} = B_{0}, \\ X_{0} *_{S} C_{0} = D_{0}, \\ A_{0} *_{N} X_{1} + A_{1} *_{N} X_{0} = B_{1}, \\ X_{0} *_{S} C_{1} + X_{1} *_{S} C_{0} = D_{1} \end{matrix} \end{matrix}$

(4)

is consistent.
$\begin{matrix} R_{A_{0}} *_{M} B_{0} = 0, D_{0} *_{T} L_{C_{0}} = 0, \\ A_{0} *_{N} D_{0} = B_{0} *_{S} C_{0}, A_{0} *_{N} D_{1} - B_{0} *_{S} C_{1} = B_{1} *_{S} C_{0} - A_{1} *_{N} D_{0}, \\ R_{A_{2}} *_{M} C_{2} = 0, C_{2} *_{S} L_{B_{2}} = 0, R_{A_{3}} *_{N} C_{3} = 0, C_{3} *_{T} L_{B_{3}} = 0, R_{A_{4}} *_{N} C_{4} *_{T} L_{B_{4}} = 0 . \end{matrix}$

Based on these circumstances, the general solution of the system (2) can be represented as

X = X_{00} + X_{01} ϵ

, where

\begin{matrix} X_{00} & = \frac{1}{8} [\begin{matrix} I_{N} & i I_{N} & j I_{N} & k I_{N} \end{matrix}] *_{N} (X_{0} + R_{N} *_{N} X_{0} *_{S} R_{S}^{T} + S_{N} *_{N} X_{0} *_{S} S_{S}^{T} + T_{N} *_{N} X_{0} *_{S} T_{S}^{T}) *_{S} [\begin{matrix} I_{S} \\ i I_{S} \\ j I_{S} \\ k I_{S} \end{matrix}], \\ X_{01} & = \frac{1}{8} [\begin{matrix} I_{N} & i I_{N} & j I_{N} & k I_{N} \end{matrix}] *_{N} (X_{1} + R_{N} *_{N} X_{1} *_{S} R_{S}^{T} + S_{N} *_{N} X_{1} *_{S} S_{S}^{T} + T_{N} *_{N} X_{1} *_{S} T_{S}^{T}) *_{S} [\begin{matrix} I_{S} \\ i I_{S} \\ j I_{S} \\ k I_{S} \end{matrix}], \\ X_{0} & = A_{0}^{†} *_{M} B_{0} + L_{A_{0}} *_{N} D_{0} *_{T} C_{0}^{†} + L_{A_{0}} *_{N} W *_{S} R_{C_{0}}, \\ X_{1} & = A_{0}^{†} *_{M} (B_{11} - A_{11} *_{N} W *_{S} R_{C_{0}}) + L_{A_{0}} *_{N} (D_{11} - L_{A_{0}} *_{N} W *_{S} C_{11}) *_{T} C_{0}^{†} \\ + L_{A_{0}} *_{N} W_{1} *_{S} R_{C_{0}}, \\ W & = F + L_{A_{2}} *_{N} L_{A_{4}} *_{N} W_{2} + W_{3} *_{S} R_{B_{4}} *_{S} R_{B_{2}} + L_{A_{2}} *_{N} W_{4} *_{S} R_{B_{3}} + L_{A_{3}} *_{N} W_{5} *_{S} R_{B_{2}}, \end{matrix}

and

W_{i} (i = \bar{1, 5})

are random tensors with proper dimensions.

Proof. (1)⇔ (2)

If condition (1) holds, it indicates that the system (2) possesses a solution. Thus, we can express the solution for the system (2) as

X = X_{00} + X_{01} ϵ \in {DQ}_{s}^{J_{1} \times \dots \times J_{N} \times K_{1} \times \dots \times K_{S}}

, where

X_{00}, X_{01} \in H_{s}^{J_{1} \times \dots \times J_{N} \times K_{1} \times \dots \times K_{S}}

. By substituting

X = X_{00} + X_{01} ϵ

into system (2), we obtain the following split quaternion tensor equations:

\begin{matrix} \{\begin{matrix} A_{00} *_{N} X_{00} = B_{00}, \\ X_{00} *_{S} C_{00} = D_{00}, \\ A_{00} *_{N} X_{01} + A_{01} *_{N} X_{00} = B_{01}, \\ X_{00} *_{S} C_{01} + X_{01} *_{S} C_{00} = D_{01} . \end{matrix} \end{matrix}

(5)

Let

X_{0} = X_{00}^{σ_{i}}, X_{1} = X_{01}^{σ_{i}}

. Apply the real representation to the system, and by (b), (c) of Proposition (2), then we have

\begin{matrix} \{\begin{matrix} A_{00}^{σ_{i}} *_{N} X_{00}^{σ_{i}} = B_{00}^{σ_{i}}, \\ X_{00}^{σ_{i}} *_{S} C_{00}^{σ_{i}} = D_{00}^{σ_{i}}, \\ A_{00}^{σ_{i}} *_{N} X_{01}^{σ_{i}} + A_{01}^{σ_{i}} *_{N} X_{00}^{σ_{i}} = B_{01}^{σ_{i}}, \\ X_{00}^{σ_{i}} *_{S} C_{01}^{σ_{i}} + X_{01}^{σ_{i}} *_{S} C_{00}^{σ_{i}} = D_{01}^{σ_{i}} . \end{matrix} \end{matrix}

(6)

i.e.,

\begin{matrix} \{\begin{matrix} A_{0} *_{N} X_{0} = B_{0}, \\ X_{0} *_{S} C_{0} = D_{0}, \\ A_{0} *_{N} X_{1} + A_{1} *_{N} X_{0} = B_{1}, \\ X_{0} *_{S} C_{1} + X_{1} *_{S} C_{0} = D_{1} . \end{matrix} \end{matrix}

(7)

Thus,

(X_{0}, X_{1})

is a pair of solutions to the system (4).

On the other hand, let

(X_{0}, X_{1})

be the solutions to the system (4). By (da) of Proposition (2), we have

\begin{matrix} \{\begin{matrix} R_{M}^{T} *_{M} A_{0} *_{N} R_{N} *_{N} X_{0} = R_{M}^{T} *_{M} B_{0} *_{S} R_{S}, \\ X_{0} *_{S} R_{S}^{T} *_{S} C_{0} *_{T} R_{T} = R_{N}^{T} *_{N} D_{0} *_{T} R_{T}, \\ R_{M}^{T} *_{M} A_{0} *_{N} R_{N} *_{N} X_{1} + R_{M}^{T} *_{M} A_{1} *_{N} R_{N} *_{N} X_{0} = R_{M}^{T} *_{M} B_{1} *_{S} R_{S}, \\ X_{0} *_{S} R_{S}^{T} *_{S} C_{1} *_{T} R_{T} + X_{1} *_{S} R_{S}^{T} *_{S} C_{0} *_{T} R_{T} = R_{N}^{T} *_{N} D_{1} *_{T} R_{T} . \end{matrix} \end{matrix}

(8)

i.e.,

\begin{matrix} \{\begin{matrix} A_{0} *_{N} R_{N} *_{N} X_{0} *_{S} R_{S}^{T} = B_{0}, \\ R_{N} *_{N} X_{0} *_{S} R_{S}^{T} *_{S} C_{0} = D_{0}, \\ A_{0} *_{N} R_{N} *_{N} X_{1} *_{S} R_{S}^{T} + A_{1} *_{N} R_{N} *_{N} X_{0} *_{S} R_{S}^{T} = B_{1}, \\ R_{N} *_{N} X_{0} *_{S} R_{S}^{T} *_{S} C_{1} + R_{N} *_{N} X_{1} *_{S} R_{S}^{T} *_{S} C_{0} = D_{1} . \end{matrix} \end{matrix}

(9)

Thus,

(R_{N} *_{N} X_{0} *_{S} R_{S}^{T}, R_{N} *_{N} X_{1} *_{S} R_{S}^{T})

represent solutions to the system of real tensor equations. Likewise,

(S_{N} *_{N} X_{0} *_{S} S_{S}^{T}, S_{N} *_{N} X_{1} *_{S} S_{S}^{T})

and

(T_{N} *_{N} X_{0} *_{S} T_{S}^{T}, T_{N} *_{N} X_{1} *_{S} T_{S}^{T})

are also solutions to the system. Then, we define

Y_{0} : = \frac{1}{4} (X_{0} + R_{N} *_{N} X_{0} *_{S} R_{S}^{T} + S_{N} *_{N} X_{0} *_{S} S_{S}^{T} + T_{N} *_{N} X_{0} *_{S} T_{S}^{T}),

Y_{1} : = \frac{1}{4} (X_{1} + R_{N} *_{N} X_{1} *_{S} R_{S}^{T} + S_{N} *_{N} X_{1} *_{S} S_{S}^{T} + T_{N} *_{N} X_{1} *_{S} T_{S}^{T}) .

Set

X_{0} = [\begin{matrix} V_{11} & V_{12} & V_{13} & V_{14} \\ V_{21} & V_{22} & V_{23} & V_{24} \\ V_{31} & V_{32} & V_{33} & V_{34} \\ V_{41} & V_{42} & V_{43} & V_{44} \end{matrix}] \in R^{J_{1} \times \dots \times 4 J_{N} \times K_{1} \times \dots \times 4 K_{S}},

X_{1} = [\begin{matrix} W_{11} & W_{12} & W_{13} & W_{14} \\ W_{21} & W_{22} & W_{23} & W_{24} \\ W_{31} & W_{32} & W_{33} & W_{34} \\ W_{41} & W_{42} & W_{43} & W_{44} \end{matrix}] \in R^{J_{1} \times \dots \times 4 J_{N} \times K_{1} \times \dots \times 4 K_{S}} .

By direct computation, we have

Y_{0} = [\begin{matrix} B_{0} & B_{1} & B_{2} & B_{3} \\ - B_{1} & B_{0} & - B_{3} & B_{2} \\ B_{2} & - B_{3} & B_{0} & - B_{1} \\ B_{3} & B_{2} & B_{1} & B_{0} \end{matrix}]

and

Y_{1} = [\begin{matrix} D_{0} & D_{1} & D_{2} & D_{3} \\ - D_{1} & D_{0} & - D_{3} & D_{2} \\ D_{2} & - D_{3} & D_{0} & - D_{1} \\ D_{3} & D_{2} & D_{1} & D_{0} \end{matrix}],

where

B_{0} = \frac{1}{4} (V_{11} + V_{22} + V_{33} + V_{44}), B_{1} = \frac{1}{4} (V_{12} - V_{21} - V_{34} + V_{43}),

B_{2} = \frac{1}{4} (V_{13} + V_{24} + V_{31} + V_{42}), B_{3} = \frac{1}{4} (V_{14} - V_{23} - V_{32} + V_{41}),

and

D_{0} = \frac{1}{4} (W_{11} + W_{22} + W_{33} + W_{44}), D_{1} = \frac{1}{4} (W_{12} - W_{21} - W_{34} + W_{43}),

D_{2} = \frac{1}{4} (W_{13} + W_{24} + W_{31} + W_{42}), D_{3} = \frac{1}{4} (W_{14} - W_{23} - W_{32} + W_{41}) .

Then, we let

X_{00} = B_{0} + B_{1} i + B_{2} j + B_{3} k = \frac{1}{2} [\begin{matrix} I_{N} & i I_{N} & j I_{N} & k I_{N} \end{matrix}] *_{N} Y_{0} *_{S} [\begin{matrix} I_{S} \\ i I_{S} \\ j I_{S} \\ k I_{S} \end{matrix}]

and

X_{01} = D_{0} + D_{1} i + D_{2} j + D_{3} k = \frac{1}{2} [\begin{matrix} I_{N} & i I_{N} & j I_{N} & k I_{N} \end{matrix}] *_{N} Y_{1} *_{S} [\begin{matrix} I_{S} \\ i I_{S} \\ j I_{S} \\ k I_{S} \end{matrix}],

where

X_{00}

and

X_{01} \in H_{s}^{J_{1} \times \dots \times J_{N} \times K_{1} \times \dots \times K_{S}}

Due to (fa) of Proposition (2),

Y_{0} = X_{00}^{σ_{i}}

Y_{1} = X_{01}^{σ_{i}}

. Thus, due to

\begin{matrix} \{\begin{matrix} A_{00}^{σ_{i}} *_{N} X_{00}^{σ_{i}} = B_{00}^{σ_{i}}, \\ X_{00}^{σ_{i}} *_{S} C_{00}^{σ_{i}} = D_{00}^{σ_{i}}, \\ A_{00}^{σ_{i}} *_{N} X_{01}^{σ_{i}} + A_{01}^{σ_{i}} *_{N} X_{00}^{σ_{i}} = B_{01}^{σ_{i}}, \\ X_{00}^{σ_{i}} *_{S} C_{01}^{σ_{i}} + X_{01}^{σ_{i}} *_{S} C_{00}^{σ_{i}} = D_{01}^{σ_{i}}, \end{matrix} \end{matrix}

(10)

we can obtain

(X_{00}, X_{01})

as the solution of system (5). And it is clear that system (2) and system (5) are equivalent. Therefore, when system (2) has solutions, system (4) also has solutions, and vice versa. In addition, we can deduce the general solution of system of dual split quaternion tensor equations by Lemma (4) as

X = X_{00} + X_{01} ϵ

, where

\begin{matrix} X_{00} = \frac{1}{8} [\begin{matrix} I_{N} & i I_{N} & j I_{N} & k I_{N} \end{matrix}] *_{N} (X_{0} + R_{N} *_{N} X_{0} *_{S} R_{S}^{T} + S_{N} *_{N} X_{0} *_{S} S_{S}^{T} + T_{N} *_{N} X_{0} *_{S} T_{S}^{T}) *_{S} [\begin{matrix} I_{S} \\ i I_{S} \\ j I_{S} \\ k I_{S} \end{matrix}], \\ X_{01} = \frac{1}{8} [\begin{matrix} I_{N} & i I_{N} & j I_{N} & k I_{N} \end{matrix}] *_{N} (X_{1} + R_{N} *_{N} X_{1} *_{S} R_{S}^{T} + S_{N} *_{N} X_{1} *_{S} S_{S}^{T} + T_{N} *_{N} X_{1} *_{S} T_{S}^{T}) *_{S} [\begin{matrix} I_{S} \\ i I_{S} \\ j I_{S} \\ k I_{S} \end{matrix}], \\ X_{0} = A_{0}^{†} *_{M} B_{0} + L_{A_{0}} *_{N} D_{0} *_{T} C_{0}^{†} + L_{A_{0}} *_{N} W *_{S} R_{C_{0}}, \\ X_{1} = A_{0}^{†} *_{M} (B_{11} - A_{11} *_{N} W *_{S} R_{C_{0}}) + L_{A_{0}} *_{N} (D_{11} - L_{A_{0}} *_{N} W *_{S} C_{11}) *_{T} C_{0}^{†} \\ + L_{A_{0}} *_{N} W_{1} *_{S} R_{C_{0}}, \\ W = F + L_{A_{2}} *_{N} L_{A_{4}} *_{N} W_{2} + W_{3} *_{S} R_{B_{4}} *_{S} R_{B_{2}} + L_{A_{2}} *_{N} W_{4} *_{S} R_{B_{3}} + L_{A_{3}} *_{N} W_{5} *_{S} R_{B_{2}}, \end{matrix}

and

W_{i} (i = \bar{1, 5})

are random tensors with suitable size.

Besides, (2) and (3) are equivalent to each other that can be easily proven using Lemma (3) and Lemma (4). We will not elaborate further on these points here. □

In the following part, we will propose equivalent conditions required when system (2) have

η

-Hermitian solutions.

Theorem 2.

Suppose that

A = A_{00} + A_{01} ϵ \in {DQ}_{s}^{I_{1} \times \dots \times I_{M} \times J_{1} \times \dots \times J_{N}}

B = B_{00} + B_{01} ϵ \in {DQ}_{s}^{I_{1} \times \dots \times I_{M} \times J_{1} \times \dots \times J_{N}}

C = C_{00} + C_{01} ϵ \in {DQ}_{s}^{J_{1} \times \dots \times J_{N} \times K_{1} \times \dots \times K_{T}}

, and

D = D_{00} + D_{01} ϵ \in {DQ}_{s}^{J_{1} \times \dots \times J_{N} \times K_{1} \times \dots \times K_{T}}

Set

\begin{matrix} A_{0} & = \{\begin{matrix} A_{00}^{σ_{i}}, & η = i, \\ {(A_{00}^{k})}^{σ_{j}}, & η = j, \\ {(A_{00}^{j})}^{σ_{k}}, & η = k, \end{matrix} A_{1} = \{\begin{matrix} A_{01}^{σ_{i}}, & η = i, \\ {(A_{01}^{k})}^{σ_{j}}, & η = j, \\ {(A_{01}^{j})}^{σ_{k}}, & η = k, \end{matrix} \\ B_{0} & = B_{00}^{σ_{i}}, B_{1} = B_{01}^{σ_{i}}, C_{0} = C_{00}^{σ_{i}}, C_{1} = C_{01}^{σ_{i}}, η = {i, j, k} \\ D_{0} & = D_{00}^{σ_{η}}, D_{1} = D_{01}^{σ_{η}}, η = {i, j, k} . \end{matrix}

Then the system (2) have η-Hermitian solutions

X = X^{η *} \in {DQ}_{s}^{J_{1} \times \dots \times J_{N} \times J_{1} \times \dots \times J_{N}}, η = {i, j, k}

, and this means that the system (4) possesses a pair of solutions

(X_{0}, X_{1})

that satisfies

X_{0} = X_{0}^{T}, X_{1} = X_{1}^{T}

, and vice versa.

Proof.

It is only necessary to demonstrate the situation for

η = j

, the other situations are identical to it, so we omit them. Let’s assume that

X = X_{00} + X_{01} ϵ \in {DQ}_{s}^{J_{1} \times \dots \times J_{N} \times J_{1} \times \dots \times J_{N}}

is a j-Hermitian solution of system (2), where

X = X^{j *}

. Then we have

\begin{matrix} X_{00} = X_{00}^{j *}, X_{01} = X_{01}^{j *} . \end{matrix}

By substituting

X = X_{00} + X_{01} ϵ

into system (2), then system (2) corresponds to the subsequent system:

\begin{matrix} \{\begin{matrix} A_{00} *_{N} X_{00} = B_{00}, \\ X_{00} *_{N} C_{00} = D_{00}, \\ A_{00} *_{N} X_{01} + A_{01} *_{N} X_{00} = B_{01}, \\ X_{00} *_{N} C_{01} + X_{01} *_{N} C_{00} = D_{01} . \end{matrix} \end{matrix}

(11)

Let

X_{0} = X_{00}^{σ_{j}}, X_{1} = X_{01}^{σ_{j}}

. Apply the real representation to the system, and by (b), (c) of Proposition (2), then we have

\begin{matrix} \{\begin{matrix} A_{00}^{σ_{j}} *_{N} V_{N} *_{N} X_{00}^{σ_{j}} = B_{00}^{σ_{j}}, \\ X_{00}^{σ_{j}} *_{N} V_{N} *_{N} C_{00}^{σ_{j}} = D_{00}^{σ_{j}}, \\ A_{00}^{σ_{j}} *_{N} V_{N} *_{N} X_{01}^{σ_{j}} + A_{01}^{σ_{j}} *_{N} V_{N} *_{N} X_{00}^{σ_{j}} = B_{01}^{σ_{j}}, \\ X_{00}^{σ_{j}} *_{N} V_{N} *_{N} C_{01}^{σ_{j}} + X_{01}^{σ_{j}} *_{N} V_{N} *_{N} C_{00}^{σ_{j}} = D_{01}^{σ_{j}} . \end{matrix} \end{matrix}

(12)

i.e.,

\begin{matrix} \{\begin{matrix} V_{M} *_{M} A_{00}^{σ_{j}} *_{N} V_{N} *_{N} X_{00}^{σ_{j}} = V_{M} *_{M} B_{00}^{σ_{j}}, \\ X_{00}^{σ_{j}} *_{N} V_{N} *_{N} C_{00}^{σ_{j}} = D_{00}^{σ_{j}}, \\ V_{M} *_{M} A_{00}^{σ_{j}} *_{N} V_{N} *_{N} X_{01}^{σ_{j}} + V_{M} *_{M} A_{01}^{σ_{j}} *_{N} V_{N} *_{N} X_{00}^{σ_{j}} = V_{M} *_{M} B_{01}^{σ_{j}}, \\ X_{00}^{σ_{j}} *_{N} V_{N} *_{N} C_{01}^{σ_{j}} + X_{01}^{σ_{j}} *_{N} V_{N} *_{N} C_{00}^{σ_{j}} = D_{01}^{σ_{j}} . \end{matrix} \end{matrix}

(13)

According to (g) of Proposition (2) and the definition of real representation, we have

\begin{matrix} V_{M} *_{M} A_{00}^{σ_{j}} *_{N} V_{N} = {(A_{00}^{k})}^{σ_{j}}, V_{M} *_{M} A_{01}^{σ_{j}} *_{N} V_{N} = {(A_{01}^{k})}^{σ_{j}}, \\ V_{M} *_{M} B_{00}^{σ_{j}} = B_{00}^{σ_{i}}, V_{M} *_{M} B_{01}^{σ_{j}} = B_{01}^{σ_{i}}, V_{N} *_{N} C_{00}^{σ_{j}} = C_{00}^{σ_{i}}, V_{N} *_{N} C_{00}^{σ_{j}} = C_{00}^{σ_{i}} . \end{matrix}

Thus, the above system can be expressed as

\begin{matrix} \{\begin{matrix} {(A_{00}^{k})}^{σ_{j}} *_{N} X_{00}^{σ_{j}} = B_{00}^{σ_{i}}, \\ X_{00}^{σ_{j}} *_{N} C_{00}^{σ_{i}} = D_{00}^{σ_{j}}, \\ {(A_{00}^{k})}^{σ_{j}} *_{N} X_{01}^{σ_{j}} + {(A_{01}^{k})}^{σ_{j}} *_{N} X_{00}^{σ_{j}} = B_{01}^{σ_{i}}, \\ X_{00}^{σ_{j}} *_{N} C_{01}^{σ_{i}} + X_{01}^{σ_{j}} *_{N} C_{00}^{σ_{i}} = D_{01}^{σ_{j}}, \end{matrix} \end{matrix}

(14)

i.e.,

\begin{matrix} \{\begin{matrix} A_{0} *_{N} X_{0} = B_{0}, \\ X_{0} *_{N} C_{0} = D_{0}, \\ A_{0} *_{N} X_{1} + A_{1} *_{N} X_{0} = B_{1}, \\ X_{0} *_{N} C_{1} + X_{1} *_{N} C_{0} = D_{1} . \end{matrix} \end{matrix}

(15)

By (e) in Proposition (2), we have

{(X_{00}^{j *})}^{σ_{j}} = {(X_{00}^{σ_{j}})}^{T}, {(X_{01}^{j *})}^{σ_{j}} = {(X_{01}^{σ_{j}})}^{T} .

Consequently,

\begin{matrix} X_{00}^{σ_{j}} = {(X_{00}^{j *})}^{σ_{j}} = {(X_{00}^{σ_{j}})}^{T}, X_{01}^{σ_{j}} = {(X_{01}^{j *})}^{σ_{j}} = {(X_{01}^{σ_{j}})}^{T}, \end{matrix}

i.e.,

X_{0} = X_{0}^{T}, X_{1} = X_{1}^{T} .

On the other hand, if system (4) has a pair of solutions

(X_{0}, X_{1})

that satisfies

X_{0} = X_{0}^{T}, X_{1} = X_{1}^{T}

, then the system (4) can be denoted as

\begin{matrix} \{\begin{matrix} {(A_{00}^{k})}^{σ_{j}} *_{N} X_{0} = B_{00}^{σ_{i}}, \\ X_{0} *_{N} C_{00}^{σ_{i}} = D_{00}^{σ_{j}}, \\ {(A_{00}^{k})}^{σ_{j}} *_{N} X_{1} + {(A_{01}^{k})}^{σ_{j}} *_{N} X_{0} = B_{01}^{σ_{i}}, \\ X_{0} *_{N} C_{01}^{σ_{i}} + X_{1} *_{N} C_{00}^{σ_{i}} = D_{01}^{σ_{j}} \end{matrix} \end{matrix}

(16)

and

\begin{matrix} X_{0} = X_{0}^{T}, X_{1} = X_{1}^{T} . \end{matrix}

As indicated by (db) in Proposition (2),

\begin{matrix} (- R_{N} *_{N} X_{0} *_{N} R_{N}^{T}, - R_{N} *_{N} X_{1} *_{N} R_{N}^{T}), \\ (- S_{N} *_{N} X_{0} *_{N} S_{N}^{T}, - S_{N} *_{N} X_{1} *_{N} S_{N}^{T}), \\ (T_{N} *_{N} X_{0} *_{N} T_{N}^{T}, T_{N} *_{N} X_{1} *_{N} T_{N}^{T}) \end{matrix}

are also solutions to the system. Next, we define

Y_{0} : = \frac{1}{4} (X_{0} - R_{N} *_{N} X_{0} *_{N} R_{N}^{T} - S_{N} *_{N} X_{0} *_{N} S_{N}^{T} + T_{N} *_{N} X_{0} *_{N} T_{N}^{T}),

Y_{1} : = \frac{1}{4} (X_{1} - R_{N} *_{N} X_{1} *_{N} R_{N}^{T} - S_{N} *_{N} X_{1} *_{N} S_{N}^{T} + T_{N} *_{N} X_{1} *_{N} T_{N}^{T}) .

Set

X_{0} = [\begin{matrix} V_{11} & V_{12} & V_{13} & V_{14} \\ V_{21} & V_{22} & V_{23} & V_{24} \\ V_{31} & V_{32} & V_{33} & V_{34} \\ V_{41} & V_{42} & V_{43} & V_{44} \end{matrix}] \in R^{J_{1} \times \dots \times 4 J_{N} \times J_{1} \times \dots \times 4 J_{N}},

X_{1} = [\begin{matrix} W_{11} & W_{12} & W_{13} & W_{14} \\ W_{21} & W_{22} & W_{23} & W_{24} \\ W_{31} & W_{32} & W_{33} & W_{34} \\ W_{41} & W_{42} & W_{43} & W_{44} \end{matrix}] \in R^{J_{1} \times \dots \times 4 J_{N} \times J_{1} \times \dots \times 4 J_{N}} .

By direct computation, we have

Y_{0} = [\begin{matrix} B_{0} & B_{1} & B_{2} & B_{3} \\ B_{1} & - B_{0} & B_{3} & - B_{2} \\ - B_{2} & B_{3} & - B_{0} & B_{1} \\ B_{3} & B_{2} & B_{1} & B_{0} \end{matrix}]

and

Y_{1} = [\begin{matrix} D_{0} & D_{1} & D_{2} & D_{3} \\ D_{1} & - D_{0} & D_{3} & - D_{2} \\ - D_{2} & D_{3} & - D_{0} & D_{1} \\ D_{3} & D_{2} & D_{1} & D_{0} \end{matrix}],

where

B_{0} = \frac{1}{4} (V_{11} - V_{22} - V_{33} + V_{44}), B_{1} = \frac{1}{4} (V_{12} + V_{21} + V_{34} + V_{43}),

B_{2} = \frac{1}{4} (V_{13} - V_{24} - V_{31} + V_{42}), B_{3} = \frac{1}{4} (V_{14} + V_{23} + V_{32} + V_{41}),

and

D_{0} = \frac{1}{4} (W_{11} - W_{22} - W_{33} + W_{44}), D_{1} = \frac{1}{4} (W_{12} + W_{21} + W_{34} + W_{43}),

D_{2} = \frac{1}{4} (W_{13} - W_{24} - W_{31} + W_{42}), D_{3} = \frac{1}{4} (W_{14} + W_{23} + W_{32} + W_{41}) .

Then, we let

\begin{matrix} X_{00} = B_{0} + B_{1} i + B_{2} j + B_{3} k = \frac{1}{2} [\begin{matrix} I_{N} & - i I_{N} & - j I_{N} & k I_{N} \end{matrix}] *_{N} Y_{0} *_{N} [\begin{matrix} I_{N} \\ i I_{N} \\ j I_{N} \\ k I_{N} \end{matrix}] \end{matrix}

and

X_{01} = D_{0} + D_{1} i + D_{2} j + D_{3} k = \frac{1}{2} [\begin{matrix} I_{N} & - i I_{N} & - j I_{N} & k I_{N} \end{matrix}] *_{N} Y_{1} *_{N} [\begin{matrix} I_{N} \\ i I_{N} \\ j I_{N} \\ k I_{N} \end{matrix}],

where

X_{00}

and

X_{01} \in H_{s}^{J_{1} \times \dots \times J_{N} \times J_{1} \times \dots \times J_{N}}

Due to (fb) of Proposition (2),

Y_{0} = X_{00}^{σ_{j}}

Y_{1} = X_{01}^{σ_{j}}

. Thus,

\begin{matrix} \{\begin{matrix} {(A_{00}^{k})}^{σ_{j}} *_{N} X_{00}^{σ_{j}} = B_{00}^{σ_{i}}, \\ X_{00}^{σ_{j}} *_{N} C_{00}^{σ_{i}} = D_{00}^{σ_{j}}, \\ {(A_{00}^{k})}^{σ_{j}} *_{N} X_{01}^{σ_{j}} + {(A_{01}^{k})}^{σ_{j}} *_{N} X_{00}^{σ_{j}} = B_{01}^{σ_{i}}, \\ X_{00}^{σ_{j}} *_{N} C_{01}^{σ_{i}} + X_{01}^{σ_{j}} *_{N} C_{00}^{σ_{i}} = D_{01}^{σ_{j}} . \end{matrix} \end{matrix}

(17)

That is,

(X_{00}^{σ_{j}}, X_{01}^{σ_{j}})

is a pair of solutions of system (4). Then,

\begin{matrix} X_{00}^{σ_{j}} & = {(X_{00}^{σ_{j}})}^{T} = {(X_{00}^{j *})}^{σ_{j}}, \\ X_{01}^{σ_{j}} & = {(X_{01}^{σ_{j}})}^{T} = {(X_{01}^{j *})}^{σ_{j}} . \end{matrix}

The above system is equivalent to

\begin{matrix} \{\begin{matrix} V_{M} *_{M} A_{00}^{σ_{j}} *_{N} V_{N} *_{N} X_{00}^{σ_{j}} = V_{M} *_{M} B_{00}^{σ_{j}}, \\ X_{00}^{σ_{j}} *_{N} V_{N} *_{N} C_{00}^{σ_{j}} = D_{00}^{σ_{j}}, \\ V_{M} *_{M} A_{00}^{σ_{j}} *_{N} V_{N} *_{N} X_{01}^{σ_{j}} + V_{M} *_{M} A_{01}^{σ_{j}} *_{N} V_{N} *_{N} X_{00}^{σ_{j}} = V_{M} *_{M} B_{01}^{σ_{j}}, \\ X_{00}^{σ_{j}} *_{N} V_{N} *_{N} C_{01}^{σ_{j}} + X_{01}^{σ_{j}} *_{N} V_{N} *_{N} C_{00}^{σ_{j}} = D_{01}^{σ_{j}}, \end{matrix} \end{matrix}

(18)

i.e.,

\begin{matrix} \{\begin{matrix} A_{00} *_{N} X_{00} = B_{00}, \\ X_{00} *_{N} C_{00} = D_{00}, \\ A_{00} *_{N} X_{01} + A_{01} *_{N} X_{00} = B_{01}, \\ X_{00} *_{N} C_{01} + X_{01} *_{N} C_{00} = D_{01} \end{matrix} \end{matrix}

(19)

and

\begin{matrix} X_{00} = X_{00}^{j *}, X_{01} = X_{01}^{j *} . \end{matrix}

It is obvious that system (19) and system (2) are equivalent. Consequently,

X = X_{00} + X_{01} ϵ = X_{00}^{j *} + X_{01}^{j *} ϵ = X^{j *}

is a j-Hermitian solution of system (2). □

Based on above theorems and lemmas, we will next present the equivalent condition when system (2) possesses a Hermitian solution. Additionally, we will put forward the equivalent criteria when two specific equations

A *_{N} X = B

and

X *_{M} C = D

have solutions, along with their general solution expressions.

Corollary 1.

Let

A = A_{00} + A_{01} ϵ

and

B = B_{00} + B_{01} ϵ \in {DQ}_{s}^{I_{1} \times \dots \times I_{M} \times K_{1} \times \dots \times K_{S}}

C = C_{00} + C_{01} ϵ

and

D = D_{00} + D_{01} ϵ \in {DQ}_{s}^{K_{1} \times \dots \times K_{S} \times S_{1} \times \dots \times S_{T}}

. Set

\begin{matrix} A_{0} & = {(A_{00}^{i})}^{σ_{1}}, A_{1} = {(A_{01}^{i})}^{σ_{1}}, B_{0} = B_{00}^{σ_{i}}, B_{1} = B_{01}^{σ_{i}}, \\ C_{0} & = C_{00}^{σ_{i}}, C_{1} = C_{01}^{σ_{i}}, D_{0} = D_{00}^{σ_{1}}, D_{1} = D_{01}^{σ_{1}} . \end{matrix}

Then the system (2) has a Hermitian solution

X = X^{*} \in {DQ}_{s}^{K_{1} \times \dots \times K_{S} \times K_{1} \times \dots \times K_{S}}

, and it means that the system of real tensor equations

\begin{matrix} \{\begin{matrix} A_{0} *_{S} X_{0} = B_{0}, \\ X_{0} *_{S} C_{0} = D_{0}, \\ A_{0} *_{S} X_{1} + A_{1} *_{S} X_{0} = B_{1}, \\ X_{0} *_{S} C_{1} + X_{1} *_{S} C_{0} = D_{1} \end{matrix} \end{matrix}

has a pair of symmetric solutions

(X_{0}, X_{1})

, and vice versa.

Corollary 2.

Let

A \in {DQ}_{s}^{I_{1} \times \dots \times I_{M} \times T_{1} \times \dots \times T_{N}}

and

B \in {DQ}_{s}^{I_{1} \times \dots \times I_{M} \times K_{1} \times \dots \times K_{S}}

, where

A = A_{00} + A_{01} ϵ, B = B_{00} + B_{01} ϵ

. Set

\begin{matrix} A_{0} = A_{00}^{σ_{i}}, A_{1} = A_{01}^{σ_{i}}, B_{0} = B_{00}^{σ_{i}}, B_{1} = B_{01}^{σ_{i}}, B_{2} = B_{1} - A_{1} *_{N} A_{0}^{†} *_{M} B_{0}, \\ A_{2} = A_{1} *_{N} L_{A_{0}}, A_{3} = R_{A_{0}} *_{M} A_{2}, C_{3} = R_{A_{0}} *_{M} B_{2} . \end{matrix}

Then the subsequent descriptions correspond to each other:

Dual split quaternion tensor equation $A *_{N} X = B$ is solvable.
The following system of real tensor equations is consistent,

$\begin{matrix} \{\begin{matrix} A_{0} *_{N} X_{0} = B_{0}, \\ A_{0} *_{N} X_{1} + A_{1} *_{N} X_{0} = B_{1} . \end{matrix} \end{matrix}$

(20)
$R_{A_{0}} *_{M} B_{0} = 0, R_{A_{3}} *_{M} C_{3} = 0$ .

Based on these circumstances, the general solution of tensor equation

A *_{N} X = B

is represented as

X = X_{00} + X_{01} ϵ

, where

\begin{matrix} X_{00} = \frac{1}{8} [\begin{matrix} I_{N} & i I_{N} & j I_{N} & k I_{N} \end{matrix}] *_{N} (X_{0} + R_{N} *_{N} X_{0} *_{S} R_{S}^{T} + S_{N} *_{N} X_{0} *_{S} S_{S}^{T} + T_{N} *_{N} X_{0} *_{S} T_{S}^{T}) *_{S} [\begin{matrix} I_{S} \\ i I_{S} \\ j I_{S} \\ k I_{S} \end{matrix}], \\ X_{01} = \frac{1}{8} [\begin{matrix} I_{N} & i I_{N} & j I_{N} & k I_{N} \end{matrix}] *_{N} (X_{1} + R_{N} *_{N} X_{1} *_{S} R_{S}^{T} + S_{N} *_{N} X_{1} *_{S} S_{S}^{T} + T_{N} *_{N} X_{1} *_{S} T_{S}^{T}) *_{S} [\begin{matrix} I_{S} \\ i I_{S} \\ j I_{S} \\ k I_{S} \end{matrix}], \end{matrix}

where

\begin{matrix} X_{0} & = A_{0}^{†} *_{M} B_{0} + L_{A_{0}} *_{N} V, \\ X_{1} & = A_{0}^{†} *_{M} (B_{2} - A_{2} *_{N} V) + L_{A_{0}} *_{N} V_{1}, \\ V & = A_{3}^{†} *_{M} C_{3} + L_{A_{3}} *_{N} V_{2}, \end{matrix}

and

V_{1}, V_{2}

are arbitrary real tensors with appropriate dimensions.

Corollary 3.

Suppose that

C = C_{0} + C_{1} ϵ \in {DQ}_{s}^{I_{1} \times \dots \times I_{M} \times J_{1} \times \dots \times J_{N}}

and

D = D_{0} + D_{1} ϵ \in {DQ}_{s}^{K_{1} \times \dots \times K_{T} \times J_{1} \times \dots \times J_{N}}

. Let

\begin{matrix} C_{0} = C_{00}^{σ_{i}}, C_{1} = C_{01}^{σ_{i}}, D_{0} = D_{00}^{σ_{i}}, D_{1} = D_{01}^{σ_{i}}, D_{2} = D_{1} - D_{0} *_{N} C_{0}^{†} *_{M} C_{1}, \\ C_{2} = R_{C_{0}} *_{M} C_{1}, B_{3} = C_{2} *_{N} L_{C_{0}}, C_{3} = D_{2} *_{N} L_{C_{0}} . \end{matrix}

Then the descriptions below correspond to each other:

Dual split quaternion tensor equation $X *_{M} C = D$ is solvable.
The following system of real tensor equations is consistent.

$\begin{matrix} \{\begin{matrix} X_{0} *_{M} C_{0} = D_{0}, \\ X_{0} *_{M} C_{1} + X_{1} *_{M} C_{0} = D_{1} . \end{matrix} \end{matrix}$

(21)
$D_{0} *_{N} L_{C_{0}} = 0, C_{3} *_{N} L_{B_{3}} = 0$ .

Based on these situations, the general solution of tensor equation

X *_{M} C = D

can be expressed as

X = X_{00} + X_{01} ϵ

, where

\begin{matrix} X_{00} = \frac{1}{8} [\begin{matrix} I_{T} & i I_{T} & j I_{T} & k I_{T} \end{matrix}] *_{T} (X_{0} + R_{T} *_{T} X_{0} *_{M} R_{M}^{T} + S_{T} *_{T} X_{0} *_{M} S_{M}^{T} + T_{T} *_{T} X_{0} *_{M} T_{M}^{T}) *_{M} [\begin{matrix} I_{M} \\ i I_{M} \\ j I_{M} \\ k I_{M} \end{matrix}], \\ X_{01} = \frac{1}{8} [\begin{matrix} I_{T} & i I_{T} & j I_{T} & k I_{T} \end{matrix}] *_{T} (X_{1} + R_{T} *_{T} X_{1} *_{M} R_{M}^{T} + S_{T} *_{T} X_{1} *_{M} S_{M}^{T} + T_{T} *_{T} X_{1} *_{M} T_{M}^{T}) *_{M} [\begin{matrix} I_{M} \\ i I_{M} \\ j I_{M} \\ k I_{M} \end{matrix}], \end{matrix}

where

\begin{matrix} X_{0} & = D_{0} *_{N} C_{0}^{†} + W *_{M} R_{C_{0}}, \\ X_{1} & = (D_{2} - W *_{M} C_{2}) *_{N} C_{0}^{†} + W_{1} *_{M} R_{C_{0}}, \\ W & = C_{3} *_{N} B_{3}^{†} + W_{2} *_{M} R_{B_{3}}, \end{matrix}

and

W_{1}, W_{2}

denote random tensors over

R

with suitable dimensions.

4. Numerical Example

This segment will show an example to substantiate Theorem (1) and an example as an application of Theorem (1).

Example 2.

Let

A = A_{00} + A_{01} ϵ

B = B_{00} + B_{01} ϵ

C = C_{00} + C_{01} ϵ

and

D = D_{00} + D_{01} ϵ

, where

\begin{matrix} {(A_{00})}_{1111} = i, {(A_{00})}_{1121} = j, {(A_{00})}_{1112} = k, {(A_{00})}_{1122} = 1, \\ {(A_{00})}_{2111} = 0, {(A_{00})}_{2121} = k, {(A_{00})}_{2112} = i, {(A_{00})}_{2122} = i + j, \\ {(A_{00})}_{1211} = - i, {(A_{00})}_{1221} = 1, {(A_{00})}_{1212} = 0, {(A_{00})}_{1222} = j, \\ {(A_{00})}_{2211} = 0, {(A_{00})}_{2221} = i, {(A_{00})}_{2212} = j, {(A_{00})}_{2222} = 1, \end{matrix}

\begin{matrix} {(A_{01})}_{1111} = j, {(A_{01})}_{1121} = k, {(A_{01})}_{1112} = i, {(A_{01})}_{1122} = 0, \\ {(A_{01})}_{2111} = 1 + j, {(A_{01})}_{2121} = i - k, {(A_{01})}_{2112} = 0, {(A_{01})}_{2122} = j \\ {(A_{01})}_{1211} = i, {(A_{01})}_{1221} = i - 2 k, {(A_{01})}_{1212} = 1, {(A_{01})}_{1222} = j, \\ {(A_{01})}_{2211} = 2, {(A_{01})}_{2221} = i, {(A_{01})}_{2212} = j, {(A_{01})}_{2222} = k \end{matrix}

\begin{matrix} {(B_{00})}_{1111} = 1, {(B_{00})}_{1121} = - 1, {(B_{00})}_{1112} = j, {(B_{00})}_{1122} = i, \\ {(B_{00})}_{2111} = 0, {(B_{00})}_{2121} = 1, {(B_{00})}_{2112} = - 1 - i - k, {(B_{00})}_{2122} = 0, \\ {(B_{00})}_{1211} = j - k, {(B_{00})}_{1221} = 1, {(B_{00})}_{1212} = - i, {(B_{00})}_{1222} = 0, \\ {(B_{00})}_{2211} = - j + k, {(B_{00})}_{2221} = - i + j, {(B_{00})}_{2212} = - 2, {(B_{00})}_{2222} = 1 + i - j, \end{matrix}

\begin{matrix} {(B_{01})}_{1111} = 1 - j, {(B_{01})}_{1121} = - k, {(B_{01})}_{1112} = - 1 + 2 j - k, {(B_{01})}_{1122} = 1 + i - j + k, \\ {(B_{01})}_{2111} = 1 - i + j, {(B_{01})}_{2121} = 1, {(B_{01})}_{2112} = i + 2 j, {(B_{01})}_{2122} = - 1 - j - k, \\ {(B_{01})}_{1211} = - 2 - 3 i + 3 k, {(B_{01})}_{1221} = - i + 2 k, {(B_{01})}_{1212} = i - j, {(B_{01})}_{1222} = - 3 - k, \\ {(B_{01})}_{2211} = - j + k, {(B_{01})}_{2221} = - 1 + 2 i + j + k, {(B_{01})}_{2212} = 2 + i, {(B_{01})}_{2222} = 2 - i, \end{matrix}

\begin{matrix} {(C_{00})}_{1111} = k, {(C_{00})}_{1121} = 0, {(C_{00})}_{1112} = i, {(C_{00})}_{1122} = 1 + j, \\ {(C_{00})}_{2111} = 1, {(C_{00})}_{2121} = j, {(C_{00})}_{2112} = i - k, {(C_{00})}_{2122} = i, \\ {(C_{00})}_{1211} = j, {(C_{00})}_{1221} = - k, {(C_{00})}_{1212} = 0, {(C_{00})}_{1222} = i, \\ {(C_{00})}_{2211} = 1 + i, {(C_{00})}_{2221} = 1, {(C_{00})}_{2212} = - j, {(C_{00})}_{2222} = k, \end{matrix}

\begin{matrix} {(C_{01})}_{1111} = 0, {(C_{01})}_{1121} = i, {(C_{01})}_{1112} = - k, {(C_{01})}_{1122} = 1, \\ {(C_{01})}_{2111} = j, {(C_{01})}_{2121} = 2, {(C_{01})}_{2112} = - i, {(C_{01})}_{2122} = 0, \\ {(C_{01})}_{1211} = k, {(C_{01})}_{1221} = i, {(C_{01})}_{1212} = j, {(C_{01})}_{1222} = - k, \\ {(C_{01})}_{2211} = 1, {(C_{01})}_{2221} = k, {(C_{01})}_{2212} = 0, {(C_{01})}_{2222} = j, \end{matrix}

\begin{matrix} {(D_{00})}_{1111} = j, {(D_{00})}_{1121} = 0, {(D_{00})}_{1112} = - 1 + j - k, {(D_{00})}_{1122} = i + j, \\ {(D_{00})}_{2111} = - 1 - i + j + 2 k, {(D_{00})}_{2121} = k, {(D_{00})}_{2112} = - 2 i, \\ {(D_{00})}_{2122} = 1 - i + j, {(D_{00})}_{1211} = - 1 + j - k, {(D_{00})}_{1221} = - i + 2 j, \\ {(D_{00})}_{1212} = - 1 - i, {(D_{00})}_{1222} = - 2 - i - j + k, {(D_{00})}_{2211} = - 1 + 2 i + j, \\ {(D_{00})}_{2221} = i, {(D_{00})}_{2212} = i - 2 k, {(D_{00})}_{2222} = - k, \end{matrix}

\begin{matrix} {(D_{01})}_{1111} = 4 k, {(D_{01})}_{1121} = 3 i + j - k, {(D_{01})}_{1112} = 1 + 2 i + j, {(D_{01})}_{1122} = 2 j - k, \\ {(D_{01})}_{2111} = 1 + k - 2 j, {(D_{01})}_{2121} = - 3 + i, {(D_{01})}_{2112} = - 1 + 2 i + 3 j + k, \\ {(D_{01})}_{2122} = - 1 + 2 i + 2 j - k, {(D_{01})}_{1211} = 1 + j - k, {(D_{01})}_{1221} = - 2 i + 2 j + k, \\ {(D_{01})}_{1212} = - 2 + i + k, {(D_{01})}_{1222} = - i, {(D_{01})}_{2211} = 2 + 2 i + j + k, \\ {(D_{01})}_{2221} = i + 2 j - k, {(D_{01})}_{2212} = - 1 + i + j + 2 k, {(D_{01})}_{2222} = - 2 + i + k . \end{matrix}

From MATLAB 7.0, it can be proven that part (3) of the Theorem (1) in this paper holds:

\begin{matrix} R_{A_{0}} *_{M} B_{0} = 0, D_{0} *_{T} L_{C_{0}} = 0, R_{A_{2}} *_{M} C_{2} = 0, C_{2} *_{S} L_{B_{2}} = 0, \\ R_{A_{3}} *_{N} C_{3} = 0, C_{3} *_{T} L_{B_{3}} = 0, R_{A_{4}} *_{N} C_{4} *_{T} L_{B_{4}} = 0, \end{matrix}

and

\begin{matrix} t (A_{0} *_{N} D_{0}) = t (B_{0} *_{S} C_{0}) = \\ [\begin{matrix} - 1 & 0 & 0 & 1 & 1 & 2 & 0 & - 1 & 0 & - 1 & 0 & 0 & 1 & 0 & 0 & - 1 \\ 1 & 1 & 0 & 1 & - 1 & 0 & 1 & 0 & - 1 & 0 & 0 & - 1 & - 1 & 1 & - 1 & 0 \\ 0 & 0 & 0 & 2 & - 1 & 0 & 1 & 0 & 0 & 0 & - 1 & 1 & - 1 & 0 & - 2 & - 1 \\ 1 & 2 & 2 & 0 & 2 & 1 & 1 & 0 & - 2 & - 1 & - 1 & - 2 & 1 & 1 & - 1 & 1 \\ - 1 & - 2 & 0 & 1 & - 1 & 0 & 0 & 1 & - 1 & 0 & 0 & 1 & 0 & - 1 & 0 & 0 \\ 1 & 0 & - 1 & 0 & 1 & 1 & 0 & 1 & 1 & - 1 & 1 & 0 & - 1 & 0 & 0 & - 1 \\ 1 & 0 & - 1 & 0 & 0 & 0 & 0 & 2 & 1 & 0 & 2 & 1 & 0 & 0 & - 1 & 1 \\ - 2 & - 1 & - 1 & 0 & 1 & 2 & 2 & 0 & - 1 & - 1 & 1 & - 1 & - 2 & - 1 & - 1 & - 2 \\ 0 & - 1 & 0 & 0 & - 1 & 0 & 0 & 1 & - 1 & 0 & 0 & 1 & - 1 & - 2 & 0 & 1 \\ - 1 & 0 & 0 & - 1 & 1 & - 1 & 1 & 0 & 1 & 1 & 0 & 1 & 1 & 0 & - 1 & 0 \\ 0 & 0 & - 1 & 1 & 1 & 0 & 2 & 1 & 0 & 0 & 0 & 2 & 1 & 0 & - 1 & 0 \\ - 2 & - 1 & - 1 & - 2 & - 1 & - 1 & 1 & - 1 & 1 & 2 & 2 & 0 & - 2 & - 1 & - 1 & 0 \\ 1 & 0 & 0 & - 1 & 0 & - 1 & 0 & 0 & 1 & 2 & 0 & - 1 & - 1 & 0 & 0 & 1 \\ - 1 & 1 & - 1 & 0 & - 1 & 0 & 0 & - 1 & - 1 & 0 & 1 & 0 & 1 & 1 & 0 & 1 \\ - 1 & 0 & - 2 & - 1 & 0 & 0 & - 1 & 1 & - 1 & 0 & 1 & 0 & 0 & 0 & 0 & 2 \\ 1 & 1 & - 1 & 1 & - 2 & - 1 & - 1 & - 2 & 2 & 1 & 1 & 0 & 1 & 2 & 2 & 0 \end{matrix}], \end{matrix}

\begin{matrix} t (A_{0} *_{N} D_{1} - B_{0} *_{S} C_{1}) = t (B_{1} *_{S} C_{0} - A_{1} *_{N} D_{0}) = \\ [\begin{matrix} - 1 & 0 & 0 & - 1 & 2 & 2 & 0 & 1 & - 1 & - 1 & 1 & - 1 & 2 & 0 & 0 & 0 \\ 1 & 0 & 0 & - 2 & 0 & 2 & 0 & - 1 & 0 & 2 & - 1 & 0 & 2 & 0 & 0 & - 3 \\ 2 & - 1 & 1 & - 1 & - 1 & 2 & - 1 & 1 & 2 & 0 & 2 & - 1 & - 1 & - 1 & 0 & - 3 \\ 1 & 1 & - 1 & - 3 & 3 & 0 & 0 & 0 & 2 & 0 & 0 & 1 & 2 & - 1 & 3 & 0 \\ - 2 & - 2 & 0 & - 1 & - 1 & 0 & 0 & - 1 & - 2 & 0 & 0 & 0 & - 1 & - 1 & 1 & - 1 \\ 0 & - 2 & 0 & 1 & 1 & 0 & 0 & - 2 & - 2 & 0 & 0 & 3 & 0 & 2 & - 1 & 0 \\ 1 & - 2 & 1 & - 1 & 2 & - 1 & 1 & - 1 & 1 & 1 & 0 & 3 & 2 & 0 & 2 & - 1 \\ - 3 & 0 & 0 & 0 & 1 & 1 & - 1 & - 3 & - 2 & 1 & - 3 & 0 & 2 & 0 & 0 & 1 \\ - 1 & - 1 & 1 & - 1 & - 2 & 0 & 0 & 0 & - 1 & 0 & 0 & - 1 & - 2 & - 2 & 0 & - 1 \\ 0 & 2 & - 1 & 0 & - 2 & 0 & 0 & 3 & 1 & 0 & 0 & - 2 & 0 & - 2 & 0 & 1 \\ 2 & 0 & 2 & - 1 & 1 & 1 & 0 & 3 & 2 & - 1 & 1 & - 1 & 1 & - 2 & 1 & - 1 \\ 2 & 0 & 0 & 1 & - 2 & 1 & - 3 & 0 & 1 & 1 & - 1 & - 3 & - 3 & 0 & 0 & 0 \\ 2 & 0 & 0 & 0 & - 1 & - 1 & 1 & - 1 & 2 & 2 & 0 & 1 & - 1 & 0 & 0 & - 1 \\ 2 & 0 & 0 & - 3 & 0 & 2 & - 1 & 0 & 0 & 2 & 0 & - 1 & 1 & 0 & 0 & - 2 \\ - 1 & - 1 & 0 & - 3 & 2 & 0 & 2 & - 1 & - 1 & 2 & - 1 & 1 & 2 & - 1 & 1 & - 1 \\ 2 & - 1 & 3 & 0 & 2 & 0 & 0 & 1 & 3 & 0 & 0 & 0 & 1 & 1 & - 1 & - 3 \end{matrix}], \end{matrix}

i.e.,

A_{0} *_{N} D_{0} = B_{0} *_{S} C_{0}, A_{0} *_{N} D_{1} - B_{0} *_{S} C_{1} = B_{1} *_{S} C_{0} - A_{1} *_{N} D_{0} .

Then, it can be deduced that the system of dual split quaternion tensor equations (2) is solvable and a solution of this system can be expressed as

X = X_{00} + X_{01} ϵ

, where

\begin{matrix} {(X_{00})}_{1111} = j, {(X_{00})}_{1121} = i, {(X_{00})}_{1112} = 1, {(X_{00})}_{1122} = 0, \\ {(X_{00})}_{2111} = j, {(X_{00})}_{2121} = - 1, {(X_{00})}_{2112} = i, {(X_{00})}_{2122} = k, \\ {(X_{00})}_{1211} = - 1, {(X_{00})}_{1221} = 0, {(X_{00})}_{1212} = i - j, {(X_{00})}_{1222} = j, \\ {(X_{00})}_{2211} = 0, {(X_{00})}_{2221} = j, {(X_{00})}_{2212} = k, {(X_{00})}_{2222} = i, \end{matrix}

and

\begin{matrix} {(X_{01})}_{1111} = 1, {(X_{01})}_{1121} = 0, {(X_{01})}_{1112} = i, {(X_{01})}_{1122} = 0, \\ {(X_{01})}_{2111} = k, {(X_{01})}_{2121} = i, {(X_{01})}_{2112} = j, {(X_{01})}_{2122} = - 1, \\ {(X_{01})}_{1211} = 0, {(X_{01})}_{1221} = 1, {(X_{01})}_{1212} = - k, {(X_{01})}_{1222} = j, \\ {(X_{01})}_{2211} = - j, {(X_{01})}_{2221} = k, {(X_{01})}_{2212} = 1, {(X_{01})}_{2222} = 0 . \end{matrix}

Example 3.

In this section, we propose a method for video encryption and decryption using Theorem (1) and provide a specific example to demonstrate this method.

Similar to quaternions [6], it has been demonstrated that split quaternions can represent color images [40]. Split quaternion tensors can represent color videos, as long as the video is segmented into multiple image slices. Then, the dual split quaternion tensor can represent two color videos.

We can encrypt two color videos through system (2) and the following model is the encryption process based on system (2):

Figure 1. The model of encrypting two videos.

It is clear that system (2) and the following system are equivalent, so we can use system (22) to encrypt and decrypt videos.

\begin{matrix} \{\begin{matrix} A_{0} *_{S} X_{0} = B_{0}, \\ X_{0} *_{S} C_{0} = D_{0}, \\ A_{0} *_{S} X_{1} + A_{1} *_{S} X_{0} = B_{1}, \\ X_{0} *_{S} C_{1} + X_{1} *_{S} C_{0} = D_{1} \end{matrix} \end{matrix}

(22)

We use two original videos

X_{0}

and

X_{1}

, each composed of 51 slices of color images of size

540 \times 540

pixels, represented as

H_{s}^{540 \times 540 \times 51}

[41]. That is,

X = X_{0} + X_{1} ϵ \in {DQ}_{s}^{540 \times 540 \times 51}

A = A_{0} + A_{1} ϵ

and

C = C_{0} + C_{1} ϵ \in {DQ}_{s}^{540 \times 540}

are the system coefficients. For simplicity, we select all

A_{0}

A_{1}

C_{0}

and

C_{1}

as real matrices and they are invertible. And we represent

B_{0}

and

B_{1} \in H_{s}^{540 \times 540 \times 51}

as keys.

D_{0}

and

D_{1} \in H_{s}^{540 \times 540 \times 51}

represent two encrypted videos. The process of encryption is described below:

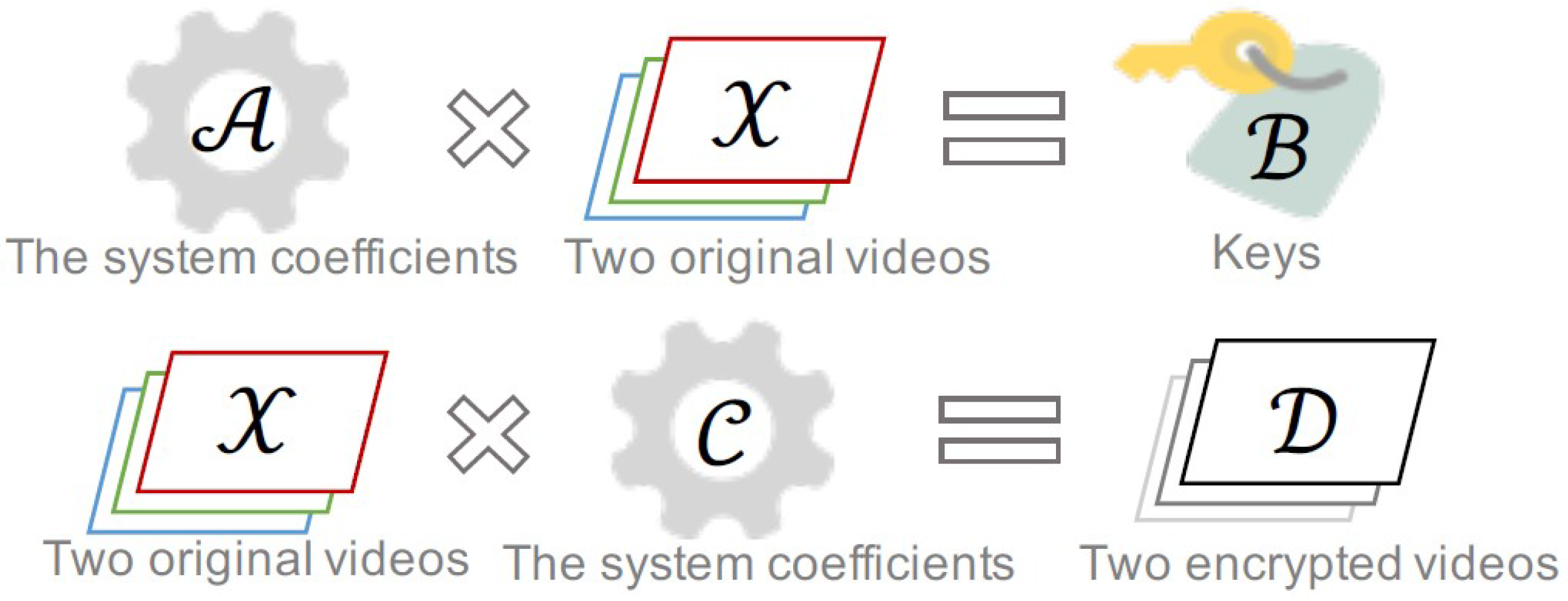
Algorithm 1 Encryption process

1:: Input:Two original videos and system coefficients.
2:: Let $X_{0}$ and $X_{1}$ represent the first original video and the second original video. Then $X_{0 i}$ and $X_{1 i}$ represent i-th slice of video $X_{0}$ and $X_{1}$ , where $i = 1, \dots, 51$ . The system coefficients are $A_{0}$ , $A_{1}$ , $C_{0}$ and $C_{1}$ .
3:: Encrypt $X_{0}$ and $X_{1}$ by the system (22).
4:: $B_{0 i}$ and $B_{1 i}$ denote keys. $D_{0 i}$ and $D_{1 i}$ represent i-th slice of the two encrypted videos, where $i = 1, \dots, 51$ . So we have obtained two encrypted videos $D_{0}$ and $D_{1}$ .
5:: Output:Two encrypted videos and keys.

For the decryption process, we use two encrypted videos,

D_{0}

and

D_{1}

, obtained from the encryption process, along with keys

B_{0}

and

B_{1}

, as well as system coefficients

A_{0}

A_{1}

C_{0}

, and

C_{1}

, to recover the two original color videos. The decryption algorithm is represented as follows:

Algorithm 2 Decryption process

1:: Input:System coefficients, keys and two encrypted videos.
2:: $B_{0}$ and $B_{1}$ represent keys. $D_{0}$ and $D_{1}$ denote the encrypted videos. $A_{0}$ , $A_{1}$ , $C_{0}$ , and $C_{1}$ are the system coefficients and they are reversible.
3:: Using the real representation, we obtain $A_{p}^{σ_{i}}$ , $B_{p}^{σ_{i}}$ , $C_{p}^{σ_{i}}$ , and $D_{p}^{σ_{i}}$ , where $p = 1, 2$ .
4:: By Theorem (1), we obtain ${XD}_{0}$ and ${XD}_{1}$ .
5:: Convert ${XD}_{0}$ and ${XD}_{1}$ into ${XD}_{00}$ and ${XD}_{01}$ using Theorem (1), respectively.
6:: Two decrypted videos are ${XD}_{00}$ and ${XD}_{01}$ , respectively.
7:: Output:Two decrypted videos.

Figure 2. The original, encrypted, and decrypted images of randomly selected slices from color videos

X_{0}

and

X_{1}

Figure 2. The original, encrypted, and decrypted images of randomly selected slices from color videos

X_{0}

and

X_{1}

The encryption’s CPU time is 59.2300 seconds and the decryption’s CPU time is 145.9600 seconds. The figure below illustrates a portion of slices from the encrypted and decrypted videos results:

To assess the quality of the encryption and decryption algorithm for color videos, we utilize the Peak Signal-to-Noise Ratio (PSNR), Structural Similarity Index Measure (SSIM) and Feature Similarity Index Measure (FSIM), with the results presented in Table 1 and Table 2. A higher PSNR value usually indicates smaller errors, meaning that the quality of the processed image is higher. The results show that the PSNR values are all greater than 30 and all SSIM and FSIM values are equal to 1, indicating a high degree of similarity between the decrypted videos and the original videos. This further demonstrates the effectiveness of our encryption and decryption algorithm.

5. Conclusions

We use the real representations of split quaternions to simplify the system of dual split quaternion tensor equations

(A *_{N} X, X *_{S} C) = (B, D)

into real tensor equations. Based on this, we put forward the equivalent conditions for this system’s solvability and the general expression of solutions. Subsequently, this proposed theorem is applied to two specific cases of dual split quaternion tensor equations. Furthermore, the paper presents the equivalent conditions when the Hermitian solution (denoted as

X = X^{*}

) and

η

-Hermitian solutions (denoted as

X = X^{η *}

) of the system (2) exist, using various real representations. Additionally, we provide a numerical example using MATLAB to validate the correctness of the key theorem presented in this paper. In the end, we use Theorem (1) to present a method for encrypting and decrypting two color videos, along with a specific example. The algorithm’s efficacy is demonstrated by PSNR, SSIM and FSIM.

Author Contributions

All authors have equal contributions in conceptualization, formal analysis, investigation, methodology, software, validation, writing an original draft, writing a review, and editing. All authors have read and agreed to the published version of the manuscript.

Funding

This research is supported by the National Natural Science Foundation of China (No. 12371023).

Data Availability Statement

Data are contained within the article.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Hamilton, W.R. Lectures on quaternions. Landmark Writings in Western Mathematics 1640–1940, 1853. [Google Scholar] [CrossRef]
Zhang, F.Z. Quaternions and matrices of quaternions. Linear Algebra Its Appl. 1997, 251, 21–57. [Google Scholar] [CrossRef]
Kösal, H.; Tosun, M. Commutative quaternion matrices. Adv. Appl. Clifford Algebr. 2014, 24, 769–779. [Google Scholar] [CrossRef]
Zhang, Y.; Wang, Q.W.; Xie, L.M. The Hermitian solution to a new system of commutative quaternion matrix equations. Symmetry. 2024, 16, 361. [Google Scholar] [CrossRef]
Cyrus, J.; Clive, C.T.; Danilo, P.M. A class of quaternion valued affine projection algorithms. Signal Process. 2013, 93, 1712–1723. [Google Scholar] [CrossRef]
Miao, J.; Kou, K.I. Color image recovery using low-rank quaternion matrix completion algorithm. IEEE Trans. Signal Process. 2021, 31, 190–201. [Google Scholar] [CrossRef]
Adler, S.L. Quaternionic quantum mechanics and quantum fields. International Series of Monographs on Physics. 1995, 88. [Google Scholar] [CrossRef]
Cockle, J. On systems of algebra involving more than one imaginary and on equations of the fifth degree. Philos. Mag. 1849, 36, 434–437. [Google Scholar] [CrossRef]
Kula, L.; Yaylı, Y. Dual split quaternions and screw motions in Minkowski 3-space. Iran. J. Sci. Technol. Trans. A Sci. 2006, 30, 245–258. [Google Scholar] [CrossRef]
Alagöz, Y.; Oral, K.H.; Yüce, S. Split quaternion matrices. Miskolc Math. Notes. 2012, 13, 223–232. [Google Scholar] [CrossRef]
Erdoğdu, M.; Özdemir, M. On eigenvalues of split quaternion matrices. Adv. Appl. Clifford Algebras. 2013, 23, 615–623. [Google Scholar] [CrossRef]
Erdoğdu, M.; Özdemir, M. On complex split quaternion matrices. Adv. Appl. Clifford Algebras. 2013, 23, 625–638. [Google Scholar] [CrossRef]
Kula, L.; Yaylı, Y. Split quaternions and rotations in semi Euclidean space E24. J. Korean Math. Soc. 2007, 44, 1313–1327. [Google Scholar] [CrossRef]
Özdemir, M.; Ergin, A.A. Rotations with unit timelike quaternions in Minkowski 3-space. J. Geom. Phys. 2006, 56, 326–332. [Google Scholar] [CrossRef]
Chen, Y.; Wang, Q.W.; Xie, L.M. Dual quaternion matrix equation AXB=C with applications. Symmetry. 2024, 16, 287. [Google Scholar] [CrossRef]
Diatta, A.; Manga, B.; Sy, F. On dual quaternions, dual split quaternions and Cartan-Schouten metrics on perfect Lie groups. arXiv:2310.02114, arXiv:2310.02114. 2023. [CrossRef]
Erdoğdu, M.; Özdemir, M. Split quaternion matrix representation of dual split quaternions and their matrices. Adv. Appl. Clifford Algebr. 2015, 13, 787–798. [Google Scholar] [CrossRef]
Atasoy, A.; Ata, E.; Yayli, Y. et al. A new polar representation for split and dual split quaternions. Adv. Appl. Clifford Algebras. 2017, 27, 2307–2319. [Google Scholar] [CrossRef]
Rao, C.R.; Mitra, S.K. Generalized inverse of matrices and its applications. Sankhyā: The Indian Journal of Statistics. 1971, 33, 289–300. [Google Scholar]
Khatri, C.G.; Mitra, S.K. Hermitian and nonnegative definite solutions of linear matrix equations. SIAM J. Appl. Math. 1976, 31, 579–585. [Google Scholar] [CrossRef]
Wang, Q.W. Bisymmetric and centrosymmetric solutions to systems of real quaternion matrix equations. Comput. Math. Appl. 2005, 49, 641–650. [Google Scholar] [CrossRef]
Li, F.L.; Hu, X.Y.; Zhang, L. The generalized reflexive solution for a class of matrix equations (AX=B,XC=D). Acta Math. Sci. 2008, 28, 185–193. [Google Scholar] [CrossRef]
Yuan, Y. Least-squares solutions to the matrix equations AX=B, XC=D. Appl. Math. Comput. 2010, 216, 3120–3125. [Google Scholar] [CrossRef]
Xie, L.M.; Wang, Q.W. A system of dual quaternion matrix equations with its applications. arXiv:2312.10037, 2023; arXiv:2312.10037. 2023. [Google Scholar] [CrossRef]
Wang, Q.W.; Lv, R.Y.; Zhang, Y. The least-squares solution with the least norm to a system of tensor equations over the quaternion algebra. Linear Multilinear Algebra. 2020, 70, 1942–1962. [Google Scholar] [CrossRef]
Wang, Q.W.; Xu, X. Iterative algorithms for solving some tensor equations. Linear and Multilinear Algebra. 2018, 67, 1325–1349. [Google Scholar] [CrossRef]
Liang, M.L.; Zheng, B.; Zhao, R.J. Tensor inversion and its application to tensor equation with Einstein product. Linear Multilinear Algebra. 2018, 67, 843–870. [Google Scholar] [CrossRef]
Xie, M.; Wang, Q.W. ; Reducible solution to a quaternion tensor equation. Front. Math. China. 2020, 15, 1047–1070. [Google Scholar] [CrossRef]
Xie, M.; Wang, Q.W.; Zhang, Y. The Minimum-Norm Least Squares Solutions to Quaternion Tensor Systems. Symmetry. 2022, 14, 1460. [Google Scholar] [CrossRef]
Qi, L.Q.; Ling, C.; Yan, H. Dual quaternions and dual quaternion Vectors. Commun. Appl. Math. Comput.. 2022, 4, 1494–1508. [Google Scholar] [CrossRef]
Einstein, A. The formal foundation of the general theory of relativity. Sitzungsber. Preuss. Akad. Wiss. Berlin (Math. Phys.), 1914; 1030–1085. [Google Scholar]
Sun, L.; Zheng, B.; Bu, C.; Wei, Y. Moore-penrose inverse of tensors via einstein product. Linear and Multilinear Algebra. 2015, 64, 686–698. [Google Scholar] [CrossRef]
Chen, C.; Surana, A.; Bloch, A.; et al. Multilinear time invariant system theory. 2019 Proceedings of the Conference on Control and its Applications. 2019, 118–125. [Google Scholar] [CrossRef]
Brazell, M.; Li, N.; Navasca, C.; Tamon, C. Solving multilinear systems via tensor inversion. SIAM J. Matrix Anal. Appl. 2013, 34, 542–570. [Google Scholar] [CrossRef]
He, Z.H.; Navasca, C.; Wang, Q.W. Tensor decompositions and tensor equations over quaternion algebra. arXiv preprint arXiv:1710.07552, arXiv:1710.07552. 2017. [CrossRef]
Liu, X.; He, Z.H. On the split quaternion matrix equation. Banach J. Math. Anal. 2020, 14, 228–248. [Google Scholar] [CrossRef]
He, Z.H.; Wang, Q.W. The general solutions to some systems of matrix equations. Linear Multilinear Algebra. 2015, 63, 2017–2032. [Google Scholar] [CrossRef]
Si, K.W.; Wang, Q.W. The General Solution to a classical matrix equation AXB=C over the dual split 1uaternion algebra. Symmetry. 2024, 16, 491. [Google Scholar] [CrossRef]
Si, K.W.; Wang, Q. W; Xie, L.M. A classical system of matrix equations over the split quaternion algebra. Adv. Appl. Clifford Algebras. 2024, 34, 51. [Google Scholar] [CrossRef]
Eduardo, B.C.; Zuleima, V.F.; Ulises, U.L. The Lorentz Group Using Conformal Geometric Algebra and Split Quaternions for Color Image Processing : Theory and Practice. IEEE Access. 2023, 11, 56785–56800. [Google Scholar] [CrossRef]
Zhang, X.F.; Li, T.; Ou, Y.G. Iterative solutions of generalized Sylvester quaternion tensor equations. Linear and Multilinear Algebra. 2023, 72, 1259–1278. [Google Scholar] [CrossRef]
Clifford, W.K. Preliminary sketch of bi-quaternions. Proc. Lond. Math. Soc. 1873, 4, 381–395. [Google Scholar] [CrossRef]

Table 1. PSNR, SSIM and FSIM of the video 1.

Video 1	PSNR	SSIM	FSIM
1	279.8545	1	1
2	280.0351	1	1
3	279.8906	1	1
4	279.4681	1	1

Table 2. PSNR, SSIM and FSIM of the video 2.

Video 2	PSNR	SSIM	FSIM
1	248.0390	1	1
2	248.2462	1	1
3	247.9977	1	1
4	246.5033	1	1

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A System of Tensor Equations over the Dual Split Quaternion Algebra with an Application

Abstract

Keywords:

Subject:

1. Introduction

2. Preliminary

2.1. Dual Split Quaternion Tensors

2.2. Basic theory with Einstein product

2.3. Real Representations of Split Quaternion Tensors

3. The General Solution to System (2)

4. Numerical Example

5. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe