The Ultimate Tensile Strength of SiC/SiC Composites: Multiscale Approach

1. Introduction

Reinforcing ceramics with continuous ceramic fibers allows inherent weaknesses of ceramics to be overcome. When the ceramics exhibit low fracture toughness, high strength sensitivity to the presence of microstructural flaws, brittle behavior, and lack of reliability, the ceramic matrix composites are damage tolerant, tough, strong and they can be flaw and notch insensitive. The ceramic matrix composites (CMCs) reinforced with continuous ceramic or carbon fibers are of interest to thermostructural applications [1]. They are lightweight, damage tolerant, and they exhibit a much greater resistance to high temperatures and aggressive environments than metals or other conventional engineering materials. Their field of applications include heat exchangers, heat engines, gas turbines, structural components in the aerospace industry, in nuclear reactors, etc. [1, 2].

The versatility of composite material is a rermarkable asset. Composites can be tailored to suit end use applications, through the sound selection and arrangement of constituents. Thus, it is important to create sound understanding of relationships between constituent properties and macroscopic behavior. Such relationships are investigated in the typical case of a SiC/SiC composite in the present paper. The ultimate strength is the mechanical property of interest.

The mechanical behavior of CMCs displays several typical features that differentiate them from the other composites (such as polymer matrix composites, metal matrix composites, etc.) and from the homogeneous (monolithic) materials. They are damage tolerant, the cracks that form in the matrix are arrested by the fibers. The damage modes in woven SiS/SiC are hierarchically organized, sequential, and stochastic as a result of microstructure features and the respective properties of constituents. Being ceramic materials, the constituents are highly sensitive to microstructural flaws. The flaw populations govern matrix cracking and fiber failures, whose strengths exhibit statistical distributions. Thus, a bottom-up multiscale approach based on micromechanics must account for the contribution of inherent fracture-inducing flaws, variability of constituent strengths, and associated size effects. Such approach is essential to understand the phenomena at low length scale that influence the behavior at macroscopic scale and to predict the mechanical behavior of CMCs. It can be the basis of an approach to composite and component design.

Various entities at increasing length scales can be defined in 2D woven SiC/SiC composites: microscopic diameter filaments, multifilament tows, microcomposites consisting of a single matrix coated filament, minicomposites consisting of a single tow of matrix coated filaments, and at the end the composite. Testspecimens of microcomposites and minicomposites can be manufactured via CVI so that all the above hierarchically organized entities can be tested separately and investigated. In very simple terms, the SiC-based matrix is deposited from gaseous reactants on to a heated substrate of fibrous preforms (SiC). As a result of chemical reaction kinetics, filaments and matrix exhibit quite close volume fractions and local sizes in the CVI made SiC/SiC composite.

The ultimate failure of a composite specimen tested in tension, in a principal fiber direction, occurs after the successive failures of constituents (filaments, matrix and interface) at the various length scales defined above. Features of mechanical behavior of CVI SiC/SiC composites with respect to microstructure, have been highlighted on the basis of large amount of modelling and experimental work [1- 3]. In CVI SiC/SiC composites, the ultimate failure is governed by the behavior of multifilement tows after matrix cracking is saturated and fiber/matrix debond is complete (ineffective length = gauge length) [3].

The approach to ultimate strength of bundles and composites has been the object of much work in the literature. Assuming constant applied stress, it was considered by most authors that « the surviving elements feel an increase of load resulting both from the increase of the external load on the bundle and the increase of load resulting from a decrease in the number of elements which share this load » [4]. Ultimate failure would occur when the failure of an additional filament at constant external load will increase the load on the survivors enough to make the progressive failure of the remaining elements possible [4]. Several models and equations relating composite ultimate tensile strength to bundle strength were proposed [5 -18]. Failure of the bundle was assumed to occur when the failure of one fiber increases the stress uniformly on all the intact fibers. The mean value of the strength of the fibers when the fibers are equal to the length (l) of the composite was considered first [6,7,8,9,10,11,12]. When comparing prediction with experimental results satisfactory agreement was not observed. Refined models considered an ineffective length (l_c) of fiber (l_c<l) [13,14,15,16,17,18], the presence of matrix cracks [11,12,13,14,15,16,17,18], and the stress sustained by the failed fibers [16,17,18]. The strength of the critical fiber is not quantified and problems arise when defining a suitable value of l_c to insert in equations. It was found that the ultimate strength of SiC/SiC minicomposites was underestimated significantly by the latter model [18,19]. Curtin indicated that the proposed equation in [18] has no rigorous applicability to the composite performance. Furthermore, the limits of the models available in the literature for describing both the ultimate strength and toughness of unidirectional fiber-reinforced ceramics were discussed in [5].

The ultimate failure of fiber tows depends on the condition of loading [20]: the loading may be either stress- or strain-controlled. The above mentioned mechanism of force increase on surviving filaments when a filament fails operates only under the force-controlled condition of loading. By contrast, under constant strain, the force on tow decreases when a filament fails, so that there is no resulting force increase on the surviving filaments. Thus, the ultimate failure of a tow is dictated theoretically by the strongest filament. In the case of stress controlled loading, the ultimate failure is caused by a critical filament much weaker than the strongest filament [20, 21]. Overloading from structural origins can cause premature fracture [20]. Laboratory tests are commonly performed under constant strain rate, whereas most theoretical approaches assume constant applied stress, as indicated above. Therefore, comparison of predictions with experimental results when the loading conditions are different is an issue. The loading mode plays a decisive role in the ultimate failure of fiber tows, so that the mechanism of ultimate failure and the definition of ultimate strength require further analysis.

The approach to ultimate strength of SiC/SiC composites proposed in the present paper considers the underlying behavior of matrix, reinforcing filaments and tows, and minicomposites. The SiC/SiC system was made of a SiC matrix and SiC continuous fibers. The test specimens were manufactured via the chemical vapor infiltration process (CVI). The significance of loading mode (strain- or stress-controlled) is highlighted. First, experimental results on tensile behavior of tows, minicomposites and composites under strain-controlled conditions provide background to the analysis. Then models of fracture of tow and of minicomposite are developed. Finally, the variability of ultimate strength of minicomposites and composites is investigated.

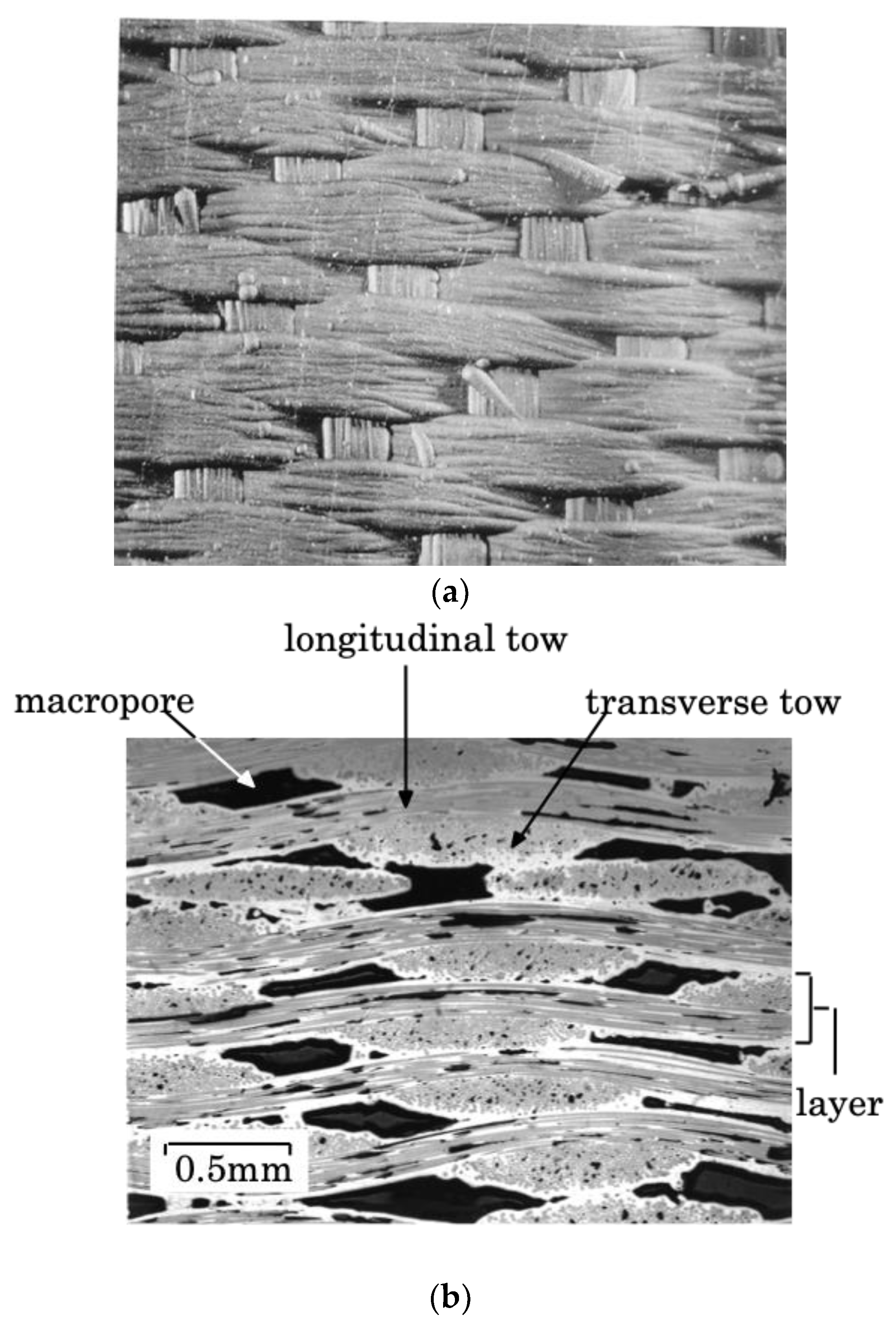
2. Background: Experimental Tensile Behavior of Filaments, Tows and Composites

This section synthezises experimental results reported in previous papers. They were generated on testspecimens representing various length scales. Figure 1 illustrates the length scales in 2D woven CVI SiC/SiC composite. Filaments and orthogonal tows of filaments coated with the matrix can be seen. Interply pores can be noted. Figure 2 shows a minicomposite testspecimen that failed during a tensile test, with the protruding filaments of underlying tow. Note on figures 1 and 2 the structural feature that the fibre and matrix volume sizes are of the same order of magnitude locally,

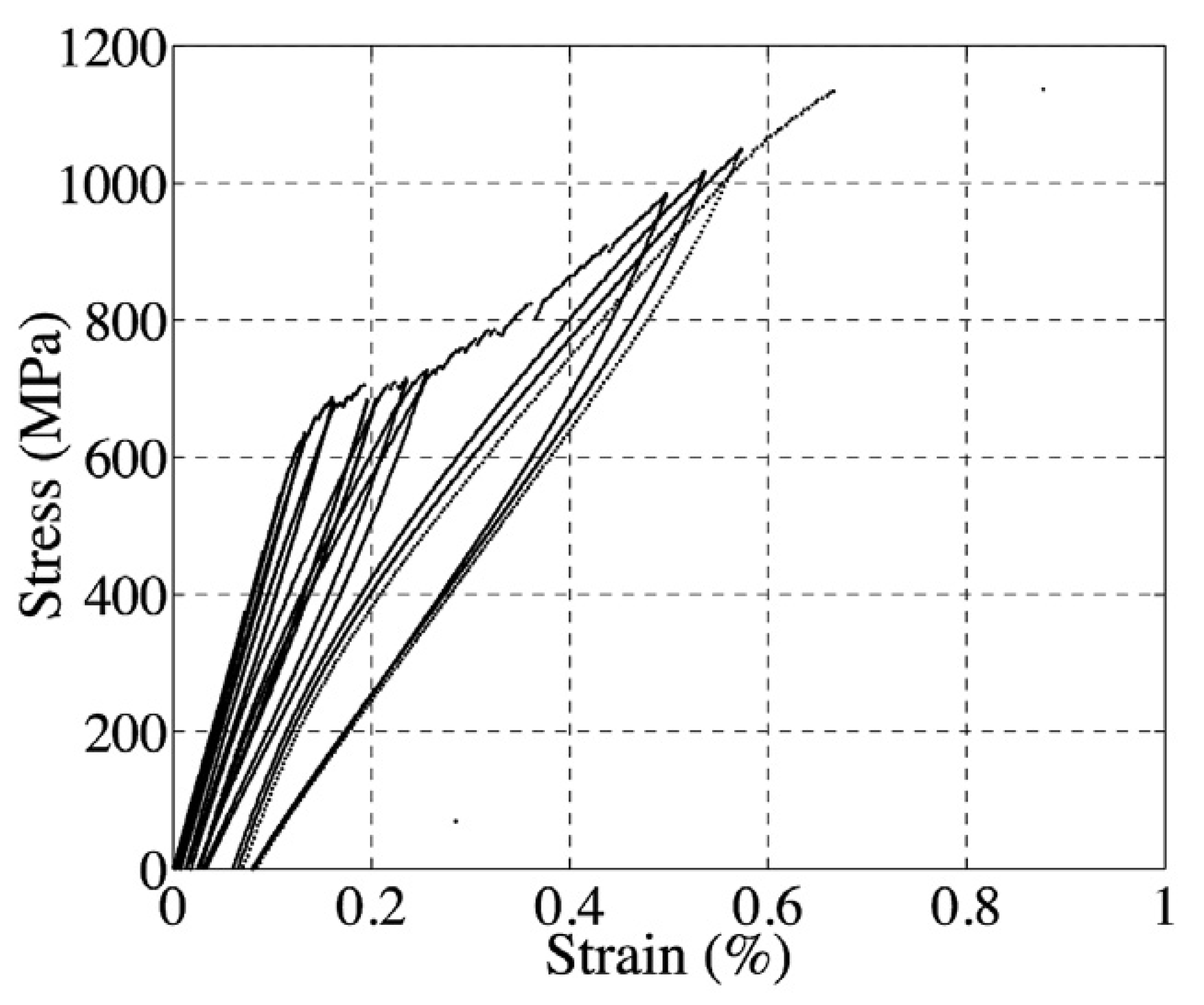
2.1. Multifilament Tows

A multifilament tow is made of hundreds or thousands of parallel filaments (Figure 2). Tensile tests on tows are commonly carried out under deformation-controlled condition. Typically the force deformation curves shown on Figure 3 were obtained on a servopneumatic testing machine at contant deformation rate (2 μm/sec). Test specimen elongation was measured using a contact extensometer (with a ± 2.5 mm elongation displacement transducer) that was clamped to the specimen using two 4-mm-long thermoretractable rings. The rings were located close to the grips. The inner distance between the rings defined the gauge length. Lubricant oil was used to avoid friction between the fibres. More details on the testing procedure are available in previous papers and ISO standard [22-25].

Figure 3 shows that close tensile curves were obtained on tows with a gauge length of 115 mm [26]. This absence of variation was attributed to the reproducibility of the population of fracture inducing flaws [26]. By contrast significant variation was displayed by the curves obtained at shorter gauge lengths [26].

The tensile behavior displays typical features as reported in a previous paper [24]: i.e., initial elastic deformations at strains <0.7% and then nonlinear deformations as a result of individual fiber breaks. Beyond the maximum, the force on the tow decreases smoothly to 0. Beyond the limit of linearity, the AE event sources looked homogeneously distributed for the 115 mm gauge length, which suggested that clusters of multiple failures were not present [24].

The behavior may be affected by artifacts. Weaker tensile behavior with lower stresses and strains as well as unstable failure has been observed in a previous paper [27]. This fracture behavior was attributed to the contribution of an extraload resulting from structural effects such as inter-fiber friction, stress wave, and load train deformation in tows without slack [27].

2.2. SiC/SiC Minicomposites

A minicomposite test specimen is a unidirectional composite reinforced by a single fiber tow (Figure 2). Such specimens were manufactured via the CVI process. To our knowledge, no alternate manufacturing techniques are available for ceramic matrix minicomposite processing. A great amount of knowledge on in-situ properties of fibers, matrix and fiber/matrix interphases has been generated from the tensile behavior of these specimens. Minicomposites represent an intermediate mesoscopic level between filaments and composite pieces reinforced by several fiber tows. The testing method is similar to that of fiber tows [25, 28]. Sample ends were glued within 40 mm long metallic tubes, that were then gripped into the testing machine. Special care was taken during specimen preparation to achieve perfect alignment of the minicomposites. The glue was introduced using a syringe. Tensile tests were performed on a rigid frame machine at room temperature at a constant displacement rate of 0.08 mm/min. Specimen elongations were measured using a LVDT extensometer mounted on the grips.

The tensile stress-strain curves of minicomposites (Figure 4) exhibit the typical elastic damage behavior of CMCs. They display successive steps as the applied deformation increases. The folowing steps were identified on Hi Nicalon/SiC minicomposites [3]:

• ⁻ at strains smaller than 0.1%, an initial linear elastic domain.
• ⁻ at strains between 0.1% and 0.3%, a non linear domain with upward curvature indicative of increasing compliance, resulting from transverse matrix cracking and associated fiber/matrix debonding (Figure 5).
• ⁻ at a strain of about 0.3%, an inflexion point that marks a transition in the damage process from matrix cracking that saturated, to a less severe process such as extension of debonding,
• ⁻ at strains comprised between 0.3% and about 0.7 a second linear domain indicative of constant compliance, that is attributed to deformation of fibres and sliding in the presence of complete debonding.
• ⁻ at strains >0.7%, a non linear domain with upward curvature, indicative of fibre successive failures.

The strains at ultimate failure were found to depend on fibre type, as indicated in table 1 that higlights a relation with fibre grain size and the resulting surface roughness [3, 29]. It can be noted that the strain-to-failure decreases with increasing grain size and fiber surface roughness, which induces increasing friction between fiber and matrix in the debonded regions.

2.3. 2D Woven SiC/SiC Made Using CVI Process

The tensile behavior was determined on dogbone shaped-specimens cut out of plates about 3.3 mm thick [30]. The specimens were tested parallel to a fibre axis at constant strain rate (4.10^-4 %/sec), using an Instron testing machine. The axial strains were measured with an extensometer over a 25 mm gauge length.Two aluminium end-tabs were affixed to the specimen ends using glue in order to prevent sliding during the tests. Furher details can be found in ISO standard [31].

The CVI 2D SiC/SiC composite exhibit linear elastic behavior to a strain of about 0.03%, and a subsequent curved domain that results essentially from transverse cracking in the matrix (the cracks are perpendicular to fibers in the loading direction) (Figure 6 and Figure 7). Saturation of matrix damage is indicated by a point of inflection at about 0.4% strain for those composites with a weak interphase (Figure 6). Saturation occurs at higher stress on those composites with a strengthened fiber/matrix interphase (Figure 6). Then the ultimate portion of the curves beyond matrix saturation stress is governed by the tows i.e., by the deformation of filaments, individual fiber breaks and sliding.

Figure 8 shows the correlative decrease of composite elastic modulus that reflects the decreasing load carrying capacity of the matrix. A significant modulus loss (70 % in 2D SiC/SiC) is caused first by the matrix cracks located in the transverse tows perpendicular to load direction (strains < 0.2 %). Then, the microcracks within the matrix of longitudinal tows are responsible for a 10 % loss only (Figure 8). The load is transferred to the matrix-coated longitudinal tows and then to the filaments in the microcracked longitudinal tows. The analysis of acoustic emission signals indicate that fracture of filaments starts at strains > 0.6%. The elastic modulus reaches a minimum dictated by the longitudinal filaments according to the following rule of mixture:

E_min = ½ E_f V_f (1)

V_f is the volume fraction of fibers oriented in the loading direction.

Ultimate failure occurred at maximum force after saturation of matrix cracking. The strain-to-failure takes comparable values in composite, minicomposite, and tow at the maximum force. The range of 0.6–1% for the 2D SiC/SiC composites was observed on test specimens with various fiber/matrix interphases, indicating an influence of fiber/matrix interface characteristics (figures 6 and 8).

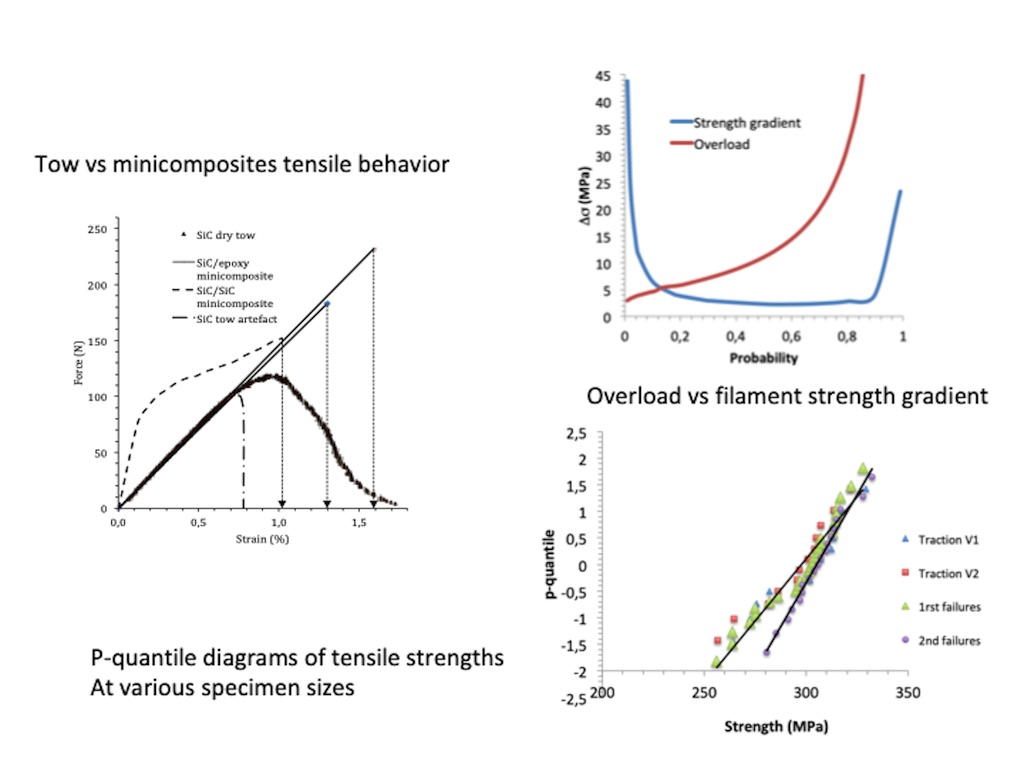
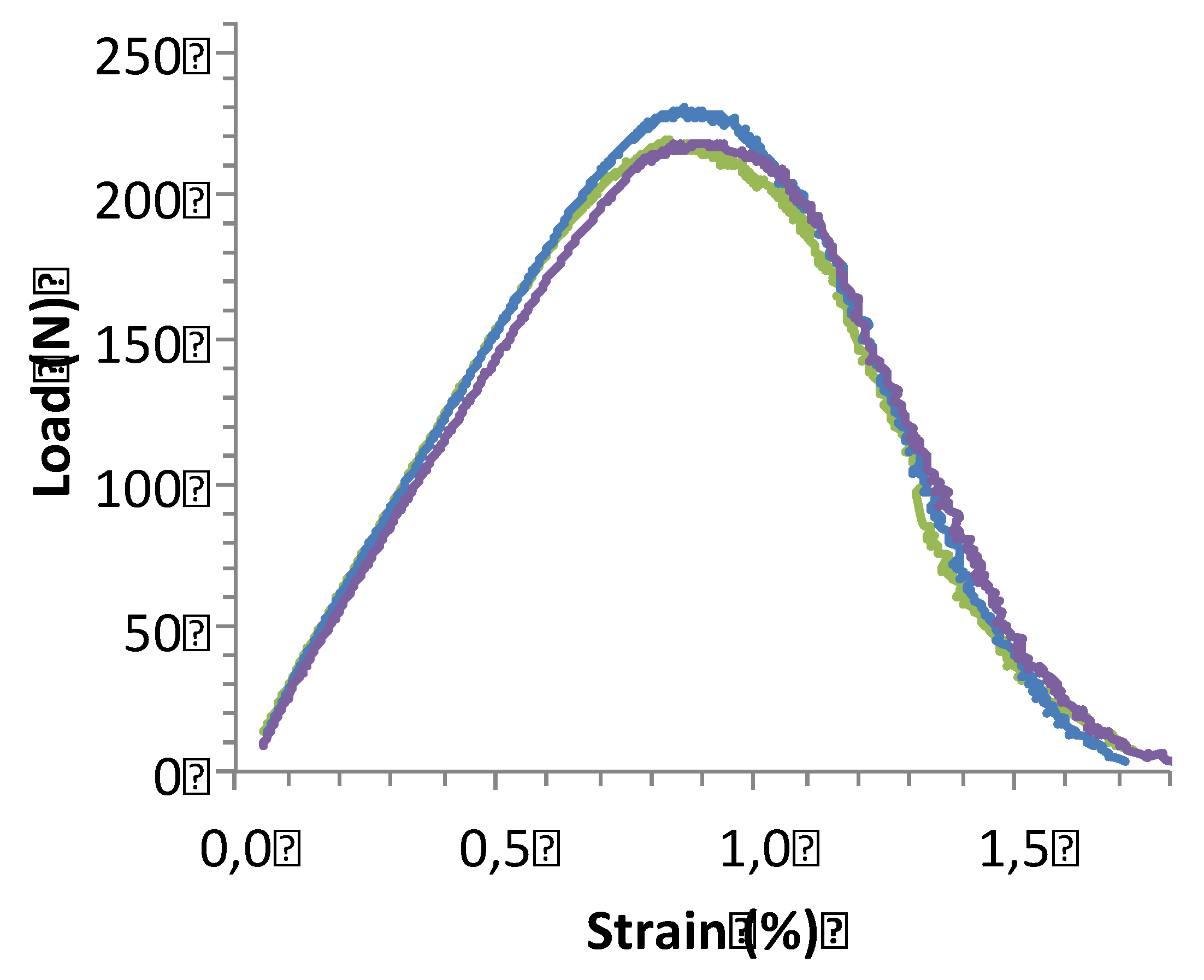
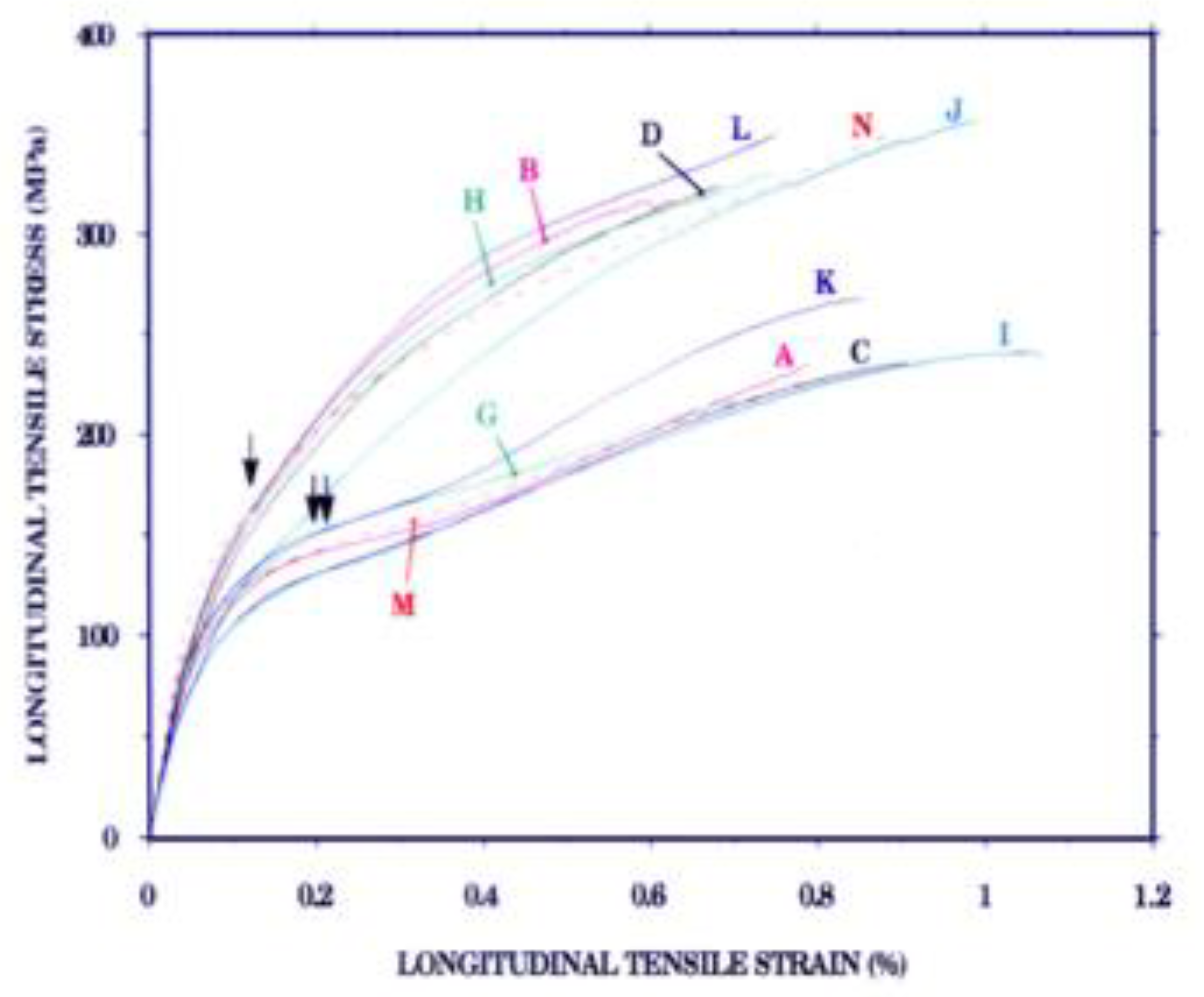
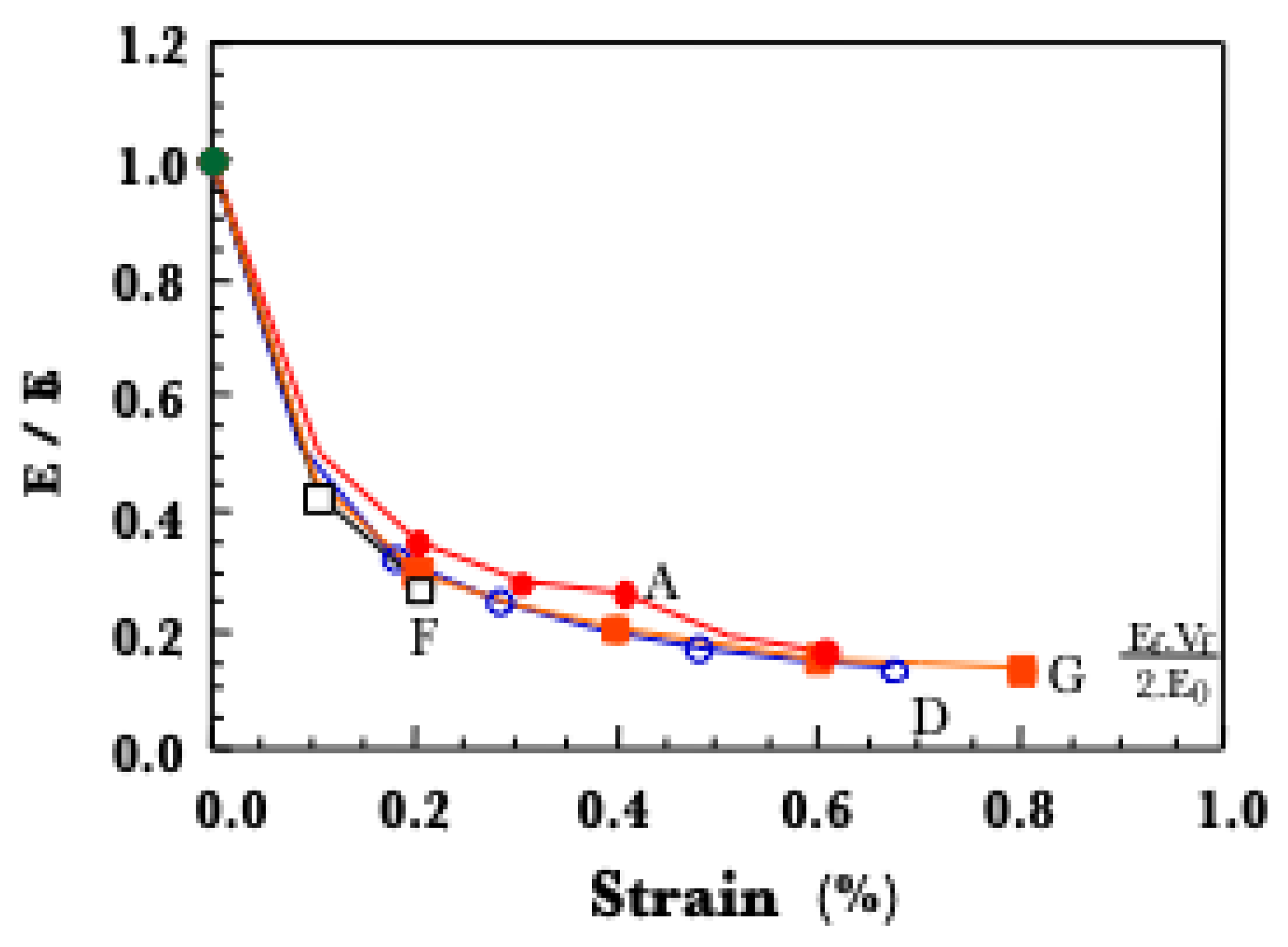
2.4. Scale Level Effect on Behavior Under Strain-Controlled Condition

Figure 8 compares the force-strain curves measured on different tow-based structures under constant strain rate: dry tows, minicomposites with stiff ceramic matrix or compliant polymer matrix. The force-strain curve of 2D SiC/SiC composite was not introduced on this figure because of its too high magnitude compared to tows and minicomposites. The same goes for filaments that exhibited too small forces.

Under the current condition of controlled deformation, the tensile behavior of ceramic minicomposites exhibits a significant difference with that of tows (Figure 2). The dry tows exhibit the typical stable failure mentioned above, whereas the minicomposite as well as the 2D woven composite specimens exhibit the unstable failure typical of force-controlled loading conditions. The ultimate failure of ceramic minicomposites and composites occurs at a strain range of 0.6–1%, in the area of the maximum force of the underlying tow. Such failure may be regarded as premature under constant strain rate, because it is inconsistent with the behavior of the underlying tows that carry essentially the load after matrix cracking saturation. This issue is investigated in a subsequent section using the proposed model. Figure 9 shows also the frequent premature failure of a tow at a strain of 0.8% that was observed experimentally when a lubricant was not used to reduce fiber interfriction. Fiber interfriction was identified by low-energy amplitude acoustic emission signals (30 dB), whereas higher-energy amplitude signals (80 dB) evidence fiber fractures [23].

The behavior of the epoxy matrix minicomposites is interesting for comparison purpose as it addresses a composite with a highly compliant matrix (E ≈ 5 GPa). Such matrix does not possess load carrying capacity when compared to the stiffness SiC fiber (E ≈ 200 GPa). Note that the Young’s modulus of the CVI SiC matrix is 400 GPa. The tensile behavior is linear elastic type (Figure 9), since the load is carried by all the fibers including the broken filaments. The ultimate failure of the epoxy minicomposites occurs close to that of the strongest filament [32], in agreement with the behavior of the underlying fiber tow under strain controlled condition. The comparison with previous results on SiC/SiC composites suggests that the SiC matrix and fiber/matrix interactions contributed to extraloading the fibers.

3. Models of Fracture of Tows and Minicomposites

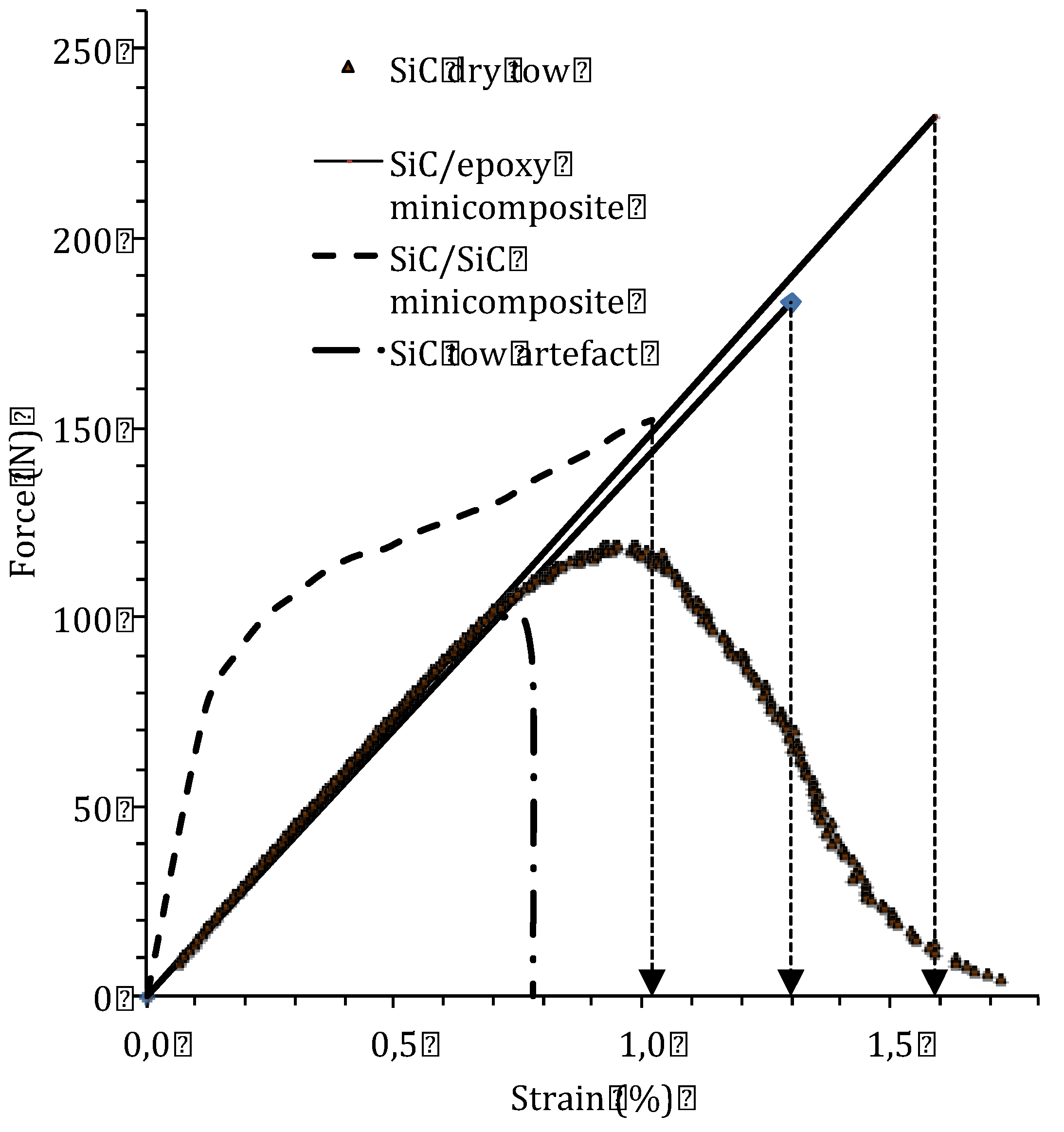
3.1. Multifilament Tows

The models of tow behavior under constant stress are based upon the following hypotheses [10, 33–35]: (i) the tow contains N₀ identical and parallel fibers that are equally loaded (equal load sharing), (ii) a broken filament does not carry load. The following models of ultimate failure of filament tows propose a criterion of initiation and propagation of filament failure as a function of loading conditions.

3.1.1. Unstable Failure Under Force Controlled Conditions

Under load-controlled conditions, the force on tow is kept constant during a filament breakage so that the force that was operating on the breaking filament is shared equally by the surviving filaments. Failure of a filament thus induces overloading on the surviving fibers by an increment:

$∆{\mathit{\sigma }}_{\mathit{a}\mathit{i}}={\displaystyle \frac{{\mathit{\sigma }}_{\mathit{a}\mathit{i}}}{{\mathit{N}}_0-\mathit{i}}}$ (2)

where i designates the fiber that failed (according to ascending strength order), σ_ai is the stress that was operating on this fiber before failure. i designates also the corresponding number of broken fibers.

Unstable failure occurs when $∆{\mathit{\sigma }}_{\mathit{a}\mathit{i}}>{\mathit{\sigma }}_{\mathit{i}+1}-{\mathit{\sigma }}_{\mathit{i}}$whatever i. σ_i+1 is the strength of the fiber having rank i+1 in the cumulative distribution of strengths. This condition is expressed as:

${\displaystyle \frac{{d\sigma }_a}{dP}}\ge {\displaystyle \frac{d\sigma }{dP}}$ (3)

where σ_a is the stress operating on filaments under force-controlled load, andσ is the filament strength. P is failure probability. It has been shown in previous papers [27] that the cumulative distribution of SiC filament tensile strengths can be described by Weibull distribution function [36]:

$P_w\left(\mathsf{\Sigma }<\sigma \right)=1-\mathrm{e}\mathrm{x}\mathrm{p}\left[{-{\displaystyle \frac{V}{V_0}}\left({\displaystyle \frac{\sigma }{{\sigma }_0}}\right)}^m\right]$ for σ > 0 (4)

where m is the shape parameter (Weibull modulus), ${\sigma }_0\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{h}\mathrm{e}$scale factor, V is the stressed volume, and V₀ = 1 m³.

Filament strength is derived from Equation (4):

$\mathit{\sigma }={\sigma }_0{\left[{\displaystyle \frac{V_0}{V}}Ln\left({\displaystyle \frac{1}{1-P}}\right)\right]}^{{\displaystyle \frac{1}{m}}}$ (5)

The stress operating on fibers under the applied force F is given by the following equation:

${\sigma }_a={\displaystyle \frac{F}{N_0(1-P)S_f}}$ (6)

with P= n/N₀ , n is the number of broken fibers.

From equations (5) and (6), it comes:

${\displaystyle \frac{d\sigma }{dP}}={\displaystyle \frac{\sigma }{m\left(1-P\right)Ln\left(\frac{1}{1-P}\right)}}$ (7)

${\displaystyle \frac{d{\sigma }_a}{dP}}={\displaystyle \frac{{\sigma }_a}{N_0(1-P)}}$ (8)

A condition of crack propagation under force controlled loading is derived from equations (3), (7) and (8):

${\sigma }_a\ge {\displaystyle \frac{\sigma \left(P\right)}{mLn\left(\frac{1}{1-P}\right)}}$ (9)

The critical stress σ(P) at instability is determined by comparing the overload and the stress gradient. The filament strength gradient in a tow, and the overload on filaments induced by the failure of a filament are respectively:

$\mathsf{\Delta }\mathsf{\sigma }={\displaystyle \frac{d\sigma }{dP}}\mathsf{\Delta }P={\displaystyle \frac{\sigma \left(P\right)}{m\left(1-P\right)Ln\left(\frac{1}{1-P}\right)}}\mathsf{\Delta }P$ (10)

$∆{\sigma }_a={\displaystyle \frac{d{\sigma }_a}{dP}}∆P={\displaystyle \frac{{\sigma }_a}{N_0(1-P)}}$ (11)

where ΔP = 1/N₀, N₀ being the initial number of filaments carrying the load, Δσ measures the difference between two successive filament strengths of the cumulative distribution.

The criterion of unstability reduces to:

${\sigma }_a=\sigma \left(P\right)$ (12)

$∆{\sigma }_a=∆\sigma$ (13)

The critical fiber in a tow for which the condition (3) is met, is determined by equating equations (10) and (11) according to Equations (12) and (13). The resulting expression of probability (P = α_c) that defines the critical filament strength σ(P=α_c) is:

$P={\alpha }_c=1-\mathrm{e}\mathrm{x}\mathrm{p}(-{\displaystyle \frac{1}{m}})$ (14)

The same expression was derived from the force-stress relation during a tensile test (equations (5) and (6)):

${\displaystyle \frac{dF}{d\sigma }}=0$ (15)

Therefore, this shows that the citical fiber that initiates unstable failure under force-controlled loading (with strength denoted σ(F_max) given by equation (15)) corresponds to the critical filament with strength σ(P=α_c).

Figure 10 compares the stress increase Δσ_a (equation (11)) under applied constant load with the strength gradient Δσin a Nicalon SiC fiber tow (equation (10)). It shows that under such loading condition, Δσ_a > Δσ${\alpha }_c)$ beyond the point of intersection of Δσ_a and Δσcurves when P = 0.17. _c = 0.17 is given by equation (14) for the value of m = 4.8.

3.1.2. Stable Failure Under Strain-Controlled Conditions

There is theoretically no overloading of surviving fibers from the failure of a filament, when the strain on filaments is kept constant by boundary conditions during fiber break. The demonstration of this statement is based on the following equations of compliances and forces when tow deformation is constant when a filament breaks:

$u=C_1{\left(n\right)F}_1\left(n\right)=C_2(n+1)F_2(n+1)$ (16)

where u is deformation, C₁ and C₂ are compliances, and F₁ and F₂ are the corresponding forces before and after failure of a filament. n is the number of filaments broken previously.

As the compliance increases with the amount of damage, C₂ > C₁ which implies that F₂ < F₁. Therefore the force induced by the applied deformation decreases when a filament breaks. There is no overload on the intact filaments. Thus Δσ_a = 0 and the condition of unstable failure is not fulfilled, unless an extra load operates. It can be generated by an artifact such as the load train deformation, and inter-fibre friction [23, 27].

The phenomenon of controlled failure of fiber tows is well illustrated by the experimental force strain curves obtained on various fiber tows. Figure 3 and Figure 9 show that the tensile force-strain curves of tows do not exhibit unstability at maximum force, but instead a stable force decrease until ultimate failure of tow. The tow strength under strain controlled condition corresponds to the strength of the strongest filament in the tow.

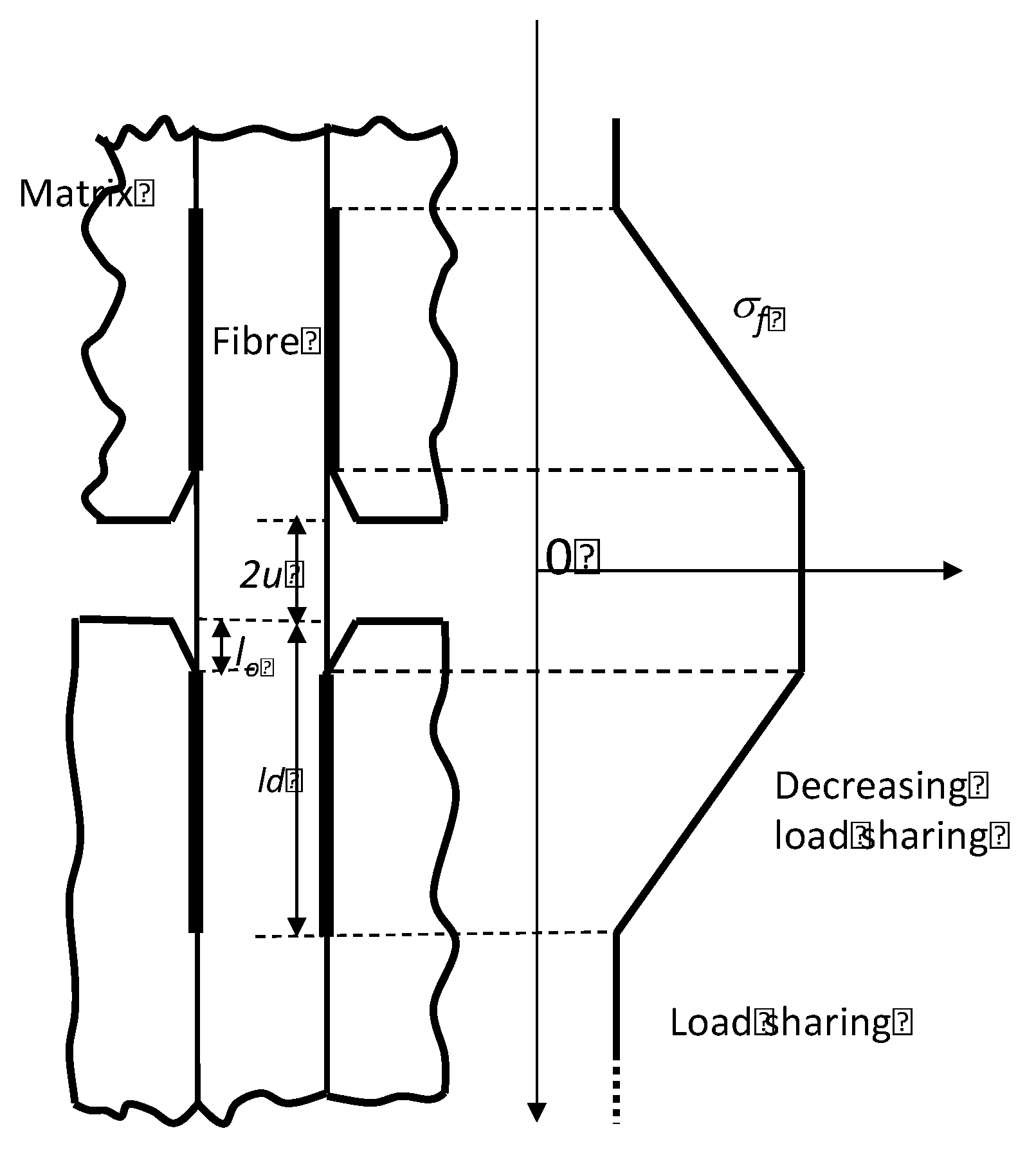
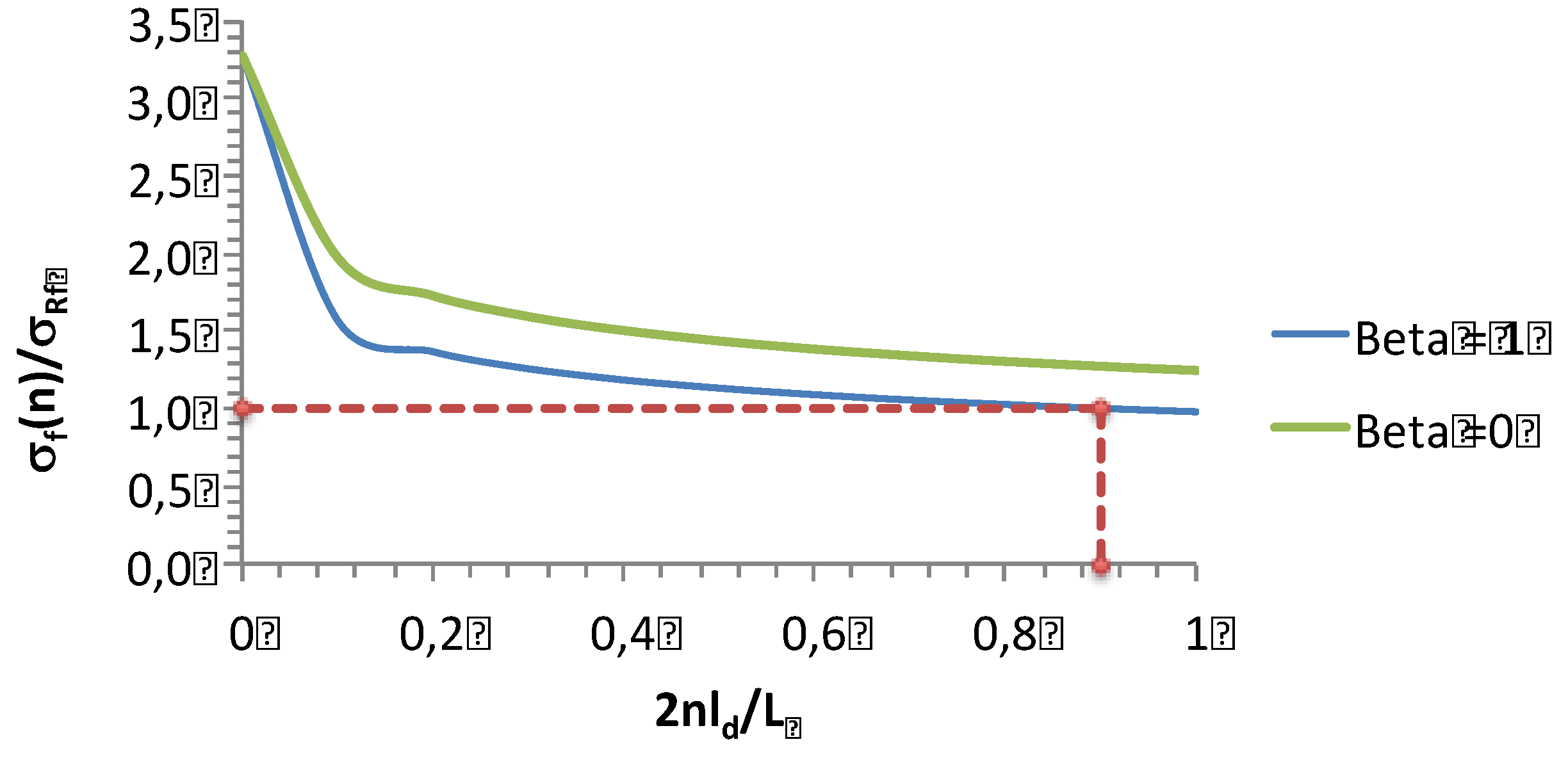
3.2. Fracture of Minicomposites

3.2.1. Model

We consider here a minicomposite reinforced by parallel continuous fibers, and subjected to a tensile load in fiber axis direction. When a crack is created in the matrix, it is perpendicular to the load direction, and it propagates throughout the matrix, leading to two new fragments with cross section S_m (Figure 4). The stress state is affected by the crack and the fiber/matrix debonding (Figure 11).

The tensile stress–strain behaviour of minicomposites is dictated by fiber deformations and failure. The stress-state in fibers is determined by the number of fragments and debonded length. For a single crack, the failure probability of a fiber can be calculated from the following Weibull equation assuming a volume-located fracture origin:

$P_f\left(1\right)=1-exp\left[-2S_f{\int }_0^L{\left({\displaystyle \frac{{\sigma }_f}{{\sigma }_{0f}}}\right)}^{m_f}dx\right]$ (17)

where S_f is the cross-sectional area of the considered fiber, m_f and σ_0f are the Weibull statistical parameters, σ_f is the stress operating on fiber, L is gauge length.

Incorporating equations of σ_f (Appendix A) in equation (17) and integrating by considering that the fiber is made of (n+1) volume elements associated to the n matrix cracks, leads to the following equation for the failure probability of the fiber in the presence of n matrix cracks [37]:

$P_f\left(n\right)=1-exp\left[-{\left({\displaystyle \frac{{\sigma }_f\left(n\right)}{{\sigma }_{0f}}}{\displaystyle \frac{1}{\left(1+a\right)}}\right)}^{m_f}{V}_{of}(2n{\displaystyle \frac{l_d}{L}}A+1)\right]$ (18)

with:

$A=\left({\displaystyle \frac{u}{l_d}}+\beta \right){(1+a)}^{m_f}-{\displaystyle \frac{1-\beta }{m_f+1}}\left({\displaystyle \frac{1-{\left(1+a\right)}^{m_f+1}}{a}}\right)-1$ (19)

with β = l₀/l_d. l_d is the length of the portion of debonded fiber, and l_o is the length of the portion of debond without fiber/matrix interaction, u is half the opening distance of a matrix crack, a =  is the load sharing parameter, V_f and V_m are the volume fractions of fiber and matrix respectively, E_f and E_m are fiber and matrix Young’s moduli.

The statistically equivalent volume of fiber V_Ef (n) under uniform stress σ_φ (n) that corresponds to the same value of probability under uniform σ_Rf on volume V_0f is:

$V_{Ef}\left(n\right)={\displaystyle \frac{V_{of}}{{\left(1+a\right)}^{m_f}}}\left[(2n{\displaystyle \frac{l_d}{L}}A+1)\right]$ (20)

The failure stress _f (n) is related to the reference strength σ_Rf of the fiber tested separately under a uniform tensile stress, by the following equation obtained by equating the corresponding equations of failure probability:

${\sigma }_f\left(n\right)={\sigma }_{Rf}{\left[{\displaystyle \frac{V_{0f}}{V_{Ef}}}\right]}^{{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$m_f$}\right.}}={\sigma }_{Rf}{(1+a)\left[(2n{\displaystyle \frac{l_d}{L}}A+1)\right]}^{{\displaystyle \raisebox{1ex}{$-1$}\!\left/ \!\raisebox{-1ex}{$m_f$}\right.}}$ (21)

3.2.2. Implications

Figure 12 shows variation of ratio σ_φ(n)/σ_rF as a function of 2nl_d/L. It appears that the resistance of filament σ_f(n) in the presence of matrix is significantly larger than the reference filament strength σ_Rf as a result of the contribution of the matrix to load carrying. As the number of matrix cracks increases, σ_f(n) approaches σ_Rf with the decreasing contribution of the matrix load carrying capacity. The curves of Figure 12 show the trend for two extreme values of β: βwhen are fiber/matrix interactions along the total debond length, and β =1 when there are no interactions in the debonded zone. Figure 12 shows that in the first case, filament failure occurs after saturation of matrix cracking (2nl_d/L >1); in the second case it occurs before matrix cracking saturation (2nl_d/L =0.9). Variability in β is thus a source of variability in the corresponding strain-to-failure.

The ratio ${\displaystyle \frac{{\sigma }_f\left(n\right)}{{\sigma }_{Rf}}}=1$ is the criterion of failure of a filament. The ultimate fracture of minicomposite requires that the failure of critical filament triggers the fracture of the filaments carrying the load. As shown in a previous section about tow unstable fracture, the criterion of propagation of filament fracture is satisfied in the case of force-controlled loading condition (Figure 10). Therefore, under force-controlled loading, a minicomposite should theoretically fail at maximum force.

By contrast, the criterion of unstable failure is not satisfied under strain-controlled condition, as discussed in previous section. To be satisfied, it requires that an overload be generated. This can result from various possible phenomena: a brutal transfer of the matrix stress onto the fibers, or fiber/matrix friction, or end effects, or dynamic effects. Calculation shows that the overload corresponding to matrix stress after saturation is too small to satisfy the criterion of unstability. Fracture from end effects was found to be erratic on tows [20], but it can operate. Dynamic effects have not been investigated deeply.

The friction of a broken filament on the matrix seems to be a plausible cause of overloading. The resistance to sliding generates a tensile stress opposite to applied stress on the matrix, given by the following equation:

${\sigma }_{\varphi }={\displaystyle \frac{2l}{r}}\tau$ (22)

where l is the sliding length i.e the length of filament after saturation of matrix cracking, r is fiber radius.τis the interfacial shear stress at fiber/matrix interface. According to friction law, τis defined as:

$\tau ={\tau }_O-\omega {\sigma }_{rr}$ (23)

where is the coefficient of friction, σ_rr is radial compressive stress on filament. The tensile overstress σ_φ is transferred onto the intact filaments by the matrix. It_increases with the number of filaments broken in order of increasing strength, which generates a loading mode of controlled-force on the fibers. Unstable failure occurs when the overstress σ_{φ }strength gradient Δσaccording to the criterion discussed in section 3.1.1.

Since the ratio l/r is very large for small diameter filaments (of the order of 10⁴), very small values of τ (of the order of magnitude of a few pascals) are required to satisfy the failure criterion shown on Figure 2. Variation of σ_φ and particularly of τ is a source of scatter on the critical fiber and consequently on the failure stress, as shown on Figure 10. σ_φ is not determined by the applied strain but instead by uncontrolled filament friction. As a consequence, the overload may take any value so that the failure strength of the minicomposite may be larger or smaller than the critical strength defined by the maximum force on tow as shown on Figure 10. The experimental data given in Table 1 support these result. σ_φ depends on interphase and fiber surface roughness. The strain-to-failure tends to decrease when roughness or grain size increases (Table 1).

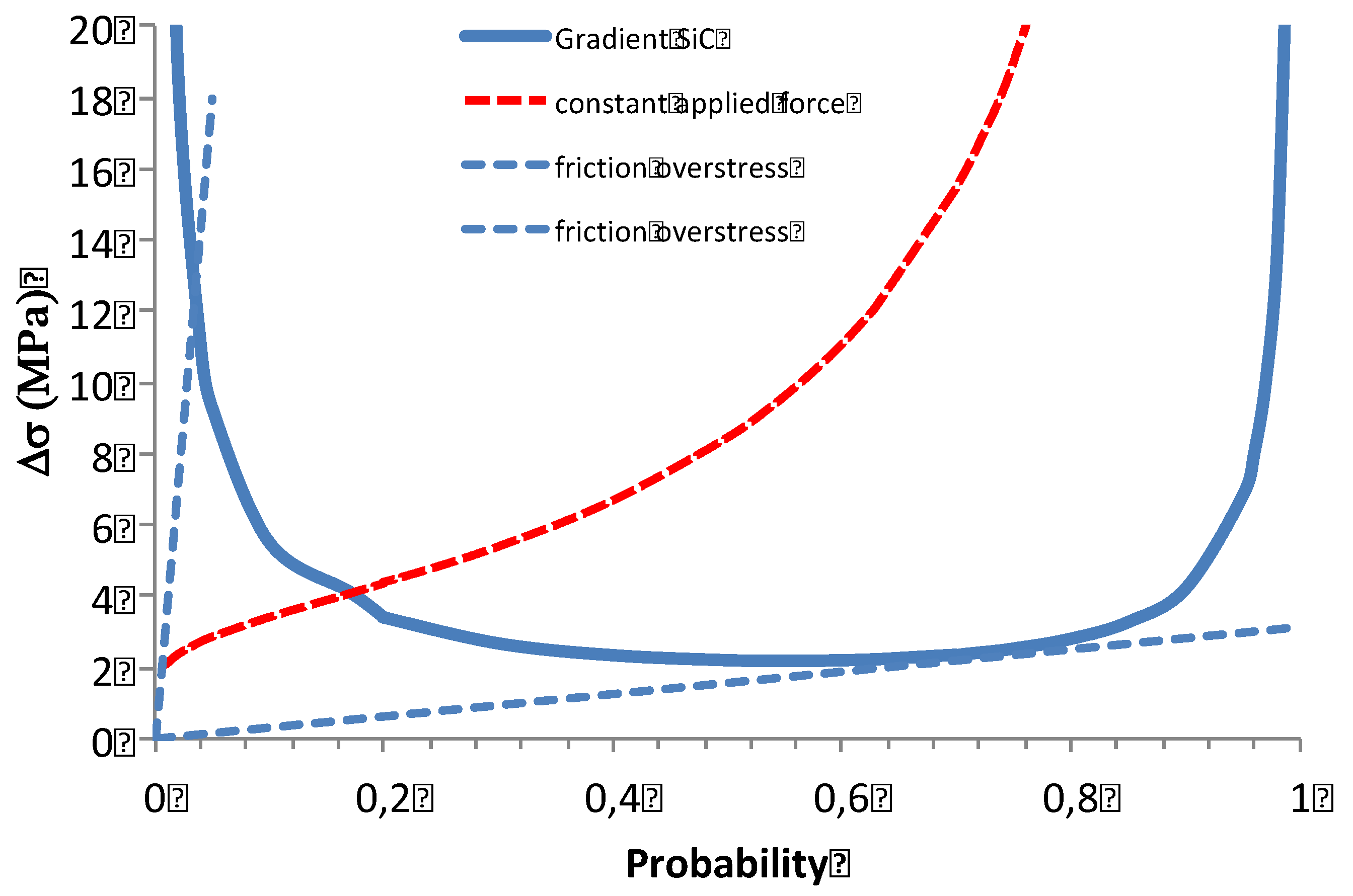
4. Variability of Ultimate Strength

4.1. Characterization of Variability

Strength variability was described using p-quantile diagrams (appendix B):

$z_p={\mathsf{\Phi }}^{-1}\left(p\right)={\displaystyle \frac{{\sigma }_p-\mu }{s}}$ (24)

where p=i/(n+1), μ = mean, s = standard deviation, σ_p is the value of strength with probability p, and Φ is the cumulative standard normal distribution of variable z.

$\mathsf{\Phi }\left(z\right)={\displaystyle \frac{1}{s\sqrt{2\pi }}}{\int }_0^z\mathrm{e}\mathrm{x}\mathrm{p}(-{\displaystyle \frac{{(t-\mu )}^2}{2s^2}})dt$ (25)

It is demonstrated (Appendix 2) that when the linearity of the plot of the p-quantile z_p vs. σ_p is linear according to equation (24) it can be concluded that the strength is a Gaussian variable.

Therefore, the normal cumulative distribution function (CDF) can be calculated using Equation (25) for the values of the mean μ and standard deviation s of the sets of experimental strength data. If necessary, Weibull parameters can be derived from  and s, using the 1st moment method [27]. The validity of Weibull function can be assessed by comparing the CDF to the reference normal distribution [27].

This approach was preferred to represent the variation of ultimate strengths, as the p-quantile diagrams provide a way to evaluate the pertinence of available distributions functions, such as the normal and then the Weibull distribution functions [25]. The ultimate strength of composites results from an erratic overload that is dictated by impredictable parameters like interface caracteristics and fiber surface. Therefore, the pertinence of a formal distribution function may be questioned a priori.

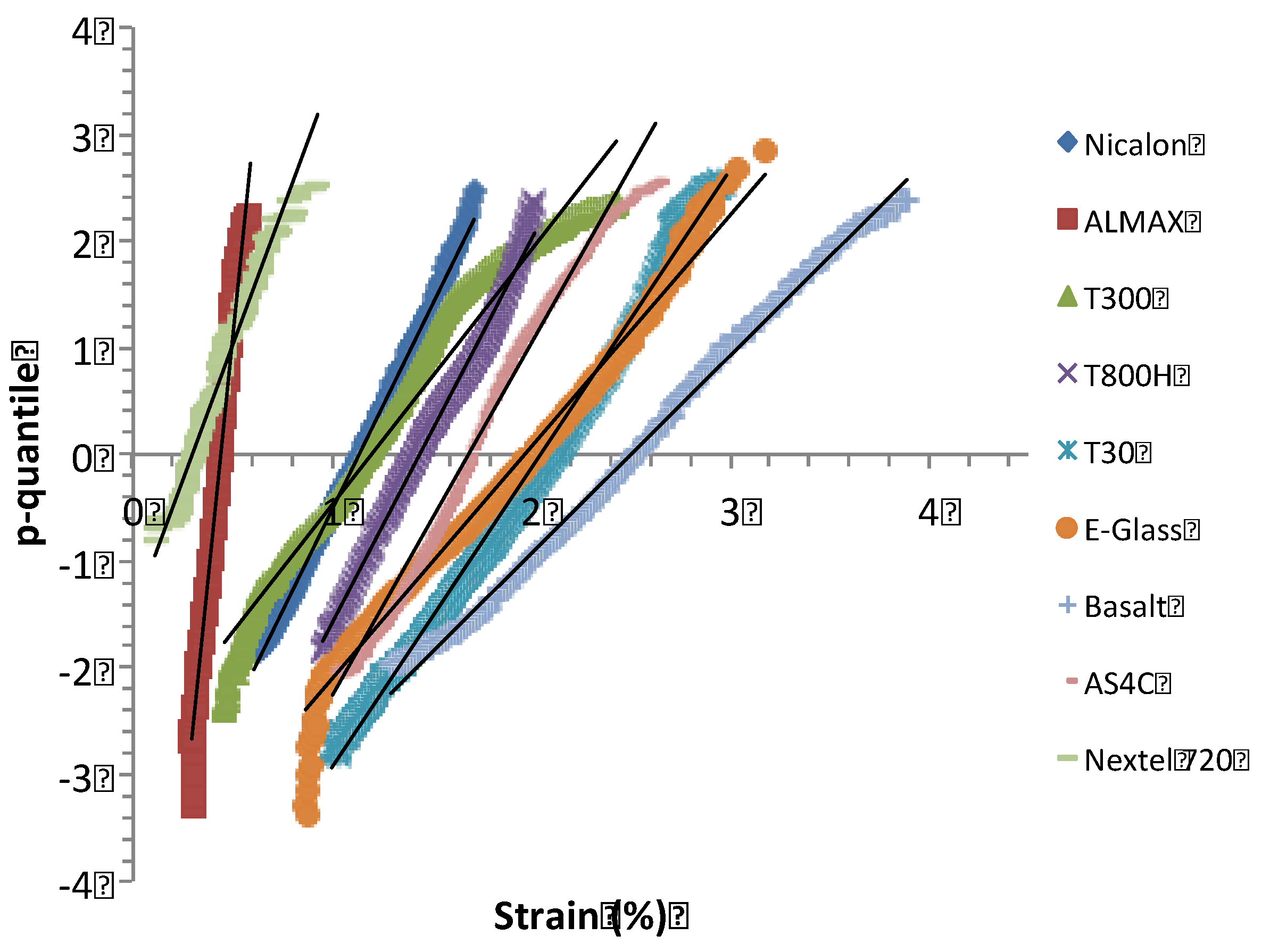
4.2. Filaments

Figure 13 shows that the plots of p-quantile z_p versus failure strain ε_p, for filaments in various fiber tow types, fit straight lines [27]. This indicates that the filaments strengths are characterized by normal distribution function. The excellent goodness of fit is characterized by high values of coefficients of linear regression (R2 > 0.99, except for T300 (R2 = 0.97)). The plots indicate clearly the respective means (for z_p = 0) and the dispersion of strength data (by the slope = 1/s). Quite identical parameters μ and s were estimated on the three SiC Nicalon fiber tows tested [26]. This remarkable result will support important conclusions on the variability of tow strengths, and the reproducibility of populations of critical flaws.

It was checked that the Weibull distribution function fitted satisfactorily the normal distribution of experimental strength data [27]. The Weibull parameters were derived from the mean and standard deviation using the moment method.

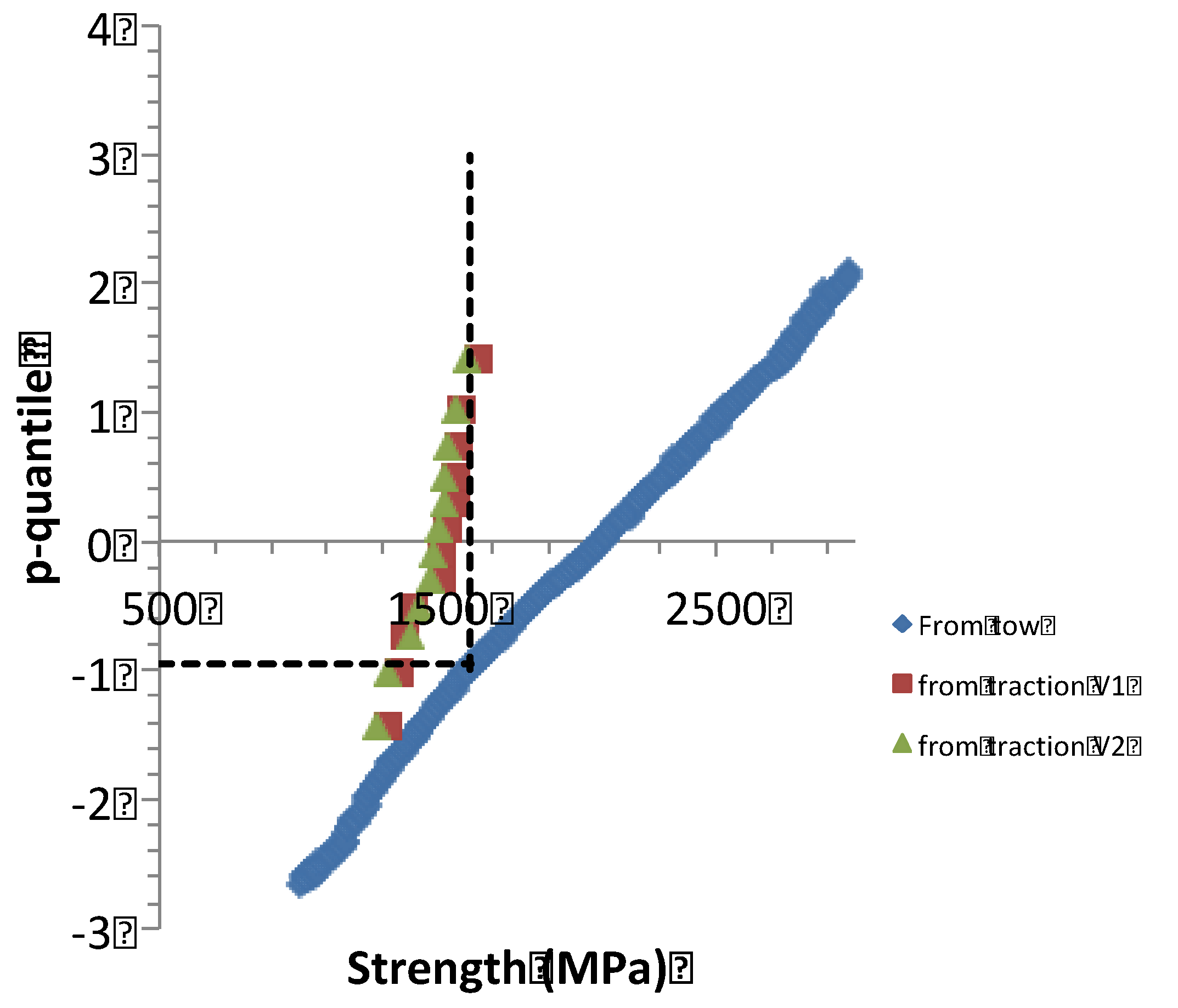
4.3. Fiber Tows

P-quantile diagrams cannot be plotted for fiber tow strengths because the tow failure stress (or strain) depends on the loading mode (strain- or force-controlled). Then, the stress at instability observed during tests under strain-controlled loading results from an artifact. Therefore, it cannot be regarded as a valuable characteristic of tow strength.

The theoretical tow strength is given by the strength of critical filament defined by P=α_c (in the distribution of filament strengths obtained during sound test under strain-controlled condition) which coincides with the stress at maximum force under force-controlled load ((F_max)). The uniqueness of this specific strength is supported by several arguments. The equations (14) and (9) respectively show that the conditions of initiation and propagation are independent of N₀ the initial number of filaments in tows. The equation (14) indicates that the critical fiber depends on m only. Then, the coefficient of variation Cv and the standard deviation of maximum force s(Fmax) approach 0 when N₀ increases, according to the following equation (24) [21, 33, 38, 39]:

$CV\left(F_{max}\right)={\displaystyle \frac{s\left(F_{max}\right)}{\mu \left(F_{max}\right)}}=\sqrt{{\displaystyle \frac{{P(F}_{max})}{N_0(1-{P(F}_{max})}}}$ (26)

where s(F_max) is the standard deviation of F_max, μ is the mean.

Typically, values as large as 500, 1000, or much more are observed on ceramic and carbon fiber tows.

Finally, it was shown on Nicalon SiC tows that when gauge lengths > 60 mm, the force-strain curves do not exhibit variability since they contain the total population of critical flaws inherent to the fibre type considered [26]. As a consequence, for this range of gauge lengths, the tow behavior is insensitive to gauge length, as well as the corresponding critical filament strength at maximum force that should show no variability.

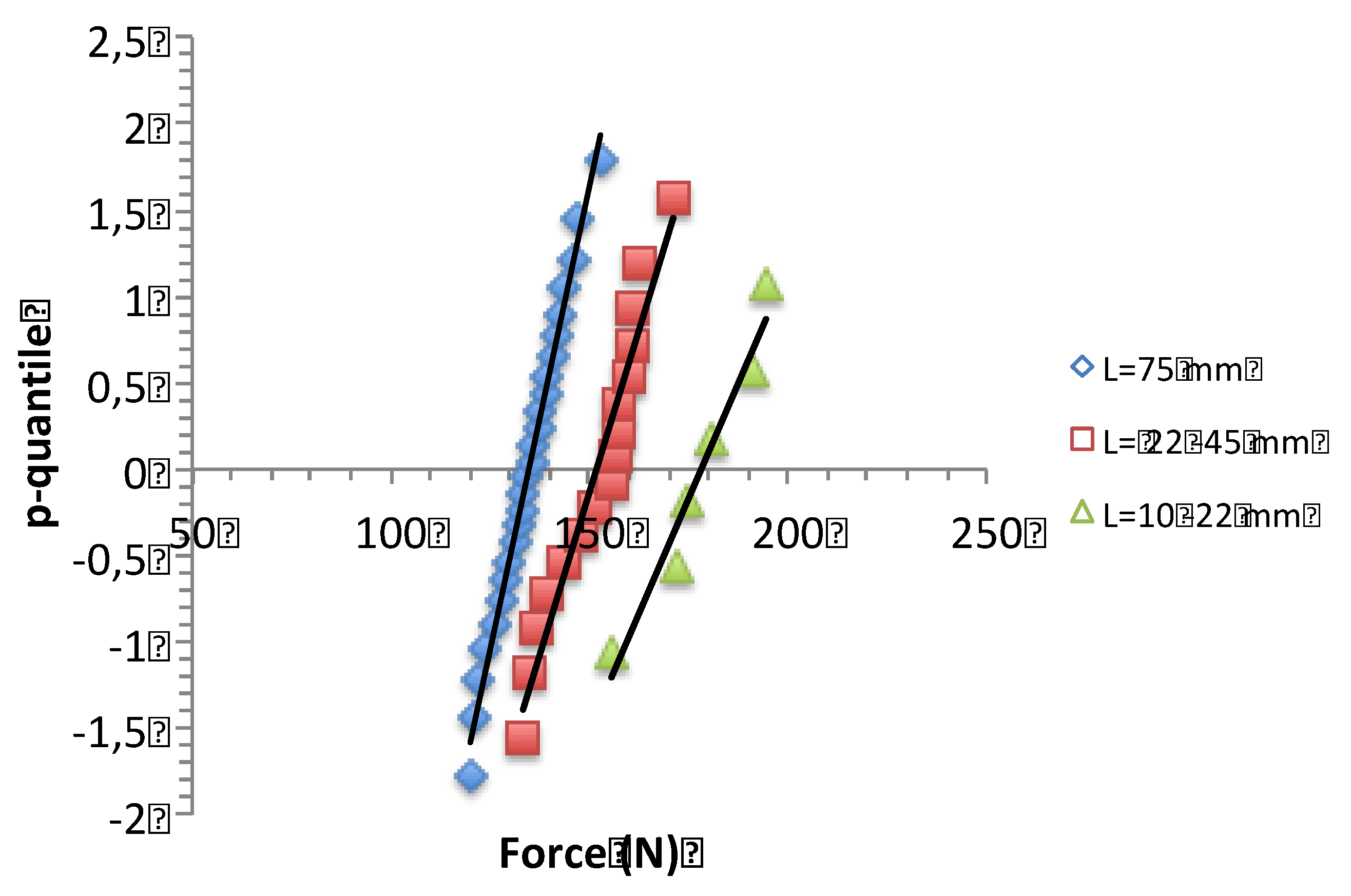
4.4. Minicomposites

Figure 14 shows the p-quantile diagrams obtained during successive tensile tests on SiC/SiC minicomposites. Failure forces instead of stresses were plotted because the load is carried essentially by the fibers as a result of the presence of transverse cracks throughout the matrix (Figure 2 and Figure 5).

A second batch of 16 tests specimens was prepared with parts of broken testspecimens from the initial batch of 26 testspecimens. A third batch of 6 specimens was obtained from the second batch. The gauge lengths were 75 mm first, then between 22 and 45 mm for the second series, and between 10 and 22 mm for the third series.

It is worth pointing out first that the p-quantile diagrams are appropriate to describe the strength variability of minicomposites, as they exhibit remarkable linearity (R2=0.99), for the specimens of the first batch. The diagrams at shorter gauge lengths show acceptable linearity with R2=0.97. These results indicate that the strength characterized by the failure force follows normal distribution.

Table 2 summarizes the values of statistical parameters. It can be noted that the Weibull modulus is whereas the coefficient of variation is much smaller larger when compared to filaments, which indicates a comparatively limited variability. The statistical parameters depend on gauge length, except the coefficient of variation. As such, the Weibull parameters do not allow predictions of minicomposite strengths at different sizes.

The strength increase with decreasing gauge length shown by Figure (Figure 14) can be logically attributed to two causes : (1) the variation in overload related to the length of the sliding zone after saturation of matrix cracking : when the minicomposite length decreases, the friction resistance decreases and the force at failure increases ; or (2) the elimination of some fraction of weaker filaments, so that the flaw population shrinks with increasing amount of stronger filaments leading to tow strengthening. This effect implies that the tow does not contain the total population of critical flaws that is inherent to the considered tow type, and hus, is not reproducible in the specimens. This point was discussed in [26]. It was shown that the Nicalon SiC tows contain the total population of critical flaws when gauge lengths > 60 mm. For the range of gauge lengths < 60 mm, the tow strength was found to be sensitive to gauge length.

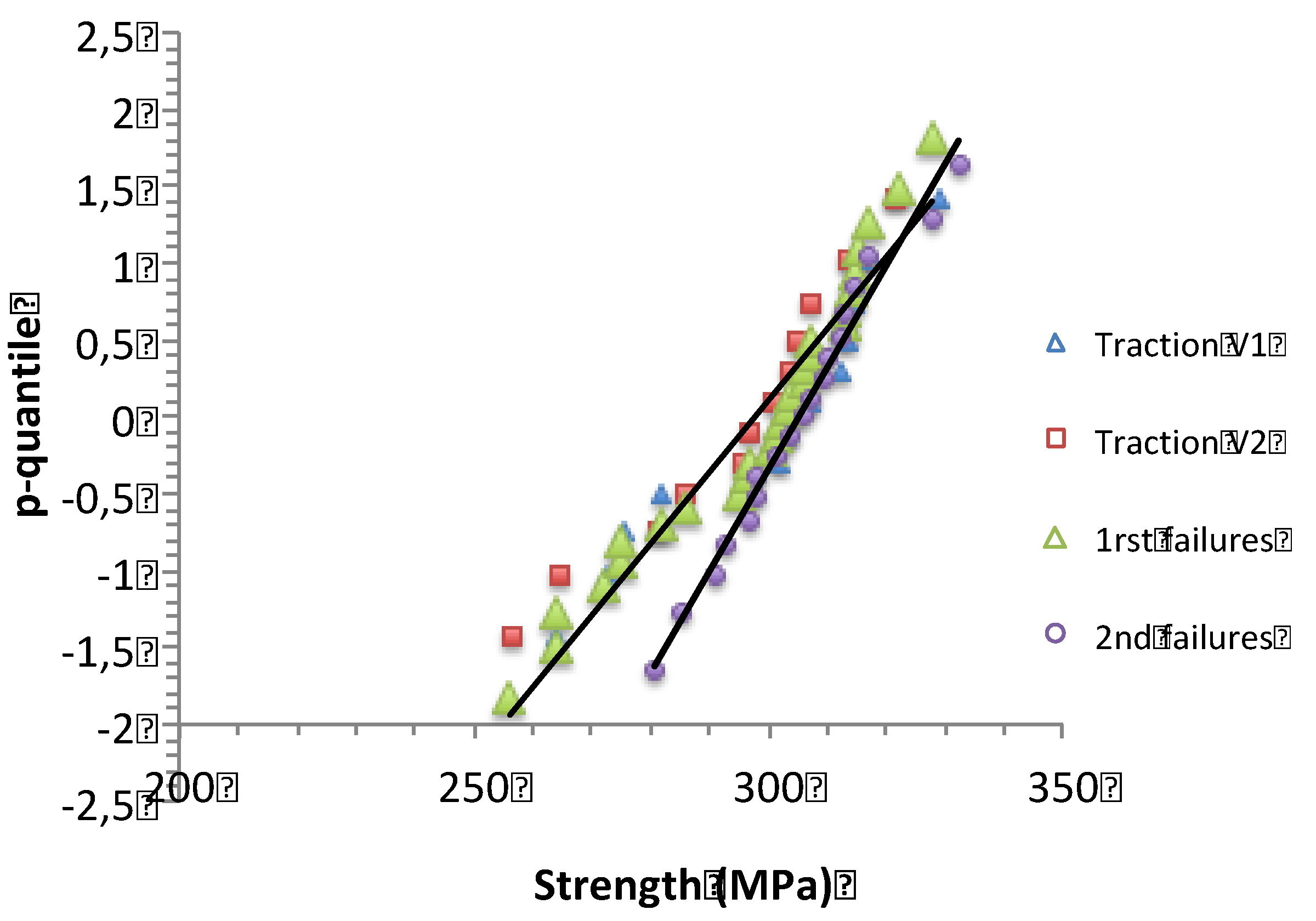
4.5. Composite Test Specimens

4.5.1. Tensile Strengths

Tensile behavior curves were determined on two batches of 12 dogbone shaped-specimens having small (V₁= 8x30x3.3 mm³) and large (V₂=16x120x3.3 mm³) volumes.

Then, additional curves were determined on batches of testspecimens made of broken parts : a batch of 19 specimens was prepared from the initial batch of 24 specimens having a 120 mm gauge length, and finally a batch of 4 specimens was prepared from the broken pieces of the second batch. The specimen gauge lengths were 120 mm for the initial batch, and between 20 and 100 mm the 2nd and 3nd batches. Two aluminium end-tabs were glued to the end of the largest piece obtained after the failure of each dogbone shaped specimen. The third series of test results was not analyzed because the number of data was considered to be insufficient.

The strain–stress curves obtained were approximately identical for all the specimens except at ultimate failure [21]. The p-quantile vs strength diagrams looked linear (Figure 15) with high values of correlation coefficients : R2=0.97 for V1, V2 and first failures, and R2 = 0.99 for the second failures. This indicates that the distributions of tensile strengths can be approximated by normal distribution function. The statistical parameters are quite close, and significantly different from those pertinent to the single filaments (Table 2). The large values of Weibull modulus and the small values of standard deviation and coefficient of variation CV characterize a limited variability. Furthermore, m and CV are close to those obtained on minicomposites.

Figure 15 also shows that the p-quantile-strengths diagrams are superimposed, despite discrepancy at the low strentgh extreme of the second failure data. Moreover, it worth pointing out that, although the second failures refer to various gauge lengths (20<L <100 mm), their distribution is very close to those obtained at a constant gauge length. Therefore, it can be concluded that all the results indicate that the composite strength does not depend on specimen size. This feature may be attributed to small variability in critical filament strength and overload, according to Figure 10. Then, the volume increase did not induce strength weakening, which means that significantly weaker critical flaws were not present in larger specimens. This suggests that the population of critical flaws in tows was reproducible and representative of the population of flaws inherent to fiber tows. Which agrees with the huge numbers of filaments in the 2D Nicalon/SiC testspecimens that contained 60 tows of 500 filaments and thus more than 30 000 critical flaws. This has been discussed and assessed in a previous paper [26].

4.5.2. Relation filament vs Composite Strengths

Strengths of critical filaments in 2D woven SiC/SiC composites were derived from the composite strengths (σ_comp) using the following commonly accepted equation:

${\sigma }_f={\displaystyle \frac{{\sigma }_{comp}}{V_f}}$ (27)

where V_f = 0.2 was the fraction of filaments in the loading direction.

Figure 15 compares the strengths of critical filaments in composite (σ_f) given by equation (27) to the strengths of filaments extracted from the typical force-strain curve of SiC Nicalon tows displayed on Figure 3. The estimated values of σ_f are close to the theoretical strength of critical filament in the tow defined by σ_φ(P=α_c). However, it is interesting to note that the σ_f estimates are smaller than σ_f(P=α_c). This result is consistent with the analysis. Furthermore, it is consistent with the catastrophic failure mode of composite at maximum force. Failure beyond the maximum force was never observed on the SiC/SiC composites. It is worth pointing out again that owing to the erratic contribution of overloading, the ultimate failure of composite under strain controlled condition is not related solely to the applied load, nor to the strength of underlying tow measured under strain-controlled condition. This is an important issue with a view to anticipate component ultimate strength when boundary conditions of loading are different from the test ones. As mentioned above, in the absence of structural effect, the ultimate failure of composite under strain controlled mode of loading would be dictated by the strength of the strongest filament in tow. The composite would exhibit smooth force decrease beyond maximum force and stable fibre pull out.

5. Conclusions

The ultimate strength of composites under strain controlled condition is not consistent with the failure of the underlying reinforcing tows. It is initiated by the failure of a critical filament, which is much weaker than the strongest filament that dictates the ultimate faillure of tows. Then, filament fracture propagates when the overstress generated by sliding of the broken filaments against the matrix exceeds the stress gradient in tow. This phenomenon can occur when the matrix fragmentation process of the matrix is saturated and the fibers are totally debonded from the matrix. In the particular case of Nicalon/SiC composites, the critical filament was found to be close to that filament defined by σ_f(P=α_c) in the distribution of filament strengths in tow, and also by the maximum force on tow loaded at a constant stress or strain rate. This discrepancy in critical fibers results from the scatter in overstress induced by erratic characteristics of fiber surface and fiber/matrix interface. The overstress depends on fiber grain size. Experimental results show that the ultimate strength of composite decreases with increasing fiber grain size and fiber/matrix interactions. The variability of these characteristics is unpredictable for a given fiber/matrix assembly.

Although the filament strength data follow normal and Weibull distributions, the critical filament defined by σ_f(P=α_c) and F_max is unique when the flaw population in tows is complete and the number of filaments is large. The saturation of flaw population was found to be effective above a critical gauge length (60 mm for Nicalon SiC filaments). Dependence of strength on gauge length was observed on minicomposites having gauge length < 75mm, whereas the composite showed independence on gauge length, and variability.

The normal distribution function was found to characterize satisfactorily minicomposite and composite strength scatter. The Weibull parameters estimated using the moment method were stable for the composite strengths but they varied with gauge length for the minicomposites. The p-quantile diagrams can be used to compare different composite sytems on testspecimens having the same size.

The ultimate failure of composites and minicomposites under strain controlled condition is not related exactly to the applied load, nor to the tow strength measured under strain-controlled condition. Contribution of overloading is an important issue with a view to anticipate component ultimate strength when boundary conditions of loading are different from the testing ones. However, the strength of the critical filament defined by σ_f(P=α_c) may provide a basis for component strength prediction and composite design, knowing that composite strength is insensitive to dimensions but it exhibits variation.