Numerical Analysis of Knudsen Number of Helium Flow Through Gas-Focused Liquid Sheet Micro-Nozzle

Preprint

Article

Numerical Analysis of Knudsen Number of Helium Flow Through Gas-Focused Liquid Sheet Micro-Nozzle

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Supplementary Material

supplementary.zip (0.53KB )

This version is not peer-reviewed

Submitted:

29 October 2024

Posted:

29 October 2024

You are already at the latest version

Alerts

Abstract

This work aims to verify whether the continuum mechanics assumption holds for the numerical simulation of a typical sample delivery system in Serial Femtosecond Crystallography (SFX). Knudsen numbers were calculated based on the numerical simulation results of helium flow through the gas-focused liquid sheet nozzle into the vacuum chamber, representing the upper limit of Knudsen number for such systems. The analysed flow is considered steady, compressible and laminar. The numerical results are mesh-independent, with a Grid Convergence Index significantly lower than 1 % for global and local analysis. The study is based on an improved definition of the numerical Knudsen number, a combination of cell Knudsen number and physical Knudsen number. In the analysis, no-slip boundary and low-pressure boundary slip conditions are compared. No significant differences are observed. The study justifies using computational fluid dynamics (CFD) analysis for SFX sample delivery systems based on the assumption of continuum mechanics.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

Serial Femtosecond Crystallography (SFX) [1] is a new technique that was enabled by intense, coherent and pulsed X-ray sources called X-ray free electron lasers (XFEL). It is used to study static and dynamic structures of protein crystals. In SFX micron-sized protein crystals are carried into an X-ray beam via very thin jets that are focused by the high-velocity gas flow. Such flow-focused jets [2], most commonly produced by Gas Dynamic Virtual Nozzles (GDVNs) [3,4], have jet diameters much smaller than Rayleigh jets. Due to the weak interaction between matter and X-rays, the diffraction of these protein crystals is rather low when the X-ray pulse hits the crystal. Signal can be increased by lowering the background scattering [5,6] coming from the water. This is done by reducing the jet diameter. Another way is to use helium as a focusing gas in a vacuum [4]. Sub-micron liquid sheet thickness jets can also reduce background scattering. Liquid sheets (also called flat jets) can be produced by colliding liquid jets [7,8,9,10,11,12,13,14,15,16,17,18] or by colliding gas jets with the middle liquid jet to achieve a sub-micron thickness [10,14,19,20,21,22].

Numerical simulations [23,24] have been used with experimental approaches to test the different nozzle designs for sample delivery systems. To choose the optimum microscopic nozzle size, gas compressibility and high velocity focusing gas, which flow along the microscopic jet in a vacuum, must be considered. The compressibility effects become important when Mach number,

M a = U / c

, a ratio of flow velocity

U

to the speed of sound

c

, is larger than 0.3. In sample delivery systems, the flow ranges from choked flow (

M a \approx 1)

[25,26] to supersonic regime (1 <

M a

< 5) [27], where the liquid sheet nozzle operates typically. Because of the gas expansion in the vacuum, its density is decreased, causing the mean free path of helium molecules to increase, where rarefied gas effects could become non-negligible.

A suitable gas flow formulation is characterised by the physical Knudsen number

{K n}_{p} = λ / L

, a ratio of the molecular mean free path

λ

to a characteristic length scale

L

. Depending on the value of Kn_p, gas flows are classified into four regimes [28]:

• Continuum regime (

{K n}_{p}

< 0.01): In this regime, the continuum assumption holds and the Navier–Stokes (N–S) equations with no-slip boundary conditions are used in numerical solutions.

• Slip flow regime (0.01 <

{K n}_{p}

< 0.1): The no-slip condition at the solid wall no longer holds, resulting in a slip velocity at the boundary. Although the Navier–Stokes equations are still applicable, slip boundary conditions are implemented to account for this effect.

• Transitional regime (0.1 <

{K n}_{p}

< 10): The continuum assumption and slip conditions start to break down.

• Free molecular regime (

{K n}_{p}

> 10): The continuum assumption is invalid, and the continuum theory can no longer be applied.

CFD solves Navier-Stokes equations based on continuum mechanics assumption. However, this approach can become questionable for the numerical simulations of micro-jets in sample delivery systems operating in a vacuum. The continuum mechanics assumption in these systems is generally justified with the evaluated integral Knudsen number based on overall global variables [24]. It was additionally shown that the cell Knudsen number should also be considered [29,30].

This study investigates the Knudsen number in detail, questioning whether the CFD approach, based on continuum mechanics assumption, is suitable for hypersonic compressible flow (

M a > 5)

in sample delivery systems considered here. Knudsen number is proportional (

{K n}_{p} \propto M a / R e

) to the ratio between Mach and Reynolds number

R e = ρ U L / μ

, the ratio between the gas density

ρ

, velocity

U

, characteristic length

L

and dynamic viscosity

μ

. Both, Mach and Reynolds numbers are proportional to the change of velocity if all other variables are kept constant. Therefore, when changing gas mass flow only, the Knudsen number remains constant since the ratio Ma/Re is independent of velocity

U

. In sample delivery systems, higher gas mass flow causes higher temperature drop. Because the speed of sound changes with temperature, the ratio Ma/Re is not constant when changing gas mass flow in these systems. However, the Knudsen number remains within the same order of magnitude, because Ma/Re does not change drastically. The investigated case in this paper is simulated for helium mass flow of 20.4 mg/min (with Mach and Reynolds number

M a \approx

R e \approx 31

), representing the upper limit for gas-focused liquid sheet nozzles, where typical helium mass flows around 10 mg/min is applied [20]. As explained before, the Knudsen number of the investigated case would remain of the same order of magnitude even for lower helium mass flows. In other sample delivery systems [25], the gas Knudsen numbers are lower due to the higher Reynolds numbers (up to 1200) and lower or similar Mach numbers. Thus, the presented study explores the upper limit of the expected Knudsen numbers in sample delivery systems.

The paper is divided into five sections. After the introduction, we define the Knudsen number and governing equations. In the third section, we introduce numerical methods and show the results of the grid convergence study. This is followed by presenting and discussing results where we focus on comparing results obtained with low-pressure boundary slip (LPBS) and no-slip boundary conditions. In the last section, we summarise our findings and conclusions.

2. Methods

2.1. Knudsen Number

Rarefied gas dynamics is characterised by the physical Knudsen number, where the free mean path

λ

is determined as:

λ = \frac{μ}{ρ} \sqrt{\frac{π m}{2 k_{B} T}},

(1)

where

μ

is dynamic viscosity,

ρ

density,

m

molecular mass,

k_{B}

Boltzmann constant and

T

temperature. As compared to the ideal gas law with

ρ = m p / (k_{B} T)

, Equation 1 can be rearranged to:

λ = \frac{μ}{p} \sqrt{\frac{π R T}{2}},

(2)

where

p

is pressure and

R

specific gas constant. For compressible flows, Knudsen number can be defined with physical Reynolds number

{R e}_{p} = ρ U L_{p} / μ

and Mach number

M a = U / c

, where

U

is fluid velocity magnitude,

L_{p}

physical characteristic length and

c = \sqrt{γ R T / M}

the speed of sound, defined by the ratio of specific heats

γ

, specific gas constant

R

, temperature

T

and molar mass

M

. The Mach, Reynolds and Knudsen numbers are related as:

{K n}_{p} = \frac{M a}{{R e}_{p}} \sqrt{\frac{γ π}{2}} .

(3)

In CFD, the cell Knudsen number

{K n}_{c} = λ / Δ x

is defined as the ratio between the mean free path

λ

to cell size

Δ x

. Alternatively, cell Knudsen number can be defined as:

{K n}_{c} = \frac{M a}{{R e}_{c}} \sqrt{\frac{γ π}{2}},

(4)

where

M a = U / c

is the local Mach number and

{R e}_{c} = ρ U Δ x / μ

is a cell Reynolds number. Hence, for the well-resolved flows, where the cell size is much smaller than the physical characteristic length, the cell Knudsen number is much larger than the physical Knudsen number

{K n}_{c}

{K n}_{p}

, meaning that the

{K n}_{c}

might exceed the continuum limit, while the

{K n}_{p}

stays in continuum regime.

The numerical Knudsen number

{K n}_{n} = λ / L_{n}

, which also affects the solution, is a combination of the physical and cell Knudsen numbers, determined by a soft-minimum function [29,30]:

{K n}_{n} = s o f t m i n ({K n}_{p}, {K n}_{c}) .

(5)

In [29], softmin function was proposed as:

{K n}_{n} = 10^{l n (\exp (\lg (K n_{p})) + \exp (\lg (K n_{c})))} .

(6)

For well-resolved flows, the numerical Knudsen number converges to a physical Knudsen number

{K n}_{n}

\to

{K n}_{p}

. At the same time, for the un-resolved flow where

{K n}_{c}

{K n}_{p}

, the numerical Knudsen number converges to cell Knudsen number

{K n}_{n}

\to

{K n}_{c}

. However, Equation 6 seems to turn the limits around because the result is closer to the higher value between

{K n}_{p}

and

{K n}_{c}

, therefore representing maximum rather than minimum, what is explained in 4.3. Definition of numerical Knudsen number. As an alternative to Equation 6 we propose:

{K n}_{n} = - l o g (e^{- {K n}_{p}} + e^{- {K n}_{c}}) .

(7)

which is a combination of softmin function and the log-exp-sum function [31-33]. Softmin function is analogous to softmax function (widely used in machine learning algorithms), while the log-exp-sum function is similar to [31].

Expression in Equation 7 has a downside for

{K n}_{p} \approx {K n}_{c} < 0

, because it returns a negative value, having no physical meaning. Furthermore, it can return

{K n}_{n} < m i n ({K n}_{p}, {K n}_{c})

which is also not expected since the numerical Knudsen number should lie within the interval (

{K n}_{p}, {K n}_{c}

) when

{K n}_{p} < {K n}_{c}

or (

{K n}_{c}, {K n}_{p})

when

{K n}_{c} < {K n}_{p}

. Therefore, we suggest the following condition for numerical Knudsen number

{K n}_{n, P}

in point

P (x, y, z)

, which limits the maximum

{K n}_{n, m a x} = m a x ({K n}_{p}, {K n}_{c})

and minimum

{K n}_{n, m i n} = m i n ({K n}_{p}, {K n}_{c})

based on

{K n}_{p}

and

{K n}_{c}

{K n}_{n, P} = \{\begin{matrix} {K n}_{n, m i n} & {K n}_{n, m i n} > {K n}_{n} \\ {K n}_{n} & {K n}_{n, m i n} < {K n}_{n} < {K n}_{n, m a x} \end{matrix} .

(8)

2.2. Governing Equations

Let us analyse steady, laminar, compressible helium flow in vacuum conditions. The flow has been resolved in ANSYS Fluent 2023R2 using a pressure-based solver. Historically, a density-based solver has been developed for compressible flows. In this paper, we used a pressure-based solver because of the intended future calculations of two-phase flow, where the Volume of Fluid (VOF) and density-based solver are incompatible. However, we did not find any difference between density-based and pressure-based solvers for typical SFX conditions, a conclusion to elaborate on in one of our future publications. The flow is described with continuity, momentum and energy equations, respectively:

\nabla \cdot (ρ v) = 0,

(9)

\nabla \cdot (ρ v v) = - \nabla p + \nabla \cdot \bar{τ},

(10)

\nabla \cdot (ρ c_{p} T v + \frac{1}{2} ρ {|v|}^{2} v) = - \nabla \cdot (v p) + \nabla \cdot (k \nabla T),

(11)

where

v

is the velocity vector,

p

pressure,

\bar{τ}

is viscous stress tensor, defined as

\bar{τ} = μ [(\nabla v) + {(\nabla v)}^{T}] - 2 / 3 μ (\nabla ∙ v) I

, where

μ

and

I

stands for dynamic viscosity and identity tensor, respectively,

c_{p}

is mass-specific heat at constant pressure,

T

is temperature, and

k

is thermal conductivity. Density is determined by the ideal gas law

ρ = p M / R T

, and dynamic viscosity from the Sutherland law

μ = A_{S} \sqrt{T} / (1 + T_{S} / T)

, with values for helium

A_{S}

= 1.48 e-06 kg/msK^1/2 and

T_{S}

= 79 K [32].

3. The Numerical Method

3.1. Spatial Discretisation

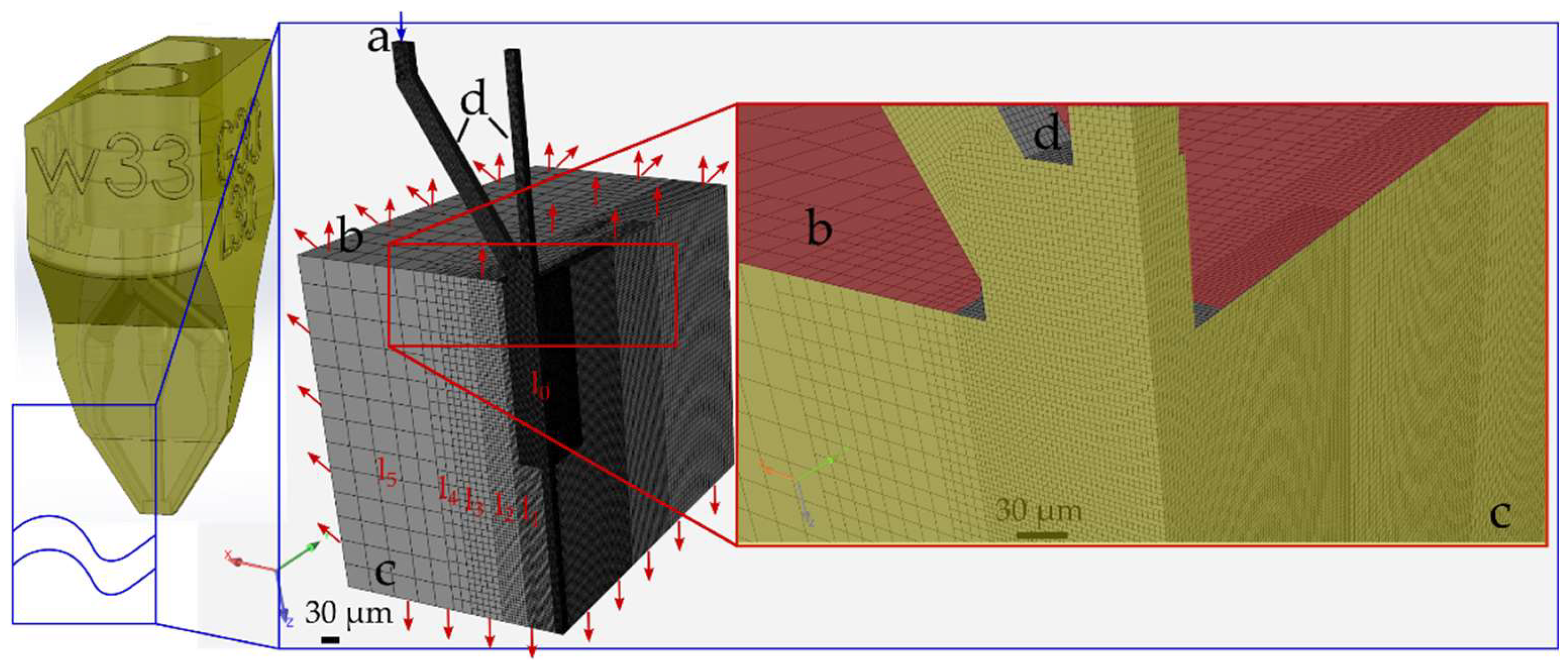
The computational fluid domain coincides with the bottom part of the gas-focused liquid sheet nozzle. Capillaries are long enough that a fully developed velocity profile is established. The computational structured mesh is hexahedral with 6 levels of refinement regions with non-conformal transitions. The cell size of the finest level is denoted as

Δ x_{0}

. The cell size of each next level is two times larger than the previous one

Δ x_{l} = 2^{l} Δ x_{0}

(level

l \in (0,5)

). Due to the symmetrical design, only a quarter of the nozzle was analysed to reduce the computational time, as shown in Figure 1, which shows the nozzle model and computational mesh. Three meshes, M1, M2, and M3, where M1 is the finest mesh and M3 is the coarsest, were generated in ANSYS Meshing to perform a grid independence study. The details of each mesh can be found in Table 1.

3.2. Boundary Conditions

The computational domain consists of four boundary patch types, i.e., mass flow inlet (20.4 mg/min), pressure outlet with zero-gauge pressure, symmetry, and wall (no-slip/LPBS, T=293 K), as demonstrated in Figure 1. The operating pressure is set to 1000 Pa.

An LPBS is used instead of no-slip boundary condition in the slip regime. Here, the gas-phase velocity at a solid surface differs from the velocity at which the wall moves and the gas temperature at the surface differs from the wall temperature. Due to their simplicity and effectiveness, Maxwell’s models are adopted in ANSYS Fluent to describe these physical phenomena [33]. The velocity slip is defined as:

U_{w} - U_{g} = (\frac{2 - α_{v}}{α_{v}}) K n L_{c} \frac{\partial U}{\partial n} \approx (\frac{2 - α_{v}}{α_{v}}) \frac{λ}{δ} (U_{g} - U_{c}),

(12)

V_{g} \equiv {(V ∙ n)}_{g} = V_{w} .

(13)

Here

U

and

V

represent the velocity components that are tangential and normal to the wall, respectively. The subscripts

g

w

and

c

indicate gas, wall and cell-centre velocities.

δ

is the distance from the cell centre to the wall.

L_{c}

is the characteristic length,

α_{v}

is the momentum accommodation coefficient of the gas mixture. Its value is calculated as the mass-fraction weighted average of each gas species in the system [33]. In our case, it equals unity. The mean free path is computed as follows:

λ = \frac{k_{B} T}{\sqrt{2} π σ^{2} p},

(14)

where

σ

is Lennard-Jones characteristic length, which equals to 260 pm for helium [34].

Equations 12 and 13 indicate that while the gas velocity component normal to the wall is the same as the normal velocity, the tangential components slip. The values lie somewhere between the cell-centre and the wall values. These two equations can be combined to give a generalised formulation [33]:

V_{g} = \frac{V_{w} + \frac{k}{δ} [(V_{w} ∙ n) n + V_{c} - (V_{c} ∙ n) n]}{1 + \frac{k}{δ}},

(15)

where

k = λ (\frac{2 - α_{v}}{α_{v}}) .

(16)

Temperature jump is defined as:

T_{w} - T_{g} = 2 (\frac{2 - α_{T}}{α_{T}}) K n L_{c} \frac{\partial T}{\partial n} \approx 2 (\frac{2 - α_{T}}{α_{T}}) \frac{λ}{δ} (T_{g} - T_{c}),

(17)

or equivalently

T_{g} = \frac{T_{w} + β T_{c}}{1 + β},

(18)

where

β = \frac{2 (2 - α_{T}) λ}{α_{T} δ},

(19)

α_{T}

is the thermal accommodation coefficient of the gas.

3.3. Solution Setup

Pressure-velocity coupling has been performed with Coupled scheme. The gradients were discretised with least square cell-based, and pressure was calculated using a Second-order equation. Density, momentum and energy equations were using the Second Order Upwind Scheme. Also, QUICK and MUSCL were tested for momentum equation, but no difference was observed except for 20-30 % longer calculation times. The solution procedure was solved using Pseudo Time Method, where Global Time Step was used. For more information, refer to [33].

3.4. Grid Convergence Study

Grid Convergence Study (GCS) was performed on meshes M1, M2 and M3 using local and global results. A well-known approach has been adopted [35,36] based on the Richardson extrapolation method. In local analysis, the calculated variables, such as velocity magnitude, pressure, temperature and density, were averaged at four different locations (lines). On the other hand, in global analysis, the maximum Mach number in the domain was selected as a representative integral variable.

In [35,36], it is suggested that for local analysis, a cell size

Δ x

is defined as a representative grid size

h = Δ x

. However, when analysing global integral quantities for three-dimensional calculations, a representative grid size is defined as:

h = {[\frac{1}{N} \sum_{i = 1}^{N} (Δ V_{i})]}^{1 / 3},

(20)

where

Δ V_{i}

is the volume of

i

-th cell, and

N

is the total number of cells used for the computations. We constructed meshes with grid refinement factor

r = h_{3} / h_{1}

larger than 1.3, recommended by Roache [35,36]. For meshes where

r_{21} = h_{2} / h_{1}

and

r_{32} = h_{3} / h_{2}

are not constant (

r_{21} \neq r_{32}

), order of convergence is defined using the following expressions:

p = \frac{|l n |\frac{ϵ_{32}}{ϵ_{21}}| + q (p)|}{\ln (r_{21})},

(21)

q (p) = \ln (\frac{r_{21}^{p} - s}{r_{32}^{p} - s}),

(22)

s = \frac{ϵ_{32} / ϵ_{21}}{|ϵ_{32} / ϵ_{21}|},

(23)

where,

ϵ_{32} = Φ_{3} - Φ_{2}

ϵ_{21} = Φ_{2} - Φ_{1}

and

Φ_{k}

denotes the solution on the

k

-th grid. As one can see, Equations 21 and 22 should be solved iteratively. Note that for

r_{21} = r_{32} = c o n s t

q (p) = 0,

and thus, there is no need for iterative calculations. The extrapolated value

Φ_{e x t}^{21}

is then calculated as:

Φ_{e x t}^{21} = \frac{r_{21}^{p} Φ_{1} - Φ_{2}}{r_{21}^{p} - 1} .

(24)

Similarly,

Φ_{e x t}^{32}

can be calculated as well. Two different errors are present: approximate relative error

e_{a}^{21}

and extrapolated relative error

e_{e x t}^{21}

, respectively:

e_{a}^{21} = |\frac{Φ_{1} - Φ_{2}}{Φ_{1}}|,

(25)

e_{e x t}^{21} = |\frac{Φ_{e x t}^{21} - Φ_{1}}{Φ_{e x t}^{21}}|,

(26)

Finally, the fine-grid convergence index is defined;

G C I^{21} = \frac{F_{S} e_{a}^{21}}{r_{21}^{p} - 1},

(27)

where the security factor

F_{S}

equals 1.25 for three meshes or more, as suggested by Roache [35].

G C I^{32}

and

e_{a}^{32}

are calculated analogously.

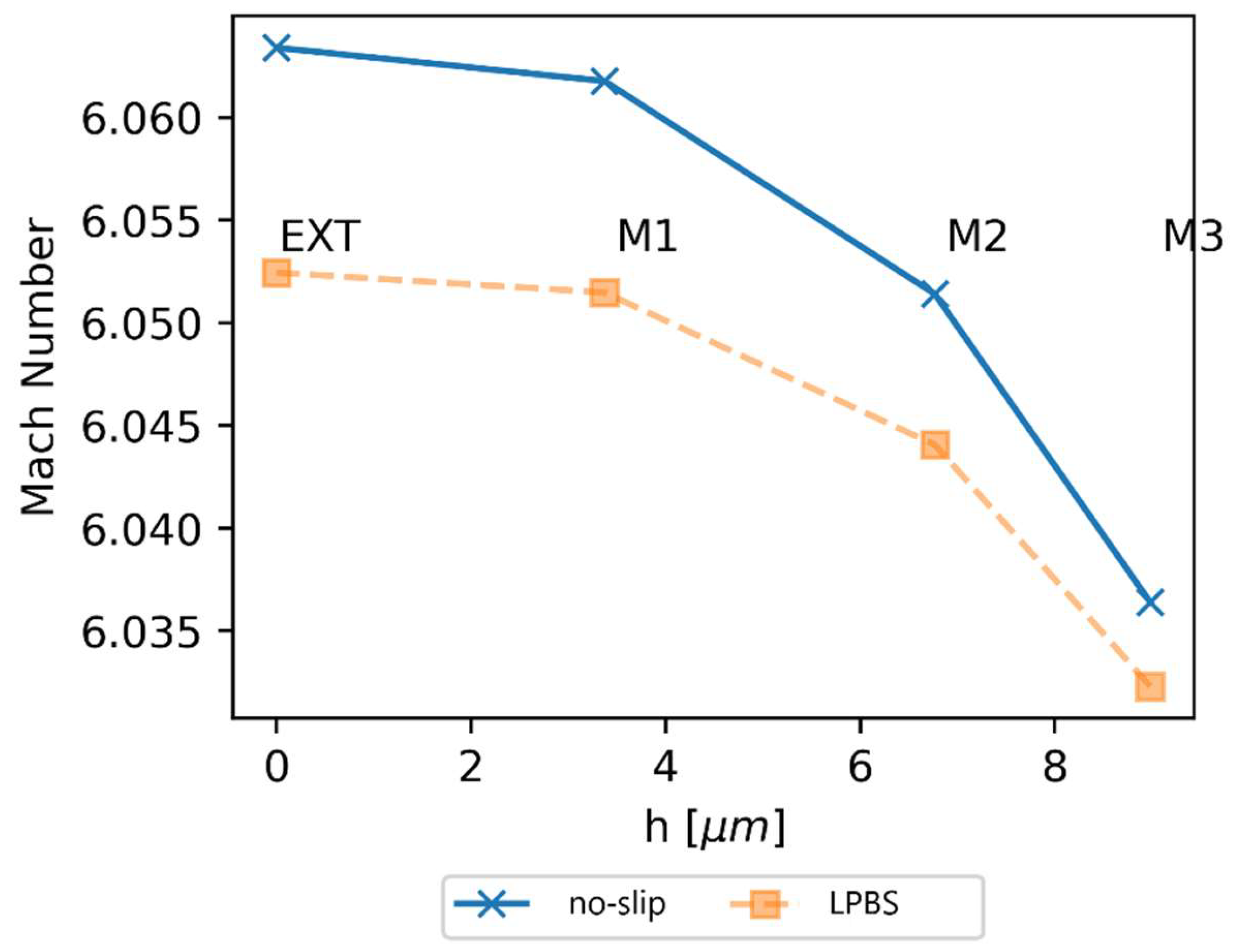
The results of the GCS (Table 2 and Figure 2) show that both

G C I^{32}

and

G C I^{21}

are low enough (< 1 %) that even the coarse mesh M3 provides a well-resolved solution. This indicates that the results are mesh-independent across all generated meshes with no significant differences observed in the local grid convergence study (Appendix A).

No major differences were found between LPBS and no-slip boundary, with maximum Mach number varying by less than 0.2 % for all three meshes and extrapolated values. Similarly, variables analysed in the local GCS match within significantly less than 1 % at most locations. Also, the

G C I^{32}

and

G C I^{21}

are significantly lower than 1 % globally and, in most cases, also locally. Thus, LPBS boundary condition does not significantly affect the solution, therefore no-slip boundary condition can be used in CFD of sample delivery systems in SFX

4. Results and Discussion

Numerical simulations using M2 and M3 meshes were performed on a desktop computer AMD Ryzen 9 7950X 16-Core Processor 4.50 GHz. Four cores were used for M3 and six for M2 mesh size. Calculations with M1 mesh were performed on multiprocessor server Supermicro SuperServer SYS-241E-TNRTTP with 4× Intel Xeon Gold 6448H processors, with a total of 132 cores, although only 4 cores were used for these calculations. Computational time (in core hours), the number of iterations and residuals criteria are listed in Table 1.

4.1. Flow Field Variables

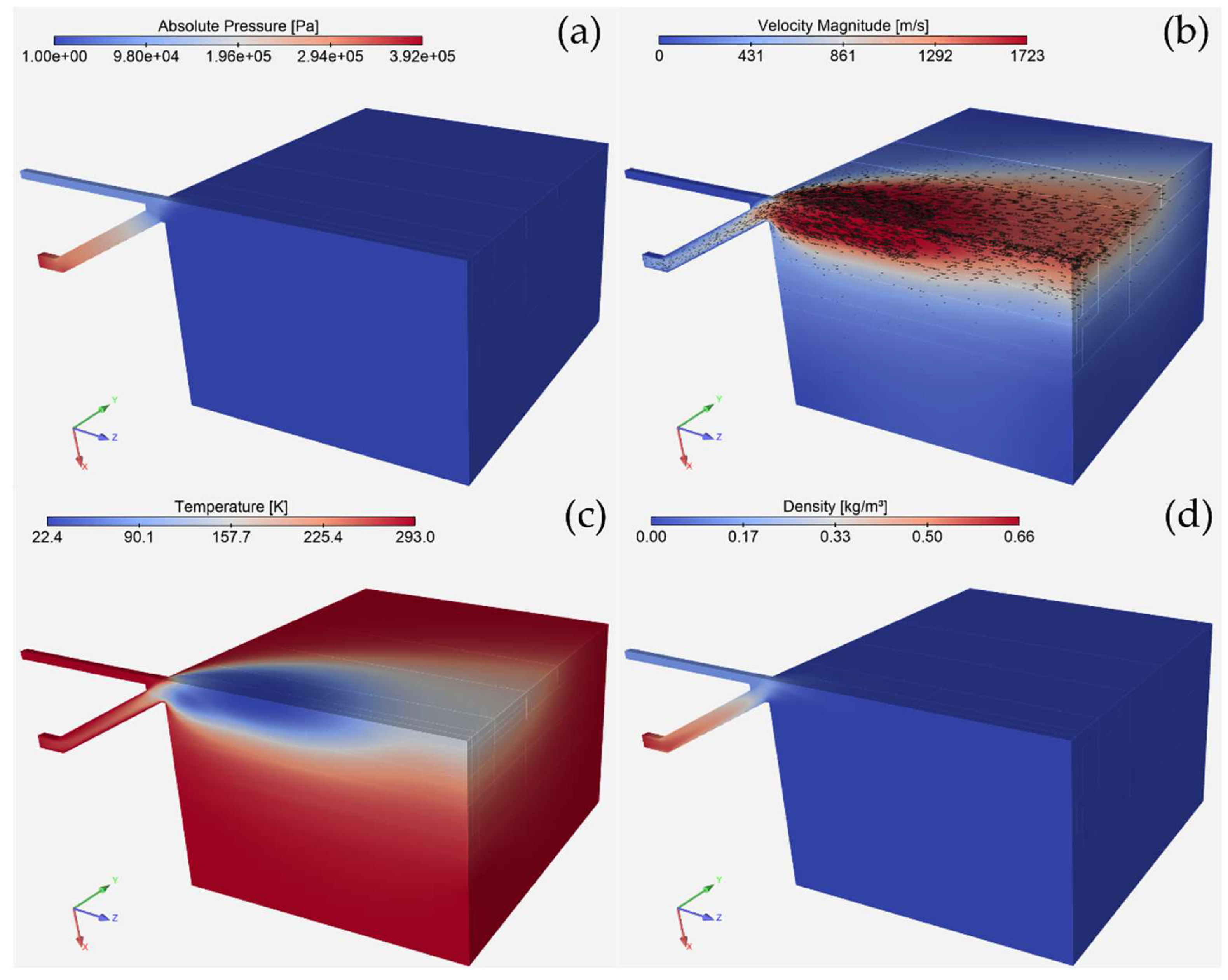
The Grid Convergence Study shows minimal differences in spatial discretisation and boundary types, so the results are presented only for M2 and no-slip boundary conditions. Figure 3 illustrates the converged solution for pressure, velocity, temperature, and density. For clarity, velocity vectors of only every 16th node are shown in Figure 3(b). When the gas from two oblique capillaries (one is across the symmetry ZY plane) collides in a common point, the gas flow expands radially. The helium jet expands after exiting the nozzle to the vacuum chamber, causing the temperature to drop, as shown in Figure 3(c). Due to the low pressure in the vacuum chamber the helium density significantly decreases (Figure 3(d)).

4.2. Dimensionless Numbers

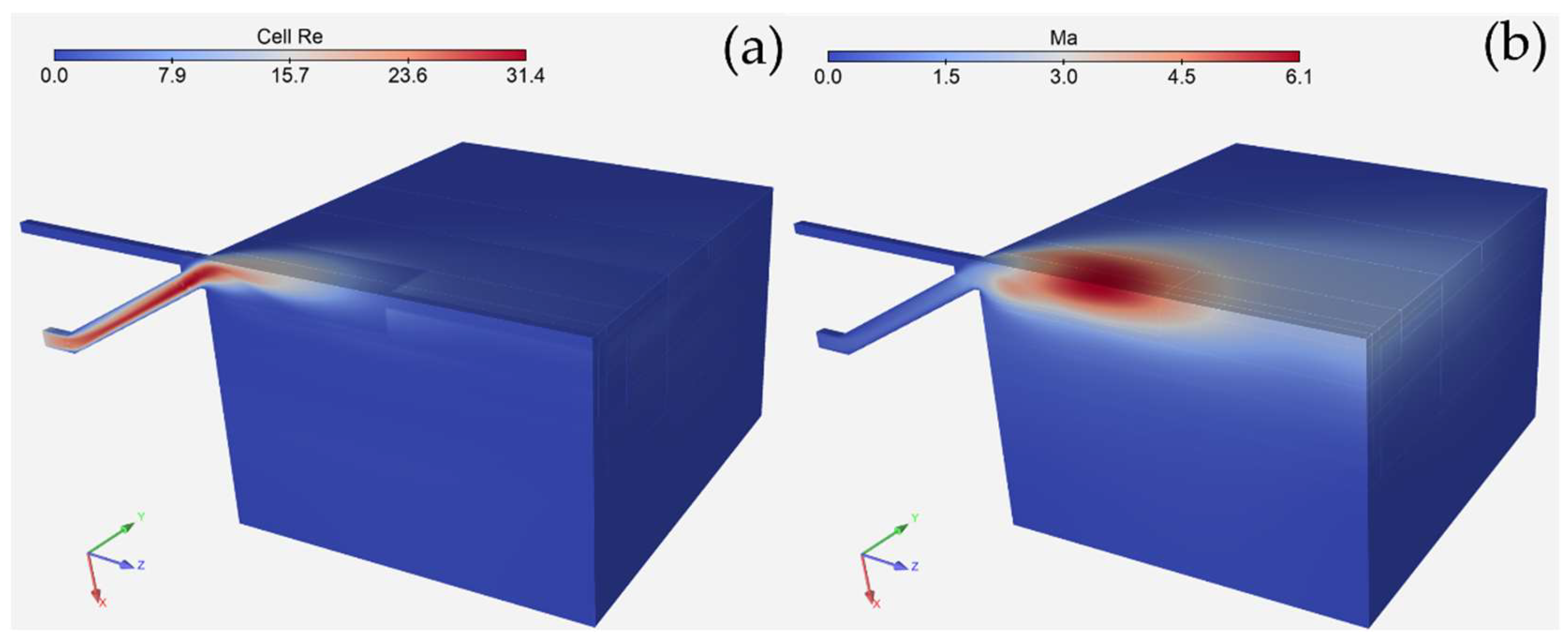
Figures 4(a) and 4(b) show Cell Reynolds number and Mach number, respectively. The helium flow through the nozzle is laminar and hypersonic in the vacuum chamber.

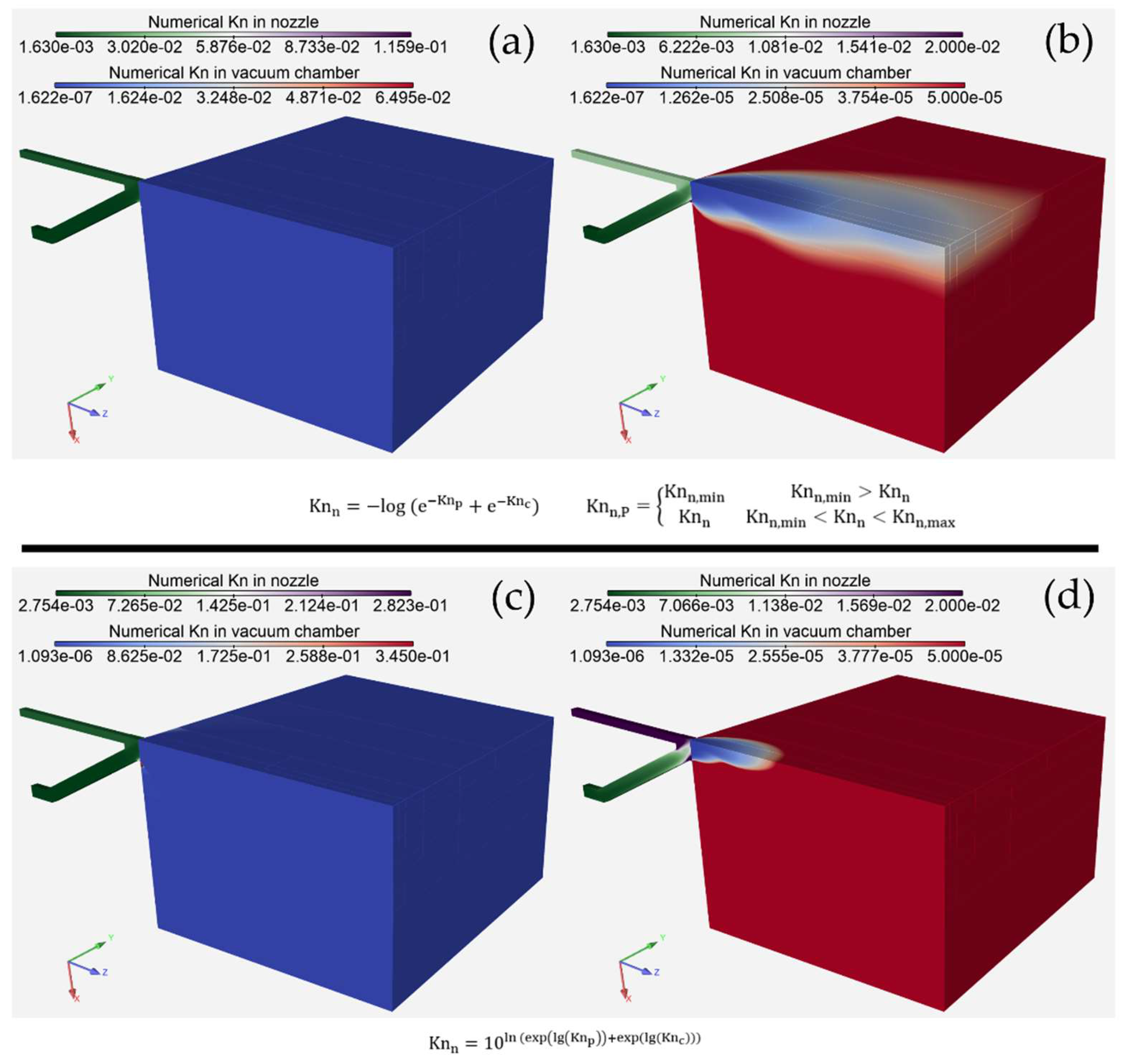
4.3. Definition of Numerical Knudsen Number

As explained in 2.1 Knudsen number, we propose Equation 8 to determine the numerical Knudsen number. Figure 5(a) shows the numerical Knudsen number, calculated by Equation 8, whose high values are removed in Figure 5(b) for clarity. Figures 5(c) and 5(d) show the numerical Knudsen number calculated by Equation 6, proposed in [29]. It can be seen (Figs 5(a) and 5(c)) that Equation 8 calculates

~

2 times lower Knudsen numbers inside the nozzle and for an order of magnitude lower Knudsen numbers in a vacuum chamber, compared to Equation 6. The reason is that

{K n}_{n}

in Equation 6 converges to the higher value between

{K n}_{c}

and

{K n}_{p}

, representing the maximum rather than the minimum. Also, in Figure 5(d) the region with higher Knudsen number is greater than in Figure 5(b), both in nozzle and vacuum chamber, confirming that Equation 6 calculates the maximum and is unsuitable for softmin function. Therefore, we propose Equation 8 to address softmin function accurately.

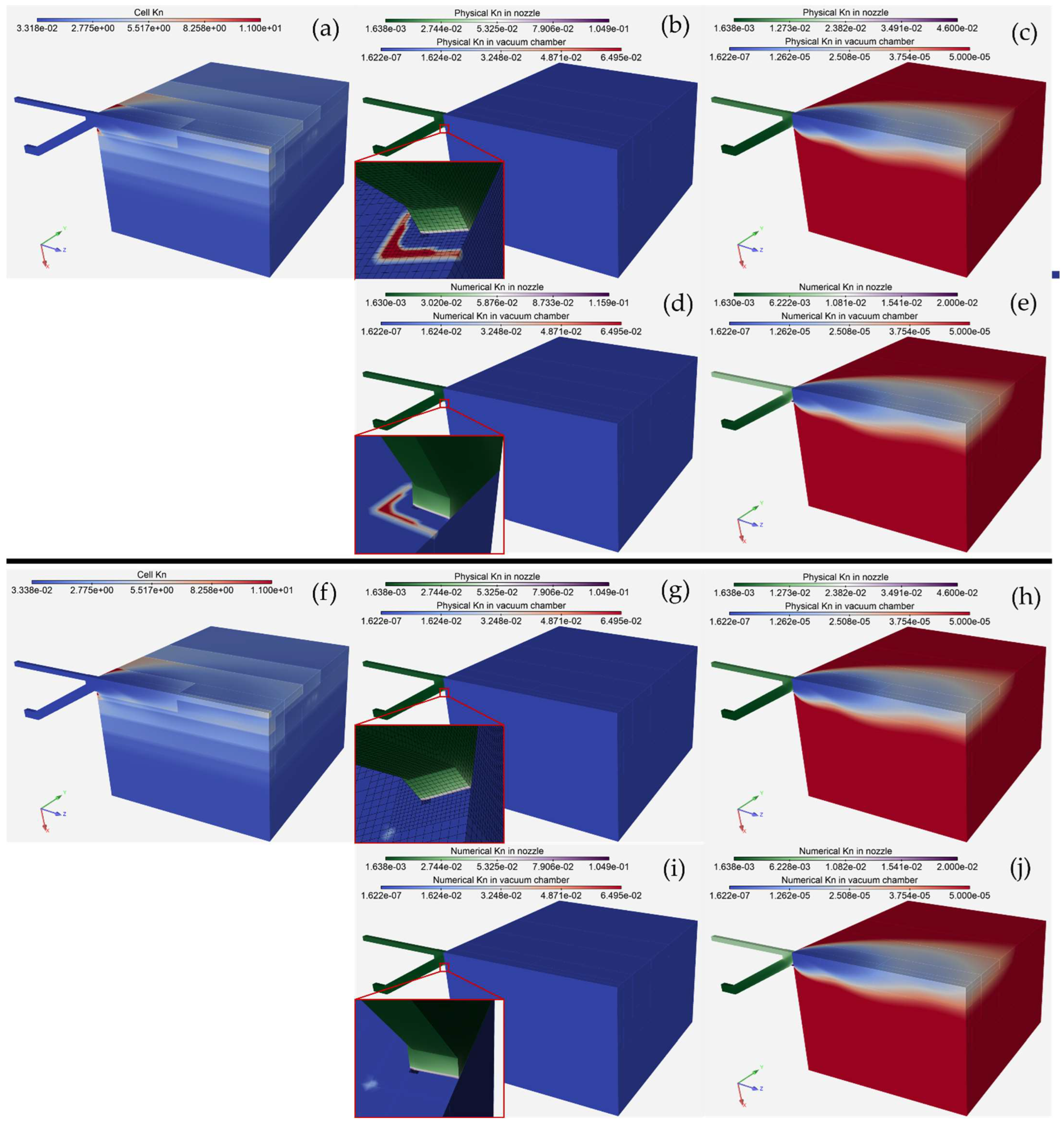
4.4. Knudsen Number

We calculated the mean free path λ of helium flow within each control volume using Equation 2. The cell Knudsen number is defined with the cell size

∆ x = {V_{c e l l}}^{1 / 3}

, representing characteristic length. We assume that helium first flows through the nozzle and later exits the nozzle into the vacuum chamber, whose characteristic length is significantly larger than the nozzle’s length. Therefore, we had to calculate the physical Knudsen number for the nozzle and vacuum chamber separately, and the calculation was done using Equation 8.

The characteristic length of the nozzle was assumed to be equal to the capillary diameter

L = 30 μ m

. The characteristic length of the vacuum chamber diameter was set at

L \approx 300 m m

to be comparable to the experimental setup in [37].

Figure 6(a) shows the Cell Knudsen number, Figure 6(b) the physical Knudsen number and Figure 6(d) the numerical Knudsen number. As seen in the zoomed-in areas of Figures 6(b) and 6(d), the regions with the transition in the cell level and on the contact between the vacuum chamber and the nozzle exhibit high physical Knudsen values. This is due to high-pressure gradients, which influence the mean free paths.

These high physical Knudsen values, which were removed in Figures 6(c) and 6(e), have no significant influence on the solution since the core of the expanded helium jet is relatively far away. High gradients in these regions can be tackled with a denser mesh.

Helium flow is mostly in the continuum regime except for a small portion of the nozzle and the cells with high-pressure gradients where flow falls in the slip regime

{K n}_{n}

> 0.1 that requires the use of LPBS. However, since most cells are in the continuum regime, LPBS has little effect on the solution. The same conclusions apply to the physical Knudsen number. The cell Knudsen number mostly falls in the slip regime except in the areas with high gradients where it exceeds this range due to fine cells. In the case of M1, the cell Knudsen number is

r_{21}

times higher than in M2, while in M3 it is

r_{32}

lower than for M2.

Figures 6(f)-6(j) demonstrate the Knudsen numbers for LPBS boundary conditions show no significant difference compared to the setup with no-slip boundary conditions. The main difference is observed in the regions with high-pressure gradients, where using LPBS boundary conditions leads to lower Knudsen values (Figs. 6(g) and 6(h)). However, both setups—using no-slip and LPBS boundary conditions—provide similar solutions, mostly within the continuum flow regime.

5. Conclusions

This work is the first detailed study of Knudsen number analysis in a sample delivery system used in SFX experiments under vacuum conditions. In simulations, most cells of the fluid domain have physical and numerical Knudsen numbers below the continuum limit (Kn < 0.01). Therefore, the CFD approach to solving Navier-Stokes equations is justified in the setup discussed here.

A few cells fall in the slip regime; therefore, the simulation with LPBS boundary conditions was tested. No significant differences were observed compared to the no-slip boundary condition. Furthermore, this is valid for all three generated meshes M1, M2 and M3, respectively, where the numerical solution is mesh-independent, as shown in local and global GCS.

In CFD, cell and physical Knudsen numbers control the numerical Knudsen number. We propose an improved equation (Equation 8) to determine the numerical Knudsen number, which is based not only on softmin and sum-log-exp function, but also respecting the physical meaning of those functions, meaning that the numerical Knudsen number is limited with min(

{K n}_{c}

and

{K n}_{p}

) and max(

{K n}_{c}

and

{K n}_{p}

), respectively.

We recommend applying this procedure to assess Knudsen numbers in various nozzle geometries beyond gas-focused liquid sheet designs for future work. The same Knudsen number evaluation approach may also be helpful for two-phase flow calculations, particularly for liquid sheets with sub-micron thicknesses approaching the continuum limit of the liquid phase.

Supplementary Materials

The following supporting information can be downloaded at: www.mdpi.com/xxx/s1, “knudsen_number.tsv”: Expressions to define cell Knudsen number, physical Knudsen number and numerical Knudsen number based on equation 8.

Author Contributions

Conceptualisation, K.K., B.Š. and S.B.; methodology, K.K.; software, K.K.; validation, K.K. and B.Š.; formal analysis, K.K.; investigation, K.K. and B.Š.; resources, B.Š and S.B.; data curation, K.K.; writing—original draft preparation, K.K.; writing—review and editing, B.Š. and S.B.; visualization, K.K.; supervision, B.Š.; project administration, B.Š.; funding acquisition, B.Š. and S.B. All authors have read and agreed to the published version of the manuscript.

Funding

Funding for this research is provided by the Centre for Free-Electron Laser Science (CFEL) under the project: Innovative Methods for Imaging with the use of X-ray Free-Electron Laser (XFEL) and Synchrotron Sources: Simulation of Gas-focused Micro-jets, and Slovenian Grant and Innovation Agency (ARIS) within core funding P2-0162, project J2-4477 and Young Researcher Program. This work was also partly funded by the Cluster of Excellence "CUI: Advanced Imaging of Matter" of the Deutsche Forschungsgemeinschaft (DFG)–EXC 2056–project ID 390715994.

Data Availability Statement

All the data generated or analysed during this study are included in this article.

Acknowledgments

The authors wish to thank Prof. Dr. Henry Chapman from DESY (Hamburg, Germany), a member of the Helmholtz Association HGF, for the opportunity to test the nozzle geometry at CFEL (Hamburg, Germany) to gain the data of helium mass flow used in this paper.

Conflicts of Interest

No potential conflict of interest was reported by the authors.

Appendix A

In Table A the results of local grid independence study are presented. Variables

Φ

were average across locations (lines) defined by two points, as follows: Line 1: (0, 0, -1e-5) and (1e-4, 0, -1e-5), Line 2: (0, 0, 1e-4) and (1e-3, 0, 1e-4), follows Line 3: (0, 0, 1e-4) and (0, 1e-3, 1e-4) and Line 4: (0, 0, -5e-5) and (0, 0, 1e-3). All points coordinates are in meters.

Table A. Local grid convergence analysis.

$Φ$	Location	Case	$Φ_{1}$	$Φ_{2}$	$Φ_{3}$	$p$	$Φ_{e x t}^{21}$	$e_{a}^{21}$ [%]	$e_{e x t}^{21}$ [%]	$G C I^{32}$ [%]	$G C I^{21}$ [%]
p [Pa]	Line 1	No-slip	69625	68950	68985	5.283	69638	0.0676	0.0189	0.0958	0.0237
p [Pa]	Line 1	LPBS	68561	68282	68237	11.07	68561	0.00438	0.000189	0.00554	0.000237
p [Pa]	Line 2	No-slip	11.66	8.713	5.586	0.9655	13.98	6.353	16.56	24.51	24.8
p [Pa]	Line 2	LPBS	9.867	8.009	4.18	4.467	9.955	2.332	0.8839	3.484	1.115
p [Pa]	Line 3	No-slip	50.17	47.75	48.35	0.5471	54.54	1.484	8.008	9.323	10.88
p [Pa]	Line 3	LPBS	47.88	47.79	47.79	0.4967	44.78	0.9932	6.914	6.807	8.084
p [Pa]	Line 4	No-slip	10654	10598	10576	4.809	10655	0.0435	0.0145	0.0634	0.0182
p [Pa]	Line 4	LPBS	10524	10501	10476	12.05	10524	0.00162	5.23E-05	0.00204	6.54E-05
$ρ$ [kg m^-3]	Line 1	No-slip	0.1758	0.1735	0.1729	2.894	0.1761	0.1931	0.1484	0.3495	0.1858
$ρ$ [kg m^-3]	Line 1	LPBS	0.1739	0.1726	0.1714	2.786	0.1742	0.1622	0.1318	0.2996	0.165
$ρ$ [kg m^-3]	Line 2	No-slip	0.00341	0.00339	0.00338	0.8286	0.00343	0.1445	0.5338	0.6329	0.6709
$ρ$ [kg m^-3]	Line 2	LPBS	0.00341	0.00339	0.00338	1.154	0.00342	0.1258	0.3184	0.4206	0.3992
$ρ$ [kg m^-3]	Line 3	No-slip	0.00393	0.0039	0.00389	2.419	0.00393	0.1174	0.1166	0.2348	0.1459
$ρ$ [kg m^-3]	Line 3	LPBS	0.00392	0.0039	0.00389	6.421	0.00392	0.0289	0.00541	0.039	0.00676
$ρ$ [kg m^-3]	Line 4	No-slip	0.0288	0.0286	0.0284	2.341	0.0289	0.1486	0.1544	0.3031	0.1933
$ρ$ [kg m^-3]	Line 4	LPBS	0.0285	0.0284	0.0282	2.323	0.0286	0.1299	0.1364	0.2661	0.1707
T [K]	Line 1	No-slip	198.72	199.47	200.3	0.602	197.6	0.1068	0.5678	0.6161	0.7057
T [K]	Line 1	LPBS	197.71	198.45	199.64	0.3577	195.08	0.1444	1.35	1.337	1.666
T [K]	Line 2	No-slip	242.49	242.2	241.53	2.806	242.54	0.0237	0.0191	0.0435	0.0238
T [K]	Line 2	LPBS	242.2	241.9	241.19	6.431	242.2	0.00786	0.00147	0.0106	0.00183
T [K]	Line 3	No-slip	234.06	234.09	234.19	2.04	234.09	0.0104	0.013	0.0231	0.0163
T [K]	Line 3	LPBS	233.83	233.91	234.01	1.819	233.95	0.037	0.0538	0.0886	0.0673
T [K]	Line 4	No-slip	101.62	102.21	102.29	2.183	101.5	0.101	0.1157	0.2149	0.1445
T [K]	Line 4	LPBS	101.66	102.11	102.37	1.144	101.28	0.1441	0.3711	0.4853	0.4622
v [m s^-1]	Line 1	No-slip	934.6	937.77	935.24	2.639	934.07	0.0649	0.0571	0.1234	0.0714
v [m s^-1]	Line 1	LPBS	940.35	942.5	938.02	11.37	940.35	0.00218	8.58E-05	0.00275	0.000107
v [m s^-1]	Line 2	No-slip	482.16	488.5	495.98	2.676	481.19	0.2346	0.2028	0.4429	0.2529
v [m s^-1]	Line 2	LPBS	482.75	488.21	496.85	3.485	482.22	0.1913	0.111	0.3161	0.1386
v [m s^-1]	Line 3	No-slip	513.05	515.37	514.89	0.7127	510.35	0.12	0.5301	0.5977	0.6591
v [m s^-1]	Line 3	LPBS	515	515.28	515.6	1.248	512.25	0.2304	0.5364	0.7253	0.667
v [m s^-1]	Line 4	No-slip	1426.3	1430.6	1432.6	1.087	1424	0.0604	0.1649	0.2119	0.2058
v [m s^-1]	Line 4	LPBS	1426.3	1428.7	1432.3	1.108	1424.2	0.0549	0.1464	0.1896	0.1828

References

Chapman, H.N.; Fromme, P.; Barty, A.; White, T.A.; Kirian, R.A.; Aquila, A.; Hunter, M.S.; Schulz, J.; DePonte, D.P.; Weierstall, U. Femtosecond X-Ray Protein Nanocrystallography. Nature 2011, 470, 73–77. [Google Scholar] [CrossRef] [PubMed]
Gañán-Calvo, A.M. Generation of Steady Liquid Microthreads and Micron-Sized Monodisperse Sprays in Gas Streams. Phys Rev Lett 1998, 80, 285–288. [Google Scholar] [CrossRef]
DePonte, D.P.; Weierstall, U.; Schmidt, K.; Warner, J.; Starodub, D.; Spence, J.C.H.; Doak, R.B. Gas Dynamic Virtual Nozzle for Generation of Microscopic Droplet Streams. J Phys D Appl Phys 2008, 41, 195505. [Google Scholar] [CrossRef]
Beyerlein, K.R.; Adriano, L.; Heymann, M.; Kirian, R.; Knoška, J.; Wilde, F.; Chapman, H.N.; Bajt, S. Ceramic Micro-Injection Molded Nozzles for Serial Femtosecond Crystallography Sample Delivery. Review of Scientific Instruments 2015, 86. [Google Scholar] [CrossRef]
Weierstall, U. Liquid Sample Delivery Techniques for Serial Femtosecond Crystallography. Philosophical Transactions of the Royal Society B: Biological Sciences 2014, 369, 20130337. [Google Scholar] [CrossRef]
Schulz, J.; Bielecki, J.; Doak, R.B.; Dörner, K.; Graceffa, R.; Shoeman, R.L.; Sikorski, M.; Thute, P.; Westphal, D.; Mancuso, A.P. A Versatile Liquid-Jet Setup for the European XFEL. J Synchrotron Radiat 2019, 26, 339–345. [Google Scholar] [CrossRef]
Kondoh, M.; Tsubouchi, M. Liquid-Sheet Jets for Terahertz Spectroscopy. Opt Express 2014, 22, 14135. [Google Scholar] [CrossRef]
Ekimova, M.; Quevedo, W.; Faube, M.; Wernet, P.; Nibbering, E.T.J. A Liquid Flatjet System for Solution Phase Soft-x-Ray Spectroscopy. Structural Dynamics 2015, 2. [Google Scholar] [CrossRef]
Galinis, G.; Strucka, J.; Barnard, J.C.T.; Braun, A.; Smith, R.A.; Marangos, J.P. Micrometer-Thickness Liquid Sheet Jets Flowing in Vacuum. Review of Scientific Instruments 2017, 88. [Google Scholar] [CrossRef]
Barnard, J.C.T.; Lee, J.P.; Alexander, O.; Jarosch, S.; Garratt, D.; Picciuto, R.; Kowalczyk, K.; Ferchaud, C.; Gregory, A.; Matthews, M.; et al. Delivery of Stable Ultra-Thin Liquid Sheets in Vacuum for Biochemical Spectroscopy. Front Mol Biosci 2022, 9. [Google Scholar] [CrossRef]
Buchmann, A.; Hoberg, C.; Havenith, M. Improvements in Windowless Spectroscopy: 3D Printed Nozzles. In Proceedings of the International Conference on Infrared, Millimeter, and Terahertz Waves, IRMMW-THz; IEEE Computer Society, 2022; Vol. 2022-August.
Yin, Z.; Luu, T.T.; Wörner, H.J. Few-Cycle High-Harmonic Generation in Liquids: In-Operando Thickness Measurement of Flat Microjets. Journal of Physics: Photonics 2020, 2, 044007. [Google Scholar] [CrossRef]
Hoffman, D.J.; van Driel, T.B.; Kroll, T.; Crissman, C.J.; Ryland, E.S.; Nelson, K.J.; Cordones, A.A.; Koralek, J.D.; DePonte, D.P. Microfluidic Liquid Sheets as Large-Area Targets for High Repetition XFELs. Front Mol Biosci 2022, 9. [Google Scholar] [CrossRef] [PubMed]
Chang, Y.P.; Yin, Z.; Balciunas, T.; Wörner, H.J.; Wolf, J.P. Temperature Measurements of Liquid Flat Jets in Vacuum. Structural Dynamics 2022, 9. [Google Scholar] [CrossRef]
Fondell, M.; Eckert, S.; Jay, R.M.; Weniger, C.; Quevedo, W.; Niskanen, J.; Kennedy, B.; Sorgenfrei, F.; Schick, D.; Giangrisostomi, E.; et al. Time-Resolved Soft X-Ray Absorption Spectroscopy in Transmission Mode on Liquids at MHz Repetition Rates. Structural Dynamics 2017, 4. [Google Scholar] [CrossRef]
George, K.M.; Morrison, J.T.; Feister, S.; Ngirmang, G.K.; Smith, J.R.; Klim, A.J.; Snyder, J.; Austin, D.; Erbsen, W.; Frische, K.D.; et al. High-Repetition-Rate ( KHz) Targets and Optics from Liquid Microjets for High-Intensity Laser–Plasma Interactions. High Power Laser Science and Engineering 2019, 7, e50. [Google Scholar] [CrossRef]
Luu, T.T.; Yin, Z.; Jain, A.; Gaumnitz, T.; Pertot, Y.; Ma, J.; Wörner, H.J. Extreme–Ultraviolet High–Harmonic Generation in Liquids. Nat Commun 2018, 9, 3723. [Google Scholar] [CrossRef]
Smith, A.D.; Balčiu̅nas, T.; Chang, Y.-P.; Schmidt, C.; Zinchenko, K.; Nunes, F.B.; Rossi, E.; Svoboda, V.; Yin, Z.; Wolf, J.-P.; et al. Femtosecond Soft-X-Ray Absorption Spectroscopy of Liquids with a Water-Window High-Harmonic Source. J Phys Chem Lett 2020, 11, 1981–1988. [Google Scholar] [CrossRef] [PubMed]
Koralek, J.D.; Kim, J.B.; Brůža, P.; Curry, C.B.; Chen, Z.; Bechtel, H.A.; Cordones, A.A.; Sperling, P.; Toleikis, S.; Kern, J.F.; et al. Generation and Characterization of Ultrathin Free-Flowing Liquid Sheets. Nat Commun 2018, 9, 1353. [Google Scholar] [CrossRef] [PubMed]
Konold, P.E.; You, T.; Bielecki, J.; Valerio, J.; Kloos, M.; Westphal, D.; Bellisario, A.; Varma Yenupuri, T.; Wollter, A.; Koliyadu, J.C.P.; et al. 3D-Printed Sheet Jet for Stable Megahertz Liquid Sample Delivery at X-Ray Free-Electron Lasers. IUCrJ 2023, 10, 662–670. [Google Scholar] [CrossRef]
Yang, J.; Nunes, J.P.F.; Ledbetter, K.; Biasin, E.; Centurion, M.; Chen, Z.; Cordones, A.A.; Crissman, C.; Deponte, D.P.; Glenzer, S.H.; et al. Structure Retrieval in Liquid-Phase Electron Scattering. Physical Chemistry Chemical Physics 2021, 23, 1308–1316. [Google Scholar] [CrossRef]
Nunes, J.P.F.; Ledbetter, K.; Lin, M.; Kozina, M.; DePonte, D.P.; Biasin, E.; Centurion, M.; Crissman, C.J.; Dunning, M.; Guillet, S.; et al. Liquid-Phase Mega-Electron-Volt Ultrafast Electron Diffraction. Structural Dynamics 2020, 7. [Google Scholar] [CrossRef]
Šarler, B.; Zahoor, R.; Bajt, S. Alternative Geometric Arrangements of the Nozzle Outlet Orifice for Liquid Micro-Jet Focusing in Gas Dynamic Virtual Nozzles. Materials 2021, 14, 1572. [Google Scholar] [CrossRef] [PubMed]
Zahoor, R.; Bajt, S.; Šarler, B. Influence of Gas Dynamic Virtual Nozzle Geometry on Micro-Jet Characteristics. International Journal of Multiphase Flow 2018, 104, 152–165. [Google Scholar] [CrossRef]
Zahoor, R.; Belšak, G.; Bajt, S.; Šarler, B. Simulation of Liquid Micro-Jet in Free Expanding High-Speed Co-Flowing Gas Streams. Microfluid Nanofluidics 2018, 22, 87. [Google Scholar] [CrossRef]
Zahoor, R.; Bajt, S.; Šarler, B. Simulation of Non-Newtonian Gas-Focused Micro-Jets in Chocked Gas Flow Regime. J Phys Conf Ser 2024, 2766, 012069. [Google Scholar] [CrossRef]
Belšak, G.; Bajt, S.; Šarler, B. Computational Modeling and Simulation of Gas Focused Liquid Micro-Sheets. International Journal of Multiphase Flow 2021, 140, 103666. [Google Scholar] [CrossRef]
Chambre, P.A.; Schaaf, S.A. Flow of Rarefied Gases; Princeton University Press, 1961; ISBN 9781400885800.
Liu, C.; Zhou, G.; Shyy, W.; Xu, K. Limitation Principle for Computational Fluid Dynamics. Shock Waves 2019, 29, 1083–1102. [Google Scholar] [CrossRef]
Liu, C.; Xu, K.; Zhou, G. Cell Size Effect on Computational Fluid Dynamics: The Limitation Principle for Flow Simulation 2018.
Ghorbel, M.; Pineau, J.; Gourdeau, R.; Javdani, S.; Srinivasa, S. A Decision-Theoretic Approach for the Collaborative Control of a Smart Wheelchair. Int J Soc Robot 2018, 10, 131–145. [Google Scholar] [CrossRef]
Kim, Y.J.; Kim, Y.-J.; Han, J.-G. Numerical Analysis of Flow Characteristics of an Atmospheric Plasma Torch 2004.
Ansys ANSYS Fluent Theory Guide 2021R1; Canonsburg, PA, 2021.
Matteucci, S.; Yampolskii, Y.; Freeman, B.D.; Pinnau, I. Transport of Gases and Vapors in Glassy and Rubbery Polymers. In Materials Science of Membranes for Gas and Vapor Separation; Wiley, 2006; pp. 1–47.
Roache, P.J. Quantification of Uncertainty In Computational Fluid. Annu Rev Fluid Mech 1997, 29, 123–160. [Google Scholar] [CrossRef]
Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J Fluids Eng 2008, 130. [Google Scholar] [CrossRef]
Zupan, B.; Peña-Murillo, G.E.; Zahoor, R.; Gregorc, J.; Šarler, B.; Knoška, J.; Gañán-Calvo, A.M.; Chapman, H.N.; Bajt, S. An Experimental Study of Liquid Micro-Jets Produced with a Gas Dynamic Virtual Nozzle under the Influence of an Electric Field. Front Mol Biosci 2023, 10. [Google Scholar] [CrossRef] [PubMed]

Figure 1. Gas-focused liquid sheet nozzle, computational domain and mesh and its details. Boundary conditions: a-mass flow inlet, b-pressure outlet, c-symmetry, d-wall.

Figure 2. Grid convergence results for the case with no-slip and LPBS boundary condition. M3, M2 and M1 represent coarse, medium and fine grid, respectively. With EXT we label extrapolated values.

Figure 3. Flow field variables: (a) Absolute pressure, (b) Velocity magnitude and velocity vectors, (c) Temperature, (d) Density.

Figure 4. Dimensionless numbers: (a) Cell Reynolds number, (b) Mach number.

Figure 5. Numerical Knudsen number: (a) Numerical Knudsen number calculated by Equation 8, (b) Numerical Knudsen number calculated by Equation 8 with rescaled values, (c) Numerical Knudsen number calculated by Equation 6, (d) Numerical Knudsen number calculated by Equation 6 with rescaled values.

Figure 6. Knudsen number for no-slip boundary conditions: (a) Cell Knudsen number, (b) Physical Knudsen number, (c) Physical Knudsen number with rescaled values, (d) Numerical Knudsen number, (e) Numerical Knudsen number with rescaled values. Knudsen number for LPBS boundary conditions: (f) Cell Knudsen number, (g) Physical Knudsen number, (h) Physical Knudsen number with rescaled values, (i) Numerical Knudsen number, (j) Numerical Knudsen number with rescaled values.

Table 1. Information about meshes and numerical simulations.

	M1	M2	M3
$Δ x_{0} [μ m]$	0.75	1.5	2
Nr. of cells	4,426,090	547,730	234,240
Nr. of iterations	260	250	226
Residuals (continuity equation)	3e-4	1e-6	1e-6
Residuals (momentum and energy equation)	2e-6	1e-9	1e-9
Calculation time [core hours]	6.9	0.63	0.21

Table 2. Global grid convergence analysis.

Case	$Φ$ and location	$r_{21}$	$r_{32}$	$Φ_{1}$	$Φ_{2}$	$Φ_{3}$	$p$	$Φ_{e x t}^{21}$	$e_{a}^{21}$ [%]	$e_{e x t}^{21}$ [%]	$G C I^{32}$ [%]	$G C I^{21}$ [%]
no-slip	Global max. Ma	2.01	1.33	6.062	6.051	6.036	2.87	6.063	0.17	0.027	0.38	0.03
LPBS	Global max. Ma	2.01	1.33	6.051	6.044	6.032	3.10	6.052	0.12	0.016	0.26	0.02

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Numerical Analysis of Knudsen Number of Helium Flow Through Gas-Focused Liquid Sheet Micro-Nozzle

Abstract

1. Introduction

2. Methods

2.1. Knudsen Number

2.2. Governing Equations

3. The Numerical Method

3.1. Spatial Discretisation

3.2. Boundary Conditions

3.3. Solution Setup

3.4. Grid Convergence Study

4. Results and Discussion

4.1. Flow Field Variables

4.2. Dimensionless Numbers

4.3. Definition of Numerical Knudsen Number

4.4. Knudsen Number

5. Conclusions

Supplementary Materials

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

Appendix A

References

MDPI Initiatives

Important Links

Subscribe