Prerpints.org logo
Preprint
Article

Mathematical Modeling of Load Capacity and Durability of Metal-Polymeric Bearings with a Composite Bushing Based on Polyamides, Polytetrafluoroethylenes, Polyetheretherketones, or Polyethylene Terephthalates

Altmetrics

Downloads

38

Views

20

Comments

0

Submitted:

28 October 2024

Posted:

30 October 2024

You are already at the latest version

Alerts
Abstract
(1) Predictive assessment of the performance characteristics of metal-polymer (MP) plain bearings at the design stage is necessary and important for engineering practice. They include bearing capacity, linear wear of the bushing, and bearing life. However, no method for their calculation has been developed. (2) The authors have created a generalized analytical method for the mathematical modeling of MP sliding bearings as a classical science-based method of contact mechanics of conformal cylindrical bodies with consideration of polymer bushing wear. (3) Contact problem of the theory of elasticity takes into account the significant difference in the elasticity characteristics of polymeric materials from those of steel: Young's modulus is 60...250 times smaller, Poisson's ratio is 1.27...1.37 times larger. The method has been used to study MP bearings with several common groups of tribopolymers used for bushings: PA, PTFE, PET, and PEEK. The maximum contact pressures and durability of dry friction bearings have been calculated taking into account the load, radial clearance, bushing thickness, elasticity characteristics of tribopolymers, their wear resistance, sliding friction coefficient, and type of tribopolymer materials. (4) The paper establishes quantitative and qualitative regularities of the influence of these factors on the maximum contact pressures and bearing durability.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Metal-polymer (MP) plain bearings are widely used in a wide variety of human activities. They have proven to be a suitable and cost-effective replacement for metal bearings in many cases. Various types of tribolgical polymeric materials (unreinforced and reinforced) are used for bushings of this type of sliding bearings for rotary (radial, axial) or reciprocating (guide) motion. They operate reliably at sufficiently high contact pressures, high sliding speeds, under dynamic loads, in chemically active and excessively humid environments, in water, in vacuum, with boundary or dry friction, do not require additional lubrication and maintenance, etc. The areas of application of plain bearings in various types of equipment are extremely diverse: engineering (machine, machine tool, automotive, instrumentation, aircraft construction, etc.; agricultural, construction, road, rocket and space, military, robotics, etc.), technological (food processing, pharmaceutical, textile, pulp, woodworking, chemical, etc.), service (computer, office, control and measuring, household, medical, diagnostic equipment, etc.), and much more. It should be noted that among the above-mentioned positive qualities of MP bearings, their ability to operate reliably in dry friction is of particular practical importance. In many cases, it is impossible to use lubrication in sliding friction units for various reasons.
Various crystalline thermoplastic, amorphous, and epoxy polymeric materials are used to manufacture bushings for mechanical bearings. To improve their strength and tribological characteristics, various types of fillers are widely used to form composites. Common ones include fiberglass (GF), carbon fiber (CF), molybdenum disulfide (MoS2), graphite (C), bronze powder, polytetrafluoroethylene (PTFE), aramid (AF), oil, etc. The most commonly used polymers for sleeves of deep groove bearings are polyamides, polyacetals (POM), and polytetrafluoroethylene. Less commonly used are polyethylene terephthalates, polyetheretherketones, polyethylene (PE-HD), etc.

2. Generalized Method of Calculation of Metal-Polymer Bearings

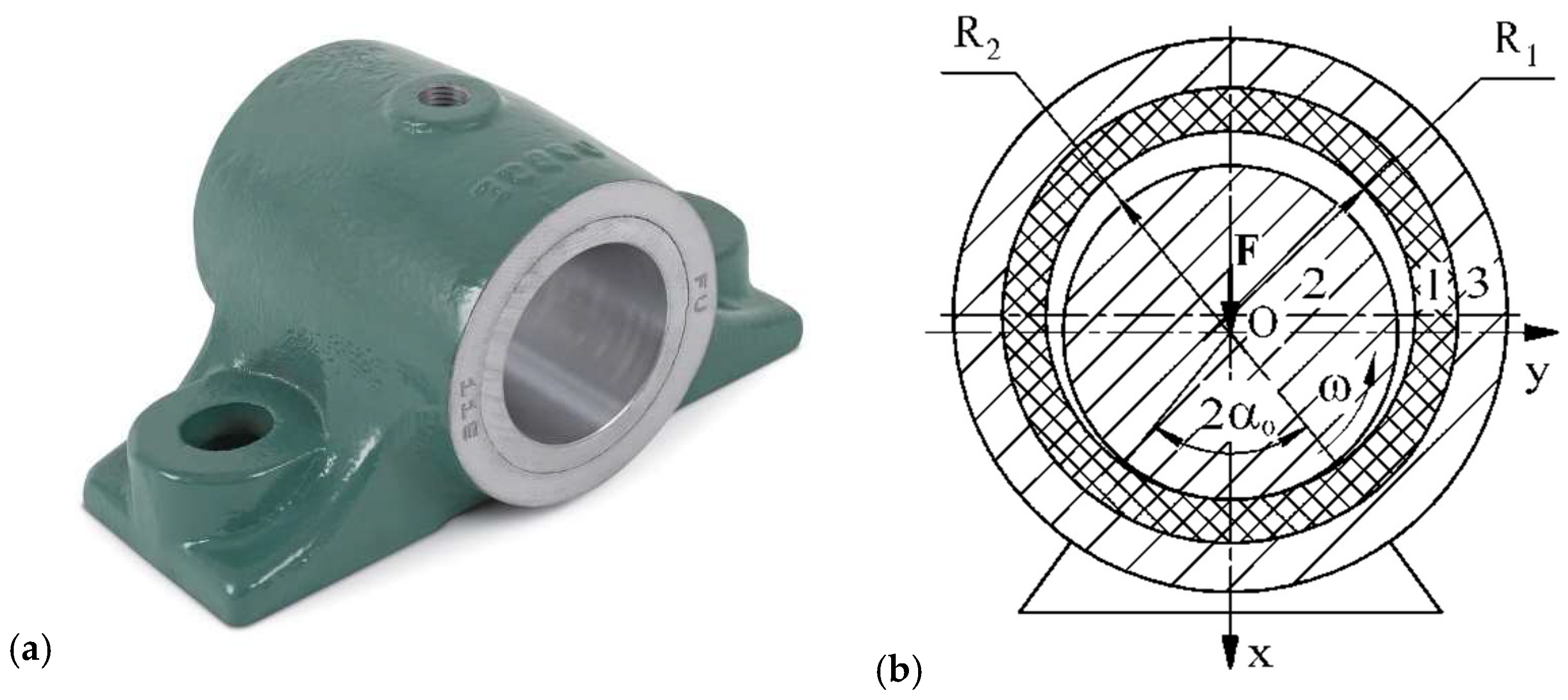
A plain bearing (Figure 1) consisting of a polymer sleeve 1, a steel shaft 2, and a housing 3 is considered. Shaft 2 is loaded with a static load N and rotates with an angular velocity ω = const. The diagram of the bearing (Fig. 1b) shows the force F = N / l reduced to the unit width l of bushing 1. When the bearing is loaded, an unknown contact pressure p α occurs, distributed along an unknown arc of contact 2 R 2 α 0 . The maximum contact pressure p m a x occurs between the shaft and the sleeve along the action line of the force F. A radial clearance ε = R 1 − R 2 ⟩ 0 must be guaranteed between the polymer sleeve 1 of inner radius R 1 and the shaft of radius R 2 . The polymer sleeve has a certain thickness S, which is selected structurally.
It is known that the mechanical properties of polymeric materials for sleeves of sliding bearings have significantly lower properties than structural steel for shafts: tensile strength by 8-10 times, Young's modulus by 60-260 times, and wear resistance by 50-150 times. Consequently, at the limit friction of such bearings, their load-bearing capacity, wear resistance, and durability will also be significantly lower than those of plain bearings with metal sleeves. Metal bearings, on the other hand, cannot operate in dry friction, in water, or process liquids. Therefore, MP bearings are indispensable here, which leads to their widespread use with a reasonable limitation of bearing capacity based on the strength properties of tribopolymers. However, except for the author's method, there are no such methods available for use at the design stage.
The generalized analytical method for studying MP sliding bearings includes the following partial methods for calculation:
- contact pressures p α and the area of their distribution, that is, the initial contact angle 2 α 0 , - maximum contact pressure p m a x ,
- taking into account bushing wear to reduce contact pressures p α h and increase the contact angle 2 α 0 h ,
- taking into account the wear of the bushing to reduce the initial maximum contact pressure,
- durability t MP of the bearing at the accepted permissible linear wear h1 of the polymer sleeve,
- maximum linear wear h1max of the bushing at a given bearing life t.
These methods are described in detail in the authors' previous publications [1,2,3,4]. Below are the basic formulas for calculating the initial maximum contact pressure p m a x in the bearing and its durability at a given wear h 1 = h 1 m a x of the polymer bushing. Here, a modified method [5,6] is used to solve the contact problem with bushing wear, which takes into account the effect of the bushing thickness S on the contact parameters.
The maximum contact pressure p m a x occurs along the force line F and is determined by the following formula:
p m a x ≈ E λ ε t a n ⁡ ( α 0 2 ) ,
where Е λ ≈ е λ / R 2 cos 2 ⁡ α 0 / 4 ,   e λ = e L , e 4 = 4 E 1 E 2 / Z , L = ( 1 + λ 4 ) , λ = R 1 / ( R 1 + S ) , 0 ⟨ α 0 ⟨ 9 0 o , Z = ( 1 + κ 1 ) ( 1 + ν 1 ) E 2 + ( 1 + κ 2 ) ( 1 + ν 2 ) E 1 , κ = 3 − 4 ν , E k , ν k are Young's modulus and Poisson's ratio of the materials of shaft 2 and sleeve 1 of the bearing, and k is the numbering of the bearing elements (Fig. 1).
The unknown angle of initial contact 2 α 0 is determined from the condition of equilibrium of the forces applied to shaft 2, i.e., the load F, and the reaction to it in the form of contact pressure p α
F = R 2 ∫ − α 0 α 0 p α cos ⁡ α d α = 4 π R 2 E λ ε sin 2 ⁡ ( α 0 / 4 ) .
Hence, taking into account the expression for E λ , the formula for the semi-angle of the angle α 0 will be
α 0 = 2 a r c sin ⁡ F / π e λ ε .
Based on the mathematical model of material wear under sliding friction [2,7] and the method for calculating contact pressures in a bearing [1,2,3,4], the durability of a sliding bearing at maximum linear wear h 1 = h 1 m a x of the bushing is calculated by the formula [8]:
t = − B 1 τ 10 m 1 v c h τ h Σ 1 1 − m k K t 1 τ − τ 10 1 − m 1 − τ − τ 10 + c h h 1 m a x Σ 1 τ h 1 − m 1 ,
where B k , m k , τ k 0 are characteristics of wear resistance of materials in a hybrid tribopair under the accepted external research conditions, which are determined by the results of model triboexperimental studies [9] (Table 1, Table 2 and Table 3); v = ω R 2 is the sliding speed, c h is the wear rate coefficient; Σ 1 = ( − K t 1 + h 1 ' ) ; K t ( 1 ) = 1 ; K t ( 2 ) = α 0 / π are the coefficients of mutual overlap of the sleeve and shaft, respectively; h 1 ' = h 2 / h 1 is the relative linear wear of the shaft to the wear of the sleeve
h 1 ' = B 1 τ 10 m 1 τ − τ 20 m 2 B 2 τ 20 m 2 τ − τ 10 m 1 K t 2
The relationship between the specific friction force τ on a tribocontact and the contact pressure p m a x is taken according to the Amonton-Coulomb law
τ = f p m a x ,
where f is the sliding friction coefficient.
Due to the wear of the bearing bushing and shaft, the pressure p m a x will decrease. In an MP bearing, the polymer bushing wears out 50-100 times faster than the steel shaft, and therefore the shaft’s wear can be neglected. The current pressure p h m a x are determined as follows:
p h m a x = p m a x − p h ,
where p h is the change in the initial pressures when the bushing wears in a mechanical bearing.
The value of p h is calculated according to the following dependence [8]:
p h ≈ E λ с h ε h t a n ⁡ ( α 0 h 2 ) ,
where c h >0 is the wear rate; ε h = h 1 m a x Σ 1 ; α 0 h ⟩ α 0 is an unknown contact angle when the bushing wears.
Therefore, during the wear process, the current contact pressure is determined by the formula
p h m a x ≈ E λ [ ε tan ⁡ α 0 2 − c h h 1 Σ 1 tan ⁡ α 0 h 2 ] .
When the polymer sleeve wears, the current specific friction force is τ h m a x < τ . Accordingly, τ h m a x = f p h m a x , and τ h = f p h . The contact angle α 0 h during wear is calculated according to the condition
F = 4 π R 2 E λ ( ε + c h ε h ) sin 2 ⁡ ( α 0 h / 4 ) = 4 π e λ cos 2 ⁡ ( α 0 / 4 ) ( ε + c h ε h ) sin 2 ⁡ ( α 0 h / 4 ) .

3. Results

Data on the materials of the bushings of the MP sliding bearings: shaft 2 - steel C45 normalized, E2=210000 MPa, ν2=0.3; tribopolymer materials of bushing 1 (Tables 1 - 3). Data for calculation: N =1500, and 3000 N, F = N / l , l = D 2 , D2 = 30 mm, F = 50, 100 N/mm, ε = 0.15 mm, S=2, 4, 6 mm, n2=100 rpm, h1=1.0 mm.
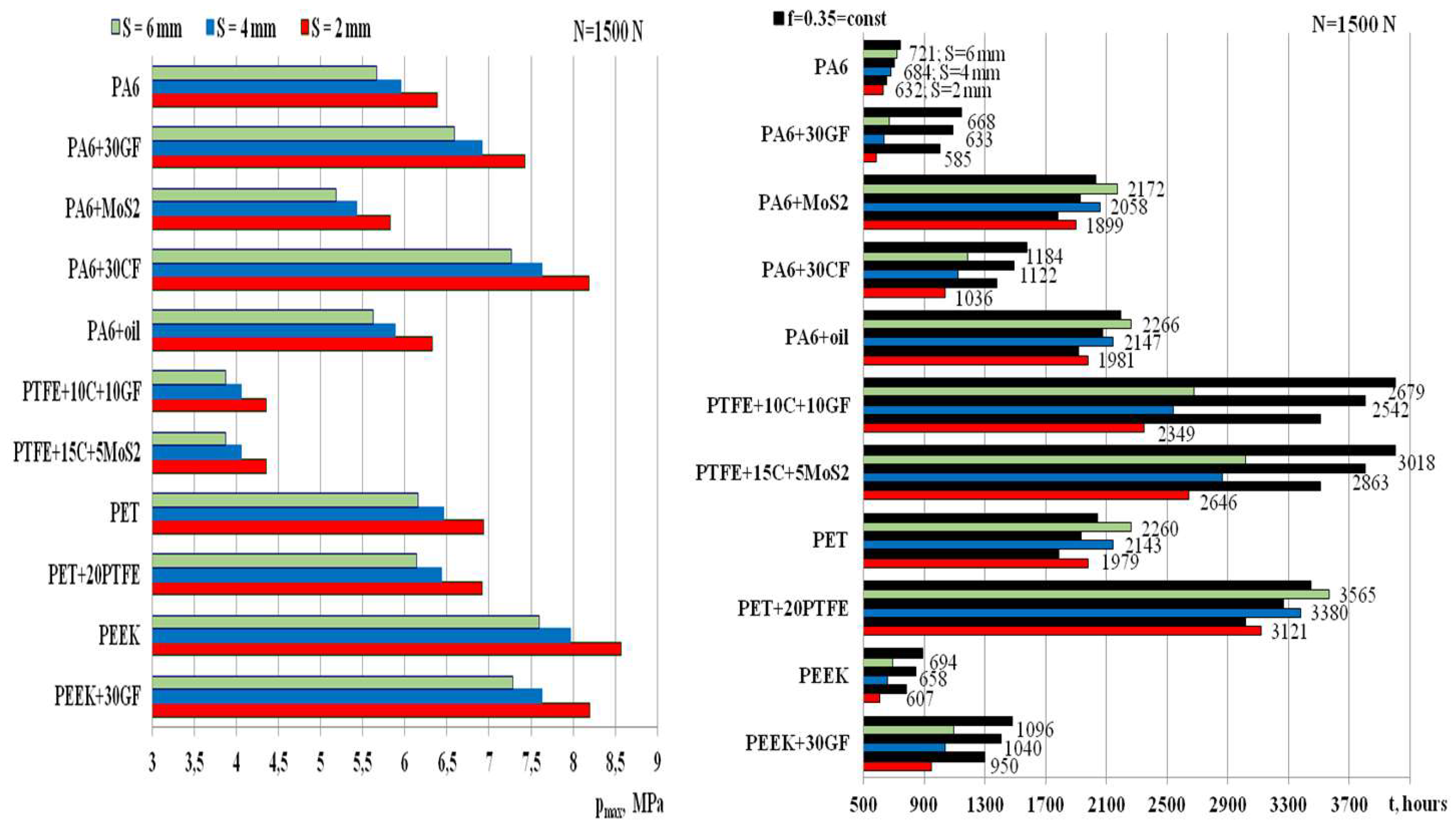
The wear resistance characteristics B 1 , m 1 , τ 10 of polymeric materials presented in the tables above were determined based on the results of their experimental studies in dry friction conditions by the method [9]. For this, a pin-on-disk tribometer [10] under controlled conditions (temperature T = 23±10C, relative humidity HR = 50±5%) was used. 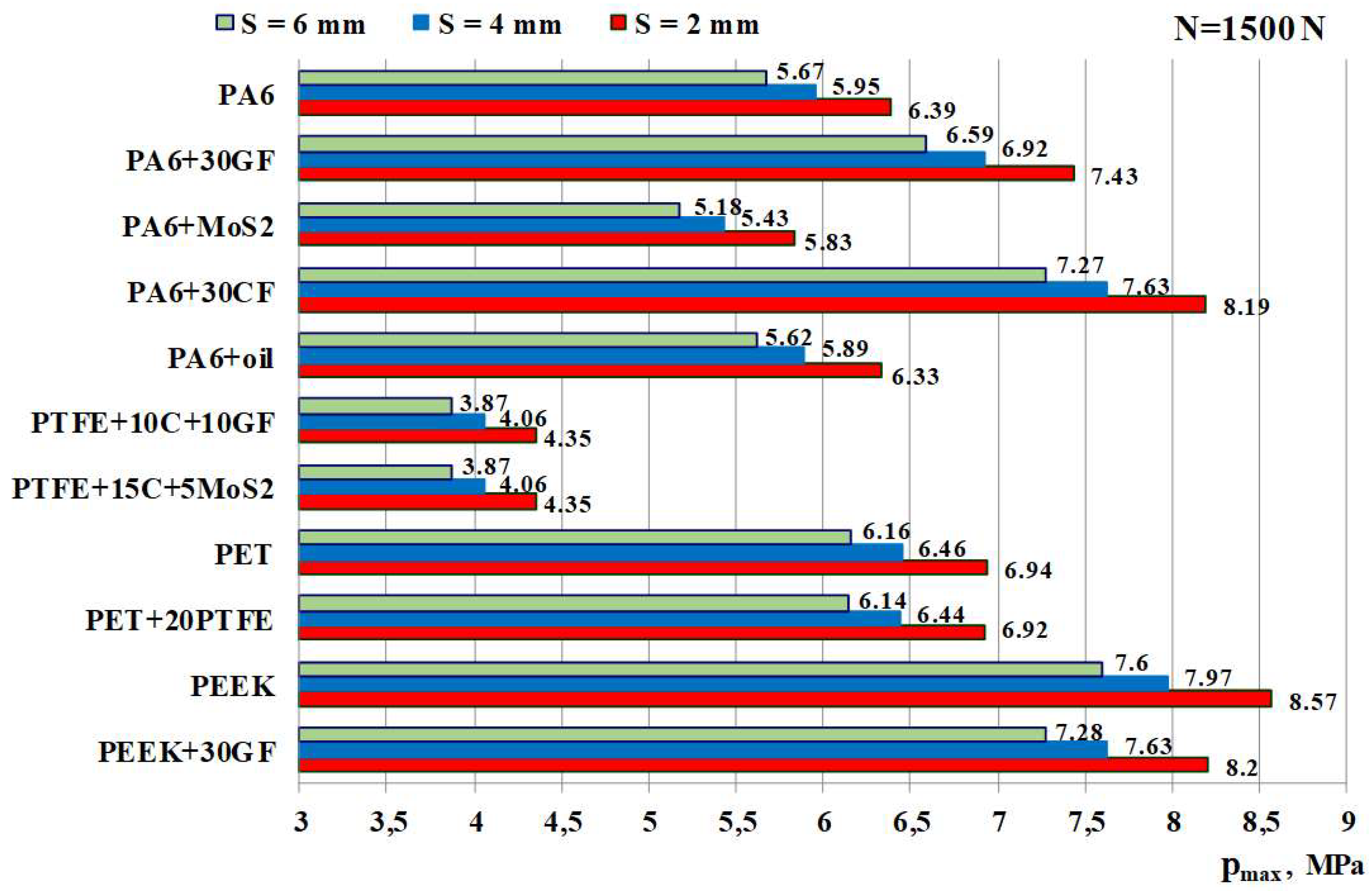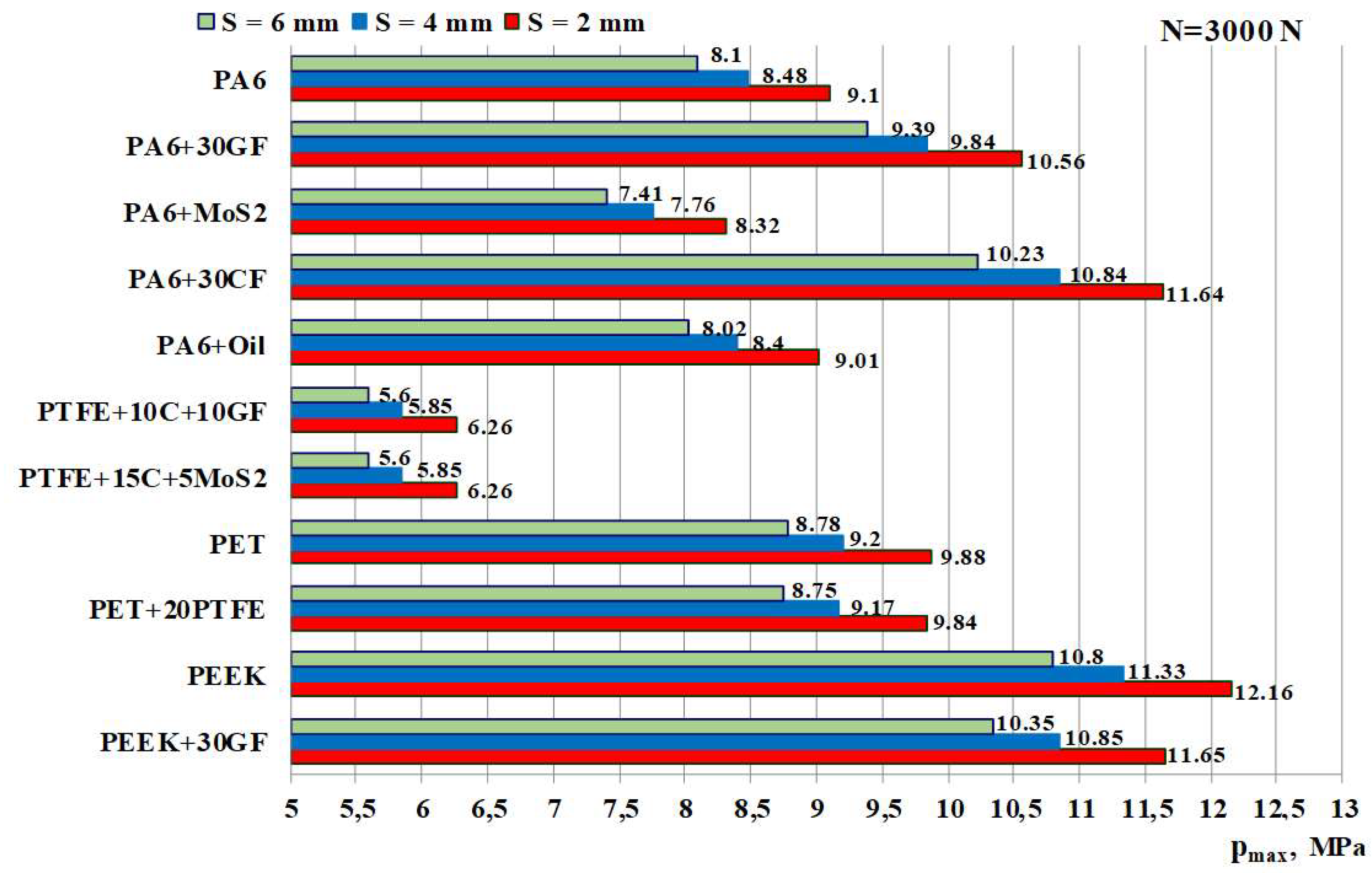The results of calculating the maximum contact pressures pmax are shown in Figure 2 and Figure 3.
Reducing the bushing thickness S from 6 to 2 mm results in a 1.126-fold increase in pmax, regardless of the type of polymeric material of the bushing. The bushing thickness S = 2 mm for a shaft diameter D2 = 30 mm is indicated for IGUS deep groove bearings Iglidur J, Iglidur G, Iglidur W300. The contact pressures in deep groove bearings increase in the following sequence depending on the type of polymeric material of the bushing: PTFE → PA6+MoS2 → PA6+oil → PA6 → PET+20PTFE → PET → PA6+30GF → PA6+30CF → PEEK+30GF → PEEK.
Fillers have a different effect on the change in contact pressures compared to unfilled (basic) polymeric materials. Fiberglass and carbon fiber in the polyamide group cause them to increase because they increase Young's modulus of the composite compared to PA6 (Table 1). The MoS2 filling reduces the pressures, while the oil filling practically does not change them. Due to the introduction of fillers into PA6, the change in pmax can be up to 1.4 times. The filling of PTFE with polyeteretherketone PET practically did not affect pmax. In the case of filling polyethylene terephthalate PEEK with glass fiber, the pressures pmax slightly decreased (by a factor of 1.045).
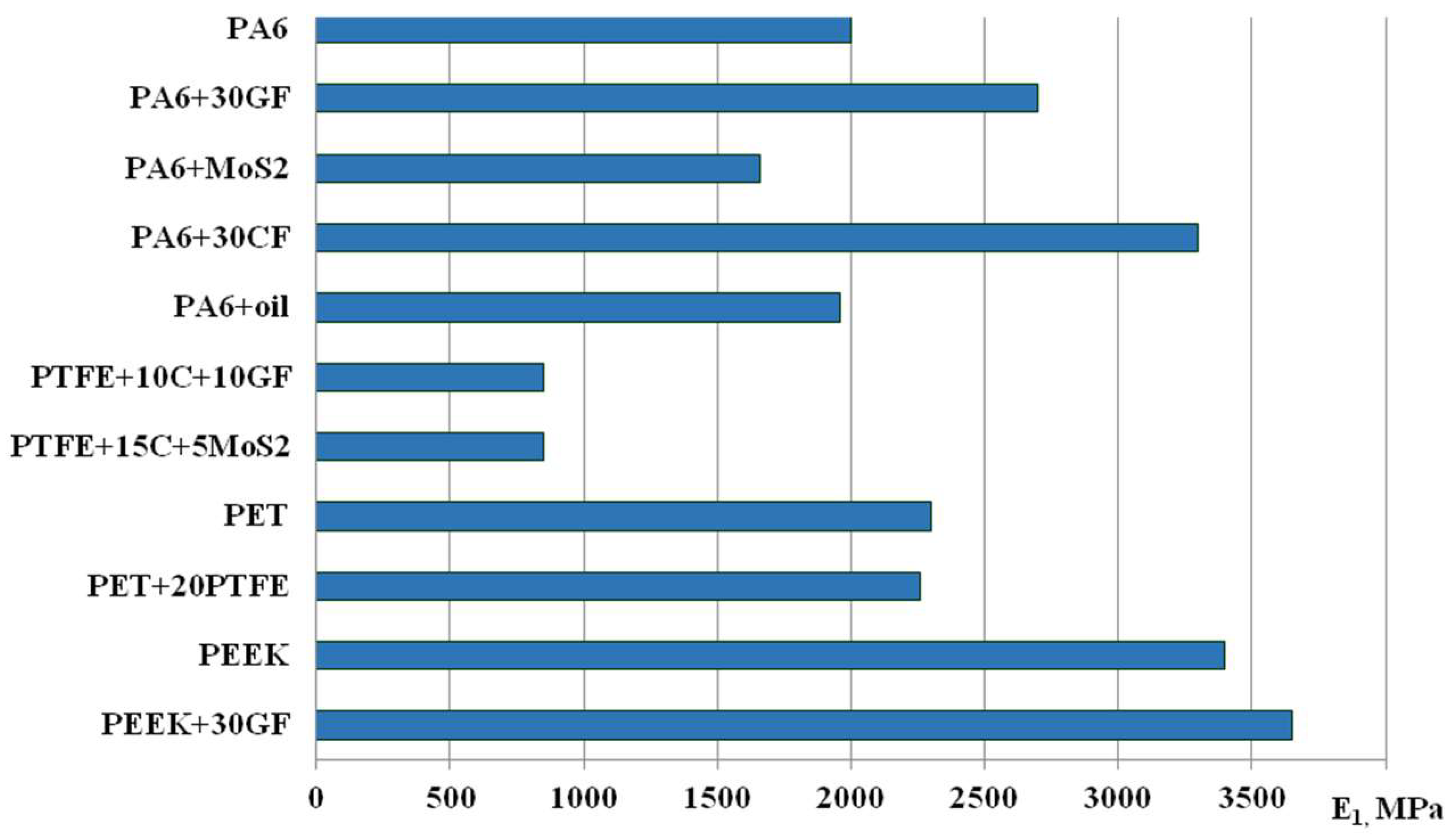
Young's modulus E1 has a significant effect on the maximum contact pressures. In polyamides, its increase reaches 2-fold (PA6+MoS2 → PA6+30CF), which, accordingly, leads to a 1.4-fold change in pmax . In the studied polymers, it increases by 4.29 times (PTFE → PEEK+30GF) (Tables 2, 3). From the analysis of Figure 2 and Figure 3, it was found that in this case, pmax increases by about 1.86 times (1.86...1.88 times at N = 1500 N, and 1.85...1.86 times at N = 3000 N).
According to the criterion of minimum contact pressures pmax, bearings with a bushing made of PTFE+10C+10GF or PTFE+15C+5MoS2 are optimal, whereas in other groups of polymers - with a bushing made of PA6+MoS2, PET, and PEEK+30GF.
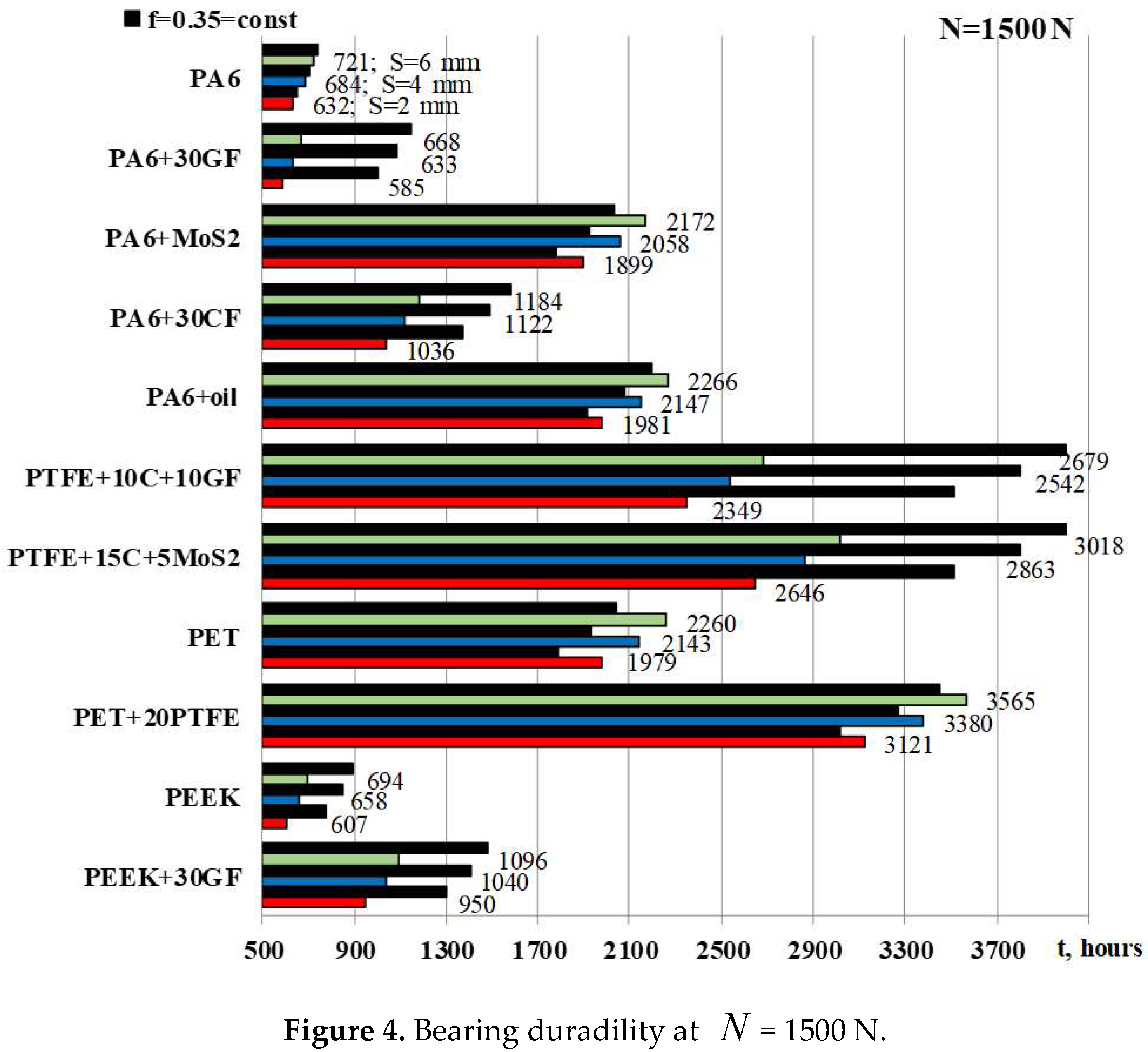
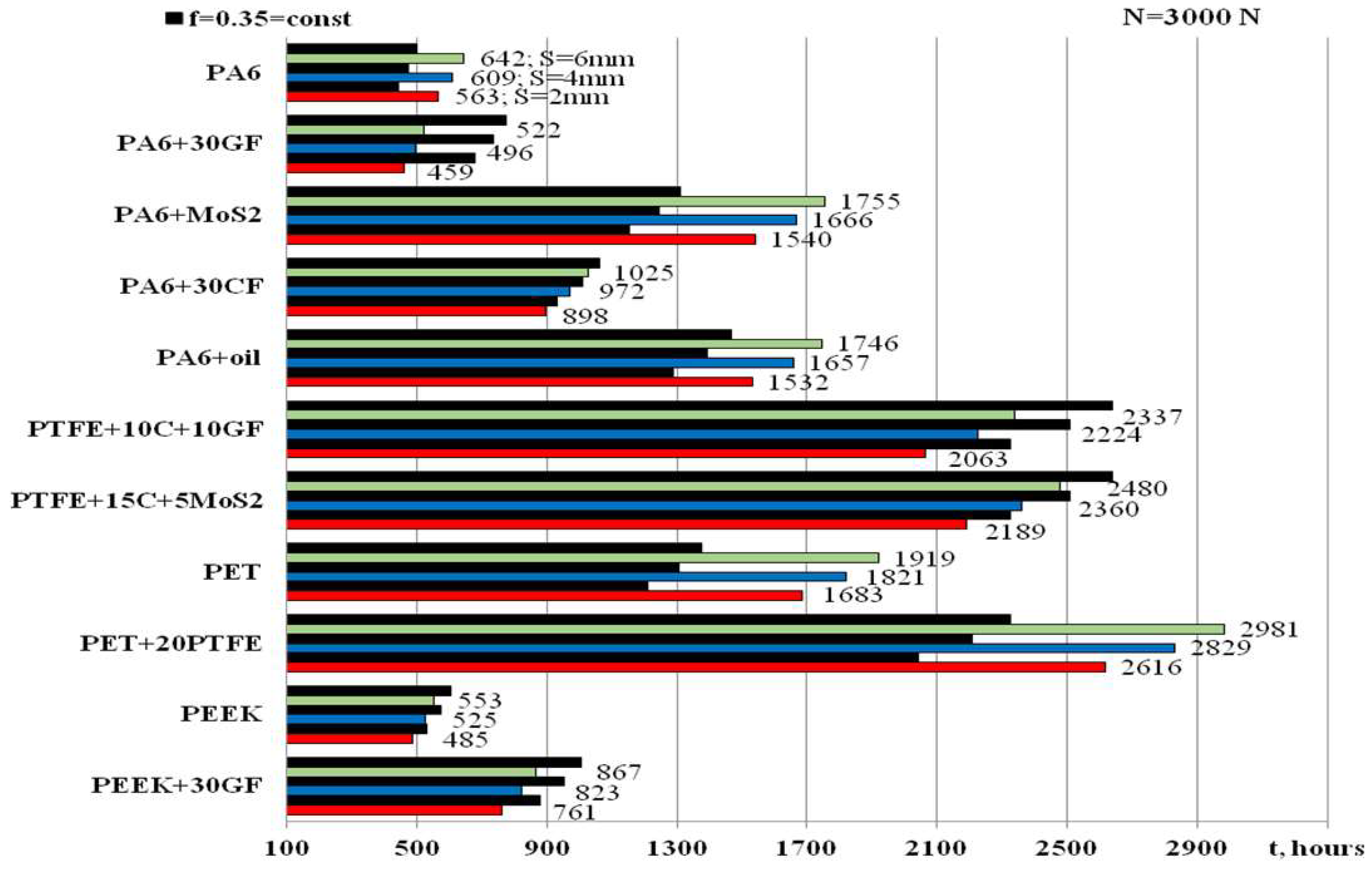
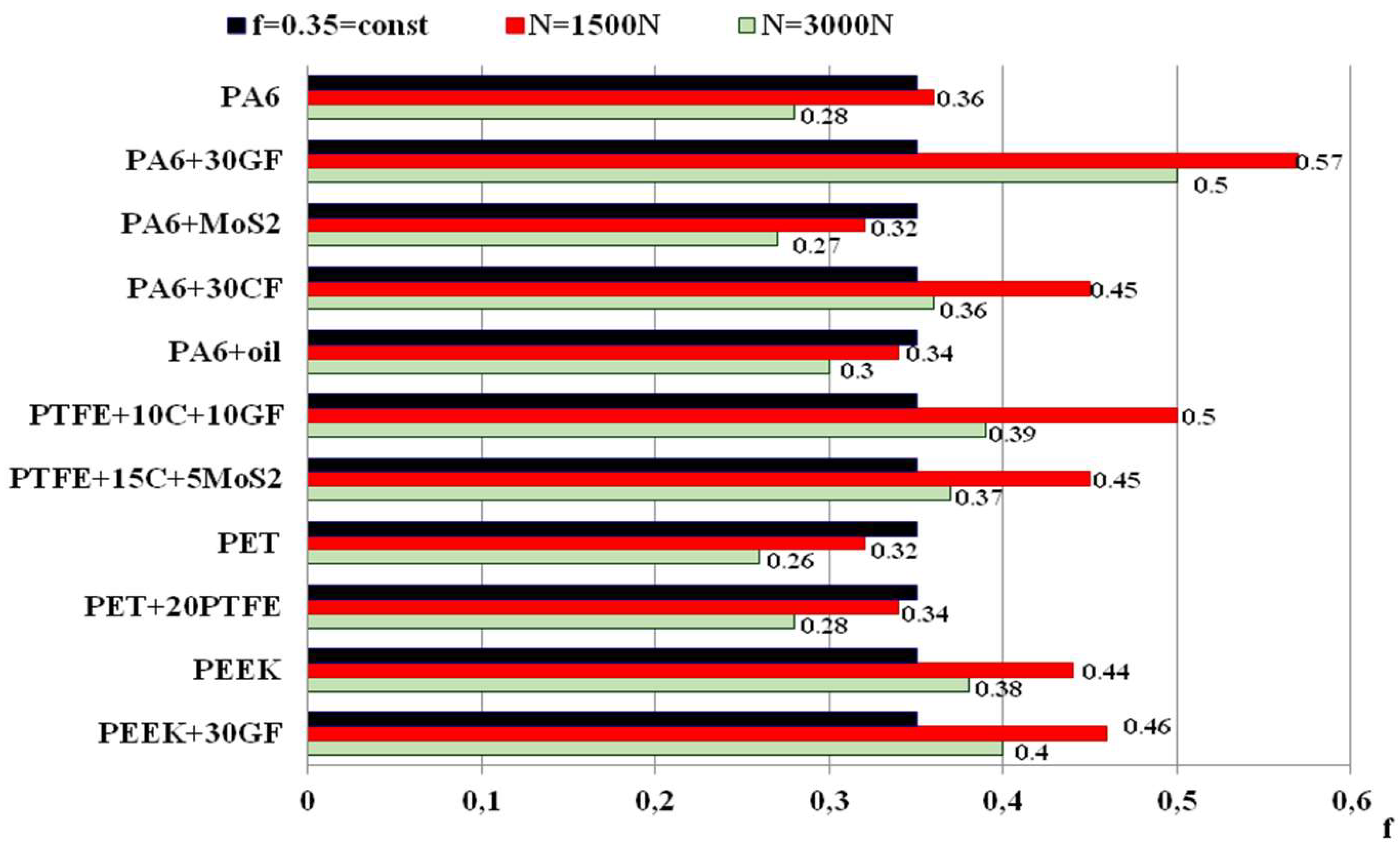
The data on the durability t of the bearings are shown in Figure 4 and Figure 5. Here, the diagrams show their durability in black at a constant friction coefficient f = 0.35. However, experimental studies have shown that in each steel-polymer pair, its values can differ significantly from the specified value (see Fig. 6). In addition, the friction coefficient decreases with increasing contact pressure. Therefore, these circumstances were taken into account when calculating the actual durability t , which is shown in the color-coded diagrams below.
When the bushing thickness S decreases from 6 to 2 mm, the bearing durability t decreases by 1.14 times for all types of polymeric materials. The bearing with a PET+20PTFE bushing has the longest durability, and the bearing with a PA6+30GF bushing has the shortest durability. The ratio of their durabilities is 5.33 at N = 1500 N and 5.7 at N = 3000 N. Bearings with a bushing made of PA6+MoS2, PA6+oil, PET have an approximate durability at N = 1500 N. At a load of N = 3000 N, it will be the same with bushings made of PA6+MoS2 and PA6+oil and slightly higher than that for PET. The lowest durabilities of bearings made of PA6, PA6+30GF, and REEK at N = 1500 N will be close, and at N = 3000 N, bearings made of PA6+30GF and PEEK will have the lowest durability. The durabilities of bearings with PA6+30CF and PEEK+30GF bushings will be somewhat higher.
Depending on the type of polymeric material of the bushing, the durability of MP bearings increases in the following sequence: PA6+30GF → PEEK → PA6 → PEEK+30GF → PA6+30CF → PA6+oil → PA6+MoS2 → PET → PTFE+10C+10GF → PTFE+15C+5MoS2 → PET+20PTFE. This sequence is significantly different from the above sequence of increasing maximum contact pressures: PTFE → PA6+MoS2 → PA6+oil → PA6 → PET+20PTFE → PET → PA6+30GF → PA6+30CF → PEEK+30GF → PEEK (Figs. 2 and 3). The increase in the linear wear resistance characteristic B1 of polymeric materials is as follows: PA6 → PEEK → PA6+30GF → PA6+MoS2 → PEEK+30GF → PA6+30CF → PET → PA6+oil → PET+20PTFE → PTFE (Table 1, Table 2 and Table 3). Friction coefficients f in these hybrid tribo-conjugations (Fig. 7) and Young's modulus E1 of polymers (Fig. 8) have other sequences of change from minimum to maximum values. Therefore, the calculated durability t of a bearing depends on the complex effect of the maximum contact pressure pmax, the wear resistance characteristics of polymeric materials B 1 , m 1 , τ 10 , Young's modulus E1, and friction coefficient f. All of these factors are included in formula (4) for calculating the bearing's mechanical life.
According to the criterion of maximum durability t, bearings with a PET+20PTFE bushing are optimal, whereas in the other groups of polymers -- with a bushing made of PA6+MoS2 or PA6+oil, PTFE+15C+5MoS2, PET+20PTFE, and PEEK+30GF.
Comparison of the pattern of change in pmax in bearings with different polymer bushings and the durability t of the bearings is shown in Figure 6. Here, it is easy to track the patterns of change in contact pressure and service life of bearings with different bushings.
Figure 7 shows the experimentally determined sliding friction coefficients at the calculated contact pressures pmax (Figure 2 and Figure 3).
Dry friction coefficients depend not only on the type of base polymer but also on the type of filler. The introduction of fiberglass into the base polymer increases the coefficient of friction of composites under dry friction on steel 45. Instead, the fillers from MoS2, oil, and PTFE as lubricants have little effect on it.
The elastic Young’s moduli of the studied polymeric materials determined by the Oliver-Farr method are shown in Figure 8.
Young's modulus of the investigated polymeric materials differs by a maximum of 4.29 times (PEEC+30GF / PTFE+10C+10GF). In the group of polyamides, the filling with CF and GF significantly increases Young's modulus compared to the base PA6 (Table 1). Filling PA6 with oil reduces it, and MoS2 practically does not change it. In polyesteretherketone, PTFE filling has a slight reducing effect on the modulus, and in polyethylene terephthalate, GF filling slightly increases it (Tables 2, 3). In all groups of polymers, fillers change Poisson's ratio slightly compared to the base materials (Table 1, Table 2 and Table 3).

4. Discussion

Despite the widespread use of sliding bearings, no relevant standards have been developed for the design calculation of their bearing capacity. Effective analytical methods are also absent in scientific publications. The calculation [11] or numerical methods [12,13] known in the literature for studying metal plain bearings are not used in engineering practice to assess the bearing capacity of MP bearings. As for the analytical methods for calculating the wear and durability of sliding bearings, there is no attempt to develop them.
In [14], an FEM study of the mechanical behavior of a large-sized MP sliding bearing with a sleeve made of a phenolic-based composite filled with PTFE and reinforced with polyester fibers was carried out. A simplified 3D FEM model was used in [15] to study the effect of clearance on contact stresses and kinematics of a polymer composite sliding bearing. Article [16] is devoted to a numerical study by the adaptive method of modeling the wear of a bearing made of a laminated polymer composite but does not provide for the possibility of estimating the durability. Here, local wear is modeled according to the Archard abrasive/adhesive wear law with a linear dependence of wear on contact pressure and sliding speed. However, [17] indicates that at friction coefficients above 0.3, which is typical for dry friction pairs, the dominant type of polymer wear is the frictional fatigue mechanism under the influence of specific friction forces. Adhesive wear can then be a secondary concomitant process. A sign of adhesive wear as the main process is the transfer of a thin adhesive film of polymeric material to a metal counterbody.
In the literature, more attention is paid to experimental studies of mechanical bearings [7,18,19,20]. In particular, their results are presented in the works [14,15,16]. Paper [21] reports on the tribological behavior during dry friction of various bearings with polymeric bushings made of polyacetal (POM-Delrin), cast polyamide PA6, etc. Work [18] is devoted to the study and evaluation of the wear resistance of bearings based on PE (polyethylene), PA, POM, PTFE, and bakelite polymers. The effect of sliding speeds, pressure, and temperature on the friction and wear of PA66 bearings, PA66+18PTFE, and PA66+20GF+25PTFE composites was studied in [22] at room temperature. A tribological analysis of the dry friction behavior of PA6 for a connecting rod plain bearing was performed in [4]. Study [19] evaluated polymeric plain bearings with PET and UHMWPE bushings and an Inconel stainless steel shaft in dry friction and water lubrication. The effect of radial clearance on the coefficient of friction, mass wear, and temperature of plain bearings with a sleeve made of the NORDEN Marine 605 composite and a shaft made of AISI 316 steel was studied in [20]. Two modes of friction in bearings were used - dry and with solid lubrication (PTFE). In [7], the wear of a sliding bearing with PEEK bushings and PEEK+30CF, PEEK+30GF, and PEEK+10CF+10C+10PTFE composites was studied.
The authors solve the problem of calculating the maximum contact pressures, wear, and durability of mechanical bearings by reasonably modifying the developed method of the elasticity theory for the study of metal bearings [1,2,3,4]. The developed method has been presented in [24], and the results of studies using it in [9,10,23,24,25,26]. Below are the results for MP bearings with bushings made of polyamides PA6, PA6+30GF, PA6+30CF, PA6+MoS2, and PA6+oil; polytetrafluoroethylenes PTFE+10C+10CF and PTFE+15C+5MoS2; polyethylene terephthalates PET and PET+20PTFE; and polyetheretherketones РEEK and PEEK+30GF.

5. Conclusions

Using a generalized analytical method, dry friction sliding bearings with a bushing made of four groups of polymeric materials for tribolgical purposes were studied. The influence of the following factors on the maximum contact pressure and durability of MP bearings was analyzed: load, radial clearance, bushing thickness, elasticity characteristics of tribopolymers, their wear resistance, sliding friction coefficient, type of tribopolymer materials, and type of fillers. It was found that Young's modulus of the polymeric material of the bushing is, in addition to the load and geometric parameters of the bearing, the main factor that has a significant effect on the maximum contact pressure. Fillers of base polymers, depending on the type, have a differential effect on the change in pmax: in PA composites, they increase (except for PA6+oil); in PET composite, they have no effect, and in PEEC composite, they slightly decrease pmax. Instead, the bearing's durability is influenced by a combination of several factors: contact pressure, polymer’s wear resistance and Young's modulus, and the coefficient of dry friction on steel. Fillers of all types of bushing polymers (except for the PA6+30GF composite) always increase bearing life. Quantitative and qualitative regularities of the influence of these factors on the maximum contact pressures and bearing life have been established.
Since the contact problem in the theory of elasticity for mechanical bearings to study their bearing capacity and durability is presented in a closed form, it is easy to solve it using appropriate computer programs. Also, the developed method can be used to optimize a bearing at the design stage according to the criteria of minimum contact pressure or maximum durability. According to the above results, this task has been solved for the accepted design data.

Author Contributions

Conceptualization, M.C. and J.Z.; methodology, M.C.; validation, J.C., J.Z.; formal analysis, M.C.; investigation, J.C.; writing—original draft preparation, M.C., J.Z.; writing—review and editing, J.C., J.Z.; funding acquisition, J.Z.

Acknowledgments

Work was financially supported by subvention within particular scientific disciplines of Lublin University of Technology.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Chernets, M.; Chernets, J. Generalized Method for Calculating the Durability of Sliding Bearings with Technological Out-of-Roundness of Details. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2015, 229, 216–226. [Google Scholar] [CrossRef]
  2. Chernets’, M.V.; Andreikiv, O.E.; Lebedeva, N.M.; Zhydyk, V.V. A Model for the Evaluation of Wear and Durability of a Plain Bearing with Small Out-of-Roundness. Mater. Sci. 2009, 45, 279. [Google Scholar] [CrossRef]
  3. Chernets, M.V. Prediction of the Life of a Sliding Bearing Based on a Cumulative Wear Model Taking into Account the Lobing of the Shaft Contour. J. Frict. Wear 2015, 36, 163–169. [Google Scholar] [CrossRef]
  4. Chernets, M.; Opielak, M.; Kornienko, A.; Radko, O. Predictive Estimation of Sliding Bearing Load-Carrying Capacity and Tribological Durability. Stroj. Vestn. – J. Mech. Eng. 2021, 67, 363–368. [Google Scholar] [CrossRef]
  5. Chernets, M.; Chernets, Y.; Skvarok, Y.; Zubrzycki, J. Investigation of Wear Resistance of Polyamide PA6 Based Composite Materials for Metal - Polymer Plain Bearings and Gears. Tribol. Ind. 2023, 45, 643–649. [Google Scholar] [CrossRef]
  6. Czerniec, M.; Zubrzycki, J. Study of Contact Pressures in Total Hip Replacement. Adv. Sci. Technol. Res. J. 2021, 15, 176–183. [Google Scholar] [CrossRef]
  7. Zhu, J.; Xie, F.; Dwyer-Joyce, R.S. PEEK Composites as Self-Lubricating Bush Materials for Articulating Revolute Pin Joints. Polymers 2020, 12, 665. [Google Scholar] [CrossRef]
  8. Chernets, M.; Zubrzycki, J. Study of Contact Parameters in Metal-On-Plastic Hip Endoprosthesis with the Analytical-Numerical Method of Contact Mechanics. Adv. Sci. Technol. Res. J. 2023, 17, 145–153. [Google Scholar] [CrossRef] [PubMed]
  9. Chernets, M.V.; Shil’ko, S.V.; Pashechko, M.I.; Barshch, M. Wear Resistance of Glass- and Carbon-Filled Polyamide Composites for Metal-Polymer Gears. J. Frict. Wear 2018, 39, 361–364. [Google Scholar] [CrossRef]
  10. Chernets, M.; Kornienko, A.; Chernets, Y. Investigations on Contact Pressures and Durability of Metal-Polymer Dry Sliding Bearings with Miniature, Small and Large Diameters. Tribol. Ind. 2022, 44, 528–539. [Google Scholar] [CrossRef]
  11. Dykha, A.; Marchenko, D. Prediction the Wear of Sliding Bearings. Int. J. Eng. Technol. 2018, 7, 4. [Google Scholar] [CrossRef]
  12. Sorokatyi, R.V.; Dykha, A.V. Analysis of Processes of Tribodamages under the Conditions of High-Speed Friction. J. Frict. Wear 2015, 36, 422–428. [Google Scholar] [CrossRef]
  13. Sorokatyi, R.V.; Pisarenko, V.G.; Dykha, M.A. Analysis of Wear Surface Geometry Formation in Plain Bearings with Misaligned Shaft and Bush Axes. J. Frict. Wear 2013, 34, 274–280. [Google Scholar] [CrossRef]
  14. Rezaei, A.; Ost, W.; Paepegem, W.V.; De Baets, P.; Degrieck, J. Experimental Study and Numerical Simulation of the Large-Scale Testing of Polymeric Composite Journal Bearings: Three-Dimensional and Dynamic Modeling. Wear 2011, 270, 431–438. [Google Scholar] [CrossRef]
  15. Rezaei, A.; Van Paepegem, W.; Ost, W.; De Baets, P.; Degrieck, J. A Study on the Effect of the Clearance on the Contact Stresses and Kinematics of Polymeric Composite Journal Bearings under Reciprocating Sliding Conditions. Tribol. Int. 2012, 48, 8–14. [Google Scholar] [CrossRef]
  16. Rezaei, A.; Van Paepegem, W.; De Baets, P.; Ost, W.; Degrieck, J. Adaptive Finite Element Simulation of Wear Evolution in Radial Sliding Bearings. Wear 2012, 296, 660–671. [Google Scholar] [CrossRef]
  17. Myshkin, N.; Kovalev, A.; Spaltman, D.; Woydt, M. Contact Mechanics and Tribology of Polymer Composites. J. Appl. Polym. Sci. 2014, 131, app–39870. [Google Scholar] [CrossRef]
  18. Ünlü, B.S.; Atik, E.; Köksal, S. Tribological Properties of Polymer-Based Journal Bearings. Mater. Des. 2009, 30, 2618–2622. [Google Scholar] [CrossRef]
  19. Nguyen, T.D.; Sukumaran, J.; De Pauw, J.; De Baets, P. TRIBOLOGICAL BEHAVIOUR OF POLYMER BEARINGS UNDER DRY AND WATER LUBRICATION. Int. J. Sustain. Constr. Des. 2013, 4. [Google Scholar] [CrossRef]
  20. Miler, D.; Škec, S.; Katana, B.; Žeželj, D. An Experimental Study of Composite Plain Bearings: The Influence of Clearance on Friction Coefficient and Temperature. Stroj. Vestn. – J. Mech. Eng. 2019, 547–556,. [CrossRef]
  21. Feyzullahoglu, E.; Saffak, Z. The Tribological Behaviour of Different Engineering Plastics under Dry Friction Conditions. Mater. Des. 2008, 29, 205–211. [Google Scholar] [CrossRef]
  22. Hua, X.; Wang, L.; Al-Hajjar, M.; Jin, Z.; Wilcox, R.K.; Fisher, J. Experimental Validation of Finite Element Modelling of a Modular Metal-on-Polyethylene Total Hip Replacement. Proc. Inst. Mech. Eng. [H] 2014, 228, 682–692. [Google Scholar] [CrossRef] [PubMed]
  23. Chernets, M.; Chernets, J.; Kindrachuk, M.; Kornienko, A. Methodology of Calculation of Metal-Polymer Sliding Bearings for Contact Strength, Durability and Wear. Tribol. Ind. 2020, 42, 572–581. [Google Scholar] [CrossRef]
  24. Chernets, M.; Pashechko, M.; Kornienko, A.; Chernets, J.; Fedorchuk, S. On the Question of Methodology of Hybrid Sliding Bearings Estimated Load Capacity and Durability Evaluation. Adv. Sci. Technol. Res. J. 2020, 14, 177–184. [Google Scholar] [CrossRef] [PubMed]
  25. Chernets, M.V.; Kornienko, A.A.; Pashechko, M.I.; Chernets, Yu.M.; Dukhota, A.I. To the Question of Calculation of Contact Pressure in MetalPolymer Plain Bearings During Wear. Trenie Iznos 2021, 42, 552–561. [Google Scholar] [CrossRef]
  26. Chernets, M.; Pashechko, M.; Kornienko, A.; Buketov, A. Study of the Influence of Temperature on Contact Pressures and Resource of Metal-Polymer Plain Bearings with Filled Polyamide PA6 Bushing. Lubricants 2022, 10, 13. [Google Scholar] [CrossRef]
Preprints 137703 g001
Figure 1. Metal-polymer plain bearing: (a) general view and (b) diagram.
Figure 1. Metal-polymer plain bearing: (a) general view and (b) diagram.
Preprints 137703 g001
Preprints 137703 g002
Figure 2. Maximum contact pressures in the MP bearing with different types of polymers: N=1500N.
Figure 2. Maximum contact pressures in the MP bearing with different types of polymers: N=1500N.
Preprints 137703 g002
Preprints 137703 g003
Figure 3. Maximum contact pressures in the MP bearing with different types of polymers: N=3000N.
Figure 3. Maximum contact pressures in the MP bearing with different types of polymers: N=3000N.
Preprints 137703 g003
Preprints 137703 g004
Figure 4. Bearing duradility at N = 1500 N.
Figure 4. Bearing duradility at N = 1500 N.
Preprints 137703 g004
Preprints 137703 g005
Figure 5. Bearing duradility at N = 3000 N.
Figure 5. Bearing duradility at N = 3000 N.
Preprints 137703 g005
Preprints 137703 g006
Figure 6. Contact pressures and durability of deep groove bearings.
Figure 6. Contact pressures and durability of deep groove bearings.
Preprints 137703 g006
Preprints 137703 g007
Figure 7. Sliding friction coefficients.
Figure 7. Sliding friction coefficients.
Preprints 137703 g007
Preprints 137703 g008
Figure 8. Modulus of elasticity of tribopolymers.
Figure 8. Modulus of elasticity of tribopolymers.
Preprints 137703 g008
Table 1. Characteristics of polyamides.
Table 1. Characteristics of polyamides.
Characteristics Polyamides
PA6 PA6+ 30GF PA6+ MoS2 PA6+ 30CF PA6+ oil
B1 ∙1010 2.26 4.12 5.58 6.53 7.03
m1 1.09 1.09 1.1 1.1 1.1
τ10, MPa 0.05 0.05 0.05 0.05 0.05
Young's modulus E1, MPa 2000 2700 1660 3300 1960
Poisson's ratio ν1 0.4 0.41 0.4 0.41 0.4
Table 2. Characteristics of polytetrafluoroethylenes.
Table 2. Characteristics of polytetrafluoroethylenes.
Characteristics Polytetrafluoroethylenes
PTFE+10C+ 10CF PTFE+15C+5MoS2
B1 ∙1010 8.2 8.2
m1 1.1 1.1
τ10, MPa 0.05 0.05
E1, MPa 850 850
ν1 0.46 0.46
Table 3. Characteristics of polyetheretherketones and polyethylene terephthalates.
Table 3. Characteristics of polyetheretherketones and polyethylene terephthalates.
Characteristics Polyetheretherketones, polyethylene terephthalates
PET PET+20PTFE PEEK PEEK+30GF
B1 ∙1010 6.81 11.45 3.76 5.95
m1 1.09 1.09 1.09 1.09
τ10, MPa 0.05 0.05 0.05 0.05
E1, MPa 2300 2260 3400 3650
ν1 0.43 0.44 0.38 0.4
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Influence of Temperature on Contact Pressures and Resource of Metal-Polymer Plain Bearings with the Filled Polyamide PA6 Bushing

Myron Chernets

et al.

,

2021

A Computational Model for Analysing the Wear Behaviour of Polymer Gears

Aljaž Ignatijev

et al.

,

2024

Design and Experimental Research on Sealing Structure for a Retrievable Packer

Yang Liu

et al.

,

2019

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated