Prerpints.org logo
Preprint
Article

On the Hypothesis of Exact Conservation of Charged Weak Hadronic Vector Current in the Standard Model

This version is not peer-reviewed.

Submitted:

30 October 2024

Posted:

31 October 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
We investigate a reliability of conservation of the vector current (CV) hypothesis in the neutron β−-decay. We calculate the contribution of the phenomenological term, responsible for the CVC in the hadronic current of the neutron β−-decay (or the CVC effect), to the neutron lifetime. We show that the CVC effect increases the neutron lifetime with a relative contribution 8.684×10−2. This leads to the increase of the neutron lifetime by 76.4 s with respect to the world averaged value τn=880.2(1.0)s (Particle Data Group, Chin. Phys. 40, 100001 (2016)). We show that since in the Standard Model (SM) there are no interactions, which are able to cancel such a huge increase of the neutron lifetime, we have to turn to the interactions beyond the SM the contribution of which to the neutron lifetime reduces to the Fierz interference term bF only. Cancelling the CVC effect at the level of the experimental accuracy we get bF=0.1219(12). If this value cannot be accepted for the Fierz interference term, the CVC effect induces irresistible problems for description and understanding of the neutron β−-decay.
Keywords: 
Subject: 
Physical Sciences  -   Nuclear and High Energy Physics

1. Introduction

The neutron lifetime with the account for the complete set of corrections of order 10 − 3 , caused by the weak magnetism, proton recoil and electromagnetic interaction, has been calculated in [1]. The theoretical value τ n = 879 . 6 ( 1 . 1 ) s agrees well with the world averaged one τ n = 880 . 2 ( 1 . 0 ) s [2] and recent experimental value τ n = 880 . 2 ( 1 . 2 ) s [3]. The theoretical uncertainty ± 1 . 1 is fully defined by the experimental uncertainties of the axial coupling constant λ = − 1 . 2750 ( 9 ) [4] and the Cabibbo-Kobayashi-Maskawa (CKM) matrix element V u d = 0 . 97425 ( 22 ) [5], which agrees well with a new value V u d = 0 . 97417 ( 21 ) [2] reported by Hardy and Tower [6]. Both values of the CKM matrix elements have been extracted from the 0 + → 0 + transitions with the errors dominated by the theoretical uncertainties caused by nuclear Coulomb distortion and radiative corrections [2,6].
According to recent analysis by Hardy and Tower [6] (see also [7]), the effect of conservation of the vector current (CVC) in the 0 + → 0 + transitions (or in the pure Fermi transitions) is being observed at the level of 1 . 2 × 10 − 4 . In turn, as has been found by Naviliat-Cuncic and Severijns [8], in the mirror decays of 19Ne, 21Na, 29P, 35Ar, and 17 K, caused by the Gamow-Teller mirror transitions, a new independent test of the CVC effect may be performed at the level of 4 × 10 − 3 [7]. Recently, the CVC effect has been investigated by Ankowski [9] and Giunti [10] in the inverse β -decay ν ¯ e + p → n + e + .

2. Precision Analysis of Neutron Lifetime to order 10 − 4

This work is addressed to the analysis of the reliability of the CVC hypothesis or the CVC effect in the neutron lifetime. The effective low-energy Lagrangian of V − A weak interactions takes the standard form [1,11]
L W ( x ) = − G F 2 V u d J μ ( x ) ψ ¯ e ( x ) γ μ 1 − γ 5 ψ ν e ( x )
where G F = 1 . 1664 × 10 − 11 MeV − 2 and V u d = 0 . 97417 ( 21 ) are the Fermi weak constant and the Cabibbo-KobayashiMaskawa (CKM) matrix element [2], respectively, J μ ( x ) is the hadronic V − A current, ψ e ( x ) and ψ ν e ( x ) are the operators of the electron and electron neutrino (antineutrino) fields. The amplitude of the neutron β − -decay n → p + e − + ν ¯ e is equal to (for more details see Appendix A)
M n → p e − ν ¯ e = − G F 2 V u d p k → p , σ p J μ ( 0 ) n k → n , σ n u ¯ e k → e , σ e γ μ 1 − γ 5 v ν k → , + 1 2
where p k → p , σ p , n k → n , σ n are the wave functions of the free proton and neutron with 3-momenta k → p and k → n = 0 → and polarizations σ p = ± 1 and σ n = ± 1 , respectively. Then, u ¯ e k → e , σ e and v ν k → ν , + 1 2 are the Dirac wave functions of the free electron and electron antineutrino with 3 − momenta k → e and k → ν and polarizations σ e = ± 1 and + 1 2 [1,11], respectively. In the Standard Model (SM) the matrix element of the hadronic current we take in the following form
p k → p , σ p J μ ( 0 ) n k → n , σ n = u ¯ p k → p , σ p γ μ − q μ q ^ q 2 + κ 2 M i σ μ ν q ν + λ − 2 M q μ q 2 − m π 2 + γ μ γ 5 u n k → n , σ n
which is similar to that used by Nowakowski et al. [12] and Leitner et al. [13], where u ¯ p k → p , σ p and u n k → n , σ n are the Dirac wave functions of the free proton and neutron. Then, − q μ q ^ / q 2 , where q = k p − k n is a 4 − momentum transferred, is the phenomenological term responsible for the CVC in the neutron β − -decay. The term κ / 2 M , where 2 M = m n + m p and m n = 939 . 5654 MeV and m p = 938 . 2720 MeV are the neutron and proton masses, defines the contribution of the weak magnetism, where κ = κ p − κ n = 3 . 7058 is the isovector anomalous magnetic moment of the nucleon, defined by the anomalous magnetic moments of the proton κ p = 1 . 7928 and the neutron κ n = − 1 . 9130 and measured in nuclear magneton [2]. The contribution of the axial current is given by the last term in Eq.(3), where λ = − 1 . 2750 ( 9 ) is the axial coupling constant [4] (see also [1,11]) and m π is the charged pion mass [2]. In the limit m π → 0 (or in the chiral limit) the axial current is also conserved [14,15]. Skipping standard calculations [1] we arrive at the rate of the neutron β − -decay given by
1 τ n = 1 τ n ( SM ) 1 + f n ( CVC ) f n
where τ n ( SM ) = 879 . 6 ( 1 . 1 ) s is the theoretical value of the neutron lifetime, calculated in [1] for λ = − 1 . 2750 ( 9 ) . It agrees perfectly well with the world averaged value τ n = 880 . 2 ( 1 . 0 ) s [2] and recent experimental one τ n = 880 . 2 ( 1 . 2 ) s [3]. Then, the phase space factor f n of the neutron, calculated order O ( 1 / M ) and O ( α / π ) caused by the contributions of the weak magnetism and proton recoil and the radiative corrections, respectively, is equal to f n = 6 . 116 × 10 − 2 MeV 5 . The phase space factor of the neutron f n ( CVC ) , caused by the CVC effect, is given by the expression
f n ( CVC ) = 1 1 + 3 λ 2 ∫ m e E 0 d E e k e E 0 − E e 2 F E e , Z = 1 ∫ d Ω e ν 4 π − 2 m e 2 Δ m e 2 + 2 E e E 0 − E e − 2 k → e · k → ν + m e 2 Δ 2 m e 2 + 2 E e E 0 − E e − 2 k → e · k → ν 2 E e − k → e · k → ν E ν
where Δ = m n − m p , E 0 = m n 2 − m p 2 + m e 2 / 2 m n = 1 . 2927 MeV is the end-point energy of the electron energy spectrum of the neutron β − -decay [1], k e = E e 2 − m e 2 is an absolute value of the electron 3 -momentum, F E e , Z = 1 is the relativistic Fermi function describing the proton-electron Coulomb final-state interaction [1]. Then, d Ω e ν is an element of the solid angle of the electron-antineutrino momentum correlations. Since we analyse the main contribution of the CVC effect, the integrand of the phase space factor f ( C V C ) is calculated to leading order in the large nucleon mass expansion. Because of the numerical value f n ( CVC ) = − 4 . 887 × 10 − 3 MeV 5 the contribution of the CVC effect to the rate of the neutron β − -decay is equal to f n ( CVC ) / f n = − 7 . 991 × 10 − 2 . This corresponds to the relative correction to the neutron lifetime Δ τ n ( CVC ) / τ n = 8 . 684 × 10 − 2 that gives Δ τ n ( CVC ) = 76 . 4 s . Unfortunately, such a huge increase of the lifetime by the CVC effect cannot be accepted for the neutron and should be substantially suppressed for the correct agreement with recent experimental data τ n = 880 . 2 ( 1 . 2 ) s [3] and world averaged value τ n = 880 . 2 ( 1 . 0 ) s [2]. In this connection it is important to emphasize that in the SM there are no contributions, which are able to diminish such a huge increase of the neutron lifetime, induced by the phenomenological term − q μ q ^ / q 2 responsible for the CVC in the neutron β − -decay [16,17,18]. Indeed, the contribution of the pseudoscalar term for a physical mass of the charged pion m π = 139 . 570 MeV decreases the neutron lifetime at the level of Δ τ n ( π ) / τ n = 4 . 691 × 10 − 6 . However, in the chiral limit m π → 0 the contribution of the charged pion may only aggravate the problem. Hence, in order to reduce a huge contribution of the CVC effect at the level of f n ( CVC ) / f n = − 7 . 991 × 10 − 2 to the level of 1 . 2 × 10 − 4 one has to turn to interactions beyond the SM.

3. Fierz Interference Term

It is well-know [20-23][20,21,22,23](see also the review papers [4,19]) that the simplest contribution of interactions beyond the SM to the neutron β − -decay is the Fierz interference term b F m e / E e , caused by scalar and tensor interactions beyond the SM. Below for the analysis of the contribution of the Fierz interference term we use the results, obtained in [1]. As has been shown in [1] all possible interactions beyond the SM [22] give the contribution to the neutron lifetime only in the form of the Fierz interference term. As a result, the Fierz interference term changes the rate of the neutron β − -decay as follows
1 τ n = 1 τ n ( SM ) 1 + b F m e E e SM
where m e / E e SM = 0 . 6556 is calculated with the electron energy spectrum density Eq.(D-59) of Ref. [1]. Taking into account the contribution of the CVC effect we get
1 τ n = 1 τ n ( SM ) 1 + f n ( CVC ) f n + b F m e E e SM
where the right-hand-side (r.h.s.) of Eq.(7) contains a complete set of phenomenological contributions within the SM and contributions beyond the SM. In the obtained expression for the neutron lifetime, given by Eq.(7), effectively the contribution of the CVC effect and the Fierz interference term can be kept at the required level of 1 . 2 × 10 − 4 if the Fierz interference term is equal to b F = 0 . 12189 ( 12 ) .

4. Conclusions

We have analyzed the CVC hypothesis in the neutron β − -decay and calculated the contribution of the CVC effect, i.e. the contribution of the phenomenological term − q μ q ^ / q 2 responsible for the CVC of the hadronic weak current of the neutron β − -decay. We have shown that the CVC effect gives a relative contribution to the rate of the neutron β − -decay at the level of f n ( CVC ) / f n = − 7 . 991 × 10 − 2 , which is one order of magnitude large compared to the level of 4 × 10 − 3 of the CVC test in the Gamow-Teller mirror transitions reported by Naviliat-Cuncic and Severijns [8]. As a result, the phenomenological term − q μ q ^ / q 2 , providing the CVC of the hadronic current in the neutron β − -decay, changes the lifetime of the neutron by Δ τ n = 76 . 4 s . Since in the SM there are no interactions, which are able to cancel such a huge increase of the neutron lifetime, we have turned to interactions beyond the SM. As has been shown in [1], the contributions of all possible interactions beyond the SM [22], which may affect the energy spectra and angular distributions of the neutron β − -decay, reduce themselves to the contribution to the neutron lifetimes in the form of the Fierz interference term only. Keeping the effective contribution, caused by the CVC effect and the Fierz interference term, at the level of the experimental uncertainty of the neutron lifetime 1 . 2 × 10 − 3 we have obtained the Fierz interference term b F = 0 . 1219 ( 12 ) , which seems to be also huge in comparison with the results b F < 0 . 01 Herczeg [24], b F = 0 . 0032 (23) Faber et al. [25], b F = − 0 . 0028 ( 26 ) Hardy and Tower [6] (see also discussion below Eq.(7) of Ref.[6]), and and b F < 0 . 03 , reported by H. Saul on behalf of the PERKEO III Collaboration [26]. Thus, if the value of the Fierz interference term b F = 0 . 1219 ( 12 ) is not acceptable one may conclude that the phenomenological realization of the CVC hypothesis in the neutron β − -decay in terms of the contribution − q μ q ^ / q 2 induces irresistible problems for description and understanding of the neutron β − -decay.

Acknowledgments

We want to thank our dear colleague Andrey Nikolaevich Ivanov, who was the main investigator of this work until he sadly passed away on December 18, 2021. We see it as our professional and personal duty to honor his legacy by continuing to publish our collaborative work. Andrey was born on June 3, 1945 in what was then Leningrad. Since 1993 he was a university professor at the Faculty of Physics, named "Peter The Great St. Petersburg Polytechnic University" after Peter the Great. Since 1995 he has been a guest professor at the Institute for Nuclear Physics at the Vienna University of Technology for several years and has been closely associated with the institute ever since. This is also were we met Andrey and have been collaborating with him closely over more than 20 years resulting in 40 scientific publications, see also [27,28,29,30,31,32,33,34,35,36,37]. We will miss Andrey as a personal friend and his immense wealth of ideas, scientific skills and his creativity. See also the official obituary for Andrey Nikolaevich Ivanov. The work of M. Wellenzohn was supported by MA 23 (p.n. 27-07 and p.n. 30-22). The sole responsibility for the content of this publication lies with the authors.

Appendix A. The Amplitude of the Rate of the Neutron Radiative β - -Decay.

In the tree-approximation the Feynman diagrams of the amplitude of the neutron radiative β − -decay are shown in Figure A1. The amplitude of the neutron radiative β − -decay, defined by the diagrams in Figure A1, we describe by the expression [1]
M n → p e − ν ¯ e γ λ ′ = e G F 2 V u d M n → p e − ν ¯ e γ λ ′
where e is the proton electric charge, G F and V u d are the Fermi weak constant and the Cabibbo-Kobayashi-Maskawa (CKM) matrix element, respectively, and the amplitude M n → p e − ν ¯ e γ λ ′ is equal to
M n → p e − ν ¯ e γ λ ′ = u ¯ p k → p , σ p ε ^ λ ′ * ( k ) 1 m p − k ^ p − k ^ − i 0 O μ u n k → n , σ n u ¯ e k → e , σ e γ μ 1 − γ 5 v ν k → , + 1 2 − u ¯ p k → p , σ p O μ u n k → n , σ n u ¯ e k → e , σ e ε ^ λ ′ * ( k ) 1 m e − k ^ e − k ^ − i 0 γ μ 1 − γ 5 v ν k → , + 1 2
where u ¯ p k → p , σ p , u n k → n , σ n , u ¯ e k → e , σ e and v ν k → ν , + 1 2 are the Dirac wave functions of the free proton, neutron, electron and electron antineutrino with 3-momenta k → p , k → n = 0 → , k → e and k → ν and polarizations σ p = ± 1 , σ n = ± 1 , σ e = ± 1 and + 1 2 [1,11], respectively, ε λ ′ * α ( k ) is the polarization vector of the photon in the polarization state λ ′ = 1 , 2 with a 4 -momentum k, obeying the constraint ε λ ′ * ( k ) · k = 0 . The amplitude Eq. A2 is gauge invariant. Indeed, one may show that, replacing ε λ ′ α * ( k ) → k α and using the Dirac equations for the free proton and electron, the amplitude Eq. A2 vanishes. Then, the matrix O μ is given by
O μ = γ μ − q μ q ^ q 2 + λ γ μ γ 5 + i κ 2 M σ μ ν k p − k n ν
where the matrix O μ , used in [ 5 , 8 ] , is modified by the term − q μ q ^ / q 2 , which is introduced according to the CVC hypothesis (see [9,12,13]) with q = k n − k p , λ is the axial coupling, which we set λ = − 1 . 2750 ( 9 ) (see [1,4,38]), κ = κ p − κ n = 3 . 7058 is the isovector anomalous magnetic moment of the nucleon, defined by the anomalous magnetic moments of the proton κ p = 1 . 7928 and the neutron κ n = − 1 . 9130 and measured in nuclear magneton [2]. In the tree-approximation the contribution of the term − q μ q ^ / q 2 to the amplitude of the neutron radiative β − -decay, calculated in the baryon non-relativistic approximation to leading order in the large baryon mass expansion, is equal to
δ M n → p e − ν ¯ e γ λ ′ = 2 m n Δ k n − k p 2 φ p † φ n u ¯ e k → e , σ e 1 2 k e · k Q e λ ′ 1 − γ 5 v ν k → , + 1 2
where Δ = m n − m p , Q e λ ′ = 2 m e k e · ε λ ′ * + 2 k e · k ε λ ′ * + m e ε ^ λ ′ * k ^ and we have used the Dirac equations for the free proton, neutron and electron antineutrino (see the Appendix of Ref. [38]). We have to emphasize that following [1,38,39] we have kept only the contribution of the photon emitted by the electron, which survives for the physical degrees of freedom of the photon. The contribution of the CVC effect to the branching ratio of the neutron radiative β − -decay is given
BR β γ ( CVC ) = τ n α π G 2 V u d 2 π 3 ∫ ω min ω max d ω ∫ m e E 0 − ω d E e E e 2 − m e 2 F E e , Z = 1 E 0 − E e − ω 2 ∫ d Ω ν e 4 π ∫ d Ω ν γ 4 π E 0 E 0 2 − k → e + ω n → k → + k → ν 2 m e 2 ω k e 2 − k → e · n → k → 2 E e − k → e · n → k → 2 + 1 E e − k → e · n → k → k e 2 − k → e · n → k → 2 + 2 E e k → e · k → ν E ν − E e E e + ω n → k → · k → ν E ν − E e E e − ω + E e + ω n → k → · k → ν E ν + ω ,
where the branching ratio is defined for the photon emitted with an energy from the interval ω min ≤ ω ≤ ω max . Then, E 0 = 1 . 2927 MeV is the end-point energy of the electron energy spectrum of the neutron β − -decay [1], F E e , Z = 1 is the relativistic Fermi function taking into account the Coulomb proton-electron final-state interaction [1,38], d Ω ν e = sin ϑ ν e d ϑ ν e d φ ν e and d Ω ν g a m m a = sin ϑ ν γ d ϑ ν γ d φ ν γ are elements of solid angles of antineutrino-electron and antineutrino-photon momentum correlations, respectively, such as k → e · k → ν = k e E 0 − E e − ω cos ϑ ν e , n → k → · k → ν = E 0 − E e − ω cos ϑ ν γ and k → e · n → k → = k e cos ϑ ν e cos ϑ ν γ + sin ϑ ν e sin ϑ ν γ cos φ ν e − φ ν γ . For the numerical analysis of the branching ratio B β γ ( CVC ) we use the theoretical value of the neutron lifetime τ n = 879 . 6 ( 1 . 1 ) s , which agrees perfectly well with the world averaged value τ n = 880 . 2 ( 1 . 0 ) s [2]. The numerical values of the branching ratio we adduce in Table A1, more details on the numerical solution of Eq. (A5) find in Appendix B.
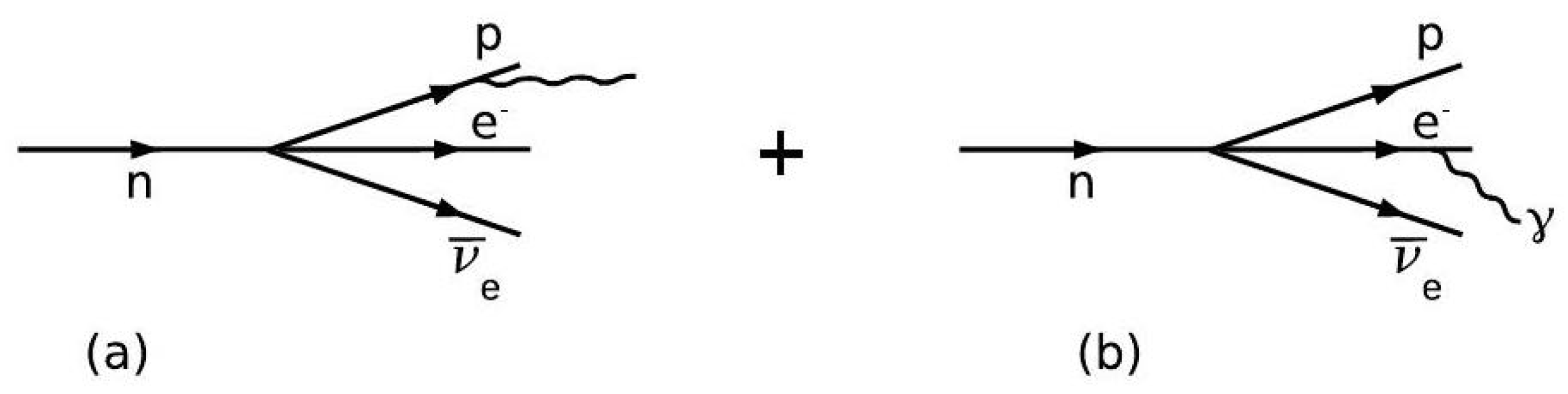
Preprints 137999 g0a1
Figure A1. Feynman diagrams, defining the amplitude of the neutron radiative β − -decay in the tree-approximation.
Figure A1. Feynman diagrams, defining the amplitude of the neutron radiative β − -decay in the tree-approximation.
Preprints 137999 g0a1
Table A1. The contribution of the CVC effect to the branching ratio of the neutron radiative β − -decay for three photon energy regions. In the last column we give a total theoretical value of the branching ratio of the neutron radiative β − -decay, calculated for three photon energy regions.
Table A1. The contribution of the CVC effect to the branching ratio of the neutron radiative β − -decay for three photon energy regions. In the last column we give a total theoretical value of the branching ratio of the neutron radiative β − -decay, calculated for three photon energy regions.
Preprints 137999 i001
The contribution of the CVC effect to the amplitude of the neutron β − -decay is equal to
M n → p e − ν ¯ e = u ¯ p k → p , σ p γ μ − q μ q ^ q 2 + λ γ μ γ 5 u n k → n , σ n u ¯ e k → e , σ e γ μ 1 − γ 5 v ν k → , + 1 2 .
This changes the neutron lifetime as follows (see also Appendix C
Δ τ n ( CVC ) = − τ n 2 G F 2 V u d 2 2 π 3 ∫ m e E 0 d E e k e E 0 − E e F E e , Z = 1 ∫ d Ω e ν 4 π E 0 m e 2 m e 2 + 2 E e E 0 − E e − 2 k → e · k → ν 2 4 E e − 3 E 0 E e E 0 − E e − k → e · k → ν − 2 m e 2 E 0 − E e .
The contribution of the CVC effect to the rate of the neutron β − -decay is defined by
λ n ( CVC ) = 1 + 3 λ 2 G F 2 V u d 2 2 π 3 f n ( CVC ) E 0
where f n ( CVC ) E 0 is given by
f n ( CVC ) E 0 = 1 1 + 3 λ 2 ∫ m e E 0 d E e k e E 0 − E e 2 F E e , Z = 1 ∫ d Ω e ν 4 π − 2 E 0 m e 2 m e 2 + 2 E e E 0 − E e − 2 k → e · k → ν + E 0 2 m e 2 m e 2 + 2 E e E 0 − E e − 2 k → e · k → ν 2 E e − k → e · k → ν E ν + λ 2 m e 2 m e 2 + 2 E e E 0 − E e − 2 k → e · k → ν E 0 − E e + k → e · k → ν E ν + m e 2 m e 2 + 2 E e E 0 − E e − 2 k → e · k → ν 2 E 0 − E e 2 + k e 2 + 2 k → e · k → ν E e − k → e · k → ν E ν

Appendix B. Numerical Analysis of the Branching Ratio in Eq. (A5)

The numerical analysis of the contribution of the CVC effect to the branching ratio of the neutron radiative β − − decay reduces to the calculation of the following in integral
I ω max , ω min = E 0 8 π ∫ ω min ω max d ω ∫ m e E 0 − ω d E e k e F E e , Z = 1 E 0 − E e − ω 2 ∫ − 1 + 1 d x ∫ − 1 + 1 d y ∫ 0 2 π d φ [ E 0 2 − k e 2 − ω 2 − E 0 − E e − ω 2 − 2 k e E 0 − E e − ω x − 2 ω E 0 − E e − ω y − 2 k e ω x y + 1 − x 2 1 − y 2 cos φ − 1 { m e 2 ω k e 2 1 − x y + 1 − x 2 1 − y 2 cos φ 2 E e − k e x y + 1 − x 2 1 − y 2 cos φ 2 + 1 E e − k e x y + 1 − x 2 1 − y 2 cos φ { k e 2 1 − x y + 1 − x 2 1 − y 2 cos φ 2 + 2 k e E e x − E e E e + ω y − E e E e − ω } + E e + ω y + ω } ,
where k e = E e 2 − m e 2 . The integral should be calculated for three intervals i) 15 × 10 − 3 MeV ≤ ω ≤ 340 × 10 − 3 MeV , ii) 14 × 10 − 3 MeV ≤ ω ≤ 782 × 10 − 3 MeV and iii) 0 . 4 × 10 − 3 MeV ≤ ω ≤ 14 × 10 − 3 MeV with E 0 = 1 . 2927 MeV and m e = 0 . 511 MeV . The Fermi function F E e , Z = 1 is equal to
F E e , Z = 1 = 1 + 1 2 γ 4 2 r p m e β 2 γ Γ 2 ( 3 + 2 γ ) e π α / β 1 − β 2 γ Γ 1 + γ + i α β 2
where β = k e / E e = E e 2 − m e 2 / E e is the electron velocity, γ = 1 − α 2 − 1 , r p = 4 . 262 × 10 − 3 MeV − 1 is the electric radius of the proton and α = 1 / 137 . 036 is the fine-structure constant.

Appendix C. Numerical Analysis of Eq. (A7)

The numerical analysis of Eq. (A7) reduces to the calculation of the integral
I = 1 2 m e 2 E 0 ∫ m e E 0 d E e E e 2 − m e 2 E 0 − E e 2 F E e , Z = 1 ∫ − 1 + 1 d x 1 m e 2 + 2 E 0 − E e E e − x E e 2 − m e 2 2 4 E e − 3 E 0 E e − x E e 2 − m e 2 − 2 m e 2
for E 0 = 1 . 2927 MeV and m e = 0 . 511 MeV with k e = E e 2 − m e 2 . The Fermi function is given by Eq.(A-2).
One has to calculate the following integral
f n ( CVC ) E 0 = 1 1 + 3 λ 2 ∫ m e E 0 d E e k e E 0 − E e 2 F E e , Z = 1 1 1 ∫ − 1 + 1 d x k 1 − 2 E 0 m e 2 m e 2 + 2 E 0 − E e E e − k e x + E 0 2 m e 2 m e 2 + 2 E 0 − E e E e − k e x 2 E e − k e x + k 2 λ 2 m e 2 m e 2 + 2 E 0 − E e E e − k e x E 0 − E e + k e x + m e 2 m e 2 + 2 E 0 − E e E e − k e x 2 E 0 − E e 2 + k e 2 + 2 E 0 − E e k e x E e − k e x
where λ = − 1 . 2750 , E 0 = 1 . 2927 MeV and m e = 0 . 511 MeV with k e = E e 2 − m e 2 . The Fermi function is given by Eq. A11). The calculation to perform for i) k 1 = k 2 = 1 , ii) k 1 = 1 and k 2 = 0 and iii) k 1 = 0 and k 2 = 1 .
Taking into account the non-vanishing mass of charged pions one has to calculate the following integral
f n ( CVC ) E 0 = 1 1 + 3 λ 2 ∫ m e E 0 d E e k e E 0 − E e 2 F E e , Z = 1 1 1 ∫ − 1 + 1 d x k 1 − 2 E 0 m e 2 m e 2 + 2 E 0 − E e E e − k e x + E 0 2 m e 2 m e 2 + 2 E 0 − E e E e − k e x 2 E e − k e x + k 2 λ 2 m e 2 m e 2 + 2 E 0 − E e E e − k e x − m π 2 E 0 − E e + k e x + m e 2 m e 2 + 2 E 0 − E e E e − k e x − m π 2 2 E 0 − E e 2 + k e 2 + 2 E 0 − E e k e x E e − k e x ,
where m π = 139 . 570 MeV , λ = − 1 . 2750 , E 0 = 1 . 2927 MeV and m e = 0 . 511 MeV with k e = E e 2 − m e 2 . The Fermi function is given by Eq.(A-2). The calculation should be performed for k 1 = 0 and k 2 = 1 .

References

  1. A. N. Ivanov, M. Pitschmann, and N. I. Troitskaya, Phys. Rev. D 88, 073002 (2013); arXiv:1212.0332v4 [hep-ph].
  2. C. Partignani et al. (Particle Data Group), Chinese Physics C 40, 100001 (2016).
  3. S. Arzumanov, L. Bondarenko, S. Chernyavsky, P. Geltenbort, V. Morozov, V. V. Nesvizhevsky, Yu. Panin, and A. Strepetov, Phys. Lett. B 745, 79 (2015).
  4. H. Abele, Progr. Part. Nucl. Phys. 60, 1 (2008).
  5. K. A. Olive et al. (Particle Data Group), Chin. Phys. A 38, 090001 (2014).
  6. J. C. Hardy and I. S. Tower, Phys. Rev. D 91, 025501 (2015).
  7. N. Severijns and O. Naviliat-Cuncic, Annu. Rev. Nucl. Part. Sci. 61, 23 (2011).
  8. O. Naviliat-Cuncic and N. Severijns, Phys. Rev. Lett. 102, 142302 (2009).
  9. A. M. Ankowski, arXiv:1601.06169v1 [hep-ph].
  10. C. Giunti, arXiv: 1602.00215 [hep-ph].
  11. A. N. Ivanov, M. Pitschmann, N. I. Troitskaya, and Ya. A. Berdnikov, Phys. Rev. C 89, 055502 (2014).
  12. M. Nowakowski, E. A. Paschos, and J. M. Rodriguez, Eur. J. Phys. 26, 545 (2005).
  13. T. Leitner, L. Alvarez-Ruso, and U. Mosel, Phys. Rev. C 73, 065502 (2006).
  14. S. L. Adler and R. Dashen, in CURrENT ALGEBRAS, Benjamin, New York 1968.
  15. V. De Alfaro, S. Fubini, G. Furlan, and C. Rossetti, in CURRENTS IN HADRON PHYSICS, North-Holland Publishing Co., Amsterdam · London, American Elsevier Publishing Co., Inc., New York, 1973.
  16. A. Sirlin, Phys. Rev. 164, 1767 (1967).
  17. E. S. Abers, D. A. Dicus, R. E. Norton, and H. R. Queen, Phys. Rev. 167, 1461 (1968).
  18. A. P. Serebrov, V. E. Varlamov, A. G. Kharitonov, A. K. Fomin, Yu. N. Pokotilovski, P. Geltenbort, I. A. Krasnoschekova, M. S. Lasakov, R. R. Taldaev, A. V. Vassiljev, and O. M. Zherebtsov, Phys. Rev. C 78, 035505 (2008).
  19. J. S. Nico, J. Phys. G: Nucl. Part. Phys. 36, 104001 (2009).
  20. J. D. Jackson, S. B. Treiman, and H. W. Wyld Jr., Phys. Rev. 106, 517 (1957); Nucl. Phys. 4, 206 (1957).
  21. M. E. Ebel and G. Feldman, Nucl. Phys. 4, 213 (1957).
  22. P. Herczeg, Progr. Part. Nucl. Phys. 46, 413 (2001).
  23. N. Severijns, M. Beck, and O. Naviliat-Cuncic, Rev. Mod. Phys. 78, 991 (2006).
  24. P. Herczeg, Beta decay and muon decay beyond the Standard Model, in PRECISION TESTS of THE StANDARD ELECTROWEAK MODEL, Edited by P. Langacker, World Scientific, Advanced Series on Directions in High Energy Physics - Vol. 14, p. 7851998.
  25. M. Faber, A. N. Ivanov, V. A. Ivanova, J. Marton, M. Pitschmann, A. P. Serebrov, N. I. Troitskaya, and M. Wellenzohn, Phys. Rev. C 80, 035503 (2009).
  26. H. Saul, Measurement of the Beta Asymmetry in Neutron Decay with PERKEO III, (the PERKEO Collaboration), Talk on 20th of January 2017 at the Institute of Atomic and Subatomic Physics, Technische Universität Wien, Stadionalle 2, A-1020 Wien, Austria.
  27. A. N. Ivanov, R. Höllwieser, N. I. Troitskaya, and M. Wellenzohn. Proton recoil energy and angular distribution of neutron radiative β-decay. Phys. Rev., D88(6):065026, 2013.
  28. A. N. Ivanov, R. Höllwieser, N. I. Troitskaya, M. Wellenzohn, and Ya A. Berdnikov. Gauge Properties of Hadronic Structure of Nucleon in Neutron Radiative Beta Decay to Order O(α/π) in Standard V - A Effective Theory with QED and Linear Sigma Model of Strong Low–Energy Interactions. Int. J. Mod. Phys. A, 33(33):1850199, 2018. [CrossRef]
  29. A. N. Ivanov, R. Höllwieser, N. I. Troitskaya, M. Wellenzohn, and Ya A. Berdnikov. Gauge and infrared properties of hadronic structure of nucleon in neutron beta decay to order O(α/π) in standard V-A effective theory with QED and linear sigma model of strong low-energy interactions. Int. J. Mod. Phys. A, 34(02):1950010, 2019. [CrossRef]
  30. Andrey N. Ivanov, Roman Höllwieser, Nataliya I. Troitskaya, Markus Wellenzohn, and Ya A. Berdnikov. Electrodisintegration of Deuteron into Dark Matter and Proton Close to Threshold. Symmetry, 13(11):2169, 2021. [CrossRef]
  31. A. N. Ivanov, R. Höllwieser, N. I. Troitskaya, M. Wellenzohn, and Ya A. Berdnikov. Tests of the standard model in neutron beta decay with polarized electrons and unpolarized neutrons and protons. Phys. Rev. D, 99(5):053004, 2019. [Erratum: Phys.Rev.D 104, 059902 (2021)]. [CrossRef]
  32. A. N. Ivanov, R. Höllwieser, N. I. Troitskaya, M. Wellenzohn, and Ya. A. Berdnikov. Corrections of order O( E r 2 / m N 2 ), caused by weak magnetism and proton recoil, to the neutron lifetime and correlation coefficients of the neutron beta decay. Results Phys., 21:103806, 2021. [CrossRef]
  33. A. N. Ivanov, R. Höllwieser, N. I. Troitskaya, M. Wellenzohn, and Ya. A. Berdnikov. Radiative corrections of order O(αEe/mN) to Sirlin’s radiative corrections of order O(α/π) , induced by the hadronic structure of the neutron. Phys. Rev. D, 103(11):113007, 2021.
  34. A. N. Ivanov, R. Höllwieser, N. I. Troitskaya, M. Wellenzohn, and Ya. A. Berdnikov. Theoretical description of the neutron beta decay in the standard model at the level of 10-5. Phys. Rev. D, 104(3):033006, 2021.
  35. A. N. Ivanov, R. Höllwieser, N. I. Troitskaya, M. Wellenzohn, and Ya. A. Berdnikov. Structure of the correlation coefficients S(Ee) and U(Ee) of the neutron β decay. Phys. Rev. C, 104(2):025503, 2021.
  36. A. N. Ivanov, R. Höllwieser, N. I. Troitskaya, M. Wellenzohn, and Ya. A. Berdnikov. On the correlation coefficient T(Ee) of the neutron beta decay, caused by the correlation structure invariant under discrete P, C and T symmetries. Phys. Lett. B, 816:136263, 2021.
  37. A. N. Ivanov, R. Höllwieser, N. I. Troitskaya, M. Wellenzohn, and Ya. A. Berdnikov. Precision analysis of pseudoscalar interactions in neutron beta decays. Nucl. Phys. B, 951:114891, 2020. [CrossRef]
  38. A. N. Ivanov, R. Höllwieser, N. I. Troitskaya, M. Wellenzohn, and Ya. A. Berdnikov, Phys. Rev. D (2017); arXiv: 1701.04613 [hep-ph].
  39. A. N. Ivanov, R. Höllwieser, N. I. Troitskaya, M. Wellenzohn, O. M. Zherebtsov, and A. P. Serebrov, Phys. Rev. C 88, 055501 (2013).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated