Submitted:
29 October 2024
Posted:
31 October 2024
You are already at the latest version
Abstract
Early detection of cervical cancer is the need of the hour to stop the fatality from this disease. There have been various CAD approaches in the past that promise to detect cervical cancer in an early stage, each of them having some constraints.This study proposes a novel ensemble deep learning model, VLR (variable learning rate), aimed at enhancing the accuracy of cervical cancer classification. The model architecture integrates VGG16, Logistic Regression, and ResNet50, combining their strengths in an offbeat ensemble design. VLR learns in two ways: firstly, by dynamic weights from three base models, each of them trained separately; secondly, by attention mechanisms used in the dense layer of the base models. Hyperparameter tuning is applied to further reduce loss, fine tune the model’s performance, and maximize classification accuracy. We performed K-fold cross-validation on VLR to evaluate any improvements in metric values resulting from hyperparameter fine tuning. We have also validated our model on images captured in three different solutions and on a secondary dataset. Our proposed VLR model outperformed existing methods in cervical cancer classification, achieving a remarkable training accuracy of 99.95% and a testing accuracy of 99.89%.
Keywords:
1. Introduction
- 1.
- VLR is an ensemble of VGG16, ResNet50 and Logistic Regression models, making it possible to harness the strength of each of these individual models by extracting high level features and also increased interpretability by reducing the chance of over fitting.
- 2.
- The VLR learning process is optimized by utilizing dynamic weights and by incorporating attention mechanisms in the dense layers of the base models. Additionally, hyperparameter tuning is applied to minimize training loss, thereby increasing validation accuracy.
- 3.
- The study aims to examine the impact of different datasets on VLR model’s accuracy. By applying VLR on different secondary datasets, the research evaluates how dataset variability affects the model’s performance.
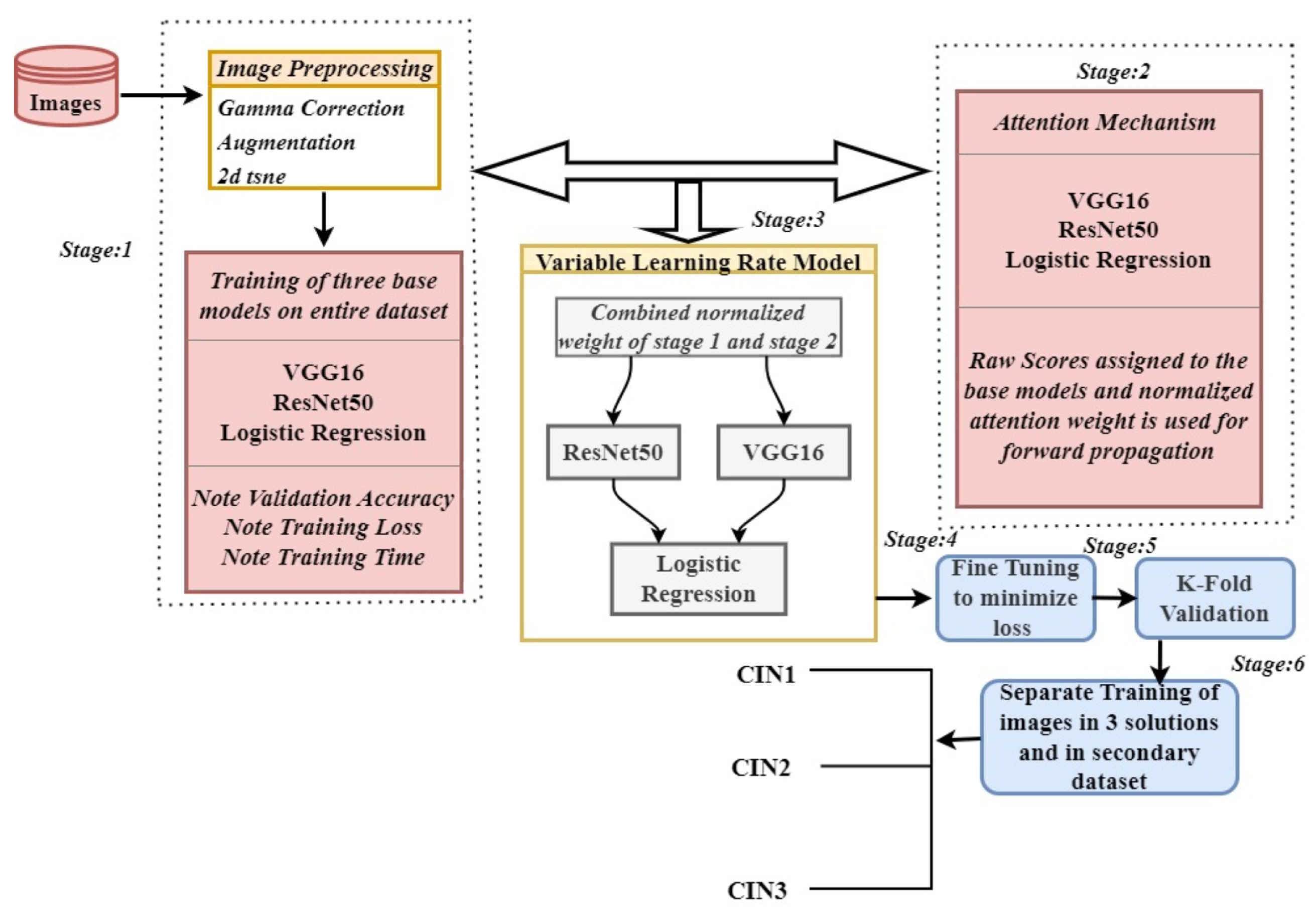
2. Proposed Methodology
2.1. Stage 1: Pre-Trained Base Models as Feature Extractor and Meta Learner
Mathematical Basis
- 1.
- Each model is trained on a dataset , where and . The training loss for each model is minimized using the binary cross-entropy loss function:where is the predicted probability for the positive class from model .
- 2.
-
The validation accuracy () for each model is denoted as:Where is an signal function that equals 1 if the predicted class matches the true label and 0 otherwise. The sum is then averaged over all n samples to compute accuracy.
- 3.
- We represent the training time () for each model simply as the time taken to train the model:
2.2. Stage 2: Attention Mechanism in Base Models
Mathematical Basis
- 1
-
Extract Features from Each ModelIn the above equation X is the input data to the base models.
- 2
-
Calculate Normalized Attention Weights Using Predefined ScoresThe attention weight for the base model i. It represents how much importance or contribution is given to a specific model’s output. The tem is the exponential function applied to the predefined score of the model i. The term is the sum of exponential values of scores for all models: VGG16, ResNet50, and LR. The summation is done over all base models, allowing normalization so that the resulting attention weights add up to 1.
- 3
- Combine Features Using Weighted Attention
2.3. Stage 3: Forward Propagation and Backward Propagation of VLR
2.4. Stage 4: Hyperparameter Fine Tuning
2.5. Stage 5: K-Fold Cross Validation
2.6. Stage 6: Validating the Model on Different Datasets
2.7. Classification
Mathematical Basis
- 1.
- Ensemble Prediction: Use stored predictions and features from base models (VGG16, ResNet50, LR) on training and validation sets to perform ensemble prediction:
- 2.
- Calculate Final Combined Weights:
- 3.
- Apply attention mechanism:
- 4.
- Combine weights:
- 5.
- Use final weights for ensemble prediction:
3. Algorithm
| Algorithm 1VLR Ensemble Model incorporating Attention Mechanism, Static Weights, Fine-Tuning, and K-Fold Cross Validation for VLR |
 |
4. Experimental Analysis
4.1. Experimental Setup
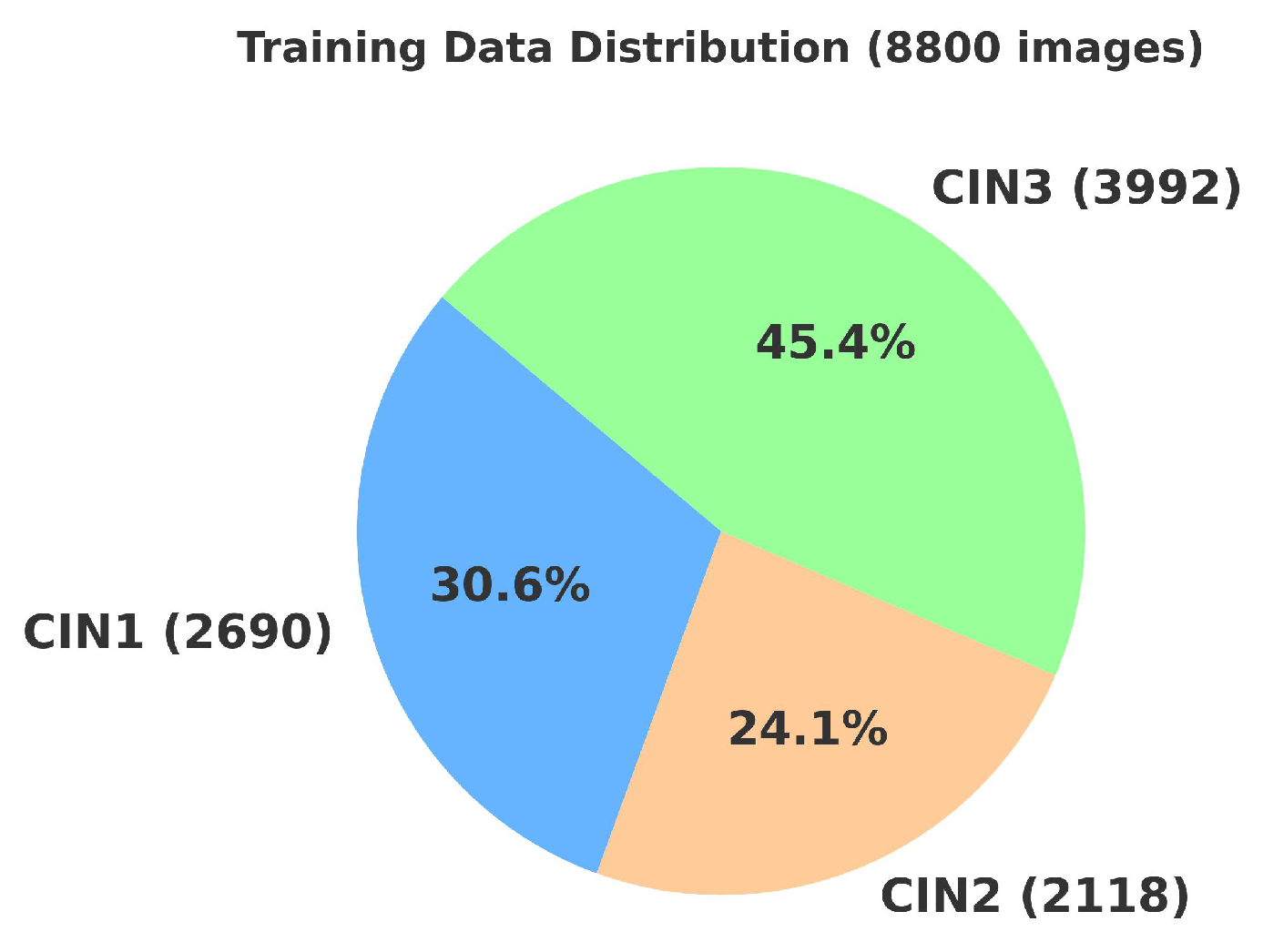
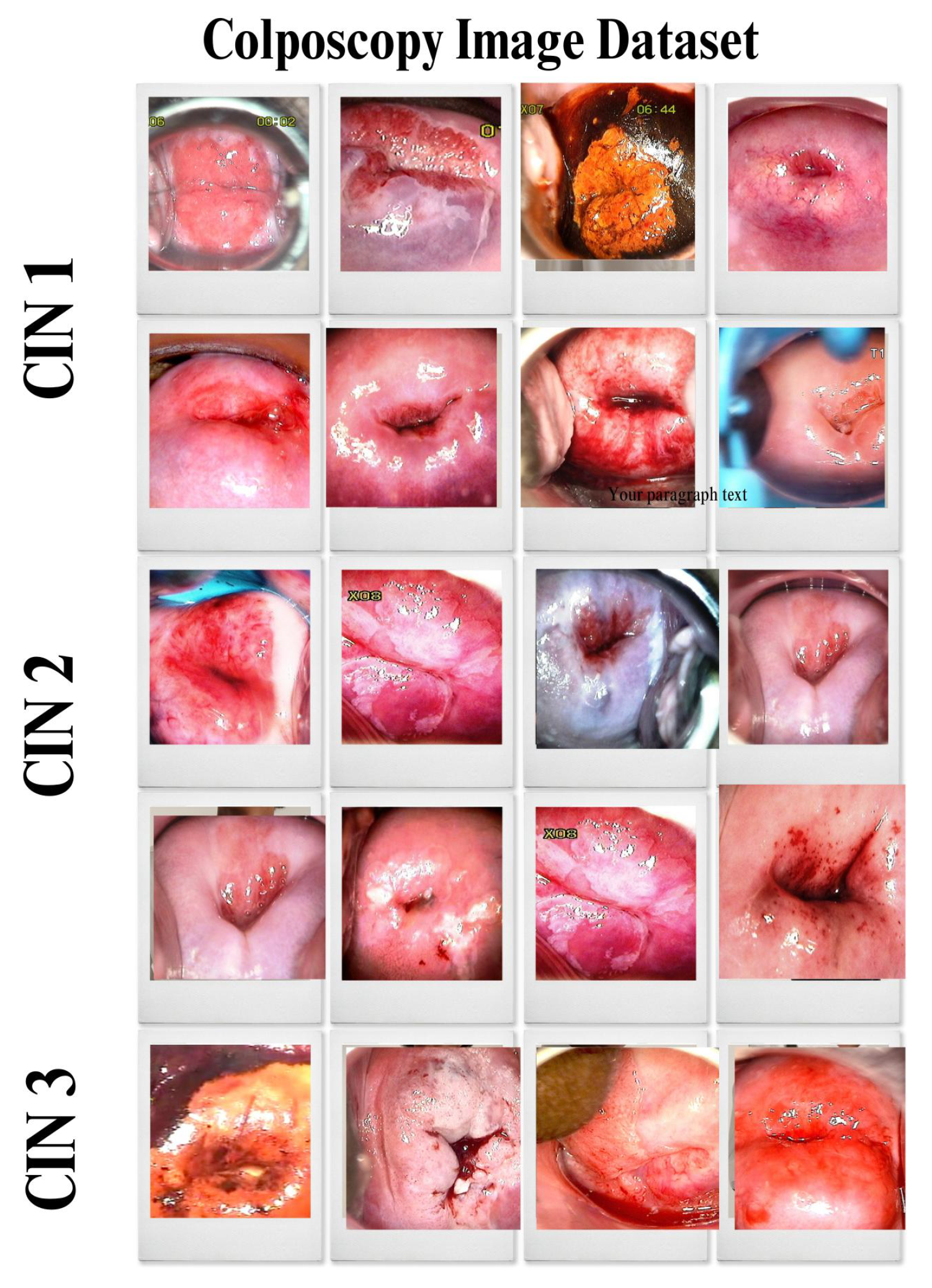
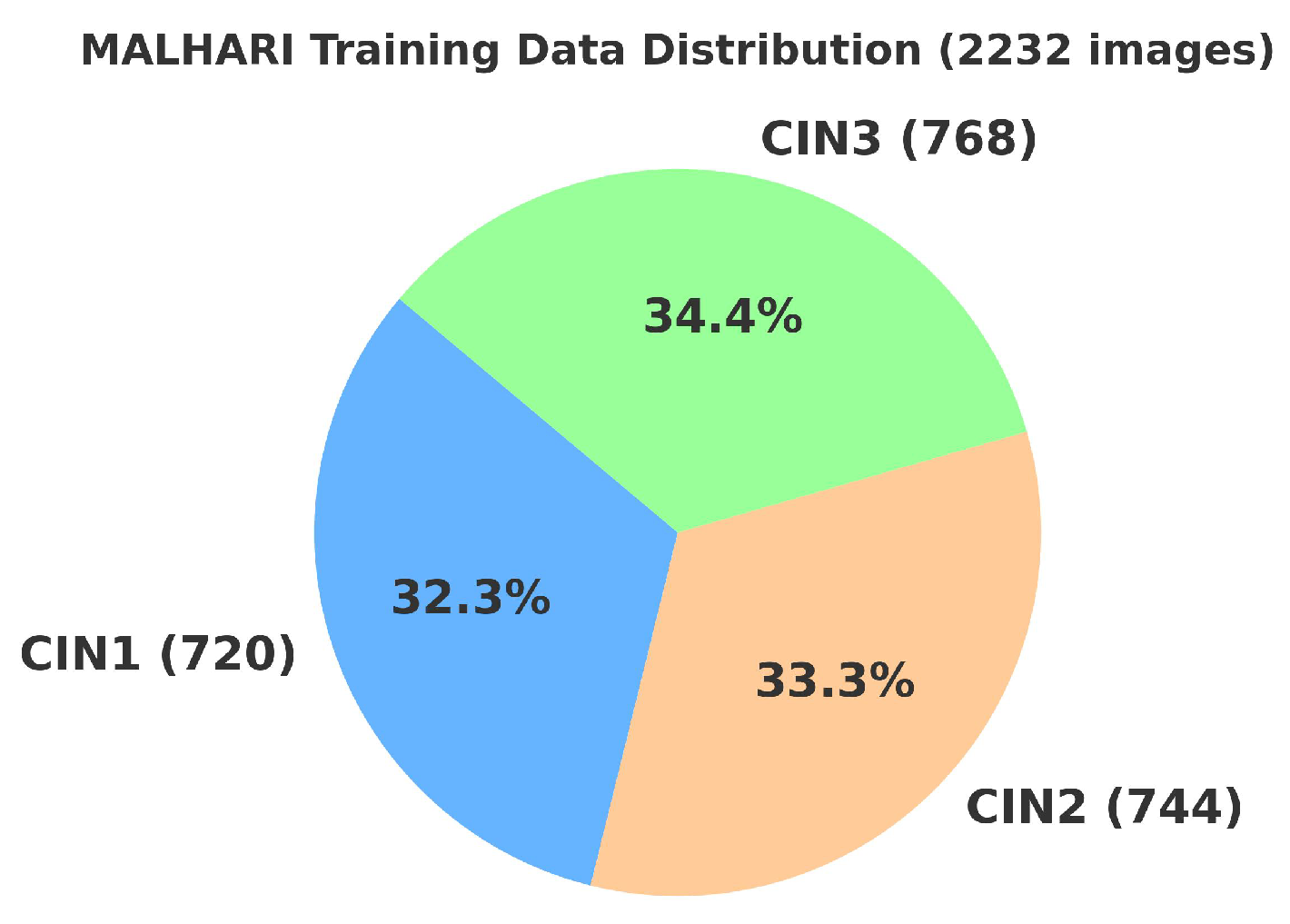
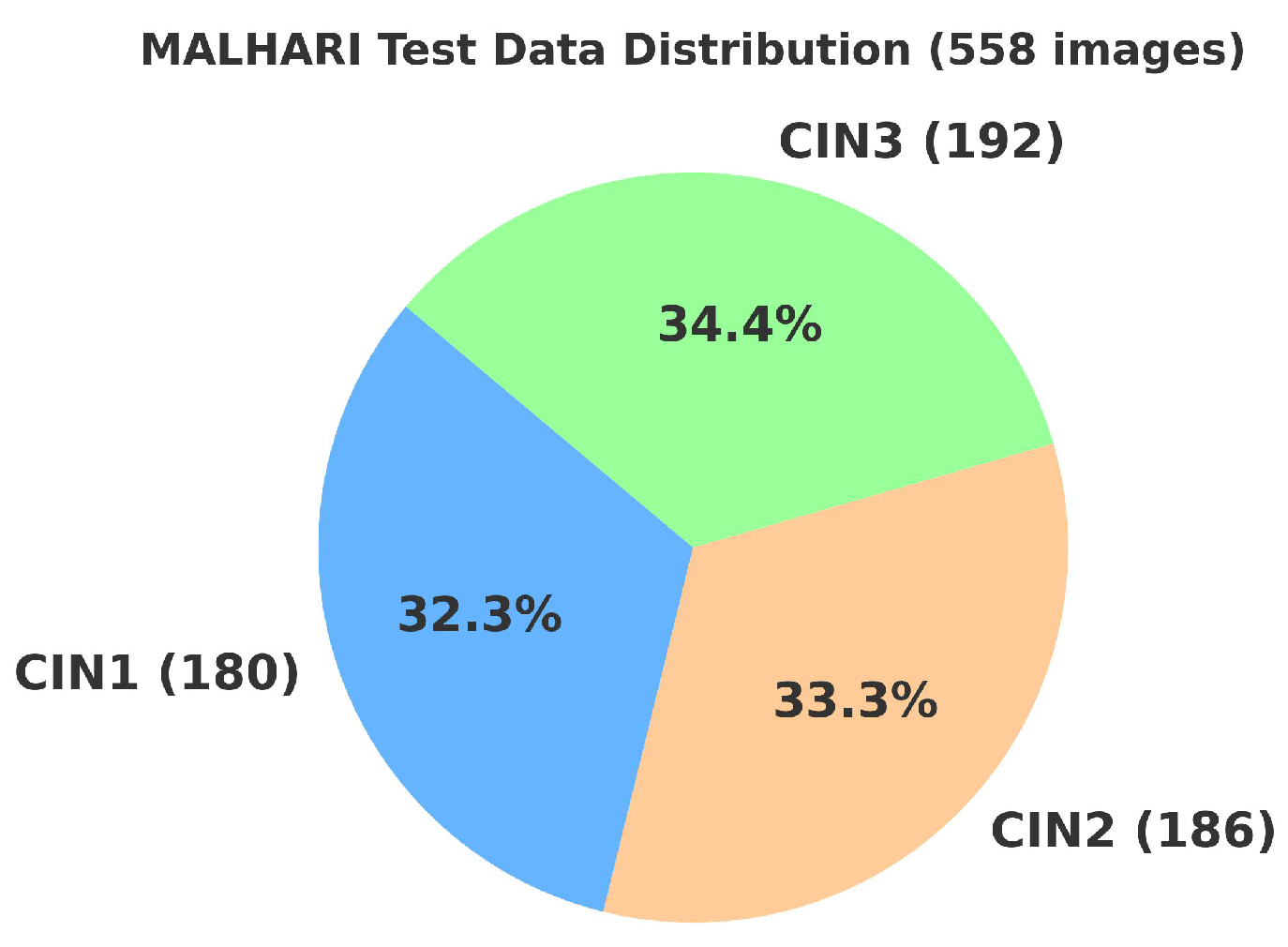
4.2. Primary Dataset
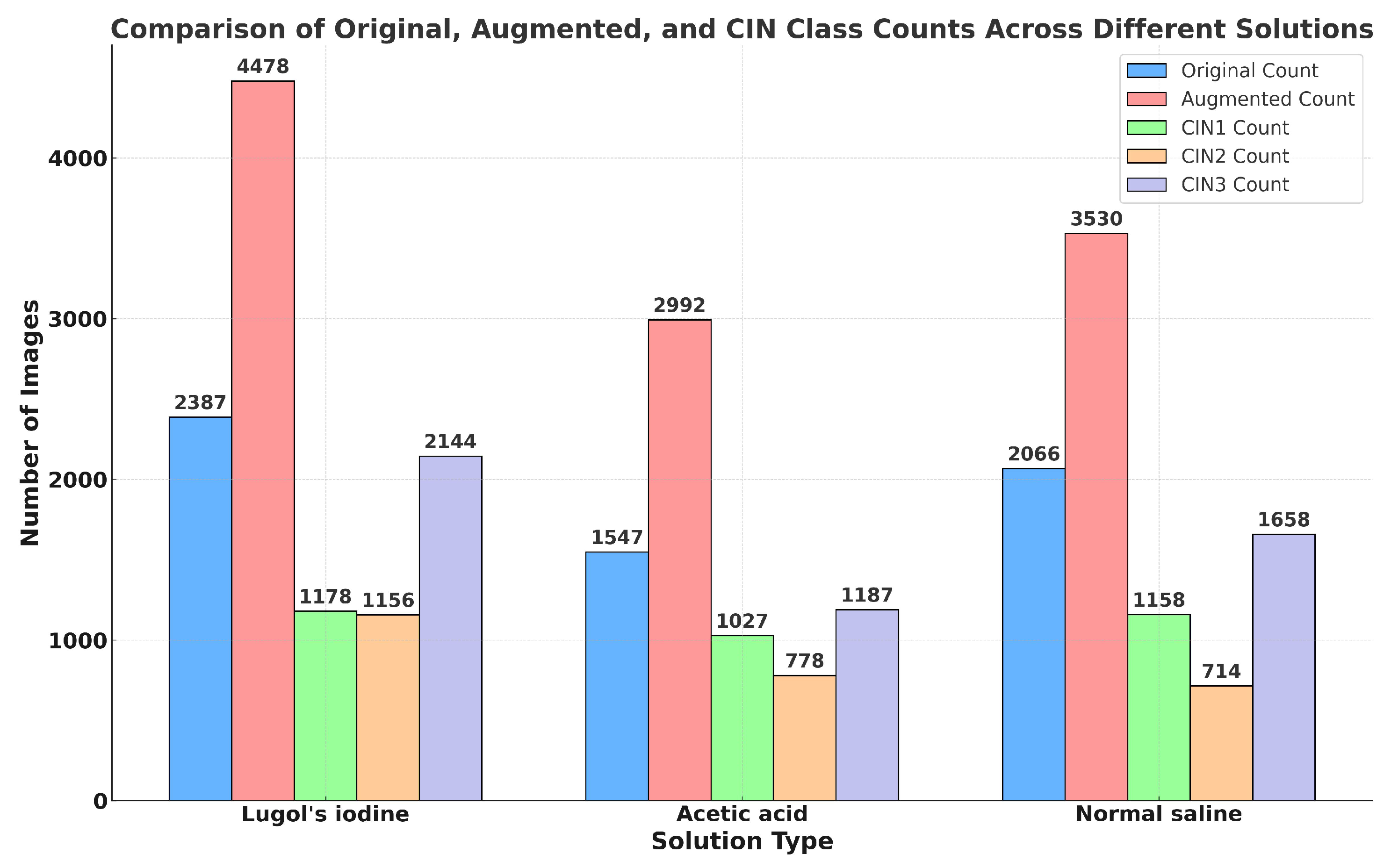
4.2.1. Details of the Primary Dataset with Respect to Three Solutions
4.3. Secondary Dataset
4.4. Data Preprocessing
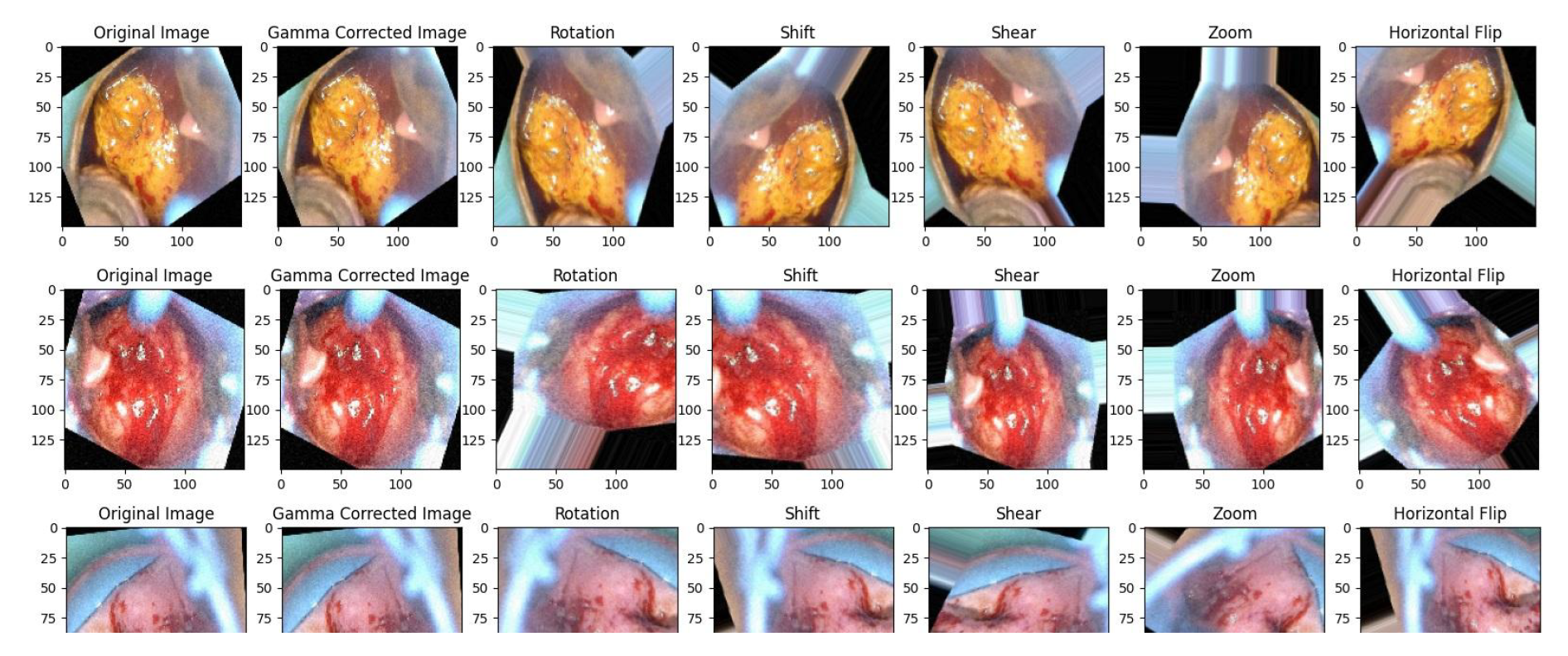
4.4.1. Gamma Correction
4.4.2. Data Augmentation
4.4.3. 2d t-sne
4.5. Experimental Setup of VLR
| Ep-och | VGG16 | ResNet50 | LR | VLR Loss Contrib | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Val-Acc (%) | Train-Loss | Train-Time (sec) | Dyn- | Val-Acc (%) | Train-Loss | Train-Time (sec) | Dyn- | Val-Acc (%) | Train-Loss | Train-Time (sec) | Dyn- | ||
| 1 | 90.05 | 0.00912 | 3240 | 0.099 | 91.22 | 0.00880 | 2640 | 0.098 | 90.87 | 0.00850 | 220 | 0.088 | 0.004423 |
| 20 | 94.12 | 0.00750 | 3600 | 0.109 | 95.67 | 0.00710 | 3200 | 0.109 | 95.80 | 0.00690 | 180 | 0.098 | 0.003753 |
| 40 | 95.13 | 0.00730 | 3960 | 0.111 | 96.12 | 0.00690 | 3520 | 0.110 | 96.50 | 0.00660 | 140 | 0.100 | 0.003666 |
| 60 | 95.65 | 0.00720 | 4320 | 0.112 | 96.75 | 0.00680 | 3840 | 0.111 | 96.90 | 0.00640 | 100 | 0.101 | 0.003620 |
| 80 | 96.25 | 0.00711 | 4560 | 0.113 | 97.20 | 0.00660 | 3960 | 0.113 | 97.30 | 0.00620 | 60 | 0.103 | 0.003554 |
| 100 | 96.55 | 0.00700 | 4700 | 0.114 | 97.65 | 0.00650 | 4100 | 0.114 | 97.80 | 0.00600 | 40 | 0.104 | 0.003505 |
| 120 | 96.77 | 0.00711 | 4800 | 0.114 | 98.10 | 0.00631 | 3920 | 0.115 | 98.02 | 0.00349 | 20 | 0.135 | 0.003315 |
| 140 | 96.77 | 0.00711 | 4840 | 0.114 | 98.23 | 0.00631 | 3960 | 0.115 | 98.92 | 0.00349 | 17 | 0.136 | 0.003317 |
| 150 | 96.77 | 0.00711 | 4860 | 0.114 | 98.23 | 0.00631 | 3960 | 0.115 | 98.92 | 0.00349 | 15 | 0.136 | 0.003317 |
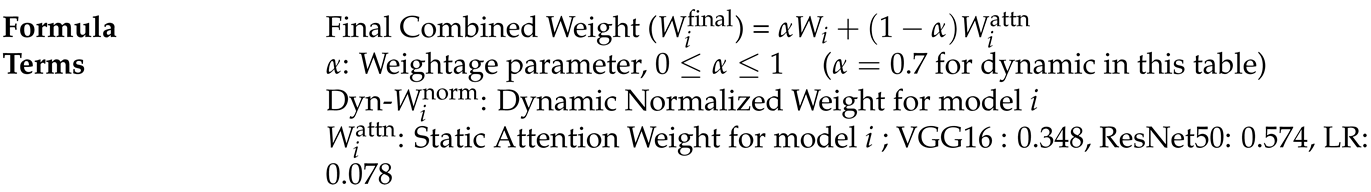 |
| Model | Raw-Score () | Exponential () | Attention-Weight-Formula () | Attention-Weight-Value () |
|---|---|---|---|---|
| ResNet50 | 3.0 | 20.09 | 0.574 | |
| VGG16 | 2.5 | 12.18 | 0.348 | |
| Logistic-Regression (LR) | 1.0 | 2.72 | 0.078 |
4.6. Experimental Setup of Hyperparameter Fine Tuning
4.7. Experimental Setup of K-Fold Cross Validation
4.8. Experimental Setup of Training of Images in Three Different Solutions and Training of Secondary Dataset
5. Results and Discussions
5.1. Results and Analysis of the Proposed Model
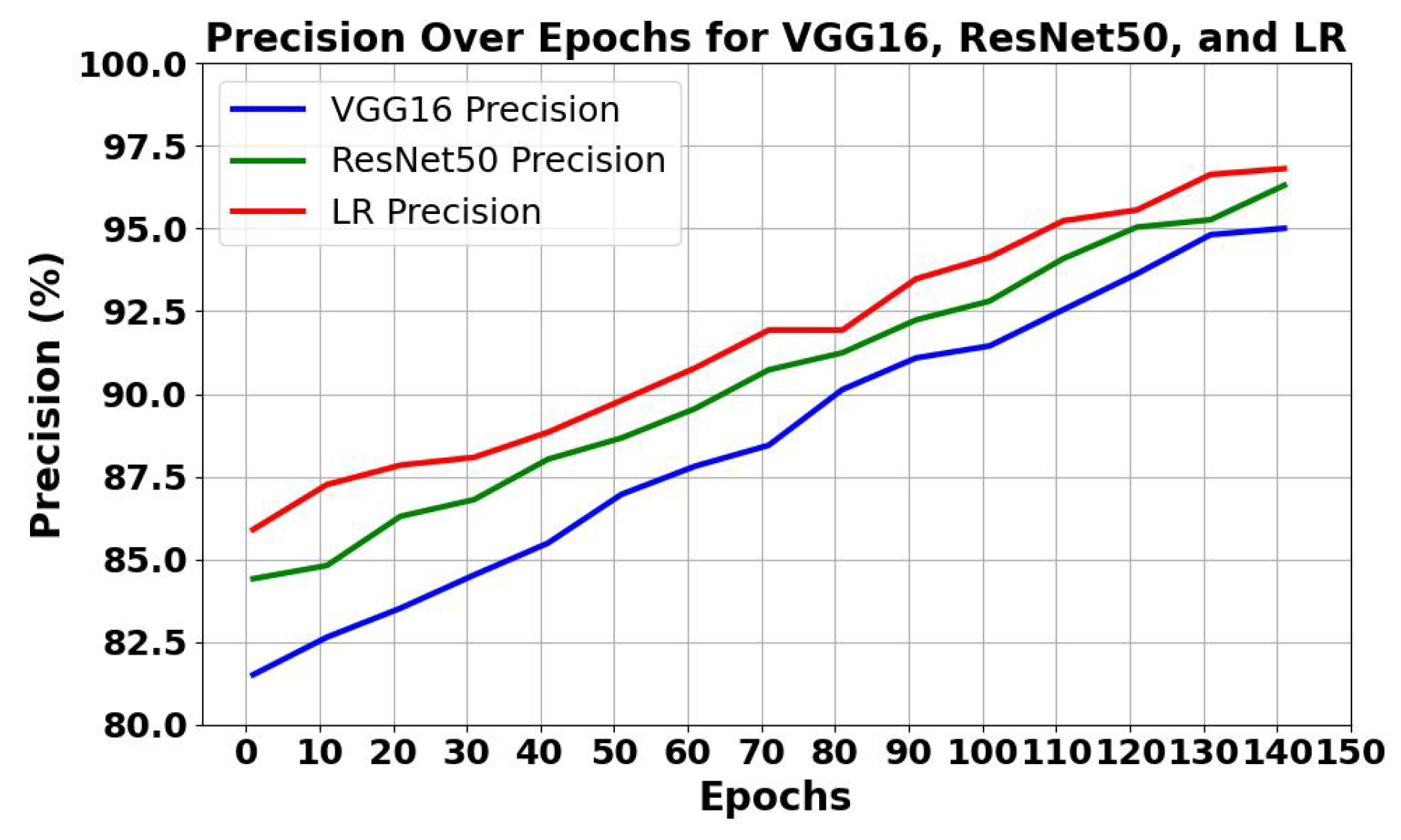
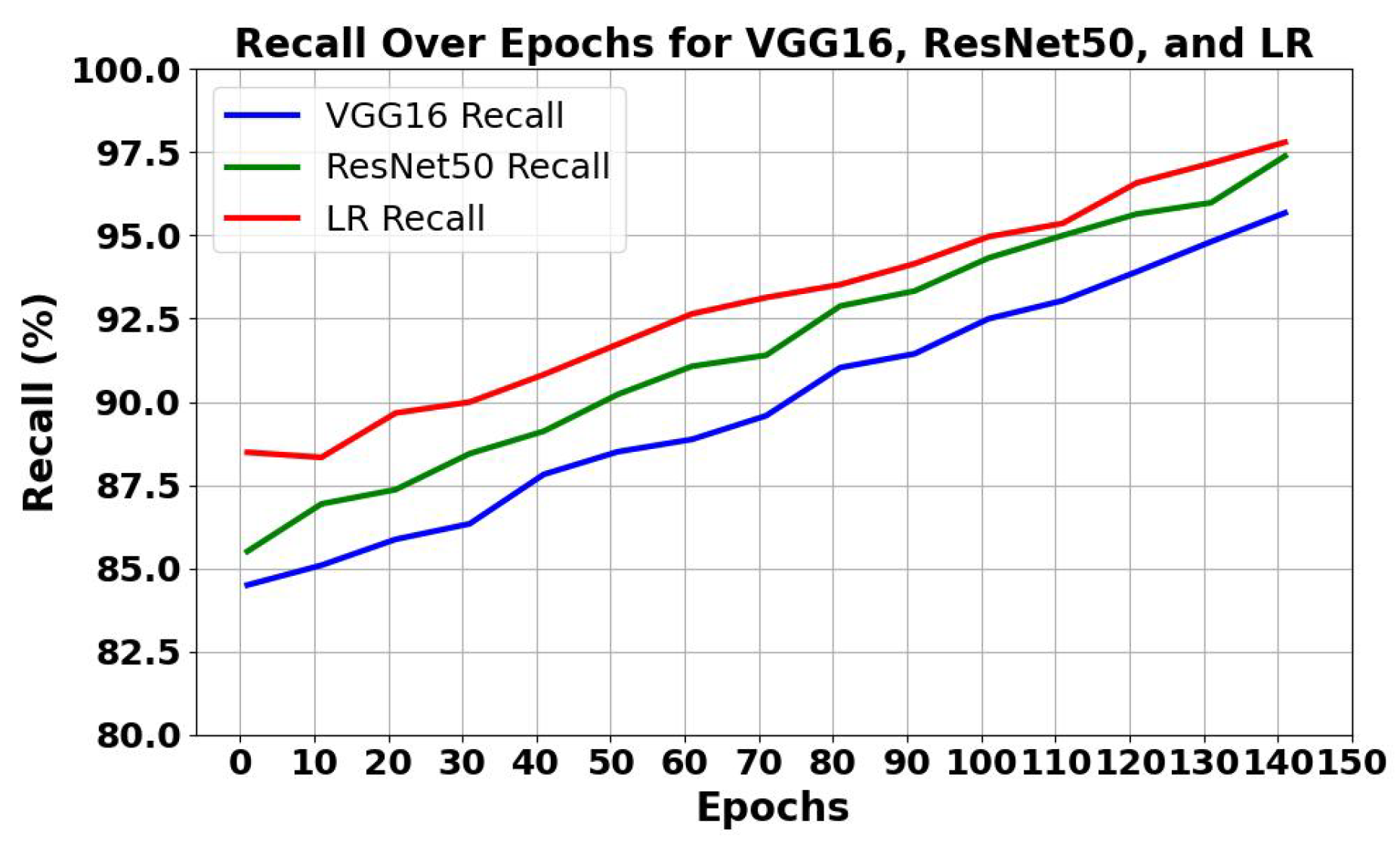
5.1.1. Analysis of Trends of Precision and Recall
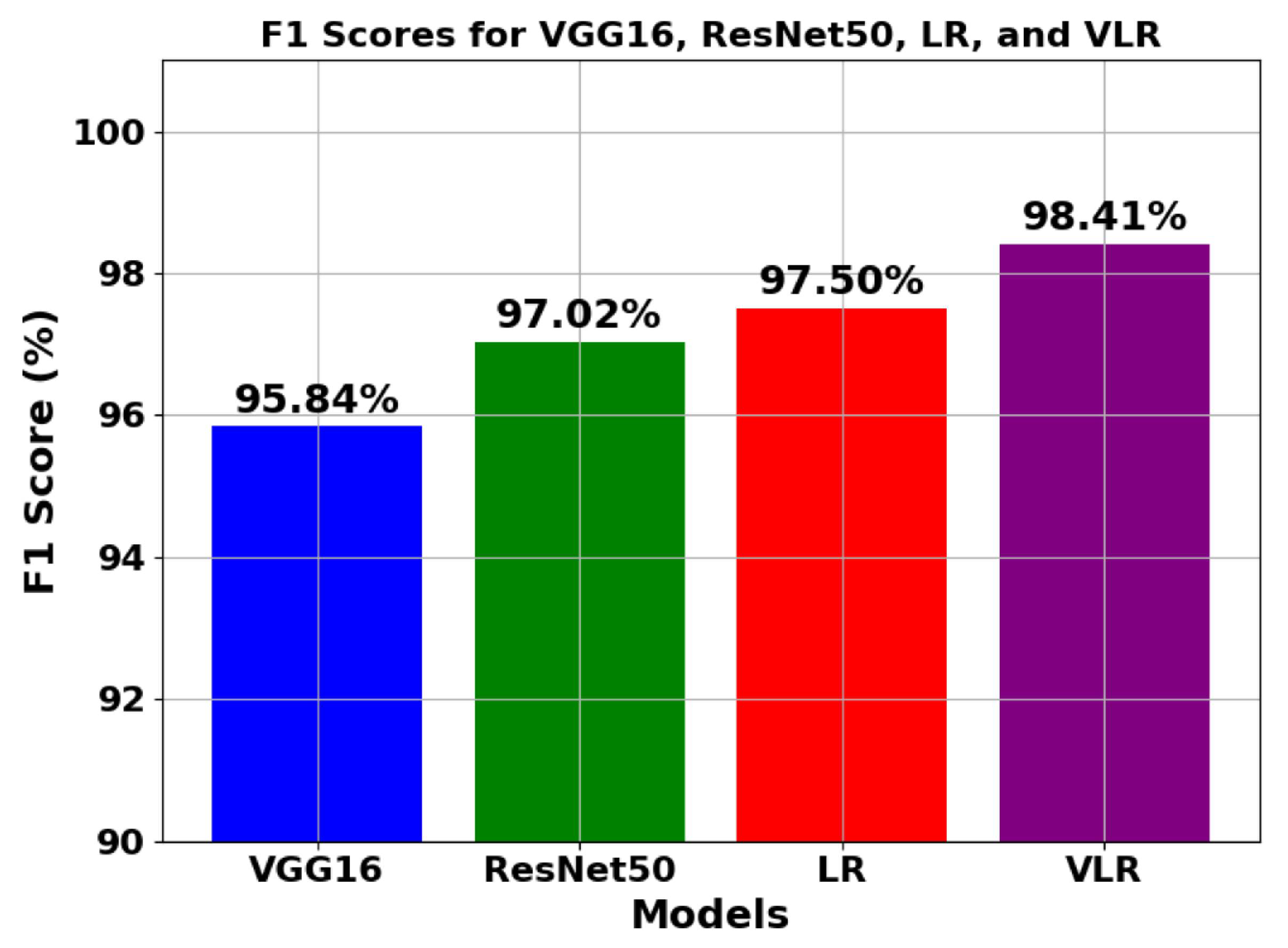
5.1.2. Analysis of trend of F1 score
5.1.3. Analysis of Using Normalized Dynamic and Static Attention Weight
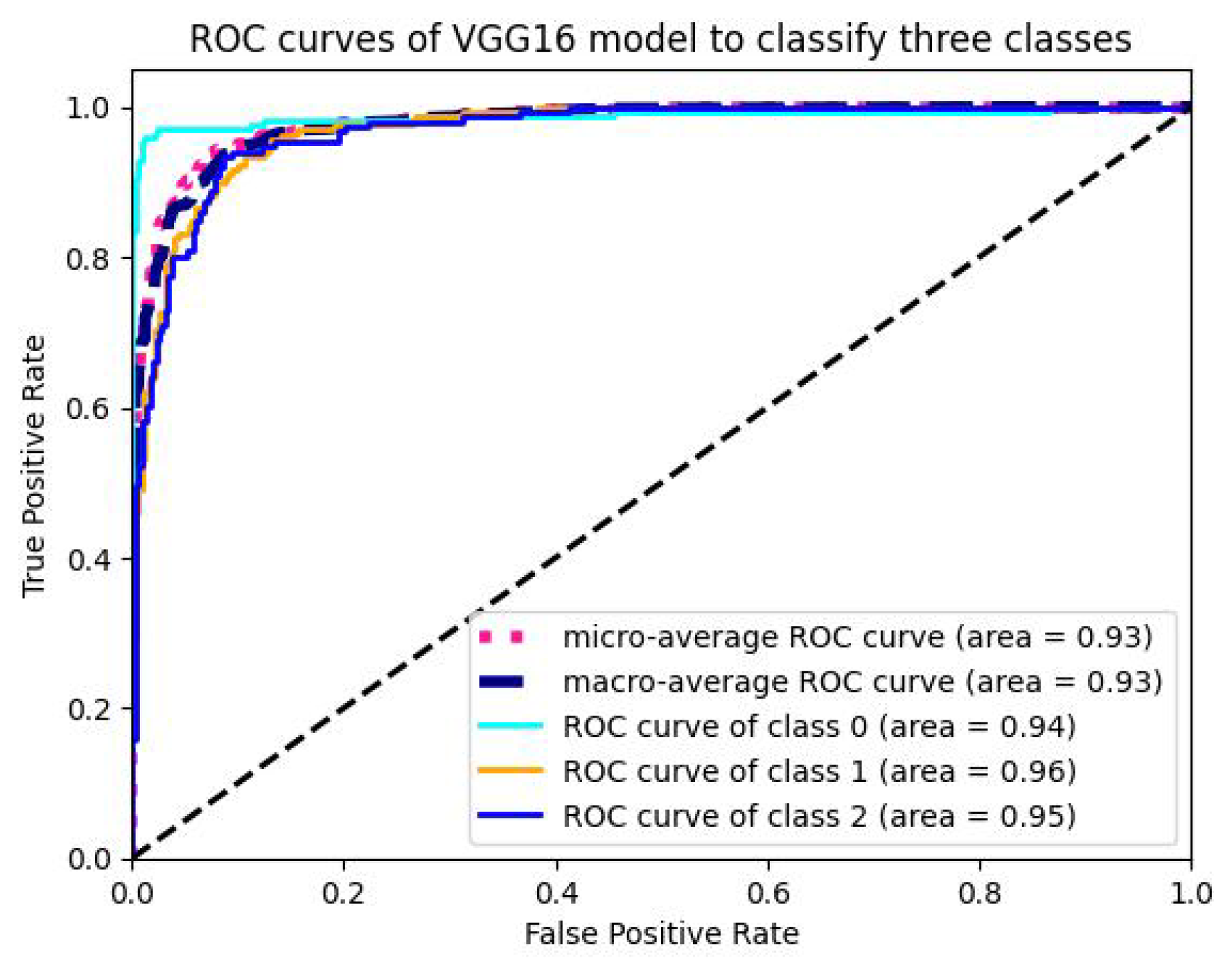
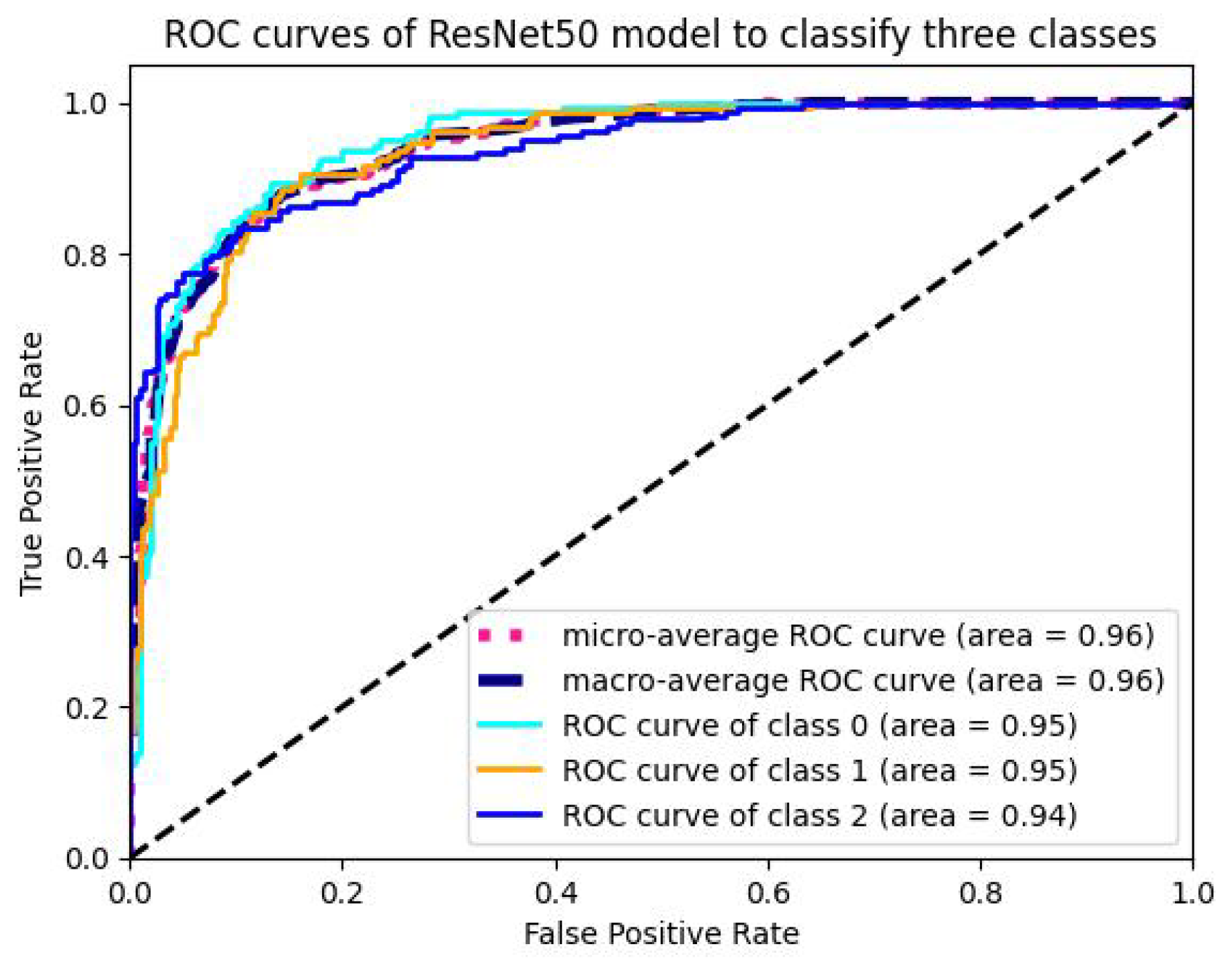
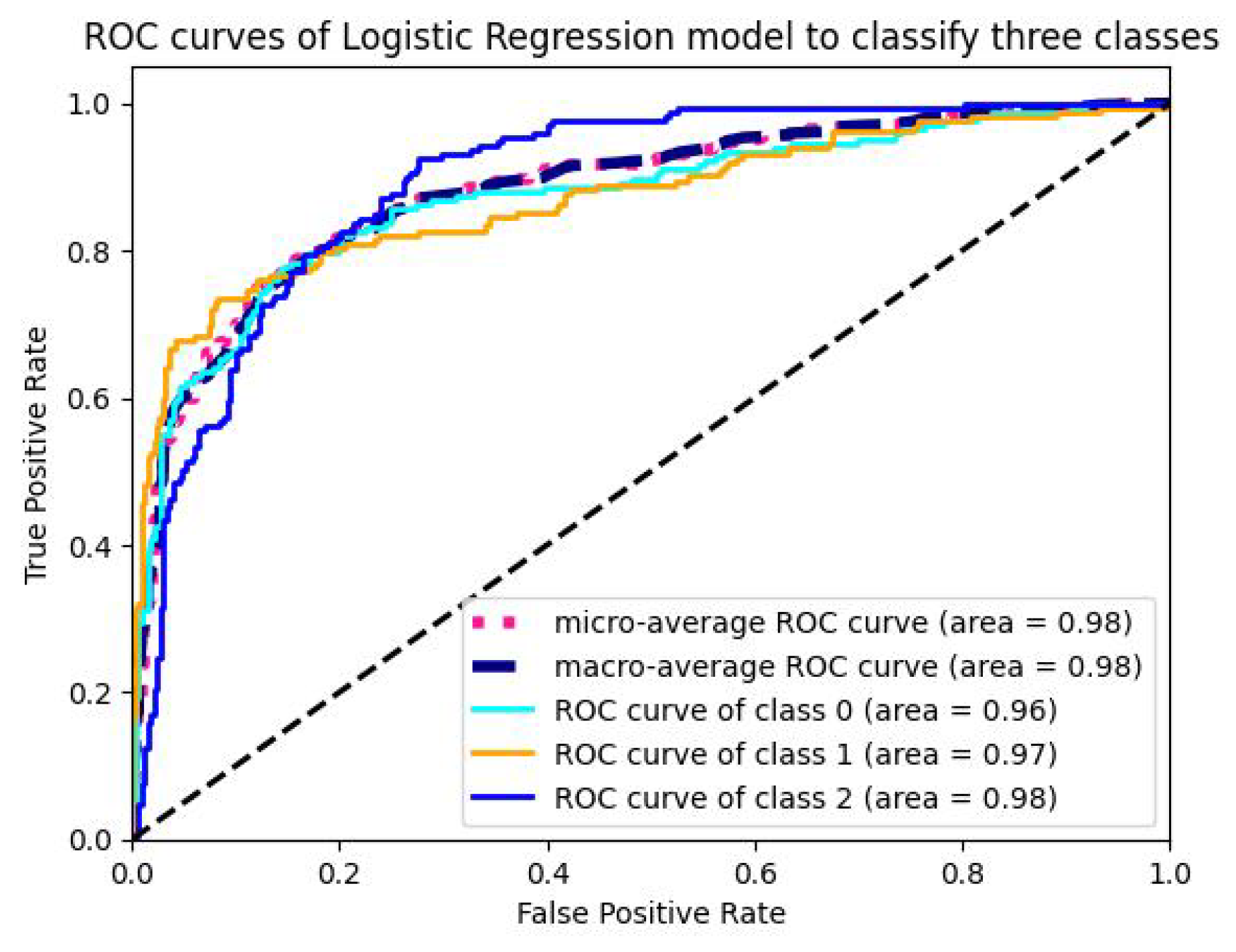
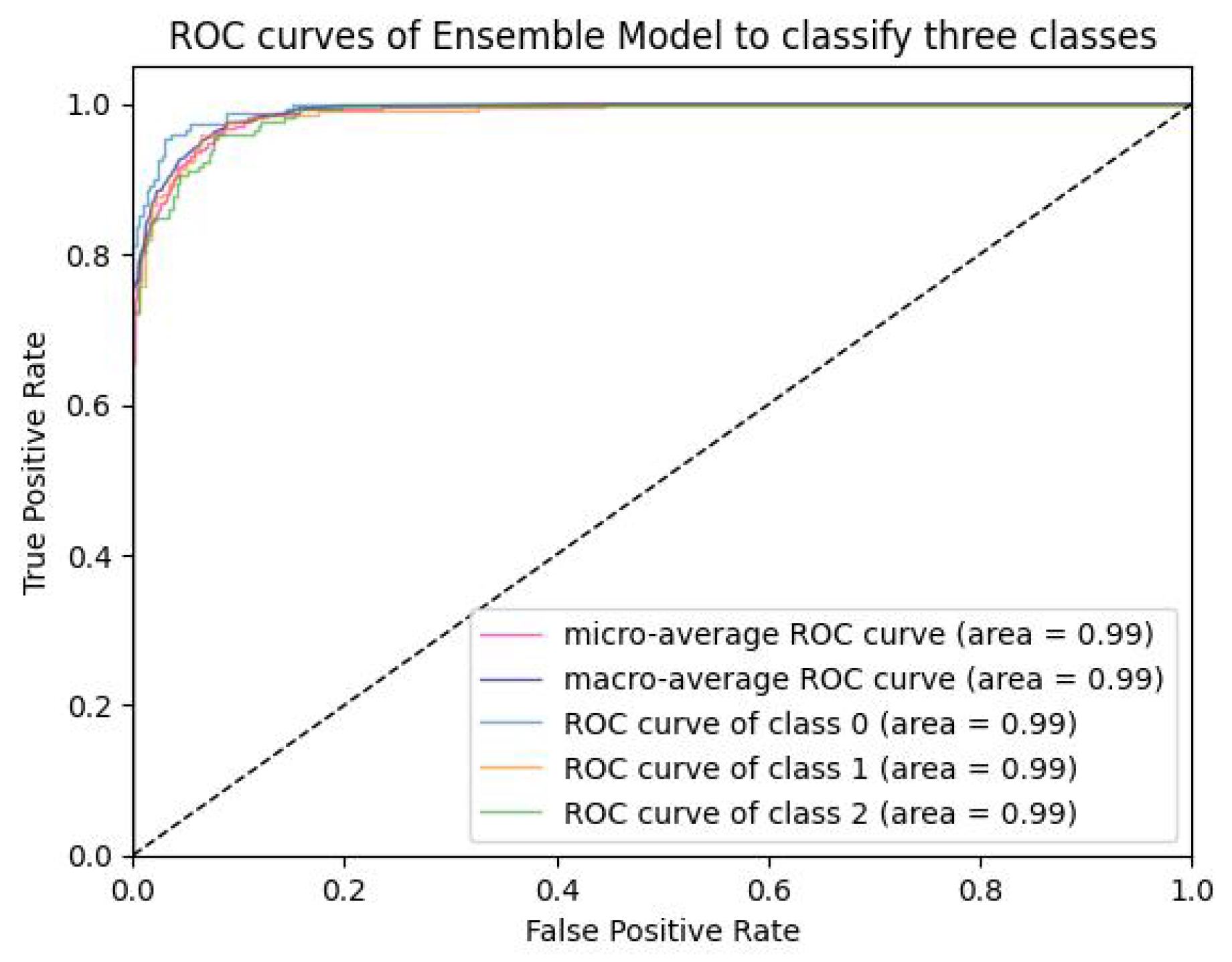
5.1.4. Analysis of ROC-AUC Graphs
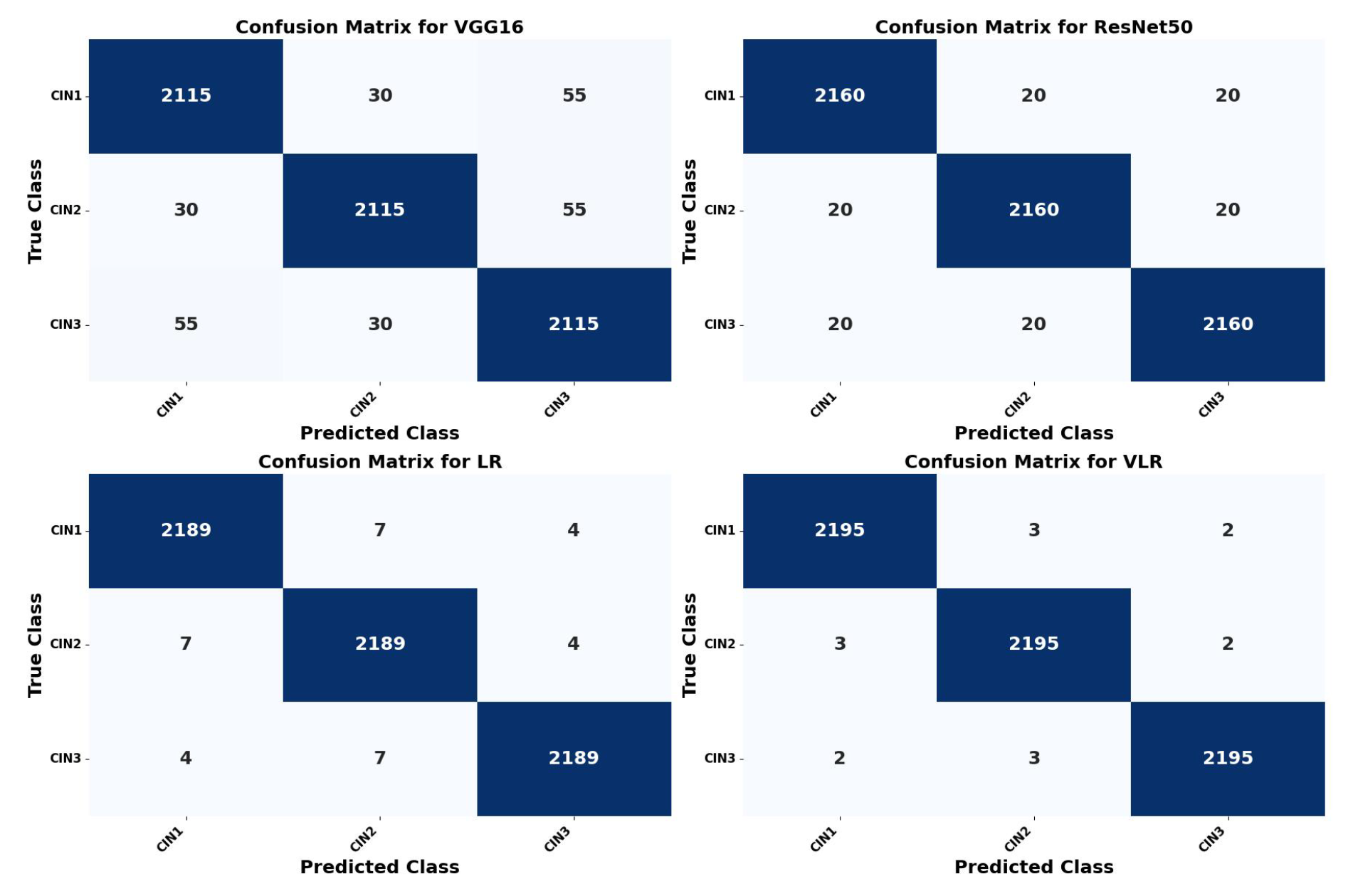
5.2. Confusion Matrix Calculation of the Four Models
5.3. K-Fold Cross Validation Results of VLR
5.4. Result Analysis of VLR on Images Captured in Three Solutions and Malhari Dataset
5.5. Final Classification by the VLR Model on the Primary Dataset
6. Related Work
6.1. Comparative Analysis Based on Colposcopy Dataset
6.2. Comparison with Existing Methods
6.3. Gaps identified and corrective measures taken
7. Conclusion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Elakkiya, R., Subramaniyaswamy, V., Vijayakumar, V., and Mahanti, A., Cervical cancer diagnostics healthcare system using hybrid object detection adversarial networks, IEEE Journal of Biomedical and Health Informatics, vol. 26, no. 4, pp. 1464–1471, 2021. [CrossRef]
- Youneszade, N., Marjani, M., and Pei, C. P., Deep learning in cervical cancer diagnosis: architecture, opportunities, and open research challenges, IEEE Access, vol. 11, pp. 6133–6149, 2023. [CrossRef]
- Li, Y., Chen, J., Xue, P., Tang, C., Chang, J., Chu, C., Ma, K., Li, Q., Zheng, Y., and Qiao, Y., Computer-aided cervical cancer diagnosis using time-lapsed colposcopic images, IEEE Transactions on Medical Imaging, vol. 39, no. 11, pp. 3403–3415, 2020. [CrossRef]
- Youneszade, N., Marjani, M., and Ray, S. K., A predictive model to detect cervical diseases using convolutional neural network algorithms and digital colposcopy images, IEEE Access, vol. 11, pp. 59882–59898, 2023. [CrossRef]
- Zhang, S., Chen, C., Chen, F., Li, M., Yang, B., Yan, Z., and Lv, X., Research on application of classification model based on stack generalization in staging of cervical tissue pathological images, IEEE Access, vol. 9, pp. 48980–48991, 2021. [CrossRef]
- Yue, Z., Ding, S., Zhao, W., Wang, H., Ma, J., Zhang, Y., and Zhang, Y., Automatic CIN grades prediction of sequential cervigram image using LSTM with multistate CNN features, IEEE Journal of Biomedical and Health Informatics, vol. 24, no. 3, pp. 844–854, 2019. [CrossRef]
- Chen, P., Liu, F., Zhang, J., and Wang, B., MFEM-CIN: A lightweight architecture combining CNN and Transformer for the classification of pre-cancerous lesions of the cervix, IEEE Open Journal of Engineering in Medicine and Biology, vol. 5, pp. 216–225, 2024. [CrossRef]
- Luo, Y.-M., Zhang, T., Li, P., Liu, P.-Z., Sun, P., Dong, B., and Ruan, G., MDFI: multi-CNN decision feature integration for diagnosis of cervical precancerous lesions, IEEE Access, vol. 8, pp. 29616–29626, 2020. [CrossRef]
- Pal, A., Xue, Z., Befano, B., Rodriguez, A. C., Long, L. R., Schiffman, M., and Antani, S., Deep metric learning for cervical image classification, IEEE Access, vol. 9, pp. 53266–53275, 2021. [CrossRef]
- Adweb, K. M. A., Cavus, N., and Sekeroglu, B., Cervical cancer diagnosis using very deep networks over different activation functions, IEEE Access, vol. 9, pp. 46612–46625, 2021. [CrossRef]
- Yue, Z., Ding, S., Li, X., Yang, S., and Zhang, Y., Automatic acetowhite lesion segmentation via specular reflection removal and deep attention network, IEEE Journal of Biomedical and Health Informatics, vol. 25, no. 9, pp. 3529–3540, 2021. [CrossRef]
- Bappi, J. O., Rony, M. A. T., Islam, M. S., Alshathri, S., and El-Shafai, W., A novel deep learning approach for accurate cancer type and subtype identification, IEEE Access, vol. 12, pp. 94116–94134, 2024. [CrossRef]
- Fang, M., Lei, X., Liao, B., and Wu, F.-X., A deep neural network for cervical cell detection based on cytology images, SSRN, vol. 13, pp. 4231806, 2022.
- Devarajan, D., Alex, D. S., Mahesh, T. R., Kumar, V. V., Aluvalu, R., Maheswari, V. U., and Shitharth, S., Cervical cancer diagnosis using intelligent living behavior of artificial jellyfish optimized with artificial neural network, IEEE Access, vol. 10, pp. 126957–126968, 2022. [CrossRef]
- Sahoo, P., Saha, S., Mondal, S., Seera, M., Sharma, S. K., and Kumar, M., Enhancing computer-aided cervical cancer detection using a novel fuzzy rank-based fusion, IEEE Access, vol. 11, pp. 145281–145294, 2023. [CrossRef]
- Al Qathrady, M., Shaf, A., Ali, T., Farooq, U., Rehman, A., Alqhtani, S. M., and Alshehri, M. S., A novel web framework for cervical cancer detection system: A machine learning breakthrough, IEEE Access, vol. 12, pp. 41542–41556, 2024. [CrossRef]
- He, Y., Liu, L., Wang, J., Zhao, N., and He, H., Colposcopic image segmentation based on feature refinement and attention, IEEE Access, vol. 12, pp. 40856–40870, 2024. [CrossRef]
- Ramzan, Z., Hassan, M. A., Asif, H. M. S., and Farooq, A., A machine learning-based self-risk assessment technique for cervical cancer, Current Bioinformatics, vol. 16, no. 2, pp. 315–332, Feb. 2021. [CrossRef]
- Parra, S., Carranza, E., Coole, J., Hunt, B., Smith, C., Keahey, P., Maza, M., Schmeler, K., and Richards-Kortum, R., Development of low-cost point-of-care technologies for cervical cancer prevention based on a single-board computer, IEEE Journal of Translational Engineering in Health and Medicine, vol. 8, pp. 1–10, 2020. [CrossRef]
- Huang, P., Zhang, S., Li, M., Wang, J., Ma, C., Wang, B., and Lv, X., Classification of cervical biopsy images based on LASSO and EL-SVM, IEEE Access, vol. 8, pp. 24219–24228, 2020. [CrossRef]
- Ilyas, Q. M., and Ahmad, M., An enhanced ensemble diagnosis of cervical cancer: A pursuit of machine intelligence towards sustainable health, IEEE Access, vol. 9, pp. 12374–12388, 2021. [CrossRef]
- Nour, M. K., Issaoui, I., Edris, A., Mahmud, A., Assiri, M., and Ibrahim, S. S., Computer-aided cervical cancer diagnosis using gazelle optimization algorithm with deep learning model, IEEE Access, 2024. [CrossRef]
- Jacot-Guillarmod, M., Balaya, V., Mathis, J., Hübner, M., Grass, F., Cavassini, M., Sempoux, C., Mathevet, P., and Pache, B., Women with cervical high-risk human papillomavirus: Be aware of your anus! The ANGY cross-sectional clinical study, Cancers, vol. 14, no. 20, pp. 5096, 2022. [CrossRef]
- Bucchi, L., Costa, S., Mancini, S., Baldacchini, F., Giuliani, O., Ravaioli, A., Vattiato, R., et al., Clinical epidemiology of microinvasive cervical carcinoma in an Italian population targeted by a screening programme, Cancers, vol. 14, no. 9, pp. 2093, 2022. [CrossRef]
- Tantari, M., Bogliolo, S., Morotti, M., Balaya, V., Buenerd, A., Magaud, L., et al., Lymph node involvement in early-stage cervical cancer: Is lymphangiogenesis a risk factor?, Cancers, vol. 14, no. 1, pp. 212, 2022. [CrossRef]
- Cho, B.-J., Choi, Y. J., Lee, M.-J., Kim, J. H., Son, G.-H., Park, S.-H., and Kim, H.-B., Classification of cervical neoplasms on colposcopic photography using deep learning, Scientific Reports, vol. 10, no. 1, pp. 13652, 2020. [CrossRef]
- Yao, K., Huang, K., Sun, J., and Hussain, A., PointNu-Net: Keypoint-assisted convolutional neural network for simultaneous multi-tissue histology nuclei segmentation and classification, IEEE Transactions on Emerging Topics in Computational Intelligence, vol. 8, no. 1, pp. 802–813, Feb. 2024. [CrossRef]
- Jiang, X., Li, J., Kan, Y., Yu, T., Chang, S., Sha, X., Zheng, H., and Wang, S., MRI-based radiomics approach with deep learning for prediction of vessel invasion in early-stage cervical cancer, IEEE/ACM Transactions on Computational Biology and Bioinformatics, vol. 18, no. 3, pp. 995–1002, 2020. [CrossRef]
- Baydoun, A., Xu, K. E., Heo, J. U., Yang, H., Zhou, F., Bethell, L. A., Fredman, E. T., et al., Synthetic CT generation of the pelvis in patients with cervical cancer: A single input approach using generative adversarial network, IEEE Access, vol. 9, pp. 17208–17221, 2021. [CrossRef]
- Kaur, M., Singh, D., Kumar, V., and Lee, H.-N., MLNet: Metaheuristics-based lightweight deep learning network for cervical cancer diagnosis, IEEE Journal of Biomedical and Health Informatics, vol. 27, no. 10, pp. 5004–5014, 2022. [CrossRef]
- Jiang, Z.-P., Liu, Y.-Y., Shao, Z.-E., and Huang, K.-W., An improved VGG16 model for pneumonia image classification, Applied Sciences, vol. 11, no. 23, pp. 11185, 2021. [CrossRef]
- Tammina, S., Transfer learning using VGG-16 with deep convolutional neural network for classifying images, International Journal of Scientific and Research Publications, vol. 9, no. 10, pp. 143–150, 2019. [CrossRef]
- Kareem, R. S. A., Tilford, T., and Stoyanov, S., Fine-grained food image classification and recipe extraction using a customized deep neural network and NLP, Computers in Biology and Medicine, vol. 175, pp. 108528, 2024. [CrossRef]
- Ali, H., and Chen, D., A survey on attacks and their countermeasures in deep learning: Applications in deep neural networks, federated, transfer, and deep reinforcement learning, IEEE Access, 2023. [CrossRef]
- Prakash, A. S. J., and Sriramya, P., Accuracy analysis for image classification and identification of nutritional values using convolutional neural networks in comparison with logistic regression model, Journal of Pharmaceutical Negative Results, pp. 606–611, 2022. [CrossRef]
- Das, P., and Pandey, V., Use of logistic regression in land-cover classification with moderate-resolution multispectral data, Journal of the Indian Society of Remote Sensing, vol. 47, no. 8, pp. 1443–1454, 2019. [CrossRef]
- Alassar, Z., Decision Tree as an Image Classification Technique, Department of City and Regional Planning, Faculty of Architecture, Akdeniz University, vol. 18, no. 4, pp. 1–7, 2020.
- Lee, J., Sim, M. K., and Hong, J.-S., Assessing Decision Tree Stability: A Comprehensive Method for Generating a Stable Decision Tree, IEEE Access, vol. 12, pp. 90061–90072, 2024. [CrossRef]
- Luo, Z., Li, J., and Zhu, Y., A deep feature fusion network based on multiple attention mechanisms for joint iris-periocular biometric recognition, IEEE Signal Processing Letters, vol. 28, pp. 1060–1064, 2021. [CrossRef]
- Chen, Z., Han, X., and Ma, X., Combining contextual information by integrated attention mechanism in convolutional neural networks for digital elevation model super-resolution, IEEE Transactions on Geoscience and Remote Sensing, vol. 62, pp. 1–16, 2024. [CrossRef]
- International Agency for Research on Cancer (IARC), IARC: International Agency for Research on Cancer, 2023. Available: https://www.iarc.who.int/.
- Jiang, X., Li, J., Kan, Y., Yu, T., Chang, S., Sha, X., Zheng, H., and Wang, S., MRI-based radiomics approach with deep learning for prediction of vessel invasion in early-stage cervical cancer, IEEE/ACM Transactions on Computational Biology and Bioinformatics, vol. 18, no. 3, pp. 995–1002, 2020. [CrossRef]
- Wang, C., Zhang, J., and Liu, S., Medical ultrasound image segmentation with deep learning models, IEEE Access, vol. 11, pp. 10158–10168, 2023. [CrossRef]
- Skerrett, E., Miao, Z., Asiedu, M. N., Richards, M., Crouch, B., Sapiro, G., Qiu, Q., and Ramanujam, N., Multicontrast Pocket Colposcopy Cervical Cancer Diagnostic Algorithm for Referral Populations, BME Frontiers, vol. 2022, pp. 9823184, 2022. [CrossRef]
- Gaona, Y. J., Malla, D. C., Crespo, B. V., Vicuña, M. J., Neira, V. A., Dávila, S., and Verhoeven, V., Radiomics diagnostic tool based on deep learning for colposcopy image classification, Diagnostics, vol. 12, no. 7, pp. 1694, 2022. [CrossRef]
- Allahqoli, L., Laganà, A. S., Mazidimoradi, A., Salehiniya, H., Günther, V., Chiantera, V., Goghari, S. K., Ghiasvand, M. M., Rahmani, A., Momenimovahed, Z., and Alkatout, I., Diagnosis of cervical cancer and pre-cancerous lesions by artificial intelligence: A systematic review, Diagnostics, vol. 12, no. 11, pp. 2771, 2022. [CrossRef]
- Zhang, T., Luo, Y.-M., Li, P., Liu, P.-Z., Du, Y.-Z., Sun, P., Dong, B., and Xue, H., Cervical precancerous lesions classification using pre-trained densely connected convolutional networks with colposcopy images, Biomedical Signal Processing and Control, vol. 55, article no. 101566, Jan. 2020. [CrossRef]
- Bai, B., Du, Y., Liu, P., Sun, P., Li, P., and Lv, Y., Detection of cervical lesion region from colposcopic images based on feature reselection, Biomedical Signal Processing and Control, vol. 57, pp. 101785, 2020. [CrossRef]
- Tanaka, Y., Ueda, Y., Kakubari, R., Kakuda, M., Kubota, S., Matsuzaki, S., Okazawa, A., Egawa-Takata, T., Matsuzaki, S., Kobayashi, E., and Kimura, T., Histologic correlation between smartphone and colposcopic findings in patients with abnormal cervical cytology: Experiences in a tertiary referral hospital, American Journal of Obstetrics and Gynecology, vol. 221, no. 3, pp. 241.e1–241.e6, Sept. 2019. [CrossRef]
- Zhang, X., and Zhao, S.-G., Cervical image classification based on image segmentation preprocessing and a CapsNet network model, International Journal of Imaging Systems and Technology, vol. 29, no. 1, pp. 19–28, 2019. [CrossRef]
- Malhari Colposcopy Dataset original, aug & combined, Malhari Colposcopy Dataset original, aug & combined, 2024. Available: https://www.kaggle.com/datasets/srijanshovit/malhari-colposcopy-dataset/suggestions?status=pending&yourSuggestions=true.

| Ep-och | Learn Rate | Batch Size | Val Loss | Train Loss | Val Acc (%) | Pre-cision (%) | Recall (%) | TP / FP / FN |
|---|---|---|---|---|---|---|---|---|
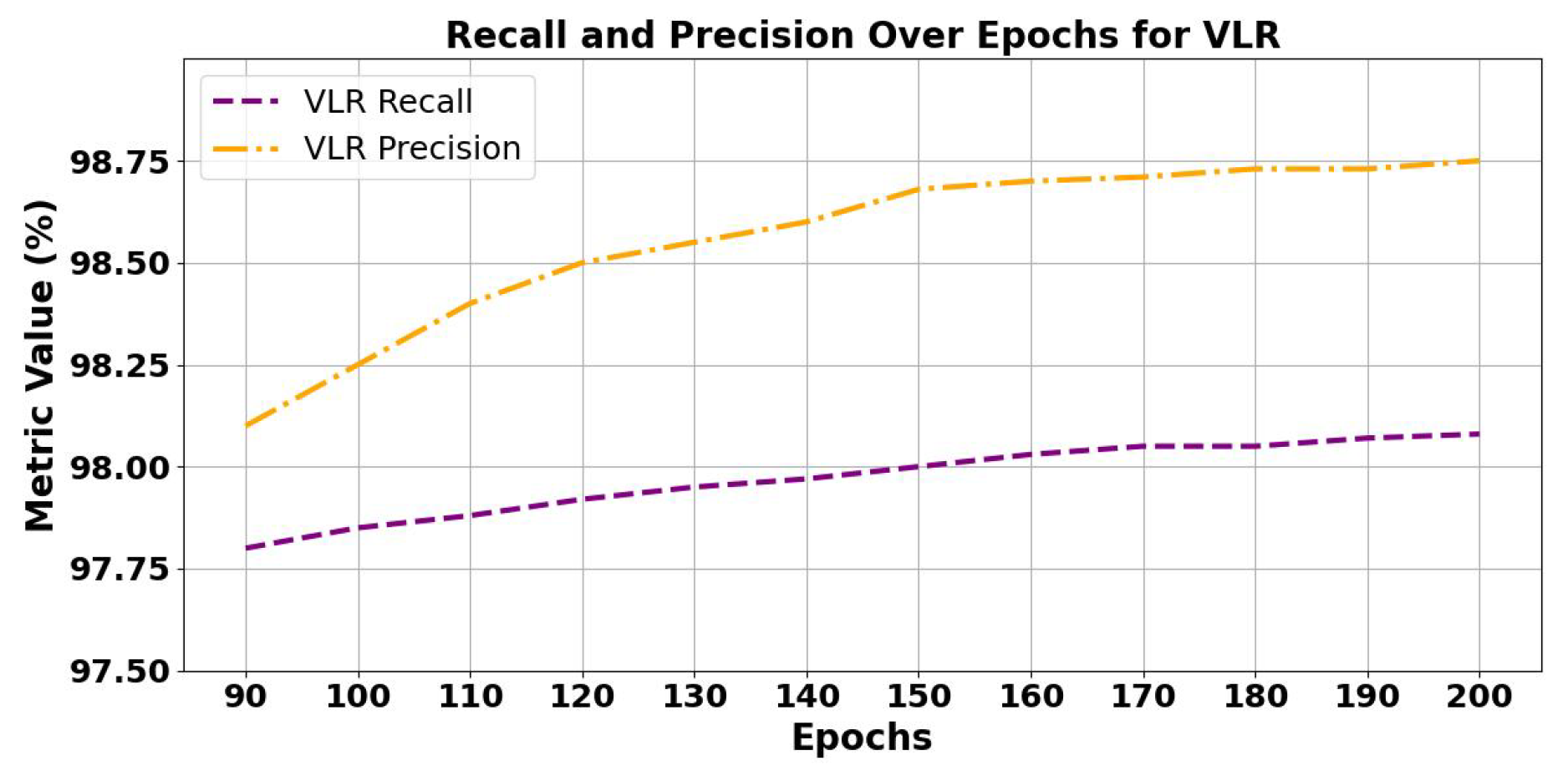
| 90 | 0.001 | 100 | 0.0065 | 0.003317 | 98.56 | 98.10 | 97.80 | 2188 / 12 / 8 |
| 100 | 0.0005 | 100 | 0.0052 | 0.003304 | 99.10 | 98.25 | 97.85 | 2189 / 11 / 7 |
| 110 | 0.0001 | 80 | 0.0041 | 0.00325 | 99.45 | 98.40 | 97.88 | 2190 / 9 / 7 |
| 120 | 0.0001 | 60 | 0.0035 | 0.00275 | 99.60 | 98.50 | 97.90 | 2191 / 8 / 6 |
| 130 | 0.00005 | 60 | 0.0030 | 0.00250 | 99.68 | 98.55 | 97.92 | 2192 / 7 / 6 |
| 140 | 0.00005 | 50 | 0.0026 | 0.00230 | 99.72 | 98.60 | 97.95 | 2193 / 6 / 5 |
| 150 | 0.00001 | 50 | 0.0023 | 0.00214 | 99.77 | 98.65 | 97.97 | 2194 / 5 / 5 |
| 160 | 0.000005 | 40 | 0.0021 | 0.00205 | 99.80 | 98.68 | 97.99 | 2194 / 5 / 4 |
| 170 | 0.000005 | 40 | 0.0019 | 0.00200 | 99.82 | 98.70 | 98.00 | 2194 / 4 / 4 |
| 180 | 0.000001 | 35 | 0.0018 | 0.00192 | 99.85 | 98.72 | 98.03 | 2194 / 4 / 3 |
| 190 | 0.000001 | 35 | 0.0017 | 0.00185 | 99.87 | 98.74 | 98.05 | 2195 / 3 / 2 |
| 200 | 0.0000005 | 30 | 0.0015 | 0.00175 | 99.89 | 98.75 | 98.08 | 2195 / 3 / 2 |
| Data-set | VGG16 | ResNet50 | LR | VLR-Loss | VLR-vali-dation-acc | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Val-Acc (%) | Train-Loss | Static | Dyn-mic | Final | Val-Acc (%) | Train-Loss | Static | Dyna-mic | Final | Val-Acc (%) | Train-Loss | Static | Dyna-mic | Final | Train-Loss-Contrib | Final-Acc | |
| Lugol’s-iodine | 91.67 | 0.00821 | 0.348 | 0.3352 | 0.3389 | 92.43 | 0.00731 | 0.574 | 0.3713 | 0.4670 | 94.42 | 0.00649 | 0.078 | 0.2935 | 0.1903 | 0.00708 | 99.21 |
| Acetic-acid | 90.17 | 0.00864 | 0.348 | 0.3360 | 0.3396 | 91.23 | 0.00791 | 0.574 | 0.3745 | 0.4705 | 92.12 | 0.00744 | 0.078 | 0.2895 | 0.1883 | 0.00746 | 99.10 |
| Normal-saline | 87.87 | 0.00978 | 0.348 | 0.3366 | 0.3400 | 88.73 | 0.00912 | 0.574 | 0.3764 | 0.4723 | 90.04 | 0.00842 | 0.078 | 0.2870 | 0.1865 | 0.00802 | 99.02 |
| Malhari | 93.45 | 0.00814 | 0.348 | 0.3332 | 0.3366 | 94.21 | 0.00701 | 0.574 | 0.3695 | 0.4642 | 95.66 | 0.00631 | 0.078 | 0.2973 | 0.1931 | 0.00695 | 99.41 |
| Model | Val-Acc (%) | Prec-ision (%) | Recall (%) | F1-Score (%) | ROC-AUC (%) | Train Time (sec-(TPU-V28) ) | Train Loss |
|---|---|---|---|---|---|---|---|
| VGG16 | 96.77 | 95.47 | 96.12 | 95.84 | 93.255 | 4860 | 0.00711 |
| ResNet50 | 98.23 | 96.65 | 97.24 | 97.02 | 95.854 | 3960 | 0.00631 |
| LR | 98.92 | 97.25 | 97.99 | 97.50 | 97.891 | 15 | 0.00349 |
| VLR | 99.89 | 98.75 | 98.08 | 98.41 | 99.991 | 5040 | 0.00175 |
| Metric | Formula | VGG16 (%) | ResNet50 (%) | LR (%) | VLR (%) |
|---|---|---|---|---|---|
| Validation Accuracy | 96.77 | 98.23 | 98.92 | 99.89 | |
| Precision (P) | 95.47 | 96.25 | 97.25 | 98.75 | |
| Recall (R) | 96.12 | 97.24 | 97.99 | 98.08 | |
| True Positives (TP) | 2115 | 2160 | 2189 | 2195 | |
| False Positives (FP) | 30 | 20 | 7 | 3 | |
| False Negatives (FN) | 55 | 20 | 4 | 2 |
| Metric | Fold 1 | Fold 2 | Fold 3 | Fold 4 | Fold 5 | Mean (%) | Standard Deviation (%) |
|---|---|---|---|---|---|---|---|
| Validation Accuracy (%) | 99.90 | 99.88 | 99.91 | 99.87 | 99.89 | 99.89 | 0.02 |
| Training Accuracy (%) | 99.96 | 99.95 | 99.95 | 99.94 | 99.95 | 99.95 | 0.01 |
| Precision (%) | 98.76 | 98.77 | 98.74 | 98.75 | 98.76 | 98.75 | 0.01 |
| Recall (%) | 98.09 | 98.08 | 98.11 | 98.06 | 98.07 | 98.08 | 0.02 |
| F1-Score (%) | 98.47 | 98.45 | 98.48 | 98.44 | 98.46 | 98.46 | 0.02 |
| ROC-AUC (%) | 99.99 | 99.98 | 99.99 | 99.98 | 99.99 | 99.99 | 0.01 |
| Training Loss | 0.00176 | 0.00174 | 0.00175 | 0.00173 | 0.00175 | 0.00175 | 0.00002 |
| Solution | Train Accuracy (%) | Validation Accuracy (%) | Pre-cision% | Recall-% | F1-Score% |
|---|---|---|---|---|---|
| Lugol’s iodine | 99.41 | 99.21 | 98.69 | 97.81 | 98.22 |
| Acetic acid | 99.23 | 99.10 | 98.14 | 97.23 | 97.64 |
| Normal saline | 99.14 | 99.02 | 97.12 | 96.04 | 96.56 |
| Malhari | 99.74 | 99.41 | 98.62 | 98.11 | 98.36 |
| Model | Accuracy (%) | Precision | Recall | F1-Score |
|---|---|---|---|---|
| MFEM-CIN[7] | 89.2 | 92.3 | 88.16 | 90.18 |
| DL[4] | 92 | 79.4 | 100 | 97.58 |
| CNN[44] | 87 | 75 | 88 | 80.55 |
| CNN[45] | 90 | NA | NA | NA |
| CNN[46] | 84 | 96 | 99 | 97.47 |
| DenseNet-CNN[47] | 73.08 | 44 | 87 | 58.44 |
| CLD Net[48] | 92.53 | 85.56 | NA | NA |
| Kappa[49] | 67 | 89 | 33 | 76.44 |
| Caps Net[50] | 99 | NA | NA | NA |
| E-GCN[3] | 81.85 | 81.97 | 81.78 | 81.87 |
| VLR | 99.95 | 98.75 | 98.08 | 98.41 |
| Reference | Dataset | Method | Accuracy | Remarks |
|---|---|---|---|---|
| [7]2024 | Colposcopy | CNN, Transformer | 89.2% | Employs a hybrid model of MFEM-CIN and Transformer. |
| [12]2024 | Pap Smear | CNN, ML, DL | 99.95% | Combines computational tools like CNN-LSTM hybrids, KNN, and SVM. |
| [16]2024 | Pap Smear | Deep Learning | 92.19% | Employs CerviSegNet-DistillPlus for classification. |
| [15]2024 | Biopsy | Machine Learning | 98.19% | Employs ensemble of machine learning algorithms for classification. |
| [17]2024 | Colposcopy | Deep Learning | 94.55% | Has used a hybrid deep neural network for segmentation. |
| [2]2023 | Pap Smear | Deep Learning | 97.18% | Uses deep learning techniques integrated with advanced augmentation techniques such as CutOut, MixUp, and CutMix. |
| [4]2023 | Colposcopy | Deep Learning | 92% | Uses predictive deep learning model. |
| [30]2022 | Pap Smear | CNN, PSO, DHDE | 99.7% | Applies CNN for a multi-objective problem, and PSO and DHDE are used for optimization. |
| [14]2022 | Cytology | ANN | 98.87% | Uses artificial Jellyfish Search optimizer combined with an ANN. |
| [9]2021 | Colposcopy | Deep Learning | 92% | Uses Deep neural techniques for cervical cancer classification. |
| [11]2021 | Colposcopy | Deep Learning | 90% | Using deep neural network generated attention maps for segmentation. |
| [10]2021 | Colposcopy | Residual Learning | 90%, 99% | Employed residual network using Leaky ReLU and PReLU for classification. |
| [29]2021 | MR-CT Images | GAN | - | Uses a conditional generative adversarial network (GAN). |
| [21]2021 | Pap Smear | Biosensors | - | Uses biosensors for higher accuracy. |
| [5]2021 | Cervical Pathology Images | SVM, k-Nearest Neighbors, CNN, RF | 90%-89.1% | Uses ResNet50 model as a feature extractor and selects k-NN, Random Forest, and SVM for classification. |
| [1]2021 | Colposcopy | CNN | 99% | Uses Faster Small-Object Detection Neural Networks. |
| [13]2021 | Pap Smear | Deep Convolutional Neural Network | 95.628% | Constructs a CNN called DeepCELL with multiple kernels of varying sizes. |
| [28]2020 | MRI Data of Cervix | Statistical Model | - | A statistical model called LM is used for outlier detection in lognormal distributions. |
| [3]2020 | Colposcopy | CNN | 81.95% | Employs a graph convolutional network with edge features (E-GCN). |
| [8]2020 | Colposcopy | Deep Learning | 83.5% | Has used K-means for classification, CNN and XGBoost to combine the CNN decesion. |
| [6]2019 | Colposcopy | CNN | 96.13% | Uses a recurrent convolutional neural network for classification of cervigrams . |
| Our Method | Colposcopy | Deep Neural Network | 99.95% | An ensemble model called Variable Learning Rate specially designed to increase the accuracy. |
| Sl.No. | Gaps | Corrective Measures |
|---|---|---|
| 1.[3,9] | less classification accuracy | VLR projects a training accuracy of 99.95% |
| 2.[12,29] | variations in dataset used for classification | correct dataset used; colposcopy |
| 3.[4,44] | recall values are higher than precision | VLR projects precision as 98.75% and recall as 98.08% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





