Prerpints.org logo
Preprint
Article

Cybercartography as a Theoretical Framework for the Design of an Expert-Topographic Map Service

Altmetrics

Downloads

54

Views

72

Comments

0

This version is not peer-reviewed

Submitted:

30 October 2024

Posted:

31 October 2024

You are already at the latest version

Alerts
Abstract
Abstract: New paradigms have emerged in mapping since the 20th century due to theoretical and practical advances in computer technology, communications, and cartography. For the design of the Expert-Topographic Map Service in Mexico, we adopted a theoretical framework of Cybercartography and expanded to incorporate expert systems and eventually other artificial intelligence resources. Using a transdisciplinary approach, our efforts could focus on the interconnection between knowledge and geotechnology to offer solutions to societal complex problems. This paper explores the theoretical pillars supporting the design of an Expert-Topographic Map Service, including cybercartography, knowledge-based systems and surface mathematical modeling. For the first time, cybercartography is applied in the realm of topographic mapping. As shown, a map conceived solely as an information system has been transformed, in the digital era, into a container of knowledge through the abstract representation of features like relief via the Triangular Irregular Network Model. Thereby, we can bridge from digital topographic maps to other knowledge-based models such as expert systems. The societal demand and empirical context for this research demonstrate that topographic maps and services are still at the core of cartographic initiatives in the 21st century.
Keywords: 
Subject: Environmental and Earth Sciences  -   Geography

1. Introduction

As Caudill et.al.[1] (p 19) explained, deeper transdisciplinary approaches are required to advance in science. These approaches can help satisfy the demand from society by expanding the interconnection between knowledge and geotechnology to offer solutions to societal complex problems. Such is the case of the design of a topographic mapping service for a country like Mexico. These ideas induced the authors to adopt Cybercartography as a theoretical framework for this endeavor. Throughout this article the reader will find references to established conceptual issues regarding topographic mapping as well as to various knowledge domains in mathematics, computer science, cartography, and geomatics. In the section of conclusions explicit cognitive interactions and conceptual convergence among these domains are explored.
Societal Empirical Context
The societal context in which the expert-topographic map service would be embedded deserves some explanation. Topographic mapping is a central facet of National Mapping Agencies as reported in the fourteenth session of the UN-GGIM [2]. In terms of Spatial Data Infrastructures is worth mentioning the advances presented by Mexico in response to the challenges of sustainable development [3]. In the following paragraphs the current and historical development of topographical mapping in Mexico is presented.
During the years 2019-2021, the National Institute of Statistics and Geography, Mexico (INEGI) undertook a project for the design of a topographic map service based on the latest theoretical and geotechnological advances in cartography and related sciences. This effort was under the leadership of the first author of this paper.
The most recent historical background of topographic mapping in Mexico can be found in the 20th century with three recognizable landmarks. The first refers to the efforts made by General Lázaro Cárdenas a former president of Mexico (1934-1940). After the end of his administration, he was nominated as the executive director of two mega-projects in regional planning (1947-1968) at the federal level, (Comisiones Hidrológicas del Tepalcatepec y del Balsas) [4]. Multiple maps of the Balsas basin from various sources and scales produced during the first half of the 20th century can be found in the Mapoteca “Manuel Orozco y Berra” [5]. These projects began the process of linking spatial information to specific projects of government and society.
The second landmark is the foundation in 1968 of a Federal Commission incorporated directly to the Office of the President of Mexico (better known as “Comisión de Estudios del Territorio Nacional, CETENAL”). The coincidence of the dates between the hydrological projects and the creation of the Commission points to the awareness of the Federal Mexican Government of the importance of topographic mapping. Accordingly, to the worldwide attention to cartography at that moment, the main project of CETENAL (later DETENAL) included the design and development of a production line for the 1:50,000 scale topographic map for the whole country. Between the years 1968 and 1988, Mexico produced 2,357 paper maps based on aerial photographs, photogrammetry, and analogic methods. This topographic map (TM) of the country is and has been the main reference for its application by an ample group of users and update processes.
In the early nineties (when CENTENAL was folded into INEGI), a large project was undertaken by INEGI to update the 1:50,000 scale TM. For this purpose, an international call for proposals was launched. As a result, the Canadian company SNC Lavalin and the Canadian Government established together with INEGI´s personnel the necessary inputs and technical issues for the updating of the TM. It is important to highlight the adoption and adaptation of the Feature Dictionary as well as the relational approach already applied by the Canadian Government for the digital conversion of the paper TM. These events mark the third landmark.
The project regarding the topographic map undertaken by INEGI (2019-2021) began with three main elements: a diagnostic of the existing maps, the conceptual design of new production processes and as a proof of concept, the implementation of two prototypes (Maya Project and Sonora State) with the newly proposed approach and production processes. As an example of the introduction to the topographic map service for the Maya Project see https://youtu.be/aueNceDBT6U
Theoretical building blocks
As was initially mentioned by Reyes et.al. [6] (p 9), much empirical work needs to be done to generate new knowledge in geomatics, and societal needs generate the problems whose solutions are the subject matter for theoretical research.
The point of departure for the Expert-Topographic Map Service (ETM) was a societal demand. In this case INEGI´s commitment towards offering a topographic map service detonated the design of the ETM taking into consideration the 21st century user requirements regarding topographic mapping.
Since the initial steps (2019), the group in charge at INEGI of this exciting and complex new project (that included C. Reyes) had the vision of implicitly adopting and empirically adapting for the design of the ETM the main ideas behind the following three theoretical approaches: cybercartography, knowledge-based systems and surface mathematical modeling. In the following paragraphs an overview of these theoretical building blocks is presented.
Cybercartography. - The cybercartographic approach has already been reported in scientific publications [7,8,9]. In this work the design elements that were derived from the initial cybercartographic theoretical framework are presented and a conceptual elaboration that expands the initial interaction space [10] (p 82) in cybercartography is discussed.
Knowledge-based systems. - As stated by Coombs [11] (Preface), “The potential value of automated knowledge-based problem solvers - or “expert systems”- is now firmly established. Since the building of the first system 15 years ago, several exemplar projects have demonstrated that computer programs are capable of expert performance in diagnostic, control, and planning tasks within a wide range of domains”.
Russell [12] mentions “Ed Feigenbaum and Raj Reddy (1994) for developing expert systems that encode human knowledge to solve real-world problems;” (p 63) and a review of the advancement of expert systems and their impact and limitations between 1968 and 1986 is also presented by Russell (p 71). For the design of the ETM and as an initial idea, basic principles of expert systems were adopted as an initial effort to explore the application of Artificial Intelligence (A.I.) into Cybercartography. It is important to mention that at INEGI the expert system implementation remained as a plan (in the year 2022).
Surface mathematical modeling. - Tom Peucker (later Poiker) [13,14] (pp 55–69) together with his research team in the seventies proposed a model for the digital representation of relief which they named the Triangular Irregular Network (TIN). The approach to the problem is a fundamental seed for a knowledge-based approach. The manner in which expert systems and surface mathematical modeling are intertwined is explored.
Scope of the paper
Due to the dimension and complexity of the INEGI project, each one of the abovementioned elements that emerged since it was initially undertaken in 2019 would require an ample presentation and most likely several scientific articles and reports. This article developed at CentroGeo with the advice of the Geomatics and Cartographic Research Center of Carleton University, focuses on the explicit description of the theoretical aspects and framework involved in the design of the of the Expert-Topographic Map Service including cybercartography, knowledge-based systems and surface mathematical modeling.
To the best of our knowledge cybercartography is for the first time adopted in the realm of topographic mapping. As shown in the article, a map conceived solely as an information system has been transformed, in the digital era, also as a container of knowledge through the abstract representation of features like relief via the Triangular Irregular Model. This fact allows bridging digital topographic maps with other knowledge-based models such as expert systems. Moreover, the theoretical bridges among the abovementioned knowledge domains are explored so that new avenues of research emerge. The last section points to new topics that could be undertaken from a transdisciplinary perspective.

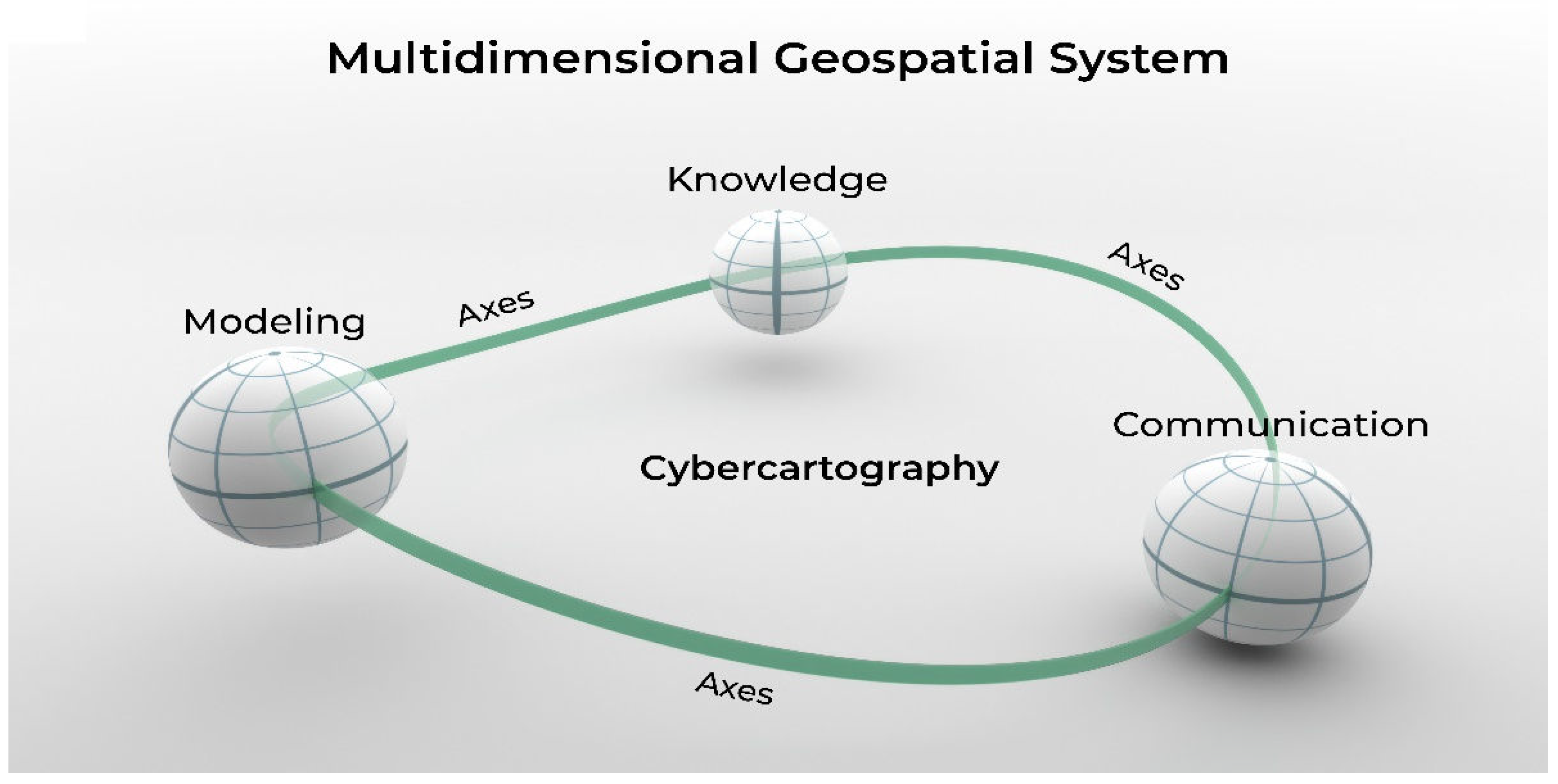
2. Theoretical Elements of the Design Method

As mentioned by Manzini [15] (p vii), “The practice of design predates professions. In fact, the practice of design-making things to serve a useful goal, making tools - predates the human race. Making tools is one of the attributes that made us human in the first place.” Design has become one of the knowledge domains explicitly recognized by academics as examples we find the work also of Simon [16], Cross [17], Telier [18], Nelson and Stolterman [19] and Dorst [20], among others.
The method applied to design the framework for an expert-topographic map service was based on the one developed by Reyes [10] (p 87) as part of the Cybercartography theoretical framework [7]. Among the premises adopted in the design process are: to explore new ways of communication and dissemination for the ETM based both on theoretical and geotechnological advances, with a knowledge-based approach to strengthen the modeling resources including computer simulations and expert systems, the service should be highly interactive and dynamic, to induce conversations with the user, to preserve the core ideas behind the analogic and virtual topographic maps, identifying good practices that could be enhanced and to adopt an organizational digital way of thinking and transformation [21] (p 4).
The concept of multidimensional system as conceived in cybercartography comes to our attention as a conceptual element for the design of the ETM.
Cybercartographic atlases are multidimensional systems composed of three axes: models, knowledge representation, and communication. Conceptually, the applications can be approached systematically from each of these perspectives. For example, a cybercartographic atlas can be viewed as a model of models or a geospatial meta-model. Alternatively, the communication process is accomplished through messages and information organized in subsystems using multiple languages. Knowledge is incorporated through implicit models derived from the suprasystem that reflect the specific interests of the users. [10] (p 77).
As shown in Figure 1, adopting the multidimensional geospatial system and the three axes that characterize cybercartography; modeling, knowledge, and communication, an initial design of the expert-topographic map was undertaken. Following is a brief description of the corresponding axes and the way in which they are theoretically intertwined.

2.1. Modeling Axes

As presented in the chapter of “Cybercartography from a Modelling Perspective” [10] (pp 63-97) these axes are fundamental and a central building block in the theoretical framework of this topic. The initial statement, “a map can be viewed as an inseparable binomial phenomenon of modeling and communication” [10] (p 73) was adopted to approach the definition of a new paradigm for the topographic map of Mexico.
Within the cybercartographic approach, the ETM is a model of models. Some of the models have been present for many centuries. For example, the geometric representation of roads and rivers, others are derived from advances of the 20th century in models of relief such as the Triangular Irregular Network, TIN [13]. The main characteristics of the different components from a modeling perspective of the ETM are briefly described below.
Geometric Component of the ETM
To build a bridge between the conception of the traditional topographic map and an expert-topographic service, there was a need to broaden the modeling perspective due to the advancement in geotechnological resources that opened new possibilities for representation. For example, as an integral component of the topographic geometry model and additional to the point, line, polygon, and surface usual elements that were represented in analogic or virtual mode, the digital terrain and surface models, contour lines and the triangular irregular network models, among others, were added to the core of the ETM.
Feature Component
To provide the user with all the features contained in the ETM service, a database model was designed. Since the topographic service offers the possibility of generating visualizations at different scales and granularities, the features, its geometric representation, and relevance for the topographic map at stake are dynamic.
Traditionally, the features were published as a catalog or as part of an inset of the map. For our purpose, the universe of features identified in the topographic maps at different scales were incorporated (in the first stage approximately one thousand) in a database. Characteristics such as names, photographs, geotexts, and videos were attached to each one of them. Using the database is possible to identify the features of interest and their geometric representation for visual mapping purposes.
Computer Simulation Component
Computer simulation has been a resource for virtual mapping in topography for more than five decades. Applications to show the terrain based on the representation of the relief were developed early in geomatics to be incorporated into national security, engineering, and scientific needs. Computer graphics is a very dynamic and important branch of computer science due to its ample application in computer games and movies.
The geomatics community has much to learn from these advancements, however, the geotechnology to obtain simulations of digital terrain models is available so that its incorporation as an integral component of the ETM Service can be easily attained.
The Meta Component
These axes comprehend the models that are derived from the different domains that are involved in the production process of the topographic map such as: geodesy, photogrammetry, remote sensing, aerial photography, and cartography. The key characteristics of the models used are contained in the Metadata components of the ETM Service as well as relevant methodological issues.

2.2. Knowledge Axes

In the design of the Cybercartographic Atlas of the Lake of Chapala, due to the context where it was to be inserted, a landscape ecology model became the central knowledge component for the narrative that would serve as an axes for the story telling [10] (p 91), [22] (p 143). In each one of the cybercartographic exercises that were undertaken by the research group of CentroGeo, an explicit knowledge model was identified and used as a guide to build the messages, narratives, and visual resources to support the communication process. In more recent research an approach that integrates knowledge and geospatial information has been adopted to advance in the Challenges of the United Nations Sustainable Development Goals [1] (p 3).
Herby special attention is given to the knowledge representation of the relief from the perspective of the knowledge axes. In this regard, surface mathematical modeling has played a key role in the development of geotechnology since the seventies.
Surface Mathematical Modeling Component
In the first stages of the digital era regarding the topographic map, the most remarkable efforts were made in the topic of the digital representation of relief which is the essence of these type of maps. The state of the art at that time can be found in the book edited by Davis and McCullagh [23] with the work of Sprunt [24] (p 173) and Peucker, Tichenor and Rase [25] (p 187) among other authors. Other researchers were also advancing in those early stages of the representation of the relief that took advantage of the resources offered by computers [26].
One should state that a map is a model of the geographical landscape, in the sense that it is an abstraction of the territory as understood by Caudill et.al. [1] (Abstract) as a holistic system where societal, political, environmental, economic, and physical issues and features are represented. It should be recognized that the cognitive framework to produce a map depends on the individual or individuals involved in its design as well as on the knowledge of each one of the domains of interest. For example, in topographic mapping, relief plays a key role. Therefore, the scientific basics on the digital representations of the relief become a key component of the theoretical framework of the ETM.
Theoretical Background.
Tom Peucker [13,27] together with his research team in the 70’s proposed a model for the digital representation of relief which they named the Triangular Irregular Network (TIN). Hereby, we explore Maxwell´s (1870) article [28]as a complement to the description of the TIN model as well as some comments based on the concepts related to Surface Topology.
Maxwell´s article. -In the introduction of Maxwell´s article he mentions:
I find that in the greater part of the substance of the following paper I have been anticipated by Professor Cayley, in a memoir “On Contour and Slope Lines” published in the Philosophical Magazine in 1859 8S. 4 Vol. xviii p. 264). An exact knowledge of the first elements of physical geography, however, is so important, and loose notions on the subject are so prevalent, that I have no hesitation in sending you what you, I hope, will have no scruple in rejecting if you think it superfluous after what has been done by Professor Cayley. Signed by J. Clerk Maxwell.
One should not be surprised by the note of Maxwell since science is the result of collaborative events that emerges through the face-to-face interaction of scientists or through bibliographic research of papers written by others. Maxwell´s paper was published, and no doubt is an important scientific contribution even for the 21st century. Maxwell (1870) in its initial statement of the paper mentions:
The results of the survey of the surface of a country are most conveniently exhibited by means of a map on which are traced contour-lines, each contour-line representing the intersection of a level surface with the surface of the earth and being distinguished by a numeral which indicates the level surface to which it belongs.
This notion of contour line nowadays prevails. Maxwell uses different terms: region of depression, region of elevation, Bar, Pass, Summits or Tops and Bottoms [28] (pp 234-235).
Using analogical reasoning between what he calls “the pure theory of surfaces” and “nature” Maxwell states the relationship between watersheds and summits and between watercourses and bottoms based on slope lines. Towards the end of the article Maxwell refers to Listing´s rule (Euler formula) regarding the algebraic relation among pits, peaks and passes in a model of the earth.
As mentioned by Firby and Gardner [29] (Author´s Preface) Surface Topology is related to geometric topology or rubber sheet geometry. The authors incorporate related topics such as graph theory, group theory, vector field theory, hyperbolic and Euclidean plane geometry, and plane tessellations.
For our purposes is of interest the formula
V-E+F=2
for a closed convex polyhedron, where V is the number of vertices, E is the number of edges, and F is the number of faces. Euler (1752) first published the result [29] (p 1). In its more general form
X(M)= V-E+F
is called the Euler characteristic [29] (p 70).
For an illustrative proof of Euler´s formula look at
https://www.youtube.com/watch?v=80EazC2_0Qo
supported by Brilliant.org/ThinkTwice [30].
It comes to our attention regarding lines of research that converge to the Euler characteristic the work of Warntz [31] and the one related to the surface of the earth mentioned by Stilwell [32] (p 2).
The study of “pits, peaks, and passes” on surfaces in R3 by Cayley (1859) and Maxwell (1870). A family of parallel planes in R3 intersects a surface S in curves we may view as curves of “constant height” (contour lines) on S. If the planes are taken to be in general position, and the surface is smooth, then S has only finitely many “pits, peaks, and passes relative to the function. It turns out that,
Number of peaks - number of passes + number of pits
Is precisely the Euler characteristic of S.
Peucker [13] used the concepts of peaks, pits, and passes as a basis in the design of the Triangular Irregular Network (TIN) to digitally represent relief. In synthesis, there are algebraic, geometric, and topological relations within the elements that conform the relief in a topographic map. By using TIN to model and represent the relief one should be aware that there is knowledge regarding physical geography and surface topology that is implicit in this digital representation.
From the knowledge base approach, the digital modeling perspective of the relief is an example of the representation of knowledge in the computer which happens to be one of the interests in Artificial Intelligence [33] (p 163).
It should be pointed that other components of the topographic map from the perspective of the knowledge axes such as road networks, hydrological and urban systems, should be analyzed.
Expert Systems Component
Artificial Intelligence (A.I.) is a scientific domain that emerges in the decade of the fifties. As Crevier [33] (p xi) mentions, “The story of A.I. consists of successes and failures, visionaries and naysayers, new hardware, and lots of programs. It is also the story of a slow but steady acquisition of knowledge about how humans think.”
According to Russell and Norvig [12] (pp 32-33) to synthetize the answer of “Can a machine think?” “The computer would need the following capabilities: natural language processing to communicate successfully in a human language; knowledge representation to store what it knows or hears; automated reasoning to answer questions and to draw new conclusions; machine learning to adapt to new circumstances and to detect and extrapolate patterns.”
Moreover, they state that “Turing viewed the physical simulation of a person as unnecessary to demonstrate intelligence. However, other researchers have proposed a total Turing test, which requires interaction with objects and people in the real world. To pass the total Turing test, a robot will need computer vision and speech recognition to perceive the world; robotics to manipulate objects and move about.”
The main identified characteristics of an expert system regarding its possible incorporation of more advanced and explicit functionalities to the ETM were established by the authors at CentroGeo and GCRC (2023-2024). These notions were related with knowledge representation of the territory and basic automated reasoning related with the needs of the user in the acquisition of the services from the ETM. In this regard, the application of Expert Systems concepts became theoretically a viable route. In the future, other A.I. capabilities such as machine learning could be explored and implemented.
Expert Systems (ES) is a term that emerged in the early seventies and was also characterized by Coombs as automated knowledge-based problem solvers. At that time, the ES had already been applied and performed “in diagnostic, interpretative, control and planning tasks” in different domains including “medicine, industry and commerce” [11] (Preface). Rusell and Nordig [12] (p 71) also characterize Expert Systems (1969–1986) in their historical revision of A.I.
Comes to our attention PROSPECTOR that was developed “to provide active consultation on problems of mineral exploration and resource evaluation” [34] (p 1) similarly for the ETM it is designed so that the cybercartographic user tells the system his/her main purpose that points to the need of the ETM and it is assumed that the user is an expert in its domain of study and has a general knowledge on topographic mapping. The expert system emulates a group of experts that would respond to the user with a certain subjective probability the characteristics of the required service (type of representation, polygons of the areas of interest, scale, granularity, features, and so on) that would better respond to the needs of the user. In this initial exercise of the incorporation into the design of the ETM of expert systems, several domain areas of knowledge are the most adequate ones to be considered in the Mexican government context: regional planning, urban planning, cadaster, and physical infrastructure development.
The expert system proposed would explore the databases that contain the description of the cartographic collection available and if the topographic map service exists then the service is given to the user. Otherwise, the system using a knowledge-based engine that determines the plausibility of the service required will give the user a suggestion for the elements of design for the topographic map service that she/he requires.
As in PROSPECTOR, the main results aid the user in obtaining new possibilities to satisfy cartographic needs and in our case, to provide elements to design its own topographic map services using the resources provided by the ETM. For example, if the result of the consultation to the expert system is a map service that can be compiled with existing mapping components or can be derived by processes offered by the system; then the system proceeds to give the instructions to the user. Such would be the case if a user requires a topographic map at a scale smaller than 1:50,000 for a specific region and with the characteristics as the one stored in the database collection. In this case the user would need to apply a generalization algorithm to obtain the required map. It is important to mention that the expert system would become relevant when the needs of the user points to a TM of larger scales than 1:50,000 and with specific needs. For example, for the Palenque prototype, the scale of the TM obtained was 1:5,000 and the features and the TM characteristics were defined at that time between the INEGI expert team and the users but, with the proposed expert system the stakeholders of the Maya project could have obtained through a consultation the characteristics of the needed TM for their basic infrastructure train component.
Similarly, as in Prospector, ETM would provide “expert consultation” that rests on a base of knowledge about topographic mapping services. The group of colleagues involved in the design of the expert system are: geocomputing and A.I. scientists, expert cartographers in topographic mapping, and users. In our case, we assume that the user is an expert in TM or has some knowledge regarding TM and is an expert in its own thematic domain/s of knowledge that are relevant for the design of the service required.
The knowledge models would be built based on a panel of cartography experts and with experts within the knowledge domains selected, that participate in a workshop using a Strabo Method [35] (p iii) based on subjective probabilities [36] (p 2). As in PROSPECTOR, the inference processes would use a traditional rule-based system, including explicit predefined constraints in the structure of the knowledge-based model by using an inference network [34] (p 13), [36] (pp 110-120).
In our case the consensus among the experts in the Strabo Method is centered around the main characteristics of the topographic map services. In this regard several assumptions are made. A special panel should be established before undertaking the application of the Strabo Method to have a consensus on the services and parameters to be adopted and used in the Strabo exercises with the different thematic panels. In addition, the practice of “having individuals rate themselves or estimate their own probability of correct response” as the basis of the approach of subjective probability should also be adopted as a good practice [35] (p 89) and the following services and parameters are established as an initial reference for the design of the Strabo exercises:
  • Services: virtual topographic maps aligned with the six possible feature groups, digital terrain models, surface terrain models, contour lines, triangular irregular networks, control points and simulation models of the terrain.
  • Parameters
    • Space time context: Definition of the polygons that cover the areas of interest, geographical characteristics of the study areas, territorial heterogeneity, and time constraints.
    • Data and geoinformation inputs: databases, aerial photographs, or satellite images, characteristics of the acquisition methods and ground verification.
    • Accuracy requirements: Geodetic assumptions and photogrammetric methods.
    • Cartographic issues: Spatial resolution, granularity, cartographic design, scale representation, geographical names, and generalization processes
    • Other key parameters: Quality standards and communication issues.
Once the knowledge-base model is built supported by the Strabo method, the input for the expert system is ready and since in this first experiment a simple inference network with subjective probabilities is proposed, the implementation resources are at hand and its implementation should not be an issue.

2.3. Communication Axes

Much has been written around the topic of the language of cartography [37] (pp 81-180), [38] (pp 313-423), [39] (pp 120-128), [40] (pp 1-49), and [41] among other books and papers. On the other hand, for the design of a cybercartographic framework for the topographic map the concept of communication was embraced from a cybernetic perspective as presented by Reyes [10] (pp 70-74).
The origin and basic building scientific ideas of cybercartography have already been mentioned. There are, however, some issues regarding the topographic map and the communication axes that are worth mentioning.
It’s important to remember the initial ideas that supported the development of cybercartography and that are relevant for our purposes; the fact that is multisensory using human senses (vision, hearing, and touch), takes advantage of the developments in multimedia and the Web, is “highly interactive and engages the user in new ways”, “the map becomes part of and information/analytical package”, cybercartography is compiled by multi/transdisciplinary teams, and there is a natural partnership with various sectors of society including academia, government, citizens, and the private sector [41] (p 3).
After almost twenty years of the publication of the advances in Cybercartography, its main assumptions and formalization challenges still stand. It has become clear that the change of paradigm in Cartography in terms of its communication axes has shown its virtues in different contexts. Because of the success of the insertion of cybercartography in societal processes, the methodologies and basic principles of this concept were incorporated into the design of the communication axes of the ETM.
Moreover, during the design of the new topographic map for Mexico it became evident that to the best of our knowledge, the best practices of cybercartography regarding modeling have not been applied in the topographic domain. Most likely because the concept was mostly embraced in the realm of science and society rather than in the domains of basic cartography and engineering. In this sense, the mathematical modeling component in topographic mapping had not been approached in a knowledge-based way from a cybercartographic perspective.
The ETM is a model of models, similarly as it had been conceptualized initially in cybercartography but with a significant difference. Besides the models that represent the geographical landscape [10] (p 79), expert systems are now explicitly incorporated. In this regard, the communication issues that emerged due to this fact have an impact in the structural subsystem as defined by [10] (p 78). A computer backbone that supports the expert system must be added as well as the theoretical advances in Artificial Intelligence as it had been foreseen [6] (p 12).
On the other hand, although the main ideas behind the communication axes in cybercartography had been embraced in the design of the ETM, in this case two different aspects were identified. The first one encompasses the needs of a user of the ETM services from the perspective of the final artifact that offers the resources of the new topographic map. The second incorporates access to the user regarding the production process of the TM that includes methodological and theoretical issues in geodesy, cartography, remote sensing, geographic information systems, photogrammetry, and field work.
As a final note in this section, we should mention that once the digital paradigm was immersed in the production process of topographic maps last century, the results could be printed or be shown virtually in computer graphic screens and looked very similar to a traditional paper map. The incorporation of the digital paradigm gave the impression that the topographic map and the communication processes to the user essentially remain the same. From our point of view, the impact of digital culture, geotechnological innovation and the advancement in cartography and other proxy sciences has been underestimated.

3. Interaction Space: modelling, knowledge, and communication

As presented by Reyes [10] (p 82) “There is conceptually a common “interaction space” among the communication, modeling, and knowledge axes.” As a result of the adoption of a cybercartography theoretical framework there are several propositions that derive from the present research.
  • In the initial proposal of Taylor [42] (p 3) different senses had to be incorporated into cybercartography. In the past, vision in its static form was predominant in the design of maps. By incorporating other ones, the cybercartographic approach intertwined with the essential purpose of artificial intelligence by considering that the computer could better emulate the human brain, designing and implementing mapping artifacts with written and spoken narratives, music, photographs, videos, and other multimedia resources.
    When the cybercartographic atlases were presented in different societal contexts the research group at CentroGeo often mentioned that the artifact was another actor in the conversation that took place in the meetings in question. Intuitively cybercartography emulated the responses and knowledge representation of a human being.
  • Moreover, since the cybercartographic artifacts allowed the users to incorporate their own information and knowledge, the artifacts were immersed in the local contexts and the conversations among the targeted communities emerged more easily.
  • The development of the Triangular Irregular Network for the digital representation of relief by Peucker [13] and his research team, was based on a knowledge-based approach. Therefore, a digital topographic map can be characterized as a digital knowledge-based representation of the relief.
    An expert system as conceived in the 20th century is a knowledge-based model therefore, this points to a conceptual bridge between the digital TM and an expert system.
  • In the introductory chapter of the book of Russell and Nordig [12], Cybernetics and Expert Systems are presented as part of the history of Artificial intelligence. The authors also mention the following capabilities of the computer that are needed in the framework of Artificial Intelligence: natural language processing, knowledge representation, automated reasoning, machine learning, computer vision and robotics.
    In the actual realm of cybercartography the following are present: natural language for the narratives (story telling), knowledge representation and visual languages.
Based on analogic reasoning, as when one is weaving with threads of distinct colors a new pattern in the textile emerges. In our case, the ideas in A.I of representing knowledge in digital computers, the advances in cybernetics and expert systems, the efforts of representing the implicit knowledge of relief in digital topographic mapping through the TIN model and the emergence of cybercartography that uses different senses to represent knowledge and emulate the human brain in its communication axes, makes it evident that these different approaches and efforts are intertwined and could produce new knowledge and most likely innovative geotechnological artifacts.
So that, the main components of the theoretical framework for the design of the ETM points to new avenues of research that undertake cybercartography or modern cartography from an artificial intelligence perspective. The rapid advances in technology in A.I. are offering resources that could transform and enhance cybercartographic artifacts both in its modeling and communication axes.

4. Discussion

Innovation often emerges in the borders of theoretical interaction among different domains of knowledge and disciplines. In our case, Cybernetics, Mathematics, Cartography and Artificial Intelligence pointed to the possibility of offering innovative digital services regarding topographic mapping by incorporating a framework that includes essential ideas of the abovementioned scientific domains.
There are several avenues for future research:
  • The advances in geotechnology allow the ETM Services to give a dynamic service changing features, scales, resolution, granularity, and scale representations, among others. Resources of computer graphics still need to be explored to enhance the cybercartographic artifacts.
  • Besides relief other fundamental features such as hydrology, vegetation, etc., could be approached from a knowledge-based perspective.
  • The current trends in theoretical, practical, and technological issues, both in Cartography and A.I. point to possible fruitful developments. Maps have been used for centuries to navigate, all kinds of robots must navigate either in the territory or in virtual spaces. Other A.I. interests such as natural language processing or knowledge representation, just to mention two topics, are also key elements in cybercartography.
  • “It turned out to be difficult to build and maintain expert systems for complex domains, in part because the reasoning methods used by the systems broke down in the face of uncertainty and in part because the systems could not learn from experience.” [12] (p. 24). So, to explore the concepts of rational agent [12] (p. 4) and knowledge agents [12] (p. 208) into the design of the topographic mapping services is a possibility.
  • As mentioned by Russell and Nordig, “We focus more on machine learning rather than handcrafted knowledge engineering, due to the increased availability of data, computing resources, and new algorithms.” [12] (Preface). In the initial stages of cybercartography the communication component of maps was substantially enhanced. As presented in this article the modeling component can also be enriched by adopting the proposed cybercartographic framework and other AI resources such as machine learning.
  • In an ideal situation one should be able to build a cybercartographic agora where a network of learning artifacts could become a common space of conversation where users and mapping services enhance their knowledge. In other words, the users learn from the cybercartographic services and new knowledge is incorporated into the services using A.I. resources.
Finally, to intertwine theoretical and practical aspects in cybercartography and artificial intelligence is a promising avenue of research. As with many other projects where transdisciplinary and polymath abilities are involved, highly specialized researchers are required as well as others that can establish theoretical bridges among different knowledge domains and towards societal actors.

Author Contributions

Conceptualization, investigation, formal analysis and writing original draft, Carmen Reyes; methodology, and writing - review & editing, D.R. Fraser Taylor, and Carmen Reyes; advice, D.R. Fraser Taylor. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Data sharing is not applicable.

Acknowledgments

We acknowledge the team from the Dirección General de Geografía y Medio Ambiente at INEGI who participated in the period from August 2018 to March 2022 in the design of the production process of the topographic map program, the implementation of the two prototypes and the technical documentation of the Project. We thank the two presidents of INEGI who were in office during this period and supported the initiative, Dra. Graciela Márquez and Dr. Julio Santaella. We also thank Dr. Pablo López, Director General of CentroGeo, who supported the theoretical work presented in this article. Thanks, are also due to Dr. Patricia Brantingham and Dr. Nicholas Chrisman for their valuable comments and suggestions. We thank Rafael García for his contribution to the design of Figure 1.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Caudill C., M. , Pulsifer P. L., Thumbadoo R. V., Taylor D. R. F. Meeting the Challenges of the UN Sustainable Development Goals through Holistic Systems Thinking and Applied Geospatial Ethics. ISPRS Int. J. Geo-Inf. 2024, 13, x. https://doi.org/10.3390/xxxxx, 2024. [Google Scholar]
  2. Geospatial World. Evolving Role of National Mapping Agencies: Transitioning to Geospatial Knowledge Infrastructure, 2024.
  3. Esparza L., G. The UN-IGIF in Mexico: Progress and Challenges in Implementation. Décima Sesión, UN-GGIM: Americas, 2023.
  4. Calderón-Mólgora M., A. , Lázaro Cárdenas del Río y las Comisiones Hidrológicas del Tepalcatepec y del Balsas. El Colegio de Michoacán, México, Cardenismo: Auge y caída de un legado político y social, in Revista de Crítica Literaria Latinoamericana, Boston, USA, 2017, 229-253.
  5. Mapoteca “Manuel Orozco y Berra”. Map Library of the Mexican Government with cartographic material from the XVII to the XX centuries, 2023. https://mapoteca.siap.gob.mx/.
  6. Reyes, C. , Taylor D. R. F., Martínez E., López-Caloca F., Geo-Cybernetics: A New Avenue of Research in Geomatics? Cartographica, 2006, Vol. 41, No 1, Spring, pp. 7-20.
  7. Taylor D. R. F. ed., Cybercartography: Theory and Practice. Elsevier B.V., The Netherlands, 2005.
  8. Taylor D. R. F. ed., Developments in the Theory and Practice of Cybercartography. Elsevier, Amsterdam, 2014.
  9. Taylor D. R., F. , Cybercartography Revisited, Chapter 1 in “Further Developments in the Theory and Practice of Cybercartography”. Elsevier, 2019.
  10. Reyes, M. del C., Cybercartography from a Modeling Perspective. In “Cybercartography: Theory and Practice”, Chapter 4. Elsevier B.V., The Netherlands, 2005.
  11. Coombs M., J. , Developments in expert systems. From a special issue of “The International Journal of Man-Machine Studies.” Academic Press Inc, London, 1984.
  12. Russell S., J. and Norvig P., Artificial Intelligence, A Modern Approach, 4th ed. Pearson Series, U.S.A., 2021.
  13. Peucker T., K. , Fowler R. J., Little J. J. and Mark D., Triangulated Irregular Networks for Representing Three-Dimensional Surfaces. Simon Fraser University, Geography Department, Burnaby, Canada, 1976.
  14. Peucker, T. K. , & Chrisman, N. Cartographic Data Structures. The American Cartographer, 2(1). 1975. [CrossRef]
  15. Manzini, E. , Design, When Everybody Designs, An Introduction to Design for Social Innovation. The MIT Press, London, England, 2015.
  16. Simon H., A. , The Sciences of the Artificial, Third Ed.; The MIT Press, Cambridge, USA, London, England, 1996.
  17. Cross, N. , Designerly Ways of Knowing, Birkhauser Verlag AG, Basel, Switzerland, Boston, USA, Berlin, Germany, 2007.
  18. Telier, A. , Design Things, Massachusetts Institute of Technology, USA, 2011.
  19. Nelson, H.G. , Stolterman E., the design way, second edition. The MIT Press, Cambridge, USA, London, England, 2014.
  20. Dorst, K. , Frame Innovation: Create New Thinking By Design. The MIT Press, Cambridge, USA, London, England, 2015.
  21. Ross W., R. , Weill P., and Robertson D. C., Enterprise Architecture as Strategy: Creating a Foundation for Business Execution. Harvard Business Review Press, 2006.
  22. Reyes, M. del C., Martínez E., Technology and Culture in Cybercartography. In “Cybercartography: Theory and Practice”, Chapter 6. Elsevier B.V., The Netherlands, 2005.
  23. Davis J., C. and Mc Cullagh M. J. eds., Display & Analysis of Spatial Data. NATO Advanced Study Institute, John Wiley & Sons, London, New York, Sydney, Toronto, 1975.
  24. Sprunt B., F. , Relief representation in automated cartography: an algorithmic approach. In, Davis J.C. and Michael J. Mc Cullagh, eds., 1975, “Display&Analysis of Spatial Data.” NATO Advanced Study Institute, John Wiley & Sons, London, New York, Sydney, Toronto, 1975.
  25. Peucker T., K. , Tichenor, and Rase W. D., The computer version of three relief representations. In Davis J. C. and Michael J. Mc Cullagh, eds., “Display & Analysis of Spatial Data.” NATO Advanced Study Institute, John Wiley & Sons, London, New York, Sydney, Toronto, 1975.
  26. Davis J., C. and Levi de López S., Compilers, Computer Mapping for Resource Analysis. Proceedings of an International Conference, A Cogeodata Conference, Kansas Geological Survey, University of Kansas, Instituto de Geografía de la UNAM, Mexico, 1978.
  27. Mark D., M. , Chrisman N., Frank A. U., McHaffie P. H., Pickles J., et al. “The GIS History Project.” UCGIS Summer Assembly, Bar Harbor, ME, USA, 1997.
  28. Maxwell J., C. , On Hills and Dales. Philosophical Magazine for December 1870, 233–240. [Google Scholar]
  29. Firby P., A. and Gardiner C. F., Surface Topology. Ellis Horwood Limited, Publishers, Chichester, and Halsted Press: a division of John Wiley and Sons, New York, Brisbane, Chichester, Toronto, 1982.
  30. Brilliant.org/ThinkTwice https://www.youtube.com/watch?v=80EazC2_0Qo.
  31. Warntz W. The Topology of a Socio-Economic Terrain and Spatial Flows, Papers in Regional Science, Volume 17, Issue 1, 1966, Pages 47-61, ISSN 1056-8190, https://doi.org/10.1111/j.1435-5597.1966.tb01341.x. (https://www.sciencedirect.com/science/article/pii/S1056819023009338).
  32. Stilwell, J. , Translator´s Introduction in “Papers on Topology, Analysis Situs and Its Five Supplements” by Henri Poincaré, July 31, 2009.
  33. Crevier, D. , AI, The Tumultuous History of the Search for Artificial Intelligence. BasicBooks. A Division of Harper Collins Publishers, Inc., New York, 1993.
  34. Hart P., E. and Duda R. O., Prospector: A Computer-Based Consultation System for Mineral Exploration. Artificial Intelligence Center, SRI International, Menlo Park California, Technical Note No. 155, 1977.
  35. Luscombe B., W. , Spatial Data Handling in Data-Poor Environments. Ph.D. Thesis, Department of Geography, Simon Fraser University, Canada, 1986. [Google Scholar]
  36. Duda R., O. and Hart P. E., The encoding and use of exploration models in the prospector system. In “Computer Mapping for Resource Analysis.” Proceedings of an International Conference, A Cogeodata Conference, Kansas Geological Survey, University of Kansas, Instituto de Geografía de la UNAM, Mexico; pp. 110–1201978.
  37. International Cartographic Association, Cartografía Básica para estudiantes y técnicos. Versión en castellano, Aguascalientes, Ags., México, INEGI, 1989.
  38. Robinson A., H. , Morrison J. L., Muehrcke P. C., Kimerling A. J., Guptill S. C., Elements of Cartography, Sixth Ed., Wiley India Pvt. Ltd., New Delhi, India, 2009.
  39. Kraak M., J. & Ormeling F. J., Cartography: Visualization of spatial data. Addison Wesley Longman Limited, England, 1996.
  40. Keates J., S. , Cartographic Design and Production, Second Edition. Longman Scientific &Technical, United Kingdom, England, John Wiley & Sons Inc., 1989.
  41. MacEachren, A. M. How maps work: representation, visualization, and design. Guilford Press. New York. 2004.
  42. Taylor D. R., F. , The Theory and Practice of Cybercartography: An Introduction. “Cybercartography: Theory and Practice” Chapter 1, Elsevier B.V., The Netherlands, 2005.
Preprints 138093 g001
Figure 1. Cybercartography can be viewed from three perspectives:.modeling, as a representation of knowledge and as a communication artifact.
Figure 1. Cybercartography can be viewed from three perspectives:.modeling, as a representation of knowledge and as a communication artifact.
Preprints 138093 g001
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated