Multi-View 3D Reconstruction Based on FEWO-MVSNet

1. Introduction

Multi-view stereo (MVS) reconstruction focus on using two or more perspective photographs to recover the geometric surface structure information of the target sceneis [1]. It has been a popular technique [2] used in the domains of actual 3D construction, historic heritage restoration and preservation, and other related areas [3]. However, the 3D reconstruction for multi-view images with weak textures and repeatitive patterns is still a challenging work in both digital photogrammetry and computer vision fields [4].

In recent years, the development of 3D reconstruction has been strongly boosted with the introduction of Convolutional Neural Networks (CNNs) into the field of scene depth estimation. Han et al. proposed MatchNet [5], which mainly consists of a metric model composed of three fully-connected layers to compute the similarity between the features to be matched. To improve the automation of the method, Yao et al. constructed the end-to-end depth estimation network MVSNet [6], which significantly improves the accuracy of the target depth information, but it also consumes a large amount of memory space when constructing the cost model and calculating the feature information of multiple views. For this reason, Yao et al. further propose the recursive stereo visual network R-MVSNet [7], which regularizes the original 2D feature cost map by gated recursive units, effectively reducing the memory occupation of the model. Zhu et al. propose to construct DCNv2 [8], which is an approach that improves the original DCN (Deep Crossing Network) by utilizing the variable sensory field convolution, which effectively improves the loss problem of feature information propagation. Gu et al. study incorporates cascaded convolutional network layers and multi-scale strategies into the network, and proposes a multi-scale depth estimation model CasMVSNet [9], and the experimental results validate the advantages of this method in terms of computational accuracy and efficiency. Wang et al. are inspired by the traditional PatchMatch algorithm, and propose the deep learning matching network PatchMatchNet [10], which quickly finds the best matching region in an image by introducing global and local optimization strategies, and the test results show that it is able to generate depth information for complex environments.

The Transformer model [11] maximizes the capture of the target itself and its contextual spatial relations based on the self-attention mechanism, which significantly enhances the representation of various features and injects a new impetus to the development of 3D reconstruction. Wang et al. proposed the depth estimation model MVSTER [12], which utilizes Transformer's polarity aggregation to enhance the correlation between semantic and spatial-geometric layers and is capable of better generating depth information in complex environments. geometric layer association, which can better match homonymous scene points and thus improve the quality of depth estimation and 3D reconstruction, however, the pole-line traversal search also reduces the efficiency of the algorithm. Ding et al. constructed a feature matching converter TransMVSNet [13] using Transformer, which utilizes the self-attention and cross-attention mechanisms for aggregating global contextual information and combines with the self-adaptive receptive field module to improve the reconstruction quality of texture-deprived regions. Aiming at the problem that weakly textured regions in multi-view images are difficult to match, Wang et al. proposed FAT-MVSNet [14], which utilizes the spatial aggregation module in Transformer to make the aggregated features more conducive to feature matching. Wang et al. proposed CT-MVSNet [15], which enhances the perception of global and local features by introducing a cross-scale adaptive matching perception Transformer that uses different combinations of interactive attention at multiple scales.

The above methods show great advantages and potentials in multi-view 3D reconstruction, and can also provide effective references for higher-level 3D reconstruction. However, the tests of the above methods in various scenarios show that they are often difficult to reconstruct a complete and reliable 3D model in repetitive or weak texture regions. Inspired by TransMVSNet, this paper proposes a 3D reconstruction algorithm based on Feature Enhancement and Weight Optimization MVSNet (FEWO-MVSNet). Our method firstly extracts global and local feature information from the multi-view images using the adaptive feature enhancement module and then introduces the adaptive optimization mechanism for weight allocation to estimate the fine depth map of the scenery with weak/repeated textures, and finally completes the reconstruction of the dense 3D point cloud. Through the training and testing of multiple international standard datasets, The test results show that our FEWO-MVSNet achieves the improvement in both accuracy and completeness.

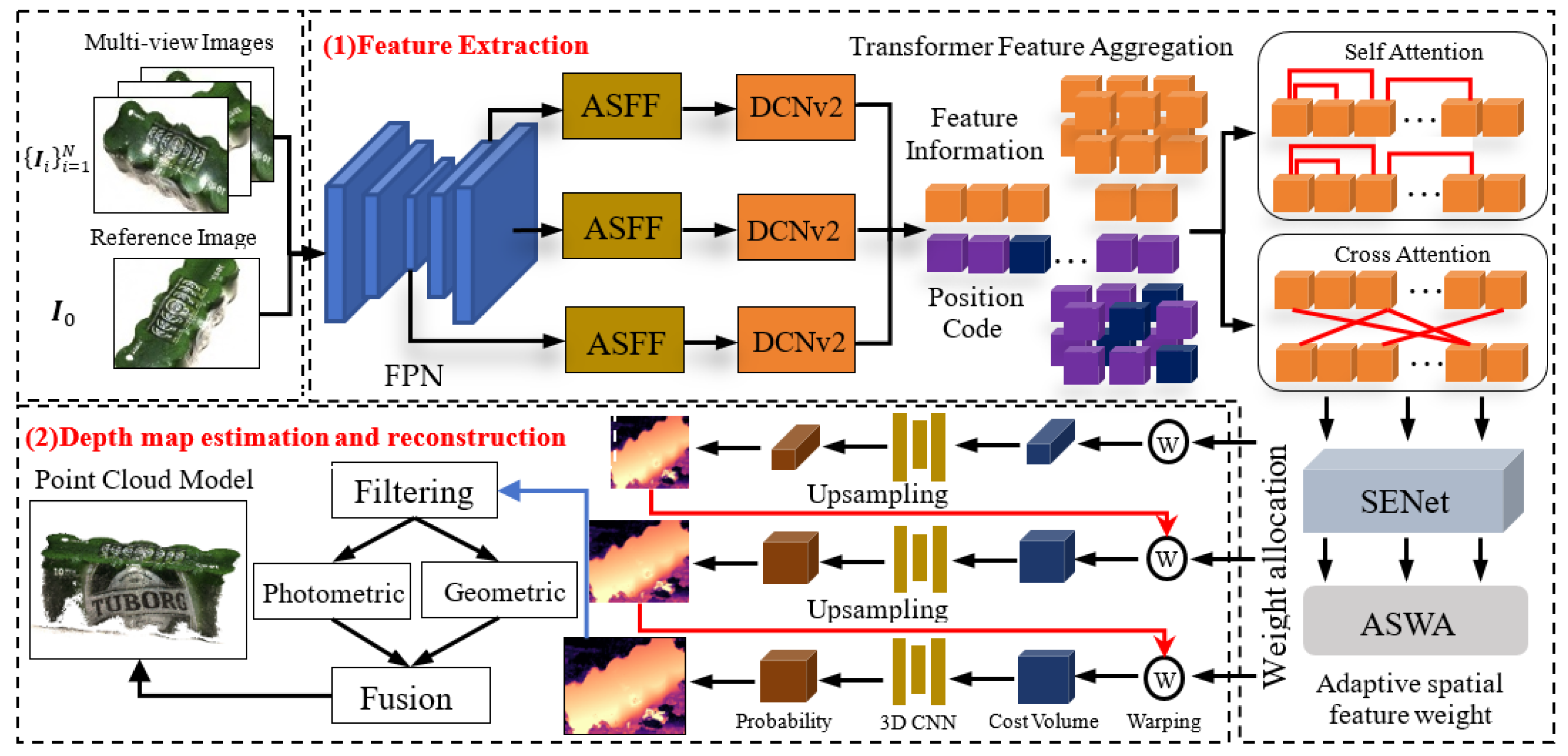
2. Methodology

AS shown in Figure 1, we design a 3D reconstruction network FEWO-MVSNet based on adaptive feature enhancement and weight allocation, using TransMVSNet as the base network. The improved work in our method includes:

• Introduce an Adaptively Spatial Feature Fusion (ASFF) module [16] on the basis of Feature Pyramid Network (FPN) to enhance the capability of capturing feature information at different scales;
• Adaptively expand the search range of features through the deformable feeler field convolution module DCNv2 [8] and combine it with the Transformer positional encoder for the enhancement of global contextual feature information aggregation;
• Design an Adaptive Space Weight Allocation (ASWA) module, which is integrated into SENet [17], to highlight the low-frequency information in the convolutional channel and color space, and then realize the dense extraction of feature information of multi-view images containing weak and repetitive texture regions.

The algorithm of FEWO-MVSNet can be briefly summarized as follows: Firstly, the multi-scale features of each image at three resolutions are extracted using the feature Pyramid FPN network; Secondly, in view of inconsistent scales between different features, the feature maps are input into the Adaptive Structural Feature Fusion (ASFF) module to achieve the information enhancement and features normalization; Thirdly, in order to improve the accuracy of the multi-view feature matching and feature aggregation, the deformable receptive field module DCNv2 and the Transformer feature aggregation module are combined to aggregate the updated feature information; for the purpose of emphasizing the adequate feature information that has been captured, we spatially label the features using SENet and ASWA; fourthly, using the differentiable homography to get the multi-view image feature mapping, and the cost volume can be generated based on depth correlation weighting method and feature transform, then the cost volume regularization is performed by 3D CNN to generate the probability volume that can predict the depth maps. lastly, we blend each depth map using a concatenated scheme and obtain a dense point clouds of the target scenery. In all, we realize the end-to-end 3D reconstruction of the model based on FEWO-MVSNet.

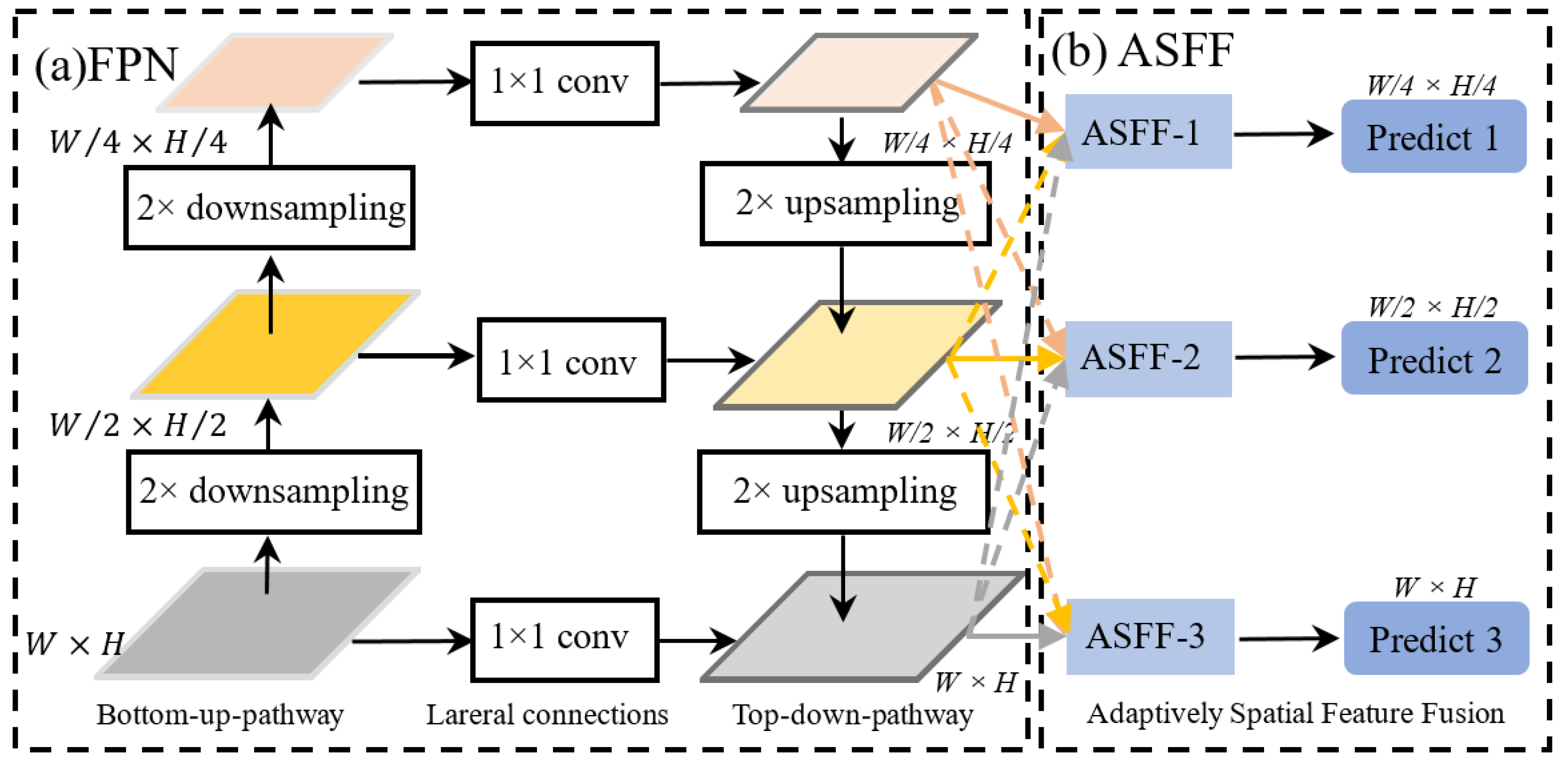
2.1. Feature Extraction Networks

The reconstruction precision of MVSNet [6] is usually low, as it uses the traditional Convolutional Neural Network (CNN), which suffers from inadequate receptive field, information disability, and low efficiency during the feature extraction. For this, we introduce FPN to replace the original CNN to realize the feature extraction with different scales from top to bottom of the pyramid network. Based on many tests, we found that in the process of hierarchical pyramidal features transfer, different scale features would be easily lost, further leading to the feature missing for output results. Therefore, the adaptive spatial feature fusion (ASFF) module is further introduced after the feature extraction network FPN to obtain the optimal weights of each channel through adaptive learning, which is conducive to maintaining the invariance of the pyramid image feature extracting ratio to realize the intelligent extraction of complex texture features.

The improved feature extraction network is shown in Figure 2. The main content of this network can be presented as follows. Firstly, given an input image with W × H resolution as well as its elements of internal and external orientation, the image is input into the bottom-up feature extraction part, which reduces the resolution of the image using 2 × 2 downsampling to increase its semantic information. Secondly, the network uses the top-down path to accomplish the fusion between high-level images and low-level images based on 2×2 upsampling. Thirdly, the top-down feature fusion path is connected to the bottom-up feature extraction path through the lateral connections, and those lateral connections combine the high-resolution information of the left part images with the rich semantic information of the right part images. Fourthly, we incorporate the Adaptive Spatial Feature Fusion (ASFF) module with the FPN network. Finally, We have three image channels with different resolutions $W/4\times H/4,W/2\times H/2,W\times H$. The adaptive weighting coefficients ($\alpha ,\beta$, and $\gamma$), and the corresponding feature layer $L_i$ merge together by weighting. The fused feature $Z_{ij}^l$ is then obtained based on the formula as follow.

$${\mathrm{Z}}_{ij}^l={\alpha }_{ij}^l\bullet L_{ij}^{1\to l}+{\beta }_{ij}^l\bullet L_{ij}^{2\to l}+{\gamma }_{ij}^l\bullet L_{ij}^{3\to l}$$

(1)

2.2. Aggregation and Enhancement for Features Based on Transformer

2.2.1. Adaptive Enlargement of Receptive Field

Due to the significant difference in the receptive field of contextual information between FPN and Transformer, the feature information can be lost easily in the process of transmission. For the purpose of correct transmission, we add the DCNv2 [8] between the modules of FPN and Transformer. In the convolution operation, the DCNv2 can compensate adaptive offsets of texture, which are generated by the learning of the network. This network can adaptively adjust the receptive field according to the local features of the image, thus it can extract texture information with different brightness and types. The adaptive offset matrix can be computed by Equation (2) as follow.

$$M\left({\mathit{x}}_0\right)=\sum _{{\mathit{x}}_n\in \mathit{R}}\epsilon \left({\mathit{x}}_n\right)\bullet l\left({\mathit{x}}_0+{\mathit{x}}_n+∆{\mathit{x}}_n\right)\bullet ∆m_k$$

(2)

where $M\left({\mathit{x}}_0\right)$ represents the offset of sampled intensity, $\epsilon \left({\mathit{x}}_n\right)$ is the deformable convolution parameter, $l$ is the input feature map, ${\mathit{x}}_0$ is the sampling point in the feature map, ${\mathit{x}}_n$ is the sampling point of the offset, $∆{\mathit{x}}_n$ is the offset matrix, and $∆m_k$ is the weight of the sampling point.

2.2.2. Feature Encoding based on Transformer

Among the existing multi-view stereo reconstruction approaches, the MVS reconstruction demands the comprehensive exploitation of information from the entire scene for depth estimation. However, the Traditional CNNs often encounter limitations when dealing with large-scale contextual information. The Transformer mechanism is capable of establishing the relationships among pixels within a global scope. it can make full use of global contextual information and improve the distinctiveness of feature information. For the purpose of enhancing the accuracy and robustness of the feature map, we employ the FPN, followed by the Transformer Feature Encoding module [18], including self-attention and cross-attention units. The extracted feature map L is flattened into one-dimensional vector. Then, we calculate the position encoding on the feature information of the flattened map by Equation (3).

$$\mathit{P}\mathit{E}=\left[\begin{array}{c}sin\left(pos/{10000}^{n/d_{model}}\right)\\ cos\left(pos/{10000}^{n/d_{model}}\right)\end{array}\right]$$

(3)

where PE denotes the position encoding, pos denotes the position information of each pixel, and $d_{model}$ represents the output dimension of the encoding-decoding model; this Equation uses the sine and cosine functions to alternately express the encoding information at each position.

Suppose that ${\mathit{Z}}_i$ represents the initial feature information, the feature enhancement for ${\mathit{Z}}_i$ can be given as follows. Firstly, three attention vectors, namely Query (Q), Key (K) and Value (V), are input into the feature encoder simultaneously. The context information of V is retrieved from the corresponding Q and K based on multi-layer stacking of the self-attention mechanism. At the same time, it captures the dependencies existing in the input sequence to produce new feature information ${\mathit{Z}}_i^{\text{'}}$. Secondly, the cross-information between the reference image and the input image is captured by the cross-attention mechanism. Finally, the updating calculation for the new feature information ${\mathit{Z}}_i^{\text{'}}$ is performed. The updated result ${\mathit{Z}}_i^{\text{'}\text{'}}$ comprises the dense features with the global and local context information.

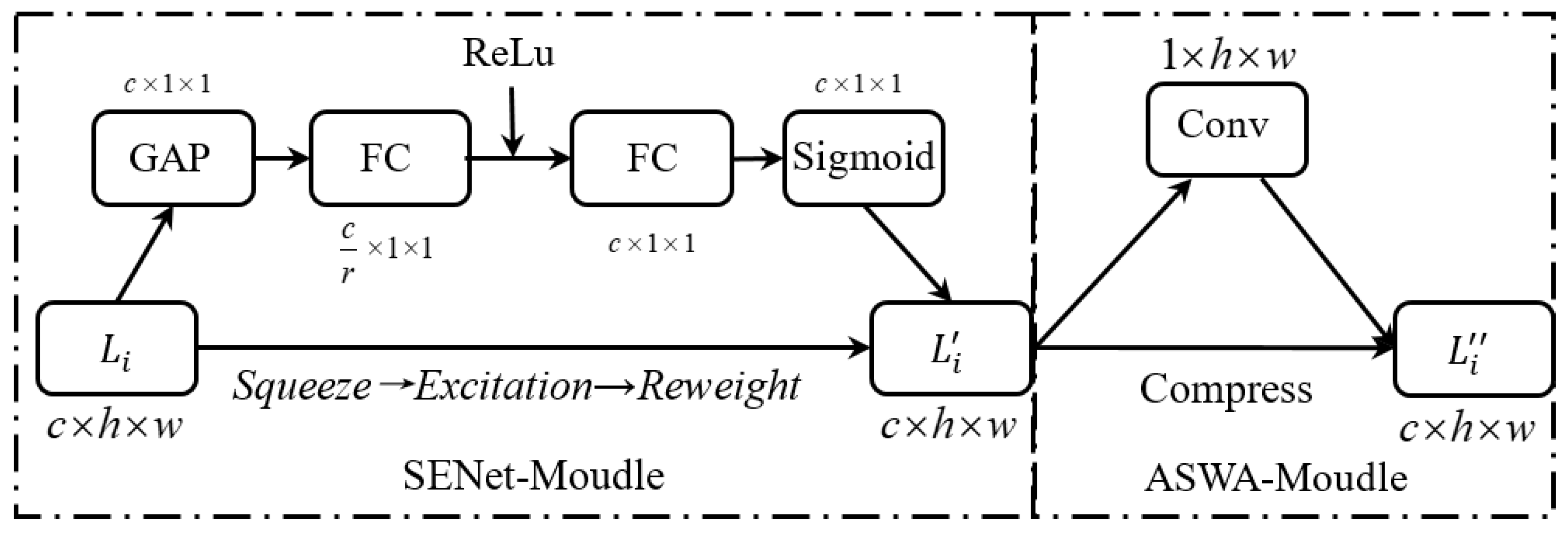
2.3. Adaptive Allocation for Feature Weights

To obtain the key feature information with adaptive dimensions, we integrate the SENet [17] with ASWA in our model to generate adaptive weight for features, which can be beneficial to deal with different view images with various types of textures. The adaptive allocation for feature weight is illustrated by Fig. 3.

Based on the aforementioned strategy of Section 2.2, it can effectively enhance the perception of model to recognize weak features as more as possible. However, it may also lead to the accumulation of redundant feature information, further resulting in high computational complexity and preventing it from capturing key features. To dynamically adjust the weights of various feature regions, we introduce SENet into our model to effectively extract weak texture features. In this part, we optimize the channel attention network SENet [17]. The correlation of feature channels is enhanced through squeeze, excitation, and adaptive weighting operation. Specifically, the key feature information ${\mathit{z}}_i$ is produced by Equation (4).

$${\mathit{z}}_i={\mathit{Z}}_i^{\text{'}\text{'}}\bullet sigmoid\left({\mathit{\phi }}_2\bullet ReLu\left({\mathit{\phi }}_1\bullet GAP\left({\mathit{L}}_i\right)\right)\right)$$

(4)

where, $sigmoid$ and $ReLu$ are the activation functions, ${\mathit{\phi }}_1$ and ${\mathit{\phi }}_2$ denote the weight factors of the fully connected layers, $GAP$ denotes the Global Average Pooling function. ${\mathit{L}}_i$ represents the arbitrary feature layer.

The SENet is trained for the adaptive adjustment of the weight coefficients ${\mathit{\phi }}_1$ and ${\mathit{\phi }}_2$ through forward and backward propagation, which guarantee the reliability of feature information in all channels. Similarly, the weight allocation for 3D spatial feature information extraction is also important. To adaptively adjust the spatial feature weights according to feature textures, the ASWA module is incorporated after the SENet. Then, the activation function $sigmoid$ is used to normalize the weight coefficients, which enables the robust capture of feature information from each spatial channel.

2.4. Correlation Volume Construction and Loss Function Estimation

2.4.1. Correlation Volume Construction

Similar to the most existing deep learning-based MVSNet methods. All the input image features ${\mathit{Z}}_i^{\text{'}\text{'}}$ can be aligned to the reference image features ${\mathit{Z}}_0^{\text{'}\text{'}}$ through the differentiable warping [19]. To start with, the transformation between the point ${\mathit{p}}_i$ of the reference image and the point ${\mathit{p}}_i^{\text{'}}$ of the input image, can be expressed by Equation (5) under the depth hypothesis $d_i$.

$${\mathit{p}}_i^{\mathrm{\text{'}}}=\mathit{K}\left[\mathit{R}\left({\mathit{K}}_0^{-1}{\mathit{p}}_i{d}_i\right)+\mathit{t}\right]$$

(5)

where R and t respectively denote the rotation and translation matrices between the input image and the reference image, ${\mathit{K}}_0$ and $\mathit{K}$ are the intrinsic matrices of the camera. Next, we calculate the correlation between corresponding points based on Equation (5) and Bilinear Interpolation method. The correlation metric is expressed by Equation (6).

$$c_{{\mathit{d}}_i}\left({\mathit{p}}_i\right)=<F_0\left({\mathit{p}}_i\right),F_{{\mathit{d}}_i}\left({\mathit{p}}_i^{\mathrm{\text{'}}}\right)>$$

(6)

where $F_0\left({\mathit{p}}_i\right)$ is the feature map of the reference image, $F_{{\mathit{d}}_i}\left({\mathit{p}}^{\text{'}}\right)$ represents the i-th feature map of the input image at depth $d_i$, $c_{{\mathit{d}}_i}\left({\mathit{p}}_i\right)$ represents the correlation coefficient of the input image and the reference image at the pixel point ${\mathit{p}}_i$. To decrease the memory consumption on regularization of correlation volume, the channel number is reduced to 1. To maintain the maximum correlation of data in the depth dimension, we introduce the Depth Correlation Weighting method [13] to aggregate the correlation volume $\mathrm{C}\left({\mathit{p}}_i\right)$ by Equation (7).

$$\mathrm{C}\left({\mathit{p}}_i\right)={\sum }_{i=1}^{X-1}max\left\{c_{d_i}\left({\mathit{p}}_i\right)\right\}\bullet c_{d_i}\left({\mathit{p}}_i\right)$$

(7)

We choose 3D CNN to make the correlation volume regularization. The 3D CNN is composed of the 3D convolutional operations and moves among all dimensions of the correlation volume. Through the 3D CNN, we can obtain the probability volume P which can predict depth information. It is also possible to acquire more information at a lower consumption of memory and computing costs.

2.4.2. Loss Function Estimation

To highlight the key information in challenging texture regions and improve the accuracy of depth estimation, we adopt the combination $\beth$ of the Focal Loss function ${\beth }_{FL}$ [20] and the Smooth Loss function ${\beth }_{SL}$ [21] by Equation(8). It can adaptively adjust the weight between the background points and the model points, and hereby improve the learning rate of the key regions.

$$\beth ={\beth }_{FL}+{\beth }_{SL}$$

(8)

$${\mathrm{\beth }}_{FL}=-{\alpha }_{FL}{\left(1-{\mathit{P}}_{d^{\mathrm{\text{'}}}}\left({\mathit{p}}_i\right)\right)}^{\gamma }\log \left({\mathit{P}}_{d^{\mathrm{\text{'}}}}\left({\mathit{p}}_i\right)\right)$$

(9)

where ${\mathit{P}}_{d^{\text{'}}}\left({\mathit{p}}_i\right)$ denotes the predicted probability at a pixel point ${\mathit{p}}_i$ at depth hypothesis $d^{\text{'}}$, $d^{\text{'}}$ denotes the depth value closest to the ground truth among all hypotheses, and $\gamma$ is the focus parameter. ${\alpha }_{FL}$ is a balancing parameter that is used to adjust the influence between the background and the model. According to experience, $\gamma =0$ is suitable for relatively simple scenarios and $\gamma =2$ fits more complicated scenarios.

$${\mathrm{\beth }}_{SL}=\left\{\begin{array}{c}{\displaystyle \frac{1}{2}}{\mathit{s}}^2,\left|\mathit{s}\right|\le 1\\ \left(\left|\mathit{s}\right|-{\displaystyle \frac{1}{2}}\right),\left|\mathit{s}\right|>1\end{array}\right.$$

(10)

where $\mathit{s}$ denotes the gaps between the predicted values and the target values. ${\beth }_{SL}$ adjusts the model more robustly through $\mathit{s}$. It can restrict the gradient of outliers from two aspects as follows. First, when $\mathit{s}$ is large, the gradient value is prevented from being excessively large. Second, when $\mathit{s}$ is small, the gradient value is sufficiently small. ${\beth }_{SL}$ also can provide a smoother response to outliers during the training process. Finally, we use the combination $\beth$ of ${\beth }_{FL}$ and ${\beth }_{SL}$ as our loss function for model training to estimate depth information.

2.4.3. D Reconstruction

In this part, we reconstruct a complete 3D point cloud model as follows. Firstly, the depth map outliers and background points can be filtered through photometric and geometric constraints. The filtering parameters are adjusted based on Dynamic operation [22]. Secondly, we generate the 3D point cloud within a pixel coordinate grid from the depth and color images. In this step, the valid pixel points are filtered out further. Thirdly, we select the color textures of 3D points according to the resolutions of multi-view images. And we convert these 3D points into the camera coordinate system. Finally, we transfer these 3D points to the world coordinate system via the extrinsic parameters of the camera. It merges all the 3D points and color data, which are saved in the PLY file for the point cloud data.

3. Results and Discussion

3.1. Experimental datasets

Three large open datasets, DTU, BlendedMVS and Tanks&Temples, are chosen to training our FEWO-MVSNet and the representative models. The detailed introduction for these datasets is showed by Table 1.

3.2. Experimental Details

We train the FEWO-MVSNet on the DTU dataset with PyTorch. In the training phase, we set the number of input data images to N=5 and the resolution to 640×512. The depth hypotheses are sampled from 425mm to 935mm. The FEWO-MVSNet adopts a three-stage cascaded network. The number of plane sweeping depth hypotheses of each section is 48, 32, and 8 respectively. To test the generalization of FEWO-MVSNet, we employ BlenedMVS to fine-tune the model. The input image data is also set to N=5, with a resolution of 768×576. The FEWO-MVSNet is trained using the Adam for 16 epochs with an initial learning rate of 0.001. The learning rate is halved respectively after the 6, 8, and 12 epochs. We used the NVIDIA GeForce GTX 3090 to train FEWO-MVSNet. The batch size is 1.

3.3. Result and analysis

3.3.1. Comparative Experiments

The FEWO-MVSNet is validated for effectiveness on the DTU dataset. We evaluate the Accuracy (Acc), Completeness (Comp), and Overall of the reconstructed 3D point cloud using the MATLAB code provided by DTU. The Acc and Comp are employed to evaluate the average distance between the ground truth point cloud and the reconstructed point cloud of the model. The Overall is the average of Acc and Comp by Equation(11).

$$Overall={\displaystyle \frac{Acc.+Comp.}{2}}$$

(11)

1)

The lower values of the three metrics Acc, Comp, and Overall indicate that the reconstructed point cloud is closer to the real point cloud. We compare the FEWO-MVSNet with the traditional methods (Gipuma, Colmap), methods of deep learning (MVSNet, R-MVSNet, CasMVSNet, DRI-MVSNet, ASPPMVSNet, PatchMatchNet), and deep learning using Transformer (MVSTR, MVSTER, TransMVSNet). The table 2 shows the quantitative comparison results of the DTU dataset. Compared to the classic deep learning algorithms MVSNet and CasMVSNet, FEWO-MVSNet improves accuracy by 8% and 1.2%, while enhancing completeness by 15% and 4.3%. The accuracy increases by 2% and 3.7% compared to the TransMVSNet and MVSTER algorithms using Transformer.

2)

Figure 4 shows the dense point cloud reconstruction. The FEWO-MVSNet improves the weak/repetitive textures by combining weight optimization and feature enhancement. In the red box in Figure 4, we can see the oscilloscope dial and side in scan11, the left and right sides of the beer packaging in scan12, the top of the cup in scan48 and the top of the sculpture in scan118. We enhance the texture information in the blank areas of these scenes. FEWO-MVSNet can produce denser and complete point clouds while preserving more details.

3.3.2. Generalization Experiments

To verify the generalization ability of the FEWO-MVSNet, we train the model by using the BlendedMVS dataset and evaluate it by using the Tanks&Temples dataset. We present the point clouds generated by FEWO-MVSNet to the official website of Tanks&Temples, that enables us to obtain the F-score. This metric indicates that a higher value means better reconstruction quality. To achieve quantitative comparison results on the intermediate set, we compare the FEWO-MVSNet with the traditional methods, methods of deep learning, and deep learning using Transformer.

Table 3. Quantitative testing results of different methods on Tanks&Temples (Inter). The bold values denote the best results and the underlined values denote the second best.

Method	Intermediate
	Mean	Fam.	Fran.	Horse	L.H.	M60	Path.	P.G.	Train
Colmap [26]	42.14	50.41	22.25	26.63	56.43	44.83	46.97	48.53	42.04
MVSNet [6]	43.48	55.99	28.55	25.07	50.79	53.96	50.86	47.90	34.69
R-MVSNet [7]	50.55	73.01	54.46	43.42	43.88	46.80	46.69	50.87	45.25
CasMVSNet [9]	56.42	76.36	58.45	46.20	55.53	56.11	54.02	58.17	46.56
DRI-MVSNet [28]	52.71	73.64	53.48	40.57	53.90	48.48	46.44	59.09	46.10
ASPPMVSNet [29]	54.03	76.50	47.74	36.34	55.12	57.28	54.28	57.43	47.54
PatchMatchNet [10]	53.15	66.99	52.64	43.25	54.87	52.87	49.54	54.21	50.81
MVSTR [30]	56.93	76.92	59.82	50.16	56.73	56.53	51.22	56.58	47.48
MVSTER [12]	60.92	80.21	63.51	52.30	61.38	61.47	58.16	58.98	51.38
TransMVSNet [13]	63.52	80.92	65.83	56.89	62.54	63.06	60.00	60.20	58.67
Ours	63.68	81.09	65.08	56.92	62.18	62.79	61.27	61.34	58.75

Table 3. Quantitative testing results of different methods on Tanks&Temples (Inter). The bold values denote the best results and the underlined values denote the second best.

Method	Intermediate
	Mean	Fam.	Fran.	Horse	L.H.	M60	Path.	P.G.	Train
Colmap [26]	42.14	50.41	22.25	26.63	56.43	44.83	46.97	48.53	42.04
MVSNet [6]	43.48	55.99	28.55	25.07	50.79	53.96	50.86	47.90	34.69
R-MVSNet [7]	50.55	73.01	54.46	43.42	43.88	46.80	46.69	50.87	45.25
CasMVSNet [9]	56.42	76.36	58.45	46.20	55.53	56.11	54.02	58.17	46.56
DRI-MVSNet [28]	52.71	73.64	53.48	40.57	53.90	48.48	46.44	59.09	46.10
ASPPMVSNet [29]	54.03	76.50	47.74	36.34	55.12	57.28	54.28	57.43	47.54
PatchMatchNet [10]	53.15	66.99	52.64	43.25	54.87	52.87	49.54	54.21	50.81
MVSTR [30]	56.93	76.92	59.82	50.16	56.73	56.53	51.22	56.58	47.48
MVSTER [12]	60.92	80.21	63.51	52.30	61.38	61.47	58.16	58.98	51.38
TransMVSNet [13]	63.52	80.92	65.83	56.89	62.54	63.06	60.00	60.20	58.67
Ours	63.68	81.09	65.08	56.92	62.18	62.79	61.27	61.34	58.75

The experiments show that the algorithm proposed in this article can achieve better reconstruction results in the case of multiple influencing factors such as outdoor scene light and noise. Figure 5 presents the results on the intermediate dataset scenarios of Family, M60, Panther, and Train. The rich texture information effects have been successfully achieved in weak texture areas like the tank tracks, gun barrels, train surfaces, and sculpture bases. The F-scores of the method in this article are better than those of existing methods. The enhancement of the effect in repetitive and weak texture regions proves that FEWO-MVSNet has a certain generalization capability.

3.4. Ablation Experiment

To examine the effect of the modules added in FEWO-MVSNet on the reconstruction results, we employ DTU as the dataset for the ablation experiments. On the basis of the baseline net CasMVSNet, we incorporate ASFF, DCNv2, and SENet-ASWA sequentially. The ablation experiments adopt the same evaluation metrics as DTU. This is done to demonstrate the effectiveness of FEWO-MVSNet.

The results of the ablation experiments in Table 4 show that each module contributes to improving point cloud reconstruction. The ASFF&DCNv2 module captures local and global feature information, which enhances the feature extraction ability of FEWO-MVSNet. The SE-ASWA module filters the extracted feature information. It extracts key information through adaptive weight allocation. These modules improve the weak /repetitive texture and detailed features. The reconstruction results show improvements in both accuracy and completeness.

4. Conclusions

We construct a novel multi-view stereo network FEWO-MVSNet, which is based on FEWO strategy and TransMVSNet framework. First, the Adaptive Structural Feature Fusion (ASFF) module is used to improve the feature learning capability of the FPN network, and then the DCNv2 and Transformer mechanisms are combined to enhance the context information of features. Next, we employ the SENet-ASWA module to optimize the redundant elements in the extracted feature and finally produce a rich and accurate 3D dense point cloud. Extensive experiments on standard datasets, such as DTU, BlendedMVS, Tanks, and Temples, demonstrate that the proposed method is superior to many existing deep learning-based methods for weak and repetitive texture regions. However, the completeness of point cloud and the complexity of our network are still to be improved, even though the FEWO-MVSNet can produce better reconstruction results at present. In the future, we will concentrate on making the point cloud more complete overall and simplifying the structure of network.