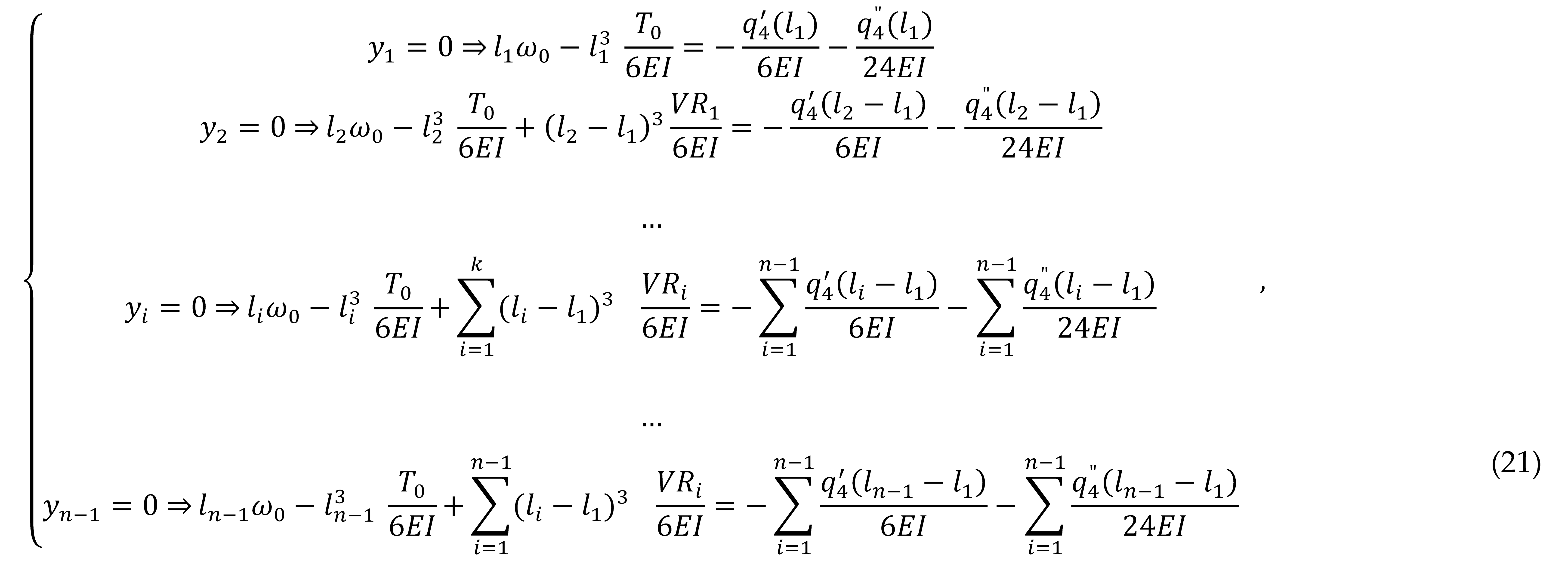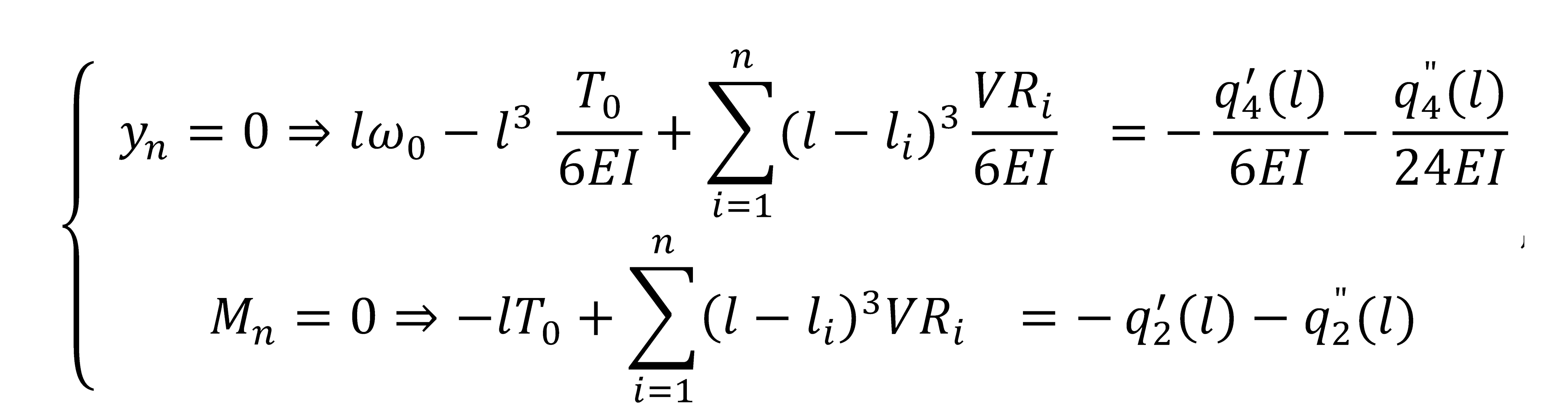1. Introduction
Interdisciplinary studies and research in many fields are very topical. This work presents a new, original and very interesting approach to a calculus problem of beams with intermediate supports by Transfer-Matrix Method (TMM), a very easy method to program to quickly obtain good results. To exemplify the applicability of this approach is given in dentistry, the calculus of a dental bridge on three poles. The dental restorations are very important for improving the general state of health as a result of improving mastication and aesthetic appearance. The approach of this study consists of to present a theoretical study about an indeterminate beam with intermediate support and after, to
particularize for an application of a dental restoration case, with a dental bridge on three poles and with two missing teeth between the three poles, assimilated to a simple static indeterminate beam, resting on three supports - the three poles and with two openings, corresponding to the two missing teeth. The results obtained in the presented case study were validated with those obtained by the classical calculation of the Resistance of Materials, with the equation of the three moments of Clapeyron.
TMM is a method used in many fields as will be presented below.
Structure calculus with TMM is presented in [
1] and the classical analytical calculus for beams with different applications is given in [
2] and [
3]. Using the TMM we can calculate different pieces as in [
4] and [
10]. The TMM is used in orthodontics and are presented in [
8] and [
17]. For the dental restauration are more papers: for dental bridges with TMM as [
12,
13,
14,
15,
16,
18] and for dental implants as [
11] and [
15]. They will be taken as starting studies [
5,
6,
7] and [
9]. A histopathological study about osseointegration of zirconium dental implants three months after insertion in rabbit femur is presented in [
19]. An
essential guide to oral pathology is [
20,
26]
is a guide to the diagnosis and treatment of conditions in the field of oral pathology and [
25] presents notions on dental preparations for fixed uni-dental prostheses. [
21] give us an in-vitro comparative study about the marginal adaptation assessment for two composite layering techniques using dye penetration, AFM, SEM and FTIR and [
24] presents an in-vitro comparative adhesion evaluation of bio-ceramic and dual-cure resin endodontic sealers using SEM, AFM, Push-Out and FTIR. [
22] presents a comparative apical sealing evaluation of two bio-ceramic endodontic sealers. [
23] we have an oral health-related knowledge about the attitude and practice among patients in rural areas around Cluj-Napoca, Romania. [
30] give us a study for ten-year survival of bridges placed in the General Dental Services in England and Wales. [
27] presents coronary reconstructions and [
28] gives a case report about ename-loplasty in interdisciplinary treatment of dental injuries. [
29] shows figures of graph partitioning by counting, sequence and layer matrices. [
31] and [
32] presents studies about bending fracture of Co-Cr dental bridges. [
33] shows an integrated construction and simulation of tool paths for milling dental crowns and bridges. [
34] and [
35] gives studies about the influence of fatigue of zirconia for dental bridge design. Research on the surface of the dental alloys with cobalt-crom base is presented in [
36]. Effects of small grit grinding and glazing on mechanical behaviors and ageing resistance of a super translucent dental zirconia show in [
37]. Other new and original case studies with different modeling and requests will be presented in the future through TMM.
2. Materials and Methods
2.1. Materials
Dental restorations for missing one or two teeth can be done by dental crowns or dental bridges on one, two or more pivots or abutments, depending on what the dentist found to exist in situ, following a specialist consultation.
Dental crowns can be made of the following materials: full zirconia, stratified zirconia - i.e. zircon and ceramic, metal and ceramic - i.e. with a metal base and a ceramic coating, or composite - used especially during prosthetic treatment as a temporary crown. Dental crowns can also be fixed on implants, which must be made of biocompatible materials.
The most suitable biocompatible materials for implants are titanium, zirconium and ceramic, materials resistant to pressure and daily wear and, at the same time, have a pleasant aesthetic appearance.
Dental bridges can be fixed or mobile. They can be semi-physiognomic or totally physiognomic. Fixed bridges can be made entirely of zirconium, ceramic, acrylic or metallic materials. Removable dentures can be made of metal - for additional structural support or acrylic resins, which can incorporate ceramic - for better aesthetics.
2.2. Methods
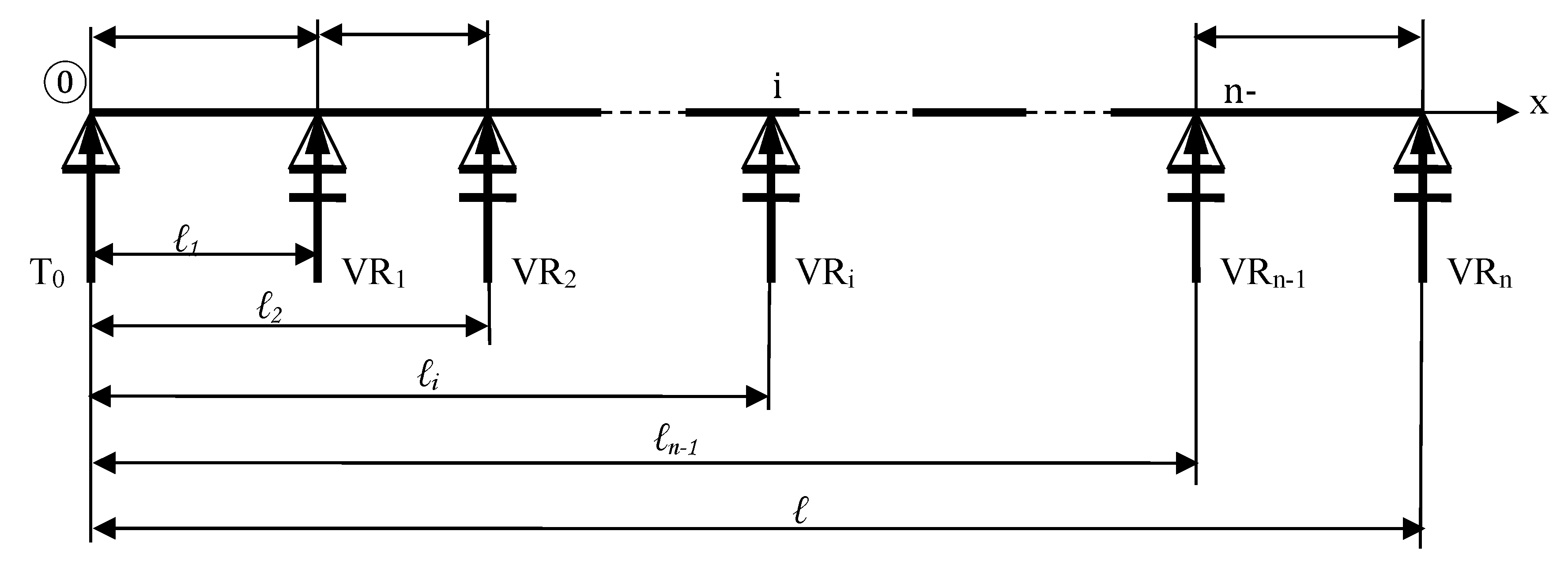
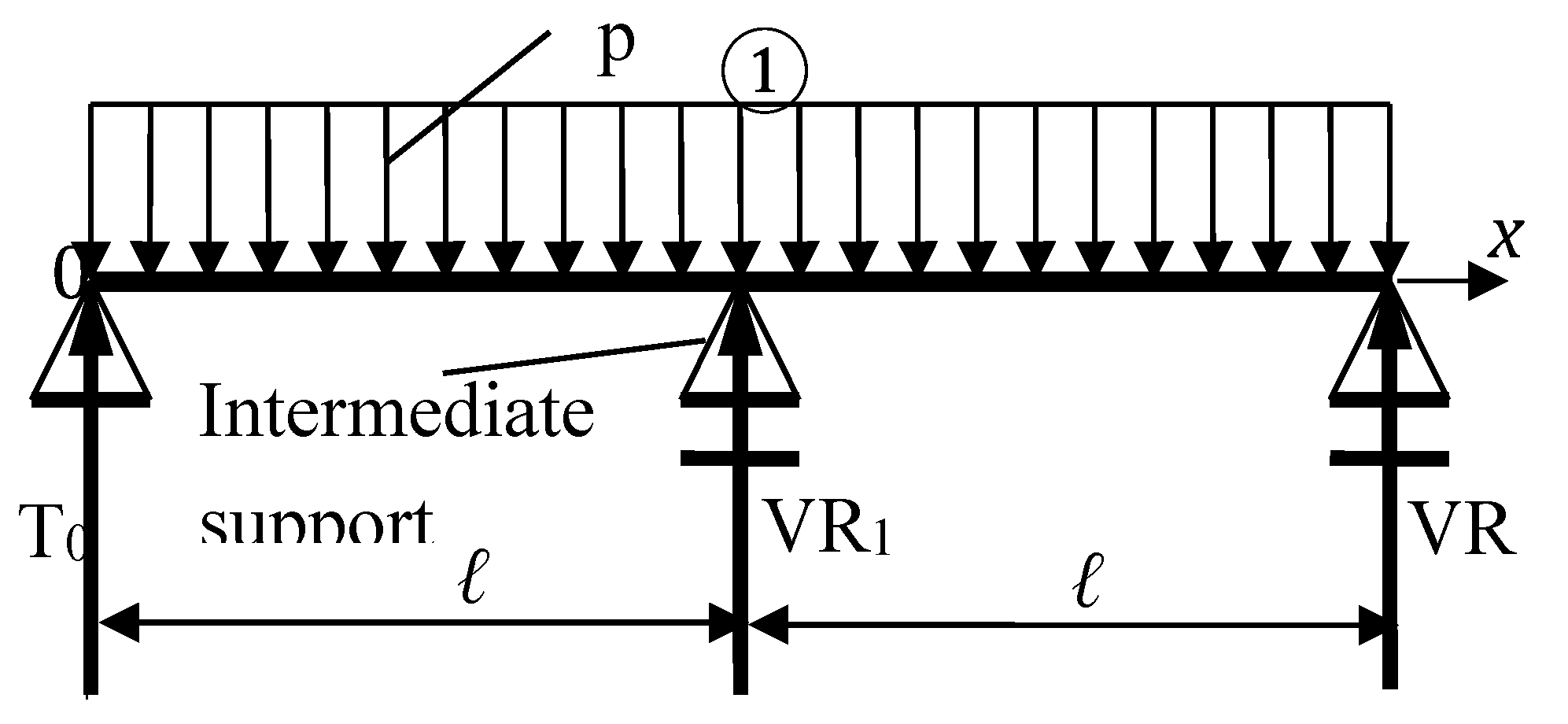
Some beams with intermediate support can be studied as statically indeterminate continuous beams. It is considered as a statically indeterminate continuous beam, articulate at the left edge, with simple support at the right edge and with intermediate supports, as in
Figure 1. The calculus is done with TMM.
2.2.1. Work Hypotheses
The beam with intermediate support that will be studied is considered as a statically indeterminate continuous beam, articulate at the left edge, with a simple support at the right edge and with
i (i=1,n-1) intermediate simple supports (
Figure 1).
The lengths of all parts of the beam are known.
The constant inertia of the entire beam is also considered.
It is considered a reference system with the origin in the left edge, the edge 0.
External vertical forces are considered to act on the beam, which can be characterized by a charge density q’(x) for the vertical concentrated loads and q”(x) is the charge density for the force uniformly distributed over the entire beam.
Due to the external forces, unknown vertical reactions arise at each edge, that are (n+1) vertical reactions. Further, these reactions will be considered as external forces with the charge density as q’”(x) .
2.2.2. Total Charge of Density for a Continuous Beam
It is considered as a statically indeterminate continuous beam, articulate at the left edge, with a simple support at the right edge and with
n intermediate supports (
Figure 1).
Thus, the total charge density
q(x) can be written as (1):
where:
q(x) is the total charge density;
q’(x) is the charge density for the exterior vertical concentrated loads;
q”(x) is the charge density for the force uniformly distributed over the entire beam;
q’”(x) is the density of charge corresponding of the vertical reaction in the edges.
The density of charge corresponding of the exterior concentrated loads q’(x), for a number j of exterior loads Fj, j=1, k, acting in the point aj, j=1, k, can be written, with Dirac’s and Heaviside’s functions and operators, as (2):
and the density of charge corresponding for the Vertical Reaction, (VRi, i=0, n) in the edges, q’”(x), with Dirac’s and Heaviside’s functions and operators too, can be written as (4):
j refers to the point where act the concentrated vertical force Fj;
Fj, j=1, k, are the exterior vertical concentrated loads;
k is the total number of the concentrated vertical force;
i refers to the edge with number i;
n+1 is the total number of edges;
p(x) is the force uniformly distributed over the entire beam;
VRi is the Vertical Reaction in the edge i.
Applying the mathematical calculus with Dirac’s and Heaviside’s functions and operators for (2), we can obtain successively the relations (5):
In the same way, the
mathematical formalism will be applied to expressions (1) and relations (6)
are obtained:
2.2.3. The State Vectors for Different Sections of the Continuous Beam
The state vectors for different sections of the continuous beam can be defined as follows.
It is noted with
{SV(x)} the
State
Vector corresponding at the section
x, at a point on the
x-axis, the abscissa measured from the origin of the reference system, which is in the left edge
0, as (7):
Elements of the state vector (7) are:
y(x) is the arrow in the section x;
ω(x) is the rotating in the section x;
M(x) is the bending moment in the section x;
T(x) is the cutting force in section x.
The state vector at the origin
{SV(0)}=, in the section
0 is as (8):
The total length
l of continuous beam is as (9):
when
ai, i=1, n is the distance between two consecutive supports.
The state vector at the last section, in the section
n, {SV(l)} =for
x=l, is as (10):
2.2.4. The Transfer-Matrix for the Section x of the Continuous Beam
The connection between the state vector from the origin, the section
0, and the state vector from some section
x, is made with relation (11):
when:
The Transfer-Matrix
[TM]x is as (12), after [
1]:
The vector for exterior forces at the section
x is as (13):
The matrix relation (11) can be developed as (14):
For the last section, for
x=l, the expression (12) can be written as (15):
The relation (15) with the developed Transfer-Matrix can be written as (16):
In matrix relation (16), the conditions on the extreme edges can be placed, in section
0, as (17):
and in section
n for
x=l, conditions are as (18):
With the conditions (17) and (18), the matrix relation (16) can be written as (19):
Also, the conditions for the arrows in each intermediate supports must be set, they must be null in each intermediate supports as (20):
or, (21):
The conditions for the right end of the beam, for x=l, are (18) and give (22):
The relations (21) and (22) can be written in a matrix relation like (23), considering that ω
0, and
are the unknowns:
Solving the system of equations given by the matrix relation (23) leads to the calculus of all unknowns. It can be also programmed very easily, thus quickly obtaining the values of the unknowns, and then, all the efforts and deformations in any section of the beam can be calculated.
3. Application and Results
3.1. Application for a Dental Restoration Case: Dental Bridge Assimilated as a Continuous Beam with Three Poles and Two Edentulous, Edentulous Are Between the Three Pole
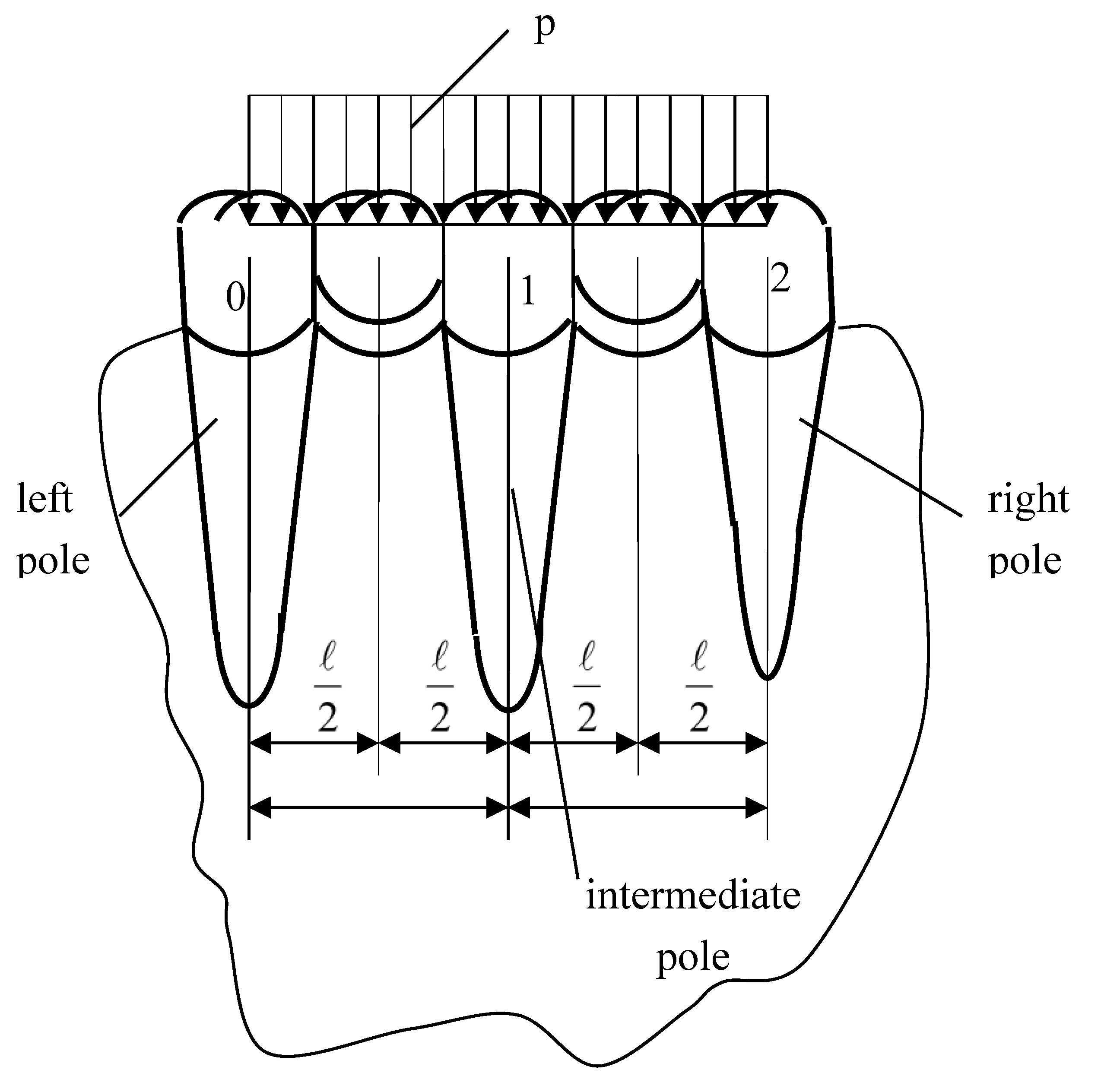
It is considered a case of double missing teeth, as in
Figure 2.
3.1.1. Conditions of Work
A dental restoration with the following characteristics was proposed:
the lengths of the two parts of the beam are known and are equal each other and are equal to l;
the constant inertia of the entire beam is also considered;
it is considered a reference system with the origin in the left edge, the edge 0.
the dental bridge should consist of three poles are the supports for the beam;
the three poles can be natural teeth, prepared to dental bridge as poles, or implants;
the left pole mast be on a stronger tooth be one degree than the second pole;
between the three poles there are two missing teeth;
the distances between the middle of the left pole and the middle of the first missing tooth, between the middle of first missing tooth and the middle of the second pole, between the middle of the second pole and the middle of the second missing tooth, between the middle of the second missing tooth and the middle of the third pole are considered equal each other;
it is considered that the uniform distributed vertical force act on the dental bridge, as a result of the action of the antagonistic teeth on the jaw, as in
Figure 2 and
Figure 3.
The dental bridge shown in
Figure 3 can be assimilated as a continuous beam, with the following characteristics:
the continuous beam is a statically indeterminate beam;
the beam is considered in the left edge articulated (in the left pole), with a simple
support in the right edge (in the right pole) and with an intermediate support on the middle (as the middle pole of the bridge);
the continuous beam is once statically indeterminate, or simply statically indeterminate beam;
the distances between the supports are noted with l.
3.1.2. Approach of Continuous Beam with an Intermediate Support by TMM
The dental bridge from
Figure 2 is assimilated as a continuous beam from
Figure 3, that is considered for this study.
It is a continuous beam, articulate at the left edge, with a simple support at the right edge and with a simple intermediate support. The simple support is considered as an intermediate support because it is between the two ends of the continuous beam, between the articulate edge of the left side and the simple support at the right side, as in
Figure 3.
The left edge is noted as 0, i.e. the articulate edge will be called the origin section, considering 0 as the origin of the reference system Ox. The second edge, the simple intermediate support, is noted with 1 and the right edge is noted with 2.
The density charge
q”(x) corresponding of exterior uniform distributed vertical load for the continuous beam from
Figure 3, is as (24):
and applying the mathematical calculus with Dirac’s and Heaviside’s functions and operators and the matrix calculus presented in § 2.2.4., for the case of
Figure 3, can be obtain the matrix relation (25):
or, (26):
It can be writing the matrix relation (26) developed in the form (27):
or, (28):
3.2. Results
(28) is a linear system of three equations with three unknowns. After calculus, the system solution is (29):
The values for
T0 and the reaction in the intermediate support
VR1 are identical to those obtained by solving the problem as a statically indetermined beam from
Figure 3, with Clapeyron's equation of the three moments, [
2].
The results (29) can be used to calculate moments and shear forces in any section of the beam, as well as deformations y and ω and after then, the stresses in any section of the beam.
4. Discussion
This work presents a new, original and very interesting approach to a calculus pro-blem of beams with intermediate supports by TMM. TMM is a very easy method to program to quickly obtain good results. Some beams with intermediate support can be stu-died as statically indeterminate continuous beams. It is considered as a statically indeterminate continuous beam, articulate at the left edge, with simple support at the right edge and with intermediate supports. The theoretical approach is presented as in § 2.2. The applicability of this approach is presented for an example in dentistry, the calculus of a dental bridge on three poles. After, that is particularized for an application of a dental restoration case, with a dental bridge on three poles and with two missing teeth between the three poles, assimilated to a simple static indeterminate beam, resting on three supports - the three poles and with two openings, corresponding to the two missing teeth, as in § 3.1. and with the results from § 3.2. The results obtained in the presented case study were validated with those obtained by the classical calculation of the Resistance of Materials, with the equation of the three moments of Clapeyron, [
2].
5. Conclusions
This study is a new, original and interesting approach about the problem of intermediate supports of a statically indeterminate beam with TMM. That is very important for many fields, both in industry and in other fields, such as medicine, in occurrence, in dentistry, in dental restorations. The application of TMM calculus can be done very easily in the case of iterative problems, i.e. those problems that require a large volume of repetitive calculus. TMM lends itself very well to its programming, which gives immediate results with fast applicability in practice.
An interesting practical application is the study of a dental crowns and bridges, such as the example presented in § 3.1.2. Due to the ease and elegance of solving various problems with TMM, their approach will continue with other new and original case studies with different modeling and requests, and they will be presented in future research.
Author Contributions
Conceptualization, M.S., D.R., M.T., O.C.-O and I.B.; methodology, M.S. and D.R.; validation, M.S., D.R. and M.T.; formal analysis, M.S.; investigation, D.R.; writing—original draft preparation, M.S. and M.T.; writing—review and editing, M.S. and M.T; visualization, M.S., D.R., M.T., I.B. and O.C.-O.; supervision, M.S.; project administration, M.S.; funding acquisition, M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding. Publication of this paper was financially supported by Technical University of Cluj-Napoca, Romania.
Data Availability Statement
Not applicable.
Acknowledgments
Publication of this paper was financially supported by Technical University of Cluj-Napoca, Romania.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Gery, P.-M.; Calgaro, J.-A. Les Matrices-Transfert dans le Calcul des Structures; Éditions Eyrolles: Paris, France, 1973. [Google Scholar]
- Suciu, M.; Tripa, M.-S. Strength of Materials; UT Press: Cluj-Napoca, Romania, 2021. [Google Scholar]
- Warren, C.Y. ROARK’’S Formulas for Stress & Strain, 6th ed.; McGrawHill Book Company: New York, NY, USA, 1989. [Google Scholar]
- Codrea, L.; Tripa, M.-S.; Opruţa, D.; Gyorbiro, R.; Suciu, M. Transfer-Matrix Method for Calculus of Long Cylinder Tube with Industrial Applications, Mathematics2023, 11(17), 3756. [CrossRef]
- Codrea, L.; Tripa, M.-S.; Opruţa, D.; Suciu, M. Studies about the bending behavior of a new sandwich composite material with COREMAT heart, Acta Technica Napocensis-Series: Applied Mathematics, Mechanics and Engineering 2023, Vol. 66, No. 2, pp. 249-254.
- Codrea, L.; Tripa, M.-S.; Opruţa, D.; Suciu, M. About bending tests for two composite materials: Fabric MAT 300 and COREMAT, Acta Technica Napocensis-Series: Applied Mathematics, Mechanics and Engineering 2023, Vol. 66, No. 2, pp. 241-248.
- Opruta, D.; Tripa, M.; Codrea, L.; Rosu, D.; Teodorescu-Draghicescu, H.; Suciu, M. , About experimental research of tensile loaded composite materials used in automative industry, Acta Technica Napocensis-Series: Applied Mathematics, Mechanics and Engineering 2022, Vol. 65, No. 3.
- Suciu, M. About an approach by Transfer-Matrix Method (TMM) for mandible body bone calculus, Mathematics 2023, 11(2), 450,. [CrossRef]
- Suciu, M. About Buckling Bio-Composite Sandwich Bars, Applied Mechanics and Materials 2013, Vol. 245, pp. 39-44, Editor Trans Tech Publications Ltd.
- Suciu, M. About the Study of Bending Beam on Elastic Environment by Transfer-Matrix Method, Applied Mechanics and Materials 2012, vol. 186, pp.149-155.
- Suciu, M. An Another Approach for Buckling Calculus of Dental Implant as a Bar on Elastic Environment by Transfer-Matrix Method (TMM), European Modern Studies Journal 2022, www.journal-ems.com, vol. 6, no. 6, ISSN 2522-9400, pp. 185-198.
- Suciu, M. About the calculus of cantilever dental bridge with a single pole in medial extension by Transfer-Matrix Method, European Modern Studies Journal 2022, www.journal-ems.com, vol. 6, no. 6, ISSN 2522-9400, pp. 300-309.
- Suciu, M. About the Analytical Calculus of Dental Bridge with Distal Extension and Single Pole Tooth Assimilated as a Beam by Transfer-Matrix Method, International Journal of Latest Research in Science and Technology 2020, Vol. 6, Issue 6, pp. 19-22.
- Suciu, M. An Approach Of A Single Dental Bridge As A Frame With Uniform Load By Transfer-Matrix Method, International Journal of Latest Research in Science and Technology 2022, Vol. 11, Issue 2.
- Tripa, M.; Şolea, G.; Sorcoi, D.; Florescu, I.; Sorcoi, A.; Păunescu, D.; Bâlc, N.; Suciu, M. About buckling calculus of straight bars on elastic environment by Transfer-Matrix Method (TMM) for dental implants, MATEC Conferences 178, 04007 (2018), IManE&E 2018. [CrossRef]
- Tripa, M.; Sorcoi, D.; Florescu, I.; Sorcoi, L.; Paunescu, D.; Suciu, M. Contributions on the analytical calculus of simple dental bridge assimilated with a beam embedded at both ends by Transfer-Matrix Method (TMM), Acta Technica Napocensis-Series: Applied Mathematics, Mechanics and Engineering 2019, Vol. 62, No. 4, pp. 573-576.
- Tripa, M.; Florescu, C.; Sorcoi, D.; Sorcoi, A.; Paunescu, D.; Suciu, M. About the Study for The Body of Mandible Bone by Transfer-Matrix Method, Journal of Multidisciplinary Engineering Science and Technology (JMEST) 2020; ISSN: 2458-9403; Vol. 7, Issue 12, December-2020, pp. 13233-13237.
- Tripa, M.; Sorcoi, D., Florescu, I.; Sorcoi, L.; Paunescu, D.; Suciu, M. About the study of frames by Transfer-Matrix Method (TMM)-similarity of dental bridges with frames, Acta Technica Napocensis-Series: Applied Mathematics, Mechanics and Engineering 2019, Vol. 62, No. 4.
- Bumbu, B. A.; Bumbu, G. A.; Berechet, M.-C.; Rus, V.; Ruxanda, F.; Miclaus, V.; Vicas, R. M.; Rotaru, D. I.; Zdrinca, C. F.; Ciobanu, M. M.; Berechet, D. Osseointegration of zirconium dental implants three months after insertion in rabbit femur. Histopathological study, Rom J Morphol Embryol 2018, 59(3):781–786.
- Chisnoiu, A. M.; Rotaru, D. I.; Chisnoiu, R. M. Essential guide to oral pathology; Editura Medicală Universitară "Iuliu Haţieganu", Cluj-Napoca, Romania, 2022.
- Chisnoiu, A. M.; Moldovan, M.; Sarosi, C.; Chisnoiu, R. M.; Rotaru, D. I.; Delean, A. G.; Pastrav, O.; Muntean, A.; Petean, I.; Tudoran, L. B.; Pastrav, M. Marginal Adaptation Assessment for Two Composite Layering Techniques Using Dye Penetration, AFM, SEM and FTIR: An In-Vitro Comparative Study, Appl. Sci. 2021, 11(12), 5657. [Google Scholar] [CrossRef]
- Chisnoiu, R.; Moldovan, M.; Chisnoiu, A.; Hrab, D.; Rotaru, D.; Păstrav, O.; Delean, A. Comparative apical sealing evaluation of two bioceramic endodontic sealers, Med Pharm Rep. 2019, Dec; 92 (Suppl No 3): S55–S60, Published online 2019 Dec 15. [CrossRef]
- Chisnoiu, R. M.; Delean, A. G.; Muntean, A.; Rotaru, D. I.; Chisnoiu, A. M.; Cimpean, S. I. Oral Health-Related Knowledge, Attitude and Practice among Patients in Rural Areas around Cluj-Napoca, Romania, Int. J. Environ. Res. Public Health 2022, 19(11), 6887; [CrossRef]
- Chisnoiu, R. M.; Moldovan, M.; Prodan, D.; Chisnoiu, A. M.; Hrab, D.; Delean, A. G.; Muntean, A.; Rotaru, D. I.; Pastrav, O.; Pastrav, M. In-Vitro Comparative Adhesion Evaluation of Bioceramic and Dual-Cure Resin Endodontic Sealers Using SEM, AFM, Push-Out and FTIR, Appl. Sci. 2021, 11(10), 4454. [CrossRef]
- Kui, A.; Chisnoiu, A. M.; Rotaru, D. I.; Zaharia, A. PROTHÈSES FIXÉES UNIDENTAIRES. Notions pratiques pour les préparations dentaires, Editura Medicală Universitară "Iuliu Haţieganu"; Cluj-Npoca, Romania, 2022.
- Rotaru, D. I.; Delean, A. G. Guide to the diagnosis and treatment of conditions in the field of oral pathology, Editura Medicală Universitară "Iuliu Haţieganu" Cluj-Napoca, Romania, 2015.
- Rotaru, D.; Chisnoiu, R.; Chisnoiu, A. Coronary reconstructions, Editura Medicală Universitară "Iuliu Haţieganu" Cluj-Napoca, Romania, 2019.
- Rotaru, D. I.; Berechet, D.; Scrobotă, I.; Moca, A.; Matei, R. I.; Dima, R. Enameloplasty in interdisciplinary treatment of dental injuries – case report, Medicine in Evolution 2022/12, Vol. 28, Issue 4, p. 6.
- Tomescu, M. A.; Jäntschi, L.; Rotaru, D. I. Figures of Graph Partitioning by Counting, Sequence and Layer Matrices, Mathematics 2021, 9(12), 1419. [CrossRef]
- Burke, F. J. T.; Lucarotti, P. S. K. Ten year survival of bridges placed in the General Dental Services in England and Wales, Journal of Dentistry 2012, vol. 40, Issue 11. [CrossRef]
- Dikova, T.; Vasilev, T. Bending fracture of Co-Cr dental bridges, produced by additive technologies: Simulation analysis and test, Engineering Fracture Mechanics 2019, 218/2019. [CrossRef]
- Dikova, T. Bending fracture of Co-Cr dental bridges, produced by additive technologies: experimental investigation, Procedia Structural Integrity 2018, 13 (2018), 461-468, Elsevier B.V. Peer-review under responsibility of the ECF22 organizers, 10.1016/j.prostr.2018.12.077.
- Gaspar, M.; Weichert, F. Integrated construction and simulation of tool paths for milling dental crowns and bridges, Computer-Aided Design 2013, 45/2013, 1170–1181.
- VerHoef, J. R. ; C. Hebert, C.; VerHoef, J. R. Arola, D. Fatigue of zirconia and dental bridge geometry: Design implications, Dental Materials 2010, 26/2010, 1133–1136. [Google Scholar] [CrossRef]
- Studart, A. R.; Filser, F.; Kocher, P.; Gauckler, L. J. Fatigue of zirconia under cyclic loading in water and its implications for the design of dental bridges, Dental Materials 2007, 23/2007,106–114. [CrossRef]
- Uriciuc, W. A.; Vermeşan, H.; Botean, A. I. Research on the surface of the dental alloys with cobalt-crom base, Acta Technica Napocensis, Series: Applied Mathematics, Mechanics and Engineering 2019, Vol. 62, Issue 3.
- Xuan Lai; Wenjie Si; Danyu Jiang; Ting Sun; Longquan Shao; Bin Deng Effects of small-grit grinding and glazing on mechanical behaviors and ageing resistance of a super translucent dental zirconia, Journal of Dentistry, 2017, 66/2017, 23-31. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).