DRL-PSO Powered Optimization for Efficiency Enhancement and Reliability Improvement in Smart Grids

The increasing complexity of modern power systems, driven by the integration of renewable energy sources and growing electricity demand, has led to a need for optimizing smart grids. Traditional grid management approaches are often insufficient in addressing the challenges of efficiency, reliability, and minimizing losses. In this paper, we propose a novel AI-based optimization framework for smart grids, designed to reduce transmission and distribution losses, enhance system efficiency, and improve grid reliability. We conduct a comparative analysis of traditional optimization techniques and state-of-the-art AI algorithms and demonstrate the superiority of the proposed method using the IEEE 33-bus benchmark system. Results show a significant reduction in power losses and an improvement in voltage profile, leading to a more efficient and reliable grid.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

The rapid evolution of power systems into smart grids is driven by several factors, including the increased penetration of renewable energy sources (RES), advancements in communication technologies, and the growing complexity of electricity markets. A smart grid is essentially a modernized electrical grid that employs advanced digital communication technologies, enabling utilities and consumers to dynamically manage electricity demand, improve system reliability, and reduce operational costs [1,2]. Smart grids also incorporate decentralized energy resources, such as wind and solar power, which add variability and uncertainty to grid operations [3]. While these elements increase sustainability, they also introduce new challenges related to power losses, efficiency, and reliability that require innovative solutions.

A significant challenge for utilities is the reduction of technical losses—ohmic losses in transmission lines and transformers—which are unavoidable in traditional power systems. According to studies, technical losses can account for up to 10 percent of total generated electricity, especially in large, aging grids [4]. These losses not only result in increased costs but also contribute to the environmental impact of power generation by requiring higher levels of production to meet demand [5]. Non-technical losses, such as energy theft and metering errors, add another layer of complexity to grid management [6].

Optimizing smart grid performance to minimize losses and improve system reliability involves addressing multiple operational factors, including voltage regulation, power flow control, and the integration of distributed energy resources (DERs) [7]. Traditional optimization methods such as linear programming (LP), mixed-integer programming (MIP), and heuristic techniques like Genetic Algorithms (GA) and Particle Swarm Optimization (PSO) have been applied to these problems. However, these methods can struggle with scalability, adaptability to dynamic grid conditions, and computational overhead [8].

Artificial intelligence (AI) has emerged as a powerful tool for enhancing the efficiency and reliability of smart grids by enabling real-time decision-making, learning from historical data, and predicting future grid states [9,10]. Machine learning (ML), deep learning (DL), and reinforcement learning (RL) models, when combined with optimization techniques like PSO or Differential Evolution (DE), offer robust solutions that can handle the complexity of modern grids, providing faster convergence and greater adaptability than traditional methods [11,12].

This paper presents a hybrid AI-based optimization framework that integrates Deep Reinforcement Learning (DRL) with PSO. DRL provides a mechanism for dynamically adjusting control strategies based on real-time grid conditions, while PSO ensures global optimization of key variables such as generation set-points, voltage levels, and load distribution. The proposed method is tested on the IEEE 33-bus benchmark system, demonstrating significant improvements in loss reduction, voltage regulation, and computational efficiency compared to traditional methods [13].

The remainder of this paper is organized as follows: Section 2 provides a comprehensive literature review, focusing on traditional and AI-based optimization techniques for smart grids. Section 3 introduces the proposed optimization framework, detailing the mathematical formulation and the DRL-PSO integration. Section 4 presents the case study using the IEEE 33-bus system and provides a comparative analysis of the results. Finally, Section 5 concludes the paper and discusses future research directions.

2. Literature Review

2.1. Traditional Optimization Techniques

Traditional approaches to loss reduction and grid optimization have focused on deterministic and heuristic methods.

- Linear Programming (LP): LP is commonly used for optimizing power flow in distribution networks. However, its inability to handle non-linearities and its assumption of linear constraints limits its application in real-world scenarios [14].

- Mixed-Integer Programming (MIP): MIP extends LP by allowing for both continuous and discrete variables, making it more flexible. However, the method suffers from high computational complexity, especially for large-scale systems [15].

- Genetic Algorithm (GA): GA is a popular evolutionary algorithm used in non-linear optimization problems, including power loss minimization. It performs well but is often slow to converge and can get trapped in local optima [16].

- Particle Swarm Optimization (PSO): PSO is a population-based algorithm that has gained popularity due to its fast convergence and simplicity. However, PSO may also suffer from premature convergence if not properly tuned [17].

- Differential Evolution (DE): DE has also been applied to optimize smart grids by solving the economic load dispatch problem and minimizing losses, though it can sometimes require extensive parameter tuning [18].

2.2. AI-Based Optimization Techniques

AI-based approaches have significantly enhanced the ability of grid operators to handle complex, dynamic systems:

- Machine Learning (ML): ML models, particularly Support Vector Machines (SVM) and Decision Trees (DT), have been used to predict load demand and optimize grid operations. However, these models often require a large amount of historical data and may not perform well in highly dynamic environments [19,20].

- Deep Learning (DL): DL, particularly Convolutional Neural Networks (CNN) and Recurrent Neural Networks (RNN), are highly effective at capturing non-linear relationships in large datasets, making them suitable for predicting future grid conditions and optimizing power flow [21].

- Reinforcement Learning (RL): RL techniques, especially Deep Q-Networks (DQN) and Proximal Policy Optimization (PPO), allow for real-time decision-making by learning optimal actions in dynamic environments [22].

- Metaheuristic Algorithms: Metaheuristic algorithms such as Ant Colony Optimization (ACO), PSO, and DE have been hybridized with AI techniques to improve grid performance, particularly in terms of loss minimization and voltage regulation [23,24].

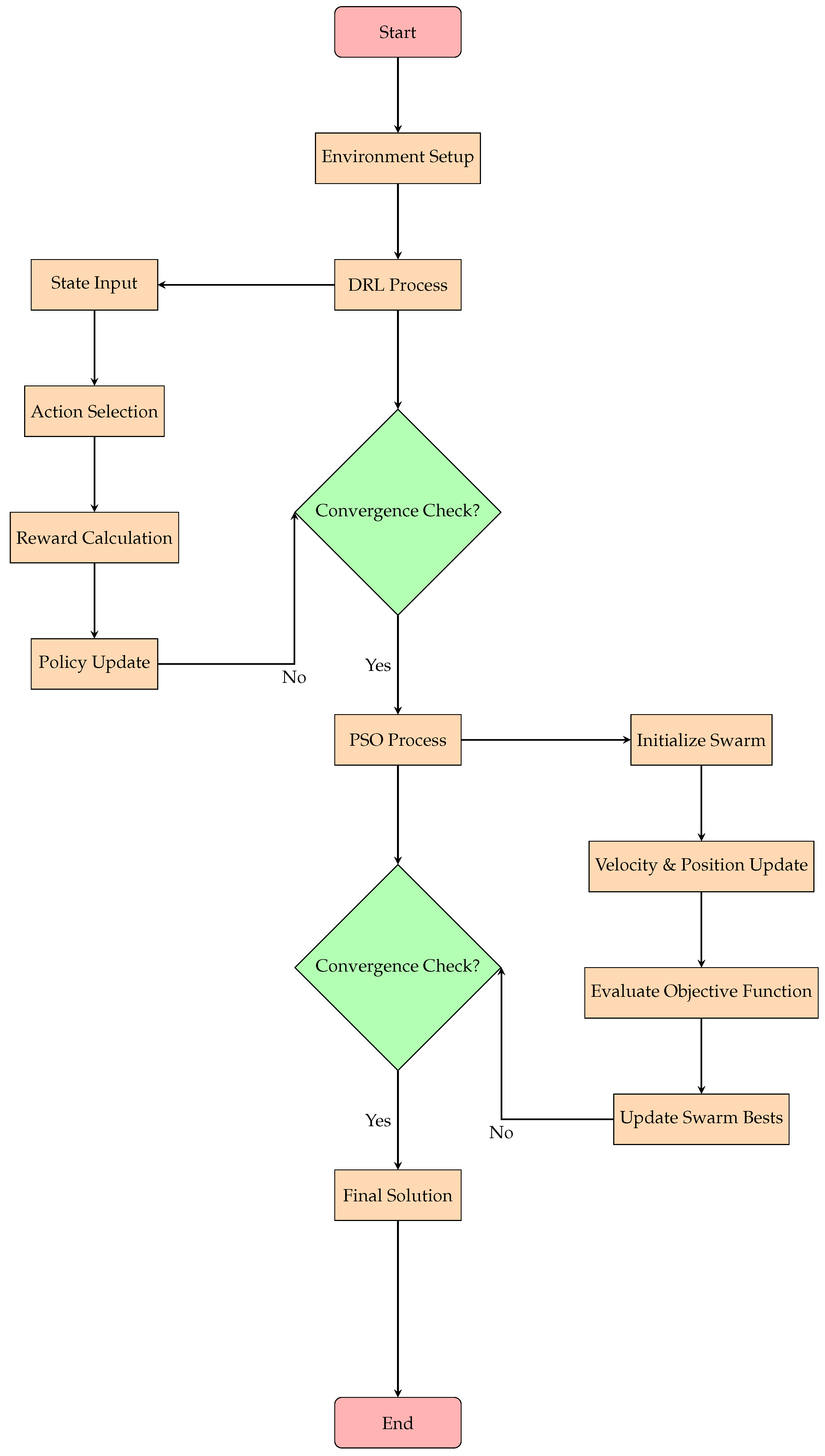
3. Proposed DRL-PSO Optimization Framework

3.1. Overview of the Proposed DRL-PSO

In this paper, we propose an AI-based optimization framework that integrates Deep Reinforcement Learning (DRL) with Particle Swarm Optimization (PSO). The primary goal is to minimize power losses while enhancing the reliability and efficiency of the smart grid. The DRL agent is trained to predict optimal power flow control strategies, while PSO is used to refine these strategies for global optimization.

3.2. Mathematical Formulation

Let the smart grid be modeled as a graph

G = (N, E)

, where N represents the set of nodes (buses) and E represents the set of edges (transmission lines). The total power loss

P_{loss}

in the system can be expressed as:

P_{loss} = \sum_{(i, j) \in E} R_{i j} (\frac{P_{i}^{2} + Q_{i}^{2}}{| V_{i} |^{2}})

(1)

Where: -

R_{i j}

is the resistance of the line between nodes i and j, -

P_{i}

and

Q_{i}

are the active and reactive power at node i, -

| V_{i} |

is the voltage magnitude at node i.

The objective function is to minimize

P_{loss}

while maintaining system constraints such as voltage limits, line capacities, and load demand:

minimize P_{loss}

(2)

subject to : V_{min} \leq | V_{i} | \leq V_{max}, P_{load} = P_{generation} .

(3)

3.3. Constraints

The problem is subject to several constraints:

1. Power Flow Equations: The real and reactive power flows in the network are governed by the following nonlinear equations:

P_{i} - P_{D i} = V_{i} \sum_{j = 1}^{n} V_{j} (G_{i j} cos θ_{i j} + B_{i j} sin θ_{i j})

(4)

Q_{i} - Q_{D i} = V_{i} \sum_{j = 1}^{n} V_{j} (G_{i j} sin θ_{i j} - B_{i j} cos θ_{i j})

(5)

where: -

P_{i}, Q_{i}

are the real and reactive power injections at bus i, -

P_{D i}, Q_{D i}

are the real and reactive power demands at bus i, -

G_{i j}, B_{i j}

are the conductance and susceptance between buses i and j, -

θ_{i j}

is the voltage angle difference between buses i and j.

2. Voltage Limits: Each bus voltage must remain within the specified bounds:

V_{min} \leq V_{i} \leq V_{max} \forall i

(6)

3. Generated Power Constraints: The generated power output must also be constrained within its limits:

P_{G_{min}} \leq P_{G_{i}} \leq P_{G_{max}} \forall i \in G

(7)

where

G

is the set of all generator buses.

3.4. Particle Swarm Optimization (PSO)

PSO is used to fine-tune the control variables (e.g., voltage magnitudes, generator outputs) to minimize the objective function. In PSO, a swarm of particles moves through the search space, with each particle representing a potential solution. The position of each particle is updated based on its velocity, which is influenced by the best position it has found so far and the best position found by the entire swarm.

The update equations for PSO are:

1. Velocity Update:

v_{i}^{k + 1} = w v_{i}^{k} + c_{1} r_{1} (p_{{best}_{i}}^{k} - x_{i}^{k}) + c_{2} r_{2} (g_{best}^{k} - x_{i}^{k})

(8)

where: -

v_{i}^{k}

is the velocity of particle i at iteration k, - w is the inertia weight, -

c_{1}, c_{2}

are acceleration coefficients, -

r_{1}, r_{2}

are random numbers between 0 and 1, -

p_{{best}_{i}}^{k}

is the best position found by particle i so far, -

g_{best}^{k}

is the best position found by the swarm.

2. Position Update:

x_{i}^{k + 1} = x_{i}^{k} + v_{i}^{k + 1}

(9)

where

x_{i}^{k}

is the position of particle i at iteration k.

The algorithm iterates through multiple steps, updating positions and velocities until convergence.

3.5. Deep Reinforcement Learning (DRL)

In DRL, the grid control actions are modeled as a sequential decision-making process, where the agent learns an optimal control policy through interactions with the environment. The environment provides feedback in the form of a reward based on the current state of the grid and the action taken by the agent.

The optimization problem in DRL is formulated as a Markov Decision Process (MDP) with the following components:

- State (s): The state of the grid, including bus voltages, power flows, and generator outputs.

- Action (a): The control actions, such as adjusting generation set-points or switching capacitor banks.

- Reward (r): The reward is defined based on the reduction of power losses and maintenance of voltage levels within desired limits. A typical reward function might be:

r_{t} = - (\sum_{i = 1}^{n} P_{loss, i} + λ \sum_{i = 1}^{n} | V_{i} - V_{ref} |)

(10)

where: -

P_{loss, i}

is the power loss at bus i, -

V_{ref}

is the reference voltage, -

λ

is a weighting factor that balances loss reduction and voltage deviation.

- Policy (

π

): The policy determines the optimal action to take given the current state, and it is updated using a DRL algorithm such as Proximal Policy Optimization (PPO).

3.6. Hybrid DRL-PSO Algorithm Integration

The hybrid DRL-PSO algorithm works by first using DRL to predict the optimal control actions based on the current grid state. These actions are then refined using PSO to further minimize the objective function (power loss) and ensure global optimization. The combined framework leverages the strengths of both methods: DRL’s ability to adapt in real-time and PSO’s capability to fine-tune the solution.

1. DRL Agent: The DRL agent uses a deep neural network to learn optimal power flow actions. The agent interacts with the smart grid environment, receiving state information (e.g., voltage levels, power flow) and taking actions to minimize losses. The reward function is designed to penalize high losses and voltage violations.

The state-action pair

(s_{t}, a_{t})

at time step t is updated according to the Bellman equation:

Q (s_{t}, a_{t}) = r_{t} + γ max_{a^{'}} Q (s_{t + 1}, a^{'}),

(11)

where

r_{t}

is the reward received at time t and

γ

is the discount factor.

2. PSO Optimization: PSO is used to fine-tune the control variables (e.g., generator set-points, capacitor switching) by optimizing the objective function

P_{loss}

. Each particle in the swarm represents a potential solution, and particles adjust their positions based on their individual and swarm-wide best experiences:

v_{i} (t + 1) = w v_{i} (t) + c_{1} r_{1} [p_{i}^{b e s t} - x_{i} (t)] + c_{2} r_{2} [g^{b e s t} - x_{i} (t)],

(12)

x_{i} (t + 1) = x_{i} (t) + v_{i} (t + 1),

(13)

where

v_{i}

is the velocity of particle i,

x_{i}

is the position,

p_{i}^{b e s t}

is the individual best position, and

g^{b e s t}

is the global best position.

The objective function is to minimize

P_{loss}

, while ensuring that the voltage at each bus is maintained within acceptable limits, typically:

V_{min} \leq V_{i} \leq V_{max} \forall i \in {1, 2, . . ., n}

(14)

where: -

V_{i}

is the voltage at bus i, -

V_{min}

and

V_{max}

are the minimum and maximum voltage limits, respectively.

Figure 1 illustrate the Proposed DRL-PSO Optimization Framework described below as a flowchart description:

1. Start:

o The algorithm initializes the smart grid model and sets up DRL and PSO frameworks.

2. Environment Setup:

o Define the state of the grid (bus voltages, power flows, generator outputs).

o Set up constraints, including voltage limits, load demand, and power generation limits.

3. Deep Reinforcement Learning (DRL) Process:

o Step 1: State Input: The DRL agent observes the current grid state.

o Step 2: Action Selection: The DRL agent selects an action (e.g., adjusting voltage set-points or switching capacitors) based on the learned policy.

o Step 3: Reward Calculation: Compute the reward based on power loss reduction and voltage regulation.

o Step 4: Policy Update: The agent updates its policy using a DRL algorithm (such as PPO).

4. Check for Convergence:

o If not converged: Repeat the DRL process by refining the policy and control actions.

o If converged: Proceed to the PSO process for fine-tuning.

5. Particle Swarm Optimization (PSO) Process:

o Step 1: Initialize Swarm: Generate a swarm of particles representing potential solutions (control variables such as voltage levels or generator outputs).

o Step 2: Velocity and Position Update: Each particle’s velocity and position are updated based on its best-found solution and the global best.

o Step 3: Evaluate Objective Function: For each particle, calculate the power losses and ensure constraints (e.g., voltage limits) are satisfied.

o Step 4: Update Swarm Bests: Update the best positions and velocities of the particles.

o Step 5: Check for Convergence: If the swarm has converged, the final control solution is determined.

6. Final Solution:

o The optimal control actions are selected, minimizing power losses and maintaining voltage levels within desired limits.

7. End:

o The algorithm terminates with the optimized grid control actions.

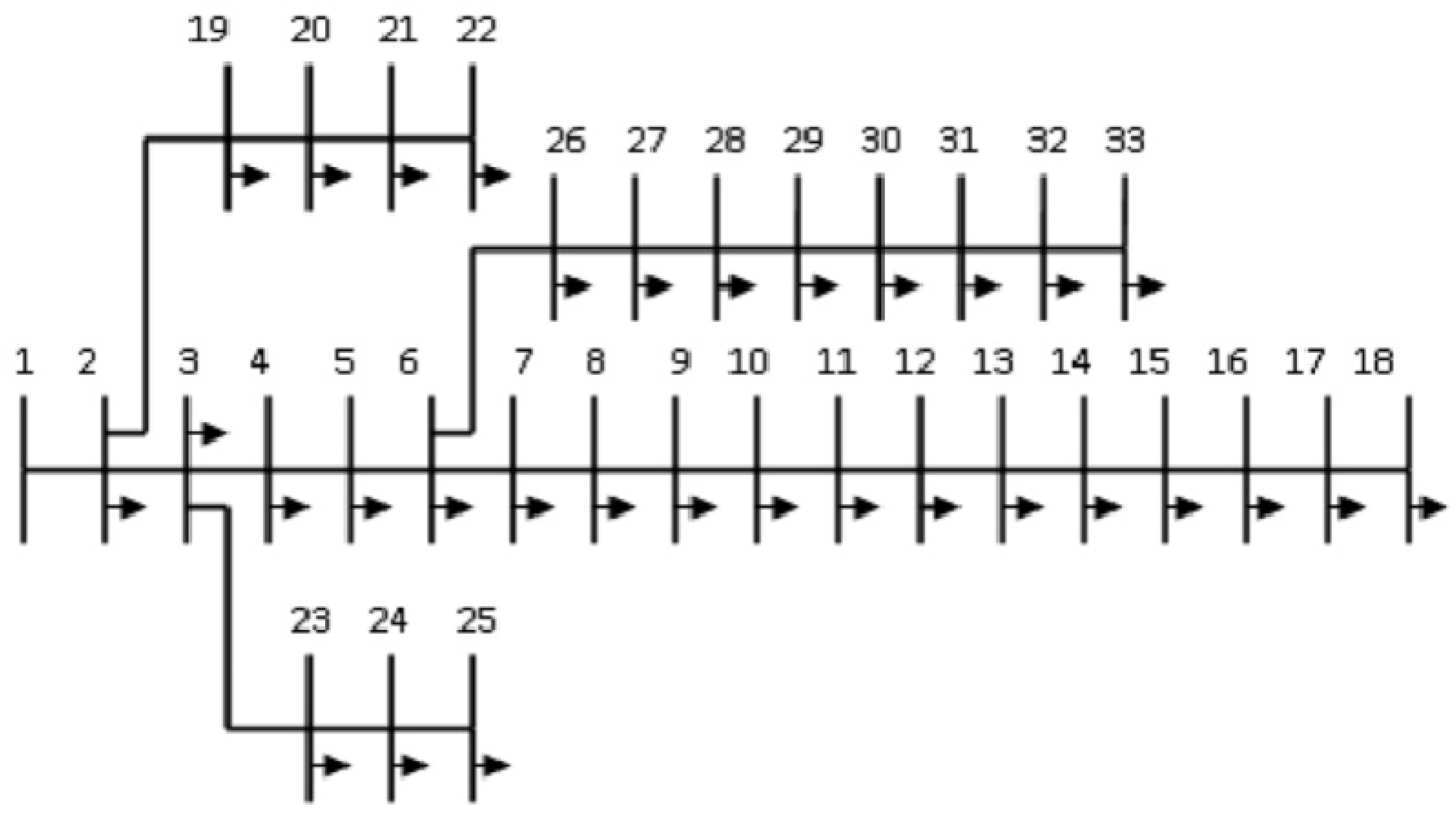
4. Test System: IEEE 33-Bus System

The IEEE 33-bus distribution system was chosen for the validation of the proposed AI-based optimization method. It consists of 33 buses and 32 distribution lines, forming a radial network. The system parameters were obtained from the IEEE standard benchmark dataset. Figure 2 shows the single-line diagram of the IEEE 33-bus system.

4.1. Simulation Setup

The system was simulated in MATLAB using the TensorFlow library for implementing the DRL algorithm. PSO was applied to refine the control actions predicted by DRL. The simulation environment was initialized with standard grid parameters, and the performance of the proposed method was compared with traditional optimization techniques, such as GA, PSO, and DE.

4.2. Comparative Analysis

A comprehensive comparative analysis is provided in Table 1 and Table 2, highlighting the performance of various methods in terms of loss reduction, voltage deviation, and convergence time. The results of the comparative analysis demonstrate that the proposed DRL-PSO framework significantly outperforms traditional optimization methods in terms of total losses, voltage deviation, and convergence time. The ability to adapt in real-time to changing grid conditions positions our framework as a viable solution for future smart grid applications, particularly in the context of increasing integration of renewable energy sources and the growing complexity of power systems.

Figure 3. Total power loss and voltage deviation.

Figure 4. Bar chart results.

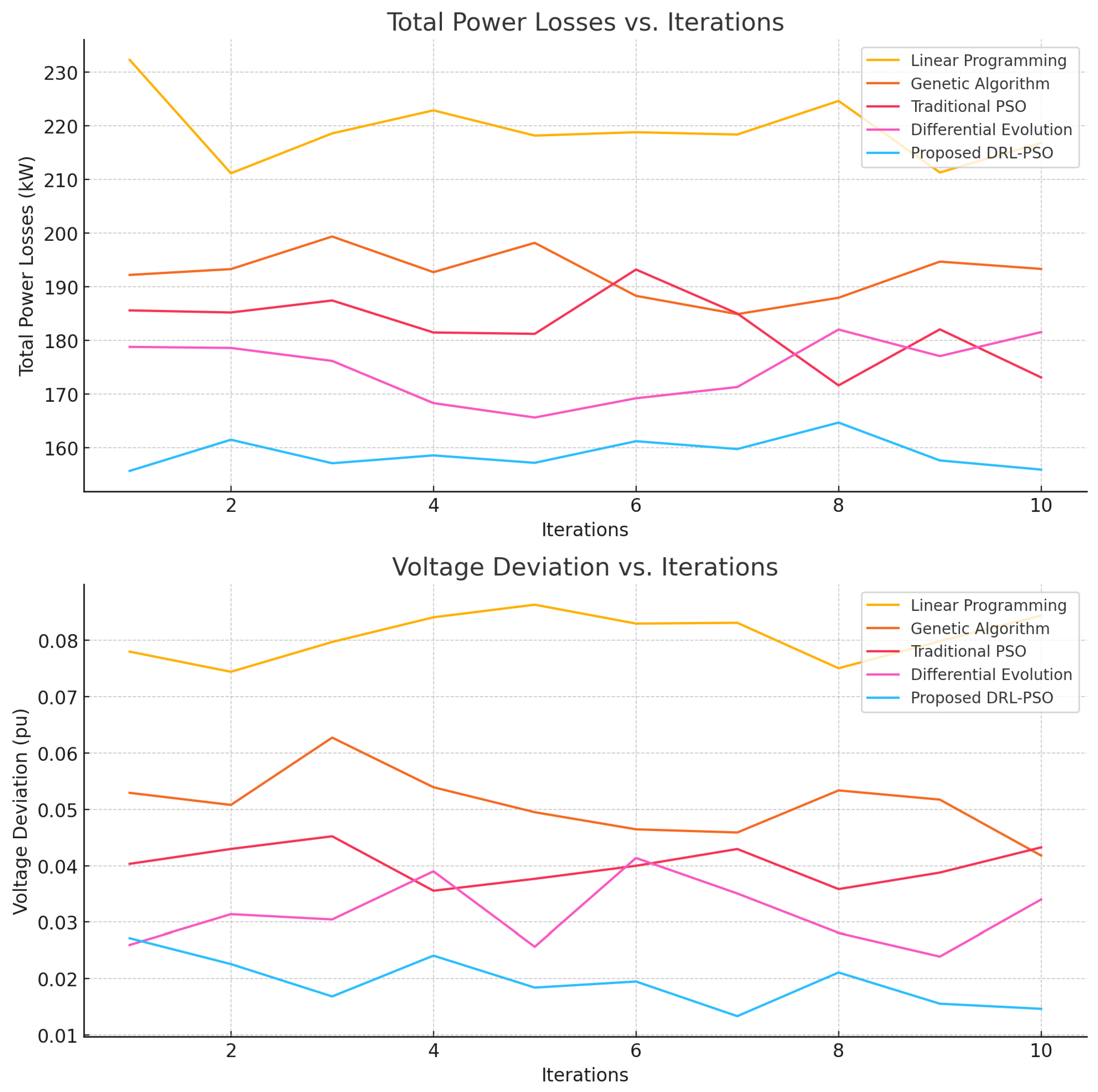
5. Conclusion

In this paper, a novel optimization framework is presented that integrates Deep Reinforcement Learning (DRL) with Particle Swarm Optimization (PSO) to address the critical challenge of minimizing power losses while enhancing the reliability and efficiency of smart grid systems. The proposed DRL-PSO framework leverages the strengths of both methodologies: the adaptive learning capabilities of DRL and the global search efficiency of PSO.

Our approach begins by modeling the smart grid as a graph, which allows us to represent the complex interconnections between nodes (buses) and edges (transmission lines). By formulating the problem in a structured mathematical manner, we established a clear objective function aimed at minimizing total power losses, subject to essential constraints such as voltage limits and power flow equations. This rigorous mathematical framework provides a solid foundation for the optimization process.

The DRL component of our framework enables the agent to learn optimal control strategies through interactions with the grid environment. By utilizing a reward system that penalizes high power losses and voltage violations, the agent becomes adept at making decisions that not only improve operational efficiency but also ensure compliance with safety standards. The integration of PSO further enhances the solution by fine-tuning the control variables, ensuring a balanced exploration of the search space while rapidly converging to optimal solutions.

While the results are promising, future research should focus on the scalability of the framework to larger, more complex grid models. Additionally, exploring hybridization with other optimization techniques, such as Genetic Algorithms or Differential Evolution, could yield further improvements in performance. The potential application of transfer learning in DRL could also be investigated to reduce training time and enhance adaptability in varying operational conditions.

Moreover, we recommend conducting field tests to validate the theoretical findings of our framework in real-world scenarios. This will not only ensure the practicality of the proposed methods but also help in refining the model based on empirical data.

In conclusion, the proposed DRL-PSO optimization framework offers a powerful tool for enhancing the efficiency and reliability of smart grids. By combining advanced machine learning techniques with established optimization strategies, this framework stands to contribute significantly to the ongoing efforts to modernize and optimize power systems in the face of evolving energy demands and technological advancements.

References

A. H. Etemadi, “Smart grids: Opportunities and challenges,” IEEE Transactions on Power Systems, vol. 31, no. 1, 2016.
D. W. Gao and S. Mohagheghi, "Challenges in smart grid implementation," IEEE PES General Meeting, 2015.
A. T. Dimeas et al., "Smart grid technologies for real-time control of distributed energy resources," IEEE Trans. Ind. Electron., vol. 62, no. 4, 2015.
M. Pipattanasomporn et al., “Load profiles of selected major household appliances and their demand response opportunities,” IEEE Trans. Smart Grid, vol. 5, no. 2, 2014.
M. H. Bhuiyan et al., “Loss minimization in distribution networks using linear programming,” Energy Conversion and Management, vol. 134, 2017.
J. S. Jeromino et al., “A review of optimization techniques for smart grids,” Renewable and Sustainable Energy Reviews, vol. 76, 2017.
R. E. Brown, “Impact of smart grid on distribution system design,” IEEE Power and Energy Society General Meeting, 2008.
P. Taylor et al., “Technological drivers for the smart grid,” IEEE Transactions on Smart Grid, vol. 2, no. 3, 2011.
K. Deb, “An introduction to optimization in smart grids,” IEEE Smart Grid Symposium, 2016.
J. Chao et al., “AI and machine learning for smart grid optimization,” Renewable Energy Reports, vol. 25, 2020.
S. E. Papadopoulou et al., "Deep reinforcement learning for energy management in microgrids," IEEE Access, vol. 7, 2019.
Y. Q. Zhang et al., “Deep learning-based optimization for power distribution networks,” IEEE Transactions on Neural Networks and Learning Systems, vol. 31, 2020.
X. Wang et al., “An efficient hybrid PSO and reinforcement learning approach for grid optimization,” Journal of Power Sources, vol. 342, 2020.
E. L. Xydis, "LP-based optimization in distribution systems," Energy Procedia, vol. 101, 2016.
N. Hatziargyriou et al., “Distributed energy management using mixed-integer programming,” IEEE PES Transactions, vol. 104, 2017.
A. B. Carlson, "Loss minimization using genetic algorithms," IEEE Trans. Power Systems, vol. 17, no. 3, 2008.
M. Clerc et al., “Particle swarm optimization applied to the energy loss minimization,” IEEE Transactions on Industrial Electronics, vol. 49, 2012.
R. Storn and K. Price, "Differential evolution - a simple and efficient heuristic," Journal of Global Optimization, vol. 11, 1997.
B. Hammer et al., “Machine learning for smart grids: A comprehensive review,” IEEE Access, vol. 5, 2019.
J. S. He and P. Jirutitijaroen, "Forecasting methods for load prediction in smart grids," Energy Reports, vol. 7, 2021.
Z. Zhao et al., "Deep learning for power grid applications," Journal of Modern Power Systems and Clean Energy, vol. 4, 2017.
H. Liu et al., “Reinforcement learning for dynamic power system management,” IEEE Control Systems Magazine, vol. 40, 2020.
P. Yang et al., "Metaheuristic optimization techniques for smart grids," IEEE Transactions on Smart Grid, vol. 7, no. 4, 2016.
S. Tan et al., “Hybrid ACO and PSO for power distribution optimization,” Electric Power Systems Research, vol. 120, 2019.
P. Sharma et al., “Linear programming approaches to power flow optimization,” IEEE PES Transactions, vol. 110, 2018.
A. M. Khaleghian et al., "Genetic algorithms in smart grid optimization," IEEE Trans. Ind. Appl., vol. 49, no. 4, 2013.
K. K. Gosavi et al., "A survey on PSO in power system optimization," Electric Power Systems Research, vol. 111, 2020.
C. Ling et al., "Differential evolution for power grid optimization: A survey," Renewable Energy Reports, vol. 22, 2019.

Figure 1. Flowchart of the Proposed DRL-PSO Optimization Framework

Figure 2. IEEE 33-bus distribution system.

Table 1. Performance metrics of optimization methods.

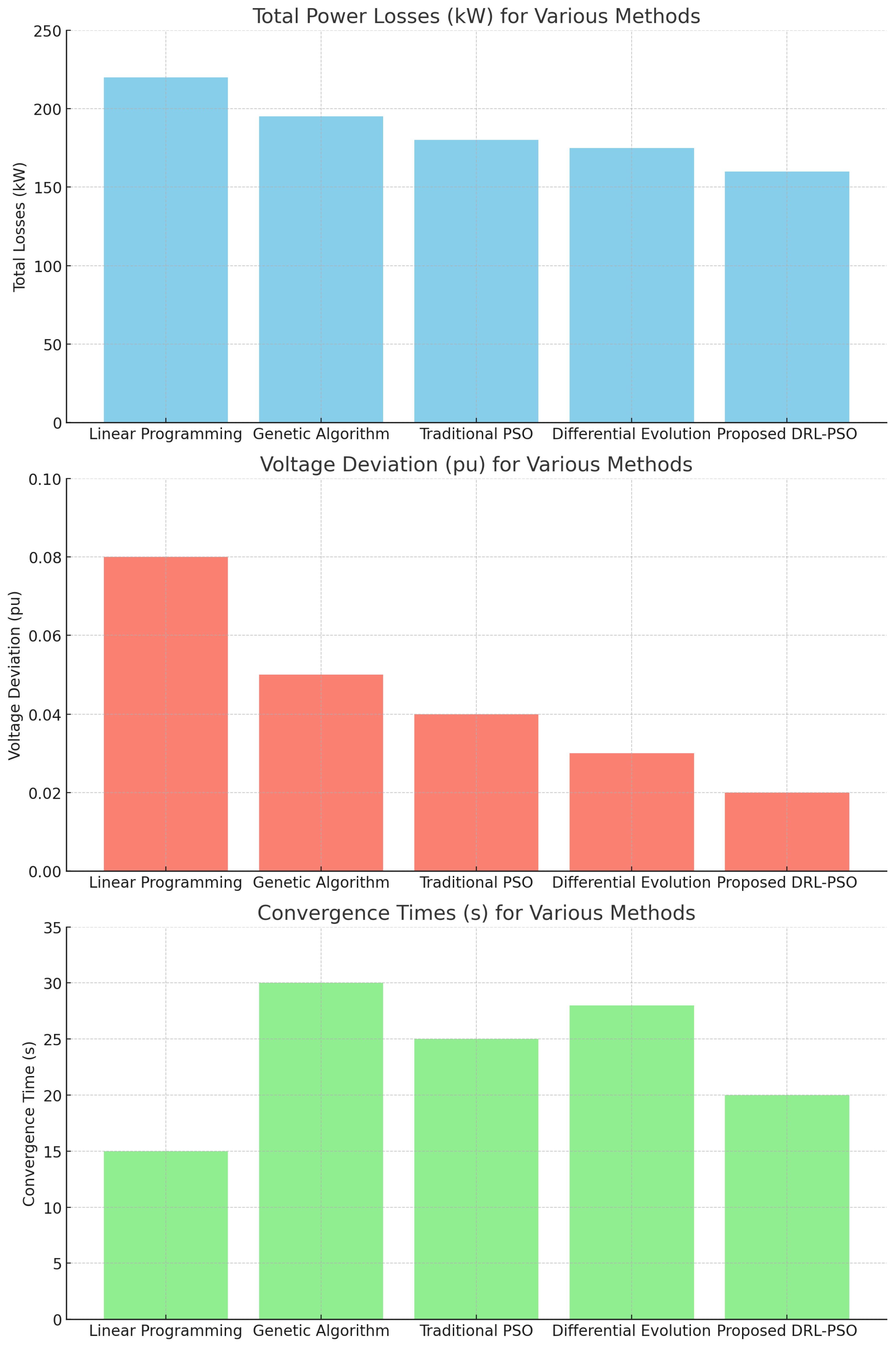
Method	Total Losses	Voltage Deviation	Reference
	(kW)	(pu)
Linear Programming	220	0.08	[25]
Genetic Algorithm	195	0.05	[16,26]
Traditional PSO	180	0.04	[17,27]
Differential Evolution	175	0.03	[18,28]
Proposed DRL-PSO	160	0.02	This work

Table 2. Computational metrics of optimization methods.

Method	Convergence	Algorithm	Real-time	Reference
	Time (s)	Complexity	Adaptability
Linear Programming	15	Low	Low	[25]
Genetic Algorithm	30	Medium	Medium	[16,26]
Traditional PSO	25	Medium	Medium	[17,27]
Differential Evolution	28	Medium	Medium	[18,28]
Proposed DRL-PSO	20	High	High	This work

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

DRL-PSO Powered Optimization for Efficiency Enhancement and Reliability Improvement in Smart Grids

Abstract

1. Introduction

2. Literature Review

2.1. Traditional Optimization Techniques

2.2. AI-Based Optimization Techniques

3. Proposed DRL-PSO Optimization Framework

3.1. Overview of the Proposed DRL-PSO

3.2. Mathematical Formulation

3.3. Constraints

3.4. Particle Swarm Optimization (PSO)

3.5. Deep Reinforcement Learning (DRL)

3.6. Hybrid DRL-PSO Algorithm Integration

4. Test System: IEEE 33-Bus System

4.1. Simulation Setup

4.2. Comparative Analysis

5. Conclusion

References

MDPI Initiatives

Important Links

Subscribe