Prerpints.org logo
Preprint
Article

A W-Band Real-Time Imaging Mini-SAR System for Unmanned Aerial Vehicles

This version is not peer-reviewed.

Submitted:

04 November 2024

Posted:

05 November 2024

You are already at the latest version

Abstract
The synthetic aperture radar (SAR) mounted on unmanned aerial vehicles (UAVs) can efficiently and rapidly acquire high-resolution geographic remote sensing data. However, the limited payload capacity and power consumption of UAVs present a challenge for the application of traditional SAR real-time imaging processing platforms based on DSP or GPU. In this paper, a real-time processor that utilizes the Xilinx Zynq Ultrascale+ZU9EG MPSoC is proposed and successfully applied to a W-band Mini-SAR system. Several essential technologies, including SAR data preprocessing, high-energy-efficient real-time processing, and lightweight motion compensation, are utilized to develop the real-time processing Mini-SAR for use in small UAVs. The total weight of the entire system is only 724 grams, and its power consumption is 38.3 watts. During the UAV flight test, the system is capable of producing SAR images with a resolution of 0.1 meters at a size of 4K x 4K in just 4.5 seconds. The discrepancy between the imaging results and the ground post-processing is less than 10-4.
Keywords: 
Subject: 
Engineering  -   Electrical and Electronic Engineering

1. Introduction

In recent years, advancements in UAV technology have led to the extensive utilization of various remote sensing payloads, including optical cameras, infrared sensors, and LiDAR systems, mounted on UAVs. They have played a significant role in environmental protection, agriculture, forestry, geological disaster monitoring, and other related fields.[1,2,3,4,5].
Synthetic Aperture Radar (SAR) employs microwaves for imaging detection and remains unaffected by clouds, fog, nighttime, and other low-light conditions. Simultaneously, it synthesizes the smaller real antenna aperture into a larger one by employing data processing techniques that take into account the relative movement of the radar and the target. SAR has an efficient antenna aperture that allows it to achieve high resolution. Because of this, SAR can be utilized on spaceborne, airborne, and UAV platforms. With the rapid development of small multi-rotor UAVs, restrictions on payload volume, weight, and power consumption have become increasingly stringent. This presents challenges for traditional SAR equipment in adapting to these changes. On the other hand, to accommodate the flexibility of UAVs, SAR needs to have real-time processing and imaging capabilities. However, SAR is a type of radar that necessitates extensive data processing. Its real-time processing encounters challenges in both algorithm design and resource consumption.
In response to research on the miniaturization of UAV-borne SAR, a series of micro-SAR products have been developed in recent years. Various types of products, ranging from kilograms to hundreds of grams, are suitable for fixed-wing UAVs, multi-rotor UAVs, unmanned helicopters, and other platforms [6,7,8,9,10]. In particular, a W-Band 3-D Integrated Mini-SAR, which was also the preliminary research result of our team in 2021, had a total volume of 67×60×50 mm³ and weighed 400 g. The system achieved a maximum resolution of 4.5 cm and was successfully captured using a DJI six-rotor drone [11]. However, this product is limited to gathering and storing raw data. The data must be exported on the ground after the flight is completed and subsequently undergo additional image processing. This process is time-consuming and impairs the maneuverability and flexibility of the UAV.
In the context of SAR real-time processing, various platforms utilizing different hardware architectures, such as FPGA, DSP, and GPU have been proposed in recent years to support a range of algorithms and application scenarios. The real-time imaging processing flow is implemented on the Virtex-7 FPGA using the chirp scaling (CS) algorithm. It takes 85.9 seconds to process an image with dimensions of 65,536 × 65,536 [12]. By simplifying the algorithm based on range-Doppler processing, the researchers utilized a 1 GHz clock DSP to process a 4k×4k size image for frequency-modulated continuous wave (FMCW) SAR, which took 2.78 seconds [13]. A real-time SAR processor has been developed using two FPGAs and six DSPs, which achieves a processing time of less than 500 milliseconds for a 1k×1k image utilizing the Range-Doppler Algorithm (RDA) [14]. Based on a similar FPGA and DSP parallel processing architecture, the CS algorithm is employed to process GF-3 SAR data, taking 24 seconds to generate a 16k×16k image [15]. A distributed SAR real-time imaging processing system has been developed using multiple embedded GPUs to process SAR images with a data size of 8k×8k on a single Jetson Nano platform. The system’s processing time is 5.86 seconds, and its actual power consumption is less than 5 watts [16]. The research findings indicate that there is currently no real-time SAR imaging system available for practical use in UAVs. The advantage of DSP lies in its optimization for handling digital signals, along with its powerful mathematical operations and data processing capabilities. However, the instruction set of DSP is relatively straightforward, offering limited programming flexibility. In situations involving high main frequency and significant computational load, the power consumption of the DSP tends to be relatively high. On the other hand, GPUs possess the advantage of parallel computing capabilities and high throughput, rendering them well-suited for processing large-scale data-parallel tasks. However, GPU memory resources are limited, and the overhead associated with management and scheduling is substantial. The advantages of FPGAs lie in their programmability, flexibility, and low latency. It is suitable for applications that have high real-time requirements. However, its development is challenging and necessitates proficiency in hardware description language programming.
Real-time imaging of SAR on micro UAVs presents several challenges. Firstly, the size, power consumption, and volume of the SAR payload must be significantly reduced. This necessitates heightened demands for system architecture, module development, and integrated assembly. Secondly, when resources are limited, real-time processing must consider the trade-off between data volume, processing speed, and processing efficiency. Developing this technology is challenging due to requirements such as processing accuracy and power consumption. At the same time, due to the challenges associated with equipping UAVs with high-precision inertial navigation systems, it is essential to utilize small, low-precision inertial navigation equipment for real-time calculation and compensation of motion errors.
This article offers a comprehensive introduction to a W-band real-time imaging Mini-SAR system, specifically designed for mounting on a UAV platform to facilitate flexible and rapid ground imaging. The primary objective is to redesign the system architecture for the W-band Mini-SAR, taking into account the requirements for real-time processing. Additionally, the radar unit requires an upgrade to facilitate data preprocessing and storage, thereby alleviating the burden of real-time processing. At the same time, the wavenumber domain algorithm (ω-k algorithm) has been optimized for real-time processing, allowing for high-speed performance on the Xilinx Zynq Ultrascale+ZU9EG MPSoC (Multiprocessor System-on-Chip). Finally, high-precision positional information is obtained using real-time kinematic (RTK) technology in conjunction with a Continuous Operational Reference System (CORS). Additionally, real-time high-precision motion compensation is achieved through SAR carried by a multi-rotor UAV.
The article is organized as follows: Chapter 2 primarily introduces the system architecture and performance indicators of the real-time imaging Mini-SAR system, while Chapter 3 emphasizes key technologies. First, the method for implementing data preprocessing on the radar unit is presented. Secondly, the algorithm optimization and hardware acceleration techniques for real-time processing are introduced. Next, we introduce a real-time motion compensation method for RTK integrated navigation that is based on a wireless mobile base station. Chapter 4 primarily presents the results of system integration and experimental verification, comparing them to existing real-time processing SAR systems.

2. System Design

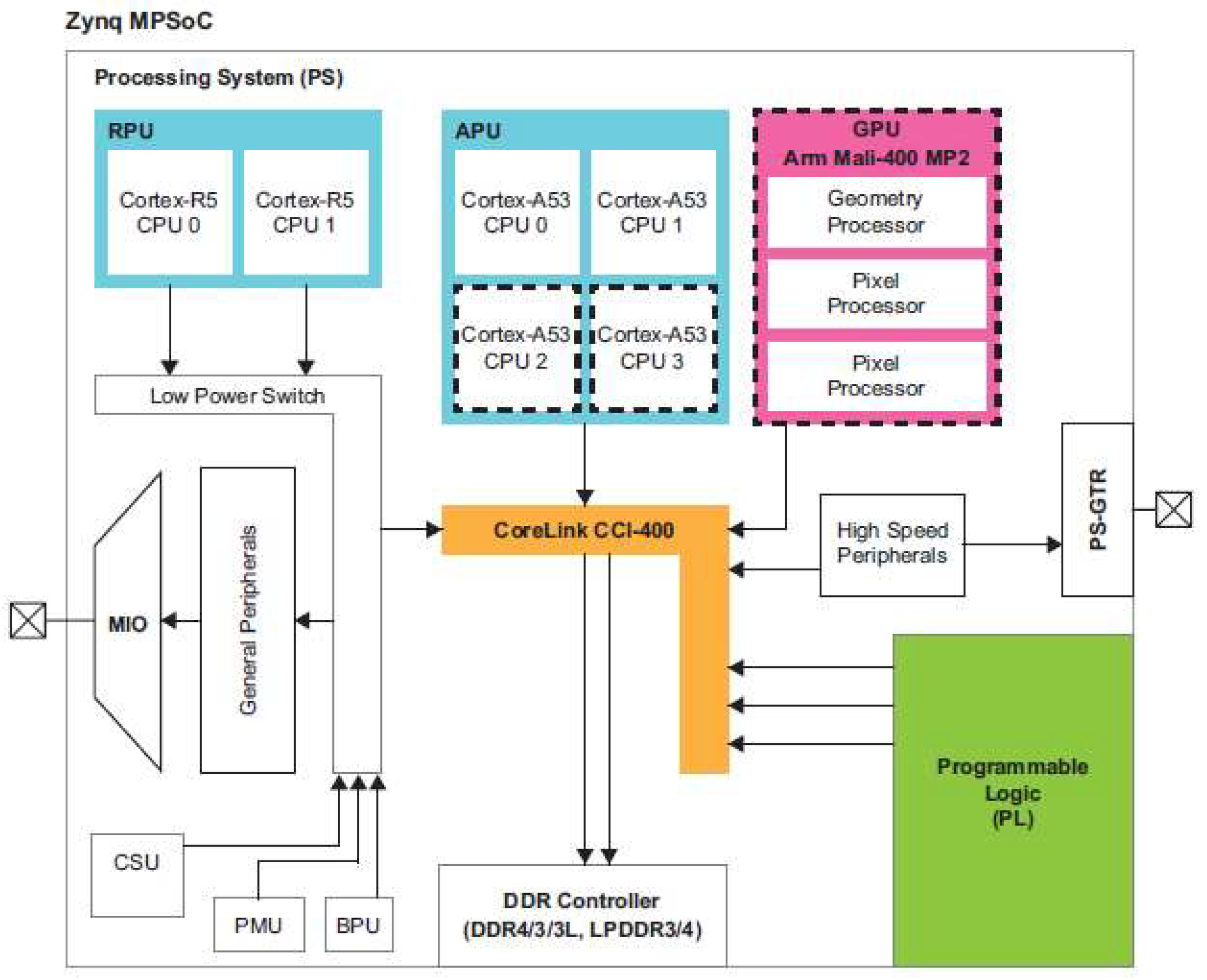
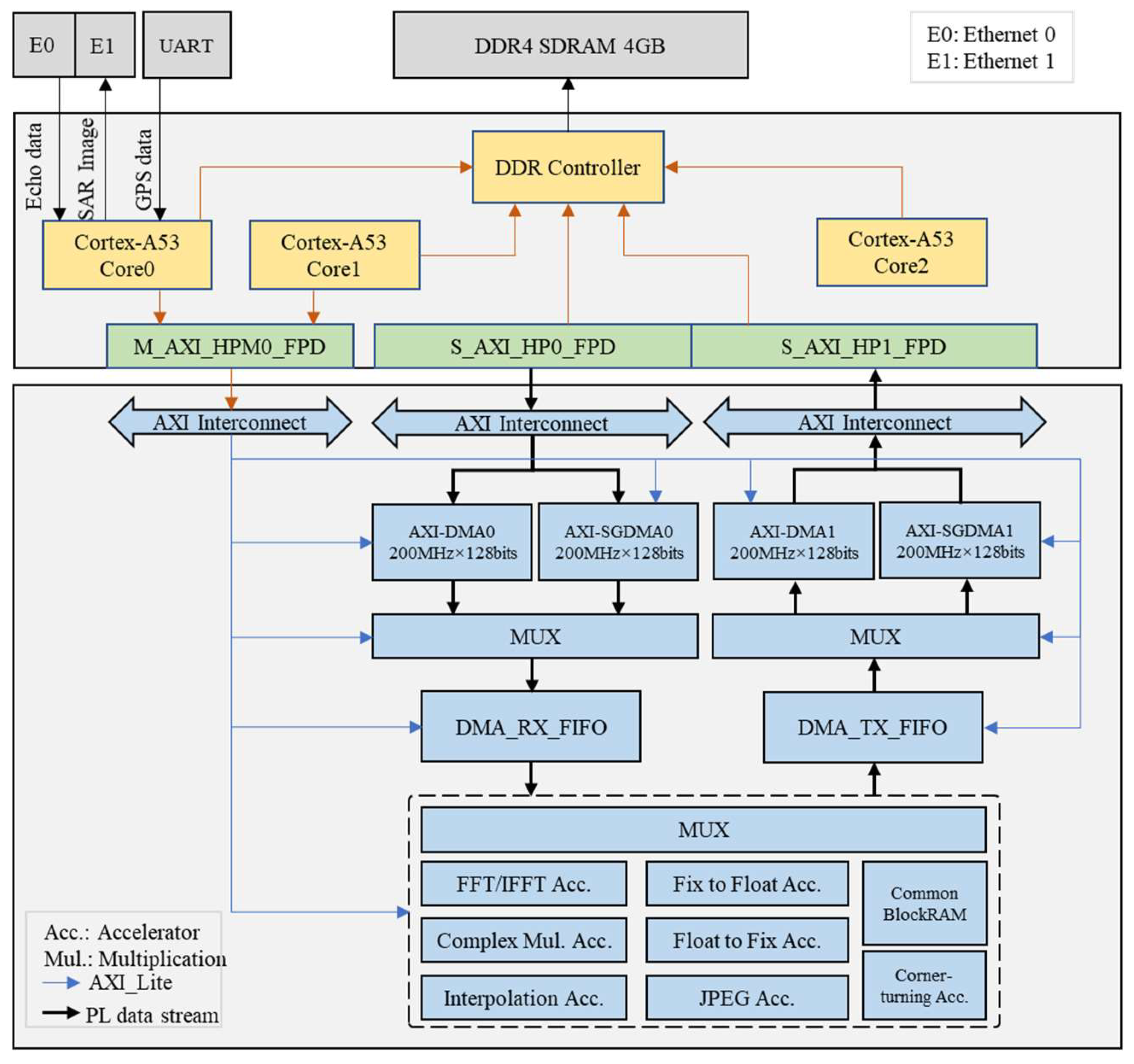
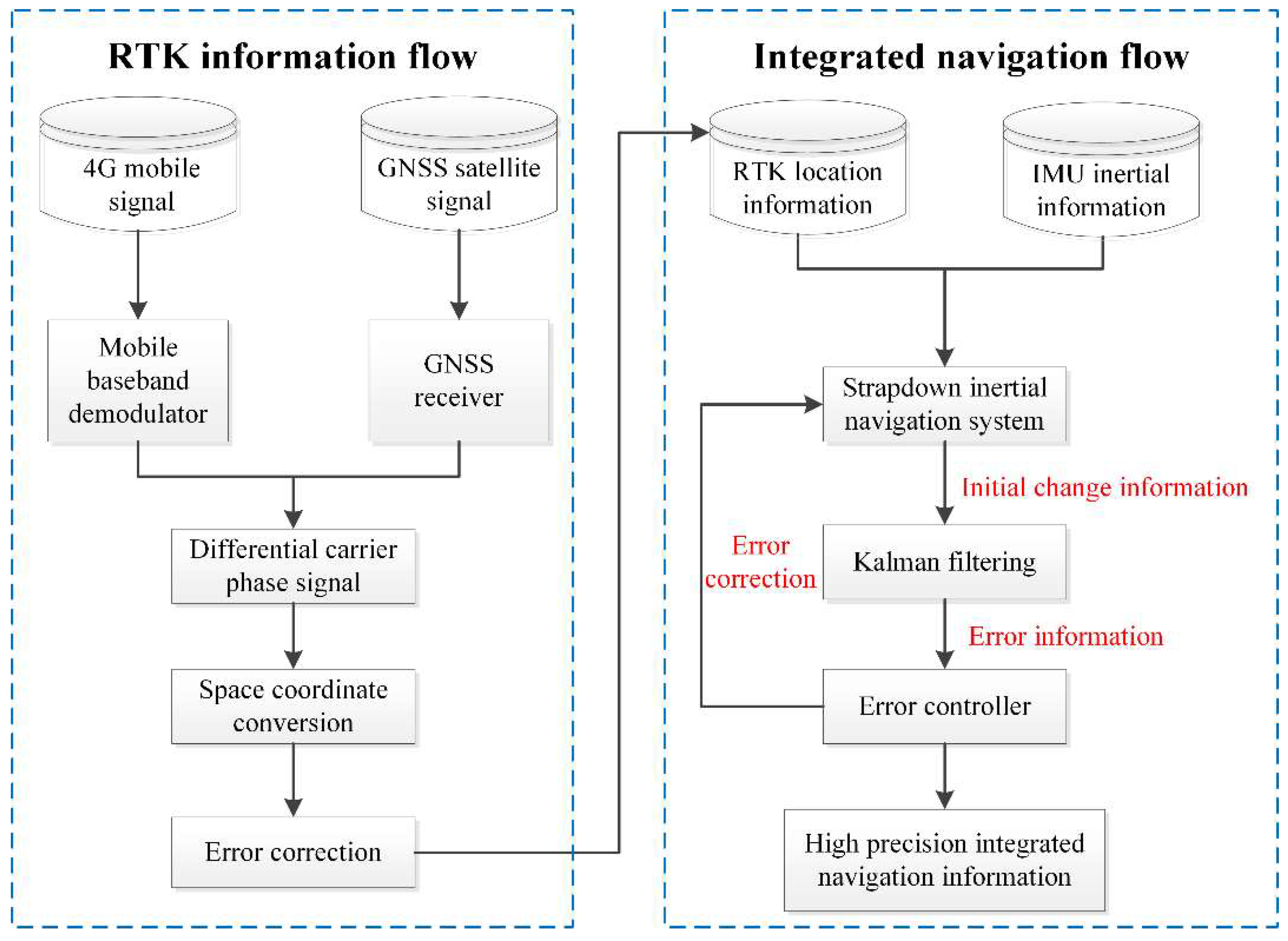
2.1. System Architecture for Real-Time Imaging Mini-SAR System

This paper proposes a lightweight, real-time processing Mini-SAR system, as illustrated in Figure 1. The system primarily consists of an integrated SAR radar unit, a real-time processor, a POS (Position and Orientation System) computing system (PCS) module, an RTK module, and an RF wireless module, along with supporting Inertial Measuring Unit (IMU), battery, and other ancillary equipment. The radar unit is responsible for transmitting, receiving, and preprocessing W-band radar signals. The real-time processor further processes and images the signals. The PCS module generates integrated navigation data in real-time by utilizing information from the IMU and RTK modules, subsequently providing it to the real-time processor. The RTK module delivers real-time, high-precision differential positioning information.
The radar unit has been optimized and enhanced based on our team’s prior work with the W-Band 3-D Integrated Mini-SAR (Mini-SAR) [11]. The Mini-SAR is a radar system that utilizes a single transmitter and receiver, operating on the Frequency Modulated Continuous Wave (FMCW) principle. The system comprises chirp signal generation based on PLL (Phase-Locked Loop) technology, a W-band transceiver channel, a high-isolation dielectric slot radiation antenna, an intermediate frequency receiving module, a digital acquisition and storage module, and a GNSS (Global Navigation Satellite System) receiver. The Mini-SAR is responsible for W-band signal generation, radiation, reception amplification, acquisition, and storage. Through high-density three-dimensional integration, the system has successfully reduced both its volume and weight. At the same time, to alleviate the burden of processed data, we have enhanced the capabilities of the radar unit’s FPGA. It now performs both radar control and preprocessing functions, rather than solely control functions. Through preprocessing functions, the data rate of the FMCW radar system is reduced by intercepting and extracting raw data.
The processing unit consists of a real-time processor, a PCS module, an RTK module, and an RF wireless module. These components collaborate to process radar data efficiently, facilitating rapid imaging and downloading. At the same time, integrated navigation data is generated using the acquired position and attitude information to apply motion compensation to SAR images.
The real-time processor performs SAR imaging processing on the preprocessed radar data and integrated navigation data. It also compresses the images and transmits them to the ground station via the RF wireless module.
The PCS module is primarily developed using DSP technology. The system utilizes attitude data from the airborne Position and Orientation System (POS) and position information from Real-Time Kinematic (RTK) technology to acquire real-time, precise motion status of the radar within the geographical coordinate system. This encompasses position, speed, and attitude, providing integrated navigation for SAR imaging. The data supports the real-time processor in executing motion compensation.
The RTK module utilizes the network differential RTK mode to obtain differential information via a wireless communication network and GNSS receiver for accurate positioning applications. The nominal positional accuracy level is approximately 2 centimeters, while the elevation accuracy is 5 centimeters.
Radar data is transmitted over Ethernet. Among them, the data transmission between the radar unit and the real-time processor utilizes a Gigabit network. The real-time processor and the RF wireless module, which are connected to the ground host computer, are linked via a 100-megabit network. This connection is primarily utilized for transmitting SAR images and for controlling the system.

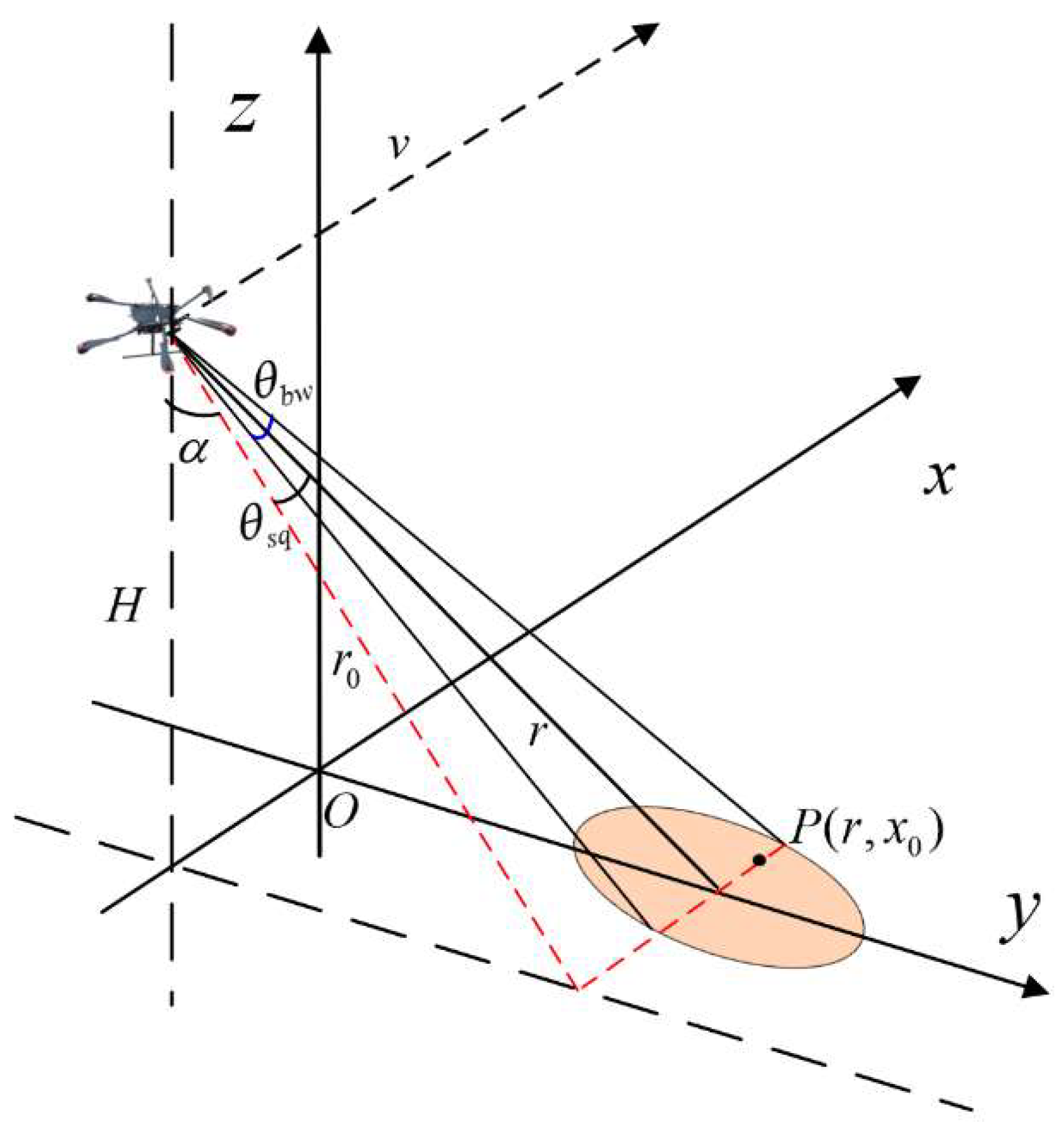
2.2. System Performance Indicators

Table 1 presents the primary performance indicators of the real-time imaging Mini-SAR system, including center frequency, maximum bandwidth, beam width, range, resolution, real-time processing image size, processing delay, image quality comparison error, volume, weight, and power consumption.
In reference [11], the radar unit and imaging parameters of the Mini SAR have been designed and tested. This includes the operating frequency band, operating range, resolution, and other specifications, all of which have remained unchanged. This article primarily focuses on the research design and experimental validation of data processing and real-time imaging following digital acquisition.

3. Key Technologies

3.1. Data Preprocessing Algorithm

Although the FMCW SAR system has reduced the sampling rate requirements through the process of dechirping, the actual data rate remains relatively high. The Mini-SAR described in this paper operates at a sampling frequency of 50 MHz and has a raw data rate of 800 Mbps, which places significant demands on lightweight real-time processing. Therefore, it is essential to preprocess the raw data. In the design of preprocessing algorithms, two primary considerations were emphasized. Firstly, the algorithm must efficiently compress SAR echo data to meet the requirements of RF wireless module transmission, while minimizing the loss of SAR echo image features to ensure high imaging quality. Secondly, the processing algorithm is designed to be concise, minimizing complex calculations to facilitate implementation on basic hardware configurations.
The methods and steps for data preprocessing and compression are based on the team’s previous research in this field [17]. By utilizing SAR’s established operating frequency band, beamwidth, sampling rate, motion speed, and other parameters, along with the compressed image size requirements, the raw data undergoes operations such as extraction, interception, and data reduction. Through actual flight test data, this method achieved a nearly 20-fold reduction in data rate without compromising image quality, effectively alleviating the burden of subsequent real-time image processing.

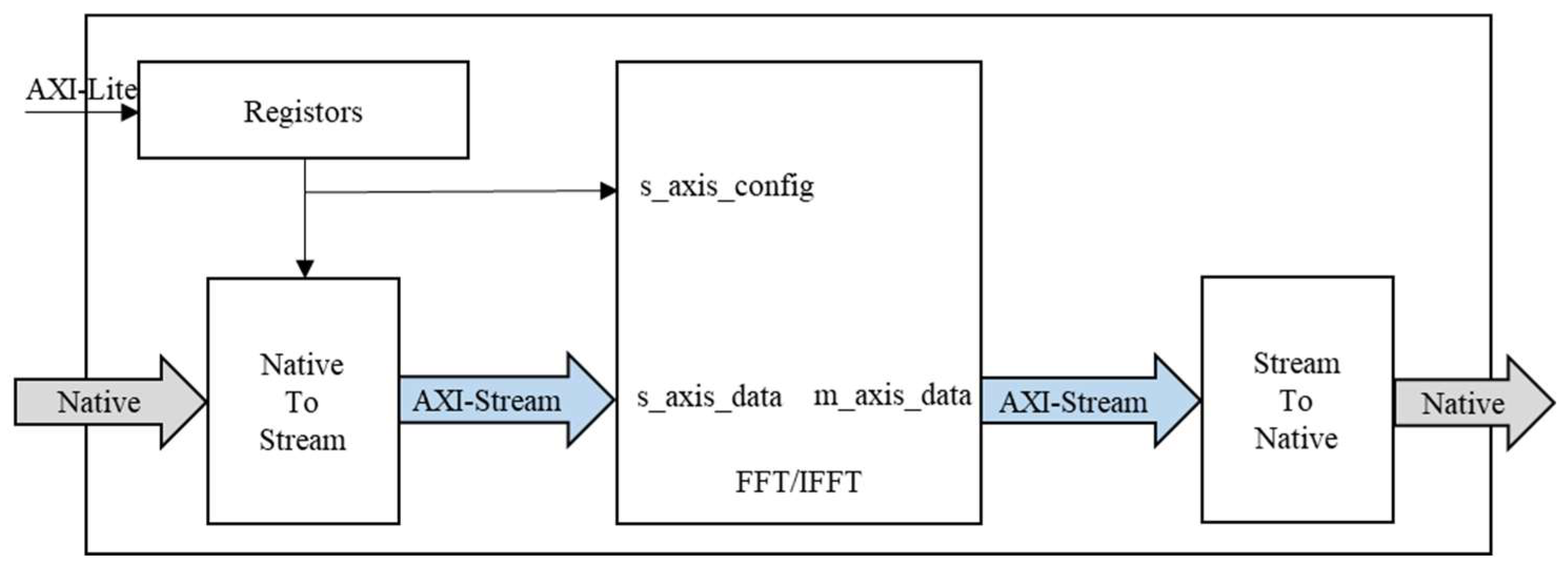
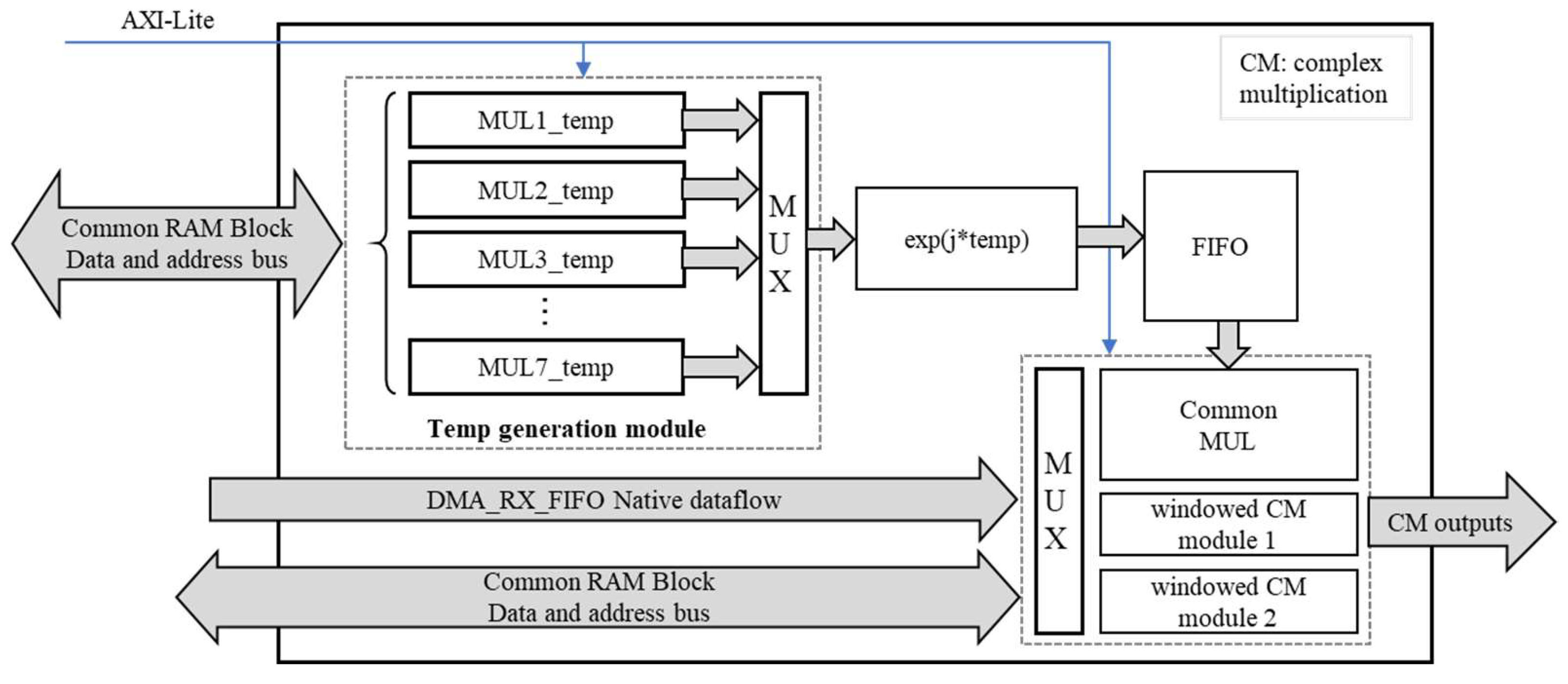
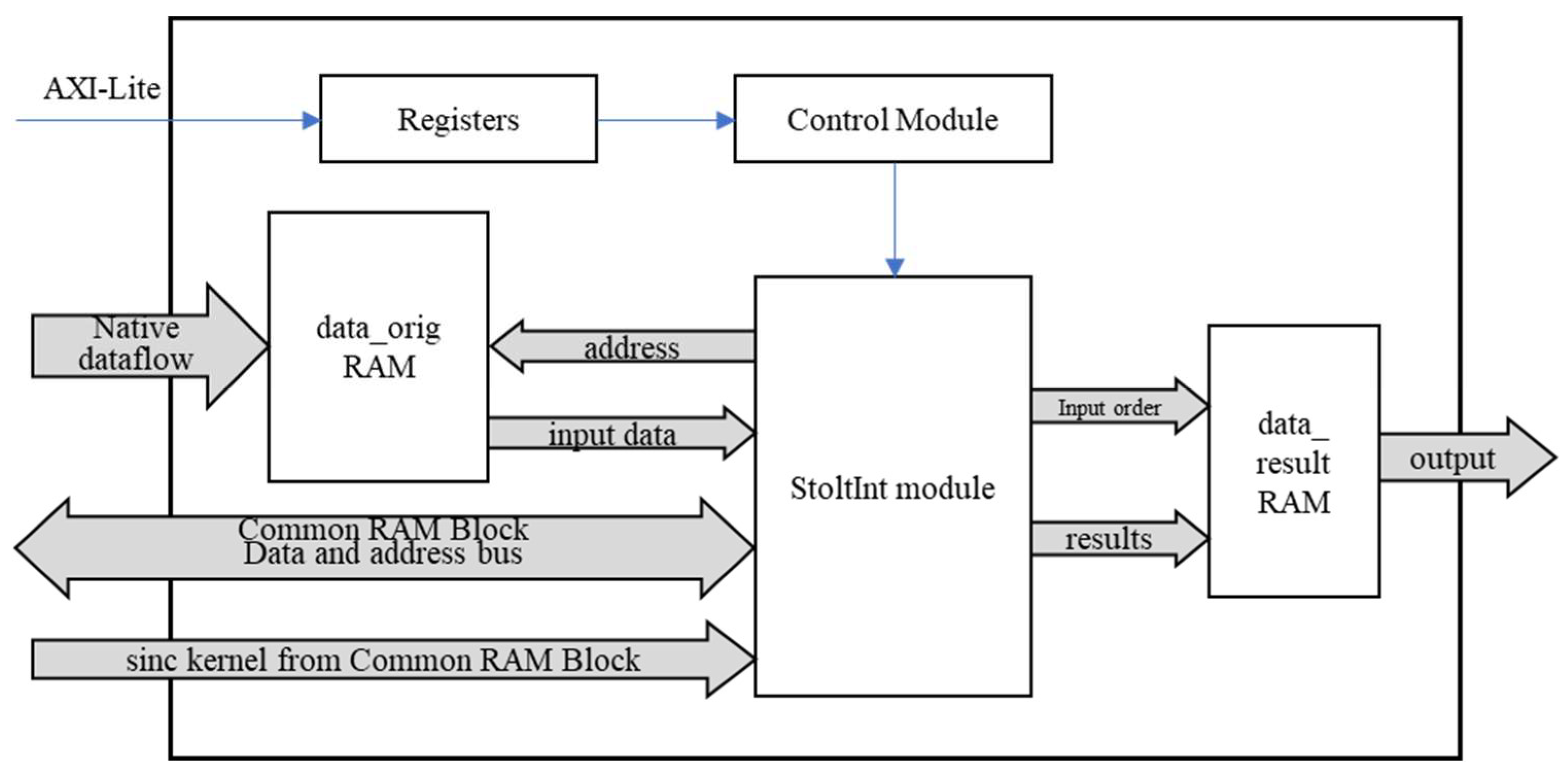
3.2. Real-Time Processing Algorithms and Hardware Acceleration

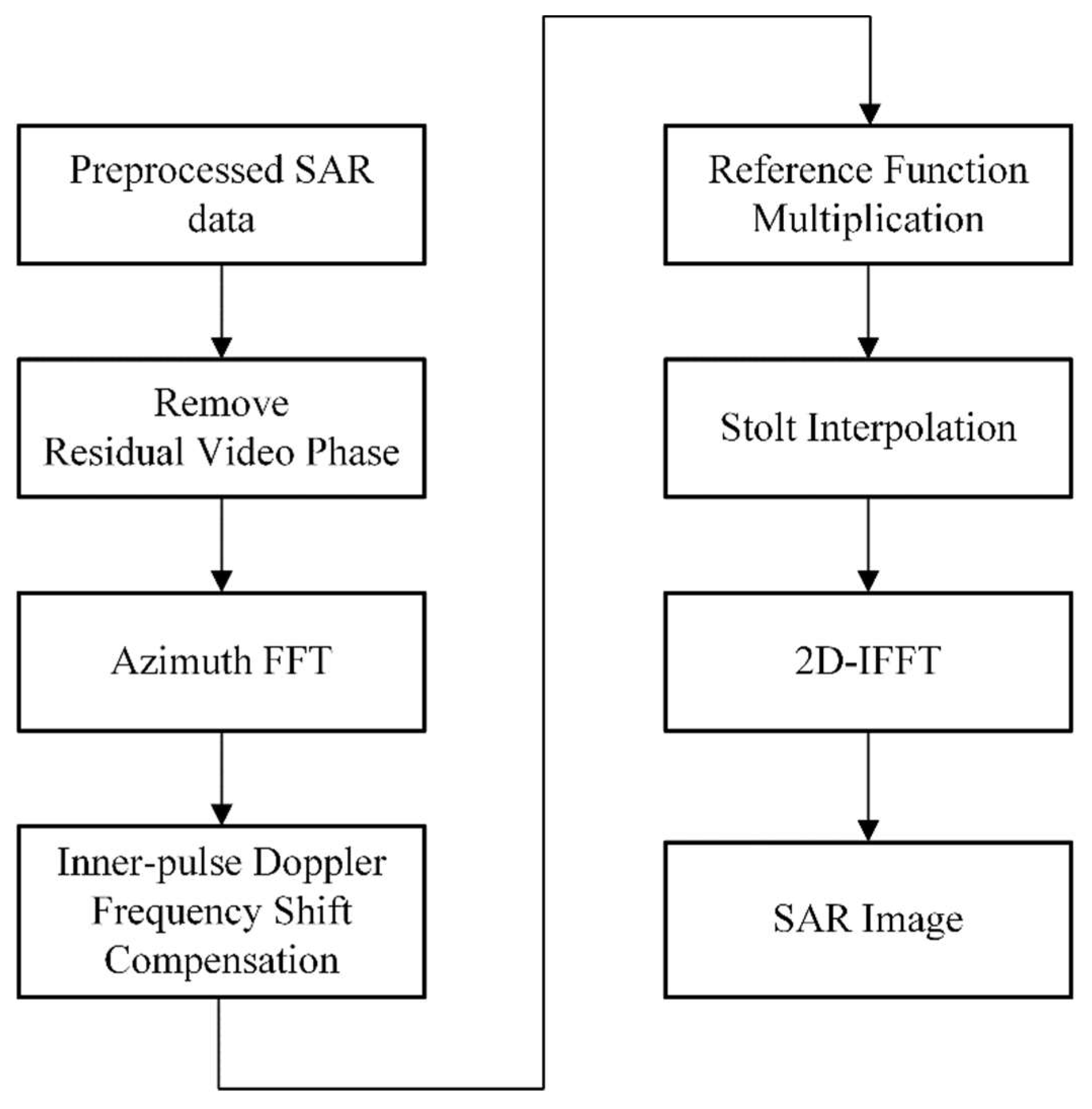
3.2.1. Principles and Structural Analysis of the ω-k Algorithm

The imaging geometry of the UAV SAR is illustrated in Figure 2, where r 0 is the minimum slant range, r is the distance from the antenna phase center (APC) to the scene center, α is the view angle, θ s q   is the squint angle, and   θ b w .is the beamwidth. Considering a target located at P ( r , x 0 ) , we can derive its instantaneous range R t as follows:
R t = r · cos ⁡ θ s q 2 + r ∙ sin ⁡ θ s q + x 0 − v t 2
where x 0 represents the ground distance from the target to the scene center and v is the forwarding velocity of the UAV.
The UAV SAR continuously transmits a linear frequency-modulated signal and receives the returned signal in dechirp mode. The transmitted signal can be expressed as:
s t t = exp ⁡ j π k t 2 + 2 f c t
where k represents the chirp rate, f c represents the central frequency of the transmitted chirp signal, and t represents the time. For simplicity, the amplitude is disregarded.. After dechirp reception of the transmitted signal, the dechirped signal from a point target P can be represented as:
s i f t = exp ⁡ ( j 2 π f c τ + j 2 π k τ t − j π k τ 2 )
where τ = 2 r / c represents the time delay of the target signal, and c is the speed of light. The final term is the Residual Video Phase (RVP) from the dechirp operation, which can be eliminated by multiplying by an RVP coefficient. After removing the RVP, the signal changes to:
s i f t = exp ⁡ ( j 2 π f c τ + j 2 π k τ t )
Define K r = 4 π f c + k t r / C as the range wavenumber, K x = 2 π f a v as the azimuth wavenumber, and X = v t as the azimuth position. Then the Equation (4) takes the following form in the wavenumber domain:
s K r , X = e x p − j K r R t
By performing the azimuth Fast Fourier Transform (FFT) and applying the principle of stationary phase (POSP), the signal in the range-azimuth two-dimensional wavenumber domain is obtained:
S K r , K x = ∫ e x p − j K r r c o s θ s q 2 + x + v t r − r s i n θ s q 2 − j K x X d X = e x p − j K r 2 − K x 2 c o s θ s q + K x s i n θ s q r + j K x v t r
The last term denotes the Doppler frequency shift induced by inner-pulse moving, which can be eliminated by multiplying a coefficient: H d o p ( K x ) = − j K x v t r . After compensating for the Doppler frequency shift, the signal can be expressed as follows:
S 1 K r , K x = e x p − j K r 2 − K x 2 c o s θ s q + K x s i n θ s q r
Taking the distance from APC to the scene center as the reference distance, r r e f , and the reference function can be constructed as:
H r e f K r , K x = e x p j K r 2 − K x 2 c o s θ s q ⋅ r r e f
H r e f K r , K x is multiplied by S 1 K r , K x to accomplish residual range migration correction (RCM) and azimuth compression, in order to obtain focused signals at the reference distance within the 2D frequency domain, as shown in Equation (12).
S 2 K r , K x = S 1 K r , K x × H r e f K r , K x = exp ⁡ − j K r 2 − K x 2 cos ⁡ θ s q ( r − r r e f ) − j K x sin ⁡ θ s q r
For cells located within other ranges, Stolt interpolation is applied to Equation (9) to achieve fully focused processing, as shown below:
S 3 K x , K y = exp ⁡ − j K x sin ⁡ θ s q r − j K y cos ⁡ θ s q ( r − r r e f )
where K y = K r 2 − K x 2 represents the vertical component of K r in the wavenumber domain. After applying the 2-D inverse FFT to Equation (10), the fully focused SAR image in the time domain is produced. The ω-k algorithm flowchart for real-time processing is depicted in Figure 3.

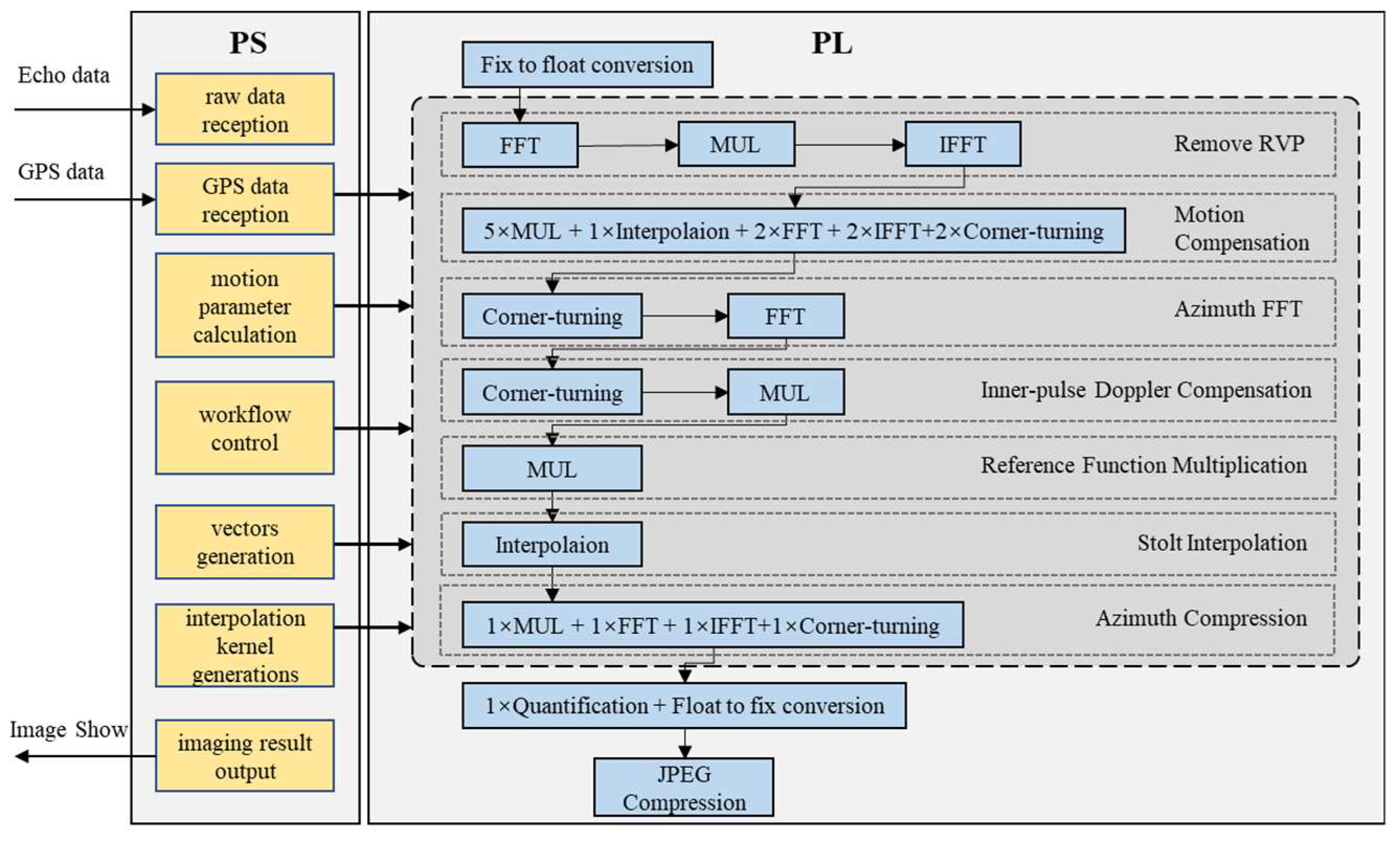
3.2.2. SAR Real-Time Processing on MPSoC

The real-time processing of UAV-SAR is implemented on the Xilinx Zynq Ultrascale+ZU9EG MPSoC. As illustrated in the architecture depicted in Figure 6, the MPSoC mainly consists of an ARM processing system (PS) and programmable logic (PL). The PS consists of four Cortex-A53 cores operating at speeds of up to 1.5 GHz and two real-time Cortex-R5 cores functioning at speeds of up to 600 MHz. This configuration is especially well-suited for high-accuracy, complex tasks. The PS supports general peripheral connectivity, including UART, SPI, and I2C, through the Multiplexed Input/Output (MIO) interface. The high-speed serial interface is facilitated by the Serial Input/Output Unit (SIOU) block, which supports various interface protocols, including PCIe, USB 3.0, DisplayPort, SATA, and Ethernet. The PL mainly consists of logic resources, such as a FPGA which is more suitable for high-speed, repetitive tasks. The integration of PS and PL can fully leverage the benefits of high precision, flexible adaptability, and configurability for complex tasks provided by the PS, along with high throughput and parallel processing capabilities offered by customized hardware in the PL. The PS and PL are interconnected by multiple groups of interconnects that comply with the Advanced eXtensible Interface (AXI) specification outlined in the ARM Advanced Microcontroller Bus Architecture (AMBA) standard. The AXI interactions between the PS and PL support the AXI4, AXI4-Lite, and AXI4-Stream protocols, with a maximum bit width of 128 bits and a maximum line rate of 250 MHz. This configuration provides a transmission bandwidth of more than 3.2GB/s in total.
1) Algorithm Partitioning. To efficiently implement the ω-k algorithm illustrated in Figure 4, it is essential to partition the algorithm into components that are favorable for hardware and software. Computations that involve low density but complex decision-making are better suited for execution on the PS without requiring specialized hardware design. Conversely, computations characterized by high computational density, which are amenable to parallelization, greatly benefit from the implementation of hardware acceleration.
Figure 5 illustrates the partitioning strategy of the ω-k algorithm on the MPSoC. To account for the non-uniform linear motion of the flight platform, a motion compensation module has been integrated into the processing workflow. The entire calculation process is divided into modules according to their mathematical operation types and functionalities. Low-density, high-complexity computations namely small batch computing, such as workflow control, motion parameter calculation, vector generation for complex multiplications, interpolation kernel generation, raw data and GPS data reception, and imaging result output, are assigned to the PS end to fully leverage its flexibility and reduce debugging time. Meanwhile, operations with high computational density namely large batch computing, such as large-scale complex multiplication, interpolation, FFT/IFFT, corner-turning, etc., are designed into hardware accelerators in the PL to achieve pipelined parallel computing.
2) Algorithm Implementation on MPSoC. According to the algorithm partitioning strategy outlined above, a real-time processing implementation of the Mini-SAR based on MPSoC is proposed, as illustrated in Figure 6. The PS side operates in a bare-metal environment and utilizes the Asymmetric Multiprocessing (AMP) approach to facilitate multi-core operation. Each core is equipped with dedicated memory, while shared memory is utilized for inter-core communication.
In our design, the Cortex-A53 core 0 is designated as the primary core responsible for system initialization and workflow management. The main core is equipped with two Gigabit Ethernet interfaces and one UART interface. One Ethernet port is designated for receiving raw data, while another port is utilized for outputting imaging results. The Universal Asynchronous Receiver-Transmitter (UART) is utilized for receiving GNSS data. The Cortex-A53 core 1 and Cortex-A53 core 2 are configured as the slave cores. Core 1 manages small batch computing and initiates DMA transfers, while Core 2 is responsible for DMA reception.
On the PL side, the algorithm’s large batch computing units, such as FFT, complex multiplication, Stolt interpolation, and corner-turning, are designed as hardware accelerators. The accelerators utilize a fully pipelined design that is parameterized, configurable, and capable of supporting single-precision floating-point operations. During real-time processing, the raw data and intermediate results are stored in the DRAM on the PS side. To configure and invoke the accelerators, one master port and two slave ports are selected. Additionally, two sets of AXI-DMA, along with several MUX modules, are initialized to facilitate data exchange between the PS and PL. Core1 in the PS is responsible for controlling the reading and writing of registers in the MUX and accelerators through AXI-Lite via the master port. It facilitates the switching and selection of DMA data paths, along with the configuration of parameters for the accelerators. Two slave ports are utilized for transmitting and receiving parameter vectors, kernel vectors, and imaging data. When transferring data to the target accelerators, the two sets of AXI-DMA operate in simple mode and Scatter/Gather (SG) mode, respectively. They utilize the AXI4-Stream interface, which allows burst transfers of unlimited size. The SG mode is specifically designed for corner-turning, as it supports the efficient transfer of 2-D memory access patterns using an AXI4-Stream channel. In addition, a standard RAM block is designed to cache parameters and kernel vectors, and it is shared among the accelerators to improve the utilization of on-chip RAM resources. A First-In-First-Out (FIFO) buffer is implemented on both the sending and receiving paths of the AXI4-Stream to enable high-speed data caching and protocol transformation.
In the implementation design, the accelerators function as callable entities within the PS. The algorithm flow within the PL, as illustrated in Figure 8, demonstrates that the FFT/IFFT, complex multiplication, interpolation, and corner-turning operations are executed 25 times out of a total of 28 during the entire process. These operations account for nearly 90% of the processing time for PL. Thus, the design of these key accelerators is illustrated below:
a) FFT/IFFT Accelerator. The algorithm requires five FFT calculations and four IFFT calculations, all of which can be performed using a single accelerator. In this design, the FFT/IFFT accelerator is implemented using the IP core from Xilinx, which leverages its runtime reconfigurability for both forward and inverse FFTs, supporting transform lengths of up to 65,536 points. The FFT IP core is configured to operate in block floating point mode with adaptive scaling, managed by the PS through AXI-Lite. It has a default transform length of 4,096 points, supporting both FFT and IFFT. To achieve faster computing speeds and higher throughput, a pipelined computing architecture is utilized. This structure entails the continuous transmission of raw data through the data input port and the reception of calculated results at the data output port. The schematic diagram of the FFT/IFFT accelerator is as depicted in Figure 7. Due to the requirement of the AXI-Stream protocol for data flow in the input and output ports of the FFT IP, protocol conversion wrappers implemented with AXI4-Stream Data FIFO IP are added at the input and output of the FFT IP to convert protocols between Native and AXI-Stream.
b) Complex Multiplication Accelerator. The algorithm involves a total of nine complex multiplication calculations. This includes two-window complex multiplications in the motion compensation step and seven complex multiplications in other steps. The schematic diagram of the complex multiplication accelerator is illustrated in Figure 10. For the two-window complex multiplications, the parameter vector is calculated by the PS and transmitted to the common RAM block. The original data and windowed parameters are continuously read at the PL end to facilitate pipelined windowed complex multiplication calculation. For the remaining seven complex multiplications, they can be uniformly represented as:
e x p ( j × t e m p ) × d a t a _ o r i g
Where j is the imaginary unit, t e m p represents a coefficient to be solved, and d a t a _ o r i g represents the original data or intermediate data during processing. In these complex multiplications, only the process of generating the t e m p values differs, while all other calculations remain unchanged. Therefore, the architecture of the complex multiplication accelerator is designed as depicted in Figure 8, with e x p ( j × t e m p ) and complex multiplication (referred to as CommonMUL module) as reusable computing resources, and the seven t e m p generation modules as independent computing resources, achieving efficient utilization of computing resources.
When executing each of the seven calculations, the t e m p generation module continuously reads the parameter vectors from the shared RAM block and performs pipeline calculations with a total of 4k×4k points. It transmits the t e m p value through MUX in order to calculate the value of the trigonometric function and store it in the synchronous FIFO. Furthermore, the values in the FIFO and the data in the DMA_TX_FIFO are read simultaneously and passed to the CommonMUL module to complete the corresponding complex multiplication operation in the algorithm process.
c) Stolt Interpolation Accelerator. The interpolation is implemented using a sinc interpolation kernel that utilizes a sinc function with 16,384 × 8 points in single-precision floating-point format. The sine interpolation kernel is precalculated on the PS side, and a Kaiser window is applied to mitigate the ringing phenomenon caused by the Gibbs effect. The kernel is then transmitted to the shared RAM block through DMA. On the PL side, the sine interpolation coefficients are determined by referencing a table. This interpolation method eliminates the need to calculate the sinc function, Kaiser window, and normalization factor for each interpolation point, thereby significantly reducing the consumption of hardware computing resources. The structural diagram of the interpolation module is presented in Figure 9. To facilitate pipeline computing, the raw data from the DMA_RX_FIFO is stored in the d a t a _ o r i g RAM frame by frame using a ping-pong method.. After the complete frame data has been cached, the interpolation calculation for the current frame is activated. The StoltInt module continuously transfers the addresses of the parameter vector to the common RAM block to retrieve the necessary parameter vectors for calculations. By continuously generating the original point coordinates and the row addresses of the sinc interpolation kernel using the parameter vectors, the system transfers the original point addresses to origRAM to obtain continuous 8-point raw data. Simultaneously, it transfers the row addresses of the sinc interpolation kernel to the common RAM block to acquire continuous 8-point sinc interpolation coefficients. Finally, the 8-point raw data and the 8-point sinc interpolation coefficients are multiplied and summed to produce the interpolation results.
d) Corner-Turning Accelerator. The corner-turning accelerator primarily utilizes the AXI-DMA operating in scatter-gather (SG) mode, which enables efficient 2-D memory access and a SRAM block. In the design, the 4k×4k data matrix, with its initial address, is divided into 4,096 smaller matrices, each containing 64×64 points. Each small matrix is written into the cache SRAM row by row and read out column by column using logical control in the PL. After the iteration, the entire process results in a 4k × 4k matrix corner-turning.

3.3. Lightweight and High-Precision Real-Time Motion Compensation System

Due to their lightweight design, multi-rotor UAVs are particularly vulnerable to interference from variations in airflow. This can lead to fluctuations in position and attitude, as well as variations in speed, which may affect the quality of SAR imaging. The integrated navigation of IMU and GNSS for motion compensation in SAR imaging is currently a widely adopted method. However, GNSS single-point positioning typically exhibits considerable error, usually at the meter level. In contrast, differential positioning necessitates the establishment of ground-based reference stations and the real-time upload of data, which is limited by constraints related to timeliness and coverage.
We aimed to transition from the traditional “mobile station on board + fixed stations on the ground” mode to a more efficient differential positioning mode based on RTK module. This was accomplished using the DOVE-E4Plus network differential RTK module, produced by Qianxun Spatial Intelligence Inc. The RTK module acquires differential observation data through a 4G mobile network and subsequently transmits it to the GNSS board via a serial port. The board processes the RTK positioning data by utilizing the differential observation data received from the CORS and subsequently transmits the processed information. The system processes relevant data using the NMEA-0183 protocol. As a result, centimeter-level, high-precision location information can be obtained in real time within a wireless communication environment, eliminating the need to establish additional base stations.
The DSP-based PCS module generates integrated navigation data in real time. First, the attitude calculation is performed using the angular velocity data provided by the IMU. The specific force measured by the accelerometer is then converted into acceleration within the navigation coordinate system. An integral operation is performed to calculate the system’s speed of motion, followed by another integral operation on the system’s velocity to determine its movement within the navigation coordinate system. The position within the navigation coordinate system. When the GNSS output is detected, the speed and position information obtained from the strap-down inertial navigation solution are subtracted from the data provided by the GNSS. This difference serves as the observation value for Kalman filtering. The estimated system error includes positional error, velocity error, attitude error, and sensor error. Error correction is applied to each module of the strap-down inertial navigation system to compensate for these errors, suppress error accumulation, and produce high-precision integrated navigation data. This process effectively mitigates errors in strap-down inertial navigation systems. The entire procedure for generating integrated navigation data is illustrated in Figure 10.
Considering the extremely short wavelength of W-band SAR and its narrow beam, any jitter in the UAV platform may result in the beam to deviate from the designated coverage area. Consequently, even if there is an error in the measurement of inertial navigation data, compensating for the loss of energy exposure will be challenging. Therefore, it is advisable to position the radar and IMU within the gimbal to ensure a stable illumination angle.

4. Results

A complete set of W-band real-time imaging Mini-SAR has been developed, as illustrated in Figure 11. Its size, weight, and power consumption (SWaP) are detailed in Table 2. The total weight of the SAR radar unit, real-time processor, PCS, and RTK is 724 grams, with a power consumption of 38.3 watts. Although GNSS/4G antennas, IMU, and cables will still contribute some weight, they can be integrated with UAVs in the future without necessitating additional resources.
The real-time processing Mini-SAR system has been successfully integrated into a six-rotor UAV. The radar unit and IMU were mounted on a one-dimensional gimbal to facilitate range-direction compensation. The real-time processor, PCS, and RTK module have been installed in the integrated enclosure. The UAV is equipped with a GNSS antenna and a 4G antenna mounted on its top. The radar is powered by the battery of the UAV. The assembly of the devices on the UAV is illustrated in Figure 12.
Subsequently, a SAR flight test was conducted. During the flight, the SAR’s downward viewing angle was set to 30°, the flight speed was 5 m/s, and the altitude was 110 m. The chirp signal was set to a center frequency of 94 GHz, a bandwidth of 4 GHz, and a pulse width of 1000 µs, resulting in a PRF of 1 kHz. The radar operates using a strip imaging model, with an imaging width of approximately 116 m. The radar data is processed in real time by the onboard processor and converted into JPEG images, which are then transmitted to the ground host via the RF wireless module. At the same time, radar data and integrated navigation data will be stored in the SAR unit. When the UAV lands, its data can be transferred via Ethernet for post-processing and compared with real-time processed images.
The real-time SAR imaging results are presented in Figure 13(a). The imaging area measures approximately 450 meters by 116 meters, and four consecutive real-time images were selected for stitching. Some typical terrain features, such as storage tanks, houses, trees, and railway tracks, are visible. A comparison with the satellite optical image from Google Maps is presented in Figure 13(b). It can be observed that the SAR image generally aligns with the optical image in terms of overall shape; however, it differs in specific details.
In another experiment, real-time image processing on the UAV was compared with ground-based post-processing of images. The real-time processing utilized preprocessed echo data and navigation data generated by onboard RTK, while the ground post-processing utilized the original radar echo data and the differential navigation data from ground base stations, along with the same IMU data. The results of the processing are illustrated in Figure 14. Post-processed images surpass real-time processed images in terms of detailed texture and edge brightness, owing to variations in data integrity and RTK results. However, there is no significant difference in typical targets, such as houses and vehicles.
To evaluate the real-time imaging capability, the hardware utilization and execution time are analyzed first. A performance evaluation method is proposed, and the corresponding evaluation results are compared with those of other designs.
The hardware utilization of the MPSoC is presented in Table 3. In total, the hardware design requires 56.2% of the Look-Up Tables (LUTs) and 42.1% of the Block RAM. From the table, it is evident that the majority of the LUTs are utilized for multiplication and interpolation, while most of the Block RAM is allocated for corner-turning and common Block RAM functions. It is noteworthy that the single FFT module requires over 8,000 LUTs and is reused nine times. It is a similar case with the corner-turning and Common Block RAM modules. The design and reuse of the FFT module and the Common BlockRAM significantly reduce the overall resource requirements, making the implementation feasible and keeping resource utilization within a reasonable range. Moreover, 36.8% of the available digital signal processing (DSP) slices are used for the efficient implementation of algorithmic functions, such as multiplication and interpolation.
The execution time of the algorithm is presented in Table 4. The size of the echo data is 128 MB (4096 × 4096 × 8 B) after preprocessing, with both the pulse length and pulse number set to 4096. For each acceleration process, data is read from the PS DDR to the accelerator and then written back to the PS DDR via AXI DMA. The AXI DMA clock frequency is set to 200 MHz, and the line width is 128. The bandwidth between the PS DDR and the accelerators is 3.2 GB/s, and the theoretical processing time for each accelerator is 80 ms (calculated as 256 MB divided by 3.2 GB/s). In our experiment, the PRF is 2.5 KHz, thus the azimuth accumulation time for raw data is 6.55s. From Table 4, the practical processing time for a single FFT/IFFT, complex multiplication, and interpolation is approximately 84 ms, which closely aligns with the theoretical value. The total imaging time for each frame is approximately 4.39 seconds, which is shorter than the accumulation time. In addition, the processing accuracy is within 3.22 × 10⁻⁴ when compared to the reference results obtained from the Visual Studio platform on an Intel CPU, which falls within the tolerable range [19]. This indicates that our design efficiently achieves real-time imaging for UAV SAR with a power consumption of only 10.8 watts.
To demonstrate the real-time imaging capabilities of Mini-SAR, a comparison was conducted with publicly available SAR real-time processing equipment, as illustrated in Table 5. The performance-to-power ratio is utilized to compare real-time processing methods across different hardware configurations, algorithms, and data sizes. It thoroughly examines the factors of image size, processing speed, and power consumption. The formula is as follows:
performance − to − power   ratio = p e r f o r m a n c e p o w e r   c o n s u m p t i o n = d a t a   s i z e / t i m e p o w e r   c o n s u m p t i o n × 100 %
Due to the typically large data size, it is normalized to megabits (Mb).
d a t a   s i z e = i m a g e   s i z e 1024 × 1024
As evident from the comparison, the SAR real-time processor discussed in this article has undergone extensive optimization regarding its processing platform, algorithms, and other aspects to better suit its application in UAVs. Although the overall energy efficiency of the processing is not particularly high, it is the only processor that has undergone actual flight test verification through the integration of the SAR radar system. Simultaneously, real-time processing will not exceed the time required to capture an image of a scene, enabling continuous rolling imaging.

115. Conclusions

This article presents a real-time processing Mini-SAR system specifically designed for deployment on small and medium-sized UAVs. The real-time processing Mini-SAR system comprises several key components, including the SAR radar unit, real-time processing unit, PCS, and RTK. The total weight is only 724 grams, and the power consumption is 38.3 watts. The radar was mounted on a multi-rotor UAV and successfully completed flight test verification. The test results indicated that this SAR achieved high-resolution imaging with a precision better than 0.1 meters and could complete real-time processing of 4k × 4k images within 4.5 seconds. The processing effect is comparable to suppressing post-processing on-site. Simultaneously, a range of essential technologies is employed in the design and implementation of SAR real-time imaging processing systems. These technologies include data preprocessing, customized algorithms, real-time imaging algorithms optimized for high energy efficiency, and lightweight, high-precision real-time motion compensation techniques.
While the real-time processing Mini-SAR system provides significant advantages in real-time imaging capabilities under resource-constrained conditions compared to existing literature, there remains potential for improvement in SAR radar performance, system integration, and high-resolution imaging algorithms. Firstly, the W-band SAR is limited at the device level, presenting opportunities for enhancements in power, noise, and other performance metrics. The integration of multifunctional on-chip components can minimize losses and enhance performance. Secondly, currently, the capabilities and integration of processing chips restrict the management of preprocessing, real-time processing, and integrated navigation generation, which are handled by three separate processors. In the future, high-efficiency ASIC chips will be employed to integrate processing, control, and various other functions into a single unit. Currently, the imaging algorithm relies solely on the fundamental ω-k algorithm to ensure efficiency. The quality of the image primarily depends on radar performance, flight attitude, and the accuracy of integrated navigation. In the future, advanced algorithms, such as autofocus, will be implemented to further enhance imaging performance.

Author Contributions

All the authors contributed to the article in different areas. Conceptualization, L.T., Y.W. and M.D.; investigation, L.T. and J.Q.; methodology, L.T., M.D.; algorithm, Y.W., J.Q. and L.T.; validation, L.T., X.M. and J.Q.; writing—original draft preparation, L.T. and Y.W.; writing—review and editing, X.W. and J. L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Key R&D Program of China (Grant No. 2022YFB3902300).

Data Availability Statement

Data sharing is not applicable.

Acknowledgments

The authors would like to express their gratitude to the colleagues who participated in the research of this Mini-SAR, as well as to the staff who supported the flight tests.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Xie, W. Research on Target Extraction System of UAV Remote Sensing Image Based on Artificial Intelligence. In Proceedings of the IEEE International Conference on Integrated Circuits Communication Systems, 2023; pp. 1-5.
  2. Yang, Z.; Yu, X.; Dedman, S.; Rosso, M.; Zhu, J.; Yang, J.; Xia, Y.; Tian, Y.; Zhang, G.; Wang, J. UAV remote sensing applications in marine monitoring: Knowledge visualization and review. The Science of the total environment 2022, 155939. [CrossRef]
  3. Lyu, X.; Li, X.; Dang, D.; Dou, H.; Wang, K.; Lou, A.J.R.S. Unmanned Aerial Vehicle (UAV) Remote Sensing in Grassland Ecosystem Monitoring: A Systematic Review. 2022, 14, 1096. [CrossRef]
  4. Sothe, C.; Dalponte, M.; Almeida, C.M.d.; Schimalski, M.B.; Lima, C.L.; Liesenberg, V.; Miyoshi, G.T.; Tommaselli, A.M.G.J.R.S. Tree Species Classification in a Highly Diverse Subtropical Forest Integrating UAV-Based Photogrammetric Point Cloud and Hyperspectral Data. 2019, 11, 1338. [CrossRef]
  5. Du, M.; Noguchi, N.J.R.S. Monitoring of Wheat Growth Status and Mapping of Wheat Yield’s within-Field Spatial Variations Using Color Images Acquired from UAV-camera System. 2017, 9, 289. [CrossRef]
  6. Caris, M.; Stanko, S.; Palm, S.; Sommer, R.; Pohl, N. Synthetic aperture radar at millimeter wavelength for UAV surveillance applications. In Proceedings of the IEEE 1st International Forum on Research Technologies for Society Industry Leveraging a better tomorrow, Turin, Italy, 16-18 September 2015.
  7. Dill, S.; Schreiber, E.; Engel, M.; Heinzel, A.; Peichl, M. A drone carried multichannel Synthetic Aperture Radar for advanced buried object detection. In Proceedings of the IEEE Radar Conference, Boston, USA, 22-26 April 2019. [CrossRef]
  8. Ding, M.; Wang, X.; Tang, L.; Qu, J.-M.; Wang, Y.; Zhou, L.; Wang, B.J.R.S. A W-Band Active Phased Array Miniaturized Scan-SAR with High Resolution on Multi-Rotor UAVs. 2022, 14, 5840. [CrossRef]
  9. Li, W.; Chen, X.; Li, G.; Bi, Y. Construction of Yunnan’s Agricultural Ecological Civilization Based on Intelligent UAV and SAR Image Analysis. In Proceedings of the 4th International Conference on Smart Systems Inventive Technology, Tirunelveli, India, 20-22 January 2022.
  10. Lort, M.; Aguasca, A.; López-Martínez, C.; Marín, T.M.J.I.J.o.S.T.i.A.E.O.; Sensing, R. Initial Evaluation of SAR Capabilities in UAV Multicopter Platforms. 2018, 11, 127-140. [CrossRef]
  11. Ding, M.; Ding, C.; Tang, L.; Wang, X.; Qu, J.-M.; Wu, R. A W-Band 3-D Integrated Mini-SAR System With High Imaging Resolution on UAV Platform. IEEE Access 2020, 8, 113601-113609. [CrossRef]
  12. Cao, Y.; Jiang, S.; Guo, S.; Ling, W.; Zhou, X.; Yu, Z. Real-Time SAR Imaging Based on Reconfigurable Computing. IEEE Access 2021, 9, 93684-93690, doi:10.1109/ACCESS.2021.3093299. [CrossRef]
  13. Jia, G.; Buchroithner, M.; Chang, W.; Li, X. Simplified real-time imaging flow for high-resolution FMCW SAR. IEEE Geoscience Remote Sensing Letters 2014, 12, 973-977.
  14. Wu, W.; Zhang, Y.; Li, Z.; Yang, H.; Wu, J.; Yang, J. A Novel High Efficiency SAR Real-Time Processing System. In Proceedings of the IGARSS 2022-2022 IEEE International Geoscience and Remote Sensing Symposium, 2022; pp. 3401-3403.
  15. Yu, W.; Xie, Y.; Lu, D.; Li, B.; Chen, H.; Chen, L. Algorithm implementation of on-board SAR imaging on FPGA+ DSP platform. In Proceedings of the 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), 2019; pp. 1-5.
  16. Yang, T.; Xu, Q.; Meng, F.; Zhang, S. Distributed Real-Time Image Processing of Formation Flying SAR Based on Embedded GPUs. IEEE Journal of Selected Topics in Applied Earth Observations Remote Sensing 2022, 15, 6495-6505. [CrossRef]
  17. Tang, L.; Qu, J.; Wang, X.; Ding, M.; Wang, Y.; Wang, B. An Efficient Real-Time Data Compression Method for Frequency-Modulated Continuous Wave SAR. In Proceedings of the 2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 2024.
  18. Xilinx, I. Zynq UltraScale+ Device Technical Reference Manual, v1.9 ed.; 2019.
  19. Xuan, Z.; Zhongjun, Y.; Yue, C.; Shuai, J. A FPGA implementation of ω⁃k algorithm. Electronic Design Engineering 2020, 28, 6.
  20. Yang, C.; Li, B.; Chen, L.; Wei, C.; Xie, Y.; Chen, H.; Yu, W.J.S. A Spaceborne Synthetic Aperture Radar Partial Fixed-Point Imaging System Using a Field- Programmable Gate Array—Application-Specific Integrated Circuit Hybrid Heterogeneous Parallel Acceleration Technique. 2017, 17. [CrossRef]
  21. Fang, R.; Sun, G.; Liu, Y.; Xing, M.-d.; Zhang, Z.-j.J.r.C.I.S.S. SAR real-time imaging pipeline technology based on multi-core DSP. 2022, 1-4.
  22. Shan-qing, H.; Hui-xing, L.; Bing-yi, L.; Yi-zhuang, X.; Liang, C.; He, C.J.T.o.B.i.o.T. The real-time imaging method for sliding spotlight SAR based on embedded GPU. Transactions of Beijing institute of Technology 2020, 40, 1018-1025.
Preprints 138458 g001
Figure 1. Schematic representation of the real-time imaging Mini-SAR system.
Figure 1. Schematic representation of the real-time imaging Mini-SAR system.
Preprints 138458 g001
Preprints 138458 g002
Figure 2. Geometric model of UAV SAR data acquisition.
Figure 2. Geometric model of UAV SAR data acquisition.
Preprints 138458 g002
Preprints 138458 g003
Figure 3. The ω-k Algorithm Flow for real-time processing.
Figure 3. The ω-k Algorithm Flow for real-time processing.
Preprints 138458 g003
Preprints 138458 g004
Figure 4. Overview of the Zynq Device Architectures [18].
Figure 4. Overview of the Zynq Device Architectures [18].
Preprints 138458 g004
Preprints 138458 g005
Figure 5. Partitioning strategy of the ω-k algorithm onto the MPSoC.
Figure 5. Partitioning strategy of the ω-k algorithm onto the MPSoC.
Preprints 138458 g005
Preprints 138458 g006
Figure 6. Implementation of real-time processing on MPSoC.
Figure 6. Implementation of real-time processing on MPSoC.
Preprints 138458 g006
Preprints 138458 g007
Figure 7. Schematic diagram of the FFT/IFFT accelerator.
Figure 7. Schematic diagram of the FFT/IFFT accelerator.
Preprints 138458 g007
Preprints 138458 g008
Figure 8. Schematic diagram of the complex multiplication accelerator.
Figure 8. Schematic diagram of the complex multiplication accelerator.
Preprints 138458 g008
Preprints 138458 g009
Figure 9. Schematic diagram of the Stolt Interpolation accelerator.
Figure 9. Schematic diagram of the Stolt Interpolation accelerator.
Preprints 138458 g009
Preprints 138458 g010
Figure 10. Integrated navigation data generation process based on 4G network RTK.
Figure 10. Integrated navigation data generation process based on 4G network RTK.
Preprints 138458 g010
Preprints 138458 g011
Figure 11. W-band real-time imaging Mini-SAR system.
Figure 11. W-band real-time imaging Mini-SAR system.
Preprints 138458 g011
Preprints 138458 g012
Figure 12. The assembly structure of the real-time imaging Mini-SAR on the UAV.
Figure 12. The assembly structure of the real-time imaging Mini-SAR on the UAV.
Preprints 138458 g012
Preprints 138458 g013aPreprints 138458 g013b
Figure 13. Comparison between real-time image and optical image. (a) The real-time SAR image. (b) The optical image of the satellite.
Figure 13. Comparison between real-time image and optical image. (a) The real-time SAR image. (b) The optical image of the satellite.
Preprints 138458 g013aPreprints 138458 g013b
Preprints 138458 g014
Figure 14. Comparison between real-time image and ground-based post-processing of image..
Figure 14. Comparison between real-time image and ground-based post-processing of image..
Preprints 138458 g014
Table 1. Main performance indicators of the real-time imaging Mini-SAR system.
Table 1. Main performance indicators of the real-time imaging Mini-SAR system.
Parameter Value
Center frequency 94 GHz
Maximum bandwidth 4 GHz
Beamwidth
Action distance		 12° × 3°
600 m
Resolution ≤ 0.05 m
Real-time imaging size 4k x 4k
Processing delay 4.5 s
Real-time imaging error ≤ 10⁻⁴
Volume 67 × 60 × 50 mm³ (Radar Unit)
Weight 724 g
Power consumption 38.3 watts
Table 2. The SWaP of the real-time imaging Mini-SAR system.
Table 2. The SWaP of the real-time imaging Mini-SAR system.
Module/Unit Size Weight/g Power consumption/watts
SAR radar 67×60×50 mm3 400 24
Real-time processor 60×60×18 mm3 110 10
PCS 67×60×14.6 mm3 120 2.5
RTK 92×54×26.5 mm3 94 1.8
IMU 90 mm (Φ)×90 mm (H) 955 5.6
GNSS antenna 89 mm (Φ)×41.5 mm (H) 195 /
4G antenna 27.5 mm (Φ)×55.6 mm (H) 18 /
Cables / 280 /
Table 3. Resource utilization of the real time processing.
Table 3. Resource utilization of the real time processing.
Module LUT Block RAM DSP
FFT/IFFT 8011 53 60
Corner Turning 197 120 0
Complex Multiplication 56572 1 477
Interpolation 68052 42 373
Common Block RAM 794 144 0
Fix to Float Conversion 744 4 0
Quantification &
Float to Fix conversion		 1361 1 8
JPEG Compression 4941 8.5 9
AXI DMA 3987 8.5 0
FIFO 258 2 0
Other 9024 0 0
Total 153941 384 927
Available 274080 912 2520
Utilization 56.2% 42.1% 36.8%
Table 4. Execution time for real-time processing of 4K x 4K echo data.
Table 4. Execution time for real-time processing of 4K x 4K echo data.
Steps Modules Time
Data Reception LwIP 865.92 ms
Real-Time Imaging Fix to Float Conversion ×1 83.91 ms
FFT/IFFT ×9 755.37 ms
Complex Multiplication ×9 755.19 ms
Interpolation ×2 167.99 ms
Corner Turning ×5 563.94 ms
Quantification and Float-to-Fix Conversion ×1 83.91 ms
JPEG ×1 83.92 ms
PS Control、Small Batch Computing 1005.32 ms
Image Output LwIP 21.82 ms
Total 2 times LwIP, 28 times acc. 4387.29 ms
Table 5. Comparison of SAR real-time processing capabilities with previous research.
Table 5. Comparison of SAR real-time processing capabilities with previous research.
Ref. Processor Algorithm Image Size Time
Consumption / s		 Power
Consumption / watts		 Performance-to-Power Ratio / % Verification
[12] FPGA
(XC7VX690T)		 CSA 65536 × 65536 85.9 38.5 1.24 Image
[20] FPGA+ASIC CSA 16384 × 16384 12 21 1.02 Image
[21] 4-chip DSP
(C6678)		 Real-Time Unified Focusing
Algorithm (RT-UFA)		 8192 × 128 0.031 46 0.70 Image
[14] 2 FPGAs+
6 DSPs		 RDA + PGA 1024 × 1024 0.462 48 0.05 Image
[22] GPU
(Jetson TX2)		 CSA 16384 × 8192 12.66 15 0.67 Image
[16] GPU
(Jetson Nano)		 CSA 8192 × 8192 5.86 5 0.55 Image
This work Xilinx Zynq Ultrascale+ZU9EG MPSoC ω-k 4096 × 4096 4.5 10 0.35 Flight Test
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated