Preprint
Article
Optimization of Temperature Measurement Method for High-Pressure Gas Flow Standard Facility Based on Sonic Nozzle Array
This version is not peer-reviewed.
Submitted:
05 November 2024
Posted:
05 November 2024
You are already at the latest version
A peer-reviewed article of this preprint also exists.
Abstract
In order to improve the accuracy of wind tunnel test, relying on the high pressure gas source of China Aerodynamic Research and Development Center, a secondary flow standard facility based on sonic nozzle array is developed, and its pressure range is (1~6)MPa, and flow range is (0.12~5.55)kg/s. At present, most facilities use the average temperature measured by the temperature array to represent the upstream temperature of the sonic nozzle array. However, the small flow calibration test results show that, the maximum temperature difference upstream of the standard sonic nozzle array is 1.97 K, the temperature field upstream of the sonic nozzle array shows non-uniformity, so the above method cannot accurately obtain the upstream temperature. To solve this problem, each nozzle used in the standard sonic nozzle array was accurately measured by temperature sensors. And the uncertainty of the facility and the discharge coefficient of the calibrated nozzle between the two methods were compared. Results show that, compared with the discharge coefficient obtained by the tempearture sensor array of 0.9902, the accurate measurement of 0.9904 is closer to National Institute of Metrology, China(NIM) traceable result of 0.9907, and the relative uncertainty of the facility is reduced from 0.124% (k=2) to 0.120% (k=2).
Keywords:
Subject:
Engineering - Industrial and Manufacturing Engineering1. Introduction
As shown in Figure 1, sonic nozzle is one of the most accurate and reliable means to measure the high-pressure gas supply flow rate. It is used in the calibration facility of the power nacelle, the dynamic simulation flow control unit, and so on [1-3]. Before use, the sonic nozzle must be calibrated to accurately measure the gas flow. The gas flow standard facility is the key equipment for the traceability verification of sonic nozzles, which has different levels: primary, secondary, and working level. The accuracy level of the original standard facility is high, and its design principles include bell type, pVTt method, mt method, etc [4]. The maximum flow range is generally within 1000 m3/h, and the expanded uncertainty is (0.025~0.10) % (k=2) . The secondary standard facility is often used to expand the flow measurement range. It is generally realized by using multiple standard flowmeters in parallel. The standard flowmeter is traced back to the original standard [5]. The sonic nozzle has the advantages of simple structure, stable performance, high measurement accuracy, and good repeatability, and is widely used as a standard flowmeter in secondary standard facilities.
At present, many metrology institutions and enterprises have established gas flow standard facilities, such as the National Institute of Standards and Technology (NIST) , Korea Institute of Standards Science (KRISS) , and the National Institute of Metrology, China (NIM) [6,7]. NIST established a high-pressure pVTt method flow standard facility. The medium is dry air, and the standard uncertainty of the sonic nozzle discharge coefficient is 0.025% (k=2) . NIST uses the pVTt method facility as the primary standard to calibrate the low-pressure sonic nozzle, and as a secondary standard nozzle to gradually increase the pressure to calibrate the medium and high-pressure sonic nozzles. The pressure measurement range of the NIST secondary standard facility for sonic nozzle calibration is (0.35~7.5) MPa, and the maximum Reynolds number is 2.8×107 [8,9]. KRISS built the original standard of the MT method. Based on the original standard, 12 sonic nozzles were calibrated and used in parallel to establish a secondary transfer standard facility. The maximum flow rate was 4000 m3/h under the maximum calibration pressure of 5 MPa [10]. NIM has established a set of high-pressure gas flow standard facility, in which the high-pressure pVTt flow standard facility is used as the original standard, the medium is dry air, the pressure calibration range is (0.1~2.5) MPa, the flow range is (0.019~1367) kg/h, and the expanded uncertainty is 0.06% (k=2) . The sonic nozzle standard meter method flow standard facility is used as a secondary standard. The facility expands the flow to 400 m3/h by a parallel combination of sonic nozzles, and the uncertainty is 0.14% (k=2) [11,12].
ISO 9300 [13] describes the basic requirements for the use of parallel combined sonic nozzles. Due to the large diameter of the pipe installed with parallel combined sonic nozzles, it is easy to have the phenomenon of an uneven temperature field, which makes it difficult to measure the upstream temperature of the parallel combined sonic nozzles. Aaron N. Johnson [14] measured the air temperature of three sections upstream of the array when measuring the temperature field of the sonic nozzle array. In each section, the average temperature was measured by inserting a circumferentially equidistant thermistor sensor. It also mentioned that during the temperature acquisition process, the temperature difference of the temperature data collected by the thermistor sensor of the same section was as high as 4.2 K. In the study of the influence of the thermal effect caused by the temperature distribution of the sonic nozzle on the discharge coefficient of the sonic nozzle, Cao et al. [15] designed two thermocouple sensor arrays for nozzle temperature acquisition. Primož Žibret [16] developed a temperature analysis model that can predict the gas flow standard facility and a temperature dynamic measurement method is realized, the method is a model-based correction.
When evaluating the measurement uncertainty of the gas flow standard facility, the temperature measurement uncertainty has a crucial impact. For the accuracy of temperature measurement, to obtain the real transient temperature value, Chao Wang, Hongbing Ding, et al. [15] used the thermodynamic model and experimental measurement and then used FLUENT software for numerical simulation. The difference between the experimental results and the model results mainly comes from the temperature distribution in the retention tank. At the same time, a dynamic temperature compensation method is proposed to reduce the uncertainty of temperature measurement. For the problem of the non-uniform spatial distribution of the temperature field, NIST [9] measured the upstream sonic nozzle array by two temperature sensor arrays at different positions to evaluate the uncertainty caused by the spatial temperature change of gas in the cross-section and axial direction. Subsequently, Aaron N. Johnson et al. [14] measured the temperature of three temperature sections upstream of the sonic nozzle array, explained the non-uniformity of spatial temperature through these measurements, and quantified the uncertainty caused by spatial sampling errors. The discharge coefficient of the sonic nozzle is significantly affected by the thermal effect of the nozzle body temperature distribution, to solve the reduction of the wall temperature of the sonic nozzle and the uncertainty of the temperature distribution caused by the heat transfer of the facility pipeline, Peijuan Cao, Chunhui Li [15] proposed an improved continuous overrelaxation method (SOR) combining SKIM and particle swarm optimization (SKIM-PSO) . Finally, through the correction of this method, the accuracy of the discharge coefficient is improved to 0.8%-0.1%.
At present, the flow range of the large-flow high-pressure sonic nozzle commonly used in dynamic simulation wind tunnel tests is (0.5~5.5) kg/s, and the working pressure range is (1~6) MPa. To analyze the upstream temperature indexing characteristics of the standard sonic nozzle array in the gas flow standard facility based on the combined standard sonic nozzle array, a positive pressure gas flow secondary standard facility is developed based on the standard sonic nozzle array (traced to NIM pVTt method flow standard facility) , relying on the 22 MPa high-pressure gas source of China Aerodynamic Research and Development Center. The design pressure range is (1~6) MPa and the flow range is (0.2~5.5) kg/s. Through the calibration test of the standard facility under different flow rates for the sonic nozzles to be calibrated with different throat diameters, the upstream temperature field of the standard sonic nozzle array at small flow rates is analyzed, and the temperature measurement accuracy caused by the upstream temperature stratification of the standard sonic nozzle array is improved. At the same time, the uncertainty of temperature measurement is reduced, thereby reducing the uncertainty of the standard facility.
2. Facility
2.1. Flow Standard Facility Based on Sonic Nozzle Array
ISO 9300 [13] describes the basic requirements for the sonic nozzles array. NIM analyzed the measurement uncertainty of the sonic nozzles array and provided the calculation formula. The following content will introduce the design principle and composition of the gas flow standard facility.
2.1.1. Principle
The design principle is that the flowmeter is to be calibrated and the standard sonic nozzle array is installed in series on the same pipe. Due to the conservation of mass, the mass flow through the standard sonic nozzle array is the same as the mass flow of the flowmeter to be calibrated. Therefore, the metering performance of the calibrated flowmeter can be measured according to the standard sonic nozzle array. Each nozzle in the standard sonic nozzle array is traced to the pVTt gas flow standard facility of NIM.
According to the different gas source systems, the gas flow standard facility is divided into the negative pressure method and the positive pressure method. To maintain the stability of the gas supply pressure, the corresponding investment cost and operation cost of the positive pressure method are much higher than the negative pressure method, and the working principle is shown in Figure 2. The sonic nozzles used in the wind tunnel test are applied under positive pressure. Therefore, based on the 22 MPa high-pressure gas source of China Aerodynamics Research and Development Center, the flow standard device is designed by the positive pressure method.
2.1.2. Structure
The structure of the standard device is shown in Figure 3. The pipe of the facility is divided into two parts. The first part is the pipe of the calibrated flowmeter, and the second is the pipe of the standard sonic nozzle array, including the variable diameter pipe, the rectifier facility, the temperature/pressure sensor, the calibrated sonic nozzle, the standard sonic nozzle array, etc.
The diameter of the first pipe is 150 mm, and the pressure is 10 MPa. At present, the throat diameter range of the sonic nozzle used in low-speed wind tunnel tests is (5.8-23.3) mm. The first pipe is connected with the second pipe through the transition section pipe, and the diameter of the pipe is changed from 150 mm to 500 mm. To weaken the jet effect of the supersonic jet of the calibrated sonic nozzle and optimize the temperature field distribution in the second pipe, the flow straightener was installed in the transition section pipe. The maximum pressure of the second pipe is 3 MPa. The sonic nozzle array consisted of 15 nozzles mounted in parallel in a mozzle holder that matched the pipe diameter, as shown in Figure 4. While calibrating, according to the calibration flow demand, open the corresponding number of the sonic nozzle.
It is necessary to measure the pressure and temperature, including the stagnation pressure, stagnation temperature, and throat temperature of the calibrated sonic nozzle, and the stagnation pressure, stagnation temperature, and pressure of the standard sonic nozzle. The installation position of the temperature and pressure sensor is designed according to ISO 9300 [13].
2.2. The Gas Supply System
The maximum working flow rate of the high-pressure gas supply system is 6.32 kg/s. The system is mainly composed of an electric ball valve, digital valve, heat exchanger, filter, pressure transmitter, and temperature transmitter. As shown in Figure 5, PT is the pressure transmitter, TT is the temperature transmitter, and M is the ball valve.
The digital valve is the core component of flow control in the gas supply system, which is composed of 16 high-pressure solenoid valves and sonic nozzles with different throat diameters. In addition, the heat exchanger in the gas supply system can heat the gas, and control the temperature of the gas flow.
2.3. Standard Sonic Nozzle Array
Figure 6 is the gas flow standard facility based on the sonic nozzle array. The sonic nozzle array consists of 15 sonic nozzles mounted in a structure matching the pipe diameter (D=500 mm) . The 15 sonic nozzles include 14 sonic nozzles with each throat diameter dth=9.028-9.062 mm and 1 sonic nozzle with throat diameter dth=6.385 mm. The ratio of the center distance of the sonic nozzle to the throat diameter is not less than 4.4 (≥39.4 mm) , and the center of the sonic nozzle has no tube wall within 4 times the throat diameter (≥36 mm) . To expand the facility to a larger flow range, the minimum distance between the nozzle center is 100 mm, and the minimum distance from the pipe wall is 70 mm, which ensures that the interference between adjacent sonic nozzles can be ignored [5].
The gas mass flow rate through the sonic nozzle array is:
where Qr,array denotes the mass flow rate of standard sonic nozzle array, i is the ith standard sonic nozzle, At,i and Cd,i represent the throat area and the discharge coefficient of the ith standard sonic nozzle, and both traced to NIM, p0 and T0 are the respective stagnation pressure and temperature, Cr* denotes critical flow function, Ru=8314.463 J/ (kmol·K) is the universal gas constant, M=28.9655 kg/kmol is the molar mass of dry air.
The material of the standard sonic nozzle is brass, and the inner surface is designed according to ISO 9300 [13]. The standard sonic nozzle is calibrated in NIM, and the calibration standard instrument is the pVTt gas flow standard facility established by NIM. The calibration Reynolds number range of each standard sonic nozzle with a throat diameter of 9 mm is Re=0.46×106~2.85×106, and the flow range is qm=0.06~0.37 kg/s; Re=0.33×106~2.02×106 and the flow range is qm=0.03~0.19 kg/s of the standard sonic nozzle with a throat diameter of 6 mm. In the range of Re and qm, the standard sonic nozzle was calibrated at stagnation pressures of 400 kPa, 1000 kPa, 1500 kPa, 2000 kPa, and 2500 kPa. The expanded uncertainty of the average discharge coefficient was 0.08% (k=2) . The relationship between the discharge coefficient of five of the sonic nozzle array (SN-45-01~SN-45-5) and Re is plotted in Figure 7. As shown in Figure 7, the variation of the discharge coefficient of each standard sonic nozzle with Re is consistent. When Re=1.2×106, the discharge coefficient is larger than the other points, ranging from 0.0003 to 0.0021. Therefore, in the test, we would like to make the upstream stagnation pressure of the standard sonic nozzle array close to the calibrated pressure, to ensure the accuracy of the discharge coefficient used in the calculation. At the same time, we will use the standard sonic nozzle discharge coefficient obtained by the interpolation method to apply it to the calculation of the mass flow.
3. Measurement System and Analysis Model
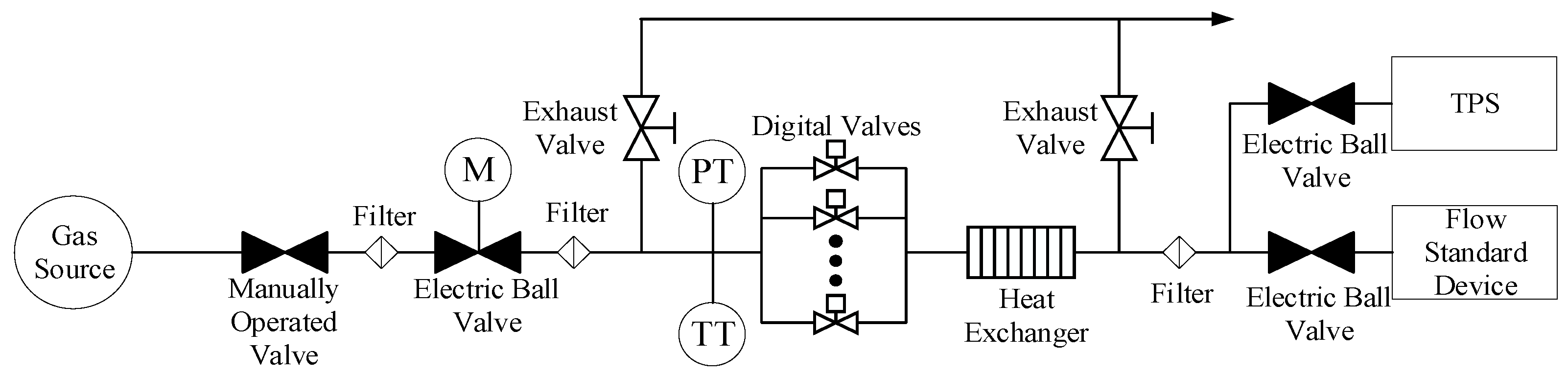
3.1. Measuring System
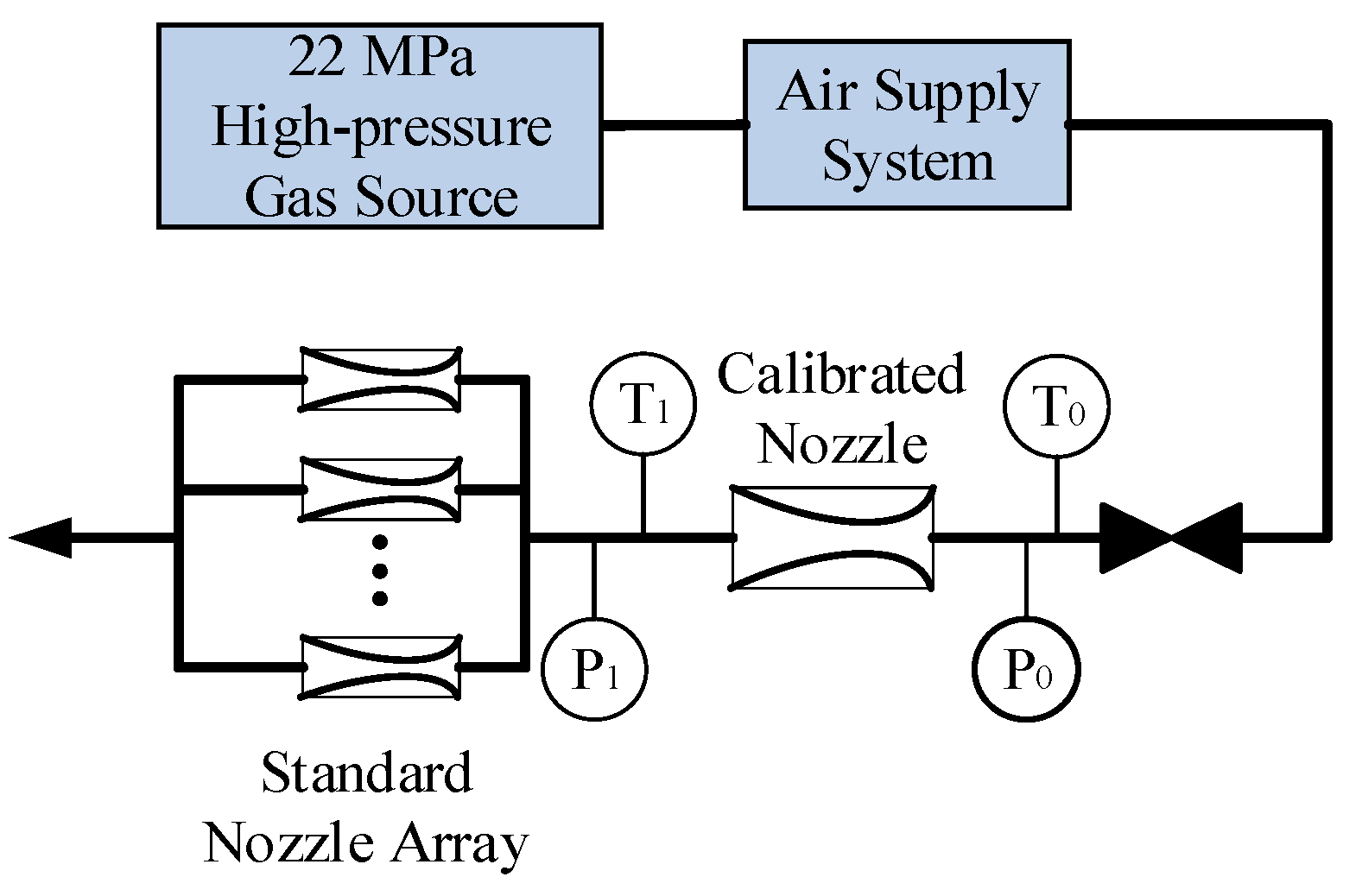
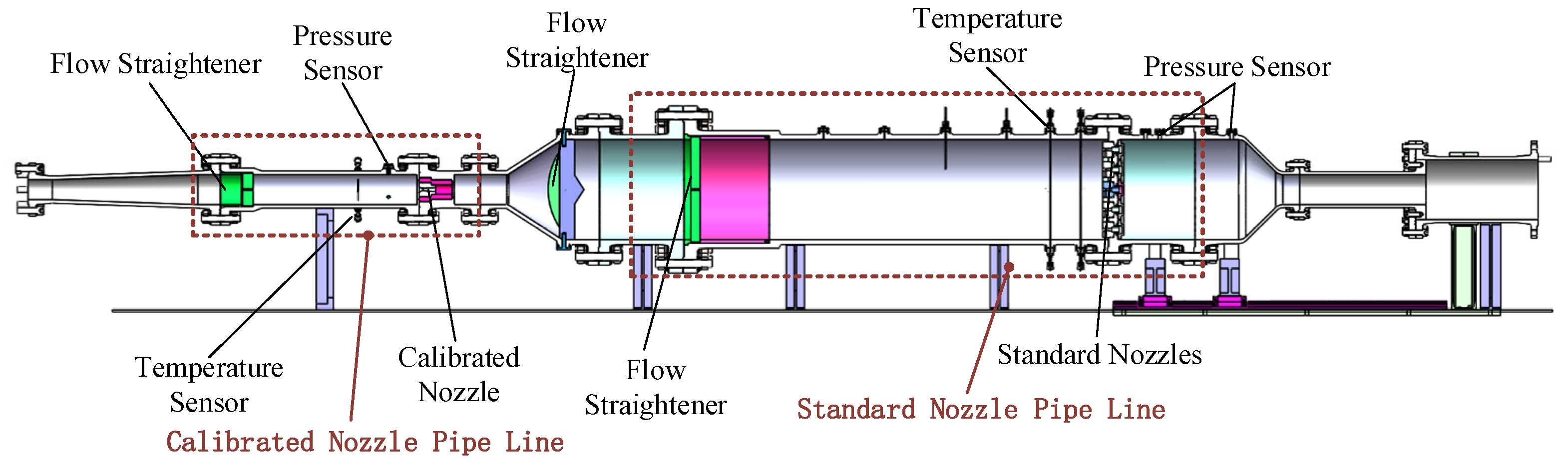
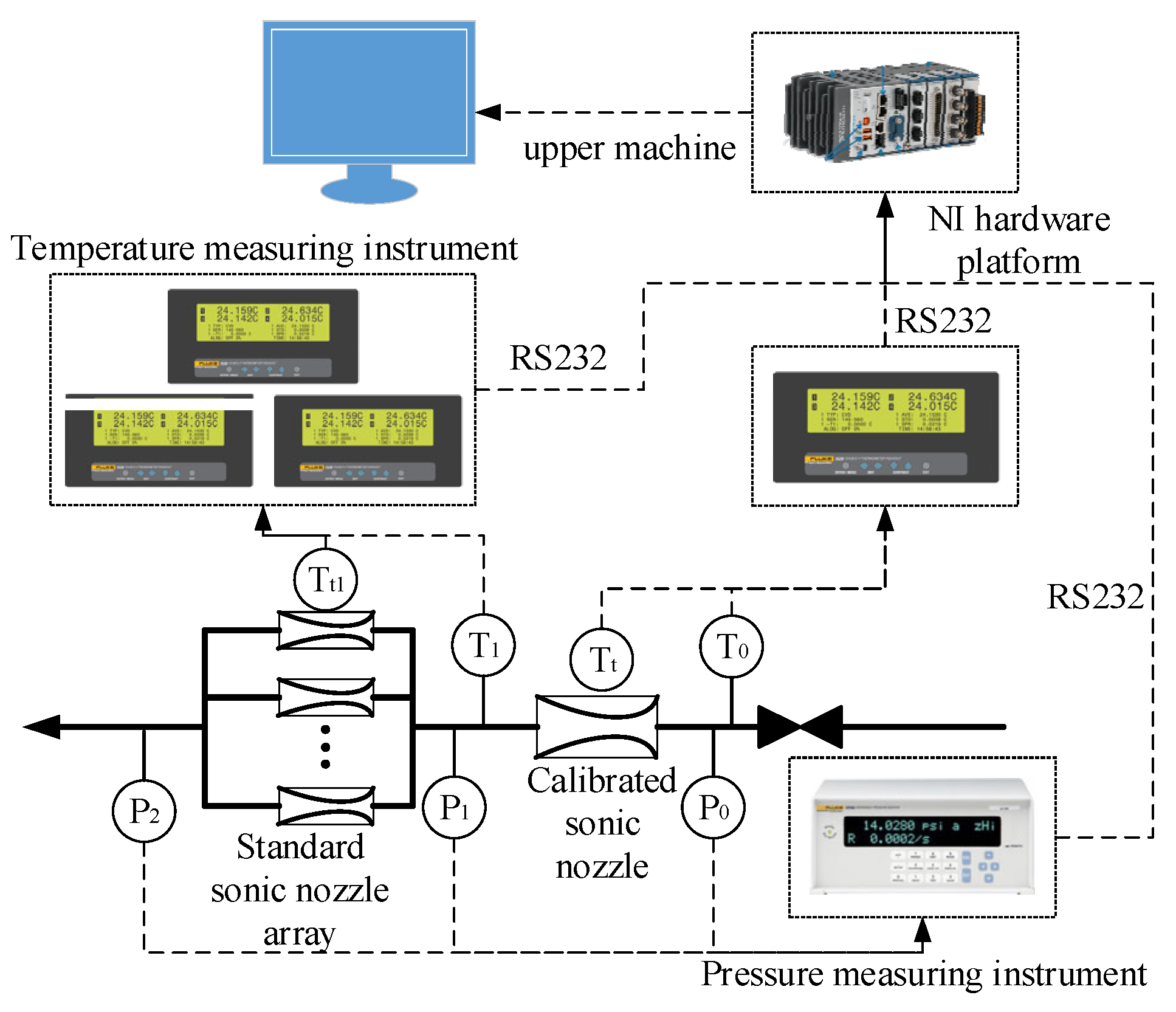
The structure of the measurement system is shown in Figure 8, and its function is to measure the atmospheric pressure, stagnation pressure, stagnation temperature, back pressure, and throat material temperature of the calibrated sonic nozzle and the standard sonic nozzle. It consists of the temperature sensor, temperature measuring instrument, pressure measuring instrument, and upper machine.
The measurement range of the temperature sensor is (0~100) ℃, with uncertainty is ±0.01 ℃, and the size of the temperature sensor is Φ3.2×229 mm; the measurement accuracy of the temperature measuring instrument is lower than ±0.01 ℃; the measurement range of the pressure measuring instrument is (0~7) MPa, and the measurement uncertainty is subdivided into 600 Pa (absolute pressure 6.0 MPa) , 300 Pa (absolute pressure 3.0 MPa) , 220 Pa (absolute pressure 2.0 MPa) . The measuring instrument communicates with the upper machine through the cluster communication port (RS232) to achieve real-time and high-precision measurement and detection.
3.2. Temperature Measurement at Different Flow Rates
We considered that the inner diameter of the second-stage pipe was 500 mm before the test, and related studies have shown [14] that due to the temperature stratification phenomenon, there will be an average temperature difference of 1.7 K on the temperature measurement profile within the larger pipe diameter. To more accurately obtain the temperature field in the second-stage pipe inner profile, the temperature of the cross-section at 12d (d: the maximum throat diameter of 9 mm in the standard nozzles) upstream of the standard sonic nozzle array was measured. 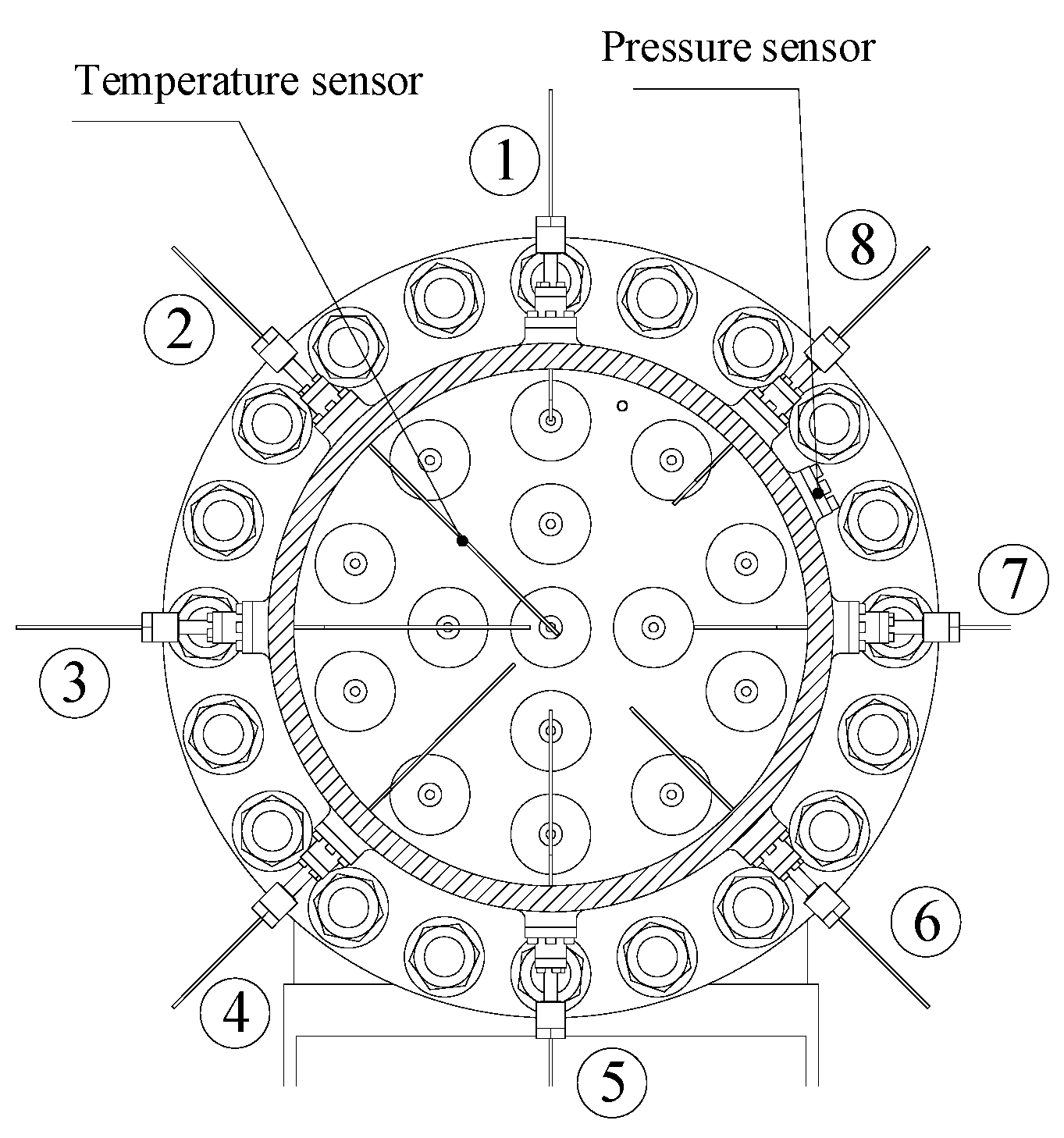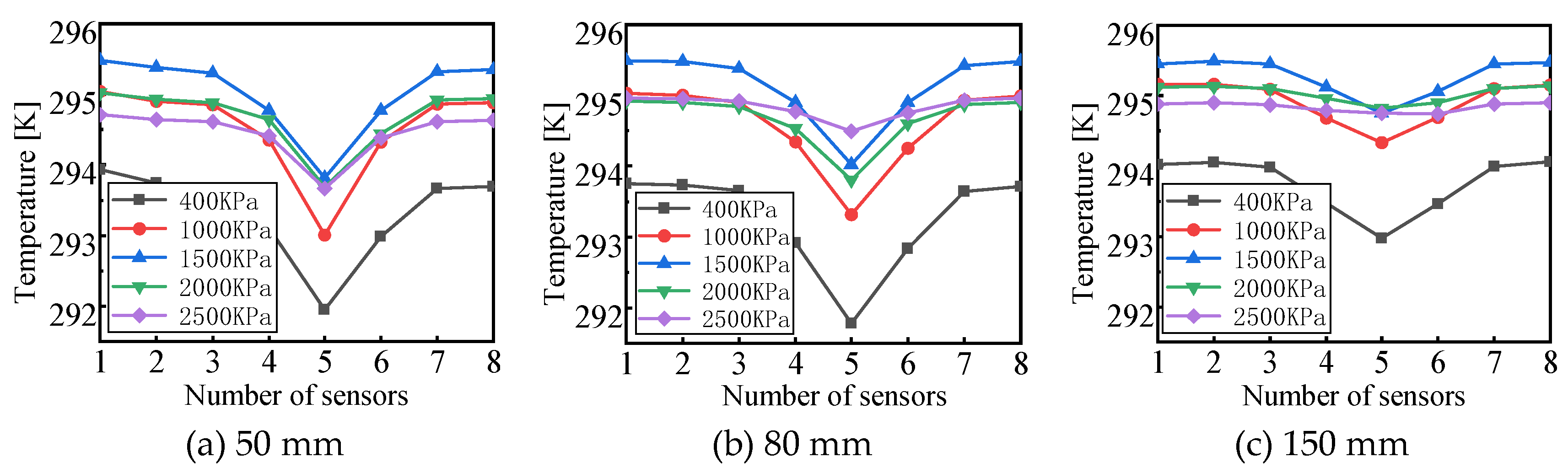As shown in Figure 9, 8 temperature sensors were installed at a distance of 12d (d=9 mm) upstream of the standard sonic nozzle array, and each sensor was inserted at a maximum depth of 150 mm and a minimum depth of 50 mm.
At present, there are different measurement methods for the upstream temperature of the sonic nozzle array. Aaron N. Johnson's method is to measure the temperature at three different distance points (Cross Section A, Cross Section B, Cross Section C) upstream of the sonic nozzle array, as shown in Figure 10, and take the average value to represent Tm,array. There is then:
If the temperature gradient among the three points is large, the temperature measurement will try to select the point close to the sonic nozzle array, i.e., Cross Section C; NIST [9] proposed that when measuring the temperature of the sonic nozzle array, two temperature sensor arrays at different locations are used to average T1. The first temperature sensor array uses 10 temperature sensors at equal distances to average Tm1, and the second temperature sensor array uses 10 uniformly distributed temperature sensors with the same insertion depth to average Tm2, as shown in Figure 11.
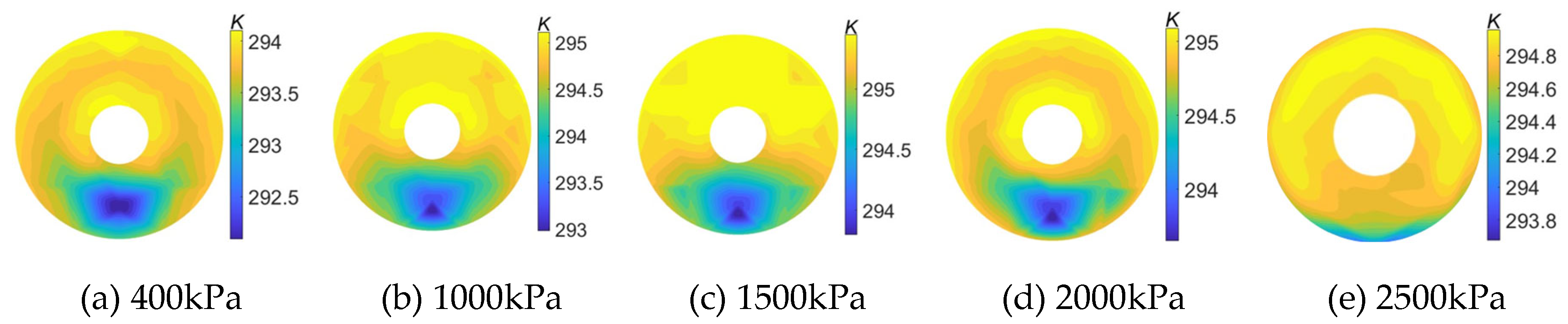
However, we found that due to the non-uniform temperature distribution shown in the temperature section upstream of the standard sonic nozzle array under different gas flow rates, at a small flow rate (qm=0.12 kg/s) , the maximum temperature of the temperature measurement section is 1.97 K, only 0.03 K when the flow rate is large (qm=3.00 kg/s) . Therefore, when measuring different flow rates, different measurement methods should be used to calculate Tm,array, and the averaging method of the temperature sensor array cannot be used.
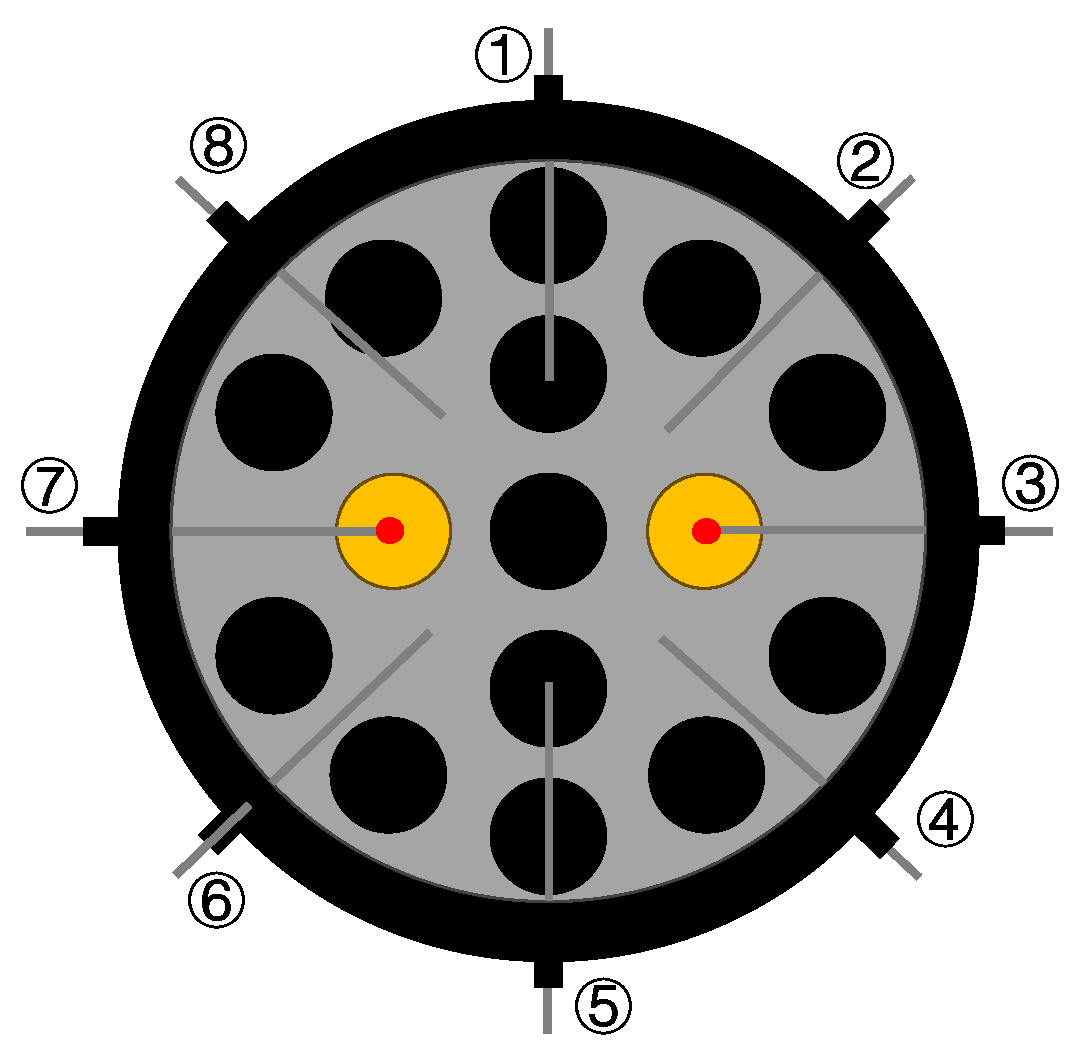
When calibrating the calibrated sonic nozzle with a small throat diameter, due to the small flow rate, the temperature difference in the same section of the pipeline is large. If the average value obtained by the temperature sensor array is used to represent Tm,array, likely, the measured temperature value is likely not the actual stagnation temperature of the standard sonic nozzle array, which will cause a large error in the calculation of the mass flow rate and the the discharge coefficient of the calibrated sonic nozzle. In the calibration test of small flow rates, relatively few standard sonic nozzles are used, so the temperature sensor array is used to directly measure the temperature upstream of the used standard sonic nozzle, and the stagnation temperature is obtained by correction. As shown in the opening method of the standard sonic nozzle array in Figure 12, we will insert the left and right temperature sensors in the temperature sensor array into the central axis of the used standard sonic nozzle to accurately measure the upstream temperature of the standard sonic nozzle, as shown in Figure 13.
Tm,array could be obtained by:
where i is the ith temperature sensor, i≤8, and Ti denotes the temperature measured by the ith temperature sensor.
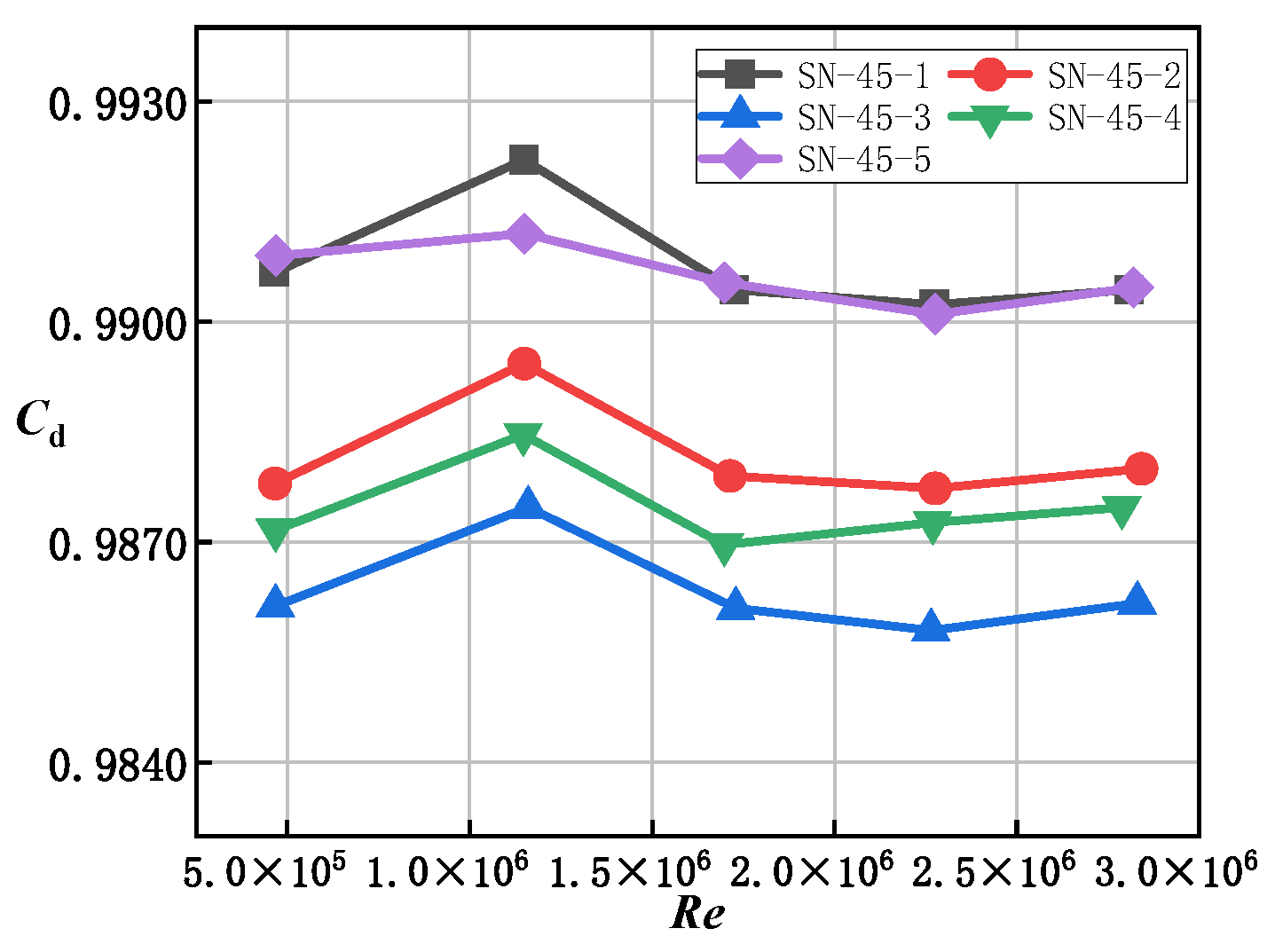
We compared the discharge coefficient of the calibrated sonic nozzle obtained by the above temperature measurement method and the method of using the average temperature obtained by the temperature sensor array with the results of NIM traceability. The discharge coefficient calculated by the average temperature measurement method is 0.9902, and the discharge coefficient calculated by the above temperature measurement method is 0.9904, which is closer to the traceability result of 0.9907, so the above temperature measurement method is more accurate.
3.3. Modified Model of Temperature and Pressure in Sonic Nozzle Array
Before the measured pressure and temperature can be converted to the stagnation pressure and the stagnation temperature, it is necessary to calculate the Mach number of the airflow at the inlet of the sonic nozzle in the pipe. The Mach number of the airflow in the pipe is [14]:
In the equation, β=d/D, d is the throat diameter or equivalent throat diameter of the sonic nozzle or sonic nozzle array, D denotes the upstream pipe inner diameter, and γ is the ratio of the constant pressure to the constant volume-specific heat.
The measured pressure pm,array and temperature Tm,array are used to compute the stagnation parray and Tarray using the following expressions [14]:
The relationship between the modified method of pressure and temperature and β is as follows:
- (1)
- When β＜0.25, the difference between the measured pressure and the stagnation pressure is less than 0.1%;
- (2)
- When β＞0.25, the difference between the measured pressure and the stagnation pressure is more than 0.5%, and it’s more obvious and should be modified. Rf=0.75 is the assumed value of the recovery factor which accounts for viscous heating of the gas as it stagnates against the temperature probe [5].
3.4. Model for Uncertainty Analysis
From the gas flow calculation Equation (1) based on the sonic nozzle array, it can be seen that the relative standard uncertainty of the flow standard facility is:
where, ur (Cd,i) is the relative uncertainty of the ith standard sonic nozzle, ur (At,i) is the relative uncertainty of throat area of the ith standard sonic nozzle, ur (C*) is the relative uncertainty of critical flow function, ur (parray) and ur (Tarray) are the respective relative uncertainty of the stagnation pressure and temperature of the sonic nozzle array, ur (M) is the relative uncertainty of molar mass, ur (Ru) is the relative uncertainty of gas constant.
Since the relative uncertainty of At,i, C*, Ru and M has been taken into account in the calculation of ur (Cd,i) , the influence of these items does not need to be considered here.
Therefore, the relative standard uncertainty of the standard facility ur (Qr,array) can be simplified as:
ur (Cd,i) has been given in the traceability and does not need to be analyzed, but ur (parray) and ur (Tarray) also contain other uncertainty components, so they need to be analyzed one by one.
ur (parray) contents:
- (1)
- Uncertainty of pressure sensor ur (parray,1) ;
- (2)
- Uncertainty of pressure stability ur (parray,2) ;
- (3)
- Uncertainty of the difference between the calibrated and traceable pressure value causes the difference in the discharge coefficient ur (parray,3) .
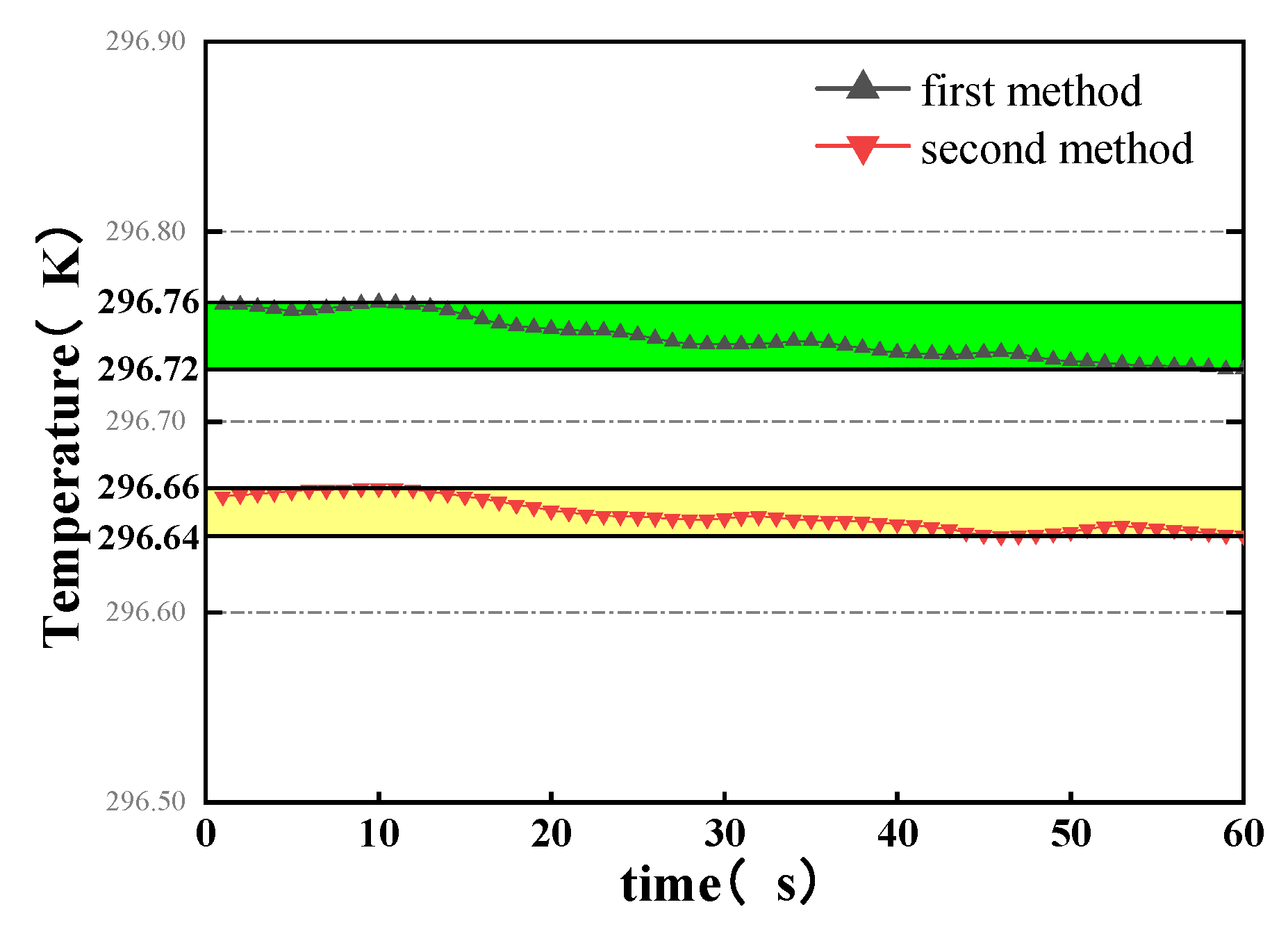
ur (parray,1) is provided by the calibration certificate, ur (parray,2) is the standard deviation divided by the mean value of the pressure during the acquisition time, so ur (parray,2) is
where is the average value of parray during the acquisition time; parray,i is the pressure value measured at the ith second, a total of 60 s.
During the measurement, the stagnation pressure upstream of the standard sonic nozzle array is kept as close as possible to the stagnation pressure at traceability, with the difference kept within 100 kPa. During data processing, the discharge coefficient of the traceability is piecewise interpolation according to the measured stagnation pressure. ur (parray,3) caused by the difference between the interpolated discharge coefficient and the actual discharge coefficient due to different stagnation pressures is as follows:
where Cd,std is the standard discharge coefficient, Cd,m is the interpolated discharge coefficient.
ur (Tarray) contents:
- (1)
- Uncertainty of temperature sensor ur (Tarray,1) ;
- (2)
- Uncertainty of temperature stability ur (Tarray,2) .
ur (Tarray,1) is provided by the calibration certificate, different temperature measurement methods upstream of the standard sonic nozzle array will affect the value of ur (Tarray,2) . ur (Tarray,2) is
where is the average value of Tarray during the acquisition time, n is the amount of data collected, Tarray,i is the temperature data collected each time.
The discharge coefficient of the calibrated sonic nozzle is
where and are the critical flow functions at the stagnation pressure and stagnation temperature corresponding to the calibrated sonic nozzle and the standard sonic nozzle array, respectively, which are obtained by querying the relevant database [17], pSN and TSN are the respective stagnation pressure and temperature of the calibrated nozzle.
According to Equation (12) , the relative uncertainty of the discharge coefficient of the calibrated sonic nozzle is
where u ( ) / ( ) is the relative uncertainty of the parameter in the bracket, uR (Cd) is repeatability measured by the repeatability test, is the change in gas mass in the space between the calibrated and the standard sonic nozzles, is the uncertainty caused by the gas storage effect of the pipe.
For the high-pressure gas flow standard facility, is a very small amount relative to Qr,array, i.e., . When the environmental conditions of the nozzle use and measurement are similar, the uncertainty caused by the critical flow function and nozzle throat diameter can be ignored.
Therefore, the relative uncertainty of the discharge coefficient of the calibrated nozzle can be simplified as follows:
ur (Cd,M) , ur (p1) and ur (T1) have been calculated in Equation (7) , therefore, Equation (14) can be further simplified as:
In the analysis of the uncertainty components of ur (Cd) , ur (Qr,array) has been given in Equation (7) , and since the pressure stability and temperature stability of ur (parray) and ur (Tarray) have been analyzed in ur (Qr,array) , the impact of their uncertainty components will not be analyzed here. ur (pSN) and ur (TSN) are only provided by the sensor. the repeatability of the discharge coefficient of the calibrated sonic nozzle uR (Cd) is
where is the average value of the discharge coefficient of the calibrated sonic nozzle, n is calibration times, Cd,i is the discharge coefficient result obtained for each calibration.
4. Results
4.1. Flow Standard Facility Test Process and Calibration Object
The test process is as follows:
- (1)
- Installation and adjustment: install the calibrated sonic nozzle in the first-stage pipe, and estimate the number and position of the standard sonic nozzles that need to be opened based on the throat diameter and flow rate of the calibrated sonic nozzle;
- (2)
- gas supply system preheating and facility inspection: turn on the heating exchanger of the gas supply system to control and stabilize the temperature of the gas at the inlet of the facility. After ventilation, gradually increase the pressure and check the air tightness;
- (3)
- adjust air flow pressure and flow: according to the calibration test requirements, change the pressure in the facility and collect data for 60 s after the pressure and temperature values stabilize;
- (4)
- test data analysis: calculate the gas flow rate, discharge coefficient, repeatability, and uncertainty of the calibrated sonic nozzle.
The throat diameters of the sonic nozzles selected for the calibration test are 8.251 mm (No.SN2-1) , 16.469 mm (No.SN5-1) and 23.246 mm (No.SN7) , and the material is brass. The calibration test of the above nozzles can include the flow range and pressure range of the standard device. The calibration test selected five pressure points, which were near 1 MPa, 2.5 MPa, 3.5 MPa, 4.5 MPa, and 6 MPa, and the specific pressure values fluctuated with the test conditions. According to the flow characteristics of the calibrated and standard sonic nozzles, it is estimated that the number of standard sonic nozzles that need to be opened for the calibrated sonic nozzles of SN2-1, SN5-1, and SN7 are 2, 8, and 15 respectively. Figure 14 shows the opening state of the standard sonic nozzle array.
4.2. Temperature Field Distribution of the Upstream of the Standard Sonic Nozzle Array
We conducted a calibration test on SN2-1 with the standard sonic nozzle array opened as shown in Figure 14 (a) . In the test, we analyzed the temperature field distribution upstream of the standard sonic nozzle array at different flow rates and observed the temperature difference phenomenon upstream of the standard sonic nozzle array at a small flow rate. At the same time, different temperature measurement methods were used to obtain Tm,array and then the discharge coefficient of SN2-1 was calculated. Then, it was compared with the discharge coefficient obtained after SN2-1 was sent to NIM for traceability to determine the more accurate temperature measurement method. The traceability results of NIM for SN2-1 are shown in Table 1.
The calibration test of SN2-1 conducted a total of three comparative measurements at three temperature sensor insertion depths (from the inner wall of the pipe: 50 mm, 80 mm, and 150 mm) .
The temperatures at the three different insertion depths of the temperature sensor are shown in Figure 15. It can be seen that the temperature field has the characteristics of up-high down low and bilateral symmetry. At the insertion depth of 50 mm and the array upstream pressure of 400 kPa, the temperature difference reached 1.97 K. As the insertion depth of the temperature sensor increased, the temperature difference decreased and reached 1.05 K at the insertion depth of 150 mm. At the same temperature sensor insertion depth and the different standard sonic nozzle array upstream pressures, the temperature difference decreases with the increase of the upstream pressure. For example, at the insertion depth of 50 mm, the temperature difference decreases from 1.97 K at 400 kPa to 1.05 K at 2500 kPa; at the insertion depth of 80 mm, the temperature difference decreases from 1.98 K at 400 kPa to 0.47 K at 2500 kPa; at the insertion depth of 150 mm, the temperature difference decreases from 1.05 K at 400 kPa to 0.13 K at 2500 kPa. To show the above phenomenon more vividly, a heat map was drawn, as shown in Figure 16.
Through the above phenomenon, we found that in the small flow calibration test, the temperature field distribution upstream of the standard sonic nozzle array is uneven. Therefore, when measuring temperature, we cannot use only the value measured at a single point or the average value of multiple points as the true temperature value. Therefore, we used two different temperature measurement methods to calculate the discharge coefficients for the three flow points of NIM traceability and determined which temperature measurement method was the most appropriate through comparison.
The first temperature measurement method is to use the average value of the temperature values collected by 8 temperature sensors installed upstream of the standard sonic nozzle array to represent T1; The second temperature measurement method is shown in Figure 13. The insertion depths of the left and right temperature sensors are adjusted to be consistent with the throat of the standard sonic nozzle. The temperature values collected by the two temperature sensors represent T1 of two different standard sonic nozzles.
Through 60s of temperature acquisition data, the temperature fluctuation curves obtained by two different temperature measurement methods are shown in Figure 17. It can be seen from the figure that the temperature value obtained by the second temperature measurement method is more stable in the time domain than the first temperature measurement method. Its stability is 0.0028%, while the first stability is 0.0038%. And the temperature stability obtained by the second temperature measurement method is more realistic.
The comparison of mass flow rate, Reynolds number, and discharge coefficient obtained by two different temperature measurement methods is shown in Table 2. From the discharge coefficient calculated by the two different measurement methods and the NIM traceability results, it can be seen that the discharge coefficient obtained by the second temperature measurement method is closer to the traceability value and therefore has higher accuracy.
Therefore, in the calibration experiment of a small flow rate, the multi-point averaging method cannot be used to represent the temperature value upstream of the standard sonic nozzle array. Instead, it is more reliable to measure the temperature of the throat of the standard sonic nozzle used by the temperature sensor.
4.3. Results of Uncertainty Analysis
4.3.1. Uncertainty of SN2-1
In the SN2-1 calibration test at a flow rate of 0.19 kg/s, we analyzed and calculated the relative standard uncertainty of the standard facility and the uncertainty of the measurement results according to the analysis method in Section 3.2. In particular, during the analysis process, we also compared the uncertainty of the two different temperature measurement methods upstream of the standard sonic nozzle arrays. The analysis results are shown in Table 3 and Table 4.
It can be seen from Table 3 and Table 4 that different temperature measurement methods have an impact on the measurement standard and the measurement results of uncertainty, and the second temperature measurement method will reduce the uncertainty results under small flow conditions compared to the first temperature measurement method.
4.3.2. Uncertainty of Measurement Standard
Through the calibration test of three calibrated sonic nozzles with different throat diameters, according to the uncertainty analysis model given by Equation (8) , the main components of the uncertainty of the measurement standard are shown in Table 5. The relative uncertainty of the measurement standard is ur (Qr,array) =0.06%. Therefore, the relative expanded uncertainty of the measurement standard is Ur (Qr,array) =0.12% (k=2).
The pressure measuring instrument is calibrated using a 0.05 class gas operated piston pressure gauge with a measurement uncertainty of 0.005% (k=2) .
The measurement range of the pressure module in the pressure measuring instrument is (0~7) MPa. The relative measurement uncertainty of the pressure measuring instrument is calculated by comparing the error between the average pressure of the positive stroke and the reverse stroke measured by the pressure measuring instrument under the standard pressure value. The measured values are shown in Table 6.
Relative to the pressure (0.4 MPa, 1.0 MPa, 1.5 MPa, 2.0 MPa and 2.5 MPa) of the standard sonic nozzle array, above 1.5 MPa, the uncertainty of the pressure caused by the error is very small and can be ignored, the maximum value is 0.004%. While below 1.5 MPa, the maximum error is 0.16 kPa. Taking this error value into account in 0.4 MPa and synthesizing it with the uncertainty of the gas operated piston pressure gauge, the relative measurement uncertainty of the pressure measuring instrument is:
The pressure data collected at five pressure points of the upstream pressure of the standard sonic nozzle array: 0.4 MPa, 1.0 MPa, 1.5 MPa, 2.0 MPa and 2.5 MPa were analyzed, and the uncertainty component ur (parray,2) was calculated as shown in Table 7.
The maximum value of 0.016% is selected as the uncertainty caused by the stagnation pressure stability, i.e., ur (parray,2) =0.016%.
The traceability results show that within the range of (400~2500) kPa, the uncertainty caused by the difference in the discharge coefficient is shown in Table 8.
The maximum value of 0.01% is selected as ur (parray,3).
ur (parray) is
The uncertainty of the temperature sensor and the data collector is obtained from the calibration certificate, which is 0.01% and 0.0025% respectively. Through synthesis, ur (Tarray,1) is
The temperature data collected at five flow rate points: 0.13 kg/s, 1.2 kg/s, 1.8 kg/s, 3.0 kg/s, and 5.5 kg/s were analyzed, and the uncertainty component caused by temperature stability was calculated as shown in Table 9.
The maximum value of 0.02% is selected as the uncertainty caused by the stagnation temperature stability, i.e., ur (Tarray,2) =0.02%.
Then there is
4.3.3. Uncertainty of Measurement Results
Through the calibration test of the calibrated sonic nozzles with three different throat diameters, according to the uncertainty analysis model given by Equation (15) , the main components of the uncertainty of the measurement results are shown in Table 10. The calculated relative synthetic standard uncertainty of the measurement standard is ur (Cd) =0.075%. Therefore, the relative expanded uncertainty of the measurement result is Ur (Cd) =0.15% (k=2) .
As shown in Section 4.3.2, relative to the pressure upstream of the calibrated sonic nozzle (1.0 MPa, 2.4 MPa, 3.6 MPa, 4.8 MPa and 6.0 MPa) , below 1.5 MPa, the maximum error is 160 Pa, then ur (pSN) is
The temperature sensor used in the calibrated sonic nozzle is the same as that used in the standard sonic nozzle array, so:
Six repeatability measurements were carried out on five flow points: 0.13 kg/s, 1.20 kg/s, 1.80 kg/s, 3.00 kg/s, and 5.55 kg/s. These five flow points cover the flow range of the standard facility and are the measuring points of the calibrated sonic nozzles. A total of three calibrated sonic nozzles with different throat diameters were selected for repeatability testing of the calibration experiment, the calibrated sonic nozzles are SN2-1, SN5-1, and SN7. The test results are shown in Table 11.
According to the test results, the repeatability of SN2-1, SN5-1 and SN7 is within 0.04%.
4.4. Stability Results
4.4.1. Stability of the Gas Supply System
The flow stability of the gas supply system affects the calibration effect. For example, the flow stability will affect the measurement stability of the stagnation pressure and stagnation temperature. The calibrated sonic nozzle SN5-1 is installed in the flow standard facility,and the actual mass flow is calculated using the standard sonic nozzle array at 5 different pressure points to analyze the stability of the flow in the facility.
According to the test results, at five different pressure points, the maximum changes of stagnation pressure within the measuring time after the gas supply reaches a stable state are 255 Pa, 428 Pa, 1433 Pa, 3622 Pa and 3653 Pa respectively; the maximum changes of stagnation temperature are 0.17 K, 0.05 K, 0.14 K, 0.38 K and 0.08 K respectively; and the maximum changes of mass flow rate are 0.26 g/s, 0.33 g/s, 1.07 g/s, 0.24 g/s and 1.06 g/s respectively. Relative to the average values of pressure, temperature and flow rate, the maximum change ratios of each parameter are 0.08%, 0.13% and 0.06% respectively. It can be seen that the gas supply system of the standard facility has good and stable gas supply capabilities.
4.4.2. Stability of the Discharge Coefficient
Every month, repeatability measurements of the discharge coefficients of four groups are performed for the flow range (0.13-5.55) kg/s, including 0.13 kg/s, 1.80 kg/s, 3.00 kg/s, and 5.55 kg/s. One group of tests is conducted six times, and the average value is taken as the measured value of the group. The maximum value of the difference between the discharge coefficients of two adjacent groups is then taken as the stability of the standard facility within the time period. The stability requirement is less than or equal to the above repeatability, i.e., ≤0.04%.
Under working environment conditions, SN2-1, SN5-1 and SN7 were selected to test the stability of the standard facility in the pressure range of (1~6) MPa and the flow range of (0.13~5.55) kg/s. The test results are shown in Table 12. The stability of the discharge coefficient calculated by the calibration test at different flow rates using three sonic nozzles with different throat diameters meets the requirements, and the stability of the standard facility performances well.
5. Conclusions
Relying on the high-pressure gas source of China Aerodynamics Research and Development Center, the gas flow secondary standard facility is based on a parallel standard sonic nozzle array, with a pressure range of (1~6) MPa and a flow range of (0.13~5.55) kg/s. Through the analysis of the test, the facility has reached the range of pressure and flow, and the following conclusions are obtained:
- (1)
- Due to the large inner diameter of the second-stage pipe of the standard facility, the temperature field of the measurement surface of the stagnation temperature of the standard sonic nozzle has obvious non-uniformity. The test shows that the non-uniformity will decrease with the increase of the gas mass flow rate;
- (2)
- In the calibration test of small flow rates, due to the non-uniformity of the temperature field, it is not possible to use only a single-point value or a multi-point average value to represent the temperature upstream of the standard sonic nozzle array. The temperature measurement should measure the temperature upstream of the standard sonic nozzle used as accurately as possible, thereby improving the accuracy of the calculated mass flow rate and the discharge coefficient of the calibrated sonic nozzle;
- (3)
- In the uncertainty analysis of the small flow calibration test, the relative uncertainty of the measurement standard obtained by the average temperature measurement method is 0.059%, and the relative uncertainty of the measurement result is 0.062%. The relative uncertainty of the measurement standard obtained by the precise temperature measurement method is 0.057%, and the relative uncertainty of the measurement result is 0.060%, which effectively reduces the uncertainty;
- (4)
- The pressure, the temperature and the flow rate of the air supply system of the standard facility are stable, which ensures the validity of the data obtained from the calibration test. In particular, the heat transfer can control the temperature of the inlet air flow, which can support the subsequent study of the effect of stagnation temperature on the discharge coefficient;
- (5)
- The standard facility has good repeatability and stability. The repeatability values of the discharge coefficient of the calibrated sonic nozzle at different pressure points are all within 0.04%, and the relative expanded uncertainty is less than 0.15% (k=2) . At the same time, the stability of the discharge coefficient of the calibrated sonic nozzle measured at different times also meets the requirements.
Author Contributions
Conceptualization, Z.Z. and J.Z.; methodology, Z.Z. and J.Z.; software, Z.Z.; validation, Z.Z. and J.Z.; formal analysis, Z.Z. and T.L.; investigation, R.Z.; resources, Z.Z.; data curation, J.Z.; writing—original draft preparation, Z.Z.; writing—review and editing, J.Z., T.L. and R.Z.; visualization, Z.Z.; supervision, R.Z. and T.L.; project administration, J.Z. and R.Z.; funding acquisition, T.L. and R.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China, grant number 52306056 and National Natural Science Foundation of China, grant number 12234015.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. All data are calculated by the author and have been included in this paper.
Conflicts of Interest
No conflict of interest exists in the submission of this manuscript, and the manuscript is approved by all authors for publication. I would like to declare on behalf of my coauthors that the work described was original research that has not been published previously, and not under consideration for publication elsewhere, in whole or in part. All the authors listed have approved the manuscript that is enclosed.
References
- Wu, H.; Liu, M. Key Parameters of a Design for a Novel Reflux Subsonic Low-Density Dust Wind Tunnel. Aerospace 2022, 9(11), 662. [Google Scholar] [CrossRef]
- Sieder-Katzmann, J.; Propst, M. Surface Pressure Measurement of Truncated, Linear Aerospike Nozzles Utilising Secondary Injection for Aerodynamic Thrust Vectoring. Aerospace 2024, 11, 507. [Google Scholar] [CrossRef]
- Choi, M.; Oh, Y. Investigation of Spray Characteristics for Detonability: A Study on Liquid Fuel Injector and Nozzle Design. Aerospace 2024, 11(6), 421. [Google Scholar] [CrossRef]
- Li, C.H.; Mickan, B. Humidity effect on the calibration of discharge coefficients of critical flow Venturi nozzles in a pVTt facility. Flow Measurement and Instrumentation 2015, 46, 125–132. [Google Scholar] [CrossRef]
- Wright, J.D.; Johnson, A.N. ASME MFC-7-2016: Measurement of gas flow by means of critical flow venturis and critical flow nozzles; National Institute of Standards and Technology: Gaithersburg, US, 2016. [Google Scholar]
- Li, C.; Wang, C. The size effect on critical back pressure ratio for sonic nozzles. International Conference on Micro/Nanoscale Heat Transfer 3918. [Google Scholar]
- Ding, H.B.; Wang, C. Flow characteristics of hydrogen gas through a critical nozzle. International journal of hydrogen energy 2014, 39(8), 3947–3955. [Google Scholar] [CrossRef]
- Johnson, A.N.; Wright, J.D. Gas flowmeter calibrations with the 26m3 pVTt standard. NIST Special Publication 2009, 1046. [Google Scholar]
- Johnson, A.N. Natural gas flow calibration service (NGFCS) NIST. NIST Special Publication 2010, 1001–1023. [Google Scholar]
- Ha, Y.C.; Park, L.A. Design of a large–Capacity flow calibration/test facility for natural gas flow meter. 16th International Flow Measurement Conference on Flow Measurement 2013, 1–4. [Google Scholar]
- Li, C.H.; Mickan, B. The bilateral comparison between NIM and PTB for small gas flow. 18th International Flow Measurement Conference on Flow Measurement 2019, 1–9. [Google Scholar]
- Cao, P.J.; Zhang, H. The influence of stagnation pressure on discharge coefficient of the sonic nozzle. 17th International Flow Measurement Conference 2016, 1–5. [Google Scholar]
- Measurement of gas flow by means of critical flow Venturi nozzles: ISO 9300: 2005; International Organization for Standardization: Switzerland, 2005; pp. 14–21.
- Johnson, A.N.; Harman, E. Blow-down calibration of a large ultrasonic flow meter. Flow Measurement and Instrumentation 2021, 77, 101848. [Google Scholar] [CrossRef]
- Cao, P.J.; Wang, C. The Thermal Effect on Discharge Coefficient of Sonic Nozzle Based on Reconstructed Body Temperature Distribution by Improved SOR Method. Transactions on Instrumentation and Measurement 2021, 1–1. [Google Scholar] [CrossRef]
- Žibret, P.; Bobovnik, G. Correction for the temperature effects in a pVTt gas flow primary standard employing a dynamic method. Measurement 2023, 207, 112375. [Google Scholar] [CrossRef]
- LEMMON E W, BELL I H. NIST standard reference database 23: reference fluid thermo-dynamic and transport properties-REFPROP, Version 9.0; National Institute of Standards and Technology: Gaitherhurg, US, 2013.
Figure 1.
Sonic nozzle object.
Figure 2.
Schematic diagram of the flow standard facility.
Figure 3.
Structure of flow standard facility based on sonic nozzle array.
Figure 4.
Installation of standard sonic nozzle array.
Figure 5.
Schematic diagram of the high-pressure gas supply system.
Figure 6.
Flow standard facility based on sonic nozzle array.
Figure 7.
Cd of the standard sonic nozzle with Re.
Figure 8.
Principles of measurement systems for flow standard facility.
Figure 9.
Distribution of temperature and pressure sensors.
Figure 10.
Aaron N. Johnson proposed a method for measuring temperature.
Figure 11.
NIST proposed a method for measuring temperature.
Figure 12.
Opening method of the standard sonic nozzle array in the small flow rate.
Figure 13.
Installation location of temperature sensors of standard sonic nozzle array.
Figure 14.
The standard sonic nozzle array open state.
Figure 15.
Temperature values of three temperature sensors at different insertion depths.
Figure 16.
Heat map under different pressures.
Figure 17.
Temperature fluctuation curves.
Table 1.
SN2-1 traceability results.
| Stagnation pressure/ (MPa) | Stagnation temperature/ (K) | Mass flow/ (kg/s) | Rent | Cd |
|---|---|---|---|---|
| 1.5 | 294.39 | 0.1883 | 1.58×106 | 0.9907 |
Table 2.
The discharge coefficients using different temperature measurement methods.
| Name | Stagnation pressure/ (MPa) | Stagnation temperature/ (K) | Mass flow/ (kg/s) | Rent | Cd |
|---|---|---|---|---|---|
| First method | 1.5 | 296.74 | 0.1873 | 1.59×106 | 0.9902 |
| Second method | 1.5 | 296.65 | 0.1874 | 1.58×106 | 0.9904 |
| NIM | 1.5 | 294.39 | 0.1883 | 1.58×106 | 0.9907 |
Table 3.
Uncertainty of measurement standards under two temperature measurement methods.
| Symbol | Source | Relative standard uncertainty/ (%) | k | ur (Qr,array) / (%) | |||
|---|---|---|---|---|---|---|---|
| First method | Second method | First method | Second method | ||||
| ur (Cd,i) | Discharge coefficient of the standard sonic nozzle | 0.040 | 1 | 0.059 | 0.057 | ||
| ur (parray,1) | calibration | Stagnation pressure | 0.040 | 1 | |||
| ur (parray,2) | Pressure stability | 0.007 | 1 | ||||
| ur (parray,3) | Pressure difference | 0.010 | 1 | ||||
| ur (Tarray,1) | calibration | Stagnation temperature | 0.010 | 1 | |||
| ur (Tarray,2) | Temperature stability | 0.004 | 0.003 | 1 | |||
Table 4.
Uncertainty of measurement results under two temperature measurement methods.
| Symbol | Source | Relative standard uncertainty/ (%) | k | ur (Cd) / (%) | ||
|---|---|---|---|---|---|---|
| First method | Second method | First method | Second method | |||
| ur (Qr,array) | Standard sonic nozzle array | 0.059 | 0.057 | 1 | 0.062 | 0.060 |
| ur (pSN) | Stagnation pressure | 0.016 | 1 | |||
| ur (TSN) | Stagnation temperature | 0.010 | 1 | |||
| uR (Cd) | Repeatability | 0.001 | 0.003 | 1 | ||
Table 5.
Uncertainty of measurement standard.
| Symbol | Source | Relative standard uncertainty/ (%) | k | ur (Qr,array) / (%) | |
|---|---|---|---|---|---|
| ur (Cd,i) | Discharge coefficient of the standard sonic nozzle | 0.040 | 1 | 0.06 | |
| ur (parray,1) | Calibration | Stagnation pressure | 0.040 | 1 | |
| ur (parray,2) | Pressure stability | 0.016 | 1 | ||
| ur (parray,3) | Pressure difference | 0.010 | 1 | ||
| ur (Tarray,1) | calibration | Stagnation temperature | 0.010 | 1 | |
| ur (Tarray,2) | Temperature stability | 0.020 | 1 | ||
Table 6.
Calibration value of the positive and reverse stroke.
| Serial number | Standard pressure value / (kPa) abs | Average value of positive stroke/ (kPa) abs | Average value of reverse stroke/ (kPa) abs | error/ (kPa) abs |
|---|---|---|---|---|
| 1 | 0 | / | / | / |
| 2 | 95.96 | 95.83 | 95.89 | 0.06 |
| 3 | 595.95 | 595.92 | 596.01 | 0.09 |
| 4 | 1095.95 | 1095.91 | 1096.01 | 0.10 |
| 5 | 1595.95 | 1595.82 | 1595.98 | 0.16 |
| 6 | 2095.95 | 2095.90 | 2095.98 | 0.08 |
| 7 | 3095.95 | 3095.92 | 3096.01 | 0.09 |
| 8 | 4095.95 | 4095.92 | 4096.00 | 0.08 |
| 9 | 5095.95 | 5095.90 | 5095.98 | 0.08 |
| 10 | 6095.95 | 6095.90 | 6095.92 | 0.02 |
| 11 | 7095.95 | 7095.83 | 7095.83 | 0.00 |
Table 7.
ur (parray,2).
| Serial number | the upstream pressure of the standard sonic nozzle array/ (MPa) | / (Pa) | Standard Deviation/(Pa) | ur (parray,2)/(%) |
|---|---|---|---|---|
| 1 | 0.4 | 400978 | 22 | 0.006 |
| 2 | 1.0 | 1003753 | 153 | 0.015 |
| 3 | 1.5 | 1505019 | 240 | 0.016 |
| 4 | 2.0 | 2010805 | 312 | 0.016 |
| 5 | 2.5 | 2554404 | 262 | 0.010 |
Table 8.
ur (parray,3).
| Serial number | Standard stagnation pressure/ (kPa) | Measured stagnation pressure/ (kPa) | Pressure difference / (kPa) | Standard Cd | Interpolation Cd | Uncertainty/ (%) |
|---|---|---|---|---|---|---|
| 1 | 398.444 | 405.966 | 7.522 | 0.9863 | 0.9863 | 0.00 |
| 2 | 1002.066 | 1035.430 | 33.364 | 0.9868 | 0.98674 | 0.01 |
| 3 | 1488.752 | 1510.038 | 21.286 | 0.9860 | 0.9860 | 0.00 |
| 4 | 1990.468 | 2051.709 | 61.241 | 0.9860 | 0.98606 | 0.01 |
| 5 | 2487.442 | 2510.088 | 22.646 | 0.9865 | 0.9865 | 0.00 |
Table 9.
ur (Tarray,2).
| Serial number | Calibrated flow rate / (kg/s) | Actual flow rate / (kg/s) | / (K) | Standard Deviation/ (K) | ur (Tarray,2) / (%) |
|---|---|---|---|---|---|
| 1 | 0.13 | 0.12 | 300.09 | 0.02 | 0.01 |
| 2 | 1.20 | 1.17 | 305.19 | 0.02 | 0.01 |
| 3 | 1.80 | 1.76 | 305.71 | 0.04 | 0.01 |
| 4 | 3.00 | 3.02 | 304.00 | 0.01 | 0.01 |
| 5 | 5.50 | 5.56 | 290.98 | 0.06 | 0.02 |
Table 10.
Uncertainty of the measurement result.
| Symbol | Source | Relative standard uncertainty/ (%) | k | ur (Cd) / (%) |
|---|---|---|---|---|
| ur (Qr,array) | Standard facility | 0.060 | 1 | 0.075 |
| ur (pSN) | Stagnation pressure | 0.016 | 1 | |
| ur (TSN) | Stagnation temperature | 0.010 | 1 | |
| uR (Cd) | Repeatability | 0.040 | 1 |
Table 11.
Repeatability test.
| Serial number | Calibrated sonic nozzles | Stagnation pressure/ (MPa) | Gas flow/ (kg/s) | Stagnation temperature/ (K) | Rent | Cd | Repeatability/ (%) |
|---|---|---|---|---|---|---|---|
| 1 | SN2-1 | 1.0 | 0.12 | 293.15 | 1.03×106 | 0.9904 | 0.001 |
| 2 | SN5-1 | 2.4 | 1.20 | 296.77 | 5.05×106 | 0.9954 | 0.035 |
| 3 | 3.6 | 1.80 | 296.80 | 7.60×106 | 0.9953 | 0.018 | |
| 4 | 6.0 | 3.00 | 292.99 | 1.32×107 | 0.9951 | 0.013 | |
| 5 | SN7 | 5.4 | 5.55 | 295.83 | 1.67×107 | 0.9965 | 0.005 |
Table 12.
Stability test.
| Serial number | Calibrated sonic nozzles | Stagnation pressure/ (MPa) | Gas flow/ (kg/s) | Cd | Cd Maximum Difference | |||
|---|---|---|---|---|---|---|---|---|
| 1th | 2nd | 3rd | 4th | |||||
| 1 | SN2-1 | 1.0 | 0.12 | 0.9904 | 0.9903 | 0.9904 | 0.9905 | 0.0002 |
| 2 | SN5-1 | 3.6 | 1.80 | 0.9952 | 0.9952 | 0.9952 | 0.9952 | 0.0000 |
| 3 | 6.0 | 3.00 | 0.9951 | 0.9951 | 0.9952 | 0.9952 | 0.0001 | |
| 4 | SN7 | 5.4 | 5.55 | 0.9964 | 0.9965 | 0.9964 | 0.9965 | 0.0001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
MDPI Initiatives
Important Links
© 2025 MDPI (Basel, Switzerland) unless otherwise stated