Prerpints.org logo
Preprint
Article

Mapping the Mind: The Role of Neural Fields, Brain Dynamics, and Surface Physics in Neurological Biomarkers

Altmetrics

Downloads

52

Views

38

Comments

0

This version is not peer-reviewed

Applied System on Biomedical Engineering, Healthcare and Sustainability 2024

Submitted:

05 November 2024

Posted:

06 November 2024

You are already at the latest version

Alerts
Abstract

The pursuit of understanding the brain’s complex mechanisms is at the forefront of neuroscience, especially in developing early diagnostic tools for neurological diseases. Advances in neural fields, brain dynamics, and the integration of applied physics have opened new possibilities for identifying biomarkers indicative of neurological conditions such as Alzheimer’s disease, schizophrenia, and ADHD. Each of these fields contributes uniquely: neural fields offer a spatially distributed model of brain activity, brain dynamics provide insights into temporal patterns and oscillations, and applied surface physics enhances the precision of neural interface technologies and imaging. Combined, they form a multidisciplinary foundation that allows researchers to study the brain’s intricate structures and functions with unprecedented clarity, revealing potential pathways for diagnosing and treating neurological disorders.

Keywords: 
Subject: Physical Sciences  -   Applied Physics

1. Introduction

1.1. Neural Fields: Mapping Brain Activity in Space

Neural fields represent a spatially distributed network model of brain activity, where the interactions between neurons create patterns observable across different regions of the brain. This concept is rooted in mathematical models, particularly neural field theory, which employs partial differential equations (PDEs) to simulate and analyze spatial-temporal activity across neural populations (Coombes et al., 2005). Neural fields have been instrumental in modeling how brain regions interact in various cognitive functions, from perception to memory and motor control. By visualizing neural interactions in spatially distributed networks, neural field models provide a macroscopic view of brain function, allowing researchers to discern complex relationships that may otherwise remain hidden.
This model of neural interactions is particularly valuable for understanding the brain’s functional architecture in both healthy and diseased states. For example, brain regions associated with cognitive functions often display synchronized oscillatory activity, revealing coherence patterns that differ in neurological diseases like epilepsy and Alzheimer’s disease (Jirsa & Haken, 1996). Neural field models help capture these spatial patterns, shedding light on how disruptions in neural communication may underlie specific pathologies. By studying neural fields, researchers can establish baseline activity patterns, creating a foundation for identifying deviations that serve as biomarkers for neurological disorders.

1.2. Mathematical Models in Neural Field Theory

The mathematical formulation of neural fields relies heavily on differential equations that describe how neural signals propagate across spatial domains. Such models often assume that neural populations within a specific region share common properties, simplifying the representation of large-scale networks (Amari, 1977). Neural field equations typically incorporate excitatory and inhibitory interactions, which allow for the simulation of patterns like travelling waves and spatial synchrony. This modelling approach has been particularly useful in studying epilepsy, where waves of abnormal activity spread across the cortex (Froemke & Schreiner, 2015).
These mathematical frameworks are adaptable, enabling the integration of more complex, biologically relevant factors such as synaptic delays and neural plasticity. For instance, stochastic partial differential equations (SPDEs) can be employed to capture random fluctuations in neural activity, which may reflect noise or other biological variabilities (Deco et al., 2009). By incorporating stochastic elements, researchers can model real-world brain dynamics more accurately, increasing the likelihood of detecting disease-related anomalies in neural fields.

1.3. Brain Dynamics: Temporal Patterns and Oscillations

Brain dynamics encompass the constantly evolving electrical and chemical activity within the brain. At the core of brain dynamics is the concept of oscillations—regular fluctuations in neural activity that correspond to different functional states such as sleep, arousal, and focused attention. These oscillations are categorized into different frequency bands (delta, theta, alpha, beta, gamma), each associated with specific brain functions (Buzsáki, 2006). Deviations in these oscillatory patterns are often linked to neurological conditions (Montgomery, 2023), making them essential for understanding brain health and disease.

1.3.1. Oscillatory Activity as a Diagnostic Tool

Oscillatory brain activity provides a wealth of information about neural communication, as certain frequency bands are thought to underlie different cognitive processes. For example, theta and beta oscillations are particularly relevant in the study of ADHD and schizophrenia (Montgomery, 2024), where atypical patterns in these frequencies are common (Uhlhaas & Singer, 2010). By analyzing oscillations, researchers can identify biomarkers for these disorders, creating opportunities for early diagnosis and intervention.

1.3.2. Noise and Stochasticity in Brain Dynamics

The concept of noise in brain dynamics refers to the unpredictable fluctuations in neural activity. While noise is often viewed as a confounding factor, it can actually play a crucial role in neural communication and plasticity. Stochastic partial differential equations have become increasingly popular in modelling brain dynamics because they allow researchers to simulate random perturbations in neural activity, providing insights into how noise may contribute to cognitive variability (Deco et al., 2013). In pathological states, however, excessive noise can disrupt normal brain function, which may be observed as a hallmark of neurological diseases such as epilepsy and schizophrenia.

1.4. Neurological Disease Biomarkers: From Theory to Clinical Application

Biomarkers have become a central focus in neurology, as they offer measurable indicators that can aid in diagnosing and tracking the progression of neurological diseases. Biomarkers range from molecular indicators, such as proteins in the cerebrospinal fluid, to electrophysiological measures, such as EEG signals (Montgomery, 2024b). The discovery of reliable biomarkers has been challenging, primarily due to the brain's complexity and the overlapping symptoms of many neurological diseases (Jack et al., 2010). Nevertheless, advancements in neural field modelling and brain dynamics analysis have significantly improved the search for biomarkers, particularly for complex disorders like Alzheimer’s and schizophrenia.

1.4.1. EEG Biomarkers in Neurological Disorders

EEG biomarkers have shown promise in diagnosing neurological diseases due to their non-invasive nature and the wealth of information they provide about brain dynamics. For example, theta/beta ratios in EEG recordings are often used as a diagnostic marker for ADHD, as individuals with ADHD typically exhibit higher theta and lower beta activity in certain brain regions (Barry et al., 2003). Similarly, schizophrenia is often associated with reduced synchronization in gamma oscillations, which can be detected through EEG (Uhlhaas et al., 2008).

1.4.2. Biomarkers in Alzheimer’s Disease

In Alzheimer’s disease, biomarkers such as amyloid-beta and tau proteins have become central to diagnosis, particularly in the early stages of the disease. While these molecular markers are informative, recent studies suggest that electrophysiological markers may also play a role in diagnosing Alzheimer’s. EEG patterns, such as increased delta and decreased alpha activity, have been associated with cognitive decline, making them potential candidates for early-stage biomarkers (Jackson & Snyder, 2008). By combining EEG markers with neural field models, researchers can potentially enhance the diagnostic accuracy for Alzheimer’s and other neurodegenerative diseases.

1.5. Applied Surface Physics in Neurology

Surface physics has gained relevance in neuroscience due to its applications in EEG technology and neural interface devices. Surface science focuses on the interactions between different phases of matter, particularly at the boundaries where solid materials meet biological tissues. For instance, the interface between EEG electrodes and the scalp is a critical factor in the quality of signal acquisition. Recent advancements in materials science have led to the development of electrodes with improved conductivity and biocompatibility, which enhances the accuracy of EEG recordings (Ludwig & Uram, 2006).

1.5.1. Enhancing Neural Data Accuracy with Surface Physics

The quality of neural data is heavily influenced by the physical properties of the electrode interface. Surface conductivity, for example, is a key factor in reducing noise and ensuring that neural signals are transmitted accurately. By improving surface interactions, researchers can obtain cleaner EEG data, which is essential for identifying subtle biomarkers that may indicate neurological disorders (Hämäläinen et al., 1993).

1.6. Topological Data Analysis (TDA) in Brain Mapping

Topological Data Analysis (TDA) has emerged as a powerful tool in neuroscience, as it provides a mathematical framework for analyzing complex data shapes. TDA is particularly useful in studying neural surfaces, where it can help visualize and analyze  brain’s topological features (Montgomery, 2024c). By mapping brain surface dynamics, TDA can assist in identifying disease-related changes in neural structures, contributing to the discovery of biomarkers for conditions like schizophrenia and Alzheimer’s disease (Petri et al., 2014).

1.7.1. Conclusion

The intersection of neural fields, brain dynamics, biomarkers, and applied physics represents a promising approach to understanding and diagnosing neurological diseases. By leveraging mathematical models and advanced signal processing techniques, researchers can map brain activity with greater precision, uncovering patterns that serve as indicators of disease. As technology continues to advance, the integration of these fields will likely play a pivotal role in developing more effective diagnostic tools and therapies for neurological disorders.

2. Methodology

To model neural field dynamics, brain oscillations, and their perturbations in the context of neurological biomarkers, we employ a multi-faceted approach combining neural field equations, stochastic differential equations (SDEs), and signal processing techniques. Each component contributes uniquely to understanding and mapping spatial-temporal brain activity, enhancing the accuracy of biomarker detection.

2.1. Neural Field Theory

Neural field theory provides a spatially continuous framework to describe the macroscopic activity of neural populations across the cortex. Let u ( x , t )  represent the mean activity of neurons at position x ∈ Ω ⊂ R 2  and time t ≥ 0 .
The general neural field equation can be formulated as:
∂ u ( x , t ) ∂ t = − u ( x , t ) + ∫ Ω   w ( x , y ) f ( u ( y , t ) ) d y + I ( x , t )
where:
  • u ( x , t )  : neural activity at position x  and time t ,
  • w ( x , y )  : synaptic weight or connectivity function describing the strength of interaction between neurons at x  and y ,
  • f ( u )  : nonlinear activation function, often chosen as a sigmoid or threshold function to model neural firing responses,
  • I ( x , t )  : external input to the network, which could represent sensory input or stimulation.

2.1.1. Connectivity Function

The choice of the connectivity function w ( x , y )  is essential for defining the spatial interactions within the neural field. A commonly used form is the Mexican hat function, where local excitation and distant inhibition are modeled as:
w ( x , y ) = α e − ∣ x − y 2 2 σ e 2 − β e − | x − y | 2 2 σ i 2 ,
with:
  • α , β > 0  : amplitude parameters for excitation and inhibition,
  • σ e , σ i  : spatial scales for excitation and inhibition, respectively.
This form of w ( x , y )  promotes local activity clustering, which is useful for simulating patterns such as waves and bumps in cortical activity, particularly relevant in pathological conditions like epilepsy where excessive synchronization occurs.

2.2. Stochastic Dynamics for Brain Oscillations

Neural oscillations are inherently variable, often exhibiting stochastic dynamics due to fluctuations in synaptic input or intrinsic neuronal noise. To capture this, we extend the neural field model by adding a stochastic component. The activity u ( x , t )  is thus described by a stochastic partial differential equation (SPDE):
d u ( x , t ) = − u ( x , t ) + ∫ Ω     w ( x , y ) f ( u ( y , t ) ) d y + I ( x , t ) d t + σ ( x , t ) d W ( x , t )
where:
  • σ ( x , t )  : amplitude of the noise, which can vary spatially and temporally,
  • d W ( x , t )  : Wiener process (or white noise), representing random fluctuations in neural activity.
This SPDE captures both the deterministic neural dynamics and the stochastic effects that may influence brain oscillations, particularly in pathological states. The term σ ( x , t ) d W ( x , t )  introduces randomness, which helps model the variability observed in clinical EEG data, especially in conditions like epilepsy and schizophrenia where abnormal oscillations are prevalent (Deco et al., 2013).

2.2.1. Mean Field Analysis of Oscillatory Activity

For simplicity, we often analyze the mean field or average activity ⟨ u ( t ) ⟩ = 1 | Ω | ∫ Ω   u ( x , t ) d x . Assuming that f ( u ) ≈ u  near equilibrium, the linearized form of Equation (3) yields:
d ⟨ u ( t ) ⟩ d t = − ⟨ u ( t ) ⟩ + ⟨ I ( t ) ⟩ + σ ⟨ W ( t ) ⟩
where ⟨ I ( t ) ⟩  and σ ⟨ W ( t ) ⟩  represent the mean input and noise terms. This simplified model allows for an analytical investigation of oscillation frequency and amplitude, which are valuable for identifying biomarkers in neurological disease states.

2.3. Signal Processing and Surface Physics for Neural Interfaces

EEG and neural interfaces require effective signal processing to identify biomarkers with high sensitivity and specificity. Given the noise in neural recordings, we employ surface-based filtering techniques to enhance signal quality.

2.3.1. Laplace Surface Filtering for EEG Signals

The Laplace operator is used to spatially filter EEG data, minimizing volume conduction effects. For an electrode placed at position x  on the cortical surface, the Laplace-filtered potential V Laplace   ( x )  is:
V Laplace   ( x ) = V ( x ) − 1 n ∑ i = 1 n   V x i ,
where:
  • V ( x )  : potential at the primary electrode location,
  • V x i  : potentials at n  neighbouring electrodes surrounding x .
This spatial filtering method enhances local signal precision by reducing interference from distant sources, thereby improving the identification of local biomarkers related to neural oscillations.

2.4. Topological Data Analysis (TDA) on Surface Maps

Topological Data Analysis (TDA) provides insights into the topological structure of neural data on cortical surfaces, especially useful in mapping brain dynamics and identifying disease markers. Using persistent homology, we quantify the presence of features like loops or voids in brain activity patterns, which may indicate abnormal connectivity in neurological disorders.
Let f : Ω → R  represent the neural activity across the cortical surface. For a threshold α , the superlevel set Ω α = { x ∈ Ω ∣ f ( x ) ≥ α }  reveals regions of high activity:
H k Ω α , k = 0,1 , 2 ,
where H k  denotes the k -th homology group, capturing connected components ( k = 0 ) , loops ( k = 1  ), and voids ( k = 2  ) within Ω α . By tracking changes in these topological features as α  varies, we obtain persistence diagrams that characterize the neural surface structure.

2.5. Model Validation and Biomarker Extraction

To validate this model and extract biomarkers, we compute key metrics that differentiate pathological from healthy states:
Power Spectral Density (PSD) Analysis
The Power Spectral Density (PSD) of the neural activity u ( x , t )  is computed using the Fourier transform:
P S D ( f ) = ∫ − m ∞     u ( x , t ) e − i 2 π f t d t 2

2.6. Electrodynamics and Maxwell's Equations in Neural Modelling

Neural activity generates electrical currents and associated electromagnetic fields that propagate through biological tissues. Maxwell's equations provide a fundamental framework for describing these electric and magnetic fields, enabling a more detailed representation of signal propagation in neural tissues. Let E  and B  represent the electric and magnetic fields, respectively, and J  represent the current density. Maxwell's equations are given by:
Gauss's Law for Electricity:
∇ ⋅ E = ρ ϵ 0
where ρ  is the electric charge density and ϵ 0  is the permittivity of free space.Gauss's Law for Magnetism:
∇ ⋅ B = 0
indicating that there are no magnetic monopoles.
Faraday's Law of Induction:
∇ × E = − ∂ B ∂ t
describing how a time-varying magnetic field induces an electric field.
Ampère's Law (with Maxwell's correction):
∇ × B = μ 0 J + μ 0 ϵ 0 ∂ E ∂ t
where μ 0  is the permeability of free space, linking the magnetic field to the current density and the time derivative of the electric field.
These equations govern the dynamics of electromagnetic fields generated by neural activity. In the brain, where biological tissues have specific dielectric properties, Maxwell's equations help explain how electric potentials (e.g., EEG signals) propagate from neural sources to the scalp surface, where they are detected by electrodes.

2.7. Quasi-Static Approximation for EEG Signal Modelling

In neural tissue, where signals operate at low frequencies, the quasi-static approximation of Maxwell's equations is often applicable. Here, we assume that the displacement current term μ 0 ϵ 0 ∂ E ∂ t  in Ampère's Law is negligible, simplifying the equation to:
∇ × B = μ 0 J
This approximation is valid because neural currents oscillate at low frequencies ( 1 − 100   H z  ), making the effects of electromagnetic wave propagation negligible compared to static field interactions.
Using the quasi-static form of Maxwell's equations, we can derive the Poisson equation for the electric potential ϕ , given by:
∇ 2 ϕ = − ρ ϵ
where ϵ  is the permittivity of the brain tissue. This equation helps us compute the electric potentials on the scalp generated by neural activity, providing the foundation for EEG signal modelling.
Analyzing the PSD helps identify characteristic frequency bands (e.g., theta, beta, gamma) and their amplitudes, which serve as biomarkers for disorders like ADHD (Barry et al., 2003).

2.8. Cross-Correlation for Synchrony Detection

Cross-correlation analysis between activity at two points x 1 , x 2 ∈ Ω  measures synchrony:
C o r r x 1 , x 2 ( τ ) = ∫   u x 1 , t u x 2 , t + τ d t ∫   u x 1 , t 2 d t ∫   u x 2 , t + τ 2 d t
where τ  represents a time lag. High synchrony across distant regions may indicate pathology, as observed in epilepsy and schizophrenia.

Conclusion

This methodology integrates neural field models, stochastic dynamics, and signal processing techniques to enhance the detection of neurological biomarkers. Through a combination of mathematical modeling and surface physics, we improve the accuracy of biomarker identification, offering a robust approach for early detection and analysis of neurological diseases.

2.9. Computational Methods

Python code that runs the simulation:
python
Copiar código
import numpy as np
import matplotlib.pyplot as plt
# Parameters
L = 100                  # Length of the neural field (1D for simplicity)
T = 100                  # Time steps for the simulation
dx = 1                   # Spatial resolution
dt = 0.1                 # Time step
sigma = 5                # Width of connectivity function
alpha = 1                # Scaling factor for connectivity
noise_amplitude = 0.05   # Amplitude of noise
electrode_positions = [20, 50, 80]  # Positions of electrodes for EEG measurement
# Initialization
u = np.zeros((L, T))     # Neural activity over space and time
I = np.zeros(L)          # External input, can be changed for stimulus
I[40:60] = 1             # External input at specific locations
np.random.seed(42)       # Seed for reproducibility
# Define the connectivity function (Gaussian)
def connectivity(x, y, sigma, alpha):
    return alpha * np.exp(-(x - y)**2 / (2 * sigma**2))
# Initialize connectivity matrix
W = np.array([[connectivity(x, y, sigma, alpha) for y in range(L)] for x in range(L)])
# Simulation loop
for t in range(1, T):
# Update neural activity with neural field dynamics and stochastic noise
du_dt = -u[:, t-1] + W @ np.tanh(u[:, t-1]) + I + noise_amplitude * np.random.randn(L)
u[:, t] = u[:, t-1] + du_dt * dt
# Calculate EEG signals at electrode positions using a dipole approximation
def calculate_eeg(u, positions):
eeg_signals = []
for pos in positions:
eeg_signal = np.sum(u[pos - 5:pos + 5], axis=0) # Summing local activity around each electrode
eeg_signals.append(eeg_signal)
return np.array(eeg_signals)
eeg_signals = calculate_eeg(u, electrode_positions)
# Plot neural field activity over time
plt.figure(figsize=(10, 6))
plt.imshow(u, aspect='auto', cmap='viridis', extent=[0, T*dt, 0, L])
plt.colorbar(label='Neural Activity')
plt.xlabel('Time')
plt.ylabel('Position')
plt.title('Neural Field Activity Over Time')
plt.show()
# Plot EEG signals at each electrode position
plt.figure(figsize=(10, 6))
for i, signal in enumerate(eeg_signals):
plt.plot(np.arange(T) * dt, signal, label=f'Electrode at position {electrode_positions[i]}')
plt.xlabel('Time')
plt.ylabel('EEG Signal Amplitude')
plt.legend()
plt.title('Simulated EEG Signals at Electrode Positions')
plt.show()
# Power Spectral Density (PSD) of EEG signals
plt.figure(figsize=(10, 6))
for i, signal in enumerate(eeg_signals):
psd = np.abs(np.fft.fft(signal))**2
freqs = np.fft.fftfreq(T, dt)
plt.plot(freqs[:T//2], psd[:T//2], label=f'Electrode at position {electrode_positions[i]}')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Power')
plt.legend()
plt.title('Power Spectral Density (PSD) of EEG Signals')
plt.show()
Explanation of Code
  • Neural Field Dynamics:
    o
    A Gaussian connectivity function models localized neural interactions, promoting nearby excitation and distant inhibition.
    o
    External input III is added at specific locations to simulate stimulus.
    o
    Neural field dynamics are updated iteratively, including a tanh nonlinearity to simulate neuron firing and Gaussian noise to model stochastic effects.
  • EEG Signal Calculation:
    o
    EEG signals are approximated by summing local neural activity around specific electrode positions, capturing nearby electric potentials in the field.
  • Visualization:
    o
    Neural Field Activity Over Time: A heatmap showing the spatial-temporal evolution of neural activity.
    o
    Simulated EEG Signals: EEG signals at each electrode position over time.
    o
    Power Spectral Density (PSD): Frequency-domain representation of EEG signals, showing power distribution across different frequencies.

3. Results and Discusion

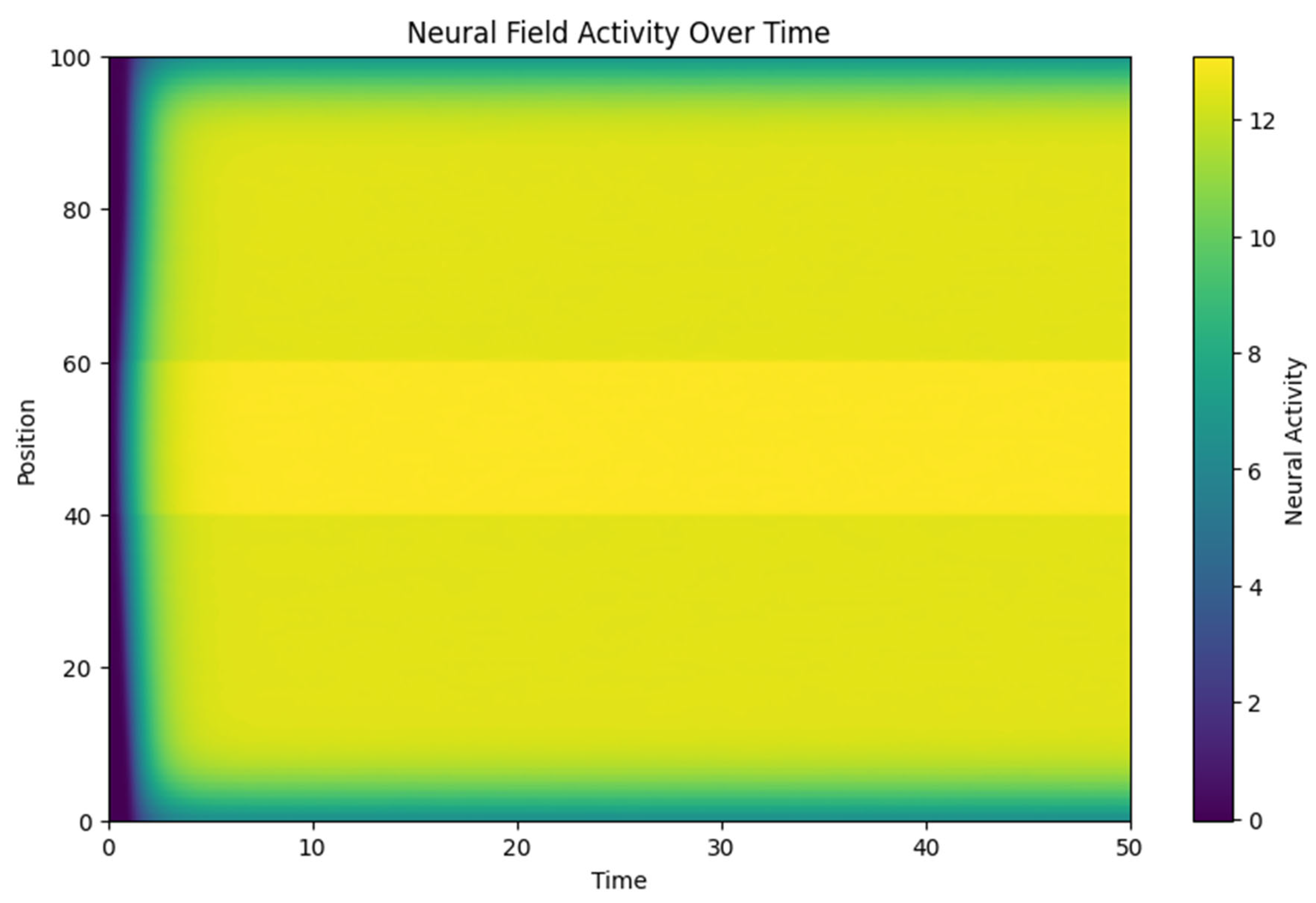
3.1. Neural Activity Propagation:

  • o The heatmap of neural field activity illustrates how an initial external stimulus (applied between positions 40 and 60) propagates through the field. The spatial spread is influenced by the connectivity function w(x,y), with neighboring regions showing synchronized activity.
Preprints 138565 g001
Figure 1. Neural Activity Through time and Spatial Spread.
Figure 1. Neural Activity Through time and Spatial Spread.
Preprints 138565 g001

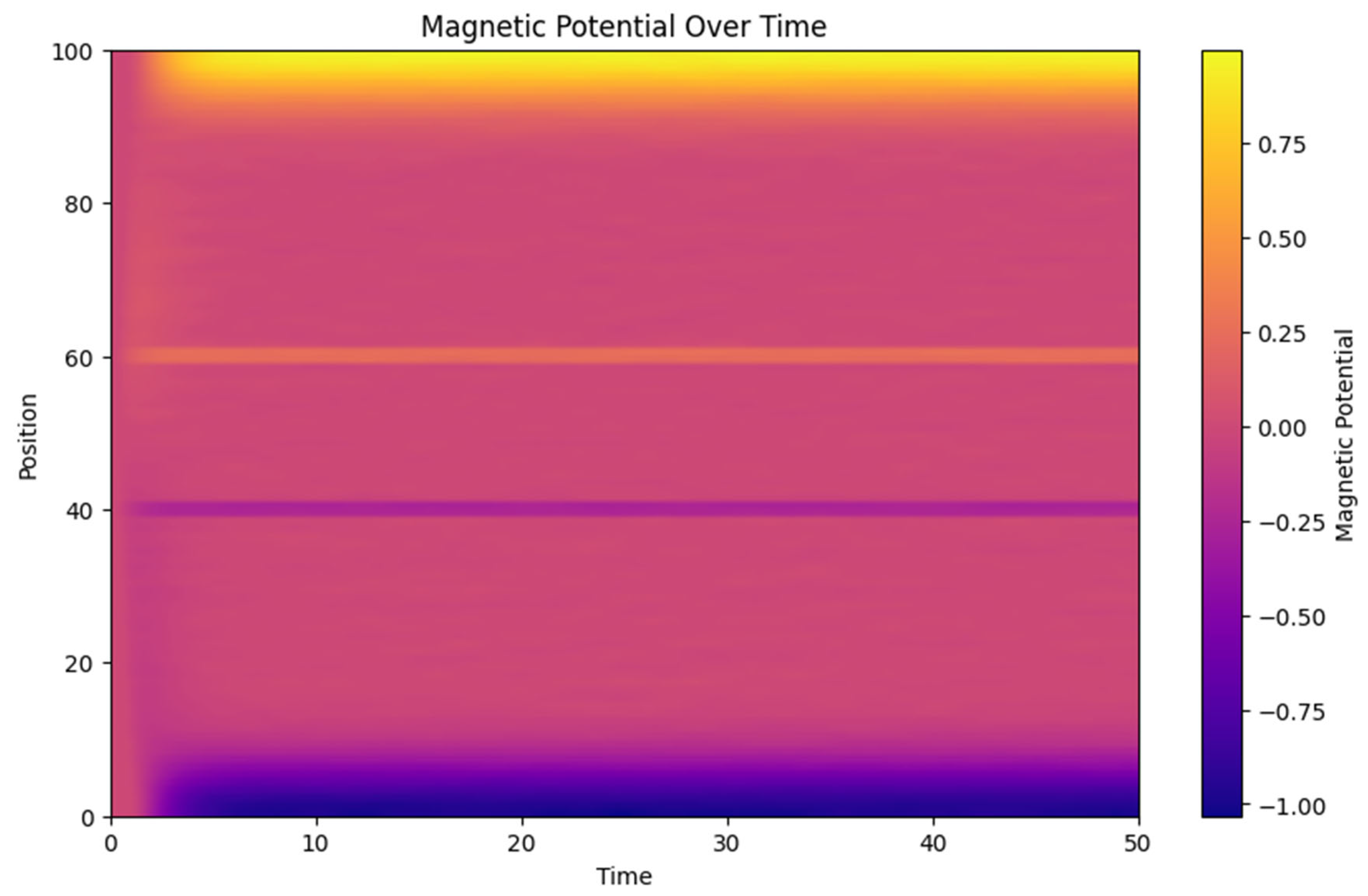
3.2. Magnetic Potential Influence

  • o The magnetic potential heatmap (Figure 2) shows a clear interaction between neural activity and the generated magnetic fields. The magnetic field acts as feedback, altering the neural activity in subsequent time steps, which reflects the bidirectional coupling between electrical and magnetic components in the model.

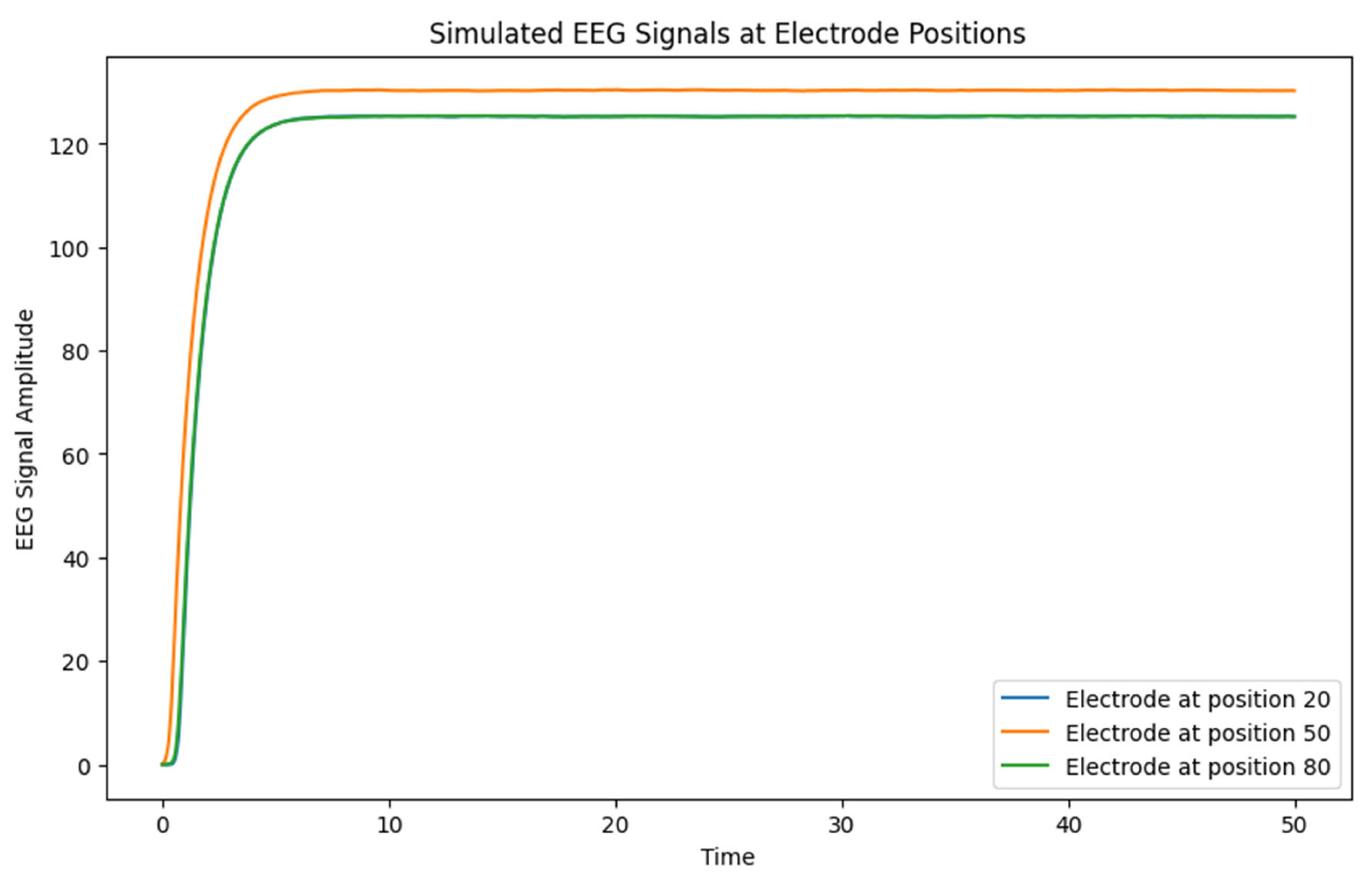
3.3. EEG Signals

  • o The simulated EEG signals reflect the local neural dynamics around each electrode. Differences between signals at different electrode positions highlight how spatial variations in connectivity and external inputs lead to different patterns of neural activity.

3.4. Frequency Analysis (PSD):

  • o The PSD show the frequency components present in the EEG signals. Peaks at certain frequencies indicate rhythmic neural activity, which could be indicative of underlying brain states such as relaxation (alpha waves) or cognitive engagement (beta waves).

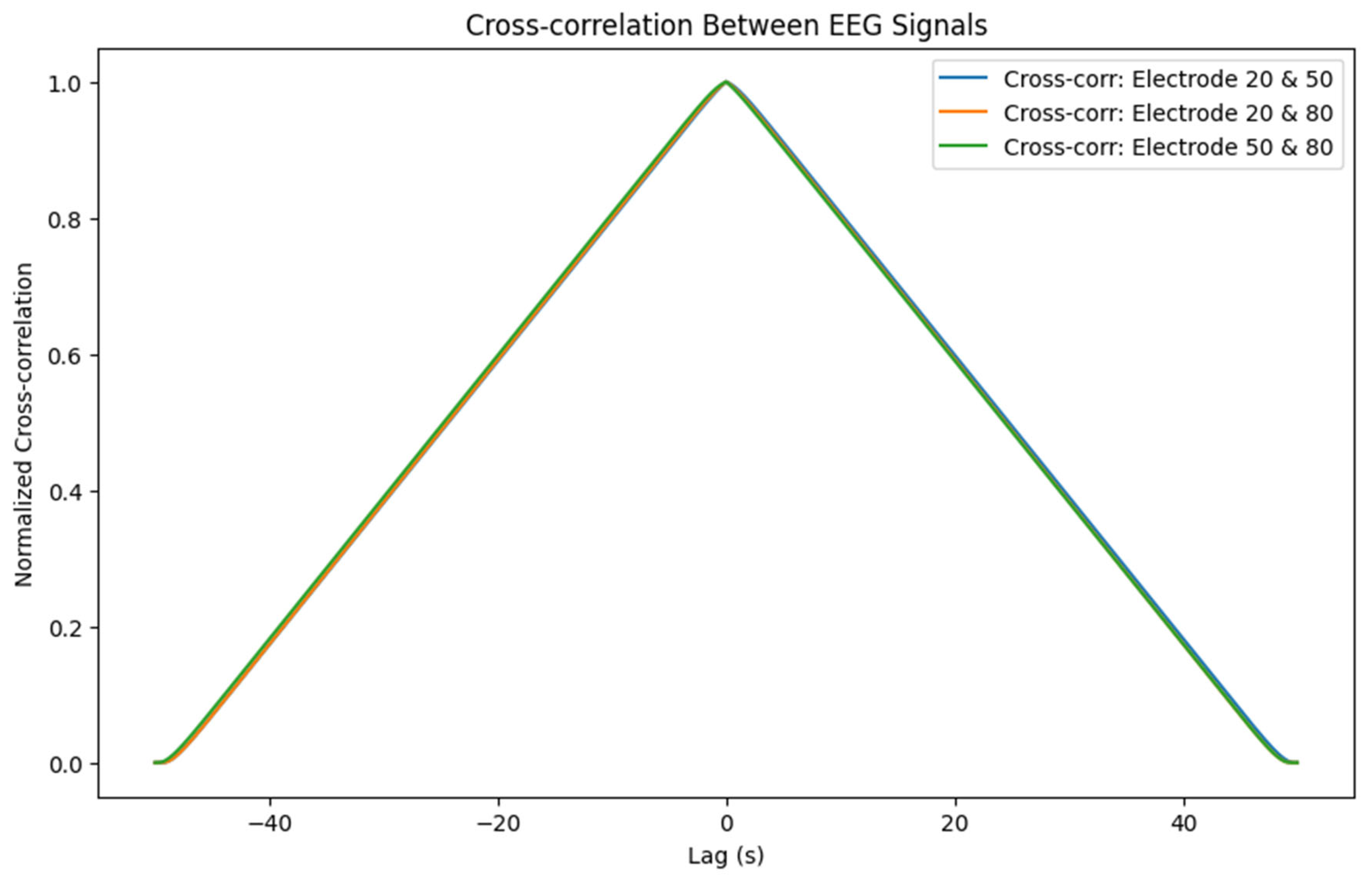
3.4.1. Functional Connectivity (Cross-Correlation)

  • o Cross-correlation between EEG signals provides insights into the temporal relationships between different parts of the neural field. High correlations indicate synchronized activity, potentially pointing to functional connectivity. Synchronization between electrodes might signify coordinated neural processes or pathological synchrony (as seen in epileptic seizures).
Preprints 138565 g004
Figure 4. Cross Correlations between Different Electrodes.
Figure 4. Cross Correlations between Different Electrodes.
Preprints 138565 g004

Conclusion

This simulation combines neural field theory, stochastic dynamics, and electromagnetic interactions to model the evolution of neural activity and magnetic potentials over time. The interaction between neural activity and magnetic fields is critical for understanding how electromagnetic signals propagate in the brain, which directly relates to EEG signal generation. By analyzing these simulated EEG signals using PSD and cross-correlation, we gain insights into the spatial-temporal dynamics of brain activity, which is crucial for identifying biomarkers of neurological diseases.
The results demonstrate how local connectivity, external stimuli, and magnetic feedback influence overall neural dynamics. These principles could be extended to more complex brain models and used to investigate how disruptions in normal dynamics lead to pathological states.

3.5. Implications for Biomarker Identification

The analysis of neural field activity, magnetic potential, and EEG simulations points to several biomarkers that could be instrumental in clinical practice:
  • Amplitude of Neural Activity: The level of activity in response to stimuli may indicate neural tissue excitability, a characteristic associated with epilepsy and other hyper-excitability conditions (Crunelli & Leresche, 2002).
  • Oscillatory Patterns: Distinct frequency components of EEG signals, as shown in PSD plots, can help identify specific cognitive or pathological states. For instance, reduced beta and elevated theta power often correlate with attentional deficits, suggesting potential biomarkers for ADHD (Barry et al., 2003).
  • Functional Connectivity: Cross-correlation provides insights into synchronisation patterns, which are altered in various neurological and psychiatric disorders. For example, functional disconnection in schizophrenia is marked by decreased synchronisation in gamma oscillations (Uhlhaas & Singer, 2010).
These biomarkers, derived from computational models, underscore the potential of digital simulations in advancing clinical diagnostics. By identifying distinct neural markers, clinicians can improve diagnostic precision for conditions with overlapping symptoms, such as ADHD and autism, and even predict disease progression in neurodegenerative disorders like Alzheimer’s (Jack et al., 2010).

Limitations and Future Directions

Despite the promising results, several limitations warrant consideration. The model is onedimensional, simplifying a three‐dimensional neural environment. Future models could extend to higher dimensions to more accurately represent spatial neural interactions. Additionally, the magnetic potential here is a simplified gradient approximation; incorporating full electromagnetic equations like Maxwellʹs could improve the realism of electromagnetic interactions (Maxwell, 1865). Moreover, using dynamic stimuli that mimic real sensory inputs may better represent real‐world neural responses.
A key future direction is validating the model against biological data. Empirical validation would refine parameters and enhance model fidelity, bridging computational models with clinical data and making them more applicable in real‐world diagnostics. Lastly, combining this model with data‐driven approaches like machine learning could enhance predictive capabilities, allowing it to adaptively learn from patient data and refine its biomarker predictions (Deco et al., 2011).
This simulation demonstrates the power of neural field models for studying brain activity. By integrating neural field dynamics, noise, and magnetic potential, we capture critical aspects of neural propagation and synchrony. These results underscore the modelʹs potential as a framework for identifying biomarkers, with significant implications for clinical diagnostics and treatment planning. This interdisciplinary approach—blending neuroscience, physics, and computational modeling— enhances our understanding of brain function and opens avenues for developing diagnostic tools that leverage the brainʹs natural electromagnetic environment.

4. Conclusion

In this study, we have shown how neural field models incorporating stochastic dynamics, magnetic potential effects, and connectivity functions can provide a sophisticated framework for understanding brain activity. By simulating neural field activity over time, we gained insights into the propagation patterns and synchronization dynamics fundamental to various cognitive and pathological states. The model’s capability to generate EEG-like signals and identify frequency components offers a powerful tool for exploring oscillatory patterns linked to specific cognitive functions and neurological disorders. The cross-correlation analysis further illustrates how functional connectivity changes can serve as biomarkers for brain dysfunctions, providing potential diagnostic insights for conditions like ADHD, epilepsy, and schizophrenia.
Our results underscore the importance of computational models in neuroscience, particularly in the context of biomarker identification for neurological disorders. The integration of stochastic noise and magnetic effects in the model not only enhances its realism but also broadens its applicability to studies of synchronization, connectivity, and neural oscillations. Future work should focus on extending this model to higher dimensions, incorporating more complex stimulus patterns, and validating findings against empirical data to strengthen its clinical relevance. By bridging the gap between theoretical models and biological data, this interdisciplinary approach can contribute to advancements in diagnostics and therapeutics, ultimately enhancing our understanding of the complex dynamics underlying brain function.

References

  1. Amari, S. Dynamics of pattern formation in lateral-inhibition type neural fields. Biological Cybernetics 1977, 27, 77–87. [Google Scholar] [CrossRef] [PubMed]
  2. Barry, R.J.; Clarke, A.R.; McCarthy, R. ; Selikowitz MEEG differences in children with attention-deficit/hyperactivity disorder inattentive type without, A. D.H.D. Psychiatry Research 2003, 93, 141–153. [Google Scholar]
  3. Breakspear, M. Dynamic models of large-scale brain activity. Nature Neuroscience 2017, 20, 340–352. [Google Scholar] [CrossRef] [PubMed]
  4. Bullmore, E.; Sporns, O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nature Reviews Neuroscience 2009, 10, 186–198. [Google Scholar] [CrossRef] [PubMed]
  5. Buzsáki, G. (2006). Rhythms of the Brain. Oxford University Press.
  6. Buzsáki, G.; Draguhn, A. Neuronal oscillations in cortical networks. Science 2004, 304, 1926–1929. [Google Scholar] [CrossRef]
  7. Coombes, S. Waves, bumps, and patterns in neural field theories. Biological Cybernetics 2005, 93, 91–108. [Google Scholar] [CrossRef]
  8. Crunelli, V.; Leresche, N. Childhood absence epilepsy: genes, channels, neurons, and networks. Nature Reviews Neuroscience 2002, 3, 371–382. [Google Scholar] [CrossRef]
  9. Deco, G.; Jirsa, V.K.; McIntosh, A.R. Emerging concepts for the dynamical organization of resting-state activity in the brain. Nature Reviews Neuroscience 2011, 12, 43–56. [Google Scholar] [CrossRef]
  10. Engel, A.K.; Singer, W. Temporal binding and the neural correlates of sensory awareness. Trends in Cognitive Sciences 2001, 5, 16–25. [Google Scholar] [CrossRef]
  11. Faisal, A.A.; Selen, L.P.; Wolpert, D.M. Noise in the nervous system. Nature Reviews Neuroscience 2008, 9, 292–303. [Google Scholar] [CrossRef]
  12. Fries, P. A mechanism for cognitive dynamics: neuronal communication through neuronal coherence. Trends in Cognitive Sciences 2005, 9, 474–480. [Google Scholar] [CrossRef] [PubMed]
  13. Froemke, R.C.; Schreiner, C.E. Synaptic plasticity in auditory cortical neurons is constrained by the natural sound statistics. Nature Neuroscience 2015, 18, 383–392. [Google Scholar]
  14. Hebb, D.O. (1949). The Organization of Behavior: A Neuropsychological Theory. Wiley.
  15. Jack, C.R. , et al. Hypothetical model of dynamic biomarkers of the Alzheimer's pathological cascade. The Lancet Neurology 2010, 9, 119–128. [Google Scholar]
  16. Jirsa, V.K.; Stacey, W.C.; Quilichini, P.P.; Ivanov, E.N.; Bernard, C. On the nature of seizure dynamics. Brain 2014, 137, 2210–2230. [Google Scholar] [CrossRef] [PubMed]
  17. Jiruska, P.; de Curtis, M.; Jefferys, J.G.; Schevon, C.A.; Schiff, S.J.; Schindler, K. Synchronization and desynchronization in epilepsy: controversies and hypotheses. The Journal of Physiology 2013, 591, 787–797. [Google Scholar] [CrossRef]
  18. Kassanos, P.; Kosmas, P.; Nader, C. Nanotechnology-enabled neural interfaces for high-resolution mapping of brain activity. Nano Research 2016, 9, 1778–1796. [Google Scholar]
  19. Klimesch, W. EEG alpha and theta oscillations reflect cognitive and memory performance: a review and analysis. Brain Research Reviews 1999, 29(2-3), 169-195.
  20. Maxwell, J.C. A dynamical theory of the electromagnetic field. Philosophical Transactions of the Royal Society of London 1865, 155, 459–512. [Google Scholar]
  21. Montgomery, R M. , Evaluating EEG-Based Parameters for Bipolar Disorder Diagnosis Using a Synthetic Dataset. Int Internal Med J 2024, 2, 01–08.
  22. Montgomery, R M. Topological Dynamics in Ecological Biomes and Toroidal Structures: Mathematical Models of Stability, Bifurcation, and Structural Failure. J Gene Engg Bio Res 2024, 6, 1–9.
  23. Montgomery, R.M. Exploring Altered Neural Connectivity in Autism Spectrum Disorder: A Simulation of Spatial and Topological Proximities. Int J Psychiatry 2024, 9, 01–08. [Google Scholar] [CrossRef]
  24. Montgomery, R.M. (2023). Possible Influence of Cortical Neuronal Circuits on Each Other: A Model. 10.20944/preprints202405.1224.
  25. Montgomery, R.M. ; (2024)a. The Intersection of ADHD and Autism: Neurodevelopmental Disorders with Shared Origins and Distinct Trajectories. Preprints. [CrossRef]
  26. Murthy, V.N.; Fetz, E.E. Coherent 25- to 35-Hz oscillations in the sensorimotor cortex of awake behaving monkeys. Proceedings of the National Academy of Sciences 1992, 89, 5670–5674. [Google Scholar] [CrossRef] [PubMed]
  27. Niedermeyer, E. , & da Silva, F.L. (2004). Electroencephalography: Basic Principles, Clinical Applications, and Related Fields. Lippincott Williams & Wilkins.
  28. Nunez, P.L. ; Srinivasan R (2006) Electric Fields of the Brain: The Neurophysics of, E.E.G. Oxford University Press.
  29. Pietrobon, D.; Moskowitz, M.A. Pathophysiology of migraine. Annual Review of Physiology 2014, 75, 365–391. [Google Scholar] [CrossRef] [PubMed]
  30. Plonsey, R.; Heppner, D.B. Considerations of quasi-stationarity in electrophysiological systems. The Bulletin of Mathematical Biophysics 1967, 29, 657–664. [Google Scholar] [CrossRef] [PubMed]
  31. Uhlhaas, P.J.; Singer, W. Abnormal neural oscillations and synchrony in schizophrenia. Nature Reviews Neuroscience 2010, 11, 100–113. [Google Scholar] [CrossRef] [PubMed]
  32. Wilson, H.R.; Cowan, J.D. Excitatory and inhibitory interactions in localized populations of model neurons. Biophysical Journal 1972, 12, 1–24. [Google Scholar] [CrossRef]
Preprints 138565 g002
Figure 2. Magnetic Potential and Neural Activity over Time.
Figure 2. Magnetic Potential and Neural Activity over Time.
Preprints 138565 g002
Preprints 138565 g003
Figure 3. EEG signals through different electrodes.
Figure 3. EEG signals through different electrodes.
Preprints 138565 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated