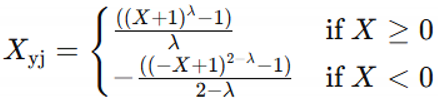Submitted:
06 November 2024
Posted:
07 November 2024
You are already at the latest version
Abstract
Clustering algorithm such as k-Means is highly sensitive to the scale of input features. A common approach to mitigate this issue is Min-Max scaling normalization, which rescales feature values to a specified range. This paper investigates an alternative form of Min-Max scaling, where the normalization is based on both the minimum (Xmin) and mean (Xmean) of the feature, rather than the maximum value. The proposed method is shown to be particularly effective in improving clustering accuracy for datasets with varying scales and distributions. Experimental results demonstrate that using this modified Min-Max scaling approach leads to better-defined clusters, enhanced performance in terms of clustering accuracy, and reduced bias in distance-based clustering algorithms. We validate the method using several standard clustering techniques, including k-Means on publicly available datasets.
Keywords:
Clustering Algorithms
; K-Means Clustering
; Clustering Performance Metrics
; Silhouette Score
; Cluster Validity
; Impact of Scaling on Clustering
; Feature Importance in Clustering
; Confusion matrix
; Accuracy
I. Introduction
Clustering is an essential technique in unsupervised machine learning, aimed at grouping similar data points based on feature similarity. Clustering algorithms, such as k-Means and DBSCAN, often rely on distance metrics (e.g., Euclidean distance) to measure the similarity between data points. However, these algorithms can be sensitive to the scale of input features. When features have differing scales, those with larger numerical ranges tend to dominate the distance calculation, potentially leading to poor clustering results [1].
A common approach to address this issue is Min-Max scaling normalization, which rescales each feature to a fixed range (usually [0, 1]). However, the traditional Min-Max scaling method uses the minimum and maximum values of the feature, which can be heavily influenced by outliers. To address this, we propose a modification to the Min-Max scaling formula by incorporating the mean of the feature instead of the maximum value, thus ensuring more robust normalization, especially when dealing with outliers or skewed distributions [2].
This paper investigates the impact of this modified Min-Max scaling on clustering performance, particularly focusing on the k-Means clustering algorithm [3].
II. Literature Review
Numerous researchers are putting up their efforts in the Normalization techniques context.
Normalization techniques can be categorized into several types, each with distinct methodologies and use cases. The following sections outline the most commonly used normalization techniques in clustering analysis.
The below are the main Normalization techniques which are present in the existing market. They were
1. Min-Max Normalization
Min-Max normalization rescales features to a specified range, typically [0, 1] [4]. The transformation is expressed mathematically as:
Xnorm=(X−Xmin) / (Xmax−Xmin)
Advantages
a. Uniform Scaling: Min-Max normalization ensures that all features contribute equally to distance metrics.
b. Interpretability: Rescaling features to a [0, 1] range makes the data more interpretable.
Disadvantages
Sensitivity to Outliers: Extreme values can skew the normalization, leading to suboptimal feature scaling.
2. Z-Score Normalization (Standardization)
Z-score normalization, or standardization, centers the data around the mean and scales it by the standard deviation [5]. The formula for this transformation is:
where μ is the mean and σ\sigma is the standard deviation of the feature.
Xstandard=(X−μ) / σ
Advantages
a. Robustness: This method is less sensitive to outliers compared to Min-Max normalization.
b. Gaussian Distribution: Standardization is effective for data that is approximately normally distributed, allowing for meaningful interpretation of standard deviations.
Disadvantages
Assumption of Normality: Z-score normalization assumes that the data follows a Gaussian distribution, which may not hold true for all datasets.
3. Robust Normalization
Robust normalization uses the median and the interquartile range (IQR) for scaling [6]. The transformation is defined as:
where Q1 and Q3Q_3Q3 are the first and third quartiles, respectively.
Xrobust=(X−Q2) / (Q3−Q1)
Advantages
Outlier Resilience: Robust normalization effectively minimizes the influence of outliers, providing a more accurate representation of the central data distribution.
Disadvantages
Less Interpretability: The scaling does not provide a straightforward interpretation as Min-Max normalization does.
4. Unit Vector Normalization
Unit vector normalization scales each feature vector to have a length of one. This method is defined as:
Xunit=X /∥X∥
Advantages
Direction Preservation: This method is particularly useful in applications where the direction of the vector is more significant than its magnitude, such as in text clustering.
Disadvantages
Not Suitable for Sparse Data: In cases where many feature values are zero, this method may not be applicable.
5. Logarithmic Transformation
Logarithmic transformation applies a logarithm function to the data, particularly effective for skewed distributions [8]:
Xlog=log(X+1)
Advantages
Skewness Mitigation: This technique can stabilize variance and make the data more normally distributed.
Disadvantages
Non-Negative Requirement: Logarithmic transformation is only applicable to non-negative data.
6. Power Transformation
Power transformation methods, such as Box-Cox and Yeo-Johnson transformations, aim to make the data more Gaussian-like [9]. They are defined as:
Box-Cox Transformation (only for positive data):
Xbox-cox=(Xλ−1) / λ where λ! =0
Yeo-Johnson Transformation (for both positive and negative data):
Advantages
Gaussian Distribution: Both transformations help stabilize variance and achieve normality, which can improve clustering performance.
Disadvantages
Parameter Estimation: Selecting the appropriate transformation parameter (e.g., λ) requires careful consideration and may complicate preprocessing.
III. Methodology
In the Min-Max Scaling change denominator with mean(x) for kmeans accuracy confusion matrix for best seed. Normally mean based accuracy improvement wit hfeature creation was there in the current era [12].
Modified Min-Max Scaling Formula
In the traditional Min-Max scaling, the normalization of each feature Xi is done using the following formula:
Where:
Xi′= (Xi−Xmin) / (Xmax−Xmin)
Xi is the original value of the feature.
Xmin and Xmax are the minimum and maximum values of the feature, respectively.
This normalization transforms the values of each feature to a fixed range, typically [0, 1]. However, the use of the maximum value can lead to issues when the feature contains outliers or extreme values. To address this, we propose an alternative formula that normalizes based on both the minimum and mean of the feature:
Where:
Xi′ = (Xi−Xmin) / Xmean
Xi is the original value of the feature.
Xmin is the minimum value of the feature.
Xmean is the mean value of the feature.
This new formula rescales each feature by the difference between its value and the minimum value, normalized by the difference between the mean and the minimum value, ensuring that features with extreme values do not unduly influence the scaling process.
To apply a modified Min-Max Scaling where we change the denominator from the range
x′=x−min(x) \ mean(x), we can follow these steps:
1. Load the Dataset: Load the Iris dataset and extract the features.
2. Apply Modified Min-Max Scaling: For each feature, normalize as x′=x−min(x) \ mean(x)
3. K-means Clustering: Perform K-means on the normalized data, testing multiple seeds to find the one with the best accuracy.
4. Evaluate Accuracy and Confusion Matrix: Track the accuracy and confusion matrix for the best-performing seed.
IV. Experimental Setup
a. Dataset Description
To evaluate the effectiveness of the modified Min-Max scaling, we conducted experiments using two datasets from the UCI Machine Learning Repository [13].
1. Iris Dataset: A classic dataset with 150 samples and 4 features (sepal length, sepal width, petal length, and petal width).
2. Wine Dataset: A dataset with 178 samples and 13 features related to the chemical composition of wines.
b. Data Preprocessing
1. Data Cleaning: Ensure the datasets are free from missing values and outliers. Outliers were identified using the IQR method and appropriately handled [14].
2. Normalization Application: Each normalization technique was applied to both datasets, transforming the feature values into the desired scale [15].
c. K-Means Clustering Algorithm
We employed the K-means clustering algorithm for our experiments. The algorithm was run with different numbers of clusters (k), ranging from 2 to 6, to evaluate its performance under various conditions [16].
For each dataset, the following steps were performed:
1. Apply the modified Min-Max scaling (based on Xmean).
2. Run k-Means clustering algorithms on the scaled and unscaled data.
3. Evaluate clustering performance using the clustering Accuracy.
d. Performance Metrics
To assess clustering performance, we used the following metrics:
1. Clustering Accuracy: Calculated by comparing the predicted cluster labels with the true class labels [17].
2. Silhouette Score: Measures the quality of clusters based on how similar an object is to its own cluster compared to other clusters [18].
3. Inertia (Within-Cluster Sum of Squares - WCSS)
Inertia measures the compactness of the clusters. It calculates the sum of squared distances between each data point and its assigned cluster's centroid [19].
4. Davies-Bouldin Index (DBI)
It measures the average similarity between clusters, with similarity defined as the ratio of the sum of the cluster's scatter (compactness) and the distance between the cluster centroids (separation) [20].
Dunn Index
The Dunn index measures the separation between clusters relative to the compactness within clusters. A higher Dunn index indicates better clustering, with well-separated and tight clusters [21].
Adjusted Rand Index (ARI)
ARI compares the clustering results to the true labels, adjusting for random chance. It measures the similarity between the predicted clusters and the true clusters [22].
Normalized Mutual Information (NMI)
NMI measures the shared information between the predicted clusters and the true labels. It normalizes mutual information to ensure values are between 0 and 1, where 1 indicates perfect agreement [23].
Fowlkes-Mallows Index (FMI)
FMI calculates the geometric mean of precision and recall for clustering, comparing the clustering results with true class labels [24].
This normalization transforms the values of each feature to a fixed range, typically [0, 1]. However, the use of the maximum value can lead to issues when the feature contains outliers or extreme values. To address this, we propose an alternative formula that normalizes based on both the minimum and mean of the feature:
V. Results and Discussion
The k-Means algorithm is sensitive to the scale of the features, as the distance between data points determines the cluster centroids. By applying the modified Min-Max scaling, we expect improved performance, especially for datasets with varying feature scales.
Table 1.
shows the clustering accuracy of k-Means with and without the modified Min-Max scaling:.
| Method | Data Set | Features Selected | Best Seed | Accuracy Obtained |
| MinMaxScaler | Iris | petal length petal width | 0 | 0.96 |
| Apply modified Min-Max Scaling | Iris | petal length petal width | 0 | 0.96 |
| MinMaxScaler | Iris | sepal length, sepal width, petal length, petal width | 3 | 0.8866666666666667 |
| Apply modified Min-Max Scaling | Iris | sepal length, sepal width, petal length, petal width | 7 | 0.96 |
| MinMaxScaler | wine | proline and nonflavanoid_phenols | 8 | 0.7191011235955056 |
| Apply modified Min-Max Scaling | wine | proline and nonflavanoid_phenols | 0 | 0.7247191011235955 |
| MinMaxScaler | wine | Proline, hue, ssstotal_phenols | 0 | 0.8764044943820225 |
| Apply modified Min-Max Scaling | wine | Proline, hue, total_phenols | 8 | 0.8876404494382022 |
5. Conclusion
This study demonstrates the effectiveness of modified Min-Max scaling normalization (using both Xmin and Xmean ) for improving the accuracy of Kmeans clustering algorithm. The results show that this method enhances the performance of k-Means, particularly when the features in the dataset have varying scales or distributions. By using the mean instead of the maximum value for scaling, the normalization process becomes more robust, reducing the influence of outliers and providing more consistent results across different clustering algorithms.
In conclusion, the modified Min-Max scaling is a valuable preprocessing step for improving clustering accuracy and should be considered when working with datasets that contain features with large scale differences or outliers.
References
- Maradana Durga Venkata Prasad, Dr. Srikanth, "A Survey on Clustering Algorithms and their Constraints", International Journal of Intelligent Systems and Applications in Engineering, JISAE, 2023, 11(6s), 165–179|165.
- H. W. Herwanto, A. N. Handayani, A. P. Wibawa, K. L. Chandrika and K. Arai, "Comparison of Min-Max, Z-Score and Decimal Scaling Normalization for Zoning Feature Extraction on Javanese Character Recognition," 2021 7th International Conference on Electrical, Electronics and Information Engineering (ICEEIE), Malang, Indonesia, 2021, pp. 1-3. [CrossRef]
- T. Li, Y. Ma and T. Endoh, "Normalization-Based Validity Index of Adaptive K-Means Clustering for Multi-Solution Application," in IEEE Access, vol. 8, pp. 9403-9419, 2020. [CrossRef]
- H. W. Herwanto, A. N. Handayani, A. P. Wibawa, K. L. Chandrika and K. Arai, "Comparison of Min-Max, Z-Score and Decimal Scaling Normalization for Zoning Feature Extraction on Javanese Character Recognition," 2021 7th International Conference on Electrical, Electronics and Information Engineering (ICEEIE), Malang, Indonesia, 2021, pp. 1-3. [CrossRef]
- N. Fei, Y. Gao, Z. Lu and T. Xiang, "Z-Score Normalization, Hubness, and Few-Shot Learning," 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 2021, pp. 142-151. [CrossRef]
- A. Fischer, M. Diaz, R. Plamondon and M. A. Ferrer, "Robust score normalization for DTW-based on-line signature verification," 2015 13th International Conference on Document Analysis and Recognition (ICDAR), Tunis, Tunisia, 2015, pp. 241-245. [CrossRef]
- Kokila M, KaviNandhini M, Vishnu R and Gandhiraj R, "Linear algebra tool box for GNU radio companion," 2015 International Conference on Communications and Signal Processing (ICCSP), Melmaruvathur, 2015, pp. 0762-0766. [CrossRef]
- T. Zhan, M. Gong, X. Jiang and S. Li, "Log-Based Transformation Feature Learning for Change Detection in Heterogeneous Images," in IEEE Geoscience and Remote Sensing Letters, vol. 15, no. 9, pp. 1352-1356, Sept. 2018. [CrossRef]
- A. Al-Saffar and H. T. Mohammed Ali, "Using Power Transformations in Response Surface Methodology," 2022 International Conference on Computer Science and Software Engineering (CSASE), Duhok, Iraq, 2022, pp. 374-379. [CrossRef]
- ABBAS CHEDDAD, "On Box-Cox Transformation for Image Normality and Pattern Classification" Received July 8, 2020, accepted August 20, 2020, date of publication August 24, 2020, date of current version September 3, 2020. [CrossRef]
- Y. Ma, P. Ke, H. Aghababaei, L. Chang and J. Wei, "Despeckling SAR Images With Log-Yeo–Johnson Transformation and Conditional Diffusion Models," in IEEE Transactions on Geoscience and Remote Sensing, vol. 62, pp. 1-17, 2024, Art no. 5215417. [CrossRef]
- Maradana Durga Venkata Prasad, Dr. Srikanth, "Global Mean Based nearest Feature object Value Selection with Feature creation Method for Clustering Accuracy Improvement", Nanotechnology Perceptions 20No.S8(2024)1396–1422. [CrossRef]
- Jingcong Wang, November 30, 2023, "UCI datasets", IEEE Dataport. [CrossRef]
- V. Kumar and C. Khosla, "Data Cleaning-A Thorough Analysis and Survey on Unstructured Data," 2018 8th International Conference on Cloud Computing, Data Science & Engineering (Confluence), Noida, India, 2018, pp. 305-309. [CrossRef]
- J. Sola and J. Sevilla, "Importance of input data normalization for the application of neural networks to complex industrial problems," in IEEE Transactions on Nuclear Science, vol. 44, no. 3, pp. 1464-1468, June 1997. [CrossRef]
- K. P. Sinaga and M. -S. Yang, "Unsupervised K-Means Clustering Algorithm," in IEEE Access, vol. 8, pp. 80716-80727, 2020. [CrossRef]
- N. Omar, A. Al-zebari and A. Sengur, "Improving the Clustering Performance of the K-Means Algorithm for Non-linear Clusters," 2022 4th International Conference on Advanced Science and Engineering (ICOASE), Zakho, Iraq, 2022, pp. 184-187. [CrossRef]
- P. Ramesh, S. Sandhiya, S. Sattainathan, L. L. A, B. P. T. V and E. S, "Silhouette Analysis Based K-Means Clustering in 5G Heterogenous Network," 2023 International Conference on Intelligent Technologies for Sustainable Electric and Communications Systems (iTech SECOM), Coimbatore, India, 2023, pp. 541-545. [CrossRef]
- A. Rykov, R. C. De Amorim, V. Makarenkov and B. Mirkin, "Inertia-Based Indices to Determine the Number of Clusters in K-Means: An Experimental Evaluation," in IEEE Access, vol. 12, pp. 11761-11773, 2024. [CrossRef]
- A. K. Singh, S. Mittal, P. Malhotra and Y. V. Srivastava, "Clustering Evaluation by Davies-Bouldin Index(DBI) in Cereal data using K-Means," 2020 Fourth International Conference on Computing Methodologies and Communication (ICCMC), Erode, India, 2020, pp. 306-310. [CrossRef]
- A. Bhadana and M. Singh, "Fusion of K-Means Algorithm with Dunn's Index for Improved Clustering," 2017 2nd International Conference on Computational Systems and Information Technology for Sustainable Solution (CSITSS), Bengaluru, India, 2017, pp. 1-5. [CrossRef]
- R. R. d. de Vargas and B. R. C. Bedregal, "A Way to Obtain the Quality of a Partition by Adjusted Rand Index," 2013 2nd Workshop-School on Theoretical Computer Science, Rio Grande, Brazil, 2013, pp. 67-71. [CrossRef]
- A. Amelio and C. Pizzuti, "Is normalized mutual information a fair measure for comparing community detection methods?," 2015 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM), Paris, France, 2015, pp. 1584-1585. [CrossRef]
- E. H. Ramirez, R. Brena, D. Magatti and F. Stella, "Probabilistic Metrics for Soft-Clustering and Topic Model Validation," 2010 IEEE/WIC/ACM International Conference on Web Intelligence and Intelligent Agent Technology, Toronto, ON, Canada, 2010, pp. 406-412. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
