Submitted:
19 November 2024
Posted:
20 November 2024
You are already at the latest version
Abstract
Electromagnetic vortex radar, with its characteristics of carrying orbital angular momentum and spiral phase wavefront, provides a new method for achieving super-resolution radar imaging. This paper combines the characteristics of vortex electromagnetic waves with the downward-looking electromagnetic vortex SAR imaging model to conduct in-depth research and analysis of SAR imaging technology based on vortex electromagnetic waves. We design corresponding imaging models, derive the imaging echo formula, and propose a novel three-dimensional ω K imaging algorithm based on fractional orbital angular momentum (OAM), specifically targeting multiple scattering targets. The three-dimensional Omega-K imaging algorithm compresses the distance by exploiting the relationship between azimuth terms in the slow time domain to obtain the azimuth information of the target; then, by combining the two-dimensional azimuth-range imaging information, the two-dimensional azimuth-range-elevation imaging information, and the elevation information of the target, the height information of the target is determined; finally, the three-dimensional imaging of the target is completed based on the Cartesian coordinate relationship. Through experimental simulation, this paper verifies the effectiveness of the proposed imaging algorithm and successfully achieves three-dimensional imaging of point targets.
Keywords:
1. Introduction
2. Imaging Model
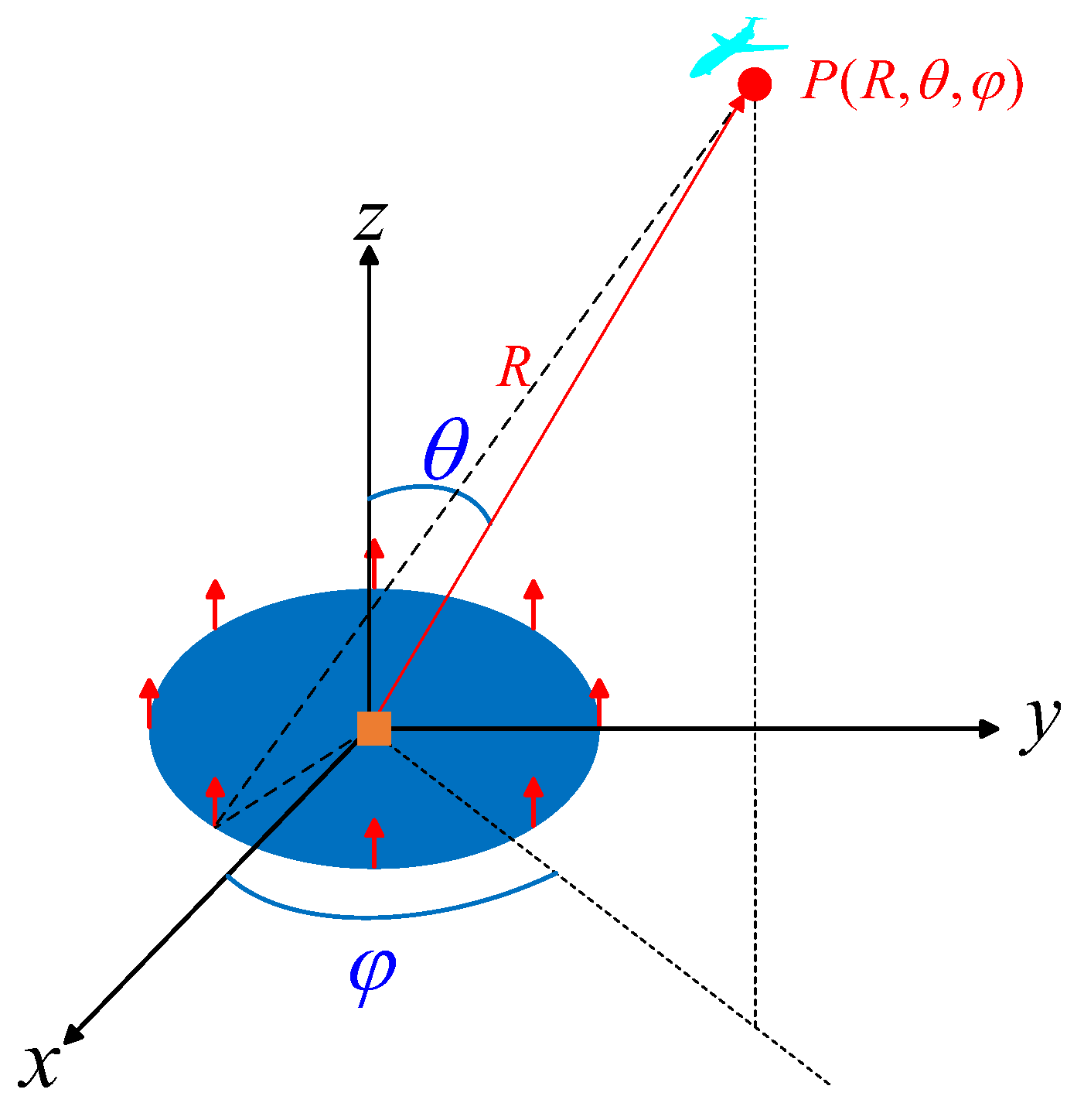
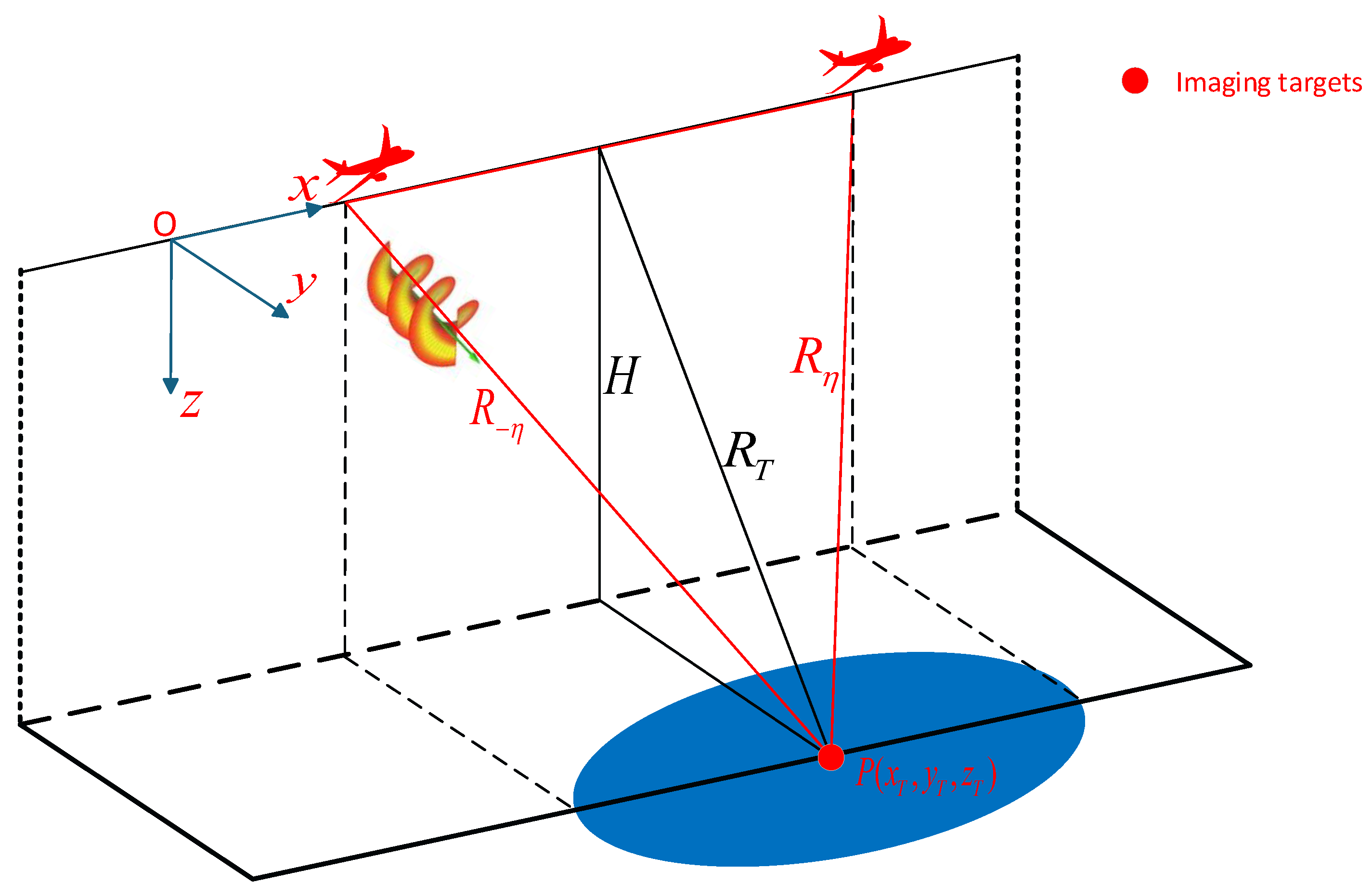
2.1. Radar-Target Imaging Model
2.2. SAR Imaging Model
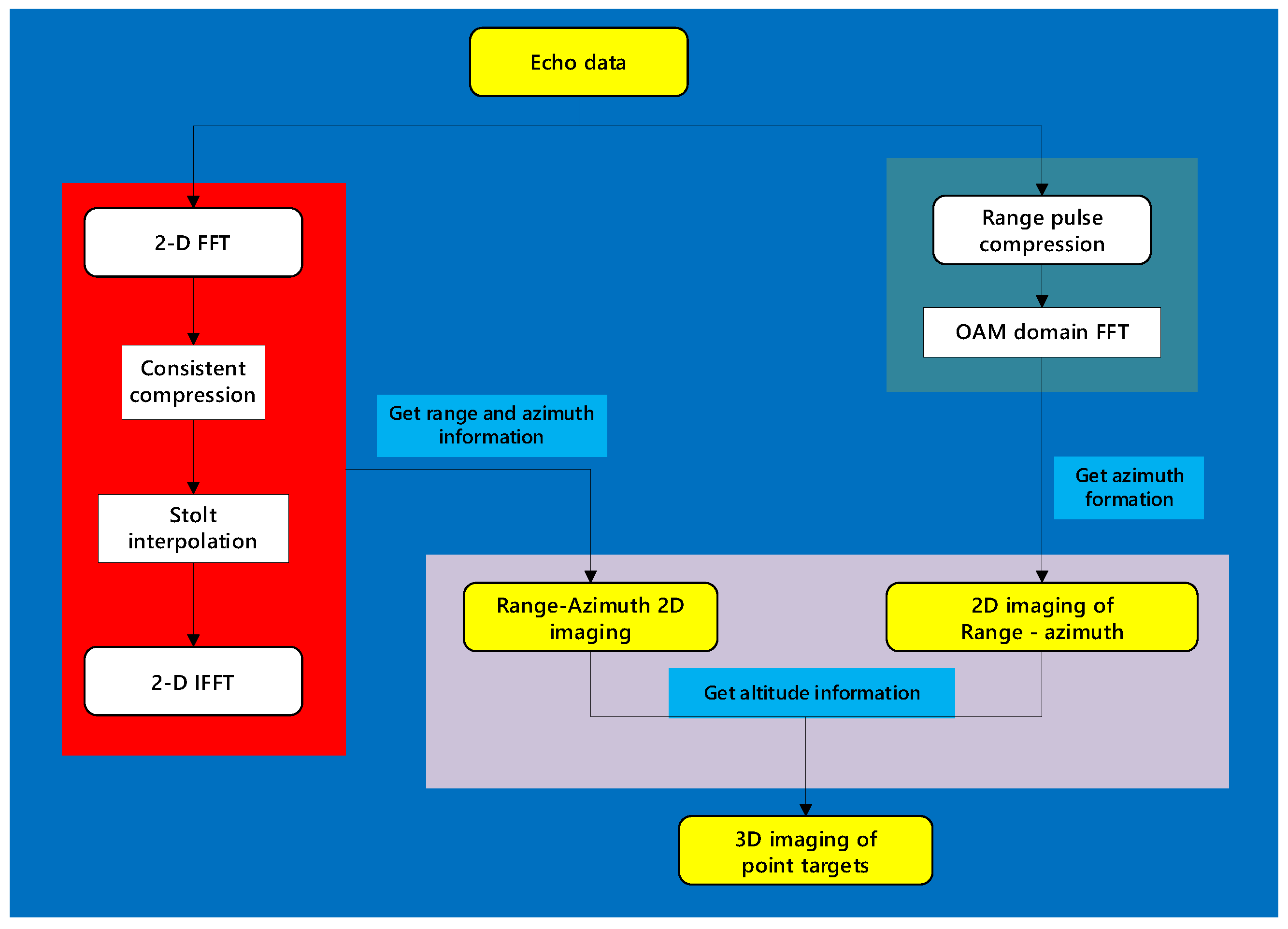
3. Omega-K 3D Imaging Algorithm
3.1. Range-Azimuth 2D Imaging
3.2. Range-Azimuth Two-Dimensional Imaging
3.3. Obtain Altitude Information
4. Imaging Simulation
| Parameters | value | Unit |
|---|---|---|
| Frequency | 10 | G Hz |
| Radar flight speed v | 150 | m / s |
| Radar flight altitude H | 2 | Km |
| Antenna center angle | 53 | ° |
| Scope of OAM mode | [-30,30] | - |
| Width of pulse | 1 | μ s |
| Bandwidth | 300 | M Hz |
| Synthetic aperture length | 25.5 | m |
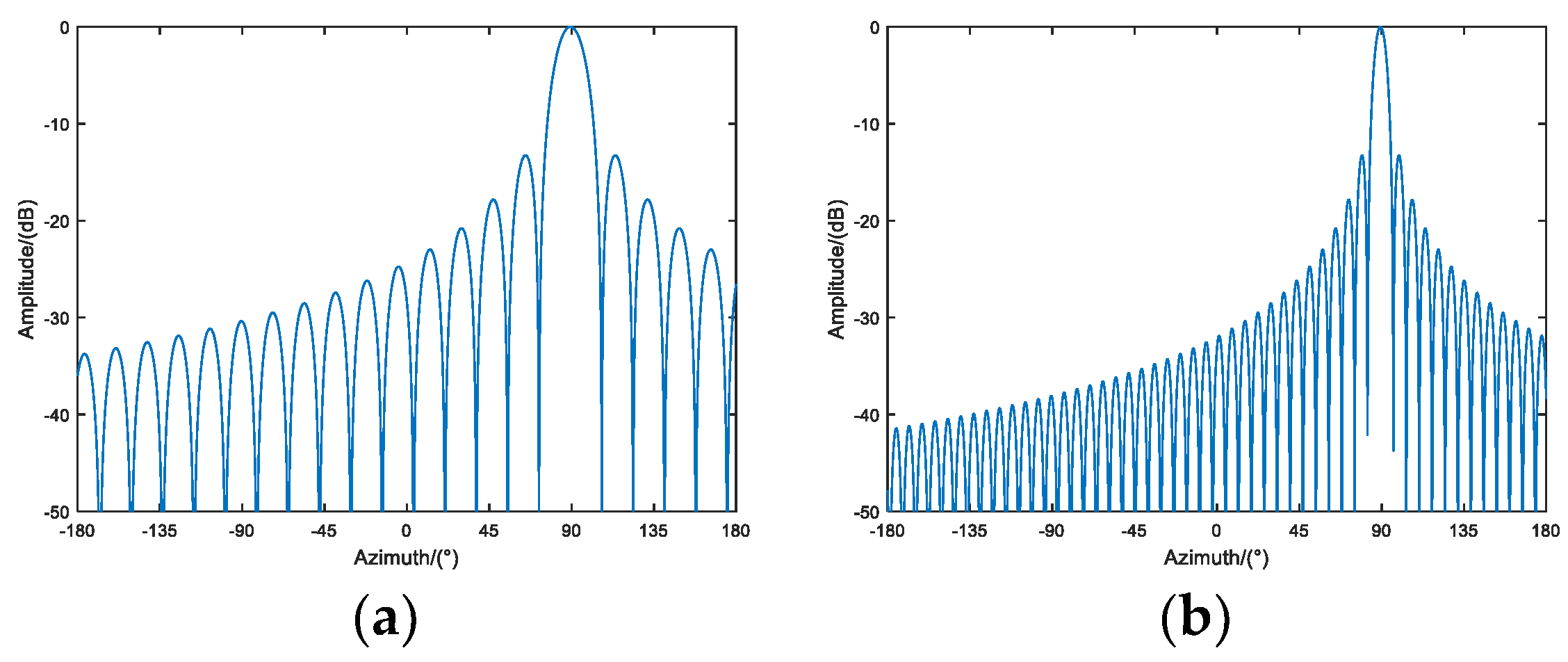
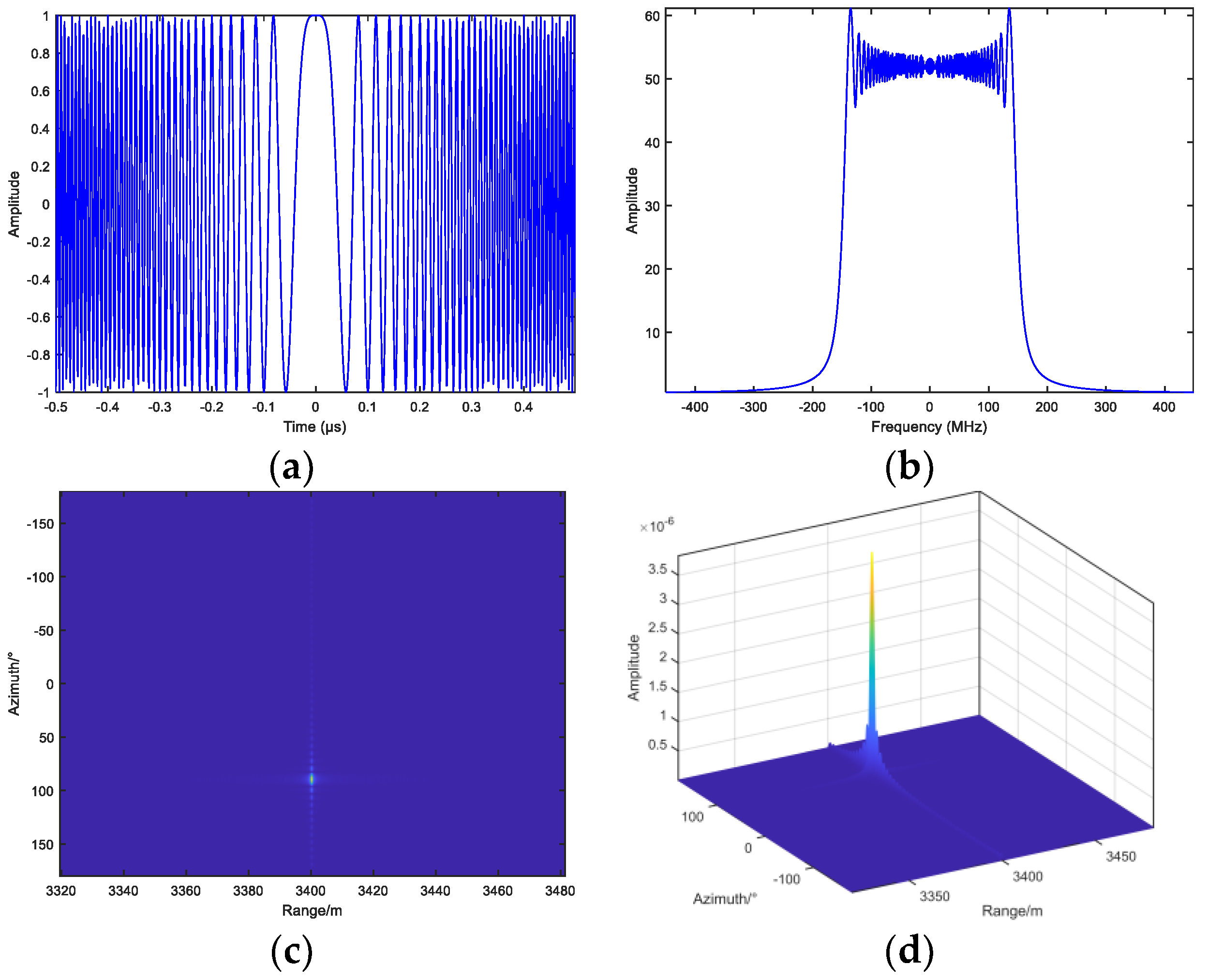
4.1. One Dimensional Imaging of Target Azimuth Angle
4.2. Range Heading Two-Dimensional Imaging
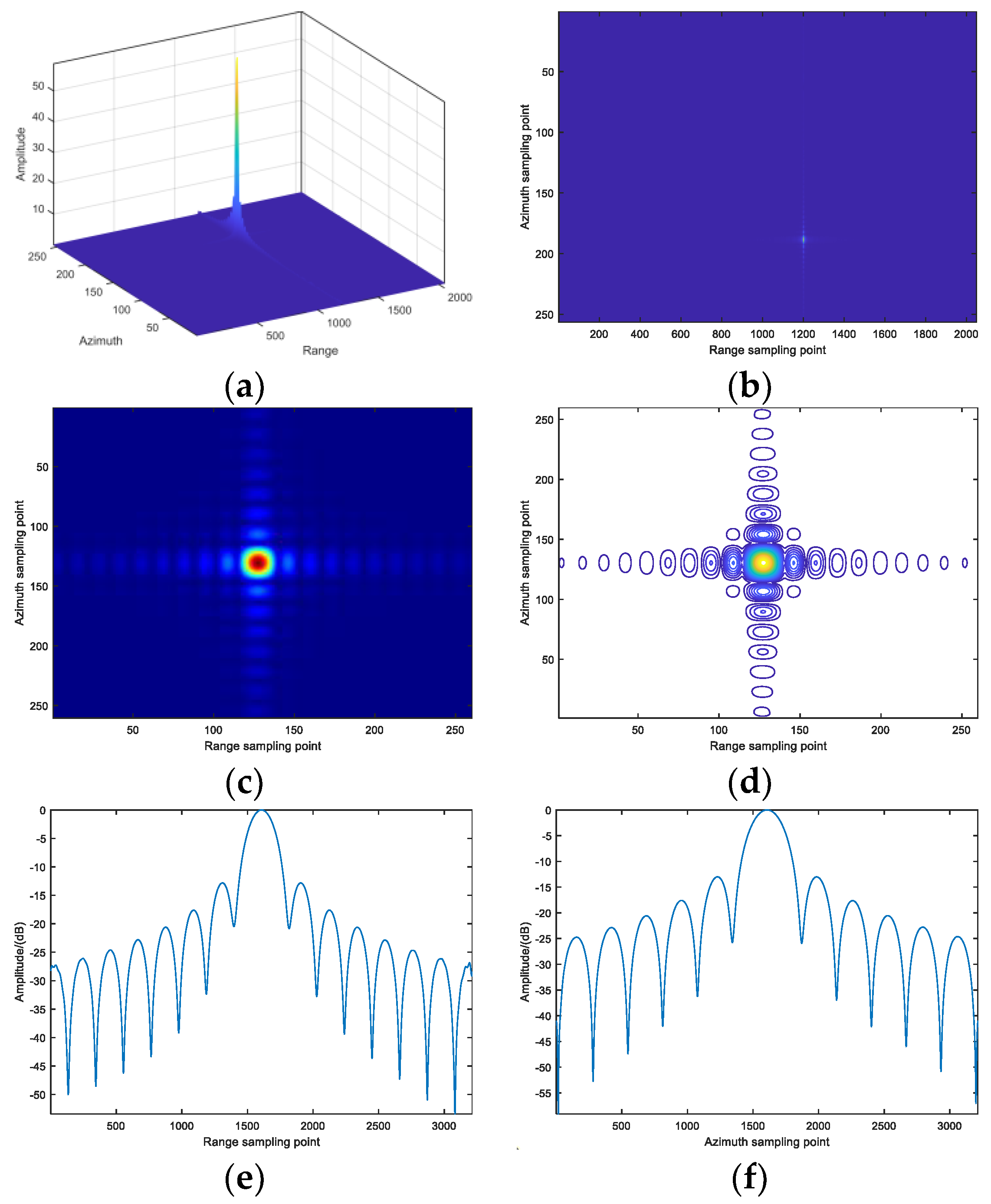
4.3. Two Dimensional Imaging Results of Target Distance and Azimuth Angle
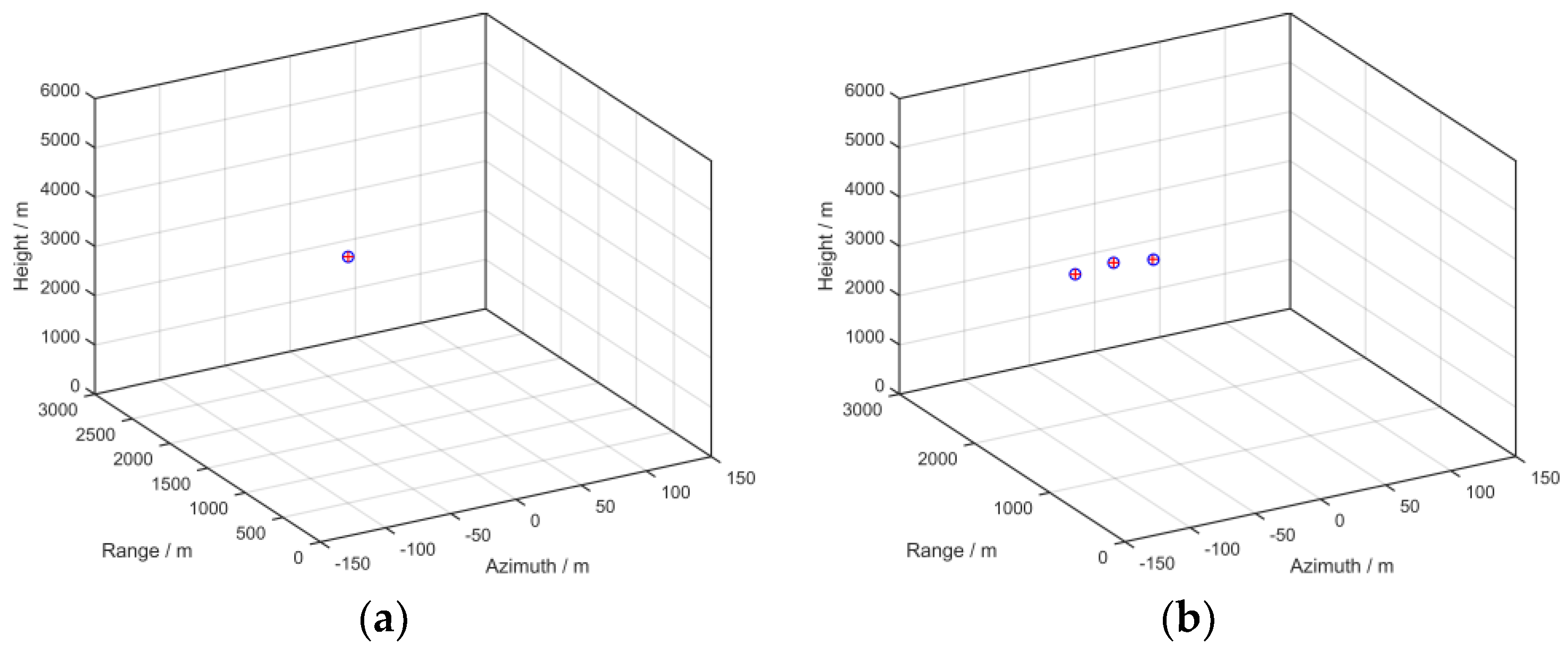
4.4. Three Dimensional Imaging Results of Point Targets
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, L.; Li, F. Beating the Rayleigh limit: Orbital-angular-momentum-based super-resolution diffraction tomography. Physical Review E—Statistical, Nonlinear, and Soft Matter Physics, 2013, 88, 033205. [Google Scholar] [CrossRef] [PubMed]
- Guo, G.; Hu, W.; Du, X. Electromagnetic vortex based radar target imaging. J. Nat. Univ. Defense Technol, 2013, 35, 71–76. [Google Scholar]
- Fang, Y.; Wang, P.; Chen, J. A Novel Imaging Formation Method for Electromagnetic Vortex SAR Based on Orbital-Angular-Momentum. 2018 China International SAR Symposium (CISS); IEEE, 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Bu, X.; Zhang, Z.; Chen, L.; et al. Implementation of vortex electromagnetic waves high-resolution synthetic aperture radar imaging. IEEE Antennas and Wireless Propagation Letters, 2018, 17, 764–767. [Google Scholar] [CrossRef]
- Wang, J.; Liu, K.; Cheng, Y.; et al. Three-dimensional target imaging based on vortex stripmap SAR. IEEE sensors journal, 2018, 19, 1338–1345. [Google Scholar] [CrossRef]
- Wang, J.; Liu, K.; Wang, H. Side-looking stripmap SAR based on vortex electromagnetic waves. 2019 IEEE International Conference on Communications Workshops (ICC Workshops); IEEE, 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Guo, S.; He, Z.; Fan, Z.; et al. CUCA based equivalent fractional order OAM mode for electromagnetic vortex imaging. IEEE Access, 2020, 8, 91070–91075. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Y.; Wang, J.; et al. Electromagnetic vortex enhanced imaging using fractional OAM beams. IEEE Antennas and Wireless Propagation Letters, 2021, 20, 948–952. [Google Scholar] [CrossRef]
- Liang, J.; Chen, Y.; Zhang, Q.; et al. Three-Dimensional Imaging of Vortex Electromagnetic Wave Radar with Integer and Fractional Order OAM Modes. Remote Sensing, 2023, 15, 2903. [Google Scholar] [CrossRef]
- Yueyue, H.; Chenlu, L.; Yongxing, D.; et al. SAR imaging based on OAM-ωK algorithm. Radio Science, 2023, 58, 1–12. [Google Scholar] [CrossRef]
- Shu, B.W.; Sheng, W.Y. Research on Radar Correlation Imaging Technology Based on Orbital Angular Momentum. Smart City Application, 2023, 6, 10–12. [Google Scholar] [CrossRef]
- Berry, M.V. Optical vortices evolving from helicoidal integer and fractional phase steps. Journal of Optics A: Pure and Applied Optics, 2004, 6, 259. [Google Scholar] [CrossRef]
- Liu, K.; Cheng, Y.; Yang, Z.; et al. Orbital-angular-momentum-based electromagnetic vortex imaging. IEEE Antennas and Wireless Propagation Letters, 2014, 14, 711–714. [Google Scholar] [CrossRef]
- Wang, L.; Tao, L.; Li, Z.; et al. Three dimensional electromagnetic vortex radar imaging based on the modified RD algorithm. 2020 IEEE Radar Conference (RadarConf20); IEEE, 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, J. Research on SAR imaging technology based on vortex electromagnetic waves. National University of Defense Technology, 2019. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





