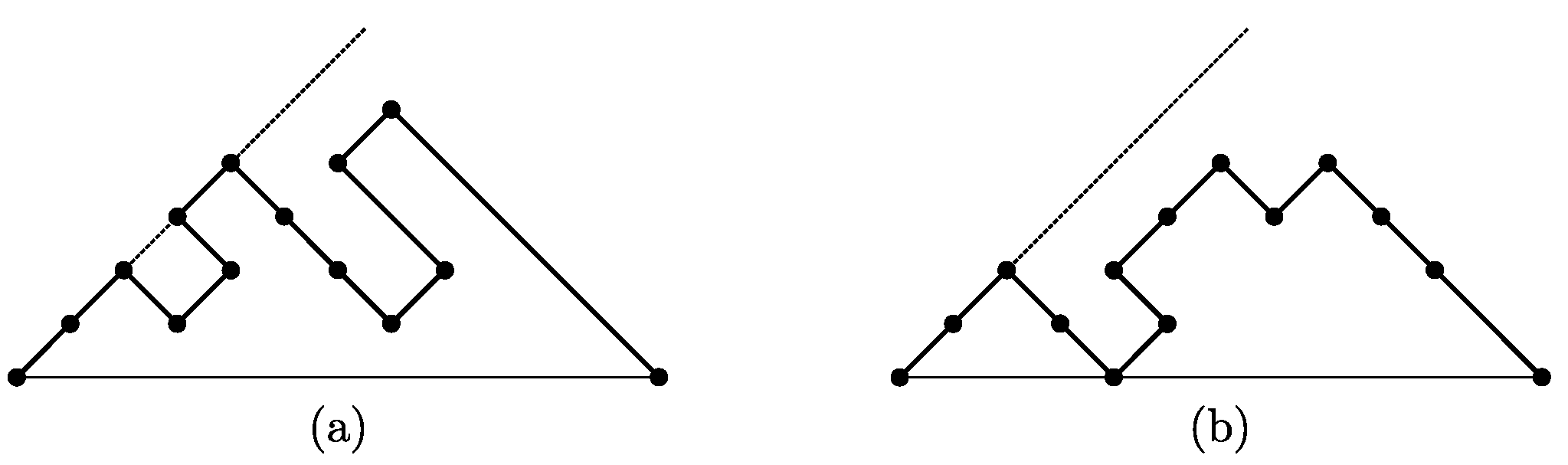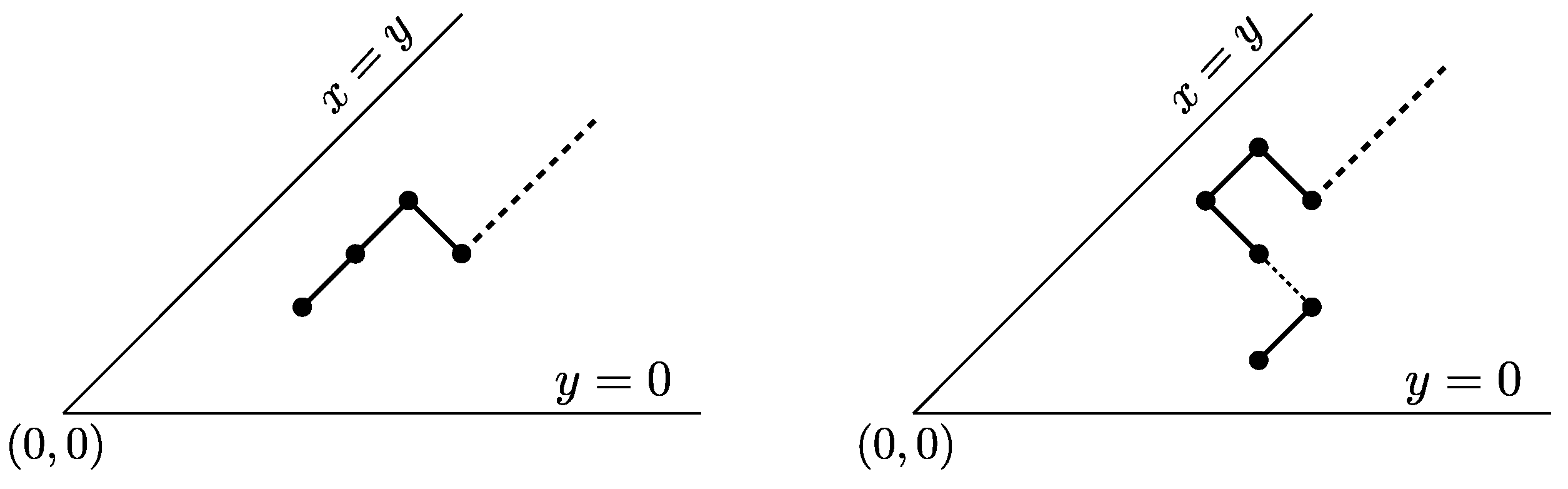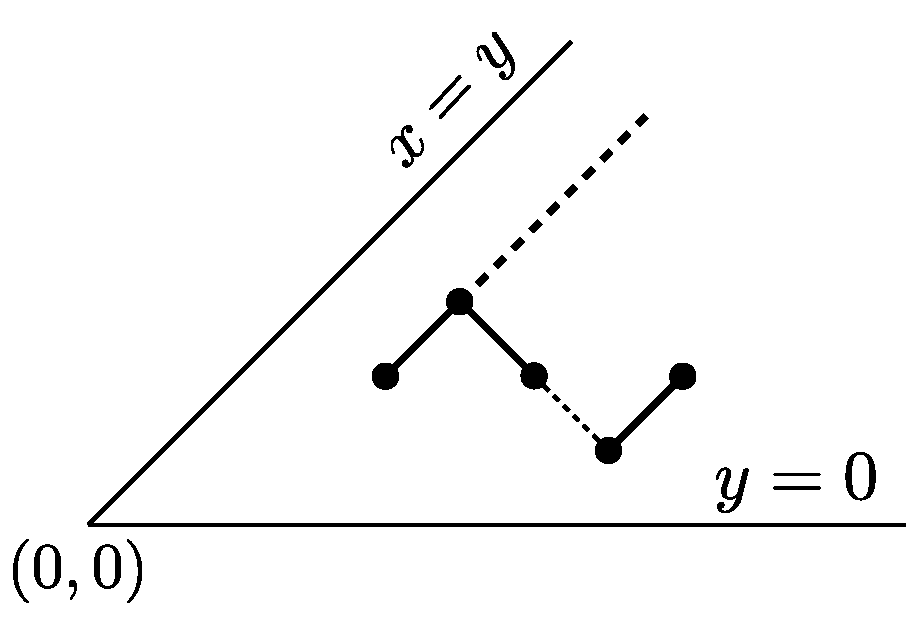4.1. The Family : Steady Paths
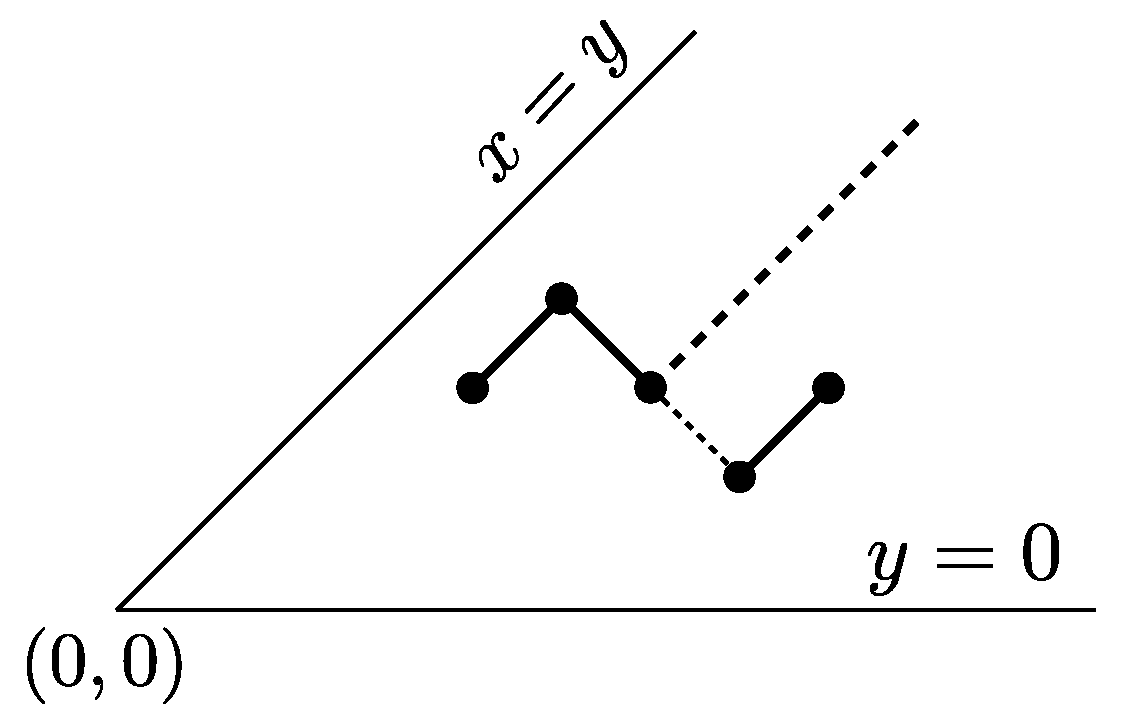
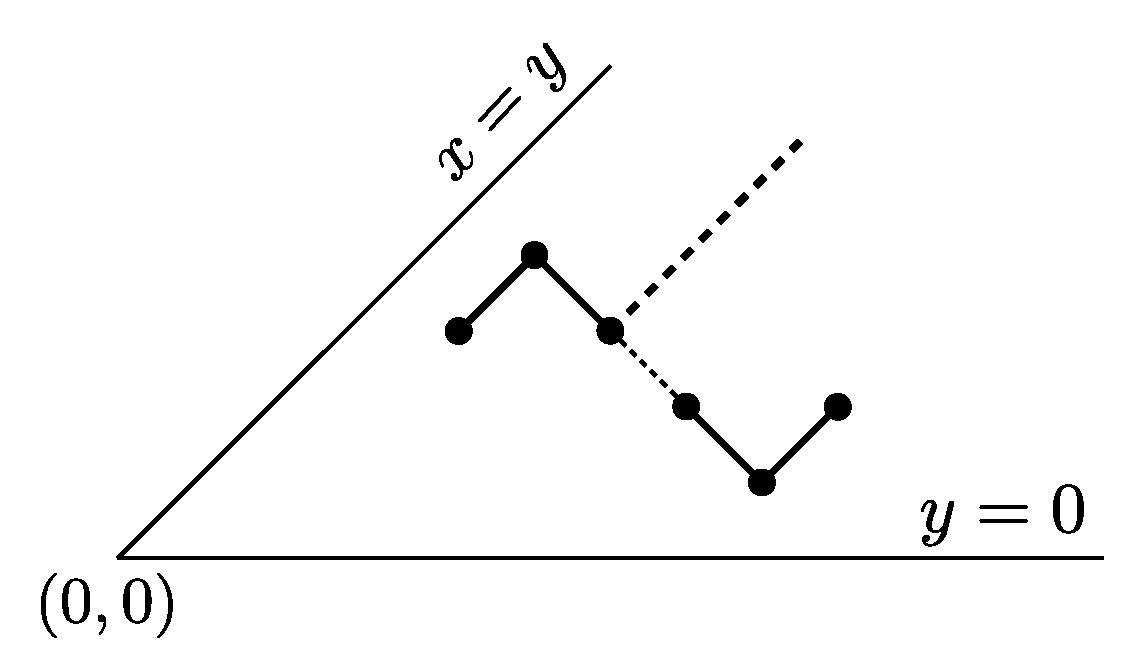
An underdiagonal path P is a steady path if the two following conditions are satisfied:
- (S1)
for every factor of P, the suffix of P following lies weakly below the line parallel to , and passing through .
- (S2)
for every factor of P, the suffix of P following lies weakly below the line parallel to , and passing through .
Clearly, a strong steady path is also a steady path, while the converse does not hold. We call the edge line of P the line , with an even integer, which supports the up step of the rightmost occurrence of either or in P.
Figure 7 (a) shows an example of a steady path whose edge line coincides with
, whereas the edge line of the steady path depicted in
Figure 7 (b) is
.
Figure 7 (c),(d) show two different examples of underdiagonal paths that are not steady paths. We also point out that steady paths are a subfamily of those “skew Dyck paths” studied in [
14].
Steady paths were introduced in [
7], as one of the several combinatorial families enumerated by powered Catalan numbers. The investigation of [
7] starts from powered Catalan inversion sequences
, and then the authors provide bijections among the families enumerated by their number sequence.
The sequence of
powered Catalan numbers is registered on [
19] as A113227, and its first terms are:
D. Callan [
10] proves that the
nth term of the sequence can be obtained as
, where
is recursively defined by:
Proposition 18 ([
13], Theorem 13).
For and , the number of powered Catalan inversion sequences having k zeros is given by the term of Equation (1). Thus, the number of powered Catalan inversion sequences of length n is , for every .
Proposition 18 can be rephrased in terms of succession rules, as done below with the rule
. More precisely, for
and
, the number of nodes at level
n that carry the label
in the generating tree associated with
is precisely the quantity
given by Equation (
1).
Proposition 19.
The family of powered Catalan inversion sequences grows according to the following succession rule
We notice that is extremely similar to the Catalan succession rule (see page ): specifically, the productions of are the same as in , but with multiplicities appearing as “powers”. Hence, the name powered Catalan.
The authors of [
7] prove the following statements (we report here the proof for the sake of completeness):
Proposition 20. Let π be a permutation of length n. Then, if and only if is a steady path.
Proof. As usual, we will proceed by contrapositive. Let P be an underdiagonal path of size n which is not steady. So, one of the two conditions (S1) or (S2) must be violated, i.e. there must be in P an up step not lying on the main diagonal such that it forms a factor either or , and an up step , which is on the right of , lying above the line parallel to and passing through . First, suppose forms a factor . Then, in , we have and , with . Let us consider then the permutation with left inversion table , i.e. such that . It holds that . Moreover, since , there is an index such that and . Therefore, is an occurrence of the pattern . On the other hand, if forms a factor , there exists such that . Then, in we have , with . Let be the permutation with left inversion table . It holds that . Moreover, since , there is an index such that and . Finally, is an occurrence of the pattern .
The above argument can be inverted proving that if
is a permutation containing an occurrence of
, then
is not steady (see also [
7]). □
We provide a growth for the family of steady paths that results in the following proposition.
Proposition 21.
The family of steady paths grows according to the following succession rule:
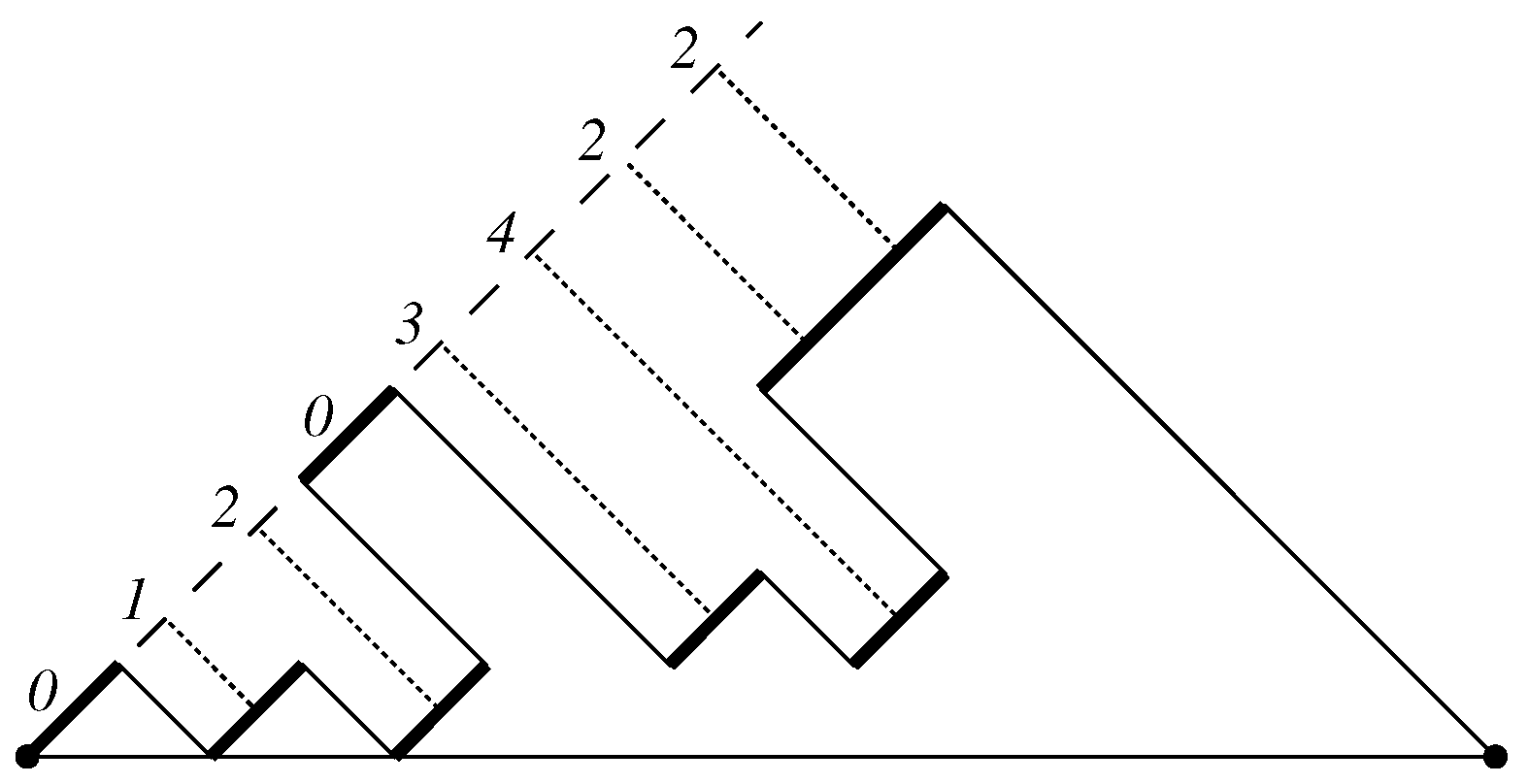
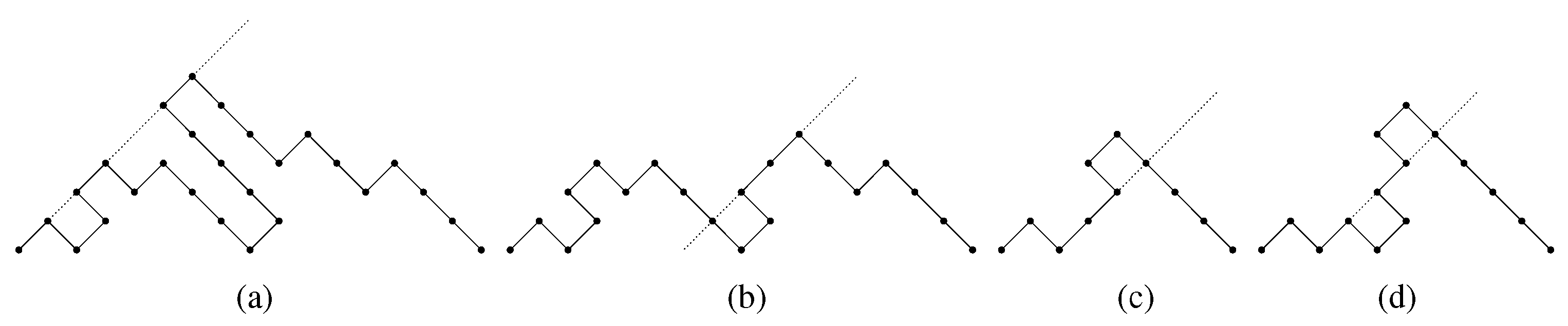
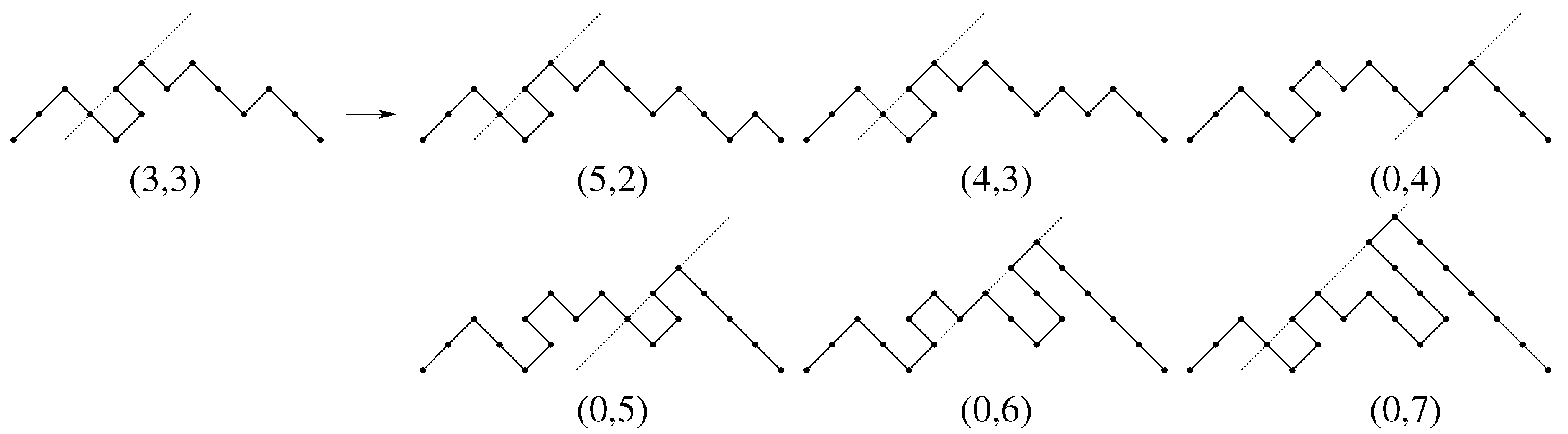
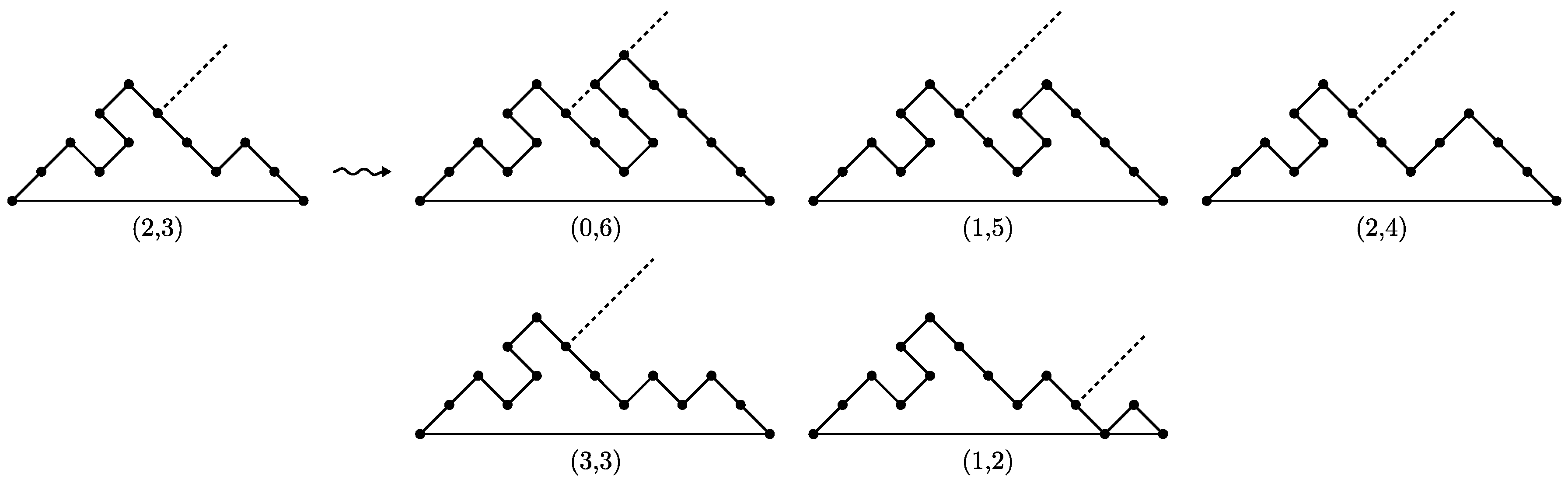
Proof. We start observing that every steady path P of size ends with a factor , with , and that removing the factor from P we obtain a steady path of size n. So, we define a recursive growth of steady paths, such that every steady path of size is uniquely produced from a steady path of size n by adding the last up step, and prove that this growth can be described by the succession rule .
Let P be a steady path of size n, ending with a factor , with . Let us denote its last up step by . We assign to P the label , where h is the distance between and the edge line, and , i.e. k is the length of P last descent plus one. Then, , whereas . The steady path of minimal length has label .
The steady path P of label produces steady paths of size , by applying the following operations:
We add an occurrence of just following a sequence of t consecutive down steps in the last descent, with . For every t, thsi operation produces a steady path with label .
We add an occurrence of just following , thus producing a factor . Therefore, the obtained steady path has edge line passing through , hence its label is .
We add an occurrence of just following , with . Therefore we obtain a new occurrence of , in the rightmost position, then the edge line of the obtained path passes through the added up step. The label of this path is .
Hence steady paths growth can be described by means of the succession rule . □
Figure 8 depicts the growth of a steady path of size
n with edge line
; for any path, the corresponding edge line is drawn.
From the proof of Proposition 20, we immediately have the following corollary (not reported in [
7]):
Corollary 22. .
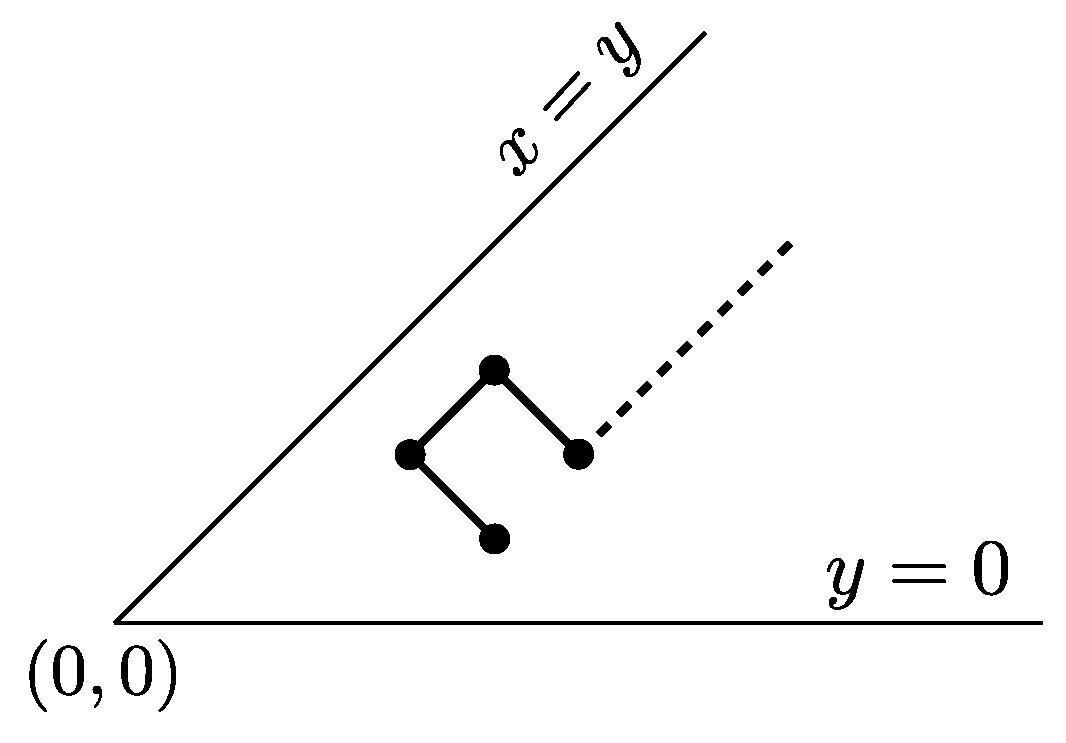
4.2. The Family : -Constrained Paths
A
-constrained path
P is a path such that, for every factor
of
P,
,
, the suffix of
P on the right of
lies weakly below the line parallel to
, and passing from
(see
Figure 9).
Again, the line the line parallel to , and passing from , will be referred to as the edge line at .
Proposition 23. Let π be a permutation of length n. Then, if and only if is -constrained.
Proof. As usual, we will proceed by contrapositive. Let P be an underdiagonal path of size n which is not -constrained. So, there are indices , , such that , , is a factor of P, and lies above the edge line at . Therefore, in we have . Let us consider then the permutation with left inversion table , i.e. such that . It holds that . Moreover, since , there is an index such that and . Finally, is an occurrence of the pattern .
The above argument can be neatly inverted proving that if is a permutation containing an occurrence of , then is not -constrained. □
Proposition 24. The number of -constrained paths of size n is the nth powered Catalan number.
Proof. We prove it by showing that
grows according to the rule:
which governs the growth of steady paths enumerated by powered Catalan numbers.
Let
. We made it grow by adding an element
on the right, and we denote by
the obtained permutation. More precisely, the entry
of
is:
We say that
x is an active entry if
avoids the pattern
. Precisely, if there are indices
, with
, such that
is an occurrence of
, i.e.
, then every entry
is not active. Actually, given an occurrence
of the pattern
, non active entries are exactly all
. Let
h (resp.
k) be the number of active entries less than (resp. greater than or equal to)
. Observe that entries 1 and
are always active, thus
, and
. The label of the the length 1 permutation is
.
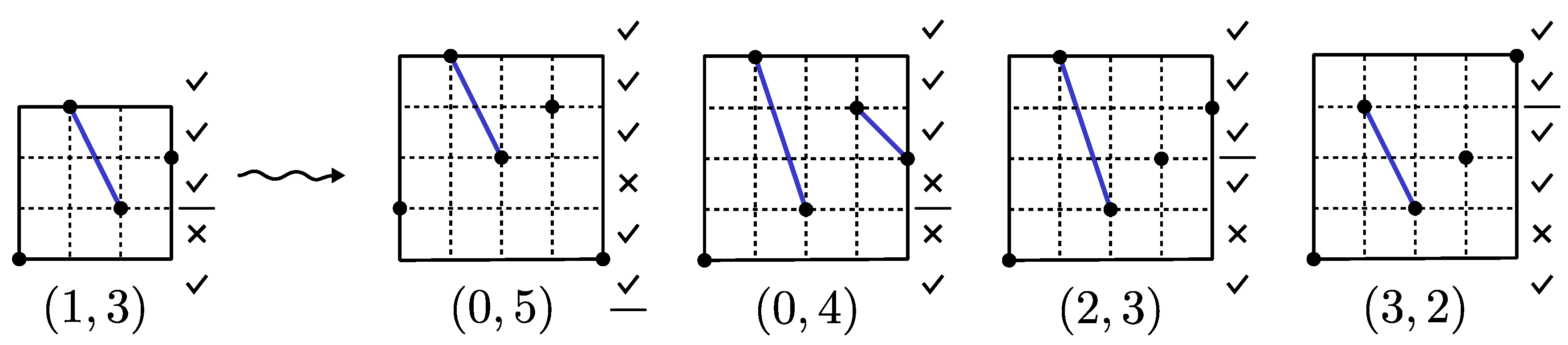
So, let
be the label of
, and let
x be an active entry of
. The labels of
are (see also the example in
Figure 10):
: in this case , for all i. The last two entries of , i.e. and 1 do not produce a new occurrence of . So, has the same active entries as , plus , so it has label .
: in this case . The entries of produce a new occurrence of , so the entries less than or equal to x become non active in . So, if x is the ith active entry for , , then has label .
: in this case . The entries of produce an ascent, so has the same active entries as , plus . So, if x is the jth active entry for , , then has label .
Then, we have that the growth of is described by the succession rule .
Figure 10.
The growth of a permutation avoiding according to the rule .
Figure 10.
The growth of a permutation avoiding according to the rule .
□
Remark 25. Although both steady paths and UDU-constrained paths are enumerated by the sequence of powered Catalan numbers, we didn’t find a direct bijection between the two families. Thus, we leave the question of establishing a correspondence as an open problem for further investigation.
From the proof of Proposition 23 it follows that:
Proposition 26. .
4.3. The Family : Strong -Constrained Paths
A strong
-constrained path
P is a path such that, for every factor
of
P,
,
, the suffix of
P on the right of the factor
lies strictly below the line parallel to
, and passing from
(see
Figure 11).
Again, the line the line parallel to , and passing from , will be referred to as the edge line at .
Proposition 27. Let π be a permutation of length n. Then, if and only if is strong -constrained.
Proof. As usual, we will proceed by contrapositive. Let be an underdiagonal path of size n which is not strong -constrained. So, there are indices , , with the factor , , and lies weakly above the edge line at . Then, in , we have , and . Accordingly, in the permutation , from , we have that . Moreover since , we have that and there is a k greater than such that . Thus the entries form an occurrence of .
The above argument can be neatly inverted proving that if is a permutation containing an occurrence of , then is not strong -constrained. □
From the proof of Proposition 27, we immediately have that is given by the inversion sequences such that there are no indices satisfying and . This property cannot be expressed in terms of classical pattern avoidance, and by abuse of notation we write this family as .
Remark 28. The permutations avoiding the pattern are the same as permutations avoiding the “barred pattern” , where a barred pattern is a pattern where some of the entries are barred. For a permutation π to avoid the barred pattern τ means that every subsequence of π which is order-isomorphic to the sequence of unbarred entries of π can be extended (exactly to the positions) to the one in π order-isomorphic to τ. So, in practice, the avoidance of in π requires that every occurrence of 2534 in π is contained in an occurrence of a 25134.
Since permutations avoiding
are enumerated by sequence A137538 in [
19], from Proposition 27 it follows:
Corollary 29. The family of strong -constrained paths is enumerated by the sequence A137538 in [19].
The first terms of A137538 are:
We point out that the reference in [
19] does not give any further information about the properties of the sequence. Therefore, in this section, our aim is to provide more information about the sequence, and we start determining a growth for the family of strong
-constrained paths by means of a generating tree.
Proposition 30.
The family of strong -constrained paths grows according to the following succession rule
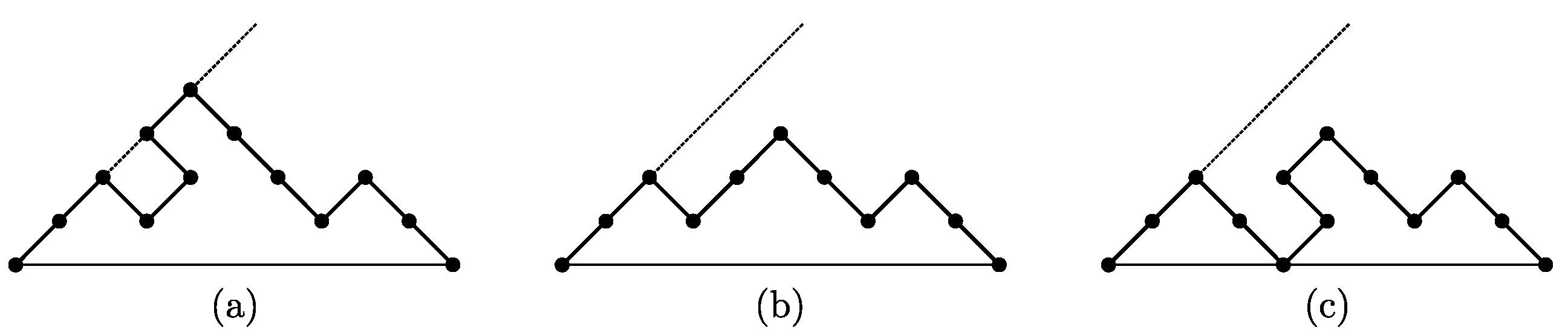
Proof. We define a a recursive growth for strong -constrained paths such that every path of size is uniquely produced from a path of size n by adding the last up step, and prove that this growth can be described by the succession rule .
Let P be a strong -constrained path of size n, and let us denote by its last up step. To P we assign the label , where h is the distance between and the edge line, and k is the length of the last descent of P plus one. Then, , and . The path of size 1 has label .
The path P with label produces strong -constrained paths of size , by applying the following operations:
add a factor following , with . For every t, this operation produces a strong -constrained path with label .
add a factor following , thus obtaining a factor . Then the obtained path has label .
add a factor following , thus obtaining a factor . Then the obtained path has label .
add a factor immediately following a sequence of t consecutive down steps in the last descent, with , thus obtaining the factor , then the obtained path has the edge line immediately below , so it has label .
Finally, strong -constrained paths grow according to the rule . □
Figure 12 depicts the growth of a strong
-constrained path of size 5; for any path, the dotted line delimiting the region forbidden to the suffix of the path is drawn.
Using standard techniques [
2,
3] we can translate the rule
into the setting of generating functions. For
and
, let
denote the generating function of strong
-constrained paths having label
and let
The generating function of strong -constrained paths is thus . The rule translates into a functional equation for the multivariate generating function of strong -constrained paths.
Proposition 31.
The generating function satisfies the following functional equation:
Proof. It follows from the productions of the rule
:
□
Replacing
in the previous equation, we obtain the following relation:
4.4. The Family : Strong -Constrained Paths
A strong
-constrained path
P is a path such that, for every factor
of
P (if any),
, the suffix of
P on the right of this factor lies strictly below the line parallel to
, and passing from
(see
Figure 13).
Again, the line the line parallel to , and passing from , will be referred to as the edge line at .
Proposition 32. Let π be a permutation of length n. Then, if and only if is strong -constrained.
Proof. As usual, we will proceed by contrapositive. Let be an underdiagonal path of size n which is not strong -constrained. So, there are indices , such that , with , is a factor of , and lies weakly above the edge line at . Therefore, in we have . Accordingly, in the permutation , from , we have that . Moreover since , we have that and there is a k greater than such that . Thus the entries form an occurrence of .
The above argument can be neatly inverted proving that if is a permutation containing an occurrence of , then is not strong -constrained. □
From the proof of Proposition 32, we immediately have that:
Corollary 33. .
We will prove that strong
-constrained paths, as strong
-constrained paths, are enumerated by the sequence A137538 in [
19]. Although we have not a direct bijection between the two families of paths, we will show a bijection between the two corresponding families of permutations, borrowed from [
5].
Proposition 34. The families and are Wilf-equivalent.
Proof. We define a recursive bijection which preserves the left-to-right minima. We recall that an entry of is a left-to-right minima if, for any , then .
So, let
. We decompose
as:
where
, and
are the left-to-right minima of
. We observe that
avoids the pattern
, since
is on the left of
, and the presence of a pattern
in
would imply a pattern
in
. Assuming that
, with
, let
be the set of entries of
on the right of
which are greater that
. Let
be the entries of
(if not empty). Let us define:
;
, with ;
.
If is empty, then we set .
All the entries of must be on the right of all the elements of , for all . Indeed, if an entry of was on the left of some entry of , , then would contain an occurrence of , where plays the role of 1, and plays the role of 3.
Repeating the same argument, we can prove that every entry of
must be on the right of all entries of
, with
. So,
can be decomposed as:
We also observe that every
should avoid the pattern
, because of the entry
on the left (being
less than every entry of
).
For a given permutation , let be the set of entries obtained by replacing the entry h by entry . We observe the mapping ′ is bijective and transforms every pattern into a pattern .
Then, for every
i such that
, let us define
as:
where
is obtained applying ′ on the reduced permutation of
. Finally, we define
as:
Then,
, and has the same left-to-right minima as
. □
Table 2.
The families of patterns of length 4 considered in
Section 4.
Table 2.
The families of patterns of length 4 considered in
Section 4.
| Permutation patterns |
Underdiagonal Paths |
Inversion Sequences |
Number Sequence |
|
Steady Paths |
|
Powered Catalan numbers |
|
-constrained |
|
Powered Catalan numbers |
|
Strong -constrained |
|
A137538 |
|
Strong -constrained |
|
A137538 |