Prerpints.org logo
Preprint
Article

Soil Moisture Retrieval Based on Ensemble Learning Models Using Landsat8 Data in Areas of High Heterogeneity

Altmetrics

Downloads

46

Views

26

Comments

0

Submitted:

04 December 2024

Posted:

05 December 2024

You are already at the latest version

Alerts
Abstract
Soil moisture (SM) is intricately connected to various components of the Earth's system and plays a critical role in human survival and development. Although significant efforts have been made in soil moisture retrieval and validation, the monitoring and assessment of high-precision, high-resolution SM networks remain limited. This study focuses on a long-term SM network (QLB-NET) located in a high-altitude plateau with significant topographic variability. Utilizing more than 20 soil moisture-related indices derived from Landsat data, along with elevation and its derivatives, we estimate soil moisture at a 30-meter resolution with the aid of ensemble Learning Models. Soil moisture is treated as the dependent variable, while the other data serve as independent variables, integrated into a dataset which is subsequently divided into training, validation, and testing sets. Four ensemble Learning Models—Random Forest (RF), Extremely Randomized Trees (ERT), Extreme Gradient Boosting (XGBoost), and Categorical Boosting (CatBoost)—were evaluated for their performance in soil moisture retrieval. The CatBoost model demonstrated the best performance, surpassing the other models across the training, validation, and test sets. In the test set, it achieved a correlation coefficient (R² = 0.83), a root mean square error (RMSE) of 0.052 m³/m³, a bias of 0.003 m³/m³, and a mean square error (MSE) of 0.003. We also used the four models to generate 30 m soil moisture maps for three different dates, providing more detailed insights into the spatial distribution of soil moisture. SHAP was employed to assess the contribution of different features to soil moisture predictions, revealing that elevation had the greatest impact. Finally, we assessed the overall heterogeneity of QLB-NET, using terrain complexity to represent local heterogeneity. Our findings indicate that the northern-central region exhibits significant local heterogeneity. Moreover, areas with higher heterogeneity also show greater uncertainty, making them a key source of model prediction error. The findings of this study contribute to more accurate retrieval of soil moisture, enhancing both new and existing methods.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

Soil provides the essential elements needed by terrestrial organisms and acts as a critical link connecting the atmosphere, hydrosphere, biosphere, and lithosphere. It is considered the central component of the Earth's critical zone [1]. SM movement, in particular, serves as the primary driver of soil physical processes [2]. Although SM constitutes only a small fraction of the Earth's total water reserves, it plays a pivotal role in numerous hydrological, biological, and biogeochemical processes. SM regulates land-atmosphere interactions, influencing climate and weather patterns [3,4], and is a crucial factor in the water and energy exchange within the soil-plant-atmosphere continuum [5]. It is also a key element governing hydrological, biological, and biogeochemical processes within ecosystems [6], as well as a determining factor for runoff potential [7]. Consequently, accurate SM information is of great importance across a wide range of research fields.
To date, the challenge of acquiring soil moisture ground truth data with both large-scale spatial coverage and temporal continuity remains a major issue for many researchers. Most soil moisture products are derived solely through remote sensing retrievals. However, as a macroscopic observation technique, remote sensing inherently introduces errors when compared to actual ground truth values, necessitating validation of these products for accuracy [8,9]. Objective and quantitative evaluations of product accuracy are essential for improving the quantitative production of remote sensing products, making them reliable sources of information. Over the years, numerous research initiatives, both domestically and internationally, have focused on obtaining ground truth data for validation. These include efforts such as establishing long-term global soil moisture observation networks [6,10], using meteorological stations and other platforms [11], or conducting short-term sampling in smaller areas to obtain accurate measurements [12,13]. Given the convenience of site selection and research objectives, most of these studies have been conducted in regions with relatively homogeneous soil moisture, such as farmlands and plains. For example, Park S-H et al. [14] employed recurrent neural network long short-term memory (RNN-LSTM) models to predict soil moisture in soybean fields, achieving an impressive R² value of 0.999. Spatial heterogeneity in soil moisture plays a critical role in processes such as evapotranspiration, runoff, precipitation, and atmospheric variability. However, this heterogeneity also complicates comparisons between in-situ observations and airborne or satellite-based remote sensing retrievals [15]. Consequently, retrieval in areas with high soil moisture heterogeneity becomes even more challenging. For instance, Abhilash Singh and Kumar Gaurav [16] used a neural network to estimate surface soil moisture from satellite imagery of the large alluvial fans in the Himalayan foreland, achieving a correlation coefficient (R) of only 0.80. Another pressing issue is the current lack of high-resolution soil moisture data. Various studies have attempted to bridge the gap between coarse-resolution soil moisture products and finer-scale observations by integrating multiple high-resolution auxiliary variables [17,18]. Soil moisture products with a 1 km resolution are commonly generated using MODIS data [18,19,20]. Although Landsat observations have the advantage of providing surface parameters at a higher spatial resolution (30 m), they are rarely explored for estimation of large-scale soil moisture products.
Estimating soil moisture using traditional statistical or physically based models is extremely challenging due to the complex and interdependent relationships between observed reflectance, surface conditions, and various climatic variables [21]. With the advent of the big data era, once reliable predictive parameters are selected and robust algorithmic models are applied, these data can be effectively leveraged to map target variables. Data-driven approaches, which account for a range of parameters (such as temperature, humidity, and other factors affecting soil moisture), have proven to significantly improve soil moisture estimation accuracy [22]. Machine learning, a form of artificial intelligence, is often faster and more efficient than traditional methods. It offers the advantage of understanding and estimating complex, non-linear mappings of distributed data without requiring prior knowledge. Moreover, it can integrate data from various poorly defined sources with unknown probability functions[23]. Machine learning techniques have rapidly advanced in predictive modeling, allowing the identification of intricate, often non-linear data structures and the generation of accurate predictive models. However, it is important to note that such empirical data-driven models require a representative set of reference samples as ground truth. Collecting ground-based reference data, however, involves significant labor and resources. Additionally, errors may occur during the measurement process, leading to invalid data that can interfere with results. Redundant data can also reduce the efficiency of machine learning algorithms, affecting both the quality and quantity of usable reference samples [23]. These models typically rely on location and sensor-specific data, as they are based on samples collected under particular operational conditions. This characteristic limits the applicability of such models across different regions and remote sensing systems, as their effectiveness depends on the availability of reference samples [24,25].
Couckuyt et al. [26] categorized machine learning (ML) techniques into three major classes: (i) classical methods, (ii) ensemble methods, and (iii) neural networks and deep learning (DL) methods. In contrast to classical methods that rely on individual base learners, ensemble learning enhances predictive performance by combining multiple base learners. This approach offers greater accuracy and robustness compared to single models, demonstrating significant advantages in tasks such as classification, regression, and other complex analyses [27]. Neural networks and DL methods, on the other hand, are capable of capturing more intricate relationships between predictors and target variables. However, due to the large and complex nature of these models, they require extensive sample data for precise predictions, making them less suitable for smaller datasets. Machine learning has already been widely applied in various domains, and one of the most valuable areas is soil moisture measurement [28]. ML has been employed to develop new algorithms capable of accurately predicting soil moisture content, which in turn can be used to improve accuracy or for other applications [29]. Umesh Acharya [30] evaluated the performance of several ML techniques in soil moisture retrieval across agricultural fields near the Red River Valley in North Dakota and Minnesota. The techniques assessed included Classification and Regression Trees (CART), Random Forest Regression (RFR), Boosted Regression Trees (BRT), Multiple Linear Regression (MLR), Support Vector Regression (SVR), and Artificial Neural Networks (ANN). Similarly, Yang Zhangjian[11] used meteorological station data and various soil moisture datasets to estimate 1 km daily surface soil moisture (SSM) across China using ML models, achieving promising results.
To improve soil moisture estimation in regions with high heterogeneity, while minimizing errors introduced by multi-source data, we employed single-source satellite data to compute soil moisture-related indices. These indices were then used as features in machine learning models, yielding excellent predictive performance and producing spatially continuous, high-resolution (30 m) surface soil moisture maps. The specific objectives of this study are as follows: (1) to collect various soil moisture-related indices and compute them using Landsat 8 data; (2) to estimate soil moisture in the QLB-NET region by integrating in-situ soil moisture measurements, satellite remote sensing data, and elevation data through multiple machine learning models, compare the performance of four models, and map the soil moisture distribution in this area; and (3) to explore the contribution of feature indices derived from auxiliary data to the prediction of soil moisture levels. (4) Evaluation of QLB-NET's overall and local heterogeneity.

2. Materials and Methods

2.1. Materials

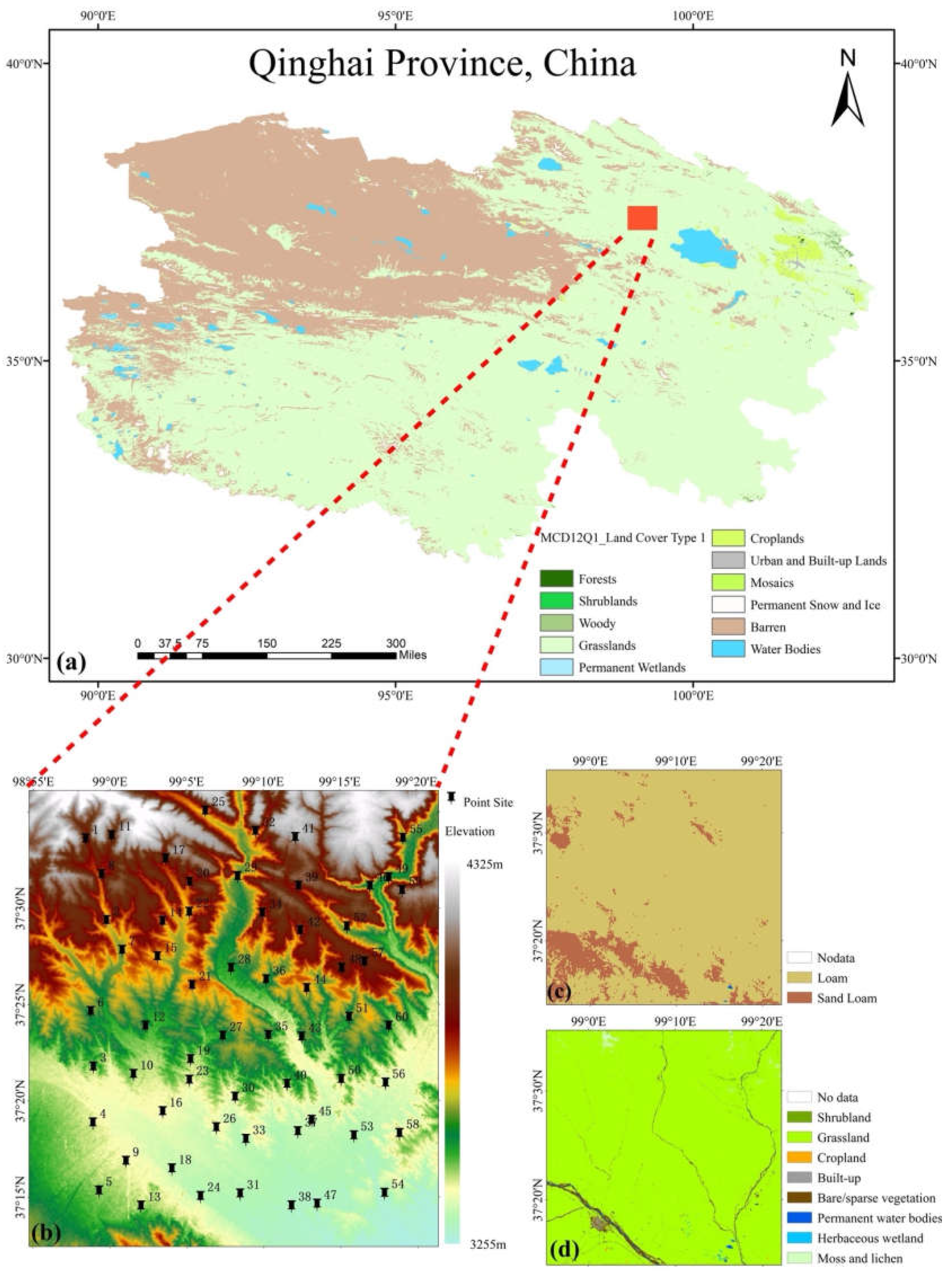
2.1.1. Study Area

The study area covers approximately 40 km × 36 km and is located in the southeastern part of TianJun County, Haixi Mongolian and Tibetan Autonomous Prefecture, Qinghai Province, China. Geographically, it lies between 98.9°E and 99.4°E longitude, and 37.2°N and 37.6°N latitude. The study area is characterized predominantly by a plateau hilly landscape, with the terrain sloping from north to south, featuring a mix of high mountains, mid-to-low mountains, valleys, and intermountain basins. The study area has an average elevation of around 3,500 meters, with significant elevation differences and steep topographic variations (see Figure 1a). Several rivers traverse the area, and wetlands are present in some regions. The study area experiences a cold plateau climate, characterized by cold temperatures and uneven precipitation throughout the year. For much of the year, temperatures remain below 0°C, with a brief warm period in the summer, during which SM is predominantly in liquid form. The soil species in the research area are mostly alpine meadow soil, with a soil thickness of 50-100cm, mainly composed of loam, and containing a large amount of gravel (see Figure 1c).

2.1.2. Data

Machine learning models typically require a large number of input features to achieve comprehensive and accurate predictions. However, the process of harmonizing different datasets can introduce errors, potentially leading to deviations in the predictive outcomes. This highlights the need for more refined models to effectively integrate or unify disparate datasets [31]. In this study, we utilized a single dataset comprising Landsat 8 reflectance data and elevation information, while also incorporating SM-related indices derived from Landsat 8. This approach not only enhances the richness of the machine learning input features but also minimizes the errors that may arise from differences between datasets, thereby improving the accuracy of SM retrieval.

2.1.2.1. Remote Sensing Datasets

The quantity and quality of datasets significantly influence the accuracy of the research methods and the choice of algorithms, while the spatial resolution of the data determines the level of detail in the spatial distribution of the results. The Landsat 8 Level 2, Collection 2, Tier 1 surface reflectance dataset serves as the foundational data for calculating many SM-related indices, offering high precision and timeliness. Collection 2 incorporates updated global digital elevation models (DEM) and improvements in calibration and validation, providing enhanced geometric accuracy. Specifically, Tier 1 includes Level-1 precision and terrain-corrected (L1TP) data, which are characterized by well-defined radiometric measurements and are cross-calibrated across different Landsat instruments. This update notably improves the absolute geographic positioning accuracy.
This dataset provides atmospherically corrected surface reflectance and land surface temperature derived from the Landsat 8 OLI/TIRS sensors. It includes five visible and near-infrared (VNIR) bands, two short-wave infrared (SWIR) bands, and one thermal infrared (TIR) band, all processed to orthorectified surface reflectance and surface temperature. With a spatial resolution of 30 meters and a temporal resolution of 15 days, this dataset offers high-resolution data for detailed analysis. Prior to use, the data undergoes pre-processing, including cloud removal and calibration. The Landsat 8 dataset, covering the period from 2019 to 2023, is accessible via Google Earth Engine (GEE, https://earthengine.google.com).

2.1.2.2. Elevation Data

The elevation data used in this study is derived from NASADEM [32], which is a reprocessed version of the SRTM dataset. The accuracy of NASADEM is enhanced through the integration of auxiliary data from ASTER GDEM, ICESat GLAS, and PRISM datasets. Key processing improvements include gap reduction through refined phase unwrapping and control using ICESat GLAS data. The dataset offers a spatial resolution of 30 meters. Slope and aspect data were calculated using ArcGIS based on this DEM.

2.1.2.3. In-Situ Measurement

The observed dataset consists of 60 sensor measurement points within a 40 km × 36 km area in TianJun County, Qinghai Lake Basin (Figure 1). The large-scale network's sensor placement was optimized using the Kriging method based on MODIS-derived apparent thermal inertia [33,34]. The data named QLB-NET for this large-scale network spans from September 3, 2019, to July 10, 2023. Additionally, there are two small-scale networks, each covering a 1 km × 1 km area with 11 sensor nodes, arranged in a spatially uniform manner. In total, these two small-scale networks comprise 22 nodes, with observations conducted from September 25, 2020, to July 1, 2023. All SM sensors used are Campbell CS655 models, with detailed performance specifications provided in Table 1. Sampling by our team occurs annually, and field SM data for the TianJun area is continuously updated. Each observation point measures SM, temperature, and electrical conductivity at depths of 5 cm, 10 cm, and 30 cm, with a measurement frequency of 30 minutes. Additionally, each observation point is marked with its latitude, longitude, and elevation. This dataset provides ground-truth data for watershed hydrological modeling, data assimilation, and remote sensing validation. Due to the limitations of optical remote sensing, which only reflects surface layer conditions, we use only the 5 cm SM data from the non-frozen period (June 15 to October 15 each year) [35].

2.2. Methods

2.2.1. Soil Moisture Retrieval

2.2.1.1. Feature Selection

The machine learning process is divided into four steps: data preparation, feature engineering, model generation, and model evaluation. After data collection, preprocessing tasks are performed, including the removal of outliers and resampling data to a uniform resolution. Feature engineering involves the construction, extraction, and selection of features. We collected various indices that can be computed from Landsat remote sensing data to characterize SM, which were then used as input features. The principles of these indices are described in the supplementary material.
Another important consideration is that having too many features can consume excessive computational resources, slow down model performance, and decrease accuracy when the number of variables significantly exceeds the optimal value [36]. After obtaining the data for each feature, we used the Boruta algorithm for feature selection. The Boruta algorithm is a wrapper built around a random forest classification algorithm, utilizing the Z-score as a measure of importance, as it accounts for fluctuations in the average accuracy loss of trees in the forest [37]. Boruta selects all relevant features related to the dependent variable rather than choosing a subset that minimizes the model’s loss function. This method ensures that the selected features are applicable across different machine learning models without the need for repeated feature selection for each model. Additionally, using the same input features for different models enhances the comparability of the results.

2.2.1.2. Machine Learning Models

Due to the limited sample size after data filtering, we found it insufficient to drive neural networks and deep learning models. Among the two remaining machine learning approaches, we adopted ensemble learning models, which combine multiple base learners for predictions. This choice is based on their advantages of reduced model variance and enhanced generalization capability. Furthermore, given that our data are not temporally continuous, we excluded time series-based methods from this study. Below, we will introduce the four ensemble learning methods utilized in our research.
The Random Forest (RF) algorithm was originally proposed by Professor Leo Breiman of the University of California, Berkeley [38]. It is an ensemble learning method that outputs predictions by averaging the results of multiple decision trees. Unlike traditional Bagging methods, Random Forest uses decision trees as base learners and applies bootstrap sampling to randomly select subsets of the data as training sets. Decision trees are constructed on these subsets, and the final model output is obtained by averaging the results of all decision trees (the mode is used for classification problems). By combining the results of multiple decision trees, Random Forest achieves high accuracy. However, because the model treats all base learners equally, it may not fully exploit the exceptional performance of particularly strong individual base learners. This limitation can affect the upper bound of the model's performance.
Extremely Randomized Trees (ERT) is an ensemble-based tree method designed for supervised classification and regression problems [39]. This approach primarily involves randomizing attributes and selecting split points when constructing decision trees. For a given numeric attribute, the algorithm randomly selects the split point, meaning the choice is independent of the target variable. At each tree node, a random subset of attributes is considered, and the best attributes are used to determine the splits. In its extreme form, the method constructs entirely random trees by selecting both the attribute and split point randomly at each node, resulting in a tree structure that is independent of the target variable.
Extreme Gradient Boosting (XGBoost), developed by Dr. Chen at the University of Washington in February 2014 [40], is an advanced boosting algorithm. Unlike traditional boosting methods that adjust weights of misclassified samples, the Gradient Boosting Decision Tree (GBDT) model iteratively learns a Classification and Regression Tree (CART) to fit the residuals between the predictions of the previous t-1 trees and the true values of the training samples. However, GBDT models are prone to overfitting in practical scenarios. To address this, Dr. Chen introduced a regularization term in the loss function. The XGBoost model optimizes performance by generating new base learners and using various approximation techniques to determine the number of features or nodes for each iteration. The model continuously adjusts to reduce the residuals from the previous round, with a shrinkage parameter (η) to mitigate potential overfitting.
Categorical Boosting (CatBoost) is an open-source machine learning framework based on gradient boosting algorithms, designed to address target leakage and prediction shift issues in gradient boosting models [41]. Similar to XGBoost, CatBoost combines multiple weak learners to form a strong learner. However, CatBoost incorporates an algorithm known as Ordered Boosting to enhance model accuracy. In Ordered Boosting, training samples are sorted by the magnitude of their feature values, and a piecewise linear model is used to fit the gradients of these values for each segment, improving the model's fitting ability. Additionally, CatBoost leverages categorical features to further enhance performance.

2.2.2. SHapley Additive exPlanations (SHAP) Method

Machine learning models are often considered black-box systems because they make predictions based on feature variables without clearly revealing how each feature affects the target variable. To address this issue, the United States Defense Advanced Research Projects Agency (DARPA) launched the Explainable Artificial Intelligence (XAI) program in 2017, aimed at improving the fairness, transparency, and explainability of machine learning algorithms [42].
The concept of SHAP (SHapley Additive exPlanations) originally emerged from game theory, where it was used to fairly distribute the combined gains among participants based on their individual contributions [43]. Lundberg and Lee [44] adapted this concept to machine learning to tackle the challenge of model interpretability inherent in black-box models. SHAP values are computed to provide feature attributions, offering insights into how each feature contributes to the model's predictions. The mathematical expression for SHAP values is as follows [45]:
∅ i   = ∑ S ⊆ N \ i S !   n   −   S   −   1 ! n ! v   S   ∪   i   −   v S  
where ∅ i is the contribution of feature i , N is the set containing all features, n is the number of features in N , S is the subset of N that contains feature i , and v N is the base value, denoting the predicted outcome for each feature in N without knowledge of the feature values.
The model outcome for each observation is estimated by adding the SHAP value of every feature for observation. For a model f and feature vector z , the model is defined as:
g   z ′ =   ∅ 0   + ∑ i = 1 M ∅ 0 z i '
where g is the explanation model, z ' ϵ   0 ,   1 M is the simplified feature vector of z (so z   =   h z z ' ). M is the number of features and ∅ i can be obtained from Eq. (1). ∅ 0 is the model output when all the features are absent ( z ' =   h z 0 ).

2.2.3. Soil Moisture Heterogeneity Analysis

2.2.3.1. Overall Heterogeneity Assessment

Soil moisture exhibits scale-dependent spatial and temporal variability as a result of the combined influences of climate, geological structure, soil characteristics, and land cover. This heterogeneity has garnered significant attention in recent research. The coefficient of variation (CV) serves as a normalized measure of the dispersion of a probability distribution, making it an important statistical indicator in soil moisture studies. It is utilized to assess the variability of soil moisture distribution [46,47,48]. By calculating the CV for different soil samples, we can evaluate the spatial and temporal non-uniformity of soil moisture. This information is crucial for formulating soil management strategies and optimizing irrigation plans, particularly in areas of high heterogeneity. A high CV may indicate the need for targeted adjustments in management practices to enhance water resource efficiency and improve crop yields. In this study, we will employ the CV to represent the overall dispersion of data samples within the research area, calculated using the following formula:
C V = SD MN * 100 %
where SD is the standard deviation of the sample and MN is the mean of the sample。

2.2.3.2. Local Heterogeneity Assessment

According to Crow et al. [9], the main physical control of soil moisture spatial variability is a function of scale, and the shades of gray in the bar chart in Figure 2 reflect the relative importance of each control factor at different scales. Considering the watershed-scale characteristics of the study area, we focus primarily on the impacts of Land Cover Patterns [49], Topographic Features, and Soil Texture and Structure [50] on soil moisture heterogeneity. Figure 1 illustrates the Land Cover Patterns and Soil Texture and Structure of the study area, revealing a relatively uniform vegetation type, primarily Grassland and loam, while the elevation distribution is more complex. Therefore, we initially hypothesize that elevation is the main factor influencing the spatial heterogeneity of soil moisture.
To address this, LU Huaxing et al. [51] constructed a Compound Terrain Complexity Index (CTCI) based on DEM data. Following the methodology of LU Huaxing et al., we employed multi-factor analysis and local window analysis, selecting four local topographic factors: local relief, local standard deviation, local ruggedness, and local total curvature. Using a moving window of 30 × 30 pixels (i.e., a 900 m × 900 m window), we calculated the local terrain complexity and ultimately derived the CTCI by integrating these four factors for each grid cell. For details of the calculation method, please refer to the method in the paper [51].

2.2.4. Evaluation Metrics

In statistics, the coefficient of determination, commonly known as R², measures the proportion of variance in the dependent variable that is predictable from the independent variables. A higher R² indicates a better fit of the model. The degree of model fit is assessed using R² and Root Mean Square Error (RMSE). Additionally, the model's accuracy is evaluated using the average bias, which directly describes the difference between predicted and observed values, and the Mean Squared Error (MSE), which is sensitive to outliers. These four evaluation metrics are used to assess the accuracy of upscaled results. The formulas for these metrics are as follows:
R 2 = 1 − ∑ i n y ^ i − y i 2 ∑ i n y ¯ i − y i 2
R M S E = 1 n ∑ i n y ^ i − y i 2
B i a s = 1 n ∑ i n y ^ i − y i
M S E = 1 n ∑ i n y ^ i − y i 2
In the formulas， y i and y ^ i represents the observed value and predicted value from the model， y ¯ i is the mean of the observed values, and n is the number of SM samples.
In this study, we used 23 indices derived from Landsat 8 reflectance, including ARVI, EVI, LSWI, and elevation data along with its derivatives, as input for four different models. Ground-measured SM data served as the dependent variable, while the indices and elevation data were used as independent variables. Before constructing the models, we performed mean normalization on the data. For each measurement point, we extracted the average value from a 3x3 grid centered on that point to account for the one to two pixel error inherent in Landsat reflectance data, thereby reducing the impact of these errors. We then extracted the corresponding dependent variables to create the input dataset. For each Landsat overpass, we averaged the ground-measured SM data collected within three hours before and after the satellite pass to represent the true SM at that time and location. To prepare the data for modeling, we selected images with good quality and no missing values from certain dates as samples. From these samples, we randomly selected 10% for the test set, while the remaining 90% were divided into training and validation sets with a 7:3 ratio. The validation set was used for hyperparameter tuning and preliminary model assessment, while the test set was used to evaluate the final model's generalization [52]. Additionally, we utilized RandomizedSearchCV for hyperparameter tuning and applied regularization to prevent overfitting. Finally, based on the In-situ measured data, we evaluated the performance of the four models during both the validation and test phases to produce the most accurate 30m SM maps.
Data preprocessing was conducted using MATLAB R²018a. The Boruta model was implemented with the Boruta package in R 4.2.2, and machine learning models along with SM heterogeneity calculations were carried out in a Python 3.8 environment, utilizing libraries such as NumPy, pandas, scikit-learn, XGBoost, and CatBoost.

3. Results

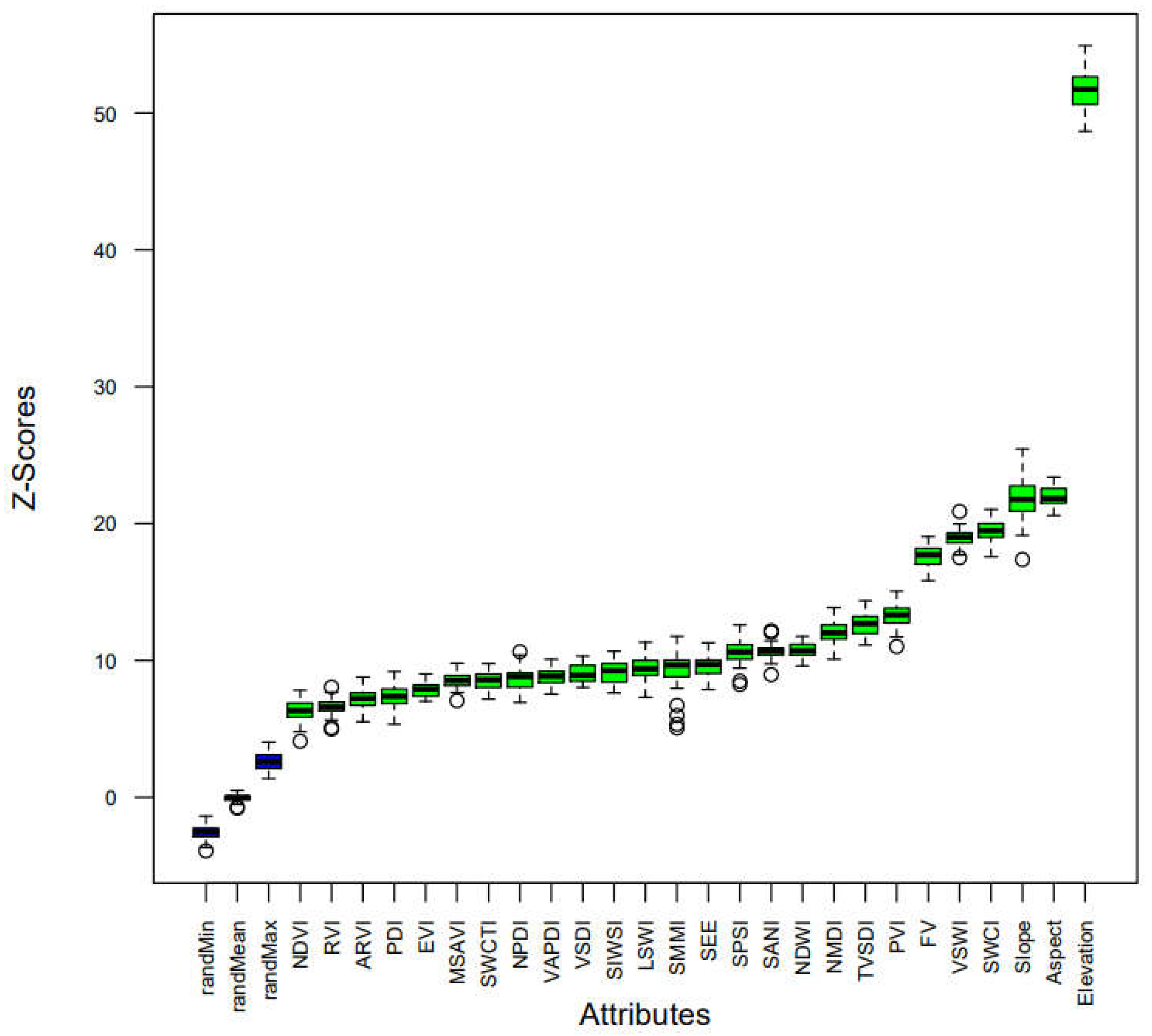
3.1. Feature Selection Analysis

Based on Landsat reflectance data, we calculated indices that characterize soil moisture. Following an analysis of the correlation between these indices and soil moisture, we identified three representative indices with strong fitting characteristics: the Normalized Difference Water Index (NDWI), Surface Water Content Index (SWCI), and Vegetation Supply Water Index (VSWI). These indices, along with elevation, slope, and aspect, are presented in scatter plots in Figure 3. Although scatter plots of slope and aspect against SM do not reveal specific patterns or trends, they play a critical role in SM retrieval [53]. The elevation exhibits a discrete pattern, which is expected, as the elevation values at the same site do not change over time, whereas soil moisture (SM) varies with temporal fluctuations. Overall, elevation is positively correlated with soil moisture. Although NDWI, SWCI, and VSWI were originally designed to represent water bodies, surface moisture content, and vegetation water supply respectively, due to the complexity of geographic factors, they also serve as key indicators for monitoring soil moisture, drought conditions, and vegetation growth [54]. In our study area, while these indices show a strong correlation with soil moisture, their fitting results are significantly weaker compared to those reported in other studies [55,56,57,58]. A likely explanation for this discrepancy is the high spatial heterogeneity of soil moisture in our research area. Single-factor models predict soil moisture based on only one variable, while integrated models combine multiple factors for prediction. Given the complexity of factors influencing soil moisture, integrated models can more comprehensively capture the interactions between these variables, thereby enhancing prediction accuracy and robustness. For this reason, we chose to use a multi-factor input approach to drive soil moisture predictions.
We utilized the Boruta algorithm, which is based on Random Forest, to evaluate feature importance. This algorithm compares the input features with random shadow features and classifies them into important, tentative, or rejected categories based on their Z-scores. Important features are those that significantly impact the target variable and should be retained for subsequent modeling; rejected features are those with minimal relevance to the target variable and should be discarded; tentative features have less clear significance and require further evaluation. Figure 4 displays the preliminary results of feature selection, with a boxplot illustrating the minimum, average, and maximum Z-scores of the features. Fortunately, all features have Z-scores significantly higher than randMax, indicating that they are all considered important. Consequently, all 26 variables will be used as input features for the machine learning models.

3.2. Evaluation of Ensemble Learning Methods and Mapping of Soil Moisture Results at 30m Resolution

As described in Section 3, we evaluated the performance of different machine learning models using four metrics (R², Bias, RMSE, MSE) on both the training and validation datasets. Figure 5 presents scatter plots showing the performance of four machine learning models during the training and validation phases. During the training phase, CatBoost performed the best, while XGBoost performed the worst, with R² values of 0.9782 and 0.9257, respectively. RMSE values were 0.0176 m³/m³ for CatBoost and 0.0333 m³/m³ for XGBoost. Notably, CatBoost demonstrated an almost zero Bias, indicating excellent unbiasedness. RF and ET showed similar performance across all four metrics in the training phase, with R² values around 0.96, RMSE approximately 0.02, and identical MSE values of 0.0006. The Bias values differed by only 0.0001.
In the validation phase, all models experienced a decline in accuracy. RF and ET showed a decrease in R² by about 0.12, whereas XGBoost's decline was around 0.06. In the validation set, XGBoost's performance surpassed that of RF and ET, becoming the second-highest in accuracy. The best performance was still achieved by CatBoost, with R² of 0.8837, RMSE of 0.0463, Bias of 0.0039, and MSE of 0.0021. ET performed the worst, with R² of only 0.8391 and RMSE exceeding 0.05. This indicates that GBDT models, compared to pure tree-based models, significantly reduce overfitting and provide results closer to the true values. From the fitted linear equations, it is observed that the slopes of all models are less than 1, indicating that high values are underestimated and low values are overestimated. This issue may be related to the setting of their loss functions. To reduce this discrepancy, the loss function's weights for high and low value regions could be adjusted after multiple experiments.
To ensure the reliability of our machine learning results, we initially set aside a small portion of the data as a test set to evaluate the model's generalization capability. This approach helps ensure that the highly fitted results are not merely a "coincidence" of overfitting to random data. The presence of a test set addresses potential data leakage issues from the validation set during data adjustments, making the results more convincing. As shown in Figure 6, the overall accuracy of all models decreased in the test set. Nonetheless, CatBoost and XGBoost remained the best-performing and second-best models, with R² values of 0.8251 and 0.8140, and RMSE values of 0.0516 and 0.0532, respectively. However, RF exhibited a lower R² and higher RMSE compared to ET, although RF's Bias was smaller and its linear model slope was closer to 1 compared to ET.
Overall, all four models performed relatively well, with minor differences in their accuracy. Comparing the test and validation sets reveals a common issue of accuracy decline due to overfitting or data leakage, with an R² loss of around 0.05 considered acceptable. Comparing Figure 3 and Figure 6, it is evident that using multiple indices as inputs for machine learning models offers more accurate SM predictions than relying on a single index. This improvement is particularly beneficial for our study area with high SM heterogeneity, significantly enhancing the accuracy of the inversion and resulting in more detailed SM spatial distribution maps (see Figure 7).
To further evaluate the spatial distribution characteristics of 30m surface SM inversion, we selected cloud-free Landsat images from each year between 2020 and 2022 to generate spatial distribution maps for three different periods (see Figure 7). The general trend observed is that SM is higher in the northern region and lower in the southern region, with a notable wetland area in the central and southern parts exhibiting relatively high SM. However, compared to low-resolution SM products, the 30m resolution maps capture finer textural details, not just broad distribution trends. In the central part of the study area, east-west trending intersecting textures may be attributed to differences in SM caused by aspects such as slope orientation or varying rock types. In the northeastern and central-southern regions, where SM content is higher due to the presence of alpine wetlands, the inversion results reveal patches of varying moisture levels. These patches likely correspond to depressions with higher moisture content and raised areas with lower moisture content. Compared to Figure 1, it is apparent that in river areas where higher SM is expected, the inversion results show SM content of less than 0.4, only outlining the river's course. This might be due to the riverbed and floodplain being composed largely of gravel, resulting in lower SM readings because the narrow and shallow river does not retain much water. For urban areas and regions with saturated SM, alternative methods for identification and exclusion might be necessary [59,60].
Among the different machine learning models, CatBoost's spatial inversion results are generally less pronounced compared to others. ET tends to predict higher SM in the northern high-altitude regions (appearing more blue), while XGBoost shows drier conditions in the southwestern dry areas (appearing more red). Over time, the selected periods indicate increasing moisture in the northern and central-southern wetland regions, with the RF model reflecting this trend more clearly. For finer details such as slope aspects and small water pools, CatBoost and XGBoost show more distinct variations, whereas RF and ET present smoother results, making these details less noticeable.

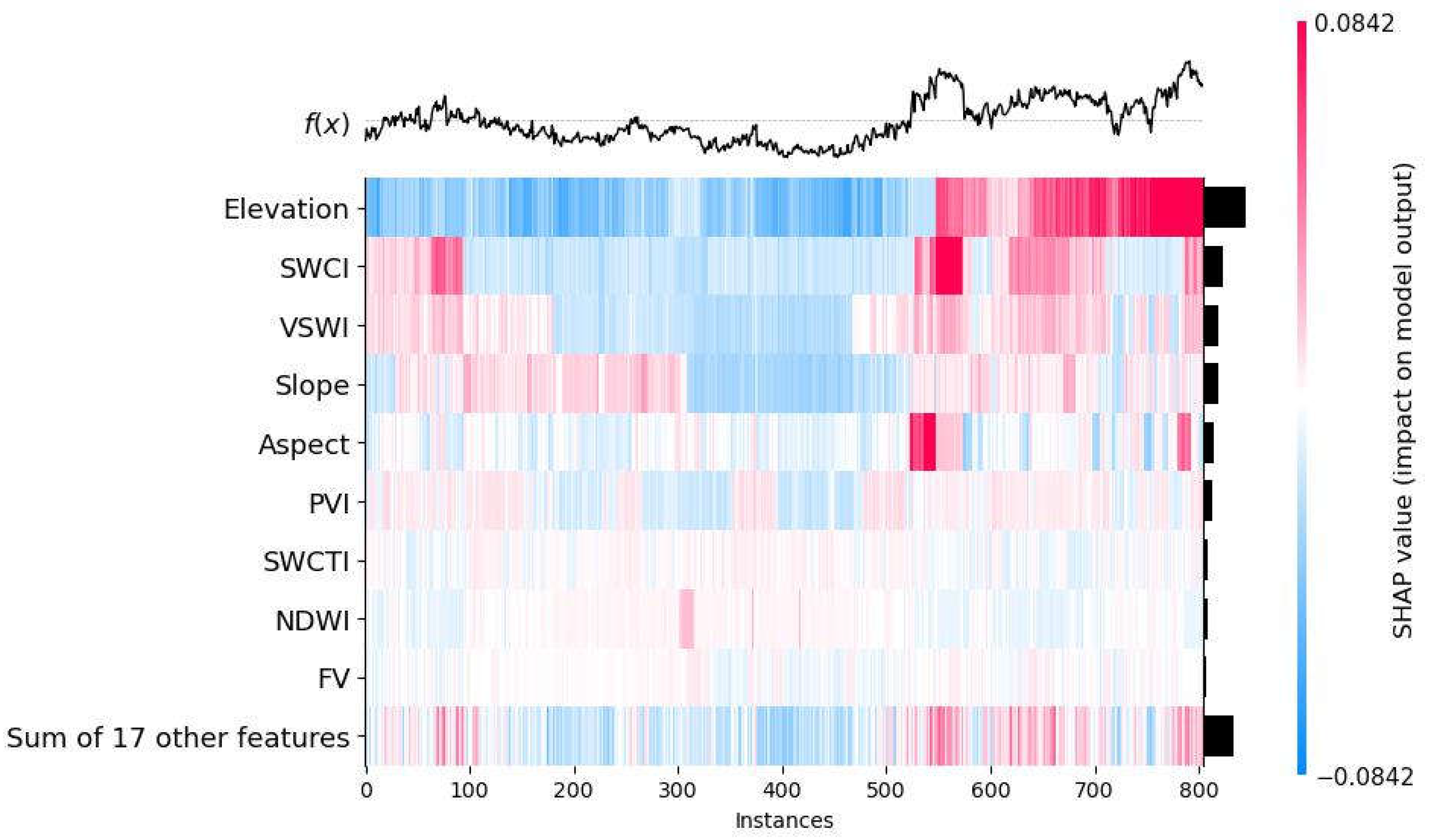
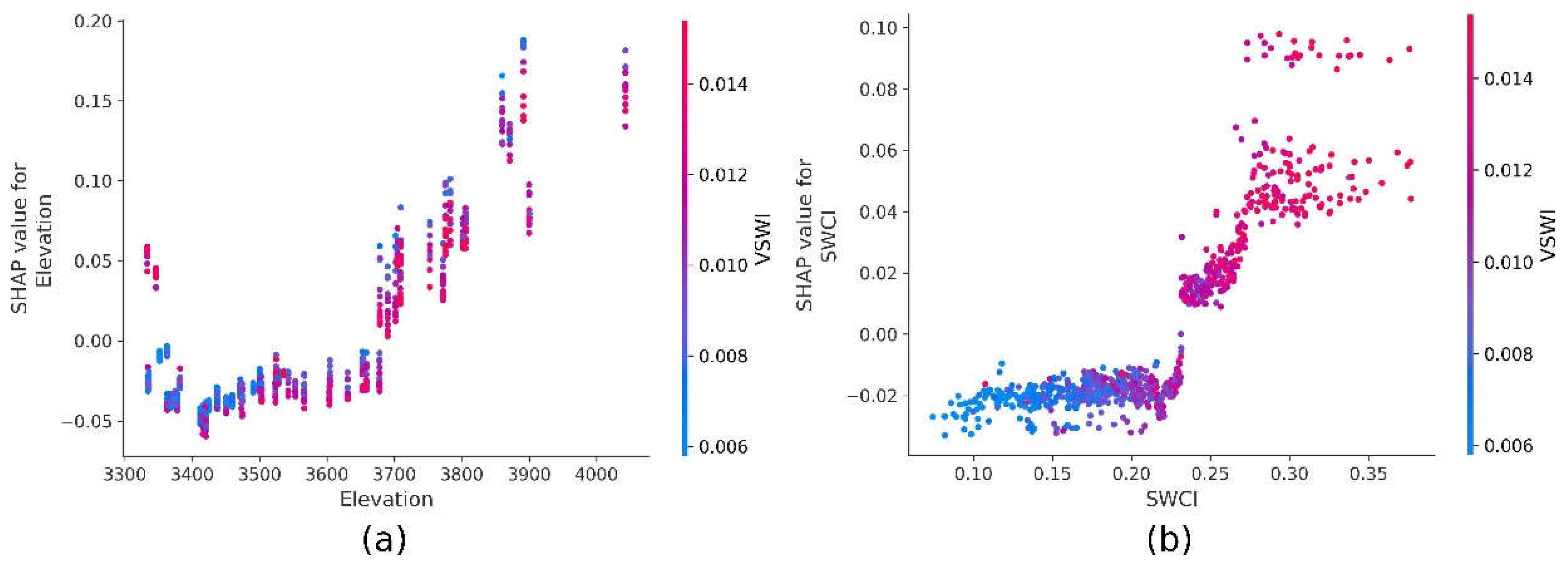
3.3. Explanation of the Features’ Contribution of SHAP to SM Prediction Results

Previously, machine learning models were often viewed as black boxes, making it difficult to describe the mathematical relationships between each feature and SM or to explain how predictions were obtained. The introduction of the SHAP model addresses this limitation by providing explanations for the impact of each feature on SM predictions. In this section, we use SHAP to elucidate the influence of various features on SM.
The normal bar plot (Figure 8a) displays the average absolute SHAP values for each feature. Since all features are continuous, the plot vertically orders them from highest to lowest based on their average impact on SM predictions, with the lowest features contributing the least and the highest contributing the most. The horizontal axis indicates the contribution of each feature to the average soil moisture prediction across all samples. It is important to note that these values are not relative; rather, the average absolute SHAP values of each feature are related to both the number of features and the average value of the target variable. Nevertheless, the bar chart provides a clear visual representation of the relative magnitudes among these contributions. From the bar plot, it is evident that Elevation, SWCI, VSWI, Slope, and Aspect are the most influential features affecting SM. The global SHAP value explanation plot (Figure 8b) illustrates both the direction and magnitude of feature impacts across different samples. Each point represents a sample, with the color indicating the value of the feature itself, ranging from blue (low value) to red (high value). It is evident from the figure that Elevation, SWCI, and VSWI exhibit a generally positive correlation with SM, which aligns with the conclusions drawn from Figure 3. Moreover, Figure 8b also reveals a positive correlation between Slope and SM, which is not as evident in Figure 3. The two most influential features identified in Figure 8b show a relatively narrow range of negative impacts on SM, whereas their positive impacts are spread over a much wider range.
Figure 9 displays SHAP values extracted for different samples under identical predictions. In this heatmap, each row represents the contribution of a single sample, while each column reflects the impact of a specific feature across all samples. By sorting the samples from low to high elevation, the heatmap clearly shows how the influence of different features on each sample changes with elevation. At high elevations, Elevation contributes positively, and SWCI and VSWI also generally contribute positively. Conversely, at low elevations, Elevation has a negative effect on SM. The positive contributions of SWCI and VSWI in the initial 100+ samples could be due to their location near marshes, wetlands, or rivers, where actual SM content remains high despite the low elevation. Since SWCI and VSWI indicate surface water and vegetation water supply, respectively, their positive contribution to SM prediction is expected.
Figure 10 illustrates the relationship between key factors influencing SM predictions and their corresponding SHAP values. The horizontal axis represents the magnitude of a given feature, while the vertical axis denotes the SHAP value for that feature in predicting SM. The color gradient reflects the values of another related feature. In Figure 10a, it is evident that as elevation increases, the corresponding SHAP values also increase. For samples located below 3,700 meters, the SHAP values of elevation are negative, indicating that elevation contributes negatively to SM prediction. Conversely, for elevations above 3,700 meters, SHAP values become positive and continue to rise, suggesting that elevation increasingly contributes to higher SM levels at higher altitudes. Notably, a few high SHAP value points are observed in low-elevation areas, likely corresponding to the wetlands shown in Figure 1. Additionally, Figure 10a shows that the Vegetation Soil Water Index (VSWI) follows a similar trend to elevation, with higher elevation points also corresponding to higher VSWI values.
In Figure 10b, a significant shift in SHAP values is observed for the Soil Water Content Index (SWCI) between 0.2 and 0.3. SHAP values are negative to the left of this transition and positive to the right, indicating that for lower SWCI values, SWCI negatively influences SM predictions, whereas for higher values, it positively contributes. As SWCI increases within this range, its positive effect on SM predictions becomes more pronounced. The color gradient from blue to red indicates that VSWI values are positively correlated with SWCI, as both exhibit similar trends. This relationship is further supported by the consistency in their contributions to SM predictions, as observed in Figure 9

3.4. Heterogeneity Analysis Results

Many studies focusing on soil moisture heterogeneity in various research areas report a coefficient of variation (CV) around 30%. In contrast, our measured data exhibits a CV value of 49.98%, indicating a particularly high level of soil moisture heterogeneity in our study area. In Figure 11, the CV values for the four ensemble learning models are 46.41%, 42.06%, 43.38%, and 44.20%, respectively.
Using the CV of the measured data as a reference for the ensemble learning predictions, we observed that CatBoost achieved the lowest degree of data compression, with its CV value being closest to that of the measured samples. Conversely, the ET model had the lowest CV value, indicating the greatest discrepancy from the measured data. Similar to Figure 5 and Figure 6, the ensemble models with CV values closer to the measured data demonstrate better fitting performance.
Figure 12 illustrates the spatial distribution of terrain complexity. When compared with Figure 1, the distribution of terrain complexity generally aligns with elevation, displaying higher values in the north and lower values in the south, although some details differ. Notably, in the northernmost region, there is a low-value area for terrain complexity that is not reflected in the elevation map, which lacks low-value patches except in valleys.
After extracting the terrain complexity for each site, we calculated the 95% confidence intervals for both the measured soil moisture and the model-predicted soil moisture at each site, as shown in Figure 13. The horizontal line at each point indicates the 95% confidence interval of the measured soil moisture, while the vertical line represents the 95% confidence interval of the model predictions. The color of the points corresponds to the terrain complexity.
It is evident from Figure 13 that points with higher terrain complexity exhibit wider horizontal confidence intervals, indicating greater data uncertainty and variability, which makes accurate prediction more challenging. Consequently, these points also show larger vertical confidence intervals. Additionally, points with higher terrain complexity tend to deviate more from the y = x fit line. This effect is less pronounced in the figure because the model predictions used to create the plot include training data, which closely approximates the true values, thereby minimizing the perceived deviation from actual predictions. Combining insights from Figure 7, Figure 12 and Figure 13, we find that regions with higher terrain complexity are associated with medium soil moisture content, spatially distributed in the upper-middle part of the study area.
We defined points with terrain complexity higher than 0.26 as high soil moisture heterogeneity points. After excluding these points, we recalculated the four evaluation metrics for the test set data, with the results shown in Figure 14. Compared to Figure 6, the performance of all models improved, with the R² of the CatBoost model increasing by 0.1, reaching a notably high value of 0.93. The R² of the other three models also improved by approximately 0.06. At the same time, RMSE, Bias, and MSE were significantly reduced. These results suggest that high soil moisture heterogeneity points are a key source of prediction error in ensemble learning models. Furthermore, ensemble learning demonstrated strong performance in predicting small sample sizes.

4. Discussion

Building on the high heterogeneity of soil moisture characteristics in the study area, we calculated over twenty indices that characterize soil moisture based on Landsat reflectance data. However, despite the good fitting results of these indices when originally proposed, they exhibited lower accuracy in representing soil moisture in our high-heterogeneity region. Therefore, we incorporated these indices, along with elevation and derived data (slope and aspect), as features for input into machine learning models. The final accuracy of the soil moisture estimations significantly improved, and we also generated spatial soil moisture maps. SHAP was used to interpret the black-box nature of the machine learning models, but both the Boruta method for feature selection and SHAP for black-box model interpretation are essentially data-driven black-box models themselves. Hence, to explore deeper mechanisms, other perspectives need to be considered.
A noticeable issue in the soil moisture image (Figure 6) is the difficulty in representing narrow rivers and areas of oversaturated soil moisture. In the image, rivers appear to be in a relatively dry state, likely due to riverbeds, floodplains, and surrounding areas being composed largely of gravel and sandy soils, which have low field water-holding capacity. Another important point to consider is that ensemble learning models are limited in their predictions—they cannot predict data for uncovered spatial or temporal scales. In areas without in-situ measured data, prediction results are less accurate compared to areas with samples. Moreover, due to the constraints of the loss function, the model tends to predict values that lean towards the mean, with larger values being underestimated and smaller values overestimated. Therefore, the actual range of values is generally wider than the predicted range.
It is well-known that machine learning outcomes are to some extent dependent on sample size[51]. When the sample size is too small, complex data-driven models cannot be employed, nor can precise results be obtained. In this study, we chose Landsat satellite data, with a revisit period of 16 days, to achieve high spatial accuracy. After filtering out low-quality remote sensing images caused by cloud cover and other factors, our sample size became quite limited, and the temporal data lacked continuity. How to obtain accurate inversion results with a small sample size remains a question worth exploring. Although neural networks and deep learning models can construct large frameworks to handle complex problems and achieve higher accuracy, they are driven by large sample sizes. Thus, we opted for the more suitable ensemble learning models among the remaining options. In regions with high soil moisture heterogeneity, if sufficient sample size is available, partitioning the study area and subsequently training models within these subregions may yield more accurate results, providing insights into the areas where the model performs well and where it does not. Future directions for improving prediction accuracy include integrating multi-source data [61,62,63], coupling data-driven models with other models [64,65], and utilizing more complex large-scale models [66,67].

5. Conclusion

Based on single-source remote sensing reflectance data and elevation data, we calculated various soil moisture-related indices to serve as features for four ensemble learning models. Using in-situ measured data as "true values," we trained these models and evaluated their predictive performance. Finally, we employed the SHAP model to address the black-box nature of machine learning models. The main findings of the study are as follows:
(1)
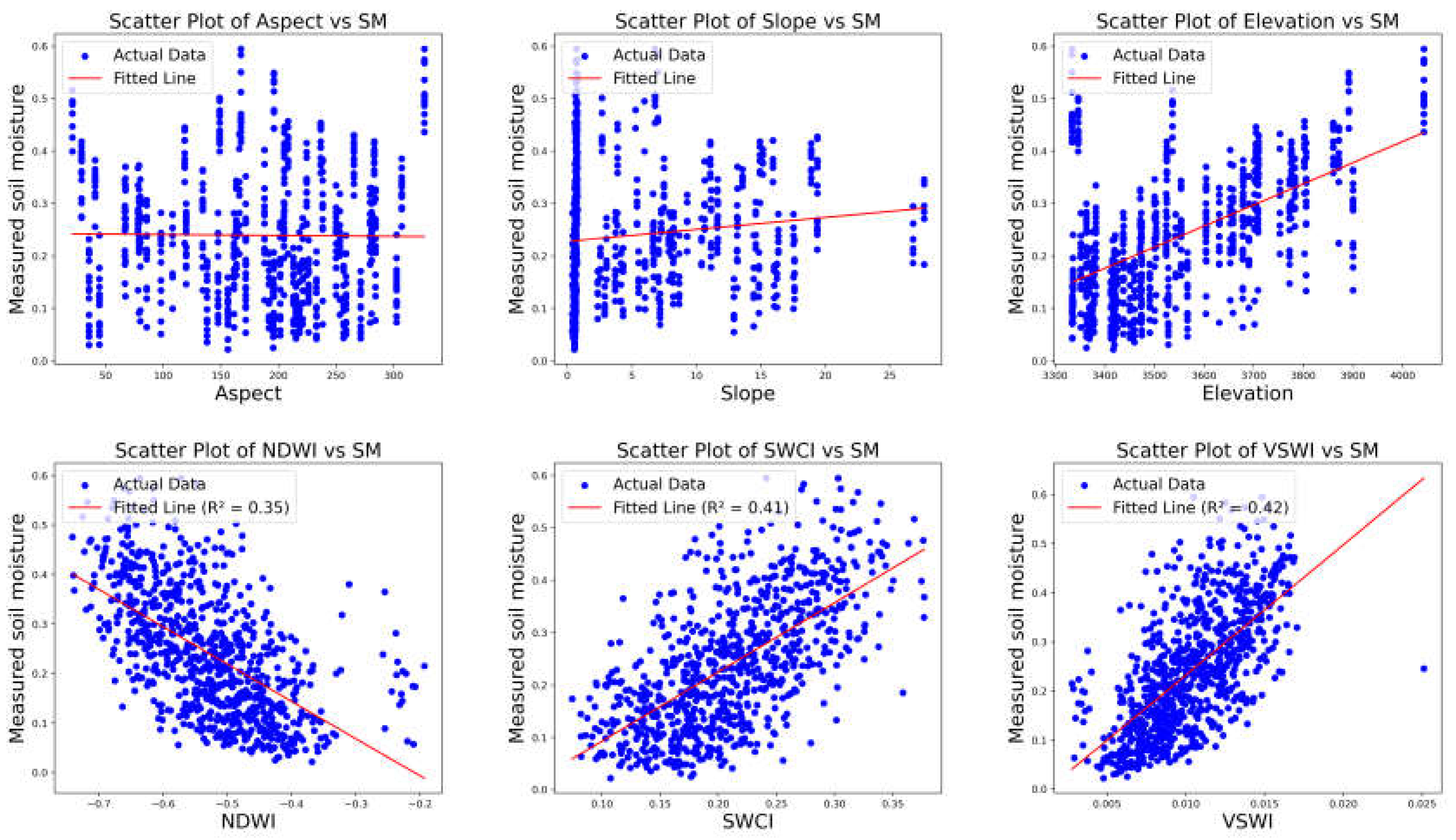
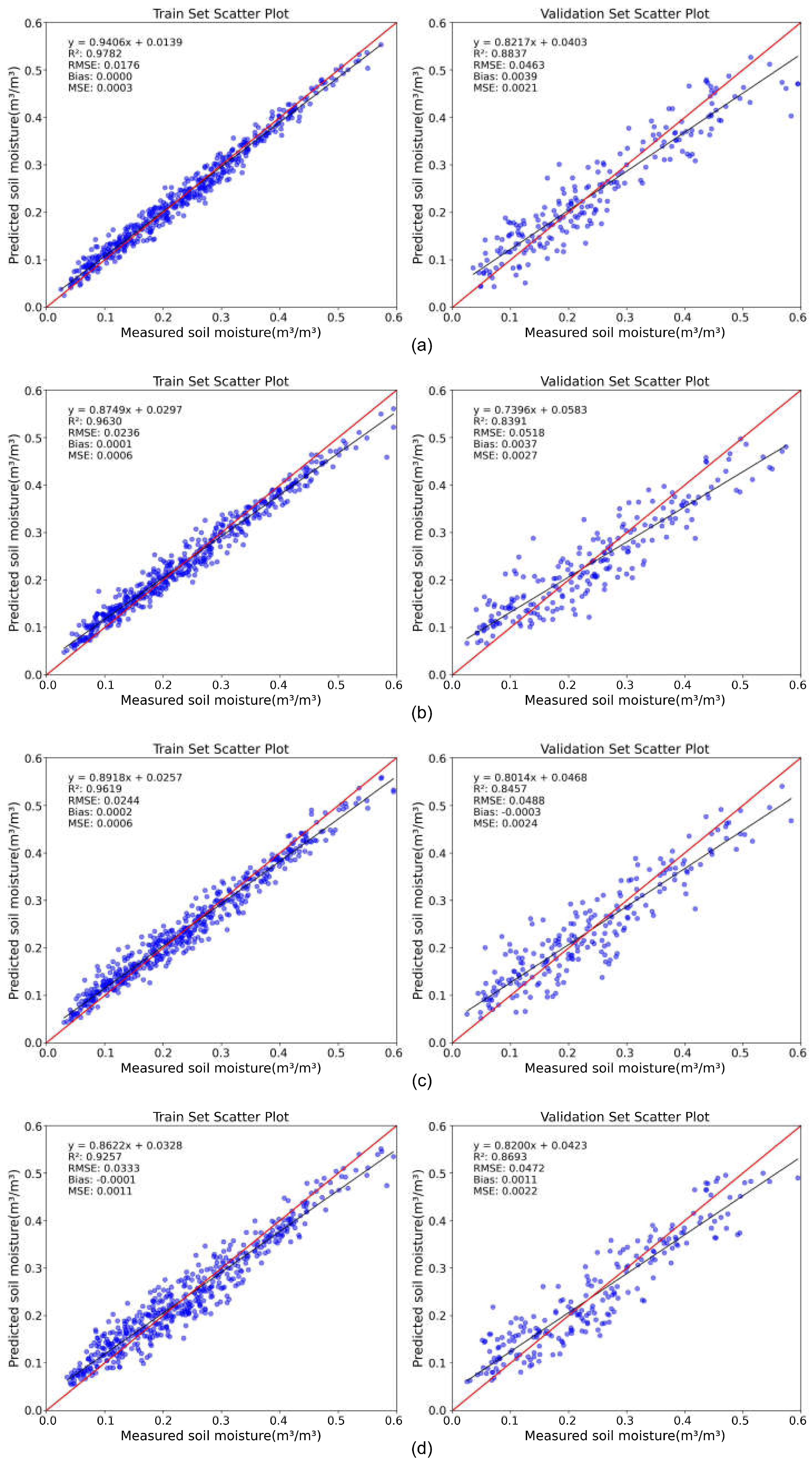
After reviewing multiple studies, we collected twenty-three indices that can characterize soil moisture based on Landsat data, including indices for vegetation and water bodies. Among these, NDWI, SWCI, and VSWI showed the best fitting results with the in-situ measured soil moisture data, achieving R² values of 0.35, 0.41, and 0.42, respectively. However, these results are significantly lower than those reported by other researchers, which we attribute to the high soil moisture heterogeneity in the study area. To address this issue, we added elevation and derived features such as slope and aspect as additional inputs for the ensemble learning models. Before this step, we employed the Boruta method for feature selection to ensure that no irrelevant features were included in the models, confirming that all input features contributed meaningfully.
(2)
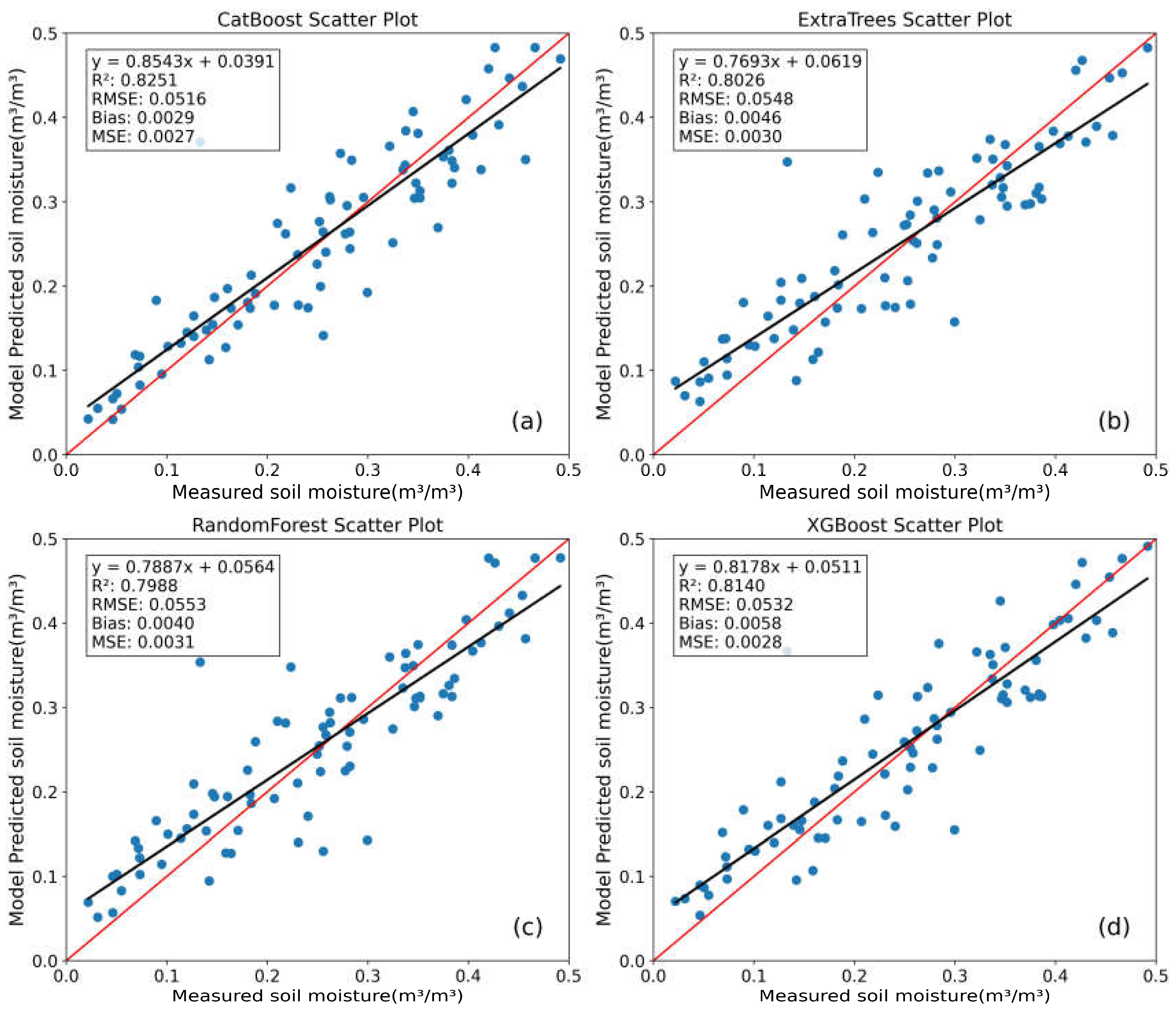
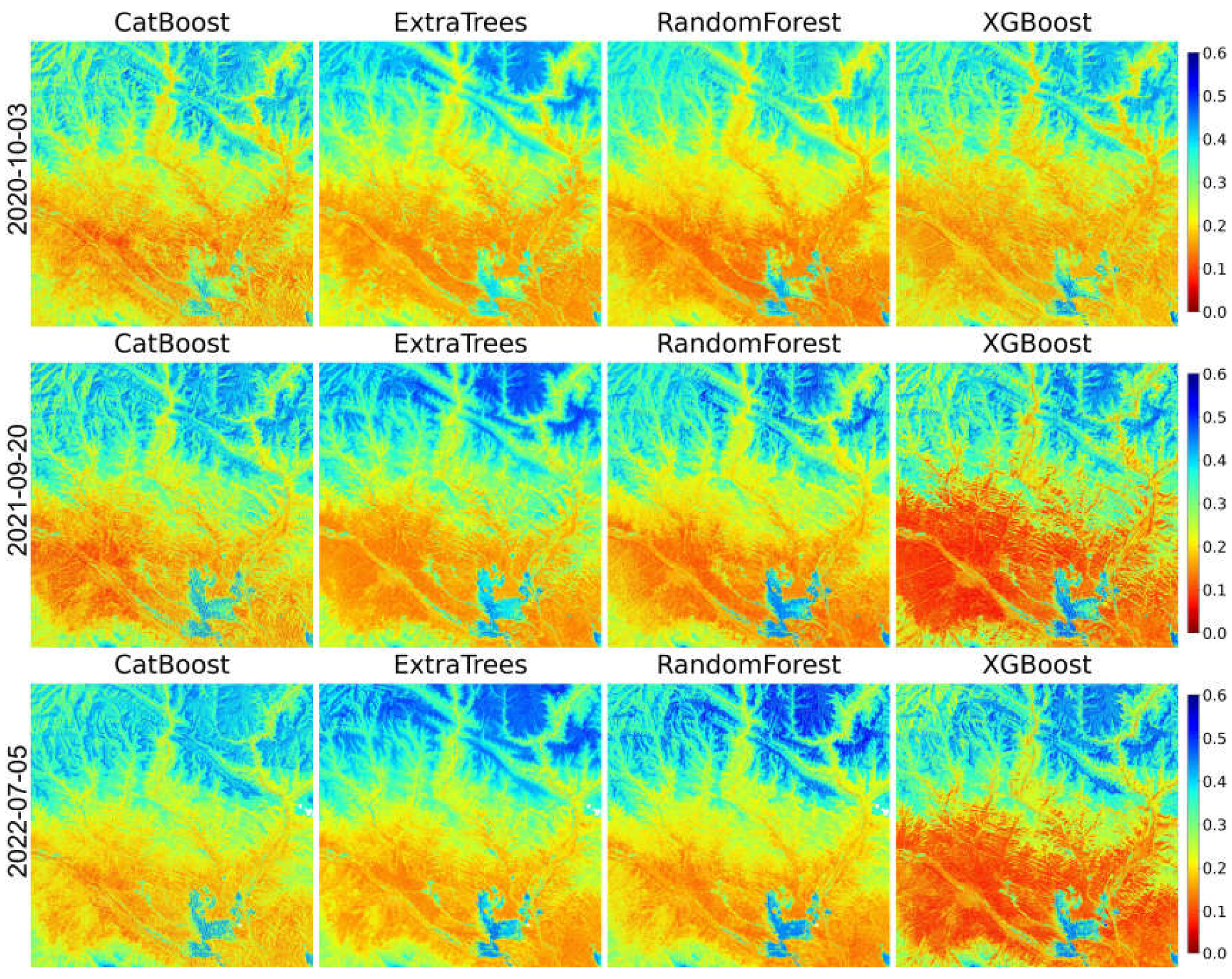
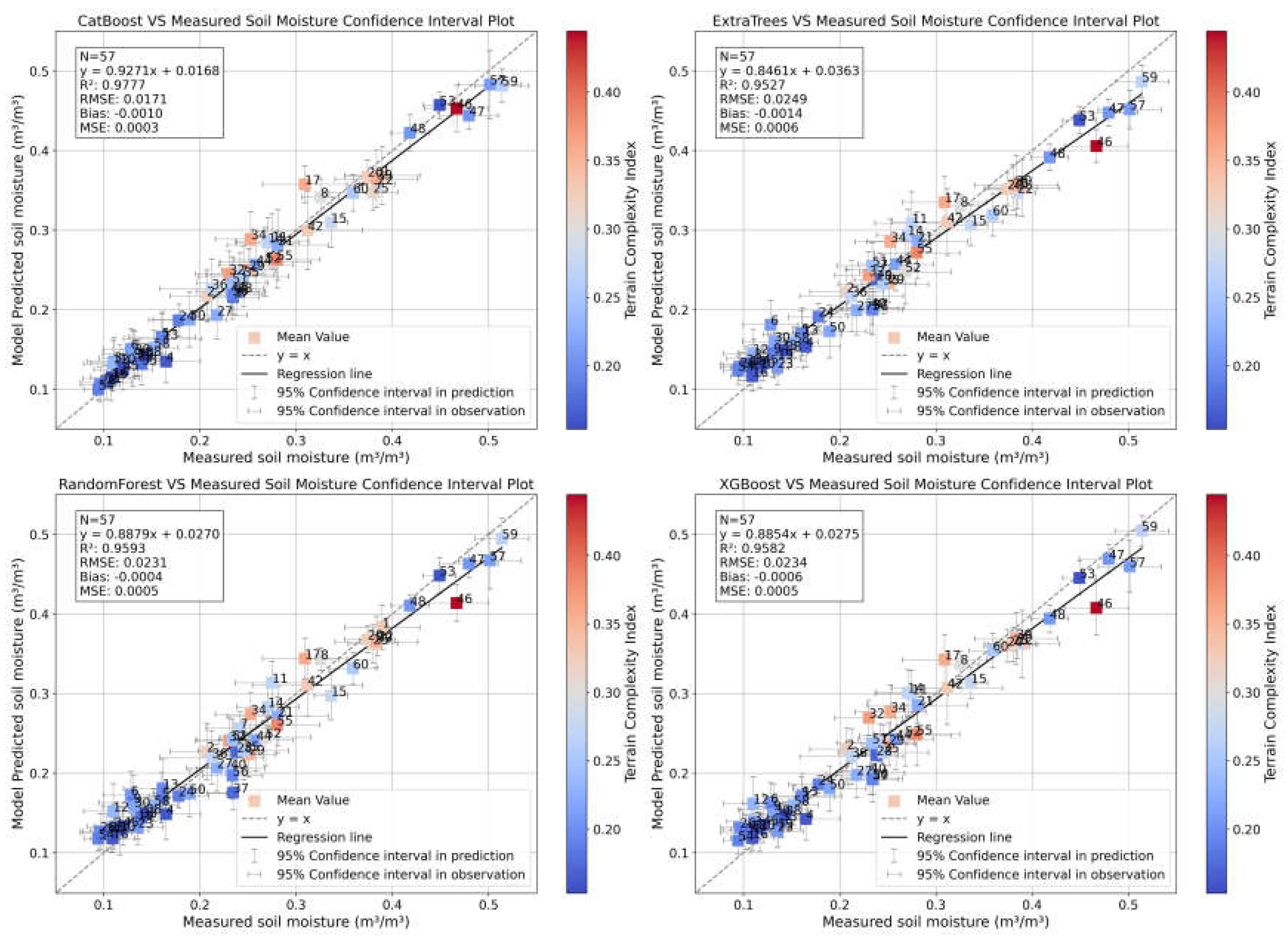
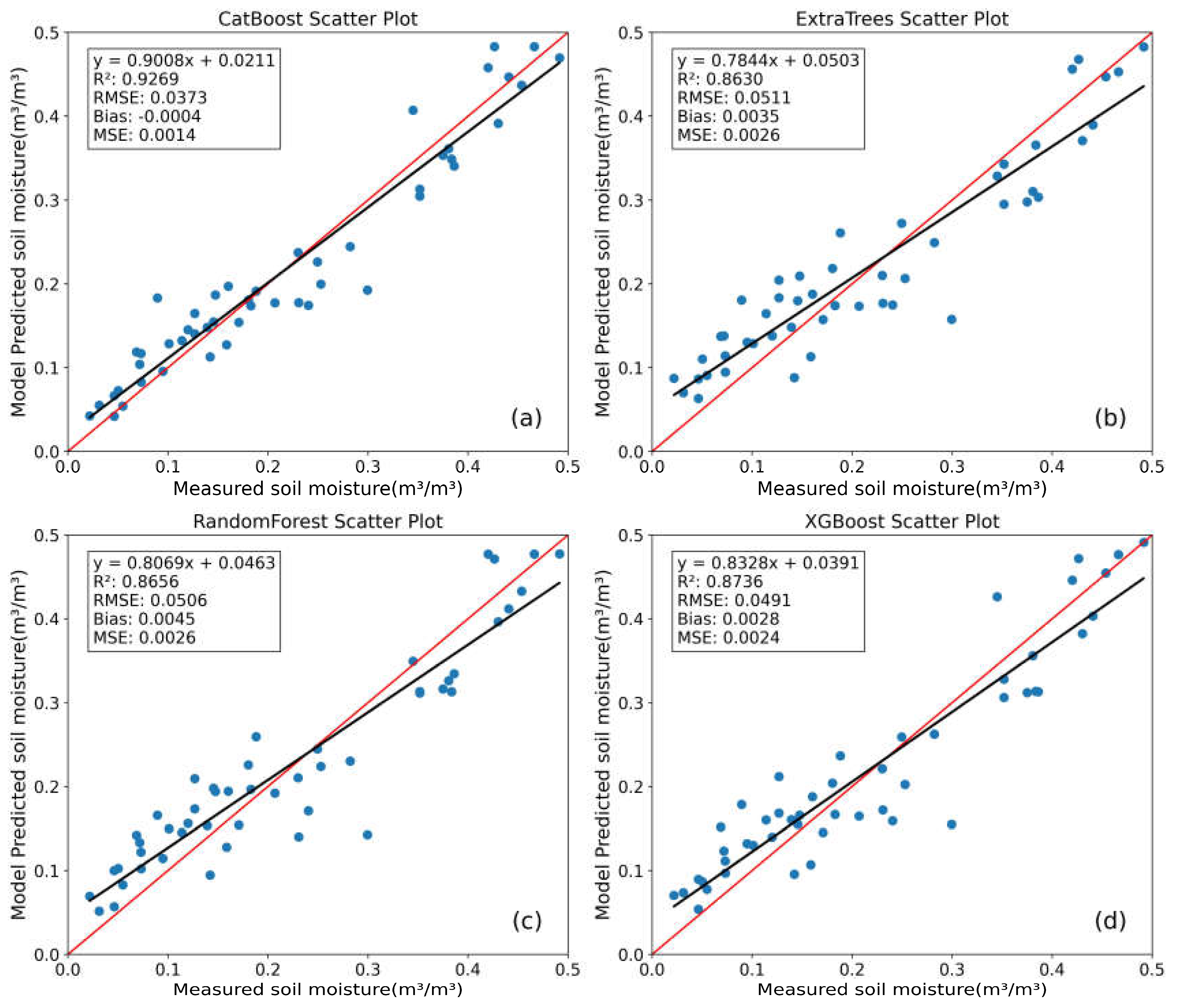
Among the four ensemble learning models, CatBoost performed the best. The soil moisture predictions made using CatBoost yielded R², RMSE, bias, and MSE values of 0.88, 0.0463, 0.0039, and 0.0021 m³/m³ for the validation dataset, and 0.83, 0.0516, 0.0029, and 0.0027 m³/m³ for the test dataset, respectively. The fitting performance of the Random Forest (RF) and Extra Trees (ET) models was relatively lower. Our results also indicate that Gradient Boosting Decision Trees (GBDT) significantly reduce overfitting compared to purely tree-based models. We used these models to generate spatial distribution maps of soil moisture in the study area, capturing detailed spatial variations.
(3)
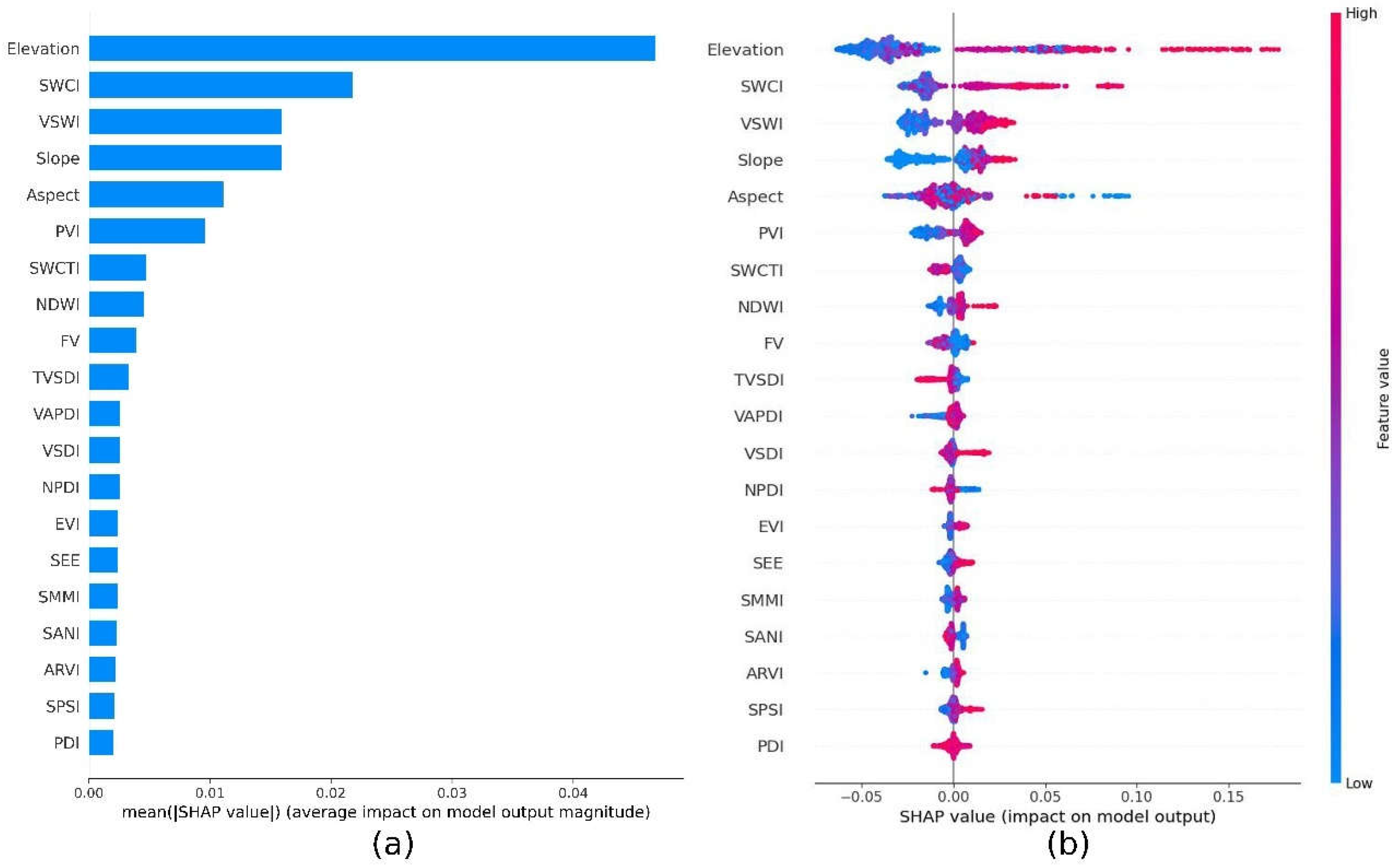
The SHAP analysis results indicate that elevation is the most critical feature among the input variables. SWCI, VSWI, slope, and aspect also play a significant role in the construction of the soil moisture model, which aligns with findings from numerous studies. Elevation has a negative predictive effect on soil moisture in lower-altitude regions, while in higher-altitude areas, its effect is positive. In the central, drier part of the study area, the SHAP values for the main features—elevation, SWCI, VSWI, slope, and aspect—are negative.
(4)
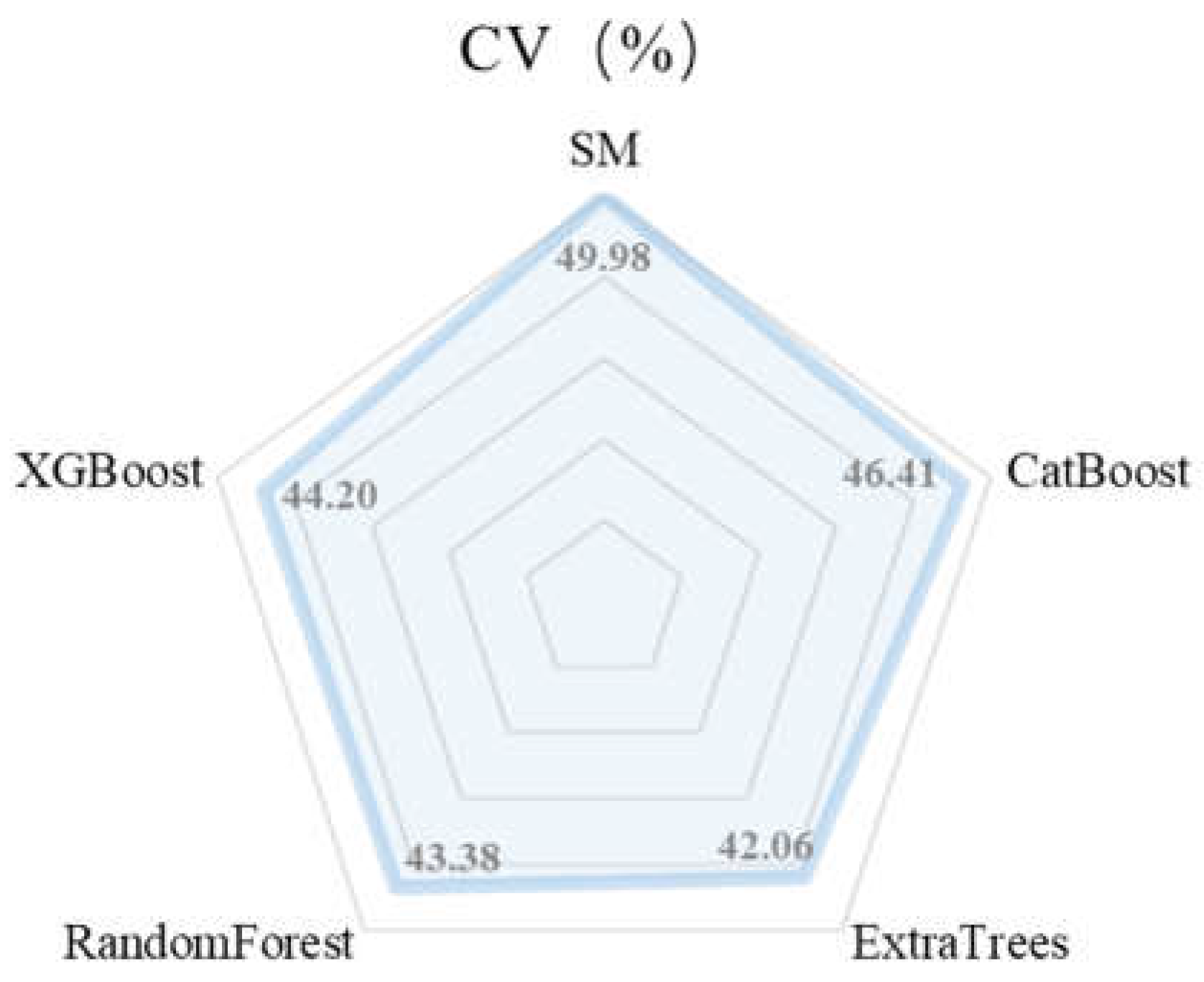
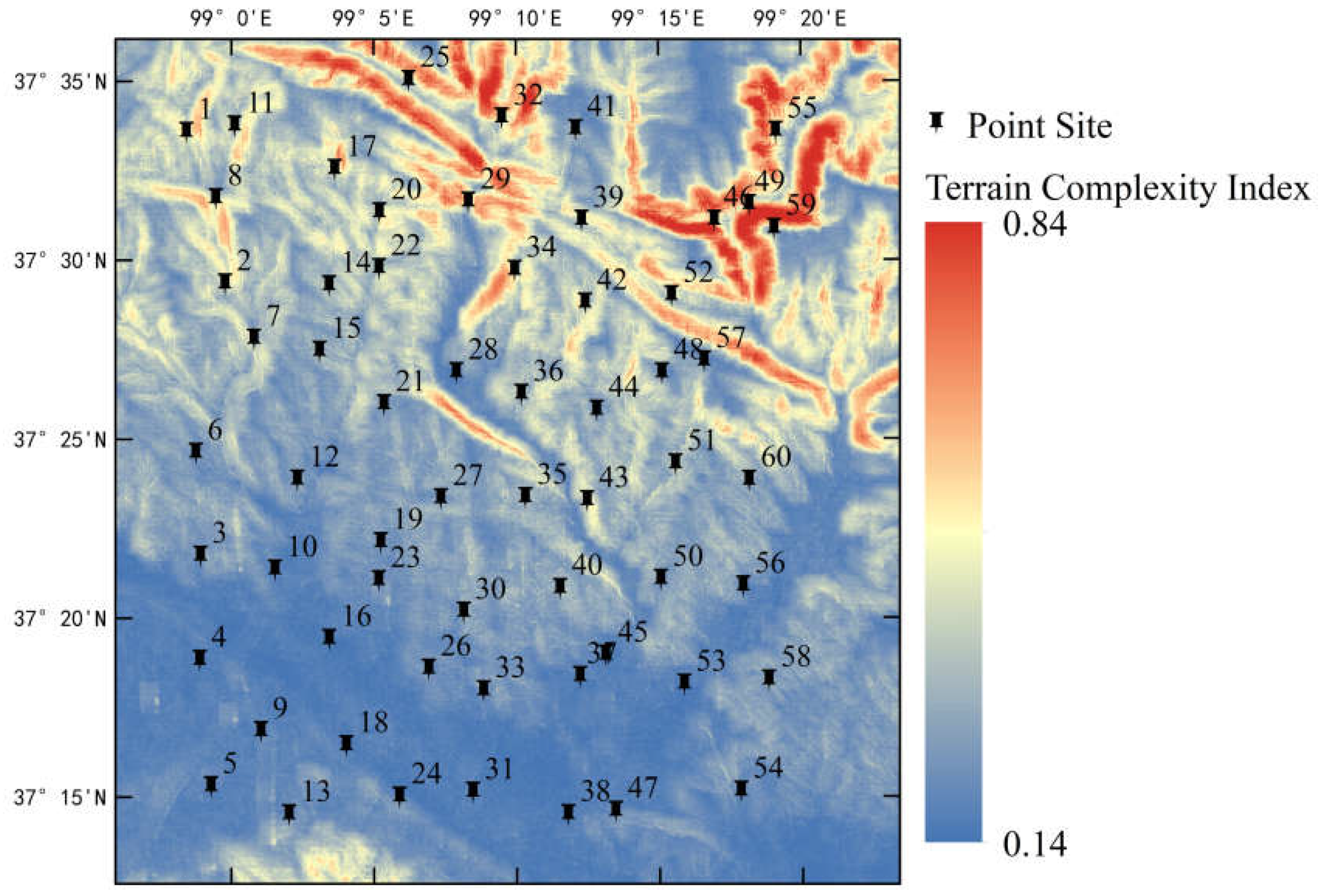
In the overall analysis of soil moisture heterogeneity, QLB-NET exhibited a high coefficient of variation (CV) value of 49.98%, indicating significant heterogeneity compared to typical soil moisture networks. In the local analysis, we represented local heterogeneity with terrain complexity, revealing a distribution pattern of higher values in the north and lower values in the south. Specifically, the northern-central region exhibited the greatest local heterogeneity. Furthermore, sites with higher heterogeneity displayed wider confidence intervals, reflecting greater uncertainty and serving as a source of model prediction error. This was corroborated by predicting the test set data using ensemble learning models after excluding high-heterogeneity data points.
Overall, applying this method to estimate SM in the TianJun region produced promising results. The study contributes significantly to understanding highly heterogeneous SM and offers valuable insights for high-altitude agriculture, water resource management, and local climate change.

Author Contributions

Conceptualization, Qingxia Wu; Data curation, Qingxia Wu; Funding acquisition, Zhongli Zhu; Investigation, Qingxia Wu and Julong Ma; Methodology, Qingxia Wu; Project administration, Zhongli Zhu; Supervision, Zhongli Zhu; Validation, Qingxia Wu; Writing – original draft, Qingxia Wu; Writing – review & editing, Zhongli Zhu, Shaomin Liu, Linna Chai and Ziwei Xu.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No. 42271337).

Data Availability Statement

The measured soil moisture data from the QLB-NET observations in this study are available online on TPDC (https://data.tpdc.ac.cn).

Acknowledgments

The authors would like to thank the United States Geological Survey (USGS) for providing the Landsat 8 data, the European Space Agency (ESA) for the global land cover map, the National Aeronautics and Space Administration (NASA) for the elevation data, and the United States Department of Agriculture (USDA) for the soil texture data.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Banwart, S.; Bernasconi, S.M.; Bloem, J.; Blum, W.; Brandao, M.; Brantley, S.; Chabaux, F.; Duffy, C.; Kram, P.; Lair, G.; et al. Soil Processes and Functions in Critical Zone Observatories: Hypotheses and Experimental Design. Vadose Zone J. 2011, 10, 974–987. [Google Scholar] [CrossRef]
  2. PENG Xinhua, W.Y.J.X. , Some key research fields of Chinese soil physics in the new era: Progresses and perspectives. Acta Pedologica Sinica, 2020. 57(5): p. 1071.
  3. Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture—Climate interactions in a changing climate: A review. Earth-Sci. Rev. 2010; 99, 125–161. [Google Scholar] [CrossRef]
  4. Mittelbach, H.; Lehner, I.; Seneviratne, S.I. Comparison of four soil moisture sensor types under field conditions in Switzerland. J. Hydrol. 2012; 430-431, 39–49. [Google Scholar] [CrossRef]
  5. Bogena, H.R.; Huisman, J.A.; Baatz, R.; Franssen, H.-J.H.; Vereecken, H. Accuracy of the cosmic-ray soil water content probe in humid forest ecosystems: The worst case scenario. Water Resour. Res. 2013, 49, 5778–5791. [Google Scholar] [CrossRef]
  6. Dobriyal, P.; Qureshi, A.; Badola, R.; Hussain, S.A. A review of the methods available for estimating soil moisture and its implications for water resource management. J. Hydrol. 2012; 458-459, 110–117. [Google Scholar] [CrossRef]
  7. D, H. , Environmental Soil Physics. 1998, San Diego: USA：Academic Press. 771.
  8. Ochsner, E.; Cosh, M.H.; Cuenca, R.; Hagimoto, Y.; Kerr, Y.H.; Njoku, E.G.; Zreda, M. State of the Art in Large-Scale Soil Moisture Monitoring. Soil Sci. Soc. Am. J. 2013, 1–32. [Google Scholar] [CrossRef]
  9. Crow, W.T.; Berg, A.A.; Cosh, M.H.; Loew, A.; Mohanty, B.P.; Panciera, R.; de Rosnay, P.; Ryu, D.; Walker, J.P. Upscaling sparse ground-based soil moisture observations for the validation of coarse-resolution satellite soil moisture products. Rev. Geophys. 2012, 50, RG200 . [Google Scholar] [CrossRef]
  10. Robock, A. , et al., The Global Soil Moisture Data Bank. 2000, American Meteorological Society: Boston MA, USA. p. 1281 - 1300.
  11. Yang, Z.; He, Q.; Miao, S.; Wei, F.; Yu, M. Surface Soil Moisture Retrieval of China Using Multi-Source Data and Ensemble Learning. Remote. Sens. 2023, 15, 2786. [Google Scholar] [CrossRef]
  12. Nie, H.; Yang, L.; Li, X.; Ren, L.; Xu, J.; Feng, Y. Spatial Prediction of Soil Moisture Content in Winter Wheat Based on Machine Learning Model. 2018 26th International Conference on Geoinformatics; pp. 1–6.
  13. Famiglietti, J.S.; Ryu, D.; Berg, A.A.; Rodell, M.; Jackson, T.J. Field observations of soil moisture variability across scales. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
  14. Park, S.; Lee, B.; Kim, M.; Sang, W.; Seo, M.C.; Baek, J.; Yang, J.E.; Mo, C. Development of a Soil Moisture Predic-tion Model Based on Recurrent Neural Network Long Short-Term Memory (RNN-LSTM) in Soybean Cultivation. Sensors 2023, 23, 1976. [Google Scholar] [CrossRef]
  15. Western, A.W.; Zhou, S.-L.; Grayson, R.B.; A McMahon, T.; Blöschl, G.; Wilson, D.J. Spatial correlation of soil moisture in small catchments and its relationship to dominant spatial hydrological processes. J. Hydrol. 2004, 286, 113–134. [Google Scholar] [CrossRef]
  16. Singh, A.; Gaurav, K. Deep learning and data fusion to estimate surface soil moisture from multi-sensor satellite images. Sci. Rep. 2023, 13, 1–20. [Google Scholar] [CrossRef] [PubMed]
  17. Wang, J.; Ling, Z.; Wang, Y.; Zeng, H. Improving spatial representation of soil moisture by integration of microwave observations and the temperature–vegetation–drought index derived from MODIS products. ISPRS J. Photogramm. Remote. Sens. 2016, 113, 144–154. [Google Scholar] [CrossRef]
  18. Xu, C.; Qu, J.J.; Hao, X.; Cosh, M.H.; Prueger, J.H.; Zhu, Z.; Gutenberg, L. Downscaling of Surface Soil Moisture Retrieval by Combining MODIS/Landsat and In Situ Measurements. Remote Sens. 2018, 10, 210. [Google Scholar] [CrossRef]
  19. Long, D.; Bai, L.; Yan, L.; Zhang, C.; Yang, W.; Lei, H.; Quan, J.; Meng, X.; Shi, C. Generation of spatially complete and daily continuous surface soil moisture of high spatial resolution. Remote. Sens. Environ. 2019, 233, 111364. [Google Scholar] [CrossRef]
  20. Wei, Z.; Meng, Y.; Zhang, W.; Peng, J.; Meng, L. Downscaling SMAP soil moisture estimation with gradient boosting decision tree regression over the Tibetan Plateau. 2019, 225, 30–44. [CrossRef]
  21. Araya, S.N.; Fryjoff-Hung, A.; Anderson, A.; Viers, J.H.; Ghezzehei, T.A. Machine Learning Based Soil Moisture Retrieval from Unmanned Aircraft System Multispectral Remote Sensing. IGARSS 2020 - 2020 IEEE International Geoscience and Remote Sensing Symposium; pp. 4598–4601.
  22. Das, B.; Rathore, P.; Roy, D.; Chakraborty, D.; Jatav, R.S.; Sethi, D.; Kumar, P. Comparison of bagging, boosting and stacking algorithms for surface soil moisture mapping using optical-thermal-microwave remote sensing synergies. CATENA 2022, 217, 106485. [Google Scholar] [CrossRef]
  23. Ali, I.; Greifeneder, F.; Stamenkovic, J.; Neumann, M.; Notarnicola, C. Review of Machine Learning Approaches for Biomass and Soil Moisture Retrievals from Remote Sensing Data. Remote. Sens. 2015, 7, 16398–16421. [Google Scholar] [CrossRef]
  24. Meroni, M.; Colombo, R.; Panigada, C. Inversion of a radiative transfer model with hyperspectral observations for LAI mapping in poplar plantations. Remote. Sens. Environ. 2004, 92, 195–206. [Google Scholar] [CrossRef]
  25. Colombo, R.; Bellingeri, D.; Fasolini, D.; Marino, C.M. Retrieval of leaf area index in different vegetation types using high resolution satellite data. Remote Sens. Environ. 2003, 86, 120–131. [Google Scholar] [CrossRef]
  26. Couckuyt, A.; Seurinck, R.; Emmaneel, A.; Quintelier, K.; Novak, D.; Van Gassen, S.; Saeys, Y. Challenges in translational machine learning. Hum. Genet. 2022, 141, 1451–1466. [Google Scholar] [CrossRef] [PubMed]
  27. Senanayake, I.P.; Arachchilage, K.R.L.P.; Yeo, I.-Y.; Khaki, M.; Han, S.-C.; Dahlhaus, P.G. Spatial Downscaling of Satellite-Based Soil Moisture Products Using Machine Learning Techniques: A Review. Remote. Sens. 2024, 16, 2067. [Google Scholar] [CrossRef]
  28. Sarwar, A.; Peters, R.T.; Mohamed, A.Z. Linear mixed modeling and artificial neural network techniques for predicting wind drift and evaporation losses under moving sprinkler irrigation systems. Irrig. Sci. 2019, 38, 177–188. [Google Scholar] [CrossRef]
  29. Ahmad, S.; Kalra, A.; Stephen, H. Estimating soil moisture using remote sensing data: A machine learning approach. Adv. Water Resour. 2010, 33, 69–80. [Google Scholar] [CrossRef]
  30. Acharya, U. , Soil Moisture Prediction using Meteorological Data, Satellite Imagery, and Machine Learning in the Red River Valley of the North. 2021, North Dakota State University.
  31. Gruber, A.; Su, C.; Crow, W.T.; Zwieback, S.; Dorigo, W.A.; Wagner, W. Estimating error cross-correlations in soil moisture data sets using extended collocation analysis. J. Geophys. Res. Atmos. 2016, 121, 1208–1219. [Google Scholar] [CrossRef]
  32. NASA JPL (2021). NASADEM Merged DEM Global 1 arc second V001 Accessed: 2024-09-11. [CrossRef]
  33. Ge, Y.; Wang, J.H.; Heuvelink, G.B.M.; Jin, R.; Li, X.; Wang, J.F. Sampling design optimization of a wireless sensor network for monitoring ecohydrological processes in the Babao River basin, China. Int. J. Geogr. Inf. Sci. 2015, 29, 92–110. [Google Scholar] [CrossRef]
  34. Jin, R.; Li, X.; Yan, B.; Li, X.; Luo, W.; Ma, M.; Guo, J.; Kang, J.; Zhu, Z.; Zhao, S. A Nested Ecohydrological Wireless Sensor Network for Capturing the Surface Heterogeneity in the Midstream Areas of the Heihe River Basin, China. IEEE Geosci. Remote. Sens. Lett. 2014, 11, 2015–2019. [Google Scholar] [CrossRef]
  35. Chai, L.; Zhu, Z.; Liu, S.; Xu, Z.; Jin, R.; Li, X.; Kang, J.; Che, T.; Zhang, Y.; Zhang, J.; et al. QLB-NET: A Dense Soil Moisture and Freeze–Thaw Monitoring Network in the Qinghai Lake Basin on the Qinghai–Tibetan Plateau. Bull. Am. Meteorol. Soc. 2024, 105, E584–E604. [Google Scholar] [CrossRef]
  36. Kohavi, R.; John, G.H. Wrappers for feature subset selection. Artificial Intelligence 1997, 97, 273–324. [Google Scholar] [CrossRef]
  37. Kursa, M.B.; Rudnicki, W.R. Feature Selection with theBorutaPackage. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef]
  38. Breiman, L. , Random forests. MACHINE LEARNING 2001, 45, 5–32. [Google Scholar] [CrossRef]
  39. Geurts, P. Ernst and L. Wehenkel, Extremely randomized trees. Machine Learning, 2006; 63, 3–42. [Google Scholar]
  40. Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. KDD '16. New York, NY, USA, 2016; pp. 785–94.
  41. Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: unbiased boosting with categorical features. NIPS'18. Red Hook, NY, USA, 2018,6639-49.
  42. Li, Z. Extracting spatial effects from machine learning model using local interpretation method: An example of SHAP and XGBoost. Comput. Environ. Urban Syst. 2022, 96. [Google Scholar] [CrossRef]
  43. Shapley, L.S. , 17. A Value for n-Person Games, H.W. Kuhn and A.W. Tucker, H.W. Kuhn and A.W. Tucker^Editors. 1953, Princeton University Press. p. 307-318.
  44. Lundberg, S.M.; Lee, S. A unified approach to interpreting model predictions. NIPS'17. Red Hook, NY, USA, 2017,4768-77.
  45. Pradhan, B.; Dikshit, A.; Lee, S.; Kim, H. An explainable AI (XAI) model for landslide susceptibility modeling. Appl. Soft Comput. 2023, 142. [Google Scholar] [CrossRef]
  46. Li, Z.; Zhao, L.; Wang, L.; Zou, D.; Liu, G.; Hu, G.; Du, E.; Xiao, Y.; Liu, S.; Zhou, H.; et al. . Retrieving Soil Moisture in the Permafrost Environment by Sentinel-1/2 Temporal Data on the Qinghai–Tibet Plateau. Remote Sens. 2022, 14, 5966.
  47. Ruichen, M.; Jinxi, S.; Bin, T.; Wenjin, X.; Feihe, K.; Haotian, S.; Yuxin, L. Vegetation variation regulates soil moisture sensitivity to climate change on the Loess Plateau. J. Hydrol. 2023, 617. [Google Scholar] [CrossRef]
  48. Srivastava, A.; Saco, P.M.; Rodriguez, J.F.; Kumari, N.; Chun, K.P.; Yetemen, O. The role of landscape morphology on soil moisture variability in semi-arid ecosystems. Hydrol. Process. 2020, 35. [Google Scholar] [CrossRef]
  49. Zanaga, D.; Van De Kerchove, R.; De Keersmaecker, W.; Souverijns, N.; Brockmann, C.; Quast, R.; Wevers, J.; Grosu, A.; Paccini, A.; Vergnaud, S. , et al.. ESA WorldCover 10 m 2020 v100.:Zenodo, 2021. [CrossRef]
  50. Hengl, T. Soil texture classes (USDA system) for 6 soil depths (0, 10, 30, 60, 100 and 200 cm) at 250 m.:Zenodo, 2018. [CrossRef]
  51. LU, H.L., U. LIUX and G. TANG, Terrain Complexity Assessment Based on Multivariate Analysis. Mountain Research, 2012. 30(05): p. 616-621.
  52. B. D. Ripley, Pattern Recognition and Neural Networks. Cambridge: Cambridge University Press, 1996.
  53. Varga, C. and C. Levente, The influence of slope aspect on soil moisture. Acta Universitatis Sapientiae, Agriculture and Environment, 2020. 12: p. 82-93.
  54. Fu, X.; Jiang, X.; Yu, Z.; Ding, Y.; Lü, H.; Zheng, D. Understanding the key factors that influence soil moisture estimation using the unscented weighted ensemble Kalman filter. Agric. For. Meteorol. 2022, 313, 108745. [Google Scholar] [CrossRef]
  55. Zhang, N.; Hong, Y.; Qin, Q.; Liu, L. VSDI: a visible and shortwave infrared drought index for monitoring soil and vegetation moisture based on optical remote sensing. Int. J. Remote. Sens. 2013, 34, 4585–4609. [Google Scholar] [CrossRef]
  56. Du, X.; Wang, S.; Zhou, Y.; Wei, H. Construction and validation of a new model for unified surface water capacity based on MODIS data. Geomatics and Information Science of Wuhan University. 2007, 32, 204–205. [Google Scholar]
  57. Hong, Z.; Zhang, W.; Yu, C.; Zhang, D.; Li, L.; Meng, L. SWCTI: Surface Water Content Temperature Index for Assessment of Surface Soil Moisture Status. Sensors 2018, 18, 2875. [Google Scholar] [CrossRef]
  58. Hegazi, E.H.; Samak, A.A.; Yang, L.; Huang, R.; Huang, J. Prediction of Soil Moisture Content from Sentinel-2 Images Using Convolutional Neural Network (CNN). Agronomy 2023, 13, 656. [Google Scholar] [CrossRef]
  59. Peng, J.; Hu, Y.N.; Liu, Y.X.; Ma, J.; Zhao, S.Q. A new approach for urban-rural fringe identification: Integrating impervious surface area and spatial continuous wavelet transform. Landsc. Urban Plan. 2018, 175, 72–79. [Google Scholar] [CrossRef]
  60. Fang-Fang, Z.; Bing, Z.; Jun-Sheng, L.; Qian, S.; Yuanfeng, W.; Yang, S. Comparative Analysis of Automatic Water Identification Method Based on Multispectral Remote Sensing. Procedia Environ. Sci. 2011, 11, 1482–1487. [Google Scholar] [CrossRef]
  61. Shi, W.; Guo, D.; Zhang, H. A reliable and adaptive spatiotemporal data fusion method for blending multi-spatiotemporal-resolution satellite images. Remote. Sens. Environ. 2022, 268, 112770. [Google Scholar] [CrossRef]
  62. Shao, Z.; Cai, J.; Fu, P.; Hu, L.; Liu, T. Deep learning-based fusion of Landsat-8 and Sentinel-2 images for a harmonized surface reflectance product. Remote. Sens. Environ. 2019, 235, 111425. [Google Scholar] [CrossRef]
  63. Mizuochi, H.; Hiyama, T.; Ohta, T.; Fujioka, Y.; Kambatuku, J.R.; Iijima, M.; Nasahara, K.N. Development and evaluation of a lookup-table-based approach to data fusion for seasonal wetlands monitoring: An integrated use of AMSR series, MODIS, and Landsat. Remote. Sens. Environ. 2017, 199, 370–388. [Google Scholar] [CrossRef]
  64. Fu, Z.; Ciais, P.; Wigneron, J.-P.; Gentine, P.; Feldman, A.F.; Makowski, D.; Viovy, N.; Kemanian, A.R.; Goll, D.S.; Stoy, P.C.; et al. Global critical soil moisture thresholds of plant water stress. Nat. Commun. 2024, 15, 1–13. [Google Scholar] [CrossRef]
  65. Han, Q.; Zeng, Y.; Zhang, L.; Wang, C.; Prikaziuk, E.; Niu, Z.; Su, B. Global long term daily 1 km surface soil moisture dataset with physics informed machine learning. Sci. Data 2023, 10, 101. [Google Scholar] [CrossRef] [PubMed]
  66. Skulovich, O.; Gentine, P. A Long-term Consistent Artificial Intelligence and Remote Sensing-based Soil Moisture Dataset. Sci. Data 2023, 10, 154. [Google Scholar] [CrossRef]
  67. O, S.; Orth, R.; Weber, U.; Park, S.K. High-resolution European daily soil moisture derived with machine learning (2003–2020). Sci. Data 2022, 9, 701. [Google Scholar] [CrossRef]
Preprints 141818 g001
Figure 1. The distribution of in-situ soil moisture stations and the land use, soil texture and elevation of the study area.
Figure 1. The distribution of in-situ soil moisture stations and the land use, soil texture and elevation of the study area.
Preprints 141818 g001
Preprints 141818 g002
Figure 2. The scale of factors affecting the spatial variability of soil moisture.
Figure 2. The scale of factors affecting the spatial variability of soil moisture.
Preprints 141818 g002
Preprints 141818 g003
Figure 3. Scatter plots of related features calculated based on elevation and indices related to SM (not all).
Figure 3. Scatter plots of related features calculated based on elevation and indices related to SM (not all).
Preprints 141818 g003
Preprints 141818 g004
Figure 4. Box plot of the Z-score obtained by the Boruta feature selection algorithm.
Figure 4. Box plot of the Z-score obtained by the Boruta feature selection algorithm.
Preprints 141818 g004
Preprints 141818 g005
Figure 5. Scatter plots of predicted SM against measured SM of the CatBoost (a), ERT (b), RF (c), and XGBoost (d) models during train (left) and validation (right).
Figure 5. Scatter plots of predicted SM against measured SM of the CatBoost (a), ERT (b), RF (c), and XGBoost (d) models during train (left) and validation (right).
Preprints 141818 g005
Preprints 141818 g006
Figure 6. Scatter plots of the four models on the test set.
Figure 6. Scatter plots of the four models on the test set.
Preprints 141818 g006
Preprints 141818 g007
Figure 7. Spatial distribution of SM in the 30-meter surface layer. Different columns represent different models, and different rows represent different dates.
Figure 7. Spatial distribution of SM in the 30-meter surface layer. Different columns represent different models, and different rows represent different dates.
Preprints 141818 g007
Preprints 141818 g008
Figure 8. A view of contribution to prediction using: (a) a bar graph of the average absolute SHAP value; and (b) SHAP global explanation.
Figure 8. A view of contribution to prediction using: (a) a bar graph of the average absolute SHAP value; and (b) SHAP global explanation.
Preprints 141818 g008
Preprints 141818 g009
Figure 9. SHAP heat map plot.
Figure 9. SHAP heat map plot.
Preprints 141818 g009
Preprints 141818 g010
Figure 10. SHAP dependence plots on (a) Elevation and VSWI, and (b) SWCI and VSWI for SM.
Figure 10. SHAP dependence plots on (a) Elevation and VSWI, and (b) SWCI and VSWI for SM.
Preprints 141818 g010
Preprints 141818 g011
Figure 11. CV values of the measured data and the predicted results of the model, where SM represents the CV of the measured sample and the other four represent the CVs of different ensemble models.
Figure 11. CV values of the measured data and the predicted results of the model, where SM represents the CV of the measured sample and the other four represent the CVs of different ensemble models.
Preprints 141818 g011
Preprints 141818 g012
Figure 12. Topographic complexity index distribution map of the study area.
Figure 12. Topographic complexity index distribution map of the study area.
Preprints 141818 g012
Preprints 141818 g013
Figure 13. Distribution of measured and model predicted values for each site in the 95% confidence interval range of the four ensemble models. where N=57, there are three sites with missing data, which are 41, 43 and 49.
Figure 13. Distribution of measured and model predicted values for each site in the 95% confidence interval range of the four ensemble models. where N=57, there are three sites with missing data, which are 41, 43 and 49.
Preprints 141818 g013
Preprints 141818 g014
Figure 14. Results of the test set of four ensemble learning models after removing high heterogeneity points.
Figure 14. Results of the test set of four ensemble learning models after removing high heterogeneity points.
Preprints 141818 g014
Table 1. Performance of Campbell-CS655 SM sensor with different indicators.
Table 1. Performance of Campbell-CS655 SM sensor with different indicators.
Performance Metrics Soil Conductivity soil moisture Volumetric Water Content Soil Temperature
Range 0-8dS/m 0-100% -50-70℃
Precision ±(5%the value+0.05dS/m) ±3% ±0.02
Accuracy 0.5% ＜0.05% ±0.5℃
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated