Prerpints.org logo
Preprint
Article

Straightforward Determination of the Average Electron-Hole Distance in Charge-Transfer States Organic Photovoltaic Donor/Acceptor Composites from Out-of-Phase Electron Spin Echo Data

Altmetrics

Downloads

26

Views

23

Comments

0

Submitted:

06 December 2024

Posted:

06 December 2024

You are already at the latest version

Alerts
Abstract

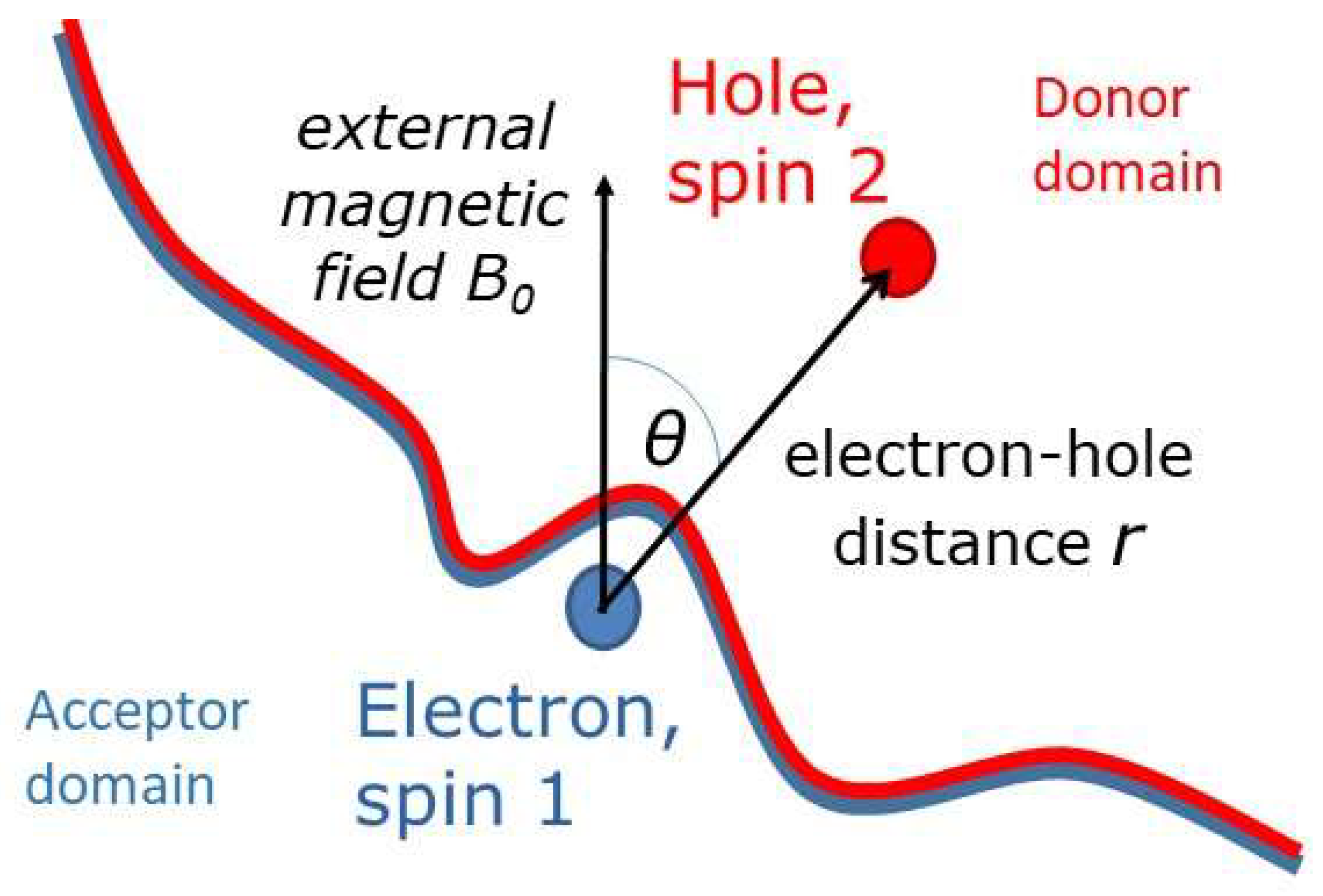
Photoinduced charge separation at donor-acceptor composites (active layer material of organic solar cells) is an important step of photoelectric energy conversion. It results in formation of the interfacial charge-transfer state (CTS), which is Coulombically bound electron-hole pair. We developed the mathematical procedure of direct quantification of the electron-hole distance on the basis of time-domain pulse electron paramagnetic resonance data, obtained in electron spin echo (ESE) experiment. For an ensemble of CTSs characterized by distribution of electron-hole distance this procedure derives the average electron-hole distance without numerical simulation of the experimental data, which is a superposition of the oscillating functions, corresponding to CTSs with the certain electron-hole distance. This procedure was tested on model distance distributions, yielding very accurate results. The data for highly efficient organic photovoltaic composite PM6/Y6 were also analyzed; the average electron-hole distance within the CTS and its dependence on temperature were determined. This procedure can be useful for tracing small changes in CTS structure during optimization of the donor-acceptor composite morphology, which is tightly related to photovoltaic efficiency of the composite.

Keywords: 
Subject: Chemistry and Materials Science  -   Electronic, Optical and Magnetic Materials

1. Introduction

Donor-acceptor composites are widely used nowadays as active layer material of organic solar cells [1,2,3]. Such devices offer promising opportunities of being thin, light-weight and flexible, which makes them more attractive than traditional silicon solar cells [4]. Additionally, organic solar cells are solution-processed, and their production can be ecologically benign, in contrast to production of silicon solar cells [5,6]. Typically, semiconducting polymer is used as the donor material of the active layer, which enables its plasticity and good film-forming properties [6,7,8,9]. For a long time, fullerene-based molecules were the preferred acceptor material [10]. Nowadays non-fullerene acceptors emerge, which outperform fullerenes in photovoltaic devices [11,12]. In efficient donor acceptor composites the donor and the acceptor molecules are properly mixed, so both phase form interpenetrating network with the domain size in order of several tens of nanometer. The composites of this type are usually called bulk heterojunction [13].
One of the major problems of organic solar cells it their relatively low photoelectric power conversion efficiency, compared to silicon solar cell. Although the efficiency of the best-performing organic solar cells reached 20% [14], typically is it significantly lower. Partly this is due to narrow width of the optical absorption spectrum of organic molecules, compared to silicon. The other possible reason is the lower yield of light-induced charge separation in organic donor-acceptor composites [15]. This is because charge photogeneration in such a composites is a complicated process [16]. It starts from light quantum (photon) absorption by either donor or acceptor molecule with formation of an exciton (electronically excited state) localized on this molecule. Then the exciton diffuses to the interface between donor and acceptor. If the exciton reaches this interface before its deactivation electron transfer from the donor to the acceptor occurs with formation of charge-transfer state (CTS), which is a geminate pair of an electron and a hole, localized on a acceptor and a donor molecules, respectively, in the vicinity of the donor/acceptor interface. Within the charge-transfer state the electron and the hole are still bound by the Coulombic attraction. These electron and hole should overcome the Coulombic attraction in order to became free charges and then contribute to photocurrent upon reaching the electrodes. Therefore, CTS is a key intermediate of photoelectric conversion in organic solar cells [17,18,19]. CTS is not formed in active layer material of solar cells of other types. It is a unique feature of organic donor/acceptor composites. The yield of the CTS dissociation with free charge formation is close to unity for some highly efficient organic photovoltaic composites, for example, PCDTBT/PCBM [20]. For other composites this yield is less than unity, which decreases their photovoltaic efficiency. This yield is determined by the competition of CTS dissociation and CTS recombination. Both these processes depend on the distance between the electron and the hole constituting the CTS: the longer is this distance, the slower is the recombination, and the higher are chances of the charges to overcome to Coulombic attraction. Therefore, the distance between the electron and the within the CTS acquired upon charge thermalization (i. e. the loss of the excess energy “inherited” from the exciton) is of primary importance for efficiency of photoelectric conversion within the given organic donor/acceptor composite.
Knowledge of the electron-hole distance within CTS in benchmark composites used in organic photovoltaics would allow targeted optimization of donor/acceptor composited of similar types. However, usually this distance is unknown or uncertain. One reason for this is complexity of donor/acceptor interface, which is characterized by energetic disorder of possible sites of electron and hole localization [21]. Therefore, in real situation the CTS in the given donor/acceptor composite is not characterized by a single electron-hole distance. Instead, broad distribution of the electron-hole distances in the ensemble of CTSs should be considered [22]. The other reason for the lack of CTS characterization in donor/acceptor composite is its elusive nature. As an intermediate of the photoelectric conversion, CTS is not stable but short-living. Furthermore, optical absorption spectra of CTS are typically weak and featureless, so its geometry can hardly be derived from steady-state of time-resolved optical measurements.
Fortunately, pulse electron paramagnetic methods based on the electron spin echo (ESE) detection has sufficient temporal resolution to capture the signal of the CTS generated by a laser pulse, at least at cryogenic temperatures, when charge diffusion is slowed down and the geometry of the CTS is fixed. Since both electron and the hole constituting the CTS have unpaired electron spin they both can be detected by EPR spectroscopy [23]. Importantly, EPR methods allow unique selectivity of the measurement of the CTS, since the rest of the composite is diamagnetic. Among the family of pulse EPR techniques, so called out-of-phase ESE is the method of choice for CTS characterization because it allows to measure the strength of the magnetic dipolar interaction between the spins of the electron and the hole forming the CTS [24]. In this experiment the CTSs are generated by a laser pulse and then they are excited by a specially designed sequence of microwave pulses. The information about the electron-hole distance is encoded in the dependence of the ESE signal intensity on the interval between the echo-forming microwave pulses τ. For a single CTS this dependence is harmonically oscillating function (so called dipolar modulation), with the frequency of the oscillation determined by the interspin distance and the orientation of the interspin vector with respect to the magnetic field of the EPR spectrometer B0. The dipolar frequency ωd in point dipolar approximation is
ω d = 2 π [ γ 2 ħ r 3 ( 1 − 3 cos 2 θ ) ]
where γ is free electron gyromagnetic ratio and ħ is the Planck constant, r is the distance between the centers of spin density distributions of the electron and the hole constituting CTS, θ is polar angle between the magnetic field B0 and the vector connecting the electron and the hole (Figure 1).
For a real sample of donor/acceptor composite the dipolar modulation should be isotropically averaged over the angle θ and then it should be also averaged over the electron-hole distance distribution function P(r). Therefore, the task of “decoding” the dipolar modulation and obtaining P(r), which is or primary importance, becomes complicated. Typically, this task is solved by numerical simulation of the experimental ESE dependence S(τ), which implies some sort of regularization of P(r). Often this is done by numerical fitting of out-of-phase ESE trace by some model function [24,25]. However, the quality of the fit depends on the choice of the fitting function, which is always imperfect. The other was is use of Tikhonov regularization [26,27,28], but the choice of the regularization parameter is somewhat arbitrary. In any case the regularization introduces additional error into the parameters of P(r). In the present work we propose regularization-free direct procedure of the obtaining the average value of the electron-hole distance within the CTS from out-of-phase ESE data. The proposed method also allows strict and unbiased estimation of the error of the average electron-hole distance. The procedure was tested on a distance distribution function model and was found to be quite accurate. Then in was applied to analyze ESE data obtained on real samples of the highly efficient organic photovoltaic composites containing polymer donor PM6 and non-fullerene acceptor Y6; dependence of the average electron-hole distance on the delay after CTS photogeneration and temperature was studied.

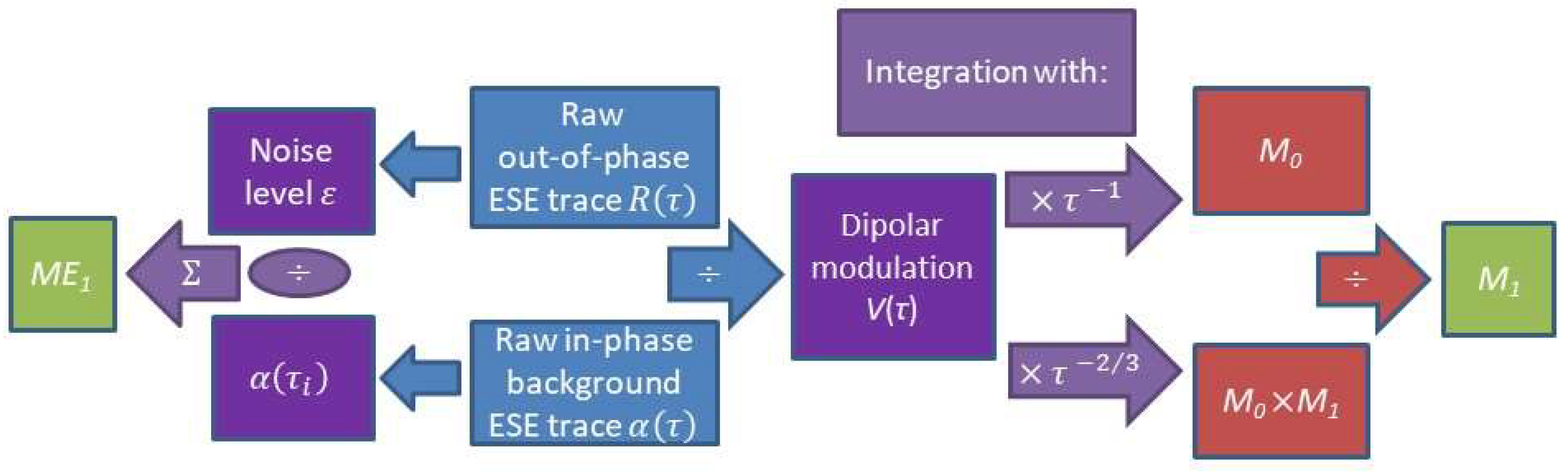
2. Theory

2.1. The Dipolar Modulation Signal and the Mellin Integral Transformation

Consider the normalized dipolar signal V(τ) for the isotropic sample without orientation selection of the dipolar modulation frequency, in the absence of exchange interaction between the spins producing the dipolar modulation, and the absence of decay caused by intermolecular spin-spin interactions other spins:
V ( τ ) = ∫ 0 ∞ P ( r ) K ( r , τ ) d r = ∫ 0 ∞ P ( r ) K ( a τ r 3 ) d r
where a =2πγ2/ħ, K ( r , τ ) is the kernel which can also be represented with a single parameter as K ( a τ r 3 ) ,
K ( r , τ ) = ∫ 0 1 Sin [ a w τ ( 1 − 3 x 2 ) ] d x = π 6 ( − Cos [ a w τ ] FSin [ a 6 π w τ ] + FCos [ a 6 π w τ ] Sin [ a w τ ] ) a w τ
Here FSin and FCos – Fresnel sine and cosine special functions, w is dipolar frequency, w=a/r3, P ( r ) is the electron-hole distance distribution function. Eq. (1) is a Fredholm equation of the first kind with the kernel in a form a product. A convenient way to solve this equation, i.e., to convert the time domain data V ( τ ) into the distance domain data P ( r ) , is to separate the variables r and τ in the kernel using the Mellin transformation [29,30,31],
Y ( s ) = ∫ 0 ∞ y ( x ) x s − 1 d x ,
which is closely related to the well-known Fourier and Laplace transformations. Applying the Mellin transformation to both sides of Eq. (1) we have
∫ 0 ∞ V ( τ ) τ s − 1 d τ = ∫ 0 ∞ ∫ 0 ∞ P ( r ) K ( a τ r 3 ) τ s − 1 d τ d r .
Substitution of new variables (r, z) ( z = τ / r 3 , d τ = r 3 d z , so that τ s − 1 = ( z r 3 ) s − 1 ) in Eq. (1) instead of the original kernel variables (r, τ ) allows to convert the double integral into a product:
∫ 0 ∞ V ( τ ) τ s − 1 d τ = ∫ 0 ∞ ∫ 0 ∞ P ( r ) K ( a τ r 3 ) ( z r 3 ) s − 1 ( r 3 d z ) d r = ∫ 0 ∞ r 3 s P ( r ) d r ∫ 0 ∞ z s − 1 K ( a z ) d z
When s = 1/3, Eq. (3) can be rearranged to give the directly calculated average distance or first moment M 1 as:
M 1 = ∫ 0 ∞ r   P ( r ) d r = ∫ 0 ∞ V ( τ ) τ − 2 / 3 d τ / ∫ 0 ∞ z − 2 / 3 K ( a z ) d z
because the is P ( r ) is a normalized probability function whose integral is unity [32].
The last integral in Eq. (3), which became the denominator in Eq. (4) with s = 1/3, has a constant analytical value:
I ( s ) = 1 a s [ 3 − s Γ [ s ] p F q [ { − 1 4 + s 2 , 1 2 + s 2 , s 2 } , { 1 2 , 3 4 + s 2 } , 1 9 ] Sin [ π s 2 ] − 1 + 2 s + 1 6 ( − 3 π Cos [ π s 2 ] Γ [ − 1 2 + s ] + 2 × 3 − s Γ [ 1 + s ] p F q [ { 1 4 + s 2 , 1 2 + s 2 , 1 + s 2 } , { 3 2 , 5 4 + s 2 } , 1 9 ] Sin [ π s 2 ] 1 + 2 s ) ]              
Which valid if − 3 < Re [ s ] < 3 / 2   . Here Γ [ s ] is Gamma function and pFq [a,b,c] is the generalized hypergeometric function. Evaluated in Mathematica v.10, I ( 1 / 3 ) = 0.284376 * a − 1 3 =   0.412772 using the free electron g-factor for each radical, so that a = 0.327 nm3/ns.
In the ideal case considered above the time domain data V(τ) is normalized dipolar modulation function. For the real case normalization coefficient V0 should be introduced, so the time domain data has is a product V0V(τ). The is normalization coefficient is a-priory unknown and also can be obtained from Eq. (3) with s = 0. This allows to calculate zeroth moment of the distance distribution from the time domain data:
M 0 = ∫ 0 ∞ V 0 × V ( τ ) τ − 1 d τ = V 0 ∫ 0 ∞ P ( r ) d r ∫ 0 ∞ z − 1 K ( a z ) d z = V 0 × 1 × 0.243
Here the last integral equals I(0) = 0.243 (see Eq. 5), ∫ 0 ∞ P ( r ) d r = 1 because P ( r ) is normalized. Therefore, V 0 = ∫ 0 ∞ V ( τ ) τ − 1 d τ / 0.243 .
We emphasize that Eq. (4) eliminates the need to calculate the distance distribution at the beginning and only after this to extract M1 from it. Applying Eq. (4) to avoid the regularization, which is typically used to obtain the distance spectrum. Both integrals on the right-hand side of Eqns. (4, 5) are more stable than the calculation of the distance spectrum by any method.
In practice, an integral like ∫ 0 ∞ V ( τ ) τ − 2 / 3 d τ in Eq. (4) can be problematic to calculate with digital data because τ − 2 / 3 diverges at τ = 0. Very mild regularization overcomes this problem. Near τ = 0, the kernel is
π 6 ( − Cos [ a w τ ] FSin [ a 6 π w τ ] + FCos [ a 6 π w τ ] Sin [ a w τ ] ) a w τ = 8 a 3 w τ 3 105 + O [ w τ ] 9 / 2
In a small interval δ τ around τ = 0, we can take V( τ ) ~ τ 3 ≈ 0, which can be considered as the only ‘regularization’ used, so that V( τ )=0 and
∫ 0 ∞ V ( τ ) τ − 2 / 3 d τ ≅ ∫ 0 δ τ 0 * τ − 2 / 3 d τ + ∫ δ τ ∞ V ( τ ) τ − 2 / 3 d τ
We conservatively use δ τ = Δ τ which is more than adequate when the parameters of signal acquisition are properly chosen: the step Δτ allows recording the signal without distortion, and the number of points N allows recording the signal completely with variation of τ within the interval NΔτ [30]. The first integral on the right-hand side of Eq. (7) is evaluated analytically, and the second term numerically from the discrete values of V ( τ ) using the trapezoid rule.
Using the Cotes formula for trapezoid rule integration,
M 1 = 1 I ( 1 / 3 ) [ 0 + Δ τ ( ( V ( τ 1 ) τ 1 − 2 / 3 + V ( τ m a x ) τ m a x − 2 / 3 ) 2 + ∑ i = 2 N − 2 V ( τ i ) τ i − 2 / 3 ) ] = Δ τ 1 / 3 I ( 1 / 3 ) [ V ( Δ τ ) 2 + ∑ i = 2 N − 2 V ( τ i ) i − 2 / 3 ]
assuming uniform sampling with τ i = i Δ τ , and that the signal goes to zero by the last point so that V ( τ m a x ) = 0 .

2.2. Testing the Procedure of the Average Distance Calculation on Model Distance Distributions

To test the efficiency of the algorithm, we take a bimodal distribution of two Gaussian functions with average distances of 2 and 3 nm, and a width of 0.3 nm, and vary the relative contribution of the first Gaussian. For each case, we construct the dipolar signal V(τ), and from the model signal we restore the first moment of P(r). Figure 2A shows the distance distribution functions, while Figure 2B shows the corresponding model signals. Table 1 summarizes the theoretical and calculated values of the first moment of the distance distribution functions. It is evident that the agreement is excellent.
In addition, the stability of the algorithm is practically independent of the width of the distance distribution function, as it is shown by the second series of model calculations. In this calculations, the distance distribution function were Gaussian functions with a fixed average distance of 4 nm and different widths (0.12, 0.2, 0.4, 0.6 and 0.8 nm), see Figure 2C. The corresponding model dipolar signals V(τ) are shown in Figure 2D. The calculated values of the first moment are given in the Table 2. It is seen that they coincide with the original value with an accuracy of 0.1%.

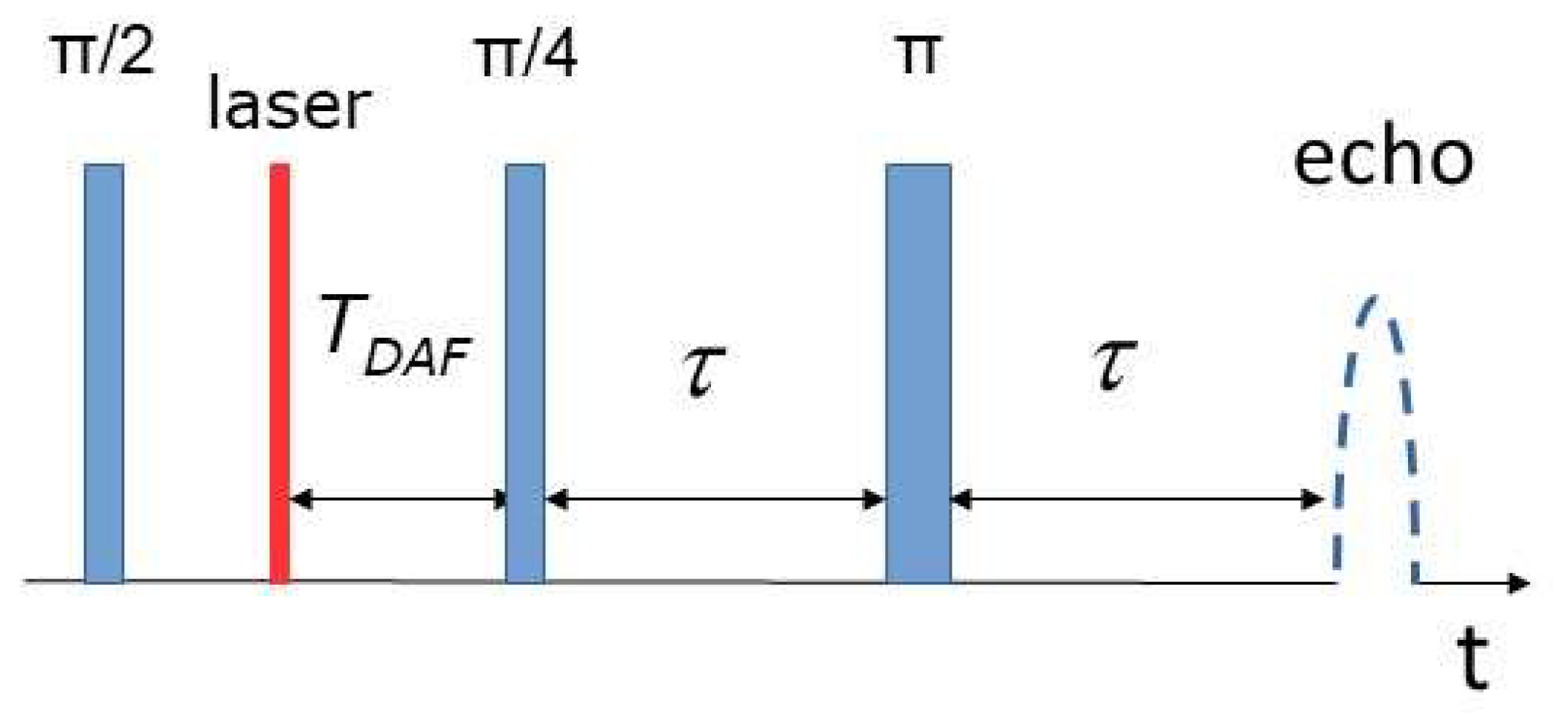
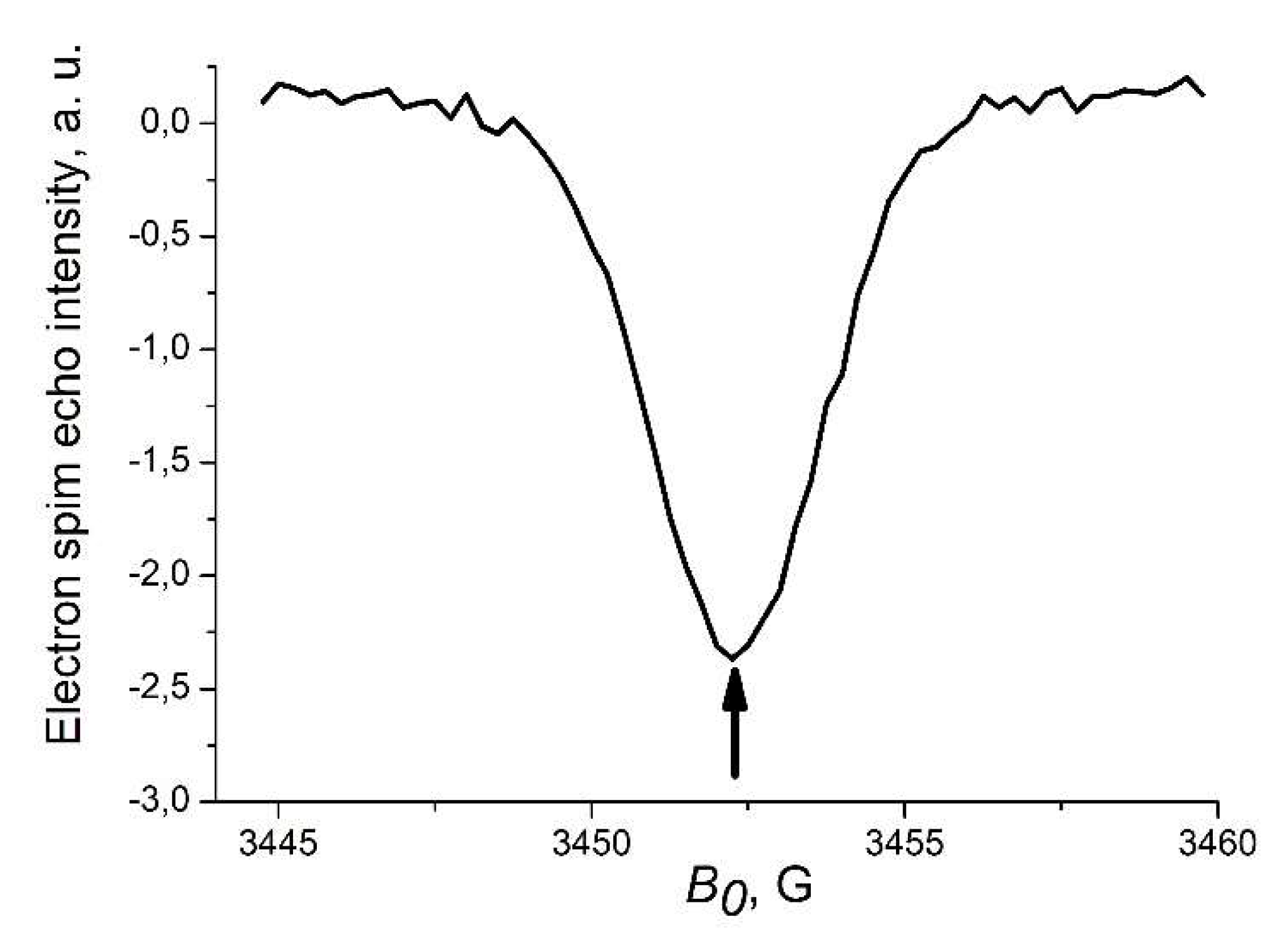
3. Experimental

PM6 and Y6 was purchased from Solarmer Inc. (China), with 99.9% purity. Chemical structures of these molecules are shown at Figure 3. To fabricate the drop-casted EPR samples, chlorobenzene solutions of PM6 with Y6 at 1:1 donor/acceptor weight ratio and total concentration 20 mg/ml were prepared. The solutions were put in the glass EPR tube of 4.5 mm outer diameter. During the evaporation of the chlorobenzene in the vacuum of about 10-3 Pa, the tube was sonicated in an ultrasonic bath. This caused the deposition of the homogeneous donor/acceptor composite on the inner wall of the EPR sample tube. The composites were annealed at 150°C for 10 minutes in the vacuum of about 10-3 Pa.
Additionally, PM6/Y6 composite was prepared by spin-coating at 700 rpm on a glass coverslip with thickness of 0.25 mm from the chloroform solution at 1:1 donor/acceptor weight ratio. This resulted in the formation of thin PM6/Y6 composite film with the thickness of about 300 nm. The coverslip with PM6/Y6 film was then cut to pieces and placed inside quartz EPR sample tube with 4.8 mm outer diameter and annealed at 150°C for 10 minutes in the vacuum of about 10-3 Pa.
ESE measurements at 80K were carried out on an X-band ELEXSYS ESP-580E EPR spectrometer equipped with an ER 4118 X-MD-5 dielectric cavity inside an Oxford Instruments CF 935 cryostat. Cold nitrogen gas flow was used to stabilize the temperature was at 80 K. As usual, the phase of the ESE signal was adjusted by the dark ESE signal of the species in thermal equilibrium. In OOP ESE experiments laser flashes generated by TECH-laser (Laser-export Co. Ltd., Russia) at wavelength 527 nm, pulse duration of about 5 ns, and pulse repetition rate of 1 kHz were used to excite the sample. The energy of the flash reaching the sample through the quartz light-guide was about 15 μJ. ESE signal was obtained using a sequence of two microwave pulses applied after a laser flash, Flash – DAF - π/4 – τ – π– τ –echo, where DAF is the Delay After laser Flash, the π-pulse was of 24 ns nominal duration. ⁠Additionally, the pre-saturating π/2-pulse was applied 2 μs prior to laser pulse in order to cancel ESE signal of the long-living paramagnetic species and to measure the OOP ESE signals of the CTS. Generally, the procedure of the experiment was similar to that in our recent OOP ESE studies of other OPV composites. The pulse sequence is illustrated in Figure 4.
ESE measurements at 30 K were carried out similarly but with some differences. Namely, cold helium flow was used for cooling the sample. The second harmonic of YAG laser at wavelength 532 nm, pulse duration of about 15 ns, and pulse repetition rate of 10 Hz and incident energy of 2 mJ was used to excite the sample.
At each temperature, the echo-detected EPR spectrum (the dependence of the ESE intensity on the magnetic field of spectrometer B0) was measured first to find the spectral position which corresponds to the maximum out-of-phase ESE intensity of CTSs (Figure 5). This spectral position is the most convenient for obtaining the ESE trace (the dependence of ESE intensity on the interval τ).
The raw out-of-phase ESE trace R(τ) (Figure 6) is a product of the non-normalized dipolar modulation V0V(τ) and the decay of ESE due to spin relaxation – the background trace. The latter trace was obtained for each temperature as in-phase ESE trace of the thermalized electrons and holes. For this experiment the same pulse sequence (Figure 4) was used with the pre-saturating microwave π/2-pulse switched off. The synchronization of the laser with the microwave pulses was also switched off. According to the previously established procedure the non-normalized dipolar modulation was obtained as a quotient of the raw out-of-phase ESE trace and background curve α(τ) [26]. Here α(τ) is obtained from in-phase ESE trace by fitting with stretched exponential decay function.

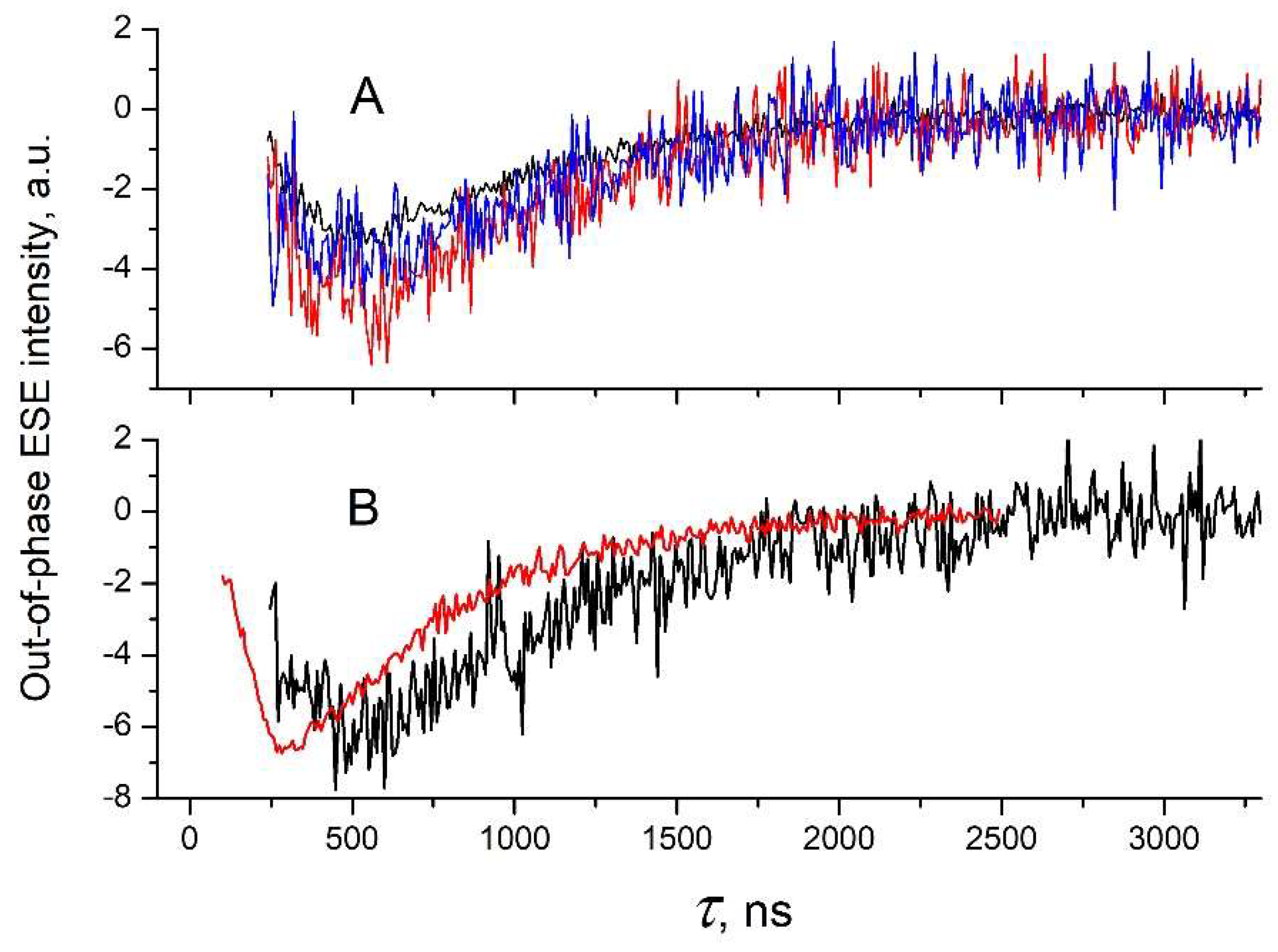
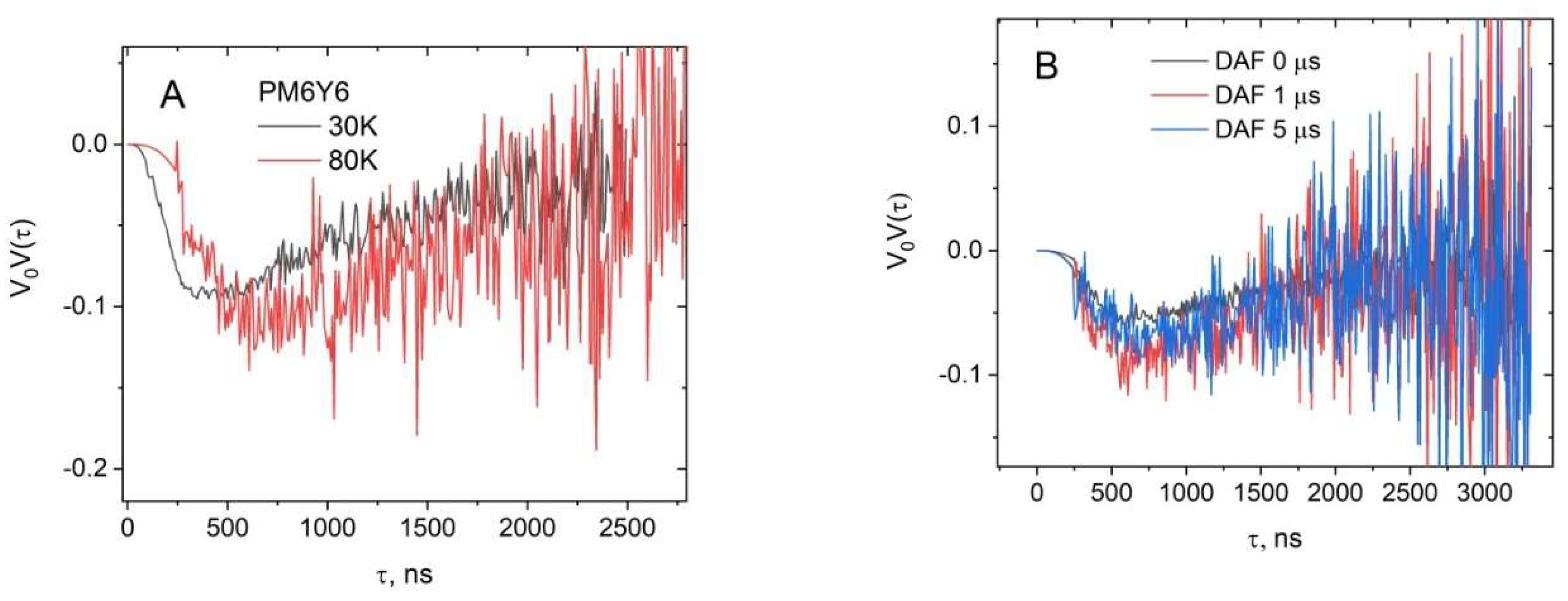
4. Results and Discussion

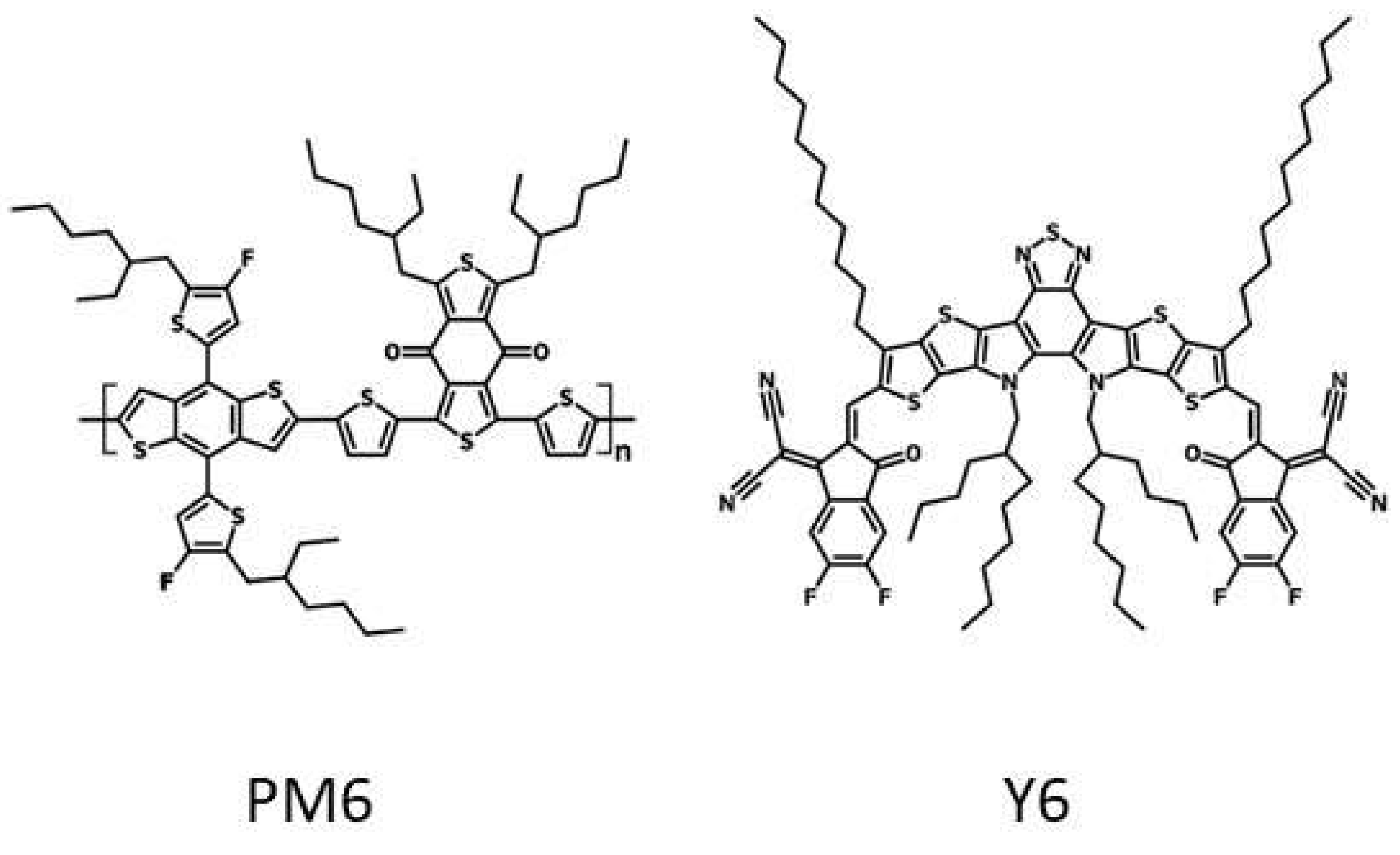
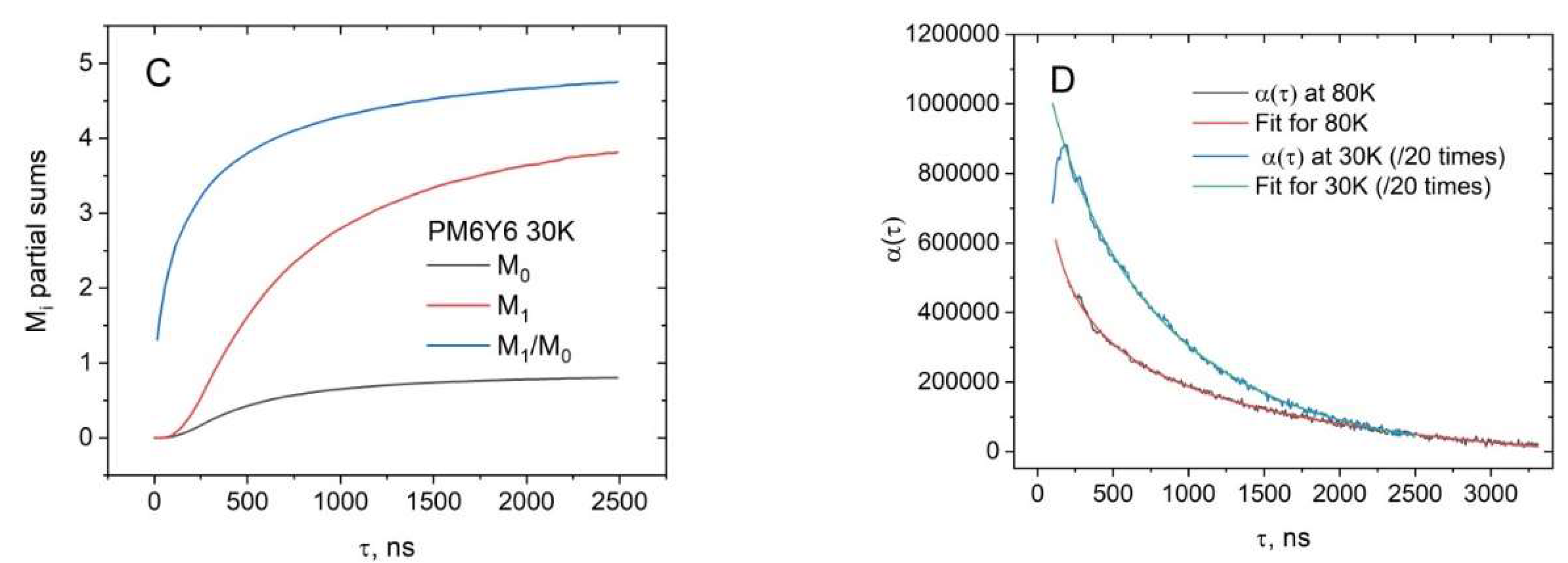
4.1. Calculation of the Average Electron-Hole Distance for CTS in Real Donor/Acceptor Composites

Figure 7 shows the data used for determination of the average electron-hole distance: dipolar modulation curves (Figure 7A and Figure 7B) and the background curves (Figure 7D). The calculation is straightforward. It results in the parameters summarized in Table 3.
For the spin-coated PM6/Y6 sample at 30K M1 = 4.75 nm, while M1 = 5.53 nm at 80K. The process of calculating the values of M1 and M0 – a sequence of partial sums for each value of τ – is shown on Figure 7C. It is evident that despite the significant experimental noise at large values of τ, the sequences M1 and M0 converge quite well. Indeed, in integrals of the type
M 1 ( τ ) = ∫ δ τ τ V ( τ ) τ − 2 / 3 d τ and   M 0 ( τ ) = ∫ δ τ τ V ( τ ) τ − 1 d τ
namely the noise at short time gives the major contribution to the fluctuation of the partial sums. Indeed, the integrand V ( τ ) τ − 2 / 3 is amplified in short times and is suppressed in long times by the factor τ − 2 / 3 .

4.2. Expression for the Error of the Average Electron-Hole Distance

The mild ‘regularization’ used to obtain M1 preserves the linearity property of the Mellin transformation [30]. This linearity enables calculation of the expected error ME1 in M1 for a proposed measurement directly from the measurement parameters and the projected noise level before making the measurement, which is an asset in planning, scheduling, and performing dipolar modulation measurement in ESE experiment.
Applying Eq. (4) to a measurement consisting of the ‘ideal’ dipolar trace V ( τ ) plus noise S ( τ ) , gives
∫ 0 ∞ ( V ( τ ) + S ( τ ) ) τ − 2 3 d τ / ∫ 0 ∞ z − 2 3 K ( a z ) d z = M 1 + E 1
E 1 = ∫ 0 ∞ S ( τ )   τ − 2 3 d τ / ∫ 0 ∞ z − 2 3 K ( a z ) d z ,
analogous to Eq. (4) and having a similar potential divergence at τ = 0. The normalization of the experimental trace uses multiple measurements or curve fitting of multiple points near τ = 0, establishing the values of V(0) and V ( τ m a x ) to much higher accuracy with much less noise compared to the other points in the experimental data trace. As a result, we can set S(0) and S ( τ m a x ) to 0, avoiding the singularity in Eq. (9) at τ = 0 and allowing the error for an experimental data trace to be written as
E 1 = Δ τ 1 / 3 I ( 1 / 3 ) ( S 1 2 + ∑ i = 2 N − 2 S i i − 2 / 3 ) ,
depending only on the noise, N, and Δ τ ; but not on V ( τ ) . This enables us to calculate the expected noise M E 1 , i.e., uncertainty of a measurement, before the measurement is made! For random experimental noise, the error E 1 has a tight distribution with an expected value M E 1 given by
M E 1 = ‖ E 1 ‖ 2 = ε Δ τ 1 / 3 I ( 1 / 3 ) α 1 − 2 4 + ∑ i = 2 N − 2 α i − 2 i − 4 / 3 )
where ε is the noise level of primary out-of-phase signal and α i is amplitude of background function, i.e. ε × α i − 1 is the rmsd of S( τ ). The sum in Eq. 12 cannot be calculated analytically. Instead, it should be calculated numerically on the basis of the expression of the background curve of non-modulated ESE decay. Typically, the background curve can be approximated by a stretched exponential:
α ( τ ) = a + b × E x p [ − ( τ d ) c ]
Approximation of out experimental data for spin-coated PM6/Y6 composite (Figure 7D) gives the following values for 30К and 80К:
a, a. u. b, a. u. c, a. u. d, ns
30K -28292.51201 1.25477∙106 0.82575 710
80K -4.53786∙106 7.20244∙107 0.18572 15
Finally we have M 1 = 4.75±0.04 nm at 30 К, and M 1 = 5.53±0.18 nm at 80 К.
We note that the integral I(s) converges at -3<s<3/2, that is, Eq. 3 formally allows us to also calculate the second, third, and fourth moments of the distance distribution function. The procedure of direct calculation of the average electron-hole distance ant the error of this value is graphically summarized in Figure 8.
Several observations can be done on the basis of the above calculations. First, the average electron-hole distance is calculated quite accurately, with the error of this value being much smaller than this value itself. Second, for temperature 80 K the, the average electron-hole distance does not depend on DAF. This can be explained by relatively long charge separation upon thermalization of the CTS, so its recombination is slow compared to our experimental timescale. On the other hand, at charge diffusion at 80 K is slow when both the electron and the hole within the CTS are thermalized. Therefore, in such condition the decay of the out-of-phase ESE of the CTS with DAF increase is governed by spin-relaxation, which is distance-independent. Third, almost the same average electron-hole distance is observed for drop-casted and spin-coated PM6/Y6 composites at 80K. This is expected because this distance is determined by the structure of the donor and the acceptor molecules forming the donor/acceptor interface in the composite. Fourth, the average electron-hole distance at 30 K is smaller than at 80K. This means that the higher thermal energy at 80 K contribute to increase of the thermalization length of electrons and/or holes, compared to 30 K. Fifth, even at the lowest temperature of our study (30 K) the average electron-hole distance is significant. Again, this is expected for highly efficient OPV composites, because long electron-hole distance within CTS facilitates its dissociation and is a prerequisite of high photon-to-charge conversion efficiency. Also, for the distance between the spin of the electron and the hole as long as several nanometers the strength of the exchange interaction is negligible, because of its exponential decay with the distance [33]. This is in line with our initial assumption that the exchange interaction between the spin of the electron and the hole is much smaller than the magnetic dipolar interaction between these spins and therefore can be neglected.

5. Conclusions

We have proposed a new method for calculating the average distance based on an analytical solution to the inverse problem and maximally independent of regularizing assumptions. The effectiveness of the method has been confirmed by model calculations. Application of this procedure to the experimental out-of-phase ESE data for highly efficient organic photovoltaic donor/acceptor composite PM6/Y6 gives very accurate estimation of the average electron-hole distance within the charge-transfer state. In addition, the proposed method allows us to estimate the error in determining the average distance based only on the parameters of the experiment - the value of the acquisition step Δτ, the number of experimental points and the amplitude of the experimental noise. The proposed method can be used to accurately compare the changes occurring within a series of similar experiments, in particular, for detecting subtle changes in CTS structure during optimization of the donor-acceptor composite morphology with volatile and non-volatile additives.

Author Contributions

Conceptualization, L.V.K. and A.G.M.; Methodology, A.G.M.; Software, A.G.M.; Formal Analysis, V.N.N.; Investigation, V. S. S., E.A.L., V. I. S., I. A. M., L. V. K.; Resources, Writing – Original Draft Preparation, L. V. K. and A.G.M.; Writing – Review & Editing, L.V.K. and A.G.M.; Funding Acquisition, A.G.M.

Funding

This work was supported by RSF grant № 24-23-00484.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Acknowledgments

The authors are thankful to Dr. S. L. Veber (International Tomography Center of Siberian Branch of Russian Academy of Sciences) for assistance in low-temperature ESE measurements.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. B.C. Thompson, J.M.J. Fréchet, Polymer–Fullerene Composite Solar Cells, Angew. Chem. Int. Ed. 47 (2008) 58–77. [CrossRef]
  2. C. Deibel, V. Dyakonov, Polymer–fullerene bulk heterojunction solar cells, Rep. Prog. Phys. 73 (2010) 096401. [CrossRef]
  3. E.S. Kobeleva, M.N. Uvarov, N.V. Kravets, A.V. Kulikova, V.A. Zinovyev, O.A. Gurova, V.I. Sysoev, A.M. Kondranova, M.S. Kazantsev, K.M. Degtyarenko, A.G. Matveeva, L.V. Kulik, Ternary Composite of Polymer, Fullerene and Fluorinated Multi-Walled Carbon Nanotubes as the Active Layer of Organic Solar Cells, J. Compos. Sci. 8 (2023) 3. [CrossRef]
  4. K. Fukuda, K. Yu, T. Someya, The Future of Flexible Organic Solar Cells, Advanced Energy Materials 10 (2020) 2000765. [CrossRef]
  5. Y. Li, W. Huang, D. Zhao, L. Wang, Z. Jiao, Q. Huang, P. Wang, M. Sun, G. Yuan, Recent Progress in Organic Solar Cells: A Review on Materials from Acceptor to Donor, Molecules 27 (2022) 1800. [CrossRef]
  6. S. Lee, D. Jeong, C. Kim, C. Lee, H. Kang, H.Y. Woo, B.J. Kim, Eco-Friendly Polymer Solar Cells: Advances in Green-Solvent Processing and Material Design, ACS Nano 14 (2020) 14493–14527. [CrossRef]
  7. M. Helgesen, R. Søndergaard, F.C. Krebs, Advanced materials and processes for polymer solar cell devices, J. Mater. Chem. 20 (2010) 36–60. [CrossRef]
  8. M. Jørgensen, K. Norrman, S.A. Gevorgyan, T. Tromholt, B. Andreasen, F.C. Krebs, Stability of Polymer Solar Cells, Advanced Materials 24 (2012) 580–612. [CrossRef]
  9. G. Li, R. Zhu, Y. Yang, Polymer solar cells, Nature Photon 6 (2012) 153–161. [CrossRef]
  10. A.V. Mumyatov, P.A. Troshin, A Review on Fullerene Derivatives with Reduced Electron Affinity as Acceptor Materials for Organic Solar Cells, Energies 16 (2023) 1924. [CrossRef]
  11. C. Yan, S. Barlow, Z. Wang, H. Yan, A.K.-Y. Jen, S.R. Marder, X. Zhan, Non-fullerene acceptors for organic solar cells, Nat Rev Mater 3 (2018) 18003. [CrossRef]
  12. J. Hou, O. Inganäs, R.H. Friend, F. Gao, Organic solar cells based on non-fullerene acceptors, Nat. Mater. 17 (2018) 119–128. [CrossRef]
  13. A.J. Heeger, 25th Anniversary Article: Bulk Heterojunction Solar Cells: Understanding the Mechanism of Operation, Advanced Materials 26 (2014) 10–28. [CrossRef]
  14. Y. Jiang, S. Sun, R. Xu, F. Liu, X. Miao, G. Ran, K. Liu, Y. Yi, W. Zhang, X. Zhu, Non-fullerene acceptor with asymmetric structure and phenyl-substituted alkyl side chain for 20.2% efficiency organic solar cells, Nat Energy 9 (2024) 975–986. [CrossRef]
  15. Y. Tamai, Charge generation in organic solar cells: Journey toward 20% power conversion efficiency: Special Issue: Emerging Investigators, Aggregate 3 (2022). [CrossRef]
  16. C. Deibel, T. Strobel, V. Dyakonov, Role of the Charge Transfer State in Organic Donor-Acceptor Solar Cells, Adv. Mater. 22 (2010) 4097–4111. [CrossRef]
  17. T.M. Burke, S. Sweetnam, K. Vandewal, M.D. McGehee, Beyond Langevin Recombination: How Equilibrium Between Free Carriers and Charge Transfer States Determines the Open-Circuit Voltage of Organic Solar Cells, Advanced Energy Materials 5 (2015) 1500123. [CrossRef]
  18. M. Causa’, J. De Jonghe-Risse, M. Scarongella, J.C. Brauer, E. Buchaca-Domingo, J.-E. Moser, N. Stingelin, N. Banerji, The fate of electron–hole pairs in polymer:fullerene blends for organic photovoltaics, Nat Commun 7 (2016) 12556. [CrossRef]
  19. M. Casalegno, R. Pastore, J. Idé, R. Po, G. Raos, Origin of Charge Separation at Organic Photovoltaic Heterojunctions: A Mesoscale Quantum Mechanical View, J. Phys. Chem. C 121 (2017) 16693–16701. [CrossRef]
  20. S.H. Park, A. Roy, S. Beaupré, S. Cho, N. Coates, J.S. Moon, D. Moses, M. Leclerc, K. Lee, A.J. Heeger, Bulk heterojunction solar cells with internal quantum efficiency approaching 100%, Nature Photon 3 (2009) 297–302. [CrossRef]
  21. C. Göhler, C. Deibel, The Role of Dynamic and Static Disorder for Charge-Transfer States in Organic Bulk Heterojunction Solar Cells, ACS Energy Lett. 7 (2022) 2156–2164. [CrossRef]
  22. A.J. Barker, K. Chen, J.M. Hodgkiss, Distance Distributions of Photogenerated Charge Pairs in Organic Photovoltaic Cells, J. Am. Chem. Soc. 136 (2014) 12018–12026. [CrossRef]
  23. J. Niklas, O.G. Poluektov, Charge Transfer Processes in OPV Materials as Revealed by EPR Spectroscopy, Adv. Energy Mater. 7 (2017) 1602226. [CrossRef]
  24. E.A. Lukina, A.A. Popov, M.N. Uvarov, E.A. Suturina, E.J. Reijerse, L.V. Kulik, Light-induced charge separation in a P3HT/PC 70 BM composite as studied by out-of-phase electron spin echo spectroscopy, Phys. Chem. Chem. Phys. 18 (2016) 28585–28593. [CrossRef]
  25. E.A. Beletskaya, E.A. Lukina, M.N. Uvarov, A.A. Popov, L.V. Kulik, Geminate recombination in organic photovoltaic blend PCDTBT/PC 71 BM studied by out-of-phase electron spin echo spectroscopy, J. Chem. Phys. 152 (2020) 044706. [CrossRef]
  26. A.A. Popov, M.N. Uvarov, L.V. Kulik, Mode of action of the third component in ternary organic photovoltaic blend PBDB-T/ITIC:PC70BM revealed by EPR spectroscopy, Synthetic Metals 277 (2021) 116783. [CrossRef]
  27. M.N. Uvarov, E.S. Kobeleva, K.M. Degtyarenko, V.A. Zinovyev, A.A. Popov, E.A. Mostovich, L.V. Kulik, Fast Recombination of Charge-Transfer State in Organic Photovoltaic Composite of P3HT and Semiconducting Carbon Nanotubes Is the Reason for Its Poor Photovoltaic Performance, IJMS 24 (2023) 4098. [CrossRef]
  28. E.A. Lukina, A.V. Kulikova, M.N. Uvarov, A.A. Popov, M. Liu, Y. Zhang, L.V. Kulik, Structure of the Charge-Transfer State in PM6/Y6 and PM6/Y6:YT Composites Studied by Electron Spin Echo Technique, Nanomanufacturing 3 (2023) 123–134. [CrossRef]
  29. A.G. Matveeva, V.M. Nekrasov, A.G. Maryasov, Analytical solution of the PELDOR inverse problem using the integral Mellin transform, Phys. Chem. Chem. Phys. 19 (2017) 32381–32388. [CrossRef]
  30. A.G. Matveeva, V.N. Syryamina, V.M. Nekrasov, M.K. Bowman, Non-uniform sampling in pulse dipolar spectroscopy by EPR: the redistribution of noise and the optimization of data acquisition, Phys. Chem. Chem. Phys. 23 (2021) 10335–10346. [CrossRef]
  31. P. Polyanin, A.V. Manzhirov, Handbook of Integral Equations, 0 ed., Chapman and Hall/CRC, 2008. [CrossRef]
  32. L. Venkataramanan, T.M. Habashy, D.E. Freed, F.K. Gruber, Continuous moment estimation of CPMG data using Mellin transform, Journal of Magnetic Resonance 216 (2012) 43–52. [CrossRef]
  33. M.L. Kirk, D.A. Shultz, D.E. Stasiw, G.F. Lewis, G. Wang, C.L. Brannen, R.D. Sommer, P.D. Boyle, Superexchange Contributions to Distance Dependence of Electron Transfer/Transport: Exchange and Electronic Coupling in Oligo( para -Phenylene)- and Oligo(2,5-Thiophene)-Bridged Donor–Bridge–Acceptor Biradical Complexes, J. Am. Chem. Soc. 135 (2013) 17144–17154. [CrossRef]
Preprints 142064 g001
Figure 1. Scheme of magnetic dipolar interaction between the spin of the electron and the hole constituting a CTS at donor/acceptor interface of a bulk heterojunction composite. The two-color red-blue line marks the boundary between the donor and the acceptor domains.
Figure 1. Scheme of magnetic dipolar interaction between the spin of the electron and the hole constituting a CTS at donor/acceptor interface of a bulk heterojunction composite. The two-color red-blue line marks the boundary between the donor and the acceptor domains.
Preprints 142064 g001
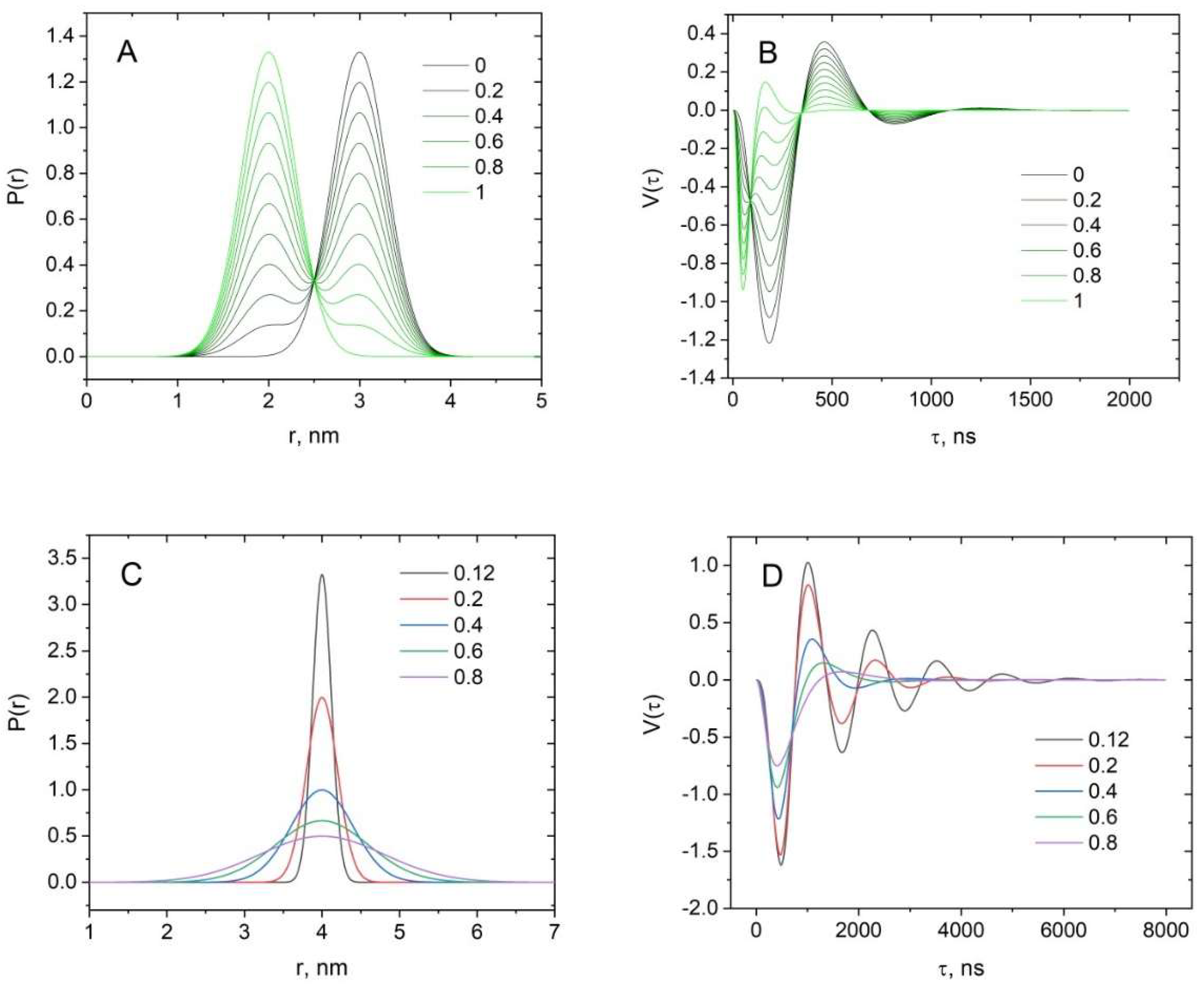
Preprints 142064 g002
Figure 2. On the right are the model distribution functions over distances, on the left are the corresponding dipole modulation curves. A: distance distribution function is a sum of two Gaussians with equal width centered at 2 and 3 nm; the relative weight of these Gaussians is varied. The figure legend indicates the weight of the component with an average distance of 2 nm; C: distance distribution function is a Gaussian with an average distance of 4 nm, the width is varied as indicated in the legend.
Figure 2. On the right are the model distribution functions over distances, on the left are the corresponding dipole modulation curves. A: distance distribution function is a sum of two Gaussians with equal width centered at 2 and 3 nm; the relative weight of these Gaussians is varied. The figure legend indicates the weight of the component with an average distance of 2 nm; C: distance distribution function is a Gaussian with an average distance of 4 nm, the width is varied as indicated in the legend.
Preprints 142064 g002
Preprints 142064 g003
Figure 3. Chemical structures of the compounds used for preparing the composites (donor: PM6, acceptor: Y6).
Figure 3. Chemical structures of the compounds used for preparing the composites (donor: PM6, acceptor: Y6).
Preprints 142064 g003
Preprints 142064 g004
Figure 4. Microwave pulse sequence used to detect out-of-phase ESE signal of CTSs in donor/acceptor composites.
Figure 4. Microwave pulse sequence used to detect out-of-phase ESE signal of CTSs in donor/acceptor composites.
Preprints 142064 g004
Preprints 142064 g005
Figure 5. Out-of-phase echo-detected EPR spectrum for CTSs in spin-coated PM6/Y6 composite taken an 30 K with DAF = 0 μs. The arrow marks the spectral position at which the ESE traces (the dependence of ESE intensity on τ) were measured.
Figure 5. Out-of-phase echo-detected EPR spectrum for CTSs in spin-coated PM6/Y6 composite taken an 30 K with DAF = 0 μs. The arrow marks the spectral position at which the ESE traces (the dependence of ESE intensity on τ) were measured.
Preprints 142064 g005
Preprints 142064 g006
Figure 6. Raw out-of-phase ESE traces for drop-cased (panel A) and spin-coated (panel B) PM6/Y6 composites. Experimental conditions: temperature 80K, DAF = 0 μs, 1 μs and 5 μs (black, red and blue lines, respectively) for panel A; temperature 30K and 80K (red and black lines, respectively), DAF = 0 μs for panel B.
Figure 6. Raw out-of-phase ESE traces for drop-cased (panel A) and spin-coated (panel B) PM6/Y6 composites. Experimental conditions: temperature 80K, DAF = 0 μs, 1 μs and 5 μs (black, red and blue lines, respectively) for panel A; temperature 30K and 80K (red and black lines, respectively), DAF = 0 μs for panel B.
Preprints 142064 g006
Preprints 142064 g007aPreprints 142064 g007b
Figure 7. A, B: experimental dipole modulation curves of the PM6Y6 sample recorded at A – different temperatures 30K and 80K, respectively; black, red and blue lines in the panel B correspond to different DAF values 0, 1 and 5 μs; C –– sequence of partial sums М1(τ), М0(τ) for calculation according to Eqs. 6 and 8, the data are taken at 30K; D – Background curves α(τ) for 80K and 30K, for details see at Eqs. 11-12.
Figure 7. A, B: experimental dipole modulation curves of the PM6Y6 sample recorded at A – different temperatures 30K and 80K, respectively; black, red and blue lines in the panel B correspond to different DAF values 0, 1 and 5 μs; C –– sequence of partial sums М1(τ), М0(τ) for calculation according to Eqs. 6 and 8, the data are taken at 30K; D – Background curves α(τ) for 80K and 30K, for details see at Eqs. 11-12.
Preprints 142064 g007aPreprints 142064 g007b
Preprints 142064 g008
Figure 8. The data flow chart of direct calculation of the average electron-hole distance M1 and the error of this value ME1. The input data are raw out-of-phase ESE trace R(τ) and raw in-phase background ESE trace α(τ), obtained in the experiment.
Figure 8. The data flow chart of direct calculation of the average electron-hole distance M1 and the error of this value ME1. The input data are raw out-of-phase ESE trace R(τ) and raw in-phase background ESE trace α(τ), obtained in the experiment.
Preprints 142064 g008
Table 1. Comparison of the average distance calculated from the dipolar modulation data for bimodal Gaussian distance distribution function with the exacts value.
Table 1. Comparison of the average distance calculated from the dipolar modulation data for bimodal Gaussian distance distribution function with the exacts value.
Contribution of the first Gaussian M1 (exact), nm M1 (calculated), nm
0 3 3.00012
0.1 2.9 2.90062
0.2 2.8 2.80108
0.3 2.7 2.70148
0.4 2.6 2.60183
0.5 2.5 2.50213
0.6 2.4 2.40237
0.7 2.3 2.30257
0.8 2.2 2.20271
0.9 2.1 2.1028
1 2 2.00284
Table 2. Comparison of the average distance calculated from the dipolar modulation data for variable-width Gaussian distance distribution function with the exacts value.
Table 2. Comparison of the average distance calculated from the dipolar modulation data for variable-width Gaussian distance distribution function with the exacts value.
Width of the Gaussian, nm M1 (calculated)
0.12 4
0.2 4.00026
0.4 4.00039
0.6 4.00094
0.8 4.00487
Table 3. Average electron-hole distance and the statistical error of this distance for CTS in PM6/Y6 composite in different conditions.
Table 3. Average electron-hole distance and the statistical error of this distance for CTS in PM6/Y6 composite in different conditions.
Sample preparation Measurement conditions: temperature; DAF M1, nm ME1, nm
Drop-casting 80K; 0us 5.52275 0.14038
Drop-casting 80K; 1us 5.48512 0.28545
Drop-casting 80K; 5us 5.61639 0.25082
Spin-coating 80K; 0us 5.52959 0.17701
Spin-coating 30K; 0us 4.75013 0.04224
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated