Prerpints.org logo
Preprint
Article

Depth Estimation Based on MMwave Radar and Camera Fusion with Attention Mechanisms and Multi-Scale Features for Autonomous Driving Vehicles

Altmetrics

Downloads

36

Views

16

Comments

0

Submitted:

06 December 2024

Posted:

06 December 2024

You are already at the latest version

Alerts
Abstract
Depth estimation is a key technology in autonomous driving, as it provides an important basis for accurately detecting traffic objects and avoiding collisions in advance. To enhance depth estimation performance in complex traffic environments, this study proposes a depth estimation method in which point clouds and images obtained from MMwave radar and cameras are fused. Firstly, a residual network is established to extract the multi-scale features of the MMwave radar point clouds and the corresponding image obtained simultaneously from the same location. Correlations between the radar points and the image are established by fusing the extracted multi-scale features. A semi-dense depth estimation is achieved by assigning the depth value of the radar point to the most relevant image region. Secondly, a bidirectional feature fusion structure with additional fusion branches is designed to enhance the richness of feature information. The information loss during the feature fusion process is reduced, and the robustness of the model is enhanced. Finally, parallel channel and position attention mechanisms are used to enhance the feature representation of key areas in the fused feature map; the interference of irrelevant areas are suppressed, and the depth estimation accuracy is enhanced. Experimental results on the public dataset nuScenes show that, compared with the baseline model, the proposed method reduces the average absolute error (MAE) by 4.7%-6.3% and the root mean square error (RMSE) by 4.2%-5.2%.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

In recent years, autonomous driving technology has developed rapidly, and environmental perception is an important part of it. The accuracy and real-time performance of environmental perception directly affect the subsequent strategies of autonomous driving systems [1].To ensure safety, autonomous driving systems typically use multiple sensors to collect environmental information, including LiDAR, millimeter-wave radar, and cameras [2]. These sensors provide reliable data support for various tasks in autonomous driving systems, such as depth estimation and obstacle avoidance [3]. Depth estimation is an important task in automatic driving systems, as it directly affects vehicle path planning and obstacle avoidance [4]. Through accurate depth estimation, autonomous vehicles can effectively determine the distance from surrounding objects, identify potential obstacles, and avoid them. However, the accuracy and real-time performance of depth estimation are affected by various factors, such as differences in sensor performance, ambient light changes, and weather conditions [5]. Therefore, autonomous driving systems need a suitable depth estimation method.
With the rapid development of convolutional neural networks, monocular depth estimation has become a research hot spot. Although the accuracy and generalizability of monocular depth estimation methods have improved with continuous advancements [6], the inherent difficulty in obtaining depth information from a monocular camera remains a challenge. To solve this problem, a common method is to fuse camera data with lidar data [7,8]. The point cloud generated by LiDAR is dense and contains depth information. However, LiDAR is highly susceptible to weather conditions, and its dense point cloud data pose challenges to the system’s processing speed [9]. Additionally, the cost of LiDAR is relatively high. 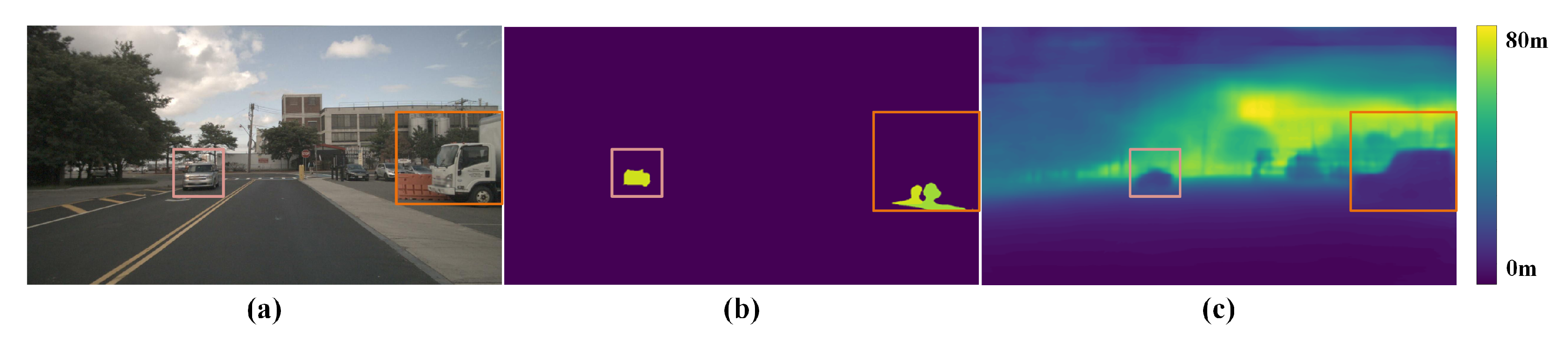Millimeter-wave radar is also a common sensor; it can not only obtain depth information but also has the characteristics of low cost and reliable operation under various weather conditions [10]. Moreover, the data volume generated by millimeter-wave radar is smaller than that generated by LiDAR, as shown in Figure 1, which reduces the hardware requirements for algorithms. Therefore, we chose millimeter-wave radar to supplement depth information in images. The depth estimation process is illustrated in Figure 2.
The point cloud data from millimeter-wave radar are relatively sparse and lack height information, which is a challenge for depth estimation based on radar points and images. Lin et al. [11] proposed the use of a two-stage network structure. In the first stage, the network filters out noise points from the millimeter-wave radar data, and, in the second stage, it refines the depth estimation results. Similarly, Long et al. [12] densified a depth map generated by radar projection, and they established correlations between radar points and image regions. Then, they used a depth completion network to obtain a complete depth estimation result.
However, the fusion methods used in these studies have certain data latency problems [13,14], which affect the accuracy of depth estimation. Additionally, the feature fusion approaches used to generate dense depth estimation results are not sufficiently effective, as they do not suppress invalid regions, leading to noise impacting the depth estimation results. To solve these problems, we propose the following improvements:
(i)We fuse a single image with a single radar frame to obtain depth information while avoiding the impact of data latency on depth estimation. By establishing correlations between radar points and image regions, we achieve semi-dense depth estimation results.
(ii)For the fusion of the image and the semi-dense depth map, we propose an improved bidirectional multi-scale feature fusion structure as the lower-layer feature fusion method. This approach effectively utilizes feature information from different scales to solve the problem of information loss during the feature fusion process, enhancing the model’s robustness in complex scenes. Furthermore, by improving the loss function, the model achieves more stable backpropagation, leading to higher depth estimation accuracy.
(iii)For the dense depth estimation stage, we propose a higher-layer feature fusion method using attention mechanisms. By using parallelly connected channel attention and spatial attention, we generate learnable attention weights to better utilize the global information from deeper layers and the local information from shallower layers. This enhances the representation of key regions, reduces the impact of redundant information, and improves the accuracy of depth estimation.

2. Related Work

2.1. Monocular Depth Estimation

Monocular depth estimation methods based on deep learning can automatically learn complex features, avoid manual feature extraction, and have gained increasing attention. Regarding supervised learning approaches, Eigen et al. [15] proposed a multi-scale network for depth prediction based on monocular image input. This method introduces the use of sparse depth labels obtained from LiDAR scans to train the depth prediction network. The algorithm uses a CNN to generate rough depth results and then restores depth details. Subsequently, Eigen et al. [16] extended the original network by adding a third-scale network to enhance image resolution. Laina et al. [17] utilized a deep residual network [18] to learn the mapping relationship between depth maps and single images. By employing a deep network for feature encoding and using an upsampling module as the decoder, they achieved high-resolution depth map outputs. Cao et al. [19] were the first to discretize depth values, transforming depth estimation into a pixel classification task rather than relying on depth continuity as in previous methods. Fu et al. [20] used regression networks for depth estimation and improved the accuracy of depth prediction by learning the sequential relationship between categories. Piccinelli et al. [21] proposed an internal discretization module for encoding internal feature representations in encoder–decoder network architectures, enhancing the generalization capability of depth estimation.
In unsupervised learning, Guizilini et al. [22] improved the network structure by employing 3D convolutions as the depth encoding–decoding network, replacing traditional pooling and upsampling operations. This approach better preserves object details in images. However, 3D convolutions significantly increase the number of network parameters, requiring more computational resources. Johnston et al. [23] proposed the use of self-attention and discrete depth to improve Monodepth2 [24]. Their approach employs ResNet101 as the depth encoder, achieving higher accuracy at the cost of a significantly increased parameter size. HR-Depth [25] introduces a nested dense skip connection design to obtain high-resolution feature maps, aiding in learning edge detail information. Additionally, a compression excitation block for feature fusion was proposed to enhance fusion efficiency. They also introduced a strategy for training a lightweight depth estimation network, achieving the performance of complex networks. FSRE-Depth [26] employs a metric learning approach, leveraging semantic segmentation results to constrain depth estimation, thereby improving edge depth estimation. Additionally, a cross-attention module was designed to promote mutual learning and perception between the two tasks. Feng et al. [27] proposed a self-teaching unsupervised monocular depth estimation method. The student network is trained on lower-resolution enhanced images under the guidance of the teacher network. This method enhances the ability of the student network to learn effectively and improves the depth prediction accuracy.

2.2. Radar-Camera Depth Estimation

As radar point clouds are sparse, effectively fusing radar point clouds with images is a key research problem. Lin et al. [11] found that noise in radar measurements is one of the main obstacles preventing the application of existing LiDAR-to-image fusion methods to radar data and images. To address this, they proposed a two-stage CNN-based network. This network takes radar data and images as inputs, where the first-stage network filters out noise in the radar data, and the second-stage network further refines the depth estimation results. Long et al. [12] proposed a radar-to-pixel association stage that learns the correspondence from radar-to-pixel mapping. They then applied a traditional depth completion method to achieve image-guided depth completion using radar and video. Lo et al. [28] introduced a depth-ordered regression network, which first converts sparse 2D radar points into height-augmented 3D measurements and then integrates radar data into the network using a post-fusion method. R4dyn [29] proposed a self-supervised depth estimation framework that utilizes radar as a supervisory signal to assist in dynamic object prediction in self-supervised monocular depth estimation. Additionally, the extra input from radar enhances the model’s robustness in depth estimation.

3. Materials and Methods

3.1. Overall Structure

We generate a dense depth estimation map from a single image I ∈ R 3 × H × W and the corresponding millimeter-wave radar point cloud P = { p n | p n ∈ R 3 , n = 0 , 1 , . . . , N − 1 } , where H and W denote the height and width of the image, and N denotes the total number of radar points. As shown in Figure 1, although the millimeter-wave radar point cloud carries depth information, the radar points are mainly distributed in the horizontal range due to the inability to obtain accurate height data. This distribution differs significantly from that of LiDAR points. Furthermore, the presence of noisy radar points adds to the difficulty in determining the depth values of the image regions.
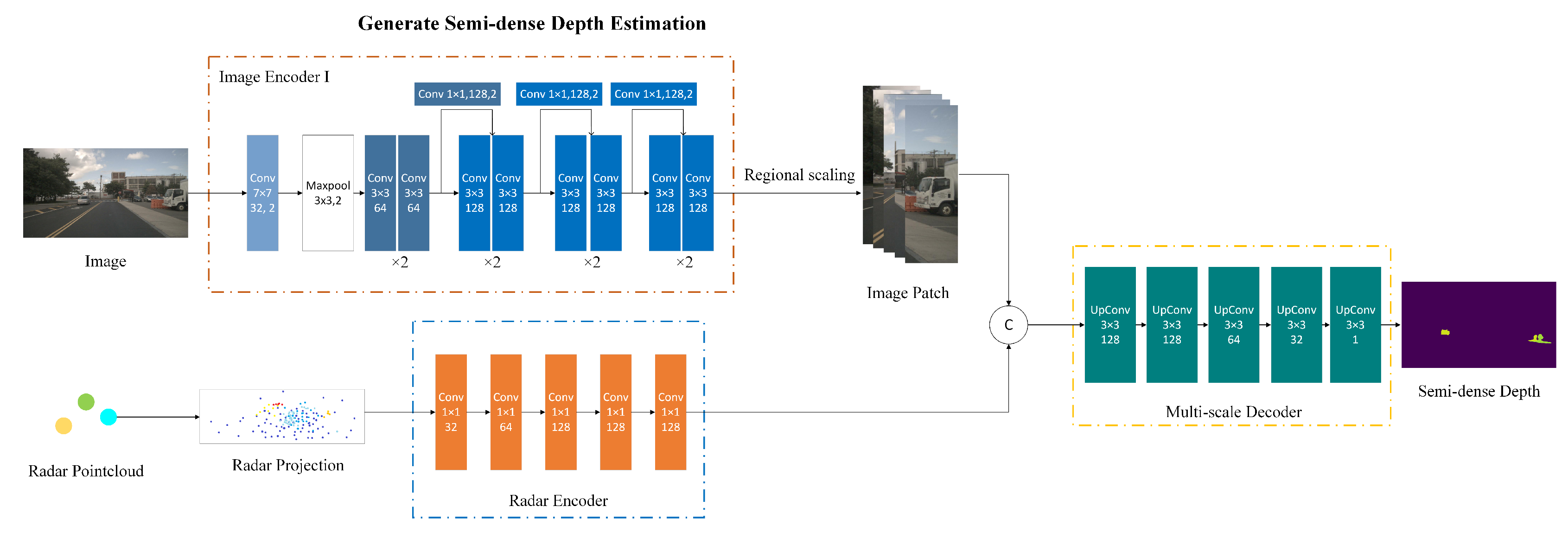
Our proposed overall framework is illustrated in Figure 3 and Figure 4. Our method consists of three stages: (i) Image features and radar features are obtained through different encoders. After concatenation, the combined features are processed through a decoder to generate a confidence map. This confidence map is used to assign depth values to image regions, resulting in a semi-dense depth estimation S d ∈ R H × W . (ii) Image I ∈ R 3 × H × W and the semi-dense depth estimation S d ∈ R H × W are processed through encoders to obtain feature maps at different scales. These feature maps are then combined through a lower layer bidirectional feature fusion to generate multi-scale fused feature maps. (iii) The multi-scale fused feature maps are processed through higher layer parallel attention methods. Following successive upsampling, the dense depth estimation D d ∈ R H × W is generated.

3.2. Generate Semi-Dense Depth Estimation

We obtain the dense depth estimation D d ∈ R H × W by fusing a single image and a single radar frame. The image encoder is based on the residual network, with the image I ∈ R 3 × H × W used as input, and the numbers of output channels for each layer are 32, 64, 128, 128, and 128. After the coordinate transformation of the radar points, they are projected into the image coordinate system to generate a radar projection map. The value at each pixel position corresponding to a radar point in the radar projection map represents the depth information of the radar point. The radar encoder consists of 5 fully connected layers, with the number of channels for each layer being 32, 64, 128, 128, and 128. After passing through the radar encoder, the radar projection map produces radar feature maps with different numbers of channels.
To address the issue of missing precise height information in radar points and to expedite the correspondence between radar points and pixel regions, we scale the area of the true position of the radar points in the image to each feature map. This further allows us to obtain the ROI areas, ensuring that each ROI corresponds to the true location of the radar points. Then, it is necessary to establish correlation matching between the radar points and pixel regions. If an image corresponds to N radar points, it is necessary to output N confidence maps C i ( I , p n ) ∈ [ 0 , 1 ] H × W to determine the image regions associated with each radar point. Each confidence map represents the probability that a pixel in I corresponds to a radar point p n . Correspondence matching involves concatenating the feature maps of the image and the radar along the channel dimension. The concatenated feature maps are then processed by a decoder composed of successive upsampling and convolutional layers to produce the confidence maps. At this stage, each pixel x h w ( h ∈ [ 0 , H ) , w ∈ [ 0 , W ) ) in the image is associated with p ∈ [ 0 , N ] radar points. Based on the confidence maps, radar points with confidence values exceeding a threshold are first selected for each pixel position. Then, the depth information of the radar point with the highest confidence is chosen as the depth estimate for each pixel position, resulting in the generation of a semi-dense depth estimation S d ∈ R H × W :
S d ( I ) = d ( p n ) , C n ( I , p n ) ( x h w , p n ) > τ 0 , o t h e r w i s e
where n = arg max i C n ( I , p n ) ( x h w , p n ) , d ( p n ) is the depth value corresponding to the pixel point and τ is the threshold value.

3.2.1. Loss Function

As some of the regions detected by lidar during the construction of the dataset may not be dense, this may result in a lack of supervised signals in these regions. For supervision, we chose to obtain the cumulative lidar depth d a c c by projecting multiple lidar frames onto the current lidar frame d g t . Pixel positions in d a c c with a radar point depth difference within 0.4 m were set to be in the positive class, thus constructing labels y l d ∈ { 0 , 1 } H × W for binary classification and minimizing the binary cross entropy loss:
L B C E = 1 | Ω | ∑ x ∈ Ω − ( y l d ( x ) log y c ( x ) + ( 1 − y l d ( x ) ) log ( 1 − y c ( x ) ) )
where Ω ⊂ R 2 denotes the image region, x ∈ Ω denotes the pixel coordinates and y c = C i ( I , p n ) denotes the confidence of the corresponding region.
As shown in Figure 5, the first stage generates the semi-dense depth estimation S d . On the far left is the original image, where yellow and blue boxes highlight significant areas. On the far right is the semi-dense depth estimation result, with preliminary depth estimation values assigned to the corresponding pedestrian or vehicle regions in the image.

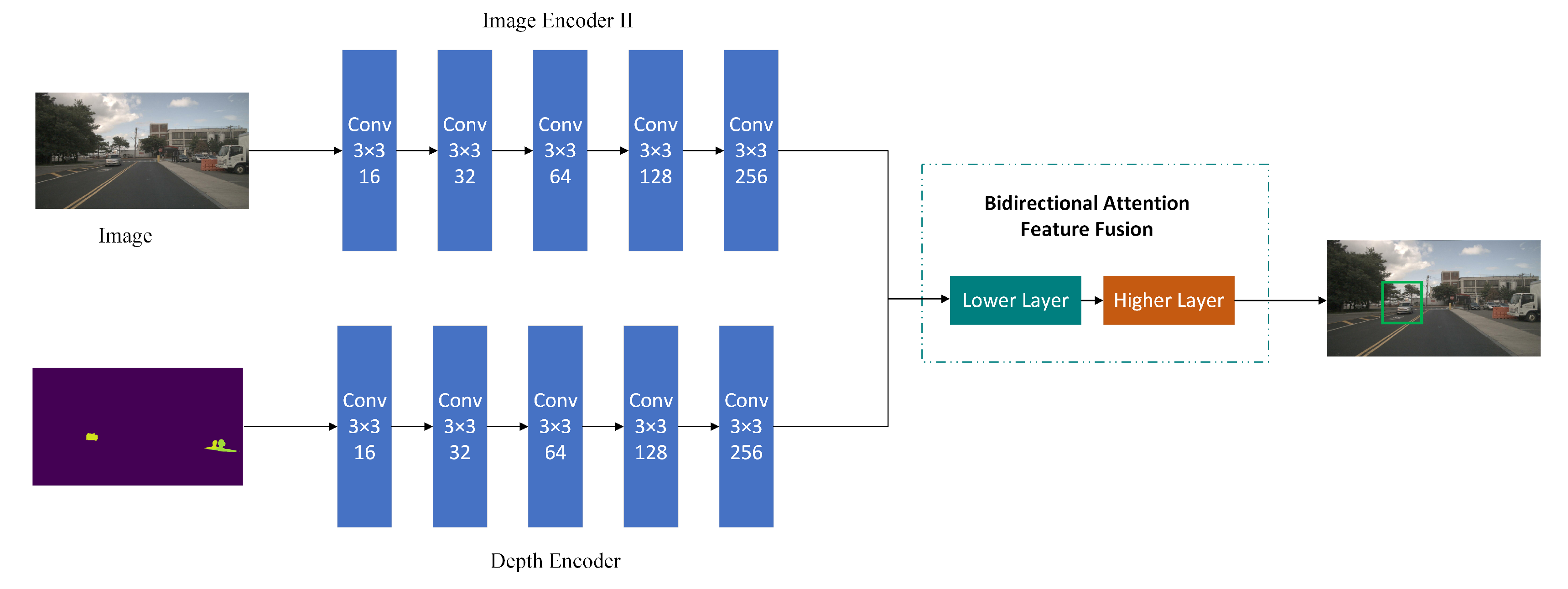
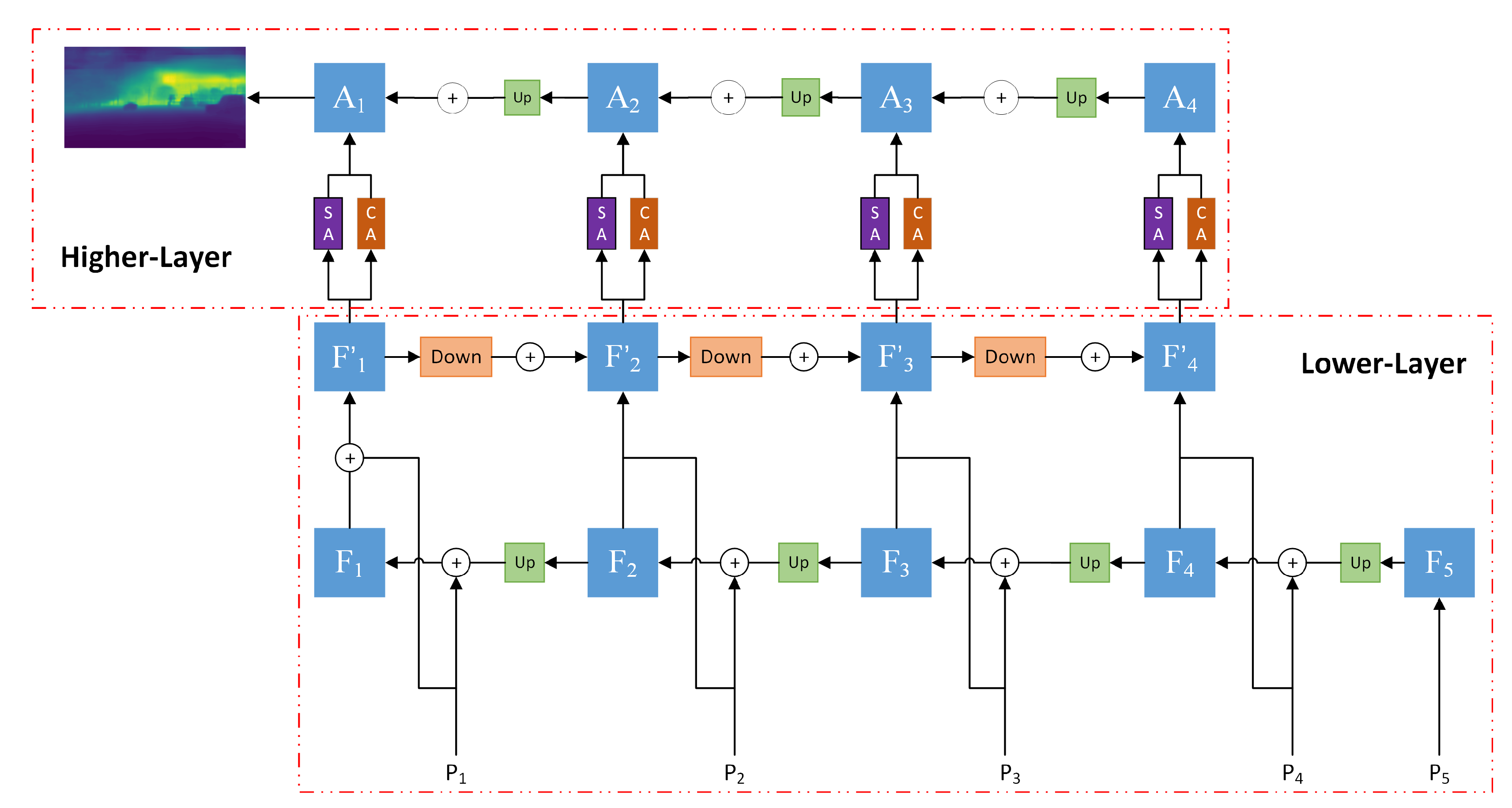
3.3. Lower-Layer Bidirectional Feature Fusion

To obtain a dense depth estimate from the semi-dense depth estimate, feature fusion between the semi-dense depth estimate and the image is required. Feature fusion is used to improve the information richness in features and combine the semantic information contained in features of different scales, which requires an understanding of the relationship between features of different scales. This is primarily based on two reasons: (i) It is difficult for the feature maps extracted by the convolutional layer to obtain both global and local information at the same time. Therefore, it is necessary to incorporate multi-scale information during the feature extraction process. (ii) Features at different levels may contain noise. Therefore, we propose a bidirectional feature fusion method so that features at different levels can better guide each other.
Using the image I ∈ R 3 × H × W and the semi-dense depth estimate S d ∈ R H × W as inputs to the feature encoder, the numbers of output channels for each layer are 16, 32, 64, 128, and 256. In order to suppress the background region, non-target region and noise influence, the depth projection weight is generated through the depth feature map D f , and then multiplied with the depth feature map to obtain the depth weight map D w . The image feature map I f ∈ R c × H × W and depth weight map D w ∈ R c × H × W with the same number of channels c are added, and then they pass through the 1 × 1 convolution layer to obtain P i , where i ∈ [ 1 , 5 ] . The equation is as follows:
D w = D f C o n v ( D f )
P i = C o n v ( I f + D w )
As shown in Figure 6, the lower-layer feature fusion path starts from F 5 . After F 5 undergoes upsampling and channel alignment, it is summed with P 4 to obtain the fused feature F 4 . Subsequently, F 3 , F 2 and F 1 are obtained through the same process. The equation is as follows:
F i = C o n v ( U p S a m p l e ( F i + 1 ) ) + P i
To obtain more information about correlated regions during the fusion process, an additional input branch is introduced. After adding F 1 and P 1 to obtain F 1 ′ , F 1 ′ is downsampled and channel aligned, and then it is added to F 2 and P 2 to obtain F 2 ′ . The subsequent F 3 ′ and F 4 ′ are obtained through the same process. The equation is as follows:
F i ′ = C o n v ( F i ) + P i , i = 1
F i ′ = C o n v ( D o w n S a m p ( F i − 1 ) ) + F i + P i , i ≥ 2

3.4. Higher-Layer Attention Mechanism and Feature Fusion

As different channels have different importance, the channel attention mechanism is used to pay more attention to channels containing more important information and pay less attention to channels containing less important information, thereby improving feature representation capabilities. [30].
As not all regions in the feature map are equally important in contributing to the model task, only regions relevant to the model task, such as the target object in a classification detection task, are of interest. The positional attention mechanism captures the spatial dependency of the feature map at any two locations by weighting all positional features and selectively aggregating features at each location, regardless of distance, and similar features are correlated with each other, thereby increasing the processing of correlated regions in different image layers in the fused feature map [31].
After the lower-layer bidirectional feature fusion, the fused feature maps at this stage retain abundant semantic information. In order to suppress the noise interference of irrelevant areas and enhance the multi-scale semantic information, we employ a parallel positional and channel attention mechanism for processing. The feature map obtained from F 4 ′ after passing through the parallel attention modules is added to obtain A 4 . After passing through the upsampling layer, A 4 is added to the feature map obtained by the parallel attention module of F 3 ′ to obtain A 3 . The subsequent A 1 and A 2 are obtained through the same process. After upsampling and convolution, A 1 produces the final dense depth estimation D d ∈ R H × W at the initial resolution. The equation is as follows:
A i = C h a n n e l ( F i ′ ) + P o s i t i o n ( F i ′ ) , i = 4
A i = C o n v ( U p S a m p ( A i + 1 ) ) + C h a n n e l ( F i ′ ) + P o s i t i o n ( F i ′ ) , 1 ≤ i ≤ 3
D d = C o n v ( U p S a m p ( A 1 ) )

3.4.1. Loss Function

Ground truth depth d g t is obtained from the lidar point cloud, and d a c c is obtained by accumulating lidar frames. During training, we minimize the difference between d, d g t , and d a c c by using a suitable L 1 penalty:
L B A F F = λ a c c l a c c ( d a c c , D d ) + λ g t l g t ( d g t , D d )
l ( d , D d ) = 1 | Ω | ∑ x ∈ Ω ( | d ( x ) − D d ( x ) | ) 2 / 2 , | d ( x ) − D d ( x ) | < 1 1 | Ω | ∑ x ∈ Ω ( | d ( x ) − D d ( x ) | − 0.5 ) , o t h e r w i s e
where Ω ⊂ R 2 denote the image region with valid values; x ∈ Ω denotes the pixel coordinates; the weight coefficient λ a c c is set to 1; and λ g t is set to 1.

3.5. Parallel Attention Mechanism

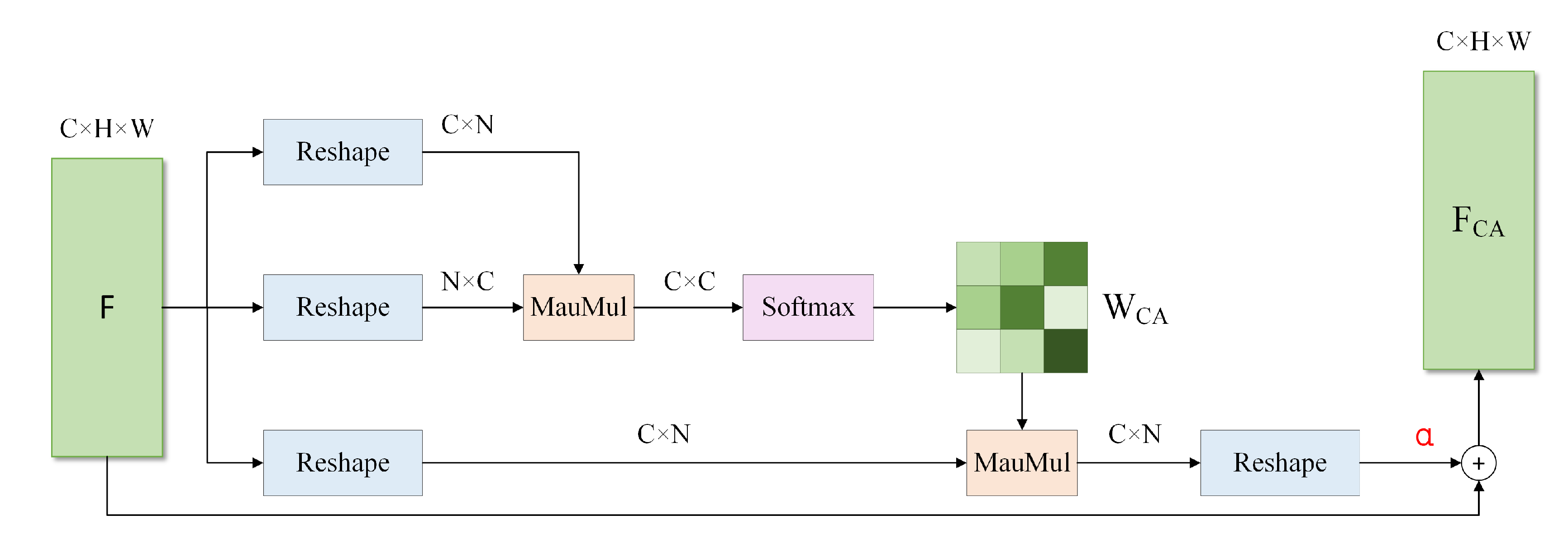
3.5.1. Channel Attention

The attention structure is shown in Figure 7. Taking the feature map F ∈ R C × H × W as input, it is transformed into matrix M 1 ∈ R C × N , where N = H × W denotes the number of pixels. Then, after transposing matrix M 1 to obtain M 2 ∈ R N × C , it is multiplied by matrix M 1 and passed through the softmax function to obtain the channel attention matrix M C A i j ∈ R C × C :
M C A i j = e x p ( M 1 i × M 2 j ) ∑ i = 1 C e x p ( M 1 i × M 2 j )
where M C A i j denotes the degree of association between the ith and jth channels. The channel attention matrix M C A i j is transformed into R C × H × W by multiplying it with matrix M 1 , which is weighted by α , and then it is added to F to obtain the channel attention feature map F C A ∈ R C × H × W :
F C A = α ( M C A i j × M 1 ) + F
where α is the learnable weight of the channel semantic information weighting feature, initialized to 0. F C A is a feature map that contains semantic dependencies between channels, which helps in accurate depth estimation.

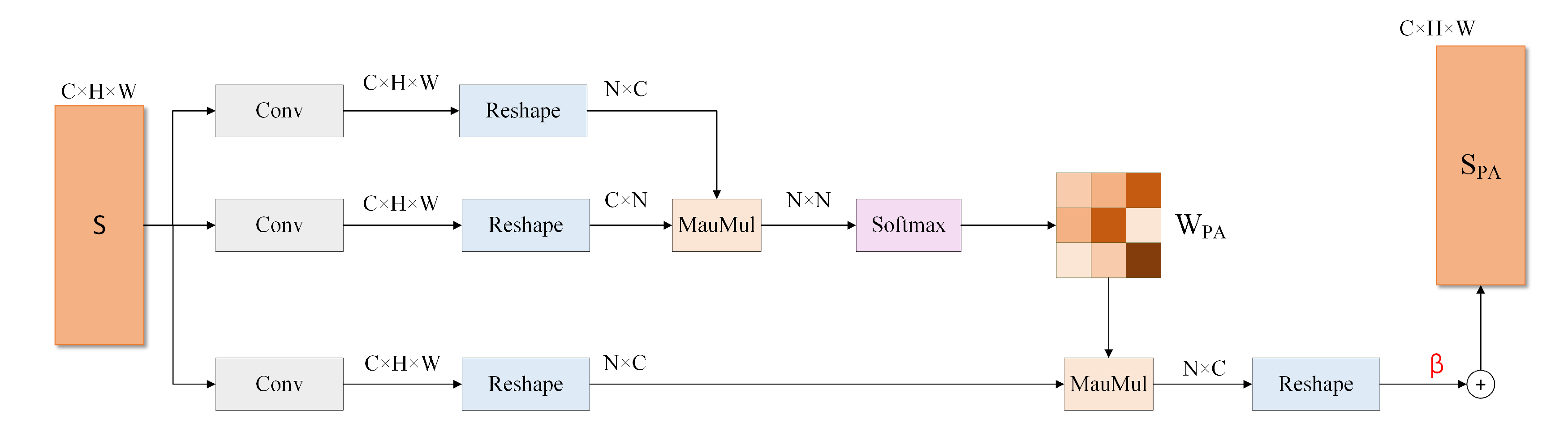
3.5.2. Position Attention

The attention structure is shown in Figure 8. Taking the feature map S ∈ R C × H × W as input, B , C , D ∈ R C × H × W are obtained by passing through three convolutional layers each; then, B , C , D are transformed into matrices M b ∈ R N × C , M c ∈ R C × N , M d ∈ R N × C ,where N = H × W . The matrices M b and M c are multiplied together and then processed by the softmax function to obtain the positional attention matrix M P A i j ∈ R N × N :
M P A i j = e x p ( M b i × M c j ) ∑ i = 1 N e x p ( M b i × M c j )
where M P A i j denotes the degree of association between the ith and jth positions. The channel attention matrix M P A i j is transformed into R C × H × W by multiplying it with matrix M d , which is weighted by β , and then it is added to S to obtain the position attention feature map S P A ∈ R C × H × W :
S P A = β ( M P A i j × M d ) + S
where β denotes the learnable weight of the position information weighted feature, initialized to 0. S P A is a feature map containing the global position information of the image, which helps to locate the target area.

4. Experiments

4.1. Datasets and Experimental Environment

We used the nuScenes dataset [32] for model training and validation. This dataset includes 1,000 scenes, capturing various driving conditions (including rainy, nighttime, and foggy scenarios). The data collection vehicles used various sensors, including MMwave radar, cameras, and LiDAR, with data collected in the Boston and Singapore areas. Each scene lasts for 20 seconds, containing 40 keyframes and corresponding radar frames, with each image having a resolution of 1600×900, totaling approximately 40,000 frames. To use the nuScenes dataset [32], we divided it into a training set with 750 scenes, a validation set with 150 scenes, and a test set with 150 scenes.
The experimental environment of this study is shown in Table 1.

4.2. Training Details and Evaluation Metrics

For training with nuScenes [32], we take the LiDAR frame corresponding to the given image as d g t , and we project the previous 80 LiDAR frames and the subsequent 80 LiDAR frames onto the current LiDAR frame d g t to obtain the accumulated LiDAR frame d a c c , during which dynamic objects are removed. We create binary classification labels y = { 0 , 1 } H × W from d a c c , where points with a depth difference of less than 0.4 meters from the radar points are labeled as positive. d g t , d a c c , and y are all used for supervision.
In the first stage of training, the input image size is 900×1600, and the cropped size during the ROI region extraction is set to 900×288. We use the Adam optimizer with β 1=0.9, β 2=0.999, and a learning rate of 2 e − 4 for 70 epochs. Our data augmentation methods include horizontal flipping, and adjustments to saturation, brightness, and contrast, each with a probability of 0.5.
In the second stage of training, we use the Adam optimizer with β 1=0.9 and β 2=0.999. We set the initial learning rate to 2 e − 4 and train for 200 epochs, and then we reduce it to 1 e − 4 and train for 200 epochs. The data augmentation methods include horizontal flipping and adjustments to saturation, brightness, and contrast, each with a probability of 0.5.
The error metrics that we use are some of those widely used in the literature for evaluating depth estimation, including the mean absolute error (MAE) and root mean square error (RMSE):
M A E = 1 | Ω | ∑ x ∈ Ω | D d g t − D d ( x ) |
R M S E = 1 | Ω | ∑ x ∈ Ω | D d g t − D d ( x ) | 2

4.3. Comparison and Analysis of Results

As shown in Table 2, we compared our method with existing methods at depths of 50 meters, 70 meters, and 80 meters, as shown in Table 1. Compared with RC-PDA [12], our method reduced the MAE by 26%, 41.6%, and 44.7%, and it reduced the RMSE by 13.6%, 31.7%, and 39.4%. Compared with DORN [28], our method reduced the MAE by 14.5%, 18.4%, and 16.8%, and it reduced the RMSE by 12.9%, 12.8%, and 16.1%. Overall, compared with the baseline model, our method reduced the MAE by 4.7%, 6.3%, and 5.8%, and reduced the RMSE by 4.2%, 5.2%, and 4.9%.
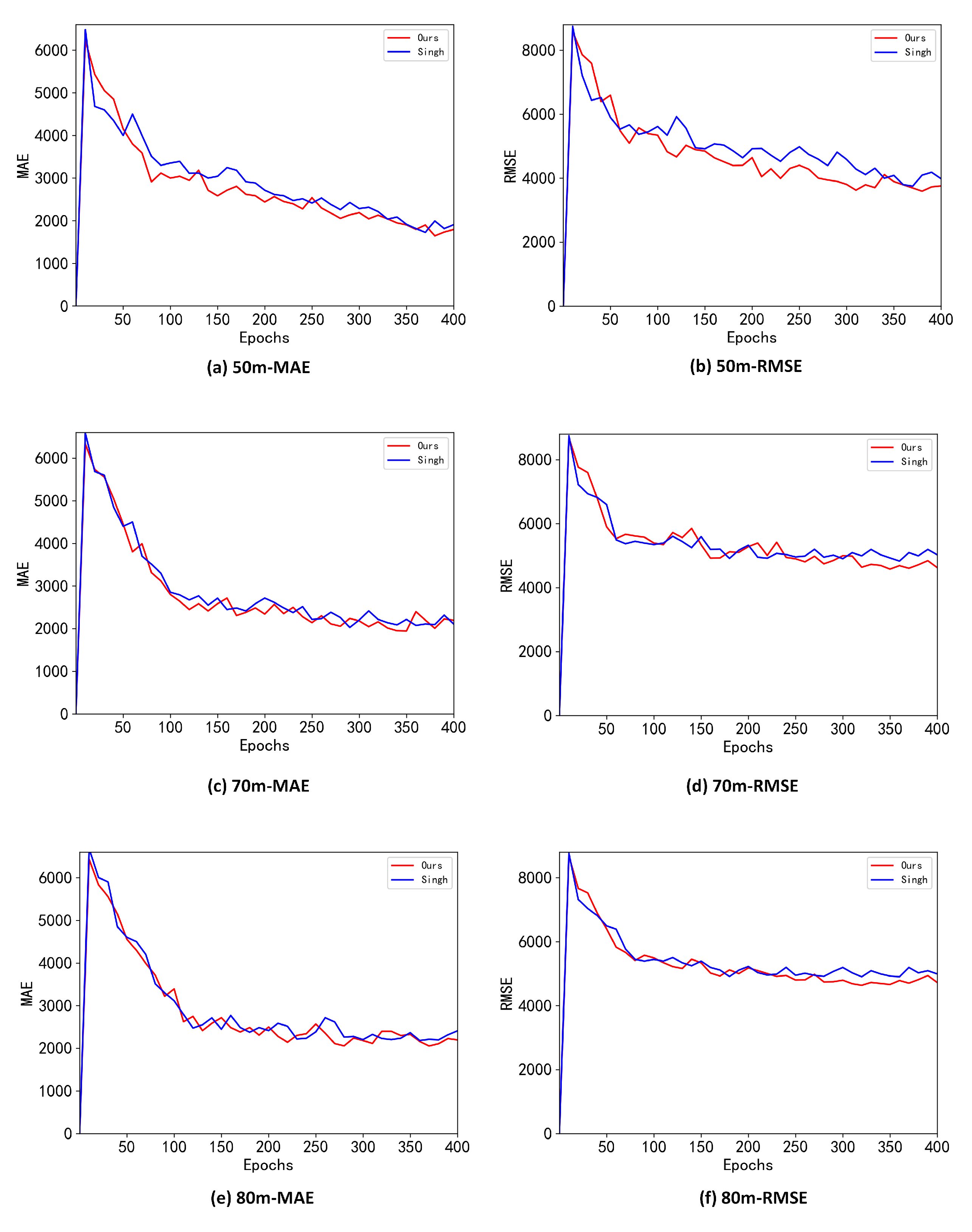
As shown in Figure 9, we plotted the MAE and RMSE curves of the different methods during the model training phase to verify the effectiveness of the proposed method.

4.3.1. Results Analysis

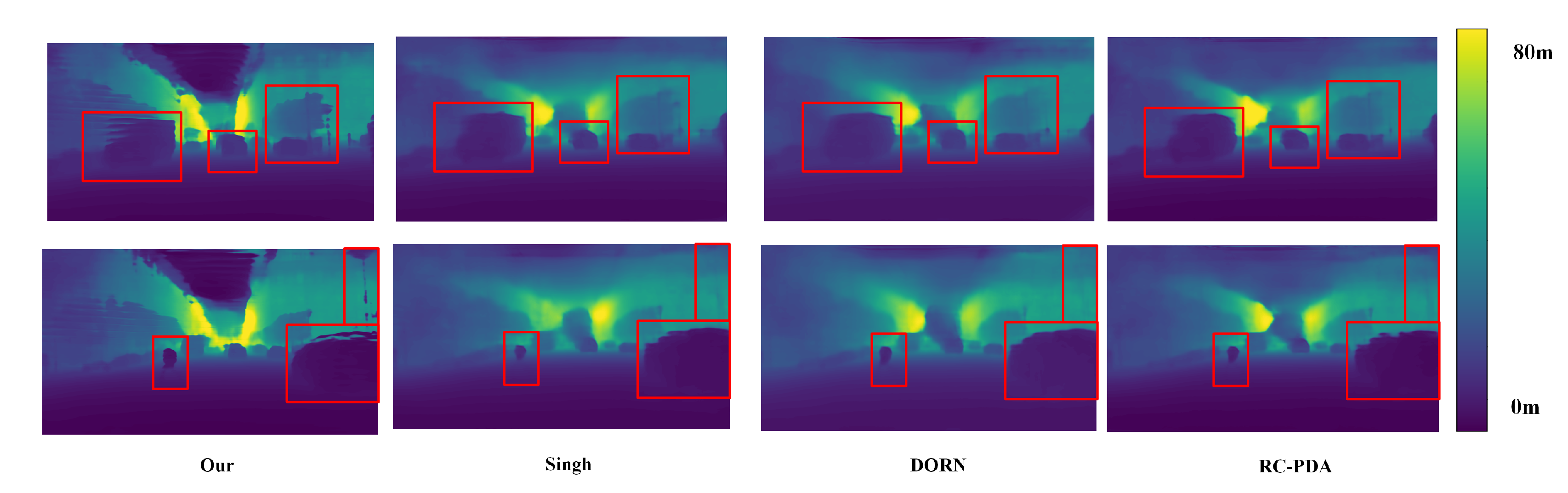
The results obtained by our method are shown in Figure 10. To compare the specific inference results, we illustrated the dense depth estimation results obtained by our methods alongside those obtained by other methods on Nuscenes, as shown in Figure 11. We selected two representative traffic scenarios: one is a multi-vehicle road scene, and the other is a pedestrian crossing an intersection. In the first column, we highlighted the prominent parts of the images using yellow and blue boxes.
In the first row, RC-PDA [12] and DORN [28] only managed to capture blurry shapes of the vehicles on the left and in the middle, with vehicle edges being indistinguishable from the background. While Singh et al. [33] could distinguish the shape of the vehicles, the edge delineation was not smooth enough, resulting in discontinuous edges in the area of the vehicle on the right. Our method, however, not only distinguished the vehicle shapes more effectively but also provided more detailed edge delineation, reducing edge discontinuities.
In the second row, the middle pedestrian is situated in a light-dark junction area, the vehicle on the right side of the scene is in a shadowed area, and there is a pole in the upper right corner. RC-PDA [12] and DORN [28] failed to capture the position of the pole, and the shapes of the middle pedestrian and the vehicle on the right were also blurry. Although Singh et al. [33] detected the pole’s position, the shape was not fully rendered. Our method provided a more complete shape and edge representation for the vehicle on the right, showed detailed depictions of both the torso and limbs of the pedestrian, and clearly captured and represented the position and shape of the pole.

4.3.2. Regional Result Analysis

We selected specific areas from the result images for a regional comparison, as shown in Figure 12. The first row displays the vehicle regions obtained by our method and other methods, which we refer to as Region-1. It is evident that the vehicle shapes obtained by our method are much clearer. The second row shows the multi-object regions, which include vehicles, trees, and street lamps, and we call this Region-2. Our method not only provides clearer object shapes but also smoother edges. We compared our method with existing methods regarding the depth range in Region-1 and Region-2, as shown in Table 3. The results demonstrate that our method consistently outperforms the other methods across different regions.

5. Conclusions

In order to enhance the performance of autonomous driving, particularly in terms of depth estimation, we propose a depth estimation method based on radar and cameras using attention mechanisms and multi-scale feature fusion. Firstly, to address the sparsity of radar point cloud data, we project radar points onto images through coordinate transformation. By learning the correlations between radar points and image regions, we establish the correspondence between radar points and image pixels. This allows the model to concentrate on target regions, assign initial depth values, and generate semi-dense depth estimations. Secondly, to further refine the depth estimation results, we re-encode the image and the semi-dense depth map. By improving the bidirectional multi-scale feature fusion structure, an additional image fusion pathway is introduced. This effectively leverages feature information at different scales, enhancing the richness and accuracy of feature representation. It also addresses the issue of information loss during feature fusion, thereby improving the model’s robustness in complex scenarios. Finally, unlike other methods that rely on the use of conventional convolutional layers as decoders for depth estimation, we employ a parallel attention mechanism to process the fused feature maps. This enhances the representation of target regions, effectively suppresses the influence of irrelevant areas and noise on the depth estimation results, and significantly improves depth estimation accuracy.
Compared with the baseline model, our method demonstrates significant performance improvements across various evaluation metrics. Within a 50 meter range, the MAE is reduced by 4.7%, and the RMSE is reduced by 4.2%. For longer ranges of 70 meters and 80 meters, the MAE is reduced by 6.3% and 5.8%, respectively, while the RMSE is reduced by 5.2% and 4.9%, respectively. These results indicate that our method outperforms the baseline model in depth estimation across various scenarios in the nuScenes dataset. It effectively handles differences in shape, size, and other attributes of targets in diverse scenes, exhibiting excellent generalization capabilities.
Moreover, to ensure that the model can effectively perform in practical applications, it is essential to account for the limitations of real-world deployment platforms, such as the demands of depth estimation tasks or complex environmental conditions. One important direction in our future work is the lightweight design of the model, with the aim of reducing its complexity and computational overhead, enabling efficient operation on resource-constrained hardware platforms. Specifically, we plan to optimize the model architecture and enhance real-time performance. While pursuing lightweight design, we will also prioritize maintaining model accuracy by experimentally exploring the trade-off between computational efficiency and depth estimation precision. Finally, we will deploy it in a test scenario and evaluate its performance in real-world applications. Insights from these test results will guide the further refinement of the model design.

Author Contributions

Conceptualization, Z.Z. and F.W.; methodology, Z.Z. and W.S.; software, Z.Z.; validation, Z.Z. and F.W.; formal analysis, Z.Z. and W.S.; investigation, F.W. and W.Z.; resources, Q.W.; data curation, Z.Z.; writing—original draft preparation, Z.Z.; writing—review and editing, F.W. and W.S.; visualization, Z.Z. and F.L.; supervision, F.W.; project administration, Z.Z.; funding acquisition, Q.W. and W.S.. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by National Science Foundation of China (Grant No. 62375196), the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (Grant No. 22KJA140002), China Jiangsu Key Disciplines of the fourteenth Five-Year Plan (Grant No. 2021135), open Project of Key Laboratory of Efficient Low-carbon Energy Conversion and Utilization of Jiangsu Provincial Higher Education Institutions (Grant No. FLOW2205), Jiangsu Province Graduate Research Innovation Program Project(Grant No. KYCX24_3430), 333 Talent Project in Jiangsu Province of China.

Data Availability Statement

The datasets are available at the following link: nuScenes:https://www.nuscenes.org/nuscenes#download.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Jiang, Y.; Wu, Y.; Zhang, J.; Wei, J.; Peng, B.; Qiu, C.W. Dilemma in optical identification of single-layer multiferroics. Nature 2023, 619, E40–E43. [Google Scholar] [CrossRef] [PubMed]
  2. Jiang, Y.; He, A.; Zhao, R.; Chen, Y.; Liu, G.; Lu, H.; Zhang, J.; Zhang, Q.; Wang, Z.; Zhao, C.; others. Coexistence of photoelectric conversion and storage in van der Waals heterojunctions. Physical Review Letters 2021, 127, 217401. [Google Scholar] [CrossRef] [PubMed]
  3. Yao, S.; Guan, R.; Huang, X.; Li, Z.; Sha, X.; Yue, Y.; Lim, E.G.; Seo, H.; Man, K.L.; Zhu, X.; others. Radar-camera fusion for object detection and semantic segmentation in autonomous driving: A comprehensive review. IEEE Transactions on Intelligent Vehicles 2023. [Google Scholar] [CrossRef]
  4. Zhang, J.; Zhang, J.; Qi, Y.; Gong, S.; Xu, H.; Liu, Z.; Zhang, R.; Sadi, M.A.; Sychev, D.; Zhao, R.; others. Room-temperature ferroelectric, piezoelectric and resistive switching behaviors of single-element Te nanowires. Nature Communications 2024, 15, 7648. [Google Scholar] [CrossRef] [PubMed]
  5. Masoumian, A.; Rashwan, H.A.; Cristiano, J.; Asif, M.S.; Puig, D. Monocular depth estimation using deep learning: A review. Sensors 2022, 22, 5353. [Google Scholar] [CrossRef] [PubMed]
  6. Jiang, Y.; He, A.; Luo, K.; Zhang, J.; Liu, G.; Zhao, R.; Zhang, Q.; Wang, Z.; Zhao, C.; Wang, L.; others. Giant bipolar unidirectional photomagnetoresistance. Proceedings of the National Academy of Sciences 2022, 119, e2115939119. [Google Scholar] [CrossRef] [PubMed]
  7. Tran, D.M.; Ahlgren, N.; Depcik, C.; He, H. Adaptive active fusion of camera and single-point lidar for depth estimation. IEEE Transactions on Instrumentation and Measurement 2023, 72, 1–9. [Google Scholar] [CrossRef]
  8. Shao, S.; Pei, Z.; Chen, W.; Liu, Q.; Yue, H.; Li, Z. Sparse pseudo-lidar depth assisted monocular depth estimation. IEEE Transactions on Intelligent Vehicles 2023. [Google Scholar] [CrossRef]
  9. Jiang, Y.; Ma, X.; Wang, L.; Zhang, J.; Wang, Z.; Zhao, R.; Liu, G.; Li, Y.; Zhang, C.; Ma, C.; others. Observation of Electric Hysteresis, Polarization Oscillation, and Pyroelectricity in Nonferroelectric p-n Heterojunctions. Physical Review Letters 2023, 130, 196801. [Google Scholar] [CrossRef] [PubMed]
  10. Wei, Z.; Zhang, F.; Chang, S.; Liu, Y.; Wu, H.; Feng, Z. Mmwave radar and vision fusion for object detection in autonomous driving: A review. Sensors 2022, 22, 2542. [Google Scholar] [CrossRef] [PubMed]
  11. Lin, J.T.; Dai, D.; Van Gool, L. Depth estimation from monocular images and sparse radar data. 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2020, pp. 10233–10240.
  12. Long, Y.; Morris, D.; Liu, X.; Castro, M.; Chakravarty, P.; Narayanan, P. Radar-camera pixel depth association for depth completion. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2021, pp. 12507–12516.
  13. Tang, J.; Tian, F.P.; Feng, W.; Li, J.; Tan, P. Learning guided convolutional network for depth completion. IEEE Transactions on Image Processing 2020, 30, 1116–1129. [Google Scholar] [CrossRef] [PubMed]
  14. Yan, Z.; Wang, K.; Li, X.; Zhang, Z.; Li, J.; Yang, J. RigNet: Repetitive image guided network for depth completion. European Conference on Computer Vision. Springer, 2022, pp. 214–230.
  15. Eigen, D.; Puhrsch, C.; Fergus, R. Depth map prediction from a single image using a multi-scale deep network. Advances in neural information processing systems 2014, 27. [Google Scholar]
  16. Eigen, D.; Fergus, R. Predicting depth, surface normals and semantic labels with a common multi-scale convolutional architecture. Proceedings of the IEEE international conference on computer vision, 2015, pp. 2650–2658.
  17. Laina, I.; Rupprecht, C.; Belagiannis, V.; Tombari, F.; Navab, N. Deeper depth prediction with fully convolutional residual networks. 2016 Fourth international conference on 3D vision (3DV). IEEE, 2016, pp. 239–248.
  18. He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778.
  19. Cao, Y.; Wu, Z.; Shen, C. Estimating depth from monocular images as classification using deep fully convolutional residual networks. IEEE Transactions on Circuits and Systems for Video Technology 2017, 28, 3174–3182. [Google Scholar] [CrossRef]
  20. Fu, H.; Gong, M.; Wang, C.; Batmanghelich, K.; Tao, D. Deep ordinal regression network for monocular depth estimation. Proceedings of the IEEE conference on computer vision and pattern recognition, 2018, pp. 2002–2011.
  21. Piccinelli, L.; Sakaridis, C.; Yu, F. idisc: Internal discretization for monocular depth estimation. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2023, pp. 21477–21487.
  22. Guizilini, V.; Ambrus, R.; Pillai, S.; Raventos, A.; Gaidon, A. 3d packing for self-supervised monocular depth estimation. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2020, pp. 2485–2494.
  23. Johnston, A.; Carneiro, G. Self-supervised monocular trained depth estimation using self-attention and discrete disparity volume. Proceedings of the ieee/cvf conference on computer vision and pattern recognition, 2020, pp. 4756–4765.
  24. Godard, C.; Mac Aodha, O.; Firman, M.; Brostow, G.J. Digging into self-supervised monocular depth estimation. Proceedings of the IEEE/CVF international conference on computer vision, 2019, pp. 3828–3838.
  25. Lyu, X.; Liu, L.; Wang, M.; Kong, X.; Liu, L.; Liu, Y.; Chen, X.; Yuan, Y. Hr-depth: High resolution self-supervised monocular depth estimation. Proceedings of the AAAI conference on artificial intelligence, 2021, Vol. 35, pp. 2294–2301.
  26. Jung, H.; Park, E.; Yoo, S. Fine-grained semantics-aware representation enhancement for self-supervised monocular depth estimation. Proceedings of the IEEE/CVF International Conference on Computer Vision, 2021, pp. 12642–12652.
  27. Feng, C.; Wang, Y.; Lai, Y.; Liu, Q.; Cao, Y. Unsupervised monocular depth learning using self-teaching and contrast-enhanced SSIM loss. Journal of Electronic Imaging 2024, 33, 013019–013019. [Google Scholar] [CrossRef]
  28. Lo, C.C.; Vandewalle, P. Depth estimation from monocular images and sparse radar using deep ordinal regression network. 2021 IEEE International Conference on Image Processing (ICIP). IEEE, 2021, pp. 3343–3347.
  29. Gasperini, S.; Koch, P.; Dallabetta, V.; Navab, N.; Busam, B.; Tombari, F. R4Dyn: Exploring radar for self-supervised monocular depth estimation of dynamic scenes. 2021 International Conference on 3D Vision (3DV). IEEE, 2021, pp. 751–760.
  30. Zhang, X.; Zhu, J.; Wang, D.; Wang, Y.; Liang, T.; Wang, H.; Yin, Y. A gradual self distillation network with adaptive channel attention for facial expression recognition. Applied Soft Computing 2024, 161, 111762. [Google Scholar] [CrossRef]
  31. Bi, M.; Zhang, Q.; Zuo, M.; Xu, Z.; Jin, Q. Bi-directional long short-term memory model with semantic positional attention for the question answering system. Transactions on Asian and Low-Resource Language Information Processing 2021, 20, 1–13. [Google Scholar] [CrossRef]
  32. Caesar, H.; Bankiti, V.; Lang, A.H.; Vora, S.; Liong, V.E.; Xu, Q.; Krishnan, A.; Pan, Y.; Baldan, G.; Beijbom, O. nuscenes: A multimodal dataset for autonomous driving. Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2020, pp. 11621–11631.
  33. Singh, A.D.; Ba, Y.; Sarker, A.; Zhang, H.; Kadambi, A.; Soatto, S.; Srivastava, M.; Wong, A. Depth estimation from camera image and mmwave radar point cloud. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2023, pp. 9275–9285.
  34. Ma, F.; Karaman, S. Sparse-to-dense: Depth prediction from sparse depth samples and a single image. 2018 IEEE international conference on robotics and automation (ICRA). IEEE, 2018, pp. 4796–4803.
  35. Wang, T.H.; Wang, F.E.; Lin, J.T.; Tsai, Y.H.; Chiu, W.C.; Sun, M. Plug-and-play: Improve depth estimation via sparse data propagation. arXiv preprint, arXiv:1812.08350 2018.
Preprints 142070 g001
Figure 1. Plotting lidar and millimeter-wave radar point clouds in images. (a) Lidar point cloud projection. (b) Millimeter-wave radar point cloud projection.
Figure 1. Plotting lidar and millimeter-wave radar point clouds in images. (a) Lidar point cloud projection. (b) Millimeter-wave radar point cloud projection.
Preprints 142070 g001
Preprints 142070 g002
Figure 2. Depth estimation using camera and millimeter-wave radar. (a) Input image. (b) Generating semi-dense depth estimation. (c) Generating dense depth estimation. Objects in the scene are highlighted.
Figure 2. Depth estimation using camera and millimeter-wave radar. (a) Input image. (b) Generating semi-dense depth estimation. (c) Generating dense depth estimation. Objects in the scene are highlighted.
Preprints 142070 g002
Preprints 142070 g003
Figure 3. Semi-dense Depth Estimation Network Structure.
Figure 3. Semi-dense Depth Estimation Network Structure.
Preprints 142070 g003
Preprints 142070 g004
Figure 4. Dense Depth Estimation Network Structure.
Figure 4. Dense Depth Estimation Network Structure.
Preprints 142070 g004
Preprints 142070 g005
Figure 5. Semi-Dense Depth Estimation.
Figure 5. Semi-Dense Depth Estimation.
Preprints 142070 g005
Preprints 142070 g006
Figure 6. Bidirectional Attention Feature Fusion Structure.
Figure 6. Bidirectional Attention Feature Fusion Structure.
Preprints 142070 g006
Preprints 142070 g007
Figure 7. Channel Attention.
Figure 7. Channel Attention.
Preprints 142070 g007
Preprints 142070 g008
Figure 8. Position Attention.
Figure 8. Position Attention.
Preprints 142070 g008
Preprints 142070 g009
Figure 9. Comparison of MAE and RMSE during training using different methods. Mae curve on the left and RMSE curve on the right.
Figure 9. Comparison of MAE and RMSE during training using different methods. Mae curve on the left and RMSE curve on the right.
Preprints 142070 g009
Preprints 142070 g010
Figure 10. The first column is the input image; The second column is the Lidar ground truth; The third column is the result of our method. Different colored bounding boxes are used to mark prominent areas in the image.
Figure 10. The first column is the input image; The second column is the Lidar ground truth; The third column is the result of our method. Different colored bounding boxes are used to mark prominent areas in the image.
Preprints 142070 g010
Preprints 142070 g011
Figure 11. The first column is the result of our method; The following columns represent the inference results of different methods. Different colored bounding boxes are used to mark prominent areas in the image.
Figure 11. The first column is the result of our method; The following columns represent the inference results of different methods. Different colored bounding boxes are used to mark prominent areas in the image.
Preprints 142070 g011
Preprints 142070 g012
Figure 12. The first column is the input image; The second column is the regional result of our method; The following columns represent the regional results of different methods. Regions in different colors are used to distinguish depths within the image.
Figure 12. The first column is the input image; The second column is the regional result of our method; The following columns represent the regional results of different methods. Regions in different colors are used to distinguish depths within the image.
Preprints 142070 g012
Table 1. Experimental Environment.
Table 1. Experimental Environment.
Experimental Platform Environment Configuration
Operating systems Ubuntu18.04
Programming Languages Python 3.8
CPU Intel(R) Xeon(R) Platinum 8352V
GPU NVIDIA RTX A5000
CUDA 11.3
Table 2. Comparison of Experimental Results.
Table 2. Comparison of Experimental Results.
Eval Distance Method Radar frames Images MAE↓ RMSE↓
5*50m RC-PDA [12] 5 3 2225.0 4156.5
RC-PDA with HG 5 3 2315.7 4321.6
DORN [28] 5(x3) 1 1926.6 4124.8
Singh [33] 1 1 1727.7 3746.8
Ours 1 1 1646.5 3589.3
5*70m RC-PDA [12] 5 3 3326.1 6700.6
RC-PDA with HG 5 3 3485.6 7002.9
DORN [28] 5(x3) 1 2380.6 5252.7
Singh [33] 1 1 2073.2 4825.0
Ours 1 1 1942.6 4574.1
10*80m RC-PDA [12] 5 3 3713.6 7692.8
RC-PDA with HG 5 3 3884.3 8008.6
DORN [28] 5(x3) 1 2467.7 5554.3
Lin [11] 3 1 2371.0 5623.0
R4Dyn [29] 4 1 N/A 6434.0
Sparse-to-dense [34] 3 1 2374.0 5628.0
PnP [35] 3 1 2496.0 5578.0
Singh [33] 1 1 2179.3 4898.7
Ours 1 1 2052.9 4658.7
Table 3. Comparison of Regional Results.
Table 3. Comparison of Regional Results.
Region Method MAE↓ RMSE↓
4*Region-1 RC-PDA [12] 24.46 41.15
DORN [28] 23.71 39.87
Singh [33] 22.84 39.42
Ours 22.61 39.17
4*Region-2 RC-PDA [12] 28.86 49.95
DORN [28] 28.64 49.76
Singh [33] 27.57 49.27
Ours 27.31 49.08
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated