1. Introduction
Steel-concrete composite beam can fully utilize the advantages of each material, presenting significant economic benefits [
1]. However, an excessive self-weight and a tendency of easily cracking of the concrete deck in negative moment zone will be some challenges, which limits the application of steel-concrete composite beam to large-span bridges [
2,
3,
4]. Ultra-high Performance Concrete (UHPC) is a newly-developed type of fiber-reinforced cementitious composite materials characterized by exceptionally high toughness and long-term durability [
5,
6,
7,
8,
9]. Combining it with steel beams can reduce the self-weight of the structure and enhance its spanning capabilities, which is potentially addressing the technical challenges of traditional steel-concrete composite beam bridges and expanding their range of applications [
10,
11,
12].
More recently, UHPC has been increasingly utilized in steel-concrete composite beam bridges with waffle UHPC bridge decks, with the objective of enhancing the strength of the waffle bridge deck and resolving the of premature cracking observed in such structures [
13,
14]. The increased strength and ductility of UHPC compared to normal concrete result in reduced consumption of UHPC materials for waffle bridge deck construction under the same loading condition. Thus, the thickness or depth of UHPC bridge deck can be reduced compared to the normal concrete that may produce the shallow bridge deck. However, this reduced depth will compromise the flexural stiffness of the cross section as well as the crack resistance of the shallow bridge deck. The waffle UHPC bridge decks are structurally composed of reinforced UHPC shallow beams with T-shaped cross-sections, namely reinforced UHPC shallow T-shaped beam. The crack resistance and crack evolution mechanisms of reinforced UHPC shallow T-shaped beam are fundamental from both a structural safety and a serviceability perspective, since excessive deflections and crack widths under service loads will significantly impair the long-term functionality and durability of these shallow structures.
For reinforced UHPC shallow T-shaped beams, the volume fraction of steel fibers within UHPC is relatively high, resulting in its crack resistance and crack evolution mechanism that differ considerably from traditional concrete beams. It is essential to ensure that the negative moment zone of reinforced UHPC shallow T-shaped beam exhibits adequate crack resistance under serviceability limit states, as this directly impacts the structural safety and durability of the structure made. To satisfy the criteria of lightweight and high strength, the incorporation of structural reinforcement is frequently utilized as a method of reducing the likelihood of cracking within the waffle UHPC bridge deck. Accordingly, an investigation into the crack evolution mechanism of reinforced UHPC shallow T-shaped beams and the development of a corresponding simplified method for crack width represent essential prerequisites for enhancing the crack resistance of steel-UHPC composite bridges. This is also crucial for advancing the development of lightweight composite bridges with waffle UHPC bridge decks. Consequently, to efficiently assess the crack resistance and crack evolution mechanisms, it is imperative to accurately predict the deflections and crack withs of reinforced UHPC shallow T-shaped beams. The prevailing methodologies for calculating UHPC crack width typically employ numerical simulations or the application of analytical formulas for ordinary concrete, which are relatively labor-intensive or time-consuming.
Researchers have conducted numerous studies on the mechanical properties of reinforced UHPC flexural specimens and have achieved notable advancement in the exploration of their crack resistance characteristics. Zheng et al. [
15,
16] devised flexural experiments for RPC rectangular beams reinforced steel bars and GFRP bars respectively. By taking into account the tensile stress in the tension zone and analyzing the distribution and propagation of cracks in the experimental beams, a formula for calculating crack width has been derived. Furthermore, Kwahk et al. [
17] and Leutbecher et al. [
18] examined the bond behavior between reinforcement and UHPC, and proposed revisions to the crack width calculation formulas in basis of the European CEB-FIP standard in their findings. Xu et al. [
19] conducted flexural tests on two non-prestressed and six prestressed T-shaped UHPC beams to investigate the cracking moment and crack development of the beams. The introduction of correction factors based on the parameters set out in the current design codes enabled the derivation of a formula for calculating the maximum allowable crack width of UHPC beams. Deng et al. [
20] employed the ordinary concrete design code to ascertain the maximum crack width, and their findings indicated that the calculated values were consistently higher than the observed values in the case of T-shaped reinforced UHPC flexural beams. Upon introducing a correction factor of 0.7, a notable alignment was observed between the calculated and the measured values. Zhao et al. [
21] conducted flexural tests on twenty reinforced UHPC rectangular slabs with the objective of investigating the effects of reinforcement protective layer thickness and reinforcement ratio on crack width. In accordance with the methodologies utilized for calculating the crack width of ordinary reinforced concrete, they employed the nonuniformity coefficient in order to assess the stress and strain exerted by the reinforcement. In consideration of the aforementioned correction factors, a formula was established for calculating the maximum crack width of UHPC slabs. Sturm et al. [
22,
23] considered the tensile effects and shrinkage creep of UHPC, deriving simplified calculation methodologies for deflection and crack width under normal service conditions of beams. Qiu et al. [
24] performed four-point bending tests on six reinforced UHPC beams to observe the evolution and dispersion of cracks. Based on the experimental data, they updated the average crack spacing, non-uniformity coefficient for reinforcement strain and characteristic force coefficient with regard to existing standards. The tensile stress in the UHPC tensile zone was considered, and formulas were established for the purpose of calculating both the reinforcement stress and crack width of reinforced UHPC flexural specimens.
Despite the existence of studies that have investigated the crack resistance of reinforced UHPC (R-UHPC) T-shaped beams, the available evidence remains limited and the methodology in need of refinement for shallow T-shaped beams. Moreover, further verification is required to ascertain the applicability of these studies. It is of great urgency to develop a reliable and practical simplified analysis method for predicting the crack width and deflection of reinforced UHPC shallow T-shaped beams. At present, there is no consensus on the calculation methods for crack width and deflection in reinforced UHPC specimens with T-shaped cross-sections. Furthermore, the current design codes do not provide specific calculation methodologies for characterizing these parameters. While the Chinese design standard GB 50010-2010 [
25] offers a method for determining the average crack spacing in ordinary concrete, this approach is not applicable to UHPC. The standard formula tends to overestimate the average crack spacing due to the favorable bond behavior between UHPC materials and reinforcement, as well as the beneficial crack-bridging effect of steel fibers. It is therefore essential to conduct flexural tests on reinforced UHPC shallow T-shaped beams to explore their cracking evolution mechanisms, with a view to developing a simplified method for predicting crack width and deflection.
This paper presents the results of an investigation in which six groups of reinforced UHPC shallow T-shaped beams are designed with varying reinforcement ratios. Based on the results of four-point bending tests, a simplified bilinear analysis model characterized with four characterization points for reinforced UHPC shallow T-shaped beams is proposed, taking into account factors such as shrinkage and creep, as well as the contribution of UHPC tension, the bond slip and tensile stiffening effect of reinforcement. The simplified analysis model is employed for forecasting the mid-span deflection and crack width in reinforced UHPC shallow T-shaped beams. Finally, the theoretical calculation values derived from the simplified analysis model are compared with the experimental data measured from bending tests to ascertain its validity, with the objective of furnishing a benchmark for the prediction of crack width and deflection of reinforced UHPC shallow T-shaped beams.
2. Segmental Analysis of Reinforced UHPC Shallow T-Shaped Beam
This section presents a detailed analysis of the stress distribution in a shallow T-shaped section beam, with consideration of the tensile constitutive responses of UHPC materials. The sectional curvature and neutral axis height are then determined using the equilibrium equation, thereby establishing the moment-curvature relationship of the flexural T-beam. Subsequently, the load-deflection and load-crack width relationships are derived through deflection-curvature conversion conditions. The solution procedure is presented in full below.
2.1. Tensile Constitutive Relationship of UHPC
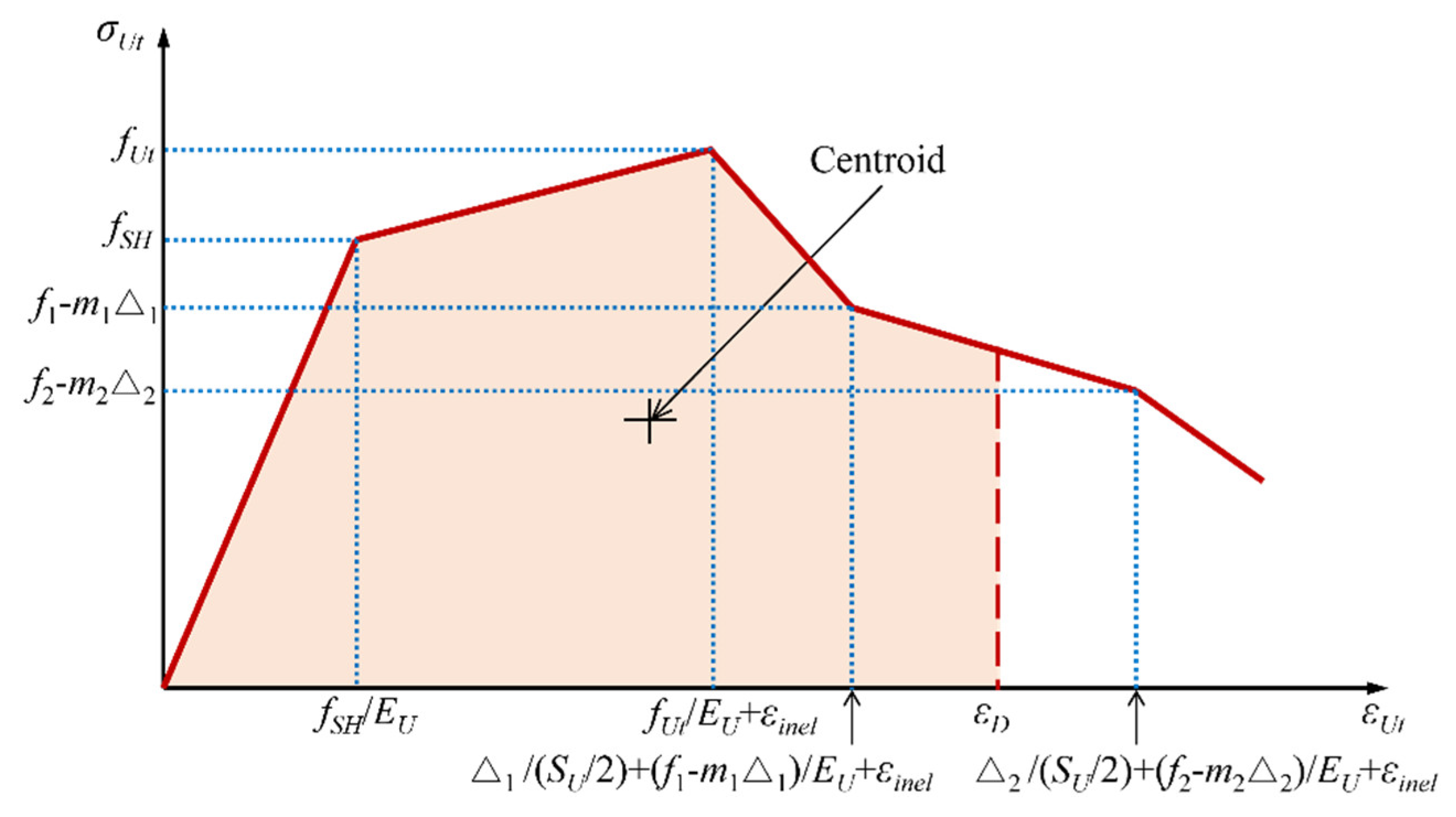
The tensile response of UHPC material can be divided into the following stages [
25,
26]: (1) a linear elastic stage before initial cracking, characterized by a linear stress-strain relationship; (2) a strain-hardening stage, marked by the development of multiple micro-cracks; (3) a strain-softening stage, characterized by rapid crack propagation and stress reduction. In the linear elastic stage, UHPC remains uncracked. During the strain-hardening stage, numerous micro-cracks are dispersed throughout the UHPC matrix. In the strain-softening stage, tensile deformation rapidly develops at the visible main cracks, as shown in
Figure 1.
Figure 1.
Tensile constitutive responses of UHPC. (a) Stress-strain relationship; (b) Stress-crack width relationship.
Figure 1.
Tensile constitutive responses of UHPC. (a) Stress-strain relationship; (b) Stress-crack width relationship.
The tensile stress
σUt of UHPC can be expressed as a piecewise linear function of strain
εUt or half crack width
Δ(Δ=w/2):
where
EU is the elastic modulus of UHPC;
fSH is the initial cracking stress;
ESH is the modulus of strain hardening;
fUt is the tensile strength of UHPC;
εinel is the permanent plastic strain caused by multiple micro-cracks;
mi and
fi are the slope and y-intercept of segment i of the stress-half crack width segmental curve, respectively;
Δi is the half crack width at the right endpoint of segment i of the stress-half crack width relationship
σ(Δ). The parameters can be obtained either through direct tensile tests or via the secondary backwards method based on flexural tests.
To simplify calculations, the stress-half crack width relationship shown in
Figure 1b is converted into an equivalent stress-strain relationship [
27]. The equivalent tensile strain within the crack zone is therefore estimated using the following formula:
where
Δ/(SU/2) is the strain caused by crack propagation;
σUt/EU is the strain caused by elastic deformation of UHPC between cracks;
εinel is the plastic strain caused by micro-cracks. By converting the stress-crack width relationship into a stress-strain relationship according to Equation (2), the stress-strain constitutive model shown in
Figure 2 is obtained.
Figure 2.
Equivalent stress-strain relationship for tensile UHPC.
Figure 2.
Equivalent stress-strain relationship for tensile UHPC.
2.2. Determination of Internal Forces in Reinforced UHPC Shallow T-Shaped Beams
2.2.1. Internal Force of UHPC in Tensile Zone
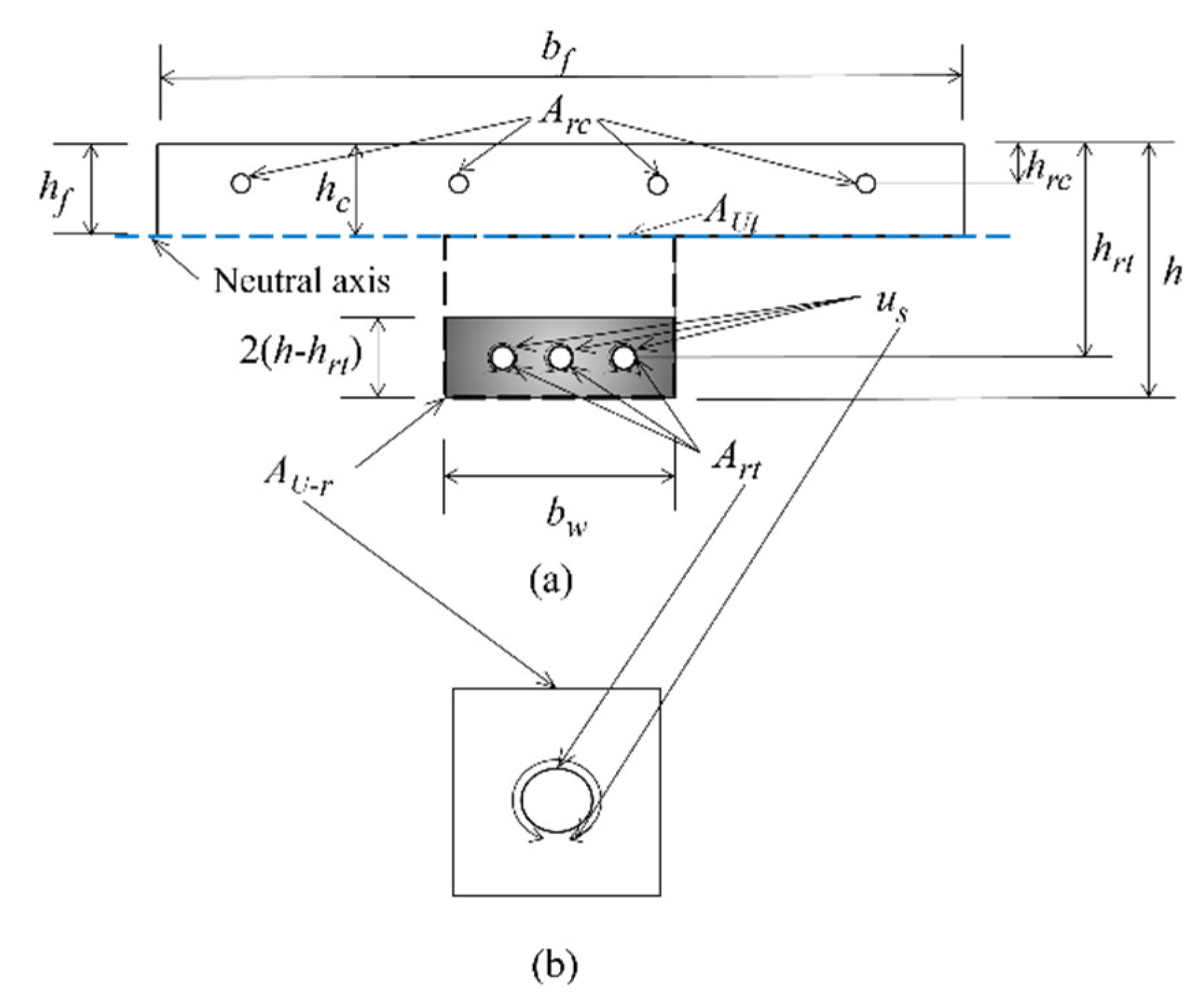
As demonstrated by the reinforced UHPC shallow T-shaped beam shown in
Figure 3, the axial force exerted in the tensile zone of UHPC can be quantitatively derived through the application of an integral, which is based on the stress-strain relationship of UHPC material as defined by Equation (1).
where
AUt is the area of the UHPC tensile zone;
h−hc is the height of the tensile zone;
is the average stress of UHPC in the tensile zone and can be determined by
The arm of force of UHPC in tensile zone is defined as
where
η is the ratio of the distance between the centroid of the tensile stress distribution and the neutral axis to the height of the tensile zone.
Figure 3.
Cross-section of reinforced UHPC shallow T-shaped beam.
Figure 3.
Cross-section of reinforced UHPC shallow T-shaped beam.
2.2.2. Internal Force of UHPC in Compressive Zone
The UHPC in the compressive zone is considered to be linear elastic as defined by the modulus of elasticity
EU. The axial force in the UHPC compressive zone is thus given by
where
φ is the curvature,
bf is the flange width, and the height of the arm of force in the compression zone relative to the neutral axis is 2/3
hc.
2.2.3. Internal Force of Reinforcement in Tensile Zone
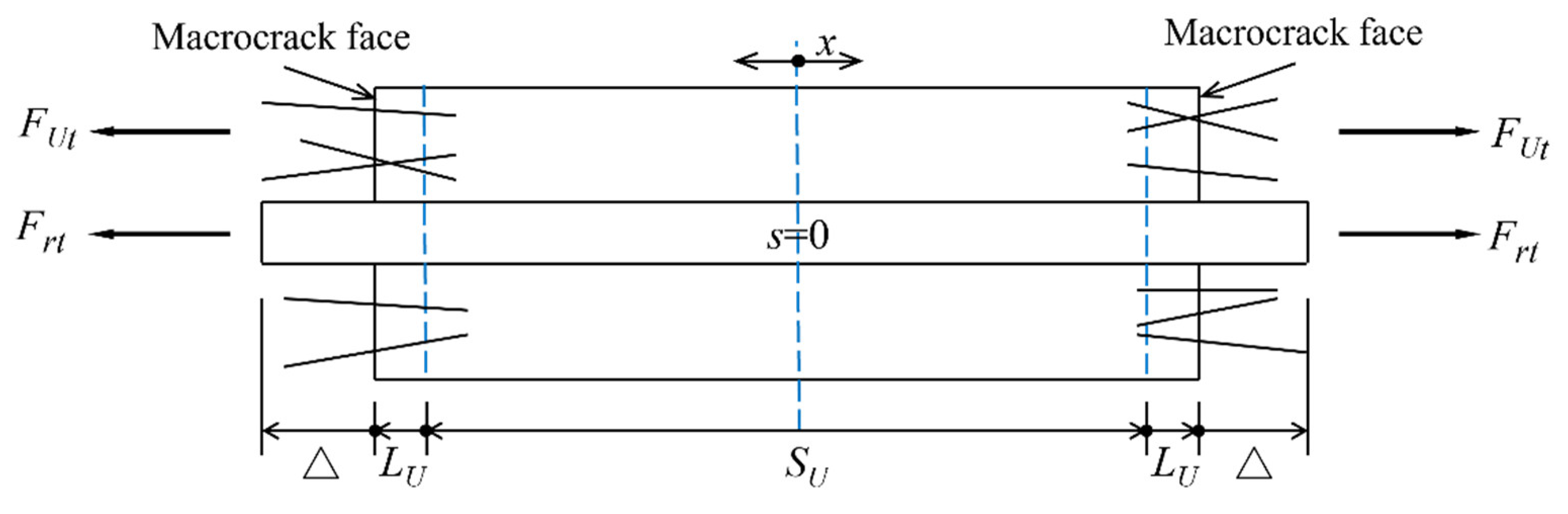
The elevation of tension-stiffening zone between two cracks for a reinforced UHPC element is shown in
Figure 4. The axial force in tension reinforcement within the T-shaped beam is given by:
where
αE is the elasticity modulus ratio of reinforcement to UHPC;
φ is the curvature;
hc is the height of the compressive zone;
γ is the increased stiffness coefficient due to tension stiffening effect. Before the formation of macro-cracks (
εD <
fUt/
EU+εinel), γ is taken as 1, and after the formation of a macro-crack (
εD ≥
fUt/
EU+εinel), γ is taken by the following expression:
Figure 4.
Elevation of tension stiffening region between cracks of reinforced UHPC beam.
Figure 4.
Elevation of tension stiffening region between cracks of reinforced UHPC beam.
2.2.4. Internal Force of Reinforcement in Compressive Zone
The reinforcement in compressive zone is as assumed to be linear elastic. Hence, the axial force of reinforcement is derived as
where, the force attributed to shrinkage strain is given by
2.3. Crack Spacing
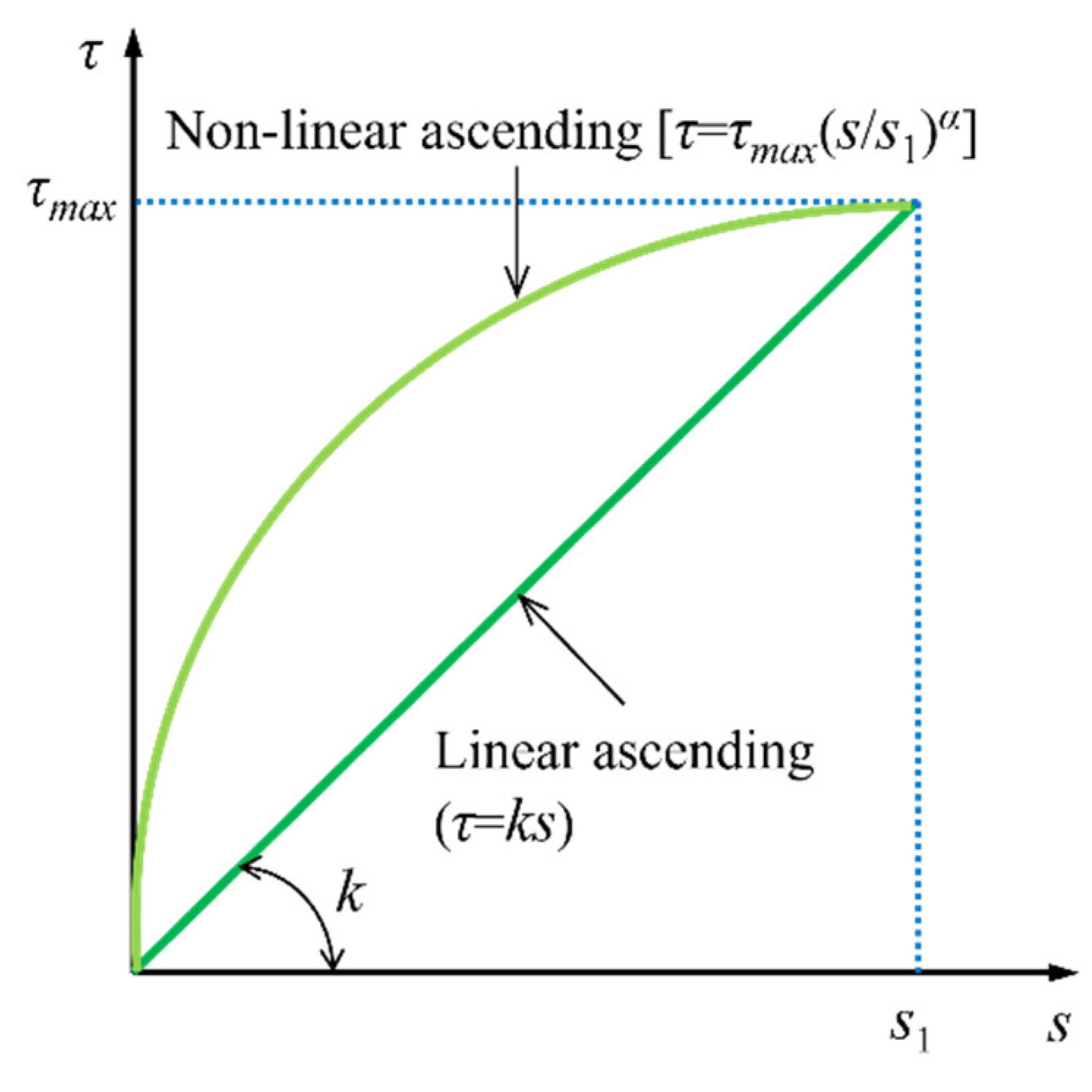
The determination of an adequate crack spacing is a fundamental aspect in the accurate calculation of crack width. Considering the bridging and crack resistance effects of steel fibers, as well as the shrinkage and creep characteristics of UHPC, the expression for crack spacing, as outlined in the literature [
22], is presented as
where
τmax is the maximum bond stress (bond strength);
s1 is the slip corresponding to the bond strength;
α is the fitted coefficient of bond behavior of the reinforcement-UHPC interface.
Figure 5 illustrates the relationship between these parameters including
τmax,
s1, and
α, which is typically determined through pull-out tests of the reinforcement within the concrete.
2.4. Segmental Analysis of Reinforced UHPC Shallow T-Shaped Beams
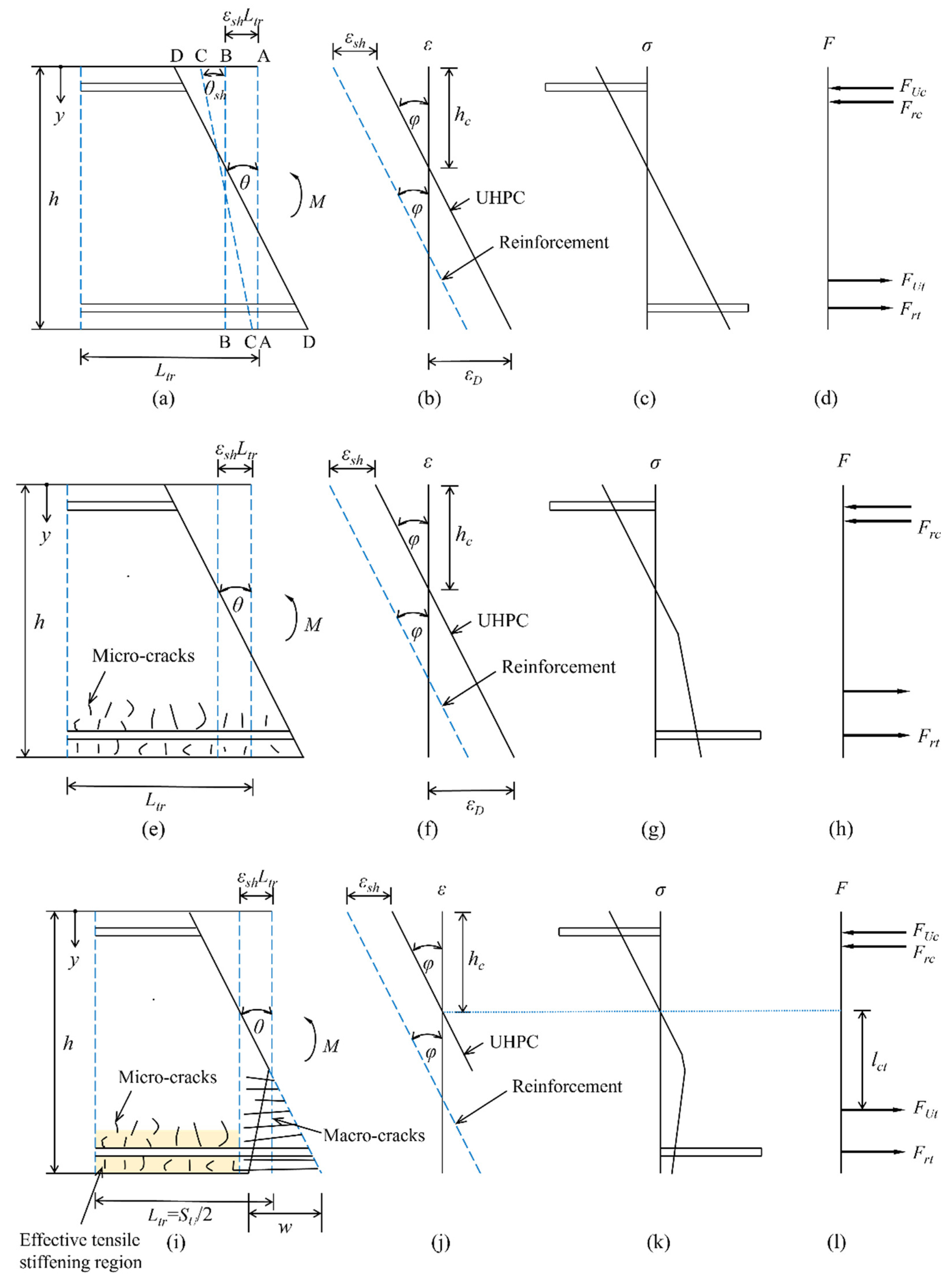
To ascertain the moment-rotation behavior of a beam, the uncracked segment as shown in
Figure 6a is initially considered. It is assumed that the stress transfer length
Ltr is equal to half the crack spacing (
SU/2), while the A-A section represents the initial position of the segment. As the shrinkage strain develops in the segment, if the reinforcement is not bonded, the resulting contraction is manifested as Section B-B. Due to the bond nature between UHPC and reinforcement, the contraction results in compressive forces being exerted on the reinforcement, while tensile forces are generated in the concrete to maintain equilibrium. This leads to the formation of Section C-C at a rotation angle
θsh. The application of an external moment results in an increase in rotation
θ to achieve equilibrium between force and moment, leading to the formation of Section D-D. For analytical purposes, the shrinkage strain
εsh can be determined by shrinkage-relevant tests of UHPC material. The influence of creep can also be incorporated through the modification of the elastic modulus of UHPC using the age-adjusted effective modulus method [
28,
29]. A division of the deformation profile in
Figure 6a by the transfer length
Ltr produces the strain profile illustrated in
Figure 6b, which represents the strain subsequent to the imposition of shrinkage strain and external moment. The sectional strain distribution of both UHPC and reinforcement is defined in
Figure 6b, where the difference in their strains representing the shrinkage strain.
Figure 6.
Detailed analysis of reinforced UHPC shallow T-shaped beam.
Figure 6.
Detailed analysis of reinforced UHPC shallow T-shaped beam.
Based on the strain distribution and constitutive relationship of UHPC material, the sectional stress distribution can be obtained as shown in Figure 6c, and its integration then produces the internal force profile in Figure 6d. By applying the force and moment equilibrium equation, the relationship between the external moment M and curvature can then be solved. As the growing of the external moment, the strain εD of UHPC bottom face will eventually reach the multi-cracking strain. Thereafter, the segment in Figure 6a is replaced by the one ass shown in Figure 6e. The emergence of microcracks leads to the stress hardening of UHPC, as illustrated in Figure 6g. Upon arriving of strain εD at the macrocracking strain, fUt/EU+εinel, macrocracks are initiated on the bottom face of beam, as represented in Figure 6i. The presence of macrocracks indicates the stress softening of tensile response, as shown in Figure 6k. In this situation, the effective stiffness of the tensile reinforcement increases due to the tensile stiffening effect. It is represented by the multiplication of the axial rigidity of the reinforcement by the tension-stiffening parameter defined by Equation (10). By employing the moment-rotation approach, this enables the derivation of the relationship between moment-curvature and moment-crack width, and further determines the deflections and crack widths in the section.
The strain at the bottom of UHPC beam
εD is applied, and then the curvature is
To determine the neutral axis depth, the force equilibrium is referred as
Substituting Equations (1), (5), (8), (14), and (18) into Equation (19), for a T-shaped section of UHPC shallow beam the following is obtained:
where
After determining the height of neutral axis from Equations (20) and (21), the curvature can be calculated using Equation (18), and then internal forces can be evaluated using Equations (3), (7), (8), and (14), thereby determining the external moment M of the section. By rearranging Equation (2), it arrives
By applying aforementioned process, it allows for the evaluation of the moment-curvature and moment-crack width relationships in a parametric manner across a range of bottom strains εD. It is noteworthy that the maximum crack width of the section can be obtained from Equation (22) under the assumptions made during the derivation of crack spacing.
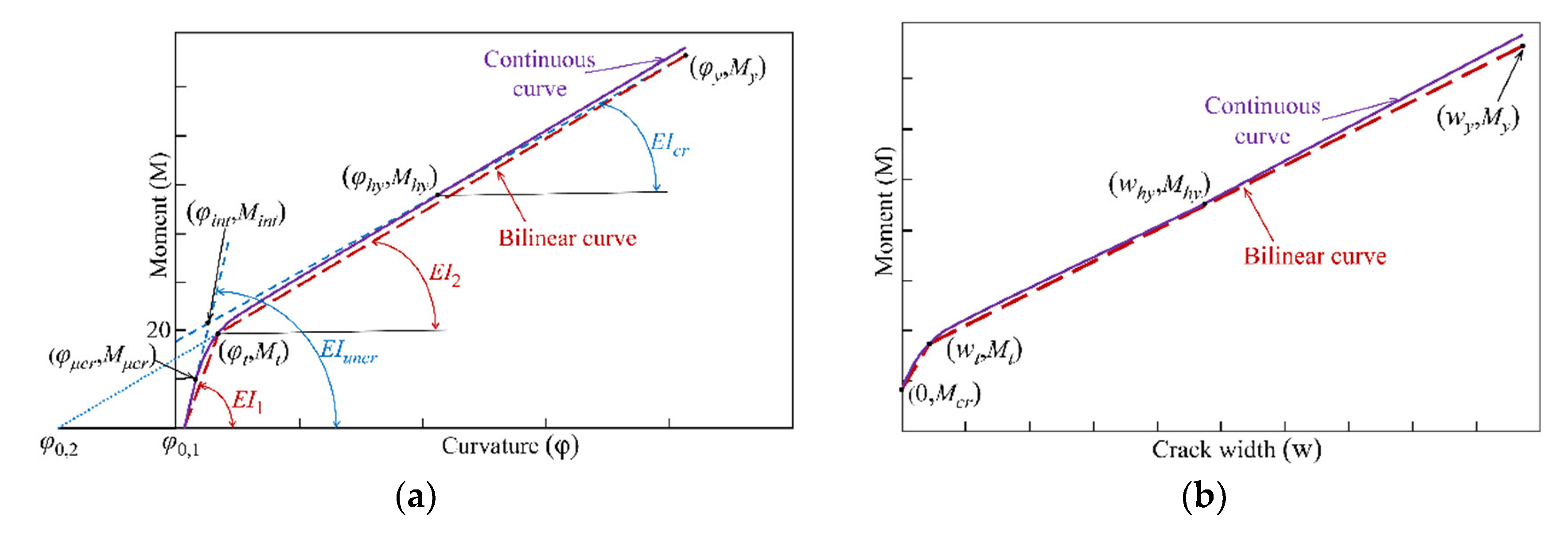
3. Simplified Analysis Model for Reinforced UHPC Shallow T-Shaped Beams
The aforementioned method requires the evaluation of bottom strain
εD to calculate the moment, curvature, and crack width to obtain a continuous smooth curve. To simplify the solution process, the continuous moment-curvature relationship, as illustrated in
Figure 7a, can be approximated by a bilinear curve, with the moment-curvature relationship expressed as follows:
where
φ0,1 is the curvature at zero moment due to shrinkage, and the first portion of the bilinear curve (flexural stiffness) is characterized by a slope as
The slope of the second portion of the bilinear curve is
The second portion of the bilinear curve intersects with the curvature axis at
Figure 7.
Simplified analysis model for moment-curvature and moment-crack width relationships: (a) Moment-curvature relationship; (b) Moment-crack width relationship.
Figure 7.
Simplified analysis model for moment-curvature and moment-crack width relationships: (a) Moment-curvature relationship; (b) Moment-crack width relationship.
3.1. Curvature at Zero Moment φ0,1
The curvature at zero moment is derived here for a reinforced UHPC beam with T-shaped cross-section, as illustrated in
Figure 3a. When UHPC is uncracked (
εD<
fSH/EU), its stress can be considered as linear elastic. The stress is thus defined as the elastic modulus with multiplication of the strain, which is related to the curvature
φ0,1, compressive zone height
hc0, and distance from the top of the section
y, that is
φ0,1(
y-
hc0). The axial force composition of UHPC is
By combining Equations (8), (14), and (25), force equilibrium provides
The solution of the curvature is obtained
where the area and first-order moment of the transformed section gives respectively to
By taking the moment at the top of the section, the moment composition of UHPC is
The moment equilibrium at the top fiber gives
where
M is the external moment applied;
and
is the moment composition carried by reinforcements in tension and in compression, respectively. The solution of the curvature is derived as
where the second-order moment of the transformed section is
By combining Equations (29) and (34), it determines the compression zone height or neutral axis depth
where
and thus
Once the compressive zone height has been quantified using Equation (38), the curvature can be calculated using either Equation (29) or Equation (34) when external moment is zero.
3.2. Moment My and Curvature φy at Reinforcement Yielding
In
Figure 2, the bottom strain
εD is unknown at the beginning of reinforcement yielding. It is however required to quantify the average stress
and the force arm
lct of the UHPC in tension. It is observed that the yielding strain
εy of reinforcement is typically significantly larger than the microcracking strain (
fSH/EU) of UHPC, which implies the height of the crack almost extends to the neutral axis. In such case, the tensile stress-strain curve prior to cracking is ignored as a simplification to obtain closed-form solutions, and is assumed to be a linear relationship providing the intersection with the stress axis at
f1 in a slope of
Ef. From Equations (4) and (6):
By establishing the axial force of reinforcement at yielding as
Frt =
fy Art and reordering Equation (8), the effective yielding strain is derived as
The curvature at yielding is
The force of tensile reinforcement is
fy Art, and the force of compressive reinforcement is given by Equation (14). Similarly, the force of UHPC in compression is calculated using Equation (7), and the force of UHPC in the tensile zone is determined by Equation (3). In this situation, the force equilibrium denotes
Substituting Equation (42) into Equation (43), it is obtained:
where
Having obtained the neutral axis height hcy using Equation (44), the curvature φy is determined using Equation (42), and the moment My can be quantified after the determination of the axial force and the force arm.
3.3. Moment Mt and Curvature φt at Transition Point
To identify the transition point, the flexural stiffness
EIuncr for the uncracked section and
EIcr for the cracked section is first required. As illustrated in
Figure 7a, the flexural stiffness of the uncracked section is determined with
where
Mμcr and
φμcr are the moment and curvature at beginning of microcracking, respectively, determined by evaluating the bottom strain
εD with
fSH /
EU.
The flexural stiffness of the cracked section can be estimated using the secant stiffness through the yield point and the point where the strain at the UHPC bottom reaches 50% of the yield strain, that is
where
Mhy and
φhy are the moment and curvature, respectively, derived by the assessing the bottom strain
εD with 0.5
φy (
h -
hcy).
Upon obtaining the flexural stiffness for both the uncracked and cracked sections, the intersection of the two curves, as shown in
Figure 7a, can be determined. By means of a direct comparison between the curvature at the intersection point, as indicated by the two curves, it can be defined as
The moment at the intersection point is derived from the rearrangement of Equation (48) as:
The selection of transition point is determined by evaluating the bottom strain same as that of the intersection point. The bottom tensile strain
εD,t at the transition point is a function of curvature and can estimated by a linear interpolation between the microcracking strain and a value of 0.5
φy (
hrt −
hc), which results in
Once the bottom strain εD,t is determined, the neutral axis height and curvature can be obtained using Equations (20) and (18), respectively. Subsequently, the forces of the reinforcement and UHPC are evaluated by Equations (3), (7), (8), and (14), and then the moment is determined by the multiplication of the forces by their level arms. Finally, the flexural stiffnesses of different parts of the curve can be assessed using Equations (24) and (25).
3.4. Estimation of Crack Width
The relationship between moment and crack width is shown in Figure 7b. The crack width can be estimated through a linear interpolation between the crack widths corresponding to microcracking, transition, half yielding, and reinforcement yielding.
3.5. Mid-Span Deflection
Based on the bending moment diagram from a four-point bending test, an expression for calculating the mid-span deflection of shallow T-shaped beams with two different flexural stiffnesses can be derived. The curvature distribution is obtained from Equations (25) and (26). By performing a double integration of the curvature distribution and considering the boundary condition of zero deflection at the supports, the mid-span deflection can be found as:
where
F is the applied load; L is the span length of the beam; a is the distance between loads;
x1 is the critical point between two different flexural stiffnesses, defined as
4. Four-Point Bending Test of Reinforced UHPC Shallow T-Shaped Beams
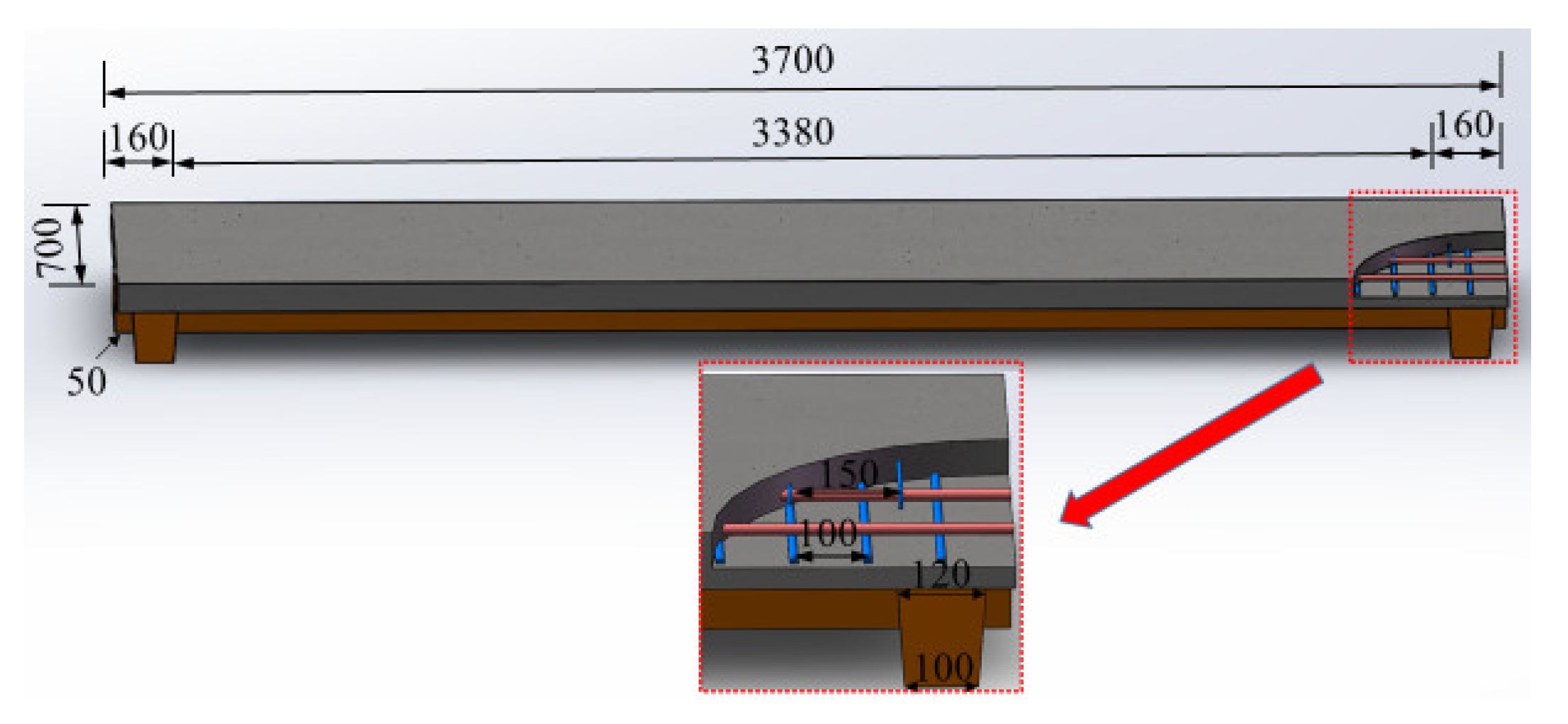
The reinforced UHPC shallow T-shaped specimens employed in the bending tests have a total length of 3.7m with a calculated diaphragm-to-diaphragm span of 3.5m. The geometric dimensions of T-shaped specimens are shown in
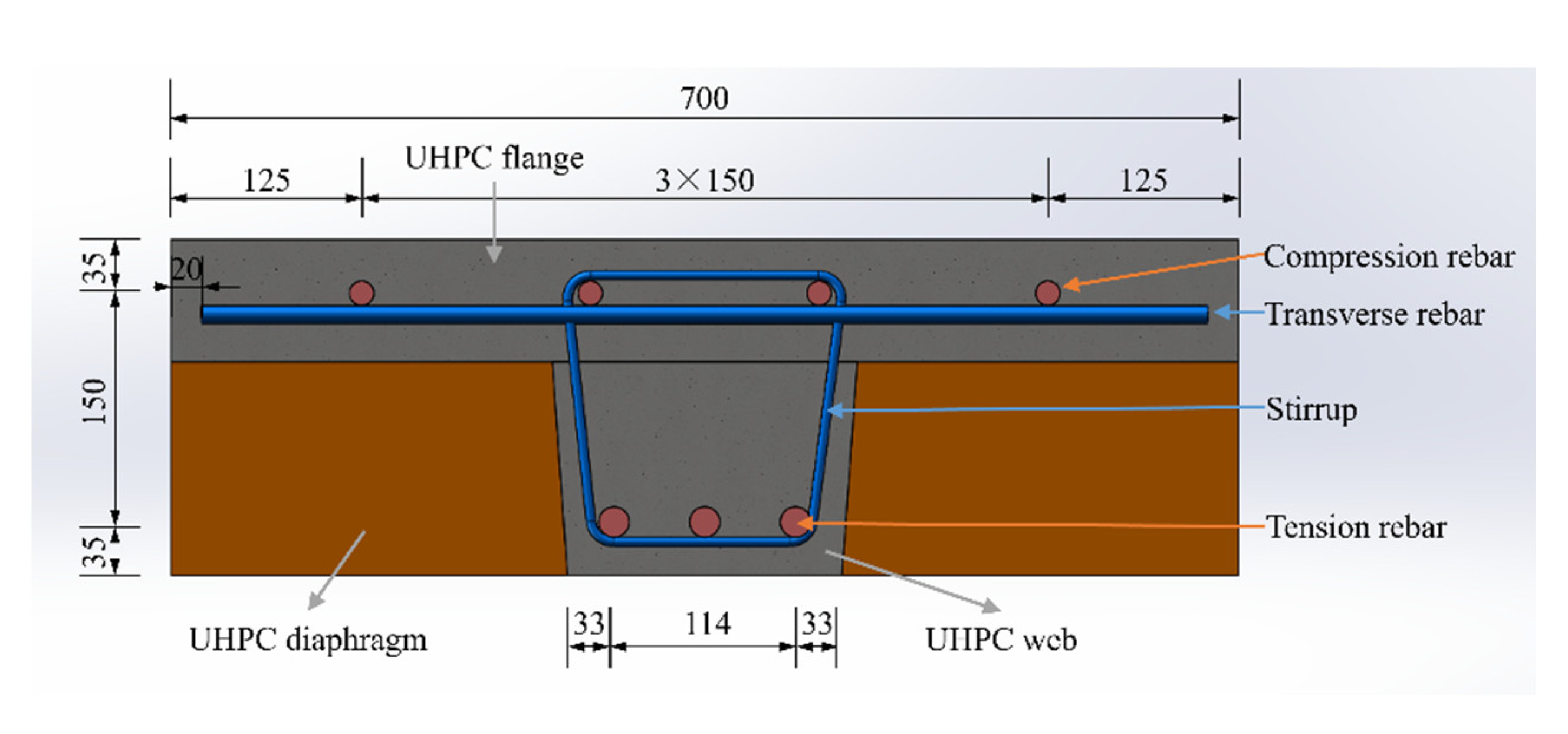
Figure 8. The dimensions of each specimen are identical, comprising a flange width of 70cm and a flange thickness of 8cm. The height of UHPC web with a linear variable width is 14cm, and its bottom width and top width are 18cm and 20cm, respectively. The specimens are longitudinally reinforced with steel reinforcements in tension side and in compression side, respectively. Additionally, some transverse reinforcements and stirrups are equipped to stabilize the longitudinal reinforcements. The details of reinforcement arrangement are illustrated in
Figure 9. A total of six reinforced UHPC shallow T-shaped specimens are designed and fabricated, with a variable type of steel fibers and a varying reinforcement ratio of longitudinal rebars in tension. The volume fraction of steel fibers within UHPC is 2.5% and the grade of steel rebars is HRB400 in China. The characteristics of the steel fibers used within UHPC are presented in
Table 1, while the design parameters of specimens and measured material properties of UHPC are shown in
Table 2.
Figure 8.
Geometric dimensions of T-shaped beam specimen (unit: mm).
Figure 8.
Geometric dimensions of T-shaped beam specimen (unit: mm).
Figure 9.
Cross-sectional reinforcement configuration of T-shaped specimen (unit: mm).
Figure 9.
Cross-sectional reinforcement configuration of T-shaped specimen (unit: mm).
Table 1.
Characteristics of steel fibers used within UHPC.
Table 1.
Characteristics of steel fibers used within UHPC.
| Fiber Type |
Fiber Shape |
Length |
Diameter |
| S-10-12 |
Straight |
10mm |
0.12mm |
| S-13-16 |
Straight |
13mm |
0.16mm |
| S-13-20 |
Straight |
13mm |
0.20mm |
| H-13-20 |
Hook-end |
13mm |
0.20mm |
Table 2.
Design parameters and measured material properties of various specimens.
Table 2.
Design parameters and measured material properties of various specimens.
| Specimen Number |
Reinforcement Ratio (%) |
Reinforcement Number |
Fiber Type |
Flexural Strength (MPa) |
Compressive Strength (MPa) |
| R-UHPC-1 |
1.75 |
2@20mm |
S-13-20 |
24.4 |
134.1 |
| R-UHPC-2 |
1.68 |
3@16mm |
S-13-20 |
24.4 |
134.1 |
| R-UHPC-3 |
2.62 |
3@20mm |
S-13-20 |
24.4 |
134.1 |
| R-UHPC-4 |
2.62 |
3@20mm |
S-13-16 |
31.8 |
126.2 |
| R-UHPC-5 |
2.62 |
3@20mm |
S-10-12 |
33.1 |
139.6 |
| R-UHPC-6 |
2.62 |
3@20mm |
H-13-20 |
21.7 |
138.7 |
All reinforced UHPC specimens are applied to four-point loading where the boundary of the specimen and the distribution beam are simply supported. To monitor the deflection variation in reinforced UHPC specimens under four-point loading, five Linear Variable Differential Transformers (LVDTs) are positioned at the mid-span and four loading sections. Within a 1.4m-long middle pure-bending zone of four-point loading, three cross-sections at the mid-span and two ends of distribution beam are selected for the purpose of measuring the strain distribution. On each cross-section chosen, five strain gauges are aligned longitudinally and each separated by a vertical spacing of 40 mm. Moreover, to quantify the deformation of UHPC at post-cracking, several LVDTs are installed on bottom surfaces of cross-sections chosen. Furthermore, the distribution and development of cracks during loading are also recorded by using a crack width measuring device.
A photo of the test setup and the loading scheme, along with the layout of the measuring points, is illustrated in Figure 10a. Four-point bending tests of reinforced UHPC specimens with shallow T-shaped sections are carried out at Hunan Provincial Key Laboratory of Wind Engineering and Bridge Engineering of Hunan University. The loading equipment used is a electro-hydraulic automatic control testing machine with a load capacity of 500 kN, as shown in Figure 10b.
Figure 10.
Photos of four-point bending tests for reinforced UHPC specimens: (a) test setup and loading scheme; (b) electro-hydraulic automatic control testing machine.
Figure 10.
Photos of four-point bending tests for reinforced UHPC specimens: (a) test setup and loading scheme; (b) electro-hydraulic automatic control testing machine.
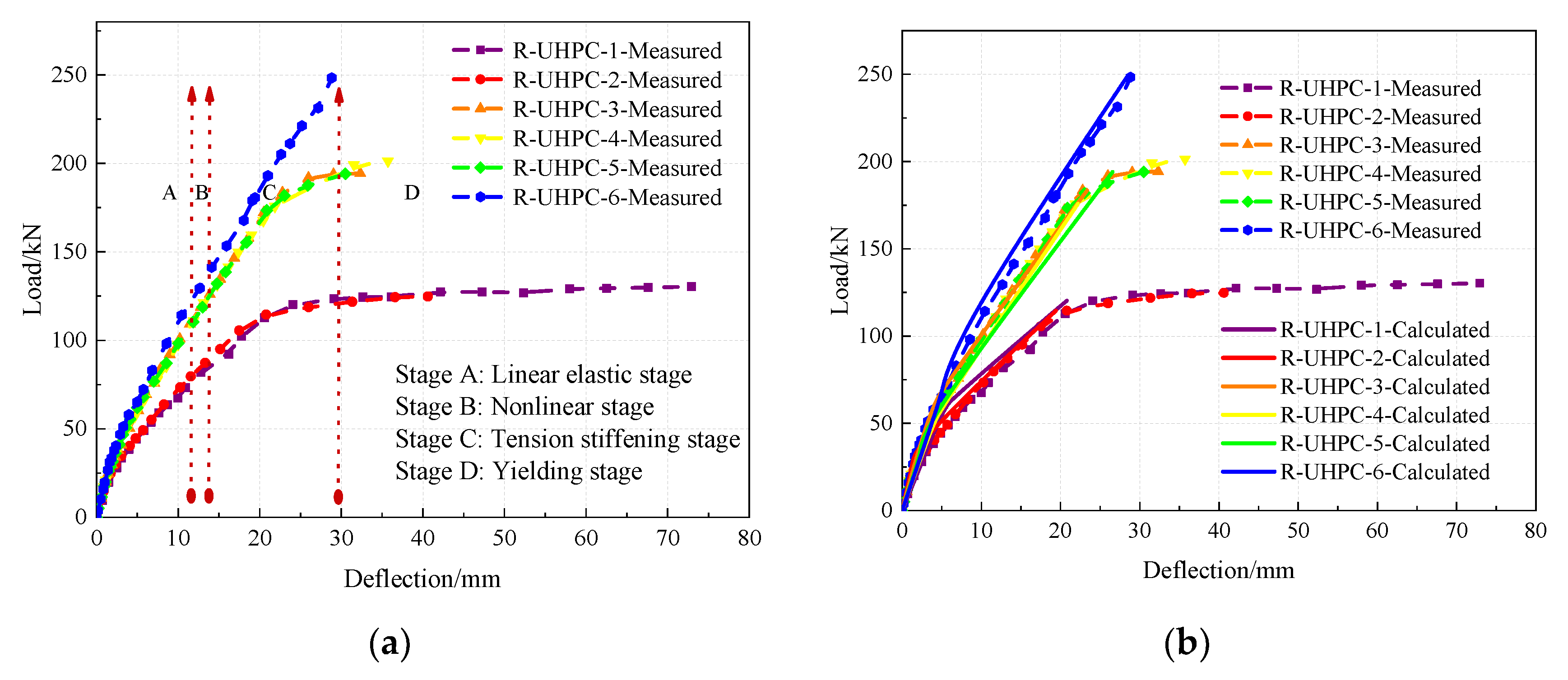
5. Result Analysis and Discussion
Figure 11a presents the load-deflection curves obtained from the static flexural tests on the reinforced UHPC shallow T-shaped beams, while Figure 11b compares the theoretical load-deflection curves derived from the proposed simplified analysis model with those obtained from the experimental tests. As illustrated in Figure 11a, a load-deflection curve can be roughly divided into four distinct stages: the linear elastic stage, the nonlinear stage with the emergence of micro-cracks, the tension stiffening stage with rapid propagation of cracks, and the yielding stage with localized macro-cracks. As evidenced by the experimental results, during the initial elastic stage, the load verse mid-span deflection curves of reinforced UHPC specimens exhibits a nearly linear trend, with the flexural stiffness comprising of the UHPC and steel reinforcement. As the applied load increases, the emergence of micro-cracks is evident within the reinforced UHPC specimens, resulting in the presence of a nonlinear relationship between load and deflection. With a growing applied load, micro-cracks develop rapidly and then a macro-crack forms in the weakest zone that most structurally vulnerable to bending moment, the pure bending zone, thereby leads to a significant reduction in flexural stiffness. This indicates the onset of the tension stiffening stage. During this period, a multitude of observed cracks commences formation, concurrently with the emergence of macro-cracks. Upon the final yielding stage, the load-bearing capacity of reinforced UHPC shallow T-shaped specimens predominantly remains stabilized despite the reinforcement yielding. This is due to the fact that the compressive UHPC has not yet fully reached its ultimate compressive strength, allowing it to maintain a certain degree of bearing capacity. In such case, the reinforced UHPC specimens exhibit a sustained increase in deflection with a notable degree of ductility which implies a characterized failure of a balanced-reinforced beam. For instance, the specimen named R-UHPC-1 is loaded gradually under a displacement control following the yielding of the reinforcement. Despite a constant load level, the mid-span deflection of the specimen is observed by a more than twofold increase, indicative of a markedly ductile failure characteristic of the reinforced UHPC T-shaped beam.
Figure 11.
Load-deflection curves of reinforced UHPC shallow T-shaped specimens. (a) Measured load-deflection curves from static four-point bending tests; (b) Comparison between theoretical and measured load-deflection curves.
Figure 11.
Load-deflection curves of reinforced UHPC shallow T-shaped specimens. (a) Measured load-deflection curves from static four-point bending tests; (b) Comparison between theoretical and measured load-deflection curves.
A favorable comparison between the theoretical values derived from simplified analysis model previously-mentioned and those obtained from measurement in Figure 11b reveals that a high degree of agreement. Particularly, with regard to the predicted mid-span deflection of reinforced UHPC specimen, it is observed to be relatively insignificant prior to the onset of reinforcement yielding. Once the reinforcement has yielded, the load-bearing level of the specimen remains approximately constant, while the mid-span deflection increases considerably. The load-bearing capacity of flexural specimen at the onset of reinforcement yielding is typically defined as the ultimate flexural capacity. From the perspective of structural safety, shallow T-shaped beams are usually not designed to enter the yielding stage for engineering application; thus, the proposed simplified analysis model is a feasible and reliable approach for predicting the mid-span deflection of reinforced UHPC beams.
The cracking behavior of the reinforced UHPC shallow T-shaped beams is monitored and documented in great detail throughout the loading process. To assess the accuracy of the theoretical model, the observed evolution of cracks within the pure bending zone is compared with the calculated results.
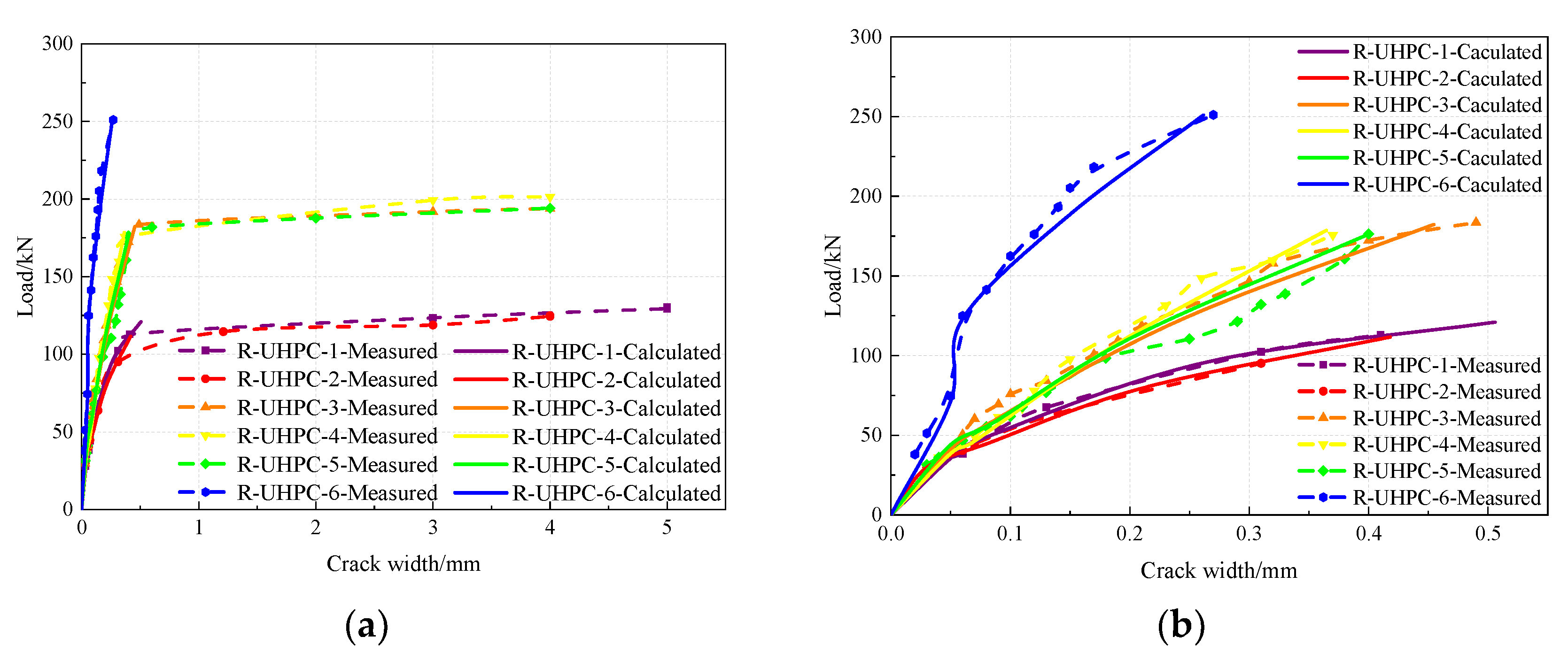
Figure 12 presents the progression of maximum crack width with applied load for each specimen. The load at which a crack width of 0.05mm is first observed is defined as the first cracking load hereafter.
Table 3 compares the measured values of the first cracking load and the crack width at reinforcement yielding with the calculation results by simplified analysis model. As illustrated in
Table 3, the theoretical analysis model is capable of accurately predicting the crack width of the reinforced UHPC flexural specimens, exhibiting a high degree of agreement between the theoretical results and experimental measurements. The ratios of first cracking loads by theoretical calculations to the counterparts from experimental measurements are found to be all within 0.95, with an average error of approximately 2.83%. This indicates that the theoretical analysis model can predict cracking loads with a high degree of accuracy. Similarly, the ratios of crack widths at reinforcement yielding theoretically calculated to those experimentally measured are all within a range of 0.9, with an average variation around 3.48%. This implies that the simplified analysis model also can accurately predict the crack width at the ultimate limit state for reinforced UHPC shallow T-shaped beams. In summary, the theoretical model proposed for the simplification analysis of reinforced UHPC shallow T-shaped beams is accessible and accurate in its prediction of deflection and crack width, thereby it is promising to provide valuable reference for the design and calculation of such beams.
Figure 12.
Load-crack width curves of reinforced UHPC shallow T-shaped specimens in static flexural tests. (a) Load-crack width curves of the whole response; (b) Load-crack width curves prior to reinforcement yielding.
Figure 12.
Load-crack width curves of reinforced UHPC shallow T-shaped specimens in static flexural tests. (a) Load-crack width curves of the whole response; (b) Load-crack width curves prior to reinforcement yielding.
6. Conclusions
A simplified analysis model has been introduced in this paper for the prediction of the mid-span deflection and crack width of reinforced UHPC shallow T-shaped beams. The feasibility and accuracy of the proposed simplified analysis model is verified by comparing the theoretical values derived by simplification analysis with the experimental results from the four-point bending tests on six reinforced UHPC shallow T-shaped specimens. The following conclusions are obtained:
1. Taking account into several factors including shrinkage and creep of UHPC, the contribution of tensile UHPC, the bond strength of the interface and tension stiffening effect, the segmental analysis method of reinforced UHPC shallow beam with T-shaped sections is first established, and then a bilinear simplified analysis model with four characteristic points is derived for determining the mid-span deflection and crack width of reinforced UHPC shallow T-shaped beams.
2. The experimental curves of load-deflection for reinforced UHPC shallow T-shaped specimens can be divided into four stages: the linear elastic stage, the nonlinear stage with the emergence of micro-cracks, the tension stiffening stage with rapid propagation of cracks, and the yielding stage with localized macro-cracks. During the initial elastic stage, the load-deflection curve exhibits a nearly linear trend. As the load increases, the emergence of a micro-crack is observed, resulting in a nonlinear relationship between load and deflection. With a growing load, micro-cracks develop rapidly and then a macro-crack forms within the pure bending zone, leading to a significant reduction in flexural stiffness. Following the onset of the tension stiffening stage, observed cracks form with the emergence of macro-cracks. Upon the yielding stage, the load-bearing capacity of reinforced UHPC shallow T-shaped specimens remains stabilized. As such, those specimens exhibit a sustained increase in deflection with a notable ductility characterized by the failure of a balanced-reinforced beam.
3. A comparison between the theoretical values derived from simplified analysis model and those results obtained from experimental measurements reveals a high degree of agreement. With regard to the predicted mid-span deflection of reinforced UHPC specimen, it is observed to be insignificant prior to reinforcement yielding. Once the reinforcement has yielded, the load-bearing level of the specimen remains nearly constant, while the mid-span deflection increases considerably. From the perspective of structural safety, the proposed simplified analysis model is a feasible and reliable approach for predicting the mid-span deflection of reinforced UHPC shallow beams.
4. The measured values of first cracking load and crack width at reinforcement yielding are compared with the calculation results by simplified analysis model. The ratios of first cracking loads and crack widths at reinforcement yielding by theoretical calculations to the counterparts from experimental measurements are found to be within a range of 0.95 and 0.9, respectively. The average error of 2.8% for the first cracking load and 3.5% for the crack width at reinforcement yielding, respectively, indicating that the theoretical analysis model is capable of predicting cracking loads and crack widths with a high degree of accuracy.
Eventually, the simplified analysis model proposed for reinforced UHPC shallow T-shaped beams is accessible and accurate in its prediction of deflection and crack width, promising to provide valuable reference for the design and calculation of such beams.
Author Contributions
Conceptualization, methodology, and funding acquisition, Z.Z; investigation, visualization, Y.W.; project administration, writing—original draft preparation, Y.C.; supervision, writing—review and editing, P.Z. All authors have read and agreed to the published version of the manuscript.
Funding
The authors appreciate the support from the Natural Science Foundation of Hunan Province, China (Grant No. 2023JJ30216), Excellent Youth Foundation from the Department of Education, Hunan Province (Grant No. 23B0576), and Natural Science Foundation of Chongqing, China (CSTB2024NSCQ-MSX1206), respectively. Besides, the authors thank the support from the National Natural Science Foundation of China (Grant No. 51808212).
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- NIE J.; Tao M.; Wu L.; et al. Advances of Research on Steel-concrete Composite Bridges[J]. China Civil Engineering Journal, 2012, 45(06): 110-122.
- NIE J. The Future of Structural Engineering in China——High-performance structural Engineering[J]. China Civil Engineering Journal, 2016, 49(09): 1-8.
- Xiang H. The future trend of the world’s bridges - inspiration from the 2011 London International Bridge Association Conference [C]. The 20th National Bridge Association Conference of China. Wuhan, China, 2012, 18-25.
- Russell H G.; Graybeal B. Ultra-high performance concrete: A state-of-the-art report for the bridge community[R]. McLean: US Department of Transportation, Federal Highway Administration, 2013.
- Shao X.; Cao J.; Yi D.; et al. Research on Basic Performance of Composite Bridge Deck System with Orthotropic Steel Deck and Thin RPC Layer[J]. China Journal of Highway and Transport, 2012, 25(02): 40-45.
- Shi C.; Wu Z.; Xiao J.; et al. A review on ultra high performance concrete: Part I. Raw materials and mixture design[J]. Construction and Building Materials, 2015, 101: 741-751. [CrossRef]
- Wang D.; Shi C.; Wu Z.; et al. A review on ultra high performance concrete: Part II. Hydration, microstructure and properties[J]. Construction and Building Materials, 2015, 96: 368-377. [CrossRef]
- Yoo D Y.; Banthia N. Mechanical properties of ultra-high-performance fiber-reinforced concrete: A review[J]. Cement and Concrete Composites, 2016, 73: 267-280. [CrossRef]
- Yoo D Y.; Yoon Y S.; A review on structural behavior, design, and application of ultra-high performance fiber-reinforced concrete[J]. International Journal of Concrete Structures and Materials, 2016, 10(2): 125-142. [CrossRef]
- Shao X.; Zhan H.; Lei W.; Zhang Z. Conceptual Design and Preliminary Experiment of Super-long-span Continuous Box-girder Bridge Composed of One-way Prestressed UHPC[J]. China Civil Engineering Journal, 2013, 46(08): 83-89.
- Shao X.; Qiu M.; Yan B.; et al. A Review on the Research and Application of Ultra-high Performance Concrete in Bridge Engineering Around the World[J]. Materials Reports, 2017, 31(23): 33-43.
- Shao X.; Cao J. Research and Application of High Performance Bridge Structures Toward Future[J]. Journal of Architecture and Civil Engineering, 2017, 34(05): 41-58.
- Shao X.; Wu J.; Liu R.; et al. Basic Performance of Waffle Deck Panel of Lightweight Steel-UHPC Composite Bridge [J]. China Journal of Highway and Transport, 2017, 30(03): 218-225+245.
- Zhu J.; Wang Y.; Yan J.; Guo X. Shear behaviour of steel-UHPC composite beams in waffle bridge deck [J]. Composite Structures, 2020, 234: 111678. [CrossRef]
- Zheng W.; Li L.; Lu S.; et al. Experimental Research Mechanical Performance of Normal Section of Reinforced Reactive Powder Concrete Beam[J]. Journal of Building Structures, 2011, 32(06): 125-134.
- Zheng W.; Lu S.; Li L.; et al. Experimental Research on Mechanical Performance of Reactive Powder Concrete Beams Reinforced with GFRP Bars[J]. Journal of Building Structures, 2011, 32(06): 115-124.
- Kwahk I L J, Kim J, et al. Evaluation of the Crack Width of the Ultra High Performance Concrete(K-UHPC) Structures[J]. Journal of the Korean Society of Safety, 2012, 27(6): 99-108.
- Leutbecher T.; Fehling E. Tensile Behavior of Ultra-High-Performance Concrete Reinforced with Reinforcing Bars and Fibers: Minimizing Fiber Content[J]. ACI Structural Journal, 2012, 109(2). [CrossRef]
- Xu H.; Deng Z. Cracking Moment and Crack Width of Ultra-high Performance Concrete Beams[J]. Journal of Harbin Institute of Technology, 2014, 46(04): 87-92.
- Deng Z.; Xiao R.; Xu H.; et al. Serviceability Research of Ultra-High performance concrete Beams Reinforced with High Strength Steel Bars[J]. Journal of Harbin Institute of Technology, 2015, 36(10): 1335-1340.
- Zhao C.; Wang C.; Li L. Experimental Study on Calculation Method of Crack Width of Reactive Powder Concrete Slab[J]. Journal of Highway and Transportation Research and Development: Applied Technology Edition, 2017, 13(08): 251-254+301.
- Sturm A B.; Visintin P.; Oehlers D J.; et al. Time-dependent tension-stiffening mechanics of fiber-reinforced and ultra-high-performance fiber-reinforced concrete[J]. Journal of Structural Engineering, 2018, 144(8): 04018122. [CrossRef]
- Sturm A B.; Visintin P.; Oehlers D J. Rational Design Approach for the Instantaneous and Time-dependent Serviceability Deflections and Crack Widths of FRC and UHPFRC Continuous and Simply Supported Beams[J]. Journal of Structural Engineering, 2019, 145(11): 4019138. [CrossRef]
- Qiu M.; Shao X.; Hu W.; et al. Calculation Method for Crack Width of Reinforced UHPC Flexural Components[J]. China Civil Engineering Journal, 2020, 53(10): 89-98+119.
- Ministry of Housing and Urban-Rural Development of China. GB 50010-2010, Code for Design of Concrete Structures[S]. China Communications Press: Beijing, China, 2010.
- Wille K.; El-Tawil S.; Naaman A E. Properties of strain hardening ultra high performance fiber reinforced concrete (UHPFRC) under direct tensile loading[J]. Cement and Concrete Composites, 2014, 48: 53-66. [CrossRef]
- Zhang Z. Bending Behaviors of Composite Bridge Deck System Composed of OSD and Reinforced UHPC Layer[D]. Hunan University, 2016.
- Hillerborg A. A model for fracture analysis[M]. Lund Institute of Technology, Division of Building materials, 1978.
- Gilbert R. I.; Ranzi G. Time-Dependent Behaviour of Concrete Structures[M]. CRC Press, 2010.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).