Submitted:
27 December 2024
Posted:
30 December 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Notations
3. Linearization Methods
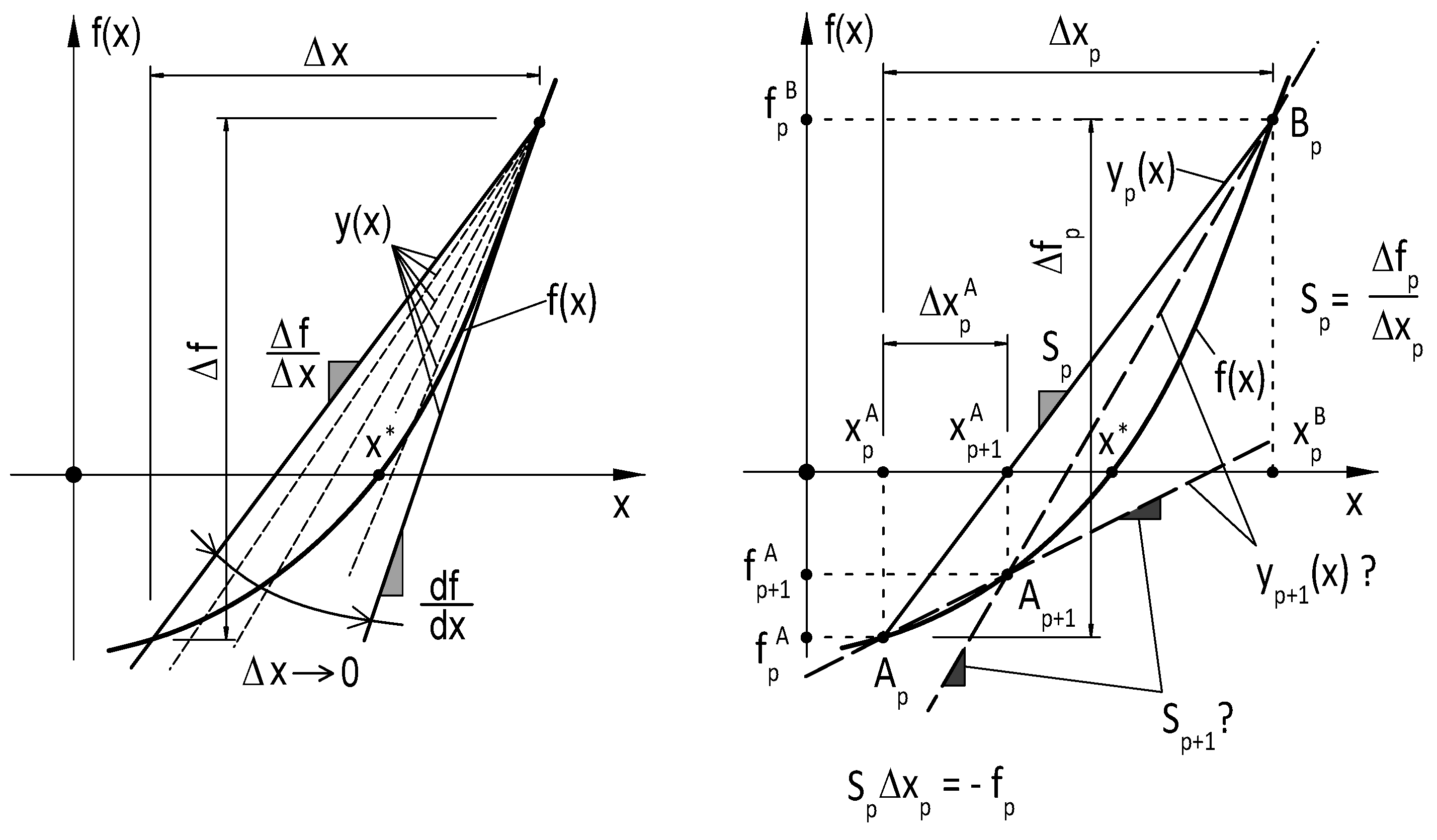
3.1. Single-Variable Case
3.2. Multi-Variable Case
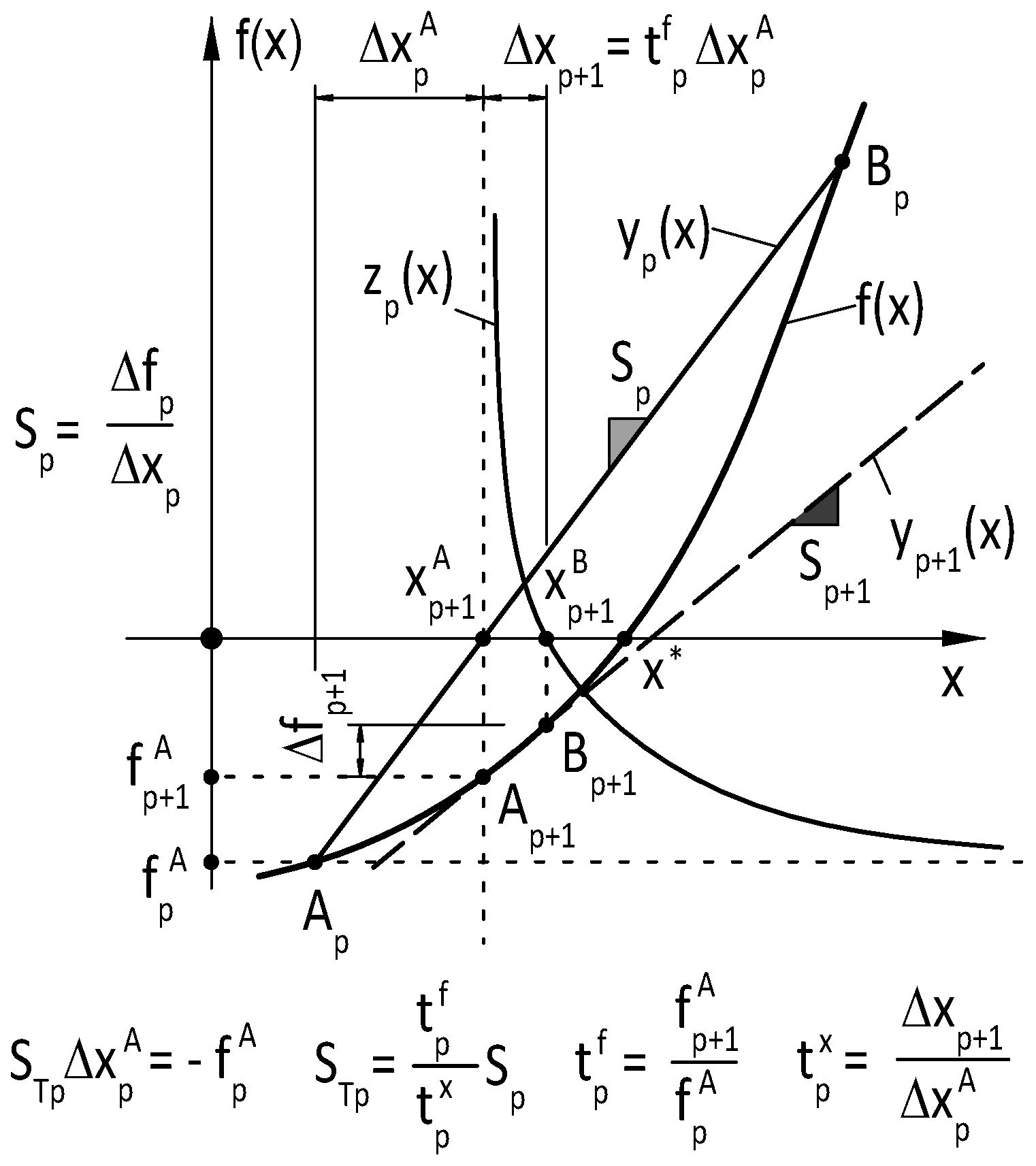
4. T-Secant Method
4.1. Single-Variable Case
4.2. Multi-Variable Case
5. Algorithm
- Step 1 : Generate a set of n additional approximates (Equation 4.14) and evaluate function values . Assure that .
- Step 2 (Classic secant update method) : Construct the Jacobian approximate matrix , determine its pseudo-inverse [31], calculate from Equation 3.21 and from Equation 5.2.
- Step 3 : If then terminate iteration, else continue with Step 4.
- Step 4 (suggested update method) : Calculate (assure that ), from Equation 4.16 and from Equation 4.24. Let and determine from Equation 4.25.
- Step 5 : Continue iteration from Step 1 with , and .
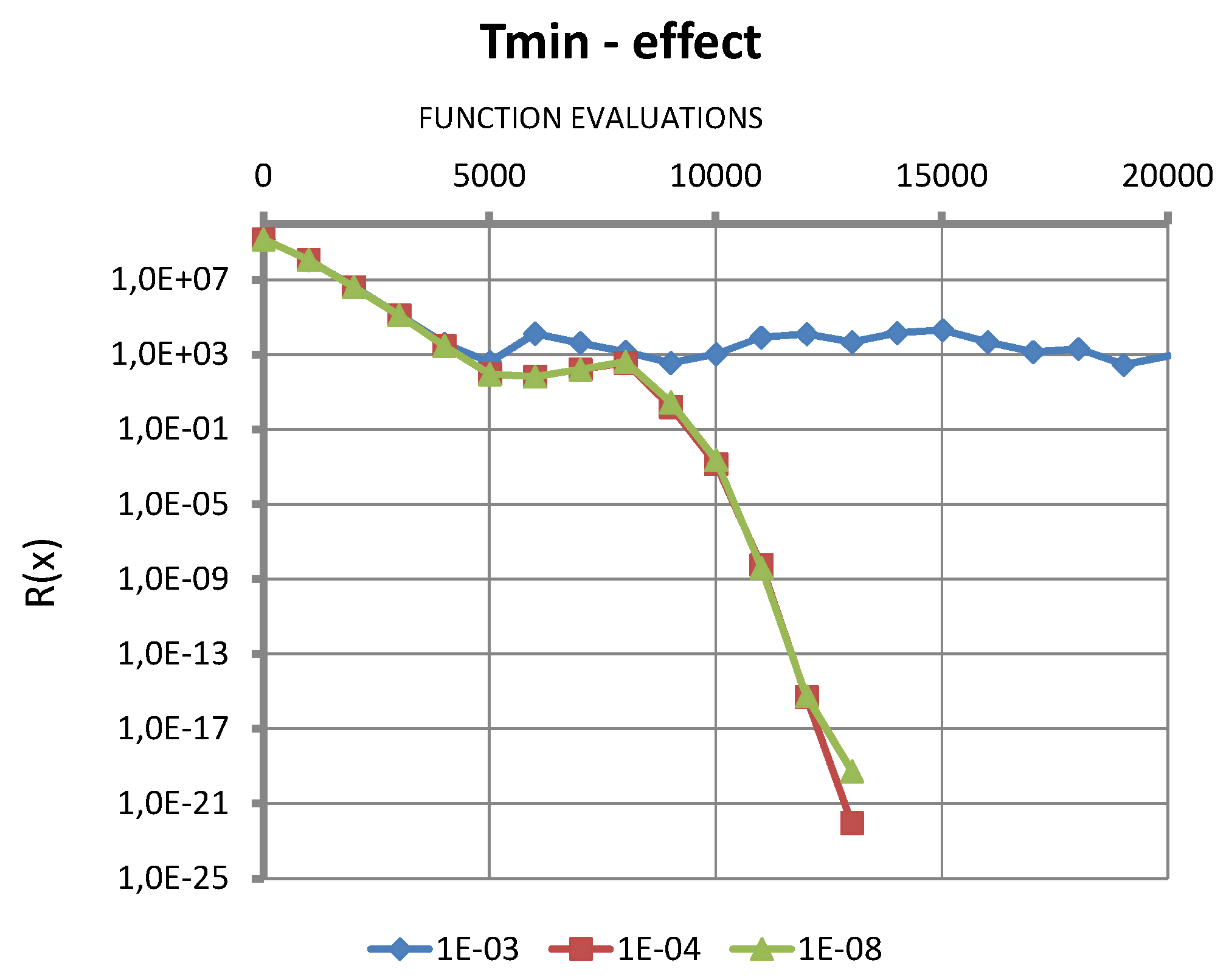
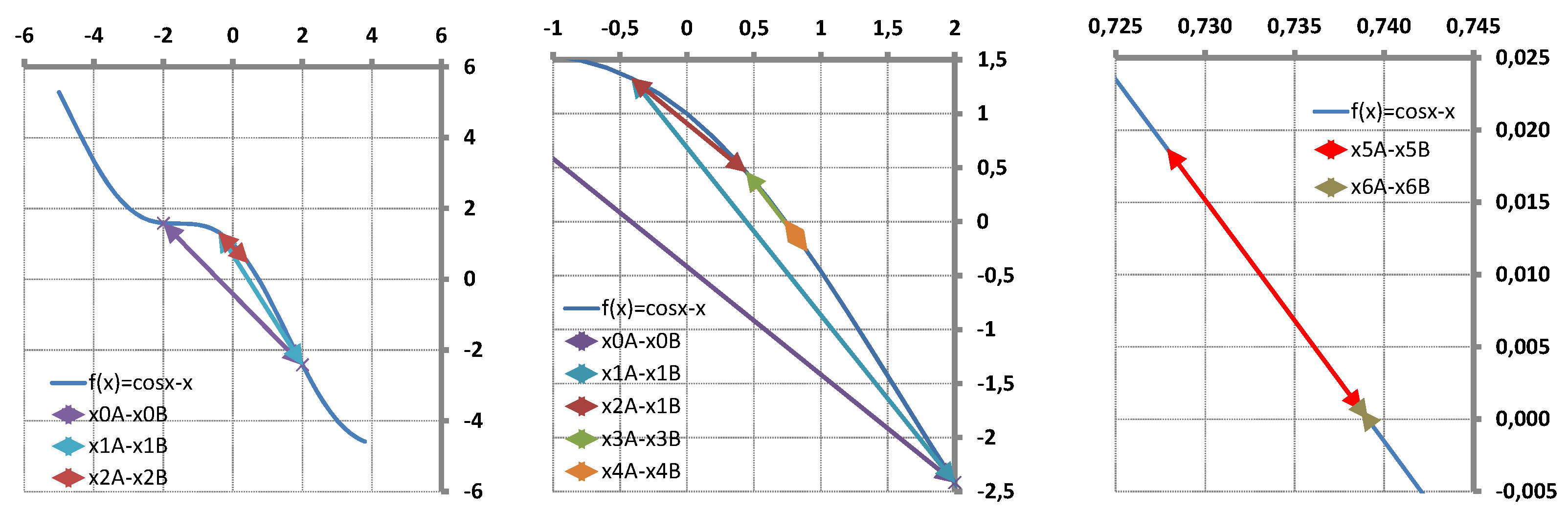
6. Numerical Tests Results
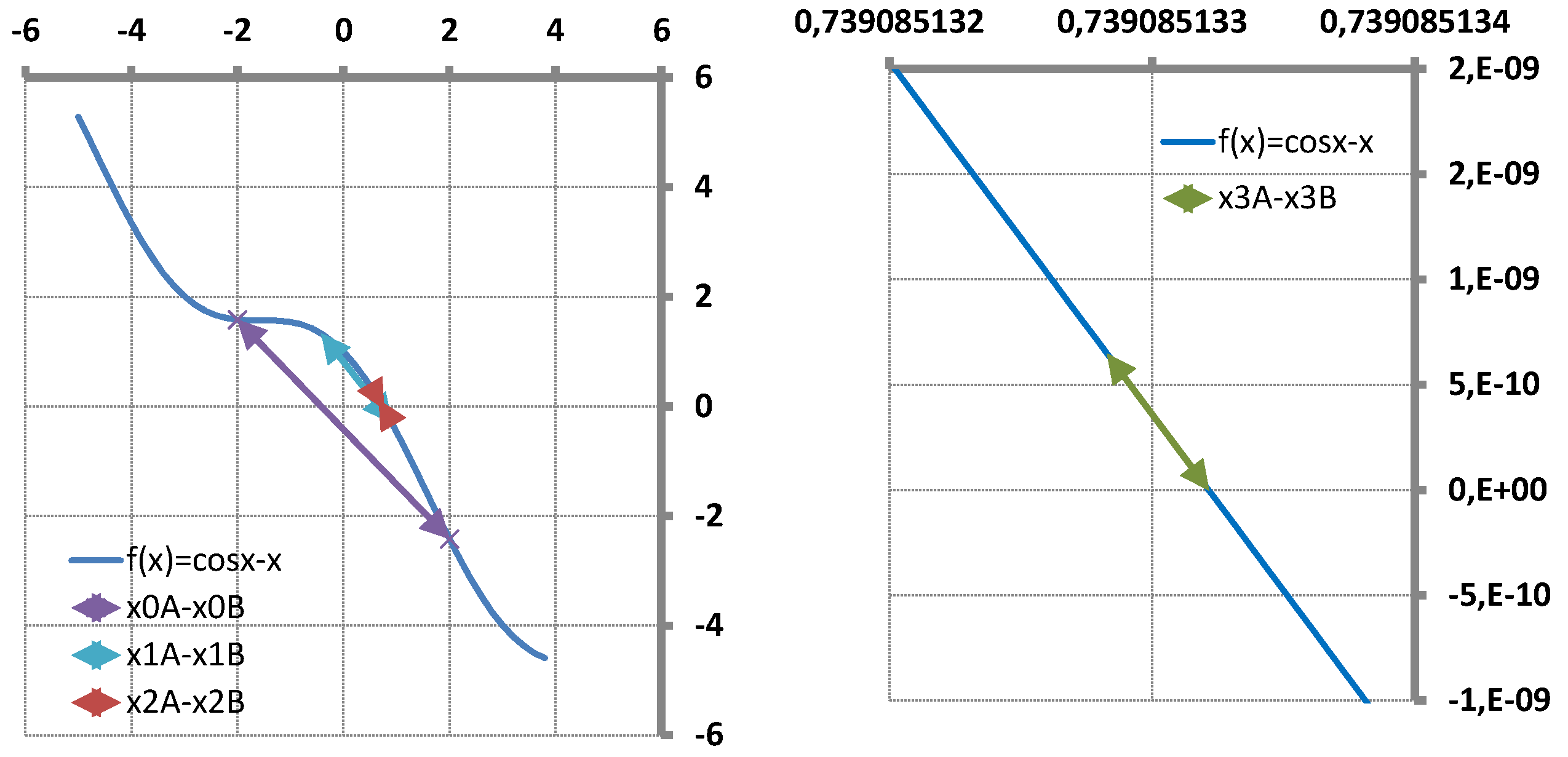
6.1. Single Variable Test Function
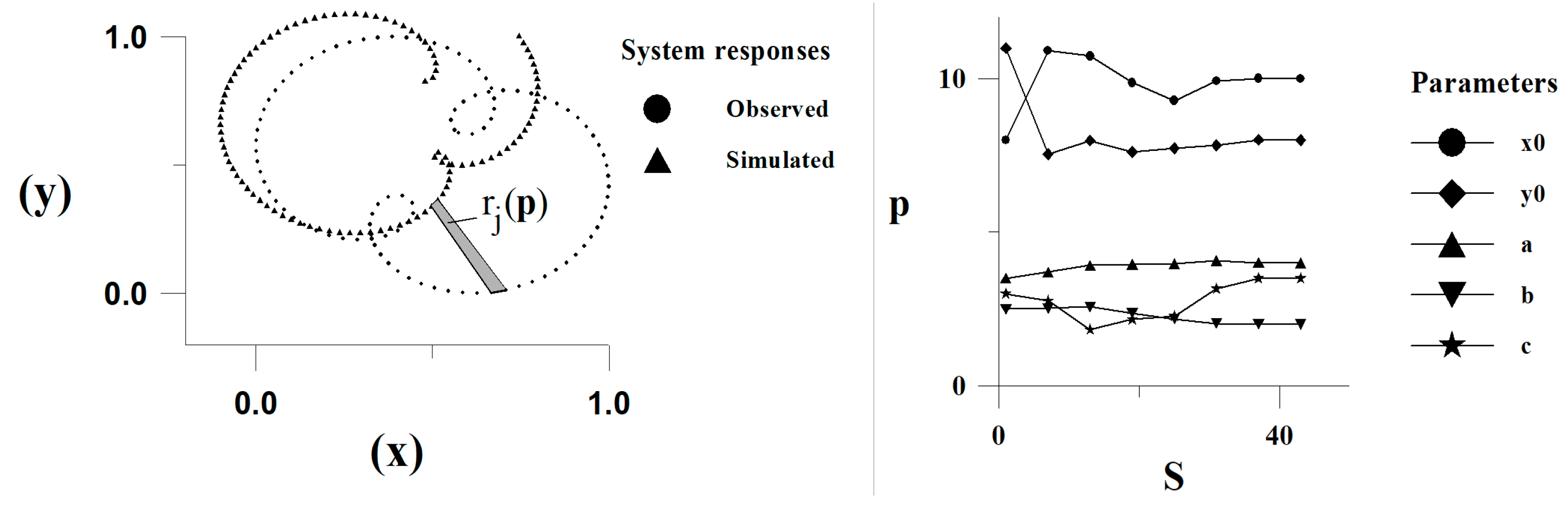
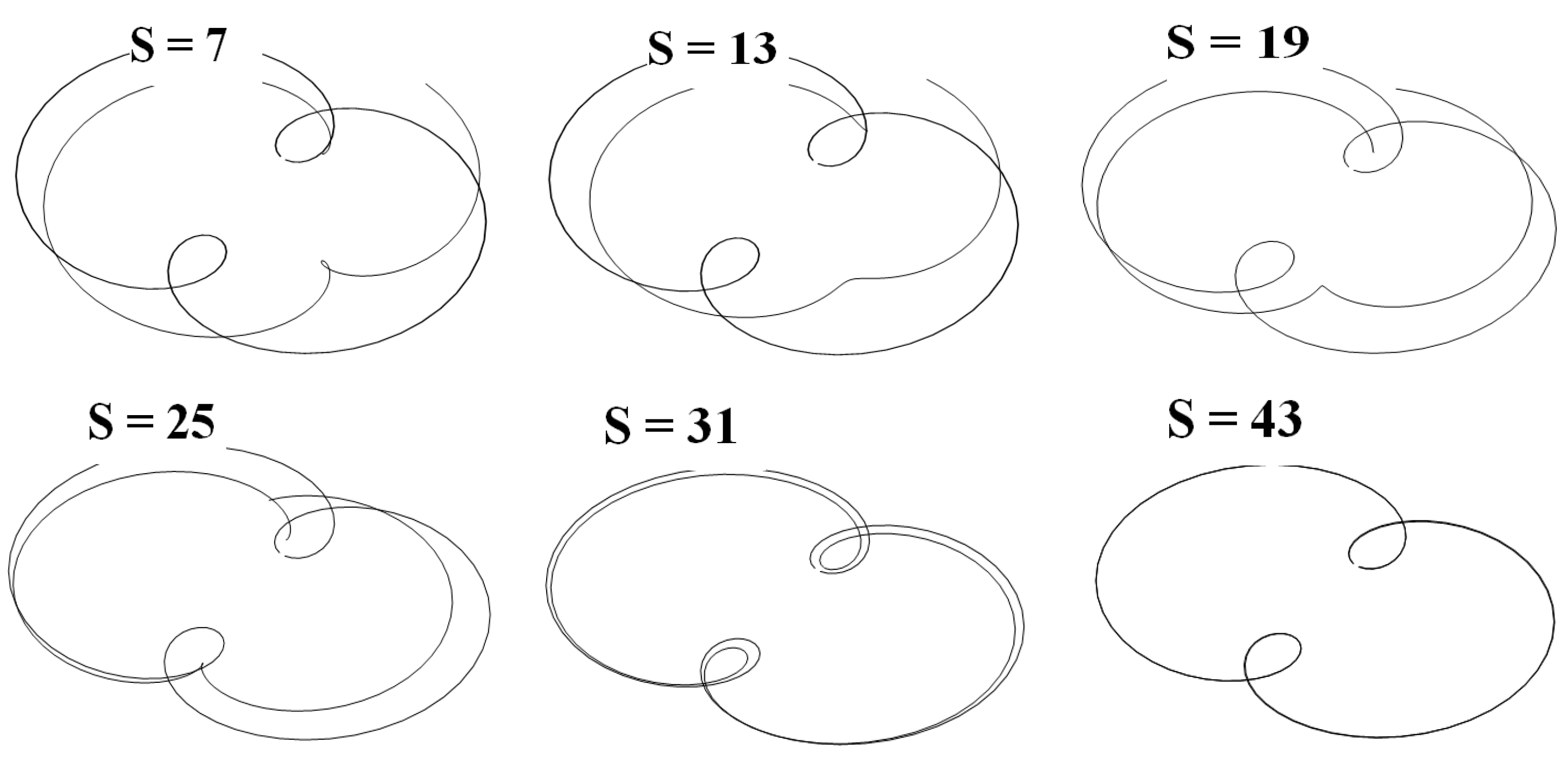
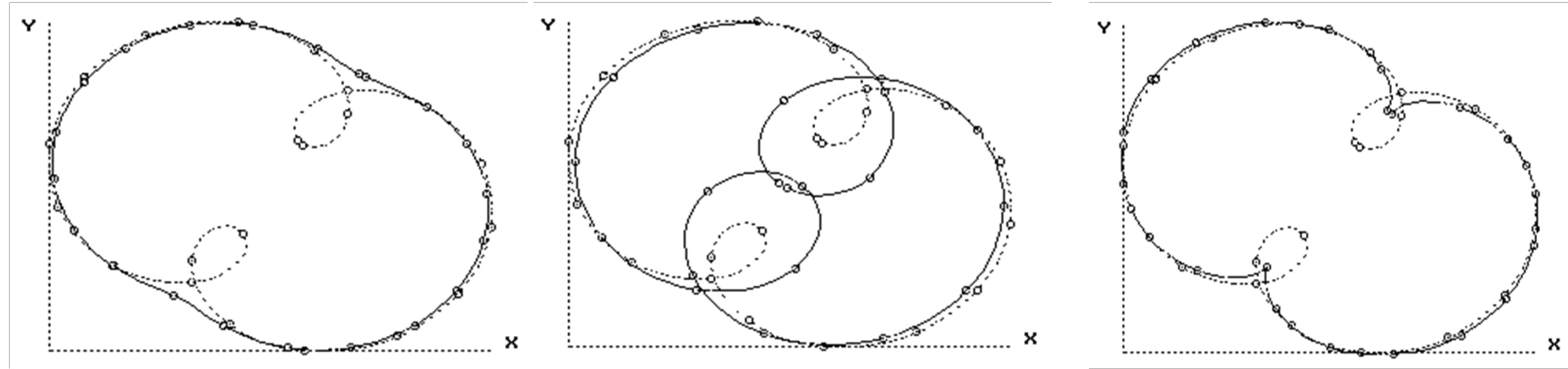
6.2. Solution of an Inverse Problem
7. Efficiency
8. Conclusions
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Amat, S.; Busquier, S.; Gutiérrez, J.M. Geometric constructions of iterative functions to solve nonlinear equations. J. Comput. Appl. Math. 2003, 157, 197–205. [Google Scholar] [CrossRef]
- Berzi, P. Convergence and Stability Improvement of Quasi-Newton Methods by Full-Rank Update of the Jacobian Approximates. MDPI AppliedMath 2024, 4, 143–181. [Google Scholar] [CrossRef]
- Berzi, P.; Beccu, R.; Lundberg, B. Identification of a Percussive Drill Rod Joint from its Response to Stress Wave Loading. International Journal of Impact Engineering 1994, 18, 281–290. [Google Scholar] [CrossRef]
- Berzi, P. Pile-Soil Interaction due to Static and Dynamic Load. Proceedings of the 13th International Conference on Soil Mechanics and Foundation Engineering, 1994, 1994-01-05, New Delhi, India, pp. 609–612.
- Berzi, P.; Popper, Gy. Evaluation of dynamic load test results on piles. Proceedings of the International Symposium on Identification of Nonlinear Mechanical Systems from Dynamic Tests (Euromech 280), 1991 1991-10-29, Ecully, France, pp. 121–128.
- Birgin, E.G.; Krejic, N.; Martinez, J.M. Globally convergent inexact quasi-Newton methods for solving nonlinear systems. Num. Algorithms. 2003, 32, 249–260. [Google Scholar] [CrossRef]
- Broyden, C. G. A class of Methods for Solving Nonlinear Simultaneous Equations. Mathematics of Computation. American Mathematical Society 1965, 19, 577–593. [Google Scholar]
- Broyden, C.G.; Dennis, J.E. , Mor, J.J. On the local and superlinear convergence of quasi-Newton methods. J. Inst. Math. Appl. 1973, 12, 223–245. [Google Scholar] [CrossRef]
- Chen, L.; Ma, Y. A new modified King–Werner method for solving nonlinear equations. Computers and Mathematics with Applications 2011, 62, 3700–3705. [Google Scholar] [CrossRef]
- Dembo, R.S.; Eisenstat, S.C.; Steihaug, T. Inexact Newton methods. SIAM J. Numer. Anal. 1971, 19, 400–408. [Google Scholar] [CrossRef]
- Dennis, J.E.; Mor, J.J. A characterization of superlinear convergence and its application to quasi-Newton methods. Mathematics and Computation 1974, 28, 543–560. [Google Scholar] [CrossRef]
- Dennis, J.E. Jr.; Schnabel, R.B. Numerical Methods for Unconstrained Optimization and Nonlinear Equations. Prentice-Hall, Englewood Cliffs, NJ, 1983.
- Gerlach, J. Accelerated convergence in Newton’s method. SIAM Rev. 1994, 36, 272–276. [Google Scholar] [CrossRef]
- Hegedus, Cs. Numerical Methods I. ELTE, Faculty of Informatics, Budapest, 2015.
- Homeier, H.H.H. On Newton-type methods with cubic convergence. J. Comput. Appl. Math. 2005, 176, 425–432. [Google Scholar] [CrossRef]
- Jisheng, K.; Yitian, L. , Xiuhua, W.; Third-order modification of Newton’s method. J. Comput. Appl. Math. 2007, 205, 1–5. [Google Scholar] [CrossRef]
- Kanwar, V.; Sharma, J.R. , Mamta J. A new family of Secant-like method with super-linear convergence. Appl. Math. Comput. 2005, 171, 104–107. [Google Scholar]
- King, R.F. ; Tangent method for nonlinear equations. Numer. Math. 1972, 18, 298–304. [Google Scholar] [CrossRef]
- Loshchilov, I.; Schoenauer, M.; Sebag, M. Adaptive Coordinate Descent. Genetic and Evolutionary Computation Conference (GECCO), ACM Press, 2011, 885–892.
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Computer Journal. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Martínez, J.M. Practical quasi-Newton methods for solving nonlinear systems. Journal of Computational and Applied Mathematics 2000, 124, 97–121. [Google Scholar] [CrossRef]
- Martinez, J.M.; Qi, L. Inexact Newton methods for solving non-smooth equations. J. Comput. Appl. Math. 1995, 60, 127–145. [Google Scholar] [CrossRef]
- Melman, A. Geometry and convergence of Euler’s and Halley’s methods. SIAM Rev. 1997, 39, 728–735. [Google Scholar] [CrossRef]
- Muller, D.E. A Method for Solving Algebraic Equations Using an Automatic Computer. Math. Tables and Other Aids to Computation 1956, 10, 208–215. [Google Scholar] [CrossRef]
- Ortega, J.M.; Rheinboldt, W.C. Iterative Solution of Nonlinear Equations in Several Variables, Academic Press, New York, 1970.
- Ostrowski, A.M. Solution of Equations and Systems of Equations. Academic Press, New York, 1966.
- Özban, A.Y. Some new variants of Newton’s method. Appl. Math. Letter. 2004, 17, 677–682. [Google Scholar] [CrossRef]
- Papakonstantinou, J.M.; Tapia, R.A. Origin and evolution of the secant method in one dimension. The American Mathematical Monthly 2013, 120/6, 500–518. [Google Scholar] [CrossRef]
- Popper, Gy. Numerical method for least square solving of nonlinear equations. Periodica Polytechnica. 1985, 29, 67–69. [Google Scholar]
- Powell, M. Powell, M.; J.; D. An efficient method for finding the minimum of a function of several variables without calculating derivatives. Computer Journal. 1964, 7, 155–162. [Google Scholar] [CrossRef]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A. , Wetterling, W.T. Numerical recepies. Cambridge University Press, Cambridge, 1986.
- Ren, H.; Wu, Q.; Bi, W. On convergence of a new secant-like method for solving nonlinear equations. Appl. Math. Comput. 2010, 217, 583–589. [Google Scholar] [CrossRef]
- Scavo, T.R.; Thoo, J.B. ; On the geometry of Halley’s method. American Math. Monthly. 1995, 102, 417–426. [Google Scholar] [CrossRef]
- Shaw, S.; Mukhopadhyay, B. An improved regula falsi method for finding simple roots of nonlinear equations. Appl. Math. and Computation 2015, 254, 370–374. [Google Scholar] [CrossRef]
- Stoer, J.; Bulirsch, R. Introduction to Numerical Analysis. Springer -Verlag, 2002.
- Strang, G. Introduction to Linear Algebra. Revised International Edition, Wellesley-Cambridge Press, 2005.
- Thukral, R. A New Secant-type method for solving nonlinear equations. Amer. J. Comput. Appl. Math. 2018, 8, 32–36. [Google Scholar]
- Traub, J.F. Iterative Methods for the Solution of Equations, 1st ed.; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1964. [Google Scholar]
- Wang, X.; Kou, J.; Gu, C. A new modified secant-like method for solving nonlinear equations. Comput. Math. Appl. 2010, 60, 1633–1638. [Google Scholar] [CrossRef]
- Weerakoon, S.; Fernando, T.G.I. ; A variant of Newton’s method with accelerated third-order convergence. Appl. Math. Letter. 2000, 13, 87–93. [Google Scholar] [CrossRef]
- Werner, W. ; Über ein Verfarhren der Ordnung 1 + √ 2 zur Nullstellenbestimmung. Numer. Math. 1979, 32, 333–342. [Google Scholar] [CrossRef]
- Wolfe, P. The Secant Method for Simultaneous Nonlinear Equations. Communications of the ACM 1959, 2, 12–13. [Google Scholar] [CrossRef]
- Zhang, H.; Li, D.-S.; Liu, Y.-Z. A new method of secant-like for nonlinear equations. Commun. Nonlinear Sci. numer. Simul. 2009, 14, 2923–2927. [Google Scholar]
| Single-variable | Multi-variable | Equations | |
|---|---|---|---|
| 1 | 3.18 | ||
| 2 | 3.17 | ||
| 3 | 3.2, 3.16 | ||
| 4 | 3.5, 3.21 | ||
| 5 | 3.8, 3.26 |
| Classic secant method | Suggested update method | Equations | |
|---|---|---|---|
| 1 | 4.14 | ||
| 2 | 3.18, 4.15 | ||
| 3 | 3.17 | ||
| 4 | 4.17 | ||
| 5 | 4.16 | ||
| 6 | 3.16, 4.19 | ||
| 7 | 3.24, 4.18 | ||
| 8 | 3.23, 4.22 | ||
| 9 | 3.22, 4.23 | ||
| 10 | 4.24 | ||
| 11 | 4.25 |
| 0 | 1.700 | 2.000 | 0.421 | -0.085 | 0.036 | 2 | 1.23 | ||
| 1 | 2.121 | 2.156 | -0.036 | -0.359 | -0.013 | 4 | 0.87 | ||
| 2 | 2.085 | 2.072 | 0.013 | -0.342 | 0.0044 | 1.08 | 6 | 0.76 | |
| 3 | 2.098 | 2.102 | -0.0044 | -0.348 | -0.0015 | 0.97 | 8 | 0.70 | |
| 4 | 2.093 | 2.092 | 0.0015 | -0.346 | 0.00053 | 1.01 | 10 | 0.67 | |
| 5 | 2.0949 | 2.0955 | -0.00053 | -0.347 | -0.00018 | 0.997 | 12 | 0.65 | |
| 6 | 2.0944 | 2.0942 | 0.00018 | -0.346 | 0.000063 | 1.001 | 14 | 0.63 | |
| 7 | 2.0946 | 2.0947 | -0.000063 | -0.346 | 0.000022 | 0.9997 | 16 | 0.62 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| Method | [38] | [26] | [7] | |||
|---|---|---|---|---|---|---|
| 1 | Secant | 1 | 1.618… | 1.618… | 1.618… | 4.0 |
| 2 | Newton | 2 | 2.0 | 1.0 | 1.414… | 3.0 |
| 3 | T-Secant | 2 | 2.618… | 1.309… | 1.618… | 4.5 |
| 4 | TS - const. | 2 | 1.0 | 0.5 | 1.0 | 0.6 |
| 5 | T-Newton | 3 | 3.0 | 1.0 | 1.442… | 3.0 |
| 6 | Chen [9] | 3 | 1.618… | 0.539… | 1.173… | − |
| 7 | Wang [39] | 5 | 1.618… | 0.323… | 1.101… | − |
| Method | ||||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | Broyden 1. [7] | 4.92 | - | 59 | 0.391 | 0.78 | |
| 2 | 2 | Broyden 2. [7] | 4.92 | - | 39 | 0.607 | 1.22 | |
| 3 | 2 | Powell [30] | 4.92 | - | 151 | 0.150 | 0.30 | |
| 4 | 2 | ACD [19] | 130.1 | - | 325 | 0.086 | 0.17 | |
| 5 | 2 | Nelder-Mead [20] | 2.00 | - | 185 | 0.127 | 0.25 | |
| 6 | 2 | T-secant [7][30] | 4.92 | 3 | 9 | 6.573 | 13.15 | |
| 7 | 2 | T-secant [19] | 130.1 | 3 | 9 | 6.937 | 13.87 | |
| 8 | 2 | T-secant [20] | 2.00 | 2 | 6 | 5.556 | 11.11 | |
| 9 | 3 | T-secant | 72.72 | 5 | 20 | 1.809 | 5.43 | |
| 10 | 3 | 32.47 | 4 | 16 | 3.815 | 11.45 | ||
| 11 | 5 | 93.53 | 8 | 48 | 0.760 | 3.80 | ||
| 12 | 5 | 7.19 | 4 | 24 | 1.351 | 6.76 | ||
| 13 | 10 | 202.6 | 14 | 154 | 0.408 | 4.08 | ||
| 14 | 200 | 92.78 | 10 | 2010 | 0.042 | 8.44 | ||
| 15 | 1000 | 212.4 | 6 | 6006 | 0.006 | 5.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




