Submitted:
09 January 2025
Posted:
10 January 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Background
2.1. GT designs
2.2. Representing univariance, multivariate, and bifactor GT designs within SEMs
2.3. Univariate GT designs
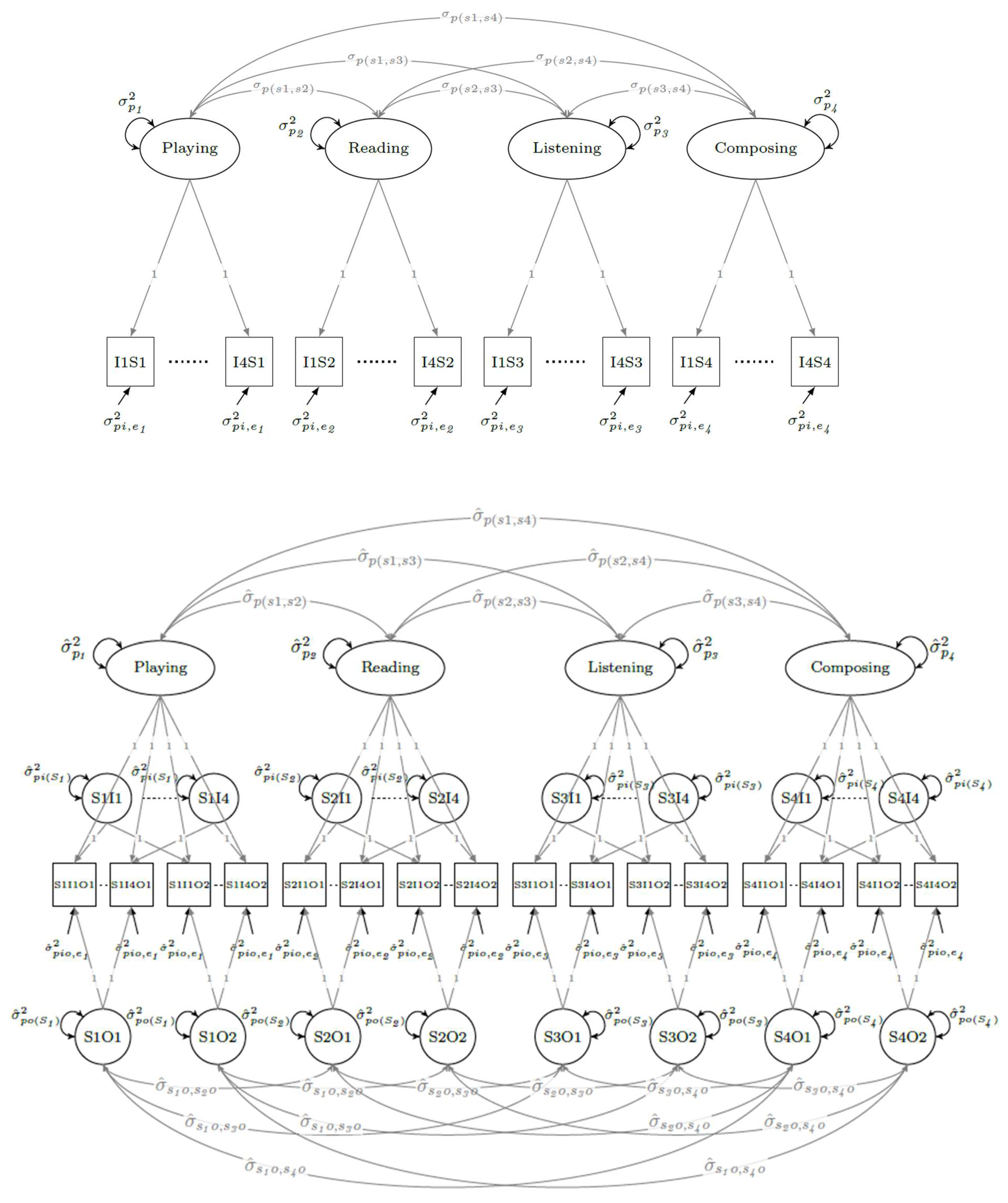
2.3. Multivariate GT designs
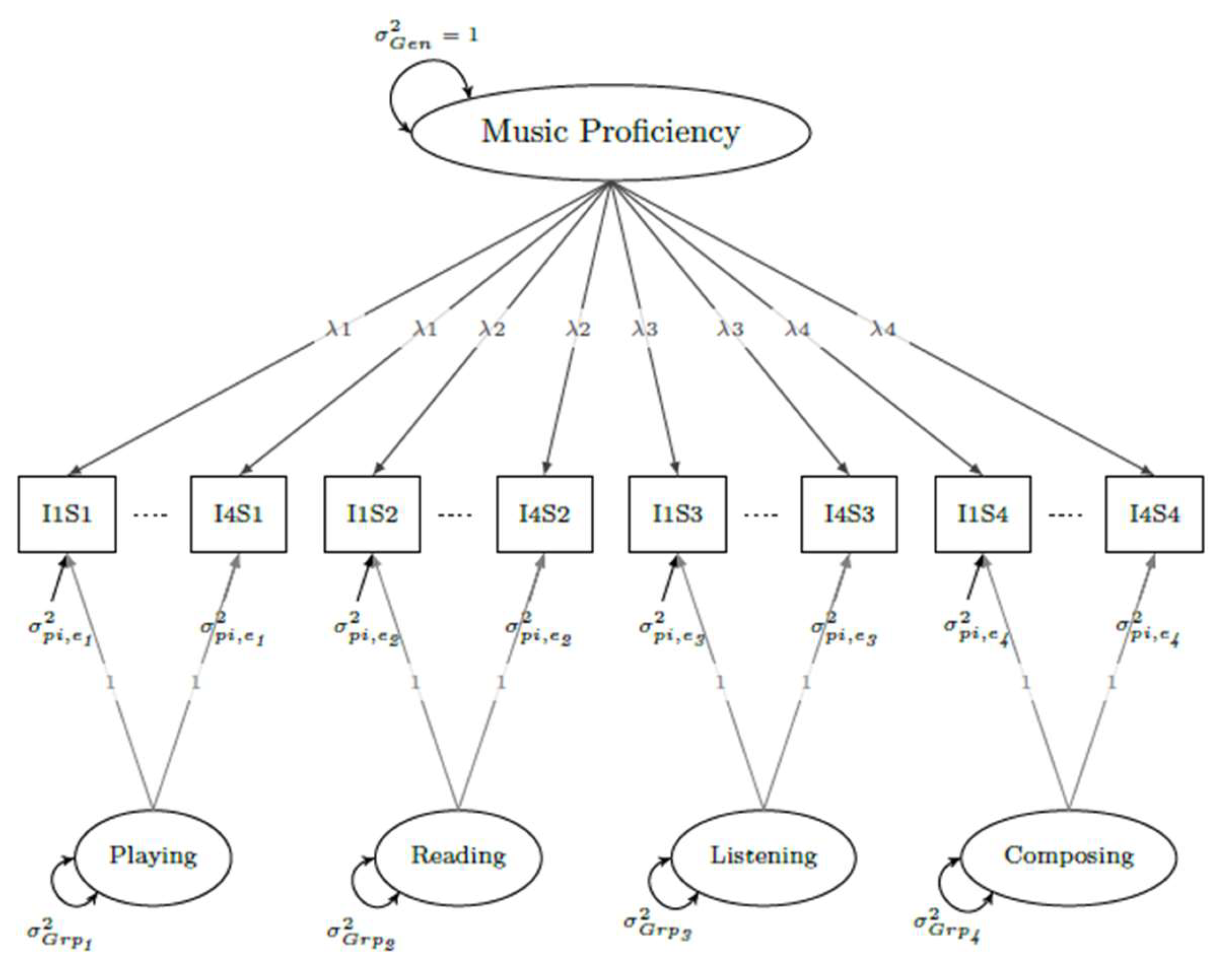
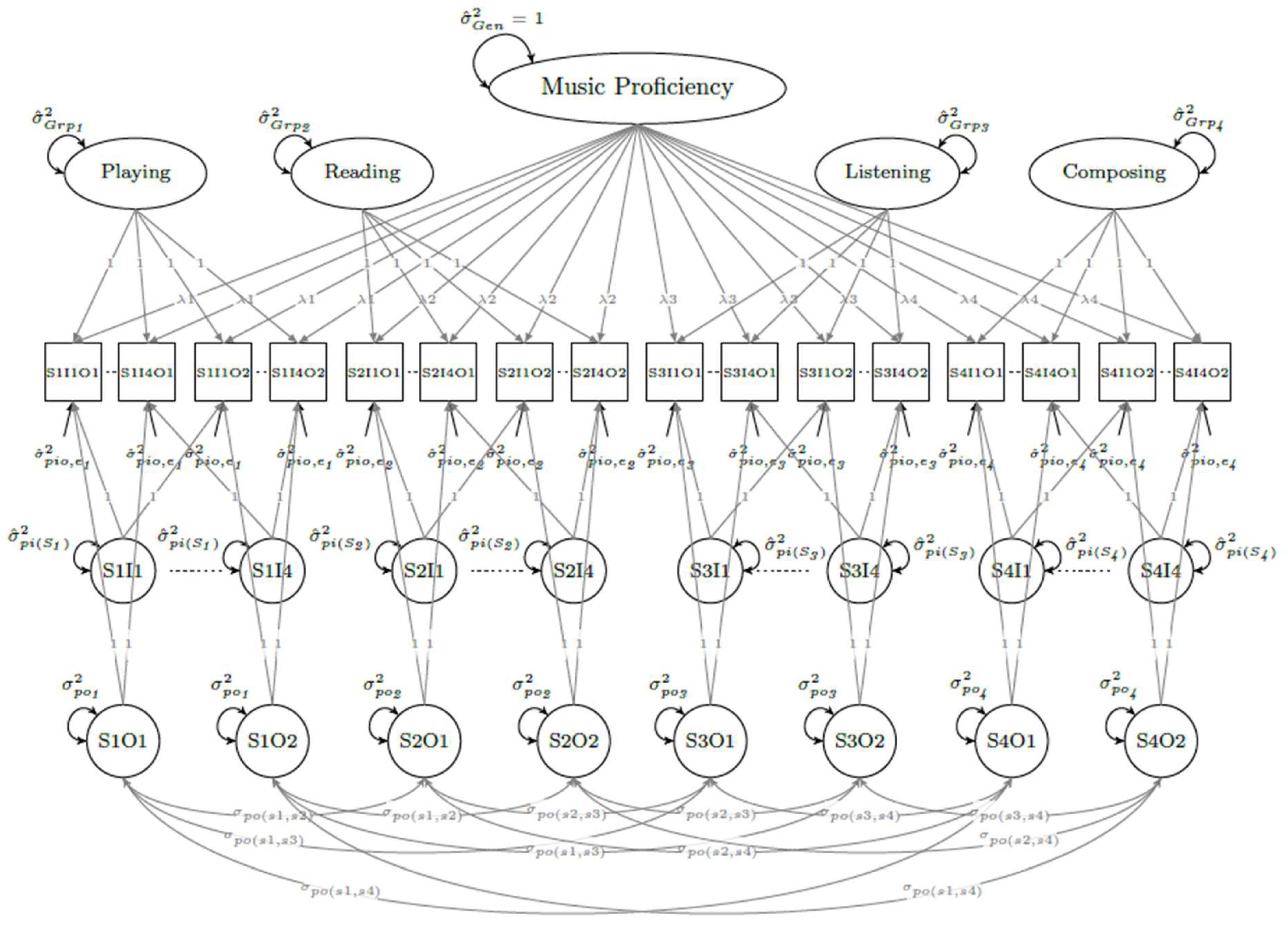
2.4. Bifactor GT designs
2.5. Using GT multivariate and bifactor designs to evaluate subscale viability.
2.6. Comparing GT univariate, multivariate, and bifactor designs.
2.7. Further advantages of using SEMs to perform GT analyses
3. This Investigation
- G coefficients, D coefficients, and variance components obtained from the GT-based univariate and multivariate SEMs will be highly congruent with those obtained from mGENOVA.
- Multivariate and bifactor GT SEMs will yield comparable G and D coefficients for subscale and composite scores.
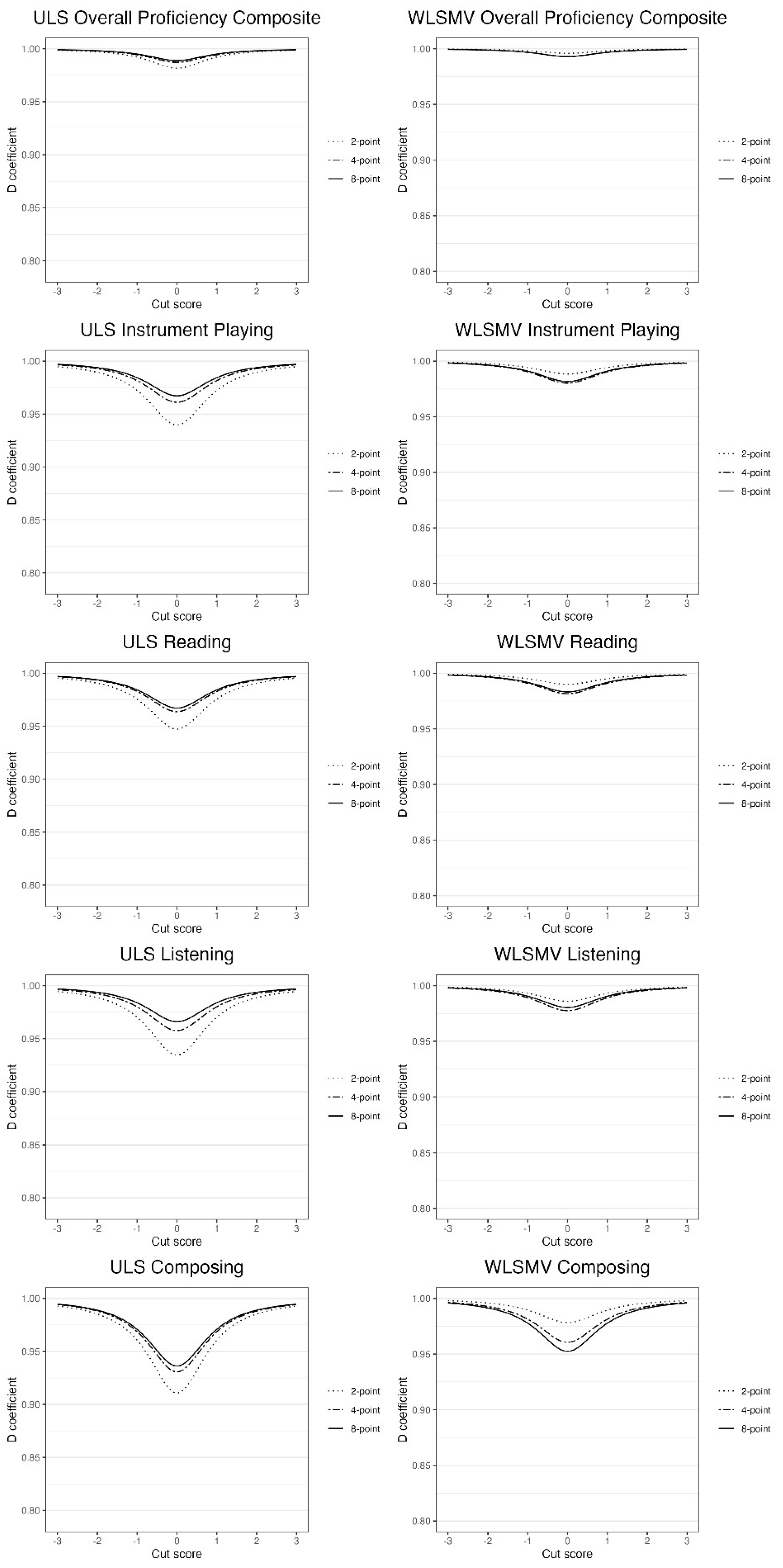
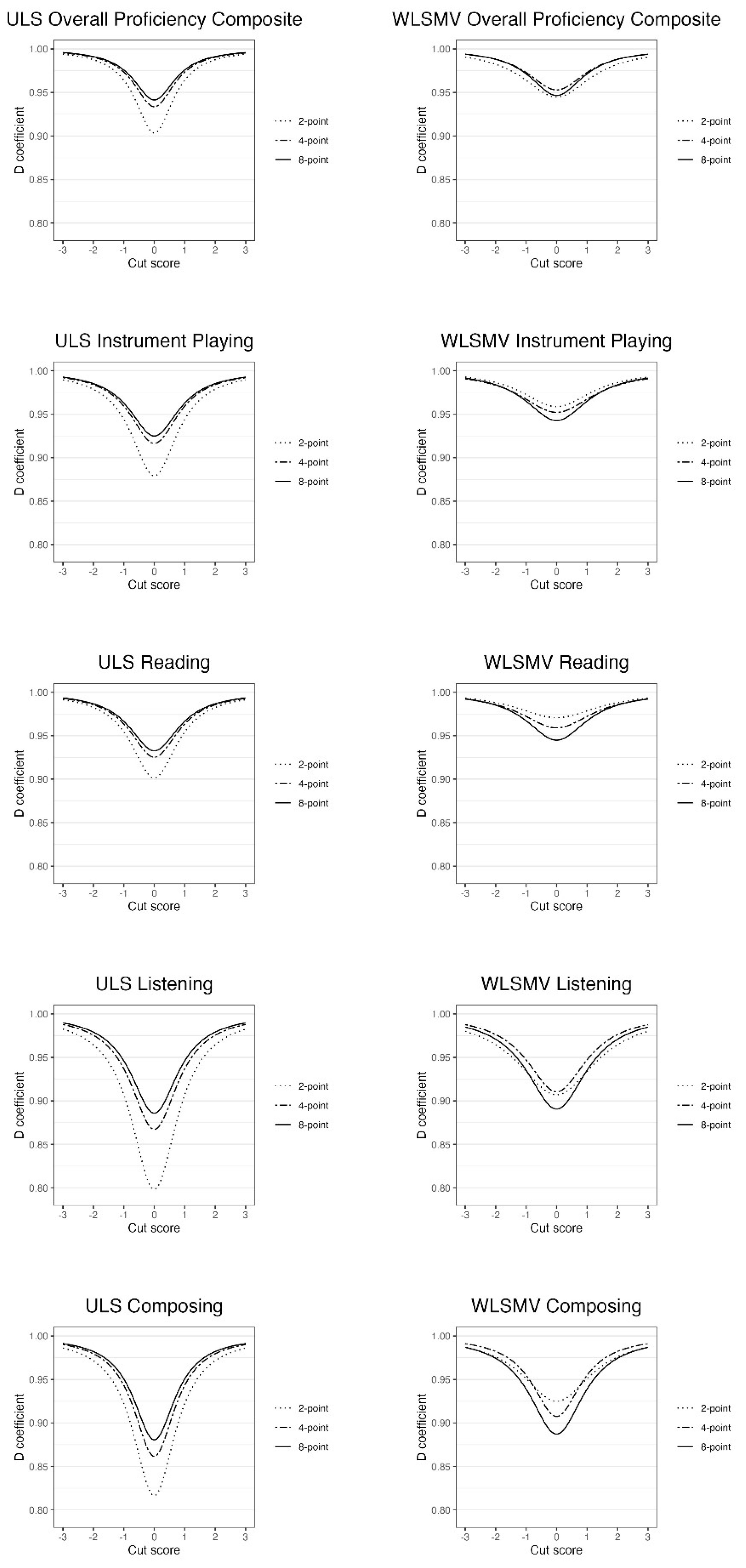
- G and D coefficients for the pi designs will exceed those for the pio designs due to control of fewer sources of measurement error.
- Across all multivariate designs, correlation coefficients between scale scores will be higher after correcting for measurement error, but the difference between corrected and uncorrected coefficients will be greater in pio than in pi designs.
- General factor effects will exceed group factor effects at both subscale and composite levels within the bifactor designs.
- Similar patterns of VARs for subscales will be found across multivariate and bifactor designs.
- Composite and subscale scores will be affected by specific-factor (method), transient (state), and response-random (within-occasion noise) measurement error within the pio designs, but those effects be greater overall at the subscale than composite level due to inclusion of fewer item scores.
- Differences in G and D coefficients for two, four, and eight item scale points will be greater on observed score than on continuous latent response variable metrics.
- G and D coefficients will be greater on continuous latent response variable than on observed score metrics but to diminishing degrees with increases in numbers of item scale points.
4. Methods
4.1. Participants, Measures, and Procedure
4.2. Analyses
5. Results
5.1. Means, Standard Deviations, and Conventional Reliability Estimates for MUSPI-S Scores
5.2. Key indices for GT pi Designs
5.2. Key indices for GT pio Designs
6. Discussion
6.1. Overview
6.2. Effectiveness of the Indicator-Mean Method
6.3. Univariate GT Analyses for Shortened and Full-Length Forms of the MUSPI-S
6.4. Multivariate GT Analyses of MUSPI-S Scores
6.5. Bifactor GT Analyses of MUSPI-S Scores
6.6. Other Noteworthy Aspects of the GT SEM Designs
7. Final Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cronbach, L.J.; Rajaratnam, N.; Gleser, G.C. Theory of generalizability: A liberalization of reliability theory. Br. J. Stat. Psychol. 1963, 16, 137–163. [Google Scholar] [CrossRef]
- Rajaratnam, N.; Cronbach, L.J.; Gleser, G.C. Generalizability of stratified-parallel tests. Psychometrika 1965, 30, 39–56. [Google Scholar] [CrossRef] [PubMed]
- Gleser, G.C.; Cronbach, L.J.; Rajaratnam, N. Generalizability of scores influenced by multiple sources of variance. Psychometrika 1965, 30, 395–418. [Google Scholar] [CrossRef] [PubMed]
- Cronbach, L.J.; Gleser, G.C.; Nanda, H.; Rajaratnam, N. The Dependability of Behavioral Measurements: Theory of Generalizability for Scores and Profiles; Wiley: New York, NY, USA, 1972. [Google Scholar]
- Brennan, R.L. Elements of Generalizability Theory (Revised Edition); American College Testing: Iowa City, IA, USA, 1992. [Google Scholar]
- Fyans, L.J. Generalizability Theory: Inferences and Practical Applications; Jossey-Bass: San Francisco, 1983. [Google Scholar]
- Shavelson, R.J.; Webb, N.M. Generalizability Theory: A Primer; Sage: Thousand Oaks, CA, USA, 1991. [Google Scholar]
- Brennan, R.L. Generalizability Theory; Springer: New York, NY, USA, 2001. [Google Scholar]
- Cardinet, J. ; Johnson. S.; Pini, G. Applying generalizability theory using EduG. Routledge: New York, 2010. [Google Scholar]
- Crocker, L.; Algina, J. Introduction to Classical and Modern Test Theory. Harcourt Brace: New York, 1986.
- McDonald, R.P. Test theory: A unified approach. Erlbaum: Mahwah, NJ, 1999.
- Raykov, T.; Marcoulides, G.A. Introduction to psychometric theory. Routledge: New York, NY, 2011.
- Marcoulides, G.A. Generalizability theory. In Handbook of Applied Multivariate Statistics and Mathematical Modeling; Tinsley, H., Brown, S., Eds.; Academic Press: San Diego, CA, 2000; pp. 527–551. [Google Scholar]
- Wiley, E.W.; Webb, N.M.; Shavelson, R.J. The generalizability of test scores. In APA Handbook of Testing and Assessment in Psychology: Vol. 1. Test Theory and Testing and Assessment in Industrial and Organizational Psychology; Geisinger, K.F., Bracken, B.A., Carlson, J.F., Hansen, J.C., Kuncel, N.R., Reise, S. P., Rodriguez, M.C., Eds.; American Psychological Association: Washington, DC, 2013; pp. 43–60. [Google Scholar]
- Webb, N.M.; Shavelson, R.J.; Steedle, J.T. Generalizability theory in assessment contexts; In Handbook on Measurement, Assessment, and Evaluation in Higher Education, Secolsky, C., Denison, D.B., Eds.; Routledge: New York, NY, 2012; pp. 152–169. [Google Scholar]
- Gao, X.; Harris, D.J. Generalizability theory. In APA Handbook of Research Methods in Psychology, Vol. 1. Foundations, Planning, Measures, and Psychometrics; Cooper, H., Camic, P.M., Long, D.L., Panter, A.T., Rindskopf, D., Sher, K.J., Eds.; American Psychological Association, 2012; pp. 661–681.
- Allal, L. Generalizability theory. In The International Encyclopedia of Educational Evaluation; Walberg, H.J., Haertel, G.D., Eds.; Pergamon: Oxford, England, 1990. [Google Scholar]
- Shavelson, R.J.; Webb, N.M. Generalizability theory. In Encyclopedia of Educational Research; Alkin, M.C., Ed.; Macmillan: New York, NY, 1992; Volume 2, pp. 538–543. [Google Scholar]
- Brennan, R.L. Generalizability theory. In The SAGE Encyclopedia of Social Science Research Methods; Lewis-Beck, M.S., Bryman, A.E., Liao, T.F., Eds.; SAGE: Thousand Oaks, CA, 2004; Volume 2, pp. 418–420. [Google Scholar]
- Shavelson, R.J.; Webb, N.M. Generalizability theory. In Encyclopedia of Statistics in Behavioral Science; Everitt, B.S., Howell, D.C., Eds.; Wiley, 2005; pp. 717–719.
- Brennan, R.L. Generalizability theory. In International Encyclopedia of Education (3rd ed.); Peterson, P., Baker, E.; McGaw, B., Eds.; Elsevier, 2010; Volume 4, pp. 61–68.
- Matt, G.E.; Sklar, M. Generalizability theory. In International Encyclopedia of the Social & Behavioral Sciences; Wright, J.D., Ed.; Elsevier, 2015; Volume 9, pp. 834–838.
- Franzen, M. Generalizability theory. In Encyclopedia of Clinical Neuropsychology; Kreutzer, J.S., DeLuca, J., Caplan, B., Eds.; Springer International Publishing: Cham, 2018; pp. 1554–1555. [Google Scholar]
- Brennan, R.L.; Kane, M.T. review. In New Directions for Testing and Measurement: Methodological Developments (No.4); Traub, R.E., Ed.; Jossey-Bass: San Francisco, CA, 1979; pp. 33–51. [Google Scholar]
- Brennan, R.L. Applications of generalizability theory. In Criterion-Referenced Measurement: The State of the Art; Berk, R.A., Ed.; The Johns Hopkins University Press: Baltimore, 1980. [Google Scholar]
- Jarjoura, D.; Brennan, R.L. Multivariate generalizability models for tests developed according to a table of specifications. In New Directions for Testing and Measurement: Generalizability Theory: Inferences and Practical Applications (No. 18); Fyans, L.J., Ed.; Jossey-Bass: San Francisco, CA, 1983; pp. 83–101. [Google Scholar]
- Webb, N.M.; Shavelson, R.J.; Maddahian, E. Multivariate generalizability theory. In New Directions in Testing and Measurement: Generalizability Theory (No. 18); Fyans, L.J., Ed.; Jossey-Bass: San Francisco, CA, 1983; pp. 67–82. [Google Scholar]
- Brennan, R.L. Estimating the dependability of the scores. In A Guide to Criterion-Referenced Test Construction; Berk, R.A., Ed.; The Johns Hopkins University Press: Baltimore, 1984; pp. 292–334. [Google Scholar]
- Allal, L. Generalizability theory. In Educational Research, Methodology, and Measurement; Keeves, J.P., Ed.; Pergamon: New York, 1988; pp. 272–277. [Google Scholar]
- Feldt, L.S.; Brennan, R.L. Reliability. In Educational Measurement (), 3rd ed.; Linn, R.L., Ed.; American Council on Education and Macmillan: New York, 1989; pp. 105–146. [Google Scholar]
- Brennan, R.L. Generalizability of performance assessments. In Technical Issues in Performance Assessments; Phillips, G.W., Ed.; National Center for Education Statistics: Washington, DC, 1996; pp. 19–58. [Google Scholar]
- Marcoulides, G.A. Applied generalizability theory models. In Modern Methods for Business Research; Marcoulides, G.A., Ed.; Erlbaum: Mahwah, NJ, 1998. [Google Scholar]
- Strube, M.J. Reliability and generalizability theory. In Reading and Understanding More Multivariate Statistics; Grimm, L.G., Yarnold, P.R., Eds.; American Psychological Association: Washington, DC, 2000; pp. 23–66. [Google Scholar]
- Haertel, E.H. Reliability. In Educational Measurement (), 4th ed.; Brennan, R.L., Ed.; American Council on Education/Praeger: Westport, CT, 2006; pp. 65–110. [Google Scholar]
- Kreiter, C.D. Generalizability theory. In Assessment in Health Professions Education; Downing, S.M., Yudkowsky, R., Eds.; Routledge: New York, 2009; pp. 75–92. [Google Scholar]
- Streiner, D.L.; Norman, G.R.; Cairney, J. Generalizability theory. In Health Measurement Scales: A Practical Guide to Their Development and Use; Oxford University Press, 2014; pp. 200–226.
- Shavelson, R.J.; Webb, N. Generalizability theory and its contribution to the discussion of the generalizability of research findings. In Generalizing from Educational Research: Beyond Qualitative and Quantitative Polarization; Ercikan, K., Roth, W., Eds.; Routledge: New York, 2019; pp. 13–32. [Google Scholar]
- Kreiter, C.D.; Zaidi, N.L.; Park, Y. S. Generalizability theory. In Assessment in Health Professions Education; Yudkowsky, R., Park, Y. S., Downing, S.M., Eds.; Routledge: New York, NY, 2020; pp. 51–69. [Google Scholar]
- Brennan, R.L. Generalizability theory. In The History of Educational Measurement: Key Advancements in Theory, Policy, and Practice; Clauser, B.E., Bunch, M.B., Eds.; Routledge: New York, NY, 2022; pp. 206–231. [Google Scholar]
- Cardinet, J.; Tourneur, Y.; Allal, L. The symmetry of generalizability theory: Applications to educational measurement. J. Educ. Meas. 1976, 13, 119–135. [Google Scholar] [CrossRef]
- Shavelson, R.J.; Dempsey Atwood, N. (1976). Generalizability of measures of teaching behavior. Rev. Educ. Res. 1976, 46, 553–611. [Google Scholar] [CrossRef]
- Cardinet, J.; Tourneur, Y.; Allal, L. Extension of generalizability theory and its applications in educational measurement. J. Educ. Meas. 1981, 18, 183–204. [Google Scholar] [CrossRef]
- Shavelson, R.J.; Webb, N.M. Generalizability theory: 1973–1980. Brit. J. Math. Stat. Psy. 1981, 34, 133–166. [Google Scholar] [CrossRef]
- Webb, N.M.; Shavelson, R.J. Multivariate generalizability of General Educational Development ratings. J. Educ. Meas. 1981, 18, 13–22. [Google Scholar] [CrossRef]
- Nußbaum, A. Multivariate generalizability theory in educational measurement: An empirical study. Appl. Psych. Meas. 1984, 8, 219–230. [Google Scholar] [CrossRef]
- Shavelson, R.J.; Webb, N.M.; Rowley, G.L. Generalizability theory. Am. Psychol. 1989, 44, 44–922. [Google Scholar] [CrossRef]
- Brennan, R.L. Generalizability theory. Educ. Meas.-Issues Pra. 1992, 11, 27–34. [Google Scholar] [CrossRef]
- Demorest, M.E.; Bernstein, L.E. Applications of generalizability theory to measurement of individual differences in speech perception. J. Acad. Reh. 1993, 26, 39–50. [Google Scholar]
- Brennan, R.L.; Johnson, E.G. Generalizability of performance assessments. Educ. Meas.-Issues Pra. 1995, 14, 9–12. [Google Scholar] [CrossRef]
- Cronbach, L.J.; Linn, R.L.; Brennan, R.L.; Haertel, E. Generalizability analysis for performance assessments of student achievement for school effectiveness. Educ. Psychol. Meas. 1997, 57, 373–399. [Google Scholar] [CrossRef]
- Lynch, B.K.; McNamara, T.F. Using G-theory and many-facet Rasch measurement in the development of performance assessments of the ESL speaking skills of immigrants. Lang. Test. 1998, 15, 15,158–180. [Google Scholar] [CrossRef]
- Hoyt, W.T.; Melby, J.N. Dependability of measurement in counseling psychology: An introduction to generalizability theory. The Counseling Psychologist 1999, 27, 325–352. [Google Scholar] [CrossRef]
- Brennan, R.L. (2000). (Mis)conceptions about generalizability theory. Educ. Meas.-Issues Pra. 2000, 19, 5–10. [Google Scholar] [CrossRef]
- Brennan, R.L. (2000). Performance assessments from the perspective of generalizability theory. Appl. Psych. Meas. 2000, 24, 339–353. [Google Scholar] [CrossRef]
- Brennan, R.L. Generalizability theory and classical test theory. Appl. Meas. Educ. 2010, 24, 1–21. [Google Scholar] [CrossRef]
- Cronbach, L.J.; Shavelson, R.J. My current thoughts on coefficient alpha and successor procedures. Educ. Psychol. Meas. 2004, 64, 391–418. [Google Scholar] [CrossRef]
- Tavakol, M.; Brennan, R.L. Medical education assessment: A brief overview of concepts in generalizability theory. Int. J. Med. Educ. 2013, 4, 221–222. [Google Scholar] [CrossRef]
- Trejo-Meja, J.A.; Snchez-Mendiola, M.; Mndez-Ramrez, I.; Martnez-Gonzlez, A. Reliability analysis of the objective structured clinical examination using generalizability theory. Med. Educ. Online 2016, 21, 31650. [Google Scholar] [CrossRef]
- Vispoel, W.P.; Morris, C.A.; Kilinc, M. Applications of generalizability theory and their relations to classical test theory and structural equation modeling. Psychol. Methods 2018, 23, 1–26. [Google Scholar] [CrossRef] [PubMed]
- Vispoel, W.P.; Morris, C.A.; Kilinc, M. Practical applications of generalizability theory for designing, evaluating, and improving psychological assessments. J. Pers. Assess. 2018, 100, 53–67. [Google Scholar] [CrossRef]
- Vispoel, W.P.; Morris, C.A.; Kilinc, M. Using generalizability theory to disattenuate correlation coefficients for multiple sources of measurement error. Multivar. Behav. Res. 2018, 53, 481–501. [Google Scholar] [CrossRef] [PubMed]
- Vispoel, W.P.; Morris, C.A.; Kilinc, M. Using generalizability theory with continuous latent response variables. Psychol. Methods 2019, 24, 153–178. [Google Scholar] [CrossRef] [PubMed]
- Vispoel, W.P.; Xu, G.; Schneider, W.S. Using parallel splits with self-report and other measures to enhance precision in generalizability theory analyses. J. Personal. Assess. 2022, 104, 303–319. [Google Scholar] [CrossRef] [PubMed]
- Vispoel, W.P.; Lee, H.; Hong, H.; Chen, T. Applying multivariate generalizability theory to psychological assessments. Psychol. Methods advance online publication. 2023, 1–23. [Google Scholar] [CrossRef]
- Andersen, S.A.W.; Nayahangan, L.J.; Park, Y.S.; Konge, L. Use of generalizability theory for exploring reliability of and sources of variance in assessment of technical skills: A systematic review and meta-analysis. Acad. Med. 2021, 96, 1609–1619. [Google Scholar] [CrossRef]
- Andersen, S.A.W.; Park, Y.S.; Sørensen, M.S.; Konge, L. Reliable assessment of surgical technical skills is dependent on context: An exploration of different variables using Generalizability Theory. Acad. Med. 2020, 95, 1929–1936. [Google Scholar] [CrossRef] [PubMed]
- Kreiter, C.; Zaidi, N.B. ; Generalizability theory's role in validity research: Innovative applications in health science education. Health Prof. Educ. 2020, 6, 282–290. [Google Scholar] [CrossRef]
- Suneja, M.; Hanrahan, K.D.; Kreiter, C.; Rowat, J. Psychometric properties of entrustable professional activity-based objective structured clinical examinations during transition from undergraduate to graduate medical education: A generalizability study. Acad. Med. 2024. [Google Scholar] [CrossRef] [PubMed]
- Anderson, T.N.; Lau, J.N.; Shi, R.; Sapp, R.W.; Aalami, L.R.; Lee, E.W.; Tekian, A.; Park, Y.S. The utility of peers and trained raters in technical skill-based assessments a generalizability theory study. J. Surg. Educ. 2022, 79, 206–215. [Google Scholar] [CrossRef]
- Jogerst, K.M.; Eurboonyanun, C.; Park, Y.S.; Cassidy, D.; McKinley, S.K.; Hamdi, I.; Phitayakorn, R.; Petrusa, E.; Gee, D.W. Implementation of the ACS/ APDS Resident Skills Curriculum reveals a need for rater training: An analysis using generalizability theory. Am. J. Surg. 2021, 222, 541–548. [Google Scholar] [CrossRef] [PubMed]
- Winkler-Schwartz, A.; Marwa, I.; Bajunaid, K.; Mullah, M.; Alotaibi, F.E.; Bugdadi, A.; Sawaya, R.; Sabbagh, A.J.; Del Maestro, R. A comparison of visual rating scales and simulated virtual reality metrics in neurosurgical training: A generalizability theory study. World Neurosurg. 2019, 127, e230–e235. [Google Scholar] [CrossRef]
- Kuru, C.A.; Sezer, R.; Çetin, C.; Haberal, B.; Yakut, Y.; Kuru, İ. Use of Generalizability Theory Evaluating Comparative Reliability of the Scapholunate Interval Measurement With X-ray, CT, and US. Acad. Radiol. 2023, 30, 2290–2298. [Google Scholar]
- Gatti, A.A.; Stratford, P.W.; Brisson, N.M.; Maly, M.R. How to optimize measurement protocols: An example of assessing measurement reliability using generalizability theory. Physiother Can. 2020, 72, 112–121. [Google Scholar] [CrossRef]
- O’Brien, J.; Thompson, M.S.; Hagler, D. Using generalizability theory to inform optimal design for a nursing performance assessment. Eval. Health Prof. 2019, 42, 297–327. [Google Scholar] [CrossRef] [PubMed]
- Peeters, M.J. Moving beyond Cronbach’s alpha and inter-rater reliability: A primer on generalizability theory for pharmacy education. Innov. Pharm. 2021, 12, 14. [Google Scholar] [CrossRef] [PubMed]
- Atilgan, H. Reliability of essay ratings: A study on Generalizability Theory. Eurasian J. Educ. Res. 2019, 19, 1–18. [Google Scholar] [CrossRef]
- Chen, D.; Hebert, M.; Wison, J. Examining human and automated ratings of elementary students’ writing quality: A multivariate generalizability theory application. Am. Educ. Res. J. 2022, 59, 1122–1156. [Google Scholar] [CrossRef]
- Deniz, K.Z.; Ilican, E. Comparison of G and Phi coefficients estimated in generalizability theory with real cases. Int. J. Assess. Tools Educ. 2021, 8, 583–595. [Google Scholar] [CrossRef]
- Wilson, J.; Chen, D.; Sandbank, M.P.; Hebert, M.; Graham, S. Generalizability of automated scores of writing quality in Grades 3-5. J. Educ. Psychol. 2019, 111, 619–640. [Google Scholar] [CrossRef]
- Eskin, D. Generalizability of Writing Scores and Language Program Placement Decisions: Score Dependability, Task Variability, and Score Profiles on an ESL Placement Test. Studies in Applied Linguistics & TESOL 2022, 21, 21–42. [Google Scholar]
- Liao, Ray J. T. The use of generalizability theory in investigating the score dependability of classroom-based L2 reading assessment. Lang. Test. 2023, 40, 86–106. [Google Scholar] [CrossRef]
- Shin, J. Investigating and optimizing score dependability of a local ITA speaking test across language groups: A generalizability theory approach. Lang. Test. 2022, 39, 313–337. [Google Scholar] [CrossRef]
- Ford, A.L.B.; Johnson, L.D. The use of generalizability theory to inform sampling of educator language used with preschoolers with autism spectrum disorder. J. Speech Lang. Hear. R. 2021, 64, 1748–1757. [Google Scholar] [CrossRef]
- Hollo, A.; Staubitz, J.L.; Chow, J.C. Applying generalizability theory to optimize analysis of spontaneous teacher talk in elementary classrooms. J. Speech Lang. Hear. R. 2020, 63, 1947–1957. [Google Scholar] [CrossRef] [PubMed]
- Van Hooijdonk, M.; Mainhard, T.; Kroesbergen, E.H.; Van Tartwijk, J. Examining the assessment of creativity with generalizability theory: An analysis of creative problem solving assessment tasks. Think. Ski. Creat. 2022, 43, 100994. [Google Scholar] [CrossRef]
- Li, G.; Xie, J.; An, L.; Hou, G.; Jian, H.; Wang, W. A generalizability analysis of the mobile phone addiction tendency scale for Chinese college students. Front. Psychiatry 2019, 10, 241. [Google Scholar] [CrossRef]
- Kumar, S.S.; Merkin, A.G.; Numbers, K.; Sachdev, P.S.; Brodaty, H.; Kochan, N.A.; Trollor, J.N.; Mahon, S.; Medvedev, O. A novel approach to investigate depression symptoms in the aging population using generalizability theory. Psychol. Assess 2022, 34, 684–696. [Google Scholar] [CrossRef] [PubMed]
- Truong, Q.C.; Krageloh, C.U.; Siegert, R.J.; Landon, J.; Medvedev, O.N. Applying generalizability theory to differentiate between trait and state in the Five Facet Mindfulness Questionnaire (FFMQ). Mindfulness 2020, 11, 953–963. [Google Scholar] [CrossRef]
- Anthony, C.J.; Styck, K.M.; Volpe, R.J.; Robert, C.R.; Codding, R.S. Using many-facet Rasch measurement and Generalizability Theory to explore rater effects for Direct Behavior Rating–Multi-Item Scales. Sch. Psychol. 2023, 38, 119–128. [Google Scholar] [CrossRef] [PubMed]
- Lyndon, M.P.; Medvedev, O.N.; Chen, Y.; Henning, M.A. Investigating stable and dynamic aspects of student motivation using generalizability theory. Aust. J. Psychol. 2020, 72, 199–210. [Google Scholar] [CrossRef]
- Sanz-Fernández, C.; Morales-Sánchez, V.; Castellano, J.; Mendo, A.H. Generalizability theory in the evaluation of psychological profile in track and field. Sports (Basel) 2024, 12, 127. [Google Scholar] [CrossRef]
- Mushquash, C.; O’Connor, B.P. SPSS and SAS programs for generalizability theory analyses. Behav. Res. Methods 2006, 38, 542–547. [Google Scholar] [CrossRef]
- Crick, J.E.; Brennan, R.L. Manual for GENOVA: A Generalized Analysis of Variance System (American College Testing Technical Bulletin No. 43). ACT, Inc.: Iowa City, IA, 1983.
- Brennan, R.L. Manual for urGENOVA (Version 2.1). University of Iowa, Iowa Testing Programs: Iowa City, IA, 2001.
- Brennan, R.L. Manual for mGENOVA (Version 2.1). University of Iowa, Iowa Testing Programs: Iowa City, IA, 2001.
- Moore, C.T. gtheory: Apply generalizability theory with R. R package version 0.1.2, 2016. [Google Scholar]
- Huebner, A.; Lucht, M. Generalizability theory in R. Pract. Assess. Res. Eval. 2019, 24. [Google Scholar]
- Jorgensen, T.D. How to estimate absolute-error components in structural equation models of generalizability theory. Psych 2021, 3, 113–133. [Google Scholar] [CrossRef]
- Vispoel, W.P.; Xu, G.; Kilinc, M. Expanding G-theory models to incorporate congeneric relationships: Illustrations using the Big Five Inventory. J. Pers. Assess. 2021, 104, 429–442. [Google Scholar] [CrossRef] [PubMed]
- Vispoel, W.P.; Xu, G.; Schneider, W.S. Interrelationships between latent state-trait theory and generalizability theory in a structural equation modeling framework. Psychol. Methods 2022, 27, 773–803. [Google Scholar] [CrossRef]
- Vispoel, W.P.; Lee, H.; Xu, G.; Hong, H. Expanding bifactor models of psychological traits to account for multiple sources of measurement error. Psychol. Assess. 2022, 32, 1093–1111. [Google Scholar] [CrossRef]
- Vispoel, W.P.; Lee, H.; Xu, G.; Hong, H. Integrating bifactor models into a generalizability theory structural equation modeling framework. J. Exp. Educ. 2023, 91, 718–738. [Google Scholar] [CrossRef]
- Vispoel, W.P.; Lee, H.; Chen, T.; Hong, H. Extending applications of generalizability theory-based bifactor model designs. Psych 2023, 5, 545–575. [Google Scholar] [CrossRef]
- Vispoel, W.P.; Lee, H. Merging generalizability theory and bifactor modeling to improve psychological assessments. Psychology and Psychotherapy: Review Study 2023, 7, 1–4. [Google Scholar]
- Vispoel, W.P.; Hong, H.; Lee, H.; Jorgensen, T.R. Analyzing complete generalizability theory designs using structural equation models. Appl. Meas. Educ. 2023, 36, 372–393. [Google Scholar] [CrossRef]
- Vispoel, W.P.; Lee, H.; Chen, T.; Hong, H. Using structural equation modeling to reproduce and extend ANOVA-based generalizability theory analyses for psychological assessments. Psych 2023, 5, 249–272. [Google Scholar] [CrossRef]
- Lee, H.; Vispoel, W.P. A robust indicator mean-based method for estimating generalizability theory absolute error and related dependability indices within structural equation modeling frameworks. Psych 2024, 6, 401–425. [Google Scholar] [CrossRef]
- Vispoel, W.P.; Hong, H.; Lee, H. Benefits of doing generalizability theory analyses within structural equation modeling frameworks: Illustrations using the Rosenberg Self-Esteem Scale [Teacher’s corner]. Struct. Equ. Model. 2024, 31, 165–181. [Google Scholar] [CrossRef]
- Vispoel, W.P.; Lee, H.; Hong, H. Analyzing multivariate generalizability theory designs within structural equation modeling frameworks [Teacher’s corner]. Struct. Equ. Model. 2024, 31, 552–570. [Google Scholar] [CrossRef]
- Vispoel, W.P.; Lee, H.; Chen, T. Multivariate structural equation modeling techniques for estimating reliability, measurement error, and subscale viability when using both composite and subscale scores in practice. Mathematics 2024, 12, 1–25. [Google Scholar] [CrossRef]
- Vispoel, W.P.; Lee, H.; Chen, T.; Hong, H. Analyzing and comparing univariate, multivariate, and bifactor generalizability theory designs for hierarchically structured personality traits. J. Personal. Assess. 2024, 106, 285–300. [Google Scholar] [CrossRef]
- Marcoulides, G.A. Estimating variance components in generalizability theory: The covariance structure analysis approach. Struct. Equ. Model. 1996, 3, 290–299. [Google Scholar] [CrossRef]
- Raykov, T.; Marcoulides, G.A. Estimation of generalizability coefficients via a structural equation modeling approach to scale reliability evaluation. Int. J. Test. 2006, 6, 81–95. [Google Scholar] [CrossRef]
- Brennan, R.L.; Kane, M.T. An index of dependability for mastery tests. J. Educ. Meas. 1977, 1977 14, 277–289. [Google Scholar] [CrossRef]
- Kane, M.T.; Brennan, R.L. Agreement coefficients as indices of dependability for domain-referenced tests. Appl. Psychol. Meas. 1980, 4, 105–126. [Google Scholar] [CrossRef]
- Morin, A.J.S.; Scalas, L.F.; Vispoel, W.; Marsh, H.W.; Wen, Z. The Music Self-Perception Inventory: Development of a short form. Psychol. Music 2016, 44, 915–934. [Google Scholar] [CrossRef]
- Scalas, L.F.; Marsh, H.W.; Vispoel, W.; Morin, A.J.S.; Wen, Z. Music self-concept and self-esteem formation in adolescence: A comparison between individual and normative models of importance within a latent framework. Psychol. Music 2017, 45, 763–780. [Google Scholar] [CrossRef]
- Fiedler, D.; Hasselhorn, J.; Katrin Arens, A.; Frenzel, A.C.; Vispoel, W.P. Validating scores from the short form of the Music Self-Perception Inventory (MUSPI-S) with seventh- to ninth-grade school students in German. Psychol. Music advance online publication. 2024, 1–22. [Google Scholar] [CrossRef]
- Vispoel, W.P.; Lee, H. ; Lee, H. Music self-concept: Structure, correlates, and differences across grade-level, gender, and musical activity groups. Psychology and Psychological Research International Journal 2024, 9, 00413. [Google Scholar] [CrossRef]
- Schmidt, F.L.; Hunter, J.E. Measurement error in psychological research: Lessons from 26 research scenarios. Psychol. Methods 1996, 1, 199–223. [Google Scholar] [CrossRef]
- Schmidt, F.L.; Le, H.; Ilies, R. Beyond alpha: An empirical examination of the effects of different sources of measurement error on reliability estimates for measures of individual differences constructs. Psychol. Methods 2003, 8, 206–224. [Google Scholar] [CrossRef] [PubMed]
- Le, H.; Schmidt, F.L.; Putka, D.J. The multifaceted nature of measurement artifacts and its implications for estimating construct-level relationships. Organ. Res. Methods 2009, 12, 165–200. [Google Scholar] [CrossRef]
- Thorndike, R.L. Reliability. In Educational Measurement; Lindquist, E.F., Ed.; American Council on Education: Washington, DC, USA, 1951; pp. 560–620. [Google Scholar]
- Spearman, C. The proof and measurement of association between two things. Am. J. Psychol. 1904, 15, 72–101. [Google Scholar] [CrossRef]
- Spearman, C. Correlation calculated from faulty data. Brit. J. Psychol. 1910, 3, 271–295. [Google Scholar] [CrossRef]
- Reise, S.P. The rediscovery of bifactor measurement models. Multivar. Behav. Res. 2012, 47, 667–696. [Google Scholar] [CrossRef] [PubMed]
- Reise, S.P.; Bonifay, W.E.; Haviland, M.G. Scoring psychological measures in the presence of multidimensionality. J. Personal. Assess. 2013, 95, 129–140. [Google Scholar] [CrossRef]
- Rodriguez, A.; Reise, S.P.; Haviland, M.G. Applying bifactor statistical indices in the evaluation of psychological measures. J. Personal. Assess. 2016, 98, 223–237. [Google Scholar] [CrossRef]
- Rodriguez, A.; Reise, S.P.; Haviland, M.G. Evaluating bifactor models: Calculating and interpreting statistical indices. Psychol. Methods 2016, 21, 137–150. [Google Scholar] [CrossRef]
- Zinbarg, R.E.; Revelle, W.; Yovel, I.; Li, W. Cronbach’s α, Revelle’s β, and McDonald’s ω H: Their relations with each other and two alternative conceptualizations of reliability. Psychometrika 2005, 70, 123–133. [Google Scholar] [CrossRef]
- Haberman, S.J. When can subscores have value? J. Educ. Behav. Stat. 2008, 33, 204–229. [Google Scholar] [CrossRef]
- Haberman, S.J.; Sinharay, S. Reporting of subscores using multidimensional item response theory. Psychometrika 2010, 75, 209–227. [Google Scholar] [CrossRef]
- Feinberg, R.A.; Jurich, D.P. Guidelines for interpreting and reporting subscores. Educ. Meas.-Issues Pract. 2017, 36, 5–13. [Google Scholar] [CrossRef]
- Sinharay, S. Added value of subscores and hypothesis testing. J. Educ. Behav. Stat. 2019, 44, 25–44. [Google Scholar] [CrossRef]
- Hjarne, M.S.; Lyrén, P.E. Group differences in the value of subscores: A fairness issue. Front. Educ. 2020, 5, 55. [Google Scholar] [CrossRef]
- Feinberg, R.A.; Wainer, H. A simple equation to predict a subscore’s value. Educ. Meas.-Issues Pra. 2014, 33, 55–56. [Google Scholar] [CrossRef]
- Rosseel, Y. lavaan: An R package for structural equation modeling. J. Stat. Softw. 2012, 48, 1–36. [Google Scholar] [CrossRef]
- Rosseel, Y.; Jorgensen, T.D.; De Wilde, L.; Package ‘lavaan’. R Package Version (0.6-17). 2023. Available online: https://cran.r-project.org/web/packages/lavaan/lavaan.pdf (accessed on 8 December 2024).
- Preacher, K.J.; Selig, J.P. Advantages of Monte Carlo confidence intervals for indirect effects. Commun. Methods Meas. 2012, 6, 77–98. [Google Scholar] [CrossRef]
- Jorgensen, T.D.; Pornprasertmanit, S.; Schoemann, A.M.; Rosseel, Y.; semTools: Useful Tools for Structural Equation Modeling. R Package Version 0.5-6. 2022. Available online: https://CRAN.R-project.org/package=semTools (accessed on 8 December 2024).
- Ark, T.K. Ordinal Generalizability Theory Using an Underlying Latent Variable Framework. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 8 December 2024. [Google Scholar]
- Vispoel, W.P. Integrating self-perceptions of music skill into contemporary models of self-concept. The Quarterly Journal of Music Teaching and Learning 1994, 5, 42–57. [Google Scholar]
- Vispoel, W.P. Integrating self-perceptions of music skill into contemporary models of self-concept. Visions of Research in Music Education 2021, 16, 33. [Google Scholar]
- Vispoel, W.P. Measuring and understanding self-perceptions of musical ability. In International Advances in Self Research; Marsh, H.W., Craven, R.G., McInerney, D.M., Eds.; Information Age Publishing: Charlotte, NC, 2003; pp. 151–180. [Google Scholar]
- Schmid, J.; Leiman, J.M. The development of hierarchical factor solutions. Psychometrika 1957, 22, 53–61. [Google Scholar] [CrossRef]
- Schmid. J. The comparability of the bi-factor and second-order factor patterns. J. Exp. Educ 1957, 25, 249–253. [Google Scholar] [CrossRef]
- American Psychological Association (APA) Technical recommendations for psychological tests and diagnostic techniques. Psychol. Bull. 1954, 51 Pt 2, 1–38. [CrossRef] [PubMed]
- Cronbach, L.J.; Schönemann, P.; McKie, D. Alpha coefficients for stratified-parallel tests. Educ. Psychol. Meas. 1965, 25, 291–312. [Google Scholar] [CrossRef]
- Holzinger, K.J.; Harman, H.H. Comparison of two factorial analyses. Psychometrika 1938, 3, 45–60. [Google Scholar] [CrossRef]
- Holzinger, K.J.; Swineford, F. The bi-factor method. Psychometrika 1937, 2, 41–54. [Google Scholar] [CrossRef]
- Rhemtulla, M.; Brosseau-Liard, P.É.; Savalei, V. When can categorical variables be treated as continuous? A comparison of robust continuous and categorical SEM estimation methods under suboptimal conditions. Psychol. Methods 2012, 17, 354–373. [Google Scholar] [CrossRef]
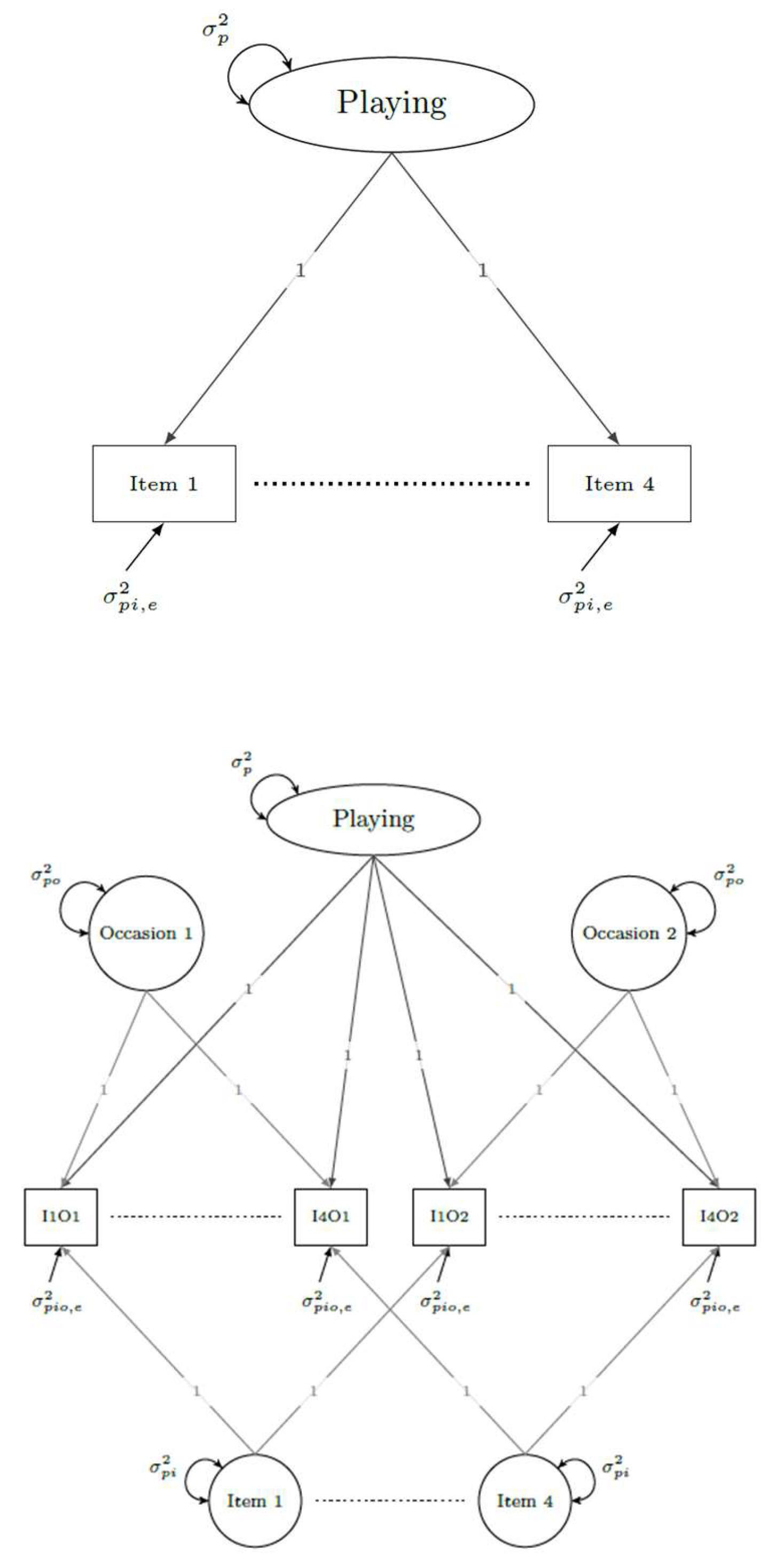
| Design/VC | Formula |
| pi design | |
| p | |
| pi,e | |
| i | . |
| pio design | |
| p | |
| pi,e | |
| po | |
| pio,e | |
| i | . |
| o | |
| io |
| Design/Index | Formula |
| pi design | |
| G | |
| G-D | |
| Cut-score-specific D | |
| Total relative error | |
| pio design | |
| G | |
| G-D | |
| Cut-score-specific D | |
| Specific-factor error | |
| Transient error | |
| Random-response error | |
| Total relative error |
| Design/VC | Formula | |
| Composite | Subscale | |
| pidesign | ||
| p | = the number of subscales | |
| pi,e | ||
| i | . | |
| piodesign | ||
| p | ||
| pi,e | ||
| po | ||
| pio,e | ||
| i | and . | |
| o | ||
| io | ||
| Design/VC | Formula | |
| Composite | Subscale | |
| pi design | ||
| General | ||
| Group | ||
| p | ||
| pi,e | ||
| i |
where = the number of items in subscale S, = intercept of item, and . |
|
| pio design | ||
| General | ||
| Group | ||
| p | ||
| pi | ||
| po | ||
| pio,e | ||
| i |
where and . |
|
| o |
where = the number of occasions in subscale S, and |
|
| io | ||
| Metric/ subscale | Occasion/index | ||||||
| Time 1 | Time 2 | ||||||
| Mean Scale (Item) |
SD Scale (Item) |
Mean Scale (Item) |
SD Scale (Item) |
Test-Retest | |||
| 2-Point | |||||||
| Composite | 22.90 (1.43) | 6.06 (0.38) | 0.954 | 23.12 (1.45) | 6.15 (0.38) | 0.957 | 0.906 |
| Instrument playing | 5.78 (1.44) | 1.83 (0.46) | 0.940 | 5.81 (1.45) | 1.85 (0.46) | 0.946 | 0.885 |
| Reading music | 5.77 (1.44) | 1.85 (0.46) | 0.948 | 5.83 (1.46) | 1.84 (0.46) | 0.942 | 0.908 |
| Listening | 5.78 (1.44) | 1.83 (0.46) | 0.935 | 6.12 (1.53) | 1.84 (0.46) | 0.940 | 0.799 |
| Composing | 5.32 (1.33) | 1.67 (0.42) | 0.911 | 5.37 (1.34) | 1.73 (0.43) | 0.934 | 0.826 |
| 4-Point | |||||||
| Composite | 35.83 (2.24) | 14.98 (0.94) | 0.967 | 36.48 (2.28) | 14.85 (0.93) | 0.971 | 0.936 |
| Instrument playing | 9.08 (2.27) | 4.46 (1.11) | 0.961 | 9.20 (2.30) | 4.41 (1.10) | 0.966 | 0.921 |
| Reading music | 9.03 (2.26) | 4.52 (1.13) | 0.964 | 9.14 (2.29) | 4.38 (1.09) | 0.971 | 0.930 |
| Listening | 9.08 (2.27) | 4.46 (1.11) | 0.958 | 9.88 (2.47) | 4.26 (1.07) | 0.959 | 0.871 |
| Composing | 8.06 (2.02) | 3.79 (0.95) | 0.932 | 8.26 (2.06) | 3.80 (0.95) | 0.950 | 0.870 |
| 8-Point | |||||||
| Composite | 63.06 (3.94) | 31.64 (1.98) | 0.971 | 64.54 (4.03) | 31.32 (1.96) | 0.975 | 0.944 |
| Instrument playing | 15.97 (3.99) | 9.42 (2.36) | 0.967 | 16.29 (4.07) | 9.24 (2.31) | 0.973 | 0.929 |
| Reading music | 15.91 (3.98) | 9.49 (2.37) | 0.968 | 16.12 (4.03) | 9.17 (2.29) | 0.978 | 0.937 |
| Listening | 15.97 (3.99) | 9.42 (2.36) | 0.966 | 17.72 (4.43) | 8.79 (2.20) | 0.967 | 0.890 |
| Composing | 14.01 (3.50) | 7.89 (1.97) | 0.937 | 14.41 (3.60) | 7.91 (1.98) | 0.958 | 0.891 |
| Metric/ Procedure | |||||||||
| Scale | 2-Point | 4-Point | 8-Point | ||||||
| mGENOVA | ULS | WLSMV | mGENOVA | ULS | WLSMV | mGENOVA | ULS | WLSMV | |
| Composite | |||||||||
| G | .977 | .977 (.964, .989) |
.996 (.995, .997) |
.985 | .985 (.983, .987) |
.993 (.992, .994) |
.988 | .988 (.987, .988) |
.993 (.992, .994) |
| TRE | .023 | .023 | .004 | .015 | .015 | .007 | .012 | .012 | .007 |
| G-D | .977 | .977 (.964, .988) |
.996 (.995, .997) |
.985 | .985 (.983, .987) |
.993 (.992, .994) |
.987 | .987 (.987, .988) |
.993 (.991, .994) |
| .140 | .140 | 1.262 | .864 | .864 | 1.093 | 3.861 | 3.861 | 1.233 | |
| .013 | .013 | .020 | .052 | .052 | .031 | .194 | .194 | .036 | |
| .000 | .000 | .000 | .000 | .000 | .000 | .002 | .003 | .001 | |
| Instrument playing | |||||||||
| G | .940 | .940 (.866, 1.000) |
.989 (.984, .993) |
.961 | .961 (.950, .973) |
.980 (.976, .984) |
.967 | .967 (.965, .970) |
.982 (.979, .985) |
| TRE | .060 | .060 | .011 | .039 | .039 | .020 | .033 | .033 | .018 |
| G-D | .940 | .940 (.863, 1.000) |
.988 (.984, .993) |
.961 | .961 (.949, .972) |
.980 (.976, .984) |
.967 | .967 (.965, .970) |
.982 (.978, .985) |
| .197 | .197 | 1.995 | 1.195 | 1.195 | 1.869 | 5.367 | 5.367 | 1.771 | |
| .050 | .050 | .092 | .192 | .192 | .150 | .722 | .722 | .131 | |
| .000 | .000 | .001 | .000 | .001 | .001 | .002 | .004 | .001 | |
| Reading music | |||||||||
| G | .948 | .948 (.876, 1.000) |
.991 (.987, .994) |
.964 | .964 (.953, .976) |
.982 (.979, .986) |
.968 | .968 (.966, .971) |
.984 (.982, .987) |
| TRE | .052 | .052 | .009 | .036 | .036 | .018 | .032 | .032 | .016 |
| G-D | .948 | .947 (.873, 1.000) |
.990 (.986, .994) |
.964 | .964 (.952, .975) |
.982 (.978, .985) |
.967 | .967 (.965, .970) |
.983 (.980, .986) |
| .202 | .202 | 1.556 | 1.230 | 1.230 | 1.364 | 5.445 | 5.445 | 1.768 | |
| .045 | .045 | .059 | .181 | .181 | .098 | .715 | .715 | .112 | |
| .000 | .000 | .003 | .003 | .003 | .004 | .021 | .022 | .008 | |
| Listening | |||||||||
| G | .935 | .935 (.860, 1.000) |
.986 (.981, .991) |
.958 | .958 (.946, .969) |
.978 (.973, .982) |
.966 | .966 (.963, .969) |
.981 (.977, .983) |
| TRE | .065 | .065 | .014 | .042 | .042 | .022 | .034 | .034 | .019 |
| G-D | .935 | .935 (.857, .998) |
.986 (.981, .991) |
.958 | .958 (.945, .969) |
.978 (.973, .982) |
.966 | .966 (.963, .969) |
.980 (.977, .983) |
| .196 | .196 | 1.546 | 1.158 | 1.158 | 1.626 | 4.927 | 4.927 | 1.413 | |
| .055 | .055 | .088 | .205 | .205 | .149 | .692 | .692 | .112 | |
| .000 | .000 | .000 | .000 | .000 | .000 | .000 | .000 | .000 | |
| Composing | |||||||||
| G | .911 | .911 (.818, .993) |
.979 (.972, .986) |
.932 | .932 (.915, .948) |
.962 (.954, .968) |
.937 | .937 (.934, .941) |
.954 (.946, .960) |
| TRE | .089 | .089 | .021 | .068 | .068 | .038 | .063 | .063 | .046 |
| G-D | .911 | .911 (.815, .990) |
.978 (.971, .986) |
.931 | .931 (.914, .947) |
.961 (.953, .967) |
.937 | .936 (.932, .940) |
.953 (.944, .959) |
| .159 | .159 | 1.026 | .837 | .837 | .595 | 3.649 | 3.649 | 1.123 | |
| .062 | .062 | .088 | .246 | .246 | .095 | .974 | .974 | .218 | |
| .000 | .000 | .003 | .003 | .003 | .002 | .016 | .018 | .006 | |
| Metric/Estimator | Correlation Coefficient | ||||
| 2-Point / ULS | Instrument playing | Reading music | Listening | Composing | |
| Instrument playing | ------ | 0.844 | 0.609 | 0.626 | |
| Reading music | 0.797 | ------ | 0.657 | 0.558 | |
| Listening | 0.571 | 0.618 | ------ | 0.646 | |
| Composing | 0.579 | 0.518 | 0.596 | ------ | |
| 2-Point / WLSMV | Instrument playing | Reading music | Listening | Composing | |
| Instrument playing | ------ | 0.920 | 0.731 | 0.749 | |
| Reading music | 0.910 | ------ | 0.778 | 0.685 | |
| Listening | 0.721 | 0.769 | ------ | 0.784 | |
| Composing | 0.737 | 0.675 | 0.770 | ------ | |
| 4-Point / ULS | Instrument playing | Reading music | Listening | Composing | |
| Instrument playing | ------ | 0.878 | 0.678 | 0.681 | |
| Reading music | 0.845 | ------ | 0.716 | 0.617 | |
| Listening | 0.650 | 0.689 | ------ | 0.689 | |
| Composing | 0.645 | 0.585 | 0.651 | ------ | |
| 4-Point / WLSMV | Instrument playing | Reading music | Listening | Composing | |
| Instrument playing | ------ | 0.915 | 0.736 | 0.736 | |
| Reading music | 0.898 | ------ | 0.776 | 0.679 | |
| Listening | 0.721 | 0.760 | ------ | 0.745 | |
| Composing | 0.715 | 0.660 | 0.722 | ------ | |
| 8-Point / ULS | Instrument playing | Reading music | Listening | Composing | |
| Instrument playing | ------ | 0.884 | 0.696 | 0.704 | |
| Reading | 0.855 | ------ | 0.727 | 0.652 | |
| Listening | 0.673 | 0.703 | ------ | 0.719 | |
| Composing | 0.671 | 0.621 | 0.684 | ------ | |
| 8-Point / WLSMV | Instrument playing | Reading music | Listening | Composing | |
| Instrument playing | ------ | 0.885 | 0.725 | 0.732 | |
| Reading music | 0.871 | ------ | 0.744 | 0.685 | |
| Listening | 0.711 | 0.731 | ------ | 0.748 | |
| Composing | 0.708 | 0.664 | 0.724 | ------ | |
| Metric/ Procedure | |||||||||
| Scale/ Index | 2-Point | 4-Point | 8-Point | ||||||
| ULS | WLSMV | ULS | WLSMV | ULS | WLSMV | ||||
| Composite | |||||||||
| G | .977 (.964, .989) | .996 (.995, .997) | .985 (.983, .987) | .993 (.991, .994) | .988 (.987, .988) | .992 (.991, .993) | |||
| .869 (.837, .899) | .938 (.925, .950) | .900 (.895, .905) | .930 (.918, .940) | .909 (.908, .910) | .924 (.913, .934) | ||||
| .108 (.073, .143) | .058 (.046, .071) | .085 (.080, .091) | .063 (.053, .073) | .078 (.077, .079) | .068 (.060, .079) | ||||
| TRE | .023 | .004 | .015 | .007 | .012 | .008 | |||
| G-D | .977 (.963, .988) | .996 (.995, .997) | .985 (.983, .987) | .992 (.991, .993) | .987 (.987, .988) | .992 (.991, .993) | |||
| .140 | 4.299 | .863 | 2.573 | 3.859 | 1.982 | ||||
| .125 | 4.050 | .789 | 2.411 | 3.553 | 1.846 | ||||
| .015 | .249 | .075 | .162 | .305 | .137 | ||||
| .013 | .071 | .052 | .078 | .194 | .060 | ||||
| .000 | .002 | .000 | .001 | .003 | .002 | ||||
| Instrument playing | |||||||||
| G | .940 (.865, 1.000) | .989 (.984, .993) | .961 (.950, .973) | .980 (.976, .984) | .967 (.965, .970) | .982 (.979, .985) | |||
| .744 (.568, .953) | .888 (.830, .948) | .806 (.774, .840) | .882 (.843, .920) | .819 (.811, .826) | .860 (.826, .890) | ||||
| .196 (.000, .394) | .101 (.042, .158) | .155 (.118, .191) | .098 (.062, .135) | .149 (.140, .157) | .122 (.094, .153) | ||||
| TRE | .060 | .011 | .039 | .020 | .033 | .018 | |||
| G-D | .940 (.863, 1.000) | .988 (.984, .993) | .961 (.949, .972) | .980 (.976, .984) | .967 (.965, .970) | .982 (.978, .984) | |||
| .197 | 5.114 | 1.195 | 4.327 | 5.367 | 2.621 | ||||
| .156 | 4.593 | 1.002 | 3.895 | 4.541 | 2.294 | ||||
| .041 | .521 | .193 | .432 | .825 | .326 | ||||
| .050 | .237 | .192 | .348 | .722 | .194 | ||||
| .000 | .004 | .001 | .002 | .004 | .002 | ||||
| Reading music | |||||||||
| G | .948 (.876, 1.000) | .991 (.987, .994) | .964 (.953, .976) | .982 (.979, .986) | .968 (.966, .971) | .984 (.982, .987) | |||
| .741 (.568, .941) | .889 (.830, .947) | .800 (.768, .833) | .881 (.842, .920) | .810 (.803, .818) | .844 (.809, .876) | ||||
| .206 (.000, .401) | .102 (.044, .159) | .165 (.128, .200) | .101 (.064, .139) | .158 (.150, .166) | .140 (.110, .174) | ||||
| TRE | .052 | .009 | .036 | .018 | .032 | .016 | |||
| G-D | .947 (.873, 1.000) | .990 (.986, .994) | .964 (.952, .975) | .982 (.978, .985) | .967 (.965, .970) | .983 (.980, .986) | |||
| .202 | 6.891 | 1.230 | 2.628 | 5.445 | 2.529 | ||||
| .158 | 6.182 | 1.020 | 2.358 | 4.557 | 2.169 | ||||
| .044 | .710 | .210 | .270 | .888 | .360 | ||||
| .045 | .263 | .181 | .189 | .715 | .161 | ||||
| .000 | .013 | .003 | .008 | .022 | .011 | ||||
| Listening | |||||||||
| G | .935 (.861, 1.000) | .986 (.981, .991) | .958 (.945, .969) | .978 (.973, .982) | .966 (.963, .969) | .981 (.977, .983) | |||
| .529 (.399, .684) | .695 (.613, .776) | .602 (.576, .628) | .674 (.614, .730) | .626 (.619, .632) | .663 (.612, .709) | ||||
| .405 (.217, .559) | .291 (.212, .373) | .356 (.325, .386) | .304 (.249, .362) | .341 (.333, .348) | .318 (.272, .367) | ||||
| TRE | .065 | .014 | .042 | .022 | .034 | .019 | |||
| G-D | .935 (.859, .999) | .986 (.981, .991) | .958 (.945, .969) | .978 (.973, .981) | .966 (.963, .969) | .980 (.977, .983) | |||
| .196 | 3.577 | 1.158 | 2.671 | 4.927 | 2.305 | ||||
| .111 | 2.522 | .727 | 1.842 | 3.190 | 1.558 | ||||
| .085 | 1.055 | .430 | .830 | 1.737 | .747 | ||||
| .055 | .204 | .205 | .245 | .692 | .183 | ||||
| .000 | .000 | .000 | .000 | .000 | .000 | ||||
| Composing | |||||||||
| G | .911 (.819, .992) | .979 (.971, .986) | .932 (.915, .948) | .962 (.954, .968) | .937 (.934, .941) | .954 (.946, .960) | |||
| .468 (.342, .626) | .651 (.562, .735) | .527 (.501, .556) | .606 (.541, .667) | .569 (.563, .576) | .626 (.574, .675) | ||||
| .443 (.237, .606) | .328 (.245, .415) | .404 (.368, .438) | .356 (.297, .417) | .368 (.360, .377) | .327 (.282, .375) | ||||
| TRE | .089 | .021 | .068 | .038 | .063 | .046 | |||
| G-D | .911 (.816, .989) | .978 (.970, .985) | .931 (.914, .947) | .961 (.953, .967) | .936 (.932, .940) | .953 (.944, .959) | |||
| .159 | 5.052 | .837 | 2.869 | 3.649 | 2.187 | ||||
| .082 | 3.358 | .474 | 1.808 | 2.216 | 1.436 | ||||
| .077 | 1.694 | .363 | 1.062 | 1.433 | .751 | ||||
| .062 | .434 | .246 | .459 | .974 | .424 | ||||
| .000 | .013 | .003 | .011 | .018 | .011 | ||||
| Design/ subscale | Metric/Estimator | |||||
| 2-Point | 4-Point | 8-Point | ||||
| ULS | WLSMV | ULS | WLSMV | ULS | WLSMV | |
| Multivariate design | ||||||
| Instrument playing | 1.196 | 1.122 | 1.154 | 1.111 | 1.145 | 1.136 |
| Reading | 1.216 | 1.134 | 1.168 | 1.120 | 1.155 | 1.154 |
| Listening | 1.338 | 1.225 | 1.278 | 1.217 | 1.268 | 1.259 |
| Composing | 1.421 | 1.305 | 1.373 | 1.367 | 1.322 | 1.289 |
| Bifactor design | ||||||
| Instrument playing | 1.185 | 1.105 | 1.146 | 1.093 | 1.137 | 1.123 |
| Reading | 1.199 | 1.098 | 1.153 | 1.113 | 1.143 | 1.137 |
| Listening | 1.363 | 1.272 | 1.299 | 1.264 | 1.287 | 1.274 |
| Composing | 1.438 | 1.263 | 1.386 | 1.292 | 1.335 | 1.263 |
| Scale/Index | Metric/ Procedure | |||||||||
| 2-Point | 4-Point | 8-Point | ||||||||
| mGENOVA | ULS | WLSMV | mGENOVA | ULS | WLSMV | mGENOVA | ULS | WLSMV | ||
| Composite | ||||||||||
| G | .904 | .904 (.853, .956) | .946 (.925, .967) | .935 | .935 (.926, .943) | .954 (.944, .964) | .943 | .943 (.941, .945) | .948 (.939, .955) | |
| SFE | .002 | .002 | .001 | .001 | .001 | .001 | .001 | .001 | .001 | |
| TE | .075 | .075 | .050 | .052 | .052 | .039 | .046 | .046 | .046 | |
| RRE | .021 | .021 | .003 | .012 | .012 | .006 | .010 | .010 | .005 | |
| TRE | .097 | .097 | .054 | .065 | .065 | .046 | .057 | .057 | .052 | |
| G-D | .904 | .904 (.851, .954) | .945 (.923, .966) | .934 | .934 (.925, .942) | .953 (.942, .963) | .942 | .942 (.939, .944) | .947 (.937, .954) | |
| .132 | .132 | 1.766 | .812 | .812 | 1.282 | 3.649 | 3.649 | 1.088 | ||
| .001 | .001 | .004 | .004 | .004 | .003 | .017 | .017 | .003 | ||
| .011 | .011 | .094 | .045 | .045 | .053 | .179 | .179 | .053 | ||
| .012 | .012 | .024 | .043 | .043 | .032 | .153 | .153 | .023 | ||
| .000 | .000 | .001 | .000 | .000 | .000 | .001 | .002 | .001 | ||
| .000 | .000 | .002 | .001 | .001 | .001 | .004 | .004 | .001 | ||
| .000 | .000 | .000 | .000 | .000 | .000 | .000 | .000 | .000 | ||
| Instrument playing | ||||||||||
| G | .880 | .879 (.740, 1.000) | .959 (.943, .976) | .917 | .917 (.892, .943) | .953 (.943, .962) | .926 | .926 (.920, .931) | .944 (.934, .952) | |
| SFE | .006 | .006 | .002 | .003 | .003 | .002 | .003 | .003 | .000 | |
| TE | .063 | .063 | .030 | .046 | .046 | .029 | .045 | .045 | .039 | |
| RRE | .051 | .051 | .009 | .033 | .033 | .017 | .027 | .027 | .017 | |
| TRE | .120 | .121 | .041 | .083 | .083 | .047 | .074 | .074 | .057 | |
| G-D | .879 | .879 (.737, 1.000) | .959 (.942, .975) | .917 | .917 (.891, .942) | .952 (.942, .962) | .925 | .925 (.919, .931) | .943 (.933, .951) | |
| .186 | .186 | 1.878 | 1.128 | 1.128 | 2.057 | 5.038 | 5.038 | 1.490 | ||
| .005 | .005 | .017 | .016 | .016 | .013 | .064 | .064 | .003 | ||
| .013 | .013 | .059 | .057 | .057 | .062 | .243 | .243 | .062 | ||
| .043 | .043 | .067 | .164 | .164 | .147 | .580 | .580 | .106 | ||
| .000 | .000 | .002 | .001 | .001 | .001 | .003 | .004 | .001 | ||
| .000 | .000 | .000 | .000 | .000 | .001 | .003 | .003 | .001 | ||
| .000 | .000 | .000 | .000 | .000 | .000 | .000 | .000 | .000 | ||
| Reading music | ||||||||||
| G | .902 | .902 (.761, 1.000) | .972 (.959, .985) | .926 | .926 (.901, .952) | .960 (.951, .968) | .934 | .934 (.928, .939) | .946 (.937, .953) | |
| SFE | .006 | .006 | .002 | .003 | .003 | .002 | .003 | .003 | .004 | |
| TE | .042 | .042 | .018 | .041 | .041 | .024 | .039 | .039 | .041 | |
| RRE | .049 | .049 | .008 | .029 | .029 | .014 | .024 | .024 | .009 | |
| TRE | .098 | .098 | .028 | .074 | .074 | .040 | .066 | .066 | .054 | |
| G-D | .902 | .902 (.757, 1.000) | .971 (.957, .984) | .926 | .925 (.899, .951) | .959 (.950, .967) | .933 | .933 (.927, .938) | .945 (.936, .953) | |
| .192 | .192 | 2.661 | 1.145 | 1.145 | 2.028 | 5.077 | 5.077 | 1.397 | ||
| .005 | .005 | .025 | .015 | .015 | .015 | .059 | .059 | .024 | ||
| .009 | .009 | .049 | .051 | .051 | .051 | .214 | .214 | .060 | ||
| .042 | .042 | .089 | .145 | .145 | .121 | .530 | .530 | .054 | ||
| .000 | .000 | .003 | .001 | .002 | .003 | .009 | .011 | .003 | ||
| .000 | .000 | .001 | .000 | .000 | .001 | .000 | .001 | .000 | ||
| .000 | .000 | .001 | .000 | .000 | .001 | .003 | .002 | .001 | ||
| Listening | ||||||||||
| G | .799 | .800 (.664, .949) | .909 (.879, .940) | .869 | .869 (.843, .895) | .912 (.895, .928) | .888 | .888 (.882, .894) | .893 (.876, .907) | |
| SFE | .000 | .000 | .000 | .002 | .002 | .001 | .001 | .001 | .001 | |
| TE | .138 | .138 | .078 | .089 | .089 | .064 | .078 | .078 | .090 | |
| RRE | .063 | .063 | .013 | .040 | .040 | .022 | .032 | .032 | .016 | |
| TRE | .201 | .201 | .092 | .131 | .131 | .088 | .112 | .112 | .107 | |
| G-D | .799 | .799 (.661, .944) | .907 (.876, .938) | .868 | .868 (.841, .893) | .911 (.893, .927) | .886 | .886 (.880, .893) | .891 (.873, .905) | |
| .168 | .168 | 2.240 | 1.019 | 1.019 | 1.316 | 4.407 | 4.407 | 1.299 | ||
| .000 | .000 | .000 | .008 | .008 | .006 | .029 | .029 | .007 | ||
| .029 | .029 | .193 | .105 | .105 | .093 | .389 | .389 | .131 | ||
| .053 | .053 | .133 | .189 | .189 | .128 | .638 | .638 | .091 | ||
| .000 | .000 | .000 | .000 | .000 | .000 | .000 | .000 | .000 | ||
| .000 | .000 | .004 | .001 | .002 | .002 | .009 | .010 | .003 | ||
| .000 | .000 | .000 | .000 | .000 | .000 | .000 | .001 | .000 | ||
| Composing | ||||||||||
| G | .818 | .818 (.661, .998) | .927 (.902, .952) | .864 | .864 (.830, .898) | .910 (.893, .924) | .883 | .883 (.875, .891) | .889 (.871, .904) | |
| SFE | .007 | .007 | .003 | .007 | .007 | .003 | .008 | .008 | .003 | |
| TE | .105 | .105 | .058 | .077 | .077 | .058 | .065 | .065 | .081 | |
| RRE | .070 | .070 | .013 | .053 | .053 | .029 | .044 | .044 | .026 | |
| TRE | .182 | .182 | .074 | .136 | .136 | .090 | .117 | .117 | .110 | |
| G-D | .817 | .817 (.657, .991) | .925 (.900, .951) | .862 | .862 (.827, .896) | .908 (.890, .923) | .881 | .881 (.873, .889) | .888 (.869, .902) | |
| .148 | .148 | 1.753 | .777 | .777 | .865 | 3.445 | 3.445 | 1.051 | ||
| .005 | .005 | .025 | .024 | .024 | .012 | .122 | .122 | .015 | ||
| .019 | .019 | .109 | .069 | .069 | .055 | .253 | .253 | .096 | ||
| .051 | .051 | .096 | .189 | .189 | .110 | .693 | .693 | .123 | ||
| .000 | .000 | .006 | .002 | .002 | .003 | .011 | .012 | .004 | ||
| .000 | .000 | .001 | .001 | .001 | .001 | .004 | .005 | .001 | ||
| .000 | .000 | .000 | .000 | .000 | .000 | .000 | .001 | .000 | ||
| Metric/Estimator | Correlation | ||||
| 2-Point / ULS | Instrument playing | Reading music | Listening | Composing | |
| Instrument playing | ------ | 0.848 | 0.660 | 0.629 | |
| Reading music | 0.756 | ------ | 0.689 | 0.571 | |
| Listening | 0.553 | 0.585 | ------ | 0.666 | |
| Composing | 0.534 | 0.491 | 0.539 | ------ | |
| 2-Point / WLSMV | Instrument playing | Reading music | Listening | Composing | |
| Instrument playing | ------ | 0.915 | 0.756 | 0.735 | |
| Reading music | 0.883 | ------ | 0.785 | 0.682 | |
| Listening | 0.706 | 0.738 | ------ | 0.779 | |
| Composing | 0.693 | 0.647 | 0.715 | ------ | |
| 4-Point / ULS | Instrument playing | Reading music | Listening | Composing | |
| Instrument playing | ------ | 0.880 | 0.701 | 0.700 | |
| Reading music | 0.811 | ------ | 0.741 | 0.650 | |
| Listening | 0.626 | 0.665 | ------ | 0.723 | |
| Composing | 0.623 | 0.581 | 0.627 | ------ | |
| 4-Point / WLSMV | Instrument playing | Reading music | Listening | Composing | |
| Instrument playing | ------ | 0.911 | 0.749 | 0.744 | |
| Reading music | 0.871 | ------ | 0.789 | 0.701 | |
| Listening | 0.698 | 0.738 | ------ | 0.767 | |
| Composing | 0.692 | 0.655 | 0.699 | ------ | |
| 8-Point / ULS | Instrument playing | Reading music | Listening | Composing | |
| Instrument playing | ------ | 0.889 | 0.715 | 0.723 | |
| Reading music | 0.826 | ------ | 0.754 | 0.680 | |
| Listening | 0.649 | 0.687 | ------ | 0.749 | |
| Composing | 0.654 | 0.617 | 0.663 | ------ | |
| 8-Point / WLSMV | Instrument playing | Reading music | Listening | Composing | |
| Instrument playing | ------ | 0.899 | 0.747 | 0.750 | |
| Reading music | 0.849 | ------ | 0.777 | 0.707 | |
| Listening | 0.686 | 0.714 | ------ | 0.775 | |
| Composing | 0.687 | 0.649 | 0.691 | ------ | |
| Scale/Index | Metric/ Procedure | ||||||||||||
| 2-Point | 4-Point | 8-Point | |||||||||||
| ULS | WLSMV | ULS | WLSMV | ULS | WLSMV | ||||||||
| Composite | |||||||||||||
| G | .904 (.854, .955) | .949 (.927, .969) | .934 (.926, .943) | .962 (.952, .971) | .942 (.940, .944) | .952 (.943, .959) | |||||||
| .813 (.761, .864) | .882 (.852, .910) | .861 (.852, .870) | .909 (.893, .924) | .875 (.873, .877) | .890 (.873, .904) | ||||||||
| .091 (.070, .119) | .066 (.054, .082) | .073 (.069, .077) | .052 (.045, .062) | .067 (.067, .068) | .062 (.054, .072) | ||||||||
| SFE | .002 | .001 | .001 | .001 | .001 | .001 | |||||||
| TE | .075 | .047 | .052 | .032 | .047 | .043 | |||||||
| RRE | .021 | .003 | .012 | .006 | .010 | .005 | |||||||
| TRE | .097 | .051 | .065 | .038 | .058 | .048 | |||||||
| G-D | .903 (.852, .953) | .948 (.925, .969) | .933 (.924, .942) | .961 (.950, .970) | .941 (.939, .943) | .951 (.942, .958) | |||||||
| .132 | 5.998 | .812 | 2.878 | 3.647 | 1.477 | ||||||||
| .118 | 5.578 | .748 | 2.721 | .017 | 1.380 | ||||||||
| .013 | .420 | .064 | .157 | .181 | .097 | ||||||||
| .001 | .015 | .004 | .007 | .153 | .004 | ||||||||
| .011 | .300 | .045 | .095 | .002 | .066 | ||||||||
| .012 | .086 | .043 | .072 | .004 | .033 | ||||||||
| .000 | .003 | .000 | .001 | .000 | .001 | ||||||||
| .000 | .005 | .001 | .003 | 3.647 | .002 | ||||||||
| .000 | .000 | .000 | .000 | .017 | .000 | ||||||||
| Instrument playing | |||||||||||||
| G | .879 (.747, 1.033) | .959 (.943, .976) | .917 (.892, .942) | .953 (.943, .962) | .926 (.920, .932) | .944 (.934, .952) | |||||||
| .712 (.574, .837) | .862 (.799, .915) | .767 (.744, .790) | .848 (.807, .884) | .782 (.777, .787) | .832 (.797, .862) | ||||||||
| .167 (.041, .360) | .097 (.050, .156) | .150 (.123, .179) | .104 (.074, .141) | .144 (.137, .150) | .112 (.087, .141) | ||||||||
| SFE | .006 | .002 | .003 | .002 | .003 | .000 | |||||||
| TE | .063 | .030 | .046 | .029 | .045 | .039 | |||||||
| RRE | .051 | .009 | .033 | .017 | .027 | .017 | |||||||
| TRE | .121 | .041 | .083 | .047 | .074 | .056 | |||||||
| G-D | .879 (.744, 1.028) | .959 (.942, .975) | .917 (.890, .941) | .952 (.942, .962) | .925 (.919, .931) | .943 (.933, .951) | |||||||
| .186 | 4.799 | 1.128 | 4.898 | 1.636 | 1.636 | ||||||||
| .151 | 4.315 | .944 | 4.361 | 4.256 | 1.441 | ||||||||
| .035 | .484 | .184 | .537 | .783 | .194 | ||||||||
| .005 | .043 | .016 | .031 | .064 | .003 | ||||||||
| .013 | .150 | .057 | .147 | .243 | .068 | ||||||||
| .043 | .172 | .164 | .351 | .580 | .116 | ||||||||
| .000 | .004 | .001 | .003 | .004 | .001 | ||||||||
| .000 | .001 | .000 | .002 | .003 | .001 | ||||||||
| .000 | .001 | .000 | .000 | .000 | .000 | ||||||||
| Reading music | |||||||||||||
| G | .902 (.766, 1.000) | .972 (.959, .985) | .926 (.901, .952) | .960 (.951, .968) | .934 (.928, .939) | .946 (.937, .954) | |||||||
| .710 (.573, .836) | .861 (.793, .917) | .778 (.755, .802) | .859 (.817, .895) | .795 (.790, .800) | .829 (.794, .858) | ||||||||
| .192 (.061, .382) | .111 (.059, .176) | .148 (.120, .177) | .101 (.069, .139) | .139 (.132, .145) | .117 (.092, .147) | ||||||||
| SFE | .006 | .002 | .003 | .002 | .003 | .004 | |||||||
| TE | .042 | .018 | .041 | .024 | .039 | .041 | |||||||
| RRE | .049 | .008 | .029 | .014 | .024 | .009 | |||||||
| TRE | .098 | .028 | .074 | .040 | .066 | .054 | |||||||
| G-D | .902 (.763, 1.000) | .971 (.957, .984) | .925 (.900, .950) | .959 (.950, .967) | .933 (.927, .939) | .945 (.936, .953) | |||||||
| .192 | 7.984 | 1.145 | 4.202 | 5.077 | 1.647 | ||||||||
| .151 | 7.076 | .962 | 3.761 | 4.324 | 1.443 | ||||||||
| .041 | .908 | .183 | .441 | .753 | .204 | ||||||||
| .005 | .074 | .015 | .031 | .059 | .029 | ||||||||
| .009 | .147 | .051 | .105 | .214 | .071 | ||||||||
| .042 | .268 | .145 | .250 | .530 | .064 | ||||||||
| .000 | .008 | .002 | .007 | .011 | .004 | ||||||||
| .000 | .004 | .000 | .001 | .001 | .000 | ||||||||
| .000 | .002 | .000 | .001 | .002 | .001 | ||||||||
| Listening | |||||||||||||
| G | .800 (.667, .951) | .909 (.878, .939) | .869 (.843, .895) | .912 (.895, .928) | .888 (.882, .894) | .893 (.876, .907) | |||||||
| .499 (.404, .600) | .660 (.578, .738) | .579 (.560, .597) | .654 (.595, .708) | .606 (.602, .611) | .640 (.589, .685) | ||||||||
| .300 (.165, .462) | .248 (.181, .324) | .290 (.264, .318) | .258 (.210, .311) | .282 (.275, .288) | .253 (.215, .295) | ||||||||
| SFE | .000 | .000 | .002 | .001 | .001 | .001 | |||||||
| TE | .138 | .078 | .089 | .065 | .078 | .090 | |||||||
| RRE | .063 | .013 | .040 | .022 | .032 | .016 | |||||||
| TRE | .201 | .092 | .131 | .088 | .112 | .107 | |||||||
| G-D | .799 (.663, .946) | .907 (.875, .938) | .868 (.841, .894) | .911 (.893, .927) | .886 (.880, .892) | .891 (.874, .905) | |||||||
| .168 | 6.950 | 1.019 | 2.338 | 4.407 | 2.119 | ||||||||
| .105 | 5.051 | .679 | 1.677 | 3.010 | 1.519 | ||||||||
| .063 | 1.899 | .340 | .661 | 1.397 | .600 | ||||||||
| .000 | -.011 | .008 | .011 | .029 | .012 | ||||||||
| .029 | .598 | .105 | .165 | .389 | .214 | ||||||||
| .053 | .413 | .189 | .227 | .638 | .149 | ||||||||
| .000 | .000 | .000 | .000 | .000 | .000 | ||||||||
| .000 | .012 | .002 | .004 | .010 | .005 | ||||||||
| .000 | .001 | .000 | .001 | .001 | .000 | ||||||||
| Composing | |||||||||||||
| G | .818 (.666, .995) | .927 (.902, .951) | .864 (.831, .899) | .910 (.893, .924) | .883 (.875, .891) | .889 (.873, .904) | |||||||
| .419 (.332, .515) | .592 (.502, .677) | .520 (.501, .539) | .592 (.530, .650) | .564 (.559, .568) | .600 (.548, .648) | ||||||||
| .399 (.246, .575) | .335 (.260, .416) | .344 (.311, .377) | .317 (.266, .373) | .319 (.312, .327) | .290 (.250, .333) | ||||||||
| SFE | .007 | .003 | .007 | .003 | .008 | .003 | |||||||
| TE | .105 | .057 | .077 | .058 | .065 | .082 | |||||||
| RRE | .070 | .013 | .053 | .029 | .044 | .026 | |||||||
| TRE | .182 | .073 | .136 | .090 | .117 | .111 | |||||||
| G-D | .817 (.661, .988) | .925 (.899, .950) | .862 (.828, .896) | .908 (.890, .923) | .881 (.873, .889) | .888 (.870, .902) | |||||||
| .148 | 9.489 | .777 | 2.499 | 3.445 | 1.680 | ||||||||
| .076 | 6.063 | .468 | 1.627 | 2.200 | 1.133 | ||||||||
| .072 | 3.427 | .309 | 0.872 | 1.245 | .547 | ||||||||
| .005 | .134 | .024 | .036 | .122 | .023 | ||||||||
| .019 | .588 | .069 | .160 | .253 | .154 | ||||||||
| .051 | .519 | .189 | .319 | .693 | .197 | ||||||||
| .000 | .033 | .002 | .007 | .012 | .006 | ||||||||
| .000 | .007 | .001 | .004 | .005 | .002 | ||||||||
| .000 | .002 | .000 | .000 | .001 | .000 | ||||||||
| Design/ subscale | Metric/Estimator | ||||||||||||||
| 2-Point | 4-Point | 8-Point | |||||||||||||
| ULS | WLSMV | ULS | WLSMV | ULS | WLSMV | ||||||||||
| Multivariate design | |||||||||||||||
| Instrument playing | 1.184 | 1.162 | 1.151 | 1.117 | 1.140 | 1.137 | |||||||||
| Reading music | 1.232 | 1.178 | 1.164 | 1.123 | 1.149 | 1.148 | |||||||||
| Listening | 1.187 | 1.157 | 1.191 | 1.191 | 1.191 | 1.157 | |||||||||
| Composing | 1.369 | 1.303 | 1.291 | 1.303 | 1.262 | 1.219 | |||||||||
| Bifactor design | |||||||||||||||
| Instrument playing | 1.176 | 1.153 | 1.145 | 1.091 | 1.135 | 1.126 | |||||||||
| Reading music | 1.218 | 1.159 | 1.154 | 1.103 | 1.140 | 1.132 | |||||||||
| Listening | 1.210 | 1.195 | 1.210 | 1.206 | 1.209 | 1.151 | |||||||||
| Composing | 1.386 | 1.250 | 1.304 | 1.263 | 1.275 | 1.206 | |||||||||
| Design/Scale | This Study MUSPI-S | Lee & Vispoel (2024) MUSPI | ||||||||
| α (occ 1) | α (occ 2) | Test-Retest | G | G-D | α (occ 1) | α (occ 2) | Test-Retest | G | G-D | |
| Mean across subscales | ||||||||||
| 2-Point | 0.933 | 0.940 | 0.858 | 0.957 | 0.960 | 0.912 | ||||
| 4-Point | 0.953 | 0.963 | 0.898 | 0.972 | 0.976 | 0.932 | ||||
| 8-Point | 0.963 | 0.970 | 0.913 | 0.976 | 0.980 | 0.936 | ||||
| persons × items (Composing subscale) | ||||||||||
| 2-Point | 0.911 | 0.934 | 0.826 | 0.911 | 0.911 | 0.942 | 0.954 | 0.894 | 0.943 | 0.940 |
| 4-Point | 0.932 | 0.950 | 0.870 | 0.932 | 0.931 | 0.959 | 0.971 | 0.911 | 0.959 | 0.957 |
| 8-Point | 0.937 | 0.958 | 0.891 | 0.937 | 0.936 | 0.965 | 0.975 | 0.919 | 0.965 | 0.962 |
| persons × items × occasions (Composing subscale) | ||||||||||
| 2-Point | 0.818 | 0.817 | 0.884 | 0.882 | ||||||
| 4-Point | 0.864 | 0.862 | 0.905 | 0.902 | ||||||
| 8-Point | 0.883 | 0.881 | 0.913 | 0.911 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





