Submitted:
13 January 2025
Posted:
14 January 2025
You are already at the latest version
Abstract
Keywords:
MSC: 35L03; 65M06; 65M12; 65M15; 65M22; 65M50
1. Introduction
2. The Problem Statement
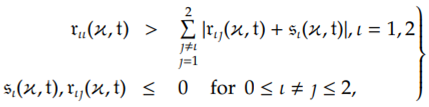
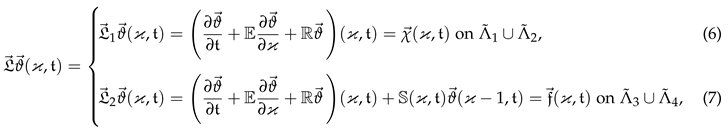
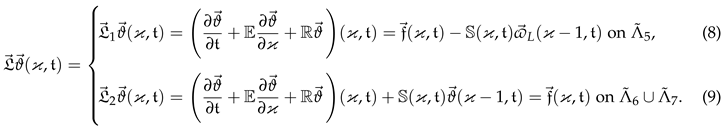
2.1. Uniqueness and Stability Analysis
3. Solution Components and Layer Functions
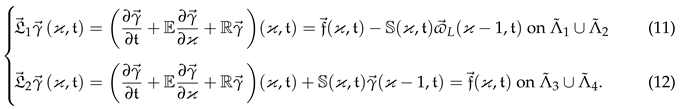
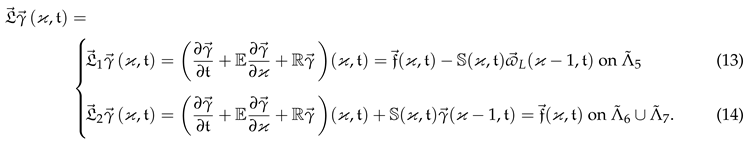
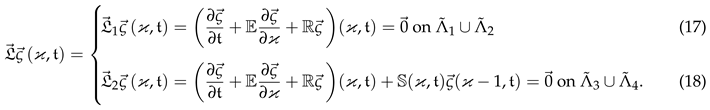
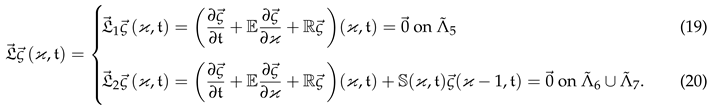
4. Solution Bounds
4.1. Sharper Estimates
4.2. Domain Discretization
5. Discrete Solution Components and Error Estimates
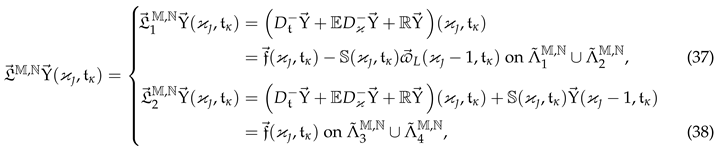
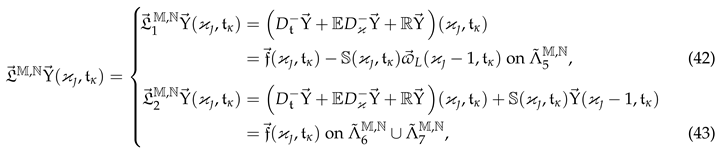
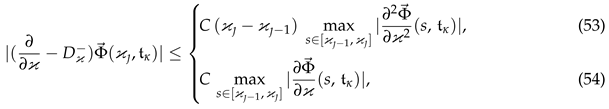
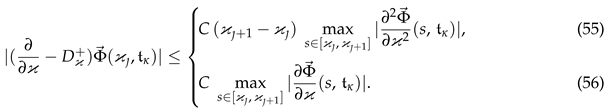
6. Numerical Illustration
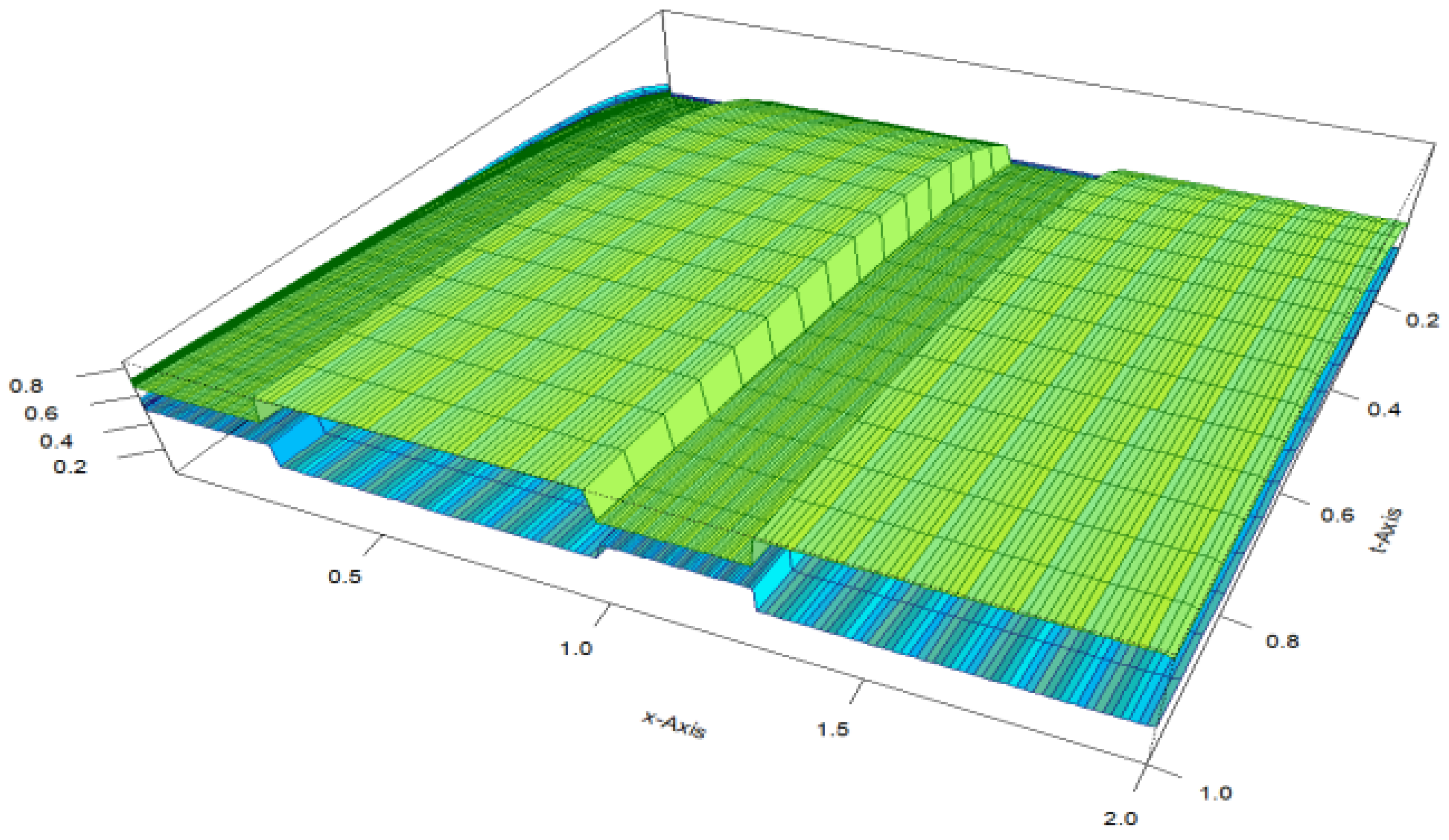
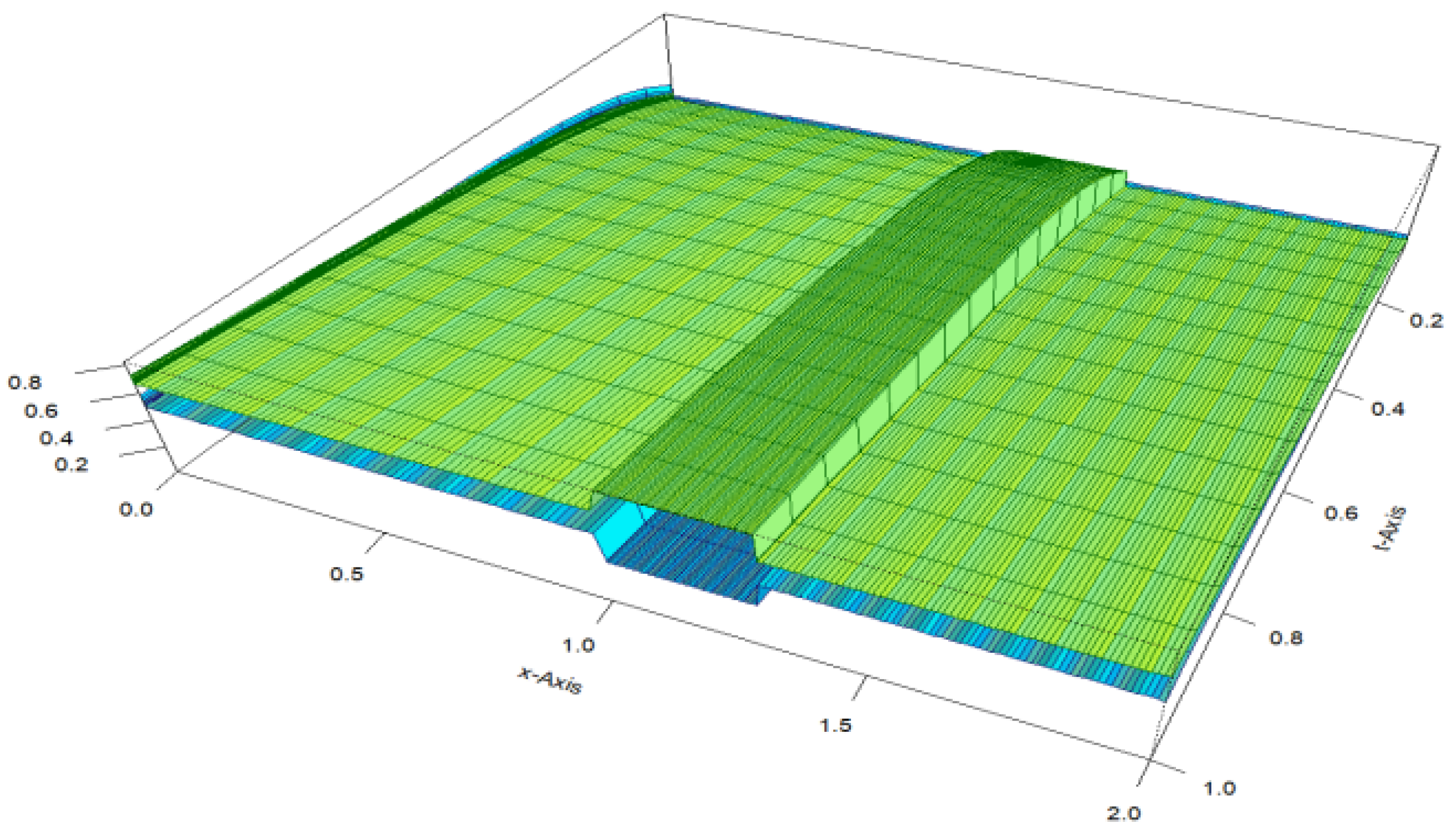
7. Conclusions
References
- Abagero, B., Duressa, G., & Debela, H. (2021). Singularly perturbed Robin-type boundary value problems with discontinuous source term in geophysical fluid dynamics. Iranian Journal of Numerical Analysis and Optimization, 11(2), 351–364.
- Ajay Singh Rathore, & Vembu Shanthi. (2024). A numerical solution of singularly perturbed Fredholm integro-differential equation with discontinuous source term. Journal of Computational and Applied Mathematics, 446, 115858. [CrossRef]
- Bharathi, K. R., Chatzarakis, G. E., Panetsos, S. L., & Paramasivam, M. J. Robust Layer Resolving Scheme for a System of Two Singularly Perturbed Time-Dependent Delay Initial Value Problems with Robin Initial Conditions. (Accepted for publication in Australian Journal of Mathematical Analysis and Applications).
- Cen, Z., Huang, J., & Xu, A. (2023). A quadratic B-spline collocation method for a singularly perturbed semilinear reaction–diffusion problem with discontinuous source term. Mediterranean Journal of Mathematics, 20, 269. [CrossRef]
- Chawla, S., Urmil, & Singh, J. (2021). A parameter-robust convergence scheme for a coupled system of singularly perturbed first-order differential equations with discontinuous source term. International Journal of Applied and Computational Mathematics, 7, 118. [CrossRef]
- Farrell, P., Hegarty, A., Miller, J. M., O’Riordan, E., & Shishkin, G. I. (2000). Robust computational techniques for boundary layers. Chapman and Hall/CRC.
- Paramasivam, M., Miller, J. J. H., & Valarmathi, S. (2014). Parameter-uniform convergence for a finite difference method for a singularly perturbed linear reaction-diffusion system with discontinuous source terms. International Journal of Numerical Analysis and Modeling, 11(2), 385–399.
- Sahoo, S. K., & Gupta, V. (2022). Higher-order robust numerical computation for singularly perturbed problems involving discontinuous convective and source terms. Mathematical Methods in the Applied Sciences, 45(8), 4876–4898. [CrossRef]
- Selvaraj, D., & Mathiyazhagan, J. P. (2021). A parameter-uniform convergence for a system of two singularly perturbed initial value problems with different perturbation parameters and Robin initial conditions. Malaya Journal of Matematik, 9(1), 498–505. [CrossRef]
- Singh, S., Choudhary, R., & Kumar, D. (2023). An efficient numerical technique for two-parameter singularly perturbed problems having discontinuity in convection coefficient and source term. Computational and Applied Mathematics, 42(62). [CrossRef]
- Soundararajan, R., Subburayan, V., & Wong, P. J. Y. (2023). Streamline diffusion finite element method for singularly perturbed 1D-parabolic convection-diffusion differential equations with line discontinuous source. Mathematics, 11(9), 2034. [CrossRef]
| ℷ | : Number of mesh points | |||
|---|---|---|---|---|
| 96 | 192 | 384 | 768 | |
| 0.100E-01 | 0.106E+00 | 0.673E-01 | 0.406E-01 | 0.236E-01 |
| 0.100E-03 | 0.106E+00 | 0.673E-01 | 0.406E-01 | 0.236E-01 |
| 0.100E-05 | 0.106E+00 | 0.673E-01 | 0.406E-01 | 0.236E-01 |
| 0.100E-07 | 0.106E+00 | 0.673E-01 | 0.406E-01 | 0.236E-01 |
| 0.100E-09 | 0.106E+00 | 0.673E-01 | 0.406E-01 | 0.236E-01 |
| 0.106E+00 | 0.673E-01 | 0.406E-01 | 0.236E-01 | |
| 0.655E+00 | 0.730E+00 | 0.782E+00 | ||
| 0.577E+01 | 0.577E+01 | 0.548E+01 | 0.501E+01 | |
| ℷ | : Number of mesh points | |||
|---|---|---|---|---|
| 144 | 288 | 576 | 1152 | |
| 0.100E-01 | 0.634E-01 | 0.385E-01 | 0.225E-01 | 0.128E-01 |
| 0.100E-03 | 0.634E-01 | 0.385E-01 | 0.225E-01 | 0.128E-01 |
| 0.100E-05 | 0.634E-01 | 0.385E-01 | 0.225E-01 | 0.128E-01 |
| 0.100E-07 | 0.634E-01 | 0.385E-01 | 0.225E-01 | 0.128E-01 |
| 0.100E-09 | 0.634E-01 | 0.385E-01 | 0.225E-01 | 0.128E-01 |
| 0.634E-01 | 0.385E-01 | 0.225E-01 | 0.128E-01 | |
| 0.721E+00 | 0.774E+00 | 0.812E+00 | ||
| 0.579E+01 | 0.579E+01 | 0.558E+01 | 0.524E+01 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





